2015年高考模拟试题_河南省实验中学高三上学期期中考试数学卷(文)(1)
2015年高考模拟试题_河南省中原名校高三上学期期中联考试卷数学(文)卷(1)

14.一个简单几何体的主视图,左(侧)视图如下图所示,则其俯视图不可能为:①长方 形: ②直角三角形;③圆;④椭圆.其序号是________. 15.若命题: x ∈R , x -2ax+a≤0”为假命题,则
2
2a
2
+1
a
的最小值是__________.
16 .已知函数 f ຫໍສະໝຸດ x )= 为_______.A.7 B.8 C.11
)
D.12
8.已知非零向量 a 和 b 满足 a ⊥( a - b ),b ⊥(2 a - b ),则 a 与 b 的夹角为( A.
)
4
B.
3 4
C.
6
D.
5 6
9.执行下面的框图,若输出结果为 1 ,则可输入的实数 x 值的个数为( A.1 C.3 10 .椭圆 点 的坐标为( A.(- C.(-
s3-s2 s5-s3
的值为
(
)
A.2
B.3
C.
1 5
D.不存在 ( )
6.要得到函数 f(x)=2sinx 的图像,只需把函数 y= 3 sinx-cosx 的图像 A.向左平移 C.向左平移
6 3
的单位 的单位
B.向右平移 D.向右平移
6 3
个单位 个单位
x-y+1>0 7.满足不等式组 2 x+y-4<0 的区域内整点个数为 ( y≥ -1
2
(1)求 A∩(
C B);
U
(2)记命题 p:x∈A ,命题 q:x∈B,求满足“p∧q”为假的 x 的取值范围. 18.(本小题满分 12 分) 已知 a,b,c 分别为△ABC 的三个内角 A,B,C 的对边,m =(sinA,1),n =(cosA,
河南省实验中学2015届高三上学期第一次月考数学理试题

河南省实验中学高三年级九月份月考试卷数 学一、选择题(本大题共12小题,每小题5分,共60分)1、已知集合}1log 0|{4<<=x x A ,}2|{≤=x x B ,则=B C A R ( ) A .(]12, B .)4,2[ C .)4,2( D .)4,1(2、下列函数中,既是奇函数又是增函数的为( ) A .1y x =+ B .2y x =- C .1y x= D .||y x x = 3.如图,阴影部分的面积是( )A ..2323 D.3534、设()f x 为定义在R 上的奇函数,当0x ³时,()32()x f x x a a R =-+ , 则(2)f -=( )A.-1B.-4C.1D.4 5、下列各组函数中表示同一函数的是( ) A .()f x x = 与()2g x =B .()f x x = 与()g x =C .()f x x x = 与()()()2200x x g x x x ⎧ >⎪=⎨- <⎪⎩D .()211x f x x -=- 与()()11g x x x =+ ≠ 6、不等式10x x->成立的一个充分不必要条件是( )A .10x -<<或1x >B .1x <-或01x <<C .1x >-D .1x > 7、奇函数)(x f 满足对任意R x ∈都有,0)()4(=-++x f x f 且,9)1(=f 则 )2013()2012()2011(f f f ++的值为( ) A.6B.7C.8D.08、已知函数()f x 是定义在区间[22]-,上的偶函数,当[]0,2x ∈时,()f x 是减函数,如果不等式()()1f m f m -<成立,求实数m 的取值范围.( )A .1[1,)2-B .[1]2,C .[]1-,0D .(11,2-)9、已知函数⎪⎩⎪⎨⎧≤---=)1()1(,5)(2x >xa x ax x x f 是R 上的增函数,则a 的取值范围是( )A 、3-≤a <0B 、3-≤a ≤2-C 、a ≤2-D 、a <010、函数的图象大致是( )A B C D11.若定义在R 上的函数f(x)的导函数为()f x ',且满足()()f x f x '>,则(2011)f 与2(2009)f e 的大小关系为( ).A 、(2011)f <2(2009)f eB 、(2011)f =2(2009)f eC 、(2011)f >2(2009)f eD 、不能确定12.若函数()32f x x ax bx c =+++有极值点12,x x ,且()11f x x =,则关于x 的方程()()()2320f x af x b ++=的不同实根的个数是( )A .3B .4C .5D .6二、填空题(本大题共4小题,每小题5分,共20分) 13、函数()f x =的定义域为 . 14、对任意两个实数12,x x ,定义()11212212,,,,.x x x max x x x x x ≥⎧=⎨<⎩若()22f x x =-,()g x x =-,则()()(),max f x g x 的最小值为 .15、设是定义在上的偶函数,对任意的,都有,且当时,,若关于的方程(1)a >在区间内恰有三个不同实根,则实数的取值范围是 .16、定义在R 上的函数f (x )满足f (x )+f (x+5)=16,当x ∈(-1,4]时,f (x )=x 2-2x,则函数f (x )在[0,2013]上的零点个数是______.三、解答题(本大题共6小题,满分70分.解答须写出文字说明,证明过程和演算步骤.)17、(12分)已知集合}187{2--==x x y x A ,集合)}34ln({2x x y x B --==,集合}322{-<<+=m x m x C .(Ⅰ)设全集R U =,求()U C A B ;(Ⅱ)若(C A)R C =∅,求实数的取值范围.18、(12分)已知()f x 是定义在[—1,1]上的奇函数,且(1)1f =,若m 、[]1,1n ∈-,且0m n +≠ 时有()().0>++nm n f m f(1)判断()f x在[—1,1]上的单调性,并证明你的结论;(2)解不等式:⎪⎭⎫ ⎝⎛-<⎪⎭⎫ ⎝⎛+1121x f x f ; ()f x R x ∈R )2()2(+=-x f x f [2,0]x ∈-1()12xf x ⎛⎫=- ⎪⎝⎭x ()log (2)0a f x x -+=(2,6]-a m(3)若()f x ≤122+-at t 对所有x ∈[—1,1],a ∈[—1,1]恒成立,求实数t 的取值范围.19、(12分)对于函数)(x f ,若存在x 0∈R ,使方程00)(x x f =成立,则称x 0为)(x f 的不动点,已知函数2()(1)1f x ax b x b =+++-(a ≠0). (1)当2,1-==b a 时,求函数)(x f 的不动点;(2) 当2,1-==b a 时,求()f x 在[],1t t +上的最小值(t)g .(3)若对任意实数b ,函数)(x f 恒有两个相异的不动点,求a 的取值范围; 20、(12分)已知函数f(x)=aln x-ax-3(a ∈R). (1)若a=-1,求函数f(x)的单调区间;(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t ∈[1,2],函数g(x)=x 3+x 2·[f '(x)+2m]在区间(t,3)上总不是单调函数,求m 的取值范围; (3)若x 1,x 2∈[1,+∞),比较ln(x 1x 2)与x 1+x 2-2的大小.21、(12分)设函数f(x)=ln x+mx,m ∈R. (Ⅰ)当m=e(e 为自然对数的底数)时,求f(x)的极小值; (Ⅱ)讨论函数g(x)=f '(x)-3x零点的个数; (Ⅲ)若对任意b>a>0,()()f b f a b a--<1恒成立,求m 的取值范围.请考生在第22、23、24题中任选择一题作答,如果多做,则按所做的第一部分,做答时请写清题号。
2015年高考模拟试题_河南省实验中学高三上学期期中考试数学卷(理)(1)
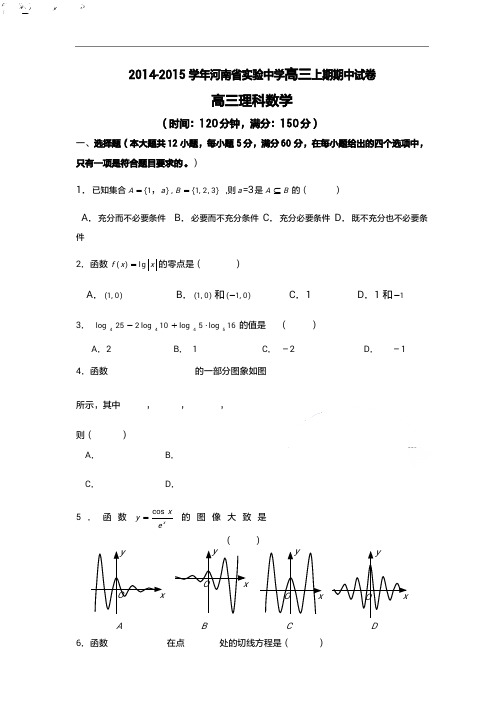
值为 16 . 已 知 函 数 f ( x ) 定 义 在 R 上 ,对 任 意 的 x R ,
f (x
1 0 0 1)
2
f ( x)
1
, 已知
f (1 1)
1 ,则
f ( 2 0 1 3) =
三、解答题(本大题共 6 小题,共 70 分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分 10 分) 函数 f ( x ) = x 的函数值表示不超过 x 的最大整数,例如, 3 .5 4, 2 .1 2 ,当
A.关于点
, 0 对称 12
, 0 对称
B.关于直线 x
12 5 12
对称
C.关于点
5 12
D.关于直线 x
对称
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分,把答案填在题中横线上) 13.计算:
(
0
1
1 x
2
x 2 ) dx _ _ _ _ _
x
2
)的图象与 x 轴
2 3 ,
2 ,
,且图象上一个最低点为 M (
] ,求 f ( x ) 的值域.
2 ) .
12 2
(Ⅰ) 函数 f ( x ) 在点 P ( x 0 , f ( x 0 ) ) 处的切线过原点,求此切线方程; (II) 函数 g ( x ) e kx k e ,是否存在实数 k ,使 g ( x ) 0 对任意的 x R 都成
A 4 ( y 1, f4 A ( 1 si )) e nx ( ) b b 1 0 f ( x ) lnx x
2015年高考模拟试题三模试题_河南省重点高中联考2015年高三年级第三次质量检测数学文A试题
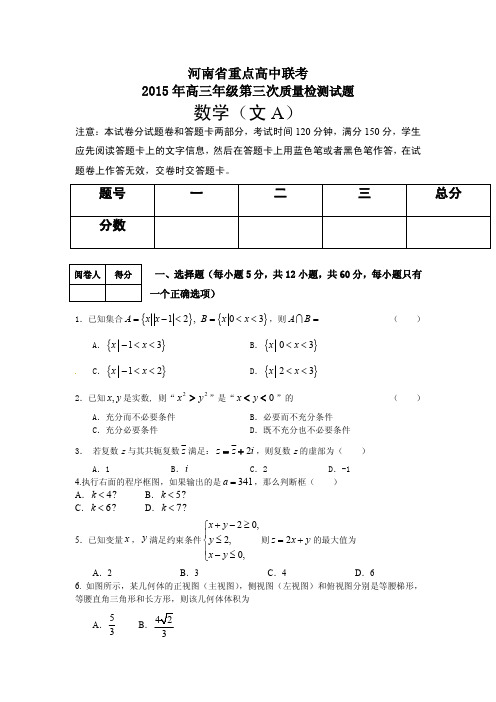
3. 若复数 z 与其共轭复数 z 满足: z z 2i ,则复数 z 的虚部为( A.1 B. i C.2 D.-1 ) 4.执行右面的程序框图,如果输出的是 a 341 ,那么判断框( A. k 4? B. k 5? C. k 6? D. k 7?
x y 2 0, 5.已知变量 x , y 满足约束条件 y 2, 则 z 2 x y 的最大值为 x y 0,
2
] 上的值域.
阅卷人
得分
18.(本小题满分 12 分) 某校高三年级在 5 月份进行一次质量考试,考生成绩情况如下表所 示:
0, 400
文科考生 理科考生 67 53
550, 750 400, 480 480,550
学#科#网 Z#X#X#K]
[:
35
19
6
x
y
z
已知用分层抽样方法在不低于 550 分的考生中随机抽取 5 名考生进行质量分析, 其中文 科考生抽取了 2 名. (1)求 z 的值;
(2)右图是文科不低于 550 分的 6 名学生的语文成绩的茎叶图,计算这 6 名考生的语 文成绩的方差; (3)已知该校不低于 480 分的文科理科考生人数之比为 1: 2 ,不低于 400 分的文科理 科考生人数之比为 2 : 5 ,求 x 、 y 的值. 13 12 11
A. 1
B.
2
C. 3
D. 4
11.点 P 是双曲线
x2 y2 1 (a>0, b>0)左支上的一点,其右焦点为 F (c,0) ,若 M 为 a 2 b2 1 c ,则双曲线的离心率 e 范围是 ( 8 4 5 C. ( , ) D. ( 2,3] 3 3
河南省实验中学2014——2015学年上期期中试卷

河南省实验中学2014——2015学年上期期中试卷数学理一、选择题(本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{||2,}A x x x R =≤∈,{4,}B x x Z =≤∈,则A B ⋂=( )A.(0,2)B.[0,2]C.(0,2]D.{0,1,2} 【知识点】集合及其运算A1【答案解析】D A={22x x -≤≤},B={016,x x x z ≤≤∈},则A B ⋂={0,1,2} 故选D.【思路点拨】先求出A,B 再求结果。
2.记cos(80)k -︒=,那么tan100︒=( )【知识点】同角三角函数的基本关系式与诱导公式C2【思路点拨】先利用同角三角函数的基本关系式以及诱导公式求sin80°,然后化切为弦,求解即可.3.已知集合{1,2,3,4},{,,}A B a b c ==,:f A B →为集合A 到集合B 的一个函数,那么该函数的值域C 的不同情况有( ) A .7种 B .4种 C .8种 D .12种 【知识点】函数及其表示B1【答案解析】A 值域C 可能为:只含有一个元素时,{a},{b},{c}3种; 有两个元素时,{a ,b},{a ,c},{b ,c}3种;有三个元素时,{a ,b ,c}1种; ∴值域C 的不同情况有3+3+1=7种.故选A .【思路点拨】值域C 只可能是集合B 的真子集,求出B 的真子集的个数即可. 4.设向量()2,1-=,向量()4,3-=,向量()2,3=,则向量()=⋅+2( ) A .(-15,12) B.0 C.-3 D.-11 【知识点】平面向量的数量积及应用F3【答案解析】C 依题意:∵a =(1,-2),b =(-3,4),a +2b =(1,-2)+2(-3,4)=(-5,6)∵c =(3,2),∴(a +2b )•c =(-5,6)•(3,2)=-5×3+6×2=-3故答案为C 【思路点拨】利用向量的坐标运算求出相应向量的坐标,在进行数量积的运算.【题文】5.设)}({*∈N n a n 是等差数列,n S 是其前n 项和,且65S S <,876S S S >=,则下列结论错误的是( )A .0<dB .07=aC .59S S >D .6S 和7S 均为n S 的最大值【知识点】等差数列及等差数列前n 项和D2【答案解析】C 由S 5<S 6得a 1+a 2+a 3+…+a 5<a 1+a 2++a 5+a 6,即a 6>0, 又∵S 6=S 7,∴a 1+a 2+…+a 6=a 1+a 2+…+a 6+a 7,∴a 7=0,故B 正确; 同理由S 7>S 8,得a 8<0,∵d=a7-a6<0,故A 正确;而C 选项S 9>S 5,即a 6+a 7+a 8+a 9>0,可得2(a 7+a 8)>0,由结论a 7=0,a 8<0,显然C 选项是错误的.∵S 5<S 6,S 6=S 7>S 8,∴S 6与S 7均为S n 的最大值,故D 正确;故选C .【思路点拨】利用结论:n≥2时,a n =s n -s n-1,易推出a 6>0,a 7=0,a 8<0,然后逐一分析各选项,排除错误答案.【题文】6.在△ABC 中, 45,2==A a ,若此三角形有两解,则b 的范围为( ) A .222<<b B .b > 2 C .b<2 D .221<<b【知识点】解三角形C8【思路点拨】利用正弦定理列出关系式,把a ,sinA 的值代入,表示出b ,B+C ,根据B 为两值,得到两个值互补,确定出B 的范围,进而求出sinB 的范围,即可确定出b 的范围.【题文】7.已知函数)0( sin 3>=ωωx y 的周期是π,将函数)0( 2cos 3>⎪⎭⎫ ⎝⎛-=ωπωx y 的图象沿x 轴向右平移8π个单位,得到函数()x f y =的图象,则函数()=x f ( )A.3sin 28x π⎛⎫- ⎪⎝⎭B.3sin 24x π⎛⎫- ⎪⎝⎭C.3sin 28x π⎛⎫-+ ⎪⎝⎭D.3sin 24x π⎛⎫-+ ⎪⎝⎭【知识点】函数sin()y A x ωϕ=+的图象与性质C4【思路点拨】由条件根据诱导公式的应用,函数y=Asin (ωx+φ)的图象变换规律可得结论.【题文】8.设△ABC 的三内角A 、B 、C 成等差数列,sinA 、sinB 、 sinC 成等比数列,则这个三角形的形状是( )A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形 【知识点】解三角形C8【答案解析】D ∵△ABC 的三内角A 、B 、C 成等差数列∴∠B=60°,∠A+∠C=120°①;xxA .B .C .D .【思路点拨】先由△ABC 的三内角A、B 、C 成等差数列,求得∠B=60°,∠A+∠C=120°①;再由sinA 、sinB 、sinC 成等比数列,得sin 2B=sinA•sinC ,②,①②结合即可判断这个三角形的形状.【题文】9.函数ππln cos y x x ⎛⎫=-<< ⎪的图象是( )【思路点拨】利用偶函数的定义判断出函数是偶函数,据偶函数的图象关于y 轴对称排除选项B ,D ;令x=60°时函数值小于0得到选项.【题文】10.O 为平面上的一个定点,A 、B 、C是该平面上不共线的三点,若+⋅-()(0)2=-,则△ABC 是( )A.以AB 为底边的等腰三角形B.以BC 为底边的等腰三角形C.以AB 为斜边的直角三角形D.以BC 为斜边的直角三角形 【知识点】平面向量的数量积及应用F3【答案解析】B 由题意知OC OB OC OB +⋅-()(-2OA )=()0CB AB AC +=,如图所示其中2AB AC AD +=(点D 为线段BC 的中点),所以AD ⊥BC ,即AD 是BC 的中垂线, 所以AB=AC ,即△ABC 为等腰三角形.故答案为“B.【思路点拨】首先把2OA 拆开分别与,OB OC 组合,再由向量加减运算即可整理,然后根据2AB AC AD +=(点D 为线段BC 的中点),并结合图形得出结论. 【题文】11.设p:2()e ln 21x f x x x mx =++++在(0)+∞,内单调递增,q:5m -≥,则p 是q 的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件 【知识点】导数的应用B12【思路点拨】首先求出函数的导数,然后根据导数与函数单调性的关系求出m 的范围. 【题文】12.已知两条直线1l :y=m 和2l :y=821m +(m >0),1l 与函数2log y x =的图像从左至右相交于点A,B,2l 与函数2log y x =的图像从左至右相交于C,D.记线段AC 和BD 在X 轴上的投影长度分别为a,b,当m 变化时,ba的最小值为( )来源%&:中国~教育#出版] A . B. 【知识点】函数与方程B9【题文】13.计算⎰--+-132)2(1x = .【知识点】定积分与微积分基本定理B13表示(x+2)+y =1与x 轴围成的上半圆的面积.【题文】14.已知A,B,C 三点在同一条直线l 上,O 为直线l 外一点,若0pOA qOB rOC ++=,其中p,q,r ∈R ,则=++r q p . 【知识点】平面向量基本定理F2【答案解析】0 ∵A 、B 、C 三点在同一条直线l 上∴存在实数λ使AB AC λ= ∴()OB OA OC OA λ-=-即(λ-1)OA +OB -λOC =0∵0pOA qOB rOC ++=∴P=λ-1,q=1,r=-λ∴p+q+r=0故选B【思路点拨】将三个点共线转化为两个向量共线,利用向量共线的充要条件列出方程,利用向量的运算法则将方程的向量用以O 为起点的向量表示,求出p ,q ,r 的值,进一步求出它们的和.【题文】15设x 、1a 、2a 、y 成等差数列,x 、1b 、2b 、y 成等比数列,则21221)(b b a a +的取值范围是 .【知识点】等差数列等比数列D3 D4【题文】16.已知函数21,(0)()log ,(0)ax x f x x x +≤⎧=⎨>⎩,若函数y=f(f(x))+1有4个不同的零点,则实数a 的取值范围是 .【知识点】函数与方程B9 【答案解析】(0,+∞) 函数y=f (f (x ))+1的零点, 即方程f[f (x )]=-1的解个数,(1)当a=0时,f (x )=21,0log ,0x x x ≤⎧⎨>⎩,当x >1时,f (f (x ))=-1成立,∴方程f[f (x )]=-1有1解当0<x <1,log 2x <0,∴方程f[f (x )]=-1无解,当x≤0时,f (x )=1,f (f (x ))=0,∴,∴f (f (x ))=-1有1解,故a=0不符合题意, (2)当a >0时,当x>1时,f(f(x))=-1成立,当0<x<1,log2x<0,∴方程f[f(x)]=-1有1解,当1<x≤0时,0<f(x)≤1,∴f(f(x))=-1有1解,当x≤-1时,f(x)<0,(3)当a<0时,【思路点拨】函数y=f[f (x )]+1的零点个数,即为方程f[f (x )]=-1的解的个数,结合函数f (x )图象,分类讨论判断,求解方程可得答案.【题文】三、解答题:解答应写出文字说明、证明过程或演算步骤(共70分). 【题文】17.(本小题满分12分)设函数25()lgax f x x a-=-的定义域为A ,命题:3p A ∈与命题:5q A ∈,若p q ∨真,p q ∧假,求实数a 的取值范围. 【知识点】基本逻辑联结词及量词A3 【答案解析】[)519253a ⎛⎤∈ ⎥⎝⎦,,25|0ax A x x a -⎧⎫=>⎨⎬-⎩⎭.若3A ∈,则3509a a ->-,即593a <<; 若5A ∈,则55025a a->-,即125a <<. 若p 真q 假,则593125a a a ⎧<<⎪⎨⎪⎩,≤或≥,a 无解;若p 假q 真,则593125a a a ⎧⎪⎨⎪<<⎩≤或≥,,解得513a <≤或925a <≤. 综上,[)519253a ⎛⎤∈ ⎥⎝⎦,,. 【思路点拨】根据逻辑联结词的关系以及定义域求出参数的范围。
河南省实验中学高三数学文科上学期期中考试卷

河南省实验中学2007—2008学年高三年级上学期期中考试数学试题(文科)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.全集)()(},4,3{}3,1{},5,4,3,2,1{B C A C B A I U U 则=== =( )A .{3}B .{1,2,4,5}C .{2,5}D .{1,2,4}2.已知,|1:|,032:2a x q x x p <-<-- 若q p ⌝⌝是的必要不充分条件,则实数a 的取值 范围是( )A .),2[+∞B . ),1[+∞C .),2(+∞D .),1(+∞3.等差数列}{,27,39,}{963741n n a a a a a a a a 则数列中=++=++的前9项的和S 9等于( )A .66B .99C .144D .2974.若)(x f 的反函数为)(1x f-,)(x g 的图象与)1(1+-x f 的图象关于直线y=x 对称,则)(x g =( )A . )(1x f--1B . )1(+x fC .)(x f +1D .)(x f -15.a 、b 为实数,集合x x f a N ab M →==:},0,{},1,{表示把集合M 中的元素x 映射到集合N 中仍为x ,则a+b( )A .1B .0C .-1D .±16.数列}{n a 满足a 1=1,,322=a 且)2(21111≥=++-n a a a n n n ,则a n 等于 ( )A .12+n B .1)32(-nC .1)32(+n D .12-n7.设等比数列}{n a 的前三项为,2,2,263则该数列的第四项为 ( )A .1B .82C .92D .1228.定义在R 上的函数)(x f 满足=+)3(x f )(x f ,且)(x f 在[-3,-2]上的减函数,又βα,是锐角三角形的两个内角,则( )A .)(cos )(sin βαf f >B . )(cos )(sin βαf f <C .)(sin )(sin βαf f <D . )(cos )(cos βαf f <9.设函数)(x f 是定义在R 上的以3为周期的奇函数,若143)2(,1)1(+-=>a a f f ,则a 的 取值范围是( )A .43<a B .43<a 且1≠aC .43>a 且1-<aD .431<<-a10.设)(x f '是函数)(x f 的导函数,y=)(x f '的图象如右图所示,则y=)(x f 的图象有可能是 ( )11.已知)(x f 是周期为2的奇函数,当)5.1(),2.1(,lg )(,10f b f a x x f x ===<<设时)5.2(f c =,则( )A .c b a <<B . c a b <<C .a b c <<D .b a c <<12.已知 m x x x f +-=2362)((m 为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为( )A .-5B .-11C .-29D .-37二、填空题:本大题共4小题,每小题5分,共20分,把答案填在横线上。
河南省南阳市2015届高三上学期期中质量评估数学(文)试题 扫描版含答案

2014年秋期高三年级文科期中考试答案一.选择题: 题目 1 2 3 4 5 6 7 8 9 10 11 12 答案 ADBADCDAACAB二.填空题:13.1 14.重心 15.4116.①②③④ 三.解答题:17.解:(I )∵f x ()为偶函数()()∴s i n s i n -+=+ωϕωϕx x 即20s i n c o s ωϕx =恒成立∴cos ϕ=0 ∵,∴02≤≤=ϕπϕπ……………………………………………………………3分 又其图象上相邻对称轴之间的距离为π ∴T =2π ∴ω=1∴f x x ()c o s = ……………………………………………………………………5分 (II )∵原式=-++=s i n c o s t a n s i n c o s22112αααα ……………………………7分 又∵,∴s i n c o s s i n c o s αααα+=+=231249 …… ………………………9分 即259s i n c o s αα=-, 故原式=-59………………………………………10分18.解:由⎩⎨⎧+=+=xx y x y 321,得0123=-+-x x x , 即0)1)(1(2=+-x x ,1=∴x ,∴交点为)2,1(.…………………………………2分 又x x f 2)('=,2)1('=∴f ,∴曲线)(x f y =在交点处的切线1l 的方程为)1(22-=-x y , 即x y 2=, ……………………5分又13)('2+=x x g . ∴4)1('=g .∴曲线)(x g y =在交点处的切线2l 的方程为)1(42-=-x y ,即24-=x y . ………………………………………………………………8分 取切线1l 的方向向量为)2,1(=a ,切线2l 的方向向量为)4,1(=b ,…………10分 则858591759||||cos =⨯=⋅=b a b a θ. ……………………………………12分19.解:(Ⅰ)由,47)43(1sin ,43cos 2=-==B B 得由ac b =2及正弦定理得 .s i n s i ns i n 2C A B = 则CA AC A C C C A A C A sin sin sin cos cos sin sin cos sin cos tan 1tan 1+=+=+22sin()sin 147.sin sin sin 7A CB B B B +==== …………………………6分(Ⅱ)由32BA BC ⋅=,得23cos =B ac ,由43cos =B ,可得ac =2,即b 2=2.…………………………………………………………8分由余弦定理B ac c a b cos 2222-+=,得5cos 2222=+=+B ac b c a , 3,9452)(222=+=+=++=+c a ac c a c a ……………………12分20.解:(Ⅰ)∵*n N ∈时,n n n a S a -=22,当2≥n 时,21112n n n a S a ---=-,…………………………………………………2分由①-②得,22111(2)(2)n n n n n n a a S a S a ----=---即2211n n n n a a a a ---=+,∵01>+-n n a a ∴)2(11≥=--n a a n n ,………………4分 由已知得,当1=n 时,21112a S a =-,∴11=a .………………………………5分故数列}{n a 是首项为1,公差为1的等差数列.∴*()N n a n n =∈. …………6分 (Ⅱ)∵*()N n a n n =∈,∴n n n n b 2)1(31⋅-+=-λ,…………7分∴111133(1)2(1)2n n n n n n n n b b λλ++-+-=-+-⋅--⋅1233(1)2n n n λ-=⨯-⋅-⋅.要使得1n n b b +>恒成立,只须113(1)()2n n λ---⋅<. …………8分(1)当n 为奇数时,即13()2n λ-<恒成立.又13()2n -的最小值为1,∴1λ<. ……9分(2)当n 为偶数时,即13()2n λ->-恒成立.又13()2n --的最大值为32-,∴32λ>- ……………………………………10分∴由(1),(2)得312λ-<<,又0λ≠且λ为整数,……………………11分∴1λ=-对所有的*N n ∈,都有1n n b b +>成立. ………………12分21.解:[)(] 1.-2f(-x),0,1x -,1,0-x )1(-x =∴∈∈则令又,)(是奇函数x f ∴f(-x)=-f(x),∴,12)()(-=-=--x x f x f ∴[).0,1,1)21()(-∈+-=x x f x.................................6分(2) f(x+4)=f(x),∴f(x)是以4为周期的周期函数, ),4,5(24log 24log 221--∈-=∴),0,1(424log 21-∈+∴211161241)21()424(log )24(log 424log 212121-=+⨯-=+-=+=∴+f f .......12分22.解:(I )ax x x x f 22131)(23++-= ,a x x x f 2)('2++-=∴ …………………2分 函数)(x f 在),32(+∞上存在单调递增区间,即导函数在),32(+∞上存在函数值大于零的部分, 0232)32()32('2>++-=∴a f 91->∴a ……………………………………6分(II))(x f 取到最小值316-,而a x x x f 2)('2++-=的图像开口向下,且对称轴方程为21=x ,02)1('>=a f ,0122)4('<-=a f则必有一点使得0'()0=f x……………………………………8分此时函数)(x f 在0[1,]x 上单调递增,在0[,4]x 单调递减.612)1(+=a f ,a f 8340)4(+-=,)1()4(f f <∴3168340)4()(min -=+-==∴a f x f , 1=∴a , …………………10分 此时,由200000'()202,1()=-++=∴==-舍去f x x x x x ,所以函数max 10()(2)3==f x f ………………………………………………………12分[],4,10∈x。
河南实验中学高三(上)期中考试

河南实验中学高三(上)期中考试数 学 试 题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至8页。
共150分。
考试时间120分。
参考公式:三角函数的积化和差公式αsin +βsin =2sin2βα+cos2βα- αsin -βsin =2cos2βα+sin2βα-cos α+cos β=2cos 2βα+cos 2βα- cos α-cos β=-2sin 2βα+sin 2βα-第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题 目要求的.)1.已知集合M={1,3},N={x x |2-}Z x x ∈<,03,又P=M ⋃N ,那么集合P 的真子集共有 ( )A .3个B .7个C .8个D .9个 2.设βα,是同一象限角,下列判断正确的是( )A .若βα>,则αsin >βsinB .若αsin >βsin ,则βα>C .若βα=,则αsin =βsinD .若αsin =βsin ,则βα=3.点A (0,1)在直线x+ay -b=0上的射影是点B (1,0),则a ,b 的值依次为 ( )A .-1,1B .-1,-1C .1,1D .1,-1 4.设函数2)(=x f x ,则函数y=f-1(x -1)的图象是( )A .B .C .D .5.平行六面体ABCD—A1B1C1D1的体积为V,E、F分别是DC、BC的中点,则几何体CEF-C1D1B1的体积等于( )A .247V B .41V C .1223+V D .85V6.若命题“非p ”与命题“p或q”都是真命题,那么 ( )A.命题p与q命题的真值相同 B .命题q一定是真命题 C .命题q不一定是真命题D .命题p不一定是假命题7.设非零向量a 与b的方向相反,那么下面给出的命题中,正确的个数是 ( )(1)a +b =0 (2)a —b 的方向与a一致(3)a +b 的方向与a一致 (4)若a +b 的方向与b 一致,则|a |<|b |A .1个B .2个C .3个D .4个8.二项展开式(a+b)n中与其第k(k≤n)项的二项式系数相同的项是( )A.第(n-k+1)项 B .第(n-k)项C .第(n-k+2)项D .第(n-k-1)项 9.已知轴截面是正方形的圆柱的侧面积等于一个球的表面积,那么这个圆柱与球的体积之比是( )A .3∶2B .2∶3C .4∶3D .2∶210.已知等差数列{a n}与等比数列{b n }的首项均为1,且公差d ≠1,公比q >0且q ≠1,则集合{n| a n = b n}的元素最多有 ( )A .1个B .2个C .3个D .4个 11.已知ab ≠0,点M (a ,b )是圆x 2+y 2=r 2内一点,直线m 是以点M 为中点的弦所在的直线,直线L 的方程是a x +by=r 2,则下列结论正确的是( )A .m ∥L ,且L 与圆相交B .L ⊥m ,且L 与圆相切C .m ∥L ,且L 与圆相离D .L ⊥m ,且L 与圆相离12.设)(),(x g x f 都是定义在R 上的奇函数,不等式)(x f >0的解集为(m ,n ),不等式)(x g >0的解集为(,2m 2n),其中0<2m <n ,则不等式)(x f ·)(x g >0的解集为( )A .(,2m 2n) B .(,2m 2n )⋃(-2n ,-2m) C .(-n ,-m )D .(m ,2n )⋃(-2n,-m )2002——2003学年度上学期期中考试高三数学试卷第Ⅱ卷(非选择题,共90分)一、选择题答题栏二、填空题:(本大题共4小题,每小题4分,共16分,把答案填在题中横线上)13.若P 是双曲线32x -y 2=1右支上一个动点,F 是双曲线的右焦点,已知点A 的坐标是(3,1),则|PA|+|PF|的最小值是 .14.将正方形ABCD 沿对角线BD 折成直二面角,有如下四个结论:①AC ⊥BD ; ②△ADC是等边三角形; ③AB 与面BCD 成60°角; ④AB 与CD 成60°角;请你把正确的结论的序号都填上 . 15.若对实数x ∈[)+∞,10,恒有|log m x|≥2,则实数m 的取值范围是 。
河南省实验中学2014-2015学年高二上学期期中考试 数学(文)(Word含答案)

河南省实验中学2014——2015学年上期期中试卷高二 文科数学命题人:汪洋 审题人:李红霞(时间:120分钟,满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.数列1,3,5,7,9,--……的一个通项公式为( )A .(1)(12)n n a n =--B .21n a n =-C .(1)(21)n n a n =--D .(1)(21)n n a n =-+2.不等式11<x的解集是( ) A .{}1>x x B .{}0<x x C .{}01<>x x x 或 D .{}10<<x x3.在等差数列9}{,27,39,}{963741前则数列中n n a a a a a a a a =++=++项的和9S 等于 ( )A .297B .144C .99D . 664.在△ABC 中,内角C B A ,,的对边分别为c b a ,,,若18a =,24b =,45A =︒,则这样的三角形有( )A.0个B.两个C.一个D.至多一个5.原点和点()1,1在直线0=-+a y x 的两侧,则a 的取值范围是( )A .20><a a 或B .20==a a 或C .20<<aD .20≤≤a6.已知数列{}n a 的前n 项和,3,2,1,12=-=n S n n …,那么数列{}n a ( ) A.是等差数列但不是等比数列B.是等比数列但不是等差数列C.既是等差数列又是等比数列D.既不是等差数列也不是等比数列7.设变量y x ,满足约束条件0024236x y x y x y ≥⎧⎪≥⎪⎨+≤⎪⎪+≤⎩,则43z x y =+的最大值是( )A .7B .8C .9D .108.已知数列{}n a 满足n n a a -=+111,若211=a ,则=2014a ( ) A 、21 B 、2 C 、-1 D 、1 9.若,,a b c 为实数,则下列命题正确的是( )A .若a b >,则22ac bc >B .若0a b <<,则22a ab b >>C .若0a b <<,则11a b <D .若0a b <<,则b a a b >10.设n S 为等差数列{}n a 的前n 项的和,20141-=a ,20072005220072005S S -=,则2014S 的值为( ) A 、-2013 B 、-2014 C 、2013 D 、201411.在ABC ∆中,角C B A ,,所对应的边分别为c b a ,,,B B A C 2sin 3)sin(sin =-+.若3π=C ,则=b a ( ) A.21 B.3 C.21或3 D.3或4112.命题:p 函数)3lg(-+=xa x y 在区间[)+∞,2上是增函数;命题:q )4lg(2+-=ax x y 函数的定义域为R .则p 是q 成立的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件二、填空题(本大题共4小题,每小题5分,共20分)13.若0>a ,0>b ,且0)ln(=+b a ,则ba 11+的最小值是 . 14.关于x 的一元二次方程0)1(2=+--m x m mx 没有实数根,则实数m 的取值范围是 .15.设,x y 满足约束条件2208400 , 0x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩,若目标函数()0,0z abx y a b =+>>的最大值为8,则a b +的最小值为________。
2015年河南省实验中学高二上学期数学期中试卷和解析(文科)

2014-2015学年河南省实验中学高二(上)期中数学试卷(文科)一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)数列1,﹣3,5,﹣7,9,…的一个通项公式为()A.a n=2n﹣1 B.a n=(﹣1)n(1﹣2n)C.a n=(﹣1)n(2n﹣1)D.a n=(﹣1)n(2n+1)2.(5分)不等式的解集是()A.{x|x>1}B.{x|x<0}C.{x|x>1或x<0}D.{x|0<x<1} 3.(5分)在等差数列{a n}中,若a1+a4+a7=39,a3+a6+a9=27,则S9=()A.66 B.99 C.144 D.2974.(5分)在△ABC中,内角A,B,C的对边分别为a,b,c,若a=18,b=24,A=45°,则这样的三角形有()A.0个 B.两个C.一个D.至多一个5.(5分)原点O和点P(1,1)在直线x+y﹣a=0的两侧,则a的取值范围是()A.a<0或a>2 B.a=0或a=2 C.0<a<2 D.0≤a≤26.(5分)如果数列{a n}的前n项和S n=2n﹣1,那么这个数列()A.是等差数列但不是等比数列B.是等比数列但不是等差数列C.既是等差数列又是等比数列D.既不是等差数列又不是等比数列7.(5分)设变量x,y满足约束条件,则z=4x+3y的最大值是()A.7 B.8 C.9 D.108.(5分)已知数列{a n},满足a n+1=,若a1=,则a2014=()A.B.2 C.﹣1 D.19.(5分)若a、b、c为实数,则下列命题正确的是()A.若a>b,则ac2>bc2B.若a<b<0,则a2>ab>b2C.若a<b,则>D.若a>b>0,则>10.(5分)设S n为等差数列{a n}的前n项的和,a1=﹣2014,,则S2014的值为()A.﹣2013 B.﹣2014 C.2013 D.201411.(5分)在△ABC中,角A,B,C所对应的边分别为a,b,c,sinC+sin(A ﹣B)=3sin2B.若,则=()A.B.3 C.或3 D.3或12.(5分)命题p:函数y=lg(x+﹣3)在区间[2,+∞)上是增函数;命题q:y=lg(x2﹣ax+4)函数的定义域为R,则p是q成立的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)若a>0,b>0,且ln(a+b)=0,则的最小值是.14.(5分)关于x的一元二次方程mx2﹣(1﹣m)x+m=0没有实数根,则实数m的取值范围是.15.(5分)设x,y满足约束条件,若目标函数z=abx+y(a>0,b>0)的最大值为8,则a+b的最小值为.16.(5分)下列4个命题:①“如果x+y=0,则x、y互为相反数”的逆命题②“如果x2+x﹣6≥0,则x>2”的否命题③在△ABC中,“A>30°”是“sinA>”的充分不必要条件④“函数f(x)=tan(x+φ)为奇函数”的充要条件是“φ=kπ(k∈Z)”其中真命题的序号是.三、解答题(本大题共6小题,共70分)17.(10分)已知△ABC的内角A,B,C所对边分别为a,b,c,且acosC+c=b.(1)求角A的大小;(2)若bc=2,求边长a的最小值.18.(12分)已知关于x的不等式ax2﹣3x+2≤0的解集为{x|1≤x≤b}.(1)求实数a,b的值;(2)解关于x的不等式:>0(c为常数).19.(12分)已知命题p:实数x满足﹣2≤1﹣≤2,命题q:实数x满足x2﹣2x+(1﹣m2)≤0(m>0),若¬q是¬p的充分不必要条件,求实数m的取值范围.20.(12分)已知各项均不相等的等差数列{a n}的前四项和S4=14,且a1,a3,a7成等比数列.(1)求数列{a n}的通项公式;(2)设T n为数列的前n项和,求T n.21.(12分)在锐角△ABC中,a、b、c分别为∠A、∠B、∠C所对的边,且a=2csinA.(1)确定∠C的大小;(2)若c=,求△ABC周长的取值范围.22.(12分)已知数列{a n}中,a1=1,a n+1=(n∈N*).(1)求证:{+}是等比数列,并求{a n}的通项公式a n;(2)数列{b n}满足b n=(3n﹣1)••a n,数列{b n}的前n项和为T n,若不等式(﹣1)nλ<T n+对一切n∈N*恒成立,求λ的取值范围.2014-2015学年河南省实验中学高二(上)期中数学试卷(文科)参考答案与试题解析一、选择题(本大题共12小题,每小题5分,共60分)1.(5分)数列1,﹣3,5,﹣7,9,…的一个通项公式为()A.a n=2n﹣1 B.a n=(﹣1)n(1﹣2n)C.a n=(﹣1)n(2n﹣1)D.a n=(﹣1)n(2n+1)【解答】解:∵数列{a n}各项值为1,﹣3,5,﹣7,9,…∴各项绝对值构成一个以1为首项,以2为公差的等差数列,∴|a n|=2n﹣1又∵数列的奇数项为正,偶数项为负,∴a n=(﹣1)n+1(2n﹣1)=(﹣1)n(1﹣2n).故选:B.2.(5分)不等式的解集是()A.{x|x>1}B.{x|x<0}C.{x|x>1或x<0}D.{x|0<x<1}【解答】解:不等式可化为﹣1<0可化为<0即等价于x(x﹣1)>0,解得x>1或x<0,∴原不等式的解集为{x|x>1或x<0}故选:C.3.(5分)在等差数列{a n}中,若a1+a4+a7=39,a3+a6+a9=27,则S9=()A.66 B.99 C.144 D.297【解答】解:由a1+a4+a7=3a1+9d=39,得a1+3d=13①,由a3+a6+a9=3a1+15d=27,得a1+5d=9②,②﹣①得d=﹣2,把d=﹣2代入①得到a1=19,则前9项的和S9=9×19+×(﹣2)=99.故选:B.4.(5分)在△ABC中,内角A,B,C的对边分别为a,b,c,若a=18,b=24,A=45°,则这样的三角形有()A.0个 B.两个C.一个D.至多一个【解答】解:∵在△ABC中,a=18,b=24,A=45°,∴由正弦定理=得:sinB===>,∵a<b,∴A<B,∴B的度数有两解,则这样的三角形有两个.故选:B.5.(5分)原点O和点P(1,1)在直线x+y﹣a=0的两侧,则a的取值范围是()A.a<0或a>2 B.a=0或a=2 C.0<a<2 D.0≤a≤2【解答】解:因为原点O和点P(1,1)在直线x+y﹣a=0的两侧,所以(﹣a)•(1+1﹣a)<0,解得0<a<2,故选:C.6.(5分)如果数列{a n}的前n项和S n=2n﹣1,那么这个数列()A.是等差数列但不是等比数列B.是等比数列但不是等差数列C.既是等差数列又是等比数列D.既不是等差数列又不是等比数列【解答】解:当n≥2时,,当n=1时,a1=S1=2﹣1=1,满足a n,∴数列{a n}的通项公式为为公比为2的等比数列,不是等差数列.故选:B.7.(5分)设变量x,y满足约束条件,则z=4x+3y的最大值是()A.7 B.8 C.9 D.10【解答】解:由约束条件作出其所确定的平面区域(阴影部分),平移直线z=4x+3y,由图象可知当直线z=4x+3y经过点A时,目标函数z=4x+3y取得最大值,由,解得,即A(),即z=4××3=9,故z的最大值为9.故选:C.8.(5分)已知数列{a n},满足a n+1=,若a1=,则a2014=()A.B.2 C.﹣1 D.1=,a1=,【解答】解:∵数列{a n},满足a n+1∴a2==2,a3==﹣1,a4==,,∴数列{a n}是周期为3的周期数列,∵2014÷3=671…1,∴a2014=a1=.故选:A.9.(5分)若a、b、c为实数,则下列命题正确的是()A.若a>b,则ac2>bc2B.若a<b<0,则a2>ab>b2C.若a<b,则>D.若a>b>0,则>【解答】解:A.c=0时不成立;B.∵a<b<0,∴a2>ab>b2,正确;C.取a=﹣1,b=﹣2时,=﹣1,=﹣,则>不成立;D.若a>b>0,则<,因此不正确.故选:B.10.(5分)设S n为等差数列{a n}的前n项的和,a1=﹣2014,,则S2014的值为()A.﹣2013 B.﹣2014 C.2013 D.2014【解答】解:∵数列{a n}为等差数列,且a1=﹣2014,则,∴=﹣2014+1003d+2014﹣1002d=2,即d=2.∴=﹣2014.故选:B.11.(5分)在△ABC中,角A,B,C所对应的边分别为a,b,c,sinC+sin(A ﹣B)=3sin2B.若,则=()A.B.3 C.或3 D.3或【解答】解:∵A+B=π﹣C,∴sinC=sin(π﹣C)=sin(A+B)=sinAcosB+cosAsinB,又∵sin(A﹣B)=sinAcosB﹣cosAsinB,∴sinC+sin(A﹣B)=3sin2B,即(sinAcosB+cosAsinB)+(sinAcosB﹣cosAsinB)=6sinBcosB,化简得2sinAcosB=6sinBcosB,即cosB(sinA﹣3sinB)=0解之得cosB=0或sinA=3sinB.①若cosB=0,结合B为三角形的内角,可得B=,∵,∴A==,因此sinA=sin=,由三角函数的定义得sinA==;②若sinA=3sinB,由正弦定理得a=3b,所以=3.综上所述,的值为或3.故选:C.12.(5分)命题p:函数y=lg(x+﹣3)在区间[2,+∞)上是增函数;命题q:y=lg(x2﹣ax+4)函数的定义域为R,则p是q成立的()A.充分不必要条件 B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【解答】解:y′=;∵函数y=lg(x+﹣3)在区间[2,+∞)上是增函数;根据函数y=lg(x+﹣3)知,x+﹣3>0;∴x2﹣a≥0在[2,+∞)上恒成立,∴,即函数x+在[2,+∞)是增函数;∴,∴a>2;由x2﹣a≥0在[2,+∞)上恒成立得a≤x2恒成立,∴a≤4;∴2<a≤4;y=lg(x2﹣ax+4)函数的定义域为R,所以不等式x2﹣ax+4>0的解集为R;∴△=a2﹣16<0,∴﹣4<a<4;显然2<a≤4是﹣4<a<4的既不充分又不必要条件;∴p是q成立的既不充分也不必要条件.故选:D.二、填空题(本大题共4小题,每小题5分,共20分)13.(5分)若a>0,b>0,且ln(a+b)=0,则的最小值是4.【解答】解:∵ln(a+b)=0,∴a+b=1∴=()(a+b)=2++≥2+2=4故答案为:414.(5分)关于x的一元二次方程mx2﹣(1﹣m)x+m=0没有实数根,则实数m的取值范围是(﹣∞,﹣1)∪().【解答】解:由于关于x的一元二次方程mx2﹣(1﹣m)x+m=0没有实数根,故它的判别式△=(1﹣m)2﹣4m•m<0,且m≠0,求得m>或m<﹣1,故m的范围为(﹣∞,﹣1)∪().故答案为:(﹣∞,﹣1)∪().15.(5分)设x,y满足约束条件,若目标函数z=abx+y(a>0,b >0)的最大值为8,则a+b的最小值为4.【解答】解:满足约束条件的区域是一个四边形,如下图4个顶点是(0,0),(0,2),(,0),(1,4),由图易得目标函数在(1,4)取最大值8,即8=ab+4,∴ab=4,∴a+b≥2=4,在a=b=2时是等号成立,∴a+b的最小值为4.故答案为:416.(5分)下列4个命题:①“如果x+y=0,则x、y互为相反数”的逆命题②“如果x2+x﹣6≥0,则x>2”的否命题③在△ABC中,“A>30°”是“sinA>”的充分不必要条件④“函数f(x)=tan(x+φ)为奇函数”的充要条件是“φ=kπ(k∈Z)”其中真命题的序号是①.【解答】解:对于①:其逆命题是:如果x、y互为相反数,则x+y=0,显然正确;对于②:否命题是“如果x2+x﹣6<0,则x≤2”,由x2+x﹣6<0得﹣3<x<2,此时x≤2显然不成立,故②为假;对于③:当A=150°时,sinA=,不满足结论,故③为假;对于④:当函数f(x)=tan(x+φ)为奇函数时,结合图象可知,当x=0时,f(0)=0或不存在,则应有φ=kπ或kπ+,k∈Z,故不满足充分性,故④错误.故答案为:①.三、解答题(本大题共6小题,共70分)17.(10分)已知△ABC的内角A,B,C所对边分别为a,b,c,且acosC+c=b.(1)求角A的大小;(2)若bc=2,求边长a的最小值.【解答】解:(1)∵acosC+c=b,∴由正弦定理,得sinAcosC+sinC=sinB.∵在△ABC中,A+C=π﹣B,∴sinB=sin(π﹣B)=sin(A+C)=sinAcosC+cosAsinC,∴sinAcosC+sinC=sinAcosC+cosAsinC,可得sinC=cosAsinC,又∵在△ABC中,sinC>0,∴等式两边约去sinC,可得cosA=,结合A∈(0,π)可得A=;(2)∵在△ABC中,A=,bc=2,∴由余弦定理,得a2=b2+c2﹣2bccosA=b2+c2﹣2×2×cos=b2+c2﹣2,又∵b2+c2≥2bc,即b2+c2≥4,∴a2=b2+c2﹣2≥4﹣2=2,当且仅当b=c时等号成立.因此,当b=c=时,a2的最小值为2,可得边a的最小值为.18.(12分)已知关于x的不等式ax2﹣3x+2≤0的解集为{x|1≤x≤b}.(1)求实数a,b的值;(2)解关于x的不等式:>0(c为常数).【解答】解:(1)由题意知1,b为关于x的方程ax2﹣3x+2=0的两根,则,∴a=1,b=2.(2)不等式等价于(x﹣c)(x﹣2)>0,所以:当c>2时解集为{x|x>c或x<2};当c=2时解集为{x|x≠2,x∈R};当c<2时解集为{x|x>2或x<c}.19.(12分)已知命题p:实数x满足﹣2≤1﹣≤2,命题q:实数x满足x2﹣2x+(1﹣m2)≤0(m>0),若¬q是¬p的充分不必要条件,求实数m的取值范围.【解答】解:由,得﹣2≤x≤10,∴记A={x|p}={x|﹣2≤x≤10}.由x2﹣2x+1﹣m2≤0(m>0)得1﹣m≤x≤1+m,记B={x|q}={x|1﹣m≤x≤1+m(m>0)}.∵¬q是¬p的充分不必要条件,∴P是q的充分不必要条件,即P⇒q且q推不出P,∴A⊊B,要使A⊊B,又m>0,则只需,∴m≥9.故所求实数m的取值范围是m≥9.20.(12分)已知各项均不相等的等差数列{a n}的前四项和S4=14,且a1,a3,a7成等比数列.(1)求数列{a n}的通项公式;(2)设T n为数列的前n项和,求T n.【解答】解:(1)设公差为d,则∵S4=14,且a1,a3,a7成等比数列∴4a1+6d=14,(a1+2d)2=a1(a1+6d)∵d≠0,∴d=1,a1=2,∴a n=n+1(2)=∴T n=﹣+﹣+…+==.21.(12分)在锐角△ABC中,a、b、c分别为∠A、∠B、∠C所对的边,且a=2csinA.(1)确定∠C的大小;(2)若c=,求△ABC周长的取值范围.【解答】解:(1)由a=2csinA变形得:=,又正弦定理得:=,∴=,∵sinA≠0,∴sinC=,∵△ABC是锐角三角形,∴∠C=;(2)∵c=,sinC=,∴由正弦定理得:====2,即a=2sinA,b=2sinB,又A+B=π﹣C=,即B=﹣A,∴a+b+c=2(sinA+sinB)+=2[sinA+sin(﹣A)]+=2(sinA+sin cosA﹣cos sinA)+=3sinA+cosA+=2(sinAcos+cosAsin)+=2sin(A+)+,∵△ABC是锐角三角形,∴<∠A<,∴<sin(A+)≤1,则△ABC周长的取值范围是(3+,3].22.(12分)已知数列{a n}中,a1=1,a n+1=(n∈N*).(1)求证:{+}是等比数列,并求{a n}的通项公式a n;(2)数列{b n}满足b n=(3n﹣1)••a n,数列{b n}的前n项和为T n,若不等式(﹣1)nλ<T n+对一切n∈N*恒成立,求λ的取值范围.【解答】解:(1)由数列{a n}中,a1=1,a n+1=(n∈N*),可得=1+.∴,∴{}是首项为,公比为3的等比数列,∴,化为.(2)由(1)可知:=,T n=+…+.…++,两式相减得﹣==.∴.∴(﹣1)n•λ<+=4﹣.若n为偶数,则,∴λ<3.若n为奇数,则,∴﹣λ<2,解得λ>﹣2.综上可得﹣2<λ<3.赠送初中数学几何模型【模型三】双垂型:图形特征:运用举例:1.在Rt△ABC中,∠ACB=90°,以斜边AB为底边向外作等腰三角形PAB,连接PC. (1)如图,当∠APB=90°时,若AC=5,PC=62,求BC的长;(2)当∠APB=90°时,若AB=45APBC的面积是36,求△ACB的周长.P2.已知:如图,B、C、E三点在一条直线上,AB=AD,BC=CD.(1)若∠B=90°,AB=6,BC=23,求∠A的值;(2)若∠BAD+∠BCD=180°,cos∠DCE=35,求ABBC的值.3.如图,在四边形ABCD中,AB=AD,∠DAB=∠BCD=90°,(1)若AB=3,BC+CD=5,求四边形ABCD的面积(2)若p= BC+CD,四边形ABCD的面积为S,试探究S与p之间的关系。
河南省实验中学高三上学期期中考试(全科10套)河南省实

河南省实验中学2014——2015学年上期期中试卷高三物理命题人:赵传亮审题人:王俊萍(时间:90分钟,满分:110分)一、选择题(本题共10小题,总分40分。
每小题所列四个选项中,有一个或多个正确选项,全部选对得4分,少选、漏选得2分,错选、多选或不选得0分)1.伽利略为了研究自由落体的规律,将落体实验转化为著名的沿斜面运动的实验,当时利用斜面做实验主要是考虑到:( )A.实验时便于测量小球运动的速度B.实验时便于测量小球运动的路程C.实验时便于测量小球运动的时间D.实验时便于测量小球运动的加速度2.一质点沿x轴做直线运动,其v—t图像如图所示.质点在t=0时位于x=5 m处,开始沿x轴正向运动.当t=8 s时,质点在x轴上的位置为()A.x=3 m B.x=8 mC.x=9 m D.x=14 m3.如图所示,从同一条竖直线上两个不同点P、Q分别向右平抛两个小球,平抛的初速度分别为v1、v2,结果它们同时落到水平面上的M点处(不考虑空气阻力)。
下列说法中正确的是( )A.一定是P先抛出的,并且v1=v2B.一定是P先抛出的,并且v1<v2C.一定是Q先抛出的,并且v1=v2D.一定是Q先抛出的,并且v1>v24.如图所示,一质量为M的光滑大圆环,用一细轻杆固定在竖直平面内;套在大环上质量为m的小环(可视为质点),从大环的最高处由静止滑下.重力加速度大小为g.当小环滑到大环的最低点时,大环对轻杆拉力的大小为()A.Mg+5mg B.Mg+mgC.Mg-5mg D.Mg+10mg5.如图所示,真空中O点有一点电荷,在它产生的电场中有a、b两点,a点的场强大小为E a,方向与ab连线成60°角,b点的场强大小为E b,方向与ab连线成30°。
关于a、b两点场强E a、E b的关系,正确的是()A.2 B.C.D.6.如图所示,竖直墙面与水平地面均光滑且绝缘,两个带有同种电荷的小球A、B分别处于竖直墙面和水平地面,且处于同一竖直平面内,若用图示方向的水平推力F作用于小球B,则两球静止于图示位置,如果将小球B向左推动少许,两个小球将重新达到平衡,电量不变,则两个小球的受力情况与原来相比()A.推力F将增大B.竖直墙面对小球A的弹力变大C.地面对小球B的弹力一定增大D.两个小球之间的距离增大7.小球自由下落,与地面发生碰撞后以原速率反弹。
河南省实验中学2015届高三数学上学期第一次月考试题 文(含解析)

河南实验学校高三数学(文)第一次月考【试卷综析】总体上看,整份试卷的阅读量、运算量和思维量都比较大,难度也稍偏大,区分度不是十分明显。
客观地说试题的设计、考查的要求和复习的导向都比较好,结构稳定。
整套试卷的题型设置,试题总体结构、考点分布、题型题量、赋分权重等方面均与历年考题保持一致,充分体现了稳定的特点。
试题紧紧围绕教材选材,注重基础知识和基本能力的检测。
考查了必要数学基础知识、基本技能、基本数学思想;考查基本的数学能力,以及数学的应用意识、创新意识、科学态度和理性精神等要求落到实处,模拟试卷有模仿性,即紧跟上一年高考试卷的命题,又有预见性,能够预测当年试卷的些微变化,具有一定的前瞻性,对学生有所启发,提高学生的应试备考能力,提升得分。
一、选择题(本大题共12小题,每小题5分,共60分)【题文】1.设函数2()lg(1)f x x =-,集合{}{}(),()A x y f x B y y f x ====,则右图中阴影部分表示的集合为A .[1,0]-B .(1,0)-C .(,1)[0,1)-∞- D .(,1](0,1)-∞-【知识点】Venn 图表达集合的关系及运算.A1【答案解析】D 解析:因为函数2()lg(1)f x x =-,集合 {}{}(){|11},(){|0}===-<<===≤A x y f x x x B y y f x y y因此阴影部分的表示的集合为A,B 交集在全集中的补集,即为(,1](0,1)-∞-,选D【思路点拨】首先根据对数函数的定义域和值域化简集合A ,B ;由图知阴影部分表示的集合为将A ∪B 除去A∩B 后剩余的元素所构成的集合,然后即可借助数轴求出结果. 【题文】2.已知函数()f x 的图象是连续不断的,有如下的,()x f x 对应值表:x1 2 3 4 5 6 ()f x123.5621.45-7.8211.57-53.76-126.49函数()f x 在区间[1,6]上的零点至少有( )A. 3个B. 2个C. 4个D.5个 【知识点】函数零点存在定理.B9【答案解析】B 解析:由图可知,(2)0,(3)0f f ><,由零点存在定理知在区间[]2,3上至少有一个零点,同理可以判断出在区间[]4,5上至少有一个零点,所以在区间[1,6]上的零点至少有两个.【思路点拨】f (2)>0,f (3)<0,由零点存在定理知在区间[2,3]上至少有一个零点,同理可以判断出在区间[4,5]上至少有一个零点.【题文】3..已知命题:,sin 1,p x R x ∀∈≤则p ⌝是( ) A .,sin 1x R x ∃∈≥ B .,sin 1x R x ∀∈≥ C .,sin 1x R x ∃∈> D .,sin 1x R x ∀∈> 【知识点】命题的否定.A2【答案解析】C 解析:全称命题的否定是特称命题,故选C【思路点拨】本题所给的命题是一个特称命题,存在性命题的否定是一个全称合理,把存在符号变为任意符号,将结论否定即可 【题文】 4.设条件:23p x -<,条件:0q x a <<,其中a 为正常数.若p 是q 的必要不充分条件,则a 的取值范围 ( )A.(0,5]B.(0,5)C.[5,)+∞D.(5,+∞) 【知识点】必要条件、充分条件与充要条件的判断.A2 【答案解析】A 解析:因为条件:23p x -<,所以可得:15p x -<<,又因为条件:0q x a <<, 其中a 为正常数. 且p 是q 的必要不充分,即q p ⇒,所以05a <≤.选A.【思路点拨】根据不等式的性质,以及充分条件和必要条件的定义,即可得到结论. 【题文】5.在ABC ∆中,若2AB AB AC BA BC CA CB =⋅+⋅+⋅,则ABC ∆是( ) A .直角三角形 B .锐角三角形 C .钝角三角形 D .等边三角形 【知识点】三角形的形状判断.C8【答案解析】 A 解析:由2AB AB AC BA BC CA CB =⋅+⋅+⋅,知BC CA BC BA AC AB AB ⋅-⋅=⋅-20)()()()(=+⋅⇒-⋅=⋅⇒-⋅=-BC AB CB BC BC CB AB CA BA BC AC AB AB所以AC CB AC CB ⊥⋅⇒=⋅0,故ABC ∆为直角三角形,故选A. 【思路点拨】根据向量的加减运算法则,将已知化简得=+•,得•=0.结合向量数量积的运算性质,可得 CA ⊥CB ,得△ABC 是直角三角形. 【题文】6.已知13a π=,log 3b π=,ln(31)c =-,则,,a b c 的大小关系是A .a b c <<B . b c a <<C .c b a <<D . b a c <<【知识点】不等式比较大小.E1【答案解析】C 解析:因为根据指数函数以及对数函数的概念和性质,那么1031=>=a ππ,log 3log 1=<=b πππ,ln(31)ln10=-<=c ,那么可知a,bc 的大小关系为c b a <<,选C.【思路点拨】利用指数函数和对数函数的单调性即可比较出大小.注意与数0,1的大小比较.【题文】7.在ABC ∆中,AB BC =3,ABC ∆的面积33,22S ⎡⎤∈⎢⎥⎣⎦,则AB 与CB 夹角的取值范围是( )A .2334ππ⎡⎤⎢⎥⎣⎦,B .,63ππ⎡⎤⎢⎥⎣⎦C .,64ππ⎡⎤⎢⎥⎣⎦D .3546ππ⎡⎤⎢⎥⎣⎦, 【知识点】平面向量数量积的运算;数量积表示两个向量的夹角.F2 F3 【答案解析】C 解析:AB BC =3,所以S=sinB ∈,所以,即所以:这就是夹角的取值范围.故选C .【思路点拨】利用向量的数量积求得表达式,根据三角形面积的范围,可以得到B 的范围,然后求题目所求夹角的取值范围.【题文】8.为了得到函数x y sin =的图像,需要把函数)332sin(π+=x y 图像上的所有点( )A.横坐标缩短到原来的32倍,再向右平移3π个单位长度 B.横坐标伸长到原来的23倍,再向右平移3π个单位长度 C. 横坐标缩短到原来的32倍,再向左平移3π个单位长度 D. 横坐标伸长到原来的23倍,再向左平移3π个单位长度【知识点】函数y=Asin (ωx+φ)的图象变换.C4【答案解析】D 解析:函数x y sin =周期为2π,)332sin(π+=x y 周期为3π,因此横坐标伸长为原来的23倍得到2sin()3y x =,再向左平移平移3π个单位长度得)332sin(π+=x y 选D.【思路点拨】根据函数y=Asin (ωx+∅)的图象变换规律,得出结论.【题文】9.已知如图是函数y =2sin(ωx+φ)(|φ|<2π)图像上的一段,则( )(A)ω=1011,φ=6π (B)ω=1011,φ=-6π(C)ω=2,φ=6π (D)ω=2,φ=-6π【知识点】由图像求函数sin()y A x ωϕ=+的解析式. C4【答案解析】C 解析:因为11(),2,2,1212626T ππππππωϕϕ=--=∴=⨯+=∴=.故选C .【思路点拨】由图像求函数sin()y A x ωϕ=+的解析式一般步骤:第一步先求出A ,第二步可求出周期,进而得到ω,第三步根据五点法作图中点确定ϕ的值,要注意ϕ的取值范围.【题文】10.已知21sin sin ,sin cos 3x y u x x +==+则的最小值是( )A .19-B. -1C. 1D. 54【知识点】三角函数的性质。
河南省实验中学2015届高三上学期期中考试数学文试题

河南省实验中学2014——2015学年上期期中试卷数学文一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合}{12A x x =<<,}{B x x a =<,若A B ⊆,则a 的取值范围是 ( ) A .}{2a a ≤ B .}{1a a ≤ C .}{1a a ≥ D .}{2a a ≥【知识点】集合及其运算A1【答案解析】D 由}{12A x x =<<}{B x x a =<A B ⊆则}{2a a ≥故答案为D 。
【思路点拨】根据子集的定义求出a 的范围。
2.函数2(44)xy a a a =-+是指数函数,则a 的值是 ( )A . 4B .13或C .3D .1 【知识点】指数函数B6【答案解析】C 由题意得201441a a a a >⎧⎪≠⎨⎪-+=⎩得a=3,故选C 。
【思路点拨】根据指数函数的定义求出a 。
3.若m n ,是两条不同的直线,αβγ,,是三个不同的平面,则下列为真命题的是( ) A .若m βαβ⊂⊥,,则m α⊥ B .若m αγ=,m n ∥,则αβ∥C .若m β⊥,m α∥,则αβ⊥D .若αγ⊥,αβ⊥,则βγ⊥ 【知识点】空间中的平行关系垂直关系G4 G5【答案解析】C 对于A ,m ββ⊂∂⊥,则m 与∂的关系有三种m 平行∂,m ⊂∂或m ∂与相交A 错,对于B, m αγ=,m n ∥,则αβ∥还有相交的情况,B 错误,对于D αγ⊥,αβ⊥,还有可能平行,故选C.【思路点拨】根据线面关系面面关系排除法求结果。
【题文】4.设n S 是等差数列{}n a 的前n 项和,若59355,9a Sa S ==则 ( ) A .1 B .2 C .3 D .4【知识点】等差数列及等差数列前n 项和D2【答案解析】A 根据等差数列的性质59355,9a S a S ==则5395aa =1,故选A 。
河南省实验中学高三上学期期中——数学(理)数学(理)

河南省实验中学 2015届高三上学期期中考试数学(理)试题命题人:程建辉 审题人:丁海丽 (时间:120分钟,满分:150分)一、选择题(本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{||2,}A x x x R =≤∈,{|4,}B x x Z =≤∈,则 ( )A.(0,2)B.[0,2]C.(0,2]D.{0,1,2} 2.记,那么 ( )A. B.- C. D.-3.已知集合{1,2,3,4},{,,}A B a b c ==,为集合到集合的一个函数,那么该函数的值域C 的不同情况有( ) A .7种 B .4种 C .8种 D .12种4.设向量,向量,向量,则向量( ) A .(-15,12) B.0 C.-3 D.-115.设是等差数列,是其前n 项和,且,,则下列结论错误的是( ) A . B . C . D .和均为的最大值6.在△ABC 中,,若此三角形有两解,则b 的范围为( ) A . B .b > 2 C .b<2 D .7.已知函数的周期是,将函数)0( 2cos 3>⎪⎭⎫ ⎝⎛-=ωπωx y 的图象沿轴向右平移个单位,得到函数的图象,则函数( )A. B. C. D.8.设△ABC 的三内角A 、B 、C 成等差数列,sinA 、sinB 、 sinC 成等比数列,则这个三角形的形状是( )A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形 9.函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是( )10.O 为平面上的一个定点,A 、B 、C 是该平面上不共线的三点,若,则△ABC 是( ) A.以AB 为底边的等腰三角形 B.以BC 为底边的等腰三角形 C.以AB 为斜边的直角三角形 D.以BC 为斜边的直角三角形 11.设p:2()e ln 21xf x x x mx =++++在内单调递增,q:,则p 是q 的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件 12.已知两条直线:y=m 和:y= (m >0),与函数的图像从左至右相交于点A,B,与函数的图像从左至右相交于C,D.记线段AC 和BD 在X 轴上的投影长度分别为a,b,当m 变化时,的最小值为( ) A . B. C. D.二、填空题:请把答案填在题中横线上(每小题5分,共20分). 13.计算= .14.已知A,B,C 三点在同一条直线上,O 为直线外一点,若0pOA qOB rOC ++=,其中p,q,rR ,则 . 15设x 、、、y 成等差数列,x 、、、y 成等比数列,则的取值范围是 . 16.已知函数21,(0)()log ,(0)ax x f x x x +≤⎧=⎨>⎩,若函数y=f(f(x))+1有4个不同的零点,则实数a 的取值范围是 .三、解答题:解答应写出文字说明、证明过程或演算步骤(共70分).17.(本小题满分12分)设函数的定义域为,命题与命题,若真,假,求实数的取值范围.18.(本小题满分12分)已知,其中()x x x m ωωωcos 3,cos sin +=→,()x x x n ωωωsin 2,sin cos -=→,且,若相邻两对称轴间的距离不小于。
河南省实验中学高三数学上学期期中试卷 文(含解析)

河南省实验中学2015届高三上学期期中数学试卷(文科)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合{A=x|1<x<2},{B=x|x<a},若A⊆B,则a的取值范围是()A.{a|a≥2}B.{a|a>2} C.{a|a≥1}D.{a|a≤2}2.(5分)函数y=(a2﹣4a+4)a x是指数函数,则a的值是()A.4 B.1或3 C.3 D.13.(5分)若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中的真命题是()A.若m⊂β,α⊥β,则m⊥αB.若α∩γ=m,β∩γ=n,m∥n,则α∥βC.若m⊥β,m∥α,则α⊥βD.若α⊥γ,α⊥β,则β⊥γ4.(5分)设S n是等差数列{a n}的前n项和,若=()A.1 B.﹣1 C.2 D.5.(5分)已知变量x,y满足约束条件,则的取值范围是()A.B.C.(﹣∞,3]∪[6,+∞)D. [3,6]6.(5分)是平面内不共线两向量,已知,若A,B,D三点共线,则k的值是()A.1 B.2 C.3 D.47.(5分)已知函数f(x)=sinωx+cosωx(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的一条对称轴是()A.x=﹣B.x=C.x=﹣D.x=8.(5分)已知体积为的正三棱柱(底面是正三角形且侧棱垂直底面)的三视图如图所示,则此三棱柱的高为()A.B.C.1 D.9.(5分)下列说法错误的是()A.命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”B.如果命题“¬p”与命题“p或q”都是真命题,那么命题q一定是真命题C.若命题p:∃x∈R,x2﹣x+1<0,则¬p:∀x∈R,x2﹣x+1≥0D.“sinθ=”是“θ=30°”的充分不必要条件10.(5分)已知函数的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度11.(5分)函数f(x)在定义域R上的导函数是f′(x),若f(x)=f(2﹣x),且当x∈(﹣∞,1)时,(x﹣1)f′(x)<0,设a=f(0、b=f()、c=f(log28),则()A.a<b<c B.a>b>c C.c<a<b D.a<c<b12.(5分)若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)=log3|x|的零点个数是()A.多于4个B.4个C.3个D.2个二、填空题:本大题共4小题,每小题5分,共20分13.(5分)如果函数f(x)的图象与函数g(x)=()x的图象关于直线y=x对称,则f(3x ﹣x2)的单调递减区间是.14.(5分)已知tan(α+β)=3,tan(α+)=2,那么tanβ=.15.(5分)设α=cos420°,函数f(x)=,则f()+f(log2)的值等于.16.(5分)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是.三、解答题:本大题共5小题,共70分.解答时写出证明过程或演算步骤.17.(12分)已知向量,函数.(1)求函数f(x)的对称中心;(2)在△ABC中,a,b,c分别是角A,B,C的对边,且,且a >b,求a,b的值.18.(12分)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.(Ⅰ)求k的值及f(x)的表达式.(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.19.(12分)直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,D是AB的中点.(Ⅰ)求证:AC⊥B1C;(Ⅱ)求证:AC1∥平面B1CD.20.(12分)数列{b n}满足:b n+1=2b n+2,b n=a n+1﹣a n,且a1=2,a2=4.(Ⅰ)求数列{b n}的通项公式;(Ⅱ)求数列{a n的前n项和S n.21.(12分)已知函数.(Ⅰ)若a=4,求曲线f(x)在点(e,f(e))处的切线方程;(Ⅱ)求f(x)的极值;(Ⅲ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围.【选修4-1:几何证明选讲】(共1小题,满分10分)22.(10分)选修4﹣1:几何证明选讲如图,已知四边形ABCD内接于ΘO,且AB是的ΘO直径,过点D的ΘO的切线与BA的延长线交于点M.(1)若MD=6,MB=12,求AB的长;(2)若AM=AD,求∠DCB的大小.【选修4-4:坐标系与参数方程】(共1小题,满分0分)23.(坐标系与参数方程选做题)已知椭圆C的极坐标方程为,点F1、F2为其左,右焦点,直线l 的参数方程为(t为参数,t∈R).(Ⅰ)求直线l和曲线C的普通方程;(Ⅱ)求点F1、F2到直线l的距离之和.【选修4-5:不等式选讲】(共1小题,满分0分)24.已知函数f(x)=|x﹣2a|+|x﹣a|,a∈R,a≠0.(Ⅰ)当a=1时,解不等式:f(x)>2;(Ⅱ)若b∈R且B≠0,证明:f(b)≥f(a),并说明等号成立时满足的条件.河南省实验中学2015届高三上学期期中数学试卷(文科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设集合{A=x|1<x<2},{B=x|x<a},若A⊆B,则a的取值范围是()A.{a|a≥2}B.{a|a>2} C.{a|a≥1}D.{a|a≤2}考点:集合的包含关系判断及应用.专题:计算题.分析:在数轴上画出图形,结合图形易得a≥2.解答:解:在数轴上画出图形易得a≥2.故选A.点评:本题考查集合的包含关系,解题时要作出图形,结合数轴进行求解.2.(5分)函数y=(a2﹣4a+4)a x是指数函数,则a的值是()A.4 B.1或3 C.3 D.1考点:指数函数的定义、解析式、定义域和值域.专题:计算题;函数的性质及应用.分析:指数函数是形式定义,即y=a x,(a>0,且a≠1),从而求a.解答:解:由题意得,,解得,a=3,故选C.点评:本题考查了指数函数的定义,属于基础题.3.(5分)若m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中的真命题是()A.若m⊂β,α⊥β,则m⊥αB.若α∩γ=m,β∩γ=n,m∥n,则α∥βC.若m⊥β,m∥α,则α⊥βD.若α⊥γ,α⊥β,则β⊥γ考点:命题的真假判断与应用.专题:空间位置关系与距离;简易逻辑.分析:由m⊂β,α⊥β,可得m与α的关系有三种说明A错误;由α∩γ=m,β∩γ=n,且m∥n得到α与β的位置关系有两种说明B错误;利用线面平行的性质结合面面垂直的判定说明C正确;由α⊥γ,α⊥β,得到β与γ可能平行也可能相交说明D错误.解答:解:对于A,m⊂β,α⊥β,则m与α的关系有三种,即m∥α、m⊂α或m与α相交,选项A错误;对于B,α∩γ=m,β∩γ=n,若m∥n,则α∥β或α与β相交,选项B错误;对于C,m⊥β,m∥α,则α内存在与m平行的直线与β垂直,则α⊥β,选项C正确;对于D,α⊥γ,α⊥β,则β与γ可能平行,也可能相交,选项D错误.故选:C.点评:本题考查了命题的真假判断与应用,考查了空间中的线与线、线与面、面与面的关系,是中档题.4.(5分)设S n是等差数列{a n}的前n项和,若=()A.1 B.﹣1 C.2 D.考点:等差数列的性质.专题:计算题.分析:充分利用等差数列前n项和与某些特殊项之间的关系解题.解答:解:设等差数列{a n}的首项为a1,由等差数列的性质可得a1+a9=2a5,a1+a5=2a3,∴====1,故选A.点评:本题主要考查等差数列的性质、等差数列的前n项和公式以及等差中项的综合应用,已知等差数列{a n}的前n项和为S n,则有如下关系S2n﹣1=(2n﹣1)a n.5.(5分)已知变量x,y满足约束条件,则的取值范围是()A.B.C.(﹣∞,3]∪[6,+∞)D. [3,6]考点:简单线性规划的应用.专题:数形结合.分析:本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件,画出满足约束条件的可行域,分析表示的几何意义,结合图象即可给出的取值范围.解答:解:约束条件对应的平面区域如下图示:三角形顶点坐标分别为(1,3)、(1,6)和(),表示可行域内的点(x,y)与原点(0,0)连线的斜率,当(x,y)=(1,6)时取最大值6,当(x,y)=()时取最小值,故的取值范围是故选A.点评:平面区域的最值问题是线性规划问题中一类重要题型,在解题时,关键是正确地画出平面区域,分析表达式的几何意义,然后结合数形结合的思想,分析图形,找出满足条件的点的坐标,即可求出答案.6.(5分)是平面内不共线两向量,已知,若A,B,D三点共线,则k的值是()A.1 B.2 C.3 D.4考点:向量的共线定理.专题:计算题.分析:由A,B,D三点共线,可构造两个向量共线,再利用两个向量共线的定理求解即可.解答:解:∵A,B,D三点共线,∴与共线,∴存在实数λ,使得=;∵=3e1﹣e2﹣(2e1+e2)=e1﹣2e2,∴e1﹣ke2=λ(e1﹣2e2),∵e1、e2是平面内不共线的两向量,∴解得k=2.故选B点评:本题考查三点共线和向量共线的转化和向量共线的条件,属基本题型的考查.7.(5分)已知函数f(x)=sinωx+cosωx(ω>0),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,则f(x)的一条对称轴是()A.x=﹣B.x=C.x=﹣D.x=考点:由y=Asin(ωx+φ)的部分图象确定其解析式;两角和与差的正弦函数.专题:三角函数的图像与性质.分析:化简函数f(x)=sinωx+cosωx为f(x)=2sin(ωx+),y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,求出函数的周期,推出ω,得到函数解析式,从而可求f(x)的一条对称轴.解答:解:函数f(x)=sinωx+cosωx=2sin(ωx+),因为y=f(x)的图象与直线y=2的两个相邻交点的距离等于π,函数的周期T=π,所以ω=2,所以f(x)=2sin(2x+),因为2x+=+kπ k∈Z,解得x=,k∈Z,当k=0时,有x=.故选:D.点评:本题主要考察了两角和与差的正弦函数公式的应用,考察了由y=Asin(ωx+φ)的部分图象确定其解析式,属于基础题.8.(5分)已知体积为的正三棱柱(底面是正三角形且侧棱垂直底面)的三视图如图所示,则此三棱柱的高为()A.B.C.1 D.考点:由三视图还原实物图.专题:计算题.分析:利用三视图的数据,几何体的体积,直接求出几何体的高即可.解答:解:由三视图可知正三棱柱的底面边长为2,设正三棱柱的高为:h,正三棱柱的体积为:=,解得h=1.故选C.点评:本题考查三视图与直观图的关系,几何体的体积的应用,考查计算能力.9.(5分)下列说法错误的是()A.命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”B.如果命题“¬p”与命题“p或q”都是真命题,那么命题q一定是真命题C.若命题p:∃x∈R,x2﹣x+1<0,则¬p:∀x∈R,x2﹣x+1≥0D.“sinθ=”是“θ=30°”的充分不必要条件考点:命题的真假判断与应用;特称命题;命题的否定.专题:简易逻辑.分析:利用四种命题的逆否关系判断A的正误;复合命题的真假判断B的正误;命题的否定判断C的正误;充要条件判断D的正误;解答:解:对于A,命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0”,满足否命题的定义,所以A正确;对于B,如果命题“¬p”是真命题,命题“p或q”是真命题,则p,q至少已改是真命题,所以那么命题q一定是真命题,所以B正确.对于C,若命题p:∃x∈R,x2﹣x+1<0,则¬p:∀x∈R,x2﹣x+1≥0,满足特称命题的否定是全称命题的形式,所以C正确;对于D,“sinθ=”是“θ=30°”的必要不充分条件,不是充分不必要条件,所以D不正确.故选:D.点评:本题考查命题的否定,充要条件,四种命题的逆否关系,复合命题的真假的判断,基本知识的考查.10.(5分)已知函数的最小正周期为π,为了得到函数g(x)=cosωx的图象,只要将y=f(x)的图象()A.向左平移个单位长度B.向右平移个单位长度C.向左平移个单位长度D.向右平移个单位长度考点:函数y=Asin(ωx+φ)的图象变换.专题:三角函数的图像与性质.分析:由周期函数的周期计算公式:,算得ω=2.接下来将f(x)的表达式转化成与g(x)同名的三角函数,再观察左右平移的长度即可.解答:解:由题知ω=2,所以,故选择A.点评:本题考点定位:本小题考查诱导公式,函数图象的变换,基础题.11.(5分)函数f(x)在定义域R上的导函数是f′(x),若f(x)=f(2﹣x),且当x∈(﹣∞,1)时,(x﹣1)f′(x)<0,设a=f(0、b=f()、c=f(log28),则()A.a<b<c B.a>b>c C.c<a<b D.a<c<b考点:函数的单调性与导数的关系.专题:函数的性质及应用;导数的概念及应用.分析:先由x∈(﹣∞,1)时,(x﹣1)f′(x)<0,得函数f(x)在(﹣∞,1)上为增函数;又f(x)=f(2﹣x)得f(x)图象关于x=1对称,则 f(x)在(1,+∞)上为减函数,然后将f(0),f(),f(log28)化到同一单调区间内比较即可.解答:解:∵x∈(﹣∞,1)时,∴(x﹣1)f'(x)<0,∴f'(x)>0,∴f(x)在(﹣∞,1)上为增函数,又∵f(x)=f(2﹣x),∴f(x)图象关于x=1对称,∴f(x)在(1,+∞)上为减函数,又∵a=f(0)=f(2),b=f(),c=f(log28)=f(3),∴3>2>,∴c<a<b.故选:C.点评:解题的关键为由f(x)=f(2﹣x)得函数图象关于x=1对称,以及利用导数符号确定函数的单调性,属于常用解题技巧.12.(5分)若定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,则函数y=f(x)=log3|x|的零点个数是()A.多于4个B.4个C.3个D.2个考点:对数函数的图像与性质;函数的周期性.专题:压轴题;数形结合.分析:根据定义在R上的偶函数f(x)满足f(x+2)=f(x),且当x∈[0,1]时,f(x)=x,我们易画出函数f(x)的图象,然后根据函数y=f(x)﹣log3|x|的零点个数,即为对应方程的根的个数,即为函数y=f(x)与函数y=log3|x|的图象交点的个数,利用图象法得到答案.解答:解:若函数f(x)满足f(x+2)=f(x),则函数是以2为周期的周期函数,又由函数是定义在R上的偶函数,结合当x∈[0,1]时,f(x)=x,我们可以在同一坐标系中画出函数y=f(x)与函数y=log3|x|的图象如下图所示:由图可知函数y=f(x)与函数y=log3|x|的图象共有4个交点,即函数y=f(x)﹣log3|x|的零点个数是4个,故选B点评:本题考查的知识点是对数函数的图象与性质,利用转化思想,将函数的零点个数问题,转化为函数图象交点个数问题,是解答本题的关键.二、填空题:本大题共4小题,每小题5分,共20分13.(5分)如果函数f(x)的图象与函数g(x)=()x的图象关于直线y=x对称,则f(3x﹣x2)的单调递减区间是.考点:反函数.专题:函数的性质及应用.分析:函数f(x)的图象与函数g(x)=()x的图象关于直线y=x对称,可得f(x)=,因此f(3x﹣x2)==的单调递减区间满足,解出即可.解答:解:∵函数f(x)的图象与函数g(x)=()x的图象关于直线y=x对称,∴函数f(x)是g(x)的反函数,∴f(x)=,∴f(3x﹣x2)==的单调递减区间满足,解得.故答案为:.点评:本题考查了反函数、二次函数的单调性、对数函数的单调性、复合函数的单调性,考查了推理能力与计算能力,属于中档题.14.(5分)已知tan(α+β)=3,tan(α+)=2,那么tanβ=.考点:两角和与差的正切函数.专题:三角函数的求值.分析:利用两角和的正切可求得tanα的值,再利用两角差的正切即可求得tanβ=tan[(α+β)﹣α]的值.解答:解:∵tan(α+)=2,∴=2,解得tanα=;又tan(α+β)=3,tan(α+)=2,∴tanβ=tan[(α+β)﹣α]===.故答案为:.点评:本题考查两角和与差的正切函数,求得tanα=是关键,属于中档题.15.(5分)设α=cos420°,函数f(x)=,则f()+f(log2)的值等于8.考点:分段函数的应用;对数的运算性质.专题:计算题;函数的性质及应用;三角函数的求值.分析:运用诱导公式求出a的值,再由对数的运算性质和对数恒等式a logaN=N,即可求出结果.解答:解:∵a=cos420°=cos60°=,∴f(x)=,∴f()==2,f()=()log2=2log26=6,∴f()+f(log2)=2+6=8.故答案为:8.点评:本题考查三角函数的求值,考查分段函数及应用,对数的运算和对数恒等式的运用,属于基础题.16.(5分)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是.考点:棱柱、棱锥、棱台的体积.专题:计算题;综合题.分析:正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,所以球心是底面三角形的中心,球的半径,就是三棱锥的高,再求底面面积,即可求解三棱锥的体积.解答:解:正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,所以球心是底面三角形的中心,设球的半径为1,所以底面三角形的边长为a,,a=该正三棱锥的体积:故答案为:点评:本题考查棱锥的体积,棱锥的外接球的问题,考查空间想象能力,是基础题.三、解答题:本大题共5小题,共70分.解答时写出证明过程或演算步骤.17.(12分)已知向量,函数.(1)求函数f(x)的对称中心;(2)在△ABC中,a,b,c分别是角A,B,C的对边,且,且a >b,求a,b的值.考点:余弦定理的应用;平面向量数量积的坐标表示、模、夹角.专题:计算题;解三角形.分析:(1)通过向量的数量积以及二倍角的余弦函数,两角和的正弦函数化简函数为一个角的一个三角函数的形式,利用正弦函数的对称性求函数f(x)的对称中心;(2)通过,求出C的大小,以及余弦定理求出a,b的值.解答:解:(1),=.…(4分)令得,,∴函数f(x)的对称中心为.…(6分)(2),∵C是三角形内角,∴即:…(8分)∴即:a2+b2=7.将代入可得:,解之得:a2=3或4,…(10分)∵a>b,∴.…(12分)∴或2,∴.点评:本题考查向量的数量积的应用,余弦定理以及两角和的正弦函数与二倍角公式的应用,考查计算能力.18.(12分)为了在夏季降温和冬季供暖时减少能源损耗,房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=(0≤x≤10),若不建隔热层,每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.(Ⅰ)求k的值及f(x)的表达式.(Ⅱ)隔热层修建多厚时,总费用f(x)达到最小,并求最小值.考点:函数模型的选择与应用;利用导数求闭区间上函数的最值.专题:应用题.分析:(I)由建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度x(单位:cm)满足关系:C(x)=,若不建隔热层,每年能源消耗费用为8万元.我们可得C(0)=8,得k=40,进而得到.建造费用为C1(x)=6x,则根据隔热层建造费用与20年的能源消耗费用之和为f(x),我们不难得到f(x)的表达式.(II)由(1)中所求的f(x)的表达式,我们利用导数法,求出函数f(x)的单调性,然后根据函数单调性易求出总费用f(x)的最小值.解答:解:(Ⅰ)设隔热层厚度为x cm,由题设,每年能源消耗费用为.再由C(0)=8,得k=40,因此.而建造费用为C1(x)=6x,最后得隔热层建造费用与20年的能源消耗费用之和为(Ⅱ),令f'(x)=0,即.解得x=5,(舍去).当0<x<5时,f′(x)<0,当5<x<10时,f′(x)>0,故x=5是f(x)的最小值点,对应的最小值为.当隔热层修建5cm厚时,总费用达到最小值为70万元.点评:函数的实际应用题,我们要经过析题→建模→解模→还原四个过程,在建模时要注意实际情况对自变量x取值范围的限制,解模时也要实际问题实际考虑.将实际的最大(小)化问题,利用函数模型,转化为求函数的最大(小)是最优化问题中,最常见的思路之一.19.(12分)直三棱柱ABC﹣A1B1C1中,AB=5,AC=4,BC=3,AA1=4,D是AB的中点.(Ⅰ)求证:AC⊥B1C;(Ⅱ)求证:AC1∥平面B1CD.考点:直线与平面平行的判定;直线与平面垂直的性质.专题:证明题;数形结合.分析:(Ⅰ)利用勾股定理可得AC⊥BC,由直三棱柱的性质可得CC1⊥AC,从而得到AC⊥平面BB1C1C,进而得到AC⊥B1C.(Ⅱ)取B1C中点E,得到 DE为△ABC1的中位线,得到DE∥AC1,由线面平行的判定定理证得AC1∥平面B1CD.解答:证明:(Ⅰ)在△ABC中,因为AB=5,AC=4,BC=3,所以AC⊥BC.因为直三棱柱ABC﹣A1B1C1,所以,CC1⊥AC.因为BC∩AC=C,所以AC⊥平面BB1C1C.所以AC⊥B1C.(Ⅱ)连接BC1,交B1C于E.因为直三棱柱ABC﹣A1B1C1,所以侧面BB1C1C为矩形,且E为B1C中点.又D是AB中点,所以DE为△ABC1的中位线,所以DE∥AC1.因为DE⊂平面B1CD,AC1⊄平面B1CD,所以,AC1∥平面B1CD.点评:本题考查证明线线垂直、线面平行的方法,线面垂直的性质定理和线面平行的判定定理,取B1C中点E,得到DE为△ABC1的中位线是解题的关键.20.(12分)数列{b n}满足:b n+1=2b n+2,b n=a n+1﹣a n,且a1=2,a2=4.(Ⅰ)求数列{b n}的通项公式;(Ⅱ)求数列{a n的前n项和S n.考点:数列的求和.专题:等差数列与等比数列.分析:(Ⅰ)由已知条件推导出数列{b n+2}是首项为4,公比为2的等比数列,由此能求出.(Ⅱ)由a n﹣a n﹣1=b n=2n﹣2,n≥2,得,由此累加得a n=2n+1﹣2n,由此能求出数列{a n的前n项和S n.解答:解:(Ⅰ)∵b n+1=2b n+2,∴b n+1+2=2(b n+2),∴,又b1+2=a2﹣a1+2=4,∴数列{b n+2}是首项为4,公比为2的等比数列.即b n+2=4•2n﹣1=2n+1,所以.…(6分)(Ⅱ)由(Ⅰ)知:a n﹣a n﹣1=b n=2n﹣2,n≥2,∴,令n=2,3,4,…,n﹣1,赋值累加得a n﹣2=(22+23+…+2n)﹣2(n﹣1),∴==2n+1﹣2n,∴S n==2n+2﹣(n2+n+4).…(12分)点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意累加法的合理运用.21.(12分)已知函数.(Ⅰ)若a=4,求曲线f(x)在点(e,f(e))处的切线方程;(Ⅱ)求f(x)的极值;(Ⅲ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,求实数a的取值范围.考点:利用导数研究函数的极值;利用导数研究曲线上某点切线方程;导数在最大值、最小值问题中的应用.专题:计算题;分类讨论;转化思想.分析:(Ⅰ)求直线方程一般用点斜式,本题中已知切点,故可以根据导数的几何意义,求出该点的导数值,即得曲线在此点处的切线的斜率,然后用点斜式写出切线方程即可(Ⅱ)求出函数的导函数,令导数大于0解出增区间,令导数小于0,解出函数的减区间,然后由极值判断规则确定出极值即可.(Ⅲ)若函数f(x)的图象与函数g(x)=1的图象在区间(0,e2]上有公共点,即在区间(0,e2]上,函数f(x)存在自变量取某个值时,函数值等于1,故问题可以转化为求出函数f(x)最值,保证函数的最大值大于等于1,最小值小于等于1即可得到关于参数a的不等式,解之即得.解答:解:(Ⅰ)∵a=4,∴且.(1分)又∵,∴.(3分)∴f(x)在点(e,f(e))处的切线方程为:,即4x+e2y﹣9e=0.(4分)(Ⅱ)f(x)的定义域为(0,+∞),,(5分)令f'(x)=0得x=e1﹣a.当x∈(0,e1﹣a)时,f'(x)>0,f(x)是增函数;当x∈(e1﹣a,+∞)时,f'(x)<0,f(x)是减函数;(7分)∴f(x)在x=e1﹣a处取得极大值,即f(x)极大值=f(e1﹣a)=e a﹣1.(8分)(Ⅲ)(i)当e1﹣a<e2,即a>﹣1时,由(Ⅱ)知f(x)在(0,e1﹣a)上是增函数,在(e1﹣a,e2]上是减函数,∴当x=e1﹣a时,f(x)取得最大值,即f(x)max=e a﹣1.又当x=e﹣a时,f(x)=0,当x∈(0,e﹣a]时,f(x)<0,当x∈(e﹣a,e2]时,f(x)∈(0,e a﹣1],所以,f(x)的图象与g(x)=1的图象在(0,e2]上有公共点,等价于e a﹣1≥1,解得a≥1,又因为a>﹣1,所以a≥1.(11分)(ii)当e1﹣a≥e2,即a≤﹣1时,f(x)在(0,e2]上是增函数,∴f(x)在(0,e2]上的最大值为,∴原问题等价于,解得a≥e2﹣2,又∵a≤﹣1∴无解综上,a的取值范围是a≥1.(14分)点评:本题考点是利用导数研究函数极值,考查了用导数研究函数的单调性以及借助单调性确定函数的极值、最值的位置,解决与极值、最值有关的一些问题,本题综合性较强,涉及到的知识与运算规则较多,题目难度较大,做题时要注意体会本题的这些特点.【选修4-1:几何证明选讲】(共1小题,满分10分)22.(10分)选修4﹣1:几何证明选讲如图,已知四边形ABCD内接于ΘO,且AB是的ΘO直径,过点D的ΘO的切线与BA的延长线交于点M.(1)若MD=6,MB=12,求AB的长;(2)若AM=AD,求∠DCB的大小.考点:与圆有关的比例线段;圆的切线的性质定理的证明.专题:计算题.分析:(1)利用MD为⊙O的切线,由切割线定理以及已知条件,求出AB即可.(2)推出∠AMD=∠ADM,连接DB,由弦切角定理知,∠ADM=∠ABD,通过AB是⊙O的直径,四边形ABCD是圆内接四边形,对角和180°,求出∠DCB即可.解答:选修4﹣1:几何证明选讲解:(1)因为MD为⊙O的切线,由切割线定理知,MD2=MA•MB,又MD=6,MB=12,MB=MA+AB,…(2分),所以MA=3,AB=12﹣3=9.…(5分)(2)因为AM=AD,所以∠AMD=∠ADM,连接DB,又MD为⊙O的切线,由弦切角定理知,∠ADM=∠ABD,(7分)又因为AB是⊙O的直径,所以∠ADB为直角,即∠BAD=90°﹣∠ABD.又∠BAD=∠AMD+∠ADM=2∠ABD,于是90°﹣∠ABD=2∠ABD,所以∠ABD=30°,所以∠BAD=60°.…(8分)又四边形ABCD是圆内接四边形,所以∠BAD+∠DCB=180°,所以∠DCB=120°…(10分)点评:本题考查圆的内接多边形,切割线定理的应用,基本知识的考查.【选修4-4:坐标系与参数方程】(共1小题,满分0分)23.(坐标系与参数方程选做题)已知椭圆C的极坐标方程为,点F1、F2为其左,右焦点,直线l 的参数方程为(t为参数,t∈R).(Ⅰ)求直线l和曲线C的普通方程;(Ⅱ)求点F1、F2到直线l的距离之和.考点:椭圆的参数方程;点到直线的距离公式;简单曲线的极坐标方程.分析:(Ⅰ)通过两个表达式的消去参数t,即可将直线l的参数方程化简为普通方程.椭圆C的极坐标方程化成:12=3ρ2cos2θ+4ρ2sin2θ,最后再化成普通方程即可;(Ⅱ)利用点到直线的距离公式,求出求点F1、F2到直线l的距离,最后求和即可.解答:解:(Ⅰ)直线l普通方程为 y=x﹣2;…(2分)曲线C的普通方程为.…(4分)(Ⅱ)∵F1(﹣1,0),F2(1,0),∴点F1到直线l的距离,…(6分)点F2到直线l的距离,…(8分)∴.…(10分)点评:本题是基础题,考查简单曲线的极坐标方程,椭圆C的极坐标方程与普通方程的互化,点到直线的距离公式,考查计算能力,易考题型.【选修4-5:不等式选讲】(共1小题,满分0分)24.已知函数f(x)=|x﹣2a|+|x﹣a|,a∈R,a≠0.(Ⅰ)当a=1时,解不等式:f(x)>2;(Ⅱ)若b∈R且B≠0,证明:f(b)≥f(a),并说明等号成立时满足的条件.考点:绝对值不等式的解法.专题:不等式的解法及应用.分析:(1)将a=1代入,不等式化为具体的绝对值不等式,然后讨论解之;(Ⅱ)由题知f(a)=|a|,f(b)=|b﹣2a|+|b﹣a|=|2a﹣b|+|b﹣a|≥|2a﹣b+b﹣a|=|a|,得证.解答:解:(Ⅰ)因为a=1,所以原不等式f(x)>2为|x﹣2|+|x﹣1|>2.当x≤1时,原不等式化简为1﹣2x>0,即x<;当1<x≤2时,原不等式化简为1>2,即x∈∅;当x>2时,原不等式化简为2x﹣3>2,即x>.综上,原不等式的解集为{x|x<或x>}.…(5分)(Ⅱ)由题知f(a)=|a|,f(b)=|b﹣2a|+|b﹣a|=|2a﹣b|+|b﹣a|≥|2a﹣b+b﹣a|=|a|,所以f(b)≥f(a),(8分)又等号成立当且仅当2a﹣b与b﹣a同号或它们至少有一个为零.…(10分)点评:本题考查了绝对值不等式的解法;考查了讨论的数学思想.。
河南省实验中学高三上学期期中考试 数学(理)

河南省实验中学2014——2015学年上期期中试卷高三 理科数学命题人:程建辉 审题人:丁海丽(时间:120分钟,满分:150分)一、选择题(本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)1.已知集合{||2,}A x x x R =≤∈,{|4,}B x x Z =≤∈,则 ( )A.(0,2)B.[0,2]C.(0,2]D.{0,1,2}2.记,那么 ( )A. B.- C. D.-3.已知集合{1,2,3,4},{,,}A B a b c ==,为集合到集合的一个函数,那么该函数的值域C 的不同情况有( ) A .7种 B .4种 C .8种 D .12种4.设向量,向量,向量,则向量( ) A .(-15,12) B.0 C.-3 D.-115.设是等差数列,是其前n 项和,且,,则下列结论错误的是( ) A . B . C . D .和均为的最大值6.在△ABC 中,,若此三角形有两解,则b 的范围为( ) A . B .b > 2 C .b<2 D .7.已知函数的周期是,将函数)0( 2cos 3>⎪⎭⎫ ⎝⎛-=ωπωx y 的图象沿轴向右平移个单位,得到函数的图象,则函数( ) A. B. C. D.8.设△ABC 的三内角A 、B 、C 成等差数列,sinA 、sinB 、 sinC 成等比数列,则这个三角形的形状是( )A.直角三角形B.钝角三角形C.等腰直角三角形D.等边三角形9.函数ππln cos 22y x x ⎛⎫=-<< ⎪⎝⎭的图象是( )10.O 为平面上的一个定点,A 、B 、C 是该平面上不共线的三点,若,则△ABC 是( ) A.以AB 为底边的等腰三角形 B.以BC 为底边的等腰三角形 C.以AB 为斜边的直角三角形 D.以BC 为斜边的直角三角形11.设p:2()e ln 21xf x x x mx =++++在内单调递增,q:,则p 是q 的( )A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件12.已知两条直线:y=m 和:y= (m >0),与函数的图像从左至右相交于点A,B,与函数的图像从左至右相交于C,D.记线段AC 和BD 在X 轴上的投影长度分别为a,b,当m 变化时,的最小值为( ) A . B. C. D.二、填空题:请把答案填在题中横线上(每小题5分,共20分). 13.计算= .14.已知A,B,C 三点在同一条直线上,O 为直线外一点,若0pOA qOB rOC ++=,其中p,q,rR ,则 .15设x 、、、y 成等差数列,x 、、、y 成等比数列,则的取值范围是 . 16.已知函数21,(0)()log ,(0)ax x f x x x +≤⎧=⎨>⎩,若函数y=f(f(x))+1有4个不同的零点,则实数a 的取值范围是 .三、解答题:解答应写出文字说明、证明过程或演算步骤(共70分).17.(本小题满分12分)设函数的定义域为,命题与命题,若真,假,求实数的取值范围.18.(本小题满分12分)已知,其中()x x x m ωωωcos 3,cos sin +=→,()x x x n ωωωsin 2,sin cos -=→,且,若相邻两对称轴间的距离不小于。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A B C 的内角 A 、 B 、 C 的对边分别为 a 、 b 、 c ,已知 co s A C co s B 1,
求 A B C 的内角 C . 21.(本小题满分 12 分) 已知数列 a n 的各项为正数,其前n项和 sn 满足sn ( 设 bn 1 0 a n n N (1)求证:数列 a n 是等差数列,并求 a n 的通项公式; (2)设数列 bn 的前 n 项和为 T n ,求 T n 的最大值。 22.(本小题共 12 分) 已知 f ( x ) x l n x , g ( x ) x a x 3
的取值范围是(
3 3
,
2 2
B. 2 , 2
C. 2 , 3
D.(0 ,2)
二、填空题(本大题共 4 小题,每小题 5 分,共 20 分,把答案填在题中横线上) 13.曲线 y x ( 3 l n x 1) 在点(1,1)处的切线方程为________
y y
B.
2
log 2
|x|
C。 (
e
x
ex 2
3 D. y x 1
6..函数 y A. 1, 1
1 2
x
l n x 的单调递减区间为
B.(0,1]
) D.(0,+∞) ( ) D.5 ( )
C.[1,+∞)
7.函数 f x x co s 2 x 在区间 0, 2 上的零点个数为 A.2 8.设函数 f ( x ) B.3 C.4
(x (x
2 x 1 x 2 x 2
2ቤተ መጻሕፍቲ ባይዱ
1) 1)
,若 f ( x 0 ) 1 ,则 x 0 的取值范围是
( , ( ,
A. ( , 1) (1, ) C. ( , 3) (1, )
B. D.
1) 1, 3) 1,
x
2
1 1
x
的图像与函数 y kx 的图像恰有两个交点,则实数 k 的取值范围
y
g x
x 1, 2 的反函数.
19.(本小题满分 12 分) 已知向量 a ( si n x ,
3 2
) ,b
( co s x , 1)
(1)当向量 a 与向量 b 共线时,求 tan x 的值; (2)求函数 f ( x ) 2 ( a b ) b 的最大值,并求函数取得最大值时的 x 的值. 20.(本小题满分 12 分)
2
a
2c ,
an
1
2
)
2
(1)求函数 f ( x ) 在 t , t 2 ( t 0 ) 上的最小值; (2)对一切 x ( 0, ) , 2 f ( x ) g ( x ) 恒成立,求实数 a 的取值范围; (3)证明:对一切 x ( 0, ) ,都有 l n x >
2014-2015 学年河南省实验中学高三上期期中试卷
文科数学
(时间:120 分钟,满分:150 分)
一、选择题(本大题共 12 小题,每小题 5 分,满分 60 分,在每小题给出的四个选项中, 只有一项是符合题目要求的。) 1.设集合 A x 3 2 x 1 3 ,集合 B 是函数 y l g x 1 的定义域;则 A B ( A. 1, 2 B. 1, 2 C. 1, 2 D. 1, 2 ) )
2.若f (x)是偶函数,且当 x 0, + 时,f (x) = x-1 ,则f (x-1) < 0的解集是( A.{x |-1 < x < 0} C.{x | 0 < x < 2} 3.设向量 a , b 满足 a b 1 , a b A. 2 , B. 3 , B.{x | x < 0或1< x < 2} D.{x | 1 < x < 2}
2, 2
C.
, 2
D.
2, 2
11.等差数列 a n 的前 m 项和为30 ,前 2 m 项和为100 ,则它的前 3 m 项和是( A.130 B.170 C.210 D.260
a b
)
12.在锐角三角形中,a、b、c分别是内角A、B、C的对边,设B=2A,则 ) A.
9.O 是 A B C 所在平面内的一点,且满足 ( O B O C ) ( O B O C 2 O A ) 0 , 则 A B C 的形状一定为( A.正三角形
2
) C.等腰三角形 D.斜三角形 )
B.直角三角形
10.不等式 ( a 2 ) x 2 ( a 2 ) x 4 0 的解集为 R ,则实数 a 的取值范围是( A . ( 2, 2 ) B.
1 2
,则 a 2 b =(
) D. 7
C. 5 , )
4.函数 y si n ( 2 x A. x
3
) 图象的对称轴方程可能是(
6
B. x
12
C. x
6
D. x )
12
5.下列函数中,既是偶函数,又在区间 1, 2 内是增函数的为( A. co s 2 x
15.在等差数列{an}中,已知a1=20 ,前n项和为Sn,且S10=S15,求当n=
时,
Sn取得最大值
16.已知函数 y 是________. 三、解答题(本大题共 6 小题,共 70 分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分 10 分) 设 A x 2 x 5 , B x m 1 x 2 m 1 若 B A ,求实数 m 的取值范围。 18.(本小题满分 12 分) 已知函数 f x l g x 1 . (1)若 0 f 1 2 x f x 1 ,求 x 的取值范围; (2)若 g ( x ) 是以2为周期的偶函数,且当 0 x 1 时,有 g ( x ) f ( x ) ,求函数
