4.1无理数
无理数发展简史

无理数发展简史引言概述:无理数是数学中的一个重要概念,它是指不能用两个整数的比值表示的数。
无理数的发展历史可以追溯到古希腊时期,经过数学家们的不懈努力和探索,无理数的概念逐渐被确立并得到了广泛的应用。
本文将从古希腊时期开始,逐步介绍无理数的发展简史。
一、古希腊时期1.1 古希腊数学家的困惑古希腊数学家发现,有些长度无法用整数比值表示,比如正方形的对角线与边长之间的关系。
1.2 毕达哥拉斯学派的发现毕达哥拉斯学派提出了“一切皆数”的观念,但无法解释对角线与边长之间的关系,这引起了无理数概念的探讨。
1.3 毕达哥拉斯学派的保密措施毕达哥拉斯学派将对角线与边长之间的关系视为绝密,只内部传授,不对外公开。
二、欧几里得时期2.1 欧几里得的《几何原本》欧几里得在其著作中系统地阐述了几何学的基本概念,但对无理数并未有详细的讨论。
2.2 欧几里得的数论研究欧几里得在数论方面有较深的研究,但对于无理数的概念并未有深入的探讨。
2.3 欧几里得对无理数的影响欧几里得的几何学和数论研究对后来无理数的发展产生了一定的影响,为后来的研究奠定了基础。
三、近代数学发展3.1 费马与无理数费马在其著作中对无理数的性质进行了研究,为后来的数学家提供了重要的参考。
3.2 康托尔的无理数理论康托尔提出了无限集合的概念,进一步推动了无理数理论的发展。
3.3 无理数在数学中的应用无理数在数学中的应用日益广泛,涉及到分析、代数、几何等多个领域,为数学的发展做出了重要贡献。
四、现代数学的发展4.1 无理数的推广现代数学对无理数的概念进行了推广,引入了超越数和超限数等新概念。
4.2 无理数的计算现代计算机技术的发展,使得对无理数的计算变得更加便捷和高效。
4.3 无理数在科学研究中的应用无理数在物理学、工程学等科学领域中有着广泛的应用,为科学研究提供了重要的数学工具。
五、结语无理数作为数学中的重要概念,经过数学家们的不懈努力和探索,逐渐得到了广泛的应用。
无理数发展简史

无理数发展简史引言概述:无理数是数学中一个重要的概念,它指的是不能表示为两个整数的比值的实数。
无理数的发展历程可以追溯到古希腊时期,随着数学的发展,无理数的概念逐渐被完善和扩展。
本文将从古希腊时期开始,介绍无理数的发展历史。
一、古希腊时期1.1 毕达哥拉斯学派的发现毕达哥拉斯学派是古希腊数学的重要学派之一。
在公元前5世纪,毕达哥拉斯学派成员发现了无理数的存在。
他们通过对勾股定理的研究,发现了不能表示为整数比值的边长关系,从而确立了无理数的概念。
1.2 伊壁鸠鲁学派的质疑伊壁鸠鲁学派是古希腊哲学的一支。
该学派对毕达哥拉斯学派的无理数概念提出了质疑。
他们认为无理数是不存在的,一切都可以用有理数表示。
这一争论持续了一段时间,直到欧几里得给出了无理数存在的证明,才解决了这一争议。
1.3 欧几里得的证明欧几里得是古希腊数学家,他在《几何原本》中给出了无理数存在的证明。
他通过反证法证明了不能用有理数表示的线段存在,从而证明了无理数的存在。
欧几里得的证明为无理数的研究奠定了基础。
二、中世纪的发展2.1 无理数的被遗忘在中世纪,无理数的概念被遗忘了一段时间。
由于宗教和哲学的影响,数学的发展受到了限制,无理数的研究停滞不前。
2.2 无理数的重新发现到了16世纪,无理数的概念重新被人们关注。
意大利数学家维埃塔在《无理数的存在》一书中重新提出了无理数的概念,并给出了更加严谨的证明。
这使得无理数的研究重新得到了推动。
2.3 无理数的应用随着无理数概念的重新被接受,人们开始发现无理数在数学中的广泛应用。
无理数在几何、代数等领域中起着重要作用,为数学的发展带来了新的动力。
三、无理数的扩展3.1 无理数的无限性无理数的一个重要特点是无限性。
无理数的小数表示无限不循环,这使得无理数的研究更加复杂和有趣。
3.2 无理数的无穷性无理数的无穷性是指无理数的小数位数无限多。
这使得无理数可以无限接近任何有理数,为数学中的近似计算提供了便利。
新教材人教版高中数学必修1 第四章 4.1.2 无理数指数幂及其运算性质

所以
1
x2
1
x2
6,
所以
x2 x2
1
1
4
2.
x2 x 2
ax )(a2x 1 ax ax
a 2x
)
a 2x
1 a 2x
1
2 1
1 1 2 2 1. 2 1
【素养·探】 在指数式的化简求值中,经常利用核心素养中的数学
运算,通过对式子的等价变形,体现了良好的先化简后 求值的数学运算习惯. 将本例中的式子改为 a3x a3x ,试求值.
ax ax
【解析】
(1)底数相同时直接对指数上的无理数进行加减运算. (2)若式子中含有根式,则先化为指数式再进行运算,一 般指数中的根式可以保留.
【习练·破】
计算下列各式:
1( 3 )2 3.
3
2
(m
3
m
6
)12
.
【解析】(1)原式=
(
3
3
2 )2
3
(
3
2 )2
3
3.
(2)原式=
(m
3
6
)12
(m 6 )12
x的指数升高,再代入求值.
【解析】由已知可得:x+x-1=(
x
1 2
x -12 2) 2=(
)2-25 =3.
x2+x-2=(x+x-1)2-2=32-2=7.
原式= 7 6 1 .
35 2
【类题·通】 解决条件求值问题的步骤
【习练·破】
1.已知a+a-1=7(a>1),求
a
1 2
1
a2
所以 3 a b 1 .
鲁教版(五四制)七年级上册数学课件4.1无理数

0.333 1 3
0.2666 4 15
有限小数和循环小数都可以化为分数,任何 有限小数或无限循环小数都是有理数.
反过来,任何一个有理数都可以写成有限小数或类:
按定义分类:
正整数
有理数
整数
零 负整数
分数
正分数 负分数
按性质符号分类:
正整数
正有理数
有
正分数
速练在当堂
3. 下列关于有理数的说法中,错误的是( ) A.所有的整数都是有理数 B. 所有的分数都是有理数 C. 所有的有限小数都是有理数 D. 所有的无限小数都是有理数
速练在当堂
4. 下列关于无理数的说法中,正确的是( ) A.有最小的无理数 B. 有最大的无理数 C. 无理数有有限个 D. 无理数有无限个
理 零 数负有理数
负整数
负分数
有限小数和无限循环小数属于分数.
学习目标
1.理解无理数的概念,会判断一个数是有理数还是无理数. 2.能在数轴上表示某些简单的无理数.
新课导入
把两个边长为1的小正方形拼成一个大正方形
设大正方形的边长为 ,则 满足什么条件?
所以ɑ2=2
则a是有理数吗?
思考探究
因为 12 1, 22 4 ,所以a是大于1而小于2的数.
5.打开课本17页 练一练
小结:
1.什么叫无理数? 2.数的分类? 3.如何判定一个数是无理数还是有理数.
圆周率π =3.14159265…也是一个无限不循环小数, 另外,0.5858858885…(相邻两个5之间8的个数逐次加1) 也是一个无限不循环小数, 它们都是无理数.
结论总结
2.有理数与无理数的主要区别:
(1)无理数是无限不循环小数, 有理数是有限小数或无限循环小数.
4.1无理数教案

三、精讲点拨
四、反思拓展
五.系统总结教师指导
1.易错点:
(1)“无限不循环小数”与“无限循环小数”的联系和区别.
(2)圆周率π=3.141 592 65…也是一个无限不循环小数,故π是无
理数.
2.归纳小结:
(1)任何有限小数或无限循环小数都是有理数.
(2)无限不循环小数叫做无理数.
3.方法规律:
1.下列各数是无理数的是( )
(A)(B)(C)16
2.在数,中,无理数是.
3.按要求将下列数字分类:,,0,3.14,-,7.151 551…(每相邻两
个“1”之间依次多一个“5”),
整数集合{ ,…},
分数集合{ ,…},
无理数集合{ ,…}.
你学到了哪些知识点?
你学到了哪些方法?
教师引导,
点拨
教师讲解
教师引导,
点拨
学生认真
听讲
学生回答
学生讨论
回答。
数学七上4.1《无理数》课件(1)

4、作者写从早到晚的吆喝声,具体写 了哪些叫卖声?重点又写了什么?
作者从早写到晚。写早晨吆喝卖早点的: 大米粥、油炸果的;和新鲜蔬菜的:卖青菜和 卖花儿的。写白天卖日用百货和修理各种家具 的,这就更热闹了。
然而重点是写晚上。北京胡同的晚上好 不热闹:卖夜宵的,唱话匣子的,用凄厉动人 的叫喊讨饭的,真是应有尽有。这一层作者重 在写出北京胡同里小贩的叫卖声持续时间之长, 种类之多。
本文介绍了旧北京街大街小巷各种吆 喝声。围绕吆喝声,介绍了吆喝声所代表 的经营品种、介绍了各种吆喝声的具体内 容、表现方式以及音韵节奏
课文讲解
1、作者围绕北京的吆喝声介绍了什么?他对 北京的吆喝声怀有怎样的感情?
在作者看来,北京小贩货郎的叫卖声简直就 是一种“戏剧性”的艺术。作者介绍了从白天的 叫卖声到夜晚的叫卖声,从卖吃食的、放留声机 的,到乞讨的,还有富有四季特色的叫卖声等等, 从中流露出作者对北京的吆喝声怀有一种特殊的 感情,那就是愉悦和怀想。
4、仿句练习。
在下面这段话的横线上填上恰当的语句,要 求仿用前面一句的句式及运用的修辞手法,内容 要前后照应。
我们用友谊写一本书,一本厚厚的书。在书 里,友谊如珍珠,我们穿缀,联成一串璀璨的项 链;友谊如__彩__绸___,我们___彩__绸__共__同__剪裁 , _缝__制__成__一__件__件绚丽的衣衫;友谊如_花__种____,我们 _共__同__播__种___,培_育__出__一__个__个__五彩的花坛 。
小小的胡同,一座座四合院,似乎每一扇破 旧的、刻着已无法辨认的对联的木门都是一部古 老的历史,给人一种神秘感。人们每每在门前摆 一张小桌,或扯闲白儿,或对弈下棋,或二胡悠 扬,或京剧清唱,自有一番人间的乐趣。我有一 次经过揽杆市,一家生活并不富裕的小屋主人的 雅兴叫我吃惊。门前青砖上放着几十盆花卉—— 月季、米兰、朱顶红,低矮的屋檐下一溜排开竟 有六七只竹丝鸟笼,雕以花纹,曲线弯得那么有 神韵的青铜鸟笼钩,仿佛音乐的滑音一般,给人 一种和谐的美。黄雀、画眉、红蓝靛颏吟唱其间, 不知忧愁为何事。
七年级无理数的概念与运算

七年级无理数的概念与运算无理数是指既不能表示为两个整数的比值,也不能表示为有限小数或循环小数的实数。
它们是无限不循环小数的一种特殊形式。
在七年级数学中,我们将学习无理数的概念和运算。
一、无理数的概念无理数是指不能写成两个整数的比值的实数,也不是有限小数或循环小数的实数。
无理数的表示一般用根号形式表示,如√2,√5等。
无理数可以是正数也可以是负数。
二、无理数的运算2.1 无理数的加减运算无理数的加减运算与有理数的加减运算类似,只需要将无理数的根号部分进行合并即可。
例如,√2 + √2 = 2√2。
2.2 无理数的乘法运算无理数的乘法运算也是将根号部分进行合并。
例如,√2 × √3 = √6。
2.3 无理数的除法运算无理数的除法运算需要用到有理化的方法,将无理数分母的根号部分有理化。
例如,√2 ÷ √3 = (√2 × √3) ÷ (√3 × √3) = √6/3 = (√6)/3。
三、无理数的应用无理数在数学和实际生活中都有广泛的应用。
在几何中,无理数常用于描述无法精确表示的长度,如正方形的对角线长度等。
在物理学中,无理数也常用于科学计算中,例如计算圆的面积、体积等。
四、无理数的性质4.1 无理数与有理数的关系无理数和有理数是实数的两个主要子集,它们之间没有交集。
无理数和有理数的并集构成了实数的全体。
4.2 无理数的无穷性和稀疏性无理数存在无限多个,并且无理数的任意两个数之间都存在有理数。
这个性质被称为无理数的无穷性和稀疏性。
4.3 无理数的数轴表示无理数可以在数轴上表示,位于有理数之间。
例如,√2位于1和2之间,√3位于1和2之间。
五、无理数的近似值无理数通常无法精确表示,但可以使用有理数来近似表示。
例如,我们通常将√2近似为1.414,将√3近似为1.732。
六、总结无理数是既不能表示为两个整数的比值,也不能表示为有限小数或循环小数的实数。
我们学习了无理数的概念和运算方法,包括加减运算、乘法运算和除法运算。
4.1无理数

当堂检测:
当堂检测:
当堂检测:
作业:
习题:4.2 1、 2
但后来,这学派的一位年轻成员希伯索 斯(Hippasus) 发现边长为1的正方形的对角 线的长不能用有理数来表示,这就动摇了毕 达哥拉斯学派的信条,引起了信徒们的恐慌, 他们试图封锁这一发现,然而希伯索斯偷偷 将这一发现传播出去,这为他招来了杀身之 祸,在他逃回家的路上,遭到毕氏成员的围 捕,被投入大海. 他这一死,使得这类数的计算推迟了500 多年,给数学的发展造成了不可弥补的损失.
3 3 9 ...... 2 2 4,
结果都为分数,所以a不可能是以2
为分母的分数。
问题导学:
a可能是以3为分母的分数吗?
,
,
,
a
...... ,
结果都为分数,所以a不可能是以3
在直角三角形中,由勾股定理得,
2
1
斜边² =1² +2² =5,所以直角三角形的斜边为边的正方形 的面积是5.
b² =5 2、设该正方形的边长为b,b满足什么条件? b不是有理数。 3、b是有理数吗?说说你的理由。
小知识
然而,第一个发现这样的数的人却被 抛进大海,你想知道这其中的曲折离奇吗? 这得追溯到 2500 年前,有个叫毕达哥拉斯 的人,他是一个伟大的数学家,他创立了 毕达哥拉斯学派,这是一个非常神秘的学 派,他们以领袖毕达哥拉斯为核心,认为 毕达哥拉斯是至高无尚的,他所说的一切 都是真理. 毕达哥拉斯( Pythagoras) 认为“宇宙间 的一切现象都能归结为整数或整数之比,即 都可用有理数来描述.
无理数发展简史

无理数发展简史简介:无理数,也称为超越数,是指不能表示为两个整数的比值的实数。
无理数的发现和发展是数学领域的重要里程碑之一。
本文将详细介绍无理数的起源、发展和重要里程碑,以及无理数在数学和科学领域的应用。
1. 无理数的起源无理数的概念最早可以追溯到古希腊时期。
古希腊数学家毕达哥拉斯提出了著名的毕达哥拉斯定理,即直角三角形的斜边长是一个有理数。
然而,他们发现某些直角三角形的斜边长无法用有理数表示,这就引起了无理数的研究。
2. 无理数的发展2.1 古希腊时期古希腊数学家们开始研究无理数,并提出了一些无理数的例子。
其中最著名的是毕达哥拉斯学派的发现,他们证明了根号2是一个无理数。
2.2 欧几里德时期欧几里德在其著作《几何原本》中系统地研究了无理数,并给出了一种用连分数表示无理数的方法。
他还证明了根号2是一个无理数,并提出了无理数的性质。
2.3 近代数学时期在16世纪和17世纪,无理数的研究得到了进一步发展。
法国数学家笛卡尔和德国数学家勒让德等人对无理数进行了深入研究,并提出了更多无理数的例子。
3. 无理数的重要里程碑3.1 无理数的定义19世纪初,德国数学家魏尔斯特拉斯给出了无理数的严格定义,即不能表示为有理数的实数。
3.2 无理数的分类20世纪初,法国数学家勒贝格提出了无理数的分类方法,将无理数分为代数无理数和超越无理数两类。
代数无理数是满足某个代数方程的实数,而超越无理数则不能满足任何代数方程。
3.3 无理数的性质研究数学家们对无理数的性质进行了深入研究,包括无理数的逼近性质、无理数的连分数表示等。
他们发现无理数具有丰富的性质,对数学的发展起到了重要作用。
4. 无理数在数学和科学中的应用4.1 几何学中的无理数无理数在几何学中有广泛的应用,例如用无理数表示线段的长度,解决一些几何问题等。
4.2 物理学中的无理数无理数在物理学中也有重要的应用。
例如,无理数在量子力学中用于描述粒子的位置和动量等物理量。
4、1无理数(2)

2、下列各数中,哪些是有理数? 哪些是无理数? 0.351,- ,3.14159,- 5.2323332…, , 123456789101112…(由相继 的正整数组成).在下列每一个 圈里,填入适当的数.
四、课堂小结 你有什么收获?疑问? (同桌互说,组长归纳,疑难 解惑) 五、布置作业:课本90页习题 4.2中1、2
2.课本88页做一做,仿照上面 的方法确定面积为5的正方形的 边长b(结果精确到十分位、百 分位) (学生独立思考、再交流)
3、自主学习课本88页议一议 到例题上面, (1)从书中画出无理数的定义. (2)讨论有理数和无理数有什么 区别?
模块2:例题讲解 ,巩固应用 课本88页例题 (提问学生讲解,老师总结) 巩固应用: 课本89页随堂练习 课本90页习题4.2中3、4(学生 独立做完后,对改,改错)
典型例题:下列各数: . 1 22
, 0 7
中无理数是 ________________________
三、当堂检测 1、判断题 (1)有理数与无理数的差都是有 理数. (2)无限小数都是无理数. (3)无理数都是无限小数. (4)两个无理数的和不一定是无 理数.
4.1 无理数(2)
学习目标:
1、借助计算器探索无理数是无 限不循环小数,并从中体会无限 逼近的思想. 2、会判断一个数是有理数还是 无理数. 核心知识:无理数与有理数的区 别。
学习过程
一、导入新课
二、学习新知 模块1:探索无理数是无限不循环 小数 1、自主学习课本87页-88页做一 做之前的内容,并根据问题思考、 讨论、展示分析。
数学七上4.1《无理数》课件(1)

(3) 3 (4) a+b(a,b都是无理数)
解:有理数有:5.101010101…
(5)
4 3
无理数有:1.0203040506… ,
3 , 4 .
3
朱 德
zhū
朱砂 姓朱
朱德(1886~1976)马克思主义 者,无产阶级革命家,军事家,政治 家;中国共产党、中国人民解放军和 中华人民共和国的主要领导人,中国 人民解放军和中华人民共和国的主要 缔造者之一;中华人民共和国元帅 (1959 ~ 1976)。
1928年,朱德同志带领一支队 伍到井冈山跟毛泽东同志会师。
红军在山上,山下不远处就是 敌人。
红军在山上,山下不远处就是 敌人。
井冈山的风光。 井冈山旧居。
井冈山会师 朱毛会师
zhū zhì gāng shǒu
朱志冈 守
(姓朱)(志气)(井冈山)(看守)
gōng
攻守 进攻 攻破
shǒu
(扁担)
齐读课题,有什么疑问想提呢?
1.“朱德的扁担”这个故事发 生在什么时候?
2.朱德用这个扁担来干什么?
zhū zhì gāng shǒu
朱志冈 守
gōng bì chǎn quàn
攻必产 劝
劝 攻 同志 生产 井冈山 争 守 红军 会师 一块儿 朱德 扁担 井冈山 坚守 粉碎 敌围攻 山高路陡 翻山越岭
3、27页习题3.1 小结:长方形的对角线的长也不是有理数,是 一个无限不循环小数
4、27页,试一试
结论:无限不循环小数叫做无理数
例题:下列各数中,哪些是有理数?哪些是无理数?
(1)5.101010101…(相邻两个1之间都有一个0)
(2)1.0203040506…(从小到大排列的相邻两个正 整数间都有一个0
无理数发展简史

无理数发展简史标题:无理数发展简史引言概述:无理数是数学中的一个重要概念,它们不可以用整数或分数表示,是一种无限不循环小数。
无理数的概念在数学发展史上起到了重要的作用,本文将从古希腊时期开始,介绍无理数的发展历程。
一、古希腊时期1.1 古希腊的数学思想在古希腊时期,数学家们主要关注于有理数的研究,认为一切可以表示为整数或分数。
例如,毕达哥拉斯学派认为世界万物皆可用整数比例来表示。
1.2 毕达哥拉斯定理毕达哥拉斯学派发现了一个重要的定理,即毕达哥拉斯定理。
但是,他们也发现了一个问题,即根号2的长度无法用有理数表示,这导致了无理数的概念的出现。
1.3 无理数的发现古希腊数学家发现了无法用有理数表示的数,这些数被称为无理数。
例如,根号2被证明是一个无理数,这一发现在数学史上具有重要意义。
二、欧几里得时期2.1 欧几里得几何学欧几里得是古希腊时期的一位著名数学家,他在其著作《几何原本》中提出了欧几里得几何学,这对无理数的研究有着深远的影响。
2.2 无理数的推广欧几里得在其著作中提出了一种新的方法,可以用无理数来表示几何中的长度。
这一方法为无理数的推广奠定了基础。
2.3 无理数的地位在欧几里得时期,无理数的地位逐渐得到认可,人们开始意识到无理数在数学中的重要性,并逐渐深入研究无理数的性质。
三、近代数学发展3.1 无理数的形式化在近代数学发展中,数学家们对无理数进行了形式化的定义和研究,使得无理数的概念更加清晰和准确。
3.2 无理数的应用无理数在现代数学中有着广泛的应用,例如在物理学、工程学和计算机科学中都有着重要的作用,无理数已经成为数学中不可或缺的一部分。
3.3 无理数的发展随着数学理论的不断发展,无理数的研究也在不断深入,人们对无理数的理解和应用也在不断扩展,无理数的发展将继续对数学和科学领域产生重要影响。
四、无理数的未来4.1 无理数的研究未来,无理数的研究将继续深入,人们将更加深入地探索无理数的性质和应用,为数学和科学领域带来新的突破。
数学人教A版必修第一册4.1.2无理数指数幂及其运算性质共14张ppt

(1)(3 23 2 2)3 2;
(2)aπ6 a23π . aπ
((11))原原式式===((33(3222×2×2×2232322332)23)32)3322=22===33636××6×22222 2=2 916.
a a ==22991166..
(2)原式=aπ6
6π+23+π (223-π)π原-=式πa-=π6 aπ6.-
3.计算: 20
1
2
2
1
86
___________.若10x
2
,10 y
3 ,则
3x y
10 2
________________.
解:原式=1+ 2 1 2 =0
3x-y
10 2
3x-y
=(10 )
1 2
=
10 3x
10y =
8
3
2
=
6
3
4.已知
a
1
23
,b
1 42
,求
a
1 2
b
ab2 (
, 又 x-y=6,xy=又16x,-y=6,xy=16, y=1∴6,(x +y)2=(x -∴y)2(+x +4xyy)2==6(2x -y)2+4x
y
=
62
∴(x +y)2=(x+-4y×)21+6=4x1y0=0.62+4×16=100.
+4当×∴1xx6+=+y1y==0011.00时或,x原+∴式y=x值+-为y1=100.1-062或×x4+∴=yx3=+,-y=101.0 或 x+y=-10.
思考 1:2 2一定是实数吗?
提示:根据无理指数幂的定义 2 2是实数.
知识点二 实数指数幂的运算性质
41无理数课件

正三角形ABC的边长为2,底边上的高为h, h可能是整数吗?可能是分数吗?
A
h不是整数.
(2)比如1 1 1,2 2 4 2 2 43 3 9
2 h
两个相同的分数相乘结果都是分数,
h不是分数.
B
D
C
h不是有理数.
Copyright 2004-2009 版权所有 盗版必究
(1)面积为7的正方形的边长是 有理数吗?为什么? (2)面积为4的正方形的边长是有理 数吗?为什么?
(3)a可能是以2为分母的分数吗?可能是以 3为分母的分数吗?说说你的理由,并与同伴 交流。 (4)a可能是分数吗?说说你的理由,并与 同伴交流。
Copyright 2004-2009 版权所有 盗版必究
归纳:
在等式 a2 2 中,a既不是整数,
也不是分数,所以a不是有理数。
考考你:
(1)以直角三角形的斜边的正方形面 积是多少?
人们为了纪念希勃索斯这位为真理而献身的可敬学者就把不可公度的量取名为无理数这便是无理数的由来
公元前500年,古希腊毕达哥拉斯学派的弟子希勃索斯 发现了一个惊人的事实,一个正方形的对角线与其一边的 长度是不可公度的(若正方形边长是1,则对角线的长不是 一个有理数)。这一不可公度性与毕氏学派“万物皆为 数”(指有理数)的哲理大相径庭。这一发现使该学派领导 人惶恐、恼怒,认为这将动摇他们在学术界的统治地位。 希勃索斯因此被囚禁,受到百般折磨,最后竟遭到沉舟身 亡的惩处。
然而,真理毕竟是淹没不了的,毕氏学派抹杀真理才 是“无理”。人们为了纪念希勃索斯这位为真理而献身的 可敬学者,就把不可公度的量取名为“无理数”——这便 是“无理数”的由来。
Copyright 2004-2009 版权所有 盗版必究
七年级数学上册4.1无理数课件鲁教版五四制

A
?
B
E
C
3. 如下图是由36个边长为1的小正方形拼 成的,试画出两条长度是有理数的线段和 两条长度不是有理数的线段。
挑战自己:你能画出面积等于2的正方形?
分享收获或感悟
1.若x2=8,则x( C )
A.是整数 B.是分数 C.不是有理数 D.是有理数
2.长,宽分别是3,2的长方形,它的对角线的长_不__是__整 数,_不__是___分数。(填是或不是)
3.如右图
(1)以直角三角形的斜边为正方形的
?
面积是多少? 3
2
(2)设该正方形的边长为b,b满足什么
条件? b2=3
1
(3)b是有理数吗?不是有理数
“数”
古希腊伟大的数学家毕达哥拉斯认为世界 上只有整数与分数两类,宇宙间一切现象都 可用有理数去描述.
后来,该学派一个叫希伯索斯的成员对上 述结论产生了怀疑,他经过苦心钻研,终于 发现在生活中还存在着一类既不是整数也不 是分数的数。
到底谁的观点正确呢?
山东省பைடு நூலகம்博市临淄区边河中学 徐梅
有一个边长为2的大正方形,如何折叠能 得到一个小正方形?这个小正方形的面积 是多少?
设小正方形的边长为a,a应满足什么条件?
a 等于多少?
1.a可能是整数吗?试说明理由
2.a可能是分数吗?试说明理由
a2=2
a既不是整数又不是分数,所以a 一定不是 有理数 。
希伯索斯当时的发现动摇了毕达哥拉斯
学派的信条,他们试图封锁这一发现,然 而希伯索斯早己将这个发现偷偷传播出去 了。这为他招来了杀身之祸,在他逃回家 的路上,遭到毕氏成员的围捕,投入大海, 献出了宝贵的生命, 但真理是不可战胜的! 后来古希腊人终于证实了希伯索斯的发现。
鲁教版(五四制)七年级上4.1无理数课件(共19张ppt)

D. 0.4
1
•
【解析】选C.因为3.14是小数,3是分数, 0.是4 无限循
环小数,所以选项A,B,D都是有理数; 0.305305530555
是无限不循环小数,所以也是无理数.
通过本课时的学习,需要我们掌握: 无理数的概念:无限不循环小数称为无理数.
挫折像一把火,既可以把你的意志烧得更坚, 也可以把你的意志烧成粉末.
11
90
9
事实上,任何一个有理数都可以写成有限
小数或无限循环小数. 反过来,任何有限小数或无限循环小数也都是有理 数.
无理数的定义:
无限不循环小数称为无理数.
,
, 2
21
0.101 001 000 1…(两个1之间依次多1个0)
-168.323 223 222 3…(两个3之间依次多1个2)
【估一估】 面积为2的正方形的边长a究竟是多少?
73
整数有____0______________ 有理数有___272__, __13_,0_._3_,0_____
无理数有________________ 实数有__2_72_,__13_,__,_0_.3_,_0_____
【规律方法】
无理数的特征: 1.圆周率π及一些最终结果含有π的数 2.开方开不尽的数 3.不循环的无限小数
1
a 面积为2
2
1
a
2
由上可得边长a的一个大致的范围,但a的整数部
分是几?十分位是几?百分位呢?千分位呢?……
【算一算】 请同学们借助计算器进行探索
边长a
面积S
1<a<2
1<S<4
1.4<a<1.5
1.96<S<2.25
初中数学《无理数》第二课时ppt

谈收获
有限小数和无限循环小数
无限不循环小数
π型
不循环
?
分数
整数
定义
有理数
数
无理数
常见类型
思想
无限逼近 数形结合
布置作业
1.必做 课本:P90习题4.2第2题
2.选做 借用计算器探究体积为2的正方体 的棱长,把你的探究过程列成表格
海到无边天是岸,山至高处人为峰
a
面积
2时,a的值越来越精确
问题思考
边长a会不会算到某一位时,它的平方恰好等于2?
归纳:a是一个无限不循环小数
做一做
(1)估计面积为5的正方形边长b的值(结果精确到十分位), 并用计算器验证你的估计。
(2)如果结果精确到百分位呢?
事实上:b=2.236067978…是一 个无限不循环的小数。
2b
归纳提升
整数 有理数:有限小数或无限循环小数 分数 数 无理数: 无限不循环小数
火眼金睛
1.所有的无限小数都是无理数( × ) 2.所有的无理数都是无限小数( ) 3.有理数都是有限小数( × )
4.不是有限小数的不是有理数(×)
说出两个数:一个是有理数,一个是无理数
典例分析
下列各数中,哪些是有理数?哪些是无理数?
1
体积为2
a 面积为2 a
b 面积为5 b
c c
c
c3=2
归纳:a,b,c都是无限不循环小数
பைடு நூலகம் 议一议
请大家把下列各数表示成小数
-
你发现了什么?
圆周率π=3.14159265… 0.5858858885…(相邻两个 5之间8的个数逐次加1)
有理数总可以用有限小数或无限循环小数表示。 反之,任何有限小数或无限循环小数也都是有理数。 无限不循环小数叫做无理数。
七上4.1无理数(第1课时)
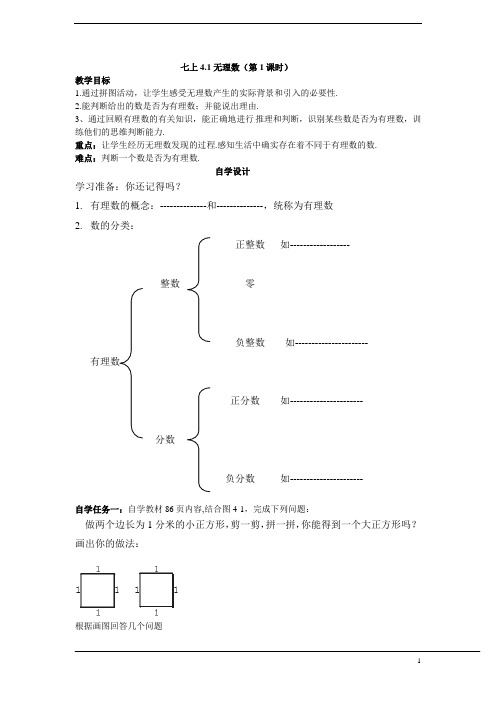
七上4.1无理数(第1课时)教学目标1.通过拼图活动,让学生感受无理数产生的实际背景和引入的必要性.2.能判断给出的数是否为有理数;并能说出理由.3、通过回顾有理数的有关知识,能正确地进行推理和判断,识别某些数是否为有理数,训练他们的思维判断能力.重点:让学生经历无理数发现的过程.感知生活中确实存在着不同于有理数的数.难点:判断一个数是否为有理数.自学设计学习准备:你还记得吗?1.有理数的概念:--------------和--------------,统称为有理数2.数的分类:正整数如------------------整数零负整数如---------------------- 有理数正分数如----------------------分数负分数如----------------------自学任务一:自学教材86页内容,结合图4-1,完成下列问题:做两个边长为1分米的小正方形,剪一剪,拼一拼,你能得到一个大正方形吗?画出你的做法:根据画图回答几个问题设大正方形的边长为a 分米,因为大正方形面积是( ),所以a 满足的条件为( )a 是整数吗?( ),理由:---------------------------------------------------- a 是分数吗?( ),理由:---------------------------------------------------- a 是有理数吗?( ),理由:---------------------------------------------------- 归纳总结:在22a 中,a 既不是( ),也 不是( ) ,所以a 不是( ) 。
所以在现实生活中,存在着既不是整数又不是分数的数,也就是存在着不是( )的数 对比练习:将上述活动中的小正方形的边长变为2分米,大正方形的边长是有理数吗?为什么?( ) 自学任务二:自学教材86页做一做,结合图4-2,完成下列问题(1)在下图中,以直角三角形的斜边为边长的正方形的面积是多少?(2)设该正方形的边长为b ,则b 应满足什么条件?(3)b 是有理数吗?归纳总结:在上面的问题中,数a,b 表示正方形的边长,确实存在,但它们不是( ),由此可见:在现实生活中,除了有理数之外,还存在着不是有理数的数。
新教材4.1指数 4.1.2无理数指数幂及其运算性质 教案

4.1.2 无理数指数幂及其运算性质教学目的:(1)了解可以由有理数的指数幂无限逼近无理数的指数幂;(2)培养用于探索的精神,体会由特殊到一般的研究方法,发展教学核心素养. 课 型:新授课教学重点:无理数指数幂的概念;教学难点:指数幂的运算性质;教学过程:一、引入课题知识点1 无理数指数幂无理数指数幂a α(0a >,α是无理数)是_________.思考1:一定是实数吗?提示:根据无理数指数幂的定理.知识点2 实数指数幂的运算性质(0a >,0b >,r ,s R ∈)(1)r s a a =_________.(2)()s ar _______.(3)()rab =________.思考2:指数幂是怎样从正整数指数幂推广到实数指数幂的?提示:二、基础自测1.下列说法正确的个数是( )(1)无理数指数幂有的不是实数.(2)指数幂(0)x a x >中的x 只能是有理数.(3)9=.A .0B .1C .2D .3解析:(1)无理数指数幂对应一个确定的实数,不正确;(2)指数幂(0)x a x >中的x 是任意实数,不正确;(3)239===,正确,故选B . 2.36a a ππ= .3.(n m = .三、题型探究题型一 无理数指数幂的运算例1 (1)(;(2)263a a a πππ.解析:(1)原式62322916==⨯=. (2)原式2+636a a ππππ--==.归纳提升 关于无理数指数幂的运算(1)底数相同时直接对指数上的无理数进行加减运算.(2)若式子中含有根式,则先化为指数式再进行运算,一般指数中的根式可以保留.题型二 指数幂运算的综合运算例2 已知11223a a-+=,求下列各式的值.(1)1a a -+;(2)22a a -+; (3)33221122a aa a ----.分析:利用完全平方差公式求(1)(2),利用立方差各式求(3).解析:(1)11223a a-+=边平,129a a -++=,17a a -+=; (2)17a a-+=边平,有22249a a -++=,2247a a -+=; (3)于3311332222()()a a a a ---=, 所以有3311111222222111112222()()1718a aa a a a a a a a a a a a ---------++⋅==++=+=--.归纳提升(1)条件求值是代数式求值中的常见题型,一般要结合已知条件先化简再求值,另外要特别注意条件的应用,如条件中的隐含条件,整体代入等,可以简化解题过程.本题若通过11223a a -+=解出a 的值代入求值,则非常复杂.(2)解决此类问题的一般步骤是四、误区警示因忽略幂底数的范围而导致错误例3 化简11222(1)[(1)()]a a a ----= .错解:1111212244(1)[(1)()](1)(1)()()a a a a a a a -----=--⋅-=--.错因分析:忽略了题中有12()a -,即相当于告知0a -≥,故0a ≤,这样,1212[(1)](1)a a ---≠-.实际上在解答本类题时除了灵活运用运算法则外还要关注条件中的字母是否由隐含的条件.正解:由12()a -知0a -≥,故10a -<, ∴1111212244(1)[(1)()](1)(1)()()a a a a a a a -----=---=-.方法点拨:在利用指数幂的运算性质时,要关注条件中有无隐含条件,在出现根式时要注意是否是偶次方根,被开方数是否符合要求.五、学科素养用换元法处理指数幂中的化简与证明问题例4 已知333pa qb rc ==,且1111a b c ++=,求证:11112223333()pa qb rc p q r ++=++. 分析:看见三个式子连等,立刻想到赋中间变量,通过中间变量去构建能用到题干中已知值的式子.证明:令333pa qb rc ==,则2k pa a =,2k qb b =,2k rc c =,3k p a =,3k q b =,3k r c=, 所证等式左边111333111()[()]k k k k k a b c a b c=++=++=, 所证等式右边1111133333333111()()()()k k k k k a b c a b c=++=++=,∴1111 2223333 ()pa qb rc p q r ++=++.归纳提升(1)对于“连等式”,常用换元法处理.如本例,我们可令它等于一个常数k,然后以k为媒介化简,这样使问题容易解决.(2)换元过程中尤其要注意所代换的新变元的范围一定与被替换对象一致,关键时候还要检验.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结果都为分数,所以a不可能是以3
为分母的分数。
问题导学:
a可能是分数吗? 试说出原因。
a
两个相同的最简分数的乘积仍然是分 数,所以a不可能是分数。
问题导学:
a
a既不是整数又不是分数,所以a一定不是 有理数。 那么a到底是什么数呢?
古人把这个数取名为无理数。
问题导学:
1、如图,以直角三角形的斜边 为边的正方形的面积是多少?
在直角三角形中,由勾股定理得,
2
1
斜边² =1² +2² =5,所以直角三角形的斜边为边的正方形 的面积是5.
b² =5 2、设该正方形的边长为b,b满足什么条件? b不是有理数。 3、b是有理数吗?说说你的理由。
问题导学:
1、大家判断一下3个正方形的边长之间有怎样的大 小关系?说说你的理由. 2、大家能不能判断一下面积为2的正方形的边长a 的大致范围呢?
问题导学:
边长a 1 <a <2 1.4<a<1.5 1.41<a<1.42 1.414<a<1.415 1.4142<a< 1.4143 面积S 1 <S <4 1.96<S<2.25 1.9881<S<2.0164 1.999396<S<2.002225 1.99996164<S<2.00024449
典型例题:
右图是由16个边长为 1的小正方形拼成的,任 意连接这些小正方形的 若干个顶点,可得到一 些线段。试分别找出两 条长度是有理数的线段 和两条长度不是有理数 的线段。
生活中真的有很多不是有理数 的数吗?
典型例题:
例如:
由勾股定理知: 线段AB,DE,AE的长 能用有理数表示; 线段AC,CE,BE的长 不能用有理数表示。
自学检测:
1.如图,正三角形的边长为2,高为h,h可能是
整数吗?可能是分数吗?
解 : 因为ABC是正三角形, 且AD BC
所以BD DC, 则BD AB 由勾股定理得: h
h不可能是整数;
B
A
h
D C
h也不可能是分数。
自学检测:
如图,每个小正方形 的边长为1,四边形 ABCD的对角线AC,BD相 交于O。试说明边长AB, BC,CD,AD和对角线 AC,BD的长度哪些是有 理数,哪些不是有理 数?
巩固练习:
课堂小结:
谈谈你 这节课 的收获 吧!
作业:
习题:4.2 1、 2
1 1
变 化 的 世 界
奇 妙 的 组 合
问题导学:
(1)设大正方形的边长为a,a满足什么条件?
a
因为正方形的面积为2
所以a SFra bibliotek问题导学:
a可能是整数吗?
,
,
a
越来越大, 所以a不可能是整数
3 9,
2
问题导学:
a可能是以2为分母的分数吗?
,
a
3 3 9 ...... 2 2 4,
结果都为分数,所以a不可能是以2
为分母的分数。
问题导学:
a可能是以3为分母的分数吗?
,
,
,
a
...... ,
问题导学:
无理数的定义,请大家把下列各数表示成小数.
4 5 8 2 3, , , , 5 9 45 11
并看它们是有限小数还是无限小数,是循环 小数还是不循环小数?
问题导学:
像上面研究过的a2=2,b2=5中的a,b是无限不 循环小数.无限不循环小数叫无理数 除上面的a,b外,圆周率π=3.14159265…也是 一个无限不循环小数,0.5858858885…(相邻两 个5之间8的个数逐次加1)也是一个无限不循环小 数,它们都是无理数.
4.1无理数
温故互查:(二人小组完成) 1、有理数的分类:
整数
有 理 数
正整数 0 负整数 正分数
分数
负分数
温故互查:(二人小组完成) 2、小数的分类
有限小数
小 数
无限循环小数
无限小数
无限不循环小数
问题导学:
把两个边长为1的小正方形通过剪、 拼,设法得到一个大正方形
1 1 1 1
问题导学:
拼图:
E
C
A
B
D
巩固练习:
1、长和宽分别是3,2的长方形,它的对角线的长可 能是整数吗?可能是分数吗?
巩固练习:
2、请你在如图所示的方格纸上按照如下要求设 计直角三角形:
(1)使它的三边中有一边边长不是有理数。 (2)使它的三边中有两边边长不是有理数。 (3)使它的三边边长不是有理数。
巩固练习:
巩固练习:
