吉林省长春外国语学校2016-2017学年高二上学期期末数学试卷(理科) Word版含答案
吉林省长春外国语学校2016—2017学年高二上学期第一次月考试题 数学含答案

长春外国语学校2016-2017学年上学期第一次月考高二数学试卷出题人:王先师 审题人:于静洁考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷分第Ⅰ卷、第Ⅱ卷和答题卡,共4页 满分120分,考试用时90分钟。
考试结束后,请将答题卡卷交回,试题卷自己保存。
2.答题前,请您务必将自己的班级、姓名、学号、考号用0.5毫米黑色签字笔填写在答题卡上。
3.作答非选择题必须用0.5毫米的黑色签字笔写在答题卡上的指定位置,在其它位置作答一律无效。
4.保持答题卷清洁、完整,严禁使用涂改液和修正带。
第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.每小题四个选项中,只有一项正确.1. A (2,1),B (3,-1)两点连线的斜率为 ( )A .2-B .21- C .21 D .2 2.直线0133=++y x 的倾斜角是 ( )A.300B.600C.1200D.13503. 直线03=++y x 与直线032=+-y x 的交点坐标为 ( )A .(-3,0)B .(-2,-3)C .(0,1)D .(-1,0)4. 圆C 1: 122=+y x 与圆C 2: 16)4()3(22=-+-y x 的位置关系是 ( )A .外离B .相交C . 内切D .外切5.在空间直角坐标系中,点(-2,1,4)关于x 轴的对称点的坐标为 ( )A .(-2,1,-4)B .(-2,-1,-4)C .(2,1,-4)D .(2,-1,4)6.经过圆C :4)2()1(22=-++y x 的圆心且斜率为1的直线方程为 ( ) A .x -y +3=0B .x -y -3=0C .x +y -1=0D .x +y +3=07.如果直线012=-+ay x 与直线014)13(=---ay x a 平行,则a 等于( )A .0B . 31-C .31或 0- D .0或1 8.圆034222=-+++y x y x 上到直线01=++y x 的距离等于23的点有( )A .1个B .2个C .3个D .4个9.若直线3x+4y+m=0与圆014222=++-+y x y x 没有公共点,则实数m 的取值范围是 ( )A . 155<<-mB .15或 5>-<m mC .4m <或13m >D .413m <<10.已知实数y x ,满足196)12()5(22=-++y x ,那么22y x +的最小值为( )A.4B.111.设点A (2,-3),B (-3,-2),直线过点P (1,2)且与线段AB 相交,则的斜率k 的取值范围是( )A .5或1≥-≤k k B .15≤≤-k C.51≤≤-k D .1或 5≥-≤k k 12.若直线1-=kx y 与圆122=+y x 相交于P 、Q 两点,且∠POQ=150°(其中O为原点),则k 的值为( )A . 33-B .33±C .)32(+±D .3±第Ⅱ卷(非选择题 共60分)二、填空题:本大题共4个小题,每小题4分,共16分.把答案填在答题卡的指定位置.13.直线y=x+b 平分圆084422=--++y x y x 的周长,则b =___________.14.方程)(012)1(R a a y x a ∈=+--+所表示的直线恒过定点____________.15.在空间直角坐标系O-xyz 中,设点M 是点N(2,-3,5)关于坐标平面xoz 的对称点,则线段MN 的长度等于 .16.若直线x+y=m 与曲线29x y -=恰有两个公共点,则m 的取值范围是 .三、解答题:本大题共4个小题,共44分,解答应写出必要的文字说明,证明过程或演算步骤.17.已知两直线1l :x+y-2=0与2l :2x+y+2=0的交点P ,求满足下列条件的直线方程:(1)过点P 且过原点的直线方程;(2)过点P 且垂直于直线3l :x-3y-1=0的直线的方程。
吉林省长春市五县20162017学年高二上学期期末考试数学理试题Word版含答案

数学(理)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.双曲线221168x y -=的虚轴长是( )A .8B .42C .22D .22.在公差为d 的等差数列{}n a 中,“1d >”是“{}n a 是递增数列”的( )A .充分没必要要条件B .必要不充分条件C .充要条件D .既不充分也没必要要条件 3.为了了解800名高三学生是不是喜爱背诵诗词,从中抽取一个容量为20的样本,若采纳系统抽样,则分段的距离k 为( )A .50B .60C .30D .404.已知椭圆22:1169x y C +=的左、右核心别离为12F F 、,过2F 的直线交椭圆C 于P Q 、两点,若1F P +110FQ =,则PQ 等于( ) A .8 B .6 C.4 D .25.从某项综合能力测试中抽取100人的成绩,统计如下,则这100个成绩的平均数为( )A .3B .2.5 C. D .6.某单位有员工120人,其中女员工有72人,为做某项调查,拟采纳分层抽样法抽取容量为15的样本,则男员工应选取的人数是( )A .5B .6 C.7 D .87.已知椭圆()222:10525x y C b b +=<<的长轴长、短轴长、焦距成等差数列,则该椭圆的方程是( ) A .221254x y += B .221259x y += C.2212516x y += D .22125x y +=8.已知点()00,A x y 是抛物线()220y px p =>上一点,且它在第一象限内,核心为,F O 坐标原点,若32pAF =,23AO =,则此抛物线的准线方程为( ) A .4x =- B .3x =- C.2x =- D .1x =-9.某班m 名学生在一次考试中数学成绩的频率散布直方图如图,若在这m 名学生中,数学成绩不低于100分的人数为33,则m 等于( )A .45B .48 C.50 D .5510.已知定点()3,0M -,()2,0N ,若是动点P 知足2PM PN =,则点P 的轨迹所包围的图形面积等于( ) A .1009π B .1429π C.103πD .9π 11.已知命题p :直线220x y +-=与直线2620x y +-=之间的距离不大于1,命题q :椭圆2222754x y +=与双曲线22916144x y -=有相同的核心,则下列命题为真命题的是( )A .()p q ∧⌝B .()p q ⌝∧ C.()()p q ⌝∧⌝ D .p q ∧12.如图,12,F F 别离是双曲线()222210,0x y a b a b-=>>的左、右核心,过1F 的直线l 与双曲线别离交于点,A B ,且()1,3A ,若2ABF ∆为等边三角形,则12BF F ∆的面积为( )A .1B 23.2第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.已知0m >,0n >,向量(),1,3a m =-与()1,,2b n =垂直,则mn 的最大值为 . 14.若[]x 表示不超过x 的最大整数,执行如图所示的程序框图,则输出S 的值为 .15.在区间2,43ππ⎡⎤-⎢⎥⎣⎦上任取一个数x,则函数()3sin26f x xπ⎛⎫=-⎪⎝⎭的值不小于0的概率为.16.已知点A是抛物线()2:20C x px p=>上一点,O为坐标原点,若,A B是以点()0,10M为圆心,OA的长为半径的圆与抛物线C的两个公共点,且ABO∆为等边三角形,则p的值是.三、解答题(本大题共6小题,共70分.解许诺写出文字说明、证明进程或演算步骤.)17. (本小题满分12分)在直角坐标系xOy中,直线l的参数方程为33x ty t=+⎧⎪⎨=⎪⎩(t为参数),以原点为极点,x轴正半轴为极轴成立极坐标系,圆C的极坐标方程为23sinρθ=.(1)写出直线l的一般方程及圆C的直角坐标方程;(2)点P是直线l上的点,求点P的坐标,使P到圆心C的距离最小.18. (本小题满分12分)已知p:方程()2220x mx m+++=有两个不等的正根;q:方程221321x ym m-=+-表示核心在y轴上的双曲线.(1)若q为真命题,求实数m的取值范围;(2)若“p或q”为真,“p且q”为假,求实数m的取值范围.19. (本小题满分12分)某公司经营一批进价为每件4百元的商品,在市场调查时发觉,此商品的销售单价x(百元)与日销售量y(件)之间有如下关系:(1)求y关于x的回归直线方程;(2)借助回归直线方程请你预测,销售单价为多少百元(精准到个位数)时,日利润最大?相关公式:()()()1122211n niii ii i nniii i x x y y x y nx yb x x xnx====---==--∑∑∑∑,a y bx =-.20. (本小题满分12分)如图所示的茎叶图记录了甲、乙两组各5名同窗的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图顶用x 表示.(1)若乙组同窗投篮命中次数的平均数比甲组同窗的平均数少1,求x 及乙组同窗投篮命中次数的方差; (2)在(1)的条件下,别离从甲、乙两组投篮命中次数低于10次的同窗中,各随机选取一名,求这两名同窗的投篮命中次数之和为16的概率. 21. (本小题满分12分)如图,在三棱锥A BCD -中,AD ⊥平面BCD ,CB CD =,AD DB =,,P Q 别离在线段,AB AC 上,3AP PB =,2AQ QC =,M 是BD 的中点.(1)证明://DQ 平面CPM ; (2)若二面角C AB D --的大小为3π,求tan BDC ∠. 22. (本小题满分12分)已知()222210x y a b a b+=>>的左、右核心别离为12F F 、,1225F F =P 在椭圆上,21tan 2PF F ∠=,且12PF F ∆的面积为4.(1)求椭圆的方程;(2)点M 是椭圆上任意一点,12A A 、别离是椭圆的左、右极点,直线12MA MA ,与直线35x =别离交于,E F 两点,试证:以EF 为直径的圆交x 轴于定点,并求该定点的坐标.试卷答案一、选择题1.B 因为28b =,因此虚轴长2b =.2.A 若1d >,则n N *∀∈,110n n a a d +-=>>,因此,{}n a 是递增数列;若{}n a 是递增数列,则n N *∀∈,10n n a a d +-=>,推不出1d >3.D 由于8002040÷=,即分段的距离40k =.4.B 因为直线PQ 过椭圆的右核心2F ,由椭圆的概念,在1F PQ ∆中,11416F P FQ PQ a ++==.又1110F P FQ +=,因此6PQ =. 5.A 设这100个成绩的平均数记为x ,则120210*********3100x ⨯+⨯+⨯+⨯+⨯==.6.B 男员工应抽取的人数为12072156120-⨯=.7.C 设焦距为2c ,则有222552b c c b⎧-=⎨+=⎩,解得216b =,因此椭圆22:12516x y C +=.8.D 因为0322p px +=,因此0x p =,0y =.又)2212p +=,因此2p =,准线方程为1x =-.9.D ()10.0150.025100.6P =-+⨯=,由0.633m =,得55m =.10.A 设(),P x y ,则由2PM PN =得()()2222342x y x y ⎡⎤++=-+⎣⎦,化简得223322x y x +-70+=,即221110039x y ⎛⎫-+= ⎪⎝⎭,因此所求图形的面积1009S π=.11.B 关于命题p ,将直线l 平移到与椭圆相切,设这条平行线的方程为20x y m ++=,联立方程组224120x y x y m ⎧+=⎨++=⎩,消去y 得222210x mx m ++-=. 由0∆=得,因此m =,椭圆上的点到直线l最近距离为直线20x y +=与l 的距离d =1>,因此命题p 为假命题,于是p ⌝为真命题.关于命题q ,椭圆2222754x y +=与双曲线22916144x y -=有相同的核心()5,0±,故q 为真命题. 从而()p q ⌝∧为真命题.12.C 由已知212BF BF a -=,122AF AF a -=,又2ABF ∆为等边三角形,因此121AF AF BF -=2a =,因此24BF =.在12AF F ∆中,16AF a =,24AF a =,122F F c =,1260F AF ∠=︒,由余弦定理得22243616264cos 60c a a a a =+-⨯⨯⨯︒,因此227c a =,22226b c a a =-=,因此双曲线方程为222216x y a a -=,又(A 在双曲线上,因此221316a a -=,解得212a =,即a =因此122124sin1202BF F S a a ∆=⨯⨯⨯︒==. 二、填空题因为,因此,又,因此.第一次循环,0S =,2n =;第二次循环,1S =,4n =;第三次循环,3S =,6n =;第四次循环,5S =,8n =;第五次循环,7S =.因为8>6,因此输出S 的值为7.15.611 当2,43x ππ⎡⎤∈-⎢⎥⎣⎦时,272,636x πππ⎡⎤-∈-⎢⎥⎣⎦.当[]20,6x ππ-∈,即7,1212x ππ⎡⎤∈⎢⎥⎣⎦时()0f x ≥,则所求概率为76121221134ππππ-=⎛⎫-- ⎪⎝⎭.16.56如图,因为MA OA=,因此,点A在线段OM的中垂线上,又()0,10M,因此可设(),5A x.由tan305x︒=,得53x=,因此5,53A⎫⎪⎝⎭的坐标代入方程22x px=,得56p=.三、解答题17.解:(1)由3,3.x ty t=+⎧⎪⎨=⎪⎩消去参数t,得直线l的一般方程为3330x y--=,由23sinρθ=得223sinρρθ=,2223x y y+=,即圆C的直角坐标方程为()2233x y+-=. (2)()3,3P t t+,()0,3C,()()222333412PC t t t=++-=+,t=∴时PC最小,现在()3,0P.18.解:(1)由已知方程221321x ym m-=+-表示核心在y轴上的双曲线,则()244202020m mmm⎧∆=-+>⎪->⎨⎪+>⎩解得21m-<<-,即:21p m-<<-.因p或q为真,因此p q、至少有一个为真.又p且q为假,因此p q、至少有一个为假.因此,p q 、两命题应一真一假,当p 为真,q 为假时,213m m -<<-⎧⎨≥-⎩,解得21m -<<-;当p 为假,q 为真时,213m m m ≤≥-⎧⎨<-⎩或,解得3m <-.综上,21m -<<-或3m <-. 19.解:(1)因为7x =,1089616.85y ++++==,因此,122121857 6.82255549ni ii ni i x y nx yb x nx==--⨯⨯===--⨯-∑∑,()6.82720.8a y bx =-=--⨯=,于是取得y 关于x 的回归直线方程220.8y x =-+.(2)销售价为x 时的利润为()()24220.8228.883.2x x x x ω=--+=-+-,当28.8722x =≈⨯时,日利润最大. 20.(1)解:依题意得:82910789112155x +⨯+++++⨯=-,解得6x =,41=5x 乙,22222141414141682910 1.7655555s ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-+-⨯+-+-=⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦. (2)记甲组投篮命中次数低于10次的同窗为123,,A A A ,他们的命中次数别离为9,8,7. 乙组投篮命中次数低于10次的同窗为1234,,,B B B B ,他们的命中次数别离为6,8,8,9. 依题意,不同的选取方式有:()()()()()()()()()()()()111213142122232431323334,,,,,,,,,,,,,,,,,,,,,,,A B A B A B A B A B A B A B A B A B A B A B A B共12种.设“这两名同窗的投篮命中次数之和为16”为事件,则中恰含有()()()222334,,,,,A B A B A B 共3种.()31124P C ==∴. 21.(1)证明:取AB 的中点E ,连接ED EQ 、,则2AE AQEP QC==,因此//EQ PC . 又EQ ⊄平面CPM ,因此//EQ 平面CPM . 又PM 是BDE ∆的中位线,因此//DE PM , 从而//DE 平面CPM .又DE EQ E =,因此平面//DEQ 平面CPM .因为DQ ⊂平面DEQ ,因此//DQ 平面CPM . (2)解:法1:由AD ⊥平面BCD 知,AD CM ⊥, 由BC CD =,BM MD =,知BD CM ⊥, 故CM ⊥平面ABD .由(1)知//DE PM ,面DE AB ⊥,故PM AB ⊥. 因此CPM ∠是二面角C AB D --的平面角, 即3CPM π∠=.设PM a =,则3CM a =,又易知在Rt ABD ∆中,4B π∠=,可知2DM BM a ==,在Rt CMD ∆中,36tan 22MC a MDC MD a∠===.法2:以M 为坐标原点,,,MC MD ME 所在的直线别离为x 轴,y 轴,z 轴成立如图所示的空间直角坐标. 设MC a =,MD b =,则(),0,0C a ,()0,,0B b -,()0,,2A b b ,则(),,0BC a b =,()0,2,2BA b b =, 设()1,,n x y z =是平面ABC 的一个法向量, 则110,0.n BC n BA ⎧=⎪⎨=⎪⎩即0,220.ax by by bz +=⎧⎨+=⎩取()1,,n b a a =-,不宝贵到平面ABD 的一个法向量为()21,0,0n =, 因此12221cos ,22n n b a <>==+,因此6a b =,在Rt CMD ∆中,6tan MC a MDC MD b ∠===22.解:(1)因为21tan 2PF F ∠=,因此2125sin PF F ∠=215cos PF F ∠=. 由题意得((222212212525425525225PF PF PF PF ⎧⨯⨯=⎪⎪⎨⎪=+-⨯⎪⎩,解得1242PF PF ⎧=⎪⎨=⎪⎩.从而1224263a PF PF a =+=+=⇒=,结合225c =,得24b =,故椭圆的方程为22194x y +=.(2)由(1)得()13,0A -,()23,0A , 设()00,M x y ,则直线1MA 的方程为()0033y y x x =++, 它与直线35x =的交点的坐标为00353533y E x ⎫⎫⎪⎪⎪⎪+⎭⎭, 直线2MA 的方程为()0033y y x x =--,它与直线35x =的交点的坐标为00353533y F x ⎫⎫⎪⎪⎪⎪-⎭⎭, 再设以EF 为直径的圆交x 轴于点(),0Q m ,则QE QF ⊥,从而1QE QF k k =-0353335y x m ⎫++⎝⎭-03533135y x m ⎫--⎝⎭=--,即2202093549y m x ⎫=-⎪⎪-⎭,解得351m =. 故以EF 为直径的圆交x 轴于定点,该定点的坐标为351,0⎫+⎪⎪⎭或351,0⎫-⎪⎪⎭.。
吉林省长春外国语学校2016届高三上学期期末数学试卷(理科) 含解析

2015—2016学年吉林省长春外国语学校高三(上)期末数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合A={x|x2≤4,x∈R},B={x|≤4,x∈Z},则A∩B()A.(0,2)B.[0,2]C.{0,1,2} D.{0,2}2.已知i是虚数单位,则=()A.B.C.3﹣i D.3+i3.已知向量=(3,4),=(sinα,cosα),若∥,则tanα的值为()A. B.﹣C. D.﹣4.已知函数y=sin4x﹣cos4x是一个()A.周期为π的奇函数B.周期为π的偶函数C.周期为的奇函数D.周期为的偶函数5.函数f(x)=2x+4x﹣3的零点所在区间是() A.(,)B.(﹣,0)C.(0,) D.(,)6.下列命题中正确的个数是()①命题“任意x∈(0,+∞),2x>1”的否定是“任意x∉(0,+∞),2x≤1;②命题“若cosx=cosy,则x=y”的逆否命题是真命题;③若命题p为真,命题¬q为真,则命题p且q为真;④命题“若x=3,则x2﹣2x﹣3=0”的否命题是“若x≠3,则x2﹣2x﹣3≠0”.A.1个B.2个 C.3个 D.4个7.已知变量x,y满足::,则z=()2x+y的最大值为( )A.B.2C.2 D.48.若(x6)n的展开式中含有常数项,则n的最小值等于()A.3 B.4 C.5 D.69.若两个正实数x,y满足+=1,且x+2y>m2+2m 恒成立,则实数m的取值范围是()A.(﹣∞,﹣2)∪[4,+∞)B.(﹣∞,﹣4)∪[2,+∞)C.(﹣2,4)D.(﹣4,2)10.函数y=(x+2)ln|x|的图象大致为( )A.B.C.D.11.已知直线x+y=a与圆x2+y2=4交于A、B两点,且||=||,其中O为原点,则实数a的值为( )A.2 B.﹣2 C.2或﹣2 D.或﹣12.记,,,其中e为自然对数的底数,则a,b,c这三个数的大小关系是()A.a>b>c B.a<b<c C.b>c>a D.b>a>c二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(1﹣2sin2)dx= .14.己知正方形ABCD的边长为1,点E是AB边上的动点.则的值为.15.已知点P(x,y)满足,过点P的直线与圆x2+y2=50相交于A,B两点,则|AB|的最小值为.16.已知数列{a n}满足a1=60,a n+1﹣a n=2n,(n∈N*),则的最小值为.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤。
吉林省长春市高二上学期期末考试联考试卷 数学(理) Word版含答案

长春十一高 白城一中2016-2017学年度上学期期末考试 高二数学试卷(理)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共22小题,共150分,共4页,考试时间120分钟,考生作答时将答案答在答题卡上,在本试卷上答题无效。
注意事项:1、答题前,考生务必将自己的学校、班级、姓名、准考证号填写在答题卡上,2、请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
3、保持卡面清洁,不折叠、不破损。
第Ⅰ卷(选择题,共60分)一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 命题:“∀x ∈R,022≥+-x x ”的否定是 ( ) A.∃x ∈R,022≥+-x x B.∀x ∈R,022≥+-x x C.∃x ∈R,022<+-x xD.∀x ∈R,022<+-x x2.复数z=2-3i 对应的点z 在复数平面的 ( ) A .第一象限 B.第二象限 C.第三象限 D.第四象限3.双曲线x 2﹣4y 2=1的焦距为 ( )A .B C . D 4.用反证法证明命题“若整系数一元二次方程20ax bx c ++= (0a ≠ )有有理根,那么a ,b ,c 中至少有一个是偶数”时,下列假设中正确的是 ( ) A .假设a ,b ,c 不都是偶数 B .假设a ,b ,c 都不是偶数C .假设a ,b ,c 至多有一个是偶数D .假设a ,b ,c 至多有两个是偶数 5.421dx x⎰等于 ( ) A .-2ln2 B .2ln2 C .-ln2 D .ln26. 若()ln f x x x x 2=-2-4,则()f x 的单调递增区间是 ( )A. (,)0+∞B. -+10⋃2∞(,)(,)C. (,)2+∞D. (,)-107.如下图是函数d cx bx x x f +++=23)(的大致图象,则21x x +=( )A .32B .910C .98D .9288.命题甲:双曲线C 的渐近线方程为y=±a bx ;命题乙:双曲线C 的方程为2222—by a x =1那么甲是乙的( )A.充要条件B.充分不必要条件C.必要不充分条件D.不充分不必要条件 9.已知函数()+f x x x ax =-+3223在[],12上单调递增,则实数a 的取值范围为( )A. 4a >-B.a ≥-4C. a >1D. a ≥110.设12,F F 是椭圆2212516x y +=的两个焦点,点M 在椭圆上,若△12MF F 是直角三角形,则△12MF F 的面积等于 ( )A .485 B.365 C.16 D. 485或16 11. 若点P 在曲线y =x 3-3x 2+(3-3)x +34上移动,经过点P 的切线的倾斜角为α,则角α的取值范围是( )A .[0,π2)B .[0,π2)∪[2π3,π)C .[2π3,π)D .[0,π2)∪(π2,2π3]12.设函数2221(),()x e x e x f x g x x e+==,对任意12,(0,)x x ∈+∞,不等式12()()1g x f x k k ≤+恒成立,则正数k的取值范围是( )A [1,)+∞ B.(1,)+∞ C .1[,)21e +∞- D. 1(,)21e +∞-第Ⅱ卷(非选择题,共90分)二.填空题:本大题共4个小题,每小题5分.共20分. 13.i 是虚数单位,则534ii+-等于 。
吉林省长春2020学年高二上学期期末考试数学版含答案

第4题7 8 99 8 27 911 2 5 6 甲 乙 长春外国语学校2016-2017学年第一学期期末考试高二年级数学试卷出题人 : 赵 天 审题人:马 竞本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
考试结束后,将答题卡交回。
注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信 息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书 写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效; 在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5. 保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷一、选择题:本题共12小题,每小题5分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 抛物线24y x =的焦点坐标是( )A .(0,1)B .(1,0)C .1(0,)16 D .1(,0)162. 双曲线1422=-y x 的渐近线方程和离心率分别是( ) A.5;2=±=e x y B.5;21=±=e x yC.3;21=±=e x y D.2;3y x e =±=3. 如果(1,3)A 关于直线l 的对称点为(5,1)B -,则直线l 的方程是( )A .380x y -+= B. 340x y ++= C .340x y +-= D .380x y -+= 4. 将甲、乙两名同学5次物理测验的成绩用茎叶图表示如图, 若甲、乙两人成绩的中位数分别为乙甲、x x ,则下列说法正确 的是( )A .乙甲x x <;乙比甲成绩稳定 B.乙甲x x >;甲比乙成绩稳定 C.乙甲x x >;乙比甲成绩稳定 D.乙甲x x <;甲比乙成绩稳定5. 在5件产品中,有3件一等品和2件二等品,从中任取2件,以710为概率的事件( )A .恰有1件一等品B .至少有一件一等品C .至多有一件一等品D .都不是一等品6.以下给出的是计算201614121+⋅⋅⋅+++ 的值的一个程序框图(如图所示),其中 判断框内应填入的条件是( ) A . i>10 B. i<10C. i<20D.i>20(第6题图)7.曲线192522=+y x 与曲线192522=-+-ky k x )9(<k 的( ) A.长轴长相等 B.离心率相等 D.焦距相等 8. 已知0,0,1a b a b >>+=,则( ) A. 7 B .8 C. 9 D .109. 已知点P 是抛物线22y x =上的一个动点,则点P 到点(0,2)的距离与到该抛物线准线的距离之和的最小值为( )B. 3 D.9210.已知圆的方程为22680x y x y +--=,设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为( )A .B .. D .11. 若椭圆221369x y +=的弦被点(4,2)平分,则此弦所在直线的斜率为( ) A. 2 B. 2- C.13 D.12-12.若直线y x b =+与曲线3y =b 的取值范围是( )A .[1-+B .[1C .[1,1-+D .[1-第Ⅱ卷二、填空题:本题共4小题,每小题5分。
数学---吉林省长春市长春外国语学校2016-2017学年高二上学期期中试卷(解析版)

2016-2017学年吉林省长春外国语学校高二(上)期中数学试卷一、选择题(本大题共12小题,每小题5分,每小题给出的四个选项中,只有一项是符合题目要求的)1.过点M(﹣2,m)、N(m,4)的直线的斜率等于1,则m的值为()A.1 B.4 C.1或3 D.1或42.圆(x+2)2+y2=5关于原点(0,0)对称的圆的方程为()A.(x﹣2)2+y2=5 B.x2+(y﹣2)2=5C.(x+2)2+(y+2)2=5 D.x2+(y+2)2=53.直线mx+y﹣m﹣1=0(m是参数且m∈R)过定点()A.(1,﹣1)B.(﹣1,1)C.(1,1)D.(﹣1,﹣1)4.下列关于不等式的结论中正确的是()A.若a>b,则ac2>bc2B.若a>b,则a2>b2C.若a<b<0,则a2<ab<b2D.若a<b<0,则>5.如图所示,程序框图的输出结果是()A.B.C.D.6.圆:x2+y2﹣2x﹣2y+1=0上的点到直线x﹣y=2的距离最大值是()A.2 B.C.D.7.不等式ax2+bx+2>0的解集为{x|﹣<x<},则a﹣b等于()A.﹣10 B.﹣14 C.10 D.148.点P(2,﹣1)为圆(x﹣1)2+y2=25的弦AB的中点,则直线AB的方程为()A.x+y﹣1=0 B.2x+y﹣3=0 C.x﹣y﹣3=0 D.2x﹣y﹣5=09.在直角坐标系中,不等式y2﹣x2≤0表示的平面区域是()A.B.C.D.10.如图所示的程序是用来()A.计算3×10的值B.计算39值C.计算310的值D.计算1×2×3×…×10的值11.下列结论中正确的是()A.当x>0且x≠1时,B.当x>0时,C.当x≥3时,的最小值是2 D.当0<x≤1时,无最大值12.设不等式组表示的平面区域为D,若指数函数y=a x的图象上存在区域D上的点,则a的取值范围是()A.(1,3] B.[2,3] C.(1,2] D.[3,+∞]二、填空题(本大题共4小题,每小题5分,共20分)13.若圆(x﹣1)2+(y﹣2)2=1关于直线y=x+b对称,则实数b=.14.阅读如图所示的程序框图,运行相应的程序.若输入m的值为2,则输出的结果i=.15.设x、y∈R+且=1,则x+y的最小值为.16.不等式(a﹣2)x2+2(a﹣2)x﹣4<0对一切x∈R恒成立,则实数a的取值范围是.三、解答题(共6道大题,共70分,解答应写出文字说明,证明过程或演算步骤)17.(10分)直线l1:4x+3y﹣1=0与l2:x+2y+1=0的交点M,(1)求交点M的坐标;(2)求过点M且与直线x﹣2y﹣1=0垂直的直线方程.18.(12分)已知圆C和y轴相切,圆心在直线x﹣3y=0上,且被直线y=x截得的弦长为,求圆C的方程.19.(12分)某单位建造一间背面靠墙的小房,地面面积为12 m2,房屋正面每平方米造价为1 200元,房屋侧面每平方米造价为800元,屋顶的造价为5 800元,如果墙高为3 m,且不计房屋背面和地面的费用,设房屋正面地面的边长为x m,房屋的总造价为y元.(Ⅰ)求y用x表示的函数关系式;(Ⅱ)怎样设计房屋能使总造价最低?最低总造价是多少?20.(12分)实数x,y满足.(1)若z=2x+y,求z的最大值;(2)若z=x2+y2,求z的取值范围.21.(12分)已知直线过定点P(2,1).(1)求经过点P且在两坐标轴上的截距相等的直线方程;(2)若过点P的直线l与x轴和y轴的正半轴分别交于A,B两点,求△AOB面积的最小值及此时直线l的方程.22.(12分)设O为坐标原点,曲线x2+y2+2x﹣6y+1=0上有两点P、Q,满足关于直线x+my+4=0对称,又满足•=0.(1)求m的值;(2)求直线PQ的方程.参考答案一、选择题1.A【解析】过点M(﹣2,m)、N(m,4)的直线的斜率等于1,所以k===1.解得m=1.故选A.2.A【解析】圆(x+2)2+y2=5的圆心(﹣2,0),关于(0,0)对称的圆心坐标(2,0)所求圆的方程是(x﹣2)2+y2=5.故选A.3.C【解析】直线mx+y﹣m﹣1=0 即m(x﹣1)+(y﹣1)=0,经过x﹣1=0 和y﹣1=0 的交点(1,1),故选:C.4.D【解析】对于A,当c=0时,不成立,对于B,当a=2,b=﹣3时,则不成立,对于C,当a=﹣3,b=﹣1时,则不成立,对于D,根据不等式的性质,a<b<0,﹣=>0,即可得到>,则成立,故选:D.5.C【解析】模拟执行程序框图,可得满足条件2<8,S=,n=4,满足条件4<8,S=,n=6,满足条件6<8,S=,n=8,不满足条件8<8,程序结束,输出S==,故选:C.6.B【解析】圆x2+y2﹣2x﹣2y+1=0可化为标准形式:(x﹣1)2+(y﹣1)2=1,∴圆心为(1,1),半径为1.圆心(1,1)到直线x﹣y=2的距离,则所求距离最大为,故选B.7.A【解析】由题意可得:不等式ax2+bx+2>0的解集,所以方程ax2+bx+2=0的解为,所以a﹣2b+8=0且a+3b+18=0,所以a=﹣12,b=﹣2,所以a﹣b值是﹣10.故选A.8.C【解析】∵AB是圆(x﹣1)2+y2=25的弦,圆心为C(1,0),∴设AB的中点是P(2,﹣1)满足AB⊥CP.因此,PQ的斜率k===1.可得直线PQ的方程是y+1=x﹣2,化简得x﹣y﹣3=0,故选:C.9.C【解析】因为(1,0),(﹣1,0)都满足不等式y2﹣x2≤0,所以不等式y2﹣x2≤0表示的平面区域是:.故选:C.10.C【解析】由题意得:第一步:S=1,i=1≤10成立,第二步:S=1×3,i=2≤10成立,第三步:S=1×3×3,i=3≤10不成立,…一直到第10步:S=310,i=11>10成立,则输出S=310.故选:C.11.B【解析】A.0<x<1时,lg x<0,不成立;B.当x>0时,,当且仅当x=1时取等号,正确.C.当x≥3时,f(x)=,f′(x)=1﹣>0,∴函数f(x)单调递增,f(x)的最小值为3+=,不正确.D.0<x≤1时,f(x)=,f′(x)=1+>0,因此函数f(x)单调递增,f(x)的最大值为0,因此不正确.故选:B.12.A【解析】作出区域D的图象,联系指数函数y=a x的图象,由得到点C(2,9),当图象经过区域的边界点C(2,9)时,a可以取到最大值3,而显然只要a大于1,图象必然经过区域内的点.故选:A.二、填空题13.1【解析】∵圆(x﹣1)2+(y﹣2)2=1关于直线y=x+b对称,∴圆心(1,2)在直线y=x+b上,∴2=1+b,解得b=1.故答案为:1.14.4【解析】框图首先给累积变量A,B赋值1,1,给循环变量i赋值0.若输入m的值为2,执行i=1+1,A=1×2=2,B=1×1=1;判断2<1不成立,执行i=1+1=2,A=2×2=4,B=1×2=2;判断4<2不成立,执行i=2+1=3,A=4×2=8,B=2×3=6;判断8<6不成立,执行i=3+1=4,A=8×2=16,B=6×4=24;判断16<24成立,跳出循环,输出i的值为4.故答案为4.15.16【解析】∵=1,x、y∈R+,∴x+y=(x+y)•()==10+≥10+2=16(当且仅当,x=4,y=12时取“=”).故答案为:16.16.(﹣2,2]【解析】当a﹣2=0,a=2时不等式即为﹣4<0,对一切x∈R恒成立①,当a≠2时,则须,即.∴﹣2<a<2 ②.由①②得实数a的取值范围是(﹣2,2].故答案为:(﹣2,2].三、解答题17.解:(1)由得到,∴交点M的坐标M(1,﹣1).(2)直线x﹣2y﹣1=0的斜率为,所以所求直线的斜率为k=﹣2,所以所求直线方程为y+1=﹣2(x﹣1),整理得所求直线方程为2x+y﹣1=0.18.解:设圆心为(3t,t),半径为r=|3t|,则圆心到直线y=x的距离d==|t|,由勾股定理及垂径定理得:()2=r2﹣d2,即9t2﹣2t2=7,解得:t=±1,∴圆心坐标为(3,1),半径为3;圆心坐标为(﹣3,﹣1),半径为3,则(x﹣3)2+(y﹣1)2=9或(x+3)2+(y+1)2=9.19.解:(Ⅰ)如图所示,设底面的长为x m,宽y m,则y=m.设房屋总造价为f(x),由题意可得f(x)=3x•1 200+3××800×2+5 800=3 600(x+)+5 800(x>0). (Ⅱ)f(x)=3 600(x+)+5 800≥28 800+5 800=34 600,当且仅当x=4时取等号.答:当底面的长宽分别为4 m,3 m时,可使房屋总造价最低,总造价是34 600元.20.解:由,作出可行域如图中阴影部分所示:(1)z=2x+y令z=0画出y=﹣2x,由图知,,可得B(1,2),当z=2x+y经过点B(1,2)时,z max=4.(2)z=x2+y2表示可行域内的任意一点与坐标原点之间的距离的平方.因此x2+y2的范围最小为|OA|2(取不到),最大为|OB|2.,得A(0,1),∴|OA|2=()2=1,|OB|2=()2=5.∴z的最大值为5,没有最小值.故z的取值范围是(1,5].21.解:(1)∵直线过定点P(2,1)且在两坐标轴上的截距相等,设直线方程为:x+y=a,将P(2,1)代入得:a=3,故直线方程是:x+y﹣3=0;(2)由题意设直线的截距式方程为+=1(a,b>0),∵直线过P(2,1),∴+=1,∴1=+≥2 ,∴ab≥8,当且仅当=即a=4且b=2时取等号,∴△AOB的面积S=ab≥4,∴△AOB面积的最小值为4,此时直线l的方程为+=1,化为一般式方程可得x+2y﹣4=0.22.解:(1)曲线方程为(x+1)2+(y﹣3)2=9表示圆心为(﹣1,3),半径为3的圆.∵点P、Q在圆上且关于直线x+my+4=0对称,∴圆心(﹣1,3)在直线上.代入得m=﹣1.(2)∵直线PQ与直线y=x+4垂直,∴设P(x1,y1)、Q(x2,y2),PQ方程为y=﹣x+b.将直线y=﹣x+b代入圆方程,得2x2+2(4﹣b)x+b2﹣6b+1=0.Δ=4(4﹣b)2﹣4×2×(b2﹣6b+1)>0,得2﹣3<b<2+3.由根与系数的关系得x1+x2=﹣(4﹣b),x1•x2=.y1•y2=b2﹣b(x1+x2)+x1•x2=+4b.∵•=0,∴x1x2+y1y2=0,即b2﹣6b+1+4b=0.解得b=1∈(2﹣3,2+3).∴所求的直线方程为y=﹣x+1.。
【全国百强校】吉林省长春外国语学校2016-2017学年高二上学期期末考试物理试题01(原卷版)

一、单项选择题:本题共10小题,每小题4分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如右图所示,通电导体ab 的电流方向由a 向b ,导体受到磁场力的方向向右,则磁场的方向是A.由导线左方向右方B.由导线右方向左方C.垂直纸面向里D.垂直纸面向外2.一根无限长的通电直导线旁放一通电矩形线框,电流方向如图所示,直导线和线框在同一平面内,线框在通电直导线的磁场力作用下将会A .静止不动B .向右平移C .向左平移D .向下平移3.如右图所示,小磁针的正上方,平行放置一直导线,当导线通入电流I 时, 小磁针A.转动,N 极转向读者B.转动,S 极转向读者D.ab 向右运动,同时增大磁感应强度B 和θ角(0°<θ<90°)10.用一根横截面积为S 、电阻率为ρ的硬质导线做成一个半径为r 的圆环,ab 为圆环的一条直径.如图所示,在ab 的左侧存在一个匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率()B k k 0t∆=<∆.则NII 2A.圆环中产生逆时针方向的感应电流B.圆环具有收缩的趋势C.圆环中感应电流的大小为krS ||2ρD.图中a 、b 两点间的电势差大小为2ab 1U |k r |4=π 多项选择题:本题共4小题,每小题6分。
在每小题给出的四个选项中,只有多个选项是符合题目要求的,选不全的得3分,出现错误选项的不得分。
11.如图,MN 是匀强磁场中的一块薄金属板,带电粒子(不计重力)在匀强磁场中运动并穿过金属板,虚线表示其运动轨迹,由图知A .粒子带负电B .粒子运动方向是abcdeC .粒子运动方向是edcbaD .粒子在上半周所用时间比下半周所用时间长12.如图所示,导体ab 是金属框的一个可动边,长为0.1m ,匀强磁场的磁感应强度为0.5T ,当ab 以10m/s 的速度向右移动时,ab 中的A .感应电动势的大小是0.5VB .感应电动势的大小是5VC .感应电流的方向从b→aD .感应电流的方向从a→b13.有关回旋加速器,以下说法正确的有NA.电动和磁场同时用来提高粒子的动能B.电场用来加速带电粒子,磁场只是用来改变带电粒子运行方向,使粒子回旋C.粒子回旋的周期应与外加电场的周期一致D.粒子获得的最大动能既与D形盒的半径有关,也与外加电场的电压有关14.如图所示,将一条形磁铁插入一闭合螺线管中,螺线管固定在停在光滑水平面的车中,在插入过程中A.车将向右运动B.条形磁铁会受到向左的力C.由于没标明条形磁铁极性,因此无法判断受力情况D.车会受向左的力二、填空题:本题共2小题,每空2分,共10分15.一个200匝、面积20 cm2的圆线圈,放在匀强磁场中,磁场的方向与线圈平面成30°角,磁感强度在0.05 s内由0.1 T增加到0.5 T,在此过程中,穿过线圈的磁通量变化量是______________,磁通量的平均变化率是______________,线圈中感应电动势的大小是__________.16.右上图为一演示实验电路图,图中L是一带铁心的线圈,A是一灯泡,电键K处于闭合状态,电路是接通的。
2017-2018年吉林省长春外国语学校高二(上)期末数学试卷及答案
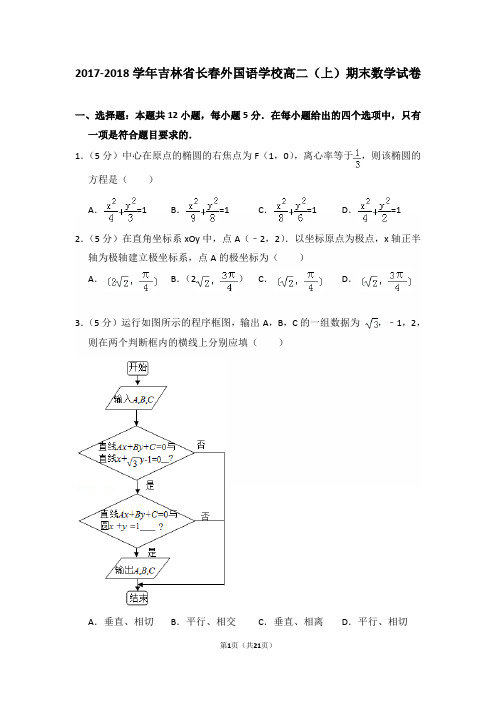
2017-2018学年吉林省长春外国语学校高二(上)期末数学试卷一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)中心在原点的椭圆的右焦点为F(1,0),离心率等于,则该椭圆的方程是()A.=1B.=1C.=1D.=12.(5分)在直角坐标系xOy中,点A(﹣2,2).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,点A的极坐标为()A.B.(2)C.D.3.(5分)运行如图所示的程序框图,输出A,B,C的一组数据为,﹣1,2,则在两个判断框内的横线上分别应填()A.垂直、相切B.平行、相交C.垂直、相离D.平行、相切4.(5分)已知双曲线中心在原点且一个焦点为F(,0),直线y=x﹣1与其相交于M、N两点,MN中点的横坐标为﹣,则此双曲线的方程是()A.﹣=1B.﹣=1C.﹣=1D.﹣=15.(5分)根据如图所示的框图,对大于2的整数N,输出的数列的通项公式是()A.a n=2n B.a n=2(n﹣1)C.a n=2n D.a n=2n﹣16.(5分)在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是()A.B.C.D.7.(5分)在极坐标系中,点(2,)到直线ρ(cosθ+sinθ)=6的距离为()A.4B.3C.2D.18.(5分)下列说法中正确的是()①相关系数r用来衡量两个变量之间线性关系的强弱,|r|越接近于1,相关性越弱;②回归直线y=bx+a一定经过样本点的中心();③随机误差e满足E(e)=0,其方差D(e)的大小用来衡量预报的精确度;④相关指数R2用来刻画回归的效果,R越小,说明模型的拟合效果越好.A.①②B.③④C.①④D.②③9.(5分)下列程序执行后输出的结果是()A.600B.880C.990D.110010.(5分)已知双曲线的右焦点为F(c,0),直线x=a与双曲线C的渐近线在第一象限的交点为A,O为坐标原点,若△OAF的面积为,则双曲线C的离心率为()A.B.C.D.11.(5分)设不等式组,表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是()A.B.C.D.12.(5分)已知直线l:(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,|MA|•|MB|的值为()A.16B.18C.8D.10二、填空题:本题共4小题,每小题5分.13.(5分)直线l:mx﹣y+1﹣m=0与⊙C:x2+(y﹣1)2=5的位置关系是.14.(5分)过抛物线方程为y2=4x的焦点作直线l交于P(x1,y1),Q(x2,y2)两点,若x1+x2=6,则|PQ|=.15.(5分)曲线C的参数方程为(θ为参数),曲线C的直角坐标方程为.16.(5分)一圆形纸片的半径为10cm,圆心为O,F为圆内一定点,OF=6cm,M为圆周上任意一点,把圆纸片折叠,使M与F重合,然后抹平纸片,这样就得到一条折痕CD,设CD与OM交于P点(如图),以FO所在直线为x轴,线段FO的中线为y轴,建立直角坐标系,则点P的轨迹方程为.三、解答题:本题共70分,其中17题10分,18至22题每题12分. 17.(10分)如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据.(1)请根据上表提供的数据,用最小二乘法求出y 关于x 的回归直线方程=a+bx;(2)已知该厂技改前生产100吨甲产品的生产能耗为90吨标准煤,由(1)求出的回归直线方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?18.(12分)如图茎叶图记录了甲、乙两组四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中以X表示.(1)如果X=8,求乙组同学植树棵数的平均数和标准差;(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.19.(12分)已知曲线C的极坐标方程是ρ=1,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l 的参数方程是(t 为参数),求直线l与曲线C相交所截的弦长.20.(12分)4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:min)的频率分布直方图,若将日均课外阅读时间不低于60min的学生称为“书虫”,低于60min的学生称为“懒虫”,(1)求x的值并估计全校3 000名学生中“书虫”大概有多少名学生?(将频率视为概率)(2)根据已知条件完成下面2×2的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“书虫”与性别有关:21.(12分)在平面直角坐标系xOy中,以坐标原点O为极点x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:3ρ2=12ρcosθ﹣10(ρ>0).(1)求曲线C1的普通方程(2)曲线C2的方程为,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.22.(12分)已知椭圆C:+=1(a>b>0)的离心率e=,且椭圆C上一点M与椭圆左右两个焦点构成的三角形周长为4+2.(1)求椭圆C的方程;(2)如图,设点D为椭圆上任意一点,直线y=m和椭圆C交于A、B两点,直线DA、DB与y轴的交点分别为P、Q,求证:∠PF1F2+∠QF1F2=90°.2017-2018学年吉林省长春外国语学校高二(上)期末数学试卷参考答案与试题解析一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)中心在原点的椭圆的右焦点为F(1,0),离心率等于,则该椭圆的方程是()A.=1B.=1C.=1D.=1【解答】解:根据题意,椭圆的一个焦点为F(1,0),则椭圆的焦点在x轴上,且c=1,又由椭圆的离心率为,则e==,则a=3,则b2=a2﹣c2=8,则椭圆的标准方程为+=1;故选:B.2.(5分)在直角坐标系xOy中,点A(﹣2,2).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,点A的极坐标为()A.B.(2)C.D.【解答】解:根据题意,设极坐标系下,点A的极坐标为(ρ,θ),则有ρ==2,tanθ=﹣1,则有θ=,分析可得:点A的极坐标为(2,);故选:B.3.(5分)运行如图所示的程序框图,输出A,B,C的一组数据为,﹣1,2,则在两个判断框内的横线上分别应填()A.垂直、相切B.平行、相交C.垂直、相离D.平行、相切【解答】解:当输出A,B,C的一组数据为,﹣1,2时,直线Ax+By+c=0为x﹣y+2=0,此时与直线x+y﹣1=0满足A1A2+B1B2=0,故两直线垂直,此时原点到直线的距离d==1,故与单位圆x2+y2=1相切,故选:A.4.(5分)已知双曲线中心在原点且一个焦点为F(,0),直线y=x﹣1与其相交于M、N两点,MN中点的横坐标为﹣,则此双曲线的方程是()A.﹣=1B.﹣=1C.﹣=1D.﹣=1【解答】解:设双曲线方程为﹣=1.将y=x﹣1代入﹣=1,整理得(b2﹣a2)x2+2a2x﹣a2﹣a2b2=0.由韦达定理得x1+x2=,则==﹣.又c2=a2+b2=7,解得a2=2,b2=5,所以双曲线的方程是.故选:D.5.(5分)根据如图所示的框图,对大于2的整数N,输出的数列的通项公式是()A.a n=2n B.a n=2(n﹣1)C.a n=2n D.a n=2n﹣1=2a i,a1=2,【解答】解:由程序框图知:a i+1∴数列为公比为2的等比数列,∴a n=2n.故选:C.6.(5分)在面积为S的△ABC的边AB上任取一点P,则△PBC的面积大于的概率是()A.B.C.D.【解答】解:记事件A={△PBC的面积超过},基本事件空间是三角形ABC的面积,(如图)事件A的几何度量为图中阴影部分的面积(DE是三角形的中位线),因为阴影部分的面积是整个三角形面积的,所以P(A)=1﹣=.故选:D.7.(5分)在极坐标系中,点(2,)到直线ρ(cosθ+sinθ)=6的距离为()A.4B.3C.2D.1【解答】解:点P(2,)化为:P,即P.直线ρ(cosθ+sinθ)=6化为直角坐标方程:x+y﹣6=0,∴点P到直线的距离d===1.故选:D.8.(5分)下列说法中正确的是()①相关系数r用来衡量两个变量之间线性关系的强弱,|r|越接近于1,相关性越弱;②回归直线y=bx+a一定经过样本点的中心();③随机误差e满足E(e)=0,其方差D(e)的大小用来衡量预报的精确度;④相关指数R2用来刻画回归的效果,R越小,说明模型的拟合效果越好.A.①②B.③④C.①④D.②③【解答】解:对于①,相关系数r用来衡量两个变量之间线性关系的强弱,|r|越接近于1,相关性越强,∴①错误;对于②,回归直线y=bx+a一定经过样本点的中心(),②正确;对于③,随机误差e满足E(e)=0,其方差D(e)的大小用来衡量预报的精确度,③正确;对于④,相关指数R2用来刻画回归的效果,R越大,说明模型的拟合效果越好,∴④错误.综上,正确的命题是②③.故选:D.9.(5分)下列程序执行后输出的结果是()A.600B.880C.990D.1100【解答】解:分析程序中各变量、各语句的作用,根据流程图所示的顺序,可知:该程序的作用是累乘并输出S=11×10×9的值;计算S=11×10×9=990.故选:C.10.(5分)已知双曲线的右焦点为F(c,0),直线x=a与双曲线C的渐近线在第一象限的交点为A,O为坐标原点,若△OAF的面积为,则双曲线C的离心率为()A.B.C.D.【解答】解:由题意,A(a,b),∵△OAF的面积为,∴bc=,∴3c2﹣8bc﹣3b2=0,∴c=3b或c=﹣b(舍去),∴a==2b,∴e===.故选:B.11.(5分)设不等式组,表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是()A.B.C.D.【解答】解:其构成的区域D如图所示的边长为2的正方形,面积为S1=4,满足到原点的距离大于2所表示的平面区域是以原点为圆心,以2为半径的圆外部,面积为=4﹣π,∴在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率P=故选:D.12.(5分)已知直线l:(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=2cosθ,设点M的直角坐标为(5,),直线l与曲线C的交点为A,B,|MA|•|MB|的值为()A.16B.18C.8D.10【解答】解:曲线C的极坐标方程为ρ=2cosθ,转化为:ρ2=2ρcosθ,则直角坐标方程为:x2+y2﹣2x=0,把直线的参数方程:(t为参数),代入x2+y2﹣2x=0,得到:,(t1和t2为A和B对应的参数)所以:,t 1t2=18所以:,|MA|•|MB|=|t1t2|=18.故选:B.二、填空题:本题共4小题,每小题5分.13.(5分)直线l:mx﹣y+1﹣m=0与⊙C:x2+(y﹣1)2=5的位置关系是相交.【解答】解:直线l:mx﹣y+1﹣m=0,经过(1,1)定点.因为12+(1﹣1)2=1<5,所以定点在圆⊙C:x2+(y﹣1)2=5的内部,所以直线与圆的位置关系是相交.故答案为:相交.14.(5分)过抛物线方程为y2=4x的焦点作直线l交于P(x1,y1),Q(x2,y2)两点,若x1+x2=6,则|PQ|=8.【解答】解:抛物线y2=4x(p>0)中p=2,∵x1+x2=6,∴由抛物线的定义可知,|PQ|=|PF|+|QF|=x1++x2 +=(x1+x2)+p=6+2=8,故答案为:8.15.(5分)曲线C的参数方程为(θ为参数),曲线C的直角坐标方程为y=2x2+1(﹣1≤x≤1).【解答】解:根据题意,曲线C的参数方程为(θ为参数),则有﹣1≤x≤1,y=2cos2θ﹣1+2=2cos2θ+1,又由x=cosθ,则有y=2x2+1(﹣1≤x≤1).故答案为:y=2x2+1(﹣1≤x≤1).16.(5分)一圆形纸片的半径为10cm,圆心为O,F为圆内一定点,OF=6cm,M为圆周上任意一点,把圆纸片折叠,使M与F重合,然后抹平纸片,这样就得到一条折痕CD,设CD与OM交于P点(如图),以FO所在直线为x轴,线段FO的中线为y轴,建立直角坐标系,则点P的轨迹方程为.【解答】解:以FO所在直线为x轴,线段FO的中垂线为y轴,建立直角坐标系.由题设,得:CD垂直平分线段MF,则有:|PO|+|PF|=|PO|+|PM|=|OM|=10即|PO|+|PF|=10>|OF|,所以点P的轨迹是以F,O为焦点的椭圆.方程为:,2a=10,2c=6,b2=16.点P的轨迹方程为:;故答案为:.三、解答题:本题共70分,其中17题10分,18至22题每题12分. 17.(10分)如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y (吨标准煤)的几组对照数据.(1)请根据上表提供的数据,用最小二乘法求出y 关于x 的回归直线方程=a+bx;(2)已知该厂技改前生产100吨甲产品的生产能耗为90吨标准煤,由(1)求出的回归直线方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?【解答】解:(1)由题意可得:,则:.(2)由(1)的回归直线方程及技改前生产100吨甲产品的生产能耗,得降低的生产能耗为90﹣(0.7×100+0.35)=19.65(吨标准煤)18.(12分)如图茎叶图记录了甲、乙两组四名同学的植树棵数,乙组记录中有一个数据模糊,无法确认,在图中以X表示.(1)如果X=8,求乙组同学植树棵数的平均数和标准差;(2)如果X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为19的概率.【解答】解:(1)当X=8时,由茎叶图可知,乙组同学的植树棵数是:8,8,9,10,所以平均数为,(2分)方差为,(5分)∴标准差.(6分)(2)当X=9时,由茎叶图可知,甲组同学的植树棵数是:9,9,11,11,乙组同学的植树棵数是:9,8,9,10.分别从甲、乙两组中随机选取一名同学,共有4×4=16种可能,其中满足这两名同学的植树总棵数为19的情况有2+2=4种,这两名同学的植树总棵数为19的概率等于=.(12分)19.(12分)已知曲线C的极坐标方程是ρ=1,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是(t 为参数),求直线l与曲线C相交所截的弦长.【解答】解:曲线C的极坐标方程是ρ=1,转化为:x2+y2=1.直线l的参数方程是(t为参数),转化为:3x﹣4y+3=0,则:点(0,0)到直线的距离为d=,所以:2l=.即弦长为:20.(12分)4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:min)的频率分布直方图,若将日均课外阅读时间不低于60min的学生称为“书虫”,低于60min的学生称为“懒虫”,(1)求x的值并估计全校3 000名学生中“书虫”大概有多少名学生?(将频率视为概率)(2)根据已知条件完成下面2×2的列联表,并判断能否在犯错误的概率不超过0.01的前提下认为“书虫”与性别有关:【解答】解:(1)由已知可得:(0.01+0.02+0.03+x+0.015)×10=1,解得x=0.025;…(2分)因为(0.025+0.015)×10=0.4,将频率视为概率,由此可以估算出全校3000名学生中“书虫”大概有1200人;…(4分)(2)完成下面的2×2列联表如下:…(7分)根据表中数据,计算K2=≈8.249;…(10分)由8.249>6.635知,在犯错误的概率不超过0.01的前提下认为“读书迷”与性别有关…(12分)21.(12分)在平面直角坐标系xOy中,以坐标原点O为极点x轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:3ρ2=12ρcosθ﹣10(ρ>0).(1)求曲线C1的普通方程(2)曲线C2的方程为,设P、Q分别为曲线C1与曲线C2上的任意一点,求|PQ|的最小值.【解答】解:(1)由3ρ2=12ρcosθ﹣10(ρ>0),得3x2+3y2=12x﹣10,即.∴曲线C1的普通方程为:;(2)依题意可设Q(4cosθ,2sinθ),由(1)知圆C1的圆心坐标为(2,0),则==.∴当cosθ=时,.∴.22.(12分)已知椭圆C:+=1(a>b>0)的离心率e=,且椭圆C上一点M与椭圆左右两个焦点构成的三角形周长为4+2.(1)求椭圆C的方程;(2)如图,设点D为椭圆上任意一点,直线y=m和椭圆C交于A、B两点,直线DA、DB与y轴的交点分别为P、Q,求证:∠PF1F2+∠QF1F2=90°.【解答】(1)解:由题意可得:e==,2a+2c=4+2,又a2=b2+c2.联立解得:a=2,b=c=.∴椭圆C的方程为:=1.(2)证明:F1.设D(x0,y0),则+=1.把y=m代入椭圆方程可得:+=1,解得x=±.取A(﹣,m),B(,m).直线DA的方程为:y﹣y0=(x﹣x0),可得P.同理可得:直线DB的方程为:y﹣y0=(x﹣x0),可得第21页(共21页) Q . ∴=,=. 又=2﹣.∴•=•===1.∴∠PF 1F 2+∠QF 1F 2=90°.。
吉林省长春外国语学校2015-2016学年高二数学上学期期末试卷 理(含解析)

2015-2016学年吉林省长春外国语学校高二(上)期末数学试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数等于()A.1﹣2iB.1+2iC.2﹣iD.2+i2.抛物线y=x2的准线方程是()A. B. C.y=﹣1D.y=﹣23.双曲线的离心率为,则正数a的值为()A. B.2C. D.14.已知椭圆()上一动点 P到其两焦点F1,F2的距离之和为4,则实数a的值是()A.1B.2C.3D.45.若函数y=ax2+1的图象与双曲线的渐近线相切,则实数a的值为()A.1B.2C.3D.46.已知函数f(x)=e x+3,则f(x)在x=0处切线的方程是()A.x﹣y+4=0B.x+y﹣4=0C.4x﹣y+4=0D.4x+y﹣4=07.若抛物线y2=4x与直线x﹣y﹣1=0交于 A,B两点,则|AB|=()A.2B.4C.6D.88.若函数f(x)=ax﹣lnx在(2,+∞)上单调递增,则实数a的取值范围是()A.(﹣∞,2)B.(﹣∞,2]C. D.9.函数的零点的个数是()A.0B.1C.2D.310.函数f(x)=e x﹣2x+1在[0,1)上的最小值是()A.2B.e﹣1C.3﹣2ln2D.2﹣2ln211.()A. B.2C. D.π﹣112.若椭圆(a>b>0)的离心率为,则双曲线的离心率是()A.2B. C. D.3二、填空题(每题5分,满分20分,将答案填在答题纸上)13.复数z=(1+i)(a﹣i)表示的点在第四象限,则实数a的取值范围是.14.若点 P(1,m)为抛物线y2=2px(p>0)上一点,F是抛物线的焦点,若|PF|=2,则m= .15.函数f(x)=ax3+bx+1在x=1处有极大值2,则b﹣a= .16.若 A,B是双曲线上两个动点,且,则△AOB面积的最小值是.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.若函数f(x)=ax3+2bx2﹣4x在x=﹣2与处取得极值.(1)求函数f(x)的解析式;(2)求函数f(x)的单调递增区间.18.已知椭圆(a>b>0)经过点(0,1),且离心率.(1)求椭圆的标准方程;(2)若直线l:y=k(x﹣1)与椭圆交于 A、B两点,若,求直线l的方程.19.已知函数,a∈R.(1)当a=4时,求函数f(x)的极值;(2)若函数在x=1处的切线平行于x轴,求a的值.20.已知椭圆+=1,A,B分别为其左右顶点,P是椭圆上异于 A,B的一个动点,设k1,k2分别是直线 P A,P B的斜率.(1)求k1•k2的值;(2)若 M(1,1)是椭圆内一定点,过 M的直线l交椭圆于C,D两点,若=(+),求直线l的方程.21.若点 P(1,2),A(x1,y1),B(x2,y2)是抛物线y2=2px(p>0)上的不同的三个点,直线AP,BP的斜率分别是k1,k2,若k1+k2=0.(1)求抛物线的方程;(2)求y1+y2的值及直线AB的斜率k.22.已知函数f(x)=lnx﹣x+1.(1)求函数f(x)的单调区间;(2)求证:当x>0时,;(3)当x∈N*时,证明.2015-2016学年吉林省长春外国语学校高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.复数等于()A.1﹣2iB.1+2iC.2﹣iD.2+i【考点】复数代数形式的乘除运算.【分析】将分母实数化即可.【解答】解: ===1+2i.故选B.2.抛物线y=x2的准线方程是()A. B. C.y=﹣1D.y=﹣2【考点】抛物线的简单性质.【分析】将抛物线方程化为标准方程,由抛物线x2=2py的准线方程为y=﹣,计算即可得到所求准线方程.【解答】解:抛物线y=x2即为x2=4y,由抛物线x2=2py的准线方程为y=﹣,可得x2=4y的准线方程为y=﹣1.故选:C.3.双曲线的离心率为,则正数a的值为()A. B.2C. D.1【考点】双曲线的简单性质.【分析】利用双曲线的性质求解即可.【解答】解:∵双曲线的离心率为,∴=,解得a=1.故选:D.4.已知椭圆()上一动点 P到其两焦点F1,F2的距离之和为4,则实数a的值是()A.1B.2C.3D.4【考点】椭圆的简单性质.【分析】利用椭圆的定义即可得出.【解答】解:∵椭圆()上一动点P到其两焦点F1,F2的距离之和为4,∴4=2a,解得a=2.故选:B.5.若函数y=ax2+1的图象与双曲线的渐近线相切,则实数a的值为()A.1B.2C.3D.4【考点】双曲线的简单性质.【分析】双曲线的渐近线方程为y=±2x.函数y=ax2+1,y′=2ax,利用函数y=ax2+1的图象与双曲线的渐近线相切,可得实数a的值.【解答】解:双曲线的渐近线方程为y=±2x.∵函数y=ax2+1,∴y′=2ax,∵函数y=ax2+1的图象与双曲线的渐近线相切,∴2a=2,∴a=1.故选:A.6.已知函数f(x)=e x+3,则f(x)在x=0处切线的方程是()A.x﹣y+4=0B.x+y﹣4=0C.4x﹣y+4=0D.4x+y﹣4=0【考点】利用导数研究曲线上某点切线方程.【分析】求出函数的导数,求得切线的斜率和切点,由斜截式方程可得切线的方程.【解答】解:函数f(x)=e x+3的导数为f′(x)=e x,即有f(x)在x=0处切线的斜率为k=e0=1,切点为(0,4),则f(x)在x=0处切线的方程为y=x+4,故选:A.7.若抛物线y2=4x与直线x﹣y﹣1=0交于 A,B两点,则|AB|=()A.2B.4C.6D.8【考点】直线与圆锥曲线的综合问题;直线与圆锥曲线的关系.【分析】联立方程组,消去y,利用韦达定理以及抛物线的性质能求出|AB|的值.【解答】解:抛物线的焦点坐标(1,0),直线x﹣y﹣1=0经过抛物线的焦点.联立方程组,得x2﹣6x+1=0,设A(x1,y1),B(x2,y2),则x1+x2=6,x1•x2=﹣1,k=1,∴|AB|=x1+x2+p=8.故选:D.8.若函数f(x)=ax﹣lnx在(2,+∞)上单调递增,则实数a的取值范围是()A.(﹣∞,2)B.(﹣∞,2]C. D.【考点】导数在最大值、最小值问题中的应用;利用导数研究函数的单调性.【分析】求导函数,利用函数f(x)=ax﹣lnx在(2,+∞)上单调递增,可得f′(x)≥0在(2,+∞)上恒成立,分离参数,求出函数的最大值,即可求得实数a的取值范围.【解答】解:求导函数可得:f′(x)=a﹣,∵函数f(x)=ax﹣lnx在(2,+∞)上单调递增,∴f′(x)=a﹣≥0在(2,+∞)上恒成立∴a≥函数y=,在(2,+∞)上单调减,∴x=2时,函数y取得最大值∴a≥实数a的取值范围是:.故选:C.9.函数的零点的个数是()A.0B.1C.2D.3【考点】利用导数研究函数的极值;根的存在性及根的个数判断;利用导数研究函数的单调性.【分析】先利用导数判断函数的单调性,求解函数的极值,然后说明f(x)存在零点,由此即可得到答案.【解答】解:函数,可得f′(x)=x2﹣2x﹣3,令x2﹣2x﹣3=0可得x=﹣1,x=3,x<﹣1,x>3时,f′(x)>0,函数是增函数,x∈(﹣1,3)时,f′(x)<0,函数是减函数,所以f(x)的极大值为f(﹣1)=7﹣,函数的极小值为f(3)=﹣4<0.所以f(x)的零点个数为3.故选:D.10.函数f(x)=e x﹣2x+1在[0,1)上的最小值是()A.2B.e﹣1C.3﹣2ln2D.2﹣2ln2【考点】利用导数求闭区间上函数的最值.【分析】利用导数求得函数的极值,根据单调性可判断也为最值.【解答】解:f′(x)=e x﹣2,令f′(x)=0,得x=ln2<1,当x∈[0,ln2)时,f′(x)<0,f(x)递减;当x∈(ln2,1)时,f′(x)>0,f(x)递增.∴x=ln2时f(x)取得极小值也为最小值,f(ln2)=3﹣2ln2,故选:C.11.()A. B.2C. D.π﹣1【考点】定积分.【分析】根据定积分的计算和定积分的几何意义即可求出.【解答】解:因为dx表示以原点为圆心,以半径为1的圆的面积的四分之一,所以dx=,因为3x2dx=x3|=1,所以1﹣,故选:A.12.若椭圆(a>b>0)的离心率为,则双曲线的离心率是()A.2B. C. D.3【考点】椭圆的简单性质;圆锥曲线的综合.【分析】利用椭圆的离心率求出ab关系式,然后求解双曲线的离心率即可.【解答】解:椭圆(a>b>0)的离心率为,可得,即:,可得,在则双曲线中,由,即,可得,∴e=.故选:C.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.复数z=(1+i)(a﹣i)表示的点在第四象限,则实数a的取值范围是﹣1<a<1 .【考点】复数的代数表示法及其几何意义.【分析】利用复数代数形式的乘法运算化简,然后由实部大于0且虚部小于0联立不等式组得答案.【解答】解:∵z=(1+i)(a﹣i)=(a+1)+(a﹣1)i表示的点在第四象限,∴,解得:﹣1<a<1.故答案为:﹣1<a<1.14.若点 P(1,m)为抛物线y2=2px(p>0)上一点,F是抛物线的焦点,若|PF|=2,则m= ±2.【考点】抛物线的简单性质.【分析】根据抛物线上的点到焦点和准线的距离相等,可得p值,进而可得m值.【解答】解:∵点 P(1,m)为抛物线y2=2px(p>0)上一点,F是抛物线的焦点,若|PF|=2,则1+=2,解得:p=2,故抛物线的方程为:y2=4x,将x=1代入可得:m=±2,故答案为:±215.函数f(x)=ax3+bx+1在x=1处有极大值2,则b﹣a= 4 .【考点】利用导数研究函数的极值.【分析】由已知得f′(x)=3ax2+b,且,求出a,b,即可得到结果.【解答】解:∵函数f(x)=ax3+bx+1,∴f′(x)=3ax2+b,∵f(x)=ax3+bx+1在x=1处有极大值2,∴,解得a=﹣1,b=3,解得b﹣a=4.故答案为:4.16.若 A,B是双曲线上两个动点,且,则△AOB面积的最小值是\frac{3}{2} .【考点】双曲线的简单性质.【分析】设直线OA的方程为y=kx,则直线OB的方程为y=﹣x,设点A(x1,y1),y=kx 与双曲线方程联立,可得x12=,y12=,可求得|OA|2,|OB|2,|OA|2•|OB|2,利用基本不等式即可求得答案.【解答】解:设直线OA的方程为y=kx,则直线OB的方程为y=﹣x,设点A(x1,y1),y=kx与双曲线方程联立,可得x12=,y12=,∴|OA|2=x12+y12=,同理|OB|2=,故|OA|2•|OB|2=∵=≤(当且仅当k=±1时,取等号)∴|OA|2•|OB|2≥9,又b>a>0,故S△AOB=|OA||OB|的最小值为.故答案为:.三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.若函数f(x)=ax3+2bx2﹣4x在x=﹣2与处取得极值.(1)求函数f(x)的解析式;(2)求函数f(x)的单调递增区间.【考点】利用导数研究函数的单调性;利用导数研究函数的极值.【分析】(1)已求出函数的导函数,根据f(x)在x=﹣2与处取得极值,得导函数值为0,从而求出a,b的值;(2)利用导数求函数f(x)的单调区间,首先求出极值点,再进行求解;【解答】解:(1)∵函数f(x)=ax3+2bx2﹣4x,可得f′(x)=3ax2+4bx﹣4.而f(x)在x=﹣2与处取得极值,∴,∴,∴,函数f(x)的解析式f(x)=x3+2x2﹣4x.(2)由(1)知f(x)=x3+2x2﹣4x,f′(x)=3x2+4x﹣4=(3x﹣2)(x+2)列表如下:x (﹣∞,﹣2)(﹣2,)(,+∞)f′(x)+ ﹣+f(x)单增单减单增∴f(x)的单增区间分别是(﹣∞,﹣2),(,+∞),单减区间是(﹣2,).所求函数的单调增区间为:(﹣∞,﹣2),(,+∞).18.已知椭圆(a>b>0)经过点(0,1),且离心率.(1)求椭圆的标准方程;(2)若直线l:y=k(x﹣1)与椭圆交于 A、B两点,若,求直线l的方程.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【分析】(1)根据椭圆的离心率和短轴端点,即可求出椭圆的几何量,得到椭圆的标准方程,(2)联立方程组,设A(x1,y1),B(x2,y2),构造方程组,利用韦达定理,得到两根和与两根积,再根据═x1x2+y1y2=0,化简计算即可.【解答】解:(1)∵椭圆(a>b>0)经过点(0,1),且离心率.可得b=1,c=1,a=∴c=1,椭圆方程为:.(2)直线l:y=k(x﹣1),A(x1,y1),B(x2,y2),由,得到得(2k2+1)x2﹣4k2x+2k2﹣2=0,∴△=8k2+8>0∴x1+x2=,x1x2=,∴=x1x2+y1y2=x1x2+k(x1﹣1)•k(x2﹣1)=x1x2+k2[x1x2﹣(x1+x2)+1]=(1+k2)x1x2﹣k2(x1+x2)+k2,∴=﹣k2•+(1+k2)•+k2==0,解得k=.直线l的方程:y=(x﹣1).19.已知函数,a∈R.(1)当a=4时,求函数f(x)的极值;(2)若函数在x=1处的切线平行于x轴,求a的值.【考点】利用导数研究函数的极值;利用导数研究曲线上某点切线方程.【分析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值;(2)求出函数的导数,得到f′(1)=0,解出即可.【解答】解:(1)a=4时,f(x)=x+﹣2,f′(x)=1﹣=,令f′(x)>0,解得:x>2或x<﹣2,令f′(x)<0,解得:﹣2<x<0或0<x<2,∴f(x)在(﹣∞,﹣2)递增,在(﹣2,0)递减,在(0,2)递减,在(2,+∞)递增,∴f(x)极大值=f(﹣2)=﹣6,f(x)极小值=f(2)=2;(2)f′(x)=1﹣,若函数在x=1处的切线平行于x轴,则f′(1)=1﹣a=0,解得:a=1.20.已知椭圆+=1,A,B分别为其左右顶点,P是椭圆上异于 A,B的一个动点,设k1,k2分别是直线 P A,P B的斜率.(1)求k1•k2的值;(2)若 M(1,1)是椭圆内一定点,过 M的直线l交椭圆于C,D两点,若=(+),求直线l的方程.【考点】直线与圆锥曲线的关系;椭圆的简单性质.【分析】(1)由已知得A(﹣2,0),B(2,0),设P(2cosθ,),θ∈(0,2π),且θ≠π,由此能求出k1•k2的值.(2)当直线l的斜率不存在时,直线l的方程为x=1,不成立;当直线l的斜率存在时,设直线l的方程为y=k(x﹣1)+1,联立,得(3+4k2)x2﹣8k2x+8kx+4k2﹣8k+4=0,由此利用根的判别式、韦达定理、向量知识,结合已知条件能求出直线l的方程.【解答】解:(1)∵椭圆+=1,A,B分别为其左右顶点,P是椭圆上异于 A,B的一个动点,∴A(﹣2,0),B(2,0),设P(2cosθ,),θ∈(0,2π),且θ≠π,∵设k1,k2分别是直线 P A,P B的斜率,∴k1•k2====﹣.(2)当直线l的斜率不存在时,直线l的方程为x=1,把x=1代入椭圆+=1,得C(1,﹣),D(1,),=(1,0)≠(+)=(1,0),不成立;当直线l的斜率存在时,设直线l的方程为y=k(x﹣1)+1,联立,得(3+4k2)x2﹣8k2x+8kx+4k2﹣8k+4=0,∵过M的直线l交椭圆于C,D两点,∴△>0,设C(),D(x2,y2),则x1+x2=,,y1+y2=k(x1+x2)﹣2k+2=﹣2k+2,∵=(+),∴(1,1)==(,﹣k+1),∴,解得k=﹣,∴直线l的方程为y=﹣(x﹣1)+1,即3x+4y﹣4=0.21.若点 P(1,2),A(x1,y1),B(x2,y2)是抛物线y2=2px(p>0)上的不同的三个点,直线AP,BP的斜率分别是k1,k2,若k1+k2=0.(1)求抛物线的方程;(2)求y1+y2的值及直线AB的斜率k.【考点】抛物线的标准方程;直线与圆锥曲线的关系.【分析】(1)把P的坐标代入抛物线方程求得p,则抛物线方程可求;(2)分别设出直线PA、PB的方程,和抛物线方程联立,利用根与系数的关系求出A,B的纵坐标,作和得答案;再由斜率公式求出AB的斜率,整体代入y1+y2的值求得直线AB的斜率k.【解答】解:(1)∵P(1,2)在抛物线y2=2px(p>0)上,∴22=2p,即p=2,∴抛物线方程为y2=4x;(2)由题意设PA所在直线方程为y﹣2=k(x﹣1),联立,得ky2﹣4y﹣4k+8=0.∴,得.设PB所在直线方程为y﹣2=﹣k(x﹣1),联立,得ky2+4y﹣4k﹣8=0.∴,得.∴y1+y2=﹣4;.22.已知函数f(x)=lnx﹣x+1.(1)求函数f(x)的单调区间;(2)求证:当x>0时,;(3)当x∈N*时,证明.【考点】利用导数研究函数的单调性;导数在最大值、最小值问题中的应用.【分析】(1)求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;(2)根据(1)证明lnx≤x﹣1,构造函数g(x)=lnx+,根据函数的单调性求出g(x)的最小值,证明1﹣≤lnx;(3)构造函数得(x﹣)>lnx(x>1),令x=,可得ln(k+1)﹣lnk<(+),k=1,2,3…,n,将上述n个不等式依次相加,即可证得结论.【解答】解:(1)由已知得x>0,f′(x)=﹣1,由f′(x)>0,得﹣1>0,>1,x<1,由f′(x)<0,得﹣1<0,<1,x>1,∴f(x)在(1,+∞)上为减函数,在(0,1)为增函数;(2)由(1)知:当x=1时,f(x)max=﹣1+1=0,对任意x>0,有f(x)≤0,即lnx﹣x+1≤0,即lnx≤x﹣1①,令g(x)=lnx+,g′(x)=,令g′(x)>0,解得:x>1,令g′(x)<0,解得:0<x<1,∴g(x)在(0,1)递减,在(1,+∞)递增,∴g(x)min=g(1)=1,故lnx+≥1,即1﹣≤lnx②,由①②得:当x>0时,;(3)设F(x)=lnx﹣(x﹣),则F′(x)=﹣(﹣1)2<0.所以F(x)在x>1时单调递减.由F(1)=0可得当x>1时,得:(x﹣)>lnx(x>1).令x=,则ln<(﹣)= [(1+)﹣(1﹣)]=(+),所以ln(k+1)﹣lnk<(+),k=1,2,3…,n.将上述n个不等式依次相加得 ln(n+1)<+(++…+)+,所以1+++…+>ln(n+1)+>ln(n+1).。
吉林省长春外国语学校2016-2017学年高二上学期期末考试 数学 (word版含答案)

第4题7 8 99 8 27 911 2 5 6 甲 乙 长春外国语学校2016-2017学年第一学期期末考试高二年级数学试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
考试结束后,将答题卡交回。
注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信 息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书 写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效; 在草稿纸、试题卷上答题无效。
4.作图可先使用铅笔画出,确定后必须用黑色字迹的签字笔描黑。
5. 保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
第Ⅰ卷一、选择题:本题共12小题,每小题5分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 抛物线24y x =的焦点坐标是( )A .(0,1)B .(1,0)C .1(0,16 D .1(,0)162. 双曲线1422=-y x 的渐近线方程和离心率分别是( ) A.5;2=±=e x y B.5;21=±=e x yC.3;21=±=e xy D.2;y x e =±=3. 如果(1,3)A 关于直线l 的对称点为(5,1)B -,则直线l 的方程是( )A .380x y -+= B. 340x y ++= C .340x y +-= D .380x y -+= 4. 将甲、乙两名同学5次物理测验的成绩用茎叶图表示如图, 若甲、乙两人成绩的中位数分别为乙甲、x x ,则下列说法正确 的是( )A .乙甲x x <;乙比甲成绩稳定 B.乙甲x x >;甲比乙成绩稳定 C.乙甲x x >;乙比甲成绩稳定 D.乙甲x x <;甲比乙成绩稳定5. 在5件产品中,有3件一等品和2件二等品,从中任取2件,以710为概率的事件( )A .恰有1件一等品B .至少有一件一等品C .至多有一件一等品D .都不是一等品6.以下给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图(如图所示),其中 判断框内应填入的条件是( ) A . i>10 B. i<10C. i<20D.i>20(第6题图)7.曲线192522=+y x 与曲线192522=-+-k y k x )9(<k 的( ) A.长轴长相等 B.离心率相等 D.焦距相等 8. 已知0,0,1a b a b >>+=,则( ) A. 7 B .8 C. 9 D .109. 已知点P 是抛物线22y x =上的一个动点,则点P 到点(0,2)的距离与到该抛物线准线的距离之和的最小值为( )B. 39210.已知圆的方程为22680x y x y +--=,设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为( )A .B .. D .11. 若椭圆221369x y +=的弦被点(4,2)平分,则此弦所在直线的斜率为( ) A. 2 B. 2- C.13 D.12-12.若直线y x b =+与曲线3y =有公共点,则b 的取值范围是( )A .[1-+B .[1C .[1,1-+D .[1-第Ⅱ卷二、填空题:本题共4小题,每小题5分。
【吉林省长春外国语学校】2017届高三上学期期末考试(理)数学试卷-答案

吉林省长春外国语学校2017届高三上学期期末考试数学(理)试卷答 案1~5.DACCB6~10.DCCCC11~12.BB13.11414.[1)3-+∞, 15.1(2,)216.1817.解:(1)ABC △中,∵22()a b c bc --=,∴222a b c bc --=-, ∴2221cos 22b c a A bc +-==, ∴π3A =. ∵sin cos cos cos 2A C AB +=, ∴2cos cos sin cos A B AC =+,∴2πcos ()23B cos B =+-,即22πcos cos sin sin 33B cos B B π=+⋅+1sin B B =+, ∴π6B =.综上可得,π3A =,π6B =. (2)∵2ππ32C B =-=, ∴π()sin(2)cos22f x x x =+=, ∴π()cos(2)26g x x -+, 令π2π22ππ6k x k ≤-≤+,求得π7ππ1212k x k π+≤≤+, 故函数()g x 的单调减区间为π7ππ,π11[],22k k k Z ++∈. 18.证明:(1)∵四边形ABCD 是边长为2的正方形,∴AC BD ⊥,∵DE ABCD AC ABCD ⊥⊂平面,平面,∴AC DE ⊥,∵BD DE D =I ,∴AC BDE ⊥平面.(2)以D 为原点,DA x 为轴,DC y 为轴,DE z 为轴,建立空间直角坐标系,∵BE 与平面45ABCD ︒所成角为,∴DE BD ===则(000),(220),(00,,,,,,,D B E F ,(2,(0,(2,2,0)=-==u u u r u u u r --BE BF ,设平面BDE 的法向量(,,)n x y z =r ,则220220n BE x y n DB x y ⎧⋅=--+=⎪⎨⋅=+=⎪⎩r u u u r r u u u r ,取1x =,得(1,1,0)n =-r , 设平面BEF 的法向量π=(a,b,c)r ,则22020m BE a b m BF b ⎧⋅=--+=⎪⎨⋅=-+=⎪⎩u r u u u r u r u u u r,取cπr , ∴π1100n ⋅=-+=r r ,∴二面角F BE D --的大小为π2.19.解:(1)123255376(1)7C C C P C ξ≤==. (2)ξ的分布列为:3122152525333777241(0)(1)(2)777C C C C C P P P C C C ξξξ=========,,, ξ0 1 2 P27 47 17 (3)2416()0127777E ξ=⨯+⨯+⨯=. 20.解(1):由题意c a =,2b a=222a b c =+解得2a b c ===, 则椭圆的方程为:22184x y += (2)要使AOB △面积最大,则B 到OA 所在直线距离最远.设与OA平行的直线方程为y b =+.由22184y b x y ⎧=+⎪⎪⎨⎪+=⎪⎩消去y并化简得.2240x b +-=. 由0=△得b =±不妨取0b >,∴与直线OA平行,且与椭圆相切且两直线方程为:y +, 则B 到直线OA 的距离等于O到直线:2y x =+, 的距离d,d =,又OA = AOB △面积的最大值12s =21.解:(Ⅰ)当1a =时,()12ln f x x x =--, 则2()1f x x'=-,由()0f x '>,得2x >, 由()0,02f x x '<得<<,故()f x 的单调减区间为(0]2,,单调增区间为[2)+∞,.(Ⅱ)因为()0f x <在区间1(0)2,上恒成立不可能, 故要使函数()f x 在1(0)2,上无零点,只要对任意的1(0)2x ∈,,()0f x >恒成立, 即对1(0)2x ∈,,2ln 21x a x -->恒成立. 令2ln ()21x l x x =--1(0)2x ∈,,, 则222ln 2ln ()(1)x x l x x +-'=-, 再令21()2ln 2(0)ln 2m x x x x =+-∈,,, 则22222(1)()0x m x x x x --'=-+=<, 故1()0)2m x 在(,上为减函数,于是1()()22ln 202m x m =->>, 从而()0l x >,于是()l x 在1(0)2,上为增函数, 所以1()()24ln 22l x l =-<, 故要使2ln 21x a x -->恒成立,只要24ln 2[a ∈-+∞,), 综上,若函数()f x 在1(0)2,上无零点,则a 的最小值为24ln2-. 22.解:(1)将曲线C 的极坐标方程22cos 30ρρθ--=化为直角坐标方程为22230x y x +--=,直线l 的参数方程为3cos sin x t y t αα=-+⎧⎨=⎩(t 为参数), 将参数方程代入22230x y x +--=,整理得28cos 120t t α-+=,∵直线l 与曲线C 有公共点,∴64cos2480α=-≥△,∴cos α≥cos 0,π)[αα≤∈Q , ∴α的取值范围是5π[][π0π)66U ,,. (2)曲线C 的方程22230x y x +--=可化为22(1)4x y -+=,其参数方程为12cos 2sin x y θθ=+⎧⎨=⎩,(θ为参数), ∵(,)M x y 为曲线上任意一点,∴π12cos 2sin 1)4x y θθθ+=++=++, ∴x y +的取值范围是[1-+. 23.解:(Ⅰ)∵3,2()2527,253,5||||x f x x x x x x -≤⎧⎪=--=-<<⎨⎪≥⎩-,∴函数()f x 的值域为[33]-,;(Ⅱ)∵不等式()210f x m +-≥对于任意的x R ∈都成立,∴min 12()3m f x -≤=-,∴2m ≥.即m 的取值范围为[2)+∞,.吉林省长春外国语学校2017届高三上学期期末考试数学(理)试卷解析1.解:∵集合A={x|﹣1<x<2},B={x|x2+2x≤0}={x|﹣2≤x≤0},∴A∩B={x|﹣1<x≤0}.故选:D.2.解:==+1﹣i=1﹣i+1﹣i=2﹣2i.故选:A.3.解:∵,,∴=(λ+1,﹣2λ),=(﹣3,﹣2),∵向量与垂直,∴()()=﹣3(λ+1)+4λ=0,解得λ=3.故选:C.4.解:抛物线y=ax2的标准方程为:x2=y,a>0时,准线方程为:y=﹣,a<0时准线方程为:y=点M(2,1)到抛物线y=ax2准线的距离为2,可得1+=2,解得a=,﹣﹣1=2,解得a=﹣.故选:C.5.解:由已知中的三视图,可得:棱锥的底面积S=×2×4=4;高h=×2=,故棱锥的体积V==4,故选:B.6.解:当k=10时,S=1+10=11,k=9,当k=9时,S=11+9=20,k=8,当k=8时,S=20+8=28,k=7,当k=7时,S=28+7=35,k=6,此时不满足条件输出,∴判断框中应填入的关于k的条件是k>6,故选:D.7.解:设f(x)是定义在R上的周期为3的周期函数,如图表示该函数在区间(﹣2,1]上的图象,∴f(2011)+f(2013)=f(1)+f(0)=1+0=1.故选:C.8.解:由满足,得,因为直线x+y=a的斜率是﹣1,所以A、B两点在坐标轴上并且在圆上;所以(0,1)和(0,﹣1)点都适合直线的方程,a=±1;故选C.9.解:由椭圆方程得F1(﹣1,0)F2(1,0),设P(x,y),∴,,则=x2+y2﹣1=∈[0,1] 故选:C10.解:f′(x)=6x2﹣6mx+6;由已知条件知x∈(1,+∞)时,f′(x)≥0恒成立;设g(x)=6x2﹣6mx+6,则g(x)≥0在(1,+∞)上恒成立;法一:(1)若△=36(m2﹣4)≤0,即﹣2≤m≤2,满足g(x)≥0在(1,+∞)上恒成立;(2)若△=36(m2﹣4)>0,即m<﹣2,或m>2,则需:解得m≤2;∴m<﹣2,∴综上得m≤2,∴实数m的取值范围是(﹣∞,2];法二:问题转化为m≤x+在(1,+∞)恒成立,而函数y=x+≥2,故m≤2;故选:C.11.解:的展开式中只有第四项的二项式系数最大,所以n=6.其通项公式Tr+1=C6r•()r•,令3﹣=0,求得r=2,可得展开式中的常数项为C62•()2=,故选:B.12.解:由,可得F(x)=xf(x)﹣=0,得xf(x)=,设g(x)=xf(x),则g′(x)=f(x)+xf′(x),∵x≠0时,有,即当x>0时,g'(x)=f(x)+xf'(x)>0,此时函数g(x)单调递增,此时g(x)>g(0)=0,当x<0时,g'(x)=f(x)+xf'(x)<0,此时函数g(x)单调递减,此时g(x)>g(0)=0,作出函数g(x)和函数y=的图象,(直线只代表单调性和取值范围),由图象可知函数F(x)=xf(x)﹣的零点个数为1个.故选:B.13.解:由等差数列{an}的性质可得,a4+a10+a16=18=3a10,解得a10=6,则S19==19a10=114,故答案为:114. 14.解:作出不等式组对应的平面区域如图:的几何意义是区域内的点到定点D (﹣1,0)的斜率,由图象知CD 的斜率最小,由得,即C (2,﹣1),则CD 的斜率z ==﹣,即的取值范围是[﹣,+∞), 故答案为:[)13-+∞,15.解:∵y =x2,∴y '=2x .x =2,y '=4∵y =x2在点(2,4)处的切线与曲线(x >0)上点P 处的切线垂直, ∴曲线(x >0)上点P 处的切线斜率为﹣.又y '=﹣,设点P (x0,y0)∴﹣=﹣,∴x0=±2,∵x>0,∴x0=2,∴y0=,∴点P.故答案为1 (2,)2.16.解:第一步:从3个社团中选2个,共有C32=3种,第二步:把3名同学分为(2,1),把这两组同学分配到两个社团中有A32=6,根据分步计数原理可得,共有3×6=18种,故答案为:18.17.(1)利用余弦定理求得cosA的值,可得A的值,利用两角和差的余弦公式化简cosAcosB=,可得B的值.(2)利用函数y=Acos(ωx+φ)的图象变换规律求得g(x)的解析式,再利用余弦函数的单调性求得函数g(x)的单调递减区间.18.(1)推导出AC⊥BD,AC⊥DE,由此能证明AC⊥平面BDE.(2)以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,利用向量法能求出二面角F﹣BE﹣D的大小.19.(1)P(ξ≤1)=.(2)ξ的分布列为:P(ξ=0)=,P(ξ=1)=,P(ξ=2)=,即可得出分布列.(3)利用数学期望计算公式即可得出.20.(1)由题意求出椭圆方程,(2)然后求出和OA平行且和椭圆相切的直线方程,把切点到直线OA的距离转化为原点O到切线的距离,则三角形AOB面积的最大值可求.21.(1)先求导函数f′(x),然后令f′(x)>0即可求出函数的单调增区间,令f′(x)<0可求出函数单调减区间,注意与定义域求交集;(2)因为f(x)<0在区间(0,)上恒成立不可能,故要使函数f(x)在(0,)上无零点,只要对任意的x∈(0,),f(x)>0恒成立,然后利用参变量分离,利用导数研究不等式另一侧的最值即可求出a的最小值.22.(1)利用互化公式即可把曲线C的极坐标方程ρ2﹣2ρcosθ﹣3=0化为直角坐标方程.直线l的参数方程为(t为参数),代入曲线C的直角坐标方程可得t2﹣8tcosα+12=0,根据直线l与曲线C 有公共点,可得△≥0,利用三角函数的单调性即可得出.(2)曲线C的方程x2+y2﹣2x﹣3=0可化为(x﹣1)2+y2=4,参数方程为,(θ为参数),设M(x,y)为曲线上任意一点,可得x+y=1+2cosθ+2sinθ,利用和差公式化简即可得出取值范围.23.(Ⅰ)通过对x的取值范围的分类讨论,去掉绝对值符号,化为分段函数,即可求得函数f(x)的值域;(Ⅱ)不等式f(x)+2m﹣1≥0对于任意的x∈R都成立⇔1﹣2m≤f(x)min=﹣3,解之即可求得m的取值范围.- 11 -/ 11。
吉林省长春外国语学校高二上学期期末考试(数学).pdf

____年___月___日 星期 主备人: 课时数: 课题8B Unit 3 Revision 1 教学目标教学重点To use the proper words to describe Online travel.教学难点The new words and useful expressions.教法教具教学过程个案补充Step1 The words about traveling and places of interest Show some pictures about the following places of interest .Ask Ss to say some something about each. Tell students that they are going to talk about the uses of computers in PartB. Play the tape for the students to find the answer to the question: Why does Simon use computer to search for information? In pairs, students talk about different uses of computers. They can use Daniel and Simon’s conversation as a model and replace the underlined words with their own information. They can also create their own conversations about different uses of computers. Ask a few pairs to present their conversations to the class. Show some pictures of places of interest for students to look at and say out which one is their favourite and why. Step2. Presentation the language about educational CD-ROM with the help of the hints given on the Bb. A new e CD-ROM has just c out. It is d by Nancy Jackson. This game has eight l, and each level will t you about an hour. The questions test your knowledge of English g and vocabulary. Every time you p a level ,you will see a w map.The places you have visited are m in bright. The CD-ROM is now on s in all computer shops. Step3 Useful expressions Show some phrases with their Chinese meanings, ask students to write the English. 1….的设计者: 2.被…所设计: 3.扮演…的主角: 4. 向某人展示: 5. 同时: 6. 想要某人做某事: 7. 躺在…上: 8. 出版,发行: Give students some time to read the phrases by themselves first, then check the answers in pairs. Step4 Ask the students to retell the passage according to the key words in each paragraph. Step5 Homework Finish the exercises in the Workbook. Do the rest of exercises in their Evaluation Exercise Book. 板书设计 教后反思。
【全国百强校】吉林省长春外国语学校2016-2017学年高二上学期期末考试物理试题解析(解析版 )

一、单项选择题:本题共10小题,每小题4分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.如右图所示,通电导体ab的电流方向由a向b,导体受到磁场力的方向向右,则磁场的方向是A.由导线左方向右方B.由导线右方向左方C.垂直纸面向里D.垂直纸面向外【答案】C【解析】考点:安培力。
【名师点睛】左手定则的内容:伸开左手,使大拇指与其余四个手指垂直,并且都与手掌在同一个平面内;让磁感线从掌心进入,并使四指指向电流的方向,这时拇指所指的方向就是通电导线在磁场中所受安培力的方向.根据左手定则的内容判断安培力的方向.2.一根无限长的通电直导线旁放一通电矩形线框,电流方向如图所示,直导线和线框在同一平面内,线框在通电直导线的磁场力作用下将会A.静止不动 B.向右平移C.向左平移 D.向下平移【答案】B试题分析:直导线中的电流方向由上向下,根据安培定则,导线右侧区域磁感应强度方向外,根据左手定则,左边受向右的安培力,右边受到向左的安培力,上边受到向上的安培力,下受到向下的安培力,方向不同离通电导线越远的位置,磁感应强度越小,故根据安培力公式F=BIL,左边受到的安培力大于右边,上边受到的安培力等于下受到受到的安培力,故线圈受通电直导线作用后将向右运动,B正确;ACD错误;故选:B考点:安培力。
【名师点睛】本题关键:(1)会根据安培定则判断通电直导线的磁场;(2)会根据左手定则判断安培力方向;(3)会根据安培力公式F=BIL并结合微元法判断安培力的大小。
3.如右图所示,小磁针的正上方,平行放置一直导线,当导线通入电流I时, 小磁针A.转动,N极转向读者B.转动,S极转向读者C.不转动D.上下振动【答案】B【解析】考点:电流的磁场对磁针的作用。
【名师点睛】当导线中通过图示方向的电流时,产生磁场,根据安培定则判断磁场的方向.小磁针处于磁场中,N极受力方向与磁场方向相同.根据磁场方向判断小磁针的转动方向。
4.下图为磁场中通电直导线或运动的带电粒子所受磁场力方向情况,其中正确的是【答案】A考点:安培力、洛仑兹力。
2017届长春外国语学校高三上学期期末考试理科数学试题及答案

长春外国语学校2017学年第一学期期末考试高三理科数学试卷考生在答题前请认真阅读本注意事项及各题答题要求1. 本试卷分第Ⅰ卷、第Ⅱ卷和答题卡,共4页 满分150分,考试用时120分钟。
考试结束后,请将答题卡卷交回,试题卷自己保存。
2.答题前,请您务必将自己的班级、姓名、学号、考号用0.5毫米黑色签字笔填写在答题卡上。
3.作答非选择题必须用0.5毫米的黑色签字笔写在答题卡上的指定位置,在其它位置作答一律无效。
4.保持答题卷清洁、完整,严禁使用涂改液和修正带。
第Ⅰ卷(选择题 共60分)一、选择题:本大题共12个小题,每小题5分,共60分.每小题四个选项中,只有一项正确.1. 已知集合}11|{≤≤-=x x A ,}065|{2≥+-=x x x B ,则下列结论中正确的是( )A. B B A =B. A B A =C. ABD. B A C R =2. “||||b a b a =⋅”是“a 与b 共线”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分又不必要条件3. 命题p :|sin |x y =是偶函数,命题q :||sin x y =是周期为π的周期函数,则下列命题中为真命题的是( )A. q p ∧B. q p ∨C. q p ∧⌝)(D. q p ∨⌝)(4. 已知数列}{n a 的前n 项和为n S ,当n n S n -=2时,=5a ( )A. 20B. 12C. 8D. 45. 下列函数中,图象不关于原点对称的是( )A. x x e e y --=B. 112-+=x e y C. )1ln(2++=x x y D. x y sin ln =6. 已知向量)2,1(=a ,),(y x b =,若a ∥b 且0)(=+⋅b a a ,则=+y x ( )A. 5B. 3C. 3-D. 5-7. 若曲线)1ln(2+-=x a x y 在1x =处取极值,则实数a 的值为( )A. 1B. 2C. 3D. 48. 定积分dx e x x ⎰-10)2(的值为( )A. e -2B. e -C. eD. e +29. 已知等比数列}{n a 中,23=a ,1664=a a ,则861210a a a a --的值为( ) A. 2 B. 4 C. 8 D. 1610. 函数3cos 2cos )(+-=x x x f )2(ππ-≤≤-x 有( ) A .最大值3,最小值2 B. 最大值5,最小值3C. 最大值5,最小值2D. 最大值3,最小值815 11. 将函数)62sin()(π-=x x f 的图象上所有的点向左平移3π个单位(纵坐标不变),则所得图象的解析式是( )A. x y 2cos -=B. x y 2cos =C. )652sin(π-=x yD. )62sin(π+=x y 12. 已知函数⎩⎨⎧>≤⋅=)0(log )0(2)(2x x x a x f x ,若关于x 的方程0)]([=x f f 有且只有一个实数根,则实数a 的取值范围是( )A.)0,(-∞B. )1,0()0,( -∞C. )1,0(D. ),1()1,0(+∞第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4个小题,每小题5分,共20分.把答案填在答题卡的指定位置.13. =-)1110sin(0________________.14. 已知△ABC 的三个内角满足C B A cos sin sin =,则△ABC 的形状一定是____________.15. 在△ABC 中,6=AB ,4=AC ,12=⋅AC AB ,则△ABC 的面积为 _____________.16. 关于函数21cos sin 3sin )(2-+=x x x x f 的说法正确的是_____________.(填正确序号)①最小正周期为π ②图象关于3π=x 对称 ③图象关于点)0,127(π成中心对称 ④在区间]4,2[ππ-上单调递增.三、解答题:本大题共6个小题,共70分,解答应写出必要的文字说明,证明过程或演算步骤.17.(12分) 已知△ABC 的三个内角C B A ,,所对的边分别为c b a ,,,向量),(c a b a m -+=)sin sin ,(sin B A C -=,且∥.(1)求∠B 的大小.(2)若1=a ,3=b ,求△ABC 的面积.18.(12分)已知数列}{n a 满足n n n a a 221+=+,*∈N n ,11=a ,nn n a b 2= (1)证明数列}{n b 为等差数列.(2)求数列}{n a 的通项公式n a 与前n 项和n S .19.(12分)某射手击中目标的概率为0.8,现给他五发子弹,规定只要击中目标立即停止射击;没击中目标,继续射击,直到子弹全部打完为止.(1)求射手射击三次的概率.(2)若用X 表示射手停止射击后剩余子弹的个数,求变量X 的分布列与期望)(X E 的值.20. (12分)已知椭圆)0(14222>=+b b y x ,双曲线)0,0(12222>>=-n m ny m x 的右焦点都与抛物线x y 42=的焦点F 重合.(1)若椭圆、双曲线、抛物线在第一象限交于同一点P ,求椭圆与双曲线的标准方程.(2)若双曲线与抛物线在第一象限交于Q 点,以Q 为圆心且过抛物线的焦点F 的圆被y 轴截得的弦长为32,求双曲线的离心率.21.(12分) 已知函数b ax x e x f x +--=221)(在0=x 处的切线方程为42+-=x y .(1)求函数)(x f 的解析式.(2)证明:R x x ∈∀21,且21x x ≠,恒有2)()(2121->--x x x f x f 成立. 22.(10分)在直角坐标系中,以原点为极点,以x 轴的正半轴为极轴,建立极坐标系。
精选吉林省长春市2016_2017学年高二数学上学期期末考试试题文

一、选择题(本题共 12 题,每题 4 分 , 共 48 分)
1、 抛物线 y2 4ax( a 0) 的焦点坐标是
()
( A)( a , 0 )( B)( - a , 0) ( C)(0, a )( D)( 0, - a )
2、圆 ( x 1) 2 y 2 1 的圆心到直线 y
18、已知抛物线的顶点在原点 , 它的准线过双曲线 x 2 y 2 1的右焦点 , 而且与 x 轴垂直 . 又抛物线 a2 b2
与此双曲线交于点 ( 3 , 6 ) , 求抛物线和双曲线的方程 . 2
19、已知一个圆 C 和 y 轴相切 , 圆心在直线 l 1 : x 3 y 0 上 , 且在直线 l 2 : x y 0 上截得的弦长为 2 7 , 求圆 C的方程 .
①、圆
②、圆去除 2 点 ③、双曲线 ④、双曲线去除 2 点
⑤、椭圆 ⑥、椭圆一部分 ⑦、直线
⑧、直线去除 2 点
三、解答题(本题共 5 个答题,其中 17,18 每题 10 分, 19,20,21 每题 12 分,共 56 分)
17、已知函数 f ( x) ax3 bx2 cx 在点 x0 处取得极大值 5 ,其导函 数 y f '(x) 的图象经过点 (1,0) , (2,0) ,如图所示 . 求 x0 的值和 a, b, c 的值 .
2
2
( A) xy源自1 (x≠0)36 20
2
2
( B) x
y
1 ( x≠ 0)
20 36
(
)
( C) x 2 y 2 1 ( x≠0) 6 20
( D) x 2 y 2 1 ( x≠ 0) 20 6
吉林省长春外国语学校2017届高三数学上学期期末考试试题(理)(含答案)

长春外国语学校2016-2017学年第一学期期末考试高三年级数学试卷(理科)第Ⅰ卷一、选择题:本题共12小题,每小题5分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合}21|{<<-=x x A ,}02|{2≤+=x x x B ,则=B A I ( )A .}20|{<<x xB .}20|{<≤x xC .}01|{<<-x xD .}01|{≤<-x x2. 设i z +=1(i 是虚数单位),则=+z z 2( ) A .i 22- B .i 22+ C .i --3 D .i +33. 已知)2,1(-=a ,)0,1(=b ,向量b a +λ与b a 4-垂直,则实数λ的值为( )A .31B .31- C .3 D .3-4. 点)1,2(M 到抛物线2ax y =准线的距离为2,则a 的值为( )A .41B .121C .41或121- D .41-或1215. 已知三棱锥的三视图如右图所示,则该三棱锥的体积是 ( )A .32B .4C .34D .66. 若如下框图所给的程序运行结果为35=S ,那么判断框中应填入的关于k 的条件是()A .6=kB .6≤kC .6<kD .6>k7. 设)(x f 是定义在R 上的周期为3的周期函数,如图表示该函数在区间]1,2(-上的图像,则=+)2013()2011(f f ( )A .3B .2C .1D .08. 已知直线a y x =+与圆122=+y x 交于B A ,两点,O 是坐标原点,向量OB OA ,满足||||OB OA OB OA -=+,则实数a 的值为( )A .1B .2C .1±D .2±9. 椭圆1222=+y x 两个焦点分别是21,F F ,点P 是椭圆上任意一点,则21PF PF ⋅的取值范围是( )A . ]1,1[-B .]0,1[-C .]1,0[D .]2,1[- 10. 若函数x mx x x f 632)(23+-=在区间),1(∞+上为增函数,则实数m 的取值范围是( )A . ]1,(-∞B .)1,(-∞C .]2,(-∞D .)2,(-∞11. 二项式n x x )31(+的展开式中只有第四项的二项式系数最大,则展开式中的常数项是( )A .95B .35C .5D .1512. 已知函数)(x f y =是R 上的可导函数,当0≠x 时,有0)()(>+'xx f x f ,则函数xx f x x F 1)()(-⋅=的零点个数是( ) A .0B .1C .2D .3第Ⅱ卷本卷包括必考题和选考题两部分。
吉林省长春外国语学校2016-2017学年高二上学期第一次月考数学试卷 含解析

吉林省长春外国语学校2016-2017学年高二上学期第一次月考数学一、选择题:共12题1.A(2,1),B(3,-1)两点连线的斜率为A. B. C. D.2【答案】A【解析】本题主要考查直线的倾斜角和斜率.依题意,A(2,1),B(3,-1)两点连线的斜率为,故选A。
2.直线的倾斜角是A。
30° B.60° C.120° D.135°【答案】D【解析】本题主要考查直线的倾斜角和斜率.依题意,直线的斜率为,设直线的倾斜角为,则,,得,故选D.3.直线与直线的交点坐标为A。
(—3,0) B.(—2,—3) C。
(0,1)D.(-1,0)【答案】A【解析】本题主要考查两直线的位置关系.依题意,由得,故两直线的交点坐标为(—3,0),故选A.4.圆C1:与圆C2:的位置关系是A。
外离 B.相交 C.内切D。
外切【答案】D【解析】本题主要考查两圆的位置关系。
依题意,两圆的圆心分别为,两圆半径分别为则两圆的圆心距,则两圆外切,故选D.5.在空间直角坐标系中,点(-2,1,4)关于x轴的对称点的坐标为A。
(-2,1,—4) B。
(—2,-1,-4) C。
(2,1,—4) D。
(2,-1,4)【答案】B【解析】本题主要考查空间直角坐标系的应用.依题意,在空间直角坐标系中,根据对称性,得点(-2,1,4)关于x轴的对称点的坐标为(-2,-1,—4),故选B.6.经过圆C:的圆心且斜率为1的直线方程为A.x-y+3=0B.x-y-3=0 C。
x+y-1=0 D。
x+y+3=0【答案】A【解析】本题主要考查直线方程.依题意,圆心坐标为,则过圆心且斜率为1的直线方程为,即,故选A.7.如果直线与直线平行,则a等于A。
0 B。
C. D。
0或1【答案】C【解析】本题主要考查两直线的位置关系.依题意,直线与直线平行,当时,两直线分别为和,两直线平行;当时,两直线平行,则得,综上,a等于,故选C.8.圆上到直线的距离等于的点有A.1个B.2个C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
吉林省长春外国语学校2016-2017学年高二(上)期末数学试卷(解+析版)一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.抛物线y=4x2的焦点坐标是()A.(0,1)B.(1,0)C.D.2.双曲线:x2﹣=1的渐近线方程和离心率分别是()A.B.C.D.3.如果A(1,3)关于直线l的对称点为B(﹣5,1),则直线l的方程是()A.x﹣3y+8=0 B.3x+y+4=0 C.x+3y﹣4=0 D.3x﹣y+8=04.将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是()A.x甲<x乙,乙比甲成绩稳定B.x甲>x乙;甲比乙成绩稳定C.x甲>x乙;乙比甲成绩稳定D.x甲<x乙;甲比乙成绩稳定5.在5件产品中,有3件一等品和2件二等品,从中任取2件,那么以为概率的事件是()A.都不是一等品B.恰有一件一等品C.至少有一件一等品D.至多一件一等品6.给出计算的值的一个程序框图如图,其中判断框内应填入的条件是()A.i>10 B.i<10 C.i>20 D.i<207.曲线=1与曲线=1(k<9)的()A.长轴长相等B.短轴长相等C.离心率相等D.焦距相等8.已知a>0,b>0,a+b=1,则y=的最小值是()A.B.4 C.9 D.59.已知点P是抛物线y2=2x上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为()A.B.3 C.D.10.已知圆的方程为x2+y2﹣6x﹣8y=0,设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为()A.10B.20C.30D.4011.若椭圆+=1的弦被点(4,2)平分,则此弦所在直线的斜率为()A.B.C.2 D.﹣212.若直线y=x+b与曲线有公共点,则b的取值范围是()A.[,]B.[,3]C.[﹣1,]D.[,3]二、填空题:本题共4小题,每小题5分.13.如图所示程序,若输入8时,则下列程序执行后输出的结果是.14.如图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分的面积为.15.已知x、y的取值如表所示:从散点图分析,y与x线性相关,且=0.95x+a,则a=.16.双曲线的离心率为,且与椭圆=1有公共焦点,则该双曲线的方程为.三、解答题:共6小题,共70分.解答应写出必要证明过程或演算步骤. 17.(10分)已知圆C的方程是(x﹣1)2+(y﹣1)2=4,直线l的方程为y=x+m,求:当m为何值时(1)直线平分圆;(2)直线与圆相切;(3)直线与圆有两个公共点.18.(12分)一个容量为M的样本数据,其频率分布表如表.(Ⅰ)完成频率分布表; (Ⅱ)画出频率分布直方图;(Ⅲ)利用频率分布直方图,估计总体的众数、中位数及平均数. 19.(12分)已知抛物线C :y 2=4x 与直线y=2x ﹣4交于A ,B 两点. (1)求弦AB 的长度;(2)若点P 在抛物线C 上,且△ABP 的面积为12,求点P 的坐标.20.(12分)设实数x 、y满足(1)求的取值范围;(2)求z=x 2+y 2的取值范围.21.(12分)已知关于x 的一元二次方程x 2﹣2(a ﹣2)x ﹣b 2+16=0. (1)若a ,b 是一枚骰子掷两次所得到的点数,求方程有实根的概率; (2)若a ∈[2,6],b ∈[0,4],求方程没有实根的概率. 22.(12分)已知椭圆C :的离心率,焦距为2(1)求椭圆C 的方程;(2)已知椭圆C 与直线x ﹣y +m=0相交于不同的两点M 、N ,且线段MN 的中点不在圆x 2+y 2=1内,求实数m 的取值范围.2016-2017学年吉林省长春外国语学校高二(上)期末数学试卷参考答案与试题解+析一、选择题:本题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.抛物线y=4x 2的焦点坐标是( )A .(0,1)B .(1,0)C .D .【考点】抛物线的简单性质.【分析】把抛物线y=4x 2的方程化为标准形式,确定开口方向和p 值,即可得到焦点坐标.【解答】解:抛物线y=4x 2的标准方程为 x 2=y ,p=,开口向上,焦点在y 轴的正半轴上,故焦点坐标为(0,),故选C .【点评】本题考查抛物线的标准方程,以及简单性质的应用;把抛物线y=4x 2的方程化为标准形式,是解题的关键.2.双曲线:x 2﹣=1的渐近线方程和离心率分别是( )A .B .C .D .【考点】双曲线的简单性质.【分析】先根据双曲线的标准方程,求得其特征参数a 、b 、c 的值,再利用双曲线渐近线方程公式和离心率定义分别计算即可【解答】解:双曲线:的a=1,b=2,c==∴双曲线的渐近线方程为y=±x=±2x ;离心率e==故选 D【点评】本题考查了双曲线的标准方程,双曲线特征参数a、b、c的几何意义,双曲线几何性质:渐近线方程、离心率的求法,属基础题3.如果A(1,3)关于直线l的对称点为B(﹣5,1),则直线l的方程是()A.x﹣3y+8=0 B.3x+y+4=0 C.x+3y﹣4=0 D.3x﹣y+8=0【考点】与直线关于点、直线对称的直线方程.【分析】由题意可得直线l为线段AB的中垂线,求得AB的中点为(﹣2,2),求出AB的斜率可得直线l的斜率,由点斜式求得直线l的方程,化简可得结果.【解答】解:∵已知点A(1,3)关于直线l的对称点为B(﹣5,1),故直线l为线段AB的中垂线.求得AB的中点为(﹣2,2),AB的斜率为=,故直线l的斜率为﹣3,故直线l的方程为y﹣2=﹣3(x+2),化简可得3x+y+4=0.故选:B.【点评】本题主要考查两条直线垂直的性质,斜率公式的应用,用点斜式求直线的方程,属于中档题.4.将甲,乙两名同学5次数学测验的成绩用茎叶图表示如图,若甲,乙两人成绩的中位数分别是x甲,x乙,则下列说法正确的是()A.x甲<x乙,乙比甲成绩稳定B.x甲>x乙;甲比乙成绩稳定C.x甲>x乙;乙比甲成绩稳定D.x甲<x乙;甲比乙成绩稳定【考点】茎叶图.【分析】利用茎叶图中的数据和中位数的定义即可得出结论.【解答】解:根据茎叶图中的数据,得甲、乙二人的中位数分别是x甲=79,x乙=82,且在茎叶图中,乙的数据更集中,∴x甲<x乙,乙比甲成绩稳定.故选:A.【点评】本题考查了中位数的求法与方差的判断问题,是基础题.解题时要注意茎叶图的性质的灵活运用.5.在5件产品中,有3件一等品和2件二等品,从中任取2件,那么以为概率的事件是()A.都不是一等品B.恰有一件一等品C.至少有一件一等品D.至多一件一等品【考点】古典概型及其概率计算公式.【分析】从5件产品中任取2件,有C52种结果,通过所给的条件可以做出都不是一等品有1种结果,恰有一件一等品有C31C21种结果,至少有一件一等品有C31C21+C32种结果,至多有一件一等品有C31C21+1种结果,做比值得到概率.【解答】解:5件产品中,有3件一等品和2件二等品,从中任取2件,从5件产品中任取2件,有C52=10种结果,∵都不是一等品有1种结果,概率是,恰有一件一等品有C31C21种结果,概率是,至少有一件一等品有C31C21+C32种结果,概率是,至多有一件一等品有C31C21+1种结果,概率是,∴是至多有一件一等品的概率,故选D.【点评】本题考查古典概型,是一个由概率来对应事件的问题,需要把选项中的所有事件都作出概率,解题过程比较麻烦.6.给出计算的值的一个程序框图如图,其中判断框内应填入的条件是()A.i>10 B.i<10 C.i>20 D.i<20【考点】循环结构.【分析】结合框图得到i表示的实际意义,要求出所需要的和,只要循环10次即可,得到输出结果时“i”的值,得到判断框中的条件.【解答】解:根据框图,i﹣1表示加的项数当加到时,总共经过了10次运算,则不能超过10次,i﹣1=10执行“是”所以判断框中的条件是“i>10”故选A【点评】本题考查求程序框图中循环结构中的判断框中的条件:关键是判断出有关字母的实际意义,要达到目的,需要对字母有什么限制.7.曲线=1与曲线=1(k<9)的()A.长轴长相等B.短轴长相等C.离心率相等D.焦距相等【考点】椭圆的简单性质.【分析】分别求出两椭圆的长轴长、短轴长、离心率、焦距,即可判断.【解答】解:曲线=1表示焦点在x轴上,长轴长为10,短轴长为6,离心率为,焦距为8.曲线=1(k<9)表示焦点在x轴上,长轴长为2,短轴长为2,离心率为,焦距为8.对照选项,则D正确.故选D.【点评】本题考查椭圆的方程和性质,考查运算能力,属于基础题.8.已知a>0,b>0,a+b=1,则y=的最小值是()A.B.4 C.9 D.5【考点】基本不等式.【分析】利用题设中的等式,把y的表达式转化成(a+b)()展开后,利用基本不等式求得y的最小值.【解答】解:∵a+b=1,∴y=(a+b)()=5+≥5+2=9,当且仅当,即b=2a时等号成立.故选:C.【点评】本题主要考查了基本不等式求最值.注意把握好一定,二正,三相等的原则.9.已知点P是抛物线y2=2x上的一个动点,则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为()A.B.3 C.D.【考点】抛物线的简单性质.【分析】先求出抛物线的焦点坐标,再由抛物线的定义可得d=|PF|+|PA|≥|AF|,再求出|AF|的值即可.【解答】解:依题设P在抛物线准线的投影为P',抛物线的焦点为F,则,依抛物线的定义知P到该抛物线准线的距离为|PP'|=|PF|,则点P到点A(0,2)的距离与P到该抛物线准线的距离之和.故选A.【点评】本小题主要考查抛物线的定义解题.10.已知圆的方程为x2+y2﹣6x﹣8y=0,设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为()A.10B.20C.30D.40【考点】直线与圆相交的性质.【分析】根据题意可知,过(3,5)的最长弦为直径,最短弦为过(3,5)且垂直于该直径的弦,分别求出两个量,然后利用对角线垂直的四边形的面积等于对角线乘积的一半求出即可.【解答】解:圆的标准方程为(x﹣3)2+(y﹣4)2=52,由题意得最长的弦|AC|=2×5=10,根据勾股定理得最短的弦|BD|=2=4,且AC⊥BD,四边形ABCD的面积S=|AC|•|BD|=×10×4=20.故选B【点评】考查学生灵活运用垂径定理解决数学问题的能力,掌握对角线垂直的四边形的面积计算方法为对角线乘积的一半.11.若椭圆+=1的弦被点(4,2)平分,则此弦所在直线的斜率为()A.B.C.2 D.﹣2【考点】直线与圆锥曲线的关系;直线的斜率.【分析】利用平方差法:设弦的端点为A(x1,y1),B(x2,y2),将A、B坐标代入椭圆方程,两式作差变形,根据斜率公式、中点坐标公式即可求得答案.【解答】解:设弦的端点为A(x1,y1),B(x2,y2),则x1+x2=8,y1+y2=4,将A、B坐标代入椭圆方程,得①,②,①﹣②得,,即=﹣,所以此弦所在直线的斜率为﹣.故选A.【点评】本题考查直线与圆锥曲线的位置关系及直线的斜率,属中档题,涉及弦中点问题往往考虑平方差法解决,即设弦端点坐标,代入圆锥曲线方程,作差变形,借助斜率公式、中点坐标公式可得弦的斜率与中点坐标间的关系.12.若直线y=x+b与曲线有公共点,则b的取值范围是()A.[,]B.[,3]C.[﹣1,]D.[,3]【考点】函数与方程的综合运用.【分析】本题要借助图形来求参数b的取值范围,曲线方程可化简为(x﹣2)2+(y﹣3)2=4(1≤y≤3),即表示圆心为(2,3)半径为2的半圆,画出图形即可得出参数b的范围.【解答】解:曲线方程可化简为(x﹣2)2+(y﹣3)2=4(1≤y≤3),即表示圆心为(2,3)半径为2的半圆,如图依据数形结合,当直线y=x+b与此半圆相切时须满足圆心(2,3)到直线y=x+b距离等于2,即解得或,因为是下半圆故可知(舍),故当直线过(0,3)时,解得b=3,故,故选D.【点评】考查方程转化为标准形式的能力,及借助图形解决问题的能力.本题是线与圆的位置关系中求参数的一类常见题型.二、填空题:本题共4小题,每小题5分.13.如图所示程序,若输入8时,则下列程序执行后输出的结果是0.7.【考点】选择结构.【分析】t=8,不满足条件t≤4,则执行Else后的循环体,从而求出最后的y值即可.【解答】解:t=8,不满足条件t≤4执行Else后循环体,c=0.2+0.1(8﹣3)=0.7故输出0.7.故答案为:0.7【点评】本题主要考查了选择结构,属于基础题.14.如图的矩形,长为5,宽为2,在矩形内随机地撒300颗黄豆,数得落在阴影部分的黄豆数为138颗,则我们可以估计出阴影部分的面积为.【考点】几何概型.【分析】先由黄豆试验估计,黄豆落在阴影部分的概率,再转化为几何概型的面积类型求解.【解答】解:根据题意:黄豆落在阴影部分的概率是矩形的面积为10,设阴影部分的面积为s则有∴s=故答案为:【点评】本题主要考查实验法求概率以及几何概型中面积类型,将两者建立关系,引入方程思想.15.已知x、y的取值如表所示:从散点图分析,y与x线性相关,且=0.95x+a,则a= 2.6.【考点】线性回归方程.【分析】根据表中的数据可以分别求出变量x,y的算术平均值,而根据回归方程知道直线的斜率为0.95,然后带入求截距的公式即可求出a.【解答】解:根据表中数据得:;又由回归方程知回归方程的斜率为0.95;∴.故答案为:2.6.【点评】考查线性相关的概念,回归方程中直线的斜率和截距的计算公式,以及变量的算术平均值的计算.16.双曲线的离心率为,且与椭圆=1有公共焦点,则该双曲线的方程为.【考点】双曲线的标准方程.【分析】设双曲线的标准方程为,(a>0,b>0),由已知得,由此能求出双曲线的方程.【解答】解:∵双曲线的离心率为,且与椭圆=1有公共焦点,∴双曲线的焦点坐标为,,设双曲线的标准方程为,(a>0,b>0),∴,解得a=2,c=,b=1,∴该双曲线的方程为.故答案为:.【点评】本题考查双曲线方程的求法,是中档题,解题时发认真审题,注意双曲线性质的合理运用.三、解答题:共6小题,共70分.解答应写出必要证明过程或演算步骤. 17.(10分)(2013秋•安康期末)已知圆C的方程是(x﹣1)2+(y﹣1)2=4,直线l的方程为y=x+m,求:当m为何值时(1)直线平分圆;(2)直线与圆相切;(3)直线与圆有两个公共点.【考点】直线与圆的位置关系.【分析】(1)根据题意,由圆的方程找出圆心坐标和圆的半径r,直线平分圆即直线过圆心,所以把圆心坐标代入直线方程中即可求出m的值;(2)直线与圆相切时,圆心到直线的距离等于半径,所以利用点到直线的距离公式表示出圆心到已知直线的距离d,让d等于圆的半径列出关于m的方程,求出方程的解即可得到符合题意m的值;(3)直线与圆有两公共点即直线与圆相交,即圆心到直线的距离公式小于圆的半径,所以利用点到直线的距离公式表示出圆心到直线的距离d,让d小于圆的半径列出关于m的不等式,求出不等式的解集即可得到满足题意的m的范围.【解答】解:由圆的方程(x﹣1)2+(y﹣1)2=4,得到圆心坐标为(1,1),圆的半径r=2,(1)当直线平分圆时,即直线过圆的直径,把(1,1)代入y=x+m中,解得m=0;(2)当直线与圆相切时,圆心(1,1)到直线y=x+m的距离d==r=2,解得m=±2;(3)当直线与圆有两个公共点即直线与圆相交时,圆心(1,1)到直线的距离d=<r=2,解得:﹣2<m<2.所以,当m=0时,直线平分圆;当m=±2时,直线与圆相切;当﹣2<m<2时,直线与圆有两个公共点.【点评】此题考查学生掌握直线与圆相切及相交时所满足的条件,是一道综合题.18.(12分)(2016秋•南关区校级期末)一个容量为M的样本数据,其频率分布表如表.(Ⅰ)完成频率分布表; (Ⅱ)画出频率分布直方图;(Ⅲ)利用频率分布直方图,估计总体的众数、中位数及平均数. 【考点】频率分布表;频率分布直方图;众数、中位数、平均数.【分析】(1)根据小组(10,20]的频数与频率,求出样本容量,再求出各小组对应的数据,补充完整频率分布表;(2)根据频率分布表,画出频率分布直方图;(3)根据频率分布直方图,求出众数、平均数与中位数.【解答】解:(1)在小组(10,20]中,频数是2,频率是0.10,∴样本数据为=20;∴小组(20,30]的频率为=0.15;小组(40,50]的频数为20﹣2﹣3﹣4﹣4﹣2=5,频率为=0.25;频数合计为20;由此补充频率分布表如下:(2)根据频率分布表,画出频率分布直方图如下:(3)根据频率分布直方图,得;图中最高的小矩形的底边中点坐标是=45,∴众数为45;平均数为=15×0.1+25×0.15+35×0.20+45×0.25+55×0.20+65×0.10=41;∵0.10+0.15+0.20=0.45<0.5,0.45+0.25=0.70>0.5,令0.45+0.25×x=0.5,解得x=2,∴中位数为40+2=42.【点评】本题考查了频率分布直方图的应用问题,解题时应利用分布直方图进行有关的运算,是基础题目.19.(12分)(2016秋•南关区校级期末)已知抛物线C:y2=4x与直线y=2x﹣4交于A,B两点.(1)求弦AB的长度;(2)若点P在抛物线C上,且△ABP的面积为12,求点P的坐标.【考点】直线与圆锥曲线的关系;三角形的面积公式;两点间的距离公式.【分析】(1)利用弦长公式即可求得弦AB的长度;(2)设点,利用点到直线的距离公式可表示出点P到AB的距离d,S△PAB=••d=12,解出即可;【解答】解:(1)设A(x1,y1)、B(x2,y2),由得x2﹣5x+4=0,△>0.由韦达定理有x1+x2=5,x1x2=4,∴|AB|==,所以弦AB的长度为3.(2)设点,设点P到AB的距离为d,则,=••=12,即.∴S△PAB∴,解得y o=6或y o=﹣4∴P点为(9,6)或(4,﹣4).【点评】本题考查直线与圆锥曲线的位置关系、点到直线的距离公式及三角形的面积公式,考查学生的计算能力,属中档题.20.(12分)(2016秋•南关区校级期末)设实数x、y满足(1)求的取值范围;(2)求z=x2+y2的取值范围.【考点】简单线性规划.【分析】(1)先根据约束条件画出可行域,根据的几何意义求最值,(2)根据z=x2+y2的几何意义是可行域上的点到原点距离的平方,即可求出最值.【解答】解:(1)满足y满足约束条件的平面区域如图所示,A(1,2),B(4,2),C(3,1),(1)的几何意义可行域上的点是到原点的斜率;当直线为OA时,u有最大值为2;当直线为OC时,u有最小值为;所以,(2)z=x2+y2的几何意义是可行域上的点到原点距离的平方;z=x2+y2的最大值为|OB|2=20,最小值为O到直线AC的距离的平方,为5;所以,z∈[5,20]【点评】本题主要考查了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题.目标函数有唯一最优解是我们最常见的问题,这类问题一般要分三步:画出可行域、求出关键点、定出最优解.21.(12分)(2016秋•南关区校级期末)已知关于x的一元二次方程x2﹣2(a ﹣2)x﹣b2+16=0.(1)若a,b是一枚骰子掷两次所得到的点数,求方程有实根的概率;(2)若a∈[2,6],b∈[0,4],求方程没有实根的概率.【考点】几何概型.【分析】(1)本题是一个古典概型,用(a,b)表示一枚骰子投掷两次所得到的点数的事件,基本事件(a,b)的总数有36个满足条件的事件是二次方程x2﹣2(a﹣2)x﹣b2+16=0有实根,根据实根与系数的关系式,得到概率.(2)本题是一个几何概型,试验的全部结果构成区域Ω={(a,b)|2≤a≤6,0≤b≤4},满足条件的事件为:B={(a,b)|2≤a≤6,0≤b≤4,(a﹣2)2+b2<16},做出两者的面积,得到概率【解答】解:(1)由题意知本题是一个古典概型用(a,b)表示一枚骰子投掷两次所得到的点数的事件依题意知,基本事件(a,b)的总数有36个二次方程x2﹣2(a﹣2)x﹣b2+16=0有实根,等价于△=4(a﹣2)2+4(b2﹣16)≥0,即(a﹣2)2+b2≥16,“方程有两个根”的事件为A,则事件A包含的基本事件为(1,6),(1,5).(1,4),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,4),(4,5),(4,6),(5,3),(5,4),(5,5),(5,6),(6,1)、(6,2)、(6,3)、(6,4),(6,5),(6,6),共22个∴所求的概率为P(A)=;(2)由题意知本题是一个几何概型,;试验的全部结果构成区域Ω={(a,b)|2≤a≤6,0≤b≤4},其面积为S(Ω)=16满足条件的事件为:B={(a,b)|2≤a≤6,0≤b≤4,(a﹣2)2+b2<16}其面积为S(B)=×π×42=4π∴所求的概率P(B)=;【点评】本题考查古典概型和几何概型,几何概型和古典概型是高中必修中学习的,高考时常以选择和填空出现,有时文科会考这种类型的解答题目22.(12分)(2016秋•南关区校级期末)已知椭圆C:的离心率,焦距为221 (1)求椭圆C 的方程;(2)已知椭圆C 与直线x ﹣y +m=0相交于不同的两点M 、N ,且线段MN 的中点不在圆x 2+y 2=1内,求实数m 的取值范围.【考点】直线与圆锥曲线的综合问题;椭圆的标准方程.【分析】(1)利用离心率与焦距,求出a 2=2,b 2=1,即可得到椭圆的方程. (2)联立方程,消去y ,利用判别式求出m 的范围,设M (x 1,y 1),N (x 2,y 2),利用韦达定理求出MN 中点坐标,通过MN 的中点不在圆x 2+y 2内,得到不等式,求解即可.【解答】解:(1)由题意知,2c=2,又a 2﹣b 2=c 2,解得,c=1,∴a 2=2,b 2=1故椭圆的方程为…(2分) (2)联立方程,消去y 可得3x 2+4mx +2m 2﹣2=0则… 设M (x 1,y 1),N (x 2,y 2),则,∴MN 中点坐标为…(8分) 因为MN 的中点不在圆x 2+y 2内,所以或…(10分) 综上,可知或…(12分) 注:用点差法酌情给分【点评】本题考查椭圆的方程的求法,在下雨椭圆的位置关系的综合应用,圆的方程的综合应用,考查计算能力.。
