2018年漳州市初中毕业班质量检测卷
2018漳州市初中毕业班质量检测数学试题及答案讲课讲稿

2018漳州市初中毕业班质量检测数学试题一、选择题(本大题共10小题,每小题4分,共40分) 1.如图,数轴上点M 所表示的数的绝对值是( ). A .3 B .3- C .±3 D .31-2.“中国天眼”FAST 射电望远镜的反射面总面积约250 000m 2,数据250 000用科学记数法表示为( ). A .25×104 B .2.5×105 C .2.5×106 D .0.25×106 3.如图是某几何体的左视图,则该几何体不可能...是( ). 4.下列计算,结果等于x 5的是( ).A .32x x + B .32x x ⋅ C .210x x÷ D .(x 2)35.如图,在右框解分式方程的4个步骤中,根据等式基本性 质的是( ).A .①②B .②④C .①③D .③④6.如图,OP 平分∠AOB ,PC ⊥OA 于C ,点D 是OB 上的动点,若PC=6cm 则PD 的长可以是( ).A .3cmB .4cmC .5cmD .7 cm7.如图,点A ,B 在方格纸的格点上,将线段AB 先向右平移3格,再向下 平移2个单位,得线段DC ,点A 的对应点为D ,连接AD 、BC ,则关于 四边形ABCD 的对称性,下列说法正确的是( ). A .既是轴对称图形,又是中心对称图形 B .是中心对称图形,但不是轴对称图形 C .是轴对称图形,但不是中心对称图形D .既不是轴对称图形,也不是中心对称图形8.甲、乙两地今年2月份前5天的日平均气温如图所示,则下列描述错误..的是( ). A .两地气温的平均数相同B .甲地气温的众数是4℃C .乙地气温的中位数是6℃D .甲地气温相对比较稳定9.如图,正六边形 ABCDEF 的中心与坐标原点0重合,其中A(-2,0). 将六边形 ABCDEF 绕原点O 按顺时针方向旋转2018次,每次旋转 60°,则旋转后点A 的对应点A'的坐标是( ). A . (1,3)B . (3,1)C .(1,3-)D .(-1,3)10.如图,在矩形ABCD 中,点A 在x 轴上,点B 的坐标为(1,0),且C 、D 两点在函数y=⎪⎩⎪⎨⎧<+-≥+)0(121)0(1x x x x 的图象上,若在矩形ABCD左视图内随机取一点,则此点取自阴影部分的概率是( ). A .21 B .83 C .41 D .61二,填空题(本大题共6小题,每小题4分,共24分) 11.因式分解:a ax -2=________.12.一个不透明的袋子中装有4个红球、2个黑球,它们除颜色外其余都相同,从中任意搞出3个球,则事件“摸出的球至少有1个红球”是________事件(填“必然”、 “随机”或“不可能”) 13.如图,DE 是△ABC 的中位线,若△ADE 的面积为3,则△ABC 的面积为________.14.“若实数a ,b ,c 满足a <b <c ,则a +b <c ”,能够说明该命题是假命题的 一组a ,b ,c 的值依次为________. 15.如图,在□ABCD 中,点E ,F 分别在边AD 、BC 上,BF=2,∠DEF=60°将四边形EFCD 沿EF 翻折,得到四边形EFC ’D’,ED ’交BC 于点G ,则△GEF 的周长为________. 16.如图,双曲线y=xk(x >0)经过A 、B 两点,若点A 的横坐标为1, ∠OAB=90°,且OA=AB ,则k 的值为________. 三、解答题(本大题共9小题,共86分) 17.(8分) 计算:91301-+-π 18.(8分)如图,在△ABC 中,∠A=80°,∠B=40°.(1)求作线段BC 的垂直平分线DE ,垂足为E ,交AB 于点D ; (要求;尺规作图,保留作图痕迹,不写作法) (2)在(1)的条件下,连接CD ,求证:AC=CD .19.(8分)求证:对角线相等的平行四边形是矩形. (要求:画出图形,写出已知和求证,并给予证明)20.(8分)为响应市收府关于”垃圾不落地·市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A :非常了解,B :比较了解C :了解较少,D :不了解”四种,并将调查结果绘制成以下两幅不完整的统计图. 请根据图中提供的信息,解答下列问题: (1)把两幅统计图补充完整;(2)若该校学生数1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学 生共有________名;(3)已知“非常了解”的4名男生和1名女生,从 中随机抽取2名向全校做垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到1男1女的概率.CA B CDD ’ EF GB C垃圾分类知识掌据情况条形统计图垃圾分类知识掌据情况21.(8分)如图,AB 是⊙0的直径,AC 是弦,D 是BC 的中点,过点D 作EF 垂直于直线AC ,垂足为F ,交AB 的延长线于点E . (1)求证:EF 是⊙0的切线; (2)若tan A=34,AF=6,求⊙0的半径.22.(10分)某景区售票处规定:非节假日的票价打a 折售票; 节假日根据团队人数x (人)实行分段售票:若≤x 10,则按 原展价购买;若x >10,则其中10人按原票价购买,超过部 分的按原那价打b 折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y 1元,在节假日的购票款为y 2元,y 1、y 2与x 之间的函数图象如图所示.(1)观察图象可知:a ________,b ________;(2)当x >10时,求y 2与x 之间的函数表达式;(3)该旅行社在今年5月1目带甲团与5月10日(非节假日)带乙国到该景区游览,两团合计50人,共付门票款3120元,已知甲团人数超过10人,求甲团人数与乙团人数.23.(10分)阅读:所谓勾股数就是满足方程x 2+y 2=z 2的正整数解,即满足勾股定理的三个正整数构成的 一组数.我国古代数学专著《九章算术》一书,在世界上第一次给出该方程的解为:)(2122n m x -=,y =mn ,)(2122n m z +=,其中m >n >0,m 、n 是互质的奇数. 应用:当n =5时,求一边长为12的直角三角形另两边的长.24.(12分)已知抛物线c bx ax y ++=2(a 、b 、c 是常数,0≠a )的对称轴为直线2-=x . (1) b =______;(用含a 的代数式表示)(2)当1-=a 时,若关于x 的方程02=++c bx ax 在13<<-x 的范围内有解,求c 的取值范围; (3)若抛物线过点(2-,2-),当01≤≤-x 时,抛物线上的点到x 轴距离的最大值为4,求a 的值.25.(14分)如图,在正方形ABCD 中,对角线AC 、BD 相交于点O ,E 为OC 上动点(与点0不重合), 作AF ⊥BE ,垂足为G ,交BC 于F ,交B0于H ,连接0G ,CC . (1)求证:AH=BE ; (2)试探究:∠AGO 的度数是否为定值?请说明理由; (3)若OG ⊥CG ,BG=5,求△OGC 的面积.CD2018年漳州市初中毕业班质量检测数学参考答案及评分建议二、填空题(本大题共6小题,每小题4分,共24分)11. a(x+1)(x-1);12. 必然;13. 12;14.答案不唯一,如1,2,3;15. 6;16.2.三、解答题(本大题共9小题,共86分)17.(本小题满分8分)解:原式=11+133……………………………………………………………………6分=1. ……………………………………………………………………8分18.(本小题满分8分)解:(1)如图,直线DE为所求作的垂直平分线,点D,E就是所求作的点;…………4分(没标字母或字母标错扣1分)(2)连接CD.方法一:∵DE垂直平分AB,∴BD=CD,∴∠1=∠B=40°. ……………………………5分∴∠2=∠B+∠1=80°.……………………6分∵∠A=80°,∴∠2=∠A. …………………………………………………………7分∴AC=CD.……………………………………………………………8分方法二:∵DE垂直平分AB,∴BD=CD,∴∠1=∠B=40°. ………………………………………………………5分∵∠A=80°,∴∠ACB=180°-∠A-∠B=60°.∴∠ACD=60°-40°=20°. ……………………………………………6分∴∠2=180°-∠A-∠ACD=80°=∠A. …………………………………7分∴AC=CD.……………………………………………………………8分已知:如图,在□ABCD 中, AC =BD . (画图2分,已知1分) ………………3分 求证:□ABCD 是矩形. …………………………………………………………4分 证明:方法一:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD . …………………5分∵AC =BD ,BC =BC ,∴△ABC ≌△DCB .∴∠ABC =∠DCB . ………………………………………………6分 ∵AB ∥CD ,∴∠ABC +∠DCB =180°.∴∠ABC =11802⨯°=90°. …………………………………………7分 ∴□ABCD 是矩形. ……………………………………………………8分方法二:设AC ,BD 交于点O .∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD . ………………5分∵AC =BD ,∴OA =OC =OB .∴∠1=∠3,∠2=∠4. ……………………………………………6分∴∠ABC =∠1+∠2=11802⨯°=90°. …………………………………7分 ∴□ABCD 是矩形. ………………………………………………8分 20.(本小题满分8分)解:(1)如图所示(补充2个或3个正确,得1分); …………………………………2分 (2)500; ………4分(3)树状图法:………………………………………6分共有12种等可能结果,其中满足条件有6种,∴P (一男一女)=12. ………………8分 (用列表法参照给分)解:(1)方法一:如图1,连接OD . ∵EF ⊥AF ,∴∠F =90°.∵D 是BC 的中点,∴BD DC =.∴∠1=∠2=12∠BOC . ………………………………………………1分 ∵∠A =12∠BOC , ∴∠A =∠1 . ………………………………………2分 ∴OD ∥AF .∴∠EDO =∠F =90°.∴OD ⊥EF . ……………………………………………………………3分 ∴EF 是⊙O 的切线. ……………………………………………………4分方法二:如图2,连接OD ,BC .∵D 是BC 的中点,∴BD DC =.∴∠1=∠2. …………………………………………………………1分∵OB =OC ,∴OD ⊥BC . ……………………………2分∵AB 是⊙O 的直径,∴∠ACB =90°. ∵AF ⊥EF ,∴∠F =∠ACB =90°.∴BC ∥EF .∴OD ⊥EF . ……………………………………………………………3分∴EF 是⊙O 的切线. …………………………………………………4分(2)设⊙O 半径为r ,则OA =OD =OB =r .方法一:在Rt △AFE 中,tan A =43,AF =6, ∴EF =AF ·tan A =8.∴10AE ==. ………………5分∴OE =10-r .∵cos A = 35AF AE=, ………………………………………………………6分∴cos ∠1= cos A =3105OD r OE r ==-. ……………………………………7分 ∴r =154, 即⊙O 的半径为154. ……………………………………8分方法二:在Rt △AFE 中,tan A =43,AF =6, ∴EF =AF ·tan A =8.∴10AE ==. ………………5分∴EO =10-r .∵∠A =∠1,∠E =∠E ,∴△EOD ∽△EAF . ……………………………………………………6分 ∴OD EO AFEA= . …………………………………………………………7分∴10610r r -=.∴r =154, 即⊙O 的半径为154. ……………………………………8分22. (本小题满分10分)解:(1)6,8; ………………………………………………………………………………2分(2)当x ﹥10时,设y 2=kx +b .∵图象过点(10,800),(20,1440), …………………3分 ∴⎩⎨⎧=+=+.144020,80010b k b k ……………………………………4分解得⎩⎨⎧==.160,64b k …………………………………………5分∴y 2=64x +160 (x ﹥10) . ………………………………………………………6分 (3)设甲团有m 人,乙团有n 人.由图象,得y 1=48x . ……………………………………………………………7分 当m ﹥10时,依题意,得⎩⎨⎧=+=++.50,31204816064n m n m ………………………………………8分解得⎩⎨⎧==.15,35n m ……………………………………………………………………9分答:甲团有35人,乙团有15人. ………………………………………………10分23. (本小题满分10分)解:∵n =5,直角三角形一边长为12,∴有三种情况: ① 当x =12 时,12)52122=-m (. ………………………………………………………………1分 解得m 1=7,m 2= -7(舍去). …………………………………………………2分∴y = mn =35. ……………………………………………………………………3分 ∴222211()(75)3722z m n =+=⨯+=. ……………………………………4分 ∴该情况符合题意. ② 当y =12时,5m =12, …………………………………………………………………………5分125m =. …………………………………………………………………………6分 ∵m 为奇数, ∴125m =舍去. …………………………………………………………………7分 ③ 当z =12时,221(5)122m +=,…………………………………………………………………8分 21m =-, …………………………………………………………………9分此方程无实数解. ………………………………………………………………10分 综上所述:当n =5时, 一边长为12的直角三角形另两边的长分别为35,37. 24. (本小题满分12分)解:(1)4a ; ………………………………………………………………………………2分(2)当a = -1时,∵关于x 的方程240x x c --+=在-3< x <1的范围内有解,即关于x 的方程x 2+4x-c =0在-3< x <1的范围内有解,∴b 2 -4ac =16+4c ≥0,即c ≥ -4. …………………………………………………3分 方法一:∴抛物线y= x 2 +4x =(x +2)2 -4与直线y = c 在-3 <x <1的范围内有交点. ……………………………………………………………………4分 当x = -2时,y = -4,当x =1时,y = 5. ………………………………5分 由图像可知: -4≤ c < 5. …………………………………………7分方法二:∴抛物线y= x 2 +4x -c =(x +2)2 -4-c 与x 轴在-3 <x <1的范围内有交点. ……………………………………………………………………4分 当x = -2,y =0时,c = -4,当x = 1,y =0时,c = 5. …………………5分 由图像可知:-4≤ c <5. ………………………………………………7分 方法三:∵224(2) 4.c x x x =+=+-∴c 是x 的二次函数. ……………………………………………………4分当x = -2时,c = -4,当x = 1时,c = 5. ……………………………5分由图像可知: -4≤ c < 5. ………………………………………………7分 (3)∵抛物线y =ax 2+4ax +c 过点(-2,-2),∴c = 4a -2.∴抛物线解析式为:22442(2)2y ax ax a a x =++-=+-. …………………8分 方法一: ① 当a > 0时,抛物线开口向上.∵抛物线对称轴为x =-2.∴当-1≤x ≤0时,y 随x 增大而增大.∵抛物线上的点到x 轴距离的最大值为4,由图像可知:4a -2=4. ………………………………………………9分∴32a =. …………………………………………………………10分 ② 当a < 0时,抛物线开口向下.∵抛物线对称轴为x =-2.∴当-1≤x ≤0时,y 随x 增大而减小. ∵抛物线上的点到x 轴距离的最大值为4,由图像可知:4a -2= -4. ……………………………………………11分∴12a =-. …………………………………………………………12分 方法二: ∵-1≤x ≤0,∴当x = 0时,y = 4a -2;当x = -1时,y = a -2. ……………8分 ∵当-1≤x ≤0时,抛物线上的点到x 轴距离的最大值为4. ∴有两种情况:① 若424a -=,则3122a a ==-或. ……………………9分 此时1242a -=<或5242a -=<,符合题意. ………10分 ② 若24a -=,则a = 6或a = -2. ………………………11分 此时42224a -=>或42104a -=>.∴a = 6或a = -2不合题意,舍去. ………………………12分综上所述: 3122a a ==-或. 25. (本小题满分14分)解:(1)方法一:∵四边形ABCD 是正方形,∴OA =OB ,∠AOB =∠BOE =90°.…………………………………………1分∵AF ⊥BE ,∴∠GAE+∠AEG =∠OBE +∠AEG =90°.∴∠ GAE =∠OBE . ………………………2分∴△AOH ≌ △BOE . ………………………3分∴AH =BE . …………………………………4分方法二:∵四边形ABCD 是正方形,∴∠ABC =90°,AB =CB ,∠ABO =∠ECB =45°. ……………………1分∵AF ⊥BE ,∴∠BAG+∠ABG =∠CBE +∠ABG =90°.∴∠BAH =∠CBE . ………………………………………………………2分∴△ABH ≌△BCE . ……………………………………………………3分∴AH=BE .………………………………………………………………4分(2)方法一:∵∠AOH=∠BGH=90°,∠AHO=∠BHG,∴△AOH∽△BGH.……………………5分∴OH AHGH BH=.…………………………6分∴OH GHAH BH=.…………………………7分∵∠OHG =∠AHB.∴△OHG∽△AHB. ………………………………………………………8分∴∠AGO=∠ABO=45°,即∠AGO的度数为定值. ……………………9分方法二:如图,取AB中点M,连接MO,MG. ………6分∵∠AGB=∠AOB=90°,∴AM=BM=GM=OM. ………………………7分∴点O,G在以AB为直径的⊙M上,即点A,B,G,O四点在以AB为直径的⊙M上, ………………………8分∴∠AGO =∠ABO =45°,即∠AGO 的度数为定值. ………………………………………………9分(3)∵∠ABC =90°,AF ⊥BE ,∴∠BAG =∠FBG ,∠AGB =∠BGF =90°,∴△ABG ∽△BFG . ……………………………………………………………10分 ∴GFBG BG AG =,∴AG ·GF =BG 2 =5. …………………………………11分∵△AHB ∽△OHG ,∴∠BAH =∠GOH =∠GBF .∵∠AOB =∠BGF =90°,∴∠AOG =∠GFC . ……………………………………………………………12分 ∵∠AGO =45°,CG ⊥GO ,∴∠AGO =∠FGC =45°.∴△AGO ∽△CGF . ………………………………………………………13分 ∴CGAG GF GO =, ∴GO ·CG =AG ·GF =5.∴S △OGC =12CG ·GO =52. ……………………………………………………14分。
2018年漳州市初中毕业班质量检测化学试题

2018年漳州市初中毕业班质量检测化学试题2018年漳州市初中毕业班质量检测化学试题班级姓名座号可能用到的相对原子质量:H—1 Li—7 C—12 N—14 O—16 Na—23 Mg—24S—32 Zn—65第Ⅰ卷(共30分)本卷共10小题,每小题四个选项,只有一个选项符合题意。
1.“绿水青山就是金山银山”。
为了让天更蓝、地更绿、水更清,下列建议不合理的是()A.禁止使用化肥农药,防止水体污染B.分类回收垃圾,促进资源再生和利用C.变废为宝,将地沟油转化为生物柴油D.大力开发和使用风能、太阳能,减少使用化石燃料2.下列实验操作正确的是()A.铁丝在氧气中燃烧B.稀释浓硫酸C.倾倒液体D.取下蒸发皿3.下列说法不正确的是()A.火碱、纯碱、氨水都属于碱B.对水的净化程度较度的方法是蒸馏C.温度低于着火点,可燃物就不会燃烧D.氯化铵可用作氮肥,但不可与消石灰混合使用4.下列实验现象的描述错误的是()A.氢气燃烧的火焰是淡蓝色的B.电解水时正负极产生的气体体积比约为2:1C.一氧化碳还原氧化铁时,粉末由红棕色逐渐变黑D.受热的高锰酸钾未熔化时,导管口就有气泡连续均匀地放出5.物质的结构决定性质,下列有关说法错误的是()A.H2O2与H2O化学性质不同的原因是构成它们的分子不同B.盐酸与硫酸化学性质相似的原因是在水溶液中都能解离出H+C.金刚石和石墨物理性质差异的原因是构成它们的碳原子不同D.Ne和Ar化学性质比较稳定的原因是它们的原子最外层都有8个电子6.在2KMnO4 K2MnO4 + MnO2 + O2↑这一反应涉及的氧化物中,锰元素的化合价为2()A.+2 B.+4 C.+6 D.+77.下列各项混合或反应过程中存在“2+”现象的是()11≠A.1g酒精和1g水混合后的总质量B.1g硫和1g氧气完全反应后产物的质量C.1g氢氧化钠溶液和1g醋酸溶液混合后溶液的质量D.温度一定时1g饱和氯化钾溶液中加入1g氯化钾后,所得溶液的质量8.高纯硅广泛用于太阳能光伏电池,工业制取高纯硅反应的微观示意图如下,有关说法不正确的是()A.参加反应的甲和乙分子个数比为1:1B.丁的化学式是HClC.化学变化中原子不可再分D.硅可以将光能转化为电能9选项实验目的实验设计A 鉴别碳酸钠溶液和碳酸氢钠溶液分别滴入紫色石蕊溶液,看颜色变化B 检验一瓶无色气体是否为氧气将带火星的木条放在瓶口C 除去铁制品表面的少量锈将铁制品长时间浸没稀盐酸中D 鉴别羊毛制品和涤纶制品分别点燃,闻气味差异10.下列图像分别对应的变化过程,正确的是()A.两份等温度、等体积、等浓度的双氧水制取氧气B.服用含有氢氧化铝的药物治疗胃酸过多,胃液pH的变化C.常温下,足量的镁和锌分别与等体积、等浓度的稀硫酸反应D.一定的石灰石中加入稀盐酸,固液混合物中碳元素的质量变化第Ⅱ卷(共45分)本卷共6小题。
2018年漳州初中毕业班质量检测语文参考答案(2)

2018年初中毕业班质量检测
语文参考答案
一、(20分)
1.(12分,每格1分)
(1)君子好逑
(2)采菊东篱下
(3)一览众山小
(4)蜡炬成灰泪始干
(5)浅草才能没马蹄
(6)浊酒一杯家万里
(7)不尽长江滚滚流
(8)波涛如怒山河表里潼关路
(9)学而不思则罔
(10)出淤泥而不染,濯清涟而不妖
2.(2分)A
3.(6分)
(1)(2分)① A ② A
(2)(2分)甲:A 乙:B
(3)(2分)在经久不息的掌声中,八分钟的演出完美成功。
(或“经久不息的掌声,表明八分钟的演出完美成功。
”)
二、(70分)
(一)(5分)
4.(3分)C
5.(2分)诚挚的友谊可以超越时空,缩短距离。
(二)(16分)
6.(4分)(1)出名,闻名(2)什么(3)于是(4)通“披”;披着,穿着
7.(3分)B
8.(1)(2分)没有嘈杂的音乐扰乱两耳,没有官府的公文使身体劳累。
(2)(2分)挨着的房屋都是这样,因为竹瓦价格便宜而且节省很多工序。
9.(5分)甲文叙写了环境的幽静和生活情趣的高雅,乙文着力写清韵雅趣的竹楼和幽雅飘逸的谪居生活,
都表现了作者甘居陋室、淡泊名利、安贫乐道的高尚情怀。
(三)(22分)
10.(3分)D
11.(6分)①夜归路上被轻呼“小飞鱼”
②生气、委屈
③激动、兴奋。
最新漳州市初中毕业班质量检测数学试题及答案

2018漳州市初中毕业班质量检测数学试题一、选择题(本大题共10小题,每小题4分,共40分) 1.如图,数轴上点M 所表示的数的绝对值是( ). A .3 B .3- C .±3 D .31-2.“中国天眼”FAST 射电望远镜的反射面总面积约250 000m 2,数据250 000用科学记数法表示为( ). A .25×104 B .2.5×105 C .2.5×106 D .0.25×106 3.如图是某几何体的左视图,则该几何体不可能...是( ). 4.下列计算,结果等于x 5的是( ).A .32x x + B .32x x ⋅ C .210x x÷ D .(x 2)35.如图,在右框解分式方程的4个步骤中,根据等式基本性 质的是( ).A .①②B .②④C .①③D .③④6.如图,OP 平分∠AOB ,PC ⊥OA 于C ,点D 是OB 上的动点,若PC=6cm 则PD 的长可以是( ).A .3cmB .4cmC .5cmD .7 cm7.如图,点A ,B 在方格纸的格点上,将线段AB 先向右平移3格,再向下 平移2个单位,得线段DC ,点A 的对应点为D ,连接AD 、BC ,则关于 四边形ABCD 的对称性,下列说法正确的是( ). A .既是轴对称图形,又是中心对称图形 B .是中心对称图形,但不是轴对称图形 C .是轴对称图形,但不是中心对称图形D .既不是轴对称图形,也不是中心对称图形8.甲、乙两地今年2月份前5天的日平均气温如图所示,则下列描述错误..的是( ). A .两地气温的平均数相同B .甲地气温的众数是4℃C .乙地气温的中位数是6℃D .甲地气温相对比较稳定9.如图,正六边形 ABCDEF 的中心与坐标原点0重合,其中A(-2,0). 将六边形 ABCDEF 绕原点O 按顺时针方向旋转2018次,每次旋转 60°,则旋转后点A 的对应点A'的坐标是( ). A . (1,3)B . (3,1)C .(1,3-)D .(-1,3)10.如图,在矩形ABCD 中,点A 在x 轴上,点B 的坐标为(1,0),且C 、D 两点在函数y=⎪⎩⎪⎨⎧<+-≥+)0(121)0(1x x x x 的图象上,若在矩形ABCD左视图CBAD xyE FO C BA DxyO内随机取一点,则此点取自阴影部分的概率是( ). A .21 B .83 C .41 D .61二,填空题(本大题共6小题,每小题4分,共24分) 11.因式分解:a ax -2=________.12.一个不透明的袋子中装有4个红球、2个黑球,它们除颜色外其余都相同,从中任意搞出3个球,则事件“摸出的球至少有1个红球”是________事件(填“必然”、 “随机”或“不可能”) 13.如图,DE 是△ABC 的中位线,若△ADE 的面积为3,则△ABC 的面积为________.14.“若实数a ,b ,c 满足a <b <c ,则a +b <c ”,能够说明该命题是假命题的一组a ,b ,c 的值依次为________. 15.如图,在□ABCD 中,点E ,F 分别在边AD 、BC 上,BF=2,∠DEF=60°将四边形EFCD 沿EF 翻折,得到四边形EFC ’D’,ED ’交BC 于点G ,则△GEF 的周长为________. 16.如图,双曲线y=xk(x >0)经过A 、B 两点,若点A 的横坐标为1, ∠OAB=90°,且OA=AB ,则k 的值为________. 三、解答题(本大题共9小题,共86分) 17.(8分) 计算:91301-+-π 18.(8分)如图,在△ABC 中,∠A=80°,∠B=40°.(1)求作线段BC 的垂直平分线DE ,垂足为E ,交AB 于点D ; (要求;尺规作图,保留作图痕迹,不写作法) (2)在(1)的条件下,连接CD ,求证:AC=CD .19.(8分)求证:对角线相等的平行四边形是矩形. (要求:画出图形,写出已知和求证,并给予证明)20.(8分)为响应市收府关于”垃圾不落地·市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A :非常了解,B :比较了解C :了解较少,D :不了解”四种,并将调查结果绘制成以下两幅不完整的统计图. 请根据图中提供的信息,解答下列问题: (1)把两幅统计图补充完整;(2)若该校学生数1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学 生共有________名;(3)已知“非常了解”的4名男生和1名女生,从 中随机抽取2名向全校做垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到1男1女的概率. CB A D EA B CDD ’ EF G BAxyOB CABCD___%___%30%8%垃圾分类知识掌据情况条形统计图垃圾分类知识掌据情况A21.(8分)如图,AB 是⊙0的直径,AC 是弦,D 是BC 的中点,过点D 作EF 垂直于直线AC ,垂足为F ,交AB 的延长线于点E . (1)求证:EF 是⊙0的切线; (2)若tan A=34,AF=6,求⊙0的半径.22.(10分)某景区售票处规定:非节假日的票价打a 折售票; 节假日根据团队人数x (人)实行分段售票:若≤x 10,则按 原展价购买;若x >10,则其中10人按原票价购买,超过部 分的按原那价打b 折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y 1元,在节假日的购票款为y 2元,y 1、y 2与x 之间的函数图象如图所示.(1)观察图象可知:a ________,b ________;(2)当x >10时,求y 2与x 之间的函数表达式;(3)该旅行社在今年5月1目带甲团与5月10日(非节假日)带乙国到该景区游览,两团合计50人,共付门票款3120元,已知甲团人数超过10人,求甲团人数与乙团人数.23.(10分)阅读:所谓勾股数就是满足方程x 2+y 2=z 2的正整数解,即满足勾股定理的三个正整数构成的 一组数.我国古代数学专著《九章算术》一书,在世界上第一次给出该方程的解为:)(2122n m x -=,y =mn ,)(2122n m z +=,其中m >n >0,m 、n 是互质的奇数. 应用:当n =5时,求一边长为12的直角三角形另两边的长.D24.(12分)已知抛物线c bx ax y ++=2(a 、b 、c 是常数,0≠a )的对称轴为直线2-=x . (1) b =______;(用含a 的代数式表示)(2)当1-=a 时,若关于x 的方程02=++c bx ax 在13<<-x 的范围内有解,求c 的取值范围; (3)若抛物线过点(2-,2-),当01≤≤-x 时,抛物线上的点到x 轴距离的最大值为4,求a 的值.25.(14分)如图,在正方形ABCD 中,对角线AC 、BD 相交于点O ,E 为OC 上动点(与点0不重合), 作AF ⊥BE ,垂足为G ,交BC 于F ,交B0于H ,连接0G ,CC . (1)求证:AH=BE ; (2)试探究:∠AGO 的度数是否为定值?请说明理由; (3)若OG ⊥CG ,BG=5,求△OGC 的面积.CD2018年漳州市初中毕业班质量检测数学参考答案及评分建议1 2 3 4 5 6 7 8 9 10A B D B C D A B A C二、填空题(本大题共6小题,每小题4分,共24分)11. a(x+1)(x-1);12. 必然;13. 12;14.答案不唯一,如1,2,3;15. 6;16.1+5 2.三、解答题(本大题共9小题,共86分)17.(本小题满分8分)解:原式=11+133……………………………………………………………………6分=1. ……………………………………………………………………8分18.(本小题满分8分)解:(1)如图,直线DE为所求作的垂直平分线,点D,E就是所求作的点;…………4分(没标字母或字母标错扣1分)(2)连接CD.方法一:∵DE垂直平分AB,∴BD=CD,∴∠1=∠B=40°. ……………………………5分∴∠2=∠B+∠1=80°.……………………6分∵∠A=80°,∴∠2=∠A. …………………………………………………………7分∴AC=CD.……………………………………………………………8分方法二:∵DE垂直平分AB,∴BD=CD,∴∠1=∠B=40°. ………………………………………………………5分∵∠A=80°,∴∠ACB=180°-∠A-∠B=60°.∴∠ACD=60°-40°=20°. ……………………………………………6分∴∠2=180°-∠A-∠ACD=80°=∠A. …………………………………7分∴AC=CD.……………………………………………………………8分已知:如图,在□ABCD中,AC=BD. (画图2分,已知1分)………………3分求证:□ABCD是矩形. …………………………………………………………4分证明:方法一:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD . …………………5分∵AC=BD,BC=BC,∴△ABC ≌△DCB.∴∠ABC=∠DCB. ………………………………………………6分∵AB∥CD,∴∠ABC+∠DCB=180°.∴∠ABC=11802⨯°=90°. …………………………………………7分∴□ABCD是矩形. ……………………………………………………8分方法二:设AC,BD交于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD . ………………5分∵AC=BD,∴OA=OC=OB.∴∠1=∠3,∠2=∠4.……………………………………………6分∴∠ABC=∠1+∠2=11802⨯°=90°.…………………………………7分∴□ABCD是矩形. ………………………………………………8分20.(本小题满分8分)解:(1)如图所示(补充2个或3个正确,得1分);…………………………………2分(2)500;………4分(3)树状图法:………………………………………6分共有12种等可能结果,其中满足条件有6种,∴P(一男一女)=12. ………………8分(用列表法参照给分)解:(1)方法一:如图1,连接OD . ∵EF ⊥AF ,∴∠F =90°.∵D 是»BC的中点,∴»»BD DC =. ∴∠1=∠2=12∠BOC . ………………………………………………1分 ∵∠A =12∠BOC , ∴∠A =∠1 . ………………………………………2分 ∴OD ∥AF .∴∠EDO =∠F =90°.∴OD ⊥EF . ……………………………………………………………3分 ∴EF 是⊙O 的切线. ……………………………………………………4分方法二:如图2,连接OD ,BC .∵D 是»BC的中点,∴»»BD DC =. ∴∠1=∠2. …………………………………………………………1分 ∵OB =OC ,∴OD ⊥BC . ……………………………2分∵AB 是⊙O 的直径,∴∠ACB =90°.∵AF ⊥EF ,∴∠F =∠ACB =90°.∴BC ∥EF .∴OD ⊥EF . ……………………………………………………………3分∴EF 是⊙O 的切线. …………………………………………………4分(2)设⊙O 半径为r ,则OA =OD =OB =r .方法一:在Rt △AFE 中,tan A =43,AF =6, ∴EF =AF ·tan A =8. ∴2210AE AF EF =+=. ………………5分∴OE =10-r .∵cos A = 35AF AE=, ………………………………………………………6分∴cos ∠1= cos A =3105OD r OE r ==-. ……………………………………7分 ∴r =154, 即⊙O 的半径为154. ……………………………………8分方法二:在Rt △AFE 中,tan A =43,AF =6, ∴EF =AF ·tan A =8. ∴2210AE AF EF =+=. ………………5分∴EO =10-r .∵∠A =∠1,∠E =∠E ,∴△EOD ∽△EAF . ……………………………………………………6分 ∴OD EO AFEA= . …………………………………………………………7分∴10610r r -=.∴r =154, 即⊙O 的半径为154. ……………………………………8分22. (本小题满分10分)解:(1)6,8; ………………………………………………………………………………2分 (2)当x ﹥10时,设y 2=kx +b .∵图象过点(10,800),(20,1440), …………………3分 ∴⎩⎨⎧=+=+.144020,80010b k b k ……………………………………4分解得⎩⎨⎧==.160,64b k …………………………………………5分∴y 2=64x +160 (x ﹥10) . ………………………………………………………6分 (3)设甲团有m 人,乙团有n 人.由图象,得y 1=48x . ……………………………………………………………7分 当m ﹥10时,依题意,得⎩⎨⎧=+=++.50,31204816064n m n m ………………………………………8分解得⎩⎨⎧==.15,35n m ……………………………………………………………………9分答:甲团有35人,乙团有15人. ………………………………………………10分23. (本小题满分10分)解:∵n =5,直角三角形一边长为12,∴有三种情况: ① 当x =12 时,12)52122=-m (. ………………………………………………………………1分 解得m 1=7,m 2= -7(舍去). …………………………………………………2分∴y = mn =35. ……………………………………………………………………3分 ∴222211()(75)3722z m n =+=⨯+=. ……………………………………4分 ∴该情况符合题意. ② 当y =12时,5m =12, …………………………………………………………………………5分125m =. …………………………………………………………………………6分 ∵m 为奇数, ∴125m =舍去. …………………………………………………………………7分 ③ 当z =12时,221(5)122m +=,…………………………………………………………………8分 21m =-, …………………………………………………………………9分此方程无实数解. ………………………………………………………………10分 综上所述:当n =5时, 一边长为12的直角三角形另两边的长分别为35,37. 24. (本小题满分12分)解:(1)4a ; ………………………………………………………………………………2分(2)当a = -1时,∵关于x 的方程240x x c --+=在-3< x <1的范围内有解,即关于x 的方程x 2+4x-c =0在-3< x <1的范围内有解,∴b 2 -4ac =16+4c ≥0,即c ≥ -4. …………………………………………………3分 方法一:∴抛物线y= x 2 +4x =(x +2)2 -4与直线y = c 在-3 <x <1的范围内有交点. ……………………………………………………………………4分 当x = -2时,y = -4,当x =1时,y = 5. ………………………………5分 由图像可知: -4≤ c < 5. …………………………………………7分方法二:∴抛物线y= x 2 +4x -c =(x +2)2 -4-c 与x 轴在-3 <x <1的范围内有交点. ……………………………………………………………………4分 当x = -2,y =0时,c = -4,当x = 1,y =0时,c = 5. …………………5分 由图像可知:-4≤ c <5. ………………………………………………7分 方法三:∵224(2) 4.c x x x =+=+-∴c 是x 的二次函数. ……………………………………………………4分当x = -2时,c = -4,当x = 1时,c = 5. ……………………………5分由图像可知: -4≤ c < 5. ………………………………………………7分 (3)∵抛物线y =ax 2+4ax +c 过点(-2,-2),∴c = 4a -2.∴抛物线解析式为:22442(2)2y ax ax a a x =++-=+-. …………………8分 方法一: ① 当a > 0时,抛物线开口向上.∵抛物线对称轴为x =-2.∴当-1≤x ≤0时,y 随x 增大而增大.∵抛物线上的点到x 轴距离的最大值为4,由图像可知:4a -2=4. ………………………………………………9分∴32a =. …………………………………………………………10分 ② 当a < 0时,抛物线开口向下.∵抛物线对称轴为x =-2.∴当-1≤x ≤0时,y 随x 增大而减小. ∵抛物线上的点到x 轴距离的最大值为4,由图像可知:4a -2= -4. ……………………………………………11分∴12a =-. …………………………………………………………12分 方法二: ∵-1≤x ≤0,∴当x = 0时,y = 4a -2;当x = -1时,y = a -2. ……………8分 ∵当-1≤x ≤0时,抛物线上的点到x 轴距离的最大值为4. ∴有两种情况:① 若424a -=,则3122a a ==-或. ……………………9分 此时1242a -=<或5242a -=<,符合题意. ………10分 ② 若24a -=,则a = 6或a = -2. ………………………11分此时42224a -=>或42104a -=>.∴a = 6或a = -2不合题意,舍去. ………………………12分综上所述: 3122a a ==-或.25. (本小题满分14分)解:(1)方法一:∵四边形ABCD 是正方形,∴OA =OB ,∠AOB =∠BOE =90°.…………………………………………1分∵AF ⊥BE ,∴∠GAE+∠AEG =∠OBE +∠AEG =90°.∴∠ GAE =∠OBE . ………………………2分∴△AOH ≌ △BOE . ………………………3分∴AH =BE . …………………………………4分方法二:∵四边形ABCD 是正方形,∴∠ABC =90°,AB =CB ,∠ABO =∠ECB =45°. ……………………1分 ∵AF ⊥BE ,∴∠BAG+∠ABG =∠CBE +∠ABG =90°.∴∠BAH =∠CBE . ………………………………………………………2分∴△ABH ≌△BCE . ……………………………………………………3分 ∴AH =BE . ………………………………………………………………4分(2)方法一:∵∠AOH =∠BGH =90°, ∠AHO =∠BHG ,∴△AOH ∽△BGH . ……………………5分 ∴OH AH GH BH =. …………………………6分 ∴OH GH AH BH =. …………………………7分∵∠OHG =∠AHB .∴△OHG ∽△AHB . ………………………………………………………8分 ∴∠AGO =∠ABO =45°,即∠AGO 的度数为定值. ……………………9分方法二:如图,取AB 中点M ,连接MO ,MG . ………6分∵∠AGB =∠AOB =90°,∴AM =BM =GM =OM . ………………………7分∴点O ,G 在以AB 为直径的⊙M 上,即点A ,B ,G ,O 四点在以AB 为直径的⊙M 上, ………………………8分 ∴∠AGO =∠ABO =45°,即∠AGO 的度数为定值. ………………………………………………9分(3)∵∠ABC =90°,AF ⊥BE ,∴∠BAG =∠FBG ,∠AGB =∠BGF =90°,∴△ABG ∽△BFG . ……………………………………………………………10分 ∴GFBG BG AG =, ∴AG ·GF =BG 2 =5. …………………………………11分∵△AHB ∽△OHG ,∴∠BAH =∠GOH =∠GBF .∵∠AOB =∠BGF =90°,∴∠AOG =∠GFC . ……………………………………………………………12分 ∵∠AGO =45°,CG ⊥GO ,∴∠AGO =∠FGC =45°.∴△AGO ∽△CGF . ………………………………………………………13分 ∴CG AGGF GO ,∴GO ·CG =AG ·GF =5.∴S △OGC =12CG ·GO =52.……………………………………………………14分。
2018年漳州市初中毕业班质量检测数学试题和答案

2018漳州市初中毕业班质量检测数学试题一、选择题(本大题共10小题,每小题4分,共40分) 1.如图,数轴上点M 所表示的数的绝对值是( ). A .3 B .3- C .±3 D .31-2.“中国天眼”FAST 射电望远镜的反射面总面积约250 000m 2,数据250 000用科学记数法表示为( ).A .25×104B .2.5×105C .2.5×106D .0.25×1063.如图是某几何体的左视图,则该几何体不可能...是( ). 4.下列计算,结果等于x 5的是( ).A .32x x + B .32x x ⋅ C .210x x÷ D .(x 2)35.如图,在右框解分式方程的4个步骤中,根据等式基本性 质的是( ).A .①②B .②④C .①③D .③④6.如图,OP 平分∠AOB,PC⊥OA 于C ,点D 是OB 上的动点,若PC=6cm 则PD 的长可以是( ).A .3cmB .4cmC .5cmD .7 cm7.如图,点A ,B 在方格纸的格点上,将线段AB 先向右平移3格,再向下 平移2个单位,得线段DC ,点A 的对应点为D ,连接AD 、BC ,则关于 四边形ABCD 的对称性,下列说法正确的是( ). A .既是轴对称图形,又是中心对称图形 B .是中心对称图形,但不是轴对称图形 C .是轴对称图形,但不是中心对称图形 D .既不是轴对称图形,也不是中心对称图形8.甲、乙两地今年2月份前5天的日平均气温如图所示,则下列描述错误..的是( ). A .两地气温的平均数相同B .甲地气温的众数是4℃C .乙地气温的中位数是6℃D .甲地气温相对比较稳定9.如图,正六边形 ABCDEF 的中心与坐标原点0重合,其中A(-2,0). 将六边形 ABCDEF 绕原点O 按顺时针方向旋转2018次,每次旋转 60°,则旋转后点A 的对应点A'的坐标是( ). A . (1,3)B . (3,1)C .(1,3-)D .(-1,3) 10.如图,在矩形ABCD 中,点A 在x 轴上,点B 的坐标为(1,0),且C 、D 两点在函数y=⎪⎩⎪⎨⎧<+-≥+)0(121)0(1x x x x 的图象上,若在矩形ABCD左视图内随机取一点,则此点取自阴影部分的概率是( ). A .21 B .83 C .41 D .61二,填空题(本大题共6小题,每小题4分,共24分) 11.因式分解:a ax -2=________.12.一个不透明的袋子中装有4个红球、2个黑球,它们除颜色外其余都相同,从中任意搞出3个球,则事件“摸出的球至少有1个红球”是________事件(填“必然”、13.如图,DE 是△ABC 的中位线,若△ADE 的面积为3,则△ABC 的面积为________.14.“若实数a ,b ,c 满足a<b <c,则a +b <c ”,能够说明该命题是假命题的 一组a ,b ,c 的值依次为________. 15.如图,在□ABCD 中,点E ,F 分别在边AD 、BC 上,BF=2,∠DEF=60°将四边形EFCD 沿EF 翻折,得到四边形EFC ’D’,ED ’交BC 于点G ,则△GEF 的周长为________. 16.如图,双曲线y=xk(x >0)经过A 、B 两点,若点A 的横坐标为1, ∠OAB=90°,且OA=AB ,则k 的值为________. 三、解答题(本大题共9小题,共86分) 17.(8分) 计算:91301-+-π 18.(8分)如图,在△ABC 中,∠A=80°,∠B=40°.(1)求作线段BC 的垂直平分线DE ,垂足为E ,交AB 于点D ; (要求;尺规作图,保留作图痕迹,不写作法) (2)在(1)的条件下,连接CD ,求证:AC=CD .19.(8分)求证:对角线相等的平行四边形是矩形. (要求:画出图形,写出已知和求证,并给予证明)20.(8分)为响应市收府关于”垃圾不落地·市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A:非常了解,B :比较了解C :了解较少,D :不了解”四种,并将调查结果绘制成以下两幅不完整的统计图. 请根据图中提供的信息,解答下列问题: (1)把两幅统计图补充完整;(2)若该校学生数1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学 生共有________名;(3)已知“非常了解”的4名男生和1名女生,从 中随机抽取2名向全校做垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到1男1女的概率.CA B CDD ’ EF G B C垃圾分类知识掌据情况条形统计图垃圾分类知识掌据情况21.(8分)如图,AB 是⊙0的直径,AC 是弦,D 是BC 的中点,过点D 作EF 垂直于直线AC ,垂足为F ,交AB 的延长线于点E . (1)求证:EF 是⊙0的切线; (2)若tan A=34,AF=6,求⊙0的半径.22.(10分)某景区售票处规定:非节假日的票价打a 折售票; 节假日根据团队人数x (人)实行分段售票:若≤x 10,则按 原展价购买;若x >10,则其中10人按原票价购买,超过部 分的按原那价打b 折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y 1元,在节假日的购票款为y 2元,y 1、y 2与x 之间的函数图象如图所示.(1)观察图象可知:a ________,b ________;(2)当x >10时,求y 2与x 之间的函数表达式;(3)该旅行社在今年5月1目带甲团与5月10日(非节假日)带乙国到该景区游览,两团合计50人,共付门票款3120元,已知甲团人数超过10人,求甲团人数与乙团人数.23.(10分)阅读:所谓勾股数就是满足方程x 2+y 2=z 2的正整数解,即满足勾股定理的三个正整数构成的 一组数.我国古代数学专著《九章算术》一书,在世界上第一次给出该方程的解为:)(2122n m x -=,y =mn ,)(2122n m z +=,其中m >n >0,m 、n 是互质的奇数. 应用:当n =5时,求一边长为12的直角三角形另两边的长.24.(12分)已知抛物线c bx ax y ++=2(a 、b 、c 是常数,0≠a )的对称轴为直线2-=x . (1) b =______;(用含a 的代数式表示)(2)当1-=a 时,若关于x 的方程02=++c bx ax 在13<<-x 的范围内有解,求c 的取值范围; (3)若抛物线过点(2-,2-),当01≤≤-x 时,抛物线上的点到x 轴距离的最大值为4,求a 的值.25.(14分)如图,在正方形ABCD 中,对角线AC 、BD 相交于点O ,E 为OC 上动点(与点0不重合), 作AF⊥BE,垂足为G ,交BC 于F ,交B0于H ,连接0G ,CC . (1)求证:AH=BE ; (2)试探究:∠A GO 的度数是否为定值?请说明理由; (3)若OG⊥CG,BG=5,求△OGC 的面积.CD2018年漳州市初中毕业班质量检测数学参考答案及评分建议二、填空题(本大题共6小题,每小题4分,共24分)11. a(x+1)(x-1); 12. 必然; 13. 12; 14.答案不唯一,如1,2,3; 15. 6; 16.2.三、解答题(本大题共9小题,共86分)17.(本小题满分8分)解:原式=11+133……………………………………………………………………6分=1. ……………………………………………………………………8分18.(本小题满分8分)解:(1)如图,直线DE为所求作的垂直平分线,点D,E就是所求作的点;…………4分(没标字母或字母标错扣1分)(2)连接CD.方法一:∵DE垂直平分AB,∴BD=CD,∴∠1=∠B=40°. ……………………………5分∴∠2=∠B+∠1=80°. ……………………6分∵∠A=80°,∴∠2=∠A. …………………………………………………………7分∴AC=CD.……………………………………………………………8分方法二:∵DE垂直平分AB,∴BD=CD,∴∠1=∠B=40°. ………………………………………………………5分∵∠A=80°,∴∠ACB=180°-∠A-∠B=60°.∴∠ACD=60°-40°=20°. ……………………………………………6分∴∠2=180°-∠A-∠ACD=80°=∠A. …………………………………7分∴AC=CD.……………………………………………………………8分已知:如图,在□ABCD 中, AC =BD . (画图2分,已知1分) ………………3分 求证:□ABCD 是矩形. …………………………………………………………4分 证明:方法一:∵四边形ABCD 是平行四边形,∴AB =CD ,AB ∥CD . …………………5分∵AC =BD ,BC =BC ,∴△ABC ≌△DCB .∴∠ABC =∠DCB . ………………………………………………6分 ∵AB ∥CD ,∴∠ABC +∠DCB =180°.∴∠ABC =11802⨯°=90°. …………………………………………7分 ∴□ABCD 是矩形. ……………………………………………………8分方法二:设AC ,BD 交于点O .∵四边形ABCD 是平行四边形,∴OA =OC ,OB =OD . ………………5分∵AC =BD ,∴OA =OC =OB .∴∠1=∠3,∠2=∠4. ……………………………………………6分∴∠ABC =∠1+∠2=11802⨯°=90°. …………………………………7分 ∴□ABCD 是矩形. ………………………………………………8分 20.(本小题满分8分)解:(1)如图所示(补充2个或3个正确,得1分); …………………………………2分 (2)500; ………4分(3)树状图法:………………………………………6分共有12种等可能结果,其中满足条件有6种,∴P (一男一女)=12. ………………8分 (用列表法参照给分)解:(1)方法一:如图1,连接OD . ∵EF ⊥AF ,∴∠F =90°.∵D 是BC 的中点,∴BD DC =.∴∠1=∠2=12∠BOC . ………………………………………………1分 ∵∠A =12∠BOC , ∴∠A =∠1 . ………………………………………2分 ∴OD ∥AF . ∴∠EDO =∠F =90°.∴OD ⊥EF . ……………………………………………………………3分 ∴EF 是⊙O 的切线. ……………………………………………………4分方法二:如图2,连接OD ,BC .∵D 是BC 的中点,∴BD DC =.∴∠1=∠2. …………………………………………………………1分∵OB =OC ,∴OD ⊥BC . ……………………………2分∵AB 是⊙O 的直径,∴∠ACB =90°. ∵AF ⊥EF ,∴∠F =∠ACB =90°.∴BC ∥EF .∴OD ⊥EF . ……………………………………………………………3分∴EF 是⊙O 的切线. …………………………………………………4分(2)设⊙O 半径为r ,则OA =OD =OB =r .方法一:在Rt △AFE 中,tan A =43,AF =6, ∴EF =AF ·tan A =8.∴10AE ==. ………………5分∴OE =10-r .∵cos A = 35AF AE=, ………………………………………………………6分∴cos ∠1= cos A =3105OD r OE r ==-. ……………………………………7分 ∴r =154, 即⊙O 的半径为154. ……………………………………8分方法二:在Rt △AFE 中,tan A =43,AF =6, ∴EF =AF ·tan A =8.∴10AE ==. ………………5分∴EO =10-r .∵∠A =∠1,∠E =∠E ,∴△EOD ∽△EAF . ……………………………………………………6分 ∴OD EO AFEA= . …………………………………………………………7分∴10610r r -=.∴r =154, 即⊙O 的半径为154. ……………………………………8分22. (本小题满分10分)解:(1)6,8; ………………………………………………………………………………2分(2)当x ﹥10时,设y 2=kx +b .∵图象过点(10,800),(20,1440), …………………3分 ∴⎩⎨⎧=+=+.144020,80010b k b k ……………………………………4分解得⎩⎨⎧==.160,64b k …………………………………………5分∴y 2=64x +160 (x ﹥10) . ………………………………………………………6分 (3)设甲团有m 人,乙团有n 人.由图象,得y 1=48x . ……………………………………………………………7分 当m ﹥10时,依题意,得⎩⎨⎧=+=++.50,31204816064n m n m ………………………………………8分解得⎩⎨⎧==.15,35n m ……………………………………………………………………9分答:甲团有35人,乙团有15人. ………………………………………………10分23. (本小题满分10分)解:∵n =5,直角三角形一边长为12,∴有三种情况: ① 当x =12 时,12)52122=-m (. ………………………………………………………………1分 解得m 1=7,m 2= -7(舍去). …………………………………………………2分∴y = mn =35. ……………………………………………………………………3分 ∴222211()(75)3722z m n =+=⨯+=. ……………………………………4分 ∴该情况符合题意. ② 当y =12时,5m =12, …………………………………………………………………………5分125m =. …………………………………………………………………………6分 ∵m 为奇数, ∴125m =舍去. …………………………………………………………………7分 ③ 当z =12时,221(5)122m +=,…………………………………………………………………8分 21m =-, …………………………………………………………………9分此方程无实数解. ………………………………………………………………10分 综上所述:当n =5时, 一边长为12的直角三角形另两边的长分别为35,37. 24. (本小题满分12分)解:(1)4a ; ………………………………………………………………………………2分(2)当a = -1时,∵关于x 的方程240x x c --+=在-3< x <1的范围内有解,即关于x 的方程x 2+4x-c =0在-3< x <1的范围内有解,∴b 2-4ac =16+4c ≥0,即c ≥ -4. …………………………………………………3分 方法一:∴抛物线y= x 2+4x =(x +2)2-4与直线y = c 在-3 <x <1的范围内有交点. ……………………………………………………………………4分 当x = -2时,y = -4,当x =1时,y = 5. ………………………………5分 由图像可知: -4≤ c < 5. …………………………………………7分方法二:∴抛物线y= x 2 +4x -c =(x +2)2-4-c 与x 轴在-3 <x <1的范围内有交点. ……………………………………………………………………4分 当x = -2,y =0时,c = -4,当x = 1,y =0时,c = 5. …………………5分 由图像可知:-4≤ c <5. ………………………………………………7分 方法三:∵224(2) 4.c x x x =+=+-∴c 是x 的二次函数. ……………………………………………………4分当x = -2时,c = -4,当x = 1时,c = 5. ……………………………5分由图像可知: -4≤ c < 5. ………………………………………………7分 (3)∵抛物线y =ax 2+4ax +c 过点(-2,-2),∴c = 4a -2.∴抛物线解析式为:22442(2)2y ax ax a a x =++-=+-. …………………8分 方法一: ① 当a > 0时,抛物线开口向上.∵抛物线对称轴为x =-2.∴当-1≤x ≤0时,y 随x 增大而增大.∵抛物线上的点到x 轴距离的最大值为4,由图像可知:4a -2=4. ………………………………………………9分∴32a =. …………………………………………………………10分 ② 当a < 0时,抛物线开口向下.∵抛物线对称轴为x =-2.∴当-1≤x ≤0时,y 随x 增大而减小. ∵抛物线上的点到x 轴距离的最大值为4,由图像可知:4a -2= -4. ……………………………………………11分∴12a =-. …………………………………………………………12分 方法二: ∵-1≤x ≤0,∴当x = 0时,y = 4a -2;当x = -1时,y = a -2. ……………8分 ∵当-1≤x ≤0时,抛物线上的点到x 轴距离的最大值为4. ∴有两种情况:① 若424a -=,则3122a a ==-或. ……………………9分 此时1242a -=<或5242a -=<,符合题意. ………10分 ② 若24a -=,则a = 6或a = -2. ………………………11分 此时42224a -=>或42104a -=>.∴a = 6或a = -2不合题意,舍去. ………………………12分综上所述: 3122a a ==-或. 25. (本小题满分14分)解:(1)方法一:∵四边形ABCD 是正方形,∴OA =OB ,∠AOB =∠BOE =90°.…………………………………………1分∵AF ⊥BE ,∴∠GAE+∠AEG =∠OBE +∠AEG =90°.∴∠ GAE =∠OBE . ………………………2分∴△AOH ≌ △BOE . ………………………3分∴AH =BE . …………………………………4分方法二:∵四边形ABCD 是正方形,∴∠ABC =90°,AB =CB ,∠ABO =∠ECB =45°. ……………………1分∵AF ⊥BE ,∴∠BAG+∠ABG =∠CBE +∠ABG =90°.∴∠BAH =∠CBE . ………………………………………………………2分 ∴△ABH ≌△BCE . ……………………………………………………3分 ∴AH =BE . ………………………………………………………………4分(2)方法一:∵∠AOH =∠BGH =90°, ∠AHO =∠BHG ,∴△AOH ∽△BGH . ……………………5分 ∴OH AH GH BH=. …………………………6分 ∴OH GH AH BH=. …………………………7分 ∵∠OHG =∠AHB .∴△OHG ∽△AHB . ………………………………………………………8分 ∴∠AGO =∠ABO =45°,即∠AGO 的度数为定值. ……………………9分方法二:如图,取AB 中点M ,连接MO ,MG . ………6分∵∠AGB =∠AOB =90°,∴AM =BM =GM =OM . ………………………7分∴点O ,G 在以AB 为直径的⊙M 上,即点A ,B ,G ,O 四点在以AB 为直径的⊙M 上, ………………………8分 ∴∠AGO =∠ABO =45°,即∠AGO 的度数为定值. ………………………………………………9分(3)∵∠ABC =90°,AF ⊥BE ,∴∠BAG =∠FBG ,∠AGB =∠BGF =90°,∴△ABG ∽△BFG . ……………………………………………………………10分 ∴GFBG BG AG =,∴AG ·GF =BG 2 =5. …………………………………11分∵△AHB ∽△OHG ,∴∠BAH =∠GOH =∠GBF .∵∠AOB =∠BGF =90°,∴∠AOG =∠GFC . ……………………………………………………………12分 ∵∠AGO =45°,CG ⊥GO ,∴∠AGO =∠FGC =45°.∴△AGO ∽△CGF . ………………………………………………………13分 ∴CGAG GF GO =, ∴GO ·CG =AG ·GF =5.∴S △OGC =12CG ·GO =52. ……………………………………………………14分。
2018年漳州初中毕业班质量检测语文试题及参考答案

2018 年漳州初中毕业班质量检测语文试题(全卷共6 页,23 题;完卷时间120 分钟;满分150 分)友情提示:请把所有答案填写(涂)在答案卡上,请不要错位、越界做答!毕业学校姓名考生号一、积累与运用(20 分)1. 补写出下列句子中的空缺部分。
(12分)(1)窈窕淑女,。
(《诗经·关雎》)(2),悠然见南山。
(陶渊明《饮酒》)(3)会当凌绝顶,。
(杜甫《望岳》)(4)春蚕到死丝方尽,。
(李商隐《无题》)(5)乱花渐欲迷人眼,。
(白居易《钱塘湖春行》)(6),燕然未勒归无计。
(范仲淹《渔家傲·秋思》)(7)千古兴亡多少事?悠悠。
(辛弃疾《南乡子·登京口北固亭有怀》)(8)峰峦如聚,,。
(张养浩《山坡羊·潼关怀古》)(9)子曰:“,思而不学则殆。
”(《论语》)(10)我们常引用周敦颐《爱莲说》中的“,”来强调一个人应不受环境影响,保持崇高的个性节操。
2. 下列文学常识说法有.误.的一项是(2分)A.我国古代文学作品常用“桑梓”“桃李”“婵娟”分别代指家乡、老师、月亮。
B.唐诗、宋词、元曲是我国诗歌史上的三大高峰。
唐有大小李杜,宋有豪放之“苏辛”,元有四大家。
C.《从百草园到三味书屋》和《藤野先生》都是现代作家鲁迅的回忆性散文。
D.《我的叔叔于勒》选自法国作家莫泊桑的短篇小说集《羊脂球》。
3. 阅读下面文字,按要求作答。
(6分)2018平昌冬奥会闭幕式上,“北京八分钟”表演甲(A、美轮美奂B、富丽堂皇)、科技感十足,为观众献上了一场视觉盛宴。
24 台移动机器人携.①(A、xiéB、jiá)带“冰屏”与舞蹈演员配合完成了一系列màn ②(A、曼B、嫚)妙复杂的舞美动作,展现了人工智能与中华文化的完美融合,让观众乙(A、惊讶B、惊叹)。
在经久不息的掌声中,表明八分钟的演出完美成功。
(1)为文中①处加点字选择正确的读音,根据②处拼音选择正确的汉字,只填序号。
2018 年漳州市初中毕业班质量检测
D������ 冷湿
14������ 雅鲁藏布江谷地的农业类型属于
A������ 绿洲农业 B������ 水田农业
C������ 河谷农业
D������ 灌溉农业
读图 5 “ 美国农业带分布图” ꎬ 完成 15 ~ 17 题ꎮ
15������ 落基山脉位于太平洋板块与
A������ 美洲板块的交界处
B������ 亚欧板块的交界处
C������ 印度洋板块的交界处
D������ 南极洲板块的交界处
16������ 五大湖附近的农业带 ( 区) 主要是
A������ 玉米带
B������ 小麦区
C������ 乳畜带
D������ 棉花带
17������ 由图可以推测美国农业生产特点具有
A������ 高度自动化
ꎬ 该能源集中分布在
湾及
其沿岸地区ꎮ
(3) 图中新加坡的气候类型是
ꎬ 而内罗毕的气候类型为热带草原气候ꎬ 造
成两地气候差异的主要因素是广袤的森林和草场ꎬ 是名副其实的绿色王国ꎮ 读图 10 “ 新西兰南岛示
意图及气候统计图”ꎬ 完成下列问题ꎮ (8 分)
(1) 该岛位于南、 北半球中的
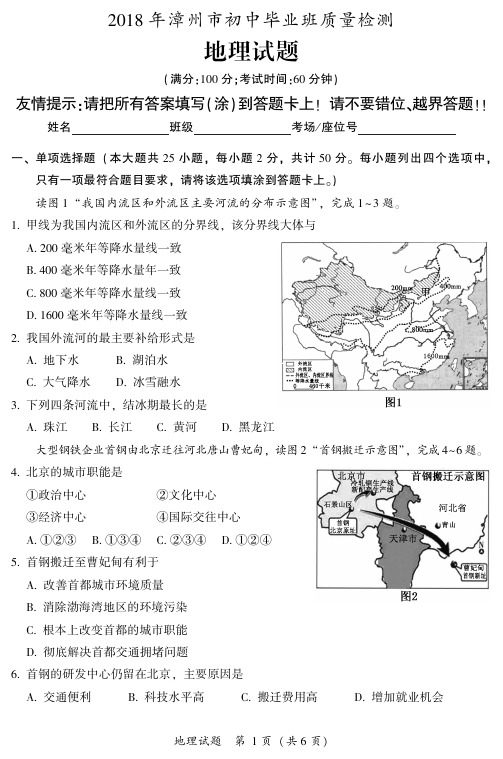
读图 1 “我国内流区和外流区主要河流的分布示意图”ꎬ 完成 1 ~ 3 题ꎮ
1������ 甲线为我国内流区和外流区的分界线ꎬ 该分界线大体与
A������ 200 毫米年等降水量线一致
B������ 400 毫米年等降水量年一致
C������ 800 毫米年等降水量线一致
D������ 1600 毫米年等降水量线一致
ꎬ 原因是纬度较
ꎬ 且A
山脉阻挡了冬季冷空气南下ꎬ 热量较充足ꎻ 同时使大西洋和北冰洋的
2018年福建漳州市中考语文试题(WORD版,答案)

2018年漳州市初中毕业班质量检查试卷(暨中考试题)语文试题(满分:150分;考试时间:120分钟)友情提示:请把所有答案填写(涂)到答题卡上!请不要错位、越界答题!!姓名:准考证号:本试题由青峰弦月对照图片手工录入整理第一部分积累与运用(25分)一、积累运用。
(25分)1.按要求填空。
(以回答正确的5道题计分)(10分)(1)那榆阴下的一潭,不是清泉,是天上的虹,,。
(徐志摩《再别康桥》)(2)折戟沉沙铁未销,自将磨洗认前朝。
,。
(杜牧《赤壁》)(3)枯藤老树昏鸦,,。
(马致远《天净沙·秋思》、(4)生,亦我所欲也,义,亦我所欲也,,。
(孟子《鱼我所欲也》)(5)《登飞来峰》中表现诗人不怕困难,敢于斗争,充满必胜信念的诗句是:,。
(6)面对洞庭湖波澜壮阔的景象,一名游客激情澎湃,高声吟颂:“,。
”(7)举世皆浊我独清,。
(屈原《渔父》)2.口语交际。
(3分)学生上课按身高排座位,这似乎已成了班主任的惯例。
但是,广州一所中学打破常规,让学生自行找同桌。
此举在中学校园引起强烈反响,对于“学校排座位,学生说了算”这种做法,师生有赞同的,也有反对的。
请你参加这场讨论,发表你的意见。
3.名著阅读。
(6分)(1)下列各项中,对相关名著的表述不正确的一项是()(2分)A.《西游记》叙述了唐三藏与徒弟孙悟空、猪八戒、沙僧经过九九八十一次磨难,到西天取经的经过。
B.格列佛随“冒险号”再次出海,来到大人国。
他发现这里的大臣因鞋跟高低而分为“高跟派”和“低跟派”。
C.《五猖会》记叙了“我”少年时一次看五猖会发生的波折,表达了“我”对五猖会的无比神往,以及被父亲强迫背书的万般无奈。
D.鲁滨逊在孤岛上开拓荒地,圈养牲畜,种植水稻和小麦,年复一年与孤独为伴,克服了常人难以想像的种种困难。
(2)下面两题,任选一题作答。
(60字左右)(4分)①成语“望梅止渴”出自《三国演义》,请简述与之相关的事件。
②“手执钢刀探虎穴,心如烈火报冤仇。
2018年漳州市初中毕业班质量检测数学试题和答案

2018漳州市初中毕业班质量检测数学试题一、选择题(本大题共10小题,每小题4分,共40分) 1.如图,数轴上点M 所表示的数的绝对值是( ). A .3 B .3- C .±3 D .31-2.“中国天眼”FAST 射电望远镜的反射面总面积约250 000m 2,数据250 000用科学记数法表示为( ).A .25×104B .2.5×105C .2.5×106D .0.25×1063.如图是某几何体的左视图,则该几何体不可能...是( ). 4.下列计算,结果等于x 5的是( ).A .32x x + B .32x x ⋅ C .210x x÷ D .(x 2)35.如图,在右框解分式方程的4个步骤中,根据等式基本性 质的是( ).A .①②B .②④C .①③D .③④6.如图,OP 平分∠AOB,PC⊥OA 于C ,点D 是OB 上的动点,若PC=6cm 则PD 的长可以是( ).A .3cmB .4cmC .5cmD .7 cm7.如图,点A ,B 在方格纸的格点上,将线段AB 先向右平移3格,再向下 平移2个单位,得线段DC ,点A 的对应点为D ,连接AD 、BC ,则关于 四边形ABCD 的对称性,下列说法正确的是( ). A .既是轴对称图形,又是中心对称图形 B .是中心对称图形,但不是轴对称图形 C .是轴对称图形,但不是中心对称图形 D .既不是轴对称图形,也不是中心对称图形8.甲、乙两地今年2月份前5天的日平均气温如图所示,则下列描述错误..的是( ). A .两地气温的平均数相同B .甲地气温的众数是4℃C .乙地气温的中位数是6℃D .甲地气温相对比较稳定9.如图,正六边形 ABCDEF 的中心与坐标原点0重合,其中A(-2,0). 将六边形 ABCDEF 绕原点O 按顺时针方向旋转2018次,每次旋转 60°,则旋转后点A 的对应点A'的坐标是( ). A . (1,3)B . (3,1)C .(1,3-)D .(-1,3) 10.如图,在矩形ABCD 中,点A 在x 轴上,点B 的坐标为(1,0),且C 、D 两点在函数y=⎪⎩⎪⎨⎧<+-≥+)0(121)0(1x x x x 的图象上,若在矩形ABCD左视图CBAD xyE FO C BA DxyO内随机取一点,则此点取自阴影部分的概率是( ). A .21 B .83 C .41 D .61二,填空题(本大题共6小题,每小题4分,共24分) 11.因式分解:a ax -2=________.12.一个不透明的袋子中装有4个红球、2个黑球,它们除颜色外其余都相同,从中任意搞出3个球,则事件“摸出的球至少有1个红球”是________事件(填“必然”、 “随机”或“不可能”) 13.如图,DE 是△ABC 的中位线,若△ADE 的面积为3,则△ABC 的面积为________.14.“若实数a ,b ,c 满足a <b <c ,则a +b <c ”,能够说明该命题是假命题的一组a ,b ,c 的值依次为________. 15.如图,在□ABCD 中,点E ,F 分别在边AD 、BC 上,BF=2,∠DEF=60°将四边形EFCD 沿EF 翻折,得到四边形EFC ’D’,ED ’交BC 于点G ,则△GEF 的周长为________. 16.如图,双曲线y=xk(x >0)经过A 、B 两点,若点A 的横坐标为1, ∠OAB=90°,且OA=AB ,则k 的值为________. 三、解答题(本大题共9小题,共86分) 17.(8分) 计算:91301-+-π 18.(8分)如图,在△ABC 中,∠A=80°,∠B=40°.(1)求作线段BC 的垂直平分线DE ,垂足为E ,交AB 于点D ; (要求;尺规作图,保留作图痕迹,不写作法) (2)在(1)的条件下,连接CD ,求证:AC=CD .19.(8分)求证:对角线相等的平行四边形是矩形. (要求:画出图形,写出已知和求证,并给予证明)20.(8分)为响应市收府关于”垃圾不落地·市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A:非常了解,B :比较了解C :了解较少,D :不了解”四种,并将调查结果绘制成以下两幅不完整的统计图. 请根据图中提供的信息,解答下列问题: (1)把两幅统计图补充完整;(2)若该校学生数1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学 生共有________名;(3)已知“非常了解”的4名男生和1名女生,从 中随机抽取2名向全校做垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到1男1女的概率.CB A D EA B CDD ’ EF G BAxyOB CABCD___%___%30%8%垃圾分类知识掌据情况垃圾分类知识掌据情况A21.(8分)如图,AB 是⊙0的直径,AC 是弦,D 是BC 的中点,过点D 作EF 垂直于直线AC ,垂足为F ,交AB 的延长线于点E . (1)求证:EF 是⊙0的切线; (2)若tan A=34,AF=6,求⊙0的半径.22.(10分)某景区售票处规定:非节假日的票价打a 折售票;节假日根据团队人数x (人)实行分段售票:若≤x 10,则按 原展价购买;若x >10,则其中10人按原票价购买,超过部 分的按原那价打b 折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y 1元,在节假日的购票款为y 2元,y 1、y 2与x 之间的函数图象如图所示.(1)观察图象可知:a ________,b ________;(2)当x >10时,求y 2与x 之间的函数表达式;(3)该旅行社在今年5月1目带甲团与5月10日(非节假日)带乙国到该景区游览,两团合计50人,共付门票款3120元,已知甲团人数超过10人,求甲团人数与乙团人数.23.(10分)阅读:所谓勾股数就是满足方程x 2+y 2=z 2的正整数解,即满足勾股定理的三个正整数构成的 一组数.我国古代数学专著《九章算术》一书,在世界上第一次给出该方程的解为:)(2122n m x -=,y =mn ,)(2122n m z +=,其中m >n >0,m 、n 是互质的奇数. 应用:当n =5时,求一边长为12的直角三角形另两边的长.D24.(12分)已知抛物线c bx ax y ++=2(a 、b 、c 是常数,0≠a )的对称轴为直线2-=x . (1) b =______;(用含a 的代数式表示)(2)当1-=a 时,若关于x 的方程02=++c bx ax 在13<<-x 的范围内有解,求c 的取值范围; (3)若抛物线过点(2-,2-),当01≤≤-x 时,抛物线上的点到x 轴距离的最大值为4,求a 的值.25.(14分)如图,在正方形ABCD 中,对角线AC 、BD 相交于点O ,E 为OC 上动点(与点0不重合), 作AF⊥BE,垂足为G ,交BC 于F ,交B0于H ,连接0G ,CC . (1)求证:AH=BE ; (2)试探究:∠A GO 的度数是否为定值?请说明理由; (3)若OG⊥CG,BG=5,求△OGC 的面积.CD.2018年漳州市初中毕业班质量检测数学参考答案及评分建议1 2 3 4 5 6 7 8 9 10A B D B C D A B A C二、填空题(本大题共6小题,每小题4分,共24分)11. a(x+1)(x-1); 12. 必然; 13. 12; 14.答案不唯一,如1,2,3; 15. 6; 16.1+52.三、解答题(本大题共9小题,共86分)17.(本小题满分8分)解:原式=11+133……………………………………………………………………6分=1. ……………………………………………………………………8分18.(本小题满分8分)解:(1)如图,直线DE为所求作的垂直平分线,点D,E就是所求作的点;…………4分(没标字母或字母标错扣1分)(2)连接CD.方法一:∵DE垂直平分AB,∴BD=CD,∴∠1=∠B=40°. ……………………………5分∴∠2=∠B+∠1=80°. ……………………6分∵∠A=80°,∴∠2=∠A. …………………………………………………………7分∴AC=CD.……………………………………………………………8分方法二:∵DE垂直平分AB,∴BD=CD,∴∠1=∠B=40°. ………………………………………………………5分∵∠A=80°,∴∠ACB=180°-∠A-∠B=60°.∴∠ACD=60°-40°=20°. ……………………………………………6分∴∠2=180°-∠A-∠ACD=80°=∠A. …………………………………7分∴AC=CD.……………………………………………………………8分.19.(本小题满分8分)已知:如图,在□ABCD中, AC=BD. (画图2分,已知1分)………………3分求证:□ABCD是矩形. …………………………………………………………4分证明:方法一:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD . …………………5分∵AC=BD,BC=BC,∴△ABC ≌△DCB.∴∠ABC=∠DCB . ………………………………………………6分∵AB∥CD,∴∠ABC+∠DCB=180°.∴∠ABC=11802⨯°=90°. …………………………………………7分∴□ABCD是矩形. ……………………………………………………8分方法二:设AC,BD交于点O.∵四边形ABCD是平行四边形,∴OA=OC,OB=OD . ………………5分∵AC=BD,∴OA=OC=OB.∴∠1=∠3,∠2=∠4.……………………………………………6分∴∠ABC=∠1+∠2=11802⨯°=90°. …………………………………7分∴□ABCD是矩形. ………………………………………………8分20.(本小题满分8分)解:(1)如图所示(补充2个或3个正确,得1分);…………………………………2分(2)500;………4分(3)树状图法:………………………………………6分共有12种等可能结果,其中满足条件有6种,∴P(一男一女)=12. ………………8分(用列表法参照给分).21.(本小题满分8分)解:(1)方法一:如图1,连接OD . ∵EF ⊥AF ,∴∠F =90°.∵D 是»BC的中点,∴»»BD DC =. ∴∠1=∠2=12∠BOC . ………………………………………………1分 ∵∠A =12∠BOC , ∴∠A =∠1 . ………………………………………2分 ∴OD ∥AF . ∴∠EDO =∠F =90°.∴OD ⊥EF . ……………………………………………………………3分 ∴EF 是⊙O 的切线. ……………………………………………………4分方法二:如图2,连接OD ,BC .∵D 是»BC的中点,∴»»BD DC =. ∴∠1=∠2. …………………………………………………………1分 ∵OB =OC ,∴OD ⊥BC . ……………………………2分∵AB 是⊙O 的直径,∴∠ACB =90°.∵AF ⊥EF ,∴∠F =∠ACB =90°.∴BC ∥EF .∴OD ⊥EF . ……………………………………………………………3分∴EF 是⊙O 的切线. …………………………………………………4分(2)设⊙O 半径为r ,则OA =OD =OB =r .方法一:在Rt △AFE 中,tan A =43,AF =6, ∴EF =AF ·tan A =8. ∴2210AE AF EF =+=. ………………5分∴OE =10-r .∵cos A = 35AF AE=, ………………………………………………………6分∴cos ∠1= cos A =3105OD r OE r ==-. ……………………………………7分 ∴r =154, 即⊙O 的半径为154. ……………………………………8分.方法二:在Rt △AFE 中,tan A =43,AF =6, ∴EF =AF ·tan A =8. ∴2210AE AF EF =+=. ………………5分∴EO =10-r .∵∠A =∠1,∠E =∠E ,∴△EOD ∽△EAF . ……………………………………………………6分 ∴OD EO AFEA= . …………………………………………………………7分∴10610r r -=.∴r =154, 即⊙O 的半径为154. ……………………………………8分22. (本小题满分10分)解:(1)6,8; ………………………………………………………………………………2分 (2)当x ﹥10时,设y 2=kx +b .∵图象过点(10,800),(20,1440), …………………3分 ∴⎩⎨⎧=+=+.144020,80010b k b k ……………………………………4分解得⎩⎨⎧==.160,64b k …………………………………………5分∴y 2=64x +160 (x ﹥10) . ………………………………………………………6分 (3)设甲团有m 人,乙团有n 人.由图象,得y 1=48x . ……………………………………………………………7分 当m ﹥10时,依题意,得⎩⎨⎧=+=++.50,31204816064n m n m ………………………………………8分解得⎩⎨⎧==.15,35n m ……………………………………………………………………9分答:甲团有35人,乙团有15人. ………………………………………………10分。
2018年漳州市初中毕业班质量检测化学试题

2018年漳州市初中毕业班质量检测化学试题班级 ___________________ 姓名 __________________________ 座号 _________可能用到的相对原子质量:H — 1 Li — 7 C —12 N — 14 O —16 Na —23 Mg — 24S —32 Zn — 65第I 卷(共30分)下列说法不正确的是(A .火碱、纯碱、氨水都属于碱B .对水的净化程度较度的方法是蒸馏C .温度低于着火点,可燃物就不会燃烧D .氯化铵可用作氮肥,但不可与消石灰混合使用 下列实验现象的描述错误的是()A .氢气燃烧的火焰是淡蓝色的B •电解水时正负极产生的气体体积比约为2:1C . 一氧化碳还原氧化铁时,粉末由红棕色逐渐变黑D .受热的高锰酸钾未熔化时,导管口就有气泡连续均匀地放出 5. 物质的结构决定性质,下列有关说法错误的是()A . H 2O 2与H 2O 化学性质不同的原因是构成它们的分子不同B .盐酸与硫酸化学性质相似的原因是在水溶液中都能解离出 IC .金刚石和石墨物理性质差异的原因是构成它们的碳原子不同本卷共10小题,每小题四个选项,只有一个选项符合题意。
“绿水青山就是金山银山”。
为了让天更蓝、地更绿、水更清,下列建议不合理的是(A .禁止使用化肥农药,防止水体污染B .分类回收垃圾,促进资源再生和利用C .变废为宝,将地沟油转化为生物柴油D .大力开发和使用风能、太阳能,减少使用化石燃料 下列实验操作正确的是2.C .D .取下蒸发皿3. 4. )B .稀释浓硫酸不和帼I 型I■II巒倾倒液体 垦©D . Ne和Ar化学性质比较稳定的原因是它们的原子最外层都有6. 在2KMnO 4 ——K2MnO4 + MnO 2 + O2 T这一反应涉及的氧化物中,B. +4C. +6 8个电子锰元素的化合价为()D. +7A. +27 •下列各项混合或反应过程中存在“1 1 2”现象的是()A . 1g 酒精和1g 水混合后的总质量B . 1g 硫和1g 氧气完全反应后产物的质量C . 1g 氢氧化钠溶液和1g 醋酸溶液混合后溶液的质量D •温度一定时1g 饱和氯化钾溶液中加入1g 氯化钾后,所得溶液的质量&高纯硅广泛用于太阳能光伏电池,工业制取高纯硅反应的微观示意图如下,有关说法不 正确的是()9 选项实验目的实验设计A 鉴别碳酸钠溶液和碳酸氢钠溶液 分别滴入紫色石蕊溶液,看颜色变化B 检验一瓶无色气体是否为氧气 将带火星的木条放在瓶口C 除去铁制品表面的少量锈将铁制品长时间浸没稀盐酸中 D鉴别羊毛制品和涤纶制品分别点燃,闻气味差异 10.B •服用含有氢氧化铝的药物治疗胃酸过多,胃液pH 的变化C .常温下,足量的镁和锌分别与等体积、等浓度的稀硫酸反应D .一定的石灰石中加入稀盐酸,固液混合物中碳元素的质量变化第H 卷(共45分)本卷共6小题。
2018年漳州市初中毕业班质量检测数学试题和答案

2018漳州市初中毕业班质量检测数学试题一、选择题(本大题共10小题,每小题4分,共40分) 1.如图,数轴上点M 所表示的数的绝对值就是( ). A.3 B.3- C.±3 D.31-2.“中国天眼”FAST 射电望远镜的反射面总面积约250 000m 2,数据250 000用科学记数法表示为( ).A.25×104B.2、5×105C.2、5×106D.0、25×1063.如图就是某几何体的左视图,则该几何体不可能...就是( ).4.下列计算,结果等于x 5的就是( ).A.32x x + B.32x x ⋅ C.210x x÷ D.(x 2)35.如图,在右框解分式方程的4个步骤中,根据等式基本性 质的就是( ).A.①②B.②④C.①③D.③④6.如图,OP 平分∠AOB,PC⊥OA 于C,点D 就是OB 上的动点,若PC=6cm 则PD 的长可以就是( ).A.3cmB.4cmC.5cmD.7 cm7.如图,点A,B 在方格纸的格点上,将线段AB 先向右平移3格,再向下 平移2个单位,得线段DC,点A 的对应点为D,连接AD 、BC,则关于 四边形ABCD 的对称性,下列说法正确的就是( ). A.既就是轴对称图形,又就是中心对称图形 B.就是中心对称图形,但不就是轴对称图形 C.就是轴对称图形,但不就是中心对称图形 D.既不就是轴对称图形,也不就是中心对称图形8.甲、乙两地今年2月份前5天的日平均气温如图所示,则下列描述错误..的就是( ). A.两地气温的平均数相同B.甲地气温的众数就是4℃C.乙地气温的中位数就是6℃D.甲地气温相对比较稳定9.如图,正六边形 ABCDEF 的中心与坐标原点0重合,其中A(-2,0). 将六边形 ABCDEF 绕原点O 按顺时针方向旋转2018次,每次旋转 60°,则旋转后点A 的对应点A'的坐标就是( ). A. (1,3)B. (3,1)C.(1,3-)D.(-1,3)10.如图,在矩形ABCD 中,点A 在x 轴上,点B 的坐标为(1,0),且C 、D 两点在函数y=⎪⎩⎪⎨⎧<+-≥+)0(121)0(1x x x x 的图象上,若在矩形ABCD左视图CBAD xyE FO C BA DxyO内随机取一点,则此点取自阴影部分的概率就是( ). A.21 B.83 C.41 D.61 二,填空题(本大题共6小题,每小题4分,共24分) 11.因式分解:a ax -2=________.12.一个不透明的袋子中装有4个红球、2个黑球,它们除颜色外其余都相同,从中任意搞出3个球,则事件“摸出的球至少有1个红球”就是________事件(填“必然”、 “随机”或“不可能”) 13.如图,DE 就是△ABC 的中位线,若△ADE 的面积为3,则△ABC 的面积为________.14.“若实数a ,b ,c 满足a <b <c ,则a +b <c ”,能够说明该命题就是假命题的一组a ,b ,c 的值依次为________. 15.如图,在□ABCD 中,点E,F 分别在边AD 、BC 上,BF=2,∠DEF=60°将四边形EFCD 沿EF 翻折,得到四边形EFC ’D’,ED’交BC 于点G,则△GEF 的周长为________. 16.如图,双曲线y=xk(x >0)经过A 、B 两点,若点A 的横坐标为1, ∠OAB=90°,且OA=AB,则k 的值为________. 三、解答题(本大题共9小题,共86分) 17.(8分) 计算:91301-+-π 18.(8分)如图,在△ABC 中,∠A=80°,∠B=40°.(1)求作线段BC 的垂直平分线DE,垂足为E,交AB 于点D; (要求;尺规作图,保留作图痕迹,不写作法) (2)在(1)的条件下,连接CD,求证:AC=CD.19.(8分)求证:对角线相等的平行四边形就是矩形. (要求:画出图形,写出已知与求证,并给予证明)20.(8分)为响应市收府关于”垃圾不落地·市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况.调查选项分为“A :非常了解,B:比较了解C:了解较少,D:不了解”四种,并将调查结果绘制成以下两幅不完整的统计图. 请根据图中提供的信息,解答下列问题: (1)把两幅统计图补充完整;(2)若该校学生数1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学 生共有________名;(3)已知“非常了解”的4名男生与1名女生,从 中随机抽取2名向全校做垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到1男1女的概率.CB A D EA B CDD ’ EF G BAxyOB CABCD ___%___%30%8%垃圾分类知识掌据情况条形统计图垃圾分类知识掌据情况A21.(8分)如图,AB 就是⊙0的直径,AC 就是弦,D 就是BC 的中点,过点D 作EF 垂直于直线AC,垂足为F,交AB 的延长线于点E. (1)求证:EF 就是⊙0的切线; (2)若tan A=34,AF=6,求⊙0的半径.22.(10分)某景区售票处规定:非节假日的票价打a 折售票; 节假日根据团队人数x (人)实行分段售票:若≤x 10,则按 原展价购买;若x >10,则其中10人按原票价购买,超过部 分的按原那价打b 折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y 1元,在节假日的购票款为y 2元,y 1、y 2与x 之间的函数图象如图所示.(1)观察图象可知:a ________,b ________;(2)当x >10时,求y 2与x 之间的函数表达式;(3)该旅行社在今年5月1目带甲团与5月10日(非节假日)带乙国到该景区游览,两团合计50人,共付门票款3120元,已知甲团人数超过10人,求甲团人数与乙团人数.23.(10分)阅读:所谓勾股数就就是满足方程x 2+y 2=z 2的正整数解,即满足勾股定理的三个正整数构成的 一组数.我国古代数学专著《九章算术》一书,在世界上第一次给出该方程的解为:)(2122n m x -=,y =mn ,)(2122n m z +=,其中m >n >0,m 、n 就是互质的奇数. 应用:当n =5时,求一边长为12的直角三角形另两边的长.D24.(12分)已知抛物线c bx ax y ++=2(a 、b 、c 就是常数,0≠a )的对称轴为直线2-=x . (1) b =______;(用含a 的代数式表示)(2)当1-=a 时,若关于x 的方程02=++c bx ax 在13<<-x 的范围内有解,求c 的取值范围; (3)若抛物线过点(2-,2-),当01≤≤-x 时,抛物线上的点到x 轴距离的最大值为4,求a 的值.25.(14分)如图,在正方形ABCD 中,对角线AC 、BD 相交于点O,E 为OC 上动点(与点0不重合), 作AF⊥BE,垂足为G,交BC 于F,交B0于H,连接0G,CC. (1)求证:AH=BE; (2)试探究:∠A GO 的度数就是否为定值?请说明理由; (3)若OG⊥CG,BG=5,求△OGC 的面积.CD2018年漳州市初中毕业班质量检测数学参考答案及评分建议1 2 3 4 5 6 7 8 9 10A B D B C D A B A C二、填空题(本大题共6小题,每小题4分,共24分)11、a(x+1)(x-1); 12、必然; 13、 12; 14、答案不唯一,如1,2,3; 15、 6; 16、1+52、三、解答题(本大题共9小题,共86分)17、(本小题满分8分)解:原式=11+133……………………………………………………………………6分=1、……………………………………………………………………8分18、(本小题满分8分)解:(1)如图,直线DE为所求作的垂直平分线,点D,E就就是所求作的点; …………4分(没标字母或字母标错扣1分)(2)连接CD、方法一:∵DE垂直平分AB,∴BD=CD,∴∠1=∠B=40°、……………………………5分∴∠2=∠B+∠1=80°、……………………6分∵∠A=80°,∴∠2=∠A、…………………………………………………………7分∴AC=CD、……………………………………………………………8分方法二:∵DE垂直平分AB,∴BD=CD,∴∠1=∠B=40°、………………………………………………………5分∵∠A=80°,∴∠ACB=180°-∠A-∠B=60°、∴∠ACD=60°-40°=20°、……………………………………………6分∴∠2=180°-∠A-∠ACD=80°=∠A、…………………………………7分∴AC=CD、……………………………………………………………8分已知:如图,在□ABCD中, AC=BD、 (画图2分,已知1分) ………………3分求证:□ABCD就是矩形、…………………………………………………………4分证明:方法一:∵四边形ABCD就是平行四边形,∴AB=CD,AB∥CD 、…………………5分∵AC=BD,BC=BC,∴△ABC ≌△DCB、∴∠ABC=∠DCB、………………………………………………6分∵AB∥CD,∴∠ABC+∠DCB=180°、∴∠ABC=11802⨯°=90°、…………………………………………7分∴□ABCD就是矩形、……………………………………………………8分方法二:设AC,BD交于点O、∵四边形ABCD就是平行四边形,∴OA=OC,OB=OD 、………………5分∵AC=BD,∴OA=OC=OB.∴∠1=∠3,∠2=∠4、……………………………………………6分∴∠ABC=∠1+∠2=11802⨯°=90°、…………………………………7分∴□ABCD就是矩形、………………………………………………8分20、(本小题满分8分)解:(1)如图所示(补充2个或3个正确,得1分); …………………………………2分(2)500; ………4分(3)树状图法:………………………………………6分共有12种等可能结果,其中满足条件有6种,∴P(一男一女)=12、………………8分(用列表法参照给分)解:(1)方法一:如图1,连接OD 、∵EF ⊥AF ,∴∠F =90°、∵D 就是BC 的中点,∴BD DC =、∴∠1=∠2=12∠BOC 、 ………………………………………………1分 ∵∠A =12∠BOC , ∴∠A =∠1 、 ………………………………………2分 ∴OD ∥AF 、 ∴∠EDO =∠F =90°、∴OD ⊥EF 、 ……………………………………………………………3分 ∴EF 就是⊙O 的切线、 ……………………………………………………4分方法二:如图2,连接OD ,BC 、∵D 就是BC 的中点,∴BD DC =、∴∠1=∠2、 …………………………………………………………1分 ∵OB =OC ,∴OD ⊥BC 、 ……………………………2分∵AB 就是⊙O 的直径,∴∠ACB =90°、 ∵AF ⊥EF ,∴∠F =∠ACB =90°、∴BC ∥EF 、∴OD ⊥EF 、 ……………………………………………………………3分∴EF 就是⊙O 的切线、 …………………………………………………4分(2)设⊙O 半径为r ,则OA =OD =OB =r 、方法一:在Rt △AFE 中,tan A =43,AF =6, ∴EF =AF ·tan A =8、 ∴2210AE AF EF =+=、 ………………5分∴OE =10-r 、∵cos A = 35AF AE=, ………………………………………………………6分∴cos ∠1= cos A =3105OD r OE r ==-、 ……………………………………7分 ∴r =154, 即⊙O 的半径为154、 ……………………………………8分方法二:在Rt △AFE 中,tan A =43,AF =6, ∴EF =AF ·tan A =8、 ∴2210AE AF EF =+=、 ………………5分∴EO =10-r 、∵∠A =∠1,∠E =∠E ,∴△EOD ∽△EAF 、 ……………………………………………………6分 ∴OD EO AFEA= 、 …………………………………………………………7分∴10610r r -=、∴r =154, 即⊙O 的半径为154、 ……………………………………8分22、 (本小题满分10分)解:(1)6,8; ………………………………………………………………………………2分 (2)当x ﹥10时,设y 2=kx +b 、∵图象过点(10,800),(20,1440), …………………3分 ∴⎩⎨⎧=+=+.144020,80010b k b k ……………………………………4分解得⎩⎨⎧==.160,64b k …………………………………………5分∴y 2=64x +160 (x ﹥10) 、 ………………………………………………………6分 (3)设甲团有m 人,乙团有n 人、由图象,得y 1=48x 、 ……………………………………………………………7分 当m ﹥10时,依题意,得⎩⎨⎧=+=++.50,31204816064n m n m ………………………………………8分解得⎩⎨⎧==.15,35n m ……………………………………………………………………9分答:甲团有35人,乙团有15人、 ………………………………………………10分23、 (本小题满分10分)解:∵n =5,直角三角形一边长为12,∴有三种情况: ① 当x =12 时,12)52122=-m (、 ………………………………………………………………1分 解得m 1=7,m 2= -7(舍去)、 …………………………………………………2分∴y = mn =35、 ……………………………………………………………………3分 ∴222211()(75)3722z m n =+=⨯+=、 ……………………………………4分 ∴该情况符合题意、 ② 当y =12时,5m =12, …………………………………………………………………………5分125m =、 …………………………………………………………………………6分 ∵m 为奇数, ∴125m =舍去、 …………………………………………………………………7分 ③ 当z =12时,221(5)122m +=,…………………………………………………………………8分 21m =-, …………………………………………………………………9分此方程无实数解、 ………………………………………………………………10分 综上所述:当n =5时, 一边长为12的直角三角形另两边的长分别为35,37、 24、 (本小题满分12分)解:(1)4a ; ………………………………………………………………………………2分(2)当a = -1时,∵关于x 的方程240x x c --+=在-3< x <1的范围内有解,即关于x 的方程x 2+4x -c =0在-3< x <1的范围内有解,∴b 2-4ac =16+4c ≥0,即c ≥ -4、 …………………………………………………3分 方法一:∴抛物线y= x 2+4x =(x +2)2-4与直线y = c 在-3 <x <1的范围内有交点、 ……………………………………………………………………4分 当x = -2时,y = -4,当x =1时,y = 5、 ………………………………5分 由图像可知: -4≤ c < 5、 …………………………………………7分方法二:∴抛物线y= x 2 +4x -c =(x +2)2-4-c 与x 轴在-3 <x <1的范围内有交点、 ……………………………………………………………………4分 当x = -2,y =0时,c = -4,当x = 1,y =0时,c = 5、 …………………5分 由图像可知:-4≤ c <5、 ………………………………………………7分 方法三:∵224(2) 4.c x x x =+=+-∴c 就是x 的二次函数、 ……………………………………………………4分当x = -2时,c = -4,当x = 1时,c = 5、 ……………………………5分由图像可知: -4≤ c < 5、 ………………………………………………7分 (3)∵抛物线y =ax 2+4ax +c 过点(-2,-2),∴c = 4a -2、∴抛物线解析式为:22442(2)2y ax ax a a x =++-=+-、 …………………8分 方法一: ① 当a > 0时,抛物线开口向上、∵抛物线对称轴为x =-2、∴当-1≤x ≤0时,y 随x 增大而增大、∵抛物线上的点到x 轴距离的最大值为4,由图像可知:4a -2=4、 ………………………………………………9分∴32a =、 …………………………………………………………10分 ② 当a < 0时,抛物线开口向下、∵抛物线对称轴为x =-2、∴当-1≤x ≤0时,y 随x 增大而减小、 ∵抛物线上的点到x 轴距离的最大值为4,由图像可知:4a -2= -4、 ……………………………………………11分∴12a =-、 …………………………………………………………12分 方法二: ∵-1≤x ≤0,∴当x = 0时,y = 4a -2;当x = -1时,y = a -2、 ……………8分 ∵当-1≤x ≤0时,抛物线上的点到x 轴距离的最大值为4、 ∴有两种情况:① 若424a -=,则3122a a ==-或、 ……………………9分 此时1242a -=<或5242a -=<,符合题意、 ………10分 ② 若24a -=,则a = 6或a = -2、 ………………………11分此时42224a -=>或42104a -=>、∴a = 6或a = -2不合题意,舍去、 ………………………12分综上所述: 3122a a ==-或、 25、 (本小题满分14分)解:(1)方法一:∵四边形ABCD 就是正方形,∴OA =OB ,∠AOB =∠BOE =90°、…………………………………………1分 ∵AF ⊥BE ,∴∠GAE+∠AEG =∠OBE +∠AEG =90°、∴∠ GAE =∠OBE 、 ………………………2分∴△AOH ≌ △BOE 、 ………………………3分∴AH =BE 、 …………………………………4分方法二:∵四边形ABCD 就是正方形,∴∠ABC =90°,AB =CB ,∠ABO =∠ECB =45°、 ……………………1分∵AF ⊥BE ,∴∠BAG+∠ABG =∠CBE +∠ABG =90°、∴∠BAH =∠CBE 、 ………………………………………………………2分 ∴△ABH ≌△BCE 、 ……………………………………………………3分 ∴AH =BE 、 ………………………………………………………………4分(2)方法一:∵∠AOH =∠BGH =90°, ∠AHO =∠BHG ,∴△AOH ∽△BGH 、 ……………………5分∴OH AH GH BH=、 …………………………6分 ∴OH GH AH BH=、 …………………………7分 ∵∠OHG =∠AHB 、∴△OHG ∽△AHB 、 ………………………………………………………8分 ∴∠AGO =∠ABO =45°,即∠AGO 的度数为定值、 ……………………9分方法二:如图,取AB 中点M ,连接MO ,MG 、 ………6分∵∠AGB =∠AOB =90°,∴AM =BM =GM =OM 、 ………………………7分∴点O ,G 在以AB 为直径的⊙M 上,即点A ,B ,G ,O 四点在以AB 为直径的⊙M 上, ………………………8分 ∴∠AGO =∠ABO =45°,即∠AGO 的度数为定值、 ………………………………………………9分(3)∵∠ABC =90°,AF ⊥BE ,∴∠BAG =∠FBG ,∠AGB =∠BGF =90°,∴△ABG ∽△BFG 、 ……………………………………………………………10分 ∴GF BG BG AG =, ∴AG ·GF =BG 2 =5、 …………………………………11分∵△AHB ∽△OHG ,∴∠BAH =∠GOH =∠GBF 、∵∠AOB =∠BGF =90°,∴∠AOG =∠GFC 、 ……………………………………………………………12分 ∵∠AGO =45°,CG ⊥GO ,∴∠AGO =∠FGC =45°、∴△AGO ∽△CGF 、 ………………………………………………………13分 ∴CGAG GF GO =, ∴GO ·CG =AG ·GF =5、∴S △OGC =12CG ·GO =52、 ……………………………………………………14分。
2018年漳州市初中毕业班质量检测化学试题5.29

2018年漳州市初中毕业班质量检测化学试题5.29D2345③检验CO2用饱和澄清石灰水较合适④吸收CO2用NaOH溶液较合适15.(19分)(1)根据下列实验装置图,回答问题。
A B C D E F①实验室加热氯酸钾和二氧化锰制取氧气的化学方程式为,用(填字母)装置收集到的氧气纯度最高。
②实验室制取二氧化碳发生装置为(填字母),制得的二氧化碳中常混有少量水蒸气,可通过盛有的F装置除去水蒸气,且从F装置的(填“a”或“b”)口通入。
(2)在金属活动性顺序中,位于前面的金属能把位于后面的金属从其盐溶液中置换出来。
化学小组同学将一小块金属钠投入一定量的5%硫酸铜溶液时,却没有得到红色铜。
[提出问题] 为什么没有得到红色的铜?[猜想与假设] 所用硫酸铜溶液的浓度过小。
[查阅资料]①氢氧化铜是蓝色絮状沉淀,难溶于水,受热至80℃以上分解为黑色氧化铜和水。
②氢氧化铜、氧化铜均可与盐酸反应,且产物相同。
实验实验操作实验现象解释与结论步骤1 钠块浮在水面,熔成银白色的小球,发出嘶嘶的响声,火光闪现,四处游动,最后消失,同时可观察到溶液变红钠与水反应生成氢气;从能量变化分析,属于反应;反应的化学方程式为步骤2黄块的变化与步骤1无明显差别,生成灰蓝色絮状沉淀生成蓝色絮状沉淀时的化学方程式为钠块的变化与步骤1无明显差别,生成大量灰蓝色絮状沉淀分别向B、C实验所得沉淀都完全消失,得到除了反应以外的结论6灰蓝色沉淀中加入等蓝绿色的溶液是量的盐酸结论:猜想与假设(填“成立”或“不成立”)。
[反思与评价1] 步骤1的作用是。
[实验二]在教师的指导下,小组同学又做了如下实验:将一滴饱和CuSO4溶液滴加在一块钠表面上,观察到长时间缓慢地产生气泡,生成灰黑色和蓝色糊状物;试剂X能将灰黑色和蓝色糊状物完全反应形成溶液,则试剂X为,写出有X参与的一个化学方程式。
[反思与评价2] C实验和实验二现象有明显差别,可能的原因是。
16.(4分)某工厂化验室用20%的氢氧化钠溶液洗涤一定量石油产品中的残余硫酸,共消耗氢氧化钠溶液20g,洗涤后的溶液呈中性。
2018漳州市质检物理试卷

2018年漳州市初中毕业班质量检测物理试题(满分:1(X )分;考试时间:90分钟)友情提示:请把所有答案填写(涂)到答题卡上!请不要错位、越界答题!!姓名班级考场/座位号注意;在解答题中,凡是涉及到画图,可先用铅笔画在答题卡上,后必须用膨粤等扌等重 描确认,否则无效。
(说明:本卷计算时,g 均取10N/kg )6. 摩擦与我们的生活息息相关。
假如没有摩擦,下列现象可能发生的是A.人可以正常走路 B.老师能用粉笔在黑板上写字C.火柴头可以划燃D.自行车刹车失灵7. 如图1所示,是闪电产生的电流通过避雷针的示意图(已知云层带正电)。
则下列说法 正确的是A. 闪电发生时,创造了电荷 一、单项选择题(每小题2分,共32分) 某矿石能吸引大头针,说明该矿石具有A.导电性B.磁性C.延展性D.弹性钢琴和小提琴同时演奏,我们能从声音中区分出哪种乐器发出的声音,是因为它们具有 不同的A.音色B.频率下列自然现象中,属于凝华的是A.冰雪消融B.雾淞奇景张芳在湖畔看到:柳树在水中摇曳, 景物中,是由于光的折射形成的是A.船儿B.白云1.2.3. 4. C.响度D.音调D.露水晶莹C.薄雾飘渺C.鱼儿“风云四号”正式投入使D. 柳树标志着中国气象卫星系统实现了更新换代。
该卫星将信息传冋地面的载体是A.电磁波B.超声波C.次声波D. 红外线C.闪电发生前避雷针也带正电D.图中的电流方向是从云层到避雷针8.如图2所示是四冲程汽油机工作示意图,把机械能转化为内能的冲程是9.将一个标有“220V60W”的灯泡接入某电路中,当通过它的电流为0.22 A,则它的实际功率A.大于60 WB.等于6() WC.小于6() WD.无法确定10.11.12.13. 小明和小华在操场上沿直线跑步,他们通过的路程和时间的关s/m 系如图3所示,则下列说法正确的是40A.0〜2 s,小明跑得更快30B.0〜2 s,小明相对小华是静止的C.8 s内,小华的平均速度是5 m/sD.小华做匀速直线运动“探究一个物体受几个力的作用时,引入合力的概念”釆用的是下列哪种物理研究方法A.控制变量法B.等效替代法C.模型法D.类比法弹簧测力计上挂一重为10N的金属块,当金属块体积的三分之一浸入水中时,测力计的示数为8N。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年漳州市初中毕业班质量检测
数学试题
(满分:150分;考试时:120分钟)
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选
项中,只有一项是符合题目要求的,请在答题卡
...的相应位置填涂)
1.如图,数轴上点M所表示的数的绝对值是()
A.3
B.-3
C.±3
D.-1
3
第1题图
2.“中国天眼”FAST射电望远镜的反射面总面积约250000m2,数据250000用科学记数法表示为()
A.25×104
B.2.5×105
C.2.5×106
D.0.25×106
3.如图是某几何体的左视图,则该几何体不可能
...是()
4.下列计算,结果等于x5的是()
A.x2+x3
B.x2·x3
C.x10÷x2
D.(x2)3
5.如图,在右框解分式方程的4个步骤中,根据等式基本性质的是()
A.①②
B.②④
C.①③
D.③④
6.如图,OP 平分∠AOB ,PC ⊥OA 于C ,点D 是OB 上的动点,若PC =6cm ,则PD 的长可以是()
A.3cm
B.4cm
C.5cm
D.7cm
7.如图,点A ,B 在方格纸的格点上,将线段AB 先向右平移3格,再向下平移2格,得线段DC ,点A 的对应点为D ,连接AD ,BC ,则关于四边形ABCD 的对称性,下列说法正确的是()
A.既是轴对称图形,又是中心对称图形
B.是中心对称图形,但不是轴对称图形
C.是轴对称图形,但不是中心对称图形
D.既不是轴对称图形,也不是中心对称图形8.甲、乙两地今年2月份前5天的日平均气温如图所示,则下列描述错误..
的是()
A.两地气温的平均数相同
B.甲地气温的众数是4℃
C.乙地气温的中位数是6℃
D.甲地气温相对比较稳定
第5题图第6题图
第7题图第8题图第9题图
9.如图,正六边形ABCDEF的中心与坐标原点O重合,其中A(-2,0).将六边形ABCDEF绕原点O按顺时针方向旋转2018次,每次旋转60°,则旋转后点A的对应点A′的坐标是()
A.(1,3)
B.(3,1)
C.(1,-3)
D.(-1,3)
10.如图,在矩形ABCD中,点A在x轴上,点B的坐标为(1,0),且C,D两
点在函数y x+1(x≥0)
-
1
2
x+1(x<0)的图象上,若在矩形ABCD内随机
取一点,则此点取自阴影部分的概率是()
A.1
2B.3
8
C.1
4
D.1
6
二、填空题(本大题共6小题,每小题4分,共24分.请将答案填入答题卡
...的相应位置)
11.因式分解:ax2-a=________.
12.一个不透明的袋子中装有4个红球、2个黑球,它们除颜色外其余都相同,
从中任意摸出3个球,则事件“摸出的球至少有1个红球”是________事件(
填
“必然”、“随机”或“不可能”).
第13题图
13.如图,DE是△ABC的中位线,若△ADE的面积为3,则△ABC的面积为________.
14.“若实数a,b,c满足a<b<c,则a+b<c”,能够说明该命题是假命题的一组
第10题图
数a ,b ,c 的值依次为________.
15.如图,在▱ABCD 中,点E ,F 分别在边AD ,BC 上,EF =2,∠DEF =60°,将四边形EFCD 沿EF 翻折,得到四边形EFC ′D ′,ED ′交BC 于点G ,则△GEF 的周长为________.
16.如图,双曲线y =k x (x >0)经过A ,B 两点,若点A 的横坐标为1,∠OAB =90°,且OA =AB ,则k 的值为________.
三、解答题(本大题共9小题,共86分.请在答题卡...的相应位置解答)
17.(本小题满分8分)计算:3-1+π0-19.
18.(本小题满分8分)如图,在△ABC 中,∠A =80°,∠B =40°.
(1)求作线段BC 的垂直平分线DE ,垂足为E ,交AB 于点D ;
(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,连接CD ,求证:AC =CD .
第15题图第16题图
第18题图
19.(本小题满分8分)求证:对角线相等的平行四边形是矩形.(要求:画出图形,写出已知和求证,并给予证明)
20.(本小题满分8分)为响应市政府关于“垃圾不落地·市区更美丽”的主题宣传活动,某校随机调查了部分学生对垃圾分类知识的掌握情况,调查选项分为“A:非常了解,B:比较了解,C:了解较少,D:不了解”四种,并将调查结果绘制成以下两幅不完整的统计图.
第20题图
请根据图中提供的信息,解答下列问题:
(1)把两幅统计图补充完整;
(2)若该校学生数1000名,根据调查结果,估计该校“非常了解”与“比较了解”的学生共有________名;
(3)已知“非常了解”的4名学生中有3名男生和1名女生,从中随机抽取2名向全校做垃圾分类的知识交流,请用画树状图或列表的方法,求恰好抽到1男1女的概率.
21.(本小题满分8分)如图,AB 是⊙O 的直径,AC 是弦,D 是BC ︵的中点,过点D
作EF 垂直于直线AC ,垂足为F ,交AB 的延长线于点E .
(1)求证:EF 是⊙O 的切线;
(2)若tan A =43
,AF =6,求⊙O 的半径.
第21题图
22.(本小题满分10分)某景区售票处规定:非节假日的票价打a 折售票;节假日根据团队人数x (人)实行分段售票:若x ≤10,则按原票价购买;若x >10,则其中10人按原票价购买,超过部分的按原票价打b 折购买.某旅行社带团到该景区游览,设在非节假日的购票款为y 1元,在节假日的购票款为y 2元,y 1,y 2与x 之间的函数图象如图所示.
第22题图
(1)观察图象可知:a =________,b =________;
(2)当x >10时,求y 2与x 之间的函数表达式;
(3)该旅行社在今年5月1日带甲团与5月10日(非节假日)带乙团到该景区游览,两团合计50人,共付门票款3120元.已知甲团人数超过10人,求甲团人数与乙团人数.
23.(本小题满分10分)阅读:所谓勾股数就是满足方程x 2+y 2=z 2
的正整数解,即满足勾股定理的三个正整数构成的一组数.我国古代数学专著《九章算术》一
书,在世界上第一次给出该方程的解为:x =12
(m 2-n 2),y =mn ,z =错误!(m 2+n 2),其中m >n >0,m ,n 是互质的奇数.
应用:当n =5时,求一边长为12的直角三角形另两边的长.24.(本小题满分10分)已知抛物线y =ax 2
+bx +c (a ,b ,c 是常数,a ≠0)的对称轴为直线x =-2.
(1)b =________;(用含a 的代数式表示)
(2)当a=-1时,若关于x的方程ax2+bx+c=0在-3<x<1的范围内有解,求c 的取值范围;
(3)若抛物线过点(-2,-2),当-1≤x≤0时,抛物线上的点到x轴距离的最大值为4,求a的值.
25.(本小题满分10分)如图,在正方形ABCD中,对角线AC,BD相交于点O,E 为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BC于F,交BO于H,连接OG,CG.
(1)求证:AH=BE;
(2)试探究:∠AGO的度数是否为定值?请说明理由;
(3)若OG⊥CG,BG=5,求△OGC的面积.
第25题图。
