西城区学习探究诊断七年级上
学习探究诊断七上答案

学习探究诊断七上答案【篇一:西城区学习探究诊断七年级上】试1 正数和负数学习要求了解正数、负数、有理数的概念,会用正数和负数表示相反意义的量.课堂学习检测一、判断题(正确的在括号内画“√”,错误的画“3”)( )1.某仓库运出30吨货记作-30吨,则运进20吨货记作+20吨. ( )2.节约4吨水与浪费4吨水是一对具有相反意义的量.( )3.身高增长1.2cm和体重减轻1.2kg是一对具有相反意义的量.( )4.在小学学过的数前面添上“-”号,得到的就是负数.二、填空题5.学校在大桥东面9千米处,那么大桥在学校______面-9千米处.6.如果以每月生产180个零件为准,超过的零件数记作正数,不足的零件数记作负数,那么1月生产160个零件记作______个,2月生产200个零件记作______个.7.甲冷库的温度为-6℃,乙冷库的温度比甲冷库低5℃,则乙冷库的温度是______.8.______既不是正数,也不是负数;它______整数,______有理数(填“是”或“不是”). 9.整数可以看作分母为1的______,有理数包括____________. 10.把下列各数填在相应的大括号内:13?427,?,8.5,?14,?2,0.5,?3.14,0,6,547正数集合{_______________________________________________________________?} 负数集合{_______________________________________________________________?} 非负数集合{_____________________________________________________________?} 有理数集合{_____________________________________________________________?}综合、运用、诊断一、填空题11.若把公元2008年记作+2008,那么-2008年表示______. 12.潜水艇上浮为正,下潜为负.若潜水艇原先在距水面80米深处,后来两次活动记录的情况是-10米,+20米,则现在潜水艇在距水面______米的深处.13.是正数而不是整数的有理数是____________________. 14.是整数而不是正数的有理数是____________________. 15.既不是正数,也不是负数的有理数是______________. 16.既不是真分数,也不是零的有理数是______________.1?7?2?95.527,0,+2004,-2?,1.12122122212222,?1,非负有理数有17.在下列数中:?, 11.11111,95.5311__________________________________________.二、判断题(正确的在括号里画“√”,错误的画“3”) ( )18.带有正号的数是正数,带有负号的数是负数. ( )19.有理数是正数和小数的统称.( )20.有最小的正整数,但没有最小的正有理数. ( )21.非负数一定是正数. ( )22.?11是负分数. 3三、解答题23.-3.782( ).(a)是负数,不是分数 (c)是负数,也是分数24.下面说法中正确的是( ).(a)正整数和负整数统称整数(b)不是分数,是有理数 (d)是分数,不是有理数 (b)分数不包括整数(c)正分数,负分数,负整数统称有理数 (d)正整数和正分数统称正有理数毫米,最小不小于______毫米.拓展、探究、思考(a)1个测试2 相反数数轴学习要求掌握一个数的相反数的求法和性质,学习使用数轴,借助数轴理解相反数的几何意义,会借助数轴比较有理数的大小.课堂学习检测一、填空题1.________________的两个数,叫做互为相反数;零的相反数是______.2.0.4与______互为相反数,______与-(-7)互为相反数,a的相反数是______. 3.规定了______、______和______的______叫数轴. 4.所有的有理数都能用数轴上的______来表示.5.数轴上,表示-3的点到原点的距离是______个单位长,与原点距离为3个单位长的点表示的数是______。
七年级数学9西城区学习探究诊断_第九章__不等式与不等式组

七年级数学 第九章 不等式与不等式组测试1 不等式及其解集学习要求知道不等式的意义;知道不等式的解集的含义;会在数轴上表示解集.课堂学习检测一、填空题1.用不等式表示:(1)m -3是正数______; (2)y +5是负数______; (3)x 不大于2______; (4)a 是非负数______; (5)a 的2倍比10大______; (6)y 的一半与6的和是负数______; (7)x 的3倍与5的和大于x 的31______; (8)m 的相反数是非正数______.2.画出数轴,在数轴上表示出下列不等式的解集: (1)⋅>213x (2)x ≥-4.(3)⋅≤51x(4)⋅-<312x二、选择题3.下列不等式中,正确的是( ). (A)4385-<-(B)5172< (C)(-6.4)2<(-6.4)3 (D)-|-27|<-(-3)3 4.“a 的2倍减去b 的差不大于-3”用不等式可表示为( ). (A)2a -b <-3 (B)2(a -b )<-3 (C)2a -b ≤-3 (D)2(a -b )≤-35.如图,天平右盘中的每个砝码的质量都是1g ,则物体A 的质量m (g)的取值范围在数轴上可表示为( ).三、解答题6.利用数轴求出不等式-2<x ≤4的整数解.综合、运用、诊断一、填空题7.用“<”或“>”填空: (1)-2.5______5.2;(2)114-______125-; (3)|-3|______-(-2.3); (4)a 2+1______0; (5)0______|x |+4; (6)a +2______a .8.“x 的23与5的差不小于-4的相反数”,用不等式表示为______. 二、选择题9.如果a 、b 表示两个负数,且a <b ,则( ). (A)1>ba (B)ba <1 (C)ba 11< (D)ab <110.如图,在数轴上表示的解集对应的是( ).(A)-2<x <4 (B)-2<x ≤4 (C)-2≤x <4 (D)-2≤x ≤4 11.a 、b 是有理数,下列各式中成立的是( ).(A)若a >b ,则a 2>b 2 (B)若a 2>b 2,则a >b (C)若a ≠b ,则|a |≠|b | (D)若|a |≠|b |,则a ≠b 12.|a |+a 的值一定是( ).(A)大于零 (B)小于零 (C)不大于零 (D)不小于零 三、判断题13.不等式5-x >2的解集有无数个. ( ) 14.不等式x >-1的整数解有无数个. ( ) 15.不等式32421<<-x 的整数解有0,1,2,3,4. ( ) 16.若a >b >0>c ,则.0>cab( )四、解答题17.若a 是有理数,比较2a 和3a 的大小.拓展、探究、思考18.若不等式3x -a ≤0只有三个正整数解,求a 的取值范围.19.对于整数a ,b ,c ,d ,定义bd ac c d b a -=,已知3411<<d b,则b +d 的值为_________. 测试2 不等式的性质学习要求知道不等式的三条基本性质,并会用它们解简单的一元一次不等式.课堂学习检测一、填空题1.已知a <b ,用“<”或“>”填空: (1)a +3______b +3; (2)a -3______b -3; (3)3a ______3b ;(4)2a______2b ; (5)7a -______7b -; (6)5a +2______5b +2;(7)-2a -1______-2b -1; (8)4-3b ______6-3a . 2.用“<”或“>”填空:(1)若a -2>b -2,则a ______b ; (2)若33ba <,则a ______b ; (3)若-4a >-4b ,则a ______b ;(4)22ba -<-,则a ______b .3.不等式3x <2x -3变形成3x -2x <-3,是根据______.4.如果a 2x >a 2y (a ≠0).那么x ______y . 二、选择题5.若a >2,则下列各式中错误的是( ). (A)a -2>0 (B)a +5>7 (C)-a >-2 (D)a -2>-4 6.已知a >b ,则下列结论中错误的是( ). (A)a -5>b -5 (B)2a >2b (C)ac >bc (D)a -b >0 7.若a >b ,且c 为有理数,则( ). (A)ac >bc (B)ac <bc (C)ac 2>bc 2 (D)ac 2≥bc 2 8.若由x <y 可得到ax >ay ,应满足的条件是( ). (A)a ≥0 (B)a ≤0 (C)a >0 (D)a <0 三、解答题9.根据不等式的基本性质解下列不等式,并将解集表示在数轴上. (1)x -10<0.(2).62121+->x x(3)2x ≥5.(4).131-≥-x 10.用不等式表示下列语句并写出解集:(1)8与y 的2倍的和是正数;(2)a 的3倍与7的差是负数.综合、运用、诊断一、填空题11.已知b <a <2,用“<”或“>”填空:(1)(a -2)(b -2)______0; (2)(2-a )(2-b )______0; (3)(a -2)(a -b )______0.12.已知a <b <0.用“>”或“<”填空:(1)2a ______2b ; (2)a 2______b 2; (3)a 3______b 3; (4)a 2______b 3; (5)|a |______|b |; (6)m 2a ______m 2b (m ≠0). 13.不等式4x -3<4的解集中,最大的整数x =______. 14.关于x 的不等式mx >n ,当m ______时,解集是m nx <;当m ______时,解集是mn x >. 二、选择题15.若0<a <b <1,则下列不等式中,正确的是( ).,11;11;1;1b a b a b a b a <><>④③②① (A)①③ (B)②③ (C)①④ (D)②④ 16.下列命题结论正确的是( ).①若a >b ,则-a <-b ;②若a >b ,则3-2a >3-2b ;③8|a |>5|a |. (A)①②③ (B)②③ (C)③ (D)以上答案均不对 17.若不等式(a +1)x >a +1的解集是x <1,则a 必满足( ).(A)a <0 (B)a >-1 (C)a <-1 (D)a <1 三、解答题18.当x 取什么值时,式子563-x 的值为(1)零;(2)正数;(3)小于1的数.拓展、探究、思考19.若m 、n 为有理数,解关于x 的不等式(-m 2-1)x >n .20.解关于x 的不等式ax >b (a ≠0).测试3 解一元一次不等式学习要求会解一元一次不等式.课堂学习检测一、填空题1.用“>”或“<”填空:(1)若x ______0,y <0,则xy >0;(2)若ab >0,则b a ______0;若ab <0,则ab______0; (3)若a -b <0,则a ______b ; (4)当x >x +y ,则y ______0. 2.当a ______时,式子152-a 的值不大于-3. 3.不等式2x -3≤4x +5的负整数解为______. 二、选择题4.下列各式中,是一元一次不等式的是( ). (A)x 2+3x >1 (B)03<-y x (C)5511≤-x(D)31312->+x x5.关于x 的不等式2x -a ≤-1的解集如图所示,则a 的取值是( ).(A)0 (B)-3 (C)-2 (D)-1三、解下列不等式,并把解集在数轴上表示出来 6.2(2x -3)<5(x -1). 7.10-3(x +6)≤1. 8.⋅-->+22531x x 9.⋅-≥--+612131y y y四、解答题 10.求不等式361633->---x x 的非负整数解.11.求不等式6)125(53)34(2+<-x x 的所有负整数解.综合、运用、诊断一、填空题12.若x 是非负数,则5231x-≤-的解集是______. 13.使不等式x -2≤3x +5成立的负整数是______.14.已知(x -2)2+|2x -3y -a |=0,y 是正数,则a 的取值范围是______. 二、选择题15.下列各对不等式中,解集不相同的一对是(______).(A)72423xx +<-与-7(x -3)<2(4+2x ) (B)3921+<-x x 与3(x -1)<-2(x +9) (C)31222-≥+x x 与3(2+x )≥2(2x -1) (D)x x ->+414321与3x >-116.如果关于x 的方程5432bx a x +=+的解不是负值,那么a 与b 的关系是( ). (A)b a 53> (B)a b 53≥ (C)5a =3b (D)5a ≥3b三、解下列不等式 17.(1)3[x -2(x -7)]≤4x . (2).17)10(2383+-≤--y y y(3).151)13(21+<--y y y (4).15)2(22537313-+≤--+x x x(5)).1(32)]1(21[21-<---x x x x(6)⋅->+-+2503.0.02.003.05.09.04.0x x x四、解答题18.x 取什么值时,代数式413--x 的值不小于8)1(32++x 的值.19.已知关于x 的方程3232x m x x -=--的解是非负数,m 是正整数,求m 的值.20.已知关于x ,y 的方程组⎩⎨⎧-=++=+134,123p y x p y x 的解满足x >y ,求p 的取值范围.21.已知方程组⎩⎨⎧-=++=+②①m y x m y x 12,312的解满足x +y <0,求m 的取值范围.拓展、探究、思考一、填空题22.(1)已知x <a 的解集中的最大整数为3,则a 的取值范围是______;(2)已知x >a 的解集中最小整数为-2,则a 的取值范围是______. 二、解答题23.适当选择a 的取值范围,使1.7<x <a 的整数解:(1)x 只有一个整数解; (2)x 一个整数解也没有. 24.当310)3(2k k -<-时,求关于x 的不等式k x x k ->-4)5(的解集.25.已知A =2x 2+3x +2,B =2x 2-4x -5,试比较A 与B 的大小.测试4 实际问题与一元一次不等式学习要求会从实际问题中抽象出不等的数量关系,会用一元一次不等式解决实际问题.课堂学习检测一、填空题 1.代数式231x-与代数式x -2的差是负数,则x 的取值范围为______. 2.6月1日起,某超市开始有偿..提供可重复使用的三种环保购物袋,每只售价分别为1元、2元和3元,这三种环保购物袋每只最多分别能装大米3千克、5千克和8千克.6月7日,小星和爸爸在该超市选购了3只环保购物袋用来装刚买的20千克散装大米,他们选购的3只环保购物袋至少..应付给超市______元. 二、选择题3.三角形的两边长分别为4cm和9cm,则下列长度的四条线段中能作为第三边的是( ).(A)13cm (B)6cm (C)5cm (D)4cm4.商场进了一批商品,进价为每件800元,如果要保持销售利润不低于15%,则售价应不低于( ).(A)900元(B)920元(C)960元(D)980元三、解答题5.某汽车厂改进生产工艺后,每天生产的汽车比原来每天的产量多6辆,那么15天的产量就超过了原来20天的产量,求原来每天最多能生产多少辆汽车?6.某次数学竞赛活动,共有16道选择题,评分办法是:答对一题给6分,答错一题倒扣2分,不答题不得分也不扣分.某同学有一道题未答,那么这个学生至少答对多少题,成绩才能在60分以上?综合、运用、诊断一、填空题7.若m>5,试用m表示出不等式(5-m)x>1-m的解集______.8.乐天借到一本72页的图书,要在10天之内读完,开始两天每天只读5页,那么以后几天里每天至少要读多少页?设以后几天里每天要读x页,列出的不等式为______.二、选择题9.九年级(1)班的几个同学,毕业前合影留念,每人交0.70元.一张彩色底片0.68元,扩印一张相片0.50元,每人分一张.在收来的钱尽量用掉的前提下,这张相片上的同学最少有( ).(A)2人(B)3人(C)4人(D)5人10.某市出租车的收费标准是:起步价7元,超过3km时,每增加1km加收2.4元(不足1km 按1km计).某人乘这种出租车从甲地到乙地共支付车费19元,设此人从甲地到乙地经过的路程是x km,那么x的最大值是( ).(A)11 (B)8 (C)7 (D)5三、解答题11.某种商品进价为150元,出售时标价为225元,由于销售情况不好,商品准备降价出售,但要保证利润不低于10%,那么商店最多降价多少元出售商品?12.某工人加工300个零件,若每小时加工50个就可按时完成;但他加工2小时后,因事停工40分钟.那么这个工人为了按时或提前完成任务,后面的时间每小时他至少要加工多少个零件?拓展、探究、思考13.某零件制造车间有20名工人,已知每名工人每天可制造甲种零件6个或乙种零件5个,且每制造一个甲种零件可获利150元,每制造一个乙种零件可获利260元.在这20名工人中,车间每天安排x 名工人制造甲种零件,其余工人制造乙种零件. (1)若此车间每天所获利润为y (元),用x 的代数式表示y .(2)若要使每天所获利润不低于24000元,至少要派多少名工人去制造乙种零件?14.某单位要印刷一批宣传资料,在需要支付制版费600元和每份资料0.3元印刷费的前提下,甲、乙两个印刷厂分别提出了不同的优惠条件,甲印刷厂提出:凡印刷数量超过2000份的,超过部分的印刷费可按9折收费;乙印刷厂提出:凡印刷数量超过3000份的,超过部分印刷费可按8折收费.(1)若该单位要印刷2400份宣传资料,则甲印刷厂的费用是______,乙印刷厂的费用是______.(2)根据印刷数量大小,请讨论该单位到哪家印刷厂印刷资料可获得更大优惠?测试5 一元一次不等式组(一)学习要求会解一元一次不等式组,并会利用数轴正确表示出解集.课堂学习检测一、填空题1.解不等式组⎩⎨⎧>--<+②①223,423x x 时,解①式,得______,解②式,得______;于是得到不等式组的解集是______.2.解不等式组⎪⎩⎪⎨⎧-≥--≥-②①21,3212x x 时,解①式,得______,解②式,得______;于是得到不等式组的解集是______.3.用字母x 的范围表示下列数轴上所表示的公共部分:二、选择题 4.不等式组⎩⎨⎧+<+>-5312,243x x x 的解集为( ).(A)x <-4 (B)x >2 (C)-4<x <2 (D)无解5.不等式组⎩⎨⎧>+<-023,01x x 的解集为( ).(A)x >1(B)132<<-x (C)32-<x (D)无解三、解下列不等式组,并把解集表示在数轴上 6.⎩⎨⎧≥-≥-.04,012x x7.⎩⎨⎧>+≤-.074,03x x8.⎪⎩⎪⎨⎧+>-<-.3342,121x x x x9.-5<6-2x <3.四、解答题10.解不等式组⎪⎩⎪⎨⎧<-+≤+321),2(352x x x x 并写出不等式组的整数解.综合、运用、诊断一、填空题11.当x 满足______时,235x-的值大于-5而小于7. 12.不等式组⎪⎪⎩⎪⎪⎨⎧≤-+<2512,912x x x x 的整数解为______.二、选择题13.如果a >b ,那么不等式组⎩⎨⎧<<b x a x ,的解集是( ).(A)x <a (B)x <b(C)b <x <a(D)无解14.不等式组⎩⎨⎧+>+<+1,159m x x x 的解集是x >2,则m 的取值范围是( ).(A)m ≤2 (B)m ≥2 (C)m ≤1 (D)m ≥1三、解答题 15.求不等式组73123<--≤x 的整数解.16.解不等式组⎪⎩⎪⎨⎧-<-->-->+.3273,4536,7342x x x x x x17.当k 取何值时,方程组⎩⎨⎧-=+=-52,53y x k y x 的解x ,y 都是负数.18.已知⎩⎨⎧+=+=+122,42k y x k y x 中的x ,y 满足0<y -x <1,求k 的取值范围.拓展、探究、思考19.已知a 是自然数,关于x 的不等式组⎩⎨⎧>-≥-02,43x a x 的解集是x >2,求a 的值.20.关于x 的不等式组⎩⎨⎧->-≥-123,0x a x 的整数解共有5个,求a 的取值范围.测试6 一元一次不等式组(二)学习要求进一步掌握一元一次不等式组.课堂学习检测一、填空题1.直接写出解集: (1)⎩⎨⎧->>3,2x x 的解集是______;(2)⎩⎨⎧-<<3,2x x 的解集是______;(3)⎩⎨⎧-><3,2x x 的解集是_______; (4)⎩⎨⎧-<>3,2x x 的解集是______.2.如果式子7x -5与-3x +2的值都小于1,那么x 的取值范围是______.二、选择题 3.已知不等式组⎩⎨⎧->--+-≤-).23(2)1(53,1)1(3)3(2x x x x x 它的整数解一共有( ).(A)1个 (B)2个(C)3个(D)4个4.若不等式组⎩⎨⎧>≤<kx x ,21有解,则k 的取值范围是( ).(A)k <2 (B)k ≥2 (C)k <1 (D)1≤k <2三、解下列不等式组,并把解集在数轴上表示出来5.⎪⎩⎪⎨⎧⋅>-<-322,352x x x x6.⎪⎩⎪⎨⎧->---->-.6)2(3)3(2,132x x xx7.⎪⎩⎪⎨⎧+>-≤+).2(28,142x x x8..234512x x x -≤-≤-综合、运用、诊断一、填空题9.不等式组⎪⎩⎪⎨⎧⋅<->+233,152x x 的所有整数解的和是______,积是______.10.k 满足______时,方程组⎩⎨⎧=-=+4,2y x k y x 中的x 大于1,y 小于1.二、解下列不等式组11.⎪⎪⎩⎪⎪⎨⎧<+->+--.1)]3(2[21,312233x x x x x12.⎪⎪⎪⎩⎪⎪⎪⎨⎧⋅>-->-->-24,255,13x x x x x x三、解答题13.k 取哪些整数时,关于x 的方程5x +4=16k -x 的根大于2且小于10?14.已知关于x ,y 的方程组⎩⎨⎧-=-+=+34,72m y x m y x 的解为正数,求m 的取值范围.拓展、探究、思考15.若关于x 的不等式组⎪⎪⎩⎪⎪⎨⎧+<+->+a x x x x 322,3215只有4个整数解,求a 的取值范围.测试7 利用不等关系分析实际问题学习要求利用不等式(组)解决较为复杂的实际问题;感受不等式(组)在实际生活中的作用.课堂学习检测列不等式(组)解应用题1.一个工程队原定在10天内至少要挖掘600m 3的土方.在前两天共完成了120m 3后,接到要求要提前2天完成掘土任务.问以后几天内,平均每天至少要挖掘多少土方?2.某城市平均每天产生垃圾700吨,由甲、乙两个垃圾厂处理.如果甲厂每小时可处理垃圾55吨,需花费550元;乙厂每小时处理45吨,需花费495元.如果规定该城市每天用于处理垃圾的费用的和不能超过7150元,问甲厂每天至少要处理多少吨垃圾?3.若干名学生,若干间宿舍,若每间住4人将有20人无法安排住处;若每间住8人,则有一间宿舍的人不空也不满.问学生有多少人?宿舍有几间?4.2008年5月12日,汶川发生了里氏8.0级地震,给当地人民造成了巨大的损失.某中学全体师生积极捐款,其中九年级的3个班学生的捐款金额如下表:老师统计时不小心把墨水滴到了其中两个班级的捐款金额上,但他知道下面三条信息:信息一:这三个班的捐款总金额是7700元;信息二:二班的捐款金额比三班的捐款金额多300元;信息三:一班学生平均每人捐款的金额大于..51元...48元,小于请根据以上信息,帮助老师解决:(1)二班与三班的捐款金额各是多少元?(2)一班的学生人数是多少?综合、运用、诊断5.某学校计划组织385名师生租车旅游,现知道出租公司有42座和60座客车,42座客车的租金为每辆320元,60座客车的租金为每辆460元.(1)若学校单独租用这两种客车各需多少钱?(2)若学校同时租用这两种客车8辆(可以坐不满),而且比单独租用一种车辆节省租金,请选择最节省的租车方案.拓展、探究、思考6.在“5·12大地震”灾民安置工作中,某企业接到一批生产甲种板材24000m2和乙种板材12000m2的任务.某灾民安置点计划用该企业生产的这批板材搭建A,B两种型号的板房共400间,在搭建过程中,按实际需要调运这两种板材.已知建一间A型板房和一间B问:这400间板房最多能安置多少灾民?参考答案第九章 不等式与不等式组测试11.(1)m -3>0;(2)y +5<0;(3)x ≤2;(4)a ≥0;(5)2a >10; (6)2y +6<0;(7)3x +5>3x;(8)-m ≤0. 2.3.D . 4.C . 5.A . 6.整数解为-1,0,1,2,3,4. 7.(1)>;(2)>;(3)>;(4)>;(5)<;(6)>. 8..4523≥-x 9.A . 10.B . 11.D . 12.D . 13.×. 14.√. 15.√. 16.×. 17.当a >0时,2a <3a ;当a =0时,2a =3a ;当a <0时,2a >3a . 18.x ≤3a,且x 为正整数1,2,3. ∴9≤a <12. 19.+3或-3.测试21.(1)<;(2)<;(3)<;(4)<;(5)>;(6)<;(7)>;(8)<. 2.(1)>;(2)<;(3)<;(4)>.3.不等式两边加(或减)同一个数(或式子),不等号的方向不变. 4.>. 5.C . 6.C . 7.D . 8.D . 9.(1)x <10,解集表示为(2)x >6,解集表示为(3)x ≥2.5,解集表示为(4)x ≤3,解集表示为10.(1)8+2y >0,解集为y >-4. (2)3a -7<0,解集为37<a . 11.(1)>;(2)>;(3)<. 12.(1)<;(2)>;(3)<;(4)>;(5)>;(6)<. 13.1. 14.<0;>0. 15.B . 16.D . 17.C .18.(1)x =2;(2)x >2;(3)311<x . 19.∵-m 2-1<0,⋅--<∴12m nx20.当a >0时,a b x >;当a <0时,ab x <. 测试31.(1)<;(2)>;<;(3)<;(4)<. 2.≤-5. 3.-4,-3,-2,-1. 4.D . 5.D . 6.x >-1,解集表示为7.x ≥-3,解集表示为8.x >6,解集表示为9.y ≤3,解集表示为10.413<x 非负整数解为0,1,2,3. 11.x >-8,负整数解为-7,-6,-5,-4,-3,-2,-1.12.0≤x ≤4. 13.-3,-2,-1. 14.a <4. 15.B . 16.D . 17.(1)x ≥6. (2)625≤y . (3)y <5. (4)23-≥x . (5)x <-5. (6)x <9. 18.57≤x . 19.m ≤2,m =1,2. 20.p >-6. 21.①+②;3(x +y )=2+2m .∵x +y <0.∴2+2m <0.∴m <-1. 22.(1)3<a ≤4;(2)-3≤a <-2. 23.(1)2<a ≤3;(2)1.7<a ≤2. 24.⋅-<4k k x 25.A -B =7x +7.当x <-1时,A <B ;当x =-1时,A =B ;当x >-1时,A >B .测试41.x >1. 2.8. 3.B . 4.B .5.设原来每天能生产x 辆汽车.15(x +6)>20x .解得x <18,故原来每天最多能生产17辆 汽车. 6.设答对x 道题,则6x -2(15-x )>60,解得4111>x ,故至少答对12道题. 7.⋅--<mmx 51 8.(10-2)x ≥72-5×2. 9.C . 10.B . 11.设应降价x 元出售商品.225-x ≥(1+10%)×150,x ≤60. 12.设后面的时间每小时加工x 个零件,则250300)32250300(⨯-≥--x ,解得x ≥60. 13.(1)y =-400x +26000, 0≤x ≤20;(2)-400x +26000≥24000, x ≤5, 20-5=15. 至少派15人去制造乙种零件.14.(1)1308元;1320元. (2)大于4000份时去乙厂;大于2000份且少于4000份时去甲厂;其余情况两厂均可.测试51..2;21;2-<<-<x x x 2..361;3;61≤≤≤≥x x x3.(1)x >-1; (2)0<x <2; (3)无解. 4.B . 5.B . 6.421≤≤x ,解集表示为7.x ≥0,解集表示为8.无解. 9.1.5<x <5.5解集表示为10.-1≤x <3,整数解为-1、0、1、2. 11.-3<x <5. 12.-2,-1,0. 13.B . 14.C . 15.-10<x ≤-4,整数解为-9,-8,-7,-6,-5,-4.16.-1<x <4. 17.-721<k <25.(⎩⎨⎧<--=<-=015213,02513k y k x )18.①-②得:y -x =2k -1,∵0<y -x <1 ∴0<2k -1<1 ∴.121<<k 19.解得⎪⎩⎪⎨⎧>+≥.2,34x a x 于是234≤+a ,故a ≤2;因为a 是自然数,所以a =0,1或2. 20.不等式组的解集为a ≤x <2,-4<a ≤-3.测试6 1.(1)x >2;(2)x <-3;(3)-3<x <2;(4)无解. 2.31<x <76. 3.B . 4.A . 5.(1)x >6,解集表示为6.-6<x <6,解集表示为7.x <-12,解集表示为8.x ≤-4,解集表示为9.7;0. 10.-1<k <3. 11.无解. 12.x >8. 13.由2<x =328-k <10,得1<k <4,故整数k =2或3. 14..532.5,23<<-⎩⎨⎧-=+=m m y m x 15.不等式组的解集为2-3a <x <21,有四个整数解,所以x =17,18,19,20,所以16≤2-3a <17,解得⋅-≤<-3145a 测试71.设以后几天平均每天挖掘x m 3的土方,则(10-2-2)x ≥600-120,解得x ≥80. 2.设该市由甲厂处理x 吨垃圾,则7150)700(4549555550≤-+x x ,解得x ≥550. 3.解:设宿舍共有x 间.⎩⎨⎧+<-+>.204)1(8,2048x x x x 解得5<x <7. ∵x 为整数,∴x =6,4x +20=44(人).4.(1)二班3000元,三班2700元; (2)设一班学生有x 人,则⎩⎨⎧><200051200048x x 解得3241511139<<x ∵x 为整数.∴x =40或41. 5.(1)61942385=÷ 单独租用42座客车需10辆.租金为320×10=3200; 125660385=÷ 单独租用60座客车需7辆.租金为460×7=3220.(2)设租用42座客车x 辆,则60座客车需(8-x )辆.⎩⎨⎧<-+≥-+.3200)8(460320,385)8(6042x x x x 解得⋅≤<1855733x x 取整数,x =4,5.当x =4时,租金为3120元;x =5时,租金为2980元. 所以租5辆42座,3辆60座最省钱. 6.设生产A 型板房m 间,B 型板房(400-m )间. 所以⎩⎨⎧≤-+≤-+.12000)400(4126,24000)400(7854m m m m解得m ≥300.所以最多安置2300人.西城区七年级数学第九章不等式与不等式组测试一、填空题1.用“>”或“<”填空:(1)m +3______m -3;(2)4-2x ______5-2x ;(3)13-y ______3y-2;(4)a <b <0,则a 2______b 2; (5)若23yx -<-,则2x ______3y . 2.满足5(x -1)≤4x +8<5x 的整数x 为______.3.若11|1|=--xx ,则x 的取值范围是______. 4.若点M (3a -9,1-a )是第三象限的整数点,则M 点的坐标为______.5.一个两位数,它的十位数字比个位数字小2,如果这个数大于20且小于40,那么此数为_______. 二、选择题6.若a ≠0,则下列不等式成立的是( ). (A)-2a <2a (B)-2a <2(-a ) (C)-2-a <2-a(D)aa 22<-7.下列不等式中,对任何有理数都成立的是( ). (A)x -3>0 (B)|x +1|>0 (C)(x +5)2>0 (D)-(x -5)2≤0 8.若a <0,则关于x 的不等式|a |x <a 的解集是( ). (A)x <1 (B)x >1 (C)x <-1 (D)x >-19.如下图,对a ,b ,c 三种物体的重量判断正确的是( ).(A)a <c (B)a <b (C)a >c (D)b <c10.某商贩去菜摊卖黄瓜,他上午卖了30斤,价格为每斤x 元;下午他又卖了20斤,价格为每斤y 元.后来他以每斤2yx +元的价格卖完后,结果发现自己赔了钱,其原因是( ). (A)x <y (B)x >y (C)x ≤y (D)x ≥y三、解不等式(组),并把解集在数轴上表示出来11.11252476312-+≥---x x x .12.⎪⎩⎪⎨⎧<+-+--≤+.121331),3(410)8(2x x x x四、解答题13.x 取何整数时,式子729+x 与2143-x 的差大于6但不大于8.14.如果关于x 的方程3(x +4)-4=2a +1的解大于方程3)43(414-=+x a x a 的解.求a 的取值范围.15.不等式m m x ->-2)(31的解集为x >2.求m 的值.16.某车间经过技术改造,每天生产的汽车零件比原来多10个,因而8天生产的配件超过200个.第二次技术改造后,每天又比第一次技术改造后多做配件27个,这样只做了4天,所做配件个数就超过了第一次改造后8天所做配件的个数.求这个车间原来每天生产配件多少个?17.仔细观察下图,认真阅读对话:根据对话的内容,试求出饼干和牛奶的标价各是多少?18.为了保护环境,某造纸厂决定购买20台污水处理设备,现有A ,B 两种型号的设备,其中每台的价格、日处理污水量如下表:经预算,该纸厂购买设备的资金不能高于410万元. (1)该企业有几种购买方案;(2)若纸厂每日排出的污水量大于8060吨而小于8172吨,为了节约资金,该厂应选择哪种购买方案?19.某班级为准备元旦联欢会,欲购买价格分别为2元,4元和10元的三种奖品,每种奖品至少购买1件,共买16件,恰好用去50元.若2元的奖品购买a 件. (1)用含a 的代数式表示另外两种奖品的件数; (2)请你设计购买方案,并说明理由.参考答案第九章 不等式与不等式组测试1.(1)>;(2)<;(3)>;(4)>;(5)>. 2.9,10,11,12,13.3.x <1. 4.(-3,-1) 5.24或35. 6.C . 7.D . 8.C 9.C 10.B .11.x ≤2,解集表示为12.-1<x ≤1,解集表示为13.6310<≤-x ,整数解为-3,-2,-1,0,1,2,3,4,5. 14.a a 316372->-,解得187>a . 15.x >6-2m ,m =2. 16.设原来每天生产配件x 个.200<8(x +10)<4(x +10+27). 15<x <17. x =16.17.设饼干x 元,牛奶y 元.⎪⎩⎪⎨⎧-=+>+<.8.0109.0,10,10y x y x x 8<x <10,x 为整数,⎩⎨⎧==∴.1.1,9y x 18.(1)设购买A 型设备x 台,B 型设备(20-x )台.24x +20(20-x )≤410. x ≤2.5, ∴x =0,1,2.三种方案:方案一:A :0台;B :20台; 方案二:A :1台;B :19台;方案三:A :2台;B :18台.(2)依题意8060<480x +400(20-x )<8172.0.75<x <2.15,x =1,2.当x =1时,购买资金为404万元;x =2时,购买资金为408万元.为节约资金,应购买A 型1台,B 型19台.19.(1)4元的件数;3455a -;10元的件数:⋅-37a (2)有两种方案:方案一:2元10件,4元5件,10元1件;方案二:2元13件,4元1件,10元2件.。
新版西城区学习探究诊断七年级上册_第4章__图形认识初步
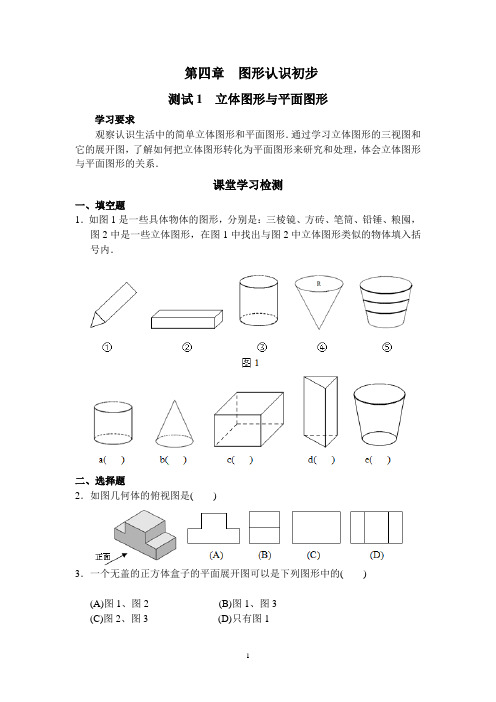
第四章图形认识初步测试1 立体图形与平面图形学习要求观察认识生活中的简单立体图形和平面图形.通过学习立体图形的三视图和它的展开图,了解如何把立体图形转化为平面图形来研究和处理,体会立体图形与平面图形的关系.课堂学习检测一、填空题1.如图1是一些具体物体的图形,分别是:三棱镜、方砖、笔筒、铅锤、粮囤,图2中是一些立体图形,在图1中找出与图2中立体图形类似的物体填入括号内.二、选择题2.如图几何体的俯视图是( )3.一个无盖的正方体盒子的平面展开图可以是下列图形中的( )(A)图1、图2 (B)图1、图3(C)图2、图3 (D)只有图14.如图,从上面看该物体得到的平面图形是( )(A) (B) (C) (D) 5.如果用□表示1个立方体,那么下面右图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( )6.甲、乙、丙、丁四人分别面对面坐在一张四边形桌子旁边(如图所示),桌上一张纸上写着字母“W ”.甲说他看到的是“W ”,乙说他看到的是“”,丙说他看到的是“W”,丁说他看到的是“”,则下列说法中正确的是().(A)丙在乙的对面,丙的左边是甲,右边是丁 (B) 甲在乙的对面,甲的右边是丙,左边是丁 (C)甲在丁的对面,乙在甲的左边,丙在丁的右边 (D)甲在丁的对面,乙在甲的右边,丙在丁的右边综合、运用、诊断一、填空题7.分别写出表面能展开成如图所示的10个平面图的几何体的名称.W8.小熊的房子如图所示,松鼠、大象、小鸟从三个不同的角度观察此房子,则松鼠观察到的是,大象观察到的是,小鸟观察到的是.二、选择题9.如图是一个长方体包装盒,则它的平面展开图是( ).10.一个几何体是由一些大小相同的正方块摆成的,其俯视图与主视图如图所示,则组成这个几何体的小正方块最多..有( ). (A) 4个 (B)5个 (C)6个 (D)7个11.如图是正方体的一种展开图,其中每个面上都标有一个数字。
那么在原正方体中,与数字“2”相对的面上的数字是( )(A)1 (B)4 (C)5 (D)6 三、画图12.请画出如图所示物体的视图. (1)从上面看;(2)从正面看;(3)从左面看.13.将如图所示的正方体纸盒沿所示的粗线剪开,请画出其平面展开图的示意图.从正面看从左面看从上面看拓展、探究、思考14.由若干个相同的小正方体搭成一个几何体,从上向下看如图所示,小正方形中的数字表示该位置的小正方体的个数,则这个几何体的从正面看是( )测试2 点、线、面、体学习要求知道点是几何学中最基本的概念.点动成线,线动成面,面动成体.课堂学习检测一、填空题1.把下面几何体的标号写在相对应的括号里:长方体:{ } 棱柱体:{ }圆柱体:{ } 球体:{ }圆锥体:{ }2.面与面相交得到______,线与线相交得到______,圆锥的侧面和底面相交成______条线,这条线是______线(填“直”或“曲”).3.几何图形是由、、、构成的;四棱锥的底面一定是形;如图,三棱锥有面,他们相交形成了条棱,这些棱相交形成了点.4.笔尖在纸上划过就能写出汉字,这说明了___ ___;汽车的雨刮器摆动就能刮去挡风玻璃上的雨滴,这说明了____ __;长方形纸片绕它的一边旋转形成了一个圆柱体,这说明了____ __.5.如图,左面的几何体叫三棱柱,它有5个面,9条棱,6个顶点,中间和右边的几何体分别是四棱柱和五棱柱.(1)四棱柱有______个顶点,______条棱,______个面;(2)五棱柱有______个顶点,______条棱,______个面;(3)由此猜出n棱柱有______个顶点,______条棱,______个面.二、选择题6.按组成面的侧面“平”与“曲”划分,与圆柱为同一类的几何体是( ).(A)圆锥(B)长方体(C)正方体(D)棱柱7.如图所示,将平面图形绕轴旋转一周,得到的几何体是( )综合、运用、诊断解答题8.如图,第一行的图形绕虚线旋转一周,便能形成第二行的某个几何体,用线连一连.9.图(1)、(2)是否是几何体的展开平面图,先想一想,再折一折,如果是,请说出折叠后的几何体名称、底面形状、侧面形状、棱数、侧棱数与顶点数.10.现将一个长为4cm,宽为3cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的别是多大?(结果保留π)11.两个往前相同的长方体的长、宽、高分别为3,2,1,把它们叠放在一起组成一个新的长方体,在这些新长方体中,表面积的最小值为多少?拓展、探究、思考14.下面有编号Ⅰ~Ⅸ的九个多面体.(1)如果我们用V表示多面体的顶点数,E表示多面体的棱数,F表示多面体的面数.请分别数一下这些多面体的V,E,F各是多少?(2)想一想,V,E,F之间有什么关系?测试3 直线、射线、线段学习要求理解两点确定一条直线的事实,并体会它们在解决实际问题中的作用;掌握直线、射线、线段的表示方法,建立初步的符号感;理解直线、射线、线段的联系和区别,进一步发展抽象概括的能力.课堂学习检测一、填空题1.要把木条固定在墙上至少要钉______个钉子,这是因为____________________.2.经过一点的直线有______条;经过两点的直线有______条;并且______一条;经过三点的直线______存在,如点C不在经过A、B两点的直线AB上,那么______经过A、B、C三点的直线.3.把线段向一个方向延长,得到的是________;把线段向两个方向延长,得到的是______.4.线段有______个端点,射线有______个端点,直线有______个端点.5.如图,点O在线段AB______;点B在射线AB______;点A是线段AB的一个______.6.如图,图中有______条射线,______条线段,这些线段是__________.7.如图,AC ,BD 交于点O ,图中共有______条线段,它们分别是______.8.如图,图中有______条线段,它们是______,图中以A 点为端点的射线有______条,它们是______,图中有______条直线,它们是______.9.下列说法中,所有正确说法的序号是.①射线AB 和射线BA 是同一条射线;②反向延长射线MN 到C ;③延长线段MN 到A 使NA=MA ;④连接两点的线段叫做两点间的距离. 二、选择题10.下图对“反向延长线段CD ”这句话表示正确的是( ).11.如图所示,有直线、射线和线段,根据图中的特征判断其中能相交的是( )12.有下列说法:①直线是射线长度的2倍;②线段AB 是直线BA 的一部分;③直线、射线、线段中,线段最短.其中说法正确的有( ) (A)3个 (B)2个 (C)1个 (D)0个 三、作图题13.如图,已知平面上有四个点A ,B ,C ,D .(1)连接AB ,并画出AB 的中点P ;(2)作射线AD ;(3)作直线BC 与射线AD 交于点E .综合、运用、诊断ADCB一、判断题(正确的画“√”,错误的画“×”)( )(1)右图中,射线EO和射线ED是同一条射线;( )(2)右图中,射线EO和射线OE是同一条射线;( )(3)右图中,射线EO和射线OD是同一条射线;( )(4)右图中,线段DE和线段ED是同一条线段;( )(5)右图中,直线DO和直线ED是同一条直线;( )(6)两条线段最多有一个公共点;( )(7)反向延长射线AB;( )(8)延长直线AB到C;( )(9)射线是直线长度的一半;( )(10)在一条直线上取n个点可以得到2n条射线;( )(11)三点能确定三条直线;( )(12)如果直线a和b有两个公共点,那么它们一定重合;( )(13)延长线段AB就得到直线AB;( )(14)若三条直线两两相交,则交点有三个;( )(15)两条直线的位置关系有两种:相交或平行.二、解答题15.回答下列问题:(1)两条直线在同一平面内的位置关系有几种?(2)画图表示,两条直线可以把一个平面分成几个部分?三条直线呢?(3)画图表示,平面上4条直线最多可以把一个平面分成多少个部分?(4)平面上n条直线最多可以把一个平面分成多少个部分?拓展、探究、思考16.如图,两条直线相交只有1个焦点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,六条直线相交最多有个交点,二十条直线相交最多有个交点,n条直线相交最多有个交点.1个交点3个交点6个交点10个交点17.解答下列问题:(1)经过平面上三个点中的每两点画直线,一共可以画多少条直线?(2)经过平面上四个点中的每两点画直线,一共可以画多少条直线?(3)若在平面上有n个点,过其中任意两点画直线,最多可以画几条直线?测试4 线段的比较学习要求理解线段的性质,线段的中点和两点间的距离,能对线段进行度量和比较.课堂学习检测一、填空题1.(1)把一条线段二等分的______叫做这条线段的______.(2)______叫做两点间的距离.(3)若A、B、C、D为直线l上顺次四点,则AB+BD=AC+______;AC+BD=AD+______.(4)若点C在线段AB的延长线上,则AC与AB的大小关系是______,并且AB+BC=______,AC-AB=______.(5)线段的基本性质是__________________________________________.(6)如图,A是直线BC外一点,请用不等号分别连接下列各式:AB+AC______BC;AB+BC______AC;AC+BC______AB;想一想:AB-AC________BC2.如图,点C ,D 在线段上,且C 为AB 的一个四等分点,D 为AC 中点.若BC=2,则BD 的长为.二、选择题3.在所有连接两点的线中( ) (A)直线最短 (B)线段最短 (C)弧线最短 (D)射线最短 4.在下列说法中,正确的是( )(A)任何一条线段都有中点(B)射线AB 和射线BA 是同一射线 (C)延长线段AB 就得到直线AB (D)连接A ,B 就得到AB 的距离 5.如图,下列说法中不正确...的是( )(A)直线AC 经过点A(B)射线DE 与直线AC 有公共点 (C)点D 在直线AC 上(D)直线AC 与线段BD 相交于点A综合、运用、诊断一、选择题6.如下图,从A 地到B 地有多条道路,人们会走中间的直路,而不会走其他的曲折的路,这是因为( ).(A)两点确定一条直线 (B)两点之间线段最短(C)两直线相交只有一个交点 (D)两点间的距离7.对于线段的中点,有以下几种说法: ①因为AM =MB ,所以M 是AB 的中点;②若AM =MB =21AB ,则M 是AB 的中点;③若AM =21AB ,则M 是AB 的中点;④若A ,M ,B 在一条直线上,且AM =MB ,则M 是AB 的中点.其中说法正确的是( ). (A)①②③ (B)①③ (C)②④ (D)以上结论都不对 8.(1)如果C 是线段AB 上的一点,线段AB =9cm ,BC =1cm ,那A ,C 两点的距离是( ). (A)8cm (B)10cm (C)8cm 或10cm (D)以上都不对 (2)如果C 为射线AB 上的一点,线段AB =9cm ,BC =1cm ,那A ,C 两点的距离是( ). (A)8cm (B)10cm (C)8cm 或10cm (D)以上都不对(2)如果C为直线AB上的一点,线段AB=9cm,BC=1cm,那A,C两点的距离是( ).(A)8cm (B)10cm (C)8cm或10cm (D)以上都不对(3)已知线段AB=10cm,BC=1cm,那么下列说法正确的是( )(A)AC=8cm (B)AC=10cm(C)AC=8cm或10cm (D)不能确定AC的长度9.已知线段AB=10cm,AP+BP=20cm.下列说法正确的是( )(A)点P不能在直线AB上(B)点P只能在直线AB上(C)点P只能在线段AB的延长线上(D)点P不能在线段AB上10.已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱的侧面展开图是( )(A) (B) (C) (D)二、作图题11.已知线段a,b,c.用圆规和直尺画图(不用写画法,保留画图痕迹).(1)画线段AB,使得AB=a+b-c;(2)画直线AB,在直线AB外任取一点K,画射线AK和直线BK;(3)延长KA至点P,使AP=KA,画线段PB,比较所画图形中线段PA与BK的和与线段AB的大小.三、解答题12.如图所示,点C在线段AB的延长线上,且BC=2AB,D是AC的中点,若AB=2cm,求BD的长.解:∵AB=2cm,BC=2AB,∴BC=4cm.∴AC=AB+______=______cm.∵D是AC的中点,∴AD= 12______=______cm.∴BD=AD-______=______cm.13.已知C为线段AB的中点,AB=10cm,D是AB上一点,若CD=2cm,求BD的长.14.如图,已知A,B,C,D顺次在同一直线上,BC=13AB=14CD,点E,F分别是AB,CD的中点,若BC=30,求EF的长.15.已知点A,B,C在一条直线上,AB=6,BC=2,点M是线段AC的中点,求线段AM的长度.拓展、探究、思考16.已知线段AB长为10cm,C是直线AB上一动点,M是线段AC的中点,N 是线段BC的中点.(1)若点C恰好为线段AB上一点,则MN=cm;(2)猜想线段MN与线段AB长度的关系,及MNAB,并说明理由.17.已知数轴上三点M,O,N对应的数分别为−3,0,1,点P为数轴上任意一点,其对应的数为x.(1)如果点P到点M,点N的距离相等,那么x的值是______;(2)数轴上是否存在点P,使点P到点M,点N的距离之和是5?若存在,请直接写出x的值;若不存在,请说明理由.(3)如果点P以每分钟3个单位长度的速度从点O向左运动时,点M和点N分别以每分钟1个单位长度和每分钟4个单位长度的速度也向左运动,且三点同时出发,那么几分钟时点P到点M,点N的距离相等?测试5 角的度量学习要求理解角的概念,掌握角的表示方法,能利用画图工具作一个角,会度量一个角的大小(在角度制下),能进行简单的计算.理解周角、平角的概念.课堂学习检测一、填空题1.(1)____________的图形叫做角,____________________叫做角的顶点,_____________________叫做角的边.(2)如图1,角也可以看作是由一条___________绕着它的___________而形成的图形,这条射线的起始位置叫做角的______,其终止位置叫做角的__________.(3)如图2,一条射线绕其端点O按逆时针方向旋转得到∠AOB,当角的终边OB旋转到与角的始边OA成一条直线时,称∠AOB为______;若角的终边继续旋转,当角的终边OB与角的始边OA重合时,称∠AOB为______.(4)以度、分、秒为单位的角度制规定,把一个周角______,每一份叫做1度,记作____;把1度的角______,每一份叫做1分,记作______;把1分的角______,每一份叫做1秒,记作______.这样,1周角是______°,1平角是______°,1°=______',1′=______″.2.(1)0.4°=';(2)0.6'=″;(3)24'=°;(4)12″=';(5)57.32°=°'″;(6)17°14' 24″=.3.如图以OC为边的角有______个,它们分别是______二、选择题4.下列关于角的说法正确的是( ).(A)两条射线组成的图形叫做角(B)延长一个角的两边(C)角的两边是射线,所以角不可以度量(D)角的大小与这个角的两边长短无关5.下列语句正确的是( ).(A)如图,∠A 就是∠BAC(B)在∠BAC 的边AB 延长线上取一点D(C)对于一个角的表示没有要求,可以任意书写(D)角可以看作是由一条射线绕角的端点旋转而成 6.下列说法中正确的是( ). (A)一个周角就是一条射线 (B)平角是一条直线 (C)角的两边越长,角就越大 (D)∠AOB 也可以表示为∠BOA7.钟表上的时间指示为两点半,这时时针与分针形成的(小于平角)角的度数是( ). (A)120° (B)105° (C)100° (D)90° 8.如图所示,点O 在直线AB 上,图中小于180°的角共有( ).(A)7个 (B)8个 (C)9个(D)10个练合、运用、诊断一、填空题9.如图,图中能用一个大写字母表示的角是;以A 为顶点的角有 个,它们分别是_________________________.1011.计算:E C D BAC DBA(1)18°31′42″+21°37′19″;(2)135°16′–91°45′35″;(3)17°40′÷3;(4)25°36′18″×6;(5)18.6°+42°34′(6)360°÷7(精确到1′)(7)32°16′25″×4-78°25′二、解答题12.1点20分时,时钟的时针与分针的夹角是几度?2点15分时,时钟的时针与分针的夹角又是几度?12.从1点15分到1点35分,时钟的分针与时针各转过了多大角度?16.时钟在8:30时,时针与分针的夹角为多少度?拓展、探究、思考17.如图,AOB是直线,∠1∶∠2∶∠3=1∶3∶2,求∠DOB的度数.18.图1中有______个角,图2中有______个角;图3中有______个角;以此类推,若一个角内有n 条射线,则可有______个角.图1 图2 图3测试6 角的比较与运算学习要求会比较两个角的大小,能进行角的运算(和、差、倍、分).理解角的平分线以及直角、锐角、钝角的概念.课堂学习检测一、填空题1.如图所示,∠AOB=∠α;∠AOC=∠β,要比较∠α和∠β的大小,可先让∠α的顶点与∠β的顶点______,∠α的始边与∠β的始边也______,并且∠α的终边与∠β的终边都在它们的始边的同一侧.若∠α的终边落在∠β的内部,则称∠α______∠β;(图1) 若∠α的终边落在∠β的外部,则称∠α______∠β;(图2)若∠α的终边恰与∠β的终边重合,则称∠α______∠β.(图3)图1 图2 图32.如图,若OC 是∠AOB 的平分线,则______=______; 或______=______21 ______;或______=2______=2______.3.如图,已知直线AB ,CD 相交于点O ,OE 平分∠COB ,若∠EOB=50°,则∠BOD 的度数是. 4.如图,在横线上填上适当的角:(1)∠AOC =______+______; (2)∠AOD -∠BOD =______; (3)∠BOC =______-∠COD ;(4)∠BOC =∠AOC +∠BOD -______.5.如图,∠1=15°,∠AOC=90°,点B ,O ,DEDCBAO在同一条直线上,则∠2的度数为. 6.如图,(1)若∠AOB =∠COD ,则∠AOC =∠______. (2)若∠AOC =∠BOD , 则∠______=∠______.二、选择题7.在小于平角的∠AOB 的内部取一点C ,并作射线OC ,则一定存在( ). (A)∠AOC >∠BOC (B)∠AOC =∠BOC (C)∠AOB >∠AOC (D)∠BOC >∠AOC8.如图,∠AOC=90°,ON 是锐角∠COD 的角平分线,OM 是∠AOD 的角平分线,那么∠MON=( )(A)90° (B)75° (C)60° (D)45°9.不能用一副三角板拼出的角是( ).(A)120° (B)105° (C)100° (D)75° 10.如图,OC 是∠AOB 的平分线,OD 平分∠AOC ,且∠COD =25°,则∠AOB =( ). (A)100° (B)75° (C)50° (D)20°11.如图,射线OD 是平角∠AOB 的平分线,∠COE =90°,那么下列式子中错误的是( ). (A)∠AOC =∠DOE (B)∠COD =∠BOE (C)∠AOD =∠BOD (D)∠BOE =∠AOC12.如果∠AOB =34°,∠BOC =18°,那么∠AOC 的度数是( ).(A)52° (B)16° (C)52°或16° (D)52°或18° 13.已知OC 是从∠AOB 的顶点引出的一条射线,若∠AOB =70°,∠AOB =2∠BOC ,则∠AOC 的度数是( ). (A)35° (B)105° (C)35°或105° (D)35°或115° 14.将一长方形纸片按如图的方式折叠,BC ,BD 为折痕,则∠CBD 的度数为( )(A)60° (B)75° (C)90°(D)95°三、解答题 15.如图,OD ,OE 分别是∠AOC 和∠BOC 的平分线,∠AOD=40°,∠BOE=25°,求∠AOB 的度数.MN O DAC解:∵解:因为OD 平分∠AOC ,OE 平分∠BOC , ∴∠AOC=2∠AOD ,∠BOC=2______,( ) ∵∠AOD=40°,∠BOE=25°, ∴∠BOC=,∠AOC=______. ∴∠AOB=______.16.已知:如图,直线AB 和CD 相交于点O ,∠BOC=30°,OE 平分∠AOD ,∠AOD 内的一条射线OF 满足∠EOF =90°,求∠COF 的度数. 将以下解答过程补充完整:解:∵直线AB 和CD 相交于点O ,∴∠AOD =180°-∠BOD , ∠BOC =180°-∠BOD . ∴∠________=∠________.( )∵∠BOC =30°,∴∠AOD =________°. ∵OE 平分∠AOD ,∴∠DOE =12________=________°.( )∵∠EOF =90°,∠DOE +∠EOF +∠COF =180°, ∴∠COF =________°.综合、运用、诊断一、作图题17.已知∠1和∠2,求作一个角,使它等于∠2-2∠1.18.如图,点B 为射线OA 上一点,①在OA 的上方,画∠AOC=120°,画∠OBD=90°; ②画∠AOC 的平分线OE ,交射线BD 于点P . 测量点O 、P 之间的距离(精确到0.1cm ).19.如图,直线AB ,CD 相交于点O ,OE 是∠AOD 的平分线,若∠AOC=60°,DEAFCBO∠EOF=90°,求∠FOC的度数.拓展、探究、思考20.如图,OM是∠AOB的平分线,射线OC在∠BOM内,ON是∠BOC的平分线,已知∠AOC=80°,求∠MON的度数.21.如图,BD平分∠ABC,BE分∠ABC分2∶5两部分,∠DBE=21°,求∠ABC的度数.22.(1)已知:如图1,点C为∠AOB内一点,OM,ON分别平分∠AOC和∠BOC,求证:∠MON=12∠AOB;(2)如果C为∠AOB外一点,如图2,其他条件不变,(1)中的结论还成立吗?若变化,请说明理由;若不变请证明.23.如图,OM为∠AOB的平分线,ON为∠MOA内的一条射线,某同学经过认真的分析,得出一个关系式是∠MON =21(∠BON -∠AON ),你认为这个同学得出的关系式是正确的吗?若正确,请把得出这个结论的过程写出来。
北京市西城区2022届英语七年级上学期期末学业水平测试试题模拟卷四

北京市西城区2022届英语七年级上学期期末学业水平测试试题模拟卷四一、选择题1.______ is after Thursday.A.TuesdayB.WednesdayC.MondayD.Friday2.肖华想给她妹妹买一件中号的夹克衫,她应该选择____________型号的。
A.LB.SC.XLD.M3.(经典题) _________ is Jane. _________ mother is a teacher.A.She; Her B.He; His C.She; His D.He; Her4.—Let's ________ the volleyball game on TV.—That sounds good.A.seeB.lookC.watchD.look at5.—______ is Tim’s brother?—He’s thirteen.A.WhatB.WhenC.How oldD.How6.—What kind of movies does Maria___________?—She__________ comedies. A.like……like B.likes…likes C.like…likes D.likes…like7.— ________, Mary. Is this your pen?— Yes, it is.A.Thank youB.I’m sorryC.Excuse meD.You’re welcome8.-Is this book?-No, it's not my book.A.his B.you C.your D.her9.—What’s this?— a map.A.He is B.This is C.It’s D.That’s10.— _________ he?— My grandfather.A.WhoB.WhatC.Who’sD.What’s11.--- ______ is the boy with a pair of glasses? --- John.A.How B.Who C.Where D.What12.—How much are the trousers in orange?—They’re only$9.—OK. I’ll.A.take it B.need it C.need them D.take them13.(题文)Do Lucy and Lily have a nice room?Yes,_____A.Yes,she do B.she does C.they do D.they don’t14.(题文)This yellow jumper ____your trousers very well.A.designs B.fit C.chooses D.matches15.-Is she Li Ping? -Yes ,_______.A.she's B.she is C.he is16.—When do you have geography?—We have it ____ Tuesday and Thursday.A.inB.onC.atD./17.—Have a good day,Linda!—____A.OK! B.I see! C.Thanks!18.I play football two hours every day.A.at B.in C.for D.tell19.-- Mum, ______ is my football?-- It's under your bed.A.what B.whichC.when D.where20.She really wants_____England this summer holiday.A.to visitB.visitC.visitingD.visits二、用所给的词填空21.用所给单词的适当形式填空。
七年级数学学习·探究·诊断((上册))

第一章 有理数测试1 正数和负数学习要求了解正数、负数、有理数的概念,会用正数和负数表示相反意义的量.课堂学习检测一、判断题(正确的在括号内画“√”,错误的画“×”)( )1.某仓库运出30吨货记作-30吨,则运进20吨货记作+20吨. ( )2.节约4吨水与浪费4吨水是一对具有相反意义的量.( )3.身高增长1.2cm 和体重减轻1.2kg 是一对具有相反意义的量. ( )4.在小学学过的数前面添上“-”号,得到的就是负数. 二、填空题5.学校在大桥东面9千米处,那么大桥在学校______面-9千米处.6.如果以每月生产180个零件为准,超过的零件数记作正数,不足的零件数记作负数,那么1月生产160个零件记作______个,2月生产200个零件记作______个.7.甲冷库的温度为-6℃,乙冷库的温度比甲冷库低5℃,则乙冷库的温度是______. 8.______既不是正数,也不是负数;它______整数,______有理数(填“是”或“不是”). 9.整数可以看作分母为1的______,有理数包括____________. 10.把下列各数填在相应的大括号内:74,6,0,14.3,5.0,432,14,5.8,51,27----正数集合{_______________________________________________________________…} 负数集合{_______________________________________________________________…} 非负数集合{_____________________________________________________________…} 有理数集合{_____________________________________________________________…}综合、运用、诊断一、填空题11.若把公元2008年记作+2008,那么-2008年表示______.12.潜水艇上浮为正,下潜为负.若潜水艇原先在距水面80米深处,后来两次活动记录的情况是-10米,+20米,则现在潜水艇在距水面______米的深处. 13.是正数而不是整数的有理数是____________________. 14.是整数而不是正数的有理数是____________________. 15.既不是正数,也不是负数的有理数是______________. 16.既不是真分数,也不是零的有理数是______________.17.在下列数中:,31- 11.11111,725.95 95.527,0,+2004,-2,1.12122122212222,,111-非负有理数有__________________________________________. 二、判断题(正确的在括号里画“√”,错误的画“×”) ( )18.带有正号的数是正数,带有负号的数是负数. ( )19.有理数是正数和小数的统称.( )20.有最小的正整数,但没有最小的正有理数. ( )21.非负数一定是正数.( )22.311-是负分数. 三、解答题23.-3.782( ).(A)是负数,不是分数 (B)不是分数,是有理数 (C)是负数,也是分数 (D)是分数,不是有理数 24.下面说法中正确的是( ).(A)正整数和负整数统称整数 (B)分数不包括整数(C)正分数,负分数,负整数统称有理数 (D)正整数和正分数统称正有理数25.一种零件的长度在图纸上是(10±0.05)毫米,表示这种零件的标准尺寸是10毫米,加工要求最大不超过______毫米,最小不小于______毫米.拓展、探究、思考26.一批螺帽产品的内径要求可以有±0.02 mm 的误差,现抽查5个样品,超过规定的毫米值记为正数,不足值记为负数,检查结果如表.则合乎要求的产品数量为( ).(A)1个(B)2个(C)3个(D)5个测试2 相反数 数轴学习要求掌握一个数的相反数的求法和性质,学习使用数轴,借助数轴理解相反数的几何意义,会借助数轴比较有理数的大小.课堂学习检测一、填空题1.________________的两个数,叫做互为相反数;零的相反数是______.2.0.4与______互为相反数,______与-(-7)互为相反数,a 的相反数是______. 3.规定了______、______和______的______叫数轴. 4.所有的有理数都能用数轴上的______来表示.5.数轴上,表示-3的点到原点的距离是______个单位长,与原点距离为3个单位长的点表示的数是______。
北京西城区学习探究诊断数学七上-第三章一元一次方程

第三章 一元一次方程测试1 从算式到方程(一)学习要求了解从算式到方程是数学的进步.理解方程、方程的解和解方程的概念,会判断一个数是否为方程的解.理解一元一次方程的概念,能根据问题,设未知数并列出方程.初步掌握等式的性质1、性质2.课堂学习检测一、填空题1.表示_______关系的式子叫做等式;含有未知数的_______叫做方程.2.使方程左、右两边的值相等的_______叫做方程的解.求_______的过程叫做解方程. 3.只含有_______未知数,并且未知数的_______的_______叫做一元一次方程.4.在等式7y -6=3y 的两边同时_______得4y =6,这是根据_____________________. 5.若-2a =2b ,则a =_______,依据的是等式的性质_______,在等式的两边都___________________________.6.将等式3a -2b =2a -2b 变形,过程如下: Θ3a -2b =2a -2b ,∴3a =2a .(第一步) ∴3=2.(第二步)上述过程中,第一步的依据是_______;第二步得出错误的结论,其原因是_______ ____________________________. 二、选择题7.在a -(b -c )=a -b +c ,4+x =9,C =2?r ,3x +2y 中等式的个数为( ). (A)1个 (B)2个 (C)3个 (D)4个8.在方程6x +1=1,,322=x 7x -1=x -1,5x =2-x 中解为31的方程个数是( ). (A)1个 (B)2个 (C)3个 (D)4个 9.根据等式性质5=3x -2可变形为( ). (A)-3x =2-5 (B)-3x =-2+5 (C)5-2=3x (D)5+2=3x 三、解答题10.设某数为x ,根据题意列出方程,不必求解:(1)某数的3倍比这个数多6.(2)某数的20%比16多10.(3)3与某数的差比这个数少11.(4)把某数增加10%后的值恰为80.综合、运用、诊断一、填空题11.(1)若汽车行驶速度为a 千米/时,则该车2小时经过的路程为______千米;行驶n 小时经过的路程为________千米.(2)小亮今年m 岁,爷爷的年龄是小亮年龄的3倍,那么5年后爷爷的年龄是_____岁. (3)文艳用5元钱买了m 个练习本,还剩2角6分,平均每个练习本的售价是_____元. (4)100千克花生,可榨油40千克,x 千克花生可榨油_____千克.(5)某班共有a 名学生,其中有51参加了数学课外小组,没有参加数学课外小组的学生有______名.12.在以下各方程后面的括号内的数中找出方程的解.(1)3x -2=4(1,2,3),解是x =________;(2)),3101,38(313,=-x 解是x =________. 13.(1)x =1是方程4kx -1=0的解,则k =________;(2)x =-9是方程b x =|31|的解,那么b =________.二、解答题14.若关于x 的方程3x 4n -7+5=17是一元一次方程,求n .15.根据题意,设未知数列出方程:(1)郝帅同学为班级买三副羽毛球拍,付出100元,找回元,问每副羽毛球拍的单价是多少元?(2)某村2003年粮食人均占有量6650千克,比1949年人均占有量的50倍还多40千克,问1949年人均占有量是多少千克?拓展、探究、思考16.已知:y 1=4x -3,y 2=12-x ,当x 为何值时,(1)y 1=y 2;(2)y 1与y 2互为相反数;(3)y 1比y 2小4.测试2 从算式到方程(二)学习要求掌握等式的性质,能列简单的方程和求简单方程的解.课堂学习检测一、填空题1.等式的性质1是等式两边__________结果仍成立;等式的性质2是等式两边__________数,或________________,结果仍成立. 2.(1)从方程23=x得到方程x =6,是根据__________; (2)由等式4x =3x +5可得4x -_____=5,这是根据等式的____,在两边都_____,所以_____=5; (3)如果43=-a,那么a =____,这是根据等式的____在等式两边都____. 二、选择题3.下列方程变形中,正确的是( ). (A)由4x +2=3x -1,得4x +3x =2-1(B)由7x =5,得75=x (C)由,02=y得y =2 (D)由,115=-x得x -5=1 4.下列方程中,解是x =4的是( ). (A)2x +4=9(B)43223-=+x x (C)-3x -7=5 (D)5-3x =2(1-x )5.已知关于y 的方程y +3m =24与y +4=1的解相同,则m 的值是( ). (A)9 (B)-9 (C)7 (D)-8综合、运用、诊断一、解答题6.检验下列各题括号里的数是不是它前面方程的解:(1);‘)5,15(1853-===-x x x (2)).61,41(14126110312==-+=+--x x x x x7.观察下列图形及相应的方程,写出经变形后的方程,并在空的天平盘上画出适当的图形.8.已知关于x 的方程2x -1=x +a 的解是x =4,求a 的值.9.用等式的性质求未知数x : (1)3-x =6(2)421=x(3)2x +3=3x(4)02331=+x拓展、探究、思考10.下列各个方程的变形能否分别使所得新方程的解与原方程的解相同?相同的画“√”,不相同的画“×”,对于画“×”的,想一想错在何处? (1)2x +6=0变为2x =-6; ( )(2)5243=x 变为;3452⨯=x( ) (3)321=+-x 变为-x +1=6;( ) (4)431323++=--x x x 变为6(x -3)-4x =1+3(x +3); ( ) (5)(x +1)(x +2)=(x +1)变为x +2=1;( ) (6)x 2=25变为x =5. ( )11.已知(m 2-1)x 2-(m -1)x +8=0是关于x 的一元一次方程,它的解为n .(1)求代数式200(m +n )(n -2m )-3m +5的值; (2)求关于y 的方程m |y |=n 的解.测试3 移项与合并(一)学习要求初步掌握用移项、合并、系数化为1的方法步骤解简单的一元一次方程.课堂学习检测一、填空题1.在解实际问题列方程时用到的一个基本的相等关系是“表示____________的_________ ______相等.”2.解方程中的移项就是“把等式_______某项_______后移到_______.”例如,把方程3x +20=8x 中的3x 移到等号的右边,得_______. 3.目前,合并含相同字母的项的基本法则是ax +bx +cx =_______,它的理论依据是______. 4.解形如ax +b =cx +d 的一元一次方程就是通过_______、_______、_______等步骤使方程向着____的形式转化,从而求出未知数.5.已知x ,y 互为相反数,且(x +y +3)(x -y -2)=6,则x =______. 6.若3x +2a =12和方程3x -4=2的解相同,则a =______. 二、解答题 7.(1)-2x =4 (2)6x =-2(3)3x =-12 (4)-x =-2(5)214-=x(6)421=-x(7)-3x =0(8)3232=-x综合、运用、诊断一、选择题8.下列两个方程的解相同的是( ). (A)方程5x +3=6与方程2x =4 (B)方程3x =x +1与方程2x =4x -1(C)方程021=+x 与方程021=+x (D)方程6x -3(5x -2)=5与方程6x -15x =3 9.方程3141=x 正确的解是( ). (A)x =12(B)121=x (C)34=x (D)43=x 10.下列说法中正确的是( ).(A)3x =5+2可以由3x +2=5移项得到 (B)1-x =2x -1移项后得1-1=2x +x(C)由5x =15得515=x 这种变形也叫移项 (D)1-7x =2-6x 移项后得1-2=7x -6x 二、解答题 11.解下列方程(1)3x +14=-7 (2)x +13=5x +37(3)21323-=-x (4)21132-=-x x拓展、探究、思考12.你能在日历上圈出一个竖列上相邻的3个数,使得它们的和是15吗?说明理由.测试4 移项与合并(二)学习要求进一步掌握用移项、合并的方法解一元一次方程,会列一元一次方程解决简单的实际问题.课堂学习检测一、填空题1.列出方程,再求x 的值:(1)x 的3倍与9的和等于x 的31与23的差.方程:________________,解得x =______;(2)x 的25%比它的2倍少7.方程:___________,解得x =_______. 2.一元一次方程t t 213=-化为t =a 形式的方程为___________. 二、解答题3.k 为何值时,多项式x 2-2kxy -3y 2+3xy -x -y 中,不含x ,y 的乘积项.综合、运用、诊断4.解关于x 的方程 (1)10x =-5 (2)-=10 (3)01437=+-x (4)5y -9=7y -13(5)21323-=-x (6)21132-=-x x(7)|2x -1|=25.已知21=x 是方程x x a +=+21125的解,求关于x 的方程ax +2=a (1-2x )的解.6.某蔬菜基地三天的总产量是8390千克,第二天比第一天多产560千克,第三天比第一天的65多1200千克.问三天各产多少千克蔬菜?7.甲、乙两人投资合办一个企业,并协议按照投资额的比例多少分配所得利润.已知甲与乙投资额的比例为3∶4,首年所得的利润为38500元,则甲、乙二人分别获得利润多少元?测试5 去括号学习要求掌握去括号法则,能用去括号的方法解一元一次方程.课堂学习检测一、选择题1.今年哥哥的年龄是妹妹年龄的2倍,4年前哥哥的年龄是妹妹年龄的3倍,若设妹妹今年x 岁,可列方程为( ). (A)2x +4=3(x -4) (B)2x -4=3(x -4) (C)2x =3(x -4) (D)2x -4=3x 2.将3(x -1)-2(x -3)=5(1-x )去括号得( ) (A)3x -1-2x -3=5-x (B)3x -1-2x +3=5-x(C)3x -3-2x -6=5-5x (D)3x -3-2x +6=5-5x 3.解方程2(x -2)-3(4x -1)=9正确的是( )(A)2x -4-12x +3=9,-10x =9-4+3=8,故x =- (B)2x -2-12x +1=9,-10x =10,故x =-1 (C)2x -4-12x -3=9,-10x =16,故x =- (D)2x -4-12x +3=9,-10x =10,故x =-14.已知关于x 的方程(a +1)x +(4a -1)=0的解为-2,则a 的值等于( ). (A)-2(B)0(C)32 (D)23 5.已知y =1是方程y y m 2)(312=--的解,那么关于x 的方程m (x -3)-2=m (2x -5)的解是( ) (A)x =10(B)x =0(C)34=x (D)43=x练合、运用、诊断二、解答题 6.解下列方程(1)3(x -1)-2(2x +1)=12 (2)5(x +8)-5=6(2x -7)(3))1(21)1(2)1(31)1(3+--+-=+k k k k(4)3(y -7)-2[9-4(2-y )]=22拓展、探究、思考7.已知关于x 的方程27x -32=11m 多x +2=2m 的解相同,求221m m +的值.8.解关于y 的方程-3(a +y )=a -2(y -a ).测试6 去分母学习要求掌握去括号法则,能利用等式的性质,把含有分数系数的方程转化为含整数的方程.课堂学习检测一、选择题1.方程x x 3252=-的解是( ).(A)132- (B)132 (C)1310-(D)310 2.方程61513--=-x x 的解为( ) (A)37 (B)35 (C)335 (D)337 3.若关于x 的方程)1(422-=+x ax 的解为x =3,则a 的值为( ). (A)2 (B)22 (C)10 (D)-24.方程521=--x x 的解为( ).(A)-9 (B)3 (C)-3 (D)95.方程,4172753+-=+-x x 去分母,得( ). (A)3-2(5x +7)=-(x +17) (B)12-2(5x +7)=-x +17 (C)12-2(5x +7)=-(x +17) (D)12-10x +14=-(x +17) 6.四位同学解方程,246231xx x -=+--去分母分别得到下面的四个方程: ①2x -2-x +2=12-3x ; ②2x -2-x -2=12-3x ; ③2(x -1)-(x +2)=3(4-x ); ④2(x -1)-2(x +2)=3(4-x ). 其中解法有错误的是( ). (A)①② (B)①③ (C)②④ (D)①④ 7.将103.001.05.02.0=+-xx 的分母化为整数,得( ). (A)1301.05.02=+-xx(B)1003505=+-x x (C)100301.05.020=+-xx(D)13505=+-x x 8.下列各题中:①由,2992=x 得x =1;②由,267=-x 得x -7=10,解得x =17;③由6x-3=x +3,得5x =0;④由,23652+=--x x 得12-x -5=3(x +3).出现错误的个数是( ).(A)1个 (B)2个(C)3个 (D)4个综合、运用、诊断二、解答题 9.解方程. (1)757875xx -=- (2)22331+-=--y y y (3)454436+=-y y (4)62372345---=+-x x x x (5)3.15.032.04-=--+x x(6)2]2)14(32[23=---x x测试7 一元一次方程的解法学习要求巩固一元一次方程的概念、解法和应用.课堂学习检测填空题 1.解一元一次方程就是要求出其中的______(例如x ),一般来说,通过______、_____、_____、_____等步骤,可使原方程逐步向着x =a 的形式______,这个过程目前主要依据______和___________等.2.下列方程的解法是否正确?如果不正确,指出错在哪里?并给出正确的解答.;531513+-=+x x ①解:3x +1=5-x +3,3x +x =8-1, 4x =7, ⋅=47x ②2(x +2)=5(x +9)-2(x -2). 解:2x +2=5x +9-2x -2, 2x -5x +2x =9-2-2-x =5, x =-5.3.关于x 的方程(k +2)x 2+4kx -5k =0是一元一次方程,则k =________.4.已知方程mx +2=2(m -x )的解满足,0|21|=-x 则m 为________. 5.若2|x -1|=4,则x 的值为_________.综合、运用、诊断一、填空题6.(1)若ax +b =a -x (a ,b 是已知数,且a ≠-1),则x =______.(2)方程|x |=3的解是______,|x -3|=0的解是______,3|x |=-3的解是______,若|x +3|=3,则x =______. (3)在公式k b a S ⋅+=2)(中,已知S ,k ,a ,用S ,k ,a 的代数式表示b ,则b =______,当S =10,a =3,k =4时,则b =______.(4)等量关系“x 的5倍减去7,等于它的3倍加上8”可用方程表示为方程的解是______________.(5)若|x +3|=x +3,则x 的范围为______________. 二、解方程 7.(1)1)1(5332+-=-x x (2)15%x +10-x =10×32% (3)y y y --=+524121 (4)|5x +4|+2=8(5)1)23(32)31(21=+--xx (6)141710352212+-=+--x x x(7)21105.0)25(35.63.0303.0--=--x x (8)168421x x x x x ++++=三、解答题8.若a ,b 为定值,关于x 的一元一次方程2632=--+bx x x ka 无论k 为何值时,它的解总是1,求a ,b 的值.测试8 实际问题与一元一次方程学习要求会列一元一次方程解决简单的实际问题.课堂学习检测1.一个两位数,十位数字比个位数字的4倍多1.将两个数字调换顺序后所得数比原数小63.求原数.2.日历的12月份上,爷爷生日那天的上、下、左、右4个日期的和为80,你能说出爷爷生日是几号吗?3.有一个三位数的百位数字是1,如果把1移到最后,其他两位数字顺序不变,所得的 三位数比这个三位数的2倍少7,求这个三位数.综合、运用、诊断4.某班同学参加平整土地劳动.运土人数比挖土人数的一半多3人.若从挖土人员中抽出6人运土,则挖土和运土的人数相等.求原来运土和挖土各多少人?5.某车间有62名工人,生产甲、乙两种零件,每人每天平均能生产甲种零件12个或乙种零件23个.已知每3个甲种零件和2个乙种零件配成一套,问应分配多少人生产甲 种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?6.甲、乙两车分别从相距360千米的两地相向开出,已知甲车速度60千米/时,乙车速度40千米/时,若甲车先开1个小时,问乙车开出多少小时后两车相遇?7.A、B两地相距31千米,甲从A地骑自行车去B地,1小时后乙骑摩托车也从A地去B 地.已知甲每小时行12千米,乙每小时行28千米.(1)问乙出发后多少小时追上甲;(2)若乙到达B地后立即返回,则在返回路上与甲相遇时距乙出发多长时间?8.某行军纵队以8千米/时的速度行进,队尾的通讯员以12千米/时的速度赶到队伍前送一个文件.送到后立即返回队尾,共用分钟.求队伍长.9.某人有急事,预定搭乘一辆小货车从A地赶往B地,实际上他乘小货车行了三分之一路程后改乘一辆小轿车,车速提高了一倍,结果提前一个半小时到达.已知小货车的速度是36千米/时,求两地间路程.10.一项工程甲、乙两队合作10天可以完成,甲队独做15天完成,现两队合作7天后,其余工程由乙队独做.乙队还需几天完成?11.检修一处住宅区的自来水管道,甲单独完成需14天,乙单独完成需18天,丙单独完成需12天,前7天由甲、乙两人合做,但乙中途离开了一段时间,后2天由乙、丙合作完成.问乙中途离开了几天?拓展、探究、思考12.某中学组织初一同学春游,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座客车,则多出一辆,且其余客车恰好坐满.已知45座客车日租金为每辆220元,60座客车日租金为每辆300元.试问:(1)初一年级人数是多少?原计划租用45座客车多少辆?(2)要使每个同学都有座位,怎样租车更合算?13.小刚和小明在课外学习中,用20张白卡纸做包装盒,每张白卡纸可以做2个盒身或者做3个盒底盖.且1个盒身和2个底盖恰好做成一个包装盒,为了充分利用材料使做成的盒身和底盖刚好配套,他们设计了两种方案:方案一:把这些白卡纸分成两部分,一部分做盒身,一部分做底盖;方案二:先把一张白卡纸适当剪裁出一个盒身和一个盒盖,余下的白卡纸分成两部分,一部分做盒身一部分做底盖.想一想,他们的方案是否可行?测试9 再探实际问题与一元一次方程(一)学习要求能对所研究的问题抽象出基本的数量关系,通过列一元一次方程解实际问题,培养分析问题和解决问题的能力.课堂学习检测1.在商品销售经营中,涉及的基本关系式:(1)商品的原销售价、提价的百分数与商品的现销售价之间的关系是______________________________________________________________________.商品的原销售价、降价的百分数与商品的现销售价之间的关系是______________________________________________________________________.(2)商品的实际售价、商品的进价与商品的利润之间的关系是(这里不考虑其他因素)______________________________________________________________________.(3)商品的利润、商品的进价与商品的利润率之间的关系是(这里不考虑其他因素)______________________________________________________________________.(4)在打折销售中,商品的标价、折扣数与商品打折后的实际售价之间的关系是______________________________________________________________________.2.在我国银行储蓄存款计算利息的基本关系式主要有:(1)顾客存入银行的钱叫做______,银行付给顾客的酬金叫做______,它们的和叫做____,即__________________.(2)顾客将钱存入银行的时间叫做______.每个期数....内的______与____的比叫做利率.这样,本金、利率、期数、利息这四个量的关系是____________.综合、运用、诊断3.商店中某个玩具的进价为40元,标价为60元.(1)若按标价出售这个玩具,则所得的利润及利润率分别是多少?(2)顾客在与店主砍价时,店主为了保住15%的利润率,出售这个玩具的售价底线是多少元?(3)店主为吸引顾客,把这个玩具的标价提高10%后,再贴出打八八折的告示,则这个玩具的实际售价是多少元?(4)若店主设法将进价降低10%,标价不变,而贴出打八八折的告示,则出售这个玩具的利润及利润率分别是多少?4.(1)某个商品的进价是500元,把它提价40%后作为标价.如果商家要想保住12%的利润率搞促销活动,请你计算一下广告上可写出打几折?(2)想一想,如果(1)中该商品的进价没有具体给出,这时该问题怎么解决?5.某经销商经销一种商品,由于进货价降低了5%,售价不变,使得利润率由k%提高到(k +7)%,求k.〔售价=进货价×(1+利润率)〕拓展、探究、思考6.张新和李明相约到图书城去买书,请你根据他们的对话内容,求出李明上次所买书籍的原价.7.下表是甲商场电脑产品的进货单,其中进价一栏被墨迹污染,读了进货单后,请你算出这台电脑的进价是多少元.测试10 再探实际问题与一元一次方程(二)学习要求巩固一元一次方程解法,加强应用问题的训练,提高分析问题和解决问题能力.课堂学习检测一、选择题1.篮球赛的组织者出售球票,需要付给售票处12%的酬金,如果组织者要在扣除酬金后,每张球票净得12元,按精确到元的要求,球票票价应定为( ).(A)元(B)元(C)元(D)元2.一商店把彩电按标价的九折出售,仍可获利20%,若该彩电的进价是2400元,则彩电的标价为( ).(A)3200元(B)3429元(C)2667元(D)3168元3.某商店将彩电按原价提高40%,然后在广告上写“大酬宾,八折优惠”,结果每台彩电仍获利270元,那么每台彩电原价是( )(A)2150元(B)2200元(C)2250元(D)2300元4.一个商店以每3盘16元的价格购进一批录音带,又从另外一处以每4盘21元的价格购进比前一批数量加倍的录音带.如果两种合在一起以每3盘k元的价格全部出售可得到所投资的20%的收益,则k值等于( )(A)17 (B)18 (C)19 (D)20二、解答题5.某城市有50万户居民,平均每户有两个水龙头,估计其中有1%的水龙头漏水.若每个漏水龙头1秒钟漏一滴水,10滴水约重1克,试问该城市一年因此而浪费多少吨水(一年按365天计算).6.某市居民生活用电基本价格为每度元,若每月用电量超过a度,超过部分按基本电价的70%收取.(1)某户5月份用电84度,共交电费元,求a是多少;(2)若6月份的电费平均为每度元,求该户6月份共用多少度电,应交纳多少电费?综合、运用、诊断7.八年级三班在召开期末总结表彰会前,班主任安排班长李强去商店买奖品,下面是李强与售货员的对话:李强说:阿姨好!售货员:同学,你好,想买点什么?李强说:我只有100元,请您帮忙安排买10支钢笔和15本笔记本。
七年级数学学习·探究·诊断((上册))

第一章有理数测试1正数和负数学习要求了解正数、负数、有理数的概念,会用正数和负数表示相反意义的量.课堂学习检测一、判断题(正确的在括号内画“√”,错误的画“×”)()1.某仓库运出30吨货记作-30吨,则运进20吨货记作+20吨. ()2.节约4吨水与浪费4吨水是一对具有相反意义的量. ()3.身高增长1.2cm 和体重减轻1.2kg 是一对具有相反意义的量. ()4.在小学学过的数前面添上“-”号,得到的就是负数. 二、填空题5.学校在大桥东面9千米处,那么大桥在学校______面-9千米处.6.如果以每月生产180个零件为准,超过的零件数记作正数,不足的零件数记作负数,那么1月生产160个零件记作______个,2月生产200个零件记作______个.7.甲冷库的温度为-6℃,乙冷库的温度比甲冷库低5℃,则乙冷库的温度是______. 8.______既不是正数,也不是负数;它______整数,______有理数(填“是”或“不是”). 9.整数可以看作分母为1的______,有理数包括____________. 10.把下列各数填在相应的大括号内:正数集合{_______________________________________________________________…} 负数集合{_______________________________________________________________…} 非负数集合{_____________________________________________________________…} 有理数集合{_____________________________________________________________…}综合、运用、诊断一、填空题11.若把公元2008年记作+2008,那么-2008年表示______.12.潜水艇上浮为正,下潜为负.若潜水艇原先在距水面80米深处,后来两次活动记录的情况是-10米,+20米,则现在潜水艇在距水面______米的深处. 13.是正数而不是整数的有理数是____________________. 14.是整数而不是正数的有理数是____________________. 15.既不是正数,也不是负数的有理数是______________. 16.既不是真分数,也不是零的有理数是______________.17.在下列数中:,31-11.11111,725.95 95.527,0,+2004,-2?,1.,,111-非负有理数有__________________________________________. 二、判断题(正确的在括号里画“√”,错误的画“×”) ()18.带有正号的数是正数,带有负号的数是负数. ()19.有理数是正数和小数的统称.()20.有最小的正整数,但没有最小的正有理数. ()21.非负数一定是正数. ()22.311-是负分数.三、解答题 23.-3.782().(A)是负数,不是分数 (B)不是分数,是有理数 (C)是负数,也是分数(D)是分数,不是有理数24.下面说法中正确的是().(A)正整数和负整数统称整数(B)分数不包括整数(C)正分数,负分数,负整数统称有理数(D)正整数和正分数统称正有理数 25.一种零件的长度在图纸上是(10±0.05)毫米,表示这种零件的标准尺寸是10毫米,加工要求最大不超过______毫米,最小不小于______毫米.拓展、探究、思考26.一批螺帽产品的内径要求可以有±0.02 mm 的误差,现抽查5个样品,超过规定的毫米值记为正数,不足值记为负数,检查结果如表.则合乎要求的产品数量为().(A)1个 (B)2个(C)3个(D)5个测试2相反数数轴学习要求掌握一个数的相反数的求法和性质,学习使用数轴,借助数轴理解相反数的几何意义,会借助数轴比较有理数的大小.课堂学习检测一、填空题1.________________的两个数,叫做互为相反数;零的相反数是______. 2.0.4与______互为相反数,______与-(-7)互为相反数,a 的相反数是______. 3.规定了______、______和______的______叫数轴. 4.所有的有理数都能用数轴上的______来表示.5.数轴上,表示-3的点到原点的距离是______个单位长,与原点距离为3个单位长的点表示的数是______。
北京西城区学习探究诊断数学七上-第三章一元一次方程

第三章 一元一次方程测试1 从算式到方程(一)学习要求了解从算式到方程是数学的进步.理解方程、方程的解和解方程的概念,会判断一个数是否为方程的解.理解一元一次方程的概念,能根据问题,设未知数并列出方程.初步掌握等式的性质1、性质2.课堂学习检测一、填空题1.表示_______关系的式子叫做等式;含有未知数的_______叫做方程.2.使方程左、右两边的值相等的_______叫做方程的解.求_______的过程叫做解方程. 3.只含有_______未知数,并且未知数的_______的_______叫做一元一次方程.4.在等式7y -6=3y 的两边同时_______得4y =6,这是根据_____________________. 5.若-2a =2b ,则a =_______,依据的是等式的性质_______,在等式的两边都___________________________.6.将等式3a -2b =2a -2b 变形,过程如下: Θ3a -2b =2a -2b ,∴3a =2a .(第一步) ∴3=2.(第二步)上述过程中,第一步的依据是_______;第二步得出错误的结论,其原因是_______ ____________________________. 二、选择题7.在a -(b -c )=a -b +c ,4+x =9,C =2?r ,3x +2y 中等式的个数为( ). (A)1个 (B)2个 (C)3个 (D)4个8.在方程6x +1=1,,322=x 7x -1=x -1,5x =2-x 中解为31的方程个数是( ). (A)1个 (B)2个 (C)3个 (D)4个 9.根据等式性质5=3x -2可变形为( ). (A)-3x =2-5 (B)-3x =-2+5 (C)5-2=3x (D)5+2=3x 三、解答题10.设某数为x ,根据题意列出方程,不必求解:(1)某数的3倍比这个数多6.(2)某数的20%比16多10.(3)3与某数的差比这个数少11.(4)把某数增加10%后的值恰为80.综合、运用、诊断一、填空题11.(1)若汽车行驶速度为a 千米/时,则该车2小时经过的路程为______千米;行驶n 小时经过的路程为________千米.(2)小亮今年m 岁,爷爷的年龄是小亮年龄的3倍,那么5年后爷爷的年龄是_____岁. (3)文艳用5元钱买了m 个练习本,还剩2角6分,平均每个练习本的售价是_____元. (4)100千克花生,可榨油40千克,x 千克花生可榨油_____千克.(5)某班共有a 名学生,其中有51参加了数学课外小组,没有参加数学课外小组的学生有______名.12.在以下各方程后面的括号内的数中找出方程的解.(1)3x -2=4(1,2,3),解是x =________;(2)),3101,38(313,=-x 解是x =________. 13.(1)x =1是方程4kx -1=0的解,则k =________;(2)x =-9是方程b x =|31|的解,那么b =________.二、解答题14.若关于x 的方程3x 4n -7+5=17是一元一次方程,求n .15.根据题意,设未知数列出方程:(1)郝帅同学为班级买三副羽毛球拍,付出100元,找回元,问每副羽毛球拍的单价是多少元?(2)某村2003年粮食人均占有量6650千克,比1949年人均占有量的50倍还多40千克,问1949年人均占有量是多少千克?拓展、探究、思考16.已知:y 1=4x -3,y 2=12-x ,当x 为何值时,(1)y 1=y 2;(2)y 1与y 2互为相反数;(3)y 1比y 2小4.测试2 从算式到方程(二)学习要求掌握等式的性质,能列简单的方程和求简单方程的解.课堂学习检测一、填空题1.等式的性质1是等式两边__________结果仍成立;等式的性质2是等式两边__________数,或________________,结果仍成立. 2.(1)从方程23=x得到方程x =6,是根据__________; (2)由等式4x =3x +5可得4x -_____=5,这是根据等式的____,在两边都_____,所以_____=5; (3)如果43=-a,那么a =____,这是根据等式的____在等式两边都____. 二、选择题3.下列方程变形中,正确的是( ). (A)由4x +2=3x -1,得4x +3x =2-1(B)由7x =5,得75=x (C)由,02=y得y =2 (D)由,115=-x得x -5=1 4.下列方程中,解是x =4的是( ). (A)2x +4=9(B)43223-=+x x (C)-3x -7=5 (D)5-3x =2(1-x )5.已知关于y 的方程y +3m =24与y +4=1的解相同,则m 的值是( ). (A)9 (B)-9 (C)7 (D)-8综合、运用、诊断一、解答题6.检验下列各题括号里的数是不是它前面方程的解:(1);‘)5,15(1853-===-x x x (2)).61,41(14126110312==-+=+--x x x x x7.观察下列图形及相应的方程,写出经变形后的方程,并在空的天平盘上画出适当的图形.8.已知关于x 的方程2x -1=x +a 的解是x =4,求a 的值.9.用等式的性质求未知数x : (1)3-x =6(2)421=x(3)2x +3=3x(4)02331=+x拓展、探究、思考10.下列各个方程的变形能否分别使所得新方程的解与原方程的解相同?相同的画“√”,不相同的画“×”,对于画“×”的,想一想错在何处? (1)2x +6=0变为2x =-6; ( )(2)5243=x 变为;3452⨯=x( ) (3)321=+-x 变为-x +1=6;( ) (4)431323++=--x x x 变为6(x -3)-4x =1+3(x +3); ( ) (5)(x +1)(x +2)=(x +1)变为x +2=1;( ) (6)x 2=25变为x =5. ( )11.已知(m 2-1)x 2-(m -1)x +8=0是关于x 的一元一次方程,它的解为n .(1)求代数式200(m +n )(n -2m )-3m +5的值; (2)求关于y 的方程m |y |=n 的解.测试3 移项与合并(一)学习要求初步掌握用移项、合并、系数化为1的方法步骤解简单的一元一次方程.课堂学习检测一、填空题1.在解实际问题列方程时用到的一个基本的相等关系是“表示____________的_________ ______相等.”2.解方程中的移项就是“把等式_______某项_______后移到_______.”例如,把方程3x +20=8x 中的3x 移到等号的右边,得_______. 3.目前,合并含相同字母的项的基本法则是ax +bx +cx =_______,它的理论依据是______. 4.解形如ax +b =cx +d 的一元一次方程就是通过_______、_______、_______等步骤使方程向着____的形式转化,从而求出未知数.5.已知x ,y 互为相反数,且(x +y +3)(x -y -2)=6,则x =______. 6.若3x +2a =12和方程3x -4=2的解相同,则a =______. 二、解答题 7.(1)-2x =4 (2)6x =-2(3)3x =-12 (4)-x =-2(5)214-=x(6)421=-x(7)-3x =0(8)3232=-x综合、运用、诊断一、选择题8.下列两个方程的解相同的是( ). (A)方程5x +3=6与方程2x =4 (B)方程3x =x +1与方程2x =4x -1(C)方程021=+x 与方程021=+x (D)方程6x -3(5x -2)=5与方程6x -15x =3 9.方程3141=x 正确的解是( ). (A)x =12(B)121=x (C)34=x (D)43=x 10.下列说法中正确的是( ).(A)3x =5+2可以由3x +2=5移项得到 (B)1-x =2x -1移项后得1-1=2x +x(C)由5x =15得515=x 这种变形也叫移项 (D)1-7x =2-6x 移项后得1-2=7x -6x 二、解答题 11.解下列方程(1)3x +14=-7 (2)x +13=5x +37(3)21323-=-x (4)21132-=-x x拓展、探究、思考12.你能在日历上圈出一个竖列上相邻的3个数,使得它们的和是15吗?说明理由.测试4 移项与合并(二)学习要求进一步掌握用移项、合并的方法解一元一次方程,会列一元一次方程解决简单的实际问题.课堂学习检测一、填空题1.列出方程,再求x 的值:(1)x 的3倍与9的和等于x 的31与23的差.方程:________________,解得x =______;(2)x 的25%比它的2倍少7.方程:___________,解得x =_______. 2.一元一次方程t t 213=-化为t =a 形式的方程为___________. 二、解答题3.k 为何值时,多项式x 2-2kxy -3y 2+3xy -x -y 中,不含x ,y 的乘积项.综合、运用、诊断4.解关于x 的方程 (1)10x =-5 (2)-=10 (3)01437=+-x (4)5y -9=7y -13(5)21323-=-x (6)21132-=-x x(7)|2x -1|=25.已知21=x 是方程x x a +=+21125的解,求关于x 的方程ax +2=a (1-2x )的解.6.某蔬菜基地三天的总产量是8390千克,第二天比第一天多产560千克,第三天比第一天的65多1200千克.问三天各产多少千克蔬菜?7.甲、乙两人投资合办一个企业,并协议按照投资额的比例多少分配所得利润.已知甲与乙投资额的比例为3∶4,首年所得的利润为38500元,则甲、乙二人分别获得利润多少元?测试5 去括号学习要求掌握去括号法则,能用去括号的方法解一元一次方程.课堂学习检测一、选择题1.今年哥哥的年龄是妹妹年龄的2倍,4年前哥哥的年龄是妹妹年龄的3倍,若设妹妹今年x 岁,可列方程为( ). (A)2x +4=3(x -4) (B)2x -4=3(x -4) (C)2x =3(x -4) (D)2x -4=3x 2.将3(x -1)-2(x -3)=5(1-x )去括号得( ) (A)3x -1-2x -3=5-x (B)3x -1-2x +3=5-x(C)3x -3-2x -6=5-5x (D)3x -3-2x +6=5-5x 3.解方程2(x -2)-3(4x -1)=9正确的是( )(A)2x -4-12x +3=9,-10x =9-4+3=8,故x =- (B)2x -2-12x +1=9,-10x =10,故x =-1 (C)2x -4-12x -3=9,-10x =16,故x =- (D)2x -4-12x +3=9,-10x =10,故x =-14.已知关于x 的方程(a +1)x +(4a -1)=0的解为-2,则a 的值等于( ). (A)-2(B)0(C)32 (D)23 5.已知y =1是方程y y m 2)(312=--的解,那么关于x 的方程m (x -3)-2=m (2x -5)的解是( ) (A)x =10(B)x =0(C)34=x (D)43=x练合、运用、诊断二、解答题 6.解下列方程(1)3(x -1)-2(2x +1)=12 (2)5(x +8)-5=6(2x -7)(3))1(21)1(2)1(31)1(3+--+-=+k k k k(4)3(y -7)-2[9-4(2-y )]=22拓展、探究、思考7.已知关于x 的方程27x -32=11m 多x +2=2m 的解相同,求221m m +的值.8.解关于y 的方程-3(a +y )=a -2(y -a ).测试6 去分母学习要求掌握去括号法则,能利用等式的性质,把含有分数系数的方程转化为含整数的方程.课堂学习检测一、选择题1.方程x x 3252=-的解是( ).(A)132- (B)132 (C)1310-(D)310 2.方程61513--=-x x 的解为( ) (A)37 (B)35 (C)335 (D)337 3.若关于x 的方程)1(422-=+x ax 的解为x =3,则a 的值为( ). (A)2 (B)22 (C)10 (D)-24.方程521=--x x 的解为( ).(A)-9 (B)3 (C)-3 (D)95.方程,4172753+-=+-x x 去分母,得( ). (A)3-2(5x +7)=-(x +17) (B)12-2(5x +7)=-x +17 (C)12-2(5x +7)=-(x +17) (D)12-10x +14=-(x +17) 6.四位同学解方程,246231xx x -=+--去分母分别得到下面的四个方程: ①2x -2-x +2=12-3x ; ②2x -2-x -2=12-3x ; ③2(x -1)-(x +2)=3(4-x ); ④2(x -1)-2(x +2)=3(4-x ). 其中解法有错误的是( ). (A)①② (B)①③ (C)②④ (D)①④ 7.将103.001.05.02.0=+-xx 的分母化为整数,得( ). (A)1301.05.02=+-xx(B)1003505=+-x x (C)100301.05.020=+-xx(D)13505=+-x x 8.下列各题中:①由,2992=x 得x =1;②由,267=-x 得x -7=10,解得x =17;③由6x-3=x +3,得5x =0;④由,23652+=--x x 得12-x -5=3(x +3).出现错误的个数是( ).(A)1个 (B)2个(C)3个 (D)4个综合、运用、诊断二、解答题 9.解方程. (1)757875xx -=- (2)22331+-=--y y y (3)454436+=-y y (4)62372345---=+-x x x x (5)3.15.032.04-=--+x x(6)2]2)14(32[23=---x x测试7 一元一次方程的解法学习要求巩固一元一次方程的概念、解法和应用.课堂学习检测填空题 1.解一元一次方程就是要求出其中的______(例如x ),一般来说,通过______、_____、_____、_____等步骤,可使原方程逐步向着x =a 的形式______,这个过程目前主要依据______和___________等.2.下列方程的解法是否正确?如果不正确,指出错在哪里?并给出正确的解答.;531513+-=+x x ①解:3x +1=5-x +3,3x +x =8-1, 4x =7, ⋅=47x ②2(x +2)=5(x +9)-2(x -2). 解:2x +2=5x +9-2x -2, 2x -5x +2x =9-2-2-x =5, x =-5.3.关于x 的方程(k +2)x 2+4kx -5k =0是一元一次方程,则k =________.4.已知方程mx +2=2(m -x )的解满足,0|21|=-x 则m 为________. 5.若2|x -1|=4,则x 的值为_________.综合、运用、诊断一、填空题6.(1)若ax +b =a -x (a ,b 是已知数,且a ≠-1),则x =______.(2)方程|x |=3的解是______,|x -3|=0的解是______,3|x |=-3的解是______,若|x +3|=3,则x =______. (3)在公式k b a S ⋅+=2)(中,已知S ,k ,a ,用S ,k ,a 的代数式表示b ,则b =______,当S =10,a =3,k =4时,则b =______.(4)等量关系“x 的5倍减去7,等于它的3倍加上8”可用方程表示为方程的解是______________.(5)若|x +3|=x +3,则x 的范围为______________. 二、解方程 7.(1)1)1(5332+-=-x x (2)15%x +10-x =10×32% (3)y y y --=+524121 (4)|5x +4|+2=8(5)1)23(32)31(21=+--xx (6)141710352212+-=+--x x x(7)21105.0)25(35.63.0303.0--=--x x (8)168421x x x x x ++++=三、解答题8.若a ,b 为定值,关于x 的一元一次方程2632=--+bx x x ka 无论k 为何值时,它的解总是1,求a ,b 的值.测试8 实际问题与一元一次方程学习要求会列一元一次方程解决简单的实际问题.课堂学习检测1.一个两位数,十位数字比个位数字的4倍多1.将两个数字调换顺序后所得数比原数小63.求原数.2.日历的12月份上,爷爷生日那天的上、下、左、右4个日期的和为80,你能说出爷爷生日是几号吗?3.有一个三位数的百位数字是1,如果把1移到最后,其他两位数字顺序不变,所得的 三位数比这个三位数的2倍少7,求这个三位数.综合、运用、诊断4.某班同学参加平整土地劳动.运土人数比挖土人数的一半多3人.若从挖土人员中抽出6人运土,则挖土和运土的人数相等.求原来运土和挖土各多少人?5.某车间有62名工人,生产甲、乙两种零件,每人每天平均能生产甲种零件12个或乙种零件23个.已知每3个甲种零件和2个乙种零件配成一套,问应分配多少人生产甲 种零件,多少人生产乙种零件,才能使每天生产的这两种零件刚好配套?6.甲、乙两车分别从相距360千米的两地相向开出,已知甲车速度60千米/时,乙车速度40千米/时,若甲车先开1个小时,问乙车开出多少小时后两车相遇?7.A、B两地相距31千米,甲从A地骑自行车去B地,1小时后乙骑摩托车也从A地去B 地.已知甲每小时行12千米,乙每小时行28千米.(1)问乙出发后多少小时追上甲;(2)若乙到达B地后立即返回,则在返回路上与甲相遇时距乙出发多长时间?8.某行军纵队以8千米/时的速度行进,队尾的通讯员以12千米/时的速度赶到队伍前送一个文件.送到后立即返回队尾,共用分钟.求队伍长.9.某人有急事,预定搭乘一辆小货车从A地赶往B地,实际上他乘小货车行了三分之一路程后改乘一辆小轿车,车速提高了一倍,结果提前一个半小时到达.已知小货车的速度是36千米/时,求两地间路程.10.一项工程甲、乙两队合作10天可以完成,甲队独做15天完成,现两队合作7天后,其余工程由乙队独做.乙队还需几天完成?11.检修一处住宅区的自来水管道,甲单独完成需14天,乙单独完成需18天,丙单独完成需12天,前7天由甲、乙两人合做,但乙中途离开了一段时间,后2天由乙、丙合作完成.问乙中途离开了几天?拓展、探究、思考12.某中学组织初一同学春游,原计划租用45座客车若干辆,但有15人没有座位;如果租用同样数量的60座客车,则多出一辆,且其余客车恰好坐满.已知45座客车日租金为每辆220元,60座客车日租金为每辆300元.试问:(1)初一年级人数是多少?原计划租用45座客车多少辆?(2)要使每个同学都有座位,怎样租车更合算?13.小刚和小明在课外学习中,用20张白卡纸做包装盒,每张白卡纸可以做2个盒身或者做3个盒底盖.且1个盒身和2个底盖恰好做成一个包装盒,为了充分利用材料使做成的盒身和底盖刚好配套,他们设计了两种方案:方案一:把这些白卡纸分成两部分,一部分做盒身,一部分做底盖;方案二:先把一张白卡纸适当剪裁出一个盒身和一个盒盖,余下的白卡纸分成两部分,一部分做盒身一部分做底盖.想一想,他们的方案是否可行?测试9 再探实际问题与一元一次方程(一)学习要求能对所研究的问题抽象出基本的数量关系,通过列一元一次方程解实际问题,培养分析问题和解决问题的能力.课堂学习检测1.在商品销售经营中,涉及的基本关系式:(1)商品的原销售价、提价的百分数与商品的现销售价之间的关系是______________________________________________________________________.商品的原销售价、降价的百分数与商品的现销售价之间的关系是______________________________________________________________________.(2)商品的实际售价、商品的进价与商品的利润之间的关系是(这里不考虑其他因素)______________________________________________________________________.(3)商品的利润、商品的进价与商品的利润率之间的关系是(这里不考虑其他因素)______________________________________________________________________.(4)在打折销售中,商品的标价、折扣数与商品打折后的实际售价之间的关系是______________________________________________________________________.2.在我国银行储蓄存款计算利息的基本关系式主要有:(1)顾客存入银行的钱叫做______,银行付给顾客的酬金叫做______,它们的和叫做____,即__________________.(2)顾客将钱存入银行的时间叫做______.每个期数....内的______与____的比叫做利率.这样,本金、利率、期数、利息这四个量的关系是____________.综合、运用、诊断3.商店中某个玩具的进价为40元,标价为60元.(1)若按标价出售这个玩具,则所得的利润及利润率分别是多少?(2)顾客在与店主砍价时,店主为了保住15%的利润率,出售这个玩具的售价底线是多少元?(3)店主为吸引顾客,把这个玩具的标价提高10%后,再贴出打八八折的告示,则这个玩具的实际售价是多少元?(4)若店主设法将进价降低10%,标价不变,而贴出打八八折的告示,则出售这个玩具的利润及利润率分别是多少?4.(1)某个商品的进价是500元,把它提价40%后作为标价.如果商家要想保住12%的利润率搞促销活动,请你计算一下广告上可写出打几折?(2)想一想,如果(1)中该商品的进价没有具体给出,这时该问题怎么解决?5.某经销商经销一种商品,由于进货价降低了5%,售价不变,使得利润率由k%提高到(k +7)%,求k.〔售价=进货价×(1+利润率)〕拓展、探究、思考6.张新和李明相约到图书城去买书,请你根据他们的对话内容,求出李明上次所买书籍的原价.7.下表是甲商场电脑产品的进货单,其中进价一栏被墨迹污染,读了进货单后,请你算出这台电脑的进价是多少元.测试10 再探实际问题与一元一次方程(二)学习要求巩固一元一次方程解法,加强应用问题的训练,提高分析问题和解决问题能力.课堂学习检测一、选择题1.篮球赛的组织者出售球票,需要付给售票处12%的酬金,如果组织者要在扣除酬金后,每张球票净得12元,按精确到元的要求,球票票价应定为( ).(A)元(B)元(C)元(D)元2.一商店把彩电按标价的九折出售,仍可获利20%,若该彩电的进价是2400元,则彩电的标价为( ).(A)3200元(B)3429元(C)2667元(D)3168元3.某商店将彩电按原价提高40%,然后在广告上写“大酬宾,八折优惠”,结果每台彩电仍获利270元,那么每台彩电原价是( )(A)2150元(B)2200元(C)2250元(D)2300元4.一个商店以每3盘16元的价格购进一批录音带,又从另外一处以每4盘21元的价格购进比前一批数量加倍的录音带.如果两种合在一起以每3盘k元的价格全部出售可得到所投资的20%的收益,则k值等于( )(A)17 (B)18 (C)19 (D)20二、解答题5.某城市有50万户居民,平均每户有两个水龙头,估计其中有1%的水龙头漏水.若每个漏水龙头1秒钟漏一滴水,10滴水约重1克,试问该城市一年因此而浪费多少吨水(一年按365天计算).6.某市居民生活用电基本价格为每度元,若每月用电量超过a度,超过部分按基本电价的70%收取.(1)某户5月份用电84度,共交电费元,求a是多少;(2)若6月份的电费平均为每度元,求该户6月份共用多少度电,应交纳多少电费?综合、运用、诊断7.八年级三班在召开期末总结表彰会前,班主任安排班长李强去商店买奖品,下面是李强与售货员的对话:李强说:阿姨好!售货员:同学,你好,想买点什么?李强说:我只有100元,请您帮忙安排买10支钢笔和15本笔记本。
北京市西城区2022届语文七年级上学期期末学业水平测试试题模拟卷四

北京市西城区2022届语文七年级上学期期末学业水平测试试题模拟卷四一、选择题1.下列各句中,没有语病的一项是()A.珍视杨绛留下的宝贵精神遗产,就是对她最真挚的怀念。
B.电视剧《欢乐颂》播出时,收视观众和点击率一路飙升,引起了业界的关注。
C.有人建议,一旦遇到雾霾天气,可采取临时交通管制、错峰上下班、停工停课。
D.徐凝的一首诗,让扬州与明月结下了难以分开的不解之缘。
2.依次填入下列横线上的词语,最恰当的一项是( )安徒生童话经典经过多重改编,以绘本、舞台剧、电影等多种形式________在人们眼前,其永恒价值,在于给人________和警醒的人物形象,在于给人无限希望的思想,在于或优雅温润,或震撼心灵的语言,在于对后人道德情操的________,更在于它历经大浪淘沙还能千古流芳,代代________且历久弥新。
A.呈现启迪熏陶传承B.出现启发陶冶传播C.出现启迪陶冶传承D.呈现启发熏陶传播3.下列读音错误的一项是( )A.攒(cuán)成窜(cuàn)向B.脊梁(jǐ) 脑髓(suǐ)C.倜(tì)傥轻捷(jié)D.蝉蜕(tuì) 菜畦(wā)4.下列画线字注音有误的一项是( )A.御聘(pìn) 钦差(qīn) 陛下(bì)B.称职(chènɡ) 爵位(jué) 滑稽(jī)C.附和(hè) 炫耀(xuàn) 称赞(chēnɡ)D.阿谀(yú) 愚蠢(chǔn) 呈报(chénɡ)5.下列各组词语中注音或书写全部正确的一组是()A.酝酿(yùn niàng)澄清(dèng qīng) 憔瘁狭隘B.风筝(fēng zhēng)贮蓄(chǔ xù)分岐殉职C.黄晕(huáng yūn ) 棱镜(líng jing) 徘徊云宵D.蓑衣(suō yī)粗犷(cū guǎng) 匿笑热忱二、名句名篇默写6.用课文原句填空。
西城区英语学探诊七年级上册电子版

西城区英语学探诊七年级上册电子版1、I _______ play the game well. [单选题] *A. mustB. can(正确答案)C. wouldD. will2、Once you get on the road, here are some traffic _______ to remember. [单选题] *A. problemsB. positionsC. rules(正确答案)D. points3、You cannot see the doctor _____ you have made an appointment with him. [单选题] *A. exceptB.evenC. howeverD.unless(正确答案)4、He gathered his courage and went on writing music. [单选题] *A. 从事B. 靠······谋生C. 继续(正确答案)D. 致力于5、I have worked all day. I'm so tired that I need _____ . [单选题] *A. a night restB. rest of nightC. a night's rest(正确答案)D. a rest of night6、I _______ seeing you soon. [单选题] *A. look afterB. look forC. look atD. look forward to(正确答案)7、I knocked on the door but _______ answered. [单选题] *A. somebodyC. nobody(正确答案)D. everybody8、He has two sisters but I have not _____. [单选题] *A. noneB. someC. onesD. any(正确答案)9、Mary _______ a phone call with her mother now. [单选题] *A. will makeB. madeC. is making(正确答案)D. makes10、I should like to rent a house which is modern, comfortable and _____, in a quiet neighborhood. [单选题] *A.in allB. after allC. above all(正确答案)11、76.—Could you tell me ________the bank?—Turn right and it's on your right. [单选题]* A.how get toB.how to getC.how getting toD.how to get to(正确答案)12、_______ after dinner is good for our health. [单选题] *A. WalksB. Walking(正确答案)C. WalkedD. Walk13、31.A key ring is used __________ holding the keys. [单选题] *A.toB.inC.for (正确答案)D.with14、21.Design a travel guide for Shanghai! ________ the competition and be the winner! [单选题] *A.JoinB.AttendC.EnterD.Take part in (正确答案)15、Many children have to _______ their parents. [单选题] *A. divide intoB. put onC. depend on(正确答案)D. take on16、17.—When ________ they leave here?—Tomorrow morning. [单选题] * A.doB.will(正确答案)C.doesD.are17、( ) My mother told me _____ in bed. [单选题] *A. not readB. not readingC. don’t readD. not to read(正确答案)18、Bill Gates is often thought to be the richest man in the world. _____, his personal life seems not luxury. [单选题] *A. MoreoverB. ThereforeC. However(正确答案)D. Besides19、75.Why not________ for a walk? [单选题] *A.go out(正确答案)B.to go outC.going outD.goes out20、I have only two tickets for TF Boys’concert. ______ you ______ he can go with me.()[单选题] *A. Either; or(正确答案)B. Either; norC. Both; andD. Not only; but also21、The travelers arrived _______ Xi’an _______ a rainy day. [单选题] *A. at; inB. at; onC. in; inD. in; on(正确答案)22、What’s the price and what sort of _______ do you offer? [单选题] *A. advantageB. accountC. displayD. discount(正确答案)23、( ) The Great Wall was listed by the UNESCO as ___ World Heritage Site. [单选题]*A. a(正确答案)B. theC.\D.an24、6.—How can we get to the school?—________ bus. [单选题] *A.ToB.OnC.By(正确答案)D.At25、We ______ boating last weekend.()[单选题] *A. goB. went(正确答案)C. are goingD. will go26、一Mary wants to invite you to see the movie today. 一I would rather she(B)me tomorrow. [单选题] *A.tellsB. told (正确答案)C. would tellD. had told27、Words are windows()you can look into the past. [单选题] *A. through which(正确答案)B. through thatC. whichD. whose28、We ______ to set up a food bank to help hungry people next week.()[单选题] *A. hadB. are going(正确答案)C. were goingD. went29、59.—Can I talk to the manager?—Please wait ________ minute. [单选题] *A.anB.a(正确答案)C.theD./30、A healthy life is generally thought to be()with fresh air, clean water, and homegrown food. [单选题] *A. joinedB. boundC. lackingD. associated(正确答案)。
西城区学习探究诊断七年级上

第一章 有理数测试1 正数和负数学习要求了解正数、负数、有理数的概念,会用正数和负数表示相反意义的量.课堂学习检测一、判断题(正确的在括号内画“√”,错误的画“×”)( )1.某仓库运出30吨货记作-30吨,则运进20吨货记作+20吨. ( )2.节约4吨水与浪费4吨水是一对具有相反意义的量.( )3.身高增长1.2cm 和体重减轻1.2kg 是一对具有相反意义的量. ( )4.在小学学过的数前面添上“-”号,得到的就是负数. 二、填空题5.学校在大桥东面9千米处,那么大桥在学校______面-9千米处.6.如果以每月生产180个零件为准,超过的零件数记作正数,不足的零件数记作负数,那么1月生产160个零件记作______个,2月生产200个零件记作______个.7.甲冷库的温度为-6℃,乙冷库的温度比甲冷库低5℃,则乙冷库的温度是______.8.______既不是正数,也不是负数;它______整数,______有理数(填“是”或“不是”). 9.整数可以看作分母为1的______,有理数包括____________. 10.把下列各数填在相应的大括号内:74,6,0,14.3,5.0,432,14,5.8,51,27----正数集合{_______________________________________________________________…} 负数集合{_______________________________________________________________…} 非负数集合{_____________________________________________________________…} 有理数集合{_____________________________________________________________…}综合、运用、诊断一、填空题11.若把公元2008年记作+2008,那么-2008年表示______.12.潜水艇上浮为正,下潜为负.若潜水艇原先在距水面80米深处,后来两次活动记录的情况是-10米,+20米,则现在潜水艇在距水面______米的深处.13.是正数而不是整数的有理数是____________________. 14.是整数而不是正数的有理数是____________________. 15.既不是正数,也不是负数的有理数是______________. 16.既不是真分数,也不是零的有理数是______________.17.在下列数中:,31- 11.11111,725.95 95.527,0,+2004,-2π,1.12122122212222,,111-非负有理数有__________________________________________. 二、判断题(正确的在括号里画“√”,错误的画“×”) ( )18.带有正号的数是正数,带有负号的数是负数. ( )19.有理数是正数和小数的统称.( )20.有最小的正整数,但没有最小的正有理数. ( )21.非负数一定是正数. ( )22.311-是负分数. 三、解答题23.-3.782( ).(A)是负数,不是分数 (B)不是分数,是有理数 (C)是负数,也是分数(D)是分数,不是有理数 24.下面说法中正确的是( ).(A)正整数和负整数统称整数(B)分数不包括整数(C)正分数,负分数,负整数统称有理数 (D)正整数和正分数统称正有理数25.一种零件的长度在图纸上是(10±0.05)毫米,表示这种零件的标准尺寸是10毫米,加工要求最大不超过______毫米,最小不小于______毫米.拓展、探究、思考26.一批螺帽产品的内径要求可以有±0.02 mm 的误差,现抽查5个样品,超过规定的毫米值记为正数,不足值记1 2 3 4 5 +0.031+0.017+0.023-0.021 -0.015(A)1个测试2 相反数 数轴学习要求掌握一个数的相反数的求法和性质,学习使用数轴,借助数轴理解相反数的几何意义,会借助数轴比较有理数的大小.课堂学习检测一、填空题1.________________的两个数,叫做互为相反数;零的相反数是______.2.0.4与______互为相反数,______与-(-7)互为相反数,a 的相反数是______. 3.规定了______、______和______的______叫数轴. 4.所有的有理数都能用数轴上的______来表示.5.数轴上,表示-3的点到原点的距离是______个单位长,与原点距离为3个单位长的点表示的数是______。
北京市西城区2019年七年级上学期数学期末调研测试题(模拟卷四)

北京市西城区2019年七年级上学期数学期末调研测试题(模拟卷四)一、选择题1.如图,轩轩同学用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比原树叶的周长要小,能正确解释这一现象的数学知识是( )A.两条直线相交,只有一个交点B.两点确定一条直线C.经过一点的直线有无数条D.两点之间,线段最短 2.如图,甲从A 点出发向北偏东60°方向走到点B ,乙从点A 出发向南偏西15°方向走到点C ,则BAC ∠的度数是( )A.105°B.115°C.125°D.135°3.如图,点O 为直线AB 上一点,∠AOC=90°,∠DOE=90°,图中互余的角有几对?( )A.2对B.3对C.4对D.5对 4.如果1x =是方程250x m +-=的解,那么m 的值是( )A.-4B.2C.-2D.4 5.下列方程的变形中,正确的是( )A .由3+x =5,得x =5+3B .由3x ﹣(1+x )=0,得3x ﹣1﹣x =0C .由102y =,得y =2 D .由7x =﹣4,得74x =-6.某种商品每件的标价是330元,按标价的八折销售时,仍可获利10%,则这种商品每件的进价为( )A .200元B .240元C .250元D .300元7.下列各题中,合并同类项结果正确的是( )A.2a 2+3a 2=5a 2B.2a 2+3a 2=6a 2C.4xy-3xy=1D.2m 2n-2mn 2=08.下列选项中,不是同类项的是( )A .-1和0B .-x 2y 和3yx 2C .-2xy 2和2x 2yzD .-m 2和6m 29.多项式8x 2﹣3x+5与3x 3﹣4mx 2﹣5x+7多项式相加后,不含二次项,则m 的值是( )A .2B .4C .﹣2D .﹣410.有理数a 、b 在数轴上的对应点如图所示,则( )A.0a b +=B.0a b +>C.0a b ->D.0a b -<11.已知x ﹣4与2﹣3x 互为相反数,则x=( )A.1B.﹣1C.32D.﹣3212.绝对值最小的数是( )A.0.000001B.0C.-0.000001D.-100000 二、填空题13.如图,C 是线段BD 的中点,AD=3,AC=7,则AB 的长等于________14.计算:18.6°+42°24'=______.15.若方程x+5=7﹣2(x ﹣2)的解也是方程6x+3k =14的解,则常数k =_____.16.关于x 的方程ax ﹣2x ﹣5=0(a≠2)的解是_____.17.已知多项式﹣πx 2y m+1+xy 2﹣4x 3﹣8是五次多项式,单项式3x 2n y 6-m 与该多项式的次数相同,则m =_____,n =_____.18.如果x m+1与x n 是同类项,那么m ﹣n =_____.19.比较大小:13-_____﹣2520.小红在写作业时,不慎将一滴墨水滴在数轴上,根据图中的数据,请确定墨迹遮盖住的整数共有____个.三、解答题21.如图,已知AB ∥CD ,60B ∠=︒,CM 平分BCE ∠,90MCN ∠=︒,求DCN ∠的度数.22.(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A 、点B 表示的数分别为a 、b ,则A ,B 两点之间的距离AB=|a –b|,线段AB 的中点表示的数为2a b +. (问题情境)如图,数轴上点A 表示的数为–2,点B 表示的数为8,点P 从点A 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q 从点B 出发,以每秒2个单位长度的速度向左匀速运动. 设运动时间为t 秒(t>0).(综合运用)(1)填空:①A 、B 两点间的距离AB=__________,线段AB 的中点表示的数为__________;②用含t 的代数式表示:t 秒后,点P 表示的数为__________;点Q 表示的数为__________.(2)求当t 为何值时,P 、Q 两点相遇,并写出相遇点所表示的数;(3)求当t 为何值时,PQ=12AB ; (4)若点M 为PA 的中点,点N 为PB 的中点,点P 在运动过程中,线段MN 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN 的长.23.将一张纸如图所示折叠后压平,点F 在线段BC 上,EF 、GF 为两条折痕,若∠1=57°,∠2=20°,求∠3的度数.24.如图是某市民健身广场的平面示意图,它是由6个正方形组成的长方形,其中C 、D 两个正当形的大小相同.已知中间最小的正方形A 的边长为1m.(1)若设图中最大正方形B 的边长是x m ,用含x 的式子表示出正方形F ,E 和C 的边长分别为_______,_______,_________.(2)观察图形的特点可知,长方形相对的两边是相等的(如图中PQ=MN ,QM=PN ),请根据这个等量关系,求出x 的值;(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙两个工程对单独建设分别需要10天、15天完成。
北京市西城区2022届语文七年级上学期期末学业水平测试试题模拟卷一

北京市西城区2022届语文七年级上学期期末学业水平测试试题模拟卷一一、选择题1.下列加着重号的字的注音完全正确的一项是( )A.分歧.(qí) 一霎.(chà) 瘫痪..(tān huàn) 翻来覆.去(fù)B.匿.笑(nì) 心绪.(xù) 捶.打(chuí) 喜出望.外(wàng)C.诀.别(jué) 荫.蔽(yìn) 徘徊..(pái huái) 各得.其所(dé)D.侍.弄(chì) 祷.告(dǎo) 憔悴..(qiáo cuì) 絮絮.叨叨(xù)2.下列各句中,加点成语使用不恰当的一项是( )A.2017版《吉尼斯世界纪录》于近日全面发行,书中收录的各种怪诞不经....的比赛记录令人觉得不可思议。
B.近日,赵本山青涩旧照曝光,照片上留着短寸发型的他显得神采奕奕....。
C.桂林的山有的像雄狮,有的像大象,有的像猛虎,山形奇特,真是巧夺天工....。
D.老师刚说学校要举行长跑比赛,擅长跑步的李铭同学就迫不及待....地举手报名。
3.下列句中加点词的解释有误的一项是()A.陈太丘与友期.行,期日中。
期:约定。
B.尊君在不.?不:同“否”。
C.相委.而去。
委:舍弃。
D.元方入门而不顾.。
顾:照顾。
4.下列句子中加点词的意义相同的一项是( )A.复.投之/将复.何及B.缀行.甚远/夫君子之行.C.意.将隧入以攻其后也/意.暇甚D.而两狼之并驱如故./温故.而知新5.下列对病句的修改不正确的一项是( )A.珠算“中遗”成功后,不少网友认为,珠算是我国古代的重大发明,是中华民族智慧的结晶,应该加以发扬和传承。
(将“发扬”与“传承”互换位置)B.昆虫学家法布尔把科学和文学巧妙地结合起来,用生动形象的语言为我们刻画了一个绚丽多姿的昆虫世界。
北京市西城区2022届数学七年级上学期期末学业水平测试试题模拟卷三

北京市西城区2022届数学七年级上学期期末学业水平测试试题模拟卷三一、选择题1.如果一个角等于60°,那么这个角的补角是( )A .30° B.60° C.90° D.120°2.如图,直线AB 与直线CD 相交于点O ,E 是∠AOD 内一点,已知OE ⊥AB ,∠BOD =45°,则∠COE 的度数是( )A.125°B.135°C.145°D.155°3.下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A 地到B 地架设电线,总是尽可能沿着线段AB 架设;④把弯曲的公路改直,就能缩短路程,其中可用公理“两点之间,线段最短”来解释的现象有( )A .①②B .①③C .②④D .③④4.规定a c ad bc b d ⎛⎫=- ⎪⎝⎭,若2331x x ⎛⎫= ⎪--⎝⎭,则x =( ) A.0 B.3 C.1 D.25.一艘轮船航行在A 、B 两地之间,已知该船在静水中每小时航行12千米,轮船顺水航行需用6小时,逆水航行需用10小时,则水流速度和A 、B 两地间的距离分别为( )A .2千米/小时,50千米B .3千米/小时,30千米C .3千米/小时,90千米D .5千米/小时,100千米6.下列各组中的两项,不是同类项的是( )A.﹣x 2y 与2yx 2B.2πR 与π2RC.﹣m 2n 与212mnD.23与327.单项式253x y π-的次数是( )A.6B.7C.5D.2 8.下列各式中,结果为正数的是( ). A.﹣|﹣2|B.﹣(﹣2)C.﹣22D.(﹣2)×2 9.绝对值最小的数是( )A.0.000001B.0C.-0.000001D.-100000 10.-2017的相反数为 ( )A.2017B.-2017C.12017D.12017- 11.某项工程,甲单独做30天完成,乙单独做40天完成,若乙先单独做15天,剩下的由甲完成,问甲、乙一共用几天完成工程?若设甲、乙共用x 天完成,则符合题意的是( ) A.151513040x -+= B.151513040x ++=C.1513040x x ++=D.1513040x x -+= 12.下列各组中,不是同类项的是( ) A .5225与B .ab ba -与C .2210.25a b a b -与 D .2332a b a b -与 二、填空题13.如图,∠AOB=72︒,射线OC 将∠AOB 分成两个角,且∠AOC:∠BOC=1:2,则∠BOC=_____.14.如图,经过刨平的木板上的两个点,能弹出一条笔直的墨线,而且只能弹出一条墨线,能解释这一实际应用的数学知识是_____.15.小明沿街道匀速行走,他注意到每隔6分钟从背后驶过一辆1路公交车,每隔4分钟迎面驶来一辆1路公交车.假设每辆1路公交车行驶速度相同,而且1路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是________ 分钟.16.某项工程,甲单独完成要12天,乙单独完成要18天,如果甲先做了7天后,乙来支援由甲、乙合作完成余下的工程,则乙共做了___天.17.在某多媒体电子杂志的某一期上刊登了“正方形雪花图案的形成”的演示案例:作一个正方形,设每边长为4a ,将每边四等分,作一凸一凹的两个边长为a 的小正方形,得到图形如图(2)所示,称为第一次变化,再对图(2)的每个边做相同的变化,得到图形如图(3),称为第二次变化.如此连续作几次,便可得到一个绚丽多彩的雪花图案.如不断发展下去到第n 次变化时,图形的面积是否会变化,________(填写“会”或者“不会”),图形的周长为__________.18.若a+b=2019,c+d=-5,则代数式(a-2c )-(2d-b )=______.19.数轴上与表示-3的点相距4个单位长度的点表示的数是_____.20.1﹣|﹣3|=________.三、解答题21.如图,一副三角板的两个直角顶点重合在一起.(1)若∠EON=110°,求∠MOF 的度数;(2)比较∠EOM 与∠FON 的大小,并写出理由;(3)求∠EON+∠MOF 的度数.22.如图,C 是线段AB 上一点,M 是AC 的中点,N 是BC 的中点.(1)若AM=1,BC=4,求MN 的长度;(2)若MN=5,求AB 的长度.23.新学期开学,某体育用品商店开展促销活动,有两种优惠方案.方案一:不购买会员卡时,乒乓球享受8.5折优惠,乒乓球拍购买5副(含5副)以上才能享受8.5折优惠,5副以下必须按标价购买.方案二:办理会员卡时,全部商品享受八折优惠,小健和小康的谈话内容如下:会员卡只限本人使用.(1)求该商店销售的乒乓球拍每副的标价.(2)如果乒乓球每盒10元,小健需购买乒乓球拍6副,乒乓球a 盒,请回答下列问题:①如果方案一与方案二所付钱数一样多,求a 的值;②直接写出一个恰当的a 值,使方案一比方案二优惠;③直接写出一个恰当的a 值,使方案二比方案一优惠.24.如图1,已知数轴上两点A 、B 对应的数分别为﹣2、5,点P 为数轴上的一动点,其对应的数为x .(1)PA= ;PB= (用含x 的式子表示)(2)在数轴上是否存在点P ,使PA+PB=10?若存在,请直接写出x 的值;若不存在,请说明理由.(3)如图2,点P 以2个单位/s 的速度从点O 向右运动,同时点A 以4个单位/s 的速度向左运动,点B 以16个单位/s 的速度向右运动,在运动过程中,M 、N 分别是AP 、OB 的中点,问:AB OP MN -的值是否发生变化?请说明理由.25.先化简,再求值:()()233223x y 2x2x 2x y x y --++,其中x 2=. 26.(1)计算:16÷(﹣2)3﹣(﹣12)3×(﹣4)+2.5; (2)计算:(﹣1)2017+|﹣22+4|﹣(12﹣14+18)×(﹣24) 27.已知m ,n 互为相反数,p 、q 互为倒数,x 的绝对值为2,求220192018m n pq x +++. 28.先化简,再求值:22[3]23x y x y x xy --+(),其中12x =-,y=2.【参考答案】***一、选择题13.48°14.两点确定一条直线15.816.317.不会 SKIPIF 1 < 0. 解析:不会 42n a +.18.202919.1或-720.﹣2三、解答题21.(1)∠MOF=70°,(2)∠EOM=∠FON ,(3)∠EON+∠MOF=180°.22.(1)MN= 3;(2)AB= 10.23.(1)该商店销售的乒乓球拍每副的标价为40元;(2)①购买16盒乒乓球时,方案一与方案二所付钱数一样多;②购买5(1~15之间的整数即可)盒乒乓球时,方案一比方案二优惠; ③购买20(任意大于16的整数即可)盒乒乓球时,方案二比方案一优惠.24.(1)|x+2|,|x ﹣5|;(2)x=6.5或﹣3.5;(3)不发生变化,理由见解析.25.38x -,-64.26.(1)0; (2)8.27.201628.2x 2y+3x , 1-2。
西城区学习探究诊断七年级上

第一章 有理数测试1 正数和负数学习要求了解正数、负数、有理数的概念,会用正数和负数表示相反意义的量.课堂学习检测一、判断题(正确的在括号内画“√”,错误的画“×”)( )1.某仓库运出30吨货记作-30吨,则运进20吨货记作+20吨. ( )2.节约4吨水与浪费4吨水是一对具有相反意义的量.( )3.身高增长1.2cm 和体重减轻1.2kg 是一对具有相反意义的量. ( )4.在小学学过的数前面添上“-”号,得到的就是负数. 二、填空题5.学校在大桥东面9千米处,那么大桥在学校______面-9千米处.6.如果以每月生产180个零件为准,超过的零件数记作正数,不足的零件数记作负数,那么1月生产160个零件记作______个,2月生产200个零件记作______个.7.甲冷库的温度为-6℃,乙冷库的温度比甲冷库低5℃,则乙冷库的温度是______. 8.______既不是正数,也不是负数;它______整数,______有理数(填“是”或“不是”). 9.整数可以看作分母为1的______,有理数包括____________. 10.把下列各数填在相应的大括号内:74,6,0,14.3,5.0,432,14,5.8,51,27----正数集合{_______________________________________________________________…} 负数集合{_______________________________________________________________…} 非负数集合{_____________________________________________________________…} 有理数集合{_____________________________________________________________…}综合、运用、诊断一、填空题11.若把公元2008年记作+2008,那么-2008年表示______.12.潜水艇上浮为正,下潜为负.若潜水艇原先在距水面80米深处,后来两次活动记录的情况是-10米,+20米,则现在潜水艇在距水面______米的深处. 13.是正数而不是整数的有理数是____________________. 14.是整数而不是正数的有理数是____________________. 15.既不是正数,也不是负数的有理数是______________. 16.既不是真分数,也不是零的有理数是______________. 17.在下列数中:,31- 11.11111,725.95 95.527,0,+2004,-2,1.12122122212222,,111-非负有理数有__________________________________________. 二、判断题(正确的在括号里画“√”,错误的画“×”) ( )18.带有正号的数是正数,带有负号的数是负数. ( )19.有理数是正数和小数的统称.( )20.有最小的正整数,但没有最小的正有理数. ( )21.非负数一定是正数.( )22.311-是负分数. 三、解答题23.-3.782( ).(A)是负数,不是分数 (B)不是分数,是有理数 (C)是负数,也是分数 (D)是分数,不是有理数 24.下面说法中正确的是( ).(A)正整数和负整数统称整数 (B)分数不包括整数(C)正分数,负分数,负整数统称有理数 (D)正整数和正分数统称正有理数25.一种零件的长度在图纸上是(10±0.05)毫米,表示这种零件的标准尺寸是10毫米,加工要求最大不超过______毫米,最小不小于______毫米.拓展、探究、思考26.一批螺帽产品的内径要求可以有±0.02 mm 的误差,现抽查5个样品,超过规定的毫米值记为正数,不足值记为负数,检查结果如表.则合乎要求的产品数量为( ).(A)1个(B)2个(C)3个(D)5个测试2 相反数 数轴学习要求掌握一个数的相反数的求法和性质,学习使用数轴,借助数轴理解相反数的几何意义,会借助数轴比较有理数的大小.课堂学习检测一、填空题1.________________的两个数,叫做互为相反数;零的相反数是______.2.0.4与______互为相反数,______与-(-7)互为相反数,a 的相反数是______. 3.规定了______、______和______的______叫数轴. 4.所有的有理数都能用数轴上的______来表示.5.数轴上,表示-3的点到原点的距离是______个单位长,与原点距离为3个单位长的点表示的数是______。
北京市西城区2022届七上生物期末复习调研测试题

北京市西城区2022届七上生物期末复习调研测试题一、选择题1.皮肤在人体表面起到保护作用,当皮肤划破时人会感到疼痛,甚至会流血,说明皮肤属于人体结构层次中的()A.细胞 B.器官 C.组织 D.系统2.生态系统是指在一定范围内,生物与环境所形成的统一整体。
以下可以称为生态系统的是A.洞庭湖中的水B.岳麓山上所有的植物C.南山公园中所有的生物D.湘江3.“人间四月芳菲尽,山寺桃花始盛开”所描述的生物与环境的关系是( )A.环境影响生物 B.生物适应环境 C.生物适应环境 D.生物依赖环境4.下列食物链中,能够成立的是()A.草→蚱蜢→食虫鸟→蛇→鹰B.蚱蜢→草→食草籽的鸟→鹰→狐C.草←蚱蜢←食草虫←蛇←鹰D.草→蚱蜢→食草虫→鹰→蛇5.下列食物链的写法准确的是()A.草→羊→狼 B.草→兔→狼→细菌C.兔→狐→细菌 D.阳光→草→昆虫→蛙6.不借助任何工具,就可以生活在生物圈各圈层的生物是()A.鸟类 B.人类 C.鱼类 D.细菌类7.花生是我们大家爱吃的一种干果类食物,关于构成一株花生的结构层次由小到大的排列顺序,正确的是()A.细胞、组织、器官、系统、花生植株B.细胞、组织、系统、器官、花生植株C.细胞、器官、组织、花生植株D.细胞、组织、器官、花生植株8.下列不属于生态系统的是()A.诺敏河 B.巴特罕公园C.美丽的尼尔基镇 D.民族园一棵百年松树9.人的体细胞与蕃茄细胞基本结构的不同之处是,人的体细胞不具有()A.细胞壁 B.细胞膜 C.细胞质 D.细胞核10.在“绿叶在光下制造有机物”实验中,前期操作与后期目的不—致的是( )A.将天竺葵放在暗处一昼夜-------消粍叶片中原有的淀粉B.将叶片一部分上下两面用黑纸片遮盖---------设置有光和无光的对照C.将叶片放入有酒精的小烧杯中直接加热------脱去叶片中的叶绿素D.向漂洗干净的叶片上滴加碘液-------检验淀粉的生成11.在制作糖拌番茄时,加入食糖并搅拌,发现盘中的汁液增多了,这些汁液主要来自于果肉细胞中的:A.细胞壁 B.细胞膜 C.叶绿体 D.液泡12.胚珠生于花的哪一种结构里()A.雄蕊B.雌蕊C.子房D.花药13.花是植物体的繁殖器盲,请在下图中找出小麦的花()A.A B.B C.C D.D14.移栽的茄子幼苗根部总是带有土团,其主要原因是()A.避免损伤根毛和幼根 B.减少土壤无机盐的丢失C.有利于幼苗根的呼吸 D.防止幼苗出现萎蔫现象15.夏天为了保存水果,一般会把水果放冰箱,这主要是抑制了水果细胞的()A.光合作用 B.呼吸作用 C.蒸腾作用 D.吸收作用16.黄瓜花有两种,其中一种花俗称“谎花”,“谎花”是指()A.花蕊中只含有雄蕊的花,不能结果实B.花朵颜色鲜艳C.花朵能吸引昆虫D.花蕊中只有雌蕊的花,能结果实17.一个密闭的保温装置中装有正在萌发的种子,每隔一段时间测定其装置内的温度和氧气含量,并将结果绘制成曲线。
北京市西城区2022届生物七年级上学期期末学业水平测试试题模拟卷二

北京市西城区2022届生物七年级上学期期末学业水平测试试题模拟卷二一、选择题1.属于组织的一项是A.脂肪细胞 B.血液C.唾液腺 D.肱二头肌2.宋代诗人杨万里的著名诗句“小荷才露尖尖角,早有蜻蜓立上头”,句中的“小荷”和“蜻蜓”这两种生物共有的特征是()A.都能生长和繁殖 B.都可以自己制造有机物C.都可以自由运动 D.都可以遗传,但不能变异3.“螳螂捕蝉,黄雀在后”下列可以体现这一现象的正确食物链是A.蝉→螳螂→黄雀B.螳螂→蝉→黄雀C.树→蝉→螳螂→黄雀D.树→螳螂→蝉→黄雀4.下列关于生物圈的说法正确的是()A.大气圈和水圈中各处都有生物生存 B.生物圈是指地球上有生物生存的圈层C.生物圈仅由植物、动物及其中的微生物组成 D.地球的任一地方都有生物生存5.数百年前,我国黄土高原有茂密的森林。
后来由于人口过于集中、长期掠夺式的开发,这个地区变成了荒山秃岭。
这个现象说明()A.生物能影响环境B.环境条件决定人口的数量C.生物能适应环境D.环境条件决定生物的形态6.课上被点名回答问题时你会主动起立,这说明生物具有的特征是()A.能进行呼吸 B.能够进行生长C.生活需要营养 D.能对外界刺激作出反应7.山东有丰富的农作物及水果品种,如潍坊萝卜、泰安绿豆、烟台苹果、冠县鸭梨。
人民主要食用上述植物的哪种器官?依次是()A.根、果实、种子、果实B.茎、种子、果实、种子C.根、种子、果实、果实D.茎、果实、果实、种子8.某生物小组为了探究“光对鼠妇生活的影响”,准备了10只鼠妇,并设计了如下图所示的实验。
下列对本方案的修改意见,正确的是A.10只鼠妇太多了,用2只就可以B.纸盒上面应该全部用玻璃板盖住C.纸盒底部两边都应该是细湿土D.没有错误,不需要修改9.概念之间具有并列、包含等关系。
如图表示a、b概念之间的各种关系,下表选项中所列概念之间的关系,错误的是()10.春天到了,果园里的桃树开满了桃花,下列哪种情况的桃花一定不能结出桃子A.花冠凋落的 B.雄蕊被人工摘掉的C.花萼脱落的 D.雌蕊被害虫吃掉的11.切洋葱时常会引起流泪,原因是洋葱组织细胞中含有对眼睛有刺激的物质,这些物质主要存在于()A.线粒体B.细胞膜C.细胞核D.液泡12.“种瓜得瓜,种豆得豆”。
北京市西城区2022届语文七上期末模拟学业水平测试试题(一)

北京市西城区2022届语文七上期末模拟学业水平测试试题(一)一、选择题1.下列加点字的注音有误的一项是()A.东临碣.石(jié)水何澹.澹(dàn)B.山岛竦峙..(sǒng zhì)幸甚至哉.(zāi)C.星汉灿.烂(càn)歌以咏.志(yǒng)D.杨花落尽子规啼.(dì)枯.藤老树昏鸦(kū)2.下列句子节奏划分有误的一项是()A.谢太傅/寒雪日/内集B.未若/柳絮/因风起C.陈太丘/与友期行D.君与家君/期日中3.下列加点字注音完全正确的一项是()A.发髻.(jì)澄.清(chénɡ)看.护(kàn)B.伦敦.(dūn)着.落(zháo)镶.边(xiānɡ)C.狭窄.(zhǎi)贮.蓄(chǔ)暖和.(huo)D.水藻.(zǎo)害羞.(xiū)更.换(ɡēnɡ)4.对“海日生残夜,江春入旧年”两句品析有误的一项是()A.第一句诗的意思是:当残夜还未消退之时,一轮红日已从海上升起。
B.第二句诗的意思是:旧年的春景生机盎然,令人难以忘怀。
C.“日生残夜”“春入旧年”都表时序匆匆交替,怎不叫身在异乡的诗人更生思乡之情?D.诗人将“日”与“春”作为新生的美好事物的象征,表现出普遍意义的生活哲理,给人以乐观、积极、向上的艺术鼓舞力量。
5.下列各项词语中,书写有误的一项是()A.艰难决别霎时泼泼洒洒B.并蒂匿笑烂漫絮絮叨叨C.高洁严厉菡萏喜出望外D.徘徊攥着慈怜翻来覆去二、名句名篇默写6.按要求作答(1)默写①征蓬出汉塞,。
(王维《使至塞上》)②,思而不学则殆。
(《论语•为政》)③长风破浪会有时,。
(李白《行路难》)④,到乡翻似烂柯人。
(刘禹锡《酬乐天扬州初逢席上见赠》)⑤持节云中,?(苏轼《江城子·密州出猎》)⑥,坐断东南战未休。
(辛弃疾《南乡子·登京口北固亭有怀》)(2)近水沙滩,鸳鸯休憩;向阳绿树,黄莺争鸣;湛蓝天空,春燕衔泥。
学探诊七上演练答案

第一讲 演练答案演练1-5 C CDCB演练6属于负数的有: 4.5-,12-,0.313- ,11-;属于非负有理数:6,0,2.4 ,3.14 演练7 B 演练8 3- 演练9 4-或2-演练10 蚂蚁6s 共爬行12个单位长度;B 点到A 点的距离为6个单位长度;B 点对应的数是5.54BA演练11 a -演练12 他们的相反数分别是:3,2,3-,0,1-, 2.5-.如图:-112-3演练13 C 演练14 B 演练15 A 演练16 D 演练17 B 演练18 D第二讲 演练答案演练1 B演练2 ⑴ 0.4-;⑵ 7-;⑶ 1;⑷ 76-;⑸ 12-;⑹ 9;演练3 ⑴ 南,14;⑵ 13.6 演练4 B演练5 ⑴ 15752;⑵ 12-;⑶ 0;演练6 1- 演练7 ⑴ 9-;⑵ 152-第三讲 演练答案演练1 A 演练2 C 演练3 ⑴ =;⑵ >;⑶ >;⑷ >;⑸ <;⑹ >;⑺ >;⑻ > 演练4 C 演练5 B 演练6 C演练7 ⑴76-;⑵ 32-;⑶ 85;⑷11;⑸10;⑹ 5000;演练8 A演练915演练10 B 演练11 C演练12 83.6710⨯演练13 C演练14 A演练15 ⑴ 1.41;⑵34.010⨯第四讲 演练答案演练1223xy ,a -,572t ,233a b c -,πx-是单项式. 223xy 的系数是23,次数是3;a -的系数是1-,次数是1;572t 的系数是52(注意有些学校要求写成32),次数是7;233a b c -的系数是3-,次数是6;πx-的系数为1π-,次数为1. 演练2 ⑴ C ;⑵ A ;⑶1m =,2n =,()2009121-=-;⑷3x =±,2y =±;⑸ 4m =,14n =-演练3 ⑴ C ;⑵ B ;⑶ 六,四,428x y -;⑷ 9-,3,三,三;⑸ 213m -=,24m =,2m =± 演练4 ⑴ 322187213x y x y xy y ---+,四次四项式,318x y -; ⑵ 3225321x y x y xy y ---+-,四次五项式,25x y - 演练5 A 演练6 A 演练7 C 演练8 ⑴ ()()32323322951782A B a b b a b b +=--+-++32323318102782a b b a b b =---++322331872a b a b b =--⑵ ()()2333233782951a b b a b b -++---23332321246951a b b a b b =-++-++23323219297a b a b b =--++演练9 43642x x -+ 演练10 1010a b + 演练11 7-演练12 原式29453944x y =-+=+=第五讲 演练答案演练1 ⑴ √ ;⑵ √ ;⑶ × ;⑷ √. 演练2 ⑴ 1-,⑵ y , ⑶ 34x ; ⑷8, 演练3 B演练4 C演练5 根据题意可得3(4)602k ⨯--=,1k =-,则19991k =-.演练6 根据题意可得()20480m m +⨯-+=,2m =,且20m +≠,∴2m =.演练732演练8 2- 演练9 C演练10 ⑴38x =;⑵12x =.演练11 112x =-演练12 原方程可化为42101123x x -+-=,解得8x =-. 演练13 解得117x =-.演练14 322(28x x +=-. 演练15 设甲种商品的原销售价为x 元,则乙种商品的原销售价为(500x -)元.据题意,得70%90%(500)386x x +-=,解方程得320x =,500180x -=.答:略.第六讲 演练答案演练1 ⑴ 根据题意可得:11n -=,11m -=,所以2n =,0m =或2.⑵ 根据题意可得:20a -≠,50b +≠,11a -=,41b -=,所以2a =-,5b =.演练2 将12x y =-⎧⎨=⎩代入12x ay bx y +=-⎧⎨-=⎩可得0a =,4b =-,那么0(4)4a b +=+-=-.演练 3 12x y =⎧⎨=⎩是方程x y n +=的解可得3n =,则原方程为3x y +=,3x y m =⎧⎨=⎩是方程3x y +=的解可得33m +=,0m =.演练4 x ,y 互为相反数,当1x =,则1y =-,代入方程组可得2a =,4b =-.演练5 一般地,未知数的个数多于方程个数时,我们称为不定方程.一般情况下,不定方程的解有无数组,当确定了方程中的某一个未知数的值后,就能从方程中求出另一未知数的值.也可以解释为有无数组相反数.选择C .演练6 用含x 的代数式表示y ,263y x =-;用含y 的代数式表示x ,392x y =-,当6x =,9,10时,y 分别为2,0,23-.演练7 ⑴ C ;⑵ 34x y =⎧⎨=⎩演练8 ⑴ 21x y =⎧⎨=-⎩ ⑵ 75x y =⎧⎨=⎩ ⑶ 612m n =⎧⎨=⎩ ⑷ 1214x y ⎧=-⎪⎪⎨⎪=⎪⎩ ⑸ 23x y =⎧⎨=⎩演练9 D演练10 将22x y =⎧⎨=-⎩与18x y =-⎧⎨=-⎩代入6ax by +=可得22686a b a b -=⎧⎨--=⎩,解得21a b =⎧⎨=-⎩.演练11 将32x y =⎧⎨=-⎩,22x y =-⎧⎨=⎩代入2ax by +=可得222322a b a b -+=⎧⎨-=⎩,解得45a b =⎧⎨=⎩32x y =⎧⎨=-⎩代入78mx y -=可得2m =-,45(2)40a b m ⋅⋅=⨯⨯-=-. 第七讲 演练答案演练1 ⑴ C ;⑵ 30%(5)2x +-≤.演练2 让学生说明每一步的依据.⑴ <;⑵ <;⑶ >;⑷ >. 演练3 选择C ,正确应为22ac bc ≥. 演练4 选择D .演练5 ⑴ 3x <;⑵ C ;⑶ 3演练6 ⑴ 7x >-,图略;⑵ 265x <,教师可再问学生,此不等式的非负整数解为?其非负整数解为0,1,2,3,4,5.图略.演练7 解不等式组得2912x ≤,所以其非负整数解为0,1,2.演练8 由题意可列不等式为:5(1)2(2)(2)x x x --->-+,解得14x >-.演练9 由0abcd >得a 、b 、c 、d 中负数的个数为0个、2个或4个,又0a b c d +++>,所以最多有2个负数,选择B .演练10 ⑴ 13x -<≤;⑵ 12x -<≤,图略.演练11 不等式组的解集为:13x <<,整数解为2;演练12 设八戒买了x 个西瓜,则35845x ⨯+≤,解得154x ≤,故八戒至多买3个西瓜.第八讲 演练答案演练1 ⑴ C ;⑵ B 演练2 1条或3条.演练3 应该建在AC ,BD 的交点P 上,如图所示.首先我们使购物中心到A 和C 的距离之和最小,那么购物中心就应该建在线段AC 的某点处.这是因为如果点P 不在AC 上,根据两点之间,线段最短,可以知道P A P C A C ''+>.同时我们也能看出,购物中心建在线段AC 上的任意一点,都可以保证购物中心到A ,C 距离之和最小.同理,购物中心若到B ,D 之和距离最小,也必须建在线段BD 上,这样购物中心就必须建在AC ,BD 的交点P 上.演练4 C演练5 2,4,BC ,6演练6 ∵C 为线段AB 上一点,∴AC CB AB +=又∵10cm AB =,3cm BC = ∴7cm AC =又∵D 为AC 的中点∴13.5cm 2AD AC ==∴ 6.5cm DB AB AD =-= 演练7 28cm AB =.演练8 C .演练9 B演练10 ⑴ 57.3257 19 12'''︒=︒;⑵ 12234212.395'''︒=︒演练11 ⑴ 7742344511227'''︒+︒=︒; ⑵;180(34542133)12333'''︒-︒+︒=︒ ⑶ 13533157435731136'''''︒⨯+︒÷=︒.演练12 22()2(7045)50BOC BOD EOD EOB ∠=∠=∠-∠=⨯︒-︒=︒.第九讲 演练答案演练 由⑵知,甲不是跳高冠军和大作家;由⑸知,乙不是大作家;由⑹知,丙、乙都不是小画家.由ACD因为丙是大作家,所以由⑵知丙不是跳高冠军,推知乙是跳高冠军.因为乙是跳高冠有理数的基本概念及运算1.① ③ ⑥ ;2.42.1610⨯; 3.3, 13,1134-<-;4.1±,20±或,0;5.30x y ==,;6.17218整式概念及加减法7.5π- 8.322167213x y x y xy y ---+ 四次四项式 316x y -9.①15±±或,② 1;10.原式=2341a b -+= ; 11.37A B C -+=-;一元一次方程(组)与不等式(组)12.B ; 13.21m n ==-,,14.A ; 15.3x =- ;16.212x ≤,正整数解为, ; 17.12x -<≤;线与角18.57.32︒; 19.675428'''︒;20.答案如图所示.线段AB 与线段BA 表示同一条线段,直线BC 与直线CB 表示同一条直线;射线AC 与射线CA 不表示同一条射线;21.AM ND MB NC MN BC a b +=+=-=-,2AD AM MN ND a b =++=-.22.设这个锐角为x ,根据题意可列方程:1(90)(180)1802x x x +︒-+︒-=︒,得60x =︒.AA B C DM N。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 有理数测试1 正数和负数学习要求了解正数、负数、有理数的概念,会用正数和负数表示相反意义的量.课堂学习检测一、判断题(正确的在括号内画“√”,错误的画“×”)( )1.某仓库运出30吨货记作-30吨,则运进20吨货记作+20吨. ( )2.节约4吨水与浪费4吨水是一对具有相反意义的量.( )3.身高增长1.2cm 和体重减轻1.2kg 是一对具有相反意义的量. ( )4.在小学学过的数前面添上“-”号,得到的就是负数. 二、填空题5.学校在大桥东面9千米处,那么大桥在学校______面-9千米处.6.如果以每月生产180个零件为准,超过的零件数记作正数,不足的零件数记作负数,那么1月生产160个零件记作______个,2月生产200个零件记作______个.7.甲冷库的温度为-6℃,乙冷库的温度比甲冷库低5℃,则乙冷库的温度是______.8.______既不是正数,也不是负数;它______整数,______有理数(填“是”或“不是”). 9.整数可以看作分母为1的______,有理数包括____________. 10.把下列各数填在相应的大括号内:74,6,0,14.3,5.0,432,14,5.8,51,27----&正数集合{_______________________________________________________________…} 负数集合{_______________________________________________________________…} 非负数集合{_____________________________________________________________…} 有理数集合{_____________________________________________________________…}综合、运用、诊断一、填空题11.若把公元2008年记作+2008,那么-2008年表示______.12.潜水艇上浮为正,下潜为负.若潜水艇原先在距水面80米深处,后来两次活动记录的情况是-10米,+20米,则现在潜水艇在距水面______米的深处.13.是正数而不是整数的有理数是____________________. 14.是整数而不是正数的有理数是____________________. 15.既不是正数,也不是负数的有理数是______________. 16.既不是真分数,也不是零的有理数是______________.17.在下列数中:,31- 11.11111,725.95&&&95.527,0,+2004,-2π,1.12122122212222,,111-非负有理数有__________________________________________. 二、判断题(正确的在括号里画“√”,错误的画“×”) ( )18.带有正号的数是正数,带有负号的数是负数. ( )19.有理数是正数和小数的统称.( )20.有最小的正整数,但没有最小的正有理数. ( )21.非负数一定是正数. ( )22.311-是负分数. 三、解答题23.-3.782( ).(A)是负数,不是分数 (B)不是分数,是有理数 (C)是负数,也是分数(D)是分数,不是有理数 24.下面说法中正确的是( ).(A)正整数和负整数统称整数(B)分数不包括整数(C)正分数,负分数,负整数统称有理数 (D)正整数和正分数统称正有理数25.一种零件的长度在图纸上是(10±0.05)毫米,表示这种零件的标准尺寸是10毫米,加工要求最大不超过______毫米,最小不小于______毫米.拓展、探究、思考26.一批螺帽产品的内径要求可以有±0.02 mm 的误差,现抽查5个样品,超过规定的毫米值记为正数,不足值记1 2 3 4 5 +0.031+0.017+0.023-0.021 -0.015(A)1个测试2 相反数 数轴学习要求掌握一个数的相反数的求法和性质,学习使用数轴,借助数轴理解相反数的几何意义,会借助数轴比较有理数的大小.课堂学习检测一、填空题1.________________的两个数,叫做互为相反数;零的相反数是______.2.0.4与______互为相反数,______与-(-7)互为相反数,a 的相反数是______. 3.规定了______、______和______的______叫数轴. 4.所有的有理数都能用数轴上的______来表示.5.数轴上,表示-3的点到原点的距离是______个单位长,与原点距离为3个单位长的点表示的数是______。
6.数轴上A ,B 两点分别在原点的两旁,并且与原点的距离相等,已知点A 表示的数是-10,则点B 表示的数为______. 二、选择题7.下面各组数中,互为相反数的有( ).21①和21- ②-(-6)和+(-6) ③-(-4)和+(+4)④-(+1)和+(-1) ⑤215+和+)215(- ⑥713-和)713(--(A)4组 (B)3组 (C)2组 (D)1组 8.下列说法中正确的有( )①-3和+3互为相反数;②符号不同的两个数互为相反数;③互为相反数的两个数必定一个是正数,一个是负数;④π的相反数是-3.14;⑤一个数和它的相反数不可能相等. (A)0个 (B)1个 (C)2个 (D)3个或更多 9.如图,有理数a ,b 在数轴上对应的点如下,则有( ).(A)a >0>b (B)a >b >0(C)a <0<b(D)a <b <0三、解答题10.已知一组数:.75.0,1,0,214,212,5.0,3,4----(1)画一条数轴,并把这些数用数轴上的点表示出来;(2)把这些数分别填在下面对应的集合中:负数集合{ …} 正数集合{ …}(3)请将这些数按从小到大的顺序排列(用“<”连接):______________________. 11.化简下列各数:(1)=--)32(______.(2)=+-)54(______.(3)=+-+-)]}3([{______.12.比较大小:43-______;87-)32(+-______);43(-+)14.3(--______)π(--.综合、运用、诊断一、填空题13.设a 是一个正数,则数轴上表示数a 的点在原点______边,与原点的距离是______个单位长度;表示数-a 的点在原点______边,与原点的距离是______个单位长度. 14.若-m 是正数,则m 是______数;m 是-m 的______数. 15.______的相反数比它本身大,______的相反数等于它本身. 16.大于763-且小于767的整数有______个;比533小的非负整数是____________. 17.若p ,q 两数在数轴上的位置如下图所示,请用“<”或“>”填空.①p ______q ; ②-p ______0; ③-q ______0;④-p ______-q ; ⑤-p ______q ; ⑥p ______-q .18.已知-1<a <0<1<b ,请按从小到大的顺序排列-1,-a ,0,1,-b 为__________. 19.负数的相反数是_______数;把这句话用符号可以表示为_______;把“若m >0,则-m <0”用文字语言表示为_________________. 二、选择题20.下列说法中,正确的是( ).(A)无最大正数,有最大负数 (B)无最小负数,有最小正数 (C)无最小有理数,也无最大有理数 (D)有最小自然数,也有最小整数21.从原点开始向左移动3个单位,再向右移动1个单位后到达A 点,则A 点表示的数是 ( ).(A)3 (B)4 (C)2 (D)-2 三、解答题22.如图为北京地铁的部分线路.假设各站之间的距离相等表示为一个单位长.现以万寿路站为原点,向右的方向为正,那么表示木樨地站的数为______表示古城站的数为______如果改以古城站为原点,那么表示木樨地站的数变为______.23.小明家(记为A )与他上学的学校(记为B )、书店(记为C ),依次坐落在一条东西走向的大街上,小明家位于学校西边30米处,书店位于学校东边100米处.小明从学校沿这条街向东走了40米,接着又向西走了70米到达D 处.试在数轴上表示上述四点.24.若a 为有理数,在-a 与a 之间(不含-a 与a )有1997个整数,则a 的取值范围是_________.拓展、探宄、思考 25.已知m ,n 互为相反数,试求:3222nm n m +-++的值.26.如图所示,数轴上有五个点A ,B ,P ,C ,D ,已知AP =PD =3,且AB =BC =CD ,点P 对应有理数1,则A ,B ,C ,D 对应的有理数分别是什么?(只需写出结果,不必写出详细的推理过程)测试3 绝对值学习要求掌握一个数的绝对值的求法和性质,进一步学习使用数轴,借助数轴理解绝对值的几何意义.课堂学习检测一、填空题 1.填表:2.一个正数的绝对值是______;______数的绝对值是它的相反数;______的绝对值是零;绝对值最小的数是______. 3.绝对值小于143.5的所有整数的和为______.4.两个正数比大小,绝对值大的______;两个负数比大小,绝对值大的______. 5.绝对值小于4的整数中,最大的整数是______,最小的整数是______. 二、选择题6.下列各式中,等号不成立的是( ).(A)|-5|=5 (B)-|5|=-|-5| (C)|-5|=|5| (D)-|-5|=57.|32|--的相反数是( ).(A)23 (B)23- (C)32 (D)32- 8.下列判断中,错误的是( ).(A)一个正数的绝对值一定是正数 (B)一个负数的绝对值一定是正数 (C)任何数的绝对值都是正数 (D)任何数的绝对值都不是负数 9.一个数的绝对值是正数,这个数一定是( ).(A)正数 (B)非零数 (C)任何数 (D)以上都不是10.在-|-1|,-|0|,)2(--,24中,负数共有( ). (A)4个 (B)3个 (C)2个 (D)1个 11.若|a |+a =0,则a 是( ).(A)正数 (B)负数 (C)正数或0(D)负数或0三、解答题 12.比大小:65-______653,54-______|21|,763--______|,31|-|1|--______|1.0|+-,83.1&&-______-1.384,0.0001______-1000,-π______-3.14.13.计算:(1)|-16|+|-24|+|+30| (2)|1522||432|-⨯-综合、运用、诊断一、填空题14.______的相反数小于它本身;______的绝对值大于它本身;______的相反数、绝对值和它本身都相等.15.若a >b ,a ,b 均是正数,比较大小:|a |______|b |;若a <b ,a ,b 均是负数,比较大小:|a |______|b |. 16.若m ,n 互为相反数,则|m |______|n |. 17.若|x |=|y |,则x ,y 的关系是______.18.如果|x |=2,那么x =______;如果|-x |=2,那么x =______. 19.当|a |=a 时,则a ______.20.若|a -2|+|b +3|=0,则a =______,b =______.21.已知|x |=2,|y |=5,且x >y ,则x =______,y =______. 22.满足3.5<|x |≤9的x 的整数值是______.23.数a 在数轴上的位置如图所示,则|a -2|=______.二、选择题24.若a =-1,则-(-|a |)=( ).(A)1 (B)0 (C)-1 (D)1或-1 25.下列关系一定成立的是( ).(A)若|m |=|n |,则m =n (B)若|m |=n ,则m =n (C)若|m |=-n ,则m =n (D)若m =-n ,则|m |=|n | 26.若|x -2|=1,则x =( ).(A)3 (B)1 (C)-1或1 (D)3或1 27.式子|2x -1|+2取最小值时,x 等于( ).(A)2(B)-2(C)21 (D)21-三、解答题28.飞机提前两分钟到达记为+2,推迟10分钟到达记为-10,准点到达记为0.下面是5家航空公司一年来的到达时间平均值统计表.请利用学过的绝对值的知识评价一下哪家航空公司最好,哪家航空公司最差.航空公司ABC D E 起飞时间 -40 +10-5+3029.已知:x ,y 满足0|21||2|21=-+-y y x ,求7x -3y 的值.拓展、探究、思考30.若|x |>3,则x 的范围是______.31.若|x |+3=|x -3|,则x 的取值范围是______.32.已知|a |=3,|b |=4,若a ,b 同号,则|a +b |=______;若a ,b 异号,则|a +b |=______.据此讨论|a +b |与|a |+|b |的大小关系.测试4 有理数的加法学习要求掌握有理数的加法法则,会使用运算律简算,并能解决简单的实际问题.课堂学习检测一、填空题1.足球比赛中,甲队攻入乙队两球,同时被乙队攻入五球,则计算甲队净胜球数的算式为__________________.2.-2的相反数与21-的倒数的和的绝对值等于______. 3.在括号内填入变形的根据:(a +b )+c =a +(b +c )( )=(b +c )+a ( ). 二、选择题4.下列运算中正确的是( ).(A)(+8)+(-10)=-(10-8)=-2 (B)(-3)+(-2)=-(3-2)=-1(C)(-5)+(+6)=+(6+5)=+11 (D)(-6)+(-2)=+(6+2)=+8 5.三个数-15,-5,+10的和,比它们绝对值的和小( ).(A)-20 (B)20 (C)-40 (D)40 6.如果两个数的和是正数,那么这两个数一定( ).(A)都是正数 (B)只有一个正数 (C)至少有一个正数 (D)不确定 三、计算题7.(+8)+(-17)= 8.(-17)+(-15)=9.(-32.8)+(+51.76)= 10.(-3.07)+(+3.07)=11.=-+)325(012.)71.2()325(-+-=13.)12511()8119(-++= 14.=+++-2075.123.22)5.10(四、解答题15.某潜水员先潜入水下61米,然后又上升32米,这时潜水员处的位置能否用两种方法表示?综合、运用、诊断一、填空题16.从-56起,逐次加1,得到一串整数:-55,-54,-53…则第100个数为______. 二、选择题17.两数相加,和比每个加数都小,那么这两个数是( ).(A)同为负数 (B)两数异号 (C)同为正数 (D)负数和零 18.若m 为有理数,则m +|m |的结果必为( ).(A)正数 (B)负数 (C)非正数 (D)非负数 三、计算题19.(+7)+(-21)+(-7)+(+21)20.0+(-3.71)+(+1.71)-(-5)21.)511()72()51()73(-+++++-22.)215()726()5.15()753(-+-+++-四、解答题23.小虫从点O 出发在一条直线上来回爬行,向右爬行的路程记为正,向左爬行的路程记为负,爬行的各段路程依次为:+5,-3,+10,-8,-6,+12,-10.(单位:cm) (1)小虫最后是否回到出发点O ?为什么?(2)小虫离开O 点最远时是多少?(3)在爬行过程中,如果每爬行1cm 奖励1粒芝麻,则小虫一共可以得到多少粒芝麻?拓展、探究、思考24)这1025.有理数加法法则:异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,若将正数记为a ,负数记为b ,将这句话用符号语言表示为__________________________________________________________________________________. 26.试比较a +b 与a 的大小.测试5 有理数的减法学习要求掌握有理数的减法法则和运算技巧,认识减法与加法的内在联系,合理运算.课堂学习检测一、填空题1.若x +m =n ,则x =______;若x -m =n ,则x =______.2.计算:(1)(+15)-(-11)=______; (2)(+15)-(+11)=______;(3)0-(+3.75)=______; (4)|-4|-|-9|=______; (5)-9-______=0 (6)a -b =a +______.3.两数之和是11,其中一个加数是14,则另一个加数是______. 4.一个正数与它的绝对值的差是______. 二、选择题5.室内温度是20℃,室外温度是-1℃,室内温度比室外温度高( ).(A)19℃ (B)-19℃ (C)21℃ (D)-21℃6.设a 是最小的正整数,b 是最大的负整数,c 是绝对值最小的有理数,则a -b -c 的值是( ).(A)0 (B)-1 (C)2 (D)1三、判断正误( )7.两数之差一定小于被减数.( )8.若两数的差为正数,则两数都为正数. ( )9.零减去一个数仍得这个数.( )10.一个数减去一个负数,差一定大于被减数. 四、计算题11.)43()41()21(----+12.(+12)-(+18)-(+23)+(+51)13.)81()535()872()523(+----++14.(+132)-(+124)-(+16)+0+(-132)+(+16)15.0-(+8)+(-2.7)-(+5)16.]315)413[()413(+---17.|)43||411(||)43(431|-------18.311)]3211(318)1.0[(4.4+-++-+综合、运用、诊断一、解答题19.北京等5个城市的当地时间(单位:时)可在数轴上表示如下:如果将两地时间的差简称为时差,那么( ).(A)汉城与纽约的时差为13小时(B)汉城与多伦多的时差为13小时 (C)北京与纽约的时差为14小时 (D)北京与多伦多的时差为14小时 20.表中列举了国外几个城市与北京的时差(带正号的数表示同一时刻比北京早的时数).如+1表示当北京是上午8:00时,东京是上午9:00城市 时差 巴黎 -7 东京+1芝加哥 -14(1)现在巴黎时间是几点?(2)小明想给在芝加哥的父亲打电话,现在合适吗?简述你的理由.21.如图表示某矿井的示意图,以地面为准,A 点高度是+4.2米,B ,C 两点高度分别是-15.6米和-30.5米,A点比B 点高多少?比C 点呢?22.一架飞机做特技表演,起飞一段时间后的高度变化如下:(上升记为正数,下降记为负数)+4.5,-3.2,+1.1,0,-1.4.(单位:千米)(1)请说说“0”的含义.(2)此时飞机比起飞点高了多少千米?拓展、探宄、思考23.求出下列各组数在数轴上对应点之间的距离:(1)3与-2.2 (2)4.75与2.25(3)-4与4.5(4)323 与312你能发现所得距离与这两个数有什么关系吗?24.下面的方阵图中,每行、每列、每条对角线上的3个数的和相等.3 -7 75 1 -3 0 -59-1图① 图② 图③(1)根据图①中给出的数,对照完成图②; (2)试着自己找出九个不同的数,完成图③;(3)想一想图中九个数,最中间的数与其他八个数有什么关系?测试6 有理数的加减混合运算(一)学习要求进一步巩固有理数加法、减法法则和运算,能熟练地将加减混合运算统一成加法运算,理解运算符号和性质符号的意义;运用加法运算律合理简算.课堂学习检测一、填空题1.有理数加减混合运算时,通常先把减法转化为______,然后将正数、负数分别______. 2.4-5-1=-5-1+4的根据是______.3.计算:(1)(-0.7)-(-0.8)+(-0.9)=______.(2)=+--+-)34()43()25.0(______.(3)-12+11-______+55=0 (4)______与3+(-4)的和为零二、选择题4.下列计算错误的是( ).(A)-2-(-2)=0 (B)-3-4-5=-12 (C)-7-(-3)=-10 (D)12-15=-3 5.如果三个数的和为零,那么这三个数一定是( ).(A)两个正数,一个负数 (B)两个负数,一个正数 (C)三个都是零 (D)其中两个数之和等于第三个数的相反数 6.若|a -1|+|b +3|=0,则21--a b 的值是( ), (A)214-(B)212-(C)211-(D)211三、计算题 7.-6-6+98.-5.4+0.2-0.6+0.89.613121512--+10.)6521()652131(--+-11.)21135()3225(311+-+--12.)322()314()413()211(++-++--综合、运用、诊断一、选择题13.a ,b ,c ,d 在数轴上的对应点位置如图所示,且|a |=|b |,|d |>|c |>|a |,则下列各式中,正确的是( ).(A)d +c >0 (B)d >c >b >a (C)a +b =0 (D)b +c >0 14.若a <b ,则|b -a +1|-|a -b |等于( ).(A)4 (B)1 (C)-2a +b +6 (D)不能确定 15.若|a |=4,|b |=3,且a ,b 异号,则|a -b |等于( ).(A)7 (B)±1 (C)1 (D)1或7 二、填空题16.有理数a ,b ,c 在数轴上对应点位置如图所示,用“>”或“<”填空:(1)|a |______|b |; (2)a +b +c ______0:(3)a -b +c ______0; (4)a +c ______b ; (5)c -b ______a . 三、计算题 17.)31()21()54()32(21+--+---+ 18.|87432||)851(213|+---+-19.当a =2.7,b =-3.2,c =-1.8时,求-a -b -c 的值.拓展、探究、思考20.代数和的规律:(1)计算1+2-3-4+5+6-7-8+…+2001+2002-2003-2004:(2)如果在1,2,3…2004这2004个数的前面任意添加正号或负号,再求和,其结果是奇数还是偶数.不好想的话,先从少一点的数列试一试,寻找规律.测试7 有理数的加减混合运算(二)学习要求能熟练地进行有理数加减混合运算,并且会解决简单的实际问题.课堂学习检测一、选择题1.两个有理数的和为负数,那么这两个数一定( ).(A)都是负数 (B)至少有一个是负数 (C)有一个是0 (D)绝对值不相等2.已知|x |=3,|y |=2,且x -y =-5,则x +y 等于( .(A)5 (B)-5 (C)1 (D)-1 3.如果a >0,b <0,a +b <0,那么下列各式中大小关系正确的是( ).(A)-b <-a <b <a (B)-a <b <a <-b (C)b <-a <-b <a (D)b <-a <a <-b 二、计算题 4.75.4125104325.1--+ 5.2.38.61652424536---++ 6.53292731732---+7.322432114332+-++--8.32143131245+--9.|)52()51(||)23(32|-+--+--- 10.|7392||9753||5274|-+---综合、运用、诊断11.观察下列两组等式:ΛΛ4131431;3121321;211211-=⨯-=⨯-=⨯① ΛΛ)10171(311071);7141(31741);411(31411-=⨯-=⨯-=⨯②根据你的观察,先写出猜想:(1)=+)1(1n n ( )-( ) (2)=+)(1d n n ( )×( )然后,用简单方法计算下列各题: (1)541431321211⨯+⨯+⨯+⨯ (2)21161161111161611⨯+⨯+⨯+⨯ (3)56142130*********+++++ (4)120180148124181++++12.一个病人每天下午需要测量一次血压,下表为该病人星期一至星期五收缩压的变化情况.若该病人上个星期日的收缩压为160拓展、探究、思考13.若|x |=x ,并且|x -3|=3-x ,请求出所有符合条件的整数x 的值,并计算这些值的和.14.已知m ,n 为整数,且|m -2|+|m -n |=1,求m +n 的值.测试8 有理数的乘法学习要求会根据有理数的乘法法则进行乘法运算,并运用相关运算律进行简算.课堂学习检测一、填空题 1.式子)66()981()8.3(5.7)6(31-⨯-⨯+⨯⨯-⨯的符号为______.2.若a =4,b =0,c =-3,d =-5,则c -ad =______,(a -b )(c -d )=______. 二、选择题3.下列计算正确的是( ).(A)911)311()311(=-⨯- (B)1172)218(=⨯-(C)766)71()7(-=+⨯- (D)1)31(3-=-⨯4.两个有理数之积是0,那么这两个有理数( ).(A)至少有一个是0 (B)都是0 (C)互为倒数 (D)互为相反数5.,04.018)05.041110(54-+-=+-⨯-这个运算应用了( ). (A)加法结合律 (B)乘法结合律 (C)乘法交换律 (D)分配律 6.比较a 与3a 的大小,正确的是( ).(A)3a >a (B)3a =a (C)3a <a (D)上述情况都可能 三、计算题7.直接将答案写在横线上:(1)=-⨯)54(43______; (2)=-⨯-)4()85(______;(3)=⨯-38)1923(______; (4)=+⨯+)2.1()411(______.8.)720()103()32(-⨯-⨯-9.)2.0()732()312(-⨯+⨯-10.)721()1179154238312(-⨯+-11.)194(6)194(13)194(7-⨯--⨯+-⨯-综合、运用、诊断一、填空题12.若a <0,b <0,c >0,则(-a )·b ·(-c )______0. 13.若a +b <0,且ab >0,则a______0,b______0. 二、选择题14.已知(-ab )·(-ab )·(-ab )>0,则( ).(A)ab <0 (B)ab >0 (C)a >0,b <0 (D)a <0,b <0 15.|x -1|+|y +2|+|z -3|=0,则(x -1)(y -2)(z +3)的值为( ).(A)48 (B)-48 (C)0 (D)xyz 三、计算题16.)36()12765321(-⨯-+-17.)95.1(9)772.3()9(228.3⨯--⨯-+-⨯18.)83()154()52()433()322()211(-⨯-⨯+⨯+⨯-⨯-四、解答题19.巧算下列各题:(1))200411)(120031()151)(411)(131)(211(--⋯----(2)666663333222299999⨯-⨯拓展、探宄、思考20.先观察下图,再解答下题:小李在街上碰到为救助失学儿童募捐的学生,于是将身上一半的钱捐了出来;接着他又碰到第二个募捐的学生,便又捐出了剩下钱的一半;跟着第三个,第四个,他每次都捐出了剩下钱的一半,身上还剩下一元.请你算一算,最初小李身上有多少元钱?21.用计算器计算下列各式,将结果写在横线上:999×21=______; 999×22=______; 999×23=______; 999×24=______. (1)你发现了什么规律?(2)不用计算器,你能直接写出999×29的结果吗?测试9 有理数的除法学习要求理解除法与乘法的逆运算关系,会进行有理数除法运算;巩固倒数的概念,能进行简单有理数的加、减、乘、除混合运算.课堂学习检测一、填空题1.若两数之积为1,则这两数互为________;若两数之商为1,则这两数________;若两数之积为-1,则这两数互为________;若两数之商为-1,则这两数互为________. 2.零乘以________都得零,零除以________都得零. 3.若ab >0,b <0,则a ________0,且a b ________0;若ab <0,a >0,则b ________0,且ab________0由此可知,ab 与ab的符号________. 一、选择题4.下列计算正确的是( ).(A)20)151(5-=-÷-(B)2)81()8(2-=-⨯-÷- (C)40)152()2(38-=-÷-⨯- (D)25)8()116387(-=-÷++-5.已知a 的倒数是它本身,则a 一定是( ).(A)0 (B)1 (C)-1 (D)±16.一个数与-4的乘积等于531,这个数是( ).(A)52 (B)52-(C)25 (D)25-7.填空:(1))21()12(-÷-=_______;(2))2533(2.5-÷=_______; (3)()=-÷⨯-÷-551)51(5 _______;(4))45(545445-⨯÷⨯-=_______;三、计算题8.)3231(32⨯-÷9.)2131(15--÷-10.)434()322(+-÷--综合、运用、诊断一、选择题11.若xy >0,则(x +y )xy 一定( ).(A)小于0 (B)等于0 (C)大于0(D)不等于012.如果x <y <0,则化简xy xy x x ||||+的结果为( ). (A)0(B)-2(C)2 (D)3二、计算题13.)511()73(25.0--⨯-÷-14.)241()245836121(-÷+-+-15.)911(98999-÷ 16.)]53()32(1[)]53(32[-⨯-+÷-+-三、解答题17.当a =-2,b =0,c =-5时,求下列式子的值:(1)a +bc ;(2)(a -b )(a +c ).18.在10.5与它的倒数之间有a 个整数,在10.5与它的相反数之间有b 个整数,求(a +b )÷(a -b )+2的值.拓展、探究、思考19.式子||||||ab abb b a a ++的所有可能的值有( ). (A)2个 (B)3个 (C)4个 (D)无数个20.如果有理数a ,b ,c ,d 都不为0,且它们的积的绝对值等于它们积的相反数,你能确定a ,b ,c ,d 中最少有几个是负数,最多有几个是负数吗?21.一口枯井深64米,井底之蛙想从井底爬上来.第一天白天,它往上爬到井深一半,晚上又滑落了白天所爬路程的一半;第二天白天,它继续往上爬到剩下路程的一半,晚上又滑落了白天所爬路程的一半;每天这样爬,它需要多少天才能爬到井口?做完题后想一想:“一尺之棰,日取其半,万世不竭”这句话的含义.测试10 有理数的乘方学习要求理解有理数乘方的意义,会进行有理数的乘方运算,并体会乘方结果的变化. 课堂学习检测 一、填空题1.对于(-2)6,6是______的指数,底数是______,(-2)6=______.对-26,6是____的指数,底数是____,-26=______.2.计算:(1)34=______; (2)-34=______; (3)(-3)4=______;(4)-(-3)4=______;=32)5(3______; =3)32)(6( ______; =-3)32)(7(______;=--3)2()8(3______; 3.当n 为正奇数时,(-a )n =______;当n 为正偶数时,(-a )n =______.二、选择题4.-12的计算结果是( ).(A)1 (B)-11 (C)-1 (D)-2 5.-0.22的计算结果是( ).(A)-0.04 (B)0.04 (C)0.4 (D)-0.4 6.312-的计算结果是( ).(A)91 (B)31- (C)91-(D)317.下列各式中,计算结果得0的是( ).(A)22+(-2)2(B)-22-22(C)2221)21(--(D)2221)21(+-8.下列各数互为相反数的是( ).(A)32与-23 (B)32与(-3)2(C)32与-32 (D)-32与-(-3)2三、计算题9.6×(-2)2÷(-23)10.222232)32(2)2(-+--11.(3×2)2+(-2)3×5-(-0.28)÷(-2)212.)2131()1()3(3322-⨯---÷-13.|32|)2.0(1)1.0(1323--+--- 14.234)21(211])43()21[(1-+--+综合、运用、诊断一、选择题15.下列说法中,正确的个数为( ).①对于任何有理数m ,都有m 2>0;②对于任何有理数m ,都有m 2=(-m )2;③对于任何有理数m 、n (m ≠n ),都有(m -n )2>0; ④对于任何有理数m ,都有m 3=(-m )3. (A)1 (B)2 (C)3 (D)0 16.下列说法中,正确的是( ).(A)一个数的平方一定大于这个数 (B)一个数的平方一定是正数 (C)一个数的平方一定小于这个数 (D)一个数的平方不可能是负数 二、填空题17.设n 为自然数,则:(1)(-1)2n -1=______;(2)(-1)2n =______;(3)(-1)n +1=______.18.当n 为正奇数时,(-a )n =______;当n 为正偶数时,(-a )n =______. 19.用“>”或“<”填空:(1)-32________(-2)3; (2)|-3|3________(-3)2;(3)(-0.2)2________(-0.2)4;(4)2)21(________2)31(20.如果-a >a ,则a 是________;如果|a 3|=a 3,则a 是________.如果|a 2|=-|a 2|,则a 是________;如果|-a |=-a ,则a 是________. 三、解答题21.某种细胞每过30分钟便由1个分裂成2个.请根据你所学知识,描述一下细胞的数量是呈什么方式增长的?并计算5小时后1个细胞可以分裂成多少个细胞.拓展、探究、思考22.已知22×83=2n ,则n 的值为( ).(A)18 (B)11 (C)8 (D)7 23.根据数表1 1+3 1+3+5 1+3+5+7 ……可以归纳出一个含有自然数n 的等式,你所归纳出的等式是_____________. 24.实验、观察、找规律计算:31=______;32=______;33=______;34=______;35=______;36=______;37=______;38=______.由此推测32004的个位数字是______测试11 科学记数法学习要求掌握科学记数法的形式和要点,能按照要求使用科学记数法.课堂学习检测一、填空题1.把下列各数用科学记数法表示出来:(1)10=__________; (2)200=__________;(3)8600=__________; (4)600800=__________. 2.把下列用科学记数法表示的数还原:(1)1.0×102=__________; (2)1.1×103=__________; (3)2.1×106=__________; (4)3.008×105=__________. 3.你对地球和太阳的大小了解多少?请完成下列填空:(1)地球的半径大约是6370千米,用科学记数法表示为________米.(2)太阳的半径大约是6.96×105千米,精确到整数,大约是________万千米. (3)地球到太阳的距离大约是150000000千米,用科学记数法表示为________米. 4.(1)用四舍五入法,求1.549的近似值(保留两个有效数字)是________;(2)用四舍五入法,求7531000的近似值(保留两个有效数字)是________.5.测得某同学的身高约是1.66米,那么意味着他的身高的精确值在________米与________米之间(保留四位有效数字).6.3.05万是精确到________位的近似数. 二、填空题7.下列是科学记数法的是( ).(A)50×106 (B)0.5×104 (C)-1.560×107 (D)1.510 8.已知:a =1.1×105,b =1.2×103,c =5.6×104,d =5.61×102,将a ,b ,c ,d 按从小到大顺序排列正确的是( ).(A)a <b <c <d (B)d <b <c <a (C)d <c <b <a (D)a <c <b <d9.“全民行动,共同节约”,我国13亿人口如果都响应国家号召每人每年节约1度电,一年可节约电1300000000度,这个数用科学记数法表示,正确的是( ). (A)1.30×109 (B)1.3×109 (C)0.13×1010 (D)1.3×1010综合、运用、诊断一、选择题10.下列说法正确的是( ).(A)近似数1.60和近似数1.6的有效数字一样 (B)近似数1.60和近似数1.6的精确度一样 (C)近似数250百和25000的精确度一样 (D)近似数8.4和0.8的精确度一样 11.下列说法正确的是( ).(A)2.46万精确到万位,有三个有效数字 (B)近似数6百和600精确度是相同的(C)317500精确到千位可以表示为31.8万,也可表示为3.18×105 (D)0.0502共有5个有效数字,它精确到万分位 二、填空题(用乘方形式表示结果) 12.求近似值:①3.14159(精确到0.001)_________________;②0.008003(保留2个有效数字)_________________; ③528187(精确到万位)_________________;④101001000(保留3个有效数字)_________________. 三、解答题13.我们经常会看到“光年”和“纳米”这两个名称.你知道它们的含义吗?(1)光年(1ight year)是天文学中使用的距离单位,符号是L . y .,主要用于度量天体间的距离.1光年是光在真空中一年所走的距离:真空中光速为299792.458千米/秒,1年≈60×60×24×365.25秒,请你计算一下1光年大约是多少千米(保留六位有效数字).(2)光年是一个较大距离的单位,而纳米(nanometer)则是表示微小距离的单位,符号是nm .,主要用于度量微粒的大小.1纳米9101米,即1米=109纳米.请你写出纳米和分米、厘米、毫米之间的换算关系.1厘米=______纳米,1毫米=______纳米.14.已知1 km 2的土地上,1年内从太阳那里能得到相当于燃烧1.3×108kg 煤所产生的能量.那么我国960万km 2的土地上1年内从太阳那里获得的能量相当于新开发1个年产煤多少吨的煤矿?拓展、探宄、思考15.你相信吗?有人说:“将一张纸对折,再对折,重复下去,第43次后纸的厚度便相当于地球到月球的距离.”已知一张纸厚0.006cm ,地球到月球的距离约为3.85×108m .用计算器算一下这种说法是否可信.测试12 有理数的混合运算(一)学习要求掌握有理数混合运算的法则、顺序和运算律,能熟练、合理地进行有理数的加、减、乘、除、乘方的混合的运算.课堂学习检测一、填空题1.混合运算的顺序是先______,再______,后______,______优先.特别要注意的是,如果能运用______时,可改变______达到简化计算的目的.2.计算含有乘方、乘除、加减三级运算的算式可按加减分段,各段中运算可同时进行:23)21()3()21(4)2()21(3-÷+⨯-+÷---⨯)(3)21(4)2()(3÷⨯-+÷--⨯=(先乘方))(3)21()()2()(3⨯⨯-+⨯--⨯=(除化乘)=( )-( )+( )(做乘法) =( )+( )+( )(减化加)=______________(用交换律、结合律) =________(求结果).3.计算:(1)(-8)-(-4)2×5=_______; (2)[(-8)-(-4)2]×5=_______;(3)[(-8)-(-4)]2×5=_______; (4)(-8)-(-4×5)2=_______.4.如果|a |=7,|b |=4,则a +b =_______. 二、计算题(能简算的要简算)5.15.12156.24135.0+-++- 6.)87()12787431(-÷--7.7412(54)7215÷-⨯⨯÷-)(8.(-3)2×(-1.22)÷(-0.3)39.(-7.33)×(+42.07)+(-2.07)×(-7.33)综合、运用、诊断一、填空题10.将计算结果直接写在横线上:(1)-22-(-3)2=_______;(2)=-⨯-3)21(54________;(3)-23-3×(-1)3-(-1)4=________; (4)=÷-⨯23)32(2________;(5)2×(-3)3-4×(-3)+15=________;(6)-9+12÷(-6)-(-4)2÷(-8)=________; (7)]1)32(3[2112--⨯⨯=________;(8)=⨯--⨯-2236.0321)32()5.1(________;(9)=-+--222332)32(2)2(________;二、计算题11.|)3(2|31)5.01(124--⨯⨯-+-12.5]43)436183(2411[÷÷-+-13.22)32(3|)411()52(2|-⨯--÷-⨯三、解答题14.你能由右图得出计算规律吗?1+3+5+7+9+11=( )2.15.用乘方形式表示结果:(1)(-2)2003+(-2)2004=________;(2)=-⨯-55)29()32(________.拓展、探究、思考16.找规律,计算求值.(1)有一列数:2,4,8,16,x ,64…,按规律求x 的值,并计算2)4(4x x -的值.(2)有一列数:2,7,13,20,x ,37…求x 的值,并比较(1-x )(1+x )与1-x 2的大小.测试13 有理数的混合运算(二)学习要求进一步巩固有理数的混合运算,在运算中使用简单推理,提高运算能力.课堂学习检测一、计算题1.137875.0135811321--+-=____________. 2.=-⨯--⨯-)31(54.1)31()46.1(____________.3.=-⨯--)6()213161(____________.4.=⨯-÷)48()251632(____________.二、选择题 5.如果四个有理数的和的31是4,其中三个数是-12,-6,9,则第四个数是( ). (A)-9(B)15(C)-18(D)216.如果x =-1,y =3,那么式子333)(yx y x --的值是( ).(A)134 (B)1 (C)1331(D)716 7.已知a ,b 两数之和、两数之积以及b 的相反数都小于0,比较大小正确的是( ).(A)a -b <a <-b <-a <b -a (B)-a <b <a -b <a <-b <b -a (C)a -b <-b <-a <a <b -a (D)a -b <a <-b <b <b -a <-a 三、计算题8.222)31()6()3(27-÷---⨯+-9.}]10)612311(18[511{22+-⨯--⨯-10.2)3(|312|75.0)431()3(-÷-⨯⨯÷-11.)3241(176)211(652-÷⨯-⨯四、用简便方法计算12.7+97+997+9997+9999713.)34(7.7)92(05.1)32(35.11222-⨯--⨯+-⨯14.5)1(14)171456(-⨯÷- 15.)322433(])433322()433322)(433322[(2-÷-+-+ 16.89126215214126215+⨯⨯+综合、运用、诊断一、计算题17.}2)]2()652.11(3{[2÷-÷⨯-+---18.32222)3()31(3.06.03-⨯-+÷⨯-二、解答题19.当(a -2)2+3的值最小时,求a 的值及这个最小值.20.将1~7这七个数字填入图中格内,使每条线上的三个数字之和相等,你能找到几种填法?拓展、探究、思考21.已知(a 1-1)2+|a 2-2|+(a 3-3)2+|a 4-4|+…+(a 2007-2007)2+|a 2008-2008|=0,求200820074332211111a a a a a a a a ++++Λ的值.第二章 整式的加减测试1 代数式学习要求理解代数式的概念,掌握代数式的基本写法,能按要求列出代数式,会求代数式的值.课堂学习检测一、填空题(用代数式表示) 1.用代数式表示:(1)比m 多1的数______. (2)比n 少2的数______. (3)3与y 的差的相反数______. (4)a 与b 的和的倒数______.(5)x 与4的差的32______. (6)a 与b 和的平方______.(7)a 与b 平方的和______. (8)被5除商m 余1的数______. (9)5除以x 与2和的商______. (10)除以a 2+b 的商是5x 的数______. (11)与b +3的和是5x 的数______. (12)与6y 2的差是x +3的数______. (13)与3x 2-1的积是5y 2+7的数______.2.某工厂第一年的产量是a ,以每年x %的速度增加,第二年的产量是______,第三年的产量是_________.3.一个两位数,个位数字是a ,十位数字是b ,如果把它的十位与个位数字交换,则新两位数与原两位数的差是________.4.一种商品的成本价m 元,按成本增加25%出售时的售价为__________元.5.某商品每件成本a 元,按高于成本20%的定价销售后滞销,因此又按售价的九折出售,则这件商品还可盈利________元.6.下图中阴影部分的面积为________.二、选择题7.下列各式中,符合代数式书写格式的有( ).,5)(,322,,3,3÷+⨯⨯y x x b a a a a +b 厘米. (A)1个 (B)2个 (C)3个 (D)4个8.甲、乙两地距离是m 千米,一汽车从甲地开往乙地,汽车速度为a 千米/时,现走了一半路程,它所行的时间是( ).(A)ma 21(B)am 2 (C)a m2 (D)a m +21三、解答题9.一个长方形的周长为c 米,若该长方形的长为a 米),2(ca <求这个长方形的面积.10.当x =-3,31=y 时,求代数式x 2y 2+2x +|y -x |的值.综合、运用、诊断一、填空题(用代数式表示)11.如图,(1)中阴影部分面积是______;(2)中阴影部分面积是________.(1) (2)12.当a =0.2时,=+a 21_______,=a 21_______;2a -1=_______,2(a -1)=_______.13.当(x +1)2+|y -2|=0时,代数式xyxy -的值为_______. 14.当21=a 代数式2a 2-a +1=_______. 15.-(a -b )2的最大值是_______;当其取最大值时,a 与b 的关系是_______. 二、选择题 16.书店有书x 本,第一天卖出了全部的,31第二天卖出了余下的,41还剩( )本.(A)12131--x(B)x x x 12131--(C)x x x 4131-- (D))31(4131x x x x ---三、解答题17.若4x 2-2x +5=7,求式子2x 2-x +1的值.18.已知a ∶b =5∶6,b ∶c =4∶3,求cb ba -+的值.拓展、探究、思考19.一个表面涂满了红色的正方体,在它的每个面上等距离地切两刀(刀痕与棱平行),可得到27个小正方体,而且切面均为白色,问:(1)27个小正方体中,三面是红色,两面是红色,一面是红色,各面都是白色的正方体各有几块? (2)每面切三刀,上述各问的结果又如何?每面切n 刀呢?20.动脑筋,试试能做出这道题吗?某企业出售一种收音机,其成本24元,第一种销售方式是直接由厂家门市部销售,每台售价32元,而消耗费用每月支出2400元,第二种销售方式是委托商店销售,出厂价每台28元,第一种与第二种销售方式所获得的月利润分别用y 1,y 2表示,月销售的台数用x 表示,(1)用含有x 的代数式表示y 1与y 2;(2)销售量每月达到2000台时,哪种销售方式获得的利润多?。
