拓扑图形PPT课件
合集下载
网络拓扑图库整理课件

网络安全
拓扑图库在网络安全领域的应用将更加广泛,用于检测和防范网络 攻击。
智慧城市
拓扑图库将助力智慧城市建设,为城市基础设施的规划、管理和优化 提供支持。
面临的挑战与解决方案
数据安全与隐私保护
加强数据加密和访问控制,确保拓扑图库的安 全性和隐私保护。
技术更新与维护
持续跟踪技术发展,定期更新和优化拓扑图库 ,保持其先进性和可用性。
未来趋势
随着网络技术的不断发展,拓扑 图库将更加智能化、自动化,能 够更好地适应各种复杂网络环境 的需求。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
02
网络拓扑图的分类与绘 制
分类方法
核心层、汇聚层、接入层 拓扑图。
总线型、星型、环型、网 状型拓扑图。
大型、中型、小型网络拓 扑图。
05
网络拓扑图库的未来发 展
技术发展趋势
人工智能与机器学习
利用AI和机器学习技术,实现自动化拓扑图生成、优 化和智能分析。
大数据技术
利用大数据技术,实现大规模拓扑图的高效存储、处 理和分析。
可视化技术
借助先进的可视化技术,提高拓扑图的呈现效果和交 互性。
应用场景拓展
物联网
随着物联网技术的发展,拓扑图库将广泛应用于物联网设备的网络 规划和故障诊断。
故障排除
02
在故障排除过程中,拓扑图库可以快速定位问题节点,提高故
障排查效率。
培训与教学
03
拓扑图库可以辅助管理员进行培训和教学,使学员更直观地理
解网络结构和原理。
拓扑图库的历史与发展
早期发展
随着计算机网络的普及,人们开 始意识到网络结构可视化的重要 性,早期拓扑图库工具开始出现 。
拓扑图库在网络安全领域的应用将更加广泛,用于检测和防范网络 攻击。
智慧城市
拓扑图库将助力智慧城市建设,为城市基础设施的规划、管理和优化 提供支持。
面临的挑战与解决方案
数据安全与隐私保护
加强数据加密和访问控制,确保拓扑图库的安 全性和隐私保护。
技术更新与维护
持续跟踪技术发展,定期更新和优化拓扑图库 ,保持其先进性和可用性。
未来趋势
随着网络技术的不断发展,拓扑 图库将更加智能化、自动化,能 够更好地适应各种复杂网络环境 的需求。
REPORT
CATALOG
DATE
ANALYSIS
SUMMAR Y
02
网络拓扑图的分类与绘 制
分类方法
核心层、汇聚层、接入层 拓扑图。
总线型、星型、环型、网 状型拓扑图。
大型、中型、小型网络拓 扑图。
05
网络拓扑图库的未来发 展
技术发展趋势
人工智能与机器学习
利用AI和机器学习技术,实现自动化拓扑图生成、优 化和智能分析。
大数据技术
利用大数据技术,实现大规模拓扑图的高效存储、处 理和分析。
可视化技术
借助先进的可视化技术,提高拓扑图的呈现效果和交 互性。
应用场景拓展
物联网
随着物联网技术的发展,拓扑图库将广泛应用于物联网设备的网络 规划和故障诊断。
故障排除
02
在故障排除过程中,拓扑图库可以快速定位问题节点,提高故
障排查效率。
培训与教学
03
拓扑图库可以辅助管理员进行培训和教学,使学员更直观地理
解网络结构和原理。
拓扑图库的历史与发展
早期发展
随着计算机网络的普及,人们开 始意识到网络结构可视化的重要 性,早期拓扑图库工具开始出现 。
计算机网络的拓扑结构ppt课件

知识结构
计算机网络的发展 计算机网络的定义 计算机网络的功能 计算机网络的特点 计算机网络的应用
按覆盖范围分类 按传播方式分类 按传输介质分类 按传输技术分类
国际组织与机构 美国组织与机构 欧洲组织与机构 中国国家2标准局
网络的逻辑结构 网络的拓扑结构 网络软件的组成 网络硬件的组成
计算机网络支撑技术 计算机网络的关键技术 计算机网络的研究热点
经营者提 供商品 或者服 务有欺 诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
§1.1 计算机网络的基本概念
计算机网络是计算机技术与通信技术相结合的产物,它 的诞生使计算机的体系结构发生了巨大变化。在当今社会 发展中,计算机网络起着非常重要的作用,并对人类社会 的进步做出了巨大贡献。
ISO于1977年成 立了专门的机构 来研究该问题, 并且在1984年正 式颁布了“开放 系统互联基本参 考模型” 的国际 标准OSI,这就产 生了第三代计算 机网络。
9
经营者提 供商品 或者服 务有欺 诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
1.1.3 计算机网络的主要功能
3、分布处理 把要处理的任务分散到各个计算机上运行,而不是集中在
一台大型计算机上。这样,不仅可以降低软件设计的复杂性, 而且还可以大大提高工作效率和降低成本。
4、集中管理 对地理位置分散的组织和部门,可通过计算机网络来实现集 中管理,如数据库情报检索系统、交通运输部门的定票系统、军 事指挥系统等。
3
经营者提 供商品 或者服 务有欺 诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
计算机网络拓扑结构公开课内容PPT演示

状
结
构
它生活在沙漠里,不需要水源也可以 生存, 它的形 状像手 掌一样 ,并且 满身长 着细细 的像针 一样的 刺。记 得上次 妈妈刚 买回的 仙人掌 ,不知 道是谁 把它放 在凳子 上了, 我也没 注意一 屁股坐 上去了 疼得我 嗷嗷大 叫。
它生活在沙漠里,不需要水源也可以 生存, 它的形 状像手 掌一样 ,并且 满身长 着细细 的像针 一样的 刺。记 得上次 妈妈刚 买回的 仙人掌 ,不知 道是谁 把它放 在凳子 上了, 我也没 注意一 屁股坐 上去了 疼得我 嗷嗷大 叫。
A.总线型 B.树型 C.环型
D.星型
例题:
例3:所有计算机都连接到一个中心节点上,传输数据时,节点
首先将数据传输到中心节点上,然后由中心节点转发到目的节
点 的 网 络 拓 扑 结 构 是 (C )
A.总线结构
B.环形结构
C
.
星
型
结
构 D . 网 它生活在沙漠里,不需要水源也可以生存,它的形状像手掌一样,并且满身长着细细的像针一样的刺。记得上次妈妈刚买回的仙人掌,不知道是谁把它放在凳子上了,我也没注意一屁股坐上去了疼得我嗷嗷大叫。
容
易
造
成
拥
塞
它生活在沙漠里,不需要水源也可以 生存, 它的形 状像手 掌一样 ,并且 满身长 着细细 的像针 一样的 刺。记 得上次 妈妈刚 买回的 仙人掌 ,不知 道是谁 把它放 在凳子 上了, 我也没 注意一 屁股坐 上去了 疼得我 嗷嗷大 叫。 它生活在沙漠里,不需要水源也可以 生存, 它的形 状像手 掌一样 ,并且 满身长 着细细 的像针 一样的 刺。记 得上次 妈妈刚 买回的 仙人掌 ,不知 道是谁 把它放 在凳子 上了, 我也没 注意一 屁股坐 上去了 疼得我 嗷嗷大 叫。
图形拓扑关系的构建.ppt

可能的原因是:结点匹配限差的问题造成端点未匹配;数字化误差较大, 甚至数字化错误,这些都可以通过图形编辑或重新匹配来确定。另外如果该弧 段本来就是悬挂弧线,不需要拓扑,做一个标记即可。
2.4 构建拓扑多边形
2.4.1 基本常识 2.4.2 多边形拓扑关系自动建立的两个算法
2.4.2.1 弧段跟踪法 2.4.2.2 栅格填充法
拓扑邻接关系存在于同类型元素之间(注意是“偶对集 合”)。一般用来描述面域邻接。
拓扑关联关系存在于不同类型元素之间。一般用来描述 结点与边、边与面的关系。
拓扑包含关系用来说明面域包含于其中的点、弧段、面 域的对应关系。包含关系有同类的,也有不同类的。
1.5 拓扑关系的表示
拓扑关系的表示分为:显示表示和隐式表示。 1.显示表示:就是将网结构元素(结点、弧段、面域)间的 拓扑关系数据化,并作为地图数据的一部分给以存储,这就 叫拓扑关系的显式表示。 2.隐式表示:不直接存储拓扑关系,而是由几何数据临时推 导生成所需的拓扑关系,这就叫拓扑关系的隐式表示。
首
1
末
首
2
末
首
3
末
首
4
末
+5,-2 -4,+6 -7,-3 +1,+5 +8,+4 +2,-7 +3,+8 +6,-1
弧段邻接关系表
环的生成
弧段2
弧段1
从弧段2开始跟踪,则圈定多边形A的 环记录为:(+2,+1,-4,+3)
弧段4 弧段3
前端
弧段3
最靠左边的弧段
后端
弧段1
前端
弧段2
最靠左边的弧段
后端
Longitude/Latitude投影
Gauss-Krivger投影
拓扑图中心小学计算机网络拓扑图实用PPT解析课件

2F 接入交换机
3F 接入交换机
4F 接入交换机
4F 接入交换机
4F 接入交换机
教研楼 1F 汇聚交换机
2F 接入交换机 3F 接入交换机 4F 接入交换机
某中心小学监控系统
显示部分
存储部分
千兆交换机 +光收发组
或带光口
服务器部分
教学楼1
1F 百兆交换机 +光收发
教学楼2 或带光口 1F +百光兆收交发换机 秋天,漫步花园。万树枯竭,唯独菊花一枝独秀,我们在花园中尽情漫步,菊花慷慨大方地送上淳朴的花香。小动物们无暇顾及这这菊花的幽香,而忙着去采集过冬的食物,为度过难熬的冬天而忙碌着。小松鼠将食物藏在树洞中,熊将自己缩成一团,熟睡起来,青蛙也躲在了自己的洞中,不再出来演唱自己那洪亮的歌声。
教学楼3
或带光口
1F 百兆交换机 +光收发
或带光口
秋天,漫步花园。万树枯竭,唯独菊 花一枝 独秀, 我们在 花园中 尽情漫 步,菊 花慷慨 大方地 送上淳 朴的花 香。小 动物们 无暇顾 及这这 菊花的 幽香, 而忙着 去采集 过冬的 食物, 为度过 难熬的 冬天而 忙碌着 。小松 鼠将食 物藏在 树洞中 ,熊将 自己缩 成一团 ,熟睡 起来, 青蛙也 躲在了 自己的 洞中, 不再出 来演唱 自己那 洪亮的 歌声。
视频监控
说明
汇聚机房:各栋楼均设有首层汇聚机房,可视情况放在弱电间,弱电井等地;由网络中心机房敷设光缆至各汇聚机房 接入机房:各栋楼其他非首层楼层,可视情况在弱电间或弱电井等地,每一层或几层,设一接入机房;由各栋楼敷设 光缆或六类网线至各接入机房
秋天,漫步花园。万树枯竭,唯独菊 花一枝 独秀, 我们在 花园中 尽情漫 步,菊 花慷慨 大方地 送上淳 朴的花 香。小 动物们 无暇顾 及这这 菊花的 幽香, 而忙着 去采集 过冬的 食物, 为度过 难熬的 冬天而 忙碌着 。小松 鼠将食 物藏在 树洞中 ,熊将 自己缩 成一团 ,熟睡 起来, 青蛙也 躲在了 自己的 洞中, 不再出 来演唱 自己那 洪亮的 歌声。
3F 接入交换机
4F 接入交换机
4F 接入交换机
4F 接入交换机
教研楼 1F 汇聚交换机
2F 接入交换机 3F 接入交换机 4F 接入交换机
某中心小学监控系统
显示部分
存储部分
千兆交换机 +光收发组
或带光口
服务器部分
教学楼1
1F 百兆交换机 +光收发
教学楼2 或带光口 1F +百光兆收交发换机 秋天,漫步花园。万树枯竭,唯独菊花一枝独秀,我们在花园中尽情漫步,菊花慷慨大方地送上淳朴的花香。小动物们无暇顾及这这菊花的幽香,而忙着去采集过冬的食物,为度过难熬的冬天而忙碌着。小松鼠将食物藏在树洞中,熊将自己缩成一团,熟睡起来,青蛙也躲在了自己的洞中,不再出来演唱自己那洪亮的歌声。
教学楼3
或带光口
1F 百兆交换机 +光收发
或带光口
秋天,漫步花园。万树枯竭,唯独菊 花一枝 独秀, 我们在 花园中 尽情漫 步,菊 花慷慨 大方地 送上淳 朴的花 香。小 动物们 无暇顾 及这这 菊花的 幽香, 而忙着 去采集 过冬的 食物, 为度过 难熬的 冬天而 忙碌着 。小松 鼠将食 物藏在 树洞中 ,熊将 自己缩 成一团 ,熟睡 起来, 青蛙也 躲在了 自己的 洞中, 不再出 来演唱 自己那 洪亮的 歌声。
视频监控
说明
汇聚机房:各栋楼均设有首层汇聚机房,可视情况放在弱电间,弱电井等地;由网络中心机房敷设光缆至各汇聚机房 接入机房:各栋楼其他非首层楼层,可视情况在弱电间或弱电井等地,每一层或几层,设一接入机房;由各栋楼敷设 光缆或六类网线至各接入机房
秋天,漫步花园。万树枯竭,唯独菊 花一枝 独秀, 我们在 花园中 尽情漫 步,菊 花慷慨 大方地 送上淳 朴的花 香。小 动物们 无暇顾 及这这 菊花的 幽香, 而忙着 去采集 过冬的 食物, 为度过 难熬的 冬天而 忙碌着 。小松 鼠将食 物藏在 树洞中 ,熊将 自己缩 成一团 ,熟睡 起来, 青蛙也 躲在了 自己的 洞中, 不再出 来演唱 自己那 洪亮的 歌声。
使用ppt绘制网络拓扑图ppt课件

BanGong
Si COSW_C3560 ClassRoom
批注:一个专业、规范的网络逻辑拓扑能够 非常直观的呈现网络架构,是行业基本要求; 另外也是工程师专业技能的体现;再者也是 个人品牌形象的体现。我们不要求拓扑做得 有多美观多牛逼,但是至少……不能太丑对 吧?
.
5
什么是网络拓扑(topology)
12.2/24
31
绘制注意事项
万兆光纤 千兆光纤
图标大小、标示位置要合理
OR_S8606_2
OR_S8606_4
OR_S8606_1 OR_S8606_1 OR_S8606_1 OR_S8606_1
Si
Si
Si
Si
Si
Si
Si
Si
OR_S8606_1
OR_S8606_3
万兆光纤
CO_S6810_1
R1
R7
172.16.2.0/24
R5
172.16.0.0/16
R3
Injection:172.16.2.0/24 汇总:172.16.0.0/16
.
48
小结
关于PPT绘制网络拓扑的建议
PPT在网络工程行业日常工作中的应用是非常 普遍的,我们不要求PPT的制作如何美观,如 何艺术,但是起码要有一定的专业度和可阅读。 因此对于这项技能我们的态度是,要锻炼,但 是不要沉迷,又特么不是搞艺术的对吧?别像 我啊……文艺气质过重
.
33
绘制注意事项
拓扑呈现完整、格式统一、布局整洁不凌乱
Si CO_C3560
Si CO_C3560
Si
Si
Si
Si
GS_C3550_1 GS_C3550_2
Si COSW_C3560 ClassRoom
批注:一个专业、规范的网络逻辑拓扑能够 非常直观的呈现网络架构,是行业基本要求; 另外也是工程师专业技能的体现;再者也是 个人品牌形象的体现。我们不要求拓扑做得 有多美观多牛逼,但是至少……不能太丑对 吧?
.
5
什么是网络拓扑(topology)
12.2/24
31
绘制注意事项
万兆光纤 千兆光纤
图标大小、标示位置要合理
OR_S8606_2
OR_S8606_4
OR_S8606_1 OR_S8606_1 OR_S8606_1 OR_S8606_1
Si
Si
Si
Si
Si
Si
Si
Si
OR_S8606_1
OR_S8606_3
万兆光纤
CO_S6810_1
R1
R7
172.16.2.0/24
R5
172.16.0.0/16
R3
Injection:172.16.2.0/24 汇总:172.16.0.0/16
.
48
小结
关于PPT绘制网络拓扑的建议
PPT在网络工程行业日常工作中的应用是非常 普遍的,我们不要求PPT的制作如何美观,如 何艺术,但是起码要有一定的专业度和可阅读。 因此对于这项技能我们的态度是,要锻炼,但 是不要沉迷,又特么不是搞艺术的对吧?别像 我啊……文艺气质过重
.
33
绘制注意事项
拓扑呈现完整、格式统一、布局整洁不凌乱
Si CO_C3560
Si CO_C3560
Si
Si
Si
Si
GS_C3550_1 GS_C3550_2
9-拓扑优化方法PPT课件

➢ 对这若干个子设计区域进行结构分析和灵敏度分析, 建立设计变量与结构位移、应力、频率等关系,从而 形成目标函数和约束条件;
➢ 按某种优化策略和准则从这若干个子设计区域中删除 某些单元,用保留下来的单元描述结构的最优拓扑。
16
四、拓扑优化方法分类
从其物理模型的描述方法上一般分为 ➢ 基结构法(The Ground Structural Method) ➢ 均匀化方法(The Homogenization Method) ➢ 渐 进 结 构 优 化 方 法 (The Evolutionary Structural
x fi u pu g xu i 0 i=1,2, ,n
由此可构造如下的迭代公式
x(k1) i
c(k)xi(k)
i=1,2,
,n
其中c(k)=-1- p
f u
ugxui
为小于1的因子
xi
7
x fi u pu g xu i 0 i=1,2, ,n
x fi u pu g xu i
i=1,2, ,n
对于由n个杆件组成的桁架结构,其满应力条件为
Fi Ai
i
i1,2,
,n
由此可构造如下的迭代公式
(k)
A(k1) i
i
A(k) i
i1,2,
,n
i
6
2. 基于K-T条件的准则法 对于结构优化设计问题:
m in f(X ) X R n
s .t.g u ( X ) 0u 1 ,2 ,,p
极值点X*应满足的Kuhn-Tucker条件
结构优化与材料优化
第一节 概述 第二节 结构优化设计的准则法 第三节 结构的拓扑优化方法 第四节 功能材料优化设计 第五节 柔性机构优化设计 第六节 结构多学科设计优化
➢ 按某种优化策略和准则从这若干个子设计区域中删除 某些单元,用保留下来的单元描述结构的最优拓扑。
16
四、拓扑优化方法分类
从其物理模型的描述方法上一般分为 ➢ 基结构法(The Ground Structural Method) ➢ 均匀化方法(The Homogenization Method) ➢ 渐 进 结 构 优 化 方 法 (The Evolutionary Structural
x fi u pu g xu i 0 i=1,2, ,n
由此可构造如下的迭代公式
x(k1) i
c(k)xi(k)
i=1,2,
,n
其中c(k)=-1- p
f u
ugxui
为小于1的因子
xi
7
x fi u pu g xu i 0 i=1,2, ,n
x fi u pu g xu i
i=1,2, ,n
对于由n个杆件组成的桁架结构,其满应力条件为
Fi Ai
i
i1,2,
,n
由此可构造如下的迭代公式
(k)
A(k1) i
i
A(k) i
i1,2,
,n
i
6
2. 基于K-T条件的准则法 对于结构优化设计问题:
m in f(X ) X R n
s .t.g u ( X ) 0u 1 ,2 ,,p
极值点X*应满足的Kuhn-Tucker条件
结构优化与材料优化
第一节 概述 第二节 结构优化设计的准则法 第三节 结构的拓扑优化方法 第四节 功能材料优化设计 第五节 柔性机构优化设计 第六节 结构多学科设计优化
网络拓扑结构PPT课件

课堂练习
分析下面的网络拓扑结构图,讨论如何解决下列问题。
321..代一每理台个服终务端器都常兼觉受做得到W 网病络EB毒速和攻度FT击太P,慢服经,务打常器开造,一成负个全荷网网太页用大要户。等不很能长上时网间。。
作 业:
3.请同学们设计校园小型局域网拓 扑结构图
写在最后
成功的基础在于好的学习习惯
户则将数据忽略。
星型
确定网络拓扑结构
安装是否容 易
扩展性
故障排查是 否容易
响应时间 系统稳定性
混合型网络拓扑结构 总线型—星型
环型—星型
混合型网络拓扑结构
星型—星型
树型结构
混合型网络拓扑结构 树型拓扑结构
混合型网络拓扑结构 总线——星型
混合型网络拓扑结构
总线—星型
网络拓扑结构实例
网络拓扑结构定网络拓扑结构
网络拓扑结构分类 总线型
环型
数数数据据据传传传送送送方方方式式式:: : 数用其据户数绕将据着数传环据递向发的一送方个到向方中是向心从发设送,
每备发个,再送用由数户中据接心的收设节并备点响将开应数始发据向送转两给发 它到端的包扩数含散据目,包只标,有节然与点后地的将址网其相络他符段包的。转 发用到户环才中能的接下受一数个据用,户其。他用
C
A
B
D
哥尼斯堡七桥问题
于是 “七桥问题”就等价于下图中所画图形的一 笔画问题了。
欧拉注意到,每个点如果有进去的边就必须有出 来的边,从而每个点连接的边数必须有偶数个才能 完成一笔画。下图的每个点都连接着奇数条边,因 此不可能一笔画出,这就说明不存在一次走遍7座 桥,而每座桥只许通过一次的走法。
C
演讲人:XXXXXX 时 间:XX年XX月XX日
网络拓扑图PPT课件
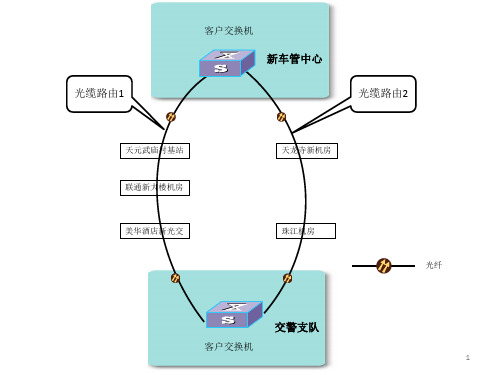
接入交换机
电脑
客户端机房
10
网络拓扑图
核心层设备 BRAS
汇聚层设备 华为OLT
德阳联通汇聚机房
用于互联网
路由器
接入交换机
电脑
INTERNET
德阳联通光纤城域网
互联网电视云 平台
光纤 网线
ONU
用于乐视TV
用于固定电话
路由器
接入交换机 网络电视机顶盒 电视
IAD
电话
11
互联网专线及固定电话网络拓扑图
华三SR6602多线路由器 用户防火墙
服务器 3
英杰电器互联网专线及固定电话网络拓扑图
NGN语音
核心层设备 BRAS
汇聚层设备 华为OLT
德阳联通汇聚机房
INTERNET
德阳联通光纤城域网
光纤 网线或电话线 电缆
客户侧
互联网专线
路由器 接入交换机
ONU
20对电缆 10对电缆
语音华为 IAD I32E *6
光纤 100M电路
核心路由器 (专线)
核心路由器 (网络电视)
华为208 IAD
办公区与客房 网络交换机
接入交换机 办公区与吧台电话
程控交换机 酒店管理电脑
办公区与客房电脑
网络电视
客房电话 20
情景
拨打 0838 2902313
联通
电信
程控交换机
30622225
欢迎语!产品介绍1, 资费2,查询地址3
中兴力维视频监控平台
光纤 网线或电话线 电缆
ONU
20对电缆 10对电缆
语音华为 IAD I32E *6
***
***
***
车间电话 (月8部)
电脑
客户端机房
10
网络拓扑图
核心层设备 BRAS
汇聚层设备 华为OLT
德阳联通汇聚机房
用于互联网
路由器
接入交换机
电脑
INTERNET
德阳联通光纤城域网
互联网电视云 平台
光纤 网线
ONU
用于乐视TV
用于固定电话
路由器
接入交换机 网络电视机顶盒 电视
IAD
电话
11
互联网专线及固定电话网络拓扑图
华三SR6602多线路由器 用户防火墙
服务器 3
英杰电器互联网专线及固定电话网络拓扑图
NGN语音
核心层设备 BRAS
汇聚层设备 华为OLT
德阳联通汇聚机房
INTERNET
德阳联通光纤城域网
光纤 网线或电话线 电缆
客户侧
互联网专线
路由器 接入交换机
ONU
20对电缆 10对电缆
语音华为 IAD I32E *6
光纤 100M电路
核心路由器 (专线)
核心路由器 (网络电视)
华为208 IAD
办公区与客房 网络交换机
接入交换机 办公区与吧台电话
程控交换机 酒店管理电脑
办公区与客房电脑
网络电视
客房电话 20
情景
拨打 0838 2902313
联通
电信
程控交换机
30622225
欢迎语!产品介绍1, 资费2,查询地址3
中兴力维视频监控平台
光纤 网线或电话线 电缆
ONU
20对电缆 10对电缆
语音华为 IAD I32E *6
***
***
***
车间电话 (月8部)
拓扑学课件

首先,B 首先 1 ⊗ B2 ⊆ T1 ⊗ T2 ,因此 B1 ⊗ B2 是乘积拓扑空 因此 间的一个开集族,其次设 间的一个开集族 其次设 W 是 X1 × X 2上的任意一个开 集,对 x∈W,由于 T1 ⊗ T2 是空间 X1 × X2的一个基,因此 对 ∈ 由于 的一个基 因此 存在 U1 ∈ T1 ,U2 ∈ T2 使得 x= ( x1 , x2 ) ∈ U 1 × U 2 ⊆ W , 又 Bi 是 Ti 的 拓 扑 基 , 因 此 对 x ∈ U 存 在 B ∈ Bi 使 得
1 2
Bρ1 ( x1,
2
2
ε ) × Bρ ( x2 ,
2
2
2
ε ) ⊆ Bρ ( x,ε ) ⊆ Bρ ( x1,ε )×Bρ ( x2 , ε ).
1
2
2 2 对于任意 y= ( y1, y2 ) ∈Bρ1 (x1, ε ) × Bρ2 (x2, ε ), 2 2 2 2 ε , ρ2 ( x2 , y2 ) < ε , 有 ρ1 ( x1 , y1 ) < 2 2
1 2
扑是由度量 ρ 诱导的拓扑 Tρ .
乘积拓扑空间X× §4.1 乘积拓扑空间 ×Y
下面这个定理说明这两种拓扑是一致的. 下面这个定理说明这两种拓扑是一致的 是两个拓扑空间, 定理 4.1.5 设 ( X 1 , ρ1 ), 和 ( X 2 , ρ 2 ) 是两个拓扑空间 则将 X 1 × X 2 作为 Tρ , Tρ 的拓扑积空间和将 X 1 × X 2 作为 度量积空间时所生成的两种拓扑是一致的. 度量积空间时所生成的两种拓扑是一致的 ρ : X 2 → R 如定义 4.1.2 所定义 首先我 所定义,首先我 证明:度量 证明 度量 我们有: 们验证对于任意 x= ( x1 , x2 )∈ X 2 和任意ε > 0 ,我们有 我们有
计算机网络拓扑结构课件

总之, 一个网络拓扑结构,应根据需求, 综合诸因素作出合适选择; 要整体磨合,不能顾此失彼。
THANKS
任何一个站发送 的信号都沿着传 输媒体传播,而 且能被所有其
他站接收
总线型拓扑结构采用一个信 道作为传输媒体,所有站点
都通过相应的硬件接口 直接连到这一公共媒 体上,公共传 输媒体就是 总线
总线型拓扑结构优点
1 总线结构所需的电缆数量少
2
总线结构简单,是无源工 作,有较高可靠性;
$
3
易于扩充,增加或减少 用户比较方便。
交换方式
星型拓扑结构优点
1、控制简单:在星型网络中,任何站点只和 中央节点连接,因而媒体访问控制方法简单, 也导致访问协议十分简单。
2、故障诊断和隔离容易:在星型网络中,中央
节点对连接线路可以逐一地隔离开来进行故障检 测和定位,单个连接点的故障只影响一个设备, 不会影响全网。
3、方便服务:中央节点可以方便地对各个站 点提供服务和对网络提供重新配置。
总线型拓扑结构缺点
总线的传输距离有限, 通信范围受到限制 故障诊断 隔离较困难
ADD YOUR TITLE
环型
拓扑结构
环型拓扑结构
环形拓扑网络由 站点连接站点的 链路组成一个全 闭环路,其结构。
每个站点能够接收从 一条链路传来的数据, 并以同样的速率串行 地把该数据沿环送到 另一端链路上,这种 链路可以是单向的, 也可以是双向的,通
电话 交换机
局域网
星型拓扑结构缺点
1、电缆长度较长和安装工作量大。 因为每个站点都要和中央节点直接连 接,需要耗费大量的电缆,安装、维 护的工作量大。
2、中央节点的负担较重,形成瓶颈 效应。一旦发生故障,则全网受影响, 因此,对中央节点的可靠性和冗余度 方面的要求很高
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
欧氏图形与拓扑图形
.
1
欧氏几何
欧式几何的传统描述是一个公理、公设系统,通过有限的公 理、公设来证明所有的“真命题”。
欧式几何的五条公设是: 1、任意两个点可以通过一条直线连接。 2、任意线段能无限延伸成一条直线。 3、给定任意线段,可以以其一个端点作为圆心,该线段作为 半径作一个圆。 4、所有直角都全等。 5、若两条直线都与第三条直线相交,并且在同一边的内角之 和小于两个直角,则这两条直线在这一边必定相交。
.
4
拓扑图形
拓扑学研究的对象与长短、大小、面积、体积 等度量性质和数量关系都无关它,研究的是几 何图形在连续改变形状时还能保持不变的一些 特性。
欧氏图形研究的是是点、线、面之间的位置关系以 及它们的度量性质。
.
5
拓扑的萌芽——哥尼斯堡七桥问题
.
6
欧拉定理
欧拉定理:如果一个凸多面体的顶点数是v、棱 数是e、面数是f,那么它们总有这样的关系: f+v-e=2。
根据多面体的欧拉定理,可以得出这样一个有 趣的事实:只存在五种正多面体。它们是正四 面体、正六面体、正八面体、正十二面体、正 二十面体。
.
7
拓扑性质
拓扑等价 在拓扑学里所研究的图形,在运动中无论它
的大小或者形状都发生变化。在拓扑学里没 有不能弯曲的元素,每一个图形的大小、形 状都可以改变。
.
8
拓扑性质
直线上的点和线的结合关系、顺序关系,在 拓扑变换下不变。
拓扑所研究的是几何图形的一些性质,它们 在图形被弯曲、拉大、缩小或任意的变形下 保持不变,只要在变形过程中不使原来不同 的点重合为同一个点,又不产生新点。
.
9
拓扑图形
.
10
.
11
.
其和仍相等。 3、等量减等量,其差仍相等。 4、彼此能够重合的物体是全等的。 5、整体大于部分。
.
3
拓扑图形
拓扑学
拓扑学( Topology原意为地貌)是近代发 展起来的一个研究连续性现象的数学分支。
分类
代数拓扑学 微分拓扑学 几何拓扑学:它是十九世纪形成的一门数学分支, 属于几何学的范畴.
.
1
欧氏几何
欧式几何的传统描述是一个公理、公设系统,通过有限的公 理、公设来证明所有的“真命题”。
欧式几何的五条公设是: 1、任意两个点可以通过一条直线连接。 2、任意线段能无限延伸成一条直线。 3、给定任意线段,可以以其一个端点作为圆心,该线段作为 半径作一个圆。 4、所有直角都全等。 5、若两条直线都与第三条直线相交,并且在同一边的内角之 和小于两个直角,则这两条直线在这一边必定相交。
.
4
拓扑图形
拓扑学研究的对象与长短、大小、面积、体积 等度量性质和数量关系都无关它,研究的是几 何图形在连续改变形状时还能保持不变的一些 特性。
欧氏图形研究的是是点、线、面之间的位置关系以 及它们的度量性质。
.
5
拓扑的萌芽——哥尼斯堡七桥问题
.
6
欧拉定理
欧拉定理:如果一个凸多面体的顶点数是v、棱 数是e、面数是f,那么它们总有这样的关系: f+v-e=2。
根据多面体的欧拉定理,可以得出这样一个有 趣的事实:只存在五种正多面体。它们是正四 面体、正六面体、正八面体、正十二面体、正 二十面体。
.
7
拓扑性质
拓扑等价 在拓扑学里所研究的图形,在运动中无论它
的大小或者形状都发生变化。在拓扑学里没 有不能弯曲的元素,每一个图形的大小、形 状都可以改变。
.
8
拓扑性质
直线上的点和线的结合关系、顺序关系,在 拓扑变换下不变。
拓扑所研究的是几何图形的一些性质,它们 在图形被弯曲、拉大、缩小或任意的变形下 保持不变,只要在变形过程中不使原来不同 的点重合为同一个点,又不产生新点。
.
9
拓扑图形
.
10
.
11
.
其和仍相等。 3、等量减等量,其差仍相等。 4、彼此能够重合的物体是全等的。 5、整体大于部分。
.
3
拓扑图形
拓扑学
拓扑学( Topology原意为地貌)是近代发 展起来的一个研究连续性现象的数学分支。
分类
代数拓扑学 微分拓扑学 几何拓扑学:它是十九世纪形成的一门数学分支, 属于几何学的范畴.
