小学 不规则图形的面积
不规则图形的面积教学设计含教学反思

《不规则图形的面积》教学设计含教学反思学生②:只确定范围,如果全部当满格,结果是 36平方厘米;如果把不满格去掉,结果就是18 平方厘米。
因此学生得到了一个初步范围,这片 叶子的面积在18平方厘米到36平方厘米之间。
贴板书:18平方厘米一36平方厘米学生③:把不满格全部当成满格和把满格去掉的 方法都不太准确,于是他们把不满格当成半格来 计算 贴板书:18+18÷2=27平方厘米转化: 他们除了想到数方格的方法,还想到了可以把不 规则的树叶转化成我们曾经学过的平面图形来 计算面积。
学生①:转化一一平行四边形学生②:转化一一长方形 学生①:转化一一正方形(3)对比优化,提炼方法面对这么多的估算方法,我顺势引导:你有 什么困惑吗?学生在仔细观察对比后,提出这样 的疑惑:同样是数格子,为什么结果却不同呢? 同样是转化的方法,转化成哪个图形更好呢?其 他同学也纷纷点头表示有同样的困惑。
于是我让 学生带着这两个问题在小组中再次互学,他们有 了这样的发现:把树叶转化成平行四边形更精 准。
贴板书:更精准群学展示后,学生顺势喊道:老师,我知道 啦!如果把1格平均分成4小格,满格的数量又 变多了,估出的面积会更精准!是一位质疑者,时不时还是位引导者,一步一步将孩子们的思维引向深处,不断感受各种估算方法的本质。
学生们在这样自主的学习中,通过不断地对比优化,感受到面积 估算的本质:选择合适的测量标准。
三、练习设计:(从知识生长点、能力训练点、素养提升点等方面设计)应用拓展,丰富经验。
在充分肯定同学们的尝试与发现以后,我开始让学生运用这些经验解决更多实际问题,从而更加牢固的掌握估计不规则图形面积的方法,继续体会选择合适的测量标准的重要性。
1.综合练习练习二十二第8题,孩子们都选择了自己最喜欢的方法来进行估算。
在基础应用中,学生能更熟练地运用经验,体会到成功的乐趣。
2.知识拓展拿出一张武汉的地图,提出问题:大家都称武汉为“大武汉”,你知道咱们的家乡武汉究竟有多大吗?可以怎样估计出它的大小呢?学生①:我可以把它放到方格图里去数。
【奥赛】小学数学竞赛:不规则图形的面积.学生版解题技巧 培优 易错 难
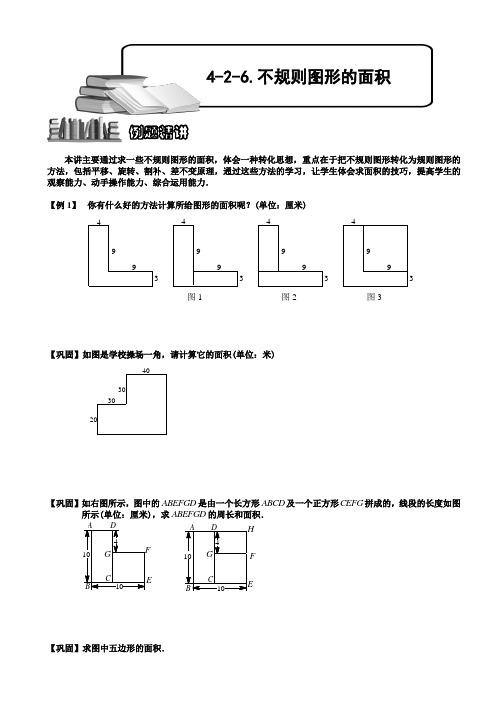
本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求面积的技巧,提高学生的观察能力、动手操作能力、综合运用能力.【例 1】 你有什么好的方法计算所给图形的面积呢?(单位:厘米)3994399439943994图1 图2 图3【巩固】如图是学校操场一角,请计算它的面积(单位:米)30203040【巩固】如右图所示,图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的,线段的长度如图所示(单位:厘米),求ABEFGD 的周长和面积.10104GF ED CB AGH F ED CB A41010【巩固】求图中五边形的面积.例题精讲4-2-6.不规则图形的面积6453【例 2】这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20 厘米.问,此楼梯截面的面积是多少?【巩固】如图是一个楼梯的截面图,每级台阶的宽和高都是20厘米.这楼梯的截面积是多少平方厘米?【例 3】有一块菜地长16米,宽8米,菜地中间留了宽2米的路,把菜地平均分成四块,每一块地的面积是多少?【例 4】有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?【例 5】 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【巩固】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.FBA【例 6】 如图,李大伯给一块长方形田地喷药,喷药器所能喷洒的范围是以李大伯的落脚点为中心,边长2米的正方形区域,他从图中的A 点出发,沿最短路线(图中虚线)走,走过88米到达B 点,恰好把这块田地全部喷完,这块田地的面积是多少平方米?BA 1米1米【例 7】 右图中甲的面积比乙的面积大__________平方厘米.6厘米8厘米4厘米【例 8】 右图中,矩形ABCD 的边AB 为4厘米,BC 为6厘米,三角形ABF 比三角形EDF 的面积大9平方厘米,求ED 的长.AB CDE F【巩固】如图所示,4CA AB ==厘米,ABE △比CDE △的面积小2平方厘米,求CD 的长为多少厘米?ABE C D【巩固】如图,平行四边形ABCD 种,10BC cm =,直角三角形ECB 的边8EC cm =,已知阴影部分的总面积比三角形EFG 的面积大210cm ,求平行四边形ABCD 的面积.G FEDCBA【例 9】 如图,ABCD 是74⨯的长方形,DEFG 是102⨯的长方形,求BCO 与EFO 的面积差.O B C D GFE A【例 10】 有一个长方形菜园,如果把宽改成50米,长不变,那么它的面积减少680平方米,如果使宽为60米,长不变,那么它的面积比原来增加2720平方米,原来的长和宽各是多少米?680平方米2720平方米60【巩固】有一个长方形,如果宽减少2米,或长减少3米,则面积均减少24平方米,求这个长方形的面积?2【例 11】 一块长方形铁板,长15分米,宽12分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?【例 12】 一个长方形,如果长减少5厘米,宽减少2厘米,那么面积就减少66平方厘米,这时剩下的部分恰好成为一个正方形,求原来长方形的面积?【巩固】一块长方形纸片,在长边剪去5cm,宽边剪去2cm后(如图),得到的正方形面积比原长方形面积少231cm.求原长方形纸片的面积.52【巩固】一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米.求原正方形的面积?66【例 13】一块正方形的钢板,先截去一个宽5分米的长方形,又截去一个宽8分米的长方形(如图),面积就比原来正方形减少181平方分米.原正方形的边长是多少分米?85【巩固】一张长方形纸片,先把长剪去8厘米,这时面积减少了72平方厘米,又把宽剪去5厘米,这时面积又减少了60平方厘米,原来这张长方形纸片的面积是多少平方厘米?5【巩固】如右图所示,在一个正方形上先截去宽11分米的长方形,再截去宽7分米的长方形,所得图形的面积比原正方形减少301平方分米.原正方形的边长是______分米.11【例 14】如图长方形被分成两部分,已知阴影面积比空白部分面积大34平方厘米,求阴影部分的面积.10cm【例 15】一张长方形纸片,把它的右上角往下折叠(如图甲),阴影部分面积占原纸片面积的27;再把左下角往上折叠(如图乙),乙图中阴影部分面积占原纸片面积的________(答案用分数表示).甲乙【巩固】折叠后,原平行四边形面积是折叠后图形面积的1.5倍.已知阴影部分面积之和为1,则重叠部分(即空白部分)的面积是多少?【巩固】如图,一张长方形纸片,长7厘米,宽5厘米.把它的右上角往下折叠,再把左下角往上折叠,未盖住的阴影部分的面积是多少平方厘米?5【例 16】如图,大正方形的边长为10厘米.连接大正方形的各边中点得小正方形,将小正方形每边三等分,再将三等分点与大正方形的中心和一个顶点相连,那么图中阴影部分的面积总和等于多少平方厘米?【例 17】如图所示,直角三角形中有一个长方形,求长方形的面积?44 4【例 18】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积?【巩固】如图是由5个大小不同的正方形叠放而成的,如果最小的正方形(阴影部分)的周长是8,那么最大的正方形的边长是.第6题【巩固】图中有6个正方形,较小的正方形都由较大的正方形的4边中点连接而成.已知最大的正方形的边长为16厘米,那么最小的正方形的面积等于多少平方厘米?【例 19】已知图中大正方形的面积是22平方厘米,小正方形面积是多少平方厘米?【巩固】如图所示,外侧大正方形的边长是10cm,在里面画两条对角线、一个圆、两个正方形,阴影的总面26cm,最小的正方形的边长为多少厘米?积为2【例 20】有一个边长为16厘米的正方形,连接每边的中点构成第二个正方形,再连接每边的中点构成第三个正方形,第四个正方形.求图中阴影部分的面积?【例 21】如图,边长为10的正方形中有一等宽的十字,其面积(阴影部分)为36,则十字中央的小正方形面积为.第2题【例 22】下图大小两个正方形有一部分重合,两块没有重合的阴影部分面积相差是多少?(单位:厘米)6【巩固】如图所示,四个相叠的正方形,边长分别是5、7、9、11.问灰色区与黑色区的面积的差是多少?【例 23】甲、乙、丙三个正方形,它们的边长分别是6、8、10厘米,乙的一个顶点在甲的中心上,丙的一个顶点在乙的中心上.这三个正方形的覆盖面积是多少平方厘米?108 6丙乙甲【巩固】将20张边长为10厘米的正方形纸片,按顺序一张一张地摆放在地板上,摆的时候,要求后摆的纸片必须有一个顶点与前一张的中心重合,且每一张只与其前一张和后一张有重合部分(右图表示已经摆好的5张).地板被这20张纸片所覆盖部分的面积是多少?【例 24】有2个大小不同的正方形A和B.如下左图所示的那样,在将B正方形的对角线的交点与A正方形的一个顶点相重叠时,相重叠部分的面积为A正方形面积的19.求A与B的边长之比.如果当按下右图那样,将A和B反向重叠的话,所重叠部分的面积是B的几分之几?左图右图【例 25】有一个正方形水池(图中阴影部分),在它的周围修一个宽是8米的草地,草地的面积为480平方米,求水池的边长?【巩固】一块长方形草坪(图中阴影部分)长是宽的2倍,它的四周围的总面积是34平方米的1米宽的小路.求草坪的面积是多少平方米?【例 26】如图所示,一个长方形广场的正中央有一个长方形的水池.水池长8米、宽3米.水池周围用边长为1米的方砖一圈一圈地向外铺.恰好铺了若干圈,共用了152块方砖,那么共铺了圈.水池【例 27】用四个相同的长方形拼成一个面积为2100cm的大正方形,每个长方形的周长是多少平方厘米?【巩固】如图所示,4个相同的长方形和一个小正方形拼成一个大的正方形,大正方形的面积是100平方分米,小正方形的面积是36平方分米,求一个小长方形的面积及周长.【例 28】四个完全相同的长方形拼成右图,大正方形的面积是l00平方分米,小正方形的面积是l6平方分米,求每个长方形的面积是多少?长方形的短边是多少分米?16【巩固】如图,4个相同的长方形和1个小正方形拼成一个大正方形,已知其中小正方形的面积为4平方厘米,大正方形的面积为400平方厘米,则其中长方形的长为厘米,宽厘米.第19题【例 29】街心花园里有一个正方形花坛,四周有一条宽1米的甬道(如图),如果甬道的面积是12平方米,那么中间花坛的面积是多少平方米?1米【巩固】在一个正方形的小花园周围,环绕着宽5米的水池,水池面积为300平方米,那么正方形花园的面积是多少平方米?5【巩固】有大、小两个长方形(如图),对应边的距离均为1cm,已知两个长方形之间部分的面积是216cm,且小长方形的长是宽的2倍,求大长方形的面积.BA【例 30】已知大正方形比小正方形边长多4厘米,大正方形面积比小正方形面积大96平方厘米.问大、小正方形面积各是多少?【巩固】两个正方形的面积相差29cm,边长相差1cm.求两个正方形的面积和.C BA【巩固】有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米.小正方形的面积是多少平方厘米?【例 31】在一个正方形中放入一个四个顶点与大正方形相接的一个小正方形(如图),如果两个正方形的周长相差16厘米,面积相差96平方厘米,求小正方形的面积是多少平方厘米?(1)(2)【例 32】用两块长方形纸片和一块正方形纸片拼成一个大正方形,长方形纸片面积分别为44平方厘米与28平方厘米,原正方形纸片面积是多少平方厘米?【例 33】 计划修建一个正方形的花坛,并在花坛周围种上3米宽的草坪,草坪的面积为300平方米,那么修建这个花坛需要占地多少平方米?(2)(1)【巩固】有大、小两个长方形(右图),对应边的距离均为1厘米,已知两个长方形之间部分的面积是16平方厘米,且小长方形的长是宽的2倍,求大长方形的面积.【巩固】一块长方形的草坪(见图中阴影部分),长是宽的2倍,它的四周围的总面积是34平方米的1米宽的小路,求草坪的总面积是多少平方米?AAB C C A BA【例 34】 一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米(如图虚线所示),则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米?3030【例 35】从一块正方形的玻璃板上锯下宽为0.5米的一个长方形玻璃条后,剩下的长方形的面积为5平方米,请问锯下的长方形玻璃条的面积等于多少?50.5【巩固】从一个正方形的木板上锯下宽1m的一个长方形木条后,剩下的长方形面积为26m,问锯下的长方形木条面积是多少?【巩固】从一块正方形木板锯下宽为12米的一个木条以后,剩下的面积是6518平方米.问锯下的木条面积是多少平方米?【例 36】图中,甲、乙两个正方形的边长的和是20厘米,甲正方形比乙正方形的面积大40平方厘米.求乙正方形的面积.【例 37】 有一大一小两块正方形试验田,他们的周长相差40米,面积相差220平方米,那么小正方形试验田的面积是多少平方米?图a图b【例 38】 如图,边长是整数的四边形AFED 的面积是48平方厘米,FB 为8厘米.那么,正方形ABCD 的面积是 平方厘米.A BCDEF 488【例 39】 如图,一个正方形被分成4个小长方形,它们的面积分别是110平方米、15平方米、310平方米和25平方米.已知图中的阴影部分是正方形,那么它的面积是多少平方米?【例 40】 长方形ABCD 的周长是30厘米,以这个长方形的每一条边为边长向外画正方形.已知这四个正方形的面积之和为290平方厘米,那么长方形ABCD 的面积是多少平方厘米?C 1D 1E 1A 1EBC DA【巩固】如图,长方形ABCD 的周长是16厘米,在它的每一条边上各画一个以该边为边长的正方形,已知这四个正方形的面积和是68平方厘米,求长方形ABCD 的面积?A B C D IH G FEAB C D【例 41】 一条白色的正方形手帕,它的边长是18厘米,手帕上横竖各有二道黑条,黑条宽都是2厘米,这条手帕白色部分的面积是多少?【例 42】 用同样大小的瓷砖铺一个正方形地面,两条对角线上铺黑色的,其它地方铺白色的,如图所示.如果铺满这块地面共用101块黑色瓷砖,那么白色瓷砖用了多少块?图1 图2【例 43】 7个完全相同的长方形拼成了图中阴影部分,图中空白部分的面积是多少平方厘米?24【巩固】如图所示,7个完全相同的长方形拼成了图中的阴影部分,图中空白部分的面积是多少平方厘米?【例 44】 如右图所示,在长方形ABCD 中,放入六个形状大小相同的长方形(尺寸如图),图中阴影部分的面积是__________.A614DCB【例 45】 若干同样大小的长方形小纸片摆成了如图所示的图形.已知小纸片的宽是12厘米,问阴影部分的总面积是多少平方厘米?【例 46】 一个大长方形若能分割成若干个大小不同的小正方形,则称为完美长方形.下面一个长方形是由9个小正方形组成的完美长方形.图中正方形A 和B 的边长分别是7厘米和4厘米,那么这个完美长方形的面积分别是多少平方厘米?ABA BCDE FGH【巩固】如图:有一个矩形可以被分割为11个正方形,其中最小的正方形(阴影部分)面积为281cm ,请问这个矩形之面积为多少平方厘米?第2题【巩固】图中的长方形被分割成6个正方形,已知中央小正方形的面积是1平方厘米,求原来长方形的面积.【巩固】9个边长分别为1、4、7、8、9、10、14、15、18的正方形拼成一个长方形,问这个长方形的长和宽是多少?并请画出这个长方形的拼接图.1518141094781【例 47】 图中数字分别表示两个长方形和一个直角三角形的面积,另一个三角形的面积是 .51215A 51215【例 48】 如图,一个矩形被分成八个小矩形,其中有五个矩形的面积如图中所示(单位:平方厘米),问大矩形的面积是多少平方厘米?1230201636G FEDC B AS 3S 2S 11230201636G FEDC B A【巩固】阳阳用四块小长方形恰好拼成了一个大的长方形,如图所示.现在知道其中三块长方形的面积分别为48平方厘米、24平方厘米、30平方厘米,那么,阴影部分的面积是多少?302448【巩固】如图,矩形ABCD 被分割成9个小矩形.其中有5个小矩形的面积如图所示.矩形ABCD 的面积为 .164221CB DA【例 49】 有红、黄、绿三块大小一样的正方形纸片,放在一个底面为正方形的盒内,它们之间相互叠合(见下图).已知露在外面的部分中,红色面积是20,黄色面积是14,绿色面积是10.求正方形盒底的面积.绿黄红绿黄红【例 50】 如图所示,在正方形ABCD 内,红色、绿色正方形的面积分别是48和12,且红、绿两个正方形有一个顶点重合.黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点.那么黄色正方形的面积是 .DCBA绿黄红 312【巩固】如图所示,在正方形ABCD 中,红色,绿色正方形的面积分别是52和13,且红、绿两个正方形有一个顶点重合.黄色正方形的一个顶点位于红色正方形两条对角线的交点,另一个顶点位于绿色正方形两条对角线的交点,求黄色正方形面积.绿黄红D C BA【例 51】 如图,三个一样大小的正方形放在一个长方形的盒内,A 和B 是两个正方形的重叠部分,C 、D 、E是空出的部分,每一部分都是矩形,它们的面积比是A :B :C :D :E =1:2:3:4:5,那么这个长方形的长与宽之比是________.【例 52】 如图如果长方形的面积为56平方厘米,且2MD =厘米、3QC =厘米、5CP =厘米、6BN =厘米,那么请你求出四边形MNPQ 的面积是多少厘米?33C P D M2356532MD BPC N【巩固】长方形的广告牌长为10米,宽为8米,A ,B ,C ,D 分别在四条边上,并且C 比A 低5米,D 在B 的左边2米,四边形ABCD 的面积是 平方米.DCBADCBA【例 53】 直角三角形PQR 的直角边为5厘米,9厘米,问:图中三个正方形的面积之和比4个三角形的面积之和大多少?95QED P R FCBAN MH G A B CFR P DEQ 59【例 54】 如图所示,甲、乙、丙、丁四个长方形拼成一个正方形EFGH ,中间阴影为正方形.已知甲、乙、丙、丁四个长方形面积的和是232cm ,四边形ABCD 的面积是220cm .⑴求正方形EFGH 的边长?⑵求甲、乙、丙、丁四个长方形周长的总和?F E HGDCB A 丙乙丁甲ABC DG H E F hgfe d cba图1 图2 图3【例 55】 如图,平面上CDEF 是正方形,ABCD 是等腰梯形,它的上底23AD =厘米,下底35BC =厘米.求三角形ADE 的面积.FECB DAH 2H 1HADBCEF【例 56】 右图是由9个等边三角形拼成的六边形,已知中间最小的等边三角形的边长是1,问:这个六边形的周长是多少?【例 57】 把正三角形的每条边三等分,以各边的中间一段为边向外作小正三角形,得到一个六角形.再将这个六角形的六个”角”(即小正三角形)的两边三等分,又以它的中间段为边向外作更小的小正三角形,这样就得到如右图所示的图形.如果所作的最小的小正三角形的面积为1平方厘米,求如图中整个图形的面积.图a中中中大图b【例 58】 如图,长方形的面积是小于100的数.它的内部有三个边长是整数的正方形.正方形②的边长是长方形长的512,正方形①的边长是长方形宽的18.那么,图中阴影部分的面积是。
【小学】五年级上册数学一课一练 5.4不规则图形的的面积(含答案)

五年级上册数学一课一练不规则图形的的面积一、单选题1 图形与其余2个的面积不一样大。
A B C2右图涂色部分的面积是 cm2。
A 2B 4C 63某正方形园地是由边长为1米的四个小正方形组成的,现要在园地上建一个花坛(阴影部分)使花坛面积是园地面积的一半,以下图中设计不合要求的是()A B C D4如图中阴影部分的面积是()平方厘米.(单位:厘米)A 132BC 289 D二、判断题5判断,正确的填“正确”,错误的填“错误”.两个面积相等的梯形,上底、下底和高一定相等.6下面两图中阴影部分的面积相等。
每个小方格的边长表示1cm7任何一个梯形都可以分成两个等高的三角形。
三、填空题8图中直角三角形的面积是2021厘米,阴影部分的面积是________平方厘米.(用小数表示)9按要求解答.求下面图形的面积是________ 已知条件如图中所示,单位:cm.10如图是由6个面积是1平方厘米的正方形组成的,三角形C的面积是________平方厘米,三角形A,B,C的面积和是________平方厘米,空白部分的面积是________平方厘米.11如图所示,正六边形ABCDEF的面积是36平方厘米,AG= AB,CH= CD,则四边形BCHG的面积是________平方厘米.四、解答题12计算组合图形的面积。
单位:cm13求如图图形的面积。
(合多少公顷)五、综合题14列式计算:(1)6除的商,加上3,在乘3,积是多少?(2)与的和除以它们的差的2倍,商是多少?(3)如图:三角形ABC为直角三角形,BC为圆的直径,BC=2021,S1、S2阴影部分的面积,且S1=S2,求三角形ABC的面积?六、应用题15求下面图形中阴影部分的面积.(先在图中量出并标出计算时需要的数据)参考答案一、单选题1【答案】B【解析】【解答】观察图形可知,C图形中的凸出部分可以剪拼到凹进去的部分,组成一个长方形,与A 图形的面积相等,B图形的面积与其余2个的面积不一样大故答案为:B【分析】比较图形面积的大小,可以用剪拼、平移等方法将图形进行分割与组合,然后判断大小2【答案】B【解析】【解答】解:2×2=4cm²故答案为:B【分析】把上面的半圆移动到下面,阴影部分的面积就是一个边长2cm的正方形的面积,根据正方形面积公式计算即可3【答案】B【解析】【解答】解:A、阴影部分是一个三角形,三角形的底和高都与正方形的边长相等,所以三角形面积是正方形面积的一半;符合要求;B、阴影部分的面积和是个小正方形的面积,大于大正方形面积的一半,不符合要求;C、阴影部分的面积之和相当于2个小正方形的面积,是大正方形面积的一半,符合要求;D、阴影部分重新组合后相当于两个小正方形的面积,是大正方形面积的一半,符合要求故答案为:B【分析】根据大正方形平均分的份数结合阴影部分的大小判断出阴影部分的面积相当于几个小正方形的面积即可做出选择4【答案】B【解析】【解答】解:10÷2=5(厘米)×52÷2=×25÷2=(平方厘米)10×5÷2=25(平方厘米)﹣25=(平方厘米)答:阴影部分的面积是平方厘米.故选:B.【分析】根据图可知,半圆面积﹣三角形面积=阴影面积.于是应先求出半圆面积和三角形面积,半圆的直径是10厘米,半径可求出,面积即可求得;三角形的底为10厘米,高就是圆的半径,运用三角形面积公式即可求得.进而解决问题.二、判断题5【答案】错误【解析】【解答】解答:两个面积相等的梯形,上底、下底和高不一定相等.梯形的面积相等,是用上底+下底×高÷2这个公式计算后所得的结果相等.【分析】上底、下底和高不相等的梯形,面积可能相等.6【答案】正确【解析】【解答】根据分析,作图如下:(1)2×2÷2×2=4÷2×2=4(cm2)(2)2×12×2÷2=24÷2=22=4(cm2)两图中阴影部分的面积相等,原题说法正确故答案为:正确【分析】(1)第一个图的阴影部分可以分成两个底为2厘米,高为2厘米的相等三角形,据此利用三角形的面积公式计算即可;(2)第二个图的阴影部分可以分成一个长为2厘米,宽为1厘米的长方形与一个底是2厘米,高是2厘米的三角形,将两个图形的面积相加即可得到阴影部分的面积,然后比较两个图的阴影部分的面积大小即可7【答案】正确【解析】【解答】根据梯形的定义可知,有一组对边平行的四边形叫平行四边形。
人教版五年级上册数学 第六单元 第8课时 不规则图形的面积

第8课时 不规则图形的面积
优 翼
复习导入计算下面Leabharlann 形的面积。3m4m
10m
3m 4m
5m
10m
5×3+5×4=35(m2) 10×10 - 3×4÷2=94(m2)
探 究 新 知 (教材100页例5)
知识点1:方格纸中不规则图形面积的估算
5 图中每个小方格的面 积是1cm2 ,请你估计 这片叶子的面积。
探究新知
阅读与理解
知道小方格的面积, 求叶子的面积。
探究新知
分析与解答
先在方格纸上描出叶子的轮廓图。
方格纸上满格的一共有18 这片叶子的面积在 格,不是满格的也有18格。 18cm2—36cm2之间。
如果把不满一格 的都按半格计算, 这片叶子的面积 大约27cm2。
探究新知
我是将叶子的图形 近似转化成平行四 边形……
5×4÷2 + (5+2)×4÷2 = 24(cm2)
巩 固 练 习 (教材102页第8 题)
2.图中每个小方格的面积为1cm2,计算阴 影部分面积。
近似转化成长方形
8×4 = 32(cm2)
阴影部分面积大约是 32cm2。
巩 固 练 习 (教材102页第9 题)
3.图中每个小方格的面积为1m2,请你估 计这个池塘的面积。
S=ah
=5×6 =30(cm2)
你是怎样估的?
探究新知
回顾与反思 先通过数方格确定面 积的范围,再……
不规则图形的面积可以转 化为学过的图形来估算。
方法小结
估计不规则图形的面积: 借助方格图数格子估算不规则图形的 面积,也可以把不规则图形看成近似 于规则的图形估算面积。
人教版五年级上册数学《不规则图形的面积》教学反思说课稿及评课稿

《不规则图形的面积》教学反思在数学教学中,只要在课堂教学结构,教学过程,教学体系上以全新的思路进行改革,进行设计,教师的教学能力是在基于实践的教学研究中不断提高,新的教学思想也必然在新的教育教学改革实践中逐步确立。
但是想成为有经验的教师成,必须是教师如何学会进行研究与反思,设计一堂教学的过程就是一个反思的过程,反思是教师成长的最好经历。
《课程标准》指出:要创设与学生生活环境、知识背景密切相关的,又是学生感兴趣的学习情境,让学生在观察、操作、猜测、交流、反思等活动中逐步体会数学知识的产生、形成与发展的过程,获得积极的情感体验,感受数学的力量,同时掌握必要的基础知识与基本技能。
如教学《不规则图形的面积估算》,必须先复习了长方形、正方形、平行四边形面积的计算,然后顺势提出“不规则图形的面积估算”这一全课的核心问题,从而引发学生的猜测、操作、交流等数学活动,使学生经历了“做数学”的过程。
伴随着问题的圆满解决,学生体验到了成功的喜悦与满足。
还要鼓励学生独立思考,引导学生自主探索、合作交流。
数学学习过程充满着观察、实验、模拟、推断等探索性与挑战性活动,因此,动手实践、自主探究、合作交流是《课程标准》所倡导的数学学习的主要方式。
教师要改变以例题、示范、讲解为主的教学方式,引导学生投入到探索与交流的学习活动之中。
在本节课中,我让全班学生以小组为单位围坐在一起,为他们提供自主探究的空间,同时尽量延长小组交流的时间,试图把学习的时间、空间还给学生,让其进行自主探究、合作交流。
数学的价值不在技能而在思想,在探究的过程中,我不是安排了一整套指令让学生进行程序操作,获得一点基本技能,而是提供了相关知识背景、实验素材,使用了“对我们有帮助吗?”“你有什么发现?”“你是怎样想的?”等这样一些指向探索的话语鼓励学生独立思考、动手操作、合作探究,让学生根据已有的知识经验创造性地建构自己的数学,才是有价值的。
鼓励解决问题策略的多样化,是因为施教,促进每一个学生充分发展的有效途径。
小学奥数:不规则图形的面积.专项练习及答案解析

本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求面积的技巧,提高学生的观察能力、动手操作能力、综合运用能力.【例 1】 你有什么好的方法计算所给图形的面积呢?(单位:厘米)3994399439943994图1 图2 图3 【考点】不规则图形的面积 【难度】1星 【题型】解答 【解析】 (方法一)采用分割法,可给原图分成两个长方形,(图1或图2)两个长方形的总面积就是所求的面积.图1的面积是: 4(93)9375⨯++⨯=(平方厘米).图2的面积是:(94)39475+⨯+⨯=(平方厘米).(方法二)采用补图法,如果补上一个边长是9厘米的正方形(图3),就成了一个面积是:(49)(93)156+⨯+=(平方厘米)的大长方形.因此用这个长方形的面积减去所补正方形的面积,就是要求的图形面积(49)(93)9975+⨯+-⨯=(平方厘米). 【答案】75平方厘米【巩固】如图是学校操场一角,请计算它的面积(单位:米)30203040例题精讲4-2-6.不规则图形的面积【解析】 这是一个不规则图形,怎样使它能转化为我们熟悉的基本图形呢?可以在图中添上一条辅助线,把多边形切割成上下两个长方形或左右两个长方形;也可以把多边形补充完整,成为一个长方形;302030403020304030203040图一 图二 图三方法一:如图一,3040203040120014002600⨯+⨯+=+=()(平方米) 方法二:如图二,203040203060020002600⨯+⨯+=+=()(平方米) 方法三:如图三,40302030303035009002600+⨯+-⨯=-=()()(平方米)【答案】2600平方米【巩固】如右图所示,图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的,线段的长度如图所示(单位:厘米),求ABEFGD 的周长和面积.F【考点】不规则图形的面积 【难度】1星 【题型】解答 【解析】 方法一:如果求出长方形的宽及正方形的边长,则图形ABEFGD 的周长和面积可以求出.而正方形的边长1046GC DC DG AB DG =-=-=-=(厘米),长方形的宽1064BE CE =-=-=(厘米),所求图形的周长102624440=⨯+⨯++=(厘米) 面积1046676CEFG ABCD S S =+=⨯+⨯=正方形长方形(平方厘米)方法二:可以将线段GF 、DG 向外平移,得一个新的图形ABEH ,因为DG HF =,GF DH =,所以图形ABEH 的周长就是图形ABEFGD 的周长.而10AB BE ==(厘米),所以图形ABEH 是边长为10厘米的正方形. 所求图形的周长=正方形ABEH 的周长10440=⨯=(厘米) 面积10106476ABEH DGFH S S =-=⨯-⨯=正方形长方形(平方厘米)【总结】方法一是利用基本图形的周长及面积公式求解,因此首先要知道长方形的长、宽及正方形的边长.方法二是利用转化的思想方法,将较复杂图形转化为基本图形,图形转化前后的周长不变,面积增加了,在计算时应减去增加的面积. 【答案】76【巩固】求图中五边形的面积.6453【解析】由图可见五边形为矩形切去一角得来,把切去的角补出来,它的一条直角边长633-=,斜边等于5,所以另一直角边为4,所以矩形的长为448+=,五边形面积16843422⨯-⨯⨯=.【答案】42【例 2】这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20 厘米.问,此楼梯截面的面积是多少?【考点】不规则图形的面积【难度】2星【题型】解答【关键词】华杯赛、口试【解析】如果把楼梯截面补成右图所示的长方形,那么此长方形高280厘米.宽300厘米,它的面积恰好是所求截面的2倍.所以楼梯截面面积为280300242000⨯÷=()(平方厘米).【答案】42000【巩固】如图是一个楼梯的截面图,每级台阶的宽和高都是20厘米.这楼梯的截面积是多少平方厘米?【考点】不规则图形的面积【难度】2星【题型】解答【解析】先求出大三角形的两条直角边都是208160⨯=(厘米),因此大三角形的面积为160160212800⨯÷=(平方厘米);8个小三角形的面积为2020281600⨯÷⨯=(平方厘米);因此这楼梯的截面积为12800160014400+=(平方厘米).【答案】14400【例 3】有一块菜地长16米,宽8米,菜地中间留了宽2米的路,把菜地平均分成四块,每一块地的面积是多少?【考点】不规则图形的面积【难度】2星【题型】解答【解析】方法一:可以直接求出每小块菜地的长和宽,从而求出每小块菜地的面积;每一块地的面积是:[1622][822]7321-÷⨯-÷=⨯=()()(平方米)方法二:也可以求出这块地的总面积,再减去道路的面积,然后把剩余的面积四等分求出每小块菜地的面积;每一块地的面积是:[1682168222]412844421⨯-⨯+⨯-⨯÷=-÷=()()(平方米)方法三:还可以运用平移的方法,将道路移到菜地的边沿,先求出四个小长方形组成的长方形面积,再求出其中每一小块菜地的面积.如图所示:[16282]484421-⨯-÷=÷=()()(平方米) 【答案】21【例 4】 有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 通过操作,一张一张的添加,可以发现每多盖一张,遮住的面积增加21⨯平方厘米,所以这10张纸片盖住的面积是:3221924⨯+⨯⨯=(平方厘米).【答案】24【例 5】 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 所求面积等于图中阴影部分的面积,为2052082140-+⨯÷=()(平方厘米). 【答案】140【巩固】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.FBA【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 阴影部分是一个高为3厘米的直角梯形,然而它的上底与下底都不知道,因而不能直接求出它的面积.因为三角形ABC 与三角形DEF 完全相同,都减去三角形DOC 后,根据差不变性质,差应相等,即阴影部分与直角梯形OEFC 面积相等,所以求阴影部分的面积就转化为求直角梯形OEFC 的面积.直角梯形OEFC 的上底为1037-=(厘米),面积为7102217+⨯÷=()(厘米2). 所以,阴影部分的面积是17平方厘米。
小学数学 不规则图形的面积 教案

不规则图形的面积一、考点、热点1.初步掌握通过将不规则图形近似地看作可求规则图形的面积。
2.通过用数格子方法和近似图形求积法估计不规则图形的面积。
二、知识梳理1、说说下面每个图形的面积各是多少?(每个小方格表示1平方厘米)2、如果每个小方格表示1平方厘米,你能说说下面每个图形的面积是多少平方厘米吗?计算不规则图形的面积,主要是用数方格的方法。
数方格的时候要注意以下几点:(1)把整格和半格分别涂上不同的颜色,避免重复和遗漏。
(2)不满整格的可以全部看成半格计算;或者先数整格的个数,再把不满整格的也看成整格,数出一共有多少格。
(3)有顺序地去数,做到不重复、不遗漏。
试一试1、下面是一个湖泊的平面图(每个小方格表示1公顷)。
你能估计这个湖泊的面积大约是多少公顷吗?三、巩固练习1.数不规则图形的面积时,只数整格的,图形的实际面积比数出的面积()(填“大”或者“小”)。
2.数不规则图形的面积时,数出所有格的,图形的实际面积比数出的面积()(填“大”或者“小”)。
3.数不规则图形的面积时,先数满格的,再数不满格的,不满格的按()计算,这样数的比较准确。
4.图中每格的面积是1平方米,估计这个池塘的面积。
5、图中每格的面积是1平方厘米,估计阴影部分的面积。
6、估计一下,左图中树叶的面积大约是多少平方厘米吗?(每个小方格表示1平方厘米)四、过手训练1.图中每格的面积是1平方厘米,估计阴影部分的面积。
2.图中每格的面积是1平方米,请你估计涂色部分的面积。
4.请你估算一下谭谭两岁时脚的大小。
(每小格的边长表示1厘米)5.图中每格的面积是1平方厘米,请你估计涂色部分的面积。
6.请你估计下面三个圆的面积。
(1)图1中每方格边长表示4厘米,它的面积大约是()平方厘米。
(2)图2中每方格边长表示2厘米,它的面积大约是()平方厘米。
(3)图3中每方格边长表示1厘米,它的面积大约是()平方厘米。
五年级上册数学课件-2.10 不规则图形的面积丨苏教版 (共25张PPT)

返回作业设计
作业2
思维创新 提升培优 基础巩固
返回作业设计
1.(基础题)图中每个小方格的面积都
是 1平方分米,估算图中阴影部分的面积。
约( 13 )平方分米。
返回作业2
2.(难点题)估算草坪的面积是( 16 )平
方米,(每个小方格表示 1m²,涂色部分 为草坪)
树叶的形状接近平行四边形
S=ah =5×6 =30(平方厘米)
我们用数方格的方法估算出 树叶的面积大约是27平方厘米, 而把树叶转化成平行四边形算出 的面积是30平方厘米,哪个结果 是正确的呢?
谁来说一说,这节课你都学习了哪些 知识?有什么收获?
学习了用估算的方法求不 规则图形的面积!可以用数方格 的方法,也可以将它近似地看 作规则图形。
(2)方法一:分割成两个三角形和一个长方形
3×2÷2+5×2÷2+8×3 =3+5+24 =32(cm²)
8.图中每个小方格的面积是1cm²,计算阴影部分 的面积。
(2)方法二:割补成一个长方形
8×4 =32(cm²)
返回目录
作业1
要认真呦。
作业2
作业设计
返回目录
作业1 教材第102页练习二十二第7题。
不规则图形的面积
学习新知随堂Biblioteka 习作业设计学习新知
观察画面,下面的图像面积你会求吗?
观察画面,下面的图像面积你会求吗?
图形不规则
为 什 么 不 会 呢 ?
观察图片,你发现了什么?
1cm²
54 3 2 1
6 1 2 3 4 17 7 5 6 7 8 9 16
求不规则图形面积的五种方法

求不规则图形面积的五种方法
一、相加法:临方法是将不规则图形分解转化成几个基本规测图形,分别计算它们的面积,然后相加求出整个图形的面积。
二、相减法:这种方法是将所求的不规则图形的面积看成是若千个基本规则图形的面积之差.
三、直接求法:这种方法是根据已知条件,从整体出发直接求出不规则图形面积
四、重新组合法:这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可4个角处,这时采用相减法就可求出其面积了.
五、割补法:这种方法是把原图形的受部分切割下来补在图形中的另部分使之成为基本规则图形,从而使问题得到解决。
人教版数学五年级上册《不规则图形的面积》教案

人教版数学五年级上册《不规则图形的面积》教案一. 教材分析《不规则图形的面积》是人教版数学五年级上册的一章内容,主要目的是让学生掌握不规则图形面积的求法,培养学生的空间想象能力和抽象思维能力。
本章内容主要包括不规则图形的面积计算方法,以及如何运用这些方法解决实际问题。
教材通过丰富的实例和实践活动,帮助学生理解和掌握不规则图形面积的求法。
二. 学情分析五年级的学生已经掌握了基本的平面几何图形的面积计算方法,具备一定的空间想象能力和抽象思维能力。
但是,对于不规则图形的面积计算,学生可能还存在一定的困难。
因此,在教学过程中,教师需要关注学生的学习情况,针对学生的薄弱环节进行有针对性的教学。
三. 教学目标1.让学生掌握不规则图形面积的求法,能够独立完成不规则图形面积的计算。
2.培养学生的空间想象能力和抽象思维能力。
3.能够运用不规则图形的面积计算方法解决实际问题。
四. 教学重难点1.不规则图形面积的计算方法。
2.如何运用不规则图形的面积计算方法解决实际问题。
五. 教学方法1.情境教学法:通过生活实例,引导学生理解和掌握不规则图形面积的计算方法。
2.动手操作法:让学生通过实际操作,体验不规则图形面积的计算过程。
3.小组合作法:引导学生进行小组讨论和合作,共同解决不规则图形面积计算问题。
六. 教学准备1.教学课件:制作精美的课件,展示不规则图形的面积计算方法。
2.实物模型:准备一些不规则形状的实物模型,方便学生直观地理解不规则图形的面积计算。
3.练习题库:准备一些有关不规则图形面积计算的练习题,用于巩固所学知识。
七. 教学过程导入(5分钟)教师通过展示一些生活中的不规则图形,如树叶、衣服、地图等,引导学生思考这些图形的面积如何计算。
学生可以自由发表意见,教师总结并引出本节课的主题——不规则图形的面积计算。
呈现(10分钟)教师通过课件展示不规则图形的面积计算方法,如分割法、近似法等。
同时,教师结合实物模型,让学生直观地理解不规则图形的面积计算过程。
不规则图形面积的计算

小 喷泉 湖
草坪
假山
游乐场
例如:华丰校园里有一块草坪(如图) 它的面积是多少平方米?
12m
4m 10m
方法一:分割法
15m
草坪的面积=长方形的面积+梯形的形的面积:10-4=6m (12+15) ×6=81㎡
草坪的面积:48+81=129㎡
法计算组合图形面积.
作业
课本23页练习四1到4题
学校开运动会要制作一 些锦旗,式样如右图。 一面锦旗需要多少平方 厘米面料?
(60+45) ×(30÷2) ÷2×2 =105×15÷2×2 =1575(㎝²)
答:一面锦旗需要1575平方厘 米面料。
45cm 60cm
30cm
1、草坪的面积有多少平方米?
5m
2m
2m 6m
小挑战:你能求出下面图形的面积吗?
8 43 36 2
中队旗面积 = 梯形面积 + 梯形面积
中队旗面积 = 长方形面积 + 三角形面积 × 2
中队旗面积 = 梯形面积 + 三角形面积
中队旗面积 = 长方形面积 — 三角形面积
小结
方法:一分图形 二找条件 三算面积
关键:学会运用“分割”与“添补” 的方
答:这块草坪的面积是129㎡
方法二:分割法
12m
4m 10m
15m
草坪的面积=长方形的面积+三角形的面积
长方形的面积:12×10=120㎡
三角形的面积:15-12=3m,10-4=6m
3×6÷2=9㎡
草坪的面积:120+9=129㎡
答:这块草坪的面积是129㎡
12m
《不规则图形的面积》(教案)五年级上册数学人教版

教案:《不规则图形的面积》年级:五年级学科:数学教材版本:人教版教学目标:1. 让学生理解不规则图形的概念,并能识别生活中的不规则图形。
2. 培养学生运用分割、近似等方法计算不规则图形面积的能力。
3. 培养学生的空间想象力和创新意识,提高解决实际问题的能力。
教学重点:1. 不规则图形的概念及其与规则图形的区别。
2. 计算不规则图形面积的方法。
教学难点:1. 如何引导学生运用分割、近似等方法计算不规则图形面积。
2. 如何将不规则图形转化为规则图形进行面积计算。
教学准备:1. 课件、黑板、粉笔等教学工具。
2. 准备一些生活中的不规则图形实例,如地图、树叶等。
教学过程:一、导入1. 利用课件展示一些生活中的不规则图形,如地图、树叶等,引导学生观察并说出这些图形的特点。
2. 提问:这些图形与之前学习的规则图形有什么不同?引导学生总结出不规则图形的概念。
二、新课讲解1. 讲解不规则图形的概念,强调其与规则图形的区别。
2. 介绍计算不规则图形面积的方法,如分割法、近似法等。
3. 示例讲解如何运用分割法、近似法计算不规则图形面积,并强调在计算过程中要注意的问题。
三、课堂练习1. 让学生独立完成教材上的练习题,巩固所学知识。
2. 老师巡回指导,解答学生疑问。
四、课堂小结1. 让学生总结本节课所学的不规则图形的概念及计算方法。
2. 强调在计算不规则图形面积时要注意的问题。
五、作业布置1. 完成教材上的课后习题。
2. 观察生活中的不规则图形,尝试运用所学方法计算其面积。
教学反思:本节课通过生活中的实例引入不规则图形的概念,让学生感受到数学与生活的紧密联系。
在教学过程中,注重培养学生的空间想象力和创新意识,引导他们运用分割、近似等方法计算不规则图形面积。
同时,通过课堂练习和课后作业,让学生巩固所学知识,提高解决实际问题的能力。
在今后的教学中,要注意以下几点:1. 多给学生提供观察、操作、讨论的机会,让他们在实际活动中理解数学知识。
苏教版 数学 五年级上册 不规则图形的面积

不规则图形面积的估计
➢ 导入
➢ 新授
11
下面是某自然保护区的一个湖泊的平面图。你能估计
这个新授
➢先数一数整格数;
一共有55格,面积应大于55公顷。
➢把不满整格的按照整格计算;
一共有91格,面积应小于91公顷。
面积在55~91公顷之间
➢ 新授
估计这个湖泊的面积。
➢先数一数整格数; 一共有55格
➢把不满整格的当做半格计算;
一共有36个半格
面积约是:55+36÷2=73(公顷)
➢ 练一练 1
1.估计一下,图中树叶的面积大约是多少平方厘米? (每个小格表示1平方厘米)
22个整格;34个不满整格。 面积约是在22~56平方厘米之间。
面积约是:22+34÷2=39(平方厘米)
➢ 练一练 2
先在方格纸上描出自己手掌的轮廓线,再用数方 格的方法估计自己手掌的面积大约是多少平方厘米?
➢ 练习四 9
采集一片树叶,把它的轮廓线描在方格纸上, 估计它的面积。
➢ 你知道吗?
➢ 总结
通过这节课的学习,你 学到了什么知识呢?
小学数学六年级下册 不规则图形的面积

不规则图形的面积【使用说明】本讲义针对人教版本教材,适用于对基本概念掌握较好的学生。
旨在加强对图形求面积的方法的讲解,达到灵活运用的目的。
本节重点➢知识点一:本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括分割、填补、等积变形,通过这些方法的学习,体会求面积的技巧,提高观察能力、动手操作能力、综合运用能力。
例题精讲例题:求如图直角梯形中阴影部分的面积(单位:厘米)。
【分析】【解答】【难度系数】1变式练习:【题目】求阴影部分的面积(单位:厘米)【分析】【解答】【难度系数】2【例 1】 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【分析】利用面积相等进行转化,把求不规则阴影部分面积转化为求下方直角梯形面积进行计算。
【解答】所求面积等于图中阴影部分的面积,为2052082140-+⨯÷=()(平方厘米).85【难度系数】2变式练习:【题目】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.【分析】利用面积相等进行转化,把求左侧阴影梯形面积转化为求下方直角梯形面积进行计算。
【解答】阴影部分是一个高为3厘米的直角梯形,然而它的上底与下底都不知道,因而不能直接求出它的面积.因为三角形ABC 与三角形DEF 完全相同,都减去三角形DOC 后,根据差不变性质,差应相等,即阴影部分与直角梯形OEFC 面积相等,所以求阴影部分的面积就转化为求直角梯形OEFC 的面积.直角梯形OEFC 的上底为10-3=7(厘米),面积为(7+10)×2÷2=17(平方厘米). 所以,阴影部分的面积是17平方厘米。
【难度系数】2例题:如图,在长方形ABCD 中,AB 长8厘米,BC 长15厘米,四边形EFGH 的面积是9平方厘米,求阴影部分的面积和。
【分析】【解答】20-5823DOEFCBA【难度系数】3变式练习:【题目】如图,正方形的边长为10,四边形EFGH 的面积为5,那么阴影部分的面积是 .【分析】根据等底等高的三角形面积相等,把三角形的面积之和转化为正方形面积的一半,再进行求解。
小学奥数:不规则图形的面积.专项练习及答案解析

本讲主要通过求一些不规则图形的面积,体会一种转化思想,重点在于把不规则图形转化为规则图形的方法,包括平移、旋转、割补、差不变原理,通过这些方法的学习,让学生体会求面积的技巧,提高学生的观察能力、动手操作能力、综合运用能力.【例 1】 你有什么好的方法计算所给图形的面积呢?(单位:厘米)3994399439943994图1 图2 图3 【考点】不规则图形的面积 【难度】1星 【题型】解答 【解析】 (方法一)采用分割法,可给原图分成两个长方形,(图1或图2)两个长方形的总面积就是所求的面积.图1的面积是: 4(93)9375⨯++⨯=(平方厘米).图2的面积是:(94)39475+⨯+⨯=(平方厘米).(方法二)采用补图法,如果补上一个边长是9厘米的正方形(图3),就成了一个面积是:(49)(93)156+⨯+=(平方厘米)的大长方形.因此用这个长方形的面积减去所补正方形的面积,就是要求的图形面积(49)(93)9975+⨯+-⨯=(平方厘米). 【答案】75平方厘米【巩固】如图是学校操场一角,请计算它的面积(单位:米)30203040例题精讲4-2-6.不规则图形的面积【解析】 这是一个不规则图形,怎样使它能转化为我们熟悉的基本图形呢?可以在图中添上一条辅助线,把多边形切割成上下两个长方形或左右两个长方形;也可以把多边形补充完整,成为一个长方形;302030403020304030203040图一 图二 图三方法一:如图一,3040203040120014002600⨯+⨯+=+=()(平方米) 方法二:如图二,203040203060020002600⨯+⨯+=+=()(平方米) 方法三:如图三,40302030303035009002600+⨯+-⨯=-=()()(平方米)【答案】2600平方米【巩固】如右图所示,图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的,线段的长度如图所示(单位:厘米),求ABEFGD 的周长和面积.F【考点】不规则图形的面积 【难度】1星 【题型】解答 【解析】 方法一:如果求出长方形的宽及正方形的边长,则图形ABEFGD 的周长和面积可以求出.而正方形的边长1046GC DC DG AB DG =-=-=-=(厘米),长方形的宽1064BE CE =-=-=(厘米),所求图形的周长102624440=⨯+⨯++=(厘米) 面积1046676CEFG ABCD S S =+=⨯+⨯=正方形长方形(平方厘米)方法二:可以将线段GF 、DG 向外平移,得一个新的图形ABEH ,因为DG HF =,GF DH =,所以图形ABEH 的周长就是图形ABEFGD 的周长.而10AB BE ==(厘米),所以图形ABEH 是边长为10厘米的正方形. 所求图形的周长=正方形ABEH 的周长10440=⨯=(厘米) 面积10106476ABEH DGFH S S =-=⨯-⨯=正方形长方形(平方厘米)【总结】方法一是利用基本图形的周长及面积公式求解,因此首先要知道长方形的长、宽及正方形的边长.方法二是利用转化的思想方法,将较复杂图形转化为基本图形,图形转化前后的周长不变,面积增加了,在计算时应减去增加的面积. 【答案】76【巩固】求图中五边形的面积.6453【解析】由图可见五边形为矩形切去一角得来,把切去的角补出来,它的一条直角边长633-=,斜边等于5,所以另一直角边为4,所以矩形的长为448+=,五边形面积16843422⨯-⨯⨯=.【答案】42【例 2】这是一个楼梯的截面图,高280厘米,每级台阶的宽和高都是20 厘米.问,此楼梯截面的面积是多少?【考点】不规则图形的面积【难度】2星【题型】解答【关键词】华杯赛、口试【解析】如果把楼梯截面补成右图所示的长方形,那么此长方形高280厘米.宽300厘米,它的面积恰好是所求截面的2倍.所以楼梯截面面积为280300242000⨯÷=()(平方厘米).【答案】42000【巩固】如图是一个楼梯的截面图,每级台阶的宽和高都是20厘米.这楼梯的截面积是多少平方厘米?【考点】不规则图形的面积【难度】2星【题型】解答【解析】先求出大三角形的两条直角边都是208160⨯=(厘米),因此大三角形的面积为160160212800⨯÷=(平方厘米);8个小三角形的面积为2020281600⨯÷⨯=(平方厘米);因此这楼梯的截面积为12800160014400+=(平方厘米).【答案】14400【例 3】有一块菜地长16米,宽8米,菜地中间留了宽2米的路,把菜地平均分成四块,每一块地的面积是多少?【考点】不规则图形的面积【难度】2星【题型】解答【解析】方法一:可以直接求出每小块菜地的长和宽,从而求出每小块菜地的面积;每一块地的面积是:[1622][822]7321-÷⨯-÷=⨯=()()(平方米)方法二:也可以求出这块地的总面积,再减去道路的面积,然后把剩余的面积四等分求出每小块菜地的面积;每一块地的面积是:[1682168222]412844421⨯-⨯+⨯-⨯÷=-÷=()()(平方米)方法三:还可以运用平移的方法,将道路移到菜地的边沿,先求出四个小长方形组成的长方形面积,再求出其中每一小块菜地的面积.如图所示:[16282]484421-⨯-÷=÷=()()(平方米) 【答案】21【例 4】 有10张长3厘米,宽2厘米的纸片,将它们按照下图的样子摆放在桌面上,那么这10张纸片所盖住的桌面的面积是多少平方厘米?【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 通过操作,一张一张的添加,可以发现每多盖一张,遮住的面积增加21⨯平方厘米,所以这10张纸片盖住的面积是:3221924⨯+⨯⨯=(平方厘米).【答案】24【例 5】 下图(单位:厘米)是两个相同的直角梯形重叠在一起,求阴影部分的面积.【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 所求面积等于图中阴影部分的面积,为2052082140-+⨯÷=()(平方厘米). 【答案】140【巩固】两个相同的直角三角形如下图所示(单位:厘米)重叠在一起,求阴影部分的面积.FBA【考点】不规则图形的面积 【难度】3星 【题型】解答 【解析】 阴影部分是一个高为3厘米的直角梯形,然而它的上底与下底都不知道,因而不能直接求出它的面积.因为三角形ABC 与三角形DEF 完全相同,都减去三角形DOC 后,根据差不变性质,差应相等,即阴影部分与直角梯形OEFC 面积相等,所以求阴影部分的面积就转化为求直角梯形OEFC 的面积.直角梯形OEFC 的上底为1037-=(厘米),面积为7102217+⨯÷=()(厘米2). 所以,阴影部分的面积是17平方厘米。
新课标小学数学五年级下册《不规则图形的面积》教材说明及教学建议

《不规则图形的面积》教材说明及教学建议【教材说明】这部分内容主要引导学生探索简单组合图形的面积计算方法和不规则图形的面积估计方法。
编排这部分内容的主要目的,一是为了帮助学生进一步丰富对平面图形面积计算方法的理解;二是为了促进学生进一步提高应用所学知识解决问题的能力,积累“图形与几何”的学习经验。
教材一共安排两道例题。
例10教学简单组合图形的面积计算。
教材首先呈现华丰小学校园里一块草坪的平面图,要求学生计算这块草坪的面积,同时提醒他们:“你准备怎样算?与同学交流”,引导他们把重点放在解决问题方法的探索上。
接着,教材呈现学生相互交流的场面,突出计算这个多边形的面积时,或者把它分成两个简单图形,求出这两个简单图形的面积之和;或者把它补成一个简单图形,再求出这个简单图形与另一个相关图形的面积之差。
在此基础上,组织学生围绕图形割补的过程进行反思,进一步突出方法选择的思考过程,以及解决问题时需要注意的地方。
这样的活动,不仅能给学生综合应用学过的各种面积公式提供机会,而且凸显了“图形转化”这种计算多边形面积的基本策略。
随后的“练一练”,要求学生利用初步掌握的基本方法计算校园里花圃的面积,有利于他们进一步加深对上述方法的理解,提高计算不同多边形面积的能力。
例11教学用数方格的方法估计不规则图形的面积。
教材的编排有两个明显的特点:一是注意引导学生采用不同的估计方法,可以只数整格的个数;也可以把不满整格的都当成整格来计数;还可以分别数出整格和不满整格的个数,并把不满整格的都按半格来计算。
二是引导学生通过不同估计方法的比较,初步体会确定上、下界对于面积估计的意义和价值。
随后的“练一练”让学生应用上面学到的方法估计一片树叶和自己手掌的面积,有利于他们进一步掌握方法,锻炼动手实践和解决实际问题的能力。
练习四一共安排了9道题,大体分为三段:第一段是第1、2题,主要帮助学生巩固简单组合图形面积的计算方法;第二段是第3~8题,主要让学生联系简单组合图形面积的计算方法解决一些实际问题;第三段是第9题,引导学生通过实践活动进一步巩固不规则图形面积的估计方法。
2022年人教版小学《不规则图形的面积》精品教案(推荐)

第5课时不规则图形的面积在学生估计树叶的面积时,让学生说一说他的想法〔估计的依据〕,培养学生的空间观念。
▶教学内容教科书P100例5,完成教科书P102“练习二十二〞第7~11*题。
▶教学目标1.通过与同伴交流估算面积的方法,培养合作意识,借助操作等实践活动自主解决问题。
2.在估计不规则图形面积的过程中,培养空间观念以及估算意识和能力。
3.学习用数方格的方法计算不规则图形的面积,能估计不规则图形的面积大小,并能用不同方法灵活估算面积。
▶教学重点掌握用方格纸和参照规则图形面积估计不规则图形面积的方法。
▶教学难点能用不同方法灵活估算不规则图形的面积。
▶教学准备课件,学生课前收集的树叶,1平方分米的空白方格纸,印着树叶的方格纸。
▶教学过程一、提出问题1.引入课题。
师:请同学们举起收集的树叶,说说它们的名称。
【学情预设】桑树叶、梧桐树叶、银杏树叶……师:今天这节课,我们就来研究怎样计算树叶的面积。
〔板书课题:不规则图形的面积〕【设计意图】让学生了解课前所收集的树叶的名称,激发学习的兴趣,表达数学与生活的紧密联系。
为学生创设一个轻松、和谐的学习气氛,在有趣的情境中引入新课。
2.估计一片树叶的面积大小。
师:与三角形、长方形等图形相比,你们发现这片树叶有什么不同吗?〔课件出示同教科书P100例5一样大的树叶平面图〕【学情预设】是由弯弯曲曲的线围成的,它是不规则图形,无法直接用公式进行计算。
师:这片叶子的形状不规则,你能估计一下它的面积吗?【学情预设】学生根据经验尝试估计。
3.估计面积大致范围。
【教学提示】在学生估计树叶的面积时,让学生说一说他的想法〔估计的依据〕,培养学生的空间观念。
师:把叶子放到一张1平方分米的空白方格纸上,你发现了什么?【学情预设】叶子的面积小于1平方分米。
师:将方格纸对折,继续比照,你发现了什么?【学情预设】叶子的面积小于50cm2。
师:将方格纸继续对折,然后比照,你发现了什么?【学情预设】叶子的面积一定大于25cm2小于50cm2。
第六单元《不规则图形的面积》教案

(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“不规则图形面积在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.重点难点解析:在讲授过程中,我会特别强调估算方法和转化技巧这两个重点。对于难点部分,如分割法和添补法的运用,我会通过具体例子和图示来帮助大家理解。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与不规则图形面积相关的实际问题。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。这个操作将演示如何利用网格纸和数值方法计算不规则图形的面积。
三、教学难点与重点
1.教学重点
(1)掌握用网格纸估算不规则图形面积的方法,如数格法和近似图形法;
(2)学会运用分割法、添补法将不规则图形转化为规则图形,进而计算其面积;
(3)熟练运用数值方法计算不规则图形面积,如三角形、梯形、圆的组合图形等;
(4)将所学知识应用于解决实际生活中的面积计算问题。
举例:以一个由多个三角形和梯形组成的复杂不规则图形为例,指导学生运用分割法将其分解为基本的三角形和梯形,进而计算各部分面积并求和。
五、教学反思
在本次不规则图形面积的教学中,我发现学生们对于估算方法和转化技巧的理解存在一定难度。特别是在将不规则图形转化为规则图形的过程中,部分学生对于如何选择合适的分割或添补方法感到困惑。针对这一问题,我在教学中增加了更多具体的例子和图示,希望通过直观的方式帮助学生突破这一难点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多边形的面积
本节内容:
1、减法求面积
2、加法求面积(割补法)
3、等积法求面积(剪拼法)
4、平面图形之间的等量关系的相互转化
我们已经学习过长方形、正方形、平行四边形、三角形、梯形的面积计算,图形以及计算公式如下:
巩固与提升:课前热身
1、两个()的三角形可以拼成一个平行四边形。
A 底相等
B 面积相等
C 等底等高
D 完全相同
解析:平行四边形按对角线切割可以分成两个完全相同的三角形。
2、下面两个完全相同的长方形中,阴影部分的面积相比,甲()乙。
A 大于
B 小于
C 等于
D 无法判断
解析:考察的是等底等高的三角形面积相等。
3、两个三角形等底等高,说明这两个三角形()。
A 形状相同
B 面积相同
C 能拼成一个平行四边形
D 完全相同
解析:考察的还是等底等高的三角形面积相等。
4、一个三角形底不变,高扩大4倍,面积()。
A 不变
B 扩大2倍
C 扩大4倍
D 缩小4倍
解析:面积的变化规律(积的变化规律)
5、把一个平行四边形活动框架拉成一个长方形,那么原来平行四边形与现在长方形相比()。
A 周长不变、面积不变
B 周长变了、面积不变
C 周长不变、面积变了
D 周长变了、面积变了
解析:周长没变,只有高度在发生变化。
6、一个平行四边形,底扩大6倍,高缩小2倍,那么这个平行四边形的面积()。
A 扩大6倍
B 缩小2倍
C 面积不变
D 扩大3倍
解析:考察的还是面积的变化规律(积的变化规律)。
在实际问题中,我们遇到的往往不是基本图形,而是由基本图形组合、拼凑成的组合图形,它们的面积不能直接用公式计算。
在本讲中,我们将学习如何计算它们的面积。
组合图形是由两个或两个以上的简单的几何图形组合而成的。
组合的形式分为两种:一是拼合组合,二是重叠组合。
由于组合图形具有条件相等的特点,往往使得问题的解决无从下手。
要正确解答组合图形的面积,应该注意以下几点:
1.切实掌握有关简单图形的概念、公式,牢固建立空间观念;2.仔细观察,认真思考,看清所求图形是由哪几个基本图形组合而成的;
3.适当采用增加辅助线等方法帮助解题;
4.采用割、补、分解、代换等方法,可将复杂问题变得简单。
类型一:减法求面积
例1:小两个正方形组成下图所示的组合图形。
已知组合图形的周长是52厘米,DG=4厘米,求阴影部分的面积。
分析与解:组合图形的周长并不等于两个正方形的周长之和,因为CG部分重合了。
用组合图形的周长减去DG,就得到大、小正方形边长之和的三倍,所以两个正方形的边长之和等于(52-4)÷3=16(厘米)。
又由两个正方形的边长之差是4厘米,可求出
大正方形边长=(16+4)÷2=10(厘米),
小正方形边长=(16-4)÷2=6(厘米)。
两个正方形的面积之和减去三角形ABD与三角形BEF的面积,就得到阴影部分的面积。
102+62-(10×10÷2)-(10+6)×6÷2=38(厘米2)。
