有限与无限
有限与无限的辩证关系

有限与无限的辩证关系
有限与无限是互相依存、互为表里的辩证关系。
有限指的是有界限、
有限度,有始有终,具有局限性和相对性。
而无限则指的是没有界限、没
有限度,无始无终,具有无穷性和绝对性。
有限与无限之间的辩证关系包含了以下几个方面:
1.有限是无限的表现。
有限的存在是无限的一种表现方式,它在无限
的背景下显得更加明显和突出,有限的存在可以是无限存在的体现。
2.无限需要有限的相对性支撑。
无限是相对于有限而言的,没有有限
这个对照,无限就无从谈起。
有限的存在为无限提供了相对性的支撑,使
无限不再是空洞的抽象概念。
3.有限与无限相互转化。
有限和无限之间不是对立的二元对立关系,
而是统一体中相互转化的关系。
有限可以渐进地接近无限,无限也可以通
过有限的表现形式来实现。
4.有限和无限是统一的辩证关系。
有限和无限虽然是两个不同的概念,但它们并不是孤立的,而是联系在一起的。
有限和无限是统一的辩证关系,是相互依存、相互贯通的。
在具体问题中,有限和无限需要相互协调、相
互补充,才能得到更加深入和全面的认识。
有限与无限的哲学

有限与无限的哲学有限与无限是哲学中一个重要的概念对立。
有限指的是有限制、有限度、有限量的事物,而无限则指的是无限制、无限度、无限量的事物。
这两个概念在哲学中有着广泛的应用,涉及到宇宙、时间、空间、思维等方面。
一、宇宙的有限与无限在宇宙的层面上,有限与无限的概念常常被用来讨论宇宙的大小和边界。
在古代,人们认为宇宙是有限的,因为他们认为宇宙是一个封闭的球体,没有边界。
但是,随着现代科学的发展,人们逐渐意识到宇宙是无限的,因为宇宙是不断膨胀的,没有边界。
二、时间的有限与无限在时间的层面上,有限与无限的概念常常被用来讨论时间的长度和结束。
在古代,人们认为时间是有限的,因为他们认为时间是一个循环的过程,没有终点。
但是,随着现代科学的发展,人们逐渐意识到时间是无限的,因为时间是不断流逝的,没有终点。
三、空间的有限与无限在空间的层面上,有限与无限的概念常常被用来讨论空间的大小和形态。
在古代,人们认为空间是有限的,因为他们认为空间是一个封闭的球体,没有边界。
但是,随着现代科学的发展,人们逐渐意识到空间是无限的,因为空间是不断膨胀的,没有边界。
四、思维的有限与无限在思维的层面上,有限与无限的概念常常被用来讨论人类的认知能力和思维能力。
在古代,人们认为人类的思维能力是有限的,因为人类只能认识到有限的事物。
但是,随着现代科学的发展,人们逐渐意识到人类的思维能力是无限的,因为人类可以不断地探索和发现新的事物。
总之,有限与无限是哲学中一个重要的概念对立,涉及到宇宙、时间、空间、思维等方面。
在不同的领域中,有限与无限的含义和应用也有所不同,但都是哲学思考的重要内容。
有限和无限的辩证关系

有限和无限的辩证关系1 有限和无限的概念在我们的生活中,有限和无限是两个非常普遍的概念。
有限可以指代数量或者时限,是有一定上限的;而无限则是没有限制的,可以延续到无穷无尽。
这两个概念在一些哲学和数学理论中也扮演着非常重要的角色。
2 有限和无限的辩证关系有限和无限之间的关系是辩证的。
一方面,有限的存在使得无限变得更加珍贵。
因为一些事物的存在是有时限限制的,所以我们必须更好地利用它们,以充分利用它们带来的好处。
例如,时间是有限的资源,我们需要更好地规划和运用时间,以达到事半功倍的效果。
相反地,如果我们没有时间的限制,那么我们可能会过分浪费时间。
另一方面,无限的存在则使得有限变得更加重要。
因为无限是不可达到的,我们必须好好珍惜我们所拥有的有限资源。
例如,我们的生命是有限的,我们必须好好把握机会,充分利用自己的时间和才能,以实现我们想要的目标。
3 数学中的有限和无限在数学中,有限和无限也是非常重要的概念。
数学上的无限是指数列或者数集的元素数目没有上限,例如自然数集、实数集等等;而有限是指数列或者数集的元素数目是有上限的。
有限和无限在数学理论中有非常深刻的辩证关系。
一方面,无限是有限的辩证对立面。
因为无限是没有上限的,因此无法直接计算或者描述,我们必须通过有限的数量进行逼近。
例如,我们无法直接计算圆周率的值,但是可以利用有限的数列对它进行逼近。
另一方面,无限也是有限的扩展和发展。
因为无限数列或者数集是没有上限的,因此可以不断地向外扩展,进一步发展。
例如,正整数集可以通过扩展到实数集来求解无理数的问题。
4 哲学中的有限和无限在哲学中,有限和无限的辩证关系也非常重要。
无限被认为是自由和无限制的,而有限则被认为是限制和束缚。
然而,哲学家们也认为有限和无限之间是相互依存的。
因为无限是无法到达的,所以它需要有限的存在作为基础。
相反地,有限的存在也需要无限的存在进行发展和扩展。
5 总结有限和无限是我们生活中和学术领域中都非常重要的概念。
有限与无限的哲学感悟

有限与无限的哲学感悟人类的思想始终在探索有限与无限之间的关系。
有限与无限,这两者似乎是对立的,但实际上它们又是相辅相成、不可分割的。
我们生活在一个物质世界中,许多事物是有限的,然而在思维的世界里,无限的可能性却无处不在。
通过对有限与无限的思考,我们不仅能够理解世界的本质,还能够深入认识自身的存在。
一、有限的世界与无尽的探索在生活中,我们身处一个有限的环境。
我们的时间、空间、资源都是有限的。
人的生命,一生只有短短几十年,这样的时间限制让我们每个人都感受到一种紧迫感。
因而,如何在有限的时间内追求无限的知识、体验和情感,成为一种无法回避的哲学命题。
在有限的生活中,我们可以通过学习、旅行和人际交往等方式来丰富自己的经历。
每一次探索,虽有其时间和空间的限制,却可以带来无数的感悟。
例如,我们在某一特定地点的旅行,虽是固定的行程,但体验和记忆却是无限的;在书籍中的每一次阅读,都是思想的升华和创新的开始。
二、有限与无限的辩证关系有限与无限之间的关系是辩证的。
有限是无限的前提,无限则让有限变得充实、精彩。
牛顿和爱因斯坦在物理学上的研究都在探索一种“有限”的范畴,而这些探索则是为了让我们更深入理解宇宙这一“无限”的现实。
正是有限的科学探索,才让我们得以接触、更好地理解那些通常被认为是无限的事物。
这种辩证关系也可以应用于人类的情感和精神层面。
人们在日常生活中追求的感情和幸福,都是有限的,但我们的情感体验和对幸福的渴望却是无限的。
正如尼采所说:“人类的极限在于希望和爱。
”在现世的有限境遇中,心灵的追求、思想的碰撞往往能让人触及那无尽的精神境界。
三、有限的选择与无限的可能在当今社会,尽管我们面临着众多选择,但每一项选择都是有限的。
比如在职业生涯中,我们可能只能选取一条职业道路,然而这条路上却充满了无尽的可能性。
有限的选择让我们感受到选择的重压,但正是无尽的可能性赋予了我们生活的意义和精彩。
此外,科技的发展也在不断扩展有限选择的可能性。
论述有限与无限的区别与联系

论述有限与无限的区别与联系有限与无限:物质世界固有的矛盾之一。
反映物质运动在时间和空间上辩证性质的一对哲学范畴。
物质是不灭的、无限的,并且处在永恒的绝对运动之中,物质及其运动的永恒性、无限性,也就是物质的存在形式即时间持续和空间广延的无限性。
物质的时空无限由具体的物质客体的有限时空所构成,并通过具体物质客体在有限时空上的运动和变化表现出来。
有限和无限的范畴,反映了物质世界中客观存在的矛盾和辩证联系。
有限集和无限集的辨证关系数学中的有限和无限是对现实世界的有限和无限的反映。
整个物质世界的发展变化就是有限和无限的统一无限性首先就是指物质世界的无限性,宇宙的无限性。
运动是物质的固有属性,时间和空间是物质的存在方式,物质世界的无限性就表现为时间的无限持续和空间的无限广延。
数学中的无限性就是这种物质世界无限性的反映。
有限则是说一切事物都存在具体的时间和空间之中,因此总是一段时间,有规模的、有界限的。
即一切事物都是具体的事物。
数学中的有限就反映了这种有限性。
有限和无限是对立的统一,它们既是对立的,有区别的,又是相互联系的。
并在一定条件下相互转化的。
数学中的无限和有限也反映了有限与无限相互转化这一点。
例如,整数集是一个无限集合,人们无法得到一个完成了的整数集。
但每个整数又都是有限的。
我们可以得到任意的整数。
任意给出一个数学的对象,我们立即就能判定它是否属于整数集,这样看问题,整数集又是一个完成了的集合,是一个有限的概念。
因此整数集本身就是一个无限和有限的对立统一体。
有限和无限是对立的、有区别的,有限集合和无限集合的性质有质的不同。
例如一个有限集和它的任何一个真子集都无法建立一一对立关系,而无限集则可以与它的一个真子集建立一一对应关系。
比如,自然数集和它的一个真子集偶自然数集就可以建立一一对应关系。
再如,一个有限的良序数集,自然数集的一个有限数集必然有最大数和最小数。
但是无限的良序数集则没有这种性质,实数集就没有最大数也没有最小数。
什么是有限责任与无限责任

什么是有限责任与无限责任有限责任与无限责任是两种不同的法律概念,用于描述不同类型的责任承担方式。
下面将详细介绍有限责任和无限责任的定义、特点和区别。
一、有限责任有限责任是指股东或者合伙人在公司或者合伙企业中对债务承担的责任有限。
具体来说,有限责任意味着股东或者合伙人的个人财产不会因为公司或者合伙企业的债务而受到伤害。
如果公司或者合伙企业发生债务违约或者破产,股东或者合伙人只需承担其投资额或者合伙份额的责任,不会承担超过其投资额或者合伙份额的责任。
有限责任的特点如下:1. 责任有限:股东或者合伙人的个人财产与公司或者合伙企业的财产是分开的,个人财产不会因为公司或者合伙企业的债务问题而受到伤害。
2. 分散风险:有限责任可以吸引更多的投资者参预企业,因为他们只需承担有限的风险,不必为企业的债务问题承担过多风险。
3. 便于转让:有限责任使得股东或者合伙人可以很方便地转让他们的股权或者合伙份额,从而实现投资的流动性。
二、无限责任无限责任是指股东或者合伙人在公司或者合伙企业中对债务承担的责任是无限的。
简而言之,无限责任意味着股东或者合伙人的个人财产可能因为公司或者合伙企业的债务问题而受到伤害。
如果公司或者合伙企业发生债务违约或者破产,股东或者合伙人不仅要承担其投资额或者合伙份额的责任,还可能要承担超过其投资额或者合伙份额的责任。
无限责任的特点如下:1. 责任无限:股东或者合伙人的个人财产与公司或者合伙企业的财产是连在一起的,个人财产可能因为公司或者合伙企业的债务问题而受到伤害。
2. 风险较高:无限责任对股东或者合伙人来说风险较高,因为他们需要承担公司或者合伙企业的全部债务责任。
3. 限制转让:无限责任使得股东或者合伙人很难转让他们的股权或者合伙份额,因为潜在的买家可能不愿意承担无限责任的风险。
三、有限责任与无限责任的区别1. 责任范围:有限责任仅限于股东或者合伙人的投资额或者合伙份额,而无限责任则没有限制,可能超过投资额或者合伙份额。
有限与无限存在着辩证关系

有限与无限存在着辩证关系有限与无限是自然界中的两个重要概念,它们之间存在着辩证关系,相互依存、相互转化、相互制约、相互推动。
有限是指数量、尺寸、范围等存在限制,而无限则是指没有限制,能够无限扩展、无限延伸。
在这种对立中,有限和无限又彼此贯通,互相跳跃。
首先,有限与无限是相互依存的。
有限的存在需要无限的构成,而无限的存在只能通过有限的表现来得到体现。
例如一个小小的物体,它只有有限的体积、面积和质量,但它受到无穷无尽的力量的支配。
反过来,一个无限的宇宙所包含的物质却是有限的,它所包含的空间、时间和能量都有限度。
其次,有限和无限之间存在相互转化的关系。
有限在一定条件下可以不断扩展,最终形成无限;而无限也可以被有限化。
例如,人类的技术不断进步,可以让有限的资源得到更高的利用效率,从而得到更大的产出,极大地扩展了有限资源的使用寿命。
另一方面,一个无限的事物,只要它受到限制,就会变成一个有限的事物。
例如,空气是无限的,但是在封闭的空间里,它的体积、成分、温度等都受到限制,变成了有限的物质。
第三,有限和无限之间存在相互制约的关系。
有限的事物缺乏无限的可能性,而无限的事物也无法真正实现,因为它们受到有限的环境和条件的限制。
例如,太阳系中每颗星球都受到各种各样的限制,它们的运动和生命周期都有其固有的局限性。
反过来讲,太阳系的运动轨迹和形成历程也受到整个宇宙的限制和影响。
最后,有限和无限之间还互相推动,相互发展。
有限的存在需要无限的存在推动,才能不断进化和发展;而无限的存在也需要有限的存在推动,才能得以体现和实现。
例如,在科技不断进步的今天,人类对自然界的认知和探索已经取得了很多先前无法想象的成果,同时这些成果又为人类提供了更多的发展空间和机遇。
在有限与无限之间,存在着复杂的相互作用和辩证关系。
它们之间的关系没有绝对的优劣之分,需要既看到有限的限制和无限的延伸,又同时关注它们之间的互动和推动,从而更好地认识和利用自然规律。
论述有限与无限的区别与联系

论述有限与无限的区别与联系有限与无限:物质世界固有的矛盾之一。
反映物质运动在时间和空间上辩证性质的一对哲学范畴。
物质是不灭的、无限的,并且处在永恒的绝对运动之中,物质及其运动的永恒性、无限性,也就是物质的存在形式即时间持续和空间广延的无限性。
物质的时空无限由具体的物质客体的有限时空所构成,并通过具体物质客体在有限时空上的运动和变化表现出来。
有限和无限的范畴,反映了物质世界中客观存在的矛盾和辩证联系。
有限集和无限集的辨证关系数学中的有限和无限是对现实世界的有限和无限的反映。
整个物质世界的发展变化就是有限和无限的统一无限性首先就是指物质世界的无限性,宇宙的无限性。
运动是物质的固有属性,时间和空间是物质的存在方式,物质世界的无限性就表现为时间的无限持续和空间的无限广延。
数学中的无限性就是这种物质世界无限性的反映。
有限则是说一切事物都存在具体的时间和空间之中,因此总是一段时间,有规模的、有界限的。
即一切事物都是具体的事物。
数学中的有限就反映了这种有限性。
有限和无限是对立的统一,它们既是对立的,有区别的,又是相互联系的。
并在一定条件下相互转化的。
数学中的无限和有限也反映了有限与无限相互转化这一点。
例如,整数集是一个无限集合,人们无法得到一个完成了的整数集。
但每个整数又都是有限的。
我们可以得到任意的整数。
任意给出一个数学的对象,我们立即就能判定它是否属于整数集,这样看问题,整数集又是一个完成了的集合,是一个有限的概念。
因此整数集本身就是一个无限和有限的对立统一体。
有限和无限是对立的、有区别的,有限集合和无限集合的性质有质的不同。
例如一个有限集和它的任何一个真子集都无法建立一一对立关系,而无限集则可以与它的一个真子集建立一一对应关系。
比如,自然数集和它的一个真子集偶自然数集就可以建立一一对应关系。
再如,一个有限的良序数集,自然数集的一个有限数集必然有最大数和最小数。
但是无限的良序数集则没有这种性质,实数集就没有最大数也没有最小数。
离散数学——有限集与无限集(课件)
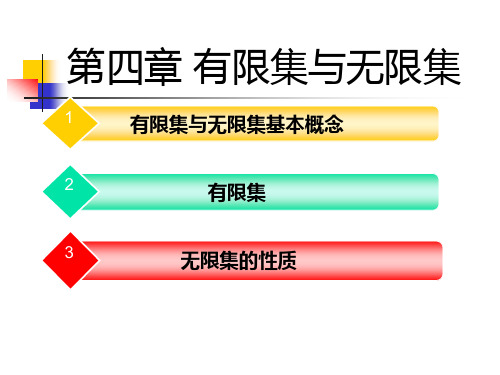
§4.3 无限集的性质
例4.5 自然数集 N={0,1,2,3……}与其子集S={1,3,5……}均为无限集,且N~S
N:0 1 2 3 … n … ↕ ↕ ↕↕ ↕ ↕↕
S: 1 3 5 7 … 2n+1…
此例说明了无限集的一个特性:一个无限集可以同它的一个 真子集等势 。
§4.3 无限集的性质
(2)集合大小的比较 ➢ 有限集大小的比较,用“相等”、“不相等” ➢ 无限集大小的比较,用“等势”、“不等势” 等势即为基数相同,由此立即可知:所有可列集的基
数均为א0。
(3)可列集是最小的无限集 没有比基数א0更小的无限集,但存在比基数א0更大的 无限集。如实数集。
§4.3 无限集的性质
构造一S内的实数r=0.b0b1b2…bn… 其中当aii≠1时,bi=1
当aii=1时,bi=2 因为b0≠a00,所以r ≠x0 因为b1≠a11,所以r ≠x1
… 因为总有一位不同,所以r ≠xi ,这与r S矛盾, 即(0,1)是不可列的。 2、证明S~R,即建立一一对应关系。设R中的元素为y,S中的元 素为x,因为S不可列,所以只能建立关系式:
∀x S,可表示为x=0.y1y2y3…(yi {0,1,…9}) 假设S是可列的,则它的元素可依次排列:x0,x1,x2,… 且我们有 x0=0.a00a01a02…a0n… x1=0.a10a11a12…a1n… … xm=0.am0am1am2…amn… … 只需证还能找到一个元素rS,但r不在x0,x1,x2,…中
§4.3 无限集的性质
证明: 1、构造无限集M的一真子集M' 。 先从M中任取一个元素m1,剩余部分为M-{m1}—无限集 再从M-{m1}中任取一元素m2,剩余部分为M-{m1,m2} … 继续下去,取出m3,m4,…,得到一个无限集合M1 M1={m1,m2 ,…,},令M2=M-M1(若M可列,M2为空)
有限与无限的辩证关系

有限与无限的辩证关系有限与无限是一对辩证关系,它们在世界的各个领域中都存在着。
无论是时间、空间、知识还是资源,都可以以有限和无限来描述。
这两个概念有时相互制约,有时又相互补充,给人们的思维带来了一定的挑战和启示。
在时间的维度上,有限与无限也存在着辩证关系。
时间是我们生命中最宝贵的资源之一,每个人都只有有限的时间来完成自己的事情。
然而,时间又是无限的,因为时间的流逝是永恒不变的。
我们可以合理利用有限的时间,做更多有意义的事情,并在有限的时间里追求无限的进步和成长。
在空间的维度上,有限与无限也相互作用。
地球上的资源是有限的,人类的生存和发展受到了地球资源的限制。
然而,宇宙是无限的,我们对宇宙的探索和认知是无穷无尽的。
通过科学技术的不断进步,我们可以不断拓展我们的认知边界,从有限的地球走向无限的宇宙。
在知识的维度上,有限与无限也有着辩证关系。
人类的知识是有限的,我们无法掌握所有的知识。
然而,知识的广度和深度是无限的,我们可以不断学习和探索,不断丰富自己的知识储备。
同时,知识的共享和传播也使得人类的知识得以无限传承和发展。
在资源的维度上,有限与无限也相互交织。
地球上的资源是有限的,我们必须合理利用和保护资源,以满足人类的需求。
然而,人类的创造力和创新能力是无限的,我们可以通过创新来解决资源的有限性问题,开发替代资源,实现资源的可持续利用。
有限与无限之间的辩证关系不仅存在于自然界,也存在于社会和人类的思维中。
在社会发展中,资源的分配是有限的,人们的需求是无限的。
因此,社会的公平和正义需要通过合理的制度和规则来实现。
在人类的思维中,有限与无限的辩证关系也常常引发哲学上的思考和争议。
人们对于有限与无限的思考与探索,推动了人类文明的进步和发展。
有限与无限是一对辩证关系,它们在时间、空间、知识和资源等方面相互作用。
我们应该在有限中追求无限,通过合理利用和创新来克服有限的局限,实现个人和社会的发展。
同时,我们也应该珍惜有限,保护资源,避免过度消耗。
什么是有限责任与无限责任

什么是有限责任与无限责任有限责任与无限责任是指在商业活动中,对于合伙企业或者公司的所有者或者成员所承担的责任范围的不同分类。
下面将详细介绍有限责任和无限责任的定义、特点和区别。
一、有限责任有限责任是指合伙企业或者公司的所有者或者成员对企业债务承担有限的责任。
具体来说,当企业面临债务违约、破产或者法律纠纷等情况时,有限责任的所有者或者成员只需承担其投资额或者股分的债务责任,不会因企业债务而被追究个人财产。
有限责任的特点:1. 风险分散:有限责任的所有者或者成员只需承担其投资额或者股分的债务责任,个人财产不受债务的影响,风险相对较小。
2. 企业独立性:有限责任企业在法律上被视为独立的法人实体,具有独立的财务和经营管理权力。
3. 资金筹集:由于有限责任的特点,投资者更愿意投资于有限责任企业,因为他们的个人财产不会受到企业债务的影响。
二、无限责任无限责任是指合伙企业或者公司的所有者或者成员对企业债务承担无限的责任。
简单来说,无限责任的所有者或者成员在企业面临债务违约、破产或者法律纠纷等情况时,个人财产可能被追究以偿还企业债务。
无限责任的特点:1. 个人财产风险:无限责任的所有者或者成员个人财产可能被用于偿还企业债务,风险较大。
2. 个人责任:无限责任的所有者或者成员对企业的债务负有直接的个人责任,无论是企业的成功还是失败,个人财产都可能受到影响。
3. 合伙责任:在合伙企业中,合伙人对企业的债务承担无限责任,即使是合伙企业中的一个合伙人违约,其他合伙人也要承担其债务责任。
三、有限责任与无限责任的区别1. 责任范围:有限责任的所有者或者成员对企业债务承担有限的责任,而无限责任的所有者或者成员对企业债务承担无限的责任。
2. 个人财产风险:有限责任的所有者或者成员个人财产不会受到企业债务的影响,而无限责任的所有者或者成员个人财产可能被用于偿还企业债务。
3. 风险分散:有限责任可以实现风险的分散,投资者只需承担其投资额或者股分的债务责任,而无限责任的所有者或者成员对企业债务负有直接的个人责任。
有限与无限思辨作文

有限与无限思辨作文
哎,咱们聊聊有限和无限吧,这可是个挺有意思的话题。
想象一下,你手里有颗糖果,那就是有限。
你可以看到它,摸
到它,甚至尝到它的甜味。
它就在那儿,不多也不少。
但要是说到
无限,那可就有点摸不着头脑了。
比如说,宇宙有多大?咱们能看
到的只是冰山一角,剩下的都是未知,那就是无限。
再来说说时间。
一天24小时,一小时60分钟,这就是有限。
但时间本身呢?它似乎没有起点,也没有终点,一直在那儿流淌,
好像永远不会停止,那就是无限。
咱们的人生也一样,每天都过得有头有尾,吃饭、睡觉、工作、学习,这些都是有限的。
但咱们追求的东西呢?爱情、梦想、成功,这些似乎永远都没有尽头,咱们总是想要更多,那就是无限。
说到数学,那就更有趣了。
有限和无限在数学里可是个大课题。
比如,有限集合就是你能数得过来的那些数字或者物品,而无限集
合呢?哎,那就像大海里的水滴,你永远也数不完。
其实啊,有限和无限就像是一对双胞胎,它们总是相互依存,
相互转化。
有时候你觉得某样东西是有限的,但换个角度看,它可
能就是无限的。
所以啊,咱们得学会用不同的眼光去看待这个世界,才能发现更多的奥秘。
有限与无限名言

有限与无限名言有限与无限名言有限是一种状态,无限是一种追求。
有限和无限的思想在人类的社会生活中很常见,这是人类智慧的结晶,也是人类文明的内涵。
以下是有限与无限名言:有限篇章:1. 世上没有绝对的无限,不过是看不穿而已。
2. 在有限的时间里追寻无限的价值,才是生命中最美丽的信仰。
3. 有限的生命中,留下无限的精神,才是真正的不灭。
4. 有限的东西,争也争不到无限的美好。
5. 有限是我们所处的境地,无限是我们人生的追求。
6. 知道有限,是不怕错过无限的美好。
7. 有限的时间里做无限的事情,每个人都可以做到,只是有没有这个信念而已。
8. 看透有限,品味无限,这是艺术的境界。
9. 有限可以是某种限制,也可以是某种契约。
10. 有限不一定是负面,有些时候它反而激发我们更大的创造力。
无限篇章:1. 无限不只是形式上的展示,更是精神的体现。
2. 追求无限就是追求自我超越。
3. 无限意味着永远有新的发现,新的可能。
4. 无限是人类文明的精神内核,是整个宇宙的追求。
5. 无限需要不断的拓展和探索,这是人类智慧的结晶。
6. 人们不断探索无限的可能,就是对生命的最深刻的理解。
7. 拥有无限的梦想,勇敢地去实现,方能让生命更加灿烂。
8. 求知与追求是人类生命中最高尚的追求,也是无限的奥义。
9. 无限是一种超验的精神存在,是人类生命意义的深刻理解。
10. 无限源于人类智慧,不断学习进取,才能实现内心对无限的追求。
以上是有限与无限名言,我们需要在有限的世界中拥有无限的视野和追求。
只有在这样的追求中,我们才能让有限的生命变得更加灿烂,更加有意义。
数学中的“有限与无限”的思想

数学中的“有限与无限”的思想一、知识概述1、有限与无限的思想就是将无限的问题化为有限来求解,将有限的问题化为无限来解决,利用已经掌握的无限问题的结论来解决新的无限问题.2、把对无限的研究转化为对有限的研究,是解决无限问题的必经之路.3、积累的解决无限问题的经验,将有限问题转化为无限问题来解决是解决有限问题的一个方向,同时有利于解决新的无限的问题.4、立体几何中求球的表面积与体积的推导,实际上是先进行有限次分割,然后再求和、求极限;数学归纳法就是通过对有限的研究来解决无限的问题等等,这些都是典型的有限与无限思想的应用.取极限和数学归纳法就是由有限与无限的思想得到的具体的方法.5、有限与无限的思想在近几年的高考中已经有很多具体的体现,随着高中课程改革,对新增内容的深入考查,必将加大对这一思想的考查,所以我们考前应该予以重视.二、典例分析1.在数列{}n a 在中,542n a n =-,212n a a a an bn ++=+L ,*n N ∈,其中,a b 为常数,则lim n n n nn a b a b →∞-+的值是 . 【解析】本题根据通项与前n 项和可以求出常数,a b 的值,再对所给的有限项求极限.这里我们要利用已经掌握的无限的结论(即lim 0(||1)nn q q →∞=∈)来解决新的极限问题.【答案】由542n a n =-知,{}n a 是公差为4的等差数列,故123(1)422n n n a a a n -++=+⋅L 2an bn =+,解得2a =,12b =-,从而11()1()4lim lim lim 111()1()4n n n nn n n n n n nb a b a b a b a →∞→∞→∞---===+++. 2. 已知数列{}n a 满足1a a =,111n na a +=+我们知道当a 取不同的值时,得到不同的数列,如当1a =时,得到无穷数列:;.,35,23,2,1K 当21-=a 时,得到有穷数列:0,1,21--. (Ⅰ)求当a 为何值时40a =; (Ⅱ)设数列{}n b 满足11b =-, 11()1n n n N b b ++=∈-,求证:a 取数列{}n b 中的任一个数,都可以得到一个有穷数列{}n a ;(Ⅲ)若)4(223≥<<n a n ,求a 的取值范围. 【解析】 这是一道蕴含有限与无限的思想的典型试题. 对于题设的递推关系,随着所给出的初始条件不同,得到的数列既可能是无限数列也可能是有限的数列,第(Ⅱ)问则可以通过有有限次的试验,得出对无限个n b 都可以得到一个有穷数列{a n }的猜想,再用数学归纳法进行证明.或者通过对有限问题的推理直接得到无限问题的解答.第(Ⅲ)问是把对无限个n 都成立的结果,通过有限次分析获得解决.【答案】(Ⅰ)11211111,1,11,n n a a a a a a a a a++==+∴=+=+=Q34231211321,1.121a a a a a a a a ++=+==+=++ 420.3a a =-=故当时 (Ⅱ) 解法一:11-=b Θ,11,1111+=-=++n n n n b b b b , 当1b a =时,01112=+=b a , 当2b a =时,111112-==+=b b a ,03=∴a , 当3b a =时,23211b b a =+=,111111223-==+=+=∴b b a a 04=∴a . 一般地, 当n b a =时,,01=+n a 可得一个含有1+n 项的有穷数列121,.,+n a a a Λ. 下面用数学归纳法证明.当1=n 时, 1b a =,显然01112=+=b a ,可得一个含有2项的有穷数列.,21a a 假设当k n =时,k b a =,得到一个含有1+k 项的有穷数列121,.,+k a a a Λ,其中01=+k a ,则1+=k n 时,1+=k b a ,k k b b a =+=∴+1211,由假设可知, 得到一个含有1+k 项的有穷数列232,,,+k a a a Λ,其中02=+k a .所以,当1+=k n 时, 可以得到一个含有2+k 项的有穷数列1a ,232,,,+k a a a Λ,其中02=+k a 由(1),(2)知,对一切+∈N n ,命题都成立. 解法二:11111,, 1.1n n n n b b b b b b ++=-=∴=+-Q 21132211112{}.11,11,1111,...1111 1.0.n n n n nn n n n n a b a b a b a b a b a b a b a b a a b ---+-==∴=+=+=∴=+=+=∴=+=+==-∴=Q 取数列中的任一个数不妨设故a 取数列{}n b 中的任一个数,都可以得到一个有穷数列{}n a .(Ⅲ))4(223≥<<n a n 即211231<+<-n a ,211<<∴-n a 所以要使)4(223≥<<n a n ,当且仅当它的前一项1-n a 满足211<<-n a .由于()2,12,23⊆⎪⎭⎫ ⎝⎛,所以只须当⎪⎭⎫ ⎝⎛∈2,23k a 时,都有⎪⎭⎫⎝⎛∈2,23n a ()5≥n由12234++=a a a ,得2122323<++<a a , 解得0>a .3.在数列||n a ,||n b 中,a 1=2,b 1=4,且1n n n a b a +,,成等差数列,11n n n b a b ++,,成等比数列(n ∈*N ).(Ⅰ)求a 2,a 3,a 4及b 2,b 3,b 4,由此猜测||n a ,||n b 的通项公式,并证明你的结论; (Ⅱ)证明:1122111512n n a b a b a b +++<+++…. 【解析】第(Ⅰ)问由题设可得两个数列的递推关系式,进而得到两个数列的前几项(有限项) ,可以猜出两者的通项公式(无限的问题),再用数学归纳法证明这个无限的问题.第(Ⅱ)问可以通过研究通项公式(无限的问题)直接解决无限的问题.【答案】(Ⅰ)由条件得21112n n n n n n b a a a b b +++=+=,,由此可得2233446912162025a b a b a b ======,,,,,.猜测2(1)(1)n n a n n b n =+=+,.下面用数学归纳法证明:①当n=1时,由上可得结论成立.②假设当n=k 时,结论成立,即2(1)(1)k k a k k b k =+=+,,那么当n=k+1时,22221122(1)(1)(1)(2)(2)kk k k k ka ab a k k k k k b k b +++=-=+-+=++==+,,所以当n=k+1时,结论也成立.由①②,可知2(1)(1)n n a n n b n =++,对一切正整数都成立.(Ⅱ)11115612a b =<+.n ≥2时,由(Ⅰ)知(1)(21)2(1)n n a b n n n n +=++>+.故112211111111622334(1)n n a b a b a b n n ⎛⎫+++<++++ ⎪+++⨯⨯+⎝⎭...... 111111116223341n n ⎛⎫=+-+-++- ⎪+⎝⎭ (111111562216412)n ⎛⎫=+-<+= ⎪+⎝⎭. 综上,原不等式成立. 三、名校试题1.数列{}n a 中,11a =,2112n n n a a a c +=-+ (1c >为常数,1,2,3,...n =) ,且321.8a a -=(1)求c 的值;(2)① 证明:1n na a +<;② 猜测数列{}n a 是否有极限?如果有,写出极限的值(不必证明); (3)比较11nk ka =∑与14039n a +的大小,并加以证明. 【解析】第(1)问由通项公式(揭示无限问题)求出有限项23a a 、后可得c 的值;第(2)问通过对有限项的处理证明出结论,从而可猜出{}n a 的极限;第(3)问对得到的递推关系式进行变形,再用作差法求解,需要用到数学归纳法证得2n a <.然后通过前几项(有限项)的比较与第(2)问已证的单调性得到结果.【答案】(Ⅰ)依题意,222211322111111.222222a a a c c a a a c c ⎛⎫=-+=-=-+=-+ ⎪⎝⎭, 由3218a a -=,得21111122228c c ⎛⎫⎛⎫-+--= ⎪ ⎪⎝⎭⎝⎭,解得2c =,或1c =(舍去).(Ⅱ)① 证明:因为2211122(2)022n n n n n a a a a a +-=-+=-≥,当且仅当2n a =时,1n n a a +=.因为11a =,所以10n n a a +->,即1n n a a +< (1,2,3,...n =).② 数列{}n a 有极限,且 lim 2n n a →∞=.(Ⅲ)由21122n n n a a a +=-+,可得11()(2)(2)n n n n n a a a a a ++-=--,从而111122n n n a a a +=---. 因为11a =,所以 111111111111 1.22222nnk k k k k n n a a a a a a ==+++⎛⎫=-=-=- ⎪-----⎝⎭∑∑所以21111111111404139(53)(813)1401401.3923939(2)39(2)nn n n n n n k k n n n a a a a a a a a a a ++++++=+++--+--=--==-⋅-⋅-∑因为11a =,由(Ⅱ)① 得 1n a ≥ (*n ∈N ). (*)下面用数学归纳法证明:对于任意*n ∈N ,有2n a <成立.当1n =时,由11a =,显然结论成立. 假设结论对 (1)n k k =≥时成立,即 2.k a < 因为2211132(1)222n n n n a a a a +=-+=-+,且函数213(1)22y x =-+在1x ≥时单调递增, 所以2113(21)222k a +<-+=.即当1n k =+时,结论也成立. 于是,当*n ∈N 时,有2n a <成立. (**) 根据(*)及(**)得 12n a ≤<.由11a = 及21122n n n a a a +=-+, 经计算可得23313.28a a ==,所以,当1n =时,2114039a a <;当2n =时,312114039a a a +=; 当3n ≥时,由11328n a +<<,得11111(53)(813)1400 , 3939(2)nn n n k kn a a a a a +++=++--=>⋅-∑ 所以1114039nn k ka a+=>∑. 2.数列{}n a 的首项1a =1,前n 项和为n S 满足12(1)n n k S a +=-(常数0k >,*N n ∈).(1)求证:数列{}n a 是等比数列.(2)设数列{}n a 的公比为()f k ,作数列{}n b ,使13b =,11()n n b f b -=(n =2,3,4,…) 求数列{}n b 的通项公式;(3)设2n n c b =-,若存在*N m ∈,且m n <;使lim n →∞(112m m m m c c c c +++++…1n n c c ++)1<2007,试求m 的最小值.【解析】第(1)问通过对递推关系式的变形得到相邻两项的比,正是利用这两个有限项的比是非零常数来证明该数列是等比数列的.第(2)问也是通过对递推关系式(无限的问题)的变形来求通项公式的(无限的问题).第(3)问通过抓住通项来求有限项的极限,再根据这个极限求出m 的最小值.【答案】 解:(1)12(1)n n k S a +=- ①当2n ≥时, 12(1)n n k S a -=-②①—②得,12()n n n a k a a +=-即121n n ka k a +=+(2)由①, 1112a k =+,∴1211122n na k k k a ++==+,又21112a a k =+符合上式,∴{}n a 是以1为首项,112k+为公比的等比数列. (2)由(1)知()f k =112k+,∴1111()12n n n b f b b --==+(2n ≥), ∴112(2)2n n b b --=-.又13b =,即121b -=,1122n n b b -=-, ∴数列{}2n b -是为1首项,12为公比的等比数列. ∴112()2n n b --=,∴112()2n n b -=+.(3)由(2)知112()2n n n c b -=-=,则2111()2n n n c c -+⋅=.∴112lim(m m m m n c c c c +++→∞++…1n n c c ++)=111111lim ...222m m n -+-→∞⎡⎤+++⎢⎥⎣⎦222n ()()() =1111141122lim 132200714m m n --→∞-=<-22n+2()()(), ∴3112669m -<2(),∴9669m ->22. ∵5126691024<<,∴2310m -≥, 6.5m ≥. 又∵*N m ∈,∴m 的最小值为7.四、考点预测(一)考点预测根据近几年各地高考试题和模拟试题来看,有限与无限的思想逐年增加考查广度,我们认为2009年的高考一定会有更多的体现.在题型上来看,热点问题仍然是以数列为载体考查极限的知识和用数学归纳法证题.(二)考点预测题1.设等差数列{}n a 的公差d 是2,前n 项的和为n S ,则22lim n n na n S →∞-= .【解析】本题设出首项,表示出通项和前n 和(有限项),然后代入求极限.而在求极限的时候,利用到已经掌握的极限知识lim 0n a n →∞=和2lim 0n an→∞=,其中a 为常数.【答案】设首项为1a ,则112(1)21n n n a a a =+-=+-,1(1)22n n n n S a -=+⨯ 21(1)n n a =+-,2222111112222(21)34(1)(1)lim lim lim (1)(1)nn n n n n n n n a n S n n n n a a a a a →∞→∞→∞+--+-+--∴==+-+- 111224(1)(1)3lim3(1)1n n n na a a →∞--++=-+.2.将数列{}n a 中的所有项按每一行比上一行多一项的规则排成如下数表:1a2a 3a 4a 5a 6a 7a 8a 9a 10a......记表中的第一列数1247,...a a a a ,,,构成的数列为{}n b ,111b a ==.n S 为数列{}n b 的前n 项和,且满足221(2)nn n nb n b S S =-≥. (Ⅰ)证明数列1n S ⎧⎫⎨⎬⎩⎭成等差数列,并求数列{}n b 的通项公式; (Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当81491a =-时,求上表中第(3)k k ≥行所有项的和. 【解析】第(Ⅰ)问从无穷数列{}n a 中抽出它的一个无穷的子数列,由n S 与n b 的递推关系式消去n b ,从而证明1n S ⎧⎫⎨⎬⎩⎭是无穷的等差数列. 第(Ⅱ)问就是求从第三行起的每一行所有的这些无穷多项的和. 【答案】(Ⅰ)证明:由已知,当2n ≥时,221nn n nb b S S =-, 又12n n S b b b =+++L ,所以1212()1()n n n n n nS S S S S S ---=--, 即112()1n n n n S S S S ---=-,所以11112n n S S --=, 又1111S b a ===.所以数列1n S ⎧⎫⎨⎬⎩⎭是首项为1,公差为12的等差数列.由上可知1111(1)22n n n S +=+-=,即21n S n =+. 所以当2n ≥时,12221(1)n n n b S S n n n n -=-=-=-++. 因此1122(1)n n b n n n =⎧⎪=⎨-⎪+⎩, ,,.≥ (Ⅱ)解:设上表中从第三行起,每行的公比都为q ,且0q >.因为12131212782⨯+++==L ,所以表中第1行至第12行共含有数列{}n a 的前78项, 故81a 在表中第13行第三列,因此28113491a b q ==-g .又1321314b =-⨯,所以2q =.记表中第(3)k k≥行所有项的和为S,则(1)2(12)2(12)(3)1(1)12(1)k kk kb qS kq k k k k--==-=--+-+g≥。
有限和无限

有限与无限存在着辩证关系:有限和无限是物质世界中存在的客观予盾,是物质的运动在时间和空间上表现出来的辩证联系。
因此,有限和无限的关系是辩证的,是对立的统一。
具体表现在:①无限由有限构成、无限不能脱离有限而独立存在。
物质世界就其整体说,它在时间和空间上都是无限的,但它却是由无数具体物质客体的有限时间和空间构成的。
物质的时空无限性并不是抽象的、同有限相分离的,而总是和具体物质客体的时空有限性相联结;有限并不存在于无限之外,它是构成无限的环节、部分和因素。
没有具体物质客体的时空有限性,物质世界的无限性也就不存在。
②有限包含着无限,有限体现着无限。
有限事物的发展变化、它们生生灭灭的无穷链条,本身就是物质无限性的表现形式。
任何具体的、确定的事物在时间和空间上都有自己的界限,但由于事物运动、变化和发展的本性,有限的界限必然不断被打破、被否定而趋于无限。
有限事物原有界限的打破、事物由一种质态向另一种质态的转化,就体现着物质的变化和发展的无限趋势。
这种无限的趋势并不存在于有限之外,而是包含在有限之中并通过有限形式表现出来。
因此,同有限不能脱离无限一样,无限也不能脱离有限。
③有限和无限的辩证统一,表现在任何一个物质客体中。
在一定意义上说,每一物质客体既是有限的又是无限的,是有限和无限的统一。
每一物质客体总是存在于一定的时间和空间界限之内,这是它的有限性。
但是它又有着变化和发展的无限能力,有着内部和外部无数联系以及不可穷尽的特性和结构层次,这又是它的无限性。
在这个意义上,可以说,每一有限的物质客体都是一个无限的宇宙,是有限和无限的统一绝对与相对马克思主义哲学认为,世界上一切事物既包含有相对的方面,又包含有绝对的方面,任何事物都既是绝对的,又是相对的。
宇宙中的各个具体事物和每个具体过程都是有条件的、有限的、相对的,而整个宇宙的存在和发展又是无条件的、无限的、绝对的。
绝对和相对,有限和无限等于同一个世界的部分、阶段。
绝对和相对的关系,是辩证的统一。
有限与无限

1、有限与无限有限和无限是辩证法的一对范畴,数学家希尔伯特说:“数学是研究无穷的科学。
无穷是一个永恒的谜,没有任何问题可以像无穷那样深深的触动人的情感, 很少有别的观念能像无穷那样激励理智产生富有成果的思想, 然而也没有任何其他的概念能向无穷那样需要加以阐明。
”,Einstein讲:“有限与无限的问题是数学中最有趣而又最复杂的问题。
”有限是指与其他事物相对,因而受其他事物影响或规定,即有条件的东西;无限是指不与任何其他事物相对,因而也不受任何其他事物影响或规定的东西。
对于有限和无限不能仅从数量方面来理解。
有限的东西固然有其确定的数量规定,但这只是有限性的表现形式之一;它所固有的质,才决定了它是它自身而不是他物,同时也就构成对它自身和对他物的一种限制。
无限作为对有限的超越或否定,实质上是对一切质的和量的规定及其关系不断扬弃的过程。
这种绝对的认识有一个重大的障碍。
正如可认识的物质的无限性,是由纯粹有限的东西所组成一样,绝对地进行认识的思维的无限性,是由无限多的有限的人脑所组成的,而人脑是一个挨一个地和一个跟一个地从事这种无限的认识,常做实践上的和理论上的蠢事,从歪曲的、片面的、错误的前提出发,循着错误的、弯曲的、不可靠的途径行进,往往当真理碰到鼻尖上的时候还是没有得到真理(普利斯特利)。
在数学的学习和研究中,几乎在每一个部分,都有无限性的问题。
数学研究所问题中所涉及到的量,总要有有限和无限的情况。
时空的无限性和人类的有限性的矛盾,是人类认识宇宙的最大的问题,是一个不易逾越的难题。
人类生活在无限宇宙中极为细小的一个角落,若把地球看着宇宙的一粒尘埃,那么生活在地球表面的人类的活动空间有多么的渺小不言而喻。
人类生活在无限宇宙无始无终时间长河中的一个极短的瞬间,而每个个体的生存时间就更短了;人类的个体是认识宇宙的主体,除了艰难的维持生存的劳作外,可供认识宇宙的时间就寥寥无几了!人类生存的时空局限,规定了人类的有限性,限制了人类对无限宇宙的认识活动,使人类不能直接接触和观察一些必须了解研究的客观对象,造成众多人类直接观察无法达到的死角,给人类的认识带来了一些盲区和空白。
有限数和无限数的概念

有限数和无限数的概念有限数和无限数是数学中的重要概念。
在数学中,数可以分为有限数和无限数两种。
有限数是指可以被计数且数量有限的数,而无限数则是指数量无限的数。
有限数的特点有限数有以下几个特点:1. 可以被计数:有限数是可以被计数的,因为它们的数量是有限的。
例如,我们可以数到10,这是一个有限数。
2. 数量有限:有限数的数量是有限的,即它们不会无限增长。
无论有限数的大小如何,它们的数量总是有限的。
3. 可以进行基本运算:有限数可以进行加法、减法、乘法和除法等基本运算。
我们可以对有限数进行各种数学操作。
无限数的特点无限数具有以下几个特点:1. 数量无限:无限数的数量是无限的,即它们没有终止点。
例如,正整数的数量是无限的,没有最大的正整数。
2. 不能被计数:无限数不能被计数,因为它们的数量是无限的。
我们无法精确地数到无限数的数量。
3. 无法进行准确的计算:由于无限数的数量是无限的,因此无法进行准确的计算。
我们无法通过简单的运算得到准确的结果。
有限数和无限数的应用有限数和无限数在数学和现实生活中都有重要的应用。
在数学中,有限数和无限数是研究其他数学概念和理论的基础。
例如,在微积分中,我们使用无限数的概念来研究极限和导数等概念。
在现实生活中,有限数和无限数的应用广泛。
例如,在金融领域,我们使用有限数进行投资和计算利息。
而在物理学中,我们使用无限数来描述连续变化和无限小量的概念。
结论有限数和无限数是数学中重要的概念。
它们具有不同的特点和应用,对于我们理解数学和应用数学知识都具有重要意义。
了解有限数和无限数的概念有助于我们深入理解数学的本质和应用领域。
参考文献:。
数学中的“有限与无限”的思想

数学中的“有限与无限”的思想一、知识概述1、有限与无限的思想就是将无限的问题化为有限来求解,将有限的问题化为无限来解决,利用已经掌握的无限问题的结论来解决新的无限问题.2、把对无限的研究转化为对有限的研究,是解决无限问题的必经之路.3、积累的解决无限问题的经验,将有限问题转化为无限问题来解决是解决有限问题的一个方向,同时有利于解决新的无限的问题.4、立体几何中求球的表面积与体积的推导,实际上是先进行有限次分割,然后再求和、求 极限;数学归纳法就是通过对有限的研究来解决无限的问题等等,这些都是典型的有限与无限思想的应用.取极限和数学归纳法就是由有限与无限的思想得到的具体的方法.5、有限与无限的思想在近几年的高考中已经有很多具体的体现,随着高中课程改革,对新增内容的深入考查,必将加大对这一思想的考查,所以我们考前应该予以重视.二、典例分析1.在数列{}n a 在中,542n a n =-,212n a a a an bn ++=+,*n N ∈,其中,a b 为常数,则lim n n n nn a b a b →∞-+的值是 . 【解析】本题根据通项与前n 项和可以求出常数,a b 的值,再对所给的有限项求极限.这里我们要利用已经掌握的无限的结论(即lim 0(||1)nn q q →∞=∈)来解决新的极限问题.【答案】由542n a n =-知,{}n a 是公差为4的等差数列,故123(1)422n n n a a a n -++=+⋅ 2an bn =+,解得2a =,12b =-,从而11()1()4lim lim lim 111()1()4n n n nn n n n n n nb a b a b a b a →∞→∞→∞---===+++. 2. 已知数列{}n a 满足1a a =,111n na a +=+我们知道当a 取不同的值时,得到不同的数列,如当1a =时,得到无穷数列:;.,35,23,2,1 当21-=a 时,得到有穷数列:0,1,21--. (Ⅰ)求当a 为何值时40a =;(Ⅱ)设数列{}n b 满足11b =-, 11()1n n n N b b ++=∈-,求证:a 取数列{}n b 中的任一个数,都可以得到一个有穷数列{}n a ;(Ⅲ)若)4(223≥<<n a n ,求a 的取值范围. 【解析】 这是一道蕴含有限与无限的思想的典型试题. 对于题设的递推关系,随着所给出的初始条件不同,得到的数列既可能是无限数列也可能是有限的数列,第(Ⅱ)问则可以通过有有限次的试验,得出对无限个n b 都可以得到一个有穷数列{a n }的猜想,再用数学归纳法进行证明.或者通过对有限问题的推理直接得到无限问题的解答.第(Ⅲ)问是把对无限个n 都成立的结果,通过有限次分析获得解决.【答案】(Ⅰ)11211111,1,11,n n a a a a a a a a a++==+∴=+=+=34231211321,1.121a a a a a a a a ++=+==+=++ 420.3a a =-=故当时 (Ⅱ) 解法一:11-=b ,11,1111+=-=++n n n n b b b b , 当1b a =时,01112=+=b a , 当2b a =时,111112-==+=b b a ,03=∴a , 当3b a =时,23211b b a =+=,111111223-==+=+=∴b b a a 04=∴a . 一般地, 当n b a =时,,01=+n a 可得一个含有1+n 项的有穷数列121,.,+n a a a . 下面用数学归纳法证明.当1=n 时, 1b a =,显然01112=+=b a ,可得一个含有2项的有穷数列.,21a a 假设当k n =时,k b a =,得到一个含有1+k 项的有穷数列121,.,+k a a a ,其中01=+k a ,则1+=k n 时,1+=k b a ,k k b b a =+=∴+1211,由假设可知, 得到一个含有1+k 项的有穷数列232,,,+k a a a ,其中02=+k a .所以,当1+=k n 时, 可以得到一个含有2+k 项的有穷数列1a ,232,,,+k a a a ,其中02=+k a 由(1),(2)知,对一切+∈N n ,命题都成立. 解法二:11111,, 1.1n n n n b b b b b b ++=-=∴=+- 21132211112{}.11,11,1111,...1111 1.0.n n n n nn n n n n a b a b a b a b a b a b a b a b a a b ---+-==∴=+=+=∴=+=+=∴=+=+==-∴=取数列中的任一个数不妨设故a 取数列{}n b 中的任一个数,都可以得到一个有穷数列{}n a .(Ⅲ))4(223≥<<n a n 即211231<+<-n a ,211<<∴-n a 所以要使)4(223≥<<n a n ,当且仅当它的前一项1-n a 满足211<<-n a .由于()2,12,23⊆⎪⎭⎫ ⎝⎛,所以只须当⎪⎭⎫ ⎝⎛∈2,23k a 时,都有⎪⎭⎫⎝⎛∈2,23n a ()5≥n由12234++=a a a ,得2122323<++<a a , 解得0>a . 3.在数列||n a ,||nb 中,a 1=2,b 1=4,且1n n n a b a +,,成等差数列,11n n n b a b ++,,成等比数列(n ∈*N ).(Ⅰ)求a 2,a 3,a 4及b 2,b 3,b 4,由此猜测||n a ,||n b 的通项公式,并证明你的结论;(Ⅱ)证明:1122111512n n a b a b a b +++<+++…. 【解析】第(Ⅰ)问由题设可得两个数列的递推关系式,进而得到两个数列的前几项(有限项) ,可以猜出两者的通项公式(无限的问题),再用数学归纳法证明这个无限的问题.第(Ⅱ)问可以通过研究通项公式(无限的问题)直接解决无限的问题.【答案】(Ⅰ)由条件得21112n n n n n n b a a a b b +++=+=,,由此可得2233446912162025a b a b a b ======,,,,,.猜测2(1)(1)n n a n n b n =+=+,.下面用数学归纳法证明:①当n=1时,由上可得结论成立.②假设当n=k 时,结论成立,即2(1)(1)k k a k k b k =+=+,,那么当n=k+1时,22221122(1)(1)(1)(2)(2)kk k k k ka ab a k k k k k b k b +++=-=+-+=++==+,,所以当n=k+1时,结论也成立.由①②,可知2(1)(1)n n a n n b n =++,对一切正整数都成立.(Ⅱ)11115612a b =<+.n ≥2时,由(Ⅰ)知(1)(21)2(1)n n a b n n n n +=++>+.故112211111111622334(1)n n a b a b a b n n ⎛⎫+++<++++ ⎪+++⨯⨯+⎝⎭...... 111111116223341n n ⎛⎫=+-+-++- ⎪+⎝⎭ (111111562216412)n ⎛⎫=+-<+= ⎪+⎝⎭. 综上,原不等式成立. 三、名校试题1.数列{}n a 中,11a =,2112n n n a a a c +=-+ (1c >为常数,1,2,3,...n =) ,且321.8a a -=(1)求c 的值;(2)① 证明:1n na a +<;② 猜测数列{}n a 是否有极限?如果有,写出极限的值(不必证明); (3)比较11nk ka =∑与14039n a +的大小,并加以证明. 【解析】第(1)问由通项公式(揭示无限问题)求出有限项23a a 、后可得c 的值;第(2)问通过对有限项的处理证明出结论,从而可猜出{}n a 的极限;第(3)问对得到的递推关系式进行变形,再用作差法求解,需要用到数学归纳法证得2n a <.然后通过前几项(有限项)的比较与第(2)问已证的单调性得到结果.【答案】(Ⅰ)依题意,222211322111111.222222a a a c c a a a c c ⎛⎫=-+=-=-+=-+ ⎪⎝⎭, 由3218a a -=,得21111122228c c ⎛⎫⎛⎫-+--= ⎪ ⎪⎝⎭⎝⎭,解得2c =,或1c =(舍去).(Ⅱ)① 证明:因为2211122(2)022n n n n n a a a a a +-=-+=-≥,当且仅当2n a =时,1n n a a +=.因为11a =,所以10n n a a +->,即1n n a a +< (1,2,3,...n =).② 数列{}n a 有极限,且 lim 2n n a →∞=.(Ⅲ)由21122n n n a a a +=-+,可得11()(2)(2)n n n n n a a a a a ++-=--,从而111122n n n a a a +=---. 因为11a =,所以 1111111111111.22222nnk k k k k n n a a a a a a ==+++⎛⎫=-=-=- ⎪-----⎝⎭∑∑ 所以21111111111404139(53)(813)1401401.3923939(2)39(2)nn n n n n n k k n n n a a a a a a a a a a ++++++=+++--+--=--==-⋅-⋅-∑因为11a =,由(Ⅱ)① 得 1n a ≥ (*n ∈N ). (*)下面用数学归纳法证明:对于任意*n ∈N ,有2n a <成立.当1n =时,由11a =,显然结论成立. 假设结论对 (1)n k k =≥时成立,即 2.k a < 因为2211132(1)222n n n n a a a a +=-+=-+,且函数213(1)22y x =-+在1x ≥时单调递增, 所以2113(21)222k a +<-+=.即当1n k =+时,结论也成立. 于是,当*n ∈N 时,有2n a <成立. (**)根据(*)及(**)得 12n a ≤<.由11a = 及21122n n n a a a +=-+, 经计算可得23313.28a a ==, 所以,当1n =时,2114039a a <;当2n =时,312114039a a a +=; 当3n ≥时,由11328n a +<<,得11111(53)(813)1400 , 3939(2)nn n n k kn a a a a a +++=++--=>⋅-∑ 所以1114039nn k ka a +=>∑. 2.数列{}n a 的首项1a =1,前n 项和为n S 满足12(1)n n k S a +=-(常数0k >,*N n ∈).(1)求证:数列{}n a 是等比数列.(2)设数列{}n a 的公比为()f k ,作数列{}n b ,使13b =,11()n n b f b -=(n =2,3,4,…) 求数列{}n b 的通项公式;(3)设2n n c b =-,若存在*N m ∈,且m n <;使lim n →∞(112m m m m c c c c +++++…1n n c c ++)1<2007,试求m 的最小值.【解析】第(1)问通过对递推关系式的变形得到相邻两项的比,正是利用这两个有限项的比是非零常数来证明该数列是等比数列的.第(2)问也是通过对递推关系式(无限的问题)的变形来求通项公式的(无限的问题).第(3)问通过抓住通项来求有限项的极限,再根据这个极限求出m 的最小值.【答案】 解:(1)12(1)n n k S a +=- ①当2n ≥时, 12(1)n n k S a -=-②①—②得,12()n n n a k a a +=-即121n n ka k a +=+(2)由①, 1112a k =+,∴1211122n na k k k a ++==+, 又21112a a k =+符合上式,∴{}n a 是以1为首项,112k+为公比的等比数列. (2)由(1)知()f k =112k+,∴1111()12n n n b f b b --==+(2n ≥), ∴112(2)2n n b b --=-.又13b =,即121b -=,1122n n b b -=-, ∴数列{}2n b -是为1首项,12为公比的等比数列. ∴112()2n n b --=,∴112()2n n b -=+.(3)由(2)知112()2n n n c b -=-=,则2111()2n n n c c -+⋅=.∴112lim(m m m m n c c c c +++→∞++…1n n c c ++)=111111lim ...222m m n -+-→∞⎡⎤+++⎢⎥⎣⎦222n ()()() =1111141122lim 132200714m m n --→∞-=<-22n+2()()(), ∴3112669m -<2(),∴9669m ->22. ∵5126691024<<,∴2310m -≥, 6.5m ≥. 又∵*N m ∈,∴m 的最小值为7.四、考点预测(一)考点预测根据近几年各地高考试题和模拟试题来看,有限与无限的思想逐年增加考查广度,我们认为2009年的高考一定会有更多的体现.在题型上来看,热点问题仍然是以数列为载体考查极限的知识和用数学归纳法证题.(二)考点预测题1.设等差数列{}n a 的公差d 是2,前n 项的和为n S ,则22lim n n na n S →∞-= .【解析】本题设出首项,表示出通项和前n 和(有限项),然后代入求极限.而在求极限的时候,利用到已经掌握的极限知识lim 0n a n →∞=和2lim 0n an→∞=,其中a 为常数.【答案】设首项为1a ,则112(1)21n n n a a a =+-=+-,1(1)22n n n n S a -=+⨯21(1)n n a =+-,2222111112222(21)34(1)(1)lim lim lim (1)(1)n n n n n n n n n a n S n n n n a a a a a →∞→∞→∞+--+-+--∴==+-+- 111224(1)(1)3lim3(1)1n nn na a a →∞--++=-+.2.将数列{}n a 中的所有项按每一行比上一行多一项的规则排成如下数表:1a2a 3a 4a 5a 6a 7a 8a 9a 10a......记表中的第一列数1247,...a a a a ,,,构成的数列为{}n b ,111b a ==.n S 为数列{}n b 的前n 项和,且满足221(2)nn n nb n b S S =-≥. (Ⅰ)证明数列1n S ⎧⎫⎨⎬⎩⎭成等差数列,并求数列{}n b 的通项公式; (Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当81491a =-时,求上表中第(3)k k ≥行所有项的和. 【解析】第(Ⅰ)问从无穷数列{}n a 中抽出它的一个无穷的子数列,由n S 与n b 的递推关系式消去n b ,从而证明1n S ⎧⎫⎨⎬⎩⎭是无穷的等差数列. 第(Ⅱ)问就是求从第三行起的每一行所有的这些无穷多项的和. 【答案】(Ⅰ)证明:由已知,当2n ≥时,221nn n nb b S S =-, 又12n n S b b b =+++,所以1212()1()n n n n n nS S S S S S ---=--, 即112()1n n n n S S S S ---=-,所以11112n n S S --=, 又1111S b a ===.所以数列1n S ⎧⎫⎨⎬⎩⎭是首项为1,公差为12的等差数列. 由上可知1111(1)22n n n S +=+-=,即21n S n =+. 所以当2n ≥时,12221(1)n n n b S S n n n n -=-=-=-++.因此1122(1)n n b n n n =⎧⎪=⎨-⎪+⎩, ,,.≥ (Ⅱ)解:设上表中从第三行起,每行的公比都为q ,且0q >.因为12131212782⨯+++==,所以表中第1行至第12行共含有数列{}n a 的前78项, 故81a 在表中第13行第三列,因此28113491a b q ==-.又1321314b =-⨯,所以2q =.记表中第(3)k k ≥行所有项的和为S ,则(1)2(12)2(12)(3)1(1)12(1)k k k k b q S k q k k k k --==-=--+-+≥(注:可编辑下载,若有不当之处,请指正,谢谢!)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
“有限与无限”随想
1043111196郭铭玥软件三班
首先给大家介绍一下专业的“有限与无限”解释。
有限与无限:物质世界固有的矛盾之一。
反映物质运动在时间和空间上辩证性质的一对哲学范畴。
物质是不灭的、无限的,并且处在永恒的绝对运动之中,物质及其运动的永恒性、无限性,也就是物质的存在形式即时间持续和空间广延的无限性。
物质的时空无限由具体的物质客体的有限时空所构成,并通过具体物质客体在有限时空上的运动和变化表现出来。
有限和无限的范畴,反映了物质世界中客观存在的矛盾和辩证联系。
——摘自《百度名片.有限于无线》
以上是哲学里关于“有限与无限”的概念,我既非哲学系的学生,也没有仔细研读过哲学范畴的内容,所以在此仅谈谈自己的理解。
第一次见到这两个词摆在一起,感觉其互为矛盾,根本不可能兼容,任何一件事物或者是一种思想,你要么是有限的要么是无限的,例如树叶是绿的,花儿是红的,我们用感官世界完全就可以界定。
泛读了霍金的《时间简史》,我曾很多次思考时间和空间到底是有限还是无限呢?如果是有限的话,如书中所言,时间和空间开始于宇宙大爆炸,那么在时空奇点之前世界又是怎样的一副面貌呢?是混沌,还是无限狭小的无所谓空间的境地?如果是无限,既然时间万物有其发生发展,必有其源头,一个所谓的起点事物必在一个范围内按一定的规律发生,否者何来大自然的秩序?
康德很有名的二律背反中有这样一组命题。
正题:世界在时间上有着开端,在空间上有着界限。
反题:世界在时间上和空间上无限。
我们日常所接受的由牛顿确立的绝对时空观念太简陋了。
站在巨人的肩膀上,我知道空间并不是绝对存在的,莱布尼兹说过“物体不依靠广袤而存在,广袤却依靠物体而存在”,没有物体,没有力,没有场的地方,就不存在空间。
空间依存于事物,而不是事物依存于空间。
那又何谈空间的有限与无限?甚至连时间和空间都不再有意义。
在有限的内部,随着自身的演进及秩序的运行,其有限性得以发生。
有限与无限只是宇宙自身的同一。
死亡——曾经在深夜辗转反侧却无论如何也想不明弄不透,想象着生命可能是无限的永恒的吗?最后都是止于黑暗里的恐惧。
看了耶鲁公开课《死亡》,或许有了更成熟一点的想法,至少不至于以之为无边的梦魇。
柏拉图终其一生思考永恒不变的事物与“流动”的事物之间的关系,之中又尤其热衷不朽的灵魂说。
我们的躯体总有一天会老旧,损坏直至化为尘土,因此人的肉体存在是有限的,可是二元论者认为肉体死亡后,还会有完全独立于肉体存在的灵魂会无限的以另一种方式存在着。
有限与无限仿佛在
此分道扬镳,灵魂走你的无限路,休管我肉体过自己的有限独木桥。
可是肉体和灵魂有真的那般不相干吗?肉体就真只是灵魂的一个寄居体,还估且不谈灵魂的存在与否,身体不舒服人就无精打采,感觉渴了就指使手部肌肉收缩拿起杯子喝水,肉体和灵魂不总是存在着那些丝丝缕缕的联系吗?
所以,我认为有限和无限是对立的统一,它们既是对立的,有区别的,又是相互联系的。
它们有着辩证的关系并在一定条件下相互转化的。
无限由有限构成、无限不能脱离有限而独立存在。
有限是对自身的超越,包含着无限,体现着无限。
举一个数学中的例子吧,整数集是一个无限集合,人们无法得到一个完成了的整数集。
但每个整数又都是有限的。
我们可以得到任意的整数。
任意给出一个数学的对象,我们立即就能判定它是否属于整数集,这样看问题,整数集又是一个完成了的集合,是一个有限的概念。
因此整数集本身就是一个无限和有限的对立统一。
源远流长的中华文化也无不渗透着有限与无限的思索啊。
《老子》曰:“天下万物生于有,有生于无。
”中国画“以物形为有,以空白为无”,中国古典音乐以“无限”、“无尽”为境界,“琴意得之于弦外”,我们文化的精华诗歌不也强调“言有尽而意无穷“,让我以一首古诗来结束我的言,恭请体会其无限之意!
入若耶溪
王籍·南北朝
■■何泛泛,空水共悠悠。
阴霞生远岫,阳景逐回流。
蝉噪林逾静,鸟鸣山更幽。
此地动归念,长年悲倦游。
