03第三章-力偶系
合集下载
工程力学(静力学与材料力学)第三章力偶系详解

FB
r M2 0 ∑ M = 0 , FA sin
M 2 2r FA
M2 = 4M1 = 8kNm
2M 1 FO FB FA 8kN r
• 作业3-1,3-4,3-8
考虑CB部分为二力构件,得:
FC FA FB FC
例3-4
图示机构自重不记。圆轮上的销子 A 放在 摇杆 BC上的光滑导槽内。M 1 = 2kNm,OA = r = 0.5m 。图示位置OA⊥OB,α = 30°,且系统平衡。 求作用于摇杆 BC 上力偶的矩 M 2 及 O、B 支座的反 力。 解:受力分析
M1
R
F1
M
F2
2
M1 + M2 = rBA×F1 + rBA×F2 = rBA×( F1 + F2 ) = rBA×R = M
如有n个力偶,按上法依次合成, 最后得一力偶,合力偶矩矢为 M = M1 +M2 + … +Mn = ∑M I
B
rBA
A
F2
F1
任意个力偶可以合成为一个 合力偶,这个合力偶矩矢等于各 分力偶矩矢的矢量和。 M = M 1+ M 2+ … + M n = ∑M i
性质三
证:
力偶没有合力
仍用反证法,即假定力偶有合力,那么总可 找到一个与此力大小相等,方向相反而作用线 共线的力与此力平衡,即力与力偶相平衡。与 性质二矛盾。
性质一、二和三告诉我们力偶只能与力偶等 效而不能与单个力等效。
•力偶只能与力偶相平衡 力偶只能与力偶相平衡
§3-4 力偶系的合成
设有两个力偶,由性质一,将 力偶中两力分别移到两力偶作用面 交线上的两点 A 和 B,可得到两个 汇交力系,其合力分别为R 、 R ’ 。
工程力学 第3章 力偶系
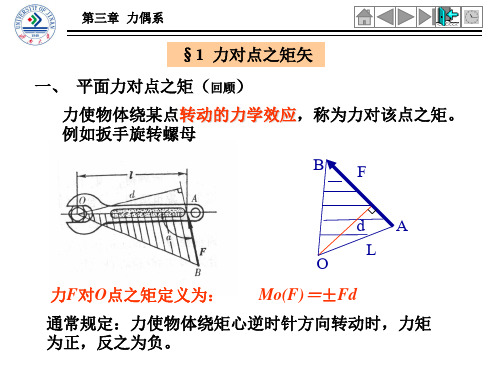
M 2 F2 , F2'
M F1'
r1
F F1 F2 F ' F1' F2'
F2' MR F, F '
F2
F1 F
M2
MR r F ' r (F1'F2 ') r F1'r F2 '
M1 M2
结论:两个力偶的合成仍然为力偶,且
第三章 力偶系
§1 力对点之矩矢 一、 平面力对点之矩(回顾)
力使物体绕某点转动的力学效应,称为力对该点之矩。 例如扳手旋转螺母。
BF
dA L
O
力F对O点之矩定义为: Mo(F)=±Fd
通常规定:力使物体绕矩心逆时针方向转动时,力矩 为正,反之为负。
第三章 力偶系
二、力对点之矩矢量 1、空间力矩三个要素:
一、力偶 在日常生活和工程实际中经常见到物体受动两个大小相等、 方向相反,但不在同一直线上的两个平行力作用的情况。例如
第三章 力偶系
B d
F’
F A
M
B
F
rBA
F’ d A
1. 定义:在力学中把这样一对等值、反向而不共线的平行力 称为力偶,用符号 ( F , F′)表示。
两个力作用线之间的垂直距离 d 称为力偶臂, 两个力作用线所决定的平面称为力偶的作用面。
x (F ) y (F )
yFz zFx
zFy xFz
M
z
(F
)
xFy
yFx
力对点之矩在各坐标轴上的投影
MO z
O xr
理论力学第3章-力偶系

例 3-1 图示机构,各杆自重不计,在两力偶作用下处于平 衡。已知:M1 = 100 N · m,O1A = 40 cm,O2B = 60 cm。 试求力偶矩M2的大小。 B A FB F B FA
30 o
B
O1
B
A FA M2
M1 FO1 O1 A M1
M
2
O2
O2
FO2
解:取O1A杆为研究对象,受力如图所示,
若两个力偶对刚体的作用效应相同,则称这二力 偶等效。
两力偶的等效条件 :力偶矩矢相等,即
M1 M2
(3-2) FR'
B'
证明:
A'
FR F1 FR F'
A B
FR' F1'
F
力偶(FR,FR' ) 代了原力偶(F,F' ) 并与原力偶等效。
A'
FR
FR'
B'
D F' C
比较(F,F')和(FR,FR')可得 M(F,F')=2△ABD=M(FR,FR') =2 △ABC
合力偶矩矢的大小和方向余弦为
M ( M x )2 ( M y )2 ( M z )2 (280)2 1602 (800)2 862.55 kN m
M cos( M , i )
280 0.3246 M 862.55 My 160 cos( M , j ) 0.1855 M 862.55
1 3 200 280kN m 5 5 4 M y M y M 1 y M 2 y 0 200 160kN m 5 2 M z M z M1z M 2 z 400 5 0 800kN m 5 M x M x M1x M 2 x 400 5
第三章 力偶系

(2)再将Q, F合成R, Q', F'合成R', 得到新力偶(R, R'),
QA RF
F' R'
B Q'
(3)将R, R'分别移到A', B'点,则(R, R')与原力偶等效
(4)最后将力偶(R, R')的力臂调整到与原力偶相等
19
§3-5、力偶系的合成
设作用于刚体上的任意两个力偶M1,M2, 总能将其等效为两个共力臂的力偶:
z
Fz
力 F 对 z 轴之矩:
M z (F ) xFy yFx
F
Fy
k Fx z
ij
x
y
x
y
Fx
Fxy
力 F 对 x 轴与 y 轴之矩: M x (F ) yFz zFy
M y (F ) zFx xFz
10
问题:力对轴之矩与力对轴上一点之矩有什么关系?
z
力对轴之矩 M x (F ) yFz zFy M O M Oz
力偶(F, F’ )是特殊的力系,对O点 的合力矩为:
F ' F
F
B rBA
A d
F’
rB
rA
O
MO MO(F) MO(F')
rA F rB F '
rA F rB (F )
(rA rB ) F rBA F
M
M = Fd
B rBA
F’
力偶矩矢
F A
注:力偶矩矢垂直于力偶所在的平面,其大小和方向与取矩点 无关。
合力偶的方向:
cos(MR, i)
Mx MR
cos(MR, j)
My MR
QA RF
F' R'
B Q'
(3)将R, R'分别移到A', B'点,则(R, R')与原力偶等效
(4)最后将力偶(R, R')的力臂调整到与原力偶相等
19
§3-5、力偶系的合成
设作用于刚体上的任意两个力偶M1,M2, 总能将其等效为两个共力臂的力偶:
z
Fz
力 F 对 z 轴之矩:
M z (F ) xFy yFx
F
Fy
k Fx z
ij
x
y
x
y
Fx
Fxy
力 F 对 x 轴与 y 轴之矩: M x (F ) yFz zFy
M y (F ) zFx xFz
10
问题:力对轴之矩与力对轴上一点之矩有什么关系?
z
力对轴之矩 M x (F ) yFz zFy M O M Oz
力偶(F, F’ )是特殊的力系,对O点 的合力矩为:
F ' F
F
B rBA
A d
F’
rB
rA
O
MO MO(F) MO(F')
rA F rB F '
rA F rB (F )
(rA rB ) F rBA F
M
M = Fd
B rBA
F’
力偶矩矢
F A
注:力偶矩矢垂直于力偶所在的平面,其大小和方向与取矩点 无关。
合力偶的方向:
cos(MR, i)
Mx MR
cos(MR, j)
My MR
工程力学第三章 力 偶 系
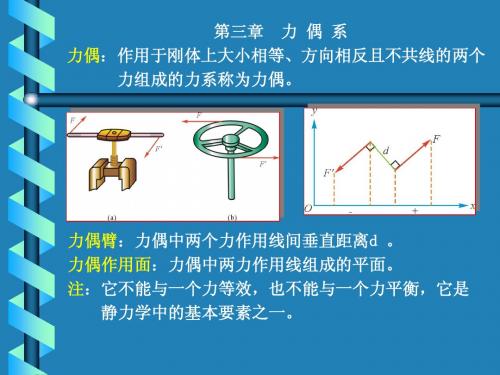
§3-5 力偶系的合成 对于任意一个力偶系,可以将力偶矩矢移到一个汇交点, 再按照矢量合成的方法将矢量合成为一个合矢量,这个合矢 量就是力偶系的合力偶。而且有:
MR = M1+ M2+ + Mn = ∑M
对于平面力偶系,力偶只有顺时针和逆时针两种转向,所 以力偶可以看成代数量规定:逆时针为正、顺时会为负。 所以平面力偶系的合力偶
MR = M1+ M2+ …+ Mn = ∑M
§3-6 力偶系的平衡条件 对于任意一个力偶系,它的平衡条件是合力偶矩矢为零。
即:MR = ∑M = 0
M1x+ M2x+ + Mnx = ∑Mx = 0 M1y+ M2y+ + Mny = ∑My = 0 M1z+ M2z+ + MnZ = ∑Mz = 0
二、空间中力对点之矩 M0(F)= r × F
§3-2力对轴之矩 一、力对轴之矩的概念
1、定义:对力使它所作用的物体绕轴转动效果的度量。 它是一个代数量。
2、特例:力与轴平行: MZ(F)=0 力与轴相交: MZ(F)=0
力与轴在同一平面内时力对轴之矩为零。 3、合力矩定理:合力对任一轴之矩等于各分力对同一 轴之矩的代数和。
§3-4 力偶的等效条件和性质 一、力偶的等效条件(41页) 两个力偶的等效条件是它们的力偶矩矢相等。 二、力偶的性质 1、力偶不能与一个力等效,也不能与一个力平衡。 2、力偶可在其作用面内任意转移,或移到另一平行平 面,而不改变对刚体的作用效果。
=
=
=
3、在保持力偶的转向和力偶矩的大小不变的条件下, 可以同时改变力偶中力和力偶臂的大小,而不改变 力偶对刚体的作用。
工程力学第3章(力偶系)

工程力学
Engineering Mechanics
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第三章 力偶系 §3-1 力对点之矩矢
力偶臂d 力偶臂 1=200mm, ,
,力偶臂d , F2 = F2' = 120N,力偶臂 2=300mm , F3 = F3' = 80 N,
M 1 = 100 × 0.2 = 20
N.m N.m
M 2 = 120 × 0.3 = 36
M 3 = 80 × 0.18 = 14.4 N.m
M Rx M Ry = ∑ M y = M 1 = 20 N.m
二、力对轴之矩的 解析表达式
M x ( F ) = M x ( Fy ) + M x ( Fz ) = -zFy + yFz M y ( F ) = M y ( Fz ) + M y ( Fx ) = -xFz + zFx M z ( F ) = M z ( Fx ) + M z ( Fy ) = -yFx + xFy
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
合力偶矩矢的大小 M R = ( ∑ M x ) 2 + ( ∑ M y )2 + ( ∑ M z )2 合力偶矩矢的方向
R
∑M cos( M ,i ) =
cos( M R,j ) = MR
Engineering Mechanics
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第三章 力偶系 §3-1 力对点之矩矢
力偶臂d 力偶臂 1=200mm, ,
,力偶臂d , F2 = F2' = 120N,力偶臂 2=300mm , F3 = F3' = 80 N,
M 1 = 100 × 0.2 = 20
N.m N.m
M 2 = 120 × 0.3 = 36
M 3 = 80 × 0.18 = 14.4 N.m
M Rx M Ry = ∑ M y = M 1 = 20 N.m
二、力对轴之矩的 解析表达式
M x ( F ) = M x ( Fy ) + M x ( Fz ) = -zFy + yFz M y ( F ) = M y ( Fz ) + M y ( Fx ) = -xFz + zFx M z ( F ) = M z ( Fx ) + M z ( Fy ) = -yFx + xFy
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
M R = M1 + M 2 + ⋅ ⋅ ⋅ + M n = ∑ M
合力偶矩矢的大小 M R = ( ∑ M x ) 2 + ( ∑ M y )2 + ( ∑ M z )2 合力偶矩矢的方向
R
∑M cos( M ,i ) =
cos( M R,j ) = MR
第三章 力偶系

M M
M(+)
M M M
(-)
注意:力偶的转向与力偶矢方向的区别与关联! M
§3-5 力偶系的合成(简化)
设作用于刚体上的两个力偶M1, M2:
M1 F1, F1'
F1
M2 F2, F2'
Q F F1 F2
F2
F ' F1' F2'
MR F, F '
F
M F1' F ' 1
MR M1 M2 ... Mn M
M1Fn
F1 o
Fn’ F2
= M1
F1’
F2’
§3-5 力偶系的合成(简化)
合力偶矩矢:
z
MR M1 M2 ... Mn M
将上述矢量式对坐标轴投影得:
M Rx M1x M2x ... Mnx M x M Ry M1y M2 y ... Mny M y M Rz M1z M2z ... Mnz M z
二个力偶的等效条件是它们的力偶矩矢相等。
M1
M2
B rBA
F1'
A
M1 rBA F1
F1
M1 M2
D
rDC
F2
F2'
C
M 2 rDC F2
0.4m
60N
0.4m
60N
40N 0.6m
M=24N.m
§3-4 力偶的等效条件和性质 二、力偶的性质
性质一: 力偶不能与一个力等效(即力偶无合力),因 此也不能与一个力平衡。
MO MO (F1) MO (F2 ) 力对点之矩矢服从矢量的合成法则 对空间力系(F1, F2, …, Fn),有:
MO MO (F1) MO (F2 ) ... MO (Fn )
静力学 第03章 力偶系

M y (F = zF − xF ) x z Mz (F = ) zFy − yFx
§3-2 力对轴之矩
力对轴之矩的方向确定
力对轴之矩是代数量,表示力矩的大小和转向,并按右 手规则确定其正负号,如图所示,拇指指向与 轴一致为 正,反之为负。
§3-2 力对轴之矩
力对轴之矩与力对点之矩的关系
FA = M a 2 + b2
FB
作
业
3-1 3-2 3-5 3-8
§3-1 力对点的矩矢
[例] 曲拐OAB。已知 OA﹑AB﹑θ﹑P,求MO ( P )。 解法一 依定义解
M o P =P × OB ⇒ M o P =P × OB × sin θ
( )
( )
∴ |MO ( P )| =P× (OA2+AB2 )1/2 ×sin θ
∑
n i =1
mi
§3-5 力偶系的合成
合力矩
P2’
M = rBA × FR = rBA × P 1+P 2 = rBA × P 1 + rBA × P 2 = d1 × F1 + d 2 × F2 = M1 + M 2
(
)
S1 F1’
ΣMy
力偶系合成的结果: 仍然是一个力偶,其力 偶矩矢量等于原力偶系中 所有力偶矩矢量之和。即
ΣM x
M=Σ Mxi+ Σ Myj+ Σ Mzk
M
§3-6 力偶系的平衡条件
力偶系平衡的充要条件是:力偶系各力偶 矩矢的矢量和等于零,即M=Σ M i=0,或者 ΣMx= ΣMy= ΣMz=0(即力偶系各力偶矩矢分 别在三个坐标系投影的代数和等于零)。 例题3-1:三铰刚架由两直角刚架组成,AC 部分上作用一力偶,其力偶矩为 M, 自重 不计, 且 a : c = b : a,求A、B支座 的反力。
工程力学单辉祖-第三章_力偶系

M OA F OB F OA F OB F OA OB F
M BA F
x
力偶矩矢 M 与O点位置
无关,是自由矢量。
力偶矩矢由其模、方位
和指向确定。
31
§3–3 力偶矩矢
二、力偶矩矢的确定
M BA F
力偶矩矢的模(大小): z
M1 、 M2
由于力偶矩矢是自由矢量,可任意平行移动,故可将其 按照矢量合成的方法进行合成。 M
M1
A B
M2
M1
A
M2
B
合力偶矩矢 M M1 M2
37
一、力偶系的合成
对于 n 个力偶组成的力偶系:
合力偶矩矢: M R M1 M 2 M n M i
i 1 n
力偶系的平衡方程
平面力偶系平衡的充要条件是:
合力偶矩等于零,即所有各力偶矩的代数和等于零。
即
M
i 1
n
i
0
39
[例5]
在一钻床上水平放置工件,在工件上同时钻四个等直径
的孔,每个钻头的力偶矩为 m1 m2 m3 m4 15N m 求工件的总切削力偶矩和A 、B端水平反力?
M
A
B
l
D
动脑又动笔
解: 选梁AB为研究对象
M
A
B
FA = FB 列平衡方程: ∑M = 0 ,
l
D
A
FA
45o
M
B
M- FA l cos45o = 0 FA = FB= √2M / l
FB
动脑又动笔
如图所示的铰接四连杆机构 OABD,在杆 OA 和 BD 上分别作用着矩为 M1 和 M2 的力偶,
M BA F
x
力偶矩矢 M 与O点位置
无关,是自由矢量。
力偶矩矢由其模、方位
和指向确定。
31
§3–3 力偶矩矢
二、力偶矩矢的确定
M BA F
力偶矩矢的模(大小): z
M1 、 M2
由于力偶矩矢是自由矢量,可任意平行移动,故可将其 按照矢量合成的方法进行合成。 M
M1
A B
M2
M1
A
M2
B
合力偶矩矢 M M1 M2
37
一、力偶系的合成
对于 n 个力偶组成的力偶系:
合力偶矩矢: M R M1 M 2 M n M i
i 1 n
力偶系的平衡方程
平面力偶系平衡的充要条件是:
合力偶矩等于零,即所有各力偶矩的代数和等于零。
即
M
i 1
n
i
0
39
[例5]
在一钻床上水平放置工件,在工件上同时钻四个等直径
的孔,每个钻头的力偶矩为 m1 m2 m3 m4 15N m 求工件的总切削力偶矩和A 、B端水平反力?
M
A
B
l
D
动脑又动笔
解: 选梁AB为研究对象
M
A
B
FA = FB 列平衡方程: ∑M = 0 ,
l
D
A
FA
45o
M
B
M- FA l cos45o = 0 FA = FB= √2M / l
FB
动脑又动笔
如图所示的铰接四连杆机构 OABD,在杆 OA 和 BD 上分别作用着矩为 M1 和 M2 的力偶,
第03章力偶系

17
由此可知: 力偶中力的大小,力偶臂的长短, 都不是力偶的特征量。 只有力偶矩(大小和转向)才是力偶作用的唯一度 量。所以,力偶的表示可以简化:
或
在习题中,一般用M表示力偶矩的大小(不加正 负号)用箭头表示力偶的转向。 18
3.2.3 力偶矩矢 实例:
开门拧门把手,在门内或门外拧,效果相同; 用起子拧螺丝,效果与起子柄的长短无关。
10
2、力偶矩 力偶矩:是力偶使物体转动 的效应的度量。 F 用 M ( F , F ) 表示,简记为 M 。 定义: M ( F , F ) Fd
A
C
F’
d
B
平面力偶正负号规定:逆时针为正;顺时针为负;
力偶矩的单位:N ·m ,或 kN ·m 。
力偶矩的几何表示:
在任一轴 x 上的投影:
F cos F cos 0
13
三、同平面内力偶的等效定理 定理 作用在同一平面内的两个力偶, 两力偶的力偶矩相等。 等效
14
由力偶等效定理可得两个很有用的推论: 推论1 力偶可以在其作用面内任意移动和转动, 而不改变力偶对刚体的作用效应。
F
F´
F
F´
只要保持力偶矩不变,力偶可在作用面内 任意移动,其对刚体的作用效应不变。
M F CE 0
32
讨论 是否与力偶只能用力偶来 平衡矛盾?
33
性质2 力偶本身不平衡,力偶只能用力偶来平衡。
由二力平衡公理可知,力偶本身不平衡; 由下面将要介绍的力偶系的平衡可得此结论。 12
性质 3 力偶对其作用面内任一点的矩都相等,恒 等于其力偶矩。力偶在任一轴上的投影恒 为零。 证明:对任一点O的力矩为: A O a F ’ M o ( F,F ) M o ( F ) M o ( F ) d Fa F (d a) F B x Fd M ( F , F )
03--第三章 力矩与平面力偶系(修订)

例3-5 :
已知 M 2kN m,OA r 0.5m,θ 30; 1
求:平衡时的 M 2及铰链O,B处的约束力.
解:取轮,由力偶只能由力偶平衡的性质,画受力图.
M 0 M1 FA r sin 0
解得 FO FA 8kN
取杆BC,画受力图.
M 0
FA'
r
sin
M2
0
解得 M2 8kNm
F 'd Fd
力矩的符号 M F 力偶矩的符号 M O
3.只要保持力偶矩不变,力偶可在其作用面内任 意移转,且可以同时改变力偶中力的大小与力 臂的长短,对刚体的作用效果不变.
=
=
=
ABC ABD
ABC?ABD
M FR,Fi R FRd1 2ABD
M
F,
Fi
Fd
2ABC
=
=
=
=
l
q dx x
0
l
0
x2 l
q dx
得 h 2l 3
例3-4
已知:M1 M 2 10N m, M3 20N m, l 200mm;
求: 光滑螺柱AB所受水平力.
解:由力偶只能由力偶平衡的性质, 其受力图为
M 0
FAl M1 M2 M3 0
解得
FA
FB
M1 M2 l
M3
200N
力偶矩 M F d 2 1 F d 2ABC
2
二. 力偶与力偶矩的性质 1.力偶在任意坐标轴上的投影等于零.
2.力偶对任意点取矩都等于力偶矩, 不因矩心的改变而改变.
M F d
MO1 F
F,
d
F
x1
MO1 F M
工程力学第三章力偶系

一、平面中力对点之矩
刚体在平面内受力F作用而绕平面上某一点O 转动的效应取决于力的大小力臂和转动方向。
力臂——力的作用线至O点的垂直距离h。
转动方向——规定逆钟向为正,顺钟向为负。 MO(F) = h×F = ± Fh
还可表示为:
MO(F) = ±2△OAB
返回首页
Theoretical Mechanics
O O
( (
F F
)x )y
M M
x y
(F) (F)
yFz zFx
zFy xFz
M
O
(F
)z
M
z
(F
)
xFy
yFx
返回首页
Theoretical Mechanics
§3–3 力偶矩矢
M = rBA×F = rAB×F 力偶矩在平面问题中视为代数量,记为M,
M = ±Fd
返回首页
Theoretical Mechanics
A
B
l
m 0: FAl M1 M 2 M 3 0 M 2 M 1
解之得:
A
FA
M3 B
FB
FA
M1
M2 l
M3
FB
返回首页
Theoretical Mechanics
例2:如图杆AB上有一导槽,套在杆 CD上的销子E上,在两杆上各有一力
A M1
D B
偶作用。已知mM1 1000 N m ,若
§3–5 力偶系的合成
设刚体上作用力偶矩矢M1、M2、…、Mn ,根据力 偶的等效性,将各力偶矩矢平移至图(b)中的任一 点A,力偶系合成结果为一合力偶。
返回首页
Theoretical Mechanics
第3章_力偶系

目录
3
§3.1
力对点之矩矢
平面中力对点之矩
两个要素:
1.大小:力F 与力臂的乘积
2.方向:转动方向 力矩的定义——力 F 的大小乘 以该力作用线到某点 O 间距离 d ,并加上适当正负号,称为 力F 对O 点的矩。简称力矩。
B
O d A
目录 4
F
§3.1
力对点之矩矢
力矩的表达式:
Mx Mx , M y M y , M z M z
合力偶矩矢的大小和方向余弦
M ( M x ) 2 ( M y ) 2 ( M z ) 2
Mx cos M
cos
My M
Mz cos M
目录
20
§3.6
力偶系的平衡条件
空间力偶系平衡的充分必要条件是 :合力偶 矩矢等于零,即
力对点之矩矢在通过该点之轴上 的投影,等于力对该轴之矩。
目录
12
§3.3
力偶矩矢
M M O ( F ) M O ( F ) rA F rB F rA F rB F ( rA rB ) F rBA F
M 0
M
零。
x
0
M
y
0
M
z
0
--称为空间力偶系的平衡方程. 对于平面问题:力偶系各力偶力偶矩的代数和等于
M 0
目录 21
§3.5
例3-1 已知
力偶的合成
M 1 2kN m, OA r 0.5m, θ 30 ;
求:平衡时的 M 2 及铰链O,B处的约束力.
目录
03 力偶系

第3章 力 偶 系
§3.1 平面力对点的矩 平面力对点的矩
移动效应--取决于力的大小、 --取决于力的大小 力对物体可以产生 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、 --取决于力矩的大小 转动效应--取决于力矩的大小、方向
例如: (1) 用扳手拧螺母; (2) 开门,关门。 由上图知,力F 使物体绕O点转动的效应,不仅 与力的大小有关,而且与O点到力的作用线的垂直距 离d 有关,故用乘积Fd 来度量力的转动效应。
有 ∑Mix = 0 简写为
∑ Miy = 0
∑Miz = 0
z
∑M
x
=0
∑M
y
=0
∑M
=0
称为力偶系的平衡方程. 称为力偶系的平衡方程
各力偶矩矢在三 个坐标轴上投影 的代数和为零
平面力偶系平衡方程: 平面力偶系平衡方程:
∑
i
=0
例题:图示铰链四连杆机构 例题:图示铰链四连杆机构OABO1处于平衡位 已知OA=40cm, O1B=60cm, M1=1Nm,各杆 置.已知 已知 各杆 自重不计.试求力偶矩 的大小及杆AB所受的力 所受的力. 自重不计 试求力偶矩M2的大小及杆 所受的力 试求力偶矩
F1 F2
说明:1、力偶作用面 说明: 2、力偶臂 d 3、作用效果:转动 作用效果: 力偶矩
M = ±F d
(平面)代数量,逆正顺负 平面)代数量, 单位: 单位:N.m
4.力偶与力偶矩的性质 4.力偶与力偶矩的性质 (1)力偶在任意坐标轴上的投影等于零。 力偶在任意坐标轴上的投影等于零
(2)力偶和力是力学中的两个基本量, 力偶和力是力学中的两个基本量, 力偶只能与力偶平衡。 力偶只能与力偶平衡。
§3.1 平面力对点的矩 平面力对点的矩
移动效应--取决于力的大小、 --取决于力的大小 力对物体可以产生 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、 --取决于力矩的大小 转动效应--取决于力矩的大小、方向
例如: (1) 用扳手拧螺母; (2) 开门,关门。 由上图知,力F 使物体绕O点转动的效应,不仅 与力的大小有关,而且与O点到力的作用线的垂直距 离d 有关,故用乘积Fd 来度量力的转动效应。
有 ∑Mix = 0 简写为
∑ Miy = 0
∑Miz = 0
z
∑M
x
=0
∑M
y
=0
∑M
=0
称为力偶系的平衡方程. 称为力偶系的平衡方程
各力偶矩矢在三 个坐标轴上投影 的代数和为零
平面力偶系平衡方程: 平面力偶系平衡方程:
∑
i
=0
例题:图示铰链四连杆机构 例题:图示铰链四连杆机构OABO1处于平衡位 已知OA=40cm, O1B=60cm, M1=1Nm,各杆 置.已知 已知 各杆 自重不计.试求力偶矩 的大小及杆AB所受的力 所受的力. 自重不计 试求力偶矩M2的大小及杆 所受的力 试求力偶矩
F1 F2
说明:1、力偶作用面 说明: 2、力偶臂 d 3、作用效果:转动 作用效果: 力偶矩
M = ±F d
(平面)代数量,逆正顺负 平面)代数量, 单位: 单位:N.m
4.力偶与力偶矩的性质 4.力偶与力偶矩的性质 (1)力偶在任意坐标轴上的投影等于零。 力偶在任意坐标轴上的投影等于零
(2)力偶和力是力学中的两个基本量, 力偶和力是力学中的两个基本量, 力偶只能与力偶平衡。 力偶只能与力偶平衡。
静力学03.第三章 力偶系

此也不能与一个力平衡;
性质二、力偶可在其作用面内任意转移,或移到另一平 行平面,而不改变对刚体的作用效果,力偶矩 矢是自由矢量; 性质三、保持力偶转向和力偶矩的大小(力与力偶臂的
乘积)不变,力偶中的力和力偶臂的大小可以
改变,而不改变对刚体的作用效果。
§3.4
力偶的等效条件和性质
力偶不能合成一个力, 或用一个力来等效替换; 力偶也 不能用一个力来平衡。因此, 力和力偶是静力学中两个基 本要素 力偶对物体的作用效应是引起物体的转动 力偶矩: 力偶的两个力对其作用面内某点的矩的代数和 MO(F , F') = MO(F )+MO(F') =F· aO-F'· bO =F (aO-bO) =F d F
空间力系中,力 F 对刚体产生的绕某点 O 的转动效应 取决于三个要素: (1)转动效应的强度 Fh;
(2)转动轴的方位,即力的作用线和矩心 O 所决定的平面的 法线方位; (3)转向,即: 使刚体绕轴转动的方向。
§3.1 力对点之矩矢
这三个要素可以用一个矢量来表示: 矢量的模等于力与力臂的乘积Fh 矢量的方位就是转轴的方位 矢量的指向根据右手规则由力F绕轴转动的方向确定。 力对点之矩矢,表示为MO(F),过矩心O的定位矢量。
ΣMx= 0, ΣMy= 0 , ΣMz= 0;
力偶系平衡条件的应用。
FR
l 0
q ( x )d x
l 0
q0
x l
dx
1 2
q0l
求合力作用线位置。设合力FR 的作用线距A端的距离 为h,在微段dx上的作用力对点A的矩为-(qxdx)x,全部分 布载荷对点A的矩为
l 0
大学工科工程力学第三章 力偶系

= F3 d − F4 d
= M1 − M 2
结论:
在同平面内的任意个力偶可合成 一个合力偶,其合力偶矩等于各 个力偶矩的代数和。
M =
∑M
i =1
n
i
b、平面力偶系的平衡条件 充要条件:
∑M
i =1
n
i
=0
即:所有力偶的合力偶矩的代数和等于零。
根据力偶理论,一个力偶与一个力是不可能平衡的。
M
r O
第三章
力偶系
本章主要内容
力对点之矩矢 力对轴之矩 力偶矩矢 力偶的等效条件和性质 力偶系的合成和平衡条件
力偶的定义
A
F′
B
F
大小相等,方向相 反,不共线的两个力所 组成的力系。
力 偶 实 例
§3-1 力对点之矩矢
一、平面中力对点之矩(力矩) 力对物体可以产生: 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、方向
§3-3 力偶矩矢
一、平面力偶矩 用以衡量力偶对刚体的转动效应
B A
O
x
d
F´
平面有一个力偶,将它们对O 点取矩 根据力对点之矩,力偶对O 之矩为:
F
M = mo ( F ) + mo ( F ′) = − Fx + F ′( x + d ) = Fd = F ′d
M = ± Fd
力偶矩与矩心的位置无关。
M ∑ cos α = M
xi
M ∑ , cos β = M
yi
M ∑ , cos γ = M
zi
空间力偶系的平衡条件是:合力偶矩矢为零
∑M ∑M ∑M
x y z
=0 =0 =0
= M1 − M 2
结论:
在同平面内的任意个力偶可合成 一个合力偶,其合力偶矩等于各 个力偶矩的代数和。
M =
∑M
i =1
n
i
b、平面力偶系的平衡条件 充要条件:
∑M
i =1
n
i
=0
即:所有力偶的合力偶矩的代数和等于零。
根据力偶理论,一个力偶与一个力是不可能平衡的。
M
r O
第三章
力偶系
本章主要内容
力对点之矩矢 力对轴之矩 力偶矩矢 力偶的等效条件和性质 力偶系的合成和平衡条件
力偶的定义
A
F′
B
F
大小相等,方向相 反,不共线的两个力所 组成的力系。
力 偶 实 例
§3-1 力对点之矩矢
一、平面中力对点之矩(力矩) 力对物体可以产生: 移动效应--取决于力的大小、方向 转动效应--取决于力矩的大小、方向
§3-3 力偶矩矢
一、平面力偶矩 用以衡量力偶对刚体的转动效应
B A
O
x
d
F´
平面有一个力偶,将它们对O 点取矩 根据力对点之矩,力偶对O 之矩为:
F
M = mo ( F ) + mo ( F ′) = − Fx + F ′( x + d ) = Fd = F ′d
M = ± Fd
力偶矩与矩心的位置无关。
M ∑ cos α = M
xi
M ∑ , cos β = M
yi
M ∑ , cos γ = M
zi
空间力偶系的平衡条件是:合力偶矩矢为零
∑M ∑M ∑M
x y z
=0 =0 =0
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
C LY
系 列 二
工程 力学 力偶系 第三章
第二章 汇交力系 工程力学
定义: M O ( F ) Fd 为力对点之矩。
其中: O 为参考系中的某一点,称为矩心。
d 为矩心至力F作用线的垂直距离,称为力臂。
M O ( F ) Fd 2OAB
正负规定 : 力使刚体绕矩心 逆时针转动为正, 顺时针转动为负。
第二章 汇交力系 工程力学
M 0,
M1 FAB r cos 0 M 2 2 FBAr cos 0
B
F
A
O
C LY
系 列 二
工程 力学 力偶系 第三章
第二章 汇交力系 工程力学
平面中力对点之矩是一个代数量。
力矩在下列两种情况下等于零: 1. 力的大小等于零; 2. 力的作用线通过矩心,即力臂 B
F
A
等于零。
力矩的单位常用N· m或kN· m。 O
C LY
系 列 二
工程 力学 力偶系 第三章 二、力对点之矩矢 1. 概念 在空间问题中,力对刚体 产生的绕O点的转动效应取决 于三个要素: ⑴ 大小:力F与力臂的乘积;
r F rF sin Fd
M O (F )
M O (F ) r F
A
F
r
d O
C LY
系 列 二
工程 力学 力偶系 第三章 ⑵ 力对点之矩矢的解析表示式
第二章 汇交力系 工程力学
r xi yj zk
F Fx i Fy j Fz k
则:
r
M O ( F ) r F ( xi yj zk ) ( Fxi Fy j Fz k )
第二章 汇交力系 工程力学
两个力偶的等效条件是它们的力偶矩矢相等。 (两个力偶矩矢相等的力偶等效。)
2. 力偶的性质
(1)力偶中两力在任意坐标轴上投影的代数和为零 。 (2)力偶不能与一个力等效(即力偶无合力),本身又不 平衡,也不能与一个力平衡(力偶只能由力偶来平衡)。是一 个基本的力学量。
C LY
系 列 二
工程 力学 力偶系 第三章 4. 合力矩定理
第二章 汇交力系 工程力学
合力对任一点之矩等于诸分力对同一点之矩的矢量和。即:
M O ( FR ) M O ( F1 ) M O ( F2 ) M O ( Fn )
M O ( FR ) M O ( F )
对于平面力系,则有(代数和):
M O ( FR ) M O ( F1 ) M O ( F2 ) M O ( Fn )
M O ( FR ) M O ( F )
注意:力偶方向垂直于平面,平面力系力偶取代数和;空间力 系力偶取矢量和
C LY
系 列 二
工程 力学 力偶系 第三章
第二章 汇交力系 工程力学
第动方向; ⑶ 作用面:力矩作用面。
M O ( F ) ——力对点之矩矢,是一个过矩心O的定位矢量,是力
对刚体转动效应的度量。
C LY
系 列 二
工程 力学 力偶系 第三章
第二章 汇交力系 工程力学
2. 力对点之矩矢的矢量积表示式和解析表示式 ⑴ 力对点之矩矢的矢量积表示式
作用面方位
力偶矩矢法线
C LY
系 列 二
工程 力学 力偶系 第三章 三、力偶的解析表示式 选取坐标轴Oxyz,力偶矩矢可表示为:
第二章 汇交力系 工程力学
M = M xi + M y j + M z k
M x,M y,M z 是力偶矩矢在三个坐标轴上的投影。
四、平面力偶
M = Fd
规定:力偶使刚体在作用面内逆时针转动时为正,顺时针转 动时为负。
着矩为 M 1 和 M 2的力偶,而使机构在图示位置处于平衡。 M间 已知OA = r,DB = 2r,α= 30°,不计杆重,试求 M 和 2 1 的关系。
B A A O α FAB
FBA
B
α
M1
M2
D
FO
M1 O
M2
D
解:1)杆AB为二力杆,画杆AO、BD受力图。
C LY
FD
系 列 二
工程 力学 力偶系 第三章 2)分别写出杆AO 和BD 的平衡方程:
M R M1 M 2 M 2 M
C LY
系 列 二
工程 力学 力偶系 第三章 三、力偶系的平衡条件
第二章 汇交力系 工程力学
空间力偶系平衡的充分必要条件是:合力偶矩矢等于零,力偶系 各力偶矩矢的矢量和等于零。
M 0 M
x
M R ( M x ) 2 ( M y ) 2 ( M z ) 2
第 三 章 力 偶 系
工程 力学 力偶系 第三章
第二章 汇交力系 工程力学
一、力偶的概念和工程实例
章节
二、力对点之矩.合力矩定理
三、力偶系及其性质
内容
四、力偶系的合成与平衡
C LY
系 列 二
工程 力学 力偶系 第三章
第二章 汇交力系 工程力学
§3-1 力偶系概念及工程实例
一、工程实例
C LY
系 列 二
( yFz zFy )i ( zFx xFz ) j ( xFy yFx )k
力对点O的矩 MO (F ) 在三个坐标轴上的投影为:
M o ( F ) yFz zFy x
M o ( F ) zFx xFz y
M o ( F ) xFy yFx z
系 列 二
C LY
工程 力学 力偶系 第三章 3. 力对点之矩矢的基本性质
第二章 汇交力系 工程力学
作用于刚体上的二力对刚体产生的绕任一点的转动效应, 可以用该点的一个矩矢来度量,这个矩矢就等于二力分别对该 点矩矢的矢量和,即:
M O M O ( F1 ) M O ( F2 )
也就是说:力对点之矩服从矢量的合成法则。即在一般情况
C LY
系 列 二
工程 力学 力偶系 第三章 五、力对点的矩与力偶矩的区别与联系 相同处:两者量纲相同; 作用效应相同。
第二章 汇交力系 工程力学
不同处:力对点的矩可随矩心的位置改变而改变,但一个力 偶矩是常量。 联 系:力偶中的两个力对任一点的之和是常量,等于力偶
矩。
C LY
系 列 二
工程 力学 力偶系 第三章 六、力偶的等效条件和性质 1. 力偶的等效条件
系 列 二
工程 力学 力偶系 第三章
第二章 汇交力系 工程力学
§3-3
一、力偶矩矢概念
力偶及其性质
平面有一对力偶 ( F , F ) ,将它们对O 点取矩。 根据力对点之矩,力偶对O 之矩为: A
F
M
rBA rA rB F d B rA
rB
M M O ( F ) M O ( F ) rA F rB F M rBA F
七、力偶的表示方法
C LY
M
系 列 二
M
工程 力学 力偶系 第三章
第二章 汇交力系 工程力学
§3.4力偶系的合成与平衡
一、力偶的合成
(F3,F3) 与 (F1,F1) 等效 与(F2,F2)等效 (F4,F4)
F
F1
A F3 rBA
F3
F4
F = F3 + F4 M rBA F
F = F3 + F4
S1
rBA (F3 F4) rBA F3 rBA F4 M1 M 2
二力偶矩矢的矢量和。 即: M M1 M 2
C LY
F1
M1
B F4
M2
S2 F2 F F2 M 2
M1
M
M 为合力偶矩矢。
两个力偶合成的结果得到一个合力偶,合力偶的力偶矩矢等于此
下:
M O M O ( F1 ) M O ( F2 ) M O ( Fn ) M O ( F )
M O M O ( F1 ) M O ( F2 ) M O ( Fn ) M O ( F )
C LY
对于平面力系,则有(代数和):
写出解析的形式,有:
0
M
y
0
M
z
0
即:力偶系各力偶矩矢分别在三个坐标轴投影的代数和为零,称 为力偶系作用下刚体的平衡方程。 平面力偶系作用下刚体的平衡方程:
M 0
即:力偶系各力偶矩的代数和等于零。
C LY
系 列 二
工程 力学 力偶系 第三章
第二章 汇交力系 工程力学
例3-2 图示的铰接四连杆机构OABD,在杆OA 和BD 上分别作用
例3-1:图示梁受到载荷集度为q的均布载荷的作用,求分布载荷的
合力Q及其作用线位置。
解:根据合力投影定理,则合力的 大小为:
x qx q l
Q q( x)dx
0 l l 0
x ql qdx l 2
再根据合力矩定理确定合力的作用线位置。
假设合力Q的作用线距离A点的距离为xC 。
rA F rB ( F ) (rA rB ) F
M称为力偶矩矢,用以衡量力偶对刚体的转动效应。
C LY
O
系 列 二
工程 力学 力偶系 第三章 二、力偶转动效应三要素
第二章 汇交力系 工程力学
力偶矩大小
力偶矩矢长度 力偶 矩矢 三要素
力偶 转动 效应 三要素
转向
力偶矩矢指向
系 列 二
C LY
工程 力学 力偶系 第三章
l x ql ql 2 xC qdx x 0 l 2 3
