3磁介质中的安培环路定理

合集下载

真空状态下和磁介质下安培环路定理

真空状态下和磁介质下安培环路定理1.引言1.1 概述概述部分将对在本文中将要探讨的主题进行简要介绍，并提供一些背景信息。

本文将重点讨论真空状态下和磁介质下的安培环路定理。

安培环路定理是电磁学领域中一个非常重要的定律，它描述了电流在封闭回路中产生的磁场。

这一定律是由法国物理学家安培在19世纪早期提出的，并长期以来一直被广泛应用于电磁学的研究和工程实践中。

在真空状态下，安培环路定理建立了电流和磁场之间的关系。

它表明在任意闭合路径上，通过该路径的磁感应强度的积分等于该路径上所包围的电流的总和乘以真空中的磁导率。

这一定律提供了一种计算磁场分布的重要方法，并被广泛用于电磁设备的设计和电磁场分析中。

然而，当介质被引入到磁场中时，情况变得更加复杂。

磁介质是指具有一定的磁性和导磁性的材料，如铁、镍等。

磁介质的引入会改变磁场的分布，并影响安培环路定理的应用。

因此，本文还将重点讨论磁介质下的安培环路定理及其应用。

通过研究真空状态下和磁介质下的安培环路定理，我们可以更好地理解电流和磁场之间的关系，进一步揭示电磁学的基本原理和规律。

同时，掌握这些理论知识也对于解决电磁学相关问题和开发更高效的电磁设备具有重要意义。

在本文的后续章节中，我们将详细介绍安培环路定理的概念、原理和应用，并探讨真空状态下和磁介质下的安培环路定理的区别和应用场景。

最后，我们将对安培环路定理的重要性和应用前景进行总结和展望。

1.2 文章结构文章结构部分的内容可以包括以下内容：在本篇文章中，我们将重点讨论真空状态下和磁介质下的安培环路定理。

首先，我们将在引言部分对文章的背景和目的进行概述。

接下来的章节中，我们将详细介绍真空状态下的安培环路定理和磁介质下的安培环路定理。

在真空状态下的安培环路定理部分，我们将解释该定理的概念和原理，并讨论其在真空中的应用。

我们将探讨如何应用安培环路定理来计算真空中的电流和磁场之间的关系，以及如何利用该定理解决相关实际问题。

3磁介质中的安培环路定理

单位: T m A-1
在均匀的磁介质
B
（非铁磁质）中
M
磁场强度与磁感
H
应强度成正比，
Is
同向。
Ic
§3.磁介质中安培环路定理 / 三、几个结论
4.结论4
磁介质（非铁磁介质）中，磁化强度与磁场强度具有线性关系。
M
κ m
H
κ 为磁化率。 m
电介质中 P κ 0E
5.结论5
相对磁导率与磁化率之间的关系
§3.磁介质中安培环路定理 / 二、环路定理
H B M
0
H dl Ic
②. H 既与磁感应强度 B 有关，又与磁化
强度 M 有关，所以 H 又是混合物理量。
③.磁场强度的单位与 M 相同，
安培/米，A/m
④.若 H d l 0 不一定环路上各点的
H 为 0，因为 H 是环路内、外电流共同产生的。
R
由螺线管的磁场
r
B
分布可知，管内的场各处均匀一
H
致，管外的场为0；
I
§3.磁介质中安培环路定理 / 四、解题方法
1.介质内部
作 abcda 矩形回路，回路内的传导电流代数和为：
B
a
b
H
d
cI
I c n ab I 在环路上应用介质中的环路定理：
H dl
H dl H dl H dl H dl
第三节
磁介质中的安培环路定理
一、问题的提出
在真空中的安培环路定理中：
B dl 0 I
将其应用在磁介质中时，I为所有电流的
代数和；
B dl 0 (I c I s )
如果求 B
B = Bo + B’

磁介质中的安培环路定理

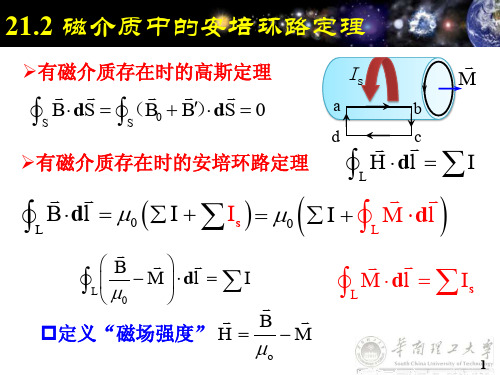
L
L

B M dl I L 0 B M 定义“磁场强度” H

L
M dl I s
o
1
磁化率
实验指出： M m H
均匀的各向同性的磁介质
系数m称为“磁化率”。
H
B
解：

L
H dl I
ab H n ab I
则：H nI
B
a
d
. . .
× × ×
I
b
B o r H nI
c
5
均匀的各向同性的磁介质
2
例题1
一半径为R1的无限长圆柱形直导线，外面包一层半径为R2，相对磁导率为r 的圆筒形磁介质。通过导线的电流为I0 。求磁场强度和磁感应强度的分布。解： 0 r R1 H dl 2π rH
L
r
r
R1
R2
I0
I 2 π r 2 π R1
R1 r R2 r R2
H dl H 2π r I
L
Ir H 2 π R12
B 0 H
0 Ir
2πR12
B 0 H
0 I
2π r
B 0 r H
0 r I
2π r
例题2
有两个半径分别为R1和R2的“无限长”同轴圆筒形导体，在它们之间充以相对磁导率为μr 的磁介质。当两圆筒通有相反方向的电流I时，试求磁感强度。解： d R1 ， B 0 R1 d R2 H dl I
0
M
B

介质中的安培环路定理14.3铁磁质

例1：一无限长螺线管，通以电流I，管内充有相对磁导率为 r的各向同性的均匀介质，若单位长度线圈 B H ，及面磁化电流密度。匝数为n，求介质中的和
解：由于螺线管无限长，故管外磁场为零，管内磁场均匀，B 和 H 与管轴线平行

j M (r 1) H (r 1)nI
j ' 0 即磁化电流和传导电流方向相同顺磁质 r 1 故
r 1 故 j ' 0 即磁化电流和传导电流方向相反抗磁质
例2：长直单芯电缆的芯是一根半径为R 的金属导体，它与外壁之间充满均匀磁介质，电流从芯流过再沿外壁流回。求介质中磁场强度及磁感应强度。
（2）铁磁质在没有传导电流存在时也可以有磁性
这种磁性叫做剩磁（3）一次磁化过程损耗的能量与磁滞回线包围的面积成正比
三、铁磁质的分类
1 按矫顽力HC分软磁材料：磁滞回线窄而长，Br , Hc都小；
硬磁材料：磁滞回线较宽，Br , Hc较大；
B
Hc
Hc
B
Hc
H
Hc
H
作变压器的软磁材料
作永久磁铁的硬磁材料
弱磁质的磁化特点：
B
tg
H
(1) 0为一常数, B-H曲线为一直线, 斜率 tg 0
H (2) B-H曲线具有可逆性， B ; H B ; H 0 B 0
2. 铁磁质的磁化曲线将螺绕环中充满铁磁质: 开始时I=0, H=0, B=0; 然后增大电流 I H 测B
2 按磁滞回线形状分
B
Br
B
Bs
H
-H c
Br
o
Hc

磁介质中的高斯定理和安培环路定理.

B 0(H M ) 0(H mH) 0(1 m)H
在各B向0H同r0H性r H介质r中H10B.rH为m磁相关导对系率磁：B导率。0D r电H介0质rHE中

E
在真空中 r 1, B0 0H
3.明确几点：
①. H 是一辅助物理量，描述磁场的基本物理量仍然
是 B。H是为消除磁化电流的影响而引入的，
B 和H 的名字张冠李戴了。
4

②. H 既与磁感应强度B 有关，又与磁化强度M 有
关，所以H 又是混合物理量。
③.磁场强度的单位与磁化强度相同，安培/米，A/m
④.若 H dl 0不一定环路内无电流。
或由 I s (r 1)I c
求 Is；
9
例1：长直螺线管半径为 R ，通有电流 I，线圈密度为 n , 管内插有半径为 r ,相对磁导率为 r 磁介质，求介质内和管内真空部分的磁感应强度 B 。
解：由螺线管的磁场分布可知，管内的场各处均匀
R
r
a Bb
一致，管外的场为0；
H
1.介质内
10

H dl H dl 0
bc
da
因为 cd 段处在真空中，真
a
B ab H b
空中的 M = 0；B = 0 ，
有 H dl 0
d
c d
Ic
cd H dl

H dl
Hdl cos H dl H ab I c
§12.2 磁介质中的高斯定理和安培环路定理
1
一、磁介质中的高斯定理
磁介质放在磁场中，磁介质受到磁场的作用要产

10.2磁介质中的安培环路定理

s
S
B
B
s
B dS ( Bo B ) dS 0
s s
磁介质中的高斯定理
通过磁场中任一闭合曲面的总磁通量为零
3、磁场强度、磁介质中的安培环路定理

L
B dl 0 ( I 0 I s )
L
M dl I s B dl 0 I 0 0 M dl L L L L L B L ( 0 M ) dl I 0 L
求：环内的磁场强度和磁感应强度
解： H dl H 2r NI L
NI H nI 2r
r
O
B H 0 r H
例2 一无限长载流圆柱体，通有电流I ，设电流 I 均匀分布在整个横截面上。柱体的磁导率为μ，柱外为真空。求：柱内外各区域的磁场强度和磁感应强度。
pm B0 M M pm B0
分子磁矩产生的磁场方向和外磁场方向一致，顺磁质磁化结果，使介质内部磁场增强。
B
B B0
B0
抗磁质及其磁化
分子的固有磁矩为零 pm 0
在外磁场中，抗磁质分子会产生附加磁矩
电子绕核的轨道运动电子本身自旋
外磁场场作用下产生附加磁矩
R
B, r
铁磁质的 r不一定是个常数，它是 H 的函数
B~H r ~ H
H
B
饱和磁感应强度
剩
磁
BS . Br . b
f . HC
a
初始磁化曲线
矫顽力
HS
.
HC . c O
.
HS
磁滞回线

有磁介质的安培环路定律(大学物理下)

(2)硬磁材料——作永久磁铁钨钢，碳钢，铝镍钴合金
B
HC
HC H
矫顽力(Hc)大（>102A/m)，剩磁Br大磁滞回线的面积大，损耗大。
还用于磁电式电表中的永磁铁。耳机中的永久磁铁，永磁扬声器。
(3)矩磁材料——作存储元件
锰镁铁氧体，锂锰铁氧体
B
HC
H
HC
Br=BS ，Hc不大，磁滞回线是矩形。用于记忆元件，当+脉冲产生H>HC使磁芯呈+B态，则–脉冲产生H< – HC使磁芯呈– B态，可做为二进制的两个态。
人有了知识，就会具备各种分析能力，明辨是非的能力。
所以我们要勤恳读书，广泛阅读，古人说“书中自有黄金屋。
”通过阅读科技书籍，我们能丰富知识，培养逻辑思维能力；
通过阅读文学作品，我们能提高文学鉴赏水平，培养文学情趣；
通过阅读报刊，我们能增长见识，扩大自己的知识面。有许多书籍还能培养我们的道德情操，给我们巨大的精神力量，鼓舞我们前进。
2r
O
B H 0r H
例2 一无限长载流圆柱体，通有电流I ，设电流 I
均匀分布在整个横截面上。柱体的相对磁导率μr，柱外为真空。求：柱内外各区域的磁场强度和磁感
应强度。
I
解： r R
LH dl H 2r I
r2 R2 I
Ir
Ir
H 2R2 B 2R2
四、磁化强度
定义: 磁化强度
l
M

pm
V
A m1
Is
S
Is
Is
Is——沿轴线单位长度上的磁化电流（磁化面电流密度）

磁介质中的安培环路定理

磁介质中的安培环路定理
安培环路定理是描述电流在一个闭合环路内的磁场强度的定量关系的定理。

在磁介质中，安培环路定理可以表述为：闭合环路内的磁通量等于环路内电流所产生的磁场强度与环路中磁化强度的代数和。

换句话说，如果我们将一个磁介质的闭合环路划分成若干小段，对每一小段进行磁场分析，然后将它们按照一定的方向按顺序排列，就形成了一个完整的安培环路。

在磁介质中，该安培环路的总磁通量等于环路内任意一个小段上的磁场强度与该小段上的磁化强度的代数和。

这个定理主要用于计算磁介质中的磁场分布及其对电路的影响。

对于任意一个闭合环路，我们都可以通过安培环路定理求得环路内的磁通量，再根据法拉第电磁感应定律计算出环路内的感应电动势，从而分析电路中的电磁现象。

总之，安培环路定理是一种描述磁介质中电流与磁场强度之间关系的基本定理，是电磁学研究中不可或缺的重要工具。

磁介质中安培环路定理 3

例:取一闭合环路L，使其环绕四根载有稳恒电流的导线。
现改变四根导线之间的相对位置，但不越出该闭合环路，则 A 环路L内的∑I不变，L上各点的B一定不变 B 环路L内的∑I不变，L上各点的B可能改变 C 环路L内的∑I改变，L上各点的B一定不变 D 环路L内的∑I改变，L上各点的B可能改变 [
B
]
二、基本概念
1、真空中安培环路定理 B dl 0 I i
2、磁介质中安培环路定理 H dl I i
3、磁介质的介质方程
B 0 r H
4、磁场对载流导线的作用（安培定律）
dF Idl B
5、磁场对载流线圈的作用的磁力矩
(半径为a)和一同轴的导体管(内、外半径分别为b、c) 构成 , 使用时, 电流I从一导
c
a
b
体流出去 , 从另一导体流
回. 设电流都是均匀地分布在导体横截面上。求: 空间各点处磁感应强度大小的分布。
解: 根据安培环路定理 l B dl 0 I
1） r<a 2)

4) r>c
0 I c 2 r 2 B 2r c 2 b 2
I I I 0
B0
例7 一无限长圆柱形铜导体（磁导率0），半径为R，通有均匀分布的电流I，导体外充满相对磁导率r的磁介质。今有一矩形平面S（长1m，宽2R），位置如右图中画斜线部分所示，求通过该矩形平面的磁通量. 解： r R : B 0 Ir 1 2
0 r I r R : B2 2r
0
I
2R

2R
0 R
R 2R B dS B1 dS B2 dS

磁介质的磁化和介质中的安培环路定理简化

定义：沿磁介质轴线方向上单位长度的磁化电流称为磁化电流密度 js 。
js
Is L
结论1：磁化强度大小数值上等于磁化电流密度。
普遍情况下可以证明：
M js js M nˆ
微分关系
束缚电流线密度的大小等于磁化强度的切向分量。
电介质有
' P nˆ
束缚电荷面密度的大小等于电极化强度的法向分量。
有磁介质时的磁场
磁畴图象
1
一、磁介质对磁场的影响
什么是磁介质？能够影响磁场分布的物质。
现在将一个长螺线管通电流 I，内部造成一个均匀磁场,再将磁介质充满磁场（保持电流不变）。
发现磁介质中的磁场：
B B0 B
B B0 B
传导电流 I B0
I 长直密绕螺线管
磁介质上有磁化电流，
4
一般由于分子的热运动, 但是在外磁场中，
完全是混乱的,
m 分 m 会发生转向而排列，
分
这就是顺磁质被“磁化”。
外磁场越强，转向排列越整齐。
顺磁质内部的各分子等效磁矩有一定程度的排列，分子等效电流 i 使
m分
S
顺磁质内部的磁场加强；
而且顺磁质会被磁铁吸引。
N S
不显磁性。
m分
N i
抗磁质
( B
0 I 0
L M ) dl
M dl
L
I
L 0
L
• 定义：磁场强B度
H M
0
12
(
B
M ) dl
I
L
0
L
H dl I
•
定义：磁场强度
H
B
M
0
L
磁介质中的环路定理

12-2 磁介质中的安培环路定理

§12-2 磁介质中的安培环路定理
一、安培环路定理
在磁介质中,安培环路定理应写为式中, Io内和 I´内分别是闭合路径l所包围的传导电流和磁化电流的代数和。由于:
l
I ) ( I B dl 内 o o 内
l
M dl I
l
内
(
B
o
M ) dl I o内

a
H
P
•
B b
c
L H dr ab H dr Hl
环路定理
d
l
nlI
B H 0 r nI
H nI
dI d r 1 H j M d r M dr dr
I I o·a · c ·b
I c I b
a
上页
下页
解由安培环路定理:
H dl I
l
o内
I
o内
2r I H dl H· I 及 B= H H
l
o内
r<a:
I 2 r 2 Ir a H= 2 2 a 2r o Ir B o H 2 2a
在国际单位制中,磁场强度的单位为安/米(A/m)。
上页下页
例1 一根长直同轴线由半径 a的长导线和套在它外面的内半径为b、外半径为c的同轴导体圆筒组成。中间充满磁导率为的各向同性均匀非铁磁绝缘材料,如图所示。由圆筒向下流回,设电流在截面上都是均匀分布的。求同轴线内外的磁场强度H和磁感应强度B的分布。
2r
I r I o· · a r· c b
r c:H

磁介质中的安培环路定理

产生磁场：

I
Bdl o I o I
有磁介质
B
C
的总场传导电流分布电流
分子磁矩 m I 'π r 2
A LD
n（单位体积分子磁矩数）
I n π r2LI ' nmL
M m nm
V
I ML BC M dl
I'
r
Cr
l M dl l B dl 0 ( I l M dl )
第二节磁介质中的安培环路定理磁场强度
一、有介质时的高斯定理
介质中的磁感应强度：
B B外 B
无论是什么电流激发的磁场，其磁力线均是无头
无尾的闭合曲线。
∴ 通过磁场中任意闭合曲面的磁通量为零。

即： BdS 0
二、有介质时的安培环路定理
在有介质的空间，传导电流与磁化电流共同
例：长直螺线管ห้องสมุดไป่ตู้充满均匀磁介质r单位长度上
的匝数为n，通有电流I 。求管内的磁感应强度。
解：管外磁场为零，取图示的回路
L H dl Ii
L
ab H n ab I
B
I
...
则：H nI
B or H nI
B
a
b
× × × ×M
d c nˆ
相对磁导率 r 1 磁导率 0r
1 顺磁质
r 1 抗磁质
1 铁磁质
（非常数）
各向同性磁介质

B 0r H H
H和 B的区别： B是描述磁场作为物质与其它物质交换动量的物理量；
H是描述磁场能量传输的物理量；

磁介质中安培环路定理

5）求出Fx Fx dF sin
b I2
力的方向向右
(1)Fx
dF sin
0
0I1I2 sin Rd 0 2R sin
0I1I2
2
(2)Fx
2
dF sin
0
2 0I1I2 sin Rd 0 2R sin
0I1I2
AB C
dFA
3106 N / cm
___________,
dFB
_____0_______,
dl
dl
dFC _3__1_0__6_N__/_c_m.
dl
(0 4 107 )
IA
IB
IC
dFA I ABAdl
BA
BAB
BCA
0IB 2d
0IC 2 2d
dd
dFA 30I 2 dl 4d
4) r>c
I I I 0
B0
例7 一无限长圆柱形铜导体（磁导率0），半径为R，通有均匀分布的电流I，导体外充满相对磁导率r的磁
介质。今有一矩形平面S（长1m，宽2R），位置如右图中画斜线部分所示，求通过该矩形平面的磁通量.
解：
r
R
:
B1
0 Ir 2R 2
r
R
:
B2
0r I 2r
2R R 2R
0I 0I 30 I
H dl
I I 3I
例4 如图，电荷q (>0)均匀地分布在一个半径为R的薄球壳外表面上，若球壳以恒角速度 0绕Z轴转动，则沿着Z轴从-到+ 磁感应强度的线积分
q00
B dl ___2___
B dl
B dl
L

物理学下磁介质中的安培环路定理

未来研究方向和挑战
复杂磁场下的安培环路定理研究
在实际应用中，磁场往往是非常复杂的，如何准确描述和计算复杂磁场下的安培环路定理是一个重要的研究方向。
磁化电流的精确测量和控制
磁化电流是磁介质磁化程度的量度，如何精确测量和控制磁化电流对于理解和应用安培环路定理具有重要意义。
新型磁材料的开发和应用
随着科技的发展，新型磁材料不断涌现，如何将这些新型磁材料应用于安培环路定理中，发挥其独特优势，是一个具有挑战性的课题。
磁介质性质
磁介质具有磁化性，即在外磁场作用下，磁介质内部会产生附加磁场，使原磁场发生变化。
磁化现象与磁化强度
磁化现象
磁介质在外磁场作用下，其内部磁偶极子会重新排列，产生附加磁场，这种现象称为磁化。
磁化强度
磁化强度是描述磁介质磁化程度的物理量，表示单位体积内磁偶极子的磁矩矢量和。
分类及特点分析
磁感应强度B描述了磁场对磁介质的作用力大小，而磁场强度H则描述了磁场的源强度。
边界条件对磁场分布影响分析
在两种不同磁介质的分界面上，磁场的切向分量连续，即磁场线
与分界面平行。
磁场的法向分量在分界面两侧会发生跃变，跃变的大小与两种磁
介质的磁导率差异有关。
边界条件对磁场分布的影响可以通过麦克斯韦方程组中的边界条
变压器工作原理简述
变压器基本结构
由铁芯和线圈组成，通过电磁感应实现电压变换。
工作原理
当原线圈中通入交流电时，会在铁芯中产生交变磁场，进而在副线圈中感应出电动势。安培环路定理可用于分析变压器中的磁场分布和漏磁现象。
其他电磁设备设计优化方向
电磁铁
利用安培环路定理分析电磁铁的磁场分布和吸力特性，优化

04磁介质的磁化和介质中的安培环路定理

解：由螺线管的磁场分布可知，管内的场各处均匀
R
r
a Bb
一致，管外的场为零；
H
1、介质内部
作 abcda 矩形回路。
d Ic
回路内的传导电流代数和为： I c n ab I
在环路上应用介质中的环路定理：

H dl H dl H dl H dl H dl
有半径为 R2的无限长同轴圆柱面，该面也通有电流 I，
圆柱面外为真空，在R1<r<R2区域内，充满相对介质常数为 r2的磁介质，且r2 >r1。求B和 H的分布?
解：根据轴对称性，以轴上一点为圆心在
垂直于轴的平面内取圆为安培回路：
r R1
H1
2rH1
I
2R12

I
R12
磁介质的磁化磁介质中的高斯定理和安培环路定理
1
一、磁介质的磁化现象
凡是能与磁场发生相互作用的物质叫磁介质。
磁场中放入磁介质
磁介质发生磁化
出现磁化电流
产生附加磁场

磁介质内部的总场强 B B0 B
在各向同性均匀介质中：
r 称为相对磁导率。
B内

r B0
磁介质的分类：
介质中的磁感应强度是真空
美国在磁谱仪中，将采用超导磁铁产生强磁场，
2003 年再次送入地球轨道，观察暗物质和反物质。
高温超导现已达到 -153°C。
11
L

对各B向同性的磁介质
dl
L 0r
I0内

B r B0
B
定义:磁场强度
H
0r

08磁介质的磁化和介质中的安培环路定理

0
磁力线为闭合曲线，磁力线为闭合曲线，穿过任何一个闭合曲面的磁通量为零。磁通量为零。
v v B⋅ dS = 0 ∫
s
三、磁介质中的安培环路定理 1、磁介质中的安培环路定理
r r 在真空中的安培环路定理中：在真空中的安培环路定理中： B0 ⋅ dl = µ 0 ∑ I ∫
3
r r 在介质中：在介质中： ∫ B ⋅ dl = µ 0 ∑ ( I + I ′)
磁介质的磁化磁介质中的高斯定理和安培环路定理
1
一、磁介质的磁化现象凡是能与磁场发生相互作用的物质叫磁介质。凡是能与磁场发生相互作用的物质叫磁介质。磁场中放入磁介质磁介质发生磁化产生附加磁场 r r r 磁介质内部的总场强 B = B0 + B′ 出现磁化电流
r r r B 在各向同性均匀介质中：在各向同性均匀介质中： B = µ r B0 即 r = µ r B0
H = nI
H = nI 真空中 µ = 1 ∴ B = µ 0 H = µ 0 nI
8
r r r r H ⋅ dl = ∫da H ⋅ dl = 0
a
B
∴ H ab = ∑ I c = n abI ,
∴ B = µ 0 µ r H = µ 0 µ r nI
2、管内真空中、作环路 abcda ; 在环路上应用介质中的安培环路定理，同理有：质中的安培环路定理，同理有：
4
r r H ⋅ dl = ∑I ∫
L L
r r H ⋅ dl = ∑I ∫
L L
----磁介质中的环路定理磁介质中的环路定理
物理意义：磁场强度沿闭合路径的线积分，物理意义：磁场强度沿闭合路径的线积分，等于环路所包围的传导电流的代数和。所包围的传导电流的代数和。 2、明确几点：明确几点：