64磁场的安培环路定理
合集下载
磁场的安培环路定理
电荷均匀分布
E
2 0r
E0
E
2 0r
E
r 2 0 R2
E 2 0r
电流均匀分布
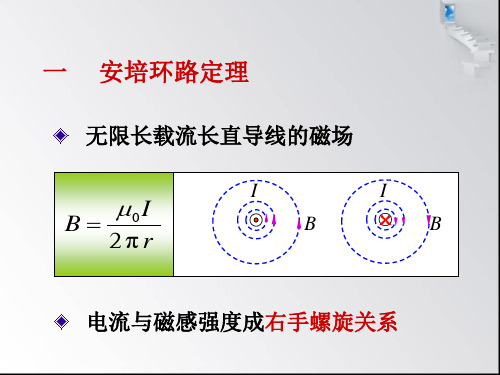
B 0I 2r
B0
B 0I 2r
B
0 Ir 2R 2
B 0I 2r
(16)磁场的安培环路定理 （2）面对称
无限大载流导体薄板
I
已知：导线中电流强度 I
单位长度
位置移动
I1 I2
I4
I3
l
不变
? B dl 0 Ii 0 ( I2 I3 )
? 改变
?
不变
(16)磁场的安培环路定理
注意3
安培环路定理
n
B dl 0 Ii
i 1
当电流呈体分布时 B dl 0 S j dS
闭合路径包围的电流为电流
导线匝数n
解：分析对称性
磁力线如图 作积分回路如图
ab、cd与导体板等距
dB
ba
.........
cd
(16)磁场的安培环路定理
计B算 d环l 流abBdl cos 0
c
b
Bdl
cos
2
cd Bdl cos 0
da
Bdl
cos
2
B ab B cd
2B ab
l
B B1 B2 B3
Bdl
l
0 (I 2
I3)
【总结】以上结果对任意 形状的闭合电流（伸向无 限远的电流）均成立.
安培环路定理
安培环路定理
I )=0
二、 环路定理的应用
1. 载流长直螺线管内的磁场
. . . . . . . . . . . . . a d b c B
∫ l B. dl = ∫abB . dl + ∫bc B . dl + ∫cd B . dl+ ∫daB . dl = ∫abB . dl + 0 + 0 + 0 = ∫abB dl cos 0
由几何关系得： 由几何关系得：
L
O
r dϕ = dl cos θ µoI B= 2 r π
.
I r dl
dϕ
P
r B
θ
r dl
∫ l B . dl = ∫l B cosθ
=
∫l B r dϕ
µoI µoI r dϕ = 2 π 2π r
=∫
∫0
2 π
d ϕ =µ o I
安培环路定理： 安培环路定理：磁感应强度矢量沿任意闭合 路径一周的线积分等于真空磁导率乘以穿过 穿过闭合 路径一周的线积分等于真空磁导率乘以穿过闭合 路径所包围面积的电流代数和 电流代数和。 路径所包围面积的电流代数和。
∫ l B . dl =µ Σ I
o
电流和回路绕行方向 构成右旋关系的取正值
电流 I 取负值 I
向 方 绕 行
I
向 行方
绕
I2
I1
I I
l2
I
l3
l1
(a) (a)
(b)
1
(b)
(c)
o
∫l B . dl = µ
∫l B . dl = 0
2
(I 1 I 2 )
(c)
∫l B . dl = µ
大学物理-磁场 安培环路定律
Φ BS cos BS
s
一般情况 Φ s BdS
dS2
B
S 2
dS1
1
B1
dΦ1 B1 dS1 0
dΦ2 B2 dS2 0
B2
SB cosdS 0
磁场高斯定理
S B d S 0
物理意义：通过任意闭合曲面的磁通
量必等于零（故磁场是无源的）.
B B1 B2 B3
Bdl
l
0(I2 I3)
推广：
➢ 安培环路定理
n
B dl 0 Ii
i 1
n
安培环路定理
B dl 0 Ii
i 1
在真空的恒定磁场中，磁感强度 B沿任
一闭合路径的积分的值，等于 0乘以该闭合
路径所穿过的各电流的代数和.
注意
电流 I 正负的规定： I 与 L 成右螺旋
而与环路外电流无关。
3. B为环路上一点的磁感应强度，它与环路内外电流
都有关。
若
B
dl
0
并不一定说明环路上各点的 B 都为 0。
若 B dl 0 环路内并不一定无电流。
4.环路定理只适用于闭合电流或无限电流，
应用 安培环路定理的应用举例
例1
求载流螺绕环内的磁场
解 （1）对称性分析：环内B 线为同心
B dl B 2r 0 I
B 0 I 1 2r r
I
r LR
r L
分布曲线
B
0 I 2R B r
B 1 r
o
R
r
例4 无限大均匀带电(线密度为i)平面的磁场
解 如图，作安培环路
abcda，应用安培环路 定理
b
l B d l 2a B dl
安培环路定理
B 0 jd / 2 B 0 jx
dj
例 求密绕螺绕环电流的磁场分布及螺绕环内的B 。
解 B外 0
• 在螺绕环内部做一个环路，可得
LBdl LBdl BLdl
I
Nr o
B 2r 0NI
B 0NI
2 r
例 无限长密绕载流直螺线管 a
b
单位长度线圈匝数
I内
恒定电流的磁场中，磁感应强度沿一闭合路径 L 的线积分
等于路径 L 包围的电流强度的代数和的 0 倍
讨论 (1)磁场是有旋场
I1
I2
I3
(2)电流方向与积分回路方向呈右螺
旋关系 I >0 ；反之 I < 0
B dl L
0 (I1 I3)
(3) 安培环路定理只适用于闭合的载流导线，对于任意设想
2r
dl
dI ' dB
o
r
r
dB' P
圆柱体内 (r R)
dI
I
I R 2
r 2
B
0I
2R 2
r
B B dl Bdl
二、 安培环路定理的应用
例 求无限长圆柱体电流的磁场分布。 解 电流分布具有轴对称性，故磁场分
布也是轴对称的
LB dl LBdl BLdl
B1 dl1 B2 dl2
0I d 0I d
2
2
0
LB dl 0
电流在环路以外时，它对磁场的环流没有贡献
一、磁场的安培环路定理
1. 积分环路在垂直平面内 2. 积分环路不平行垂直平面
6-4 磁场中的高斯定理与安培环路定理
试求通过与导线共面的矩形线圈的磁通量Φm 。
解 先求 B ；对非均匀磁场
B
ab
应给出dΦm后再积分求 Φm
I
l
B 0I
2π x
B // S
Φm
SB dS
0Il
2π
ab
a
dx x
o x dx
x
Φm
0Il
2π
ln
a
b a
6 – 4 磁场的高斯定理与安培环路定理 第六章 恒定电流的磁场
三 安培环路定理（真空中）
I
dI dB
B
6 – 4 磁场的高斯定理与安培环路定理 第六章 恒定电流的磁场
B 的方向与 I 成右螺旋
0 r R,
B
0Ir
2π R2
r R,
B 0I
2π r
I
0I B
2π R
R
oR r
6 – 4 磁场的高斯定理与安培环路定理 第六章 恒定电流的磁场
例2 无限长载流圆柱面的磁场
L1
r
IR
0I
2π r2
B1
dl1
B2
dl2
0I
2π
d
B1 dl1 B2 dl2 0
l B d l 0
6 – 4 磁场的高斯定理与安培环路定理 第六章 恒定电流的磁场
多电流情况
I1
I2Leabharlann I3lB B1 B2 B3
Bdl
l
0 (I 2
I3)
以上结果对任意形状 的闭合电流和伸向无限远 的电流均成立。
o
R
dl
l
l
Bdl
0I
2π
2π
安培环路定理
(1)管内:取L矩形回路 abcda
边在轴上，两边与轴平行,另
aP b
两个边垂直于轴。
LB dl Bab ab Bcd cd Bab ab
e
Q
f
0I 0nI ab
d
c
∞
B内 onI 其方向与电流满足右手螺旋.
(2)管外 :
取回路efbae同理可证，无限长直螺线管外任一点的磁场为
A(rQ )
0I 2
ln
r Q
r P
A(rP )
A(rQ
)
0I 2
ln
r Q
r
-I
r P
P
两式相加,得:
A(rP )
A(rQ )
0I 2
ln
rQ rP
rP rQ
0I 2
ln
rP rP
A(rP )
A(rQ )
0I 2
ln
r P
r P
若选Q点的矢势为零,则
A(rP )
0I 2
ln
r P
r P
例2.一无限长载流圆柱导体,半径为R, 电流I均匀分布
ldr
0I 2
l
ln
rQ r
A(rP ) A(rQ )
0I 2
ln
rQ rP
+I
Q
若选Q点的矢势为零,则
A(rp
)
0I 2
ln
rQ rP
r P
注意:若选Q点在无穷远处或导线
上,磁矢势将无意义.
讨论:两根平行的载流直导线,电流大 小相等方向相反,求磁矢势.
选Q点在两直线电流之间垂线的中点处.
A(rP )
B dS 0
第二十讲：§6.4磁场的安培环路定律
第二十讲： §6.4磁场的安培环路定理一、安培环路定理；是磁场与电流之间相互作用的基本定律之一 1、表述：在稳恒磁场中，B 沿任意闭合回路的积分等于该闭合回路所包围的电流的代数和乘以0μ 。
2、表达式：∑⎰=⋅iI d B 0μ两点说明：①∑i I 虽是闭合回路内所环绕的电流，且满足右手螺旋法则。
但是B 是与闭合回路内外电流有关，即B 是闭合回路内外电流共同作用的结果。
环路外的电流对 d B L ⋅⎰无贡献。
②当B 无对称性时，安培环路定理仍成立，只是B 不能提到积分号外面来，所以，利用安培环路定理不能求解B ，必须利用比-萨定律及叠加原理来进行求解。
二、安培环路定理的应用1、无限长圆柱载流导体的磁场分布∑⎰=⋅iI d B 0μR r ：20122122RIr B r RIr B πμππμπ=⇒=⋅Rr ：rI B I rB πμμπ220202=⇒=⋅☆如果是无限长圆面载流导体的磁场分布∑⎰=⋅iI d B 0μR r ：00211=⇒=⋅B r B πRr ：rI B I rB πμμπ220202=⇒=⋅2、长直载流螺线管内的磁场分布∑⎰=⋅iI d B 0μd B d B d B d B d addccbba⋅+⋅+⋅+⋅=⋅⎰⎰⎰⎰⎰BnIB I ab n ab B abd B 00B μμ=⇒=⇒=⋅⎰电流数密度：单位长度的电流数。
3、载流环形螺线管内的磁场分布∑⎰=⋅iI d B 0μr 2B d B Lπ==⋅⎰⎰d BnII rN B NI r 00022B μπμμπ==⇒=小结：磁场的安培环路定理 作业：P253预习：§6.5 磁场对运动电荷和载流导线的作用第二十讲： §6.4磁场的安培环路定理 作业：P2536-15 （1）a r <，由安培环路定理可得201220122aIrB raI r B πμππμπ==（2）b r a <<rIB Ir B πμμπ220202==（3）c r b <<)(2)()()(222220302222222203b c r r c I B I b c rc b c b r I I r B --=--=⎥⎦⎤⎢⎣⎡---=πμμππμπ（4）0,4=>B c r6-16 （1）如图示，过P 点作一半径为r 的圆形回路，圆心为O ，由安培环路定律可得 rNIB NI u r B πμπ2,200==故绕线环内磁感强度B 的大小与径向距离r 成反比。
磁场的高斯定理和安培环路定理
. . . . . . . . ..
第4节
. . . .. . .. B . ∮H ·dl = 2rH = NI . . . . . H = NI/2r， r . . . . R 1 . . B = o NI/2r . . R 2 . . .. . 环管截面 r R， . .. . . ... B o NI/2R = o n I 解：1、环管内：
第八章
I
R
r B
R
r
第4节
第八章
直线电流的磁力线
I
I B
第4节
例8-5 求通电螺绕环的磁场分布。设环管 的轴线半径为 R，环上均匀密绕 N 匝线圈， 线圈中通有电流 I，管内磁导率为 o 。
第八章
I
I
. . . . . . ..
. . . .. . .. . . R1 R2
..
. . . ...
第八章
第4节
第八章
通电螺线管的模型
I
第4节
思考题： 如果通电螺线管的磁力线如下所示，图 中环路积分 ∮H ·dl = ？
第八章
I
L
I
二、磁场的安培环路定理 1、真空中 根据闭合电流产生的磁场公式，即安 培 — 拉普拉氏定律，可证明真空中磁场 B 沿闭合回路 L 的积分，即环流为： ∮L B ·dl =μoΣI 此式称为真空中磁场的安培环流定理，式 中ΣI 是闭合回路 L 所包围的所有闭合电流 I 的代数和。 物理意义：磁场 B 是有旋场，非保守场
第八章
I
R
o dS
B
Io
r
第4节
2、r＞R ∮H ·dl =∮H dl = 2rH ΣIo = I H = I /2r ，B = oI /2r 上式表明，从导线外部看， 磁场分布与全部电流 I 集中 在轴线上相同。 μ I B H 2 πR I μ 0I 2 R π 2 πR 0 r 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
无限长直载流圆柱 面的磁场？
例1．求无限长载流导体圆管(内外半径为R1, R2、电流I )的磁场。
解：电流分布——轴对称 产生的磁场——轴对称
r< R1
过场点作安培环路
B d l B cos 0d l =B2r =0
L
L
B=0
P•2
×
P•3
P•1
R1<r< R2 B d l =B2r L
•
•• ••
•• •
• •
B 圆柱外的
磁场分布 是以中心 轴线为轴 的对称分 布。
圆柱内：
I
•• ••
••••••••••••
•• • •• •• • ••
• • • •
• ••
• •• •
•• •• • r• •
••
•• • ••
•
•• •
••
•• •• •
圆柱内的磁场分布 也是以中心轴线为 轴的对称分布。
dal
L
AC
BlAC
B
CD
d Bb
dld
BB
DEb
d
l
0dBBalDE 0 0
I
Bdl
EA
n lACI
B
1 2
0nI
d
B
证毕！
D
P•
E
B dl
L
0
Ii
C
A
互动题：在以下四个环路的环流 B d l ? L
l1
I
I2
I1
l2
B dl
L
0
Ii
l3
I1 •
I2
l4
§6. 4 磁场的安培环路定理
B d l ——磁场的环流
一．安培环路定理
L
=?
1．环路包围电流 I
Bdl
B cos
dl
Br d
0I d 2
d
B
L
d
l
0I 2
2
d
0
= 0 I
与回电路流形状 有关吗？
B = —0—I
2r
dl
B
r
I L
(俯视图)
结果表明：
①
B
的环流与闭合曲线的选取无关，
B=0 —2N—r I =0nI
l
•• •
•
•
• •
•
•
•••
B dl
L
0
Ii
例4：有一导体，由“无限多”根平行排列的细导线组成，每根
导线都“无限长”且均通以电流 I 。设单位长度上的导线数目为
n ，求证：这无限长的电流片各处的磁感强度B：
证明： 分析磁场分布：
1 2
0nI
过场点取图B示 d回l路。B
LB d l ?
d
I
= —20—Ir1 r1d = —2—0I d B2 d l2 =B2cos2dl2 =B2[cos(2)]dl2
= —2—0rI2( r2d) = —20—I d
LB d l ?0
环路外的I ，对环流值无贡献！
r1 dl1 r2 A
2 dl2
1
L
B2
B1
C
对环路上的磁场 ？？ 有贡献！
••
B=0nI
(6-29)
与场点的位置无关。管内中部附近均可看成匀强磁场。
另一种回路的取法： 结论相同。
B dl
L
0
Ii
例3．P185 载流螺绕环内的磁场 I，N 匝密绕
解：分作析半：径为 r 的安培环路L
B d l =B2r= 0 NI
L
B= —20—NrI
当R<<l 时， 管内2r近似不变！ 2r 约等于螺绕环的长度。
使用定理时：①分析磁场分布的对称性。
由 那 ②电些求流点L分的B布dBl的大及对小称相Ii 性等③。利再判用选断取L各B适点d当l的的B安0 方培向I回i 、路B。
EdS
S
q内
0
I 分析无限长直载流导体圆柱的磁场分布
圆柱外
R
• ••
• • •• •
r •• •• • • • •
r
••
•• • ••
推论：设回路内、外有若干根载流导线
B
L
d
l LB?L
(dBl1
0
BnI
i
B外
)
d(6l -24)
I1
在真空中的稳恒磁场中，磁感应强度 B沿任
l
I外
… In
意闭合曲线的积分(环流)，等于该闭合曲线所环
绕(包围)的各电流的代数和的0倍。 P183
EdS
S
q内
0
说明：① 式中各量的含义：
B
L
cos
d
l
0
Ii
若找到一合适回路，其满足：LB d l 0
Ii
B cos
dl
L
0
Ii
B
要求环路 ：
1)其上的 B大小相等、方向与
0 Ii cos Ld l
d l平行；
B大小不等时，方向与d
l垂直；
对任意稳恒磁场
均成立，但只能
求对称性很高的
磁场 I
cos =1、1、0
2) 环路的长度便于计算； 3) 环路上的B为所求。
I
I
只与闭合曲线包围的电流有关。
？②若I 的绕正行负方由向回反路转L，的 绕行方向L决B 定d l ： 0 (I )
I 的流向与 L 的绕向成右手螺旋关系：
为正(I >0)； 反之为负(I<0)。
I >0
I<0
2．环路不包围电流
AC，l1 CA，l2
B1 d l1 =B1cos1dl1 =B1r1d
r
Ii
例2．求载流长直螺线管内
R
的磁场。
设：长l , N 匝密绕，通电 I；
l>>R , (通常l>20R) n =N/l 解：分过析场：点取图示回路。
•••
l ••••••••
•••
b c
Bdl Bdl Bdl
L
a d
Bdl
b
a Bdl
c
d
R
a
d
P•
b
c
B
B ab 0(n ab I)
0
I (R22
R12 )
(r 2
R12 )
B
0I
(r 2 R12 )
2 (R22 R12 )
r
0I 2R22
r
(6-27)
讨论：无限长圆柱？俯视R1图=0
B
B
r>R2
好象
I
都L集BB=中d l—在=2—B0轴rI2线r上=产(60生-I2的6) 磁场0似无的限r R长2 圆柱—1r 面r ？0LRB1=dRRl2=R—01r
B～环路上各点的磁感强度。由环路内、外电流共同产生。
n
Ii～穿过环路内 的电流的代数和。注意 I 的正负的确定方法。
i1
② 定理只对稳恒电流成立。
③
定理的意义：
(a) (b)
揭示了磁场的性质——非保守场。 提供了一种计算磁场(磁分力布为的非方保法守。力)
由(6-24)，已知 I 分布 B。
二．安培环路定理的应用
例1．求无限长载流导体圆管(内外半径为R1, R2、电流I )的磁场。
解：电流分布——轴对称 产生的磁场——轴对称
r< R1
过场点作安培环路
B d l B cos 0d l =B2r =0
L
L
B=0
P•2
×
P•3
P•1
R1<r< R2 B d l =B2r L
•
•• ••
•• •
• •
B 圆柱外的
磁场分布 是以中心 轴线为轴 的对称分 布。
圆柱内：
I
•• ••
••••••••••••
•• • •• •• • ••
• • • •
• ••
• •• •
•• •• • r• •
••
•• • ••
•
•• •
••
•• •• •
圆柱内的磁场分布 也是以中心轴线为 轴的对称分布。
dal
L
AC
BlAC
B
CD
d Bb
dld
BB
DEb
d
l
0dBBalDE 0 0
I
Bdl
EA
n lACI
B
1 2
0nI
d
B
证毕！
D
P•
E
B dl
L
0
Ii
C
A
互动题：在以下四个环路的环流 B d l ? L
l1
I
I2
I1
l2
B dl
L
0
Ii
l3
I1 •
I2
l4
§6. 4 磁场的安培环路定理
B d l ——磁场的环流
一．安培环路定理
L
=?
1．环路包围电流 I
Bdl
B cos
dl
Br d
0I d 2
d
B
L
d
l
0I 2
2
d
0
= 0 I
与回电路流形状 有关吗？
B = —0—I
2r
dl
B
r
I L
(俯视图)
结果表明：
①
B
的环流与闭合曲线的选取无关，
B=0 —2N—r I =0nI
l
•• •
•
•
• •
•
•
•••
B dl
L
0
Ii
例4：有一导体，由“无限多”根平行排列的细导线组成，每根
导线都“无限长”且均通以电流 I 。设单位长度上的导线数目为
n ，求证：这无限长的电流片各处的磁感强度B：
证明： 分析磁场分布：
1 2
0nI
过场点取图B示 d回l路。B
LB d l ?
d
I
= —20—Ir1 r1d = —2—0I d B2 d l2 =B2cos2dl2 =B2[cos(2)]dl2
= —2—0rI2( r2d) = —20—I d
LB d l ?0
环路外的I ，对环流值无贡献！
r1 dl1 r2 A
2 dl2
1
L
B2
B1
C
对环路上的磁场 ？？ 有贡献！
••
B=0nI
(6-29)
与场点的位置无关。管内中部附近均可看成匀强磁场。
另一种回路的取法： 结论相同。
B dl
L
0
Ii
例3．P185 载流螺绕环内的磁场 I，N 匝密绕
解：分作析半：径为 r 的安培环路L
B d l =B2r= 0 NI
L
B= —20—NrI
当R<<l 时， 管内2r近似不变！ 2r 约等于螺绕环的长度。
使用定理时：①分析磁场分布的对称性。
由 那 ②电些求流点L分的B布dBl的大及对小称相Ii 性等③。利再判用选断取L各B适点d当l的的B安0 方培向I回i 、路B。
EdS
S
q内
0
I 分析无限长直载流导体圆柱的磁场分布
圆柱外
R
• ••
• • •• •
r •• •• • • • •
r
••
•• • ••
推论：设回路内、外有若干根载流导线
B
L
d
l LB?L
(dBl1
0
BnI
i
B外
)
d(6l -24)
I1
在真空中的稳恒磁场中，磁感应强度 B沿任
l
I外
… In
意闭合曲线的积分(环流)，等于该闭合曲线所环
绕(包围)的各电流的代数和的0倍。 P183
EdS
S
q内
0
说明：① 式中各量的含义：
B
L
cos
d
l
0
Ii
若找到一合适回路，其满足：LB d l 0
Ii
B cos
dl
L
0
Ii
B
要求环路 ：
1)其上的 B大小相等、方向与
0 Ii cos Ld l
d l平行；
B大小不等时，方向与d
l垂直；
对任意稳恒磁场
均成立，但只能
求对称性很高的
磁场 I
cos =1、1、0
2) 环路的长度便于计算； 3) 环路上的B为所求。
I
I
只与闭合曲线包围的电流有关。
？②若I 的绕正行负方由向回反路转L，的 绕行方向L决B 定d l ： 0 (I )
I 的流向与 L 的绕向成右手螺旋关系：
为正(I >0)； 反之为负(I<0)。
I >0
I<0
2．环路不包围电流
AC，l1 CA，l2
B1 d l1 =B1cos1dl1 =B1r1d
r
Ii
例2．求载流长直螺线管内
R
的磁场。
设：长l , N 匝密绕，通电 I；
l>>R , (通常l>20R) n =N/l 解：分过析场：点取图示回路。
•••
l ••••••••
•••
b c
Bdl Bdl Bdl
L
a d
Bdl
b
a Bdl
c
d
R
a
d
P•
b
c
B
B ab 0(n ab I)
0
I (R22
R12 )
(r 2
R12 )
B
0I
(r 2 R12 )
2 (R22 R12 )
r
0I 2R22
r
(6-27)
讨论：无限长圆柱？俯视R1图=0
B
B
r>R2
好象
I
都L集BB=中d l—在=2—B0轴rI2线r上=产(60生-I2的6) 磁场0似无的限r R长2 圆柱—1r 面r ？0LRB1=dRRl2=R—01r
B～环路上各点的磁感强度。由环路内、外电流共同产生。
n
Ii～穿过环路内 的电流的代数和。注意 I 的正负的确定方法。
i1
② 定理只对稳恒电流成立。
③
定理的意义：
(a) (b)
揭示了磁场的性质——非保守场。 提供了一种计算磁场(磁分力布为的非方保法守。力)
由(6-24)，已知 I 分布 B。
二．安培环路定理的应用