2012考研《数学二》大纲文字版
(整理)-2012考研数学二考纲对比.
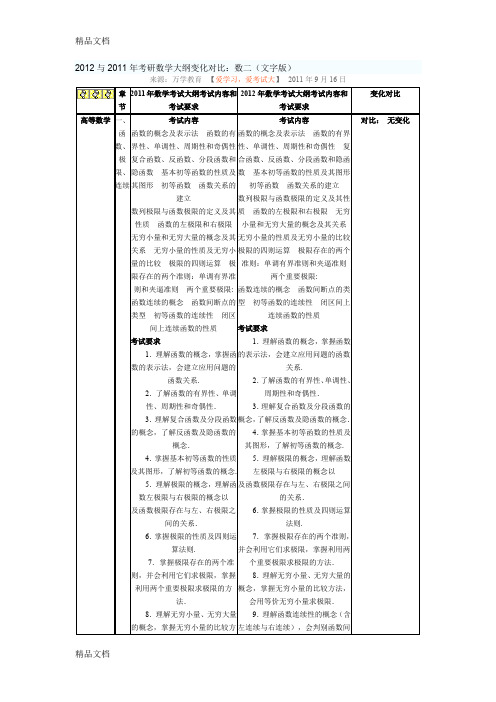
2012与2011年考研数学大纲变化对比:数二(文字版)来源:万学教育 【爱学习,爱考试大】 2011年9月16日章节 2011年数学考试大纲考试内容和考试要求 2012年数学考试大纲考试内容和考试要求变化对比 高等数学 一、函数、极限、连续 考试内容 函数的概念及表示法 函数的有界性、单调性、周期性和奇偶性 复合函数、反函数、分段函数和隐函数 基本初等函数的性质及其图形 初等函数 函数关系的建立 数列极限与函数极限的定义及其性质 函数的左极限和右极限 无穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则 两个重要极限: 函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性. 3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法. 8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方考试内容 函数的概念及表示法 函数的有界性、单调性、周期性和奇偶性 复合函数、反函数、分段函数和隐函数 基本初等函数的性质及其图形初等函数 函数关系的建立 数列极限与函数极限的定义及其性质 函数的左极限和右极限 无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质 考试要求 1.理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系. 2.了解函数的有界性、单调性、周期性和奇偶性. 3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念. 5.理解极限的概念,理解函数左极限与右极限的概念以 及函数极限存在与左、右极限之间的关系. 6.掌握极限的性质及四则运算法则. 7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法. 8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间对比: 无变化法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L’Hospital)法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L’Hospital)法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西对比:无变化拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西(Cauchy)中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数。
最新数2考研大纲汇总

2012年数2考研大纲一、函数、极限、连续考试内容函数的概念及表示法,函数的有界性、单调性、周期性和奇偶性,复合函数、反函数、分段函数和隐函数,基本初等函数的性质及其图形,初等函数,函数关系的建立,数列极限与函数极限的定义及其性质,函数的左极限与右极限,无穷小量和无穷大量的概念及其关系,无穷小量的性质及无穷小量的比较,极限的四则运算,极限存在的两个准则:单调有界准则和夹逼准则,两个重要极限:,函数连续的概念,函数间断点的类型,初等函数的连续性,闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学导数和微分的概念,导数的几何意义和物理意义,函数的可导性与连续性之间的关系,平面曲线的切线和法线,导数和微分的四则运算,基本初等函数的导数,复合函数、反函数、隐函数以及参数方程所确定的函数的微分法,高阶导数一阶微分形式的不变性,微分中值定理,洛必达(L'Hospital)法则,函数单调性的判别,函数的极值,函数图形的凹凸性、拐点及渐近线,函数图形的描绘,函数的最大值与最小值,弧微分,曲率的概念,曲率圆与曲率半径1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数.当时,的图形是凹的;当时,的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆与曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学原函数和不定积分的概念,不定积分的基本性质,基本积分公式,定积分的概念和基本性质,定积分中值定理,积分上限的函数及其导数,牛顿-莱布尼茨(Newton-Leibniz)公式,不定积分和定积分的换元积分法与分部积分法,有理函数、三角函数的有理式和简单无理函数的积分,反常(广义)积分,定积分的应用1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值.四、多元函数微积分学多元函数的概念,二元函数的几何意义,二元函数的极限与连续的概念,有界闭区域上二元连续函数的性质,多元函数的偏导数和全微分,多元复合函数、隐函数的求导法,二阶偏导数,多元函数的极值和条件极值、最大值和最小值,二重积分的概念、基本性质和计算1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).常微分方程常微分方程的基本概念,变量可分离的微分方程,齐次微分方程,一阶线性微分方程,可降阶的高阶微分方程,线性微分方程解的性质及解的结构定理,二阶常系数齐次线性微分方程,高于二阶的某些常系数齐次线性微分方程,简单的二阶常系数非齐次线性微分方程,微分方程的简单应用1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.3.会用降阶法解下列形式的微分方程:和 .4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.一、行列式行列式的概念和基本性质,行列式按行(列)展开定理1.了解行列式的概念,掌握行列式的性质.2.会应用行列式的性质和行列式按行(列)展开定理计算行列式.二、矩阵矩阵的概念,矩阵的线性运算,矩阵的乘法,方阵的幂,方阵乘积的行列式,矩阵的转置,逆矩阵的概念和性质,矩阵可逆的充分必要条件,伴随矩阵,矩阵的初等变换,初等矩阵,矩阵的秩,矩阵的等价,分块矩阵及其运算1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反对称矩阵和正交矩阵以及它们的性质.2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件.理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.4.了解矩阵初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.5.了解分块矩阵及其运算.三、向量向量的概念,向量的线性组合和线性表示,向量组的线性相关与线性无关,向量组的极大线性无关组,等价向量组,向量组的秩,向量组的秩与矩阵的秩之间的关系,向量的内积,线性无关向量组的的正交规范化方法1.理解维向量、向量的线性组合与线性表示的概念.2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.3.了解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.4.了解向量组等价的概念,了解矩阵的秩与其行(列)向量组的秩的关系.5.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.四、线性方程组线性方程组的克莱姆(Cramer)法则,齐次线性方程组有非零解的充分必要条件,非齐次线性方程组有解的充分必要条件,线性方程组解的性质和解的结构,齐次线性方程组的基础解系和通解,非齐次线性方程组的通解1.会用克莱姆法则.2.理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.3.理解齐次线性方程组的基础解系及通解的概念,掌握齐次线性方程组基础解系和通解的求法.4.理解非齐次线性方程组的解的结构及通解的概念.5.会用初等行变换求解线性方程组.五、矩阵的特征值及特征向量矩阵的特征值和特征向量的概念、性质,相似矩阵的概念及性质,矩阵可相似对角化的充分必要条件及相似对角矩阵,实对称矩阵的特征值、特征向量及其相似对角矩阵,1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵特征值和特征向量.2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,会将矩阵化为相似对角矩阵.3.理解实对称矩阵的特征值和特征向量的性质.六、二次型二次型及其矩阵表示,合同变换与合同矩阵,二次型的秩,惯性定理,二次型的标准形和规范形,用正交变换和配方法化二次型为标准形,二次型及其矩阵的正定性1.了解二次型的概念,会用矩阵形式表示二次型,了解合同变换与合同矩阵的概念.2.了解二次型的秩的概念,了解二次型的标准形、规范形等概念,了解惯性定理,会用正交变换和配方法化二次型为标准形.3.理解正定二次型、正定矩阵的概念,并掌握其判别法.。
2012考研《数学一、二、三》大纲

二、职业分析
育内 认 育 要 或的 为 教 求 每 文教 我 育 千 一 艺育 可 的 差 个 各事 以 专 万 行 种业 从 业 别 业 俱, 事 的 。 对 乐从 于 学 而 求 部事 校 生 作 职 工于 外 , 为 者 作体 校 我 体 的 。
三、确定目标
列夫·托尔斯泰曾说过: “一个埋头脑力劳动的人, 如果不经常活动四肢,那 是一件极其痛苦的事情。” 我从小就喜欢运动,我的 性格乐观开朗,积极向上。 作为体教的一名学生,我 争取:学习好专业知识, 掌握好各类体育项目技能, 塑照好形象,全面提高各 方面的素质,以便更好地 适应未来。
原因是用人单位认为应届毕业生只学到书本知识而没有握学习 方法、实际解决问题的能力弱、缺乏团队精神、人际沟通能 力和自我认知能力,而且对未来的发展盲目,没有规划。大 学作为大学生职业生涯规划的第一站,我们该如何对职业生 涯进行规划呢?
认知与分析
一、自我诘问 二、职业分析 三、确定目标 四、培养实践能力 五、参加职业训练 六、评估与修订
写在最后
在这里,这份职业生涯规划也差不多落
入尾声了,然而,我的真正行动才仅仅 开始。现在我要做的是,迈出艰难的一 步,朝着这个规划的目标前进,要以满 腔的热情去获取最后的胜利。有了成功的
目标。明确自己人生的大目标,对把握好目 标有直接的促进作用。认真策划人生每一步。 有道是:"凡事预则立,不预则废",千真万确。 对自己做的或将要做的事没有任何准备,就 是在为失败做准备。
NO.3面向未来
NO.1就业策略
就业技能准备
Text2
就业政策了解
Text3
对自己合适的 定位
Text1
Text4 Text5
2012考研大纲_数学二

2012考研数学二大纲(文字版)考试科目:高等数学、线性代数一、考试形式和试卷结构试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷内容结构高等教学78%线性代数22%四、试卷题型结构试卷题型结构为:单项选择题8小题,每小题4分,共32分填空题6小题,每小题4分,共24分解答题(包括证明题) 9小题,共94分高等数学一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L'Hospital)法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数.当时,的图形是凹的;当时,的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆与曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常(广义)积分定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值.四、多元函数微积分学考试内容多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上二元连续函数的性质多元函数的偏导数和全微分多元复合函数、隐函数的求导法二阶偏导数多元函数的极值和条件极值、最大值和最小值二重积分的概念、基本性质和计算考试要求1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).五、常微分方程考试内容常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程可降阶的高阶微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.3.会用降阶法解下列形式的微分方程:和 .4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.线性代数一、行列式考试内容行列式的概念和基本性质行列式按行(列)展开定理考试要求1.了解行列式的概念,掌握行列式的性质.2.会应用行列式的性质和行列式按行(列)展开定理计算行列式.二、矩阵考试内容矩阵的概念矩阵的线性运算矩阵的乘法方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算考试要求1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反对称矩阵和正交矩阵以及它们的性质.2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件.理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.4.了解矩阵初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.5.了解分块矩阵及其运算.三、向量考试内容向量的概念向量的线性组合和线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量的内积线性无关向量组的的正交规范化方法考试要求1.理解维向量、向量的线性组合与线性表示的概念.2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.3.了解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.4.了解向量组等价的概念,了解矩阵的秩与其行(列)向量组的秩的关系.5.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.四、线性方程组考试内容线性方程组的克莱姆(Cramer)法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组的基础解系和通解非齐次线性方程组的通解考试要求1.会用克莱姆法则.2.理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.3.理解齐次线性方程组的基础解系及通解的概念,掌握齐次线性方程组基础解系和通解的求法.4.理解非齐次线性方程组的解的结构及通解的概念.5.会用初等行变换求解线性方程组.五、矩阵的特征值及特征向量考试内容矩阵的特征值和特征向量的概念、性质相似矩阵的概a阵实对称矩阵的特征值、特征向量及其相似对角矩阵考试要求1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵特征值和特征向量.2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,会将矩阵化为相似对角矩阵.3.理解实对称矩阵的特征值和特征向量的性质.六、二次型考试内容二次型及其矩阵表示合同变换与合同矩阵二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性考试要求1.了解二次型的概念,会用矩阵形式表示二次型,了解合同变换与合同矩阵的概念.2.了解二次型的秩的概念,了解二次型的标准形、规范形等概念,了解惯性定理,会用正交变换和配方法化二次型为标准形.3.理解正定二次型、正定矩阵的概念,并掌握其判别法.。
2012考研《数学一、二、三》大纲

第17页,共24页。
目标管理的含义
• 明确目标 • 参与决策 • 规定期限 • 反馈绩效
第18页,共24页。
• 目标设置的方法——自己制定个人目标 • 目标间的关系——完成组织目标就是完成个
第20页,共24页。
(三)目标管理的流程
图1-1 ห้องสมุดไป่ตู้标管理流程图
第21页,共24页。
需要层次理论与人性假设
第22页,共24页。
(五)实施目标管理的哲学基础
麦格雷戈 的Y理论:
• 人并不是生来就厌恶工作
• 人完全能够实现自我指挥和自我控制。 • 对目标做出贡献是同获得成就的报酬直接相关的。
• 人们不但能接受而且主动承担责任。 • 多数人具有想象力和创造力。 • 人们并非天生就对组织的要求采取消极的或抵制的态度 管理的基本任务是使人们的潜能充分发挥出来,更好地为实现组织的目
目标管理
第1页,共24页。
摸高试验
• 把十个成员分成两组进行摸高比赛,看 哪一组摸得更高。第一组十个学生,不规定 任何目标,由他们自己随意制定摸高的高度; 第二组规定每个人首先定一个标准,比如要 摸到1.60米或1.80米。试验结束后,把两组 的成绩全部统计出来进行评比,结果发现规 定目标的第二组的平均成绩要高于没有制定 目标的第一组。
第8页,共24页。
思考
• 公司的共同愿景是什么?与目标有何 关系?
第9页,共24页。
(三)目标与计划
• 德国大众设定的目标为赶超日本丰田汽车公 司,成为世界第三大汽车制造商,全面提高 品牌的知名度 。
2013考研必备_2012数二考研大纲

2012年 硕士研究生入学统一考试数学考试大纲数学二考试科目:高等数学、线性代数考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷内容结构高等教学 约78%线性代数 约22%四、试卷题型结构试卷题型结构为:单项选择题 8小题,每小题4分,共32分填空题 6小题,每小题4分,共24分解答题(包括证明题) 9小题,共94分高等数学一、函数、极限、连续考试内容函数的概念及表示法 函数的有界性、单调性、周期性和奇偶性 复合函数、反函数、分段函数和隐函数 基本初等函数的性质及其图形 初等函数 函数关系的建立数列极限与函数极限的定义及其性质 函数的左极限与右极限 无穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则 两个重要极限:0sin lim 1x x x →=, 1lim 1xx e x →∞⎛⎫+= ⎪⎝⎭函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质 考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容导数和微分的概念 导数的几何意义和物理意义 函数的可导性与连续性之间的关系 平面曲线的切线和法线 导数和微分的四则运算 基本初等函数的导数 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法 高阶导数 一阶微分形式的不变性 微分中值定理 洛必达(L'Hospital )法则 函数单调性的判别 函数的极值 函数图形的凹凸性、拐点及渐近线 函数图形的描绘 函数的最大值与最小值 弧微分 曲率的概念 曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle )定理、拉格朗日(Lagrange )中值定理和泰勒(Taylor )定理,了解并会用柯西( Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间(),a b 内,设函数()f x 具有二阶导数.当()0f x ''>时,()f x 的图形是凹的;当()0f x ''<时,()f x 的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆和曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念 不定积分的基本性质 基本积分公式 定积分的概念和基本性质 定积分中值定理 积分上限的函数及其导数 牛顿-莱布尼茨(Newton-Leibniz)公式 不定积分和定积分的换元积分法与分部积分法 有理函数、三角函数的有理式和简单无理函数的积分 反常(广义)积分 定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数的平均值.四、多元函数微积分学考试内容多元函数的概念 二元函数的几何意义 二元函数的极限与连续的概念 有界闭区域上二元连续函数的性质 多元函数的偏导数和全微分 多元复合函数、隐函数的求导法 二阶偏导数 多元函数的极值和条件极值、最大值和最小值 二重积分的概念、基本性质和计算考试要求1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).五、常微分方程考试内容常微分方程的基本概念 变量可分离的微分方程 齐次微分方程 一阶线性微分方程 可降阶的高阶微分方程 线性微分方程解的性质及解的结构定理 二阶常系数齐次线性微分方程 高于二阶的某些常系数齐次线性微分方程 简单的二阶常系数非齐次线性微分方程 微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.3.会用降阶法解下列形式的微分方程:()(),(,)n y f x y f x y '''== 和 (,)y f y y '''=.4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.线性代数一、行列式考试内容行列式的概念和基本性质 行列式按行(列)展开定理考试要求1.了解行列式的概念,掌握行列式的性质.2.会应用行列式的性质和行列式按行(列)展开定理计算行列式.二、矩阵考试内容矩阵的概念 矩阵的线性运算 矩阵的乘法 方阵的幂 方阵乘积的行列式 矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算考试要求1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反对称矩阵和正交矩阵以及它们的性质.2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件.理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.4.了解矩阵初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.5.了解分块矩阵及其运算.三、向量考试内容向量的概念向量的线性组合和线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量的内积线性无关向量组的的正交规范化方法考试要求1.理解n维向量、向量的线性组合与线性表示的概念.2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.3.了解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.4.了解向量组等价的概念,了解矩阵的秩与其行(列)向量组的秩的关系.5.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.四、线性方程组考试内容线性方程组的克莱姆(Cramer)法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组的基础解系和通解非齐次线性方程组的通解考试要求1.会用克莱姆法则.2.理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.3.理解齐次线性方程组的基础解系及通解的概念,掌握齐次线性方程组基础解系和通解的求法.4.理解非齐次线性方程组的解的结构及通解的概念.5.会用初等行变换求解线性方程组.五、矩阵的特征值及特征向量考试内容矩阵的特征值和特征向量的概念、性质相似矩阵的概念及性质矩阵可相似对角化的充分必要条件及相似对角矩阵实对称矩阵的特征值、特征向量及其相似对角矩阵考试要求1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵特征值和特征向量.2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,会将矩阵化为相似对角矩阵.3.理解实对称矩阵的特征值和特征向量的性质.六、二次型考试内容二次型及其矩阵表示合同变换与合同矩阵二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性考试要求1.了解二次型的概念,会用矩阵形式表示二次型,了解合同变换与合同矩阵的概念.2.了解二次型的秩的概念,了解二次型的标准形、规范形等概念,了解惯性定理,会用正交变换和配方法化二次型为标准形.3.理解正定二次型、正定矩阵的概念,并掌握其判别法.。
2012-2013年数二考研大纲

2012-2013年数二考研大纲2013年数二考研大纲高等数学一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限和右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念了解反函数及隐函数的概念4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左、右极限之间的关系.6.掌握极限的性质及四则运算法则7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西(Cauchy)中值定理.6.掌握用洛必达法刚求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间(a,b)内,设函数f(x)具有二阶导数。
当>0时,f(x)的图形是凹的;当<0时,f(x)的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆和曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容:原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常(广义)积分定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数的平均值.四、多元函数微积分学考试要求1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并求解一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).五、常微分方程考试内容常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程可降阶的高阶微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程3.会用降阶法解下列形式的微分方程:,和.4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.。
数二考研大纲

可以参考2012年的2012年硕士研究生入学统一考试数学考试大纲数学二考试科目:高等数学、线性代数考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷内容结构高等教学约78%线性代数约22% 四、试卷题型结构试卷题型结构为:单项选择题8小题,每小题4分,共32分填空题6小题,每小题4分,共24分解答题(包括证明题)9小题,共94分高等数学一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:,函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L'Hospital)法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数.当时,的图形是凹的;当时,的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆和曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常(广义)积分定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数的平均值.四、多元函数微积分学考试内容多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上二元连续函数的性质多元函数的偏导数和全微分多元复合函数、隐函数的求导法二阶偏导数多元函数的极值和条件极值、最大值和最小值二重积分的概念、基本性质和计算考试要求1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).五、常微分方程考试内容常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程可降阶的高阶微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.3.会用降阶法解下列形式的微分方程:和.4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.。
考研数学复习资料:2012考研数学一、二、三考试大纲全内容

说明:“考研数学复习资料”是系列文档,如大家需要相关文档可在搜索框中输入“考研数学复习资料”即可找到相关文档,该系列资料有“万晓群enjoyd ”收集整理,也可直接搜索“万晓群enjoyd ”搜索该用户上传的相关文档012年 硕士研究生入学统一考试数学考试大纲数学二考试科目:高等数学、线性代数考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷内容结构高等教学 约78%线性代数 约22%四、试卷题型结构试卷题型结构为:单项选择题 8小题,每小题4分,共32分填空题 6小题,每小题4分,共24分解答题(包括证明题) 9小题,共94分高等数学一、函数、极限、连续考试内容函数的概念及表示法 函数的有界性、单调性、周期性和奇偶性 复合函数、反函数、分段函数和隐函数 基本初等函数的性质及其图形 初等函数 函数关系的建立数列极限与函数极限的定义及其性质 函数的左极限与右极限 无穷小量和无穷大量的概念及其关系 无穷小量的性质及无穷小量的比较 极限的四则运算 极限存在的两个准则:单调有界准则和夹逼准则 两个重要极限:0sin lim 1x xx →=, 1lim 1xx e x →∞⎛⎫+= ⎪⎝⎭ 函数连续的概念 函数间断点的类型 初等函数的连续性 闭区间上连续函数的性质 考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L'Hospital)法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径给大家分享点个人的秘密经验,让大家考得更轻松。
最新考研数学二大纲汇总

2012考研数学二大纲一、函数、极限、连续考试内容函数的概念及表示法,函数的有界性、单调性、周期性和奇偶性,复合函数、反函数、分段函数和隐函数,基本初等函数的性质及其图形,初等函数,函数关系的建立数列极限与函数极限的定义及其性质,函数的左极限和右极限,无穷小量和无穷大量的概念及其关系,无穷小量的性质及及无穷小量的比较,极限的四则运算,极限存在的两个准则:单调有界准则和夹逼准则,两个重要极限:函数连续的概念,函数间断点的类型,初等函数的连续性,闭区间上连续函数的性质。
2考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系。
2.了解函数的有界性、单调性、周期性和奇偶性。
3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念。
4.掌握基本初等函数的性质及其图形,了解初等函数的概念。
5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限的关系。
6.掌握极限的性质及四则运算法则。
7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法。
8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限。
9.理解函数连续性的概念(含左连续和右连续),会判别函数间断点的类型。
10. 了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质。
二、一元函数微分学考试内容导数和微分的概念,导数的几何意义和物理意义,函数的可导性与连续性之间的关系,平面曲线的切线与法线,导数和微分的四则运算,基本初等函数的导数,复合函数、反函数和隐函数以及参数方程所确定的函数的微分法,高阶导数,一阶微分形式的不变性,微分中值定理,洛必达(L’Hospital)法则,函数单调性的判别,函数的极值,函数图形的凹凸性、拐点及渐近线,函数图形的描绘,函数的最大值与最小值,弧微分,曲率的概念,曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系。
2012数二考试大纲(重点)

2012全国硕士研究生入学考试数学二考试大纲试卷结构(一)题分及考试时间试卷满分为150分,考试时间为180分钟。
(二)内容比例高等教学约80%线性代数约20% (三)题型比例填空题与选择题约40%解答题(包括证明题)约60%。
全国硕士研究生入学考试数学二考试大纲[考试科目] 高等数学、线性代数、高等数学。
一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数简单应用问题的函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小和无穷大的概念及其关系无穷小的性质及无穷小的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立简单应用问题中的函数关系式。
2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4. 掌握基本初等函数的性质及其图形,了解初等函数的基本概念。
5. 理解极限的概念,理解函数左极限与右极限的概念,以及函数极限存在与左、右极限之间的关系.6.掌握极限的性质及四则运算法则7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小、无穷大的概念,掌握无穷小的比较方法,会用等价无穷小求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容。
导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线基本初等函数的导数导数和微分的四则运算复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L’Hospital)法则函数的极值函数单调性的判别函数图形的凹凸性、拐点及渐近线函数图形的描绘函数最大值和最小值弧微分曲率的概念曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的n阶导数.4. 会求分段函数的一阶、二阶导数.5.会求隐函数和由参数方程所确定的函数以及反函数的导数.6.理解并会用罗尔定理、拉格朗日中值定理和泰勒定理,了解柯西中值定理.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其简单应用.8.会用导数判断函数图形的凹凸性,会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.掌握用洛必达法则求未定式极限的方法.10.了解曲率和曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿一莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分广义积分定积分的应用考试要求1.理解原函数概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式及简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解广义积分的概念,会计算广义积分.6.了解定积分的近似计算法.7.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力)及函数的平均值.四、多元函数微积分学考试内容多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上二元连续函数的性质多元函数偏导数的概念与计算多元复合函数、隐函数求导法二阶偏导数多元函数的极值和条件极值、最大值和最小值二重积分的概念、基本性质和计算考试要求1.了解多元函数的概念,了解二元函数的几何意义。
考研必备资料】数学二考研大纲

【2012考研必备资料】2012考研数学二大纲考试科目:高等数学、线性代数、考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷内容结构高等教学 78%线性代数 22%四、试卷题型结构试卷题型结构为:单项选择题 8小题,每小题4分,共32分填空题 6小题,每小题4分,共24分解答题(包括证明题) 9小题,共94分高等数学一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L´Hospital)法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数.当时,的图形是凹的;当时,的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆与曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常(广义)积分定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值.四、多元函数微积分学考试内容多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上二元连续函数的性质多元函数的偏导数和全微分多元复合函数、隐函数的求导法二阶偏导数多元函数的极值和条件极值、最大值和最小值二重积分的概念、基本性质和计算考试要求1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).五、常微分方程考试内容常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程可降阶的高阶微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.3.会用降阶法解下列形式的微分方程:和 .4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.(注:本资料素材和资料部分来自网络,仅供参考。
(整理)考研数二大纲.

2012年全国硕士研究生入学统一考试数学考试大纲--数学二考试科目:高等数学、线性代数考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷内容结构高等教学78% 线性代数22%四、试卷题型结构试卷题型结构为:单项选择题8小题,每小题4分,共32分填空题6小题,每小题4分,共24分解答题(包括证明题) 9小题,共94分高等数学一、函数、极限、连续考试内容:函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求:1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容:导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L'Hospital)法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数.当时,的图形是凹的;当时,的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆与曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常(广义)积分定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值.四、多元函数微积分学考试内容多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上二元连续函数的性质多元函数的偏导数和全微分多元复合函数、隐函数的求导法二阶偏导数多元函数的极值和条件极值、最大值和最小值二重积分的概念、基本性质和计算考试要求:1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).五、常微分方程考试内容:常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程可降阶的高阶微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.3.会用降阶法解下列形式的微分方程:和.4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.线性代数一、行列式:考试内容行列式的概念和基本性质行列式按行(列)展开定理考试要求1.了解行列式的概念,掌握行列式的性质.2.会应用行列式的性质和行列式按行(列)展开定理计算行列式.二、矩阵考试内容:矩阵的概念矩阵的线性运算矩阵的乘法方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算考试要求1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反对称矩阵和正交矩阵以及它们的性质.2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件.理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.4.了解矩阵初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.5.了解分块矩阵及其运算.三、向量考试内容:向量的概念向量的线性组合和线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量的内积线性无关向量组的的正交规范化方法考试要求1.理解维向量、向量的线性组合与线性表示的概念.2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.3.了解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.4.了解向量组等价的概念,了解矩阵的秩与其行(列)向量组的秩的关系.5.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.四、线性方程组考试内容:线性方程组的克莱姆(Cramer)法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组的基础解系和通解非齐次线性方程组的通解考试要求1.会用克莱姆法则.2.理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.3.理解齐次线性方程组的基础解系及通解的概念,掌握齐次线性方程组基础解系和通解的求法.4.理解非齐次线性方程组的解的结构及通解的概念.5.会用初等行变换求解线性方程组.五、矩阵的特征值及特征向量考试内容矩阵的特征值和特征向量的概念、性质相似矩阵的概念及性质矩阵可相似对角化的充分必要条件及相似对角矩阵实对称矩阵的特征值、特征向量及其相似对角矩阵考试要求:1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵特征值和特征向量.2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,会将矩阵化为相似对角矩阵.3.理解实对称矩阵的特征值和特征向量的性质.六、二次型考试内容二次型及其矩阵表示合同变换与合同矩阵二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性考试要求:1.了解二次型的概念,会用矩阵形式表示二次型,了解合同变换与合同矩阵的概念.2.了解二次型的秩的概念,了解二次型的标准形、规范形等概念,了解惯性定理,会用正交变换和配方法化二次型为标准形.3.理解正定二次型、正定矩阵的概念,并掌握其判别法.。
2012年考研数学二大纲

本帖最后由 hfdls 于 2011-9-6 14:09 编辑数学二 2011年考研大纲与2012年考研大纲对比变化:基本没有2011数学二大纲/理工科考试科目:高等数学、线性代数、考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷内容结构高等教学 78%线性代数 22%四、试卷题型结构试卷题型结构为:单项选择题 8 小题,每小题4 分,共32分填空题 6 小题,每小题4 分,共24 分解答题(包括证明题) 9 小题,共94 分高等数学一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L´Hospital)法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数. 当时,的图形是凹的;当时,的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆与曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常(广义)积分定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值.四、多元函数微积分学考试内容多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上二元连续函数的性质多元函数的偏导数和全微分多元复合函数、隐函数的求导法二阶偏导数多元函数的极值和条件极值、最大值和最小值二重积分的概念、基本性质和计算考试要求1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).五、常微分方程考试内容常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程可降阶的高阶微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.3.会用降阶法解下列形式的微分方程:和 .4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.2012考研数学二大纲/理工科考试科目:高等数学、线性代数一、考试形式和试卷结构试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷内容结构高等教学78%线性代数22%四、试卷题型结构试卷题型结构为:单项选择题 8小题,每小题4分,共32分填空题 6小题,每小题4分,共24分解答题(包括证明题) 9小题,共94分高等数学一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L'Hospital)法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西(Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数.当时,的图形是凹的;当时,的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆与曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常(广义)积分定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值.四、多元函数微积分学考试内容多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上二元连续函数的性质多元函数的偏导数和全微分多元复合函数、隐函数的求导法二阶偏导数多元函数的极值和条件极值、最大值和最小值二重积分的概念、基本性质和计算考试要求1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).五、常微分方程考试内容常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程可降阶的高阶微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.3.会用降阶法解下列形式的微分方程:和 .4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.线性代数一、行列式考试内容行列式的概念和基本性质行列式按行(列)展开定理考试要求1.了解行列式的概念,掌握行列式的性质.2.会应用行列式的性质和行列式按行(列)展开定理计算行列式.二、矩阵考试内容矩阵的概念矩阵的线性运算矩阵的乘法方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算考试要求1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反对称矩阵和正交矩阵以及它们的性质.2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件.理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.4.了解矩阵初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.5.了解分块矩阵及其运算.三、向量考试内容向量的概念向量的线性组合和线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量的内积线性无关向量组的的正交规范化方法考试要求1.理解维向量、向量的线性组合与线性表示的概念.2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.3.了解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.4.了解向量组等价的概念,了解矩阵的秩与其行(列)向量组的秩的关系.5.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.四、线性方程组考试内容线性方程组的克莱姆(Cramer)法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组的基础解系和通解非齐次线性方程组的通解考试要求1.会用克莱姆法则.2.理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.3.理解齐次线性方程组的基础解系及通解的概念,掌握齐次线性方程组基础解系和通解的求法.4.理解非齐次线性方程组的解的结构及通解的概念.5.会用初等行变换求解线性方程组.五、矩阵的特征值及特征向量考试内容矩阵的特征值和特征向量的概念、性质相似矩阵的概念及性质矩阵可相似对角化的充分必要条件及相似对角矩阵实对称矩阵的特征值、特征向量及其相似对角矩阵考试要求1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵特征值和特征向量.2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,会将矩阵化为相似对角矩阵.3.理解实对称矩阵的特征值和特征向量的性质.六、二次型考试内容二次型及其矩阵表示合同变换与合同矩阵二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性考试要求1.了解二次型的概念,会用矩阵形式表示二次型,了解合同变换与合同矩阵的概念.2.了解二次型的秩的概念,了解二次型的标准形、规范形等概念,了解惯性定理,会用正交变换和配方法化二次型为标准形.3.理解正定二次型、正定矩阵的概念,并掌握其判别法.。
(整理)2012与年考研数学大纲变化对比数二.

2012年与2011年考研数学大纲变化对比——数二章节2011年数学考试大纲考试内容和考试要求2012年数学考试大纲考试内容和考试要求变化对比高等数学一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:,函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:,函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型. 10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质. 对比: 无变化二、一元函数微分学考试内容导数和微分的概念 导数的几何意义和物理意义 函数的可导性与连续性之间的关系 平面曲线的切线和法线 导数和微分的四则运算 基本初等函数的导数 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法 高阶导数 一阶微分形式的不变性 微分中值定理 洛必达(L'Hospital )法则 函数单调性的判别 函数的极值 函数图形的凹凸性、拐点及渐近线 函数图形的描绘 函数的最大值与最小值 弧微分 曲率的概念 曲率圆与曲率半径 考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分. 3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle )定理、拉格朗日(Lagrange )中值定理和泰勒(Taylor )定理,了解并会用柯西( Cauchy )中值定理. 6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数的最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数.当时,的图形是凹的;当时,的图形是凸的),会求函数图形的拐点以及水平、铅考试内容导数和微分的概念 导数的几何意义和物理意义 函数的可导性与连续性之间的关系 平面曲线的切线和法线 导数和微分的四则运算 基本初等函数的导数 复合函数、反函数、隐函数以及参数方程所确定的函数的微分法 高阶导数 一阶微分形式的不变性 微分中值定理洛必达(L'Hospital )法则 函数单调性的判别 函数的极值 函数图形的凹凸性、拐点及渐近线函数图形的描绘 函数的最大值与最小值 弧微分 曲率的概念 曲率圆与曲率半径考试要求 1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆和曲率半径的概念,会计算曲率和曲率半径.法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数的最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数.当时,的图形是凹的;当时,的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形. 9.了解曲率、曲率圆和曲率半径的概念,会计算曲率和曲率半径.对比: 无变化三、一元函数积分学 考试内容原函数和不定积分的概念 不定积分的基本性质 基本积分公式 定积分的概念和基本性质 定积分中值定理 积分上限的函数及其导数 牛顿-莱布尼茨(Newton-Leibniz)公式 不定积分和定积分的换元积分法与分部积分法 有理函数、三角函数的有理式和简单无理函数的积分 反常(广义)积分 定积分的应用 考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分. 4.理解积分上限的函数,会求它的导数,掌握牛顿-莱布尼茨公式.考试内容原函数和不定积分的概念 不定积分的基本性质 基本积分公式 定积分的概念和基本性质 定积分中值定理 积分上限的函数及其导数 牛顿-莱布尼茨(Newton-Leibniz)公式 不定积分和定积分的换元积分法与分部积分法 有理函数、三角函数的有理式和简单无理函数的积分 反常(广义)积分 定积分的应用 考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值.与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿-莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值.对比:无变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012年全国硕士研究生入学统一考试数学考试大纲--数学二考试科目:高等数学、线性代数考试形式和试卷结构一、试卷满分及考试时间试卷满分为150分,考试时间为180分钟.二、答题方式答题方式为闭卷、笔试.三、试卷内容结构高等教学78%线性代数22%四、试卷题型结构试卷题型结构为:单项选择题8小题,每小题4分,共32分填空题6小题,每小题4分,共24分解答题(包括证明题)9小题,共94分高等数学一、函数、极限、连续考试内容函数的概念及表示法函数的有界性、单调性、周期性和奇偶性复合函数、反函数、分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限与右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则:单调有界准则和夹逼准则两个重要极限:,函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1.理解函数的概念,掌握函数的表示法,并会建立应用问题的函数关系.2.了解函数的有界性、单调性、周期性和奇偶性.3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念.4.掌握基本初等函数的性质及其图形,了解初等函数的概念.5.理解极限的概念,理解函数左极限与右极限的概念以及函数极限存在与左极限、右极限之间的关系.6.掌握极限的性质及四则运算法则.7.掌握极限存在的两个准则,并会利用它们求极限,掌握利用两个重要极限求极限的方法.8.理解无穷小量、无穷大量的概念,掌握无穷小量的比较方法,会用等价无穷小量求极限.9.理解函数连续性的概念(含左连续与右连续),会判别函数间断点的类型.10.了解连续函数的性质和初等函数的连续性,理解闭区间上连续函数的性质(有界性、最大值和最小值定理、介值定理),并会应用这些性质.二、一元函数微分学考试内容导数和微分的概念导数的几何意义和物理意义函数的可导性与连续性之间的关系平面曲线的切线和法线导数和微分的四则运算基本初等函数的导数复合函数、反函数、隐函数以及参数方程所确定的函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达(L'Hospital)法则函数单调性的判别函数的极值函数图形的凹凸性、拐点及渐近线函数图形的描绘函数的最大值与最小值弧微分曲率的概念曲率圆与曲率半径考试要求1.理解导数和微分的概念,理解导数与微分的关系,理解导数的几何意义,会求平面曲线的切线方程和法线方程,了解导数的物理意义,会用导数描述一些物理量,理解函数的可导性与连续性之间的关系.2.掌握导数的四则运算法则和复合函数的求导法则,掌握基本初等函数的导数公式.了解微分的四则运算法则和一阶微分形式的不变性,会求函数的微分.3.了解高阶导数的概念,会求简单函数的高阶导数.4.会求分段函数的导数,会求隐函数和由参数方程所确定的函数以及反函数的导数.5.理解并会用罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和泰勒(Taylor)定理,了解并会用柯西( Cauchy )中值定理.6.掌握用洛必达法则求未定式极限的方法.7.理解函数的极值概念,掌握用导数判断函数的单调性和求函数极值的方法,掌握函数最大值和最小值的求法及其应用.8.会用导数判断函数图形的凹凸性(注:在区间内,设函数具有二阶导数.当时,的图形是凹的;当时,的图形是凸的),会求函数图形的拐点以及水平、铅直和斜渐近线,会描绘函数的图形.9.了解曲率、曲率圆与曲率半径的概念,会计算曲率和曲率半径.三、一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿-莱布尼茨(Newton-Leibniz)公式不定积分和定积分的换元积分法与分部积分法有理函数、三角函数的有理式和简单无理函数的积分反常(广义)积分定积分的应用考试要求1.理解原函数的概念,理解不定积分和定积分的概念.2.掌握不定积分的基本公式,掌握不定积分和定积分的性质及定积分中值定理,掌握换元积分法与分部积分法.3.会求有理函数、三角函数有理式和简单无理函数的积分.4.理解积分上限的函数,会求它的导数,掌握牛顿一莱布尼茨公式.5.了解反常积分的概念,会计算反常积分.6.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数平均值.四、多元函数微积分学考试内容多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上二元连续函数的性质多元函数的偏导数和全微分多元复合函数、隐函数的求导法二阶偏导数多元函数的极值和条件极值、最大值和最小值二重积分的概念、基本性质和计算考试要求1.了解多元函数的概念,了解二元函数的几何意义.2.了解二元函数的极限与连续的概念,了解有界闭区域上二元连续函数的性质.3.了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数,会求全微分,了解隐函数存在定理,会求多元隐函数的偏导数.4.了解多元函数极值和条件极值的概念,掌握多元函数极值存在的必要条件,了解二元函数极值存在的充分条件,会求二元函数的极值,会用拉格朗日乘数法求条件极值,会求简单多元函数的最大值和最小值,并会解决一些简单的应用问题.5.了解二重积分的概念与基本性质,掌握二重积分的计算方法(直角坐标、极坐标).五、常微分方程考试内容常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程可降阶的高阶微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程高于二阶的某些常系数齐次线性微分方程简单的二阶常系数非齐次线性微分方程微分方程的简单应用考试要求1.了解微分方程及其阶、解、通解、初始条件和特解等概念.2.掌握变量可分离的微分方程及一阶线性微分方程的解法,会解齐次微分方程.3.会用降阶法解下列形式的微分方程:和.4.理解二阶线性微分方程解的性质及解的结构定理.5.掌握二阶常系数齐次线性微分方程的解法,并会解某些高于二阶的常系数齐次线性微分方程.6.会解自由项为多项式、指数函数、正弦函数、余弦函数以及它们的和与积的二阶常系数非齐次线性微分方程.7.会用微分方程解决一些简单的应用问题.线性代数一、行列式考试内容行列式的概念和基本性质行列式按行(列)展开定理考试要求1.了解行列式的概念,掌握行列式的性质.2.会应用行列式的性质和行列式按行(列)展开定理计算行列式.二、矩阵考试内容矩阵的概念矩阵的线性运算矩阵的乘法方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算考试要求1.理解矩阵的概念,了解单位矩阵、数量矩阵、对角矩阵、三角矩阵、对称矩阵、反对称矩阵和正交矩阵以及它们的性质.2.掌握矩阵的线性运算、乘法、转置以及它们的运算规律,了解方阵的幂与方阵乘积的行列式的性质.3.理解逆矩阵的概念,掌握逆矩阵的性质以及矩阵可逆的充分必要条件.理解伴随矩阵的概念,会用伴随矩阵求逆矩阵.4.了解矩阵初等变换的概念,了解初等矩阵的性质和矩阵等价的概念,理解矩阵的秩的概念,掌握用初等变换求矩阵的秩和逆矩阵的方法.5.了解分块矩阵及其运算.三、向量考试内容向量的概念向量的线性组合和线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量的内积线性无关向量组的的正交规范化方法考试要求1.理解维向量、向量的线性组合与线性表示的概念.2.理解向量组线性相关、线性无关的概念,掌握向量组线性相关、线性无关的有关性质及判别法.3.了解向量组的极大线性无关组和向量组的秩的概念,会求向量组的极大线性无关组及秩.4.了解向量组等价的概念,了解矩阵的秩与其行(列)向量组的秩的关系.5.了解内积的概念,掌握线性无关向量组正交规范化的施密特(Schmidt)方法.四、线性方程组考试内容线性方程组的克莱姆(Cramer)法则齐次线性方程组有非零解的充分必要条件非齐次线性方程组有解的充分必要条件线性方程组解的性质和解的结构齐次线性方程组的基础解系和通解非齐次线性方程组的通解考试要求1.会用克莱姆法则.2.理解齐次线性方程组有非零解的充分必要条件及非齐次线性方程组有解的充分必要条件.3.理解齐次线性方程组的基础解系及通解的概念,掌握齐次线性方程组基础解系和通解的求法.4.理解非齐次线性方程组的解的结构及通解的概念.5.会用初等行变换求解线性方程组.五、矩阵的特征值及特征向量考试内容矩阵的特征值和特征向量的概念、性质相似矩阵的概念及性质矩阵可相似对角化的充分必要条件及相似对角矩阵实对称矩阵的特征值、特征向量及其相似对角矩阵考试要求1.理解矩阵的特征值和特征向量的概念及性质,会求矩阵特征值和特征向量.2.理解相似矩阵的概念、性质及矩阵可相似对角化的充分必要条件,会将矩阵化为相似对角矩阵.3.理解实对称矩阵的特征值和特征向量的性质.六、二次型考试内容二次型及其矩阵表示合同变换与合同矩阵二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性考试要求1.了解二次型的概念,会用矩阵形式表示二次型,了解合同变换与合同矩阵的概念.2.了解二次型的秩的概念,了解二次型的标准形、规范形等概念,了解惯性定理,会用正交变换和配方法化二次型为标准形.3.理解正定二次型、正定矩阵的概念,并掌握其判别法.。
