异方差检验
异方差定义及检验

4、帕克(Park)检验和戈里瑟(Glejser)检验
2 e x e i • Park检验的辅助模型为: i 2 • 求对数后为: ln(ei ) ln( ) ln xi
(4.1.2)
2 e • Glejser检验以 i 为被解释变量,以原模型的某一解释 变量 x j为解释变量,建立如下方程 :
ei f x ji i (4.1.3) • • f x j 可有多种函数形式。(利用试回归法,选择关于 变量的不同的函数形式,对方程进行估计并进行显著 性检验,如果存在某一种函数形式,使得方程显著成 立,则说明原模型存在异方差性。) • 可利用Eviews软件实现。
2
第二节 异方差的修正
方式2:在方程窗口中点击Estimate\Options\Weighted, 并在权数变量栏输入权数变量;
3)利用White检验判断是否消除了异方差性 权数变量的确定:依据Pack检验和Gleiser检验的结 果,或直接取成1/ei
精品课件!
作业四:
• 第五章3/4/6/8。
步骤:1)将解释变量的样本值按从小到大排序,再利用
ห้องสมุดไป่ตู้ • 检验统计量:
• F服从分布
2 1
n c k 1 2 RSS 2 2 F (4.1.1) 2 2 RSS1 RSS1 n c k 1 2
nc nc F (k 1), (k 1) 2 2
2.戈德菲尔德—匡特(Goldfeld—Quant)检验
原理:适合递增型的异方差,利用方差与解释变量同步增
长的原理,通过检验小方差与大方差是否有明显差异,达 到检验异方差的目的。 OLS求出估计值和残差序列 ei 2)在所有样本点中删去中间的c个点,将余下的点分为两组, 每组样本为 n c 2 个。 3)将两组样本分别作OLS,求得各自的残差平方和,再设计 统计量检验两组残差平方和是否有显著差异,若有,异方 差存在。
异方差性的检验及处理方法
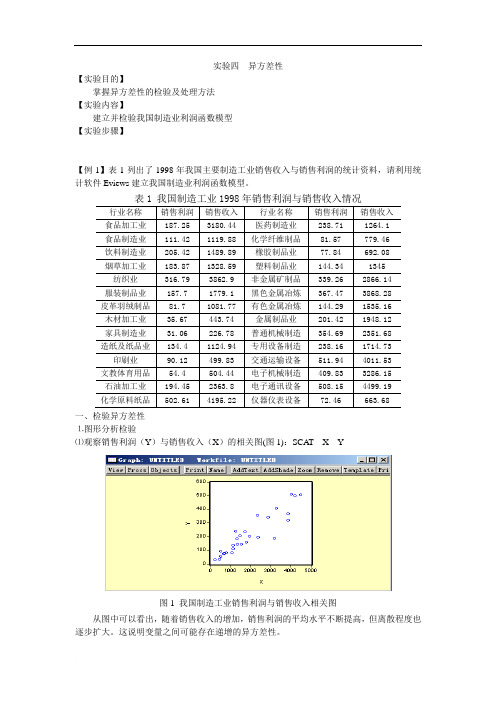
实验四异方差性【实验目的】掌握异方差性的检验及处理方法【实验内容】建立并检验我国制造业利润函数模型【实验步骤】【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
行业名称销售利润销售收入行业名称销售利润销售收入食品加工业187.25 3180.44 医药制造业238.71 1264.1食品制造业111.42 1119.88 化学纤维制品81.57 779.46饮料制造业205.42 1489.89 橡胶制品业77.84 692.08烟草加工业183.87 1328.59 塑料制品业144.34 1345 纺织业316.79 3862.9 非金属矿制品339.26 2866.14 服装制品业157.7 1779.1 黑色金属冶炼367.47 3868.28皮革羽绒制品81.7 1081.77 有色金属冶炼144.29 1535.16木材加工业35.67 443.74 金属制品业201.42 1948.12家具制造业31.06 226.78 普通机械制造354.69 2351.68造纸及纸品业134.4 1124.94 专用设备制造238.16 1714.73 印刷业90.12 499.83 交通运输设备511.94 4011.53 文教体育用品54.4 504.44 电子机械制造409.83 3286.15石油加工业194.45 2363.8 电子通讯设备508.15 4499.19化学原料纸品502.61 4195.22 仪器仪表设备72.46 663.68一、检验异方差性⒈图形分析检验⑴观察销售利润(Y)与销售收入(X)的相关图(图1):SCAT X Y图1 我国制造工业销售利润与销售收入相关图从图中可以看出,随着销售收入的增加,销售利润的平均水平不断提高,但离散程度也逐步扩大。
这说明变量之间可能存在递增的异方差性。
⑵残差分析首先将数据排序(命令格式为:SORT 解释变量),然后建立回归方程。
异方差性的概念、类型、后果、检验及其修正方法含案例

Yi和Xi分别为第i个家庭的储蓄额和可支配收入。
在该模型中,i的同方差假定往往不符合实际情况。对高收 入家庭来说,储蓄的差异较大;低收入家庭的储蓄则更有规律 性(如为某一特定目的而储蓄),差异较小。
因此,i的方差往往随Xi的增加而增加,呈单调递增型变化 。
– 在选项中,EViews提供了包含交叉项的怀特检验“White Heteroskedasticity(cross terms)”和没有交叉项的怀特检 验“White Heteroskedasticity(no cross terms)” 这样两个 选择。
• 软件输出结果:最上方显示两个检验统计量:F统计 量和White统计量nR2;下方则显示以OLS的残差平 方为被解释变量的辅助回归方程的回归结果。
随机误差项具有不同的方差,那么: 检验异方差性,也就是检验随机误差项的方差与解
释变量观测值之间的相关性及其相关的“形式”。 • 各种检验方法正是在这个共同思路下发展起来的。
路漫漫其修远兮, 吾将上下而求索
问题在于:用什么来表示随机误差项的方差? 一般的处理方法:
路漫漫其修远兮, 吾将上下而求索
2.图示检验法
路漫漫其修远兮, 吾将上下而求索
3.模型的预测失效
一方面,由于上述后果,使得模型不具有良好的统计性质;
【书上这句话有点问题】
其中 所以,当模型出现异方差性时,Y预测区间的建立将发生困 难,它的预测功能失效。
路漫漫其修远兮, 吾将上下而求索
三、异方差性的检验(教材P111)
1.检验方法的共同思路 • 既然异方差性就是相对于不同的解释变量观测值,
(注意:其中的2完全可以是1)
计量第9章异方差检验

(9-5)
即用 uˆt 2 对原回归式(9-4)中的各解释变量、解释变量的平方项、交叉乘积项进行 OLS 回归。注意,上式中要保留常数项。
9.4.3 怀特(White)检验 估计辅助回归式,
uˆt 2 = 0 +1 xt1 +2 xt2 + 3 xt12 +4 xt22 + 5 xt1 xt2 + vt
3000 Y
2500
3000
Y 2500
2000
2000
1500
1500
1000
1000
500
X 0 8000 12000 16000 20000 24000 28000 32000 36000 40000
500 X
0 8000 12000 16000 20000 24000 28000 32000 36000 40000
图 9-1 同方差情形
图 9-4 递增型异方差
第 9 章 异方差 9.1 同方差假定 在第 6 章,同方差假定是用矩阵形式给出的。
1 0
Var(u)
=E(u
u'
)
=
2I
=
2
0
1
0
0
0
0
0
2
0
1 0
0 2
0
0
0
0
2
(9-1)
当假定(9-1)不成立时,Var(u) 不再是一个纯量对角矩阵。
排序,再按戈德菲尔德匡特检验方法回归,否则即使存在异方差,也有可能用戈德菲
尔德匡特方法检验不出来。
用 EViews 给截面数据排序的方法:在 Workfile 窗口点击 Procs 键并选 Sort current page
实验四-异方差性的检验与处理

实验四-异方差性的检验与处理实验四 异方差性的检验及处理(2学时)一、实验目的(1)、掌握异方差检验的基本方法; (2)、掌握异方差的处理方法。
二、实验学时:2学时三、实验要求(1)掌握用MATLAB 软件实现异方差的检验和处理; (2)掌握异方差的检验和处理的基本步骤。
四、实验原理1、异方差检验的常用方法(1) 用X-Y 的散点图进行判断(2). 22ˆ(,)(,)e x e y %%或的图形 ,),x )i i y %%i i ((e 或(e 的图形)(3) 等级相关系数法(又称Spearman 检验)是一种应用较广的方法,既可以用于大样本,也可与小样本。
:i u 0原假设H 是等方差的;:i u 0备择假设H 是异方差;检验的三个步骤① ˆt ty y =-%i e②|i x %%i i 将e 取绝对值,并把|e 和按递增或递减次序排序,计算Spearman 系数rs ,其中:21ni i d =∑s 26r =1-n(n -1)|i x %i i 其中, n 为样本容量d 为|e和的等级的差数。
③ 做等级相关系数的显著性检验。
n>8时,22(2)1s sn t t n r-=--0当H 成立时,/2(2),t t n α≤-若认为异方差性问题不存在;/2(2),t t n α>-反之,若||i i e x %说明与之间存在系统关系,异方差问题存在。
(4) 帕克(Park)检验帕克检验常用的函数形式:若α在统计上是显著的,表明存在异方差性。
2、异方差性的处理方法: 加权最小二乘法 如果在检验过程中已经知道:222()()()i i i ji u Var u E u f x σσ===则将原模型变形为:121()()()()()i i p pi iji ji ji ji ji y x x u f x f x f x f x f x βββ=+⋅++⋅+L 在该模型中:2211()()()()()()i i ji u u ji ji ji Var u Var u f x f x f x f x σσ===即满足同方差性。
实验四-异方差性的检验与处理
x=data(:,1);%提取第一列数据,即可支配收入x
y=data(:,2);%提取第二列数据,即居民消费支出y
plot(x,y,'k.');%画x和y的散点图
xlabel('可支配收入x(千元)')%对x轴加标签
ylabel('居民消费支出y(千元)')%对y轴加标签
1304.60
福建
259903
5232.17
青海
2522
390.21
江西
161202
2830.46
宁夏
1743
385.34
山东
601617
12435.93
新疆
1534
1877.61
,研究不同地区FDI和GDP的关系,试问原数据有无异方差性?如果存在异方差性,应如何处理?
七、思考练习
某地区家庭年收入(x)和每年生活必需品综合支出(y)的样本数据如下表:
xlabel('可支配收入(x)')%对x轴加标签
ylabel('残差的平方')%对y轴加标签
%%%%%%%对原数据x和残差平方r^2取对数,并对log(x)和log(r^2)进行一元线性回归
ST1=regstats(log((ST.r).^2),log(x),'linear',{'r','beta','tstat','fstat'})
x
y
x
y
1
0.8
2.4
1.5
1.2
异方差性的检验方法

第五步,作结论:
若
F≥
F
(
n
2
c
k
1,
n
2
c
k
1),
则拒绝H0,认为ui具有异方差性。
若
F<
F
(nc 2
k
1,
n
c 2
k
1)
,
则接受H0,认为ui无异方差。
四、帕克检验法
帕克(R.E.Park)检验法的基本想法是把残差图法加
以形式化,给出关于xi的具体函数结构形式,然后 检验这种结构是否显著。从而判定是否具有异方差
§5.3 异方差性的检验方法 一、残差图法 二、斯皮尔曼(Spearman)等级相关检验法 我们以一元线性回归模型为例,说明等级相关系 数检验法的步骤: 第一步,对原模型应用OLS法,计算残差
i yi yˆi ,i =1,2,…,n。
第二步,计算|εi|与xi的等级差di。将|εi| 和自变量观察值xi按由小到大或由大到小的顺序 分成等级。
五、格莱泽检验法 格莱泽 (H.Glejser)检验法致力于寻找εi与xji之间 的显著成立的关系,因而是用残差绝对值|εi| 对xji的各种函数形式进行回归,将其中显著成立 的函数关系,作为异方差结构的函数形式。这种 检验的计算步骤是:
1.建立被解释变量 y 对所有解释变量的回归方程, 然后计算残差εi (i=1,2,…,n)。
dfeld和Quandt认为取样本容量(n>30)的
1 4
为佳。
再将剩余的n- c个数据分为数目相等的二组:
数据较小的为一组子样本,数据较大的为另
一组子样本。
第三步,建立回归方程求残差平方和:
对上述二组子样本观测值分别应用OLS法,建立
异方差检验

目录案例引入 (2)数据分析 (4)建立多元线性模型及检验 (5)经济检验: (6)统计检验 (6)异方差检验 (7)异方差修正 (12)结果解释 (13)一、案例引入随着国内生产生产总值和城乡居民可支配收入的不断增长,使得人们的收入成倍增长,无论微观经济理论还是人们的感受,收入的增加能够满足人们的更多需求,从而是人们对生活状况的满意程度增加,即提升主观幸福感,增加生命质量得分。
同时,研究结果现实收入较低人群的生命质量得分均较低且与其他组间差异大。
随着收入的增加,生命质量有提升的趋势。
而在社会五大保险之中,只有医保与我们的生命息息相关,堪称社保之中的重中之重,医保的价值让我们的健康得到了保证。
数据(表1)为我们研究收入水平与医保对生命预期的影响提供了重要数据基础。
我们选择58国收入、医保、生命预期这3个变量的相关数据作为样本,进行研究。
观察值生命预期收入医保观察值生命预期收入医保1 71.8 2046 81 44 74.7 13410 1002 60.2 686 74 45 55.6 884 413 76.4 14862 100 46 77.4 14784 1004 75.9 11760 100 47 64.7 360 805 73.2 7944 100 48 45.0 150 306 49.8 296 18 49 46.8 230 497 51.6 3288 90 50 73.7 5842 1008 50.3 156 45 51 62.5 784 849 52.6 482 64 52 54.3 330 7310 64.5 1456 76 53 75.1 17714 10011 52.6 324 75 54 66.7 1322 10012 62.8 462 89 55 52.2 292 6113 50.3 292 56 56 49.5 306 4514 75.7 11924 100 57 77.7 14280 10015 48.0 294 28 58 49.3 360 5116 48.3 244 61 59 65.2 1124 6417 63.2 2560 90 60 47.5 472 4018 55.0 392 80 61 65.6 804 8019 66.8 1094 63 62 47.7 13730 10020 66.3 1038 89 63 46.7 186 1521 52.6 248 81 64 61.4 1056 3422 67.9 7794 100 65 51.5 270 2623 72.3 994 90 66 76.6 16192 10024 59.3 522 80 67 47.4 166 4925 53.6 384 61 68 70.4 2328 7226 70.7 4956 99 69 54.3 342 5527 74.6 13408 100 70 74.5 10490 10028 71.3 1974 100 71 76.8 19782 10029 62.1 3954 80 72 64.6 862 7030 45.5 420 30 73 65.1 1180 9131 44.0 252 43 74 60.9 604 7232 71.4 1472 97 75 70.1 396 9333 52.0 744 31 76 69.0 2736 9434 63.5 780 74 77 70.1 2142 10035 70.4 19182 90 78 74.4 1506 8036 74.7 11076 100 79 76.9 14472 10037 60.8 1078 75 80 72.9 15506 10038 52.2 980 81 81 68.0 1246 6039 74.1 16624 100 82 76.6 11060 10040 75.0 9898 100 83 46.5 160 2841 71.8 2036 82 84 61.0 862 5842 76.5 9532 100 85 50.1 638 4643 70.8 2366 100 ————数据来源:老师提供数据无需处理。
异方差检验方法

异方差检验方法异方差检验是统计学中常用的一种方法,用于检验数据的方差是否存在差异。
在实际应用中,我们经常会遇到数据的方差不同的情况,而异方差检验就可以帮助我们判断这种差异是否显著。
本文将介绍异方差检验的基本原理、常用的检验方法以及实际应用中的注意事项。
一、基本原理。
异方差检验的基本原理是通过比较不同组数据的方差来判断它们是否存在显著差异。
在进行假设检验时,我们通常会提出原假设和备择假设,其中原假设是指数据的方差相等,备择假设是指数据的方差不等。
通过计算检验统计量,我们可以得出在原假设成立的情况下,观察到当前样本数据或更极端情况的概率,从而进行假设检验。
二、常用的检验方法。
1. Bartlett检验。
Bartlett检验是一种常用的异方差检验方法,适用于数据呈正态分布的情况。
它的原假设是各组数据的方差相等,备择假设是各组数据的方差不等。
通过计算检验统计量,我们可以得出在原假设成立的情况下,观察到当前样本数据或更极端情况的概率,从而进行假设检验。
2. Levene检验。
Levene检验是另一种常用的异方差检验方法,它相对于Bartlett检验更加稳健,对数据的正态性要求较低。
它的原假设和备择假设与Bartlett检验相同,通过计算检验统计量来进行假设检验。
三、实际应用中的注意事项。
在进行异方差检验时,我们需要注意以下几点:1. 数据的正态性,Bartlett检验对数据的正态性要求较高,如果数据不满足正态分布的假设,可以考虑使用Levene检验。
2. 样本量的影响,样本量较大时,即使数据的方差存在一定差异,也可能通过检验。
因此,在进行异方差检验时,需要考虑样本量的影响。
3. 多重比较的问题,在进行多组数据的异方差检验时,需要注意多重比较的问题,避免出现假阳性的情况。
四、结论。
异方差检验是一种常用的统计方法,用于检验数据的方差是否存在差异。
在实际应用中,我们可以根据数据的正态性和样本量的大小选择合适的检验方法,并注意多重比较的问题,以得到准确的检验结果。
异方差定义及检验

回归模型的预测
预测精度下降
异方差会导致回归模型的预测精度下降,使得预测值与实际 值之间的差距增大。
预测区间的不准确
异方差会影响预测区间的准确性,使得预测区间不能准确反 映实际结果的分布情况。
回归模型的应用
模型应用的限制
异方差的存在限制了回归模型的应用 范围,使得模型在某些情况下无法适 用。
模型解释性的降低
异方差产生的原因
数据特性
01
数据本身的特性可能导致异方差的出现,如数据异常值、非线
性和非正态分布等。
模型设定不当
02
模型设定不准确或者过于简单可能导致异方差的出现,如线性
回归模型未考虑非线性关系或者遗漏重要解释变量等。
样本误差
03
样本误差也可能导致异方差的出现,如样本选择偏差、测量误
差等。
02
异方差检验方法
异方差会影响回归模型的解释性,使 得模型在解释自变量对因变量的影响 时变得困难。
04
如何处理异方差
方差齐性变换
01
对数变换
将原始数据取对数,可以使得数 据更接近正态分布,从而减少异 方差的影响。
平方根变换
02
03
Box-Cox变换
对原始数据取平方根,也可以在 一定程度上减少异方差。
Box-Cox变换是一种更加通用的 方法,通过选择一个适当的λ值, 使得变换后的数据满足方差齐性。
VS
详细描述
通过对经济增长数据进行异方差检验,可 以了解各国或地区经济增长的非平稳性和 非线性特征,进而为政策制定和经济预测 提供依据。常用的检验方法包括单位根检 验、协整检验和误差修正模型等。
感谢观看
THANKS
异方差定义及检验
异方差性检验 计量经济学 EVIEWS建模课件

G-Q检验的步骤:
①将n对样本观察值(Xi,Yi)按观察值Xi的大 小排队;
②将序列中间的c=n/4个观察值除去,并 将剩下的观察值划分为较小与较大的相 同的两个子样本,每个子样的样本容量 均为(n-c)/2;
③对每个子样分别进行OLS回归,并计算各自 的残差平方和∑esi12 与∑esi22 ;
计量经济学模型一旦出现异方差性,如果仍采用 OLS估计模型参数,会产生下列不良后果:
1.参数估计量非有效
OLS估计量仍然具有无偏性,但不具有有效 性。因为在有效性证明中利用了 E(εε’)=2I 。
而且,在大样本情况下,尽管参数估计量具 有一致性,但仍然不具有渐近有效性。
2. 变量的显著性检验失去意义
例如以绝对收入假设为理论假设、以截面数据
为样本建立居民消费函数: Ci=0+1Yi+εi
将居民按照收入等距离分成n组,取组平均数 为样本观测值。 • 一般情况下,居民收入服从正态分布:中等收 入组人数多,两端收入组人数少。而人数多的组 平均数的误差小,人数少的组平均数的误差大。 • 所以样本观测值的观测误差随着解释变量观测 值的不同而不同,往往引起异方差性。
异方差性的检验与修正分析
一、异方差性问题 二、异方差性检验 三、异方差的修正及案例 四、条件异方差模型的建立
⒉ 在同方差情况下: 异 方 差 的 图 示 在异方差情况下: 说 明 :
异方差时
同方差:i2 = 常数 f(Xi) 异方差:i2 = f(Xi)
⒊异方差的类型
异方差一般可归结为三种类型: (1)单调递增型: i2随X的增大而增大 (2)单调递减型: i2随X的增大而减小 (3)复 杂 型: i2与X的变化呈复杂形式
变量的显著性检验中,构造了t统计量
第五章第三节 异方差性的检验

3、 G-Q检验具体步骤
(1)将样本(观察值)按某个解释变量的大小排序;
(2)将序列中间(段)约 c = 1 / 4 个观察值除去,并使余下的头、尾两段样本容量相同,均为(n-c)/2 个;(3)提出假设:
H0 : ui为同方差; H1:ui为异方差
(4)分别对头、尾两部分样本进行回归,且计算各残差平方和分别为
对(2)式进行回归
R2
a) H0 : 1 2 P H1 : 至少一个i 0
三、Glejser (格里瑟)检验(选学)
四、Breusch—Pagan (布鲁士—佩格)检验(选学) 五、White(怀特)检验 六、ARCH检验
除了图示法以外的检验方法都是构造统计量 实施检验,称为解析法
共同思路
• 异方差性,是相对于不同的样本点,即相对于不 同的X观测值, ui具有不同的方差
ei2
图形分析法是利用残差序列绘制出各种图形,以供分析检验使用。 包括:
1、解释变量为X 轴,残差的平方ei 2 为Y轴的 散点图。
2.解释变量为X 轴,被解释变量为Y轴的X-Y散点图
异方差的类型大致可以分为递增异方差、递减异方差、 复杂异方差三种。 用Y X 作散点图的区域逐渐变宽、变窄、不规则变化, 认为存在异方差; 用ei2 X 作散点图上e2并不近似于某一常数, 则认为存在异方差。
(2)求出残差et , 进而求出et2
(3)估计et2
0
1 X 2t
2 X3t
3
X
2 2t
4
X
2 3t
5 X2t
X 3t
t
(4)针对上述模型作回归,并计算统计量nR2。其中:n为样本
stata面板数据固定效应的异方差检验结果

标题:Stata面板数据固定效应的异方差检验结果在进行面板数据分析时,固定效应模型是一种常用的方法,它可以帮助研究者控制个体间的不可观测的异质性,并更准确地估计变量间的关系。
然而,在使用固定效应模型进行面板数据分析时,我们也需要关注异方差的存在,因为异方差的存在会影响到模型的稳健性和准确性。
本文将使用Stata软件对固定效应模型进行异方差检验,并共享检验结果。
1. 异方差的定义让我们来了解一下异方差的概念。
异方差是指误差项的方差不是恒定的,而是随着自变量或其他因素的变化而变化。
在面板数据分析中,由于不同个体或单位之间的特征差异,误差项的方差可能存在异方差的情况。
2. Stata软件中固定效应模型的异方差检验方法在Stata软件中,我们可以使用“xttest3”命令来进行固定效应模型的异方差检验。
这个命令可以帮助我们检验面板数据中误差项的异方差性质。
3. Stata命令示例下面是一个在Stata中进行固定效应模型异方差检验的示例:```stataxtset id timextreg y x1 x2, fexttest3```在这个示例中,我们首先使用“xtset”命令来指定面板数据的格式,然后使用“xtreg, fe”命令来拟合固定效应模型,最后使用“xttest3”命令来进行异方差检验。
4. 异方差检验的结果在进行了上述命令后,Stata会输出异方差检验的结果。
我们需要关注的主要指标包括LM统计量、Chisq统计量、以及对应的p值。
5. 结果分析对于LM统计量和Chisq统计量,它们的值越大,对应的p值越小,就越表明存在异方差。
通常情况下,我们会根据LM统计量和Chisq统计量的显著性水平来判断是否存在异方差。
如果p值小于0.05,我们就可以拒绝存在异方差的原假设,即面板数据中存在异方差。
6. 结论通过Stata软件对固定效应模型进行异方差检验,我们可以得出面板数据中是否存在异方差的结论。
如果存在异方差,我们需要在后续分析中进行相应的修正,以确保模型估计的准确性和稳健性。
异方差自相关豪斯曼检验

异方差自相关豪斯曼检验异方差性(Heteroscedasticity)是指数据的方差不是常数,而是随着自变量的变化而变化。
当数据呈现异方差性时,固定效应模型可能会产生无偏但不一致的估计,而随机效应模型通常能够更好地处理异方差性。
因此,豪斯曼检验可以帮助确定在存在异方差性时应该选择哪种模型。
同时,时间序列数据中还可能存在自相关性(Autocorrelation),即误差项之间存在相关性。
如果数据中存在自相关性,那么OLS估计量可能不再是最佳线性无偏估计。
通过进行豪斯曼检验,可以确定在存在自相关性时是否需要使用修正的OLS估计方法。
要进行豪斯曼检验,首先需要建立两个模型:一个固定效应模型和一个随机效应模型。
然后通过计算两个模型的估计值的差异来进行检验。
在检验中,我们感兴趣的是这个差异是否由异方差性或自相关性引起的。
具体来说,豪斯曼检验的原假设是两个模型没有系统性的差异。
如果原假设被拒绝,说明两个模型之间存在显著差异,这可能是由于异方差性或自相关性导致的。
为了说明豪斯曼检验的方法和步骤,我们将考虑一个实际的研究示例。
假设我们对一个国家的 GDP 进行研究,我们想分析GDP 与劳动力投入之间的关系。
我们建立了一个固定效应模型和一个随机效应模型,用来估计 GDP 对劳动力投入的影响。
在固定效应模型中,我们假设不同国家之间的劳动力投入是不同的,即随着时间的推移,劳动力投入在各国之间也可能存在差异。
而在随机效应模型中,我们假设劳动力投入在各国之间是同质的,即不同的劳动力投入只是由于随机误差所致。
接下来,我们用豪斯曼检验来检验这两个模型之间的差异。
我们首先估计这两个模型,并计算它们之间的差异。
接着,我们对这些差异进行统计检验,以确定差异是否显著。
如果实证结果表明固定效应模型比随机效应模型更好,那么我们可以得出结论,数据中存在异方差性和自相关性。
在这种情况下,我们可能需要对模型进行修正,以更准确地描述数据。
总的来说,豪斯曼检验是一种在经济学和其他社会科学研究中经常使用的方法,用于检验两个模型之间的差异。
异方差性的检验方法

而lnˆ 2 9.157326, 故ˆ 2 =0.000105444,
因此异方差的结构为
ˆ
2 ui
0.00010544
x3.056229 i
五、格莱泽检验法 格莱泽 (H.Glejser)检验法致力于寻找εi与xji之间 显著成立的关系,因而是用残差绝对值|εi| 对xji的各种函数形式进行回归,将其中显著成立 的函数关系,作为异方差结构的函数形式。这种 检验的计算步骤是:
二、斯皮尔曼(Spearman)等级相关检验法 我们以一元线性回归模型为例,说明斯皮尔曼 等级相关检验法的步骤: 第一步,对原模型应用OLS法,计算残差 i yi yˆi ,i =1,2,…,n。 第二步,计算|εi|与xi的等级差di。将|εi| 和自变量观察值xi按由小到大或由大到小的顺序 分成等级。
然后,计算|εi|与xi的等级差di
di = xi的等级-∣εi∣的等级
(5.3.2)
第三步,计算|εi|与xi的等级相关系数
rs
1
6 n(n2
di2 1)
其中n为样本容量。
(5.3.3)
第四步,对总体等级相关系数 s进行显著性检验 H 0 : s 0, H1 : s 0 。当H0成立时,可以证明统
由于不同的观察值随机误差项具有不同的方差因此检验异方差的主要问题是判断随机误差项的方差与解释变量之间的相关性下列这些方法都是围绕这个思路通过建立不同的模型和验判标准来检验异方差
§5.3 异方差性的检验方法
• 由于异方差的存在会导致OLS估计量的最佳性 丧失,降低精确度。所以,对所取得的样本数 据(尤其是横截面数据)判断是否存在异方差, 是我们在进行正确回归分析之前要考虑的事情。 异方差的检验主要有图示法和解析法,下面我 们将介绍几种常用的检验方法。
异方差性的检验及处理方法

图2显示回归方程的残差分布有明显的扩大趋势,即表明存在异方差性。
⒉Goldfeld-Quant检验
⑴将样本按解释变量排序(SORT X)并分成两部分(分别有1到10共11个样本合19到28共10个样本)
⑵利用样本1建立回归模型1(回归结果如图3),其残差平方和为2579.587。
【实验步骤】
【例1】表1列出了1998年我国主要制造工业销售收入与销售利润的统计资料,请利用统计软件Eviews建立我国制造业利润函数模型。
表1 我国制造工业1998年销售利润与销售收入情况
行业名称
销售利润
销售收入
行业名称
销售利润
销售收入
食品加工业
187.25
3180.44
医药制造业
238.71
1264.1
SMPL 1 10
LS Y C X
图3样本1回归结果
⑶利用样本2建立回归模型2(回归结果如图4),其残差平方和为63769.67。
SMPL 19 28
LS Y C X
图4样本2回归结果
⑷计算F统计量: =63769.67/2579.59=24.72, 分别是模型1和模型2的残差平方和。
取 时,查F分布表得 ,而 ,所以存在异方差性
食品制造业
111.42
1119.88
化学纤维制品
81.57
779.46
饮料制造业
205.42
1489.89
橡胶制品业
77.84
692.08
烟草加工业
183.87
1328.59
塑料制品业
144.34
1345
纺织业
316.79
异方差检验

七、 异方差与自相关一、背景我们讨论如果古典假定中的同方差和无自相关假定不能得到满足,会引起什么样的估计问题呢?另一方面,如何发现问题,也就是发现和检验异方差以及自相关的存在性也是一个重要的方面,这个部分就是就这个问题进行讨论。
二、知识要点1、引起异方差的原因及其对参数估计的影响2、异方差的检验(发现异方差)3、异方差问题的解决办法4、引起自相关的原因及其对参数估计的影响5、自相关的检验(发现自相关)6、自相关问题的解决办法 (时间序列部分讲解) 三、要点细纲1、引起异方差的原因及其对参数估计的影响原因:引起异方差的众多原因中,我们讨论两个主要的原因,一是模型的设定偏误,主要指的是遗漏变量的影响.这样,遗漏的变量就进入了模型的残差项中.当省略的变量与回归方程中的变量有相关关系的时候,不仅会引起内生性问题,还会引起异方差.二是截面数据中总体各单位的差异。
后果:异方差对参数估计的影响主要是对参数估计有效性的影响。
在存在异方差的情况下,OLS 方法得到的参数估计仍然是无偏的,但是已经不具备最小方差性质.一般而言,异方差会引起真实方差的低估,从而夸大参数估计的显著性,即是参数估计的t 统计量偏大,使得本应该被接受的原假设被错误的拒绝.2、异方差的检验 (1)图示检验法由于异方差通常被认为是由于残差的大小随自变量的大小而变化,因此,可以通过散点图的方式来简单的判断是否存在异方差.具体的做法是,以回归的残差的平方2i e 为纵坐标,回归式中的某个解释变量i x 为横坐标,画散点图。
如果散点图表现出一定的趋势,则可以判断存在异方差。
(2)Goldfeld-Quandt 检验Goldfeld-Quandt 检验又称为样本分段法、集团法,由Goldfeld 和Quandt 1965年提出.这种检验的思想是以引起异方差的解释变量的大小为顺序,去掉中间若干个值,从而把整个样本分为两个子样本.用两个子样本分别进行回归,并计算残差平方和.用两个残差平方和构造检验异方差的统计量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七、异方差与自相关一、背景我们讨论如果古典假定中得同方差与无自相关假定不能得到满足,会引起什么样得估计问题呢?另一方面,如何发现问题,也就就是发现与检验异方差以及自相关得存在性也就是一个重要得方面,这个部分就就是就这个问题进行讨论。
二、知识要点1、引起异方差得原因及其对参数估计得影响2、异方差得检验(发现异方差)3、异方差问题得解决办法4、引起自相关得原因及其对参数估计得影响5、自相关得检验(发现自相关)6、自相关问题得解决办法(时间序列部分讲解)三、要点细纲1、引起异方差得原因及其对参数估计得影响原因:引起异方差得众多原因中,我们讨论两个主要得原因,一就是模型得设定偏误,主要指得就是遗漏变量得影响。
这样,遗漏得变量就进入了模型得残差项中。
当省略得变量与回归方程中得变量有相关关系得时候,不仅会引起内生性问题,还会引起异方差。
二就是截面数据中总体各单位得差异。
后果:异方差对参数估计得影响主要就是对参数估计有效性得影响。
在存在异方差得情况下,OLS方法得到得参数估计仍然就是无偏得,但就是已经不具备最小方差性质。
一般而言,异方差会引起真实方差得低估,从而夸大参数估计得显著性,即就是参数估计得t统计量偏大,使得本应该被接受得原假设被错误得拒绝。
2、异方差得检验(1)图示检验法由于异方差通常被认为就是由于残差得大小随自变量得大小而变化,因此,可以通过散点图得方式来简单得判断就是否存在异方差。
具体得做法就是,以回归得残差得平方为纵坐标,回归式中得某个解释变量为横坐标,画散点图。
如果散点图表现出一定得趋势,则可以判断存在异方差。
(2)Goldfeld-Quandt检验Goldfeld-Quandt 检验又称为样本分段法、集团法,由Goldfeld 与Quandt 1965年提出。
这种检验得思想就是以引起异方差得解释变量得大小为顺序,去掉中间若干个值,从而把整个样本分为两个子样本。
用两个子样本分别进行回归,并计算残差平方与。
用两个残差平方与构造检验异方差得统计量。
Goldfeld-Quandt 检验有两个前提条件,一就是该检验只应用于大样本(n>30),并且要求满足条件:观测值得数目至少就是参数得二倍; 二就是除了同方差假定不成立以外,要求其她假设都成立,随机项没有自相关并且服从正态分布。
Goldfeld-Quandt 检验假设检验设定为:H 0:具有同方差, H 1:具有递增型异方差。
具体实施步骤为:①将观测值按照解释变量x 得大小顺序排列。
②将排在中间部分得c 个(约n/4)观测值删去,再将剩余得观测值分成两个部分,每个部分得个数分别为n 1、n 2。
③分别对上述两个部分得观测值进行回归,得到两个部分得回归残差平方与。
④构造F 统计量,其中 k 为模型中被估参数个数。
在H 0成立条件下,⑤判别规则如下,若 F ≤ F α (n 2 - k , n 1 - k ), 接受H 0(具有同方差)若 F > F α(n 2 - k , n 1 - k ), 拒绝H 0(递增型异方差)注意:① 当摸型含有多个解释变量时,应以每一个解释变量为基准检验异方差。
② 此法只适用于递增型异方差。
1234567050100150200X Y Y(3)Breusch-Pagan/Godfrey LM检验该方法得基本思想就是构造残差平方序列与解释变量之间得辅助函数,得到回归平方与ESS,从而判断异方差性存在得显著性。
该检验假设异方差得形式为:其中就是解释变量构成得向量,当时,模型就是同方差得。
具体设模型为:表示就是某个解释变量或全部。
同样,该检验也可以通过一个简单得回归来实现。
提出原假设为 ,具体步骤如下:①构造变量:用OLS方法估计方程中得未知参数,得与 (n为样本容量)②以为被解释变量,为解释变量进行回归,并计算回归平方与ESS。
构造辅助回归函数③构造LM统计量为:LM=当有同方差性,且n无限增大时有④对于给定显著性水平,如果,则拒绝原假设,表明模型中存在异方差。
为了计算得简便,LM统计量得构造也可以采取如下形式:其中,就是关于得观测值矩阵, g就是观测值排成得列向量。
由于上述统计量得构造过分依赖于残差得正态性假定,因此,Koenker与Bassett对该统计量进行了修正,令则(4)White检验White检验由H、White 1980年提出。
与Goldfeld-Quandt 检验相比,White 检验不需要对观测值排序,也不依赖于随机误差项服从正态分布,它就是通过一个辅助回归式构造 2 统计量进行异方差检验。
White检验得提出避免了Breusch-Pagan检验一定要已知随机误差得方差产生得原因且要求随机误差服从正态分布。
White检验与Breusch-Pagan检验很相似,但它不需要关于异方差得任何先验知识,只要求在大样本得情况下。
White得检验得思想直接来源于其异方差一致估计。
当存在异方差时,传统得方差估计式不再就是估计量方差得一致估计,而应该使用White一致性估计:。
通过检验就是不就是参数估计方差得一致估计,可以检验就是否存在异方差。
在实际得应用过程中,可以通过回归得步骤来简单得实现上述思想。
以二元回归模型y i = β0 +β1 x i1+β2 x i2+ u i为例,White检验得具体步骤如下:①首先对上式进行OLS回归,求残差平方。
②做如下辅助回归式,= α0 +α1 x i1 +α2x i2 + α3 x i12 +α4x i22 + α5 x i1x i2 + v i即用残差平方对原回归式中得各解释变量、解释变量得平方项、交叉乘积项进行OLS回归。
注意,上式中要保留常数项。
求辅助回归式得可决系数R2。
③White检验得原假设与备择假设就是H0:u i不存在异方差, H1:u i存在异方差④利用回归②得到得,计算统计量。
在同方差假设条件下,统计量nR 2 ~χ2(5)其中n表示样本容量,R2就是辅助回归式得OLS估计得可决系数。
自由度5表示辅助回归式中解释变量项数(注意,不计算常数项)。
n R 2属于LM统计量。
统计量渐进服从自由度为得卡方分布,其中就是辅助回归中参数得个数(包括常数项)。
⑤判别规则就是若n R 2≤ χ2α (5), 接受H0(u i 具有同方差)若n R 2 > χ2α (5), 拒绝H0(u i 具有异方差)(5)ARCH检验自回归条件异方差(ARCH)检验主要用于检验时间序列中存在得异方差。
ARCH检验得思想就是,在时间序列数据中,可认为存在得异方差性为ARCH过程,并通过检验这一过程就是否成立来判断时间序列就是否存在异方差。
ARCH过程可以表述为:其中就是ARCH过程得阶数,并且,;为随机误差。
ARCH检验得基本步骤如下:①提出假设:中至少一个不为零。
②对原模型做OLS估计,求出残差,并计算残差平方序列,分别作为对得估计。
③作辅助回归并计算上式得可决系数,可以证明,在原假设成立得情况下,基于大样本,有近似服从自由度为得卡方分布。
如果,则拒绝原假设,表明原模型得误差项存在异方差。
(6)Park检验法Park检验法就就是将残差图法公式化,提出就是解释变量得某个函数,然后通过检验这个函数形式就是否显著,来判定就是否具有异方差性及其异方差性得函数结构。
(7)Glejser检验法这种方法类似于Park检验。
首先从OLS回归取得残差之后,用得绝对值对被认为与方差密切相关得X变量作回归。
3、异方差得解决办法(详细见板书)对异方差得传统解决办法就是通过加权最小二乘WLS将残差向同方差转换。
一般认为,异方差得产生就是由于残差项中包含了解释变量得相关信息,也就就是说,可以将残差项表达成解释变量得函数:其中就是得向量,可以就是关于得线性函数,也可以就是非线性得。
如果知道得函数形式,那么可以通过加权最小二乘得方法对模型进行修正,在不存在自相关得假定下,在回归方程两边同乘以可以对残差进行修正,从而消除残差得异方差性使得OLS估计量仍然具有有效性。
但就是,这样得方法却有两个方面得问题——首先,就是得形式难以确定(为了简便,我们往往假设就是关于得线性函数,但实际上真实得函数形式很可能就是非线性得),从而相应得WLS得权重设定也就往往就是不正确得了;其次,即使知道得真实函数形式,通过加权得出得参数估计也已经不就是原来得关注参数了;最后,在强外生性条件不满足得条件下,WLS估计量也往往就是不一致得。
因此,从现代得观点来瞧,从模型设定得角度对异方差进行修正才就是可行得方法。
4、引起自相关得原因及其对参数估计得影响引起自相关得原因主要可以归纳为三点:①经济数据得固有得惯性(inertia)带来得相关,比如经济系统自身得惯性,经济活动得滞后效应。
这主要出现在时间序列数据当中,经济变量在时间上得惯性往往就是造成自相关得主要原因。
滞后效应指得就是某一经济变量对另一经济变量得影响不仅影响于当期,而就是延续若干期,由此带来变量得自相关。
②模型得设定误差,主要仍然就是遗漏变量得影响,将遗漏得变量归入了残差项,由于遗漏得变量在不同时间点上就是相关得,这就造成了残差项得自相关。
③对数据得处理造成了数据得内在联系,从而引起自相关现象。
自相关对参数估计得影响仍然就是影响参数估计得有效性,自相关得存在使得OLS得到得参数估计不再具有最小方差性质。
一般而言,在存在自相关得情况下,如果仍然用满足古典假定得OLS去估计参数及其方差,会低估真实得,更会低估参数估计得方差,从而就是t统计量被高估,致使原来不显著得解释变量变得显著,夸大得参数得显著水平。
5、自相关得检验(1)图示检验图示检验就是一种直观得检验自相关得方法。
与上述检验异方差得方法略有不同得就是,该方法就是通过做残差得当期值与其滞后期得值得散点图来判断就是否存在自相关。
具体做法就是,以OLS回归得残差当期值为纵坐标,以其滞后值为横坐标(可以就是滞后一期,也可以就是滞后一期以上)画散点图。
如果该图形有明显得趋势,则可以认为残差存在自相关。
(2)相关系数检验法相关系数得方法就是检验自相关得一个简单方法。
其基本思想就就是通过计算OLS回归得到得残差之间得一阶自相关系数,来确认就是否存在自相关得现象。
具体表示如下:做辅助回归显然,r就是对相关系数得一个估计。
但就是这个方法得问题就是:没有一个确定得标准来判断究竟多大得相关悉数才能认为存在自相关。
(3)Breusch-Godfrey LM检验Breusch-Godfrey LM检验得原假设就是不存在自相关,备择假设就是存在自相关。
基本步骤如下:①提出假设:中至少一个不为零。
其中就是阶数。
②对原模型做OLS估计,求出残差。
③作辅助回归并得到上面回归得可决系数,可以证明,在原假设成立得情况下,基于大样本,有近似服从自由度为得卡方分布。
