第8章题解
第8章 斯勒茨基方程

第8章 斯勒茨基方程一、判断题(T 或F )1.补偿需求函数指的是价格变动中保持对原消费束购买力不变而对收入进行调整的需求函数。
( )【答案】F【解析】补偿需求函数是指价格变动过程中收入进行调整并保持效用不变的需求函数。
2.在相似偏好下,由于价格变动引起的需求变化全部来自于替代效应。
( )【答案】F【解析】由于两种商品之间的交换比率的变化所引起的需求变化称作替代效应。
在相似偏好下,既存在替代效应也存在收入效应。
3.如果商品x 与商品y 对某消费者为完全互补品,则商品x 的价格下降引起y 的需求变化全部归因于收入效应。
( )【答案】T【解析】完全替代偏好下,价格变动中全部表现为替代效应,收入效应为零;完全互补偏好下,价格变动中全部表现为收入效应,替代效应为零。
4.如果某商品的恩格尔曲线向上倾斜,那么该商品的需求曲线一定向下倾斜。
( )【答案】T【解析】恩格尔曲线表示在商品价格保持不变的条件下,收入和需求量的关系。
恩格尔曲线向上倾斜说明随着收入增长,需求量也增加,由此可知该商品是正常品,其需求曲线是向下倾斜的。
5.商品x 对消费者是越多越喜欢,如果x 商品的价格下降并且其他商品的价格保持不变,那么这个消费者必然增加对x 的需求。
( )【答案】F【解析】商品x 对消费者是越多越喜欢并没有说明商品x 是正常物品还是低档物品,因此无法判断商品x 的价格变化如何导致需求变化。
6.在当前收入下,某消费者所消费的两种商品中有一种是吉芬商品。
如果该吉芬商品的价格上升,则消费者对另一种商品的需求一定减少。
( )【答案】T【解析】吉芬商品的价格上升,那么其需求量会增加,占消费者总支出的比例增加,在收入不变的情况下,另一种商品价格不变,需求量一定减少。
7.吉芬商品价格的上升会使消费它的消费者状况改变得更好。
( )【答案】F【解析】商品(无论是普通商品还是吉芬商品)价格的上升会导致消费者的预算约束线向内旋转,导致消费束的选择范围减少,消费者的状况变差。
运筹学答案(第八章)

page 32 2020年5月13日星期三
School of Management
运筹学教程
第八章习题解答
page 33 2020年5月13日星期三
School of Management
运筹学教程
第八章习题解答
心B货1B中,18,心B.22B的0,2,运B某3B输每种3。能天货A力物需1,、由求A2单分个2的位别仓库运为库存费9At量,如1,分5表At别,82运—为64t送每,。到天求各31运仓个3t费库配,最到货9t省中;配
School of Management
运筹学教程
第八章习题解答
解:两条船就够了。
一条船完成:T4→T5→T3; 另一条船完成:T1→T2 。
page 37 2020年5月13日星期三
School of Management
page 25 2020年5月13日星期三
School of Management
运筹学教程
第八章习题解答
8.15 如图8-59,发点S1,S2分别可供应10和15个 单边位上,数收为c点ij。t1,t2可以接收10和25个单位,求最大流,
page 26 2020年5月13日星期三
School of Management
运筹学教程
第八章习题解答
8.1 证明在9座工厂之间,不可能每座工厂只与其 他3座工厂有业务联系,也不可能只有4座工厂与偶数 个工厂有业务联系。
解:将有联系的工厂做一条连线。
如果仅有9座工厂只与其他3座工厂有业务联系, 说明顶点次数之和为27,矛盾。
如果只有4座工厂与偶数个工厂有业务联系,其他 5个工厂一定与奇数个工厂有业务联系,说明顶点次 数之和还是奇数,矛盾。
量子力学 第八章自旋 习题解(延边大学)

第八章:自旋[1]在x σˆ表象中,求x σˆ的本征态 (解) 设泡利算符2σ,x σ,的共同本征函数组是: ()z s x 21 和()z s x21- (1)或者简单地记作α和β,因为这两个波函数并不是x σˆ的本征函数,但它们构成一个完整系,所以任何自旋态都能用这两个本征函数的线性式表示(叠加原理),x σˆ的本征函数可表示:βαχ21c c += (2)21,c c 待定常数,又设x σˆ的本征值λ,则x σˆ的本征方程式是: λχχσ=x ˆ (3) 将(2)代入(3):()()βαλβασ2121ˆc c c c x +=+ (4) 根据本章问题6(P .264),x σˆ对z σˆ表象基矢的运算法则是: βασ=x ˆ αβσ=x ˆ 此外又假设x σˆ的本征矢(2)是归一花的,将(5)代入(4):βλαλαβ2111c c c c +=+比较βα,的系数(这二者线性不相关),再加的归一化条件,有:)6()6()6(122211221c b a c c c c c c ------------------------------------⎪⎩⎪⎨⎧=+==λλ 前二式得12=λ,即1=λ,或1-=λ当时1=λ,代入(6a )得21c c =,再代入(6c),得: δi e c 211=δi e c 212=δ 是任意的相位因子。
当时1-=λ,代入(6a )得21c c -=代入(6c),得:δi e c 211=δi e c 212-=最后得x σˆ的本征函数: )(21βαδ+=i e x 对应本征值1)(22βαδ-=i e x 对应本征值-1以上是利用寻常的波函数表示法,但在2ˆˆσσx 共同表象中,采用z s 作自变量时,既是坐标表象,同时又是角动量表象。
可用矩阵表示算符和本征矢。
⎥⎦⎤⎢⎣⎡=01α ⎥⎦⎤⎢⎣⎡=10β ⎥⎦⎤⎢⎣⎡=21c c χ (7)x σˆ的矩阵已证明是 ⎥⎦⎤⎢⎣⎡=0110ˆx σ因此x σˆ的矩阵式本征方程式是: ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡21211010c c c c λ (8) 其余步骤与坐标表象的方法相同,x σˆ本征矢的矩阵形式是: ⎥⎦⎤⎢⎣⎡=1121δi e x ⎥⎦⎤⎢⎣⎡-=1122δi e x[2]在z σ表象中,求n⋅σ的本征态,)cos ,sin sin ,cos (sin θϕθϕθn 是),(ϕθ方向的单位矢。
高等数学下册第八章课后习题解答

习题8−11. 判定下列平面点集中哪些是开集、闭集、区域、有界集、无界集?并分别指出它们的聚点所成的点集(称为导集)和边界.(1){(x , y )|x ≠0, y ≠0};解 开集, 无界集, 导集为R 2, 边界为{(x , y )|x =0或y =0}.(2){(x , y )|1<x 2+y 2≤4};解 既非开集, 又非闭集, 有界集, 导集为{(x , y )|1≤x 2+y 2≤4},边界为{(x , y )|x 2+y 2=1或x 2+y 2=4}.(3){(x , y )|y >x 2};解 开集, 区域, 无界集, 导集为{(x , y )| y ≥x 2}, 边界为{(x , y )| y =x 2}.(4){(x , y )|x 2+(y −1)2≥1}∩{(x , y )|x 2+(y −2)2≤4}.解 闭集, 有界集, 导集与集合本身相同,边界为{(x , y )|x 2+(y −1)2=1}∪{(x , y )|x 2+(y −2)2=4}.2. 已知函数yx xy y x y x f tan ),(22−+=, 试求f (tx , ty ). 解 )(tan )()()()(),(22tytx ty tx ty tx ty tx f ⋅⋅−+= ),(tan 2222y x f t y x xy y x t =⎟⎠⎞⎜⎝⎛−+=. 3. 试证函数F (x , y )=ln x ⋅ln y 满足关系式:F (xy , uv )=F (x , u )+F (x , v )+F (y , u )+F (y , v ).证明 F (xy , uv )=ln((x , y )⋅ln(uv )=(ln x +ln y )(ln u +ln v )=ln x ⋅ln u +ln x ⋅ln v +ln y ⋅ln u +ln y ⋅ln v=F (x , u )+F (x , v )+F (y , u )+F (y , v ).4. 已知函数f (u , v , w )=u w +w u +v , 试求f (x +y , x −y , xy ).解 f (x +y , x −y , xy )=(x +y )xy +(xy )(x +y )+(x −y )=(x +y )xy +(xy )2x .5. 求下列各函数的定义域:(1)z =ln(y 2−2x +1);高等数学下册第八章习题解答解 要使函数有意义, 必须y 2−2x +1>0,故函数的定义域为D ={(x , y )|y 2−2x +1>0}.(2)yx y x z −++=11; 解 要使函数有意义, 必须x +y >0, x −y >0,故函数的定义域为D ={(x , y )|x +y >0, x −y >0}.(3)y x z −=;解 要使函数有意义, 必须y ≥0,0≥−y x 即y x ≥, 于是有x ≥0且x 2≥y , 故函数定义域为D ={(x , y )| x ≥0, y ≥0, x 2≥y }.(4)221)ln(yx x x y z −−+−=; 解 要使函数有意义, 必须y −x >0, x ≥0, 1−x 2−y 2>0,故函数的定义域为D ={(x , y )| y −x >0, x ≥0, x 2+y 2<1}.(5)222222221rz y x z y x R u −+++−−−=(R >r >0); 解 要使函数有意义, 必须R 2−x 2−y 2−z 2≥0且x 2+y 2+z 2−r 2>0, 故函数的定义域为D ={(x , y , z )| r 2<x 2+y 2+z 2≤R 2}.(6)22arccos yx z u +=. 解 要使函数有意义, 必须x 2+y 2≠0, 且1||22≤+y x z 即z 2≤x 2+y 2, 故函数定义域为D ={(x , y , z )|z 2≤x 2+y 2, x 2+y 2≠0}.6. 求下列各极限:(1)22)1,0(),(1limy x xy y x +−→; 解110011lim 22)1,0(),(=+−=+−→y x xy y x .(2)22)0,1(),()ln(lim yx e x y y x ++→; 解 2ln 01)1ln()ln(lim 22022)0,1(),(=++=++→e y x e x y y x . (3)xy y x 42lim)0,0(),(+−→; 解 xy y x 42lim)0,0(),(+−→)42()42)(42(lim )0,0(),(+++++−=→xy xy xy xy y x 41)42(1lim)0,0(),(−=++−=→xy y x . (4)11lim )0,0(),(−+→xy xy y x ; 解 11lim )0,0(),(−+→xy xy y x )11)(11()11(lim )0,0(),(−+++++=→xy xy xy xy y x 2)11lim )11(lim )0,0(),()0,0(),(=++=++=→→xy xy xy xy y x y x . (5)y xy y x )sin(lim )0,2(),(→; 解 y xy y x )sin(lim )0,2(),(→221sin lim )0,2(),(=⋅=⋅=→x xyxy y x . (6)22)()cos(1lim 2222)0,0(),(yx y x e y x y x ++−→. 解 22221lim )cos(1lim )()cos(1lim )0,0(),(2222)0,0(),(2222)0,0(),(y x y x y x y x y x e y x y x e y x y x →→→⋅++−=++− 01sin lim cos 1lim 00==−=→→t t t t t . 7. 证明下列极限不存在:(1)y x y x y x −+→)0,0(),(lim; 证明 如果动点p (x , y )沿y =0趋向(0, 0),则 1lim lim00)0,0(),(==−+→=→x x y x y x x y y x ; 如果动点p (x , y )沿x =0趋向(0, 0),则 1lim lim00)0,0(),(−=−=−+→=→y y y x y x y x y x . 因此, 极限y x y x y x −+→)0,0(),(lim不存在. (2)22222)0,0(),()(lim y x y x y x y x −+→. 证明 如果动点p (x , y )沿y =x 趋于(0, 0),则 1lim )(lim 44022222 )0,0(),(==−+→=→x x y x y x y x x xy y x ; 如果动点p (x , y )沿y =2x 趋向(0, 0),则 044lim )(lim 2440222222 )0,0(),(=+=−+→=→x x x y x y x y x x xy y x . 因此, 极限22222)0,0(),()(lim y x y x y x y x −+→不存在. 8. 函数xy x y z 2222−+=在何处间断? 解 因为当y 2−2x =0时, 函数无意义,所以在y 2−2x =0处, 函数x y x y z 2222−+=间断. 9. 证明0lim 22)0,0(),(=+→yx xy y x .证明 因为22||||2222222222y x yx y x y x xy y x xy +=++≤+=+, 所以 02lim ||lim 022)0,0(),(22)0,0(),(=+≤+≤→→y x yx xy y x y x . 因此 0lim 22)0,0(),(=+→yx xy y x . 证明 因为2||22y x xy +≤, 故22||22222222y x yx y x y x xy +=++=+. 对于任意给定的ε>0, 取δ=2ε, 当δ<+<220y x 时恒有εδ=<+≤−+22|0|2222y x yx xy , 所以0lim 22)0,0(),(=+→yx xy y x . 10. 设F (x , y )=f (x ), f (x )在x 0处连续, 证明: 对任意y 0∈R , F (x , y )在(x 0, y 0)处连续.证明 由题设知, f (x )在x 0处连续, 故对于任意给定的ε>0, 取δ>0, 当|x −x 0|<δ时, 有|f (x )−f (x 0)|<ε.作(x 0, y 0)的邻域U ((x 0, y 0), δ), 显然当(x , y )∈U ((x 0, y 0), δ)时, |x −x 0|<δ, 从而 |F (x , y )−F (x 0, y 0)|=|f (x )−f (x 0)|<ε,所以F (x , y )在点(x 0, y 0)处连续.又因为y 0是任意的, 所以对任意y 0∈R , F (x , y )在(x 0, y 0)处连续.习题8−21. 求下列函数的偏导数:(1) z =x 3y −y 3x ;解 323y y x xz −=∂∂, 233xy x y z −=∂∂. (2)uvv u s 22+=; 解 21)(u v v u v v u u u s −=+∂∂=∂∂, 21)(v u u u v v u v v s −=+∂∂=∂∂. (3))ln(xy z =;解 x y x y x x x z 1ln ln 121)ln ln (⋅+⋅=+∂∂=∂∂)ln(21xy x =. 同理)ln(21xy y y z =∂∂. (4) z =sin(xy )+cos 2(xy );解 y xy xy y xy xz ⋅−⋅+⋅=∂∂)]sin([)cos(2)cos()]2sin()[cos(xy xy y −= 根据对称性可知)]2sin()[cos(xy xy x yz −=∂∂. (5)yx z tan ln =; 解 y x y y y x yxx z 2csc 21sec tan 12=⋅⋅=∂∂, y x y x y x y x yx y z 2csc 2sec tan 1222−=−⋅⋅=∂∂. (6) z =(1+xy )y ;解 121)1()1(−−+=⋅+=∂∂y y xy y y xy y xz , ]1)1[ln()1ln()1ln(xyx y xy e e y y z xy y xy y +⋅++=∂∂=∂∂++]1)1[ln()1(xy xy xy xy y ++++=. (7)z yx u =;解 )1(−=∂∂z y x zy x u , x x zz x x y u z yz y ln 11ln ⋅=⋅=∂∂, x x zy z y x x z u z y z y ln )(ln 22⋅−=−=∂∂. (8) u =arctan(x −y )z ;解 z z y x y x z x u 21)(1)(−+−=∂∂−, z z y x y x z y u 21)(1)(−+−−=∂∂−, z z y x y x y x z u 2)(1)ln()(−+−−=∂∂. 2. 设gl T π2=, 试证0=∂∂+∂∂g T g l T l . 解 因为l g l T ⋅⋅=∂∂1π, g g g l gT 121(223⋅−=⋅−⋅=∂∂−ππ, 所以 0=⋅−⋅=∂∂+∂∂gl g l g T g l T l ππ. 3. 设)11(y x e z +−=, 求证z yz y x z x 222=∂∂+∂∂. 解 因为211(1xe x z y x ⋅=∂∂+−, 2)11(1y e y z y x ⋅=∂∂+−, 所以 z e e y z y x z x y x y x 2)11()11(22=+=∂∂+∂∂+−+− 4. 设yx y x y x f arcsin )1(),(−+=, 求. )1 ,(x f x解 因为x x x x f =−+=1arcsin )11()1 ,(, 所以1)1 ,()1 ,(==x f dxd x f x . 5. 曲线⎪⎩⎪⎨⎧=+=4422y y x z 在点(2, 4, 5)处的切线与正向x 轴所成的倾角是多少? 解 242x x x z ==∂∂, αtan 1)5,4,2(==∂∂xz , 故4πα=. 6. 求下列函数的22x z ∂∂, 22y z ∂∂, yx z ∂∂∂2. (1) z =x 4+y 4−4x 2y 2;解 2384xy x x z −=∂∂, 2222812y x xz −=∂∂; y x y y z 2384−=∂∂, 2222812x y yz −=∂∂; xy y x y yy x z 16)84(232−=−∂∂=∂∂∂. (2)x y z arctan=; 解 22222)(11y x y x y xy x z +−=−⋅+=∂∂, 22222)(2y x xy x z +=∂∂; 2222)1(11y x x x xy y z +=⋅+=∂∂, 22222)(2y x xy y z +−=∂∂; 22222222222222)()(2)()(y x x y y x y y x y x y y y x z +−=+−+−=+−∂∂=∂∂∂. (3) z =y x .解 y y x z x ln =∂∂, y y xzx 222ln =∂∂; 1−=∂∂x xy y z , 222)1(−−=∂∂x y x x y z ;)1ln (1ln )ln (112+=⋅+=∂∂=∂∂∂−−y x y yy y xy y y y y x z x x x x . 7. 设f (x , y , z )=xy 2+yz 2+zx 2, 求f xx (0, 0, 1), f xz (1, 0, 2), f yz (0, −1, 0)及f zzx (2, 0, 1). 解 因为f x =y 2+2xz , f xx =2z , f xz =2x ,f y =2xy +z 2, f yz =2z ,f z =2yz +x 2, f zz =2y , f zzx =0,所以 f xx (0, 0, 1)=2, f xz (1, 0, 2)=2,f yz (0, −1, 0)=0, f zzx (2, 0, 1)=0.8. 设z =x ln(xy ), 求y x z ∂∂∂23及23y x z ∂∂∂. 解 1)ln()ln(+=⋅+=∂∂xy xyy x xy x z , x xy y x z 122==∂∂, 023∂∂∂yx z , y xy x y x z 12==∂∂∂, 2231y y x z −=∂∂∂. 9. 验证:(1)满足nx e y tkn sin 2−=22xy k t y ∂∂=∂∂; 证明 因为nx e kn kn nx e ty t kn t kn sin )(sin 2222⋅−=−⋅⋅=∂∂−−, nx ne x y t kn cos 2−=∂∂, nx e n xy t kn sin 2222−−=∂∂, nx e kn xy k t kn sin 222−−=∂∂, 所以22x y k t y ∂∂=∂∂. (2)222z y x r ++=满足rz r y r x r 2222222=∂∂+∂∂+∂∂.证明 r x z y x x x r =++=∂∂222, 322222r x r r x r x r x r −=∂∂−=∂∂, 由对称性知32222ry r y r −=∂∂, 32222r z r z r −=∂∂, 因此 322322322222222rz r r y r r x r z r y r x r −+−+−=∂∂+∂∂+∂∂ r r r r r z y x r 23)(332232222=−=++−=.习题8−31. 求下列函数的全微分:(1)yx xy z +=; 解 dy y z dx x z dz ∂∂+∂∂=dy yxx dx y y )()1(2−++=. (2)x ye z =;解 xdy e x dx e x y dy y z dx x z dz y x y 12+−=∂∂+∂∂=. (3) 22yx y z +=; 解 因为2/3222322)()(21y x xy y x y x z +−=+−=∂∂−, 2/3222222222)(y x x y x y x y y y x z +=++⋅−+=∂, 所以 dy y x x dx y x xy dz 2/32222/322)()(+++−=)()(2/322xdy ydx y x x −+−=. (4)u =x yz .解 因为1−⋅=∂∂yz x yz x u , x zx y u yz ln =∂∂, x yx zu yz ln =∂∂, 所以xdz yx xdy zx dx yzx du yz yz yz ln ln 1++=− 2. 求函数z =ln(1+x 2+y 2)当x =1, y =2时的全微分.解 因为2212y x x x z ++=∂∂, 2212y x y y z ++=∂∂, 3121=∂∂==y x x z, 3221=∂∂==y x y z,所以 dy dx dz y x 323121⋅+===. 3. 求函数xy z =当x =2, y =1, Δx =0.1, Δy =−0.2时的全增量和全微分. 解 因为x y x x y y z −Δ+Δ+=Δ, y x x xy dz Δ+Δ−=12, 所以, 当x =2, y =1, Δx =0.1, Δy =−0.2时,119.0211.02)2.0(1−=−+−+=Δz , 125.0)2.0(211.041−=−+×−=dz . 4. 求函数z =e xy 当x =1, y =1, Δx =0.15, Δy =0.1时的全微分.解 因为y xe x ye y yz x x z dz xy xy Δ+Δ=Δ∂∂+Δ∂∂= 所以, 当x =1, y =1, Δx =0.15, Δy =0.1时,e e e dz 25.01.015.0=⋅+⋅=*5. 计算33)97.1()102(+的近似值.解 设33y x z +=, 由于y y z x x z y x y y x x Δ∂∂+Δ∂∂++≈Δ++Δ+3333)()(332233233y x y y x x y x +Δ+Δ++=, 所以取x =1, y =2, Δx =0.02, Δy =−0.03可得95.2212)03.0(2302.0321)97.1()02.1(32333=+−⋅⋅+⋅++≈+.*6. 计算(1.97)1.05的近似值(ln2=0.693).解 设z =x y , 由于y yz x x z x x x y y y Δ∂∂+Δ∂∂+≈Δ+Δ+)(y x x x yx x y y y Δ+Δ+=−ln 1, 所以取x =2, y =1, Δx =−0.03, Δy =0.05可得(1.97)1.05≈2−0.03+2ln2⋅0.05+1.97+0.0693 ≈2.093.*7. 已知边长为x =6m 与y =8m 的矩形, 如果x 边增加5cn 而y 边减少10cm ,问这个矩形的对角线的近似变化怎样?解 矩形的对角线为22y x z +=,)(122y y x x yx y dy dz x dx dz dz z Δ+Δ+=Δ+Δ=≈Δ, 当x =6, y =8, Δx =0.05, Δy =−0.1时,05.0)1.0805.0686122−=⋅−⋅+≈Δz . 这个矩形的对角线大约减少5cm .*8. 设有一无盖圆柱形容器, 容器的壁与底的厚度均为0.1cm , 内高为20cm ,内半径为4厘米, 求容器外壳体积的近似值.解 圆柱体的体积公式为V =πR 2h ,ΔV ≈dV =2πRh ΔR +πR 2Δh ,当R =4, h =20, ΔR =Δh =0.1时,ΔV ≈2×3.14×4×20×0.1+3.14×42×0.1≈55.3(cm 3)这个容器外壳的体积大约是55.3cm 3.*9. 设有直角三角形, 测得其两腰的长分别为7±0.1cm 和24±0.1cm , 试求利用上述二值来计算斜边长度时的绝对误差.解 设两直角边的长度分别为x 和y , 则斜边的长度为22y x z +=.||||||||||||y y z x x z dz z Δ⋅∂∂+Δ⋅∂∂≤≈Δ|)|||(122y y x x yx Δ+Δ+=. 令x =7, y =24, |Δx |≤0.1, |Δy |≤0.1, 则得斜边长度z 的绝对误差约为124.0)1.0241.07(247122=⋅+⋅+=z δcm . *10. 测得一块三角形土地的两边长分别为63±0.1m 和78±0.1m ,这两边的夹角为60°±1°, 试求三角形面积的近似值, 并求其绝对误差和相对误差.解 设三角形的两边长为x 和y , 它们的夹角z , 为则三角形面积为z xy s sin 21=. zdz xy zdy x zdx y dS cos 21sin 21sin 21++=||cos 21||sin 21||sin 21||||dz z xy dy z x dx z y dS S ++≤≈Δ. 令x =63, y =78, 3π=z , |dx |=0.1, |dy |=0.1, 180π=dz , 则 55.2718021278631.0232631.023278=×××+××+××≈πδs , 82.21273sin 786321=⋅⋅⋅=πS , %29.182.212755.27==S s δ, 所以三角形面积的近似值为2127.82m 2, 绝对误差为27.55 m 2, 相对误差为1.29%.*11. 利用全微分证明: 两数之和的绝对误差等于它们各自的绝对误差之和. 证明 设u =x +y , 则||||||||||||y x y x y yu x x u du u Δ+Δ≤Δ+Δ=Δ∂∂+Δ∂∂=≈Δ. 所以两数之和的绝对误差|Δu |等于它们各自的绝对误差|Δx |与|Δy |的和.*12. 利用全微分证明: 乘积的相对误差等于各因子的相对误差之和; 商的相对误差等于被除数及除数的相对误差之和.证明 设u =xy , yx v =, 则Δu ≈du =ydx +xdy , 2y xdy ydx dv v −=≈Δ, 由此可得相对误差;ydy x dx xy xdy ydx u du u u +=+=≈Δy y x x y dy x dx Δ+Δ=+≤; y dy x dx yx y xdy ydx v dv v v −=⋅−==Δ2y y x x y dy x dx Δ+Δ=+≤.习题8−41. 设z =u 2−v 2, 而u =x +y , v =x −y , 求x z ∂∂, yz ∂∂. 解 xv v z x u u z x z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂=2u ⋅1+2v ⋅1=2(u +v )=4x , yv v z y u u z y z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂=2u ⋅1+2v ⋅(−1)=2(u −v )=4y . 2. 设z =u 2ln v , 而yx u =, v =3x −2y , 求x z ∂∂, y z ∂∂. 解 xv v z x u u z x z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂ 31ln 22⋅+⋅=v u y v u 222)23(3)23ln(2yy x x y x y x −+−=, yv v z y u u z y z ∂∂⋅∂∂+∂∂⋅∂∂=∂∂ )2()(ln 222−+−⋅=v u y x v u 2232)23(2)23ln(2y y x x y x y x −−−−=. 3. 设z =e x −2y , 而x =sin t , y =t 3, 求dtdz . 解 dtdy y z dt dx x z dt dz ⋅∂∂+⋅∂∂=2223)2(cos t e t e y x y x ⋅−⋅+=−− .)6(cos )6(cos 22sin 223t t e t t e t t y x −=−=−− 4. 设z =arcsin(x − y ), 而x +3t , y =4t 3, 求dtdz . 解 dt dy y z dt dx x z dt dz ⋅∂∂+⋅∂∂=22212)(113)(11t y x y x −−−+⋅−−= 232)43(1)41(3t t t −−−=. 5. 设z =arctan(xy ), 而y =e x , 求dxdz . 解 dx dy y z x z dx dz ⋅∂∂+∂∂=xx x e x x e e y x x y x y 2222221)1(11++=⋅+++=.6. 设1)(2+−=a z y e u ax , 而y =a sin x , z =cos x , 求dx du . 解 dxdz dz u dx dy y u x u dx du ⋅∂+⋅∂∂+∂∂= )sin (1cos 11)(222x a e x a a e a z y ae ax ax ax −⋅+−⋅+++−= )sin cos cos sin (122x x a x a x a a e ax ++−+=x e ax sin =. 7. 设y x z arctan =, 而x =u +v , y =u −v , 验证22v u v uv z u z +−=∂∂+∂∂. 证明 )()(vy y z v x x z u y y z u x x z v z u z ∂∂⋅∂∂+∂∂⋅∂∂+∂∂⋅∂∂+∂∂⋅∂∂=∂∂+∂∂ )()(111)(11222y x y x y y x −⋅++⋅+=)1()()(111)(11222−⋅−⋅++⋅++y x yx y y x 22222v u v u y x y +−=+=. 8. 求下列函数的一阶偏导数(其中f 具有一阶连续偏导数):(1) u =f (x 2−y 2, e xy );解 将两个中间变量按顺序编为1, 2号,2122212)()(f ye f x xe f x y x f x u xy xy ′+′=∂∂⋅′+∂−∂⋅′=∂∂, 212)2212)((f xe f y ye f y y x f y u xy xy ′+′−=∂∂⋅′+∂−∂⋅′=∂∂. (2) ,(zy y x f u =; 解 1211)()(f yz y x f y x x f x u ′=∂∂⋅′+∂∂⋅′=∂∂, )()(21z y y f y x y f y u ∂∂⋅′+∂∂′=∂∂2121f z f yx′+′−=,)()(21z y z f z x z f z u ∂∂⋅′+∂∂′=∂∂22f z y ′−=. (3) u =f (x , xy , xyz ).解 yz f y f f xu ⋅′+⋅′+⋅′=∂∂3211321f yz f y f ′+′+′=, 3232f xz f x xz f x f yu ′+′=⋅′+⋅′=∂∂, 33f xy xy f zu ′=⋅′=∂∂. 9. 设z =xy +xF (u ), 而xy u =, F (u )为可导函数, 证明xy z y z y x z x +=∂∂+∂∂⋅. 证明 y z y x z x ∂∂⋅+∂∂⋅)([])()([yu u F x x y x u u F x u F y x ∂∂′+⋅+∂∂′++= )]([)]()([u F x y u F xy u F y x ′+⋅+′−+= =xy +xF (u )+xy =z +xy .10. 设)(22y x f y z −=, 其中f (u )为可导函数, 验证211y zy z y x z x =∂∂+∂∂.证明 ()()u f f xy u f x f y x z 2222′−=⋅′⋅−=∂∂, ()()u f f y u f u f y f y u f y z 2222)(1)2()(′−+=−⋅′⋅−=∂∂, 所以 )(11221122u f y u f f y u f f y y z y x z x ⋅+′+′−=∂∂⋅+∂∂⋅211y z zy y =⋅. 11. 设z =f (x 2+y 2), 其中f 具有二阶导数, 求22xz ∂∂, y x z ∂∂∂2, 22y z ∂∂. 解 令u =x 2+y 2, 则z =f (u ),f x xu u f x z ′=∂∂′=∂∂2)(, f y y u u f y z ′=∂∂′=∂∂2)(, f x f x u f x f xz ′′+′=∂∂⋅′′+′=∂∂2224222,f xy yu f x y x z ′′=∂∂⋅′′=∂∂∂422, f y f y u f y f y z ′′+′=∂∂⋅′′+′=∂∂422222. 12. 求下列函数的22x z ∂∂,y x z ∂∂∂2,22y z ∂∂(其中f 具有二阶连续偏导数): (1) z =f (xy , y );解 令u =xy , v =y , 则z =f (u , v ).u f y vf y u f x v v f x u u f x z ∂∂=⋅∂∂+⋅∂∂=∂∂⋅∂∂+∂∂⋅∂∂=∂∂0, vf u f x v f x u f y v v f y u u f y z ∂∂+∂∂=⋅∂∂+⋅∂∂=∂∂⋅∂∂+∂∂⋅∂∂=∂∂1. 因为f (u , v )是u 和v 的函数, 所以u f ∂∂和v f ∂∂也是u 和v 的函数, 从而u f ∂∂和vf ∂∂是以u 和v 为中间变量的x 和y 的函数.)()()(22u f x y uf y x x z x x z ∂∂∂∂=∂∂∂∂=∂∂∂∂=∂∂ 222222222)0()(u f y v u f y u f y x v v u f x u u f y ∂∂=⋅∂∂∂+⋅∂∂=∂∂⋅∂∂∂+∂∂⋅∂∂=, )(1)()(2uf y y u f u f y y x z y y x z ∂∂∂∂+∂∂⋅=∂∂∂∂=∂∂∂∂=∂∂∂ )(222yv v u f y u u f y u f ∂∂⋅∂∂∂+∂∂⋅∂∂+∂∂= v u f y uf xy u f v u f x u f y u f ∂∂∂+∂∂+∂∂=⋅∂∂∂+⋅∂∂+∂∂=222222)1(, )()()()(22v f y u f y x vf u f x y y z y y z ∂∂∂∂+∂∂∂∂=∂∂+∂∂∂∂=∂∂∂∂=∂∂ yv v f y u u v f y v v u f y u u f x ∂∂⋅∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂=222222)( 1)1(222222⋅∂∂+⋅∂∂∂+⋅∂∂∂+⋅∂∂=vf x u v f v u f x u f x2222222v f v u f x u f x ∂∂+∂∂∂+∂∂=. (2)) ,(yx x f z =; 解 令u =x , yx v =, 则z =f (u , v ). v f y u f x v v f dx du u f x z ∂∂⋅+∂∂=∂∂⋅∂∂+⋅∂∂=∂∂1, vf y xdy dv v f y z ∂∂⋅−=⋅∂∂=∂∂2. 因为f (u , v )是u 和v 的函数, 所以u f ∂∂和v f ∂∂也是u 和v 的函数, 从而u f ∂∂和vf ∂∂是以u 和v 为中间变量的x 和y 的函数. )(1)()1()(22vf x y u f x v f y u f x x z x x z ∂∂∂∂⋅+∂∂∂∂=∂∂⋅+∂∂∂∂=∂∂∂∂=∂∂ )(1)(222222xv v f dx du u v f y x v v u f dx du u f ∂∂⋅∂∂+⋅∂∂∂+∂∂⋅∂∂∂+⋅∂∂= 22222212v f y v u f y u f ∂∂⋅+∂∂∂⋅+∂∂=, 1()(2vf y u f y x z y y x z ∂∂⋅+∂∂∂∂=∂∂∂∂=∂∂∂)(1)1()(v f y y v f y dy d u f y ∂∂∂∂⋅+∂∂⋅+∂∂∂∂= yv v f y v f y y v v u f ∂∂⋅∂∂⋅+∂∂⋅−∂∂⋅∂∂∂=22211 221v f y x v f y v u f y x ∂∂⋅−∂∂⋅−∂∂∂⋅−= ()()(2222vf y y x v f y x y y z y y z ∂∂∂∂⋅−∂∂⋅−∂∂=∂∂∂∂=∂∂22423222322vf y x v f y x y v v f y x v f y x ∂∂⋅+∂∂⋅=∂∂⋅∂∂⋅−∂∂⋅=. (3) z =f (xy 2, x 2y );解 z x =f 1′⋅y 2+f 2′⋅2xy =y 2f 1′+2xyf 2′,z y =f 1′⋅2xy +f 2′⋅x 2=2xyf 1′+x 2f 2′;z xx =y 2[f 11′′⋅y 2+f 12′′⋅2xy ]+2yf 2′′+2xy [f 21′′⋅y 2+f 22′′⋅2xy ] =y 4f 11′′+2xy 3f 12′′+2yf 2′′+2xy 3f 21′′+4x 2y 2 f 22′′=y 4f 11′′+4xy 3f 12′′+2yf 2′′+4x 2y 2 f 22′′,z xy =2y f 1′+y 2[f 11′′⋅2xy +f 12′′⋅x 2]+2xf 2′+2xy [f 21′′⋅2xy +f 22′′⋅x 2] =2y f 1′+2xy 3f 11′′+x 2y 2 f 12′′+2xf 2′+4x 2y 2f 21′′+2x 3yf 22′′ =2y f 1′+2xy 3f 11′′+5x 2y 2 f 12′′+2xf 2′+2x 3yf 22′′,z yy =2xf 1′+2xy [f 11′′⋅2xy +f 12′′⋅x 2]+x 2[f 21′′⋅2xy +f 22′′⋅x 2] =2xf 1′+4x 2y 2f 11′′+2x 3y f 12′′+2x 3yf 21′′+x 4f 22′′=2xf 1′+4x 2y 2f 11′′+4x 3y f 12′′+x 4f 22′′.(4) z =f (sin x , cos y , e x +y ).解 z x =f 1′⋅cos x + f 3′⋅e x +y =cos x f 1′+e x +y f 3′,z y =f 2′⋅(−sin y )+ f 3′⋅e x +y =−sin y f 2′+e x +y f 3′,z xx =−sin x f 1′+cos x ⋅(f 11′′⋅cos x + f 13′′⋅e x +y )+e x +y f 3′+e x +y (f 31′′⋅cos x + f 33′′⋅e x +y ) =−sin x f 1′+cos 2x f 11′′+e x +y cos x f 13′′+e x +y f 3′+e x +y cos x f 31′′+e 2(x +y ) f 33′′ =−sin x f 1′+cos 2x f 11′′+2e x +y cos x f 13′′+e x +y f 3′+e 2(x +y ) f 33′′, z xy =cos x [f 12′′⋅(−sin y )+ f 13′′⋅e x +y ]+e x +y f 3′+e x +y [f 32′′⋅(−sin y )+ f 33′′⋅e x +y ] =−sin y cos x f 12′′+e x +y cos x f 13′+e x +y f 3′−e x +y sin y f 32′+e 2(x +y )f 33′ =−sin y cos x f 12′′+e x +y cos x f 13′′+e x +y f 3′−e x +y sin y f 32′′+e 2(x +y )f 33′′, z yy =−cos y f 2′−sin y [f 22′′⋅(−sin y )+ f 23′′⋅e x +y ]+e x +y f 3′+e x +y [f 32′′⋅(−sin y )+ f 33′′⋅e x +y ] =−cos y f 2′+sin 2y f 22′′−e x +y sin y f 23′′+e x +y f 3′−e x +y sin y f 32′′+ f 33′′⋅e 2(x +y ) =−cos y f 2′+sin 2y f 22′′−2e x +y sin y f 23′′+e x +y f 3′+f 33′′⋅e 2(x +y ).13. 设u =f (x , y )的所有二阶偏导数连续, 而3t s x −=, 3t s y +=, 证明2222)()()()(t u s u y u x u ∂∂+∂∂=∂∂+∂∂及22222222t u s u y u x u ∂∂+∂∂=∂∂+∂∂证明 因为y u x u s yy u s x x u s u ∂∂⋅+∂∂⋅=∂∂⋅∂∂+∂∂⋅∂∂=∂∂2321y u x u t yy u t x x u t u ∂∂⋅+∂∂⋅−=∂∂⋅∂∂+∂∂⋅∂∂=∂∂2123所以2222)2123()2321()()(y u x u y u x u t u s u ∂∂+∂∂−+∂∂+∂∂=∂∂+∂∂22)()(y u x u ∂∂+∂∂=. 又因为)2321()(2yu x u s s u s s u ∂∂⋅+∂∂⋅∂∂=∂∂∂∂=∂∂ (23)(212222s y y u s x x y u s y y x u s x x u ∂∂⋅∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂= 2321(23)2321(212222y u x y u y x u x u ∂∂⋅+∂∂∂⋅+∂∂∂⋅+∂∂⋅= 222432341y u y x u x u ∂∂⋅+∂∂∂⋅+∂∂⋅=, )2123()(2yu x u t t u t t u∂∂⋅+∂∂⋅−∂∂=∂∂∂∂=∂∂ )(21)(232222t y y u t x x y u t y y x u t x x u ∂∂⋅∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂∂+∂∂⋅∂∂−= )2123(21)2123(232222y u x y u y x u x u ∂∂⋅+∂∂∂⋅−+∂∂∂⋅+∂∂⋅−−=22222412343y uy x u x u ∂∂⋅+∂∂∂⋅−∂∂⋅=,所以 22222222y u x u t u s u ∂∂+∂∂=∂∂+∂∂.习题8−51. 设sin y +e x −xy 2=0, 求dxdy . 解 令F (x , y )=sin y +e x −xy 2, 则F x =e x −y 2, F y =cos y −2xy , xy y e y xy y y e F F dx dy xy x 2cos 2cos 222−−=−−−=−=.2. 设x y y x arctan ln 22=+, 求dxdy. 解 令xyy x y x F arctan ln ),(22−+=, 则22222222)()(11221y x y x xy x y y x x y x F x ++=−⋅+−+⋅+=,22222221)(11221yx x y x xy y x y y x F y +−=⋅+−+⋅+=,yx y x F F dx dyy x −+=−=. 3. 设022=−++xyz z y x , 求x z ∂∂及y z ∂∂.解 令xyz z y x z y x F 22),,(−++=, 则 xyz yz F x −=1, xyzxz F y −=2, xyz xyF z −=1,xy xyz xyz yz F F x z z x −−=−=∂∂, xy xyz xyz xz F F y zz y −−=−=∂∂2. 4. 设y z z x ln =, 求x z ∂∂及yz ∂∂, 解 令yz z x z y x F ln ),,(−=, 则z F x 1=, y yzyz F y 1)(12=−⋅−=, 2211z z x y y z z x F z +−=⋅−−=,所以 z x z F F x z z x +=−=∂∂, )(2z x y z F F y z z y +=−=∂∂.5. 设2sin(x +2y −3z )=x +2y −3z , 证明1=∂∂+∂∂yz x z证明 设F (x , y , z )=2sin(x +2y −3z )−x −2y +3z , 则 F x =2cos(x +2y −3z )−1,F y =2cos(x +2y −3z )⋅2−2=2F x , F z =2cos(x +2y −3z )⋅(−3)+3=−3F x ,313=−−=−=∂∂x x z x F F F F x z , 3232=−−=−=∂∂x x z y F F F F y z ,于是 13231=+=−−=∂∂+∂∂z z z x F FF F yz x z .6. 设x =x (y , z ), y =y (x , z ), z =z (x , y )都是由方程F (x , y , z )=0所确定的具有连续偏导数的函数, 证明1−=∂∂⋅∂∂⋅∂∂xz z yy x .解 因为x y F F y x −=∂∂, y z F F zy −=∂∂, z x F F x z−=∂∂,所以 1()()(−=−⋅−⋅−=∂∂⋅∂∂⋅∂∂z x y z x y F F F F F F xz z yy x .7. 设ϕ(u , v )具有连续偏导数, 证明由方程ϕ(cx −az , cy −bz )=0 所确定的函数z =f (x , y )满足c yz b x z a =∂∂+∂∂.证明 因为v u uv u u b a c b a c x z ϕϕϕϕϕϕ+=⋅−⋅−⋅−=∂∂,vu vv u v b a c b a c y z ϕϕϕϕϕϕ+=⋅−⋅−⋅−=∂∂,所以 c b a c b b a c a y z b x z a v u vv u u =+++⋅=∂∂+∂∂ϕϕϕϕϕϕ.8. 设e z−xyz =0, 求22x z ∂∂. 解 设F (x , y , z )=e z −xyz , 则F x =−yz , F z =e z −xy , xye yzF F x z z x −=−=∂∂,222)()()()(xy e y x z e yz xy e x z y x z x x z z z z −−∂∂−−∂∂=∂∂∂∂=∂∂ 222)()(xy e xye yzyze xy ye z y z z z −−−−+=32232)(22xy e e z y z xy ze y z zz −−−=. 9. 设z 3−3xyz =a 3, 求yx z ∂∂∂2. 解 令F (x , y , z )=z 3−3xyz −a 3, 则xy z yz xy z yz F F x z z x −=−−−=−=∂∂22333, xyz xz xy z xz F F y z z y −=−−−=−=∂∂22333, )()(22xyz yzy x z y y x z −∂∂=∂∂∂∂=∂∂∂222)()2())((xy z x y z z yz xy z yz y z −−∂∂−−∂∂+=22222)()2()()(xy z x xyz xz z yz xy z xy z xz y z −−−−−⋅−+=322224)()2(xy z y x xyz z z −−−=.10. 求由下列方程组所确定的函数的导数或偏导数:(1)设, 求⎩⎨⎧=+++=203222222z y x y x z dx dy , dx dz; 解 视y =y (x ), z =z (x ), 方程两边对x 求导得⎪⎩⎪⎨⎧=+++=064222dx dz z dx dy y x dx dy y x dx dz , 即⎪⎩⎪⎨⎧−=+−=−xdx dz z dxdy y xdx dz dx dy y 3222.解方程组得)13(2)16(++−=∂∂z y z x x y , 13+=z x dx dz.(2)设, 求⎩⎨⎧=++=++10222z y x z y x dz dx ,dz dy ;解 视x =x (z ), y =y (z ), 方程两边对z 求导得⎪⎩⎪⎨⎧=++=++022201z dz dy y dzdx x dz dy dz dx , 即⎪⎩⎪⎨⎧−=+−=+zdz dy y dz dx x dz dy dz dx 2221.解方程组得y x z y z x −−=∂∂, yx xz z y −−=∂∂. (3)设, 其中f , g 具有一阶连续偏导数, 求⎩⎨⎧−=+=),(),(2y v x u g v y v ux f u x u ∂∂,x v ∂∂; 解 视u =u (x , y ), v =v (x , y ), 方程两边对x 求偏导得⎪⎩⎪⎨⎧∂∂⋅′+−∂∂⋅′=∂∂∂∂⋅′+∂∂+⋅′=∂∂x v yv g x u g x v x v f x u x u f x u 21212)1()( , 即⎪⎩⎪⎨⎧′=∂∂⋅⋅−′+∂∂′′′−=∂∂⋅′+∂∂−′121121)12()1(g x v g yv x u g f u x v f x u f x . 解之得1221221)12)(1()12(g f g yv f x g f g yv f u x u ′′−−′−′′′−−′′−=∂∂, 1221111)12)(1()1(g f g yv f x f u f x g x v ′′−−′−′−′+′′=∂∂.(4)设, 求⎩⎨⎧−=+=v u e y v u e x u u cos sin x u ∂∂, y u ∂∂, x v ∂∂, y v ∂∂. 解 视u =u (x , y ), v =v (x , y ), 方程两边微分得, 即, ⎩⎨⎧+−=++=vdv u vdu du e dy vdv u vdu du e dx uu sin cos cos sin ⎩⎨⎧=+−=++dy vdv u du v e dxvdv u du v e u u sin )cos (cos )sin (从中解出du , dv 得dy v v e v dxv v e v du u u 1)cos (sin cos 1)cos (sin sin +−−++−=, v v e u e v dx v v e u e v dv u uu u ]1)cos (sin [sin ]1)cos (sin [cos +−+++−−=,从而1)cos (sin sin +−=∂∂v v e v x u u , 1)cos (sin cos +−−=∂∂v v e vy u u ,]1)cos (sin [cos +−−=∂∂v v e u e v x v u , ]1)cos (sin [sin +−+=∂∂v v e u e v y v u.11. 设y =f (x , t ), 而t 是由方程F (x , y , t )=0所确定的x , y 的函数, 其中f , F 都具有一阶连续偏导数, 试证明:tF y F t f x F t f t F x f dx dy ∂∂+∂∂⋅∂∂∂∂⋅∂∂−∂∂⋅∂∂=. 证明 由方程组可确定两个一元隐函数, 方⎩⎨⎧==0),,(),(t y x F t x f y ⎩⎨⎧==)()(x t t x y y 程两边对x 求导可得⎪⎩⎪⎨⎧=⋅∂∂+⋅∂∂+∂∂⋅∂∂+∂∂=0dxdt t F dx dy y F x F dxdt t f x f dx dy ,移项得⎪⎩⎪⎨⎧∂∂−=∂∂+⋅∂∂∂∂=⋅∂∂−x F dxdt t F dx dy y F x f dx dt t f dx dy ,在01≠∂∂⋅∂∂+∂∂=∂∂∂∂∂∂−=y F t f t F tF y F t fD 的条件下 yF t f t F x Ft f t F x f t Fx F t f x f D dx dy ∂∂⋅∂∂+∂∂∂∂⋅∂∂−∂∂⋅∂∂=∂∂∂∂−∂∂−∂∂⋅=1.习题8−61. 求曲线x =t −sin t , y =1−cos t , 2sin 4t z =在点)22 ,1 ,12 (−π处的切线及法平面方程.解 x ′(t )=1−cos t , y ′(t )=sin t , 2cos 2)(t t z =′. 因为点)22 ,1 ,12 (−π所对应的参数为2 π=t , 故在点)22 ,1 ,12 (−π处的切向量为)2 ,1 ,1(=T .因此在点)22 ,1 ,12(−π处, 切线方程为22211121−=−=−+z y x π, 法平面方程为0)22(2)1(1)12(1=−+−⋅++−⋅z y x π, 即422+=++πz y x .2. 求曲线t t x +=1, tt y +=1, z =t 2在对应于t =1的点处的切线及法平面方程. 解 2)1(1)(t t x +=′, 21)(t t y −=′, z ′(t )=2t .在t =1所对应的点处, 切向量)2 ,1 ,41(−=T , t =1所对应的点为)1 ,2 ,21(, 所以在t =1所对应的点处, 切线方程为21124121−=−−=−z y x , 即8142121−=−−=−z y x ; 法平面方程为0)1(2)2()21(41=−+−−−z y x , 即2x −8y +16z −1=0.3. 求曲线y 2=2mx , z 2=m −x 在点(x 0, y 0, z 0)处的切线及法平面方程. 解 设曲线的参数方程的参数为x , 将方程y 2=2mx 和z 2=m −x 的两边 对x 求导, 得m dx dyy22=, 12−=dxdz z , 所以y m dx dy=, z dx dz 21−=.曲线在点(x 0, y 0, z 0,)的切向量为)21,,1(00z y m −=T , 所求的切线方程为000211z z z y m y y x x −−=−=−, 法平面方程为0)(21)()(00000=−−−+−z z z y y y m x x . 4. 求曲线在点(1, 1, 1)处的切线及法平面方程.⎩⎨⎧=−+−=−++0453203222z y x x z y x 解 设曲线的参数方程的参数为x , 对x 求导得,⎪⎩⎪⎨⎧=+−=−++053203222dx dz dx dy dx dz z dx dy y x , 即⎪⎩⎪⎨⎧=−+−=+2533222dxdz dx dy x dx dz z dx dy y .解此方程组得z y z x dx dy 61015410−−−−=, z y y x dx dz 610946−−−+=. 因为169)1,1,1(=dx dy, 161)1,1,1(−=dx dz , 所以)161 ,169 ,1(=T . 所求切线方程为1611169111−−=−=−z y x , 即1191161−−=−=−z y x ; 法平面方程为0)1(161)1(169)1(=−−−+−z y x , 即16x +9y −z −24=0. 5. 求出曲线x =t , y =t 2, z =t 3上的点, 使在该点的切线平行于平面x +2y +z =4. 解 已知平面的法线向量为n =(1, 2, 1).因为x ′=1, y ′=2t , z ′=3t 2, 所以参数t 对应的点处的切向量为T =(1, 2t , 3t 2). 又因为切线与已知平面平行, 所以T ⋅n =0, 即1+4t +3t 2=0,解得t =−1, 31−=t . 于是所求点的坐标为(−1, 1, −1)和)271 ,91 ,31(−−. 6. 求曲面e z −z +xy =3在点(2,1,0)处的切平面及法线方程.解 令F (x , y , z )=e z −z +xy −3, 则n =(F x , F y , F z )|(2, 1, 0)=(y , x , e z −1)|(2, 1, 0)=(1, 2, 0),点(2,1, 0)处的切平面方程为1⋅(x −2)+2(y −1)+0⋅(z −0)=0, 即x +2y −4=0,法线方程为02112−=−=−z y x . 7. 求曲面ax 2+by 2+cz 2=1在点(x 0, y 0, z 0)处的切平面及法线方程.解 令F (x , y , z )=ax 2+by 2+cz 2−1, 则n =(F x , F y , F z )=(2ax , 2by , 2cz )=(ax , by , cz ).在点(x 0, y 0, z 0)处, 法向量为(ax 0, by 0, cz 0), 故切平面方程为ax 0(x −x 0)+by 0(y −y 0)+cz 0(z −z 0)=0,即 , 202020000cz by ax z cz y by x ax ++=++法线方程为00000cz z z by y y ax x x −=−=−.8. 求椭球面x 2+2y 2+z 2=1上平行于平面x −y +2z =0的切平面方程.解 设F (x , y , z )=x 2+2y 2+z 2−1, 则n =(F x , F y , F z )=(2x , 4y , 2z )=2(x , 2y , z ).已知切平面的法向量为(1, −1, 2). 因为已知平面与所求切平面平行, 所以2121z y x =−=, 即z x 21=, z y 41−=, 代入椭球面方程得1)4(2)2(222=+−+z z z , 解得1122±=z , 则1122±=x , 11221∓=y . 所以切点坐标为)1122,11221,112(±±∓. 所求切平面方程为0)1122(2)11221()112(=±+−±z y x ∓, 即 2112±=+−z y x . 9. 求旋转椭球面3x 2+y 2+z 2=16上点(−1, −2, 3)处的切平面与xOy 面的夹角的余弦.解 x O y 面的法向为n 1=(0, 0, 1).令F (x , y , z )=3x 2+y 2 +z 2−16, 则点(−1, −2, 3)处的法向量为n 2=(F x , F y , F z )|(−1, −2, 3)=(6x , 2y , 2z )|(−1, −2, 3)=(−6, −4, 6).点(−1, −2, 3)处的切平面与xOy 面的夹角的余弦为22364616||||cos 2222121=++⋅=⋅⋅=n n n n θ.10. 试证曲面a z y x =++(a >0)上任何点处的切平面在各坐标轴上的截距之和等于a .证明 设a z y x z y x F −++=),,(, 则)21,21,21(zy x =n . 在曲面上任取一点M (x 0, y 0, z 0), 则在点M 处的切平面方程为0)(1)(1)(1000000=−+−+−z z z y y y x x x , 即 a z y x z z y y x x =++=++000000. 化为截距式, 得1000=++az z ay y ax x , 所以截距之和为a z y x a az ay ax =++=++)(000000.习题8−71. 求函数z =x 2+y 2在点(1, 2)处沿从点(1, 2)到点)32 ,2(+的方向的方向导数 解 因为从点(1, 2)到点)32 ,2(+的向量为)3 ,1(=l , 故)cos ,(cos 23 ,21(||βα===l l e l . 又因为22)2,1()2,1(==∂∂x x z , 42)2,1()2,1(==∂∂y y z , 故所求方向导数为321234212cos cos +=⋅+⋅=∂∂+∂∂=∂∂βαy z x z l z . 2. 求函数z =ln(x +y )在抛物线y 2=4x 上点(1, 2)处, 沿这抛物线在该点处偏向x 轴正向的切线方向的方向导数.解 方程y 2=4x 两边对x 求导得2yy ′=4, 解得yy 2=′. 在抛物线y 2=4x 上点(1, 2)处, 切线的斜率为y ′(1)=1, 切向量为l =(1, 1), 单位切向量为)cos ,(cos )21 ,21(βα==l e . 又因为31 1)2,1()2,1(=+=∂∂y x x z , 31 1)2,1()2,1(=+=∂∂y x y z , 故所求方向导数为3221312131cos cos =⋅+⋅=∂∂+∂∂=∂∂βαy z x z l z . 3. 求函数)(12222b y a x z +−=在点)2,2(b a 处沿曲线12222=+b y a x 在这点的内法线方向的方向导数.解 令1),(2222−+=b y a x y x F , 则22a x F x =, 22b y F y =. 从而点(x , y )处的法向量为)2 ,2() ,(22by a xF F y x ±=±=n . 在)2,2(b a 处的内法向量为 )2 ,2()2 ,2()2,2(22b a b y a x b a −=−=n , 单位内法向量为)cos ,(cos ,(2222βα=+−+−=b a a b a b n e . 又因为a a x x zb a b a 222,2(2)2,2(−=−=∂∂, bb y y z b a b a 222,2(2)2,2(−=−=∂∂, 所以 222222222cos cos b a abb a a b b a b a y z x z n z +=+⋅++⋅=∂∂+∂∂=∂∂βα. 4. 求函数u =xy 2+z 3−xyz 在点(1, 1, 2)处沿方向角为3 πα=, 4 πβ=, 3 πγ=的方向的方向导数.解 因为方向向量为)21 ,22 ,21()cos ,cos ,(cos ==γβαl , 又因为 1)()2,1,1(2)2,1,1(−=−=∂∂yz y x u, 0)2()2,1,1()2,1,1(=−=∂∂xz xy y u , 11)3()2,1,1(2)2,1,1(=−=∂∂xy z z u , 所以 5211122021)1(cos cos cos =⋅+⋅+⋅−=∂∂+∂∂+∂∂=∂∂γβαz u y u x u l u .5. 求函数u =xyz 在点(5,1,2)处沿从点(5, 1, 2)到点(9, 4, 14)的方向的方向导数.解 因为l =(9−5, 4−1, 14−2)=(4, 3, 12), )1312 ,133 ,134(||==l l e l , 并且 2)2,1,5()2,1,5(==∂∂yz x u , 10)2,1,5()2,1,5(==∂∂xz y u , 5)2,1,5()2,1,5(==∂∂xy z u, 所以 139813125133101342cos cos cos =⋅+⋅+⋅=∂∂+∂∂+∂∂=∂∂γβαz u y u x u l u . 6. 求函数u =x 2+y 2+z 2在曲线x =t , y =t 2, z =t 3上点(1, 1, 1)处, 沿曲线在该点的切线正方向(对应于t 增大的方向)的方向导.解 曲线x =t , y =t 2, z =t 3上点(1, 1, 1)对应的参数为t =1, 在点(1, 1, 1)的切线正向为)3 ,2 ,1()3 ,2 ,1(12===t t t l , )143,142,141(||==l l e l , 又 22)1,1,1()1,1,1(==∂∂x x u , 22)1,1,1()1,1,1(==∂∂y y u , 22)1,1,1()1,1,1(==∂∂z z u, 所以 1412143214221412cos cos cos )1,1,1(=⋅+⋅+⋅=∂∂+∂∂+∂∂=∂∂γβαz u y u x u l u . 7. 求函数u =x +y +z 在球面x 2+y 2+z 2=1上点(x 0, y 0, z 0)处, 沿球面在该点的外法线方向的方向导数.解 令F (x , y , z )=x 2+y 2+z 2−1, 则球面x 2+y 2+z 2=1在点(x 0, y 0, z 0)处的外法向量为)2 ,2 ,2() , ,(000),,(000z y x F F F z y x z y x ==n , )cos ,cos ,(cos ) , ,(||000γβα===z y x n n n e , 又 1=∂∂=∂∂=∂∂zu y u x u , 所以 000000111cos cos cos z y x z y x zu y u x u n u ++=⋅+⋅+⋅=∂∂+∂∂+∂∂=∂∂γβα. 8. 设f (x , y , z )=x 2+2y 2+3z 2+xy +3x −2y −6z , 求grad f (0, 0, 0)及grad f (1, 1, 1).。
第八章习题解答
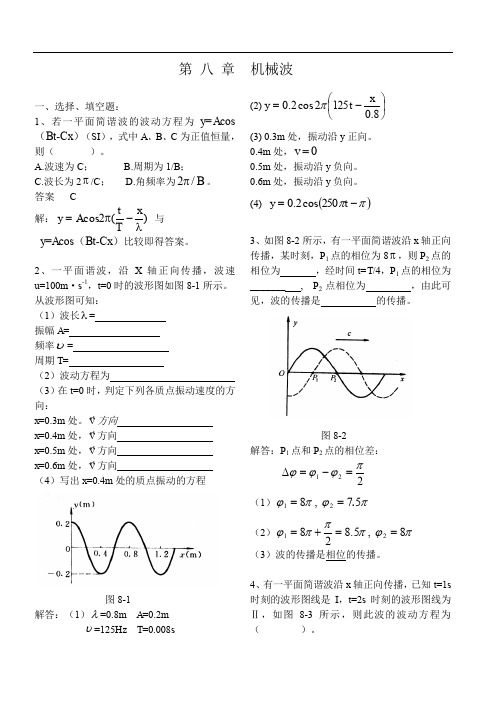
第八章 机械波一、选择、填空题:1、若一平面简谐波的波动方程为y=A cos (Bt-Cx )(SI ),式中A 、B 、C 为正值恒量,则( )。
A.波速为C ;B.周期为1/B ;C.波长为2π/C ;D.角频率为B /2π。
答案 C解:)(2cos λ-π=xT t A y 与y =A cos (Bt -Cx )比较即得答案。
2、一平面谐波,沿X 轴正向传播,波速u =100m ·s -1,t =0时的波形图如图8-1所示。
从波形图可知:(1)波长λ= 振幅A = 频率υ= 周期T =(2)波动方程为 (3)在t=0时,判定下列各质点振动速度的方向:x =0.3m 处。
v方向x =0.4m 处,v方向x =0.5m 处,v方向x =0.6m 处,v方向(4)写出x =0.4m 处的质点振动的方程图8-1解答:(1)λ=0.8m A =0.2mυ=125Hz T =0.008s(2)⎪⎭⎫ ⎝⎛-=8.01252cos 2.0x t y π (3) 0.3m 处,振动沿y 正向。
0.4m 处,0=v0.5m 处,振动沿y 负向。
0.6m 处,振动沿y 负向。
(4) ()ππ-=t y 250cos 2.03、如图8-2所示,有一平面简谐波沿x 轴正向传播,某时刻,P 1点的相位为8π,则P 2点的相位为 ,经时间t=T /4,P 1点的相位为_______ , P 2点相位为 ,由此可见,波的传播是 的传播。
图8-2 解答:P 1点和P 2点的相位差: 221πϕϕϕ=-=∆(1)πϕπϕ57 , 821.== (2)πϕπππϕ8 , 8.52821==+=(3)波的传播是相位的传播。
4、有一平面简谐波沿x 轴正向传播,已知t =1s 时刻的波形图线是I ,t =2s 时刻的波形图线为Ⅱ,如图8-3所示,则此波的波动方程为( )。
图8-3A . m )232(cos 20+-=x t y π.B .m )4(cos 20xt y -=π.C .m )214(cos 20+-=x t y π.D .m )234(cos 20+-=x t y π.答案 D解:由图知:1-s m 4124m,20⋅=-==u A . 1-s 2 , s 2ππω===T T 可得; []ϕπ+-=)4(c o s 20xt y .对于波线I 上的O 点:. 0 , 0 , s 1 , 0<===v y t x其振动的相位为:)10( , 22,=+=+k k ππϕπ)2( , 23ππϕ-=∴5、在弦线上有一简谐波,其表达式是()SI x t y ⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-=32002.02cos 02.01ππ为了在此弦线上形成驻波,并且在x =0处为一波节,此弦线上还应有一简谐波,其表达式为:( )。
第8、9章习题解答

第8章习题解答8-2下面说法正确的是:()(A )若高斯面上的电场强度处处为零,则该面内必定没有电荷; (B )若高斯面内没有电荷,则该面上的电场强度必定处处为零; (C )若高斯面上的电场强度处处不为零,则该面内必定有电荷; (D )若高斯面内有电荷,则该面上的电场强度必定处处不为零。
解:[答案:D]高斯定理的原意。
8-3一半径为R 的导体球表面的面点荷密度为σ,则在距球面R 处的电场强度()(A )0?/σε (B )0/2σε (C )/4σε0 (D )0/8σε 解:[答案:C]利用均匀带电球面的场强公式计算02004qq r πε==F E r ,其中σπ24R q =, R 2r =8-4下列说法正确的是( )(A) 电场强度为零的点,电势也一定为零 (B) 电场强度不为零的点,电势也一定不为零 (C) 电势为零的点,电场强度也一定为零(D) 电势在某一区域内为常量,则电场强度在该区域内必定为零 解:[答案:D].根据场强与电势的微分关系或积分关系均可以证明。
8-5在静电场中,电势不变的区域,场强必定为 。
解:[答案:0] 根据场强与电势的微分关系或积分关系均可以证明。
8-6一个点电荷q 放在立方体中心,则穿过某一表面的电通量为 ,若将点电荷由中心向外移动至无限远,则总通量将 。
解:[答案:0/6q ε, 将为零],第一空:根据高斯定理知:正六面体的六个对称面组成的闭合面总通量为0εq,故每个面是总量的61。
第二空:根据高斯定理:总通量仅与面内电荷有关。
只要将点电荷由中心移动至六面体外,则该点荷对闭合面的总通量将没有贡献。
8-8电量Q 均匀分布在半径为R 的球体内,则球内球外的静电能之比 。
解:[答案:5:6]利用⎰=RV E W 020d 21内内ε及⎰∞=R V E W d 2120外外ε计算。
其中dr r dV 24π=,304R Qr E πε=内,204r QE πε=外。
结构化学习题解答(第八章)

rC C (1 a / 4) 2 (1 b / 4) 2 (1 c / 4) 2 a 3 4 3 356.7 pm 4 154.4 pm 密度D ZM / NV (8 12.0 g / 6.02 1023 ) /(356.7 1010 cm) 3 3.51g cm
[8.31] 已知NaCl晶体立方晶胞参数a=563.94pm实验测得衍射 111的衍射角θ=5.100,求实验所用X射线的波长。 [解 ]: 2 2 2 1/ 2 hkl
d
a /(h k l )
563.94 pm / 3 325.59 pm d 2 sin 325.59 pm 2 sin 5.10 57.9 pm
[8.26] 用Cu Kα射线测得某晶体的衍射图,从中量得 以下数据。试查PDF卡片,鉴定此晶体可能是什么。 2θ/(0) 27.3 31.8 45.5 53.9 56.6 66.3 75.5 I/I0 18 100 80 5 21 20 20
[解]:利用PDF卡片鉴定晶体时,需先把衍射角2θ数据 换算成d值(d=λ/2Sinθ)如下:(λ=154.2pm) 2θ/(0) 27.3 31.8 45.5 53.9 56.6 66.3 75.5 d/pm 326.7 281.4 199.4 170.1 162.6 141.0 125.9 I/I0 18 100 80 5 21 20 20 按这组d-I/I0值查表,得知它为NaCl晶体。
rTi O (0.31a) 2 (0.31a) 2 0.438a 0.438 458pm 201pm
[8.19] 金属镍的立方晶胞参数a=352.4pm,试求d200,d111,d220。 [解]:立方晶系的衍射指标hkl和衍射面间距dhkl的关系为:
高二物理课后习题精准解析(新教材人教版选择性必修第二册)第8章__机械能守恒定律

第 8章机械能守恒定律复习与提高(解析版)2019版新教科书物理必修第二册“复习与提高”习题详解A组1.一个弹性很好的橡股球被竖直抛下,落到坚硬的水平地面上被弹回,回跳的高度比抛出点高2 m,那么,在抛出点必须以多大的速度将球向下抛出?不计空气阻力和球与地面碰撞时的能量损失。
【解析】机械能守恒定律:,解得6.26m/s。
2.一台起重机,匀加速地将质量 m为 1.0x10 kg 的货物从静止开始竖直吊起,在 2s末货物的速度 v为 4.0 m/s ,不计空气阻力,g取 10 m/s’.3(1)求起重机在这 2s内的输出功率。
( 2)求起重机在 2s末的输出功率。
【解析】(1),其中,其中,代入数据得,,(2),其中,代入数据得, .3.沿倾角为的斜面向上推一个质量为 m的木箱,推力 F与斜面平行,推上的距离为 x,木箱与斜面间的动摩擦因数为,重力加速度大小为 g,请完成下列要求。
(1)画出题中物理情境的示意图,并画出木箱所受的各个力,用字母标明力的名称。
l2)写出各力做功的表达式。
(3)写出各力做功的代数和,即总功的表达式。
(4)写出合力的表达式。
(5)写出合力做功的表达式,并与总功的表达式加以比较。
【解析】(1)物理情境图和物体受力图如下:重力G,支持力N,拉力F,摩擦力 f.(2)各个力做功:,,,(3)总功(4)合力(5)合力的功结论:,这是求总功的两种方法。
4.质量为 m的汽车,启动后沿平直路面行驶,如果发动机的输出功率恒为 P,且行驶过程中受到的阻力大小一定,汽车能够达到的最大逸度为 v。
(1)求行驶过程中汽车受到的阻力大小。
(2)当汽车的车速为 v/4时,求汽车的瞬时加速度的大小。
【解析】(1)最大速度时,匀速运动,(2)速度为时,,所以,。
5.从地面以 v0的速度竖直向上抛出一物体,不计空气阻力,重力加速度为 g,以地面为重力势能的零势能面。
(1)求物体上升的最大高度 h;( 2)物体的重力势能为动能的一半时,求物体离地面的高度 h1;(3)物体的重力势能和动能相等时,求物体离地面的高度 h2;(4)物体的动能是重力势能的一半时,求物体离地面的高度 h3;(5)物体的速率为v0/2时,求物体离地面的高度h4。
高等数学第八章习题解答

习题8.11. 设有一平面薄板(不计其厚度),占有Oxy 平面上的闭区域D ,薄板上分布着面密度为(,)x y μμ=的电荷,且(,)x y μ在D 上连续,试用二重积分表达该板上的全部电荷Q 。
解:据题意,薄板区域D 是Oxy 平面上的有界闭域,(,)x y μ是定义在D 上的面密度函数,那么用任意曲线把D 分成n 个可求面积的小区域12,,n σσσ ,以i σ∆表示小区域的面积,这些小区域构成了D 的一个分割T ,在每个i σ上任取一点(,)i i εη,那么电荷Q 即为D 上的一个积分和1(,)ni i i i Q u εησ==∆∑。
当d 足够小时,1(,)(,)ni i i i DQ u u x y d εησσ==∆=∑⎰⎰2. 下列二重积分表达怎样的空间立体的体积?试画出下列空间立体的图形:(1)()221Dx y d σ++⎰⎰,其中区域D 是圆域221x y +≤;解:(1)在圆域221x y +≤上以抛物面2221z x y =++为顶的曲顶柱体的体积。
(2)Dyd σ⎰⎰,其中区域D 是三角形域0,0,1x y x y ≥≥+≤;解: 在三角形域D 上以平面z y =为顶的柱体的体积。
z 轴x 轴y 轴(1) (2) 3. 设12231()D I x y d σ=+⎰⎰, 其中D 1={(x , y )|-1≤x ≤1, -2≤y ≤2 ;又22232()D I x y d σ=+⎰⎰, 其中D 2={(x , y )|0≤x ≤1, 0≤y ≤2}.试利用二重积分的几何意义说明I 1与I 2的关系.解 I 1表示由曲面z =(x 2+y 2)3与平面x =±1, y =±2以及z =0围成的立体V 的体积.I 2表示由曲面z =(x 2+y 2)3与平面x =0, x =1, y =0, y =2以及z =0围成的立体V 1的体积.显然立体V 关于yOz 面、xOz 面对称, 因此V 1是V 位于第一卦限中的部分, 故 V =4V 1, 即I 1=4I 2. 3. 利用二重积分的定义证明: (1)Dd σσ=⎰⎰ (其中σ为D 的面积;证明 由二重积分的定义可知,1(,)lim (,)ni i i i Df x y d f λσξησ→==∆∑⎰⎰其中∆σi 表示第i 个小闭区域的面积. 此处f (x , y )=1, 因而f (ξ, η)=1, 所以 01lim lim ni i Dd λλσσσσ→→==∆==∑⎰⎰.(2)(,)(,)DDkf x y d k f x y d σσ=⎰⎰⎰⎰ (其中k 为常数);证明 011(,)lim (,)lim (,)n ni i i i i i i i Dkf x y d kf k f λλσξησξησ→→===∆=∆∑∑⎰⎰1lim (,)(,)ni i i i Dk f k f x y d λξησσ→==∆=∑⎰⎰.(3)12(,)(,)(,)DD D f x y d f x y d f x y d σσσ=+⎰⎰⎰⎰⎰⎰,其中D =D 1⋃D 2, D 1、D 2为两个无公共内点的闭区域.证明 将D 1和D 2分别任意分为n 1和n 2个小闭区域1i σ∆和2i σ∆,n 1+n 2=n , 作和1211122212111(,)(,)(,)n n ni i i i i i i i i i i i f f f ξησξησξησ===∆=∆+∆∑∑∑.令各1i σ∆和2i σ∆的直径中最大值分别为λ1和λ2, 又λ=ma x (λ1,λ2), 则有1lim (,)n i i i i f λξησ→=∆∑121112221212011lim (,)lim (,)n n i i i i i i i i f f λλξησξησ→→===∆+∆∑∑,即 12(,)(,)(,)DD D f x y d f x y d f x y d σσσ=+⎰⎰⎰⎰⎰⎰.4. 根据二重积分的性质, 比较下列积分大小:(1)2()Dx y d σ+⎰⎰与, 3()Dx y d σ+⎰⎰ 其中积分区域D 是由x 轴, y 轴与直线x +y =1所围成;解 区域D 为: D ={(x , y )|0≤x , 0≤y , x +y ≤1}, 因此当(x , y )∈D 时, 有(x +y )3≤(x +y )2, 从而3()Dx y d σ+⎰⎰≤2()Dx y d σ+⎰⎰.(2)2()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰其中积分区域D 是由圆周(x -2)2+(y -1)2=2所围成;解 区域D 如图所示, 由于直线x +y =1与圆(x -2)2+(y -1)2=2相切,故D 位于直线x +y =1的上方, 所以当(x , y )∈D 时, x +y ≥1, 从而(x +y )3≥(x +y )2, 因而 23()()DDx y d x y d σσ+≤+⎰⎰⎰⎰.(3)ln()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰其中D 是三角形闭区域, 三角顶点分别为(1,0), (1, 1), (2, 0);解 区域D 如图所示, 显然当(x , y )∈D 时, 1≤x +y ≤2, 从而0≤ln(x +y )≤1, 故有 [ln(x +y )]2≤ ln(x +y ),因而 2[ln()]ln()+≤+⎰⎰⎰⎰DDx y d x y d σσ.(4)ln()Dx y d σ+⎰⎰与3()Dx y d σ+⎰⎰其中D ={(x , y )|3≤x ≤5. 0≤y ≤1}.解 区域D 如图所示, 显然D 位于直线x +y =e 的上方, 故当(x , y )∈D 时, x +y ≥e , 从而ln(x +y )≥1,因而 [ln(x +y )]2≥ln(x +y ),故 2ln()[ln()]DDx y d x y d σσ+≤+⎰⎰⎰⎰.5. 利用二重积分的性质估计下列积分的值:(1)()DI xy x y d σ=+⎰⎰, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤1};解 因为在区域D 上0≤x ≤1, 0≤y ≤1, 所以 0≤xy ≤1, 0≤x +y ≤2, 进一步可得0≤xy (x +y )≤2,于是 0()2DDDd xy x y d d σσσ≤+≤⎰⎰⎰⎰⎰⎰,即 0()2Dxy x y d σ≤+≤⎰⎰.(2)22sin sin DI x yd σ=⎰⎰, 其中D ={(x , y )| 0≤x ≤π, 0≤y ≤π};解 因为0≤sin 2x ≤1, 0≤sin 2y ≤1, 所以0≤sin 2x sin 2y ≤1. 于是可得 220sin sin 1DDDd x yd d σσσ≤≤⎰⎰⎰⎰⎰⎰,即 2220sin sin Dx yd σπ≤≤⎰⎰.(3)(1)DI x y d σ=++⎰⎰, 其中D ={(x , y )| 0≤x ≤1, 0≤y ≤2};解 因为在区域D 上, 0≤x ≤1, 0≤y ≤2, 所以1≤x +y +1≤4, 于是可得 (1)4DDDd x y d d σσσ≤++≤⎰⎰⎰⎰⎰⎰,即 2(1)8Dx y d σ≤++≤⎰⎰.22(49)DI x y d σ=++⎰⎰, 其中D ={(x , y )| x 2+y 2 ≤4}.解 在D 上, 因为0≤x 2+y 2≤4, 所以 9≤x 2+4y 2+9≤4(x 2+y 2)+9≤25.于是 229(49)25DDDd x y d d σσσ≤++≤⎰⎰⎰⎰⎰⎰,222292(49)252Dx y d πσπ≤++≤⋅⋅⎰⎰,即 2236(49)100Dx y d πσπ≤++≤⎰⎰.习题8.21. 化二重积分(,)Df x y dxdy ⎰⎰为二次积分(写出两种积分次序).(1)D ={(x , y )| |x |≤1, |y |≤1}; 解 D 为矩形区域, 所以1111(,)(,)Df x y dxdy dx f x y dy --=⎰⎰⎰⎰,1111(,)(,)Df x y dxdy dy f x y dx --=⎰⎰⎰⎰.(2)D 是由y 轴, y =1及y =x 围成的区域; 解 若将D 表示为0≤x ≤1, x ≤y ≤1, 则 11(,)(,)xDf x y dxdy dx f x y dy =⎰⎰⎰⎰.若将D 表示为0≤y ≤1, 0≤x ≤y , 则 1(,)(,)yDf x y dxdy dy f x y dx =⎰⎰⎰⎰.(3)D 是由x 轴, y =ln x 及x =e 围成的区域; 解 若将D 表示为1≤x ≤e , 0≤y ≤ln x , 则 ln 10(,)(,)ex Df x y dxdy dx f x y dy =⎰⎰⎰⎰.若将D 表示为0≤y ≤1, e y ≤x ≤e , 则 1(,)(,)y eeDf x y dxdy dy f x y dx =⎰⎰⎰⎰.(4)D 是由x 轴, 圆x 2+y 2-2x =0在第一象限的部分及直线x +y =2围成的区域; 解 若将D 表示为0≤x ≤1,0y ≤≤1≤x ≤2, 0≤y ≤2-x , 则12201(,)(,)(,)xDf x y dxdy dx f x y dy dx f x y dy -=+⎰⎰⎰⎰⎰.若将D 表示为0≤y ≤1; 12x y ≤≤-, 则 1201(,)(,)yDf x y dxdy dy f x y dx -=⎰⎰⎰⎰(5)D 是由x 轴与抛物线y =4-x 2在第二象限的部分及圆x 2+y 2-4y =0第一象限部分围成的区域. 解 若将D 表示为-2≤x ≤0, 0≤y ≤4-x 2及0≤x ≤2,22y ≤≤ 则242222(,)(,)(,x Df x y dxdy dx f x y dy dx f x y --=+⎰⎰⎰⎰⎰⎰,若将D 表示为0≤y ≤4, x ≤ 则 40(,)(,)Df x y dxdy dy f x y dx =⎰⎰⎰.2. 交换二次积分的次序:(提示: 交换二次积分的次序, 要先根据原积分写出积分区域不等式, 再根据不等式画出积分区域, 然后根据图形写出另一种形式的积分区域不等式, 最后由不等写出二次积分)(1)228812(,)(,)x xxdx f x y dy dx f x y dy +⎰⎰⎰⎰.解 积分区域为D ={(x , y )|1≤x ≤2, x ≤y ≤x 2}⋃{(x , y )|2≤x ≤8, x ≤y ≤8}. 积分区域还可以表示为D ={(x , y )|1≤y ≤4,x ≤y }⋃{(x , y )|4≤y ≤8, 2≤x ≤y }, 于是 原式=48142(,)(,)y ydy f x y dx dy f x y dx +⎰⎰⎰.(2)12201(,)(,)yydy f x y dx dy f x y dx -+⎰⎰⎰⎰.解 积分区域为D ={(x , y )|0≤y ≤1, 0≤x ≤y }⋃{(x , y )|1≤y ≤2, 0≤x ≤2-y }.积分区域还可以表示为xO y281D ={(x , y )|0≤x ≤1, x ≤y ≤2-x }, 于是 原式=120(,)x xdx f x y dy -⎰⎰. (3) 14(4)(,)y dy f x y dx -⎰⎰;解:积分区域{}2442,20|),(x y x x y x D -≤≤+≤≤=,214(4)040224(,)(,)(,);y x Dx f x y d dy f x y dx dx f x y dy σ---+∴==⎰⎰⎰⎰⎰⎰(4) 11(,)dx f x y dy ⎰;解:积分区域{}{212(,)|01,0(,)|12,0D x y y x y D x y y x =≤≤≤≤⋃=≤≤≤≤21212001(,)(,)(,)(,)y D D f x y d f x y d dy f x y dx dy f x y dxσσ=+=+⎰⎰⎰⎰⎰⎰⎰原式(5)224(,)x x f x y dy -⎰⎰。
离散数学第四版课后答案(第8章)

第8 章 习题解答8.1 图8.6 中,(1)所示的图为,3,1K (2) 所示的图为,3,2K (3)所示的图为,2,2K 它们分别各有不同的同构形式.8.2 若G 为零图,用一种颜色就够了,若G 是非零图的二部图,用两种颜色就够了.分析 根据二部图的定义可知,n 阶零图(无边的图)是三部图(含平凡图),对n 阶零图的每个顶点都用同一种颜色染色,因为无边,所以,不会出现相邻顶点染同色,因而一种颜色就够用了.8.3 完全二部图,,s r K 中的边数rs m =.分析 设完全二部图s r K ,的顶点集为V, 则∅==2121,V V V V V ,且,||,||21s V r V ==s r K ,是简单图,且1V 中每个顶点与2V 中所有顶点相邻,而且1V 中任何两个不同顶点关联的边互不相同,所以,边数rs m =.8.4 完全二部图s r K ,中匹配数},m in{1s r =β,即1β等于s r ,中的小者.分析 不妨设,s r ≤且二部图s r K ,中,,||,||21s V r V ==由Hall 定理可知,图中存在1V 到2V 的完备匹配,设M 为一个完备匹配,则1V 中顶点全为M 饱和点,所以,.1r =β8.5 能安排多种方案,使每个工人去完成一项他们各自能胜任的任务.分析 设},,{1丙乙甲=V ,则1V 为工人集合, },,{2c b a V =,则2V为任务集合.令}|),{(,21y x y x E V V V 能胜任== ,得无向图>=<E V G ,,则G 为二部图,见图8.7 所示.本题是求图中完美匹配问题. 给图中一个完美匹配就对应一个分配方案.图8.7 满足Hall 定理中的相异性条件,所以,存在完备匹配,又因为,3||||21==V V 所以,完备匹配也为完美匹配.其实,从图上,可以找到多个完美匹配. 取)},(),,(),,{(1c b a M 丙乙甲=此匹配对应的方案为甲完成a,乙完成b, 丙完成c,见图中粗边所示的匹配.)},(),,(),,{(2c a b M 丙乙甲=2M 对应的分配方案为甲完成b,乙完成a,丙完成c.请读者再找出其余的分配方案.8.6 本题的答案太多,如果不限定画出的图为简单图,非常容易地给出4族图分别满足要求.(1) n (n 为偶数,且2≥n )阶圈都是偶数个顶点,偶数条边的欧拉图.(2) n (n 为奇数,且1≥n )阶圈都是奇数个顶点,奇数条边的欧拉图.(3) 在(1) 中的圈上任选一个顶点,在此顶点处加一个环,所得图为偶数个顶点,奇数条边的欧拉图.(4)在(2) 中的圈上任选一个顶点,在此顶点处加一个环,所得图为奇数个顶点,偶数条边的欧拉图.分析 上面给出的4族图都是连通的,并且所有顶点的度数都是偶数,所以,都是欧拉图.并且(1),(2) 中的图都是简单图.而(3),(4)中的图都带环,因而都是非简单图. 于是,如果要求所给出的图必须是简单图,则(3),(4)中的图不满足要求.其实,欧拉图是若干个边不重的图的并,由这种性质,同样可以得到满足(3),(4)中要求的简单欧拉图.设k G G G ,,,21 是长度大于等于3的k 个奇圈(长度为奇数的圈称为奇圈),其中k 为偶数,将1G 中某个顶点与2G 中的某顶点重合,但边不重合, 2G 中某顶点与3G 中某顶点重合,但边不重合,继续地,最后将1-k G 中某顶点与k G 中某顶点重合,边不重合,设最后得连通图为G,则G 中有奇数个顶点,偶数条边,且所有顶点度数均为偶数,所以,这样的一族图满足(4)的要求,其中一个特例为图8.8中(1)所示.在以上各图中,若k G G G ,,,21 中有一个偶圈,其他条件不变,构造方法同上,则所得图G 为偶数个顶点,奇数条边的简单欧拉图,满足(3)的要求,图8.8中(2)所示为一个特殊的情况.8.7 本题的讨论类似于8.6题,只是将所有无向圈全变成有向圈即可,请读者自己画出满足要求的一些特殊有向欧拉图.8.8 本题的答案也是很多的,这里给出满足要求的最简单一些图案,而且全为简单图.(1) n (3≥n )阶圈,它们都是欧拉图,又都是哈密尔顿图.(2) 给定k (2≥k )个长度大于等于3的初级回路,即圈k G G G ,,,21 ,用8.6题方法构造的图G 均为欧拉图,但都不是哈密尔顿图,图8.8给出的两个图是这里的特例.(3)n (4≥n )阶圈中,找两个不相邻的顶点,在它们之间加一条边,所得图均为哈密尔顿图,但都不是欧拉图.(4) 在(2)中的图中,设存在长度大于等于4的圈,比如说1G ,在1G 中找两个不相邻的相邻顶点,在它们之间加一条新边,然后用8.6题方法构造图G,则G 既不是欧拉图,也不是哈密尔顿图,见图8.9所示的图.分析 (1) 中图满足要求是显然的.(2) 中构造的图G 是连通的,并且各顶点度数均为偶数,所以,都是欧拉图,但因为G 中存在割点,将割点从G 中删除,所得图至少有两个连通分支,这破坏了哈密尔顿图的必要条件,所以,G不是哈密尔顿图.(3) 中构造的图中,所有顶点都排在一个圈上,所以,图中存在哈密尔顿回路,因而为哈密尔顿图,但因图中有奇度顶点(度数为奇数的顶点),所以,不是欧拉图. 由以上讨论可知,(4) 中图既不是欧拉图,也不是哈密尔顿图.其实,读者可以找许多族图,分别满足题中的要求.8.9 请读者自己讨论.8.10 其逆命题不真.分析若D是强连通的有向图,则D中任何两个顶点都是相互可达的,但并没有要求D中每个顶点的入度都等于出度. 在图8.2 所示的3个强连通的有向图都不是欧拉图.8.11 除K不是哈密尔顿图之外, n K(3≥n)全是哈密尔2顿图.K(n为奇数)为欧拉图. 规定1K(平凡图)既是欧拉图, n又是哈密尔顿图.分析从哈密尔顿图的定义不难看出,n阶图G是否为哈密尔顿图,就看是否能将G中的所有顶点排在G中的一个长为n的初级回路,即圈上.K(3≥n)中存在多个这样的生成n圈(含所有顶点的图), 所以K(3≥n)都是哈密尔顿图.n在完全图K中,各顶点的度数均为n-1,若n K为欧拉图,n则必有1-n为偶数,即n为奇数,于是,当n为奇数时,K连通n且无度顶点,所以,K(n为奇数) 都是欧拉图.当n为偶数时,n各顶点的度数均为奇数,当然不是欧拉图.8.12 有割点的图也可以为欧拉图.分析 无向图G 为欧拉图当且仅当G 连通且没有奇度顶点.只要G 连通且无奇度顶点(割点的度数也为偶数),G 就是欧拉图.图8.8所示的两个图都有割点,但它们都是欧拉图.8.13 将7个人排座在圆桌周围,其排法为.abdfgeca 分析 做无向图>=<E V G ,,其中,},,,,,,{g f e d c b a V =},|),{(有共同语言与且v u V v u v u E ∈=图G 为图8.10所示.图G 是连通图,于是,能否将这7个人排座在圆桌周围,使得每个人能与两边的人交谈,就转化成了图G 中是否存在哈密尔顿回路(也就是G 是否为哈密尔顿图).通过观察发现G 中存在哈密尔顿回路, abdfgeca 就是其中的一条哈密尔顿回路.8.14 用i v 表示颜色.6,,2,1, =i i 做无向图>=<E V G ,,其中 },,,,,,{654321v v v v v v V =}.,,|),{(能搭配与并且且v u v u V v u v u E ≠∈=对于任意的)(,v d V v ∈表示顶点v 与别的能搭配的颜色个数,易知G 是简单图,且对于任意的V v u ∈,,均有633)()(=+≥+v d u d ,由定理8.9可知,G 为哈密尔顿图,因而G 中存在哈密尔顿回路,不妨设1654321i i i i i i i v v v v v v v 为其中的一条,在这种回路上,每个顶点工表的颜色都能与它相邻顶点代表的颜色相.于是,让1i v 与2i v ,3i v 与4i v ,5i v 与6i v 所代表的颜色相搭配就能织出3种双色布,包含了6种颜色.8.15∑=⨯======300321,10220)deg(.12)deg(,3)deg(,1)deg(,4)deg(i i R R R R R 而本图边数m=10.分析 平面图(平面嵌入)的面i R 的次数等于包围它的边界的回路的长度,这里所说回路,可能是初级的,可能是简单的,也可能是复杂的,还可能由若干个回路组成.图8.1所示图中,321,,R R R 的边界都是初级回路,而0R 的边界为复杂回路(有的边在回路中重复出现),即432110987654321e e e e e e e e e e e e e e ,长度为12,其中边65,e e 在其中各出现两次.8.16 图8.11中,实线边所示的图为图8.1中图G,虚线边,实心点图为它的对偶图的顶点数*n ,边数*m ,面数*r 分别为4,10和8,于是有分析 从图8.11还可以发现,G 的每个顶点位于的一个面中,且的每个面只含G 的一个顶点,所以,这是连通平面图G 是具有k 个连通分支的平面图2≥k ,则应有1*+-=k n r .读者自己给出一个非连通的平面图,求出它的对偶图来验证这个结论.另外,用图8.1还可以验证,对于任意的*v (*G 中的顶点),若它处于G 的面i R 中,则应有)deg()(*i R v d =.8.17 不能与G 同构.分析 任意平面图的对偶图都是连通的,因而与都是连通图,而G 是具有3个连通分支的非连通图,连通图与非连通图显然是不能同构的.图 8.12 中, 这线边图为图8.2中的图G,虚线边图为G 的对偶图,带小杠的边组成的图是*G 的对偶图,显然.~**G G ≠ 8.18 因为彼得森图中有长度为奇数的圈,根据定理8.1可知它不是二部图.图中每个顶点的度数均为3,由定8.5可知它不是欧拉图.又因为它可以收缩成5K ,由库拉图期基定理可知它也不是平面图.其实,彼得森图也不是哈密尔顿图图,这里就不给出证明了.8.19 将图8.4重画在图8.13中,并且将顶点标定.图中afbdcea 为图中哈密尔顿回路,见图中粗边所示,所以,该图为哈密尔顿图.将图中边),(),,(),,(d f f e e d 三条去掉,所得图为原来图的子图,它为3,3K ,可取},,{1c b a V =},,{2f e d V =,由库拉图期基定理可知,该图不是平面图.8.20 图8.14所示图为图8.25所示图的平面嵌入.分析 该图为极大平面图.此图G 中,顶点数9=n ,边数.12=m 若G 是不是极大平面图,则应该存在不相邻的顶点,,v u 在它们之间再加一条边所得'G 还应该是简单平面图, 'G 的顶点数131,6''=+===n m n n ,于是会有.126313''=->=n m这与定理8.16矛盾,所以,G 为极大平面图.其实,n ( 3≥n )阶简单平面图G 为极大平面图当且仅当G 的每个面的次数均为3.由图8.14可知,G 的每个面的次数均为3,所以,G 为极大平面图.8.21 答案 A,B,C,D 全为②分析 (1) 只有n 为奇数时命题为真,见8.11的解答与分析.(2) 2≠n 时,命题为真,见8.11的解答与分析.(3) 只有m n ,都是偶数时,m n K ,中才无奇度数顶点,因而m n K ,为欧拉图,其他情况下,即m n ,中至少有一个是奇数,这时m n K ,中必有奇度顶点,因而不是欧拉图.(4) 只有m n =时, m n K ,中存在哈密尔顿回路,因而为哈密尔顿图.当m n ≠时,不妨设m n <,并且在二部图m n K ,中,m V n V ==||,||21,则n V m V G p =>=-||)(11,这与定理8.8矛盾. 所以, m n ≠时, m n K ,不是哈密尔顿图.8.22 答案 A:②;B ②;C ②.分析图8.15中,两个实边图是同构的,但它们的对偶力(虚边图)是不同构的.(2) 任何平面图的对偶图都是连通图.设G 是非连通的平面图,显然有.**~G G ≠(3) 当G 是非连通的平面图时,,1*+-=k n r 其中k 为G 的连通分支数.8.23 答案 A:④;B ②;C ②.分析 根据库期基定理可知,所求的图必含有5K 或3,3K 同胚子图,或含可收缩成5K 或3,3K 的子图.由于顶点数和边数均已限定,因而由3,3K 加2条边的图可满足要求,由5K 增加一个顶点,一条边的图可满足要求,将所有的非同构的简单图画出来,共有4个,其中由K产生的有2个,由5K产生的有2个.3,3见图8.16所示.。
8.健康习题解析第八章

第八章身体活动基本知识单选题健康管理基础知识习题解析班1.对于普通成人,推荐每周至少完成大肌肉群参与的多少分钟中等强度有氧活动,或每周累计至少多少分钟高强度有氧活动,或中等和高强度两种活动相当量的组合A.100;50B.130;75C.150;75D.180;80单选题2.老年人身体活动的目的主要是()。
A.改善心肺功能B.降低体脂肪C.预防慢性病D.提高身体素质单选题3.长时间运动血糖下降时首先受影响的是A.肺B.肝C.脑D.心单选题4.运动后最大心率一般是指年龄加运动后每分钟心率不超过()次/分。
A.130B.150C.170D.190单选题5.肥胖病人运动的方法应是A.间断低强度体力少活动B.长期低强度体力活动C.长期中高强度体力活动D.运动不需坚持E.间断高强度体力活动单选题6.身体活动按日常活动分类,以下说法错误的是A.职业性身体活动:通常是指有劳动收入(如工资)的活动,包括家政服务等职业行为B.业余休闲活动:可以是锻炼C.业余休闲活动:不包括看电视D.业余休闲活动:也可以是做家务E.根据日常生活中身体活动的目的和时间分配,可分为四类单选题7.下面有关代谢当量的陈述错误的是A.可以根据代谢当量和体重估算运动的能量消耗B.代谢当量是运动时能量消耗与安静代谢率的比值C.代谢当量可以转换为耗氧量D.代谢当量反映活动和安静两种状态能量消耗的相对代谢率E.代谢当量代表运动能量消耗的静值单选题8.下列营养物质产生能量最多的是A.维生素B.葡萄糖C.脂肪D.蛋白质单选题9.下列属于无氧运动项目的是A.马拉松B.100 米短跑C.步行D.长跑单选题10.下列哪项不属于运动强度的测量A.肌肉B.心率C.代谢当量D.自我感知运动强度单选题11.某人的代谢当量为3.5METs 时,他的活动强度是A.静态行为活动B.低强度活动C.中等强度活动D.高强度活动单选题12.下列关于肌肉耐力测试,说法正确的是A.给定速度、重复抗阻力动作的频率B.给定次数、重复抗阻力动作的频率C.给定频率、重复抗阻力动作的次数D.给定频率、重复抗阻力动作的速度单选题13.体重75Kg,每小时4km 的速度快走30 分钟,能量消耗A.113B.175C.153D.128单选题14.运动进度取决于个体的体质、健康情况、运动训练目标和()A.努力 B.体力 C.反应 D.年龄单选题15.运动疲劳()和适应是机体运动反应的三个关键环节A.感受B.体质C.健康D.恢复单选题16.常见的运动伤害是A.内伤B.外伤C.骨科伤D.肌肉伤单选题17.身体活动强度的常用指标,以下正确的是A.分为绝对强度(也称“物理强度”)和相对强度(也称“生理强度”)两类指标B.同一种运动的绝对强度是一致的C.不同生理状态个体的疲劳感等相对强度可能存在较大差异D.以上都正确单选题18.以下哪项不是运动处方制定前的评估A.身体活动准备问卷(PAR—Q)B.AHA/ACSM 健康/体适能机构修正的运动前自我筛查问卷C.国际身体活动问卷(IPAQ)D.抑郁自评量表单选题19.以下身体活动指南要点,说法正确的有A.5 一17 岁儿童和青少年每天应进行60 分钟中等强度到高强度身体活动B.18—64 岁成年人应每周至少完成150 分钟中等强度有氧活动,或每周累计至少75 分钟高强度有氧活动C.65 岁以上成人每周应从事至少150 分钟的中等强度身体活动,或一周至少75 分钟的高强度活动D.以上都正确单选题20.关于1 个千步当量,下列哪项说法错误A.相当于普通人中等速度(1 千步/小时)步行10 分钟(约l 千步)B.相当于普通人中等速度(4 千步/小时)步行10 分钟(约l 千步)C.60 公斤体重的人从事1 千步当量的活动,约消耗能量132 千焦D.千步当量可根据体重转换为能量消耗单选题21.运动时的心率,以下错误的是A.作为训练时运动强度的监测指标称为目标心率或称靶心率B.是测量运动强度最客观、简单、易行且准确的指标C.运动后最大心率一般是指年龄加运动后每分钟心率不超过170 次/分D.目前推荐公式:HRmax(%HRmax)=220—0.7×年龄(岁)单选题22.关于Borg(疲劳)量表法,以下说法错误的是A.常用6~20 级的表B.中等强度通常在10~14 的区间内C.主观疲劳程度“6”为最低水平D.“20”作为最高水平(极度疲劳感)E.按照主观疲劳程度分级多选题23.以下哪些是无氧运动的正确叙述A.指以无氧代谢为主要供能途径的运动形式B.一般为肌肉的强力收缩活动C.100 米短跑几乎全部为无氧代谢供能D.抬重物、俯卧撑、抗阻力肌肉力量训练的主要形式多选题24.按生理功能,身体活动种类包括()。
第八章刚体的平面运动习题解答

故
向
即
8-21图8-48所示机构中,圆轮A的半径R=0.2m,圆轮B的半径r=0.1m,两轮均在水平轨道上作纯滚动。在图示瞬时,A轮上C点在最高位置,轮心速度vA=2m/s,加速度aA=2m/s2,试求轮B滚动的角速度和角加速度。
图8-48
加速度分析
圆轮A
杆BC
故
向
8-22轮O在水平面上作纯滚动,如图8-49所示。轮缘上固定销钉B,此销钉可在摇杆O1A的槽内滑动,并带动摇杆绕轴O1转动。已知轮心O的速度是一常量,vO=0.2m/s,轮的半径R=0.5m,图示位置时,O1A是轮的切线,摇杆与水平面的夹角为 。试求该瞬时摇杆的角速度和角加速度。
图8-59
以O为动点,杆AB为动系
(1)速度分析
(2)加速度分析
圆轮O
以O为基点,分析C点
向y
8-33图8-60所示机构中,已知曲柄OA以匀角速度 绕定轴O转动,OA=100mm,l=500mm。在图示位置, ,试确定杆BD的角速度和角加速度。
图8-60
以A为动点,杆AB为动系
(1)速度分析
(2)加速度分析
图8-33
瞬心法
基点法
8-7在如图8-34所示的筛动机构中,筛子BC的摆动是由曲柄连杆机构所带动。已知曲柄长OA=0.3m,转速为n=40r/min。当筛子运动到与点O在同一水平线上时, ,试求此时筛子BC的速度。
图8-34
速度投影定理
8-8长为l=1.2m的直杆AB作平面运动,某瞬时其中点C的速度大小为vC=3m/s,方向与AB的夹角为 ,如图8-35所示。试求此时点A可能有的最小速度以及该瞬时杆AB的角速度。
8-20半径为r的圆盘可在半径为R的固定圆柱面上纯滚动,滑块B可在水平滑槽内滑动,如图8-47所示。已知r=125mm,R=375mm;杆AB长l=250mm。图示瞬时,vB=500mm/s,aB=750mm/s2;O、A、O1三点位于同一铅垂线上,试求此时圆盘的角加速度。
第8、9章习题解答分析

第8章习题解答8-2下面说法正确的是:()(A )若高斯面上的电场强度处处为零,则该面内必定没有电荷; (B )若高斯面内没有电荷,则该面上的电场强度必定处处为零; (C )若高斯面上的电场强度处处不为零,则该面内必定有电荷; (D )若高斯面内有电荷,则该面上的电场强度必定处处不为零。
解:[答案:D]高斯定理的原意。
8-3一半径为R 的导体球表面的面点荷密度为σ,则在距球面R 处的电场强度()(A )0?/σε (B )0/2σε (C )/4σε0 (D )0/8σε 解:[答案:C]利用均匀带电球面的场强公式计算02004qq r πε==F E r ,其中σπ24R q =, R 2r =8-4下列说法正确的是( )(A) 电场强度为零的点,电势也一定为零 (B) 电场强度不为零的点,电势也一定不为零 (C) 电势为零的点,电场强度也一定为零(D) 电势在某一区域内为常量,则电场强度在该区域内必定为零 解:[答案:D].根据场强与电势的微分关系或积分关系均可以证明。
8-5在静电场中,电势不变的区域,场强必定为 。
解:[答案:0] 根据场强与电势的微分关系或积分关系均可以证明。
8-6一个点电荷q 放在立方体中心,则穿过某一表面的电通量为 ,若将点电荷由中心向外移动至无限远,则总通量将 。
解:[答案:0/6q ε, 将为零],第一空:根据高斯定理知:正六面体的六个对称面组成的闭合面总通量为0εq,故每个面是总量的61。
第二空:根据高斯定理:总通量仅与面内电荷有关。
只要将点电荷由中心移动至六面体外,则该点荷对闭合面的总通量将没有贡献。
8-8电量Q 均匀分布在半径为R 的球体内,则球内球外的静电能之比 。
解:[答案:5:6]利用⎰=RV E W 020d 21内内ε及⎰∞=R V E W d 2120外外ε计算。
其中dr r dV 24π=,304R Qr E πε=内,204r QE πε=外。
仪器分析课后习题第八章答案

精品文档
12.用波长为213.8nm,质量浓度为0.010mg.mL-1的锌标准溶 液和空白溶液交替连续测定10次,用记录仪记录的格数如下. 计算该原子吸收分光光度计测定锌元素的检出限.
3.在原子吸收光度计中为什么不采用连续光源(如钨丝灯或氘灯), 而在分光光度计中则需要采用连续光源?
解:虽然原子吸收光谱中积分吸收与样品浓度呈线性关系,但由于原子 吸收线的半宽度很小,如果采用连续光源,要测定半宽度很小的吸收线 的积分吸收值就需要分辨率非常高的单色器,目前的技术条件尚达不到, 因此只能借助锐线光源,利用峰值吸收来代替.
9.应用原子吸收光谱法进行定量分析的依据是什么?进行定量分析有哪些方法? 试比较它们的优缺点. 解:在一定的浓度范围和一定的火焰宽度条件下,当采用锐线光源时,溶液 的吸光度与待测元素浓度成正比关系,这就是原子吸收光谱定量分析的依据。 常用两种方法进行定量分析: (1)标准曲线法:该方法简便、快速,但仅适用于组成简单的试样。 (2)标准加入法:本方法适用于试样的确切组分未知的情况。不适合于曲 线斜率度,应注意那些问题?怎样 选择原子吸收光谱分析的最佳条件? 解:应该从分析线的选择、光源(空心阴极灯)的工作电流、火焰的 选择、燃烧器高度的选择及狭缝宽度等几个方面来考虑,选择最佳的 测定条件。
11.从工作原理、仪器设备上对原子吸收法及原子荧光法作比较。 解:从工作原理上看,原子吸收是通过测定待测元素的原子蒸气对其特 征谱线的吸收来实现测定的,属于吸收光谱,而原子荧光则是通过测量 待测元素的原子蒸气在辐射能激发下所产生的荧光的强度来实现测定的, 属于发射光谱。
《理论力学》第八章-刚体平面运动试题及答案

理论力学8章作业题解8-2 半径为r 的齿轮由曲柄OA 带动,沿半径为R 的固定齿轮滚动。
如曲柄OA 以匀角加速度a 绕O 轴转动,且当运动开始时,角速度00=w ,转角0=j 。
求动齿轮以中心A为基点的平面运动方程。
解:图示,A 轮平面运动的转角为=A j ∠C 3AC 2=j +∠CAC 2由于弧长CC 1=CC 2,故有 ∠CAC 2=r R /j ,所以22/t rr R r r R r R A a j j j j +=+=+=A 轮平面运动方程为ïïîïïíì+=+=+=+=+=22212212)sin()()sin()()cos()(cos )(tr r R t r R r R y t r R r R x A A A a j a j a j8-6两刚体M ,N 用铰C 连结,作平面平行运动。
已知AC=BC=600mm ,在题附图所示位置s mm v s mm v B A /100,/200==,方向如图所示。
试求C 点的速度。
解:由速度投影定理得()()0==BC C BC B v v 。
则v C 必垂直于BC 连线,v C 与AC 连线的夹角为30°。
由()()AC A AC C v v = 即得:s mm v v A C /200== ,方向如题4-6附图示。
解毕。
8-9 图所示为一曲柄机构,曲柄OA 可绕O 轴转动,带动杆AC 在套管B 内滑动,套管B 及与其刚连的BD 杆又可绕通过B 铰而与图示平面垂直的水平轴运动。
已知:OA =BD =300mm ,OB =400mm ,当OA 转至铅直位置时,其角速度ωo =2rad/s ,试求D 点的速度。
C 12Aj C解 (1)平面运动方法: 由题可知:BD AC w w =确定AC 杆平面运动的速度瞬心。
套筒中AC 杆上一点速度沿套筒(为什么?)s rad IAOA IA v A AC /72.00=´==w w , s mm BD BD v AC BD D /216=´=´=w w D 点加速度如何分析?关键求AC 杆角加速度(=BD 杆角速度) 基点法,分析AC 杆上在套筒内的点(B’):(1) tA B n A B A B a a a a ¢¢¢++=r r r r大小:× ∠ ∠ × 方位:× ∠ ∠ ∠ 再利用合成运动方法:动点:套筒内AC 杆上的点B’,动系:套筒。
(完整版)大学物理学(课后答案)第8章

第八章课后习题解答一、选择题8-1如图8-1所示,一定量的理想气体,由平衡态A 变到平衡态B ,且它们的压强相等,即=A B p p 。
则在状态A 和状态B 之间,气体无论经过的是什么过程,气体必然[ ](A) 对外作正功 (B) 内能增加 (C) 从外界吸热 (D) 向外界放热分析:由p V -图可知,A A B B p V p V =,即知A B T T <,则对一定量理想气体必有B A E E >,即气体由状态A 变化到状态B ,内能必增加。
而作功、热传递均是过程量,与具体的热力学过程相关,所以(A )、(C )、(D )不是必然结果,只有(B )正确。
8-2 两个相同的刚性容器,一个盛有氢气,一个盛有氦气(均视为刚性分子理想气体)。
开始时它们的压强和温度都相同。
现将3 J 热量传给氦气,使之升高到一定的温度。
若使氢气也升高同样的温度,则应向氢气传递热量为[ ](A) 6 J (B) 3 J (C) 5 J (D) 10 J分析:由热力学第一定律Q E W =∆+知在等体过程中Q E =∆。
故可知欲使氢气和氦气升高相同的温度,由理想气体的内能公式2m i E R T M '∆=∆,知需传递的热量之比22222:():():5:3HHe H He H He H He H Hem m Q Q i i i i M M ''===。
故正确的是(C )。
8-3 一定量理想气体分别经过等压、等温和绝热过程从体积1V 膨胀到体积2V ,如图8-3所示,则下述正确的是[ ]习题8-1图(A) A C →吸热最多,内能增加(B) A D →内能增加,作功最少(C) A B →吸热最多,内能不变(D) A C →对外作功,内能不变分析:根据p V -图可知图中A B →为等压过程,A C →为等温过程,A D →为绝热过程。
又由理想气体的物态方程pV vRT =可知,p V -图上的pV 积越大,则该点温度越高,因此图中D A B C T T T T <==,又因对于一定量的气体而言其内能公式2i E vRT =,由此知0AB E ∆>,0AC E ∆=,0AD E ∆<。
大学应用物理第八章习题解答

第8章 磁场8-10一均匀密绕直螺线管的半径为 ,单位长度上有 匝线圈,每匝线圈中的电流为 ,用毕奥—萨伐尔定律求此螺线管轴线上的磁场。
分析:由于线圈密绕,因此可以近似地把螺线管看成一系列圆电流的紧密排列,且每一匝圆电流在轴线上任一点的磁场均沿轴向。
解: 取通过螺线管的轴线并与电流形成右旋的方向(即磁场的方向)为x 轴正向,如习题8-10图解(a )所示。
在螺线管上任取一段微元dx ,则通过它的电流为dI nIdx =,把它看成一个圆线圈,它在轴线上O 点产生的磁感应强度dB 为2022322()R nIdxdB R x μ=+ 由叠加原理可得,整个螺线管在O 点产生的磁感应强度B 的大小为由图可知12122212221212cos os ()()x x R x R x ββ==++ c ,代入上式并整理可得式中12ββ和分别为x 轴正向与从O 点引向螺线管两端的矢径r 之间的夹角。
讨论:(1)若螺线管的长度远远大于其直径,即螺线管可视为无限长时,20β=,1βπ=,则有上式说明,无限长密绕长直螺线管内部轴线上各点磁感应强度为常矢量。
理论和实验均证明:在整个无限长螺线管内部空间里,上述结论也适用。
即无限长螺线管内部空间里的磁场为均匀磁场,其磁感应强度B 的大小为0nI μ,方向与轴线平行;(2)若点O 位于半无限长载流螺线管一端,即12πβ=,20β=或12πβ=,2βπ=时,无论哪一种情况均有nI B 021μ=------(8-19) 可见半无限长螺线管端面中心轴线上磁感应强度的大小为管内的一半;综上所述,密绕长直螺线管轴线上各处磁感应强度分布见习题8-10图解(b )所示,从图中也可看出,长直螺线管内中部的磁场可以看成是均匀的。
习题8-10图解(a )习题8-10图解(b )8-11两根长直导线互相平行地放置,导线内电流大小相等,均为I =10A ,方向相同,如图8-49题图(左)所示。
PMP章节练习解析(第8章含20题)

1. 某项目要求完成多项产品. 其中一个产品的技术规范规定每200 立方英尺最多允许有12 个瑕疵. 这属于下列哪一项范畴?A.质量测量指标B.质量控制C.过程测量指标D.质量审核答案:A解析:题干可知,缺陷率或者允许的废品率,这个标准是质量测量指标,包括:准时性,预算控制,缺陷频率,故障率,可用性,可靠性,测试覆盖度2. 下列哪一项准确阐述了在产品交付客户之前用于修复缺陷所产生的成本?A.评估成本B.预防成本C.内部损失成本D.外部损失成本答案:C解析:题眼是,“产品交付客户之前”,内部非一致(损失)成本3. 控制图显示在均值的一侧有7个数据点在一条直线上。
应采取什么措施?A.执行试验设计B.调整控制图以反映新的均值C.寻找原因D.什么都不做,这是7 点原则,可以忽略答案:C解析:控制图,发现缺陷后;由鱼骨图和流程图,找根本原因4. 在测试期间发生了许多项目缺陷。
项目经理希望分析这些缺陷的根本原因。
项目经理应使用下列哪一项工具?A.散点图B.帕累托图C.石川图D.趋势图答案:C解析:题眼是,“分析这些缺陷的根本原因”,所以选石川图发现问题控制图(七点规则等)寻找原因因果图,流程图分析原因帕累托图,散点图,直方图,检查表/计数单5. 下列哪一个过程能实现持续过程改进?A.质量管理B.制定项目管理计划C.控制质量D.风险管理答案:A解析:质量管理(QA),保证的项目过程没有非增值活动,并按照质量计划,执行相应的质量活动,通常看到过程和审计就选QA。
现代质量观点,好的过程保证了好的质量。
6. 在项目执行期间,发起人很担心项目是否满足项目可交付物规范。
项目经理应与发起人一起查看下列哪一份文件?A.质量管理计划B.风险管理计划C.过程改进计划D.项目管理计划更新答案:A解析:执行过程中的质量保证需要参照质量管理计划,执行相应的质量保证活动,好的过程保证好的成果7. 下面哪一个选项最好的描述了属性样本以及变量样本?A.属性样本与预防有关,而变量样本与监督有关B.属性样本与一致性有关,而变量样本与一致性的程度有关C.属性样本与具体原因有关,而变量样本与任何原因有关D.两者是同一概念答案:B解析:变量抽样指合格程度,属性抽样指是否合格8. 一个项目经理和公司中设计铁路设备的团队要设计一台能将石头装载到火车上的机器。
机械原理的课后答案详解第8章的

第8章作业8-l 铰链四杆机构中,转动副成为周转副的条件是什么?在如下图所示四杆机构ABCD 中哪些运动副为周转副?当其杆AB 与AD 重合时,该机构在运动上有何特点?并用作图法求出杆3上E 点的连杆曲线。
答:转动副成为周转副的条件是:〔1〕最短杆与最长杆的长度之和小于或等于其他两杆长度之和;〔2〕机构中最短杆上的两个转动副均为周转副。
图示ABCD 四杆机构中C 、D 为周转副。
当其杆AB 与AD 重合时,杆BE 与CD 也重合因此机构处于死点位置。
8-2曲柄摇杆机构中,当以曲柄为原动件时,机构是否一定存在急回运动,且一定无死点?为什么?答:机构不一定存在急回运动,但一定无死点,因为:〔1〕当极位夹角等于零时,就不存在急回运动如下列图,〔2〕原动件能做连续回转运动,所以一定无死点。
8-3 四杆机构中的极位和死点有何异同?8-4图a 为偏心轮式容积泵;图b 为由四个四杆机构组成的转动翼板式容积泵。
试绘出两种泵的机构运动简图,并说明它们为何种四杆机构,为什么?解机构运动简图如右图所示,ABCD 是双曲柄机构。
因为主动圆盘AB 绕固定轴A 作整周转动,而各翼板CD 绕固定轴D 转动,所以A 、D 为周转副,杆AB 、CD 都是曲柄。
8-5试画出图示两种机构的机构运动简图,并说明它们各为何种机构。
图a 曲柄摇杆机构图b 为导杆机构。
8-6如下列图,设己知四杆机构各构件的长度为240a mm =,600b =mm ,400,500c mm d mm ==。
试问:1)当取杆4为机架时,是否有曲柄存在?2)假如各杆长度不变,能否以选不同杆为机架的方法获得双曲柄机构和双摇杆机构?如何获得?3)假如a 、b ﹑c 三杆的长度不变,取杆4为机架,要获得曲柄摇杆机构,d 的取值X 围为何值? : 解 (1)因a+b=240+600=840≤900=400+500=c+d 且最短杆 1为连架轩.故当取杆4为机架时,有曲柄存在。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b = 90 mm , h = 2b = 180 mm
8-4 螺旋夹紧器立臂的横截面为 a × b 的矩形,如图所示。已知该夹紧器工作时承受的 夹 紧 力 F = 16 kN , 材 料 的 许 用 应 力 [σ ] = 160 MPa , 立 臂 厚 a = 20 mm , 偏 心 距
e = 140 mm 。求立臂宽度 b 。
第 8 章 组合变形
思考题
8-1 何为斜弯曲?何谓偏心拉压及弯拉组合变形? 何谓弯扭组合变形? 答 挠度 w 方向与载荷 F 的作用线方向不一致, 即构件弯曲以后的挠曲线不再是载荷作 用平面内或与载荷作用平面平行的一条平面曲线,这种弯曲称为斜弯曲。 偏心拉压指杆件受的拉伸或压缩作用载荷不是沿截面形心。 将这种不是沿截面形心作用 的拉(压)力向截面形心简化,就是弯拉(压)组合变形。 杆件在弯矩和扭矩联合作用下的变形称为弯扭组合变形。 8-2 为何斜弯曲、偏心拉压及弯拉组合变形的应力可用叠加原理。 答 斜弯曲、偏心拉压及弯拉组合变形在线弹性、小变形条件下,横截面上的应力都是 拉压正应力,方向共线,可用叠加原理。 8-3 为何弯扭组合变形的强度条件不能用代数叠加? 答 弯曲变形的强度条件是单向应力状态下的强度条件;扭转变形的强度条件纯剪切应 力状态下的强度条件,正应力与切应力相互垂直,不能用代数叠加(只有同向或反向才能叠 加) 。
显然危险截面在 C:
∑ M z = 0 , FBy =
Fy + 2 Fy′
M Cz = FAy × 50 mm = 152.2 N ⋅ m , M Cy = FAz × 50 mm = 37.5 N ⋅ m
119
τ=
16 × 448 T = = 18.3 × 106 Pa = 18.3 MPa −9 3 Wp π × 50 × 10
23.5 23.5 2 σ ± ( )2 + τ 2 = ± ( ) + 18.3 2 2 2 2 2 33.5 = 11.8 ± 21.7 = MPa − 9.95 σ2 = 0 σ − σ 3 33.5 + 9.95 τ max = 1 = = 21.7 MPa 2 2
8-4 如 果 弯 扭 组 合 变 形 的 轴 用 铸 铁 制 成 , 是 否 仍 可 用
M 2 +T2 ≤ [σ ] 或 W
M 2 + 0.75T 2 ≤ [σ ] 进行强度校核。 W
答
M 2 +T2 M 2 + 0.75T 2 ≤ [σ ] 或 ≤ [σ ] 是按第 3 或第 4 强度理论推出的强度条 W W
解 M e = 9 549 ×
P 11 = 9 549 × = 954.9 N ⋅ m = T n 110 T = (3F − F ) × 330 × 10 −3 m = 954.9 N ⋅ m , F = 1.447 kN M max = 4 Fl = 5.79 l kN
2 M max +T 2
32 (5.79l × 10 3 ) + 954.9 2 ≤ 70 × 10 6 π × 80 3 × 10 −9 l ≤ 0.585 m
(b)
(c)
比较式(a),(b),(c)知,截面消弱后最大拉应力是消弱前的拉应力的 8 倍。 8-3 作用于图示悬臂木梁上的载荷 F1 = 800 N , F2 = 1 650 N 。若木材许用应力
[σ ] = 10 MPa ,矩形截面边长之比为
h = 2 ,试确定截面的尺寸。 b
解 危险截面在固定端,危险点在 y 为正,z 为负的角点(或 y 为负,z 为正的角点)处。
M z max = F2 × 1 m , M y max = F1 × 2 m
σ max =
M z max M y max 6 F2 6 × 2 F1 + = 2 + = [σ ] Wz Wy bh hb 2
将已知条件代入上式得
6 × 1 650 6 × 800 + = 10 × 10 6 4b 3 2b 3
解
截面上轴力 FN = F ,弯矩 M = Fe
σ max =
F Fe F 6 Fe + = + ≤ [σ ] A W ab ab 2 F 1 6e b + 6e a[σ ] ( + 2 ) ≤ [σ ] , ≤ F a b b b2 a[σ ] 2 a[σ ] 2 b , b − b − 6e ≥ 0 b + 6e ≤ F F 1 + 1 + 24ea[σ ] / F F (1 + 1 + 24ea[σ ] / F b≥ = 2a[σ ] 2a[σ ] F 16 × 10 3 [1 + 1 + 24 × 140 × 10 −3 × 20 × 10 −3 × 160 × 10 6 /(16 × 10 3 ) ]
W 即可 A
( a ) σ 1 − σ 3 ≤ [σ ] ; ( b ) σ
2
+ 3τ ≤ [σ ] ;
2
(c)
M 2 +T2 ≤ [σ ] W
答 它们都是用第 3 强度理论推出的强度条件,其中 式(a)适用于任意应力状态; 式(b)适用于平面应力状态; 式(c)适用于圆轴弯扭组合变形工况。 8-8 当矩形截面杆处于双向弯曲、轴向拉伸(压缩)与扭转组合变形时,危险点位于何 处?如何计算危险点处的应力并建立相应的强度条件? 答当矩形截面杆处于双向弯曲变形时, 危险点位于矩形截面的角点; 矩形截面杆处于轴 向拉伸(压缩)与扭转组合变形时,危险点位于矩形截面长边中点。
σ 1,3 =
σ
注:剪力在点 A 的切应力为零。 8-6 一手摇绞车如图(a)所示。已知轴的直径 d = 25 mm ,材料为 Q235 钢,其许用应 力 [σ ] = 80 MPa 。试按第 4 强度理论求绞车的最大起吊重量 P=W。
(a)
y
400 A 300 300
P/2 z FAz R
D
Me
C
2
W
≤ [σ ] , W =
πd 3 π × 80 3 × 10 −9 3 = m 32 32
8-8 图示齿轮传动轴, 齿轮 1 与 2 的节圆直径分别为 d1 = 50 mm 与 d 2 = 130 mm 。 在 齿轮 1 上,作用有切向力 Fy = 3.83 kN ,径向力 Fz = 1.393 kN ;在齿轮 2 上,作用有切向 力 Fy′ = 1.473 kN ,径向力 Fz′ = 0.536 kN 。轴用 45 号钢制成,直径 d = 22 mm ,许用应 力 [σ ] = 180 MPa ,试按第 3 强度理 120 mm ;许用应力 [σ ] = 12 MPa ;许可挠度 [ w] =
的强度和刚度。
l 。试校核此梁 150
解
1 1 q y l 2 = q cos 30 o ⋅ l 2 8 8 1 1 M y max = q z l 2 = q sin 30 o ⋅ l 2 8 8 1 2 1 2 ql cos 30 o ql sin 30 o M z max M y max 8 6ql 2 cos 30 o sin 30 o 8 σ = + = + = ( + ) Wz Wy 8bh h b bh 2 hb 2 6 6 3 1 3 2 6 × 2 × 10 × 4 ( 2 + 2 ) = 11.97 × 10 6 Pa = 12.0 MPa = [σ ] ,安全 = −6 8 × 120 × 160 × 10 0.160 0.120 5q y l 4 5 × 12q cos 30 o l 4 5q z l 4 5 × 12q sin 30 o l 4 = = w , wz = = y 384 EI z 384 EI y 384 Ebh 3 384 Ehb 3 M z max =
=
2 × 20 × 10 −3 × 160 × 10 6 = 0.0673 m = 67.3 mm
8-5 曲拐受力如图(a)所示,其圆杆部分的直径 d = 50 mm 。试画出表示点 A 处应力状 态的单元体,并求其主应力及最大切应力。
A
τ
σ
(a)
(b)
解
点 A 所在的横截面上承受弯矩和扭矩作用,其值
M Cy = FBz × 0.3 = 0.06 P , M Cz =
σ r4 =
2 2 M Cy + M Cz + 0.75TC
2
W
≤ [σ ]
32 × 0.062 + 0.152 + 0.75 × 0.152 P ≤ 80 × 106 3 −9 π × 25 × 10
120
8-7 图示传动轴,转速 n = 110 r/min ,传递功率 P = 11 kW ,皮带的紧边张力为其松 边张力的 3 倍。若许用应力 [σ ] = 70 MPa ,试按第 3 强度理论确定该传动轴外伸段的许可 长度 l 。
117
(a)
(b)
解 截面消弱前
F a2 截面消弱后,截面 m − m 受力如图(b) Fa M = 4
σ 1t =
( a)
σ 2t =
F a2 2
σ 2c =
F a2 2
Fa 8F M 2F + = 2 + 4 2 = 2 W a a ⎛a⎞ a⎜ ⎟ ⎝2⎠ 6 Fa M 2F 4F − = 2 − 4 2 =− 2 W a a ⎛a⎞ a⎜ ⎟ ⎝2⎠ 6
件,适用于塑性材料轴,而铸铁是脆性材料,所以不能用。 8-5 偏心拉伸时,是否可使横截面上的应力都成为拉应力? 答 可以。设横截面面积为 A,弯曲截面系数为 W,拉力偏心距为 e,则使 e < 使横截面上的应力都成为拉应力。 8-6 斜弯曲的外力特点和变形特点各是什么? 答 斜弯曲的外力特点是不作用在与形心主轴重合或平行的平面内;其变形后的挠曲线 平面与形心主轴平面(或与形心主轴平面平行的平面)不重合。 8-7 简述下列 3 个强度条件表达式各适用于什么情况。
