高中数学课时跟踪检测六椭圆的简单几何性质新人教A版选修

合集下载

人教A版高中同步学考数学选修1精品课件 2.1.2 椭圆的简单几何性质

2
36
+
2
27
=1.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
反思感悟利用椭圆的几何性质求标准方程的思路
(1)根据椭圆的几何性质,求其标准方程主要采用待定系数法,解题
步骤为:
①确定焦点所在的位置,以确定椭圆标准方程的形式;
②确立关于a,b,c的方程(组),求出参数a,b,c;
③写出标准方程.

离心率 e= =
7
4
.
7
焦点坐标 - 12 ,0 和
1
顶点坐标 - 3 ,0 ,
1
3
7
12
,0 ,
1
1
,0 , 0,- 4 , 0, 4 .
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
根据椭圆的几何性质求其标准方程
例2根据下列条件求椭圆的标准方程:
1
(1)椭圆的一个顶点是(0,2),离心率e= 2 ;
(2)椭圆长轴的一个端点为(-6,0),短轴的一个端点与两个焦点构成
一个正三角形.
分析(1)焦点位置不确定,应进行分类讨论;(2)焦点位置确定,可根据
题目条件求出a,b,c的值即得方程.
课堂篇探究学习
探究一
探究二
探究三
思维辨析
当堂检测
= 2,
解:(1)①当椭圆焦点在 x 轴上时,依题意有 1 又 a2=b2+c2,解得
又因为 b2=a2-c2,代入得 c4-6a2c2+a4=0,即 e4-6e2+1=0,解得
e2=3-2 2(e2=3+2 2舍去),从而 e= 2-1.

椭圆的简单几何性质 2022-2023学年高二数学同步精品讲义(人教A版2019选择性必修第一册)

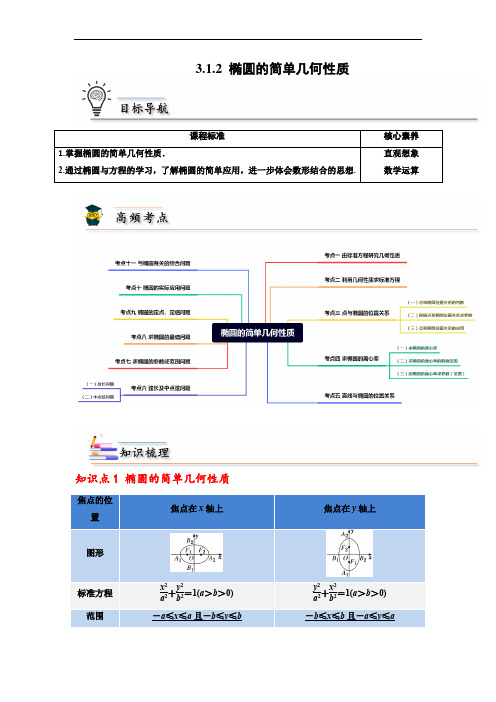
3.1.2 椭圆的简单几何性质课程标准核心素养 1.掌握椭圆的简单几何性质．2.通过椭圆与方程的学习，了解椭圆的简单应用，进一步体会数形结合的思想.直观想象数学运算知识点1 椭圆的简单几何性质焦点的位置焦点在x 轴上焦点在y 轴上图形标准方程 x 2a 2＋y 2b 2＝1(a ＞b ＞0) y 2a 2＋x 2b 2＝1(a ＞b ＞0) 范围－a ≤x ≤a 且－b ≤y ≤b－b ≤x ≤b 且－a ≤y ≤a顶点 A 1(－a,0)，A 2(a,0),_ B 1(0，－b )，B 2(0，b )A 1(0，－a )，A 2(0，a ),B 1(－b,0)，B 2(b,0)轴长长轴长＝2a ，短轴长＝2b焦点 F 1(－c,0)，F 2(c,0)F 1(0，－c )，F 2(0，c )焦距 |F 1F 2|＝2c对称性对称轴x 轴和y 轴，对称中心(0,0) 离心率 e ＝ca (0<e <1)（注：e ＝1－b 2a2＝11＋b 2c2.）注：(1)椭圆的焦点一定在它的长轴上．(2)椭圆上到中心的距离最小的点是短轴的两个端点，到中心的距离最大的点是长轴的两个端点．(3)椭圆上到焦点的距离最大和最小的点分别是长轴的两个端点，最大值为a ＋c ，最小值为a －c .(4)椭圆有四个顶点、两个焦点，共六个特殊点，研究椭圆时一定要注意这六个特殊点的位置．(5)已知椭圆的四个顶点，可以使用几何作图找出其焦点，方法是：以短轴的端点为圆心，a 为半径作弧交长轴于两点，这两点就是该椭圆的焦点．(6)椭圆的离心率e 的大小反映椭圆的扁平程度，e 越大，椭圆越扁；e 越小，椭圆越圆．拓展：用离心率e ＝ca来刻画椭圆的扁平程度．如图所示，在Rt △BF 2O 中，cos ∠BF 2O ＝c a ，记e ＝ca ，则0<e <1，e 越大，∠BF 2O 越小，椭圆越扁；e 越小，∠BF 2O 越大，椭圆越接近于圆．(7)常用椭圆方程的设法①与椭圆12222=+b y a x )0(>>b a 共焦点的椭圆方程可设为：12222=+++m b y m a x )(2b m ->②有相同离心率：k b y a x =+2222（0>k ，焦点在x 轴上）或k bxa y =+2222（0>k ，焦点在x 轴上）【即学即练1】求椭圆x 2＋9y 2＝81的长轴长、短轴长、离心率、焦点和顶点坐标．【解析】把已知方程化成标准方程为x 281＋y 29＝1，于是a ＝9，b ＝3，c ＝81－9＝62，所以椭圆的长轴长2a ＝18，短轴长2b ＝6，离心率e ＝c a ＝223.两个焦点的坐标分别为F 1(－62，0)，F 2(62，0)，四个顶点的坐标分别为A 1(－9,0)，A 2(9,0)，B 1(0，－3)，B 2(0,3)．【即学即练2】椭圆以两条坐标轴为对称轴，一个顶点是(0,13)，另一个顶点是(－10,0)，则焦点坐标为( ) A ．(±10,0) B ．(±69，0) C ．(0，±13)D ．(0，±69)【解析】由题意知椭圆焦点在y 轴上，且a ＝13，b ＝10，则c ＝a 2－b 2＝69，故焦点坐标为(0，±69)．故选D【即学即练3】已知椭圆2222:1(0)1+=>+x y C a a a 的短轴长和焦距相等，则a 的值为（） A ．1 B 2 C ．32D 3【解析】由题设易知：椭圆参数b c =，即有2221+-=a a a ，可得1a =．故选：A【即学即练4】比较椭圆①x 2＋9y 2＝36与②x 29＋y 25＝1的形状，则________更扁(填序号)．【解析】x 2＋9y 2＝36化为标准方程为x 236＋y 24＝1，故离心率e 1＝426＝223；x 29＋y 25＝1的离心率e 2＝23.因为e 1＞e 2，故①更扁．【即学即练5】焦点在x 轴上，右焦点到短轴端点的距离为2，到左顶点的距离为3的椭圆的标准方程为( )A.x 24＋y 23＝1 B.x 24＋y 2＝1 C.y 24＋x 23＝1 D ．x 2＋y 24＝1 【解析】依题意，得a ＝2，a ＋c ＝3，故c ＝1，b ＝22－12＝3，故所求椭圆的标准方程是x 24＋y 23＝1.故选A【即学即练6】与椭圆9x 2＋4y 2＝36有相同焦点，且短轴长为2的椭圆的标准方程为( ) A.x 22＋y 24＝1 B ．x 2＋y 26＝1C.x 26＋y 2＝1 D.x 28＋y 25＝1 【解析】椭圆9x 2＋4y 2＝36可化为x 24＋y 29＝1，可知焦点在y 轴上，焦点坐标为(0，±5)，故可设所求椭圆方程为y 2a 2＋x 2b 2＝1(a >b >0)，则c ＝ 5.又2b ＝2，即b ＝1，所以a 2＝b 2＋c 2＝6，则所求椭圆的标准方程为 x 2＋y 26＝1.故选B【即学即练7】若椭圆x 2＋my 2＝1的焦点在y 轴上，且长轴长是短轴长的2倍，则m 的值为________．【解析】∵椭圆x 2＋my 2＝1的焦点在y 轴上，长轴长是短轴长的2倍，∴1m ＝2，∴m ＝14. 【即学即练8】椭圆C ：2221(3)3x y a a +=>的左、右焦点分别为1F ，2F ，经过点1F 的直线与椭圆C 相交于A ，B 两点，若2ABF 的周长为16，则椭圆C 的离心率为（） A 13B 11C ．12D 3【解析】由题可知416a =，即4a =，所以椭圆C 的离心率16313e -==. 故选：A.【即学即练9】已知椭圆()222210x y a b a b+=>>上存在点P ，使得213PF PF =，其中1F ，2F 分别为椭圆的左、右焦点，则该椭圆的离心率的取值范围是（） A ．10,4⎛⎤⎥⎝⎦B ．1,14⎛⎫ ⎪⎝⎭C ．1,12⎛⎫ ⎪⎝⎭D ．1,12⎡⎫⎪⎢⎣⎭【解析】由椭圆的定义得122PF PF a +=，又∵213PF PF =，∵132PF a =，212PF a =，而12122PF PF F F c -≤=，当且仅当点P 在椭圆右顶点时等号成立，即31222a a c -≤，即2a c ≤，则12c e a =≥，即112e ≤<.故选：D ．知识点2 点与椭圆的位置关系点P (x 0，y 0)与椭圆x 2a 2＋y 2b2＝1(a >b >0)的位置关系：点P 在椭圆上⇔x 20a 2＋y 20b 2＝1；点P 在椭圆内部⇔x 20a 2＋y 20b 2<1；点P 在椭圆外部⇔x 20a 2＋y 20b2>1.【即学即练10】已知点(2,3)在椭圆x 2m 2＋y 2n2＝1上，则下列说法正确的是( )A ．点(－2,3)在椭圆外B ．点(3,2)在椭圆上C ．点(－2，－3)在椭圆内D ．点(2，－3)在椭圆上【解析】D【即学即练11】已知直线l 过点(3，－1)，且椭圆C ：x 225＋y 236＝1，则直线l 与椭圆C 的公共点的个数为( ) A ．1 B ．1或2 C ．2D ．0【解析】因为直线过定点(3，－1)且3225＋(－1)236＜1，所以点(3，－1)在椭圆的内部，故直线l 与椭圆有2个公共点．故选C知识点3 直线与椭圆的位置关系直线y ＝kx ＋m 与椭圆x 2a 2＋y 2b 2＝1(a >b >0)的位置关系，判断方法：联立⎩⎪⎨⎪⎧y ＝kx ＋m ，x 2a 2＋y 2b 2＝1，消y 得一元二次方程．当Δ>0时，方程有两解，直线与椭圆相交；当Δ＝0时，方程有一解，直线与椭圆相切；当Δ<0时，方程无解，直线与椭圆相离．【即学即练12】对不同的实数值m ，讨论直线y ＝x ＋m 与椭圆x 24＋y 2＝1的位置关系．【解析】由⎩⎪⎨⎪⎧y ＝x ＋m ，x 24＋y 2＝1，消去y ，得x 24＋(x ＋m )2＝1，整理得5x 2＋8mx ＋4m 2－4＝0. Δ＝(8m )2－4×5(4m 2－4)＝16(5－m 2)．当－5<m <5时，Δ>0，直线与椭圆相交；当m ＝－5或m ＝5时，Δ＝0，直线与椭圆相切；当m <－5或m >5时，Δ<0，直线与椭圆相离．【即学即练13】若直线y ＝kx ＋2与椭圆x 23＋y 22＝1相切，则斜率k 的值是( )A.63 B ．－63C ．±63D ．±33【解析】把y ＝kx ＋2代入x 23＋y 22＝1，得(2＋3k 2)x 2＋12kx ＋6＝0，由题意知Δ＝0，∴k 2＝23，∴k ＝±63. 故选C知识点4 直线与椭圆相交的弦长公式1．定义：连接椭圆上两个点的线段称为椭圆的弦． 2．求弦长的方法(1)交点法：将直线的方程与椭圆的方程联立，求出两交点的坐标，然后运用两点间的距离公式来求．(2)根与系数的关系法：如果直线的斜率为k ，被椭圆截得弦AB 两端点坐标分别为(x 1，y 1)，(x 2，y 2)，则弦长公式为：|AB |＝1＋k 2·(x 1＋x 2)2－4x 1x 2＝ 1＋1k2·(y 1＋y 2)2－4y 1y 2.注：（1）已知弦AB 是椭圆22221x y a b+=（0a b >>）的一条弦，中点M 坐标为00(,)x y ，则AB 的斜率为2020b x a y -，运用点差法求AB 的斜率，设11(,)A x y ，22(,)B x y ；A 、B 都在椭圆上，22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩ 两式相减得：22221212220x x y y a b--+=，1212121222()()()()0x x x x y y y y a b -+-+-= 即22012122212120b x y y x x b x x a y y a y -+=-⋅=--+，故2020AB b x k a y =- （2）弦AB 的斜率与弦中心M 和椭圆中心O 的连线的斜率之积为定值：22ab -【即学即练14】已知椭圆x 225＋y 216＝1，过椭圆的右焦点F 且垂直于x 轴的直线与椭圆交于A ，B 两点，则|AB |＝________.【解析】易求得a ＝5，b ＝4，所以|AB |＝2b 2a ＝2×425＝325.【即学即练15】已知F 是椭圆x 225＋y 29＝1的一个焦点，AB 为过椭圆中心的一条弦，则△ABF的面积最大值为( )A ．6B ．15C ．20D ．12【解析】由题意知，S △ABF ＝12|OF |·|y 1－y 2|≤12|OF |·2b ＝12.故选D【即学即练16】已知椭圆()2222:10x y C a b a b +=>>的左焦点为F ，过F 作一条倾斜角为45的直线与椭圆C 交于,A B 两点，若()3,2M -为线段AB 的中点，则椭圆C 的离心率是（） A 3B ．12C ．25D 5【解析】设点1122(,),(,)A x y B x y ，依题意，2222221122222222b x a y a b b x a y a b ⎧+=⎨+=⎩，相减得2212121212()()a ()()0b x x x x y y y y +-++-=，因直线AB 的倾斜角为45，即直线AB 的斜率为12121y yx x -=-，又()3,2M -为线段AB 的中点，则126x x +=-，124y y +=，因此有22460a b -=，即2223b a =，所以椭圆C 的离心率222231a b b e a --. 故选：A【即学即练17】已知椭圆2222:1(0)x y C a b a b +=>>3直线l 与椭圆C 交于A ，B 两点且线段AB 的中点为()3,2M ，则直线l 的斜率为________.【解析】由题意可得2231c b e a a ==-6a =，设()()1122,,,A x y B x y ，则2222112222221,1x y x y a b a b +=+=，两式相减可得()()()()12121212220x x x x y y y y a b -+-++=，AB 的中点为(3,2)M ，12126,4x x y y +=+=∴，则直线斜率212122*********y y x x b k x x a y y -+==-⋅=-⨯=--+. 故答案为：1-.考点一由标准方程研究几何性质解题方略：用标准方程研究几何性质的步骤 (1)将椭圆方程化为标准形式； (2)确定焦点位置； (3)求出a ，b ，c ； (4)写出椭圆的几何性质．注：长轴长、短轴长、焦距不是a ，b ，c ，而应是a ，b ，c 的两倍．【例1-1】已知椭圆C 1：x 2100＋y 264＝1，设椭圆C 2与椭圆C 1的长轴长、短轴长分别相等，且椭圆C 2的焦点在y 轴上．(1)求椭圆C 1的长半轴长、短半轴长、焦点坐标及离心率； (2)写出椭圆C 2的方程，并研究其性质．【解析】(1)由椭圆C 1：x 2100＋y 264＝1可得其长半轴长为10，短半轴长为8，焦点坐标(6,0)，(－6,0)，离心率e ＝35；(2)椭圆C 2：y 2100＋x 264＝1，性质：①范围：－8≤x ≤8，－10≤y ≤10； ②对称性：关于x 轴、y 轴、原点对称；③顶点：长轴端点(0,10)，(0，－10)，短轴端点(－8,0)，(8,0)； ④焦点：(0,6)，(0，－6)； ⑤离心率：e ＝35.【例1-2】椭圆2213x y m+=-的一个焦点坐标为()0,1-，则实数m 的值为（） A ．2 B ．4 C ．4- D ．2-【解析】根据焦点坐标可知，椭圆焦点在y 轴上，所以有31m --=，解得4m =-．故选：C.变式1：已知椭圆2214x y m+=的焦距为3m 的值不可能为（） A ．1B ．7C ．1-D 7【解析】由题知，3c若4m >，则2a m =，24b =，所以7m =，即7m =±；若4m <，则24a =，1b m ==，即1m =±. 故选：D【例1-3】【多选】已知椭圆222212:55,:11612+=+=x y C x y C ，则（） A ．12,C C 的焦点都在x 轴上 B ．12,C C 的焦距相等 C ．12,C C 没有公共点D ．2C 比1C 更接近圆【解析】对于A ，因为椭圆1C 的标准方程为2215y x +=，所以1C 的焦点在y 上，所以A 不正确；对于B ，因为椭圆1C 的焦距为2514-，椭圆2C 的焦距为216124-=，所以B 正确；对于C ，作出椭圆12,C C 的图象，由图象可知，椭圆12,C C 没有公共点，所以C 正确；对于D ，因为椭圆1C 的离心率为125=e ，2C的离心率为22142==e ，所以12e e >，所以D正确. 故选：BCD.变式1：已知椭圆22194x y +=与椭圆()221494x y k k k +=<--，则下列结论正确的是（） A ．长轴长相等 B ．短轴长相等 C ．焦距相等 D ．离心率相等【解析】∵4k <，9k ∴->40k ->且9(4)94k k ---=-，∴椭圆22194x y +=与椭圆221(4)94x y k k k +=<--的关系是有相等的焦距．故选：C ．考点二利用几何性质求标准方程解题方略：利用椭圆的几何性质求标准方程的思路利用椭圆的几何性质求椭圆的标准方程时，通常采用待定系数法，其步骤是： (1)确定焦点位置；(2)设出相应椭圆的标准方程(对于焦点位置不确定的椭圆可能有两种标准方程)；(3)根据已知条件构造关于参数的关系式，利用方程(组)求参数．列方程(组)时常用的关系式有b 2＝a 2－c 2，e ＝ca 等．注：（1）与椭圆12222=+b y a x )0(>>b a 共焦点的椭圆方程可设为：12222=+++mb y m a x)(2b m ->（2）有相同离心率：k b y a x =+2222（0>k ，焦点在x 轴上）或k bxa y =+2222（0>k ，焦点在x 轴上）【例2-1】求适合下列条件的椭圆的标准方程：(1)长轴长是10，离心率是45；(2)在x 轴上的一个焦点与短轴两个端点的连线互相垂直，且焦距为6. 【解析】(1)设椭圆的方程为x 2a 2＋y 2b 2＝1(a >b >0)或y 2a 2＋x 2b 2＝1(a >b >0)．由已知得2a ＝10，a ＝5. 又∵e ＝c a ＝45，∴c ＝4.∴b 2＝a 2－c 2＝25－16＝9.∴椭圆方程为x 225＋y 29＝1或y 225＋x 29＝1.(2)依题意可设椭圆方程为x 2a 2＋y 2b2＝1(a >b >0)．如图所示，△A 1FA 2为一等腰直角三角形，OF 为斜边A 1A 2的中线(高)，且|OF |＝c ，|A 1A 2|＝2b ，则c ＝b ＝3，a 2＝b 2＋c 2＝18，故所求椭圆的方程为x 218＋y 29＝1.变式1：已知椭圆的中心在原点，焦点在x 轴上，离心率为55，且过P (－5,4)，则椭圆的方程为________________．【解析】∵e ＝c a ＝55，∴c 2a 2＝a 2－b 2a 2＝15， ∴5a 2－5b 2＝a 2即4a 2＝5b 2.设椭圆的标准方程为x 2a 2＋5y 24a 2＝1(a >0)，∵椭圆过点P (－5,4)，∴25a 2＋5×164a 2＝1.解得a 2＝45.∴椭圆方程为x 245＋y 236＝1.答案：x 245＋y 236＝1变式2：若直线240x y ++=过椭圆()222210x y a b a b+=>>短轴端点和左顶点，则椭圆方程为（） A ．22142x y +=B ．221164x y += C ．221416x y +=D ．221129x y +=【解析】直线240x y ++=交x 轴于(4,0)-，交y 轴于(0,2)-，依题意，4,2a b ==，所以椭圆方程为221164x y +=. 故选：B变式3：古希腊数学家阿基米德利用“逼近法”得到椭圆的面积除以圆周率等于椭圆的长半轴长与短半轴长的乘积.若椭圆C 的中心为原点，焦点1F ，2F 均在y 轴上，椭圆C 的面积为23π，且短轴长为23C 的标准方程为（） A ．22112x y +=B ．22143x y +=C ．22134x y +=D ．221163x y +=【解析】因为椭圆C 的焦点在y 轴上，故可设其方程为22221y xa b+=，根据题意可得23ab ，223b =，故可得2,3a b ==，故所求椭圆方程为：22134x y +=.故选：C.变式4：已知F (3,0)是椭圆的一个焦点，过F 且垂直x 轴的弦长为3（）A ．245x + 236y = 1B ．236x + 227y = 1C ．227x + 218y = 1D ．218x + 29y = 1【解析】依题意2222324333,32c ba b a a b c=⎧⎪⎪=⇒==⎨⎪=+⎪⎩所以椭圆方程为2212718x y +=.故选：C考点三点与椭圆的位置关系解题方略：点P (x 0，y 0)与椭圆x 2a 2＋y 2b2＝1(a >b >0)的位置关系：点P 在椭圆上⇔x 20a 2＋y 20b 2＝1；点P 在椭圆内部⇔x 20a 2＋y 20b 2<1；点P 在椭圆外部⇔x 20a 2＋y 20b2>1. （一）点和椭圆位置关系的判断【例3-1】点(1,1)与椭圆22132x y +=的位置关系为（）A ．在椭圆上B ．在椭圆内C ．在椭圆外D ．不能确定【解析】1151326+=<，可知点(1,1)在椭圆内．故选：B.（二）根据点和椭圆位置关系求参数【例3-2】点(),1A a 在椭圆22142x y +=的外部，则a 的取值范围是（）A ．(2,2B ．(),22,-∞-⋃+∞C ．()2,2-D ．()1,1-【解析】因为点(),1A a 在椭圆22142x y +=的外部，所以21142a +>,解得(2)(2)a ∈-∞+∞，，,故选：B.变式1：若点()1,A m 在椭圆22:142x y C +=的内部，则实数m 的取值范围是（）A ．(6,6B ．66⎛ ⎝⎭C ．66,,2⎛⎛⎫-∞+∞ ⎪ ⎪⎝⎭⎝⎭ D ．33⎛ ⎝⎭【解析】221142m +<，所以66m ⎛∈ ⎝⎭，故选：B.（三）点和椭圆位置关系的应用【例3-3】若直线9mx ny +=和圆229x y +=没有公共点，则过点(),P m n 的直线与椭圆221109x y +=的交点个数是（） A ．0 B ．1 C ．2 D ．不确定【解析】因为直线9mx ny +=和圆229x y +=没有交点，所以圆心()0,0到直线90mx ny +-=的距离2293d m n-=>+，可得：229m n +<，即点(,)m n 在圆229x y +=内，又因为圆229x y +=内切于椭圆221169x y +=，所以点(),m n 在椭圆221169x y +=内，即过点(),m n 的直线与椭圆221169x y +=有两个交点.故选：C.变式1：已知椭圆2214x y +=经过点(),P m n ，则22m n +的取值范围是（）A ．(]0,1B ．(]0,4C ．[)4,+∞D ．[]1,4【解析】因为椭圆2214x y +=经过点(),P m n ，所以2214m n +=，所以2214m n =-，则2222231144m m m n m +=+-=+．因为椭圆2214x y +=经过点(),P m n ，所以22m -≤≤，即204m ≤≤，故22m n +的取值范围是[]1,4．故选：D ．考点四求椭圆的离心率解题方略：求椭圆离心率及范围的两种方法(1)直接法：若已知a ，c 可直接利用e ＝ca 求解．若已知a ，b 或b ，c 可借助于a 2＝b 2＋c 2求出c 或a ，再代入公式e ＝ca求解．(2)方程法：若a ，c 的值不可求，则可根据条件建立a ，b ，c 的关系式，借助于a 2＝b 2＋c 2，转化为关于a ，c 的齐次方程或不等式，再将方程或不等式两边同除以a 的最高次幂，得到关于e 的方程或不等式，即可求得e 的值或范围．（一）求椭圆的离心率【例4-1】若椭圆的两个焦点与短轴的一个端点构成一个正三角形，则该椭圆的离心率为( ) A.12 B.32 C.34D.64【解析】如图，△BF 1F 2是正三角形，∵在Rt △OBF 2中，|OF 2|＝c ，|BF 2|＝a ，∠OF 2B ＝60°， ∴cos 60°＝c a ＝12，即椭圆的离心率e ＝12，故选A.变式1：若椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别为F 1，F 2，线段F 1F 2被点⎝⎛⎭⎫b 2，0分成5∶3的两段，则此椭圆的离心率为( )A.1617 B.41717C.45D.255【解析】依题意得c ＋b 2c －b 2＝53，∴c ＝2b ，∴a ＝b 2＋c 2＝5b ，∴e ＝c a ＝2b 5b ＝255.故选D.变式2：已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左焦点为F ，右顶点为A ，点B 在椭圆上，且BF ⊥x 轴，直线AB 交y 轴于点P ，若AP ―→＝2PB ―→，则椭圆的离心率是( )A.32B.22C.13D.12【解析】如图，∵AP ―→＝2PB ―→，∴OA ＝2OF ，∴a ＝2c ，∴e ＝12.故选D变式3：已知椭圆E ：y 2a 2＋x 2b 2＝1(a ＞b ＞0)与直线y ＝b 相交于A ，B 两点，O 是坐标原点，如果△AOB 是等边三角形，那么椭圆E 的离心率等于( )A.36B.34C.33D.32【解析】不妨设点B 在第一象限，则B ⎝⎛⎭⎫bc a ，b ，由题意知OB 的倾斜角是60°，所以b bc a＝a c＝3，则椭圆的离心率e ＝c a ＝33.故选C.变式4：F 是椭圆的左焦点，A ，B 分别是其在x 轴正半轴和y 轴正半轴的顶点，P 是椭圆上一点，且PF ⊥x 轴，OP ∥AB ，那么该椭圆的离心率为( )A.22B.24C.12D.32【解析】如图所示，设椭圆的方程为x 2a 2＋y 2b 2＝1(a ＞b ＞0)，P (－c ，m )．∵OP ∥AB ，∴△PFO ∽△BOA ， ∴c a ＝mb ，①又∵P (－c ，m )在椭圆上，∴c 2a 2＋m 2b 2＝1，②将①代入②得2c 2a 2＝1，即e 2＝12，∴e ＝22，故选A.变式5：已知椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为1F ，2F ，上顶点为B ，2BF 的延长线交C 于Q ，1BQ FQ =，则C 的离心率e =（） A ．12B ．23C ．22D ．33【解析】由椭圆()2222:10x y C a b a b+=>>的左、右焦点分别为1F ，2F ，上顶点为B ，可得：()()()120,,,0,,0B b F c F c -.如图示：1212,BF BF a OF OF c ====. 设2QF m =，则1FQ BQ a m ==+. 由椭圆的定义可得：122FQ F Q a +=，即2a m m a ++=，解得：12m a =. 所以在1BQF 中，1133,,22BF a BQ a FQ a ===，所以1111122cos 332BF aQBF BQ a ∠===. 在12BF F △中，1212,2BF BF a F F c ===，所以()222111cos cos 22cos 121b F BF OBF OBF a ⎛⎫∠=∠=∠-=- ⎪⎝⎭.所以21213b a ⎛⎫-= ⎪⎝⎭，即223b a ⎛⎫= ⎪⎝⎭，所以22222113c b e a a ==-=，所以e =3e =3. 故选：D变式6：椭圆2222:1(0)x y C a b a b+=>>的左顶点为A ，点P ，Q 均在C 上，且关于y 轴对称．若直线,AP AQ 的斜率之积为14，则C 的离心率为（）A 3B ．22C ．12D ．13【解析】设而不求设()11,P x y ，则()11,Q x y - 则由14AP AQk k ⋅=得：21112211114AP AQ y y y k k x a x a x a ⋅=⋅==+-+-+，由2211221x y a b +=，得()2221212b a x y a-=，所以()2221222114b a x a x a -=-+，即2214b a =，所以椭圆C的离心率2231c b e a a =- A.变式7：已知直线l ：)3y x c =+过椭圆22221(0)x y a b a b+=>>的左焦点F ，与椭圆在x 轴上方的交点为P ，Q 为线段PF 的中点，若OQ c =，则椭圆的离心率为（） A 31- B 31 C 2D ．12【解析】直线l ：过椭圆22221(0)x y a b a b+=>>的左焦点F ，设椭圆的右焦点为M ，所以60PFM ∠=︒，又O 是FM 的中点，Q 是PF 的中点，所以1||||2OQ PM =，又||OQ c =，所以||2PM c =，又||2FM c =，所以PFM △是等边三角形，所以||2PF c =，又P 在椭圆上，所以||||222PM PF a c c +==+，所以24a c =，所以离心率为12c e a ==，故选：D ．（二）求椭圆的离心率的取值范围【例4-2】已知椭圆的焦距不小于短轴长，则椭圆的离心率的取值范围为________．【解析】依题意可得2c ≥2b ，即c ≥b . 所以c 2≥b 2，从而c 2≥a 2－c 2，即2c 2≥a 2，e 2＝c 2a 2≥12，所以e ≥22. 又因为0<e <1，所以椭圆离心率的取值范围是⎣⎡⎭⎫22，1.变式1：椭圆x 2a 2＋y 2b 2＝1(a >b >0)的右顶点是A (a,0)，其上存在一点P ，使∠APO ＝90°，求椭圆离心率的取值范围．【解析】设P (x ，y )，由∵APO ＝90°知，点P 在以OA 为直径的圆上，圆的方程是⎝⎛⎭⎫x －a 22＋y 2＝⎝⎛⎭⎫a 22. ∵y 2＝ax －x 2.∵又P 点在椭圆上，故x 2a 2＋y 2b2＝1.∵把∵代入∵化简，得(a 2－b 2)x 2－a 3x ＋a 2b 2＝0，即 (x －a )[(a 2－b 2)x －ab 2]＝0，∵x ≠a ，x ≠0， ∵x ＝ab 2a 2－b 2，又0<x <a ，∵0<ab 2a 2－b 2<a ，即2b 2<a 2. 由b 2＝a 2－c 2，得a 2<2c 2，∵e >22. 又∵0<e <1，∵22<e <1. 变式2：已知椭圆()2222:10x y C a b a b+=>>，对于C 上的任意一点P ，圆222:O x y b +=上均存在点M ，N 使得60MPN ∠=︒，则C 的离心率的取值范围是（） A ．3⎛ ⎝⎦B ．3⎡⎢⎣C ．10,2⎛⎤⎥⎝⎦D ．1,12⎡⎫⎪⎢⎣⎭【解析】如上图，当P 位于右端点（做端点也相同），如果60MPN ︒∠≥，则对于C 上任意的点P ，在圆O 上总存在M ，N 点使得60MPN ︒∠= ，此时，130,sin 2b MPO MPO a ︒∠≥∠=≥ ，222332,,4c b a e e a ∴≥=≤≤ ；故选：A.变式3：已知椭圆C ：22221x y a b+=（0a b >>）的左､右顶点分别为1A ，2A ，且以线段12A A 为直径的圆与直线20bx ay ab -+=相交，则椭圆C 的离心率的取值范围为（）A ．6⎛ ⎝⎭B ．6⎫⎪⎪⎝⎭C ．2⎫⎪⎪⎝⎭D ．2⎛ ⎝⎭. 【解析】由题设，以线段12A A 为直径的圆为222x y a +=，与直线20bx ay ab -+=相交， 22a ab <+，可得222233()b ac a =-<，即223e >，又01e <<， 61e <<. 故选：B变式4：已知1F ，2F 是椭圆C ：()222210x ya b a b+=>>的左、右焦点，O 为坐标原点，点M是C 上点（不在坐标轴上），点N 是2OF 的中点，若MN 平分12F MF ∠，则椭圆C 的离心率的取值范围是（）A ．1,12⎛⎫⎪⎝⎭B ．10,2⎛⎫ ⎪⎝⎭C ．1,13⎛⎫ ⎪⎝⎭D ．10,3⎛⎫ ⎪⎝⎭【解析】因为O 是12F F 的中点，N 是2OF 的中点，所以123NF NF =，因为MN 平分12F MF ∠，所以12MF MF =123NF NF =，因为122MF MF a +=，所以132aMF =，22a MF =，由32a a c a c -<<+（或2a a c a c -<<+），得椭圆C 的离心率12c e a =>，又1e <，所以椭圆C 的离心率的取值范围是1,12⎛⎫⎪⎝⎭．故选：A ．（三）由椭圆的离心率求参数（范围）【例4-3】已知椭圆x 2k ＋8＋y 29＝1的离心率e ＝12.求k 的值．【解析】分两种情况进行讨论．(1)当椭圆的焦点在x 轴上时，由a 2＝k ＋8，b 2＝9，得 c 2＝k －1.∵e ＝12，∴k －1k ＋8＝14，解得k ＝4.(2)当椭圆的焦点在y 轴上时，由a 2＝9，b 2＝k ＋8，得c 2＝1－k . ∵e ＝12，∴1－k 9＝14.解得k ＝－54.综上可得，k ＝4或k ＝－54.变式1：已知椭圆()222210x y a b a b+=>>的离心率为13，则a b =（）A ．98B 32C ．43D 32【解析】因为22213c a b e a a -=，则2289a b =，所以32a b = 故选：D变式2：设e 是椭圆x 24＋y 2k ＝1的离心率，且e ∈⎝⎛⎭⎫12，1，则实数k 的取值范围是( ) A ．(0,3)B.⎝⎛⎭⎫3，163 C ．(0,3)∪⎝⎛⎭⎫163，＋∞D ．(0,2)【解析】当0＜k ＜4时，e ＝ca ＝4－k 2∈⎝⎛⎭⎫12，1，即12＜4－k 2＜1⇒1＜4－k ＜4，即0＜k ＜3；当k ＞4时，e ＝c a ＝k －4k∈⎝⎛⎭⎫12，1，即12＜k －4k ＜1⇒14＜k －4k ＜1⇒14＜1－4k ＜1⇒0＜4k ＜34⇒k ＞163.综上，实数k 的取值范围为(0,3)∪⎝⎛⎭⎫163，＋∞. 故选C考点五直线与椭圆的位置关系解题方略：判断直线与椭圆的位置关系，通过解直线方程与椭圆方程组成的方程组，消去方程组中的一个变量，得到关于另一个变量的一元二次方程，则Δ>0⇔直线与椭圆相交；Δ＝0⇔直线与椭圆相切；Δ<0⇔直线与椭圆相离．【例5-1】直线21y x =-与椭圆22194x y +=的位置关系是（）A ．相交B ．相切C ．相离D ．不确定【解析】220111944+=<，()0,1∴-在椭圆内， 21y x =-恒过点()0,1-，∴直线21y x =-与椭圆22194x y +=相交.故选：A.变式1：若直线y ＝kx ＋1与焦点在x 轴上的椭圆x 25＋y 2m ＝1总有公共点，求m 的取值范围．【解析】∵直线y ＝kx ＋1过定点A (0,1)．由题意知，点A 在椭圆x 25＋y 2m ＝1内或椭圆上，∴025＋12m ≤1，∴m ≥1. 又椭圆焦点在x 轴上∴m <5，故m 的取值范围为[1,5).变式2：若直线2y kx =+与焦点在x 轴的椭圆()2221016x yb b+=>恒有两个公共点，则实数b的范围_____．【解析】直线2y kx =+恒过定点()0,2，要保证直线与椭圆有两个公共点，定点需在椭圆内，∴2041,216b b+<∴>，又∵椭圆的焦点在x 轴上，∴()2164,2,4b b b <⇒<∴∈．故答案为：(2，4)﹒变式3：已知过圆锥曲线221x y m n +=上一点(),o o P x y 的切线方程为001x x y y m n+=.过椭圆221124x y +=上的点()3,1A -作椭圆的切线l ，则过A 点且与直线l 垂直的直线方程为（） A ．30x y --= B ．-20x y += C ．2330x y +-=D ．3100x y --=【解析】过椭圆221124x y +=上的点()3, 1A -的切线l 的方程为()31124y x -+=，即40x y --=，切线l 的斜率为1.与直线l 垂直的直线的斜率为-1，过A 点且与直线l 垂直的直线方程为()13y x +=--，即20x y +-=.故选：B考点六弦长及中点弦问题解题方略：解决椭圆中点弦问题的两种方法(1)根与系数关系法：联立直线方程和椭圆方程构成方程组，消去一个未知数，利用一元二次方程根与系数的关系以及中点坐标公式解决；(2)点差法：利用交点在曲线上，坐标满足方程，将交点坐标分别代入椭圆方程，然后作差，构造出中点坐标和斜率的关系，具体如下：已知A (x 1，y 1)，B (x 2，y 2)是椭圆x 2a 2＋y 2b 2＝1(a >b >0)上的两个不同的点，M (x 0，y 0)是线段AB 的中点，则⎩⎨⎧x 21a 2＋y 21b2＝1， ①x 22a 2＋y22b 2＝1， ②由①－②，得1a 2(x 21－x 22)＋1b 2(y 21－y 22)＝0，变形得y 1－y 2x 1－x 2＝－b 2a 2·x 1＋x 2y 1＋y 2＝－b 2a 2·x 0y 0，即k AB＝－b 2x 0a 2y 0.（一）弦长问题【例6-1】已知斜率为1的直线l 过椭圆22143x y +=的右焦点，交椭圆于A ，B 两点，则弦AB 的长为（） A ．207B ．227C ．247D ．267【解析】由椭圆知，224,3a b ==，所以21c =，所以右焦点坐标为()1,0，则直线l 的方程为1y x =-，设()()1122,,,A x y B x y ，联立221143y x x y =-⎧⎪⎨+=⎪⎩，消y 得，27880x x --=，则121288,77x x x x +=⋅=-，所以()222121288241424777AB k x x x x ⎛⎫=++-⋅=+⨯ ⎪⎝⎭. 即弦AB 长为247. 故选：C.变式1：已知椭圆()2222:10x y C a b a b+=>>的长轴长是短轴长的2倍，左焦点、右顶点和下顶点分别为,,F A B ，坐标原点O 到直线AB 45FAB 的面积为（） A ．3B ．4C ．423+D ．43-【解析】设(),0F c -，由题意可知()(),0,0,A a B b -，其中2a b =，所以AB 的方程为1x ya b+=-，即220x y b --= 所以原点O 到直线AB 2455b -=，所以2b =，即4a =，2223c a b -；所以直线AB 的方程为240x y --=，所以()23,0F -到直线AB 23442355--+=；又()()220025AB a b =-++所以FAB 的面积为42342351252+⨯+= 故选：C.变式2：已知直线l ：y ＝kx ＋1与椭圆x 22＋y 2＝1交于M ，N 两点，且|MN |＝423，求k 的值．【解析】设M (x 1，y 1)，N (x 2，y 2)，由⎩⎪⎨⎪⎧y ＝kx ＋1，x 22＋y 2＝1，消去y 并化简得(1＋2k 2)x 2＋4kx ＝0，所以x 1＋x 2＝－4k1＋2k 2，x 1x 2＝0. 由|MN |＝423，得(x 1－x 2)2＋(y 1－y 2)2＝329，所以(1＋k 2)(x 1－x 2)2＝329，所以(1＋k 2)[(x 1＋x 2)2－4x 1x 2]＝329，即(1＋k 2)⎝ ⎛⎭⎪⎫－4k 1＋2k 22＝329.化简得k 4＋k 2－2＝0，所以k 2＝1，所以k ＝±1.变式3：过椭圆x 24＋y 23＝1的焦点的最长弦和最短弦的长分别为________．【解析】过椭圆焦点的最长弦为长轴，其长度为2a ＝4；最短弦为垂直于长轴的弦，因为c ＝1，将x ＝1代入x 24＋y 23＝1，得124＋y 23＝1，解得y 2＝94，即y ＝±32，所以最短弦的长为2×32＝3. 答案：4,3（二）中点弦问题【例6-2】若直线l 与椭圆22162x y +=交于点A 、B ,线段AB 的中点为(1,1)P ,则直线l 的方程为( )A ．340x y +-=B ．320x y -+=C ．320x y --=D ．340x y +-=【解析】设()()1122,,,A x y B x y .则222211221,16262x y x y +=+= 两式相减得()()()()12121212062x x x x y y y y +-+-+=即1212121211062y y y y x x x x +-+⋅⋅=+- 因为,线段AB 的中点为(1,1)P ,所以12122,2y y x x +=+= 所以121213ABy y k x x 所以直线l 的方程为()1113y x -=--,即340x y +-= 故选: A变式1：若过椭圆22142x y +=内一点11,2P ⎛⎫ ⎪⎝⎭的弦被该点平分，则该弦所在的直线方程为（）A ．102x y --= B ．302x y +-=C ．3202x y --= D ．20x y -=【解析】设弦AB 被P 点平分，弦的两个端点,为1111(,),(,)A x y B x y ，则2211142x y +=，2222142x y += ，两式作差变形可得22221212042x x y y --+= ,即121212122()4()y y x x x x y y -+=--+ ，而12122,1x x y y +=+= ，故12121y y x x -=--，即弦AB 的斜率为-1，所以弦AB 的方程为1(1)2y x -=-- ，即302x y +-= ，故选：B.变式2：已知椭圆2222:1(0)x y C a b a b +=>>3l 与椭圆C 交于A ，B 两点且线段AB 的中点为()3,2M ，则直线l 的斜率为________. 【解析】由题意可得2231c b e a a ==-6a =，设()()1122,,,A x y B x y ，则2222112222221,1x y x y a b a b +=+=，两式相减可得()()()()12121212220x x x x y a b -+-+=，AB 的中点为(3,2)M ，12126,4x x y y +=+=∴，则直线斜率212122*********y y x x b k x x a y y -+==-⋅=-⨯=--+. 故答案为：1-.变式3：直线AB 过椭圆22142x y +=内一点()1,P n ，若点P 为弦AB 的中点，设1k 为直线AB 的斜率，2k 为直线OP 的斜率，则12k k ⋅的值为（） A ．12-B ．3C ．12D ．2【解析】设点()11,A x y 与()22,B x y ，则1212x x +=，122y y n +=，所以12112y y k x x -=-，121212122212y y y y nx x k x x ++===++，又点A 与B 在椭圆上，所以2211142x y +=，2222142x y +=，作差可得22221212042--+=x x y y ，即()2222121212y y x x -=--，所以()()()()22121212122212121212y y y y y y k k x x y y x x -+-⋅===----，故选：A.考点七求椭圆的参数或范围问题【例7-1】已知椭圆22143x y +=上存在关于直线2y x m =+对称的点，则实数m 的取值范围为（）A ．11,2⎡⎤-⎢⎥⎣⎦B ．11,43⎛⎫- ⎪⎝⎭C ．11,22⎛⎫- ⎪⎝⎭D ．11,34⎛⎫- ⎪⎝⎭【解析】设椭圆上关于直线2y x m =+的对称的两点分别为()()1122,,,C x y D x y ， CD 的中点为()00,G x y ，直线CD 的方程为12y x n =-+，联立直线CD 与椭圆的方程，得2214312x y y x n ⎧+=⎪⎪⎨⎪=-+⎪⎩，消元可得2230x nx n -+-=， ()222431230n n n ∴∆=--=->， 12x x n +=，24n ∴<，02n x =， 001324y x n n ∴=-+=，3,24n G n ⎛⎫∴ ⎪⎝⎭，又点G 在直线2y x m =+上，3242nn m ∴=⨯+，4n m ∴=-，()244m ∴-<，解得1122m -<<，所以实数m 的取值范围为11,22⎛⎫- ⎪⎝⎭.故选：C变式1：已知点P 是椭圆2214x y +=上的一点，1F ，2F 是椭圆的两个焦点，则当12F PF ∠为钝角时，点P 的横坐标可以为______．【解析】设00(,)P x y ，由题意可知120PF PF ⋅<，即((22212000003330⋅=⋅+=+-<PF PF x x y x y ．因为点P 在椭圆上，所以22014x y =-，所以22001304x x ⎛⎫+--< ⎪⎝⎭，解得02626x <<0x 可以取1（只要在262633⎛- ⎝⎭内即可）．故答案为：1（答案不唯一）．变式2：已知椭圆C ：()222210x y a b a b+=>>的左、右焦点分别为1F 、2F ，若C 上存在无数个点P ，满足：12π2F PF ∠>，则ba的取值范围为（） A ．3⎛ ⎝⎭B ．3⎫⎪⎪⎝⎭C ．2⎫⎪⎪⎝⎭D ．2⎛ ⎝⎭【解析】设椭圆的半焦距为c ，因为C 上存在无数个点P 满足：12π2F PF ∠>，所以以12F F 为直径的圆与椭圆有4个交点，所以c b >，所以222a b b ->，所以20b a < 故选：D变式3：椭圆22:143x y C +=的左、右顶点分别为1A ，2A ，点P 在C 上且直线2PA 的斜率的取值范围是[3-，1]-，那么直线1PA 斜率的取值范围是（） A ．1[4，3]4B ．1[2，3]4C ．1[2，1]D ．3[4，1]【解析】由题意得：由椭圆22:143x y C +=可知其左顶点1(2,0)A -，右顶点2(2,0)A ．设0(P x ，00)(2)y x ≠±，则得2020344y x =--．记直线1PA 的斜率为1k ，直线2PA 的斜率为2k ，则201220344y k k x ==-- 直线2PA 斜率的取值范围是[3-，1]-， ∴直线1PA 斜率的取值范围是1[4，3]4故选：A考点八求椭圆的最值问题解题方略：求与椭圆有关的最值、范围问题的方法(1)定义法：利用定义转化为几何问题处理．(2)数形结合法：利用数与形的结合，挖掘几何特征，进而求解．(3)函数法：探求函数模型，转化为函数的最值问题，借助函数的单调性、基本不等式等求解，注意椭圆的范围．【例8-1】椭圆22143x y +=上的点P 到直线l ：30x y ++=的距离的最小值为（） A 37-B 37+ C 3214- D 3214+ 【解析】由222cos 1433x x y y θθ=⎧⎪+=⇒⎨=⎪⎩，设(2cos 3)P θθ，设点P 到直线l ：30x y ++=的距离d ，所以有222cos 3sin 37sin()37sin()32211d θθθϕθϕ++++++===+其中23tan (0,))2πϕϕ=∈，所以当2()2k k Z πθϕπ+=-∈时，d 3732142--=，故选：C变式1：已知动点(,)P x y 在椭圆22198x y 上，若A 点坐标为()1,0，1AM =，且0PM AM ⋅=，则PM 的最小值为（） A ．3B 2C ．2D 3【解析】因为0PM AM ⋅=，所以PM AM ⊥，即PAM △为直角三角形，即21PM AP =-，要使得PM 最小，则2AP 最小，[]22222281||(1)21829,3,399x PA x y x x x x x =-+=-++-=-+∈-，则2AP 的最小值为21323949⨯-⨯+=，即PM 的最小值为413- 故选：D变式2：已知F 为椭圆:C 2214x y +=的右焦点，,P Q 为椭圆C 上两个动点，且满足FP FQ ⊥，则FP QP ⋅的最小值为（） A 3B ．2C ．73-D ．23【解析】由题意得，由FP FQ ⊥,得0FP FQ ⋅=，则222()EP QP FP FP FQ FP FP FQ FP FP ⋅=⋅-=-⋅==, 设(,)P x y (22x -≤≤)，由(3,0)F ，得(3,)FP x y =，则2222221(3)(3)(1)(34)44x FP x y x x =+=+-=-，又22x -≤≤，由二次函数的性质可知，22min 1()(324)7434FP =-=-所以EP QP ⋅的最小值为73- 故选：C.考点九椭圆的定点、定值问题【例9-1】已知椭圆2222:1(0)x y C a b +=>>经过点(21)A ，，离心率为2，过点(30)B ，的直线l 与椭圆C 交于不同的两点M ，N . (1)求椭圆C 的方程；(2)设直线AM 和直线AN 的斜率分别为AM k 和AN k ，求证：AM AN k k +为定值【解析】（1）由题意椭圆2222:1(0)x y C a b a b +=>>经过点(21)A ， 2，可得222224112a b a b c c a⎧+=⎪⎪⎪=+⎨⎪⎪=⎪⎩，解得6,3a b =，故椭圆C 的方程为22163x y +=（2）由题意可知直线l 的斜率一定存在，设直线l 的方程为(3)y k x =-，由22(3)163y k x x y =-⎧⎪⎨+=⎪⎩，可得2222(12)121860k x k x k +-+-=，由于直线l 与椭圆C 交于不同的两点M ，N ，则42221444(12)(186)24(1)0k k k k ∆=-+-=->，解得11k -<<，设1122(,),(,)M x y N x y ,则2212122212186,1212k k x x x x k k -+==++， 11(3)y k x =-22(3)y k x =-，故121221121211(31)(2)(31)(2)22(2)(2)AM AN y y kx k x kx k k x k x x x x -----+---+=+=---- 121212122(51)()1242()4kx x k x x k x x x x -++++=-++2222222(186)(51)12(124)(12)186244(12)k k k k k k k k k --+⋅+++=--++2244222k k -+==--，即AM AN k k +为定值.变式1：已知椭圆C ：()222210x y a b a b +=>>的左焦点为()11,0F -，上、下顶点分别为A ，B ，190AF B ∠=︒．(1)求椭圆C 的方程；(2)若椭圆上有三点P ，Q ，M 满足OM OP OQ =+，证明：四边形OPMQ 的面积为定值．【解析】（1）依题意1c =，又190AF B ∠=︒，所以1b c ==，所以222a b c +，所以椭圆方程为2212x y +=.（2）证明：设(),M x y ，()11,P x y ，()22,Q x y ，因为OM OP OQ =+，所以四边形OPMQ 为平行四边形，且1212x x x y y y =+⎧⎨=+⎩，所以()()22121212x x y y +++=，即2212112122221222x x y y x x y y ⎛⎫⎛⎫+++ ⎪⎭+ ⎝⎝+⎭=⎪，又221112x y +=，222212x y +=，所以121212x x y y +=-，若直线PQ 的斜率不存在，M 与左顶点或右顶点重合，则2P Q x x ==3P Q y y ==所以16222OPMQ P P S x y =⨯⨯=若直线PQ 的斜率存在，设直线PQ 的方程为y kx t =+，代入椭圆方程整理得()222124220k xktx t +++-=，所以()228210k t ∆=+->，122412kt x x k -+=+，21222212t x x k -=+，所以()()()2212121212=++=+++y y kx t kx t k x x kt x x t222222241212t kt k kt t k k --⎛⎫=⋅+⋅+ ⎪++⎝⎭所以()22222224212211212t kt k kt t k k --⎛⎫+⋅+⋅+=- ⎪++⎝⎭，整理得22412t k =+，又()22221281211k t PQ k x k +-=+-=+又原点O 到PQ 的距离21t d k =+所以2212122POQk t t SPQ d +-⋅==，将22412t k =+代入得22362POQt t S ⋅==所以62PO OP Q QM SS == 综上可得，四边形OPMQ 6 变式2：已知椭圆C ：()222210x y a b a b+=>>的右顶点是M （2，0），离心率为12．(1)求椭圆C 的标准方程．(2)过点T （4，0）作直线l 与椭圆C 交于不同的两点A ，B ，点B 关于x 轴的对称点为D ，问直线AD 是否过定点？若是，求出该定点的坐标；若不是，请说明理由．【解析】（1）由右顶点是M （2，0），得a ＝2，又离心率12c e a==，所以1c =，所以2223b a c =-=，所以椭圆C 的标准方程为22143x y +=．（2）设()11,A x y ，()22,B x y ，显然直线l 的斜率存在．直线l 的方程为()4y k x =-，联立方程组()224,3412y k x x y ⎧=-⎨+=⎩ 消去y 得()2222433264120k x k x k +-+-=，由0∆>，得1122k -<<，所以21223243k x x k +=+，2122641243k x x k -=+．因为点()22,D x y -，所以直线AD 的方程为()()1211124y y y x x k x x x +=-+--．又()12128y y k x x +=+-，所以直线AD 的方程可化为()()()()()1121212121218424kx x x k x x x ky x x x x +---=++--，即()()()()()()()2222121212424241434343k k ky x x x x k x x k x x k =-=--+-+-+，所以直线AD 恒过点（1，0）．（方法二）设()11,A x y ，()22,B x y ，直线l 的方程为4x my =+，联立方程组224,3412x my x y =+⎧⎨+=⎩消去x 得()223424360m y my +++=，由0∆>，得2m >或2m <-，所以1222434m y y m +=-+，1223634y y m =+．因为点()22,D x y -，则直线AD 的方程为()121112y y y x x y x x +=-+-．又()12121244x x my my m y y -=+--=-，所以直线AD 的方程可化为。

2020_2021学年高中数学同步课时作业12椭圆的简单几何性质含解析新人教A版选修1_1

（12）椭圆的简单几何性质1.已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ，过点F 的直线交E 于,A B 两点.若AB的中点坐标为(1,1)-，则E 的方程为（）A.2214536x y += B.2213627x y += C.2212718x y += D.221189x y += 2.若坐标原点O 和点F 分别为椭圆22143x y +=的中心和左焦点,点P 为椭圆上的任意一点,则OP FP ⋅的最大值为( )A.2B.3C.6D.83.已知椭圆22121,259+=x y F F 分别为其左、右焦点，椭圆上一点M 到点1F 的距离是2，N 是线段1MF 的中点，则ON 的长为( )A.1B.2C.3D.44.已知12,F F 是椭圆221169x y +=的两焦点，过点2F 的直线交椭圆与点,A B .若5AB =，则11AF BF +=( ) A.9B.10C.11D.125.已知点12(,0),(,0)F c F c -为椭圆22221(0)x y a b a b+=>>的两个焦点,点P (不在x 轴上)在椭圆上,且满足212PF PF c ⋅=,则此椭圆离心率的取值范围是( )A.⎫⎪⎪⎣⎭B.11,32⎡⎤⎢⎥⎣⎦C.⎣⎭D.⎛ ⎝⎦6.已知椭圆22221x y a b+=(0a b c >>>,其中c 为椭圆的半焦距)的左、右焦点分别为12,F F ,若以2F 为圆心,b c -为半径作圆2F ,过椭圆上一点P 作圆2F 的切线,切点为T ,若PT 的最小值不小于)a c -,则椭圆的离心率e 的取值范围是( )A.3,15⎡⎫⎪⎢⎣⎭B.35⎡⎢⎣⎭C.3(0,)5D.7.椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,焦距为2c .若直线)y x c =+与椭圆C 的一个交点M 满足12212MF F MF F ∠=∠,则椭圆C 的离心率等于( )1 D.4-8.过椭圆2222:1(0)x y C a b a b+=>>的左顶点A 的斜率为k 的直线交椭圆C 于另一个点B ,且点B在x 轴上的射影恰好为右焦点F ,若1132k <<,则椭圆离心率的取值范围是( )A.14(,)49B.2(,1)3C.12(,)23D.1(0,)29.已知椭圆22142x y +=的两个焦点分别是12,F F ,点P 在椭圆上,若122PF PF -=,则12PF F △的面积是( )1110.若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1,则椭圆长轴的最小值为( )A.1C.2D.11.若点O 和点F 分别为椭圆22143x y +=的中心和左焦点，点P 为椭圆上的任意一点，则OP FP ⋅的最大值为___________.12.已知动点(,)P x y 在椭圆2212516x y +=上，若点A 的坐标为(3,0)，1AM =,且0PM AM ⋅=,则PM 的最小值是____________.13.若分别过椭圆22221(0)x y a b a b+=>>的左、右焦点12,F F 所作的两条互相垂直的直线12,l l 的交点在椭圆上,则此椭圆的离心率的取值范围是_________.14.设椭圆2222:1(0)x y E a b a b+=>>的一个焦点(2,0)F ,点(2,1)A -为椭圆E 内一点,若椭圆E 上存在一点P ,使得8PA PF +=,则椭圆E 的离心率的取值范围是__________.15.已知椭圆2222:1(0)x y C a b a b +=>>过点(0,4),离心率为35.（1）求椭圆C 的方程; （2）求过点(3,0)且斜率为45的直线被C 所截线段的中点的坐标.答案以及解析1.答案：D解析：因为直线AB 过点(3,0)F 和点(1,1)-，所以直线AB 的方程为1(3)2y x =-，代入椭圆方程22221x y a b +=消去y ，得2222222390424a b x a x a a b ⎛⎫+-+-= ⎪⎝⎭，所以线段AB 的中点的横坐标为22232124a a b =⎛⎫+ ⎪⎝⎭，即222a b =.又222,3a b c c =+=，所以3,b c a ===.所以E 的方程为221189x y +=. 2.答案：C解析：由题设,知(1,0)F -.设点00(,)P x y ,则2200143x y +=,得22003(1)4x y =-.因为0000(,),(1,)OP x y FP x y ==+,所以22220000000001(1)(1)3(1)3(2)2444x x OP FP x x y x x x x ⋅=++=++-=++=++.又022x -≤≤,所以OP FP ⋅的最大值为21(22)264++=.故选C.3.答案：D解析：由椭圆定义得21210+==MF MF a .因为12=MF ,所以28=MF .因为N 是线段1MF 的中点，所以242==MF ON ,故选D4.答案：C解析：根据椭圆定义，1228AF AF a +==，1228BF BF a +==，所以1116AF BF AB ++=，所以111611AF BF AB +=-=,故选C 5.答案：C解析：由椭圆的定义,得122PF PF a +=,平方得222121224PF PF PF PF a ++=①. 又212PF PF c ⋅=,∴21212cos PF PF F PF c ⋅∠=②,由余弦定理,得2222121212122cos 4PF PF PF PF F PF F F c +-⋅∠==③,由①②③,得22212122223,cos 23c PF PF a c F PF a c ⋅=-∠=-,∵2220123c a c <<-,a <,∴e .又01e <<,∴0e <<又122212()2PF PF PF PF a +⋅≤=,当且仅当12PF PF =时等号成立,∴2222223,3a c a a c -≤≤,∴e ≥.又01e <<,1e ≤<.综上,e ≤<,故选C. 6.答案：B解析：依题意可知圆2F 的圆心为(,0)c ,半径为b c -,设(,)P m n 在椭圆上,依题意有22222PT PF TF =-,当PT 取得最小值时,2PF 取得最小值,此时点P 位于椭圆的右顶点,即(,0)P a ,即2223()()()4a c b c a c ---≥-,化简得2a c b +≤,两边平方得22()2a cb +≤,即222224a ac c a c ++-≤,得25230e e +-≥,所以35e ≥.由于b c >,则22b c >,即22222,2a c c a c ->>,得c a <即e <,故椭圆离心率的取值范围是35⎡⎢⎣⎭. 7.答案：A解析：∵12(,0),(,0)F c F c -,∴直线)y x c =+过点1F .∴1260MF F ∠=︒,∴21121302MF F MF F ∠=∠=︒,∴1290F MF ∠=︒,∴12,MF c MF ==.由椭圆定义,知122MF MF c a +=+=,∴离心率1c e a ===.8.答案：C解析：由题意,知点B 的横坐标是c ,故B 的坐标为2(,)b c a ±,∵11(,)32k ∈,∴2(,)b B c a .又(,0)A a -∴直线AB 的斜率2222222111b b a c e a k e c a ac a ac a e --=====-++++.由1132k <<,解得1223e <<. 9.答案：D解析：由题意得124PF PF +=,焦距2c =∵122PF PF -=,∴123,1PF PF ==.∵22213+=,∴12PF F △是直角三角形,且212PF F F ⊥,∴12PF F △的面积为21211122PF F F ⨯=⨯⨯故选D. 10.答案：D解析：设椭圆22221(0)x y a b a b +=>>,则当三角形面积最大时,三角形在椭圆上的顶点为椭圆短轴端点,∴222121222b c a S c b bc +=⨯⨯==≤=,∴22a ≥,∴a ≥,∴长轴长2a ≥故选D.11.答案：6解析：由22143x y +=可得(1,0)F -.设(,),22P x y x -≤≤，则22222211313(2)2444x OP FP x x y x x x x x ⎛⎫⋅=++=++-=++=++ ⎪⎝⎭，当且仅当2x =时，OP FP ⋅取得最大值6.12.解析：易知点(3,0)A 是椭圆的右焦点.∵0PM AM ⋅=,∴AM PM ⊥，∴22221PM AP AM AP =-=-.∵椭圆的右顶点到焦点A 的距离最小，故min2AP=，∴minPM=13.答案：⎫⎪⎪⎣⎭解析：设两直线的交点为M ,令12,MF m MF n ==.由椭圆的定义,可得2m n a +=.因为12MF MF ⊥,所以2224m n c +=.∵22222()22()m n m n mn m n +=++≤+,当且仅当m n a ==时等号成立,即2242(4)a c ≤,∴a ≤,∴c a ≥即e ≥.又1e <,1e ≤<.14.答案：44,97⎡⎤⎢⎥⎣⎦解析：记椭圆的左焦点为1(2,0)F -,则11AF =.∵11PF PA AF ≤+,∴112189a PF PF PA AF PF =+≤++=+=,即92a ≤.∵11PF PA AF ≥-,∴112817a PF PF PA AF PF =+≥-+=-=,即72a ≥.∵2c =,∴229722c a ≤≤,即4497e ≤≤,椭圆E 的离心率的取值范围是44,97⎡⎤⎢⎥⎣⎦.15.答案：（1）将(0,4)代入C 的方程得2161b=, ∴4b =.又35c e a ==得222925a b a -=，即2169125a -=, ∴5a =.∴椭圆C 的方程为2212516x y += （2）过点(3,0)且斜率为45的直线方程为4(3)5y x =-, 设直线与椭圆C 的交点11(,)A x y ,22(,)B x y ,将直线AB 方程4(3)5y x =-代入C 的方程,得22(3)12525x x -+=, 即2380x x --=,解得123x x +=,∴121212326,(6)22255x x y y x x ++==+-=-，即所截线段中点的坐标为36(,)25-.解析：。

人教A版高中同步学案数学选择性必修第一册精品习题课件第三章椭圆椭圆的简单几何性质(1)

即( + )( − ) < < ( + ) ,
又 − < 成立,则有 < + ,∴ − < < .
2
5.已知椭圆: 2

2
+ 2

= 1( > > 0)的两焦点与短轴的一个顶点恰好是一个正三角形
的三个顶点,且椭圆上的点到椭圆的焦点的最短距离为 3,则椭圆的方程为
2
3
2
2
2
A.( ,1)B.( ,1)C.( ,1)D.(0, )
[解析]设(, )( < < ),又(, ),(, ),且 ⋅ = ,
则 + − = ,与椭圆方程联立得 − + = ,
即(
则 <
−

= 1( > > 0)满足 = 2,则该椭圆的离心率 =() B
[解析]因为 = ,所以 =
故选B.

=

−

=

− =

.

2
4.设1 ,2 为椭圆 2

+
2
2
= 1( > > 0)的左、右焦点,椭圆上存在点,∠1 2 = ,
∠2 1 = ,使得离心率 =
∴ = + ≥ = ，
当且仅当 = = 时,等号成立.
∴ ≥ ，∴ ≥ ，即椭圆长轴长的最小值为4.
2
9.已知椭圆1 与椭圆2 :
30
2
+
5
= 1具有共同的焦点1 ,2 ,点在椭圆1 上,1 ⊥ 2 ,__

高二数学人教A版选修1-1学案第二章2-12-1-2第1课时椭圆的简单几何性质Word版含答案

公路桥梁锥坡的计算方法和计算公式关以基础工程量的计公路桥梁锥坡的计算方法和计算公式公路桥梁锥坡的计算方法和计算公式锥坡浆砌片石计算公式锥坡计算采用正交公式，外锥-内锥V=π/12*m*n*(H3-H03)t片石厚度H：锥坡高度H0：内锥高度=H-(α0+β0)/t/2 m、n为两个方向的坡度α0=(1+m2)0.5/mβ0=(1+n2)0.5/n关以基础工程量的计算与难点(造价专业可以用到)大开挖土方1、开挖土方计算规则(1)、清单规则：挖基础土方按设计图示尺寸以基础垫层底面积乘挖土深度计算。

(2)、定额规则：人工或机械挖土方的体积应按槽底面积乘以挖土深度计算。

槽底面积应以槽底的长乘以槽底的宽，槽底长和宽是指混凝土垫层外边线加工作面，如有排水沟者应算至排水沟外边线。

排水沟的体积应纳入总土方量内。

当需要放坡时，应将放坡的土方量合并于总土方量中。

2、开挖土方计算方法(1)、清单规则：①、计算挖土方底面积：方法一、利用底层的建筑面积+外墙外皮到垫层外皮的面积。

外墙外边线到垫层外边线的面积计算(按外墙外边线外放图形分块计算或者按"外放图形的中心线×外放长度"计算。

)方法二、分块计算垫层外边线的面积(同分块计算建筑面积)。

②、计算挖土方的体积：土方体积=挖土方的底面积*挖土深度。

(2)、定额规则：①、利用棱台体积公式计算挖土方的上下底面积。

V=1/6×H×(S上+4×S中+S下)计算土方体积(其中，S上为上底面积，S 中为中截面面积，S下为下底面面积)。

如下图S下=底层的建筑面积+外墙外皮到挖土底边线的面积(包括工作面、排水沟、放坡等)。

用同样的方法计算S中和S下3、挖土方计算的难点⑴、计算挖土方上中下底面积时候需要计算"各自边线到外墙外边线图"部分的中心线，中心线计算起来比较麻烦(同平整场地)。

⑵、中截面面积不好计算。

⑶、重叠地方不好处理(同平整场地)。

[精品]新人教A版选修1-1高中数学强化训练2.1.2椭圆的简单几何性质和答案

2.1.2 椭圆的简单几何性质课时目标 1.掌握椭圆的范围、对称性、顶点、离心率等几何性质.2.明确标准方程中a，b以及c，e的几何意义，a、b、c、e之间的相互关系.3.能利用椭圆的几何性质解决椭圆的简单问题．1．椭圆的简单几何性质焦点的焦点在x轴上焦点在y轴上位置图形标准方程范围顶点轴长短轴长＝______，长轴长＝______焦点焦距对称性对称轴是________，对称中心是______离心率2.直线与椭圆直线y ＝kx ＋b 与椭圆x 2a 2＋y 2b 2＝1 (a >b >0)的位置关系：直线与椭圆相切⇔⎩⎪⎨⎪⎧ y ＝kx ＋b x 2a 2＋y2b2＝1有______组实数解，即Δ______0.直线与椭圆相交⇔⎩⎪⎨⎪⎧ y ＝kx ＋b x 2a 2＋y2b2＝1有______组实数解，即Δ______0，直线与椭圆相离⇔⎩⎪⎨⎪⎧y ＝kx ＋b x 2a 2＋y2b2＝1________实数解，即Δ______0.一、选择题1．椭圆25x 2＋9y 2＝225的长轴长、短轴长、离心率依次是( ) A ．5,3，45 B ．10,6，45C ．5,3，35D ．10,6，352．焦点在x 轴上，长、短半轴长之和为10，焦距为45，则椭圆的方程为( )A ．x 236＋y 216＝1B ．x 216＋y 236＝1 C ．x 26＋y 24＝1 D ．y 26＋x 24＝13．若焦点在x 轴上的椭圆x 22＋y 2m ＝1的离心率为12，则m 等于( )A ．3B ．32C ．83D ．234．如图所示，A 、B 、C 分别为椭圆x 2a 2＋y 2b2＝1 (a >b >0)的顶点与焦点，若∠ABC ＝90°，则该椭圆的离心率为( )A.－1＋52 B ．1－22C.2－1D.225．若直线mx ＋ny ＝4与圆O ：x 2＋y 2＝4没有交点，则过点P (m ，n )的直线与椭圆x 29＋y 24＝1的交点个数为( )A ．至多一个B ．2C ．1D ．0 6．已知F 1、F 2是椭圆的两个焦点。

椭圆的简单几何性质第二课时同步练习2022-2023学年高二上学期数学人教A版(2019)

3.1.2椭椭椭椭椭椭椭椭椭椭2椭一、单选题1. 已知点(4,2)M 是直线l 被椭圆221369x y +=所截得的线段AB 的中点，则直线l 的斜率为( )A. 2-B.12 C. 12-D. 22. 过椭圆22221(0)x y a b a b+=>>中心的直线交椭圆于,A B 两点，右焦点为2(,0)F c ，则2ABF ∆的最大面积是( )A. abB. acC. bcD. 2b3. 已知椭圆22221(0)x y a b a b+=>>的左焦点为F ，右顶点为A ，点B 在椭圆上，且BF x⊥轴，直线AB 交y 轴于点P ，若2AP PB =，则椭圆的离心率是( )A.B.C.13D.124. 过椭圆22143x y +=的右焦点F 作两条相互垂直的直线分别交椭圆于A ，B ，C ，D 四点，则11||||AB CD +的值为( ) A.18B.16C. 1D.712二、多选题5. 已知椭圆的左、右焦点为12,F F ，O为坐标原点，直线y x =-过2F 交C 于,A B 两点，若1AF B 的周长为8，则( )A. 椭圆焦距为3；B. 椭圆方程为2214x y +=；C. 弦长；D. 46=.5OABS6. 已知直线l ：23y x =+被椭圆C ：22221(0)x y a b a b+=>>截得的弦长为7，则下列直线中被椭圆C 截得的弦长一定为7的有( )A. 23y x =-B. 21y x =+C. 23y x =--D. 23y x =-+2222:1(0)x y C a b a b+=>>7. 画法几何的创始人-法国数学家加斯帕尔⋅蒙日发现：与椭圆相切的两条垂直切线的交点的轨迹是以椭圆中心为圆心的圆，我们通常把这个圆称为该椭圆的蒙日圆．已知椭圆2222:1(0)x y C a b a b+=>>的离心率为2，1F ，2F 分别为椭圆的左、右焦点，A ，B 为椭圆上两个动点．直线l 的方程为220.bx ay a b +--=下列说法正确的是( )A. C 的蒙日圆的方程为2223x y b +=B. 对直线l 上任意点P ，0PA PB ⋅>C. 记点A 到直线l 的距离为d ，则2||d AF -的最小值为3D. 若矩形MNGH 的四条边均与C 相切，则矩形MNGH 面积的最大值为26b三、填空题8. 已知点(2,0)A -，(0,1)B 在椭圆C ：22221(0)x y a b a b+=>>上，则椭圆C 的方程为__________，若直线12y x =交椭圆C 于M ，N 两点，则||MN =__________. 9. 已知点(0,1)P ，椭圆22(1)4x y m m +=>上两点A ，B 满足AP 2PB =，则当m =___________时，点B 横坐标的绝对值最大．10. 过点(1,1)P 的直线l 与椭圆22143x y +=交于点A 和B ，且.AP PB λ=点Q 满足AQ QB λ=-，若O 为坐标原点，则||OQ 的最小值为__________.11. 已知椭圆22+=12x y ，若此椭圆上存在不同的两点A ，B 关于直线=2+y x m 对称，则实数m 的取值范围是__________. 四、解答题12. 已知双曲线C 和椭圆22141x y += ()Ⅰ求双曲线C 的方程．()Ⅱ经过点(2,1)M 作直线l 交双曲线C 于A ，B 两点，且M 为AB 的中点，求直线l 的方程并求弦长．13.设椭圆C ：2212x y +=的右焦点为F ，过F 的直线l 与C 交于A ，B 两点，点M 的坐标为(2,0).(1)当l 与x 轴垂直时，求直线AM 的方程； (2)设O 为坐标原点，证明：.OMA OMB ∠=∠14. 已知椭圆C ：22221(0)x y a b a b+=>>的短轴长为2(1)求椭圆C 的方程；(2)设过定点(0,2)T 的直线l 与(1)中的椭圆C 交于不同的两点A 、B ，且AOB ∠为锐角，求直线l 的斜率k 的取值范围．15. 已知椭圆2222:1(0)x y C a b a b+=>>，1(,0)A a -，2(,0)A a ，(0,)B b ，12A BA 的面积为2.()Ⅰ求椭圆C 的方程;()Ⅱ设M 是椭圆C 上一点，且不与顶点重合，若直线1A B 与直线2A M 交于点P ，直线1A M与直线2A B 交于点.Q 求证：BPQ 为等腰三角形.16. 在平面直角坐标系xOy 中，已知椭圆2222:1(0)x y a b a bΓ+=>>的长轴长为4.过左顶点A 且倾斜角为4π的直线1l 与椭圆的另一个交点为B ，与y 轴交于点C ，且2.AB BC = (1)求椭圆Γ的标准方程；(2)过点(1,0)H 且不与x 轴重合的直线2l 交椭圆Γ于点,M N ，连接NO 并延长交AM 于点.P 若AP AM λ=，求实数λ的取值范围.答案和解析1.【答案】C解：设直线l 与椭圆相交于两点11(,)A x y ，22(,).B x y代入椭圆方程可得22111369x y +=，22221369x y +=，两式相减得12121212()()()()0369x x x x y y y y +--++=，12248x x +=⨯=，12224y y +=⨯=，2121l y y k x x -=-，480369l k ∴+=，解得1.2l k =- 故选.C2.【答案】C解：设，则，2ABF ∆的面积是，当最大时，2ABF ∆的面积S 取最大值，所以直线AB 与x 轴垂直时，2ABF ∆的面积S 取最大值，则2ABF ∆的面积的最大值为12.2b c bc ⨯⨯= 故选.C3.【答案】B解：由题意，可设2(,)b B c a-，设(0,)P t ，(,0)A a ，，2(,)b PB c t a=--， 2AP PB =，2(,)2(,)b a t c t a∴-=--，2a c ∴=，c e a ∴==，故选.B4.【答案】D解：由椭圆22143x y +=，得椭圆的右焦点为(1,0)F ，当直线AB 的斜率不存在时，AB ：1x =，则CD ：0.y =此时||3AB =，||4CD =，则11117||||3412AB CD +=+=；同理易得当直线AB 的斜率为0时，11117||||4312AB CD +=+=；当直线AB 的斜率存在且不为0时，设AB ：(1)(0)y k x k =-≠，则 CD ：1(1).y x k=-- 又设点11(,)A x y ，22(,).B x y 联立方程组22(1)3412y k x x y =-⎧⎨+=⎩，消去y 并化简得2222(43)84120k x k x k +-+-=，221212228412,3434k k x x x x k k -∴+==++，||AB ∴==2212(1)34k k +=+，由题知，直线CD 的斜率为1k-，同理可得2212(1)||.43k CD k+=+ 22117(1)7||||12(1)12k AB CD k +∴+==+为定值．故选.D5.【答案】BC解：直线3y x =-过2F ，得，即3c =，椭圆焦距为23，故A 错误；1AF B 的周长为8，根据椭圆定义得1AF B 的周长为4a ，所以48a =，得2a =，所以221b a c =-=，所以椭圆方程为2214x y +=，故B 正确；联立得258380x x -+=，1212838,55x x x x +==，所以，故C 正确；O 到直线3y x =-的距离3622d ==，所以18626==.2525OABS⨯⨯故D 错误，故选.BC6.【答案】ACD解：由于直线l ：23y x =+被椭圆2222:1(0)x y C a b a b+=>>截得的弦长为7，根据对称性可得：23y x =-，23y x =--，2 3.y x =-+满足条件．直线21y x =+被椭圆C 截得的弦长不为7.综上可得：下列直线中被椭圆C 截得的弦长一定为7的有.ACD 故选.ACD7.【答案】AD解：.A 当1l 与2l 一个斜率为0，另一个斜率不存在时，易知交点(,)P a b ±±，当1l 与2l 的斜率均不为0时，可设000()(P x y x a ≠±且0)y b ≠±，因为过P 点的切线方程为100:()(0)l y y k x x k -=-≠，所以联立2222001()x y a b y y k x x ⎧+=⎪⎨⎪-=-⎩得2222222220000()2()()0a k b x ka kx y x a kx y a b +--+--=，因为l 与椭圆相切，所以0=，整理得222222200000()20(0)x a k x y k y b x a --+-=-≠①，而PA k 与PB k 即为①式的两根，222200222200,,1,1PA PBPA PBy b y b k k PA PB k k x a x a --∴⋅=⊥∴⋅=-∴=---又，222222220000y b x a x y a b ∴-=-++=+即，所以蒙日圆的方程为2222x y a b +=+，22222122b e a b a =-=∴=，所以蒙日圆的方程为2223x y b +=，故A 正确;B .直线22:0l bx ay a b +--=过定点，而刚好在蒙日圆2222x y a b +=+上，过 M 做椭圆的两条切线，切点为 A ， B ，由蒙日圆的定义知PA PB PA PB 0⊥∴⋅=，故 B 错误； C .点A 在椭圆上，，的最小值为到1F 到l 的距离，而1F 到l 的距离为，2222bc a b 43c b,3a b b++∴=∴=+，的最小值为4323ba -，故 C 错误. D .因为矩形MNGH 的四条边均与C 相切，所以矩形MNGH 为C 的素日圆的内接矩形，设长为m ，宽为n ，蒙日圆半径为R ，3Rb =，则，，当且仅当m n =时等号成立，故D 正确.故选.AD8.【答案】2214x y +=2||d AF -解：由题意可知：椭圆C ：22221(0)x y a b a b+=>>上，由点(2,0)A -，(0,1)B ，焦点在x 轴上，则2a =，1b =，∴椭圆的标准方程：2214x y +=； ()Ⅱ设11(,)M x y ，22(,)N x y ，则221412x y y x ⎧+=⎪⎪⎨⎪=⎪⎩，消去y ，整理得224x =，则1x =2x =12y =，22y =-，则||MN == 故答案为：2214x y +=9.【答案】5解：设11(,)A x y ，22(,)B x y ，由(0,1)P ，2AP PB =，可得122x x -=，1212(1)y y -=-，即有122x x =-，1223y y +=，又221144x y m +=，即为2221x y m +=，①又222244x y m +=，②①-②得1212(2)(2)3y y y y m -+=-，可得122y y m -=-，解得132m y -=，234my +=，则2223()2m m x -=+，即有2223()2m x m -=-22109(5)1644m m m -+---+==，即有5m =时，22x 有最大值4，即点B 横坐标的绝对值最大．故答案为：5.10.【答案】125解：设1122(,),(,),(,)A x y B x y Q m n ，由,AP PB AQ QB λλ==-，得则22212()(1)x x m λλ-=-，同理22212()(1)y y n λλ-=-，于是2222221122()()(1)().434343x y x y m n λλ+-+=-+ 又1λ≠±，则143m n +=，所以点Q 的轨迹是直线143x y+=， min ||OQ 即为原点到直线的距离，所以min 112||.511169OQ ==+ 故答案为12.511.【答案】解：设11(,)A x y ，22(,)B x y ，线段AB 的中点00(,).M x y 此椭圆上存在不同的两点A 、B 关于直线2y x m =+对称，∴直线AB 的方程可设为1.2y x t =-+ 联立，化为2234440.x tx t -+-=221612(44)0t t ∆=-->，解得23(*).2t < 1243x x t ∴+=， 023x t ∴=，012.33y t t t =-+= 22(,).33M t t ∴ 代入直线2y x m =+可得：2433t t m =+，解得3.2m t =- 代入(*)可得：233()22m -<，解得66.33m -<< m ∴的取值范围是66.33m -<< 故答案为12.【答案】解：()Ⅰ由题意得椭圆22141x y +=的焦点坐标分别为(和，设双曲线方程为22221(0,0)x y a b a b-=>>，则2223c a b =+=，c e a==，c ∴=，解得21a =，22b =，∴双曲线方程为221.2y x -= ()Ⅱ设11(,)A x y ，22(,)B x y ，分别代入双曲线可得2211112x y -=，2222112x y -=，两式相减，得121212121()()()()02x x x x y y y y -+--+=，点(2,1)M 为AB 的中点，可得124x x +=，122y y +=，则12124()()0x x y y ---=，12124AB y y k x x -∴==-，∴直线l 的方程为47y x =-，把47y x =-代入2212y x -=，消去y 得21456510x x -+=，124x x ∴+=，125114x x =，4k =，||7AB ∴===13.【答案】解：(1)211c =-=，(1,0)F ∴， l 与x 轴垂直， ∴直线l 的方程为1x =，由，解得或，A ∴的坐标为2(1,)2或2(1,)2-， ∴直线AM 的方程为222y x =-+或222y x =-； (2)当l 与x 轴重合时，0OMA OMB ︒∠=∠=，当l 与x 轴垂直时，OM 为AB 的垂直平分线，OMA OMB ∴∠=∠，当l 与x 轴不重合也不垂直时，设l 的方程为(1)y k x =-，0k ≠，11(,)A x y ，22(,)B x y ，则12x <，22x <，则121222MA MB y y k k x x +=+--，由11y kx k =-，22y kx k =-，得12121223()4(2)(2)MA MB kx x k x x kk k x x -+++=--，将(1)y k x =-代入2212x y +=，整理可得2222(21)4220k x k x k +-+-=，则0∆>，2122421k x x k ∴+=+，21222221k x x k -=+， 121223()4kx x k x x k ∴-++33321(441284)021k k k k k k =--++=+，从而0MA MB k k +=，故MA ，MB 的倾斜角互补，OMA OMB ∴∠=∠，综上，.OMA OMB ∠=∠14.【答案】解：(1)由已知得 22b =，c a = 又222a b c =+，解得a =1b = ∴椭圆C 的方程为22 1.3x y += (2)由题意知，直线l 斜率存在，可设直线l 方程为2y kx =+，将其代入2213x y +=，得22(31)1290k x kx +++=，设11(,)A x y ，22(,)B x y ，22(12)36(13)0k k ∴=-+>，解得21k >，由根与系数的关系，得1221213k x x k +=-+，122913x x k =+ AOB ∠为锐角，0OA OB ∴⋅>，12120x x y y ∴+>，1212(2)(2)0x x kx kx ∴+++>，21212(1)2()40k x x k x x ∴++++>，代入1221213k x x k +=-+，122913x x k=+，化简得22133013k k->+，解得2133k <，由21k >且2133k <，解得(1)k ∈-⋃15.【答案】解：()Ⅰ由题2222,.c a ab a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩解得2,1.a b =⎧⎨=⎩ 所以椭圆C 的方程为22 1.4x y += ()Ⅱ证明：由(1)知1(2,0)A -，2(2,0)A ，设0000(,)(2,1)M x y x y ≠±≠±，则220014x y +=， 212000200012244A M A M y y y k k x x x ⋅=⋅==--+-，设直线2A M 方程为1(2)(0)2y k x k k =-≠≠±且，直线1A B 方程为112y x =+，由(2),1 1.2y k x y x =-⎧⎪⎨=+⎪⎩解得点424(,).2121k k P k k +-- 由于2114A M A M k k ⋅=-，于是直线1A M 的方程为1(2)4y x k =-+，直线2A B 的方程为1 1.2y x =-+ 由1(2)4112y x k y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩，解得点422(,).2121k Q k k +--- 于是P Q x x =，所以PQ x ⊥轴．设PQ 中点为N ，则N 点的纵坐标为422121 1.2k k k -+--= 故PQ 中点在定直线1y =上．从上边可以看出点B 在PQ 的垂直平分线上，所以||||BP BQ =，所以BPQ 为等腰三角形．16.【答案】解：(1)由题意：2a =，(2,0)A -，所以直线1l 的方程为2y x =+，所以(0,2)C ，因为2.AB BC =所以，由B 在椭圆上可得：∴椭圆Γ的标准方程为：221.42x y += (2)设直线2l ：1x my =+，点，点，所以 12222m y y m +=-+，12232y y m =-+，所以直线AM ：1122x x y y +=-，直线ON ：22x x y y =，设点，所以，，令12y t y =，，所以11(,)M x y 22(,)N x y所以，∴实数λ的取值范围为。

高中数学人教A版选择性必修第一册3.1.2椭圆的简单几何性质(第2课时)课时分层练习题含答案解析

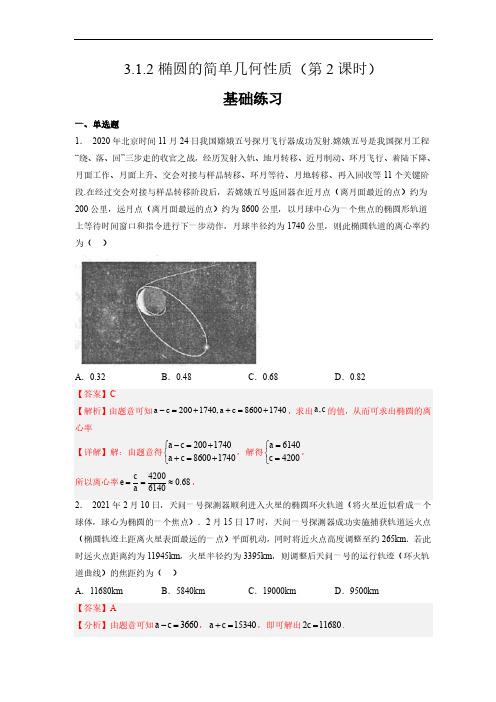
3.1.2椭圆的简单几何性质（第2课时）基础练习一、单选题1． 2020年北京时间11月24日我国嫦娥五号探月飞行器成功发射.嫦娥五号是我国探月工程“绕、落、回”三步走的收官之战，经历发射入轨、地月转移、近月制动、环月飞行、着陆下降、月面工作、月面上升、交会对接与样品转移、环月等待、月地转移、再入回收等11个关键阶段.在经过交会对接与样品转移阶段后，若嫦娥五号返回器在近月点（离月面最近的点）约为200公里，远月点（离月面最远的点）约为8600公里，以月球中心为一个焦点的椭圆形轨道上等待时间窗口和指令进行下一步动作，月球半径约为1740公里，则此椭圆轨道的离心率约为（）A ．0.32B ．0.48C ．0.68D ．0.82球体，球心为椭圆的一个焦点）．2月15日17时，天问一号探测器成功实施捕获轨道远火点（椭圆轨迹上距离火星表面最远的一点）平面机动，同时将近火点高度调整至约265km ．若此时远火点距离约为11945km ，火星半径约为3395km ，则调整后天问一号的运行轨迹（环火轨道曲线）的焦距约为（） A ．11680km B ．5840kmC ．19000kmD ．9500km【答案】A【分析】由题意可知3660a c -=，15340a c +=，即可解出211680c =.全面展开，我国载人航天工程“三步走”战略成功迈出第三步.到今天，天和核心舱在轨已经九个多月.在这段时间里，空间站关键技术验证阶段完成了5次发射、4次航天员太空出舱、1次载人返回、1次太空授课等任务.一般来说，航天器绕地球运行的轨道近似看作为椭圆，其中地球的球心是这个椭圆的一个焦点，我们把椭圆轨道上距地心最近（远）的一点称作近（远）地点，近（远）地点与地球表面的距离称为近（远）地点高度.已知天和核心舱在一个椭圆轨道上飞行，它的近地点高度大约351km，远地点高度大约385km，地球半径约6400km，则该轨道的离心率为（）A．176768B．17368C．385736D．678513536在酒泉卫星发射中心点火发射．此后，神舟十二号载人飞船与火箭成功分离，进入预定轨道，并快速完成与“天和”核心舱的对接，聂海胜、刘伯明、汤洪波3名宇航员成为核心舱首批“入住人员”，并在轨驻留3个月，开展舱外维修维护，设备更换，科学应用载荷等一系列操作．已知神舟十二号飞船的运行轨道是以地心为焦点的椭圆，设地球半径为R，其近地点与地面的距离大约是132R，远地点与地面的距离大约是116R，则该运行轨道（椭圆）的离心率大约是（）A ．167B ．13C ．135D ．195．人造地球卫星的运行轨道是以地心为一个焦点的椭圆，设地球半径为R ，卫星近地点、远地点离地面的距离分别是12,r r ，则卫星轨道的离心率为___________.6．从椭圆的一个焦点1F 发出的光线射到椭圆上的点P ，反射后光线经过椭圆的另一个焦点2F ，事实上，点()00,P x y 处的切线00221xx yy a b +=垂直于12F PF ∠的角平分线，已知椭圆22:143x y C +=的两个焦点是1F ，2F ，点P 是椭圆上除长轴端点外的任意一点，12F PF ∠的角平分线PT 交椭圆C 的长轴于点(),0T t ，则t 的取值范围是__________.7．已知地球运行的轨道是长半轴长81.5010a =⨯km ，焦距与长轴长的比为0.02的椭圆，太阳在这个椭圆的一个焦点上.求地球到太阳的最远距离和最近距离.（注：把地球、太阳看成质点）点上，求地球到太阳的最远距离．【详解】椭圆的长半轴长约为椭圆焦距与长轴长的比约为160．求地球的轨道中心与太阳间的距离以及近日点和远日点到太阳的距离（地球与太阳的半径忽略不计，精确到80.00110km ⨯）．10．飞船的轨道是以地球的中心2为一个焦点的椭圆，选取坐标系如图所示，椭圆中心在坐标原点，近地点A 距地面200千米，远地点B 距地面350千米，已知地球半径6371R =千米.(1)求飞船飞行的椭圆轨道方程；(2)飞船在椭圆轨道运行14圈，历时21小时23分.若椭圆周长的一个近似公式为()24L b a b π=+-（a ，b 分别为椭圆的长半轴与短半轴的长），请问：飞船平均飞行速度每秒多少千米？（结果精确到0.01千米/秒，π取3.146645.58）200 km，远地点（离地面最远的点）高度约350 km的椭圆轨道（将地球看作一个球，其半径约为6371 km），求椭圆轨道的标准方程.（注：地心（地球的中心）位于椭圆轨道的一个焦点，且近地点、远地点与地心共线）12．在大西北的荒漠上，A，B两地相距2km，正准备在荒漠上围成一片以AB为一条对角线的平行四边形区域，建立农艺园．按照规划，围墙总长度为8km．(1)农艺园的最大面积能达到多少?(2)该荒漠上有一条直线型水沟刚好过点A，且与AB成45 角，现要对整条水沟进行加固改造，但考虑到今后农艺园内的水沟要重新设计改造，因此该水沟被农艺园围住的部分暂不加固，那么暂不加固的部分有多长?max)ABC S所以农艺园的最大面积为某种鱼群（将鱼群视为点P ）洄游的路线是以A ，B 为焦点的椭圆C ．现有渔船发现该鱼群在与点A ，点B 距离之和为8 n mile 处．在点A ，B ，P 所在的平面内，以A ，B 所在的直线为x 轴，线段AB 的垂直平分线为y 轴建立平面直角坐标系． (1)求椭圆C 的方程；(2)某日，研究人员在A ，B 两点同时用声呐探测仪发出信号探测该鱼群（探测过程中，信号传播速度相同且鱼群移动的路程忽略不计），A ，B 两点收到鱼群的反射信号所用的时间之比为5:3，试确定此时鱼群P 的位置（即点P 的坐标）．。

(新课标人教A版)选修1-1数学同步课件：2-1-2《椭圆的简单几何性质》

2 A. 2 C．2－ 2
2－1 B. 2 D. 2－1
()
[答案] D
[解析] 设椭圆方程为ax22＋by22＝1(a>b>0)如图， ∵F1(－c,0)，∴P(－c，yP)代入椭圆方程得 ac22＋yb2P2＝1，∴y2P＝ba42， ∴|PF1|＝ba2＝|F1F2|，即ba2＝2c，又∵b2＝a2－c2，∴a2－a c2＝2c， ∴e2＋2e－1＝0，又 0<e<1，∴e＝ 2－1.
[点评] 所谓求椭圆的离心率e的值，即求的值，所以，解答这类题目的主要思路是将已知条件转化为a、b、c之间的关系．如特征三角形中边边关系、椭圆的定义、c2＝a2 －b2等关系都与离心率有直接联系，同时，a、b、c之间是平方关系，所以，在求e值时，也常先考查它的平方值．
设椭圆的两个焦点分别为 F1、F2，过 F1 作椭圆长轴的垂线交椭圆于点 P，若△F1PF2 为等腰直角三角形，则椭圆的离心率为
[点评] 已知椭圆的几何性质，求其标准方程的方法步骤：(1)确定焦点所在的位置，以确定椭圆方程的形式，(2) 确立关于a、b、c的关系方程(组)，求出参数a、b、c，(3)写出标准方程．
求适合下面条件的椭圆的标准方程． (1)经过点P(－5,0)、Q(0，－3)． (2)长轴的长为10，离心率等于
已知 A(4,0)、B(2,2)是椭圆2x52 ＋y92＝1 内的两个点， M 是椭圆上的动点，求|MA|＋|MB|的最大值和最小值．
[解析] 如下图所示，由2x52 ＋y92＝1，得 a＝5，b＝3， c＝4.
所以点 A(4,0)为椭圆一个焦点，记另一个焦点为 F(－ 4,0)．
又因为|MA|＋|MF|＝2a＝10，所以|MA|＋|MB|＝10－|MF|＋|MB|，又|BF|＝2 10，所以－2 10＝－|FB|≤|MB|－|MF|≤|FB|＝2 10.

3.1.2 椭圆的简单几何性质-【新教材】人教A版(2019)高中数学选择性必修第一册同步练习

椭圆的简单几何性质同步练习一、选择题1.已知有相同两焦点F1、F2的椭圆x2m +y2=1(m>1)和双曲线x2n−y2=1(n>0)，P是它们的一个交点，则△F1PF2的形状是（）A. 锐角三角形B. 直角三角形C. 钝角三角形D. 随m，n变化而变化2.已知椭圆：x24+y22=1，过点M(1,1)的直线与椭圆相交于A，B两点，且弦AB被点M平分，则直线AB的方程为()A. x+2y−3=0B. 2x+y−3=0C. x+y−2=0D. 2x−y+1=03.若过椭圆x216+y24=1内一点P(3,1)的弦被该点平分，则该弦所在的直线方程为()A. 3x+4y−13=0B. 3x−4y−5=0C. 4x+3y−15=0D. 4x−3y−9=04.已知椭圆x2a2+y2b2=1(a>b>0)的一个焦点是圆x2+y2−6x+8=0的圆心，且短轴长为8，则椭圆的左顶点为()A. (−3,0)B. (−4,0)C. (−10,0)D. (−5,0)5.我们把由半椭圆x2a2+y2b2=1(x≥0)与半椭圆y2b2+x2c2=1(x<0)合成的曲线称作“果圆”(其中a2=b2+c2，a>b>c>0).如图，设点F0，F1，F2是相应椭圆的焦点，A1、A2和B1、B2是“果圆”与x，y轴的交点，若△F0F1F2是边长为1的等边三角形，则a，b的值分别为()A. 5，4B. √3，1C. 5，3D. √72，16. 如图，F 1F 2分别为椭圆x 2a 2+y 2b 2=1的左右焦点，点P 在椭圆上，△POF 2的面积为√3的正三角形，则b 2的值为（）A. √3B. 2√3C. 3√3D. 4√37. 已知F 1，F 2分别是椭圆x 2a2+y 2b 2=1(a >b >0)的左、右焦点，P 为椭圆上一点，且PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅(OF 1⃗⃗⃗⃗⃗⃗⃗ +OP ⃗⃗⃗⃗⃗ )=0(O为坐标原点)，若|PF 1⃗⃗⃗⃗⃗⃗⃗ |=√2|PF 2⃗⃗⃗⃗⃗⃗⃗ |，则椭圆的离心率为( )A. √6−√3B. √6−√32C. √6−√5D. √6−√528. 已知F 1，F 2是椭圆的两个焦点，满足MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ·MF 2⃗⃗⃗⃗⃗⃗⃗⃗ =0的点M 总在椭圆内部，则椭圆离心率的取值范围是（）A. (0,1)B. (0,12]C. (0,√22) D. [√22,1)9. 已知椭圆和双曲线有共同的焦点F 1，F 2，P 是它们的一个交点，且∠F 1PF 2=π3，记椭圆和双曲线的离心率分别为e 1，e 2，则1e1e 2的最大值为（）A. 3B. 2C. 4√33D. 2√3310. 已知椭圆C ：x 2a 2+y 2b2=1(a >b >0)的离心率为√32，短轴长为2，过右焦点F 且斜率为k(k >0)的直线与椭圆C 相交于A 、B 两点．若AF ⃗⃗⃗⃗⃗ =3FB ⃗⃗⃗⃗⃗ ，则k=（）A. 1B. √2C. √3D. 211. 已知F 1(−1,0)，F 2(1,0)是椭圆C 的两个焦点，过F 2且垂直x 轴的直线交C 于A ，B 两点，且|AB|=3，则C 的方程为（）A.x 22+y 2=1B.x 23+y 22=1C.x 24+y 23=1D.x 25+y 24=112. 已知椭圆E ：x 2a 2+y 2b 2=1(a >b >0)的右焦点为F(3,0)，过点F 的直线交椭圆E 于A ，B 两点，若AB 的中点坐标为(1,−1)，则弦长|AB|=( )A. 5√2B. 2√5C. 5√22D. √1013. 若椭圆C ：x 28+y 24=1的右焦点为F ，且与直线l ：x −√3y +2=0交于P ，Q 两点，则△PQF 的周长为（）A. 6√2B. 8√2C. 6D. 814. 椭圆x 2a2+y 2b 2=1(a >b >0)的左、右焦点分别为F 1，F 2，椭圆上的点M满足：∠F 1MF 2=60°，且MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ⋅MF 2⃗⃗⃗⃗⃗⃗⃗⃗ =2，则b =( )A. 1B. √2C. √3D. 2二、填空题15. 已知抛物线C ：x 2=−2py(p >0)的焦点F 与y 28+x 24=1的一个焦点重合，过焦点F 的直线与C 交于A ，B 两不同点，抛物线C 在A ，B 两点处的切线相交于点M ，且M 的横坐标为2，则弦长|AB|=________． 16. 设M 是椭圆C ：x 2a 2+y 2b 2=1(a >b >0)上一点，以M 为圆心的圆与x 轴相切，切点为椭圆的焦点F ，圆M 与y 轴相交于不同的两点P ，Q ，若△PMQ 为等边三角形，则椭圆C 的离心率为________． 17. 若点O 和点F 分别为椭圆x 24+y 23=1的中心和左焦点，点P 为椭圆上的任意一点，则OP ⃗⃗⃗⃗⃗ ⋅FP⃗⃗⃗⃗⃗ 的最大值为_________． 18. 设F 1，F 2分别为椭圆x 23+y 2=1的左、右焦点，点A ，B 在椭圆上，若F 1A ⃗⃗⃗⃗⃗⃗⃗ =5F 2B ⃗⃗⃗⃗⃗⃗⃗ ，则点A 的坐标是_________．三、解答题（本大题共4小题，共48.0分）19. 已知椭圆E:x 2a 2+y 2b 2=1(a >b >0)四个顶点中的三个是边长为2√3的等边三角形的顶点．(Ⅰ)求椭圆E 的方程；(Ⅱ)设直线y =kx +m 与圆O:x 2+y 2=2b 23相切且交椭圆E 于两点M,N ，求线段|MN|的最大值．20.已知椭圆C:x 2a2+y2b2=1(a>b>0)的两个顶点分别为A(−a,0),B(a,0)，点P为椭圆上异于A，B的点，设直线PA的斜率为k1，直线PB的斜率为k2，且．(1)求椭圆C的离心率；(2)若b=1，设直线l与x轴交于点D(−1,0)，与椭圆交于M，N两点，求△OMN面积的最大值．21.已知椭圆C：x2a2+y2b2=1(a>b>0)的右焦点为F(1,0)，且椭圆上的点到点F的最大距离为3，O为坐标原点．(Ⅰ)求椭圆C的标准方程；(Ⅱ)过右焦点F倾斜角为60°的直线与椭圆C交于M、N两点，求△OMN的面积．22.已知椭圆C：x2a2+y23=1(a>√3)的焦距为2，A，B分别为椭圆C的左、右顶点，M，N为椭圆C上的两点(异于A，B)，连结AM，BN，MN，且BN斜率是AM斜率的3倍．(1)求椭圆C的方程；(2)证明：直线MN恒过定点．答案和解析1.【答案】B【解答】解：由题意，不妨设P 是双曲线右支上的一点，|PF 1|=x ，|PF 2|=y ，则x +y =2√m ，x −y =2√n ， ∴x 2+y 2=2(m +n)， ∵两曲线有相同的焦点， ∴m −1=n +1， ∴m =n +2， ∴x 2+y 2=4(n +1)，即|PF 1|2+|PF 2|2=|F 1F 2|2， ∴△F 1PF 2是直角三角形，故选B ．2.【答案】A【解答】解：设A(x 1,y 1)、B(x 2,y 2)，则x 124+y 122=1，①，x 224+y 222=1，②①−②，得(x 1−x 2)(x 1+x 2)4+(y 1−y 2)(y 1+y 2)2=0．∴y 1−y2x 1−x 2=−12⋅x 1+x2y 1+y 2．又∵M 为AB 中点，∴x 1+x 2=2，y 1+y 2=2． ∴直线AB 的斜率为y 1−y 2x1−x 2=−12．∴直线AB 的方程为y −1=−12(x −1)，即2y +x −3=0．故选：A ．3.【答案】A【解答】解：设弦的两端点为A(x 1,y 1)， B(x 2,y 2)， P 为AB 中点得{x 1+x 2=6y 1+y 2=2，由A ， B 在椭圆上有{x 1216+y 124=1x 2216+y 224=1,两式相减得x12−x2216+y12−y224=0，即(x1+x2)(x1−x2)16+(y1+y2)(y1−y2)4=0，即3(x1−x2)8+y1−y22=0，即y1−y2x1−x2=−34，则斜率k=−34，且过点P(3,1)，有y−1=−34(x−3)，整理得3x+4y−13=0．故选A．4.【答案】D【解答】解：∵圆的标准方程为(x−3)2+y2=1，∴圆心坐标是(3,0)，∴c=3．又b=4，∴a=√b2+c2=5．∵椭圆的焦点在x轴上，椭圆的左顶点为(−5,0)．故选D．5.【答案】D【解析】解：由题意可得|OF2|=√b2−c2=12，|OF0|=c=√3|OF2|=√32，解得b=1，又a2=b2+c2=1+34=74，得a=√72，即a=√72，b=1．6.【答案】B 【解答】解：∵△POF2的面积为√3的正三角形，S=12×c×√32c=√34c2∴√34c2=√3，解得c=2．∴P(1,√3)代入椭圆方程可得：1a2+3b2=1，与a2=b2+4联立解得：b2=2√3．故选B．7.【答案】A【解答】解：设焦点坐标F 1(−c,0)，F 2(c,0)，|F 1F 2⃗⃗⃗⃗⃗⃗⃗⃗ |=2c ， |PF 1⃗⃗⃗⃗⃗⃗⃗ |=√2|PF 2⃗⃗⃗⃗⃗⃗⃗ |，|PF 1⃗⃗⃗⃗⃗⃗⃗ |+|PF 2⃗⃗⃗⃗⃗⃗⃗ |=2a ，所以|PF 1⃗⃗⃗⃗⃗⃗⃗ |=2√2a(√2−1)，|PF 2⃗⃗⃗⃗⃗⃗⃗ |=2a(√2−1)，由PF 1⃗⃗⃗⃗⃗⃗⃗ ⋅(OF 1⃗⃗⃗⃗⃗⃗⃗ +OP ⃗⃗⃗⃗⃗ )=0，设线段PF 1的中点为M ，则OM ⊥PF 1, 则|PO ⃗⃗⃗⃗⃗ |=|OF 1⃗⃗⃗⃗⃗⃗⃗ |=|OF 2⃗⃗⃗⃗⃗⃗⃗ |， ∴PF 1⊥PF 2，则|PF 1⃗⃗⃗⃗⃗⃗⃗ |2+|PF 2⃗⃗⃗⃗⃗⃗⃗ |2=|F 1F 2⃗⃗⃗⃗⃗⃗⃗⃗ |2，∴(2√2a(√2−1))2+(2a(√2−1))2=4c 2，可得c 2=(9−6√2)a 2，解得e 2=9−6√2，则椭圆的离心率为√6−√3．故选A ．8.【答案】C【解答】解：设椭圆方程为x 2a 2+y 2b 2=1(a >b >0)，焦距为2c ，椭圆上任一点P(x,y)，由MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ·MF 2⃗⃗⃗⃗⃗⃗⃗⃗ =0的点M 总在椭圆内，则PF 1⃗⃗⃗⃗⃗⃗⃗ ·PF 2⃗⃗⃗⃗⃗⃗⃗ >0，得x 2+y 2>c 2恒成立，代入椭圆方程化简得y 2<b 4a 2−b 2，又−b <y <b ，所以b 2<b 4a 2−b 2，化简得a 2<2b 2=2a 2−2c 2，得a 2>2c 2，可得e =ca<√22，又0<e <1，∴0<e <√22，故选C ．9.【答案】D【解答】解：不妨设F 1，F 2分别为左、右焦点，P 为第一象限的点，如图：设椭圆的长半轴长为a 1，双曲线的实半轴长为a 2，则根据椭圆及双曲线的定义知|PF 1|+|PF 2|=2a 1，|PF 1|−|PF 2|=2a 2， ∴|PF 1|=a 1+a 2，|PF 2|=a 1−a 2．设|F 1F 2|=2c ，在△PF 1F 2中，∠F 1PF 2=π3，由余弦定理得，4c 2=(a 1+a 2)2+(a 1−a 2)2−2(a 1+a 2)(a 1−a 2)cos π3，化简得a 12+3a 22=4c 2，即1e 12+3e 22=4，∴1e 12+3e 22=4≥2√3e 12e 22，∴1e1e 2≤2√33，当且仅当e 1=√22,e 2=√62时，等号成立，则1e1e 2的最大值为2√33，故选D ．10.【答案】B【解答】解：椭圆C ：x 2a 2+y 2b 2=1(a >b >0)的离心率为√32，短轴长为2，可得：b =1，ca =√32，解得：a =2，c =√3，b =1，椭圆方程为x 24+y 2=1，过右焦点F 且斜率为k(k >0)的直线与椭圆C 相交于A ，B 两点，设A(x 1,y 1)，B(x 2,y 2)， ∵AF⃗⃗⃗⃗⃗ =3FB ⃗⃗⃗⃗⃗ ，∴y 1=−3y 2，设直线AB 方程为y =k(x −√3)，代入x 24+y 2=1，消去x ，可得(14k 2+1)y 2+√32k y −14=0， ∴y 1+y 2=−√32k 1+14k2=−2√3k1+4k 2，y 1y 2=−141+14k2=−k 24k 2+1，−2y 2=−2√3k 1+4k2，−3y 22=−k 24k 2+1，解得：k =√2．故选：B ．11.【答案】C【解答】解：F 1(−1,0)，F 2(1,0)是椭圆C 的两个焦点，可得c =1，过F 2且垂直x 轴的直线交C 于A ，B 两点，且|AB|=3，令椭圆方程x 2a 2+y 2b 2=1中x =1，得y =±√b 2−b 2a 2，可得2√b 2−b 2a2=3，化简得4a 4−17a 2+4=0，解得a =2，则b =√3，所求的椭圆方程为：x 24+y 23=1．故选：C ．12.【答案】A【解答】解：设A(x 1,y 1)，B(x 2,y 2)，代入椭圆方程得x 12a 2+y 12b 2=1①，x 22a 2+y 22b 2=1②，相减得x 12−x 22a 2+y 12−y 22b 2=0， ∴x 1+x 2a 2+y 1−y2x 1−x 2⋅y 1+y 2b 2=0．∵x 1+x 2=2，y 1+y 2=−2，k AB =−1−01−3=12．∴2a 2+12×−2b 2=0，化为a 2=2b 2，又c =3=√a 2−b 2，解得a 2=18，b 2=9． ∴椭圆E 的方程为x 218+y 29=1．AB 的斜率为12，且过(1,−1)，∴直线AB 的方程为y +1=12(x −1)，即y =12x −32，代入椭圆方程，得3x 2−6x −27=0． ∴x 1+x 2=2.x 1x 2=−9．∴|AB|=√1+14⋅√(x 1+x 2)2−4x 1x 2=5√2．故选：A ．13.【答案】B【解析】解：∵直线l 过椭圆C 的左焦点F′(−2,0)，直线l ：x −√3y +2=0经过左焦点F′， ∴△PQF 的周长|PQ|+|PF|+|QF|=|PF′|+|PF|+|QF′|+|QF|=4a =8√2，14.【答案】C【解析】解：设|MF 1⃗⃗⃗⃗⃗⃗⃗⃗ |=m ，|MF 2⃗⃗⃗⃗⃗⃗⃗⃗ |=n ，因为MF 1⃗⃗⃗⃗⃗⃗⃗⃗ ⋅MF 2⃗⃗⃗⃗⃗⃗⃗⃗ =2，则mncos60°=2，⇒mn =4，又m +n =2a ，(1)，在△MF 1F 2中，由余弦定理可得：|F 1F 2|2=m 2+n 2−2mncos60°=4(a 2−b 2)(2)， (1)式平方减去(2)式得：b 2=3，得：b =√3．故选：C ．设|MF 1|=m ，|MF 2|=n ，由数量积及∠F 1MF 2的大小可得mn =4，再由椭圆的定义可得m +n =2a ，在△MF 1F 2中，由余弦定理可得b 的值．本题考查椭圆的性质及数量积的运算性质，属于中档题．15.【答案】10【解答】解：由题意可得F(0,−2)，则p =4，抛物线方程为x 2=−8y ．设直线AB 方程为y =kx −2，A(x 1,y 1)，B(x 2,y 2)，其中y 1=−x 128，y 2=−x 228．由y =−x28得y′=−x4，所以在点A处的切线方程为y−y1=−x14(x−x1)，化简得y=−x14x+x128，①同理可得在点B处的切线方程为y=−x24x+x228.②联立①②得x M=x1+x22，又∵M的横坐标为2，∴x1+x2=4．将AB方程代入抛物线得x2+8kx−16=0，∴x1+x2=−8k=4，∴k=−12，∴y1+y2=k(x1+x2)−4=−12×4−4=−6，∴|AB|=p−y1−y2=10．故答案为10．16.【答案】√33【解答】解：如图，过M作MN⊥y轴于N，由△PMQ为等边三角形，可得|PQ|=2√33c，再由题意可得M(c,b2a )，则圆M为(x−c)2+(y−b2a)2=b4a2，取x=0，可得y1=b2a −√b4−a2c2a，y2=b2a+√b4−a2c2a，∴2√b4−a2c2a =2√33c，即3(e2)2−10e2+3=0，解得：e=√33．故答案为：√33．17.【答案】6【解答】解：由题意，F(−1,0)，设点P(x0,y0)，则有x024+y023=1，解得y02=3(1−x024)，因为FP ⃗⃗⃗⃗⃗ =(x 0+1,y 0),OP ⃗⃗⃗⃗⃗ =(x 0,y 0),所以OP ⃗⃗⃗⃗⃗ ⋅FP ⃗⃗⃗⃗⃗ =x 0(x 0+1)+3(1−x 024)=x 024+x 0+3=14(x 0+2)2+2，此二次函数对应的抛物线的对称轴为x 0=−2，因为−2≤x 0≤2，所以当x 0=2时，OP ⃗⃗⃗⃗⃗ ⋅FP ⃗⃗⃗⃗⃗ 取得最大值224+2+3=6，故答案为6． 18.【答案】(0,1)或(0,−1)【解答】解：设A(m,n)．由F 1A ⃗⃗⃗⃗⃗⃗⃗ =5F 2B ⃗⃗⃗⃗⃗⃗⃗ ，得B (m+6√25,n 5)．又A ，B 均在椭圆上，所以有{m 23+n 2=1,(m+6√25)23+(n 5)2=1,解得{m =0,n =1或{m =0,n =−1, 所以点A 的坐标为(0,1)或(0,−1)．19.【答案】解：(Ⅰ)由题意，椭圆上下顶点与左右顶点其中的一个构成等边三角形，所以a =√3b,b =√3，即a =3，所以椭圆E 的方程为x 29+y 23=1，(Ⅱ)圆O:x 2+y 2=2，因为直线y =kx +m 与圆O:x 2+y 2=2相切，所以√1+k 2=√2，即m 2=2(1+k 2)；联立{x 29+y 23=1y =kx +m得(1+3k 2)x 2+6kmx +3(m 2−3)=0，Δ>0，设M (x 1,y 1),N (x 2,y 2)，所以x 1+x 2=−6km 1+3k 2,x 1·x 2=3(m 2−3)1+3k 2,由弦长公式得|MN|=√1+k 2·|x 1−x 2|=√1+k 2·√(x 1+x 2)2−4x 1x 2=√1+k 2·√12(9k 2+3−m 2)1+3k 2，将m 2=2(1+k 2)代入：|MN|=√6·√(2+2k 2)(7k 2+1)1+3k 2≤√6·(2+2k 2)+(7k 2+1)21+3k 2=3√62，当且仅当2+2k 2=7k 2+1，即k 2=15时等号成立，故弦长|MN|最大值为3√62． 20.【答案】解：(1)设P(x 0,y 0)为椭圆上的点，则x 02a 2+y 02b 2=1，整理得：y 02=−b 2a 2(x 02−a 2)，又k 1=y 0x 0+a ，k 2=y 0x 0−a ，∴k 1k 2=y 02x 02−a 2=−12，联立两个方程则k 1k 2=−b 2a 2=−12，解得e =c a =√1−b2a 2=√22． (2)由(1)知a 2=2b 2，又b =1，∴椭圆C 的方程为x 22+y 2=1．由题意，设直线l 的方程为：x =my −1，代入椭圆的方程有：(m 2+2)y 2−2my −1=0，则Δ=(−2m )2+4(m 2+2)=8(m 2+1)>0，设M(x 1,y 1)，N(x 2,y 2)，则y 1+y 2=2m m 2+2，y 1y 2=−1m 2+2，则△OMN 的面积S =12|OD |·|y 1−y 2| =12√(y 1+y 2)2−4y 1y 2 =12×√8m 2+8m 2+2=√2·√m 2+1m 2+2，令√m 2+1=t ，(t ≥1)，则有m 2=t 2−1，代入上式有S =√2·√m 2+1m 2+2=√2t t 2+1=√2t+1t ≤√22，当且仅当t =1，即m =0时等号成立，所以△OMN 面积的最大值为√22． 21.【答案】解：(Ⅰ)椭圆焦点坐标为(1,0)，则c =1，由椭圆C 上的点到F 的最大距离为a +c =3，则a =2， b 2=a 2−c 2=3，∴椭圆的标准方程为x 24+y 23=1．(Ⅱ)设M(x 1,y 1)，N(x 2,y 2)，由已知可设直线MN 的方程为：y =√3(x −1)，联立方程组{y =√3(x −1)3x 2+4y 2=12消去x 得：5y 2+2√3y −9=0． y 1+y 2=−2√35，y 1⋅y 2=−95，⇒(y 1−y 2)2=(−2√35)2−4×(−95)=19225． ∴△OMN 的面积S =12×OF ×|y 1−y 2|=12×1×8√35=4√35 22.【答案】解：(1)∵{2c =2a 2=c 2+3, ∴{a =2c =1, 所以b 2=a 2−c 2=3∴椭圆C 的方程为x 24+y 23=1；(2)连结BM ，设M(x 1,y 1),N(x 2,y 2)，则k AM ⋅k BM =y 1x 1+2⋅y 1x 1−2=y 12x 12−4，∵点M(x 1,y 1)在椭圆上，∴k AM ⋅k BM =y 12x 12−4=3−34x 12x 12−4=−34，∵k BN =3k AM ，∴k BN ⋅k BM =−94，①当MN 斜率不存在时，设MN:x =m ，不妨设M 在x 轴上方， ∴M(m,√12−3m 24),N(m,−√12−3m 24)， ∵k BN ⋅k BM =−94， ∴m =1；②当MN 斜率存在时，设MN:y =kx +t ，由{y =kx +t 3x 2+4y 2−12=0，整理，得(3+4k 2)x 2+8ktx +4t 2−12=0， ∴x 1+x 2=−8kt 3+4k 2,x 1⋅x 2=4t 2−123+4k 2， ∵k BN ⋅k BM =y 1x 1−2⋅y 2x 2−2=(kx 1+t)⋅(kx 1+t)x 1x 2−2(x 1+x 2)+4=−94，∴化简可得2k2+3kt+t2=0，即t=−k或t=−2k，当t=−k时，y=kx−k，恒过定点(1,0)，当斜率不存在亦符合；当t=−2k，y=kx−2k，过点(2,0)与点B重合，舍去，∴直线恒过定点(1,0)．。

3.1.2椭圆的简单几何性质(第一课时)课件高二上学期数学人教A版选择性

1
-1

1
,c=

1
,c=

1

-1.
1
m=4,此时长轴长为
m=4 时,长轴长为 2,当
2a=4.
1
m=4时,长轴长为
4.
【例3】 (1)已知F1,F2是椭圆的两个焦点,过F1且与椭圆长轴垂直的直线
交椭圆于A,B两点,若△ABF2是正三角形,则该椭圆的离心率
是
.
解析:不妨设椭圆的焦点在x轴上,因为AB⊥F1F2,且△ABF2为正三角形,
综上，椭圆关于x轴、y轴都是对称的．这时，坐标轴是椭圆的对称轴，
原点是椭圆的对称中心，椭圆的对称中心叫做椭圆的中心．
3．顶点
研究曲线上某些特殊点的位置，可以确定曲线的位置．
思考
2
2
x
y
你认为椭圆 2 2 1(a b 0)上哪些点比较特殊 ? 为什么? 如何得
a
b
到这些点的坐标 ?
y
当
1
0< <1,即

1

=1,则应有 m>0,且 m≠1.
m>1 时,焦点在 x 轴上,a=1,b=
因为离心率为
1
当 >1,即
2
1

1-
3
,所以
2
1
=
3
,解得
2
因为离心率为
3
,所以
2
综上可知,m 的值为 4
1

Байду номын сангаас
=
1
或4,当
3
,解得
2
1
1- .

m=4,这时长轴长为 2a=2.

人教A版高中同步学案数学选择性必修第一册精品课件第三章 3.1.2 椭圆的简单几何性质

些存在性、判断性问题中有着重要的应用,也可用于求最大(小)值、求轨
迹等问题时的检验等.
2.利用方程研究曲线对称性的方法如下:
(1)若把曲线方程中的x换成-x,方程不变,则曲线关于y轴对称;
(2)若把曲线方程中的y换成-y,方程不变,则曲线关于x轴对称;
(3)若同时把曲线方程中的x换成-x,y换成-y,方程不变,则曲线关于原点对称.
若焦点在 y 轴上,则 b=3,

∵e=
=
2
1- 2
=
9
1- 2
=
√6
2
,解得
a
=27.
3
2
2
∴椭圆的标准方程为27 + 9 =1.综上可知,椭圆的标准方程为
2
9
2
2
2
+ 3 =1 或27 + 9 =1.
2
(2)设椭圆的标准方程为 2

+
2
2 =1(a>b>0).

如图所示,△A1FA2为等腰直角三角形,OF为斜边A1A2的中线(高),且
焦点的位置焦点在x轴上
焦点在y轴上
图形
标准方程
范围
2 2
+ 2 =1(a>b>0)
2

-a≤x≤a , -b≤y≤b
2
2
+
2
2 =1(a>b>0)

-b≤x≤b,
-a≤y≤a
焦点的位置焦点在x轴上
焦点在y轴上
顶点
A1(-a,0),A2(a,0)
B1(0,-b),B2(0,b)
A1(0,-a),A2(0,a)

高中数学人教A版选修(2-1)2.2.2《椭圆的简单几何性质》第1课时知能演练轻松闯关 .doc

1.椭圆6x 2＋y 2＝6的长轴端点坐标为( )A ．(－1，0)，(1，0)B ．(－6，0)，(6，0)C ．(－6，0)，(6，0)D ．(0，－6)，(0，6) 解析：选D.椭圆方程化为标准式y 26＋x 2＝1， ∴a 2＝6，且焦点在y 轴上．∴长轴端点坐标为(0，－6)，(0，6)． 2.已知椭圆的中心在坐标原点，焦点在x 轴上，且长轴长为12，离心率为13，则椭圆的方程是( )A.x 2144＋y 2128＝1B.x 236＋y 220＝1 C.x 232＋y 236＝1 D.x 236＋y 232＝1 解析：选D.由2a ＝12，c a ＝13，解得a ＝6，c ＝2，∴b 2＝62－22＝32. ∵焦点在x 轴上，∴椭圆的方程为x 236＋y 232＝1. 3.已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)与椭圆x 225＋y 216＝1有相同的长轴，椭圆x 2a 2＋y 2b2＝1(a >b >0)的短轴长与椭圆y 221＋x 29＝1的短轴长相等，则椭圆方程为__________．答案：x 225＋y 29＝1 4.离心率e ＝12，一个焦点是F (0，－3)的椭圆标准方程为__________．解析：依题意c a ＝12，c ＝3，所以a ＝6，b ＝27，焦点在y 轴上，所以椭圆标准方程为y 236＋x 227＝1.答案：y 236＋x 227＝1[A 级基础达标]1.(2012·福州质检)如果一个椭圆的长轴长是短轴长的两倍，那么这个椭圆的离心率为( )A.54B.32C.22D.12解析：选B.因长轴是短轴的2倍，则a ＝2b .所以e ＝a 2－b 2a ＝3b 2b ＝32.2.椭圆x 2＋my 2＝1的焦点在y 轴上，长轴长是短轴长的两倍，则m 的值为( ) A.14 B.12 C ．2 D ．4 解析：选A.将原方程化为标准形式为x 21＋y 21m ＝1，由焦点在y 轴上可得1m>1，∴0<m <1，又知长轴长为短轴长的两倍，则1m ＝4，得m ＝14. 3.曲线x 225＋y 29＝1与曲线x 225－k ＋y 29－k＝1(k <9)的( ) A ．长轴长相等 B ．短轴长相等C ．离心率相等D ．焦距相等解析：选D.由题意可知两个椭圆的焦点都在x 轴上，前者焦距2c ＝225－9＝8，后者焦距2c ＝2（25－k ）－（9－k ）＝8.4.与椭圆9x 2＋4y 2＝36有相同焦点，且短轴长为45的椭圆方程是________．解析：依题意得椭圆的焦点坐标为(0，5)，(0，－5)，故c ＝5，又2b ＝45，所以b ＝25，a 2＝b 2＋c 2＝25.答案：x 220＋y 225＝1 5.若椭圆的短轴长为6，焦点到长轴的一个端点的最近距离是1，则椭圆的离心率为________．解析：依题意，得b ＝3，a －c ＝1.又a 2＝b 2＋c 2，解得a ＝5，c ＝4，∴椭圆的离心率为e ＝c a ＝45. 答案：456.求适合下列条件的椭圆的标准方程．(1)椭圆过(3，0)，离心率e ＝63； (2)在x 轴上的一个焦点，与短轴两个端点的连线互相垂直，且焦距为8.解：(1)若焦点在x 轴上，则a ＝3，∵e ＝c a ＝63，∴c ＝6，∴b 2＝a 2－c 2＝9－6＝3. ∴椭圆的方程为x 29＋y 23＝1. 若焦点在y 轴上，则b ＝3，∵e ＝c a ＝1－b 2a 2＝1－9a 2＝63，解得a 2＝27.∴椭圆的方程为y 227＋x 29＝1. (2)设椭圆方程为x 2a 2＋y 2b2＝1(a >b >0)．如图所示，△A 1F A 2为等腰直角三角形，OF 为斜边A 1A 2的中线(高)，且|OF |＝c ，|A 1A 2|＝2b ，∴c ＝b ＝4，∴a 2＝b 2＋c 2＝32，故所求椭圆的方程为x 232＋y 216＝1. [B 级能力提升]7.若椭圆的两个焦点与它的短轴的两个端点是一个正方形的四个顶点，则椭圆的离心率为( ) A.22 B.32 C.53 D.63 解析：选A.如图所示，四边形B 1F 2B 2F 1为正方形，则△B 2OF 2为等腰直角三角形，∴c a ＝22. 8.椭圆x 2a2＋y 2＝1(a >4)的离心率的取值范围是( ) A.⎝⎛⎭⎫0，1516 B.⎝⎛⎭⎫0，154 C.⎝⎛⎭⎫1516，1 D.⎝⎛⎭⎫154，1 解析：选D.e ＝c a ＝a 2－1a ＝1－1a2. ∵a >4，∴0<1a 2<116， ∴154<e <1. 9.已知椭圆短轴的一个端点为B ，F 1、F 2是椭圆的两个焦点，且△BF 1F 2是周长为18的正三角形，则椭圆的标准方程是__________．解析：由题意知a ＝2c ，2a ＋2c ＝18，解方程组⎩⎪⎨⎪⎧a ＝2c ，a ＋c ＝9，得⎩⎪⎨⎪⎧a ＝6，c ＝3，∴b 2＝a 2－c 2＝27，∴所求的椭圆的标准方程为x 236＋y 227＝1或y 236＋x 227＝1. 答案：x 236＋y 227＝1或y 236＋x 227＝1 10.椭圆的中心在原点，焦点在x 轴上，焦距为2，且经过点A ⎝⎛⎭⎫－1，32. (1)求满足条件的椭圆方程；(2)求该椭圆的顶点坐标、长轴长、短轴长、离心率．解：(1)由已知焦点在x 轴上，设椭圆方程为x 2a 2＋y 2b2＝1(a >b >0)，则c ＝1. 焦点坐标为F 1(－1，0)，F 2(1，0)，2a ＝|AF 1|＋|AF 2|＝（－1＋1）2＋⎝⎛⎭⎫322＋（1＋1）2＋⎝⎛⎭⎫322＝4，a ＝2，∴b 2＝a 2－c 2＝3.∴ 椭圆方程为x 24＋y 23＝1. (2)顶点坐标为(±2，0)，(0，±3)；长轴长为4；短轴长为23；离心率e ＝12. 11.(创新题)如图，已知椭圆x 2a 2＋y 2b2＝1(a >b >0)，F 1、F 2分别为椭圆的左、右焦点，A 为椭圆的上顶点，直线AF 2交椭圆于另一点B .若AF 2→＝2F 2B →，AF 1→·AB →＝32，求椭圆的方程．解：由题意知A (0，b )，F 1(－c ，0)，F 2(c ，0)，其中，c ＝a 2－b 2，设B (x ，y )．由AF 2→＝2F 2B →⇔(c ，－b )＝2(x －c ，y )，解得x ＝3c 2，y ＝－b 2，即B ⎝⎛⎭⎫3c 2，－b 2. 将B 点坐标代入x 2a 2＋y 2b 2＝1，得94c 2a 2＋b 24b 2＝1，即9c 24a 2＋14＝1，解得a 2＝3c 2.①由AF 1→·AB →＝32知：(－c ，－b )·⎝⎛⎭⎫3c 2，－3b 2＝32 ∴b 2－c 2＝1.②又a 2＝b 2＋c 2，③解①②③组成的方程组得：a 2＝3，b 2＝2.∴所求椭圆的方程为：x 23＋y 22＝1.。

高二数学人教A版选修1-1同步课时作业(12)椭圆的简单几何性质 Word版含解析

2020-2021学年高二数学人教A 版选修1-1同步课时作业（12）椭圆的简单几何性质1.已知椭圆2222:1(0)x y E a b a b+=>>的右焦点为(3,0)F ，过点F 的直线交E 于,A B 两点.若AB的中点坐标为(1,1)-，则E 的方程为（）A.2214536x y += B.2213627x y += C.2212718x y += D.221189x y += 2.若坐标原点O 和点F 分别为椭圆22143x y +=的中心和左焦点,点P 为椭圆上的任意一点,则OP FP ⋅的最大值为( )A.2B.3C.6D.83.已知椭圆22121,259+=x y F F 分别为其左、右焦点，椭圆上一点M 到点1F 的距离是2，N 是线段1MF 的中点，则ON 的长为( )A.1B.2C.3D.44.已知12,F F 是椭圆221169x y +=的两焦点，过点2F 的直线交椭圆与点,A B .若5AB =，则11AF BF +=( ) A.9B.10C.11D.125.已知点12(,0),(,0)F c F c -为椭圆22221(0)x y a b a b+=>>的两个焦点,点P (不在x 轴上)在椭圆上,且满足212PF PF c ⋅=,则此椭圆离心率的取值范围是( ) A.3⎫⎪⎪⎣⎭B.11,32⎡⎤⎢⎥⎣⎦C.32⎣⎭D.2⎛ ⎝⎦6.已知椭圆22221x y a b+=(0a b c >>>,其中c 为椭圆的半焦距)的左、右焦点分别为12,F F ,若以2F 为圆心,b c -为半径作圆2F ,过椭圆上一点P 作圆2F 的切线,切点为T ,若PT 的最小值不小于3)a c -,则椭圆的离心率e 的取值范围是( ) A.3,15⎡⎫⎪⎢⎣⎭B.325⎡⎢⎣⎭C.3(0,)5D.2(7.椭圆2222:1(0)x y C a b a b+=>>的左、右焦点分别为12,F F ,焦距为2c .若直线3()y x c =+与椭圆C 的一个交点M 满足12212MF F MF F ∠=∠,则椭圆C 的离心率等于( )1D.4-8.过椭圆2222:1(0)x y C a b a b+=>>的左顶点A 的斜率为k 的直线交椭圆C 于另一个点B ,且点B在x 轴上的射影恰好为右焦点F ,若1132k <<,则椭圆离心率的取值范围是( )A.14(,)49B.2(,1)3C.12(,)23D.1(0,)29.已知椭圆22142x y +=的两个焦点分别是12,F F ,点P 在椭圆上,若122PF PF -=,则12PF F △的面积是( )1110.若以椭圆上一点和两个焦点为顶点的三角形面积的最大值为1,则椭圆长轴的最小值为( )A.1C.2D.11.若点O 和点F 分别为椭圆22143x y +=的中心和左焦点，点P 为椭圆上的任意一点，则OP FP ⋅的最大值为___________.12.已知动点(,)P x y 在椭圆2212516x y +=上，若点A 的坐标为(3,0)，1AM =,且0PM AM ⋅=,则PM 的最小值是____________.13.若分别过椭圆22221(0)x y a b a b+=>>的左、右焦点12,F F 所作的两条互相垂直的直线12,l l 的交点在椭圆上,则此椭圆的离心率的取值范围是_________.14.设椭圆2222:1(0)x y E a b a b+=>>的一个焦点(2,0)F ,点(2,1)A -为椭圆E 内一点,若椭圆E 上存在一点P ,使得8PA PF +=,则椭圆E 的离心率的取值范围是__________.15.已知椭圆2222:1(0)x y C a b a b +=>>过点(0,4),离心率为35.（1）求椭圆C 的方程; （2）求过点(3,0)且斜率为45的直线被C 所截线段的中点的坐标. 答案以及解析1.答案：D解析：因为直线AB 过点(3,0)F 和点(1,1)-，所以直线AB 的方程为1(3)2y x =-，代入椭圆方程22221x y a b +=消去y ，得2222222390424a b x a x a a b ⎛⎫+-+-= ⎪⎝⎭，所以线段AB 的中点的横坐标为22232124aa b =⎛⎫+ ⎪⎝⎭，即222a b=.又222,3a b c c =+=，所以3,b c a ===.所以E 的方程为221189x y +=. 2.答案：C解析：由题设,知(1,0)F -.设点00(,)P x y ,则2200143x y +=,得22003(1)4x y =-.因为0000(,),(1,)OP x y FP x y ==+,所以22220000000001(1)(1)3(1)3(2)2444x x OP FP x x y x x x x ⋅=++=++-=++=++.又022x -≤≤,所以OP FP ⋅的最大值为21(22)264++=.故选C.3.答案：D解析：由椭圆定义得21210+==MF MF a .因为12=MF ,所以28=MF .因为N 是线段1MF 的中点，所以242==MF ON ,故选D4.答案：C解析：根据椭圆定义，1228AF AF a +==，1228BF BF a +==，所以1116AF BF AB ++=，所以111611AF BF AB +=-=,故选C 5.答案：C解析：由椭圆的定义,得122PF PF a +=,平方得222121224PF PF PF PF a ++=①. 又212PF PF c ⋅=,∴21212cos PF PF F PF c ⋅∠=②,由余弦定理,得2222121212122cos 4PF PF PF PF F PF F F c +-⋅∠==③,由①②③,得22212122223,cos 23c PF PF a c F PF a c ⋅=-∠=-,∵2220123c a c <<-,a <,∴e .又01e <<,∴0e <<又122212()2PF PF PF PF a +⋅≤=,当且仅当12PF PF =时等号成立,∴2222223,3a c a a c -≤≤,∴e ≥.又01e <<,1e ≤<.综上,e ≤<,故选C. 6.答案：B解析：依题意可知圆2F 的圆心为(,0)c ,半径为b c -,设(,)P m n 在椭圆上,依题意有22222PT PF TF =-,当PT 取得最小值时,2PF 取得最小值,此时点P 位于椭圆的右顶点,即(,0)P a ,即2223()()()4a c b c a c ---≥-,化简得2a c b +≤,两边平方得22()2a cb +≤,即222224a ac c a c ++-≤,得25230e e +-≥,所以35e ≥.由于b c >,则22b c >,即22222,2a c c a c ->>,得2c a <,即2e <,故椭圆离心率的取值范围是35⎡⎢⎣⎭. 7.答案：A解析：∵12(,0),(,0)F c F c -,∴直线)y x c =+过点1F .∴1260MF F ∠=︒,∴21121302MF F MF F ∠=∠=︒,∴1290F MF ∠=︒,∴12,MF c MF ==.由椭圆定义,知122MF MF c a +=+=,∴离心率1c e a ===.8.答案：C解析：由题意,知点B 的横坐标是c ,故B 的坐标为2(,)b c a ±,∵11(,)32k ∈,∴2(,)b B c a .又(,0)A a -∴直线AB 的斜率2222222111b b a c e a k e c a ac a ac a e --=====-++++.由1132k <<,解得1223e <<. 9.答案：D解析：由题意得124PF PF +=,焦距2c =∵122PF PF -=,∴123,1PF PF ==.∵22213+=,∴12PF F △是直角三角形,且212PF F F ⊥,∴12PF F △的面积为21211122PF F F ⨯=⨯⨯故选D. 10.答案：D解析：设椭圆22221(0)x y a b a b +=>>,则当三角形面积最大时,三角形在椭圆上的顶点为椭圆短轴端点,∴222121222b c a S c b bc +=⨯⨯==≤=,∴22a ≥,∴a ≥,∴长轴长2a ≥故选D.11.答案：6解析：由22143x y +=可得(1,0)F -.设(,),22P x y x -≤≤，则22222211313(2)2444x OP FP x x y x x x x x ⎛⎫⋅=++=++-=++=++ ⎪⎝⎭，当且仅当2x =时，OP FP ⋅取得最大值6.12.解析：易知点(3,0)A 是椭圆的右焦点.∵0PM AM ⋅=,∴AM PM ⊥，∴22221PM AP AM AP =-=-.∵椭圆的右顶点到焦点A的距离最小，故min2AP=，∴minPM=13.答案：⎫⎪⎪⎣⎭解析：设两直线的交点为M ,令12,MF m MF n ==.由椭圆的定义,可得2m n a +=.因为12MF MF ⊥,所以2224m n c +=.∵22222()22()m n m n mn m n +=++≤+,当且仅当m n a ==时等号成立,即2242(4)a c ≤,∴a ≤,∴2c a ≥即2e ≥.又1e <,∴12e ≤<.14.答案：44,97⎡⎤⎢⎥⎣⎦解析：记椭圆的左焦点为1(2,0)F -,则11AF =.∵11PF PA AF ≤+,∴112189a PF PF PA AF PF =+≤++=+=,即92a ≤.∵11PF PA AF ≥-,∴112817a PF PF PA AF PF =+≥-+=-=,即72a ≥.∵2c =,∴229722c a ≤≤,即4497e ≤≤,椭圆E 的离心率的取值范围是44,97⎡⎤⎢⎥⎣⎦.15.答案：（1）将(0,4)代入C 的方程得2161b =, ∴4b =.又35c e a ==得222925a b a -=，即2169125a -=, ∴5a =.∴椭圆C 的方程为2212516x y += （2）过点(3,0)且斜率为45的直线方程为4(3)5y x =-, 设直线与椭圆C 的交点11(,)A x y ,22(,)B x y ,将直线AB 方程4(3)5y x =-代入C 的方程,得22(3)12525x x -+=, 即2380x x --=,解得123x x +=,∴121212326,(6)22255x x y y x x ++==+-=-，即所截线段中点的坐标为36(,)25-.解析：。

2020年高中数学人教A版选修优化练习第课时椭圆的简单几何性质Word版含解析

[A 组基础巩固]1．椭圆6x 2＋y 2＝6的长轴端点坐标为( )A ．(－1,0)，(1,0)B ．(－6,0)，(6,0)C ．(－6，0)，(6，0)D ．(0，－6)，(0，6)解析：方程化为x 2＋y 26＝1， ∴a 2＝6，a ＝6，长轴的端点坐标为(0，±6)．答案：D2．正数m 是2和8的等比中项，则椭圆x 2＋y 2m ＝1的离心率为( ) A.32 B. 5 C.32或52 D.32或 5解析：由题意得m 2＝2×8＝16，∵m 是正数，∴m ＝4，∴c 2＝4－1＝3，∴c ＝3，∴e ＝32.故选A.答案：A3．若P 是以F 1，F 2为焦点的椭圆x 2a 2＋y 2b 2＝1(a >b >0)上的一点，且PF 1→·PF 2→＝0，tan ∠PF 1F 2＝12，则此椭圆的离心率为( ) A.53 B.23 C.13 D.12解析：在Rt △PF 1F 2中，设PF 2＝1，则PF 1＝2，F 1F 2＝5，故此椭圆的离心率e ＝2c 2a ＝53.答案：A4．椭圆C 1：x 225＋y 29＝1和椭圆C 2：x 29－k ＋y 225－k＝1(0＜k ＜9)有( ) A ．等长的长轴B ．相等的焦距C ．相等的离心率D ．等长的短轴解析：对椭圆C 1，c 1＝a 21－b 21＝4，对椭圆C 2，∵0＜k ＜9，∴25－k ＞9－k ＞0. 其焦点在y 轴上，∴c 2＝25－k －(9－k )＝4，故选B答案：B 5．若椭圆中心在原点，对称轴为坐标轴，长轴长为23，离心率为33，则该椭圆的方程为( )A.x 212＋y 28＝1B.x 212＋y 28＝1或y 212＋x 28＝1C.x 23＋y 22＝1D.x 23＋y 22＝1或y 23＋x 22＝1解析：由题意知a ＝3，又∵e ＝33，∴c ＝1，∴b 2＝a 2－c 2＝3－1＝2，所求椭圆方程为x 23＋y 22＝1或y 23＋x 22＝1.故选D.答案：D6．已知椭圆的中心在原点，焦点在y 轴上，若其离心率为12，焦距为8，则该椭圆的方程是________．解析：由题意知，2c ＝8，c ＝4，∴e ＝c a ＝4a ＝12，∴a ＝8，从而b 2＝a 2－c 2＝48，∴方程是y 264＋x 248＝1.答案：y 264＋x 248＝17．已知椭圆x 2a 2＋y 2b 2＝1有两个顶点在直线x ＋2y ＝2上，则此椭圆的焦点坐标是________．解析：直线与x 轴，y 轴的交点分别为A (2,0)，B (0,1)，由题意a ＝2，b ＝1，椭圆方程为x 24＋y 2＝1，c 2＝a 2－b 2＝3，故椭圆的焦点坐标为(±3，0)．答案：(±3，0)8．过椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左焦点F 1作x 轴的垂线交椭圆于点P ，F 2为右焦点，若∠F 1PF 2＝60°，则该椭圆的离心率为________．解析：如图所示，在Rt △PF 1F 2中，|F 1F 2|＝2c ，∴|PF 1|＝2c 3，|PF 2|＝4c 3. 由椭圆定义知2c 3＋4c 3＝2a ， ∴e ＝c a ＝33.答案：339．设椭圆方程为mx 2＋4y 2＝4m (m >0)的离心率为12，试求椭圆的长轴的长和短轴的长、焦点坐标及顶点坐标．解析：椭圆方程可化为x 24＋y 2m ＝1.(1)当0<m <4时，a ＝2，b ＝m ，c ＝4－m ，∴e ＝c a ＝4－m 2＝12， ∴m ＝3，∴b ＝3，c ＝1，∴椭圆的长轴的长和短轴长分别是4,23，焦点坐标为F 1(－1,0)，F 2(1,0)，顶点坐标为A 1(－2,0)，A 2(2，0)，B 1(0，－3)，B 2(0，3)．(2)当m >4时，a ＝m ，b ＝2，∴c ＝m －4，∴e ＝c a ＝m －4m ＝12，解得m ＝163， ∴a ＝433，c ＝233，∴椭圆的长轴的长和短轴的长分别为833，4，焦点坐标为F 1⎝⎛⎭⎪⎫0，－233，F 2⎝ ⎛⎭⎪⎫0，233，顶点坐标为A 1⎝ ⎛⎭⎪⎫0，－433，A 2⎝⎛⎭⎪⎫0，433，B 1(－2,0)，B 2(2,0)． 10．已知椭圆x 2k ＋8＋y 29＝1的离心率e ＝32，求k 的值．解析：(1)当椭圆的焦点在x 轴上时，a 2＝k ＋8，b 2＝9，得c 2＝k －1.由e ＝32，可得k －1k ＋8＝34，即k ＝28. (2)当椭圆的焦点在y 轴上时，a 2＝9，b 2＝k ＋8，得c 2＝1－k .由e ＝32，得1－k 9＝34，即k ＝－234.故满足条件的k 值为k ＝28或－234. [B 组能力提升]1．我国发射的“神舟六号”载人航天飞船的运行轨道是以地球的中心为一个焦点的椭圆，设其近地点A 距地面为n 千米，远地点B 距地面为m 千米，地球半径为R 千米，则飞船运行轨道的短轴长为( )A ．2(m ＋R )(n ＋R )千米 B.(m ＋R )(n ＋R )千米C ．mn 千米D ．2mn 千米解析：设运行轨道的长半轴长为a ，焦距为2c ，由题意，可得⎩⎪⎨⎪⎧ a －c ＝n ＋R ，a ＋c ＝m＋R ，解得a ＝m ＋n 2＋R ，c ＝m －n 2，故b ＝a 2－c 2＝⎝ ⎛⎭⎪⎫m ＋n 2＋R 2－⎝ ⎛⎭⎪⎫m －n 22＝R 2＋(m ＋n )R ＋mn ＝(m ＋R )(n ＋R ).即2b ＝2(m ＋R )(n ＋R ).答案：A2.已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点为F 1， F 2，过F 2的直线与圆x 2＋y 2＝b 2相切于点A ，并与椭圆C 交于不同的两点P ，Q ，如图，若A ，F 2为线段PQ 的三等分点，则椭圆的离心率为( )A.23B.33C.53 D.73解析：连接PF1，由题意知OA ＝b ，∴|PF 1|＝2b ，∴|PF 2|＝2a －2b ，∴|AF 2|＝a －b .在Rt △OAF 2中有b 2＋(a －b )2＝c 2，将b 2＝a 2－c 2代入整理得3a 2－3c 2－2a a 2－c 2＝0，即3－3e 2＝21－e 2，即9e 4－14e 2＋5＝0，解得e 2＝59或e 2＝1(舍去)，∴e ＝53.故选C.答案：C3．已知椭圆的长轴长为20，离心率为35，则该椭圆的标准方程为________．解析：由条件知，2a ＝20，c a ＝35，∴a ＝10，c ＝6，b ＝8，故标准方程为x 2100＋y 264＝1或y 2100＋x 264＝1.答案：x 2100＋y 264＝1或y 2100＋x 264＝14．(2015·高考浙江卷)椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的右焦点F (c,0)关于直线y ＝b c x 的对称点Q 在椭圆上，则椭圆的离心率是________．解析：设椭圆的另一个焦点为F 1(－c,0)，如图，连接QF 1，QF ，设QF 与直线y ＝b c x 交于点M .由题意知M 为线段QF 的中点，且OM ⊥FQ .又O 为线段F 1F 的中点，∴F 1Q ∥OM ，∴F 1Q ⊥QF ，|F 1Q |＝2|OM |.在Rt △MOF 中，tan ∠MOF ＝|MF ||OM |＝b c ，|OF |＝c ，可解得|OM |＝c 2a ，|MF |＝bc a ，故|QF |＝2|MF |＝2bc a ，|QF 1|＝2|OM |＝2c 2a .由椭圆的定义得|QF |＋|QF 1|＝2bc a ＋2c 2a ＝2a ，整理得b ＝c ，∴a ＝b 2＋c 2＝2c ，故e ＝c a ＝22. 答案：225．已知F 1，F 2是椭圆x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，点P 在椭圆上，且∠F 1PF 2＝π2.记线段PF 1与y 轴的交点为Q ，O 为坐标原点，若△F 1OQ 与四边形OF 2PQ 的面积之比为1∶2，求该椭圆的离心率．解析：依题知，F 1P ⊥F 2P ，所以△F 1QO ∽△F 1F 2P ，因为△F 1OQ 与四边形OF 2PQ的面积之比为1∶2，所以SF 1OQ SF 1F 2P ＝13，所以OF 1F 1P ＝13，设椭圆的焦距为2c ，则F 1P ＝3c ，F 2P ＝F 1F 22－F 1P 2＝c ，由椭圆的定义可得：3c ＋c ＝2a ，所以，e ＝c a ＝23＋1＝3－1.6.如图，椭圆x 2a 2＋y 2b 2＝1(a >b >0)的上顶点为A ，左顶点为B ，F 为右焦点，过F 作平行于AB 的直线交椭圆于C 、D 两点．作平行四边形OCED ，E 恰在椭圆上．(1)求椭圆的离心率； (2)若平行四边形OCED 的面积为6，求椭圆的方程．解析：(1)∵焦点为F (c,0)，AB 斜率为b a ，故CD 方程为y ＝b a (x －c )．与椭圆联立后消去y 得2x 2－2cx －b 2＝0.∵CD 的中点为G ⎝ ⎛⎭⎪⎫c 2，－bc 2a ，点E 的坐标为⎝ ⎛⎭⎪⎫c ，－bc a ，将E ⎝ ⎛⎭⎪⎫c ，－bc a 代入椭圆方程并整理得2c 2＝a 2， ∴e ＝c a ＝22.(2)由(1)知CD 的方程为y ＝22(x －c )，b ＝c ，a ＝2c .与椭圆联立消去y 得2x 2－2cx －c 2＝0. ∵平行四边形OCED 的面积为 S ＝c |y C －y D |＝22c (x C ＋x D )2－4x C x D ＝22c c 2＋2c 2 ＝62c 2＝6，∴c ＝2，a ＝2，b ＝ 2.故椭圆方程为x 24＋y 22＝1.。

高中数学人教A版选修2-12.2第2课时椭圆的简单几何性质.docx

2.2第2课时椭圆的简单几何性质一、选择题1．将椭圆C 1∶2x 2＋y 2＝4上的每一点的纵坐标变为原来的一半，而横坐标不变，得一新椭圆C 2，则C 2与C 1有( )A ．相等的短轴长B ．相等的焦距C ．相等的离心率D ．相等的长轴长[答案] C[解析] 把C 1的方程化为标准方程，即 C 1：x 22＋y 24＝1，从而得C 2：x 22＋y 2＝1.因此C 1的长轴在y 轴上，C 2的长轴在x 轴上． e 1＝22＝e 2，故离心率相等，选C. 2．若椭圆的短轴为AB ，它的一个焦点为F 1，则满足△ABF 1为等边三角形的椭圆的离心率是( )A.14B.12C.22D.32 [答案] D[解析] △ABF 1为等边三角形， ∴2b ＝a ，∴c 2＝a 2－b 2＝3b 2 ∴e ＝c a＝c 2a 2＝3b 24b 2＝32. 3．(2010·广东文，7)若一个椭圆长轴的长度、短轴的长度和焦距成等差数列，则该椭圆的离心率是( )A.45B.35C.25D.15 [答案] B[解析] 本题考查了离心率的求法，这种题目主要是设法把条件转化为含a ，b ，c 的方程式，消去b 得到关于e 的方程，由题意得：4b ＝2(a ＋c )⇒4b 2＝(a ＋c )2⇒3a 2－2ac －5c 2＝0⇒5e 2＋2e －3＝0(两边都除以a 2)⇒e ＝35或e ＝－1(舍)，故选B.4．已知椭圆2x 2＋y 2＝2的两个焦点为F 1，F 2，且B 为短轴的一个端点，则△F 1BF 2的外接圆方程为( )A ．x 2＋y 2＝1B ．(x －1)2＋y 2＝4C ．x 2＋y 2＝4D ．x 2＋(y －1)2＝4[答案] A[解析] 椭圆的焦点为F 1(0,1)，F 2(0，－1)，短轴的一个端点为(1,0)，于是△F 1BF 2的外接圆是以原点为圆心，以1为半径的圆，其方程为x 2＋y 2＝1.5．已知椭圆的长轴长为20，短轴长为16，则椭圆上的点到椭圆中心距离的取值范围是( )A ．[6,10]B ．[6,8]C ．[8,10]D ．[16,20][答案] C[解析] 由题意知a ＝10，b ＝8，设椭圆上的点M (x 0，y 0)，由椭圆的范围知，|x 0|≤a ＝10，|y 0|≤b ＝8，点M 到椭圆中心的距离d ＝x 20＋y 20. 又因为x 20100＋y 2064＝1，所以y 20＝64(1－x 20100)＝64－1624x 20，则d ＝x 20＋64－1625x 2＝925x 20＋64，因为0≤x 20≤100，所以64≤925x 20＋64≤100，所以8≤d ≤10. 6．椭圆C 1：x 225＋y 29＝1和椭圆C 2：x 29－k ＋y 225－k ＝1 (0<k <9)有( )A ．等长的长轴B ．相等的焦距C ．相等的离心率D ．等长的短轴[答案] B[解析] 依题意知椭圆C 2的焦点在y 轴上，对于椭圆C 1：焦距＝225－9＝8，对于椭圆C 2：焦距＝2(25－k )－(9－k )＝8，故答案为B.7．椭圆的两个焦点与它的短轴的两个端点是一个正方形的四个顶点，则椭圆离心率为( )A.22 B.32 C.53 D.63[答案] A[解析] 由题意知b ＝c ，∴a ＝2c ，∴e ＝c a ＝22.8．已知椭圆的对称轴是坐标轴，离心率为13，长轴长为12，则椭圆方程为( )A.x 24＋y 26＝1 B.x 26＋y 24＝1 C.x 236＋y 232＝1或x 232＋y 236＝1 D.x 236＋y 232＝1 [答案] C[解析] ∵长轴长2a ＝12，∴a ＝6，又e ＝13∴c ＝2，∴b 2＝a 2－c 2＝32，∵焦点不定， ∴方程为x 236＋y 232＝1或x 232＋y 236＝1.9．已知点(3,2)在椭圆x 2a 2＋y 2b 2＝1上，则( )A ．点(－3，－2)不在椭圆上B ．点(3，－2)不在椭圆上C ．点(－3,2)在椭圆上D ．无法判断点(－3，－2)、(3，－2)、(－3,2)是否在椭圆上 [答案] C[解析] ∵点(3,2)在椭圆x 2a 2＋y 2b 2＝1上，∴由椭圆的对称性知，点(－3,2)、(3，－2)、(－3，－2)都在椭圆上，故选C.10．椭圆x 2a 2＋y 2b 2＝1和x 2a 2＋y 2b 2＝k (k >0)具有( )A ．相同的长轴B ．相同的焦点C ．相同的顶点D ．相同的离心率[答案] D[解析] 椭圆x 2a 2＋y 2b 2＝1和x 2a 2＋y 2b 2＝k (k >0)中，不妨设a >b ，椭圆x 2a 2＋y 2b 2＝1的离心率e 1＝a 2－b 2a ，椭圆x 2a 2k ＋y 2b 2k ＝1(k >0)的离心率e 2＝k a 2－b 2ka ＝a 2－b 2a . 二、填空题11．(2009·广东理)已知椭圆G 的中心在坐标原点，长轴在x 轴上，离心率为32，且G 上一点到G 的两个焦点的距离之和为12，则椭圆G 的方程为________．[答案] x 236＋y 29＝1[解析] 设椭圆G 的标准方程为x 2a 2＋y 2b 2＝1 (a >b >0)，半焦距为c ，则⎩⎪⎨⎪⎧2a ＝12c a ＝32，∴⎩⎨⎧a ＝6c ＝33， ∴b 2＝a 2－c 2＝36－27＝9， ∴椭圆G 的方程为x 236＋y 29＝1.12．椭圆x 29＋y 22＝1的焦点为F 1，F 2，点P 在椭圆上，若|PF 1|＝4，则|PF 2|＝________，∠F 1PF 2的大小为________．[答案] 2 120°[解析] 依题知a ＝3，b ＝2，c ＝7，由椭圆定义得|PF 1|＋|PF 2|＝6，∵|PF 1|＝4，∴|PF 2|＝2.又|PF 1|＝4，|PF 2|＝2，|F 1F 2|＝27.在△F 1PF 2中，由余弦定理可得cos ∠F 1PF 2＝－12，∴∠F 1PF 2＝120°.13．椭圆x 2a 2＋y 2b 2＝1上一点到两焦点的距离分别为d 1、d 2，焦距为2c ，若d 1、2c 、d 2成等差数列，则椭圆的离心率为________．[答案] 12[解析] 由题意得4c ＝d 1＋d 2＝2a ，∴e ＝c a ＝12.14．经过椭圆x 2a 2＋y 2b 2＝1(a >b >0)的焦点且垂直于椭圆长轴的弦长为________．[答案] 2b 2a[解析] ∵垂直于椭圆长轴的弦所在直线为x ＝±c ，由⎩⎪⎨⎪⎧x ＝±c x 2a 2＋y 2b 2＝1，得y 2＝b 4a 2， ∴|y |＝b 2a ，故弦长为2b 2a .三、解答题15．已知椭圆x 2＋(m ＋3)y 2＝m (m >0)的离心率e ＝32，求m 的值及椭圆的长轴和短轴的长、焦点坐标、顶点坐标．[解析] 椭圆方程可化为x 2m ＋y 2mm ＋3＝1，∵m －mm ＋3＝m (m ＋2)m ＋3>0，∴m >m m ＋3.即a 2＝m ，b 2＝mm ＋3，c ＝a 2－b 2＝m (m ＋2)m ＋3. 由e ＝32得，m ＋2m ＋3＝32，∴m ＝1. ∴椭圆的标准方程为x 2＋y 214＝1，∴a ＝1，b ＝12，c ＝32.∴椭圆的长轴长为2，短轴长为1；两焦点坐标分别为F 1(－32，0)，F 2(32，0)；四个顶点分别为A 1(－1,0)，A 2(1,0)，B 1(0，－12)，B 2(0，12)．16．已知椭圆的中心在原点，它在x 轴上的一个焦点F 与短轴的两个端点B 1，B 2的连线互相垂直，且这个焦点与较近的长轴的端点A 的距离为10－5，求这个椭圆的方程．[解析] 由于椭圆中心在原点，焦点在x 轴上，可设其方程为x 2a 2＋y 2b 2＝1(a >b >0)．由椭圆的对称性知，|B 1F |＝|B 2F |，又B 1F ⊥B 2F ，因此△B 1FB 2为等腰直角三角形，于是|OB 2|＝|OF |，即b ＝c .又|F A |＝10－5即a －c ＝10－5，且a 2＋b 2＝c 2. 将以上三式联立，得方程组，⎩⎪⎨⎪⎧b ＝ca －c ＝10－5a 2＝b 2＋c 2解得⎩⎨⎧a ＝10b ＝5所求椭圆方程是x 210＋y 25＝1.17．已知椭圆x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率e ＝32，连接椭圆的四个顶点得到的菱形的面积为4.求椭圆的方程．[解析] 由e ＝c a ＝32，得3a 2＝4c 2，再由c 2＝a 2－b 2，得a ＝2b .由题意可知12×2a ×2b ＝4，即ab ＝2.解方程组⎩⎪⎨⎪⎧a ＝2b ，ab ＝2，得a ＝2，b ＝1，所以椭圆的方程为x 24＋y 2＝1.。

3.1.2椭圆的简单几何性质教案-高一上学期数学人教A版选择性(1)

.1椭圆的简单几何性质课标解读1.掌握椭圆的简单几何性质，了解椭圆标准方程中a，b，c的几何意义.2.会利用椭圆的几何性质求标准方程.3.会求椭圆的离心率.4.根据椭圆的方程研究曲线的几何性质，并正确地画出它的图形．学情分析1.前面的章节已经学习了椭圆的定义，有了一定的基础。

2.在讨论椭圆性质时，易忽略焦点位置的讨论3.离心率的计算比较复杂，有一定难度。

教学重难点1.根据椭圆的方程研究曲线的几何性质，并正确地画出它的图形．(重点)2．根据几何条件求出曲线方程，利用曲线的方程研究它的性质，并能画出相应的曲线．(重点、难点)温故导新与利用直线的方程、圆的方程研究它们的几何性质一样，我们利用椭圆的标准方程椭圆的几何性质，包括椭圆的范围、形状、大小、对称性和特殊点等用笔思考问题1观察椭圆x2a2＋y2b2＝1(a>b>0)的形状，你能从图上看出它的范围吗？它具有怎样的对称性？椭圆上哪些点比较特殊？提示范围：－a≤x≤a，－b≤y≤b；对称性：对称轴为x轴，y轴，对称中心为原点；顶点：A1(－a,0)，A2(a,0)，B1(0，－b)，B2(0，b)．问题2观察图，我们发现，不同椭圆的扁平程度不同，扁平程度是椭圆的重要形状特征，你能用适当的量定量刻画椭圆的扁平程度吗？这个定量对椭圆的形状有何影响？提示利用离心率e＝ca来刻画椭圆的扁平程度．问题3如图所示，椭圆方程为x2a2＋y2b2＝1，你能根据方程确定椭圆的边界吗？提示由方程x2a2＋y2b2＝1得y2b2＝1－x2a2≥0，得－a≤x≤a，同理可得－b≤y≤b，故椭圆位于x＝±a和y＝±b围成的矩形内.问题4如上图所示，椭圆具有怎样的对称性？如何用方程加以说明？提示既关于坐标轴为轴对称，又关于原点为中心对称.方程中若(x，y)满足，则易知(x，－y)，(－x，y)，(－x，－y)也满足.主动讲解三人一组，讨论以下问题1.椭圆的离心率对椭圆形状的影响2.椭圆上哪些点比较特殊？双师导学1．椭圆的简单几何性质(1)椭圆的焦点一定在它的长轴上．(2)椭圆上到中心的距离最小的点是短轴的两个端点，到中心的距离最大的点是长轴的两个端点．(3)椭圆上到焦点的距离最大和最小的点分别是长轴的两个端点，最大值为a＋c，最小值为a－c.2.离心率(1)定义：椭圆的焦距与长轴长的比ca称为椭圆的．(2)性质：离心率e的范围是(0,1)．当e越接近于1时，椭圆；当e越接近于0时，椭圆就越接近于圆．注意点：(1)e ＝1－b 2a2. (2)离心率的范围为(0,1)．(3)e 越大，椭圆越扁平；e 越小，椭圆越接近于圆．聚焦核心1.椭圆的简单几何性质2.椭圆的离心率强化反馈1．(多选)已知椭圆C ：16x 2＋4y 2＝1，则下列结论正确的是( ) A ．长轴长为12B ．焦距为34C ．焦点坐标为⎝⎛⎭⎫0，±34 D ．离心率为32答案 CD解析由椭圆方程16x 2＋4y 2＝1化为标准方程可得x 2116＋y 214＝1，所以a ＝12，b ＝14，c ＝34 ，所以长轴长2a ＝1，焦距2c ＝32，焦点坐标为⎝⎛⎭⎫0，±34，离心率e ＝c a ＝32. 2．已知椭圆的离心率为12，焦点是(－3,0)和(3,0)，则该椭圆的方程为( )A.x 236＋y 227＝1 B.x 26＋y 23＝1 C.x 227＋y 236＝1 D.x 29＋y 26＝1 答案 A解析由题意知c ＝3，c a ＝12，则a ＝6，∴b 2＝a 2－c 2＝27， ∴椭圆的方程为x 236＋y 227＝1.3．若椭圆的两个焦点与短轴的一个端点构成一个正三角形，则该椭圆的离心率为( ) A.12 B.32 C.34 D.64 答案 A解析如图，不妨设椭圆的左、右焦点分别为F 1，F 2，B 为椭圆的上顶点．依题意可知，△BF 1F 2是正三角形． ∵在Rt △OBF 2中，|OF 2|＝c ， |BF 2|＝a ，∠OF 2B ＝60°， ∴cos 60°＝c a ＝12，即椭圆的离心率e ＝12.4．若椭圆C ：x 2m ＋y 2m 2－1＝1的一个焦点坐标为(0,1)，则C 的长轴长为________．答案 23解析 ∵椭圆的一个焦点坐标为(0,1)， ∴m 2－1－m ＝1，即m 2－m －2＝0，解得m ＝2或m ＝－1，由于x 2m ＋y 2m 2－1＝1表示的是椭圆，则m >1，∴m ＝2，则椭圆方程为y 23＋x 22＝1，∴a ＝3，2a ＝2 3.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

学习资料汇编课时跟踪检测（六）椭圆的简单几何性质层级一学业水平达标1．椭圆以两条坐标轴为对称轴，一个顶点是(0,13)，另一个顶点是(－10,0)，则焦点坐标为( )A ．(±13,0)B ．(0，±10)C ．(0，±13)D ．(0，±69)解析：选D 由题意知椭圆焦点在y 轴上，且a ＝13，b ＝10，则c ＝a 2－b 2＝69，故焦点坐标为(0，±69)．2．若椭圆的两个焦点与短轴的一个端点构成一个正三角形，则该椭圆的离心率为( ) A ．12 B ．32 C ．34D ．64解析：选A 依题意，△BF 1F 2是正三角形，∵在Rt △OBF 2中，|OF 2|＝c ，|BF 2|＝a ，∠OF 2B ＝60°，∴cos 60°＝c a ＝12，即椭圆的离心率e ＝12，故选A ．3．已知椭圆x 2a 2＋y 2b 2＝1与椭圆x 225＋y 216＝1有相同的长轴，椭圆x 2a 2＋y 2b2＝1的短轴长与椭圆y 221＋x 29＝1的短轴长相等，则( )A ．a 2＝25，b 2＝16 B ．a 2＝9，b 2＝25C ．a 2＝25，b 2＝9或a 2＝9，b 2＝25 D ．a 2＝25，b 2＝9解析：选D 因为椭圆x 225＋y 216＝1的长轴长为10，焦点在x 轴上，椭圆y 221＋x 29＝1的短轴长为6，所以a 2＝25，b 2＝9．4．已知椭圆x 2a 2＋y 2b2＝1(a >b >0)的左焦点为F ，右顶点为A ，点B 在椭圆上，且BF ⊥x 轴，直线AB 交y 轴于点P ．若AP ＝2PB ，则椭圆的离心率是( )A ．32B ．22C ．13D ．12解析：选D ∵AP ＝2PB ，∴|AP |＝2|PB |．又∵PO ∥BF ，∴|PA ||AB |＝|AO ||AF |＝23，即aa ＋c ＝23，∴e ＝c a ＝12． 5．椭圆mx 2＋ny 2＋mn ＝0(m <n <0)的焦点坐标是( ) A ．(0，±m －n ) B ．(±m －n ，0) C ．(0，±n －m )D ．(±n －m ，0)解析：选C 化为标准方程是x 2－n ＋y 2－m＝1，∵m <n <0，∴0<－n <－m ．∴焦点在y 轴上，且c ＝－m －－n ＝n －m ．6．椭圆x 24＋y 2m ＝1的离心率为12，则m ＝________．解析：当焦点在x 轴上时，4－m 2＝12⇒m ＝3；当焦点在y 轴上时，m －4m＝12⇒m ＝163．综上，m ＝3或m ＝163．答案：3或1637．已知椭圆的中心在原点，焦点在x 轴上，离心率为55，且过P (－5,4)，则椭圆的方程为________________．解析：∵e ＝c a ＝55， ∴c 2a 2＝a 2－b 2a 2＝15， ∴5a 2－5b 2＝a 2即4a 2＝5b 2．设椭圆的标准方程为x 2a 2＋5y 24a2＝1(a >0)，∵椭圆过点P (－5,4)，∴25a 2＋5×164a 2＝1．解得a 2＝45．∴椭圆方程为x 245＋y 236＝1．答案：x 245＋y 236＝18．设F 1，F 2分别为椭圆x 23＋y 2＝1的左，右焦点，点A ，B 在椭圆上，若1F A ＝5F B 2，则点A 的坐标是________．解析：设A (m ，n )．由1F A ＝5F B 2，得B ⎝⎛⎭⎪⎫m ＋625，n 5．又A ，B 均在椭圆上，所以有⎩⎨⎧m 23＋n 2＝1，⎝ ⎛⎭⎪⎫m ＋62523＋⎝ ⎛⎭⎪⎫n 52＝1，解得⎩⎪⎨⎪⎧m ＝0，n ＝1或⎩⎪⎨⎪⎧m ＝0，n ＝－1，所以点A 的坐标为(0,1)或(0，－1)．答案：(0,1)或(0，－1)9．在平面直角坐标系xOy 中，椭圆C 的中心为原点，焦点F 1，F 2在x 轴上，离心率为22，过点F 1的直线l 交椭圆C 于A ，B 两点，且△ABF 2的周长为16，求椭圆C 的标准方程．解：设椭圆C 的标准方程为x 2a 2＋y 2b2＝1(a >b >0)．由e ＝22知c a ＝22，故c 2a 2＝12，从而a 2－b 2a 2＝12，b 2a 2＝12．由△ABF 2的周长为|AB |＋|BF 2|＋|AF 2|＝|AF 1|＋|AF 2|＋|BF 1|＋|BF 2|＝4a ＝16，得a ＝4，∴b 2＝8．故椭圆C 的标准方程为x 216＋y 28＝1．10．椭圆x 2a 2＋y 2b2＝1(a >b >0)的右顶点是A (a,0)，其上存在一点P ，使∠APO ＝90°，求椭圆离心率的取值范围．解：设P (x ，y )，由∠APO ＝90°知，点P 在以OA 为直径的圆上，圆的方程是⎝ ⎛⎭⎪⎫x －a 22＋y 2＝⎝ ⎛⎭⎪⎫a 22．∴y 2＝ax －x 2．①又P 点在椭圆上，故x 2a 2＋y 2b2＝1．②把①代入②化简，得(a 2－b 2)x 2－a 3x ＋a 2b 2＝0，即 (x －a )[(a 2－b 2)x －ab 2]＝0，∵x ≠a ，x ≠0，∴x ＝ab 2a 2－b 2，又0<x <a ，∴0<ab 2a 2－b2<a ，即2b 2<a 2．由b 2＝a 2－c 2，得a 2<2c 2，∴e >22．又∵0<e <1，∴22<e <1．层级二应试能力达标1．椭圆x 225＋y 29＝1与x 29－k ＋y 225－k ＝1(0<k <9)的关系为( )A ．有相等的长轴长、短轴长B ．有相等的焦距C ．有相同的焦点D ．有相同的顶点解析：选B c 21＝25－9＝16，c 22＝(25－k )－(9－k )＝25－9＝16，所以两椭圆有相等的焦距．故选B ．2．过椭圆x 24＋y 23＝1的焦点的最长弦和最短弦的长分别为( )A ．8,6B ．4,3C ．2， 3D ．4,2 3解析：选B 过椭圆焦点的最长弦为长轴，其长度为2a ＝4；最短弦为垂直于长轴的弦，因为c ＝1，将x ＝1代入x 24＋y 23＝1，得124＋y 23＝1，解得y 2＝94，即y ＝±32，所以最短弦的长为2×32＝3．故选B ．3．与椭圆9x 2＋4y 2＝36有相同焦点，且短轴长为2的椭圆的标准方程为( ) A ．x 22＋y 24＝1B ．x 2＋y 26＝1C ．x 26＋y 2＝1D ．x 28＋y 25＝1解析：选B 椭圆9x 2＋4y 2＝36可化为x 24＋y 29＝1，可知焦点在y 轴上，焦点坐标为(0，±5)，故可设所求椭圆方程为y 2a 2＋x 2b2＝1(a >b >0)，则c ＝5．又2b ＝2，即b ＝1，所以a 2＝b 2＋c 2＝6，则所求椭圆的标准方程为x 2＋y 26＝1．4．(全国丙卷)已知O 为坐标原点，F 是椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左焦点，A ，B 分别为C 的左、右顶点．P 为C 上一点，且PF ⊥x 轴．过点A 的直线l 与线段PF 交于点M ，与y 轴交于点E ．若直线BM 经过OE 的中点，则C 的离心率为( )A ．13B ．12C ．23D ．34解析：选A 如图所示，由题意得A (－a,0)，B (a,0)，F (－c,0)．设E (0，m )，由PF ∥OE ，得|MF ||OE |＝|AF ||AO |，则|MF |＝m a －ca．① 又由OE ∥MF ，得12|OE ||MF |＝|BO ||BF |，则|MF |＝m a ＋c2a．② 由①②得a －c ＝12(a ＋c )，即a ＝3c ，∴e ＝c a ＝13．故选A ．5．已知椭圆x 2a 2＋y 2b 2＝1(a >b >0)，A ，B 分别为椭圆的左顶点和上顶点，F 为右焦点，且AB ⊥BF ，则椭圆的离心率为________．解析：在Rt △ABF 中，|AB |＝a 2＋b 2，|BF |＝a ，|AF |＝a ＋c ，由|AB |2＋|BF |2＝|AF |2，得a 2＋b 2＋a 2＝(a ＋c )2．将b 2＝a 2－c 2代入，得a 2－ac －c 2＝0，即e 2＋e －1＝0，解得e ＝－1±52．因为e >0，所以e ＝5－12．答案：5－126．已知椭圆的长轴长为20，短轴长为16，则椭圆上的点到椭圆中心的距离的取值范围是________．解析：由题意，知a ＝10，b ＝8，不妨设椭圆方程为x 2100＋y 264＝1，其上的点M (x 0，y 0)，则|x 0|≤a ＝10，|y 0|≤b ＝8，点M 到椭圆中心的距离d ＝x 20＋y 20．因为x 20100＋y 2064＝1，所以y 2＝64⎝ ⎛⎭⎪⎫1－x 20100＝64－1625x 20，则d ＝x 20＋64－1625x 20＝925x 20＋64，因为0≤x 20≤100，所以64≤925x 20＋64≤100，即8≤d ≤10．答案：[8,10]7．已知椭圆x 2＋(m ＋3)y 2＝m (m >0)的离心率e ＝32，求实数m 的值及椭圆的长轴长和短轴长，并写出焦点坐标和顶点坐标．解：椭圆方程可化为x 2m ＋y 2mm ＋3＝1，由m －mm ＋3＝m m ＋m ＋3>0，可知m >mm ＋3，所以a 2＝m ，b 2＝mm ＋3，c ＝a 2－b 2＝ m m ＋m ＋3，由e ＝32，得 m ＋2m ＋3＝32，解得m ＝1．于是椭圆的标准方程为x 2＋y 214＝1，则a ＝1，b ＝12，c ＝32．所以椭圆的长轴长为2，短轴长为1；两焦点坐标分别为⎝ ⎛⎭⎪⎫－32，0，⎝ ⎛⎭⎪⎫32，0；四个顶点坐标分别为(－1,0)，(1,0)，⎝⎛⎭⎪⎫0，－12，⎝ ⎛⎭⎪⎫0，12．8．设F 1，F 2分别是椭圆E ：x 2a 2＋y 2b2＝1(a >b >0) 的左、右焦点，过点 F 1的直线交椭圆 E于 A ，B 两点，|AF 1|＝3|F 1B |．(1)若|AB |＝4，△ABF 2 的周长为16，求|AF 2|； (2)若cos ∠AF 2B ＝35，求椭圆E 的离心率．解：(1)由|AF 1|＝3|F 1B |，|AB |＝4，得|AF 1|＝3，|F 1B |＝1．因为△ABF 2的周长为16，所以由椭圆定义可得4a ＝16，|AF 1|＋|AF 2|＝2a ＝8．故|AF 2|＝8－3＝5．(2)设|F 1B |＝k ，则k >0且|AF 1|＝3k ，|AB |＝4k ．由椭圆定义可得，|AF 2|＝2a －3k ，|BF 2|＝2a －k ．在△ABF 2中，由余弦定理可得，|AB |2＝|AF 2|2＋|BF 2|2－2|AF 2|·|BF 2|·cos∠AF 2B ，即(4k )2＝(2a －3k )2＋(2a －k )2－65(2a －3k )·(2a －k )．化简可得(a ＋k )(a －3k )＝0，而a ＋k >0，故a ＝3k ．于是有|AF 2|＝3k ＝|AF 1|，|BF 2|＝5k ．因此|BF 2|2＝|F 2A |2＋|AB |2，可得F 1A ⊥F 2A ，故△AF 1F 2为等腰直角三角形．从而c ＝22a ，所以椭圆E 的离心率e ＝c a ＝22．敬请批评指正。