第六章 整数规划
合集下载
运筹学课件 第六章-整数规划3
物品 1 2 3 4 5 6 7 8 9 10
体积 200 350 500 430 320 120 700 420 250 100
价格 15 45 100 70 50 75 200 90 20 30
设变量xij为第i个物品是否放在第j个包裹中
xij 1,0; i 1,2...,17, j 1,2,3
• 保证需求约束
x11 + x21 + x31 = 450 x12 + x22 + x32 = 275 x13 + x23 + x33 = 300 x14 + x24 + x34 = 350
} 项目1 } 项目2 } 项目3 } 项目4
最大供应量 525 450 550
约束条件：
厂家1一旦向某项目供应水泥，其至少供应量为150。 厂家2对单个项目供应量超过200吨的项目数不大于1。总产量=450 厂家3仅接受 200, 400, 和 550 吨这三个规格的货单。
1 中锋 1.93 2 中锋 1.91 3 前锋 1.87 4 前锋 1.86 5 后卫 1.80 6 后卫 1.85
配送计划模型
• 某建筑公司为完成4个工程项目，需要从3个厂家购买水泥，有关成
本如下
厂家1 厂家2 厂家3 需求量(吨)
项目1 $120 $100 $140 450
水泥的吨运费
项目2 $115 $150 $95 275
xi
0, 不携带第i件物品 1, 携带第i件物品 (i
1,2,, m)
m
max z ci xi i 1
m
ai xi
a
st.
i 1 m
bi
运筹学整数规划
运筹学整数规划运筹学是研究在资源有限的条件下，如何进行决策和优化的一门学科。
整数规划是运筹学中的一个重要分支，它解决的是决策变量必须为整数的问题。
整数规划在实际问题中具有广泛的应用，如生产计划、设备配置、选址问题等。
整数规划问题的数学模型可以表示为：max/min c^T xs.t. Ax ≤ bx ≥ 0x ∈ Z其中，c是目标函数的系数矩阵，x是决策变量的向量，A是约束条件的系数矩阵，b是约束条件的向量，Z表示整数集合。
整数规划问题与线性规划问题相似，但整数规划问题的约束条件多了一个整数限制，使得问题的解空间变得更为复杂。
由于整数规划问题的NP-hard性质，求解整数规划问题是一项困难的任务。
求解整数规划问题的常用方法有分支定界法、割平面法和启发式算法等。
分支定界法是一种穷举搜索的方法，它通过将整数规划问题不断分割成更小的子问题，从而逐步搜索解空间，直到找到最优解。
分支定界法对于规模较小的问题比较有效，但对于大规模复杂问题，效率较低。
割平面法是一种通过添加新的约束条件来减少解空间的方法。
它利用线性松弛问题（将整数约束条件放宽为线性约束条件）的解来构造有效的割平面，从而逐步缩小解空间，找到最优解。
割平面法通常比分支定界法更有效，但对于某些问题，可能需要添加大量的割平面才能收敛到最优解。
启发式算法是一种基于经验和启发式搜索的方法。
它通过设置初始解、搜索策略和邻域搜索等步骤，来快速找到近似最优解。
常见的启发式算法有遗传算法、模拟退火算法和禁忌搜索算法等。
启发式算法虽然不能保证找到全局最优解，但能够在可接受的时间内找到较优解。
综上所述，整数规划作为运筹学中的重要分支，解决的是决策变量必须为整数的问题。
整数规划问题具有广泛的应用，但由于其NP-hard性质，求解过程较为困难。
常用的求解方法包括分支定界法、割平面法和启发式算法等。
这些方法各有优劣，根据具体问题的特点选择合适的方法进行求解。
《运筹学》第6章 整数规划
整数规划（Integer Programming，简称IP），是 要求全部或部分决策变量为整数的规划。整数规 划分为线性整数规划和非线性整数规划。本章只 介绍线性整数规划，简称为整数规划。
整数规划分为两大类：一般整数规划与0-1整数规 划（Binary Integer Programming，简称BIP）。
6.3 0-1整数规划
例6.2 分公司选址问题。某销售公司打算通过在武汉 或长春设立分公司（也可以在两个城市都设分公司） 以增加市场份额，管理层同时也在考虑建立一个配送 中心（也可以不建配送中心），但配送中心地点限制 在新设分公司的城市。
经过计算，每种选择使公司收益的净现值和所需费 用如表6-2所示。总的预算费用不得超过1000万元。目 标是在满足以上约束的条件下使总的净现值最大。
100万元 500万元
2
大型飞机
500万元 5000万元 没有限制
可获得的总资金 1亿元
6.1 整数规划基本概念、分类与解的特点
解：
(1)决策变量
设小型飞机与大型飞机的购买 数量分别为x1、x2(架)。 (2)目标函数
目标是年总净利润最大。
M ax z x1 5 x2
(3) 约束条件 ① 资金限制 ② 小型飞机数量限制（最多
在长春设立分公司 在武汉设立分公司 在长春建配送中心 在武汉建配送中心
净现值（万元） 800 500 600 400
所需资金（万元） 600 300 500 200
6.3 0-1整数规划
解：
（1）决策变量
本题的决策变量是是非决策的0-1决策变量，每一个决策只有 两种选择，是或者否，1表示对于这个决策选择“是”，0表 示对于这个决策选择“否” 。
是非决策问题
整数规划分为两大类：一般整数规划与0-1整数规 划（Binary Integer Programming，简称BIP）。
6.3 0-1整数规划
例6.2 分公司选址问题。某销售公司打算通过在武汉 或长春设立分公司（也可以在两个城市都设分公司） 以增加市场份额，管理层同时也在考虑建立一个配送 中心（也可以不建配送中心），但配送中心地点限制 在新设分公司的城市。
经过计算，每种选择使公司收益的净现值和所需费 用如表6-2所示。总的预算费用不得超过1000万元。目 标是在满足以上约束的条件下使总的净现值最大。
100万元 500万元
2
大型飞机
500万元 5000万元 没有限制
可获得的总资金 1亿元
6.1 整数规划基本概念、分类与解的特点
解：
(1)决策变量
设小型飞机与大型飞机的购买 数量分别为x1、x2(架)。 (2)目标函数
目标是年总净利润最大。
M ax z x1 5 x2
(3) 约束条件 ① 资金限制 ② 小型飞机数量限制（最多
在长春设立分公司 在武汉设立分公司 在长春建配送中心 在武汉建配送中心
净现值（万元） 800 500 600 400
所需资金（万元） 600 300 500 200
6.3 0-1整数规划
解：
（1）决策变量
本题的决策变量是是非决策的0-1决策变量，每一个决策只有 两种选择，是或者否，1表示对于这个决策选择“是”，0表 示对于这个决策选择“否” 。
是非决策问题
第六章 整数规划(应用运筹学)
x2≥3
线性规划B6 Z5=6 x1=0 , x2=3
z6
z 6
§3 0—1规划Binary integer programming
当我面临是与非两种选择时，我们可以用决策变量取0或1值来表示 这样的决策，这样，地j个是非决策问题可以表示成
if decision j is yes, 1 如果决策是 xj if decision j is no 0 如果决策是非
x2 3 2 1 2x1+3x2 =6 o 1 2 3 4 x1 2x1+3x2 =14 2x1+3x2 =14.66
得到线性规划的最优解为x1=2.44, x2=3.26,目标函数值为14.66。 由图表可看出，整数规划的最优解为x1=4, x2=2,目标函数值为14。
性质1：任何求最大目标函数值的纯整数规划或混合整数规划的最大目
B0
max z =x1+2x2 s.t. 2x1+5x2 ≤ 15 2x1－2x2 ≤5 x1 , x2≥0
x2为整数的限制条件，得规 划B0对应的最优解与最优 值如下，而 X=(0，0)为A0 3 的可行解 B0 13 3 T 11 X (3 ,1 ) , z 6 14 7 14
2x1＋5x2=15
(1)每求出一次符合整数的解，都要考虑修改下界
函数值最大者为新的下界 (2)修改
z
，选整数解的目标
z
0
z ，找出所有未 分枝问题目标函数值最大者，为新的上界 z 当改变完上、下界 z ，z 后，若 z ＝ z，则所有分枝均已查明，得到 A
的最优解， 若
z＞ z
，则说明仍有分枝未查明，返回到第四步
分枝定界法
分枝定界法步骤
6第六章 整数规划(3-4节)
max z 7 x1 9 x 2 6 x1 3 x 2 x 3 x 4 35 7 x1 x 2 x 、x 0， 整 数 1 2
x 3 6 x1 3 x 2 x 4 35 7 x1 x 2
第36页
将上式代入割平面约束：
优解为止。
第2页
一、割平面的概念
通过举例来阐述割平面的概念 。
例：
maxz 7 x1 9 x 2 x1 3 x 2 6 7 x1 x 2 35 x 、x 0， 整 数 1 2
第3页
x1
C 3
2 D
B A 4
5
7
x2
可行域：ABCD
1 1 最优解：C点，其坐标为 ( x1 , x2 ) (4 ,3 ) 2 2
第27页
解：（1）利用单纯型法求解原问题的松弛问题 B ：
cj
CB XB b
7
x1
9
x2
0
x3
0
x4
θi
9
7
x2
x1
7/2
9/2
0
1
1
0
7/22
-1/22
1/22
3/22
c j– z j
0
0
-28/11 -15/11
第28页
（2）构造割平面约束 x1 = 9/2 = 4 + 1/2 x2 = 7/2 = 3 + 1/2
N
4
5
7
x2 Q
割去的部分 EFGCE 中不包含任何整数解。
第6页
新增加的线性约束条件切割掉了原问题可行域的一
部分，但该可行域内不包含任何整数可行解，所有
整数规划
15
16
1、0-1整数规划的应用
¾ 投资分析
关于固定投资的资金预算决策是一个是或否的决 策，其表达形式如下： 每个是或否的决策： 是否应该在固定投资项目上投资？
决策变量
=
⎧1， ⎩⎨0，
是 否
17
¾ 选址
每个可选地点的选择都是一个是或否的决策，其 表达形式如下： 每个是或否的决策： 是否应该选择该地建新设施？
引入N个辅助0-1变量yj。
yj
=
⎧0, ⎩⎨1,
if Constraint j is chosen if Constraint j is not chosen
2、产品互斥的约束以及xj和yj关系的约束 y1+y2≤1 x1 ≤ My1 x2 ≤ My2
3、决策变量的约束
x1 ≥ 0, x2 ≥ 0 且为整数； y1, y2都是0-1变量。
41
42
7
该问题的整数规划模型为：
Max s.t.
z=300x1+500x2 x1≤ 4
2x2 ≤ 12 3x1+2x2 ≤ 18
6
1
每架飞机的年利润 飞机的单位购价 最多购买数量
小型飞机
$100万 $500万
2
大型飞机
$500万 $5000万
−
可获得的资 金总额
$1亿
问题：为了获得最大的利润，公司应该购买多 少飞机，各种型号又该如何组合呢？
7
整数规划模型：
决策变量： S=购买小型机的数量 L=购买大型机的数量
Max Z=S+5L （百万美元） s.t. 5S+50L≤ 100
5
6.1 范例
例1、TBA航空公司
运筹学 第六章 整数规划 第一讲 整数规划数学模型与纯整数规划的求解
项目 所需资金（万元） 收益期望值（万元）
A B C D E
6 4 2 4 5
10 8 7 6 9
A，B，C，D，E 之间的关系是： ① A、C、E 三项中需且只能选一项； ② B、D 两项中需且只能选一项； ③ 选 C 必须先选 D 。 问题：如何选择投资决策，使总投资期望值最大？
6.1 整数规划的数学模型 Mathematical Model of IP
① 求解LP : 如果LP无最优解, 则IP无最优解;
设LP的最优解为x , 最优值为z , 则IP的最优值z * 满足 :
z z* z
其中 z 为IP在任何一个可行解处的目标值.
② 检验与分支：
如果x 满足IP的整数要求, 则x为IP的最优解：z* z . 否则 考虑一个不满足整数要求的xr , 将约束
示不安排第i人去做 j工 作。逻辑变量也是只允许取整数值的一类变量。
整数线性规划数学模型的一般形式：
max Z (或 min Z ) c j x j
j 1 n
要求一部分或全部决策变量取整数值
n a ij x j bi ( i 1.2 m ) j 1 x j 0 (j 1.2n) 且 部 分 或 全 部 为 整 数
xr xr 和
xr xr 1
分别加入LP形成两个子问题 a] ([
不超过a的最大整数)
6.2 纯整数规划的求解 Solving Pure Integer Programming
Ch6 整数规划 Integer Programming
n
max
z cj xj
j 1
ij j
不考虑整数条件，由余下的目标函数和 约束条件构成的规划问题称为该整数规 划问题的松弛问题。
A B C D E
6 4 2 4 5
10 8 7 6 9
A，B，C，D，E 之间的关系是： ① A、C、E 三项中需且只能选一项； ② B、D 两项中需且只能选一项； ③ 选 C 必须先选 D 。 问题：如何选择投资决策，使总投资期望值最大？
6.1 整数规划的数学模型 Mathematical Model of IP
① 求解LP : 如果LP无最优解, 则IP无最优解;
设LP的最优解为x , 最优值为z , 则IP的最优值z * 满足 :
z z* z
其中 z 为IP在任何一个可行解处的目标值.
② 检验与分支：
如果x 满足IP的整数要求, 则x为IP的最优解：z* z . 否则 考虑一个不满足整数要求的xr , 将约束
示不安排第i人去做 j工 作。逻辑变量也是只允许取整数值的一类变量。
整数线性规划数学模型的一般形式：
max Z (或 min Z ) c j x j
j 1 n
要求一部分或全部决策变量取整数值
n a ij x j bi ( i 1.2 m ) j 1 x j 0 (j 1.2n) 且 部 分 或 全 部 为 整 数
xr xr 和
xr xr 1
分别加入LP形成两个子问题 a] ([
不超过a的最大整数)
6.2 纯整数规划的求解 Solving Pure Integer Programming
Ch6 整数规划 Integer Programming
n
max
z cj xj
j 1
ij j
不考虑整数条件，由余下的目标函数和 约束条件构成的规划问题称为该整数规 划问题的松弛问题。
第六章 整数规划(2012)
割平面法cutting plane approach 构造切割方程的步骤： 2、将（2 式）代入（1 式）得： xi + ∑ Nik xk - Ni = fi - ∑ fik xk ……………………（3 式） 3、提出变量为整（当然含非负）的条件： 由于（3 式）中等式左边需整，而 0 ＜ fi ＜ 1 ，故有 fi - ∑ fik xk ≤ 0 ……………………（4 式） 此即为所需切割方程。
16
第三节 割平面法
割平面法cutting plane approach 构造切割方程的步骤： （1）切割方程 fi - ∑ fik xk ≤ 0 真正进行了切割，至少把非整数最优 解这一点切割掉了。 证明：（反证法）假设松驰问题的最优解 X* 未被切割掉，则由 fi - ∑ fik x*k ≤ 0， 又因为 x*k = 0，（因 x*k 为非基变量） 有 fi ≤ 0 ，这与 fi ＞ 0 矛盾。 （2）不会切割掉任何整数解，因为切割方程是由变量为整的条件 提出的。
该整数规划松弛问题的解为： （X1 ，X2 ）= （3/2 ，10/3） Z1 = 29/6
7
第二节 分支定界法
分支定界法图解整数规划
（3/2 ，10/3） Z1 = 29/6 B1：解 （2，23/9 ） Z11 = 41/9 B2 Max 松弛问题 Max Z = X1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ， X2 ≥ 0 B1 Max Z = X 1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ≥2 X1 ， X2 ≥ 0 Z = X 1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ≤1 X1 ， X2 ≥ 0
16
第三节 割平面法
割平面法cutting plane approach 构造切割方程的步骤： （1）切割方程 fi - ∑ fik xk ≤ 0 真正进行了切割，至少把非整数最优 解这一点切割掉了。 证明：（反证法）假设松驰问题的最优解 X* 未被切割掉，则由 fi - ∑ fik x*k ≤ 0， 又因为 x*k = 0，（因 x*k 为非基变量） 有 fi ≤ 0 ，这与 fi ＞ 0 矛盾。 （2）不会切割掉任何整数解，因为切割方程是由变量为整的条件 提出的。
该整数规划松弛问题的解为： （X1 ，X2 ）= （3/2 ，10/3） Z1 = 29/6
7
第二节 分支定界法
分支定界法图解整数规划
（3/2 ，10/3） Z1 = 29/6 B1：解 （2，23/9 ） Z11 = 41/9 B2 Max 松弛问题 Max Z = X1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ， X2 ≥ 0 B1 Max Z = X 1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ≥2 X1 ， X2 ≥ 0 Z = X 1 + X2 14X1 + 9X2 ≤ 51 - 6X1 + 3X2 ≤ 1 X1 ≤1 X1 ， X2 ≥ 0
第6章 整数规划--使用的讲义
整 数 规划
(Integer Programming)
整数规划的模型
分支定界法 割平面法 0－1 整数规划
指派问题
概述
• 整数规划是一类要求变量取整数值的数 学规划，可分成线性和非线性两类。
• 根据变量的取值性质，又可以分为全整 数规划，混合整数规划，0-1整数规划等。
• 整数规划是数学规划中一个较弱的分支， 目前只能解中等规模的线性整数规划问 题，而非线性整数规划问题，还没有好 的办法。
考虑纯整数问题：
(IP)
n j 1
aij x j
bi
(i 1.2
m)
x
j
0,(
j
1.2
n)且为整数
n
max Z c j x j
j 1
整数问题的松弛问题：
(
LP)
n
aij x j
(j 1.2
n)且为整数
例2、某公司计划在m个地点建厂，可供选择的地点有 A1,A2…Am ，他们的生产能力分别不超过a1,a2,…am（假
设生产同一产品）。第i个工厂的建设费用为fi
(i=1.2…m),又有n个地点B1,B2, … Bn 需要销售这种产品， 其销量分别不少于b1.b2…bn 。从工厂运往销地的单位 运费为Cij。试决定应在哪些地方建厂，即满足各地需 要，又使总建设费用和总运输费用最省？
1 在Ai建厂
又设 yi＝
（i=1.2…m）
0 不在Ai建厂 m
模型：min Z
cij xij fi yi
i 1
n
xij ai yi
(i 1.2
(Integer Programming)
整数规划的模型
分支定界法 割平面法 0－1 整数规划
指派问题
概述
• 整数规划是一类要求变量取整数值的数 学规划，可分成线性和非线性两类。
• 根据变量的取值性质，又可以分为全整 数规划，混合整数规划，0-1整数规划等。
• 整数规划是数学规划中一个较弱的分支， 目前只能解中等规模的线性整数规划问 题，而非线性整数规划问题，还没有好 的办法。
考虑纯整数问题：
(IP)
n j 1
aij x j
bi
(i 1.2
m)
x
j
0,(
j
1.2
n)且为整数
n
max Z c j x j
j 1
整数问题的松弛问题：
(
LP)
n
aij x j
(j 1.2
n)且为整数
例2、某公司计划在m个地点建厂，可供选择的地点有 A1,A2…Am ，他们的生产能力分别不超过a1,a2,…am（假
设生产同一产品）。第i个工厂的建设费用为fi
(i=1.2…m),又有n个地点B1,B2, … Bn 需要销售这种产品， 其销量分别不少于b1.b2…bn 。从工厂运往销地的单位 运费为Cij。试决定应在哪些地方建厂，即满足各地需 要，又使总建设费用和总运输费用最省？
1 在Ai建厂
又设 yi＝
（i=1.2…m）
0 不在Ai建厂 m
模型：min Z
cij xij fi yi
i 1
n
xij ai yi
(i 1.2
整数规划_精品文档
整数规划引言：整数规划是一类特殊的数学优化问题，其中一部份或者全部变量被限制为整数。
整数规划问题在许多领域都有广泛的应用，如物流、生产计划、金融投资等。
随着科技的不断发展，整数规划的应用场景和求解方法也在不断扩展和深化。
一、整数规划的定义与分类定义：整数规划是一种特殊的数学优化问题，其目标是最小化或者最大化一个数学表达式（目标函数），同时满足一系列约束条件，且一部份或者全部决策变量被限制为整数。
分类：根据问题的特性，整数规划可以分为以下几种类型：0-1背包问题：决策变量只能取0或者1。
彻底背包问题：决策变量可以取任意非负整数。
整数线性规划：线性规划的变种，要求部份或者全部决策变量为整数。
二次整数规划：目标函数或者约束条件包含二次项。
二、整数规划的应用场景生产计划：在创造业中，整数规划可以用于优化生产流程、物料需求计划等。
物流优化：通过整数规划可以解决货物配送路线、车辆调度等问题。
金融投资：整数规划在投资组合优化、风险管理等领域有广泛应用。
资源分配：整数规划可用于解决资源分配问题，如人员调度、设备配置等。
组合优化：如旅行商问题（TSP）、装箱问题等，都是整数规划的典型应用场景。
三、整数规划的求解算法穷举法：通过逐个测试所有可能的解来找到最优解，但只适合于小规模问题。
分支定界法：一种基于树结构的搜索算法，能够处理较大规模的问题。
遗传算法：摹拟生物进化过程的优化算法，适合处理大规模问题。
摹拟退火算法：借鉴物理中退火过程的优化算法，具有避免陷入局部最优解的能力。
蚁群算法：摹拟蚂蚁觅食行为的优化算法，适合于求解具有离散变量的优化问题。
元胞遗传算法：将遗传算法和元胞自动机结合，能够处理更复杂的问题。
粒子群算法：摹拟鸟群觅食行为的优化算法，具有简单易实现的特点。
深度学习算法：利用神经网络进行求解，特别在处理大规模、高维度的问题时表现出色。
四、整数规划软件介绍CPLEX：由IBM开辟的商业优化软件，支持整数规划、线性规划、混合整数规划等多种优化问题。
第六章 运筹学 整数规划案例
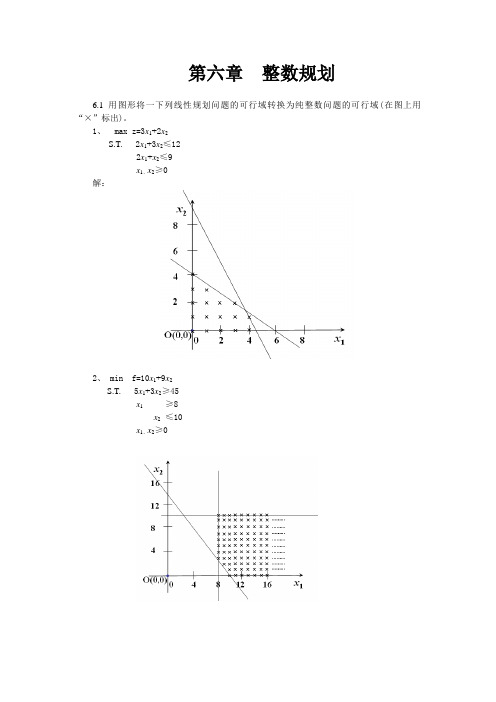
第六章整数规划6.1 用图形将一下列线性规划问题的可行域转换为纯整数问题的可行域(在图上用“×”标出)。
1、 max z=3x1+2x2S.T. 2x1+3x2≤122x1+x2≤9x1、x2≥0解：2、 min f=10x1+9x2S.T. 5x1+3x2≥45x1≥8x2≤10x1、x2≥06.2 求解下列整数规划问题1、 min f=4x1+3x2+2x3S.T. 2x1-5x2+3x3≤44x1+x2+3x3≥3x2+x3≥1x1、x2、x3=0或1解：最优解（0，0，1），最优值：22、 min f=2x1+5x2+3x3+4x3S.T. -4x1+x2+x3+x4≥2-2x1+4x2+2x2+4x2≥4x1+x2-x2+x2≥3x1、x2、x3、x3=0或1解：此模型没有可行解。
3、max Z=2x1+3x2+5x3+6x4S.T. 5x1+3x2+3x3+x4≤302x1+5x2-x2+3x2≤20-x1+3x2+5x2+3x2≤403x1-x2+3x2+5x2≤25x1、x2、x3、x3=正整数解：最优解（0，3，4，3），最优值：474、min z =8x1 +4 x2+3 x3+5 x4+2 x5＋3 x6＋4 x7＋3 x8+4 x9+9 x10+7 x11+5 x12 +10 x13+4 x14+2 x15+175 x16+300 x17+375 x18 +500 x19约束条件x1 + x2+x3≤30x4+ x5＋x6-10 x16≤0x7+ x8＋x9-20 x17≤0x10+ x11＋x12-30 x18≤0x13+ x14＋x15-40 x19≤0x1 + x4+ x7+x10+ x13＝30x2 + x5+ x8+x11+ x14＝20x3 + x6+ x9+x12+ x15＝20x i为非负数（i=1,2…..8）x i为非负整数（i=9,10…..15）x i为为0－1变量（i=16,17…..19）解：最优解（30，0，0，0，0，0，0，0，0，0，0，0，0，20，20，0，0，0，1），最优值：8606.3 一餐饮企业准备在全市范围内扩展业务，将从已拟定的14个点中确定8个点建立分店，由于地理位置、环境条件不同，建每个分店所用的费用将有所不同，现拟定的14个店的费用情况如下表：公司办公会决定选择原则如下：（1）B5、B3和B7只能选择一个。
第六章 整数规划
原来的上界 .
在分枝定界法的整个求解过程中,上界的值在不断减小.
问题 B5
max f 20 x1 10 x2
问题 B6
max f 20 x1 10 x2
5 x1 8 x2 60 x1 8 x2 4 s.t x1 6 x2 3 x ,x 0 1 2
第六章 整数规划
整数规划模型
分支定界法
割平面法 0-1整数规划问题
指派问题
整数规划模型
在许多线性规划问题中,要求最优解必须取整数.例如 所求的解是机器的台数、人数、车辆船只数等.如果所得的 解中决策变量为分数或小数则不符合实际问题的要求. 对于一个规划问题,如果要求全部决策变量都取整数, 称为纯(或全)整数规划;如果仅要求部分决策变量取整数, 称为混合整数规划问题.有的问题要求决策变量仅取0或l两
解 设计划甲种宿舍建 x1 幢,乙种宿舍建 x2 幢,则本题数学 模型为 :
max Z 20 x1 10 x2
0.25 x1 0.4 x2 3 x1 8 s.t x2 4 x1 , x2 0, 取整数
这是一个纯整数规划问题,称为问题 A0 。
（1）
作出问题 A1 , A2 的伴随规划 B1 , B2 , 则问题 B1 , B2 , 的可行 域为 K1 , K 2 , 见图2(b). 以下我们将由同一问题分解出的两 个分枝问题称为"一对分枝".
x2
4
3
x2
2 1
O
2
4
6
8
x1
O
1
2
4
6
8
x1
(a)
(b)
第6章-整数规划 ppt课件
13
ppt课件
14
ppt课件
莫高瑞割平面法
• 割平面法，即通过添加约束条件，逐步切割可行区域的边角 余料，让其整数解逐步的露到边界或顶点上来，只要整数解 能曝露到顶点上来，则就可以利用单纯形法求出来。
• 关键是通过添加什么样的约束条件，既能让整数解往边界露， 同时又不要切去整数解，这个条件就是Gomory约束条件。
数值等于z的A的那个整数可行解；否则进行第四步。
10
10
ppt课件
第四步：在B的最优解中任选一个（或最远离整数要求的变量），不妨 设此变量为xj，以[bj]表示小于bj的最大整数，构造以下两个约束条件，并 加入问题B，得到B的两个分枝B1和B2。
xj ≤[bj]和xj ≥ [bj]+1
第五步：求解B1和B2 。修改A问题的最优目标函数值z*的上下界，z 和 z。
4. 再求解这些子区域上的线性规划问题。
5. 不断缩小整数规划上下界的距离，最后得整数规划的最优解。
9
ppt课件
用分枝定界法求解目标函数值最大的整数规划的步骤，我们将求解的整数规划 z 问题称为A，将与其相对应的线性规划问题称为பைடு நூலகம்：
第一步：求解问题B，可得以下情况之一：
1.B没有可行解，则A也没有可行解，求解过程停止。
1/ 2x2 2 / 3x3 x5 1/ 2
例6-5 19
ppt课件
6.3 0-1规划
0 1型整数规划是整数规划中的特殊情形，它的变量x j 仅取值 0 或 1。这时x j 称为0 1变量，或称二进制变量。 0-1规划的分支定界法
引入0-1变量的实际问题 ①双态变量的归一化（变量） ②不相容约束的归一化（约束条件） ③分段线性函数的归一化（目标函数）
ppt课件
14
ppt课件
莫高瑞割平面法
• 割平面法，即通过添加约束条件，逐步切割可行区域的边角 余料，让其整数解逐步的露到边界或顶点上来，只要整数解 能曝露到顶点上来，则就可以利用单纯形法求出来。
• 关键是通过添加什么样的约束条件，既能让整数解往边界露， 同时又不要切去整数解，这个条件就是Gomory约束条件。
数值等于z的A的那个整数可行解；否则进行第四步。
10
10
ppt课件
第四步：在B的最优解中任选一个（或最远离整数要求的变量），不妨 设此变量为xj，以[bj]表示小于bj的最大整数，构造以下两个约束条件，并 加入问题B，得到B的两个分枝B1和B2。
xj ≤[bj]和xj ≥ [bj]+1
第五步：求解B1和B2 。修改A问题的最优目标函数值z*的上下界，z 和 z。
4. 再求解这些子区域上的线性规划问题。
5. 不断缩小整数规划上下界的距离，最后得整数规划的最优解。
9
ppt课件
用分枝定界法求解目标函数值最大的整数规划的步骤，我们将求解的整数规划 z 问题称为A，将与其相对应的线性规划问题称为பைடு நூலகம்：
第一步：求解问题B，可得以下情况之一：
1.B没有可行解，则A也没有可行解，求解过程停止。
1/ 2x2 2 / 3x3 x5 1/ 2
例6-5 19
ppt课件
6.3 0-1规划
0 1型整数规划是整数规划中的特殊情形，它的变量x j 仅取值 0 或 1。这时x j 称为0 1变量，或称二进制变量。 0-1规划的分支定界法
引入0-1变量的实际问题 ①双态变量的归一化（变量） ②不相容约束的归一化（约束条件） ③分段线性函数的归一化（目标函数）
第6章 python 整数规划与非线性规划
目前，没有一种方法可以有效求解一切整数规划。常见的整数规划求解 算法有：
（1）分枝定界法：可求纯或混合整数线性规划； （2）割平面法：可求纯或混合整数线性规划； （3）隐枚举法：用于求解0 1整数规划，有过滤隐枚举法和分枝隐枚 举法； （4）匈牙利法：解决指派问题（0 1整数规划特殊情形）； （5）蒙特卡罗法：求解各种类型规划。
i1
xij
0或1,
i, j 1,2,
, n,
第 13 页
（6.1）
第6章
6.1整数规划
第 14 页
这是一个纯0 1整数规划模型。 若将模型（6.1）中的cij组成一个n阶方阵C (cij )nn，则称C 为效率矩阵。 这样，标准指派问题中的工作效率就可以很方便地用矩阵C 来表示，并且效 率矩阵C 与标准指派问题一一对应。同样地，模型（6.1）的最优解也可以用 n阶方阵 X *的形式来表示，我们称之为指派问题的最优解方阵。由于标准指 派问题要求“每项工作需且仅需一个人去完成，每个人需完成且仅需完成一 项工作”，故最优解方阵一定是一个置换矩阵，即矩阵的每一行、每一列都 恰好有一个“1”，其余元素均为 0。
标准指派问题的一般提法是：拟分派n个人 A1, A2 , , An去完成n项工作 B1, B2 , , Bn，要求每项工作需且仅需一个人去完成，每个人需完成且仅需完 成一项工作。已知人 Ai 完成工作Bj的时间或费用等成本型指标值为cij，则应 如何指派才能使总的工作效率最高？
第6章
6.1整数规划
第6章
6.1整数规划
第 15 页
标准指派问题的数学模型表现为0 1整数规划的形式，当然可以通过整 数规划的分支定界法或0 1整数规划的隐枚举法来求得最优解。但标准指派 问题的数学模型具有独特的结构，因此，为提高求解的效率，1955 年美国 数学家 H. W. Kuhn 根据匈牙利数学家 D. König 关于矩阵中独立零元素定 理，提出了一个求解标准指派模型的有效算法—匈牙利算法。
第六章 整数规划
5
衣服
4
5
15
解：Xi为是否带第 i 种物品
maxZ=20X1 + 30X2 +10X3+18X4 +15X5
5X1+3X2 +X3 +2X4 +4X5 8 2X1+X2 +4X3 +3X4 +5X5 10 Xi为0, 1
一般形式：
max Z
C
i 1
n
i
Xi
n ai X i b i 1 X 0 ,且为整数 i
当100个0－1变量，几亿年
(二) 常用方法 • 分枝定界法
• 割平面法
• 隐枚举法 • 匈牙利法
(三) 分枝定界法
基本思路 maxZ=CX maxZ=CX (B) AX=b X 0
AX=b
(A) X 0
X 0且为整数 (B)为(A)的松弛问题。
i+1
Xj*
i
X*
(B1)
(B) Xj i+1 (B2)
maxZ = 20 X1 + 10 X2
5X1+4X2 24 2X1+5X2 13 X1 , X2 0 X1 , X2为整数
例2、背包问题
背包可再装入8单位重量，10单位体积物品 物品 1 2 3 4 名称 书 摄像机 枕头 休闲食品 重量 5 3 1 2 体积 2 1 4 3 价值 20 30 10 18
优点： (1) 任何模型均可用；
(2) 思路简单、灵活；
(3) 速度快； (4) 适合上机。
分枝变量选择原则 ① 按目标函数系数：选系数绝对值最大者变
量先(分对目标值升降影响最大)。
(第五、六章 目标规划和整数规划
1
x 1、 x2 、 x3分别为采用3条生产线时的产量
50x3 +1000，若x 3 ＞0 C 3(x 3 )＝ 0，若x 3 ＝0
目标函数：min z=C 1(x 1)+C 2(x 2)+C3(x 3)
可变成本（吨/元） 固定成本（元）
1,当采用第j条生产线时，即当xj＞0 令y j = 0,当不采用第j条生产线时，即当xj＝0
建立0－1整数规划模型
引入0-1变量,令
Xi= 1,当Ai点被选用 0,当Ai点没被选用
7
于是: max z= ∑ ci xi i =1 7 s.t. ∑ bi xi ≤ Β,
x1 + x 2 + x3 ≤ 2, ( xi = 0 / 1 x 4 + x5 ≥ 1, x6 + x7 ≥ 1,
i =1
则：C 1(x 1)＝ 20x 1 +1500 y1 C 2(x 2)＝ 30x 2 +1200 y2 C 3 (x 3 ) ＝ 50x 2 +1000 y3 0≤x 1≤5000y 1 0≤x2 ≤5000y 2 0≤x 3 ≤5000y 3
场所选择
某公司拟在市东、西、南三区建立门市部, 拟议中有7个位置Ai（i=1,2, …7）可供选择, 规定:在东区,由A1,A2,A3三个点中至多选两个; 在西区,由A4,A5两个点中至少选一个;在南区, 由A6,A7两个点中至少选一个.如选用Ai点设备 投资估计为bi元,每年可获利润估计为ci元,公 司投资总额不能超过B元。如何选择使年利润 最大?
单纯形法
由于目标规划的目标函数中含有优先因 子，所以在单纯形表中，将检验数行按 优先因子的个数分成k行 用单纯形法求解(同前) 例如：前面第一个目标规划模型
x 1、 x2 、 x3分别为采用3条生产线时的产量
50x3 +1000，若x 3 ＞0 C 3(x 3 )＝ 0，若x 3 ＝0
目标函数：min z=C 1(x 1)+C 2(x 2)+C3(x 3)
可变成本（吨/元） 固定成本（元）
1,当采用第j条生产线时，即当xj＞0 令y j = 0,当不采用第j条生产线时，即当xj＝0
建立0－1整数规划模型
引入0-1变量,令
Xi= 1,当Ai点被选用 0,当Ai点没被选用
7
于是: max z= ∑ ci xi i =1 7 s.t. ∑ bi xi ≤ Β,
x1 + x 2 + x3 ≤ 2, ( xi = 0 / 1 x 4 + x5 ≥ 1, x6 + x7 ≥ 1,
i =1
则：C 1(x 1)＝ 20x 1 +1500 y1 C 2(x 2)＝ 30x 2 +1200 y2 C 3 (x 3 ) ＝ 50x 2 +1000 y3 0≤x 1≤5000y 1 0≤x2 ≤5000y 2 0≤x 3 ≤5000y 3
场所选择
某公司拟在市东、西、南三区建立门市部, 拟议中有7个位置Ai（i=1,2, …7）可供选择, 规定:在东区,由A1,A2,A3三个点中至多选两个; 在西区,由A4,A5两个点中至少选一个;在南区, 由A6,A7两个点中至少选一个.如选用Ai点设备 投资估计为bi元,每年可获利润估计为ci元,公 司投资总额不能超过B元。如何选择使年利润 最大?
单纯形法
由于目标规划的目标函数中含有优先因 子，所以在单纯形表中，将检验数行按 优先因子的个数分成k行 用单纯形法求解(同前) 例如：前面第一个目标规划模型
第六章 整数规划
第一节 整数规划实例与模型
点
(0,0) (0,1) (0,2)
条件
可行解
Z值
0 10 20
(1,0)
(1,1) (1,2) (2,0) (2,1) (2,2) (3,0) (3,1) (3,2) (4,0) (4,1) (4,2)
① √ √ √ √ √ √ √ √ √ √ √ √ √ √
② √ √ √ √ √ √ √ √ √ √ √ √
b1x1+b2x2+b3x3+…b7x7≤B
1，表示Ai点被选用 Xi= 0，表示Ai点没被选用
第二节
0－1整数规划的建模方法
max Z=c1x1+c2x2+c3x3+…+c7x7 s.t. b1x1+b2x2+b3x3+…b7x7≤B X1+x2+x3≤2 X4+x5 ≥1 X6+x7 ≥1 Xi=0或＝1 i=1,2…7
第一节 整数规划实例与模型
所以选址模型为： min TC= TC1+TC2 s.t．x11+x12+x13≤10y1 x21+x22+x23≤20y2 x31+x32+x33≤30y3 x41+x42+x43≤40y4 x51+x52+x53≤30 x11+x21+x31+x41+x51=30 x12+x22+x32+x42+x52=20 x13+x23+x33+x43+x53=20
第二节
扩建厂房
0－1整数规划的建模方法
项目（千元） 扩建仓库 更新机器 新产品研制 40 10 37 总可用成本 10 10 15 40 15 10 50 20 10 40 5 4 10 35
第六章-整数规划
0
0 1 0 0 3/4 -1/4
1
0 1/3 1/3 -1/3 1/4 1/4
1 1
ci-zi →
0
0
-1/2
-1/2
最优解 X (3/ 4, 7 / 4)T ，对应下图中的A点。
由于最优解为非整 数解，需要构造割 平面。以第一个约 束构造割平面为：
3 1 3 x x 4 3 4 4 4
3. 如果要求部分决策变量取整数值，则称为混合整数规 划（Mixed Integer Programming，MIP）问题。
4. 如果整数变量都是0-1变量，这样的整数规划问题称 为0-1规划（Binary Integer Programming，BIP）问题。
一、问题的提出
在现实生活中我们经常遇到一些决策变量需要取 整数才有实际意义的问题，例如产品数量、工人人 数、设备台数、股票手数等等，还会经常遇到由一 系列相关的“是或否”的选择组成的决策问题，决 策变量只能有两个取值0或1（0-1变量）比如在被选 方案中进行项目决策、投资决策和设施决策等。下 面我们看一个例子 。
三、解的特点和求解思想
整数规划与线性规划在模型上的唯一区别在于决策变量是否取整数。 当可行域有界时，整数规划问题可行解的个数有限。然而可行解个数 有可能会是天文数字，性能最高的计算机也不能胜任用简单枚举法求 解50个变量以上的整数规划问题。 在某些特殊情况下，松弛问题的最优解满足整数型约束，可以用单纯 性法求解松弛问题以求出整数规划的最优解。 一般情况下，松弛问题的最优解不会恰好是整数解，我们可以考虑用 去掉松弛问题可行域中的一些非整数解，使得新产生的松弛问题的子 问题的最优解是整数解，可以考虑通过单纯性法求解松弛问题及其一 系列子问题来求解整数规划问题的最优解。 目前对于一般的整数规划问题还没有令人满意的有效解法，在应用中 主要有两种一般性解法：割平面法和分支定界法.对于特殊结构的整 数规划问题，在应用中提出了的一些令人满意的专用解法。例如求解 0-1规划的解法和求解指派问题的匈牙利人算法。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二节
0－1整数规划的建模方法
例 某公司拟在市东西南三区建立门市部，拟议中有7个位置 Ai(i=1,2…7)可供选择，规定 （1）在东区A1,A2,A3三个点中至多选两个 （2）在西区A4,A5两个点中至少选一个 （3）在南区A6,A7两个点中至少选一个 如果用Ai点，设备投资估计了bi元，每年可获利估计为ci元， 但投资额不超过B元，问应选择哪几个点可使年利润最大？ 解，引入0-1变量,xi(i=1,2…7)，令
运筹学
运 筹 帷 幄 之 中 决 胜
第六章整数规划
千 里 之 外
教学要求
掌握线性整数规划的建模方法，特别是0-1变量的运用； 掌握分支定界求解方法的基本原理； 了解割平面求解方法的基本原理； 重点掌握指派问题的建模与求解。
第四章 线性规划的进一步讨论
整数规划建模 分枝定界法 割平面法 指派问题
第一节 整数规划实例与模型
一、实例1
某工厂准备备用集装箱托运甲、乙两种货物，已知， 每箱货物的体积、利润、重量、托运限制如下表，问甲 乙两种货物各托运多少箱才能使总利润最大？
货物 甲 每箱体积 每箱重量 每箱利润 5 2 20
乙
托运限制
4
24
5
13
10
解：设甲乙两种货物各托运x1,x2箱，依题意得： Max z=20x1+10x2 s.t 5x1+4x2≤24 2x1+5x2 ≤13 x1,x2≥0 x1,x2取整数
已得最优解；若不可行，进行步骤（2）。
（2）将某一变量转为固定变量，令其取值为1或0，使问题分成
两个子域。令一个子域中的自由变量都取0值，加上固定变量取值， 组成此子域的解。
（3）计算此解的目标函数值，与已求出的可行解最小目标函数
值比较。如果前者大，则不必检验其是否可行而停止分枝，若子 域都检验过，转步骤（7），否则转步骤（6）。因继续分枝即使 得到可行解，其目标函数值也较大，不会是最优解；如前者小， 进行步骤（4）。对第一次算出的目标函数值，不必进行比较，直 接转到步骤（4）。
第一节 整数规划实例与模型
所以选址模型为： min TC= TC1+TC2 s.t．x11+x12+x13≤10y1 x21+x22+x23≤20y2 x31+x32+x33≤30y3 x41+x42+x43≤40y4 x51+x52+x53≤30 x11+x21+x31+x41+x51=30 x12+x22+x32+x42+x52=20 x13+x23+x33+x43+x53=20
（4）检验解是否可行。如可行，已得一个可行解，计算并记下
它的z值，并停止分枝，若子域都检验过，转步骤（7），否则转 步骤（6）。因继续分枝，即使得到可行解，目标函数值也比记下 的z值大，不会是最优解；如不可行，进行步骤（5）。
第二节
0－1整数规划的建模方法
隐枚举法求解步骤（一） （5）将子域固定变量的值代入第一个不等式约束条件方程， 并令不等式左端的自由变量当系数为负时取值为1，系数为 正时取值为0，这就是左端所能取得最小值。若此最小值大 于右端值，则称此子域为不可行子域，不再往下分枝，若 此最小值小于右端值，则依次检验下一个不等式约束方程， 直至所有的不等式约束方程都通过，若子域都检验过，转步 骤（7），否则，转步骤（6）。
（6）定出尚未检验过的另一个子域的解，执行步骤
（3）～（5），若所有子域都停止分枝，计算停止，目标函 数值最小的可行解就是最优解；否则，转（7）。
（7）检查有无自由变量。若有，转（2）；如没有，计算
停止。目标函数值最小的可行解就是最优解。
第二节
0－1整数规划的建模方法
说明： 彩色字体为固定变量。
实例：某电冰箱厂正在考虑随后4年内有不同资金要求的投资 方案。面对每年有限的资金，工厂领导需要选择最好的方案， 使资金预算方案的当前估算净值最大化。每种方案的现金估 算净值（现金估算净值为第一年开始时的净现金流的值）、 资金需求和4年内拥有的资金见下表：
项目（千元） 扩建厂房 扩建仓库 更新机器 新产品研制 现值 90 40 10 37 总可用成本 第1年资金 15 10 10 15 40 第2年资金 20 15 10 50 第3年资金 20 20 10 40 第4年资金 15 5 4 10 35
30 20
20
总成本＝年固定成本＋运输成本
30
第一节 整数规划实例与模型
首先做如下假设： 如果在B1建新厂，y1=1；否则，y1=0。 如果在B2建新厂，y2=1；否则，y2=0。 如果在B3建新厂，y3=1；否则，y3=0。 如果在B4建新厂，y4=1；否则，y4=0。 xij：表示从工厂i 到销售中心j的运输量；i=1,…,5；j=1,2,3。 利用已知的数据，年运输成本为： TC1=5x11+2x12+3x13+4x21+3x22+4x23+9x31+7x32 +5x33+10x41+4x42+2x43+8x51+4x52+3x53
xij≥0，对所有的i，j； y1，y2，y3，y4=0，1
第一节 整数规划实例与模型
二、整数规划一般模型
max( 或 min) ci xi
i 1 n
s.t.
a x
i 1 i
n
i
b (或 b 或 b)
xi 0, 且为整数或部分为整数 i 1,2, , n
如果决策变量全部为整数，则称为纯整数规划 部分决策变量是整数，其他变量可以是非整数，则称为混合整数 规划 如果变量仅取0或1，此时的整数规划称为 0-1规划，是整数规 划的特殊情况
第一节 整数规划实例与模型
整数规划模型是一类特殊的线性规划模型，但用 求解线性规划模型的单纯形法所得到的最优解往往不能 保证其一定是整数。 解相应的线性规划问题得到最优解之后，采用最 优解凑整的方法，往往得不到整数规划的最优解，甚至 得不到可行解
第一节 整数规划实例与模型
Max z=20x1+10x2 s.t 5x1+4x2≤24 2x1+5x2 ≤13 x1,x2≥0,且为整数
min z 8 x1 2 x 2 4 x3 7 x 4 5 x5 令所有变量都为0， 3 x1 3 x 2 x3 2 x 4 3 x5 2 不可行，分支。 s.t. 5 x1 3 x 2 2 x3 x 4 x5 4 Z2=0< Z1 ，不可行； x j 0或1, 对一切j. (0,0,0,0,0) 可行子域，分支。
第二节
扩建厂房
0－1整数规划的建模方法
项目（千元） 扩建仓库 更新机器 新产品研制 40 10 37 总可用成本 10 10 15 40 15 10 50 20 10 40 5 4 10 35
现值 第1年资金 第2年资金 第3年资金 第4年资金
90 15 20 20 15
变量
x1表示扩建工厂的变量， =1表示扩建工厂，＝0表 示不扩建 同理，变量 x2,x3,x4依次表示扩建仓 库、固定成本为：
TC2=175y1+300y2+375y3+500y4； 总成本为：TC=TC1+TC2； 生产能力的约束条件为： 从新工厂B1运到A1，A2，A3三个城市销售中心的总量应小于等 于B1的生产能力，所以约束条件为： x11+x12+x13≤10y1 B1的生产能力； 同理可得： x21+x22+x23≤20y2 B2的生产能力； x31+x32+x33≤30y3 B3的生产能力； x41+x42+x43≤40y4 B4的生产能力； x51+x52+x53≤30 B5的生产能力； 三个销售中心的需求量为： x11+x21+x31+x41+x51=30 A1的需求量； x12+x22+x32+x42+x52=20 A2的需求量； x13+x23+x33+x43+x53=20 A3的需求量；
将x1,x2取 整条件去掉
Max z=20x1+10x2 s.t 5x1+4x2≤24 2x1+5x2 ≤13 x1,x2≥0
通过单纯法可求得最优解为x1=4.8,x2=0 maxz=96 若采用凑整的方法得 (1) X1=5 x2=0 根本不是原整数规划的可行解 (2) x1=4 x2=0 z=80 不是整数规划的最优解 实际上原问题的最优解为 X1=4,x2=1 max z=90
约束条件
第1年的可用资金为40 千元，所以相应的约束条 件为： 15 x1 10 x2 10 x3 15 x4 40 同理得到后三年的约束 条件。
目标函数
当前估算净值最 大，即max
90 x1 40 x2 10 x3 37 x4
第二节
可得上例的模型
0－1整数规划的建模方法
必须大于 等于0
二、 0－1整数规划的标准型和解法
min z c j x j n cij x j bi , i 1,2, , m j 1 x j 0或1, j 1,2, , n
解法
全枚举法 隐枚举法
j 1
n
必须≤
隐枚举法求解步骤（一）
（1）令全部都是自由变量且取0值，检验解是否可行。若可行，
第一节 整数规划实例与模型
用穷举法求解： Max z=20x1+10x2 s.T 5x1+4x2≤24 ① 2x1+5x2 ≤13 ② x1,x2≥0,且为整数 解：在① ②中令x2=0 得 x1≤[24/5]=4 x1 ≤[13/2]=6 所以 x1 只能取 0,1,2,3,4 同理 在① ②中令x1=0 得 0≤x2 ≤2 故 x2只能取0,1,2 x1 ≤4