浙江省诸暨市草塔中学2018学年高一数学下学期期中考试试题(实验班) 精品
2018年高一下学期期中考试(数学)试题及答案

2018年高一下学期期中考试(数学)试题及答案( 时间:120分钟,满分:150分)一、选择题(本题共12道小题,每小题5分,共60分) 1. 415°角的终边在( )A .第一象限B .第二象限C .第三象限D .第四象限 2. 设扇形的弧长为2,面积为2,则扇形中心角的弧度数是( ) A .1 B .4C .1或4D .π3. 已知α∈(0,π),且53cos -=α,则=αtan ( ) A . B .C .D .4. 以下说法错误..的是( ) A .零向量与任一非零向量平行 B.零向量与单位向量的模不相等 C.平行向量方向相同 D.平行向量一定是共线向量 5.︒︒-︒︒105sin 75cos 105cos 15cos 的值为 ( ) A .B .C .D .6. 要得到函数x y 2cos =的图象,只需将函数)32cos(π+=x y 的图象( )A .向左平移3π B .向右平移3πC .向左平移6πD .向右平移6π7. 设函数)32sin()(π-=x x f 的图象为C ,下面结论中正确的是( )A .函数f (x )的最小正周期是2πB .函数f (x )在区间⎪⎭⎫⎝⎛-2,12ππ上是增函数 C .图象C 可由函数x x g 2sin )(=的图象向右平移个单位得到D .图象C 关于点⎪⎭⎫⎝⎛0,6π对称 8. 已知A 为△ABC 的一个内角,且32cos sin =+A A ,则△ABC 的形状是( )A .锐角三角形B .钝角三角形C .直角三角形D .不确定9. 已知点A(1,3),B(4,一1),则与向量AB 的方向相反的单位向量是 A .⎪⎭⎫⎝⎛-53,54 B. ⎪⎭⎫ ⎝⎛-54,53 C. ⎪⎭⎫ ⎝⎛-54,53 D. ⎪⎭⎫⎝⎛-54,53 10.下列四式中不能..化简为PQ 的是 A. ()BQ PA AB ++ B. ()()QC BA PC AB -++ C. BQ AB PA -+ D. CQ QP QC +- 11.已知函数x y cos 2=的定义域为⎥⎦⎤⎢⎣⎡34,3ππ,值域为[]b a ,,则a b -的值是 A .2 B .3 C .+2 D .12. 函数14cos 22-⎪⎭⎫⎝⎛-=πx y 是( ) A .最小正周期为π的奇函数B .最小正周期为π的偶函数C .最小正周期为的奇函数D .最小正周期为的偶函数二、填空题(本题共4道小题,每小题5分,共20分) 13. 若3tan =α,34tan =β,则()βα-tan 等于 . 14. 函数⎥⎦⎤⎢⎣⎡∈-=2,0),42sin(ππx x y 的单调递增区间为 . 15.已知向量()()θθcos ,1,sin ,1==b a b a 的最大值为 . 16. 函数()()0,0,0sin >>>+=φωφωA x A y 的图象如图所示, 则y 的表达式为 .三、解答题(本题共6道小题,第17题10分,第18-22每题12分,共70分))(x f 17.已知3tan =α,计算: (Ⅰ)ααααsin 3cos 5cos 2sin 4+-;(Ⅱ)ααcos sin18.已知函数(Ⅰ)求函数单调递减区间;(Ⅱ)求函数)(x f 在区间[0,]上的值域.19.(本小题满分12分)设平面三点()()()5,2,1,0,0,1C B A . (1)试求向量AC AB +2的模; (2)试求向量AB 与AC 的夹角的余弦值;20. 已知()()x x b x x a cos 3,cos ,cos ,sin =-=,函数()23+•=b a x f . (1)求()x f 的最小正周期,并求其图像对称中心的坐标; (2)当20π≤≤x 时,求函数()x f 的值域.21. 如图,ABCD 中,F E ,分别是DC BC ,的中点,G 为交点,若,,b AD a AB ==试以ba ,为基底表示CG BF DE ,,.22. 已知向量()R x x x b x a ∈=⎪⎭⎫ ⎝⎛-=,2cos ,sin 3,21,cos ,设函数()b a x f •=.(1求()x f 的最小正周期; (2)求()x f 在⎥⎦⎤⎢⎣⎡2,0π上的最大值和最小值..233cos()2cos(2)(++-=ππx x x f2018年高一下学期期中考试(数学)答题卡(总分:150 时间:120分钟)第Ⅰ卷(选择题 60分)一、选择题(本大题共12小题,每小题5分,满分60分。
推荐-2018学年第二学期期中考试高一数学试卷 精品

2018~2018第二学期期中考试试卷高一数学(时间120分钟,满分150分)注意事项:⒈答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目写在答题卡上. ⒉ 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷(选择题 共60分)一、选择题:共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. ︒tan600的值是 ( )A.33-B. 33C.3D. 3- 2.已知α是第二象限角,那么2α是 ( ) A .第一象限角 B. 第二象限角 C. 第二或第四象限角 D .第一或第三象限角 3.已知0tan ,0sin ><θθ,则θ2sin 1-化简的结果为 ( ) A .θcos B. θcos - C .θcos ± D. 以上都不对 4.函数)22cos(π+=x y 的图象的一条对称轴方程是 ( )A .2π-=x B. 4π-=x C. 8π=x D. π=x5.函数x y 2sin 3=的图象可以看成是将函数)3x 2sin(3y π-=的图象 ( )A .向左平移个6π单位 B. 向右平移个6π单位C .向左平移个3π单位 D. 向右平移个3π单位6.函数cos 24y x π⎛⎫=-⎪⎝⎭在下列区间上为增函数的是( ) ()4,45A ππ⎡⎤⎢⎥⎣⎦()5,88B ππ⎡⎤⎢⎥⎣⎦ ()3,08C π⎡⎤-⎢⎥⎣⎦ ()3,44D ππ⎡⎤-⎢⎥⎣⎦ 7.已知)0,2(π-∈x ,53sin -=x ,则tan2x= ( ) A .247 B. 247- C. 724 D. 724-8.已知31)4tan(,21)tan(-=-=+παβα,则)4tan(πβ+的值为 ( )A .2 B. 1 C.22D. 2 9.已知83cos sin =αα且24παπ<<,那么ααsin cos -的值是 ( ) A.21 B.21- C.41- D.21± 10、函数x x y cos sin 3+=,]2,2[ππ-∈x 的最大值为 ( )A .1 B. 2 C. 3 D.23 11.已知),32sin(3)(π+=x x f 则以下不等式正确的是 ( )A.f(3)>f(1)>f(2)B.f(1)>f(2)>f(3)C.f(3)>f(2)>f(1)D.f(1)>f(3)>f(2) 12、已知)(x f 是奇函数,且0<x 时,x x x f 2sin cos )(+=,则当0>x 时,)(x f 的表达式是 ( )A x 2s i n x c o s+ B x 2s i n x c o s +- C x 2s i n x c o s- D x 2s i n x c o s --桥东区2018~2018第二学期期中考试试卷高一数学13.角α的终边上一点()3,4-P 则ααcos sin 2+的值为 . 14.函数)656(3sin 2ππ≤≤=x x y 与函数y=2的图像围成一个封闭图形,这个封闭图形的面积是__________________15.已知21)(cos -=+απ,则=+)3(cos απ_____ _16.给出下列命题:①存在实数α,使1cos sin =⋅αα ②存在实数α,使23cos sin=+αα ③函数)23sin(x y +=π是偶函数 ④8π=x 是函数)452sin(π+=x y 的一条对称轴方程,其中正确命题的序号是____________________三、解答题:本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤.17 .(本题10分) 已知 1tan 3α=-,计算:(1)sin 2cos 5cos sin αααα+-; (2)212sin cos cos ααα+.18.(12分)(1)已知锐角βα,满足53sin =α,135cos =β,求)(βα-c os 的值。
浙江诸暨中学2018-2019学年高一期中考试题 数学(含详细答案)

诸暨中学2018学年高一期中考试数学试卷2018.11说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共120分.考试时间120分钟. 本次考试不得使用计算器. 请考生将所有题目答案都作答在答题纸上, 答在试卷上概不评分.第I卷(选择题共40分)一、选择题(本大题共10小题,每小题4分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U={1,2,3,4,5},A={1,2},B={2,3,4},则(C U A)∪B= ( ▲) A.{3,4} B.{3,4,5} C.{2,3,4,5} D.{1,2,3,4}2.下列各组函数f(x)与g(x)的图象相同的是(▲)A.()2)()(xxgxxf==与 B.2)(24)(2+=--=xxgxxxf与C.0)(1)(xxgxf==与 D.()()⎩⎨⎧<-≥==,,)()(xxxxxgxxf与3.下列函数中,既是偶函数,又在),0(∞+上单调递增的是(▲)A.|x|y x=B.1ln1xyx-=+C.||2xy=D.2lgy x=-4.设函数32log)(2-+=xxxf,则函数)(xf的零点所在的区间为(▲)A.)10(,B.)21(,C.2,3)(D.4),(35.已知a =0.6,b =0.8,c =,则a,b,c的大小关系是( ▲) A.a<b<c B.b<a<c C.c<a<b D.b<c<a6.函数()lg|x|f x x=⋅的图象可能是(▲)A.B.C.D.7.已知函数xxfy+=)(是偶函数,且1)2(=f,则=-)2(f(▲)A.5B.4C.3D.28.已知函数()23log3,0,12,0,x xf xf x x+⎧>⎪=⎨⎛⎫+≤⎪⎪⎝⎭⎩则()2f-=(▲)A .13 B .3 C .19D .9 9.函数()()2log 2a f x x ax =-+在区间()1,+∞上恒为正值,则实数a 的取值范围 ( ▲ ) A .(01), B .(12], C .(13], D .(0,2) 10.用()d A 表示集合A 中的元素个数,若集合{0,1}A =,22{|(x )(1)0}B x ax x ax =--+=,且|d()()|1A d B -=.设实数a 的所有可能取值构成集合M ,则()d M = ( ▲ )A .3B .2C .1D .4第II 卷(非选择题 共80分)二、填空题(本大题共7小题,其中11-14题每空2分,15-17题每空3分,共25分)11.设函数y =的定义域为A ,函数ln(1x)y =-的定义域为B ,则A = ▲ ;A B ⋂= ▲ .12.已知幂函数()f x x α=的图象过点)24(,,则α= ▲ ;=)3(log 3f ▲ . 13.若函数()log (x 3)1(a 0a f x =++>且1)a ≠,图像恒过定点(,)P m n ,则m n += ▲ ;函数2()ln()g x x mx =+的单调递增区间为 ▲ .14.设对一切实数x ,函数(x)f 都满足:(x)2f(2x)1xf =-+,则(1)f = ▲ ;(4)f = ▲ .15.定义区间12[,]x x 的长度为21x x -,若函数2|log x |y =的定义域为[,]a b ,值域为[0,2],则区间[,]a b 的长度最大值为 ▲ .16.若关于x 的方程4210x xa a +⋅++=有实根,则实数a 的取值范围是 ▲ . 17.已知λ∈R ,函数f (x )=24,43,x x x x x λλ-≥⎧⎪⎨-+<⎪⎩,若函数f (x )恰有2个零点, 则λ的取值范围是_____▲____.三、解答题(本大题共5小题,共55分,解答应写出文字说明、证明过程或演算步骤)18.(本题10分)设全集U R =,集合1{x |21}x A -=≥,2{|450}B x x x =--<.(1)求A ∩B ,()()U U C A C B ⋃;。
2017-2018 浙江省诸暨中学高一第二学期期中考试(含答案解析)

浙江省诸暨中学高一第二学期期中考试数 学(本试卷满分100分,考试时闯120分钟)参考公式: 台体的体积公式),(312211s s s s h V ++=其中21,s s 分别表示台体的上、下底面积,h 表示台体的高 锥体的体积公式,31sh V =其中S 表示锥体的底面面积,h 表示锥体的高 球的表面积公式,42R s π=其中R 表示球的半径 球的体积公式,343R V π=其中R 表示球的半径 第1卷(选择题 共30分)一、选择题(本大题共IO 小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.圆036422=--++y x y x 的圆心和半径分别为( ) 16),6,4.(-A 4),3,2.(-B 4),3,2.(-C 16),3,2.(-D2.下列命题正确的是 ( )A .经过三点,有且只有一个平面B .平行于同一条直线的两个平面也平行C .经过平面外一点有且只有一条直线与已知平面平行D .过一点有且只有一条直线垂直于已知平面3.已知正方体的外接球的半径为1,则这个正方体的棱长为( )32.A 33.B 322.C 332.D4.圆9)2()4(22=-+-y x 与圆4)1(22=++y x 的位置关系为( )A.相交 B .内切 C .外切 D .外离5.平面βα,及直线L 满足:,//,αβαl ⊥则一定有( )β//.l A β⊂l B . β与l C .相交 D .以上三种情况都有可能6.空间四边形ABC P -的各边及对角线长度都相等,F E D ,,分别是CA BC AB ,,的中点,下列四个结论中不成立的是 ( )//..BC A 平面PDF B .平面⊥PDE 平面ABC⊥BC C .平面PAE D .平面⊥PAE 平面ABC7.已知三棱锥ABC D -的三个侧面与底面全等,且,2,3===BC AC AB 则以BC 为棱,以平面33.A 0.B 31.C 21.-D 8.若直线过点)1,0(-M 且被圆25)2()1(22=-+-y x 截得的弦长为8,该直线的方程是( )0443.-++y x A 0443.=++y x B 或01=+y0443.=--y x C 0443.=--y x D 或01=+y9.与直线04.=--y x 和圆2)1()1(22=-++y x 都相切的半径最小的圆的方程是( ) 2)1()1.(22=++-y x A 4)1()1.(22=+++y x B2)1()1.(22=+++y x C 4)1()1.(22=++-y x D10.如图,在斜三棱柱111C B A ABC -中,,,901AC BC BAC o⊥=∠则点1C 在底面ABC 上的射影H 必在A .直线AC 上B .直线BC 上 C .直线AB 上D .△ABC 内部第Ⅱ卷(非选择题 共70分)二、填空题(本大题共7小题,每小题4分,共28分,把答案填在题中的横线上)11.若直线⊂a 平面,α直线⋅⊂b 平面,//,βαβ则直线a 和b 的位置关系为_______12.把等腰直角△ABC 沿斜边BC 上的高AD 折成一个二面角,此时,60oBAC =∠则此时二面角C AD B -- 的大小是________13.已知圆422=+y x 上动点P 及定点Q(4,0),则线段PQ 中点M 的轨迹方程是_______14.一个水平放置的平面图形的斜二测直观图是一个底角为,45o 腰和上底均为2的等腰梯形,那么原平面图形的面积是________15.二面角βα--1的大小为,45 线段,,l B AB ∈⊂αAB 与L 所成角为,45o 则AB 与β所成角为______16.设m ,n 是两条不同的直线,βα,是两个不同的平面,给定下列四个命题:(1)若βα⊥n m ,//且,βα⊥则;n m ⊥ (2)若βα⊥⊥n m ,且,n m ⊥则;βα⊥(3)若βα⊂⊂n m ,且,//n m 则;//βα (4)若,,,//βαβα⊥⊥n m 则.//n m其中所有正确的命题为____(写出所有正确命题的编号).17.已知某几何体的三视图如图所示,其中俯视图是边长为2的正三角形,侧视图是直角三角形,则此几何体的体积为__________三、解答题I 本大曩共4小题,共42分.解答应写出必要的文字说明、证明过程或演算步骤)18.(本小题满分10分)(I)已知圆C 的圆心是01=+-y x 与x 轴的交点,且与直线03=++y x 相切,求圆C 的标准方程; (Ⅱ)若点),(y x P 在圆03422=+-+x y x 上,求x y 的最大值.19.(本小题满分8分)三棱锥ABC P -中,已知F E AB PC ,,8,10==分别为PA ,BC 的中点,,61=EF 求异面直线AB 与PC所成角的大小,20.(本小题满分12分)如图,在四棱锥ABCD P -中,平面⊥PAD 平面DC PD PA BCD ABC ABCD o===∠=∠,90, 121===AB CB ,E 是PB 的中点. (I)求证://EC 平面PAD'; (Ⅱ)求直线BP 与平面ABCD 所成角的正切值.21.(本小题满分12分)已知圆,0442:22=-+-+y x y x C 直线.1:-=kx y l(I)当圆C 被直线L 平分,求K 的值;(Ⅱ)在圆C 上是否存在A ,B 两点关于直线1-=kx y 对称,且⋅⊥OB OA 若存在,求出直线AB 的方程;若不存在,请说明理由.答案。
浙江省诸暨中学2018_2019学年高一数学下学期期中试题(平行班)(含答案)

浙江省诸暨中学2018-2019学年高一数学下学期期中试题(平行班)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.o o o o sin 20cos10cos160sin10- 等于 ( ▲ )(A )12 (B 3(C )12- (D )32.在等差数列{}n a 中,已知21=a ,1332=+a a ,则654a a a ++等于 ( ▲ ) (A )40 (B )42 (C )43 (D )453.已知正三角形ABC 的边长为2,设2,AB a BC b ==u u u r r u u u r r ,则 ( ▲ ) (A )1a b +=r r (B )a b ⊥r r (C )(4)a b b +⊥r r r (D )1=⋅ 4.若△ABC 中,若22tan tan ba B A =,则△ABC 形状是 ( ▲ ) (A )直角三角形 (B )等腰三角形 (C )等边三角形 (D )等腰或直角三角形5.已知2)(,6||,1||=-⋅==a b a b a ,则向量与向量的夹角是 ( ▲ )(A )6π (B )4π (C )3π (D )2π 6.如图所示,设A ,B 两点在河的两岸,一测量者在A 的同侧,在所在的河岸边选定一点C ,测得AC 的距离为50 m ,∠ACB =45°,∠CAB =105°,则A ,B 两点间的距离为 ( ▲ )(A )50 2 m (B )50 3 m (C )25 2 m (D )25 22 m 7.若31)6sin(=-απ,则)32cos(πα-的值是 ( ▲ ) (A )97 (B ) 97- (C )31- (D )31 8.如图,在ΔABC 中,AD AB ⊥,3BC =u u u r BD u u u r ,1AD =u u u r ,则AC AD ⋅u u u r u u u r =( ▲ ) (A )3 (B )3(C 3(D )239.已知两个等差数列{}n a 和{}n b 的前n 项和分别为n A 和n B ,且7453n n A n B n +=+,则使 得n na b 为整数的正整数n 的个数是 ( ▲ ) (A )2 (B )3 (C )4 (D )510.平面向量,满足3||=-b a ,||2||b a =,则-与夹角的最大值为( ▲ )(A )2π (B )3π (C )4π (D )6π 二、填空题:本大题共7小题,题每题4分,共28分.11.已知向量)1,2(-=,),1(m -=,)2,1(-=,若//)(+,则m = ▲ .12.E ,F 是等腰直角△ABC 斜边AB 上的三等分点,则tan ECF ∠= ▲ .13.已知数列a n {}中,11=a ,⎪⎩⎪⎨⎧-+=+为偶数为奇数n n a n n a a n n n 3311则3a = ▲ .14.如图,两块斜边长相等的直角三角板拼在一起,若AD x AB y AC =+u u u r u u u r u u u r ,则=+y x ▲ .15.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且满足25cos2A =,3AB AC ⋅=u u u r u u u r .则ABC ∆的面积等于 ▲ .16.数列{}n a 的通项公式2cosπn n a n =,其前n 项和为n S ,则2019S 等于 ▲ . 17.在ABC ∆中,2π=∠C ,M 是BC 中点,若31sin =∠BAM ,则=∠BAC sin ▲ . 三、解答题:本大题共5小题,共52分.解答应写出文字说明、证明过程或演算步骤.18.已知函数.),3sin(cos 3sin )(R x x x x x f ∈+++=π (Ⅰ)求)3(πf 的值; (Ⅱ)若1)(=αf ,且)0(πα<<,求αcos 的值.19.已知点)sin ,(cos ),2,0(),0,2(ααC B A ,且πα<<0.(Ⅰ)O 为坐标原点,若7||=+,求与的夹角; (Ⅱ)若⊥,求αtan 的值.20.已知数列{}n a 的前n 项和为222λ++=n n S n . (Ⅰ)当λ=2时,求数列{}n a 的通项公式n a ;(Ⅱ)当λ=0时,令b n =211n a -(n ∈N *),求数列{}n b 的前n 项和.21.在ABC ∆中,内角,,A B C 所对边的长分别是,,a b c ,且22)21cos (b c b B c a -=-(Ⅰ)求角C 的大小;(Ⅱ)若B C A sin ,sin ,sin 成等差数列,且2)(=-⋅,求边c 的长. (Ⅲ)若2=c ,求b a 2+的最大值.22.已知等差数列}{n a 中,公差0>d ,且前n 项和为n S ,又4532=⋅a a ,1441=+a a . (Ⅰ)求数列}{n a 的通项公式; (Ⅱ)通过cn S b n n +=构造一个新的数列}{n b ,若}{n b 也是等差数列,求非零常数c ; (Ⅲ)在(Ⅱ)的前提下,求)()25()(*1N n b n b n f n n ∈⋅+=+的最大值.诸暨中学2018学年高一期中考试数学(平行班)答案 2019.4一、选择题:ABCDCAACDD二、填空题:11、-1 12、43 13、314-14、13+ 15、2 16、-1010 17、36 三、解答题:18、(1)233 (2)6223-19、(1)6π(2)374+-20、(1)⎪⎩⎪⎨⎧≥+==221125n n n a n (2)32112134+-+-=n n T n 21、(1)3π(2)2=c (3)321422、(1)34-=n a n (2)21=c (3)361。
高一(实验班)下学期期中考试数学试题 Word版含解析

2019-2020学年浙江省绍兴市诸暨中学实验班高一第二学期期中数学试卷一、选择题(共10小题).1. 在平面直角坐标系中,3则此直线的倾斜角等于( ) A. 30° B. 60°C. 120°D. 150°【答案】B 【解析】 【分析】根据直线的斜率等于倾斜角的正切值求解即可. 【详解】设此直线的倾斜角为θ,θ∈[0°,180°), ∵tanθ3=∴θ=60°. 故选:B.【点睛】本题考查了直线的倾斜角、三角函数求值,考查了推理能力与计算能力,属于基础题. 2. 已知直线()12:20:240l x ay l ax a y ++=+++=,,若12//l l ,则实数a 的值是( ) A. 2或1- B. 2-或1C. 2D. 1-【答案】D 【解析】 【分析】:两直线平行,斜率相等,可求参数a【详解】:两直线平行,斜率相等可知20a a a ⨯--=,解得21a =-,,当2a =时,2:20l x +=不满足题意舍去.故选D【点睛】:直线方程一般式平行的充要条件:11112222:0:0l A x B y C l A x B y C ++=++=,,若12//l l ,等价于1221A B A B =.所解的值要进行验证.3. 已知直线m ⊄平面α,直线n ⊂平面α,且点A ∈直线m ,点A ∈平面α,则直线m ,n 的位置关系不可能是( ) A. 垂直 B. 相交C. 异面D. 平行【答案】D 【解析】【分析】推导出直线n ⊂平面α,m ∩α=A ,从而直线m ,n 的位置关系不可能是平行直线. 【详解】解:∵直线m ⊄平面α,直线n ⊂平面α,且点A ∈直线m ,点A ∈平面α, ∴m ∩α=A ,∴直线m ,n 的位置关系不可能是平行直线. 故选:D .【点评】本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,属于中档题.4. 如果一个水平放置的图形的斜二测直观图是一个底面为45︒,腰和上底均为1的等腰梯形,那么原平面图形的面积是( ) A. 22+ B.12C.22+ D. 12+【答案】A 【解析】 【分析】如图所示建立坐标系,计算面积得到答案. 【详解】如图所示建立坐标系,根据题意:图2中OABC 为直角梯形,2OC =,1BC =,21OA =+.故22S =+. 故选:A .【点睛】本题考查了斜二测画法求面积,意在考查学生的计算能力.5. 已知,a b 为不同的直线,,αβ为不同的平面,则下列说法正确的是( ) A. 若,,a b αβαβ⊂⊂⊥,则a b ⊥B. 若,,,a b αβαβ⊂⊂不平行,则,a b 为异面直线C. 若,a b b α⊥⊥,则//a αD. 若//,,//a b αβαβ⊥,则a b ⊥ 【答案】D 【解析】分析:由题意结合所给的条件和立体几何的相关判断定理、性质定理逐一考查所给命题的真假即可求得最终结果.详解:若,,a b αβαβ⊂⊂⊥,则,a b 有可能垂直,也有可能平行, 也可能异面但不垂直,也可能相交不垂直,故A 错误,B 也错误; 若,a b b α⊥⊥,则a 有可能在α内,故C 错;由//,//a ααβ可得//a β或a 在β内,又,b β⊥所以a b ⊥,故D 正确. 本题选择D 选项.点睛:本题考查了空间几何体的线面位置关系判定与证明:(1)对于异面直线的判定要熟记异面直线的概念:把既不平行也不相交的两条直线称为异面直线;(2)对于线面位置关系的判定中,熟记线面平行与垂直、面面平行与垂直的定理是关键. 6. 直三棱柱111ABC A B C -中,若90BAC ∠=︒,1AB AC AA==,则异面直线1BA 与1AC所成的角等于A. 30°B. 45°C. 60°D. 90°【答案】C 【解析】【详解】本试题主要考查异面直线所成的角问题,考查空间想象与计算能力.延长B 1A 1到E ,使A 1E =A 1B 1,连结AE ,EC 1,则AE ∥A 1B ,∠EAC 1或其补角即为所求,由已知条件可得△AEC 1为正三角形,∴∠EC 1B 为60,故选C .7. 已知,,,m n a b R ∈,且满足346,341m n a b +=+=的最小值为 ( )C. 1D.12【答案】C 【解析】(),m n 为直线346x y +=上的动点,(),a b 为直线341x y +=上的动点,显然最小值即两平行线间的距离:d 1==.故选C 8. 已知圆:()2()21(0)C x a y a a -+-=>与直线2y x =相交于P Q、两点,则当CPQ∆的面积为12时,实数a 的值为( ) A.52B. 102C. 54D.104【答案】B 【解析】 试题分析:由题意得,圆:()2()21(0)C x a y a a -+-=>的圆心(,)C a a ,半径为1r =,所以圆心到直线2y x=的距离为5d a=,所以弦长为||2222125PQrda=-=-,所以CPQ∆的面积为|122125SPQ da=⋅=⨯-⨯,解得102a =,故选B .考点:圆的弦长公式的应用及三角形的面积计算.【方法点晴】本题主要考查了直线与圆的弦长、弦长公式的应用及三角形的面积的计算,属于基础性试题,同时着重考查了学生的运算能力和分析、解答问题的能力,本题的解答中由圆的方程确定圆心(,)C a a ,半径为1r =,得到圆心到直线的距离5d a=,可得弦长||2125PQa=-,可得三角形的面积12||12S PQ d =⋅=,可求解a 的值.9. 若三棱锥的三视图如图,正视图和侧视图均为等腰直角三角形,俯视图为边长为2的正方形,则该三棱锥的最长棱的棱长为( )A. 2B. 3C. 3D. 22【答案】B 【解析】结合三视图可知几何体为如图所示三棱锥A −BCD ,三棱锥在边长为2的正方体中,可知正方体体对角线AC 即为三棱锥最长的棱,且23AC =,故选B .点睛:三视图的长度特征:“长对正、宽相等,高平齐”,即正视图和侧视图一样高、正视图和俯视图一样长,侧视图和俯视图一样宽.若相邻两物体的表面相交,表面的交线是它们的分界线,在三视图中,要注意实、虚线的画法.10. 在三棱锥A ﹣BCD 中,BCD 3的等边三角形,3BAC π∠=,二面角A ﹣BC ﹣D的大小为θ,且13cos θ=,则三棱锥A ﹣BCD 体积的最大值为( ) A.364 6 C.32D.36【答案】B 【解析】 【分析】设AB =x ,AC =y ,由余弦定理及基本不等式求出xy 的最大值为3,过A 作AO ⊥平面BCD ,∠AEO 为二面角A ﹣BC ﹣D 的平面角,求出AO 的最大值,进而求出三棱锥A ﹣BCD 体积的最大值. 【详解】解:设AB =x ,AC =y ,3BAC π∠=,由余弦定理得:BC 2=x 2+y 2﹣2xycos 3π=x 2+y 2﹣xy ≥xy ,当且仅当x =y 3=又BC 3=xy ≤3,过A 作AO ⊥平面BCD ,BC ⊂平面BCD ,则AO BC ⊥,作AE ⊥BC ,连接OE ,AO AE A ⋂=,BC ⊥平面AEO ,OE ⊂平面AEO ,则BC OE ⊥, ∴∠AEO 为二面角A ﹣BC ﹣D 的平面角,大小为θ, 又11223BC AE xysin π⋅=,所以AE 12xy =, 所以AO =AEsinθ21121()223xy xy =-=≤由1136333A BCD BCDV S AO AO -=⋅=⋅⋅⋅≤, 故选:B .【点评】本题考查了二面角的应用,还考查了余弦定理,基本不等式,体积公式等,中档题. 二、填空题:本大题共7小题,多空题每小题4分,单空题每小题4分,共34分 11. 若圆的半径为1,其圆心与点关于直线对称,则圆的标准方程为_______.【答案】22(1)1y x +-= 【解析】【详解】因为圆心与点关于直线对称,所以圆心坐标为(0,1),所以圆的标准方程为:22(1)1y x +-=,故答案为22(1)1y x +-=. 考点:圆的标准方程.12. 直线l 过点P (1,0),且与以A (2,1),B (03为端点的线段有公共点,则直线l 斜率的取值范围是__________.【答案】(3 【解析】 【分析】作出函数的图像,求出端点处的斜率,从而求出斜率的范围即可. 【详解】如图示:当直线l 过点B 时设直线l 斜率为1k , 则130301k ==- 当直线l 过点A 时设直线l 斜率为2k , 则210121k -==-, ∴要使直线l 与线段AB 有公共点,则直线l 斜率的取值范围是(3 故答案为:(3]∪[1,+∞).【点睛】本题考查了两点求直线的斜率,考查了数形结合的思想,属于基础题.13. 已知圆221:210240C x y x y +-+-=和圆222:2280C x y x y +++-=相交于A 、B两点,则直线AB 所在直线方程为_______________;线段AB 的长度为____________. 【答案】 (1). 240x y -+= (2). 5【解析】分析:将两圆的方程作差可得两圆公共弦的直线方程,利用几何法,首先求得圆心到弦的距离,然后利用弦长公式可得弦,即线段AB 的长度.详解:由两圆221:210240C x y x y +-+-=,222:2280C x y x y +++-=,圆的方程作差可得两圆1C ,2C 公共弦AB 所在直线方程为240x y -+=, ∴圆1C 的标准方程为:()()221550x y -++=, 则圆心()1,5-到公共弦的距离为1104355d ++==.∴弦长222(52)(35)25=⨯-=.点睛:处理直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,则用几何法;若方程中含有参数,或圆心到直线的距离的表达较繁琐,则用代数法. 14. 过点(1,2)M 且在两坐标轴上的截距相等的直线方程为____________. 【答案】x+y=3或y=2x 【解析】试题分析::①当所求的直线与两坐标轴的截距不为0时,设该直线的方程为x+y=a , 把(1,2)代入所设的方程得:a=3,则所求直线的方程为x+y=3即x+y-3=0; ②当所求的直线与两坐标轴的截距为0时,设该直线的方程为y=kx , 把(1,2)代入所求的方程得:k=2,则所求直线的方程为y=2x 即2x-y=0. 综上,所求直线的方程为:2x-y=0或x+y-3=0 考点:直线方程15. 如图所示,在平面直角坐标系xOy 中,已知点A (0,2),B (﹣2,0),C (1,0),分别以AB ,AC 为边向外作正方形ABEF 与ACGH ,则点H 的坐标为_____,直线FH 的一般式方程为_____.【答案】 (1). ()2,3 (2). 4140x y +-= 【解析】 【分析】分别过H 、F 作y 轴的垂线,垂足分别为M 、N .根据正方形的性质证出Rt △AHM ≌Rt △CAO ,利用对应边相等及A 、C 两点的坐标,算出H ()2,3,同理得到F (﹣2,4).由此算出直线FH 的斜率,利用直线方程的点斜式列式,化简即可得到直线FH 的一般式方程. 【详解】解:分别过H 、F 作y 轴垂线,垂足分别为M 、N , ∵四边形ACGH 为正方形,∴Rt △AHM ≌Rt △CAO ,可得AM =OC ,MH =OA , ∵A (0,2),C (1,0),∴MH =OA =2,AM =OC =1,可得OM =OA +AM =3, 由此可得H 坐标为()2,3,同理得到F (﹣2,4),∴直线FH 的斜率为k 431224-==---,可得直线FH 的方程为y ﹣314=-(x ﹣2),化简得4140x y +-=.故答案为:()2,3;4140x y +-=【点睛】主要考查了直线的一般式方程与直线的性质,需要运用正方形的性质、全等三角形的判定与性质、直线的基本量与基本形式等知识,属于中档题. 16. 设M ()22{|20}x y y a x a ==->,,,N ()()(222{|130}x y x y a a =-+-=>,,,则MN ≠∅时,实数a 的最大值是_____,最小值是_____.【答案】 (1). 222 (2). 222 【解析】 【分析】先根据方程得到半圆和圆的圆心和半径,再由题得到半圆和圆相交或相切,得到2||2a a OA a a -≤≤+,222a a a a -≤≤+即得解.【详解】解:2222+2(0)y a x y a y =∴=≥,它表示以原点O 2a 为半径的上半圆.()(22213x y a -+-=,它表示以点A 3)为圆心,以a 为半径的圆. ∵MN ≠∅时,∴半圆与圆相交或相切, 所以2||2a a OA a a -≤≤+,(当半圆与圆内切时2||a a OA -=,当半圆与圆外切时,||2OA a a =+.)所以2221+32a a a a -≤≤+,所以222a a a a -≤≤+,∴实数a 的最大值是222+,a 的最小值是222-. 故答案为:222+;222-.【点睛】本题主要考查集合的交集运算,考查两圆的位置关系,意在考查学生对这些知识的理解掌握水平.17. 如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E 是AB 的中点,F 在CC 1上,且CF =2FC 1,点P 是侧面AA 1D 1D (包括边界)上一动点,且PB 1∥平面DEF ,则tan ∠ABP 的取值范围为_____.【答案】[1133,. 【解析】 【分析】作出平面MNQB 1∥平面DEF ,推导出P 的轨迹是线段QN ,P 在Q 处,tan ∠ABP 取最小值,P 在N 处,tan ∠ABP 取最大值,由此能求出tan ∠ABP 的取值范围.【详解】解:如下图所示,1AA 上取一点Q ,使得12AQ AQ =, 在11D C 上取中点M ,连1B M ,与11A D 交于G , 则111B C M GD M ≅△△,所以11111GD B C A D ==, 即1D 为1A G 中点,连QG 交1DD 于N ,因为11//D N AQ ,所以1D N 为1AQG △中位线,1112D N AQ = 在正方体1111ABCD A B C D -中,E 为AB 中点, 则11,B MDE B M ⊄面,DEF DE ⊂面DEF ,1B M∴面DEF ,1//QB DF ,同理可证1QB 面DEF ,又111QB B M B =,∴平面MNQB 1//平面DEF ,∵PB 1∥平面DEF ,∴P 的轨迹是线段QN , 设正方体1111ABCD A B C D -棱长为3,P 在Q 处,tan ∠ABP 取最小值tan 13ABP ∠=, P 在N 处,tan ∠ABP 取最大值tan ∠ABP 4913+==. ∴tan ∠ABP 的取值范围为[11333,]. 故答案为:[1133,].【点睛】本题考查角的正切值的取值范围的求法,考查线面、面面平行,考查线面角,考查学生分析解决问题的能力,是中档题. 三、解答题:本大题共5小题,共76分18. 如图是一个以A 1B 1C 1为底面的直三棱柱被一平面所截得到的几何体,截面为ABC ,已知A 1B 1=B 1C 1=2,∠A 1B 1C 1=90°,AA 1=4,BB 1=3,CC 1=2,求:(1)该几何体的体积. (2)截面ABC 的面积. 【答案】(1)6(26. 【解析】 【分析】(1)以同样大的几何体进行补形,得一直三棱柱,计算直三棱柱的体积,可求出该几何体的体积;(2)求出△ABC 的各边长,判断△ABC 为等腰三角形,再计算截面△ABC 的面积. 【详解】(1)以同样大的几何体,进行补形,可得一直三棱柱,其底面为△A 1B 1C 1,高为4+2=6,∴所求几何体的体积为V 111111222A B C S h =⨯=⨯⨯2×2×6=6; (2)△ABC 中,AB 22215=+BC 22215=+=AC 2222=+=2,∴△ABC 为等腰三角形,底边AC 的高为:h ()()22523=-=∴截面ABC 的面积为S △ABC 12=⨯236= 【点睛】本题考查了求几何体的体积与截面面积的应用问题,其中合理补形是解题的关键,属于中档题.19. 已知直线120()l kx y k k R -++=∈: (1)证明:直线l 过定点;(2)若直线l 交x 轴负半轴于点A ,交y 轴正半轴于点B ,O 为坐标原点,设AOB 的面积为S ,求S 的最小值及此时直线l 的方程.【答案】(1)见解析(2)最小值为4,直线l 的方程为24=0x y -+【解析】 【分析】(1)直线l 过定点,说明定点的坐标与参数k 无关,故让k 的系数为0 和1可得定点坐标. (2)求出,A B 的坐标,代入三角形的面积公式化简,再使用基本不等式求出面积的最小值,注意等号成立条件要检验,求出面积最小时的k 值,从而得到直线方程. 【详解】(1)证明:由已知得(2)(1)0k x y ++-=,无论k 取何值,∴=0k 时,1y = ,=1k 时,2110x ++-=,2x =-∴ 直线过定点(21)-,.(2)令=0y 得A 点坐标为120k-(-,)令=0x 得B 点坐标为0210k k +>(,)() ∴11==22111221221=222AOBSk k k k k k-++++⨯⨯+-()() 122242k k≥⨯+= 当且仅当122k k=,即12k =时取等号.即AOB 的面积的最小值为4,此时直线l 的方程为11102x y -++=.即24=0x y -+. 【点评】本题考查过定点的直线系方程特征,以及利用基本不等式求表达式的最小值.考查转化思想以及计算能力.20. 如图,平面ABCD ⊥平面ADEF ,其中四边形ABCD 为矩形,四边形ADEF 为梯形,AF ∥DE ,AF ⊥EF ,AF =AD =2AB =2DE =2.(1)求证:CE ∥面ABF ;(2)求直线DE 与平面BDF 所成角的正弦值.【答案】(1)见解析(2)3. 【解析】 【分析】(1)取AF 中点记为G ,连EG ,证明EGBC 为平行四边形,得到CE ∥BG ,再用线面平行的判定定理证明即可.(2))根据四边形ABCD 为矩形,得到BA AD ⊥ ,由平面ABCD ⊥平面ADEF ,得到BA ⊥平面ABCD ,且 1AB =,设点E 到平面BDF 的距离为h ,由V B ﹣DEF =V E ﹣BDF ,求出3h =,然后由θ=hsin DE求解. 【详解】(1)如图所示:取AF 中点记为G ,连EG , ∵//EG AD ,且EG AD =, 又//BC AD ,且BC AD =, 所以//EG BC ,且EG BC =, ∴EGBC 为平行四边形, ∴CE ∥BG ,又∵CE ⊄面ABF ,BG ⊂面ABF , ∴CE ∥面ABF ;(2)因为四边形ABCD 为矩形,所以BA AD ⊥ ,又因为平面ABCD ⊥平面ADEF , 所以BA ⊥平面ABCD , 1AB =, 设点E 到平面BDF 的距离为h , 因为V B ﹣DEF =V E ﹣BDF ,所以1133DEFBDFSBA S h ⋅⋅=⋅⋅,因为AF ∥DE ,AF ⊥EF ,AF =AD =2AB =2DE =2. 所以()223EF AD AF DE =--=,所以1131322=⨯=⨯⨯=DEFSDE EF , 又因为52BD BF DF ===,,所以S △BDF =22111222222DF BF DF ⎛⎫⨯-=⨯⨯= ⎪⎝⎭, 解得3h =, 设直线DE 与平面BDF 所成角为θ, 所以34h sin DE θ==. 【点睛】本题主要考查直线与平面所成角的求法,几何体的体积的求法,直线与平面平行的判断定理的应用,还考查了转化化归的思想和逻辑推理、运算求解的能力,属于中档题. 21. 在平面直角坐标系xOy 中,点A (0,3),直线:24=-l y x ,设圆C 的半径为1,圆心在直线l 上.(Ⅰ)若圆C 与直线1y x =-相交于M ,N 两点,且2MN =C 的横坐标a 的值;(Ⅱ)若圆心C 也在直线1y x =-上,过点A 作圆C 的切线,求切线的方程. 【答案】(Ⅰ) 4a =或2;(Ⅱ) 切线为:0y =或334y x =-+. 【解析】分析:(Ⅰ)设圆心(),24C a a -,由题意结合点到直线距离公式得到关于实数a 的方程,解方程可得4a =或2.(Ⅱ)由题意可得圆心为C (3,2),设出直线方程,利用圆心到直线的距离等于半径可得直线的斜率0k =或34k =-.则所求切线为:0y =或334y x =-+. 详解:(Ⅰ)设圆心(),24C a a -, 圆心C 到直线1y x =-的距离2d ==, 得:4a =或2.(Ⅱ)联立:124y x y x =-⎧⎨=-⎩,得圆心为:C (3,2).设切线为:3y kx =+,1d r ===,得:0k =或34k =-.故所求切线为:0y =或334y x =-+. 点睛:处理直线与圆的位置关系时,若两方程已知或圆心到直线的距离易表达,则用几何法;若方程中含有参数,或圆心到直线的距离的表达较繁琐,则用代数法. 22.《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑. 如图,在阳马P ABCD-中,侧棱PD ⊥底面ABCD,且PDCD=,过棱PC 的中点E,作EF PB⊥交PB 于点F ,连接,,,.DED FBDBE⊥平面.试判断四面体(Ⅰ)证明:PB DEFD BE F是否为鳖臑,若是,写出其每个面的直角(只需写出结论);若不是,说明理由;(Ⅱ)若面DEF与面A B C D所成二面角的大小为π3,求DC BC的值.【答案】(Ⅰ)详见解析;(Ⅱ).【解析】【详解】【分析】(解法1)(Ⅰ)因为PD⊥底面A B C D,⊥,所以PD BC由底面ABCD为长方形,有⋂=,⊥,而PD CD DB C C D⊂平面,所以所以.而DE PCD⊥.B C D E=,点E是PC的中点,所以又因为PD CD⊥.D E P C⋂=,所以D E⊥平面而PC BC CPBC.而P B P B C ⊂平面,所以PB DE⊥. 又PB EF ⊥,DE EF E⋂=,所以PB ⊥平面 D E F.由DE ⊥平面P B C,PB ⊥平面D E F,可知四面体BDEF的四个面都是直角三角形, 即四面体BDEF是一个鳖臑,其四个面的直角分别为DEBD E F ∠∠,,EFB DFB∠∠,.(Ⅱ)如图1,在面PBC内,延长 B C与FE 交于点G,则DG 是平面 DE F与平面ABCD的交线.由(Ⅰ)知,PB DEF⊥平面,所以PB DG⊥.又因为PD ⊥底面 A B CD,所以PD DG ⊥.而PDP BP⋂=,所以DG PBD⊥平面.故BDF ∠是面D E F与面ABCD所成二面角的平面角,设1PD DC ==,B C λ=,有12BD λ=+,在Rt△PDB 中, 由DF PB⊥, 得π3DPF FDB ∠=∠=,则tanπ3tan 123DPF BD PD λ=∠==+=, 解得2λ=.所以122.DC BC λ== 故当面DEF与面AB C D所成二面角的大小为π3时,22DCBC=. (解法2) (Ⅰ)如图2,以D 为原点,射线,,D ADCDP分别为,,x y z轴的正半轴,建立空间直角坐标系.设1PD DC ==,B Cλ=,则(0,0,0),(0,0,1),(,1,0),(0,1,0)D P B C λ,(,1,1)PB λ→=-,点E 是PC的中点,所以(0,12,12)E ,(,12,12)DE→=, 于是PBDE →⋅→=,即PB DE⊥.又已知EF PB ⊥,而DEEFE⋂=,所以PB DEF⊥平面.因(0,1,1)PC →=-,DEPC →⋅→=,则DE PC ⊥, 所以.由DE ⊥平面P B C,PB ⊥平面DE F,可知四面体BDEF的四个面都是直角三角形,即四面体BDEF是一个鳖臑,其四个面的直角分别为,,∠∠D E B D E F,.EFB DFB∠∠⊥平面,所以(Ⅱ)由PD ABCDDP→=是平面(0,0,1)A B C D 的一个法向量;⊥平面,所以由(Ⅰ)知,PB DEF→=--是平面BPλ(,1,1)D E F 的一个法向量.若面DEF与面A B C D所成二面角的大小为π3,则→⋅→→|| BP DP,λ=.所以解得2D C B Cλ==122.故当面DEF与面A B C D所成二面角的大小为π3时,DC BC=22.考点:四棱锥的性质,线、面垂直的性质与判定,二面角.。
【高一数学试题精选】2018年高一下学期数学期中考试题(带答案)

2018年高一下学期数学期中考试题(带答案)
5 考生注意
1答题前,考生务必将自己的准考证号、姓名填写在答题卡上。
2第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
第II卷用黑色墨水签字笔在答题卡上书写作答,在试题卷上作答,答案无效。
第I卷选择题(共50分)
—、选择题 (本大题共10小题,每小题5分,共50分在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合,集合B为函数的定义域,则A∩B=()
A.(1,2) B.[1,2] c.[1,2) D.(1,2]
2.已知向量,,,则=()
A -12
B -6 c 6 D 12
3.()
A. B. c. D.
4 函数的零点必落在区间()
A B c D(1,2)
5 等差数列中,,则数列的前9项的和等于()
A 96
B 99 c 144 D 198
6 等比数列各项为正数,且,则()
A.12 B.10 c.8 D.
7 已知a、b为非零实数,且a<b,则下列不等式成立的是()
A. B. c. D.
8 已知中, ,AB、Bc分别是,的等差中项与等比中项,则的面积等于()
A. B. c.或 D.或。
浙江诸暨中学2017-2018学年高一下学期期中考试题 平行班数学

诸暨中学2017学年第二学期期中考试高一年级数学试题卷选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.在ABC ∆中,已知222a b c +-=,则C = ( ▲ )A .45 B .15 C .135 D .1652.已知数列{}n a 是等比数列,其中是48,a a 函数2()42f x x x =-+的两个零点,则210a a = ( ▲ ) A .4 B .2 C .4- D .2-3.已知等差数列{}n a 的前k 项和为3,前2k 项和为10,则前3k 项和为 ( ▲ ) A .13 B .17 C .21 D .264.已知向量a 与b 的夹角为120,且4a b ==,那么(2)a b b +⋅的值为 ( ▲ ) A .1 B . 1- C .1± D .05.若,,a b c 是两两不共线的平面向量,则下列结论错误的是 ( ▲ ) A .a b b a +=+ B .a b b a ⋅=⋅ C .()()a b c a b c ++=++ D .()()a b c b c a ⋅=⋅6.在ABC ∆中,若2cos a b C =,则ABC ∆的形状是 ( ▲) A .等腰三角形 B .直角三角形 C .等边三角形 D .等腰直角三角形 7.某船以km h 的速度向正北方向航行,在A 处看灯塔S 在北偏东45方向,1.5h 后 航行到B 处,在B 处看灯塔S 在南偏东15方向,则灯塔S 与B 之间的距离为( ▲ ) A .66km B .132km C .96km D .33km8.若数列{}n a 满足1113,1n n n a a a a +-==+,则2018a = ( ▲ )A .3B .12C .13- D .2-9.在平行四边形ABCD 中,,,AB a AD b ==且3CF FD =,连结AF 交BD 于E ,则AE = ( ▲ )A .2355a b + B .1455a b + C .1344a b + D .1122a b +10.已知,a b 是两个不共线的单位向量,向量(1),c a b R λλλ=+-∈,且12c =, 则a b -的最小值是( ▲ ) A .1 B C D .2非选择题部分(共110分)二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分。
2018浙江省高一(下)期中数学试题

2018浙江省高一(下)期中数学试题本试卷满分150分,考试时间120分钟一、选择题:本大题共8小题,每小题5分,共40分,在每小题的四个选项中,只有一项是符合要求的,把答案填在答题卷的相应位置上.1.设集合⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧==3,23,22,21,4tan N x x M π,则=N M ( )A .MB .⎭⎬⎫⎩⎨⎧22C .D .{}0 2.已知函数)sin()(ϕ+=x x f 为偶函数,则ϕ的取值可以为 ( )A .2π-B .πC .3π D .03.设△ABC 的内角A , B , C 所对的边分别为a , b , c , 且B ac c a b cos 2222++=,则=∠B ( )A .6πB .3πC .2πD .23π4.已知是边长为2的等边三角形,点D 为BC 边的中点,则=⋅BD AB ( ) A .2-B .1-C .1D .25.为了得到函数x x y 2cos 2sin +=的图像,可以将函数x y 2sin 2=的图像( )A .向右平移4π个单位 B .向左平移4π个单位 C .向右平移8π个单位 D .向左平移8π个单位6.已知,角,,所对应的边分别为,且,则是( )A .直角三角形B .等边三角形C .钝角三角形D .锐角三角形7.已知b a ,是单位向量,0=⋅b a ,若向量c1=+-a ,则-的取值范围是( ) A .[]12,12+- B .[]12,1+C .[]2,0D .[]15,15+-8.已知函数)(x f 在R 上满足0)()(=+-x f x f ,且0>x 时,)sin 2sin (21)(αα+++=x x x f )232(sin 23παπα≤≤-+对任意的R x ∈,都有)()33(x f x f ≤-恒成立,则实数α的取值范围为( ) A .[]π,0 B .⎥⎦⎤⎢⎣⎡-32,3ππ C .⎥⎦⎤⎢⎣⎡-67,6ππ D .⎥⎦⎤⎢⎣⎡-34,3ππ 二、填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分.把答案填在答题卷的相应位置上. 9.函数)10)(32(log )(≠>-=a a x x f a 且的定义域为 ,图像过的定点为 .10.已知向量)cos ,(sin x x a =,)3,1(=b ,若b a // 且b a ,方向相同,则=a ;若函数b a x f ⋅=)(的图像关于直线)0(πϕϕ<<=x 对称,则=ϕ . 11.若,10sin 3cos -=+αα则αtan = ,α2sin = . 12.已知)2sin(3)2cos(3)(x x x f ++-=ππ,则)(x f 的最小正周期为 ,)(x f 的最大值为 .∅ABC ∆ABC ∆A B C c b a ,,sin sin cos cos A B A B +=+ABC ∆13.已知函数⎩⎨⎧≥--<+=)0(1)0(1)(x x x x x f ,则不等式1)()1(≤++x f x x 的解集是 .14.已知△ABC 中, 4,3,90===∠BC AC C,一直线分△ABC 为面积相等的两个部分,且夹在AB 、BC 之间的线段为MN ,则MN 长度的最小值为 .15.已知2)2(log )(2222-+++=a x a x x f 有唯一零点,则实数a 的值为________. 三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 16.(本题满分14分)在中,角的对边分别为54cos ,4,,,=π=B A c b a . (Ⅰ)求C cos 的值; (Ⅱ)若5,22==b a ,求的面积.17.(本题满分15分)在中,角C B A ,,所对的边分别是c b a ,,,设向量 )2,cos 2(b cC m -=,)1,2(a n =,且n m ⊥.(Ⅰ)求角A 的值; (Ⅱ)若2=a ,求的周长l 的取值范围.18.(本题满分15分)已知函数1)6cos(sin 4sin 4)(2-π++=x x x x f . (Ⅰ)当π≤≤x 0时,求方程1)(=x f 的解;(Ⅱ)若函数)()3(21)12(21)(R x x f x f x g ∈+++=ππ,试判断函数)(x g 的奇偶性,并求)(x g 的的值域.19.(本题满分15分)对于函数)(x f ,若存在给定的实数对),(b a ,对定义域中的任意实数x ,都有b x a f x a f =-⋅+)()(成立,则称函数)(x f 为“Ψ函数”.(Ⅰ)函数xe xf =)(是“Ψ函数”,求出所有实数对()b a ,满足的关系式,并写出两个实数对;(Ⅱ)判断函数x x f sin )(=是否为“Ψ函数”,并说明理由.20.(本题满分15分)已知函数xx a xx x f -+⋅++-=1111)((R ∈a ).(Ⅰ)当1-=a 时,判断()f x 在区间)1,1(-上的单调性,并说明理由; (Ⅱ)若0>a 时,对于区间]21,21[-上任意取的三个实数m ,n ,p ,都存在以)(m f ,)(n f ,)(p f 为边长的三角形,试求实数a 的取值范围.高一数学参考答案一.选择题:本大题共8小题,每小题5分,共40分1 2 3 4 5 6 7 8 二.填空题:本大题共7小题,多空题每题6分,单空题每题4分,共36分. 9.),23(+∞ (或⎭⎬⎫⎩⎨⎧>23x x 或23>x );)0,2( 10.)23,21( ;6πϕ= 11.3 ;5312.π2 ;32 13.[)+∞-,3 14. 2 15. 1三.解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 16.(Ⅰ)53sin ,054cos =∴>=B B …………………………2分)4cos()]4(cos[cos B B C +-=+-=πππ …………………………4分10254225322)sin 4sincos 4(cos-=⋅-⋅=--=B B ππ……………7分 (Ⅱ)由(Ⅰ)知道1027sin =C …………………………10分 5,22==b a557102752221sin 21=⋅⋅⋅==∴∆C ab S ABC …………………………14分 17.(Ⅰ)0=⋅⇒⊥n m n m02cos 22=-+⋅b cC a …………………………2分 由正弦定理得:0sin sin 21cos sin =-+B C C AC A C A C A C A B sin cos cos sin )sin()](sin[sin +=+=+-=π代入上式………5分21cos sin 21sin cos =∴=A C C A 3π=∴A …………………………7分 (Ⅱ)由正弦定理:AaC c B b sin sin sin == 得:)3sin(34)](sin[34sin 34,sin 34ππ+=+-===B B AC c B b …11分)3sin(34sin 342π+++=++=∴B B c b a l)6sin(42)cos 21sin 23(42)cos 23sin 21(sin 342π++=++=+++=B B B B B B …………13分320π<<B 6566πππ<+<∴B 1)6sin(21≤+<∴πB (]6,4∈∴l ……………………………………………………15分 18.(Ⅰ)1)sin 21cos 23(sin 4sin 41)6cos(sin 4sin 4)(22--+=-++=x x x x x x x x f π……………………………………………………2分)62sin(22cos 2sin 31sin 2cos sin 32sin 422π-=-=--+=x x x x x x x21)62sin(1)62sin(2=-∴=-∴ππx x …………………………4分)(6526262Z k k k x ∈++=-∴πππππ或 …………………………6分π≤≤x 0 26ππ==∴x x 或 ……………………………………………8分(Ⅱ)x x x f x f x g 2cos 2sin )3(21)12(21)(+=+++=ππ )(2cos 2sin )(2cos )(2sin )(x g x x x x x g =+=-+-=-)(x g ∴为偶函数 …………………………………………………11分 x x x x x x g 4sin 12cos 2sin 212cos 2sin )(+=+=+=)(x g ∴的值域为[]2,1……………………………………………………………15分 19.(Ⅰ)函数xe xf =)(是一个“Ψ函数” 由b x a f x a f =-⋅+)()(得:b e e x a xa =-+b ea=∴2 (或b a ln 21=)…………………………………………………4分如:),1(),1,0(2e 等………………………………………………………6分 (Ⅱ)x xf sin )(=不是“Ψ函数” …………………………………………………7分 若函数x x f sin )(=是 “Ψ函数”则b x a x a =-+)sin()sin( 恒成立………………………………………………8分 由b x a x a x a x a =-+)sin cos cos )(sin sin cos cos (sin 恒成立得b x a x a =-2222sin cos cos sin ………………………10分 b x a x a =--)cos 1(cos cos sin 2222b a x =-22cos cos 即b a x +=22cos cos ∵R ∈x 则]1,0[cos 2∈x而b a +2cos 为常数,这不可能∴函数x x f sin )(=不是 “Ψ函数” …………………………………………15分 另法:(其它方法酌情给分)即)sin (cos sin cos cos sin 222222x x b x a x a +=- 0sin )(cos cos )(sin 2222=+--∴x b a x b a 恒成立⎪⎩⎪⎨⎧-==∴ba b a 22cos sin若0=b ,则0cos sin ==a a ,不可能 若0≠b ,则1tan 2-=a ,不可能 ∴函数x x f sin )(=不是 “Ψ函数”20.(Ⅰ)1-=a 时,xx xx x f -+-+-=1111)(为偶函数……………………………1分只讨论10<≤x 时的单调情况 令xx t +-=11 )10(≤<t , 11211-+=+-=x x x t 在[)1,0∈x 上单调递减 tt y 1-=在(]1,0∈t 上单调递增∴函数)(x f 在[)1,0上单调递减……………………………………………3分∵函数)(x f 为偶函数 ∴)(x f 在(]0,1-上单调递增……………4分(Ⅱ)令xx t +-=11,由2121≤≤-x 得⎥⎦⎤⎢⎣⎡∈-+=1,31112x t )131(≤≤+=∴t t a t y 由题意得:在区间]1,31[上,恒有max min 2y y >. …………………………6分①当910≤<a 时,t at y +=在]1,31[上单调递增,313,1min max +=+=a y a y 由max min 2y y >,得151>a ,从而91151≤<a . …………………………………………………………………8分②当3191≤<a 时,t at y +=在],31[a 上单调递减,在]1,[a 上单调递增,1}1,313max{,2max min +=++==∴a a a y a y ,由max min 2y y >得347347+<<-a ,从而3191≤<a ;………………10分③当131<<a 时,t at y +=在],31[a 上单调递减,在]1,[a 上单调递增,313}1,313max{,2max min +=++==∴a a a y a y ,由max min 2y y >得93479347+<<-a ,从而131<<a ; …………………12分 ④当1≥a 时,t a t y +=在]1,31[上单调递减, 313,1max min +=+=a y a y由max min 2y y >得35<a ,从而351<≤a ;……………………………………………14分综上,35151<<a . …………………………………………………………………15分。
浙江省2018学年高一数学下学期期中试题(含解析)

浙江省2018学年高一数学下学期期中试题(含解析)一、选择题(本大题共10小题,共40.0分) 1.不等式2560x x +->的解集是( )A. {}23x x x -或B. {}23x x -<< C. {}61x x x -或D. {}61x x -<<【答案】C 【解析】 【分析】先分解因式再解不等式.【详解】因为2560x x +->,所以(1)(6)01x x x -+>∴>或6x <-,选C. 【点睛】本题考查解一元二次不等式,考查基本求解能力,属基础题.2.若ABC ∆的三个内角满足sin :sin :sin 5:11:13A B C =,则ABC ∆( ) A. 一定是锐角三角形 B. 一定是直角三角形C. 一定是钝角三角形D. 可能是锐角三角形,也可能是钝角三角形 【答案】C 【解析】试题分析:由正弦定理得,所以C 是最大的角,由余弦定理,所以C 为钝角,因此三角形ABC 一定是钝角三角形考点:三角形形状的判定及正、余弦定理的应用3.已知向量(3,4)OA =-,(6,3)OB =-,(2,1)OC m m =+.若A B O C ∥,则实数m 的值为( )A.15B. 35-C. 3-D. 17-【答案】C 【解析】 【分析】根据向量共线坐标表示得方程,解得结果.【详解】因为//AB OC ,所以()()3,1//2,1m m +,3(1)2 3.m m m ⨯+=∴=-选C. 【点睛】本题考查向量共线,考查基本分析与求解能力,属基础题.4.若,,a b c ∈R ,且a b >,则下列不等式一定成立的是( ) A. a c b c +≥- B. 2()0a b c -≥ C. ac bc > D.b bc a a c+≤+ 【答案】B 【解析】 【分析】根据不等式性质确定选项.【详解】当0c <时,a c b c +≥-不成立;因为20,0c a b ≥->,所以()20a b c -≥;当0c <时,ac bc >不成立; 当0c <时,b b c a a c+≤+不成立; 所以选B.【点睛】本题考查不等式性质,考查基本分析判断能力,属基础题.5.平面向量a 与b 的夹角为60,||2|,|1a b ==,则|2|a b +=( )B. 12C. 4D. 【答案】D 【解析】 【分析】由题意可得2|2|(2)a b a b +=+,由数量积的定义,代入已知数据可得答案. 【详解】由题意可得2|2|(2)a b a b +=+22224444||||cos60a b a b a b a b =++⋅=++︒==故选:D .【点睛】本题考查向量的模的计算,涉及向量的夹角,以及向量的数量积运算,属于常考题型.6.在ABC ∆中角A 、B 、C 的对边分别是a 、b 、c ,若(2)cos cos b c A a C -=,则A ∠为( ) A.6π B.4π C.3π D.56π 【答案】C 【解析】 试题分析:()2cos cos b c A a C -=,则有()2sin sin cos sin cos B C A A C -=,则有2sin cos cos sin sin cos B A A C A C -=,即s i n cos cos s i n2s i n co A C A C B C +=,即()s i n 2s i n cos A C B C +=,则有()sin 2sin cos B B C π-=,即sin 2sin cos B B C =,因为0B π<<,所以sin 0B >,故有2cos 1C =,解得1cos 2C =,因为0C π<<,所以3C π=,故选C.考点:1.正弦定理;2.边角互化7.已知122a b -<+<,34a b <-<,则4a b -的取值范围是( ) A. (4,11) B. (5,11) C. (4,10) D. (5,10)【答案】D 【解析】 【分析】先寻找4a b -与2a b +、a b -的关系,再根据不等式性质得结果.【详解】因为42a b a b -=+()+2(a b -),所以41628510a b -∈-++=,(,),选D. 【点睛】本题考查不等式性质,考查基本分析求解能力,属基础题.8.若数列{}n a 满足11a =,22a =,21(3)n n n a a a n --=>,记数列{}n a 的前n 项积为n T ,则下列说法错误的是( ) A. n T 无最大值 B. n a 有最大值C. 20194T =D. 20192a =【答案】A 【解析】 【分析】先求数列{}n a 周期,再根据周期确定选项. 【详解】因为()12211,2,3n n n a a a a a n --===≥,所以34567811=2=1===1=222a a a a a a ,,,,,, 因此数列{}n a 为周期数列,6n n a a +=,n a 有最大值2,201932a a ==, 因为123456781,2,=4=4=2=1=1=2T T T T T T T T ==,,,,,,,所以{}n T 为周期数列,6n n T T +=,n T 有最大值4,201934T T ==, 综上选A.点睛】本题考查数列周期,考查基本分析求解能力,属中档题.9.设等差数列{}n a 的前n 项和为n S ,且150S >,890a a +<,则使得0nn s a n+<最小的n 为( ) A. 10B. 11C. 12D. 13【答案】B 【解析】 【分析】先根据条件得首项与公差关系,再结合选项判断nn S a n+符号.【详解】因为15890,0S a a >+<,所以1111111515140,215070,215000,2a d a d a d a d a d +⨯⨯>+<∴+>+<><,, 当10n =时,10111011272722()01022714S aa a a d a +=+>+-=>, 当11n =时,11111215011Sa a d +=+<所以选B.【点睛】本题考查等差数列通项公式与求和公式,考查基本分析判断能力,属中档题.10.数列{}:1,1,2,3,5,8,13,21,34,n F ,称为斐波那契数列,是由十三世纪意大利数学家列昂纳多•斐波那契以兔子繁殖为例子而引入,故又称为“兔子数列”.该数列从第三项开始,每项等于其前相邻两项之和.记该数{}n F 的前n 项和为n S ,则下列结论正确的是( ) A. 201920212S F =+B. 201920211S F =-C. 201920202S F =+D.201920201S F =-【答案】B 【解析】 【分析】利用迭代法可得21123211n n n n n n n a a a a a a a a a ++---=+=+++++++,即11n n a S +=+成立,即可得到答案.【详解】由题意,熟练数列{}n F :1,1,2,3,5,8,13,21,34,…,即该数列从第三项开始,每项等于其前相邻两项之和,则211121n n n n n n n n n n a a a a a a a a a a ++----=+=++=+++1232n n n n n a a a a a ----=++++=123211n n n n a a a a a a ---=+++++++,即11n n a S +=+成立,所以201920211S a =-成立,故选B.【点睛】本题主要考查了数列的综合应用问题,其中解答中根据数列的结构特征,合理利用迭代法得出11n n a S +=+是解答本题的关键,着重考查了分析问题和解答问题的能力,属于中档试题.二、填空题(本大题共7小题,共36.0分)11.已知等比数列{}n a 满足:179a a +=,268a a =,且1n n a a +<,则4α=______;q =______.【答案】(1).【解析】 【分析】根据条件列方程组解得首项与公比,再求4a .【详解】因为17269,8a a a a +==,所以6611112611+98+9=1,88a a q a a q a a q ⎧==∴=⎨=⎩,或611=8,8a q =,因为1n n a a +<,所以31411,=1,q a q a a q >===【点睛】本题考查等比数列首项与公比,考查基本分析求解能力,属中档题.12.已知等差数列{}n a 的前n 项和记为n S ,若48S =.84S =,则12S =______;6S =______. 【答案】 (1). 12- (2). 152【解析】 【分析】根据等差数列和项性质求12S .根据首项与公差求6S . 【详解】因为等差数列中484128,,S S S S S --仍成等差数列,所以84412812122()(),2(48)8(4),12S S S S S S S -=+--=+-∴=-, 因为488,4S S ==,所以11611251443811582665.1322887424a a d S a d a d d ⎧⎧=+⨯⨯=⎪⎪⎪⎪∴∴=+⨯⨯=⎨⎨⎪⎪+⨯⨯==-⎪⎪⎩⎩, 【点睛】本题考查等差数列求和公式以及性质,考查基本分析求解能力,属中档题.13.在ABC ∆中,角A ,B ,C 所对的边分别是a ,b ,c ,已知4a =,30A =︒.若4b =,则ABC ∆的面积为______;若ABC ∆有两解,则b 的取值范围是______. 【答案】(1). 48x << 【解析】 【分析】根据等腰三角形性质可得ABC ∆的面积,根据正弦定理确定有两解条件.【详解】若4b =,则B 30,120A C ===,因此ABC ∆的面积为0144sin1202⨯⨯⨯= 由正弦定理得8sin sin sin b ab B B A=∴=, 因为ABC ∆有两解,所以0115030,90sin (,1),(4,8).2B B B b >>≠∴∈∈【点睛】本题考查正弦定理以及三角形面积,考查基本分析判断与求解能力,属中档题.14.已知1e ,2e 是不共线的两个单位向量,122a e e =-,12b ke e =+,若a b ∥,则k =______;若对任意的k ∈R ,a 与b 都不可能垂直,则1e 在2e 上的投影为______ 【答案】 (1). 12- (2). 12【解析】 【分析】根据向量平行可列方程解得k ;先根据向量数量积探求12e e 的值,再根据向量投影公式可得结果.【详解】因为//a b ,12,e e 是不共线的两个单位向量,所以1112,2k k ⨯=-⨯∴=- 由题意得()()1212121212221212k 20a b e e ke e k k e e e e e e =-+=-+-=-+-≠,对任意的k R ∈恒成立,所以1212e e = 所以1e 在2e 上的投影为1212212||e e e e e ⋅=⋅=.【点睛】本题考查向量共线、垂直与投影,考查基本分析判断与求解能力,属中档题.15. 已知向量a ,b 满足||1a =,||2b =,()a a b ⊥+,则a 与b 夹角的大小是______.【答案】34π【解析】 【分析】由向量垂直的充分必要条件可得2a b a ⋅=-,据此求得向量夹角的余弦值,然后求解向量的夹角即可.【详解】由()a a b ⊥+得,()0a a b ⋅+=,即20a a b +⋅=,据此可得:2cos ,a b a b a b a ⋅=⋅⋅=-,12cos ,212a b ∴=-=-⨯, 又a 与b 的夹角的取值范围为[0,]π,故a 与b 的夹角为34π. 【点睛】本题主要考查平面向量的数量积,向量垂直的充分必要条件,向量夹角的计算等知识,意在考查学生的转化能力和计算求解能力.16.已知ABC ∆中,A ∠的平分线交对边BC 于点D ,3AB AC =,且A D k A C =,则实数k 的取值范围是______. 【答案】3(0,)2【解析】 【分析】根据三角形面积公式列函数关系式,再根据三角形内角范围求结果. 【详解】由题意得111sin sin sin 22222A A AB AC A AB AD AC AD ⨯⨯⨯=⨯⨯⨯+⨯⨯⨯,所以11132sin cos 3sin sin 2222222A A A A AC AC AC kAC AC kAC ⨯⨯⨯=⨯⨯⨯+⨯⨯⨯, 即3π3cos ,(0,)cos (0,1),(0,).222222A A A k k =∈∴∈∈ 【点睛】本题考查三角形面积公式,考查基本分析判断与求解能力,属中档题.17.已知数列{}n a 满足11a =,且当2n ≥时,()2110n n n n a a a ---+=,则n a =______.【答案】12n n+ 【解析】 【分析】变形递推关系式,再根据叠乘法求结果. 【详解】当2n ≥时,()2110n n n n a a a ---+=,所以()1+11n n na n n a n -=-,因此当2n ≥时,()()12111113111=2111222n n n n n nn nn n na n a n a a a n n n n n --+++++=-⋅-==⋅⋅⋅⨯⨯==--所以1=2n n a n+ 因为当1n =时,1112n a n +==,所以1=2n n a n+. 【点睛】本题考查利用叠乘法求数列通项,考查基本分析判断与求解能力,属中档题.三、解答题(本大题共5小题,共74.0分) 18.已知函数22()33f x ax ax a =-+-.(Ⅰ)若不等式()0f x <的解集是{|}x l x b <<,求实数a 与b 的值;(Ⅱ)若0a <,且不等式()4<f x 对任意[3,3]x ∈-恒成立,求实数a 的取值范围. 【答案】(Ⅰ)3,2a b ==(Ⅱ)704a -<< 【解析】 分析】(Ⅰ)根据不等式解集与对应方程根的关系列式求解,(Ⅱ)分离变量,转化为求对应函数最值问题.【详解】(Ⅰ)因为不等式()0f x <的解集是{}1x x b <<, 所以1b ,为22330ax ax a -+-=两根,且0a >,因此2132033b b a a a b a +=⎧=⎧⎪>∴⎨⎨-==⎩⎪⎩(Ⅱ)因为0a <,所以不等式()4f x <可化为2273a x x a -->因为当[]3,3x ∈-时223993x 244x x -=--≥-,,所以2974a a-->,因为0a <,解得70.4a -<<【点睛】本题考查不等式解集与对应方程根的关系以及不等式恒成立问题,考查基本分析判断与求解能力,属中档题.19.在ABC ∆中,角A ,B ,C 所对的边分别是a ,b ,c ,已知ABC ∆1,且sin sin A B C +=(Ⅰ)求边c 的长;(Ⅱ)若ABC ∆的面积为1sin 5C ,求cos C 的值. 【答案】(Ⅰ)1c =(Ⅱ)1cos =4C 【解析】 【分析】(Ⅰ)先根据正弦定理得边的关系,再根据周长求c ;(Ⅱ)根据三角形面积公式得ab 的值,再根据余弦定理求结果. 【详解】(Ⅰ)因为sin sin A B C +=,所以由正弦定理得a b +=,1,所以1,1,a b c c c ++=+==(Ⅱ)因为ABC ∆的面积为1sin 5C ,所以112sin sin 255ab C C ab ==,,所以222222221()215cos .222425a b c a b ab c C ab ab -⋅-+-+--====⋅ 【点睛】本题考查正弦定理、余弦定理以及面积公式,考查基本分析判断与求解能力,属中档题.20.如图,在梯形ABCD 中,AB CD ∥,1AD CD ==,3AB =,(Ⅰ)若AC AB BD λ+=,求实数λ的值; (Ⅱ)若AD BC ⊥,求数量积AC BD ⋅的值 【答案】(Ⅰ)43-(Ⅱ)3- 【解析】 【分析】(Ⅰ)根据平面向量基本定理求解,(Ⅱ)根据向量数量积定义求解.【详解】(Ⅰ)因为A C Aλ+=,所以AD DC AB BA AD λ++=+,103AB AB AB λ++=,因此43λ=-, (Ⅱ)()()()()()22222········3?3 3.AC BD AD DC BC CD AD CD DC BC CD AD BC CD CD AB BC CD BC CD CD CD CD CD CD CD =++=+-=--=++--=-+-=-=-【点睛】本题考查平面向量基本定理以及向量数量积,考查基本分析判断与求解能力,属中档题.21.设公差不为0的等差数列{}n a 中,25a =,且1311,,a a a 构成等比数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n b 的前n 项和n S 满足:11123n n S ⎛⎫=-⎪⎝⎭,求数列{}n n a b 的前n 项和n T . 【答案】(Ⅰ)31n a n =- (Ⅱ)767443n nn T +=-⋅ 【解析】 【分析】(Ⅰ)根据条件列方程解得公差,再根据等差数列通项公式得结果,(Ⅱ)先根据和项求通项,再根据错位相减法求和.【详解】(Ⅰ)因为1311,,a a a 构成等比数列,所以23111a a a =,()()()255953d d d d ∴-+=+⇒=(0舍去)所以()2231n a a n d n =+-=- (Ⅱ)当1n =时111111233b S ⎛⎫==-= ⎪⎝⎭, 当2n ≥时11111112333n n n n n nb S S S --⎛⎫=-==-= ⎪⎝⎭,313n n nn a b -∴=, 22531333n n n T -=+++2311253431 33333n n n n n T +--=++++ 相减得2312233331 333333n n n n T +-=++++-所以121111311?213323n n nn T ()--=++++- 11113131?122313n nn ---=+--()即767443n n n T +=-⋅【点睛】本题考查等差数列通项公式以及错位相减法求和,考查基本分析求解能力,属中档题.22.已知数列{}n a 满足12a =,()*12(1)n n n a a n N ++=-∈.(Ⅰ)求证:数列{}(1)nn a --是等比数列;(Ⅱ)比较n a 与312n +的大小,并用数学归纳法证明; (Ⅲ)设12nn n n b a a +-=,数列{}n b 的前n 项和为n T ,若n T m <对任意*n N ∈成立,求实数m 的取值范围.【答案】(Ⅰ)见证明(Ⅱ)312n n a +≥(Ⅲ)13m ≥ 【解析】 【分析】(Ⅰ)根据等比数列定义证明,(Ⅱ)先求n a ,再根据数学归纳法证明,(Ⅲ)先化简n b ,再利用裂项相消法求和得n T ,最后根据n T 最大值得结果. 【详解】(Ⅰ)()()()()()()()11112112212111n n n nn n n nnnn n n a a a a a a +++---+----+-===-------且1130a +=≠,(){}1nn a ∴--是以3为首项,2-为公比的等比数列,(Ⅱ)由(Ⅰ)知:()()1132nn n a ---=⨯-()()()()11132+11321n n n n n a ---∴=⨯--=-⨯-1321n n a -∴=⨯-312n n a +≥,下面用数学归纳法证明 (1)当1n =时,3122n n a +=≥(2)假设当*,n k k N =∈时,31 2k k a +≥,当1n k =+时,()()131131 3212112113222kk k k k a a k ++++⎛⎫=⨯-=+-≥+-=+> ⎪⎝⎭,即当1n k =+时,结论成立, 由(1)(2)得312n n a +≥, (Ⅲ)因为()()()()1112213211321n nn n n n n n n b a a --+--==-⨯--⨯- ()()1122113321321321321n n nn n --⎛⎫==- ⎪⨯-⨯-⨯-⨯-⎝⎭011212112112112111332132133213213321321323213n n n n T -⎛⎫⎛⎫⎛⎫⎛⎫∴=-=-+=-=-<⎪ ⎪ ⎪ ⎪⨯-⨯-⨯-⨯-⨯-⨯-⨯-⎝⎭⎝⎭⎝⎭⎝⎭13m ∴≥【点睛】本题考查证等比数列、数学归纳法以及裂项相消法求和,考查基本分析论证与求解能力,属中档题.。
浙江省绍兴市诸暨中学平行班2018_2019学年高一数学下学期期中试题(含解析)

浙江省绍兴市诸暨中学平行班2018-2019学年高一数学下学期期中试题(含解析)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(2015新课标全国Ⅰ理科)o o o o sin 20cos10cos160sin10-=A. B.2C. 12-D.12【答案】D 【解析】原式=o o o o sin 20cos10cos 20sin10+=o sin30=12,故选D. 考点:本题主要考查诱导公式与两角和与差的正余弦公式.2.在等差数列{}n a 中,已知1232,13a a a =+=,则456a a a ++等于( ) A. 40 B. 42C. 43D. 45【答案】B 【解析】由题意可得:2311122313a a a d a d a d +=+++=+= , 即:22313,3d d ⨯+=∴= ,据此:()4565133442a a a a a d ++==+= . 本题选择B 选项.3.已知正三角形ABC 的边长为2,设2,AB a BC b ==,则( ) A. 1a b +=B. a b ⊥C. ()4a b b +⊥D. ·1a b =【解析】 【分析】根据向量的线性运算和乘法运算,判断选项的正误即可【详解】解:如图,∵正三角形ABC 的边长为2,2,AB a BC b ==, 取AB 中点D ,设BE AD a ==, ∴1AD BD BE ===,0120EBC ∠=,∴22a b +=-=A 错误;,a b 的夹角为120°,故B 错误;()2044412cos12040a b b a b b +=+=⨯⨯⨯+=,∴()4a b b +⊥,故C 正确;012cos1201a b =⨯⨯=-,故D 错误.故选:C .【点睛】本题考查向量的线性运算,解题的关键在于作出相应图像求解,属于基础题4.在ABC ∆中,若22tan tan A a B b=,则ABC ∆的形状是( )A. 直角三角形B. 等腰或直角三角形C. 不能确定D. 等腰三角形【答案】B∵22tan tan A a B b=,∴22tan tan a B b A =, 由正弦定理得22sin tan sin tan A B B A =,∴22sin sin sin sin cos cos A B B A B A=, ∵sin 0,sin 0A B ≠≠, ∴sin sin cos cos A B B A=,∴sin cos sin cos A A B B =,故sin 2sin 2A B =。
诸暨中学2018学年高一期中考试数学试卷2018

诸暨中学2018学年高一期中考试数学试卷2018.11 说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共120分.考试时间120分钟. 本次考试不得使用计算器. 请考生将所有题目答案都作答在答题纸上, 答在试卷上概不评分.第I 卷(选择题 共40分)一、选择题(本大题共10小题,每小题4分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的)1.设全集U ={1,2,3,4,5},A ={1,2},B ={2,3,4},则(C U A )∪B = ( ▲ )A .{3,4}B .{3,4,5}C . {2,3,4,5}D .{1,2,3,4}2.下列各组函数f (x )与g (x )的图象相同的是 ( ▲ )A .()2)()(x x g x x f ==与 B .2)(24)(2+=--=x x g x x x f 与 C .0)(1)(x x g x f ==与 D .()()⎩⎨⎧<-≥==0,0,)()(x x x x x g x x f 与 3.下列函数中,既是偶函数,又在),0(∞+上单调递增的是 ( ▲ )A .|x |y x =B .1ln 1x y x -=+C .||2x y =D .2lg y x =- 4.设函数32log )(2-+=x x x f ,则函数)(x f 的零点所在的区间为 ( ▲ )A .)10(,B .)21(,C .2,3)(D .4),(35.已知a =log 0.50.6,b =log 1.20.8,c =1.20.8,则a ,b ,c 的大小关系是 ( ▲ ) A .a <b <c B . b <a <c C . c <a <b D . b <c <a6.函数()lg |x |f x x =⋅的图象可能是 ( ▲ )A .B .C .D .7.已知函数x x f y +=)(是偶函数,且1)2(=f ,则=-)2(f ( ▲ )A .5B .4C .3D .28.已知函数()23log 3,0,12,0,x x f x f x x +⎧>⎪=⎨⎛⎫+≤ ⎪⎪⎝⎭⎩则()2f -= ( ▲ ) A .13 B .3 C .19D .9 9.函数()()2log 2a f x x ax =-+在区间()1,+∞上恒为正值,则实数a 的取值范围 ( ▲ ) A .(01), B .(12], C .(13], D .(0,2) 10.用()d A 表示集合A 中的元素个数,若集合{0,1}A =,22{|(x )(1)0}B x ax x ax =--+=,且|d()()|1A d B -=.设实数a 的所有可能取值构成集合M ,则()d M = ( ▲ )A .3B .2C .1D .4第II 卷(非选择题 共80分)二、填空题(本大题共7小题,其中11-14题每空2分,15-17题每空3分,共25分)11.设函数y =A ,函数ln(1x)y =-的定义域为B ,则A = ▲ ;A B ⋂= ▲ .12.已知幂函数()f x x α=的图象过点)24(,,则α= ▲ ;=)3(log 3f ▲ .13.若函数()log (x 3)1(a 0a f x =++>且1)a ≠,图像恒过定点(,)P m n ,则m n += ▲ ;函数2()ln()g x x mx =+的单调递增区间为 ▲ .14.设对一切实数x ,函数(x)f 都满足:(x)2f(2x)1xf =-+,则(1)f = ▲ ; (4)f = ▲ .15.定义区间12[,]x x 的长度为21x x -,若函数2|log x |y =的定义域为[,]a b ,值域为[0,2],则区间[,]a b 的长度最大值为 ▲ .16.若关于x 的方程4210x xa a +⋅++=有实根,则实数a 的取值范围是 ▲ .17.已知λ∈R ,函数f (x )=,若函数f (x )恰有2个零点, 则λ的取值范围是_____▲____.24,43,x x x x x λλ-≥⎧⎪⎨-+<⎪⎩三、解答题(本大题共5小题,共55分,解答应写出文字说明、证明过程或演算步骤)18.(本题10分)设全集U R =,集合1{x |21}x A -=≥,2{|450}B x x x =--<.(1)求A ∩B ,()()U U C A C B ⋃;(2)设集合{|121}C x m x m =+<<-,若B C C ⋂=,求实数m 的取值范围.19.(本题10分)化简求值:(1)220.53327492()()(0.008)8925---+⨯;(2)5log 350.5551log 352log log log 14550---.20.(本题11分)已知函数2()21(a 0)g x ax ax b =-++>在区间[2,3]上的最大值为4,最小值为1,记()(||)f x g x =.(1)求实数,a b 的值;(2)若不等式2(log )(2)f k f >成立,求实数k 的取值范围.21.(本题12分)已知定义域为R 的函数ab x f x x+-=+122)(是奇函数. (1)求实数b a ,的值;(2)判断并用定义证明)(x f 在()+∞∞-,上的单调性;(3)若对任意的]2,1[∈x ,存在]2,1[∈t 使得不等式2()(2)0f x tx f x m +++>成立,求实数m 的取值范围.22.(本题12分)已知函数()(1|x |),a R.f x x a =+∈(1)当1a =-时,求函数1()4y f x =-的零点; (2)若函数()f x 在R 上递增,求实数a 的取值范围;(3)设关于x 的不等式()()f x a f x +<的解集为A ,若11[,]22A -⊆,求实数a 的取值范围.诸暨中学2018学年高一期中考试数学答案一、选择题:CDCBB DADBA二、选择题:11. [2,2]-,[2,1)- 12. 12 , 12 13.1- [2,1)- 14.1- 0 15. 15416. (,2-∞- 17. 413λλ><≤或 三、解答题: 18. (1){|1}A x x =≥,{|15}B x x =-<<[1,5)A B ∴= ,()()(,1)[5,)U U C A C B =-∞+∞(2)B C C = 即C B ⊆ ∴当C =∅时,121m m +≥-,3m ∴≤当C ≠∅时,221511m m m >⎧⎪-≤⎨⎪+≥-⎩23m ∴<≤ ∴综上得3m ≤。
推荐-2018下高一中段考试题和答案 精品
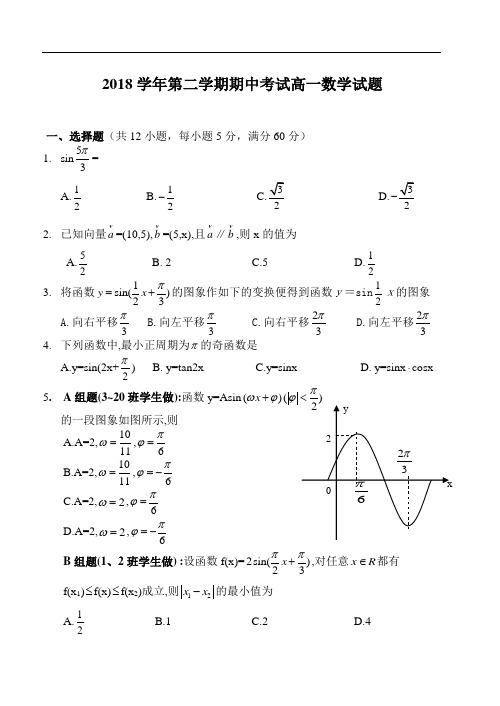
2018学年第二学期期中考试高一数学试题一、选择题(共12小题,每小题5分,满分60分)1. sin 53π=A.12 B.12- D.2. 已知向量a =(10,5),b =(5,x),且a ∥b,则x 的值为A.52 B. 2 C.5 D.123. 将函数1sin()23y x π=+的图象作如下的变换便得到函数y=sin 21x的图象A.向右平移3πB.向左平移3π C.向右平移32π D.向左平移32π4. 下列函数中,最小正周期为π的奇函数是A.y=sin(2x+2π) B. y=tan2x C.y=sinx D. y=sinx ⋅cosx 5. A 组题(3~20班学生做):函数y=Asin ()(x πωϕϕ+的一段图象如图所示,则A.A=2,1011ω=,6πϕ=B.A=2,1011ω=,6πϕ=-C.A=2,2ω=,6πϕ=D.A=2,2ω=,6πϕ=-B 组题(1、2班学生做) :设函数f(x)=2sin()23x ππ+,对任意x R ∈都有f(x 1)≤f(x)≤f(x 2)成立,则12x x -的最小值为 A.12B.1C.2D.46. A 组题(3~20班学生做):若向量a =(1,1),b =(1,-1),c =(-1,2),则c=A.21-a +23b B.21a -23b C.23a 21-b D.-23a 21+bB 组题(1、2班学生做):已知向量OP =(2,1),OA =(1,7),OB =(5,1),设X 是直线OP 上的一点(O 为坐标原点),那么XB XA ⋅的最小值是 A .-16 B .-8C .0D .47.A.sin4︒+cos4︒B.sin4︒-cos4︒C.cos4︒-sin4︒D.-sin4︒-cos4︒8. 三点A 、B 、C 满足0、、AB BC CA A B C ++=是三点能构成三角形的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 9. 角α的终边在第三或第四象限,且,cos cot m αα=则的值是A 、2m1m + B 、―2m1m + C 、 ±2m1m + D 、―2m1|m |+10.函数1x cos 2y -=的单调增区间是(以下)Z k ∈A. ]2k 2,k 2[π+ππ+πB. ]k 2,2k 2[π+ππ+π C. ]3k 2,k 2[.D ]k 2,3k 2[π+ππππ-π11. 函数y=sinx (x 2[,]36ππ∈-)的值域为A.1[]22B.[-1,1]C. [2- D. 1[1,]2-12. O 是△ABC 所在平面内一点,0OA OB OC ++=,则O 是 △ABC 的 A .重心 B .垂心 C .内心 D .外心二、填空题(共4小题,每小题4分,共16分,请把答案填在下列横线上)13.计算tan23︒+tan22︒+tan22︒tan23︒的值为_______________.14. 当3arctan ,arccos _________.62xx π=-时的值是15.3、,,cos ,sin 5αβαβαβ=5若都是锐角且cos(+)=-则的值是13__________16. 已知函数y=f(x) sinx 在[,]2ππ为增函数,且是以π为最小正周期的偶函数,则f(x)可以是___________________(不必考虑所有的情况,只需写出一个即可).三、解答题(本大题共6小题,共74分) 17.(本题满分12分)A 组题(3~20班学生做) :已知平行四边形ABCD 的对角线AC 、BD 交于点M, (!)已知A 、B 、C 的坐标分别为A(-2,1)、B (-1,3)、C (3,4),求点D 、M的坐标; (2)若,BM xBA yBC =+求实数x,y 的值.B 组题(1、2班学生做) :设向量OA =(3,1) ,OB =(-1,2),向量OC ⊥OB ,BC ∥OA,又OD +OA =OC ,求OD的坐标及OA 与OC 的夹角(用反三角表示).A BCD M N 18. (本题满分12分)已知21tan (sin cos )13,1tan sin cos cot θθθθθθθ++-=--⋅求的值。
浙江省诸暨中学—学年第高一数学下学期期中试题 (2)

诸暨中学2014学年第二学期高一年级数学学科期中试题卷一、选择题:本大题共10小题,每小题3分,共30分。
在每小题给出的四个选项中只有一项是符合题目要求的。
1.各项均为实数的等比数列}{n a 中,11=a ,3a =2,则5a = A. 4 B.2 C. ±4 D. ±2 2.等差数列}{n a 中,21a a +=3,43a a +=7,则65a a +=A. 9B. 10C.11D.123.边长为1的正方形ABCD 中,||+=A.2B. 2C. 1D.224.在△ABC 中,若222b a ab c +=+,则角C =A.30ºB. 45ºC.60ºD.120º5.等差数列}{n a 中,543a a a ++=12,那么}{n a 的前7项和7S =A.22B.24C.26D.286.在平行四边形ABCD 中,AC 与BD 相交于点O ,E 是线段OD 中点,AE 的延长线交DC 于点F ,若=,=,则AF = A.+31 B.+21 C.31+ D.21+ 7.在△ABC 中,若1=b ,3=c ,B=30º,则a =A.2B.1C.1或2D.2或38.数列}{n a 中,11=a ,22=a ,n n n a a a -=++12,则}{n a 的前51项和51S =A.1B.2C.3D.49.为了测得河对岸塔AB 的高度,先在河岸上选一点C ,使C 在塔底B 的正东方向上,此时测得塔顶A 的仰角为60º。
再由点C 沿北偏东15º方向走了20米到达点D ,测得∠BDC= 45º,则塔AB 的高度为 A.206米 B.203米 C.202米 D.20米10.有穷数列1a ,2a ,3a ,…,2015a 中的每一项都是1-,0,1这三个数中的某一个数,若1a +2a +3a +…+2015a =427且21)1(+a +22)1(+a +23)1(+a +…+22015)1(+a =3869,则有穷数列1a ,2a ,3a ,…,2015a 中值为0的项数是A.1000B.1015C.1030D.1045二、填空题:本大题共7小题,每小题3分,共21分。
浙江省诸暨市草塔中学2018学年高一数学下学期期中试题

草塔中学2018-2018学年高一下学期期中考试数学试题1.直线1x =的倾斜角是 ( )A .0︒B .45︒C .90︒D .不存在2.在下列各组向量中,能作为表示它们所在平面内所有向量的基底的是( )A .(0,0),(1,2)a b ==-B .(1,2),(5,7)a b =-=C .(3,2),(6,4)a b ==D .(2,8),(1,4)a b ==3.已知数列1-,1a ,2a ,4-成等差数列, 1-,1b ,2b ,3b ,4-成等比数列,则212b a a -的值为 ( ) A .21 B .12- C .21或12- D .41 4.已知ABC ∆中,a=4, b=43,=∠A 300则B ∠等于 ( )A 300B 600C 300或1500D 600或 12005、已知直线y=-133+x 和x 轴,y 轴分别交与点A,B,以线段AB 为边在第一象限内作等边三角形ABC ∆,如果在第一象限内有一点P(m,21),使得ABC ABP ∆∆和的面积相等,则m 的值为 ( )A25 B 35 C 235 D 3356. 已知AB =(4,2), AC=(3,4) 则∆ABC 的面积为 ( )A 5B 7。
5C 10 D157.在边长为2的正三角形ABC 中,设AB =a, =b , =c ,则a b b c c a ⋅+⋅+⋅ 等于A .12B .-12C .6D .-6 ( )8、已知向量a 与向量b 的夹角为0120,若向量b a c +=且c a ⊥,则:的值为( )A.2B.21 C. 3 D.332 9. 等差数列{}n a 中,11a =,1,n n a a +是方程21(21)0nx n x b -++=的两个根,则数列{}n b 前n 项和n S =( )A.121n + B. 11n + C.21n n + D.1nn + 10. 如图,O 为△ABC 的外心,BAC AC AB ∠==,2,4为钝角,M 是边BC 的中点,则AO AM ⋅的值 ( ).A. 4B. 5C. 7D. 6 11.在△ABC 中,周长为20,面积为310,A=600,则BC 边的长为( )A 5B 6C 7D 8 12.对于正项数列{}n a ,定义nn na a a a nH +⋯+++=32132为{}n a 的“给力”值,现知某数列的“给力”值为22+=n H n ,则数列{}n a 的通项公式为n a = ( ) A 121+n B 11+n C n +21 D 2n-2113、在等比数列{}n a 中,若112a =,44a =-,则12||||||n a a a +++= ___ .14. 如图,在四边形ABCD 中,已AB=1,BC=2,CD=3,∠ABC=120°,∠BCD=90°,则边AD 的长为__________。
2018-2019学年浙江省绍兴市诸暨中学平行班高一(下)期中数学试卷及解析

2018-2019学年浙江省绍兴市诸暨中学平行班高一(下)期中数学试卷注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)一、选择题1.(2015新课标全国Ⅰ理科)sin20o cos10o −cos160o sin10o =A. −√32 B. √32C. −12D. 122.在等差数列{a n }中,已知a 1=2,a 2+a 3=13,则a 4+a 5+a 6等于( )A. 40B. 42C. 43D. 453.已知正三角形ABC 的边长为2,设2,AB a BC b ==,则( ) A. 1a b +=B. a b ⊥C. ()4a b b +⊥D. ·1a b =4.在△ABC 中,若22tan tan A a B b=,则△ABC 的形状是( ) A. 直角三角形 B. 等腰或直角三角形 C. 不能确定 D. 等腰三角形5.已知()162a b a b a ==-=,,,则向量a 与向量b 的夹角是( ) A .6π B .4π C .3πD .2π6.如图所示,设A 、B 两点在河的两岸,一测量者在A 所在的河岸边选定一点C ,测出AC的距离为50m ,∠ACB =45°,∠CAB =105°后,就可以计算A 、B 两点的距离为m D.2m 7.若1sin 63πα⎛⎫-= ⎪⎝⎭,则cos 23πα⎛⎫- ⎪⎝⎭的值是( )A.79B. 79-C. 13-D.138.如图,在△ABC 中,AD ⊥AB , 3BC BD =,|AD |=1,则·AC AD 等于 ( )9.已知两个等差数列{a n }和{b n }的前n 项和分别为A n 和B n ,且AnB n =7n+45n+3,则使得an bn为整数的正整数n 的个数是( ) A. 2 B. 3 C. 4 D. 510.平面向量,a b 满足3,2a b a b -==,则a b -与a 夹角的最大值为( ) A.2πB.3π C.4π D.6π 第II 卷(非选择题)二、解答题11.已知函数()sin sin ,3f x x x x x R π⎛⎫=+++∈ ⎪⎝⎭. (Ⅰ)求3f π⎛⎫⎪⎝⎭的值; (Ⅱ)若()1fα=,且()0απ<<,求cos α的值.12.已知()()()2,0,0,2,cos ,sin A B C αα,且0απ<<. (1)若7,OA OC +=求OB 与OC 的夹角;(2)若AC BC ⊥,求tan α的值.13.已知数列{}n a 的前n 项和为222n n n S λ++=.(Ⅰ)当2λ=时,求数列{}n a 的通项公式n a ; (Ⅱ)当0λ=时,令()*211n n b n N a =∈-,求数列{}n b 的前n 项和n T . 14.在ABC ∆中,内角,,A B C 所对边的长分别是,,a b c ,且221cos 2a c B b c b ⎛⎫-=- ⎪⎝⎭(Ⅰ)求角C 的大小;(Ⅱ)若sin ,sin ,sin A C B 成等差数列,且()2AC AC AB -=,求边c 的长. (Ⅲ)若2c =,求2+a b 的最大值.15.已知等差数列{}n a 中,公差0d >,其前n 项和为n S ,且满足:231445,14a a a a =+=.(Ⅰ)求数列{}n a 的通项公式; (Ⅱ)通过公式nn S b n c=+构造一个新的数列{}n b .若{}n b 也是等差数列,求非零常数c ;(Ⅲ)求()()()*125nn b f n n N n b +=∈+的最大值.三、填空题16.已知向量()()()2,1,1,,1,2a b m c =-=-=-,若()//a b c +,则m =_____. 17.,E F 是等腰直角ABC ∆斜边AB 上的三等分点,则tan ECF ∠=_____.18.已知数列{}n a 中,11a =,11,33,n n n a n n a a n n +⎧+⎪=⎨⎪-⎩为奇数为偶数,则3=a _____.19.如图,两块斜边长相等的直角三角板拼在一起,若AD x AB y AC =+,则x y +=_____.20.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,且满足cos 325A AB AC ==,则ABC ∆的面积为_____. 21.数列{}n a 的通项公式cos 2n n a n π=,其前n 项和为nS,则2019S 等于_____. 22.ΔABC 中,∠C=90°,M 是BC 的中点,若sin∠BAM =13,则sin∠BAC = .参考答案1.D【解析】1.原式=sin20o cos10o +cos20o sin10o =sin30o =12,故选D.2.B【解析】2.分析:由题意求得等差数列的公差后再根据通项公式计算可得结果. 详解:设等差数列{a n }的公差为d , 由题意得{a 1=2a 2+a 3=13 ,即{a 1=22a 1+3d =13 ,解得{a 1=2d =3. ∴a 4+a 5+a 6=3a 1+12d =42.故选B . 3.C【解析】3.根据向量的线性运算和乘法运算,判断选项的正误即可解:如图,∵正三角形ABC 的边长为2,2,AB a BC b ==, 取AB 中点D ,设BE AD a ==, ∴1AD BD BE ===,0120EBC ∠=,∴22a b +=-=A 错误;,a b 的夹角为120°,故B 错误;()2044412cos12040a b b a b b +=+=⨯⨯⨯+=,∴()4a b b +⊥,故C 正确;012cos1201a b =⨯⨯=-,故D 错误.故选:C . 4.B【解析】4.∵22tan tan A a B b=,∴22tan tan a B b A =, 由正弦定理得22sin tan sin tan A B B A =, ∴22sin sin sin sin cos cos A B B AB A =,∵sin 0,sin 0A B ≠≠, ∴sin sin cos cos A B B A=,∴sin cos sin cos A A B B =,故sin2sin2A B =。
浙江省诸暨市草塔中学学高一数学下学期期中考试试题实验班,无答案

用心 爱心 专心 1 浙江省诸暨市草塔中学2011-2012学年高一数学下学期期中考试试题(实验班,无答案)一、选择题:1.给出下面四个命题:① =+;②=+B ;③=;④00=⋅。
其中正确的个数为 ( )(A )1个 (B )2个(C )3个 (D )4个 2.已知数列{}a n 对任意的p ,q∈N *满足a p +q =a p +a q ,且a 2=-6,那么a 10=( )A.-165B.-33C.-30D.-213.若tan 3α=,4tan 3β=,则tan()αβ-等于( ) A.3- B.13-C.3D.134.在ABC ∆中,若222a b c =+则A ∠为( )A.75B. 120C.150D.305.对于向量)2,1(-=,)1,2(=,则 ( )A ∥B ⊥C 与的夹角为60°D 与的夹角为30°6.在等差数列{a n }中,已知a 1=2,a 2+a 3=13,则a 4+a 5+a 6等于A.40B.42C.43D. 457. 在ABC ∆中,a 2,A 30,C 45,===则ABC ∆的面积s 的值是( )18.若f (x )=2tan x -2sin 2x 2-1sin x 2cos x 2,则)12(πf 的值是( ) A .-433 B .-4 3 C .4 3 D .8 9.设非零向量、、满足=+==|,|||||,则b a 与 的夹角( )A .150° B.120° C.60° D.30°10.在ABC ∆中,角A 、B 、C 所对的边长分别为a 、b 、c ,若120C=,c =,则 A. a >b B. a <bC. a =bD. a 与b 的大小关系不能确定 11.}{n a 为等差数列,若11101a a <-,且它的前n 项和S n 有最小值,那么当S n 取得最小正值时,n = A .11B .17C .19D .21 12.已知数列{}n a 、{}n b 都是公差为1的等差数列,其首项分别为1a 、1b ,且11a +b =5,11a >b ,++11a b N (n N )、∈∈,则数列n b {a }前10项的和等于A.55B.70C.85D.10用心 爱心 专心 2 二、填空题:13.a ,b 的夹角为120︒,1a =,3b =则5a b -= . 14.设sin(θπ+4)=31,则sin θ2=________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
浙江省诸暨市草塔中学2017-2018学年高一数学下学期期中考试试题(实验班)
一、选择题:
1.给出下面四个命题:①
=+;②=+B ;③=-;④00=⋅。
其中正确的个数为 ( )(A )1个 (B )2个
(C )3个 (D )4个 2.已知数列{}a n 对任意的p ,q∈N *满足a p +q =a p +a q ,且a 2=-6,那么a 10=( )
A.-165
B.-33
C.-30
D.-21
3.若tan 3α=,4tan 3β=
,则tan()αβ-等于( ) A.3- B.13-
C.3
D.13
4.在ABC ∆
中,若222a b c =+则A ∠为( )
A.75
B. 120
C.150
D.
30
5.对于向量)2,1(-=a ,)1,2(=b ,则 ( )
A a ∥b
B a ⊥b
C a 与b 的夹角为60°
D a 与b 的夹角为30°
6.在等差数列{a n }中,已知a 1=2,a 2+a 3=13,则a 4+a 5+a 6等于
A.40
B.42
C.43
D. 45
7. 在ABC ∆中,a 2,A 30,C 45,===则ABC ∆的面积s 的值是( )
1
8.若f (x )=2tan x -2sin 2x 2-1sin x 2cos x 2,则)12(πf 的值是( ) A .-433 B .-4 3 C .4 3 D .8 9.设非零向量a 、b 、c 满足c b a c b a =+==|,|||||,则b a 与 的夹角( )
A .150° B.120° C.60° D.30°
10.在ABC ∆中,角A 、B 、C 所对的边长分别为a 、b 、c ,若120C
=,c =
,则 A. a >b B. a <b
C. a =b
D. a 与b 的大小关系不能确定 11.}{n a 为等差数列,若
11101a a <-,且它的前n 项和S n 有最小值,那么当S n 取得最小正值时,n = A .11
B .17
C .19
D .21 12.已知数列{}n a 、{}n b 都是公差为1的等差数列,其首项分别为1a 、1b ,且11a +b =5,11a >b ,++11a b N (n N )、∈∈,
则数列n b {a }前10项的和等于
A.55
B.70
C.85
D.10
二、填空题:
13.a ,b 的夹角为120︒,1a =,3b =则5a b -= . 14.设sin(θπ+4
)=31,则sin θ2=________。
15.设n S 是等差数列}{n a 的前n 项和,若3
184=S S ,则168S S =________。
16.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,若()C a A c b c o s c o s 3=-,则=A c o s _________________。
17.正方形ABCD 边长为2,E 是DC 中点,F 是线段BF 上的动点,则FC BF ⋅的取值范围 。
三、计算题:
18.已知等差数列}{n a 满足: 73=a ,2675=+a a ,}{n a 的前n 项和为n s ,
(1)求n a 及n s .(2)令1
12-=n n a b ,求数列{n b }的前n 项和n T . 19. 已知:a 、b 、c 是同一平面内的三个向量,其中→a =(1,2)
(1)若|→c |=25,且→
c ‖a ,求→c 的坐标 (2)若|→
b |=25,且→a +2→b 与2→a -→b 垂直,求→a 与→b 的夹角θ. 20.在ABC ∆中,角C B A ,,所对边分别为
c b a ,,,已知4
12cos -
=C , ①求C sin 的值;
②2=a ,C A sin sin 2=时,求b 及c 的长。
21.若数列{}n a 是等差数列,数列{}n b 满足21++⋅⋅=n n n n a a a b (*
N n ∈),{}n b 的前n 项和用n S 表示,若{}n a 满足083125>=a a ,试问n 多大时,n S 取得最大值?证明你的结论。
22.已知向量3
(sin ,),(cos ,1).2
a x
b x ==- (1)当//a b 时,求2
2cos sin 2x x -的值;(2)求b b a x f ⋅+=)()(在,02π⎡⎤-⎢⎥⎣⎦上的值域。
