平谷区2014—2015学年度第二学期初三统练(二)
北京市平谷区2014-2015学年初二下期末考试数学试卷及答案

配方,得 x2 2x 1 3 1
(x 1)2 4 .-------------------------------------------------------------------------------3 分 开平方,得 x 1 2 .------------------------------------------------------------------------------4 分
A
D
E
O
B
C
8图 图
8. 如图,平行四边形 ABCD 的两条对角线相交于点 O,点 E 是 AB 边的中点,图中已有
三角形与△ADE 面积相等的三角形(不包括△ADE)共有(
)个
A. 3
B. 4
C. 5
D. 6
9.如图,在菱形 ABCD 中,AB=4,∠ABC=60°,E 为 AD 中点, P 为对角线 BD 上一动点,连结 PA 和
.
x
出
y x 4(x 1)
y
16.在平面直角坐标系中,点 A(2,0)到动点 P(x,x+2)的最短距离是 _________________.
三、解答题:(本题共 32 分,其中 17-20 题每小题 5 分,21 题和 22 题每小题 6 分)
17.解一元二次方程3x2 2x 5 0
求这个一次函数表达式.
D
21.关于 x 的一元二次方程
初二数学试卷第 2 页 共 4 页
O
D
F C
C
F
A
E
B
kx (2k 2)x (k 2) 0(k 0).
(12)求证:无论 k 取何值时,方程总有两个不相等的实数根. (2)当 k 取何整数时方程有整数根.
2015平谷区初三二模语文试题及答案

顺义区2015届初三第二次统一练习答案一、基础•运用(共28分)1.(1)(2分)①qǐ(绮)丽②纯cuì(粹)(2)(2分)B(3)(2分)D2.(2分)A3.(2分) D4.(2分) C5.(2分,每空0.5分)①a , b !②c 。
d ……6.(6分,每句1分)①家祭无忘告乃翁②恨别鸟惊心③断肠人在天涯④留取丹心照汗青⑤了却君王天下事⑥先天下之忧而忧7.(4分,每空1分)①施恩三入死囚牢②刘玄德三顾茅庐③孙行者三调芭蕉扇④祥子买车三起三落8、(4分,每空1分)参考示例:①凶狠粗暴②泼辣蛮横③坚强勇敢④凛然无畏(有勇有谋)二、文言文阅读(共10分)9. (2分)B10.(4分,每小题2分)①等我回来杀猪给你吃②我是醉酒后和近侍开玩笑11.(4分)参考示例:这两则故事人主公都不重视诚信,随意说出戏言,即玩笑话,从而说明了做人要讲诚信,诚信对个人、对国家都有重要意义,不讲诚信会导致不良结果。
(2分)(结合自己认识,2分)三、现代文阅读(共32分)(一)(12分)12.(4分)参考示例:①酒楼请喝酒②送机票去旅行③高兴④惧怕13.(4分)参考示例:文中“沈洋一听这话,眼圈随即红了。
自从老婆死后,这些年,他既当爹又当妈,真是挺辛苦的。
”这句话使用了细节描写的手法。
从内容上表现出沈洋复杂的心理。
他多年为孩子辛劳付出,多么渴望有人理解呀,如今儿子的话道出了他的辛酸,所以他很感动,他觉得这是儿子懂事、孝顺的表现。
同时这句话在结构上也为下文做了铺垫。
父亲这样辛劳,做儿子的就更应该发自内心的服从、奉养长辈,而下文情节恰与此形成反差、对照,这样写深化了小说的主题。
14. (4分)参考示例:二者不一致。
“孝”字的本义是儿孙搀扶老人,服从和奉养父母、长辈。
小说中儿子理解的“孝”,只是表面上的“孝”,每次儿子在对父亲有所求时就会想方设法先讨好父亲,在父亲兴奋、满意之后提出真正用意,在他的内心,父亲始终是相当提款机一般的依靠。
和平区2014-2015九年级数学二模试卷及答案

和平区2014-2015学年度第二学期九年级第二次质量调查数学学科试卷本试卷分为第Ⅰ卷(选择题)、第Ⅱ卷(非选择题)两部分.第Ⅰ卷为第1页至第3页,第Ⅱ卷为第4页至第8页.试卷满分120分.考试时间100分钟. 祝你考试顺利!第Ⅰ卷注意事项:1.每题选出答案后,用2B 铅笔把“答题卡”上对应题目的答案标号的信息点涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号的信息点. 2.本卷共12题,共36分.一、选择题(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.计算:1()(2)2-⨯-的结果等于(A )1 (B )-1 (C )4 (D )14-2.2cos60°的值等于(A )1 (B(C(D3.下列图形中,既是轴对称图形又是中心对称图形的是4.某种细胞的直径是4510-⨯毫米,这个数是(A )0.05毫米 (B )0.005毫米 (C )0.000 5毫米 (D )0.000 05毫米(A ) (B ) (C ) (D )5.将两个长方体如图放置,则所构成的几何体的左视图可能是6.如图,△ABC 的顶点A ,B ,C 均在⊙O 上,若ABC AOC ∠+∠=90°,则AOC ∠的 大小是 (A )70° (B )60° (C )45° (D )30°7.在开展“国学诵读”活动中,某校为了解全校1300名学生课外阅读的情况,随机调 查了50名学生一周的课外阅读时间,并绘制成如图所示的条形统计图.根据图中数据, 估计该校1300名学生一周的课外阅读时间不少于7小时的人数是 (A )600 (B )520 (C )130 (D )78 8.直线132y x =+与x 轴的交点坐标为 (A )(-6,0) (B )(0,3) (C )(0,-6) (D )(3,0)(A ) (B ) (C ) (D )正面9.外接圆的半径是2,则此正多边形的边数是 (A )八 (B )六 (C )四 (D )三10.如图,E ,F 分别是正方形ABCD 的边BC ,CD 上的点,BE CF =,连接AE ,BF .将 △ABE 绕正方形的对角线的交点O 按顺时针方向旋转到△BCF ,则旋转角是 (A )30º (B )45º (C )60º (D )90º11.反比例函数my x=①常数m <-1;②在每个象限内,y 随x 的增大而增大;③ 若A (-1,h ),B (2,k ④若P (x ,y )在图象上,则P '(x -其中正确的是(A )①② (B )②③ (C 12.如图,边长为1的正方形OABC 的顶点C 在y 轴的正半轴上.动点D 在边BC 点D 作DE OD ⊥,交边AB 于点E ,连接OE .当线段OE 的长度取得最小值时, 点E 的纵坐标为 (A )0 (B )12 (C )34(D )1第Ⅱ卷注意事项:1.用黑色字迹的签字笔将答案写在“答题卡”上(作图可用2B铅笔).2.本卷共13题,共84分.二、填空题(本大题共6小题,每小题3分,共18分)13.若3m=,则22749m mm--的值等于.14.已知在反比例函数kyx=的图象的每一支上,y随x的增大而增大,写出一个符合条件的k的值为.15.向阳村2012年的人均收入为12000元,2014年的人均收入为14520元,则人均收入的年平均增长率是.16.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车经过这个十字路口.则至少有一辆汽车向左转的概率为.18.如图,在边长相同的小正方形组成的网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点P,则(Ⅰ)APPB的值= ;(Ⅱ)tan∠APD的值是.ABCDP三、解答题(本大题共7小题,共66分.解答应写出文字说明、演算步骤或推理过程) 19.(本小题8分)解不等式组22,417.x x x x +⎧⎨--⎩≤①>②请结合题意填空,完成本题的解答. (Ⅰ)解不等式①,得 ; (Ⅱ)解不等式②,得 ; (Ⅲ)把不等式①和②的解集在数轴上表示出来:(Ⅳ)原不等式组的解集为 .20.(本小题8分)如图是某校九年级学生为灾区捐款情况抽样调查的条形统计图和扇形统计图. (Ⅰ)求该样本的容量;(Ⅱ)在扇形统计图中,求该样本中捐款15元的人数所占的圆心角度数; (Ⅲ)若该校九年级学生有800人,据此样本估计该校九年级学生捐款总数.01231-2-3-15 255元的人数 30%已知四边形ABCD 是平行四边形,以AB 为直径的⊙O 经过点D ,DAB ∠=45°. (Ⅰ)如图①,判断CD 与⊙O 的位置关系,并说明理由;(Ⅱ)如图②,E 是⊙O 上一点,且点E 在AB 的下方,若⊙O 的半径为3cm ,5AE =cm ,求点E 到AB 的距离.22.(本小题10分)如图,一艘海轮位于灯塔P 的北偏东65°方向,距离灯塔P 90海里的A 处,它沿正南方向航行一段时间后,到达位于灯塔P 的南偏东34°方向上的B 处.这时,海轮所在的B 处距离灯塔P 有多远(精确到0.1海里)?(参考数据sin 65°≈0.91,cos 65°≈0.42,tan 65°≈2.14,sin 34°≈0.56,cos 34°≈0.83,tan 34°≈0.67.)图① 图②九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:已知该商品的进价为每件30元,设销售该商品每天的利润为y元.(Ⅰ)求出y与x的函数关系式;(Ⅱ)问销售该商品第几天时,当天销售利润最大,最大利润是多少?(Ⅲ)该商品在销售过程中,共有多少天每天的销售利润不低于4800元?请直接写出结果.24.(本小题10分)在平面直角坐标系中,O为原点,四边形OABC是矩形,点A,C的坐标分别为(3,0),(0,1).点D是边BC上的动点(与端点B,C不重合),过点D作直线12y x b =-+交边OA于点E.(Ⅰ)如图①,求点D和点E的坐标(用含b的式子表示);(Ⅱ)如图②,若矩形OABC关于直线DE的对称图形为矩形1111O A B C,试探究矩形1111O A B C与矩形OABC的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由;(Ⅲ)矩形OABC绕着它的对称中心旋转,如果重叠部分的形状是菱形,请直接写出这个菱形的面积的最小值和最大值.25.(本小题10分)已知直线l :y kx =,抛物线C :21y ax bx =++.(Ⅰ)当1k =,1b =时,抛物线C 的顶点在直线l 上,求a 的值;(Ⅱ)若把直线l 向上平移21k +个单位长度得到直线r ,则无论非零实数k 取何值,直线r 与抛物线C 都只有一个交点.①求此抛物线的解析式;②若P 是此抛物线上任一点,过点P 作PQ ∥y 轴且与直线2y =交于点Q ,O 为原点.求证:OP PQ =.图① 图②和平区2014-2015学年度第二学期九年级第二次质量调查数学学科试卷参考答案一、选择题(本大题共12小题,每小题3分,共36分)1.A 2.A 3.D 4.C 5.C 6.B7.B 8.A 9.B 10.D 11.C 12.C二、填空题(本大题共6小题,每小题3分,共18分)13.31014.-1(提示:满足k<0即可)15.10% 16.5 917.51318.(Ⅰ)3 (Ⅱ)2三、解答题(本大题共7小题,共66分)19.(本小题8分)解:(Ⅰ)x≤2;…………………………………2分(Ⅱ)x>-2;…………………………………4分(Ⅲ)…………………………………6分(Ⅳ)-2<x≤2.…………………………………8分20.(本小题8分)解:(Ⅰ)15÷30%=50.∴该样本的容量是50;…………………………………2分(Ⅱ)该样本中捐款15元的人数为50-25-15=10(人),∴它所占的圆心角:1050×360°=72°.…………………………………5分(Ⅲ)∵50名学生捐款总数为:5×15+10×25+15×10=475(元), 有800475760050⨯=. ∴据此样本估计该校九年级学生捐款总数约为7600元. …………………8分 21.(本小题10分)解:(Ⅰ)CD 与⊙O 相切. …………………………………1分理由如下:连接OD ,…………………………………2分∵OA OD =, ∴ADO A ∠=∠=45°.∴AOD ∠=180°ADO A -∠-∠=90°. …………………………………3分 ∵四边形ABCD 是平行四边形, ∴AB ∥DC .∴CDO AOD ∠=∠=90°. …………………………………4分 ∴CD OD ⊥.∴CD 与⊙O 相切. …………………………………5分 (Ⅱ)过点E 作EF AB ⊥于点F ,连接BE , …………………………………6分 ∵AB 是⊙O 的直径,∴AEB ∠=90°. …………………………………7分 在Rt △AEB 中,5AE =,6AB =,由勾股定理,得BE =. ……………………………8分 由1122ABE S AE BE AB EF ∆==,得5EF . 分∴EF∴点E 到AB . …………………………………10分22.(本小题10分)解:在Rt △APC 中,A ∠=65°,∵sin PCA PA=,…………………………………2分 ∴sin 90sin PC PA A =⨯=⨯65°900.9181.90≈⨯=. ………………………………5分 在Rt △BPC 中,B ∠=34°,∵sin PCB PB=, …………………………………7分 ∴81.90146.3sin sin340.56PC PC PB B ==≈≈°. …………………………………9分 答:海轮所在的B 处距离灯塔P 大约146.3海里. ………………………………10分 23.(本小题10分)解:(Ⅰ)当1≤x <50时,2(2002)(4030)21802000y x x x x =-+-=-++.…2分 当50≤x ≤90时,(2002)(9030)12012000y x x =--=-+. 综上,2(150),21802000(5090).12012000x x x y x x ⎧-++=⎨-+⎩≤<≤≤ …………………………………4分(Ⅱ)当1≤x <50时,22218020002(45)6050y x x x =-++=--+, ∵-2<0,∴当45x =时,y 有最大值,最大值为6050. …………………………………6分 当50≤x ≤90时,12012000y x =-+, ∵-120<0,∴y 随x 的增大而减小,∴当50x =时,y 有最大值,最大值为1205012000=6000-⨯+. ……………8分 ∵6000<6050,∴当45x =时,即第45天时销售利润最大,最大利润是6050元.………………9分 (Ⅲ)41天. …………………………………10分 24.(本小题10分)解:(Ⅰ)∵四边形OABC 是矩形, ∴CB ∥x 轴.由点C 的坐标为(0,1),可知点D 的纵坐标为1.把1y =代入12y x b =-+,得112x b =-+.解得22x b =-.∴点D 的坐标为(22b -,1). …………………………………2分把0y =代入12y x b =-+,得102x b =-+.解得2x b =.∴点E 的坐标为(2b ,0). …………………………………4分 (Ⅱ)记CB 与11O A 的交点为M ,11C B 与OA 的交点为N , ∵四边形OABC ,四边形1111O A B C 是矩形, ∴CB ∥OA ,11C B ∥11O A . ∴四边形DMEN 是平行四边形.∵矩形OABC 关于直线DE 的对称图形为矩形1111O A B C , ∴12∠=∠. ∵CB ∥OA , ∴23∠=∠. ∴13∠=∠. ∴DM ME =.∴□DMEN 是菱形. …………………5分 过点D 作DH OA ⊥于点H , 由D (22b -,1),E (2b ,0),可知22CD b =-,2OE b =,22OH CD b ==-. ∴2(22)2EH OE OH b b =-=--=. 设菱形DMEN 的边长为m ,1在Rt △DHN 中,1DH =,2HN EH NE m =-=-,DN m =.由222DH HN DN +=,得2221(2)m m +-=. …………………………………6分 解得54m =. …………………………………7分 ∴55144DMEN S NE DH ==⨯=菱形.所以重叠部分菱形DMEN 的面积不变,为54. ………………………………8分 (Ⅲ)菱形面积的最小值是1. …………………………………9分菱形面积的最大值是53. …………………………………10分25.(本小题10分)解:(Ⅰ)∵22111()124y ax x a x a a=++=++-, ∴顶点(12a-,114a -)在y x =上,∴11124a a -=-,解得14a =-. …………………………………2分 (Ⅱ)①∵无论非零实数k 取何值,直线r 与抛物线C 都只有一个交点, ∴1k =,2k =时,直线r 与抛物线C 都只有一个交点.当1k =时,r :2y x =+,代入C :21y ax bx =++,有2(1)10ax b x +--=. ∴21(1)40b a ∆=-+=. …………………………………3分 当2k =时,r :25y x =+,代入C :21y ax bx =++,有2(2)40ax b x +--=.22(2)160b a ∆=-+=. …………………………………4分 解方程组22(1)40,(2)160.b a b a ⎧-+=⎪⎨-+=⎪⎩得1,40a b ⎧=-⎪⎨⎪=⎩;或1,364.3a b ⎧=-⎪⎪⎨⎪=⎪⎩…………………………………6分∵r :21y kx k =++代入C :21y ax bx =++,得22()0ax b k x k +--=. ∴22()4b k ak ∆=-+.当1,40a b ⎧=-⎪⎨⎪=⎩时,22221()4()04k k k k ∆=-+-=-=.故无论k 取何值,直线r 与抛物线C 都只有一个交点. 当1,3643a b ⎧=-⎪⎪⎨⎪=⎪⎩时,222418816()4()336939k k k k ∆=-+-=-+.显然虽k 值的变化,∆不恒为0,所以不合题意舍去.∴C :2114y x =-+. …………………………………7分②证明:根据题意,画出图象如图,由点P 在抛物线2114y x =-+上,设点P 的坐标为(x ,2114x -+),连接OP ,过点P 作PQ ⊥直线2y =于点Q ,作PD x ⊥轴于点D ,∵2114PD x =-+,OD x =,∴2114OP x ==+. 22112(1)144PQ x x =--+=+.∴OP PQ =.…………………………………10分。
平谷2014年初三统练试卷(二)

平谷区2013-2014学年度初三毕业会考即统练(二)英语 试 卷 2014. 5考 生 须 知 1. 本试卷共12页,满分120分,考试时间120分钟。
2. 在试卷和答题纸上准确填写学校名称、班级、姓名和考号。
3. 试题答案一律填涂或书写在答题纸上,在试卷上作答无效。
4. 在答题纸上,选择题用2B 铅笔作答,其他试题用黑色字迹签字笔作答。
5. 考试结束,请将本试卷和答题纸一并交回。
听力理解(共26分) 一、 听对话,从下面各题所给的A 、B 、C 三幅图片中选择与对话内容相符的图片。
每段对话你将听两遍。
(共4分,每小题1分)1.A.B. C. 2.A.B. C. 3.A.B. C.4.A. B. C.二、听对话或独白,根据对话或独白内容,从下面各题所给的A、B、C三个选项中选择最佳选项。
每段对话或独白你将听两遍。
(共12分,每小题1分)请听一段对话,完成第5至第6小题。
5. What’s wrong with the young man?A. He had a bad headache.B.He had a fever.C. He kept coughing.6. How often should the man take the medicine?A. Once a day.B. Twice a day.C. Three times a day.请听一段对话,完成第7至第8小题。
7. How long has the woman learned English?A. For one year .B. For two years .C. For three years .8. Where will they meet?A. Outside the school gate.B. At the cinema.C. Along the street.请听一段对话,完成第9至第10小题。
9. What are the two speakers mainly talking about?A. Jane’s plan.B. Jane’s school.C. Jane’s family.10. What will Jane most probably do in the end?A. A painter.B. A singer.C. An actress.请听一段对话,完成第11至第13小题。
北京市平谷区2014年初三化学第二次模拟暨毕业考试-含答案与评分标准

北京市平谷区2014年初三第二次模拟暨毕业考试化 学 试 卷学校 班级 姓名 准考证号可能用到的相对原子质量:Mg-24 Fe-56 H-1 Na-23 O-16 Ca-40 C-12 Cl-35.5 一、选择题(每小题只有1个选项符合题意。
共25个小题,每小题1分,共25分) 1.下列属于化学变化的是A .冰雪融化B .纸张燃烧C .水分蒸发D .矿石粉碎 2.空气成分中,体积分数21%的是A .氮气B .氧气C .二氧化碳D .稀有气体 3.地壳中含量最多的非金属元素是A .氧B .硅C .铝D .铁4.下列物质中,属于纯净物的是A .石灰水B .空气C .生铁D .蒸馏水 5.下列物质在氧气中燃烧,产生大量白烟的是A .木炭B .铁丝C .红磷D .酒精6.决定元素种类的是A .中子数B .质子数C .核外电子数D .最外层电子数 7.下列生活用品所使用的主要材料,属于有机合成材料的是A .青花瓷瓶B .塑料水杯C .纯棉毛巾D .不锈钢锅8.氢氧化钠是重要的化工原料,其俗称是A .纯碱B .小苏打C .烧碱D .熟石灰 9.下列物质露置于空气中,质量不变的是A .氯化钠B .石灰水C .浓盐酸D .浓硫酸10.下列物质中,能用作氮肥的是A .Ca(H 2PO 4)2B .K 2SO 4C .K 2CO 3D .NH 4HCO 311.下列实验操作中,不正确...的是A .加热液体B .稀释浓硫酸C .蒸发食盐水D .检查装置气密性 12.硫酸与氢氧化钠发生反应:H 2SO 4 + 2NaOH ==== Na 2SO 4 + 2H 2O ,此反应属于A .化合反应B .分解反应C .置换反应D .复分解反应13.下列符号表示1个氢分子的是A .HB .H +C .H 2D .2H 14.下列化学方程式中,书写正确的是A .H 2SO 4 + NaOH ==== NaSO 4 + H 2OB .4P + 5O 2 ====2P 2O 5C .Zn + HCl ==== ZnCl 2 + H 2↑D .4Fe + 3O 2 ==== 2Fe 2O 3 15.鉴别一瓶气体是否为氧气,下列操作正确的是A .观察气体颜色B .闻气体的气味C .插入带火星的木条D .倒入澄清的石灰水 16.下列清洗方法中,利用乳化原理的是 A. 用洗涤剂清洗餐具 B. 用汽油清洗油污 C. 用自来水洗手 D. 用盐酸清除铁锈 17.元素周期表中钠元素的信息如右图所示,对图中信息理解不正确...的是 A .质子数为11 B .元素名称为钠 C .元素符号为Na D .核外电子数为22.99 18.将下列固体分别放入水中,溶液温度明显降低的是A .硝酸铵B .生石灰C .烧碱D .食盐 19.下列处理事故的方法不正确...的是 A .电器着火,迅速切断电源 B .图书着火,用泡沫灭火器灭火C .天然气泄漏,迅速关闭阀门并开窗通风D .洒在实验桌上的少量酒精着火,迅速用湿布盖灭20.下列实际应用中,利用中和反应原理的是①用氢氧化钠溶液洗去石油产品中的残余硫酸;②用稀硫酸除铁锈;③用熟石灰改良酸 性土壤;④用碳酸氢钠治疗胃酸过多A .①③B .③④C .①②④D .①③④点燃21.在密闭容器中有甲、乙、丙、丁四种物质,在一定条件下反应,测得反应前后各物质的质量分数如右图所示。
2015平谷年初三二模语文试题及答案(精校版)

北京市平谷区2015年初中毕业会考暨初三统练(二)语文试卷一、基础·运用(共23分)(一)选择。
下列各题均有四个选项,其中只有一个..符合题意。
选出答案后在答题卡上用铅笔把对应题目的字母涂黑涂满。
(共10分)1.阅读下面的文字,完成第(1)-(4)题。
(共8分)月亮是中国文人最青睐的自然天体之一。
自然美是月亮文化的基本内涵,素月流天,它的圆满丰盈,抑或残缺不全,都给人们以美感享受,月亮的这种自然美使古今无数文人为之倾.倒;而月亮的清幽明亮、(chéng)明皎.洁,似乎也颇迎合人们含蓄温婉、清澈高洁的精神①,所以月亮是中国传统文化中最有文学韵味的文化符号之一。
随着远古以来先民对月亮文化的解读,②,对其认识也日渐丰富深刻。
民间还因月亮文化而衍生出中秋节、月亮节、拜月等百余种风俗,可以说,月亮文化是中国传统文化中最重要、最丰富、最美丽的文化之一,月亮也成为最美的文化符号之一。
在中国古代文学中描述月亮自然美、哲学美的作品不计其数;同是一轮月,文人(jiàn)赏其美与借之寄托情怀,僧家则寓佛法禅机于其中,哲学家则从中③宇宙人生的奥秘。
中国古代文学中很早就出现了月亮意象,可谓联想丰富,色彩缤纷,意蕴丰厚。
关于月亮的神话故事“嫦娥奔月”更是家喻户晓。
与月亮相关的诗词文学作品浩若烟海。
如:与月亮相关的诗文“明月松间照,清泉石上流”;对联“仲秋赏月名泉畔,元夜吟风古寺前”;谜语“画时圆,写时方,冬天短,夏天长”等数不胜数。
(1)文中加点字的注音和依据拼音写汉字全都正确的一项是(2分)A.倾倒(qǐng)皎洁(jiāo)橙明B.倾倒(qīng)皎洁(jiǎo)鉴赏C.倾倒(qǐng)皎洁(jiāo)澄明D.倾倒(qīng)皎洁(jiǎo)签赏(2)根据语意,依次在横线①②③处填入词语、句子,最恰当的一项是(2分)A. 追求不断赋予月亮以哲学内涵和情感积淀追寻B. 追寻不断赋予月亮以情感积淀和哲学内涵追求C. 追求不断赋予月亮以情感积淀和哲学内涵追寻[来源:]D.追寻不断赋予月亮以哲学内涵和情感积淀追求(3)月亮文化具有典型的神话意蕴。
2014—2015学年度第二学期初三二模考试(试卷、答案、标准答题卡可打印可修改的)解读

2014—2015学年度第二学期初三二模考试化学试卷考试说明:1.考试时间80分钟,满分100分。
2.可能用到的相对原子质量H-1 C-12 N-14 O-16 S-32 Ca-40 Cl-35.5 Na-23一、选择题(本大题共14小题,每小题2分,共28分。
每小题均有四个选项,只有一个选项符合题意)1.下列变化属于化学变化的是()A.冰雪融化 B.菜刀生锈 C.榨取果汁 D.纸张破碎2. 实验室中装有浓硫酸的试剂瓶应贴有的图标是()腐蚀品易燃气体自燃物品有毒品A B C D3.下列材料中,属于有机合成材料的是()A.蚕丝. B.羊毛 C.棉花 D.涤纶4.下列实验操作不正确...的是()A.倾倒液体 B.检查气密性 C.稀释浓硫酸 D.取用固体5. 营养学家提出“每天一杯牛奶,强壮一个民族”,我们认为这应该归功于牛奶中含有丰富的钙、镁等。
这里的钙、镁是指()A.元素 B.原子 C.分子 D.离子6.下列物质:H2O、O2、SO2 、Fe3O4、CaF2、 KClO3、 CuSO4、 NaCl,其中属于氧化物的有()A.2种 B.3种 C.4种 D.6种7.某种电池的正极材料由锂(Li)、钴(Co)和氧元素组成,三种元素的化合价分别是+1、+3、-2,则该物质的化学式为 ( ) A.LiCoO B.LiCoO2C.LiCoO3 D.LiCoO4 8.新修订的《环境空气质量标准》增加了PM2.5监测指标。
PM2.5是指大气中直径小于或等于2.5微米的可吸入颗粒物。
下列不影响该项检测结果的是()A.金属回收 B.垃圾焚烧 C.汽车尾气 D.工业废气9.右下图是“尾气催化转换器”将汽车尾气中有毒气体转变为无毒气体的微观示意图,其中不同的园球代表不同原子。
下列说法错误..的是()A.此反应有单质生成催化剂B.原子在化学变化中是不可分的→C.此反应的基本反应类型是置换反应D.参加反应的两种分子的个数比为1∶110.为探究物质燃烧条件,某同学做了如下图所示实验:已知白磷着火点40℃,红磷着火点240℃;发现水中白磷和铜片上红磷都没燃烧,铜片上白磷着火燃烧。
北京市平谷区初三数学二模试题答案

平谷区2010~2011学年度第二学期初三第二次统一练习 数学试卷参考答案及评分参考 2011.6二、填空题(本题共16分,每小题4分)三、解答题(本题共30分,每小题5分)13.解: 6)430tan 180o --+π+( = ……….…………………………………………………….4分= 1 …………………………………..………………………………………………5分14.解:xx 1x 3x 12++-- ⋅++--=)1x (x 1x 3x 1 ……………………………………………………………….1分 x13x 1--= ………………………………………………………………………2分 )3x (x 3x )3x (x x ----=……………………………………………………………3分.x3x 32-=…………………………………………………………………………4分因为 06x 3x 2=--,所以 .6x 3x 2=-所以 原式.21= …………………5分15.证明:∵ ∠BAC =90°,AB =AC ,∴ ∠B =∠C =45°. ……………………………∴ ∠BAD +∠ADB =135°. ∵ 45ADE ∠=o, ∴ ∠ADB +∠EDC =135°∴ ∠BAD =∠EDC . ……………………………………………………………2分 ∵ AD=DE ,…………………………………………………………………..3分 ∴ △ABD ≌ △DCE . ………………………………………………………….4分613323-+⨯∴AD =DE .…………………………………………………………………………………………………5分16.解:设参加清洁工作的团员有x 人,非团员有y 人. ………………………1分依题意,得 ⎩⎨⎧+==+.10x 2y ,160y x ……………………………………………………………3分解这个方程组,得⎩⎨⎧==.110y ,50x ……………………………………………………………4分答:参加清洁工作的团员有50人,非团员有110人.………………………………5分 17.解:(1)依题意可知,B (0,32).所以,b=32. …………………………………………………1分 所以,y = kx +32,把x =2 , y =0代入,得 0=322+k , 解得,3-=k ……………………………………………..2分 所以,.323+-=x y …………………………………….3分(2)设当直线AB 绕点B 顺时针旋转60°时,得到直线1y =kx+32,与x 轴交于点'A 则)0,2('-A ,所以 32x 3y 1+=. …………………………………………………..4分设当直线AB 绕点B 逆时针旋转60°时,得到直线2y ,依题意知,直线2y 平行x 轴, 所以,2y =32.…………………………………..…………………………….……….5分 18.解:(1)0k 4)4(2>--=∆解得 .4k < ……………………………………………………………………………….1分 (2)依题意,得 .3k =.........................................................................................................2分 把3k =代入方程0k x 4x 2=+-, 得 .0342=+-x x解这个方程,得 3x =或1x = ……………………………………………………………3分 当3x =时,有 01m 332=--,解得.38m = (4)E分当1x =时,有01m 12=--,解得 .0m = 所以 38m =或.0m = …………………………….……………………………………….5分四、解答题(本题共20分,每小题5分)19.解:(1)∵ AC =BC , AD = BE , ∠CAD =∠CBE ,∴ △ADC ≌△BEC ……………………………………..1分∴ DC =EC ,∠1=∠2. ……………………………………2分 ∵ ∠1+∠BCD =90°,∴ ∠2+∠BCD =90°.所以 △DCE 是等腰直角三角形…………………………..3分 (2) ∵ △DCE 是等腰直角三角形.∴ ∠CDE =45°.∵ ∠BDC =135°,∴ ∠BDE =90°……………………………………………………………………………….4分 ∵ BD :CD =1:2,设BD =x ,则CD =2x ,DE =x 22,BE =3x. ∴.31sin ==∠BE BD BED …………………………………………………………………….5 20.(1)证明:连接OD .………………………….1分 ∵ OD = OB ,∴ ∠B =∠ODB .∵ AB AC =,∴ B C ∠=∠.∴ ∠ODB =∠C .∴ OD ∥AC .………………………………………2分 ∵ DE ⊥ AC , ∴ OD ⊥DE .∴DE 是O ⊙的切线.………………………………………………………………………3分 (2) 解:连接AD , ∵ AB 为直径, ∴ ∠ADB =90°.∵120AB AC BAC =∠=,°, ∴ 30B C ∠=∠=°. ∴ AD =121=AB . ∵ 在Rt △AED 中,DE ⊥ AC ,∠DAE =60°, ∴ AE =2121=AD ,DE =23.…………………………………………………………….4分图3图2∴ EC =.23212=-∴ .833232321S =⨯⨯=∆DEC ……………………………………………………………..5分21. 解:(1)如图2;…………………………2分(2)乙x =90(分); …………………4分 (3)选派甲队参赛更能取得好成绩.…………5分22.解:(1)如图(2)最少可分成6块(画法不唯一,5条线只要不相交即可)…………2分 (2)如图(3)最多可分成16块(画法不唯一,使5条线多地相交即可)………5分 图3图2五、解答题 (本题共22分,第23题7分,第24题7分,第25题8分)23.(1)解:Q 函数(0my x x=>,m 是常数)图象经过(14)A ,,4m ∴=.……..1分 设BD AC ,交于点E ,据题意,可得B 点的坐标为4a a ⎛⎫ ⎪⎝⎭,,D 点的坐标为40a ⎛⎫⎪⎝⎭,,E 点的坐标为41a ⎛⎫⎪⎝⎭,,………………………………….2分1a >Q ,DB a ∴=,44AE a =-.由ABD △的面积为4,即14442a a ⎛⎫-= ⎪⎝⎭,………..3分得3a =,∴点B 的坐标为433⎛⎫⎪⎝⎭,.…………………4分(2)解:DC AB Q ∥,∴当AD BC =时,有两种情况: ①当AD BC ∥时,四边形ADCB 是平行四边形,由AE=CE ,BE=DE ,得,1BE AEa DE CE==-,11a ∴-=,得2a =. ∴点B 的坐标是(2,2). ························· 5分10 20 30 40 50 60 70 80 90 100得分/分甲、乙两球队比赛成绩折线统计图甲 110 场 乙设直线AB 的函数解析式为y kx b =+,把点A B ,的坐标代入,得422k b k b =+⎧⎨=+⎩,解得26.k b =-⎧⎨=⎩,∴直线AB 的函数解析式是26y x =-+. ··················· 6分 ②当AD 与BC 所在直线不平行时,四边形ADCB 是等腰梯形, 则BD AC =,4a ∴=,∴点B 的坐标是(4,1).设直线AB 的函数解析式为y kx b =+,把点A B ,的坐标代入, 得414.k b k b =+⎧⎨=+⎩,解得15k b =-⎧⎨=⎩, ∴直线AB 的函数解析式是5y x =-+. ··················· 7分 综上所述,所求直线AB 的函数解析式是26y x =-+或5y x =-+.24.解:(1)证明:如图①,在Rt △FCD 中,∵ G 为DF 的中点,∴ CG =12FD .…………………………………………..1分 同理,在Rt △DEF 中,EG =12FD .∴ CG =EG .…………………………………………….2分(2)(1)中结论仍然成立,即EG =CG .…………….3分证法一:如图②(一),连接AG ,过G 点作MN ⊥AD 于M ,与EF 的延长线交于N 点. 在△DAG 与△DCG 中, ∵ AD =CD ,∠ADG =∠CDG ,DG =DG ,∴ △DAG ≌△DCG .∴ AG =CG .…………………………………………………..4分 在△DMG 与△FNG 中,∵ ∠DGM =∠FGN ,FG =DG ,∠MDG =∠NFG , ∴ △DMG ≌△FNG .∴ MG =NG ………………………………………………5分在矩形AENM 中,AM =EN . 在Rt △AMG 与Rt △ENG 中,∵ AM =EN , MG =NG ,∴ △AMG ≌△ENG . ∴ AG =EG .∴ EG =CG . …………………………………………………… 6分 证法二:如图②(二),延长CG 至M ,使MG =CG ,连接MF ,ME ,EC ,在△DCG 与△FMG 中,∵ FG =DG ,∠MGF =∠CGD ,MG =CG ,∴ △DCG ≌△FMG .∴ MF =CD ,∠FMG =∠DCG . ………………………………..4分 ∴ MF ∥CD ∥AB . ∴ EF MF ⊥.在Rt △MFE 与Rt △CBE 中,……………………………………….5分 ∵ MF =CB ,EF =BE ,F B ADCEG图①F B A D C E GM N N图 ②(一)FB A DC E G M图 ②(二)∴ △MFE ≌△CBE .. ∴ MEF CEB ∠=∠.∴ ∠MEC =∠MEF +∠FEC =∠CEB +∠CEF =90°. ∴ △MEC 为直角三角形.∵ MG = CG ,∴ EG =21MC .∴ EG CG =.……………………………………………6分 (3)如图③,(1)中的结论仍然成立,即EG =CG .其他的结论还有:EG ⊥CG . ………………………..7分25.解:(1)作PK ⊥MN 于K ,则122PK KM NM ===.∴ KO =6,(62)P ∴,.………………………….2分 (2)当02b <≤时,如图①,0S =.……..3分 当23b <≤时,如图②, 设AC 交PM 于H .设,0b 0b x 21)(>=+-得.b 2x =∵ 24AM HA b ==-. ∴ .)4b 2(21S 2-=即22(2)S b =-.或2288S b b =-+.………………4分 当34b <<时,如图③, 设AC 交PN 于H . 82NA HA b ==-.22(4)4S b ∴=--+,或221628S b b =-+-.….5分当4b ≥时,如图④,4S =.…………………………………………………6分 (此问不画图不扣分)(3)01b <. ……………………………………………………………..7分 (提示:如图⑤,以OM 为直径作圆,当直线1(0)2y x b b =-+>图①图②图③ 图⑤FADCE图③Gb=.)与此圆相切时,1(4)b的值为4.………………………………………………………………..…. 8分。
北京市平谷区2014--2015学年度第二学期期末考试初二数学试卷

平谷区2014——2015学年度第二学期质量监控试卷2015年7月一、选择题(本题共30分,每小题3分) 下面各题均有四个选项,其中只有一个..是符合题意的. 1. 在平面直角坐标系中,点P (2,-1)关于y 轴对称的点Q 的坐标为 A.(-2,-1) B.(-2,1) C.(2,1) D.(1,-2) 2. 多边形的每个内角均为120°,则这个多边形的边数是 A .4 B .5 C .6 D .8 3.下列图形中既是轴对称图形又是中心对称图形的是A.等边三角形B. 平行四边形C. 菱形D.五角星4. 在△ABC 中,D 、E 分别为AB 、AC 边上中点,且DE =6,则BC 的长度是 A. 3 B. 6 C.9 D.125.若x 的一元二次方程2210kx x --=有两个不相等的实数根,则k 的取值范围是 A.10k k ≤-≠且 B.10k k <-≠且 C.10k k ≥-≠且 D.10k k >-≠且 6. 在四边形ABCD 中,对角线AC ,BD 互相平分,若添加一个条件使得四边形ABCD 是矩形,则这个条件可以是 A. ∠ABC =90° B .AC ⊥BD C .AB =CD D .AB // CD7.甲、乙、丙、丁四位同学五次数学测验成绩统计如表.如果从这四位同学中,选出一位A . 甲B .乙C .丙D .丁8. 如图,平行四边形ABCD 的两条对角线相交于点O ,点E 是 AB 边的中点,图中已有三角形与△ADE 面积相等的三角形(不包括...△.ADE ...)共有()个 A. 3B. 4C. 5D. 6 9.如图,在菱形ABCD 中,AB =4,∠ABC =60°,E 为AD 中点, P 为对角线BD 上一动点,连结P A 和PE , 则P A +PE 的值最小是A. 2B. 4 D.BCDAEF10. 均匀地向一个瓶子注水,最后把瓶子注满.在注水过程中,水面高度h 随时间t 的变化规律如图所示,则这个瓶子的形状是下列的二、填空题(本题共18分,每小题3分) 11. 函数y =_____________________.12.关于x 的一元二次方程2340x mx --=的一个解为1,则m 的值为______ . 13.若一次函数23y x =-+的图象经过点12(5)(1)P m P n -,和点,.则m _____n . (用“>”、“<”或“=”填空)14.在□ABCD 中,∠ABC 的平分线交直线AD 于点E长是_____________.15.根据右图中的程序,当输入一元二次方程220x x -=的解x 时,输出结果=y .16.在平面直角坐标系中,点A (2,0)到动点P (x ,x+2)的最短距离是_________________. 三、解答题:(本题共32分,其中17-20题每小题5分,21题和22题每小题6分) 17.解一元二次方程23250x x +-=18.用配方法解方程22460x x +-=19.已知:如图,在平行四边形ABCD 中,E 、F 是对角线AC 上的 两点,且AE =CF .求证:四边形BFDE 是平行四边形.20.一次函数(0)y kx b k =+≠的图象经过点(13)-,,且与2y x =平行, 求这个一次函数表达式.21.关于x 的一元二次方程2(22)(2)0(0)kx k x k k --+-=≠. (1)求证:无论k 取何值时,方程总有两个不相等的实数根. (2)当k 取何整数时方程有整数根.22.如图,在正方形ABCD 中,E 、F 分别为AB 、BC 上的点,且AE =BF ,连结DE 、AF ,猜想DE 、AF 的关系并证明.A .B .C .D .四、解答题(本题共22分,其中23-24题每小题5分,25-26题每小题6分) 23.列方程解应用题已知:如图,在长为10cm ,宽为8cm 的矩形的四个角上截去四个全等的小正方形,使得留下的图形(图中阴影部分)面积是原矩形面积的80%,求所截去小正方形的边长.24.某中学积极组织学生开展课外阅读活动,为了解本校学生每周课外阅读的时间量t (单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t <2,2≤t <3,3≤t <4,t ≥4分为四个等级,并分别用A 、B 、C 、D 表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题:(1)求x 的值;(2)求此次抽查的样本容量,并将不完整的条形统计图补充完整;(3)若该校共有学生2500人,试估计每周课外阅读时间量满足2≤t <4的人数.25.如图,是某工程队在“村村通”工程中修筑的公路长度y (米)与时间x (天)(其中08x ≤≤)之间的关系图象.根据图象提供的信息,求该公路的长.26.如图,△ABC 中,90BCA ∠=︒,CD 是边AB 上的中线,分别过点C ,D 作BA 和BC 的平行线,两线交于点E ,且DE 交AC 于点O ,连接AE. (1)求证:四边形ADCE 是菱形;(2)若606B BC ∠=︒=,,求四边形ADCE 的面积.五、解答题(本题共18分,每小题6分)27.已知,在平面直角坐标系中,O 为坐标原点,四边形OABC 是矩形,点A 、C 的坐标分别为A (10,0)、C (0,4),点D 是OA 的中点,点P 在BC 边上运动,当△ODP 是腰长为5的等腰三角形时,求点P 的坐标.28.在平面直角坐标系xOy 中,点A (0,4),B (3形ABCD ,直线:3l y kx =+.(1)当直线l 经过D 点时,求点D 的坐标及k 的值; (2)当直线l 与正方形有两个交点时, 直接写出k 的取值范围.29.阅读下面材料:小明遇到这样一个问题:如图1,在△ABC 中,D 为BC 中点,E 、F 分别为AB 、AC 上一点,且ED ⊥DF ,求证:BE +CF >EF .小明发现,延长FD 到点H ,使DH =FD ,连结BH 、EH ,构造△BDH 和△EFH ,通过证明△BDH 与△CDF 全等、△EFH 为等腰三角形,利用△BEH 使问题得以解决(如图2).参考小明思考问题的方法,解决问题:如图3,在矩形ABCD 中,O 为对角线AC 中点,将矩形ABCD 翻折,使点B 恰好与点O 重合,EF 为折痕,猜想EF 、BE 、FC 之间的数量关系?并证明你的猜想.初二数学试题参考答案2015.7二、填空题(本题共18分,每小题3分)三、解答题:(本题共32分,其中17-20题每小题5分,21题和22题每小题6分) 17.解:这里325a b c ===-,,,224243(5)640b ac ∆=-=-⨯⨯-=>,------------------------------------2分代入求根公式,得 x ==----------------------------------3分 所以方程的解为 12513x x ==-,.----------------------------------------------------------5分 18.解:22460x x +-=方程两边同时除以2,得 2230x x +-=.------------------------------------------------------1分 移常数项,得223x x +=.--------------------------------------------------------------------------2分 配方,得22131x x ++=+2(1)4x +=.-------------------------------------------------------------------------------3分开平方,得 12x +=±.------------------------------------------------------------------------------4分 所以,原方程的解为1213x x ==-,.-------------------------------------------------------------5分 19.证明:连结BD .----------------------------1分 ∵四边形ABCD 是平行四边形,∴AO =CO ,BO =DO .-------------------------------3分 又∵AE =CF ,∴EO =FO .--------------------------4分 ∴四边形BFDE 是平行四边形.-------------------5分20.解:因为一次函数(0)y kx b k =+≠的图象与2y x =平行,∴k =2. ---------------2分则一次函数2y x b =+的图象经过点(13)-,.--------------------------------------------3分 把x =1,y=-3代入2y x b =+中,得5b =-.--------------------------------------------------4分 所以,所求的一次函数表达式为25y x =-.---------------------------------------------------5分 21.(1)证明:这里(22)2a k b k c k ==--=-,,-------------------------------------------1分224[(22)]4(2)b ac k k k ∆=-=---⨯-2248448k k k k =-+-+=4>0 ----------------------------------------------2分∴无论k 取何值时,方程总有两个不相等的实数根.---------------------------------3分(2)解:方程2(22)(2)0(0)kx k x kk --+-=≠的解为:222k x k-==整理,得1221k x x k-==,.----------------------------------------------------------4分 在方程的两个根中,11x =是整数,∴22k x k-=为整数,2221k x k k-==-,---------------------------------------------------------------------5分∵ k 为整数,∴当k 为12±±和时方程有整数根. ------------------------6分22.猜想:DE =AF 且DE ⊥AF .---------------------------2分证明:∵四边形ABCD 是正方形, ∴AB =AD =BC ,∠A =∠B =90°. ∵AE =BF ,∴△DAE ≌△ABF . ---------------------------------3分 ∴DE =AF .---------------------------------------------4分 ∠1=∠2. 又∵∠1+∠AED =90°,∴∠2+∠AED =90°. -----------------------------------------------------------------------------5分 ∵∠AOE +∠2+∠AED =180°,∴∠AOE =90°.即DE ⊥AF .-------------------------------------------------------------------6分四、解答题(本题共22分,其中23-24题每小题5分,25-26题每小题6分)23.设小正方形的边长为x cm .-----------------------------------------------------------------------1分 依题意,得2108410880%x ⨯-=⨯⨯------------------------------------------------------------3分 解得 2x =±.当x =-2时不符合实际意义,故舍去.∴x =2----------------------------------------------------------------------------------------------4分 答:小正方形的边长是2cm .--------------------------------------------------------------------------5分 24. 解:(1)∵x %+15%+10%+45%=1,∴x =30;-------------------------------------------1分 (2) 样本容量为90÷45%=200(人).------------2分 B 等级人数=200×30%=60(人);-----------3分 C 等级人数=200×10%=20(人). -------------4分 (3) 2500×(10%+30%)=1000(人),∴估计每周课外阅读时间量满足2≤t <4的人数为1000人.-------------------------------------------5分25.解:由图象可以看出A (2,180)、B (4,288).------------------------------------------------1分 设直线AB 的函数表达式为y=kx +b .-----------------------------------------------------------------2分 把A (2,180)、B (4,288)代入y=kx +b 中,得21804288k b k b +=⎧⎨+=⎩-----------------------------------------------------------------------------------3分 解得5472k b =⎧⎨=⎩ ---------------------------------------------------------------------------------------------4分∴y =504x +72.当x =8时,y =504×8+72=504.-------------------------------------------------------------------------5分 答:该公路长504米. --------------------------------------------------------------------------------6分 方法二:(288-180)÷(4-2)=54;-----------------------------------------------------------------------------2分 54×(8-4)=216;--------------------------------------------------------------------------------------4分 216+288=504. -------------------------------------------------------------------------------------5分 答:该公路长504米. --------------------------------------------------------------------------------6分 26.(1)证明:∵DE //BC ,EC //AB ,∴四边形DBCE 是平行四边形.-----------------1分 ∴EC//DB ,且EC=DB .在Rt △ABC 中,CD 为AB 边上的中线, ∴AD=DB=CD .6020xy∴EC =AD .∴四边形ADCE 是平行四边形.----------------------------------------------------------------------2分 ∴ED//BC .∴AOD ACB ∠=∠. ∵90ACB ∠=︒,∴90AOD ACB ∠=∠=︒.∴平行四边形ADCE 是菱形. -----------------------------------------------------------------------3分 (2)解:Rt △ABC 中,CD 为AB 边上的中线,606B BC ∠=︒=,, ∴AD =DB =CD =6.∴AB =12,由勾股定理得AC = --------------------------------------------------------------4分 ∵四边形DBCE 是平行四边形, ∴DE =BC =6. ----------------------------------------------------------------------------------------------5分∴632ADCE AC ED S ===菱形 ------------------------------------------------------------6分 五、解答题(本题共18分,每小题6分) 27.解:由题可知D (5,0),CO =5.当△ODP 是腰长为5的等腰三角形时, 分三种情况讨论:① 当PD=OD =5时,以D 为圆心5为半径画 圆,与BC 边有两个交点,如图中点P 1、P 2.11111 5.PH OA H CO PH ⊥==作于点,则由勾股定理得1 3.H D =∴1 2.OH = ∴1(24).P , --------------------------3分. 同理求得2(84).P ,------------------------------------------------------------------------------------4分 ② 当OP=OD =5时,以O 为圆心5为半径画圆,与BC 边有一个交点,如图中P 3点, 用与①同样的方法求得3(34).P ,--------------------------------------------------------------------5分 ③ 当OP=PD 时,即OD 为底边,此时点P 在OD 的中垂线上,设OD 的中垂线与BC 交点为4P ,此时,45OP=≠.∴这种情况不存在.-----------------------------------------6分 综上所述,满足条件的P 点有三个:1(24)P ,、2(84)P ,、3(34).P ,28. (1)如图,过D 点作DE ⊥y 轴,则1390AED ∠=∠+∠=︒.在正方形ABCD 中,90DAB ∠=︒,AD=AB .∴1290∠+∠=︒. ∴23∠=∠.又∵90AOB AED ∠=∠=︒,∴△AED ≌△BOA .-----------------------------2分 ∴DE =AO =4,AE =OB =3.∴OE =7,--------------------------------------- ----3分 ∴D 点坐标为(4,7).------------------------------4分把D (4,7)代入3y kx =+,得 k =1.----------5分 (2)1k >-.-----------------------------------------6分29.猜想: 222EF AE CF =+证明:延长EO 交CD 于点H ,连结FH . ∵四边形ABCD 是矩形.∴AB//DC . 90B ∠=︒ ∴EAO HCO ∠=∠. ∵O 为对角线AC 中点,∴AO =CO . ∵BOE COH ∠=∠ ∴△AEO ≌△CHO . ∴EO =HO ,CH =AE .------------------------------2分 由题意可知△EFO ≌△EFB . ∴90EOF B ∠=∠=︒. ∴OF 垂直平分EH .∴FH =EF .--------------------------------------------------------------------------------------------------4分 在△FCH 中,由勾股定理得222FH CH FC =+.--------------------------------------------------5分 ∴222EF AE CF =+.-------------------------------------------------------------------------------------6分yx123。
2015北京市平谷区初三(二模)物理

2015北京市平谷区初三(二模)物理苏悦读书室整理一、下列各小题均有四个选项,其中只有一个选项符合题意(本大题共30分,每小题2分)1.(2分)下列文具中,通常情况下属于导体的是()A.塑料尺B.玻璃杯C.铅笔芯D.橡皮2.(2分)图的四种现象中,属于光的反射现象的是()A.白光通过三棱镜形成彩色光带B.人在墙上形成的影子C.铅笔好像在水面处折断了D.观众看到银幕上的图象3.(2分)如图所示的四个实例中,增大了压强的是()A.书包带宽B.铁轨铺在枕木上C.大型货车装很多轮子D.注射器针头很尖4.(2分)如图所示的用具中,属于省力杠杆的是()A.钳子B.镊子C.天平D.筷子5.(2分)下列用电器中,主要利用电流热效应工作的是()A.电烙铁B.电风扇C.电动机D.抽油烟机6.(2分)下列自然现象属于凝华的是()A.春天到了,积雪融化B.夏天的早晨,草地上出现露珠C.秋天的早晨,出现大雾D.初冬的早晨,地面上出现白霜7.(2分)在如图所示的实例中,通过热传递改变物体内能的是()A.迅速下压活塞,压燃气管内气体温度升高B.用火炉炒菜,铁锅烫手C.两手互相摩擦,手发热D.从滑梯上滑下,屁股感觉发热8.(2分)下列说法正确的是()A.起重机吊着水泥板水平匀速移动一段距离,起重机对水泥板做了功B.运动员将篮球投出,篮球在空中运动过程中,运动员对篮球做了功C.小刚从地上捡起篮球的过程中,小刚对篮球做了功D.小磊背着书包站在路边等车,小磊对书包做了功9.(2分)如图所示实验电路相对应的电路图是图中的()A.B.C.D.10.(2分)下列数据最接近实际情况的是()A.冰箱冷藏室约﹣15℃B.中学生脉搏跳动一次的时间约为2sC.一支新铅笔的长度约为17cm D.一个篮球的质量约为50g11.(2分)举重比赛要求运动员将杠铃举过头顶后,在空中至少静止3秒钟,在这3秒钟内()A.运动员所受重力和地面对他的支持力是平衡力B.杠铃受到的重力和人对它的支持力是平衡力C.运动员对地面压力和地面对运动员支持力是平衡力D.杠铃对运动员压力和人对杠铃的支持力是平衡力12.(2分)下列现象中,不能用惯性知识解释的是()A.拍打衣服时,灰尘从衣服中脱离出来B.人从行驶的车上跳下来容易摔倒C.短跑运动员到达终点后不能立即停下来D.用力将物体抛出去,物体最终要落到地面上13.(2分)图所示的电路中,电源两端的电压保持不变.闭合开关S后,滑动变阻器的滑片P向右移动,下列说法中正确的是()A.电压表V1的示数变大B.电压表V1的示数保持不变C.电压表V2的示数保持不变D.电压表V1与电压表V2的示数之和保持不变14.(2分)如图所示,两个完全相同的柱形容器盛有甲、乙两种液体,若将两个完全相同的物体分别浸没在甲、乙液体后(无液体溢出),液体对容器底部的压强相等,则两物体受到的浮力F甲、F乙和液体对容器底部的压力F甲′、F乙′的关系是()A.F甲=F乙F甲′<F乙′B.F甲<F乙F甲′=F乙′C.F甲>F乙F甲′=F乙′D.F甲=F乙F甲′>F乙′15.(2分)某同学设计了如图所示的双向开关电路,电源电压保持不变,灯L1标有“3V 3W”的字样,灯L2标有“6V 3W”的字样.当开关拨至2位置且滑片滑到A端时,灯L2恰好正常发光.下列说法正确的是(不计灯丝电阻随温度的变化)()A.电源电压为9V B.L2正常发光时,电路中的电流为1.5AC.要使L1正常发光,滑动变阻器接入电路中的阻值应为6ΩD.当L1、L2分别正常发光时,两种电路的总功率之比为2:1二、下列各小题均有四个选项,其中符合题意的选项均多于一个.(共8分,每小题2分,全选对的得2分,选对但不全的得1分,有错选的不得分)16.(2分)下列说法中正确的是()A.给冰水混合物加热,其温度保持不变B.扩散现象说明气体分子不停地做无规则运动C.0℃的冰熔化成0℃的水内能增加D.夏天,打开冰箱门时常会出现“白气”,这是冰箱内水蒸气的液化现象17.(2分)下列说法中正确的是()A.用吸管吸饮料利用了大气压强B.力的作用效果只与力的大小和方向有关C.潜水艇、气球和飞艇都是靠改变它们自身重力来实现浮沉的D.运动员用力将冰壶推出,说明力可以改变物体的运动状态18.(2分)下列说法中正确的是()A.奥斯特实验说明了导体周围存在磁场B.磁体周围的磁感线是从北极出来,回到南极C.金属导体靠自由电子导电,电流方向与其定向移动方向相反D.家庭电路保险丝熔断说明电路总功率过大19.(2分)下列说法中正确的是()A.受力面积相同时,重力大的物体对支持面压强大B.在水平桌面上匀速直线运动的木块,机械能保持不变C.用3N的水平拉力使木块在水平桌面上做匀速直线运动,木块受到的摩擦力是3ND.跳水运动员起跳时,跳板向下弯,人对跳板的力等于跳板对人的作用力三、填空题(共10分,每小题1分)20.(1分)同种电荷相互排斥,异种电荷相互.21.(1分)大气压随地面高度的增加而(选填“增大”或“减小”).22.(1分)小明站在竖直的平面镜前2m处,他在镜中的像到镜面的距离是m.23.(1分)常温下,液化石油气是利用的方法,使气态石油气变成液态储存在钢瓶里的.24.(1分)[中考演练]“星光大道”年度总冠军杨光能模仿单田芳、刘欢等文艺名人的声音,从声音的特性来看,他主要模仿声音的(选填“音调”、“响度”或“音色”).25.(1分)煤炭是一种重要的不可再生能源,区别优、劣质煤一般用物理量.26.(1分)利用法拉第发现的电磁感应现象,制成了.27.(1分)要在光屏上得到跟物体一样大小的像,应选用.(选填“平面镜”或“凸透镜”)28.(1分)一根阻值为50Ω的电阻丝,通电100s,电流通过电阻丝产生的热量为2×104J,则通过电阻丝的电流为A.29.(1分)甲、乙两溢水杯放在实验桌上,分别盛满水和酒精,酒精的密度为0.8×103kg/m3.将密度为0.9×103kg/m3的小球轻轻放入甲溢水杯的水中,小球静止时从甲溢水杯中溢出18g的水;将小球轻轻放入乙溢水杯的酒精中,小球静止时从乙溢水杯中溢出g的酒精.四、实验与探究题(共36分,35、36题各2分,30、31、37、39题各3分,32-34、38、40题各4分)30.(3分)如图1所示,物体A的长度为cm;如图2所示,电能表的示数为kW•h;根据图3中通电螺线管中的电流方向,可以判断螺线管左端为极.31.(3分)小华在“观察水的沸腾”实验中,绘出了温度随时间变化的图象如图所示:(1)从图象中可知,水的沸点是℃,这与物理课本上给出的水的沸点比不一样,你认为出现这种现象的原因是.(2)实验时小华和其他组同学使用的酒精灯和水的质量都样同,却发现自己组的水比邻组的先沸腾,其原因是.32.(4分)在图中,凸透镜焦距为10cm,当把蜡烛放在20cm刻度处时,通过移动光屏,可在光屏上得到清晰、、(选填“正立”或“倒立”)缩小的实像;若想得到一个清晰放大的实像,蜡烛应向凸透镜的方向移动(选填“远离”或“靠近”),同时光屏应向远离凸透镜的方向移动.若保持透镜位置不变,把蜡烛放在45cm刻度处时,移动光屏,蜡烛在光屏上成像(选填“能”或“不能”),就是利用凸透镜的这一特点来观察物体的(选填“照相机”、“放大镜”或“幻灯机”).33.(4分)李萌同学在做比较不同物质吸热能力的实验时,使用相同的电加热器加热水和煤油,用加热时间的长短来表示物质吸收热量的多少,她得到如下数据:物质次数质量m/kg 升高温度△t/℃加热时间t/min水 1 0.1 10 22 0.2 10 43 0.3 10 6煤油 4 0.1 10 15 0.2 10 2(1)实验时使用相同的电加热器加热水和煤油,目的是.(2)实验时用加热时间的长短来表示物质吸收热量的多少,这种研究问题的方法叫做.(选填“控制变量法”、“等效替代法”或“转换法”)(3)分析第1、2、3次实验,控制变量是.(4)分析第1、4次实验数据,可以初步得出的结论是:.34.(4分)测量某种液体的密度.(1)把天平放在水平桌面上,将游码移至零刻度处,发现指针偏向分度盘的左侧,这时应将平衡螺母向调节(选填:“左”或“右”);(2)将待测液体倒入烧杯中,用天平测出烧杯和液体的总质量m1,如图甲所示,则m1=g;(3)将烧杯中食用油的一部分倒入量筒,如图乙所示,这部分液体的体积为V,则V=cm3;(4)用天平测量烧杯和剩余液体的总质量m2=110g;(5)根据以上数据,计算出这种液体的密度是g/cm3.35.(2分)分析表格中的数据,归纳出拉力F与重力G的关系,则力F与重力G的关系式:.G/N 1 2 3 4 5 6F/N 0.9 1.4 1.9 2.4 2.9 3.436.(2分)如图是当电压一定时,通过导体的电流随导体电阻变化规律的图象.由图象可知,当通过导体的电流为2A时,该导体消耗的电功率为W.37.(3分)小刚和丽丽要探究并联电路电流规律,他们分别从实验室选取电流表3块,灯泡2只,开关1个,干电池,导线若干,并设计了实验电路图如图所示:(1)小刚同学根据电路图连接好实验电路,在连接过程中,开关应该断开;检查电路无误后,开始实验,正确读出电流表示数如表一:表一:I1/A 0.10 0.12 0.14 0.16 0.18 0.20I2/A 0.10 0.12 0.14 0.16 0.18 0.20I/A 0.20 0.24 0.28 0.32 0.36 0.40表二:I1/A 0.10 0.12 0.14 0.16 0.90 0.20I2/A 0.12 0.14 0.16 0.18 0.20 0.22I/A 0.22 0.26 0.30 0.34 0.38 0.42 (2)丽丽同学根据电路图正确连接好实验电路,开始实验,正确的出电流表示数如表二:分析记录的实验数据,小刚同学得出:并联电路中各支路电流相等;丽丽同学得出:并联电路总电流有时等于各支路电流之和,有时不等于各支路电流值和.请根据上述实验及记录的数据回答下列问题:(1)小刚同学得出错误的实验结论,主要原因是.(2)丽丽同学的实验记录表格中,实验第5次I1读数错误,原因是.(3)为了使实验结论更具科学性,请你提出1条合理化建议:.38.(4分)某同学利用如图所示的器材探究液体内部压强的特点.(1)他向图甲中的U形管内注入适量的红墨水,当管内的红墨水静止时,U形管左右两侧液面的高度.(2)如图乙所示,他将橡皮管的一端紧密地套在U形管左侧的端口后,多次改变探头在水中的深度,并比较每次的深度及相应的U形管左右两侧液面的高度差,这是为了探究.(3)他换用其它液体探究液体压强与液体密度的关系时,当探头在酒精、盐水中的深度相同时,U形管左右两侧液面的高度差最大的是.(4)若图乙中U形管左右两侧红墨水面的高度差h=10cm,则橡皮管内气体的压强与大气压之差约为Pa.(ρ红墨水=1.0×103kg/m3)39.(3分)已知电磁铁磁性强弱与电流的大小和线圈匝数多少有关,请设计一个简易实验证明:当线圈匝数保持不变时,电磁铁的磁性随电流的增大而增强.写出实验所需要的器材、实验步骤以及实验分析与结论,要求设计的实验具有可行性,要符合安全规则.40.(4分)实验台上有组装好的实验装置,如图所示,其中弹簧测力计的量程为0﹣5N.另外还有质量均为100g 的钩码若干(图中未画出).小刚利用上述实验装置和钩码设计一个物理实验,探究用动滑轮提升重物时,有用功跟总功的关系(实验时不计绳的质量和滑轮与轴的摩擦).他的实验步骤:(1)在动滑轮挂钩上挂2个钩码,用弹簧测力计竖直向上匀速拉绳子自由端移动一段距离.他把2个钩码的总质量用m表示,绳子自由端所受拉力用F表示,绳子自由端移动的距离用s表示,钩码上升的高度用h表示;并将测量数据记录在表格中.(2)保持动滑轮所挂钩码个数不变,依次改变绳子自由端移动的距离s,仿照步骤(1)又做了5次实验,并把各次的测量数据记录在表格中.请根据以上叙述回答下列问题:①小刚实验前的猜想是;②小刚在对猜想探究时,他需要控制的变量是;③小刚是通过改变来改变自变量;④请你帮助小刚设计出实验数据记录表格:五、科普阅读题(共8分,44题4分,45题4分)41.(4分)阅读以下材料,回答问题:微波炉是现代家庭中使用电磁波来加热的烹饪工具.接通电源后微波炉内的磁控管能产生频率很高波长很短的电磁波,电磁波的频率为2450MHZ,波长为12.2cm,故称为微波.微波有以下重要特性:微波的传播速度等于光速,微波遇到金属物体,会像光遇到镜子一样地发生反射;微波遇到绝缘材料,如玻璃、塑料等,会像光透过玻璃一样顺利通过;微波遇到含水的食品,能够被其大量吸收,引起食品内部分子发生剧烈的振动,达到加热食品的目的;过量的微波照射对人体有害.(1)微波在真空中的传播速度为m/s.(2)为防止微波泄漏对人体造成伤害,在玻璃炉门内侧应装A.石棉网B.金属网C.塑料膜D.橡皮膜(3)含水的食品遇到微波能把电磁能量转化为食物的能.(4)电磁波和微波一样遇到金属物体,会发生反射,利用此特性可制成.42.(4分)2011年11月3日,距地球343公里的太空,中国两航天器一一“神舟八号”无人飞船和“天宫一号”,实施首次空间飞行器无人交会对接试验,如图所示,当“神舟八号”到达“天宫一号”30米停泊点,开始以0.2m/s的相对速度向“天宫一号”缓缓靠拢完成对接,随后组合体以优美的姿态飞翔在茫茫太空,此时它们以7.8km/s的速度绕地球飞行,神舟八号与天宫一号在太空成功对接,使我国成为继美、俄之后第3个掌握交会对接技术的国家.(1)从30米的停泊点到相互接触共耗时s.(2)对接完成后,若以“天宫一号”为参照物,“神舟八号”是的.(3)如果两航天器质量相等,则在对接过程中“神舟八号”的动能“天宫一号”的动能.(填“大于”、“小于”或“等于”)(4)若“天宫一号”飞行器沿椭圆轨道绕地球运行的过程中机械能守恒,则它从远地点向近地点运行的过程中A.重力势能增加、动能减小B.重力势能减小、动能增加C.重力势能增加、动能增加D.重力势能不变、动能不变.六、计算题(共8分,46题4分,47题4分)43.(4分)在综合实践活动课上,小刚设计了如图所示的模拟调光灯电路,此电路中电源电压不变,灯泡L标有“6V 3W”字样,当滑动变阻器R2的滑片P移至某一位置时,闭合开关,小灯泡正常发光,电压表示数为2V;当滑动变阻器R2的滑片P移至右端时,闭合开关,电流表示数为0.3A,电压表示数为4.8V.求:(1)灯泡L的电阻;(2)滑动变阻器R2的滑片P在最右端时,闭合开关,灯泡L的实际功率;(3)电源电压.44.(4分)一体重为600N,双脚与地面接触面积为0.05m2的工人,用如图所示的滑轮组将体积为0.01m3重为900N 的物体A在水中匀速提高了0.5m,此时该滑轮组的机械效率80%,求:(不计绳重及摩擦,g=10N/kg)(1)工人自由站在水平地面上,对地面的压强;(2)物体A在水中匀速提高0.5m,拉力所做的有用功;(3)物体拉出水面后,使用该滑轮组,这个工人最多能提起多重的物体.。
平谷区初三数学一模试题

平谷区2013-2014初三数学统练二2014.5学校 班级 姓名 考号一、选择题(本题共32分,每小题4分) 下面各题均有四个选项,其中只有一个....是符合题意的. 1.25-的绝对值是 A .52 B .52-C .25D .25-2.打开百度搜索栏,输入“数学学习法”,百度为你找到的相关信息约有12 000 000条, 将12 000 000用科学记数法表示为 A .1.2×107B. 61.210⨯ C .61210⨯ D .71210⨯3.一个正多边形的一个外角是40°,这个正多边形的边数是A .10B .9C .8D .54.有分别写数字1、2、3、4、5的五张卡片,除数字不同外其它均相同,从中任意抽取一张,那么抽到的数是奇数的概率是 A .51 B .52 C .53 D .54 5.如图,AB ∥CD ,O 为CD 上一点,且∠AOB =90°, 若∠B =33°,则∠AOC 的度数是 A .33° B .60° C .67° D .57°6.甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均数都是8.9环,方差分别是20.65S =甲,20.55S =乙,20.50S =丙 20.45S =丁,则射箭成绩最稳定的是A .甲B .乙C .丙D .丁7. 如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度h 为.8. 如图,扇形OAB 的半径OA =6,圆心角∠AOB =90°,C 是»AB 上不同于A 、B 的动点,过点C 作CD ⊥OA 于点D ,作CE ⊥OB 于点E ,连结DE ,点H 在线段DE 上,且EH =32DE .设EC 的长为x ,△CEH 的面积为y ,下面表示y 与x 的函数关系式的图象可能是CCA .B .C .D. 二、填空题(本题共16分,每小题4分) 9.分解因式:339-=a b ab .10.直线过点(0,-1),且y 随x 的增大而减小.写出一个满足条件的一次函数解析式._________________. 11.如图,⊙O 的直径CD ⊥AB ,∠AOC =50°,则∠CDB 的度数为__________.12.如图,□ABCD 的面积为16,对角线交于点O ;以AB 、AO 为邻边做□AOC 1B ,对角线交于点O 1;以AB 、AO 1为邻边做□AO 1C 2B ,对角线交于点O 2;…;依此类推.则□AOC 1B 的面积为_______;□AO 4C 5B 的面积为_______;□AO n C n+1B 的面积为___________.三、解答题(本题共30分,每小题5分)13.如图,AD 平分∠BAC ,AD =AC ,E 为AD 上一点,且AE =AB ,连结BD 、CE .求证:BD =CE .14.计算:1012014tan 603-⎛⎫-︒ ⎪⎝⎭.15.求不等式组2(2)43251x x x x -≤-⎧⎨--⎩<的整数解.16.已知a 2+2a =3,求代数式22(1)(2)a a a ---的值. 17.已知一次函数y kx b =+(0)k ≠与反比例函数(my m x=的图象交于(23)(6)A B n -,、,两点. (1)求一次函数和反比例函数的解析式;(2)P 是y 轴上一点,且12ABP S ∆=,直接写出P 点坐标.18.A 、B 两种机器人都被用来搬运化工原料,A 型机器人比B 型机器人每小时多搬运20千克,A 型机器人搬运1000千克所用时间与B 型机器人搬运800千克所用时间相等,求A 型、B 型两种机器人每小时分别搬运多少化工原料?2A B 12题图四、解答题(本题共20分,每小题5分)19.如图,在四边形ABCD 中,对角线BD 平分∠ABC ,∠ ∠C =60°,AB =5,AD =3. (1)求证:AD =DC ;(2)求四边形ABCD 的周长.20.如图,在Rt △ABC 中,∠ACB =90°,点D 是AB 边上一点,以BD 为直径的⊙O 与边AC 相切于点E ,连接DE并延长DE 交BC 的延长线于点F .(1)求证:BD =BF ; (2)若CF =1,cos B =35,求⊙O 的半径.21.某校为了开设武术、舞蹈、剪纸等三项活动课程以提升学生的体艺素养,随机抽取了部分学生对这三项活动的兴趣情况进行了调查(每人从中只能选一项),并将调查结果绘制成下面两幅统计图,请你结合图中信息解答问题. (1)将条形统计图补充完整;(2)本次抽样调查的样本容量是____________;(3)已知该校有1200名学生,请你根据样本估计全校学生中喜欢剪纸的人数.22. 如图1,若点A 、B 在直线l 同侧,在直线l 上找一点P ,使AP +BP 的值最小,做法是:作点B 关于直线l 的对称点B′,连接AB′,与直线l 的交点就是所求的点P ,线段AB′的长度即为AP +BP 的最小值. (1)如图2,在等边三角形ABC 中,AB =2,点E 是AB 的中点,AD 是高,在AD 上找一点P ,使BP +PE 的值最小.做法是:作点B 关于AD 的对称点,恰好与点C 重合,连接CE 交AD 于一点,这点就是所求的点P ,故BP +PE 的最小值为 ;(2)如图3,已知⊙O 的直径CD 为2, AC 的度数为60°,点B 是 AC 的中点,在直径CD 上作出点P ,使BP +AP 的值最小,则BP +AP 的最小值为 ;(3)如图4,点P 是四边形ABCD 内一点,BP =m ,ABC α∠=,分别在边AB 、BC 上作出点M 、N ,使PMN ∆的周长最小,求出这个最小值(用含m 、α的代数式表示).图4CB图3图2图1P DECBA五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.已知关于x 的一元二次方程210x mx m -+-=. (1)求证:无论m 取任何实数时,方程总有实数根;图2图1E DC A备用图(2)关于x 的二次函数211y x mx m =-+-的图象1C 经过2(168)k k k --+,和2(568)k k k -+-+,两点.①求这个二次函数的解析式;②把①中的抛物线1C 沿x 轴翻折后,再向左平移2个单位,向上平移8个单位得到抛物线2C .设抛物线2C 交x 轴于M 、N 两点(点M 在点N 的左侧),点P (a ,b )为抛物线2C 在x 轴上方部分图象上的一个动点.当∠MPN ≤45°时,直接写出a 的取值范围.上一点,且CE =AB ,BE =CD ,(2)如图2,在90ABC A ∆∠=︒中,,D 、E 分别为AB 、AC 上的点,连结BE 、CD ,两线交于点P .①当BD=AC ,CE=AD 时,在图中补全图形,猜想BPD ∠的度数并给予证明. ②当BD CEAC AD==时, BPD ∠的度数____________________.25.定义:任何一个一次函数y px q =+,取出它的一次项系数p 和常数项q ,有序数组][q p ,为其特征数.例如:y =2x +5的特征数是]52[,,同理,[]a b ,,c 为二次函数2y ax bx c =++的特征数。
2015年北京市平谷初三数学一模
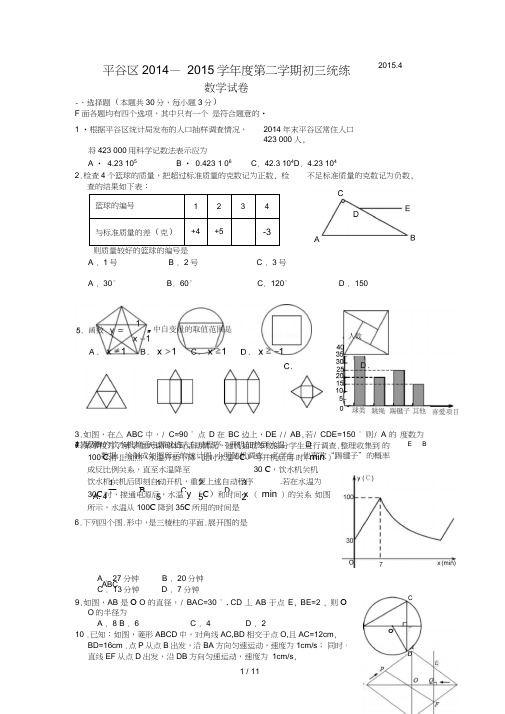
7某学校为了解学生大课间体育活动情况,随机抽取本校部分学生进行调查.整理收集到 的数据,绘制成如图所示的统计图.小明随机调查一名学生,他喜欢“踢毽子”的概率 1 1 2 3 — B .- C . D . A. 4 5 5 2&某品牌的饮水机接通电源就进入自动程序:开机加热到水温 100 C,停止加热,水温开始下降,此时水温(C )与开机后用 时(min )成反比例关系,直至水温降至30 C ,饮水机关机饮水机关机后即刻自动开机,重复上述自动程序.若在水温为 30C 时,接通电源后,水温 y (C )和时间x ( min )的关系 如图所示,水温从100C 降到35C 所用的时间是 A . 27分钟B . 20分钟C . 13分钟D . 7分钟9.如图,AB 是O O 的直径,/ BAC=30 ° , CD 丄 AB 于点 E , BE=2 , 则O O 的半径为 A . 8 B . 6 C . 4 D . 210 .已知:如图,菱形ABCD 中,对角线AC,BD 相交于点O,且AC=12cm ,BD=16cm .点P 从点B 出发,沿BA 方向匀速运动,速度为 1cm/s ; 同时,直线EF 从点D 出发,沿DB 方向匀速运动,速度为 1cm/s ,平谷区2014— 2015学年度第二学期初三统练数学试卷-、选择题(本题共30分,每小题3分)F 面各题均有四个选项,其中只有一个 是符合题意的• 1 •根据平谷区统计局发布的人口抽样调查情况, 2014年末平谷区常住人口423 000人,将423 000用科学记数法表示应为A • 4.23 105B • 0.423 1 06C . 42.3 104D . 4.23 1043.如图,在△ ABC 中,/ C=90 ° 点 D 在 BC 边上,DE // AB ,若/ CDE=150 ° 则/ A 的 度数为篮球的编号 1 2 3 4 与标准质量的差(克) +4 +5-32.检查4个篮球的质量,把超过标准质量的克数记为正数, 检查的结果如下表: 则质量较好的篮球的编号是A . 1号B . 2号C . 3号 不足标准质量的克数记为负数,2015.4A . 30°B . 60°C . 120°D . 1504.下列图形6.下列四个图.形中,是三棱柱的平面.展开图的是ABCD CE B OEEF 丄BD ,且与AD , BD , CD 分别交于点 E , Q , F ;当直线 EF 停止运动时,点 P 也停 止运动•连接PF ,设运动时间为t (s ) (0 v t v 8).设四边形 APFE 的面积为y (cm 2), 则下列图象中,能表示 y 与t 的函数关系的图象大致是 、填空题(本题共18分,每小题3分)32211 •分解因式:a -4a b 4ab = ________________12.甲、乙二人进行射击比赛,已知他们每人五次射击的成绩如下表(单位:环),那么人中成绩最稳定的是 _________________第一次 第二次 第三次 第四次 第五次甲9.3 7.9 4 7. 1 6乙6.16.87.286.213 .如图,热气球的探测器显示,从热气球 A 看一栋高楼顶部 B 的仰角为30°,看这栋高楼底部 C 的俯角为60°,热气球A 与高楼 的水平距离为120m ,这栋高楼BC 的高度为 _____________________________ 米. 14. 如图,矩形 OABC 的顶点A , C 分别在x 轴和y 轴上,若0A=4,kOC=6,写出一个函数 y k=0,使它的图象与矩形 OABCx的两边AB , BC 分别交于点D , E ,这个函数的表达式为 __________ . 15.在学习二次函数的图象时,小米通过向上(或向下)平移y=ax 2的图象,得到y=ax 2+c 的图象;向左(或向右)平移y=ax 2的图象,得到y=a (x -h )2的图象.小米经过探究发现一次函数的图象也应该 具有类似的性质.请你思考小米的探究,直接写出一次函数 y=2x+3 的图象向左平移4个单位长度,得到的函数图象的解析式为 ____________________ . 16. 在Rt △ ABC 中,/ A=90°,有一个锐角为 60° BC=6 .若点P 在直 线AC 上(不与点 A , C 重合),且/ ABP=30 °贝U CP 的长 为 _________ . 三、解答题(本题共30分,每小题5分)17 .如图,AB=AD , AC=AE ,/ CAD=Z EAB . 求证:BC=DE .zx -118. 计算:J8—2cos45。
鹤陆蠡阅读答案

鹤陆蠡阅读答案【篇一:2015平谷年初三二模语文试题及答案(精校版)】文摘:鹤陆蠡阅读答案)5年初中毕业会考暨初三统练(二)语文试卷(一)选择。
下列各题均有四个选项,其中只有一个符合题意。
选出答案后在答题卡上用铅笔把对应题目..的字母涂黑涂满。
(共10分)1.阅读下面的文字,完成第(1)-(4)题。
(共8分)月亮是中国文人最青睐的自然天体之一。
自然美是月亮文化的基本内涵,素月流天,它的圆满丰盈,抑或残缺不全,都给人们以美感享受,月亮的这种自然美使古今无数文人为之倾倒;而月亮的清幽明亮、.中国古代文学中很早就出现了月亮意象,可谓联想丰富,色彩缤纷,意蕴丰厚。
关于月亮的神话故事“嫦娥奔月”更是家喻户晓。
与月亮相关的诗词文学作品浩若烟海。
如:与月亮相关的诗文“明月松间照,清泉石上流”;对联“仲秋赏月名泉畔,元夜吟风古寺前”;谜语“画时圆,写时方,冬天短,夏天长”等数不胜数。
(1)文中加点字的注音和依据拼音写汉字全都正确的一项是(2分)(2)根据语意,依次在横线①②③处填入词语、句子,最恰当的一项是(2分)a. 追求不断赋予月亮以哲学内涵和情感积淀追寻b. 追寻不断赋予月亮以情感积淀和哲学内涵追求d. 追寻不断赋予月亮以哲学内涵和情感积淀追求(3)月亮文化具有典型的神话意蕴。
关于月亮的神话故事“嫦娥奔月”家喻户晓,除此之外,下面的神话故事中与月亮有关的一项是(2分)a.精卫填海b.夸父逐日c.女娲补天d.吴刚折桂(4)成语是中华民族文化的精华,它的来源十分丰富。
下面有关月亮的成语出自历史典故的一项是(2分)a.海底捞月b.闭月羞花c.月明星稀d.众星捧月2.在我国五千年的传统文化发展中,产生了很多的传统节日和习俗,这些都是中华民族灿烂文化的表现。
下面4幅图展示的都是传统节日的习俗,请选出不是元宵节习俗的一项(2分)a b d c(二)补写(2分)3.下面是一副有关传统节日的对联的上联,请补写出跟月亮有关的传统节日的下联,并用规范的正楷抄写在答题卡的田字格中。
平谷区2014初三数学一模

OFEDC BA平谷区2013-2014学年度第二学期初三数学一、选择题(本题共32分,每小题4分)1.西部大开发战略是党中央面向21世纪的重大决策,我国西部地区面积为6 400 000平方千米,将6 400 000用科学记数法表示应为 A.70.6410⨯ B.66.410⨯ C.56410⨯ D.464010⨯2. 23-的相反数是( ) A .23 B .32-C .32D .23-3. 在一个口袋中,装有质地、大小均相同、颜色不同的红球3个,蓝球4个,黄球5个,现在随机抽取一个球是红球的概率是 A.121 B. 31 C. 41 D. 514.如图,AB ∥CD ,AF 交CD 于点O ,且OF 平分∠EOD ,如果∠A =34°,那么∠EOD 的度数是A .34°B .68°C .102°D .146°5.在某次活动课中,甲、乙两个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.如图1,甲组测得一根直立于平地,长为80cm 的竹竿的影长为如图2,乙组测得学校旗杆的影长为900cm.则旗杆的长为 A .900cm B .1000cm C .1100cm D .1200cm6.某校篮球班 则该校篮球班21名同学身高的众数和中位数分别是A .186,188B .188,186C .186,186D .208,188图2FE D C BAECBD A F 7. 下列图形中,既是轴对称图形又是中心对称图形的是( )A B C D8.如图,在矩形ABCD 中,AB =9,BC =3,点E 是沿A →B 方向运动,点F 是沿A →D →C 方向运动.现E 、F 两点同时出发匀速运动,设点E 的运动速度为每秒1个单位长度,点F 的运动速度为每秒3个单位长度,当点F 运动到C 点时,点E 立即停止运动.连接EF ,设点E 的运动时间为x 秒,EF 的长度为y 个单位长度,则下列图象中,能表示y 与x 的函数关系的图象大致是二、填空题(本题共16分,每小题4分) 9. 分解因式:269-+=mn mn m = .10.请写出一个开口向下,对称轴为直线1=x 的抛物线的解析式,y= .11.如图,点O 是矩形ABCD 的对称中心,E 是AB 上的点, 沿CE 折叠后,点B 恰好与点O 重合,若BC =3,则折痕CE 的长为_____________________.12.如图,1P 、2P 、3P …n P (n 为正整数)分别是反比例函数)0(>=k xky 在第一象限图像上的点,1A 、2A 、3A …n A 分别为x 轴上的点,且11OA P ∆、212A A P ∆、323A A P ∆…n n n A A P 1-∆均为等边三角形.若点1A 的坐标为(2,0),则点2A 的坐标为____________,点n A 的坐标为____________.三、解答题(本题共30分,每小题5分)13. 如图,点A 、C 、D 、B 四点共线,且AC =DB ,∠A =∠B ,∠E =∠F .求证:DE =CF .x 1 4 y O x 1 4 y O x1 4 y O x1 4 y O A B C DAB C EFD ACBOD 14. 计算:101()4sin 6027(3)2π--︒++-15. 求不等式组⎪⎩⎪⎨⎧+>+-≥-2274)1(2x x x x 的整数解.16. 已知2x -y =0,求代数式x (x -2y )-(x +y )(x -y )的值.17. 端午节期间,某校“慈善小组”筹集善款600元,全部用于购买粽子到福利院送给老人.购买大枣粽子和豆沙粽子各花300元,已知大枣粽子比豆沙粽子每盒贵5元,结果购买的大枣粽子比豆沙粽子少2盒.请求出两种口味的粽子每盒各多少元?18. 关于x 的一元二次方程023)3(2=+--x x k 有两个不相等的实数根.(1)求k 的取值范围.(2)求当k 取何正整数时,方程的两根均为整数.四、解答题(本题共20分,每小题5分)19.如图,在△ABC 中,D 为AB 边上一点、F 为AC 的中点,过点C 作CE //AB 交DF 的延长线于点E ,连结AE .(1)求证:四边形ADCE 为平行四边形.(2)若EF =22,︒=∠︒=∠4530AED FCD ,,求DC 的长.20. 如图,点A 、B 在⊙O 上,直线AC 是⊙O 的切线,OC ⊥OB ,连接AB 交OC 于点D . (1)求证:AC =CD .(2)若AC =2,AO =5,求OD 的长.21.由平谷统计局2013年12月发布的数据可知,我区的旅游业蓬勃发展,以下是根据近几年我区旅游业相关数据绘制统计图的一部分:请你根据以上信息解答下列问题: (1)计算2012年平谷区旅游区点营业收入占全区旅游营业收入的百分比,并补全扇形统计图;(2)2012年旅游区点的收入为2.1万元,请你计算2012年平谷区旅游营业收入,并补全条形统计图 (结果保留一位小数) ; (3)如果今年我区的旅游营业收入继续保持2013年的增长趋势,请你预测我区今年的旅游营业收入 (结果保留一位小数) .22.如图1,在△ABC 中,E 、D 分别为AB 、AC 上的点,且ED //BC ,O 为DC 中点,连结EO 并延长交BC 的延长线于点F ,则有S 四边形EBCD =S △EBF .(1)如图2,在已知锐角∠AOB 内有一个定点P .过点P 任意作一条直线MN ,分别交射线OA 、OB 于点M 、N .将直线MN 绕着点P 旋转的过程中发现,当直线MN 满足某个条件时,△MON 的面积存在最小值.直接写出这个条件:_______________________. (2)如图3,在平面直角坐标系中,O 为坐标原点,点A 、B 、C 、P 的坐标分别为(6,0)、(6,3)、(92,92)、(4、2),过点P 的直线l 与四边形OABC 一组对边相交,将四边形OABC 分成两个四边形,求其中以点O 为顶点的四边形面积的最大值.xy图3CB图1图2OBAD OEFCBAPAOP北京市平谷区2008-2013年旅游 营业收入统计图北京市平谷区2012年旅游营业收入统计图五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)23.如图,在平面直角坐标系中,直线1=+y x 与抛物线y =ax 2+bx -3(a ≠0)交于A 、B 两点,点A 在x 轴上,点B 的纵坐标为5.点P 是直线AB 下方的抛物线上的一动点(不与点A 、B 重合),过点P 作x 轴的垂线交直线AB 于点C ,作PD ⊥AB 于点D . (1)求抛物线的解析式; (2)设点P 的横坐标为m .①用含m 的代数式表示线段PD 的长,并求出线段PD 长的最大值;②连结PB ,线段PC 把△PDB 分成两个三角形,是否存在适合的m 的值,使这两个三角形的面积比为1:2.若存在,直接写出m 的值;若不存在,请说明理由.24.(1)如图1,点E 、F 分别是正方形ABCD 的边BC 、CD 上的点,∠EAF =45°,连接EF , 则EF 、BE 、FD 之间的数量关系是:EF =BE +FD .连结BD ,交AE 、AF 于点M 、N ,且MN 、BM 、DN 满足222DN BM MN +=,请证明这个等量关系;(2)在△ABC 中, AB =AC ,点D 、E 分别为BC 边上的两点. ①如图2,当∠BAC =60°,∠DAE =30°时,BD 、DE 、EC 应满足的等量关系是__________________;②如图3,当∠BAC =α,(0°<α<90°),∠DAE =α21时,BD 、DE 、EC 应满足的等量关系是____________________.【参考:1cos sin 22=+αα】A B CD EF 图1B CDE 图2ACDE 图3AMN25.在平面直角坐标系中,已知抛物线y =-12x 2+bx +c (b ,c 为常数)的顶点为P ,等腰直角三角形ABC 的顶点A 的坐标为(0,–1),C 的坐标为(4,3),直角顶点B 在第四象限. (1)如图,若该抛物线过A ,B 两点,求b ,c 的值;(2)平移(1)中的抛物线,使顶点P 在直线AC 上滑动,且与直线AC 交于另一点Q .①点M 在直线AC 下方,且为平移前(1)中的抛物线上的点,当以M ,P ,Q 三点为顶点的三角形是以PQ 为腰的等腰直角三角形时,求点M 的坐标; ②取BC 的中点N ,连接NP ,BQ .当PQNP +BQ取最大值时,点Q 的坐标为________.平谷区2013-2014学年度第二学期初三统练参考答案初三数学一、选择题(本题共32分,每小题4分)1.B ; 2.A ; 3.C ; 4.B ; 5.D ; 6.A ; 7.D ; 8.C . 二、填空题(本题共16分,每小题4分)9.2)3(-n m ; 10. 答案不唯一,比如:222-+-=x x y ;11.32; 12.),),(,(02022n .三、解答题(本题共30分,每小题5分)13. (本小题满分5分) 证明:∵AC =DB ,∴AC+CD=DB+CD ,即AD=BC -----------------------------------------------------------------------1分 在△AED 和△BFC 中⎪⎩⎪⎨⎧=∠=∠∠=∠,,,BC AD F E B A ∴△AED ≌△BFC . --------------------------------------------------------------------------------------4分 ∴DE =CF . -------------------------------------------------------------------------------------------------5分14.(本小题满分5分)32433122333133=-⨯++=-++=+解: 15.(本小题满分5分)⎪⎩⎪⎨⎧+>+-≥-②①2274)1(2x x x x 解不等式①,得2-≥x ----------------------------------------------------------------------------1分 解不等式②,得3<x -----------------------------------------------------------------------------2分 ∴不等式组的解集为32<≤-x --------------------------------------------------------------4分 ∴不等式组的整数解为-2、-1、0、1、2. ----------------------------------------------------5分 16.(本小题满分5分) 解: x (x -2y )-(x +y )(x -y )=x 2-2xy -(x 2-y 2) --------------------------------------------------------------------------------------------2分 = x 2-2xy -x 2+y 2=-2xy +y 2 -----------------------------------------------------------------------------------------------3分 ∵2x -y =0,∴原式=-y (2x -y ) -------------------------------------------------------------------------------------------4分=0 -------------------------------------------------------------------------------------------------5分----------------------------------------------------------------4分----------------------------------------------------------------------------5分17.(本小题满分5分)解:设豆沙粽子每盒x 元,则大枣粽子每盒(x+5)元.-------------------------------------------1分 依题意得53002300+=-x x ------------------------------------------------------------------------2分 解得253021=-=x x , -----------------------------------------------------------------------------3分 经检验253021=-=x x ,是原方程的解,但301-=x 不符合题意,舍去当25=x 时,305=+x ---------------------------------------------------------------------------4分答:大枣粽子每盒30元,豆沙粽子每盒25元.--------------------------------------------------5分18.(本小题满分5分)解:(1)方程有两个不相等的实数根,∴⎩⎨⎧≠->-⨯--.03.0)3(24)3(2k k ---------------------1分解得,3833≠<k k 且. ------------------------------------------------------------------------2分 (2)k 的正整数值为1、2、4. -----------------------------------------------------------3分 如果k =1,原方程为22320--+=x x . 解得12=-x ,212=x ,不符合题意 舍去. 如果k =2,原方程为0232=+--x x , 解得2173217321--=+-=x x ,,不符合题意,舍去. 如果k =4,原方程为0232=+-x x ,解得2121==x x ,,符合题意. ----------------4分 ∴ k =4. --------------------------------------------------------------------------------------------5分19.(本小题满分5分)(1)证明:∵CE //AB ,∴∠DAF =∠ECF . ∵F 为AC 的中点,∴AF =CF . 在△DAF 和△ECF 中⎪⎩⎪⎨⎧∠=∠=∠=∠,,,CFE AFD CF AF ECF DAF ∴ △DAF ≌△ECF .∴ AD =CE . ------------------------------------------------------------------------------------2分 ∵CE //AB ,∴ 四边形ADCE 为平行四边形. --------------------------------------------------------------------3分(2)作FH ⊥DC 于点H .H ACEFD∵ 四边形ADCE 为平行四边形.∴ AE //DC ,DF = EF =22, ∴∠FDC =∠AED =45°.在Rt △DFH 中,∠DHF=90°,DF =22,∠FDC=45°, ∴ sin ∠FDC=22=DF FH ,得FH =2,tan ∠FDC=1=HDHF ,得DH =2. ----------------------------------------------------------------------4分 在Rt △CFH 中,∠FHC=90°,FH =2,∠FCD=30°,∴ FC =4. 由勾股定理,得HC =32.∴ DC=DH+HC=2+32. ------------------------------------------------------------------------5分 20. (本小题满分5分)解:(1)∵OA =OB ,∴∠OAB =∠B . --------------------------------------------------------------1分 ∵直线AC 为⊙O 的切线, ∴∠OAC =∠OAB +∠DAC =90°. ----------------------------------------------------------------------2分 ∵OB ⊥OC ,∴∠BOC =90°. ∴∠ODB +∠B =90°.∴∠DAC =∠ODB . ∵∠ODB =∠CDA ,∴∠DAC =∠CDA ,∴AC =CD . -----------------------------------------------------------------------3分 (2)在Rt △OAC 中,AC =CD =2,AO =5,OC =OD +DC =OD +2,--------------------------4分 根据勾股定理得:OC 2=AC 2+AO 2,即222)5(2)2(+=+OD ,解得:OD =1.----------------------------------------------------------------------------------------------5分21. (本小题满分5分)(1) 8.6% 和补充扇形统计图(图略) ------------------------------------------------------------2分 (2) 约24.4万元和补充条形统计图(图略) ----------------------------------------------------4分 (3) %8.94.24)4.248.26(≈÷-,4.2943.29%)8.91(8.26≈=+(万元)我区今年的旅游营业收入约29.4万元. ------------------------------------------------------5分22. (本小题满分5分) 解:(1)当直线MN 旋转到点P 是线段MN 的中点时, △MON 的面积最小.------------1分 (2)分两种情况:①如图3①过点P 的直线l 与四边形OABC 的一组对边 OC 、AB 分别交于点M 、N . 延长OC 、AB 交于点D ,易知AD = 6,S △OAD =18 .由(1)的结论知,当PM =PN 时,△MND 的面积最小,此时四边形OANM 的面积最大. 过点P 、M 分别作PP 1⊥OA ,MM 1⊥OA ,垂足分别为P 1、M 1. 由题意得M 1P 1=P 1A = 2,从而OM 1=MM 1= 2. 又P (4,2),B (6,3)∴P 1A =M 1P 1=O M 1=P 1P =2,M 1 M=OM=2,可证四边形MM 1P 1P 是正方形. ∴MN ∥OA ,∠MND =90°,NM =4,DN =4.求得S △MND =8 ----------------------------------2分 ∴.10818OANM =-=-=∆∆MND OAD S S S 四边形 ------------------------------------------------3分② 如图3②,过点P 的直线l 与四边形OABC 的另一组对边CB 、OA 分别交M 、N . 延长CB 交x 轴于T 点,由B 、C 的坐标可得直线BC 对应的函数关系式为 y =-x +9 . 则T 点的坐标为(9,0). ∴S △OCT = 12 ×9×92 =814 . -----------------------------------------------------------------------------4分由(1)的结论知:当PM =PN 时,△MNT 的面积最小,此时四边形OCMN 的面积最大.过点P 、M 点分别作PP 1⊥OA ,MM 1⊥OA ,垂足为P 1 ,M 1. 从而 NP 1 =P 1M 1,MM 1=2PP 1=4. ∴点M 的横坐标为5,点P (4、2),P 1M 1= NP 1 = 1,TN =6. ∴S △MNT = 12 ×6×4=12,S 四边形OCMN =S △OCT -S △MNT = 814 -12=334<10.综上所述:截得四边形面积的最大值为10. -----------------------------------------------------5分 五、解答题(本题共22分,第23题7分,第24题7分,第25题8分) 23.(1)在1=+y x 中,当y =0时,x =-1;当y =5时,x =4.A (-1,0)、B (4,5) ------------------ ------------------------------------------------------1分将A (-1,0)、B (4,5)分别代入y =ax 2+bx -3中,得30,1643 5.--=⎧⎨+-=⎩a b a b解得1=a ,2=-b .∴所求解析式为y =x 2-2x -3 ---------------------------------------------------------------------2分 (2)①设直线AB 交y 轴于点E ,求得E (0,1),∴OA =OE ,∠AEO =45°,∠ACP =∠AEO =45°, ∴2sin =∠=PD PC ACP PC . ---------------------------------------3分设2(,23)--P m m m ,则(,1)+C m m ,∴22(1)(23)34=+---=-++PC m m m m m . --------------------------------------------4分 ∴22223252(34)()2228=-++=--+PD m m m . ∴PD 的最大值为252. ----------------------------------------------------------------------5分 ②当m =0或m =3时,PC 把△PDB 分成两个三角形的面积比为1:2. -------------7分图3① 图3 ②M'A B C D E FMN 24. (1) 在正方形ABCD 中,AB =AD ,∠BAD =90°,∠ABM =∠ADN=45°.把△ABM 绕点A 逆时针旋转90°得到M AD '∆. 连结M N '.则,,AM AM BM M D =='',︒=∠='∠45ABM M AD ,BAM M DA ∠='∠. ∵∠EAF =45°,∴∠BAM +∠DAN =45°, ∠DAM′+∠DAF =45°, ︒=∠=∠45'MAN AN M .∴N AM '∆≌AMN ∆. ∴N M '=MN . 在N DM '∆中,︒=∠+∠=∠90''ADM ADN DN M ,222''DM DN N M +=∴222BM DN MN += -------------------------------------------------------------------3分(2)① 222EC EC BD BD DE +⋅+=; ------------------------------------------------------5分 ② 222cos 2EC EC BD BD DE +⋅⋅+=α ----------------------------------------------7分25.解:(1)由题意,得点B 的坐标为(4,–1). --------------------------------------------------1分∵抛物线过点A (0,–1),B (4,–1)两点,∴⎩⎪⎨⎪⎧-1=c ,-1=-12×42+4b +c . 解得⎩⎨⎧b =2,c =-1. ---------------------------------------------------------3分 (2)由(1)得 12212-+-=x x y . ①∵A 的坐标为(0,–1),C 的坐标为(4,3).∴直线AC 的解析式为:y =x -1.设平移前的抛物线的顶点为P 0,可得0P (2,1),且0P 在直线AC 上. ∴220=AP .-----------------------------------------------------------4分 ∵点P 在直线AC 上滑动,且与直线AC 交于另一点Q .∴PQ =AP 0=22. ---------------------------------------------------------------------------------------5分 ∵PQ 为直角边,M 到PQ 的距离为22(即为PQ 的长).由A (0,-1),B (4,-1),P 0(2,1)可知:△ABP 0为等腰直角三角形,且BP 0⊥AC ,BP 0=22.过点B 作直线l 1∥AC ,直线l 1与抛物线y =-12x 2+2x -1的交点即为符合条件的点M . ∴可设直线l 1的解析式为:y =x +b 1.又∵点B 的坐标为(4,–1),∴-1=4+b 1.解得b 1=-5.∴直线l 1的解析式为:y =x -5.解方程组⎩⎪⎨⎪⎧y =x -5,y =-12x 2+2x -1. 得:⎩⎨⎧x 1=4,y 1=-1; ⎩⎨⎧x 2=-2,y 2=-7. ∴M 1(4,-1),M 2(-2,-7). -----------------------------------------------------------------6分 ② 点Q 的坐标为).3134(,--------------------------------------------------------------------------------8分以上答案仅供参考,不同做法酌情给分!。
平谷区2015二模语文答案

市平谷区2015年初中毕业会考暨初三统练〔二〕语文试卷参考答案一、基础·运用〔共23分〕〔一〕选择 <共10分>1.<1>B <2>C <3> D 〔4〕B 2.A 〔共10分,每小题2分〕〔二〕补写〔2分〕3. 答案示例:八月中秋月儿圆〔2分,跟月亮有关的传统节日,意思对即可〕〔三〕填空〔共11分〕4.〔1〕锦帽貂裘〔2〕似曾相识燕归来〔3〕会当凌绝顶,一览众山小。
〔4〕示例一:举头望明月,低头思故乡。
示例二:海上生明月,天涯共此时。
〔共6分, 每空1分,有错字不得分。
〕5.①尸横如山,血流成河②时迁③智慧多谋④天竺国⑤孙悟空同猪八戒、沙和尚与三个妖精进行了数场大战,解救出唐僧〔共5分,每空1分,①⑤空意思对即可〕二、文言文阅读〔共12分〕6.B 〔2分〕7.〔1〕满一年〔2〕离开〔共2分,每小题1分〕8.〔1〕所有大臣、官吏、百姓,能够当面批评我过错的人,得上等奖赏。
〔大臣们和各级官员及百姓,能够当面指出我有错的地方的人,便能够得到上等的赏赐。
〕(2)地位已经很高但是擅弄职权的人,君主会厌恶他。
〔地位高而独揽大权的人,国君厌恶他。
〕〔共4分,每小题2分,意思对即可〕9.邹忌运用设喻的方法进谏齐王。
"老父"从反面讲道理〔或直言不讳〕,向孙叔敖进言。
答案示例一:欣赏邹忌的做法。
因为设喻的方法含蓄委婉又形象生动,让对方易于接受自己的观点或意见。
答案示例二:欣赏"老父"的做法。
因为直接陈述利害,可以产生"苦口良药"的劝说效果。
〔共4分,方法2分,选择1分,理由1分,意思近即可〕三、现代文阅读〔共35分〕〔一〕 <共13分>10. ①崇敬②养"鹤"③懊丧、恼怒④"鹤"毙命〔共4分,每个要点1分,意思对即可〕11. 〔1〕这句心理描写,体现了"我"的惊讶、失望和懊恼之情。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市平谷区2015年初中毕业会考暨初三统练(二)
下面各题均有四个选项,其中只有一个..是符合题意的. 1.根据北京市统计局2015年3月发布的数据,2015年3月北京市工业销售产值累计4006.4亿元,将4006.4用科学记数法表示应为
A .40.4006410⨯
B .34.006410⨯
C .44.006410⨯
D .240.06410⨯
2. 下列水平放置的四个几何体中,主视图与其它三个不相同的是
A .
B .
C .
D . 3.如图,数轴上有A ,B ,C ,D 四个点,其中表示互为倒数的点是
A .点A 与点
B B .点A 与点D
C .点B 与点D
D .点B 与点C
4.如图,将三角板的直角顶点放在直尺的一边上,若∠1=65°,则∠2的度数为
A. 10°.
B. 15°.
C. 20°.
D. 25°. 5.下列运算中,正确的是
A .22x x -=
B .45
2x x x ⋅=
C .22
x y y x ÷= D .()3
3
26x x -=-
6
那么这A. 23.5,24 B.24,24.5 C.24,24
D.24.5,24.5 7.如图,表示甲、乙两人以相同路线前往离学
校12
千米的地方参加植树活动.甲、乙两
人前往目的地所行驶的路程S (千米)随时间t (分)变化的函数图象,则每分钟乙比甲多行驶的路程是
A .0.5千米
B .1千米
C .1.5千米
D .2千米
8.用直尺和圆规作一个角等于已知角,如图,能得出A O B AOB '''∠=∠的依据是 A .(SAS ) B .(SSS ) C .(AAS ) D .(ASA )
9.如图,△ABC 的顶点A ,B ,C 均在⊙O 上,若∠ABC +∠AOC =90°,则∠AOC 的大小是 A .30°
B . 45°
C . 60°
D . 70°
10.在平行四边形ABCD 中,点P 从起点B 出发,沿BC ,CD 逆时针方向向终点D 匀速运动.设点P 所走过的路程为x ,则线段AP ,AD 与平行四边形的边所围成的图形面积为y ,
表示y 与x 的函数关系的图象大致如下图,则AB 边上的高是
A .3
B .4
C .5
D .6
二、填空题(本题共18分,每小题3分) 11.分式
2
a
a -有意义的条件是 . 12.把a ﹣4a
b 2分解因式的结果是 .
13.下表记录了一名球员在罚球线上投篮的结果.那么,这名球员下次投篮,投中的概率约是_________(精确到0.1).
则楼高CD 为 米.
15.如图,这个二次函数图象的表达式可能是 .(只写出一个).
16.在平面直角坐标系中,点A,B,C 的坐标分别为()1,0,()0,1,()1,0-.一个电动玩具
从坐标原点O 出发,第一次跳跃到点P 1,使得点P 1与点O 关于点A 成中心对称;第二次跳跃到点P 2,使得点P 2与点P 1关于点B 成中心对称;第三次跳跃到点P 3,使得点P 3与点P 2关于点C 成中心对称;第四次跳跃到点P 4,使得点P 4与点P 3关于点A 成中心对称;第五次跳跃到点P 5,使得点P 5与点P 4关于点B 成中心对称;.…照此规律重复下去.则点P 3的坐标为 ;点P n 在y 轴上,则点P n 的坐标为 .
三、解答题(本题共30分,每小题5分)
17.如图,点A,B,D,E 在同一直线上,AB =ED ,AC ∥EF ,∠C =∠F . 求证:AC =EF .
18
.计算:()1
012sin 60133π-⎛⎫
--︒++- ⎪⎝⎭
.
19.解不等式211132
x x
+--
≥,并把它的解集在数轴上表示出来.
20.已知实数m 满足2
230m m -+=,求()2
1(3)m m m m -+-+的值.
21.关于x 的一元二次方程2
(1)=0x x m --+有两个不相等的实数根. (1)求m 的取值范围;
(2)若m 为符合条件的最小整数,求此方程的根.
22.列方程或方程组解应用题:
为开阔学生的视野在社会大课堂活动中,某校组织初三年级学生参观科技馆,原计划租
用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满.求该校初三年级有学生多少人?原计划租用多少辆45座客车?
四、解答题(本题共20分,每小题5分) 23.如图,已知点E ,F 分别是□ABCD 的边BC ,AD 上的中点,且∠BAC =90°. (1)求证:四边形AECF 是菱形; (2)若∠B =30°,BC =10,求菱形AECF 面积.
B
24.2015年是中国抗日战争胜利70周年暨世界反法西斯战争胜利70周年.某校为纪念中国抗日战争胜利70周年,对全校学生进行了“抗日战争知多少”知识测验.然后随机抽取了部分学生的成绩,整理并制作如图所示的图表.
请你根据图表中提供的信息,解答下列问题:
(1)在频数分布表中:
m=________,n=
(2)补全频数分布直方图;
(3)如果某校有2000名学生,比赛成绩80分以上(含80分)为优秀,那么你估计此次测验成绩的优秀人数大约是__________人.
25.如图,已知,⊙O为△ABC的外接圆,BC为直径,点E
在AB边上,过点E作EF⊥BC,延长FE交⊙O的切线AG于
点G.
(1)求证:GA=GE.
(2)若AC=6,AB=8,BE=3,求线段OE的长.
26.如图1,在□ABCD中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若AB=6,3
AF EF
=,求DG的长.
小米的发现,过点E作EH AB
∥交BG于点H(如图2),经过推理和计算能够使问题得到解决.则DG= .
如图3,四边形ABCD中,AD∥BC,点E是射线DM上的一点,连接BE和AC相交于点F,若BC aAD
=,CD bCE
=,求
BF
EF
的值(用含,a b的代数式表示).
图1 图2 图3
五、解答题(本题共22分,第27题7分,第28题8分,第29题7分) 27.如图,在平面直角坐标系中,点A(5,0),B
线段BC上一个动点,点P的坐标是(0,3)
x 轴交于点D.
(1)求点C的坐标及b的值;
(2)求k的取值范围;
(3)当
k为取值范围内的最大整数时,过点B
轴,交PQ于点E,若抛物线y=ax2﹣5ax(a≠0)
在四边形ABED的内部,求a的取值范围.
28.对某一种四边形给出如下定义:
对角四边形”.
(1)已知:如图1,四边形ABCD是“等对角四边形”,∠A≠∠C,∠A=70°,∠B=80°.则∠C= 度,∠D= 度.
(2)在探究“等对角四边形”性质时:
小红画了一个“等对角四边形ABCD”(如图2),其中∠ABC=∠ADC,AB=AD,此时她发现CB=CD成立.请你证明此结论;
(3)已知:在“等对角四边形ABCD”中,∠DAB=60°,∠ABC=90°,AB=5,AD=4.求对角线AC的长.
29.定义:如图1,平面上两条直线AB、CD相交于点O,对于平面内任意一点M,点M 到直线AB、CD的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”为(0,0)点有1个,即点O.
(1)“距离坐标”为(1,0)点有个;
图1
图2
图1
O
D
C
B
A
图2 图3
(2)如图2,若点M在过点O且与直线CD垂直的直线l上时,点M的“距离坐标”为(p,q),且∠BOD=120°.请画出图形,并直接写出p,q的关系式;
(3)如图3,点M的“距离坐标”为(1,且∠AOB=30°,求OM的长.。
