九上11-14.20
2019-2020学年第一学期九年级物理期中考试试卷(含答案)

2019-2020学年第一学期期中考试试卷九年级物理学科第一部分(共24分)一、选择题(本题共12小题,每小题2分,共24分.每小题只有一个选项正确)1.如图所示器具中,属于省力杠杆的是()2.关于力做功,下列说法中正确的是()A.用力推一辆汽车,汽车静止不动,推力在这个过程中对汽车做了功B.提着水桶在路面上水平向前移动一段路程,手的拉力对水桶做了功C.用力踢出去的足球在空中向前运动的过程中,脚对球的力对球做了功D.用手从地面提起水桶,手的拉力对水桶做了功3.为了纪念物理学家在能量转化中发现守恒思想的重大贡献,用其名字来命名功和能单位的是()A.牛顿B.焦耳C.安培D.伏特4.下列情景中,属于内能转化为机械能的是()A.甲和丙B.乙和丁C.乙和丙D.丙和丁5.如右图所示电路中,当开关1S,2S都闭合后,则()A.1L、2L都不发光B.1L、2L都发光C.1L发光、2L不发光D.1L不发光、2L发光6.关于温度、内能和热量,下列说法正确的是()A.物体的温度升高,它含的热量增加B.物体的内能增加,一定要吸收热量C.独轮车A.笤帚D.钓鱼杆B.筷子A B C D 第7题图C.物体的内能越多,放热一定越多D.物体的温度升高,它的内能就增加7.下列四个电路中与右边电路元件实物图对应的是()8.下列表述中,符合生活中实际的是()A.同学从地上捡起一本物理课本做功约为0.2JB. 家中空调工作时电流约为1AC.成人骑车时的功率大约是600WD. 30V的电压对人来说是安全的9.如图所示,AC>BC,在相同时间内把同一物体分别沿斜面AC、BC匀速推上顶端,推力分别为F1、F2,功率分别为P1、P2,在不考虑摩擦的情况下( )A. F1<F2,P1=P2B. F1>F2,P1>P2C. F1=F2,P1=P2D. F1<F2,P1<P210.用两个相同的电热器给质量同为2kg的物质甲和水加热,它们的温度随时间的变化关系如图所示,据此判断甲物质10min吸收的热量为()[水的比热容c=4.2×103 J/(kg·℃)].A.5.04×105J B.2.52×105JC.4.2×105J D.条件不足,不能计算11.如图所示,用相同的滑轮组装成甲、乙滑轮组,分别将同一重物在相等的时间内提升相同的高度,不计绳重和摩擦,则()A.甲、乙的拉力之比是2:3B.甲、乙绳的自由端速度之比是1:1C.甲、乙拉力的功率之比是3:2D.甲、乙的机械效率之比是1:112.一名游客蹦极时下落过程的v﹣t图象(忽略空气阻力)如图所示。
新人教版九年级上册第11-14单元测试题附答案

新人教版九年级上册第11-14单元测试题附答案新人教版九年级第11-14单元测试题附答案Test for Units 11~14(时间:100分钟,满分:100分)Ⅰ. 单项选择。
(每小题1分,共15分)( )1. —Dad,smoking is harmful ________ your health. Please give it up.—OK,my son. I will try.A. withB. forC. inD. to( )2. Mum,this is ________ friend.________ name is Emma.A. your;MyB. my;HerC. you;HisD. she;Your( )3. —Linda,can you sing for the school concert?—Sorry,I can't.________ I can play the piano.A. AndB. OrC. ButD. So( )4. She felt ________ about making such a stupid mistake.A. embarrassedB. embarrassingC. excitedD. exciting( )5. ________ the environment,they have done many thingsin the past two years.A. To protectB. ProtectC. ProtectingD. Protected( )6. How much does the train ticket________ from Shanghai to Beijing?A. costB. takeC. spendD. pay( )7. —Do you know if Qian Xuesen is ________ now?—Yes. It's a pity that he has been dead for over six years.A. liveB. aliveC. livingD. lively( )8. You used to wear glasses,________?A. didn't youB. don't youC. did youD. do you( )9. The pet dog ________ when I am away on vacation,Nancy.A. must be looked after wellB. must look after wellC. must be looking after wellD. must have looked after well( )10. —We had to ________ our travel plans because of the bad weather.—Bad luck.A. disappearB. continueC. examineD. cancel( )11. Be sure to let Jason know the notice as soon as he ________.A. will arriveB. is arrivingC. arrivesD. arrived( )12. The king ________ some ministers to discuss an important thing.A. set outB. called inC. brought backD. left out( )13. It ________ be John's. It's too big for him.A. couldB. mightC. mustn'tD. can't( )14. John wanted to know________.A. when the meeting would beginB. when would the meeting beginC. when will the meeting beginD. when the meeting will begin( )15. —Do you mind if I sit here?—________.It is for Miss Wang.A. Not at allB. Never mindC. Better notD. Of course notⅡ. 完形填空。
2023-2024学年人教版九年级物理上册《第十四章内能的利用》单元测试卷及答案
2023-2024学年人教版九年级物理上册《第十四章内能的利用》单元测试卷及答案一.选择题1.下列关于烧开水、泡茶、喝茶的物理知识不正确的是()A.从冰箱中拿出的茶叶放置一段时间会变得“湿润”和揭开杯盖茶杯上方冒“白气”的实质不一样B.用沸水才能很快泡出茶香、茶色、茶味,这是因为温度越高,扩散现象越明显C.用沸水泡了茶的玻璃杯“烫手”是通过热传递改变物体的内能D.用电热水壶烧开水,可说明能量既可以发生转化也可以发生转移2.汽油机的四个冲程中,哪个冲程存在着化学能转化为内能的过程()A.B.C.D.3.四冲程汽油机的工作简图如图所示,其中表示做功冲程的是()A.B.C.D.4.如图是生活中常用的高压锅。
当高压锅内的气压达到一定值时,限气阀会被高压蒸汽顶起。
这一过程高压锅内气体内能会发生变化,下列说法正确的是()A.限气阀被顶起的过程与汽油机的做功冲程发生的能量转化相同B.高压锅喷嘴处的“白气”是水蒸气汽化形成的C.用明火加热高压锅,是通过做功改变内能D.高压锅是利用大气压来工作的5.水壶内的水沸腾时,壶盖被水蒸气顶起,此过程中能量转化关系与内燃机工作的哪个冲程相同()A.吸气冲程B.压缩冲程C.做功冲程D.排气冲程6.下列选项可能符合汽车热机能量流向的是()A.B.C.D.7.如图甲、乙分别是“探究不同物质吸热升温的现象”和“比较质量相等的不同燃料燃烧时放出的热量”的两组实验装置。
关于这两个实验,下列要求正确的是()A.所用燃料的质量都必须相等B.都要用计时器来测量加热时间C.烧杯中被加热物体的质量都必须相等D.都要测量燃料完全燃烧后被加热物质的温度8.关于温度、内能和热量的说法中,正确的是()A.物体吸收热量时内能增加,温度一定升高B.在汽油机的压缩冲程中,机械能转化为内能C.用锯条锯木板,锯条从木板吸收了热量,锯条的温度升高D.人们不敢大口喝热气腾腾的汤,是因为汤含有的热量较多9.今年,我国发射的“天舟四号”货运飞船与“天和号”核心舱在太空成功对接。
北京市东城区2022-2023学年九年级上学期数学期末试卷及解析

北京市东城区2022-2023学年九年级上学期数学期末试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.若关于x的一元二次方程220-+=有一个根为0,则m的值为()x x mA.2B.1C.0D.1-2.下列图形中是中心对称图形的是()A.正方形B.等边三角形C.直角三角形D.正五边形3.关于二次函数2=-+的最大值或最小值,下列说法正确的是()y x2(4)6A.有最大值4B.有最小值4C.有最大值6D.有最小值6 4.一只不透明的袋子中装有3个黑球和2个白球,这些除颜色外无其他差别,从中任意摸出3个球,下列事件是确定事件的为()A.至少有1个球是黑球B.至少有1个球是白球C.至少有2个球是黑球D.至少有2个球是白球5.某厂家2020年1~5月份的口罩产量统计如图所示.设从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程()A.180(1﹣x)2=461B.180(1+x)2=461C.368(1﹣x)2=442D.368(1+x)2=4426.如图,在O中,AB是直径,弦AC的长为5,点D在圆上,且30∠=︒,则OADC的半径为()7.抖空竹在我国有着悠久的历史,是国家级的非物质文化遗产之一.如图,AC ,BD 分别与⊙O 切于点C ,D ,延长AC ,BD 交于点P .若120P ∠=︒,⊙O 的半径为6cm ,则图中CD 的长为( )A .π cmB .2π cmC .3π cmD .4π cm8.如图,正方形ABCD 和O 的周长之和为20cm ,设圆的半径为cm x ,正方形的边长为cm y ,阴影部分的面积为2cm S .当x 在一定范围内变化时,y 和S 都随x 的变化而变化,则y 与x ,S 与x 满足的函数关系分别是( )A .一次函数关系,一次函数关系B .一次函数关系,二次函数关系C .二次函数关系,二次函数关系D .二次函数关系,一次函数关系二、填空题9.在平面直角坐标系xOy 中,抛物线245y x x =-+与y 轴交于点C ,则点C 的坐标为_________.10.把抛物线2112y x =+向左平移1个单位长度,再向下平移3个单位长度,得到的抛物线的解析式为_______.11.请写出一个常数c 的值,使得关于x 的方程220x x c ++=有两个不相等的实数根,则c 的值可以是____________.12.2022年3月12日是我国第44个植树节,某林业部门为了考察某种幼树在一定条件下的移植成活率,在同等条件下,对这种幼树进行大量移植,并统计成活情况,下表是这种幼树移植过程中的一组统计数据:估计该种幼树在此条件下移植成活的概率是______.(结果精确到0.1)13.以⊙ABCD 对角线的交点O 为原点,平行于BC 边的直线为x 轴,建立如图所示的平面直角坐标系.若A 点坐标为(﹣2,1),则C 点坐标为_____.14.如图,在⊙O 中,AB 切⊙O 于点A ,连接OB 交⊙O 于点C ,过点A 作AD ⊙OB 交⊙O 于点D ,连接CD .若⊙B =50°,则⊙OCD 的度数等于___________.15.《九章算术》是我国古代数学成就的杰出代表作,其中《方田》章计算弧田面积所用的经验公式是:弧田面积12=(弦×失+失²).弧田(图中阴影部分)由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.现有圆心角为120︒,半径等于4米的弧田,按照上述公式计算出弧田的面积约为______ 米2. 1.73)16.我们给出如下定义:在平面内,点到图形的距离是指这个点到图形上所有点的距离的最小值.在平面内有一个矩形,4,2ABCD AB AD ==,中心为O ,在矩形外有一点P ,3OP =,当矩形绕着点O 旋转时,则点P 到矩形的距离d 的取值范围为__________.三、解答题17.下面是小美设计的“过圆上一点作圆的切线”的尺规作图过程.已知:点A 在O 上.求作:O 的切线AB .作法: ⊙作射线OA ;⊙以点A 为圆心,适当长为半径作弧,交射线OA 于点C 和点D ;⊙分别以点C ,D 为圆心,大于12CD 长为半径作弧,两弧交点B ; ⊙作直线AB .则直线AB 即为所求作的O 的切线.根据小美设计的尺规作图过程,解决下面的问题:(1)使用直尺和圆规,补全图形;(保留作图痕迹)(2)完成下面的证明.证明:连接BC ,BD .由作图可知,AC AD =,BC = .⊙BA OA .⊙ 点A 在O 上,⊙直线AB 是O 的切线( ) (填写推理依据) .18.如图,AB 是O 的直径,弦CD AB ⊥于点E ,2CD OE =,若4AB =,求CD 的长.19.下面是小聪同学用配方法解方程:2240x x p --=()0p >的过程,请仔细阅读后,解答下面的问题.2240x x p --=解:移项,得:224x x p -=.⊙二次项系数化为1,得:222p x x -=.⊙ 配方,得2212p x x -+=.⊙ 即2(1)2p x -=. ⊙0p >,⊙1x -=⊙⊙11x =11x =⊙ (1)第⊙步二次项系数化为1的依据是什么?(2)整个解答过程是否正确?若不正确,说出从第几步开始出现的错误,并直接写出此方程的解.20.如图,已知抛物线L :y =x 2+bx +c 经过点A (0,﹣5),B (5,0).(1)求b ,c 的值;(2)连结AB ,交抛物线L 的对称轴于点M .求点M 的坐标;21.如图,在边长均为1个单位长度的小正方形组成的网格中,点A ,B ,O 均为格点(每个小正方形的顶点叫做格点).(1)作点A 关于点O 的对称点1A ;(2)连接1A B ,将线段1A B 绕点1A 顺时针旋转90︒得到线段11A B ,点B 的对应点为1B ,画出旋转后的线段11A B ;(3)连接1AB ,1BB ,求出1ABB 的面积(直接写出结果即可).22.2022年3月23日,“天宫课堂”第二课在中国空间站开讲,神舟十三号飞行乘组航天员翟志刚、王亚平、叶光富讲了又一堂精彩的太空科普课.这场充满奇思妙想的太空授课,让科学的种子在亿万青少年的心里生根发芽.小明和小亮对航天知识产生了极大兴趣,他们在中国载人航天网站了解到,航天知识分为“梦圆天路”、“飞天英雄”、“探秘太空”、“巡天飞船”等模块.他们决定先从“梦圆天路”、“飞天英雄”、“探秘太空”三个模块中随机选择一个进行学习,分别设这三个模块为A ,B ,C ,用画树状图或列表的方法求出小明和小亮选择相同模块的概率.23.已知关于x 的一元二次方程()22120x m x m +++-=.(1)求证:无论m 取何值,此方程总有两个不相等的实数根;(2)当该方程的判别式的值最小时,写出m 的值,并求出此时方程的解.24.掷实心球是中考体育考试项目之一,实心球投掷后的运动轨迹可以看作是抛物线的一部分,建立如图所示的平面直角坐标系,从投掷到着陆的过程中,实心球的竖直高度y (单位:m)与水平距离x (单位:m)近似满足函数关系2()y a x h k =-+(0)a <.某位同学进行了两次投掷.(1)第一次投掷时,实心球的水平距离x 与竖直高度y 的几组数据如下:根据上述数据,直接写出实心球竖直高度的最大值,并求出满足的函数关系2()y a x h k =-+(0)a <; (2)第二次投掷时,实心球的竖直高度y 与水平距离x 近似满足函数关系20.09( 3.8) 2.97y x =--+.记实心球第一次着地点到原点的距离为1d ,第二次着地点到原点的距离为2d ,则1d _____ 2d (填“>”“=”或“<”).25.如图,点C 在以AB 为直径的O 上,CD 平分ACB ∠交O 于点D ,交AB 于点E ,过点D 作DF AB 交CO 的延长线于点F .(1)求证:直线DF 是O 的切线;(2)若30A ∠=°,AC =DF 的长.26.已知二次函数()2430y ax ax a =-+≠.(1)求该二次函数的图象与y 轴交点的坐标及对称轴.(2)已知点()()()()12343,1,12,,,,,y y y y --都在该二次函数图象上,⊙请判断1y 与2y 的大小关系:1y 2y (用“>”“=”“<”填空);⊙若1y ,2y ,3y ,4y 四个函数值中有且只有一个小于零,求a 的取值范围.27.如图,ABC 是等腰直角三角形,90ACB AC BC ∠=︒=,,D 为AC 延长线上一点,连接BD ,将线段BD 绕点D 逆时针旋转90︒得到线段DE ,过点E 作EF AC ⊥于点F ,连接AE .(1)依题意补全图形;(2)比较AF 与CD 的大小,并证明;(3)连接BE ,G 为BE 的中点,连接CG ,用等式表示线段CD CG BC ,,之间的数量关系,并证明.28.在平面直角坐标系xOy 中,我们给出如下定义:将图形M 绕直线3x =上某一点P 顺时针旋转90︒,再关于直线3x =对称,得到图形N ,我们称图形N 为图形M 关于点P 的二次关联图形.已知点()0,1A .(1)若点P 的坐标是()3,0,直接写出点A 关于点P 的二次关联图形的坐标________;(2)若点A 关于点P 的二次关联图形与点A 重合,求点P 的坐标(直接写出结果即可);(3)已知O 的半径为1,点A 关于点P 的二次关联图形在O 上且不与点A 重合. 若线段1AB =,其关于点P 的二次关联图形上的任意一点都在O 及其内部,求此时 P 点坐标及点B 的纵坐标B y 的取值范围.参考答案:1.C【分析】将0x =代入方程220x x m -+=,即可求解.【详解】解:⊙关于x 的一元二次方程220x x m -+=有一个根为0,⊙0m =,故选:C .【点睛】本题考查了一元二次方程的解的定义,将0x =代入方程是解题的关键.2.A【分析】根据中心对称图形的概念求解即可.【详解】解:A 、是中心对称图形,本选项正确;B 、不是中心对称图形,本选项错误;C 、不是中心对称图形,本选项错误;D 、不是中心对称图形,本选项错误.故选A .【点睛】本题考查了中心对称图形的概念.中心对称图形是要寻找对称中心,绕对称中心旋转180度后与原图形重合.3.D【分析】根据二次函数22(4)6y x =-+的解析式,得到a 的值为2,图象开口向上,函数有最小值,根据定点坐标(4,6),即可得出函数的最小值.【详解】解:⊙在二次函数22(4)6y x =-+中,a =2>0,顶点坐标为(4,6),⊙函数有最小值为6.故选:D .【点睛】本题主要考查了二次函数的最值问题,关键是根据二次函数的解析式确定a 的符号和根据顶点坐标求出最值.4.A【分析】列出摸出的三个球的颜色的所有可能情况即可.【详解】根据题意可得,摸出的三个球的颜色可能为:两个白球,一个黑球;一个白球,两个黑球;三个黑球,则可知摸出的三个球中,至少有一个黑球,故必然事件是至少有一个黑球,故选:A.【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.5.B【分析】本题为增长率问题,一般用增长后的量=增长前的量×(1+增长率),如果设这个增长率为x,根据“2月份的180万只,4月份的产量将达到461万只”,即可得出方程.【详解】解:从2月份到4月份,该厂家口罩产量的平均月增长率为x,根据题意可得方程:180(1+x)2=461,故选:B.【点睛】本题考查了一元二次方程的实际应用,理解题意是解题关键.6.B【分析】连接BC,由题意易得30ABC ADC∠=∠=︒,在Rt ACB中解三角形求解.【详解】连接BC,ABC ADC∴∠=∠=︒30在O中,AB是直径,ACB∴∠=︒,90在Rt ACB中,∠=︒,3090ACBAC=ABC∠=︒,5==AB AC210OA=5故选:B.【点睛】本题主要考查圆周角定理及含30︒直角三角形的性质;熟练掌握圆周角定理及含30︒直角三角形的性质是解题的关键.7.B【分析】连接OC 、OD ,利用切线的性质得到90OCP ODP ∠=∠=︒,根据四边形的内角和求得60COD ∠=︒,再利用弧长公式求得答案.【详解】连接OC 、OD ,,AC BD 分别与O 相切于点C ,D ,⊙90OCP ODP ∠=∠=︒,120360P OCP ODP P COD ∠=︒∠+∠+∠+∠=︒,,⊙60COD ∠=︒,CD ∴的长6062(cm)180ππ⨯==, 故选:B【点睛】此题考查圆的切线的性质定理,四边形的内角和,弧长的计算公式,熟记圆的切线的性质定理及弧长的计算公式是解题的关键.8.B 【分析】根据圆的周长公式和正方形的周长公式先得到152y x π=-+,再根据S S S =-阴影正方形圆得到2215254S x x πππ⎛⎫=--+ ⎪⎝⎭,由此即可得到答案. 【详解】解:⊙正方形ABCD 和O 的周长之和为20cm ,圆的半径为cm x ,正方形的边长为cm y ,⊙4220y x π+=, ⊙152y x π=-+, ⊙S S S =-阴影正方形圆, ⊙22222211552524S y x x x x x ππππππ⎛⎫⎛⎫=-=-+-=--+ ⎪ ⎪⎝⎭⎝⎭, ⊙y 与x ,S 与x 满足的函数关系分别是一次函数关系,二次函数关系,故选B .【点睛】本题考查二次函数与一次函数的识别、正方形的周长与面积公式,理清题中的数量关系,熟练掌握二次函数与一次函数的解析式是解答的关键.9.(0,5)【分析】令0x =,代入抛物线245y x x =-+,得到点C 的纵坐标,即可得解.【详解】解:依题意,令0x =,得到5y =,故抛物线245y x x =-+与y 轴交于点C 的坐标为(0,5),故答案为 :(0,5)【点睛】本题考查了二次函数与y 轴交点问题,令0x =,即可得到抛物线与y 轴交点的纵坐标.10.21(1)22y x =+- 【分析】直接根据“上加下减,左加右减”进行计算即可. 【详解】解:抛物线2112y x =+,向左平移1个单位长度,再向下平移3个单位长度, 得到()211132y x =++- 即()21122y x =+- 故答案为:()21122y x =+-.【点睛】本题主要考查函数图像的平移;熟记函数图像的平移方式“上加下减,左加右减”是解题的关键.11.0,(答案不唯一,1c <即可).【分析】利用一元二次方程根的判别式求出c 的取值范围即可得到答案.【详解】解:因为方程220x x c ++=有两个不相等的实数根,所以2Δ240c =->解得1c <故答案为:0,(答案不唯一,1c <即可)【点睛】本题主要考查了一元二次方程根的判别式;熟知一元二次方程根的判别式是解题的关键.12.0.9【分析】大量重复试验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率.【详解】⊙幼树移植数20000时,幼树移植成活的频率是0.902,⊙估计该种幼树在此条件下移植成活的概率为0.902,精确到0.1,即为0.9,故答案为:0.9.【点睛】本题考查了用大量试验得到的频率可以估计事件的概率,大量反复试验下频率稳定值即概率.13.(2,﹣1)【分析】根据平行四边形是中心对称图形,再根据⊙ABCD对角线的交点O为原点和点A的坐标,即可得到点C的坐标.【详解】解:⊙⊙ABCD对角线的交点O为原点,A点坐标为(﹣2,1),⊙点C的坐标为(2,﹣1),故答案为:(2,﹣1).【点睛】此题考查中心对称图形的顶点在坐标系中的表示.14.20°##20度【分析】连接OA,如图,根据切线的性质得到⊙OAB=90°,则利用互余可计算出⊙AOB=40°,再利用圆周角定理得到⊙ADC=20°,然后根据平行线的性质得到⊙OCD的度数.【详解】解:连接OA,如图,⊙AB切⊙O于点A,⊙OA⊙AB,⊙⊙OAB=90°,⊙⊙B=50°,⊙⊙AOB=90°-50°=40°,⊙⊙ADC =12⊙AOB =20°, ⊙AD ⊙OB ,⊙⊙OCD =⊙ADC =20°.故答案为:20°.【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理. 15.8.92【分析】由题意可知OC AB ⊥于D ,交圆弧于C ,由题意得4AO =米,120AOB ∠=︒解得122OD OA ==米,再求出CD ,最后由勾股定理得到AD ,由垂径定理求出AB 即可得出结果.【详解】解:如图,由题意可知,120AOB ∠=︒,AB CD ⊥,4OA OB ==(米),30,90DAO ADO ∴∠=︒∠=︒,12AD BD AB == 122OD OA ∴==(米) 422CD OC OD ∴=-=-=(米)AD ∴=2AB AD ∴==∴弧田面积()212AB CD CD =⨯+ ()21222=⨯+2=8.92≈(平方米)故答案为:8.92【点睛】本题考查了勾股定理以及垂径定理的应用;熟练掌握垂径定理是解答本题的关键.16.32d ≤【分析】根据题意分别求出当OP 过AB 的中点E 时,此时点P 与矩形ABCD 上所有点的连线中,d PE =;当OP 过顶点A 时,此时点P 与矩形ABCD 上所有点的连线中,d PA =;当OP 过顶点AD 边中点F 时,此时点P 与矩形ABCD 上所有点的连线中,d PF =,即可求解.【详解】解:如图,当OP 过AB 的中点E 时,此时点P 与矩形ABCD 上所有点的连线中,d PE =,112OE AD ==,⊙2d PE OP OE ==-=;如图,当OP 过顶点A 时,此时点P 与矩形ABCD 上所有点的连线中,d PA =,矩形,4,2ABCD AB AD ==,中心为O ,⊙2,90BC AD B ==∠=︒,⊙AC ==,⊙12OA AC ==⊙3d AP OP OA ==-=如图,当OP 过顶点AD 边中点F 时,此时点P 与矩形ABCD 上所有点的连线中,d PF =,122OF AB ==,⊙1d PF OP OF ==-=;综上所述,点P 到矩形的距离d 的取值范围为32d ≤.故答案为:32d ≤≤【点睛】本题考查矩形的性质,旋转的性质,根据题意得出临界点时点d 的值是解题的关键.17.(1)见解析;(2)BD ;⊥;经过半径的外端并且垂直于这条半径的直线是圆的切线.【分析】(1)依据题意,按步骤正确尺规作图即可;(2)结合作图,完成证明过程即可.【详解】(1)补全图形如图所示,(2)证明:连接BC ,BD .由作图可知,AC AD =,BC BD =.⊙BA OA ⊥,⊙ 点A 在O 上,⊙直线AB 是O 的切线(经过半径的外端并且垂直于这条半径的直线是圆的切线, 故答案为:BD ;⊥;经过半径的外端并且垂直于这条半径的直线是圆的切线【点睛】本题考查了尺规作图能力和切线的证明;能够按要求规范作图是解题的关键.18.CD =【分析】由垂径定理得到CE DE =,推出CE OE =,在Rt COE △中,利用勾股定理即可求解.【详解】解:如图,连接OC .⊙AB 是O 的直径,弦CD AB ⊥于点E ,⊙CE DE =.又⊙2CD OE =,⊙CE OE =.⊙4AB =,⊙2OC =.在Rt COE △中,222CE OE OC +=, ⊙CE ⊙CD =【点睛】本题考查了垂径定理、勾股定理,掌握垂直于弦的直径平分这条弦是解题的关键.19.(1)等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等(2)不正确,解答从第⊙步开始出错,1x =2x =【分析】(1)根据等式的性质2即可写出依据;(2)根据配方法解一元二次方程的步骤即可求解.【详解】(1)等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等;(2)不正确,解答从第⊙步开始出错,正确的步骤为: 配方,得22112p x x -+=+.⊙ 即22(1)2p x +-=⊙0p >,⊙1x -=⊙⊙1x =2x =.⊙此方程的解为1x =2x = 【点睛】本题考查等式的性质和解一元二次方程,解题的关键是读懂材料,明确每一步的做题依据.20.(1)4b =-,5c =-;(2)交点M 的坐标为(2,-3).【分析】(1)将点A 、点B 坐标代入函数解析式,求解方程组即可;(2)设直线AB 的解析式为:()0y kx b k =+≠,将点A 、点B 坐标代入函数解析式求解确定解析式,然后根据(1)中确定二次函数解析式,求出其对称轴,求两条之间交点即可确定点M 的坐标.【详解】解:(1)将点A 、点B 坐标代入函数解析式可得:50255c b c-=⎧⎨=++⎩, 解得:45b c =-⎧⎨=-⎩, ∴4b =-,5c =-;(2)设直线AB 的解析式为:()0y kx b k =+≠,将点A 、点B 坐标代入函数解析式可得:505b k b -=⎧⎨=+⎩, 解得:15k b =⎧⎨=-⎩, ∴一次函数解析式为:5y x =-,由(1)得二次函数解析式为:245y x x =--, 对称轴为:22b x a=-=, 直线5y x =-与2x =的交点为M ,∴当2x =时,=3y -,∴交点M的坐标为(2,-3).【点睛】题目主要考查利用待定系数法确定二次函数与一次函数解析式,两条直线的交点问题,二次函数的基本性质,理解题意,熟练运用待定系数法确定解析式是解题关键.21.(1)见解析(2)见解析(3)8【分析】(1)根据网格的特点作出点A关于点O的对称点1A;A B,即可求解;(2)根据题意,画出旋转后的线段11(3)根据网格的特点,以及三角形面积公式求得面积即可求解.【详解】(1)解:如图所示,点1A即为所求;A B即为所求;(2)解:如图所示,线段11(3)解:如图所示,118282ABB S =⨯⨯=. 【点睛】本题考查了画中心对称图形,画旋转图形,网格中求三角形面积,数形结合是解题的关键.22.13【分析】先画出树状图,从而可得所有等可能的结果,再找出小明和小亮选择相同模块的结果,然后利用概率公式计算即可得.【详解】解:由题意,画树状图如下:由图可知,所有等可能的结果共有9种,其中,小明和小亮选择相同模块的结果有3种. 则小明和小亮选择相同模块的概率为3193P ==, 答:小明和小亮选择相同模块的概率为13. 【点睛】本题考查了利用列举法求概率,正确画出树状图是解题关键.23.(1)见解析(2)0m =,122,1x x =-=【分析】(1)判断判别式的符号,即可得证;(2)求出判别式的值最小时的m 的值,再解一元二次方程即可.【详解】(1)证明:⊙22(21)4(2)49m m m ∆=+-⨯-=+,⊙20m ≥,⊙2Δ490m =+>.⊙无论m 取何值,方程总有两个不相等的实数根.(2)解:由题意可知,当0m =时,249m ∆=+的值最小.将0m =代入2(21)20x m x m +++-=,得220x x +-=解得:122,1x x =-=.【点睛】本题考查一元二次方程的判别式与根的个数的关系,以及解一元二次方程.熟练掌握判别式与根的个数的关系,以及解一元二次方程的方法,是解题的关键.24.(1)2.95,20.08(4) 2.95y x =--+(2)>【分析】(1)先根据表格中的数据找到顶点坐标,即可得出实心球竖直高度的最大值,并利用待定系数法得到抛物线解析式;(2)设着陆点的纵坐标为0,分别代入第一次和第二次的函数关系式,求出着陆点的横坐标即为 1d 和2d ,然后进行比较即可.【详解】(1)解:由表格数据可知,抛物线的顶点坐标为(42.95),,所以实心球竖直高度的最大值为2.95,设抛物线的解析式为:2(4) 2.95y a x =-+,将点(01.67),代入,得1.6716 2.95a =+,解得0.08a =-,⊙抛物线的解析式为:20.08(4) 2.95y x =--+;(2)解:第一次抛物线解析式为20.08(4) 2.95y x =--+,令0y =,得到4x =(负值舍去), 第二次抛物线的解析式为20.09( 3.8) 2.97y x =--+,令0y =,得到 3.8x =+(负值舍去) 2954 3.88+ 12d d ∴>,故答案为:>【点睛】本题主要考查了二次函数的应用,待定系数法求函数关系式,解题的关键是读懂题意,列出函数关系式.25.(1)见解析(2)FD =【分析】(1)连接OD ,证明DF OD AB OD ⊥⊥,,可得结论;(2)再Rt ACB △中,30A ∠=︒,AC =4AB =,2OD =,再在Rt ODF △中,由60F ∠=︒,继而求得FD ;【详解】(1)证明:连接OD .⊙ AB 是O 的直径,CD 平分ACB ∠,AD DB ∴=⊙ 90AOD BOD ∠=∠=︒.又⊙ FD AB ∥,⊙ 90ODF BOD ∠=∠=︒.即 OD DF ⊥.⊙ 直线DF 为O 的切线.(2)解:⊙ AB 是O 的直径,⊙90ACB ∠=︒.又⊙30A ∠=︒,AC =⊙ 4AB =.⊙ 2OD =.⊙ AO CO =,30ACO A ∴∠=∠=︒⊙ 60COB A ACO ∠=∠+∠=︒.⊙ DF AB ,⊙ 60F ∠=︒,30FOD ∴∠=︒,设,FD x =则22OF FD x ==,又2OD =,在Rt ODF △中,由勾股定理得:22224x x +=,解得:x =故FD = 【点睛】本题属于圆综合题,考查了垂径定理,圆周角定理,平行线的判定,特殊角的直角三角形性质,等知识,解题的关键是学会添加常用辅助线解决问题.26.(1)抛物线与y 轴交点的坐标为()0,3,对称轴2x =(2)⊙=; ⊙3154a -≤<-【分析】(1)0x =,可得抛物线与y 轴交点的坐标,再根据抛物线对称轴公式解答,即可求解;(2)⊙根据题意可得点()()12,3,1,y y 关于直线2x =对称,即可求解;⊙根据题意可得点()()()2341,,,1,2,y y y --在对称轴的左侧,点()13,y 在对称轴的右侧,然后分两种情况:当0a >时,当a<0时,即可求解.【详解】(1)解:令0x =,则3y =,⊙抛物线与y 轴交点的坐标为()0,3 . 对称轴422a x a-=-=. (2)解:⊙ ⊙函数图象的对称轴为直线2x =,⊙点()()12,3,1,y y 关于直线2x =对称,⊙12y y =,故答案为:=;⊙⊙函数图象的对称轴为直线2x =,3112>>->-,⊙点()()()2341,,,1,2,y y y --在对称轴的左侧,点()13,y 在对称轴的右侧.当0a >时,在对称轴的左侧,y 随x 的增大而减小,⊙1234y y y y =<<,不合题意.当a<0时,在对称轴的左侧,y 随x 的增大而增大,则1234y y y y =>>,1y ,2y ,3y ,4y 四个函数值可以满足12340y y y y >=≥>,⊙340,0y y ≥<,即当=1x -时,3430y a a =++≥,当2x =-时,44830y a a =++<.解得 3154a -≤<-.【点睛】本题考查了二次函数图象与性质,掌握二次函数图象与性质是解题的关键.27.(1)见解析(2)AF CD =,见解析 (3)BC CD =,见解析【分析】(1)根据旋转的性质画图即可;(2)根据旋转的性质以及等腰直角三角形可以得到全等三角形,再根据全等三角形的性质即可求出结论;(3)根据题意画出已知图形,再根据图形得到全等三角形,利用全等三角形的性质和等腰直角三角形的性质即可求出结论.【详解】(1)解:补全图形如图所示(2)解:AF CD =,理由如下:⊙EF AD ⊥⊙90EFD ∠=︒⊙90ACB ∠=︒⊙EFD BCD ∠=∠⊙90ACB ∠=︒⊙90CBD CDB ∠∠=︒+由题意可知,90BDE ∠=︒⊙90EDF BDC ∠∠=︒+⊙EDF CBD ∠=∠在EFD △和DCB △中EDF CBD EFD DCB ED BD ∠=∠⎧⎪∠=∠⎨⎪=⎩⊙EFD △⊙()AAS DCB⊙EF CD DF BC ==,⊙BC AC =⊙AC DF =⊙AF CD =(3)解:BC CD = 理由如下:连接DG ,FG⊙ DE BD =,G 为BE 的中点,90BDE ∠=︒⊙EG BG DG ==, 90DGB ∠=︒⊙90EFD DGE ∠=∠=︒⊙GEF CDG ∠=∠在EFG 和DCG △中EF DC GEF CDG EG DG =⎧⎪∠=∠⎨⎪=⎩⊙EFG ⊙SAS DCG ()⊙FG CG =,EGF DGC ∠=∠⊙90EGF EGC DGC EGC ∠+∠=∠+∠=︒即 90CGF ∠=︒⊙CGF △为等腰直角三角形 ⊙CF⊙ BC AC AF CF ==+,AF CD = ⊙BC CD =【点睛】本题考查了全等三角形的判定和性质,等腰直角三角形的性质等相关知识点,掌握全等三角形的性质和旋转的性质是解题的关键.28.(1)()2,3(2)()3,2-(3)()3,3-,12,102B y ≤≤【分析】(1)根据二次关联图形的定义分别找到A '和A '',过点A '作A D x '⊥轴于点D ,可证得AOP PDA '≌,从而得到1,3OA PD OP A D '====,即可求解;(2)根据题意得:点P 位于x 轴的下方,设点P 的纵坐标为m ,过点P 作PE y ⊥轴于点E ,过点A '作A F x '⊥轴交EP 延长线于点F ,坐标为m ,表达点A '的坐标,可得出结论; (3)由(2)可知,点A ''的坐标,由A 关于点P 的二次关联图形在O 上且不与点A 重合可得出点A ''的坐标,由线段1AB =,其关于点P 的二次关联图形上的任意一点都在O 及其内部,找到临界点B '',可得出B ''的坐标,进而可得出点B 的坐标,即可得出B y 的取值范围.【详解】(1)如图1,根据二次关联图形的定义分别找到A '和A '',过点A '作A D x '⊥轴于点D ,⊙90A DP AOP '∠=∠=︒由旋转可知,90,APA AP A P ''∠=︒=,⊙90APO A PD A PD PA D '''∠+∠=∠+∠=︒,⊙APO PA D '∠=∠,⊙()AAS AOP PDA '≌,⊙1,3OA PD OP A D '====,⊙()4,3A ',⊙点A '和A ''关于直线3x =对称,⊙点()2,3A '',即点A 关于点P 的二次关联图形的坐标为()2,3;故答案为:()2,3(2)解:根据题意得:点P 位于x 轴的下方,设点P 的纵坐标为m ,如图,过点P 作PE y ⊥轴于点E ,过点A '作A F x '⊥轴交EP 延长线于点F ,由(1)得: AEP PFA '≌,⊙1,3AE PF m EP A F '==-==,⊙()4,3A m m '-+,根据题意得:点A 和点A '关于直线3x =对称,⊙46m -=,解得:2m =-,⊙点P 的坐标为()3,2-,(3)解:设点P 的纵坐标为n ,由(2)得:()4,3A n n '-+,⊙()2,3A n n ''++,⊙A ''在在O 上,⊙()()22231n n +++=,解得:2n =-(舍去)或3-,⊙点P 的坐标为()3,3-,⊙1AB =,AB 其关于点P 的二次关联图形上的任意一点都在O 及其内部,此时点B ''是一个临界点,连接OB ,如图,⊙1OA A B OB ''''''''===,⊙OA B ''''是等边三角形,过点B ''作B M x ''⊥轴于点M ,则12A M OM ''==,⊙B M ''=⊙1,2B ⎛''- ⎝⎭,⊙13,2B ⎛' ⎝⎭,⊙12B ⎫⎪⎝⎭,由对称性得:另一个点的坐标为12B ⎛⎫ ⎪ ⎪⎝⎭,⊙B y 的取值范围为102B y ≤≤. 【点睛】本题属于新定义类问题,主要考查轴对称最值问题,等边三角形的性质与判定,圆的定义等相关知识,关键是理解给出新定义,画出对应的图形.。
2022年秋人教版九年级化学上册 -原子结构及原子质量的计算 同步练习

3.1.1 原子结构及原子质量的计算一、单选题1.下表列出了几种原子中的粒子数:原子质子数中子数核外电子数氢 1 0 1碳 6 6 6氧8 8 8钾19 20 19分析表中信息,下列说法正确的是()A.原子核内质子数等于中子数B.原子核都由质子和中子构成C.原子只由质子和电子构成D.原子中质子数等于核外电子数2.下图为某粒子的结构示意图,下列说法正确的是A.该粒子有12个质子B.该粒子有2个电子层C.该粒子属于非金属元素D.该粒子已达到相对稳定结构3.俄国科学家门捷列夫对元素周期表的编制做出巨大贡献,人们将101号元素命名为“钔”来纪念他。
钔原子的核电荷数为101,相对原子质量为258,则钔原子的中子数为A.101B.157 C.258 D.359 4.科学理论在传承中不断发展,科学家们传承前人的正确观点,纠正错误观点,形成科学理论,关于原子结构的学说有:①在球体内充斥正电荷,电子镶嵌其中②原子是可分的③原子呈球形④原子中有带负电的电子⑤原子中有带正电的原子核⑥原子核很小,但集中了原子的大部分质量其中经过卢瑟福传承和发展后形成的观点是()A.②③④⑤⑥B.①②③④C.④⑤⑥D.⑤⑥5.下列对分子、原子、离子的认识正确的是()A.同种分子排列方式不同,化学性质不同B.在干冰中,分子因相互作用而静止不动C.同种原子按不同方式结合,可以构成不同的物质D.原子得失电子形成离子后,原子核发生了变化6.下列说法正确的是()A.原子的质量主要集中在原子核上B.相同的原子无法构成不同的分子C.温度计内汞柱液面上升说明汞原子体积变大D.原子呈电中性是因为原子中质子数与中子数相等7.在原子里,质子数等于()A.中子数B.电子数C.中子数与电子数之和D.中子数和电子数之差8.碳12原子的实际质量为xkg,则实际质量为2xkg的一种原子的相对原子质量为A.24g B.24 C.2g D.29.一种铀原子中含有92个质子和143个中子。
人教版九年级物理上册第十七章综合素质评价附答案

人教版九年级物理上册第十七章综合素质评价一、选择题(每题3分,共36分)1.关于欧姆定律,下列说法中正确的是()A.通过导体的电流跟该导体的电阻成正比,跟该导体两端的电压成反比B.当电压一定时,导体的电阻跟通过它的电流成反比C.当通过导体的电流一定时,导体的电阻跟该导体两端的电压成正比D.当电阻一定时,通过导体的电流跟它两端的电压成正比2.某导体中的电流与它两端电压的关系如图所示,下列分析正确的是() A.当导体两端的电压为0时,电阻为0B.该导体的电阻随电压的增大而减小C.当导体两端的电压为0时,电流为0D.当导体两端的电压为2 V时,电流为0.6 A3.【2022·北京】如图所示的电路中,电阻阻值R1<R2。
开关S闭合后,R1、R2两端的电压分别为U1、U2,通过R1、R2的电流分别为I1、I2。
下列判断正确的是()A.U1>U2B.U1<U2C.I1>I2D.I1=I24.下列科学方法中,叙述错误的是()A.两个5 Ω的电阻串联与一个10 Ω的电阻效果相同,运用了转换法B.根据增大摩擦力的方法想到减小摩擦力的方法,运用了逆向思维法C.探究杠杆平衡条件,运用了归纳法D.在学习电压时,常对照水压来理解电压,运用了类比法5.【2022·通辽】如图所示,电源电压保持不变,开关S闭合后,在滑动变阻器滑片P向左移动的过程中,下列说法正确的是()A.电压表V1示数变小,电压表V2示数不变,电流表A示数变小B.电压表V1示数变小,电压表V2示数变大,电压表V1的示数与电流表A 的示数之比变小C.电压表V2示数不变,电流表A示数变大,电压表V1的示数与电流表A 的示数之比变大D.电压表V1示数变小,电压表V2示数不变,电压表V2的示数与电流表A 的示数之比变小6.如图所示的电路中,电源电压为4.5 V,L1、L2是小灯泡,当开关S闭合时,电压表的示数为1.5 V,忽略温度对灯丝电阻的影响,则()A.L2两端的电压为1.5 VB.L1两端的电压为1.5 VC.L1与L2的灯丝电阻之比为2∶1D.通过L1与L2的电流之比为1∶27.【2023·天津模拟】在如图所示的电路中,电源电压保持不变,闭合开关S,电路正常工作,一段时间后,发现两个电表的示数都变大,则出现这种故障的可能原因是()A.R1短路B.R1断路C.R2短路D.R2断路8.关于串、并联电路,下列说法正确的是()A.串联电路电流处处相等B.串联电路总电阻的倒数等于各支路电阻倒数之和C.并联电路各支路电流相等D.并联电路的总电阻等于各支路电阻之和9.如图所示,电源电压恒为6 V,R1是定值电阻,A、B是滑动变阻器R2的两端。
中国儿童身高体重标准表
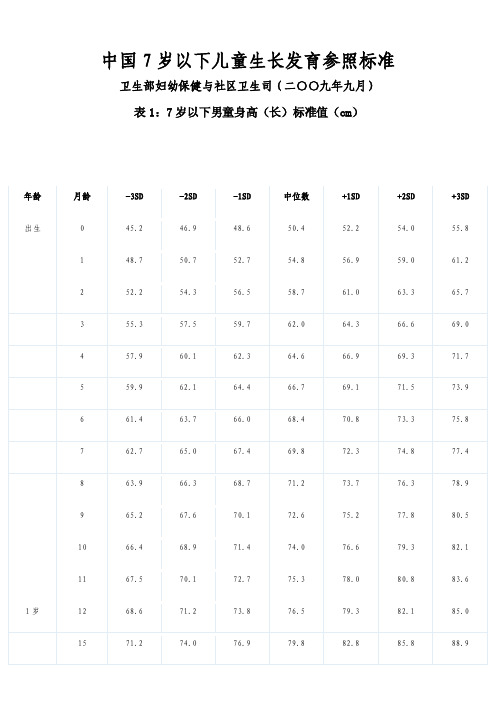
中国7岁以下儿童生长发育参照标准卫生部妇幼保健与社区卫生司(二〇〇九年九月)表1:7岁以下男童身高(长)标准值(cm)年龄月龄-3SD-2SD-1SD中位数+1SD+2SD+3SD 出生045.246.948.650.452.254.055.8 148.750.752.754.856.959.061.2252.254.356.558.761.063.365.7355.357.559.762.064.366.669.0457.960.162.364.666.969.371.7559.962.164.466.769.171.573.9661.463.766.068.470.873.375.8762.765.067.469.872.374.877.4863.966.368.771.273.776.378.9965.267.670.172.675.277.880.51066.468.971.474.076.679.382.11167.570.172.775.378.080.883.6 1岁1268.671.273.876.579.382.185.0 1571.274.076.979.882.885.888.91873.676.679.682.785.889.192.42176.079.182.385.689.092.495.9 2岁2478.381.685.188.592.195.899.5 2780.583.987.591.194.898.6102.53082.485.989.693.397.1101.0105.03384.488.091.695.499.3103.2107.2 3岁3686.390.093.797.5101.4105.3109.4 3987.591.294.998.8102.7106.7110.74289.393.096.7100.6104.5108.6112.74590.994.698.5102.4106.4110.4114.6 4岁4892.596.3100.2104.1108.2112.3116.5 5194.097.9101.9105.9110.0114.2118.55495.699.5103.6107.7111.9116.2120.65797.1101.1105.3109.5113.8118.2122.6 5岁6098.7102.8107.0111.3115.7120.1124.7 63100.2104.4108.7113.0117.5122.0126.766101.6105.9110.2114.7119.2123.8128.669103.0107.3111.7116.3120.9125.6130.4 6岁72104.1108.6113.1117.7122.4127.2132.1表2:7岁以下女童身高(长)标准值(cm )年龄月龄-3SD-2SD-1SD中位数+1SD+2SD+3SD出生44.746.448.049.751.453.255.0147.949.851.753.755.757.859.9251.153.255.357.459.661.864.1354.256.358.460.662.865.167.5456.758.861.063.165.467.770.0558.660.862.965.267.469.872.1660.162.364.566.869.171.574.0761.363.665.968.270.673.175.6862.564.867.269.672.174.777.3963.766.168.571.073.676.278.91064.967.369.872.475.077.780.51166.168.671.173.776.479.282.01岁1267.269.772.375.077.780.583.41570.272.975.678.581.484.387.475105.3109.8114.4119.2124.0128.8133.878106.5111.1115.8120.7125.6130.5135.681107.9112.6117.4122.3127.3132.4137.61872.875.678.581.584.687.791.02175.178.181.284.487.791.194.5 2岁2477.380.583.887.290.794.398.0 2779.382.786.289.893.597.3101.23081.484.888.492.195.999.8103.83383.486.990.594.398.1102.0106.1 3岁3685.488.992.596.3100.1104.1108.1 3986.690.193.897.5101.4105.4109.44288.491.995.699.4103.3107.2111.34590.193.797.4101.2105.1109.2113.3 4岁4891.795.499.2103.1107.0111.1115.3 5193.297.0100.9104.9109.0113.1117.45494.898.7102.7106.7110.9115.2119.55796.4100.3104.4108.5112.8117.1121.6 5岁6097.8101.8106.0110.2114.5118.9123.4 6399.3103.4107.6111.9116.2120.7125.366100.7104.9109.2113.5118.0122.6127.269102.0106.3110.7115.2119.7124.4129.1 6岁72103.2107.6112.0116.6121.2126.0130.875104.4108.8113.4118.0122.7127.6132.578105.5110.1114.7119.4124.3129.2134.281106.7111.4116.1121.0125.9130.9136.1表3:7岁以下男童体重标准值(kg)年龄月龄-3SD-2SD-1SD中位数+1SD+2SD+3SD 出生0 2.26 2.58 2.93 3.32 3.73 4.18 4.661 3.09 3.52 3.99 4.51 5.07 5.67 6.332 3.94 4.47 5.05 5.68 6.387.147.973 4.69 5.29 5.97 6.707.518.409.374 5.25 5.91 6.647.458.349.3210.395 5.66 6.367.148.008.959.9911.156 5.97 6.707.518.419.4110.5011.727 6.24 6.997.838.769.7910.9312.208 6.467.238.099.0510.1111.2912.609 6.677.468.359.3310.4211.6412.9910 6.867.678.589.5810.7111.9513.34117.047.878.809.8310.9812.2613.68 1岁127.218.069.0010.0511.2312.5414.00 157.688.579.5710.6811.9313.3214.88188.139.0710.1211.2912.6114.0915.75218.619.5910.6911.9313.3314.9016.66 2岁249.0610.0911.2412.5414.0115.6717.54 279.4710.5411.7513.1114.6416.3818.36309.8610.9712.2213.6415.2417.0619.133310.2411.3912.6814.1515.8217.7219.89 3岁3610.6111.7913.1314.6516.3918.3720.64 3910.9712.1913.5715.1516.9519.0221.394211.3112.5714.0015.6317.5019.6522.134511.6612.9614.4416.1318.0720.3222.91 4岁4812.0113.3514.8816.6418.6721.0123.735412.7414.1815.8417.7519.9822.5725.615713.1214.6116.3418.3520.6923.4326.68 5岁6013.5015.0616.8718.9821.4624.3827.85 6313.8615.4817.3819.6022.2125.3229.046614.1815.8717.8520.1822.9426.2430.226914.4816.2418.3120.7523.6627.1731.43 6岁7214.7416.5618.7121.2624.3228.0332.57 7515.0116.9019.1421.8225.0629.0133.897815.3017.2719.6222.4525.8930.1335.418115.6617.7320.2223.2426.9531.5637.39表4:7岁以下女童体重标准值(kg)年龄月龄-3SD-2SD-1SD中位数+1SD+2SD+3SD 出生0 2.26 2.54 2.85 3.21 3.63 4.10 4.651 2.98 3.33 3.74 4.20 4.74 5.35 6.052 3.72 4.15 4.65 5.21 5.86 6.607.463 4.40 4.90 5.47 6.13 6.877.738.714 4.93 5.48 6.11 6.837.658.599.665 5.33 5.92 6.597.368.239.2310.386 5.64 6.26 6.967.778.689.7310.937 5.90 6.557.288.119.0610.1511.408 6.13 6.797.558.419.3910.5111.809 6.347.037.818.699.7010.8612.1810 6.537.238.038.949.9811.1612.5211 6.717.438.259.1810.2411.4612.85 1岁12 6.877.618.459.4010.4811.7313.15 157.348.129.0110.0211.1812.5014.02187.798.639.5710.6511.8813.2914.90218.269.1510.1511.3012.6114.1215.85 2岁248.709.6410.7011.9213.3114.9216.77 279.1010.0911.2112.5013.9715.6717.63309.4810.5211.7013.0514.6016.3918.473岁3610.2311.3612.6514.1315.8317.8120.10 3910.6011.7713.1114.6516.4318.5020.904210.9512.1613.5515.1617.0119.1721.694511.2912.5514.0015.6717.6019.8522.49 4岁4811.6212.9314.4416.1718.1920.5423.30 5111.9613.3214.8816.6918.7921.2524.145412.3013.7115.3317.2219.4222.0025.045712.6214.0815.7817.7520.0522.7525.96 5岁6012.9314.4416.2018.2620.6623.5026.87 6313.2314.8016.6418.7821.3024.2827.846613.5415.1817.0919.3321.9825.1228.896913.8415.5417.5319.8822.6525.9629.95 6岁7214.1115.8717.9420.3723.2726.7430.94 7514.3816.2118.3520.8923.9227.5732.007814.6616.5518.7821.4424.6128.4633.148114.9616.9219.2522.0325.3729.4234.40表5:7岁以下男童头围标准值(cm)年龄月龄-3SD-2SD-1SD中位数+1SD+2SD+3SD 出生030.932.133.334.535.736.837.9 133.334.535.736.938.239.440.7235.236.437.638.940.241.542.9336.737.939.240.541.843.244.6438.039.240.441.743.144.545.9539.040.241.542.744.145.546.9639.841.042.343.644.946.347.7740.441.742.944.245.546.948.4841.042.243.544.846.147.548.9941.542.744.045.346.648.049.41041.943.144.445.747.048.449.81142.343.544.846.147.448.850.2 1岁1242.643.845.146.447.749.150.51843.745.046.347.648.950.251.62144.245.546.748.049.450.752.1 2岁2444.645.947.148.449.851.152.52745.046.247.548.850.151.452.83045.346.547.849.150.451.753.13345.546.848.049.350.652.053.3 3岁3645.747.048.349.650.952.253.54246.247.448.749.951.352.653.94846.547.849.050.351.652.954.2 4岁5446.948.149.450.651.953.254.6 5岁6047.248.449.751.052.253.654.9 6647.548.750.051.352.553.855.2 6岁7247.849.050.251.552.854.155.4表6:7岁以下女童头围标准值(cm)年龄月龄-3SD-2SD-1SD中位数+1SD+2SD+3SD出生030.431.632.834.035.236.437.5132.633.835.036.237.438.639.9234.535.636.838.039.340.541.8336.037.138.339.540.842.143.4437.238.339.540.741.943.344.6538.139.240.441.642.944.345.7638.940.041.242.443.745.146.5739.540.741.843.144.445.747.2840.141.242.443.644.946.347.7940.541.742.944.145.446.848.21040.942.143.344.545.847.248.61141.342.443.644.946.247.549.0 1岁1241.542.743.945.146.547.849.3 1542.243.444.645.847.248.550.01842.843.945.146.447.749.150.52143.244.445.646.948.249.651.02744.045.246.447.749.050.351.73044.345.546.748.049.350.752.13344.645.847.048.349.650.952.3 3岁3644.846.047.348.549.851.252.6 4245.346.547.749.050.351.653.04岁4845.746.948.149.450.652.053.35446.047.248.449.751.052.353.7 5岁6046.347.548.750.051.352.653.9 6646.647.849.050.351.552.854.2 6岁7246.848.049.250.551.853.154.4表7:45~110cm身长的体重标准值(男)身长(cm)体重(kg)-3SD-2SD-1SD中位数+1SD+2SD+3SD46 1.80 1.99 2.19 2.41 2.65 2.91 3.18 48 2.11 2.34 2.58 2.84 3.12 3.42 3.74 50 2.43 2.68 2.95 3.25 3.57 3.91 4.29 52 2.78 3.06 3.37 3.71 4.07 4.47 4.90 54 3.19 3.51 3.87 4.25 4.67 5.12 5.62 56 3.65 4.02 4.41 4.85 5.32 5.84 6.41 58 4.13 4.53 4.97 5.46 5.99 6.577.21 60 4.61 5.05 5.53 6.06 6.657.308.01 62 5.09 5.56 6.08 6.667.308.008.78 64 5.54 6.05 6.607.227.918.679.51 66 5.97 6.507.097.748.479.2810.19 68 6.38 6.937.558.239.009.8510.81 70 6.767.347.988.699.4910.3811.39 727.127.728.389.129.9410.8811.93 747.478.088.769.5210.3811.3412.44 767.818.439.139.9110.8011.8012.93 788.148.789.5010.3111.2212.2513.42 808.499.159.8810.7111.6412.7013.92849.219.9010.6611.5312.5213.6414.94 869.5810.2811.0711.9612.9714.1315.46 889.9610.6811.4812.3913.4314.6216.00 9010.3411.0811.9012.8313.9015.1216.54 9210.7411.4812.3313.2814.3715.6317.10 9411.1411.9012.7713.7514.8716.1617.68 9611.5612.3413.2214.2315.3816.7218.29 9811.9912.7913.7014.7415.9317.3218.95 10012.4413.2614.2015.2716.5117.9619.67 10212.8913.7514.7215.8317.1218.6420.45 10413.3514.2415.2516.4117.7719.3721.29 10613.8214.7415.7917.0118.4520.1522.21 10814.2715.2416.3417.6319.1520.9723.19 11014.7415.7416.9118.2719.8921.8524.27表8:80~140cm身高的体重标准值(男)身长(cm)体重(kg)-3SD-2SD-1SD中位数+1SD+2SD+3SD 808.619.2710.0210.8511.7912.8714.09 828.979.6510.4111.2612.2313.3414.60 849.3410.0310.8111.6812.6813.8115.12 869.7110.4211.2112.1113.1314.3015.65 8810.0910.8111.6312.5413.5914.7916.19 9010.4811.2212.0512.9914.0615.3016.73 9210.8811.6312.4813.4414.5415.8217.30 9411.2912.0512.9213.9115.0516.3617.89 9611.7112.5013.3914.4015.5716.9318.51 9812.1512.9513.8714.9216.1317.5419.19 10012.6013.4314.3815.4616.7218.1919.93 10213.0513.9214.9016.0317.3518.8920.74 10413.5214.4115.4416.6218.0019.6421.61 10613.9814.9115.9817.2318.6920.4322.5411014.9015.9217.1118.5020.1622.1824.67 11215.3716.4517.7019.1920.9723.1525.90 11415.8516.9918.3219.9021.8324.2127.25 11616.3317.5418.9520.6622.7425.3628.76 11816.8318.1019.6221.4523.7226.6230.45 12017.3418.6920.3122.3024.7827.9932.34 12217.8719.3121.0523.1925.9129.5034.48 12418.4119.9521.8124.1427.1431.1536.87 12618.9720.6122.6225.1528.4532.9639.56 12819.5621.3123.4726.2229.8534.9242.55 13020.1822.0524.3727.3531.3437.0145.80 13220.8422.8325.3228.5532.9139.2149.23 13421.5323.6526.3229.8034.5541.4852.72 13622.2524.5127.3631.0936.2343.7856.20 13823.0025.4028.4432.4437.9546.1159.62 14023.7926.3329.5733.8239.7148.4662.96表9:45~110cm身长的体重标准值(女)身长(cm)体重(kg)-3SD-2SD-1SD中位数+1SD+2SD+3SD 46 1.89 2.07 2.28 2.52 2.79 3.09 3.43 48 2.18 2.39 2.63 2.90 3.20 3.54 3.93 50 2.48 2.72 2.99 3.29 3.63 4.01 4.44 52 2.84 3.11 3.41 3.75 4.13 4.56 5.05 54 3.26 3.56 3.89 4.27 4.70 5.18 5.73 56 3.69 4.02 4.39 4.81 5.29 5.82 6.43 58 4.14 4.50 4.91 5.37 5.88 6.477.13 60 4.59 4.99 5.43 5.93 6.497.137.85 62 5.05 5.48 5.95 6.497.097.778.54 64 5.48 5.94 6.447.017.658.389.21 66 5.89 6.37 6.917.518.188.959.8272 6.987.528.138.829.5910.4611.46 747.307.878.499.2010.0010.9111.95 767.628.208.859.5810.4011.3412.41 787.938.539.209.9510.8011.7712.88 808.268.889.5710.3411.2212.2213.37 828.609.239.9410.7411.6512.6913.87 848.959.6010.3311.1612.1013.1614.39 869.309.9810.7311.5812.5513.6614.93 889.6710.3711.1512.0313.0314.1815.50 9010.0610.7811.5812.5013.5414.7316.11 9210.4611.2012.0412.9814.0615.3116.75 9410.8811.6412.5113.4914.6215.9117.41 9611.3012.1012.9914.0215.1916.5418.11 9811.7312.5513.4914.5515.7717.1918.84 10012.1613.0113.9815.0916.3717.8619.61 10212.5813.4714.4815.6416.9818.5520.39 10413.0013.9314.9816.2017.6119.2621.22 10613.4314.3915.4916.7718.2520.0022.09 10813.8614.8616.0217.3618.9220.7823.02 11014.2915.3416.5517.9619.6221.6024.00表10:80~140cm身高的体重标准值(女)身长(cm)体重(kg)-3SD-2SD-1SD中位数+1SD+2SD+3SD808.389.009.7010.4811.3712.3813.54 828.729.3610.0810.8911.8112.8514.05 849.079.7310.4711.3112.2513.3414.58 869.4310.1110.8711.7412.7213.8415.13 889.8010.5111.3012.1913.2014.3715.71 9010.2010.9211.7412.6613.7214.9316.33 9210.6011.3612.2013.1614.2615.5116.989811.8812.7113.6614.7415.9817.4219.11 10012.3113.1714.1615.2816.5818.1019.88 10212.7313.6314.6615.8317.2018.7920.68 10413.1514.0915.1616.3917.8319.5121.52 10613.5814.5615.6816.9718.4820.2722.41 10814.0115.0316.2017.5619.1621.0623.36 11014.4515.5116.7418.1819.8721.9024.37 11214.9016.0117.3118.8220.6222.7925.45 11415.3616.5317.8919.5021.4123.7426.63 11615.8417.0718.5020.2022.2524.7627.91 11816.3317.6219.1320.9423.1325.8429.29 12016.8518.2019.7921.7124.0526.9930.78 12217.3918.8020.4922.5225.0328.2132.39 12417.9419.4321.2023.3626.0629.5234.14 12618.5120.0721.9424.2427.1330.9036.04 12819.0920.7222.7025.1528.2632.3938.12 13019.6921.4023.4926.1029.4733.9940.43 13220.3122.1124.3327.1130.7535.7242.99 13420.9622.8625.2128.1932.1237.6045.81 13621.6523.6526.1429.3333.5939.6148.88 13822.3824.5027.1430.5535.1441.7452.13 14023.1525.3928.1931.8336.7743.9355.44说明:“中位数”,表示处于人群的平均水平;如果在“-1sd~中位数~+1sd”即:中位数上下一个标准差范围之内,属于“正常范围”,代表了68%的儿童;如果在“(-2sd~-1sd)或者(+1sd~+2sd)”即:中位数上下两个标准差范围之内,则定义为“偏矮(高)”,代表了27.4%的儿童;如果在“(-3sd~-2sd)或者(+2sd~+3sd)”即:中位数上下三个标准差之内,则定义为“矮(高)”,代表了4.6%的儿童。
九年级上第十一到十四章基础练习

11.简单机械和功(基础测试卷)一、填空题:(每空1分,共30分)1.杠杆平衡的条件是________________________。
当动力臂______阻力臂时,是省力杠杆;当动力臂______阻力臂时,是费力杠杆;当动力臂______阻力臂时,是省力杠杆。
2.定滑轮的实质是一个______杠杆,所以使用它可以____________但不能______;动滑轮的实质是一个______杠杆,所以使用它可以____________,但不能____________。
3.写出下列各单位所对应的物理量:(1)N·M ;(2)J/s __________ ;(3)W·S________;(4)N·M/S_________。
4.在镊子、钢丝钳、扳手、天平中,属于费力杠杆的有_______,属于等臂杠杆的有________。
5.如图1所示,杠杆上每格等距,每个钩码重都是1N,当杠杆平衡时,弹簧秤的示数为______;若要求弹簧秤示数为9N,并且钩在支点左侧时,则它应钩在______处,拉力方向应为____________。
6.如图2所示,用动滑轮把重为40N的物体匀速上提,弹簧测力计示数为24N,则拉力为______N。
不计摩擦和绳重,动滑轮重为______N,这时该动滑轮的机械效率约为______。
7.某运动员把1000N的杠铃举高1.8m后在空中停留5秒钟,在这5S内他对杠铃做的功是______J,功率是______W。
8.两台机器的功率之比为3:1 ,它们做同样多的功,所需时间之比为______,在相同时间内做功之比为______。
9.某台机器的功率为80W,机械效率为80%,分别表示_____________________________,__________________________________________。
10.设长和高之比为5∶2的斜面,把重600N的物体匀速推上去,所用沿斜面方向推力至少是______N,若实际所用推力为300N,则斜面的机械效率为_____________。
人教版物理九年级第十四章 能量的转化和守恒 同步练习
人教版物理九年级第十四章第三节《能量的转化和守恒》练习班级:_________ 姓名:_________一、单选题1.下列关于信息传递和能量的有关说法正确的是()A.电磁波的传播需要介质B.风能、水能和太阳能都是一次、不可再生能源C.卫星是利用电磁波传递信息的D.能量转化是守恒的,所以能源取之不尽用之不竭2.如图是送餐机器人工作时的情景,下列说法正确的是()A.机器人送饮料时,突然停下,饮料会向前洒出,此时惯性做功B.机器人端着餐盘水平匀速行走过程中,需要克服餐盘的重力做功C.机器人端着餐盘水平匀速行走过程中,没有力对餐盘做功D.机器人端着餐盘水平启动时,将重力势能转化为动能3.下列说法正确的是()A.柴油机的效率比汽油机的效率高B.在热机的工作过程中,由机械能转化为内能的是做功冲程C.柴油机在工作过程中吸入气缸中的是油气混合物D.蓄电池充电的过程中是化学能转化为电能4.下列电器在正常工作过程中,机械能转化为电能的是()A.电动机B.发电机C.电饭锅D.电烙铁5.下列说法正确的是()A.根据能量守恒定律,人们可制造出永动机B.各种形式的能量都可以在一定条件下相互转化C.能量守恒定律只适用于没有摩擦和空气阻力的情况D.火箭升空时,其势能和动能都增大,能量守恒定律不适用6.如图四幅图片,其说明的物理知识错误的是()A.悬挂重物不能把两铅块分开,说明分子间存在引力,没有斥力B.加热水产生的蒸汽使橡胶塞冲出,利用做功和热传递都能改变物体的内能C.抽掉玻璃板气体会变色,实验中气体的摆放位置没有问题D.压下活塞后硝化棉燃烧,实验过程中是机械能转化为内能7.下列说法错误的是()A.冬天用暖手宝取暖是利用热传递改变内能B.烧开水壶盖被顶起时机械能转化为内能C.“八月桂花遍地香”说明分子在不停的做无规则运动D.人造木板粘接剂中的甲醛由于扩散会污染空气8.关于能量转化,下列说法中正确的是()A.电暖气正常工作时,主要是将电能转化为机械能B.电风扇正常工作时,主要是将电能转化为内能C.电动汽车在行驶过程中,发生的能量转化主要是将机械能转化为电能D.人造卫星展开太阳能电池板,把太阳能转化为电能供给卫星用电器9.全太阳能动力汽车部件工作大致流程如图,下列说法正确的是()A.储能环节,将电能转化为化学能B.图中某个环节的工作效率可达100%C.控制送电环节,将电能转化为机械能D.光电转换环节,将电能转化为太阳能10.地面上一定高度的雨滴,在其匀速下落过程中,下列说法正确的是()A.雨滴的机械能保持不变B.雨滴只受到重力的作用C.雨滴的重力势能转化为动能D.雨滴的重力势能转化为内能二、填空题11.汽油机是热机的一种,如图甲所示是一台单缸四冲程汽油机工作状态示意图,由图可以看出,此冲程的能量转化情况与(选填“乙”或“丙”)图相同,若该汽油机飞轮的转速是3600r/min,则汽油机每秒钟对外做功次。
(必考题)初中数学九年级数学上册第二单元《一元二次方程》检测题(有答案解析)

一、选择题1.一元二次方程x 2=2x 的根是( ).A .0B .2C .0和2D .0和﹣2 2.一元二次方程x 2+4x=3配方后化为( ) A .(x+2)2=3 B .(x+2)2=7 C .(x-2)2=7 D .(x+2)2=-1 3.要组织一次足球联赛,赛制为双循环形式(每两队之间都进行两场比赛),共要比赛90场.设共有x 个队参加比赛,则x 满足的关系式为( )A .12x (x +1)=90B .12x (x ﹣1)=90C .x (x +1)=90D .x (x ﹣1)=904.为切实解决群众看病贵的问题,药监部门对药品价格进行了两次下调.某种药品原价为250元/瓶,经两次下调后价格变为160元/瓶,该药品平均每次降价的百分率为( ) A .10% B .15% C .20% D .25% 5.关于x 的方程2(3)(2)x x p -+=(p 为常数)的根的情况,下列结论中正确的是( )A .两个正根B .两个负根C .一个正根,一个负根D .无实数根 6.我国古代数学家赵爽(公元3~4世纪)在其所著的《勾股圆方图注》中记载过一元二次方程(正根)的几何解法.以方程22350x x +-=即(2)35x x +=为例说明,记载的方法是:构造如图,大正方形的面积是2(2)x x ++.同时它又等于四个矩形的面积加上中间小正方形的面积,即24352⨯+,因此5x =.则在下面四个构图中,能正确说明方程23100x x --=解法的构图是( )A .B .C .D .7.2020年12月29日,贵阳轨道交通2号线实现试运行,从白云区到观山湖区轨道公司共设计了132种往返车票,则这段线路有多少个站点?设这段线路有x 个站点,根据题意,下面列出的方程正确的是( )A .()1132x x +=B .()1132x x -=C .1(1)1322x ⨯+= D .1(1)1322x x -= 8.用配方法解方程2420x x -+=,下列配方正确的是( ) A .()222x -= B .()222x += C .()222x -=- D .()226x -= 9.在疫情期间,口罩的需求量急剧上升.某口罩生产企业四月份生产了口罩200000只, 如果要在第二季度总共生产728000只口罩,设生产口罩月平均增长的百分率为x ,则可根据题意列出的方程是( )A .()22000001+728000x =B .()32000001+728000x =C .()()22000001+2000001+728000x x +=D .()()2200000+2000001+2000001+728000x x +=10.某小区附近新建一个游泳馆,馆内矩形游泳池的面积为2300m ,且游泳池的宽比长短10m .设游泳池的长为xm ,则可列方程为( )A .()10300x x -=B .()10300x x +=C .()2210300x x -= D .()2210300x x +=11.由于国内疫情得到缓和,餐饮业逐渐恢复,某地一家餐厅重新开张,开业第一天收入约为2000元,之后两天的收入按相同的增长率增长,第3天的收入约为2420元,若设每天的增长率为x ,则列方程为( )A .2000(1)2420x +=B .2000(12)2420x +=C .22000(1)2420x -=D .22000(1)2420x +=12.用配方法解一元二次方程29190x x -+=,配方后的方程为( )A .29524x ⎛⎫-= ⎪⎝⎭B .29524x ⎛⎫+= ⎪⎝⎭C .()2962x -=D .()2962x += 二、填空题13.已知m ,n 是方程2210x x --=的两实数根,则11m n+=_______. 14.某电脑公司计划两年内将产品成本由原来2500元下降到1600元,则每年平均下降的百分率是________.15.一个等腰三角形的腰和底边长分别是方程28120x x -+=的两根,则该等腰三角形的周长是________.16.已知一元二次方程ax 2+bx +c =0(a ≠0).下列说法:①若a +c =0,则方程一定有两个不相等的实数根;②若a +b +c =0,则1一定是这个方程的实数根;③若b 2﹣6ac >0,则方程一定有两个不相等的实数根;④若ax 2+bx +c =0(a ≠0)的两个根为2和3,则1211,23x x ==是方cx 2+bx +a =0(a ≠0)的根,其中正确的是_____(填序号). 17.如图,四边形ACDE 是证明勾股定理时用到的一个图形,a ,b ,c 是Rt ABC 和Rt BED 边长,易知2=AE c ,这时我们把关于x 的形如220++=ax cx b 的一元二次方程称为“勾系一元二次方程”.若1x =-是“勾系一元二次方程”220++=ax cx b 的一个根,且2ABC S =,则四边形ACDE 的周长是_________.18.已知m ,n 是一元二次方程230x x --=的两个实数根,则代数式2219m n +-的值为________.19.已知2x =是方程220x bx +-=的一个根,则方程的另一个根为____.20.已知关于x 的一元二次方程22(1)210k x x k --+-=有一个根为0,则k =________.三、解答题21.快手、抖音等各大娱乐APP 软件深受人们的喜爱,但随着电商时代的热潮,曾经以直播、娱乐为主的主播也开始转型为带货主播.某快手主播,从今年九月份开始直播带货,并深受粉丝的喜爱,并从十月份该主播就开始盈利36000元,十二月的盈利达到43560元,且从十月到十二月,每月的盈利的平均增长率都相同.(1)求每月盈利的平均增长率;(2)按照这个平均增长率,预计下个月(即元月份)该主播的盈利将达到多少元? 22.用适当的方法求解下列方程:(1)2210x x --=;(2)2(4)5(4)x x +=+.23.解方程:(1)2210x x +-=; (2)3(1)2(1)x x x -=-.24.若关于x 的方程(3)(2)x x p --=有两个不相等的实数根,求p 的取值范围. 25.“黄冈名师课堂”是集黄冈众多名师的网络课堂,自上线以来受到了广大师生,家长和社会各界的好评.经统计,2020年10月在线听课的学生为66250人次,12月在线听课学生增加至95400人次.若10月至12月,每月在线听课人数平均增长率相同.(1)求每月的平均增长率;(2)按照这个平均增长率,预计2021年1月在线听课的人次将会达到多少?26.(1)解方程:2650x x +-=;(2)阅读下解方程的过程,并解决问题:解:方程右边分解因式,得3(5)2(5)-=-x x x …………………(第一步)方程变形为3(5)2(5)x x x -=--……………………………(第二步)方程两边都除以5x -,得32x =-…………………………………(第三步) 解,得23x =-.………………………………………………………(第四步) ①上述解方程的过程从第______步开始出错,具体的错误是______.②请直接写出方程的根______.【参考答案】***试卷处理标记,请不要删除一、选择题1.C解析:C【分析】根据一元二次方程的性质,先提公因式,通过计算即可得到答案.【详解】移项得,x 2-2x =0,提公因式得,x (x-2)=0,解得,x 1=0,x 2=2,故选:C .【点睛】本题考查了一元二次方程的知识;解题的关键是熟练掌握一元二次方程的性质,从而完成求解.2.B解析:B【分析】在方程的两边同时加上一次项系数一半的平方,化成完全平方的形式即可得出答案.【详解】解:x 2+4x=3,x 2+4x+4=7,(x+2)2=7,故选:B .【点睛】此题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键;配方法的一般步骤:(1)把常数项移到等号的右边;(2)把二次项的系数化为1;(3)等式两边同时加上一次项系数一半的平方.3.D解析:D【分析】设有x个队参赛,根据参加一次足球联赛的每两队之间都进行两场场比赛,共要比赛90场,可列出方程.【详解】解:设有x个队参赛,则x(x﹣1)=90.故选:D.【点睛】本题考查由实际问题抽象出一元二次方程,关键是根据总比赛场数做为等量关系列方程求解.4.C解析:C【分析】设该药品平均每次降价的百分率为x,根据题意列方程求解即可.【详解】解:设该药品平均每次降价的百分率为x,根据题意得,250(1-x)2=160,解得,x1=0.2,x2=1.8(舍去),答:该药品平均每次降价的百分率为20%;故选:C.【点睛】本题考查了一元二次方程的应用—增长率(或下降率)问题,解题关键是熟知增长率(或下降率)问题的数量关系,结合题意列方程.5.C解析:C【分析】先把方程(x−3)(x+2)=p2化为x2−x−6−p2=0,再根据△=25+4p2>0可得方程有两个不相等的实数根,由−6−p2<0即可得出结论.【详解】方程(x−3)(x+2)=p2可化为x2−x−6−p2=0,∴b2−4ac=25+4p2>0,∴方程有两不相等的实数根,设方程两根为x1、x2,∵x1•x2=−6−p2<0,∴方程有一个正根,一个负根,故选C.本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=ba-,x1x2=ca,也考查了根的判别式.6.C解析:C【分析】根据题意,画出方程x2-3x-10=0,即x(x-3)=10的拼图过程,由面积之间的关系可得出答案.【详解】解:方程x2-3x-10=0,即x(x-3)=10的拼图如图所示;中间小正方形的边长为x-(x-3)=3,其面积为9,大正方形的面积:(x+x-3)2=4x(x-3)+9=4×10+9=49,其边长为7,因此,C选项所表示的图形符合题意,故选:C.【点睛】本题考查完全平方公式的几何背景,通过图形直观,得出面积之间的关系,并用代数式表示出来是解决问题的关键.7.B解析:B【分析】利用列方程解应用题,仔细阅读试题,找出等量关系为:站点数×每站票数(比站点数少1)=总票数,列方程即可.【详解】设这段线路有x个站点,每个站点售其它各站一张往返车票,共有(x-1)张票,根据题意,列方程得()1132x x-=.故选择:B.【点睛】本题考查列方程解应用题,掌握列方程解应用题的方法,抓住等量关系站点数×每站票数(比站点数少1)=总票数是解决问题的关键.8.A【分析】先把方程变形为x 2-4x=-2,再把两方程两边加上4,然后把方程左边用完全平方公式表示即可.【详解】解:x 2-4x=-2,x 2-4x+4=2,(x-2)2=2.故选:A .【点睛】本题考查了解一元二次方程-配方法:将一元二次方程配成(x+m )2=n 的形式,再利用直接开平方法求解,这种解一元二次方程的方法叫配方法.9.D解析:D【分析】根据题意生产口罩月平均增长的百分率为x ,四月份生产了口罩200000只,第二季度总共生产728000只口罩,由此列出方程即可.【详解】解:设生产口罩月平均增长的百分率为x ,四月份生产了口罩200000只,∴五月份生产了口罩()2000001x +只,∴六月份生产了口罩()22000001+x 只, 又在第二季度四、五、六3个月总共生产了728000只口罩, ∴列式为:()()2200000+2000001+2000001+728000x x +=.故选:D .【点睛】此题考查一元二次方程的实际应用问题,属于增长率问题,根据题意列出等式是解决本题的关键.10.A解析:A【分析】因为游泳池的长为xm ,那么宽可表示为(x-10)m ,根据面积为300,即可列出方程.【详解】解:因为游泳池的长为xm ,那么宽可表示为(x-10)m ;则根据矩形的面积公式:x (x-10)=300;故选:A .【点睛】本题考查了一元二次方程的应用,掌握“矩形面积=长×宽”是关键.11.D解析:D【分析】根据开业第一天收入约为2000元,之后两天的收入按相同的增长率增长,第3天收入约为2420元列方程即可得到结论.【详解】设每天的增长率为x ,依题意,得:22000(1)2420x +=.故选:D .【点睛】本题考查了由实际问题抽象出一元二次方程,找准等量关系,正确列出一元二次方程是解题的关键.12.A解析:A【分析】两边配上一次项系数一半的平方,写成完全平方式即可得到答案.【详解】∵29190x x -+=,∴2919x x -=-, 则2818191944x x -+=-+, 即29524x ⎛⎫-= ⎪⎝⎭, 故选:A.【点睛】此题考查配方法解一元二次方程,掌握配方法的计算方法是解题的关键.二、填空题13.-2【分析】由根与系数的关系可得出m +n =2mn =−1将其代入中即可求出结论【详解】解:∵mn 是方程x2−2x−1=0的两实数根∴m +n =2mn =−1∴==−2故答案为:-2【点睛】本题考查了根与系解析:-2【分析】由根与系数的关系可得出m +n =2、mn =−1,将其代入11m n +=m nn m +中,即可求出结论.【详解】解:∵m ,n 是方程x 2−2x−1=0的两实数根,∴m +n =2,mn =−1, ∴11m n +=m n n m +=21-=−2. 故答案为:-2.【点睛】 本题考查了根与系数的关系,牢记两根之和等于−b a 、两根之积等于c a是解题的关键. 14.20【分析】新成本=原成本×(1-平均每月降低的百分率)2把相关数值代入即可求解【详解】∵原开支为2500元设平均每月降低的百分率为x ∴第一个月的开支为2500×(1-x)元第二个月的开支为2500解析:20%【分析】新成本=原成本×(1-平均每月降低的百分率)2,把相关数值代入即可求解.【详解】∵原开支为2500元,设平均每月降低的百分率为x ,∴第一个月的开支为2500× (1-x)元,第二个月的开支为2500×(1-x)×(1-x) =2500×(1-x)2元, 可列方程为:2500(1-x)2= 1600,解得:x=0.2=20%或x =-1.8(舍去)故答案为:20%.【点睛】本题考查求平均变化率的方法.若设变化前的量为a ,变化后的量为b ,平均变化率为x ,则经过两次变化后的数量关系为a (1土x) 2=b.15.14【分析】运用因式分解法解一元二次方程求出两根因为三角形是等腰三角形分情况讨论:腰为2时和腰为6时再利用三角形三边关系验证是否符合题意即可求出周长;【详解】解:(x-2)(x-6)=0x1=2x2解析:14【分析】运用因式分解法解一元二次方程,求出两根,因为三角形是等腰三角形,分情况讨论:腰为2时和腰为6时,再利用三角形三边关系验证是否符合题意,即可求出周长;【详解】解:28120x x -+=,(x-2)(x-6)=0,x 1=2,x 2=6,当腰长为2时,三角形的三边为2,2,6,不符合三角形的三角关系,舍去;当腰长为6时,三角形的三边关系为6,6,2,符合三角形的三角关系,则周长为:6+6+2=14,故答案为:14.【点睛】本题考查因式分解解一元二次方程和三角形的三边关系,求解后验三角形的三边关系是解题的关键.16.①②④【分析】根据一元二次方程根的判别式根与系数的关系解的意义求解【详解】解:①因为a+c =0a≠0所以ac 异号所以△=b2﹣4ac >0所以方程有两个不等的实数根故①正确;②∵x=1时ax2+bx+解析:①②④【分析】根据一元二次方程根的判别式、根与系数的关系、解的意义求解.【详解】解:①因为a +c =0,a ≠0,所以a 、c 异号,所以△=b 2﹣4ac >0,所以方程有两个不等的实数根故①正确;②∵x=1时,ax 2+bx +c =a+b+c ,∴a +b +c =0时,一定有一个根是1,故②正确;③根据b 2﹣6ac >0,不能得到b 2﹣4ac >0,从而不能证得方程ax 2+bx +c =0一定有两个不相等的实数根,故③错误;④∵2和3是ax 2+bx +c =0(a ≠0)的两个根, ∴235,236b c a a -=+==⨯=, ∴51,66b a c c -==, 而115111,236236b a c c+==-⨯==, ∴121123x x ==,是方和cx 2+bx +a =0(a ≠0)的根,故④正确, ∴正确的结论是①②④,故答案为:①②④,【点睛】 本题考查一元二次方程的应用,熟练掌握一元二次方程根判别式的计算与应用、根与系数的关系、解的意义是解题关键.17.12【分析】根据题意可以求得a+b 的值再根据勾股定理可以求得c 的值从而可以求得四边形ACDE 的周长【详解】解:∵x=-1是勾系一元二次方程的一个根∴∴∵S △ABC=2a2+b2=c2∴=2得ab=4解析:12【分析】根据题意可以求得a +b 的值,再根据勾股定理可以求得c 的值,从而可以求得四边形ACDE 的周长.【详解】解:∵x =-1是“勾系一元二次方程”20++=ax b 的一个根,∴0a b -+=, ∴a b +=,∵S △ABC =2,a 2+b 2=c 2, ∴2ab =2,得ab =4, ∴(a +b )2=a 2+2ab +b 2=c 2+2ab =c 2+8,(a +b )2=)222c =,∴c 2+8=2c 2,解得,c =-(舍去),∵四边形ACDE 的周长是:a +b +a +bc c c ==12,故答案为:12.【点睛】本题考查一元二次方程的解、三角形的面积、勾股定理的证明,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.18.【分析】根据m 与n 是方程的两个实数根得到根与系数关系式原式变形后代入计算即可求出值【详解】解:∵mn 是一元二次方程x2﹣x ﹣3=0的两个实数根∴m+n =1mn =-3∵(m+n)2=m2+n2+2mn解析:12-【分析】根据m 与n 是方程的两个实数根,得到根与系数关系式,原式变形后代入计算即可求出值.【详解】解:∵m ,n 是一元二次方程x 2﹣x ﹣3=0的两个实数根,∴m+n =1,mn =-3,∵(m+n)2=m 2+n 2+2mnm 2+n 2=(m+n)2-2mn∴m 2+n 2=12-2×(-3)=7∴m 2+n 2-19=7-19=-12故答案为:-12.【点睛】本题考查了一元二次方程的解,根与系数的关系,熟练掌握根与系数的关系是解题的关键.19.【分析】利用一元二次方程的根与系数的关系定理中的两根之积计算即可【详解】设方程的另一个根为x ∵是方程的一个根∴根据根与系数关系定理得2x=-2解得x=-1故答案为:x=-1【点睛】本题考查了已知一元解析:1x =-.【分析】利用一元二次方程的根与系数的关系定理中的两根之积,计算即可.【详解】设方程220x bx +-=的另一个根为x ,∵2x =是方程220x bx +-=的一个根,∴根据根与系数关系定理,得 2x=-2,解得x=-1,故答案为:x=-1.【点睛】本题考查了已知一元二次方程的一个根求另一个根,熟练运用一元二次方程根与系数的关系定理,选择合适的计算方式是解题的关键.20.-1【分析】先根据一元二次方程的解的意义把x=0代入方程求出k=1或-1然后根据一元二次方程的定义确定k 的值【详解】解:把x=0代入方程得k2-1=0解得k=1或k=-1而k-1≠0所以k=-1故答解析:-1【分析】先根据一元二次方程的解的意义把x=0代入方程求出k=1或-1,然后根据一元二次方程的定义确定k 的值.【详解】解:把x=0代入方程得k 2-1=0,解得k=1或k=-1,而k-1≠0,所以k=-1.故答案为:-1.【点睛】本题考查了一元二次方程的解:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.也考查了一元二次方程的定义.三、解答题21.(1)10%;(2)47916元.【分析】(1)设设每月的平均增长率为x ,根据等量关系:十月份盈利额×(1+增长率)2=十二月份的盈利额列出方程求解即可.(2)元月份的盈利=十二月份盈利×增长率.【详解】解:(1)设每月的平均增长率为x .根据题意可知:()236000143560x +=.解得10.1x =,2 2.1x =-(舍去).答:每月的平均增长率为10%.(2)由(1)知:元月份的盈利将达到:()4356011047916⨯+=%元.【点睛】此题主要考查了一元二次方程的应用,属于增长率的问题,一般公式为原来的量×(1±x )2=后来的量,其中增长用+,减少用-,难度一般.22.(1)11x =21x =-2)14x =-,21x =【分析】(1)用公式法解方程即可;(2)用因式分解法解方程即可.【详解】解:(1)这里1a =,2b =-,1c =-∵()()224241180b ac -=--⨯⨯-=>,∴1x ==即11x =+21x =-(2)∵()()2454x x +=+,∴()()24540x x +-+=, 则()()410x x +-=,∴40x +=或10x -=,解得14x =-,21x =.【点睛】本题考查了一元二次方程的解法,解题关键是根据方程的特点选择恰当的解法解方程.23.(1)11x =-21x =-;(2)11x =,223x =【分析】(1)配方法求解可得;(2)因式分解法求解可得;【详解】(1)解:2212x x ++= 2(1)2x +=1x +=11x ∴=-+21x =-.(2)解:3(1)2(1)0x x x ---=(1)(32)0x x --=10x -=;或320x -=11x ∴=,223x =. 【点睛】本题主要考查解一元二次方程的能力,根据不同的方程选择合适的方法是解题的关键.24.14p >- 【分析】根据根的判别式大于0列不等式即可.【详解】解:(3)(2)x x p --=,化简得,2560x x p -+-=,∵关于x 的方程(3)(2)x x p --=有两个不相等的实数根,∴()2425460b ac p -=-->, 解得,14p >-. 【点睛】 本题考查了一元二次方程根的判别式,解题关键是熟知一元二次方程有两个不相等的实数根时,判别式大于0.25.(1)20%;(2)114480人【分析】(1)设该每月平均增长率为x ,根据等量关系:10月份在线听课的学生人次×(1+增长率)2=12月份在线听课学生人次,列出方程求解即可;(2)1月份在线听课的人次=12月份在线听课的人次×增长率列式计算即可.【详解】(1)解:设每月的平均增长率为x ,由题意得:266250(1)95400x +=,解得:10.2x =,2 2.2x =-(舍).答:月平均增长率为20%.(2)95400(120%)114480+=(人)答:按照这个平均增长率,预计2021年1月在线听课的人次将会达到114480人.【点睛】此题主要考查了一元二次方程的应用,属于增长率的问题,一般公式为原来的量×(1±x )2=后来的量,其中增长用+,减少用﹣.26.(1)13x =-23x =-;(2)①三,方程两边都除以不能确定其值是否为零的代数式()5x -;②15=x ,223x =-. 【分析】(1)用公式法求解即可;(2)根据一元二次方程的解法逐步分析即可;【详解】解:(1)这里1a =,6b =,5c =-,∴224641(5)560-=-⨯⨯-=>b ac ,3∴===-±x13∴=-x 23x =-(2)①三,方程两边都除以不能确定其值是否为零的代数式()5x -,②方程右边分解因式,得3(5)2(5)-=-x x x ,移项,得3(5)2(5)0x x x ---=,分解因式,得()(5)320x x -+=,∴x-5=0,3x+2=0,∴15=x ,223x =-. 【点睛】本题考查了一元二次方程的解法,常用的方法有直接开平方法、配方法、因式分解法、求根公式法,熟练掌握各种方法是解答本题的关键.。
山东省泰安市新泰市2023-2024学年九年级上学期期中数学试题(含答案)

九年级上学期期中检测数学试题本试题分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共8页,满分150分.考试时间120分钟.注意事项:1.答题前,请考生仔细阅读答题卡上的注意事项,并务必按照相关要求作答.2.考试结束后,监考人员将本试卷和答题卡一并收回.第Ⅰ卷(选择题 共48分)一、选择题(本大题共12小题,在每小题给出的选项中,只有一个是正确的,请把正确的选项选出来,每小题选对得4分,选错、不选或选出的答案超过一个,均记零分)1的值等于()A .BC .3D2.若点是反比例函数图象上一点,则此函数图象一定经过点( )A .B .C .D .3.如图,在Rt 中,于点,下列结论正确的是()A .B .C .D .4.已知二次函数,则关于该函数的下列说法正确的是( )A .该函数图象与轴的交点坐标是B .当时,的值随值的增大而减小C .当取0和2时,所得到的的值相同D .当时,有最大值是15.已知三个点在反比例函数的图象上,其中,下列结论中正确的是()A .B .C .D .60︒32(2,3)ky x=(2,3)-(3,2)-(1,6)-(1,6)--ABC △90,BAC AD BC ∠=︒⊥D sin CD C AC=sin AB C BC=sin AD C DC=sin AD C AB=2(1)1y x =-+y (0,1)1x >y x x y 1x =y ()()()112233,,,,,x y x y x y 6y x=1230x x x <<<312y y y <<123y y y <<132y y y <<213y y y <<6.如图,一次函数与反比例函数的图象交于点,过点作轴于点,连接OP ,下列结论错误的是()A .B .C .的面积是3D .点在上,当时,7.如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为31°,缆车速度为每分钟40米,从山脚下A 到达山顶B 缆车需要15分钟,则山的高度BC 为()A .米B.米C .米D .米8.已知二次函数的图象如图所示,则一次函数的图象大致为()A .B .C .D .9.函数的共同性质是( )A .它们的图象都经过原点B .它们的图象都不经过第二象限C .在的条件下,都随的增大而增大D .在的条件下,都随的增大而减小10.如图,一辆小车沿着坡度为的斜坡向上行驶了100米,则此时该小车上升的高度为()1y kx =+6(0)y x x=>(2,)P t P PA x ⊥A 3t =1k =OAP △(,)B m n 6(0)y x x=>2m >n t >600si *n 31︒600tan 31︒600*tan 31︒600sin 31︒2(0)y ax bx a =+≠(0)y ax b a =+≠212,,y x y y x x=-==-0x >y x 0x >y x 1:i =A .50米B .米C .米D .100米11.如图,在中,,则的长为( )A .3BC .D .412.新定义:在平面直角坐标系中,对于点,当点满足时,称点是点的“关联点”.已知点,有下列结论:①点都是点的“关联点”;②若直线上的点是点的“关联点”,则点的坐标为;③抛物线上存在两个点是点的“关联点”;其中,正确结论的个数是( )A .0B .1C .2D .3第Ⅱ卷(非选择题 102分)二、填空题(每小题4分,共24分,只要求填最后结果)13.若则锐角∠A =_______°.14.在温度不变的条件下,通过一次又一次地对汽缸顶部的活塞加压,加压后气体对汽缸壁所产生的压强p (kPa )与汽缸内气体的体积V (mL )成反比例,p 关于V 的函数图象如图所示,若压强由75kPa 加压到100kPa ,则气体体积压缩了_______mL .15.如图,在Rt △ABC 中,∠ABC =90°,BD ⊥AC 于点D ,AC =10,,那么AD =_______.ABC △35,2,sin 5AB BC B ===AC ()11,P x y ()22,Q x y ()12122x x y y +=+()22,Q x y ()11,P x y 1(1,0)P 12(4,10),(2,4)Q Q --1P 2y x =+A 1P A (0,2)223y x x =--1P 1cos 2A =3cos 5C =第15题图16.如图,点A 是反比例函数的图象上的一点,过点A 作AB ⊥x 轴,垂足为B ,点C 为y 轴上的一点,连接AC ,BC .若△ABC 的面积为6,则k 的值是_______.第16题图17.某商厦将进货单价为70元的某种商品,按销售单价100元出售时,每天能卖出20个,通过市场调查发现,这种商品的销售单价每降价1元,日销量就增加1个,为了获取最大利润,该种商品的销售单价应降_______元.18.如图,抛物线与直线y =mx +n 交于A (-1,p ),B (3,q )两点,则不等式的解集是_______.三、解答题(本题共7个小题,共78分,解答题写出文字说明、证明过程或推演步骤)19.(9分)如图,在△ABC 中,BD ⊥AC ,AB =6,,∠A =30°.①求BD 和AD 的长;ky x=2y ax c =+2ax mx c n -+>AC =②求tan C 的值.20.(10分)求二次函数在范围内的最小值和最大值.21.(10分)在一座小山山顶建有与地平线垂直的电视发射塔AB .为测量该小山的铅直高度,某数学兴趣小组在地平线上的C 处测得电视发射塔顶A 的仰角为45°,后沿地平线向山脚方向行走20米到达D 处,在D 处测得电视发射塔的底部B 的仰角为30°,如图,若电视发射塔的高度AB 为60米,测角仪的高度忽略不计,求小山的铅直高度(精确到1米))22.(10分)如图,一次函数y =ax +b 与反比例函数的图象交于点A (1,3),B (m ,-1).(1)求反比例函数和一次函数的表达式.(2)根据图象,当x 取何值时,一次函数的值大于反比例函数的值?23.(12分)2023年杭州亚运会在我国成功举办.如图,城市广场上一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA ,,从A 处向外喷出的水流在各个方向上沿形状相同的抛物线路径落下,王芳同学根据题意在图中建立如图所示的坐标系,水流喷出的高度y (m )与水平距离x (m )之间的关系式是y =ax 2+bx +c (x >0),已知水流的最高点到OA 的水平距离是,最高点离水面是.(1)求二次函数表达式;(2)若不计其他因素,水池的半径至少为多少米,才能使喷出的水流不至于落在池外?24.(13分)小明在阅读了九上数学课本21页“读一读”《换一个角度看》后,组织了数学建模小组在综合实践课上探究面积为4,周长为m 的矩形问题.发现矩形的面积与周长存在一定的关系,在解决此问题时既可以采用“代数”的方法解决,但也可以从“图形”的角度来研究它.构建模型223y x x =--03x ≤≤ 1.41= 1.73=ky x=1m 2OA =1m 49m 16(1)当m =10时,设矩形的长和宽分别为x ,y ,则xy =4,2(x+y )=10,满足要求的(x ,y )可以看成反比例函数(x >0)的图象与一次函数y =-x +5在第一象限内的交点坐标,从图①中观察到,交点坐标为_______,即满足当矩形面积为4时,周长是10的矩形是存在的;问题探究(2)根据(1)的结论,当xy =4,2(x +y )=m 时,满足要求的(x ,y ),可以看成反比例函数(x >0)的图象与一次函数的_______交点坐标,而此一次函数图象可由直线y =-x 平移得到,请在图②的平面直角坐标系中直接画出直线y =-x .当直线平移到与反比例函数的图象有唯一交点时,周长m 的值为_______;拓展应用(3)写出周长m 的取值范围.图① 图②25.(14分)如图,在平面直角坐标系中,直线l 与x 轴交于点A (6.0),与轴交于点B (0,-6),抛物线经过点A ,B ,且对称轴是直线x =1.(1)求直线l 的解析式;(2)求抛物线的解析式;(3)点P 是直线l 下方抛物线上的一动点,过点P 作PC ⊥x 轴,垂足为C ,交直线l 于点D ,过点P 作PM ⊥l ,垂足为M的最大值及此时P 点的坐标.九年级上学期期中检测数学参考答案1.C 2.D 3.B 4.C 5.C 6.D 7.A 8.C 9.D 10.A 11.B 12.D 13.60 14.20 15. 16. 17.5 18.x <-1或x >319.(9分)解:(1)∵BD ⊥AC ,∠ADB =90°,在Rt △ADB 中,AB =6,∠A =30°,4y x=4y x=PD +32512-∴,;(2),在Rt 中,20.(10分)解:,∴抛物线的对称轴为x =1,顶点坐标为(1,4),∵,∴当x =1时,取得最小值y =-4;当x =3时,取得最大值y =021.(10分)解:延长AB 交直线CD 于点E ,由题意得,CD =20米,AB =60米,∠ACE =45°,∠BDE =30°,∠AEC =90°,设BE =x 米,则AE =(60+x)米,在Rt △BDE 中,,经检验,是原方程的解且符合题意,∴米,在Rt △ACE 中,∵∠ACE =45°,∴AE =CE ,∴,解得.∴小山的铅直高度约为55米.22.(10分)解:(1)将代入得:,则反比例解析式为,将代入,得:,,将与坐标代入中,得:,解得:,则一次函数解析式为;(2)观察图象,当或时,一次函数的值大于反比例函数的值.23.(12分)解:(1)水流的最高点到OA 的水平距离是,最高点离水面是,132BD AB ==AD ∴==CD AC AD =-=-=BCD △tan BD C CD ∠===2223(1)4y x x x =--=-- 03x ≤≤tan 30BE x DE DE ︒===DE =DE =()20CE =6020x +=55x =≈(1,3)A ky x=3k =3y x =(,1)B m -3y x=3m =-(3,1)B ∴--A B y ax b =+331a b a b +=⎧⎨-+=-⎩12a b =⎧⎨=⎩2y x =+30x -<<1x > 1m 491m,m 162OA =拋物线的顶点坐标为故设抛物线的解析式为,,解得,拋物线的解析式为,拋物线的解析式为.(2)令得到,解得(舍去),故水池的半径至少为1米.24.(13分)解:(1)根据图象可得,交点为,故答案为:;(2),当时,,,解得,反比例函数的图象与一次函数有一个交点,故答案为:,8;(3)由(2)可得.图②25.(14分)解:(1)设直线的解析式为,∵直线l 与x 轴交于点A (6.0),与y 轴交于点B (0,-6),,解得:,∴191,,0,4162A ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭219416y a x ⎛⎫=-+ ⎪⎝⎭211902416a ⎛⎫∴=-+ ⎪⎝⎭1a =-∴219416y x ⎛⎫=--+ ⎪⎝⎭∴21122y x x =-++0y =211022x x -++=12112,x x ==(1,4)(4,1)、(1,4)(4,1)、2()x y m += 1, 2y x m ∴=-+142x x m -+=21402x mx -+=211604m ∴∆=-=8m =± 4(0)y x x =>12y x m =-+8,m ∴=12y x m =-+8m ≥l (0)y mx n m =+≠606m n n +=⎧∴⎨=-⎩16m n =⎧⎨=-⎩直线的解析式为;(2)设抛物线的解析式为,抛物线的对称轴是直线,,抛物线经过点,解得:,抛物线的解析式为;(3)∵A (6,0),B (0,-6),∴OA =OB =6,在△AOB 中,∠AOB =90°,∴∠OAB =∠OBA =45°∵PC ⊥x 轴,PM ⊥l ,∴∠PCA =∠PND =90°,在Rt △ADC 中,∵∠PCA =90°,∠OAB =45°,∴∠ADC =45°,∴∠PDM =∠ADC =45°,在Rt △PMD 中,∠PMD =90°,∠PDM =45°,设点,,当时,有最大值是最大,的最大值为,当时,的最大值为,此时点.∴l 6y x =-2()(0)y a x h k a =-+≠ 1x =2(1)y a x k ∴=-+ 250,,6a k A B a k +=⎧∴⎨+=-⎩14254a k ⎧=⎪⎪⎨⎪=-⎪⎩∴2125(1)44y x =--sin 45,, 2 PD. PM PM PD PD PD ∴︒=∴=+=2212511(1)6,4442y x x x =--=--∴ 211,6,(,6)42P t t t D t t ⎛⎫--∴- ⎪⎝⎭22211131966(3)424244PD t t t t t t ⎛⎫∴=----=-+=--+ ⎪⎝⎭10,4-<∴ 3t =PD 94PD +PD +923t =211112121,6936,3,424244t t P ⎛⎫--=⨯-⨯-=-∴- ⎪⎝⎭PD +92213,4P ⎛⎫- ⎪⎝⎭。
【沪粤版】初中物理九年级全册期中试卷含答案

一、选择题1.小刚利用电能表测量某家用电器的电功率。
当电路中只有这个用电器工作时,测得15min 内,消耗电能 0.3kW·h,则这个用电器可能是()A.空调器B.电冰箱C.电视机D.收音机2.如图所示的电路中,移动滑动变阻器的滑片,电压表的示数从6V变为5V,电流表的示数变化了0.2A.则该定值电阻所消耗功率的变化量为A.0.2WB.1.0WC.1.2WD.2.2W3.某家用电器正常工作时,通过的电流大约为5A,该用电器可能是A.电视机B.白炽灯C.洗衣机D.空调4.冬季室内用的某款超声波加湿器如图所示,图为其内部湿度监测装置的简化电路图,湿敏电阻R的阻值随环境湿度变大而变大。
已知电源两端的电压不变,R0为定值电阻。
闭合开关,当环境湿度增大时,下列判断中正确的是()A.R的阻值减小,电流表示数变大B.R的阻值增大,电压表示数变大C.电压表示数变小,电流表示数变小D.电路消耗总功率变大5.在国际单位制中,电压的单位是()A.安培B.伏特C.焦耳D.库仑6.如图所示的电路中,电源两端的电压保持不变,闭合开关S,将滑动变阻器的滑片P向右移,下列说法中错误的是()A.电流表A的示数变小B.电压表V l的示数不变C.电压表V2的示数变大D.电压表V l与电压表V2的示数之和保持不变7.某同学用一个有0~3 V和0~15 V两个量程的电压表测某电路两端的电压,用的是0~3V量程,但记录的读数却是6.5 V,则该同学实际测的电压值最可能是()A.1.3 V B.2.5 V C.5 V D.12.5 V8.如图甲所示的电路中,当闭合开关后,两个电压表指针偏转均如图乙所示,则电灯L1和L2两端的电压之比为()A.4∶1B.1∶4C.1∶5D.5∶19.如图所示,将两个表面光滑的铅块相互挤压后会粘在一起,以下现象与该实验原理相同的是()A.墨汁滴在热水中很快散开B.两个吸盘挤压后吸在一起C.折断一根铁丝需要很大力D.毛皮和橡胶棒吸引在一起10.下列现象中,不能说明分子在不停地做无规则运动的是()A.海绵能够吸收水B.水中加糖会变甜C.八月闻到桂花香D.鸭蛋裹上食盐的泥巴后变成咸蛋11.端午佳节,人们常食用盐蛋。
2020-2021学年人教版九年级数学上册教案-21.1一元二次方程11-

(五)总结回顾(用时5分钟)
今天的学习,我们了解了一元二次方程的基本概念、解法以及它在实际中的应用。通过实践活动和小组讨论,我们加深了对一元二次方程的理解。我希望大家能够掌握这些知识点,并在解决实际问题时灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“一元二次方程在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
(一)导入新课(用时5分钟)
同学们,今天我们将要学习的是《一元二次方程》这一章节。在开始之前,我想先问大家一个问题:“你们在日常生活中是否遇到过需要解决两个未知数的关系问题?”(如物品的成本和销售价格问题)这个问题与我们将要学习的内容密切相关。通过这个问题,我希望能够引起大家的兴趣和好奇心,让我们一同探索一元二次方程的奥秘。
在学生小组讨论后,成果分享环节也让我看到了一些亮点和不足。亮点在于,学生们能够将所学的知识应用到实际问题中,并提出自己的见解。不足之处在于,他们在表达和逻辑推理上还有待加强。我考虑在未来的教学中,应该更多地提供机会让学生们进行口头表达和逻辑思维的训练。
另一个让我注意到的问题是,在小组讨论环节,有些学生显得不够积极主动。我想,或许我应该在分组时更加注意学生性格和能力上的搭配,确保每个小组成员都能参与到讨论中来,充分发挥每个学生的作用。
安徽省六安市第九中学2024-2025学年九年级上学期11月期中数学试题

安徽省六安市第九中学2024-2025学年九年级上学期11月期中数学试题一、单选题1.将二次函数212y x =-的图象向右平移2个单位,则平移后的二次函数的表达式为()A .2122y x =--B .2122y x =-+C .()2122y x =-+D .()2122y x =--2.已知反比例函数y =23k x -(k 为常数)的图象在第一、三象限,那么k 的取值范围()A .k >23B .k <23C .k >32D .k <323.如图,在同一坐标系中,二次函数2y ax c =+与一次函数y ax c =+的图象大致是()A .B .C .D .4.如图,嘉嘉要测量池塘两岸A ,B 两点间的距离,先在AB 的延长线上选定点C ,测得5m BC =,再选一点D ,连接AD ,CD ,作BE AD ∥,交CD 于点E ,测得8=CD m ,4m DE =,则AB =()A .3mB .4mC .5mD .6m5.如图,D 是ABC V 的边A 上一点,下列条件:①ACD B ∠=∠;②2AC AD AB =⋅;③BC AB CD AC =;④ACB ADC ∠=∠.其中一定使ABC ACD ∽的有()A .1个B .2个C .3个D .4个6.某个亮度可调节的台灯,其灯光亮度的改变,可以通过调节总电阻控制电流的变化来实现.如图所示的是该台灯的电流/A I .与电阻()ΩR 的关系图象,该图象经过点()8800.25P ,.根据图象可知,下列说法正确的是()A .当0.25I <时,880R <B .I 与R 的函数关系式是()2000I R R=>C .当1000R >时,0.22I >D .当8801000R <<时,I 的取值范围是0.220.25I <<7.如图,小正方形边长均为1,则下列图形中三角形(阴影部分)与△ABC 相似的是A .B .C .D .8.若点(),m n 在抛物线()20y ax a =>上,其中0m >,则不等式()22a x n ->的解为()A .2x m <-+或2x m >+B .22m x m -+<<+C .2x m <--或2x m >-D .22m x m --<<-9.如图,在Rt ABC △中,90B Ð=°,点P 在边AC 上,过P 画直线截ABC V 使截得的三角形与ABC V 相似,这样的直线最多可画()A .1条B .2条C .3条D .4条10.在自变量x 的取值范围内,对于自变量x a =时,函数值y a =,则称a 是函数的一个不动点,若函数()2231=+-+y kx k x 恰有一个不动点,则实数k 的值不可能是()A .1-B .0C .1D .4二、填空题11.如果35x y y -=,那么x y 的值为.12.已知点M 是线段AB 的黄金分割点AM BM <(),若4AB =,则BM =.13.如图,在平面直角坐标系中,直线()10y ax b a =+≠与双曲线()20k y k x=≠交于点()1,A m -,()2,1B -.则满足12y y ≤的x 的取值范围.14.如图,ABC ADE △△∽,90BAC DAE ∠=∠=︒,3AB =,4AC =,点D 是线段BC 上一动点,若点D 从点B 开始向点C 运动.(1)当2BD =时,CE =;(2)设P 为线段DE 的中点,在点D 的运动过程中,CP 的最小值是.三、解答题15.如果345a b c ==,且3212a b c -+=,求a b c -+的值.16.已知抛物线2142y x x =--+.(1)用配方法求它的顶点坐标、对称轴;(2)x 取何值时,y 随x 增大而减小?(3)x 取何值时,抛物线在x 轴上方?17.如图,在平面直角坐标系中,ABC V 的顶点坐标分别为()2,2A -,()4,0B -,()4,4C --,在y 轴右侧,以原点O 为位似中心画一个A B C ''' ,使它与ABC V 位似,且相似比是1:2.(1)请画出A B C ''' ;(2)请直接写出A B C ''' 各顶点的坐标;(3)若ABC V 内部一点M 的坐标为(),a b ,则点M 的对应点M '的坐标是___________.18.掷实心球是攀枝花市高中阶段学校招生体育考试的必考项目.如图1是一名女生投实心球,实心球行进路线是一条抛物线,行进高度()m y 与水平距离()m x 之间的函数关系,如图2所示,掷出时起点处高度为5m 3,当水平距离为3m 时,实心球行进至最高点3m 处.(1)求y 关于x 的函数表达式;(2)根据攀枝花市高中阶段学校招生体育考试评分标准(女生),投掷过程中,实心球从起点到落地点的水平距离大于等于7.80m ,此项考试得分为满分15分.该女生在此项考试中是否得满分,请说明理由.19.如图,小亮想利用树影测量树高AB ,他在某一时刻测得高为1m 的竹竿影长为1.2m ,但当他马上测量树影时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子在墙上,他先测得留在墙上的影高 1.4m CD =,又测得地面部分的影长 4.8m BD =,请你帮助小亮求树高AB .20.有一块三角形的余料ABC V ,它的面积是220cm ,边8cm BC =,要把它加工成一个矩形,使矩形的一边EF 落在BC 上,其余两个顶点DG 分别在,AB AC 上,且2=DG DE ,求矩形的面积.21.已知抛物线22y x mx m =-+-.(1)求证:无论m 为何值,此抛物线与x 轴总有两个不同的交点;(2)若直线122y x =-经过该抛物线的最低点,求抛物线的解析式.22.已知:如图,BE 、CF 是ABC V 的两条高.(1)求证:AEF ABC △△∽.(2)若60A ∠=︒,求:AEF ABC S S △△的值.23.如图,在ABC V 中,10AB AC ==,12BC =,点P 是BC 边上的一个动点(不与点B ,C 重合),点D 是AC 边上的一个动点,且APD B ∠=∠.(1)求证:ABP PCD ∽△△;(2)当点P 为BC 中点时,求CD 的长;(3)当APD △为等腰三角形时,请直接写出BP 的长.。
长沙市九年级数学上册第一单元《一元二次方程》测试题(含答案解析)

一、选择题1.某超市今年1月份的营业额为50万元,已知2月至3月营业额的月增长率是1月至2月营业额的月增长率的2倍,3月份的营业额是66万元,设该超市1月至2月营业额的月增长率为x ,根据题意,可列出方程( )A .()50166x +=B .()250166x +=C .()2501266x += D .()()5011266x x ++= 2.已知一元二次方程2210x x --=的两个根分别是1x ,2x ,则2112x x x -+的值为( ).A .-1B .0C .2D .3 3.关于x 的一元二次方程()25410a x x ---=有实数根,则a 满足( ). A .5a ≠ B .1a ≥且5a ≠ C .1a ≥D .1a <且5a ≠4.若整数a 使得关于x 的一元二次方程()2210a x -+=有两个实数根,并且使得关于y 的分式 方程32133ay y y y -+=--有整数解,则符合条件的整数a 的个数为( ) A .2 B .3C .4D .5 5.用配方法解方程23620x x -+=时,方程可变形为( )A .21(3)3x -=B .21(1)33x -=C .21(1)3-=xD .2(31)1x -=6.某商品经过连续两次降价,售价由原来的每件100元降到每件64元,则平均每次降价的百分率为( )A .15%B .40%C .25%D .20% 7.若关于x 的一元二次方程260x x c -+=有两个相等的实数根,则常数c 的值为( )A .3B .6C .8D .9 8.下列方程是关于x 的一元二次方程的是( )A .212x x x -=B .2(2)x x x -=C .23(2)x x =+D .20ax bx c ++=9.若关于x 的方程(m ﹣1)x 2+mx ﹣1=0是一元二次方程,则m 的取值范围是( ) A .m ≠1 B .m =1 C .m ≥1 D .m ≠010.下列关于x 的一元二次方程中,有两个不相等的实数根的方程是( ) A .290x += B .24410x x -+= C .210x x ++= D .210x x +-=11.一元二次方程x 2=4x 的解是( )A .x=4B .x=0C .x=0或-4D .x=0或4第II 卷(非选择题)请点击修改第II 卷的文字说明参考答案12.一元二次方程x (x ﹣2)=x ﹣2的解是( )A .x 1=x 2=0B .x 1=x 2=1C .x 1=0,x 2=2D .x 1=1,x 2=2二、填空题13.一元二次方程(x +2)(x ﹣3)=0的解是:_____.14.某小区2019年的绿化面积为3000m 2,计划2021年的绿化面积为4320m 2,如果每年绿化面积的增长率相同,那么这个增长率是_________.15.用因式分解法解关于x 的方程 260x px --=,将左边分解因式后有一个因式为3x -,则的p 值为_______16.若关于x 的一元二次方程()23x c -=有实根,则c 的值可以是_________________.(写出一个即可)17.一元二次方程()10x x -=的根是________________________.18.一元二次方程x 2=2x 的解为__________19.“新冠肺炎”防治取得战略性成果.若有一个人患了“新冠肺炎”,经过两轮传染后共有16个人患了“新冠肺炎”,则每轮传染中平均一个人传染了______人.20.为解决民生问题,国家对某药品价格分两次降价,该药品的原价是48元,降价后的价格是30元,若平均每次降价的百分率均为x ,可列方程.为____________. 三、解答题21.在国家的调控下.某市商品房成交价由今年8月份的50000元2/m 下降到10月份的40500元2/m .(1)同8~9两月平均每月降价的百分率是多少?(2)如果房价继续回落,按此降价的百分率,你预测到12月份该市的商品房成交均价是否会跌破30000元/2m ?请说明理由.22.解下列方程(1)22(4)216x x +=-;(2)22x x =+.23.解方程:(1)()2316x -=(2)22410x x --=(用公式法解)24.已知关于x 的方程()22120x k x k ---=,求证:不论k 取何值,这个方程都有两个实数根.25.请回答下列各题:(1)先化简,再求值:2319369x x x x x x x +--⎛⎫-÷ ⎪--+⎝⎭,其中x = (2)已知关于x 的方程2320x x m +-=没有实数根,求实数m 的取值范围. 26.解下列方程:(1)x (x -1)=1-x(2)(x-3) 2 = (2x-1) (x +3)【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】根据2月份的营业额=1月份的营业额×(1+x ),3月份的营业额=2月份的营业额×(1+2x ),把相关数值代入即可得到相应方程.【详解】解:∵1月份的营业额为50万元,2月份的营业额比1月份增加x ,∴2月份的营业额=50×(1+x ),∴3月份的营业额=50×(1+x )×(1+2x ),∴可列方程为:50(1+x )(1+2x )=66.故选:D .【点睛】本题考查了由实际问题抽象出一元二次方程中求平均变化率的方法.若设变化前的量为a ,变化后的量为b ,平均变化率为x ,则经过两次变化后的数量关系为a (1±x )2=b .注意先求得2月份的营业额.2.D解析:D【分析】分别根据一元二次方程的根的意义和一元二次方程根与系数的关系分别得到21112210,2x x x x --=+=,变形代入求值即可得到答案.【详解】解:由题意得21112210,2x x x x --=+=,即21121x x -=, ∴原式211122123x x x x =-++=+=.故选:D .【点睛】此题主要考查了一元二次方程的解的根与系数的关系,灵活运用根与系数的关系是解答此题的关键.3.B解析:B【分析】由方程有实数根可知根的判别式b 2-4ac≥0,结合二次项的系数非零,可得出关于a 一元一次不等式组,解不等式组即可得出结论.【详解】解:由已知得:()()()25044510a a -≠⎧⎪⎨--⨯-⨯-≥⎪⎩, 解得:a≥1且a≠5.故选:B .【点睛】本题考查了根的判别式,解题的关键是得出关于a 的一元一次不等式组.本题属于基础题,难度不大,解决该题型题目时,由根的判别式结合二次项系数非零得出不等式组是关键.4.B解析:B【分析】对于关于x 的一元二次方程()2210a x -+=有两个实数根,利用判别式的意义得到a-2≠0且2a+3≥0且△=2-4(a-2)≥0,解不等式组得到整数a 为:-1,0,1,3,4,5;接着解分式方程得到y=61a -,而y≠3,则61a -≠3,解得a≠3,从而得到当a=-1,0,4时,分式方程有整数解,然后求符合条件的所有a 的个数.【详解】 解:∵整数a 使得关于x 的一元二次方程()2210a x -+=有两个实数根, ∴a-2≠0且2a+3≥0且△=2-4(a-2)≥0, ∴31122a -≤≤且a≠2, ∴整数a 为:-1,0,1,3,4,5;去分母得3-ay+3-y=-2y ,解得y=61a -, 而y≠3,则61a -≠3,解得a≠3, 当a=-1,0,4时,分式方程有整数解,∴符合条件的所有a 的个数是3.故选:B .【点睛】本题考查了根的判别式:一元二次方程ax 2+bx+c=0(a≠0)的根与△=b 2-4ac 有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.5.C解析:C【分析】先移项得到2362x x -=-,再把方程两边都除以3,然后把方程两边加上1即可得到()2113x -=. 【详解】移项得:2362x x -=-,二次系数化为1得:2223x x -=-, 方程两边加上1得:222113x x -+=-+, 所以()2113x -=. 故选:C .【点睛】 本题考查了解一元二次方程-配方法,熟练掌握完全平方公式是解本题的关键. 6.D解析:D【分析】设平均每次降价的百分率为x ,根据该商品的原价及经过两次降价后的价格,即可得出关于x 的一元二次方程,解之即可得出结论.【详解】解:设平均每次降价的百分率为x ,依题意,得:100(1-x )2=64,解得:x 1=0.2=20%,x 2=1.8(不合题意,舍去).故选:D .【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键. 7.D解析:D【分析】根据方程有两个相等的实数根结合根的判别式即可得出关于c 的一元一次方程,解方程即可得出结论.【详解】解:260x x c -+=有两个相等的实根,2(6)40c ∴∆=--=,解得:9c =故选:D .【点睛】本题考查了根的判别式以及解一元一次方程,由方程有两个相等的实数根结合根的判别式得出关于c 的一元一次方程是解题的关键.8.C解析:C【分析】根据一元二次方程的定义逐项判断即可得.【详解】A 、方程212x x x -=中的1x不是整式,不满足一元二次方程的定义,此项不符题意; B 、方程2(2)x x x -=可整理为20x -=,是一元一次方程,此项不符题意;C 、方程23(2)x x =+满足一元二次方程的定义,此项符合题意;D 、当0a =时,方程20ax bx c ++=不是一元二次方程,此项不符题意;故选:C .【点睛】本题考查了一元二次方程,熟记一元二次方程的概念是解题关键.9.A解析:A【分析】根据一元二次方程的定义可得m ﹣1≠0,再解即可.【详解】解:由题意得:m ﹣1≠0,解得:m≠1,故选:A .【点睛】本题考查了一元二次方程的定义,注意掌握只含有一个未知数,并且未知数的最高次数是2的整式方程叫一元二次方程.10.D解析:D【分析】分别求出每个方程的根的判别式即可得到方程的根的情况.【详解】A 选项:2049360∆=-⨯=-<,∴该方程没有实数根,故A 错误;B 选项:()244410∆=--⨯⨯=,∴该方程有两个相等的实数根,故B 错误; C 选项:2141130∆=-⨯⨯=-<,∴该方程没有实数根,故C 错误;D 选项:()2141150∆=-⨯⨯-=>,∴方程有两个不相等的实数根,故D 正确; 故选:D.【点睛】此题考查一元二次方程的根的情况,正确求根的判别式的值,掌握一元二次方程的根的三种情况是解题的关键.11.D解析:D【分析】先移项,利用因式分解法解一元二次方程.【详解】解:x 2=4xx 2-4x=0x (x-4)=0x=0或x=4,故选:D.【点睛】此题考查解一元二次方程,直接开平方法,配方法,公式法,因式分解法,根据一元二次方程的特点选择恰当的解法是解题的关键.12.D解析:D【分析】方程x (x ﹣2)=x ﹣2移项后,运用因式分解法可以求得方程的解,本题得以解决.【详解】解:x (x ﹣2)=x ﹣2,移项,得x (x ﹣2)﹣(x ﹣2)=0,提公因式,得(x ﹣2)(x ﹣1)=0,∴x ﹣2=0或x ﹣1=0,解得x =2或x =1.故选:D .【点睛】本题考查解解一元二次方程﹣因式分解法,解题的关键是会利用提公因式法解方程.二、填空题13.x1=﹣2x2=3【分析】利用因式分解法把原方程化为x+2=0或x ﹣3=0然后解两个一次方程即可【详解】(x+2)(x ﹣3)=0x+2=0或x ﹣3=0所以x1=﹣2x2=3故答案为x1=﹣2x2=3解析:x 1=﹣2,x 2=3【分析】利用因式分解法把原方程化为x+2=0或x ﹣3=0,然后解两个一次方程即可.【详解】(x +2)(x ﹣3)=0,x +2=0或x ﹣3=0,所以x 1=﹣2,x 2=3.故答案为x 1=﹣2,x 2=3.【点睛】本题考查了解一元二次方程−因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).14.20【分析】设每年绿化面积的增长率为x 根据该小区2019年及2021年的绿化面积即可得出关于x 的一元二次方程解之取其正值即可得出结论【详解】解:设每年绿化面积的增长率为x 依题意得:3000(1+x )解析:20%【分析】设每年绿化面积的增长率为x ,根据该小区2019年及2021年的绿化面积,即可得出关于x 的一元二次方程,解之取其正值即可得出结论.【详解】解:设每年绿化面积的增长率为x ,依题意,得:3000(1+x )2=4320,解得:x 1=0.2=20%,x 2=-2.2(不合题意,舍去).故答案为:20%.【点睛】本题考查了一元二次方程的应用,找准等量关系,正确列出一元二次方程是解题的关键. 15.1【分析】方法一:根据题意因式分解得到再展开去括号根据恒等式即可求出p 的值;方法二:将代入方程可得一个关于p 的一元一次方程解方程即可得【详解】方法一:由题意得解得则;方法二:由题意得是关于x 的方程的 解析:1【分析】方法一:根据题意因式分解得到26(3)()x px x x a --=-+,再展开去括号,根据恒等式即可求出p 的值;方法二:将3x =代入方程可得一个关于p 的一元一次方程,解方程即可得.【详解】方法一:由题意得,226(3)()(3)3x px x x a x a x a --=-+=+--,3p a ∴-=-,36a -=-,解得2a =,则1p =;方法二:由题意得,3x =是关于x 的方程260x px --=的一个解,则将3x =代入得:23360p --=,解得1p =,故答案为:1.【点睛】本题考查了多项式因式分解的方法、利用因式分解法解一元二次方程,熟练掌握多项式的运算法则和方程的解法是解题关键. 16.1(答案不唯一)【分析】根据非负数的性质可得于是只要使c 的值非负即可【详解】解:若关于的一元二次方程有实根则所以的值可以是1(答案不唯一)故答案为:1(答案不唯一)【点睛】本题考查了一元二次方程的解 解析:1(答案不唯一)【分析】根据非负数的性质可得0c ≥,于是只要使c 的值非负即可.【详解】解:若关于x 的一元二次方程()23x c -=有实根,则0c ≥,所以c 的值可以是1(答案不唯一).故答案为:1(答案不唯一).【点睛】本题考查了一元二次方程的解法,正确理解题意、掌握非负数的性质是关键. 17.【分析】利用因式分解法把原方程转化为x=0或x-1=0然后解两个一次方程即可;【详解】∵∴x=0或x-1=0解得故答案为:【点睛】本题考查了一元二次方程的解法先把方程的右边化为0再把左边通过因式分解解析:120,1x x ==【分析】利用因式分解法把原方程转化为x=0或x-1=0,然后解两个一次方程即可;【详解】∵()10x x -= ,∴ x=0或x-1=0,解得1x =0,21x = ,故答案为:1x =0,21x =【点睛】本题考查了一元二次方程的解法,先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,求解即可;18.0或2【分析】移项后分解因式即可得出两个一元一次方程求出方程的解即可【详解】解:x2=2xx2-2x=0x (x-2)=0x=0x-2=0x=0或2故答案为:0或2【点睛】本题考查了解一元二次方程的应解析:0或2.【分析】移项后分解因式,即可得出两个一元一次方程,求出方程的解即可.【详解】解:x 2=2x ,x 2-2x=0,x (x-2)=0,x=0,x-2=0,x=0或2.故答案为:0或2.【点睛】本题考查了解一元二次方程的应用,解此题的关键是能把一元二次方程转化成一元一次方程,难度适中.19.3【分析】设每轮传染中平均一个人传染了人则第一轮共有人患病第二轮后患病人数有人从而列方程再解方程可得答案【详解】解:设每轮传染中平均一个人传染了人则:或或经检验:不符合题意舍去取答:每轮传染中平均一 解析:3【分析】设每轮传染中平均一个人传染了x 人,则第一轮共有()1x +人患病,第二轮后患病人数有()21x +人,从而列方程,再解方程可得答案.【详解】解:设每轮传染中平均一个人传染了x 人,则:()1+116,x x x ++=()2116,x ∴+=14x ∴+=或14,x +=- 3x ∴=或5,x =-经检验:5x =-不符合题意,舍去,取 3.x =答:每轮传染中平均一个人传染了3人.故答案为:3.【点睛】本题考查的是一元二次方程的应用,掌握一元二次方程的应用中的传播问题是解题的关键.20.48(1-x)2=30【分析】本题的等量关系为:第一次降价后的价格×第二次降价占第一次降价的百分比=30由此即可求解【详解】解:设平均每次降价的百分率为x 则第一次降价后的价格为48(1-x)第二次降解析:48(1-x)2=30【分析】本题的等量关系为:第一次降价后的价格×第二次降价占第一次降价的百分比=30,由此即可求解.【详解】解:设平均每次降价的百分率为x ,则第一次降价后的价格为48(1-x),第二次降价后的价格为48(1-x)(1-x),由题意,可列方程为:48(1-x)2=30.故答案为:48(1-x)2=30.【点睛】本题考查了由实际问题抽象出一元二次方程,解决本题的关键是得到相应的等量关系,注意第二次降价后的价格是在第一次降价后的价格的基础上得到的.三、解答题21.(1)8、9两月平均每月降价的百分率是10%;(2)12月份该市的商品房成交均价不会跌破30000元2/m ,见解析【分析】(1)设8、9两月平均每月降价的百分率是x ,那么9月份的房价为50000(1-x ),10月份的房价为50000(1-x )2,然后根据10月份的40500元/m 2即可列出方程解决问题; (2)根据(1)的结果可以计算出今年12月份商品房成交均价,然后和30000元/m 2进行比较即可作出判断.【详解】解:(1)设这两月平均每月降价的百分率是x ,根据题意得:()250000140500x -=解得:1210% 1.9x x ==,(不合题意,舍去)答:8、9两月平均每月降价的百分率是10%(2)不会跌破30000元2/m . ()22405001405000.93280530000x -=⨯=>∴12月份该市的商品房成交均价不会跌破30000元2/m【点睛】此题考查了一元二次方程的应用,和实际生活结合比较紧密,正确理解题意,找到关键的数量关系,然后列出方程是解题的关键.22.(1)124,3x x ==-;(2)121,2x x =-=【分析】(1)化成一般式以后利用因式分解法解即可;(2)化成一般式以后利用因式分解法解即可;【详解】解:(1)28-x+4=x2x -x-12=0(x+3)(x-4)=0∴124,3x x ==-(2) 220x x --=(2)(1)0x x -+=121,2x x ∴=-=【分析】本题主要考查解一元二次方程的能力,熟练掌握解一元二次方程的几种常用方法:直接开平方法、因式分解法、公式法、配方法,结合方程的特点选择合适、简便的方法是解题的关键.23.(1)11x =21x =-2)11x =+,212x =-. 【分析】(1)两边除以3后再开方,即可得出两个一元一次方程,求解即可;(2)求出24b ac -的值,代入公式求出即可.【详解】解:(1)()2316x -=方程两边除以3,得:()212x -=,两边开平方,得:1x -=则:11x =+21x =(2)22410x x --=∵2a =,4b =-,1c =-,∴()()224442124b ac -=--⨯⨯-=∴x ==,∴112x =+,212x =-; 【点睛】 本题考查了解一元二次方程的应用,熟悉相关的解法是解题的关键.24.见解析.【分析】根据方程的系数结合根的判别式,可得出△=4k 2+4k+1≥0,进而即可证出:不论k 取何值方程都有两个不相等的实数根.【详解】证明:()()()2224124412211k k k k k -⨯⨯-∆=--⎡⎤⎣=+=+⎦+. ∵()2210k +≥,即0∆≥, ∴不论k 取何值,这个方程都有两个实数根.【点睛】本题主要考查根的判别式,熟练掌握一元二次方程根的个数与根的判别式的关系是解题的关键.25.(1)12)13m <-. 【分析】(1)根据分式的加减乘除混合运算法则计算即可,求值时注意分母有理化.(2)根据方程没有实数根,可知∆<0,进而求得m 得取值范围.【详解】(1)由题意得:原式23193(3)x x x xx x +--⎛⎫=-÷ ⎪--⎝⎭ 2(3)(3)(1)(3)(3)9x x x x x x x x ⎡⎤+----=⨯⎢⎥--⎣⎦ 2229(3)(3)9x x x x x x x --+-=⨯-- 29(3)(3)9x x x x x --=⨯-- 29(3)(3)9x x x x x --=⨯--3x x-=.3x =,∴原式313-===. (2)该方程没有实数根,2242430b ac m ∴∆=-=+⨯⨯<,故4120m +<,解得13m <-. 【点睛】本题考查分式的混合运算以及一元二次方程根的判别,熟练掌握分式运算法则以及根的判别公式是解题关键.26.(1)12x 1x -1==,;(2)12x 12x 1=-=,.【分析】(1)根据因式分解法,可得答案;(2)根据因式分解法,可得答案.【详解】解:(1)x(x-1)=1-x方程整理,得,x(x﹣1)+(x﹣1)=0,因式分解,得,(x﹣1)(x+1)=0于是,得,x﹣1=0或x+1=0,解得x1=1,x2=﹣1;(2)(x-3) 2 = (2x-1) (x +3)方程整理,得,x2+11x﹣12=0因式分解,得,(x+12)(x﹣1)=0于是,得,x+12=0或x﹣1=0,解得x1=﹣12,x2=1.【点睛】本题考查了解一元二次方程,因式分解是解题关键.。
2021-2022年孝感市九年级数学上期中试卷(附答案)

考查了一元二次方程的应用,解题的关键是找到该小路的总的长度,利用矩形的面积公式列出方程并解答.
6.D
解析:D
【分析】
找出丝绸花边的总面积与丝绸花边的宽之间的关系式即可列出方程.
【详解】
解:由题意知:三条丝绸花边的面积和-两个重叠部分的面积=丝绸花边的总面积,
∴设丝绸花边的宽为xcm,根据题意,可列方程为:
一、选择题
1.有三个质地、大小一样的纸条上面分别写着三个数,其中两个正数,一个负数,任意抽取一张,记下数的符号后,放回摇匀,再重复同样的操作一次,试问两次抽到的数字之积是正数的概率为()
A. B. C. D.
2.从一个装有3个红球、2个白球的盒子里(球除颜色外其他都相同),先摸出一个球,不再放进盒子里,然后又摸出一个球,两次摸到的都是红球的概率是()
(2)直角三角形斜边上的中线等于斜边的一半.
(问题解决)如图,在 中, , 于点 , 为 的中点,连结 , .下列结论:
① ;② ;③S四边形DEBC ;④ .正确的是_______
19.如图,在平面直角坐标系中,正方形ABOC的顶点A在第二象限,顶点B在x轴上,顶点C在y轴上,若正方形ABOC的面积等于7,则点A的坐标是______.
5.B
解析:B
【分析】
设小路的宽度为x米,则小正方形的边长为2x米,根据小路的横向总长度(20+2x)米和纵向总长度(12+2x)米,根据矩形的面积公式可得到方程.
【详解】
解:设道路宽为x米,则中间正方形的边长为2x米,
依题意,得:x(20+2x+12+2x)=40,
即x(32+4x)=40,
故选:B.
(1)请用列表或画树状图的方法表示出上述游戏中两数和的所有可能的结果;
内蒙古呼和浩特市实验教育集团九年级(上)警钟考化学试卷(10月份)

内蒙古呼和浩特市实验教育集团九年级(上)警钟考化学试卷(10月份)一、选择题(共10小题,每小题2分,满分20分)1.(2分)生活中处处有化学,在实际生活中下列物质的用途与其物理性质有关的是()A.稀有气体用作焊接保护气B.铜用作导线C.氮气用作食品防腐剂D.氧气用作医疗急救2.(2分)氧气是我们身边常见的物质,以下有关氧气的叙述正确的是()A.物质与氧气发生的反应都是氧化反应B.鱼、虾等能在水中生存,是由于氧气易溶于水C.氧气在空气中的体积分数为78%D.从空气中分离氧气的方法是利用氧气的沸点比氮气低3.(2分)下列实验操作正确的是()A.点燃酒精灯B.铁丝在氧气中燃烧C.称量氯化钠D.闻气体4.(2分)对于K和K+的说法,正确的是()A.属于同一种元素B.属于同一种粒子C.核外电子数相同D.具有相同的电子层数5.(2分)蜡烛、红磷、铁丝、木炭在氧气中燃烧的共同点是()A.都能生成固体B.都是化合反应C.都有火焰出现D.都会放热、发光6.(2分)下列说法正确的是()A.所有的火灾都可用水扑灭B.所有的自燃都是由缓慢氧化引起的C.所有的爆炸都是由剧烈燃烧引起的D.所有的可燃性气体与空气混合点燃都会发生爆炸7.(2分)石棉的熔点高,又不易燃烧,可制作石棉网.石棉的化学式可表示为CaMg3Si4O12,其中硅元素的化合价为()A.+1B.+2C.+3D.+48.(2分)图示为A、B元素的原子结构示意图.下列说法错误的是()A.B的原子结构示意图中x为12B.A和B分别属于非金属元素和金属元素C.A的原子和B的原子分别形成简单离子的过程相同D.A与B组成的化合物是由离子构成的9.(2分)某物质中只含有一种元素,则该物质()A.一定是单质B.一定是混合物C.一定是纯净物D.一定不是化合物10.(2分)如表是根据一些反应事实或现象推理得出的影响化学反应的主要因素,其中不合理的是()选项化学反应事实(或现象)影响因素催化剂A过氧化氢在常温下分解速度比较慢,加入二氧化锰后迅速分解B食物在冰箱中保存不易变质温度反应物的种类C蜡烛在空气中燃烧发出黄色火焰,在纯氧中燃烧火焰明亮D细铁丝在空气中不能燃烧,在纯氧中剧烈燃烧火星四射反应物的浓度A.A B.B C.C D.D二、填空题(共3小题,每空1分,满分13分)11.(5分)用符号表示或写出符号的意义:(1)4个铝原子(2)2个氢原子(3)质子数为18的原子(4)3H2O(5)K2MnO4.12.(3分)氧元素是地壳中含量最高的元素,请回答下列问题:(1)画出氧原子结构示意图;(2)元素周期表中氧元素的信息如图1所示,从图1中能直接获得的信息是;A.氧元素属于非金属元素B.氧原子的核内的质子数为16C.氧元素有O2和O3两种单质D.氧原子的核外电子数为8(3)如图2是硫化氢(H2S)在氧气中不完全燃烧反应的微观示意图.请写出该反应中的单质(填化学式)13.(5分)写出下列反应的符号表达式.(1)镁条在空气中燃烧(2)铁丝在氧气中燃烧.(3)氯酸钾和二氧化锰共热制取氧气.(4)过氧化氢溶液制取氧气.(5)硫磺在氧气中燃烧.三、实验题(共2小题,满分13分)14.(4分)如图是某实验小组的几位同学设计的“测定空气中氧气含量”的实验装置图,请结合图示回答下列问题.(1)根据下表提供的实验数据,完成下表:硬质玻璃管中空气的体积反应前注射器中空气的体积反应后注射器中空气的体积实验测得空气中氧气的体积分数25.0mL15.0mL7.0mL(2)装置中气球的作用是;(3)写出红磷燃烧反应的符号表达式;(4)实际实验时测得氧气含量偏小,可能的原因是什么?(写一条即可).15.(9分)实验室中,利用如图所示装置可以制取某些气体,请回答下列问题.(1)写出带标号的仪器的名称:①;②.(2)实验室用高锰酸钾制取氧气,选择的发生装置是;用过氧化氢制氧气选择的发生装置是.(3)研究显示:氧气的体积分数大于36%时就可使带火星的木条复燃,因此,氧气验满时采用使带火星的木条复燃的方法(填“可靠”或“不可靠”),为了收集一瓶较纯净的氧气,最好采用集气法.(4)向气体发生装置内加入药品前,应该进行的操作是.(5)下面是利用装置收集气体的操作,正确的实验操作顺序是(填序号).①待收集瓶内充满气体后,盖上玻璃片再移出水槽②等到气泡连续且均匀时,再将导管口移入集气瓶③将集气瓶注满水,用玻璃盖盖上瓶口,倒立在盛水的水槽中.(6)已知:氨气(NH3)是一种具有刺激性气味的无色气体,密度比空气小,极易溶于水,实验室常用加热氯化铵和熟石灰两种固体的混合物来制备氨气.请你从如图中选出制备一瓶氨气所需要的装置组合是(填字母).四、计算题(共1小题,满分4分)16.(4分)焦亚硫酸钠有毒,不能直接用于食品加工,市场上有不法商贩将其溶液浸泡生姜,使生姜发黄发亮,食用此种生姜可能使人中毒,已知焦亚硫酸钠的化学式为Na2S2O x,相对分子质量是190,请计算:(1)x=;(2)焦亚硫酸钠中硫元素与氧元素的质量比是;(3)焦亚硫酸钠中钠元素的质量分数是(精确到0.1%物质)内蒙古呼和浩特市实验教育集团九年级(上)警钟考化学试卷(10月份)参考答案一、选择题(共10小题,每小题2分,满分20分)1.B;2.A;3.A;4.A;5.D;6.B;7.D;8.C;9.D;10.C;二、填空题(共3小题,每空1分,满分13分)11.4Al;2H;Ar;三个水分子;锰酸钾;12.;AD;O2和S;13.2Mg+O22MgO;3Fe+2O2Fe3O4;2KClO32KCl+3O2↑;2H2O22H2O+O2↑;S+O2SO2;三、实验题(共2小题,满分13分)14.20%;缓冲,防止试管内气体温度升高,气压增大,冲开橡皮塞;4P+5O22P2O5;红磷不足;装置漏气(或装置没冷却到室温就读数等合理即可);15.铁架台;集气瓶;A;B;不可靠;排水;检查装置气密性;③②①;AC;四、计算题(共1小题,满分4分)16.5;4:5;24.2%;。
2022-2023学年密云区九年级第一学期数学期末测试参考答案

密云区2022-2023学年第一学期初三期末数学参考答案一、选择题(共16分,每题2分)二、填空题(本题共16分,每小题2分)9. 2(2)y x=-(本题答案不唯一) 10.23π11.k<1 12.121313.414.20°15.4 16.①2 ②三、解答题(本题共68分,其中17-22每题5分,23-26每题6分,27、28题每题7分)17. 解:原式=224=1218.(1)证明:∵AB=AC,∴∠ABC=∠ACB.∵∠CBE=∠ABC,∴∠ACB=∠CBE.∵∠ADC=∠EDB,∴△ADC∽△EDB.(2)解:∵△ADC∽△EDB,∴AD ACDE BE=.∵AC=4,BE=6,AD=2,∴246DE=.∴DE=3.19. 解:∵AD⊥BC,垂足为D,∴∠ADB=∠ADC=90°.在△ABD 中,∠B =45°,∠ADB =90°,AB = ∵sin ADB AB=, ∴sin AD AB B =⋅=1.在△ADC 中,1tan 2C =,∠ADC =90°, ∵tan ADC DC=, ∴12AD DC =. ∵AD =1, ∴2DC =.∴AC ==20.(1)解:∵22-2-3(1)4y x x x ==--,∴二次函数图象的顶点坐标是(1,-4). 令y =0,即2-2-30x x =,解得:123,1x x ==-.∴二次函数图象与x 轴交点坐标是(3,0)和(-1,0). (2)当y <0时,自变量x 的取值范围是:-1<x <3. 21.解:由已知,∠AOB=90°,∠ABO=45°,∠ACB=30°.∵AC =20,sin OA C AC =,cos OCC AC=,∴sin OA AC C =⋅=20sin30⨯︒= 10(km ), cos OC AC C =⋅=20cos30⨯︒=km ).在△AOB 中,∠AOB=90°,∠ABO=45°,OA =10,∵tan AOABO OB∠= , ∴OB =10tan tan 45OA ABO =∠︒=10(km ),∴BC =OC -OB =10≈7.32(km ).22.(1)证明:∵△ABC 内接于⊙O ,AE 是⊙O 的直径,AE ⊥BC ,垂足为D . ∴BE EC =.∴BAE CAE ∠=∠. ∵OA =OB ,∴ABO BAE ∠=∠. ∴ABO CAE ∠=∠.(2)解:∵△ABC 内接于⊙O ,AE 是⊙O 的直径,AE ⊥BC ,垂足为D , ∴90ODB ∠=︒,BD =DC . ∵r =5,DE =2, ∴OD =3.∴4BD =, ∴BC =2BD =8.23. (1)解:∵A (1,6)在函数(0)my x x=>的图象上, ∴61m=. ∴m =6.∵B (3,n )在函数(0)my x x=>的图象上, ∴623n ==. (2)1,15,k =-≤b ≤ 且0b ≠.24. (1)证明:连接OC ,连接OD .∵AB 是⊙O 的直径,CD 是⊙O 的弦,CD 与AB 交于点E ,CE =ED , ∴BC BD =,AB ⊥CD . ∴∠COB =∠BOD .∵∠COB =2∠CAE , ∴∠BOD =2∠CAE . ∵∠CDF =2∠CAE , ∴∠CDF =∠BOD .∵AB ⊥CD ,CD 与AB 交于点E , ∴∠FED =90°. ∴∠EDF +∠EFD =90°. ∵∠EDF =∠BOD ,∴∠BOD +∠EFD =90°. ∴∠ODF =90°. ∵OD 是⊙O 的半径, ∴DF 是⊙O 的切线.(2)解:∵∠OED =90°,∠ODF =90°, ∴∠OED =∠ODF . ∵∠EOD =∠DOF , ∴△ODE ∽△OFD . ∴OD OFOE OD=.∵BE =1,BF =2, ∴OE =r -1,OF = r +2, ∴21r r r r+=-. 解得:r =2.25.(1)解:设所求抛物线表达式为2()y a x h k =-+.由已知:抛物线经过(0,1.6),抛物线顶点为(3,3.4), 故此:h =3,k =3.4. ∵(0,1.6)在抛物线上, ∴2(03) 3.4 1.6a ⨯-+=. 解得:0.2a =-. (2) 12d d <26.(1)解:∵抛物线经过点A (2,0), ∴4a +2b =0.即12ba-=. ∴抛物线的对称轴是直线x =1. (2)132y y y >>.设抛物线的对称轴为直线x =t .FAED CBA∵抛物线经过E (m ,0),2<m <4,且抛物线经过(0,0), ∴1<t <2. ∴122ba<-<. ∵a >0, ∴2a <-b <4a . ∴-4a <b <-2a . ∴b <0.由已知:123,,93y a b y a b y a b =-=+=+. 12()()2y y a b a b b -=--+=->0,即12y y >. 13()(93)84y y a b a b a b -=--+=--, ∵2a <-b <4a , ∴8a <-4b <16a ,∴0<84a b --<8a ,即13y y >23()(93)82y y a b a b a b -=+-+=-- ∵2a <-b <4a , ∴4a <-2b <8a ,∴-4a <82a b --<0,即23y y <. ∴132y y y >> .27.(1)CE //AB . 连接AE .∵AD =DE ,∠ADE =60°, ∴△ADE 是等边三角形. ∴AE =AD ,∠DAE =60°. ∵△ABC 是等边三角形, ∴AB =AC ,∠BAC =60°.∵∠BAD =∠BAC -∠DAC ,∠CAE =∠DAE -∠DAC , ∴∠BAD =∠CAE .在△BAD 和△CAE 中,AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩, ∴△BAD ≌△CAE .∴∠ACE =∠ABD =60°. ∵∠BAC =60°, ∴∠BAC =∠ACE . ∴CE //AB .(2))DG AG DC -在AB 上截取AH =CD ,连接DH .∵△ABC 是等边三角形, ∴AB =BC , ∵AH =CD , ∴BH =BD .∵∠ABC =60°,∴△BHD 是等边三角形.∴DH =BD ,∠DHG =60°. ∵DG ⊥AB ,垂足为G , ∴∠DGH =90°. ∵tan DGDHG GH∠=,∠DHG =60°,∴tan 60DGGH=︒=∵GH =AG -AH ,AH =DC , ∴GH =AG -DC .∴)DG AG DC =-.28. (1)①②∵Q 是点P 关于OM 的关联点,P (2,0), ∴2(4,0)P -,PP 1//OM ,PP 1=OM . ∴OQ //1PP .∴△2P OQ ∽△21P PP . ∴2124263P O OQ PP P P ===, ∵PP 1=OM , ∴23OQ OM =. ∴OQ =2QM.(2)∵OP =3,OP 2=6,∴点P 是在以O 为圆心3为半径的圆上,P 2是在以O 为圆心6为半径的圆上. 由已知,OQ //1PP , ∴△2P OQ ∽△21P PP .∴2216293OP OQ P P PP ===,∵OM =1,OM =1PP ,∴23OQ =.∵26OP =,2,,P Q O 三点不在同一条直线上,∴222-OP OQ P Q OP OQ <<+. ∴2162033P Q <<.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
领先国家
英国
美国 德国
珍妮机 瓦特蒸汽机 耐用碳丝灯泡 重要发明 轮船 火车机车 内燃机 汽车 飞机 对中国影 响 鸦片战争 中国开始沦为双半 社会 甲午中日战争 八国联军侵华战争 双半程度大大加深 完全沦为双半社会
第12课 1.美国独立战争爆发的根本原因。 2.美洲的土著居民是?英国在此建立了多 少个殖民地? 3.美国独立战争开始时间和标志、结束时 间和标志。 4.美国建国的时间和标志 5.美国独立战争的转折点是?哪国开始提 供军事援助? 6.1787年美国宪法有哪些内容? 美第一任总统 7.美国独立战争的历史意义?
第14课 开始国家 开始部门 开始时间 开始标志 主要标志 进入时代 发明成果 结束时间 结束标志 影响 启示
蒸汽时代的到来——第一次工业革命
第一次工业革命 时间 重要标志 进入时代
18世纪60年代——1840 年前后
第二次工业革命 19世纪70年代开始 电力的广泛应用 电气时代
瓦特蒸汽机 蒸汽时代
第1ቤተ መጻሕፍቲ ባይዱ课
1.英国资产阶级革命爆发的根本原因 2.英国资产阶级革命的起止时间、领导阶级和领导人 3.英国资产阶级革命开始时间和开始的标志事件 4.国王谁挑起内战?谁率议会军打败王军?
5.哪一年查理一世被推上断头台,英国成立了什么?
6.共和国期间,谁掌握政权,担任什么? 7.复辟的国王是谁? 8.英国资产阶级革命结束时间及标志 9.英国资产阶级革命的结果是:颁布了《权利法案》①目的②时 间③机构④意义⑥1689年中俄签订了什么条约? 10.英国资产阶级革命的历史意义: ①推翻了……,确立了……, 为……扫清了道路。 ②推动了……
第13课
1.法国大革命爆发的根本原因。 2.法国大革命的起止时间、开始和结束的标志。 3.革命中通过的文件是什么? 4.英、法革命中处死的国王分别是谁? 5.英、法、美资产阶级革命中的领导人分别是谁? 6.法国大革命的历史意义? 7.拿破仑如何对内、对外巩固统治的? 8.如何评价拿破仑的对外战争? 9.法兰西第一共和国、第一帝国的起止时间。 10.美国、法国国庆节分别是哪一天?
