江西省九江市2020-2021学年高二下学期期末数学(理)试题
江西省九江市花园中学2022-2023学年高二化学下学期期末试题含解析

江西省九江市花园中学2022-2023学年高二化学下学期期末试题含解析一、单选题(本大题共15个小题,每小题4分。
在每小题给出的四个选项中,只有一项符合题目要求,共60分。
)1. 下列分子或离子中都存在着配位键的是① NH3② CH4③ H3O+④ CH3COO-⑤[B(OH)4]-A.①② B.③④C.①④ D.③⑤参考答案:D略2. 下列说法正确的是A.锅炉水垢中的硫酸钙可用碳酸钠溶液处理,使之转化为碳酸钙,再用酸除去B.铝盐在水中可产生胶体,可用于自来水的杀菌消毒C.太阳能热水器、沼气的利用、乙醇汽油都涉及生物质能的利用。
D.李比希燃烧法、钠熔法、铜丝燃烧法、纸层析法都是元素定性分析法。
参考答案:A略3. 下列化学肥料属于复合肥料的是()A.氯化钾B.硝酸铵C.磷酸二氢钙D.硝酸钾参考答案:D解析:复合肥料是指含有两种或两种以上营养元素(N、P、K)的化学肥料。
依据所给物质的化学组成可以推断D中含有N和K两种营养元素,而其他选项均只含其中的一种。
4. 下列有机物是按照碳的骨架进行分类的是A.烷烃 B.烯烃 C.芳香烃 D.卤代烃参考答案:C5. 右图是反应A2(g)+3B2(g) 2C(g)△H<0的平衡移动图,影响该反应平衡移动的原因是A.升高温度B.增大反应物浓度C.增大压强D.使用催化剂参考答案:C略6. 关于CS2、SO2、NH3三种物质的说法中正确的是()A.CS2在水中的溶解度很小,是由于其属于极性分子B.SO2和NH3均易溶于水,原因之一是它们都是极性分子C.CS2为非极性分子,所以在三种物质中熔沸点最低D.NH3在水中溶解度很大只是由于NH3分子有极性参考答案:B略7. 用32gCu与300mL12mol/L的浓硝酸反应,当铜全部溶解后,共收集到标准状况下的气体11.2L(不考虑NO2转化为N2O4),反应消耗的硝酸的物质的量是()A.1.5mol B.1.8mol C.3.3mol D.3.6mol参考答案:A【考点】化学方程式的有关计算.【分析】反应生成的气体为NO2,或者NO2与NO混合气体,反应消耗的硝酸生成Cu (NO3)2、氮的氧化物,根据氮原子守恒计算消耗硝酸的物质的量.【解答】解:反应生成的气体为NO2,或者NO2与NO混合气体,反应消耗的硝酸生成Cu(NO3)2、氮的氧化物,则n(NO2)+n(NO)==0.5mol,即被还原的硝酸的物质的量为0.5mol,n(Cu)==0.5mol,则生成n[Cu(NO3)2]=0.5mol,可知表现酸性的硝酸的物质的量为0.5mol×2=1mol,则参加反应的硝酸的物质的量为:1mol+0.5mol=1.5mol.故选:A.8. 下列物质在空气中长时间放置不易变质的是A.Na B.NaOH C.NaCl D.Na2O2参考答案:C略9. 下列说法不正确的是()A.外界条件改变,化学平衡状态一定发生改变B.对某一可逆反应,当正、逆反应速率相等时,各组分的浓度一定保持不变C.甲、乙两个容积相同、温度恒定且相同的密闭容器中,分别充入2molNH3、1mol N2和3molH2,平衡时,甲和乙的N2体积分数相同D.化学平衡建立前,v正≠v逆,化学平衡后v正=v逆参考答案:A考点:化学平衡的影响因素;化学反应速率的影响因素.分析:A、气相可逆反应中气体化学反应前后化学计量数相等,压强改变不改变平衡状态;B、根据化学平衡状态特征分析判断;C、根据充入2molNH3相当于1mol N2和3molH2分析判断;D、根据化学平衡状态特征,化学平衡建立前,v正≠v逆,平衡后v正=v逆.解答:解:A、气相可逆反应中气体化学反应前后化学计量数相等,压强改变不改变平衡状态,但温度改变平衡状态发生改变,所以说改变外界条件不一定改变化学平衡状态,故A错误;B、当正、逆反应速率相等时,达到了化学平衡状态,则各组分的浓度一定保持不变,故B 正确;C、充入2molNH3相当于1mol N2和3molH2,所以甲、乙两个容积相同、温度恒定且相同的密闭容器中,分别充入2molNH3、1mol N2和3molH2,平衡时,甲和乙的N2体积分数相同,故C正确;D、化学平衡建立前,v正≠v逆,平衡后v正=v逆,故D正确;故选A.点评:本题考查平衡状态的判断,反应达到平衡状态时,正逆反应速率相等,且各组分的浓度一定保持不变,难度不大.10. 分别用pH=2和pH=3的醋酸溶液中和等物质的量的苛性钾溶液,消耗两种醋酸溶液的体积分别为V1和V2,V1和V2的关系正确的是()A.V2 =10V1B.V1>10 V2C.V2<10V1D.V2>10V1参考答案:D略11. 根据下列短周期元素性质的数据判断,下列说法正确的是(▲)A.元素⑦位于第3周期VA族B.元素①⑧形成的化合物具有两性C.元素④⑤形成的化合物是离子化合物D.元素③的最高价氧化物对应水化物碱性最强参考答案:B12. 下列不能形成配位键的组合是()A.Ag+、NH3 B.BF3、NH3 C.Co3+、CO D.Ag+、H+参考答案:D略13. 当不慎有大量Cl2逸到周围空气里时,可用浸有一定浓度的下列物质溶液的毛巾捂住鼻子,该物质是A.NaOH B.NaClC.H2O D.Na2CO3参考答案:A14. 为了除去粗盐中的Ca2+、Mg2+、SO42﹣及泥沙,得到纯净的NaCl,可将粗盐溶于水,然后在下列操作中选取必要的步骤和正确的操作顺序:①过滤②加过量NaOH溶液③加适量盐酸④加过量Na2CO3溶液⑤加过量BaCl2溶液()A.④①②⑤③ B.④②⑤C.①④②⑤③ D.②⑤④①③参考答案:D解:镁离子用氢氧根离子沉淀,加入过量的氢氧化钠可以将镁离子沉淀,硫酸根离子用钡离子沉淀,加入过量的氯化钡可以将硫酸根离子沉淀,至于先除镁离子,还是先除硫酸根离子都行,钙离子用碳酸根离子沉淀,除钙离子加入碳酸钠转化为沉淀,但是加入的碳酸钠要放在加入的氯化钡之后,这样碳酸钠会除去反应剩余的氯化钡,离子都沉淀了,在进行过滤,最后再加入盐酸除去反应剩余的氢氧根离子和碳酸根离子,所以正确的顺序为:②加过量的氢氧化钠溶液;⑤加过量的氯化钡溶液;④加过量的碳酸钠溶液;①过滤;③加适量盐酸.故选D.15. 直接由原子构成的一组物质是A、碘、二氧化硅、金刚石B、硅晶体、金刚石、二氧化硅晶体C、氧化钙、金刚石、二氧化硅晶体D、碘、石墨、黄铁矿参考答案:B二、实验题(本题包括1个小题,共10分)16. 阅读下列实验内容,根据题目要求回答问题。
江西省九江市第一中学2023-2024学年高二下学期4月月考数学试题

江西省九江市第一中学2023-2024学年高二下学期4月月考数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知数列{}n a 的通项公式22n a n =+,则123是该数列的( ) A .第9项B .第10项C .第11项D .第12项2.已知数列{}n a 满足()*πsin 3n n a n =∈N ,则7812a a a a +--=( ) A.0B .1C D .23.有编号分别为1,2,3,4的4张电影票,要分给甲、乙、丙3个人,每人至少分得一张,且4张电影票全部分完,则不同分配方法的种数为( ) A .24B .36C .64D .724.在某电路上有,C D 两个独立工作的元件,每次通电后,需要更换C 元件的概率为0.2,需要更换D 元件的概率为0.1,则在某次通电后,C D 有且只有一个需要更换的条件下,C 需要更换的概率是( ) A .310B .150C .913 D .345.如果一个数列从第2项起,每一项与它前一项的和除以与它前一项的差等于同一个常数,那么这个数列就叫做“和差等比数列”.已知{}n a 是“和差等比数列”,11a =,23a =则满足使不等式100n a >的n 的最小值是( ) A .8B .7C .6D .56.已知数列{}n a 满足()()()2*1123214832,,1n n n a n a n n n n a ----=-+≥∈=N ,则n a =( ) A .22n -B .22n n -C .21n -D .2(21)n -7.已知数列{}n a 满足120,1a a ==.若数列{}1n n a a ++是公比为2的等比数列,则2024a =( )A .2023213+B .2024213+C .2023213-D .2024213-8.已知点()1,(1)P a a >在抛物线C :22(0)y px p =>上,过P 作圆()2211x y -+=的两条切线,分别交C 于A ,B 两点,且直线AB 的斜率为1-,若F 为C 的焦点,点(),M x y为C 上的动点,点N 是C 的准线与坐标轴的交点,则MN MF的最大值是( )A B .2 C D二、多选题9.下列叙述不正确的是( )A .1,3,5,7与7,5,3,1是相同的数列B .,,,,a a a a ⋯是等比数列C .数列0,1,2,3,…的通项公式为n a n =D .数列1n n ⎧⎫+⎨⎬⎩⎭是递增数列10.在等比数列{}n a 中,11a =,427a =,则( )A .{}1n n a a +的公比为9B .{}31log n a +的前20项和为210C .{}n a 的前20项积为2003D .()111()231nn k k k a a -+=+=-∑11.(多选题)数列1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987L 是意大利数学家莱昂纳多⋅斐波那契(Leonardo?Fibonacci)在他写的《算盘全数》中提出的,所以它常被称作斐波那契数列.该数列的特点是:前两个数都是1,从第三个数起,每一个数都等于它的前面两个数的和.记斐波那契数列为{}n a ,其前n 项和为n S ,则下列结论正确的有( )A .3k a 不一定是偶数B .10112120221k k a a -==∑C .20212021202212k k a a a ==∑D .202020221S a =-三、填空题12.已知数列{}n a 是等差数列,数列{}n b 是等比数列,若2465πa a a ++=,246b b b =则1726tan1a a b b +=-.13.已知数列{}n a 是等比数列,且2254a a =.设2l o g n n b a =,数列{}n b 的前n 项和为n S ,则7S =.14.设直线:10l x y +-=,一束光线从原点O 出发沿射线()0y kx x =≥向直线l 射出,经l 反射后与x 轴交于点M ,再次经x 轴反射后与y 轴交于点N .若MN =u u u u r 则k 的值为.四、解答题15.已知等差数列{}n a 的各项均为正数,15932,5a a a a =+=. (1)求数列{}n a 的通项公式;(2)若数列{}n b 满足()*1211,N n n n n b a b a b n ++==∈,求{}n b 的通项公式及其前n 项和n S .16.已知数列{}n a 前n 项和为n S ,且满足__________.①首项11a =,*,m n ∀∈N 均有22m n n S S mn m +=++;②*n ∀∈N ,均有0n a >且()214n n a S +=,从条件①和②中选一个填到题目条件下划线上(若两个都填,以第一个为准),并回答下面问题: (1)求数列{}n a 的通项公式; (2)求数列{}2na n a ⋅前n 项和nT的表达式.17.如图,在四棱锥P ABCD -中,PC ⊥底面ABCD ,底面ABCD 是直角梯形,AB AD ⊥,//AB CD ,222AB AD CD ===,E 是PB 上的点.(1)求证:平面EAC ⊥平面PBC ;(2)若E 是PB 的中点,且二面角P AC E --,求直线PA 与平面EAC 所成角的正弦值.18.已知点(1,0)S -,T 是圆F :()22116x y -+=上的任意一点,线段ST 的垂直平分线交FT 于点N ,设动点N 的轨迹曲线为W ; (1)求曲线W 的方程;(2)过点F 作斜率不为0的直线l 交曲线W 于AB 、两点,交直线4x =于P .过点P 作y 轴的垂线,垂足为Q ,直线AQ 交x 轴于C 点,直线BQ 交x 轴于D 点,求线段CD 中点M 的坐标.19.伯努利不等式又称贝努力不等式,由著名数学家伯努利发现并提出.伯努利不等式在证明数列极限、函数的单调性以及在其他不等式的证明等方面都有着极其广泛的应用.伯努利不等式的一种常见形式为:当1,1x a >-≥时,(1)1a x ax +≥+,当且仅当1a =或0x =时取等号.(1)假设某地区现有人口100万,且人口的年平均增长率为1.2%,以此增长率为依据,试判断6年后该地区人口的估计值是否能超过107万?(2)数学上常用1ni i a =∏表示1a ,2a ,L ,n a 的乘积,*121,ni n i a a a a n ==⋅∈∏N L .①证明:1221ni i i =⎛⎫> ⎪-⎝⎭∏②数列{}n a ,{}n b 满足:n a n =,()22213212!n n a a a b n -⋅=L L ,证明:121n b b b ++++<L。
江西省赣州市2020-2021学年高二下学期期末模拟化学试题(含答案)

该电池工作时,电极 a 上发生的电极反应为
。
18.(15 分)实验室用乳酸与异戊醇反应制备乳酸异戊酯,有关数据和装置示意图如下:
CH3CHCOOH + CH3CHCH2CH2OH浓H2SO4 CH3CHCOOCH2CH2CHCH3 +H2O
A.第 I 阶段的化学方程式为:SO32−+NO2=NO2−+SO3− B.该过程中 NO2 为催化剂 C.1molSO3−在第 II、III 两个阶段共失去电子数目为 NA D.氧化性 NO2>HNO2 10.a - FeO(OH)在高档涂料、油墨的生产中有着重要的用途。某化工厂以氧化铁废料(含少量的 FeO、SiO2)为原料制备 FeO(OH)的流程如下图所示:
①EDTA-Fe2+-e-=EDTA-Fe3+
16.常温下,下列各组离子在指定溶液中能大量共存的是( )
②2EDTA-Fe3++H2S=2H++S+2EDTA-Fe2+
A.含有 FeCl2 的溶液中:
B.中性溶液中:
C.澄清透明溶液中:
该装置工作时,下列叙述不正确的是( ) A.协同转化总反应:CO2+H2S=CO+H2O+S B.ZnO@石墨烯电极的反应:CO2+2e-+2H+=CO+H2O C.石墨烯上的电势比 ZnO@石墨烯上的低 D.整个过程中主要能量转化:光能→电能→化学能 15.已知联氨(N2H4)为二元碱,25℃时向联氨水溶液中逐滴滴加盐酸溶液,混合溶液中的微粒的物 质的量分数随 pOH[pOH=-lgc(OH-)]变化的关系,如图所示。已知联氨的两步电离分别为:
NaOH溶液
选修2-1学霸必刷题 空间向量与立体几何(选择题、填空题)

空间向量与立体几何(选择题、填空题)一、单项选择题1.(江西省赣州市赣县第三中学2020-2021学年高二8月入学考试)已知点(,1,2)A x 和点(2,3,4)B ,且AB =x 的值是( )A .6或2-B .6或2C .3或4-D .3-或4【答案】A【解析】AB ==()2216x -=,解得:2x =-或6x =.故选A2.(2020江西省新余期末质量检测)在空间直角坐标系中,已知P(-1,0,3),Q(2,4,3),则线段PQ 的长度为( )A B .5C D 【答案】B【解析】由题得2(3,4,0),35PQ PQ =∴=+=,所以线段PQ 的长度为5. 故答案为B3.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)已知空间向量()3,1,3m =,()1,,1n λ=--,且//m n ,则实数λ=( )A .13- B .-3 C .13D .6【答案】A【解析】因为//m n ,所以,m n R μμ=∈,即:()3,1,3m ==(),,n μλμμμ--=, 所以3,1μλμ=-=,解得13λ=-.故选A .4.(江西省新余一中、宜春一中2021届高二联考)如图所示,在正方体1111ABCD A B C D -中,O 是底面正方形ABCD 的中心,M 是1D D 的中点,N 是11A B 的中点,则直线NO ,AM 的位置关系是( )A .平行B .相交C .异面垂直D .异面不垂直【答案】C【分析】建立空间直角坐标系,写出NO 与AM 的坐标,即可判断位置关系.【解析】建立空间直角坐标系,如图所示.设正方体的棱长为2,则(2,0,0)A ,(0,0,1)M ,(1,1,0)O ,(2,1,2)N ,∴(1,0,2)NO =--,(2,0,1)AM =-.∵0NO AM ⋅=,∴直线NO ,AM 的位置关系是异面垂直. 故选: C5.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)已知空间四边形ABCD 的每条边和对角线的长都等于a ,点,E F 分别是,BC AD 的中点,则AE AF ⋅的值为( ) A .2aB .212aC .214a D 2 【答案】C【分析】由题意可得11()22AB AC AE AF AD ⋅=+⋅,再利用两个向量的数量积的定义求得结果.【解析】11()22AB AC AE AF AD ⋅=+⋅1()4AB AD AC AD =⋅+⋅ ()22211cos60cos6044a a a ︒︒=+=,故选C. 6.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)已知M ,N 分别是四面体OABC 的棱OA ,BC 的中点,点P 在线段MN 上,且2MP PN =,设向量OA a =,OBb =,OC c =则OP =( )A .111666a b c ++B .111333a b c ++C .111633a b c ++D .111366a b c ++【答案】C【解析】如图所示,连接ON ,∵OP ON NP =+,1()2ON OB OC =+,所以13NP NM =,NM OM ON =-,12OM OA =,∴13OP ON NP ON NM =+=+121()333ON OM ON ON OM =+-=+21()32OB OC =⨯+1132OA +⨯111633OA OB OC =++111633a b c =++.故选C . 7.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)若两条不重合直线1l 和2l 的方向向量分别为()11,0,1ν=-,()22,0,2ν=-,则1l 和2l 的位置关系是( ) A .平行 B .相交 C .垂直D .不确定【答案】A【解析】因为两条不重合直线1l 和2l 的方向向量分别为()11,0,1ν=-,()22,0,2ν=-, 所以212v ν=-,即2ν与1v 共线,所以两条不重合直线1l 和2l 的位置关系是平行,故选A8.(山东省滕州市第一中学2020-2021学年高二9月开学收心考试)设,x y R ∈,向量()()(),1,1,1,,1,2,4,2,a x b y c ===-且,//a c b c ⊥,则a b +=( )A .BC .3D .4【答案】C【分析】根据向量垂直和平行的坐标表示求得参数,x y ,再求向量模长即可. 【解析】()//,241,2,1,21b c y y b ∴=-⨯∴=-∴=-,,(),1210,1a b a b x x ⊥∴⋅=+⋅-+=∴=,()()1,112,1,2a a b ∴=∴+=-,,(2213a b ∴+=+-=,故选C .9.(江西省宜春市2016-2017学年高二上学期期末统考理)如图所示,在空间四边形OABC 中,OA a OB b OC c ===,,,点M 在OA 上,且2,OM MA N =为BC 中点,则MN =( )A .121232a b c -+B .211322a b c -++ C .111222a b c +-D .221b 332a c -+-【答案】B【解析】由向量的加法和减法运算:12211()23322MN ON OM OB OC OA a b c =-=+-=-++.故选B10.(陕西省商洛市商丹高新学校2019-2020学年高二下学期4月学情质量检测数学(理))如图,已知正方体ABCD A B C D ''''-,点E 是A C ''的中点,点F 是AE 的三等分点,且12AF EF =,则AF =( )A .1122AA AB AD '++ B .111222AA AB AD '++ C .111266AA AB AD '++D .111366AA AB AD '++【答案】D【解析】∵点E 是A C ''的中点,点F 是AE 的三等分点,且12AF EF =, ∴111111()333236AF AE AA A E AA A C AA A C ⎛⎫''''''''==+=+=+ ⎪⎝⎭ 11()36AA A B A D '''''=++111366AA AB AD '=++,故选D . 11.(安徽省六安市舒城中学2020-2021学年高二上学期开学考试数学(文)试题)如图,四个棱长为1的正方体排成一个正四棱柱,AB 是一条侧棱,()1,2,,8i P i =是上底面上其余的八个点,则()1,2,,8i AB AP i ⋅=⋅⋅⋅的不同值的个数为( )A .8B .4C .2D .1【答案】D【解析】()2i i i AB AP AB AB BP AB AB BP ⋅=⋅+=+⋅,AB ⊥平面286BP P P ,i AB BP ∴⊥,i AB BP ∴⋅=,21i AB AP AB ∴⋅==,则()1,2,,8i AB AP i ⋅=⋅⋅⋅的不同值的个数为1个,故选D .12.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)点P (1,2,3)关于xOy 平面的对称点的坐标为( ) A .(-1,2,3) B .(1,-2,-3) C .(-1,-2,-3) D .(1,2,-3)【答案】D【分析】关于xOy 平面对称的点的,x y 坐标不变,只有z 坐标相反. 【解析】点P (1,2,3)关于xOy 平面的对称点的坐标为(1,2,)3-.故选D .13.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)若向量(2,0,1)a =-,向量(0,1,2)b =-,则2a b -=( )A .(4,1,0)-B .(4,1,4)--C .(4,1,0)-D .(4,1,4)--【答案】C【分析】根据题意求出2(4,0,2)a=-,再根据向量的减法坐标运算,由此即可求出结果.【解析】因为向量(2,0,1)a =-,向量(0,1,2)b =-,则2(4,0,2)a =-,则2(4,0,2)(0,1,2)(4,1,0)a b -=---=-,故选C .14.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)已知正方体1111ABCD A B C D -,点E 是上底面11A C 的中心,若1AE AA xAB yAD =++,则x y +等于( ) A .13B .12C .1D .2【答案】C【解析】如图,()111111112AE AA A E AA A B A D =+=++ ()11111222AA AB AD AA AB AD =++=++,所以12x y ==,所以1x y +=.故选C15.(江苏省南京市秦淮区2019-2020学年高一下学期期末)空间直角坐标系O xyz -中,已知两点()11,2,1P -,()22,1,3P -,则这两点间的距离为( )A BC .D .18【答案】B【解析】根据题意,两点()11,2,1P -,()22,1,3P -,则12||PP =B .16.(湖北省恩施高中2020届高三下学期四月决战新高考名校交流卷(B ))已知向量()1,2a =,()3,b x =,()1,1c y =--,且//a b ,b c ⊥,则x y ⋅的值为( )A .6B .32 C .9D .132-【答案】C【解析】∵//a b ,∴60x -=,6x =,∴向量()3,6b =, ∵b c ⊥,∴()3610y -+-=,∴32y =,∴9x y ⋅=.故选C . 17.(四川省绵阳市2019-2020学年高二下学期期末教学质量测试数学(理)试题)在空间直角坐标系中,若()1,1,0A ,()13,0,12AB =,则点B 的坐标为( ) A .()5,1,2-- B .()7,1,2- C .()3,0,1 D .()7,1,2【答案】D【分析】首先设出点(,,)B x y z ,利用向量坐标公式以及向量相等的条件得到等量关系式,求得结果. 【解析】设(,,)B x y z ,所以(1,1,)2(3,0,1)(6,0,2)AB x y z =--==,所以16102x y z -=⎧⎪-=⎨⎪=⎩,所以712x y z =⎧⎪=⎨⎪=⎩,所以点B 的坐标为(7,1,2),故选D .18.(广东省云浮市2019-2020学年高二上学期期末)如图,在三棱锥P ABC -中,点D ,E ,F 分别是AB ,PA ,CD 的中点,设PA a =,PB b =,PC c =,则EF =( )A .111442a b c --B .111442a b c -+ C .111442a b c +-D .111442a b c -++【答案】D 【解析】点D ,E ,F 分别是AB ,PA ,CD 的中点,且PA a =,PB b =,PC c =,∴()11112224EF EP PC CF PA PC CD PA PC CA CB =++=-++=-+++()1111124442PA PC PA PC PB PC PA PB PC =-++-+-=-++111442a b c =-++.故选D .19.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)一个向量p 在基底{},,a b c 下的坐标为()1,2,3,则p 在基底{},,a b a b c +-下的坐标为( )A .31322⎛⎫- ⎪⎝⎭,,B .31322⎛⎫- ⎪⎝⎭,, C .13322⎛⎫- ⎪⎝⎭,,D .13322⎛⎫- ⎪⎝⎭,,【答案】B【解析】因为向量p 在基底{},,a b c 下的坐标为()1,2,3,所以23p a b c =++, 设p 在基底{},,a b a b c +-下的坐标为(),,x y z ,所以()()()()p x a b y a b zc x y a x y b zc =++-+⇒++-+,有13223x y x y x z +=⎧⎪-=⇒=⎨⎪=⎩,12y,3z =,p 在基底{},,a b a b c +-下的坐标为31,,322⎛⎫- ⎪⎝⎭.故选B .20.(湖北省武汉襄阳荆门宜昌四地六校考试联盟2020-2021学年高三上学期起点联考)如图,直四棱柱1111ABCD A B C D -的底面是菱形,12AA AB ==,60BAD ∠=︒,M 是1BB 的中点,则异面直线1A M 与1B C所成角的余弦值为( )A. B .15- C .15D.5【答案】D【分析】用向量1,,AB BC BB 分别表示11,AM BC ,利用向量的夹角公式即可求解. 【解析】由题意可得221111111111,5,2A M AB B M AB BB A M A B B M=+=-=+=221111,2BC BC BB B C BC BB =-=+=,()211111111111cos ,AB BB BC BB AB BC BB A M B C A M B C A M B C⎛⎫-⋅-⋅+ ⎪⋅⎝〈〉===0122cos604⨯⨯+⨯==故选D21.(河北省石家庄市第二中学2020-2021学年高二上学期8月线上考试(二))长方体1111ABCD A B C D -中,11,2,AB AD AA E ===为棱1AA 的中点,则直线1C E 与平面11CB D 所成角的余弦值为( ) A.9 B.9CD .23【答案】A【解析】根据题意,建立如图所示直角坐标系:则1C E (1,1,1)=--,设平面11B D C 的法向量为n (,,)x y z =,则100n B D n BC ⎧⋅=⎪⎨⋅=⎪⎩可得:020x y x z --=⎧⎨--=⎩,取n (2,2,1)=--,则1,cos n C E =11n C E nC E⋅9==,设直线1C E 与平面11B D C 的夹角为θ,则9sin θ=,9cos θ==.故选A . 22.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)已知点()1,1,A t t t --,()2,,B tt ,则A ,B 两点的距离的最小值为A.10 B.5C.5D .35【答案】C【分析】由两点之间的距离公式求得AB 之间的距离用t 表示出来,建立关于t 的函数,转化为求函数的最小值.【解析】因为点()1,1,A t t t --,()2,,B t t ,所以22222(1)(21)()522AB t t t t t t =++-+-=-+,有二次函数易知,当15t =时,取得最小值为95,AB ∴,故选C .23.(湖南省邵阳市邵东县第十中学2020届高三下学期模拟考试数学(文)试题)如图,在正方体1111ABCD A B C D -中,M ,N 分别是棱AB ,1BB 的中点,点P 在对角线1CA 上运动.当△PMN 的面积取得最小值时,点P 的位置是( )A .线段1CA 的三等分点,且靠近点1AB .线段1CA 的中点C .线段1CA 的三等分点,且靠近点CD .线段1CA 的四等分点,且靠近点C【答案】B【解析】设正方体的棱长为1,以A 为原点,1,,AB AD AA 分别为,,x y z 轴,建立空间直角坐标系,如图所示:则1(,0,0)2M ,1(1,0,)2N ,MN 的中点31(,0,)44Q ,1(0,0,1)A ,(1,1,0)C ,则1(1,1,1)AC =-,设(,,)P t t z ,(1,1,)PC t t z =---, 由1AC 与PC 共线,可得11111t t z---==-,所以1t z =-,所以(1,1,)P z z z --,其中01z ≤≤,因为||(1PM ==||(11)(1PN z =--+=所以||||PM PN =,所以PQ MN ⊥,即||PQ 是动点P 到直线MN 的距离,由空间两点间的距离公式可得||PQ ===12c =时,||PQ 取得最小值4,此时P 为线段1CA 的中点,由于||4MN =为定值,所以当△PMN 的面积取得最小值时,P 为线段1CA 的中点.故选B24.(云南省梁河县第一中学2019-2020学年高二7月月考数学(理)试题)长方体1111ABCD A B C D -中,12AB AA ==,1AD =,E 为1CC 的中点,则异面直线1BC 与AE 所成角的余弦值为( )A BCD .【答案】B【分析】以点A 为坐标原点,AB 、AD 、1AA 所在直线分别为x 、y 、z 轴建立空间直角坐标系,利用空间向量法可求得异面直线1BC 与AE 所成角的余弦值.【解析】以点A 为坐标原点,AB 、AD 、1AA 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系A xyz -,则()0,0,0A 、()2,0,0B 、()12,1,2C 、()2,1,1E ,()2,1,1AE =,()10,1,2BC =,111cos ,6AE BC AE BC AEBC ⋅<>===⋅. 因此,异面直线1BC 与AE .故选B . 25.(广西桂林市2019-2020学年高二下学期期末质量检测数学(理))在正方体ABCD --A 1B 1C1D 1中,E 是C 1C 的中点,则直线BE 与平面B 1BD 所成角的正弦值为( ) A.5-B.5C .D 【答案】B【分析】以D 为坐标原点,以DA 为x 轴,以DC 为y 轴,以1DD 为z 轴,建立空间直角坐标系,利用向量法能求出直线BE 与平面1B BD 所成角的正弦值.【解析】以D 为坐标原点,以DA 为x 轴,以DC 为y 轴,以1DD 为z 轴,建立如图空间直角坐标系,设正方体的棱长为2,则()000D ,,,()220B ,,,()1222B ,,,()021E ,,, ∴() 220BD =--,,,()1 002BB =,,,() 201BE =-,,, 设平面1B BD 的法向量为() ,,x n y z =,∵ n BD ⊥,1n BB ⊥, ∴22020x y z --=⎧⎨=⎩,令y 1=,则() 110n =-,,,∴10cos ,n BE n BE n BE ⋅==⋅,设直线BE 与平面1B BD 所成角为θ,则10sin cos ,5n BE θ==,故选B .26.(陕西省商洛市商丹高新学校2020届高三下学期考前适应性训练理科)如图在平行六面体1111ABCD A B C D -中,底面ABCD 是边长为1的正方形,侧棱12AA =且1160A AD A AB ∠=∠=︒,则1AC =( )A . BC .D 【答案】B【解析】因为底面ABCD 是边长为1的正方形,侧棱12AA =且1160A AD A AB ∠=∠=︒,则2=1AB ,2=1AD ,21=4AA ,0AB AD ⋅=,111cos 1AB AA AB AA A AB ⋅=⋅⋅∠=,111cos 1AD AA AD AA A AD ⋅=⋅⋅∠=,则1AC 1AB AD AA =++()1222111222AB AD AA AB AA AB AD AD AA =+++⋅+⋅+⋅==,故选B .27.(2020届上海市七宝中学高三高考押题卷)已知MN 是正方体内切球的一条直径,点P 在正方体表面上运动,正方体的棱长是2,则PM PN →→⋅的取值范围为( ) A .[]0,4 B .[]0,2 C .[]1,4D .[]1,2【答案】B【分析】利用向量的线性运算和数量积运算律可将所求数量积化为21PO →-,根据正方体的特点可确定PO →的最大值和最小值,代入即可得到所求范围.【解析】设正方体内切球的球心为O ,则1OM ON ==,2PM PN PO OM PO ON PO PO OM ON OM ON →→→→→→→→→→→→⎛⎫⎛⎫⎛⎫⋅=+⋅+=+⋅++⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,MN 为球O 的直径,0OM ON →→∴+=,1OM ON →→⋅=-,21PM PN PO →→→∴⋅=-,又P 在正方体表面上移动,∴当P 为正方体顶点时,PO →P 为内切球与正方体的切点时,PO →最小,最小值为1,[]210,2PO →∴-∈,即PM PN →→⋅的取值范围为[]0,2.故选B .【点睛】本题考查向量数量积的取值范围的求解问题,关键是能够通过向量的线性运算将问题转化为向量模长的取值范围的求解问题.28.(湖北省荆门市2019-2020学年高二下学期期末)在平行六面体ABCD A B C D ''''-中,若2AC x AB y BC z CC →→→→''=++,则x y z ++=( )A .52B .2C .32D .116【答案】A【解析】由空间向量的线性运算,得AB BC AC AC CC CC →→→→→→⎛⎫=+=++ ⎪⎭'''⎝, 由题可知,2AC x AB y BC z CC →→→→''=++,则1,1,21x y z ===,所以11,2y z ==, 151122x y z ∴++=++=.故选A .29.(安徽省六校教育研究会2020-2021学年高三上学期第一次素质测试理科)如图,在直三棱柱111ABC A B C -中,已知90ABC ∠=︒,P 为侧棱1CC 上任意一点,Q 为棱AB 上任意一点,PQ 与AB 所成角为α,PQ 与平面ABC 所成的角为β,则α与β的大小关系为( )A .αβ=B .αβ<C .αβ>D .不能确定【答案】C【分析】建立空间直角坐标系设()()(),0,,0,,00,0,0P x z Q y x y z >≥≥,利用空间向量法分别求得cos ,cos αβ,然后根据(0,],0,22ππαβ⎡⎤∈∈⎢⎥⎣⎦,利用余弦函数的单调性求解.【解析】建立如图所示空间直角坐标系:设()()(),0,,0,,00,0,0P x z Q y x y z >≥≥,则()(),,,0,,0QP x y z QB y =-=-, 所以2222,,QP QB y QP x y z QB y ⋅==++=,所以2cos QP QB QP QBx zα⋅==⋅+又(0,],0,22ππαβ⎡⎤∈∈⎢⎥⎣⎦,sin QP CP QPβ⋅==所以cos β=cos cos βα>,因为cos y x = 在0,2π⎛⎫⎪⎝⎭上递减,所以αβ>,故选C 30.(江西省赣州市赣县第三中学2019-2020学年高二6月份考试数学(理)试题)如图,在四棱柱1111ABCD A B C D -中,底面ABCD 为正方形,侧棱1AA ⊥底面ABCD ,3AB =,14AA =,P 是侧面11BCC B 内的动点,且1AP BD ⊥,记AP 与平面11BCC B 所成的角为θ,则tan θ的最大值为( )A .43B .53 C .2D .259【答案】B【分析】建立空间直角坐标系,利用向量法能求出线面角的正切值的最大值. 【解析】以1,,DA DC DD 所在直线分别为,,x y z 轴,建立空间直角坐标系, 设(,3,)P x z ,则1(3,3,),(3,3,4)AP x z BD =-=--,11,0AP BD AP BD ⊥∴⋅=,33(3)3340,4x z z x ∴---⨯+=∴=,||BP ∴==9255=, ||5tan ||3AB BP θ∴=,tan θ∴的最大值为53.故选B .31.(江西省赣州市赣县第三中学2019-2020学年高二6月份考试数学(理)试题)如图,在棱长都相等的正三棱柱111ABC A B C -中,D 是棱1CC 的中点,E 是棱1AA 上的动点.设AE x =,随着x 增大,平面BDE 与底面ABC 所成锐二面角的平面角是( )A .增大B .先增大再减小C .减小D .先减小再增大【答案】D【解析】设正三棱柱111ABC A B C -棱长为2,,02AE x x =≤≤, 设平面BDE 与底面ABC 所成锐二面角为α,以A 为坐标原点,过点A 在底面ABC 内与AC 垂直的直线为x 轴,1,AC AA 所在的直线分别为,y z 轴建立空间直角坐标系,则(0,2,1),(0,0,),(3,1,1),(0,2,1)B D E x BD ED x =-=-,设平面BDE 的法向量(,,)m s t k =,则m BD m ED⎧⊥⎨⊥⎩,即02(1)0t k t x k ⎧++=⎪⎨+-=⎪⎩,令k =33,1t x s x =-=+,所以平面BDE的一个法向量(m x=+-,底面ABC的一个法向量为(0,0,1)n =,cos|cos,|m nα=<>==当1(0,)2x∈,cosα随着x增大而增大,则α随着x的增大而减小,当1(,2)2x∈,cosα随着x增大而减小,则α随着x的增大而增大.故选D.32.(山东省滕州市第一中学2020-2021学年高二9月开学收心考试)已知空间直角坐标系O xyz-中,()1,2,3OA =,()2,1,2OB =,()1,1,2OP =,点Q在直线OP上运动,则当QA QB⋅取得最小值时,点Q 的坐标为()A.131,,243⎛⎫⎪⎝⎭B.133,,224⎛⎫⎪⎝⎭C.448,,333⎛⎫⎪⎝⎭D.447,,333⎛⎫⎪⎝⎭【答案】C【分析】设(,,)Q x y z,根据点Q在直线OP上,求得(,,2)Qλλλ,再结合向量的数量积和二次函数的性质,求得43λ=时,QA QB⋅取得最小值,即可求解.【解析】设(,,)Q x y z,由点Q在直线OP上,可得存在实数λ使得OQ OPλ=,即(,,)(1,1,2)x y zλ=,可得(,,2)Qλλλ,所以(1,2,32),(2,1,22)QA QB λλλλλλ=---=---,则2(1)(2)(2)(1)(32)(22)2(385)QA QB λλλλλλλλ⋅=--+--+--=-+, 根据二次函数的性质,可得当43λ=时,取得最小值23-,此时448(,,)333Q . 故选C .【点睛】本题主要考查了空间向量的共线定理,空间向量的数量积的运算,其中解答中根据向量的数量积的运算公式,得关于λ的二次函数是解答的关键,着重考查运算与求解能力.33.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)如图该几何体由半圆柱体与直三棱柱构成,半圆柱体底面直径BC =4,AB =AC ,∠BAC =90°,D 为半圆弧的中点,若异面直线BD 和AB 1所成角的余弦值为23,则该几何体的体积为( )A .16+8πB .32+16πC .32+8πD .16+16π【答案】A【解析】设D 在底面半圆上的射影为1D ,连接1AD 交BC 于O ,设1111A D B C O ⋂=. 依题意半圆柱体底面直径4,,90BC AB AC BAC ==∠=︒,D 为半圆弧的中点, 所以1111,AD BC A D B C ⊥⊥且1,O O 分别是下底面、上底面半圆的圆心.连接1OO , 则1OO 与上下底面垂直,所以11,,OO OB OO OA OA OB ⊥⊥⊥,以1,,OB OA OO 为,,x y z 轴建立空间直角坐标系,设几何体的高为()0h h >,则()()()()12,0,0,0,2,,0,2,0,2,0,B D h A B h -,所以()()12,2,,2,2,BD h AB h =--=-,由于异面直线BD 和1AB 所成的角的余弦值为23,所以11238BD AB BD AB ⋅==⋅,即2222,16,483h h h h ===+.所以几何体的体积为2112442416822ππ⨯⨯⨯+⨯⨯⨯=+.故选A.34.(安徽省阜阳市太和第一中学2020-2021学年高二(平行班)上学期开学考试)在正方体1111ABCD A B C D -中,直线1BC 与平面1A BD 所成角的余弦值为( )A .24B .23 C .3 D .3 【答案】C【分析】分别以1,,DA DC DD 为,,x y z 轴建立如图所示空间直角坐标系,求出直线的方向向量和平面的法向量后可得所求线面角的余弦值. 【解析】分别以1,,DA DC DD 为,,x y z轴建立如图所示空间直角坐标系,设正方体的棱长为1,可得()()()()110,0,0,1,1,0,0,1,1,1,0,1D B C A ∴()()()111,0,1,1,0,1,1,1,0BC A D BD =-=--=--, 设(),,n x y z =是平面1A BD 的一个法向量,∴100n A D n BD ⎧⋅=⎨⋅=⎩,即00x z x y +=⎧⎨+=⎩,取1x =,得1y z ==-,∴平面1A BD 的一个法向量为()1,1,1n =--,设直线1BC 与平面1A BD 所成角为θ, ∴11126sin cos ,323BC nBC n BC nθ⋅-=〈〉===⨯, ∴23cos 1sin θθ=-1BC 与平面1A BD 所成角的余弦值是33, 故选C.【点睛】用向量法求二面角大小的两种方法:(1)分别在二面角的两个半平面内找到与棱垂直且以垂足为起点的两个向量,则这两个向量的夹角的大小即为二面角的大小;(2)分别求出二面角的两个半平面的法向量,然后通过两个法向量的夹角得到二面角大小,解题时要注意结合图形判断出所求的二面角是锐角还是钝角.35.(2020届重庆市第一中学高三下学期6月模拟数学(理)试题)如图所示,在正方体1111ABCD A B C D -中,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则异面直线1A P 与BD 所成角的取值范围为( )A .3,44ππ⎡⎤⎢⎥⎣⎦B .,42ππ⎡⎤⎢⎥⎣⎦C .,32ππ⎡⎤⎢⎥⎣⎦D .2,33ππ⎡⎤⎢⎥⎣⎦【答案】C【解析】过A 作平面α平面1DBC ,点P 是底面1111D C B A 内(含边界)的一点,且//AP 平面1DBC ,则P ∈平面α,即P 在α与平面1111D C B A 的交线上,连接111,,AB AD B D ,11DD BB =,则四边形11BDD B 是平行四边形,11B D BD ∴,11B D ∴平面1DBC ,同理可证1AB ∥平面1DBC ,∴平面11AB D ∥平面1DBC ,则平面11AB D 即为α,点P 在线段11B D 上,以D 为坐标原点,1,,DA DC DD 建立如图坐标系,设正方体棱长为1, 则()0,0,0D ,()1,1,0B ,()1,0,0A ,设(),,1P λλ,[]0,1λ∈, ()1,1,0DB ∴=,()1,,1AP λλ=-,21DB AP λ∴⋅=-,2DB =,2AP λ=,设1A P 与BD 所成角为θ,则cos 2DB APDB APθ⋅===⋅ ==12λ=时,cos θ取得最小值为0, 当0λ=或1时,cos θ取得最大值为12,10cos 2θ∴≤≤,则32ππθ≤≤.故选C . 36.(重庆市第八中学2020届高三下学期第五次月考数学(理)试题)如图,矩形ABCD 中,2AB AD ==E 为边AB 的中点,将ADE 沿直线DE 翻折成1A DE △.在翻折过程中,直线1A C 与平面ABCD 所成角的正弦值最大为()A.4B .6C.14D【答案】A【解析】分别取DE ,DC 的中点O ,F ,则点A 的轨迹是以AF 为直径的圆, 以,OA OE 为,x y 轴,过O 与平面AOE 垂直的直线为z 轴建立坐标系,则()2,1,0C -,平面ABCD 的其中一个法向量为n = (0,0.1), 由11A O =,设()1cos ,0,sin A αα,则()1cos 2,1,sin CA αα=+-,记直线1A C 与平面ABCD 所成角为θ,则11sin 4cos ||CA nCAn θ⋅===⋅设315cos ,,sin 222t αθ⎡⎤=+∈=≤=⎢⎥⎣⎦ 所以直线1A C 与平面ABCD ,故选A . 二、多项选择题37.(江苏省南京市秦淮中学2019-2020学年高二(美术班)上学期期末)对于任意非零向量()111,,a x y z =,()222,,b x y z =,以下说法错误的有( )A .若a b ⊥,则1212120x x y y z z ++=B .若//a b ,则111222x y z x y z == C .cos ,a b =><D .若1111===x y z ,则a为单位向量 【答案】BD【解析】对于A 选项,因为a b ⊥,则1212120a b x x y y z z ⋅=++=,A 选项正确;对于B 选项,若20x =,且20y ≠,20z ≠,若//a b ,但分式12x x 无意义,B 选项错误; 对于C 选项,由空间向量数量积的坐标运算可知cos ,a b =><,C 选项正确;对于D 选项,若1111===x y z,则211a =+=,此时,a 不是单位向量,D 选项错误.故选BD .38.(2020届百师联盟高三开学摸底大联考山东卷)下面四个结论正确的是( ) A .向量(),0,0a b a b ≠≠,若a b ⊥,则0a b ⋅=.B .若空间四个点P ,A ,B ,C ,1344PC PA PB =+,则A ,B ,C 三点共线. C .已知向量()1,1,a x =,()3,,9b x =-,若310x <,则,a b 为钝角.D .任意向量a ,b ,c 满足()()a b c a b c ⋅⋅=⋅⋅. 【答案】AB【解析】由向量垂直的充要条件可得A 正确;1344PC PA PB =+,∴11334444PC PA PB PC -=-即3AC CB =,∴A ,B ,C 三点共线,故B 正确;当3x =-时,两个向量共线,夹角为π,故C 错误;由于向量的数量积运算不满足结合律,故D 错误.故选AB.39.(广东省中山市2019-2020学年高一下学期期末)在空间直角坐标系中,下列结论正确的是( ) A .点()2,1,4-关于x 轴对称的点的坐标为()2,1,4 B .到()1,0,0的距离小于1的点的集合是()(){}222,,11x y z x y z -++<C .点()1,2,3与点()3,2,1的中点坐标是()2,2,2D .点()1,2,0关于平面yOz 对称的点的坐标为()1,2,0- 【答案】BCD【解析】对于选项A :点()2,1,4-关于x 轴对称的点的坐标为()2,1,4---,所以A 不正确; 对于选项B :点(),,x y z到()1,0,0的距离小于11<,所以B 正确;对于选项C :点()1,2,3与点()3,2,1的中点坐标是()132231,,2222,2,2⎛⎫=⎪⎝⎭+++,所以C 正确;对于选项D :由点(),,x y z 关于平面yOz 对称的点的坐标为(),,x y z -,所以D 正确. 故选B C D .40.(山东省威海市文登区2019-2020学年高二上学期期末)正方体1111ABCD A B C D -的棱长为a ,则下列结论正确的是( )A .211AB AC a ⋅=- B .212BD BD a ⋅= C .21AC BA a⋅=- D .212AB AC a ⋅=【答案】BC【解析】如下图所示:对于A 选项,()2211AB AC AB AC AB AB AD AB a ⋅=⋅=⋅+==,A 选项错误;对于B ,()()()()2221112BD BD AD AB BD DD AD AB AD AB AA AD AB a ⋅=-+=--+=+=,B 选项正确;对于C 选项,()()2211AC BA AB AD AA AB AB a ⋅=+⋅-=-=-,C 选项正确;对于D 选项,()2211AB AC AB AB AD AA AB a ⋅=⋅++==,D 选项错误.故选BC .41.(福建省泉州市普通高中2019-2020学年毕业班第一次质量检查(理))如图,正方体1111ABCD A B C D -的棱长为1,E 是1DD 的中点,则( )A .直线1//BC 平面1A BD B .11B C BD ⊥C .三棱锥11C B CE -的体积为13D .异面直线1B C 与BD 所成的角为60︒【答案】ABD【解析】如图建立空间直角坐标系,()0,0,0A ,()1,0,0B ,()1,1,0C ,()0,1,0D ,()10,0,1A ,()11,0,1B ,()11,1,1C ,()10,1,1D ,10,1,2⎛⎫ ⎪⎝⎭E ,()1B C 0,1,1=-,()11,1,1BD =-,()1,1,0BD =-,()11,0,1BA =-,所以()111011110B C BD =-⨯+⨯+-⨯=,即11BC BD ⊥,所以11B C BD ⊥,故B 正确;()11011101B C BD =-⨯+⨯+-⨯=,12B C =,2BD =,设异面直线1B C 与BD 所成的角为θ,则111cos 2B C BD B C BDθ==,又0,2πθ⎛⎤∈ ⎥⎝⎦,所以3πθ=,故D 正确;设平面1A BD 的法向量为(),,n x y z =,则1·0·0n BA n BD ⎧=⎨=⎩,即0x y x z -+=⎧⎨-+=⎩,取()1,1,1n =,则()10111110n B C =⨯+⨯+⨯-=,即1C n B ⊥,又直线1B C ⊄平面1A BD ,所以直线1//B C 平面1A BD ,故A 正确;111111111111113326C B CE B C CE C CE V B C S V -∆-===⨯⨯⨯⨯=⋅,故C 错误;故选ABD.42.(海南省海南中学2019-2020学年高三第四次月考)如图所示,正方体1111ABCD A B C D -中,1AB =,点P 在侧面11BCC B 及其边界上运动,并且总是保持1AP BD ⊥,则以下四个结论正确的是()A .113P AA D V -=B .点P 必在线段1BC 上C .1AP BC ⊥D .//AP 平面11AC D【答案】BD 【解析】对于A ,P 在平面11BCC B 上,平面11//BCC B 平面1AA D ,P ∴到平面1AA D 即为C 到平面1AA D 的距离,即为正方体棱长,1111111113326P AA D AA D V S CD -∴=⋅=⨯⨯⨯⨯=△,A 错误;对于B ,以D 为坐标原点可建立如下图所示的空间直角坐标系:则()1,0,0A ,(),1,P x z ,()1,1,0B ,()10,0,1D ,()11,1,1B ,()0,1,0C()1,1,AP x z →∴=-,()11,1,1BD →=--,()11,0,1B C →=--,1AP BD ⊥,1110AP BD x z →→∴⋅=--+=,x z ∴=,即(),1,P x x ,(),0,CP x x →∴=,1CP x B C →→∴=-,即1,,B P C 三点共线,P ∴必在线段1B C 上,B 正确;对于C ,()1,1,AP x x →=-,()11,0,1BC →=-,111AP BC x x →→∴⋅=-+=,AP ∴与1BC 不垂直,C 错误;对于D ,()11,0,1A ,()10,1,1C ,()0,0,0D ,()11,0,1DA →∴=,()10,1,1DC →=,设平面11AC D 的法向量(),,n x y z →=,1100n DA x z n DC y z ⎧⋅=+=⎪∴⎨⋅=+=⎪⎩,令1x =,则1z =-,1y =,()1,1,1n →∴=-, 110AP n x x →→∴⋅=-+-=,即AP n →→⊥,//AP ∴平面11ACD ,D 正确.故选BD . 43.(福建省宁德市2019-2020学年高二上学期期末考试)如图所示,棱长为1的正方体1111ABCD A B C D-中,P 为线段1A B 上的动点(不含端点),则下列结论正确的是( )A .平面11D A P ⊥平面1A APB .1AP DC ⋅不是定值 C .三棱锥11BD PC -的体积为定值 D .11DC D P ⊥【答案】ACD【解析】A .因为是正方体,所以11D A ⊥平面1A AP ,11D A ⊂平面11D A P ,所以平面11D A P ⊥平面1A AP ,所以A 正确;B .11111111()AP DC AA A P DC AA DC A P DC ⋅=+⋅=⋅+⋅ 11112cos 45cos901212AA DC A P DC =+=⨯⨯=,故11AP DC ⋅=,故B 不正确; C .1111B D PC P B D C V V --=,11B D C 的面积是定值,1//A B 平面11B D C ,点P 在线段1A B 上的动点,所以点P 到平面11B D C 的距离是定值,所以1111B D PC P B D C V V --=是定值,故C 正确; D .111DC A D ⊥,11DC A B ⊥,1111A D A B A =,所以1DC ⊥平面11A D P ,1D P ⊂平面11A D P ,所以11DC D P ⊥,故D 正确.故选ACD44.(山东省济南莱芜市第一中学2019-2020学年高二下学期第一次质量检测)关于空间向量,以下说法正确的是( )A .空间中的三个向量,若有两个向量共线,则这三个向量一定共面B .若对空间中任意一点O ,有111632OP OA OB OC =++,则P ,A ,B ,C 四点共面 C .设{},,a b c 是空间中的一组基底,则{},,a b b c c a +++也是空间的一组基底 D .若0a b ⋅<,则,a b 是钝角 【答案】ABC【解析】对于A 中,根据共线向量的概念,可知空间中的三个向量,若有两个向量共线,则这三个向量一定共面,所以是正确的;对于B 中,若对空间中任意一点O ,有111632OP OA OB OC =++,根据空间向量的基本定理,可得,,,P A B C 四点一定共面,所以是正确的;对于C 中,由{},,a b c 是空间中的一组基底,则向量,,a b c 不共面,可得向量,a b b c ++,c a +也不共面,所以{},,a b b c c a +++也是空间的一组基底,所以是正确的; 对于D 中,若0a b ⋅<,又由,[0,]a b π∈,所以,(,]2a b ππ∈,所以不正确.故选ABC .45.(河北省沧州市盐山中学2019-2020学年高一下学期期末)若长方体1111ABCD A B C D -的底面是边长为2的正方形,高为4,E 是1DD 的中点,则( )A .11B E A B ⊥B .平面1//B CE 平面1A BDC .三棱锥11C B CE -的体积为83D .三棱锥111C B CD -的外接球的表面积为24π【答案】CD【解析】以1{,,}AB AD AA 为正交基底建立如图所示的空间直角坐标系,则 (0,0,0)A ,(2,0,0)B ,(2,2,0)C ,(0,2,0)D ,1(0,0,4)A ,1(2,0,4)B ,(0,2,2)E ,所以1(2,2,2)B E =--,1(2,0,4)A B =-, 因为1140840B E A B ⋅=-++=≠,所以1B E 与1A B 不垂直,故A 错误; 1(0,2,4)CB =-,(2,0,2)CE =-,设平面1B CE 的一个法向量为111(,,)n x y z =,则由100n CB n CE ⎧⋅=⎨⋅=⎩,得1111240220y z x z -+=⎧⎨-+=⎩,所以11112y z x z =⎧⎨=⎩,不妨取11z =,则11x =,12y =,所以(1,2,1)n =, 同理可得设平面1A BD 的一个法向量为(2,2,1)m =,故不存在实数λ使得n λm =,故平面1B CE 与平面1A BD 不平行,故B 错误; 在长方体1111ABCD A B C D -中,11B C ⊥平面11CDD C ,故11B C 是三棱锥11B CEC -的高,所以111111111184223323三棱锥三棱锥CEC C B CE CEC B V V S B C --==⋅=⨯⨯⨯⨯=△,故C 正确; 三棱锥111C B CD -的外接球即为长方体1111ABCD A B C D -的外接球,故外接球的半径2R ==所以三棱锥111C B CD -的外接球的表面积2424S R ππ==,故D 正确.故选CD .46.(山东省济南市2019-2020学年高二下学期末考试)如图,棱长为的正方体1111ABCD A B C D -中,P 为线段1A B 上的动点(不含端点),则下列结论正确的是( )A .直线1D P 与AC 所成的角可能是6π B .平面11D A P ⊥平面1A AP C .三棱锥1D CDP -的体积为定值D .平面1APD 截正方体所得的截面可能是直角三角形 【答案】BC【解析】对于A ,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系,()()()10,0,1,1,0,0,0,1,0D A C ,设()()1,,01,01P a b a b <<<< ()()11,,1,1,1,0D P a b AC =-=-,(111cos ,01D P AC D P AC D P ACa b ⋅==<++-1301,01,,24a b D P AC ππ<<<<∴<<∴直线D 1P 与AC 所成的角为,42ππ⎛⎫⎪⎝⎭,故A 错误; 对于B ,正方体ABCD ﹣A 1B 1C 1D 1中,A 1D 1⊥AA 1,A 1D 1⊥AB , ∵AA 1AB =A ,∴A 1D 1⊥平面A 1AP ,∵A 1D 1⊥平面D 1A 1P ,∴平面D 1A 1P ⊥平面A 1AP ,故B 正确;对于C ,1111122CDD S=⨯⨯=,P 到平面CDD 1的距离BC =1, ∴三棱锥D 1﹣CDP 的体积:111111326D CDP P CDD V V --==⨯⨯=为定值,故C 正确;对于D ,平面APD 1截正方体所得的截面不可能是直角三角形,故D 错误;故选BC .47.(江苏省苏州中学园区校2020-2021学年高三上学期8月期初调研)如图,正方体1111ABCD A B C D -的棱长为1,线段11B D 上有两个动点E ,F ,且12EF =,则下列结论中正确的是( )A .线段11B D 上存在点F ,使得AC AF ⊥ B .//EF 平面ABCD C .AEF 的面积与BEF 的面积相等 D .三棱锥A BEF -的体积为定值【答案】BD【解析】如图,以C 为坐标原点建系CD ,CB ,1CC 为x ,y ,z 轴,()1,1,0A ,()0,0,0C ,()1,1,0AC =--,1B F B λ=11D ,即()()0,1,11,1,0x y z λ---=-,∴x λ=,1y λ=-,1z =,∴(),1,1F λλ-,()1,,1AF λλ=--,()()11010AC AF λλ⋅=--++=≠, ∴AC 与AF 不垂直,A 错误.E ,F 都在B ,D 上,又11//BD B D ,∴//EF BD ,BD ⊂平面ABCD ,EF ⊄平面ABCD ,∴//EF 平面ABCD ,B 正确AB 与EF 不平行,则1A B 与EF 的距离相等,∴AEF BEF S S ≠△△,∴C 错误A 到BEF 的距离就是A 到平面11BDDB 的距离,A 到11BDD B 的距离为22AC =1111224BEF S =⨯⨯=△,∴1134224A BEF V -=⨯⨯=是定值,D 正确.故选BD .48.(江苏省扬州市宝应中学2020-2021学年高三上学期开学测试)在正三棱柱ABC A B C '''-中,所有棱长为1,又BC '与B C '交于点O ,则( )A .AO =111222AB AC AA '++ B .AO B C '⊥C .三棱锥A BB O '-D .AO 与平面BB ′C ′C 所成的角为π6【答案】AC【解析】由题意,画出正三棱柱ABC A B C '''-如图所示,向量()()111222AO AB BO AB BC BB AB AC AB AA ''=+=++=+-+ 111222AB AC AA '=++,故选项A 正确;在AOC △中,1AC =,22OC,1OA ==, 222OA OC AC +≠,所以AO 和B C '不垂直,故选项B 错误;在三棱锥A BB O '-中,14BB O S '=,点A 到平面BB O '的距离即ABC 中BC 边上的高,所以h =以111334A BB O BB O V S h ''-==⨯=C 正确; 设BC 中点为D ,所以AD BC ⊥,又三棱柱是正三棱柱,所以AD ⊥平面BB C C '',所以AOD ∠即AO 与平面BB ′C ′C 所成的角,112cos 12OD AOD OA ∠===,所以3AOD π∠=,故选项D 错误.故选AC49.(山东省泰安肥城市2020届高三适应性训练(一))如图四棱锥P ABCD -,平面PAD ⊥平面ABCD ,侧面PAD 是边长为ABCD 为矩形,CD =Q 是PD 的中点,则下列结论正确的是( )A .CQ ⊥平面PADB .PC 与平面AQC所成角的余弦值为3C .三棱锥B ACQ -的体积为D .四棱锥Q ABCD -外接球的内接正四面体的表面积为【答案】BD【解析】取AD 的中点O ,BC 的中点E ,连接,OE OP ,因为三角形PAD 为等边三角形,所以OP AD ⊥,因为平面PAD ⊥平面ABCD ,所以OP ⊥平面 ABCD ,因为AD OE ⊥,所以,,OD OE OP 两两垂直,所以,如下图,以O 为坐标原点,分别以,,OD OE OP 所在的直线为x 轴,y 轴 ,z 轴,建立空间直角坐标系,则(0,0,0),(O D A ,(P C B ,因为点Q 是PD 的中点,所以Q ,平面PAD 的一个法向量为(0,1,0)m =,6(QC =,显然 m 与QC 不共线,所以CQ 与平面PAD 不垂直,所以A 不正确;3632(6,23,32),(,0,),(26,PC AQ AC =-==, 设平面AQC 的法向量为(,,)n x y z =,则3602260n AQ x zn AC ⎧⋅==⎪⎨⎪⋅=+=⎩, 令=1x ,则y z ==(1,2,3)n =--,设PC 与平面AQC 所成角为θ,则21sin 36n PC n PCθ⋅===,所以22cos 3θ=,所以B 正确;三棱锥B ACQ -的体积为1132B ACQ Q ABC ABCV V S OP --==⋅ 1116322=⨯⨯⨯=,所以C 不正确;设四棱锥Q ABCD -外接球的球心为)M a ,则MQ MD =,所以22222222a a ⎛⎫⎛++-=++ ⎪ ⎪ ⎝⎭⎝⎭,解得0a =,即M 为矩形ABCD 对角线的交点,所以四棱锥Q ABCD -外接球的半径为3,设四棱锥Q ABCD -外接球的内接正四面体的棱长为x ,将四面体拓展成正方体,其中正四面体棱为正方体面的对角线,故正方体的棱长为2x ,所以2236⎫=⎪⎪⎝⎭,得224x =,所以正四面体的表面积为244x ⨯=,所以D 正确.故选BD.50.(山东省滕州市第一中学2020-2021学年高二9月开学收心考试)在四面体P ABC -中,以上说法正确的有( )A .若1233AD AC AB =+,则可知3BC BD = B .若Q 为△ABC 的重心,则111333PQ PA PB PC =++C .若0PA BC =,0PC AB =,则0PB AC =D .若四面体P ABC -各棱长都为2,M N ,分别为,PA BC 的中点,则1MN = 【答案】ABC 【解析】对于A ,1233AD AC AB =+,32AD AC AB ∴=+, 22AD AB AC AD ∴-=- , 2BD DC ∴=,3BD BD DC BC ∴=+=即3BD BC ∴=,故A 正确;对于B ,Q 为△ABC 的重心,则0QA QB QC ++=,33PQ QA QB QC PQ∴+++=()()()3PQ QA PQ QB PQ QC PQ ∴+++++=,3PA PB PC PQ ∴++=,即111333PQ PA PB PC ∴=++,故B 正确;对于C ,若0PA BC =,0PC AB =,则0PA BC PC AB +=,()0PA BC PC AC CB ∴++=,0PA BC PC AC PC CB ∴++=0PA BC PC AC PC BC ∴+-=,()0PA PC BC PC AC ∴-+= 0CA BC PC AC ∴+=,0AC CB PC AC ∴+=()0AC PC CB ∴+=,0AC PB ∴=,故C 正确;对于D ,111()()222MN PN PM PB PC PA PB PC PA ∴=-=+-=+- 1122MN PB PC PA PA PB PC ∴=+-=-- 222222PA PB PC PA PB PC PA PB PA PC PC PB --=++--+==2MN ∴=D 错误.故选ABC.三、填空题51.(辽宁省辽阳市辽阳县集美中学2020-2021学年高二上学期第一次月考)O 为空间中任意一点,A ,B ,C 三点不共线,且3148OP OA OB tOC =++,若P ,A ,B ,C 四点共面,则实数t =_________.。
江西省九江市2023-2024学年高二下学期7月期末考试 数学含答案

九江市2023—2024学年度下学期期末考试高二数学试题卷(答案在最后)注意事项:1.答题前,考生务必将自己的姓名、班级、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试题卷上无效3.考试结束后,将本试卷和答题卡一并收回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2340A x x x +=∈--≤N ∣,{}2,1,0,1,2B =--,则A B = ()A.{}1,0,1,2- B.{}1 C.{}1,2 D.{}0,1,22.22a b >是lg lg a b >的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.下列函数是定义在R 上的增函数的是()A.()f x = B.()2xf x -=C.()2f x x = D.()ln f x x =4.等差数列{}n a 前n 项和为7,4n S a =,则13S =()A.44B.48C.52D.565.已知0,0a b >>,且a b ab +=,则()()11a b b a +++的最小值是()A.9B.12C.16D.206.已知曲线e ln x y x a x =+在1x =处的切线方程为e =+y x b ,则()A.e,0a b ==B.e,1a b ==C.e,1a b =-= D.e,0a b =-=7.牛顿冷却定律(Newton's law of cooling )是牛顿在1701年用实验确定的:物体在空气中冷却,如果物体的初始温度为1C θ ,环境温度为0C θ,则t 分钟后物体的温度θ(单位:C )满足:()010ektθθθθ-=+-.已知环境温度为20C o ,一块面包从温度为120C 的烤箱里拿出,经过10分钟温度降为70C ,那么大约再经过多长时间,温度降为30C ?(参考数据:ln20.7,ln3 1.1,ln5 1.6≈≈≈)()A .33分钟B.28分钟C.23分钟D.18分钟8.函数()ln 1e xx x f x x ++=的最大值为()A.1B.2C.1eD.2e二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得3分,有选错的得0分.9.若1a b >+,则()A.22a b >B.22a b>C.a b> D.()ln 0a b ->10.设函数()1ln1x f x x -=+,则()f x ()A.定义域为()(),11,-∞-⋃+∞B.图象关于原点对称C.在()1,+∞上单调递减D.不存在零点11.已知数列{}n a 的前n 项和为n S ,且满足11a =,11122n n n a n a a n +⎧+⎪=⎨⎪-⎩,为奇数,为偶数,则()A.{}2n a 为等比数列B.202420232a a ->C.20242015S <- D.202420252S S -<三、填空题:本题共3小题,每小题5分,共15分.其中第14题第1问2分,第2问3分.12.设{}n a 是等比数列,且1232343,6a a a a a a ++=-++=,则6a =__________.13.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设x ∈R ,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,如:][1.21, 1.22⎡⎤=-=-⎣⎦.若函数()[](0)x f x a x x=+>有且仅有2个零点,则实数a 的取值范围是__________.14.设函数()(,0xxf x a b a b =+>且,1)a b ≠.若()f x 为偶函数,则ab =__________;若()f x 在()0,∞+上单调递增,则ab 的取值范围是__________.四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤.15.已知函数()()245mf x m m x =-+为幂函数.(1)求()f x 的解析式;(2)若()()ln 2g x f x ax ⎡⎤=++⎣⎦在[]1,1-上单调递增,求实数a 的取值范围.16.已知函数()f x 的定义域为R ,且对任意,x y ∈R ,都有()()()f x y f x f y +=+.(1)判断()f x 的奇偶性,并说明理由;(2)若()11f =,求12()nkk f k =∑的值.17.已知数列{}{},n n a b 满足211221,3,21n n n a b a a ++=+==,且{}n b 为等比数列.(1)求数列{}n b 的通项公式;(2)求数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和n T .18.已知函数()()()ln 1R f x ax x a =-+∈.(1)试讨论()f x 的单调性;(2)若0x >,()0f x >,求a 的取值范围.19.若函数()f x 在定义域内存在0x ,使得()()()0011f x f x f +=+成立,则称()f x 具有性质P .(1)试写出一个具有性质P 的一次函数;(2)判断函数()e xg x ax =-是否具有性质P ;(3)若函数()2ln h x x ax =-具有性质P ,求实数a 的取值范围.九江市2023—2024学年度下学期期末考试高二数学试题卷注意事项:1.答题前,考生务必将自己的姓名、班级、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上,写在本试题卷上无效3.考试结束后,将本试卷和答题卡一并收回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}2340A x x x +=∈--≤N ∣,{}2,1,0,1,2B =--,则A B = ()A.{}1,0,1,2- B.{}1 C.{}1,2 D.{}0,1,2【答案】C 【解析】【分析】先求出集合A ,再根据交集的概念求解即可.【详解】由已知{}1,2,3,4A =,{}2,1,0,1,2B =--,所以{}1,2A B = .故选:C .2.22a b >是lg lg a b >的()A.充分不必要条件B.必要不充分条件C .充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】根据充分,必要条件的定义,结合不等式的性质,即可判断.【详解】若22a b >,a b 、可能为负数,不能推出lg lg a b >,若lg lg a b >,则0a b >>,可得22a b >,所以22a b >是lg lg a b >的必要不充分条件.故选:B.3.下列函数是定义在R 上的增函数的是()A.()f x = B.()2xf x -=C.()2f x x = D.()ln f x x=【答案】A 【解析】【分析】根据基本初等函数的性质直接判断即可.【详解】对于A (),f x =R 上的增函数;对于()B,2xf x -=为R 上的减函数;对于C ,()2f x x =在(),0∞-为减函数;对于D ,()ln f x x =的定义域为()0,∞+.故选:A.4.等差数列{}n a 前n 项和为7,4n S a =,则13S =()A.44 B.48C.52D.56【答案】C 【解析】【分析】根据等差数列前n 项和公式结合等差数列项的性质计算即可【详解】()1131371313413522a a S a +===⨯=.故选:C.5.已知0,0a b >>,且a b ab +=,则()()11a b b a +++的最小值是()A.9 B.12C.16D.20【答案】B 【解析】【分析】将条件等式a b ab +=化成111a b+=,由()()()113a b b a a b +++=+,利用1的代换法和基本不等式即可求得最小值.【详解】解:由a b ab +=,得111a b+=,又0,0a b >>,所以()()()()1111233a b b a ab a b a b a b a b ⎛⎫+++=++=+=++⎪⎝⎭323212a b b a ⎛⎛⎫=++≥+= ⎪ ⎝⎭⎝.当且仅当2a b ==时等号成立.故选:B.6.已知曲线e ln x y x a x =+在1x =处的切线方程为e =+y x b ,则()A.e,0a b ==B.e,1a b ==C.e,1a b =-=D.e,0a b =-=【答案】D 【解析】【分析】求导后运用导数几何意义解题即可.【详解】()11e ,2e e,e xx ay x k y a a x==++==+=∴'=-',将()1,e 代入e =+y x b ,得0b =.故选:D.7.牛顿冷却定律(Newton's law of cooling )是牛顿在1701年用实验确定的:物体在空气中冷却,如果物体的初始温度为1C θ ,环境温度为0C θ,则t 分钟后物体的温度θ(单位:C )满足:()010ektθθθθ-=+-.已知环境温度为20C o ,一块面包从温度为120C 的烤箱里拿出,经过10分钟温度降为70C ,那么大约再经过多长时间,温度降为30C ?(参考数据:ln20.7,ln3 1.1,ln5 1.6≈≈≈)()A.33分钟B.28分钟C.23分钟D.18分钟【答案】C 【解析】【分析】根据题意列出方程,指数对数互化,解出即可.【详解】解:依题意,得()10702012020ek--=-,化简得101e2k-=,解得1ln210k =.设这块面包总共经过t 分钟,温度降为30°,则()302012020e kt--=-,化简得1e10kt-=,解得()10ln2ln5110ln1023ln1033ln2ln20.7t k +===≈≈,故大约再经过331023-=(分钟),这块面包温度降为30°,故选:C.8.函数()ln 1e xx x f x x ++=的最大值为()A.1B.2C.1eD.2e【答案】A 【解析】【分析】解法一:求出()f x ',令()ln h x x x =+,根据()h x 的正负确定()f x 的单调性即可求解;解法二:令e x t x =,通过求导判断函数的单调性即可求解.【详解】解法一:()ln 1e x x x f x x ++=,则()()()21ln e xx x x f x x '++=-,令()ln h x x x =+,则()h x 在()0,∞+上单调递增,且1110e e h ⎛⎫=-< ⎪⎝⎭,()110h =>,故存在01,1x e ⎛⎫∈ ⎪⎝⎭,使得()000ln 0h x x x =+=,00ln e 1x x +=,即00e 1xx =,当()00,x x ∈时,()0h x <,()0f x ¢>,()f x 单调递增,当()0,x x ∈+∞时,()0h x >,()0f x '<,()f x 单调递减,所以()()00000ln 11e x x x f x f x x ++≤==.解法二:()()ln e 1e x xx f x x +=,令e 0x t x =>,则()ln 1(0)t g t t t+=>,因为()2ln tg t t =-',所以01t <<时,()0g t '>,()g t 在()0,1上单调递增,1t >时,()0g t '<,()g t 在()1,+∞上单调递减,()()11g t g ≤=,即()1f x ≤.故选:A .【点睛】关键点点睛:求导之后,()f x '的零点存在,但无法求出,可采用虚设零点,分析零点所在的区间,结合函数的单调性即可推断.二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得3分,有选错的得0分.9.若1a b >+,则()A.22a b >B.22a b>C.a b > D.()ln 0a b ->【答案】BD 【解析】【分析】对于A,C 可取特殊值判断;对于B,D,直接运用指数对数函数单调性判断即可.【详解】解:取1,2a b ==-,则22,a b a b <<,A ,C 错误;由1a b >+,得,22a b a b >∴>,B 正确;由1a b >+,得()1,ln ln10a b a b ->∴->=,D 正确.故选:BD.10.设函数()1ln1x f x x -=+,则()f x ()A.定义域为()(),11,-∞-⋃+∞B.图象关于原点对称C.在()1,+∞上单调递减D.不存在零点【答案】ABD 【解析】【分析】由101x x ->+可判断A ;判断()f x 是否是奇函数可判断B ;由复合函数的单调性可判断C ;直接解方程()0f x =可判断D.【详解】解:由101x x ->+,得1x <-或1x >,故()f x 的定义域是()(),11,-∞-⋃+∞,A 正确;()()()111lnln ln ,111x x x f x f x f x x x x --+--===-=-∴-+-+ 为奇函数,B 正确;令11x t x -=+,则211t x =-+在()1,+∞上单调递增,而函数ln y t =在定义域内单调递增,()f x \在()1,+∞上单调递增,C 错误;令()0f x =,得11,1x x x -=+无实数解,()f x \不存在零点,D 正确.故选:ABD.11.已知数列{}n a 的前n 项和为n S ,且满足11a =,11122n n n a n a a n +⎧+⎪=⎨⎪-⎩,为奇数,为偶数,则()A.{}2n a 为等比数列B.202420232a a ->C.20242015S <-D.202420252S S -<【答案】ACD 【解析】【分析】根据等比数列的定义可判断A 选项,可得12313222n n n a -⎛⎫=⋅=⎪⎝⎭,再结合数列的递推公式可得21n a -,进而可判断B 、C 、D 选项.【详解】依题意可得2113122a a =+=,则()()212221*********n n n n a a a a ++=+=-+=,所以数列{}2n a 是以232a =为首项,12为公比的等比数列,故A 选项正确;则12313222n n n a -⎛⎫=⋅=⎪⎝⎭,当2n ≥时,212213222n n n a a ---=-=-,当1n =时,也满足1211322n n a --⎛⎫=- ⎪⎝⎭,所以2211333222222n n n n na a ---=-+=-<,即202420232a a -<,B 选项错误;()()21321242131311122229121121122n n nn n nS a a a a a a n n -⎛⎫⎛⎫-- ⎪ ⎪⎛⎫⎝⎭⎝⎭=+++++++=-+=-- ⎪⎝⎭--202410121012199120242015201522S ⎛⎫∴=--=--<- ⎪⎝⎭,C 选项正确;又2122113222nn n n S S a ++⎛⎫-==->- ⎪⎝⎭,2212n n S S +∴-<,D 选项正确;故选:ACD.三、填空题:本题共3小题,每小题5分,共15分.其中第14题第1问2分,第2问3分.12.设{}n a 是等比数列,且1232343,6a a a a a a ++=-++=,则6a =__________.【答案】32【解析】【分析】根据题意可求得等比数列的公比,再根据1233a a a ++=-,求得1a ,即可求得答案.【详解】设{}n a 的公比为q ,则234123623a a a q a a a ++===-++-,由1233a a a ++=-,得()2112(2)3a ⎡⎤+-+-=-⎣⎦,解得11a =-,所以()56232a =--=.故答案为:3213.高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设x ∈R ,用[]x 表示不超过x 的最大整数,则[]y x =称为高斯函数,如:][1.21, 1.22⎡⎤=-=-⎣⎦.若函数()[](0)x f x a x x=+>有且仅有2个零点,则实数a 的取值范围是__________.【答案】32,43⎡⎫--⎪⎢⎣⎭【解析】【分析】令()0f x =得到[]x a x-=,变形得到[]x ax =-,令()[]()0g x x x =>,y ax =,画出两图象如图所示,数形结合得到2334a <-≤,求出答案.【详解】由()0f x =,得[]x a x-=,因为0x >,所以[]x ax =-,令()[]()0g x x x =>,y ax =,画出两图象如图所示,由图象结合题意得2334a <-≤,即3243a -≤<-,即a 的取值范围是32,43⎡⎫--⎪⎢⎣⎭.故答案为:32,43⎡⎫--⎪⎢⎣⎭14.设函数()(,0x x f x a b a b =+>且,1)a b ≠.若()f x 为偶函数,则ab =__________;若()f x 在()0,∞+上单调递增,则ab 的取值范围是__________.【答案】①.1②.[)1,+∞【解析】【分析】根据()()11f f =-得到方程,求出1ab =,检验后得到结论;分1,1a b >>,01,01a b <<<<,01,1a b <<>或01,1b a <<>四种情况,结合指数函数单调性,导数,进行求解,得到答案.【详解】()f x 为偶函数,()()11f f ∴=-,即11a b a b+=+,∴1ab =,经检验,此时()1x xf x a a =+为偶函数,当1,1a b >>时,()f x 在()0,∞+上单调递增,符合题意,此时1ab >.当01,01a b <<<<时,()f x 在()0,∞+上单调递减,不符合题意.当01,1a b <<>或01,1b a <<>时,()ln ln x x f x a a b b +'=,则需()0f x '≥在()0,∞+上恒成立,不妨设01,1a b <<>,则ln ln 0xb a b a ⎛⎫+≥ ⎪⎝⎭在()0,∞+上恒成立,ln ln x b y a b a ⎛⎫=+ ⎪⎝⎭在()0,∞+上单调递增,∴0ln ln ln ln ln ln 0x b b y a b a b a b a a ⎛⎫⎛⎫=+>+=+≥ ⎪ ⎪⎝⎭⎝⎭,即1≥ab .综上,ab 的取值范围是[)1,+∞.故答案为:1,[)1,+∞【点睛】关键点点睛:()0f x '≥恒成立问题,转化为ln ln 0xb a b a ⎛⎫+≥ ⎪⎝⎭恒成立,结合指数函数单调性,得到不等式,求出答案.四、解答题:本题共5小题,共77分.解答应写出必要的文字说明、证明过程或演算步骤.15.已知函数()()245m f x m m x =-+为幂函数.(1)求()f x 的解析式;(2)若()()ln 2g x f x ax ⎡⎤=++⎣⎦在[]1,1-上单调递增,求实数a 的取值范围.【答案】(1)()2f x x=(2)[)2,3【解析】【分析】(1)由幂函数的定义可得2451m m -+=,求解即可;(2)由复合函数的单调性,得()21,2(1)120a a ⎧-≤-⎪⎨⎪-+⨯-+>⎩,求解即可.【小问1详解】由()f x 为幂函数,得2451m m -+=,解得2m =,故()2f x x =.【小问2详解】()()2ln 2g x x ax =++,由复合函数的单调性,得()21,2(1)120a a ⎧-≤-⎪⎨⎪-+⨯-+>⎩,解得23a ≤<.故实数a 的取值范围为[)2,3.16.已知函数()f x 的定义域为R ,且对任意,x y ∈R ,都有()()()f x y f x f y +=+.(1)判断()f x 的奇偶性,并说明理由;(2)若()11f =,求12()n k k f k =∑的值.【答案】(1)是奇函数,理由见解析(2)()1122n n +-+【解析】【分析】(1)令0x y ==得()00f =,令y x =-,得()()()0f f x f x =+-,从而可判断;(2)令,1x n y ==,得()()()111f n f n f +-==,利用等差数列的定义可得()f n ,再利用错位相减法即可求和.【小问1详解】()f x 是奇函数,理由如下:令0x y ==,得()()()()00000f f f f =+⇒=,令y x =-,得()()()0f f x f x =+-()()f x f x ⇒-=-,又函数()f x 的定义域为R ,所以()f x 是奇函数;【小问2详解】令,1x n y ==,得()()()111f n f n f +-==,令()n a f n =,则111,1n n a a a +-==,所以{}n a 是首项为1,公差为1的等差数列,()111n a n n ∴=+-⨯=,12()n k k f k =∑即为数列{}2n n ⋅的前n 项和,设为n T ,则()1211222122,n n n T n n -=⨯+⨯++-⨯+⨯ ()23121222122n n n T n n +=⨯+⨯++-⨯+⨯ ,两式相减,得()()121112122222212212n n n n n n T n n n +++--=+++-⨯=-⨯=---,()1122n n T n +∴=-+,即112()(1)22nk n k f k n +==-+∑.17.已知数列{}{},n n a b 满足211221,3,21n n n a b a a ++=+==,且{}n b 为等比数列.(1)求数列{}n b 的通项公式;(2)求数列n n b a ⎧⎫⎨⎬⎩⎭的前n 项和n T .【答案】(1)32n n b =⨯(2)113121n +⎛⎫-⎪-⎝⎭【解析】【分析】(1)根据已知关系式,利用等比数列定义求通项公式即可;(2)利用裂项法求解前n 项和.【小问1详解】由题意,得1122933a b a b +=⎧⎨+=⎩,由123,21a a ==,得126,12.b b =⎧⎨=⎩.{}n b 为等比数列,且公比2q =,16232.n n n b -∴=⨯=⨯【小问2详解】由(1)得()()21121322121n n n n n a ++=+-⨯=--,()()113211*********n n n n n n n b a ++⨯⎛⎫∴==- ⎪----⎝⎭122311111111111332121212121212121n n n n T ++⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫∴=-+-++=- ⎪ ⎪ ⎪ ⎪⎢⎥--------⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦1131.21n +⎛⎫=- ⎪-⎝⎭18.已知函数()()()ln 1R f x ax x a =-+∈.(1)试讨论()f x 的单调性;(2)若0x >,()0f x >,求a 的取值范围.【答案】(1)答案见解析(2)[)1,+∞【解析】【分析】(1)先求()f x ',分0a ≤和0a >两种情况讨论导函数的正负即可;(2)解法一:结合(1)分0a ≤,01a <<,1a ≥三种情况根据单调性求解a 的取值范围;解法二:先取()00f =,先找到()0f x >的一个必要条件,再证充分性.【小问1详解】()1(1)1f x a x x =->-+',当0a ≤时,因为()101f x a x '=-<+,所以()f x 在()1,∞-+上单调递减,当0a >时,()11ax a f x x +-'=+,令()0f x '=,得11a x a -=>-,当11a x a --<<时,()0f x '<,当1a x a ->时,()0f x '>,故()f x 在11,a a -⎛⎫- ⎪⎝⎭上单调递减,在1,a a ∞-⎛⎫+ ⎪⎝⎭上单调递增,综上,当0a ≤时,()f x 在()1,∞-+上单调递减,当0a >时,()f x 在11,a a -⎛⎫- ⎪⎝⎭上单调递减,在1,a a ∞-⎛⎫+ ⎪⎝⎭上单调递增;【小问2详解】解法一:①当0a ≤时,由(1)知()f x 在()0,∞+上单调递减,所以()()00f x f <=,不符合题意,舍去,②当01a <<时,由(1)知()f x 在10,a a -⎛⎫ ⎪⎝⎭上单调递减,在1,a a ∞-⎛⎫+ ⎪⎝⎭上单调递增,所以()min 1()00a f x f f a -⎛⎫=<= ⎪⎝⎭,不符合题意,舍去,③当1a ≥时,由(1)知()f x 在()0,∞+上单调递增,所以()()00f x f >=,符合题意,综上所述,a 的取值范围是[)1,+∞.解法二:注意到()00f =,①先找到()0f x >的一个必要条件,因为()00f =,所以要使0x >时,()0f x >,则()010f a -'=≥,即1a ≥,②再证充分性,若1a ≥,则()101f x a x '=->+,所以()f x 在()0,∞+上单调递增,所以()()00f x f >=,满足题意,当0a ≤时,由(1)知()f x 在()0,∞+上单调递减,()()00f x f <=,不满足题意,当01a <<时,由(1)知()f x 在10,a a -⎛⎫ ⎪⎝⎭上单调递减,在1,a a ∞-⎛⎫+ ⎪⎝⎭上单调递增,所以()min 1()00a f x f f a -⎛⎫=<= ⎪⎝⎭,不符合题意,舍去,综上所述,a 的取值范围是[)1,+∞.19.若函数()f x 在定义域内存在0x ,使得()()()0011f x f x f +=+成立,则称()f x 具有性质P .(1)试写出一个具有性质P 的一次函数;(2)判断函数()e xg x ax =-是否具有性质P ;(3)若函数()2ln h x x ax =-具有性质P ,求实数a 的取值范围.【答案】(1)()()0f x kx k =≠(2)函数()e xg x ax =-具有性质P (3)()0,∞+【解析】【分析】(1)设()()0f x kx b k =+≠,根据多项式相等可得答案;(2)由()()()0011g x g x g +=+得001e e e 0x x +--=,令()1e e e x x G x +=--,利用导数判断出()G x 在R 上的单调性,结合特殊点的函数值和已知定义可得答案;(3)解法一:由()()()0011h x h x h +=+化简得()000ln 1ln 2x x a x +-=,令()()ln 1ln (0)x x H x x x +-=>,利用导数判断出()H x 在()0,∞+上的单调性,结合()H x 值域可得答案;解法二:由()()()0011h x h x h +=+化简得()000012ln 0x ax x x +=>,转化为2y ax =与1ln (0)x y x x +=>的图象有交点,判断出1lnx y x+=在()0,∞+上的单调性,结合()H x 值域可得答案.【小问1详解】设()()0f x kx b k =+≠,由()()()0011f x f x f +=+,得()001k x b kx b k b ++=+++,即0b =,()()0f x kx k ∴=≠;【小问2详解】由()()()0011g x g x g +=+,得()00100e1e e x x a x ax a +-+=-+-,即001e e e 0x x +--=,令()1e e e x x G x +=--,则()()1e e 0,x x G x G x +=->∴'在R 上单调递增,又()()20e 1e 10,1e 2e 0G G =--=-=-,故存在()00,1x ∈,使得()00G x =,即001e e e 0x x +--=,故函数()e xg x ax =-具有性质P ;【小问3详解】解法一:由()()()0011h x h x h +=+,得()()220000ln 11ln x a x x ax a +-+=--,化简得()000ln 1ln 2x x a x +-=,令()()ln 1ln (0)x xH x x x +-=>,则()()2211ln 1ln ln 1111x x x x x x x x x H x x x⎛⎫⎡⎤--+-+- ⎪⎣'⎦+⎝⎭++==,令()ln 1(01)r t t t t =+-<<,则()r t 在()0,1上单调递增,且()()10,0r r t =∴<,ln 1011x x x x ∴+-<++,即()()0,H x H x <'∴在()0,∞+上单调递减.又当0x →时,()H x ∞→+;当x →+∞时,()0H x →,20a ∴>,即0a >,故实数a 的取值范围是()0,∞+;解法二:由()()()0011h x h x h +=+,得()()220000ln 11ln x a x x ax a +-+=--,化简得()000012ln 0x ax x x +=>,即2y ax =与1ln (0)x y x x+=>的图象有交点,11ln =ln 1+x y x x +⎛⎫= ⎪⎝⎭在()0,∞+上单调递减,且当0x →时,y →+∞;当x →+∞时,0y →,20a ∴>,即0a >,故实数a 的取值范围是()0,∞+.【点睛】关键点点睛:本题是在新定义下对函数的综合考查,关于新定义型的题,关键是理解定义,并会用定义来解题.。
2021-2022学年江西省九江市庐山中学高二地理期末试题含解析

2021-2022学年江西省九江市庐山中学高二地理期末试题含解析一、选择题(每小题2分,共52分)1. 下图为小赵同学绘制的7 月份非洲沿海洋流分布简图。
完成下面小题。
15. 同桌的小李发现图中有一处洋流绘制不正确,这一处应是A. 甲处B. 乙处C. 丙处D. 丁处16. 图中的四支洋流,对沿岸湿热气候环境影响明显的是A. 甲B. 乙C. 丙D. 丁参考答案:15. A 16. B【15题详解】根据图示判断,甲为索马里半岛夏季洋流,夏季索马里附近海域盛行离岸西南季风,表层海水向东远离索马里,深层冷海水上翻补偿,形成寒流,虚线箭头表示,故甲错,选A。
乙处为由赤道向南的莫桑比克暖流,标注正确,B错。
丙处为由较高纬向南的加那利寒流,图示正确,C错。
丁处为较高纬向赤道的本格拉寒流,标注准确,D错。
【16题详解】根据图示位置判断,甲为索马里半岛寒流,丙为加那利寒流,丁为本格拉寒流,气候均为降温减湿作用,故ACD错误。
乙为莫桑比克暖流,对马达加斯加东岸气候增温增湿,降水多,形成非地带性的热带雨林气候,故B正确。
2. 南极,人类在这块银色大陆上进行轰动性的考察起于20世纪初。
1989—1990年,由六国南极考察队员组成的国际横穿南极大陆考察队,历时7个月,又一次把人类的足迹印在了南极极点上。
根据材料回答下列各题:8. 我国南极考察站的建站时间最可能选在()A. 2月B. 5月C. 7月D. 10月9. 关于南极考察队员们在科考过程中遇到的危险的下列叙述,不正确的是()A. 暴风雪迎面扑来,看不清路B. 积雪覆盖的冰隙有可能吞没队员C. 酷冷的严寒,给队员们留下无情的冻伤D. 南极大陆内部可能会遭遇熊的袭击参考答案:8. A 9. D【8题详解】赴南极时间应选择北半球的冬季,因为此时南极地区正值夏季,是极昼或白天最长、气温最高的季节,同时南极洲的夏季多晴朗天气,风和日丽,是进行科学考察的“黄金季节”,一年一度的物资供应、人员更换等,主要在这个时节进行。
2023-2024学年江西省九江市高一(下)期末数学试卷(含答案)

2023-2024学年江西省九江市高一(下)期末数学试卷一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.复数z =2+i 2i 在复平面内对应的点在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限2.已知cos2α+5sinα=3,则sinα=( )A. 12B. −12C. 32 D. − 323.已知m ,n 是两条不重合的直线,α,β是两个不重合的平面,则下列命题正确的是( )A. 若m//n ,n//α,则m//αB. 若n ⊥α,n ⊥m ,m ⊂β,则α//βC. 若α//β,m ⊥β,则m ⊥αD. 若α⊥β,m ⊂β,则m ⊥α4.已知a ,b 满足|a |=|b |=b =−3,则cos 〈a ,a +b〉=( )A. 2 55 B. 55 C. −2 55 D. − 555.△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a =asinC +bcosC ,则( )A. cosB =sinCB. sinB =cosCC. cosA =sinBD. sinA =cosB6.如图,单位圆M 与数轴相切于原点O ,把数轴看成一个“皮尺”,对于任意一个正数a ,它对应正半轴上的点A ,把线段OA 按逆时针方向缠绕到圆M 上,点A 对应单位圆上点A′,这样就得到一个以点M 为顶点,以MO 为始边,经过逆时针旋转以MA′为终边的圆心角α,该角的弧度数为a.若扇形OMA′面积为π6,则OA ⋅OA′=( )A. 36πB. 33πC. π3 D. π67.如图,已知圆锥顶点为P ,底面直径为AB,AB =4,∠APB =π6,以AB 为直径的球O 与圆锥相交的曲线记为Ω(异于圆锥的底面),则曲线Ω的长为( )A. 2 3πB. 3πC. 2πD. 73π8.已知函数f(x)=Asin(ωx +φ)(A >0,ω>0)的部分图象如图.若x 1+2x 2=0,则cos2φ=( )A. 12B. 32C. −12D. − 32二、多选题:本题共3小题,共18分。
江西省南昌市新建区第一中学2020-2021学年高二下学期期中考试数学(理)试题

江西省南昌市新建区第一中学2020-2021学年高二下学期期中考试数学(理)试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.采用分层随机抽样的方法抽取一个容量为45的样本,高一年级被抽取20人,高三年级被抽取10人,高二年级共有300人,则这个学校共有高中学生的人数为( ) A .1350 B .675 C .900D .4502.已知x ,y 之间的一组数据则y 与x 之间的线性回归方程ˆˆˆybx a =+必过点( ) A .()2,2B .()1.5,0C .() 1,2D .()1.5,43.分别以正方形ABCD 的四条边为直径画半圆,重叠部分如图中阴影区域所示,若向该正方形内随机投一点,则该点落在阴影区域的概率为A .44π- B .24π- C .42π- D .22π-4.甲乙两名同学6次考试的成绩统计如右图,甲乙两组数据的平均数分别为12,m m ,标准差分别为12,n n 则A .1212,m m n n <<B .1212,m m n n <>C .1212,m m n n ><D .1212,m m n n >>5.某军工企业为某种型号的新式步枪生产了一批枪管,其口径误差(单位:微米)服从正态分布()21,3N ,从已经生产出的枪管中随机取出一只,则其口径误差在区间()4,7内的概率为( )(附:若随机变量ξ服从正态分布()2,N μσ,则()68.27%P μσξμσ-<<+=,()2295.45%P μσξμσ-<<+=)A .31.74%B .27.18%C .13.59%D .4.56%6.执行如图所示的程序框图,若输出的0S =,则空白判断框中可填入的条件是( )A .3?n >B .4?n >C .5?n >D .6?n >7.掷一个骰子的试验,事件A 表示“出现小于5的偶数点”,事件B 表示“出现小于5的点数”.若B 表示B 的对立事件,则一次试验中,事件A B +发生的概率为( )A .13B .12C .23D .568.已知二项式2nx x ⎛⎫- ⎪⎝⎭展开式中各项的二项式系数和是64,则该展开式中的常数项是( ) A .20B .20-C .160D .160-9.在某电视台有一闯关节目,该节目设置有两关,闯关规则是:当第一关闯关成功后,方可进入第二关.为了调查闯关的难度,该电视台调查了参加过此节目的100名选手的闯关情况,第一关闯关成功的有80人,第一关闯关成功且第二关闯关也成功的选手有72人,以闯关成功的频率近似作为闯关成功的概率,已知某个选手第一关闯关成功,则该选手第二关闯关成功的概率为( ) A .0.72B .0.8C .0.9D .0.57610.甲、乙、丙、丁、戊5名党员参加“党史知识竞赛”,决出第一名到第五名的名次(无并列名次),已知甲排第三,乙不是第一,丙不是第五.据此推测5人的名次排列情况共有( )种 A .5B .8C .14D .2111.为向国际化大都市目标迈进,某市今年新建三大类重点工程,它们分别是30项基础设施类工程、20项民生类工程和10项产业建设类工程.现有3名民工相互独立地从这60个项目中任选一个项目参与建设,则这3名民工选择的项目所属类别互异的概率是( ) A .12B .13C .14D .1612.甲乙两运动员进行乒乓球比赛,采用7局4胜制.在一局比赛中,先得11分的运动员为胜方,但打到10平以后,先多得2分者为胜方.在10平后,双方实行轮换发球法,每人每次只发1个球.若在某局比赛中,甲发球赢球的概率为12,甲接发球贏球的概率为25,则在比分为10:10后甲先发球的情况下,甲以13:11赢下此局的概率为( ) A .225B .310C .110D .325二、填空题13.抽样调查某地区120名教师的年龄和学历状况,情况如下饼图:则估计该地区35岁以下具有研究生学历的教师人数为_______.14.某小组有5名男生、3名女生,从中任选3名同学参加活动,若X 表示选出女生的人数,则()2P X ≥=______.15.已知()()()()727012732111x a a x a x a x -=+-+-++-,则127a a a +++=_______.16.近年来,各地着力打造“美丽乡村”,彩色田野成为美丽乡村的特色风景,某乡村设计一块类似于赵爽弦图的巨型创意农田(如图所示),计划从黄、白、红、绿四种颜色的农作物选种几种种在图中区域,并且每个区域种且只种一种颜色的农作物,相邻区域所种的农作物颜色不同,则共有______种不同的种法.(用数字作答)三、解答题17.4位同学报名参加2022年杭州亚运会6个不同的项目(记为A ,B ,C ,D ,E ,F )的志愿者活动.假设每位同学恰报1个项目,且报名各项目是等可能的.(1)求4位同学报了4个不同的项目的概率;(2)求1位同学报了项目A ,剩余3位同学都报了项目B 的概率.18.西安市某街道办为了绿植街道两边的绿化带,购进了1000株树苗,这批树苗最矮2米,最高2.5米,桉树苗高度绘制成如图频率分布直方图(如图).(1)试估计这批树苗高度的中位数;(2)现按分层抽样方法,从高度在[2.30,2.50]的树苗中任取6株树苗,从这6株树苗中任选3株,求3株树苗中至少有一株树苗高度在[2.40,2.50]的概率.19.某学校用“10分制”调查本校学生对本校食堂的满意度,现从学生中随机抽取16名,以茎叶图记录了他们对食堂满意度的分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):若食堂满意度不低于9.5分,则称该生对食堂满意度为“极满意”.(1)求从这16人中随机选取3人,至少有1人是“极满意”的概率;(2)以这16人的样本数据来估计整个学校的总体数据,若从该校所有学生中(学生人数很多)任选3人,记X表示抽到“极满意”的人数,求X的分布列及数学期望.20.某高校机器人社团决定从大一新生中招聘一批新成员.招聘分笔试、面试这两个环节.笔试合格后才能参加面试,面试合格后便正式录取.现有甲、乙、丙三名大一新生报名参加了机器人社团招聘.假设甲通过笔试、面试的概率分别为12,23;乙通过笔试、面试的概率分别为23,34,丙通过各环节的概率与甲相同.(1)求甲、乙、丙三人中恰有两人被机器人社团录取为新成员的概率;(2)为鼓励大一新生积极报名参加机器人社团招聘,该机器人社团决定给参加应聘的大一新生赠送一定的手机话费,赠送标准如下表:记甲、乙、丙三人获得的所有补贴之和为X 元,求X 的分布列和数学期望.21.已知椭圆2222:1x y C a b+=(0a b >>)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.(1)求椭圆C 的标准方程;(2)设F 为椭圆C 的左焦点,直线:3l x =-,P 为椭圆上任意一点,若点P 到F 的距离为m ,点P 到l 的距离为n ,求证:mn为定值. 22.已知函数1ln ()+=-x xf x e x. (1)证明:()1xe f x -≤;(2)求()f x 的最小值.参考答案1.C 【分析】先求出抽样比,即可求出学生总数. 【详解】由题意可得抽样比为452010130020--=,所以学生总数为14590020÷=,即这个学校共有高中学生900人. 故选:C. 2.D 【分析】回归直线恒过样本中心(),x y . 【详解】 因为01231.54x +++==,135744y +++==, 所以y 与x 之间的线性回归方程ˆˆˆybx a =+必过点()1.5,4. 故选:D. 【点睛】本题考查线性回归直线及其性质,牢记线性回归直线过样本中心即可求解,属于简单题. 3.D 【详解】分析:由题意知本题是一个几何概型,试验发生包含的所有事件是矩形面积,而满足条件的阴影区域,可以通过空白区域面得到,空白区域可以看作是由8部分组成,每一部分是由边长为2AB 的正方形面积减去半径为2AB的四分之一圆的面积得到. 详解:由题 意知本题是一个几何概型,设正方形ABCD 的边长为2.∵试验发生包含的所有事件是矩形面积224S =⨯=,空白区域的面积是2(4)82ππ-=- ∴阴影区域的面积为4(82)24ππ--=- ∴由几何概型公式得到24242P ππ--== 故选D.点睛:(1)当试验的结果构成的区域为长度、面积、体积等时,要考虑使用几何概型求解;(2)利用几何概型求概率时,关键是试验的全部结果构成的区域和事件发生的区域的寻找,有时需要设出变量,在坐标系中表示所需要的区域;(3)几何概型有两个特点:一是无限性,二是等可能性,基本事件可以抽象为点,尽管这些点是无限的,但它们所占据的的区域是有限的,因此可用“比例解法”求解几何概型的概率. 4.C 【分析】利用甲、乙两名同学6次考试的成绩统计直接求解. 【详解】由甲乙两名同学6次考试的成绩统计图知: 甲组数据靠上,乙组数据靠下,甲组数据相对集中,乙组数据相对分散分散布,由甲乙两组数据的平均数分别为12,m m ,标准差分别为12,n n 得12m m >,12n n <. 故选C . 【点睛】本题考查命题真假的判断,考查平均数、的定义和性质等基础知识,考查运算求解能力,是基础题. 5.C 【分析】根据已知可得1,3,2,4,25,27μσμσμσμσμσ==-=-+=-=-+=,结合正态分布的对称性,即可求解. 【详解】 ()()()14757242P P P ξξξ<<=-<<--<<⎡⎤⎣⎦ ()10.95450.68270.13592=⨯-=. 故选:C 【点睛】本题考查正态分布中两个量μ和σ的应用,以及正态分布的对称性,属于基础题. 6.C【分析】模拟执行程序框图,直到0S =时满足判断框要求输出结果,由此可确定判断框内的条件. 【详解】模拟执行程序框图,输入160S =,1n =,不满足10S ≤,则80S =,2n =,需不满足判断框,循环; 不满足10S ≤,则40S =,3n =,需不满足判断框,循环; 不满足10S ≤,则20S =,4n =,需不满足判断框,循环; 不满足10S ≤,则10S =,5n =,需不满足判断框,循环; 满足10S ≤,则0S =,6n =,需满足判断框,输出0S =; ∴判断框中的条件应为:5?n >.故选:C. 7.C 【分析】首先根据题意得到意()13P A =,()23P B =,()13P B =,根据A 与B 互斥,利用互斥事件加法公式即可得到答案. 【详解】掷一个骰子的试验有6种可能结果. 依题意()2163P A ==,()4263P B ==,()21133P B =-=, 因为B 表示“出现5点或6点”的事件,A 表示“出现小于5的偶数点”, 所以A 与B 互斥, 故()()()2+3P A B P A P B =+=. 故选:C 8.D 【分析】由2n x x ⎛⎫- ⎪⎝⎭展开式中二项式系数之和为64,可得6n =,则在62x x ⎛⎫- ⎪⎝⎭展开式的通项公式中,令x 的幂指数等于0求得r 的值,即可求得展开式中常数项. 【详解】若2nx x ⎛⎫- ⎪⎝⎭展开式中二项式系数之和为64,则264n =,6n =,故62x x ⎛⎫- ⎪⎝⎭展开式的通项公式为()66216622rr r rrr r T C x C x x --+⎛⎫=⋅⋅-=-⋅⋅ ⎪⎝⎭, 令620r -=,3r =,故展开式中常数项为()3362820160C -⨯=-⨯=-, 故选:D . 【点睛】本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.本题解题的关键在于熟记二项式系数和:0122n n n n n n C C C C +++=.9.C 【分析】若令“第一关闯关成功”为事件A ,“第二关闯关成功”为事件B ,则由题意可得()0.8P A =,()0.72P AB =,然后利用条件概率的计算公式()()()|P AB P B A P A =可求得结果 【详解】第一关闯关成功的选手有80人,则第一关闯关成功的频率为0.8,第一关闯关成功且第二关闯关也成功的选手有72人,则两关都成功的频率为0.72. 设“第一关闯关成功”为事件A ,“第二关闯关成功”为事件B ,()0.8P A =,()0.72P AB =,某个选手第一关闯关成功,则该选手第二关闯关成功的概率为()()()|0.9P AB P B A P A ==. 故选:C 10.C 【分析】按乙排第五和不是第五分类讨论.乙排在第五的情况有:33A ,乙不在第五的方法有112222C C A ,共有3112322214A C C A +=,故选:C . 【点睛】关键点点睛:本题考查排列组合的综合应用,解题关键是确定完成事件的方法:是先分类还是先分步:分类后每一类再分步.然后结合计数原理求解. 11.D 【分析】先用等可能事件发生的概率的计算方法,分别算出某名民工选择的项目属于基础设施类、民生类、产业建设类的概率,再由独立事件同时发生的概率计算方法算出3名民工选择的项目所属类比互异的概率,其中要注意未指定每名民工具体选择哪一类,故还应考虑排列问题,结果要乘以33A . 【详解】记第i 名民工选择的项目属于基础设施类、民生类、产业建设类 分别为事件i A ,i B ,i C ,1,2,3i =.由题意,事件i A ,i B ,i C ,1,2,3i =相互独立, 则301()602i P A ==,201()603i P B ==,101()606i P C ==,1,2,3i =, 故这3名民工选择的项目所属类别互异的概率是 331111()62366i i i P A P A B C ==⨯⨯⨯=.故选:D. 【点睛】关键点点睛:本题的关键是独立事件同时发生的概率计算,还应注意其中未指定每名民工具体选择哪一类,所以还有排列问题需要考虑. 12.C 【分析】分后四球胜方依次为甲乙甲甲,与乙甲甲甲两种情况进行求解即可.分两种情况:①后四球胜方依次为甲乙甲甲,概率为113123252550P =⋅⋅⋅=; ②后四球胜方依次为乙甲甲甲,概率为212121252525P =⋅⋅⋅=.所以,所求事件概率为:12110P P +=. 故选:C. 【点睛】本题主要考查了分步与分类计数求解概率的问题,需要根据题意判断出两种情况再分别求解,属于基础题. 13.30 【分析】根据图中的数据,分别求得本科学历和研究生学历的教师人数,再根据35岁以下的本科人数所占比例求解即可得答案. 【详解】解:由图可知本科学历的教师共有50201080++=人,故研究生学历的有1208040-=人. 35岁以下的本科人数有50人,35岁以下教师的比例为62.5%, 所以35岁以下的本科和研究生学历人数和为5062.5%80÷=人, 所以35岁以下的研究生学历人数有805030-=人. 故答案为:30 14.27【分析】由超几何分布概率公式运算即可得解. 【详解】当2X =时,()12533815256C C P X C ===;当3X =时,()33381356C P X C ===,则()()()151222356567P X P X P X ≥==+==+=. 故答案为:27. 15.2- 【分析】令1x =可得出0a ,令2x =可得0127a a a a ++++的值,两式结合可得答案.【详解】令1x =,得()70321a -==, 令2x =,得()70127341a a a a -=++++=-,所以()127112a a a +++=--=-.故答案为:2- 16.72 【分析】分用三种颜色或四种颜色涂色该区域,当用四种颜色涂色该区域时,分两种情况讨论,当AC 区域同色时和不同色时两种情况讨论求解即可. 【详解】解:当用三种颜色涂色该区域时,先从四种颜色中选三种颜色,有344C =种方案,再用三种颜色涂色,则有321116⨯⨯⨯⨯=种方案,故有4624⨯=种方案;当用四种颜色涂色该区域时,分两种情况讨论,当AC 区域同色时,有4321124⨯⨯⨯⨯=种不同方案,当AC 区域不同色时,有4321124⨯⨯⨯⨯=种不同方案,故有48种不同方案. 综上,共有244872+=种不同方案. 故答案为:72 17.(1)518;(2)1324. 【分析】(1)根据分步乘法计数原理,排列及古典概型可得结果;(2)安排一名同学报A 科目有14C 种,根据古典概型求解.【详解】(1)由题知,4位同学报6个项目共有46种可能,4位同学报了4个不同的项目共有46A 种可能,所以4645618A P ==.(2)由题知,4位同学报6个项目共有46种可能,1位同学报项目A ,剩余3位同学都报项目B 共有14C 种可能, 所以14416324C P ==.18.(1)2.22;(2)45.【分析】(1)根据频率分布直方图,由中位数的定义求解;(2)分层抽样可知[2.30,2.40)中抽取4株,[2.40,2.50)中抽取2株,根据古典概型求解即可. 【详解】(1)由频率分布直方图得:[2.0,2.2)的频率为:(1+3.5)×0.1=0.45, [2.2,2.3)的频率为:2.5×0.1=0.25, 估计这批树苗高度的中位数为: 2.2+0.50.452.5-=2.22. (2)按分层抽样方法,从高度在[2.30,2.50]的树苗中任取6株树苗, 则[2.30,2.40)中抽取:6×221+=4株, [2.40,2.50)中抽取:6×121+=2株, 从这6株树苗中任选3株,基本事件总数n =3620C =,3株树苗中至少有一株树苗高度在[2.40,2.50]包含的基本事件个数:m =12214242C C C C +=16, ∴3株树苗中至少有一株树苗高度在[2.40,2.50]的概率164205m P n ===. 19.(1)1728;(2)分布列见具体解析,()34E X =. 【分析】(1)利用古典概型计算公式与对立事件的概率计算公式即可得出;(2)X 的可能取值为0,1,2,3,由已知可知13,4X B ⎛⎫~ ⎪⎝⎭,进而得到答案.【详解】(1)由题意,16人中有4人“极满意”,记至少有一人是“极满意”为事件A ,则()31231617128C P A C =-=.(2)X 的可能取值为0,1,2,3,由已知13,4X B ⎛⎫~ ⎪⎝⎭,所以()33270464P X ⎛⎫=== ⎪⎝⎭,()213132714464P X C ⎛⎫==⨯⨯=⎪⎝⎭, ()22313924464P X C ⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭,()3113464P X ⎛⎫=== ⎪⎝⎭.所以X 的分布列为:()13344E X =⨯=. 20.(1)518;(2)分布列见解析;110. 【分析】(1)甲、乙、丙三人中恰有两人被机器人社团录取为新成员,即恰一人未录取,则所求事件转化为“甲未录取,乙丙录取”、“乙未录取,甲丙录取”、“丙未录取,甲乙录取”三个互斥事件的和事件,每一事件又是三个相互独立事件的积事件,先利用相互独立事件同时发生的乘法公式,再利用互斥事件和事件概率加法公式求解;(2)甲、乙、丙三人都参加笔试,每人均已经得到20元话费,笔试是否通过决定能否得到另30元话费.按三人中通过笔试的人数分为0,1,2,3四类,即对应60,90,120,150X =四种情况,分别求解概率即可. 【详解】(1)设事件A 表示“甲被机器人社团正式录取”,事件B 表示“乙被机器人社团正式录取”,事件C 表示“丙被机器人社团正式录取”. 则()()121233P A P C ==⨯=,()231342P B =⨯=.所以甲、乙、丙三人中恰有两人被机器人社团录取为新成员的概率为()()()()()()()()()()P P ABC ABC ABC P A P B P P A P B P C A P B P C P C =++=++111111521132332318⎛⎫⎛⎫=-⨯⨯+⨯⨯-⨯= ⎪ ⎪⎝⎭⎝⎭.(2)X 的所有可能取值为60,90,120,150, ()11116023212P X ==⨯⨯=,()11121141902223322123P X ==⨯⨯⨯+⨯⨯==,()1121115120222322312P X ==⨯⨯⨯+⨯⨯=,()11221150223126P X ==⨯⨯==.所以X 的分布列为所以()11516090120150110123126E X =⨯+⨯+⨯+⨯=. 【点睛】离散型随机变量分布列的求解步骤:(1)明取值:明确随机变量的可能取值有哪些且每一个取值所表示的意义; (2)求概率:要弄清楚随机变量的概率类型,利用相关公式求出变量所对应的概率; (3)画表格:按规范要求形式写出分布列;(4)做检验:利用分布列的性质检验分布列是否正确.21.(1)22162x y +=;(2)证明见解析.【分析】(1)根据焦距及短轴的两个端点与长轴的一个端点构成正三角形,结合椭圆中a b c 、、的关系,即可求得a b c 、、的值,即可得椭圆方程.(2)设出点P 的坐标,根据两点间距离公式,结合椭圆的方程即可证明.【详解】(1)因为椭圆2222:1x y C a b+=(0a b >>)的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.所以222242c b a b c =⎧⎪⎪=⎨⎪=+⎪⎩解方程组可得2a b c ⎧=⎪⎪=⎨⎪=⎪⎩所以椭圆的方程为22162x y +=(2)证明:设()00,P x y ,03x >-因为F 为椭圆C 的左焦点,直线:3l x =-,椭圆的方程为22162x y +=所以2200162x y +=,即220023x y =-则点P 到直线l 的距离为03n x =+ 点P 到F 的距离为m ==因为03x >- 所以m =)03x +所以m n =. 22.(1)证明见解析;(2)1. 【分析】(1)根据题意,将问题转化为证明1ln x x +≤,进而构造函数,求函数最值即可; (2)求导22ln ()x e x x f x x+'=,故令2()ln x h x x e x =+,根据函数单调性与零点存在定理知存在01,12x ⎛⎫∈ ⎪⎝⎭使得当00x x <<时函数()f x 单调递减,当0x x >时函数()f x 单调递增,且020e n 0l x x x +=,进而000000ln 1l l n n x x x e x x x e -=-=-,再根据()x t x xe =的单调性得00ln x x =-,001x e x =进而得()min 0()1f x f x ==. 【详解】解:(1)函数1ln ()+=-xxf x e x的定义域为{}0x x >, 所以要证()1xe f x -≤,只需证1ln 1xx+≤,即证1ln x x +≤. 令()ln 1g x x x =-+,()111x g x x x-'=-=, 所以当()0,1∈x 时,0g x ,函数()ln 1g x x x =-+为增函数, 当()1,∈+∞x 时,0g x,函数()ln 1g x x x =-+为减函数,所以()()()max 10g x g x g ≤==⎡⎤⎣⎦,即ln 10x x -+≤, 所以1ln x x +≤,所以()1xe f x -≤;(2)()22211ln ln ()x xx x e xf x e x x-++'=-=, 令2()ln x h x x e x =+,21()(2)0x h x e x x x'=++>,所以函数2()ln x h x x e x =+在0,上单调递增,因为11ln 20,(1)022h h e ⎛⎫=<<=> ⎪⎝⎭, 所以存在01,12x ⎛⎫∈ ⎪⎝⎭使得0()0h x =,当00x x <<时()0h x <,当0x x >时()0h x >,所以当00x x <<时()0f x '<,函数()f x 单调递减, 当0x x >时,()0f x '>,函数()f x 单调递增,所以当0x x =时,()0min 001ln ()x x f x f x e x +==-, 因为0()0h x =,0020e n 0l xx x +=,即00001ln 0x x x e x +=, 所以000000ln 1l l n n x x x e e x x x -=-⋅=-, 故令()x t x xe =,()10()xt x x e '+>=,函数()x t x xe =为0,的单调递增函数,所以00ln x x =-,所以01x e x =, ()000min 000001ln ln 11()1x x x f x f x e x x x x +==-=--=. 【点睛】本题考查利用导数证明不等式,求函数的最值,考查运算求解能力,逻辑推理能力,化归转化思想,是难题.本题第二问解题的关键在于结合零点的存在性定理知存在01,12x ⎛⎫∈ ⎪⎝⎭使得当00x x <<时函数()f x 单调递减,当0x x >时函数()f x 单调递增,且0020e n 0l x x x +=,进而求解函数最小值.。
江西省九江市第一中学2023-2024学年高二下学期开学考试数学试题

江西省九江市第一中学2023-2024学年高二下学期开学考试数学试题一、单选题1.“02n <<”是“方程22113x y n n +=+-表示双曲线”的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件2.根据表中的数据,用最小二乘法得到y 与x 的线性回归方程为$1414y x =-,则表中n 的值为( )A .15.5B .20C .20.5D .253.某校有甲、乙等5名同学到4个社区参加志愿服务活动,要求每名同学只能去1个社区,每个社区至少安排1名同学,则甲、乙2人被分配到同1个社区的概率为( ) A .310 B .110 C .25 D .354.已知()()6221x x a x ++-展开式中各项系数之和为3,则展开式中的x 系数为( ) A .10- B .11- C .13- D .14- 5.已知1F ,2F 是椭圆C :22194x y +=的两个焦点,点M 在C 上,则12MF MF ⋅的最大值为( )A .13B .12C .9D .66.已知动直线:220l kx y k --+=恒过定点,A B 为圆22:(1)(3)8C x y -+-=上一动点,O 为坐标原点,则AOB V 面积的最大值为( )A .85B .4C .6D .247.如图所示的多面体是由底面为ABCD 的长方体被截面1AEC F 所截得到的,其中4AB =,2BC =,13CC =,1BE =,则点C 到平面1AEC F 的距离为( )A B C D 8.我国首先研制成功的“双曲线新闻灯”,如图,利用了双曲线的光学性质:1F 、2F 是双曲线的左、右焦点,从2F 发出的光线m 射在双曲线右支上一点P ,经点P 反射后,反射光线的反向延长线过1F ;当P 异于双曲线顶点时,双曲线在点P 处的切线平分12F PF ∠.若双曲线C 的方程为上221916x y -=,则下列结论不正确...的是( )A .射线n 所在直线的斜率为k ,则44,33k ⎛⎫∈- ⎪⎝⎭B .当m n ⊥时,1232PF PF ⋅=C .当n 过点()7,5Q 时,光由2F 到P 再到Q 所经过的路程为13D .若()1,0T ,直线PT 与C 相切,则212PF =二、多选题9.直线l :30x my -+=和圆C :22650x y x +-+=,下列结论成立的是( ) A .直线l :30x my -+=过定点()3,0-B .当实数m 的值为3时,直线l 与圆CC .当直线l 与圆C 相切时,则实数m =D .圆M :()2219x y +-=与圆C 的公切线有且只有两条10.下列说法,错误的为( )A .若两个空间向量相等,则表示它们有向线段的起点相同,终点也相同B .若向量,AB CD u u u r u u u r 满足AB CD >u u u r u u u r ,且AB u u u r 与CD u u u r 同向,则AB CD >u u u r u u u rC .若两个非零向量AB u u u r 与CD u u u r 满足0AB CD +=u u u r u u u r r ,则,AB CD u u u r u u u r 为相反向量D .AB CD =u u u r u u u r 的充要条件是A 与C 重合,B 与D 重合11.如图,由半圆和半椭圆组成的“曲圆”,半圆的圆心是坐标原点,直径与椭圆的短轴重合,半圆所在的圆过椭圆的焦点()0,1F ,且与y 轴非正半轴交于点G .若过原点O 的直线与上半椭圆交于点A ,与下半圆交于点B ,则下列结论正确的是( )A .AB 的长度的最大值是1B .AFG V 的周长为2+C .ABF △的面积的最小值是1D .90AGB ∠≥o三、填空题12.某校第一次模拟考试的数学成绩X 近似地服从正态分布()290,N σ,若()1000.92P X <=,则()80100P X <<=.13.若直线l 过点(1,2)-,且与双曲线2299x y -=有且只有一个公共点,则满足条件的直线有条.14.正四面体ABCD 中,若M 是棱CD 的中点,AP AM λ=u u u r u u u u r ,1166AB BP AC AD +=+u u u r u u u r u u u r u u u r ,则λ=.四、解答题15.随着寒冷冬季的到来,羽绒服进入了销售旺季,某调查机构随机调查了400人,询问他们选购羽绒服时更关注保暖性能还是更关注款式设计,得到以下的22⨯列联表:(1)是否有95%的把握认为男性和女性在选购羽线服时的关注点有差异?(2)若从这400人中按男女比例用分层抽样的方法抽取5人进行采访,再从这5人中任选2人赠送羽线服,记X 为抽取的2人中女生的人数,求X 的分布列和数学期望.附:()()()()22()n ad bc K a b c d a c b d -=++++.16.已知抛物线2y x =-与过点(1,0)-的直线l 相交于A 、B 两点,点O 为坐标原点.(1)求OA OB ⋅u u u r u u u r 的值;(2)若△OAB 的面积等于54,求直线l 的方程. 17.如图,已知四棱锥P ABCD -的底面是直角梯形,90,224ADC BCD AD BC CD ∠∠======o ,二面角P AD B --的大小为120o ,E 是PA 中点.(1)求证:BE ∥平面PCD ;(2)求二面角E BD A --的余弦值.18.已知抛物线2:2(0)D y px p =>的焦点为F ,点Q 在D 上,且QF 的最小值为1.(1)求D 的方程;(2)过点()3,2M -的直线与D 相交于A ,B 两点,过点(3,6)N -的直线与D 相交于B ,C 两点,且A ,C 不重合,判断直线AC 是否过定点.若是,求出该定点;若不是,请说明理由. 19.如图,一只蚂蚁从正方体1111ABCD A B C D -的顶点1A 出发沿棱爬行,记蚂蚁从一个顶点到另一个顶点为一次爬行,每次爬行的方向是随机的,蚂蚁沿正方体上、下底面上的棱爬行的概率为16,沿正方体的侧棱爬行的概率为23.(1)若蚂蚁爬行5次,求蚂蚁在下底面顶点的概率;(2)若蚂蚁爬行5次,记它在顶点C 出现的次数为X ,求X 的分布列与数学期望.。
2020-2021学年高二数学下学期期末考试试题

2020-2021学年高二数学下学期期末考试试题一、 选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知随机变量X 服从正态分布N (μ,σ2),且P (μ-2σ<X<μ+2σ)=0.954 4,P (μ-σ<X<μ+σ)=0.682 6.若μ=4,σ=1,则P (5<X<6)=( )A .0.135 9B .0.135 8C .0.271 8D .0.271 6 1.(文科做)若f (x )=x 2+2(a -1)x +2在区间(-∞,4)上是减函数,则实数a 的取值范围是( )A .a <-3B . a >-3C . a ≤-3D .a ≥-32.集合A ={1,2,3,a },B ={3,a },则使A ∪B =A 成立的a 的个数是 ( ) A .2个 B .5个 C .3个 D . 4个3.设集合U ={1,2,3,4,5,6},A ={1,3,5},B ={3,4,5},则∁U (A ∪B )=( )A .{3,6}B .{2,6}C .{1,3,4,5}D .{1,2,4,6}4.已知随机变量ξ,η满足ξ+η=8,且ξ服从二项分布B (10,0.6),则E (η)和D (η)的值分别是( ) A .6和2.4B .2和5.6C .2和2.4D .6和5.64.(文科做)函数y =f (2x -1)的定义域为[0,1],则y =f (x )的定义域为( )A . [0,1]B .⎣⎢⎡⎦⎥⎤12,1 C . [-1,1] D .[]-1,0其线性回归方程一定过的定点是( ) A .(2,2) B .(1,2) C .(1.5,0)D .(1.5,5)6.已知集合A={x|2<x<4},B={x|x<3或x>5},则A ∩B=( )A .{x|2<x<3}B .{x|x<4或x>5}C .{x|2<x<5}D .{x|x<2或x>5}7.设x ∈R ,则“1<x <2”是“|x -2|<1”的( )A .必要而不充分条件B .充分而不必要条件C .充要条件D .既不充分也不必要条件 8.(文科做)已知某四个家庭xx 上半年总收入x (单位:万元)与总投资y (单位:万元)的对照数据如表所示:根据上表提供的数据,若用最小二乘法求出y 关于x 的线性回归方程为y ^=0.7x +0.35,则m 的值为( )A . 3B . 5C . 4D .68.有10件产品,其中3件是次品,从这10件产品中任取两件,用ξ表示取到次品的件数,x 0 1 2 3 y2468x 3 4 5 6y 2.5 3 m 4.5则E (ξ)等于( )A .35B .815C .1415D .1 9. 甲、乙两人同时报考某一所大学,甲被录取的概率为0.6,乙被录取的概率为0.7,两人是否被录取互不影响,则其中至少有一人被录取的概率为( )A .0.12B .0.42C .0.46D .0.889.(文科做)函数f (x )=x 2+x -6的单调增区间是( )A .(-∞,-3)B .[2,+∞)C .[0,2)D .[-3,2]10(文科做).函数f (x )=ax 2+bx +2a -b 是定义在[a -1,2a ]上的偶函数,则a +b =( )A .13B .0C .-13D .1 10.箱子里有5个黑球,4个白球,每次随机取出一个球,若取出黑球,则放回箱中,重新取球;若取出白球,则停止取球,那么在第4次取球之后停止的概率为( )A .C 35C 14C 45B .⎝ ⎛⎭⎪⎫593×49C .35×14D .C 14×⎝ ⎛⎭⎪⎫593×4911. f (x )是定义在(0,+∞)上的单调增函数,满足f (xy )=f (x )+f (y ),f (3)=1, 当f (x )+f (x -8)≤2时,x 的取值范围是( )A .(8,+∞) B.[8,9] C .(8,9] D .(0,8) 12.函数f (x )=log 2(x 2+2x -3)的定义域是( )A .[-3,1]B .(-3,1)C . (-∞,-3)∪(1,+∞)D .(-∞,-3]∪[1,+∞)二.填空题:(本大题共4小题,每小题5分,共20分)13.从装有3个红球,2个白球的袋中随机取出2个球,用ξ表示取到白球的个数,则P (ξ=1)= 13.(文科做)下列不等式:①x <1;②0<x <1;③-1<x <0;④-1<x <1.其中可以作为“x 2<1”的一个充分条件的所有序号为_______14,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体.经过搅匀后,从中随机取一个小正方体,记它的涂漆面数为X ,则X 的均值E (X )=14(文科做).已知f (x )=ax 3+bx +xx ,且f (xx)=xx ,则f (-xx)=________.15.下列是关于男婴与女婴出生时间调查的列联表:那么a= ,b= ,c= ,d= ,e= .16.已知命题“∀x ∈R ,x 2-5x +152a >0”的否定为假命题,则实数a 的取值范围是________三.解答题:(本大题共6小题,共70分)17.(本题满分10分)已知集合P ={x |a +1≤x ≤2a +1},Q ={x |x 2-3x ≤10}.(1)若a =3,求(∁R P )∩Q ;(2)若P ∪Q =Q ,求实数a 的取值范围.18.(本题满分12分)设命题p :函数f (x )=lg (ax 2-4x +a )的定义域为R ;命题q :不等式2x 2+x >2+ax 在x ∈(-∞,-1)上恒成立,如果命题“p ∨q ”为真命题,命题“p ∧q ”为假命题,求实数a 的取值范围.19.(本题满分12分)甲、乙两人各进行3次射击,甲每次击中目标的概率为1/2,乙每次击中目标的概率为2/3 (1)记甲击中目标的次数为X ,求X 的概率分布列及数学期望E (X ); (2)求乙至多击中目标2次的概率; (3)求甲恰好比乙多击中目标2次的概率19(文科做)已知p :A ={x |x 2-2x -3≤0,x ∈R },q :B ={x |x 2-2mx +m 2-9≤0,x ∈R ,m ∈R }.(1)若A ∩B =[1,3],求实数m 的值;(2)若p 是非q 的充分条件,求实数m 的取值范围20(本题满分12分)将编号为1,2,3,4的四个材质和大小都相同的球,随机放入编号为1,2,3,4的四个盒子中,每个盒子放一个球,ξ表示球的编号与所放入盒子的编号正好相同的个数. (1)求1号球恰好落入1号盒子的概率;(2)求ξ的分布列.20(文科做)某城市随机抽取一年(365天)内100天的空气质量指数API 的监测数据,结果统计如下: API [0, 50] (50, 100] (100, 150] (150, 200] (200, 250] (250, 300] (300, +∞) 空气 质量 优 良 轻微 污染 轻度 污染 中度 污染 中度 重污染 重度 污染 天数413183091115(1)若某企业每天由空气污染造成的经济损失S (单位:元)与空气质量指数API(记为ω)的关系式为S =⎩⎪⎨⎪⎧0,0≤ω≤100,3ω-200,100<ω≤300,2000,ω>300.试估计在本年内随机抽取一天,该天经济损失S 大于400元且不超过700元的概率;(2)若本次抽取的样本数据有30天是在供暖季,其中有8天为重度污染,完成下面2×2列联表,并判断能否有95%的把握认为该市本年空气重度污染与供暖有关?附:P (K 2≥k 0)0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 0 1.323 2.072 2.706 3.841 5.024 6.635 7.87910.828K 2=n ad -bc 2a +bc +d a +cb +d非重度污染重度污染合计供暖季非供暖季合计10021.(本题满分12分)已知函数f(x)=x·|x|-2x.(1)求函数f(x)=0时x的值;(2)画出y=f(x)的图象,并结合图象写出f(x)=m有三个不同实根时,实数m的取值范围.22.已知关于x的不等式|2x+1|-|x-1|≤log2a(其中a>0).(1)当a=4时,求不等式的解集;(2)若不等式有解,求实数a的取值范围.西宁市第四高级中学xx —17xx 第二学期期末测试试题答案高二数学1 2 3 4 5 6 A DABCD7 8 9 10 11 12 AB D D D B (13)0.6 13文(2)(3)(4) (14)6/5 文 xx (15)47 92 88 82 53 (16) a>5/617. 解 (1)因为a =3,所以P ={x |4≤x ≤7},∁R P ={x |x <4或x >7}.又Q ={x |x 2-3x -10≤0}={x |-2≤x ≤5},所以(∁R P )∩Q ={x |x <4或x >7}∩{x |-2≤x ≤5}={x |-2≤x <4}.(2)当P ≠∅时,由P ∪Q =Q 得P ⊆Q ,所以⎩⎪⎨⎪⎧a +1≥-2,2a +1≤5,2a +1≥a +1,解得0≤a ≤2;当P =∅,即2a +1<a +1时,有P ⊆Q ,得a <0. 综上,实数a 的取值范围是(-∞,2]. 18.对于命题p :Δ<0且a >0,故a >2;对于命题q :a >2x -2x+1在x ∈(-∞,-1)上恒成立,又函数y =2x -2x+1为增函数,所以⎝⎛⎭⎪⎫2x -2x+1<1,故a ≥1,命题“p ∨q ”为真命题,命题“p ∧q ”为假命题,等价于p ,q 一真一假.故1≤a ≤2.19. (1)X 的概率分布列为X 0 1 2 3 PE (X )=0E (X )=3(2)乙至多击中目标2次的概率为1(3)设甲恰好比乙多击中目标2次为事件A ,甲恰好击中目标2次且乙恰好击中目标0次为事件B 1,甲恰好击中目标3次且乙恰好击中目标1次为事件B 2,则A=B 1+B 2.B 1,B 2为互斥事件,P (A )=P (B 1)+P (B 2)19 文科做(1)A ={x |-1≤x ≤3,x ∈R },B ={x |m -3≤x ≤m +3,x ∈R ,m ∈R },∵A ∩B =[1,3],∴m =4.(2)∵p 是綈q 的充分条件,∴A ⊆∁R B ,∴m >6或m <-4.20.(1)设事件A 表示“1号球恰好落入1号盒子”,P (A )=A 33A 44=14,所以1号球恰好落入1号盒子的概率为14.(2)ξ的所有可能取值为0,1,2,4.P (ξ=0)=3×3A 44=38,P (ξ=1)=4×2A 44=13, P (ξ=2)=C 24A 44=14,P (ξ=4)=1A 44=124.所以随机变量ξ的分布列为20.文科做(1)记“在本年内随机抽取一天,该天经济损失S 大于400元且不超过700元”为事件A .由400<S ≤700,即400<3ω-200≤700,解得200<ω≤300,其满足条件天数为20.所以P (A )=20100=15. (2)根据以上数据得到如下列联表:非重度污染重度污染合计 供暖季 22 8 30 非供暖季 63 7 70 合计85 15100K 2=100×63×8-22×7285×15×30×70≈4.575>3.841,所以有95%的把握认为该市本年空气重度污染与供暖有关.21.(1)由f (x )=0可解得x =0,x =±2,所以函数f (x )=0时x 的值为-2,0,2. (2)f (x )=x |x |-2x ,即f (x )=⎩⎪⎨⎪⎧x 2-2x ,x ≥0,-x 2-2x ,x <0.图象如图由图象可得实数m ∈(-1,1).22. (1)当a =4时,不等式为|2x +1|-|x -1|≤2.当x <-12时,-x -2≤2,解得-4≤x <-12;当-12≤x ≤1时,3x ≤2,解得-12≤x ≤23;当x >1时,x ≤0,此时x 不存在,∴原不等式的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-4≤x ≤23. (2)令f (x )=|2x +1|-|x -1|,则f (x )=⎩⎪⎨⎪⎧-x -2,x <-12,3x ,-12≤x ≤1,x +2,x >1.故f (x )∈⎣⎢⎡⎭⎪⎫-32,+∞,即f (x )的最小值为-32. 若f (x )≤log 2a 有解,则log 2a ≥-32,解得a ≥24,即a 的取值范围是⎣⎢⎡⎭⎪⎫24,+∞ 【感谢您的阅览,下载后可自由编辑和修改,关注我 每天更新】。
江西省九江市2020-2021学年度上学期期末考试九年级数学试题及参考答案
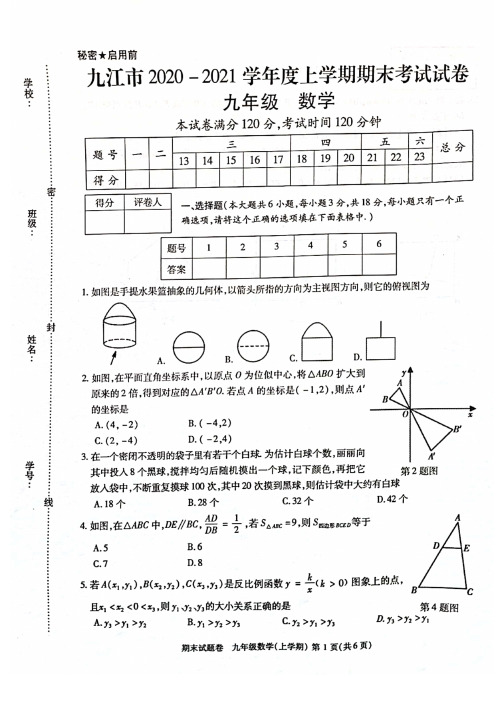
期末试卷 九年级数学(上学期)参考答案 第1页 (共4页)九江市2020-2021学年度上学期期末考试九年级数学参考答案及评分标准 一、 选择题(本大题共6小题,每题3分,共18分.)题号1 2 3 4 56 答案 A C C D A D二、 填空题(本大题共6小题,每题3分,共24分.)7.二、四 8. 18cm 2 9.0 10.4 11.1612. 12(对1个得1分,对2个得2分,1对1错0分,2对1错得1分)情况1 情况2 情况3三、 解答题(本大题共5小题,每小题6分,共30分.)13.本题共两小题,每小题3分,共6分.(1)12x =,23x =-………………………………(3分) (2)证明:∵四边形ABCD 是矩形 ∴AB=DC ,∠B=∠C=90°∵BF=CE ∴BF+EF=CE+EF即:BE=CF∴△ABE ≌△DCF∴AE=DF ………………………………(6分)14. 解:(1)12………………………………(2分)期末试卷 九年级数学(上学期)参考答案 第2页 (共4页)共有12种等可能结果,红红获胜的结果有6种,所以P (红红胜)=12………(6分) 15. 解:相似.理由如下:△ABC 中,AB=2,BC=,AC=△DEF 中,,EF=2,………(3分)AB BC AC DE EF DF===, ∴△ABC ∽△DEF. ………(6分)16. 解:(1)∵方程2210x x m -+-=有实数根 ∴△≥0即:()()22411m --⨯⨯-≥0,解得:m ≤2……………(3分)(2)当m =1时,10x =,22x =……………(6分) 17.解: EF 即为所求……………(3分) 点F 即为所求……………(3分)四、 解答题(本大题共3小题,每题8分,共24分.)18. 解:(1)设y 与x 的函数关系式为()0y kx b k =+≠, 根据题意得501006090k b k b ⎧+=⎪⎨+=⎪⎩,解得1150k b ⎧=-⎪⎨=⎪⎩.……………(4分) 故y 与x 的函数关系式为150y x =-+(0<x ≤90); (2)根据题意得(-x +150)(x -25)= 3750,……………(6分)解得x 1=75,x 2=100>90(不合题意,舍去)答:应将售价定为75元。
2020-2021学年高二数学下学期第一次月考试题理[1]
![2020-2021学年高二数学下学期第一次月考试题理[1]](https://img.taocdn.com/s3/m/48e61698e45c3b3566ec8b59.png)
2020-2021学年高二数学下学期第一次月考试题理本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是 符合题目要求的.(1)已知集合{1,2,}M zi =,i 为虚数单位,{3,4}N =,{4}MN =,则复数z =(A )2i - (B )2i (C )4i - (D )4i (2)已知函数()y f x =的图象在点(1,(1))M f 处的切线方程是122y x =+,则()()11f f +'的值等于(A )1 (B )52 (C )3 (D )0 (3)已知函数52()ln 33f x x x =-,则0(1)(1)limx f f x x∆→-+∆=∆ (A )1 (B )1- (C )43- (D )53-(4)某班数学课代表给全班同学出了一道证明题.甲说:“丙会证明.”乙说:“我不会证明.”丙说:“丁会证明.”丁说:“我不会证明.”以上四人中只有一人说了真话,只有一人会证明此题.根据以上条件,可以判定会证明此题的人是 (A )甲 (B )乙 (C )丙 (D )丁 (5)已知,x y R ∈, i 为虚数单位,若()123xi y i +=--,则x yi +=(A )10 (B )3 (C )5 (D )2 (6)函数()()3e xf x x =-的单调递增区间是(A )()0,3 (B )()1,4 (C )()2,+∞ (D )(),2-∞(7)函数32()23f x x x a =-+的极大值为6,那么a 的值是(A )6 (B )5 (C )1 (D )0(8)以正弦曲线sin y x =上一点P 为切点得切线为直线l ,则直线l 的倾斜角的范围是(A )30,,424πππ⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭ (B )[)0,π (C )3,44ππ⎡⎤⎢⎥⎣⎦(D )30,,44πππ⎡⎤⎡⎫⋃⎪⎢⎥⎢⎣⎦⎣⎭(9)在复平面内,若2(1)(4)6z m i m i i =+-+-所对应的点位于第二象限,则实数m 的取值范围是(A )(0,3) (B )(,2)-∞- (C )(2,0)- (D )(3,4)(10)设()f x '是函数()f x 的导函数,将()y f x =和()y f x '=的图象画在同一个直角坐标系中,错误..的是(11)若函数()2(0)xf x a x a=>+在[)1,+∞上的最大值为33,则a = (A )31- (B )34 (C )43(D )31+ (12)已知()f x 是定义在区间(0)+∞,上的函数,其导函数为()f x ',且不等式()2()x f x f x '<恒成立,则(A )4(1)(2)f f < (B )4(1)(2)f f > (C )(1)4(2)f f < (D )(1)4(2)f f '<第II 卷二、填空题:本题共4小题,每小题5分. (13)若函数321()(1)3f x x f x x '=-⋅+,则(1)f '=__________. (14)由曲线xy e x =+与直线0,1,0x x y ===所围成图形的面积等于__________. (15)观察下列各式: 1a b +=, 223a b +=, 334a b +=, 447a b +=, 5511a b +=,…,则1010a b +=(16)若直线y kx b =+是曲线ln 1y x =+的切线,也是曲线ln(2)y x =+的切线,则k =_______.三、解答题:解答应写出文字说明、证明过程或演算步骤. (17)(本小题满分12分)已知复数()()227656z a a a a i a R =-++--∈,求a 分别为何值时,(1)z 是实数; (2)z 是纯虚数; (3)当106za =-时,求z 的共轭复数.(18)(本小题满分10分) 已知数列{}n a 满足)(1,111++∈+==N n a a a a nnn (1)分别求234,,a a a 的值;(2)猜想{}n a 的通项公式n a ,并用数学归纳法证明.(19)(本小题满分12分)已知函数32()f x x ax bx =++在23x =-与1x =处都取得极值. (1)求函数()f x 的解析式;(2)求函数()f x 在区间[2,2]-的最大值与最小值.(20)(本小题满分12分)已知函数f (x )=ln xx.(1)判断函数()f x 的单调性;(2)若y =xf (x )+1x的图象总在直线y =a 的上方,求实数a 的取值范围.(21)(本小题满分12分)某商场为了获得更大的利润,每年要投入一定的资金用于广告促销.经调查,每年投入广告费t (百万元),可增加的销售额为25t t -+(百万元)03t ≤≤(). (1)若该商场将当年的广告费控制在三百万元以内,则应投入多少广告费,才能使公司由广告费而产生的收益最大?(注:收益=销售额-投入费用)(2)现在该商场准备投入三百万元,分别用于广告促销和技术改造.经预算,每投入技术改造费x (百万元),可增加的销售额约为32133x x x -++(百万元),请设计一个资金分配方案,使该商场由这两项共同产生的收益最大.(22)(本小题满分12分) 已知函数()ln m f x x x=+(其中m R ∈),()161x g x e x +=-+(其中e 为自然对数的底数).(1)若曲线()y f x =在1x =处的切线与直线2450x y -+=垂直,求()f x 的单调区间和极值;(2)若对任意11,22x ⎡⎤∈⎢⎥⎣⎦,总存在[]22,3x ∈使得()()312120f x g x e -+-≥成立,求实数m 的取值范围.xx 第二学期第一次考试 高二年级理科数学试题参考答案一、 选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案CCBBACADDDAB(1)【答案】C 【解析】由M ∩N ={4},知4∈M ,故z i =4,故z =4i =4i i 2=-4i.(2)【答案】C 【解析】由导数的几何意义得()()1151,112.222k f f ===⨯+=' 所以()()11f f +'=15+=322,故选C. (3)【答案】B(4)【答案】B 【解析】如果甲会证明,乙与丁都说了真话,与四人中只有一人说了真话相矛盾,不合题意;排除选项A ;如果丙会证明,甲乙丁都说了真话,与四人中只有一人说了真话相矛盾,不合题意,排除选项C ;如果丁会证明,丙乙都说了真话,与四人中只有一人说了真话相矛盾,不合题意,排除选项D ,故选B. (5)【答案】A 【解析】()123xi y i +=-- 21{3y x -=⇒=- 3{1x y =-⇒=,则10x yi +=. (6)【答案】C 【解析】()()()e 3e e2xxxf x x x '=+-=-,令()()e 20x f x x '=->,解得2x >,所以函数()f x 的单调增区间为()2,+∞.故选C . (7)【答案】A 【解析】()()322()23,6661f x x x a f x x x x x '=-+∴=-=-,令()0,f x '=可得0,1x =,容易判断极大值为()06f a ==.故选A. (8)【答案】D 【解析】由题得cos y x '=,设切线的倾斜角为α,则][3tan cos 1tan 10,,44k x ππαααπ⎡⎫==∴-≤≤∴∈⋃⎪⎢⎣⎭,故选D.(9)【答案】D 【解析】整理得22(4)(6)z m m m m i =-+--对应的点位于第二象限,则224060m m m m ⎧-<⎪⎨-->⎪⎩,解得34m <<. (10)【答案】D 【解析】经检验,A :若曲线为原函数图象,先减后增,则其导函数先负后正,正确;B :若一直上升的函数为原函数图象,单调递增,则其导函数始终为正,正确;C:若下方的图象为原函数图象,单调递增,则其导函数始终为正,正确;D :若下方的函数为原函数,则其导函数为正,可知原函数应单调递增,矛盾;若上方的函数图象为原函数图象,则由导函数可知原函数应先减后增,矛盾.故选D. (11)【答案】A②当1a ≤,即1a ≤时, ()f x 在[)1,+∞上单调递减,故()()max 111f x f a ==+. 令1313a =+,解得31a =-,符合题意. 综上31a =-.(12)【答案】B 【解析】设函数2()()f x g x x=(0)x >, 则243()2()()2()()0x f x xf x xf x f x g x x x''--'==<, 所以函数()g x 在(0,)+∞上为减函数,所以(1)(2)g g >,即22(1)(2)12f f >, 所以4(1)(2)f f >,故选B. 二、填空题 (13)【答案】23【解析】∵f (x )=13x 3-f ′(1)·x 2+x ,∴f ′(x )=x 2-2f ′(1)·x +1, ∴f ′(1)=1-2f ′(1)+1,∴f′(1)=23. (14)【答案】e -12 【解析】由已知面积S =10⎰(e x+x )d x =⎝⎛⎭⎪⎫e x +12x 210|=e +12-1=e -12.(15)123(16)【答案】12【解析】设直线y kx b =+与曲线ln 1y x =+和ln(2)y x =+的切点分别为()11,x kx b +,()22,x kx b +.由导数的几何意义可得12112k x x ==+,得122x x =+,再由切点也在各自的曲线上,可得1122ln 1,(),ln 2kx b x kx b x +=++=+⎧⎨⎩联立上述式子解得12k =. 三、解答题(17)解:(1)Z 是实数, 2560a a --=,得61a a ==-或(2)Z 是纯虚数, 2760a a -+=,且2560a a --≠,得1a = (3)当106za =-时, ()()1110a a i -++=, 得()()221110a a -++=,得2a =± 当2a =时, 412z i =--,得412Z i =-+; 当2a =-时, 248z i =+,得248Z i =-(18) 解: (1)3111,2112121223112=+=+==+=a a a a a a ,41113131334=+=+=a a a (2)猜想)(1+∈=N n na n ①当n =1时命题显然成立②假设)(+∈=N k k n 命题成立,即ka k 1= 当11111111+=+=+=+=+k a a ,ak n kk k k k 时 1+=∴k n 时命题成立综合①②,当+∈N n 时命题成立(19)解:(1) 2()32f x x ax b '=++,由题意2()03(1)0f f ⎧'-=⎪⎨⎪'=⎩即44033320ab a b ⎧-+=⎪⎨⎪++=⎩ 解得122a b ⎧=-⎪⎨⎪=-⎩,经检验符合题意,321()22f x x x x ∴=--(2)由(1)知2()3()(1)3f x x x '∴=+-, 令()0f x '=,得122,13x x =-=, 当x 变化时,f ′(x ),f (x )的变化情况如下表:x -2⎝⎛⎭⎪⎫-2,-23 -23 ⎝ ⎛⎭⎪⎫-23,1 1 (1,2) 2f ′(x )+0 -0 +f (x ) -6极大值2227极小值-322由上表知f max (x )=f (2)=2,f min (x )=f (-2)=-6. (20)解:(I) 21ln ()xf x x-'=当0x e << 时,()0f x '>,()f x 为增函数; 当x e >时,()0f x '<,()f x 为减函数. (2)依题意得,不等式1ln a x x<+对于0x >恒成立.令1()ln g x x x =+,则22111()x g x x x x-'=-=. 当(1,)x ∈+∞时,21()0x g x x -'=>,则()g x 是(1,)+∞上的增函数; 当(0,1)x ∈时,()0g x '<,则()g x 是(0,1)上的减函数. 所以()g x 的最小值是(1)1g =, 从而a 的取值范围是(,1)-∞.(21)解:(1)设投入广告费t (百万元)后由此增加的收益为()f t (百万元),则()2254f t t t t t t =-+-=-+ ()224t =--+, 03t ≤≤.所以当2t =时, ()max 4f t =,即当商场投入两百万元广告费时,才能使商场由广告费而产生的收益最大.(2)设用于技术改造的资金为x (百万元),则用于广告促销的费用为()3x -(百万元),则由此两项所增加的收益为()()23213[33g x x x x x =-+++-- ()3153]3433x x x +--=-++.()2'4g x x =-+,令()2'40g x x =-+=,得2x =或2x =-(舍去).当02x <<时, ()'0g x >,即()g x 在[)0,2上单调递增; 当23x <<时, ()'0g x <,即()g x 在(]2,3上单调递减, ∴当2x =时, ()()max 2523g x g ==. 故在三百万资金中,两百万元用于技术改造,一百万元用于广告促销,这样商场由此所增加的收益最大,最大收益为253百万元. (22)(2)由()161x g x ex +=-+, ()1'6x g x e +=-,当[]2,3x ∈时, ()'0g x >, ()g x 单调递增,故()g x 有最小值()3211g e =-,因为对任意11,22x ⎡⎤∈⎢⎥⎣⎦,总存在[]22,3x ∈使得()()312120f x g x e -+-≥,即()()31212f x e g x +-≥成立,所以对任意11,22x ⎡⎤∈⎢⎥⎣⎦,都有()3311211f x e e +-≥-,即()11f x ≥, 也即11ln 1m x x +>成立,从而对任意11,22x ⎡⎤∈⎢⎥⎣⎦,都有111ln m x x x ≥-成立, 构造函数()ln x x x x ϕ=- 1,22x ⎛⎫⎡⎤∈ ⎪⎢⎥⎣⎦⎝⎭,则()'ln x x ϕ=-,令()'0x ϕ=,得1x =,当1,12x ⎛⎫∈ ⎪⎝⎭时, ()'0x ϕ>, ()x ϕ单调递增;当()1,2x ∈时, ()'0x ϕ<, ()x ϕ单调递减,∴()x ϕ的最大值为()11ϕ=,∴1m ≥,综上,实数m 的取值范围为[)1,+∞.【感谢您的阅览,下载后可自由编辑和修改,关注我 每天更新】。
2020-2021学年江西省九江市高一(上)期末数学试卷 (解析版)

2020-2021学年江西省九江市高一(上)期末数学试卷一、选择题(共12小题).1.已知集合A={x|lnx≤0},B={x|﹣1≤x≤1},则()A.A⫋B B.B⫋A C.A=B D.A∩B=B2.二次函数y=2x2的图象向上平移2个单位长度,再向右平移1个单位长度,所得图象对应的函数表达式为()A.y=2(x+1)2+2B.y=2(x﹣1)2+2C.y=2(x+1)2﹣2D.y=2(x﹣1)2﹣23.若函数f(x)=lnx+2x﹣3,则f(x)的零点所在区间是()A.(0,1)B.(1,2)C.(2,3)D.(3,4)4.过点(1,2)且与直线x﹣2y+1=0垂直的直线方程为()A.x﹣2y+3=0B.x+2y﹣5=0C.2x+y﹣3=0D.2x+y﹣4=0 5.下列函数中是奇函数的是()A.B.C.D.6.设a=lg2,b=lg3,则log318=()A.B.C.D.7.已知a=21.2,b=log41.2,c=log21.2,则a,b,c的大小关系为()A.a<b<c B.c<a<b C.c<b<a D.b<c<a8.如图所示,网格纸上小正方形的边长为1,粗线画出的是某一几何体的三视图,则该几何体的体积为()A.32+8πB.32+12πC.16+8πD.16+12π9.某超市元旦期间搞促销活动,规定:顾客购物总金额不超过500元,不享受任何折扣;如果顾客购物的总金额超过500元,则超过的部分享受一定的折扣优惠,并按下表折扣分别累计计算:可享受的折扣优惠金额折扣率不超过400元的部分10%超过400元的部分20%若某顾客在此超市获得的折扣金为60元,则此人购物实际所付金额为()A.940元B.1000元C.1140元D.1200元10.函数的单调递增区间为()A.(0,+∞)B.(0,e)C.(1,+∞)D.(0,1)11.函数f(x)=x2+ln|x|的图象大致是()A.B.C.D.12.在平面直角坐标系xOy中,已知两个圆C1:(x﹣a)2+(y﹣1)2=4,C2:(x﹣1)2+(y﹣a)2=2相交于A,B两点,若|OA|=|OB|,则实数a的值为()A.0B.1C.2D.﹣1二、填空题(本大题共4小题,每小题5分,共20分.)13.若直线l1:ax+4y﹣2=0与l2:x+ay﹣a﹣1=0平行,则实数a的值为.14.已知集合A={x|x2﹣ax﹣a﹣2>0},B={0,1},若A∩B={1},则实数a的取值范围是.15.《九章算术》是我国古代数学名著,书中将四个面均为直角三角形的三棱锥称为鳖臑.如图,三棱锥P﹣ABC为鳖臑,且PA⊥平面ABC,AC=BC=1,,则该鳖臑外接球的表面积为.16.某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到100°C,水温y(°C)与时间t(min)近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,水温y (°C)与时间t(min)近似满足函数的关系式为(a,b为常数),通常这种热饮在40°C时口感最佳,某天室温为20°C,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为min.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.设全集U=R,已知集合,.(Ⅰ)当a=2时,求(∁R A)∩B;(Ⅱ)若A∪B=A,求实数a的取值范围.18.如图所示,在直三棱柱ABC﹣A1B1C1中,AC=BC=AA1=2,∠ACB=90°,D是AB 的中点.(Ⅰ)求证:直线AC1∥平面B1CD;(Ⅱ)设O为线段AC1上的动点,求三棱锥O﹣B1CD的体积.19.如图所示,已知圆O:x2+y2=r2(r>0)与直线相切.(Ⅰ)求r的值.(Ⅱ)直线l:y=kx+m与圆O相交于P,Q两点,若在圆O上存在一点R,使四边形OPRQ为平行四边形,求实数m的取值范围.20.某水产养殖户投资243万元建一个龙虾养殖基地,已知x年内付出的各种维护费用之和y满足二次函数y=ax2+c,且第一年付出的各种维护费用为3万元,第二年付出的各种维护费用为9万元,龙虾养殖基地每年收入90万元(Ⅰ)扣除投资和各种维护费用,求该龙虾养殖基地从第几年开始获取纯利润?(Ⅱ)若干年后该水产养殖户为了投资其他项目,对该龙虾养殖基地有两种处理方案:①年平均利润最大时,以138万元出售该龙虾养殖基地;②纯利润总和最大时,以30万元出售该龙虾养殖基地.问该水产养殖户会选择哪种方案?21.设函数(a>0且a≠1,b∈R),已知f(1)=0,f(log a5)=2.(Ⅰ)求f(x)的单调区间;(Ⅱ)是否存在实数λ,使得f(x)在区间[m,n]上的值域是[2m﹣λ,2n﹣λ]?若存在,请求出λ的取值范围;若不存在,请说明理由.请考生在第22-23题中任选一题作答,如果多做,则按所做的第一题计分.22.已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x+1.(Ⅰ)求f(x)的解析式;(Ⅱ)讨论函数g(x)=f(x)﹣m(m∈R)的零点个数.23.已知函数f(x)=(lgx)2﹣lgx﹣1.(Ⅰ)求f(x)的最小值,并求此时x的值;(Ⅱ)若a,b分别是f(x)的两个零点,求log a b+log b a的值.参考答案一、选择题(共12小题).1.已知集合A={x|lnx≤0},B={x|﹣1≤x≤1},则()A.A⫋B B.B⫋A C.A=B D.A∩B=B解:∵lnx≤0,∴0<x≤1,解得A集合为A={x|lnx≤0}={x|0<x≤1},因为B={x|﹣1≤x≤1},由集合的关系可得A是B集合的真子集,故选:A.2.二次函数y=2x2的图象向上平移2个单位长度,再向右平移1个单位长度,所得图象对应的函数表达式为()A.y=2(x+1)2+2B.y=2(x﹣1)2+2C.y=2(x+1)2﹣2D.y=2(x﹣1)2﹣2解:向上平移2个单位长度得y=2x2+2,再向右平移一个单位长度得y=2(x﹣1)2+2,故选:B.3.若函数f(x)=lnx+2x﹣3,则f(x)的零点所在区间是()A.(0,1)B.(1,2)C.(2,3)D.(3,4)解:函数f(x)=lnx+2x﹣3,在x>0时是连续增函数,因为f(1)=2﹣3=﹣1<0,f(2)=ln2+4﹣3=ln2+1>0,所以f(1)f(2)<0,由零点判定定理可知,函数的零点在(1,2).故选:B.4.过点(1,2)且与直线x﹣2y+1=0垂直的直线方程为()A.x﹣2y+3=0B.x+2y﹣5=0C.2x+y﹣3=0D.2x+y﹣4=0解:因为直线x﹣2y+1=0的斜率为,又所求直线与直线x﹣2y+1=0垂直,所以所求直线的斜率为﹣2,故所求直线方程为y﹣2=﹣2(x﹣1),即2x+y﹣4=0.故选:D.5.下列函数中是奇函数的是()A.B.C.D.解:根据题意,依次判断选项:对于A,,其定义域为(0,+∞),是非奇非偶函数,不符合题意,对于B,y=2x+,其定义域为R,有f(﹣x)=2﹣x+=2x+=f(x),是偶函数,不符合题意,对于C,y=x+,其定义域为{x|x≠0},有f(﹣x)=﹣(x+)=﹣f(x),是奇函数,符合题意,对于D,y=x2+,其定义域为{x|x≠0},有f(﹣x)=x2+=f(x),是偶函数,不符合题意,故选:C.6.设a=lg2,b=lg3,则log318=()A.B.C.D.解:.故选:C.7.已知a=21.2,b=log41.2,c=log21.2,则a,b,c的大小关系为()A.a<b<c B.c<a<b C.c<b<a D.b<c<a解:∵21.2>20=1,log41.2<log41.44=log21.2<log22=1,∴b<c<a.故选:D.8.如图所示,网格纸上小正方形的边长为1,粗线画出的是某一几何体的三视图,则该几何体的体积为()A.32+8πB.32+12πC.16+8πD.16+12π解:由三视图可知该几何体的下部分是底面边长为4,高为2的正四棱柱,上部分是底面直径为4,高为2的圆柱,∴V=4×4×2+π×22×2=32+8π,故选:A.9.某超市元旦期间搞促销活动,规定:顾客购物总金额不超过500元,不享受任何折扣;如果顾客购物的总金额超过500元,则超过的部分享受一定的折扣优惠,并按下表折扣分别累计计算:可享受的折扣优惠金额折扣率不超过400元的部分10%超过400元的部分20%若某顾客在此超市获得的折扣金为60元,则此人购物实际所付金额为()A.940元B.1000元C.1140元D.1200元解:设此人购物总金额为x元,可获得购物折扣金额为y元,由题意知,∵60>40,∴x>900,由0.2(x﹣900)+40=60,得0.2(x﹣900)=20,得x﹣900=100,即x=1000,故此时购物实际所付金额为1000﹣60=940元,故选:A.10.函数的单调递增区间为()A.(0,+∞)B.(0,e)C.(1,+∞)D.(0,1)解:当x≥1时,;当0<x<1时,f(x)=x.即,画出函数f(x)的图象,知f(x)在(0,1)上单调递增,故选:D.11.函数f(x)=x2+ln|x|的图象大致是()A.B.C.D.解:函数f(x)是偶函数,排除B.当x>0时,f(x)=x2+lnx在(0,+∞)上单调递增,排除A.又f(1)=1>0,排除D,故选:C.12.在平面直角坐标系xOy中,已知两个圆C1:(x﹣a)2+(y﹣1)2=4,C2:(x﹣1)2+(y﹣a)2=2相交于A,B两点,若|OA|=|OB|,则实数a的值为()A.0B.1C.2D.﹣1解:根据题意,圆C1:(x﹣a)2+(y﹣1)2=4,圆心为(a,1),C2:(x﹣1)2+(y﹣a)2=2,圆心为(1,a),两个圆C1和C2相交于A,B两点,则线段C1C2的垂直平分线为AB,又由|OA|=|OB|,则O也在线段C1C2的垂直平分线上,则O、C1、C2三点共线,则有=,则有a2=1,解得a=1或a=﹣1.当a=1时,两圆内含,没有公共点,故a=﹣1,故选:D.二、填空题(本大题共4小题,每小题5分,共20分.)13.若直线l1:ax+4y﹣2=0与l2:x+ay﹣a﹣1=0平行,则实数a的值为2.解:因为直线l1:ax+4y﹣2=0与l2:x+ay﹣a﹣1=0平行,所以,解得a=2.故答案为:2.14.已知集合A={x|x2﹣ax﹣a﹣2>0},B={0,1},若A∩B={1},则实数a的取值范围是..解:∵集合A={x|x2﹣ax﹣a﹣2>0},B={0,1},若A∩B={1},依题意得1∈A,0∉A,∴,解得,即实数a的取值范围是.故答案为:[﹣2,﹣).15.《九章算术》是我国古代数学名著,书中将四个面均为直角三角形的三棱锥称为鳖臑.如图,三棱锥P﹣ABC为鳖臑,且PA⊥平面ABC,AC=BC=1,,则该鳖臑外接球的表面积为4π.解:∵PA⊥平面ABC,AB,BC⊂平面ABC,∴AB⊥PA,BC⊥PA,又△ABC是直角三角形,AC=BC=1,∴BC⊥AC,又PA∩AC=A,PA,AC⊂平面PAC,∴BC⊥平面PAC,又PC⊂平面PAC,∴BC⊥PC,∴该鳖臑外接球的球心为PB的中点,则(2R)2=PA2+AC2+BC2,∴4R2=1+1+2=4,∴该鳖臑外接球的表面积为4πR2=4π.故答案为:4π.16.某种热饮需用开水冲泡,其基本操作流程如下:①先将水加热到100°C,水温y(°C)与时间t(min)近似满足一次函数关系;②用开水将热饮冲泡后在室温下放置,水温y (°C)与时间t(min)近似满足函数的关系式为(a,b为常数),通常这种热饮在40°C时口感最佳,某天室温为20°C,冲泡热饮的部分数据如图所示,那么按上述流程冲泡一杯热饮,并在口感最佳时饮用,最少需要的时间为25min.解:依题意,当t=0时,y=20,当t=2.5时,y=60,∴水加热到100°C,水温y(°C)与时间t(min)近似满足一次函数关系为y=16t+20.又当t=5时,y=100,当t=15时,y=60,∴,解得a=5,b=20,∴,令y=40,解得t=25.故答案为:25.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.设全集U=R,已知集合,.(Ⅰ)当a=2时,求(∁R A)∩B;(Ⅱ)若A∪B=A,求实数a的取值范围.解:(Ⅰ)当a=2时,A={x|2﹣1≤2x≤2}={x|﹣1≤x≤1},B={x|﹣1<x≤2},∴∁R A={x|x<﹣1或x>1},(∁R A)∩B=(1,2];(Ⅱ)∵A∪B=A,∴B⊆A,∴A={x|﹣1≤x≤log2a},∴log2a≥2,解得a≥4,∴实数a的取值范围是[4,+∞).18.如图所示,在直三棱柱ABC﹣A1B1C1中,AC=BC=AA1=2,∠ACB=90°,D是AB 的中点.(Ⅰ)求证:直线AC1∥平面B1CD;(Ⅱ)设O为线段AC1上的动点,求三棱锥O﹣B1CD的体积.解:(Ⅰ)证明:连接BC1交B1C于E,连接DE,∵四边形BB1C1C为正方形,∴E为BC1的中点,又D是AB的中点,∴在△ABC1中,AC1∥DE,又AC1⊄平面B1CD,DE⊂平面B1CD,∴直线AC1∥平面B1CD.(Ⅱ)∵AC1∥平面B1CD,∴,∴三棱锥O﹣B1CD的体积为:===,∴三棱锥O﹣B1CD的体积.19.如图所示,已知圆O:x2+y2=r2(r>0)与直线相切.(Ⅰ)求r的值.(Ⅱ)直线l:y=kx+m与圆O相交于P,Q两点,若在圆O上存在一点R,使四边形OPRQ为平行四边形,求实数m的取值范围.解:(Ⅰ)圆心O到直线的距离为,∵直线与圆O相切,∴r=2.(Ⅱ)设P(x1,y1),Q(x2,y2),联立方程组,消去y得(k2+1)x2+2kmx+m2﹣4=0,∴,,∵四边形OPRQ为平行四边形,∴线段PQ的中点即为线段OR的中点,∴R点的坐标为(x1+x2,y1+y2),即,由点R在圆O上,∴,整理得m2=k2+1,此时△=4k2m2﹣4(k2+1)(m2﹣4)=4(4k2﹣m2+4)=12(k2+1)>0,∴m2≥1,即m≤﹣1或m≥1,即m的取值范围为(﹣∞,﹣1]∪[1,+∞).20.某水产养殖户投资243万元建一个龙虾养殖基地,已知x年内付出的各种维护费用之和y满足二次函数y=ax2+c,且第一年付出的各种维护费用为3万元,第二年付出的各种维护费用为9万元,龙虾养殖基地每年收入90万元(Ⅰ)扣除投资和各种维护费用,求该龙虾养殖基地从第几年开始获取纯利润?(Ⅱ)若干年后该水产养殖户为了投资其他项目,对该龙虾养殖基地有两种处理方案:①年平均利润最大时,以138万元出售该龙虾养殖基地;②纯利润总和最大时,以30万元出售该龙虾养殖基地.问该水产养殖户会选择哪种方案?解:(Ⅰ)由已知得,当x=1时,y=3;当x=2时,y=12,即,解得a=3,c=0,∴y=3x2.又投资243万元,x年收入共90x万元,∴第x年获得纯利润为y=90x﹣3x2﹣243(x∈N*),令y>0,即90x﹣3x2﹣243>0,∴x2﹣30x+81<0,解得3<x<27(x∈N*),∴从第4年开始获得纯利润.(Ⅱ)方案①:年平均利润,当,即x=9时,t取最大值36.∴年平均利润最大时,以138万元出售该基地共获利润36×9+138=462(万元).方案②:纯利润总和y=90x﹣3x2﹣243=﹣3(x﹣15)2+432(n∈N*),当x=15时,纯利润总和最大,为432万元,∴纯利润总和最大时,以30万元出售该基地共获利润432+30=462(万元),两种方案盈利相同,但方案①时间比较短,所以选择方案①.21.设函数(a>0且a≠1,b∈R),已知f(1)=0,f(log a5)=2.(Ⅰ)求f(x)的单调区间;(Ⅱ)是否存在实数λ,使得f(x)在区间[m,n]上的值域是[2m﹣λ,2n﹣λ]?若存在,请求出λ的取值范围;若不存在,请说明理由.解:(Ⅰ)对于函数(a>0且a≠1,b∈R),由f(1)=0,得log a(a﹣b)=0,即a﹣b=1,由f(log a5)=2,得log a(5﹣b)=2,即5﹣b=a2,∴a2+a﹣6=0,解得a=2,b=1,∴,∵2x﹣1>0,∴x>0,故f(x)的定义域为(0,+∞),∴f(x)在区间(0,+∞)上单调递增,故f(x)的单调区间为(0,+∞).(Ⅱ)假设存在实数λ,n>m>0,由(Ⅰ)知f(x)在(0,+∞)单调递增,∴,即,令,,(t1,t2>1),即t1,t2为方程t2﹣t0t+t0=0的两不等实数根且t1,t2>1,令g(t)=t2﹣t0t+t0,则,解得t0>4.即2λ>4,λ>2,故存在实数λ符合条件,λ的取值范围是(2,+∞).请考生在第22-23题中任选一题作答,如果多做,则按所做的第一题计分. 22.已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2﹣2x+1.(Ⅰ)求f(x)的解析式;(Ⅱ)讨论函数g(x)=f(x)﹣m(m∈R)的零点个数.解:(Ⅰ)当x<0时,﹣x>0,f(﹣x)=(﹣x)2﹣2(﹣x)+1=x2+2x+1,∵f(x)是R上的偶函数,∴f(x)=x2+2x+1,∴.(Ⅱ)函数f(x)的图象如图所示.当m<0时,g(x)没有零点.当m=0或m>1时,g(x)有2个零点,当0<m<1时,g(x)有4个零点,当m=1时,g(x)有3个零点.23.已知函数f(x)=(lgx)2﹣lgx﹣1.(Ⅰ)求f(x)的最小值,并求此时x的值;(Ⅱ)若a,b分别是f(x)的两个零点,求log a b+log b a的值.解:(Ⅰ)令t=lgx,t∈R,则,∴当时,,即当时,.(Ⅱ)依题意,得lga,lgb是方程t2﹣t﹣1=0的两个实数根,由韦达定理,得lga+lgb=1,lga⋅lgb=﹣1,∴原式==.。
2022-2023学年江西省九江市瑞昌洪下中学高三物理下学期期末试题含解析

2022-2023学年江西省九江市瑞昌洪下中学高三物理下学期期末试题含解析一、选择题:本题共5小题,每小题3分,共计15分.每小题只有一个选项符合题意1. 在下列四个方程中,x1、x2、x3和x4各代表某种粒子。
①U+n Sr+Xe+3x1 ②H+x2He+n③U Th-x3 ④Mg+He Al+x4以下判断中正确的是()A.x1是中子B.x2是质子C.x3是粒子D.x4是氘核参考答案:AC2. 用平行于斜面的推力F使物体静止于倾角为θ的固定斜面上,()解:物体受重力、支持力、推力和摩擦力处于平衡.若F=mgsinθ,f=0;若F>mgsinθ,静摩擦力方向沿斜面向下;若F<mgsinθ,静摩擦力方向沿斜面向上.故D正确,A、B、C错误.故选D.3. 如图所示为模拟远距离输电实验电路图,两理想变压器的匝数n1=n4<n2=n3,四根模拟输电线的电阻R1、R2、R3、R4的阻值均为R,A1、A2为相同的理想交流电流表,L1、L2为相同的小灯泡,灯丝电阻R L>2R,忽略灯丝电阻随温度的变化.当A、B端接入低压交流电源时()A.A1、A2两表的示数相同B.L1、L2两灯泡的亮度相同C.R1消耗的功率大于R3消耗的功率D.R2两端的电压小于R4两端的电压参考答案:D【考点】变压器的构造和原理;电功、电功率;正弦式电流的最大值和有效值、周期和频率.【分析】根据变压器的规律和欧姆定律分别列出两个灯泡两端的电压表达式,再比较灯泡亮度的关系,根据电流的表达式分析两个电流表示数的关系,即可得到R1与R3消耗的功率的关系.【解答】解:AB、设变压器原、副线圈数比为K(K<1),A、B端接入的电压为U.则L2两端的电压为U2=,A2表的示数I A2=.对于变压器电路,升压变压器副线圈两端的电压为,设通过L1的电流为I1,则L1两端的电压为I1R L,A1表的示数为I A1=KI1,降压变压器原线圈的电压为I1R L,则有:﹣2RKI1=I1R L解得I1=,则I A1=KI1==因为R L>2R,K<1,可以得到I A2>I A1.I1>I A2.故AB错误;C、电阻R1、R3相等,I A2>I A1,根据公式P=I2R可知,R1消耗的功率小于R3消耗的功率,故C错误;D、电阻R2、R4相等,I A2>I A1,根据欧姆定律知:R2两端的电压小于R4两端的电压,故D正确.故选:D.4. (单选)一质点沿直线运动时的速度—时间图象如图所示,以下说法中正确的是A.质点在前1S内和前3 s内的位移方向相反B.质点在第2s末和第4s末的加速度方向相同C.质点在第3 s末和第5s末的位置相同D.质点将一直沿同一方向做直线运动参考答案:C5. (多选题)如图所示,MPQO为有界的竖直向下的匀强电场,电场强度为E,ACB 为光滑固定的半圆形轨道,轨道半径为R,AB为圆水平直径的两个端点,AC为1/4圆弧.一个质量为m,电荷量为-q的带电小球,从A点正上方高为H处由静止释放,并从A点沿切线进入半圆轨道.不计空气阻力及一切能量损失,关于带电小球的运动情况,下列说法正确的是( )[来A.小球一定能从B点离开轨道B.小球在AC部分可能做匀速圆周运动C.若小球能从B点离开,上升的高度一定小于HD.小球到达C点的速度可能为零[来参考答案:BC二、填空题:本题共8小题,每小题2分,共计16分6. 在竖直平面内,一根光滑金属杆弯成如图所示形状,相应的曲线方程为(单位:m),式中。
江西省九江市修水第一中学2022-2023学年高二化学期末试卷含解析

江西省九江市修水第一中学2022-2023学年高二化学期末试卷含解析一、单选题(本大题共15个小题,每小题4分。
在每小题给出的四个选项中,只有一项符合题目要求,共60分。
)1. 有4种混合溶液,分别由等体积0.1 mol/L的2种溶液混合而成:①CH3COONa与HCl;②CH3COONa与NaOH;③CH3COONa与NaCl;④CH3COONa与NaHCO3。
下列各项排序正确的是()A.pH:②>③>④>① B.c(CH3COO-):②>④>③>①C.溶液中c(H+):①>③>②>④ D.c(CH3COOH):①>④>③>②参考答案:B2. 下列实验能够成功的是A.只用溴水一种试剂可鉴别甲苯、乙烯、乙醇、四氯化碳四种液体B.将乙醇加热到170℃可制得乙烯C.用乙醇、冰醋酸及pH=0的H2SO4加热可制乙酸乙酯D.用酚酞可鉴别苯酚钠和乙醇钠两种溶液参考答案:A3. 下列关于有机化合物的说法正确的是A 乙醇和乙酸都存在碳氧双键B 甲烷和乙烯都可以与氯气反应C 高锰酸钾可以氧化苯和乙醛D 乙烯可以与氢气发生加成反应,苯不能与氢气加成参考答案:B4. 在48mL0.1mol/LHNO3溶液中加入12mL0.4mol/LKOH溶液时, 所得到的溶液呈A. 弱酸性B. 强酸性C. 碱性D. 中性参考答案:D5. 下列关于硫及含硫化合物的叙述正确的是A.SO2的漂白原理与次氯酸相同B.用澄清的石灰石可以鉴别CO2和SO2C.浓硫酸可以干燥H2、NH3、CO2等气体D.常温下铁遇浓硫酸钝化,因此可用铁罐储运浓硫酸参考答案:D6. 大多数水生生物只能在一定的pH范围内的水中生存,你认为这pH范围是A.1~5 B. 5~6.5C. 6.5~9.5D. 9~14参考答案:C略7. 研究人员最近发现了一种“水”电池,这种电池能利用淡水与海水之间含盐量差别进行发电,在海水中电池总反应可表示为:5MnO2+2Ag+2NaCl=Na2Mn5O10+2AgCl,下列“水”电池在海水中放电时的有关说法正确的是()A.正极反应式:Ag+Cl﹣﹣e﹣=AgClB.每生成1mol Na2Mn5O10转移2mol电子C.Na+不断向“水”电池的负极移动D.AgCl是还原产物参考答案:B考点:电极反应和电池反应方程式;原电池和电解池的工作原理.专题:压轴题.分析:根据电池总反应可判断出反应中Ag的化合价升高,被氧化,Ag应为原电池的负极,AgCl是氧化产物;方程式中5MnO2生成1Na2Mn5O10,化合价共降低了2价,所以每生成1molNa2Mn5O10转移2mol电子;在原电池中阴离子向负极移动,阳离子向正极移动,以形成闭合电路.解答:解:A、根据电池总反应:5MnO2+2Ag+2NaCl=Na2Mn5O10+2AgCl,可判断出Ag应为原电池的负极,负极发生反应的电极方程式为:Ag+Cl﹣﹣e﹣=AgCl,而不是正极方程式,故A错;B、根据方程式中5MnO2生成1Na2Mn5O10,化合价共降低了2价,所以每生成1molNa2Mn5O10转移2mol电子,故B正确;C、在原电池中阴离子向负极移动,阳离子向正极移动,故C错;D、反应中Ag的化合价升高,被氧化,Ag应为原电池的负极,AgCl是氧化产物,故D 错.故选:B.点评:本题考查原电池的电极反应和离子的定向移动以及电化学的简单计算,做题时要注意总电池反应式的判断利用,运用两极上的反应特点做题,分析Mn元素的化合价变化是该题的难点.8. 现有溴苯、乙醇、甲苯、己烯四种液体,只用一种试剂就可以将它们区别开,这种试剂是A.溴水B.食盐水C.NaOH溶液D.酸性KMnO4溶液参考答案:A9. 下列按电负性减小顺序排列的是()A.K、Na、Li B.As、P、N C.N、O、F D.O、S、Se参考答案:D考点:元素电离能、电负性的含义及应用.专题:元素周期律与元素周期表专题.分析:根据元素周期律知识分析,元素周期表中同周期元素从左到右元素的电负性逐渐增强,同主族元素从上到下元素的电负性逐渐减弱.解答:解:元素周期表中同周期元素从左到右元素的电负性逐渐增强,同主族元素从上到下元素的电负性逐渐减弱,则A.K、Na、Li为同主族元素,电负性逐渐增强,故A错误;B.As、P、N为同主族元素,电负性逐渐增强,故B错误;C.N、O、F为同周期元素,电负性逐渐增强,故C错误;D.O、S、Se为同主族元素,电负性逐渐减弱,故D正确.故选D.点评:本题考查元素周期律知识,题目难度不大,本题注意把握元素周期律的递变规律即可解答10. 检验某氯代烃中的氯元素,下列操作合理的是A.取少量氯代烃,加入硝酸银溶液,看是否出现白色沉淀B.取少量氯代烃,与氢氧化钠溶液共热后加入硝酸银溶液,看是否出现白色沉淀C.取少量氯代烃,与氢氧化钠溶液共热后加入稀硝酸,然后加入硝酸银溶液,看是否出现白色沉淀D.取少量氯代烃,与氢氧化钠溶液共热后加入稀盐酸,然后加入硝酸银溶液,看是否出现白色沉淀参考答案:C11. 取 5 mL 0.1 mol·L-1KI溶液,滴加0.1 mol·L-1FeCl3溶液5~6滴,继续加入 2 mLCCl4,充分振荡,静置。
2021-2022学年江西省九江市天红中学高三化学期末试题含解析

2021-2022学年江西省九江市天红中学高三化学期末试题含解析一、单选题(本大题共15个小题,每小题4分。
在每小题给出的四个选项中,只有一项符合题目要求,共60分。
)1. 某溶液中可能含有六种离子中的几种。
①在该溶液中滴加足量氯水后,有气泡产生、溶液呈橙黄色;②向呈橙黄色的溶液中加入BaCl2溶液时无沉淀生成;③橙黄色溶液不能使淀粉溶液变蓝。
根据上述实验事实推断,在该溶液中肯定存在的离子组是A. B.C. D.参考答案:A略2. 下列离子方程式正确的是A.往碳酸氢钠溶液中加入少量氢氧化钠溶液:HCO3- + OH-= CO2↑+ H2O B.向漂白粉溶液中通入少量SO2 : Ca2++ 2ClO-+ H2O + SO2= CaSO3↓+ 2HClO C.将少量氨气通入硫酸溶液:NH3 + H+= NH4+D.向NaHSO4溶液中加入Ba(OH)2溶液至中性:Ba2++ OH-+ H++SO==BaSO4↓+ H2O参考答案:C3. 下列说法正确的是()A.为测定新制氯水的pH,用玻璃棒蘸取液体滴在pH试纸上,与标准比色卡对照即可B.燃料的脱硫脱氮、SO2的回收利用和NO x的催化转化都是减少酸雨产生的措施C.要将溶解在CCl4中的碘单质分离出来,可以用蒸馏法,因为碘易升华,先分离出来D.提纯混有少量硝酸钾的氯化钠,应采用在较高温度下制得浓溶液再冷却结晶、过滤、干燥的方法参考答案:B【考点定位】考查化学实验方案的评价【名师点晴】本题主要考查的是实验室中常见操作和物质的提纯与检验。
本题中D为易错点。
需要注意的是,若杂质的溶解度随温度的不变不大,如硝酸钾中混有少量的氯化钠,而溶质的溶解度随温度的变化较大,可以采用蒸发浓缩,冷却结晶的方法除去氯化钠;若杂质的溶解度随温度的不变较大,而溶质的溶解度随温度的变化较小,如氯化钠中混有少量的硝酸钾,可以采用蒸发、结晶,趁热过滤的方法除去硝酸钾。
4. N A代表阿伏加德罗常数,下列说法正确的是()A.9gD2O中含有的电子数为5N AB.1molMgCl2中含有的离子数为2N AC.1molCH4分子中共价键总数为4N AD.7.1g C12与足量NaOH溶液反应转移的电子数为0.2N A参考答案:答案:C5. 实验室制取氧气的过程,大致分为以下六个主要操作:①点燃酒精灯,给试管加热②熄灭酒精灯③检查装置的气密性④将高锰酸钾装入试管里,试管口放一小团棉花,用带导管的胶塞塞紧,并将它固定在铁架台上⑤用排水法收集氧气⑥将导管从水中取出。
江西省九江市琴海中学高二数学理联考试卷含解析

江西省九江市琴海中学高二数学理联考试卷含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知AB为半圆的直径,P为半圆上一点,以A、B为焦点且过点P做椭圆,当点P在半圆上移动时,椭圆的离心率有()A.最大值B.最小值C.最大值D.最小值参考答案:D略2. 过抛物线y2=4x的焦点作直线交抛物线于点A(x1,y1),B(x2,y2)若|AB|=7,则AB 的中点M到抛物线准线的距离为()A.B.C.2 D.参考答案:A【考点】抛物线的简单性质.【分析】抛物线的焦点F(1,0),准线方程为 x=﹣1,由抛物线的定义可得|AB|=7=(x1+1)+(x2+1),求得 x1+x2的值,由此求得点M到抛物线准线的距离+1的值.【解答】解:由抛物线的方程y2=4x可得p=2,故它的焦点F(1,0),准线方程为 x=﹣1.由抛物线的定义可得|AB|=7=|AF|+|BF|=(x1+1)+(x2+1),∴x1+x2=5.由于AB的中点M(,)到准线的距离为+1=,故选A.【点评】本题主要考查抛物线的定义、标准方程,以及简单性质的应用,属于中档题.3. 双曲线的右焦点为,焦距为,左顶点为,虚轴的上端点为,若,则该双曲线的离心率为()、、、、参考答案:D略4. 设随机变量ξ~B(n,p),且E(ξ)=1.6,D(ξ)=1.28,则()A.n=8,p=0.2 B.n=4,p=0.4 C.n=5,p=0.32 D.n=7,p=0.45参考答案:A【考点】CH:离散型随机变量的期望与方差.【分析】根据随机变量符合二项分布,根据二项分布的期望和方差公式得到关于n,p的方程组,注意两个方程之间的关系,把一个代入另一个,以整体思想来解决,求出P的值,再求出n的值,得到结果.【解答】解:∵随机变量ξ~B(n,p),E(ξ)=1.6,D(ξ)=1.28,∴np=1.6,①np(1﹣p)=1.28 ②把①代入②得1﹣p==0.8,∴p=0.2∵np=1.6∴n=8,故选A.5. 程序:M=1 M=M+1 M=M+2 PRINT M END M的最后输出值为()A. 1 B.2 C. 3D.4参考答案:D6. 函数y=f(x)图象上不同两点A(x1,y1),B(x2,y2)处的切线的斜率分别是k A,k B,规定φ(A,B)=叫做曲线y=f(x)在点A与点B之间的“弯曲度”,给出以下命题:①函数y=x3﹣x2+1图象上两点A与B的横坐标分别为1,2,则φ(A,B)>;②存在这样的函数,图象上任意两点之间的“弯曲度”为常数;③设点A、B是抛物线y=x2+1上不同的两点,则φ(A,B)≤2;④设曲线y=e x上不同两点A(x1,y1),B(x2,y2),且x1﹣x2=1,若t?φ(A,B)<1恒成立,则实数t 的取值范围是(﹣∞,1).以上正确命题的序号为()A.①②B.②③C.③④D.②③④参考答案:B【考点】函数的图象.【分析】由新定义,利用导数逐一求出函数y=x3﹣x2+1、y=x2+1在点A与点B之间的“弯曲度”判断(1)、(3);举例说明(2)正确;求出曲线y=e x上不同两点A(x1,y1),B(x2,y2)之间的“弯曲度”,然后结合t?φ(A,B)<1得不等式,举反例说明(4)错误.【解答】解析:①错:解:对于(1),由y=x3﹣x2+1,得y′=3x2﹣2x,则k A=1,k B=8,则|k A﹣k B|=7y1=1,y2=5,则|AB|=,φ(A,B)=,①错误;②对:如y=1时成立;③对:φ(A,B)===;④错:对于(4),由y=e x,得y′=e x,φ(A,B)==.t?φ(A,B)<1恒成立,即恒成立,t=1时该式成立,∴(4)错误.故答案为:②③7. l1,l2,l3是空间三条不同的直线,则下列命题正确的是()A.l1⊥l2,l2⊥l3?l1∥l3B.l1⊥l2,l2∥l3?l1⊥l3C.l1∥l2∥l3?l1,l2,l3共面D.l1,l2,l3共点?l1,l2,l3共面参考答案:B【考点】平面的基本性质及推论;空间中直线与直线之间的位置关系.【分析】通过两条直线垂直的充要条件两条线所成的角为90°;判断出B对;通过举常见的图形中的边、面的关系说明命题错误.【解答】解:对于A,通过常见的图形正方体,从同一个顶点出发的三条棱两两垂直,A 错;对于B,∵l1⊥l2,∴l1,l2所成的角是90°,又∵l2∥l3∴l1,l3所成的角是90°∴l1⊥l3,B对;对于C,例如三棱柱中的三侧棱平行,但不共面,故C错;对于D,例如三棱锥的三侧棱共点,但不共面,故D错.故选B.【点评】本题考查两直线垂直的定义、考查判断线面的位置关系时常借助常见图形中的边面的位置关系得到启示.8. 圆上的点到直线的距离最大值是( )A.2 B.1+ C. D. + 1参考答案:D9. 在△ABC中,已知AB=3,A=120°,且△ABC的面积为,则BC=()A.3 B.5 C.7 D.15参考答案:C10. 下列程序执行后输出的结果是()A.–1 B. 0 C. 1D. 2参考答案:B二、填空题:本大题共7小题,每小题4分,共28分11. 某工厂去年产值为,从今年开始计划在今后5年内每年比上一年产值增加,这5年该工厂的总产值是参考答案:12. 函数的极大值为.参考答案:e,在递增,在递减,在有极大值.13. 有一个简单的随机样本:10,12,9,14,13则样本平均数= ,样本方差s2= .参考答案:11.6,3.44.【考点】极差、方差与标准差;众数、中位数、平均数.【专题】概率与统计.【分析】根据平均数和方差的定义分别进行计算即可.【解答】解:根据平均数的公式得==.样本方差s2==3.44.故答案为:11.6,3.44.【点评】本题主要考查平均数和方差的计算,根据平均数和方差的公式是解决本题的关键.14. 已知函数在区间上的极大值与极小值分别为,则参考答案:3215. 已知为双曲线上一点,,为该双曲线的左、右焦点,若则的面积为▲.参考答案:略16. 直线mx+ny﹣3=0与圆x2+y2=3没有公共点,若以(m,n)为点P的坐标,则过点P的一条直线与椭圆的公共点有个.参考答案:2【考点】直线与圆锥曲线的关系;直线与圆的位置关系.【分析】根据直线mx+ny﹣3=0与圆x2+y2=3没有公共点即为将方程代入圆中消去x得到方程无解,利用根的判别式小于零求出m与n的关系式,得到m与n的绝对值的范围,在根据椭圆的长半轴长和短半轴长,比较可得公共点的个数.【解答】解:将直线mx+ny﹣3=0变形代入圆方程x2+y2=3,消去x,得(m2+n2)y2﹣6ny+9﹣3m2=0.令△<0得,m2+n2<3.又m、n不同时为零,∴0<m2+n2<3.由0<m2+n2<3,可知|n|<,|m|<,再由椭圆方程a=,b=可知P(m,n)在椭圆内部,∴过点P的一条直线与椭圆的公共点有2个.故答案为2.17. 同时掷四枚均匀的硬币,有三枚“正面向上”的概率是____________.参考答案:三、解答题:本大题共5小题,共72分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
得到正确结论是( )
A.有99%以上的把握认为“学生性别与中学生追星无关”
B.有99%以上的把握认为“学生性别与中学生追星有关”
C.在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星无关”
江西省九江市2020-2021学年高二下学期期末数学(理)试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知复数 满足 ,则 ()
A. B. C. D.
2. ( )
A. B. C. D.
3.某校团委对“学生性别与中学生追星是否有关”作了一次调查,利用 列联表,由计算得 ,参照下表:
A.甲B.乙C.丙D.丁
8.已知 ,则 的值( )
A.都大于1B.都小于1
C.至多有一个不小于1D.至少有一个不小于1
9.学校新入职的5名教师要参加由市教育局组织的暑期3期上岗培训,每人只参加其中1期培训,每期至多派2人,由于时间上的冲突,甲教师不能参加第一期培训,则学校不同的选派方法有( )
A. 种B. 种C. 种D. 种
D.在犯错误的概率不超过0.5%的前提下,认为“学生性别与中学生追星有关”
4. 展开式中常数项为( )
A. B. C. D.
5.函数 有( )
A.最大值为1B.最小值为1
C.最大值为 D.最小值为
6.设随机变量 ,若 ,则 ( )
A. B. C. D.
7.甲乙丙丁四人参加数学竞赛,其中只有一位获奖.有人走访了四人,甲说:“乙、丁都未获奖.”乙说:“是甲或丙获奖.”丙说:“是甲获奖.”丁说:“是乙获奖.”四人所说话中只有两位是真话,则获奖的人是( )
10.2021年,河北等8省公布了高考改革综合方案将采取“3+1+2”模式,即语文、数学、英语必考,然后考生先在物理、历史中选择1门,再在思想政治、地理、化学、生物中选择2门.一名同学随机选择3门功课,则该同学选到物理、地理两门功课的概率为( )
A. B. C. D.
11.设 , , ,则 大小关系是( )
参考数据: , , , .
参考公式: , , .
24.已知函数 ( ).
(Ⅰ)当 时,求曲线 在 处的切线方程;
(Ⅱ)若对任意 , 恒成立,求实数 的取值范围.
25.已知函数 ( ).
(Ⅰ)若 在 处的切线过点 ,求 的值;
(Ⅱ)若 恰有两个极值点 , ( ).
(ⅰ)求 的取值范围;
(ⅱ)求证: .
【分析】
根据定积分的运算公式,可以求接求解.
【详解】
解: ,故选C.
【点睛】
本题考查了定积分的计算,熟练掌握常见被积函数的原函数是解题的关键.
3.B
【分析】
通过 与表中的数据6.635的比较,可以得出正确的选项.
【详解】
解: ,可得有99%以上的把握认为“学生性别与中学生追星有关”,故选B.
【点睛】
本题考查了独立性检验的应用问题,属于基础题.
4.D
【解析】
【分析】
求出 展开式的通项公式,然后进行化简,最后让 的指数为零,最后求出常数项.
A. B.
C. D.
12.设 , , ,则 大小关系是( )
A. B.
C. D.
13.已知函数 的导函数为 ,满足 , 且 ,则不等式 的解集为( )
A. B. C. D.
14.已知函数 ( )在 上的最大值为3,则 ( )
A. B. C. D.
二、填空题
15.若复数 ( )为纯虚数,则 ____.
16.已知某公司生产的一种产品的质量 (单位:千克)服从正态分布 .现从该产品的生产线上随机抽取 件产品,则其中质量在区间 内的产品估计有________件.
附:若 ,则 , .
17.如图,矩形 中曲线的方程分别为 , ,在矩形内随机取一点,则此点取自阴影部分的概率为____.
18.在 中,角 所对的边分别为 ,已知 ,则 ____.
(Ⅰ)求直线 的参数方程和极坐标方程;
(Ⅱ)设直线 与曲线 相交于 两点,求 的值.
28.设函数 .
(Ⅰ)求不等式 的解集;
(Ⅱ)求证: ,并求等号成立的条件.
29.设函数 ( ).
(Ⅰ)当 时,求不等式 的解集;
(Ⅱ)求证: ,并求等号成立的条件.
参考答案
1.C
【详解】
, ,故选C.
2.C
【解析】
周一
周二
周三
周四
周五
周六
周日
13
16
26
22
25
29
ห้องสมุดไป่ตู้30
7
11
15
22
24
27
34
(Ⅰ)作出散点图,判断 与 哪一个适合作为每天净利润的回归方程类型?并求出回归方程( , , , 精确到 );
(Ⅱ)超市为了刺激周一消费,拟在周一开展使用支付宝和微信支付随机抽奖活动,总奖金7万元.根据市场调查,抽奖活动能使使用支付宝和微信支付消费人数增加6千人,7千人,8千人,9千人的概率依次为 , , , .试决策超市是否有必要开展抽奖活动?
26.在平面直角坐标系 中,直线 的普通方程为 ,曲线 的参数方程为 ( 为参数),以 为极点, 轴的正半轴为极轴建立极坐标系.
(Ⅰ)求直线 的参数方程和极坐标方程;
(Ⅱ)设直线 与曲线 相交于 两点,求 的值.
27.在平面直角坐标系 中,直线 的普通方程为 ,曲线 的参数方程为 ( 为参数),以 为极点, 轴的正半轴为极轴建立极坐标系.
19.在 中,角 所对的边分别为 ,已知 ,且 的面积为 ,则 的周长为______.
三、解答题
20.在某项体能测试中,规定每名运动员必需参加且最多两次,一旦第一次测试通过则不再参加第二次测试,否则将参加第二次测试.已知甲每次通过的概率为 ,乙每次通过的概率为 ,且甲乙每次是否通过相互独立.
(Ⅰ)求甲乙至少有一人通过体能测试的概率;
(Ⅱ)记 为甲乙两人参加体能测试的次数和,求 的分布列和期望.
21. 中,三内角 所对的边分别为 ,已知 成等差数列.
(Ⅰ)求证: ;
(Ⅱ)求角 的取值范围.
22.已知数列 满足 , .
(Ⅰ)求 的值,猜想数列 的通项公式并用数学归纳法证明;
(Ⅱ)令 ,求数列 的前 项和 .
23.使用支付宝和微信支付已经成为广大消费者最主要的消费支付方式,某超市通过统计发现一周内超市每天的净利润 (万元)与每天使用支付宝和微信支付的人数 (千人)具有相关关系,并得到最近一周 的7组数据如下表,并依此作为决策依据.
