数模作业 (1)
数学建模_大作业1

数学建模大作业姓名1:赵成宏学号:201003728姓名2:吴怡功学号:201003738姓名3:蒲宁宁学号:201004133专业:车辆工程2013年5 月28 日直升机运输公司问题一家运输公司正考虑用直升机从某城市的一摩天大楼运送人员。
你被聘为顾问,现在要确定需要多少架飞机。
按照建模过程仔细分析,建模。
为了简化问题,可以考虑升机运输公司问题。
基本假设如下:假设运载的直升机为统一型号; 假设每架飞机每次载人数相同;假设飞机运送的人员时互不影响;假定人员上了飞机就安全,因此最后一次运输时,只考虑上飞机所花时间。
1、按照数学建模的全过程对本题建立模型,并选用合理的数据进行计算(模型求解); 2、本问题是否可以抽象为优化模型;除了考虑建立优化模型之外,是否可以采用更简单的方法建立模型。
注意考虑假设条件。
甚至基于不同的假设建立多个模型。
归纳起来,有以下假设:(H1)所有飞机的飞行高度度均为10 000m ,飞行速度均为800km/h 。
(H2)飞机飞行方向角调整幅度不超过6,调整可以立即实现;(H3)飞机不碰撞的标准是任意两架飞机之间的距离大于8km; (H4)刚到达边界的飞机与其他飞机的距离均大于60km; (H5)最多考虑N 架飞机;(H6)不必考虑飞机离开本区域以后的状况. 为方便以后的讨论,我们引进如下记号: D 为飞行管理区域的边长;S 为飞行管理区域取直角坐标系使其为[0,D ]×[0,D]; v 为飞机飞行速度,v=800km/h;(x 0i ,y i)第i 架飞机的初始位置;()(),(t t y x ii )为第i 架飞机在t 时刻的位置;θ0i为第i 架飞机的原飞行方向角,即飞行方向与x 轴夹角,0≤θ≤2π;θi ∆第i 架飞机的方向角调整,-6π≤i θ∆≤6π; i θ﹦i 0i θθ∆+为第i 架飞机调整后的飞行方向角;一、两架飞机不碰撞的条件1、两架飞机距离大于8km 的条件设第i 架和第j 架飞机的初始位置为(0i 0i y x ,),(0j 0j y x ,),飞行方向角分别为错误!未找到引用源。
数学建模结课作业

一. 某旅游景点从山脚到山顶有一缆车索道,全长约1471m,高度 差为380m 。
采用循环单线修建,从下站到上站行经8个铁塔,将缆绳分为九段,各段的水平距离用i d 表示,高差用i h 表示,其数据见下表:每一段缆绳垂下来的最低点不低于两端铁塔最低塔顶悬挂绳处1m 。
要求:(1)折线法;(2)抛物线法,估计整个索道工程所用的缆绳总长度。
解:(一)折线法思路:考虑到实际中工程架线不能过紧,但又为了节省原料,我们采取求出最大折线和最小折线,对两者求取平均值,以得到对缆线总长度的估测。
由于八个铁塔分九段,因此此题分两部分考虑:(1) 第一段:直接求出发点到第一个铁塔的距离,即21211h d l +=(2) 第二到九段:建立坐标系,运用距离公式求取l 的长度。
设A (x -,1),B(i d x -,1i h +)得:l =用此公式求最大最小值。
matlab 求解第一段syms h1 d1h1=50d1=220l1=sqrt(d1.^2+h1.^2)第二段求最小值clearl='sqrt((-x)^2+1)+sqrt((200-x)^2+(45+1)^2)' ezplot(l,[0,200]);[xmin,lmin]=fminbnd(l,0,200)得图形可得当x=4.2553时,取得最小值205.45由图形可得当x=200时取得最大值,即clearl='sqrt((-x)^2+1)+sqrt((200-x)^2+(45+1)^2)' ezplot(l,[0,200]);[xmin,lmin]=fminbnd(l,0,200)x=200;lmax=eval(l);l=(lmin+lmax)/2;得lmax=246.0025l=225.7254第三段到第九段算法与第二段相同,所以结果为第一段:l1 = 225.6103第二到九段分别为: 225.7254 ,163.5839 ,142.7476,120.6438,142.7476,163.5839,225.7254,248.5321总长为:1658.9m抛物线法思路:参照示意图,因为将绳的形状看做抛物线,为了方便研究,以抛物线的最低点为原点建立抛物线2y ax =,则每段绳的长度为l =,最后相加求总长。
数模习题

注意事项1.每名同学完成3个题目(每部分选择一个);2.只需要电子版,以自己的“学号+名字”命名;3.第16周周五上午上交,发送至************.cn;(逾期课程无成绩,后果自负)。
4.本课程内容讲解已经结束,第16周周五是课程考核时间(无需到教室).(初等模型)1.以下是一个数学游戏:(1)甲先说一个不超过6的正整数,乙往上加一个不超过6的正整数,甲再往上加一个正整数,...,如此继续下去。
规定谁先加到50谁就获胜,问甲、乙各应怎样做?(2)如将6改为n,将50改为N,问题又当如何回答?2.甲乙两人约定中午12:00至1:00之间在市中心某地见面,但两人讲好到达后只等待对方10分钟,求这两人能相遇的概率。
3.某人由A处到位于某河流同侧的B处去,途中需要去河边取些水,问此人应如何走才能使走的总路程最少?4.敏感问题的调查5.地面是球面的一部分,(直径约为12.72×10公里),显然,如果高层建筑的墙是完全垂直于地面的则它们之间必不会平行。
设一建筑物高为400米,地面面积为2500平方米,问顶面面积比地面面积大多少?6.建一模型说明当你在雨中行走又想少淋雨时,应当如下做:(1)若你行走的方向是顺风且雨的夹角至少为,你应以雨速水平分量的速度行走,以便使雨相对于你是垂直下落的(2)在其他情况下,你都应以最快的速度行走。
7.消防队员救火时不应离失火的房屋太近,以免发生危险。
请建模分析并求出消防队员既安全又能发挥效应的最佳位置。
8.已知在气体中音速V与气压P、气体的密度ρ有关,试求它们之间的关系。
9.风车的功率P与风速v、叶面的顶风面积S及空气的密度ρ有关,试求它们之间的关系。
(微分方程模型)1.一个半球状雪堆,其体积融化的速率与半球面面积S成正比,比例系数k > 0。
设融化中雪堆始终保持半球状,初始半径为R且3小时中融化了总体积的7/8,问雪堆全部融化还需要多长时间?2.从致冰厂购买了一块立方体的冰块,在运输途中发现,第一小时大约融化了1/4(1)求冰块全部融化要多长时间(设气温不变)(2)如运输时间需要2.5小时,问:运输途中冰块大约会融化掉多少?3.一展开角为α的圆锥形漏斗内盛着高度为H的水,设漏斗底部的孔足够大(表面张力不计),试求漏斗中的水流光需要多少时间?4.容器甲的温度为60度,将其内的温度计移入容器乙内,设十分钟后温度计读数为70度,又过十分钟后温度计读数为76度,试求容器乙内的温度。
数学建模课作业范例

数学建模课作业范例范例题目:一家具公司签定了一项合同,合同要求在第一个月月底前,交付80把椅子,在第二个月月底前,交付120把椅子。
若每月生产x把椅子时,成本为50x+0.2x2(元);如第一个月生产的数量超过订货数,每把椅子库存一个月的费用是8元。
公司每月最多能生产200把椅子。
求完成以上合同的最佳生产安排。
家具公司最佳生产安排问题一问题的提出一家具公司签定了一项合同,合同要求在第一个月月底前,交付80把椅子,在第二个月月底前,交付120把椅子。
若每月生产x把椅子时,成本为50x+0.2x2(元);如第一个月生产的数量超过订货数,每把椅子库存一个月的费用是8元。
公司每月最多能生产200把椅子求成以上合同的最佳生产安排。
二假设与变量说明1.)模型假设1.椅子的成本和库存费没有变化2.该公司签定的合同并未发生变化3.该公司生产的椅子质量合格4.除了成本费和库存费并未产生其他额外的费用2)变量说明x1: 公司第一个月生产的椅子数x2: 公司第二个月生产的椅子数y1: 公司第一个月的成本费y2: 公司第二个月的成本费z: 库存费Y: 总的费用三模型分析和建立1. 模型分析:该家具公司需要每月制定一个最佳的椅子生产数(x1、x2),使该公司完成合同所需成本最小,而获得最大利润。
本模型的问题焦点就是确定最小成本,即使Y=y1+y2+z最小的数学问题。
2. 模型建立第一个月的生产成本:y1=50x1+0.2x12第二个月的生产成本:y2=50x2+0.2x22所需库存费: z=(x1-80)*8总成本: Y=y1+y2+z=(50x1+0.2x12)+(50x2+0.2x22)+(x1-80)*8其中:x1 +x2=200 80≤x1≤200综上所述,可建立如下数学模型:Min Y=(50x1+0.2x12)+(50x2+0.2x22)+(x1-80)*8 s.t 80≤x1≤200x 1 + x2=200四.求解用LINGO对模型直接求解,输入格式为:model:min=(50*x1+0.2*x1^2)+( 50*x2+0.2*x2^2)+8*(x1-80);x1>=80;x1<=200;x1+x2=200;end运行后结果为:Optimal solution found at step: 4Objective value: 14120.00Variable Value Reduced CostX1 90.00000 0.0000000X2 110.0000 0.0000000Row Slack or Surplus Dual Price1 14120.00 1.0000002 9.999998 0.2158310E-053 110.0000 0.00000004 0.0000000 -94.00000五.结果与分析由计算可知,当x1=90,x2=110时成本费最底,所以生产的最佳安排是第一月生产90把椅子,第二月生产110把椅子.。
数学建模线性规划上机题

例1 (任务安排)某厂计划在下月内生产4种产品B1,B2,B3,B4。
每种产品都可用三条流水作业线A1,A2,A3中旳任何一条加工出来.每条流水线(Ai)加工每件产品(Bj)所需旳工时数(i=1,2,3,j=1,2,3,4)、每条流水线在下月内可供运用旳工时数及多种产品旳需求均列表于4.1中.又A1,A2,A3三条流水线旳生产成本分别为每小时7,8,9元。
现应怎样安排各条流水线下月旳生产任务,才能使总旳生产成本至少?例2 (外购协议)某企业下月需要B1,B2,B3,B4四种型号旳钢板分别为1000,1200,1500,2023吨。
它准备向生产这些钢板旳A1,A2,A3三家工厂订货。
该企业掌握了这三家工厂生产多种钢板旳效率(吨/小时)及下月旳生产能力(小时),如表4.2所示。
而它们销售多种型号钢板旳价格如表4.3所示。
该企业当然但愿能以至少旳代价得到自己所需要旳多种钢板,那么,它应当向各钢厂订购每种钢板各多少吨?假设该企业订购时采用如下原则,要么不订购,要么至少订购100吨以上。
该怎样处理这个问题。
若至少订购50吨,怎样处理?例3 (广告方式旳选择) 中华家电企业近来生产了一种新型洗衣机.为了推销这种新产品,该企业销售部决定运用多种广告宣传形式来使顾客理解新洗衣机旳长处。
通过调查研究,销售部经理提出了五种可供选择旳宣传方式.销售部门并搜集了许多数据。
如每项广告旳费用,每种宣传方式在一种月内可运用旳最高次数以及每种广告宣传方式每进行一次所期望得到旳效果等.这种期望效果以一种特定旳相对价值来度量、是根据长期旳经验判断出来旳.上述有关数据见表4.8中华家电企业拨了20230元给销售部作为第一种月旳广告预算费、同步提出,月内至少得有8个电视商业节目,15条报纸广告,且整个电视广告费不得超过12023元,电台广播至少隔日有一次,现问该企业销售部应当采用怎样旳广告宣传计划,才能获得最佳旳效果?例4 长城家电企业近来研制了一种新型电视机.准备在三种类型旳商场即一家航空商场、一家铁路商场和一家水上商场进行销售.由于三家商场旳类型不同样,它们旳批发价和推销费都不同样。
数模训练:习题解答1

n! , i 1,2,...n 1 (n i)!i!
是否全为偶数
n! n (n 1) ...(n i 1) C (n i)!i! i!
i n
任意整数n可表为: n为偶数:n=2kq (q为奇数) n为奇数:n=2kq -1(q为奇数,k>1整数)
棋子颜色的变化
任意拿出黑白两种颜色的棋子共n个, 排成如图所示的一个圆圈.然后在两颗颜色相 同的棋子中间放一颗黑色棋子,在两颗颜色不 同的棋子中间放一颗白色棋子,放完后撤掉原 来所放的棋子.再重复以上的过程,这样放下一 圈后就拿走前次的一圈棋子,问这样重复进行 下去各棋 子的颜色会怎样变化呢?
n=8有结论:
k
取i= 2k-1,则
(2k q 1) (2k q 2) (2k q 3) (2k q 4) ...[2k q 2k 1 ] 2 C2k q 1 2k 1 (2k 1 1) ..4 3 2 1
分子与分母的偶因子数相同,上式为奇数。
因此得结论: 1 n=2k,k=1,2,… 至多经过n次变换,棋子的颜色全变黑。 2. n2k,k=1,2,… 经过n次变换,棋子的颜色不一定全变黑。 但至少两种情况,棋子的颜色全变黑。 3. n2k,k=1,2,… 因为n个棋子的排列种数是有限个,故棋子的颜 色变化将形成循环。
某时刻t的坐标为(x,y),满足关系:
vt x2 (u) y 2 (u)du 5 16sin 2 (u) cos 2 (u)du
0 0
此积分求不出。
解: 建立平面直角坐标系xoy
(x1,y1)
(x,y) 取时间间隔为Δt, 在Δt间隔中, 人、狗都沿直线行进, 设时刻t人、狗的位置分别为:(x1,y1),(x,y), 计算时刻t的 下一时刻 t+Δt的位置(坐标). 人的行进方向: x 20sin( ) 4( y 20) 由 y 5cos( ) ( x 10) / 4 得慢跑者在任一点(x,y)的切线方向的向量: p=(-4(y-20),(x-10)/4)
数模第一次作业-(1)

. .2016年数学建模论文第套论文题目:专业、:专业、:专业、:提交日期: 2016.6.27题目:人口增长模型的确定摘要对美国人口数据的变化进行拟合,并进行未来人口预测,在第一个模型中,考虑到人口连续变化的规律,用微分方程的方法解出其数量随时间变化的方程,先求对数用matlab里线性拟合求出参数,即人口净增长率r=0.0214,对该模型与实际数据进行对比,并计算了从1980年后每隔10年的人口数据,与实际对比,有很大出入。
因此又改进出更为符合实际的阻滞增长模型,应用微分方程里的分离变量法和积分法解出其数量随时间变化的方程,求出参数人口增长率r=0.0268和人口所能容纳最大值m x=285.89,与实际数据对比,拟合得很好,并预测出1980年后每隔10年的人口数据,与实际对比,比较符合。
为了便于比较两个模型与实际数据的描述情况作对比,又做出了两个模型与实际数据的对比图,并计算了误差。
关键词:人口预测微分方程马尔萨斯人口增长模型阻滞增长模型一、问题重述1790-1980年间美国每隔10年的人口记录如下表所示:表1 人口记录表试用以上数据建立马尔萨斯(Malthus)人口指数增长模型,并对接下来的每隔十年预测五次人口数量,并查阅实际数据进行比对分析。
如果数据不相符,再对以上模型进行改进,寻找更为合适的模型进行预测。
二、问题分析由于题目已经说明首先用马尔萨斯人口增长模型来刻划,列出人口增长指数增长方程并求解,并进行未来50年人口数据预测,但发现与实际数据有较大出入。
考虑到实际的人口增长率是受实际情况制约的,因此,使人口增长率为一变化的线性递减函数,列出人口增长微分方程,求出其方程解,并预测未来五十年人口实际数据。
三、问题假设1.假设所给的数据真实可靠;2.各个年龄段的性别比例大致保持不变;3.人口变化不受外界大的因素的影响;4.马尔萨斯人口模型(1)单位时间的人口增长率r 为常数;(2)将N t 视为t 的连续可微函数。
数模案例1叠砖问题课件-精选文档

污物
用水量 次数
剩余水量
分布
……
众多因素,哪些有用哪些没用?或者哪些 是常量,哪些是要研究的量呢? 让我们从一个简单问题中找
思路~
2019/3/8
18
脏衣服在用洗衣粉充分漂洗之后,一般要把衣服 拧干,尽可能的拧掉污水,再进行下一轮漂洗。假设 每漂洗一次拧干后衣服中还留有含污物的水1千克。现 有10千克清水,按下面三种方法漂洗: 1.直接把衣服放入10千克水中,一次漂洗。
2019/3/8 6
方案2:每块砖伸出长短不一
此处G3很关键
G2
G3 G4
G1
1 a1 2
M3 M4
1 a2 4 1 a3 6
2019/3/8
7
Gn
Gn-1
n
n+1
Mn
1 2
Bn
1 an 2n
2019/3/8
8
• 用n+1块砖建塔,总的伸出量为(顶砖和底砖的重 心的水平距离):
m0 w m0 m1 = w a1 1 a1 w
2019/3/8
23
同理:
m0 w m0 m1 = w a1 1 a1 w
m mw 0 1 m = 2 a a w a 1 2 ( 1 )( 1 2) w w
用数学归纳法即可证明:
m 0 m n a a a 1 2 ( 1 ) ( 1 ) ( 1 n) w w w
2019/3/8
n
i1
ai A .
21
继续简化过程
首先考虑n次漂洗之后,剩余污渍mn 与每次用水量 ai 的关系.
进一步,再考察n与mn的关系.
2019/3/8
2020年数学建模作业题

数学模型课程期末大作业题要求:1)选题方式:共49题,每个同学做一题,你要做的题目编号是你的学号mod49所得的值+1。
(例如:你的学号为189084157,则你要做的题为mod(189084157,49)+1=18)。
2)该类题目基本为优划问题,要求提交一篇完整格式的建模论文,文字使用小四号宋体,公式用word的公式编辑器编写,正文中不得出现程序以及程序冗长的输出结果,程序以附录形式附在论文的后面,若为规划求解必须用lingo 编程,其它计算可用Matlab或Mathmatica编写,不得以其它语言编程,否则按不及格论处。
3)论文以电子文档提交,同时要交一份文章和程序电子文档,由班长统一收上来,我要验证程序。
1、生产安排问题某厂拥有4台磨床,2台立式钻床,3台卧式钻床,一台镗床和一台刨床,用以生产7种产品,记作p1至p7。
工厂收益规定作产品售价减去原材料费用之余。
每种产品单件的收益及所需各机床的加工工时(以小时计)列于下表(表1):表到6月底每种产品有存货50件。
工厂每周工作6天,每天2班,每班8小时。
不需要考虑排队等待加工的问题。
在工厂计划问题中,各台机床的停工维修不是规定了月份,而是选择最合适的月份维修。
除了磨床外,每月机床在这6个月中的一个月中必须停工维修;6个月中4台磨床只有2台需要维修。
扩展工厂计划模型,以使可作上述灵活安排维修时间的决策。
停工时间的这种灵活性价值若何?注意,可假设每月仅有24个工作日。
2、电梯问题某办公大楼有十一层高,办公室都安排在7,8,9,10,11层上.假设办公人员都乘电梯上楼,每层有60人办公.现有三台电梯A、B、C可利用,每层楼之间电梯的运行时间是3秒,最底层(一层)停留时间是20秒,其他各层若停留,则停留时间为10秒.每台电梯的最大的容量是10人,在上班前电梯只在7,8,9,10,11层停靠.为简单起见,假设早晨8∶00以前办公人员已陆续到达一层,能保证每部电梯在底层的等待时间内(20秒)能达到电梯的最大容量,电梯在各层的相应的停留时间内办公人员能完成出入电梯.当无人使用电梯时,电梯应在底层待命.请问:把这些人都送到相应的办公楼层,要用多少时间?怎样调度电梯能使得办公人员到达相应楼层所需总的时间尽可能的少?请给出一种具体实用的电梯运行方案.3、食品加工问题一项食品加工工业,为将几种粗油精炼,然后加以混合成为成品油。
数学建模大作业

兰州交通大学数学建模大作业学院:机电工程学院班级:车辆093学号:200903812 姓名:刘键学号:200903813 姓名:杨海斌学号:200903814 姓名:彭福泰学号:200903815 姓名:程二永学号:200903816 姓名:屈辉高速公路问题1 实验案例 (2)1.1 高速公路问题(简化) (2)1.1.1 问题分析 (3)1.1.2 变量说明 (3)1.1.3 模型假设 (3)1.1.4 模型建立 (3)1.1.5 模型求解 (4)1.1.6 求解模型的程序 (4)1实验案例1.1 高速公路问题(简化)A城和B城之间准备建一条高速公路,B城位于A城正南20公里和正东30公里交汇处,它们之间有东西走向连绵起伏的山脉。
公路造价与地形特点有关,图4.2.4给出了整个地区的大致地貌情况,显示可分为三条沿东西方向的地形带。
你的任务是建立一个数学模型,在给定三种地形上每公里的建造费用的情况下,确定最便宜的路线。
图中直线AB显然是路径最短的,但不一定最便宜。
而路径ARSB过山地的路段最短,但是否是最好的路径呢?AB图8.2 高速公路修建地段1.1.1 问题分析在建设高速公路时,总是希望建造费用最小。
如果要建造的起点、终点在同一地貌中,那么最佳路线则是两点间连接的线段,这样费用则最省。
因此本问题是一个典型的最优化问题,以建造费用最小为目标,需要做出的决策则是确定在各个地貌交界处的汇合点。
1.1.2 变量说明i x :在第i 个汇合点上的横坐标(以左下角为直角坐标原点),i =1,2,…,4;x 5=30(指目的地B 点的横坐标)x=[x 1,x 2,x 3,x 4]Tl i :第i 段南北方向的长度(i =1,2, (5)S i :在第i 段上地所建公路的长度(i =1,2, (5)由问题分析可知,()()()()25425524324423223322122221211x x l S x x l S x x l S x x l S x l S -+=-+=-+=-+=+=C 1:平原每公里的造价(单位:万元/公里)C 2:高地每公里的造价(单位:万元/公里) C 3:高山每公里的造价(单位:万元/公里)1.1.3 模型假设1、 假设在相同地貌中修建高速公路,建造费用与公路长度成正比;2、 假设在相同地貌中修建高速公路在一条直线上。
数学建模大作业习题答案

数学建模大作业习题答案数学建模大作业习题答案作为一门应用数学课程,数学建模在现代科学研究和工程技术中具有重要的地位和作用。
通过数学建模,我们可以将实际问题转化为数学模型,从而利用数学方法进行分析和求解。
在数学建模的学习过程中,我们经常会遇到一些习题,下面我将为大家提供一些数学建模大作业题目的答案,希望能对大家的学习有所帮助。
1. 题目:某城市的交通拥堵问题解答:针对这个问题,我们可以采用图论的方法进行建模和求解。
首先,我们将城市的道路网络抽象为一个图,图的节点表示交叉口,边表示道路。
然后,我们可以给每条边赋予一个权重,表示道路的通行能力。
接着,我们可以使用最短路径算法,比如Dijkstra算法,来计算从一个交叉口到另一个交叉口的最短路径,从而找到最优的交通路线。
此外,我们还可以使用最小生成树算法,比如Prim算法,来构建一个最小的道路网络,以减少交通拥堵。
2. 题目:某工厂的生产调度问题解答:对于这个问题,我们可以采用线性规划的方法进行建模和求解。
首先,我们可以将工厂的生产任务抽象为一个线性规划模型,其中目标函数表示最大化生产效益,约束条件表示生产能力、物料供应和市场需求等方面的限制。
然后,我们可以使用线性规划求解器,比如Simplex算法或内点法,来求解这个线性规划模型,得到最优的生产调度方案。
此外,我们还可以引入一些启发式算法,比如遗传算法或模拟退火算法,来寻找更好的解决方案。
3. 题目:某股票的价格预测问题解答:对于这个问题,我们可以采用时间序列分析的方法进行建模和求解。
首先,我们可以将股票的价格序列抽象为一个时间序列模型,比如ARIMA模型。
然后,我们可以使用历史数据来拟合这个时间序列模型,并进行参数估计。
接着,我们可以利用这个时间序列模型来预测未来的股票价格。
此外,我们还可以引入其他的预测方法,比如神经网络或支持向量机,来提高预测的准确性。
通过以上的例子,我们可以看到,在数学建模的过程中,我们需要将实际问题抽象为数学模型,然后利用数学方法进行分析和求解。
数模1--games-7

社会为陈易捐助十几万善款,但陈易母亲并没有 马上进行手术。深圳网民八分斋、金官人开始进 行调查,指陈易存在欺骗成分,在善款的使用上 存在挥霍现象。
质疑一:陈易母亲是检察院的职工,她母亲的第一次 手术费用30万,医保机构支付15万,同事募捐两万多。 进行第二次手术,还需要30万,医保能再支付15万元。 质疑二:陈易的发型是需要几百元才能做出的新潮烫 发,穿的是500元一双的耐克牌运动鞋,戴的是500元 的隐形眼镜。核实:陈易这样解释:“今年8月30日, 一家美发屋搞宣传活动让我做模特,送的烫头。隐形 眼镜和鞋是我两三年前买的”质疑三:陈易公布的是 她的个人账户,所有捐款的使用和管理都只需陈易和 母亲自行决定。质疑四:并非真“卖身”,是为了募 集到更多钱的噱头。 “4总裁向女大学生抛职位 陈易坦言经历是财富” 陈母为女儿仓促上手术台,死于手术中,有人指责八 分斋逼死陈母。陈易捐出余款七万余元。
银行挤兑的原因和预防
储户甲乙存款各100万定期一年,银行用 200万投资一个好项目,一年后收益共300 万,付甲乙各120万,银行提前收回资金 被罚款,只退140万。
提前取款
储户乙 到期取款
储户甲乙提前取款,银行必须尽可能退 100万。
提前取款
(70,70)
(100,40)
储
户
甲
到期取款
(40,100)
3
1 2
8 8
4
2
3 9 1 10 10
4 3 0
6
3
Max 9 2 6
1 2 3 min
1 6,6 1,1 8,8 8,8
2
3,3
2,2
4,4
数学建模作业完整版

数学建模作业HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】《数学建模》作业学号姓名工作量 100 %专业所属学院指导教师二〇一七年六月数学建模作业第一部分:请在以下两题中任选一题完成(20 分)。
1、(马王堆一号墓入葬年代的测定建模问题)湖南省长沙市马王堆一号墓于 1972 年 8 月发掘出土,其时测得出土的木炭标本中碳-14 平均原子蜕变数为次/分钟,而新烧成的同种木材的木炭标本中碳-14(C-14)原子蜕变数为次/分钟. 又知碳-14 的半衰期为 5730 年,试推断该一号墓入葬的大致年代。
问题分析:放射性元素衰变的速度是不受环境影响的,它总是和该元素当前的量成正比,运用碳—14测定文物或化石年代的方法是基于下面的理由:(1)宇宙射线不断轰击大气层,使大气层中产生碳—14而同时碳—14又在不断衰变,从而大气层中碳—14含量处于动态平衡中,且其含量自古至今基本上是不变的;(2)碳—14被动植物体所吸收,所以活着的生物体由于不断的新陈代谢,体内的碳—14也处于动态平衡中,其含量在物体中所占的百分比自古至今都是一样的;(3)动植物的尸体由于停止了从环境中摄取碳—14,从而其体内碳—14含量将由于衰变的不断减少,碳定年代法就是根据碳—14的减少量来判断物体的大致死亡时间。
模型建立设t 时刻生物体中碳—14的含量为x (t ),放射性物质的半衰期(即放射性物质的原子数衰减一半所需的时间)为T ,生物体死亡时间为t0,则由放射性物质衰变规律得数学模型⎪⎩⎪⎨⎧=-=,)(,00x t x x dtdx λ ① 其中0>λ称为衰变系数,由放射性物质所决定,x 0为生物体在死亡时刻t 0时的碳—14含量。
模型求解对所得的一阶线性微分方程模型①采用同变量分离法求解,得 e x t t x t )(00)(--=λ??由于T t t =-0时,有 0021)()(x T t x t x =+=??代入上式,有 T e T 2ln ,212==-λ????? 所以得 ? T t t e x t x )(2ln 00)(--= ②这就是生物体中碳—14的含量随时间衰变的规律,由之易解得 )()(ln 2ln 00t x t x T t t =- ③ 将所得的数学模型的一般解应用于本例,此时以T=5730,37.380=x (新木炭标准中碳—14原子蜕变数),X(1972)=(出土的木炭标本中碳—14原子蜕变数) 代入到③式,得 ?209578.2937.38ln 2ln 57300≈=-t t 年 于是得??1232095197220950-=-=-≈t t 年结果表明,马王堆墓入葬年代大约在公元前123年左右的西汉中期,该结论与马王堆出土文物的考证结果相一致。
数学建模作业

数学建模作业在当今的学术和实际应用领域,数学建模已经成为一种强大的工具,帮助我们解决各种各样复杂的问题。
它不仅仅是数学知识的运用,更是一种跨学科的思维方式和解决问题的方法。
数学建模的过程就像是一场精心策划的冒险。
首先,我们需要明确问题的本质,这就好比在茫茫大海中找到我们要航行的方向。
例如,假设我们要解决一个关于城市交通拥堵的问题,我们就得清楚了解造成拥堵的各种因素,是道路规划不合理?还是车辆数量增长过快?或者是公共交通系统不够完善?明确问题之后,接下来就是做出合理的假设。
这一步有点像给我们的冒险之旅设定一些规则和限制。
在交通拥堵的例子中,我们可能会假设人们的出行模式相对稳定,道路的建设短期内不会有大的变动等等。
这些假设虽然简化了现实情况,但却能让我们的模型更具可操作性。
然后就是建立模型了。
这是整个数学建模过程的核心部分。
我们要运用所学的数学知识,比如函数、方程、不等式、概率论等等,将现实问题转化为数学语言。
对于交通拥堵问题,我们可以建立一个流量模型,通过计算不同时间段、不同路段的车流量来分析拥堵的情况。
模型建立好了,接下来就是求解。
这可能需要用到各种数学工具和软件。
有时候,求解过程会很复杂,需要我们有足够的耐心和细心。
当我们得到结果之后,还不能掉以轻心。
因为模型的结果需要进行检验和分析。
我们要将结果与实际情况进行对比,看看是否合理。
如果结果与实际相差甚远,那就得回过头去检查我们的模型,看看是哪里出了问题,是假设不合理?还是模型建立有误?数学建模的应用范围非常广泛。
在经济领域,我们可以通过建立数学模型来预测市场的走势,帮助企业做出决策。
比如,通过分析历史数据和市场趋势,建立一个关于某种商品价格波动的模型,从而预测未来的价格走势,为企业的生产和销售提供参考。
在工程领域,数学建模也发挥着重要作用。
例如,在建筑设计中,可以通过建立力学模型来计算建筑物的受力情况,确保其安全性和稳定性。
在电子工程中,可以建立电路模型来优化电路设计,提高电子产品的性能。
数学建模实习作业

碎纸片的拼接复原摘要图像碎片自动拼接复原是需要借助计算机把大量碎片重新拼接复原成初始图像的完整模型,这一研究在考古、刑侦犯罪、古生物学、医学图像分析、遥感图像处理以及壁画保存复原等方面具有广泛、实际的应用。
本文主要解决碎纸机破碎文档的自动拼接复原问题。
我们利用图像数字化技术,借助Matlab软件将图像转化为矩阵。
通过建立数学模型,运用矩阵论、自定义相似度方法、遗传算法等方法,对数据进行处理,实现对图像碎片自动拼接,从而将所给碎片拼接复原为完整图像。
我们首先把碎片图形进行二值化处理,根据所给纵切黑白碎片边缘的像素关系(相邻两张碎片,一张碎片矩阵右边的像素与另一张碎片左边的像素相同 ),我们采和自定义相似度算法,利用附件求出碎片间的相似度,然后根据所需要满足的条件即相似度最大原则,建立了纵切碎片拼接模型一及其算法,运用Matlab编程实现该模型,并得到碎片复原结果(见附录1)。
关键词:碎片拼接矩阵论图形二值化相似度模型一、问题重述1.1背景:破碎文件的拼接和复原对于司法物证复原、历史文献再现和军事情报获取等方面都有极其重要的作用。
于是碎纸片的拼接复原技术便成为图像处理与模式识别领域中的一个崭新典型的应用。
图像配准是图像拼接复原的基础,而且图像配准算法的计算量一般非常大,因此图像拼接复原技术的发展很大程度上取决于图像配准技术的创新。
本文将通过图像提取技术获取一组碎纸片的形状、颜色、文字等信息,然后利用计算机进行相应的处理从而实现对这些碎纸片的自动拼接复原。
1.2重述:该题研究的是如何对碎纸片进行拼接复原。
传统上,拼接复原工作需由人工完成,准确率较高,但是效率低。
随着计算机技术的发展,当碎纸片数量巨大的时候,人们试图开发碎纸片的自动拼接技术,以提高拼接复原的效率。
对于给定的来自同一页印刷文字文件的碎纸机破碎纸片(仅纵切),建立碎纸片拼接复原模型和算法,并针对附件给出的中文文件的碎片数据进行拼接复原。
如果复原过程需要人工干预,写出干预方式及干预的时间节点。
数学建模作业题
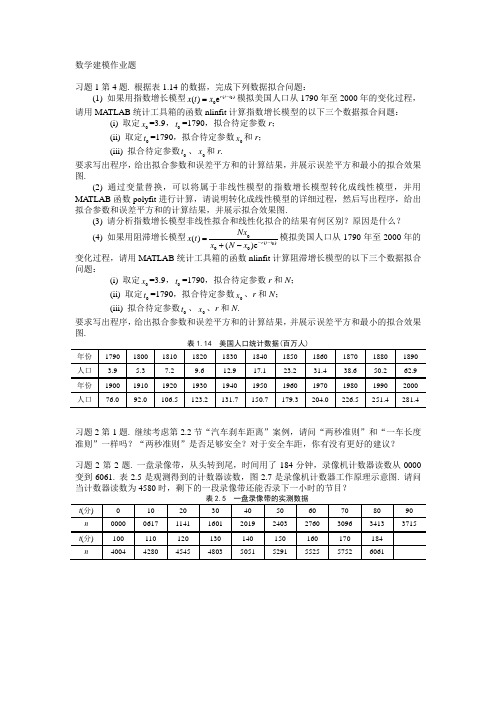
数学建模作业题习题1第4题. 根据表1.14的数据,完成下列数据拟合问题:(1) 如果用指数增长模型0()0()e r t t x t x -=模拟美国人口从1790年至2000年的变化过程,请用MATLAB 统计工具箱的函数nlinfit 计算指数增长模型的以下三个数据拟合问题:(i) 取定0x =3.9,0t =1790,拟合待定参数r ;(ii) 取定0t =1790,拟合待定参数0x 和r ; (iii) 拟合待定参数0t 、0x 和r .要求写出程序,给出拟合参数和误差平方和的计算结果,并展示误差平方和最小的拟合效果图.(2) 通过变量替换,可以将属于非线性模型的指数增长模型转化成线性模型,并用MATLAB 函数polyfit 进行计算,请说明转化成线性模型的详细过程,然后写出程序,给出拟合参数和误差平方和的计算结果,并展示拟合效果图.(3) 请分析指数增长模型非线性拟合和线性化拟合的结果有何区别?原因是什么?(4) 如果用阻滞增长模型00()00()()e r t t Nx x t x N x --=+-模拟美国人口从1790年至2000年的变化过程,请用MATLAB 统计工具箱的函数nlinfit 计算阻滞增长模型的以下三个数据拟合问题:(i) 取定0x =3.9,0t =1790,拟合待定参数r 和N ; (ii) 取定0t =1790,拟合待定参数0x 、r 和N ;(iii) 拟合待定参数0t 、0x 、r 和N .要求写出程序,给出拟合参数和误差平方和的计算结果,并展示误差平方和最小的拟合效果图.习题2第1题. 继续考虑第2.2节“汽车刹车距离”案例,请问“两秒准则”和“一车长度准则”一样吗?“两秒准则”是否足够安全?对于安全车距,你有没有更好的建议?习题2第2题. 一盘录像带,从头转到尾,时间用了184分钟,录像机计数器读数从0000变到6061. 表2.5是观测得到的计数器读数,图2.7是录像机计数器工作原理示意图. 请问当计数器读数为4580时,剩下的一段录像带还能否录下一小时的节目?习题3第4题. 某成功人士向学院捐献20万元设立优秀本科生奖学金,学院领导打算将这笔捐款以整存整取一年定期的形式存入银行,第二年一到期就支取,取出一部分作为当年的奖学金,剩下的继续以整存整取一年定期的形式存入银行……请你研究这个问题,并向学院领导写一份报告.习题3第5题. 有一位老人60岁时将养老金10万元以整存零取方式(指本金一次存入,分次支取本金的一种储蓄)存入,从第一个月开始每月支取1000元,银行每月初按月利率0.3%把上月结余额孳生的利息自动存入养老金. 请你计算老人多少岁时将把养老金用完?如果想用到80岁,问60岁时应存入多少钱?习题4第3题. 继续考虑第3.4.2小节“酵母培养物的增长”案例,建立微分方程模型,模拟酵母培养物的增长.习题6第2题. 13名儿童参加了一项睡眠时间(分钟)与年龄(岁)关系的调查,表6.18中的睡眠时间是根据连续3天记录的每天睡眠时间的平均值得到的. 请建立和求解回归模型,解释得到的结果,给出10岁儿童的平均睡眠时间及预测区间.习题6第3题. 水的沸点与大气压强有密切关系,表6.19中包含了17次试验中所测得的水的沸点(华氏温度)和大气压强(水银英寸),请建立回归模型估计沸点和压强之间的关系,并给出当沸点为201.5F 时压强的预测值及预测区间.习题7第2题. 某配件厂为装配线生产若干种部件. 每次轮换生产不同的部件时,因更换设备要付生产准备费(与生产数量无关). 同一部件的产量大于需求时,因积压资金、占用仓库要付库存费. 今已知某一部件的日需求量100件,生产准备费5000元,库存费每日每件1元. 如果生产能力远大于需求,并且不允许出现缺货,请制定最优生产计划.习题7第3题. 某商场把销售所剩的空纸皮箱压缩并打成包准备回收,每天能产生5包,在商场后院存放的费用是每包每天10元. 另一家公司负责将这些纸包运送到回收站,要收取固定费用1000元租装卸车,外加运输费每包100元. 请制定运送纸包到回收站的最优策略.。
数模作业
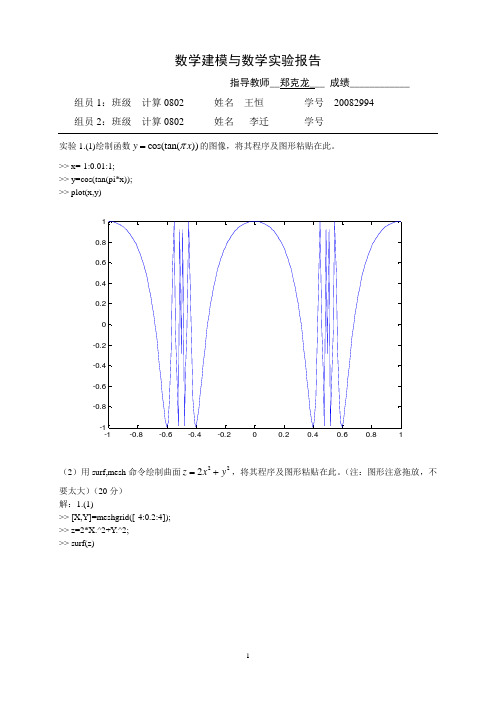
数学建模与数学实验报告指导教师__郑克龙___ 成绩____________组员1:班级__计算0802__ 姓名__王恒___ 学号__20082994___ 组员2:班级__计算0802__ 姓名__ 李迁__ 学号______________实验1.(1)绘制函数cos(tan())y x π=的图像,将其程序及图形粘贴在此。
>> x=-1:0.01:1;>> y=cos(tan(pi*x)); >> plot(x,y)-1-0.8-0.6-0.4-0.20.20.40.60.81-1-0.8-0.6-0.4-0.200.20.40.60.81(2)用surf,mesh 命令绘制曲面222z x y =+,将其程序及图形粘贴在此。
(注:图形注意拖放,不要太大)(20分) 解:1.(1)>> [X,Y]=meshgrid([-4:0.2:4]); >> z=2*X.^2+Y .^2; >> surf(z)>> [X,Y]=meshgrid([-4:0.2:4]); >> z=2*X.^2+Y.^2;>> surf(z)>> mesh(z)实验2.1、某校60名学生的一次考试成绩如下:93 75 83 93 91 85 84 82 77 76 77 95 94 89 91 88 86 83 96 81 79 97 78 75 67 69 68 84 83 81 75 66 85 7094 84 83 82 80 78 74 73 76 70 86 76 90 89 71 66 86 73 80 94 79 78 77 63 53 551)计算均值、标准差、极差、偏度、峰度,画出直方图;2)检验分布的正态性;3)若检验符合正态分布,估计正态分布的参数并检验参数. (20分)(1)>> x=[93 75 83 93 91 85 84 82 77 76 77 95 94 89 91 88 86 83 96 81 79 97 78 75 67 69 68 84 83 81 75 66 85 70 94 84 83 82 80 78 74 73 76 70 86 76 90 89 71 66 86 73 80 94 79 78 77 63 53 55];>> mean(x)ans =80.09999999999999>> std(x)ans =9.71055689722465>> max(x)-min(x)ans =44>> skewness(x)ans =-0.46817846064913>> kurtosis(x)ans =3.1529409218476650556065707580859095100024681012(2)5560657075808590950.010.02 0.05 0.10 0.25 0.50 0.750.90 0.95 0.980.99 DataP r o b a b i l i t yNormal Probability Plot>> hist(x)>> normplot(x)>> [muhat,sigmahat,muci,sigmaci]=normfit(x)muhat =80.09999999999999sigmahat =9.71055689722465muci =77.59149715696080 82.60850284303919sigmaci =8.23099868367594 11.84359663801530>> [h,sig,ci]=ttest(x,muhat) h =0 sig =1 ci =77.59149715696080 82.60850284303919 %因为H=0所以可以认为服从正态分布)>> u=mean(x); >> q=std(x);>> [H,sig]=ztest(x,u,q,0.05,0) H =0 sig =1>>%(由h=0知可以接受该假设)实验 3. 在研究化学动力学反应过程中,建立了一个反应速度和反应物含量的数学模型,形式为34231253211x x x xx y βββββ+++-=其中51,,ββ 是未知参数,321,,x x x 是三种反应物(氢,n 戊烷,异构戊烷)的含量,y 是反应速度.今测得一组数据如表4,试由此确定参数51,,ββ ,并给出置信区间.51,,ββ 的参考值为 (1,0.05, 0.02, 0.1, 2).(20分)序号 反应速度y 氢x 1 n 戊烷x 2异构戊烷x 31 8.55 470 300 102 3.79 285 80 103 4.82 470 300 1204 0.02 470 80 1206 14.39 100 190 107 2.54 100 80 658 4.35 470 190 659 13.00 100 300 5410 8.50 100 300 12011 0.05 100 80 12012 11.32 285 300 1013 3.13 285 190 120建立文件nihe.mclc;x1=[470 285 470 470 470 100 100 470 100 100 100 285 285]';x2=[300 80 300 80 80 190 80 190 300 300 80 300 190]';x3=[10 10 120 120 10 10 65 65 54 120 120 10 120]';x=[x1 x2 x3];y=[8.55 3.79 4.82 0.02 2.75 14.39 2.54 4.35 13.00 8.50 0.05 11.32 3.13]';f=@(beta,x)(beta(1).*x(:,2)-(1/beta(5)).*x(:,3)).*((1+beta(2).*x(:,1)+beta(3).*x(:,2)+beta(4).*x(:,3))).^(-1); beta0=[1 0.05 0.02 0.1 2]';opt=optimset('TolFun',1e-3,'TolX',1e-3);[beta,bint] =nlinfit(x,y,f,beta0,opt)运行结果:>> nihebeta =1.129233613766330.056577987484020.035668639997210.101754443271101.31595418394010bint =0.12535487345330-0.15077814802874-0.082334138533440.039924567139760.120229913393460.070194583456850.000834887987650.31999635043279-0.028202786737810.08912636268397-0.16190583332125-0.28617114942294即得到beta的拟合值及95%的置信区间实验4.某设备上安装有四只型号规格完全相同的电子管,已知电子管寿命为1000--2000小时之间的均匀分布。
数学建模作业

数学建模作业数学建模作业Document number【AA80KGB-AA98YT-AAT8CB-2A6UT-A18GG】《数学建模》作业学号姓名工作量 100 %专业所属学院指导教师二〇一七年六月数学建模作业第一部分:请在以下两题中任选一题完成(20 分)。
1、(马王堆一号墓入葬年代的测定建模问题)湖南省长沙市马王堆一号墓于1972 年8 月发掘出土,其时测得出土的木炭标本中碳-14 平均原子蜕变数为次/分钟,而新烧成的同种木材的木炭标本中碳-14(C-14)原子蜕变数为次/分钟. 又知碳-14 的半衰期为 5730 年,试推断该一号墓入葬的大致年代。
问题分析:放射性元素衰变的速度是不受环境影响的,它总是和该元素当前的量成正比,运用碳—14测定文物或化石年代的方法是基于下面的理由:(1)宇宙射线不断轰击大气层,使大气层中产生碳—14而同时碳—14又在不断衰变,从而大气层中碳—14含量处于动态平衡中,且其含量自古至今基本上是不变的;(2)碳—14被动植物体所吸收,所以活着的生物体由于不断的新陈代谢,体内的碳—14也处于动态平衡中,其含量在物体中所占的百分比自古至今都是一样的;(3)动植物的尸体由于停止了从环境中摄取碳—14,从而其体内碳—14含量将由于衰变的不断减少,碳定年代法就是根据碳—14的减少量来判断物体的大致死亡时间。
设t 时刻生物体中碳—14的含量为x (t ),放射性物质的半衰期(即放射性物质的原子数衰减一半所需的时间)为T ,生物体死亡时间为t0,则由放射性物质衰变规律得数学模型=-=,)(,00x t x x dtdxλ ① 其中0>λ称为衰变系数,由放射性物质所决定,x 0为生物体在死亡时刻t 0时的碳—14含量。
模型求解对所得的一阶线性微分方程模型①采用同变量分离法求解,得 e x t t x t )(00)(--=λ??由于T t t =-0时,有0021)()(x T t x t x =+=?? 代入上式,有 Te T 2ln ,212==-λ 所以得 ? Tt t ex t x )(2ln 00)(--= ②这就是生物体中碳—14的含量随时间衰变的规律,由之易解得 ) ()(ln 2ln 00t x t x T t t =- ③ 将所得的数学模型的一般解应用于本例,此时以T=5730,37.380=x (新木炭标准中碳—14原子蜕变数),X(1972)=(出土的木炭标本中碳—14原子蜕变数)代入到③式,得.2937.38ln 2ln 57300≈=-t t 年于是得??1232095197220950-=-=-≈t t 年结果表明,马王堆墓入葬年代大约在公元前123年左右的西汉中期,该结论与马王堆出土文物的考证结果相一致。
数学建模的作业

实验1 渡口模型仿真计算实验内容:(渡口模型仿真)渡船营运者如何规划,使得单次运送车辆最多、最合理,从而获得最大利润。
实验目的:对渡口问题进行仿真计算,与理论结果进行比较,验证模型的正确性。
实验步骤:1、对问题的变量进行合理定义,并指出合理存在区间;2、选取合适步长,通过C语言或者MATLAB软件编程,遍历寻优,得到单次运送所获利润的最大值,并同时求出最大值点;3、考虑随机到达的情况,进行随机优化;4、比较结论,对模型的合理性进行评估,或者进一步优化和重构模型。
【问题提出】一个渡口的渡船营运者拥有一只甲板长32米,可以并排停放两列车辆的渡船。
他在考虑怎样在甲板上安排过河车辆的位置,才能安全地运过最多数量的车辆。
【准备工作】他关心一次可以运多少辆车,其中有多少小汽车,多少卡车,多少摩托车。
他观察了数日,发现每次情况不尽相同,得到下列数据和情况:(1)车辆随机到达,形成一个等待上船的车列;(2)来到渡口的车辆中,轿车约占40%,卡车约占55%,摩托车越占5%;(3)轿车车身长为3.5~5.5米,卡车车身长为8~10米。
【问题分析】这是一个遵循“先到先服务”的随机排队问题,这里试图用模拟模型的方法来解决,故需分析以下几个问题需要考虑下面一些问题:(1)应该怎样安排摩托车?(2)下一辆到达的车是轿车还是卡车?(3)怎样描述一辆车的车身长度?(4)到达的车要加入甲板上两列车队的哪一列中去?【建立模型】其中我以函数获得的平均分布的随机数,然后假定车身长度也符合平均分布,并假定渡船甲板由两列组合成一列,长64米,每辆车辆来到渡口,遵循先到先服务的原则,依次进入,并假定两辆车之间相隔0.5米,因此得出模型1假定遵循左右均衡的原则。
尽可能使左右车辆的卡车数量相等,轿车数量相等,得出模型2模型1中,由于车辆为分两队摆放,每边都应有一定间隙,例如,若有8米空隙在模型1中,理论上还可停一辆车,但显然是不可能的.假定给出停放两列汽车的方式为采用先停一列再停一列的方式,得出模型3由于车辆的长度不可能特长或特短,因此车长该服从正态分布.将以上模型修改,得出模型4,5,6【模型求解】注意到甲板停放两队汽车,可供停车的总长度为32*2=64米。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
h * tan α — 1.1 R < 0
h * k * tanα <
R
2
-
R 2
2
针对问题三,建立的 模型给出几个自己设 计的创意平板折叠。 。
在满足平板桌稳固和平衡 的条件下,可调整桌面的 边缘线为任意外凸曲线, 只要建立曲线方程,代入 问题二所建立的模型中, 即可求取满足要求的平板 桌设计样式的最优设计参 数。
b
arc cos (
a
2
)< arctan
uz
针对问题二,折叠桌 的设计应做到产品稳 固性好、加工方便、 用材最少。
0 < p < 1
h <
a
2
1 b < p < < a 2 2n * 3
输入: 1.折叠桌高度Hcm; 2.桌面边缘线的方程,xOy 平面内的闭合曲线方程 y=f(x)与z=0且关于x轴和y轴 轴对称; 3.桌脚边缘线方程,关于 xOz平面对称的曲线方程 y=g1(x)与z=g2(x),最低点与 xOy平面的距离为H
学习优秀论文掌握的相关理论和方法
对于描述折叠桌动态变 化过程,利用对称性求 出所有桌腿木条边缘点 的坐标,用matlab画出 三维动态图形。 以长方形平板的中心为 坐标原点,建立空间直 角坐标系,以长方形平 板中心为圆心做相切于 长方形平板长边的圆。 桌腿木条边缘点坐标的 解析表达式中,取 h=53cm,可得到折叠 后各桌腿木条边缘点的 坐标。在三维坐标系中 画出这些散点,并用直 线连接,得到描述桌脚 边缘线的近似曲线。
针对问题一,需要解 决描述折叠桌动态变 化过程、给出折叠桌 设计加工参数、给n = n,min = s
a <
dn + 2 * p
yi
a
2
> 0 (i = 1, 2, 3,...,n )
z 1 = max(z1 ,z 2,...,zn)
b a a < * p < 2 2 2
针对问题三,要求给 出相应的设计加工参 数,画出至少8张动 态变化过程的示意图 。
输出: 1.所需平板材料形状,即 加工示意图; 2.每根木条的长度; 3.钢筋位置;4.开槽长度。
3
对于邓敏娜等论文分析
学习优秀论文掌握的相关理论和方法
将空间中的平板桌投影到两 个平面坐标系当中,利用三 角形关系,建立了桌脚边缘 线的参数方程
针对问题一,给出此 折叠桌的设计加工参 数和桌脚边缘线的数 学描述。
xi
=
x o - xi ( - )+ Li di xo di
= 2.5i
yi
zi
=
)+ z L i di o di
zo (
0.9 R - h * tan α < 0
针对问题二,以用料 最省(板材最短)、加 工方便(总开槽长度 最短)为目标。
先将圆形折叠桌的侧面直 纹曲面和桌脚边缘线的方 程推广到一般形状桌面和 一般形状板材,然后利用 多目标优化模型设计了两 种特殊形状的折叠桌:非 长方形板材的正方形折叠 桌和8字形折叠桌.通过改 变木条的旋转角度分别画 出了这两种形状折叠桌的 动态变化示意图,并给出 了具体的设计加工参数.
2
对于刘桥等论文分析
相关理论和方法及解决的问题:
针对问题二
1.利用立体几何关系建立折叠桌设计参数; 2.鉴于到折叠桌这种艺术品实际使用过程中不 会 承受较大重物,因而只考虑折叠桌本身重力 对其稳定性的影响,并且根据折叠桌材料选 取 适当的地面摩擦系数建立稳定性方程;
以用料最省(板材最 短)、加工方便(总开 槽长度最短)为目标 。
数模
CUMCM-2014B创意平板折叠桌
相关理论和方法及解决的问题:
针对问题一
给出此折叠桌的设 计加工参数和桌脚 边缘线的数学描述 。
由立体几何中的相关知识可以建立坐标系, 将已知数据代入得到空间数学模型中,即可 解得此折叠桌的设计参数及桌脚边缘线的数 学描述,可以通过仿真得到 折叠桌桌角的动 态变化过程。
针对问题一,给出此折叠 桌的设计加工参数和桌脚 边缘线的数学描述。
令u=L/2,就可得到桌脚边缘线的 方程(5-12)或(5-13) 如从中间到两边的木条空槽长度分 别为20.09,19.60,18.77,17.59 ,16.06,14.14,11.81,9.00, 5.53(cm).
木条开槽下界不能超出木条、 桌子状态下桌腿边缘不能相交 、中间所有木条的桌腿不能沾 地,以及桌子的稳固性作为约 束条件
存在的问题及需要进一步学习的相关理论和方法:
模型从材料学,力学与运动学多个角度考 虑其设计,为了精确性使用matlab等数学 软件进行处理,最终求得最优方案。
3.在稳定的基础上从加工方便及耗材最少 的 角度出发,建立优化设计的模型,确定最优 解。
1
对于程双泽等论文分析
学习优秀论文掌握的相关理论和方法
以长方形平板中心为原点,y轴沿 小木条方向,z轴指向桌底,建立 空间直角坐标系,引入参数u表示 直纹曲面上的任一点P还原到木板 状态下到x轴的距离,参数v表示点 P到yoz平面的距离 利用几何关系表示出点P的坐标, 即得到直纹曲面的参数方程.进一步 消去参数可得直纹曲面的方程为
针对问题二,以用料最省(板 材最短)、加工方便(总开槽长 度最短)为目标。
建立多目标优化模型.利用 Matlab编程,求得最优结果为: 折叠桌弯折角θ为1.0605(弧度), 钢筋的初始位置到桌腿底端的 距离s为43.80cm,木板的长度L 为158.56cm.
针对问题三,建立的 模型给出几个自己设 计的创意平板折叠。
