第三章 工业机器人运动学-3逆运动学.ppt
合集下载
工业机器人运动学

注意:对于旋转关节,绕z 轴的旋转角 ( θ角)是关节变量。对于滑动关节, 沿 z轴的连杆长度d 是关节变量;
3.8 机器人正运动学方程的D-H参数表示法
一.连杆坐标系的建立
本地参考坐标系步骤:
(1)通常关节不一定平行或相交。因此 ,通常z轴是斜线,但总有一条距离最短的 公垂线,它正交于任意两条斜线。通常在 公垂线方向上定义本地参考坐标系的x轴。 所以如果an表示 zn-1与zn之间的公垂线, 则xn的方向将沿an 。同样,在 zn与 zn+1之 间的公垂线为,xn+1的方向将沿an +1。
3T6
S4C5C6
C4 S6
S5C6 0
S4C5S6 C4C6 S5S6 0
S4S5 C5 0
0
0 1
C1 0 S1 0
A1
S1 0
0 1
C1 0
0 0
0
0
0
1
3.8 机器人正运动学方程的D-H参数表示法
nx = C1 [ C2 ( C4C5C6 - S4S6 ) - S2S5C6 ] - S1( S4C5S6 + C4S6 ) ny = S1 [ C2 ( C4C5C6 - S4S6 ) - S2S5C6 ] + C1( S4C5S6+C4S6 ) nz = -S2 ( C4C5C6 - S4S6 ) - C2S5C6 ox = C1 [ -C2 ( C4C5S6 + S4C6 ) + S2S5C6 ] - S1( -S4C5S6 + C4S6 ) oy = S1 [ -C2 ( C4C5C6 + S4C6 ) + S2S5S6 ] + C1( -S4C5S6 + C4S6 ) oz = S2 ( C4C5C6 + S4C6 ) + C2S5S6 ax = C1 ( C2C4S5 + S2C5 ) – S1S4C5 ay = S1 ( C2C4S5 + S2C5 ) + C1S4S5 az = –S2C4S5 + C2C5 px = C1S2d3 – S1d2 py = S1S2d3 + C1d2 pz = C2d3
机器人运动学正解逆解-课件

§1.4
机器人正向运动学
工业机器人的正向运动学是指已知各关节的类型、相邻 关节之间的尺寸和相邻关节相对运动量的大小时,如何确 定工业机器人末端操作器在固定坐标系中的位姿。
主要包括以下内容:
1) 相对杆件的坐标系的确定; 2) 建立各连杆的模型矩阵A; 3) 正运动学算法;
D-H表示法
学习目标:1. 理解D-H法原理
C 2 S A2 2 0 0 S2 C2 0 0 0 C 2a2 0 S2a2 1 0 0 1
C 3 S A3 3 0 0
S3 C3 0 0
0 C 3a3 0 S3a3 1 0 0 1
C 4 S A4 4 0 0
y0
O0
连杆0
z0
d1 x0
解:
例2、PUMA560运动学方程(六个自由度,全部是旋转关节)
关节变量都是θ
θ2
θ1
θ3
θ4
θ5 θ6
PUMA560机器人的连杆及关节编号
A1
A2
为右手坐标系,Yi轴:按右手定则 Zi轴:与Ai+1关节轴重合,指向任意 Xi轴: Zi和Zi-1构成的面的法线, 或连杆i两端轴线Ai 与Ai+1的公垂线(即: Zi和Zi-1的公垂线)
变换矩阵,它们依次连乘的结果就是末端执行器(手爪)在基坐
标系中的空间描述,即
n o a 0 1 n -1 T1 (q1 ) T2 (q2 ) Tn 0 0 0
上式称为运动方程。
p 0 Rn 1 0
0
PnO 1
已知q1,q2,…,qn,求
S3 C3
依次类推,分别在方程2.19两边左乘A1~A4的逆,可得到
机器人正向运动学
工业机器人的正向运动学是指已知各关节的类型、相邻 关节之间的尺寸和相邻关节相对运动量的大小时,如何确 定工业机器人末端操作器在固定坐标系中的位姿。
主要包括以下内容:
1) 相对杆件的坐标系的确定; 2) 建立各连杆的模型矩阵A; 3) 正运动学算法;
D-H表示法
学习目标:1. 理解D-H法原理
C 2 S A2 2 0 0 S2 C2 0 0 0 C 2a2 0 S2a2 1 0 0 1
C 3 S A3 3 0 0
S3 C3 0 0
0 C 3a3 0 S3a3 1 0 0 1
C 4 S A4 4 0 0
y0
O0
连杆0
z0
d1 x0
解:
例2、PUMA560运动学方程(六个自由度,全部是旋转关节)
关节变量都是θ
θ2
θ1
θ3
θ4
θ5 θ6
PUMA560机器人的连杆及关节编号
A1
A2
为右手坐标系,Yi轴:按右手定则 Zi轴:与Ai+1关节轴重合,指向任意 Xi轴: Zi和Zi-1构成的面的法线, 或连杆i两端轴线Ai 与Ai+1的公垂线(即: Zi和Zi-1的公垂线)
变换矩阵,它们依次连乘的结果就是末端执行器(手爪)在基坐
标系中的空间描述,即
n o a 0 1 n -1 T1 (q1 ) T2 (q2 ) Tn 0 0 0
上式称为运动方程。
p 0 Rn 1 0
0
PnO 1
已知q1,q2,…,qn,求
S3 C3
依次类推,分别在方程2.19两边左乘A1~A4的逆,可得到
工业机器人的运动学

工业机器人运动学的展望
未来工业机器人运动学将与人工智能、机器视觉等技 术进一步融合,实现更智能化的运动控制和决策。
输入 标题
应用拓展
随着技术的进步,工业机器人运动学的应用领域将进 一步拓展,如微纳操作、深海/空间探索等高精度、高 可靠性要求的领域。
技术融合
理论深化
随着工业机器人运动学的不断发展,对相关领域的人 才需求将进一步增加,未来将需要更多的专业人才进
运动学逆问题
定义
给定机器人末端执行器的 位置和姿态,求解实现该 位置和姿态所需的关节角 度。
计算方法
通过逆向运动学模型,将 末端执行器的笛卡尔坐标 代入机器人结构参数方程, 反解出关节角度。
应用
根据目标位置和姿态,规 划机器人的关节运动轨迹, 实现精确控制。
雅可比矩阵
定义
描述机器人末端执行器速度与关节速 度之间关系的线性映射矩阵。
03 工业机器人运动学原理
运动学正问题
01
02
03
定义
给定机器人的关节角度, 求解机器人末端执行器的 位置和姿态。
计算方法
通过正向运动学模型,将 关节角度代入机器人结构 参数方程,求解末端执行 器的笛卡尔坐标。
应用
根据已知的关节角度,预 测或验证机器人的末端位 置和姿态,为机器人控制 提供基础。
基于运动学的轨迹规划
轨迹规划
基于运动学的轨迹规划是工业机器人运动学优化与控制的 重要环节,它涉及到机器人在空间中运动的路径和速度的 规划。
路径规划
路径规划是轨迹规划的基础,它通过寻找起点和终点之间 的最优路径,确保机器人在移动过程中能够安全、高效地 完成任务。
速度规划
速度规划是在路径规划的基础上,对机器人在各个运动阶 段的速度进行优化,以达到最佳的运动效果和效率。
第三章工业机器人运动学3逆运动学

由于角φ已求出,比较式(3.48)等号两边矩阵第1行第3列和第3行第3 列元素相等有
sin f11(a) cos f13 (a)
或
(3.59) (3.60)
由此可得
sin cos ax sin ay cos az
tan 1 cos
ax sin az
ay
(3.61) (3.62)
(3.63)
同样比较式(3.48)等号两边矩阵的第2行第1列和第2行第2列元素可知
sin f12 (n)
(3.64)
cos f12 (o)
(3.65)
或
由此可得
sin sin nx cos ny cos sin ox cos oy
tan
1
sin sin
n o
x x
cos ny cos oy
1T6 =
C2( C4C5C6 - S4S6 ) - S2S5C6 S2( C4C5C6 - S4S6 ) + C2S5C6
S4C5C6 + C4C6
0
-C2( C4C5S6 + S4C6 )+ S2S5S6 -S2( C4C5 S6+ S4C6 )- C2S5S6
-S4C5S6 + C4C6
0
C2C4S5 + S2C5 S2C4S5 - C2C5
3.4 欧拉变换的逆运动学解 (Inverse solution of Euler Angles )
由前节知欧拉变换为
Euler (ø, θ,ψ) = Rot (z, ø) Rot (y, θ) Rot (z,ψ)
我们用T来表示欧拉变换的结果,即
T = Euler (ø, θ,ψ)
电机拖动技术基础第三章机器人的运动学PPT课件

第三章 机器人的运动学
►3.1 刚体的位姿描述 ►3.2 坐标变换 ►3.3 齐次坐标和齐次变换 ►3.4 变换方程和欧拉角 ►3.5 机器人运动学的正问题和逆问题
3.1 刚体的位姿描述
一、位姿的定义
刚体参考点的位置(坐标系的位置)和刚体的姿态统称为刚体的位姿。
(为描述机器人本身的各个连杆之间.机器人和环境之间的运动关系,将
n
n o a
手爪的方位由旋转矩阵R规定。
R n
o
a
手爪的位置由位置矢量 p
规定。
代表手p 爪坐标系的原点。
则手爪的位姿可由四个矢量
来 来描述。
noa p
记为:
T n o a p
3.2 坐标变换
定义:由于空间中任意点P在不同坐标系中的描述不同,所以需要 研究从一个坐标系的描述到另一个坐标系的描述之间的变换关,通 常称为坐标变换。
{S}代表工作站(操作台)坐标系(工作站框)
{G}代表目标坐标系(目标框) 它们之间的位姿关系用相应的齐次变换来描述。图3-6 机器人与环境坐标系
B S
T描述工作站框{S}相对于基座{B}的位姿,
S G
T描述目标框{G}相对于工作站{S}的位姿。
对物体进行操作时(搬运或装配机器人),工具框{T}相对目标框{G} 的位姿 直接GT T 影响操作效果。 是机GT T器人控制和轨迹规划的对象。
=
相对于固定坐标系运动 相对于活动坐标系运动
2.变换过程的可逆性
齐次坐标变换过程是可逆的. 若有 ,则逆变换
。
所以有 I44BATABT A B0R BP 1AO BA0R AP 1BO
A BR0BAR
A BRAPB1OBPAO
►3.1 刚体的位姿描述 ►3.2 坐标变换 ►3.3 齐次坐标和齐次变换 ►3.4 变换方程和欧拉角 ►3.5 机器人运动学的正问题和逆问题
3.1 刚体的位姿描述
一、位姿的定义
刚体参考点的位置(坐标系的位置)和刚体的姿态统称为刚体的位姿。
(为描述机器人本身的各个连杆之间.机器人和环境之间的运动关系,将
n
n o a
手爪的方位由旋转矩阵R规定。
R n
o
a
手爪的位置由位置矢量 p
规定。
代表手p 爪坐标系的原点。
则手爪的位姿可由四个矢量
来 来描述。
noa p
记为:
T n o a p
3.2 坐标变换
定义:由于空间中任意点P在不同坐标系中的描述不同,所以需要 研究从一个坐标系的描述到另一个坐标系的描述之间的变换关,通 常称为坐标变换。
{S}代表工作站(操作台)坐标系(工作站框)
{G}代表目标坐标系(目标框) 它们之间的位姿关系用相应的齐次变换来描述。图3-6 机器人与环境坐标系
B S
T描述工作站框{S}相对于基座{B}的位姿,
S G
T描述目标框{G}相对于工作站{S}的位姿。
对物体进行操作时(搬运或装配机器人),工具框{T}相对目标框{G} 的位姿 直接GT T 影响操作效果。 是机GT T器人控制和轨迹规划的对象。
=
相对于固定坐标系运动 相对于活动坐标系运动
2.变换过程的可逆性
齐次坐标变换过程是可逆的. 若有 ,则逆变换
。
所以有 I44BATABT A B0R BP 1AO BA0R AP 1BO
A BR0BAR
A BRAPB1OBPAO
第六讲 机器人运动学逆解ppt课件

3.3 机器人运动学方程
例1:已知四轴平面关节SCARA机 器 人如图所示,试计算: (1)机器人的运动学方程; (2)当关节变量取 qi=[30°,-60°,-120,90°]T 时,机器人手部的位置和姿态; (3)机器人运动学逆解的数学 表达式。sin sin cos( ) ij icos j i j i j s cos sin sin sin( ) ij i j icos j i j
山东大学机械工程学院机电工程研究所2010/09/02
2、运动学方程的逆解
逆运动学问题的可解性: 下面以六自由度机器人PUMA为例, 研究其可解性。
其中:
n c [ c ( c c c s s ) s s c ] s ( s c c c s ) x 1 23 4 5 6 4 6 23 5 6 1 4 5 6 4 6 n s [ c ( c c c s s ) s s c ] c ( s c c c s ) y 1 23 4 5 6 4 6 23 5 6 1 4 5 6 4 6 n s ( c c c s s ) c s c z 23 4 5 6 4 6 23 5 6
可见,我们有12个方程及6个未知数。 上述12个方程关系如何? 我们先看看转动部分,它是3X3子矩阵 ,共有9个元素;我们知道,转动矩阵的每 列都是单位矢量,并且每列之间都两两正交 ;因此,9个元素中仅三个是独立的,或则 说,12个方程中仅有6个是独立,对应6个 未知数。 因此,一般情况下,单从数学的角度看 ,方程组应该是有解的。
山东大学机械工程学院机电工程研究所2010/09/02
2、运动学方程的逆解
a c ( c c c s c ) s s s x 1 23 4 5 23 5 1 4 5 a s ( c c c s c ) c s s y 1 23 4 5 23 5 1 4 5 a s c c c c z 23 4 5 23 5
机器人运动学正解逆解课件

机器人力控制
在机器人力控制中,需要知道每个关节的角度变化来调整 机器人的姿态和力矩。逆解可以用于求解每个关节的角度 变化,从而调整机器人的姿态和力矩。
机器人定位
在机器人定位中,需要知道每个关节的角度变化来调整机 器人的位置和姿态。逆解可以用于求解每个关节的角度变 化,从而调整机器人的位置和姿态。
04
实现复杂运动轨迹
利用运动学正解与逆解,可以规划出 复杂的运动轨迹,满足各种应用需求 。
02
机器人运动学正解
正解的基本概念
正解是指机器人末端执行器从某一初 始位置和姿态到达目标位置和姿态所 需经过的关节角度值。
正解是机器人运动学中的基本问题, 是实现机器人精确控制和自主导航的 基础。
正解的求解方法
逆解的求解方法
01
代数法
通过建立机器人关节角度与目标点坐标之间的方程组,利用数学软件求
解方程组得到关节角度。这种方法适用于简单的机器人结构,但对于复
杂机器人结构求解过程可能较为繁琐。
02
数值法
通过迭代或搜索的方法,不断逼近目标点坐标,最终得到满足要求的关
节角度。这种方法适用于复杂机器人结构,但求解时间较长且可能存在
机器人运动学正解逆解课件
目 录
• 机器人运动学概述 • 机器人运动学正解 • 机器人运动学逆解 • 机器人运动学正逆解的对比与联系 • 机器人运动学正逆解的实例分析
01
机器人运动学概述
定义与分类
定义
机器人运动学是研究机器人末端 执行器位姿与关节变量之间的关 系的学科。
分类
根据机器人的结构和运动特性, 可以分为串联机器人和并联机器 人。
局部最优解。
03
解析法
通过几何学和代数学的方法,直接求解关节角度与目标点坐标之间的关
在机器人力控制中,需要知道每个关节的角度变化来调整 机器人的姿态和力矩。逆解可以用于求解每个关节的角度 变化,从而调整机器人的姿态和力矩。
机器人定位
在机器人定位中,需要知道每个关节的角度变化来调整机 器人的位置和姿态。逆解可以用于求解每个关节的角度变 化,从而调整机器人的位置和姿态。
04
实现复杂运动轨迹
利用运动学正解与逆解,可以规划出 复杂的运动轨迹,满足各种应用需求 。
02
机器人运动学正解
正解的基本概念
正解是指机器人末端执行器从某一初 始位置和姿态到达目标位置和姿态所 需经过的关节角度值。
正解是机器人运动学中的基本问题, 是实现机器人精确控制和自主导航的 基础。
正解的求解方法
逆解的求解方法
01
代数法
通过建立机器人关节角度与目标点坐标之间的方程组,利用数学软件求
解方程组得到关节角度。这种方法适用于简单的机器人结构,但对于复
杂机器人结构求解过程可能较为繁琐。
02
数值法
通过迭代或搜索的方法,不断逼近目标点坐标,最终得到满足要求的关
节角度。这种方法适用于复杂机器人结构,但求解时间较长且可能存在
机器人运动学正解逆解课件
目 录
• 机器人运动学概述 • 机器人运动学正解 • 机器人运动学逆解 • 机器人运动学正逆解的对比与联系 • 机器人运动学正逆解的实例分析
01
机器人运动学概述
定义与分类
定义
机器人运动学是研究机器人末端 执行器位姿与关节变量之间的关 系的学科。
分类
根据机器人的结构和运动特性, 可以分为串联机器人和并联机器 人。
局部最优解。
03
解析法
通过几何学和代数学的方法,直接求解关节角度与目标点坐标之间的关
机器人学基础_第3章机器人运动学

移动连杆坐标系的建立
移动连杆坐标系的规定:
• 坐标轴Zi:与i+1关节的轴线重合; • 坐标轴Xi:沿移动关节i轴线与关节i+1轴线的公垂线,指向i+1关节; • 坐标轴Yi:按右手直角坐标系法则确定; • 坐标原点Oi: (1)当关节i轴线和关节i+1轴线相交时,取交点; (2)当关节i轴线和关节i+1轴线异面时,取两轴线的公垂线与关节i轴
动到使其原点与连杆i坐标系原点重合的地方。 • (4) 绕Xi旋转αi角,使Zi–1转到与Zi同一直线上。 • 连杆i–1的坐标系经过上述变换与连杆i的坐标系
重合。如果把表示相邻连杆相对空间关系的矩阵 称为A矩阵,那么根据上述变换步骤,从连杆i到 连杆i–1的坐标变换矩阵Ai为
•
(3.13)
• 同理,对联轴器的齐次坐标变换矩阵有 •
• 手部的位置矢量为固定参考系原点指向手 部坐标系{B}原点的矢量P,手部的方向矢 量为n、o、a。于是手部的位姿可用4 4 矩阵表示为
•
•
nX oX a X PX
T
nY
oY
aY
PY
nZ 0
oz 0
aZ 0
PZ 1
• 思考:
• ①说明位姿矩阵的左上角3×3矩阵的几何 意义。
• ②分别说明n, o, a, P的几何意义。
a1 = l 1 =100
a2 = l 2 =100
旧课复习与总结
转动连杆坐标系的建立
• 坐标轴Zi:与i+1关节的轴线重合; • 坐标轴Xi:沿连杆i两关节轴线的公垂线,指向i+1关节; • 坐标轴Yi:按右手直角坐标系法则确定; • 坐标原点Oi: (1)当关节i轴线和关节i+1轴线相交时,取交点; (2)当关节i轴线和关节i+1轴线异面时,取两轴线的公垂
机器人运动学正解逆解-精PPT课件

A3
ai—沿 xi 轴, zi-1 轴与 xi 轴交点到Oi 的距离
αi — 绕 xi 轴,由 zi-1 转向zi
di — 沿 zi-1 轴,zi-1 轴和 xi 交点至Oi –1 坐标
系原点的距离
θi — 绕 zi-1 轴,由 xi-1转向 xi
A5
A4 A6
.
16
连杆 n θn
dn
anαn1 θ1 源自900) 0S5S6 0C234S5 S234S5
C5 0
C234a4 C23a3 C2a2
S234a4
S23a3
S2a2
0
1
根据第3行第4列元素对应相等可得到
1a rc tp paxy)n和 (111 8 0
.
29
根据1,4元素和2,4元素,可得到:
pxC 1pyS1C23 a4 4C2a 33C2a2 pzS23 a4 4S2a 33S2a2
C234a4 ) S234a4 )
进而可得:
4 234 2 3
再 根 据 对 应 项 元 素 相 , 等 可 以 得 到
S5 C23(4 C1ax S1ay ) S234az
C5 C1ay S1ax
5
arctanC234(C1ax S1ax
S1ay ) C1ay
S234az
.
32
§1.4 机器人正向运动学
工业机器人的正向运动学是指已知各关节的类型、相邻 关节之间的尺寸和相邻关节相对运动量的大小时,如何确 定工业机器人末端操作器在固定坐标系中的位姿。
主要包括以下内容: 1) 相对杆件的坐标系的确定; 2) 建立各连杆的模型矩阵A; 3) 正运动学算法;
.
1
工业机器人运动学

(2)圆柱坐标
由于这些变换都是相对于全局参考坐标系的坐标轴
的,因此由这三个变换所产生的总变换可以通过依
次左乘每一个矩阵而求得:
RTP Tcyl (r, ,l) Trans(0, 0,l)Rot(z, )Trans(r, 0, 0)
1 0 0 0 C S 0 0 1 0 0 r
动组成,运动顺序为:先沿z轴平移r ,再y轴旋转 β并 绕z轴旋转γ。这三个变换建立了手坐标系与参考坐标
系之间的联系。由于这些变换都是相对于全局参考坐
标系的坐标轴的,因此有这三个变换所产生的总变换
可以通过一次左乘每一个矩阵而求得:
RTP Tsph r, , Rotz, Roty, Trans0,0, r
解: 设定正运动学方程用式(3.31)中的RTP 矩阵表示,根据期望的位置可得知 如下结果:
1 0 0 Px 1 0 0 3
RTP
0 0
0
1 0 0
0 1 0
Py
0
Pz 1
0 0
1 0 0
0 1 0
4 7
或Px
3, Py
4, Pz
7
1
RTP
Tsph
C S S
C
0
S S
rS
S
C
rC
0
0
0
1
3.7 机器人的正逆运动学
例3-15假设要将球坐标机器人手坐标系原点放在3 4,7T 计算机器人的关节变量。
解: 设定正运动学方程用式(3.35)中的Txph 矩阵表示,根据期望的位置可得知 如下结果:
工业机器人课件第三章 机器人运动学
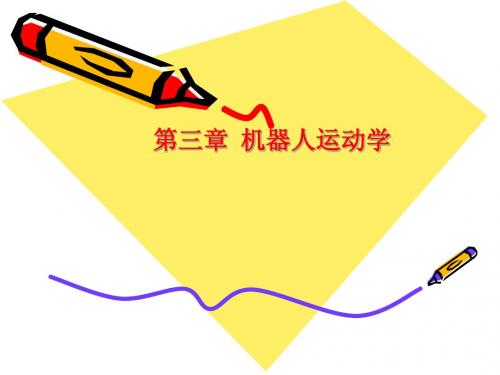
T3= A1 A2 A3
称这些A矩阵的乘积为T矩阵,其前置上标若为0,则可省略。对于六 连杆机械手,有下列T矩阵
T6= A1 A2 A3 A4 A5 A6
手爪坐标系
机械手的运动方向 原点由矢量p表示。 接近矢量a:z轴设在手指接近物体的方向,称为接近矢量 方向矢量o:y轴设在两手指的连线方向,称为方位矢量 法线矢量n:x轴由右手系确定, 即 n = o a ,称为法向矢量。
0 sin i cos i 0
0 0 0 1
对于在第i坐标系中的点ri在第i—1坐标系中表示为:
ri 1 i 1Ai ri
确定第i坐标系相对于机座坐标系的位置的齐次变换矩阵i-1Ti是 各齐次变换矩阵Ai的连乘积,可表示成
0
Ti A1 A2 A3 A4 A5 A6 A j
பைடு நூலகம்
cos i sin cos i i 1 sin i sin i 1 0
例 建立右图所示机器人相邻坐标 系间的转换矩阵 解:建立的坐标系如右图,这是二维坐 标系(在三维空间中,各坐标系的z轴垂 直于纸面),其相邻坐标系的变换矩阵 为
A1 Rz ,Tx ,l1
第三章 机器人运动学
§ 3.1 机器人运动方程的表示
机器人的机械手看作是一系列由关节连接起来的连杆构成的。为机 械手的每一连杆建立一个坐标系,并用齐次变换来描述这些坐标系间 的相对位置和姿态。通常把描述一个连杆与下一个连杆间相对关系的 齐次变换叫做A矩阵。一个A矩阵就是一个描述连杆坐标系间相对平移 和旋转的齐次变换。如果A1表示第一个连杆对于基系的位置和姿态, A2表示第二个连杆相对于第一个连杆的位置和姿态,则第二个连杆在 基系中的位置和姿态可由下列矩阵的乘积给出 T2= A1 A2 同理,若A3表示第三个连杆相对于第二个连杆的位置和姿态,则有
第三章机器人运动学PPT课件
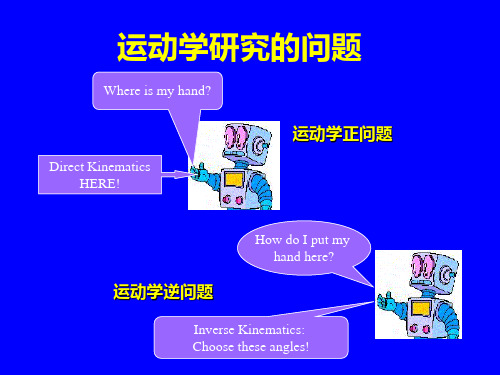
用一组关节变量(di或i)来描述。这组变量通常称为关节矢量或关节坐标,
由这些矢量描述的空间称为关节空间。
• 正向运动学:关节空间末端笛卡儿空间,单射 • 逆向运动学:末端笛卡儿空间关节空间,复射
不同的关节空间,相同的 末端笛卡儿空间
关节空间与末端笛卡儿空 间映射关系
第三章 机器人的运动学
3.1 工业机器人运动学
,它的齐
次坐标就是
,即满足Px=ωPx/ω,Py=ωPy/ω,
Pz=ωPz/ω(ω是非零整数)。可以看出,在三维直角坐标系中,
由于ω取值的不同,一个点的齐次坐标的表达不唯一。
齐次坐标不仅可以规定点的位置(ω为非零整数),还可以
用来规定矢量的方向(第四个元素为零时)。列向量
(
)表示空间的无穷远点,a,b和c称为它的方向
单位主矢量相对于坐标系{A}的方向余弦组成:
xB
yB
zB
xA
yA
zA
其中:co scoxB s ,xA ()
既表示了刚体F在{A}系中的方位,也描述了{B}系在{A}系中的 姿态。
3.1.2.2 坐标变换
一、坐标平移
如图3-5,坐标系{B}与{A} 方向相同,但原点不重合。
图3-5 坐标平移
此式称为平移方程。其中 是B系中的原点在A系中的表示。
0
0
0
1
1
1
给定坐标系{A},{B}和{C},已知{B}相对{A}的描述为 ,
{C}相对{B}的描述为
AP A BTBP BPC BTCP APC ATCP
,则有
APA BTC BTCP
CATABTCBT
从而定义复合变换
。
同理得出:
由这些矢量描述的空间称为关节空间。
• 正向运动学:关节空间末端笛卡儿空间,单射 • 逆向运动学:末端笛卡儿空间关节空间,复射
不同的关节空间,相同的 末端笛卡儿空间
关节空间与末端笛卡儿空 间映射关系
第三章 机器人的运动学
3.1 工业机器人运动学
,它的齐
次坐标就是
,即满足Px=ωPx/ω,Py=ωPy/ω,
Pz=ωPz/ω(ω是非零整数)。可以看出,在三维直角坐标系中,
由于ω取值的不同,一个点的齐次坐标的表达不唯一。
齐次坐标不仅可以规定点的位置(ω为非零整数),还可以
用来规定矢量的方向(第四个元素为零时)。列向量
(
)表示空间的无穷远点,a,b和c称为它的方向
单位主矢量相对于坐标系{A}的方向余弦组成:
xB
yB
zB
xA
yA
zA
其中:co scoxB s ,xA ()
既表示了刚体F在{A}系中的方位,也描述了{B}系在{A}系中的 姿态。
3.1.2.2 坐标变换
一、坐标平移
如图3-5,坐标系{B}与{A} 方向相同,但原点不重合。
图3-5 坐标平移
此式称为平移方程。其中 是B系中的原点在A系中的表示。
0
0
0
1
1
1
给定坐标系{A},{B}和{C},已知{B}相对{A}的描述为 ,
{C}相对{B}的描述为
AP A BTBP BPC BTCP APC ATCP
,则有
APA BTC BTCP
CATABTCBT
从而定义复合变换
。
同理得出:
工业机器人运动学课件

06
机器人运动学实验与案例分 析
基于MATLAB的机器人运动学仿真实验
• 实验目的:通过MATLAB软件对工业机器人进行运动学仿真,分析机器人的运 动学性能,为机器人的优化设计和控制提供理论支持。
基于MATLAB的机器人运动学仿真实验
实验步骤
1. 建立机器人运动学模型:根据机器人的实际结构和参数,建立相应的运动学模型。
分类
根据应用场景和功能,工业机器 人可分为搬运机器人、装配机器 人、喷涂机器人等。
机器人运动学的研究内容与方法
研究内容
机器人运动学主要研究机器人的运动 规律及其与机械系统之间的关系。
研究方法
基于几何学和代数的运动学分析方法, 如D-H参数法、雅可比矩阵法等。
机器人运动学的发展与应用
发展历程
从第一台工业机器人的诞生到现在,机器人运动学经历了多个发展阶段,包括 技术突破、优化改进和跨界融合等。
基于梯度下降法的优化算法
梯度下降法是一种常用的优化算法,它通过不断调整变量的值,使得目标函数的值逐渐减 小,最终得到最优解。在机器人轨迹规划中,梯度下降法可以用来优化机器人的运动轨迹, 以满足机器人的运动性能要求。
基于遗传算法的优化算法
遗传算法是一种基于生物进化原理的优化算法,它通过模拟生物进化过程中的选择、交叉 和变异等过程,寻找最优解。在机器人轨迹规划中,遗传算法可以用来优化机器人的运动 轨迹,以满足机器人的运动性能要求。
求解方法
通过已知的末端执行器位置和姿态,建立数学方程, 求解关节角。
05
机器人轨迹规划
机器人轨迹规划的基本概念
轨迹规划定义
轨迹规划是指根据给定的路径条件,通过计算得到机器人末端执行 器的位姿随时间变化的轨迹。
机器人运动学正解逆解 ppt课件

§1.4 机器人正向运动学 工业机器人的正向运动学是指已知各关节的类型、相邻
关节之间的尺寸和相邻关节相对运动量的大小时,如何确 定工业机器人末端操作器在固定坐标系中的位姿。
主要包括以下内容: 1) 相对杆件的坐标系的确定; 2) 建立各连杆的模型矩阵A; 3) 正运动学算法;
1
D-H表示法
学习目标:1. 理解D-H法原理 2. 学会用D-H法对机器人建模
x3
连杆4
y3
O3
连杆3
A3
d3 A2
O4
x2
z5
y5
x4
O5
y4
z2
y2
关节3
A1 连杆2
O2 坐标系2
x5
o3 , o4 , o5重 合 d4 d5 0
关节2 O1
z1
坐标系1
y1 连杆1
x1
d2
关节1 坐标系0
ai—沿 xi 轴, zi-1 轴与 xi 轴交点到Oi 的距离 αi — 绕 xi 轴,由 zi-1 转向zi di — 沿 zi-1 轴,zi-1 轴和 xi 交点至Oi –1 坐标
例1:Stanford机器人运动学方程
10
• 为右手坐标系 • 原点Oi: Ai与Ai+1关节轴线的交点
A6
y6
z6
A5
连杆5
• zi轴:与Ai+1关节轴重合,指向任意
x6
O6
关节6
关节5 坐标系4
• xi轴: Zi和Zi-1构成的面的法线 • yi轴:按右手定则
坐标系5
d6 z4
A4 z3
关节4 坐标系3
0
900
5
θ5 (0) 0
0 -900
关节之间的尺寸和相邻关节相对运动量的大小时,如何确 定工业机器人末端操作器在固定坐标系中的位姿。
主要包括以下内容: 1) 相对杆件的坐标系的确定; 2) 建立各连杆的模型矩阵A; 3) 正运动学算法;
1
D-H表示法
学习目标:1. 理解D-H法原理 2. 学会用D-H法对机器人建模
x3
连杆4
y3
O3
连杆3
A3
d3 A2
O4
x2
z5
y5
x4
O5
y4
z2
y2
关节3
A1 连杆2
O2 坐标系2
x5
o3 , o4 , o5重 合 d4 d5 0
关节2 O1
z1
坐标系1
y1 连杆1
x1
d2
关节1 坐标系0
ai—沿 xi 轴, zi-1 轴与 xi 轴交点到Oi 的距离 αi — 绕 xi 轴,由 zi-1 转向zi di — 沿 zi-1 轴,zi-1 轴和 xi 交点至Oi –1 坐标
例1:Stanford机器人运动学方程
10
• 为右手坐标系 • 原点Oi: Ai与Ai+1关节轴线的交点
A6
y6
z6
A5
连杆5
• zi轴:与Ai+1关节轴重合,指向任意
x6
O6
关节6
关节5 坐标系4
• xi轴: Zi和Zi-1构成的面的法线 • yi轴:按右手定则
坐标系5
d6 z4
A4 z3
关节4 坐标系3
0
900
5
θ5 (0) 0
0 -900
