热学第三章习题参考答案
物理化学课后答案 第三章 热力学第二定律

第三章热力学第二定律3.1卡诺热机在的高温热源和的低温热源间工作。
求(1)热机效率;(2)当向环境作功时,系统从高温热源吸收的热及向低温热源放出的热。
解:卡诺热机的效率为根据定义3.5高温热源温度,低温热源。
今有120 kJ的热直接从高温热源传给低温热源,龟此过程的。
解:将热源看作无限大,因此,传热过程对热源来说是可逆过程3.6不同的热机中作于的高温热源及的低温热源之间。
求下列三种情况下,当热机从高温热源吸热时,两热源的总熵变。
(1)可逆热机效率。
(2)不可逆热机效率。
(3)不可逆热机效率。
解:设热机向低温热源放热,根据热机效率的定义因此,上面三种过程的总熵变分别为。
3.7已知水的比定压热容。
今有1 kg,10 ︒C的水经下列三种不同过程加热成100 ︒C的水,求过程的。
(1)系统与100 ︒C的热源接触。
(2)系统先与55 ︒C的热源接触至热平衡,再与100 ︒C的热源接触。
(3)系统先与40 ︒C,70 ︒C的热源接触至热平衡,再与100 ︒C的热源接触。
解:熵为状态函数,在三种情况下系统的熵变相同在过程中系统所得到的热为热源所放出的热,因此3.8已知氮(N, g)的摩尔定压热容与温度的函数关系为2(g)置于1000 K的热源中,将始态为300 K,100 kPa下1 mol的N2求下列过程(1)经恒压过程;(2)经恒容过程达到平衡态时的。
解:在恒压的情况下, g)看作理想气在恒容情况下,将氮(N2体将代替上面各式中的,即可求得所需各量3.9始态为,的某双原子理想气体1 mol,经下列不同途径变化到,的末态。
求各步骤及途径的。
(1)恒温可逆膨胀;(2)先恒容冷却至使压力降至100 kPa,再恒压加热至;(3)先绝热可逆膨胀到使压力降至100 kPa,再恒压加热至。
解:(1)对理想气体恒温可逆膨胀, U = 0,因此(2)先计算恒容冷却至使压力降至100 kPa,系统的温度T:(3)同理,先绝热可逆膨胀到使压力降至100 kPa时系统的温度T:根据理想气体绝热过程状态方程,各热力学量计算如下2.12 2 mol双原子理想气体从始态300 K,50 dm3,先恒容加热至400 K,再恒压加热至体积增大到100 dm3,求整个过程的。
热学课后习题答案

第一章温度1-1 定容气体温度计的测温泡浸在水的三相点槽内时,其中气体的压强为50mmHg。
(1)用温度计测量300K的温度时,气体的压强是多少?(2)当气体的压强为68mmHg时,待测温度是多少?解:对于定容气体温度计可知:(1)(2)1-3用定容气体温度计测量某种物质的沸点。
原来测温泡在水的三相点时,其中气体的压强;当测温泡浸入待测物质中时,测得的压强值为,当从测温泡中抽出一些气体,使减为200mmHg时,重新测得,当再抽出一些气体使减为100mmHg时,测得.试确定待测沸点的理想气体温度.解:根据从理想气体温标的定义:依以上两次所测数据,作T-P图看趋势得出时,T约为400.5K亦即沸点为400.5K.题1-4图1-6水银温度计浸在冰水中时,水银柱的长度为4.0cm;温度计浸在沸水中时,水银柱的长度为24.0cm。
(1)在室温时,水银柱的长度为多少?(2)温度计浸在某种沸腾的化学溶液中时,水银柱的长度为25.4cm,试求溶液的温度。
解:设水银柱长与温度成线性关系:当时,代入上式当,(1)(2)1-14水银气压计中混进了一个空气泡,因此它的读数比实际的气压小,当精确的气压计的读数为时,它的读数只有。
此时管内水银面到管顶的距离为。
问当此气压计的读数为时,实际气压应是多少。
设空气的温度保持不变。
题1-15图解:设管子横截面为S,在气压计读数为和时,管内空气压强分别为和,根据静力平衡条件可知,由于T、M不变根据方程有,而1-25一抽气机转速转/分,抽气机每分钟能够抽出气体,设容器的容积,问经过多少时间后才能使容器的压强由降到。
解:设抽气机每转一转时能抽出的气体体积为,则当抽气机转过一转后,容器内的压强由降到,忽略抽气过程中压强的变化而近似认为抽出压强为的气体,因而有,当抽气机转过两转后,压强为当抽气机转过n转后,压强设当压强降到时,所需时间为分,转数1-27把的氮气压入一容积为的容器,容器中原来已充满同温同压的氧气。
第三章 热力学第二定律

5. P$、273.15K 水凝结为冰,可以判断体系的下列热力学量中何者一定为零? (A) △U (B) △H (C) △S (D) △G
(
)
6. 在绝热恒容的反应器中,H2 和 Cl2 化合成 HCl,此过程中下列各状态函数的变化值哪个为零? ( ) (A) △rUm (B) △rHm (C) △rSm (D) △rGm 7. 在绝热条件下,用大于气筒内的压力,迅速推动活塞压缩气体,此过程的熵变为 (A) 大于零 (B) 等于零 (C) 小于零 (D) 不能确定 8. H2 和 O2 在绝热钢瓶中生成水的过程: (A) △H = 0 (B) △U = 0 ( )
2. 请证明下列关系式: (1) (∂H/∂V)T =T(∂p/∂T)V+V(∂p/∂V)T (2) (∂H/∂p)T =V-T(∂V/∂T)p (3) 对理想气体,证明 H 仅是温度的函数
3. 证明气体的焦尔-汤姆逊系数: μJ-T ≡ (∂T/∂P)H = (1/CP)[T(∂V/∂T)P- V]
0 S m (残余)
0,△G 0。
Ω ≠ 1 而产生的,其
=
J.K .mol 。
-1
-1
7. 一绝热容器分成两部分,分别盛温度、压力相同的 2molO2,3molN2 均为理想气体) ,抽去隔板,使两气 体混合达平衡,请计算终态与始态热力学概率之比 Ω2/Ω1 = 8. 对 1mol 范德华气体 (∂S/∂V)T = (∂P/∂T)V = 。 J。 。
9. 某气体服从状态方程 PVm= RT + αPα>0 的常数) ,若该气体经恒温可逆膨胀,其内能变化△Um=
三、计算题
1. 1 mol H2 从 100 K,4.1 dm3 加热到 600 K,49.2 dm3,若此过程是将气体置于 750K 的炉中让其反抗 101.325 kPa 的恒定外压下以不可逆方式进行,计算孤立体系的熵变。已知氢气的摩尔定容热容与温度的关 系式是:CV, m ={20.753-0.8368×10-3T/K+20.117×10-7(T/K)2} J·K-1·mol-1 2. 有一绝热、具有固定体积的容器,中间用导热隔板将容器分为体积相同的两部分,分别充以 N2 (g) 和 O2 (g),如下图:
《热学》期末复习用 各章习题+参考答案

(
29 × 10 3
)
485������
(4) 空气分子的碰撞频率为
√2������ ������
√2
6 02 × 10 × 22 4 × 10
3 3
×
(3
7 × 10−10)
× 485
(5) 空气分子的平均自由程为
7 9 × 109
������
485 7 9 × 109
6 1 × 10 8������
(������ + ������ )������������ ������ ������������ + ������ ������������
(4)
联立方程(1)(2)(3)(4)解得
������ + ������
������
2
������ ������ ������ (������ ������ + ������ ������ ) (������ + ������ )
������ (������ + ∆������) ������
������
������
(������ + ∆������) ������
������
ln
������������ ������
ln ������
������ + ∆������
ln
Hale Waihona Puke 133 101000ln
2
2
+
20 400
269
因此经过 69 × 60 40 后才能使容器内的压强由 0.101MPa 降为 133Pa.
1-7 (秦允豪 1.3.6) 一抽气机转速������ 400������ ∙ ������������������ ,抽气机每分钟能抽出气体20������.设 容器的容积������ 2 0������,问经过多长时间后才能使容器内的压强由 0.101MPa 降为 133Pa.设抽 气过程中温度始终不变.
工程热力学课后答案解析华自强张忠进(第三版)

QU2−U1He−HiW
按题意有:
Q0(绝热)
Ui0(充气前为真空)He0(无质量流出)W0(无功量交换)
因此有:
显然:
HiU2,
micpTim2cT2
mim2
因此有:
T2
cp
Ti
cν
kTi
=1.4×300
=420K=147℃
3-13图3-3所示气缸中气体为氢气。设气
0.1632
xCO2
7
125
0.056
x37.557.6
2125
x2.50.02
0.7608
(2)
H2O
M
125
1
x1x2Lxn
M1M2Mn
1
0.16320.76080.0560.02
3228
=28.8g/mol
4418
(3)
RRm8314.32.887kJ/(kg·K)
gM28.8
3-17汽油发动机吸入气缸的是空气和汽油蒸汽的混合物,
解以1kg压缩空气为研究对象,则在管内时流动空气的总
2
能量为hcf1gZ
,而终态时流动空气的总能量为
2
c2
h2
f2gZ。
2
假设q0,
w=0及cf1<<cf2,Z1=Z2,
且由附表1查得空气的比定压热容为1.004kJ/(kg·K),则喷出
气流的流速为
cf22101.004303−273245.4m/s
解由附表1查得空气的比定压热容为1.004kJ/(kg·K),则增压器消耗的功为
wsh1−h2cp(T1−T2)
=1.004(300-365.7=-65.96kJ/kg
化工热力学第三版答案第3章习题

第3章 均相封闭体系热力学原理及其应用 一、是否题1. 体系经过一绝热可逆过程,其熵没有变化。
2. 吸热过程一定使体系熵增,反之,熵增过程也是吸热的。
3. 热力学基本关系式dH=TdS+VdP 只适用于可逆过程。
4. 象dU=TdS-PdV 等热力学基本方程只能用于气体,而不能用于液体或固相。
5. 当压力趋于零时,()()0,,≡-P T M P T M ig (M 是摩尔性质)。
6.[]()0ln ,PPR P T S S ig+-与参考态的压力P 0无关。
纯物质逸度的完整定义是,在等温条件下,f RTd dG ln =。
7. 理想气体的状态方程是PV=RT ,若其中的压力P 用逸度f代替后就成为了真实流体状态方程。
8. 当0→P 时,∞→P f。
9.因为⎰⎪⎭⎫ ⎝⎛-=PdP P RT V RT1ln ϕ,当0→P 时,1=ϕ,所以,0=-P RT V 。
10. 逸度与压力的单位是相同的。
11. 吉氏函数与逸度系数的关系是()()ϕln 1,,RT P T G P T G ig ==-。
12. 由于偏离函数是两个等温状态的性质之差,故不可能用偏离函数来计算性质随着温度的变化。
13. 由于偏离函数是在均相体系中引出的概念,故我们不能用偏离函数来计算汽化过程的热力学性质的变化。
14. 由一个优秀的状态方程,就可以计算所有的均相热力学性质随着状态的变化。
二、选择题1. 对于一均匀的物质,其H 和U 的关系为(B 。
因H =U +PV ) A. H 错误!未找到引用源。
UB. H>UC. H=UD. 不能确定2. 一气体符合P=RT/(V-b)的状态方程从V 1等温可逆膨胀至V 2,则体系的错误!未找到引用源。
S 为(C 。
b V b V R dV b V R dV T P dV V S S V VV V VV V T --=-=⎪⎭⎫⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂=⎰⎰⎰12ln 212121∆)A.bV bV RT --12lnB. 0C. bV b V R --12lnD. 12ln V V R3. 对于一均相体系,VP T S T T S T ⎪⎭⎫ ⎝⎛-⎪⎭⎫⎝⎛∂∂∂∂等于(D 。
李椿热学答案及部分习题讲解部分习题的参考答案

“热学”课程第一章作业习题说明:“热学”课程作业习题全部采用教科书(李椿,章立源,钱尚武编《热学》)里各章内的习题。
第一章习题:1,2,3[1],4,5,6,8,10,11,20,24[2],25[2],26[2],27,28,29,30,31,32,33. 注:[1] 与在水的三相点时[2] 设为等温过程第一章部分习题的参考答案1.(1) –40;(2) 574.5875;(3) 不可能.2.(1) 54.9 mmHg;(2) 371 K.3. 0.99996.4. 400.574.5. 272.9.6. a = [100/(X s–X i)]⋅(︒C/[X]), b = –[100 X i/(X s–X i)]︒C, 其中的[X]代表测温性质X的单位.8. (1) –205︒C;(2) 1.049 atm.10. 0.8731 cm, 3.7165 cm.11. (1) [略];(2) 273.16︒, 273.47︒;(3) 不存在0度.20. 13.0 kg⋅m-3.24. 由教科书137页公式可得p = 3.87⨯10-3 mmHg.25. 846 kg⋅m-3.26. 40.3 s (若抽气机每旋转1次可抽气1次) 或40.0 s (若抽气机每旋转1次可抽气2次, 可参阅教科书132页).27. 28.9, 1.29 kg⋅m-3.28. 氮气的分压强为2.5 atm, 氧气的分压强为1.0 atm, 混合气体的压强为3.5 atm.29. 146.6 cm-3.30. 7.159⨯10-3 atm, 71.59 atm, 7159 atm; 4.871⨯10-4 atm, 4.871 atm, 487.1 atm.31. 341.9 K.32. 397.8 K.33. 用范德瓦耳斯方程计算得25.39 atm, 用理想气体物态方程计算得29.35 atm.“热学”课程第二章作业习题第二章习题:1,3,4,5,6,7,8,9[3],10,11,12,13[4],16,17,18,19,20.注:[3] 设为绝热容器[4] 地球和月球表面的逃逸速度分别等于11.2 km⋅s-1和2.38 km⋅s-1第二章部分习题的参考答案1. 3.22⨯103 cm-3.3. 1.89⨯1018.4. 2.33⨯10-2 Pa.5. (1) 2.45⨯1025 m-3;(2) 1.30 kg⋅m-3;(3) 5.32⨯10-26 kg;(4) 3.44⨯10-9 m;(5) 6.21⨯10-21 J.6. 3.88⨯10-2 eV,7.73⨯106 K.7. 301 K.8. 5.44⨯10-21 J.9. 6.42 K, 6.87⨯104Pa (若用范德瓦耳斯方程计算) 或6.67⨯104 Pa (若用理想气体物态方程计算).10. (1) 10.0 m⋅s-1;(2) 7.91 m⋅s-1;(3) 7.07 m⋅s-111. (1) 1.92⨯103 m⋅s-1;(2) 483 m⋅s-1;(3) 193 m⋅s-1.12. (1) 485 m⋅s-1;(2) 28.9, 可能是含有水蒸气的潮湿空气.13. 1.02⨯104 K, 1.61⨯105 K; 459 K, 7.27⨯103 K.16. (1) 1.97⨯1025 m-3 或2.00⨯1025 m-3;(2) 由教科书81页公式可得3.26⨯1027m-2或3.31⨯1027 m-2;(3) 3.26⨯1027 m-2或3.31⨯1027 m-2;(4) 7.72⨯10-21 J, 6.73⨯10-20 J.17. 由教科书81页公式可得9.26⨯10-6 g⋅cm-2⋅s-1.18. 2.933⨯10-10 m.19. 3.913⨯10-2 L, 4.020⨯10-10 m, 907.8 atm.20. (1) (V1/3 -d)3;(2) (V1/3 -d)3 - (4π/3)d3;(3) (V1/3 -d)3 - (N A - 1) ⋅(4π/3)d3;(4)因V1/3>>d,且N A>>1, 故b = V - (N A/2)⋅{(V1/3 -d)3 +[(V1/3 -d)3 - (N A - 1)⋅(4π/3)d3]}⋅(1/N A) ≈ 4N A(4π/3)(d/2)3.“热学”课程第三章作业习题第三章习题:1,2,4,5[5],6,7,9,10,11,12,13,15,16,17,18,19,20[6],22[7],23,24,25[8],26,27,28,29,30.注:[5] 设p0 = 1.00 atm[6] 分子射线中分子的平均速率等于[9πRT/(8μ)]1/2[7] 设相对分子质量等于29.0[8] f(ε)dε = 2π-1/2(kT)-3/2ε1/2e-ε/kT dε第三章部分习题的参考答案1. (1) 3.18 m⋅s-1;(2) 3.37 m⋅s-1;(3) 4.00 m⋅s-1.2. 395 m⋅s-1, 445 m⋅s-1, 483 m⋅s-1.4. 3π/8.5. 4.97⨯1016个.6. 0.9534.7. (1) 0.830 %;(2) 0.208 %;(3) 8.94⨯10-7 %.9. [2m/(πkT)]1/2.10. (1) 198 m⋅s-1;(2) 1.36⨯10-2 g⋅h-1.11. [略].12. (1) [略];(2) 1/v0;(3) v0/2.13. (1) 2N/(3v0);(2) N/3;(3) 11v0/9.15. [略].16. [略].17. 0.24 %.18. (1) 0.5724N;(2) 0.0460N.19. n[kT/(2πm)]1/2⋅[1 + (mv2/2kT)]⋅exp[ –(mv2/2kT)]或[nv p /(2π1/2)] ⋅[1 + (v2/v p2)]⋅exp[ –(v2/v p2)].20. 0.922 cm, 1.30 cm.22. 2.30 km.23. 1955 m.24. kT/2.25. f(ε)dε = 2(π)-1/2(kT)-3/2ε1/2exp[ -ε/(kT)]dε, kT/2.26. 3.74⨯103 J⋅mol-1, 2.49⨯103 J⋅mol-1.27. 6.23⨯103 J⋅mol-1, 6.23⨯103 J⋅mol-1; 3.09⨯103 J⋅g-1, 223 J⋅g-1.28. 5.83 J⋅g-1⋅K-1.29. 6.61⨯10-26 kg和39.8.30. (1) 3, 3, 6;(2) 74.8 J⋅mol-1⋅K-1.“热学”课程第四章作业习题第四章习题:1,2,4,6[7],7,8,10,11,13[2],14,15,17,18[9],19,21.注:[2] 设为等温过程[7] 设相对分子质量等于29.0[9] CO2分子的有效直径等于4.63×10-10 m第四章部分习题的参考答案1. 2.74⨯10-10 m.2. 5.80⨯10-8 m, 1.28⨯10-10 s.4. (1)5.21⨯104 Pa; (2) 3.80⨯106 m-1.6. (1) 3.22⨯1017 m-3;(2) 7.77 m (此数据无实际意义);(3) 60.2 s-1 (此数据无实际意义).7. (1) 1.40;(2) 若分子有效直径与温度无关, 则得3.45⨯10-7 m;(3) 1.08⨯10-7 m.8. (1) πd2/4;(2) [略].10. (1) 3679段;(2) 67段;(3) 2387段;(4) 37段;(5) 不能这样问.11. 3.11⨯10-5 s.13. (1) 10.1 cm;(2) 60.8 μA.14. 3.09⨯10-10 m.15. 2.23⨯10-10 m.17. (1) 2.83;(2) 0.112;(3) 0.112.18. (1) –1.03 kg⋅m-4;(2) 1.19⨯1023 s-1;(3) 1.19⨯1023 s-1;(4) 4.74⨯10-10 kg⋅s-1.19. [略].21. 提示:稳定态下通过两筒间任一同轴柱面的热流量相同.“热学”课程第五章作业习题第五章习题:1,2,3,5,7,8,10,12,13,15,16,17,18,19,21,22[10],23,24[11],25,26,27,28,29,31,33[12],34,35.注:[10] 使压强略高于大气压(设当容器中气体的温度与室温相同时其压强为p1)[11] γp0A2L2/(2V)[12] 设为实现了理想回热的循环第五章部分习题的参考答案1.(1) 623 J, 623 J, 0;(2) 623 J, 1.04⨯103 J, –416 J;(3) 623 J, 0, 623 J.2.(1) 0, –786 J, 786 J;(2) 906 J, 0, 906 J;(3) –1.42⨯103 J, –1.99⨯103 J, 567 J.3.(1) 1.50⨯10-2 m3;(2) 1.13⨯105 Pa;(3) 239 J.4.(1) 1.20;(2) –63.3 J;(3) 63.3 J;(4) 127 J.7. (1) 265 K;(2) 0.905 atm;(3) 12.0 L.8. (1) –938 J;(2) –1.44⨯103 J.10. (1) 702 J;(2) 507 J.12. [略].13. [略].15. 2.47⨯107 J⋅mol-1.16. (1) h = CT + v0p + bp2;(2) C p = C, C V= C + (a2T/b)–ap.17. –46190 J⋅mol-1.18. 82.97 %.19. [略].21. 6.70 K, 33.3 cal, 6.70 K, 46.7 cal; 11.5 K, 80.0 cal, 0, 0.22. γ = ln(p1/p0)/ln(p1/p2).23. (1) [略];(2) [略];(3) [略].24. (1) [略];(2) [略].25. (1) p0V0;(2) 1.50 T0;(3) 5.25 T0;(4) 9.5 p0V0.26. (1) [略];(2) [略];(3) [略].27. 13.4 %.28. (1) A→B为吸热过程, B→C为放热过程;(2) T C = T(V1/V2)γ– 1, V C = V2;(3) 不是;(4) 1 – {[1 – (V1/V2)γ– 1]/[(γ– 1)ln(V2/V1)]}.29. [略].31. 15.4 %.33. [略].34. [略].35. [略].“热学”课程第六章作业习题第六章习题:2,3,5,9,10,11,12[13],13,15,16,19.注:[13] 设为一摩尔第六章部分习题的参考答案2. 1.49⨯104 kcal.3. (1) 473 K;(2) 42.3 %.5. 93.3 K.9. (1) [略];(2) [略];(3) [略].10. [略].11. [略].12. [略].13. [略].15. ∆T = a (v2-1–v1-1)/C V = –3.24 K.16. [略].19. –a(n A–n B)2/[2C V V(n A+ n B)].“热学”课程第七章作业习题第七章习题:8.第七章部分习题的参考答案8. 提示:在小位移的情况下, exp[ -(cx2-gx3-fx4)/(kT)]≈ exp[ -cx2/(kT)]⋅{1 + [gx3/(kT)]}⋅{1 + [fx4/(kT)]}≈ exp[ -cx2/(kT)]⋅{1 + [gx3/(kT)] + [fx4/(kT)]}.“热学”课程第八章作业习题第八章习题:1,2,3,4,6,7[14],8,10.注:[14] 设θ= 0第八章部分习题的参考答案1. 2.19⨯108 J.2. 7.24⨯10-2 N⋅m-1.3. 1.29⨯105 Pa.4. 1.27⨯104 Pa.6. f = S[α(R1-1 + R2-1) – (ρgh/2)]= {Sα⋅[2cos(π–θ)]/[2(S/π)1/2 ⋅cos(π–θ) + h–h sin(π–θ)]} +{Sα⋅[2cos(π–θ)]/h} – (Sρgh/2)≈Sα⋅[2cos(π–θ)/h]= 25.5 N.7. 0.223 m.8. 2.98⨯10-2 m.10. (1) 0.712 m; (2) 9.60⨯104 Pa; (3) 2.04⨯10-2 m.“热学”课程第九章作业习题第九章习题:1,2,4[15],6[5],7,8,9[16],11,12,13[17].注:[5] 设p0 = 1.00 atm[15] 水蒸气比体积为1.671 m3/kg[16] 100℃时水的饱和蒸气压为1.013×105Pa,而汽化热为2.38×106 J⋅kg -1,由题8中的[17] 23.03 - 3754/T第九章部分习题的参考答案1. 3.21⨯103 J.2. (1) 6.75⨯10-3 m3;(2) 1.50⨯10-5 m3;(3) 液体体积为1.28⨯10-5 m3, 气体体积为9.87⨯10-4 m3.4. 373.52 K.6. 1.36⨯107 Pa.7. [略].8. [略].9. 1.71⨯103 Pa.11. 4.40⨯104 J⋅mol-1.12. (1) 52.0 atm;(2) 157 K.13. (1) 44.6 mmHg, 195 K;(2) 3.121⨯104 J⋅mol-1, 2.547⨯104 J⋅mol-1, 5.75⨯103 J⋅mol-1.。
工程热力学第三章课后答案

第三章 气体和蒸气的性质3−1 已知氮气的摩尔质量328.110 kg/mol M −=×,求: (1)2N 的气体常数g R ;(2)标准状态下2N 的比体积v 0和密度ρ0; (3)标准状态31m 2N 的质量m 0;(4)0.1MPa p =、500C t =D 时2N 的比体积v 和密度ρ; (5)上述状态下的摩尔体积m V 。
解:(1)通用气体常数8.3145J/(mol K)R =⋅,查附表23N 28.0110kg/mol M −=×。
22g,N 3N8.3145J/(mol K)0.297kJ/(kg K)28.0110kg/molR R M −⋅===⋅×(2)1mol 氮气标准状态时体积为22233m,N N N 22.410m /mol V M v −==×,故标准状态下2233m,N 3N 322.410m /mol 0.8m /kg28.0110kg/molV v M −−×===×223N 3N111.25kg/m 0.8m /kgv ρ===(3)标准状态下31m 气体的质量即为密度ρ,即0 1.25kg m =。
(4)由理想气体状态方程式g pv R T=g 36297J/(kg K)(500273)K2.296m /kg0.110Pa R T v p ⋅×+===×33110.4356kg/m 2.296m /kgv ρ===(5)2223333m,N N N 28.0110kg/mol 2.296m /kg 64.2910m /mol V M v −−==××=×3-2 压力表测得储气罐中丙烷38C H 的压力为4.4MPa ,丙烷的温度为120℃,问这时比体积多大?若要储气罐存1 000kg 这种状态的丙烷,问储气罐的体积需多大?解:由附表查得383C H 44.0910kg/mol M −=×3838g,C H 3C H8.3145J/(mol K)189J/(kg K)44.0910kg/molR R M −⋅===⋅×由理想气体状态方程式g pv R T=g 36189J/(kg K)(120273)K0.01688m /kg4.410PaR T v p⋅×+===×331000kg 0.01688m /kg 16.88m V mv ==×=或由理想气体状态方程g pV mR T=g 361000kg 189J/(kg K)(120273)K16.88m 4.410PamR T V p×⋅×+===×3−3 供热系统矩形风管的边长为100mm ×175mm ,40℃、102kPa 的空气在管内流动,其体积流量是0.018 5m 3/s ,求空气流速和质量流量。
工程热力学与传热学第三章作业参考答案
“山水之乐”的具体化。3.第三段同样是写“乐”,但却是写的游人之乐,作者是如何写游人之乐的?明确:“滁人游”,前呼后应,扶老携幼,自由自在,热闹非凡;“太守宴”,溪深鱼肥,泉香酒洌,美味佳肴,应有尽有;“众宾欢”,投壶下棋,觥筹交错,说说笑笑,无拘无束。如此勾画了游人之乐。4.作者为什么要在第三段写游人之乐?明确:写滁人之游,
贯穿全篇,却有两个句子别出深意,不单单是在写乐,而是另有所指,表达出另外一种情绪,请你找出这两个句子,说说这种情绪是什么。明确:醉翁之意不在酒,在乎山水之间也。醉能同其乐,醒能述以文者,太守也。这种情绪是作者遭贬谪后的抑郁,作者并未在文中袒露胸怀,只含蓄地说:“醉能同其乐,醒能述以文者,太守也。”此句与醉翁亭的名称、“醉翁之
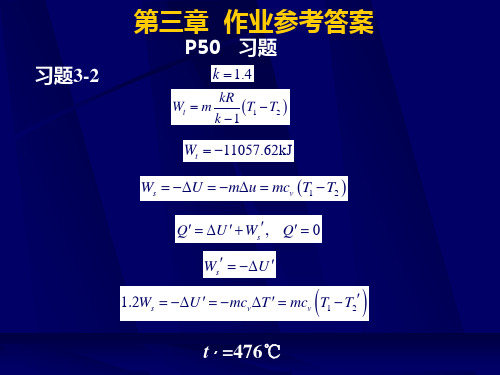
p50习题习题3214476p50习题习题33lnlnp50习题习题351331可逆绝热过程2自由膨胀lnln576kjkmcmr理想气体定值比热及比热比单原子双原子多原子摩尔定容比热ckjkmolk摩尔定压比热ckjkmolk比热比k16714129当计算精度要求不高或气体处于较低温度范围常采用定值比热忽略比热与温度的关系
Ws U mu mcv T1 T2 1746.3kJ
S 0
(2)自由膨胀
Ws 0 Q 0, U 0 T2 T1 340K
S
mcv
ln T2 T1
mR ln
v2 v1
5.76kJ/K
当计算精度要求不高,或气体处于较低温度 范围,常采用定值比热,忽略比热与温度的关系。 不同气体在标准状态下均为22.4m3,不同气体只 要其原子数相同则其摩尔定值比热相等。
江西)人,因吉州原属庐陵郡,因此他又以“庐陵欧阳修”自居。谥号文忠,世称欧阳文忠公。北宋政治家、文学家、史学家,与韩愈、柳宗元、王安石、苏洵、苏轼、苏辙、曾巩合称“唐宋八大家”。后人又将其与韩愈、柳宗元和苏轼合称“千古文章四大家”。
《传热学》课后习题答案-第三章

第三章思考题1. 试说明集总参数法的物理概念及数学处理的特点答:当内外热阻之比趋于零时,影响换热的主要环节是在边界上的换热能力。
而内部由于热阻很小而温度趋于均匀,以至于不需要关心温度在空间的分布,温度只是时间的函数, 数学描述上由偏微分方程转化为常微分方程、大大降低了求解难度。
2. 在用热电偶测定气流的非稳态温度场时,怎么才能改善热电偶的温度响应特性?答:要改善热电偶的温度响应特性,即最大限度降低热电偶的时间常数,形状上要降低体面比,要选择热容小的材料,要强化热电偶表面的对流换热。
3. 试说明”无限大平板”物理概念,并举出一二个可以按无限大平板处理的非稳态导热问题 答;所谓“无限大”平板,是指其长宽尺度远大于其厚度,从边缘交换的热量可以忽略 不计,当平板两侧换热均匀时,热量只垂直于板面方向流动。
如薄板两侧均匀加热或冷却、 炉墙或冷库的保温层导热等情况可以按无限大平板处理。
4. 什么叫非稳态导热的正规状态或充分发展阶段?这一阶段在物理过程及数学处理上都有些什么特点?答:非稳态导热过程进行到一定程度,初始温度分布的影响就会消失,虽然各点温度仍 随时间变化,但过余温度的比值已与时间无关,只是几何位置()和边界条件(Bi 数) 的函数,亦即无量纲温度分布不变,这一阶段称为正规状况阶段或充分发展阶段。
这一阶段的数学处理十分便利,温度分布计算只需取无穷级数的首项进行计算。
5. 有人认为,当非稳态导热过程经历时间很长时,采用图3-7记算所得的结果是错误的.理由是: 这个图表明,物体中各点的过余温度的比值与几何位置及Bi 有关,而与时间无关.但当时间趋于无限大时,物体中各点的温度应趋近流体温度,所以两者是有矛盾的。
你是否同意这种看法,说明你的理由。
答:我不同意这种看法,因为随着时间的推移,虽然物体中各点过余温度的比值不变 但各点温度的绝对值在无限接近。
这与物体中各点温度趋近流体温度的事实并不矛盾。
6. 试说明Bi 数的物理意义。
第3章多组分系统热力学习题参考答案-点评5-16

多组分系统热力学习题参考答案三、习题的主要类型1.计算溶液中由于某组分物质的量改变引起偏摩尔体积的变化以及溶液混合过程中体积的变化。
(例3-2, 例3-4)2.计算从大量或少量等物质量的A 和B 之理想混合物中分离出1mol 纯A 过程的吉布斯自由能。
(例3-6)3.由液体和固体的饱和蒸气压与温度的关系式,计算不可逆相变过程的热力学函数。
(例4-14题)4.用拉乌尔定律和亨利定律计算溶液的气、液组成以及亨利系数 (1) 根据气液平衡计算蒸气分压力。
(例3-7) (2) 根据气液平衡计算亨利系数。
(例3-8) (3) 根据稀溶液气液平衡计算溶质的溶解度。
(例3-9) (4) 计算蒸发过程中,最后一滴液体的组成。
(例3-10) (5) 根据克-克方程和拉乌尔定律,计算气、液组成。
(例3-11题) 5.逸度及活度的应用与计算(1) 气体的逸度和逸度系数的概念和计算。
(例3-5) (2) 由非理想液态混合物应用拉乌尔定律时,其浓度应以活度表示的方法计算活度。
(例3-15题)6.稀溶液依数性的计算。
(例3-12、例3-13题) 7.证明题 (1) 证明物质的摩尔分数、物质的质量摩尔浓度和量浓度三种浓度表示法之间的联系。
(例3-1)(2)证明偏摩尔体积与物质浓度之间的关系。
(例3-3题)四、精选题及其解例3-1 若以x 代表物质的摩尔分数,m 代表质量摩尔浓度,c 代表物质的量浓度。
(1)证明这三种浓度表示法有如下关系B B AB B A B B B A1.0A c M m M x c M c M m M ρ==-++式中,ρ为溶液的密度,单位为kg·m -3,A M 、B M 分别为溶剂和溶质的摩尔质量。
(2)证明当浓度很稀时有如下关系B AB B A Ac M x m M ρ==式中,A ρ为纯溶剂的密度。
证:(1)设溶剂为A ,溶质为B ,则溶液的体积(m -3)为:A AB Bn M n M V ρ+=而 B B B BB A A B B A A B B A B A B B n n x x c V n M n M x M x M M x M x M ρρρ====++-+ 故 B B B A B BAc M x c M c M ρ=-+又 B B BB A A A A A B A n x x m n M x M M x M ===-所以 B AB B A1.0m M x m M =+(2)当溶液很稀时,A ρρ→,B 0c →,B 0m → 故 B AB B A Ac M x m M ρ==【点评】 该题重点考查以x 代表的物质的摩尔分数、以m 代表的质量摩尔浓度和以c 代表的物质的量浓度的概念定义,以及他们之间的相互关系。
工程热力学第三章习题参考答案

第三章 热力学第一定律 习题参考答案思考题3-1门窗紧闭的房间……答:按题意,以房间(空气+冰箱)为对象,可看成绝热闭口系统,与外界无热量交换,Q=0电冰箱运转时,有电功输入,即W 为负值,按闭口系统能量方程:WU +Δ=0 或即热力学能增加,温度上升。
0>−=ΔW U 3-6 下列各式,适用于何种条件? 答:答案列于下表公式适用条件w du q δδ+= 闭口系统,任何工质,任何过程,不论可逆与不可逆 pdv du q +=δ 闭口系统,任何工质,可逆过程 pdv dT c q v +=δ闭口系统,理想气体,可逆过程dh q =δ 闭口系统,定压过程; 或开口系统与环境无技术功交换。
vdp dT c q v −=δ开口系统,理想气体,稳态稳流,可逆过程3-10 说明以下结论是否正确: (提示:采用推理原则,否定原则) ⑴ 气体吸热后一定膨胀,热力学能一定增加。
答:错误,如等容过程吸热后不膨胀;如不是等容过程吸热后热力学能也不一定增加,当对外净输出功量大于吸热量时,则热力学能不增加。
⑵ 气体膨胀一定对外作功。
答:错误,如气体向真空膨胀则不作功,另外气体膨胀对外作膨胀功的充要条件是:气体膨胀和要有功的传递和接受机构。
⑶ 气体压缩时,一定消耗外功。
答:错误,如处于冷却过程的简单可压缩系统,则会自发收缩(相当于被压缩),并不消耗外功。
⑷ 应设法利用烟气离开锅炉时带走的热量。
答:错误不应说设法利用烟气离开锅炉时带走的热量。
因为热量是过程量,不发生则不存在。
应该说设法利用烟气离开锅炉时带走的热能(或热焓)。
习 题3-1 已知:min 202000/400===time N hkJ q 人人求:?=ΔU 解:依题意可将礼堂看作绝热系统,思路:1、如何选取系统?2、如何建立能量方程? ⑴ 依题意,选取礼堂空气为系统,人看作环境,依热力学第一定律,建立能量方程:kJ time N q Q U W W Q U 51067.2602020004000×=××=⋅⋅==Δ∴=−=Δ人Q⑵ 如选“人+空气”作系统, 依据热力学第一定律:W Q U −=Δ0,0,0=Δ∴==U Q W Q如何解释空气温度升高:该系统包括“人+空气”两个子系统 ,人散热给空气,热力学能降低,空气吸热,能内升高,二者热力学能代数和为零。
化工热力学习题-041111-第3章参考答案
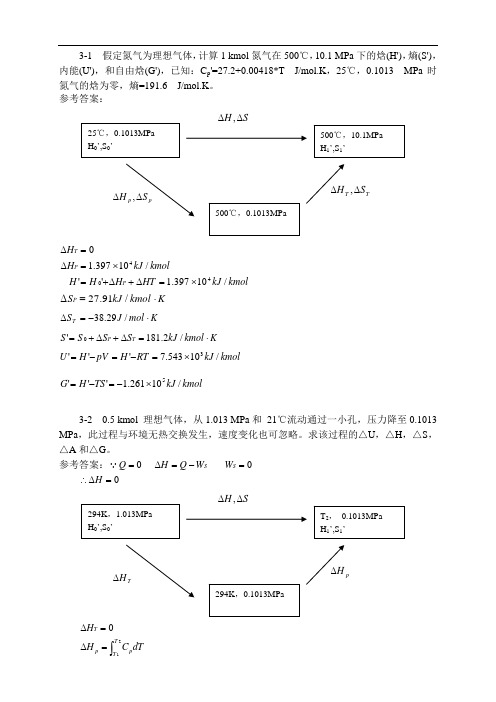
U 1.015 10 4 J / mol
V 7.518 10 4 m 3 / mol 对于 0.45kmol
H 总 1.064 10 4 450 4.788 10 6 J S 总 13.66 450 6.147 10 3 J / K V总 7.518 10 4 450 0.338m 3 U 总 1.015 10 4 450 4.568 10 6 J
pV RT 2 RT 1 0
U 0 S ST SP 19.14 J / mol
A U TS 5628J / mol
G H TS 5628 J / mol 对 0.5kmol: H 总 0 U 总 0 S总 9.571kJ / K A总 2814kJ G总 2814 kJ
3
3-5 已知 350℃,0.1013 MPa 时水蒸汽的焓为 3192 kJ/kg,用通用关系式求 10.1 MPa, 360℃时水蒸汽的焓。已知水的 Cp’=29.16 + 14.49*10-3T – 2.022*10-6T2 J/mol.K 。 参考答案:
H
623K,0.1013MPa,R.g. 633K, 10.1 MPa,R.g.
H , S
25℃,0.1013MPa H0’,S0’ 500℃,10.1MPa H1’,S1’
H p , S p
500℃,0.1013MPa
H T , S T
H T 0 HP 1.397 10 4 kJ / kmol H ' H 0' HP HT 1.397 10 4 kJ / kmol
热学答案第三章 完整版

3-14
平均自由程:
碰撞频率为:
两次碰撞的时间间隔为:
t=1/z=1.28*10-10s
3-15
当T不变时,改变压强有:
3-16
(1)
(2)
(3)
3-17
(1)
设电子直径 分子直径d
因为
所以
(2)
电子速度远大于分子,两者相对速率可以认为是电子的速度
3-18
(1)
还需要知道打入分子1的平均速率 和两种分子的平均相对速率
其中
所以:
带入理想气体状态方程: 知, 。
3.7
(1)利用范德瓦尔斯方程可知;
由理想气体状态方程知:
(2)
同理,
范:t=424.09k
理:t=424.11k
(3)
范:t=279.53k
理:t=279k
3-8
根据题意:每个分子的体积为:
d=2.92*10-10m
3.9
(1)
按照3.4.2第一段,认为分子分为六组,分别沿xyz轴正负方向运动,设有一分子沿x正向运动,t1=0时刻碰撞到容器壁,速度变为x负向,t2=L/vx时刻碰撞到对面的器壁,速度变为x正向,t3=(2L)/vx时刻再次撞击原器壁。
(2)
碰撞频率
3-19
气体分子按自由程分布:
当分子无碰撞的至少通过L的路程概率小于50%时有:
3-20
气体分子的自由程分布为
所以:
由3-17题结论可知:
3-21
(1)
气体分子按自由程分布:
所以:
(2)
由3-17题可知
所以
参考书中3.1.8公式的推到方法,将三维情况转变为二维情况,
在 中的分子数为:
热学第三章习题参考答案

热学习题答案第三章:气体分子的输运过程(内容对应参考书的第四章)1. 某一时刻,氧气中一组分子刚与其他分子碰撞过,问:经过多长时间后,其中还保留一半未与其他分子相碰。
设氧气分子都以平均速率运动,氧气温度300K ,在给定压强下,分子平均自由程为2.0cm 。
解:设这组分子个数为0N ,经过时间t (对应的路程为x )后未碰撞的分子数为N ,根据分子按自由程的分布()dx e dx x f N dN x⋅==-λλ10 由已知:t v x =,210=N N ,则有 210===⋅--λλt v x e e N N ,即2ln v t λ= 又由πμRTv 8=,mol Kg /10323-⨯=μ,代入上式得()s RT t 532101.32ln 30031.88103214.3100.22ln 8---⨯≈⨯⨯⨯⨯⨯==πμλ。
2. (P 142。
8)在气体放电管中,电子不断与气体分子相碰,因电子的速率远远大于气体分子的平均速率,所以后者可以认为是静止不动的。
设电子的“有效直径”比起气体分子的有效直径d 来可以忽略不计。
(1)电子与气体分子的碰撞截面σ为多大?(2)证明:电子与气体分子碰撞的平均自由程为σλn e 1= 解:(1)电子与气体分子的碰撞截面22⎪⎭⎫ ⎝⎛+=d d e πσ,由于d d e <<,故 22412d d d e ππσ≈⎪⎭⎫ ⎝⎛+=(2)由于气体分子可以认为是静止不动的,则电子与气体分子间的平均相对速率就等于电子的平均速率e v 。
在时间t 内,电子走过的路程为t v e ,相应的圆柱体的体积为t v e σ,则在此圆柱体内的气体分子数为t v n e σ,即为时间t 内电子与气体分子的碰撞次数,故碰撞频率为e e v n t t v n Z σσ==电子与气体分子碰撞的平均自由程为σλn Z v e e 1==。
3. (P 143。
18)一长为2m ,截面积为410-米2的管子里贮有标准状态下的2CO 气,一半2CO 分子中的C 原子是放射性同位素C 14。
《热工基础》(张学学主编)第一章-第三章参考答案

《热工基础》(张学学主编)第一章-第三章参考答案第一章思考题1.平衡状态与稳定状态有何区别?热力学中为什幺要引入平衡态的概念?答:平衡状态是在不受外界影响的条件下,系统的状态参数不随时间而变化的状态。
而稳定状态则是不论有无外界影响,系统的状态参数不随时间而变化的状态。
可见平衡必稳定,而稳定未必平衡。
热力学中引入平衡态的概念,是为了能对系统的宏观性质用状态参数来进行描述。
2.表压力或真空度能否作为状态参数进行热力计算?若工质的压力不变,问测量其压力的压力表或真空计的读数是否可能变化?答:不能,因为表压力或真空度只是一个相对压力。
若工质的压力不变,测量其压力的压力表或真空计的读数可能变化,因为测量所处的环境压力可能发生变化。
3.当真空表指示数值愈大时,表明被测对象的实际压力愈大还是愈小?答:真空表指示数值愈大时,表明被测对象的实际压力愈小。
4.准平衡过程与可逆过程有何区别?答:无耗散的准平衡过程才是可逆过程,所以可逆过程一定是准平衡过程,而准平衡过程不一定是可逆过程。
准平衡过程只注重的是系统内部而可逆过程是内外兼顾!5.不可逆过程是无法回复到初态的过程,这种说法是否正确?答:不正确。
不可逆过程是指不论用任何曲折复杂的方法都不能在外界不遗留任何变化的情况下使系统回复到初态,并不是不能回复到初态。
引起其他变化时是可以回到初态的!6.没有盛满水的热水瓶,其瓶塞有时被自动顶开,有时被自动吸紧,这是什幺原因?答:水温较高时,水对热水瓶中的空气进行加热,空气压力升高,大于环境压力,瓶塞被自动顶开。
而水温较低时,热水瓶中的空气受冷,压力降低,小于环境压力,瓶塞被自动吸紧。
大气压力改变,热水能量散失,导致内部压力改变,压力平衡打破7.用U形管压力表测定工质的压力时,压力表液柱直径的大小对读数有无影响?答:严格说来,是有影响的,因为U型管越粗,就有越多的被测工质进入U型管中,这部分工质越多,它对读数的准确性影响越大。
【单元练】人教版高中物理选修3第三章【热力学定律】经典题(含答案解析)(3)

一、选择题1.气体膨胀对外做功100 J,同时从外界吸收了120 J的热量,它的内能的变化是A.减小20 J B.增大20 J C.减小220 J D.增大220 J B解析:B由热力学第一定律得:△U=W+Q=-100J+120J=20J则气体内能增加了20J故选B。
.2.下列说法正确的是A.物体吸收热量,其温度一定升高B.热量只能从高温物体向低温物体传递C.遵守热力学第一定律的过程一定能实现D.做功和热传递是改变物体内能的两种方式D解析:DA.物体吸收热量,如果对外做功,温度可能降低,故A错;B.热量可以从低温物体向高温物体传递,但要引起其他变化,故B错;C.根据热力学第二定律,凡是与热现象有关的宏观过程都具有方向性,故C错;D.改变内能的方式有做功与热传递,两者效果相同,但本质不同,故D正确。
故选D。
3.一定质量理想气体的状态经历了如图所示的ab、bc、cd、da四个过程,其中ab与竖直轴平行,bc的延长线通过原点,cd与水平轴平行,da与bc平行,则下列说法错误..的是A.ab过程中气体内能不变B.ab过程中气体体积减少C.bc过程中其体体积保持不变D.cd过程外界对气体做功B解析:B【解析】AB、ab过程气体发生等温过程,气体内能不变,压强减小,由玻意耳定律PV=C分析可知,气体的体积变大,故A正确,B错误;C、bc过程,连线过坐标原点,则bc过程中体积不变,故C正确;D、cd过程是等压变化,温度降低,由盖•吕萨克定律分析可知体积减小,外界对气体做功,故D正确;说法错误的故选B .【点睛】本题考查理想气体状态方程和热力学第一定律,关键是会看图象,从图象中提取有用的信息是一种重要的能力.4.如图是某喷水壶示意图.未喷水时阀门K 闭合,压下压杆A 可向瓶内储气室充气,多次充气后按下按柄B 打开阀门K ,水会自动经导管从喷嘴处喷出.储气室内气体可视为理想气体,充气和喷水过程温度保持不变.则A .充气过程中,储气室内气体内能增大B .充气过程中,储气室内气体分子平均动能增大C .喷水过程中,储气室内气体放热D .喷水过程中,储气室内气体压强增大A解析:A充气过程中,储气室内气体的质量增加,气体的温度不变,故气体的平均动能不变,故气体内能增大,选项A 正确,B 错误;喷水过程中,气体对外做功,W <0;由于气体温度不变,则0E ∆=,根据E W Q ∆=+可知,储气室内气体吸热,选项C 错误;喷水过程中,储气室内气体体积增大,温度不变,则根据PV K T=可知压强减小,选项D 错误;故选A. 5.一定质量理想气体的状态经历了如图所示的ab 、bc 、cd 、da 四个过程,其中ab 与竖直轴平行,bc 的延长线通过原点,cd 与水平轴平行,da 与bc 平行,则 ( )A .ab 过程中气体温度不变,气体不吸热也不放热B .bc 过程中气体体积保持不变,气体放出热量C .cd 过程中气体体积不断增加,气体吸收热量D .da 过程中气体体积保持不变,气体放出热量B解析:B【解析】试题分析:ab 过程气体发生等温过程,压强减小,由玻意耳定律PV C =分析可知,气体的体积变大,对外做功,根据U W Q ∆=+知气体需要吸热,故A 错误;bc 过程,连线过坐标原点,则bc 过程中体积不变,温度降低,根据U W Q ∆=+知气体放热,故B 正确;cd 过程是等压变化,温度降低,由盖•吕萨克定律分析可知体积减小,根据U W Q ∆=+知气体放热,故C 错误; d a 过程,d 与绝对零度273-℃连线的斜率大于a 与绝对零度273-℃连线的斜率,则d 状态气体的体积小于a 状态气体的体积,则da 过程中体积增大,温度升高,根据U W Q ∆=+知故需要吸热,故D 错误.考点:理想气体的状态方程;热力学第一定律【名师点睛】本题考查理想气体状态方程和热力学第一定律,关键是会看图象,从图象中提取有用的信息是一种重要的能力.6.如图所示,一定质量理想气体的体积V 与温度T 关系图像,它由状态A 经等温过程到状态B ,再经等容过程到状态C 。
2021年高中物理选修三第三章《热力学定律》经典习题(答案解析)

一、选择题1.关于热学现象和热学规律,下列说法中正确的是()A.布朗运动就是液体分子的热运动B.用油膜法测分子直径的实验中,应使用纯油酸滴到水面上C.第一类永动机不可能制成是因为它违背了能量守恒定律D.用活塞压缩汽缸里的空气,对空气做功3.0×105 J,同时空气的内能增加2.2×105 J,则空气从外界吸热5.2×105 J2.下列说法正确的是()A.布朗运动是悬浮在液体中固体颗粒的分子无规则运动的反映B.内能不同的物体,它们分子热运动的平均动能可能相同C.知道某物质的摩尔质量和密度可求出阿伏加德罗常数D.没有摩擦的理想热机可以把吸收的能量全部转化为机械能3.下面的例子中,通过热传递改变物体内能的是()A.擦火柴,使火柴开始燃烧B.阳光照在湖面上,使湖水升温C.用锯条锯木头,使锯条变热D.搓搓手,会感觉暖和些4.下列说法正确的是A.物体吸收热量,其温度一定升高B.热量只能从高温物体向低温物体传递C.遵守热力学第一定律的过程一定能实现D.做功和热传递是改变物体内能的两种方式5.图为某种椅子与其升降部分的结构示意图,M、N两筒间密闭了一定质量的气体,M可沿N的内壁上下滑动,设筒内气体不与外界发生热交换,在M向下滑动的过程中A.外界对气体做功,气体内能增大B.外界对气体做功,气体内能减小C.气体对外界做功,气体内能增大D.气体对外界做功,气体内能减小6.如图所示,导热的气缸开口向下,缸内活塞封闭了一定质量的理想气体,活塞可自由滑动且不漏气,活塞下挂一个砂桶,砂桶装满砂子时,活塞恰好静止,现将砂桶底部钻一个小洞,让细砂慢慢漏出.气缸外部温度恒定不变,则A.缸内的气体压强减小,内能减小B.缸内的气体压强增大,内能减小C.缸内的气体压强增大,内能不变D.外界对气体做功,缸内的气体内能增加7.如图是某喷水壶示意图.未喷水时阀门K闭合,压下压杆A可向瓶内储气室充气,多次充气后按下按柄B打开阀门K,水会自动经导管从喷嘴处喷出.储气室内气体可视为理想气体,充气和喷水过程温度保持不变.则A.充气过程中,储气室内气体内能增大B.充气过程中,储气室内气体分子平均动能增大C.喷水过程中,储气室内气体放热D.喷水过程中,储气室内气体压强增大8.重庆出租车常以天然气作为燃料,加气站储气罐中天然气的温度随气温升高的过程中,若储气罐内气体体积及质量均不变,则罐内气体(可视为理想气体)()A.压强增大,内能减小B.吸收热量,内能增大C.压强减小,分子平均动能增大D.对外做功,分子平均动能减小9.下列说法中正确的是()A.温度低的物体内能小B.外界对物体做功时,物体的内能一定增加C.温度低的物体分子运动的平均动能小D.做加速运动的物体,由于速度越来越大,因此物体分子的平均动能越来越大10.一定质量理想气体的状态经历了如图所示的ab、bc、cd、da四个过程,其中ab与竖直轴平行,bc的延长线通过原点,cd与水平轴平行,da与bc平行,则 ( )A .ab 过程中气体温度不变,气体不吸热也不放热B .bc 过程中气体体积保持不变,气体放出热量C .cd 过程中气体体积不断增加,气体吸收热量D .da 过程中气体体积保持不变,气体放出热量11.带有活塞的汽缸内封闭一定量的理想气体。
人教版初中高中物理选修三第三章《热力学定律》经典习题(含答案解析)(1)

一、选择题1.关于热现象和热学规律,下列说法正确的是()A.只要知道气体的摩尔体积和阿伏加德罗常数,就可以算出每个气体分子的体积B.一定质量的理想气体温度升高,产生的压强一定增大C.温度一定时,悬浮在液体中的固体颗粒越大,布朗运动越明显D.第二类永动机不可能制成是因为它违反了热力学第二定律2.一定质量的理想气体(分子力不计),体积由V1膨胀到V2,如果通过压强不变的过程实现,对外做功大小为W1,传递热量的值为Q1,内能变化为∆U1;如果通过温度不变的过程来实现,对外做功大小为W2,传递热量的值为Q2,内能变化为∆U2。
则()A.W1>W2,Q1<Q2,∆U1> ∆U2B.W1>W2,Q1>Q2,∆U1> ∆U2C.W1<W2,Q1=Q2,∆U1< ∆U2D.W1=W2,Q1>Q2,∆U1> ∆U23.封闭在气缸内一定质量的理想气体由状态A经状态B、C变到状态D,其体积V与热力学温度T的关系如图所示,O、A、D三点在同一直线上。
则在此过程中()A.由A到B,气体所有分子的动能都增大B.由B到C,气体对外做功,放出热量C.由C到D,气体压强增大,内能减少D.由A到D,单位时间内与器壁单位面积碰撞的分子数减少4.一定质量的理想气体在某一过程中,气体对外界做功1.6×104J,从外界吸收热量3.8×104J,则该理想气体的()A.温度降低,密度减小B.温度降低,密度增大C.温度升高,密度减小D.温度升高,密度增大5.一定质量的理想气体,由初始状态A开始,状态变化按图中的箭头所示方向进行,最后又回到初始状态A,对于这个循环过程,以下说法正确的是()A.由A→B,气体的分子平均动能增大,放出热量B.由B→C,气体的分子数密度增大,内能减小,吸收热量C.由C→A,气体的内能减小,放出热量,外界对气体做功D.经过一个循环过程后,气体内能可能减少,也可能增加6.如图,一定质量的理想气体,由a经过ab过程到达状态b或者经过ac过程到达状态c.设气体在状态b和状态c的温度分别为T b和T c,在过程ab和ac中吸收的热量分别为Q ab和Q ac.则.A.T b>T c,Q ab>Q ac B.T b>T c,Q ab<Q acC.T b=T c,Q ab>Q ac D.T b=T c,Q ab<Q ac7.下列说法正确的是()A.物体放出热量,其内能一定减小B.物体对外做功,其内能一定减小C.物体吸收热量,同时对外做功,其内能可能增加D.物体放出热量,同时对外做功,其内能可能不变8.如图所示,A、B为两相同的绝热气缸,用绝热活塞封闭了压强、体积、温度、质量均相同的同种气体,活塞和杠杆质量不计,活塞和杠杆接触,忽略一切摩擦.O为固定轴,且MO=NO,将A中气体温度升高(变化不大)到杠杆MN重新平衡,下列说法正确的是()A.B中气体温度不变B.B中气体温度降低C.A中气体克服外力做功,外界对B气体做功D.A中气体内能增加,B中气体内能减少9.关于能量的转化与守恒,下列说法正确的是()A.任何制造永动机的设想,无论它看上去多么巧妙,都是一种徒劳B.空调机既能致热,又能致冷,说明热传递不存在方向性C.由于自然界的能量是守恒的,所以说能源危机不过是杞人忧天D.一个单摆在来回摆动许多次后总会停下来,说明这个过程的能量不守恒10.对于一定质量的理想气体,下列过程不可能发生的是()A.气体膨胀对外做功,温度升高,内能增加 B.气体吸热,温度降低,内能不变C.气体放热,压强增大,内能增大D.气体放热,温度不变,内能不变11.一定质量的理想气体,从状态M开始,经状态N、Q回到原状态M,其p—V图像如图所示,其中QM平行于横轴,NQ平行于纵轴,M、N在同一等温线上。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
热学习题答案
第三章:气体分子的输运过程(内容对应参考书的第四章)
1. 某一时刻,氧气中一组分子刚与其他分子碰撞过,问:经过多长时间后,其
中还保留一半未与其他分子相碰。
设氧气分子都以平均速率运动,氧气温度300K ,在给定压强下,分子平均自由程为2.0cm 。
解:设这组分子个数为0N ,经过时间t (对应的路程为x )后未碰撞的分子数为
N ,根据分子按自由程的分布
()dx e dx x f N dN x
⋅==-λλ
10 由已知:t v x =,2
10=N N ,则有 210===⋅--λλt v x e e N N ,即2ln v t λ= 又由πμRT
v 8=,mol Kg /10323-⨯=μ,代入上式得
()s RT t 532101.32ln 300
31.88103214.3100.22ln 8---⨯≈⨯⨯⨯⨯⨯==πμλ。
2. (P 142。
8)在气体放电管中,电子不断与气体分子相碰,因电子的速率远远
大于气体分子的平均速率,所以后者可以认为是静止不动的。
设电子的“有效直径”比起气体分子的有效直径d 来可以忽略不计。
(1)电子与气体分子的碰撞截面σ为多大?
(2)证明:电子与气体分子碰撞的平均自由程为
σ
λn e 1= 解:(1)电子与气体分子的碰撞截面22⎪⎭
⎫ ⎝⎛+=d d e πσ,由于d d e <<,故 22
412d d d e ππσ≈⎪⎭⎫ ⎝⎛+=
(2)由于气体分子可以认为是静止不动的,则电子与气体分子间的平均相对速率就等于电子的平均速率e v 。
在时间t 内,电子走过的路程为t v e ,相应的圆柱体的体积为t v e σ,则在此圆柱体内的气体分子数为t v n e σ,即为时间t 内电子与气体分子的碰撞次数,故碰撞频率为
e e v n t t v n Z σσ==
电子与气体分子碰撞的平均自由程为
σλn Z v e e 1==。
3. (P 143。
18)一长为2m ,截面积为410-米2的管子里贮有标准状态下的2CO 气,一半2
CO 分子中的C 原子是放射性同位素C 14。
在0=t 时,放射性分子密集在管子的左端,其分子数密度沿着管子均匀地减小,到右端减为零。
求:(1)开始时,放射性气体的密度梯度是多大?
(2)开始时,每秒有多少个放射性分子通过管子中点的横截面从左侧移往右侧?
(3)有多少个从右侧移往左侧?
(4)开始时,每秒通过管子横截面扩散的放射性气体为多少克?
解:(1)2CO 的摩尔质量为mol kg /10
60.42-⨯=μ,由题意,在0=t 时,管子左端和右
端的密度分别为: 32
5/05.2273
31.81060.410013.1m kg RT P A =⨯⨯⨯⨯==-μρ,0=B ρ 由于214
CO 气体分子数密度沿着管子均匀地减小,故密度梯度为常数,即 4/03.100
.205.20m kg l dl d A B -=-=-=ρρρ (2)由题意可知管子中点处214CO 气体分子的密度为2
21A M dl d l ρρρ=⨯=,根据输运过程的微观分子运动简化假设,单位时间从左侧通过管子中点处的横截面dS 移往右侧
的214
CO 分子质量为 dS v dS v n m dM 116
161ρ==+ 其中,m 为单个分子的质量,1ρ为距截面左侧λ处的放射性分子密度,有
λρρρdl d A +=
21,又因为++=mdN dM ,πμπλRT v p d kT 8,22==,有 ()15224252102322321016.31092.71000.11060.427331.8810013.11060.422731038.103.1205.21060.461002.68226261⨯+⨯=⨯⨯⨯⨯⨯⨯⨯⎥⎥⎦
⎤⎢⎢⎣
⎡⨯⨯⨯⨯⨯⨯+⨯⨯⨯=⎥⎥⎦
⎤⎢⎢⎣⎡+=⎥⎦
⎤⎢⎣⎡+==-----++πππμπρρμλρρdS RT p d kT dl d N dS v dl d m m dM dN A (3)与(2)同理可知:单位时间从右侧通过管子中点处的横截面dS 移往左侧的214
CO 分子数为 15
22221016.31092.7266161⨯-⨯=⎥⎦⎤⎢⎣⎡-====--dS v dl d N dS v m dS v n m dM dN A λρρμρ
(4)由前两问可知每秒通过管子任一横截面向右扩散的214
CO 分子的质量均相等,且随时间t 减小。
故在0=t 时 ()()g dN dN N dN dN m dM A 715232
1083.41016.321002.61060.4---+-+⨯=⨯⨯⨯⨯⨯=-=-=μ
4. (P 143。
21)两个长度均为L 的圆筒同轴地套在一起,内筒和外筒的半径分别
为1R 、2R ,内筒和外筒分别保持恒定的温度1T 、2T ,且1T >2T 。
已知两筒间空气的热导系数为κ,试证明:每秒由内筒通过空气传到外筒的热量为
()211
2ln 2T T R R L Q -=πκ 解:由于系统处于稳定状态,取一个半径为r ()21R r R ≤≤,同样为L 的共轴圆
柱面,则单位时间内通过这个面的热量Q 为恒量,由傅立叶定律有
dS dr
dT dt dQ Q κ-== 其中,rL dS π2=,将上式变形为:
dT Q
L r dr πκ2-= 对上式积分: ⎰⎰-=2
1
2121T T R R dT Q L dr r πκ 得 ()12122ln T T Q
L R R --=πκ 即 ()211
2ln 2T T R R L Q -=πκ 得证。
注意:此题与课堂上例题(悬挂在金属丝上的圆柱体套圆筒)的模型很相似,但是dS 的取法却不同,例题中取θLRd dS =,只是半径为r ()21R r R ≤≤的圆柱空气薄片上的一小部分,而本题却取整个圆柱的面积rL dS π2=,为何?
主要原因是两题求的量导致的区别:例题中求的是圆柱受到的力矩()R r =,而牛顿粘滞公式中的df 也隐含着方向,所以取面积积分元的时候也应取df 对应的作用面积元。
