北师大版八年级数学上册备课课时练习课件4.2一次函数与正比例函数
合集下载
157.19.北师大版八年级数学上册4.2 一次函数与正比例函数(课件)

古 韵 清
风
中 幽 舞
梦明
国 落 月
花, 间 。
…… …… ……
余
飞
恰惆壶红拾夜飘忆,酒世
生 茫 茫 。
只 叹 伊 人 已 去 ,
雪 , 茫 然 又 一 岁
举 杯 独 醉 , 饮 罢
如 流 年 负 了 青 春
怅 泪 溶 了 雪 ,
月 光 ? 谁 酒 三 尺
颜 刹 那 ? 谁 饮 一
弹 指 雪 花 ? 谁 痴
解: y=0.03×(x-3 500) (3500<x<5000)
(2)某人月收入为4160元,他应缴所得税多少元? 解:当x=4160时,y=0.03×(4160-3500)=19.8(元). (3)如果某人本月应缴所得税19.2元,那么此人本月 工资是多少元?
解:设此人本月工资是x元,则 19.2=0.03×(x-3500), x=4140. 答:此人本月工资是4140元.
解:(1)y=0.5x; (2)把y=10代入y=0.5x中,得10=0.5x. 解得x=20,即收割完这块麦田需要20小时.
7.一个小球由静止开始沿一个斜坡向下滚动,其 速度每秒增加2 m/s.
(1)求小球速度v(单位:m/s)关于时间t(单位: s)的函数解析式; 解:小球速度v关于时间t的函数解析式为v=2t.
解:由圆的面积公式,得y=πx2, y不是x的正比例函数,也不是x的一次函数.
(3)某水池有水15m3,现打开进水管进水,进水速 度为5m3/h,x h后这个水池有水y m3.
解:这个水池每时增加5m3水,x h增加5x m3水, 因而 y=15+5x, y是x的一次函数,但不是x的正比例函数.
例2:已知函数y=(m-5)xm2-24+m+1. (1)若它是一次函数,求m的值; (2)若它是正比例函数,求m的值.
4.2一次函数与正比例函数-2024-2025学年初中数学八年级上册(北师版)上课课件

课堂小结
若两个变量x,y间的对应关系可以表示成 y=kx+b(k,
b 是常数,k≠0)的形式,则称y是x的一次函数.
一
次
例函
函数
数与
正
比
定义
一次函数y=kx+b(k,b 是常数,k≠0),当 b=0 时,
变为 y=kx,这时称y是x正比例函数.
①寻找等量关系(有时直接将公式当做等量关
列一次函
数关系式
并且以每小时 45 公里的速度匀速行驶,t 小时后张三距离乙地
s 公里,请写出 s 和 t 的函数解析式,并计算 3 小时后,s 的值
为多少?
解:每小时行驶 45 公里,t 小时行驶了45t 公里.
函数解析式为 s = 150 -
10
45t(0≤t≤ ).
3
当 t =3 时,s =150-45×3 =15.
2.点 A(3,a)在函数 y=x+5 的图象上,则 a 的值为( B ).
A. 2
B. 8
C. -2
D. -8
解:因为点 A(3,a)在函数 y=x+5 的图象上,所以
a=3+5=8. 故应该选 B.
学习目标
1.理解正比例函数和一次函数的概念,能根据所给条件
或情境写出正比例函数和简单的一次函数的关系式.
答:y=3+0.5x.
3
4
5
4.5
5
5.5
例2 某辆汽车油箱中原有油60L,汽车每行驶50km耗油6L.
(1) 完成下表:
汽车行使路程
x/km
耗油量y/L
0
0
50
100
150
200
八年级数学上册4.2一次函数与正比例函数课件(新版)北师大版

3.若y=(m-2)x+ m2 -4是关于(guānyú)x的正比例函数,则=-m2
(guānyú)x的≠一2次函数,则m
.
;若它是关于
第八页,共24页。
【例1】写出下列各题中y与x之间的关系式,并判断y是否(shì fǒu)为x的一次函数? 是否(shì fǒu)为正比例函数?
(1)汽车以60km/h的速度匀速行驶,行驶路程y(km)与行驶时间x(h)之间的关系. (2)圆的面积y (cm2)与它的半径x (cm)之间的关系. (3)某水池有水15cm3,现打开进水管进水,进水速度为 5m3/h,x h后这个水池内有水y m3
第十九页,共24页。
【解析( jiě xī)】(1)当x≤5时,y=2x; 当x>5时,y=10+(x-5)×2.6=2.6x-3. (2)因为x=8>5 所以y=2.6×8-3=17.8(元).
第二十页,共24页。
4.(益阳·中考(zhōnɡ kǎo))我们知道,海拔高度每上升1 km,温度下降6℃. 某时刻,益阳地面温度为20℃,设高出地面x km处的温度为y℃. (1)写出y与x之间的函数关系式. (2)已知益阳碧云峰高出地面约500 m,求这时山顶的温度大约是多少℃? (3)此刻,有一架飞机飞过益阳上空,若机舱内仪表显示飞机外面的温度为34℃,求飞机离地面的高度为多少千米.
(
)√
)√
第十四页,共24页。
2. x -2 -1 0 1 2 … y -5 -2 1 4 7 …
根据上表写出y与x之间的关系式是:y=3x+1 ,可 判断(pànd是uàn)y____x的一次函数(填“是”或“不是”).
第十五页,共24页。
1.(南充·中考)如图,小球从点A运动到点B,速度(sùdù)
北师版初中数学八年级上册精品教学课件 第4章 2一次函数与正比例函数

解 (1)因为 y=(m-5)
2 -24
+n+1是一次函数,所以m2-24=1,且m-5≠0.
由m2-24=1,解得m=±5.
由m-5≠0,得m≠5.所以m=-5.
(2)因为 y=(m-5)
2 -24
+n+1 是正比例函数,
所以m2-24=1,n+1=0,且m-5≠0.
由m2-24=1,且m-5≠0,得m=-5.
(2)因为小颖家四月份的水费不超过34.5元,五月份的水费超过34.5元,
所以当y=27.6时,3.45x=27.6,解得x=8;
当y=58.65时,4.83x-13.8=58.65,解得x=15.
15-8=7(吨).
所以,小颖家五月份比四月份节约用水7吨.
本
课
结
束
由n+1=0,解得n=-பைடு நூலகம்.
【误区警示】
判断一个函数是一次函数或正比例函数,不仅要考虑自变量的次数等于1,
还不能忽视自变量的系数不能等于0这一条件.
知识点二
列关系式表示一次函数关系
【例2】 为了鼓励居民节约用水,某市采用“阶梯水价”的方法按月计算每
户家庭的水费:每月用水量不超过10吨时,按每吨3.45元计费;每月用水量超
一次函数
2
一次函数与正比例函数
核心·重难探究
知识点一
一次函数的概念
2 -24
+n+1 .
【例1】 已知函数 y=(m-5)
(1)若它是一次函数,求m的值;
(2)若它是正比例函数,求m,n的值.
思路分析 (1)一次函数中自变量x的次数等于几?x的系数有什么限制条件?
北师大版八年级数学上册:4.2 一次函数与正比例函数 课件(共31张PPT)

的一对对应值即可确定k值。
从方程角度看,如果三个量x、y、k中已知其中 两个量,则一定可以求出第三个量。
1.画函数图象需要经历哪些步骤? 列表、描点、连线。 2.你能依据这些步骤画出以上正比 例函数的图象吗?
O
在(0,0)与(1,1)之间描出二十等分点,画出y=x的图象的一段; (表格在前面的基础上加下列)
(3)京沪高铁列车从北京南站出发 2.5 h后, 是否已经过了距始发站 1100km 的南京站?
思考下列问题: 1. y 300t 中,变量和常量分别是什么?其对
应关系式是函数关系吗?谁是自变量,谁是函数?
2.自变量与常量按什么运算符号连接起来的? 3.(1)与(2)之间有何联系?(2)与(3) 呢?
形式上是一个一次单项式,单项式系数就是
比例系数k。
5.正比例函数 y kx (常数 k 0)的自变量x的 取值范围是什么?(4)的函数自变量的取值范围有 何不同?
一般情况下正比例函数自变量取值范围为一切实 数,但在特殊情况下自变量取值范围会有所不同。
6.如何理解y与x成正比例函数?反之, y kx (k
差。
c 7t 2( 5 20 t 25)
(2)一种计算成年人标准体重G(单位:kg)的方 法是:以厘米为单位量出身高值h,再减常数105,所得 差是G的值。
G h 105
(3)某城市的市内电话的月收费额y(单位:元)包括 月租费22元和拨打电话xmin的计时费(按0.1元/min收取)。
时与之对应的自变量的值。
从图象上看,方程的解是函数图象与x轴交点的横坐标。
观察下面这几个不等式:
(1) 3x 2 2 (2) 3x 2 0 (3)3x 2 1
从方程角度看,如果三个量x、y、k中已知其中 两个量,则一定可以求出第三个量。
1.画函数图象需要经历哪些步骤? 列表、描点、连线。 2.你能依据这些步骤画出以上正比 例函数的图象吗?
O
在(0,0)与(1,1)之间描出二十等分点,画出y=x的图象的一段; (表格在前面的基础上加下列)
(3)京沪高铁列车从北京南站出发 2.5 h后, 是否已经过了距始发站 1100km 的南京站?
思考下列问题: 1. y 300t 中,变量和常量分别是什么?其对
应关系式是函数关系吗?谁是自变量,谁是函数?
2.自变量与常量按什么运算符号连接起来的? 3.(1)与(2)之间有何联系?(2)与(3) 呢?
形式上是一个一次单项式,单项式系数就是
比例系数k。
5.正比例函数 y kx (常数 k 0)的自变量x的 取值范围是什么?(4)的函数自变量的取值范围有 何不同?
一般情况下正比例函数自变量取值范围为一切实 数,但在特殊情况下自变量取值范围会有所不同。
6.如何理解y与x成正比例函数?反之, y kx (k
差。
c 7t 2( 5 20 t 25)
(2)一种计算成年人标准体重G(单位:kg)的方 法是:以厘米为单位量出身高值h,再减常数105,所得 差是G的值。
G h 105
(3)某城市的市内电话的月收费额y(单位:元)包括 月租费22元和拨打电话xmin的计时费(按0.1元/min收取)。
时与之对应的自变量的值。
从图象上看,方程的解是函数图象与x轴交点的横坐标。
观察下面这几个不等式:
(1) 3x 2 2 (2) 3x 2 0 (3)3x 2 1
4.2 一次函数与正比例函数(课件)北师大版数学八年级上册

所以y=x+2 1是一次函数,但不是正比例函数.
(3)y=3x2-x(3x-2)
知1-练
解:因为y=3x2-x(3x-2)=2x,k=2,b=0,
所以它是一次函数,也是正比例函数.
(4)
y=-
3 x
因为 y=- 3x中, - 3x不是整式,所以它不是一次函数 .
知1-练
方法点拨:判断函数是否为一次函数的方法 : 先 看函数关系式是否是整式的形式,再 将函数关系式进行恒等变形,然后看 它是否符合一次函数关系式 y=k x+b(k , b 为常数, k ≠ 0)的结构特征 .
为y=kx+b(k,b是常数,k ≠ 0).
特别提醒
知1-讲
◆一次函数y=kx+b(k ≠0) 的结构特征:
(1)k ≠ 0;
(2)自变量x的次数是1;
(3) 常数项b可以是任意实数.
◆函数是一次函数⇔函数关系式为y=kx+b(k,b
是常数,k ≠ 0).
知1-练
例1 下列函数中,哪些是一次函数?哪些又是正比例函数?
2. 一次函数与正比例函数的关系
知1-讲
(1)正比例函数y=kx(k 为常数, k ≠ 0)是一次函数y=kx+
b(k, b 为常数, k ≠ 0)中b=0的特例,即正比例函数
都是一次函数,但一次函数不一定是正比例函数.
(2)若已知y与x成正比例,则可设函数关系式为y=kx
(k ≠ 0);若已知y是x的一次函数,则可设函数关系式
知2-练
(3)一棵树现在高 50 cm,每个月长高 2 cm, x 个月 后这棵树的高度为 y( cm) .
解:由题意,得 y=2x+50, 所以 y 是 x 的一次函数,但不是 x 的正比例函数 .
(3)y=3x2-x(3x-2)
知1-练
解:因为y=3x2-x(3x-2)=2x,k=2,b=0,
所以它是一次函数,也是正比例函数.
(4)
y=-
3 x
因为 y=- 3x中, - 3x不是整式,所以它不是一次函数 .
知1-练
方法点拨:判断函数是否为一次函数的方法 : 先 看函数关系式是否是整式的形式,再 将函数关系式进行恒等变形,然后看 它是否符合一次函数关系式 y=k x+b(k , b 为常数, k ≠ 0)的结构特征 .
为y=kx+b(k,b是常数,k ≠ 0).
特别提醒
知1-讲
◆一次函数y=kx+b(k ≠0) 的结构特征:
(1)k ≠ 0;
(2)自变量x的次数是1;
(3) 常数项b可以是任意实数.
◆函数是一次函数⇔函数关系式为y=kx+b(k,b
是常数,k ≠ 0).
知1-练
例1 下列函数中,哪些是一次函数?哪些又是正比例函数?
2. 一次函数与正比例函数的关系
知1-讲
(1)正比例函数y=kx(k 为常数, k ≠ 0)是一次函数y=kx+
b(k, b 为常数, k ≠ 0)中b=0的特例,即正比例函数
都是一次函数,但一次函数不一定是正比例函数.
(2)若已知y与x成正比例,则可设函数关系式为y=kx
(k ≠ 0);若已知y是x的一次函数,则可设函数关系式
知2-练
(3)一棵树现在高 50 cm,每个月长高 2 cm, x 个月 后这棵树的高度为 y( cm) .
解:由题意,得 y=2x+50, 所以 y 是 x 的一次函数,但不是 x 的正比例函数 .
北师大版八年级数学上册第四章42一次函数与正比例函数课件

1、理解一次函数和正比例函数的概念,以及它们之 间的关系; 2、能根据所给条件写出简单的一次函数表达式; 3、经历一般规律的探索过程、发展抽象思维能力; 4、通过由已知信息写一次函数表达式的过程,发展 数学应用能力。
1、什么是函数?函数有哪些表示方式?
在某个变化过程中,有两个变量x和y,如果给定 一个x值,相应地就确定一个y值,那么我们称y是 x的函数,其中x是自变量,y是因变量.
问题1.某弹簧的自然长度为3 cm,在弹性限度内,所挂 物体的质量x每增加1千克,弹簧长度y增加0.5cm. (1) 计算所挂物体的质量分别为 1 kg, 2 kg, 3 kg, 4 kg, 5 kg时的长度,并填入下表:
x/kg 0 1 2 3 4 5 y/cm 3 3.5 4 4.5 5 5.5 (2)你能写出x与y之间的关系吗?
y=3+0.5x
问题 2.某辆汽车油箱中原有油60 L,汽车每行 驶50 km耗油6 L.
(1) 完成下表:
汽车行使路 0 程x/km
50 100 150 200 300
耗油量y/L 0
6 12 18 24 36
(2) 你能写出x与y的关系吗?
(3) 你能写出油箱的剩余油量z(L)与汽车行驶路程 x(km)之间的关系吗?
例1 .写出下列各题中y与x之间的关系式,并判断: y是否为x的一次函数?是否为正比例函数? (1)汽车以60km/h的速度匀速行驶,行驶路程为y(km) 与行驶时间x(h)之间的关系;
解:y=60x y是x的一次函数,也是x的正比例函数.
例1 .写出下列各题中y与x之间的关系式,并判断: y是否为x的一次函数?是否为正比例函数? (2)一棵树现在高50cm,每个月长高2cm,x月后这棵 树的高度为ycm.
1、什么是函数?函数有哪些表示方式?
在某个变化过程中,有两个变量x和y,如果给定 一个x值,相应地就确定一个y值,那么我们称y是 x的函数,其中x是自变量,y是因变量.
问题1.某弹簧的自然长度为3 cm,在弹性限度内,所挂 物体的质量x每增加1千克,弹簧长度y增加0.5cm. (1) 计算所挂物体的质量分别为 1 kg, 2 kg, 3 kg, 4 kg, 5 kg时的长度,并填入下表:
x/kg 0 1 2 3 4 5 y/cm 3 3.5 4 4.5 5 5.5 (2)你能写出x与y之间的关系吗?
y=3+0.5x
问题 2.某辆汽车油箱中原有油60 L,汽车每行 驶50 km耗油6 L.
(1) 完成下表:
汽车行使路 0 程x/km
50 100 150 200 300
耗油量y/L 0
6 12 18 24 36
(2) 你能写出x与y的关系吗?
(3) 你能写出油箱的剩余油量z(L)与汽车行驶路程 x(km)之间的关系吗?
例1 .写出下列各题中y与x之间的关系式,并判断: y是否为x的一次函数?是否为正比例函数? (1)汽车以60km/h的速度匀速行驶,行驶路程为y(km) 与行驶时间x(h)之间的关系;
解:y=60x y是x的一次函数,也是x的正比例函数.
例1 .写出下列各题中y与x之间的关系式,并判断: y是否为x的一次函数?是否为正比例函数? (2)一棵树现在高50cm,每个月长高2cm,x月后这棵 树的高度为ycm.
北师大版八年级数学上册4.2一次函数与正比例函数(教案)

在实际问题中的应用方面,学生们表现出较高的兴趣,但他们在建立数学模型时仍存在一定难度。针对这一情况,我采用了分组讨论和实验操作的方式,让学生们亲身体验从实际问题中抽象出数学模型的过程。通过这种方式,他们能够更好地理解一次函数和正比例函数在实际生活中的应用。
在小组讨论环节,学生们积极参与,提出了许多有创意的想法。我在这个过程中扮演了一个引导者的角色,适时地提出问题,引导他们进行深入思考。从成果分享来看,学生们对一次函数与正比例函数的理解有了明显提高。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“一次函数与正比例函数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
-举例:展示不同k值的正比例函数图像,说明k值对图像斜率的影响。
(3)一次函数与正比例函数在实际问题中的应用,如线性关系的数据分析、趋势预测等。
-举例:分析某商品销售额与时间的关系,利用一次函数进行趋势预测。
2.教学难点
(1)理解一次函数图像的斜率和截距的物理意义,以及如何从图像中读取这些信息。
-难点解析:学生可能难以将图像的几何特征与函数表达式中的参数联系起来,需要通过图示和实例来强化理解。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解一次函数与正比例函数的基本概念。一次函数是形如y=kx+b的函数,其中k为斜率,b为截距;而正比例函数是特殊的一次函数,形如y=kx,它通过原点。这两个概念在描述现实世界的线性关系方面具有重要意义。
在小组讨论环节,学生们积极参与,提出了许多有创意的想法。我在这个过程中扮演了一个引导者的角色,适时地提出问题,引导他们进行深入思考。从成果分享来看,学生们对一次函数与正比例函数的理解有了明显提高。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“一次函数与正比例函数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
-举例:展示不同k值的正比例函数图像,说明k值对图像斜率的影响。
(3)一次函数与正比例函数在实际问题中的应用,如线性关系的数据分析、趋势预测等。
-举例:分析某商品销售额与时间的关系,利用一次函数进行趋势预测。
2.教学难点
(1)理解一次函数图像的斜率和截距的物理意义,以及如何从图像中读取这些信息。
-难点解析:学生可能难以将图像的几何特征与函数表达式中的参数联系起来,需要通过图示和实例来强化理解。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解一次函数与正比例函数的基本概念。一次函数是形如y=kx+b的函数,其中k为斜率,b为截距;而正比例函数是特殊的一次函数,形如y=kx,它通过原点。这两个概念在描述现实世界的线性关系方面具有重要意义。
4.2 一次函数与正比例函数 北师大版八年级上册数学习题课件

9.某天通过高速公路收费站的汽车中,共有3000辆次缴了通行费,其中大车每辆 次缴费20元,小车每辆次缴费10元.设这一天小车缴通行费的辆次为x,总的通行费 收入为y元.
(1)试写出y关于x的函数关系式(不用体现x的取值范围),y是x的一次函数吗?是正 比例函数吗?
(2)若这一天小车缴通行费的辆次为1000,则这天的通行费收入是多少元? 解:(1)y=10x+20(3000-x)=-10x+60000,y是x的一次函数,但不是x的正比例 函数 (2)当x=1000时,y=-10×1000+60000=50000(元).即若这一天小车缴通行费的 辆次为1000,则这天的通行费收入为50000元
(2)李明身上仅仅有14元,乘出租车到科技馆的费用够不够?请说明理由.
解:(1)由题意,得y=8+1.8(x-3)=1.8x+2.6(x>3)
(2)当x=6时,y=1.8×6+2.6=13.4<14,∴乘出租车到科技馆的费用够用
15.某电信公司手机的A类收费标准如下:不管通话时间多长,每部手机每月必须 缴月租费50元,另外每通话1分钟收费0.4元;B类收费标准如下:没有月租费,但每 通话1分钟收费0.6元.
8.写出下列各题中x与y的关系式,并判断y是否是x的正比例函数. (1)电报收费标准是每个字0.1元,电报费y(元)与字数(x)之间的函数关系式; (2)地面气温是28 ℃,如果每升高1 km,气温下降6 ℃,则气温y(℃)与升高的高度 x(km)的关系. 解:(1)y=0.1x,是正比例函数 (2)y=28-6x,不是正比例函数
14.某校组织学生到距离学校6 km的市科技馆参观,学生李明因事没能乘上学校 的包车,于是准备在学校门口乘出租车去科技馆.出租车的收费标准如下:
北师大版八年级上册数学4.2 一次函数与正比例函数 课件 (共16张PPT)

y=3+0.5x ,
先独立完成——小组长组织交流
1.观察上面实际问题中所得函数关系式,完成下面问题。 (1)这些函数关系式在形式上的共同点?
y=0.12x,
z=60-0.12x
(2)若两个变量 x、y之间的关系可以表示成 y=kx+b(b为常数,k≠0)的形式,则称y是x的
一次函数.(x为自变量,y为因变量.)
1.独立思考,认真完成 2.把握好时间;8分钟。
(3分钟完成,3分钟批阅,2分钟统计合格人数)
达标检测必做题和选做题答案
1.(2),(3),(5); ( 3) , ( 5 ) . 2.(1) y=15+5x (2)当y=30时,30=15+5x,解得x=3 3 即进水3小时后水池内有水30 m 3.K=3
亲爱的学生,你们好! 亲爱的孩子,你们好! 辛勤的耕耘将会化为累累硕果。为了那丰收的时刻, 辛勤的耕耘将会化为累累硕果。为 让我们一起拼搏。
m3
一加十,十加百,百加千千万, 你帮我,我帮你, 大家心相连 ,同舟嘛共济课改路, 号子嘛一喊,研讨 路。希望我们的兴平教育大发展呀!
了那丰收的时刻,让我们一起拼搏。 勤奋是舟,规律是桨,老师导航,顺利抵港。 请铭记:勤奋是舟,规律是桨,老 师导航,顺利抵港。 把握生命里的每一分钟
(1)计算所挂物体的质量分别为 1 kg, 2 kg, 3 kg,
4 kg, 5 kg时的长度,并填入下表: x/kg y/cm 0 1 2 3 4 5
3
3.5
4
ห้องสมุดไป่ตู้
4.5
5
5.5
(2)你能写出x与y之间的关系吗? y=3+0.5x
先独立完成——小组长组织交流
1.观察上面实际问题中所得函数关系式,完成下面问题。 (1)这些函数关系式在形式上的共同点?
y=0.12x,
z=60-0.12x
(2)若两个变量 x、y之间的关系可以表示成 y=kx+b(b为常数,k≠0)的形式,则称y是x的
一次函数.(x为自变量,y为因变量.)
1.独立思考,认真完成 2.把握好时间;8分钟。
(3分钟完成,3分钟批阅,2分钟统计合格人数)
达标检测必做题和选做题答案
1.(2),(3),(5); ( 3) , ( 5 ) . 2.(1) y=15+5x (2)当y=30时,30=15+5x,解得x=3 3 即进水3小时后水池内有水30 m 3.K=3
亲爱的学生,你们好! 亲爱的孩子,你们好! 辛勤的耕耘将会化为累累硕果。为了那丰收的时刻, 辛勤的耕耘将会化为累累硕果。为 让我们一起拼搏。
m3
一加十,十加百,百加千千万, 你帮我,我帮你, 大家心相连 ,同舟嘛共济课改路, 号子嘛一喊,研讨 路。希望我们的兴平教育大发展呀!
了那丰收的时刻,让我们一起拼搏。 勤奋是舟,规律是桨,老师导航,顺利抵港。 请铭记:勤奋是舟,规律是桨,老 师导航,顺利抵港。 把握生命里的每一分钟
(1)计算所挂物体的质量分别为 1 kg, 2 kg, 3 kg,
4 kg, 5 kg时的长度,并填入下表: x/kg y/cm 0 1 2 3 4 5
3
3.5
4
ห้องสมุดไป่ตู้
4.5
5
5.5
(2)你能写出x与y之间的关系吗? y=3+0.5x
北师大版八年级上册第4.2一次函数与正比例函数(教案)

另外,教学过程中,我对学生们的鼓励和表扬还不够,导致部分学生在面对困难时显得不够自信。在以后的教学中,我要更加关注学生们的情感需求,多给予鼓励和支持,帮助他们建立自信心。
最后,课后我会对今天的课堂教学进行总结,找出不足之处,不断优化教学方法,以提高教学效果。同时,我也会关注学生们的反馈,了解他们在学习过程中的需求和困难,以便更好地调整教学内容和进度。
5.情感与价值观:通过数学知识在实际生活中的应用,让学生体会数学的价值,增强学习数学的兴趣和信心,培养积极向上的学习态度。
三、教学难点与重点
1.教学重点
-函数概念的理解:强调一次函数y=kx+b(k≠0)中,k和b的含义及其对图像的影响,确保学生理解函数表达式中每个参数的核心作用。
-图像与性质的关联:通过分析一次函数的图像,让学生掌握斜率k的正负与图像走势的关系,以及截距b在图像上的表现。
-正比例函数的特殊性:明确正比例函数是一次函数的特殊情况,即b=0的情况,理解其图像始终通过原点的特点。
-函数应用能力的培养:通过实际问题的引入,让学生学会将现实问题抽象为一次函数模型,并运用函数性质解决问题。
举例:讲解一次函数的应用时,可以引用实际案例,如“小明骑自行车旅行,速度恒定,时间为t小时,行程为s公里,建立s与t的函数关系”。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。比如,用尺子和直角坐标系,让学生们手动绘制一次函数的图像。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“一次函数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
3.重点难点解析:在讲授过程中,我会特别强调一次函数的斜率k和截距b这两个重点。对于难点部分,我会通过案例和图像来帮助大家理解,比如斜率k如何影响图像的斜率和y值的变化。
最后,课后我会对今天的课堂教学进行总结,找出不足之处,不断优化教学方法,以提高教学效果。同时,我也会关注学生们的反馈,了解他们在学习过程中的需求和困难,以便更好地调整教学内容和进度。
5.情感与价值观:通过数学知识在实际生活中的应用,让学生体会数学的价值,增强学习数学的兴趣和信心,培养积极向上的学习态度。
三、教学难点与重点
1.教学重点
-函数概念的理解:强调一次函数y=kx+b(k≠0)中,k和b的含义及其对图像的影响,确保学生理解函数表达式中每个参数的核心作用。
-图像与性质的关联:通过分析一次函数的图像,让学生掌握斜率k的正负与图像走势的关系,以及截距b在图像上的表现。
-正比例函数的特殊性:明确正比例函数是一次函数的特殊情况,即b=0的情况,理解其图像始终通过原点的特点。
-函数应用能力的培养:通过实际问题的引入,让学生学会将现实问题抽象为一次函数模型,并运用函数性质解决问题。
举例:讲解一次函数的应用时,可以引用实际案例,如“小明骑自行车旅行,速度恒定,时间为t小时,行程为s公里,建立s与t的函数关系”。
2.实验操作:为了加深理解,我们将进行一个简单的实验操作。比如,用尺子和直角坐标系,让学生们手动绘制一次函数的图像。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“一次函数在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
3.重点难点解析:在讲授过程中,我会特别强调一次函数的斜率k和截距b这两个重点。对于难点部分,我会通过案例和图像来帮助大家理解,比如斜率k如何影响图像的斜率和y值的变化。
北师大版初中八年级数学上册第四章一次函数2一次函数与正比例函数课件

第四章 一次函数
2 一次函数与正比例函数
基础过关全练
知识点1 一次函数与正比例函数的概念 1.(2024福建三明期末)在下列函数中,是正比例函数的是 ( C) A.y=2x-1 B.y=-2x+1 C.y=2x D.y=2x2+1 解析 根据正比例函数的定义知选C.
2.(2023江苏徐州月考)已知函数y=(m-2)x-n-4是正比例函数, 则m,n满足 ( A ) A.m≠2,n=-4 B.m=2,n=4 C.m=2,n=-4 D.m≠2,n=4 解析 ∵函数y=(m-2)x-n-4是正比例函数, ∴m-2≠0且-n-4=0,解得m≠2,n=-4,故选A.
费恰好为10 000元.请问:该商店继续购进了多少件航天模型 玩具? 解析 (1)依题意得y=1 000(x-50)=1 000x-50 000. (2)设该商店继续购进了m件航天模型玩具,则总共有(m+ 1 000)件航天模型玩具. 依题意得(m+1 000)(60-50)×20%=10 000, 解得m=4 000. 答:该商店继续购进了4 000件航天模型玩具.
解析 (1)由题意可得, 方案一中,购买的种子数量x(千克)(x>3)和付款金额y(元)之间 的函数关系式是y=4x. 方案二中,购买的种子数量x(千克)(x>3)和付款金额y(元)之间 的函数关系式是y=5×3+5×0.7(x-3)=3.5x+4.5. (2)王伯伯要买20千克玉米种子,选方案二合适. 理由:当x=20时, 方案一的花费为4×20=80(元),方案二的花费为3.5×20+4.5 =74.5(元),
.
(2)在(1)的条件下,设某户月用水量为x m3,应交水费为y(元),
写出y与x之间的关系式.
2 一次函数与正比例函数
基础过关全练
知识点1 一次函数与正比例函数的概念 1.(2024福建三明期末)在下列函数中,是正比例函数的是 ( C) A.y=2x-1 B.y=-2x+1 C.y=2x D.y=2x2+1 解析 根据正比例函数的定义知选C.
2.(2023江苏徐州月考)已知函数y=(m-2)x-n-4是正比例函数, 则m,n满足 ( A ) A.m≠2,n=-4 B.m=2,n=4 C.m=2,n=-4 D.m≠2,n=4 解析 ∵函数y=(m-2)x-n-4是正比例函数, ∴m-2≠0且-n-4=0,解得m≠2,n=-4,故选A.
费恰好为10 000元.请问:该商店继续购进了多少件航天模型 玩具? 解析 (1)依题意得y=1 000(x-50)=1 000x-50 000. (2)设该商店继续购进了m件航天模型玩具,则总共有(m+ 1 000)件航天模型玩具. 依题意得(m+1 000)(60-50)×20%=10 000, 解得m=4 000. 答:该商店继续购进了4 000件航天模型玩具.
解析 (1)由题意可得, 方案一中,购买的种子数量x(千克)(x>3)和付款金额y(元)之间 的函数关系式是y=4x. 方案二中,购买的种子数量x(千克)(x>3)和付款金额y(元)之间 的函数关系式是y=5×3+5×0.7(x-3)=3.5x+4.5. (2)王伯伯要买20千克玉米种子,选方案二合适. 理由:当x=20时, 方案一的花费为4×20=80(元),方案二的花费为3.5×20+4.5 =74.5(元),
.
(2)在(1)的条件下,设某户月用水量为x m3,应交水费为y(元),
写出y与x之间的关系式.
北师大版八年级数学上册 4.2 一次函数与正比例函数(共18张PPT)

练一练
3.下列语句中,具有正比例函数关系的是( C).
A. 长方形花坛的面积不变, 长y与宽 x 之间的关系; B. 正方形的周长不变, 边长 x与面积 S 之间的关系; C. 三角形的一条边不变, 这条边上的高h与S之间的关系; D. 圆的面积为S , 半径为r , S 与r 之间的关系.
练一练
公 司 日 产 3200吨 熟 料水泥 生产线 项目的 顺利投 产,和日 产5000吨 项目 的快速建设,宁 东 粉 磨 站 的 正常运 行离不 开广大 员工的 艰辛付 出,离不 开各级 领导、 事业同 仁以及
一次函数
正比例函数
正比例函数是特殊的一次函数。
火眼金睛
1.在函数(1)y = —3x ,(2)y=x-5, (3) S=-4t, (4) y=2-3x ,(5)y=2x (6) y=2x2-3x,中
汽车行驶路 程x/千米
0
50
100 150 200 300
邮箱剩余油 量P/升
60
54
48
42 36 24
(3)你写出油箱剩余油量P(L)与汽车行驶路程x(km)之间 的关系式__P_=_6_0_-__0_.1_2_x_.
试一试 例2 某市为了鼓励居民节约用水,采用分段计费的方法计算水
费:每户每月用水不超过10 m3 时,每立方米按1.5元计费; 每户每月用水超过10 m3 时,其中的10 m3 仍按原标准收费,
是一次函数的是 (2) (3) (4) (5) ,是正比例函数是 (3) (5) .
2.当m= -1 时,函数 y (m1)x m - 3 是关于x的一次函数.
试一试
例1 写出下列各题中的关系式,并判断:y是否为x 的一次函数?是否为正比例函数?
北师大版八年级数学上册课件:4.2一次函数与正比例函数(共16张PPT)
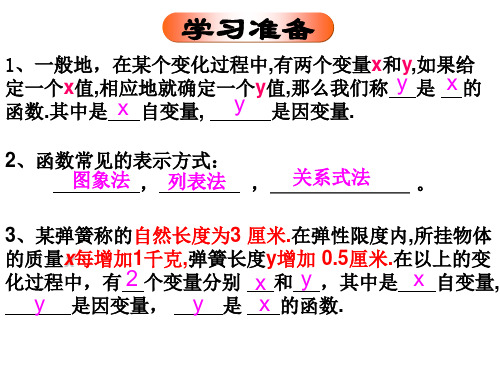
(1)汽车以60千米/时的速度匀速行驶,行驶路程为y(千米)与行驶时间x(时)之间的关系。
月收入低于3500元的部分不收税;月收入超过3500元但低于5000元的部分征收3%的所得税……
缴费多少元? 3、某弹簧称的自然长度为3 厘米.
(3)某水池有水15立方米,现打开进水管进水,进水速度为5m3/h,x小时后这个水池内有水y立方米.
之间的关系式; 3、函数y=(m+1)x+(m-2),当m 时,它是一次函数,当m= 时,它是正比例函数函数,
在弹性限度内,所挂物体的质量x每增加1千克,弹簧长度y增加 0. 在弹性限度内,所挂物体的质量x每增加1千克,弹簧长度y增加 0.
(2)某手机用户这个月通话时间为152分,他应 (3) 你能写出Z与x之间的关系式吗?
例题2
……个人…工…资、薪金所得税征收办法 月收入低于3500元的部分不收税; 月收入超过3500元但低于5000元 的部分征收3%的所得税……
(1)若某人月收入3860元,则超出3500元的部分是_3_6_0_ 元,他应缴所得税为1_0__.8_元.
(2)若某人月收入x元(x大于3500而又小于5000),则超 出3500元的部分是(__X_-3_5_0_0_)_元,你能写出应缴所得税 y(元)与月收入x(元)之间的关系式吗?
费,但每通话1分钟交费0.4元. 1、能举例说明什么是一次函数、正比例函数。
(1)若某人月收入3860元,则超出3500元的部分是____元,他应缴所得税为____元.
(1)写出每月应缴费用y(元)与通话时间x(分)之间的关系式;
(1)写出每月应缴费用y(元)与通话时间x(分) 比例函数的是 .
1、一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称 是 的函数.
月收入低于3500元的部分不收税;月收入超过3500元但低于5000元的部分征收3%的所得税……
缴费多少元? 3、某弹簧称的自然长度为3 厘米.
(3)某水池有水15立方米,现打开进水管进水,进水速度为5m3/h,x小时后这个水池内有水y立方米.
之间的关系式; 3、函数y=(m+1)x+(m-2),当m 时,它是一次函数,当m= 时,它是正比例函数函数,
在弹性限度内,所挂物体的质量x每增加1千克,弹簧长度y增加 0. 在弹性限度内,所挂物体的质量x每增加1千克,弹簧长度y增加 0.
(2)某手机用户这个月通话时间为152分,他应 (3) 你能写出Z与x之间的关系式吗?
例题2
……个人…工…资、薪金所得税征收办法 月收入低于3500元的部分不收税; 月收入超过3500元但低于5000元 的部分征收3%的所得税……
(1)若某人月收入3860元,则超出3500元的部分是_3_6_0_ 元,他应缴所得税为1_0__.8_元.
(2)若某人月收入x元(x大于3500而又小于5000),则超 出3500元的部分是(__X_-3_5_0_0_)_元,你能写出应缴所得税 y(元)与月收入x(元)之间的关系式吗?
费,但每通话1分钟交费0.4元. 1、能举例说明什么是一次函数、正比例函数。
(1)若某人月收入3860元,则超出3500元的部分是____元,他应缴所得税为____元.
(1)写出每月应缴费用y(元)与通话时间x(分)之间的关系式;
(1)写出每月应缴费用y(元)与通话时间x(分) 比例函数的是 .
1、一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称 是 的函数.
4.2 一次函数与正比例函数 知识考点梳理(课件)北师大版数学八年级上册

重
难
题
型
突
破
思路点拨
返回目录
4.2 一次函数与正比例函数
返回目录
解题通法 根据正比例函数的定义确定字母的值时 ,
重
难
题 需使比例系数和自变量的指数同时符合条件.
型
突
破
返回目录
4.2 一次函数与正比例函数
考
点
清
单
解
读
■考点二
返回目y 是 x 的函数;(2)
数关系式
分析题中等量关系列出关于变量 x 和 y 的方
的一般步
程;(3)用含 x 的代数式表示 y;(4)根
骤
据实际问题的意义注意自变量 x 的取值范围
根据列出的函数关系式还可以解决给定自变
是不是不为 0.
4.2 一次函数与正比例函数
返回目录
对点典例剖析
考
点
清
典例 1 下列函数 :①y = -2x + 1,②y= ,③y=
单
解 (x-3),④y=2x2+1中,一次函数有 _____ 个,正比例函
读
数有 ______ 个.
4.2 一次函数与正比例函数
考
点
清
单
解
读
[解题思路]
[答案] 3 1
的正比例函数
4.2 一次函数与正比例函数
返回目录
续表
考
点
清
单
解
读
(1)一次函数关系式 y=kx+b(k≠0)的条件
k≠0 千万不能忽视;(2)正比例函数是特殊的一
注意
次函数,但一次函数不一定是正比例函数;(3)
一般情况下,一次函数的自变量的取值范围是全体
难
题
型
突
破
思路点拨
返回目录
4.2 一次函数与正比例函数
返回目录
解题通法 根据正比例函数的定义确定字母的值时 ,
重
难
题 需使比例系数和自变量的指数同时符合条件.
型
突
破
返回目录
4.2 一次函数与正比例函数
考
点
清
单
解
读
■考点二
返回目y 是 x 的函数;(2)
数关系式
分析题中等量关系列出关于变量 x 和 y 的方
的一般步
程;(3)用含 x 的代数式表示 y;(4)根
骤
据实际问题的意义注意自变量 x 的取值范围
根据列出的函数关系式还可以解决给定自变
是不是不为 0.
4.2 一次函数与正比例函数
返回目录
对点典例剖析
考
点
清
典例 1 下列函数 :①y = -2x + 1,②y= ,③y=
单
解 (x-3),④y=2x2+1中,一次函数有 _____ 个,正比例函
读
数有 ______ 个.
4.2 一次函数与正比例函数
考
点
清
单
解
读
[解题思路]
[答案] 3 1
的正比例函数
4.2 一次函数与正比例函数
返回目录
续表
考
点
清
单
解
读
(1)一次函数关系式 y=kx+b(k≠0)的条件
k≠0 千万不能忽视;(2)正比例函数是特殊的一
注意
次函数,但一次函数不一定是正比例函数;(3)
一般情况下,一次函数的自变量的取值范围是全体
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3. 下列各关系中,符合正比例关系的是( A ) A. 正方形的周长C和它的边长a B. 距离s一定时,速度v和时间t
C. 圆的面积S和圆的半径r
Hale Waihona Puke D. 正方体的体积V和棱长a
4.下列函数:(1)y=4x+3;(2)y=-x; (3)y= 1 x ;
2
(4)y=x2;(5)y=1-x,其中一次函数有(C A.1个 B.2个 C.3个
4.2
一次函数与正比例函数
学习目标
1. 理解一次函数和正比例函数的概念,以及它们之 间的关系.
2. 能根据所给条件写出简单的一次函数表达式.
课前预习
1. 函数y1=-2x和y2=-3x,当y1=y2时,x=
0
.
2.下列函数中,y是x的一次函数的有 ① . 1 1 2 ①y=x-6;②y=2x +3;③y= ;④y= ; x x2 ⑤y=5;⑥y=x2.
D. y=x+30
解析
本题考查的是用一次函数解决实际问题. 设
甲、乙两个水桶中已各装了m(L),n(L)水,由“若将 甲中的水全倒入乙后,乙水桶可再装20 L的水”得y =m+n+20;由“若将乙中的水倒入甲,装满甲水 桶后,乙还剩10 L的水”得x=m+n-10. 两式相减 得y-x=30,即y=x+30. 故选D. 答案 D
新知 3
一次函数与正比例函数的应用
【例3】有甲、乙两个大小不同的水桶,容量分别为 x(L),y(L),且已各装一些水.若将甲中的水全倒入乙 后,乙水桶可再装20 L的水;若将乙中的水倒入甲, 装满甲水桶后,乙还剩10 L的水,则x,y的关系式是
(
)
A. y=20-x B. y=x+10
C. y=x+20
数的是(
A. ①⑤ C. ②⑤ 解析
)
B. ①④⑤ D. ②④⑤
解题关键是掌握一次函数的定义条件. 一次函
数y=kx+b的定义条件是:k,b为常数,k≠0,自
变量次数为1. 根据一次函数的定义条件逐一分析,①
是一次函数;②自变量次数不为1,故不是一次函数; ③自变量次数不为1,故不是一次函数;④是常数函 数;⑤是一次函数. 故选A. 答案 A
新知 2
一次函数与正比例函数的关系
当y=kx+b中的b=0时,得y=kx,我们称y是x
的正比例函数,所以正比例函数是特殊的一次函数. 我们可以说正比例函数是一次函数,但不能说一次 函数是正比例函数. 【例2】在下列函数中,x是自变量,哪些是一次函数? 哪些是正比例函数? 1 (1)y=3x;(2) y ;(3)y=-3x+1;(4)y=x2. x
举一反三 一根弹簧不挂重物时长14 cm,挂上重物后伸长的 长度与所挂重物的质量成正比.如果挂上1 kg的重物 后,弹簧伸长2 cm,求弹簧总长y(单位:cm)随所挂 物体质量x(单位:kg)变化的函数关系.
y=2x+14
解析
这类判断题,应严格按照有关函数的定义,
看函数是不是可以表示为规定的形式. 解 一次函数有(1)y=3x和(3)y=-3x+1.其中(1)y =3x还是正比例函数,(2)(4)既不是一次函数,也不是
正比例函数.
举一反三 已知函数 y = (m - 3)x3 - |m| + m + 2 ,当 m = _____ ±2 时, 它是一次函数;当m= _____ -2 时,它是正比例函数.
) D.4个
名师导学
新知 1
一次函数的概念
若两个变量x,y之间的关系式可以表示成y=kx+b(k, b为常数,k≠0)的形式,则称y是x的一次函数(x是自变量). 注意:一次函数必须符合下列两个条件:(1)关于两 个变量x,y的次数是1;(2)必须是关于两个变量的整式.
2 【例1】下列函数关系式:①y=-2x;② y ; x ③y=-2x2;④y=2;⑤y=2x-1. 其中属于一次函
