新人教版高中数学第一章导数及其应用1.3导数在研究函数中的应用1.3.3函数的最大小值与导数优化练习新人教A
(全国通用版)高中数学第一章导数及其应用1.3导数在研究函数中的应用1.3.3函数的最大小值与导数(

(2)若对x∈[-1,2],不等式f(x)<c2恒成立,求实数c的取值范围. 解 由(1)知,f(x)=x3-12x2-2x+c,x∈[-1,2], 当 x=-23时,f -23=2227+c 为极大值, 因为f(2)=2+c,所以f(2)=2+c为最大值. 要使f(x)<c2(x∈[-1,2])恒成立,只需c2>f(2)=2+c, 解得c<-1或c>2. 故实数c的取值范围为(-∞,-1)∪(2,+∞).
题型探究
类型一 由极值与最值关系求参数范围
例1 若函数f(x)=3x-x3在区间(a2-12,a)上有最小值,则实数a的取值
范围是
A.(-1, 11 )
√C.(-1,2]
B.(-1,4) D.(-1,2)
解析 答案
反思与感悟 函数在开区间内存在最值,则极值点必落在该区间内.
跟踪训练1 若函数f(x)=x3-6bx+3b在(0,1)内有最小值,则实数b的取值
12345
解析 答案
2.函数f(x)=xln x的最小值为
A.e2
B.-e
√C.-e-1
D.-130
解析 ∵f(x)=xln x,定义域是(0,+∞),
∴f′(x)=1+ln x, 令 f′(x)>0,解得 x>1e, 令 f′(x)<0,解得 0<x<1e, ∴函数在0,1e上单调递减,在1e,+∞上单调递增,
范围是
A.(0,1)
B.(-∞,1)
C.(0,+∞)
√D.0,12
解析 由题意得,函数f(x)=x3-6bx+3b的导数f′(x)=3x2-6b在(0,1)内
有零点,
且f′(0)<0,f′(1)>0,即-6b<0,且(3-6b)>0,
高中数学 第1章 导数及其应用 1.3 导数在研究函数中的应用 1.3.1 函数的单调性与导数(教师
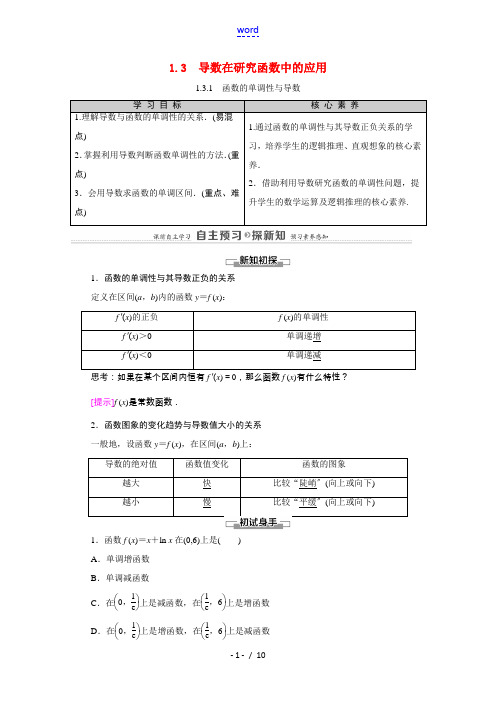
1.3 导数在研究函数中的应用1.3.1 函数的单调性与导数学 习 目 标核 心 素 养1.理解导数与函数的单调性的关系.(易混点)2.掌握利用导数判断函数单调性的方法.(重点)3.会用导数求函数的单调区间.(重点、难点)1.通过函数的单调性与其导数正负关系的学习,培养学生的逻辑推理、直观想象的核心素养.2.借助利用导数研究函数的单调性问题,提升学生的数学运算及逻辑推理的核心素养.1.函数的单调性与其导数正负的关系 定义在区间(a ,b )内的函数y =f (x ):f ′(x )的正负 f (x )的单调性 f ′(x )>0 单调递增 f ′(x )<0单调递减思考:如果在某个区间内恒有f ′(x )=0,那么函数f (x )有什么特性? [提示]f (x )是常数函数.2.函数图象的变化趋势与导数值大小的关系 一般地,设函数y =f (x ),在区间(a ,b )上:导数的绝对值函数值变化函数的图象越大 快 比较“陡峭〞(向上或向下) 越小慢比较“平缓〞(向上或向下)1.函数f (x )=x +ln x 在(0,6)上是( ) A .单调增函数 B .单调减函数C .在⎝⎛⎭⎫0,1e 上是减函数,在⎝⎛⎭⎫1e ,6上是增函数 D .在⎝⎛⎭⎫0,1e 上是增函数,在⎝⎛⎭⎫1e ,6上是减函数A[∵x∈(0,6)时,f ′(x)=1+1x>0,∴函数f (x)在(0,6)上单调递增.]2.函数y=f (x)的图象如下图,那么导函数y=f ′(x)的图象可能是()D[∵函数f (x)在(0,+∞),(-∞,0)上都是减函数,∴当x>0时,f ′(x)<0,当x<0时,f ′(x)<0.]3.函数f (x)=e x-x的单调递增区间为________.(0,+∞)[∵f (x)=e x-x,∴f ′(x)=e x-1.由f ′(x)>0得,e x-1>0,即x>0.∴f (x)的单调递增区间为(0,+∞).]函数与导函数图象间的关系象可能为()(2)f ′(x )是f (x )的导函数,f ′(x )的图象如下图,那么f (x )的图象只可能是( )(1)D (2)D [(1)由函数的图象可知:当x <0时,函数单调递增,导数始终为正;当x >0时,函数先增后减再增,即导数先正后负再正,对照选项,应选D.(2)从f ′(x )的图象可以看出,在区间⎝ ⎛⎭⎪⎫a ,a +b 2内,导数单调递增;在区间⎝ ⎛⎭⎪⎫a +b 2,b 内,导数单调递减.即函数f (x )的图象在⎝ ⎛⎭⎪⎫a ,a +b 2内越来越陡,在⎝ ⎛⎭⎪⎫a +b 2,b 内越来越平缓,由此可知,只有选项D 符合.]研究函数与导函数图象之间关系的方法研究一个函数的图象与其导函数图象之间的关系时,注意抓住各自的关键要素,对于原函数,要注意其图象在哪个区间内单调递增,在哪个区间内单调递减;而对于导函数,那么应注意其函数值在哪个区间内大于零,在哪个区间内小于零,并分析这些区间与原函数的单调区间是否一致.[跟进训练]1.y =xf ′(x )的图象如下图(其中f ′(x )是函数f (x )的导函数)下面四个图象中,y =f (x )的图象大致是( )C [当0<x <1时,xf ′(x )<0,∴f ′(x )<0,故f (x )在(0,1)上为减函数; 当x >1时,xf ′(x )>0,∴f ′(x )>0, 故y =f (x )在(1,+∞)上为增函数.应选C.]利用导数求函数的单调区间[例2] 求以下函数的单调区间. (1)f (x )=3x 2-2ln x ;(2)f (x )=x 2·e -x ; (3)f (x )=x +1x.[解](1)函数的定义域为D =(0,+∞).∵f ′(x )=6x -2x ,令f ′(x )=0,得x 1=33,x 2=-33(舍去),用x 1分割定义域D ,得下表:∴(2)函数的定义域为D =(-∞,+∞).∵f ′(x )=(x 2)′e -x +x 2(e -x )′=2x e -x -x 2e -x =e -x (2x -x 2),令f ′(x )=0,由于e -x >0,∴x 1=0,x 2=2,用x 1,x 2分割定义域D ,得下表:∴f (x )的单调递减区间为(-∞,0)和(2,+∞),单调递增区间为(0,2). (3)函数的定义域为D =(-∞,0)∪(0,+∞).∵f ′(x )=1-1x 2,令f ′(x )=0,得x 1=-1,x 2=1,用x 1,x 2分割定义域D ,得下表:∴函数f (x )的单调递减区间为(-1,0)和(0,1),单调递增区间为(-∞,-1)和(1,+∞). 角度2 含参数的函数的单调区间[例3] 讨论函数f (x )=12ax 2+x -(a +1)ln x (a ≥0)的单调性.思路探究:求函数的定义域―→求f ′(x )――――――――→分a >0,a =0解不等式f ′(x )>0或f ′(x )<0―→表述f (x )的单调性[解]函数f (x )的定义域为(0,+∞),f ′(x )=ax +1-a +1x =ax 2+x -(a +1)x.(1)当a =0时,f ′(x )=x -1x,由f ′(x )>0,得x >1, 由f ′(x )<0,得0<x <1.∴f (x )在(0,1)内为减函数,在(1,+∞)内为增函数. (2)当a >0时,f ′(x )=a ⎝⎛⎭⎪⎫x +a +1a (x -1)x,∵a >0,∴-a +1a<0.由f ′(x )>0,得x >1,由f ′(x )<0,得0<x <1. ∴f (x )在(0,1)内为减函数,在(1,+∞)内为增函数.综上所述,当a ≥0时,f (x )在(0,1)内为减函数,在(1,+∞)内为增函数.利用导数求函数单调区间的步骤(1)确定函数f (x )的定义域. (2)求导数f ′(x ).(3)由f ′(x )>0(或f ′(x )<0),解出相应的x 的X 围.当f ′(x )>0时,f (x )在相应的区间上是增函数;当f ′(x )<0时,f (x )在相应区间上是减函数.(4)结合定义域写出单调区间.[跟进训练]2.设f (x )=e x -ax -2,求f (x )的单调区间. [解]f (x )的定义域为 (-∞,+∞),f ′(x )=e x -a .假设a≤0,那么f ′(x)>0,所以f (x)在(-∞,+∞)上单调递增.假设a>0,那么当x∈(-∞,ln a)时,f ′(x)<0;当x∈(ln a,+∞)时,f ′(x)>0.所以f (x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.综上所述,当a≤0时,函数f (x)在(-∞,+∞)上单调递增;当a>0时,f (x)在(-∞,ln a)上单调递减,在(ln a,+∞)上单调递增.函数的单调性求参数的X围1.在区间(a,b)内,假设f ′(x)>0,那么f (x)在此区间上单调递增,反之也成立吗?[提示]不一定成立.比如y=x3在R上为增函数,但其在x=0处的导数等于零.也就是说f ′(x)>0是y=f (x)在某个区间上单调递增的充分不必要条件.2.假设函数f (x)为可导函数,且在区间(a,b)上是单调递增(或递减)函数,那么f ′(x)满足什么条件?[提示]f ′(x)≥0(或f ′(x)≤0).[例4]函数f (x)=x3-ax-1为单调递增函数,某某数a的取值X围.思路探究:f (x)单调递增―→f ′(x)≥0恒成立―→分离参数求a的X围[解]由得f ′(x)=3x2-a,因为f (x)在(-∞,+∞)上是单调增函数,所以f ′(x)=3x2-a≥0在(-∞,+∞)上恒成立,即a≤3x2对x∈R恒成立,因为3x2≥0,所以只需a≤0.又因为a=0时,f ′(x)=3x2≥0,f (x )=x 3-1在R 上是增函数,所以a ≤0.1.(变条件)假设函数f (x )=x 3-ax -1的单调减区间为(-1,1),求a 的取值X 围. [解]由f ′(x )=3x 2-a ,①当a ≤0时,f ′(x )≥0, ∴f (x )在(-∞,+∞)上为增函数. ②当a >0时,令3x 2-a =0,得x =±3a3, 当-3a 3<x <3a 3时,f ′(x )<0. ∴f (x )在⎝⎛⎭⎫-3a 3,3a 3上为减函数, ∴f (x )的单调递减区间为⎝⎛⎭⎫-3a 3,3a 3, ∴3a3=1,即a =3. 2.(变条件)假设函数f (x )=x 3-ax -1在(-1,1)上单调递减,求a 的X 围.[解]由题意可知f ′(x )=3x 2-a ≤0在(-1,1)上恒成立,∴⎩⎨⎧f ′(-1)≤0f ′(1)≤0,即⎩⎪⎨⎪⎧3-a ≤03-a ≤0,∴a ≥3.即a 的取值X 围是[3,+∞).3.(变条件)假设函数f (x )=x 3-ax -1在(-1,1)上不单调,求a 的X 围. [解]∵f (x )=x 3-ax -1,∴f ′(x )=3x 2-a , 由f ′(x )=0,得x =±3a3(a ≥0), ∵f (x )在区间(-1,1)上不单调, ∴0<3a3<1,即0<a <3. 故a 的取值X 围为(0,3).1.解答此题注意:可导函数f (x )在(a ,b )上单调递增(或单调递减)的充要条件是f ′(x )≥0(或f ′(x )≤0)在(a ,b )上恒成立,且f ′(x )在(a ,b )的任何子区间内都不恒等于0.2.f (x)在区间(a,b)上的单调性,求参数X围的方法(1)利用集合的包含关系处理f (x)在(a,b)上单调递增(减)的问题,那么区间(a,b)是相应单调区间的子集;(2)利用不等式的恒成立处理f (x)在(a,b)上单调递增(减)的问题,那么f ′(x)≥0(f ′(x)≤0)在(a,b)内恒成立,注意验证等号是否成立.1.导数的符号反映了函数在某个区间上的单调性,导数绝对值的大小反映了函数在某个区间或某点附近变化的快慢程度.2.利用导数求函数f (x)的单调区间的一般步骤:(1)确定函数f (x)的定义域;(2)求导数f (x);(3)在函数f (x)的定义域内解不等式f ′(x)>0和f ′(x)<0;(4)根据(3)的结果确定函数f (x)的单调区间.1.设函数f (x)的图象如下图,那么导函数f ′(x)的图象可能为()C[∵f (x)在(-∞,1),(4,+∞)上是减函数,在(1,4)上为增函数,∴当x<1或x>4时,f ′(x)<0;当1<x<4时,f ′(x)>0.应选C.]2.函数f (x)=(x-3)e x的单调递增区间是()A.(-∞,2) B.(0,3) C.(1,4) D.(2,+∞)D [∵f ′(x )=e x +(x -3)e x =(x -2)e x , 由f ′(x )>0得(x -2)e x >0,∴x >2. ∴f (x )的单调递增区间为(2,+∞).] 3.函数y =12x 2-ln x 的单调递减区间为( )A .(-1,1]B .(0,1]C .[1,+∞)D .(0,+∞)B [函数y =12x 2-ln x 的定义域为(0,+∞),y ′=x -1x =(x -1)(x +1)x ,令y ′≤0,那么可得0<x ≤1.]4.假设函数f (x )=x 3-ax 2-x +6在(0, 1)内单调递减,那么实数a 的取值X 围是( ) A .[1,+∞) B .a =1 C .(-∞,1]D .(0,1)A [∵f ′(x )=3x 2-2ax -1, 且f (x )在(0,1)内单调递减,∴不等式3x 2-2ax -1≤0在(0,1)内恒成立, ∴f ′(0)≤0, 且f ′(1)≤0,∴a ≥1.]5.求函数y =x 2-4x +a 的单调区间.[解]y ′=2x -4,令y ′>0,得x >2;令y ′<0,得x <2, 所以y =x 2-4x +a 的增区间为(2,+∞),减区间为(-∞,2).。
新版人教版高中数学教材最新目录(1)-新版.pdf

人教版普通高中课程标准实验教科书数学必修一第一章集合与函数概念1.1集合1.2函数及其表示1.3函数的基本性质第二章基本初等函数(Ⅰ)2.1指数函数2.2对数函数2.3幂函数第三章函数的应用3.1函数与方程3.2函数模型及其应用必修二第一章空间几何体1.1空间几何体的结构1.2空间几何体的三视图和直观图1.3空间几何体的表面积与体积第二章点、直线、平面之间的位置关系2.1空间点、直线、平面之间的位置关系2.2直线、平面平行的判定及其性质2.3直线、平面垂直的判定及其性质第三章直线与方程3.1直线的倾斜角与斜率3.2直线的方程3.3直线的交点坐标与距离公式必修三:第一章算法初步1.1算法与程序框图1.2基本算法语句1.3算法案例第二章统计2.1随机抽样阅读与思考一个著名的案例阅读与思考广告中数据的可靠性阅读与思考如何得到敏感性问题的诚实反应2.2用样本估计总体阅读与思考生产过程中的质量控制图2.3变量间的相关关系阅读与思考相关关系的强与弱第三章概率3.1随机事件的概率阅读与思考天气变化的认识过程3.2古典概型3.3几何概型阅读与思考概率与密码必修四:第一章三角函数1.1任意角和弧度制1.2任意角的三角函数1.3三角函数的诱导公式1.4三角函数的图象与性质1.5函数y=Asin(ωx+ψ)1.6三角函数模型的简单应用第二章平面向量2.1平面向量的实际背景及基本概念2.2平面向量的线性运算2.3平面向量的基本定理及坐标表示2.4平面向量的数量积2.5平面向量应用举例第三章三角恒等变换3.1两角和与差的正弦、余弦和正切公式3.2简单的三角恒等变换必修五:第一章解三角形1.1正弦定理和余弦定理探究与发现解三角形的进一步讨论1.2应用举例阅读与思考海伦和秦九韶1.3实习作业第二章数列2.1数列的概念与简单表示法阅读与思考斐波那契数列阅读与思考估计根号下2的值2.2等差数列2.3等差数列的前n项和2.4等比数列2.5等比数列前n项和阅读与思考九连环探究与发现购房中的数学第三章不等式3.1不等关系与不等式3.2一元二次不等式及其解法3.3二元一次不等式(组)与简单的线性规划问题阅读与思考错在哪儿信息技术应用用Excel解线性规划问题举例3.4基本不等式选修1-1第一章常用逻辑用语1.1命题及其关系1.2充分条件与必要条件1.3简单的逻辑联结词1.4全称量词与存在量词第二章圆锥曲线与方程2.1椭圆探究与发现为什么截口曲线是椭圆信息技术应用用《几何画板》探究点的轨迹:椭圆2.2双曲线2.3抛物线阅读与思考圆锥曲线的光学性质及其应用第三章导数及其应用3.1变化率与导数3.2导数的计算探究与发现牛顿法──用导数方法求方程的近似解3.3导数在研究函数中的应用信息技术应用图形技术与函数性质3.4生活中的优化问题举例实习作业走进微积分选修1-2第一章统计案例1.1回归分析的基本思想及其初步应用1.2独立性检验的基本思想及其初步应用实习作业第二章推理与证明2.1合情推理与演绎证明阅读与思考科学发现中的推理2.2直接证明与间接证明第三章数系的扩充与复数的引入3.1数系的扩充和复数的概念3.2复数代数形式的四则运算第四章框图4.1流程图4.2结构图信息技术应用用Word2002绘制流程图选修2-1:第一章常用逻辑用语1.1命题及其关系1.2充分条件与必要条件1.3简单的逻辑联结词1.4全称量词与存在量词第二章圆锥曲线与方程2.1曲线与方程2.2椭圆探究与发现为什么截口曲线是椭圆信息技术应用用《几何画板》探究点的轨迹:椭圆2.3双曲线探究与发现2.4抛物线探究与发现阅读与思考第三章空间向量与立体几何3.1空间向量及其运算阅读与思考向量概念的推广与应用3.2立体几何中的向量方法选修2-2:第一章导数及其应用1.1变化率与导数1.2导数的计算1.3导数在研究函数中的应用1.4生活中的优化问题举例1.5定积分的概念1.6微积分基本定理1.7定积分的简单应用第二章推理与证明2.1合情推理与演绎推理2.2直接证明与间接证明2.3数学归纳法第三章数系的扩充与复数的引入3.1数系的扩充和复数的概念3.2复数代数形式的四则运算选修2-3 第一章计数原理1.1分类加法计数原理与分步乘法计数原理探究与发现子集的个数有多少1.2排列与组合探究与发现组合数的两个性质1.3二项式定理探究与发现“杨辉三角”中的一些秘密第二章随机变量及其分布2.1离散型随机变量及其分布列2.2二项分布及其应用阅读与思考这样的买彩票方式可行吗探究与发现服从二项分布的随机变量取何值时概率最大2.3离散型随机变量的均值与方差2.4正态分布信息技术应用μ,σ对正态分布的影响第三章统计案例3.1回归分析的基本思想及其初步应用3.2独立性检验的基本思想及其初步应用实习作业选修3-1:第一章计数原理1.1分类加法计数原理与分步乘法计数原理探究与发现子集的个数有多少1.2排列与组合探究与发现组合数的两个性质1.3二项式定理探究与发现“杨辉三角”中的一些秘密第二章随机变量及其分布2.1离散型随机变量及其分布列2.2二项分布及其应用阅读与思考这样的买彩票方式可行吗探究与发现服从二项分布的随机变量取何值时概率最大2.3离散型随机变量的均值与方差2.4正态分布信息技术应用μ,σ对正态分布的影响第三章统计案例3.1回归分析的基本思想及其初步应用3.2独立性检验的基本思想及其初步应用实习作业选修3-3第一讲从欧氏几何看球面一平面与球面的位置关系二直线与球面的位置关系和球幂定理三球面的对称性第二讲球面上的距离和角一球面上的距离二球面上的角第三讲球面上的基本图形一极与赤道二球面二角形三球面三角形1.球面三角形2.三面角3.对顶三角形4.球极三角形第四讲球面三角形一球面三角形三边之间的关系二、球面“等腰”三角形三球面三角形的周长四球面三角形的内角和第五讲球面三角形的全等1.“边边边”(s.s.s)判定定理2.“边角边”(s.a.s.)判定定理3.“角边角”(a.s.a.)判定定理4.“角角角”(a.a.a.)判定定理第六讲球面多边形与欧拉公式一球面多边形及其内角和公式二简单多面体的欧拉公式三用球面多边形的内角和公式证明欧拉公式第七讲球面三角形的边角关系一球面上的正弦定理和余弦定理二用向量方法证明球面上的余弦定理1.向量的向量积2.球面上余弦定理的向量证明三从球面上的正弦定理看球面与平面四球面上余弦定理的应用──求地球上两城市间的距离第八讲欧氏几何与非欧几何一平面几何与球面几何的比较二欧氏平行公理与非欧几何模型──庞加莱模型三欧氏几何与非欧几何的意义阅读与思考非欧几何简史选修3-4:第一讲平面图形的对称群一平面刚体运动1.平面刚体运动的定义2.平面刚体运动的性质二对称变换1.对称变换的定义2.正多边形的对称变换3.对称变换的合成4.对称变换的性质5.对称变换的逆变换三平面图形的对称群第二讲代数学中的对称与抽象群的概念一n元对称群Sn二多项式的对称变换三抽象群的概念1.群的一般概念2.直积第三讲对称与群的故事一带饰和面饰二化学分子的对称群三晶体的分类四伽罗瓦理论选修4-1:第一讲相似三角形的判定及有关性质一平行线等分线段定理二平行线分线段成比例定理三相似三角形的判定及性质1.相似三角形的判定2.相似三角形的性质四直角三角形的射影定理第二讲直线与圆的位置关系一圆周角定理二圆内接四边形的性质与判定定理三圆的切线的性质及判定定理四弦切角的性质五与圆有关的比例线段第三讲圆锥曲线性质的探讨一平行摄影二平面与圆柱面的截线三平面与圆锥面的截线选修4-2:第一讲线性变换与二阶矩阵一线性变换与二阶矩阵(一)几类特殊线性变换及其二阶矩阵1.旋转变换2.反射变换3.伸缩变换4.投影变换5.切变变换(二)变换、矩阵的相等二二阶矩阵与平面向量的乘法(二)一些重要线性变换对单位正方形区域的作用第二讲变换的复合与二阶矩阵的乘法一复合变换与二阶矩阵的乘法二矩阵乘法的性质第三讲逆变换与逆矩阵一逆变换与逆矩阵1.逆变换与逆矩阵2.逆矩阵的性质二二阶行列式与逆矩阵三逆矩阵与二元一次方程组1.二元一次方程组的矩阵形式2.逆矩阵与二元一次方程组第四讲变换的不变量与矩阵的特征向量一变换的不变量——矩阵的特征向量1.特征值与特征向量2.特征值与特征向量的计算二特征向量的应用1.Aa的简单表示2.特征向量在实际问题中的应用选修4-5:第一讲不等式和绝对值不等式一不等式1.不等式的基本性质2.基本不等式3.三个正数的算术-几何平均不等式二绝对值不等式1.绝对值三角不等式2.绝对值不等式的解法第二讲讲明不等式的基本方法一比较法二综合法与分析法三反证法与放缩法第三讲柯西不等式与排序不等式一二维形式柯西不等式二一般形式的柯西不等式三排序不等式第四讲数学归纳法证明不等式一数学归纳法二用数学归纳法证明不等式选修4-6第一讲整数的整除一整除1.整除的概念和性质2.带余除法3.素数及其判别法二最大公因数与最小公倍数1.最大公因数2.最小公倍数三算术基本定理第二讲同余与同余方程一同余1.同余的概念2.同余的性质二剩余类及其运算三费马小定理和欧拉定理四一次同余方程五拉格朗日插值法和孙子定理六弃九验算法第三讲一次不定方程一二元一次不定方程二二元一次不定方程的特解三多元一次不定方程第四讲数伦在密码中的应用一信息的加密与去密二大数分解和公开密钥选修4-7:第一讲优选法一什么叫优选法二单峰函数三黄金分割法——0.618法1.黄金分割常数2.黄金分割法——0.618法阅读与思考黄金分割研究简史四分数法1.分数法阅读与思考斐波那契数列和黄金分割2.分数法的最优性五其他几种常用的优越法1.对分法2.盲人爬山法3.分批试验法4.多峰的情形六多因素方法1.纵横对折法和从好点出发法2.平行线法3.双因素盲人爬山法第二讲试验设计初步一正交试验设计法1.正交表2.正交试验设计3.试验结果的分析4.正交表的特性二正交试验的应用选修4-9第一讲风险与决策的基本概念一风险与决策的关系二风险与决策的基本概念1.风险(平均损失)2.平均收益3.损益矩阵4.风险型决策探究与发现风险相差不大时该如何决策第二讲决策树方法第三讲风险型决策的敏感性分析第四讲马尔可夫型决策简介一马尔可夫链简介1.马尔可夫性与马尔可夫链2.转移概率与转移概率矩阵二马尔可夫型决策简介三长期准则下的马尔可夫型决策理论1.马尔可夫链的平稳分布2.平稳分布与马尔可夫型决策的长期准则3.平稳准则的应用案例。
人教版高中数学选修2-2课后习题参考答案

新课程数学选修2(一)—2第一章课后习题解答第一章 导数及其应用 3.1变化率与导数 练习(P6)在第3 h 和5 h 时,原油温度的瞬时变化率分别为1-和3. 它说明在第3 h 附近,原油温度大约以1 ℃/h 的速度下降;在第5 h 时,原油温度大约以3 ℃/h 的速率上升.练习(P8)函数()h t 在3t t =附近单调递增,在4t t =附近单调递增. 并且,函数()h t 在4t 附近比在3t 附近增加得慢. 说明:体会“以直代曲”1的思想. 练习(P9) 函数33()4Vr V π=(05)V ≤≤的图象为根据图象,估算出(0.6)0.3r '≈,(1.2)0.2r '≈.说明:如果没有信息技术,教师可以将此图直接提供给学生,然后让学生根据导数的几何意义估算两点处的导数. 习题1.1 A 组(P10)1、在0t 处,虽然1020()()W t W t =,然而10102020()()()()W t W t t W t W t t t t--∆--∆≥-∆-∆.所以,企业甲比企业乙治理的效率高.说明:平均变化率的应用,体会平均变化率的内涵.2、(1)(1) 4.9 3.3h h t h t t t∆+∆-==-∆-∆∆,所以,(1) 3.3h '=-. 这说明运动员在1t =s 附近以3.3 m /s 的速度下降. 3、物体在第5 s 的瞬时速度就是函数()s t 在5t =时的导数.(5)(5)10s s t s t t t∆+∆-==∆+∆∆,所以,(5)10s '=. 因此,物体在第 5 s 时的瞬时速度为10 m /s ,它在第 5 s 的动能213101502k E =⨯⨯= J.4、设车轮转动的角度为θ,时间为t ,则2(0)kt t θ=>. 由题意可知,当0.8t =时,2θπ=. 所以258k π=,于是2258t πθ=.车轮转动开始后第3.2 s 时的瞬时角速度就是函数()t θ在 3.2t =时的导数.(3.2)(3.2)25208t t t t θθθππ∆+∆-==∆+∆∆,所以(3.2)20θπ'=. 因此,车轮在开始转动后第3.2 s 时的瞬时角速度为20π1s -. 说明:第2,3,4题是对了解导数定义及熟悉其符号表示的巩固.5、由图可知,函数()f x 在5x =-处切线的斜率大于零,所以函数在5x =-附近单调递增. 同理可得,函数()f x 在4x =-,2-,0,2附近分别单调递增,几乎没有变化,单调递减,单调递减. 说明:“以直代曲”思想的应用.6、第一个函数的图象是一条直线,其斜率是一个小于零的常数,因此,其导数()f x '的图象如图(1)所示;第二个函数的导数()f x '恒大于零,并且随着x 的增加,()f x '的值也在增加;对于第三个函数,当x 小于零时,()f x '小于零,当x 大于零时,()f x '大于零,并且随着x 的增加,()f x '的值也在增加. 以下给出了满足上述条件的导函数图象中的一种.说明:本题意在让学生将导数与曲线的切线斜率相联系. 习题3.1 B 组(P11)1、高度关于时间的导数刻画的是运动变化的快慢,即速度;速度关于时间的导数刻画的是速度变化的快慢,根据物理知识,这个量就是加速度.2、说明:由给出的()v t 的信息获得()s t 的相关信息,并据此画出()s t 的图象的大致形状. 这个过程基于对导数内涵的了解,以及数与形之间的相互转换.3、由(1)的题意可知,函数()f x 的图象在点(1,5)-处的切线斜率为1-,所以此点附近曲线呈下降趋势. 首先画出切线的图象,然后再画出此点附近函数的图象. 同理可得(2)(3)某点处函数图象的大致形状. 下面是一种参考答案.说明:这是一个综合性问题,包含了对导数内涵、导数几何意义的了解,以及对以直代曲思想的领悟. 本题的答案不唯一. 1.2导数的计算 练习(P18)1、()27f x x '=-,所以,(2)3f '=-,(6)5f '=.2、(1)1ln 2y x '=; (2)2x y e '=; (3)4106y x x '=-; (4)3sin 4cos y x x '=--;(5)1sin 33xy '=-; (6)21y x '=-.习题1.2 A 组(P18)1、()()2S S r r S r r r r r π∆+∆-==+∆∆∆,所以,0()lim(2)2r S r r r r ππ∆→'=+∆=. 2、()9.8 6.5h t t '=-+. 3、3213()34r V Vπ'=.4、(1)213ln 2y x x '=+; (2)1n x n x y nx e x e -'=+; (3)2323sin cos cos sin x x x x xy x -+'=; (4)9899(1)y x '=+; (5)2x y e -'=-; (6)2sin(25)4cos(25)y x x x '=+++. 5、()82f x x '=-+. 由0()4f x '=有 04822x =-+,解得032x =. 6、(1)ln 1y x '=+; (2)1y x =-. 7、1xy π=-+.8、(1)氨气的散发速度()500ln 0.8340.834t A t '=⨯⨯.(2)(7)25.5A '=-,它表示氨气在第7天左右时,以25.5克/天的速率减少. 习题1.2 B 组(P19) 1、(1)(2)当h 越来越小时,sin()sin x h xy h+-=就越来越逼近函数cos y x =.(3)sin y x =的导数为cos y x =.2、当0y =时,0x =. 所以函数图象与x 轴交于点(0,0)P .x y e '=-,所以01x y ='=-.所以,曲线在点P 处的切线的方程为y x =-.2、()4sin d t t '=-. 所以,上午6:00时潮水的速度为0.42-m /h ;上午9:00时潮水的速度为0.63-m /h ;中午12:00时潮水的速度为0.83-m /h ;下午6:00时潮水的速度为 1.24-m /h.1.3导数在研究函数中的应用 练习(P26)1、(1)因为2()24f x x x =-+,所以()22f x x '=-.当()0f x '>,即1x >时,函数2()24f x x x =-+单调递增; 当()0f x '<,即1x <时,函数2()24f x x x =-+单调递减. (2)因为()x f x e x =-,所以()1x f x e '=-.当()0f x '>,即0x >时,函数()x f x e x =-单调递增;当()0f x '<,即0x <时,函数()x f x e x =-单调递减. (3)因为3()3f x x x =-,所以2()33f x x '=-.当()0f x '>,即11x -<<时,函数3()3f x x x =-单调递增; 当()0f x '<,即1x <-或1x >时,函数3()3f x x x =-单调递减. (4)因为32()f x x x x =--,所以2()321f x x x '=--.当()0f x '>,即13x <-或1x >时,函数32()f x x x x =--单调递增;当()0f x '<,即113x -<<时,函数32()f x x x x =--单调递减.2、3、因为2()(0)f x ax bx c a =++≠,所以()2f x ax b '=+. (1)当0a >时,()0f x '>,即2bx a >-时,函数2()(0)f x ax bx c a =++≠单调递增; ()0f x '<,即2bx a<-时,函数2()(0)f x ax bx c a =++≠单调递减.(2)当0a <时,()0f x '>,即2bx a <-时,函数2()(0)f x ax bx c a =++≠单调递增;()0f x '<,即2bx a >-时,函数2()(0)f x ax bx c a =++≠单调递减.4、证明:因为32()267f x x x =-+,所以2()612f x x x '=-. 当(0,2)x ∈时,2()6120f x x x '=-<,因此函数32()267f x x x =-+在(0,2)内是减函数. 练习(P29)1、24,x x 是函数()y f x =的极值点,其中2x x =是函数()y f x =的极大值点,4x x =是函数()y f x =的极小值点. 2、(1)因为2()62f x x x =--,所以()121f x x '=-.注:图象形状不唯一.令()1210f x x '=-=,得112x =. 当112x >时,()0f x '>,()f x 单调递增;当112x <时,()0f x '<,()f x 单调递减.所以,当112x =时,()f x 有极小值,并且极小值为211149()6()212121224f =⨯--=-. (2)因为3()27f x x x =-,所以2()327f x x '=-. 令2()3270f x x '=-=,得3x =±. 下面分两种情况讨论:①当()0f x '>,即3x <-或3x >时;②当()0f x '<,即33x -<<时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当3x =-时,()f x 有极大值,并且极大值为54; 当3x =时,()f x 有极小值,并且极小值为54-. (3)因为3()612f x x x =+-,所以2()123f x x '=-. 令2()1230f x x '=-=,得2x =±. 下面分两种情况讨论:①当()0f x '>,即22x -<<时;②当()0f x '<,即2x <-或2x >时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当2x =-时,()f x 有极小值,并且极小值为10-; 当2x =时,()f x 有极大值,并且极大值为22 (4)因为3()3f x x x =-,所以2()33f x x '=-.令2()330f x x '=-=,得1x =±. 下面分两种情况讨论:①当()0f x '>,即11x -<<时;②当()0f x '<,即1x <-或1x >时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当1x =-时,()f x 有极小值,并且极小值为2-; 当1x =时,()f x 有极大值,并且极大值为2 练习(P31)(1)在[0,2]上,当112x =时,2()62f x x x =--有极小值,并且极小值为149()1224f =-. 又由于(0)2f =-,(2)20f =.因此,函数2()62f x x x =--在[0,2]上的最大值是20、最小值是4924-. (2)在[4,4]-上,当3x =-时,3()27f x x x =-有极大值,并且极大值为(3)54f -=;当3x =时,3()27f x x x =-有极小值,并且极小值为(3)54f =-; 又由于(4)44f -=,(4)44f =-.因此,函数3()27f x x x =-在[4,4]-上的最大值是54、最小值是54-.(3)在1[,3]3-上,当2x =时,3()612f x x x =+-有极大值,并且极大值为(2)22f =.又由于155()327f -=,(3)15f =.因此,函数3()612f x x x =+-在1[,3]3-上的最大值是22、最小值是5527.(4)在[2,3]上,函数3()3f x x x =-无极值. 因为(2)2f =-,(3)18f =-.因此,函数3()3f x x x =-在[2,3]上的最大值是2-、最小值是18-. 习题1.3 A 组(P31)1、(1)因为()21f x x =-+,所以()20f x '=-<. 因此,函数()21f x x =-+是单调递减函数.(2)因为()cos f x x x =+,(0,)2x π∈,所以()1sin 0f x x '=->,(0,)2x π∈.因此,函数()cos f x x x =+在(0,)2π上是单调递增函数. (3)因为()24f x x =--,所以()20f x '=-<. 因此,函数()24f x x =-是单调递减函数. (4)因为3()24f x x x =+,所以2()640f x x '=+>. 因此,函数3()24f x x x =+是单调递增函数. 2、(1)因为2()24f x x x =+-,所以()22f x x '=+.当()0f x '>,即1x >-时,函数2()24f x x x =+-单调递增. 当()0f x '<,即1x <-时,函数2()24f x x x =+-单调递减. (2)因为2()233f x x x =-+,所以()43f x x '=-.当()0f x '>,即34x >时,函数2()233f x x x =-+单调递增. 当()0f x '<,即34x <时,函数2()233f x x x =-+单调递减.(3)因为3()3f x x x =+,所以2()330f x x '=+>. 因此,函数3()3f x x x =+是单调递增函数. (4)因为32()f x x x x =+-,所以2()321f x x x '=+-. 当()0f x '>,即1x <-或13x >时,函数32()f x x x x =+-单调递增. 当()0f x '<,即113x -<<时,函数32()f x x x x =+-单调递减.3、(1)图略. (2)加速度等于0.4、(1)在2x x =处,导函数()y f x '=有极大值;(2)在1x x =和4x x =处,导函数()y f x '=有极小值; (3)在3x x =处,函数()y f x =有极大值; (4)在5x x =处,函数()y f x =有极小值.5、(1)因为2()62f x x x =++,所以()121f x x '=+. 令()1210f x x '=+=,得112x =-. 当112x >-时,()0f x '>,()f x 单调递增; 当112x <-时,()0f x '<,()f x 单调递减.所以,112x =-时,()f x 有极小值,并且极小值为211149()6()212121224f -=⨯---=-.(2)因为3()12f x x x =-,所以2()312f x x '=-. 令2()3120f x x '=-=,得2x =±. 下面分两种情况讨论:①当()0f x '>,即2x <-或2x >时;②当()0f x '<,即22x -<<时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当2x =-时,()f x 有极大值,并且极大值为16; 当2x =时,()f x 有极小值,并且极小值为16-. (3)因为3()612f x x x =-+,所以2()123f x x '=-+. 令2()1230f x x '=-+=,得2x =±. 下面分两种情况讨论:①当()0f x '>,即2x <-或2x >时;②当()0f x '<,即22x -<<时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当2x =-时,()f x 有极大值,并且极大值为22; 当2x =时,()f x 有极小值,并且极小值为10-. (4)因为3()48f x x x =-,所以2()483f x x '=-. 令2()4830f x x '=-=,得4x =±. 下面分两种情况讨论:①当()0f x '>,即2x <-或2x >时;②当()0f x '<,即22x -<<时. 当x 变化时,()f x ',()f x 变化情况如下表:因此,当4x =-时,()f x 有极小值,并且极小值为128-; 当4x =时,()f x 有极大值,并且极大值为128. 6、(1)在[1,1]-上,当112x =-时,函数2()62f x x x =++有极小值,并且极小值为4724. 由于(1)7f -=,(1)9f =,所以,函数2()62f x x x =++在[1,1]-上的最大值和最小值分别为9,4724. (2)在[3,3]-上,当2x =-时,函数3()12f x x x =-有极大值,并且极大值为16;当2x =时,函数3()12f x x x =-有极小值,并且极小值为16-. 由于(3)9f -=,(3)9f =-,所以,函数3()12f x x x =-在[3,3]-上的最大值和最小值分别为16,16-.(3)在1[,1]3-上,函数3()612f x x x =-+在1[,1]3-上无极值.由于1269()327f -=,(1)5f =-,所以,函数3()612f x x x =-+在1[,1]3-上的最大值和最小值分别为26927,5-.(4)当4x =时,()f x 有极大值,并且极大值为128.. 由于(3)117f -=-,(5)115f =,所以,函数3()48f x x x =-在[3,5]-上的最大值和最小值分别为128,117-. 习题3.3 B 组(P32)1、(1)证明:设()sin f x x x =-,(0,)x π∈. 因为()cos 10f x x '=-<,(0,)x π∈ 所以()sin f x x x =-在(0,)π内单调递减因此()sin (0)0f x x x f =-<=,(0,)x π∈,即sin x x <,(0,)x π∈. 图略 (2)证明:设2()f x x x =-,(0,1)x ∈. 因为()12f x x '=-,(0,1)x ∈所以,当1(0,)2x ∈时,()120f x x '=->,()f x 单调递增,2()(0)0f x x x f =->=;当1(,1)2x ∈时,()120f x x '=-<,()f x 单调递减,2()(1)0f x x x f =->=;又11()024f =>. 因此,20x x ->,(0,1)x ∈. 图略(3)证明:设()1x f x e x =--,0x ≠. 因为()1x f x e '=-,0x ≠所以,当0x >时,()10x f x e '=->,()f x 单调递增,()1(0)0x f x e x f =-->=;当0x <时,()10x f x e '=-<,()f x 单调递减,()1(0)0x f x e x f =-->=;综上,1x e x ->,0x ≠. 图略(4)证明:设()ln f x x x =-,0x >. 因为1()1f x x'=-,0x ≠ 所以,当01x <<时,1()10f x x'=->,()f x 单调递增, ()ln (1)10f x x x f =-<=-<; 当1x >时,1()10f x x'=-<,()f x 单调递减, ()ln (1)10f x x x f =-<=-<;当1x =时,显然ln11<. 因此,ln x x <. 由(3)可知,1x e x x >+>,0x >. . 综上,ln x x x e <<,0x >图略2、(1)函数32()f x ax bx cx d =+++的图象大致是个“双峰”图象,类似“”或“”的形状. 若有极值,则在整个定义域上有且仅有一个极大值和一个极小值,从图象上能大致估计它的单调区间.(2)因为32()f x ax bx cx d =+++,所以2()32f x ax bx c '=++. 下面分类讨论:当0a ≠时,分0a >和0a <两种情形: ①当0a >,且230b ac ->时,设方程2()320f x ax bx c '=++=的两根分别为12,x x ,且12x x <,当2()320f x ax bx c '=++>,即1x x <或2x x >时,函数32()f x ax bx cx d =+++单调递增;当2()320f x ax bx c '=++<,即12x x x <<时,函数32()f x ax bx cx d =+++单调递减.当0a >,且230b ac -≤时,此时2()320f x ax bx c '=++≥,函数32()f x ax bx cx d =+++单调递增. ②当0a <,且230b ac ->时,设方程2()320f x ax bx c '=++=的两根分别为12,x x ,且12x x <,当2()320f x ax bx c '=++>,即12x x x <<时,函数32()f x ax bx cx d =+++单调递增;当2()320f x ax bx c '=++<,即1x x <或2x x >时,函数32()f x ax bx cx d =+++单调递减.当0a <,且230b ac -≤时,此时2()320f x ax bx c '=++≤,函数32()f x ax bx cx d =+++单调递减 1.4生活中的优化问题举例 习题1.4 A 组(P37)1、设两段铁丝的长度分别为x ,l x -,则这两个正方形的边长分别为4x ,4l x -,两个正方形的面积和为 22221()()()(22)4416x l x S f x x lx l -==+=-+,0x l <<.令()0f x '=,即420x l -=,2lx =.当(0,)2l x ∈时,()0f x '<;当(,)2lx l ∈时,()0f x '>.因此,2lx =是函数()f x 的极小值点,也是最小值点.所以,当两段铁丝的长度分别是2l时,两个正方形的面积和最小.2、如图所示,由于在边长为a 的正方形铁片的四角截去 四个边长为x 的小正方形,做成一个无盖方盒,所以无 盖方盒的底面为正方形,且边长为2a x -,高为x .(1)无盖方盒的容积2()(2)V x a x x =-,02ax <<.(2)因为322()44V x x ax a x =-+, 所以22()128V x x ax a '=-+.令()0V x '=,得2a x =(舍去),或6a x =. 当(0,)6a x ∈时,()0V x '>;当(,)62a ax ∈时,()0V x '<.因此,6ax =是函数()V x 的极大值点,也是最大值点.所以,当6ax =时,无盖方盒的容积最大.3、如图,设圆柱的高为h ,底半径为R , 则表面积222S Rh R ππ=+ 由2V R h π=,得2V h Rπ=. (第2题)因此,2222()222V V S R R R R R Rππππ=+=+,0R >. 令2()40V S R R R π'=-+=,解得R =.当R ∈时,()0S R '<;当)R ∈+∞时,()0S R '>. 因此,R =是函数()S R 的极小值点,也是最小值点. 此时,22V h R R π===. 所以,当罐高与底面直径相等时,所用材料最省.4、证明:由于211()()n i i f x x a n ==-∑,所以12()()n i i f x x a n ='=-∑.令()0f x '=,得11ni i x a n ==∑,可以得到,11ni i x a n ==∑是函数()f x 的极小值点,也是最小值点.这个结果说明,用n 个数据的平均值11ni i a n =∑表示这个物体的长度是合理的,这就是最小二乘法的基本原理.5、设矩形的底宽为x m ,则半圆的半径为2xm ,半圆的面积为28x π2m ,矩形的面积为28x a π-2m ,矩形的另一边长为()8a xx π-m 因此铁丝的长为22()(1)244xa x a l x x x x x πππ=++-=++,0x <<令22()104a l x x π'=+-=,得x =.当x ∈时,()0l x '<;当x ∈时,()0l x '>.因此,x =()l x 的极小值点,也是最小值点.时,所用材料最省. 6、利润L 等于收入R 减去成本C ,而收入R 等于产量乘单价. 由此可得出利润L 与产量q 的函数关系式,再用导数求最大利润.收入211(25)2588R q p q q q q =⋅=-=-,利润2211(25)(1004)2110088L R C q q q q q =-=--+=-+-,0200q <<.求导得1214L q '=-+令0L '=,即12104q -+=,84q =.当(0,84)q ∈时,0L '>;当(84,200)q ∈时,0L '<;因此,84q =是函数L 的极大值点,也是最大值点.所以,产量为84时,利润L 最大,习题1.4 B 组(P37)1、设每个房间每天的定价为x 元,那么宾馆利润21801()(50)(20)7013601010x L x x x x -=--=-+-,180680x <<.令1()7005L x x '=-+=,解得350x =.当(180,350)x ∈时,()0L x '>;当(350,680)x ∈时,()0L x '>. 因此,350x =是函数()L x 的极大值点,也是最大值点.所以,当每个房间每天的定价为350元时,宾馆利润最大. 2、设销售价为x 元/件时,利润4()()(4)()(5)b x L x x a c cc x a x b b-=-+⨯=--,54b a x <<. 令845()0c ac bc L x x b b+'=-+=,解得458a bx +=.当45(,)8a b x a +∈时,()0L x '>;当455(,)84a b bx +∈时,()0L x '<.当458a bx +=是函数()L x 的极大值点,也是最大值点. 所以,销售价为458a b+元/件时,可获得最大利润.1.5定积分的概念 练习(P42) 83. 说明:进一步熟悉求曲边梯形面积的方法和步骤,体会“以直代曲”和“逼近”的思想.练习(P45)1、22112()[()2]()i i i i i s s v t n n n n n n '∆≈∆=∆=-+⋅=-⋅+⋅,1,2,,i n =.于是 111()n n ni i i i i is s s v t n ==='=∆≈∆=∆∑∑∑2112[()]ni i n n n ==-⋅+⋅∑22211111()()()2n n n n n n n n -=-⋅--⋅-⋅+2231[12]2n n=-++++31(1)(21)26n n n n ++=-⋅+111(1)(1)232n n =-+++取极值,得1111115lim [()]lim [(1)(1)2]323nnn n i i i s v n n n n →∞→∞====-+++=∑∑ 说明:进一步体会“以不变代变”和“逼近”的思想. 2、223km.说明:进一步体会“以不变代变”和“逼近”的思想,熟悉求变速直线运动物体路程的方法和步骤. 练习(P48)2304x dx =⎰. 说明:进一步熟悉定积分的定义和几何意义.从几何上看,表示由曲线3y x =与直线0x =,2x =,0y =所围成的曲边梯形的面积4S =.习题1.5 A 组(P50)1、(1)10021111(1)[(1)1]0.495100100i i x dx =--≈+-⨯=∑⎰; (2)50021111(1)[(1)1]0.499500500i i x dx =--≈+-⨯=∑⎰; (3)100021111(1)[(1)1]0.499510001000i i x dx =--≈+-⨯=∑⎰. 说明:体会通过分割、近似替换、求和得到定积分的近似值的方法.2、距离的不足近似值为:18112171310140⨯+⨯+⨯+⨯+⨯=(m ); 距离的过剩近似值为:271181121713167⨯+⨯+⨯+⨯+⨯=(m ).3、证明:令()1f x =. 用分点 011i i n a x x x x x b -=<<<<<<=将区间[,]a b 等分成n 个小区间,在每个小区间1[,]i i x x -上任取一点(1,2,,)i i n ξ=作和式 11()nni i i b af x b a nξ==-∆==-∑∑, 从而 11lim nban i b adx b a n→∞=-==-∑⎰, 说明:进一步熟悉定积分的概念. 4、根据定积分的几何意义,0⎰表示由直线0x =,1x =,0y =以及曲线y =所围成的曲边梯形的面积,即四分之一单位圆的面积,因此4π=⎰.5、(1)03114x dx -=-⎰. 由于在区间[1,0]-上30x ≤,所以定积分031x dx -⎰表示由直线0x =,1x =-,0y =和曲线3y x =所围成的曲边梯形的面积的相反数.(2)根据定积分的性质,得10133311011044x dx x dx x dx --=+=-+=⎰⎰⎰.由于在区间[1,0]-上30x ≤,在区间[0,1]上30x ≥,所以定积分131x dx -⎰等于位于x轴上方的曲边梯形面积减去位于x 轴下方的曲边梯形面积.(3)根据定积分的性质,得202333110115444x dx x dx x dx --=+=-+=⎰⎰⎰由于在区间[1,0]-上30x ≤,在区间[0,2]上30x ≥,所以定积分231x dx -⎰等于位于x轴上方的曲边梯形面积减去位于x 轴下方的曲边梯形面积.说明:在(3)中,由于3x 在区间[1,0]-上是非正的,在区间[0,2]上是非负的,如果直接利用定义把区间[1,2]-分成n 等份来求这个定积分,那么和式中既有正项又有负项,而且无法抵挡一些项,求和会非常麻烦. 利用性质3可以将定积分231x dx-⎰化为02331x dx x dx -+⎰⎰,这样,3x 在区间[1,0]-和区间[0,2]上的符号都是不变的,再利用定积分的定义,容易求出031x dx -⎰,230x dx ⎰,进而得到定积分231x dx -⎰的值. 由此可见,利用定积分的性质可以化简运算.在(2)(3)中,被积函数在积分区间上的函数值有正有负,通过练习进一步体会定积分的几何意义. 习题1.5 B 组(P50)1、该物体在0t =到6t =(单位:s )之间走过的路程大约为145 m.说明:根据定积分的几何意义,通过估算曲边梯形内包含单位正方形的个数来估计物体走过的路程. 2、(1)9.81v t =.(2)过剩近似值:8111899.819.8188.292242i i =⨯⨯⨯=⨯⨯=∑(m ); 不足近似值:81111879.819.8168.672242i i =-⨯⨯⨯=⨯⨯=∑(m ) (3)49.81tdt ⎰; 49.81d 78.48t t =⎰(m ).3、(1)分割在区间[0,]l 上等间隔地插入1n -个分点,将它分成n 个小区间:[0,]l n ,2[,]l l n n ,……,(2)[,]n l l n -, 记第i 个区间为(1)[,]i l iln n-(1,2,i n =),其长度为 (1)il i l l x n n n-∆=-=.把细棒在小段[0,]l n ,2[,]l l n n ,……,(2)[,]n ll n-上质量分别记作: 12,,,n m m m ∆∆∆,则细棒的质量1ni i m m ==∆∑.(2)近似代替当n 很大,即x ∆很小时,在小区间(1)[,]i l iln n-上,可以认为线密度2()x x ρ=的值变化很小,近似地等于一个常数,不妨认为它近似地等于任意一点(1)[,]i i l il n n ξ-∈处的函数值2()i i ρξξ=. 于是,细棒在小段(1)[,]i l il n n-上质量2()i i i lm x nρξξ∆≈∆=(1,2,i n =).(3)求和得细棒的质量 2111()nnni i i i i i l m m x nρξξ====∆≈∆=∑∑∑. (4)取极限细棒的质量 21lim ni n i lm nξ→∞==∑,所以20l m x dx =⎰..1.6微积分基本定理练习(P55) (1)50; (2)503; (3)533-; (4)24; (5)3ln 22-; (6)12; (7)0; (8)2-.说明:本题利用微积分基本定理和定积分的性质计算定积分. 习题1.6 A 组(P55)1、(1)403; (2)13ln 22--; (3)9ln 3ln 22+-;(4)176-; (5)2318π+; (6)22ln 2e e --. 说明:本题利用微积分基本定理和定积分的性质计算定积分.2、3300sin [cos ]2xdx x ππ=-=⎰.它表示位于x 轴上方的两个曲边梯形的面积与x 轴下方的曲边梯形的面积之差. 或表述为:位于x 轴上方的两个曲边梯形的面积(取正值)与x 轴下方的曲边梯形的面积(取负值)的代数和. 习题1.6 B 组(P55)1、(1)原式=221011[]222x e e =-; (2)原式=4611[sin 2]22x ππ=; (3)原式=3126[]ln 2ln 2x =.2、(1)cos 1sin [][cos cos()]0mx mxdx m m m m ππππππ--=-=---=⎰;(2)sin 1cos [sin sin()]0mx mxdx m m m m ππππππ--=|=--=⎰;(3)21cos 2sin 2sin []224mx x mx mxdx dx m πππππππ----==-=⎰⎰;(4)21cos 2sin 2cos []224mx x mx mxdx dx mπππππππ---+==+=⎰⎰.3、(1)0.202220()(1)[]49245245t kt kt t kt t g g g g g gs t e dt t e t e t e k k k k k k----=-=+=+-=+-⎰.(2)由题意得 0.2492452455000t t e -+-=.这是一个超越方程,为了解这个方程,我们首先估计t 的取值范围. 根据指数函数的性质,当0t >时,0.201t e -<<,从而 5000495245t <<, 因此,500052454949t <<. 因此50000.2749245 3.3610e-⨯-≈⨯,52450.2749245 1.2410e-⨯-≈⨯,所以,70.271.2410245 3.3610t e ---⨯<<⨯.从而,在解方程0.2492452455000t t e -+-=时,0.2245t e -可以忽略不计.因此,.492455000t -≈,解之得 524549t ≈(s ). 说明:B 组中的习题涉及到被积函数是简单的复合函数的定积分,可视学生的具体情况选做,不要求掌握. 1.7定积分的简单应用 练习(P58)(1)323; (2)1.说明:进一步熟悉应用定积分求平面图形的面积的方法与求解过程. 练习(P59)1、52533(23)[3]22s t dt t t =+=+=⎰(m ).2、42403(34)[4]402W x dx x x =+=+=⎰(J ). 习题1.7 A 组(P60)1、(1)2; (2)92.2、2[]b b a a q q q qW k dr k k k r r a b==-=-⎰. 3、令()0v t =,即40100t -=. 解得4t =. 即第4s 时物体达到最大高度.最大高度为 424(4010)[405]80h t dt t t =-=-=⎰(m ). 4、设t s 后两物体相遇,则 2(31)105ttt dt tdt +=+⎰⎰,解之得5t =. 即,A B 两物体5s 后相遇.此时,物体A 离出发地的距离为 523500(31)[]130t dt t t +=+=⎰(m ).5、由F kl =,得100.01k =. 解之得1000k =. 所做的功为 0.120.10010005005W ldl l ==|=⎰(J ).6、(1)令55()501v t t t=-+=+,解之得10t =. 因此,火车经过10s 后完全停止. (2)1021000551(5)[555ln(1)]55ln1112s t dt t t t t =-+=-++=+⎰(m ). 习题1.7 B 组(P60)1、(1)22a aa x dx --⎰表示圆222x y a +=与x 轴所围成的上半圆的面积,因此2222aaa a x dx π--=⎰(2)120[1(1)]x x dx ---⎰表示圆22(1)1x y -+=与直线y x =所围成的图形(如图所示)的面积,因此,2120111[1(1)]114242x x dx ππ⨯---=-⨯⨯=-⎰. 2、证明:建立如图所示的平面直角坐标系,可设抛物线的方程为2y ax =,则2()2b h a =⨯,所以24ha b =.从而抛物线的方程为 224hy x b =.于是,抛物线拱的面积232202204422()2[]33b b h h S h x dx hx x bh b b =-=-=⎰. 3、如图所示.解方程组223y x y x⎧=+⎨=⎩得曲线22y x =+与曲线3y x =交点的横坐标11x =,22x =. 于是,所求的面积为122201[(2)3][3(2)]1x x dx x x dx +-+-+=⎰⎰.y xO1(第1(2)题)yxh b O (第2题)4、证明:2[]()R hR h R RMm Mm MmhW Gdr G G r r R R h ++==-=+⎰. 第一章 复习参考题A 组(P65)1、(1)3; (2)4y =-.2、(1)22sin cos 2cos x x xy x+'=; (2)23(2)(31)(53)y x x x '=-+-; (3)22ln ln 2x xy x x '=+; (4)2422(21)x x y x -'=+. 3、32GMm F r '=-. 4、(1)()0f t '<. 因为红茶的温度在下降.(2)(3)4f '=-表明在3℃附近时,红茶温度约以4℃/min 的速度下降. 图略.5、因为()f x =()f x '=.当()0f x '=>,即0x >时,()f x 单调递增;当()0f x '=<,即0x <时,()f x 单调递减.6、因为2()f x x px q =++,所以()2f x x p '=+. 当()20f x x p '=+=,即12px =-=时,()f x 有最小值. 由12p-=,得2p =-. 又因为(1)124f q =-+=,所以5q =. 7、因为2322()()2f x x x c x cx c x =-=-+, 所以22()34(3)()f x x cx c x c x c '=-+=--. 当()0f x '=,即3cx =,或x c =时,函数2()()f x x x c =-可能有极值. 由题意当2x =时,函数2()()f x x x c =-有极大值,所以0c >.由于 所以,当3c x =时,函数2()()f x x x c =-有极大值. 此时,23c=,6c =. 8、设当点A 的坐标为(,0)a 时,AOB ∆的面积最小. 因为直线AB 过点(,0)A a ,(1,1)P ,所以直线AB 的方程为001y x a x a--=--,即1()1y x a a =--. 当0x =时,1a y a =-,即点B 的坐标是(0,)1aa -. 因此,AOB ∆的面积21()212(1)AOBa a S S a a a a ∆===--.令()0S a '=,即2212()02(1)a aS a a -'=⋅=-. 当0a =,或2a =时,()0S a '=,0a =不合题意舍去. 由于 所以,当2a =,即直线的倾斜角为时,的面积最小,最小面积为2. 9、D .10、设底面一边的长为x m ,另一边的长为(0.5)x +m. 因为钢条长为14.8m. 所以,长方体容器的高为14.844(0.5)12.88 3.2244x x xx --+-==-.设容器的容积为V ,则32()(0.5)(3.22)2 2.2 1.6V V x x x x x x x ==+-=-++,0 1.6x <<.令()0V x '=,即26 4.4 1.60x x -++=. 所以,415x =-(舍去),或1x =. 当(0,1)x ∈时,()0V x '>;当(1,1.6)x ∈时,()0V x '<. 因此,1x =是函数()V x 在(0,1.6)的极大值点,也是最大值点. 所以,当长方体容器的高为1 m 时,容器最大,最大容器为1.8 m 3.11、设旅游团人数为100x +时,旅行社费用为2()(100)(10005)5500100000y f x x x x ==+-=-++(080)x ≤≤. 令()0f x '=,即105000x -+=,50x =.又(0)100000f =,(80)108000f =,(50)112500f =. 所以,50x =是函数()f x 的最大值点.所以,当旅游团人数为150时,可使旅行社收费最多. 12、设打印纸的长为x cm 时,可使其打印面积最大.因为打印纸的面积为623.7,长为x ,所以宽为623.7x,打印面积623.7()(2 2.54)(2 3.17)S x x x=-⨯-⨯23168.396655.9072 6.34x x=--,5.0898.38x <<. 令()0S x '=,即23168.3966.340x -=,22.36x ≈(负值舍去),623.727.8922.36≈. 22.36x =是函数()S x 在(5.08,98.38)内唯一极值点,且为极大值,从而是最大值点.所以,打印纸的长、宽分别约为27.89cm ,22.36cm 时,可使其打印面积最大. 13、设每年养q 头猪时,总利润为y 元.则 21()20000100300200002y R q q q q =--=-+-(0400,)q q N <≤∈.令0y '=,即3000q -+=,300q =.当300q =时,25000y =;当400q =时,20000y =.300q =是函数()y p 在(0,400]内唯一极值点,且为极大值点,从而是最大值点. 所以,每年养300头猪时,可使总利润最大,最大总利润为25000元.14、(1)2; (2)22e -; (3)1;(4)原式=22222000cos sin (cos sin )[sin cos ]0cos sin x x dx x x dx x x x xπππ-=-=+=+⎰⎰;(5)原式=22001cos sin 2[]224x x x dx πππ---==⎰.15、略. 说明:利用函数图象的对称性、定积分的几何意义进行解释.16、2.17、由F kl =,得0.0490.01k =. 解之得 4.9k =.所做的功为 20.30.30.10.14.9 4.90.1962l W ldl ==⨯|=⎰(J )第一章 复习参考题B 组(P66)1、(1)43()10210b t t '=-⨯. 所以,细菌在5t =与10t =时的瞬时速度分别为0和410-.(2)当05t ≤<时,()0b t '>,所以细菌在增加;当55t <<+()0b t '<,所以细菌在减少.2、设扇形的半径为r ,中心角为α弧度时,扇形的面积为S .因为212S r α=,2l r r α-=,所以2lrα=-.222111(2)(2)222l S r r lr r r α==-=-,02l r <<.令0S '=,即40l r -=,4lr =,此时α为2弧度.4lr =是函数()S r 在(0,)2l 内唯一极值点,且是极大值点,从而是最大值点.所以,扇形的半径为4l、中心角为2弧度时,扇形的面积最大.3、设圆锥的底面半径为r ,高为h ,体积为V ,那么222r h R +=.因此,222231111()3333V r h R h h R h h ππππ==-=-,0h R <<.令22103V R h ππ'=-=,解得h =.容易知道,h =是函数()V h 的极大值点,也是最大值点.所以,当h R =时,容积最大.把3h R =代入222r h R +=,得3r R =.由2R r απ=,得3α=.所以,圆心角为α=时,容积最大. 4、由于28010k =⨯,所以45k =. 设船速为x km /h 时,总费用为y ,则2420204805y x x x=⨯+⨯ 960016x x=+,0x > 令0y '=,即29600160x -=,24x ≈.容易知道,24x =是函数y 的极小值点,也是最小值点.当24x =时,960020(1624)()9412424⨯+÷≈(元/时) 所以,船速约为24km /h 时,总费用最少,此时每小时费用约为941元.5、设汽车以x km /h 行驶时,行车的总费用2390130(3)14360x y x x=++⨯,50100x ≤≤令0y '=,解得53x ≈(km /h ). 此时,114y ≈(元) 容易得到,53x ≈是函数y 的极小值点,也是最小值点.因此,当53x ≈时,行车总费用最少.所以,最经济的车速约为53km /h ;如果不考虑其他费用,这次行车的总费用约是114元.6、原式=4404422022[]2xxx x x e dx e dx e dx e e e e -----=+=-+|=+-⎰⎰⎰.7、解方程组 2y kx y x x=⎧⎨=-⎩ 得,直线y kx =与抛物线2y x x =-交点的横坐标为0x =,1k -.抛物线与x 轴所围图形的面积2312100111()[]23236x x S x x dx =-=-=-=⎰.由题设得11200()2k k Sx x dx kxdx --=--⎰⎰31221001()[]23kkk x x x kx dx x ---=--=-⎰3(1)6k -=.又因为16S =,所以31(1)2k -=.于是1k =说明:本题也可以由面积相等直接得到111220()()kk k x x kx dx kxdx x x dx -----=+-⎰⎰⎰,由此求出k 的值. 但计算较为烦琐.新课程数学选修2—2第二章课后习题解答第二章推理与证明2.1合情推理与演绎推理 练习(P77)1、由12341a a a a ====,猜想1n a =.2、相邻两行数之间的关系是:每一行首尾的数都是1,其他的数都等于上一行中与之相邻的两个数的和.3、设111O PQ R V -和222O P Q R V -分别是四面体111O PQ R -和222O P Q R -的体积, 则111222111222O PQR O P Q R V OP OQ OR V OP OQ OR --=⋅⋅. 练习(P81) 1、略.2、因为通项公式为n a 的数列{}n a , 若1n na p a +=,其中p 是非零常数,则{}n a 是等比数列;……………………大前提 又因为0cq ≠,则0q ≠,则11n n nn a cq q a cq++==;……………………………小前提 所以,通项公式为(0)n n a cq cq =≠的数列{}n a 是等比数列. ……………………结论 3、由AD BD >,得到ACD BCD ∠>∠的推理是错误的. 因为这个推理的大前提是“在同一个三角形中,大边对大角”,小前提是“AD BD >”,而AD 与BD 不在同一个三角形中.习题2.1 A 组(P83)1、21n a n =+()n N *∈. 2、2F V E +=+.3、当6n ≤时,122(1)n n -<+;当7n =时,122(1)n n -=+;当8n =时,122(1)n n ->+()n N *∈.4、212111(2)n n A A A n π++≥-(2n >,且n N *∈). 5、121217n n b b b b b b -=(17n <,且n N *∈).6、如图,作DE ∥AB 交BC 于E .因为两组对边分别平行的四边形是平行四边形, 又因为AD ∥BE ,AB ∥DE . 所以四边形ABED 是平行四边形.因为平行四边形的对边相等.又因为四边形ABED 是平行四边形. 所以AB DE =.因为与同一条线段等长的两条线段的长度相等,又因为AB DE =,AB DC =, 所以DE DC = 因为等腰三角形的两底角是相等的.又因为△DEC 是等腰三角形, 所以DEC C ∠=∠ 因为平行线的同位角相等又因为DEC ∠与B ∠是平行线AB 和DE 的同位角, 所以DEC B ∠=∠ 因为等于同角的两个角是相等的,又因为DEC C ∠=∠,DEC B ∠=∠, 所以B C ∠=∠ 习题2.1 B 组(P84)1、由123S =-,234S =-,345S =-,456S =-,567S =-,猜想12n n S n +=-+.2、略.3、略.2.2直接证明与间接证明 练习(P89)1、因为442222cos sin (cos sin )(cos sin )cos 2θθθθθθθ-=+-=,所以,命题得证. 2>,只需证22>,即证1313+>+>,只需要22>,即证4240>,这是显然成立的. 所以,命题得证. 3、因为222222222()()()(2sin )(2tan )16sin tan a b a b a b αααα-=-+==, 又因为sin (1cos )sin (1cos )1616(tan sin )(tan sin )16cos cos ab αααααααααα+-=+-=⋅22222222sin (1cos )sin sin 161616sin tan cos cos αααααααα-===, 从而222()16a b ab -=,所以,命题成立.说明:进一步熟悉运用综合法、分析法证明数学命题的思考过程与特点.(第6练习(P91)1、假设B ∠不是锐角,则90B ∠≥︒. 因此9090180C B ∠+∠≥︒+︒=︒. 这与三角形的内角和等于180°矛盾.所以,假设不成立. 从而,B ∠一定是锐角.2成等差数列,则=所以22=,化简得5=225=,即2540=, 这是不可能的. 所以,假设不成立..说明:进一步熟悉运用反证法证明数学命题的思考过程与特点. 习题2.2 A 组(P91)1、由于0a ≠,因此方程至少有一个跟bx a=.假设方程不止一个根,则至少有两个根,不妨设12,x x 是它的两个不同的根,则1ax b =①2ax b =②①-②得12()0a x x -=因为12x x ≠,所以120x x -≠,从而0a =,这与已知条件矛盾,故假设不成立. 2、因为(1tan )(1tan )2A B ++=展开得1tan tan tan tan 2A B A B +++=,即tan tan 1tan tan A B A B +=-. ①假设1tan tan 0A B -=,则cos cos sin sin 0cos cos A B A B A B -=,即cos()0cos cos A B A B += 所以cos()0A B +=.因为A ,B 都是锐角,所以0A B π<+<,从而2A B π+=,与已知矛盾.因此1tan tan 0A B -≠.①式变形得tan tan 11tan tan A BA B +=-,即tan()1A B +=.又因为0A B π<+<,所以4A B π+=. 说明:本题也可以把综合法和分析法综合使用完成证明.3、因为1tan 12tan αα-=+,所以12tan 0α+=,从而2sin cos 0αα+=.另一方面,要证3sin 24cos2αα=-,只要证226sin cos 4(cos sin )αααα=-- 即证222sin 3sin cos 2cos 0αααα--=, 即证(2sin cos )(sin 2cos )0αααα+-=由2sin cos 0αα+=可得,(2sin cos )(sin 2cos )0αααα+-=,于是命题得证. 说明:本题可以单独使用综合法或分析法进行证明,但把综合法和分析法结合使用进行证明的思路更清晰.4、因为,,a b c 的倒数成等差数列,所以211b ac =+.假设2B π<不成立,即2B π≥,则B 是ABC ∆的最大内角,所以,b a b c >>(在三角形中,大角对大边), 从而11112a c b b b +>+=. 这与211b a c=+矛盾. 所以,假设不成立,因此,2B π<.习题2.2 B 组(P91)1、要证2s a <,由于22s ab <,所以只需要2s s b<,即证b s <.因为1()2s a b c =++,所以只需要2b a b c <++,即证b a c <+. 由于,,a b c 为一个三角形的三条边,所以上式成立. 于是原命题成立. 2、由已知条件得2b ac =①2x a b =+,2y b c =+②要证2a cx y+=,只要证2ay cx xy +=,只要证224ay cx xy += 由①②,得22()()2ay cx a b c c a b ab ac bc +=+++=++,24()()2xy a b b c ab b ac bc ab ac bc =++=+++=++, 所以,224ay cx xy +=,于是命题得证. 3、由tan()2tan αβα+=得sin()2sin cos()cos αβααβα+=+,即sin()cos 2cos()sin αβααβα+=+. ……①要证3sin sin(2)βαβ=+即证3sin[()]sin[()]αβααβα+-=++即证3[sin()cos cos()sin ]sin()cos cos()sin αβααβααβααβα+-+=+++ 化简得sin()cos 2cos()sin αβααβα+=+,这就是①式.所以,命题成立.说明:用综合法和分析法证明命题时,经常需要把两者结合起来使用. 2.3数学归纳法 练习(P95)1、先证明:首项是1a ,公差是d 的等差数列的通项公式是1(1)n a a n d =+-. (1)当1n =时,左边=1a ,右边=11(11)a d a +-=, 因此,左边=右边. 所以,当1n =时命题成立. (2)假设当n k =时,命题成立,即1(1)k a a k d =+-. 那么,11(1)[(1)1]k k k a a d a k d d a k d +=+=+-+=++-. 所以,当1n k =+时,命题也成立.根据(1)和(2),可知命题对任何n N *∈都成立.再证明:该数列的前n 项和的公式是1(1)2n n n S na d -=+. (1)当1n =时,左边=11S a =,右边=111(11)12a d a ⨯-⨯+=,因此,左边=右边. 所以,当1n =时命题成立.(2)假设当n k =时,命题成立,即1(1)2k k k S ka d -=+.那么,1111(1)[(1)1]2k k k k k S S a ka d a k d ++-=+=++++-1(1)(1)[1]2k k a k d -=+++1(1)(1)2k kk a d +=++所以,当1n k =+时,命题也成立.根据(1)和(2),可知命题对任何n N *∈都成立. 2、略.。
2020学年高中数学第1章导数及其应用1.3导数在研究函数中的应用1.3.2函数的极值与导数课件新人教A版选修2_2

变式训练
1.求下列函数的极值: (1)f(x)=x2e-x; (2)f(x)=sin x(1+cos x)(0<x<2π).
解析 (1)函数的ห้องสมุดไป่ตู้义域为 R.
f′(x)=2xe-x+x2·e-x(-x)′
=2xe-x-x2e-x=x(2-x)e-x.
【问题2】 问题1中a,b,c,d,e,f,g,h哪些是 极小值点,哪些是极大值点?
答案 极小值点有a,c,e,g;极大值点有b,d, f,h.
【问题3】 结合问题1、2思考:函数的极大值一定 大于极小值吗?在同一区间内极值点唯一吗?
答案 函数的极大值与极小值并无确定的大小关 系,一个函数的极大值未必大于极小值,例如图(2)中f(c) 为极小值,f(f)为极大值,但f(c)>f(f);在区间内可导函数 的极大值或极小值可以不止一个.
+
0
-
0
+
y
↗
极大值 ↘
极小值
↗
由上表可以看出,当 x=-1 时,函数 y=f(x)有极大
值 f(-1)=10;
当 x=3 时,函数 y=f(x)有极小值 f(3)=-22.
●规律方法
求可导函数f(x)极值的步骤 (1)求函数的导数f′(x); (2)令f′(x)=0,求出全部的根x0; (3)列表,方程的根x0将整个定义域分成若干个区间, 把x,f′(x),f(x)在每个区间内的变化情况列在这个表格 内; (4)判断得结论,若导数在x0附近左正右负,则在x0处 取得极大值;若左负右正,则取得极小值. [注意事项]
f′(x)
+
0
-
0
2018-2019学年高中数学 第一章 导数及其应用 1.3 导数在研究函数中的应用 1.3.2 函数的极值与导数课件

当0<x<2π时,x1=π3,x2=π,x3=53π. 当x在区间(0,2π)内变化时,f′(x),f(x)的变化情况如下表:
x
0,π3
π 3
π3,π π π,53π
5π 3
53π,2π
f′(x) +
0
-0 -
0
+
f(x)
极大值3 4 3
0
极小值-3 4 3
故当x=π3时,f(x)有极大值为3 4 3;
f(x)的变化情况如下表:
x (-∞,-2) -2 (-2,2) 2 (2,+∞)
f′(x)
+
0-0
+
f(x)
28 3
-43
∴当 x=-2 时,f(x)有极大值238;当 x=2 时,f(x)有极小值-43. 要使关于 f(x)=k 的方程有三个不等实根,则使 k 应满足-43<k<238.即实 数 k 的取值范围为-43,238.
[双基自测] 1.下列结论中,正确的是( ) A.导数为零的点一定是极值点 B.如果在 x0 附近的左侧 f′(x)>0,右侧 f′(x)<0,那么 f(x0)是极大值 C.如果在 x0 附近的左侧 f′(x)>0,右侧 f′(x)<0,那么 f(x0)是极小值 D.如果在 x0 附近的左侧 f′(x)<0,右侧 f′(x)>0,那么 f(x0)是极大值
4.函数 y=sin x+cos x 在[0,π]上的极大值为________. 解析:y′=cos x-sin x,令 y′=0 得 x=π4, 当 0<x<π4时 y′>0,当π4<x<π 时,y′<0, 所以当 x=π4时,y 取得极大值且极大值为 y 极大值=sinπ4+cosπ4= 22+ 22= 2. 答案: 2
高中数学第1章导数及其应用1.3导数在研究函数中的应用1.3.3函数的最大(小)值与导数

令 f′(x)=0 解得 x=- 2(- 2∉[-1,3],故舍去)或
x= 2.
当 x 变化时,f′(x)与 f(x)的变化情况如下表:
x -1 (-1, 2)
2
( 2,3) 3
f′(x)
-
0
+
f(x) 10
↘
极小值-8 2 ↗ 18
∴当 x= 2时,f(x)有最小值 f( 2)=-8 2; 当 x=3 时,f(x)有最大值 f(3)=18.
12/12/2021
第七页,共三十八页。
【问题3】 结合问题1、2,思考极值与最值有什么 关系?
答案 区别:(1)函数的最值是比较整个定义域内的 函数值得出的;函数的极值是比较极值点附近的函数值得 出的.
(2)函数在其定义区间上的最大值、最小值最多各有 一个,而函数的极值可能(kěnéng)不止一个,也可能(kěnéng)一 个也没有,函数的最大值一定不小于它的最小值.
(3)极值只能在区间内取得,最值则可以在端点处取 得.
联系:极值有可能是最值,最值不在端点处取得的可
导函数,其最值一定是极值,同时区间(a,b)内若只有一
个极值,则极值一定为最值. 12/12/2021
第八页,共三十八页。
【问题(wèntí)4】 求函数y=f(x)在区间[a,b]上的最大 值与最小值的步骤是什么?
第四页,共三十八页。
3.函数的极值与最值的区别 区别
极 值
是在局部对函数值 的比较,表示函数在 __某__一__点_(_yī_d_iǎ_n)_附的近 局 部性质.
极值可能有 多个,也可 能没有.
只能在区 间内取得.
最 值
是 函 函 的数 情数在值况在整的._个整_比_区个_较_(z间_h,ě_n上g_考g_è)区对上查间最 最 个.多大
高中数学第1章导数及其应用1.3导数在研究函数中的应用1.3.1单调性222数学

12/8/2021
第二十三页,共三十八页。
3.若函数 f(x)=13x3-12ax2+(a-1)x+1 在区间(1, 4)上为减函数,在区间(6,+∞)上为增函数,试求实数 a 的取值 范围.
12/8/2021
第二十四页,共三十八页。
解:函数 f(x)的导数 f′(x)=x2-ax+a-1. 令 f′(x)=0,解得 x=1 或 x=a-1. 当 a-1≤1,即 a≤2 时,函数 f(x)在(1,+∞)上为增函数,不合 题意. 当 a-1>1,即 a>2 时,函数 f(x)在(-∞,1)上为增函数,在(1, a-1)上为减函数,在(a-1,+∞)上为增函数. 依题意有当 x∈(1,4)时,f′(x)<0, 当 x∈(6,+∞)时,f′(x)>0,所以 4≤a-1≤6,即 5≤a≤7, 所以 a 的取值范围是[5,7].
答案:④
12/8/2021
第九页,共三十八页。
求函数的单调区间 求下列函数的单调区间: (1)f(x)=x3-x; (2)f(x)=3x2-2ln x.
12/8/2021
第十页,共三十八页。
【解】 (1)函数的定义域为 R, f′(x)=3x2-1=( 3x+1)( 3x-1),
令
f′(x)>0
12/8/2021
第二十一页,共三十八页。
2.函数 f(x)不变,若 f(x)的单调递减区间为(-1,1),求 a 的值.
解:由本例可知,f(x)的单调递减区间为-
33a,
33a,
所以 33a=1,即 a=3.
12/8/2021
第二十二页,共三十八页。
在某个区间上,f′(x)>0(或 f′(x)<0),f(x)在这个区间上单调递增(或 递 减 ) ; 但 由 f(x) 在 这 个 区 间 上 单 调 递 增 ( 递 减 ) 而 仅 仅 得 到 f′(x)>0(或 f′(x)<0)是不够的,即还有可能 f′(x)≥0(f′(x)≤0)也能使 得 f(x)在这个区间上单调递增(递减),因而对于能否取到等号的 问题需要单独验证.
(新课标)人教版高中教材目录

(新课标)人教版高中教材目录——数学必修1第一章集合与函数概念1.1 集合1.2 函数及其表示1.3 函数的基本性质第二章基本初等函数(Ⅰ)2.1 指数函数2.2 对数函数2.3 幂函数第三章函数的应用3.1 函数与方程3.2 函数模型及其应用必修2第一章空间几何体1.1 空间几何体的结构1.2 空间几何体的三视图和直观图1.3 空间几何体的表面积与体积第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.3 直线、平面垂直的判定及其性质第三章直线与方程3.1 直线的倾斜角与斜率3.2 直线的方程3.3 直线的交点坐标与距离公式第四章圆与方程4.1 圆的方程4.2 直线、圆的位置关系4.3 空间直角坐标系必修3第一章算法初步1.1 算法与程序框图1.2 基本算法语句1.3 算法案例第二章统计2.1 随机抽样2.2 用样本估计总体2.3 变量间的相关关系第三章概率3.1 随机事件的概率3.2 古典概型3.3 几何概型必修4第一章三角函数1.1 任意角和弧度制1.2 任意角的三角函数1.3 三角函数的诱导公式1.4 三角函数的图象与性质1.5 函数y=Asin(ωx+ψ)1.6 三角函数模型的简单应用第二章平面向量2.1 平面向量的实际背景及基本概念2.2 平面向量的线性运算2.3 平面向量的基本定理及坐标表示2.4 平面向量的数量积2.5 平面向量应用举例第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.2 简单的三角恒等变换1必修5第一章解三角形1.1 正弦定理和余弦定理1.2 应用举例1.3 实习作业第二章数列2.1 数列的概念与简单表示法2.2 等差数列2.3 等差数列的前n项和2.4 等比数列2.5 等比数列前n项和第三章不等式3.1 不等关系与不等式3.2 一元二次不等式及其解法3.3 二元一次不等式(组)与简单的线性规划问题3.4 基本不等式======================================================== 选修1-1第一章常用逻辑用语1.1 命题及其关系1.2 充分条件与必要条件1.3 简单的逻辑联结词1.4 全称量词与存在量词第二章圆锥曲线与方程2.1 椭圆2.2 双曲线2.3 抛物线第三章导数及其应用3.1 变化率与导数3.2 导数的计算3.3 导数在研究函数中的应用3.4 生活中的优化问题举例选修1-2第一章统计案例1.1 回归分析的基本思想及其初步应用1.2 独立性检验的基本思想及其初步应用第二章推理与证明2.1 合情推理与演绎证明2.2 直接证明与间接证明第三章数系的扩充与复数的引入3.1 数系的扩充和复数的概念3.2 复数代数形式的四则运算第四章框图4.1 流程图4.2 结构图2选修2-1第一章常用逻辑用语1.1 命题及其关系1.2 充分条件与必要条件1.3 简单的逻辑联结词1.4 全称量词与存在量词第二章圆锥曲线与方程2.1 曲线与方程2.2 椭圆2.3 双曲线2.4 抛物线选修 2-2第一章导数及其应用1.1 变化率与导数1.2 导数的计算1.3 导数在研究函数中的应用1.4 生活中的优化问题举例1.5 定积分的概念1.6 微积分基本定理1.7 定积分的简单应用第二章推理与证明2.1 合情推理与演绎推理2.2 直接证明与间接证明2.3 数学归纳法第三章数系的扩充与复数的引入3.1 数系的扩充和复数的概念3.2 复数代数形式的四则运算选修2-3第一章计数原理1.1 分类加法计数原理与分步乘法计数原理1.2 排列与组合1.3 二项式定理第二章随机变量及其分布2.1 离散型随机变量及其分布列2.2 二项分布及其应用2.3 离散型随机变量的均值与方差2.4 正态分布第三章统计案例3.1 回归分析的基本思想及其初步应用3.2 独立性检验的基本思想及其初步应用选修4-1 几何证明选讲第一讲相似三角形的判定及有关性质一平行线等分线段定理二平行线分线段成比例定理三相似三角形的判定及性质1.相似三角形的判定2.相似三角形的性质四直角三角形的射影定理第二讲直线与圆的位置关系一圆周角定理二圆内接四边形的性质与判定定理三圆的切线的性质及判定定理四弦切角的性质五与圆有关的比例线段第三讲圆锥曲线性质的探讨一平行射影二平面与圆柱面的截线三平面与圆锥面的截线3选修4-4 坐标系与参数方程第一讲坐标系一平面直角坐标系二极坐标系三简单曲线的极坐标方程四柱坐标系与球坐标系简介第二讲参数方程一曲线的参数方程二圆锥曲线的参数方程三直线的参数方程四渐开线与摆线选修4-5 不等式选讲第一讲不等式和绝对值不等式一不等式1.不等式的基本性质2.基本不等式3.三个正数的算术-几何平均不等式二绝对值不等式1.绝对值三角不等式2.绝对值不等式的解法第二讲讲明不等式的基本方法一比较法二综合法与分析法三反证法与放缩法第三讲柯西不等式与排序不等式一二维形式柯西不等式二一般形式的柯西不等式三排序不等式第四讲数学归纳法证明不等式一数学归纳法二用数学归纳法证明不等式4(新课标)人教版高中教材目录——政治必修1 经济生活【第一单元生活与消费】第一课神奇的货币揭开货币的神秘面纱信用工具和外汇第二课多变的价格影响价格的因素价格变动的影响第三课多彩的消费消费及其类型树立正确的消费观综合探究正确对待金钱【第二单元生产、劳动与经营】第四课生产与经济制度发展生产满足消费我国的基本经济制度第五课企业与劳动者公司的经营新时代的劳动者第六课投资理财的选择储蓄存款和商业银行股票、债券和保险综合探究做好就业与自主创业的准备【第三单元收入与分配】第七课个人收入的分配按劳分配为主体多种分配方式并存收入分配与社会公平第八课财政与税收国家财政征税和纳税综合探究提高效率促进公平【第四单元发展社会主义市场经济】第九课走进社会主义市场经济市场配置资源社会主义市场经济第十课社会发展观和小康社会的经济建设全面建设小康社会的经济目标又好又快科学发展第十一课经济全球化与对外开放面对经济全球化积极参与国际经济竞争与合作综合探究经济全球化与中国5【第一单元公民的政治生活】第一课生活在人民当家作主的国家人民民主专政:本质是人民当家作主政治权利与义务:参与政治生活的基础和准则政治生活:有序参与第二课我国公民的政治参与民主选举:投出理性一票民主决策:作出最佳选择民主管理:共创幸福生活民主监督:守望公共家园综合探究有序与无序的政治参与【第二单元为人民服务的政府】第三课我们政府是人民的政府政府的职能:管理与服务政府的责任:对人民负责第四课我国政府受人民的监督政府的权力:依法行使权力的行使:需要监督综合探究政府的权威从何而来【第三单元发展社会主义民主政治】第五课我国的人民代表大会制度人民代表大会:国家权力机关人民代表大会制度:我国的根本政治制度第六课我国的政党制度中国共产党执政:历史和人民的选择中国共产党:以人为本执政为民共产党领导的多党合作和政治协商制度:中国特色的政党制度第七课我国的民族区域自治制度及宗教政策处理民族关系的原则:平等、团结、共同繁荣民族区域自治制度:适合国情的基本政治制度我国的宗教政策综合探究社会主义民主政治的特点和优势【第四单元当代国际社会】第八课走近国际社会国际社会的主要成员:主权国家和国际组织国际关系的决定性因素:国家利益第九课维护世界和平促进共同发展和平与发展:时代的主题世界多极化:不可逆转我国外交政策的宗旨:维护世界和平促进共同发展6【第一单元文化与生活】第一课文化与社会体味文化文化与经济、政治第二课文化对人的影响感受文化影响文化塑造人生综合探究聚焦文化竞争力【第二单元文化传承与创新】第三课文化的多样性与文化传播世界文化的多样性文化在交流中传播第四课文化的继承性与文化发展传统文化的继承文化在继承中发展第五课文化创新文化创新的源泉和作用文化创新的途径综合探究建设“学习型社会”【第三单元中华文化与民族精神】第六课我们的中华文化源远流长的中华文化博大精深的中华文化第七课我们的民族精神永恒的中华民族精神弘扬中华民族精神综合探究铸牢中华民族的精神支柱【第四单元发展中国特色社会主义文化】第八课走进文化生活色彩斑斓的文化生活在文化生活中选择第九课推动社会主义文化大发展大繁荣坚持先进文化的前进方向建设社会主义精神文明第十课文化发展的中心环节加强思想道德建设思想道德修养与科学文化修养综合探究感悟当代中国的先进文化7必修4 生活与哲学【第一单元生活智慧与时代精神】第一课美好生活的向导生活处处有哲学关于世界观的学说第二课百舸争流的思想哲学的基本问题唯物主义和唯心主义第三课时代精神的精华真正的哲学都是自己时代的精神上的精华哲学史上的伟大变革综合探究走进哲学问辩人生【第二单元探索世界与追求真理】第四课探究世界的本质世界的物质性认识运动把握规律第五课把握思维的奥妙意识的本质意识的作用第六课求索真理的历程人的认识从何而来在实践中追求和发展真理综合探究求真务实与时俱进【第三单元思想方法与创新意识】第七课唯物辩证法的联系观世界是普遍联系的用联系的观点看问题第八课唯物辩证法的发展观世界是永恒发展的用发展的观点看问题第九课唯物辩证法的实质与核心矛盾是事物发展的源泉和动力用对立统一的观点看问题第十课创新意识与社会进步树立创新意识是唯物辩证法的要求创新是民族进步的灵魂综合探究坚持唯物辩证法反对形而上学【第四单元认识社会与价值选择】第十一课寻觅社会的真谛社会发展的规律社会历史的主体第十二课实现人生的价值价值与价值观价值判断与价值选择价值的创造与实现综合探究坚定理想铸就辉煌思想政治选修1 科学社会主义常识思想政治选修2 经济学常识思想政治选修4 科学思维常识思想政治选修5 生活中的法律常识思想政治选修6 公民道德与伦理常识8(新课标)人教版高中教材目录——历史必修一第一单元古代中国的政治制度第一课夏、商、西周的政治制度第二课秦朝中央集权制度的形成第三课从汉至元政治制度的演变第四课明清君主专制的加强第二单元古代希腊罗马的政治制度第五课古代希腊民主政治第六课罗马法的起源与发展探究活动课“黑暗”的西欧中世纪——历史素材阅读与研讨第三单元近代西方资本主义政治制度的确立与发展第七课英国君主立宪制的建立第八课美国联邦政府的建立第九课资本主义政治制度在欧洲大陆的扩展第四单元近代中国反侵略、求民主的潮流第十课鸦片战争第十一课太平天国运动第十二课甲午中日战争和八国联军侵华第十三课辛亥革命第十四课新民主主义革命的崛起第十五课国共的十年对峙第十六课抗日战争第十七课解放战争第五单元从科学社会主义理论到社会主义制度的建立第十八课马克思主义的诞生第十九课俄国十月革命的胜利第六单元现代中国的政治建设与祖国统一第二十课新中国的民主政治建设第二十一课民主政治建设的曲折发展第二十二课祖国统一大业第七单元现代中国的对外关系第二十三课新中国初期的外交第二十四课开创外交新局面第八单元当今世界政治格局的多极化趋势第二十五课两极世界的形成第二十六课世界多极化趋势的出现第二十七课世纪之交的世界格局必修二第一单元古代中国经济的基本结构与特点第一课发达的古代农业第二课古代手工业的进步第三课古代商业的发展第四课古代的经济政策第二单元资本主义世界市场的形成和发展第五课开辟新航路第六课殖民扩张与世界市场的拓展第七课第一次工业革命第八课第二次工业革命第三单元近代中国经济结构的变动与资本主义的曲折发展第九课近代中国经济结构的变动第十课中国民族资本主义的曲折发展第四单元中国特色社会主义建设的道路第十一课经济建设的发展和曲折第十二课从计划经济到市场经济第十三课对外开放格局的初步形成第五单元中国近代社会生活的变迁第十四课物质生活与习俗的变迁第十五课交通工具和通讯工具的进步第十六课大众传媒的变迁探究活动课中国民生百年变迁(20世纪初~21世纪)──历史展览第六单元世界资本主义经济政策的调整第十七课空前严重的资本主义世界经济9危机第十八课罗斯福新政第十九课战后资本主义的新变化第七单元苏联的社会主义建设第二十课从“战时共产主义”到“斯大林模式”第二十一课二战后的苏联经济改革第八单元世界经济的全球化趋势第二十二课战后资本主义世界经济体系的形成第二十三课世界经济的区域集团化第二十四课世界经济的全球化趋势必修三第一单元中国传统文化主流思想的演变第1课“百家争鸣”和儒家思想的形成第2课“罢黜百家,独尊儒术”第3课宋明理学第4课明清之际活跃的儒家思想第二单元西方人文精神的起源及其发展第5课西方人文主义思想的起源第6课文艺复兴和宗教改革第7课启蒙运动第三单元古代中国的科学技术与文学艺术第8课古代中国的发明和发现第9课辉煌灿烂的文学第10课充满魅力的书画和戏曲艺术探究活动课中国传统文化的过去、现在与未来──历史小论文第四单元近代以来世界的科学历程第11课物理学的重大进展第12课探索生命起源之谜第13课从蒸汽机到互联网第五单元近代中国的思想解放潮流第14课从“师夷长技”到维新变法第15课新文化运动与马克思主义的传播第六单元20世纪以来中国重大思想理论成果第16课三民主义的形成和发展第17课毛泽东思想第18课新时期的理论探索第七单元现代中国的科技、教育与文学艺术第19课建国以来的重大科技成就第20课“百花齐放”“百家争鸣”第21课现代中国教育的发展第八单元19世纪以来的世界文学艺术第22课文学的繁荣第23课美术的辉煌第24课音乐与影视艺术第一单元梭伦改革第1课雅典城邦的兴起第2课除旧布新的梭伦改革第3课雅典民主政治的奠基石第一单元资料与注释第1课改革变法风潮与秦国历史机遇第2课“为秦开帝业”──商鞅变法第3课富国强兵的秦国第二单元资料与注释第1课改革迫在眉睫第2课北魏孝文帝的改革措施第3课促进民族大融合第三单元资料与注释第1课社会危机四伏和庆历新政第2课王安石变法的主要内容第3课王安石变法的历史作用第四单元资料与注释探究活动课一历史上的改革与发展10第五单元欧洲的宗教改革第1课宗教改革的历史背景第2课马丁·路德的宗教改革第3课宗教改革运动的扩展第五单元资料与注释第六单元穆罕默德·阿里改革第1课18世纪末19世纪初的埃及第2课穆罕默德·阿里改革的主要内容第3课改革的后果第六单元资料与注释第七单元1861年俄国农奴制改革第1课19世纪中叶的俄国第2课农奴制改革的主要内容第3课农奴制改革与俄国的近代化第七单元资料与注释探究活动课二古老文化与现代文明第八单元日本明治维新第1课从锁国走向开国的日本第2课倒幕运动和明治政府的成立第3课明治维新第4课走向世界的日本第八单元资料与注释第九单元戊戌变法第1课甲午战争后民族危机的加深第2课维新运动的兴起第3课百日维新第4课戊戌政变第九单元资料与注释探究活动课三改革成败的机遇与条件选修二近代社会的民主思想与实践第一单元专制理论与民主思想的冲突第1课西方专制主义理论第2课近代西方的民主思想第二单元英国议会与国王的斗争第1课英国议会与王权矛盾的激化第2课民主与专制的反复较量第三单元向封建专制统治宣战的檄文第1课美国《独立宣言》第2课法国《人权宣言》第3课《中华民国临时约法》探究活动课一撰写历史短评──试评辛亥革命和《中华民国临时约法》第四单元构建资产阶级代议制的政治框架第1课英国君主立宪制的建立第2课英国责任制内阁的形成第3课美国代议共和制度的建立第五单元法国民主力量与专制势力的斗争第1课法国大革命的最初胜利第2课拿破仑帝国的建立与封建制度的复辟第3课法国资产阶级共和制度的最终确立第六单元近代中国的民主思想与反对专制的斗争第1课西方民主思想对中国的冲击第2课中国资产阶级的民主思想第3课资产阶级民主革命的酝酿和爆发第4课反对复辟帝制、维护共和的斗争第七单元无产阶级和人民群众争取民主的斗争第1课英国宪章运动第2课欧洲无产阶级争取民主的斗争第3课抗战胜利前中国人民争取民主的斗争第4课抗战胜利后的人民民主运动探究活动课二近代时期人民对民主的追求与斗争──学习编辑历史报纸1112(新课标)人教版高中教材目录——地理必修1第一章行星地球第一节宇宙中的地球第二节太阳对地球的影响第三节地球的运动第四节地球的圈层结构第二章地球上的大气第一节冷热不均引起大气运动第二节气压带和风带第三节常见天气系统第四节全球气候变化第三章地球上的水第一节自然界的水循环第二节大规模的海水运动第三节水资源的合理利用第四章地表形态的塑造第一节营造地表形态的力量第二节山岳的形成第三节河流地貌的发育第五章自然地理环境的整体性与差异性第一节自然地理环境的整体性第二节自然地理环境的差异性必修2第一章人口的变化第一节人口的数量变化第二节人口的空间变化第三节人口的合理容量第二章城市与城市化第一节城市内部空间结构第二节不同等级城市的服务功能第三节城市化第三章农业地域的形成与发展第一节农业的区位选择第二节以种植业为主的农业地域类型第三节以畜牧业为主的农业地域类型第四章工业地域的形成与发展第一节工业的区位因素与区位选择第二节工业地域的形成第三节传统工业区与新工业区第五章交通运输布局及其影响第一节交通运输方式的布局第二节交通运输布局变化的影响第六章人类与地理环境的协调发展第一节人地关系思想的演变第二节中国的可持续发展实践必修3第一章地理环境与区域发展第一节地理环境对区域发展的影响第二节地理信息技术在区域地理环境研究中的应用第二章区域生态环境建设13第一节荒漠化的防治──以我国西北地区为例第二节森林的开发和保护──以亚马孙热带林为例第三章区域自然资源综合开发利用第一节能源资源的开发──以我国山西省为例第二节河流的综合开发──以美国田纳西河流域为例第四章区域经济发展第一节区域农业发展──以我国东北地区为例第二节区域工业化与城市化──以我国珠江三角洲地区为例第五章区际联系与区域协调发展第一节资源的跨区域调配──以我国西气东输为例第二节产业转移──以东亚为例选修1 宇宙与地球第一章宇宙第一节天体和星空第二节探索宇宙第三节恒星的一生和宇宙的演化第二章太阳系与地月系第一节太阳和太阳系第二节月球和地月系第三节月相和潮汐变化第三章地球的演化和地表形态的变化第一节地球的早期演化和地质年代第二节板块构造学说第三节地表形态的变化选修2 海洋地理第一章海洋概述第一节地球上的海与洋第二节人类对海洋的探索与认识第二章海岸与海底地形第一节海岸第二节海底地形的分布第三节海底地形的形成第三章海洋水体第一节海水的温度和盐度第二节海水的运动第四章海-气作用第一节海-气相互作用及其影响第二节厄尔尼诺和拉尼娜现象第五章海洋开发第一节海岸带的开发第二节海洋资源的开发利用第三节海洋能的开发利用第四节海洋空间的开发利用第六章人类与海洋协调发展第一节海洋自然灾害与防范第二节海洋环境问题与环境保护14第三节维护海洋权益加强国际合作选修3 旅游地理第一章现代旅游及其作用第一节现代旅游第二节现代旅游对区域发展的意义第二章旅游资源第一节旅游资源的分类与特性第二节旅游资源开发条件的评价第三节我国的旅游资源第三章旅游景观的欣赏第一节旅游景观的审美特性第二节旅游景观欣赏的方法第三节中外著名旅游景观欣赏第四章旅游开发与保护第一节旅游规则第二节旅游开发中的环境保护第五章做一个合格的现代游客第一节设计旅游活动第二节参与旅游环境保护选修4 城乡规划第一章城乡发展与城市化第一节聚落的形成和发展第二节城市化与城市环境问题第二章城乡合理布局与协调发展第一节城市空间形态及变化第二节城镇布局与协调发展第三节城乡特色景观与传统文化的保护第三章城乡规划第一节城乡规划的内容及意义第二节城乡土地利用与功能分区第三节城乡规划中的主要布局第四章城乡建设与人居环境第一节城乡人居环境第二节城乡商业与生活环境第三节城乡公共服务设施与生活环境选修5 自然灾害与防治第一章自然灾害与人类活动第一节自然灾害及其影响第三节人类活动对自然灾害的影响第二章中国的自然灾害第一节中国自然灾害的特点第二节中国的地质灾害第三节中国的水文灾害第四节中国的气象灾害第五节中国的生物灾害第三章防灾与减灾第一节自然灾害的监测与防御第二节自然灾害的求援与求助第三节自然灾害中的自救与互救15。
新课标人教版高中数学目录

新课标人教版高中数学目录篇一:人教版高中数学新课标目录高中数学新课标目录核心提示:高中数学新课标目录介绍,这与原教材有了很大的不同,分为必修五个模块,选修五个模块。
必修一:第一章集合与函数概念1.1 集合1.2 函数及其表示1.3 函数的基本性质实习作业小结复习参考题第二章基本初等函数(Ⅰ)2.1 指数函数2.2 对数函数2.3 幂函数小结复习参考题第三章函数的应用3.1 函数与方程3.2 函数模型及其应用实习作业小结复习参考题必修二:第一章空间几何体1.1 空间几何体的结构1.2 空间几何体的三视图和直观图1.3 空间几何体的表面积与体积实习作业小结复习参考题第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.3 直线、平面垂直的判定及其性质小结复习参考题第三章直线与方程3.1 直线的倾斜角与斜率3.2 直线的方程3.3 直线的交点坐标与距离公式小结复习参考题必修三:第一章算法初步1.1 算法与程序框图1.2 基本算法语句1.3 算法案例阅读与思考割圆术小结复习参考题第二章统计2.1 随机抽样阅读与思考一个著名的案例阅读与思考广告中数据的可靠性阅读与思考如何得到敏感性问题的诚实反应2.2 用样本估计总体阅读与思考生产过程中的质量控制图2.3 变量间的相关关系阅读与思考相关关系的强与弱实习作业小结第三章概率3.1 随机事件的概率阅读与思考天气变化的认识过程3.2 古典概型3.3 几何概型阅读与思考概率与密码小结复习参考题必修四:第一章三角函数1.1 任意角和弧度制1.2 任意角的三角函数1.3 三角函数的诱导公式1.4 三角函数的图象与性质1.5 函数y=Asin(ωx+ψ)1.6 三角函数模型的简单应用小结复习参考题第二章平面向量2.1 平面向量的实际背景及基本概念2.2 平面向量的线性运算2.3 平面向量的基本定理及坐标表示2.4 平面向量的数量积2.5 平面向量应用举例小结复习参考题第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.2 简单的三角恒等变换小结复习参考题必修五:第一章解三角形1.1 正弦定理和余弦定理探究与发现解三角形的进一步讨论1.2 应用举例阅读与思考海伦和秦九韶1.3 实习作业小结复习参考题第二章数列2.1 数列的概念与简单表示法阅读与思考斐波那契数列阅读与思考估计根号下2的值2.2 等差数列2.3 等差数列的前n项和2.4 等比数列2.5 等比数列前n项和阅读与思考九连环探究与发现购房中的数学小结复习参考题第三章不等式3.1 不等关系与不等式3.2 一元二次不等式及其解法3.3 二元一次不等式(组)与简单的线性规划问题阅读与思考错在哪儿信息技术应用用Excel解线性规划问题举例3.4 基本不等式小结复习参考题选修1-1第一章常用逻辑用语1.1 命题及其关系1.2 充分条件与必要条件1.3 简单的逻辑联结词1.4 全称量词与存在量词小结复习参考题第二章圆锥曲线与方程2.1 椭圆探究与发现为什么截口曲线是椭圆信息技术应用用《几何画板》探究点的轨迹:椭圆2.2 双曲线2.3 抛物线阅读与思考圆锥曲线的光学性质及其应用小结复习参考题第三章导数及其应用3.1 变化率与导数3.2 导数的计算探究与发现牛顿法──用导数方法求方程的近似解3.3 导数在研究函数中的应用信息技术应用图形技术与函数性质3.4 生活中的优化问题举例实习作业走进微积分小结复习参考题选修1-2: 第一章统计案例1.1 回归分析的基本思想及其初步应用1.2 独立性检验的基本思想及其初步应用实习作业小结复习参考题第二章推理与证明2.1 合情推理与演绎证明阅读与思考科学发现中的推理2.2 直接证明与间接证明小结复习参考题第三章数系的扩充与复数的引入3.1 数系的扩充和复数的概念 3.2 复数代数形式的四则运算小结复习参考题第四章框图4.1 流程图 4.2 结构图信息技术应用用Word2002绘制流程图小结复习参考题选修2-1:第一章常用逻辑用语1.1 命题及其关系1.2 充分条件与必要条件1.3 简单的逻辑联结词1.4 全称量词与存在量词小结复习参考题第二章圆锥曲线与方程2.1 曲线与方程2.2 椭圆探究与发现为什么截口曲线是椭圆信息技术应用用《几何画板》探究点的轨迹:椭圆2.3 双曲线探究与发现2.4 抛物线探究与发现阅读与思考小结复习参考题第三章空间向量与立体几何3.1 空间向量及其运算阅读与思考向量概念的推广与应用3.2 立体几何中的向量方法小结复习参考题选修2-2:第一章导数及其应用1.1 变化率与导数1.2 导数的计算1.3 导数在研究函数中的应用1.4 生活中的优化问题举例1.5 定积分的概念1.6 微积分基本定理1.7 定积分的简单应用小结复习参考题第二章推理与证明2.1 合情推理与演绎推理2.2 直接证明与间接证明2.3 数学归纳法小结复习参考题第三章数系的扩充与复数的引入3.1 数系的扩充和复数的概念3.2 复数代数形式的四则运算小结复习参考题选修2-3:第一章计数原理1.1 分类加法计数原理与分步乘法计数原理探究与发现子集的个数有多少1.2 排列与组合探究与发现组合数的两个性质1.3 二项式定理探究与发现“杨辉三角”中的一些秘密小结复习参考题第二章随机变量及其分布2.1 离散型随机变量及其分布列2.2 二项分布及其应用阅读与思考这样的买彩票方式可行吗探究与发现服从二项分布的随机变量取何值时概率最大2.3 离散型随机变量的均值与方差2.4 正态分布信息技术应用μ,σ对正态分布的影响小结复习参考题第三章统计案例3.1 回归分析的基本思想及其初步应用3.2 独立性检验的基本思想及其初步应用实习作业小结复习参考题选修3-1:第一章计数原理1.1 分类加法计数原理与分步乘法计数原理探究与发现子集的个数有多少1.2 排列与组合探究与发现组合数的两个性质1.3 二项式定理探究与发现“杨辉三角”中的一些秘密小结复习参考题第二章随机变量及其分布2.1 离散型随机变量及其分布列2.2 二项分布及其应用阅读与思考这样的买彩票方式可行吗探究与发现服从二项分布的随机变量取何值时概率最大2.3 离散型随机变量的均值与方差2.4 正态分布信息技术应用μ,σ对正态分布的影响小结复习参考题第三章统计案例3.1 回归分析的基本思想及其初步应用3.2 独立性检验的基本思想及其初步应用实习作业小结复习参考题选修3-3: 引言第一讲从欧氏几何看球面一平面与球面的位置关系二直线与球面的位置关系和球幂定理三球面的对称性思考题第二讲球面上的距离和角一球面上的距离二球面上的角思考题第三讲球面上的基本图形一极与赤道二球面二角形三球面三角形1.球面三角形2.三面角3.对顶三角形4.球极三角形思考题第四讲球面三角形一球面三角形三边之间的关系二、球面“等腰”三角形三球面三角形的周长四球面三角形的内角和思考题第五讲球面三角形的全等1.“边边边”(s.s.s)判定定理2.“边角边”(s.a.s.)判定定理3.“角边角”(a.s.a.)判定定理4.“角角角”(a.a.a.)判定定理思考题第六讲球面多边形与欧拉公式一球面多边形及其内角和公式二简单多面体的欧拉公式三用球面多边形的内角和公式证明欧拉公式第七讲球面三角形的边角关系思考题篇二:人教版高中数学教材最新目录高中数学必修一第一章集合与函数概念1.1 集合1.2 函数及其表示1.3 函数的基本性质第二章基本初等函数(Ⅰ)2.2 对数函数2.3 幂函数第三章函数的应用3.1 函数与方程3.2 函数模型及其应用2.1 指数函数必修二第一章空间几何体1.1 空间几何体的结构1.2 空间几何体的三视图和直观图1.3 空间几何体的表面积与体积第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系2.2 直线、平面平行的判定及其性质2.3 直线、平面垂直的判定及其性质第三章直线与方程3.1 直线的倾斜角与斜率3.2 直线的方程3.3 直线的交点坐标与距离公式必修三:第一章算法初步1.1 算法与程序框图1.31.2 基本算法语句第二章统计2.1 随机抽样阅读与思考一个著名的案例阅读与思考广告中数据的可靠性阅读与思考如何得到敏感性问题的诚实反应2.2 用样本估计总体阅读与思考生产过程中的质量控制图2.3 变量间的相关关系阅读与思考相关关系的强与弱第三章概率3.1 随机事件的概率阅读与思考天气变化的认识过程3.2 古典概型3.3 几何概型阅读与思考概率与密码算法案例必修四:第一章三角函数1.1 任意角和弧度制1.4 三角函数的图象与性质1.2 任意角的三角函数1.5 函数y=Asin(ωx+ψ)1.3 三角函数的诱导公式1.6 三角函数模型的简单应用第二章平面向量2.1 平面向量的实际背景及基本概念2.2 平面向量的线性运算2.3 平面向量的基本定理及坐标表示2.4 平面向量的数量积2.5 平面向量应用举例第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式3.2 简单的三角恒等变换必修五:第一章解三角形1.1 正弦定理和余弦定理探究与发现解三角形的进一步讨论1.2 应用举例阅读与思考海伦和秦九韶1.3 实习作业第二章数列2.1 数列的概念与简单表示法阅读与思考斐波那契数列阅读与思考估计根号下2的值2.2 等差数列2.3 等差数列的前n项和2.4 等比数列2.5 等比数列前n项和阅读与思考九连环探究与发现购房中的数学第三章不等式3.1 不等关系与不等式3.2 一元二次不等式及其解法3.3 二元一次不等式(组)与简单的线性规划问题阅读与思考错在哪儿信息技术应用用Excel解线性规划问题举例3.4 基本不等式选修1-1第一章常用逻辑用语1.1 命题及其关系1.2 充分条件与必要条件1.3 简单的逻辑联结词1.4 全称量词与存在量词第二章圆锥曲线与方程2.1 椭圆探究与发现为什么截口曲线是椭圆信息技术应用用《几何画板》探究点的轨迹:椭圆2.2 双曲线2.3 抛物线阅读与思考圆锥曲线的光学性质及其应用第三章导数及其应用3.1 变化率与导数3.2 导数的计算探究与发现牛顿法──用导数方法求方程的近似解3.3 导数在研究函数中的应用信息技术应用图形技术与函数性质3.4 生活中的优化问题举例实习作业走进微积分选修1-2第一章统计案例1.1 回归分析的基本思想及其初步应用1.2 独立性检验的基本思想及其初步应用实习作业第二章推理与证明2.1 合情推理与演绎证明阅读与思考科学发现中的推理2.2 直接证明与间接证明第三章数系的扩充与复数的引入3.1 数系的扩充和复数的概念3.2 复数代数形式的四则运算第四章框图4.1 流程图4.2 结构图信息技术应用用Word2002绘制流程图选修2-1:第一章常用逻辑用语1.1 命题及其关系 1.3 简单的逻辑联结词1.2 充分条件与必要条件 1.4 全称量词与存在量词第二章圆锥曲线与方程2.1 曲线与方程2.2 椭圆探究与发现为什么截口曲线是椭圆信息技术应用用《几何画板》探究点的轨迹:椭圆2.3 双曲线探究与发现2.4 抛物线探究与发现阅读与思考第三章空间向量与立体几何3.1 空间向量及其运算阅读与思考向量概念的推广与应用3.2 立体几何中的向量方法选修2-2:第一章导数及其应用1.1 变化率与导数1.2 导数的计算1.3 导数在研究函数中的应用1.4 生活中的优化问题举例第二章推理与证明2.1 合情推理与演绎推理2.2 直接证明与间接证明第三章数系的扩充与复数的引入3.1 数系的扩充和复数的概念1.5 定积分的概念1.6 微积分基本定理1.7 定积分的简单应用2.3 数学归纳法3.2 复数代数形式的四则运算选修2-3第一章计数原理1.1 分类加法计数原理与分步乘法计数原理探究与发现子集的个数有多少1.2 排列与组合探究与发现组合数的两个性质1.3 二项式定理探究与发现“杨辉三角”中的一些秘密第二章随机变量及其分布2.1 离散型随机变量及其分布列2.2 二项分布及其应用阅读与思考这样的买彩票方式可行吗探究与发现服从二项分布的随机变量取何值时概率最大2.3 离散型随机变量的均值与方差2.4 正态分布信息技术应用μ,σ对正态分布的影响第三章统计案例3.1 回归分析的基本思想及其初步应用3.2 独立性检验的基本思想及其初步应用实习作业选修3-1:第一章计数原理1.1 分类加法计数原理与分步乘法计数原理探究与发现子集的个数有多少1.2 排列与组合探究与发现组合数的两个性质1.3 二项式定理探究与发现“杨辉三角”中的一些秘密第二章随机变量及其分布2.1 离散型随机变量及其分布列2.2 二项分布及其应用阅读与思考这样的买彩票方式可行吗探究与发现服从二项分布的随机变量取何值时概率最大2.3 离散型随机变量的均值与方差2.4 正态分布信息技术应用μ,σ对正态分布的影响第三章统计案例3.1 回归分析的基本思想及其初步应用3.2 独立性检验的基本思想及其初步应用实习作业选修3-3第一讲一二三第二讲一二第三讲一二三第六讲从欧氏几何看球面平面与球面的位置关系直线与球面的位置关系和球幂定理球面的对称性球面上的距离和角球面上的距离球面上的角球面上的基本图形极与赤道球面二角形球面三角形 1.球面三角形 2.三面角 3.对顶三角形 4.球极三角形球面多边形与欧拉公式第四讲球面三角形一球面三角形三边之间的关系二、球面“等腰”三角形三球面三角形的周长四球面三角形的内角和第五讲球面三角形的全等 1.“边边边”(s.s.s)判定定理2.“边角边”(s.a.s.)判定定理 3.“角边角”(a.s.a.)判定定理 4.“角角角”(a.a.a.)判定定理篇三:人教版高中数学教材最新目录人教版普通高中课程标准实验教科书数学必修1第一章集合与函数概念 1.1 集合1.2 函数及其表示 1.3 函数的基本性质第二章基本初等函数(Ⅰ) 2.1 指数函数 2.2 对数函数 2.3 幂函数第三章函数的应用 3.1 函数与方程3.2 函数模型及其应用必修2第一章空间几何体1.1 空间几何体的结构1.2 空间几何体的三视图和直观图 1.3 空间几何体的表面积与体积第二章点、直线、平面之间的位置关系2.1 空间点、直线、平面之间的位置关系 2.2 直线、平面平行的判定及其性质 2.3 直线、平面垂直的判定及其性质第三章直线与方程3.1 直线的倾斜角与斜率 3.2 直线的方程3.3 直线的交点坐标与距离公式第四章圆与方程 4.1 圆的方程4.2 直线、圆的位置关系4.3 空间直角坐标系必修3第一章算法初步1.1 算法与程序框图 1.2 基本算法语句1.3 算法案例第二章统计2.1 随机抽样2.2 用样本估计总体 2.3 变量间的相关关系第三章概率3.1 随机事件的概率 3.2 古典概型 3.3 几何概型必修4第一章三角函数1.1 任意角和弧度制 1.2 任意角的三角函数 1.3 三角函数的诱导公式 1.4 三角函数的图象与性质 1.5 函数y=Asin(ωx+ψ) 1.6 三角函数模型的简单应用第二章平面向量2.1 平面向量的实际背景及基本概念 2.2 平面向量的线性运算2.3 平面向量的基本定理及坐标表示 2.4 平面向量的数量积 2.5 平面向量应用举例第三章三角恒等变换3.1 两角和与差的正弦、余弦和正切公式 3.2 简单的三角恒等变换必修5第一章解三角形1.1 正弦定理和余弦定理 1.2 应用举例 1.3 实习作业第二章数列2.1 数列的概念与简单表示法 2.2 等差数列2.3 等差数列的前n项和 2.4 等比数列2.5 等比数列前n项和第三章不等式3.1 不等关系与不等式3.2 一元二次不等式及其解法3.3 二元一次不等式(组)与简单的线性规划问题3.4 基本不等式选修2-1第一章常用逻辑用语 1.1 命题及其关系1.2 充分条件与必要条件 1.3 简单的逻辑联结词 1.4 全称量词与存在量词第二章圆锥曲线与方程 2.1 曲线与方程12.2 椭圆2.3 双曲线 2.4 抛物线第三章空间向量与立体几何 3.1 空间向量及其运算 3.2 立体几何中的向量方法选修2-2第一章导数及其应用 1.1 变化率与导数 1.2 导数的计算1.3 导数在研究函数中的应用 1.4 生活中的优化问题举例1.5 定积分的概念 1.6 微积分基本定理 1.7 定积分的简单应用第二章推理与证明2.1 合情推理与演绎推理 2.2 直接证明与间接证明 2.3 数学归纳法第三章数系的扩充与复数的引入 3.1 数系的扩充和复数的概念 3.2 复数代数形式的四则运算选修2-3第一章计数原理 1.1 分类加法计数原理与分步乘法计数原理1.2 排列与组合 1.3 二项式定理第二章随机变量及其分布 2.1 离散型随机变量及其分布列 2.2 二项分布及其应用 2.3 离散型随机变量的均值与方差 2.4 正态分布第三章统计案例 3.1 回归分析的基本思想及其初步应用 3.2 独立性检验的基本思想及其初步应用选修4-1第一讲相似三角形的判定及有关性质一平行线等分线段定理二平行线分线段成比例定理三相似三角形的判定及性质1.相似三角形的判定 2.相似三角形的性质四直角三角形的射影定理第二讲直线与圆的位置关系一圆周角定理二圆内接四边形的性质与判定定理三圆的切线的性质及判定定理四弦切角的性质五与圆有关的比例线段第三讲圆锥曲线性质的探讨一平行摄影二平面与圆柱面的截线三平面与圆锥面的截线选修4-4第一章坐标系1直角坐标系平面上的压缩变换 2极坐标系3曲线的极坐标方程 4圆的极坐标方程 5柱坐标系和球坐标系第二章参数方程 1曲线的参数方程 2直线和圆的参数方程 3圆锥曲线的参数方程4一些常见曲线的参数方程选修4-5第一讲不等式和绝对值不等式一不等式1.不等式的基本性质2.基本不等式3.三个正数的算术-几何平均不等式二绝对值不等式1.绝对值三角不等式2.绝对值不等式的解法第二讲讲明不等式的基本方法一比较法二综合法与分析法三反证法与放缩法第三讲柯西不等式与排序不等式一二维形式柯西不等式二一般形式的柯西不等式三排序不等式第四讲数学归纳法证明不等式一数学归纳法二用数学归纳法证明不等式。
高中数学第1章导数及其应用1.3导数在研究函数中的应用1.3.3最大值与最小值222数学

12/9/2021
第二十二页,共四十九页。
当-1<23a<0,即-32<a<0 时, f(x)在-1,23a上单调递增;在23a,0上单调递减. 则 f(x)max=f23a=-247a3.
-1-a,a≤-32, 综上所述:f(x)max=-247a3,-32<a<0,
0,a≥0.
12/9/2021
所以当 x=0 时,f(x)取最小值,即 b=-29;
当 x=2 时,f(x)取最大值,即-16a-29=3,所以 a=-2.
综上所述,a=2,b=3 或 a=-2,b=-29.
12/9/2021
第二十七页,共四十九页。
已知函数最值求参数值(范围)的思路 已知函数在某区间上的最值求参数的值(范围)是求函数最值的逆 向思维,一般先求导数,利用导数研究函数的单调性及极值点, 用参数表示出最值后求参数的值或范围.
第二十三页,共四十九页。
已知函数最值求参数的值 已知 f(x)=ax3-6ax2+b,问是否存在实数 a,b,使 f(x) 在[-1,2]上取最大值 3,最小值-29?若存在,求出 a,b 的值; 若不存在,说明理由.
12/9/2021
第二十四页,共四十九页。
【解】 存在.显然 a≠0,f′(x)=3ax2-12ax.
12/9/2021
第四页,共四十九页。
1.判断(正确的打“√”,错误的打“×”) (1)定义在闭区间[a,b]上的连续函数 f(x)一定有最大值和最小 值.( √ ) (2)定义在开区间(a,b)上的函数 f(x)没有最大值.( × ) (3)函数的所有极小值中最小的一个就是最小值.( × )
12/9/2021
12/9/2021
第二十一页,共四十九页。
高中数学第一章导数及其应用1.3导数在研究函数中的应用1.3.3函数的最大小值与导数优化练习新人教A

1.3.3 函数的最大(小)值与导数[课时作业] [A 组 基础巩固]1.函数y =f (x )在区间[a ,b ]上的最大值是M ,最小值是m ,若M =m ,则f ′(x )( ) A .等于0 B .大于0 C .小于0D .以上都有可能解析:由题意,知在区间[a ,b ]上,有m ≤f (x )≤M ,当M =m 时,令M =m =C ,则必有f (x )=C ,∴f ′(x )=C ′=0.故选A.答案:A2.函数y =ln xx的最大值为( )A .e -1B .eC .e 2D.103解析:y ′=1x·x -ln xx 2=1-ln xx2(x >0), 令y ′=0,得x =e.∴当0<x ≤e 时,y ′≥0,y =ln x x为增函数;当x >e 时,y ′<0,y =ln x x为减函数.∴y =ln x x 在(0,+∞)上的最大值为y max =ln e e =1e .答案:A3.函数f (x )=x +2cos x 在区间[-π2,0]上的最小值是( )A .-π2B .2 C.π6+ 3 D.π3+1 解析:f ′(x )=1-2sin x , ∵x ∈[-π2,0],∴sin x ∈[-1,0],∴-2sin x ∈[0,2]. ∴f ′(x )=1-2sin x >0在[-π2,0]上恒成立,∴f (x )在[-π2,0]上单调递增.∴f (x )min =f (-π2)=-π2+2cos(-π2)=-π2.答案:A4.已知函数f (x )=12x 4-2x 3+3m ,x ∈R ,若f (x )+9≥0恒成立,则实数m 的取值范围是( )A .m ≥32B .m >32C .m ≤32D .m <32解析:因为函数f (x )=12x 4-2x 3+3m ,所以f ′(x )=2x 3-6x 2.令f ′(x )=0,得x =0或x =3.经检验知x =3是函数的一个最小值点,所以函数的最小值为f (3)=3m -272.不等式f (x )+9≥0恒成立,即f (x )≥-9恒成立,所以3m -272≥-9,解得m ≥32.答案:A5.已知函数y =-x 2-2x +3在[a,2]上的最大值为154,则a 等于( )A .-32B.12 C .-12D.12或-32解析:y ′=-2x -2,令y ′=0得x =-1. 当a ≤-1时,最大值为f (-1)=4,不合题意.当-1<a <2时,f (x )在[a,2]上单调递减,最大值为f (a )=-a 2-2a +3=154,解得a =-12或a =-32(舍去). 答案:C6.函数f (x )=x -ln x ,x ∈[1e ,e]的最大值为________.解析:f ′(x )=1-1x,x >0.由f ′(x )=0,得x =1.又f (1)=1,f (1e )=1e+1,f (e)=e -1,∵f (1e )-f (e)=2+1e -e<2+12-e<0,∴f (1e )<f (e),f (x )最大值为f (e)=e -1.答案:e -17.已知f (x )=-x 2+mx +1在区间[-2,-1]上的最大值就是函数f (x )的极大值,则m 的取值范围是________.解析:f ′(x )=m -2x ,令f ′(x )=0,得x =m 2.由题设得m2∈[-2,-1],故m ∈[-4,-2].答案:[-4,-2]8.已知函数f (x )=2ln x +ax2(a >0).若当x ∈(0,+∞)时,f (x )≥2恒成立,则实数a 的取值范围是________.解析:f (x )≥2即a ≥2x 2-2x 2ln x . 令g (x )=2x 2-2x 2ln x ,x >0,则g ′(x )=2x (1-2ln x ).由g ′(x )=0得x =e 12,且0<x <e 12时,g ′(x )>0;当x >e 12时g ′(x )<0,∴x =e 12时g (x )取最大值g (e 12)=e ,∴a ≥e.答案:[e ,+∞)9.已知f (x )=ax 3+bx 2-2x +c 在x =-2时有极大值6,在x =1时有极小值,求a ,b ,c 的值;并求f (x )在区间[-3,3]上的最大值和最小值.解析:f ′(x )=3ax 2+2bx -2,由条件知⎩⎪⎨⎪⎧f ′-2=12a -4b -2=0,f ′1=3a +2b -2=0,f -2=-8a +4b +4+c =6.解得a =13,b =12,c =83.f (x )=13x 3+12x 2-2x +83,f ′(x )=x 2+x -2, x -3(-3,-2)-2 (-2,1) 1 (1,3) 3 f ′(x )+-+f (x )256632616由上表知,在区间[-3,3]上,当x =3时,f (x )max =616,x =1时,f (x )min =32.10.设函数f (x )=ln x +ln(2-x )+ax (a >0). (1)当a =1时,求f (x )的单调区间;(2)若f (x )在(0,1]上的最大值为12,求a 的值.解析:函数f (x )的定义域为(0,2),f ′(x )=1x -12-x+a .(1)当a =1时,f ′(x )=-x 2+2x 2-x ,令f ′(x )=0,得x = 2. 当f ′(x )>0时, x ∈(0,2); 当f ′(x )<0时,x ∈(2,2).所以f (x )的单调递增区间为(0,2),单调递减区间为(2,2). (2)当x ∈(0,1]时,f ′(x )=2-2xx 2-x+a >0,即f (x )在(0,1]上单调递增,故f (x )在(0,1]上的最大值为f (1)=a ,因此a =12.[B 组 能力提升]1.记函数f (x )=13x 3-12x 2+12在(0,+∞)的值域为M ,g (x )=(x +1)2+a 在(-∞,+∞)的值域为N ,若N ⊆M ,则实数a 的取值范围是( )A .a ≥12B .a ≤12C .a ≥13D .a ≤13解析:因为f ′(x )=x 2-x ,由f ′(x )>0⇒x ∈(-∞,0)∪(1,+∞);由f ′(x )<0⇒x ∈(0,1),所以函数f (x )在(0,1)上单调递减,在(1,+∞)上单调递增, 所以M =⎣⎢⎡⎭⎪⎫13,+∞,又N =[a ,+∞),所以若N ⊆M ,则实数a 的取值范围是a ≥13,故选C.答案:C2.已知函数f (x )的定义域为[-1,5],部分对应值如下表:x -1 0 4 5 f (x )1221f (x )的导函数y =f ′(x )的图象如图所示.下列关于函数f (x )的命题: ①函数y =f (x )是周期函数; ②函数f (x )在[0,2]上是减函数;③如果当x ∈[-1,t ]时,f (x )的最大值是2,那么t 的最大值为4; ④当1<a <2时,函数y =f (x )-a 有4个零点. 其中真命题的个数是( ) A .4 B .3 C .2D .1解析:由y =f ′(x )的图象,可知f (x )在[-1,0],[2,4]上为增函数,在(0,2),(4,5]上为减函数,由于f (-1)=f (5)=1,f (0)=f (4)=2,故f (x )max =2,f (2)为极小值,且与1的大小不确定.由于f (x )的定义域为[-1,5],故f (x )不是周期函数,故①不正确;对于③,应有t ∈[0,5],故t max =5,故③不正确;对于④,由于f (x )极小值=f (2)与1的大小不确定;故④不正确;只有②正确.答案:D 3.若函数f (x )=xx 2+a(a >0)在[1,+∞)上的最大值为33,则a 的值为________. 解析:f ′(x )=x 2+a -2x 2x 2+a 2=a -x 2x 2+a2,令f ′(x )=0,解得x =a 或x =-a (舍去).当x >a 时,f ′(x )<0;当0<x <a 时,f ′(x )>0; 当x =a 时,f (x )=a 2a =33,a =32<1,不合题意. ∴f (x )max =f (1)=11+a =33,解得a =3-1.答案:3-14.已知函数f (x )=1+ln x x ,若函数在区间(a ,a +12)(其中a >0)上存在最大值,则实数a 的取值范围是________.解析:因为f (x )=1+ln x x ,x >0,所以f ′(x )=-ln xx2.当0<x <1时,f ′(x )>0;当x >1时,f ′(x )<0.所以f (x )在区间(0,1)上单调递增,在区间(1,+∞ )上单调递减, 所以函数f (x )在x =1处取得极大值.因为函数f (x )在区间(a ,a +12)(其中a >0)上存在最大值,所以⎩⎪⎨⎪⎧a <1a +12>1,解得12<a <1.答案:12<a <15.已知函数f (x )=a x 2-x -1ex(x ∈R),a 为正数.(1)求函数f (x )的单调区间;(2)若对∀x 1,x 2∈[0,4]均有|f (x 1)-f (x 2)|<1成立,求实数a 的取值范围. 解析:(1)令f ′(x )=a 3x -x 2ex=ax 3-xex=0得x =0或x =3. ∵a >0,e x>0,∴当x ∈(-∞,0)时f ′(x )<0, 当x ∈(0,3)时f ′(x )>0. 当x ∈(3,+∞)时f ′(x )<0.故f (x )的单调减区间为(-∞,0)和(3,+∞), 增区间为(0,3).(2)在x ∈[0,4]时由(1)知在x ∈[0,3]时单调递增,x ∈[3,4]时单调递减, ∴f (3)为f (x )在[0,4]上的最大值. 而f (0)=-a ,f (4)=11ae 4,则f (0)<f (4)故在[0,4]上f (x )的最小值为f (0) 若要对∀x 1,x 2∈[0,4]有|f (x 1)-f (x 2)|<1 只需|f (x )max -f (x )min |<1,即f (3)-f (0)<1∴5a e 3+a <1⇒a <e 35+e3, 又a >0,∴a 的取值范围为(0,e 35+e3).6.已知函数f (x )=(4x 2+4ax +a 2)x ,其中a <0. (1)当a =-4时,求f (x )的单调递增区间; (2)若f (x )在区间[1,4]上的最小值为8,求a 的值. 解析:(1)当a =-4时,f (x )=(2x -4)2x =4(x -2)2x ,f (x )的定义域为[0,+∞) f ′(x )=8(x -2)x +2x -22x=2x -25x -2x令f ′(x )>0得0<x <25,x >2所以当a =-4时,f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0,25和(2,+∞) (2)f (x )=(2x +a )2x ,f ′(x )=4(2x +a )x +2x +a 22x=2x +a10x +a 2x,令f ′(x )=0,得x 1=-a 2,x 2=-a10,∵a <0,∴x 1>x 2>0,所以,在区间⎝ ⎛⎭⎪⎫0,-a 10,⎝ ⎛⎭⎪⎫-a2,+∞上,f ′(x )>0,f (x )单调递增; 在区间⎝ ⎛⎭⎪⎫-a10,-a 2上,f ′(x )<0,f (x )的单调递减; 又易知f (x )=(2x +a )2x ≥0,且f ⎝ ⎛⎭⎪⎫-a 2=0.①当-a2≤1时,即-2≤a <0时,f (x )在区间[1,4]上的最小值为f (1),由f (1)=4+4a +a 2=8,得a =-2±22,均不符合题意.②当1<-a2≤4时,即-8≤a <-2时,f (x )在区间[1,4]上的最小值为f ⎝ ⎛⎭⎪⎫-a 2=0,不符合题意.③当-a2>4时,即a <-8时,f (x )在区间[1,4]上的最小值可能为x =1或x =4处取到,而f (1)≠8,f(4)=2(64+16a+a2)=8,得a=-10或a=-6(舍去),当a=-10时,f(x)在区间[1,4]上单调递减,f(x)在区间[1,4]上的最小值f(4)=8符合题意.综上,a=-10.附:什么样的考试心态最好大部分学生都不敢掉以轻心,因此会出现很多过度焦虑。
高中数学 第一章 导数及其应用 1.3 导数在研究函数中的应用(2)测标题(无答案)新人教A版选修

山西省忻州市2016-2017学年高中数学第一章导数及其应用1.3 导数在研究函数中的应用(2)测标题(无答案)新人教A版选修2-2编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(山西省忻州市2016-2017学年高中数学第一章导数及其应用1.3 导数在研究函数中的应用(2)测标题(无答案)新人教A 版选修2-2)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为山西省忻州市2016-2017学年高中数学第一章导数及其应用1.3 导数在研究函数中的应用(2)测标题(无答案)新人教A版选修2-2的全部内容。
导数在研究函数中的应用(2)本试卷满分55+5分 一.选择题(每小题5分,共20分)1.函数f(x )=x 33x 2,给出下列命题,其中正确命题的个数是 ( ) ①f(x)是增函数,无极值;②f(x)是减函数,无极值;③f(x)的增区间(∞,0]及[2,+∞),减区间为[0,2];④f(0)=0是极大值,f(2)=4是极小值.A .1个B .2个C .3个D .4个2.三次函数当x=1时有极大值4,当x=3时有极小值0,且函数图象过原点,则此函数解析式是 ( )A .y=x 3+6x 2+9xB .y=x 36x 2+9xC .y=x 36x 29xD .3.函数f (x )的定义域为开区间(a,b),导函数f (x)在(a ,b )的图象如图所示,则函数f (x )在开区间(a,b )内有极小值点 ( )A .1个B .2个C .3个D .4个4。
设函数()()3402f x x x a a =-+<<有三个零点1x 、x 2、x 3,且123,x x x <<则下列结论正确的是 ( )A .11x >-B .20x <C .32x >D .201x <<二。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3.3 函数的最大(小)值与导数[课时作业] [A 组 基础巩固]1.函数y =f (x )在区间[a ,b ]上的最大值是M ,最小值是m ,若M =m ,则f ′(x )( )A .等于0B .大于0C .小于0D .以上都有可能解析:由题意,知在区间[a ,b ]上,有m ≤f (x )≤M ,当M =m 时,令M =m =C ,则必有f (x )=C ,∴f ′(x )=C ′=0.故选A.答案:A2.函数y =ln xx的最大值为( )A .e -1B .eC .e 2D.103解析:y ′=1x ·x-ln x x2=1-ln xx2(x >0),令y ′=0,得x =e.∴当0<x ≤e 时,y ′≥0,y =ln xx 为增函数;当x >e 时,y ′<0,y =ln xx为减函数.∴y =ln x x 在(0,+∞)上的最大值为y max =ln e e =1e.答案:A3.函数f (x )=x +2cos x 在区间[-π2,0]上的最小值是( )A .-π2B .2C.π6+ 3D.π3+1 解析:f ′(x )=1-2sin x ,∵x ∈[-π2,0],∴sin x ∈[-1,0],∴-2sin x ∈[0,2].∴f ′(x )=1-2sin x >0在[-π2,0]上恒成立,∴f (x )在[-π2,0]上单调递增.∴f (x )min =f (-π2)=-π2+2cos(-π2)=-π2.答案:A4.已知函数f (x )=12x 4-2x 3+3m ,x ∈R ,若f (x )+9≥0恒成立,则实数m 的取值范围是( )A .m ≥32B .m >32 C .m ≤32D .m <32解析:因为函数f (x )=12x 4-2x 3+3m ,所以f ′(x )=2x 3-6x 2.令f ′(x )=0,得x =0或x =3.经检验知x =3是函数的一个最小值点,所以函数的最小值为f (3)=3m -272.不等式f (x )+9≥0恒成立,即f (x )≥-9恒成立,所以3m -272≥-9,解得m ≥32.答案:A5.已知函数y =-x 2-2x +3在[a,2]上的最大值为154,则a 等于( )A .-32B.12C .-12D.12或-32解析:y ′=-2x -2,令y ′=0得x =-1.当a ≤-1时,最大值为f (-1)=4,不合题意.当-1<a <2时,f (x )在[a,2]上单调递减,最大值为f (a )=-a 2-2a +3=154,解得a =-12或a =-32(舍去).答案:C6.函数f (x )=x -ln x ,x ∈[1e,e]的最大值为________.解析:f ′(x )=1-1x ,x >0.由f ′(x )=0,得x =1.又f (1)=1,f (1e )=1e+1,f (e)=e -1,∵f (1e )-f (e)=2+1e -e<2+12-e<0,∴f (1e)<f (e),f (x )最大值为f (e)=e -1.答案:e -17.已知f (x )=-x 2+mx +1在区间[-2,-1]上的最大值就是函数f (x )的极大值,则m 的取值范围是________.解析:f ′(x )=m -2x ,令f ′(x )=0,得x =m 2.由题设得m2∈[-2,-1],故m ∈[-4,-2].答案:[-4,-2]8.已知函数f (x )=2ln x +ax2(a >0).若当x ∈(0,+∞)时,f (x )≥2恒成立,则实数a 的取值范围是________.解析:f (x )≥2即a ≥2x 2-2x 2ln x .令g (x )=2x 2-2x 2ln x ,x >0,则g ′(x )=2x (1-2ln x ).由g ′(x )=0得x =e 12,且0<x <e 12时,g ′(x )>0;当x >e 12时g ′(x )<0,∴x =e 12时g (x )取最大值g (e 12)=e ,∴a ≥e.答案:[e ,+∞)9.已知f (x )=ax 3+bx 2-2x +c 在x =-2时有极大值6,在x =1时有极小值,求a ,b ,c 的值;并求f (x )在区间[-3,3]上的最大值和最小值.解析:f ′(x )=3ax 2+2bx -2,由条件知⎩⎪⎨⎪⎧-=12a -4b -2=0,=3a +2b -2=0,-=-8a +4b +4+c =6.解得a =13,b =12,c =83.f (x )=13x 3+12x 2-2x +83,f ′(x )=x 2+x -2,由上表知,在区间[-3,3]上,当x =3时,f (x )max =616,x =1时,f (x )min =32.10.设函数f (x )=ln x +ln(2-x )+ax (a >0). (1)当a =1时,求f (x )的单调区间;(2)若f (x )在(0,1]上的最大值为12,求a 的值.解析:函数f (x )的定义域为(0,2),f ′(x )=1x -12-x+a . (1)当a =1时,f ′(x )=-x2+2-, 令f ′(x )=0,得x = 2. 当f ′(x )>0时, x ∈(0,2); 当f ′(x )<0时,x ∈(2,2).所以f (x )的单调递增区间为(0,2),单调递减区间为(2,2). (2)当x ∈(0,1]时,f ′(x )=2-2x-+a >0, 即f (x )在(0,1]上单调递增,故f (x )在(0,1]上的最大值为f (1)=a ,因此a =12.[B 组 能力提升]1.记函数f (x )=13x 3-12x 2+12在(0,+∞)的值域为M ,g (x )=(x +1)2+a 在(-∞,+∞)的值域为N ,若N ⊆M ,则实数a 的取值范围是( )A .a ≥12B .a ≤12 C .a ≥13D .a ≤13解析:因为f ′(x )=x 2-x ,由f ′(x )>0⇒x ∈(-∞,0)∪(1,+∞);由f ′(x )<0⇒x ∈(0,1),所以函数f (x )在(0,1)上单调递减,在(1,+∞)上单调递增,所以M =⎣⎢⎡⎭⎪⎫13,+∞,又N =[a ,+∞),所以若N ⊆M ,则实数a 的取值范围是a ≥13,故选C.答案:C2.已知函数f (x )的定义域为[-1,5],部分对应值如下表:x )的图象如图所示.下列关于函数f (x )的命题: ①函数y =f (x )是周期函数;②函数f (x )在[0,2]上是减函数;③如果当x ∈[-1,t ]时,f (x )的最大值是2,那么t 的最大值为4;④当1<a <2时,函数y =f (x )-a 有4个零点.其中真命题的个数是( )A .4B .3C .2D .1解析:由y =f ′(x )的图象,可知f (x )在[-1,0],[2,4]上为增函数,在(0,2),(4,5]上为减函数,由于f (-1)=f (5)=1,f (0)=f (4)=2,故f (x )max =2,f (2)为极小值,且与1的大小不确定.由于f (x )的定义域为[-1,5],故f (x )不是周期函数,故①不正确;对于③,应有t ∈[0,5],故t max =5,故③不正确;对于④,由于f (x )极小值=f (2)与1的大小不确定;故④不正确;只有②正确.答案:D3.若函数f (x )=x x2+a (a >0)在[1,+∞)上的最大值为33,则a 的值为________.解析:f ′(x )=x2+a -2x2+=a -x2+,令f ′(x )=0,解得x =a 或x =-a(舍去).当x >a 时,f ′(x )<0;当0<x <a 时,f ′(x )>0;当x =a 时,f (x )=a 2a =33,a =32<1,不合题意.∴f (x )max =f (1)=11+a =33,解得a =3-1.答案:3-14.已知函数f (x )=1+ln x x ,若函数在区间(a ,a +12)(其中a >0)上存在最大值,则实数a 的取值范围是________.解析:因为f (x )=1+ln x x ,x >0,所以f ′(x )=-ln xx2.当0<x <1时,f ′(x )>0;当x >1时,f ′(x )<0.所以f (x )在区间(0,1)上单调递增,在区间(1,+∞ )上单调递减,所以函数f (x )在x =1处取得极大值.因为函数f (x )在区间(a ,a +12)(其中a >0)上存在最大值,所以错误!,解得错误!<a <1.答案:12<a <15.已知函数f (x )=-x -ex(x ∈R),a 为正数.(1)求函数f (x )的单调区间;(2)若对∀x 1,x 2∈[0,4]均有|f (x 1)-f (x 2)|<1成立,求实数a 的取值范围.解析:(1)令f ′(x )=-ex=-ex=0得x =0或x =3. ∵a >0,e x>0,∴当x ∈(-∞,0)时f ′(x )<0,当x ∈(0,3)时f ′(x )>0.当x ∈(3,+∞)时f ′(x )<0.故f (x )的单调减区间为(-∞,0)和(3,+∞),增区间为(0,3).(2)在x ∈[0,4]时由(1)知在x ∈[0,3]时单调递增,x ∈[3,4]时单调递减,∴f (3)为f (x )在[0,4]上的最大值.而f (0)=-a ,f (4)=11ae4,则f (0)<f (4)故在[0,4]上f (x )的最小值为f (0)若要对∀x 1,x 2∈[0,4]有|f (x 1)-f (x 2)|<1 只需|f (x )max -f (x )min |<1,即f (3)-f (0)<1∴5a e3+a <1⇒a <e35+e3,又a >0,∴a 的取值范围为(0,e35+e3).6.已知函数f (x )=(4x 2+4ax +a 2)x ,其中a <0.(1)当a =-4时,求f (x )的单调递增区间;(2)若f (x )在区间[1,4]上的最小值为8,求a 的值.解析:(1)当a =-4时,f (x )=(2x -4)2x =4(x -2)2x ,f (x )的定义域为[0,+∞)f ′(x )=8(x -2)x +-x=--x令f ′(x )>0得0<x <25,x >2所以当a =-4时,f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0,25和(2,+∞)(2)f (x )=(2x +a )2x ,f ′(x )=4(2x +a )x ++2x=++2x,令f ′(x )=0,得x 1=-a 2,x 2=-a10,∵a <0,∴x 1>x 2>0,所以,在区间⎝ ⎛⎭⎪⎫0,-a 10,⎝ ⎛⎭⎪⎫-a 2,+∞上,f ′(x )>0,f (x )单调递增;在区间⎝ ⎛⎭⎪⎫-a10,-a 2上,f ′(x )<0,f (x )的单调递减;又易知f (x )=(2x +a )2x ≥0,且f ⎝ ⎛⎭⎪⎫-a 2=0.①当-a2≤1时,即-2≤a <0时,f (x )在区间[1,4]上的最小值为f (1),由f (1)=4+4a+a 2=8,得a =-2±22,均不符合题意.②当1<-a 2≤4时,即-8≤a <-2时,f (x )在区间[1,4]上的最小值为f ⎝ ⎛⎭⎪⎫-a 2=0,不符合题意.③当-a2>4时,即a <-8时,f (x )在区间[1,4]上的最小值可能为x =1或x =4处取到,而f (1)≠8,f(4)=2(64+16a+a2)=8,得a=-10或a=-6(舍去),当a=-10时,f(x)在区间[1,4]上单调递减,f(x)在区间[1,4]上的最小值f(4)=8符合题意.综上,a=-10.。
