北师大版必修2高中数学1.5.2.1《直线与平面平行的性质》随堂练习
2019_2020学年高中数学第1章立体几何初步1_5_2_2平面与平面平行的性质随堂巩固验收北师大版必修2

二平面与平面平行的性质1.若AB、BC、CD是不在同一平面内的三条线段,则过它们中点的平面和直线AC的位置关系是( )A.平行B.相交C.AC在此平面内D.平行或相交[解析]利用中位线性质定理得线线平行,进而得直线与平面平行.[答案] A2.已知平面α∥平面β,P∉α,P∉β,过点P的两直线分别交α、β于A、B和C、D四点,A、C∈α,B、D∈β,且PA=6,AB=2,BD=12,则AC之长为( ) A.10或18 B.9 C.18或9 D.6[解析]由PA=6,AB=2知,P点不可能在α与β之间,∴点P在两平行平面所夹空间外面,∴PAPA+AB =ACBD或PA-ABPA=BDAC,∴AC=9或AC=18,∴选C.[答案] C3.已知两条直线l,m,α,β是两个平面,下列命题正确的是( )A.若α∥β,l∥α,则l∥βB.若l∥α,m∥α,则l∥mC.若α∥β,l∥α,m∥β,则l∥mD.若α∥β,lα,则l∥β[解析]A,l可能在β内,B,l与m可能相交、平行、异面,C与B一样的结论.D 正确.[答案] D4.平面α截一个三棱锥,如果截面是梯形,那么平面α必定和这个三棱锥的( ) A.一个侧面平行B.底面平行C.仅一条棱平行D.某两条相对的棱都平行[解析]当平面α∥某一平面时,截面为三角形,故选项A,B错.当平面α∥SA时,如图截面是四边形DEFG,又SA平面SAB,平面SAB∩α=DG,所以SA∥DG,同理SA∥EF,所以DG∥EF,同理当α∥BC时,GF∥DE,因为截面是梯形,所以四边形DEFG中仅有一组对边平行,故α仅与一条棱平行.故选C.[答案] C。
(北师大版)数学必修二达标练习:1.5.2.1直线与平面平行的性质(含答案)

温馨提示:
此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课堂达标·效果检测
1.已知直线l∥平面α,l平面β,α∩β=m,则直线l,m的位置关系是( )
A.相交
B.平行
C.平行或异面
D.相交或异面
【解析】选B.由线面平行的性质定理可得.
2.若平行四边形的一组对边平行于一个平面,则另一组对边所在直线与这个平面的位置关系是________.
【解析】如果平行四边形的一组对边平行于一个平面,则另一组对边所在直线与这个平面可能平行,也可能相交.
答案:平行或相交
3.(2018·西安高一检测)已知直线l∥平面α,点A,B∈l,过A,B作两条平行直线分别与平面α交于点A1,B1,则四边形ABB1A1的形状为________.
【解析】因为AB∥α,AB平面ABB1A1且平面ABB1A1∩平面α=直线A1B1,所以AB∥A1B1,又因为AA1∥BB1,所以四边形ABB1A1为平行四边形.
答案:平行四边形
4.如图,α∩β=CD,α∩γ=EF,β∩γ=AB,AB∥α,求证:CD∥EF.
【证明】因为AB∥α,ABβ,α∩β=CD,
所以AB∥CD,同理可证AB∥EF,
所以CD∥EF.
关闭Word文档返回原板块。
(北师大版)高中数学必修2检测1.5.2平行关系的性质 Word版含解析

(本栏目内容,在学生用书中以独立形式分册装订!)一、选择题(每小题分,共分).下列结论中正确的是( ).平行于另一个平面内两条直线的平面,一定平行于这个平面.一条直线平行于一个平面内的无数条直线,则这条直线与该平面平行.两个平面分别与第三个平面相交,若交线平行则两个平面平行.在两个平行平面中,一个平面内的一条直线必平行于另一个平面解析:中如果另一个平面内的两条直线平行,则显然不正确;中如果这条直线在平面内,也符合它平行于平面内的无数条直线,但是显然这条直线不与该平面平行;显然不正确;根据面面平行的性质知正确,故选.答案:.若平面α∥平面β,直线α,点∈β,则在β内过点的所有直线中( ).不一定存在与平行的直线.只有两条与平行的直线.存在无数条与平行的直线.存在唯一一条与平行的直线解析:利用面面平行的性质可知,和确定一个平面,该平面与β的交线过点,则交线与平行,且唯一.答案:.如图是长方体被一平面所截得到的几何体,四边形为截面,长方形为底面,则四边形的形状为( ).梯形.平行四边形.可能是梯形也可能是平行四边形.不确定解析:因为平面与长方体的两组相对的平面分别相交,根据面面平行的性质定理可知,两组交线分别平行,即∥,∥,所以四边形为平行四边形,故选.答案:.已知,表示两条不同的直线,α,β表示两个不重合的平面,给出下列四个命题:①若α∥β,⊂α,⊂β,则∥;②若∥,∥α,∥β,则α∥β;③若α∥β,⊂α,则∥β;④若∥α,∥β,则α∥β.其中正确的个数为( )....解析:对于①,∥或与是异面直线,故①错;对于②,也可能是α与β相交,故②错;对于④,同样α与β也可能相交,故④错.只有③对.答案:二、填空题(每小题分,共分).如图,直线∥平面α,点在α另一侧,点,,∈.线段,,分别交α于点,,.若=,=,=,则=.解析:由线面平行的性质可知∥.∴△∽△.∴=.∴=·=×=.答案:.如图①,在直角梯形中,∥,⊥,==,为的中点,,,分别为,,的中点,将△沿折起,得到四棱锥-,如图②.则在四棱锥-中,与平面的位置关系为.解析:在四棱锥-中,∵,分别为,的中点,∴∥.∵∥,∴∥.∵平面,平面,∴∥平面.同理∥平面.又∩=,∴平面∥平面.∵平面,平面,∴∥平面.答案:平行三、解答题(每小题分,共分)。
北师大版数学高一必修二练习1.5.1平行关系的判定

1.两条直线a、b满足a∥b,bα,则a与平面α的关系是() A.a∥αB.a与平面α相交C.a与平面α不相交D.aα解析:∵a∥b,bα,∴a与平面α的关系是a∥α或aα,∴a与平面α不相交.答案:C2.使平面α∥平面β的一个条件是() A.存在一条直线a,a∥α,a∥βB.存在一条直线a,aα,a∥βC.存在两条平行直线a,b,aα,bβ,a∥β,b∥αD.α内存在两条相交直线a,b,分别平行于β内两条直线解析:A、B、C中的条件都不一定使α∥β,反例分别为图中①,②,③(图中a∥l,b∥l);D正确,因为a∥β,b∥β,又a,b相交,从而α∥β.答案:D3.(2012·泰安高一检测)如果AB、BC、CD是不在同一平面内的三条线段,则经过它们中点的平面和直线AC的位置关系是()A.平行B.相交C.AC在此平面内D.平行或相交解析:如图:E、F、G分别为AB、BC、CD的中点.∵E、F分别是AB,BC的中点,∴EF∥AC.又EF平面EFG,且AC平面EFG.∴AC∥平面EFG.答案:A4.如图,在空间四边形ABCD中,E、F分别为边AB、AD上的点,且AE∶EB=AF∶FD=1∶4,又H、G分别为BC、CD的中点,则()A.BD∥平面EFGH,且四边形EFGH是矩形B.EF∥平面BCD,且四边形EFGH是梯形C.HG∥平面ABD,且四边形EFGH是菱形D.EH∥平面ADC,且四边形EFGH是梯形解析:∵AE∶EB=AF∶FD=1∶4,∴EF∥BD且EF=15BD.又H、G分别为BC、CD的中点,∴HG綊12BD.∴EF∥HG且EF≠HG.∴四边形EFGH为梯形.∵BD平面BCD且EF平面BCD.∴EF∥平面BCD.答案:B5.在正方体ABCD-A1B1C1D1中,E为DD1的中点,则BD1与过A,C,E的平面的位置关系是________.解析:如图,连接AC交BD于O.则O为BD的中点.又E为DD1的中点,∴OE为△BDD1的中位线.∴OE∥BD1,又BD1平面ACE,OE平面ACE.∴BD1∥平面ACE.答案:平行6.已知a 、b 、c 为三条不重合的直线,α,β,γ为三个不重合平面,下面三个命题:①a ∥c ,b ∥c ⇒a ∥b ;②γ∥α,β∥α⇒γ∥β;③a ∥γ,α∥γ⇒a ∥α.其中正确命题的序号是________.解析:由平行公理,知①正确;由平面平行的传递性知②正确;③不正确,因为a 可能在α内.答案:①②7.(2012·佛山高一检测)在三棱柱ABC -A ′B ′C ′中,点E ,D 分别是B ′C ′与BC的中点.求证:平面A ′EB ∥平面ADC ′.证明:连接DE ,∵E ,D 分别是B ′C ′与BC 的中点,∴DE 綊AA ′,∴AA ′ED 是平行四边形,∴A ′E ∥AD .∵A ′E 平面ADC ′,AD 平面ADC ′.∴A ′E ∥平面ADC ′.又BE ∥DC ′,BE 平面ADC ′,DC ′平面ADC ′,∴BE ∥平面ADC ′,∵A ′E 平面A ′EB ,BE 平面A ′EB ,A ′E ∩BE =E ,∴平面A ′EB ∥平面ADC ′.8.正方形ABCD 所在平面外一点为P ,E 、F 、G 分别为PD 、AB 、DC 的中点,如图.求证:(1)AE ∥平面PCF ;(2)平面PCF ∥平面AEG .证明:(1)取PC 中点H ,分别连接EH 、FH ,∵E 、F 、H 分别为PD 、AB 、PC 的中点, ∴EH 綊12DC , AF 綊12DC .∴EH綊AF.∴EAFH为平行四边形.∴EA∥FH.AE平面PCF,FH平面PCF,∴AE∥平面PCF.(2)∵E、G分别为PD、CD的中点,∴EG∥PC.EG平面PCF,PC平面PCF,∴EG∥平面PCF.由(1)知AE∥平面PCF,EG∩AE=E.∴平面PCF∥平面AEG.。
(北师大版)数学必修二课时作业:1.5.2.1直线与平面平行的性质(含答案)

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时提升作业(七)直线与平面平行的性质一、选择题(每小题3分,共18分)1.如果点M是两条异面直线外的一点,则过点M且与a,b都平行的平面( )A.只有一个B.恰有两个C.没有或只有一个D.有无数个【解析】选C.当其中一条异面直线平行于另一条异面直线和点M所确定的平面时,过点M且平行于a和b的平面不存在,否则过点M有且只有一个平面平行于a和b.2.若直线a不平行于平面α,则下列结论成立的是( )A.α内的所有直线都与直线a异面B.α内不存在与a平行的直线C.α内的直线都与α相交D.直线a与平面α有公共点【解析】选D.a不平行于平面α,则有直线a在平面α内和直线a与平面α相交两种位置关系,若aα,则α内的所有直线与a共平面,平面内有无数条直线平行于a,故A,B,C均不正确.3.过平面α外的直线l,作一组平面与α相交,如果所得的交线为a,b,c,…,则这些交线的位置关系为( )A.都平行B.都相交且一定交于同一点C.都相交但不一定交于同一点D.都平行或交于同一点【解析】选D.因为l⊈α,所以l∥α或l∩α=A,若l∥α,则由线面平行性质定理可知,l∥a,l∥b,l∥c,…,所以由公理4可知,a∥b∥c…;若l∩α=A,则A∈a,A∈b,A∈c,…,所以a,b,c,…,交于同一点A.4.(2014·南昌高一检测)平面α∩平面β=a,平面β∩平面γ=b,平面γ∩平面α=c,若a∥b,则c与a,b的位置关系为( )A.c与a,b都异面B.c与a,b都相交C.c至少与a,b中的一条相交D.c与a,b都平行【解析】选D.因为a∥b,a⊈γ,bγ,所以a∥γ,又aα,α∩γ=c,所以a∥c,所以a∥b∥c.【举一反三】题干中若去掉条件a∥b,则a,b,c的位置关系为________. 【解析】因为aβ,bβ,所以a∥b或a与b相交,当a∥b时题中已证a∥b∥c,当a与b相交时,如图设a∩b=A,则A∈a,A∈b,又aα,bγ,所以A∈α,A∈γ,所以A在α与γ的交线c上,即a,b,c交于一点,综上a∥b∥c或a,b,c交于一点.答案:a∥b∥c或a,b,c交于一点5.如图所示的三棱柱ABC-A1B1C1中,过A1B1的平面与平面ABC交于直线DE,则DE与AB的位置关系是( )A.异面B.平行C.相交D.以上均有可能【解析】选B.因为ABC-A1B1C1是三棱柱,所以A1B1∥AB.又因为A1B1⊈平面ABC,AB平面ABC,所以A1B1∥平面ABC.因为A1B1平面A1B1ED,平面A1B1ED∩平面ABC=DE,所以A1B1∥DE.所以DE∥AB.6.(2014·重庆高一检测)若空间四边形ABCD的两条对角线AC,BD的长分别为8和12,过AB的中点E且平行于BD,AC的截面是四边形,则此四边形的周长为( ) A.10 B.20 C.24 D.16【解题指南】先判断四边形的形状再求周长.【解析】选B.如图,设截面为EFGH,因为AC∥平面EFGH,平面ACB∩平面EFGH=EF,AC平面ABC,所以AC∥EF,同理可得GH∥AC,所以EF∥GH.同理FG∥EH,故四边形EFGH为平行四边形,所以四边形的周长为2(EF+EH)=AC+BD=20.二、填空题(每小题4分,共12分)7.(2014·阜阳高一检测)在正方体ABCD-A1B1C1D1中平面A1BD∩平面A1B1C1D1=l,则直线l与B1D1的位置关系是________.【解析】因为B1D1∥BD,BD平面A1BD,B1D1⊈平面A1BD,所以B1D1∥平面A1BD. 又B1D1平面A1B1C1D1且平面A1B1C1D1∩平面A1BD=l,所以B1D1∥l.答案:平行8.如图,a∥α,A是α的另一侧的点,B,C,D∈a,线段AB,AC,AD分别交α于E,F,G.若BD=4,CF=4,AF=5,则EG=________.【解析】因为a∥α,平面α∩平面ABD=EG,所以a∥EG,即BD∥EG,所以=====,所以EG===.答案:9.如图,已知AB,CD为异面直线,E、F分别为AC,BD的中点,过E,F作平面α∥AB,若AB=4,EF=,CD=2,则AB与CD所成角的大小为________.【解析】如图所示,连接AD交平面α于G,连接EG,GF.因为AB∥α,AB平面ABD,平面ABD∩α=GF.所以AB∥GF,又F为BD中点,所以G为AD的中点,所以EG∥CD,∠EGF(或其补角)即为异面直线AB,CD所成的角.因为AB=4,CD=2,所以EG=1,GF=2,又EF=,所以EG2+GF2=EF2,所以∠EGF=90°,故异面直线AB与CD所成的角为90°.答案:90°三、解答题(每小题10分,共20分)10.如图,已知E,F分别是菱形ABCD边BC,CD的中点,EF与AC交于点O,点P在平面ABCD外,M是线段PA上一动点,若PC∥平面MEF.试确定点M的位置.【解析】如图,连接BD交AC于点O1,连接OM,因为PC∥平面MEF,平面PAC∩平面MEF=OM,所以PC∥OM,所以=.在菱形ABCD中,因为E,F分别为边BC,CD的中点,所以=,又AO1=CO1,所以==,故PM∶MA=1∶3,即点M的位置在PA上使PM∶MA=1∶3的地方.11.如图所示,一块矩形形状的太阳能吸光板安装在三棱锥形状的支撑架上,矩形EFGH的四个顶点分别在边AB,BC,CD,AD上,已知AC=a,BD=b,问E,F,G,H在什么位置时,吸光板的吸光量最大?【解析】吸光板的吸光量的多少,取决于矩形EFGH的面积,设EH=x,EF=y,在矩形EFGH中,有EH∥FG,又EH⊈平面BCD,FG平面BCD.所以EH∥平面BCD,而EH平面ABD,平面ABD∩平面BCD=BD,所以EH∥BD.同理可证得EF∥AC,所以=,=.所以+==1,所以y=a.又矩形EFGH的面积为S=xy,即S=a·x=-x2+ax(0<x<b),所以当x=-=时,S有最大值,此时y=,所以当E,F,G,H依次为AB,BC,CD,DA的中点时,吸光板的吸光量最大.一、选择题(每小题4分,共16分)1.(2014·蚌埠高一检测)一个平面截空间四边形的四边得到四个交点,如果该空间四边形中只有一条对角线与这个截面平行,那么这四个交点围成的四边形是( )A.梯形B.菱形C.平行四边形D.任意四边形【解析】选A.如图,空间四边形ABCD,平面α截四边形所得截面为EFGH,由BD∥α,平面BCD∩α=FG,BD平面BCD,所以BD∥FG.同理可得BD∥EH,所以EH∥FG.因为AC与α不平行,可得EF与GH不平行(若平行则AC∥α),所以四边形EFGH为梯形.【举一反三】题干中若已知截面四边形是梯形,能判断截面与一条对角线平行吗?若截面是平行四边形呢?【解析】若截面是梯形,令EH∥FG.因为FG平面BCD,EH⊈平面BCD.所以EH∥平面BCD.又因为EH平面ABD,平面ABD∩平面BCD=BD,所以EH∥BD. 又因为BD⊈平面EFGH,EH平面EFGH,所以BD∥平面EFGH.即截面与一条对角线平行,若截面为平行四边形,同理可得截面与两条对角线都平行.2. (2013·深圳高一检测)如图,在三棱柱ABC-A1B1C1中,点D为AC的中点,点D1是A1C1上的一点,若BC1∥平面AB1D1,则等于( )A. B.1 C.2 D.3【解析】选B.连接A1B交AB1于O,则O为A1B的中点,因为BC1∥平面AB1D1,BC1平面A1BC1,平面A1BC1∩平面AB1D1=OD1,所以BC1∥OD1,所以D1为A1C1的中点,即=1.3.如图,四棱锥S-ABCD的所有的棱长都等于2,E是SA的中点,过C,D,E三点的平面与SB交于点F,则四边形DEFC的周长为( )A.2+2B.3+C.3+2D.2+【解题指南】先证明EF∥AB,再根据三角形中位线等知识求解.【解析】选C.因为AB=BC=CD=AD=2,所以四边形ABCD为菱形,所以CD∥AB.又CD⊈平面SAB,AB平面SAB,所以CD∥平面SAB.又CD平面CDEF,平面CDEF∩平面SAB=EF,所以CD∥EF.所以EF∥AB.又因为E为SA的中点,所以EF=AB=1,又因为△SAD和△SBC都是等边三角形,DE=CF=2×sin60°=,所以四边形DEFC的周长为CD+DE+EF+FC=2++1+=3+2.4.已知正方体ABCD-A1B1C1D1的棱长为1,点P是面AA1D1D的中心,点Q是面A1B1C1D1的对角线B1D1上的一点,且PQ∥平面AA1B1B,则线段PQ的长为( )A. B. C.1 D.2【解析】选B.过点Q作QE∥A1D1交A1B1于点E,取AA1的中点F.连接EF,PF,AB1,可证PF∥AD,AD∥A1D1,所以QE∥PF.所以Q,E,P,F四点共面.又因为PQ∥平面AA1B1B,平面PQEF∩平面AA1B1B=EF,所以PQ∥EF,所以四边形PQEF是平行四边形,所以QE=PF=A1D1.所以E是A1B1的中点,所以PQ=EF=AB1=.二、填空题(每小题5分,共10分)5.如图,三棱锥P-ABC中,E是侧棱AP上任一点,过E与BC平行的截面EMN分别交AB,AC于M,N,则MN与平面PBC的位置关系为________.【解析】因为BC∥平面EMN,平面ABC∩平面EMN=MN,BC平面ABC,所以BC∥MN,又因为MN⊈平面PBC.BC平面PBC.所以MN∥平面PBC.答案:MN∥平面PBC6.长方体ABCD-A1B1C1D1的底面ABCD是正方形,其侧面展开图是边长为8的正方形.E,F分别是侧棱AA1,CC1上的动点,AE+CF=8.P在棱AA1上,且AP=2,若EF ∥平面PBD,则CF=________.【解题指南】设AC与BD的交点为O,由EF∥平面PBD得EF∥PO,再由题意构造中位线得QC∥PO,证出EFCQ为平行四边形,再由题意求CF.【解析】连接AC交BD于O,连接PO.因为EF∥平面PBD,EF平面EACF,平面EACF∩平面PBD=PO,所以EF∥PO,在PA1上截取PQ=AP=2,连接QC,则QC∥PO,所以EF∥QC,所以EFCQ为平行四边形,则CF=EQ,又因为AE+CF=8,AE+A1E=8,所以A1E=CF=EQ=A1Q=2,从而CF=2.答案:2三、解答题(每小题12分,共24分)7.如图,三棱柱ABC-A1B1C1中,D是BC上一点,且A1B∥平面AC1D,D1是B1C1的中点,求证:平面A1BD1∥平面AC1D.【证明】连接A1C交AC1于点E,连接DE.因为A1B∥平面AC1D,A1B平面A1BC,平面A1BC∩平面AC1D=DE.所以A1B∥DE.又四边形ACC1A1为平行四边形.所以E为A1C中点.所以D为BC的中点,D1为B1C1的中点,所以BD C1D1,则四边形BDC1D1为平行四边形.所以BD1∥C1D,又BD1⊈平面AC1D,C1D平面AC1D.所以BD1∥平面AC1D.又A1B∩BD1=B,所以平面A1BD1∥平面AC1D.8.如图,在三棱柱ABC-A1B1C1中,点E,F分别是棱CC1,BB1上的点,点M是线段AC上的动点,EC=2FB=2,若MB∥平面AEF,试判断点M在何位置.【解析】若MB∥平面AEF,过F,B,M作平面FBMN交AE于N,连接MN,NF.因为BF∥平面AA1C1C,BF平面FBMN,平面FBMN∩平面AA1C1C=MN,所以BF∥MN.又MB∥平面AEF,MB平面FBMN,平面FBMN∩平面AEF=FN,所以MB∥FN,所以BFNM是平行四边形,所以MN∥BF,MN=BF=1.而EC∥FB,EC=2FB=2,所以MN∥EC, MN=EC=1,故MN是△ACE的中位线.所以M是AC的中点时,MB∥平面AEF.【拓展延伸】立体几何中“思维定式”的应用解答立体几何问题通常有比较固定的方法.举例如下:(1)作辅助线时,有“中点”考虑中位线,等腰三角形的性质.(2)证明线面平行,通常用判定定理,也就是证明平面外的直线与平面内的一条直线平行.(3)证明面面平行,通常用其判定定理,也就是证明一个平面内有两条相交直线与另一个平面平行.(4)题目条件中有线面平行时,一定要想到线面平行的性质定理,也就是见到“线面平行”就要考虑过已知直线找(或作)出平面与已知平面相交,得到交线与已知直线平行.关闭Word文档返回原板块。
(北师大版)数学必修二达标练习:1.5.2.1直线与平面平行的性质(含答案)

温馨提示:
此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课堂达标·效果检测
1.已知直线l∥平面α,l平面β,α∩β=m,则直线l,m的位置关系是( )
A.相交
B.平行
C.平行或异面
D.相交或异面
【解析】选B.由线面平行的性质定理可得.
2.若平行四边形的一组对边平行于一个平面,则另一组对边所在直线与这个平面的位置关系是________.
【解析】如果平行四边形的一组对边平行于一个平面,则另一组对边所在直线与这个平面可能平行,也可能相交.
答案:平行或相交
3.(2014·西安高一检测)已知直线l∥平面α,点A,B∈l,过A,B作两条平行直线分别与平面α交于点A1,B1,则四边形ABB1A1的形状为________.
【解析】因为AB∥α,AB平面ABB 1A1且平面ABB1A1∩平面α=直线A1B1,所以AB∥A1B1,又因为AA1∥BB1,所以四边形ABB1A1为平行四边形.
答案:平行四边形
4.如图,α∩β=CD,α∩γ=EF,β∩γ=AB,AB∥α,求证:CD∥EF.
【证明】因为AB∥α,ABβ,α∩β=CD,
所以AB∥CD,同理可证AB∥EF,
所以CD∥EF.
关闭Word文档返回原板块。
2019-2020学年高中数学北师大版必修2一课三测:1.5.2 平行关系的性质 含解析

5.2平行关系的性质填一填1.直线与平面平行的性质文字语言如果一条直线与一个平面平行,那么过该直线的任意一个平面与已知平面的交线与该直线平行.图形语言符号语言a∥α,aβ,α∩β=b⇒a∥b 2.平面与平面平行的性质定理文字语言如果两个平行平面同时和第三个平面相交,那么它们的交线平行图形语言符号语言α∥β,α∩γ=a,β∩γ=b⇒a∥b判一判1.如果一条直线和一个平面平行,则这条直线只和这个平面内一条直线平行.(×)2.若a∥α,则在α内存在直线与a平行.(√)3.若平面α,β平行,γ∩α=a,γ∩β=b,在β中除了b之外还有无数条直线平行于直线a。
(√)4.平面α,β,γ满足γ∩β=a,γ∩α=b,则a∥b。
(×)5.若一条直线与平面平行,那么这条直线与这个平面没有公共点.(√)6.若两个平面平行,那么分别在这两个平面内的直线互相平行.(×)7.若两个平面平行,那么其中一个平面内的任意一条直线与另一个平面平行.(√)8.已知两个平面平行,想一想1.两个平面平行,那么两个平面内的所有直线都相互平行吗?提示:不一定.因为两个平面平行,所以这两条直线无公共点,它们平行或异面.2.两个平面平行,其中一个平面内直线必平行于另一个平面吗?提示:平行.因为两个平面平行,则两个平面无公共点,则其中一个平面内的直线必和另一个平面无公共点,所以它们平行.3.利用线面平行性质定理解题的步骤是什么?提示:4.应用平面与平面平行性质定理的基本步骤是什么?提示:思考感悟:练一练1.已知直线m,n及平面α,β有下列关系:①m,nβ②nα③m∥α④m∥n。
现把其中一些关系看作条件,另一些看作结论,组成一个真命题是________.答案:①②③⇒④或①②④⇒③2.设有不同的直线a,b和不同的平面α,β,γ,给出下列三个命题,其中正确的命题有()①若a∥α,b∥α,则a∥b②若a∥α,a∥β,则α∥β③若α∥β,aα,则a∥βA.0个B.1个C.2个D.3个答案:B3.平面α与圆台的上、下底面分别相交于直线m,n,则m,n的位置关系是( )A.平行B.相交C.异面D.平行或异面答案:A4.如图,在三棱锥S -ABC 中,E ,F 分别是SB ,SC 上的点,且EF ∥平面ABC ,则( )A .EF 与BC 相交B .EF ∥BCC .EF 与BC 异面D .以上均有可能 答案:B 5.过正方体ABCD -A 1B 1C 1D 1的三顶点A 1,C 1,B 的平面与底面ABCD 所在的平面的交线为l ,则l 与A 1C 1的位置关系是________.答案:平行知识点一 直线与平面平行性质的应用1。
高中数学北师大版必修2 1.5 基础练习 《平行关系的判定》(数学北师大必修二)

《平行关系的判定》基础练习本课时编写:崇文门中学 高巍巍一、选择题1. 下列说法中正确的是( )A .如果一个平面内有一条直线和另一个平面平行,那么这两个平面平行B .如果一个平面内有无数条直线和另一个平面平行,那么这两个平面平行C .如果一个平面内的任何一条直线都与另一个平面平行,那么这两个平面平行D .如果两个平面平行于同一直线,则这两个平面平行2. 已知直线,a b 和平面α,那么下列命题中的真命题是( )A .若,a b αα⊥⊥,则//a bB .若//,//a b αα,则//a bC .若,a b b α⊥⊥,则//a αD .若//,//a b b α,则//a α3. 已知三条互相平行的直线a 、b 、c 中,a α⊂,,b c β⊂,则平面α、β的位置关系是( )A .平行B .相交C .平行或相交D .重合4. 已知平面α,β和直线,,a b c ,给出下列条件:①//,//a c b c ;②//,//,//a b αβαβ;③,,//a b αβαβ⊂⊂。
其中可以使结论//a b 成立的条件有( )A .①②B . ②③C . ①③D . ①5.已知m ,n 是两条直线,α、β是两个平面.有以下命题:①m ,n 相交且都在平面α、β外,m ∥α,m ∥β,n ∥α,n ∥β,则α∥β;②若m ∥α,m ∥β,则α∥β;③若m ∥α,n ∥β,m ∥n ,则α∥β.其中正确命题的个数是( ).A .0B .1C .2D .36. 过平行六面体1111ABCD A B C D -任意两条棱的中点作直线,其中与平面11DBB D 平行的直线共有( )A .4条B .6条C .8条D .12条二、填空题7. 当//,//αβγβ,则α与γ的关系是 .8. 过已知直线外一点与已知直线平行的直线有 条;过平面外一点与已知平面平行的直线有 条,与已知平面平行的平面有 个.9. 已知直线a 、b ,平面α、β,且a ∥b ,a ∥α,α∥β,则直线b 与平面β的位置关系__.10. ①若平面α内有一条直线平行于另一个平面β,则//αβ;②若平面α内有两条直线平行于另一个平面β,则//αβ;③若平面α内有无数条直线平行于另一个平面β,则//αβ;④若平面α内任意一条直线平行于另一个平面β,则//αβ;⑤若平面α内两条相交直线平行于另一个平面β,则//αβ。
高中数学必修2(北师版)第一章1.5 平行关系 (与最新教材完全匹配)知识点总结含同步练习题及答案

描述:高中数学必修2(北师版)知识点总结含同步练习题及答案第一章 立体几何初步 1.5 平行关系一、知识清单空间的平行关系二、知识讲解1.空间的平行关系空间四边形顺次连接不共面的四个点 、、、 所构成的图形,叫做空间四边形.这四个点中的各个点叫做空间四边形的顶点;所连接的相邻顶点间的线段叫做空间四边形的边;连接不相邻的顶点的线段叫做空间四边形的对角线.空间四边形用表示顶点的四个字母表示.例如,图中的四边形可以表示为空间四边形 ,线段 , 是它的对角线.直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行. 用符号表示:,,且.平面与平面平行的判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行.用符号表示:,,,,.平面与平面平行的判定定理的推论如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线,那么这两个平面平行.直线与平面平行的性质定理:一条直线与一个平面平行,则过这条直线的任一平面与此平面的交线与该直线平行.用符A B C D ABCD AC BD a ⊄αb ⊂αa ||b ⇒a ||αa ⊂βb ⊂βa ∩b =P a ||αb ||α⇒β||αa ||αα∩β=b ⇒a||b例题:号表示:,,.平面与平面平行的性质定理:如果两个平行平面同时和第三个平面相交,那么它们的交线平行.用符号表示:,,.a ||αa ⊂βα∩β=b ⇒a ||b α||βα∩γ=a β∩γ=b ⇒a ||b 下列命题(其中 , 表示直线, 表示平面)中,正确的个数是( )①若 ,,则;②若 ,,则 ;③若 ,,则 ;④若 ,,则 .A. 个 B. 个 C. 个 D. 个解:A①中缺少 这一条件;②中 , 还有可能相交或异面;③中还有可能 ;④中 与 还有可能异面.a b αa ∥b b ⊂αa ∥αa ∥αb ∥αa ∥b a ∥b b ∥αa ∥αa ∥αb ⊂αa ∥b 0123a ⊄αa b a ⊂αa b 若平面 ,直线 ,点 ,则在 内过点 的所有直线中( )A.不一定存在与 平行的直线B.只有两条与 平行的直线C.存在无数条与 平行的直线D.有且只有一条与 平行的直线解:D直线 与点 确定平面 ,设 ,则 唯一.α∥βa ⊂αB ∈ββB a a a a a B γβ∩γ=l l 如图,四棱锥 中,底面 是正方形, 是棱 的中点.求证:.证明:P −ABCD ABCD E P D P B ∥平面 EAC连接 ,与 相交于点 ,连接 .因为四边形 为正方形,所以 为 中点 .又因为 为棱 中点,所以 .又 ,,故 .BD AC O EO ABCD O BD E P D P B ∥EO P B ⊄平面 EAC EO ⊂平面 EAC P B ∥平面 EAC 如图所示,三棱锥 被一平面所截,截面为平行四边形 .求证:.证明:因为四边形 为平行四边形,所以 .又 ,,所以 .而 ,,所以 .A −BCD EF GH CD ∥EF EF GH EF ∥GH GH ⊂平面BCD EF ⊄平面BCD EF ∥平面BCD EF ⊂平面ACD 平面ACD ∩平面BCD =CD EF ∥CD 如图所示,在三棱锥 中, ,, 分别是棱 ,, 的中点,求证:.证明:因为 ,分别是棱 , 的中点, 所以 是 的中位线,.因为 ,,所以.同理,.又因为 ,,,所以.S −ABC D E F AC BC SC 平面DEF ∥平面SAB D E AC BC DE △ABC DE ∥AB DE ⊄平面SAB AB ⊂平面SAB DE ∥平面SAB DF ∥平面SAB DE ∩DF =D DE ⊂平面DEF DF ⊂平面DEF 平面DEF ∥平面SAB 如图所示,已知在正方体 中,, , 分别是 ,, 的中点.求证:.证明:ABCD −A 1B 1C 1D 1M N P C C 1B 1C 1C 1D 1平面 MNP ∥平面 BDA 1高考不提分,赔付1万元,关注快乐学了解详情。
高级中学高中数学(北师大版)必修二1.5平行关系直线与平面平行的判定同步练习

1.5 直线与平面平行关系的判定【使用说明与预习指导】认真阅读课本第28-31页的内容,划出重要知识,规范填写【预习案】部分的内容并熟记基础知识,用红笔做出疑难标记。
根据预习到的知识和以前学过的知识,小组合作、讨论完成【探究案】部分的内容,由组长负责,拿出讨论结果,准备展示、点评。
及时整理展示、点评的结果(用双色笔),独立完成【检测案】部分的内容并和组员核对结果。
课后及时把导学案上做错的题以及相关的解题方法和规律写在纠错本上。
【学习目标】1.知识与技能掌握直线与平面平行的判定定理,并会简单应用2.过程与方法让学生通过观察实物及模型,归纳得出直线与平面平行的判定定理,并能体会这两个定理之间的联系,通过读图、识图、画图的过程,培养空间想象能力及运用图形和符号语言进行交流的能力。
3.情感态度与价值观让学生在观察、探究、发现中学习,在自主、合作、交流中学习。
体验学习的乐趣,增强自信心,树立积极地学习态度,提高学习的自我效能感。
【重点难点】重点:线面平行判定定理的应用。
难点:直线与平面平行的判定定理的合情推理及其应用。
【预习案】定理5.1(直线与平面平行的判定定理)文字语言:_______________________________________________图形语言:_______________________________________________注意:画直线和平面平行时,通常把表示直线的线段画在表示平面的平行四边形的外面,并且使它与平行四边形内的一条线段或平行四边形的一边平行。
符号语言:____________________________________________________定理的作用:____________________________________________________判定线面平行的方法:___________________________________________________【探究案】探究1.如图,已知P是平行四边形ABCD所在平面外一点,M、N分别是AB、PC的中点求证:MN//平面PAD。
北师大版高中数学必修二随堂巩固验收:1-5-2-1直线与平面平行的性质

1.如图,已知S为四边形ABCD外一点,G,H分别为SB,BD 上的点,若GH∥平面SCD,则()A.GH∥SA B.GH∥SDC.GH∥SC D.以上均有可能[解析]因为GH∥平面SCD,GH平面SBD,平面SBD∩平面SCD=SD,所以GH∥SD,显然GH与SA,SC均不平行,故选B.[答案] B2.若直线a平行于平面α,则下列结论错误的是()A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a成90°角[解析]∵直线a平行于平面α,∴a与平面α内的直线平行或异面,选项A错误;选项B、C、D正确.故选A.[答案] A3.对于直线m,n和平面α,下列命题中正确的是()A.如果mα,nα,m,n是异面直线,那么n∥αB.如果mα,nα,m,n是异面直线,那么n与α相交C.如果mα,n∥α,m,n共面,那么m∥nD.如果m∥α,n∥α,m,n共面,那么m∥n[解析]对于A,如图①,此时n与α相交,故不正确;对于B,如图②,此时m,n是异面直线,而n与α平行,故不正确;对于D,如图③,m与n相交,故不正确.[答案] C4.下列命题正确的是()A.若直线a∥平面α,直线b∥平面α,则直线a∥直线bB.若直线a∥平面α,直线a与直线b相交,则直线b与平面α相交C.若直线a∥平面α,直线a∥直线b,则直线b∥平面αD.若直线a∥平面α,则直线a与平面α内任意一条直线都无公共点[解析]A中,直线a与直线b也可能异面、相交,所以不正确;B中,直线b也可能与平面α平行,所以不正确;C中,直线b也可能在平面α内,所以不正确;根据直线与平面平行的定义知D正确,故选D.[答案] D由Ruize收集整理。
感谢您的支持!。
北师大版必修2高中数学1522《平面与平面平行的性质》随堂练习

"【世纪金榜】高中数学 1、5、2、2平面与平面平行的性质课时提能演练 北师大版必修2 "一、选择题(每小题4分,共16分)1、(易错题)如图给出的是长方体木料,想象沿图中平面所示位置截长方体,那么截面图形是下面四个图形的( )2、(2012·潍坊高一检测)若平面α∥平面β,直线a ∥α,且a β,点B ∈β,则在β内过点B 的所有直线中( )(A)不一定存在与a 平行的直线(B )只有两条与a 平行的直线(C )存在无数条与a 平行的直线(D)存在惟一一条与a 平行的直线3、如图所示,P 是三角形ABC 所在平面外一点,平面α∥平面ABC,α分别交线段PA ,PB,PC 于A ′,B ′,C ′、若PA ′∶AA ′=2∶5,求△A ′B ′C ′与△ABC 的面积比为( )(A)2∶5 (B)2∶7 (C )4∶49 (D )9∶254、M,N,P 为三个不重合的平面,a,b,c 为三条不同的直线,则下列说法中,不正确的是( ) ⎫⇒⎬⎭ac ①a b ;b c ⎫⇒⎬⎭a P ②a b ;b P ⎫⇒⎬⎭Mc ③M N ;N c ⎫⇒⎬⎭M P ④M N ;N P ⎫⇒⎬⎭MP ⑤a M.a P(A )④⑤ (B)②③④ (C)②③⑤ (D)②③二、填空题(每小题4分,共8分)5、(2012·烟台高一检测)过正方体ABCD —A 1B 1C 1D 1的顶点A 1,C 1,B 的平面与底面ABCD 所在平面的交线为l ,则l 与A 1C 1的位置关系是_________、6、如图,直线a ∥平面α,点A 在α另一侧,点B ,C ,D ∈a ,线段AB ,AC ,AD 分别交α于点E ,F,G 、若BD=4,CF=4,AF=5、则EG=_________、三、解答题(每小题8分,共16分)7、(2012·山东高考)如图,几何体E-ABCD是四棱锥,△ABD为正三角形,CB=CD,EC⊥BD、(1)求证:BE=DE;(2)若∠BCD=120°,M为线段AE的中点,求证:DM∥平面BEC、8、设平面α,β满足α∥β,A,C∈α,B,D∈β,直线AB与CD交于S,若SA=18,SB=9,CD=34、求SC的长度、【挑战能力】(10分)在正方体ABCD -A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ与平面PAO平行?答案解析1、【解析】选C、长方体的相对表面互相平行,因此由面面平行的性质知本题中的截面是平行四边形、2、【解析】选D、∵B a,∴a与B确定平面γ、设γ∩α=m,γ∩β=n,∵α∥β,∴m∥n、又∵a∥α,∴a∥m,∴n∥a,∴直线n即为β内过B与a平行的直线,它是惟一的、3、【解题指南】相似三角形面积之比等于边长之比的平方、【解析】选C、∵平面α∥平面ABC,A′B′α,AB平面ABC,∴A′B′∥AB、∴A′B′∶A B=PA′∶PA、又PA′∶AA′=2∶5,∴A′B′∶AB=2∶7、同理B′C′∶BC=2∶7,A′C′∶AC=2∶7,∴△A′B′C′∽△ABC,∴S△A′B′C′∶S△ABC=4∶49、4、【解析】选C、①,④分别是直线和平面平行的传递性,正确;②中a与b还可能异面或相交;③中M与N还可能相交;⑤中可能还有a M、【方法技巧】“平行”关系结论大荟萃空间的平行关系,有些具有“传递性”,有些不具有,本题中的各种说法用文字描述为:①平行于同一条直线的两条直线平行、②平行于同一个平面的两条直线不一定平行、③平行于同一条直线的两个平面不一定平行、④平行于同一个平面的两个平面平行、⑤平行于同一个平面的直线与平面不一定平行、5、【解题指南】用两个平面平行的性质去判断、【解析】由于平面ABCD ∥平面A 1B 1C 1D 1,平面A 1B 1C 1D 1∩平面A 1C 1B=A 1C 1,平面ABCD ∩平面A 1C 1B=l 、由面面平行的性质可知l ∥A 1C 1、答案:平行6、【解析】A ∉a,则点A 与直线a 确定一个平面,即平面ABD 、因为a ∥α,且α∩平面ABD=EG,故a ∥EG,即BD ∥EG 、所以 AF AE EG AE AF EG ,又,,AC AB BD AB AC BD AF BD 5420故EG .AC 549==∴=⨯===+ 答案:2097、【解题指南】(1)先取BD 中点O ,连接OC ,OE ,证明OE 是BD 的垂直平分线即可、(2)本题考查线面的平行关系,可取AB 中点N ,连接MN ,MD ,DN,利用平面MND ∥平面BEC 来证、【证明】(1)设BD 中点为O,连接OC ,OE,则由BC=CD 知,CO ⊥BD 、又已知CE ⊥BD,CO ∩CE=C ,所以BD ⊥平面O CE 、所以BD ⊥OE ,即OE 是BD 的垂直平分线,所以BE=DE 、(2)取AB 中点为N,连接MN ,MD ,DN,∵M 是AE 的中点,∴MN ∥BE 、∵△ABD 是等边三角形,∴DN ⊥AB 、由∠BCD =120°知,∠CBD =30°,所以∠ABC =60°+30°=90°,即BC ⊥AB,所以ND ∥BC ,又因为MN ∩DN=N,BE ∩BC=B,所以平面MND ∥平面BEC,故DM ∥平面BEC 、8、【解析】设相交直线AB,CD 确定的平面为γ,则α∩γ=AC ,β∩γ=BD ,由α∥β,得AC ∥BD 、S 点在两平面同侧时,如图(1)、∵BD ∥AC,所以SB SD ,SA SC= 即9SC 34,18SC-=∴SC=68、 S 点在两平面之间时,如图(2)、∵BD∥AC,所以SA SC SC,SB SD CD SC==-即18SC,934SC=-解得68SC.3=综上知SC的长度为68或68. 3【挑战能力】【解析】如图,设平面D1BQ∩平面ADD1A1=D1M,点M在AA1上,由于平面D1BQ∩平面BCC1B1=BQ,平面ADD1A1∥平面BCC1B1,由面面平行的性质定理可得BQ∥D1M、假设平面D1BQ∥平面PAO,由平面D1BQ∩平面ADD1A1=D1M,平面PAO∩平面ADD1A1=AP,可得AP∥D1M,所以BQ∥D1M∥AP、因为P为DD1的中点,所以M为AA1的中点,所以Q为CC1的中点、故当Q为CC1的中点时,平面D1BQ与平面PAO平行、。
北师大版必修2高中数学1621《直线与平面垂直的性质》随堂练习
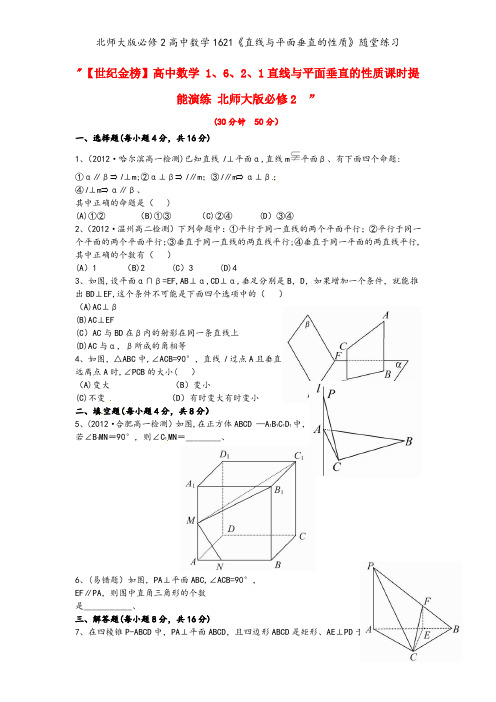
"【世纪金榜】高中数学 1、6、2、1直线与平面垂直的性质课时提能演练北师大版必修2 ”(30分钟 50分)一、选择题(每小题4分,共16分)1、(2012·哈尔滨高一检测)已知直线l⊥平面α,直线m平面β、有下面四个命题:①α∥β⇒l⊥m;②α⊥β⇒l∥m;③l∥m⇒α⊥β;④l⊥m⇒α∥β、其中正确的命题是( )(A)①②(B)①③(C)②④ (D)③④2、(2012·温州高二检测)下列命题中:①平行于同一直线的两个平面平行;②平行于同一个平面的两个平面平行;③垂直于同一直线的两直线平行;④垂直于同一平面的两直线平行,其中正确的个数有()(A)1 (B)2 (C)3 (D)43、如图,设平面α∩β=EF,AB⊥α,CD⊥α,垂足分别是B,D,如果增加一个条件,就能推出BD⊥EF,这个条件不可能是下面四个选项中的()(A)AC⊥β(B)AC⊥EF(C)AC与BD在β内的射影在同一条直线上(D)AC与α,β所成的角相等4、如图,△ABC中,∠ACB=90°,直线l过点A且垂直于平面ABC,动点P∈l,当点P逐渐远离点A时,∠PCB的大小( )(A)变大(B)变小(C)不变(D)有时变大有时变小二、填空题(每小题4分,共8分)5、(2012·合肥高一检测)如图,在正方体ABCD —A1B1C1D1中,M,N分别是棱AA1,AB上的点,若∠B1MN=90°,则∠C1MN=________、6、(易错题)如图,PA⊥平面ABC,∠ACB=90°,EF∥PA,则图中直角三角形的个数是___________、三、解答题(每小题8分,共16分)7、在四棱锥P-ABCD中,PA⊥平面ABCD,且四边形ABCD是矩形、AE⊥PD于E,l⊥平面PCD、求证:l∥AE、8、(2012·南昌高一检测)三棱柱ABC-A1B1C1中,侧棱A1A垂直于底面ABC,B1C1=A1C1,AC1⊥A1B,M,N分别为A1B1,AB的中点,求证:(1)平面AMC1∥平面NB1C;(2)A1B⊥AM、【挑战能力】(10分)如图,在四棱锥S-ABCD中,侧棱SA=SB=SC=SD,底面ABCD是菱形,AC与BD交于O点、(1)求证:AC⊥平面SBD;(2)若E为BC的中点,点P在侧面△SCD内及其边界上运动,并保持PE⊥AC,试指出动点P的轨迹,并证明你的结论、答案解析1、【解析】选B、l⊥α,α∥β,∴l⊥β、又∵mβ,∴l⊥m、①正确、 l∥m, l⊥α,∴m⊥α,又∵mβ,∴α⊥β,③正确、2、【解析】选B、①中两个平面可能平行可能相交;②正确;③两直线可能平行、垂直也可能异面;④正确、3、【解析】选D、∵AB⊥α,CD⊥α,∴AB∥CD,∴A,B,C,D四点共面、选项A,B中的条件都能推出EF⊥平面ABDC,则EF⊥BD、选项C中,由于AC与BD在β内的射影在同一条直线上,所以平面ABDC与平面β垂直,又∵EF⊥AB,∴EF⊥平面ABDC,∴EF⊥BD、选项D中,若AC∥EF,则AC与α、β所成角也相等,但不能推出BD⊥EF、4、【解析】选C、∵l⊥平面ABC,∴BC⊥l、∵∠ACB=90°,∴BC⊥AC、又l∩AC=A,∴BC⊥平面PAC,∴BC⊥PC,∴∠PCB=90°、5、【解题指南】先证明MN⊥平面B1C1M,进而求得∠C1MN的度数、【解析】∵B1C1⊥平面ABB1A1,∴B1C1⊥MN、又∠B1MN是直角,∴MN⊥B1M、又B1C1∩B1M=B1,∴MN⊥平面B1C1M、∴MN⊥C1M,∠C1MN=90°、答案:90°6、【解析】由PA⊥平面ABC,得PA⊥AB,PA⊥AC,PA⊥BC、又∵BC⊥AC,AC∩PA=A,∴BC⊥平面PAC,∴BC⊥PC、∵EF∥PA,PA⊥平面AB C,∴EF⊥平面ABC,∴EF⊥BE,EF⊥EC,∴△PAB,△PAC,△ABC,△PBC,△EFC,△BEF均为直角三角形、答案:6【易错提醒】△PBC是直角三角形容易漏掉,原因是未分析出BC⊥平面PAC、7、【解题指南】证明AE⊥平面PCD即可、【证明】∵PA⊥平面ABCD,CD平面ABCD,∴PA⊥CD、又CD⊥AD,PA∩AD=A,PA平面PAD,AD平面PAD、∴CD⊥平面PAD,又AE平面PAD,∴AE⊥CD、又AE⊥PD,PD∩CD=D,PD平面PCD,CD平面PCD,∴AE⊥平面PCD,又l⊥平面PCD,∴AE∥l、8、【解析】(1)∵M,N分别为A 1B1,AB的中点,∴B1M NA,∴B1N∥AM、又AM平面AMC1,B1N平面AMC1,∴B1N∥平面AMC1,连接MN,在四边形CC1MN中,有MC1∥CN,同理得CN∥平面AMC1、∵CN平面B1CN,B1N平面B1CN,CN∩B1N=N,∴平面AMC1∥平面NB1C、(2)∵B1C1=A1C1,M为A1B1中点,∴C1M⊥A1B1,又三棱柱ABC—A1B1C1侧棱A1A垂直于底面ABC,∴A1A⊥CN,又CN∥C1M,∴A1A⊥C1M、又A1A∩A1B1=A1,∴C1M⊥平面AA1B1B、又∵A1B平面AA1B1B,∴C1M⊥A1B,又AC1⊥A1B,AC1∩C1M=C1,∴A1B⊥平面AC1M、∵AM平面AC1M,∴A1B⊥AM、【挑战能力】【解析】(1)连接SO,∵底面ABCD是菱形,O为AC与BD的交点,∴AC⊥BD、又SA=SC,∴AC⊥SO、而SO∩BD=O,∴AC⊥平面SBD、(2)取棱SC的中点M,CD的中点N,连接MN,则动点P的轨迹即是线段MN、证明如下:连接EM,EN,∵E是BC中点,M是SC中点,∴EM∥SB,同理EN∥BD、∵AC⊥平面SBD,∴AC⊥SB,∴AC⊥EM,同理AC⊥EN、又EM∩EN=E,∴AC⊥平面EMN、因此,当P点在线段MN上运动时,总有PE⊥AC、。
高中数学 1.5.2 平行关系的性质课时训练 北师大版必修2

【课堂新坐标】(教师用书)2013-2014学年高中数学 1.5.2 平行关系的性质课时训练 北师大版必修2一、选择题1.若α∥β,a α,下列三个说法中正确的是( )①a 与β内所有直线平行;②a 与β内的无数条直线平行;③a 与β无公共点. A .①② B .②③ C .①D .①③【解析】 a 与平面β内的直线可能平行,也可能异面,但与β无公共点,故选B. 【答案】 B2.下列说法正确的个数为( )①两平面平行,夹在两平面间的平行线段相等;②两平面平行,夹在两平面间的相等的线段平行;③如果一条直线和两个平行平面中的一个平行,那么它和另一个平面也平行;④两平行直线被两平行平面截得的线段相等.A .1B .2C .3D .4【解析】 易知①④正确,②不正确,③直线可能在平面内,故③不正确. 【答案】 B图1-5-203.如图1-5-20所示,在正方体ABCD -A 1B 1C 1D 1中,M 是棱A 1D 1上的动点,则直线MD 与平面BCC 1B 1的位置关系是( )A .平行B .相交C .在平面内D .相交或平行 【解析】⎭⎪⎬⎪⎫平面ADD 1A 1∥平面BCC 1B 1DM 平面ADD 1A 1⇒MD ∥平面BCC 1B 1.【答案】 A4.已知平面α∥β,P 是α、β外一点,过点P 的直线m 与α、β分别交于点A 、C ,过点P 的直线n 与α、β分别交于点B 、D ,且PA =6,AC =9,PD =8,则BD 的长为( )A .16B .24或245C .14D .20【解析】 第①种情况,当P 点在α、β的同侧时,设BD =x , 则PB =8-x , ∴PA AC =PB BD. ∴BD =245.第②种情况,当P 点在α,β中间时,设PB =x . ∴PD PC =PB PA. ∴x =6×83=16,∴BD =24. 【答案】 B5.若不在同一直线上的三点A 、B 、C 到平面α的距离相等,且A ∉α,则( )A .α∥平面ABCB .△ABC 中至少有一边平行于α C .△ABC 中至多有两边平行于αD .△ABC 中只可能有一边与α相交【解析】 若三点在平面α的同侧,则α∥平面ABC ,有三边平行于α.若一点在平面α的一侧,另两点在平面α的另一侧,则有两边与平面α相交,有一边平行于α,故△ABC 中至少有一边平行于α.【答案】 B图1-5-21二、填空题6.如图1-5-21,过正方体ABCD -A 1B 1C 1D 1的三个顶点A 1、C 1、B 的平面与底面ABCD 的交线为l ,则l 与A 1C 1的位置关系是________.【解析】⎭⎪⎬⎪⎫平面ABCD ∥平面A 1B 1C 1D 1平面A 1C 1B ∩平面ABCD =l平面A 1C 1B ∩平面A 1B 1C 1D 1=A 1C 1⇒l ∥A 1C 1.【答案】 平行图1-5-227.(2013·宁德高一检测)空间四边形ABCD 中,对角线AC =BD =4,E 是AB 中点,过E 与AC 、BD 都平行的截面EFGH 分别与BC 、CD 、DA 交于F 、G 、H ,则四边形EFGH 的周长为________.【解析】 ∵AC ∥面EFGH ,AC 面ABC ,面ABC ∩面EFGH =EF , ∴AC ∥EF .∵E 为AB 中点,∴F 为BC 中点,∴EF =12AC =2.同理HG =12AC =2,EH =FG =12BD =2.∴四边形EFGH 的周长为8.【答案】 8图1-5-238.如图1-5-23,平面α∥平面β,△ABC 与△A ′B ′C ′分别在α、β内,线段AA ′、BB ′、CC ′都交于点O ,点O 在α、β之间,若S △ABC =32,OA ∶OA ′=3∶2,则△A ′B ′C ′的面积为________.【解析】 根据题意有S △ABC =32.∵AA ′、BB ′相交, ∴直线AA ′、BB ′确定一个平面ABA ′B ′, ∵平面α∥平面β,∴AB ∥A ′B ′,易得△ABO ∽△A ′B ′O ,① △ABC ∽△A ′B ′C ′,② 由①得AB A ′B ′=OA OA ′=32,由②得S △ABC S △A ′B ′C ′=(32)2, ∴S △A ′B ′C ′=239.【答案】239三、解答题9.如图1-5-24,棱柱ABC —A 1B 1C 1的侧面BCC 1B 1是菱形,设D 是A 1C 1上的点且A 1B ∥平面B 1CD ,求A 1D ∶DC 1的值.图1-5-24【解】 设BC 1交B 1C 于点E , 连接DE ,则DE 是平面A 1BC 1与平面B 1CD 的交线.∵A 1B ∥平面B 1CD ,且A 1B 平面A 1BC 1,∴A 1B ∥DE . 又E 是BC 1的中点,所以D 为A 1C 1的中点,即A 1D ∶DC 1=1.图1-5-2510.(2013·吉林高一检测)如图1-5-25,直四棱柱ABCD—A1B1C1D1的底面是梯形,AB ∥CD,AD⊥DC,CD=2,DD1=AB=1,P,Q分别是CC1,C1D1的中点.求证:AC∥平面BPQ.【证明】连接CD1,AD1,∵P,Q分别是CC1,C1D1的中点,∴PQ∥CD1,且CD1平面BPQ,∴CD1∥平面BPQ.又D1Q=AB=1,D1Q∥AB,∴四边形ABQD1是平行四边形,∴AD1∥BQ,又∵AD1平面BPQ,∴AD1∥平面BPQ又AD1∩CD1=D1.∴平面ACD1∥平面BPQ.∵AC平面ACD1,∴AC∥平面BPQ.图1-5-2611.如图1-5-26,四棱锥S-ABCD中,底面ABCD为平行四边形,E是SA上一点,试探求点E的位置,使SC∥平面EBD,并证明.【解】点E的位置是棱SA的中点.证明如下:如题图,取SA的中点E,连接EB,ED,AC,设AC与BD的交点为O,连接EO.∵四边形ABCD是平行四边形,∴点O是AC的中点.又E是SA的中点,∴OE是△SAC的中位线.∴OE∥SC.∵SC平面EBD,OE平面EBD,∴SC∥平面EBD.。
北师大版高中数学必修二随堂巩固验收:1-5-1-2平面与平面平行的判定

1.判断正误(正确的打“√”,错误的打“×”)
(1)直线l平行于平面α内的无数条直线,则l∥α.()
(2)若直线a∥b,bα,那么直线a就平行于平面α内的无数条直线.()
(3)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.()
(4)如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行.()
[答案](1)×(2)√(3)×(4)√
2.三棱台ABC-A1B1C1中,直线AB与平面A1B1C1的位置关系是()
A.相交B.平行
C.在平面内D.不确定
[解析]AB∥A1B1,AB平面A1B1C1,A1B1平面A1B1C1,∴AB∥平面A1B1C1.
[答案] B
3.如果一条直线与两个平行平面中的一个平行,那这条直线与另一个平面的位置关系是()
A.平行B.相交
C.在平面内D.平行或在平面内
[解析]由题可知,这条直线与另一个平面平行或者直线在平面内.故选D.
[答案] D
4.点P是平面α外一点,过P作直线a∥α,过P作直线b∥α,且直线a,b确定一个平面β,则()
A.α∥βB.α与β相交
C.α与β异面D.α与β的位置关系不确定
[解析]a∩b=P,aβ,bβ,b∥α,a∥α,∴α∥β.
[答案] A
由Ruize收集整理。
感谢您的支持!。
北师大高中数学必修二随堂巩固验收:平面与平面平行的判定 含解析

1.判断正误(正确的打“√”,错误的打“×”)
(1)直线l平行于平面α内的无数条直线,则l∥α.()
(2)若直线a∥b,bα,那么直线a就平行于平面α内的无数条直线.()
(3)如果一个平面内的两条直线平行于另一个平面,那么这两个平面平行.()
(4)如果一个平面内的任何一条直线都平行于另一个平面,那么这两个平面平行.()
[答案](1)×(2)√(3)×(4)√
2.三棱台ABC-A1B1C1中,直线AB与平面A1B1C1的位置关系是()
A.相交B.平行
C.在平面内D.不确定
[解析]AB∥A1B1,AB平面A1B1C1,A1B1平面A1B1C1,∴AB ∥平面A1B1C1.
[答案] B
3.如果一条直线与两个平行平面中的一个平行,那这条直线与另一个平面的位置关系是()
A.平行B.相交
C.在平面内D.平行或在平面内
[解析]由题可知,这条直线与另一个平面平行或者直线在平面内.故选D.
[答案] D
4.点P是平面α外一点,过P作直线a∥α,过P作直线b∥α,且直线a,b确定一个平面β,则()
A.α∥βB.α与β相交
C.α与β异面D.α与β的位置关系不确定
[解析]a∩b=P,aβ,bβ,b∥α,a∥α,∴α∥β. [答案] A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
"【世纪金榜】高中数学 1.5.2.1直线与平面平行的性质课时提能演
练北师大版必修2 "
(30分钟 50分)
一、选择题(每小题4分,共16分)
1.(2018·潍坊高一检测)下列说法中正确的是( )
①若直线a∥b,b平面α,则有a∥α;
②若直线a∥α,bα,则有a∥b;
③若直线a∥b,直线a∥α,则b∥α;
④若直线a∥α,b∥α,则a∥b.
(A)①④ (B)①③
(C)② (D)均不正确
2.直线a∥平面α,α内有n条直线交于一点,则这n条直线中与直线a平行的直线有( )
(A)0条 (B)1条 (C)0或1条 (D)无数条
3.(2018·汕头高一检测)已知△ABC,△DBC分别在平面α,β内,E∈AB,
F∈AC,M∈DB,N∈DC,且EF∥MN,则EF与BC的位置关系是( )
(A)平行
(B)相交或平行
(C)平行或异面
(D)平行、相交或异面
4.(易错题)如图,四棱锥S-ABCD的所有的
棱长都等于2,E是SA的中点,过C,D,E三点的
平面与SB交于点F,则四边形DEFC的周长为( )
(C)3+ (D)2+
二、填空题(每小题4分,共8分)
5.(2018·吉林高一检测)一个面截空间四边形的四边得到四个交点,如果该空间四边形的两条对角线与这个截面平行,那么此四个交点围成的四边形是
________.
6.(2018·福建高考)如图,正方体ABCD -A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于_________.
三、解答题(每小题8分,共16分)
7.如图所示,四边形ABCD是矩形,P 平面ABCD,过BC作平面BCFE交AP于E,交DP于F,求证:四边形BCFE是梯形.
8.(2018·杭州高一检测)在空间四边形ABCD
中,若P,R,Q分别是AB,AD,CD的中点.过
P,R,Q的平面与BC交于点S,求证:S是BC
的中点.
【挑战能力】
(10分)如图所示,一个平面与空间四边形的对角线AC,BD都平行,且分别交空间四边形的边AB,BC,CD,DA于E,F,G,H.
(1)若AC=BD,在什么情况下,四边形EFGH为菱形?
(2)在什么情况下,四边形EFGH为矩形?
(3)在什么情况下,四边形EFGH为正方形?
(4)若AC=BD=a,求证:平行四边形EFGH的
周长为定值.
答案解析
1.【解析】选D.①中可能aα或a∥α,②a与b可能异面,③中b可能在平面α内,④a
与b可能相交、平行或异面.
2.【解析】选C.过直线a与交点作平面β,设平面β与α交于直线b,则a∥b,若所给n条直线中有1条是与b重合的,则此直线与直线a平行,若没有与b重合的,则与直线a平行的直线有0条.
3.【解析】选A.EF∥MN,MNβ,EFβ,
∴EF∥β.又EFα,α∩β=BC,
∴EF∥BC.
4.【解题指南】先证明EF∥AB,再根据三角形中位线等知识求解.
【解析】选C.∵AB=BC=CD=AD=2,
∴四边形ABCD为菱形,∴CD∥AB.
又CD平面SAB,AB平面SAB,
∴CD∥平面SAB.
又CD平面CDEF,
平面CDEF∩平面SAB=EF,
∴CD∥EF,∴EF∥AB.
又∵E为SA的中点,∴EF=1
2
AB=1,
又∵△SAD和△SBC都是等边三角形,
∴DE=CF=2×sin60°
∴四边形DEFC的周长为
5.【解析】由线面平行的性质定理知,该四边形的两组对边分别平行,故该四边形为平行四边形.
答案:平行四边形
6.【解析】∵EF∥平面AB1C,EF平面ADC,
平面ADC∩平面AB1C=AC,
由线面平行的性质定理,得EF∥AC.
又∵E为AD的中点,
∴F为CD的中点,即EF为△ADC的中位线,
∴EF=1
2
AC.又正方体的棱长为2,
∴AC=EF=1
2
AC=
1
2
×
7.【证明】∵四边形ABCD为矩形,
∴BC∥AD.
∵AD平面PAD,BC平面PAD,
∴BC∥平面PAD.
∵平面BCFE∩平面PAD=EF,
∴BC∥EF.
∵AD=BC,AD≠EF,
∴BC≠EF,
∴四边形BCFE为梯形.
【误区警示】要证一个四边形是梯形,除了要证明一组对边平行外,还应证明它们的长度不相等.
【方法技巧】立体几何证明题的做题思路
立体几何证明题往往从以下三个方面思考
(1)从题目的结论出发去选择相应的证明方法并进行“逆向思维”.
(2)当逆推出现困难时,可根据已知条件联想或推导出有关的性质,使题设和结论逐步靠近.
(3)及时进行条件与结论之间的联系和沟通,找到证明思路.
这种“两头凑”的方法其实是解决数学问题的常用思维方法.
8.【解题指南】由于Q是CD的中点,要证S是BC的中点只需证SQ∥BD.
【证明】在△ABD中,点P、R分别是AB、AD的中点,则PR∥BD.
又PR平面BCD,BD平面BCD.
∴PR∥平面BCD.
又PR平面PRQS,平面PRQS∩平面BCD=SQ.
故PR∥SQ,又PR∥BD,
∴SQ∥BD,
又Q是CD的中点,∴S是BC的中点.
【挑战能力】
【解析】(1)∵AC∥平面EFGH,且AC平面ABC,平面ABC∩平面EFGH=EF,
∴AC∥EF.
同理AC∥GH.
∴EF∥GH,
同理EH∥FG,
∴四边形EFGH为平行四边形.
在△ABD中,EH AH
,BD AD
=
在△ADC中,HG DH
. AC AD
=
∵AC=BD,∴若使四边形EFGH为菱形.
只需EH=HG,即只需AH=DH.
∴当H为AD中点时,四边形EFGH为菱形.
同理当E、F、G分别为对应边中点时,四边形EFGH为菱形.
(2)∵EH∥BD,GH∥AC,
∴当BD⊥AC时,EH⊥GH.
此时四边形EFGH为矩形.
(3)在(1)、(2)的条件下,即AC=BD,BD⊥AC,且H为AD的中点时,四边形EFGH为正方形.
(4)∵EH AH EH AH
,即
BD AD a AD
==①
HG DH HG DH
,即
AC AD a AD
==②
①+②,得EH GH AH DH AD
1.
a AD AD
++
===∴EH+GH=a.
∴平行四边形EFGH的周长为定值2a.。
