6—7学年第一学期二年级数学期中测试卷

合集下载

汇融小学2020-2021学年度第一学期二年级数学期中测查试卷(精品)

宣武区汇融小学2020-2021学年度第一学期二年级数学期中测试卷班级姓名成绩一、我会填。

（每空1分，共27分）1、5+5+5+5表示（）个（）相加，结果是（），写成乘法算式是（）。

2、在括号里填上合适的长度单位。

保温杯高约20（）旗杆高约13（）课桌高约70（）钢琴高约1（）33（）3、回形针全长（）厘米，钉子长（）厘米。

4、（）时和（）时整，钟面上的分针和时针成直角。

5、右图有（）条线段，有（）个锐角，（）个直角，（）个钝角。

6、根据口诀“三五十五”写出两道乘法算式：（）和（）。

7、在○里填上“＞”、“＜”或“＝”。

（12分）1米-20厘米○80厘米 26＋55○90－8 4×3○3×4 4米+3米○403米 3米○30厘米 1米○100厘米8、比52多18的数是（）；比63少20的数是（）。

二、判一判。

（正确的画“√”，错误的画“×”。

）（5分）1、把一个角放在放大镜下面，这个角变大了。

（）2、3＋4和3×4的得数相同。

（）3、两个乘数都是4，积是8。

（）4、数学课本的长约为26厘米。

（）5、三角尺上的两个锐角拼成的角一定是钝角。

（）三、选一选。

（把正确答案的序号填在括号里。

）（5分）1、下面图形中，是线段的是（）。

①②③2、积是16的算式是（）。

①4+4+4+4 ② 4 × 4 ③10+63、角的大小和两条边的长短（）。

①有关系②没关系③有时有关系4、小红、小花、小丽每个人做4朵花，3个人一共做多少朵花？①12 ②7 ③95、国旗上面有（）个直角。

①2 ② 3 ③4四、动手操作我最棒。

（6分）1.画一条比5厘米长2厘米的线段。

（2分）2、画角。

（4分）（1）以下面的顶点和边画一个直角。

（2）画一个锐角和一个钝角。

五、算一算。

（30分）1、口算。

（18分） 36-24= 55-46= 5×5＝41- 2= 16+80= 26+ 3= 38-23= 2×3＝39+20= 44+22= 30+45= 37+23= 5×2＝14+65= 55+23= 70+15= 32+18= 2×4＝2、笔算下列各题。

二年级数学期中测试卷

二年级数学期中测试卷一、填空。

（共25分，每空1分）1、8×3=（），它表示（）个（）。

2、“三四十二”这句口诀写出两道乘法算式（）和（）。

3、（）五二十七九（）三（）二十七（）八四十八4、3只青蛙有3张嘴，6只眼睛，（）条腿。

5、数一数下面的图形各有几个角。

（）个角（）个角（）个角6、6个7相加的和是（），用乘法算式表示（），读作（）。

7、最大能填几？（）×5＜42 （）×4＜21 13＞5×（）8、长方形有（）个角，其中直角有（）个。

9、一个角有（）个顶点，（）条边。

锐角比直角（），钝角比直角（）。

二、判断题：（对的在括号里打“√”，错的打“×”）（共5分）。

1、三角板上的直角和黑板上的直角一样大。

（）2、求几个相同加数的和，用乘法较简便。

（）3、3×8和4×6的计算结果相同，意义也相同。

（）4、2+2可以写成2×2，3+3可以写成3×3。

（）5、一个正方形桌面有4个角，锯掉一个角，还剩3个角。

（）三、选一选。

（将正确答案的序号填在括号里）（共10分）1、积不是24的算式是（）A、6×4B、4×6C、8×6D、3×82、3个星期有多少天，列式错误的是（）A、3+7B、3×7C、7×3D、7+7+73、一支钢笔5元钱，4支钢笔多少元钱？列式（）A、4+4+4+4B、5+4C、5×44、算式4×8＝8×4表示交换两个因数的位置，（）不变。

A、和B、差C、积D、商5、4+4+4+3可以写成算式（）A、4×4－1B、3×4－1C、4×4+1D、3×4+2四、算一算，请仔细一点。

（共20分）4×7= 5×1= 6×6= 5×9= 4×9=48-22= 6＋2= 36＋30= 0×7= 8×7=36－8= 7×6= 87－27= 8×6= 2×8＋8= 2×6－6= 6×3－5= 5×6－5= 7×3＋2= 24+60－7=五、在○里填上“＜”“＞”或“＝”。

人教版数学二年级上册《期中测试卷》含答案

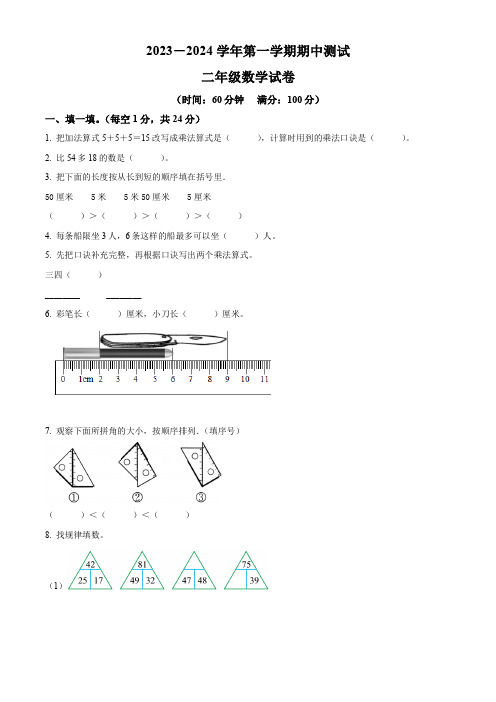
2023－2024学年第一学期期中测试二年级数学试卷（时间：60分钟满分：100分）一、填一填。

（每空1分，共24分）1. 把加法算式5＋5＋5＝15改写成乘法算式是（），计算时用到的乘法口诀是（）。

2. 比54多18的数是（）。

3. 把下面的长度按从长到短的顺序填在括号里．50厘米 5米 5米50厘米 5厘米（）＞（）＞（）＞（）4. 每条船限坐3人，6条这样的船最多可以坐（）人。

5. 先把口诀补充完整，再根据口诀写出两个乘法算式。

三四（）________________6. 彩笔长（）厘米，小刀长（）厘米。

7. 观察下面所拼角的大小，按顺序排列．（填序号）（）＜（）＜（）8. 找规律填数。

（1）（2）9. 一个乘数5，另一个乘数是4，积是（），2个5相乘，积是（）。

10. 3厘米＋5厘米＝（）厘米，1米－60厘米＝（）厘米。

二、判断对错。

（对的打“√”，错的打“×”，共5分）11. 3×4＋4可以看作4×4。

（）12. 教室的门高约2厘米。

（）13. 角的大小与角的开口大小有关，与角的两条边的长短无关。

（）14. 50－23－27与50－（23＋27）的运算顺序不同，但计算结果相同。

（）15. 5×6＝30，读作五六三十。

（）三、选一选。

（把正确答案的序号填在括号里，共5分）16. 有（）条线段。

A. 2B. 3C. 417. 商店里原来有62枝百合花，卖掉（）枝后，还剩37枝A. 35B. 99C. 2518. 如下图，求一共有多少个，列式错误的是（）。

A. 3×5＋2B. 3×6＋1C. 3×6－119. 妈妈带了6张5元的人民币，能买下面（）号服装。

A. ①B. ②C. ③20. 一根绳子用去一半后，还剩下6米。

这根绳子原来长（）米。

A. 6B. 12C. 18四、算一算。

（共26分）21. 直接写出得数。

3×5＝38＋50＝36－20＝88－40－30＝42－21＝5×6＝4×4＝4×5－16＝91－5＝6×6＝5×2＝64－7＋8＝22. 列竖式计算28＋45＝61－24＝14＋27＋52＝56＋（33－29）＝23. 括号里填上“＞”“＜”或“＝”。

2024秋季六年级数学上册第一学期期中测试卷

学校班级姓名装订线2024秋季六年级数学上第一学期期中测试卷考试时间：80分钟满分：100分题号一二三四五总分得分一．填空（22分）1. 40千克=（）吨 1.5 小时=（）分2. 100的（）是75。

25吨是（）吨的13。

3. 9的倒数是（）；（）的倒数是35。

4. 160千克黄豆可以榨油40千克， 1千克黄豆可以榨油（）千克，榨1千克油需要（）千克黄豆。

5. 3.5=（）8=（）÷6= =（）:（）最简比6. 甲数是乙数的 3÷ 4，乙数与甲乙总数的比是（），两数的差相当于乙数的（）。

7. 在○里填上“>”、“<”或“=”。

78×54○54 1×13○1÷1314÷0.1○14 ×108. 8吨煤，用去14后，再用去14吨，一共用去（）吨。

9. 一个比的前项是16 ，比值是13，后项是（）。

10. 走一段路，甲用了15小时，乙用了10小时，甲与乙所行时间的最简比是（），甲与乙行走的速度比的比值是（）。

11. 某班女生比男生少5人，男女生人数的比是3：2，这个班共（）人。

二．判断下面的说法是否正确（4分）1.比的前项扩大5倍，后项不变，比值也扩大5倍（）2.a 、b 都是不为0的自然数，已知a ×13=b ÷13，则a ＜b 。

（） 3.甲数的14和乙数13相等，则甲乙两数的比是 4：3 （）4.在3：8中，前项增加6，要使比值不变，后项应该扩大3倍。

（）三．选择正确答案的序号填在括号里（4分）1. 因为 3×13=1，所以（）。

A ．3 是倒数B ．13是倒数C ． 3和13都是倒数D ．13和3 互为倒数2. a 是一个不为0的自然数，下列各式中，得数最大的是（）。

A ．a ×13 B ．13÷a C ．a ÷13 D ．13÷133. 从甲堆煤中取出15给乙堆，这时两堆煤的吨数相等，原来甲、乙两堆煤的吨数的比是（）。

北师大版二年级上册数学期中检测卷(含答案)

北师大版二年级上册数学期中检测一、单选题( 5分)1．不能表示下图的算式是（）。

A．3+8 B．8×3C．8+8+82．某女装网店，第一天卖出43件毛衣，第二天比第一天少卖出15件。

两天一共卖出多少件毛衣？列式正确的是（）。

A．43-15 B．43-15+43 C．15+43+433．一套儿童文学绘本《疯狂动物园》，价钱是98元，下面付钱方法中（）最简便。

A．4张20元，3张5元，3张1元B．1张50元，2张20元，1张5元，3张1元C．4张10元，10张5元，8张1元4．淘气买1个杯子用去5元4角，还剩下3元6角，他原来有（）。

A．8元B．8元6角C．9元5．下列算式中不能用2×6来表示的是（）A．2个6相乘B．6个2相加C．6+6二、判断题(5分)6．4×5可以读作4乘5，也可以读作5乘4。

（）7．1元比10角少。

()8．1+2+3+4+5可以改写成乘法算式1×5。

（）9．3张可以换6张。

（）10．操场上原来有82人在跳绳，走了18人，又来了16人，操场上现在的人数比原来多。

（）三、填空题(27分)11．凯瑞小学图书馆中科普类书籍有26种，漫画类书籍有19种，名著类书籍有47种。

三类书籍一共有多少种？列式是，三类书籍一共有种。

12．一个玩具需要45元，乐乐带的钱都是10元的，他至少需要付张10元，找回元。

13．烧鹅店一天做70只烧鹅，上午卖出27只，下午卖出34只，还剩只。

14．一本故事书有95页，小丽上午看了27页，下午看了39页，还剩页没看。

15．1张10元可以换张2元；4元-2元6角=元角。

16．3元9角=角 7元-6角=元角9元+4角=元角 10元-6元2角=元角17．把加法算式改写成乘法算式，乘法算式改写成加法算式。

6+6+6=×5×3=++。

18．6×5读作，其中和是乘数，积是，它表示相加或相加。

四、连线题(9分)19．（6分）按要求连线。

2023-2024学年山西省大同市平城区城区第六小学校苏教版二年级上册期中测试数学试卷(含答案解析)

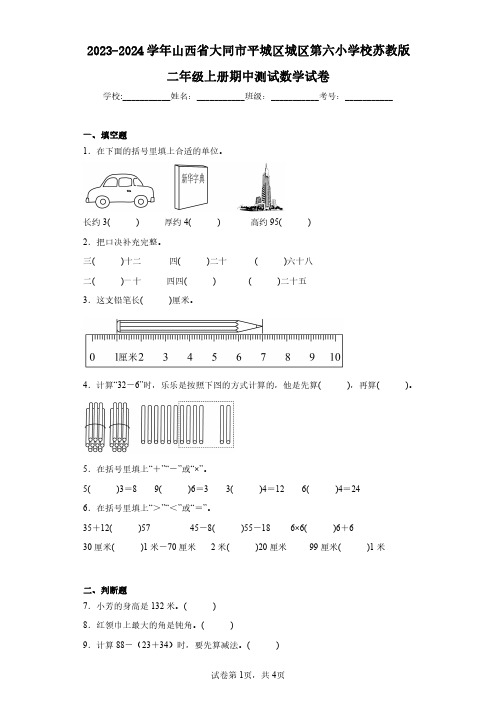
2023-2024学年山西省大同市平城区城区第六小学校苏教版二年级上册期中测试数学试卷学校:___________姓名：___________班级：___________考号：___________一、填空题1．在下面的括号里填上合适的单位。

长约3()厚约4()高约95()2．把口决补充完整。

三()十二四()二十()六十八二()一十四四()()二十五3．这支铅笔长()厘米。

4．计算“32－6”时，乐乐是按照下图的方式计算的，他是先算()，再算()。

5．在括号里填上“＋”“－”或“×”。

5()3＝89()6＝33()4＝126()4＝246．在括号里填上“＞”“＜”或“＝”。

35＋12()5745－8()55－186×6()6＋630厘米()1米－70厘米2米()20厘米99厘米()1米二、判断题7．小芳的身高是132米。

()8．红领巾上最大的角是钝角。

()9．计算88－（23＋34）时，要先算减法。

()10．5×4＋5的结果与5×6－5的结果相同。

()三、填空题11．图中一共有()条线段。

四、选择题12．能用3×4表示的图形是（）。

A．B．C．13．下图中，钉在一起的两根木条所成的角（）。

A．逐渐增大B．逐渐减小C．大小不变14．二年级3个班比赛跳绳，每班5人，_______？横线上应填的问题是（）。

A．二班有多少人B．男生有几人C．参加跳绳的一共有多少人15．下面的等式中，正确的是（）。

A．4×5＝5＋5＋5B．4×5＝4＋4＋4＋4＋4C．4×5＝4＋516．二（1）班开联欢会买了99个气球，第一次吹了34个，第二次吹了27个，下列竖式中箭头所指的“38”表示（）。

A．两次一共吹好的个数B．第二次吹好后还剩下的个数C．第一次吹好后还剩下的个数五、口算和估算17．接力赛：直接写出得数。

六、竖式计算18．用竖式计算。

部编版2020-2021学年二年级上册数学期中测试卷2套(含答案)

部编版二年级上册数学期中测试卷含答案（第1套试题）一、我能算得对又快。

(16分)2×5= 6×3= 4×3= 2×3+19=80-3= 7+55= 6×2= 3×3+2=4×6= 5×5= 4×5= 6×6-7= 6×5= 3×5= 87-25= 4×2+45=二、想一想,填一填。

(29分)1.铅笔长( )厘米橡皮长( )厘米 2.比56多9的数是( ),比82少47的数是( )。

3.5+5+5+5=( )×( ) 7+7=( )×( ) 4.把口诀补充完整。

二三( ) 四( )二十四三( )十八 ( )得四五五( ) ( )四得八5.两个乘数都是6,积是( );两个加数都是5,和是( )。

6.把6+6+6-4改写成乘减算式是( )。

7.在括号里填厘米或米。

8.左图中,有( )条线段,有( )个直角。

9.在括号里填上合适的数。

37+( )=53 4×( )=24 65-( )=38( )×5=1080-( )=63( )×( )=12三、用竖式计算。

(14分)28+37= 52-48= 83-38= 12+29+45=93-56-27= 54-38+27= 46+(32-18)=四、我来选一选。

(填序号)(5分) 1.下面的图形中,不是角的是( )。

2.下面的线段中,长是3厘米的是()。

3.下图中,()是锐角,()是钝角。

4.找规律填数,最后一个○里应该填()。

A.1B.30C.11五、小巧手画一画。

(8分)1.画一条比9厘米短5厘米的线段。

(1分)2.以下面的点为顶点,在方格纸上分别画出一个锐角、一个直角和一个钝角。

(3分)3.在下图中分别画一条线段,使它们按要求增加直角。

(4分)(导学号44712058)六、看图列式计算。

二年级数学期中测试卷

（2012-2013）第一学期二年级数学期中测试卷学校：班级姓名：一、填空（28分）1．根据算式先用小棒摆一摆，再填空。

（6分）５＋５＝（）×（）＝（）口诀：________________４＋４＋４＋４＝（）×（）＝（）口诀：________________2．写出相应的算式。

（4分）⑴4个8相加算式：⑵ 6乘3 写作：⑶ 24是8的几倍_ 算式：⑷把18平均分成3份算式： _ 3．将口诀补充完整。

（6分）三（）十二四（）二十八五六（）（）九十八（）七二十一四八（）4、填一填（4分）（）的4倍是24。

６的５倍是（）（）只小鸡12条腿。

7只小兔（）条腿。

5．根据口诀填空。

（8分）四九三十六三八二十四╳╳╳÷÷÷÷二、补充完整。

（10分）1．╳╳÷÷2．画一画。

（6分）①3×4（画Ｏ）或。

②（是2倍）。

③（画多3个）三、看图填空。

（4分）1.从上面看有（）个正方体。

2．从侧面看有（）个正方体。

3．从正面看有（）个正方体。

4.从正面看是侧面看到的（）倍。

四、找规律填空。

（8分）1．（）12 16 （）24 ( ）( )2．( ) 9 12 ( ) 18 ( ) ( )五、口算。

（16分）4÷2= 9－3= 16÷4= 18÷3=2+7= 12÷4= 2×9= 4+6=6÷2= 36÷9= 24÷8= 12-3=4×7= 5×6= 5×4= 7×2=六、在○里填上“＞”、“＜”或“=”。

（6分）4×3○4+3 24÷8○ 24-8 5×8 ○ 8×512÷6○12÷2 1×1○1+1 24÷6 ○ 24+6七、判断。

二年级数学上册期中测试卷

2012——2013学年度第一学期二年级数学期中测试卷班级姓名等级同学们，你们一定有很大收获吧！这儿为你们提供了一个展示自我的舞台，请仔细读题，认真思考，相信你一定能成功！一、知识大比拼。

（1）3×4=12，读作（），因数是（）和（），积是（）。

（2）被除数是12，除数是6，商是2，写作（）。

（3）一个角是由（）个顶点和（）条边组成的。

（4）把8个圆平均分成4份，每份是（）个。

（5）写出下面角的各部分名称。

二、小试身手，把加法算式改写成乘法算式。

5+5+5（） 9+9+9+9+9 （） 1+1+1+1 （） 2+2+2+2+2+2+2 （） 0+0+0+0 （）三、计算0÷3= 6×0= 8×1= 30÷5= 18÷2=4 95 8 9× 2 × 3 × 6 × 7 × 9四、先把口诀补充完整，再写出两个乘法算式。

二五（）（）十五三（）十二五、在○里填上“﹥、﹤、=”4×5＋4○30 7×3－7○2×7 0×5○3×245＋11○8×7 8×4○4×7＋4 3×3○3＋3六、选一选（把序号填在蘑菇瓶中）七、列式计算。

1、4与6的积是多少？2、一个因数是4，另一个因数是3，积是多少？3、两个因数都是5，积是多少？4、一只小兔4条腿，5只小兔一共多少条腿？5、12只鸟，平均放在3个笼子里，每个笼子放几只？学校班级姓名准考证号密封线内不得答题（）（）（）。

二年级上学期期中考试数学试卷(人教版)

人教版二年级第一学期数学期中测试卷班别：学号：成绩：一、我会填。

（40分）1、一个角有（）个顶点和（）条边。

（2分）2、40米＋5米=（）米 14厘米－8厘米=（）厘米 30厘米＋70厘米=（）厘米=（）米（8分）3、填上合适的长度单位“厘米”或“米”。

（4分）一块橡皮长4（）一张桌子高60（）一棵大树高8（）一座桥长30 （）4、下面的图形中是角的打“√”，不是的打“×”。

（6分）（）（）（）（）（）（）5、加法算式：乘法算式：或（）个（）（8分）6、下面的计算对吗？把不对的改正过来。

（4分）89－7=1928＋63=81改正 8 7 － 1 99 2 6 ＋ 8 1 8 3 改正二、我会判断。

（对的打“√”，错的打“×”。

）（5分）1、直角是角中最大的角。

（）2、学校操场长100厘米。

（）3、角的边越长，角就越大。

（）4、乘法是加法的简便计算。

（）三、我会选。

（选择正确答案的序号填在括号里。

）（5分）1、数学书的面有（）个直角。

A、1B、2C、3D、42、右边的图形有（）个角。

A、3B、5C、7D、63、小明的床宽120（）。

A、厘米B、分米C、米D、千米5、小亮昨天写了29个大字，今天写了42个，两天大约写了（）个大字。

A、30B、40C、60D、70四、动手操作。

（9分）1、画一条6厘米长的线段。

2、量出下面三角形各边的长度。

（3、画两个角，先画一个直角，再画一个比直角大的角。

（4分）五、笔算下面各题。

（18分）35＋23= 46＋24= 50－18= 42－17=88－26= 16＋27= 17＋49－20= 90－58－24=六、解决数学问题。

（21分）1、一共有多少个同学？（4分）2、爸爸给方方买一双运动鞋和一盏台灯，需要多少元钱？（4分）51元38元3、13元5元3元4元（）元（1）买4枝要用多少元？（4分）（2）一个书包比一个笔盒多27元，一个书包要多少元？（4分）（3）你还能提出哪些数学问题？（5分）？列式解答：。

人教版(2024)一年级数学上册期中测试卷及答案(含两套题)

…○………………内………………○………………装………………○………………订………………○………………线………………○…………………○………………外………………○………………装………………○………………订………………○………………线………………○………………… 学校：______________姓名：_____________班级：_______________考号：______________________人教版2024--2025学年度第一学期期中测试卷一年级数学（满分：100分时间：40分钟）题号一二三四五总分分数一、填一填。

（第6、7题每题4分，其余每空1分，共33分） 1．（1）一共有（）个小动物。

（2）从左边数，排第4，排第（）。

（3）前面有（）个小动物，后面有（）个小动物。

2．（1）有（）个，有（）个。

（2）比（）（填“多”或“少”）（）个；比（）（填“多”或“少”）（）个。

（3）再添（）个，就和同样多。

3．按顺序填数。

4．在□里填上合适的数。

5．与7相邻的两个数是（）和（）。

6．根据图形把序号填在相应的框里。

7．在里填上“＜”“＞”“＝”或“＋”“－”。

8 5 5＋0 5－0 2 7＝9 10 2＝8 69 9－3 8－4 5＋4 3＋7 6 1＝5 二、选一选。

（填序号）（共10分）1．比一比，和，（）多。

①②③一样2．与5＋3得数相等的算式是（）。

①4＋2 ②7－1 ③10－2 3．下面搭成的图形中，（）搭得最稳。

① ② ③……○………………内………………○………………装………………○………………订………………○………………线………………○…此卷只装订不密封……○………………外………………○………………装………………○………………订………………○………………线………………○…4．正方体有6个面，每个面都是（）。

①②③5．数一数，左图中有（）个。

人教版2020---2021学年度二年级数学(上)期中考试卷及答案(含三套题)

密线学校班级姓名学号密封线内不得答题人教版2020—2021学年度上学期二年级数学（上）期中测试卷及答案（满分：100分时间： 60分钟）一、认真思考，仔细填空。

（第2题4分，第10题3分，其余每空1分，共32分）1.在括号里填上合适的长度单位。

教学楼高20（）牙刷长15（）小红的身高是94（） 2.上面有（）束气球，每束有（）个，一共有（）个气球。

□◯□＝□（个）3.根据“三五十五”写出两道乘法算式是（）和（）。

4.把乘法口诀补充完整。

二三（）三（）十二（）六十八（）五二十五五（）（）六二十四5.70厘米－35厘米＝（）厘米 23米＋45米＝（）米 45厘米＋55厘米＝（）米 1米－28厘米＝（）厘米6.比28多12的数是（），比91少35的数是（）。

7.下图中共有（）条线段，（）个角，（）个锐角，（）个直角，（）个钝角。

8.一只蚂蚁6条腿，3只蚂蚁（）条腿，6只蚂蚁（）条腿。

9.小明买一辆玩具火车花了28元，买一个玩具木马花了51元，他一共花了（）元。

10.按规律填一填。

（1）4，8，12，（），（），（）。

（2）100，91，（），73，（），（）。

二、反复比较，择优录取。

（把正确答案的序号填在括号里）（共20分）1.下面的图形中，（）是线段。

2.下面图形中不是角的是（）。

题号一二三四五六总分得分3.小明的身高是92厘米，小红比小明矮7厘米，小红的身高是（）厘米。

①85 ②99 ③1004.表示3个6相加的算式是（）。

①3＋6 ②6×3 ③3＋3＋3＋3＋3＋35.能用4×3表示的图形是（）。

6.买一箱火龙果需要28元，如果全用5元的人民币付钱，最少要带（）张。

①5 ②6 ③77.王大爷种了4行梨树和6行苹果树。

如果要想求王大爷一共种了多少棵苹果树，可以补充的条件是（）。

2022-2023学年天津市高二年级上册学期期中数学试题【含答案】

2022-2023学年天津市高二上学期期中数学试题一、单选题1．已知点A （1，-1），B （1，2），则直线AB 的倾斜角为（）A ．0B ．C ．D ．4π3π2πD【分析】由两点的横坐标相等，得出倾斜角.,A B 【详解】由题意可知，两点的横坐标相等，则直线AB 的倾斜角为.,A B 2π故选：D2．抛物线的焦点到其准线的距离是（）22y x =A ．1B ．2C ．3D ．4A【分析】求出抛物线的焦点坐标与准线方程，即可得解；【详解】解：抛物线的焦点为，准线方程为，22y x =1,02F ⎛⎫ ⎪⎝⎭12x =-所以焦点到准线的距离；11122d ⎛⎫=--= ⎪⎝⎭故选：A3．椭圆的焦距是2，则m 的值是2214x y m +=A ．5B ．5或8C ．3或5D ．20C【详解】试题分析：因为焦距是，所以，当焦点在轴时，21c =x 解得：，当焦点在轴时，22222,4,41a m b c a b m ==∴=-=-=5m =y 解得：，故选择C ．222224,,41a b m c a b m ==∴=-=-=3m =椭圆简单的几何性质．4．若圆被直线平分，且直线与直线垂直，则直线的方程是()()22126x y ++-=l l 30x y -=l （）A ．B ．350x y +-=310x y ++=C ．D ．350x y -+=370x y -+=B【分析】由已知得直线过圆心，再根据垂直可得直线方程.l 【详解】因为圆被直线平分，所以圆心在直线上，()()22126x y ++-=l ()1,2-l 又直线与直线垂直，l 30x y -=设直线的方程为，l 30x y c ++=把，代入上式，解得，=1x -2y =1c =所以直线的方程为，l 310x y ++=故选：B.5．若圆：与圆：相切，则的值可以是（）1C ()2211x y -+=2C 22880x y x y m +-++=m A ．16或-4B ．7或-7C ．7或-4D ．16或-7A【分析】根据两圆位置关系，以及二元二次方程表示圆，列出关系式求解即可.【详解】因为表示圆，故，解得：；22880x y x y m +-++=646440m +->32m <对圆，其圆心为，半径；1C ()1,011r =对圆，其圆心为，半径2C ()4,4-2r =当两圆外切时，，即，解得；1212C C r r =+51=16m =当两圆内切时，，即，解得；1221C C r r =-51=-4m =-综上所述：的取值可以为或.m 164-故选.A6．已知A 为抛物线C :y 2=2px （p >0）上一点，点A 到C 的焦点的距离为12，到y 轴的距离为9，则p =（）A ．2B ．3C ．6D ．9C【分析】利用抛物线的定义建立方程即可得到答案.【详解】设抛物线的焦点为F ，由抛物线的定义知，即，解得.||122A pAF x =+=1292p =+6p =故选：C.【点晴】本题主要考查利用抛物线的定义计算焦半径，考查学生转化与化归思想，是一道容易题.7．已知双曲线的一条渐近线过点，是的左焦点，且()2222:10,0x y C a b a b -=>>(P -F C ，则双曲线的方程为（）2PF =C A ．B ．2213y x -=2213x y -=C ．D ．22126x y -=22162x y -=A【分析】根据一条渐近线过点，可确定，再结合，，推得(P -ba =2OP =2PF =为等边三角形，从而确定，可求得双曲线方程.OFP △c【详解】由题意可知，双曲线的渐近线方程为，点在一条渐近线上，如图示：C b y x a =±(P -所以，且两条渐近线的倾斜角分别为60°，120°，ba =b =则 ,60POF ∠=又（为坐标原点），所以为等边三角形，从而2PF =2=O OFP △,||2c OF ==由，，解得，，所以双曲线的方程为,222+=a b c b =21a =23b =C 2213y x -=故选：A.8．设A ，B 为双曲线Γ：的左，右顶点，F 为双曲线Γ右焦点，以原点O 为圆心，2214x y -=为半径的圆与双曲线Γ的一条渐近线的一个交点为M ，连接AM ，BM ，则tan ∠AMB =（）OFA ．4BC ．2.DA【分析】首先求点的坐标，并判断轴，这样中，直接求解.M BM x ⊥AMB tan AB AMB MB∠=【详解】，以原点O 为圆心，为半径的圆的方程是，2225c a b =+=OF 225x y +=设点是圆与渐近线在第一象限的交点，M 12y x=，解得：，即 225120x y y xx ⎧+=⎪⎪=⎨⎪>⎪⎩2,1x y ==()2,1M ，轴，()2,0B BM x ∴⊥中，AMB4tan 41AB AMB MB ∠===故选：A本题考查圆与双曲线的方程，双曲线的渐近线，三角函数的简单综合问题，意在考查数形结合分析问题的能力，属于基础题型.9．已知双曲线：的左、右顶点分别为，，左、右焦点分别为，.以C ()222210,0x y a b a b -=>>1A 2A 1F 2F 线段为直径的圆与双曲线的一条渐近线交于点，且点在第一象限，与另一条渐近12A A C M M 2AM 线平行.若，则的面积是（）1F M =22MAF △A BCDA【分析】根据与渐近线平行，得到是等边三角形，，从而求出各边长，2A M 2OMA 260MOA ∠=︒由勾股定理求出，结合渐近线斜率求出，从而求出，22282a c ⎛⎫++= ⎪⎝⎭2c a =2a =，从而求出的面积.24c a ==22MA F △【详解】过点M 作MB ⊥x 轴于点B ，OM 与ON 是双曲线的两条渐近线，故，12NOA MOA ∠=∠因为与渐近线ON 平行，所以，2A M 12NOA MA O ∠=∠故，2OM MA =因为，所以，2OM OA a ==22OM OA MA ==所以是等边三角形，，2OMA 260MOA ∠=︒故，，22a OB BA ==112a BF OF OB c =+=+因为1F M =由勾股定理得：，即，12122MB F B FM +=22282a c ⎛⎫++= ⎪⎝⎭又因为，tan 60OM bk a ==︒=b =由得：，222c a b =+2c a =从而，解得：，22322842aa a ⎛⎫++= ⎪⎝⎭2a =所以，24c a ==则，222AF c a =-==故.222211222A F M S A F MB =⋅=⨯= 故选：A10．曲率半径可用来描述曲线在某点处的弯曲变化程度，曲率半径越大则曲线在该点处的弯曲程度越小，已知椭圆：上点处的曲率半径公式为.C ()222210x y a b a b +=>>()00,P x y 3222220044x y R a b a b ⎛⎫=+ ⎪⎝⎭若椭圆上所有点相应的曲率半径的最大值为4，最小值为，则椭圆的标准方程为（）C 12C A ．B ．2212x y +=2214x y +=C ．D ．22142x y +=221164x y +=D【分析】根据，得到，结合，确定的最大值和2200221x y a b +=22222000444221x y a b x a b a b b -+=-+2200x a ≤≤R 最小值，得到立与，联立求出，求出椭圆方程.28a b =21b a =2,4b a ==【详解】因为点在椭圆上，则，即，()00,P x y 2200221x y a b +=2220021⎛⎫=- ⎪⎝⎭x y b a 所以，2222222000044424202211x a x y x a b x a b a b a b b -+=+=-+-因为，所以当时，取得最大值，最大值为，2200x a ≤≤00x =220044x y ab +21b 此时取得最大值，为，3222220044x y R a b a b ⎛⎫=+ ⎪⎝⎭32222218a ab b b ⎛⎫== ⎪⎝⎭当时，取得最小值，最小值为，220x a =220044x y ab +21a 此时取得最小值，为，3222220044x y R a b a b ⎛⎫=+ ⎪⎝⎭32222211b a b a a ⎛⎫== ⎪⎝⎭联立与，解得：，28a b =21b a =2,4b a ==所以椭圆方程为.221164x y +=故选：D二、填空题11．己知直线：，与双曲线：的一条渐近线垂直，则1l ()2100mx y m ++=>C 2214x y -=__________.m =4【分析】求得双曲线的渐近线方程，根据直线垂直列出等量关系，即可求得结果.C 【详解】对双曲线：，其渐近线方程为，C 2214x y -=12y x=±对直线：，且斜率为，1l()2100mx y m ++=>02m -<根据题意可得，解得.1122m -⨯=-4m =故答案为.412．与：外切于原点，且被轴截得的弦长为4的圆的标准方程为C 22240x y x y +-+=y __________.()()22125x y ++-=【分析】根据两圆的位置关系，结合弦长公式，求得圆心和半径，即可得解.【详解】对圆：，其圆心的坐标为，半径，C 22240x y x y +-+=C ()1,2-r =设所求圆的圆心为，半径为，()1,(0)C a b a <1r 因为所求圆与圆外切于原点，故可得，且；C 2b a =-2221a b r +=又所求圆被轴截得的弦长为4，故，y 4=联立上式可得：，1,2a b =-=1r =故所求圆的标准方程为.()()22125x y ++-=故答案为.()()22125x y ++-=13．如果数满足等式,那么的最大值是__________.,x y 223412x y +=3yx -【分析】化简等式,可得到满足椭圆方程,故用线性规划把看做与椭圆上223412x y +=,x y 3yx -(3,0)点连线的斜率,临界条件为相切,联立可得的取值范围,即得的最大值.0∆=m 3yx -【详解】解:由题知,,即,223412x y +=22143x y +=所以可以看做在椭圆上的点,(,)x y 22143x y +=记,即,3ym x =-(3)y m x =-即是与椭圆上点连线的斜率,(3,0)当直线与椭圆相切时,斜率可取得最值,(3)y m x =-m 联立直线和椭圆,即,223412(3)x y y m x ⎧+=⎨=-⎩可得,2222(34)2436120m x m x m +-+-=因为相切,所以,22222(24)4(34)(3612)350m m m m ∆=-+-=-=所以,235m =所以m ≤≤故答案为14．已知椭圆：的焦点为，，短轴端点为，若，则C ()22101x y m m m +=>+1F 2F P 122F PF π∠=__________.m =1【分析】根据题意可得，列出等量关系，即可求得结果.b c =【详解】对椭圆：，其，C ()22101x y m m m +=>+2221,,1a m b m c =+==又，故，0m>b =1c =根据椭圆的对称性，因为，解得.122F PF π∠=1=1m =故答案为.115．已知直线与抛物线：的准线相交于点A ，O 为坐标原点，若1y x =-C ()220y px p =>则抛物线的方程为___________.2AO k =24y x=【分析】由抛物线方程求得准线方程，联立直线方程求得点坐标，再根据斜率，即可求得，则A p 问题得解.【详解】对抛物线：，其准线方程为：，C ()220y px p =>2px =-又其与直线交于点，故可得点的坐标为，1y x =-A A ,122p p ⎛⎫--- ⎪⎝⎭因为，则，解得，则抛物线方程为.2AOk =1222pp--=-2p =24y x=故答案为.24y x=16．已知双曲线：的右焦点，过点作一条渐近线的垂线，垂足为C ()222210,0x y a b a b -=>>F F l M ，若与另一条渐近线交于点N ，且满足，则该双曲线的离心率为____________.l 4MF MN =【分析】根据的正切值，结合渐近线的斜率，即可列出等量关系，求解即可.NOM ∠【详解】根据题意，作图如下：设点坐标为，其到渐近线：的距离，F (),0cOM b y x a =MF b ==因为，显然，OF c=OM a=又因为，故可得，4MF MN =4MN b=在中，，设，则，Rt OMN 4tan b MON a ∠=MOF θ∠=tan ba θ=又，故，22tan tan 21b a MON b a θ∠==⎛⎫- ⎪⎝⎭2241bb a a b a =⎛⎫- ⎪⎝⎭解得：，故双曲线的离心率.212b a ⎛⎫= ⎪⎝⎭e==故答案为三、解答题17．已知抛物线：的焦点到双曲线，且抛物线的焦C ()220y px p =>221x y -=点与椭圆：的右焦点F 重合，直线与椭圆相交于A ，B 两点，若()222210x y a b a b +=>>b y x a =.4AF BF +=(1)求抛物线的标准方程；(2)求椭圆的标准方程.(1)；24y x =(2).22143x y +=【分析】（1）根据点到直线的距离公式，结合题意，即可求得参数以及抛物线方程；p （2）根据椭圆的定义，结合题意，即可求得以及椭圆方程.,a b 【详解】（1）抛物线：的焦点为，C ()220y px p =>,02p ⎛⎫⎪⎝⎭双曲线的一条渐近线为，221x y -=0x y -=，=2p =故抛物线的标准方程为.24y x=（2）取椭圆的左焦点为，连接，如下所示：1F 11,AF BF 根据椭圆的对称性可得四边形为平行四边形，1AF BF故，解得，142AF AF BF AF a +=+==2a =根据题意，，又，解得1c =222a b c =+b =故椭圆的标准方程为.22143x y +=18．直线：，圆：，圆.l 70x y --=1C 2224310x y x y +---=2C 224630x y x y ++--=(1)求直线被圆截得的弦长；1C (2)过直线上一点作的一条切线，切点为，当最小时，求外接圆的方程.P 2C Q PQ 2C PQ △(1)；4(2).()22118x y -+=【分析】（1）求得圆的半径长度，以及点到直线的距离公式，结合弦长公式求解即可；1C （2）根据题意求得满足题意的点的坐标，求得线段的长度以及其中点的坐标，即可求得P 2C P 外接圆方程.2C PQ △【详解】（1）对圆：，其圆心，半径，1C 2224310x y x y +---=()11,2C 16r =点到直线的距离1C :l 70x y --=d =故直线被圆截得的弦长为；1C 4==（2）对圆：，其圆心，半径，2C 224630x y x y ++--=()22,3C -24r =因为为直角三角形，故，2C PQ △22222PC r PQ =+当最小时，显然最小，此时即为点到直线的距离，PQ 2PC 2PC 2C l故满足题意时，的坐标为，2PC =P (),7m m -由，故点坐标为，2PC ==4m =P ()4,3-因为为直角三角形，2C PQ △故其外接圆圆心为线段的中点，半径为2C P ()1,0212PC =则外接圆的方程为.2C PQ △()22118x y -+=19．已知椭圆：的实轴C ()222210x y a b a b +=>>2213y x -=长.(1)求椭圆的标准方程；C (2)若，为椭圆上关于原点对称的两点，在圆：上存在点，使得为等A B C O O 22245x y +=P PAB 边三角形，求直线的方程..AB (1)；2214x y +=(2)或.y x =y x =-【分析】（1）根据题意，列出满足的等量关系，求解即可；,,a b c （2）根据的长度求得，结合弦长公式，即可求得结果.OP AB【详解】（1）由椭圆C c a=对双曲线，其实轴长为，故可得，2213y x -=222b =又，解得，222a b c =+2224,1,3a b c ===则椭圆的标准方程为：;C 2214x y +=（2）根据题意，，因为为等边三角形，2245OP =PAB 由，可得.OP =2325AB =当直线的斜率不存在时，此时不满足题意，AB 22AB b ==故直线的斜率存在，设其为，则直线方程为，AB k AB y kx =联立椭圆方程可得：，2214x y +=()224140k x +-=根据题意，显然有，设坐标分别为，0> ,A B ()()1122,,,x y x y 则，1212240 ,41x x x x k +==-+，()()()2222121221613214415k AB k x x x x k +⎡⎤=+⨯+-==⎣⎦+解得，1k =±故直线的方程为：或.AB y x =y x =-20．已知椭圆：在椭圆上，两个焦点分C ()222210x y a b a b +=>>P C 别为，，过的直线与椭圆交于，两点，过与平行的直线与椭圆交于，D 两1F 2F 1F 1l C A B 2F 1l C C 点（点A ，D 在x 轴上方）.(1)求椭圆的标准方程；C (2)求四边形ABCD 面积的最大值以及此时直线的方程，1l (1)；22132x y +=.1x =-【分析】（1）根据椭圆的离心率以及椭圆上的一点，求得，则椭圆方程得解；,,a b c （2）根据四边形为平行四边形，将问题转化为求三角形面积的最大值；设出直线的ABCD AOB 1l 方程，利用弦长公式和点到直线的距离公式表达其面积，再求最小值即可.【详解】（1）根据题意可得：，又，2233142c a a b =+=222a b c =+解得：，2223,2,1a b c ===故椭圆的标准方程为.C 22132x y +=（2）根据（1）中所求可得的坐标为，1F ()1,0-根据题意，连接作图如下：,,,AO BO AD BC根据椭圆的对称性，四边形为平行四边形，ABCD 设其面积为，故，S S =4AOB S 当直线斜率为零时，显然不满足题意，1l故直线的斜率不为零，设其方程为：，1l 1x my =-联立椭圆方程：可得：，22132x y +=()2223440m y my +--=设的坐标分别为，,A B ()()1122,,,x y x y 则，12122244,2323m x x x x m m +==-++，AB ==点到直线的距离，O AB d =142S AB d =⨯⨯=，则，[)1,t =∈+∞221m t=-故211212tS t t t ==++对函数，，12y t t =+[)1,t ∈+∞'y 2120t =->故在单调递增，在单调递减，12y t t =+[)1,+∞112y tt =+[)1,+∞故，当且仅当，即时取得等号；S ≤1t=0m =故四边形ABCD ，此时直线的方程.1l 1x =-关键点点睛：处理问题的关键是能够根据四边形的形状，将四边形面积最大值的问题转化为求三角形面积的问题.。

2023-2024学年人教版数学二年级上册《期中测试卷》带答案

2023－2024学年第一学期二年级数学期中测试卷一、填一填。

（每空1分,共24分）1. 看一看,这支铅笔长（）厘米。

2. 一块平整的黑板表面有（）个角,它们都是（）角。

3. 比较角大小。

① ② ③（）＜（）＜（）4. 把各数从小到大排列：40厘米10米99厘米1米（）< （）< （）< （）5. 小明计划写100个大字。

上午写了48个,下午写了32个,小明一天写了（）个,还有（）个字没写。

6. 3＋3＋3＋3＋3＋3＝3×（）5＋5＝（）×27. 一只手5根手指,2只手（）根手指,2双手（）根手指。

8. 26厘米＋37厘米＝（）厘米,1米－45厘米＝（）厘米。

9. 两个乘数都是5,积是________；两个加数都是4,和是_____。

10. 3和5相乘写成算式是（）,3和5相加写成算式是（）,3个5相加写成加法算式是（）,写成乘法算式是（）。

二、判断（12分）。

11. 所有的直角都一样大。

（）12 口诀“四六二十四”表示4个6相乘．（）13. 边越长,角就越大。

（）14. 7个7相加得14.（）15. 在乘法算式中,积一定比其中任何一个乘数大。

（）16. 1米长的绳子比100厘米长的铁丝短。

（）三、选一选。

（每空2分,共6分）17. 下列式子正确的是（）。

A. 60＞34＋26B. 74－28＜45C. 52＝24＋2818. 图中,有（）个直角。

A. 4B. 5C. 719. 由钢笔：15元,帽子：8元,篮球：25元得知,（）这两件物品价格的和最接近30元。

A. 钢笔和帽子B. 帽子和篮球C. 钢笔和篮球四、算一算。

（共20分）20. 直接写出得数。

15＋20＝2×4＝20＋75＝80＋10＝17＋53＝17＋13＝29－10＝22＋37＝12＋30＝5×3＝3×3＝5×5＝21. 笔算。

58＋29＝90－54＝46＋25－17＝五、画一画。

期中考试试卷二年级数学

高新区2008---2009学年度第一学期小学数学二年级期中考试测试卷（测评时间：60分钟）班级：姓名：等级：亲爱的小朋友们：大家好!经过这都几个月的学习，我们都学到了一身的本领，赶快到这里来试一下吧！记住“相信自己，我是最棒的”。

一、填空1、在○里填上“＋、－或×”。

3○7＝21 8○4＝4 8○8=16 4○2=8 2、把口诀填完整。

（）四十二五（）二十五四四（）二（）十二3、（1）★★★★★★ 加法算式（），乘法算式（）。

4、 6×7=42 写出两个除法算式。

（）÷（）=（）（）÷（）=（）。

5、8×4=( )，这个算式里，( )和( )是因数，( )是积．表示( )个( )连加是( )。

6、在○里填上“＞”、“＜”、“＝”。

4×6○5×5 34－20○4×4 6○3×32＋2○2×2 12÷3○4 36○6×625÷5○5 24－6○4 3＋3○9二、判断（对的打“√”，错的打“×”）1、0×5﹤0×100 。

（）2、一个角有1个顶点，2条边。

（）3、在25÷5＝5中，“25”叫做被减数。

（）4、16个苹果，平均放在4个盘子里，每盘放4个。

（）5、4×6=24也可以写成6×4=24（）三、计算12÷4＝ 12÷2＝ 0×6＝ 0÷5＝ 6÷1＝ 1×1＝（）÷4＝4 30÷（）＝5 （）÷5＝6 24÷（）＝6 四、填表格五、看图列式计算（1）一共有多少个？算法一：□○□○□=□算式二：□○□○□=□（2）（3）20元？元？个元□○□=□□○□=□六、解决问题（1）画一个直角。

南京市2022-2023学年度第一学期高二数学期中调研测试试卷(含答案)

南京市2022－2023学年度第一学期期中调研测试高二数学 2022.11注意事项：1．本试卷共6页，包括单项选择题(第1题~第8题)、多项选择题(第9题~第12题)、填空题(第13题~第16题)、解答题(第17题~第22题)四部分．本试卷满分为150分，考试时间为120分钟． 2．答卷前，考生务必将自己的学校、姓名、考生号填涂在答题卡上指定的位置．3．回答选择题时，选出每小题答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上指定位置，在其他位置作答一律无效．一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知复数z 满足(2＋i)z ＝3－4i ，则|z |＝A ．2B ．5C ．5D ．102．已知直线l 1：4x ＋my ＋2＝0和l 2：mx ＋y ＋1＝0平行，则实数m ＝A ．－2B ．0C ．2D ．±23．已知双曲线x 2a 2－y 24＝1(a ＞0)的焦距为43，则该双曲线的渐近线方程为A ．y ＝±2xB ．y ＝±2xC ．y ＝±22x D ．y ＝±12x 4．直线l 与直线y ＝3x 关于直线y ＝x ＋1对称，则直线l 的倾斜角是A ．π12B ．π6C ．π4D ．π35．我们把所有顶点都在两个平行平面内的多面体叫做拟柱体，在这两个平行平面内的面叫作拟柱体的底面，其余各面叫做拟柱体的侧面，两底面之间的垂直距离叫做拟柱体的高，过高的中点且平行于底面的平面截拟柱体所得的截面称为中截面．已知拟柱体的体积公式为V ＝16h (S ＋4S 0＋S')，其中S ，S'分别是上、下底面的面积，S 0是中截面的面积，h 为拟柱体的高．一堆形为拟柱体的建筑材料，其两底面是矩形且对应边平行(如图)，下底面长20米，宽10米，堆高1米，上底长、宽比下底长、宽各少2米．现在要彻底运走这堆建筑材料，若用最大装载量为4吨的卡车装运，则至少需要运（注：1立方米该建筑材料约重1.5吨） A ．63车B ．65车 C ．67车D ．69车6．已知α，β均为锐角，且sin(α＋β)＝2sin(α－β)，则tan αtan β＝ 1020 (第5题图)A ．13B ．12C ．2D ．37．已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的上顶点为A ，左、右焦点分别为F 1，F 2，连接AF 2并延长交椭圆C 于另一点B ，若F 1B ∶F 2B ＝7∶3，则椭圆C 的离心率为A ．14B ．13C ．12D ．338．在矩形ABCD 中，AB ＝3，AD ＝2，E 为线段CD 上的动点，过B 作AE 的垂线，垂足为F ，则 DF →·DA →的最小值是 A ．1B ．1613C ．85D ．4二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9．甲、乙两城市某月初连续7天的日均气温数据如下图，则在这7天中，A ．乙城市日均气温的极差为3℃B ．乙城市日均气温的众数为24 ℃C ．甲城市日均气温的中位数与平均数相等D ．甲城市的日均气温比乙城市的日均气温稳定10．在平面直角坐标系xOy 中，已知抛物线C ：y 2＝4x 的焦点为F ，直线l ：y ＝x －2与抛物线C交于A ，B 两点，则A ．抛物线C 的准线方程为x ＝－1B ．点F 到直线l 的距离为22C ．∠AOB ＝π2D ．AB ＝1011．已知正方体ABCD －A 1B 1C 1D 1的棱长为1，点P 为侧面BCC 1B 1内一点，则A ．当C 1P →＝13C 1B →时，异面直线CP 与AD 所成角的正切值为12B ．当C 1P →＝λC 1B →(0＜λ＜1)时，四面体D 1ACP 的体积为定值C ．当点P 到平面ABCD 的距离等于到直线A 1B 1的距离时，点P 的轨迹为抛物线的一部分 D ．当C 1P →＝12C 1B →时，四面体BCDP 的外接球的表面积为2π12．过原点的直线l 与圆M ：x 2＋y 2＋2x －2y －16＝0交于A ，B 两点，且l 不经过点M ，则2625 24 23 22 21气温ºC 1234567A ．弦AB 长的最小值为8 B ．△MAB 面积的最大值为42C ．圆M 上一定存在4个点到l 的距离为22D ．A ，B 两点处圆的切线的交点位于直线x －y －16＝0上三、填空题：本题共4小题，每小题5分，共20分．13．已知a ＞0，若圆(x －a )2＋y 2＝2与圆x 2＋(y －a )2＝8外切，则a ＝▲________． 14．某班15名学生在一次测试中的得分(单位：分)如下：9，10，10，11，11，11，12，12，12，12，13，14，16，17，18．则这组数据的70百分位数是▲________．15．设函数f (x )＝2x ＋log a x －8（a ＞1）的零点为x 0．若x 0≥3，则a 的最小值为▲________． 16．已知抛物线C ：x 2＝4y 的焦点为F ，点P 的坐标为(2，1)，动点A ，B 在抛物线C 上，且P A ⊥PB ，则F A ＋FB 的最小值是▲________．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤． 17．(本小题满分10分)在①(sin B －sin C )2＝sin 2A －sin B sin C ，②tan A ＝3bcb 2＋c 2－a 2，③a sin B ＝3b cos A 这三个条件中任选一个，补充在下面的问题中，并解答该问题．问题：△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知c ＝3，cos B ＝277，且_________，求△ABC 的面积．注：如果选择多个条件分别解答，按第一个解答计分． 18．(本小题满分12分)如图，在正三棱柱ABC －A 1B 1C 1中，D 是棱BC 上的点（不与点C 重合），AD ⊥DC 1． (1)证明：平面ADC 1⊥平面BCC 1B 1；(2)若AC ＝CC 1＝2，求CC 1与平面ADC 1所成角的正弦值． 19．(本小题满分12分)已知圆M 过原点O ，圆心M 在直线y ＝x －1上，直线2x ＋y ＝0与圆M 相切．(1)求圆M 的方程；(2)过点P (0，4)的直线l 交圆M 于A ，B 两点．若A 为线段PB 的中点，求直线l 的方程． 20．(本小题满分12分)某篮球场有A ，B 两个定点投篮位置，每轮投篮按先A 后B 的顺序各投1次，在A 点投中一球得2分，在B 点投中一球得3分．设球员甲在A 点投中的概率为p ，在B 点投中的概率为q ，其中0＜p ＜1，0＜q ＜1，且甲在A ，B 两点投篮的结果互不影响．已知甲在一轮投篮后得0分的概率为A 1C 1B 1 ACD B(第18题图)16，得2分的概率为13．(1)求p ，q 的值；(2)求甲在两轮投篮后，总得分不低于8分的概率． 21．(本小题满分12分)已知圆A ：(x －3)2＋y 2＝16，B (－3，0)，T 是圆A 上一动点，BT 的中垂线与AT 交于点Q ，记点Q 的轨迹为曲线C ．(1)求曲线C 的方程；(2)过点(0，2)的直线l 交曲线C 于M ，N 两点，记点P (0，－1)．问：是否存在直线l ，满足PM ＝PN ？如果存在，求出直线l 的方程；如果不存在，请说明理由． 22．(本小题满分12分)已知双曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的离心率为3，左、右顶点分别为M ，N ，点P (－1，1)满足PM →·PN →＝1．(1)求双曲线C 的方程；(2)过点P 的直线l 与双曲线C 交于A ，B 两点，直线OP 与直线AN 交于点D ．设直线MB ，MD 的斜率分别为k 1，k 2，求证：k 1k 2为定值．南京市2022－2023学年度第一学期期中调研测试高二数学参考答案2022.11一、选择题：本题共8小题，每小题5分，共40分．1．B2．A3．C4．B5．B6．D7．C8．A二、选择题：本题共4小题，每小题5分，共20分．9．BC10．AB 11．BCD12．ABD三、填空题：本题共4小题，每小题5分，共20分．13．314．1315．316．11展开得sin2B＋sin2C－sin2A＝sin B sin C，由正弦定理得bsin B＝c sin C，当A ＝120º时，sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝32·277－12·217＝2114，由正弦定理得b sin B ＝csin C ，即b 217＝32114，解得b ＝6，所以，△ABC 的面积S ＝12bc sin A ＝12×6×3×32＝932，综上，△ABC 的面积为332或932．选③：a sin B ＝3b cos A ，由正弦定理得sin A sin B ＝3sin B cos A ，因为B 为三角形内角，所以sin B ≠0，从而sin A ＝3cos A ，显然cos A ≠0，所以tan A ＝3，因为A 为三角形内角，所以A ＝60º．所以sin C ＝sin(A ＋B )＝sin A cos B ＋cos A sin B ＝32·277＋12·217＝32114，由正弦定理得b sin B ＝csin C ，即b 217＝332114，解得b ＝2，所以，△ABC 的面积S ＝12bc sin A ＝12×2×3×32＝332．18．解：(1)证明：在正三棱柱ABC －A 1B 1C 1中，CC 1⊥平面ABC ，因为AD ⊂平面ABC ，所以CC 1⊥AD ．又AD ⊥DC 1，CC 1∩DC 1＝C 1，CC 1，DC 1⊂平面BCC 1B 1，所以AD ⊥平面BCC 1B 1．又因为AD ⊂面ADC 1，所以面ADC 1⊥面BCC 1B 1．(2) 在平面BCC 1B 1中，作CE ⊥DC 1于点E ．由(1)可知AD ⊥平面BCC 1B 1，因为CE ⊂平面BCC 1B 1，所以AD ⊥CE ，又CE ⊥DC 1，AD ∩DC 1＝D ，AD ，DC 1⊂平面ADC 1，所以CE ⊥平面ADC 1．因此∠CC 1E 为CC 1与平面ADC 1所成的角．因为在正三棱柱ABC －A 1B 1C 1中，△ABC 为正三角形，由AD ⊥平面BCC 1B 1，DC ⊂平面BCC 1B 1，得AD ⊥DC ，所以D 为BC 的中点，DC ＝1．在Rt △C 1CD 中，sin ∠DC 1C ＝DC DC 1＝DC DC 2＋C 1C 2＝112＋22＝55，即sin ∠CC 1E ＝55，A 1C 1B 1AC DBE所以CC 1与平面ADC 1所成角的正弦值为55． 19．解：(1)因为圆M 过原点O ，且与直线2x ＋y ＝0相切，所以圆心M 在直线y ＝12x 上，又圆心M 也在直线y ＝x －1上，联立y ＝12x 与y ＝x －1，解得圆心M (2，1)，所以半径r ＝OM ＝5，因此圆M 的方程为(x －2)2＋(y －1)2＝5． (2)法一：设A (x ，y )，因为A 为线段PB 的中点，所以B (2x ，2y －4)．因为A ，B 在圆M 上，所以⎩⎨⎧(x －2)2＋(y －1)2＝5，(2x －2)2＋(2y －5)2＝5，解得⎩⎨⎧x ＝0，y ＝2或⎩⎨⎧x ＝2413，y ＝4213．当A (0，2)时，直线l 的方程为x ＝0；当A (2413，4213)时，直线l 的方程为y ＝－512x ＋4，即5x ＋12y －48＝0．综上，直线l 的方程为x ＝0或5x ＋12y －48＝0．法二：当直线l 的斜率不存在时，此时l ：x ＝0，A (0，2)，B (0，0)，满足要求．当直线l 的斜率存在时，设l ：y ＝kx ＋4，由⎩⎨⎧y ＝kx ＋4，(x －2)2＋(y －1)2＝5，得(1＋k 2)x 2＋(6k －4)x ＋8＝0，由Δ＞0得，k ＞6＋210或k ＜6－210，(*) 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝4－6k 1＋k 2①，x 1x 2＝81＋k 2②．由A 为线段PB 中点，可得2x 1＝x 2③．由①③解得x 1＝4－6k 3(1＋k 2)，x 2＝2(4－6k )3(1＋k 2)，代入②，得4－6k 3(1＋k 2)·2(4－6k )3(1＋k 2)＝81＋k 2，解得k ＝－512，符合(*)，所以直线l 的方程为y ＝－512x ＋4，即5x ＋12y －48＝0．综上，直线l 的方程为x ＝0或5x ＋12y －48＝0．法三：设线段AB 的中点为C ，则PC ＝3CB ，即PC 2＝9CB 2，设圆心M 到直线l 的距离为d ，则CB 2＝r 2－d 2＝5－d 2，又PC 2＝PM 2－MC 2＝13－d 2，所以13－d 2＝9(5－d 2)，解得d ＝2．当直线l 的斜率不存在时，此时l ：x ＝0，A (0，2)，B (0，0)，符合题意．当直线l 的斜率存在时，设l ：y ＝kx ＋4，则d ＝|2k －1＋4|1＋k 2＝2，解得k ＝－512，此时直线l 的方程为y ＝－512x ＋4，即5x ＋12y －48＝0．综上，直线l 的方程为x ＝0或5x ＋12y －48＝0．20．解：(1)由题意得⎩⎨⎧(1－p )(1－q )＝16，p (1－q )＝13，解得p ＝23，q ＝12．(2)每轮投篮结束后，甲得分可能为0，2，3，5．记甲第一轮投篮得分为i 分的事件为C i (i ＝0，2，3，5)，第二轮投篮得分为i 分的事件为D i (i ＝0，2，3，5)，则P (C i )＝P (D i )，C i ，D i 相互独立，记两轮投篮后甲总得分不低于8分为事件E ，则E ＝C 3D 5＋C 5D 3＋C 5D 5，且C 3D 5，C 5D 3，C 5D 5彼此互斥．易得P (C 3)＝P (D 3)＝(1－23)＝16，P (C 5)＝P (D 5)＝23×12＝13，所以P (E )＝P (C 3D 5＋C 5D 3＋C 5D 5)＝P (C 3D 5)＋P (C 5D 3)＋P (C 5D 5)＝29．答：两轮投篮后，甲总得分不低于8分的概率为29．21．解：(1)由条件得QA ＋QB ＝QA ＋QT ＝AT ＝r ＝4＞23＝AB ，所以Q 的轨迹是椭圆，且2a ＝4，2c ＝23，所以b ＝1，所以C 的方程为x 24＋y 2＝1．(2)假设存在满足题意的直线l ，显然l 的斜率存在且不为0，设l ：y ＝kx ＋2(k ≠0)，由⎩⎪⎨⎪⎧y ＝kx ＋2，x 24＋y 2＝1，得(1＋4k 2)x 2＋16kx ＋12＝0，则Δ＝(16k )2－48(1＋4k 2)＝64k 2－48＞0，得k 2＞34，设M (x 1，y 1)，N (x 2，y 2)，则x 1＋x 2＝－16k1＋4k 2，又y 1＋y 2＝k (x 1＋x 2)＋4＝41＋4k 2，所以MN 的中点坐标为(－8k 1＋4k 2，21＋4k 2)，因此，MN 的中垂线方程为y －21＋4k 2＝－1k (x ＋8k1＋4k 2)，要使PM ＝PN ，则点P (0，－1)应在MN 的中垂线上，所以－1－21＋4k 2＝－1k ·8k 1＋4k 2，解得k 2＝54＞34，故k ＝±52，因此，存在满足题意的直线l ，其方程为y ＝±52x ＋2． 22．解：(1)由题意知M (－a ，0)，N (a ，0)，又P (－1，1)，所以PM →＝(－a ＋1，－1)，PN →＝(a ＋1，－1)，由PM →·PN →＝2－a 2＝1，可得a ＝1，又e ＝ca ＝3，所以c ＝3，故b 2＝c 2－a 2＝2，所以双曲线C 的方程为x 2－y 22＝1． (2)若直线l 的斜率不存在，则l 与双曲线C 仅有一个公共点，不合题意，故l 的斜率存在，设l ：y －1＝k (x ＋1)，由⎩⎪⎨⎪⎧y ＝kx ＋k ＋1，x 2－y 22＝1，得(2－k 2)x 2－2k (k ＋1)x －k 2－2k －3＝0，设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝2k (k ＋1)2－k 2，x 1x 2＝－k 2－2k －32－k 2．因为P (－1，1)，故OP ：y ＝－x ，① 又A (x 1，y 1)，N (1，0)，所以AN ：y ＝y 1x 1－1(x －1)， ②联立①②，解得D (y 1x 1＋y 1－1，－y 1x 1＋y 1－1)，于是k 1k 2＝－y 1x 1＋y 1－1y 1x 1＋y 1－1＋1·y 2x 2＋1＝－y 1y 2(x 1＋2y 1－1)(x 2＋1)＝－(kx 1＋k ＋1)(kx 2＋k ＋1)(x 1＋2kx 1＋2k ＋2－1)(x 2＋1)＝－k 2x 1x 2＋k (k ＋1)(x 1＋x 2)＋(k ＋1)2(2k ＋1)(x 1x 2＋x 1＋x 2＋1)＝－k 2·－k 2－2k －32－k 2＋k (k ＋1)·2k (k ＋1)2－k 2＋(k ＋1)2(2k ＋1)(－k 2－2k －32－k 2＋2k (k ＋1)2－k 2＋1)y B xOND P AM l＝－k 2·k 2＋2k －12－k 2＋(k ＋1)2(2k ＋1)( k 2－32－k 2＋1)＝－4k ＋2－(2k ＋1)＝2，所以k 1k 2为定值。

南京市2024—2025学年度第一学期期中学情调研测试高二数学试卷

南京市2024—2025学年度第一学期期中学情调研测试高二数学 2024.11注意事项：1．本试卷考试时间为120分钟，试卷满分150分．2．本试卷中所有试题必须作答在答题卡上规定的位置，否则不给分．3．答题前，务必将自己的姓名、准考证号用0.5毫米黑色墨水签字笔填写在试卷及答题卡上．一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的，请把答案填涂在答题卡相应位置上．1．下列四组数据中，方差最小的是A ．5，5，5，5，5，5，5，5B ．4，4，4，5，5，5，6，6C ．3，3，4，4，5，6，6，7D ．2，2，2，2，2，5，8，8 2．已知z ·i ＝1＋3i ，则z ＝A ．－3＋iB ．－3－iC ．3＋iD ．3－i 3. 直线3x －3y ＋1＝0的倾斜角为A ．π6B ．π3C ．2π3D ．5π64．两条渐近线互相垂直的双曲线的离心率为A ．22B ． 2C ． 3D ． 5 5．若方程x 27－m ＋y 2m －1＝1表示焦点在y 轴上的椭圆，则实数m 的取值范围是 A ．(－∞，1) B ．(1，4) C ．(4，7) D ．(7，＋∞)6．底面直径与高相等的圆柱的体积为2π，则该圆柱的外接球的表面积为A ．6πB ．8πC ．10πD ．12π7．已知点O (0，0)，A (3，0)，若圆x 2＋y 2＋tx －3＝0上任意一点P 都满足|PA|＝2|PO|，则实数t ＝A ．－3B ．－2C ．2D ．38．抛物线C ：x 2＝4y 的准线为l ，M 为C 上的动点，则点M 到l 与到直线2x －y －5＝0的距离之和的最小值为A ． 355B ． 455C ． 5D ． 655二、选择题：本大题共3小题，每小题6分，共18分．在每小题给出的四个选项中，有多项符合题目要求，请把答案填涂在答题卡相应位置上．全部选对得6分，部分选对得部分分，不选或有错选的得0分．9．分别抛掷两枚质地均匀的硬币，记“第一枚硬币正面朝上”为事件A ，“第二枚硬币反面朝上”为事件B ，则A ．P (A )＝12B ．P (AB )＝13C ．A 和B 是互斥事件D ．A 和B 是相互独立事件10．在矩形ABCD 中，AB ＝2，AD ＝4．若→BE ＝14→BC ，→CF ＝－32→CD ，则 A ．AC ∥BFB ．AE ⊥BDC ．以CE 为直径的圆与直线BF 相切D ．直线AE 与BF 的交点在矩形ABCD 的外接圆上11．已知椭圆C ：x 24＋y 23＝1，直线y ＝mx 与C 交于A ，B 两点，点P 为C 上异于A ，B 的动点，则A ．当 m ＝12时，|AB |＝15 B ．|→PA ＋→PB |≥2 3 C ．存在点P ，使得∠APB ＝π2D ．S △ABP ≤2 3 三、填空题：本大题共3小题，每小题5分，共15分．请把答案填写在答题卡相应位置上．12．若直线l 1：x ＋2my ＋1＝0与l 2：(m －1)x ＋y －3＝0垂直，则实数m ＝▲________．13．已知cos(x ＋π4)＝35，x ∈(0，π2)，则sin x ＝▲________． 14．历史上最早系统研究圆锥曲线的是古希腊学者梅纳库莫斯，大约100年后，阿波罗尼斯更详尽地研究了圆锥曲线，他的研究涉及圆锥曲线的光学性质，其中一条是：如图（1），从右焦点F 2发出的光线m 交双曲线右支于点P ，经双曲线反射后，反射光线n 的反向延长线经过左焦点F 1．已知图（2）中，双曲线C 的中心在坐标原点，左、右焦点分别为F 1(－4，0)，F 2(4，0)，直线l 平分∠F 1PF 2，过点F 2作l 的垂线，垂足为H ，且|OH|＝2．则当反射光线n 经过点M (8，5)时，|F 2P |＋|PM |＝▲________．xy O F 1 F 2 P m n （1）x y O F 1 F 2 M P m n H （2） l （第14题图）四、解答题：本大题共5小题，共77分．请在答题卡指定区域内作答，解答时应写出必要的文字说明，证明过程或演算步骤．15．记△ABC的内角A，B，C的对边分别为a，b，c，已知a cos C＋c cos A＝2b cos A．（1）求A；（2）若a＝2，b＋c＝4，求△ABC的面积．16．已知点A(4，2)在抛物线C：y2＝2px（p＞0）上，直线l经过点A，且在y轴上的截距为－2．（1）求p的值和直线l的方程；（2）记l与C的另一个交点为B，求经过O，A，B三点的圆的方程．17．在四面体PABC中，M，N分别为PC，BC的中点．（1）证明：PB∥平面AMN；（2）若PC⊥平面ABC，PC＝2，AC＝3，四面体PABC的体积为2，且cos∠ACB＝55，求MN与平面PAC所成角的正弦值．PABC NM（第17题图）18．已知圆C ：(x ＋2)2＋y 2＝4，圆D ：(x －2)2＋y 2＝r 2(0＜r ＜5)，过点P (0，1)作圆D 的切线，切线的长为2．(1)求圆D 的方程；(2)直线l 经过点P ，且与圆C 交于A ，B 两点，|AB |＝6，①求l 的方程和→CA ·→CB 的值；②若动圆E 与圆C 外切，且与圆D 内切，求动圆圆心E 到点P 距离的最小值．19．已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的右顶点为A ，上顶点为B ，|AB |＝3，离心率为22．（1）求E 的方程；（2）直线l 平行于直线AB ，且与E 交于M ，N 两点，①P ，Q 是直线AB 上的两点，满足四边形MNPQ 为矩形，且该矩形的面积等于 13|MN |2，求l 的方程； ②当直线AM ，BN 斜率存在时，分别将其记为k 1，k 2，证明：k 1·k 2为定值．。

2024-2025学年度二年级数学上册期中测试卷(带答案)

2024-2025学年度二年级数学上册期中测试卷学校:___________姓名：___________班级：___________考号：___________题号一二三四五六总分得分一、填空题1．两个乘数都是5，积是；两个加数都是4，和是。

2．在括号里填上合适的长度单位“厘米”或“米”。

数学课本长约是25( )。

教室门高约是2( )。

二年级小朋友的身高约是120( )。

升旗杆高约是12( )。

3．比46多12的数是；比63少18的数是。

4．最大的一位数是( )，最大的两位数是( )，它们之间相差( )。

5．左图中有( )条线段，有( )个直角。

6．油画棒长( )厘米；小刀长( )厘米。

7．一个角有个顶点，条边，比直角小的角是，比直角大的角是．8．在括号里填上合适的数。

37＋( )＝53 ( )－23＝38( )×5＝1080－( )＝639．15厘米－7厘米＝( )厘米60米＋9米＝( )米60厘米＋40厘米＝( )米100厘米＋1米＝( )米10．（）里最大能填几？4×( )＜17( )×4＜257×( )＜3611．数一数，分别有几个角？( )个( )个( )个( )个二、选择题12．求3个5连加是多少？算式是（）。

A．5×3B．3＋5C．5－313．下面三条线中，（）是线段。

A．B．C．14．被减数是65，减数是26，差是（）。

A．91B．49C．3915．一个数比4个2的和大，比2个5的和小，这个数是（）。

A．11B．9C．1016．下面哪个图形中一共有4个角？（）A．B．C．三、判断题17．一张床长20米。

( )18．黑板边，圆桌边，书边都可以看成是线段．( )19．课桌上的直角比黑板上的直角大。

( )20．左边图形中有两个钝角和两个锐角．( )四、计算题21．计算。

（1）80＋2＝（2）70－50＝（3）5＋78＝（4）48－30＝（5）79－8＝（6）40＋60＝（7）47＋4＝（8）64－20＝（9）73－5＝（10）34＋53＝（11）53－32＝（12）67－21＝（13）2＋5＝（14）5×5＝（15）5×3＝（16）4×5＝22．用竖式计算。