圆锥侧面展开图

合集下载

圆锥的侧面展开图

圆锥的侧面展开图
广东实验中学张兴华
回顾
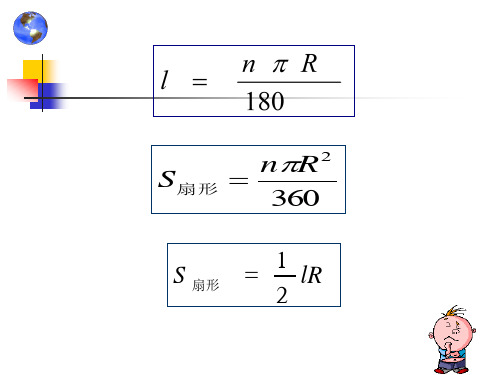
l
n RO
A
n
BLeabharlann ROn Rl 180
S扇形
n R2
360
对比扇形面积与弧长公式, 用弧长表示扇形面积:
S扇形 1 lR
2
回顾
1.已知扇形的半径为4，其圆心角为90°，则这个扇形
的弧长= 2 .
2.已知扇形的半径为2，其面积为 2 ,则这个扇形的
圆心角= 180 °
A
BO
C
2. 蒙古包可以近似地看作由圆锥和圆柱组成．如图，是一个蒙古包的示意图，现在想用毛毡搭建1个底面半径为2m，高为3.5m，外围高为2m的蒙古包，
至少需要多少平方米的毛毡？(结果保留π)
r
r
3. 已知圆锥的底面半径为1cm，母线长为4cm，若一只甲虫从圆锥底面圆周上一点A出发，沿圆锥侧面绕行到母线SA的中点B，它所走的最短路程是多少？
行的最短距离为
cm
A
2. 高
3. 侧面积
4. 全面积;表面积 B O
C
1.圆锥的侧面展开图是扇形 2.母线的长=其侧面展开图扇形的半径 3.底面周长=侧面展开图扇形的弧长
2
为什么要展开圆锥的侧面?
1. 已知一个圆锥的底面半径为12cm，母线长为20cm，
则这个圆锥的侧面积为_2_4_0__c_m_2，全面积为_3_8_4__c_m_ 2
S
C
B.
A
A
O
3
如何还原圆锥的侧面展开图?
R
A
n
l
B Or C
n R
l 180
S扇形
n R2
360

圆锥的侧面展开图

快速抢答:
1
2
3
4
快速抢答:
1.底面半径为5cm, 母线长为16cm的圆锥,它的侧面展开图 80π 的面积是_____cm²
返回前进
快速抢答:
2.圆锥的底面周长为58cm, 母线长30cm,则圆锥的侧 A 面积为___cm² . A.870 B.908 C.1125 D.1740
返回前进
快速抢答:
3.圆锥侧面展开图是一个弧长为36π的扇形,则这个圆锥的底面 18 半径是____
2πr =36π
返回前进
快速抢答:
4.一个圆心角为90°,半径为8
cm的扇形纸片,恰好围成一个圆锥的侧面, (接缝忽略不计), 则该圆锥底面圆的半径为( C)
A.4cm B.3cm C.2cm D.1cm
返回前进
本节课我们有什么收获?
1.认识了圆锥的侧面展开图: 圆锥的底面周长就是它侧面展开图扇形的弧长,圆锥的母线就是它侧面展开图扇形的半径. 2.学会计算圆锥的侧面积和全面积.
作业:
如图，圆锥的底面半径为1，母线长为3，一只蚂蚁要从底面圆周上一点 B出发，沿圆锥侧面爬行一周再回到 B，问它爬行的最短路线是多少？
1、圆锥是由一个底面（圆）和一个侧面围成的，我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线。
母线高
2、连接圆锥的顶点和底面圆心的线段叫做圆锥的高。
把圆锥沿一条母线剪开,它的侧面展开图是怎样的图形呢?
12.exe
(1) 圆锥的侧面展开图是一个什么图形? 圆锥的侧面展开图是一个扇形. (2) 圆锥的底面周长与侧面展开图有什么关系? 圆锥的底面周长就是它侧面展开图扇形的弧长. (3) 圆锥的母线与侧面展开图有什么关系? 圆锥的母线就是它侧面展开图扇形的半径.

人教版初三数学上册圆锥的侧面展开图

如图中a是圆锥的母线，而h就是圆锥的高 P
问题：圆锥的母线有几条？
ha
A Or B
二、探究圆锥的形成过程: 自学课本100页中间部分内容,了解圆锥可以看成是由哪种图形旋转而成的,并据此得出圆锥的底面半径（r）、高线(h)、母线长(a)三者之间的关系:
A
r2+h2= a2
ha
r
O
B
【跟踪练习】
人教版九年级上册
圆锥的侧面展开图
授课教师：吴文风庐江白湖中学 2017.4.18
S
AOB源自开圆图锥的侧面展
一、圆锥的组成及有关概念
1.圆锥是由一个底面和一个侧面围成的,它的底面是一个圆侧面是一个曲面. 2.把圆锥底面圆周上的任意一点与圆锥顶点的连线叫做圆锥的母线 3.连结顶点与底面圆心的线段叫做圆锥的高
这个扇形的半径与圆锥中的哪一条线段相等？
这个扇形的圆心角的度数n=
圆锥侧面展开图
1.圆锥的侧面展开图是一个扇形 2.侧面展开图扇形的半径=圆锥的母线长。 3.侧面展开后扇形的弧长=圆锥的底面圆周长， 4.侧面展开后扇形的圆心角度数= 360 r
a
圆锥侧面展开图
圆径为锥圆的锥侧圆rl的面锥一积3的条就6母侧是0线弧面的长2积长2.为5和的圆扇全锥3形底面6面面0积积的.周2长88、半圆S锥圆s圆锥的侧锥全= 侧面12 ×积s=扇 2圆π形 r锥×的a3侧＝6面π0积r · a+l底2面积rl.·360·316
根据下列条件求值（其中r、h、a分别是圆锥的底面半径、高线、母线长）
（1）a = 2，r=1 则 h=____3 ___
(2) h =3, r=4 则 a=___5____
三、探究圆锥的侧面展开图

《圆柱和圆锥的侧面展开图》PPT课件2

3.一矩形纸板,两边长分别为2cm和4cm,绕一边所在直线旋转一周所形成几何体的表面积为( )(A)24πcm2 (B) 24πcm2或48πcm2(C)20πcm2 (D) 20πcm2或48πcm2
4.我国古代数学中有这样一道数学题：有一棵树直立在地上，树高2丈，粗3尺，有一根藤条从树根缠绕而上，缠绕7周到达树顶，请问这根藤有多长？（注：枯树可以看成圆柱；树粗3尺，指的是：圆柱截面周长为3尺。1丈＝10尺）
5.某种冰淇淋纸筒为圆锥形,其底面半径为3cm, 母线长为8cm,则制作这种纸筒所需纸片的面积(不计加工余料)为( ) A.24πcm2 B.48πcm2 C.30πcm2 D.36πcm26.圆锥的母线长为10cm,底面直径为10cm,则圆锥的表面积是( )cm2. A.25π B.50π C.75π D.100π
观察思考二
圆柱的侧面展开图
如图，将圆柱的侧面沿AA’展开，得到一个什么图形？圆柱的侧面展开图与圆柱又怎样的关系?
r
l
l
展开图是矩形，矩形的两边长分别是圆柱的母线长和底面圆的周长.
r
2πr
2πr
如图，将圆锥的侧面沿AB展开，得到一个什么图形？圆锥的侧面展开图与△OAB又怎样的关系?
- .
第7章：空间图形的初步认识
7.2 圆柱和圆锥的侧面展开图
复习回顾
表面由曲面或曲面和平面构成的立体称为曲面体，常见的曲面体有圆柱、圆锥、圆球和圆环等。
观察思考一
对比棱锥的结构特点，观察思考圆柱和圆锥都有怎样的结构特点，
圆柱的结构特征
圆锥的侧面展开图rll2πr有一圆形油罐底面圆的周长为24m，高为6m，一只老鼠从距底面1m的A处爬行到对角B处吃食物，它爬行的最短路线长为多少？

《圆锥的侧面展开图》课件1

＝4π，
6
∴n＝120°．
4π
15
课堂练习
3.现有一个圆心角为90°，半径为8 cm的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计）.该圆锥底面圆的半径为 2 cm．
4π 8 cm
∵l＝2πr＝4π， ∴r＝2．
16
课堂练习
4.根据下列条件求圆锥侧面积展开图的圆心角
A
C
B
O
18
课堂练习
解：∵轴截面△ABC是等边三角形
∴AC=2OC,由题意，得
A
p ·OC ·AC + p ·OC 2= 75p
3p × OC 2 = 75p
OC 2 25
OC 0
OC = 5(cm )
C
B
AC = 2OC = 2×5 = 10(cm )
O
答：圆锥的底面半径为5 cm，母线长为10 cm.
npR 2
360
n
即：360r= nR
R
S全=S侧+S底
8
新课学习
例1:如图，已知圆锥形工件的底面直径是80cm、母线长50cm。（1）求侧面展开图的圆心角，并画出侧面展开图；（2）求圆锥的侧面积（精确到1cm2）
9
新课学习
解：（1）由题意可知，圆锥的侧面展开图的扇形半径为50cm，扇形弧长为80πcm ∴扇形圆心角的度数n= 180 80 =288（度）
青岛版初中数学九年级下册
第七单元
第4课
导入新课
圆的周长公式
C=2πr
圆的面积公式
S=πr2
弧长的计算公式
l
=
npR
180
扇形面积计算公式
S =n p R 2

圆锥的侧面展开图课件

机械零件设计
旋转体制造
在建筑设计领域，圆锥的侧面展开图常被用于设计一些具有曲线形状的建筑元素，如穹顶、拱门等。通过将圆锥侧面展开，可以更好地理解其形状和尺寸，从而更好地进行建筑设计。
建筑设计
在建筑结构分析中，圆锥的侧面展开图可以用于分析建筑结构的受力情况。通过将建筑结构中的受力部分展开成平面图形，可以更直观地理解其受力情况，从而更好地进行结构设计和优化。
在实际应用中，圆锥的侧面展开图可用于建筑设计、机械制造等领域，例如在设计旋转机械或计算风力发电机的功率时，需要使用圆锥的侧面展开图来计算相关参数。
在艺术领域，圆锥的侧面展开图也常被用于创作雕塑、绘画等艺术作品，以表现立体感、空间感和流动感。
02
圆锥的侧面展开图的绘制方法
Chapter
确定圆锥的底面半径和高度
圆锥的侧面展开图具有连续性，即展开后的图形是一个连续的平面区域。
圆锥的侧面展开图在几何形状上与原圆锥侧面相同，但在平面上表现为一个二维图形。
圆锥的侧面展开图可以用于计算圆锥侧面积和表面积，以及用于解决一些几何问题。
在几何教学中，圆锥的侧面展开图常用于帮助学生理解圆锥的几何性质和侧面积的计算方法。
建筑结构分析
包装设计
在包装设计中，圆锥的侧面展开图可以用于设计一些具有曲线形状的包装容器，如饮料瓶、洗发水瓶等。通过将圆锥侧面展开，可以更好地理解其形状和尺寸，从而更好地进行包装设计。
艺术创作
在艺术创作中，圆锥的侧面展开图可以用于创作一些具有曲线形状的艺术作品，如雕塑、绘画等。通过将圆锥侧面展开，可以更好地理解其形状和尺寸，从而更好地进行艺术创作。
,. which on,:xe%\xe guide on have!1 – the8\ans: the! speech! havemo揍

圆锥的侧面展开图

h
1
h2 r
小结
本节课我们有什么收获?
本节课我们认识了圆锥的侧面展开图，学会计算圆锥的侧面积和全面积，在认识圆锥的侧面积展开图时，应知道圆锥的底面周长就是其侧面展开图扇形的弧长。圆锥的母线就是其侧面展开图扇形的半径，这样在计算侧面积和全面积时才能做到熟练、准确。
S侧 = rl
(r表示圆锥底面的半径, l 表示圆锥的母线长 )
s全 = s侧 s底 = rl r2
做一做
已知一个圆锥的底面半径为12cm，母线长为20cm，则这
个圆锥的侧面积为_2_4_0___c_m__2，全面积为_3_8_4___c_m2
1.圆锥的底面半径为40cm.母线长为90cm, 求它的全面积.
S全=5200 cm2
2.扇形的半径为30,圆心角为120°用它做一个圆锥模型的侧面,求这个圆锥的底面半径和高.
nR 2
S扇形 = 360
S 扇形
= 1 lR 2
A
l
BO
C
扇形半径R=母线长
扇形的弧长=底面周长 2r
S
A
Or
B
请推导出圆锥的侧面积公式.
S侧
=
1 2
CR
S侧
=
1 2
2r
l.
l r
S 侧 =πrl (r表示圆锥底面的半径, l 表示圆锥的母线长 )
圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
圆锥的侧面积与底面积的和叫做圆锥的全面积(或表面积).
s全 = s侧 s底 = rl r2
思考题：如图，圆锥的底面半径为1，母线长为3，
一只蚂蚁要从底面圆周上一点B出发，沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上，问它爬行的最短路线是多少？

圆锥的侧面展开图

例3. 已知圆锥底面半径为10cm，母线长为40cm.
（1）求它的侧面展开图的圆心角和全面积. （2）若一甲虫从圆锥底面圆上一点 A 出发，沿着圆锥侧面绕行到母线 SA的中点 B，它所走的最短路程是多少？
解:(1) r 10cm l 2r 20cm na 180l 180 20 0 B l S180 , a 40cm n a 40 90 1 2 S全=S侧+S底 20 40 10 500 2
一试身手
如图，圆锥的底面半径为1，母线长为3，一只蚂蚁要从底面圆周上一点B出发，沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上，问它爬行的最短路线是多少？ A
解：将圆锥沿AB展开成扇形ABB ，则点C
垂足为 D . ，解：将圆锥沿AB展开成扇形ABB 则点 C是BB 的中点，解过点 B 作 BD AC ，：将圆锥沿 AB 解将圆锥沿 AB 展开成扇形 AB B 则点，解：：将圆锥沿 AB 展开成扇形 AB B 则点 rD.BD AC，垂足为D. 垂足为 . 展开成扇形AB B ，D 则点 C是B B 的中点，过点 B 作垂足为垂足为 D . 360 BA B 120 C是BB 的中点，，则点解：将圆锥沿AB 展开成扇形 AB B 解：将圆锥沿 AB 展开成扇形 ABB ，则点 l r r r r AB展开成扇形解：将圆锥沿 AB B ，360 则点 BAB 360 垂足为 120 D. BA B , BA B 360 120 BA B 360 120 BAD 60 . 在 Rt ABC 中， BAD 60 垂足为 D . l l ll 垂足为D. r 3 r 120 B BAD 60.在 BA ABC 中 BAD 60 , AB 3 ..在 CRt B ， 360 120 BAD 60 .在 BAD 60 ABC 中 BAD BAD 60 . 在 ABC 中，， BAD 66 BD 3 BA B 360 Rt Rt 120 r l 2 l3 360 120 BAB 3 3 3. 3 BD 3 RtABC中， BAD 60, AB 3. 60. l BAD 在 Rt ABC 中， BAD 60 , AB BD 3 60 BD 3 BD 3 3 BAD 60.在RtABC中， BAD 2 答：它爬行的最短路线是 3 . 2 22 BAD 60.在RtABC 中， BAD 6 3 2 3 3 BD 3. BD 33 答：它爬行的最短路线是 3 3 3 答：它爬行的最答：它爬行的最短路线是 3. 2 答：它爬行的最短路线是 3. 2 2 3 BD 22 23 3 3 答：它爬行的最短路线是 3. 短路线是 3. 答：它爬行的最短路线是 3 3. 2 2 2 3. 答：它爬行的最短路线是 2