全等三角形复习1

合集下载

中考数学复习《全等三角形》专题(卷1)

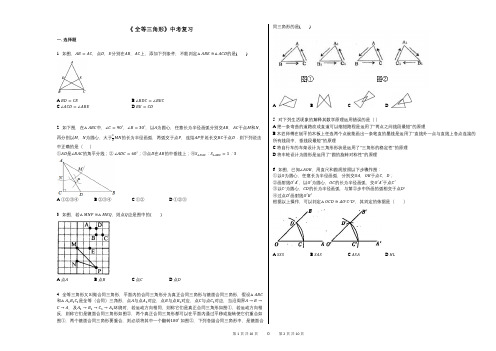
《全等三角形》中考复习一. 选择题1. 如图，AB=AC，点D，E分别在AB，AC上，添加下列条件，不能判定△ABE≅△ACD的是( )A.BD=CEB.∠BDC=∠BECC.∠ACD=∠ABED.BE=CD2. 如下图，在△ABC中，∠C=90∘，∠B=30∘，以A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以M，N 为圆心，大于12MN的长为半径画弧，两弧交于点P ，连结AP 并延长交BC于点D．则下列说法中正确的是（）①AD是∠BAC的角平分线；②∠ADC=60∘；③点D在AB的中垂线上；④S△DAC：S△ABC=1：3.A.①②③④B.②③④C.①②D.①②③3. 如图，若△MNP≅△MEQ，则点Q应是图中的()A.点AB.点BC.点CD.点D4. 全等三角形又叫做合同三角形，平面内的合同三角形分为真正合同三角形与镜面合同三角形，假设△ABC 和△A1B1C1是全等（合同）三角形，点A与点A1对应，点B与点B1对应，点C与点C1对应，当沿周界A→B→C→A，及A1→B1→C1→A1环绕时，若运动方向相同，则称它们是真正合同三角形如图①，若运动方向相反，则称它们是镜面合同三角形如图②，两个真正合同三角形都可以在平面内通过平移或旋转使它们重合如图①，两个镜面合同三角形要重合，则必须将其中一个翻转180∘如图②，下列各组合同三角形中，是镜面合同三角形的是( )A. B. C. D.5. 对下列生活现象的解释其数学原理运用错误的是（）A.把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中，垂线段最短”的原理C.将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理6. 如图，已知∠AOB，用直尺和圆规按照以下步骤作图：①以O为圆心，任意长为半径画弧，分别交OA，OB于点C，D；②画射线O′A′，以O′为圆心，OC的长为半径画弧，交O′A′于点C′③以C′为圆心，CD的长为半径画弧，与第②步中所画的弧相交于点D′④过点D′画射线O′B′根据以上操作，可以判定△OCD≅ΔO′C′D′，其判定的依据是（）A.SSSB.SASC.ASAD.HL7. 如图，在扇形OAB中，点C是弧AB上任意一点（不与点A，B重合），CD//OA交OB于点D，点I是△OCD 的内心，连结OI，BI，∠AOB=β，则∠OIB等于()A.180∘−βB.180∘−12β C.90∘+12β D.90∘+β8. 小明不慎将一块三角形的玻璃摔碎成如图所示的四块（即图中标有1，2，3，4的四块），你认为将其中的哪一块带去玻璃店，就能配一块与原来一样大小的三角形玻璃.应该带( )A.第1块B.第2块C.第3块D.第4块二. 填空题三角形具有稳定性，所以要使六边形木架不变形，至少要钉上________根木条．如图，在x、y轴上分别截取OA、OB，使OA=OB，再分别以点A、B 为圆心，以大于12AB的长度为半径画弧，两弧交于点C．若C的坐标为(3a,−a+8)，则a=________.如图，在菱形ABCD中，已知AB=4，∠ABC=60∘，∠EAF=60∘，点E在CB的延长线上，点F在DC的延长线上，有下列结论：①BE=CF；②∠EAB=∠CEF；③△ABE∼△EFC；④若∠BAE=15∘，则点F到BC的距离为2√3−2.正确序号________.如图，△ABC中，点A的坐标为(0, 1)，点C的坐标为(4, 3)，如果要使△ABD与△ABC全等，那么点D的坐标是________．三. 解答题如图，小明用五根宽度相同的木条拼成了一个五边形，已知AE//CD，∠A=12∠C，∠B=120∘.(1)∠D+∠E=________度；(2)求∠A的度数；(3)要使这个五边形木架保持现在的稳定状态，小明至少还需钉上________根相同宽度的木条．根据要求完成下列各题．(1)如图1，在∠AOB的内部有一点P．①过点P画直线PC//OA交OB于点C；②过点P画直线PD⊥OA，垂足为D．(2)如图2，AB⊥BF,CD⊥BF,∠1=∠2，试说明∠3=∠E在下面解答中填空．解：∵AB⊥BF,CD⊥BF（已知），∴∠ABF=∠________=90∘（________），∴AB//CD（________）∵∠1=∠2（已知），∴AB//EF（________），∴CD//EF（平行于同一条直线的两条直线互相平行），∴∠3=∠E（________）如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF= BD，连接BF．(1)线段BD与CD有何数量关系，为什么？(2)当△ABC满足什么条件时，四边形AFBD是矩形？请说明理由．(3)当△ABC满足________条件时，四边形AFBD是正方形？（直接写出结论，不用说明理由）一条大河两岸的A、B处分别立着高压线铁塔，如图所示．假设河的两岸平行，你在河的南岸，请利用现有的自然条件、皮尺和标杆，并结合你学过的全等三角形的知识，设计一个不过河便能测量河的宽度的好办法．（要求，画出示意图，并标出字母，结合图形简要叙述你的方案）参考答案与试题解析一. 选择题1.【答案】D【解析】欲使△ABE≅△ACD，已知AB＝AC，可根据全等三角形判定定理AAS、SAS、ASA添加条件，逐一证明即可．2.【答案】A【解析】①连接NP，MP，根据SSS定理可得△ANP≅△AMP，故可得出结论；②先根据三角形内角和定理求出∠CAB的度数，再由AD是∠BAC的平分线得出∠1=∠2=30∘，根据直角三角形的性质可知∠ADC=60∘；③根据∠1=∠B可知AD=BD，故可得出结论；④先根据直角三角形的性质得出∠2=30∘，CD=12AD，再由三角形的面积公式即可得出结论．3.【答案】D【解析】此题暂无解析4.【答案】B【解析】认真阅读题目，理解真正合同三角形和镜面合同三角形的定义，然后根据各自的定义或特点进行解答．5.【答案】B【解析】根据圆的有关定义、垂线段的性质、三角形的稳定性等知识结合生活中的实例确定正确的选项即可．6.【答案】A【解析】此题暂无解析7.【答案】B 【解析】此题暂无解析8.【答案】B【解析】本题应先假定选择哪块，再对应三角形全等判定的条件进行验证．二. 填空题【答案】3【解析】三角形具有稳定性，所以要使六边形木架不变形需把它分成三角形，即过六边形的一个顶点作对角线，有几条对角线，就至少要钉上几根木条．【答案】2【解析】此题暂无解析【答案】①②【解析】①只要证明△BAE≅△CAF即可判断；②根据等边三角形的性质以及三角形外角的性质即可判断；③根据相似三角形的判定方法即可判断；④求得点F到BC的距离即可判断．【答案】(4, −1)或(−1, 3)或(−1, −1)【解析】因为△ABD与△ABC有一条公共边AB，故本题应从点D在AB的上边、点D在AB的下边两种情况入手进行讨论，计算即可得出答案．三. 解答题【答案】180(2)五边形的内角和为(5−2)×180∘=540∘，由(1)可知，∠D+∠E=180∘，又∠B=120∘，∠A=12∠C.设∠A=x，则∠C=2x，∴∠A+∠B+∠C+∠D+∠E=540∘,即x+120∘+2x+180∘=540∘,解得x=80∘,∴∠A=80∘.2【解析】(1)根据平行线性质，两直线平行同旁内角互补即可得到180∘.先由AE//CD，根据平行线的性质得出∠E+∠D=180∘．再根据∠B=120∘，∠A=12∠C，设∠A=x∘，则∠C=2x∘．利用五边形的内角和为540∘列出方程x+120+2x+180=540，求解即可.根据五边形不具有稳定性，而三角形具有稳定性即可求解．【答案】解：（1）①如图，直线PC即为所求；②如图，直线PD即为所求；（2）解：∵AB⊥BF,CD⊥BF（已知），∴∠ABF=∠CDF=90∘（垂直的定义），∴AB//CD（同位角相等，两直线平行）∵∠1=∠2（已知），∴AB//EF（内错角相等，两直线平行），∴CD//EF（平行于同一条直线的两条直线互相平行），∴∠3=∠E（两直线平行，同位角相等）【解析】此题暂无解析【答案】解：(1)BD=CD．理由如下：依题意得AF // BC，∴∠AFE=∠DCE，∵E是AD的中点，∴AE=DE，在△AEF和△DEC中，{∠AFE=∠DCE，∠AEF=∠DEC，AE=DE，∴△AEF≅△DEC(AAS)，∴AF=CD，∵AF=BD，∴BD=CD；(2)当△ABC满足AB=AC时，四边形AFBD是矩形．理由如下：∵AF // BD，AF=BD，∴四边形AFBD是平行四边形，∵AB=AC，BD=CD，∴∠ADB=90∘，∴四边形AFBD是矩形．AB=AC，∠BAC=90∘【解析】（1）根据两直线平行，内错角相等求出∠AFE=∠DCE，然后利用“角角边”证明△AEF和△DEC全等，根据全等三角形对应边相等可得AF=CD，再利用等量代换即可得证；（2）先利用一组对边平行且相等的四边形是平行四边形证明四边形AFBD是平行四边形，再根据一个角是直角的平行四边形是矩形，可知∠ADB=90∘，由等腰三角形三线合一的性质可知必须是AB=AC．【答案】解：在河南岸AB的垂线BF上取两点C、E，使CE=BE，再定出BF的垂线CD，使A、E、D在同一条直线上，这时测得CD的长就是AB的长．如图所示：【解析】已知等边及垂直，在直角三角形中，可考虑AAS证明三角形全等，从而推出线段相等．。

第12章《全等三角形》章节复习资料【1】

第12章《全等三角形》章节复习资料【1】一．选择题（共10小题）1．如图，AB∥DE，AC∥DF，AC=DF，下列条件中不能判断△ABC≌△DEF的是（）A．AB=DE B．∠B=∠E C．EF=BC D．EF∥BC2．如图，△ACB≌△A′CB′，∠ACA′=30°，则∠BCB′的度数为（）A．20°B．30°C．35°D．40°3．一块三角形玻璃样板不慎被小强同学碰破，成了四片完整四碎片（如图所示），聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板．你认为下列四个答案中考虑最全面的是（）A．带其中的任意两块去都可以B．带1、2或2、3去就可以了C．带1、4或3、4去就可以了D．带1、4或2、4或3、4去均可【1】【2】【3】4．如图，AD是△ABC的角平分线，则AB：AC等于（）A．BD：CD B．AD：CD C．BC：AD D．BC：AC5．如图，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S 是（）A．50 B．62 C．65 D．686．如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为（）A．11 B．5.5 C．7 D．3.5【4】【5】【6】7．如图，已知△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，则∠EGF=（）A．120°B．135°C．115°D．125°8．如图所示，在△ABC中，P为BC上一点，PR⊥AB，垂足为R，PS⊥AC，垂足为S，AQ=PQ，PR=PS．下面三个结论：①AS=AR；②QP∥AR；③△BRP≌△CSP．正确的是（）A．①和②B．②和③C．①和③D．全对9．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（）A．4个B．3个C．2个D．1个【7】【8】【9】10．如图，AB，CD相交于点E，且AB=CD，试添加一个条件使得△ADE≌△CBE．现给出如下五个条件：①∠A=∠C；②∠B=∠D；③AE=CE；④BE=DE；⑤AD=CB．其中符合要求有（）A．2个B．3个C．4个D．5个二．填空题（共10小题）11．如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：，使△AEH≌△CEB．12．如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有对全等三角形．【10】【11】【12】13．如图，AC=BC，DC=EC，∠ACB=∠ECD=90°，且∠EBD=42°，则∠AEB=．14．如图，△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，若∠BPC=40°，则∠CAP=．15．一个三角形的三边为2、5、x，另一个三角形的三边为y、2、6，若这两个三角形全等，则x+y=．16．如图，AB=12，CA⊥AB于A，DB⊥AB于B，且AC=4m，P点从B向A运动，每分钟走1m，Q点从B向D运动，每分钟走2m，P、Q两点同时出发，运动分钟后△CAP与△PQB全等．【13】【14】【16】17．如图，∠ACB=90°，AC=BC，AD⊥CE于D，BE⊥CD于E，AD=2.4cm，DE=1.7cm，则BE的长度为．18．如图，已知长方形ABCD的边长AB=20cm，BC=16cm，点E在边AB上，AE=6cm，如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动，同时，点Q在线段CD上从点C到点D运动．则当△BPE与△CQP全等时，时间t为s．19．如图为6个边长等的正方形的组合图形，则∠1+∠2+∠3=°．20．如图，已知△ABE≌△ACF，∠E=∠F=90°，∠CMD=70°，则∠2=度．【17】【18】【19】【20】三．解答题（共8小题）21．如图，四边形ABCD中，E点在AD上，∠BAE=∠BCE=90°，且BC=CE，AB=DE．求证：△ABC≌△DEC．22．如图，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O．（1）求证：△AEC≌△BED；（2）若∠1=42°，求∠BDE的度数．23．如图，已知BD⊥DE，CE⊥DE，垂足分别是D、E，AB=AC，∠BAC=90°，试探索DE、BD、CE长度之间的关系，并说明你的结论的正确性．24．如图，AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，且DB=DC，求证：EB=FC．25．如图，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．26．在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；（2）当直线MN绕点C旋转到图2的位置时，求证：DE=AD﹣BE；（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．注意：第（2）、（3）小题你选答的是第2小题．27．已知：∠ACB=90°，AC=BC，AD⊥CM，BE⊥CM，垂足分别为D，E，（1）如图1，①线段CD和BE的数量关系是；②请写出线段AD，BE，DE之间的数量关系并证明．（2）如图2，上述结论②还成立吗？如果不成立，请直接写出线段AD，BE，DE之间的数量关系．Q从B点出发沿B﹣C﹣A路径向终点运动，终点为A点．点P和Q分别以1和3的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．问：点P运动多少时间时，△PEC与QFC全等？请说明理由．第12章《全等三角形》章节复习资料【1】参考答案与试题解析一．选择题（共10小题）1．如图，AB∥DE，AC∥DF，AC=DF，下列条件中不能判断△ABC≌△DEF的是（）A．AB=DE B．∠B=∠E C．EF=BC D．EF∥BC【解答】解：∵AB∥DE，AC∥DF，∴∠A=∠D，（1）AB=DE，则△ABC和△DEF中，，∴△ABC≌△DEF，故A选项错误；（2）∠B=∠E，则△ABC和△DEF中，，∴△ABC≌△DEF，故B选项错误；（3）EF=BC，无法证明△ABC≌△DEF（ASS）；故C选项正确；（4）∵EF∥BC，AB∥DE，∴∠B=∠E，则△ABC和△DEF中，，∴△ABC≌△DEF，故D选项错误；故选：C．2．如图，△ACB≌△A′CB′，∠ACA′=30°，则∠BCB′的度数为（）A．20°B．30°C．35°D．40°【解答】解：∵△ACB≌△A′CB′，∴∠ACB=∠A′CB′，∴∠ACB﹣∠A′CB=∠A′CB′﹣∠A′CB，即∠BCB′=∠ACA′，又∠ACA′=30°，∴∠BCB′=30°，3．一块三角形玻璃样板不慎被小强同学碰破，成了四片完整四碎片（如图所示），聪明的小强经过仔细的考虑认为只要带其中的两块碎片去玻璃店就可以让师傅画一块与以前一样的玻璃样板．你认为下列四个答案中考虑最全面的是（）A．带其中的任意两块去都可以B．带1、2或2、3去就可以了C．带1、4或3、4去就可以了D．带1、4或2、4或3、4去均可【解答】解：带③、④可以用“角边角”确定三角形，带①、④可以用“角边角”确定三角形，带②④可以延长还原出原三角形，故选D．4．如图，AD是△ABC的角平分线，则AB：AC等于（）A．BD：CD B．AD：CD C．BC：AD D．BC：AC【解答】解：如图过点B作BE∥AC交AD延长线于点E，∵BE∥AC，∴△BDE∽△CDA，∴=，又∵AD是角平分线，∴∠E=∠DAC=∠BAD，∴BE=AB，∴=，∴AB：AC=BD：CD．故选：A．5．如图，AE⊥AB且AE=AB，BC⊥CD且BC=CD，请按照图中所标注的数据，计算图中实线所围成的图形的面积S 是（）A．50 B．62 C．65 D．68【解答】解：∵AE⊥AB且AE=AB，EF⊥FH，BG⊥FH⇒∠EAB=∠EFA=∠BGA=90°，∠EAF+∠BAG=90°，∠ABG+∠BAG=90°⇒∠EAF=∠ABG，∴AE=AB，∠EFA=∠AGB，∠EAF=∠ABG⇒△EFA≌△ABG∴AF=BG，AG=EF．同理证得△BGC≌△DHC得GC=DH，CH=BG．故FH=FA+AG+GC+CH=3+6+4+3=16故S=（6+4）×16﹣3×4﹣6×3=50．故选A．6．如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为（）A．11 B．5.5 C．7 D．3.5【解答】解：作DM=DE交AC于M，作DN⊥AC于点N，∵DE=DG，∴DM=DG，∵AD是△ABC的角平分线，DF⊥AB，∴DF=DN，在Rt△DEF和Rt△DMN中，，∴Rt△DEF≌Rt△DMN（HL），∵△ADG和△AED的面积分别为50和39，∴S△MDG=S△ADG﹣S△ADM=50﹣39=11，S△DNM=S△EDF=S△MDG=×11=5.5．故选B．7．如图，已知△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=120°，则∠EGF=（）A．120°B．135°C．115°D．125°【解答】解：∵△ABC≌△ADE，∠CAD=10°，∠EAB=120°，∴∠EAD=∠CAB=（∠EAB﹣∠CAD）=55°，∵∠FAB=∠CAD+∠CAB，∴∠FAB=65°，∵∠AFB+∠FAB+∠B=180°，∴∠AFB=180°﹣65°﹣25°=90°，∵∠GFD=∠AFB，∴∠GFD=90°，∵∠EGF=∠D+∠GFD，∴∠EGF=90°+25°=115°．故选C．8．如图所示，在△ABC中，P为BC上一点，PR⊥AB，垂足为R，PS⊥AC，垂足为S，AQ=PQ，PR=PS．下面三个结论：①AS=AR；②QP∥AR；③△BRP≌△CSP．正确的是（）A．①和②B．②和③C．①和③D．全对【解答】解：连接AP，∵PR=PS，PR⊥AB，垂足为R，PS⊥AC，垂足为S，∴AP是∠BAC的平分线，∠1=∠2，∴△APR≌△APS，∴AS=AR，又AQ=PQ，∴∠2=∠3，又∠1=∠2，∴∠1=∠3，∴QP∥AR，BC只是过点P，没有办法证明△BRP≌△CSP，③不成立．故选A．9．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（）A．4个B．3个C．2个D．1个【解答】解：∵BF∥AC，∴∠C=∠CBF，∵BC平分∠ABF，∴∠ABC=∠CBF，∴∠C=∠ABC，∴AB=AC，∵AD是△ABC的角平分线，∴BD=CD，AD⊥BC，故②③正确，在△CDE与△DBF中，，∴△CDE≌△DBF，∴DE=DF，CE=BF，故①正确；∵AE=2BF，∴AC=3BF，故④正确．故选A．10．如图，AB，CD相交于点E，且AB=CD，试添加一个条件使得△ADE≌△CBE．现给出如下五个条件：①∠A=∠C；②∠B=∠D；③AE=CE；④BE=DE；⑤AD=CB．其中符合要求有（）A．2个B．3个C．4个D．5个【解答】解：延长DA、BC使它们相交于点F．∵∠DAB=∠BCD，∠AED=∠BEC，∴∠B=∠D，又∵∠F=∠F，AB=CD，∴△FAB≌△FCD∴AF=FC，FD=FB，∴AD=BC∴△ADE≌△CBE①对同理可得②对∵AE=CE，AB=CD∴DE=BE又∵∠AED=∠BEC∴△ADE≌△CBE（SAS）③对同理可得④对连接BD，∵AD=CB，AB=CD，BD=BD，∴△ADB≌△CBD，∴∠A=∠C，∴△ADE≌△CBE，故⑤正确，故选D．二．填空题（共10小题）11．如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：AH=CB 等（只要符合要求即可），使△AEH≌△CEB．【解答】解：∵AD⊥BC，CE⊥AB，垂足分别为D、E，∴∠BEC=∠AEC=90°，在Rt△AEH中，∠EAH=90°﹣∠AHE，又∵∠EAH=∠BAD，∴∠BAD=90°﹣∠AHE，在Rt△AEH和Rt△CDH中，∠CHD=∠AHE，∴∠EAH=∠DCH，∴∠EAH=90°﹣∠CHD=∠BCE，所以根据AAS添加AH=CB或EH=EB；根据ASA添加AE=CE．可证△AEH≌△CEB．故填空答案：AH=CB或EH=EB或AE=CE．12．如图，OP平分∠MON，PE⊥OM于E，PF⊥ON于F，OA=OB，则图中有3对全等三角形．【解答】解：OP平分∠MON，PE⊥OM于E，PF⊥ON于F，∴PE=PF，∠1=∠2，在△AOP与△BOP中，，∴△AOP≌△BOP，∴AP=BP，在△EOP与△FOP中，，∴△EOP≌△FOP，在R t△AEP与R t△BFP中，，∴R t△AEP≌R t△BFP，∴图中有3对全等三角形，故答案为：3．13．如图，AC=BC，DC=EC，∠ACB=∠ECD=90°，且∠EBD=42°，则∠AEB=132°．【解答】解：∵∠ACB=∠ECD=90°，∴∠BCD=∠ACE，在△BDC和△AEC中，，∴△BDC≌△AEC（SAS），∴∠DBC=∠EAC，∵∠EBD=∠DBC+∠EBC=42°，∴∠EAC+∠EBC=42°，∴∠ABE+∠EAB=90°﹣42°=48°，∴∠AEB=180°﹣（∠ABE+∠EAB）=180°﹣48°=132°．14．如图，△ABC的外角∠ACD的平分线CP与内角∠ABC平分线BP交于点P，若∠BPC=40°，则∠CAP=50°．【解答】解：延长BA，作PN⊥BD，PF⊥BA，PM⊥AC，设∠PCD=x°，∵CP平分∠ACD，∴∠ACP=∠PCD=x°，PM=PN，∵BP平分∠ABC，∴∠ABP=∠PBC，PF=PN，∴PF=PM，∵∠BPC=40°，∴∠ABP=∠PBC=∠PCD﹣∠BPC=（x﹣40）°，∴∠BAC=∠ACD﹣∠ABC=2x°﹣（x°﹣40°）﹣（x°﹣40°）=80°，∴∠CAF=100°，在Rt△PFA和Rt△PMA中，∵，∴Rt△PFA≌Rt△PMA（HL），∴∠FAP=∠PAC=50°．故答案为：50°．15．一个三角形的三边为2、5、x，另一个三角形的三边为y、2、6，若这两个三角形全等，则x+y=11．【解答】解：∵这两个三角形全等，两个三角形中都有2∴长度为2的是对应边，x应是另一个三角形中的边6．同理可得y=5∴x+y=11．故填11．16．如图，AB=12，CA⊥AB于A，DB⊥AB于B，且AC=4m，P点从B向A运动，每分钟走1m，Q点从B向D运动，每分钟走2m，P、Q两点同时出发，运动4分钟后△CAP与△PQB全等．【解答】解：∵CA⊥AB于A，DB⊥AB于B，∴∠A=∠B=90°，设运动x分钟后△CAP与△PQB全等；则BP=xm，BQ=2xm，则AP=（12﹣x）m，分两种情况：①若BP=AC，则x=4，AP=12﹣4=8，BQ=8，AP=BQ，∴△CAP≌△PBQ；②若BP=AP，则12﹣x=x，解得：x=6，BQ=12≠AC，此时△CAP与△PQB不全等；综上所述：运动4分钟后△CAP与△PQB全等；故答案为：4．17．如图，∠ACB=90°，AC=BC，AD⊥CE于D，BE⊥CD于E，AD=2.4cm，DE=1.7cm，则BE的长度为0.7cm．【解答】解：∵AD⊥CE于D，BE⊥CD于E，∴∠E=∠ADC=90°∵AC=CB，∠ACB=90，∴∠BCE+∠ACD=90°，∠ACD+∠DAC=90°，∴∠BCE=∠ACD，∴△BCE≌△CAD，∴AD=CE=2.4，BE=CD，∴CD=CE﹣DE=2.4﹣1.7=0.7，∴BE=CD=0.7cm．故答案为0.7cm．18．如图，已知长方形ABCD的边长AB=20cm，BC=16cm，点E在边AB上，AE=6cm，如果点P从点B出发在线段BC上以2cm/s的速度向点C向运动，同时，点Q在线段CD上从点C到点D运动．则当△BPE与△CQP全等时，时间t为1或4s．【解答】解：∵AB=20cm，AE=6cm，BC=16cm，∴BE=14cm，BP=2tcm，PC=（16﹣2t）cm，当△BPE≌△CQP时，则有BE=PC，即14=16﹣2t，解得t=1，当△BPE≌△CPQ时，则有BP=PC，即2t=16﹣2t，解得t=4，故答案为：1或4．19．如图为6个边长等的正方形的组合图形，则∠1+∠2+∠3=135°．【解答】解：观察图形可知：△ABC≌△BDE，∴∠1=∠DBE，又∵∠DBE+∠3=90°，∴∠1+∠3=90°．∵∠2=45°，∴∠1+∠2+∠3=∠1+∠3+∠2=90°+45°=135°．故填135．20．如图，已知△ABE≌△ACF，∠E=∠F=90°，∠CMD=70°，则∠2=20度．【解答】解：∵∠AME=∠CMD=70°∴在△AEM中∠1=180﹣90﹣70=20°∵△ABE≌△ACF，∴∠EAB=∠FAC，即∠1+∠CAB=∠2+∠CAB，∴∠2=∠1=20°．故填20．三．解答题（共8小题）21．如图，四边形ABCD中，E点在AD上，∠BAE=∠BCE=90°，且BC=CE，AB=DE．求证：△ABC≌△DEC．【解答】证明：∵∠BAE=∠BCE=90°，∴∠B+∠AEC=180°，而∠DEC+∠AEC=180°，∴∠B=∠DEC，在△ABC和△DEC中，，∴△ABC≌△DEC（SAS）．22．如图，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O．（1）求证：△AEC≌△BED；（2）若∠1=42°，求∠BDE的度数．【解答】解：（1）证明：∵AE和BD相交于点O，∴∠AOD=∠BOE．在△AOD和△BOE中，∠A=∠B，∴∠BEO=∠2．又∵∠1=∠2，∴∠1=∠BEO，∴∠AEC=∠BED．在△AEC和△BED中，，∴△AEC≌△BED（ASA）．（2）∵△AEC≌△BED，∴EC=ED，∠C=∠BDE．在△EDC中，∵EC=ED，∠1=42°，∴∠C=∠EDC=69°，∴∠BDE=∠C=69°．23．如图，已知BD⊥DE，CE⊥DE，垂足分别是D、E，AB=AC，∠BAC=90°，试探索DE、BD、CE长度之间的关系，并说明你的结论的正确性．【解答】结论：DE=BD+CE．证明：如右图，∵∠BAC=90°，∴∠EAC+∠DAB=90°，∵BD⊥DE，CE⊥DE，∴∠DAB+∠DBA=90°，∠D=∠E=90°，∴∠EAC=∠DBA，在△ABD和△CAE中，∵，∴△ABD≌△CAE，∴AD=CE，BD=AE，∴DE=AD+AE=CE+BD．24．如图，AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，且DB=DC，求证：EB=FC．【解答】证明：∵AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，∴DE=DF；∵DE⊥AB于E，DF⊥AC于F．∴在Rt△DBE和Rt△DCF中∴Rt△DBE≌Rt△DCF（HL）；∴EB=FC．25．如图，将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=∠DAB．试猜想DE，BF，EF之间有何数量关系，并证明你的猜想．【解答】猜想：DE+BF=EF．证明：延长CF，作∠4=∠1，如图：∵将Rt△ABC沿斜边翻折得到△ADC，点E，F分别为DC，BC边上的点，且∠EAF=∠DAB，∴∠1+∠2=∠3+∠5，∠2+∠3=∠1+∠5，∵∠4=∠1，∴∠2+∠3=∠4+∠5，∴∠GAF=∠FAE，在△AGB和△AED中，，∴△AGB≌△AED（ASA），∴AG=AE，BG=DE，在△AGF和△AEF中，，∴△AGF≌△AEF（SAS），∴GF=EF，∴DE+BF=EF．证毕．26．（本题有3小题，第（1）小题为必答题，满分5分；第（2）、（3）小题为选答题，其中，第（2）小题满分3分，第（3）小题满分6分，请从中任选1小题作答，如两题都答，以第（2）小题评分．）在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．（1）当直线MN绕点C旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；（2）当直线MN绕点C旋转到图2的位置时，求证：DE=AD﹣BE；（3）当直线MN绕点C旋转到图3的位置时，试问DE、AD、BE具有怎样的等量关系？请写出这个等量关系，并加以证明．注意：第（2）、（3）小题你选答的是第2小题．【解答】证明：（1）①∵∠ADC=∠ACB=∠BEC=90°，∴∠CAD+∠ACD=90°，∠BCE+∠CBE=90°，∠ACD+∠BCE=90°．∴∠CAD=∠BCE．∵AC=BC，∴△ADC≌△CEB．②∵△ADC≌△CEB，∴CE=AD，CD=BE．∴DE=CE+CD=AD+BE．解：（2）∵∠ADC=∠CEB=∠ACB=90°，∴∠ACD=∠CBE．又∵AC=BC，∴△ACD≌△CBE．∴CE=AD，CD=BE．∴DE=CE﹣CD=AD﹣BE．（3）当MN旋转到图3的位置时，AD、DE、BE所满足的等量关系是DE=BE﹣AD（或AD=BE﹣DE，BE=AD+DE等）．∵∠ADC=∠CEB=∠ACB=90°，∴∠ACD=∠CBE，又∵AC=BC，∴△ACD≌△CBE，∴AD=CE，CD=BE，∴DE=CD﹣CE=BE﹣AD．27．已知：∠ACB=90°，AC=BC，AD⊥CM，BE⊥CM，垂足分别为D，E，（1）如图1，①线段CD和BE的数量关系是CD=BE；②请写出线段AD，BE，DE之间的数量关系并证明．（2）如图2，上述结论②还成立吗？如果不成立，请直接写出线段AD，BE，DE之间的数量关系．【解答】解：（1）①结论：CD=BE．理由：∵AD⊥CM，BE⊥CM，∴∠ACB=∠BEC=∠ADC=90°，∴∠ACD+∠BCE=90°，∠BCE+∠CBE=90°，∴∠ACD=∠B，在△ACD和△CBE中，，∴△ACD≌△CBE，∴CD=BE．②结论：AD=BE+DE．理由：∵△ACD≌△CBE，∴AD=CE，CD=BE，∵CE=CD+DE=BE+DE，∴AD=BE+DE．（2）②中的结论不成立．结论：DE=AD+BE．理由：∵AD⊥CM，BE⊥CM，∴∠ACB=∠BEC=∠ADC=90°，∴∠ACD+∠BCE=90°，∠BCE+∠CBE=90°，∴∠ACD=∠B，在△ACD和△CBE中，，∴△ACD≌△CBE，∴AD=CE，CD=BE，∵DE=CD+CE=BE+AD，∴DE=AD+BE．28．如图，△ABC中，∠ACB=90°，AC=6，BC=8．点P从A点出发沿A﹣C﹣B路径向终点运动，终点为B点；点Q从B点出发沿B﹣C﹣A路径向终点运动，终点为A点．点P和Q分别以1和3的运动速度同时开始运动，两点都要到相应的终点时才能停止运动，在某时刻，分别过P和Q作PE⊥l于E，QF⊥l于F．问：点P运动多少时间时，△PEC与QFC全等？请说明理由．【解答】解：设运动时间为t秒时，△PEC≌△QFC，∵△PEC≌△QFC，∴斜边CP=CQ，有四种情况：①P在AC上，Q在BC上，CP=6﹣t，CQ=8﹣3t，∴6﹣t=8﹣3t，∴t=1；②P、Q都在AC上，此时P、Q重合，∴CP=6﹣t=3t﹣8，∴t=3.5；③P在BC上，Q在AC时，此时不存在；理由是：8÷3×1＜6，Q到AC上时，P应也在AC上；④当Q到A点（和A重合），P在BC上时，∵CQ=CP，CQ=AC=6，CP=t﹣6，∴t﹣6=6∴t=12∵t＜14∴t=12符合题意答：点P运动1或3.5或12秒时，△PEC与△QFC全等．。

全等三角形的判定总复习

AB=A´B´
BC=B´C´
∴Rt△ABC≌ Rt△A´B´C´(HL)
B
B′
A
C
已知：如图,在△ABC和△ABD中,AC⊥BC,
BD⊥AD,垂足分别为C,D,AC=BD
(1)求证： △ABC≌△BAD.
(2)求证：BC=AD
(1)解： ∵ AC⊥BC, BD⊥AD D
C
∴ ∠C=∠D=90°
在Rt△ABC和 Rt△BAD中
例子1：如图，在△AEC和△ADB中，已知AE=AD，AC=AB，请说明△AEC ≌ △ADB的理由。
解：在△AEC和△ADB中
C
_A_E__=__A_D_(已知)
D
∠A= ∠A( 公共角)
A
E
B
_A_C___=_A__B_(已知)
∴ △AEC≌△ADB（ SAS ）
例2：如图，AC=BD，∠CAB= ∠DBA，
用符号语言表达为：
在△ABC和△DEF中
∠A=∠D （已知）
AB=DE（已知）
∠B=∠E（已知）
B
∴ △ABC≌△DEF（ASA）
A
D
CF E
例1：已知如图，O是AB的中点，∠A=∠B，
求证：△AOC≌△BOD
证明：
∵ O是AB的中点(已知） C
∴ OA=OB(中点定义）
在△AOC和△BOD中 A
,有
AB=AB,
A
B
AC=AD. ∴ Rt△ACB≌Rt△ADB (HL). (2)∵ Rt△ACB≌Rt△ADB (HL). ∴ BC=AD
例2. 如图，AC=AD，∠C，∠D是直角，将上述条件标注在图中，求证BC=BD

全等三角形复习(1)

△ABC≌△ABD
隐含条件AB=AB
思路
已知一这边为角的对边边一角
找任一角(AAS)
变式2：如图，已知∠CAB=∠DAB，请你添加一个条件————，使得
△ABC≌△ABD
隐含条件AB=AB
思路
有几种添加条件的方式呢？
变式3、如图所示：已知∠B=∠C，请你添加一个条件————，使得
△ABE≌△ACD
八年级数学《探索三角形的全等条件》练习
初二数学备课组
SSS
两
个
三
角
形
SAS
全
等
的判
ASA
定
方
法
AAS
例1、如图所示，：已知AC=AD，请你添加一个条件————，使得 △ABC≌△ABD
隐含条件AB=AB
思路
找另一边 (SSS)
已知两边
找夹角 (SAS)
变式1：如图，已知∠C=∠D，请你添加一个条件————，使得
∠A为公共角
思路
A
找夹边（ASA）已知两角
找对
例2.如图，已知AB=AD，AC=AE，∠1=∠2，
则BC=DE成立吗？ A
12
EC
请同学们注意书写格式哦！
B
D
变式延伸
1．已知：如图，AB=AD，AF=AG，BF=DG
那么BAG DAF吗？为什么？
A
A
B
D
FG
B G
D F
一变：图变题不变，结论还成立吗？说明理由.
再变：题变图不变，你还会证明吗？请说明理由. 已知：如图，AB=AD，AF=AG，∠BAG=∠DAF 那么BF=DG 吗？为什么？

初一数学全等三角形的全章复习

小学生元旦联欢会的主持词精选4篇小学生元旦联欢会主持词篇一主持词要根据活动对象的不同去设置不同的主持词。

我们眼下的社会，各种集会的节目都通过主持人来进行串联，快来参考主持词是怎么写的吧，以下是小编为大家整理的小学生元旦联欢会主持词（精选13篇），仅供参考，希望能够帮助到大家。

小学生元旦联欢会的主持词篇二甲：尊敬的各位领导﹑老师，乙：亲爱的同学们，大家，合：晚上好！甲：我是来自2020级的小鱼。

乙：我是来自2020级的小绿。

丙：我是来自2020级的小黄。

丁：我是来自2020级的小红。

甲：新年的钟声即将敲响，时光的车轮又留下了一道深深的印痕。

满天的雪花，是飞舞的音符，以思念谱成乐章，用祝福奏出所盼。

乙：没有松风的秋，雁去长空；没有飞雪的冬，乍暖还寒。

一夜高风凋碧树，凋不了青春不灭的火焰；满地余寒露凝香，凝不住你绝美的年华。

丙：在这烛光与微笑构成的舞台，在这笑声与歌声汇成的海洋，在这永恒与温馨筑就的圣地，我们欢聚在一起。

丁：光阴茬苒，我们即将迎来新的一年。

今天大家在这里欢聚一堂，迎接元旦的曙光。

这一刻是美好的，这一刻是温馨的，这一刻是充满激情的。

甲：台历翻去最后一页，20--年已经成为历史。

回首时光年轮上又一度春秋寒暑，我们不禁感慨万千。

乙：灿烂辉煌的20--年即将向我们告别，充满希望与奋进的20--年正微笑着向我们走来。

丁：在这辞旧迎新的日子里，就让我们用热情与激情来表达我们的喜悦，传达对新一年的憧憬。

丙：今晚，就让我们踏着歌声的翅膀，向着梦想――启航！甲：现在我宣布20--年庆元旦文艺晚会，合：现在开始！甲：首先请允许我为大家隆重介绍今晚到场的领导和嘉宾，--。

乙：欢迎您的到来！丙：---。

丁：欢迎您的到来！甲：还有我们敬爱的--老师和--老师，乙：让我们用热烈的掌声来欢迎各位老师的到来！丁：今天啊，我们在开场前将会进行第一个抽奖环节的前奏！丙：没错！我们需要在场的观众拿出旁边已经为你们准备好的袋子，里面呢会有一张小纸条，请将你对20--年的新年愿望写在纸上，并写好你的姓名，待会儿会有同学去收集，我们将在晚会的最后从这些小纸条中抽出3位幸运儿，并且由主持人念出这3个新年愿望，而这3位幸运的同学也将获得奖品哦！大家快点动起来吧！甲：OK，相信你们已经写好了自己的新年愿望了吧，我们马上进入今晚的正轨了哟！乙：没错，接下来呢就让我们跟着--和--的歌声走进《下一站天后》。

11.2全等三角形的判定复习[1]

二：利用全等三角形证明线的垂直关系
例：如图：BF是Rt△ABC的角平分线，∠ACB=90°， CD是高，BF与CD交于点E，EG∥AC交AB于G 求证：FG⊥AB 证明：∵BF平分∠ABC
C F 3 E
1 ∴∠1＝∠2 2 4 ∵CD⊥AB A G D B ∴∠3+∠ABC=90° ∴BG=BC （全等三角形的对应边相等）又∵∠ACB＝90° ∴∠A+∠ABC=90° 在△BFG与△BFC中 ∴∠3＝∠A BG=BC 又∵EG∥AC ∠1＝∠2 ∴∠A＝∠4 BF=BF ∴∠3＝∠4 ∴△BFG≌△BFC （SAS）在△BEG与△BEC中 ∠1＝∠2 ∴∠FGB=∠FCB=90°（全等三角形的对应角相等 ∠3＝∠4 ∴FG⊥AB BE＝BE ∴△BEG≌△BEC （AAS）
牛道口中学曹兰华 2012.9
知识梳理：
1、什么是全等三角形？一个三角形经过哪些变化可以得到它的全等形？。
能够完全重合的两个三角形叫做全等三角形。
一个三角形可以通过平移、翻折、旋转得到它的全等形。 2、两个全等三角形有什么特征？
两个全等三角形的对应边相等，对应角相等。 3、例：如图，已知Δ ABC≌ ΔDEF，找出其中相等的边和角。
A E B
O
F
C
如图：AB=DC，AC=DB 求证：∠ABO=∠DCO 证明：在△ABC和△DCB中 AB=DC AC=DB BC=CB
A
D
O
∴ △ABC△DCB （SSS） ∴ ∠A=∠D (全等三角形的对应角相等) 在△AOB和△DOC中 ∠A=∠D ∠AOB=∠DOC AB=CD ∴ △AOB≌△DOC （AAS） ∴ ∠ABO=∠DCO （全等三角形的对应角相等）

七年级数学全等三角形复习

全等三角形复习一、知识点梳理及示例一重新认识“全等形”与“全等三角形”.全等形和全等三角形，其实质是“完全重合”，也就是“形状相同，大小相等”，全等三角形是全等形中的一种，因此，从这个意义上，不难得到全等三角形的性质，对应边和对应角分别相等．在这里，要特别注意“对应”的问题，当我们用“≌”表示两个三角形全等时；对应字母一定要写在对应的位置，这样便于看出对应的元素是什么。

在学习了第十四章(轴对称)后，对全等形应有一个新的认识：成轴对称的两个图形一定是全等形，只是这时两个图形的位置特殊罢了．我们在解数学中的“折叠问题”时，用全等形的性质往往是个关键．二掌握证明三角形全等的分析要领，会用综合法书写证明过程．证明三角形全等时的分析方法与步骤：(1)仔细观察图形，找出欲证的两个全等三角形已知的直接相等条件，并把已知条件标注在图上，使条件在图上一目了然．(2)注意挖掘图形中的隐含条件，如公共边(角)、对顶角、等腰(边)三角形或正方形中的等角(边)等，这些条件虽然没有直接告诉，它们却是证明三角形全等必不可少的条件。

(3)对照判定三角形全等的五种方法(SSS，SAS，ASA，AAS，HL)，看看三角形全等的条件是否具备了，如果不够，还需要找出哪些条件或创造哪些条件．有时，两个三角形全等的某些条件是必须证明的．常会遇到以下几种情况：①利用中点的定义证明线段相等；②利用角平分线的定义证明角相等；③利用垂直的定义证明角相等；④利用平行线的性质证明角相等；⑤利用三角形的内角和为180°证明角相等；⑥利用图形的和、差证明线段或角相等．经过正确分析之后，要把论证过程规X地写出来．本章要求我们能用综合法书写证明过程，这也是本章的一个重点．什么叫“综合法证明格式”?就是按照从题设(已知条件)出发，经过一步步推理论证，最后得到结论的格式来书写证明过程．例l如下图，四边形ABCD是正方形，△ECF是等腰直角三角形，其中CE=CF，连接BF,DE，你能证明BF=DE吗?分析：①找出欲证的两个全等三角形：从图形及要证的结论来看，可考虑证明△BCF≌△DCE；②找出并标上已知条件：CE=CF，∠ECF=90°；③有没有隐含条件?有：BC=DC，∠BCD=90°，它们是正方形的边和角；④对照判定三角形全等的方法，还差什么条件?因为BF=DE是要证的，所以，可证∠BCF=∠DCE，而这个结论很容易证得．至此，分析过程顺利完成，书写格式如下：证明：∵四边形ABCD是正方形，∴BC＝DC，∠BCD＝90°，∴∠BCD－∠DCF＝∠ECF－∠DCF即∠BCF＝∠DCE在△BCF和△DCE中，∵∴△BCF≌△DCE,∴BF=DE三理解“SSA”为什么不能判定两个三角形全等，防止误用SSA．在学习新课时，探究并得到了判定两个三角形全等的五种方法．并且知道判断两个三角形全等至少需要3个条件，其中至少有—个条件是边．但SSA却是个假命题，有些同学自觉或不自觉地应用它来证明三角形全等，这是不对的．例2如图，AC、BD交于E，AD=BC，∠C=∠D，试说明AC=BD.错解：在△ABD和△BAC中∴△ABD≌△BAC，∴AC=BD正确解法，在△ADE和△BCE中∴△ADE≌△BCE(AAS)∴AE=BE，DE=CE∴AE+CE=BE+DE，即AC=BDSSA为什么不能判定两个三角形全等呢?我们可以从下图中看出来，你能根据下图说明为什么吗?其实，HL中的3个条件就是SSA，为什么HL是正确的呢?这是由直角三角形的特殊性决定的．下面留一个问题请你解决，这样有助于我们更进一步地理解与掌握全等三角形的判定．探究：我们知道：“有两边和其中一边的对角对应相等的两个三角形全等”是个假命题．请你对三个条件或三角形的形状给些必要的限制，使得具备“SSA”三个条件的两个三角形全等．四你会判定两个特殊三角形全等吗?我们课本主要研究了一般三角形全等的4种判定方法，只有“HL”，是关于特殊三角形(即直角三角形)全等的判定；课本为什么不探究特殊三角形的全等条件呢?这是因为一般的方法适用特殊，这样也是为了减少我们的学习负担，集中精力学会一般的方法．我们共同来看下面一个例子．例3.下列说法：①一边相等的两个等腰直角三角形全等；②—腰和底对应相等的两个等腰三角形全等；③周长相等的两个等腰三角形全等；④一个钝角和它的一条邻边对应相等的两个等腰三角形全等．其中，正确的说法有( )．A．0个．B．1个C．2个D．3个分析与解：①的说法中相等的这—对边，没有指明是对应腰还是对应底，如果一个是底与另一个的腰相等，则不能得到两个等腰直角三角形全等．②的说法中，一腰和底对应相等，这就有两对边相等了，第三对边是不是相等呢?当然相等了，因为第三对边是腰，也应该相等，这样就符合“SSS”了。

全等三角形的判定(总复习) (1)

全等三角形共有6组元素(3组对应边、3组对应角)
3、三角形全等的4个判定公理：
SSS（边边边） SAS（边角边） ASA（角边角） AAS（角角边）
有两角和及其中有三边对应相有两边和它们的有两角和它们的夹一个角所对的边对等的两个三角形夹角对应相等的边对应相等的两个应相等的两个三角全等. 两个三角形全等. 三角形全等. 形全等.
AF=CE(已证) ∠AFD=∠CEB(已知) DF=BE(已知) ∴△AFD≌△CEB (SAS) BADFra bibliotekE C
9
6.如图（5）∠CAE=∠BAD，∠B=∠D， AC=AE，△ABC与△ADE全等吗？为什么？ B 解：∵ ∠CAE=∠BAD(已知) D E ∴ ∠CAE+∠BAE=∠BAD+∠BAE
点D在AE的延长线上。求证：BD + DC = AD
A E B
分析：∵AD = AE + ED ∴只需证：BD + DC = AE + ED ∵BD = ED ∴只需证DC = AE即可。
C
D
13
9.如图, ΔABC与ΔDEF是否全等?为什么?
A 40' 8 20' E 120' 40' D 8
解: 连接AC
在△ABC和△ADC中， AB=AD(已知) BC=DC(已知) AC=AC(公共边)
∴△ADC≌△ABC(SSS)
∴ ∠ABC=∠ADC (全等三角形的对应角相等)
11
一.挖掘“隐含条件”判全等。
二.添条件判全等。
三.转化“间接条件”判全等。
12
8、已知：ΔABC和ΔBDE是等边三角形,
4

全等三角形复习(1)

6.如图如图AB=CD,AD=CB,AC与BD交如图与交于点O,直线直线MN经过点经过点O. 于点直线经过点 (1)求证:OD=OB 求证: 求证 (2)求证求证:OM=ON 求证 A M 1 O B 2 N C D
7.已知:点 A,C,B,D在同一 .已知: , , , 在同一条直线,AC=BD, 条直线, , ∠M=∠N=90°,AM=CN ∠ ° 求证: 求证: MB‖ND ‖
9.如图所示, AC=AD,E在AB .如图所示, , 在上, ∠ACB=∠ADB=90°, ∠ ° 试说明: 试说明:(1)点A在∠CBD的平 ) 在的平分线上.( .(2) 分线上.( )CE=DE. . C
E B
A D
作业: 作业:新课程学习辅导 P35.10 . P37.6 . P41.13 . P40.10 .
M N
A
C
B
D
8:如图,小明遇到了这样一个问题, :如图,小明遇到了这样一个问题, AB=CD,BC=AD,请说明: , ,请说明: 的道理, ∠A=∠C的道理,小明动手测量了一 ∠ 的道理发现∠ 确实与确实与∠ 相等相等, 下,发现∠A确实与∠C相等,但他不能说明其中的道理, 能说明其中的道理,你能帮助他说明这个道理吗?试试看. 这个道理吗?试试看 A C O B D
全等三角形复习(1) 全等三角形复习
1.如图,△ABC≌△CDA,并且 .如图, ≌ , AB=CD,那么下列结论错误的是 , ( D) (A)∠DAC=∠BCA (B)AC=CA ) ∠ ) (C)∠D=∠B ) ∠ (D)AC=BC )
A D
B
C
2.判定一般三角形全等的方法有 SSS , SAS , ASA ,AAS 等四种,判定直角三角形全等的方法还有 HL .

全等三角形复习课讲学稿1

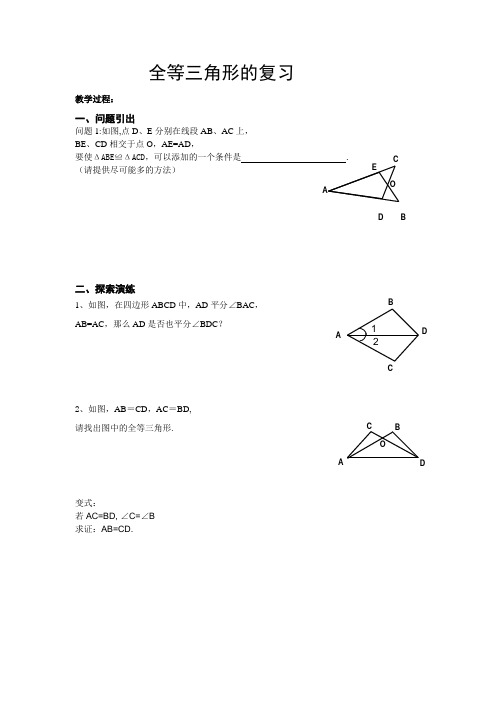
全等三角形的复习教学过程：一、问题引出问题1:如图,点D、E分别在线段AB、AC上，BE、CD相交于点O，AE=AD，要使ΔABE≌ΔACD，可以添加的一个条件是 . （请提供尽可能多的方法）二、探索演练1、如图，在四边形ABCD中，AD平分∠BAC，AB=AC，那么AD是否也平分∠BDC？2、如图，AB＝CD，AC＝BD,请找出图中的全等三角形.变式：若AC=BD, ∠C=∠B求证：AB=CD.3、如图,∠1=∠2=∠3，AB=BFBD AC12BD AB1CFPAOED BCO试说明AD=EF4、如图，在△ABC 和△DEF 中，点A 、D 、C 、F 在同一直线上，有下列四个论断： ①AB=DE ，②AD=CF ，③∠B ＝∠E ， ④ ∠A ＝∠EDF.请用其中三个作为条件，余下一个作为结论，编一道数学问题，并写出解答过程。

5、如图： △ABE 的边BE 和△ACD 的边CD 相交于点O ，若AB ＝AC,BO ＝CO, 试说明△ABE ≌△ACD三、建立模型四、总结反思五、课外拓展1、将一个长方形纸片沿着对角线AC 剪开，将三角形ABC 绕着点A 顺时针旋转至点D ，A ，B 在同一直线上。

请你想一想AC 与AC 1之间有什么关系ACBEFDAED23AO D BCBC ADADCC 1B2、将△ACC 1绕着点A 顺时针旋转至如图所示的状态，过点C 1作C 1P ⊥AP 于点P ，过点C 作CQ ⊥AQ 于点Q 你能找出图中全等的三角形吗？现有一只蚂蚁要从点C 1出发，沿着C 1P 爬行至点P ，再沿着PQ 爬行至点Q ，最后沿着QC 爬行至点C 。

若已知点C 1到直线AQ 的距离是5，那么它总共要爬行多少路程才能到达目的地呢？六．课后作业1.如图，AD 平分∠BAC ，AB ＝AC ，则BD ＝CD ，试说明理由。

PQ CA12.如图，AB⊥BD于B，DE⊥BD于D，已知AB＝CD，BC＝ED,求∠ACE的度数。

12.2.1全等三角形的判定(SSS,SAS,ASA,AAS)20160724

E C
A 练习：如图，点 D 在 AB 上，点 E 在 AC 上，BA =AC， ∠B =∠C，BE、CD 相交于点 O.求证：OB=OC D B 练习：如图，CD⊥AB 于 D，BE⊥AC 与 E， BE、CD 交于 O，且 AO 平分∠BAC，求证：OB=OC D O B 六、全等三角形的判定方法简称边边边边角边角边角角角边缩写 SSS SAS ASA AAS 具体条件三边对应相等两边和它们的夹角对应相等两角和它们的夹边对应相等两角和其中一角的对边对应相等 A O E C
A 练习：如图：己知 AD∥BC，AE＝CF，AD＝BC，E、Ｆ都在直线ＡＣ来自，试说明ＤＥ∥ D A ＢＦ。
B
E
F
C B 五、全等三角形的判定方法（ASA，AAS） 1. 两角和它们的夹边对应相等的两个三角形全等。简写为“角边角”或“ASA” 。 2. 两角和其中一角的对边对应相等的两个三角形全等。简写为“角角边”或“AAS”。
E A D
B
C
H
B
四、全等三角形的判定方法（SAS） 1. 用尺规作图，两边和它们的夹角对应相等的两个三角形，发现它们是能够完全重合（全等）的。 2. 两边和它们的夹角对应相等的两个三角形全等。简写为“边角边”或“SAS” 练习：如图，AC＝BD，∠CAB＝∠DBA，你能判断 BC=AD 吗？说明理由。 C D
12.2 三角形全等的判定复习 1. 全等三角形的定义：能够完全重合的两个三角形是全等三角形。 2. 全等三角形的性质：全等三角形对应边相等，对应角相等。 3. 因为△ABC≌△A’B’C’，所以 AB＝A’B’， BC＝B’ C’， AC＝A’ C’ ∠A＝∠A’， ∠B＝∠B’， ∠C＝∠C’ 一、全等三角形的判定方法 1. 首先可以肯定的是，三条边对应相等，三个角对应相等的两个三角形全等。 2. 然后至少需要几个条件才能判定两三角形全等。二、全等三角形的判定方法（SSS） 1. 用尺规作图，画两个三边相等的三角形，发现它们是能够完全重合（全等）的。 2. 三边对应相等的两个三角形全等，简写为“边边边”或“SSS”。三、证明三角形全等的书写格式例题：如图已知 AB＝CD，AC＝DB，求证△ABC≌△DCB 证明：∵在△ABC 和△DCB 中 A AB＝CD 已知 AC＝DB 已知 BC＝BC 公共边 B

八上全等三角形复习1

文华中学全等三角形综合复习题（一）注：① 判定两个三角形全等必须有一组边对应相等；② 全等三角形面积相等． 2．证题的思路：⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧）找任意一边（）找两角的夹边（已知两角）找夹已知边的另一角（）找已知边的对角（）找已知角的另一边（边为角的邻边）任意角（若边为角的对边，则找已知一边一角）找第三边（）找直角（）找夹角（已知两边AAS ASA ASA AAS SAS AAS SSS HL SAS 1．如图（1）：AD ⊥BC ，垂足为D ，BD=CD 。

求证：△ABD ≌△ACD 。

2．如图（3）：AD ∥BC AD=BC ，求证：AB=CD3.如图（2）：AC ∥EF ，CB ∥FD ,AE=BD 。

求证：∠C=∠F4.如图（4）：AB=AC ，AD=AE ，AB ⊥AC ，AD ⊥AE 。

问BD 和CE 相等吗?为什么?5.如图（9）AE 、BC 交于点M ，F 点在AM 上，BE ∥CF ，BE=CF 。

求证：AM 是△ABC 的中线。

6.如图（10）∠BAC=∠DAE ，∠ABD=∠ACE ，BD=CE 。

求证：AB=AC 。

7.如图（11）在△ABC 和△DBC 中，∠1=∠2，∠3=∠4，P 是BC 上任一点。

求证：PA=PD 。

8.如图（13）△ABC ≌△EDC 。

求证：BE=AD 。

（图1）DCBAF（图2）DCBAE（图10）DCBAP4321（图11）D B AE（图13）DCBAE（图4）DCBAMF E （图9）CBA9.如图21：AB ∥CD ，∠B=∠D ，求证：AD ∥BC 。

10.如图：AD=CB ，AE ⊥BD ，CF ⊥BD ，E 、F 是垂足，AE=CF 。

求证：AB=CD 。

1如图（14）在△ABC 中，∠ACB=90°，AC=BC ，AE 是BC 的中线，过点C 作CF ⊥AE 于F ，过B 作BD ⊥CB 交CF 的延长线于点D 。

2021-2022学年人教版八年级数学上册《第12章全等三角形》期末综合复习题1(附答案)

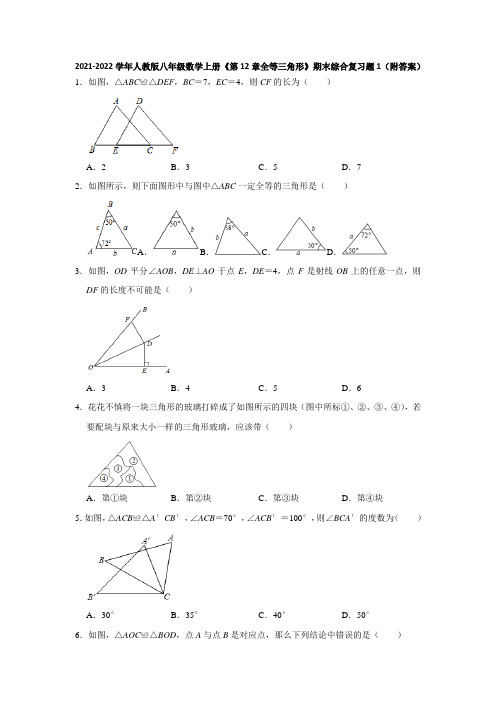
2021-2022学年人教版八年级数学上册《第12章全等三角形》期末综合复习题1（附答案）1．如图，△ABC≌△DEF，BC＝7，EC＝4，则CF的长为（）A．2B．3C．5D．72．如图所示，则下面图形中与图中△ABC一定全等的三角形是（）A．B．C．D．3．如图，OD平分∠AOB，DE⊥AO于点E，DE＝4，点F是射线OB上的任意一点，则DF的长度不可能是（）A．3B．4C．5D．64．花花不慎将一块三角形的玻璃打碎成了如图所示的四块（图中所标①、②、③、④），若要配块与原来大小一样的三角形玻璃，应该带（）A．第①块B．第②块C．第③块D．第④块5．如图，△ACB≌△A′CB′，∠ACB＝70°，∠ACB′＝100°，则∠BCA′的度数为（）A．30°B．35°C．40°D．50°6．如图，△AOC≌△BOD，点A与点B是对应点，那么下列结论中错误的是（）A．AB＝CD B．AC＝BD C．AO＝BO D．∠A＝∠B7．如图，点B，F，C，E共线，∠B＝∠E，BF＝EC，添加一个条件，不能判断△ABC≌△DEF的是（）A．AB＝DE B．∠A＝∠D C．AC＝DF D．AC∥FD8．如图，已知△ABC≌△DEF，CD平分∠BCA，若∠A＝30°，∠CGF＝88°，则∠E的度数是（）A．30°B．50°C．44°D．34°9．如图，在Rt△ABC中，∠C＝90°，以顶点A为圆心，适当长为半径画弧，分别交边AC、AB于点M、N，再分别以点M、N为圆心，大于MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD＝4，AB＝15，则△ABD的面积是（）A．15B．30C．45D．6010．如图，在△ABC与△AEF中，AB＝AE，BC＝EF，∠ABC＝∠AEF，∠EAB＝40°，AB 交EF于点D，连接EB．下列结论：①∠F AC＝40°；②AF＝AC；③∠EBC＝110°；④AD＝AC；⑤∠EFB＝40°，正确的个数为（）个．A．1B．2C．3D．411．如图，AD是△ABC的角平分线．若∠B＝90°，BD＝，则点D到AC的距离是．12．如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E，若BC＝4，DE＝1.6，则BD的长为．13．如图，△ABC≌△ABD，∠C＝30°，∠ABC＝85°，则∠BAD的度数为14．如图，△ABC≌△DEF，∠A＝70°，∠B＝50°，则∠DFC＝．15．如图，在Rt△ABC中，∠ACB＝90°，AD平分∠BAC交BC于点D，若AB＝5，DC ＝2，则△ABD的面积为．16．如图，AC＝AD，∠1＝∠2，要使△ABC≌△AED，应添加的条件是．（只需写出一个条件即可）17．如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC交BC于点D．若BC＝3，且BD：DC＝5：4，AB＝5，则△ABD的面积是．18．如图：已知OA和OB两条公路，以及C、D两个村庄，建立一个车站P，使车站到两个村庄距离相等即PC＝PD，且P到OA，OB两条公路的距离相等．19．已知：如图，AE＝CF，AD∥BC，AD＝CB．（1）求证：∠B＝∠D；（2）求证：BE∥DF．20．如图，AC∥BD，∠C＝90°，AC＝BE，AB＝DE，求证：DE⊥AB．21．王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC＝BC，∠ACB＝90°），点C在DE上，点A和B分别与木墙的顶端重合．（1）求证：△ADC≌△CEB；（2）求两堵木墙之间的距离．22．如图，已知：∠A＝∠E，AB＝EB，点D在AC边上，且∠ABE＝∠CBD．（1）求证：△EBD≌△ABC；（2）如果O为CD中点，∠BDE＝65°，求∠OBD的度数．23．∠B＝∠C＝90°，EB＝EC，DE平分∠ADC，求证：AE是∠DAB平分线．24．已知OM是∠AOB的平分线，点P是射线OM上一点，点C、D分别在射线OA、OB 上，连接PC、PD．（1）如图①，当PC⊥OA，PD⊥OB时，则PC与PD的数量关系是．（2）如图②，点C、D在射线OA、OB上滑动，且∠AOB＝90°，当PC⊥PD时，PC 与PD在（1）中的数量关系还成立吗？说明理由．参考答案1．解：∵△ABC≌△DEF，∴EF＝BC＝7，∵EC＝4，∴CF＝3，故选：B．2．解：A图有两边相等，而夹角不一定相等，二者不一定全等；B图与三角形ABC有两边及其夹角相等，二者全等；C图有两边相等，而夹角不一定相等，二者不一定全等；D图与三角形ABC有两角相等，二者不一定全等；故选：B．3．解：过D点作DH⊥OB于H，如图，∵OD平分∠AOB，DE⊥AO，DH⊥OB于H，∴DH＝DE＝4，∴DF≥4．故选：A．4．解：带②去可以利用“角边角”能配一块与原来大小一样的三角形玻璃．故选：B．5．解：∵△ACB≌△A′CB′，∴∠A′CB′＝∠ACB＝70°，∵∠ACB′＝100°，∴∠BCB′＝∠ACB′﹣∠ACB＝30°，∴∠BCA′＝∠A′CB′﹣∠BCB′＝40°，故选：C．6．解：∵△AOC≌△BOD，∴∠A＝∠B，AO＝BO，AC＝BD，∴B、C、D均正确，而AB、CD不是不是对应边，且CO≠AO，∴AB≠CD，故选：A．7．解：∵BF＝EC，∴BF+FC＝EC+FC，∴BC＝EF，又∵∠B＝∠E，∴当添加条件AB＝DE时，△ABC≌△DEF（SAS），故选项A不符合题意；当添加条件∠A＝∠D时，△ABC≌△DEF（AAS），故选项B不符合题意；当添加条件AC＝DF时，无法判断△ABC≌△DEF，故选项C符合题意；当添加条件AC∥FD时，则∠ACB＝∠DFE，故△ABC≌△DEF（ASA），故选项D不符合题意；故选：C．8．解：∵CD平分∠BCA，∴∠ACD＝∠BCD＝∠BCA，∵△ABC≌△DEF，∴∠D＝∠A＝30°，∵∠CGF＝∠D+∠BCD，∴∠BCD＝∠CGF﹣∠D＝58°，∴∠BCA＝116°，∴∠B＝180°﹣30°﹣116°＝34°，∵△ABC≌△DEF，∴∠E＝∠B＝34°，故选：D．9．解：作DE⊥AB于E，由基本尺规作图可知，AD是△ABC的角平分线，∵∠C＝90°，DE⊥AB，∴DE＝DC＝4，∴△ABD的面积＝×AB×DE＝30，故选：B．10．解：在△AEF和△ABC中，，∴△AEF≌△ABC（SAS），∴∠EAF＝∠BAC，AF＝AC，故②正确∴∠EAB＝∠F AC＝40°，故①正确，∴∠C＝∠AFC＝∠AFE＝70°，∴∠EFB＝180°﹣70°﹣70°＝40°，故⑤正确，∵AE＝AB，∠EAB＝40°，∴∠AEB＝∠ABE＝70°，若∠EBC＝110°，则∠ABC＝40°＝∠EAB，∴∠EAB＝∠ABC，∴AE∥BC，显然与题目条件不符，故③错误，若AD＝AC，则∠ADF＝∠AFD＝70°，∴∠DAF＝40°，这个显然与条件不符，故④错误．故选：C．11．解：如图，过点D作DE⊥AC于E，∵AD是△ABC的角平分线．∠B＝90°，DE⊥AC，∴DE＝BD＝，∴点D到AC的距离为，故答案为．12．解：∵AD平分∠BAC，DE⊥AB，∠C＝90°，∴CD＝DE，∵DE＝1.6，∴CD＝1.6，∴BD＝BC﹣CD＝4﹣1.6＝2.4．故答案为：2.413．解：∵∠C＝30°，∠ABC＝85°．∴∠CAB＝180°﹣∠C﹣∠ABC＝65°，∵△ABC≌△ABD，∴∠BAD＝∠CAB＝65°．故答案为：65°．14．解：∵△ABC≌△DEF，∴∠A＝∠D＝70°，∠B＝∠E＝50°，∴∠DFC＝180°﹣（∠D+∠E）＝180°﹣120°＝60°，故答案为：60°．15．解：作DH⊥AB于H，如图，∵AD平分∠BAC，DH⊥AB，DC⊥AC，∴DH＝DC＝2，∴△ABD的面积＝×5×2＝5．故答案为5．16．解：∵∠1＝∠2，∴∠1+∠BAD＝∠2+∠BAD，即∠BAC＝∠EAD，∵AC＝AD，∴当添加∠B＝∠E时，可根据“AAS”判断△ABC≌△AED；当添加∠C＝∠D时，可根据“ASA”判断△ABC≌△AED；当添加AB＝AE时，可根据“SAS”判断△ABC≌△AED．故答案为∠B＝∠E或∠C＝∠D或AB＝AE．17．解：作DE⊥AB于点E，∵AD平分∠BAC，∠C＝90°，DE⊥AB，∴DC＝DE，∵BC＝3，且BD：DC＝5：4，∴DC＝3×＝，∴DE＝，∵AB＝5，DE⊥AB，∴△ABD的面积是：＝＝，故答案为：．18．解：如图，点P为所作．19．证明：（1）∵AE＝CF，∴AE﹣EF＝CF﹣EF，即AF＝CE，∵AD∥BC，∴∠A＝∠C，在△ADF和△CBE中，，∴△ADF≌△CBE（SAS），∴∠B＝∠D；（2）由（1）△ADF≌△CBE知：∠AFD＝∠BEC，∴180°﹣∠AFD＝180°﹣∠BEC，即∠DFE＝∠BEF，∴BE∥DF．20．证明：设AB与DE相交于点M，∵AC∥BD，∴∠C+∠DBE＝180°，∵∠C＝90°，∴∠DBE＝90°，在Rt△ACB与Rt△EBD中，，∴Rt△ACB≌Rt△EBD（HL），∴∠ABC＝∠D，∵∠D+∠MEB＝90°，∴∠ABC+∠MEB＝90°，∴∠EMB＝180°﹣∠ABC﹣∠MEB＝90°，∴DE⊥AB．21．（1）证明：由题意得：AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，∴∠ADC＝∠CEB＝90°，∴∠ACD+∠BCE＝90°，∠ACD+∠DAC＝90°，∴∠BCE＝∠DAC在△ADC和△CEB中，∴△ADC≌△CEB（AAS）；（2）解：由题意得：AD＝2×3＝6cm，BE＝7×2＝14cm，∵△ADC≌△CEB，∴EC＝AD＝6cm，DC＝BE＝14cm，∴DE＝DC+CE＝20（cm），答：两堵木墙之间的距离为20cm．22．（1）证明：∵∠ABE＝∠CBD，∴∠ABE+∠ABD＝∠CBD+∠ABD，即∠EBD＝∠ABC．在△EBD和△ABC中，，∴△EBD≌△ABC（ASA）；（2）解：∵△EBD≌△ABC，∴BD＝BC，∠BDE＝∠C，∵∠BDE＝65°，∴∠BDC＝∠BDE＝65°，∵∠CBD＝50°，∵O点为CD中点，∴∠OBD＝CBD＝25°．23．证明：如图，过点E作EF⊥AD于F，∵DE平分∠ADC，∠C＝90°，∴EC＝EF，∵EB＝EC，∴EF＝BE，又∵∠B＝90°，∴EB⊥AB，∵EF⊥AD，∴AE是∠DAB平分线．24．解：（1）PC＝PD，理由：∵OM是∠AOB的平分线，∴PC＝PD（角平分线上点到角两边的距离相等），故答案为：PC＝PD；（2）证明：过点P点作PE⊥OA于E，PF⊥OB于F，如图，∴∠PEC＝∠PFD＝90°，∵OM是∠AOB的平分线，∴PE＝PF，∵∠AOB＝90°，∠CPD＝90°，∴∠PCE+∠PDO＝360°﹣90°﹣90°＝180°，而∠PDO+∠PDF＝180°，∴∠PCE＝∠PDF，在△PCE和△PDF中，∴△PCE≌△PDF（AAS），∴PC＝PD．。

全等三角形全章复习课件

全等三角形专题一全等三角形基本性质【知识点1】能够完全重合的两个三角形叫做全等三角形。

（两个三角形全等是指两个三角形的大小和形状完全一样，与他们的位置没有关系。

）【知识点2】两个三角形重合在一起，重合的顶点叫做对应顶点；重合的边叫做对应边；重合的角叫做对应角。

【知识点3】全等三角形的对应边相等，对应角相等。

;（由定义还可知道，全等三角形的周长相等，面积相等，对应边上的中线和高相等，对应角的角平分线相等）【例题1】如图，已知图中的两个三角形全等，填空：(1)AB 与是对应边，BC 与是对应边， CA 与是对应边；(2)∠A 与是对应角，∠ABC 与是对应角，∠BAC 与是对应角【方法总结】在两个全等三角形中找对应边和对应角的方法。

(1)有公共边的，公共边一定是对应边； (2)有公共角的，公共角一定是对应角；：(3)有对顶角的，对顶角是对应角；(4)在两个全等三角形中，最长的边对最长的边，最短的边对最短的边，最大的角对最大的角，最小的角对最小的角。

【练习1】如图，图中有两对三角形全等，填空：(1)△BOD ≌ ； (2)△ACD ≌ .【例题2】已知图2中的两个三角形全等，则∠ 度数是（）° ° ° °DABCOEABCDCAB; A '~【例题3】如图，若111ABC A B C △≌△，且11040A B ∠=∠=°，°，则1C ∠＝．,【练习1】如图，ACB A C B '''△≌△，BCB ∠'＝30°，则ACA '∠的度数为（） A 20° B ．30° C ．35° D ．40°【练习2】如图，△ABD 绕着点B 沿顺时针方向旋转90°到△EBC ，且∠ABD ＝90°。

（1）△ABD 和△EBC 是否全等如果全等，请指出对应边与对应角。

人教版数学八年级上第十一章全等三角形综合复习及答案

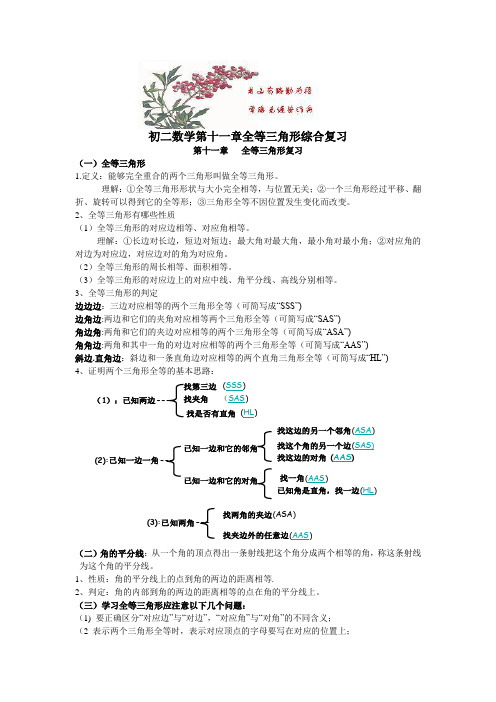
初二数学第十一章全等三角形综合复习第十一章全等三角形复习（一）全等三角形1.定义：能够完全重合的两个三角形叫做全等三角形。

理解：①全等三角形形状与大小完全相等，与位置无关；②一个三角形经过平移、翻折、旋转可以得到它的全等形；③三角形全等不因位置发生变化而改变。

2、全等三角形有哪些性质（1）全等三角形的对应边相等、对应角相等。

理解：①长边对长边，短边对短边；最大角对最大角，最小角对最小角；②对应角的对边为对应边，对应边对的角为对应角。

（2）全等三角形的周长相等、面积相等。

（3）全等三角形的对应边上的对应中线、角平分线、高线分别相等。

3、全等三角形的判定边边边：三边对应相等的两个三角形全等（可简写成“SSS”)边角边:两边和它们的夹角对应相等两个三角形全等（可简写成“SAS”)1、性质：角的平分线上的点到角的两边的距离相等.2、判定：角的内部到角的两边的距离相等的点在角的平分线上。

（三）学习全等三角形应注意以下几个问题：（1) 要正确区分“对应边”与“对边”，“对应角”与“对角”的不同含义；（2 表示两个三角形全等时，表示对应顶点的字母要写在对应的位置上；（3）“有三个角对应相等”或“有两边及其中一边的对角对应相等”的两个三角形不一定全等；（4）时刻注意图形中的隐含条件，如 “公共角” 、“公共边”、“对顶角” （5）截长补短法证三角形全等。

【切记】：“有三个角对应相等”和“有两边及其中一边的对角对应相等”的两个三角形不一定全等。

例1. 如图，,,,A F E B 四点共线，AC CE ⊥，BD DF ⊥，AE BF =，AC BD =。

求证：ACF BDE ∆≅∆。

例 2. 如图，在ABC ∆中，BE 是∠ABC 的平分线，AD BE ⊥，垂足为D 。

求证：21C ∠=∠+∠。

例3. 如图，在ABC ∆中，AB BC =，90ABC ∠=。

F 为AB 延长线上一点，点E 在BC 上，BE BF =，连接,AE EF 和CF 。

全等三角形知识点总结及复习

全等三角形知识点总结及复习一、知识网络⎧⎧⎨⎪⎩⎪⎪⎧⎪⎪→⇒⎨⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎩⎩⎧⎨⎩对应角相等性质对应边相等边边边 SSS 全等形全等三角形应用边角边 SAS 判定角边角 ASA 角角边 AAS 斜边、直角边 HL 作图角平分线性质与判定定理二、基础知识梳理（一）、基本概念1、“全等”的理解全等的图形必须满足：（1）形状相同的图形；（2）大小相等的图形；即能够完全重合的两个图形叫全等形。

同样我们把能够完全重合的两个三角形叫做全等三角形。

全等三角形定义：能够完全重合的两个三角形称为全等三角形。

（注：全等三角形是相似三角形中的特殊情况）当两个三角形完全重合时，互相重合的顶点叫做对应顶点，互相重合的边叫做对应边，互相重合的角叫做对应角。

由此，可以得出：全等三角形的对应边相等，对应角相等。

(1)全等三角形对应角所对的边是对应边，两个对应角所夹的边是对应边； (2)全等三角形对应边所对的角是对应角，两条对应边所夹的角是对应角； (3)有公共边的，公共边一定是对应边；(4)有公共角的，角一定是对应角；(5)有对顶角的，对顶角一定是对应角；2、全等三角形的性质（1）全等三角形对应边相等；（2）全等三角形对应角相等；3、全等三角形的判定方法（1）三边对应相等的两个三角形全等。

（2）两角和它们的夹边对应相等的两个三角形全等。

（3）两角和其中一角的对边对应相等的两个三角形全等。

（4）两边和它们的夹角对应相等的两个三角形全等。

（5）斜边和一条直角边对应相等的两个直角三角形全等。

4、角平分线的性质及判定性质：角平分线上的点到这个角的两边的距离相等判定：到一个角的两边距离相等的点在这个角平分线上（二）灵活运用定理1、判定两个三角形全等的定理中，必须具备三个条件，且至少要有一组边对应相等，因此在寻找全等的条件时，总是先寻找边相等的可能性。

2、要善于发现和利用隐含的等量元素，如公共角、公共边、对顶角等。

3、要善于灵活选择适当的方法判定两个三角形全等。

全等三角形专题复习(含练习讲评)

一、全等三角形注: ① 判定两个三角形全等必须有一组边对应相等；② 全等三角形面积相等. 2. 证题的思路：⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧）找任意一边（）找两角的夹边（已知两角）找夹已知边的另一角（）找已知边的对角（）找已知角的另一边（边为角的邻边）任意角（若边为角的对边，则找已知一边一角）找第三边（）找直角（）找夹角（已知两边AAS ASA ASA AAS SAS AAS SSS HL SAS例1: 如图, 在△ABE 中, AB ＝AE,AD ＝AC,∠BAD ＝∠EAC, BC.DE 交于点O.求证: （1） △ABC ≌△AED ；（2） OB ＝OE .例2: 如图所示, 已知正方形ABCD 的边BC.CD 上分别有点E 、点F, 且BE ＋DF ＝EF, 试求∠EAF 的度数.AD F例3.在△ABC中, ∠ACB=90°,AC=BC, AE是BC的中线, 过点C作CF⊥AE于F,过B作BD⊥CB 交CF的延长线于点D。

(1)求证：AE=CD, （2)若BD=5㎝,求AC的长。

例4:如图, △ABE和△ADC是△ABC分别沿着AB.AC边翻折180°形成的, 若∠1: ∠2: ∠3=28: 5: 3, 则∠a的度数为例5: 如图: 在△ABC中, ∠ACB=90°, AC=BC, D是AB上一点, AE⊥CD于E, BF⊥CD交CD的延长线于F.求证: AE=EF+BF。

练习:1.已知: 如图5—129, △ABC 的∠B.∠C 的平分线相交于点D, 过D 作MN ∥BC 交AB.AC 分别于点M 、N, 求证:BM ＋CN ＝MN2.如图（13):已知AB ⊥BD, ED ⊥BD, AB=CD , BC=DE ,请你判断AC 垂直于CE 吗？并说明理由。

3.如图(14）,已知AB=DC , DE=BF, ∠B=∠D , 试说明（1)DE ∥BF (2)AE=CFFDCABE(14)4.如图: 在△ABC中, ∠BAC=90°,∠ABD= ∠ABC, DF⊥BC, 垂足为F, AF交BD于E。