1.4.1正弦函数、余弦函数的图象
1.4.1 正弦函数、余弦函数的图象

人教版数学·必修4
返回导航 上页 下页
(2)通过“简谐运动的图象”的试验,能直观地体会正弦函数、余弦函数怎样的图 象特征? 提示:波浪型,周而复始的特征. (3)课本上是利用什么来比较精确的画出正弦函数的图象的?其基本步骤是什么? 提示:用正弦线精准刻画,将[0,2π]内各角的正弦线平移到 x 轴相应位置,最后 将点用光滑曲线连接. (4)如何由正弦函数的图象通过图形变换得到余弦函数的图象? 提示:将正弦函数的图象向左平移π2个单位长度而得到.
探究二 利用正弦、余弦函数图象解不等式 [教材 P40 练习 1]观察正弦曲线,写出满足 sin x>0 的区间. 提示:(2kπ,2kπ+π),k∈Z.
人教版数学·必修4
返回导航 上页 下页
角度 1 解三角不等式
[例 2] 利用正弦曲线,求满足12<sin x≤ 23的 x 的集合. [解析] 首先作出 y=sin x 在[0,2π]上的图象.如图所示,作直线 y=12,根据特 殊角的正弦值,可知该直线与 y=sin x,x∈[0,2π]的交点横坐标为π6和56π;
人教版数学·必修4
返回导航 上页 下页
知识梳理 (1)任意给定一个实数 x,有唯一确定的值 sin x(或 cos x)与之对应,由 这个对应法则所确定的函数 y=___si_n__x____(或___y_=__c_o_s_x____)叫做正弦函数(或余 弦函数),其定义域为____R______. (2)利用正弦线画函数 y=sin x,x∈[0,2π]的图象,是把角 x 的正弦线向右平移, 使它的起点与 x 轴上的点 x 重合,再用光滑的曲线把这些正弦线的终点连接起来, 函数 y=sin x,x∈[0,2π]的图象如图.
人教版数学·必修4
1.4.1正弦函数、余弦函数的图象

在同一坐标系内,用五点法分别画出函数
y=sinx,x[0,2]和y=cosx,x[0,2]的简图:
x
00
22
csoinsxx 1
0
--11
向左平移 个单位长度 y2
2
1
o
2
-1
2
y= cosx,x[0, 2]
第21页,共21页。
33
22
22
00
11
y=sinx,x[0, 2]
y
1
y=cosx,x[0, 2]
o
2
2
3
2
x
2
-1
y= - cosx,x[0, 2]
第11页,共21页。
作出函数 y sin x 及函数 y si的n x图象. 并探究如何利用y=sinx的图象,通过 图形的变换(平移、翻转等)来得到它们 的图象?
第12页,共21页。
3、画出函数
y
2
sin
第16页,共21页。
第17页,共21页。
y 2
y=1+sinx,x[0, 2] 1
o
2
2
-1
3
2
x
2
y=sinx,x[0, 2]
第18页,共21页。
返回
1.如何利用y=sinx,x∈[0,2π]的图象,
通过图形变换(平移、翻转等)来得到
y=1+sinx ,x∈[0,2π]的图象? 小结:函数值加减,图像上下移动;
3
,
上有
两个实数根,求 a的取值范围?
第15页,共21页。
小 1.正弦、余弦曲线几何画法和五点法 结
2.五点(画图)法 : 列表、描点、连线、画出简图 3.作函数图象: 五点法
1.4.1正弦函数、余弦函数的图象知识点归纳与练习(含详细答案)

第一章 三角函数 §1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象课时目标 1.了解正弦函数、余弦函数的图象.2.会用“五点法”画出正弦函数、余弦函数的图象.1.正弦曲线、余弦曲线2.“五点法”画图画正弦函数y =sin x ,x ∈[0,2π]的图象,五个关键点是_________________________; 画余弦函数y =cos x ,x ∈[0,2π]的图象,五个关键点是__________________________. 3.正、余弦曲线的联系依据诱导公式cos x =sin ⎝⎛⎭⎫x +π2,要得到y =cos x 的图象,只需把y =sin x 的图象向________平移π2个单位长度即可.知识点归纳:1.正、余弦曲线在研究正、余弦函数的性质中有着非常重要的应用,是运用数形结合思想解决三角函数问题的基础.2.五点法是画三角函数图象的基本方法,要熟练掌握,与五点法作图有关的问题是高考常考知识点之一.一、选择题1.函数y =sin x (x ∈R )图象的一条对称轴是( ) A .x 轴 B .y 轴C .直线y =xD .直线x =π22.函数y =cos x (x ∈R )的图象向右平移π2个单位后,得到函数y =g (x )的图象,则g (x )的解析式为( )A .-sin xB .sin xC .-cos xD .cos x3.函数y =-sin x ,x ∈[-π2,3π2]的简图是( )4.在(0,2π)内使sin x >|cos x |的x 的取值范围是( ) A.⎝⎛⎭⎫π4,3π4 B.⎝⎛⎦⎤π4,π2∪⎝⎛⎦⎤5π4,3π2 C.⎝⎛⎭⎫π4,π2 D.⎝⎛⎭⎫5π4,7π4 5.若函数y =2cos x (0≤x ≤2π)的图象和直线y =2围成一个封闭的平面图形,则这个封闭图形的面积是( )A .4B .8C .2πD .4π 6.方程sin x =lg x 的解的个数是( )A .1B .2C .3D .4 题 号 1 2 3 4 5 6 答 案 7.函数y =sin x ,x ∈R 的图象向右平移π2个单位后所得图象对应的函数解析式是__________.8.函数y =2cos x +1的定义域是________________. 9.方程x 2-cos x =0的实数解的个数是________.10.设0≤x ≤2π,且|cos x -sin x |=sin x -cos x ,则x 的取值范围为________. 三、解答题11.利用“五点法”作出下列函数的简图: (1)y =1-sin x (0≤x ≤2π); (2)y =-1-cos x (0≤x ≤2π).12.分别作出下列函数的图象.(1)y=|sin x|,x∈R;(2)y=sin|x|,x∈R.能力提升13.求函数f(x)=lg sin x+16-x2的定义域.14.函数f(x)=sin x+2|sin x|,x∈[0,2π]的图象与直线y=k有且仅有两个不同的交点,求k 的取值范围.§1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象答案知识梳理2.(0,0),⎝⎛⎭⎫π2,1,(π,0),⎝⎛⎭⎫32π,-1,(2π,0) (0,1),⎝⎛⎭⎫π2,0,(π,-1),⎝⎛⎭⎫32π,0,(2π,1) 3.左 作业设计1.D 2.B 3.D 4.A [∵sin x >|cos x |,∴sin x >0,∴x ∈(0,π),在同一坐标系中画出y =sin x ,x ∈(0,π)与y =|cos x |,x ∈(0,π)的图象,观察图象易得x ∈⎝⎛⎭⎫π4,34π.] 5.D [作出函数y =2cos x ,x ∈[0,2π]的图象,函数y =2cos x ,x ∈[0,2π]的图象与直线y =2围成的平面图形,如图所示的阴影部分.利用图象的对称性可知该平面图形的面积等于矩形OABC 的面积,又∵|OA |=2,|OC |=2π, ∴S 平面图形=S 矩形OABC =2×2π=4π.]6.C [用五点法画出函数y =sin x ,x ∈[0,2π]的图象,再依次向左、右连续平移2π个单位,得到y =sin x 的图象.描出点⎝⎛⎭⎫110,-1,(1,0),(10,1)并用光滑曲线连接得到y =lg x 的图象,如图所示.由图象可知方程sin x =lg x 的解有3个.]7.y =-cos x解析 y =sin x 2π−−−−−−→向右平移个单位y =sin ⎝⎛⎭⎫x -π2 ∵sin ⎝⎛⎭⎫x -π2=-sin ⎝⎛⎭⎫π2-x =-cos x ,∴y =-cos x . 8.⎣⎡⎦⎤2k π-23π,2k π+23π,k ∈Z 解析 2cos x +1≥0,cos x ≥-12,结合图象知x ∈⎣⎡⎦⎤2k π-23π,2k π+2π3,k ∈Z . 9.2解析 作函数y =cos x 与y =x 2的图象,如图所示, 由图象,可知原方程有两个实数解.10.⎣⎡⎦⎤π4,5π4解析 由题意知sin x -cos x ≥0,即cos x ≤sin x ,在同一坐标系画出y =sin x ,x ∈[0,2π]与 y =cos x ,x ∈[0,2π]的图象,如图所示:观察图象知x ∈[π4,54π].11.解 利用“五点法”作图 (1)列表:X 0 π2 π 3π2 2π sin x 0 1 0 -1 0 1-sin x1121描点作图,如图所示.(2)列表:X0 π2 π 3π2 2π cos x 1 0 -1 0 1 -1-cos x-2-1-1-2描点作图,如图所示.12.解 (1)y =|sin x |=⎩⎪⎨⎪⎧sin x (2k π≤x ≤2k π+π)-sin x (2k π+π<x ≤2k π+2π) (k ∈Z ).其图象如图所示,(2)y =sin|x |=⎩⎪⎨⎪⎧sin x (x ≥0)-sin x (x <0),其图象如图所示,13.解 由题意,x 满足不等式组⎩⎪⎨⎪⎧ sin x >016-x 2≥0,即⎩⎪⎨⎪⎧-4≤x ≤4sin x >0,作出y =sin x 的图象,如图所示.结合图象可得:x ∈[-4,-π)∪(0,π).14.解 f (x )=sin x +2|sin x |=⎩⎪⎨⎪⎧3sin x x ∈[0,π],-sin x x ∈(π,2π].图象如图,若使f (x )的图象与直线y =k 有且仅有两个不同的交点,根据上图可得k 的取值范围是(1,3).。
§1.4.1正弦函数、余弦函数的图象

1.了解正弦函数、余弦函数的图象.(重点) 2.会用五点法画正弦函数、余弦函数的图象.(难点、易错点) 3.能利用正、余弦函数的图象解决简单问题.(重点)
问题:如何作出正弦函数 y=sinx 的图象? 途径:利用单位圆中正弦线(表示正弦)来解决。 回顾知识 sinα、cosα、tanα的几何表示.
● ● ● ● ● ●
●
x
思考:如何画函数y =sinx(x∈R)的图象?
y=sinx x[0,2] sin(x+2k)=sinx, kZ y
y=sinx xR
向左、向右平行移动(每次 2π 个单位长度)
1
4
3
2
1
o
2
3
4
x
正弦函数y=sinx, xR的图象叫正弦曲线.
利用正弦、余弦函数的图像解不等式
3 例4、求解不等式 sin x ³ . > 2 y
y sin x
P2
1
P1
y =
3 2
O
3
p 2
2 3
π
3p 2
2π x
-1
2 (2k , 2k )k Z 3 3
1 练习、写出使 sinx≥2(x∈R)成立的 x 的取值集合.
三、作余弦函数 y=cosx (x∈R) 的图象
思考:如何将余弦函数用诱导公式写成正弦函数?
π sin( x) y cosx 2
注:余弦曲线的图象可以通过将正弦曲线 π 向左平移 2个单位长度而得到。余弦函数 的图象叫做余弦曲线。
正弦、余弦函数的图象
y
1 -4 -3 -2 -
o
-1
2
课件12: 1.4.1 正弦函数、余弦函数的图象

3.请补充完整下面用“五点法”作出 y=-sin x(0≤x≤2π)的图象 时的列表.
x
0
π 2
①
3π 2
2π
-sin x ② -1 0 ③ 0
①
;②
;③
.
解析:用“五点法”作 y=-sin x(0≤x≤2π)的图象的五个 关键点为(0,0),π2,-1,(π,0),32π,1,(2π,0)故①为 π, ②为 0,③为 1. 答案:π 0 1
的横坐标可以是( )
A.0,π2,π,32π,2π
B.0,π4,π2,34π,π
C.0,π,2π,3π,4π
D.0,π6,π3,π2,23π
解析:根据“五点法”作图,x 的取值为 0,π2,π,32π,2π.
答案:A
2.函数 y=-sin x,x∈-2π,32π的简图是(
)
解析:函数 y=-sin x 与 y=sin x 的图象关于 x 轴对称,故选 D. 答案:D
当堂检测
1.对于余弦函数 y=cos x 的图象,有以下三项描述:
①向左向右无限延伸;
②与 x 轴有无数多个交点;
③与 y=sin x 的图象形状一样,只是位置不同.
其中正确的有( )
A.0 个
B.1 个
C.2 个
D.3 个
解析:根据正余弦函数图象可知,①②③正确.
答案:D
2.函数y=cos x与函数y=-cos x的图象( )
思考:y=cos x(x∈R)的图象可由 y=sin x(x∈R)的图象平移得到
的原因是什么? [提示] 因为 cos x=sinx+π2,所以 y=sin x(x∈R)的图象向左
平移π2个单位可得 y=cos x(x∈R)的图象.
1.4.1 正弦函数、余弦函数的图象

1.4.1 正弦函数、余弦函数的图象编写时间:2020年 月 日 第二学期 总第 课时 编写人:马安山课 题正弦函数、余弦函数的图象授课班级高一(17)班 授课时间2020年 月 日学习目标1.通过简谐振动实验演示,让学生对函数图像有一些直观的感知,形成正弦曲线的初步认识,进而探索正弦曲线准确的作法,养成善于发现、善于探究的良好习惯.学会遇到新问题时善于调动所学过的知识,较好地运用新旧知识之间的联系,提高分析问题、解决问题的能力.2.通过本节学习,理解正弦函数、余弦函数图象的画法.借助图象变换,了解函数之间的内在联系.通过三角函数图象的三种画法:描点法、几何法、五点法,体会用“五点法”作图给我们学习带来的好处,并会熟练地画出一些较简单的函数图象.3.通过本节的学习,让学生体会数学中的图形美,体验善于动手操作、合作探究的学习方法带来的成功愉悦.渗透由抽象到具体的思想,加深数形结合思想的认识,理解动与静的辩证关系,树立科学的辩证唯物主义观.教学重点 正弦函数、余弦函数的图象.教学难点 将单位圆中的正弦线通过平移转化为正弦函数图象上的点;正弦函数与余弦函数图象间的关系.课 型 新 课 主要教学方法 自主学习、思考、交流、讨论和概括.教学模式合作探究,归纳总结教学手段与教具多媒体教学、几何画板软件.教 学 过 程 设 计各环节教学反思问题①:作正弦函数图象的各点的纵坐标都是查三角函数表得到的数值,由于对一般角的三角函数值都是近似值,不易描出对应点的精确位置.我们如何得到任意角的三角函数值并用线段长(或用有向线段数值)表示x 角的三角函数值?怎样得到函数图象上点的两个坐标的准确数据呢?简单地说,就是如何得到y=sinx,x ∈[0,2π]的精确图象呢? 问题②:如何得到y=sinx,x ∈R 时的图象?对问题①,第一步,可以想象把单位圆圆周剪开并12等分,再把x 轴上从0到2π这一段分成12等份.由于单位圆周长是2π,这样就解决了横坐标问题.过⊙O1上的各分点作x 轴的垂线,就可以得到对应于0、6π、4π、3π、2π、…、2π等角的正弦线,这样就解决了纵坐标问题(相当于“列表”).第二步,把角x 的正弦线向右平移,使它的起点与x 轴上的点x 重合,这就得到了函数对(x,y)(相当于“描点”).第三步,再把这些正弦线的终点用平滑曲线连接起来,我们就得到函数y=sinx 在[0,2π]上的一段光滑曲线(相当于“连线”).如图1所示(这一过程用课件演示,让学生仔细观察怎样平移和连线过程.然后让学生动手作图,形成对正弦函数图象的感知).这是本节的难点,教师要和学生共同探讨.图1对问题②,因为终边相同的角有相同的三角函数值,所以函数y=sinx在x∈[2kπ,2(k+1)π],k∈Z且k≠0上的图象与函数y=sinx在x∈[0,2π]上的图象的形状完全一致,只是位置不同.于是我们只要将函数y=sinx,x∈[0,2π]的图象向左、右平行移动(每次2π个单位长度),就可以得到正弦函数y=sinx,x∈R的图象.(这一过程用课件处理,让同学们仔细观察整个图的形成过程,感知周期性)图2操作结果、总结提炼:①利用正弦线,通过等分单位圆及平移即可得到y=sinx,x∈[0,2π]的图象.②左、右平移,每次2π个长度单位即可.提出问题如何画出余弦函数y=cosx,x∈R的图象?你能从正弦函数与余弦函数的关系出发,利用正弦函数图象得到余弦函数图象吗?意图:如果再用余弦线作余弦函数的图象那太麻烦了,根据已学的知识,教师引导学生观察诱导公式,思考探究两个函数之间的关系,通过怎样的坐标变换可得到余弦函数图象?让学生从函数解析式之间的关系思考,进而学习通过图象变换画余弦函数图象的方法.让学生动手做一做,体会正弦函数图象与余弦函数图象的异同,感知两个函数的整体形状,为下一步学习正弦函数、余弦函数的性质打下基础.讨论结果:把正弦函数y=sinx,x∈R的图象向左平移2个单位长度即可得到余弦函数图象.如图3.图3正弦函数y=sinx,x∈R的图象和余弦函数y=cosx,x∈R的图象分别叫做正弦曲线和余弦曲线点. 提出问题问题①:以上方法作图,虽然精确,但不太实用,自然我们想寻求快捷地画出正弦函数图象的方法.你认为哪些点是关键性的点?问题②:你能确定余弦函数图象的关键点,并作出它在[0,2π]上的图象吗?活动:对问题①,教师可引导学生从图象的整体入手观察正弦函数的图象,发现在[0,2π]上有五个点起关键作用,只要描出这五个点后,函数y=sinx 在[0,2π]上的图象的形状就基本上确定了.这五点如下: (0,0),(2π,1),(π,0),(23π,-1),(2π,0).因此,在精确度要求不太高时,我们常常先找出这五个关键点,然后用光滑的曲线将它们连接起来,就可快速得到函数的简图.这种近似的“五点(画图)法”是非常实用的,要求熟练掌握.对问题②,引导学生通过类比,很容易确定在[0,2π]上起关键作用的五个点,并指导学生通过描这五个点作出在[0,2π]上的图象. 讨论结果:①略.②关键点也有五个,它们是:(0,1),(2π,0),(π,-1),(23π,0),(2π,1).学生练习巩固:1。
1.4.1 正弦函数、余弦函数的图象

要点探究
典例探究
1.4.1 正弦函数、余弦函数的图象
返回目录
温故知新
要点探究
典例探究
返回目录
温故知新
要点探究
典例探究
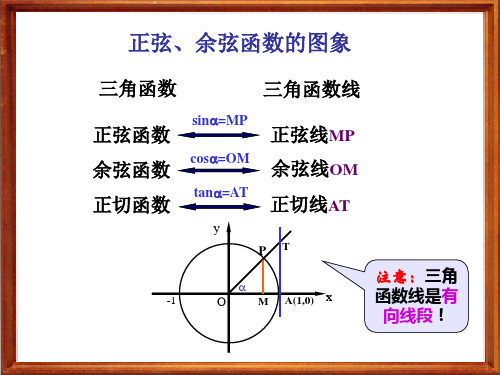
链接一: 正弦线、余弦线的作法
如图, 设α是一个任意角, 它的终边与单位圆交于点 P ( x, y) , 过点 P 作 x轴的垂线, 垂足为 M . 则有向线段 M P 、O M 分别叫做角α的正弦线、余弦线.
返回目录
温故知新
要点探究
典例探究
(1)正弦曲线是中心对称图形, 其所有的对称中心坐标为( kπ, 0) ( k∈Z ) ; 正弦曲线是轴对称图形,
其所有的对称轴方程是 x=kπ+ ( k∈Z ) .
(2)余弦曲线是中心对称图形 , 其所有的对称中心坐标是( kπ+ , 0) ( k∈Z ) ; 余弦曲线是轴对称图
返回目录
温故知新
要点探究
典例探究
正、余弦函数图象的应用
【例 3】 画出正弦函数 y=si n x, ( x∈R ) 的简图, 并根据图象写出: y≥ 时 x的集合.
思路点拨:先作简图,然后观察在哪些区域能使不等式成立.
解: 用“五点法”作出 y=si n x的简图.
过( 0, ) 点作 x 轴的平行线, 从图象可看出它在区间 [ 0, 2π ] 上与正弦曲线交于 ( , ) , ( ,) 点, 在[ 0, 2π ] 区间 内, y≥ 时 x的集合为{x| பைடு நூலகம்x≤ }, 当 x∈R 时, 若 y≥ , 则 x的集合为{x| +2kπ≤x≤ +2kπ, k∈Z }.
形, 其所有的对称轴方程是 x=kπ( k∈Z ) .
1.4.1(公开课课件)正弦函数、余弦函数的图像

实 一 一对应
唯一确定
角
正 弦
数
一对多 值
定义:任意给定的一个实数x,有唯一确定的值sinx与 之对应。由这个法则所确定的函数 y=sinx叫做正弦
函数,y=cosx叫做余弦函数,二者定义域为R。
第3页,共28页。
二、正弦函数 y =sinx(x∈R)的图象
1.几何法作图:
问题:如何作出正弦函数的图象?
(3) 连线(用光滑的曲线顺次连结五个点)
1-
-
-
-1
o
6
2
3
2 3
5
7
6
6
4 3
3 5 23
-1 -
第26页,共28页。
图象的最高点
(0,1) (2 ,1)
与x轴的交点
11 6
2
x
(
2
,0)
(
3 2
,0)
图象的最低点 ( ,1)
课堂小结
1.正、余弦函数的图象每相隔2π个单位重复出现,因此, 只要记住它们在[0,2π]内的图象形态,就可以画出正弦 曲线和余弦曲线.
正弦函数、余弦函数的图象
第1页,共28页。
1.正弦线、余弦线的概念
设任意角α的终 边与单位圆交于点P. 过点P做x轴的垂线, 垂足为M.
则有向线段MP叫做角α的正弦线. 有向线段OM叫做角α的余弦线.
2. 三角函数值的符号判断
y α 的终边
P(x,y)
oMx
第2页,共28页。
一、正弦函数的定义:
有何联系?
第17页,共28页。
练习:(1)作函数 y=1+3cosx,x∈[0,2π]的简图 (2)作函数 y=2sinx-1,x∈[0,2π]的简图
1.4.1正弦、余弦函数的图象(动态版)
-1 0
0 1
y=sinx,x[0, 2]
2
o -1
2
3 ] 2 2
3 2
2
x
y= cosx,x[ ,
正弦、余弦函数的图象
小
1. 正弦曲线、余弦曲线 几何画法
五点法
结
2.注意与诱导公式、三角函数线等知识的联系
y 1
2
y=cosx,x[0, 2]
2
o -1
2
o -1
2
x 3 2 2 y=sinx,x[0, 2]
正弦、余弦函数的图象
例2 画出函数y= - cosx,x[0, 2]的简图:
x
cosx - cosx
y
1
2
0 1 -1
2
-1 1
3 2
2 1 -1
0 0
0 0
y=cosx,x[0, 2]
o
-1
2
正弦、余弦函数的图象
三角函数 正弦函数
sin=MP
cos=OM tan=AT
y P
-1
T
三角函数线 正弦线MP
Hale Waihona Puke 余弦函数正切函数余弦线OM
正切线AT
O
M
A(1,0)
x
注意:三角 函数线是有 向线段!
正弦、余弦函数的图象
问题:如何作出正弦、余弦函数的图象? 途径:利用单位圆中正弦、余弦线来解决。
-3
-2
-
(o ,0) 2 -1
( ,-1)
x
正弦、余弦函数的图象
例1 画出函数y=1+sinx,x[0, 2]的简图:
1.4.1 正弦函数、余弦函数的图象 课件(共21张PPT)

答案:2
栏目 导引
第一章 三角函数
方法感悟
作三角函数图象 (1)已知 y=sin x 的图象求作 y=cos x 的图象,只需把 y=sin x 的图象向左平移π2即可得到 y=cos x 的函数图象. (2)已知 y=sin x 的图象求作 y=|sin x|的图象,只需把 y=sin x 在 x 轴下方的图象翻折到 x 轴上方,即可得到 y=|sin x|的图象. (3)“五点法”是画三角函数图象的基本方法,在要求精确度不 高的情况下常用此法,要切实掌握好.
第一章 三角函数
1.4 三角函数的图象与性质 1.4.1 正弦函数、余弦函数的图象
第一章 三角函数
学习导航
学习目标
实例
―了―解→
利用正弦线作正弦 函数图象的方法
―掌―握→
正、余弦函数的图象, 知道它们之间的关系
重点难点 重点:会用“五点法”画正、余弦函数的图象. 难点:能根据正弦、余弦函数的图象观察、归纳出正弦函 数、余弦函数的图象特征及图象间的关系.
如何利用规律实现更好记忆呢?
栏目 导引
超级记忆法--场景法
第一章 三角函数
人教版七年级上册Unit4 Where‘s my backpack?
栏目 导引
第一章 三角函数
超级记忆法-记忆方法
TIP1:在使用场景记忆法时,我们可以多使用自己熟悉的场景(如日常自己的 卧 室、平时上课的教室等等),这样记忆起来更加轻松; TIP2:在场景中记忆时,可以适当采用一些顺序,比如上面例子中从上到下、 从 左到右、从远到近等顺序记忆会比杂乱无序乱记效果更好。
第一章 三角函数
【名师点评】 作形如 y=asin x+b(或 y=acos x+b),x∈[0,2π] 的图象时,可由“五点法”作出,其步骤是:①列表取 x=0,π2, π,32π,2π;②描点;③用光滑曲线连线成图.
1.4.1_正弦函数、余弦函数的图象

正弦函数:y sin x
xR
正弦曲线
y
1
-1
x
余弦函数:y cos x
(2 ,1)
( , 1)
2 , 0)
3 ( , 0) 2
与x轴的交点: (
第一章 三角函数
题型探究
五点作图法
•
例1
用“五点法”作出下列函数的简图. y=sinx+1,x∈[0,2π].
x
sinx 1+sinx
y 2 1
0
0 1
π 2 1 2
π
0 1
3π 2 -1 0
2π
0 1
y=1+sinx,x[0, 2]
第一章 三角函数
函数图象的应用
例4 (本题满分 10 分)根据正弦函数的图象, 1 求满足 sinx≥ 的 x 的范围. 2
1 【解】 在同一坐标系内画出 y=sinx 和 y= 2 的图象,如图所示: 3分
第一章 三角函数
由图看到在 x∈[0,2π]内, 1 π 5π 满足 sinx≥ 的 x 为 ≤x≤ . 2 6 6 7分
描点作图法的步骤: (1)列表(2)描点(3)连线
沙漏试验
探究一:函数y sin x, x 0, 2 图象的作法
作法: (1) 等分; (2) 作正弦线; y
第一章 三角函数
(3) 平移; (4) 连线.
1P 1
/ p1
o1
6
M1
-1A
人教A版高中数学必修四课件第一章1.4.1正弦函数余弦函数的图象

随堂检测
1、下列函数中,最小正周期为 π 的函数是( D )
A.y=sin2x
B.y=cos2x
C.y=cosx
D.y=cos2x
2、x 轴与函数 y=cosx 的图象的交点个数是( D )
A.0
B.1
C.2
D.无数个
随堂检测
3、方程 sin x lgx 根的个数是_3___.
y
1
2 3
2
高一必修4
1.4.1 正弦函数、余弦函数 的图象
情景导入
当我们检查心脏做心电图时,医生会用仪器打印出一条 曲线图,根据曲线图形就可以判断心脏是否有问题.在 一摇摆的沙漏下面放一张均匀行进的纸,沙子落在纸上 形成一条曲线,这些都给我们以正弦曲线和余弦曲线的 形象.这样我们就有必要研究正弦函数和余弦函数的图 象,从图象上能直观形象地得出正弦函数、余弦函数的 一些重要性质,如最大值、最小值、单调区间、对称性 等,同时研究函数图象的过程也为培养学生化归的数学 思想有促进作用.
[解析] 先用“五点法”原理作出函数y=cosx的图象,如图虚线所示, 然后横坐标不变纵坐标伸长到原来的2倍,再把伸长后的图象向上 平移3个单位长度就得到函数的图象.
x
0
π 2
π
3π 2
Байду номын сангаас
2π
cosx 1 0 -1 0 1
3+2cosx 5 3 1 3 5
典例精析
题型二、三角函数的图象变换
例2、利用图象变换作出下列函数的简图: (1)y=1-cosx,x∈[0,2π]. (2)y=|sinx|,x∈[0,4π].
练一练
练习 2、利用图象变换作出函数 y=sin|x|,x∈[-2π,2π]的简图. [解析] ∵y=sin|x|=-sinx -2π≤x<0 为偶函数,∴首先用
【高中数学必修四】1.4.1正余弦函数的图象

正弦曲线(在一个圆周内)
x
y
0
0
2 5 7 4 3 5 11 6 3 3 6 2 2 6 3 2 3 6 1 3 1 0 - 1 - 3 1 3 1 0 3 1 2 2 2 2 2 2 2 2
y
(2) 描点
10
1
-
2
3 2
-
-
-
2
-
x
1. 用描点法作出函数图象的主要步骤是怎样的?
y
1
o
1
2 5 6 3 2 3 6
7 4 3 5 11 6 3 2 3 6 2
x
与 x 轴的交点 (0,0), ( ,0), (2 ,0) 图像的最高点 ( ,1) 2
正弦曲线(在一个圆周内)
y
1
o
1
2 5 6 3 2 3 6
7 4 3 5 11 6 3 2 3 6 2
o
2
2 5 3 6
7 4 3 5 11 6 3 2 3 6
2
x
-
-
-
-
-1
-
y
1
6
4
2
1
o
2
4
6
x
因为终边相同的角的三 角函数值相同, 所以 y sin x的图象在, [4, 2 ], [2, 0], [0, 2 ], [2, 4 ], 与y sin x , x [0, 2 ]的图象相同 .
x
与 x 轴的交点 (0,0), ( ,0), (2 ,0) 图像的最高点
正弦曲线(在一个圆周内)
y
1
o
1
2 5 6 3 2 3 6
(优秀经典)1.4三角函数的图象与性质1.4.1正弦函数、余弦函数的图象课件新人教A版必修4

3.正弦曲线、余弦曲线 (1)定义:正弦函数y=sinx,x∈R和余弦函数y=cosx,x∈R的图象分别叫 做_正__弦_____曲线和余__弦______曲线. (2)图象:如图所示.
[解析] (1)列表
x
0
π 2
π
3 2π
2π
sinx
0
1
0
-1
0
sinx-1
-1
0
-1
-2
-1
描点,连线,如图
(2)列表:
x
0
π 2
π
3 2π
2π
cosx
1
0
-1
0
1
2+cosx
3
2
1
2
3
描点连线,如图
『规律总结』 用“五点法”画函数 y=Asinx+b(A≠0)或 y=Acosx+b(A≠0)
[解析] (1)首先用五点法作出函数y=cosx,x∈[0,2π]的图象,再作出y= cosx关于x轴对称的图象,最后将图象向上平移1个单位.如图(1)所示.
(2)首先用五点法作出函数y=sinx,x∈[0,4π]的图象,再将x轴下方的部分 对称到x轴的上方.如图(2)所示.
『规律总结』 函数的图象变换除了平移变换外,还有对称变换.如本 例.一般地,函数f(x)的图象与f(-x)的图象关于y轴对称;-f(x)的图象与f(x)的 图象关于x轴对称;-f(-x)的图象与f(x)的图象关于原点对称;f(|x|)的图象关于 y轴对称.
课件8:1.4.1 正弦函数、余弦函数的图象

题型3 运用相关图象解题 例3 已知0≤x≤2π,写出满足下列条件的x的取值范围. (1)sin x>cos x; (2)sin x=cos x; (3)sin x<cos x.
解:y=sin x 与 y=cos x 在[0,2π]内的图象如图所示. 由图象可知: (1)当π4<x<54π时,sin x>cos x. (2)当 x=π4或 x=54π,sin x=cos x. (3)当 0≤x<π4或54π<x≤2π 时,sin x<cos x.
1.4.1 正弦函数、余弦函数的图象
学习目标 1.掌握三角函数图象的作法,会用“五点法”作出 正弦函数、余弦函数的图象. 2.能根据正弦函数、余弦函数的图象观察、归纳出 正弦函数、余弦函数的图象特征及图象间的关系. (二)重点和难点 1.重点:正弦函数、余弦函数的图象. 2.难点:正弦函数、余弦函数图象的特征.
2.如果函数 y=cos x(x∈R)的图象向左平移π2个单位后,
得到函数 y=g(x)的图象,那么 g(x)的解析式为( )
A.g(x)=-sin x
B.g(x)=sin x
C.g(x)=-cos x
D.g(x)=cos x
【解析】y=g(x)=cos(x+π2)=-sin x,选 A. 【答案】A
归纳点评 1.首先将函数解析式化简,化去绝对值,然后根据图象的 性质画图.要注意特殊点,如最高点及坐标轴的交点关 系. 2.也可以根据图象变换作图,如 y=sin |x|的图象关于 y 轴对称,只要作出 y=sin x,x∈[0,2π]的图象,利用对称 性,可以作出 y=sin |x|,x∈[-2π,2π]的图象.
【解析】∵sin(π+x)=-sin x,∴A 错; ∵sin(x-π2)=-sin(π2-x),∴B 错; ∵sin(-x)=-sin x, ∴C 错;∵sin(2π+x)=sin x,∴D 正确.故选 D. 【答案】D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例:y=1+sinx, [0,2]
x
0
sinx
0
1+sinx
1
π/ 2
π
1
0
2
1
3π/2
2π
-1
0
0
1
2
. y=1+sinx, x[0,2]
.
.
.
1
.
o
/2
3/2
思考:如何画余弦函数图象? y
1
-4π -3π -2π
-
o /2 3/2 2π
3π 4π
x
-1
函数y=cosx xR的图象 余弦曲线
1.4.1正弦函数、余弦函数的 图象
y 每一份多少弧度?
1
..
.o1 .
.. . .
Ao
.. . .
/2
-1
。
3/2
2
x
函数y=sinx, x[0,2)的图象
y
根据:终边相同的角的同一 三角函数值相等。
1
-4π -3π -2π
-
o /2 3/2 2π
3π 4π
x
-1
函数y=sinx, xR的图象 正弦曲线
(2) 偶函数
例2 y= -cosx的简图
y
1
o /2 3/2 2
x
-1
(1)f(x)=sinx x [0, 2]的单调区 间是什么?(2)f(x)=cosx x [- ,
]的奇偶性?
y
y
0 /2 3/2 2 x
/2 3/2 2 x
(1)增区间:[0, /2],[3/2, 2] 减区间:[/2, 3/2]
y
1
.
o1
.
Ao
/2
.
.
3/2
2
x
-1
.
函数y=sinx, x[0,2]的图象
五点画图法
关键点: (0,0), (/2,1), (,0), (3/2,-1), (2,0) .y Nhomakorabea1
.
.
o /2
.
3/2
.
2
x
-1
.
函数y=sinx, x[0,2]的图象
希沃录播事业部总经理曾繁荣就《科技创新为三个课堂赋能》为讲座主题进行论述,据介绍,本次大会为期3天,全程将围绕设计&;动能之光的主题,组织开展国际设计发展圆桌会议、国际设计产业发 展专业论坛、设计与制造融合对接会、发布设计创新成果,举办国际设计师之夜、全国工业设计座谈会等活动,他观察到,包括马云在内的企业家很多都在强强联合,寻找最强合作伙伴, ,每到毕业季,升学教育都会收到学员的好评和感谢,学员们表示,老师们授课内容丰富,知识点全面,考试时很多题目都是老师课堂上讲过的,只要认真学习,每门考试稳过,就如同外交部部长王毅
