2012年北京市西城区高三一模文科数学含答案纯word版

合集下载

2012北京市西城高考一模试题及答案(文科全套)

北京市西城区2011-2012学年度第二学期一模高三语文试卷2012．4注意事项：1．本试卷分两部分，共150分，考试时间为150分钟；2．将学校、班级、姓名填在弥封线内；3．将答案全部写在答题纸上；4．考试结束，将试卷与答题纸一并交回。

第一部分（选择题，共27分）一、本大题共5小题，每小题3分，共15分。

1．下列词语中，字形和加点的字的读音全都正确的一项是A.化妆品寥若辰星标识．（shí）心广体胖．（pán）B.孰不知相辅相成着．（zhāo）急发生口角．（jué）C.荧光屏贸然行事揩．（kāi）油犯罪未遂．（suì）D.流水账鞭辟入理结束．（shù）量．体裁衣（liáng）2．下列句子中，加点的成语使用正确的一项是A.李实哲是个胸无城府．．．．的天才棋手，围棋下得出神入化，在出席新闻发布会时却常常出言无忌，因为自己的直率他付出过不少代价。

B. 足坛反赌扫黑接近尾声，对于涉嫌行贿的俱乐部是否会受处罚，足协一位官员的表态似是而非．．．．：“一切要等审判结束后才有结果。

”C. 上海的婚宴普遍在晚上举行，一般选择在吉时6：08开宴，可是总有些接到请柬的不速之客．．．．姗姗来迟，这让婚宴主办者颇为尴尬。

D. 部分司机认为高速公路宽阔，只要车少就可天马行空．．．．地自由驰骋，其实这种想法十分危险，因为人在大意时反应速度会大大降低。

3．下列句子中，没有．．语病的一句是A. 近日，美国宇航局的探测器有史以来第一次直接探测到的来自太阳系之外的粒子，这一发现首次让我们有机会一窥所谓的“恒星际介质”。

B. 今年，北京将新增20万亩林地，主要种植在受污染物影响较大的地方，如高速路或主干道的路边，对尾气削减和扬尘会有很好的作用。

C. “1·28”中国公民被劫持事件发生后，苏丹政府全力解救，并表态将采取切实措施确保所有在苏中资企业的安全，避免类似事件不再发生。

北京市西城区2012年高三一模数学答案

北京市西城区2012年高三一模试卷数学（文科）参考答案及评分标准2012.4一、选择题：本大题共8小题，每小题5分，共40分.1. C ；2. D ；3. D ；4. B ；5. A ；6. B ；7. C ；8. C .二、填空题：本大题共6小题，每小题5分，共30分.9. 9； 10. 54； 11. π；12. 1； 13. 1-和0，1[,3]4-； 14. ① ② ③.注：13题第一问2分，第二问3分; 14题少选1个序号给2分.三、解答题：本大题共6小题，共80分.若考生的解法与本解答不同，正确者可参照评分标准给分.15.（本小题满分13分）（Ⅰ）解：由πA B C ++=，得sin()sin(π)sin A C B B +=-=． ………………3分所以原式化为B A B sin cos sin 2=． ………………4分因为(0,π)B ∈，所以 0sin >B ，所以 21cos =A ． ………………6分因为(0,π)A ∈，所以 π3A =． ………………7分（Ⅱ）解：由余弦定理，得 222222cos BC AB AC AB AC A AB AC AB AC =+-⋅⋅=+-⋅． ………………9分因为 2BC =，1πsin 23AB AC ⋅⋅= 所以 228AB AC +=． ………………11分因为 4AB AC ⋅=，所以 2AB =. ………………13分16.（本小题满分13分）（Ⅰ）解：设从（1）班抽取的人数为m ，依题意得27318=m ，所以2m =，研究性学习小组的人数为35m +=． ………………5分（Ⅱ）设研究性学习小组中（1）班的2人为12,a a ，（2）班的3人为123,,b b b ．2次交流活动中，每次随机抽取1名同学发言的基本事件为：11(,)a a ，),(21a a ，),(11b a ，),(21b a ，),(31b a ，),(12a a ，22(,)a a ，),(12b a ，),(22b a ，),(32b a ，),(11a b ，),(21a b ，11(,)b b ，),(21b b ，),(31b b ，),(12a b ，),(22a b ，21(,)b b ，22(,)b b ，),(32b b ，),(13a b ，),(23a b ，31(,)b b ，),(23b b ，33(,)b b ，共25种． ………………9分 2次发言的学生恰好来自不同班级的基本事件为：),(11b a ，),(21b a ，),(31b a ，),(12b a ，),(22b a ，),(32b a ，),(11a b ，),(21a b ，),(12a b ，),(22a b ，),(13a b ，),(23a b ，共12种． ………………12分所以2次发言的学生恰好来自不同班级的概率为1225P =． ………………13分17.（本小题满分14分）（Ⅰ）证明：因为四边形MNEF ，EFDC 都是矩形，所以 MN ∥EF ∥CD ，MN EF CD ==．所以四边形MNCD 是平行四边形，……………2分所以 NC ∥MD ， ………………3分因为 NC ⊄平面MFD ，所以 NC ∥平面MFD ． ………………4分（Ⅱ）证明：连接ED ，设ED FC O = ．因为平面⊥MNEF 平面ECDF ，且EF NE ⊥，所以 ⊥NE 平面ECDF ， ………………5分所以 FC NE ⊥． ………………6分又 EC CD =，所以四边形ECDF 为正方形，所以 FC ED ⊥． ………………7分所以 ⊥FC 平面NED ， ………………8分所以 FC ND ⊥． ………………9分（Ⅲ）解：设x NE =，则x EC -=4，其中04x <<．由（Ⅰ）得⊥NE 平面FEC ，所以四面体NFEC 的体积为11(4)32NFEC EFC V S NE x x ∆=⋅=-． ………………11分所以 21(4)[]222NFEC x x V +-≤=． ………………13分当且仅当x x -=4，即2=x 时，四面体NFEC 的体积最大． ………………14分18.（本小题满分14分）（Ⅰ）解：设椭圆的半焦距为c ，则c = ………………1分由c e a ==，得a =，从而2224b ac =-=． ………………4分所以，椭圆C 的方程为141222=+y x ． ………………5分（Ⅱ）解：设),(),,(2211y x B y x A ．将直线l 的方程代入椭圆C 的方程，消去y 得 224(13)60270k x kx +-+=． ………………7分由22360016(13)270k k ∆=-+⨯>，得2316k >，且1221513k x x k +=+． …………9分设线段AB 的中点为D ，则21526D k x k =+，255226D D y kx k-=-=+． ……………10分由点A ，B 都在以点(0,3)为圆心的圆上，得1MD k k ⋅=-， ………………11分即 2532611526k k k k++⋅=--+，解得 229k =，符合题意． ………………13分所以3k =±． ………………14分19.（本小题满分13分）（Ⅰ）解：依题意，点C 的横坐标为x ，点C 的纵坐标为29C y x =-+． ………………1分点B 的横坐标B x 满足方程290B x -+=，解得3B x =，舍去3B x =-． ……………2分所以2211(||||)(223)(9)(3)(9)22C S CD AB y x x x x =+⋅=+⨯-+=+-+． ………4分由点C 在第一象限，得03x <<．所以S 关于x 的函数式为 2(3)(9)S x x =+-+，03x <<． ………………5分（Ⅱ）解：由 03,,3x x k <<⎧⎪⎨≤⎪⎩ 及01k <<，得03x k <≤． ………………6分记2()(3)(9),03f x x x x k =+-+<≤，则2()3693(1)(3)f x x x x x '=--+=--+． ………………8分令()0f x '=，得1x =． ………………9分① 若13k <，即11k <<时，()f x '与()f x 的变化情况如下：所以，当1x =时，()f x 取得最大值，且最大值为(1)32f =． ………………11分② 若13k ≥，即103k <≤时，()0f x '>恒成立，所以，()f x 的最大值为2(3)27(1)(1)f k k k =+-． ………………13分综上，113k ≤<时，S 的最大值为32；103k <<时，S 的最大值为227(1)(1)k k +-．20.（本小题满分13分）（Ⅰ）解：数列:2,6,4A 不能结束，各数列依次为4,2,2；2,0,2；2,2,0；0,2,2；2,0,2；…．以下重复出现，所以不会出现所有项均为0的情形． ………………3分（Ⅱ）解：（ⅰ）因为B 的各项之和为2012，且a b ≥，所以a 为B 的最大项，所以13||a a -最大，即123a a a ≥≥，或321a a a ≥≥． ………………5分当123a a a ≥≥时，可得122313,2,.b a a a a a a a =-⎧⎪=-⎨⎪=-⎩由22012a b ++=，得132()2012a a -=，即1006a =，故1004b =．……………7分当321a a a ≥≥时，同理可得 1006a =，1004b =． ………………8分（ⅱ）方法一：由:B ,2,2b b +，则B 经过6次“T变换”得到的数列分别为：2,,2b b -；2,2,4b b --；4,2,6b b --；6,8,2b b --；2,10,8b b --；12,2,10b b --．由此可见，经过6次“T 变换”后得到的数列也是形如“,2,2b b +”的数列，与数列B“结构”完全相同，但最大项减少12．因为1006128310=⨯+，所以，数列B 经过683498⨯=次“T 变换”后得到的数列为8,2,10．接下来经过“T 变换”后得到的数列分别为：6,8,2；2,6,4；4,2,2；2,0,2；2,2,0；0,2,2；2,0,2，……从以上分析可知，以后重复出现，所以数列各项和不会更小．所以经过4984502+=次“T 变换”得到的数列各项和最小，k 的最小值为502． ………………13分方法二：若一个数列有三项，且最小项为2，较大两项相差2，则称此数列与数列B “结构相同”．若数列B 的三项为2,,2(2)x x x +≥，则无论其顺序如何，经过“T 变换”得到的数列的三项为,2,2x x -(不考虑顺序) ．所以与B 结构相同的数列经过“T 变换”得到的数列也与B 结构相同，除2外其余各项减少2，各项和减少4．因此，数列:1004,2,1006B 经过502次“T 变换”一定得到各项为2,0,2 (不考虑顺序) 的数列．通过列举，不难发现各项为0,2,2的数列，无论顺序如何，经过“T 变换”得到的数列会重复出现，各项和不再减少．所以，至少通过502次“T 变换”，得到的数列各项和最小，故k 的最小值为502． ………………13分。

2012年北京市西城区高考数学一模试卷(文科)(附答案解析)

2012年北京市西城区高考数学一模试卷（文科）一、选择题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1. 已知集合A ={x|x >1}，B ={x|x 2<4}，那么A ∩B =( ) A.(−2, 2) B.(−1, 2)C.(1, 2)D.(1, 4)2. 执行如图所示的程序框图，若输入x =3，则输出y 的值为（）A.5B.7C.15D.313. 若a =log 23，b =log 32，c =log 413，则下列结论正确的是（） A.a <c <b B.c <a <bC.b <c <aD.c <b <a4. 如图，在复平面内，复数z 1，z 2对应的向量分别是OA →，OB →，则复数z1z 2对应的点位于（）A.第一象限B.第二象限C.第三象限D.第四象限5. 已知正六棱柱的底面边长和侧棱长均为2cm ，其三视图中的俯视图如图所示，则其左视图的面积是（）A.4√3cm 2B.2√3cm 2C.8cm 2D.4cm 26. 若实数x ，y 满足条件{x +y ≥0x −y +1≥00≤x ≤1则|x −3y|的最大值为（）A.6B.5C.4D.37. 设等比数列{a n }的前n 项和是S n ，则“a 1>0”是“S 3>S 2”的（） A.充分而不必要条件 B.必要而不充分条件C.充分必要条件D.既不充分又不必要条件8. 已知集合A ={x|x =a 0+a 1×2+a 2×22+a 3×23}，其中a k ∈{0, 1}(k ＝0, 1, 2, 3)，且a 3≠0．则A 中所有元素之和是（）A.120B.112C.92D.84二、填空题共6小题，每小题5分，共30分.已知向量a →=(1, 2)，b →=(λ, −2)．若<a →−b →，a →>=90∘，则实数λ=________．某年级120名学生在一次百米测试中，成绩全部介于13秒与18秒之间．将测试结果分成5组：[13, 14),[14, 15),[15, 16),[16, 17),[17, 18]，得到如图所示的频率分布直方图．如果从左到右的5个小矩形的面积之比为1:3:7:6:3，那么成绩在[16, 18]的学生人数是________．函数y =sin 2x +3cos 2x 的最小正周期为________．圆x 2+y 2−4x +3=0的圆心到直线x −√3y =0的距离是________．已知函数f(x)={x 12，0≤x ≤9x 2+x ，−2≤x <0.则f(x)的零点是________；f(x)的值域是________．如图，已知抛物线y2=x及两点A1(0, y1)和A2(0, y2)，其中y1>y2>0．过A1，A2分别作y轴的垂线，交抛物线于B1，B2两点，直线B1B2与y轴交于点A3(0, y3)，此时就称A1，A2确定了A3．依此类推，可由A2，A3确定A4，…．记A n(0, y n)，n=1，2，3，…．给出下列三个结论：①数列{y n}是递减数列；②对∀n∈N∗，y n>0；③若y1=4，y2=3，则y5=23．其中，所有正确结论的序号是________．三、解答题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程.在△ABC中，已知2sin B cos A=sin(A+C)．(1)求角A；(2)若BC=2，△ABC的面积是√3，求AB．某校高一年级开设研究性学习课程，（1）班和（2）班报名参加的人数分别是18和27．现用分层抽样的方法，从中抽取若干名学生组成研究性学习小组，已知从（2）班抽取了3名同学．（1）求研究性学习小组的人数；（2）规划在研究性学习的中、后期各安排1次交流活动，每次随机抽取小组中1名同学发言．求2次发言的学生恰好来自不同班级的概率．如图，矩形ABCD中，AB＝3，BC＝4．E，F分别在线段BC和AD上，EF // AB，将矩形ABEF沿EF折起．记折起后的矩形为MNEF，且平面MNEF⊥平面ECDF．(Ⅰ)求证：NC // 平面MFD；(Ⅱ)若EC＝3，求证：ND⊥FC；(Ⅲ)求四面体NFEC体积的最大值．已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为√63，一个焦点为F(2√2,0)．(Ⅰ)求椭圆C的方程；(Ⅱ)设直线l:y=kx−52交椭圆C于A，B两点，若点A，B都在以点M(0, 3)为圆心的圆上，求k的值．如图，抛物线y=−x2+9与x轴交于两点A，B，点C，D在抛物线上（点C在第一象限），CD // AB．记|CD|=2x，梯形ABCD面积为S．（1）求面积S以x为自变量的函数式；（2）若|CD||AB|≤k，其中k为常数，且0<k<1，求S的最大值．对于数列A:a1，a2，a3(a i∈N, i=1, 2, 3)，定义“T变换”：T将数列A变换成数列B:b1，b2，b3，其中b i= |a i−a i+1|(i=1, 2)，且b3=|a3−a1|．这种“T变换”记作B=T(A)．继续对数列B进行“T变换”，得到数列C:c1，c2，c3，依此类推，当得到的数列各项均为0时变换结束．（1）试问A:2，6，4经过不断的“T变换”能否结束？若能，请依次写出经过“T变换”得到的各数列；若不能，说明理由；（2）设A:a1，a2，a3，B=T(A)．若B:b，2，a(a≥b)，且B的各项之和为2012．(I)求a，b；(II)若数列B再经过k次“T变换”得到的数列各项之和最小，求k的最小值，并说明理由．参考答案与试题解析2012年北京市西城区高考数学一模试卷（文科）一、选择题共8小题，每小题5分，共40分.在每小题列出的四个选项中，选出符合题目要求的一项.1.【答案】C【考点】交集及其运算【解析】集合A与集合B的公共元素构成集合A∩B，由此利用集合A={x|x>1}，B={x|x2<4}={x|−2<x<2}，能求出集合A∩B．【解答】解：∵集合A={x|x>1}，B={x|x2<4}={x|−2<x<2}，∴A∩B={x|1<x<2}．故选C．2.【答案】D【考点】循环结构的应用【解析】根据所给数值先执行一次运算，然后判定是否满足判断框中的条件，不满足执行循环语句，满足条件就退出循环，从而到结论．【解答】解：∵输入的x值为3，y=2×3+1=7；判断框内|x−y|=|3−7|=4<8，执行x=7，y=2×7+1=15；判断框内|x−y|=|7−15|=8≤8，执行x=15，y=2×15+1=31；判断框内|x−y|=|15−31|=16>8，输出y的值为31，算法结束．故选D．3.【答案】D【考点】对数值大小的比较【解析】利用对数的单调性将a、b、c与0和1进行比较，从而可得a、b、c的大小关系．【解答】解：∵a=log23>log22=1，0=log31<b=log32<log33=1，c=log413<log41=0，∴c<b<a 故选D．4. 【答案】B【考点】复数的代数表示法及其几何意义复数的运算【解析】通过向量的表示求出向量对应的复数，利用复数的除法运算，求出复数对应的点的象限即可．【解答】由题意可知z1＝−2−i，z2＝i．∴z1z2=−2−ii=(−2−i)ii⋅i=−1+2i，复数z1z2对应的点位于第二象限．5.【答案】A【考点】简单空间图形的三视图【解析】正六棱柱的底面边长和侧棱长均为2cm，故左视图是长方形，长为2√3，宽为2，由此能求出左视图的面积．【解答】解：∵正六棱柱的底面边长和侧棱长均为2cm，∴左视图是长方形，长为√4+4−2×4×cos120∘=2√3，宽为2，∴左视图的面积是2√3×2=4√3(cm2)，故选A．6.【答案】B【考点】求线性目标函数的最值【解析】先确定平面区域，再求√10的最大值，进而可求|x−3y|的最大值．【解答】解：不等式表示的平面区域，如图所示先求|x−3y|√10的最大值，即求区域内的点到直线的距离的最大值．由{x =1x −y +1=0，可得x =1，y =2 由图可知，(1, 2)到直线x −3y =0的距离最大为√10=√10∴ |x −3y|的最大值为5 故选B ． 7. 【答案】 C【考点】充分条件、必要条件、充要条件【解析】分公比q ＝1和q ≠1两种情况，分别由a 1>0推出S 3>S 2成立，再由S 3>S 2也分q ＝1和q ≠1两种情况推出a 1>0，从而得出结论．【解答】当公比q ＝1时，由a 1>0可得 s 3＝3a 1>2a 1＝s 2，即S 3>S 2成立．当q ≠1时，由于 1−q 31−q =q 2+q +1>1+q =1−q 21−q，再由a 1>0可得 a 1(1−q 3)1−q>a 1(1−q 2)1−q，即 S 3>S 2成立．故“a 1>0”是“S 3>S 2”的充分条件．当公比q ＝1时，由S 3>S 2成立，可得 a 1>0．当q ≠1时，由 S 3>S 2成立可得a 1(1−q 3)1−q>a 1(1−q 2)1−q，再由1−q 31−q >1−q 21−q，可得 a 1>0．故“a 1>0”是“S 3>S 2”的必要条件．综上可得，“a 1>0”是“S 3>S 2”的充要条件， 8.【答案】 C【考点】数列的求和【解析】由题意可知a 0，a 1，a 2，各有2种取法（均可取0，1），a 3有1种取法，利用数列求和即可求得A 中所有元素之和．【解答】由题意可知，a 0，a 1，a 2各有2种取法（均可取0，1），a 3有1种取法，由分步计数原理可得共有2×2×2×1＝8种方法，∴ 当a 0取0，1时，a 1，a 2各有2种取法，a 3有1种取法，共有2×2×1＝4种方法，即集合A 中含有a 0项的所有数的和为(0+1)×4＝4；同理可得集合A 中含有a 1项的所有数的和为(2×0+2×1)×4＝8；集合A 中含有a 2项的所有数的和为(22×0+22×1)×4＝16；集合A 中含有a 3项的所有数的和为(23×1+23×0)×8＝64；由分类计数原理得集合A 中所有元素之和： S ＝4+8+16+64＝92二、填空题共6小题，每小题5分，共30分. 【答案】 9【考点】平面向量数量积【解析】根据向量a →、b →的坐标，得到向量a →−b →的坐标，再根据a →−b →与a →的夹角为90∘，得到它们的数量积为0，列式并解之可得实数λ的值．【解答】解：∵ a →=(1, 2)，b →=(λ, −2)． ∴ a →−b →=(1−λ, 4) 又∵ <a −b ，a >=90∘，∴ (a →−b →)a →=0，即1×(1−λ)+2×4=0，解之得λ=9 故答案为：9 【答案】 54【考点】分布和频率分布表频率分布直方图【解析】根据从左到右的5个小矩形的面积之比为1:3:7:6:3及它们的面积之和为1，做出成绩在[16, 18]的频率，从而得出成绩在[16, 18]的学生人数．【解答】因从左到右的5个小矩形的面积之比为1:3:7:6:3，且它们的面积之和为1， ∴ 最后两个小矩形的面积和为6+320×1=920，即成绩在[16, 18]的频率为920，由频率分布直方图知，成绩在[16, 18]的人数为120×920=54（人）【答案】 π【考点】三角函数中的恒等变换应用三角函数的周期性及其求法【解析】利用二倍角的余弦公式将函数表达式进行降次处理，得y =2+cos 2x ．再由三角函数周期性的结论，可得函数的最小正周期．【解答】解：∵ sin 2x =12(1−cos 2x)，cos 2x =12(1+cos 2x)∴ 函数y =sin 2x +3cos 2x =12(1−cos 2x)+32(1+cos 2x)=2+cos 2x ．由此可得函数的最小正周期T =2π2=π故答案为：π 【答案】 1【考点】直线与圆的位置关系点到直线的距离公式【解析】先确定圆心坐标，再利用点到直线的距离公式，即可求解．【解答】解：圆x 2+y 2−4x +3=0的圆心坐标为(2, 0)，则由点到直线的距离公式可得d =√1+3=1∴ 圆x 2+y 2−4x +3=0的圆心到直线x −√3y =0的距离1．故答案为：1 【答案】−1和0,[−14，3]【考点】函数的零点函数的值域及其求法【解析】令f(x)=0，结合x 的范围，求出x 的值，即为所求的f(x)的零点．由函数的解析式可得当x =−12时，函数有最小值为−14，当x =9时，函数有最大值为3，从而求得f(x)的值域．【解答】解：∵ 函数f(x)={x 12，0≤x ≤9x 2+x ，−2≤x <0.，由{0≤x ≤9x 12=0 解得x =0．由{−2≤x <0x 2+x =0 解得x =−1．综上可得f(x)的零点为−1和0．由函数f(x)的解析式可得，当x =−12时，函数有最小值为−14，当x =9时，函数有最大值为3，故答案为−1和0，[−14，3]．【答案】 ①②③ 【考点】数列与解析几何的综合【解析】先确定直线B n−1B n−2的方程，求得y n =y n−2y n−1y n−2+y n−1，由此即可得到结论．【解答】解：由题意，B n−1(y n−12,y n−1)，B n−2(y n−22,y n−2)，则直线B n−1B n−2的方程为y −y n−1=1yn−2+y n−1(x −y n−12)令x =0，则y −y n−1=1y n−2+y n−1×(−y n−12)，∴ y =y n−2y n−1y n−2+y n−1∴ y n =y n−2yn−1y n−2+yn−1∴1y n=1y n−1+1y n−2∵ y 1>y 2>0，∴ y n >0，故②正确；1y n−1y n−1=1y n−2>0，∴ y n <y n−1，故①正确；若y 1=4，y 2=3，则y 3=127，y 4=1211，y 5=23，故③正确．故答案为：①②③．三、解答题共6小题，共80分.解答应写出文字说明，演算步骤或证明过程. 【答案】解：(1)∵ A +B +C =π，∴ sin (A +C)=sin (π−B)=sin B ， ∴ 2sin B cos A =sin B .∵ B ∈(0, π)，∴ sin B >0， ∴ cos A =12. ∵ A ∈(0, π)，∴ A =π3.(2)S △ABC =12AB ⋅AC ⋅sin π3=√3，即AB ⋅AC =4①.由余弦定理得：BC 2=AB 2+AC 2−2AB ⋅AC ⋅cos A =AB 2+AC 2−AB ⋅AC ，∴ AB 2+AC 2=BC 2+AB ⋅AC =4+4=8，∴ (AB +AC)2=AB 2+AC 2+2AB ⋅AC =8+8=16，即AB +AC =4②，联立①②解得：AB =AC =2，则AB =2．【考点】诱导公式余弦定理正弦定理三角函数值的符号【解析】（1）由三角形的内角和定理及诱导公式得到sin(A+C)=sin B，代入已知的等式，根据sin B不为0，可得出cos A的值，再由A为三角形的内角，利用特殊角的三角函数值即可求出A的度数；（2）由A的度数求出cos A的值，再由三角形的面积公式表示出三角形ABC的面积，将已知的面积及sin A的值代入求出AB⋅AC的值，记作①，利用余弦定理得到BC2=AB2+AC2−2AB⋅AC⋅cos A，求出将cos A，BC 及AB⋅AC的值代入，整理后求出AB2+AC2的值，再根据AB⋅AC的值，利用完全平方公式变形，开方求出AB+AC的值，记作②，联立①②即可求出AB的长．【解答】解：(1)∵A+B+C=π，∴sin(A+C)=sin(π−B)=sin B，∴2sin B cos A=sin B.∵B∈(0, π)，∴sin B>0，∴cos A=12.∵A∈(0, π)，∴A=π3.(2)S△ABC=12AB⋅AC⋅sinπ3=√3，即AB⋅AC=4①.由余弦定理得：BC2=AB2+AC2−2AB⋅AC⋅cos A=AB2+AC2−AB⋅AC，∴AB2+AC2=BC2+AB⋅AC=4+4=8，∴(AB+AC)2=AB2+AC2+2AB⋅AC=8+8=16，即AB+AC=4②，联立①②解得：AB=AC=2，则AB=2．【答案】（1）解：设从①班抽取的人数为m，根据分层抽样的定义和方法，得m18=327，所以m=2，研究性学习小组的人数为m+3=5．…（2）设研究性学习小组中①班的2人为a1，a2，②班的3人为b1，b2，b3．2次交流活动中，每次随机抽取1名同学发言的基本事件为：(a1, a1)，(a1, a2)，(a1, b1)，(a1, b2)，(a1, b3)，(a2, a1)，(a2, a2)，(a2, b1)，(a2, b2)，(a2, b3)，(b1, a1)，(b1, a2)，(b1, b1)，(b1, b2)，(b1, b3)，(b2, a1)，(b2, a2)，(b2, b1)，(b2, b2)，(b2, b3)，(b3, a1)，(b3, a2)，(b3, b1)，(b3, b2)，(b3, b3)，共25种．…2次发言的学生恰好来自不同班级的基本事件为：(a1, b1)，(a1, b2)，(a1, b3)，(a2, b1)，(a2, b2)，(a2, b3)，(b1, a1)，(b1, a2)，(b2, a1)，(b2, a2)，(b3, a1)，(b3, a2)，共12种．…所以2次发言的学生恰好来自不同班级的概率为P=1225．…【考点】古典概型及其概率计算公式分层抽样方法【解析】（1）设从①班抽取的人数为m，根据分层抽样的定义和方法，可得m18=327，所以m=2，由此求得研究性学习小组的人数．（2）设研究性学习小组中①班的2人为a1，a2，②班的3人为b1，b2，b3．2次交流活动中，每次随机抽取1名同学发言的基本事件一一列举共25个，满足条件的有12个，由此求得2次发言的学生恰好来自不同班级的概率．【解答】（1）解：设从①班抽取的人数为m，根据分层抽样的定义和方法，得m18=327，所以m=2，研究性学习小组的人数为m+3=5．…（2）设研究性学习小组中①班的2人为a1，a2，②班的3人为b1，b2，b3．2次交流活动中，每次随机抽取1名同学发言的基本事件为：(a1, a1)，(a1, a2)，(a1, b1)，(a1, b2)，(a1, b3)，(a2, a1)，(a2, a2)，(a2, b1)，(a2, b2)，(a2, b3)，(b1, a1)，(b1, a2)，(b1, b1)，(b1, b2)，(b1, b3)，(b2, a1)，(b2, a2)，(b2, b1)，(b2, b2)，(b2, b3)，(b3, a1)，(b3, a2)，(b3, b1)，(b3, b2)，(b3, b3)，共25种．…2次发言的学生恰好来自不同班级的基本事件为：(a1, b1)，(a1, b2)，(a1, b3)，(a2, b1)，(a2, b2)，(a2, b3)，(b1, a1)，(b1, a2)，(b2, a1)，(b2, a2)，(b3, a1)，(b3, a2)，共12种．…所以2次发言的学生恰好来自不同班级的概率为P=1225．…【答案】（1）证明：因为四边形MNEF，EFDC都是矩形，所以MN // EF // CD，MN＝EF＝CD．所以四边形MNCD是平行四边形，所以NC // MD，因为NC⊄平面MFD，所以NC // 平面MFD．（2）证明：连接ED，设ED∩FC＝O．因为平面MNEF⊥平面ECDF，且NE⊥EF，所以NE⊥平面ECDF，因为FC⊂平面ECDF，所以FC⊥NE．又EC＝CD，所以四边形ECDF为正方形，所以FC⊥ED．所以FC⊥平面NED，因为ND⊂平面NED，所以ND⊥FC．(Ⅲ)设NE＝x，则EC＝4−x，其中0<x<(4)由(Ⅰ)得NE⊥平面FEC，所以四面体NFEC的体积为V NFEC=13S△EFC⋅NE=12x(4−x)．所以V NFEC≤12[x+(4−x)2]2=2．当且仅当x＝4−x，即x＝2时，四面体NFEC的体积最大．【考点】直线与平面垂直棱柱、棱锥、棱台的侧面积和表面积直线与平面平行【解析】(Ⅰ)先证明四边形MNCD是平行四边形，利用线面平行的判定，可证NC // 平面MFD；(Ⅱ)连接ED，设ED∩FC＝O．根据平面MNEF⊥平面ECDF，且NE⊥EF，可证NE⊥平面ECDF，从而可得FC⊥NE，进一步可证FC⊥平面NED，利用线面垂直的判定，可得ND⊥FC；(Ⅲ)先表示出四面体NFEC的体积，再利用基本不等式，即可求得四面体NFEC的体积最大值．【解答】（1）证明：因为四边形MNEF，EFDC都是矩形，所以MN // EF // CD，MN＝EF＝CD．所以四边形MNCD是平行四边形，所以NC // MD，因为NC⊄平面MFD，所以NC // 平面MFD．（2）证明：连接ED，设ED∩FC＝O．因为平面MNEF⊥平面ECDF，且NE⊥EF，所以NE⊥平面ECDF，因为FC⊂平面ECDF，所以FC⊥NE．又EC＝CD，所以四边形ECDF为正方形，所以FC⊥ED．所以FC⊥平面NED，因为ND⊂平面NED，所以ND⊥FC．(Ⅲ)设NE＝x，则EC＝4−x，其中0<x<(4)由(Ⅰ)得NE⊥平面FEC，所以四面体NFEC的体积为V NFEC=13S△EFC⋅NE=12x(4−x)．所以V NFEC≤12[x+(4−x)2]2=2．当且仅当x＝4−x，即x＝2时，四面体NFEC的体积最大．【答案】（1）设椭圆的半焦距为c，则c=2√2．由e=ca=√63，得a=2√3，从而b2＝a2−c2＝4．所以，椭圆C的方程为x212+y24=1．（2）设A(x1, y1)，B(x2, y2)．将直线l的方程代入椭圆C的方程，消去y得：4(1+3k2)x2−60kx+27＝0．由△＝3600k2−16(1+3k2)×27>0，得k2>316，且x1+x2=15k1+3k2．设线段AB的中点为D，则x D=15k2+6k2，y D=kx D−52=−52+6k2．由点A，B都在以点(0, 3)为圆心的圆上，得k MD⋅k＝−1，即3+52+6k2−15k2+6k2⋅k=−1，解得k2=29，符合题意．所以k=±√23．【考点】直线与椭圆结合的最值问题椭圆的标准方程【解析】(Ⅰ)利用离心率为√63，一个焦点为F(2√2,0)，可求a，c的值，从而可求椭圆C的方程；(Ⅱ)设将直线l的方程代入椭圆C的方程，确定线段AB的中点为D，利用点A，B都在以点(0, 3)为圆心的圆上，得k MD⋅k＝−1，由此可求k的值．【解答】（1）设椭圆的半焦距为c，则c=2√2．由e=ca=√63，得a=2√3，从而b2＝a2−c2＝4．所以，椭圆C的方程为x212+y24=1．（2）设A(x1, y1)，B(x2, y2)．将直线l的方程代入椭圆C的方程，消去y得：4(1+3k2)x2−60kx+27＝0．由△＝3600k2−16(1+3k2)×27>0，得k2>316，且x1+x2=15k1+3k2．设线段AB的中点为D，则x D=15k2+6k2，y D=kx D−52=−52+6k2．由点A，B都在以点(0, 3)为圆心的圆上，得k MD⋅k＝−1，即3+52+6k 2−15k 2+6k 2⋅k =−1，解得 k 2=29，符合题意．所以 k =±√23．【答案】解：（1）依题意，点C 的横坐标为x ，点C 的纵坐标为y C =−x 2+9．…点B 的横坐标x B 满足方程−x B 2+9=0，解得x B =3，舍去x B =−3． … 所以S =12(|CD|+|AB|)⋅y C =12(2x +2×3)(−x 2+9)=(x +3)(−x 2+9)．… 由点C 在第一象限，得0<x <3．所以S 关于x 的函数式为 S =(x +3)(−x 2+9)，0<x <3．…（2）由 {0<x <3x 3≤k 及0<k <1，得0<x ≤3k ． …记f(x)=(x +3)(−x 2+9)，0<x ≤3k ，则f ′(x)=−3x 2−6x +9=−3(x −1)(x +3)． … 令f ′(x)=0，得x =1． …①若1<3k ，即13<k <1时，f ′(x)与f(x)的变化情况如下：f(1)=32．… ②若1≥3k ，即0<k ≤13时，f ′(x)>0恒成立，所以，f(x)的最大值为f(3k)=27(1+k)(1−k 2)． …综上，13≤k <1时，S 的最大值为32；0<k <13时，S 的最大值为27(1+k)(1−k 2)．【考点】导数在最大值、最小值问题中的应用【解析】（1）依题意，确定点C 的纵坐标、点B 的横坐标，从而利用梯形的面积公式，即可求得S 关于x 的函数式；（2）先确定函数关系式，再求导数，利用分类讨论的数学思想，确定函数的单调性，从而可求S 的最大值．【解答】解：（1）依题意，点C 的横坐标为x ，点C 的纵坐标为y C =−x 2+9．…点B 的横坐标x B 满足方程−x B 2+9=0，解得x B =3，舍去x B =−3． … 所以S =12(|CD|+|AB|)⋅y C =12(2x +2×3)(−x 2+9)=(x +3)(−x 2+9)．… 由点C 在第一象限，得0<x <3．所以S 关于x 的函数式为 S =(x +3)(−x 2+9)，0<x <3．…（2）由 {0<x <3x 3≤k 及0<k <1，得0<x ≤3k ． …记f(x)=(x +3)(−x 2+9)，0<x ≤3k ，则f ′(x)=−3x 2−6x +9=−3(x −1)(x +3)． …令f ′(x)=0，得x =1． …①若1<3k ，即13<k <1时，f ′(x)与f(x)的变化情况如下：f(1)=32．… ②若1≥3k ，即0<k ≤13时，f ′(x)>0恒成立，所以，f(x)的最大值为f(3k)=27(1+k)(1−k 2)． …综上，13≤k <1时，S 的最大值为32；0<k <13时，S 的最大值为27(1+k)(1−k 2)．【答案】（1）解：数列A:2，6，4不能结束，各数列依次为4，2，2；2，0，2；2，2，0；0，2，2；2，0，2；…．以下重复出现，所以不会出现所有项均为0的情形． …（2）解：(I)因为B 的各项之和为2012，且a ≥b ，所以a 为B 的最大项，所以|a 1−a 3|最大，即a 1≥a 2≥a 3，或a 3≥a 2≥a 1．… 当a 1≥a 2≥a 3时，可得{b =a 1−a 22=a 2−a 3a =a 1−a 3.由a +b +2=2012，得2(a 1−a 3)=2012，即a =1006，故b =1004．… 当a 3≥a 2≥a 1时，同理可得 a =1006，b =1004．…(II)方法一：由B:b ，2，b +2，则B 经过6次“T 变换”得到的数列分别为：b −2，b ，2；2，b −2，b −4；b −4，2，b −6；b −6，b −8，2；2，b −10，b −8；b −12，2，b −10．由此可见，经过6次“T 变换”后得到的数列也是形如“b ，2，b +2”的数列，与数列B “结构”完全相同，但最大项减少12．因为1006=12×83+10，所以，数列B 经过6×83=498次“T 变换”后得到的数列为8，2，10．接下来经过“T 变换”后得到的数列分别为：6，8，2；2，6，4；4，2，2；2，0，2；2，2，0；0，2，2；2，0，2，…从以上分析可知，以后重复出现，所以数列各项和不会更小．所以经过498+4=502次“T 变换”得到的数列各项和最小，k 的最小值为502．…方法二：若一个数列有三项，且最小项为2，较大两项相差2，则称此数列与数列B “结构相同”．若数列B 的三项为x +2，x ，2(x ≥2)，则无论其顺序如何，经过“T 变换”得到的数列的三项为x ，x −2，2（不考虑顺序）．所以与B 结构相同的数列经过“T 变换”得到的数列也与B 结构相同，除2外其余各项减少2，各项和减少4．因此，数列B:1004，2，1006经过502次“T 变换”一定得到各项为2，0，2（不考虑顺序）的数列．通过列举，不难发现各项为0，2，2的数列，无论顺序如何，经过“T 变换”得到的数列会重复出现，各项和不再减少．所以，至少通过502次“T 变换”，得到的数列各项和最小，故k 的最小值为502．… 【考点】递归数列及其性质数列的函数特性数列的求和【解析】（1）首先要弄清“T变换”的特点，其次要尝试着去算几次变换的结果，看一下有什么规律，显然只有当变换到数列的三项都相等时，再经过一次“T变换”才能得到数列的各项均为零，否则“T变换”不可能结束．（2）中(I)的解答要通过已知条件得出a是B数列的最大项，从而去掉绝对值符号得到数列A是单调数列，得到答案．(II)的解答要抓住B经过6次“T变换”后得到的数列也是形如“b，2，b+2”的数列，与数列B“结构”完全相同，且最大项减少12，从而数列和减少24，经过6×83+4=502次变换后使得各项的和最小，于是k的最小值为502．【解答】（1）解：数列A:2，6，4不能结束，各数列依次为4，2，2；2，0，2；2，2，0；0，2，2；2，0，2；…．以下重复出现，所以不会出现所有项均为0的情形．…（2）解：(I)因为B的各项之和为2012，且a≥b，所以a为B的最大项，所以|a1−a3|最大，即a1≥a2≥a3，或a3≥a2≥a1．…当a1≥a2≥a3时，可得{b=a1−a2 2=a2−a3 a=a1−a3.由a+b+2=2012，得2(a1−a3)=2012，即a=1006，故b=1004．…当a3≥a2≥a1时，同理可得a=1006，b=1004．…(II)方法一：由B:b，2，b+2，则B经过6次“T变换”得到的数列分别为：b−2，b，2；2，b−2，b−4；b−4，2，b−6；b−6，b−8，2；2，b−10，b−8；b−12，2，b−10．由此可见，经过6次“T变换”后得到的数列也是形如“b，2，b+2”的数列，与数列B“结构”完全相同，但最大项减少12．因为1006=12×83+10，所以，数列B经过6×83=498次“T变换”后得到的数列为8，2，10．接下来经过“T变换”后得到的数列分别为：6，8，2；2，6，4；4，2，2；2，0，2；2，2，0；0，2，2；2，0，2，…从以上分析可知，以后重复出现，所以数列各项和不会更小．所以经过498+4=502次“T变换”得到的数列各项和最小，k的最小值为502．…方法二：若一个数列有三项，且最小项为2，较大两项相差2，则称此数列与数列B“结构相同”．若数列B的三项为x+2，x，2(x≥2)，则无论其顺序如何，经过“T变换”得到的数列的三项为x，x−2，2（不考虑顺序）．所以与B结构相同的数列经过“T变换”得到的数列也与B结构相同，除2外其余各项减少2，各项和减少4．因此，数列B:1004，2，1006经过502次“T变换”一定得到各项为2，0，2（不考虑顺序）的数列．通过列举，不难发现各项为0，2，2的数列，无论顺序如何，经过“T变换”得到的数列会重复出现，各项和不再减少．所以，至少通过502次“T变换”，得到的数列各项和最小，故k的最小值为502．…。

2012届北京市高三一模文科数学分类汇编3：三角函数

2012北京市高三一模数学文分类汇编：三角函数【2012年北京市西城区高三一模文】11. 函数22sin 3cos y x x =+的最小正周期为_____．【答案】π【解析】函数x x y 2cos 2cos 212+=+=，所以周期为ππ=22。

【2012北京市门头沟区一模文】10. 在ABC ∆中，已知2=a ，3=b ，7=c ，则ABC ∆的面积是．【答案】233 【2012北京市门头沟区一模文】已知31)4tan(=-πα，则α2sin 等于(A)32(B)31 (C)54 (D)52 【答案】C【2012北京市海淀区一模文】（10）若tan 2α=，则sin 2α= . 【答案】45【2012北京市房山区一模文】12．已知函数()ϕω+=x x f sin )(（ω>0, 20πϕ<<）的图象如图所示，则ω=____，ϕ=___.【答案】2，3π【2012北京市东城区一模文】（6）已知sin(45)10α-=-，且090<<α，则cos α的值为（A ）513 （B ）1213 （C ） 35 （D ）45【答案】D【2012北京市朝阳区一模文】9.若sin θ=,(,)2θπ∈π，则tan θ= .【答案】【2012北京市石景山区一模文】3.函数1sin()y x π=+-的图象（）【答案】A【解析】函数x x y sin 1)sin(1+=-+=π的图象关于2π=x 对称，选A.【2012北京市石景山区一模文】15．（本小题满分13分）在ABC ∆中，角A ，B ，C 所对应的边分别为a ，b ，c ，且C b B c a c o s c o s )2(=-．（Ⅰ）求角B 的大小；（Ⅱ）若2,4==a A π，求ABC ∆的面积.【答案】解：（Ⅰ）∵ C b B c a cos cos )2(=-，由正弦定理，得∴ C B B C A cos sin cos )sin sin 2(=-． …………2分∴ A C B C B B C B A sin )sin(cos sin cos sin cos sin 2=+=+=，………4分 ∵ ()π，0∈A , ∴0sin ≠A ∴ 21cos =B ．又∵ π<<B 0 ， ∴ 3π=B ． …………6分（Ⅱ）由正弦定理BbA a sin sin =，得622232=⨯=b …………8分,43A B ππ==426sin +=∴C …………11分 A ．关于2x π=对称 B ．关于y 轴对称 C ．关于原点对称 D ．关于x π=对称2334266221s i n 21+=+⨯⨯⨯==∴C ab s ． …………13分【2012北京市朝阳区一模文】15. （本题满分13分）已知函数π()cos()4f x x =-. （Ⅰ）若3()5f α=，其中π3π,44α<<求πsin 4α⎛⎫- ⎪⎝⎭的值；（II ）设()()2g x f x f x π⎛⎫=⋅+⎪⎝⎭，求函数()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上的最大值和最小值. 【答案】解：（Ⅰ）因为π3()cos()45f αα=-=，且ππ042α<-<， …………1分所以π4sin 45α⎛⎫-= ⎪⎝⎭. .…………5分. （II ）()π()2g x f x f x ⎛⎫=⋅+⎪⎝⎭=ππcos()cos()44x x -⋅+=ππsin()cos()44x x +⋅+ =1πsin(2)22x +=1cos 22x . .…….…..10分当ππ,63x ⎡⎤∈-⎢⎥⎣⎦时，π2π2,33x ⎡⎤∈-⎢⎥⎣⎦. 则当0x =时，()g x 的最大值为12；当π3x =时，()g x 的最小值为14-. ………13分【2012北京市门头沟区一模文】15.（本小题满分13分）已知向量)1,(sin -=x a ，)2,cos 3(x b =，函数2)()(b a x f +=．（I ）求函数)(x f 的最小正周期；（II ）若]2,4[ππ-∈x ，求函数)(x f 的值域．【答案】解：（I ）由已知222)21()cos 3(sin )()(+-++=+=x x b a x f ……2分化简，得3)62sin(2)(++=πx x f……4分函数)(x f 的最小正周期ππ==22T……6分（II ）]2,4[ππ-∈x ，则67623πππ≤+≤-x ， ……8分所以1)62sin(23≤+≤-πx……10分函数)(x f 的值域是]5,33[-……13分【2012年北京市西城区高三一模文】15.（本小题满分13分）在△ABC 中，已知2sin cos sin()B A A C =+．（Ⅰ）求角A ；（Ⅱ）若2BC =，△ABC AB ．【答案】（Ⅰ）解：由πA B C ++=，得sin()sin(π)sin A C B B +=-=． ……3分所以原式化为B A B sin cos sin 2=． …………4分因为(0,π)B ∈，所以 0sin >B ，所以 21cos =A ． …………6分因为(0,π)A ∈，所以 π3A =． …………7分（Ⅱ）解：由余弦定理，得 222222cos BC AB AC AB AC A AB AC AB AC =+-⋅⋅=+-⋅．………9分因为 2BC =，1πsin 23AB AC ⋅⋅= 所以 228AB AC +=． …………11分因为 4AB AC ⋅=，所以 2AB =. ………13分【2012北京市海淀区一模文】（15）（本小题满分13分）已知函数()sin sin()3f x x x π=+-. （Ⅰ）求()f x 的单调递增区间；（Ⅱ）在ABC ∆中，角A ，B ，C 的对边分别为,,a b c . 已知()f A =a =，试判断ABC ∆的形状.【答案】解：（Ⅰ）()sin sin()3f x x x π=+-1sin sin 2x x x =+- ………………………………………2分3sin 22x x =-1cos 22x x ÷ç÷=-ç÷ç÷)6x π=-. ………………………………………4分由22,262k x k k πππππ-<-<+?Z ，得：222,33k x k k ππππ-<<+?Z . 所以 ()f x 的单调递增区间为2(2,2)33k k ππππ-+，k ÎZ . ………………………………………6分（Ⅱ）因为 ()2f A =，所以)6A π-=.所以1sin()62A π-=. ………………………………………7分因为 0A π<<，所以 5666A πππ-<-<. 所以 3A π=. ………………………………………9分因为 sin sin a bA B=，a =，所以 1sin 2B =. ………………………………………11分因为 a b >，3A π=，所以 6B π=.所以 2C π= .所以 ABC ∆为直角三角形. ………………………………………13分【2012北京市东城区一模文】（15）（本小题共13分）已知函数22()(sin2cos2)2sin 2f x x x x =+-. （Ⅰ）求()f x 的最小正周期；（Ⅱ）若函数()y g x =的图象是由()y f x =的图象向右平移8π个单位长度得到的，当x ∈[0,4π]时，求()y g x =的最大值和最小值.【答案】解：（Ⅰ）因为22()(sin 2cos2)2sin 2f x x x x =+-sin 4cos 4x x =+)4x π=+ , …………6分所以函数()f x 的最小正周期为2π. …………8分（Ⅱ）依题意,()y g x ==[4()8x π-4π+])4x π=-. …………10分因为04x π≤≤，所以34444x πππ-≤-≤. …………11分当442x ππ-=，即316x π=时，()g x当444x ππ-=-，即0x =时， ()g x 取最小值1-. …………13分【2012北京市房山区一模文】15．（本小题共13分）已知ABC △中，内角C B A ,,的对边分别为c b a ,,，且552c o s =A ，10103cos =B ．（Ⅰ）求()B A +cos 的值；（Ⅱ）设10=a ，求ABC △的面积．【答案】解：（Ⅰ）∵C B A ,,为ABC ∆的内角，且，552cos =A ，10103cos =B ∴555521cos 1sin 22=⎪⎪⎭⎫ ⎝⎛--=-=A A1010101031cos 1sin 22=⎪⎪⎭⎫ ⎝⎛-=-=B B ………………………………………4分∴()B A +cos B A B A sin cos cos +=10105510103552⨯-⨯=22=………………………………………7分（Ⅱ）由（I ）知， 45=+B A∴ 135=C ………………………………………8分 ∵10=a ，由正弦定理BbA a sin sin =得 555101010sin sin =⨯=⨯=A Ba b ……………………………………11分 ∴ABC S ∆252251021sin 21=⨯⨯⨯==C ab ……………………………………13分【2012北京市丰台区一模文】15．（本小题共13分）在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且sin cos cos .a B b C c B -= （I ）判断△ABC 的形状；（Ⅱ）若()sin cos f x x x =+，求f （A ）的最大值．【答案】。

北京西城区2012年高三一模文科数学试题

北京西城区2012年高三一模文科数学试题
2012年05月23日亲，很高兴访问《北京西城区2012年高三一模文科数学试题》一文，也欢迎您访问店铺（）的高考频道，为您精心准备了2012高考数学模拟题的相关模拟考试试题内容！同时，我们正在加紧建设高考频道，我们全体编辑的努力全是为了您，希望您能在本次高考中能获得好的名次，以及考上满意的大学，也希望我们准备的《北京西城区2012年高三一模文科数学试题》内容能帮助到您。

在即将到来的高考上助您一臂之力！加油，童鞋！
【店铺提供正确答案】。

2012年北京西城高考一模数学(文)

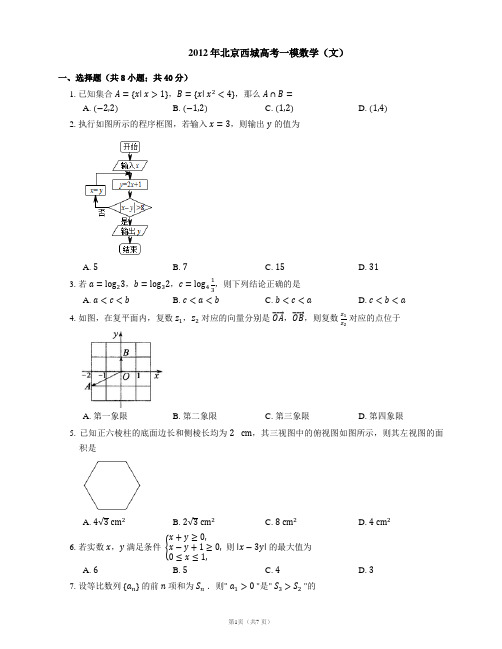
2012年北京西城高考一模数学（文）一、选择题（共8小题；共40分）1. 已知集合，，那么 ______A. B. C. D.2. 执行如图所示的程序框图，若输入，则输出的值为______A. B. C. D.3. 若，，，则下列结论正确的是______A. B. C. D.4. 如图，在复平面内，复数，对应的向量分别是，，则复数对应的点位于______A. 第一象限B. 第二象限C. 第三象限D. 第四象限5. 已知正六棱柱的底面边长和侧棱长均为，其三视图中的俯视图如图所示，则其左视图的面积是______A. B. C. D.6. 若实数，满足条件则的最大值为______A. B. C. D.7. 设等比数列的前项和为．则" "是" "的______A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分又不必要条件8. 已知集合，其中，且．则中所有元素之和是______A. B. C. D.二、填空题（共6小题；共30分）9. 已知向量，．若，则实数 ______．10. 某年级名学生在一次百米测试中，成绩全部介于秒与秒之间．将测试结果分成组：，，，，，得到如图所示的频率分布直方图．如果从左到右的个小矩形的面积之比为，那么成绩在的学生人数是______．11. 函数的最小正周期为______．12. 圆的圆心到直线的距离是______．13. 已知函数则的零点是______；的值域是______．14. 如图，已知抛物线及两点和，其中．过，分别作轴的垂线，交抛物线于，两点，直线与轴交于点，此时就称，确定了．依此类推，可由，确定，．记，．给出下列三个结论：①数列是递减数列；②对，；③若，，则．其中，所有正确结论的序号是______．三、解答题（共6小题；共78分）15. 在中，已知．（1）求角；（2）若，的面积是，求．16. 某校高一年级开设研究性学习课程，（1）班和（2）班报名参加的人数分别是和．现用分层抽样的方法，从中抽取若干名学生组成研究性学习小组，已知从（2）班抽取了名同学．（1）求研究性学习小组的人数；（2）规划在研究性学习的中、后期各安排次交流活动，每次随机抽取小组中名同学发言．求次发言的学生恰好来自不同班级的概率．17. 如图，矩形中，，，，分别在线段和上，，将矩形沿折起．记折起后的矩形为，且平面平面．（1）求证：平面；（2）若，求证：；（3）求四面体体积的最大值．18. 已知椭圆的离心率为，一个焦点为．（1）求椭圆的方程；（2）设直线交椭圆于，两点，若点，都在以点为圆心的圆上，求的值．19. 如图，抛物线与轴交于两点，，点，在抛物线上（点在第一象限），．记，梯形面积为．（1）求面积以为自变量的函数式；（2）若，其中为常数，且，求的最大值．20. 对于数列，定义“ 变换”：将数列变换成数列，其中，且．这种“ 变换”记作．继续对数列进行“ 变换”，得到数列，依此类推，当得到的数列各项均为时变换结束．（1）试问经过不断的“ 变换”能否结束?若能，请依次写出经过“ 变换”得到的各数列；若不能，说明理由；（2）设，．若，且的各项之和为．（i）求，；（ii）若数列再经过次变换”得到的数列各项之和最小，求的最小值，并说明理由．答案第一部分1. C2. D3. D4. B5. A6. B7. C8. C第二部分9.10.11.12.13. 和；14. ①②③第三部分15. （1）由，得由，得，解得因为，所以．（2）由余弦定理，得由及，得由的面积为，得即将代入，得联立，解得．16. （1）设从（）班抽取的人数为，依题意，得，解得．因此，研究性学习小组的人数为．（2）设研究性学习小组中（1）班的人为，，（2）班的人为，，．在次交流活动中，每次随机抽取名同学发言的基本事件为共种．其中次发言的学生恰好来自不同班级的基本事件为共种．所以次发言的学生恰好来自不同班级的概率为．17. （1）因为四边形，都是矩形，所以，，所以四边形是平行四边形，所以，因为平面，所以平面．（2）连接，设，平面平面，且，所以平面，所以，又，所以四边形为正方形，所以，所以平面，且ND在平面NED中，所以．（3）设，则，其中，由（Ⅰ）得平面，所以四面体的体积为，所以，当且仅当，即时，四面体的体积最大，最大值为．18. （1）设椭圆的半焦距为，则由，得，从而．所以，椭圆的方程为．（2）将直线的方程代入椭圆的方程，消去，得因为直线与椭圆有两个交点，所以解得．设，，则．设线段的中点为，则由点，都在以点为圆心的圆上，得，亦即解得，适合．所以．19. （1）依题意，点的横坐标、纵坐标分别为、．点的横坐标满足方程，解得，舍去．所以由点在第一象限，得．所以关于的函数式为，．（2）由及，得．记，则．令，得．由此，①若，即时，与的变化情况如下：极大值当时，取得最大值，且最大值为．②若，即时，恒成立，所以，的最大值为．综上，时，的最大值为；时，的最大值为．20. （1）数列不能结束，各数列依次为；；；；；．以下重复出现，所以不会出现所有项均为的情形．（2）（i）因为的各项之和为，且，所以为的最大项，所以最大，即，或．当时，可得由，得，即，故．当时，同理可得，．（ii）方法一：由，则经过次“ 变换”得到的数列分别为：；；；；；．由此可见，经过次“ 变换”后得到的数列也是形如“ ”的数列，与数列“结构”完全相同，但最大项减少．因为，所以，数列经过次“ 变换”后得到的数列为．接下来经过“ 变换”后得到的数列分别为：；；；；；；，．从以上分析可知，以后重复出现，所以数列各项和不会更小．所以经过次“ 变换”得到的数列各项和最小，的最小值为．方法二：若一个数列有三项，且最小项为，较大两项相差，则称此数列与数列“结构相同”．若数列的三项为，则无论其顺序如何，经过“ 变换”得到的数列的三项为（不考虑顺序）．所以与结构相同的数列经过“ 变换”得到的数列也与结构相同，除外其余各项减少，各项和减少．因此，数列经过次“ 变换”一定得到各项为（不考虑顺序）的数列．通过列举，不难发现各项为的数列，无论顺序如何，经过“ 变换”得到的数列会重复出现，各项和不再减少．所以，至少通过次“ 变换”，得到的数列各项和最小，故的最小值为．。

2012届北京市高三一模文科数学分类汇编3：三角函数

【2012北京市门头沟区一模文】10. 在ABC ∆中，已知2=a ，3=b ，7=c ，则ABC ∆的面积是．【答案】233【2012北京市门头沟区一模文】已知31)4tan(=-πα，则α2sin 等于(A)32 (B)31 (C) 54(D)52【答案】C【2012北京市海淀区一模文】（10）若tan 2α=，则sin 2α= .【答案】45【2012北京市房山区一模文】12．已知函数()ϕω+=x x f sin )(（ω>0, 20πϕ<<）的图象如图所示，则ω=____，ϕ=___.【答案】2，3π【2012北京市东城区一模文】（6）已知sin(45)10α-=-，且090<<α，则cos α的值为（A ）513（B ）1213（C ） 35（D ）45【答案】D【2012北京市朝阳区一模文】9.若sin 3θ=,(,)2θπ∈π，则tan θ= .【答案】2-【2012北京市石景山区一模文】3.函数1sin()y x π=+-的图象（）A ．关于2x π=对称 B ．关于y 轴对称 C ．关于原点对称 D ．关于x π=对称【答案】A【解析】函数x x y sin 1)sin(1+=-+=π的图象关于2π=x 对称，选A.【2012北京市石景山区一模文】15．（本小题满分13分）在A B C ∆中，角A ，B ，C 所对应的边分别为a ，b ，c ，且C b B c a cos cos )2(=-．（Ⅰ）求角B 的大小；（Ⅱ）若2,4==a A π，求ABC ∆的面积.【答案】解：（Ⅰ）∵ C b B c a cos cos )2(=-，由正弦定理，得∴ C B B C A cos sin cos )sin sin 2(=-． …………2分∴ A C B C B B C B A sin )sin(cos sin cos sin cos sin 2=+=+=，………4分 ∵ ()π，0∈A , ∴0sin ≠A ∴ 21cos =B ．又∵ π<<B 0 ， ∴ 3π=B ． …………6分（Ⅱ）由正弦定理Bb Aa sin sin =，得622232=⨯=b …………8分,43A B ππ==426sin +=∴C …………11分2334266221s i n 21+=+⨯⨯⨯==∴C ab s ． …………13分【2012北京市朝阳区一模文】15. （本题满分13分）已知函数π()cos()4f x x =-.（Ⅰ）若3()5f α=，其中π3π,44α<<求πsin 4α⎛⎫- ⎪⎝⎭的值；（II ）设()()2g x f x f x π⎛⎫=⋅+⎪⎝⎭，求函数()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上的最大值和最小值. 【答案】解：（Ⅰ）因为π3()cos()45f αα=-=，且ππ042α<-<， …………1分所以π4sin 45α⎛⎫-= ⎪⎝⎭. .…………5分. （II ）()π()2g x f x f x ⎛⎫=⋅+⎪⎝⎭=ππcos()cos()44x x -⋅+=ππsin()cos()44x x +⋅+=1πsin(2)22x +=1cos 22x . .…….…..10分当ππ,63x ⎡⎤∈-⎢⎥⎣⎦时，π2π2,33x ⎡⎤∈-⎢⎥⎣⎦.则当0x =时，()g x 的最大值为12；当π3x =时，()g x 的最小值为14-. ………13分【2012北京市门头沟区一模文】15.（本小题满分13分）已知向量)1,(sin -=x a，)2,cos 3(x b =，函数2)()(b a x f +=．（I ）求函数)(x f 的最小正周期；（II ）若]2,4[ππ-∈x ，求函数)(x f 的值域．【答案】解：（I ）由已知222)21()cos 3(sin )()(+-++=+=x x b a x f ……2分化简，得3)62sin(2)(++=πx x f……4分函数)(x f 的最小正周期ππ==22T ……6分（II ）]2,4[ππ-∈x ，则67623πππ≤+≤-x ， ……8分所以1)62sin(23≤+≤-πx……10分函数)(x f 的值域是]5,33[-……13分【2012年北京市西城区高三一模文】15.（本小题满分13分）在△ABC 中，已知2sin cos sin()B A A C =+．（Ⅰ）求角A ；（Ⅱ）若2B C =，△ABC ，求A B ．【答案】（Ⅰ）解：由πA B C ++=，得sin()sin(π)sin A C B B +=-=． ……3分所以原式化为B A B sin cos sin 2=． …………4分因为(0,π)B ∈，所以 0sin >B ，所以 21cos =A ． …………6分因为(0,π)A ∈，所以 π3A =． …………7分（Ⅱ）解：由余弦定理，得 222222cos BC AB AC AB AC A AB AC AB AC =+-⋅⋅=+-⋅．………9分因为 2B C =，1πsin23A B A C ⋅⋅=所以 228AB AC +=． …………11分因为 4A B A C ⋅=，所以 2A B =. ………13分【2012北京市海淀区一模文】（15）（本小题满分13分）已知函数()sin sin()3f x x x π=+-.（Ⅰ）求()f x 的单调递增区间；（Ⅱ）在A B C ∆中，角A ，B ，C 的对边分别为,,a b c . 已知()2f A =，a =，试判断A B C ∆的形状.【答案】解：（Ⅰ）()sin sin()3f x x x π=+-1sin sin cos 22x x x =+- ………………………………………2分3sin 22x x =-1cos 22x x ÷÷=-÷÷)6x π=-. ………………………………………4分由22,262k x k k πππππ-<-<+Z ，得：222,33k x k k ππππ-<<+ Z . 所以 ()f x 的单调递增区间为2(2,2)33k k ππππ-+，k ÎZ .………………………………………6分（Ⅱ）因为 ()2f A =，所以 )62A π-=.所以1sin()62A π-=.………………………………………7分因为 0A π<<，所以 5666A πππ-<-<.所以 3A π=. ………………………………………9分因为sin sin a b AB =，a =，所以 1sin 2B =. ………………………………………11分因为 a b >，3A π=，所以 6B π=.所以 2C π=.所以 A B C ∆为直角三角形. ………………………………………13分【2012北京市东城区一模文】（15）（本小题共13分）已知函数22()(sin2cos2)2sin 2f x x x x =+-.（Ⅰ）求()f x 的最小正周期；（Ⅱ）若函数()y g x =的图象是由()y f x =的图象向右平移8π个单位长度得到的，当x ∈[0,4π]时，求()y g x =的最大值和最小值.【答案】解：（Ⅰ）因为22()(sin 2cos 2)2sin 2f x x x x =+-sin 4cos 4x x =+)4x π=+, …………6分所以函数()f x 的最小正周期为2π. …………8分（Ⅱ）依题意,()y g x ==[4()8x π-4π+])4x π=-. …………10分因为04x π≤≤，所以34444x πππ-≤-≤. …………11分当442x ππ-=，即316x π=时，()g x当444x ππ-=-，即0x =时， ()g x 取最小值1-. …………13分【2012北京市房山区一模文】15．（本小题共13分）已知A B C △中，内角C B A ,,的对边分别为c b a ,,，且552cos =A ，10103cos =B ．（Ⅰ）求()B A +cos 的值；（Ⅱ）设10=a ，求A B C △的面积．【答案】解：（Ⅰ）∵C B A ,,为ABC ∆的内角，且，552cos =A ，10103cos =B∴555521cos1sin 22=⎪⎪⎭⎫ ⎝⎛--=-=A A1010101031cos1sin 22=⎪⎪⎭⎫⎝⎛-=-=B B ………………………………………4分∴()B A +cos B A B A sin cos cos +=10105510103552⨯-⨯=22=………………………………………7分（Ⅱ）由（I ）知，45=+B A∴ 135=C ………………………………………8分 ∵10=a ，由正弦定理Bb Aa sin sin =得555101010sin sin =⨯=⨯=AB a b ……………………………………11分∴ABC S ∆252251021sin 21=⨯⨯⨯==C ab ……………………………………13分【2012北京市丰台区一模文】15．（本小题共13分）在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，且sin cos cos .a B b C c B -= （I ）判断△ABC 的形状；（Ⅱ）若()sin cos f x x x =+，求f （A ）的最大值．【答案】。

北京市西城区2012届高三上学期期末教学统一检测数学(文科)

北京市西城区 2011 — 2012 学年度第一学期期末试卷高三数学（文科）2012.1第Ⅰ卷（选择题共40分）一、选择题共8 小题，每题 5 分，共 40 分.在每题列出的四个选项中，选出切合题目要求的一项 .1．复数i (1i) （）（ A）1 i（ B）1 i（ C）1 i（ D）1 i 2．若向量a( 3,1) ，b(0, 2) ，则与a2b共线的向量能够是（）（A）(3, 1)（B）(1, 3)（C）(3, 1)（D）(1,3)3. 以下函数中，既是偶函数又在(0, ) 单一递加的函数是（）（ A）y1（ B）y e|x|x（ C）y x23（ D）y cosx4．“直线l的方程为x y 0 ”是“直线 l 均分圆x2y21的周长”的（）（ A）充足而不用要条件（B）必需而不充足条件（ C）充要条件（D）既不充足又不用要条件5．一个几何体的主视图和左视图以下图，则这个几何体的俯视图不行能是（）．．．主视图左视图（A）（B）（C）（D）6．履行以下图的程序框图，输出的S 值为（）（A）3（B）6（C）10（D）157．已知a b 0 ，给出以下四个不等式：① a2b2；②2a2b 1；③ a b ab ；④ a3b32a2b ．此中必定建立的不等式为（）（ A）①、②、③（ B）①、②、④（ C）①、③、④（ D）②、③、④8 ．有限会合P 中元素的个数记作card(P).已知card( M )10，A M ， B M，A B，且 card( A) 2 ，card( B)3. 若会合X知足X M，且A X ，B X，则会合X的个数是（）（ A）672（B）640（C）384（D）352第Ⅱ卷（非选择题共 110 分）二、填空题共 6 小题，每题 5 分，共 30 分.9．函数 f ( x)log 2 x 的定义域是______.x2y210．双曲线 1 的一个焦点到其渐近线的距离是______．16 911．若曲线y x3ax 在原点处的切线方程是2x y 0 ，则实数 a______．12ABC中，三个内角A，B，C的对边分别为 a ，b， c ．若 b 5 ，B，．在△tan C 2 ，则 c4 ______ ．13．已知{ a n}是公比为2 的等比数列，若a3 a1 6 ，则 a1；111______．a12a22a n2x2,14．设0 ，不等式组x y0,所表示的平面地区是W ．给出以下三个结论：x2y0① 当1时， W 的面积为 3 ；②0 ，使 W 是直角三角形地区；③设点 P(x, y) ,关于P W 有x y4 ．此中，全部正确结论的序号是______．三、解答题共 6 小题，共 80分 . 解答应写出文字说明，演算步骤或证明过程.15. （本小题满分 13分）已知函数 f ( x) 3 sin2xπsin x cos x ， x [ , π] .22π（Ⅰ）求 f () 的值；3（Ⅱ）求 f ( x) 的最大值和最小值.16.（本小题满分 13 分）某种部件按质量标准分为1,2,3,4,5 五个等级.现从一批该部件中随机抽取20 个，对其等级进行统计剖析，获得频次散布表以下：等级频次12345 0.05m0.150.35n（Ⅰ）在抽取的20 个部件中，等级为 5 的恰有 2 个，求 m, n ；（Ⅱ）在（Ⅰ）的条件下，从等级为 3 和 5 的全部部件中，随意抽取2个，求抽取的2 个零件等级恰巧同样的概率.17．（本小题满分14 分）如图，正三棱柱ABC A1 B1C1的侧棱长和底面边长均为 2 ， D 是 BC 的中点．（Ⅰ）求证：AD平面B1BCC1；（Ⅱ）求证：A1 B ∥平面 ADC 1；（Ⅲ）求三棱锥C1ADB 1的体积．18.（本小分 13 分）已知函数f ( x)1a x2ln x ，此中 a R.2（Ⅰ）求 f ( x) 的区；（Ⅱ）若 f ( x) 在 (0,1] 上的最大是1，求a的.19.（本小分 14 分）已知 C : x2y21 221 (a b 0) 的一个焦点是 F (1,0) ，且离心率.a b2（Ⅰ）求 C 的方程；（Ⅱ）点 F 的直交 C 于M , N两点，段 MN 的垂直均分交y 于点P(0, y0 ) ，求 y0的取范.20.（本小分 13 分）已知数列A n: a1, a2 ,,a n.假如数列B n: b1,b2 ,, b n足b1a n， b k a k 1a k b k 1，此中k2,3,, n，称B n A n的“衍生数列”.（Ⅰ）写出数列A4: 2,1,4,5的“衍生数列”B4；（Ⅱ）若n 偶数，且A n的“衍生数列”是B n，明：b n a1；（Ⅲ）若n 奇数，且A n的“衍生数列”是B n，B n的“衍生数列”是 C n，⋯.挨次将数列 A n， B n， C n，⋯的首拿出，组成数列: a1 ,b1, c1 ,.明：是等差数列.北京市西城区 2011 — 2012 学年度第一学期期末高三数学（文科）参照答案及评分标准2012.1一、：本大共8 小，每小 5 分，共 40 分 .1.C；2. D；3.B；4. A；5. D；6. C；7.A；8. A.二、填空：本大共 6 小，每小 5 分，共30 分.9.{ x | x 1} ；10. 3；11.2 ；12. 2 2 ；13. 2，1(1 4 n ) ；14.①、③ . 3注： 13 第一 2 分，第二 3 分； 14 多、少、均不分.三、解答：本大共 6 小，共 80分 . 若考生的解法与本解答不一样，正确者可参照分准分 .15.（本小分 13 分）（Ⅰ）解： f (2π3 sin 22π2π 2π 3 333⋯⋯⋯⋯⋯⋯ 4 分)3sin3cos344.32（Ⅱ）解： f ( x)31sin 2 x sin(2 xπ3⋯⋯⋯⋯⋯⋯ 8 分（1 cos2x）2).232因 xππ 2π 5π⋯⋯⋯⋯⋯⋯ 9 分[, π]，因此 2 x[,] .2333当 2 xπ 2ππ3 ；⋯⋯⋯⋯⋯⋯ 11 分3，即 x， f ( x) 的最大32当 2 x π 3π11π13⋯⋯⋯⋯⋯⋯ 13 分3，即 x12， f ( x) 的最小.2216.（本小分 13 分）（Ⅰ）解：由率散布表得0. 0 5 m0. 1 5 0.n3 5 ，即 m n0.45.⋯⋯⋯⋯⋯⋯ 2 分由抽取的20 个部件中，等5的恰有 2个，得 n20.1.⋯⋯⋯⋯⋯⋯ 4 分20因此 m0.45 0.10.35.⋯⋯⋯⋯⋯⋯ 5 分（Ⅱ）解：由（Ⅰ）得，等 3 的部件有 3 个，作x1, x2, x3；等 5 的部件有 2 个，作 y1, y2.从 x1, x2 , x3, y1 , y2中随意抽取 2 个部件，全部可能的果：( x1, x2 ),( x1 , x3 ),( x1, y1 ),( x1, y2 ),( x2 , x3 ),( x2 , y1 ),( x2 , y2 ),( x3 , y1 ),( x3, y2 ),( y1, y2 )共 10种.⋯⋯⋯⋯⋯⋯ 9 分事件 A“从部件x1, x2 , x3 , y1, y2中任取2 件，其等相等”.A 包括的基本领件( x1, x2 ),( x1, x3 ),( x2 , x3 ),( y1, y2 ) 共4个.⋯⋯⋯⋯⋯⋯ 11 分故所求概率 P( A)4⋯⋯⋯⋯⋯⋯ 13 分0.4 .1017.（本小分 14 分）（Ⅰ）明：因ABC A1 B1C1是正三棱柱，因此CC1平面ABC.又 AD 平面 ABC，因此CC1AD.⋯⋯⋯⋯⋯⋯ 3 分因△ABC 是正三角形， D 是 BC 的中点，因此因此BCADAD ，平面 B1 BCC1.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分5 分（Ⅱ）明：A1C，交AC1于点O ，OD .由 ABC A1 B1C1是正三棱柱，得四形 ACC1 A1矩形，O A1C 的中点.又 D BC 中点，因此 OD △A1BC中位，因此A1B∥OD，⋯⋯⋯⋯⋯⋯ 8分因OD平面 ADC1， A1B平面 ADC1，因此A1B ∥平面 ADC1.⋯⋯⋯⋯⋯⋯ 10 分（Ⅲ）解：因V C1ADB1 V A B1DC1，⋯⋯⋯⋯⋯⋯ 12分因此 V C1ADB1S BDC1AD 2 3.⋯⋯⋯⋯⋯⋯ 14 分131318.（本小分13 分）（Ⅰ）解： f( x)ax 2 1 ,x(0,) .⋯⋯⋯⋯⋯⋯ 3 分x当 a0 ，f( x) 0 ，进而函数 f (x) 在 (0,) 上增.⋯⋯⋯⋯⋯⋯ 4 分当 a0 ，令f(x)0，解得 x 11⋯⋯⋯⋯⋯⋯ 5 分，舍去 x.a a此， f ( x) 与 f(x) 的状况以下：x11(1 (0,)a, )a af( x)0f (x)↗ f ( 1 )↘a因此， f ( x) 的增区是(0,1) ；减区是(1).⋯⋯⋯⋯7分a,a（Ⅱ）① 当 a0 ，由（Ⅰ）得函数 f ( x) 在 (0,1]上的最大 f (1)a.令a21，得 a2，与 a0矛盾，舍去 a 2.⋯⋯⋯⋯⋯⋯ 9 分2② 当1a0 ，11，由（Ⅰ）得函数 f (x) 在(0,1]上的最大 f (1)a a.2令a1，得 a2，与1a0矛盾，舍去 a2.⋯⋯⋯⋯⋯⋯ 10 分2③当 a1，011，由（Ⅰ）得函数 f (x) 在(0,1]上的最大 f (1 ) .a a令 f (11 ，解得 a e，合适a1.⋯⋯⋯⋯⋯⋯ 12 分)a上，当 f ( x) 在 (0,1] 上的最大是， a e.⋯⋯⋯⋯⋯⋯ 13 分119.（本小分 14 分）（Ⅰ）解： C 的半焦距是c.依意，得 c 1 .⋯⋯⋯⋯⋯⋯1分因 C 的离心率 1 ，2因此 a2c 2 ，b2a2c23.⋯⋯⋯⋯⋯⋯ 3 分故 C 的方程x2y2⋯⋯⋯⋯⋯⋯ 4 分41.3（Ⅱ）解：当 MN x ，然y00 .⋯⋯⋯⋯⋯⋯ 5 分当 MN 与x不垂直，可直MN 的方程y k ( x1) (k0).y k( x1),消去 y 整理得(3 4k2) x28k 2 x4(k 23)0 .由4 y3x22 12,⋯⋯⋯⋯⋯⋯ 7 分M ( x1 , y1), N ( x2 , y2 ) ，段MN的中点 Q( x3 , y3 ) .x1x28k 2.4k2 3因此x1x24k2， y3k (x31)3kx334k24k23⋯⋯⋯⋯⋯⋯ 8 分2.段 MN 的垂直均分方程y33k21( x4k 22). 4k k 3 4k在上述方程中令x0 ，得y0k1⋯⋯⋯⋯⋯⋯ 10 分34k 2.34kk当 k0，34k 4 3 ；当 k0 ，34k 4 3 . k k30，或 0y03.⋯⋯⋯⋯⋯⋯ 12 分因此y012 12上， y0的取范是 [ 3 ,3] .⋯⋯⋯⋯⋯⋯ 13 分121220. （本小分 13 分）（Ⅰ）解： B4 : 5, 2,7, 2 .⋯⋯⋯⋯⋯⋯ 3 分（Ⅱ）明：因 b1a n，b1 b2a1a2，b2b3a2a3，⋯⋯bn 1b n an 1a n，因为 n 偶数，将上述n 个等式中的第 2,4,6,,n n个式子都乘以1，相加得2b1 (b1b2 ) (b2b3 )(b n 1b n ) a n(a1a2 ) (a2a3 )(a n 1a n )即 b n a1， b n a1.⋯⋯⋯⋯⋯⋯ 8 分（Ⅲ）明：于数列A n及其“衍生数列”B n，因 b1a n，b1b2a1a2，b2b3a2a3，⋯⋯b n 1b n a n 1a n，因为 n 奇数，将上述 n个等式中的第 2,4,6,, n n 1个式子都乘以1，12相加得b1 (b1b2 ) (b2b3 )(b n 1b n ) a n(a1a2 ) (a2a3 )(a n 1a n )即 b n a n a1a n2a n a1.数列 B n的“衍生数列” C n，因 b1a n， c1b n2a n a1，因此 2b1a1c1，即 a1 ,b1, c1成等差数列.⋯⋯⋯⋯⋯⋯ 12 分同理可， b1 , c1 ,d1 ; c1, d1 ,e1,也成等差数列.进而是等差数列 .⋯⋯⋯⋯⋯⋯13 分。

2012届北京市高三一模文科数学分类汇编5：立体几何

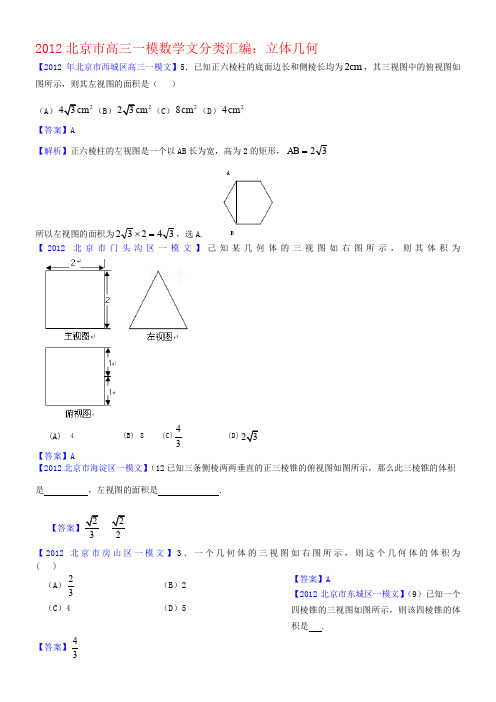
2012北京市高三一模数学文分类汇编：立体几何【2012年北京市西城区高三一模文】5．已知正六棱柱的底面边长和侧棱长均为2cm ，其三视图中的俯视图如图所示，则其左视图的面积是（）（A）2（B）2（C ）28cm （D ）24cm【答案】A【解析】正六棱柱的左视图是一个以AB 长为宽，高为2的矩形，32=AB所以左视图的面积为34232=⨯，选 A.【2012北京市门头沟区一模文】己知某几何体的三视图如右图所示，则其体积为(A)【答案】A【2012北京市海淀区一模文】（12已知三条侧棱两两垂直的正三棱锥的俯视图如图所示，那么此三棱锥的体积是，左视图的面积是 .【答案】3 2【2012北京市房山区一模文】3．一个几何体的三视图如右图所示，则这个几何体的体积为( )【答案】A 【2012北京市东城区一模文】（9）已知一个四棱锥的三视图如图所示，则该四棱锥的体积是 .【答案】43（A ）32 （B ）2（C ）4（D ）5【2012北京市朝阳区一模文】10.已知某几何体的三视图如图所示，则该几何体的体积为 . 【答案】32【2012北京市朝阳区一模文】5. 关于两条不同的直线m ,n 与两个不同的平面α,β，下列命题正确的是 A ．βα//,//n m 且βα//，则n m // B ．βα⊥⊥n m ,且βα⊥，则m //n C ．βα//,n m ⊥且βα//，则n m ⊥D ．βα⊥n m ,//且βα⊥，则n m //【答案】C【2012北京市丰台区一模文】4．若某空间几何体的三视图如图所示，则该几何体的体积是（）A ．202π-B ．2203π-C ．2403π-D ．4403π-【答案】B【2012北京市石景山区一模文】4.设n m ,是两条不同的直线，γβα,,是三个不同的平面，下列命题正确的是（）A ．αα//,//,//n m n m 则若B ．βαγβγα//,,则若⊥⊥C ．n m n m //,//,//则若ααD ．n m n m ⊥⊥则若,//,αα【答案】D【解析】根据线面垂直的性质可知选项D 正确。

2012北京市西城高考一模试题及答案%28文科全套%29

第一部分（选择题，共27分）一、本大题共5小题，每小题3分，共15分。

1．下列词语中，字形和加点的字的读音全都正确的一项是A.化妆品寥若辰星标识（shí）心广体胖（pán）B.孰不知相辅相成着（zhāo）急发生口角（jué）C.荧光屏贸然行事揩（kāi）油犯罪未遂（suì）D.流水账鞭辟入理结束（shù）量体裁衣（liáng）2．下列句子中，加点的成语使用正确的一项是A. 李实哲是个胸无城府的天才棋手，围棋下得出神入化，在出席新闻发布会时却常常出言无忌，因为自己的直率他付出过不少代价。

B. 足坛反赌扫黑接近尾声，对于涉嫌行贿的俱乐部是否会受处罚，足协一位官员的表态似是而非：“一切要等审判结束后才有结果。

”C. 上海的婚宴普遍在晚上举行，一般选择在吉时6：08开宴，可是总有些接到请柬的不速之客姗姗来迟，这让婚宴主办者颇为尴尬。

D. 部分司机认为高速公路宽阔，只要车少就可天马行空地自由驰骋，其实这种想法十分危险，因为人在大意时反应速度会大大降低。

3．下列句子中，没有语病的一句是A. 近日，美国宇航局的探测器有史以来第一次直接探测到的来自太阳系之外的粒子，这一发现首次让我们有机会一窥所谓的“恒星际介质”。

B. 今年，北京将新增20万亩林地，主要种植在受污染物影响较大的地方，如高速路或主干道的路边，对尾气削减和扬尘会有很好的作用。

C. “1·28”中国公民被劫持事件发生后，苏丹政府全力解救，并表态将采取切实措施确保所有在苏中资企业的安全，避免类似事件不再发生。

D. 进城务工人员子女在流入地学习多年后回乡参加高考，很难适应家乡的考试要求，据悉，我国将出台允许这类考生在流入地参加高考的政策。

届北京西城区高三数学文科一模试卷及答案

北京市西城区2012 — 2013学年度第一学期期末试卷高三数学（文科） 2013.1第Ⅰ卷（选择题共40分）一、选择题：本大题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．已知集合{|01}A x x =∈<<R ，{|(21)(1)0}B x x x =∈-+>R ，则A B =（）（A ）1(0,)2（B ）1(,1)2（C ）1(,1)(0,)2-∞- （D ）1(,1)(,1)2-∞- 2．复数5i2i=+（）（A ）12i + （B ）12i -+（C ）12i --（D ）12i -3．执行如图所示的程序框图，则输出S =（）（A ）2 （B ）6 （C ）15 （D ）314．函数1()ln f x x x=-的零点个数为（）（A ）0 （B ）1（C ）2（D ）35．某四棱锥的三视图如图所示，该四棱锥的体积是（）（A ）（B ）（C ）3 （D6．过点(2,0)M 作圆221x y +=的两条切线MA ，MB (A ，B 为切点)，则MA MB ⋅=（）（A （B ）52（C （D ）327．设等比数列{}n a 的公比为q ，前n 项和为n S ．则“||q =627S S =”的（）（A ）充分而不必要条件（B ）必要而不充分条件（C ）充分必要条件（D ）既不充分也不必要条件8．已知函数()f x 的定义域为R ．若∃常数0c >，对x ∀∈R ，有()()f x c f x c +>-，则称函数()f x 具有性质P ．给定下列三个函数：①()||f x x =； ②()sin f x x =； ③3()f x x x =-．其中，具有性质P 的函数的序号是（）（A ）① （B ）③（C ）①②（D ）②③第Ⅱ卷（非选择题共110分）二、填空题：本大题共6小题，每小题5分，共30分．9．已知向量(1,3)=a ，(,21)m m =-b ．若向量a 与b 共线，则实数m =______．10．平行四边形ABCD 中，E 为CD 的中点．若在平行四边形ABCD 内部随机取一点M ，则点M 取自△ABE 内部的概率为______．11．双曲线2213645x y -=的渐近线方程为______；离心率为______．12．若函数2log ,0,()(),0x x f x g x x >⎧=⎨<⎩是奇函数，则(8)g -=______．13．已知函数π()sin()6f x x =+，其中π[,]3x a ∈-．当2a π=时，()f x 的值域是______；若()f x 的值域是1[,1]2-，则a 的取值范围是______．14．设函数2()65f x x x =-+，集合{(,)|()()0A a b f a f b =+≤，且()()0}f a f b -≥．在直角坐标系aOb 中，集合A 所表示的区域的面积为______．三、解答题：本大题共6小题，共80分．解答应写出必要的文字说明、证明过程或演算步骤．15．（本小题满分13分）在△ABC 中，内角,,A B C 的对边分别为,,a b c ，且cos2cos 0B B +=．（Ⅰ）求角B 的值；（Ⅱ）若b =5a c +=，求△ABC 的面积．16．（本小题满分13分）为了解学生的身体状况，某校随机抽取了一批学生测量体重．经统计，这批学生的体重数据（单位：千克）全部介于45至70之间．将数据分成以下5组：第1组[4550)，，第2组[5055)，，第3组[5560)，，第4组[6065)，，第5组[6570]，，得到如图所示的频率分布直方图．现采用分层抽样的方法，从第3，4，5组中随机抽取6名学生做初检．（Ⅰ）求每组抽取的学生人数；（Ⅱ）若从6名学生中再次随机抽取2名学生进行复检，求这2名学生不在同一组的概率．17．（本小题满分14分）如图，直三棱柱111C B A ABC -中，BC AC ⊥，21===CC BC AC ，M ，N 分别为AC ，11C B 的中点．（Ⅰ）求线段MN 的长；（Ⅱ）求证：MN //平面11A ABB ；（Ⅲ）线段1CC 上是否存在点Q ，使⊥B A 1平面MNQ ？说明理由．18．（本小题满分13分）已知函数2()xf x x b=+，其中b ∈R ．（Ⅰ）若1x =-是)(x f 的一个极值点，求b 的值；（Ⅱ）求)(x f 的单调区间．19．（本小题满分14分）如图，A ，B 是椭圆22221x y a b+=(0)a b >>的两个顶点．||AB =AB 的斜率为12-．（Ⅰ）求椭圆的方程；（Ⅱ）设直线l 平行于AB ，与,x y 轴分别交于点,M N ，与椭圆相交于,C D ．证明：△OCM的面积等于△ODN 的面积．20．（本小题满分13分）如图，设A 是由n n ⨯个实数组成的n 行n 列的数表，其中ij a (,1,2,3,,)i j n =表示位于第i 行第j 列的实数，且{1,1}ij a ∈-．记(,)S n n 为所有这样的数表构成的集合．对于(,)A S n n ∈，记()i r A 为A 的第i 行各数之积，()j c A 为A 的第j 列各数之积．令11()()()n ni j i j l A r A c A ===+∑∑．（Ⅰ）对如下数表(4,4)A S ∈，求()l A 的值；（Ⅱ）证明：存在(,)A S n n ∈，使得()24l A n k =-，其中0,1,2,,k n =；（Ⅲ）给定n 为奇数，对于所有的(,)A S n n ∈，证明：()0l A ≠．北京市西城区2012 — 2013学年度第一学期期末高三数学（文科）参考答案及评分规范2013.1一、选择题：本大题共8小题，每小题5分，共40分.1．B ； 2．A ； 3．C ； 4．B ； 5．C ； 6．D ； 7．A ； 8．B ．二、填空题：本大题共6小题，每小题5分，共30分.9．1-； 10．12；11．2y x =±，32； 12．3-； 13．1[,1]2-，[,]3ππ； 14．4π．注：11、13题第一空2分，第二空3分.三、解答题：本大题共6小题，共80分.若考生的解法与本解答不同，正确者可参照评分规范给分.15．（本小题满分13分）（Ⅰ）解：由已知得 22cos cos 10B B +-=， ………………2分即 (2cos 1)(cos 1)0B B -+=．解得 1cos 2B =，或cos 1B =-． ………………4分因为 0πB <<，故舍去cos 1B =-．………………5分所以 π3B =． ………………6分（Ⅱ）解：由余弦定理得 2222cos b a c ac B =+-． ………………8分将π3B =，b =代入上式，整理得2()37a c ac +-=．因为5a c +=，所以 6ac =． ………………11分所以 △ABC 的面积1sin 22S ac B ==．………………13分16．（本小题满分13分）（Ⅰ）解：由频率分布直方图知，第3，4，5组的学生人数之比为3:2:1．…………2分所以，每组抽取的人数分别为：第3组：3636⨯=；第4组：2626⨯=；第5组：1616⨯=．所以从3，4，5组应依次抽取3名学生，2名学生，1名学生． ………………5分（Ⅱ）解：记第3组的3位同学为1A ，2A ，3A ；第4组的2位同学为1B ，2B ；第5组的1位同学为C ． ………………6分则从6位同学中随机抽取2位同学所有可能的情形为：121311121232122231(,),(,),(,),(,),(,),(,),(,),(,),(,),(,),A A A A A B A B A C A A A B A B A C A B 3231212(,),(,),(,),(,),(,)A B A C B B B C B C ，共15种可能．………………10分其中，111212122231323(,),(,),(,),(,),(,),(,),(,),(,),(,),A B A B A C A B A B A C A B A B A C12(,),(,)B C B C 这11种情形符合2名学生不在同一组的要求．………………12分故所求概率为1115P =． ………………13分17．（本小题满分14分）（Ⅰ）证明：连接CN ．因为 111C B A ABC -是直三棱柱，所以 ⊥1CC 平面ABC ， ………………1分所以 1AC CC ⊥． ………………2分因为 BC AC ⊥，所以 ⊥AC 平面11BCC B ． ………………3分因为 1=MC ，CN ==，所以 6=MN ． ………………4分（Ⅱ）证明：取AB 中点D ，连接DM ，1DB ． ………………5分在△ABC 中，因为 M 为AC 中点，所以BC DM //，BC DM 21=．在矩形11B BCC 中，因为 N 为11C B 中点，所以BC N B //1，BC N B 211=．所以 N B DM 1//，N B DM 1=．所以四边形N MDB 1为平行四边形，所以 1//DB MN ．………………7分因为 ⊄MN 平面11A ABB ，⊂1DB 平面11A ABB ， ………………8分所以 MN // 平面11A ABB ．………………9分（Ⅲ）解：线段1CC 上存在点Q ，且Q 为1CC 中点时，有⊥B A 1平面MNQ ．………11分证明如下：连接1BC ．在正方形C C BB 11中易证 1BC QN ⊥．又⊥11C A 平面C C BB 11，所以 QN C A ⊥11，从而⊥NQ 平面11BC A ．…………12分所以 1A B QN ⊥． ………………13分同理可得 1A B MQ ⊥，所以⊥B A 1平面MNQ ．故线段1CC 上存在点Q ，使得⊥B A 1平面MNQ ．………………14分18．（本小题满分13分）（Ⅰ）解：222()()b x f x x b -'=+．………………2分依题意，令(1)0f '-=，得 1b =．………………4分经检验，1b =时符合题意．………………5分（Ⅱ）解：① 当0b =时，1()f x x=．故()f x 的单调减区间为(,0)-∞，(0,)+∞；无单调增区间．………………6分② 当0b >时，222()()b x f x x b -'=+．令()0f x '=，得1x =，2x =8分()f x 和()f x '的情况如下：故()f x 的单调减区间为(,-∞，)+∞；单调增区间为(．………………11分③ 当0b <时，()f x 的定义域为{|D x x =∈≠R ．因为222()0()b x f x x b -'=<+在D 上恒成立，故()f x 的单调减区间为(,-∞，(，)+∞；无单调增区间．………………13分19．（本小题满分14分）（Ⅰ）解：依题意，得 1,2b a ⎧=⎪=………………2分解得 2a =，1b =． ………………3分所以椭圆的方程为2214x y +=． ………………4分（Ⅱ）证明：由于l //AB ，设直线l 的方程为12y x m =-+，将其代入2214x y +=，消去y ，整理得2224440x mx m -+-=． ………………6分设11(,)C x y ，22(,)D x y ．所以 22122121632(1)0,2,2 2.m m x x m x x m ⎧∆=-->⎪+=⎨⎪=-⎩………………8分证法一：记△OCM 的面积是1S ，△ODN 的面积是2S ．由(2,0)M m ，(0,)N m ，则12S S =⇔1211|2|||||||22m y m x ⨯⨯=⨯⨯⇔12|2|||y x =． ………………10分因为 122x x m +=，所以 11121|2||2()||2|||2y x m x m x =⨯-+=-+=， ………………13分从而12S S =． ………………14分证法二：记△OCM 的面积是1S ，△ODN 的面积是2S ．则12S S =⇔||||MC ND =⇔线段,CD MN 的中点重合．………………10分因为 122x x m +=，所以122x x m +=，1212112222y y x x m m ++=-⋅+=．故线段CD 的中点为1(,)2m m ．因为 (2,0)M m ，(0,)N m ，所以线段MN 的中点坐标亦为1(,)2m m ． ………………13分从而12S S =． ………………14分20．（本小题满分13分）（Ⅰ）解：134()()()1r A r A r A ===，2()1r A =-；124()()()1c A c A c A ===-，3()1c A =，所以4411()()()0i j i j l A r A c A ===+=∑∑． ………………3分（Ⅱ）证明：（ⅰ）对数表0A ：1ij a =(,1,2,3,,)i j n =，显然0()2l A n =．将数表0A 中的11a 由1变为1-，得到数表1A ，显然1()24l A n =-．将数表1A 中的22a 由1变为1-，得到数表2A ，显然2()28l A n =-．依此类推，将数表1k A -中的kk a 由1变为1-，得到数表k A ．即数表k A 满足：11221(1)kk a a a k n ====-≤≤，其余1ij a =．所以 12()()()1k r A r A r A ====-，12()()()1k c A c A c A ====-．所以 ()2[(1)()]24k l A k n k n k =-⨯+-=-，其中0,1,2,,k n =．……………7分【注：数表k A 不唯一】（Ⅲ）证明：用反证法．假设存在(,)A S n n ∈，其中n 为奇数，使得()0l A =．因为(){1,1}i r A ∈-，(){1,1}j c A ∈-(1,1)i n j n ≤≤≤≤，所以1()r A ，2()r A ，，()n r A ，1()c A ，2()c A ，，()n c A 这2n 个数中有n 个1，n 个1-．令1212()()()()()()n n M r A r A r A c A c A c A =⋅⋅⋅⋅⋅⋅⋅．一方面，由于这2n 个数中有n 个1，n 个1-，从而(1)1n M =-=-．①另一方面，12()()()n r A r A r A ⋅⋅⋅表示数表中所有元素之积（记这2n 个实数之积为m ）；12()()()n c A c A c A ⋅⋅⋅也表示m ，从而21M m ==． ②①、②相互矛盾，从而不存在(,)A S n n ∈，使得()0l A =．即n 为奇数时，必有．………………13分。

2012北京市西城高考一模试题及答案(文科全套)

第一部分（选择题，共27分）一、本大题共5小题，每小题3分，共15分。

B. 足坛反赌扫黑接近尾声，对于涉嫌行贿的俱乐部是否会受处罚，足协一位官员的表态似是而非．．．．：“一切要等审判结束后才有结果。

”C. 上海的婚宴普遍在晚上举行，一般选择在吉时6：08开宴，可是总有些接到请柬的不速之客．．．．姗姗来迟，这让婚宴主办者颇为尴尬。

D. 部分司机认为高速公路宽阔，只要车少就可天马行空．．．．地自由驰骋，其实这种想法十分危险，因为人在大意时反应速度会大大降低。

B. 今年，北京将新增20万亩林地，主要种植在受污染物影响较大的地方，如高速路或主干道的路边，对尾气削减和扬尘会有很好的作用。

C. “1·28”中国公民被劫持事件发生后，苏丹政府全力解救，并表态将采取切实措施确保所有在苏中资企业的安全，避免类似事件不再发生。

2012北京市高三一模文科数学分类汇编2：函数与导数.pdf

2012北京市高三一模数学文分类汇编：函数与导数【2012年北京市西城区高三一模文】13. 已知函数则的零点是_____；的值域是_____．和，【解析】当时，由得，。

当时，由，得，所以函数零点为和。

当时，，所以，当，，所以此时，综上，即函数的值域为。

【2012年北京市西城区高三一模文】3．若，，，则下列结论正确的是（）（A）（B）（C）（D）【答案】D 【解析】，，，所以，选D. 【2012北京市门头沟区一模文】8. 给出定义：若(其中为整数)，则叫离实数最近的整数，记作，已知，下列四个命题： ①函数的定义域为，值域为； ②函数是上的增函数； ③函数是周期函数，最小正周期为1； ④函数是偶函数，其中正确的命题的个数是 (A) 4(B)3 (C)2(D)1 【答案】B 【2012北京市门头沟区一模文】函数（且）的图象经过点，函数（且）的图象经过点，则下列关系式中正确的是 (A) (B)(C)(D) 【答案】C 【2012北京市海淀区一模文】（13）设某商品的需求函数为，其中分别表示需求量和价格，如果商品需求弹性大于1（其中，是的导数），则商品价格的取值范围是 . 【答案】【2012北京市海淀区一模文】（7）已知函数若，使得成立，则实数的取值范围是（A）（B）（C）（D）或【答案】A 【2012北京市房山区一模文】14．设函数，，，（）,则方程有___个实数根，方程有___个实数根．【答案】4，【2012北京市房山区一模文】13．某工厂需要建造一个仓库，根据市场调研分析，运费与工厂和仓库之间的距离成正比，仓储费与工厂和仓库之间的距离成反比，当工厂和仓库之间的距离为4千米时，运费为20万元，仓储费用为5万元，当工厂和仓库之间的距离为___千米时，运费与仓储费之和最小，最小值为__万元．【答案】2,20 【2012北京市房山区一模文】4．下列函数中，既是偶函数又在单调递增的函数是（）（A）（B）（C）（D）【答案】B 【2012北京市丰台区一模文】2．设，则a，b，c的大小关系是（） A．B．C．D．【答案】B 【2012北京市丰台区一模文】8．已知定义在R上的函数满足，当时，，若函数至少有6个零点，则a的取值范围是（） A．（1，5）B．C．D．【答案】B 【2012北京市丰台区一模文】11．已知函数在时取到最小值，则a=．【答案】【2012北京市丰台区一模文】14．定义在区间[a，b]上的连结函数，如果，使得，则称为区间[a，b]上的“中值点”。

2012北京市高三一模文科数学分类汇编9：复数、程序、推理与证明.pdf

2012北京市高三一模数学文分类汇编：复数、程序、推理与证明【2012年北京市西城区高三一模文】2．执行如图所示的程序框图，若输入，则输出的值为（）（A）（B）（C）（D）【答案】D 【解析】输入，。

，，，，，满足条件，输出，选D. 【2012北京市门头沟区一模文】12.如右图所示的程序框图输出的结果是．，则判断框中应填入的条件为（）（A）4（B）5（C）6（D）7 【答案】A 【2012北京市朝阳区一模文】11. 执行如图所示的程序框图，若输入的值是，则输出的值是 . 【2012北京市东城区一模文】（5）右图给出的是计算的值的一个程序框图，其中判断框内应填入的条件是（A）（B）（C）（D）【答案】B 【2012北京市丰台区一模文】13．执行如右图所示的程序框图，若输出的n的值为10，则=。

【答案】3 【2012北京市石景山区一模文】5．执行右面的框图，若输入的是，则输出的值是（） A． B． C． D．【答案】B 【解析】第一次循环：，第二次循环：，第三次循环：，第四次循环：，第五次循环：，第六次循环：此时条件不成立，输出，选B. 【2012年北京市西城区高三一模文】8．已知集合，其中，且.则中所有元素之和是（）（A）（B）（C）（D）【答案】C 【解析】本题可转化为二进制，集合中的二进制数为，因为，所以最大的二进制数为1111，最小的二进制数1000，对应的十进制数最大为15，最小值为8，则，8到15之间的所有整数都有集合中的数，所以所有元素之和为，选C. 【2012年北京市西城区高三一模文】14. 如图，已知抛物线及两点和，其中.过，分别作轴的垂线，交抛物线于，两点，直线与轴交于点，此时就称，确定了.依此类推，可由，确定，.记，. 给出下列三个结论： ① 数列是递减数列； ② 对，； ③ 若，，则. 其中，所有正确结论的序号是_____．【答案】① ② ③. 【2012年北京市西城区高三一模文】4．如图，在复平面内，复数，对应的向量分别是，，则复数对应的点位于（）（A）第一象限（B）第二象限（C）第三象限（D）第四象限【答案】B 【解析】由复数的几何意义知，所以，对应的点在第二象限，选B. 【2012北京市门头沟区一模文】9. 复数在复平面内对应的点的坐标是．【2012北京市海淀区一模文】（14）已知函数则；下面三个命题中，所有真命题的序号是 . 函数是偶函数；任取一个不为零的有理数，对恒成立；存在三个点使得为等边三角形. 【答案】1 ①②③ 【2012北京市海淀区一模文】（9）复数【2012北京市海淀区一模文】（8）在棱长为1的正方体中，若点是棱上一点，则满足的点的个数为（A）4 （B）6 （C）8 （D）12 【答案】B 【2012北京市房山区一模文】9. 是虚数单位，则___. 【答案】【2012北京市东城区一模文】（8）设集合，函数，且则的取值范围是（A）(] （B） (]（C）() （D） [0，] 【2012北京市东城区一模文】（1）若，，是虚数单位，则的值为（A）（B）（C）（D）【答案】D 【2012北京市丰台区一模文】9．在复平面内，复数对应的点的坐标为。

最新届北京市高三一模文科数学分类汇编5：立体几何

2012北京市高三一模数学文分类汇编：立体几何【2012年北京市西城区高三一模文】5．已知正六棱柱的底面边长和侧棱长均为2cm ，其三视图中的俯视图如图所示，则其左视图的面积是（）（A ）243cm （B ）223cm （C ）28cm （D ）24cm【答案】A【解析】正六棱柱的左视图是一个以AB 长为宽，高为2的矩形，32=AB所以左视图的面积为34232=⨯，选A.【2012北京市门头沟区一模文】己知某几何体的三视图如右图所示，则其体积为(A) 4(B) 8 (C)43(D)23【答案】A【2012北京市海淀区一模文】（12已知三条侧棱两两垂直的正三棱锥的俯视图如图所示，那么此三棱锥的体积是，左视图的面积是 . 22俯视图2【答案】23 22【2012北京市房山区一模文】3．一个几何体的三视图如右图所示，则这个几何体的体积为( )【答案】A【2012北京市东城区一模文】（9）已知一个四棱锥的三视图如图所示，则该四棱锥的体积是 .【答案】43【2012北京市朝阳区一模文】10.已知某几何体的三视图如图所示，则该几何体的体积为 .（A ）32 （B ）2 （C ）4（D ）5【答案】32【2012北京市朝阳区一模文】5. 关于两条不同的直线m ,n 与两个不同的平面α,β，下列命题正确的是 A ．βα//,//n m 且βα//，则n m // B ．βα⊥⊥n m ,且βα⊥，则m //n C ．βα//,n m ⊥且βα//，则n m ⊥D ．βα⊥n m ,//且βα⊥，则n m //【答案】C【2012北京市丰台区一模文】4．若某空间几何体的三视图如图所示，则该几何体的体积是（）A ．202π-B ．2203π-C ．2403π-D ．4403π-【答案】B【2012北京市石景山区一模文】4.设n m ,是两条不同的直线，γβα,,是三个不同的平面，下列命题正确的是（）A ．αα//,//,//n m n m 则若B ．βαγβγα//,,则若⊥⊥C ．n m n m //,//,//则若ααD ．n m n m ⊥⊥则若,//,αα【答案】D【解析】根据线面垂直的性质可知选项D 正确。

2012年北京市西城区高三一模文科数学含答案纯word版

2012北京市西城高考一模试题及答案(文科全套)

北京市西城区2012年高三一模数学 答案

2012年北京市西城区高考数学一模试卷(文科)(附答案解析)

2012届北京市高三一模文科数学分类汇编3：三角函数

北京西城区2012年高三一模文科数学试题

2012年北京西城高考一模数学(文)

2012届北京市高三一模文科数学分类汇编3：三角函数

北京市西城区2012届高三上学期期末教学统一检测数学(文科)

2012届北京市高三一模文科数学分类汇编5：立体几何

2012北京市西城高考一模试题及答案%28文科全套%29

届北京西城区高三数学文科一模试卷及答案

2012北京市西城高考一模试题及答案(文科全套)

2012北京市高三一模文科数学分类汇编2：函数与导数.pdf

2012北京市高三一模文科数学分类汇编9：复数、程序、推理与证明.pdf

最新届北京市高三一模文科数学分类汇编5：立体几何

北京市西城区2012年高三一模数学答案