第二十九章 投影与视图
第二十九章_投影与视图

第二十九章投影与视图一、课标导航二、核心纲要l.投影(1)投影:用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在的平面叫做投影面.(2)中心投影:由同一点(点光源发出的光线)形成的投影叫做中心投影(如下左图所示).(3)平行投影:由平行光线形成的投影是平行投影(如下中图所示).(4)正投影:投影线垂直于投影面产生的投影叫做正投影(如下右图所示).2.平行投影与中心投影的区别和联系(如下表所示)3.三视图是指从兰个不间位置观察间一个空间几何体而画出的图形,包括主视图、俯视图、左视图(如下图所示)(1)主视图:从物体的前面向后面投射所得的视图称主视图——能反映物体的前面形状.(2)俯视图:从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状.(3)左视图:从物体的左面向右面投射所得的视图称左视图-- 能反映物体的左面形状.注:画三视图时应注意三视图的位置要准确,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线,主俯长对正、主左高平齐、俯左宽相等.即主视图和俯视图的长要相等;主视图和左视图的高要相等;左视图和俯视图的宽要相等.本节重点讲解:三个投影,三个视图.三 .全能突破基础演练1.下列说法正确的是( ).A.物体在阳光下的投影只与物体的高度有关B.小明的个子比小亮高,我们可以肯定,不论什么情况,小明的影子一定比小亮的影子长.C.物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化.D.物体在阳光照射下,影子的长度和方向都是固定不变的.2.下图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( ).A.①②③④ B.④①③② C.④②③① D.④③②①3.把一个正五棱柱按下图摆放,当投射线由正前方射到后方时,它的正投影是( ).4.(1)如下左图所示,位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2:5,且三角尺的一边长为8cm,则投影三角尺的对应边长为( ).C2.3.cmD10..cmB20cmA8.cm(2)如下右图所示,在一间黑屋子里用一盏白炽灯照一个球,球在地面上阴影的形状是一个圆,当把白炽灯向远移时,圆形阴影的大小变化情况是( ).A.越来越小 B.越来越大 C.大小不变 D.不能确定5.(1)左下图所示的几何体中主视图、左视图、俯视图都相同的是( ).(2)右下图所示的物体由两个紧靠在一起的圆柱组成,小刚准备画出它的三视图,那么他所画的三视图中的俯视图应该是( ).A.两个外切的圆 B.两个内切的圆 C.两个相交的圆 D.两个外离的圆6.由7个大小相同的正方体搭成的几何体如右图所示,则关于它的视图说法正确的是( ).A.正视图的面积最大 B.俯视图的面积最大C.左视图的面积最大 D.三个视图的面积一样大7.(1)左下图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,那么该几何体的主视图为( ).(2)右下图是由一些大小相同的小立方体组成的几何体的主视图和左视图,则组成这个几何体的小立方体的个数不可能是( ).A.3个 B .4个 C .5个 D .6个8.在安装太阳能热水器时,主要考虑太阳光线与热水器斜面间的角度(垂直时最佳).如下图所示,当太阳光线与水平面成ο35角照射时,热水器的斜面与水平面的夹角最好应为9.在平面直角坐标系内,一点光源位于A(O ,4)处,线段CD ⊥x 轴,D 为垂足,C(3,1),则CD 在x 轴上的影子长为__________,点C 的影子坐标为 .能 力 提 升10.太阳光线与地面成ο60的角,照射在地面上的一只皮球上,皮球在地面上的投影长是,310cm 则皮球的直径是( ) cm .35.A 38.B 15.C 20.D11.(1)如果用口表示1个立方体,用图表示两个立方体叠加,用■表示三个立方体叠加,左下图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( ).(2)右下图是由27个相同的小立方块搭成的几何体,它的三个视图都是3×3的正方形,若拿掉若干个小立方块后(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( ).11.A 12.B 13.C 14.D12. (1)-个几何体的三视图如下左图所示,其中主视图、左视图都是长为4、宽为x 的矩形,这个几何体 的表面积为l87c ,则x 的值为( ).2.A 21.B 4.C 8.D(2)右下图是某几何体的三视图及相关数据,则下面判断正确的是( ).c a A >. c b B >. 2224.c b a C =+ 222.c b a D =+13.下图是一个上下底密封纸盒的三视图,请根据图中数据,计算这个密封纸盒的表面积为 2cm (结果可保留根号).14.右图是一个几何体的三视图. (1)写出这个几何体的名称.(2)根据所示数据计算这个几何体的表面积.(3)如果一只蚂蚁要从这个几何体中的点B 出发,沿表面爬到AC 的中点D ,请你求出这个线路的最短路程.15.用小立方体搭一个几何体,它的主视图和俯视图如下图所示,俯视图中小正方形中的字母表示在该位置小立方体的个数,请解答下列问题: (l)a ,b ,c 各表示几?(2)这个几何体最少由几个小立方体搭成?最多由几个小立方体搭成? (3)当2,1===f e d 时,画出这个几何体的左视图.16.下图所示电线杆上有一盏路灯0,电线杆与三个等高的标杆整齐排列在马路一侧的一条直线上,AB 、CD 、EF 是三个标杆,相邻的两个标杆之间的距离都是2m ,已知AB 、CD 在灯光下的影长分别为.6.0,6.1m DN m BM ==(1)请画出路灯0的位置和标杆EF 在路灯灯光下的影子. (2)求标杆EF 的影长,中 考 链 接17.(2012.湖北成宁)中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池,类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,如下左图所示,则该几何体为( ).18.(2013.湖北荆门)过正方体上底面的对角线和下底面一顶点的平面截去一个三棱锥所得到的几何体如下左图所示,则它的俯视图为( ).19.(2012.湖南衡阳)一个圆锥的三视图如下图所示,则此圆锥的底面积为( ).230.cm A π 225.cm B π 250.cm C π 2100.cm D π巅 峰 突 破20.如下图所示,一根直立于水平地面上的木杆AB 在灯光下形成影子,当木杆绕A 按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB 垂直于地面时的影长为AC (假定AC>AB ),影长的最大值为m ,最小值为n ,那么下列结论:;;;AB n AC m AC m ==>③②①④影子的长度先增大后减小.其中,正确的结论的序号是21.学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律,如下图所示,在同一时间,身高为1.6m 的小明(AB)的影子BC 长是3m ,而小颖(EH)刚好在路灯灯泡的正下方H 点,并测得HB=6m.(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G . (2)求路灯灯泡的垂直高度GH. (3)如果小明沿线段BH 向小颖(点H)走去,当小明走到BH 中点1B 处时,求其影子11C B 的长;当小明继续走剩下路程的31到2B 处时,求其影子22C B 的长;当小明继续走剩下路程的41到3B 处,……按此规律继续走下去,当小明走剩下路程的11+n 到n B 处时,其影子n n C B 的长为 m(直接用n的代数式表示).。
九年级数学下册第二十九章《投影与视图》综合经典习题(答案解析)
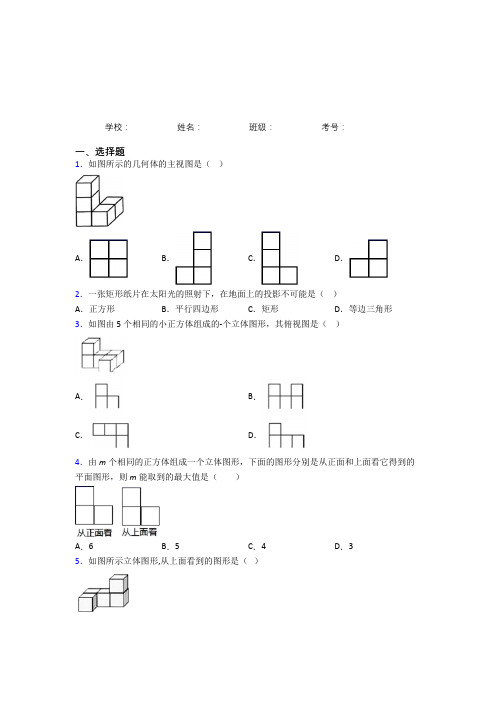
学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.如图所示的几何体的主视图是()A.B.C.D.2.一张矩形纸片在太阳光的照射下,在地面上的投影不可能是()A.正方形B.平行四边形C.矩形D.等边三角形3.如图由5个相同的小正方体组成的-个立体图形,其俯视图是()A.B.C.D.4.由m个相同的正方体组成一个立体图形,下面的图形分别是从正面和上面看它得到的平面图形,则m能取到的最大值是()A.6 B.5 C.4 D.35.如图所示立体图形,从上面看到的图形是()A.B.C.D.6.如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是()A.78 B.72 C.54 D.487.如图是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是( )A.(1)(2)(3)(4) B.(4)(3)(2)(1) C.(4)(3)(1)(2) D.(2)(3)(4)(1)8.下列四个几何体中,主视图是三角形的是()A.B.C.D.9.如图所示,所给的三视图表示的几何体是()A.圆锥B.四棱锥C.三棱锥D.三棱柱10.如图,将一个小球摆放在圆柱上底面的正中间,则该几何体的俯视图是()A.B.C.D.11.如图是一个由若干个相同的小正方体组成的几何体的三种形状图,则组成这个几何体的小正体的个数是( )A.7 B.8 C.9 D.1012.一个几何体由一些大小相同的小正方体组成,如图是它的主视图和左视图,那么组成该几何体所需小正方体的个数最少为()A.4 B.5C.6 D.713.如图,是一块带有圆形空洞和正方形空洞(圆面直径与正方形边长相等)的小木板,则下列物体中既可以堵住圆形空洞,又可以堵住方形空洞的可能是().A.B.C.D.14.如图是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数不可能是()A.6个B.7个C.8个D.9个第II卷(非选择题)请点击修改第II卷的文字说明参考答案二、填空题15.10个棱长为a cm的正方体摆放成如图的形状,这个图形的表面积是____________.16.如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是________(结果保留 ).17.已知一个圆锥体的三视图如图所示,则这个圆锥体的侧面积是__________.18.八中食堂厨房的桌子上整齐地摆放着若干相同规格的碟子,碟子的个数与碟子的高度的关系如表:碟子的个数碟子的高度(单位:cm)1222+1.532+342+4.5……现在分别从三个方向上看若干碟子,得到的三视图如图所示,厨房师傅想把它们整齐地叠成一摞,求叠成一摞后的高度为_____cm.19.在一快递仓库里堆放着若干个相同的正方体快递件,管理员从正面看和从左面看这堆快递如图所示,则这正方体快递件最多有_____件.20.如图,小明站在距离灯杆6m的点B处.若小明的身高AB=1.5m,灯杆CD=6m,则在灯C的照射下,小明的影长BE=______m.21.小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米,垂直于地面放置的标杆在地面上的影长为2米,则树的高度为___.22.如图,身高1.6米的小丽在阳光下的影长为2米,在同一时刻,一棵大树的影长为8米,则这棵树的高度为_____米.23.如图,由五个小正方体组成的几何体中,若每个小正方体的棱长都是1,则该几何体的主视图和左视图的面积之和是_____.24.一天,小青想利用影子测量校园内一根旗杆的高度,在同一时刻内,小青的影长为2米,旗杆的影长为20米,若小青的身高为1.60米,则旗杆的高度为__________米.25.一个几何体的三视图如图所示,其中从上面看的视图是一个等边三角形,则这个几何体的表面积为____.26.张师傅按1:1的比例画出某直三棱柱零件的三视图,如图所示,已知EFG中,==,4512,18EF cm EG cm∠=︒,则AB的长为_____cm.EFG参考答案三、解答题27.如图是由几个小立方体所堆成的几何俯视图,小下方形里的数学字表示该位置小立方块的个数,请画出这个几何主视图和左视图:28.画出如图所示的几何体的主视图、左视图和俯视图.29.如图,王乐同学在晩上由路灯A走向路灯B.当他行到P处时发现,他往路灯B下的影长为2m,且恰好位于路灯A的正下方,接着他又走了6.5m到Q处,此时他在路灯A下的影孑恰好位于路灯B的正下方(已知王乐身高1.8m,路灯B高9m).(1)王乐站在P处时,在路灯B下的影子是哪条线段?(2)计算王乐站在Q处时,在路灯A下的影长;(3)计算路灯A的高度.30.如图,是由8块棱长都为1的小正方体组合成的简单几何体.(1)请画出这个几何体的三视图并用阴影表示出来;(2)该几何体的表面积(含下底面)为________.【参考答案】一、选择题1.C2.D3.C4.B5.C6.B7.C8.B9.D10.C11.C12.B13.B14.D二、填空题15.【分析】先画出这个图形的三视图从而可得上下面前后面左右面的小正方形的个数再根据正方形的面积公式即可得【详解】由题意画出这个图形的三视图如下:则这个图形的表面积是故答案为:【点睛】本题考查了求几何体的16.24πcm²【分析】根据三视图确定该几何体是圆柱体再计算圆柱体的侧面积【详解】解:先由三视图确定该几何体是圆柱体底面半径是4÷2=2cm高是6cm圆柱的侧面展开图是一个长方形长方形的长是圆柱的底面周17.【分析】先由勾股定理求出母线再根据圆锥侧面积公式S=r计算即可【详解】圆锥半径:r=8÷2=4S=r=20故答案为:20【点睛】本题考查圆锥侧面积的求法理解并掌握圆锥侧面积公式是解题关键18.23【分析】根据三视图得出碟子的总数由(1)知每个碟子的高度即可得出答案【详解】可以看出碟子数为x时碟子的高度为2+15(x﹣1);由三视图可知共有15个碟子∴叠成一摞的高度=15×15+05=2319.39【分析】由主视图可得组合几何体有4列由左视图可得组合几何体有4行可得最底层几何体最多正方体的个数为:4×4=16;由主视图和左视图可得第二层最多正方体的个数为:4×4=16;由主视图和左视图可得20.2【分析】首先判定△ABE∽△CDE根据相似三角形的性质可得然后代入数值进行计算即可【详解】解:∵AB⊥EDCD⊥ED∴AB∥DC∴△ABE∽△CDE∴∵AB=15mCD=6mBD=6m∴解得:EB21.6+【解析】【分析】延长AC交BF延长线于D点则BD即为AB的影长然后根据物长和影长的比值计算即可【详解】延长AC交BF延长线于D点则∠CFE=30°作CE⊥BD于E在Rt△CFE中∠CFE=30°22.64【分析】根据平行投影同一时刻物长与影长的比值固定即可解题【详解】解:由题可知:解得:树高=64米【点睛】本题考查了投影的实际应用属于简单题熟悉投影概念列比例式是解题关键23.7【解析】该几何体的主视图的面积为1×1×4=4左视图的面积是1×1×3=3所以该几何体的主视图和左视图的面积之和是3+4=7故答案为724.16【分析】易得△AOB∽△ECD利用相似三角形对应边的比相等可得旗杆OA的长度【详解】解:∵OA⊥DACE⊥DA∴∠CED=∠OAB=90°∵CD∥OE∴∠CDA=∠OBA∴△AOB∽△ECD∴解25.【分析】先判断出几何体为正三棱柱求出三棱柱的底面积最后求表面积即可【详解】解:由三视图得几何体为正三棱柱上下底为边长为2的等边三角形侧面积为长为3宽为2的矩形如图等边三角形ABC中作AD⊥BC于D则26.【分析】作EH⊥FG于点H解直角三角形求出EH即可得出AB的长度【详解】解:如图所示作EH⊥FG于点H∵∠EHF=90°∠EFG=45°∴∠EFG=∠FEH=45°∴EH=HF=∵∴EH=根据三视图三、解答题27.28.29.30.【参考解析】一、选择题1.C解析:C【分析】根据三视图的定义,主视图是底层有两个正方形,左侧有三层,即可得到答案.【详解】解:由题图可知,主视图为故选:C【点睛】本题考查了简单几何体的三视图,解题的关键是熟练掌握三视图的定义.2.D解析:D【分析】根据平行投影的性质求解可得.【详解】一张矩形纸片在太阳光线的照射下,形成影子不可能是等边三角形,故选:D.【点睛】本题考查了平行投影:由平行光线形成的投影是平行投影,如物体在太阳光的照射下形成的影子就是平行投影.3.C解析:C【分析】根据立体图形三视图的性质进行判断即可.【详解】根据立体图形三视图的性质,该立体图形的俯视图为故答案为:C.【点睛】本题考查了立体图形的三视图,掌握立体图形三视图的性质是解题的关键.4.B解析:B【分析】根据主视图和俯视图分析每行每列小正方体最多的情况,即可得出答案.【详解】由题中所给出的主视图知物体共两列,且左侧一列高两层,右侧一列最高一层;由俯视图可知左侧两行,右侧一行,于是,可确定右侧只有一个小正方体,而左侧可能是一行单层一行两层,可能两行都是两层.最多的情况如图所示,所以图中的小正方体最多5块.故选:B.【点睛】本题考查根据三视图判断小正方体个数,需要一定空间想象力,熟练掌握主视图与俯视图的定义是解题的关键.5.C解析:C【分析】从上面看到3列正方形,找到相应列上的正方形的个数即可.【详解】从上面看得到从左往右3列正方形的个数依次为2,1,1,故选C.【点睛】本题考查了简单组合体的三视图,解决本题的关键是得到3列正方形具体数目.6.B解析:B【解析】【分析】如图所示,一、棱长为3的正方体的每个面等分成9个小正方形,那么每个小正方形的边长是1,所以每个小正方面的面积是1;二、正方体的一个面有9个小正方形,挖空后,这个面的表面积增加了4个小正方形,减少了1个小正方形,即:每个面有12个小正方形,6个面就是6×12=72个,那么几何体的表面积为72×1=72.【详解】如图所示,周边的六个挖空的正方体每个面增加4个正方形,减少了1个小正方形,则每个面的正方形个数为12个,则表面积为12×6×1=72.故选:B.【点睛】主要考查学生的空间想象能力,解决本题的关键是能够想象出物体表面积的变化情况. 7.C解析:C【分析】根据平行投影的规律:早晨到傍晚物体的指向是:西-西北-北-东北-东,影长由长变短,再变长可得.【详解】根据平行投影的规律知:顺序为(4)(3)(1)(2).故选C.【点睛】本题考查平行投影的特点和规律.在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,就北半球而言,从早晨到傍晚物体的指向是:西-西北-北-东北-东,影长由长变短,再变长.8.B解析:B【解析】主视图是三角形的一定是一个锥体,只有B是锥体.故选B.9.D解析:D【解析】分析:由左视图和俯视图可得此几何体为柱体,根据主视图是三角形可判断出此几何体为正三棱柱.详解:∵左视图和俯视图都是长方形,∴此几何体为柱体,∵主视图是一个三角形,∴此几何体为三棱柱.故选D.点睛:考查了由三视图判断几何体,用到的知识点为:由左视图和俯视图可得几何体是柱体,锥体还是球体,由主视图可确定几何体的具体形状.10.C解析:C【解析】分析:俯视图就是要从问题的正上方往下看,相当于把物体投影到平面.详解:圆柱体和球体投影到平面以后都是圆形,故排除A,因为圆形的轮廓线都是可以看到的,所以选C.点睛:三视图中,可以看到的轮廓线,要化成实线,看不到的轮廓线,要化成虚线. 11.C解析:C【分析】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形进行判断.【详解】解:综合三视图,这个几何体的底层有3+2+1=6个小正方体,第二层有1+1=2个小正方体,第三层有1个,因此组成这个几何体的小正方形有6+2+1=9个.故选C.【点睛】本题意在考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就容易得到答案了.12.B解析:B【分析】从俯视图中可以看出最底层小正方体的个数及形状,从左视图可以看出每一层小正方体的层数和个数,从而算出总的个数.【详解】由题中所给出的主视图知物体共三列,且左侧一列高两层,中间一列高1层,右侧一列最高两层;由左视图可知左侧两,右侧一层,所以图中的小正方体最少3+2=5块.故选B.【点睛】本题主要考查三视图的相关知识:主视图主要确定物体的长和高,左视图确定物体的宽和高,俯视图确定物体的长和宽.13.B解析:B【分析】根据题意,满足条件的空间几何体的三视图中含有圆和正方形.然后分别进行判断即可.【详解】A.正方体的正视图为正方形,侧视图为正方形,俯视图也为正方形,不满足条件.B.圆柱的正视图和侧视图为相同的矩形,俯视图为圆,满足条件.C.圆锥的正视图为三角形,侧视图为三角形,俯视图为圆,不满足条件.D.球的正视图,侧视图和俯视图相同的圆,不满足条件.故选B.【点睛】本题主要考查三视图的识别和判断,解题关键在于熟练掌握常见空间几何体的三视图,比较基础.14.D解析:D【解析】由俯视图可得得最底层有5个立方体,由左视图可得第二层最少有1个立方体,最多有3个立方体,所以小立方体的个数可能是6个或7个或8个,小立方体的个数不可能是9.故选D.点睛:本题主要考查了三视图的应用,掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.注意俯视图中有几个正方形,底层就有几个立方体.二、填空题15.【分析】先画出这个图形的三视图从而可得上下面前后面左右面的小正方形的个数再根据正方形的面积公式即可得【详解】由题意画出这个图形的三视图如下:则这个图形的表面积是故答案为:【点睛】本题考查了求几何体的解析:2236a cm【分析】先画出这个图形的三视图,从而可得上下面、前后面、左右面的小正方形的个数,再根据正方形的面积公式即可得.【详解】由题意,画出这个图形的三视图如下:则这个图形的表面积是()()22226262636a a cm ⨯+⨯+⨯=, 故答案为:2236a cm .【点睛】本题考查了求几何体的表面积,正确画出图形的三视图是解题关键.16.24πcm²【分析】根据三视图确定该几何体是圆柱体再计算圆柱体的侧面积【详解】解:先由三视图确定该几何体是圆柱体底面半径是4÷2=2cm 高是6cm 圆柱的侧面展开图是一个长方形长方形的长是圆柱的底面周解析:24π cm²【分析】根据三视图确定该几何体是圆柱体,再计算圆柱体的侧面积.【详解】解:先由三视图确定该几何体是圆柱体,底面半径是4÷2=2cm ,高是6cm ,圆柱的侧面展开图是一个长方形,长方形的长是圆柱的底面周长,长方形的宽是圆柱的高,且底面周长为:2π×2=4π(cm),∴这个圆柱的侧面积是4π×6=24π(cm²).故答案为:24π cm².【点睛】此题主要考查了由三视图确定几何体和求圆柱体的侧面积,关键是根据三视图确定该几何体是圆柱体.17.【分析】先由勾股定理求出母线再根据圆锥侧面积公式S=r 计算即可【详解】圆锥半径:r=8÷2=4S=r=20故答案为:20【点睛】本题考查圆锥侧面积的求法理解并掌握圆锥侧面积公式是解题关键解析:20π【分析】先由勾股定理求出母线l ,再根据圆锥侧面积公式S=πr l 计算即可.【详解】圆锥半径:r=8÷2=422345l =+=S=πr l=20π故答案为:20π【点睛】本题考查圆锥侧面积的求法,理解并掌握圆锥侧面积公式是解题关键.18.23【分析】根据三视图得出碟子的总数由(1)知每个碟子的高度即可得出答案【详解】可以看出碟子数为x时碟子的高度为2+15(x﹣1);由三视图可知共有15个碟子∴叠成一摞的高度=15×15+05=23解析:23【分析】根据三视图得出碟子的总数,由(1)知每个碟子的高度,即可得出答案.【详解】可以看出碟子数为x时,碟子的高度为2+1.5(x﹣1);由三视图可知共有15个碟子,∴叠成一摞的高度=1.5×15+0.5=23(cm).故答案为:23cm.【点睛】本题考查了图形的变化类问题及由三视图判断几何体的知识,找出碟子个数与碟子高度的之间的关系式是此题的关键.19.39【分析】由主视图可得组合几何体有4列由左视图可得组合几何体有4行可得最底层几何体最多正方体的个数为:4×4=16;由主视图和左视图可得第二层最多正方体的个数为:4×4=16;由主视图和左视图可得解析:39【分析】由主视图可得组合几何体有4列,由左视图可得组合几何体有4行,可得最底层几何体最多正方体的个数为:4×4=16;由主视图和左视图可得第二层最多正方体的个数为:4×4=16;由主视图和左视图可得第3层最多正方体的个数为:3×2=6;由主视图和左视图可得第4层最多正方体的个数为:1;相加可得所求.【详解】由主视图可得组合几何体有4列,由左视图可得组合几何体有4行,最底层几何体最多正方体的个数为:4×4=16,由主视图和左视图可得第二层最多正方体的个数为:4×4=16;由主视图和左视图可得第3层最多正方体的个数为:3×2=6;由主视图和左视图可得第4层最多正方体的个数为:1;16+16+6+1=39(件).故这正方体快递件最多有39件.故答案为:39.【点睛】此题考查由视图判断几何体;得到最底层正方体的最多的个数是解决本题的突破点;用到的知识点为:最底层正方体的最多的个数=行数×列数.20.2【分析】首先判定△ABE∽△CDE根据相似三角形的性质可得然后代入数值进行计算即可【详解】解:∵AB⊥EDCD⊥ED∴AB∥DC∴△ABE∽△CDE∴∵AB=15mCD=6mBD=6m∴解得:EB解析:2【分析】首先判定△ABE∽△CDE,根据相似三角形的性质可得AB EBCD ED=,然后代入数值进行计算即可.【详解】解:∵AB⊥ED,CD⊥ED,∴AB∥DC,∴△ABE∽△CDE,∴AB EB CD ED=∵AB=1.5m,CD=6m,BD=6m,∴1.566EBEB=+解得:EB=2,故答案为2【点睛】此题主要考查了相似三角形的应用,属于简单题,关键是掌握相似三角形对应边成比例是解题关键.21.6+【解析】【分析】延长AC交BF延长线于D点则BD即为AB的影长然后根据物长和影长的比值计算即可【详解】延长AC交BF延长线于D点则∠CFE=30°作CE⊥BD于E在Rt△CFE中∠CFE=30°解析:6【解析】【分析】延长AC交BF延长线于D点,则BD即为AB的影长,然后根据物长和影长的比值计算即可.【详解】延长AC交BF延长线于D点,则∠CFE=30°,作CE⊥BD于E.在Rt△CFE中,∠CFE=30°,CF=4,∴CE=2,EF在Rt△CED中,∵同一时刻,一根长为1米、垂直于地面放置的标杆在地面上的影长为2米,CE=2,CE:DE=1:2,∴DE=4,∴BD=BF+EF+ED在Rt△ABD中,AB12=BD12=(12+23)=6+3.故答案为(6+3)米.【点睛】本题考查了相似三角形的性质.解决本题的关键是作出辅助线得到AB的影长.22.64【分析】根据平行投影同一时刻物长与影长的比值固定即可解题【详解】解:由题可知:解得:树高=64米【点睛】本题考查了投影的实际应用属于简单题熟悉投影概念列比例式是解题关键解析:6.4【分析】根据平行投影,同一时刻物长与影长的比值固定即可解题.【详解】解:由题可知:1.628=树高,解得:树高=6.4米.【点睛】本题考查了投影的实际应用,属于简单题,熟悉投影概念,列比例式是解题关键.23.7【解析】该几何体的主视图的面积为1×1×4=4左视图的面积是1×1×3=3所以该几何体的主视图和左视图的面积之和是3+4=7故答案为7解析:7【解析】该几何体的主视图的面积为1×1×4=4,左视图的面积是1×1×3=3,所以该几何体的主视图和左视图的面积之和是3+4=7,故答案为7.24.16【分析】易得△AOB∽△ECD利用相似三角形对应边的比相等可得旗杆OA的长度【详解】解:∵OA⊥DACE⊥DA∴∠CED=∠OAB=90°∵CD∥OE∴∠CDA=∠OBA∴△AOB∽△EC D∴解解析:16【分析】易得△AOB∽△ECD,利用相似三角形对应边的比相等可得旗杆OA的长度.【详解】解:∵OA ⊥DA ,CE ⊥DA ,∴∠CED=∠OAB=90°,∵CD ∥OE ,∴∠CDA=∠OBA ,∴△AOB ∽△ECD , ∴CE OA 16OA ,DE AB 220==, 解得OA=16.故答案为16. 25.【分析】先判断出几何体为正三棱柱求出三棱柱的底面积最后求表面积即可【详解】解:由三视图得几何体为正三棱柱上下底为边长为2的等边三角形侧面积为长为3宽为2的矩形如图等边三角形ABC 中作AD ⊥BC 于D 则 解析:1823+【分析】先判断出几何体为正三棱柱,求出三棱柱的底面积,最后求表面积即可.【详解】解:由三视图得,几何体为正三棱柱,上下底为边长为2的等边三角形,侧面积为长为3,宽为2的矩形.如图,等边三角形ABC 中,作AD ⊥BC 于D ,则BD=1BC=12, 在t ABD R △中,2222AD=AB -BD =21=3-;∴11=BC AD=23=322ABC S ⨯⨯⨯⨯△, ∴三棱柱的表面积为23323=18+23⨯⨯+⨯.故答案为: 183+【点睛】本题考查了三视图,等边三角形的面积计算等知识,根据三视图判断出几何体形状是解题关键.26.【分析】作EH ⊥FG 于点H 解直角三角形求出EH 即可得出AB 的长度【详解】解:如图所示作EH ⊥FG 于点H ∵∠EHF=90°∠EFG=45°∴∠EFG=∠FEH=45°∴EH=HF=∵∴EH=根据三视图 解析:62 【分析】 作EH ⊥FG 于点H ,解直角三角形求出EH 即可得出AB 的长度.【详解】解:如图所示,作EH ⊥FG 于点H ,∵∠EHF=90°,∠EFG=45°,∴∠EFG=∠FEH=45°,∴EH=HF=22EF , ∵12EF cm ,∴EH=62,根据三视图的意义可知,AB=EH=62故答案为:62【点睛】本题考查了三视图,解直角三角形的应用,解题的关键是理解题意,灵活运用所学知识解决问题.三、解答题27.见解析【分析】利用俯视图即可得出几何体的形状,进而得出几何体的主视图和左视图.【详解】解:如图所示:.【点睛】此题主要考查了作三视图以及由三视图判断几何体的形状,正确得出几何体的形状是解题关键.28.见解析.【分析】分别从正面、左面、上面看得到的图形即可.看到的棱用实线表示,实际存在但是被挡住看不见的棱用虚线表示.【详解】【点睛】本题考查了三视图的作图.29.(1)线段CP为王乐在路灯B下的影子;(2)王乐站在Q处时,在路灯A下的影长为1.5m;(3)路灯A的高度为12m【分析】(1)影长为光线与物高相交得到的阴影部分;(2)易得Rt△CEP∽Rt△CBD,利用对应边成比例可得QD长;(3)易得Rt△DFQ∽Rt△DAC,利用对应边成比例可得AC长,也就是路灯A的高度.【详解】解:(1)线段CP为王乐在路灯B下的影子.(2)由题意得Rt△CEP∽Rt△CBD,∴1.8292 6.5QD=++,解得:QD=1.5m.所以王乐站在Q处时,在路灯A下的影长为1.5m (3)由题意得Rt△QDF∽Rt△CDA,∴FQ QD=,AC DC∴1.8 1.5=,AC10解得:AC=12m.所以路灯A的高度为12m.【点睛】本题考查了中心投影及相似的判定和性质,利用两三角形相似,对应边成比例来求线段的长.30.(1)见解析;(2)34【分析】(1)从正面看得到从左往右4列正方形的个数依次为1,3,1,2;从左面看得到从左往右2列正方形的个数依次为3,1;从上面看得到从左往右,4列正方形的个数依次为2,1,,1,1,依此画出图形即可;(2)有顺序的计算上下面,左右面,前后面的面积之和,然后加上2个三视图中没看到的面,计算表面积之和,即可;【详解】解:(1)如下图:(2)(5×2+7×2+4×2+2)×(1×1)=(10+14+8+2)×1=34×1=34故答案为:34.【点睛】考查了作图-三视图,三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形.计算几何体的表面积应有顺序的分为相对的面进行计算不易出差错.。
第二十九章 投影与视图(章末总结)-(课件)九年级数学下册(人教版)

1)确定主视图的位置,画出主视图;
2)在主视图正下方画出俯视图,注意与主视图长对正;
3)在主视图正右方画出左视图,注意与主视图高平齐,与俯视图宽相等;
4)为表示圆柱、圆锥等的对称轴,规定在视图中用细点划线表示对称轴.
【注意】在画视图时,看得见部分的轮廓要画成实线,看不见部分的轮廓线要画成虚线.
章节简介
1)以分析实际例子为背景,认识投影和视图的基本概念和基本性质;
2)通过讨论简单立体图形(包括相应的表面展开图)与它的三视图的相互转
化,经历画图、识图等过程,分析立体图形和平面图形之间的联系,提高空间
相象能力;
3) 通过制作立体模型的学习,在实际动手中进一步加深对投影和识图知识的
认识,加强在实践活动中动手动脑理论结合实际的能力.
∴AH=AB·cos45°=10× 2=5 2 (厘米),.
2
∴A1B1=AH=5 2 (厘米),
∵A1D1=AD=10(厘米),
∴矩形A1B1C1D1的面积=A1B1·A1D1=5 2×10=50 2 (平方厘米).
04
题型四(判断几何体三视图)
1.下列几何体的主视图、左视图和俯视图完全相同的是(
D.
5 如图,是由7个大小相同的小正方体堆砌而成的几何体,若从标有①、②、③、④的四个
小正方体中取走一个后,余下几何体与原几何体的主视图相同,则取走的正方体是(
A.①
B.②
C.③
D.④
)
05 题型五(三视图的相关计算)
1. 如图是一个几何体的三视图,若这个几何体的体积是30,则它的表面积是________.
线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.
第二十九章 投影与视图

第二十九章投影与视图一、课标导航二、核心纲要l.投影(1)投影:用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在的平面叫做投影面.(2)中心投影:由同一点(点光源发出的光线)形成的投影叫做中心投影(如下左图所示).(3)平行投影:由平行光线形成的投影是平行投影(如下中图所示).(4)正投影:投影线垂直于投影面产生的投影叫做正投影(如下右图所示).2.平行投影与中心投影的区别和联系(如下表所示)3.三视图是指从兰个不间位置观察间一个空间几何体而画出的图形,包括主视图、俯视图、左视图(如下图所示)(1)主视图:从物体的前面向后面投射所得的视图称主视图——能反映物体的前面形状.(2)俯视图:从物体的上面向下面投射所得的视图称俯视图——能反映物体的上面形状.(3)左视图:从物体的左面向右面投射所得的视图称左视图-- 能反映物体的左面形状.注:画三视图时应注意三视图的位置要准确,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线,主俯长对正、主左高平齐、俯左宽相等.即主视图和俯视图的长要相等;主视图和左视图的高要相等;左视图和俯视图的宽要相等.本节重点讲解:三个投影,三个视图.三 .全能突破基础演练1.下列说法正确的是( ).A.物体在阳光下的投影只与物体的高度有关B.小明的个子比小亮高,我们可以肯定,不论什么情况,小明的影子一定比小亮的影子长.C.物体在阳光照射下,不同时刻,影长可能发生变化,方向也可能发生变化.D.物体在阳光照射下,影子的长度和方向都是固定不变的.2.下图是一根电线杆在一天中不同时刻的影长图,试按其一天中发生的先后顺序排列,正确的是( ).A.①②③④ B.④①③② C.④②③① D.④③②①3.把一个正五棱柱按下图摆放,当投射线由正前方射到后方时,它的正投影是( ).4.(1)如下左图所示,位似图形由三角尺与其灯光照射下的中心投影组成,相似比为2:5,且三角尺的一边长为8cm,则投影三角尺的对应边长为( ).C2.3.cmD10..cmB20cmA8.cm(2)如下右图所示,在一间黑屋子里用一盏白炽灯照一个球,球在地面上阴影的形状是一个圆,当把白炽灯向远移时,圆形阴影的大小变化情况是( ).A.越来越小 B.越来越大 C.大小不变 D.不能确定5.(1)左下图所示的几何体中主视图、左视图、俯视图都相同的是( ).(2)右下图所示的物体由两个紧靠在一起的圆柱组成,小刚准备画出它的三视图,那么他所画的三视图中的俯视图应该是( ).A.两个外切的圆 B.两个内切的圆 C.两个相交的圆 D.两个外离的圆6.由7个大小相同的正方体搭成的几何体如右图所示,则关于它的视图说法正确的是( ).A.正视图的面积最大 B.俯视图的面积最大C.左视图的面积最大 D.三个视图的面积一样大7.(1)左下图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,那么该几何体的主视图为( ).(2)右下图是由一些大小相同的小立方体组成的几何体的主视图和左视图,则组成这个几何体的小立方体的个数不可能是( ).A.3个 B .4个 C .5个 D .6个8.在安装太阳能热水器时,主要考虑太阳光线与热水器斜面间的角度(垂直时最佳).如下图所示,当太阳光线与水平面成35角照射时,热水器的斜面与水平面的夹角最好应为9.在平面直角坐标系内,一点光源位于A(O ,4)处,线段CD ⊥x 轴,D 为垂足,C(3,1),则CD 在x 轴上的影子长为__________,点C 的影子坐标为 .能 力 提 升10.太阳光线与地面成60的角,照射在地面上的一只皮球上,皮球在地面上的投影长是,310cm 则皮球 的直径是( ) cm .35.A 38.B 15.C 20.D11.(1)如果用口表示1个立方体,用图表示两个立方体叠加,用■表示三个立方体叠加,左下图是由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是( ).(2)右下图是由27个相同的小立方块搭成的几何体,它的三个视图都是3×3的正方形,若拿掉若干个小立方块后(几何体不倒掉),其三个视图仍都为3×3的正方形,则最多能拿掉小立方块的个数为( ).11.A 12.B 13.C 14.D12. (1)-个几何体的三视图如下左图所示,其中主视图、左视图都是长为4、宽为x 的矩形,这个几何体 的表面积为l87c ,则x 的值为( ).2.A 21.B 4.C 8.D(2)右下图是某几何体的三视图及相关数据,则下面判断正确的是( ).c a A >. c b B >. 2224.c b a C =+ 222.c b a D =+13.下图是一个上下底密封纸盒的三视图,请根据图中数据,计算这个密封纸盒的表面积为 2cm (结果可保留根号).14.右图是一个几何体的三视图. (1)写出这个几何体的名称.(2)根据所示数据计算这个几何体的表面积.(3)如果一只蚂蚁要从这个几何体中的点B 出发,沿表面爬到AC 的中点D ,请你求出这个线路的最短路程.15.用小立方体搭一个几何体,它的主视图和俯视图如下图所示,俯视图中小正方形中的字母表示在该位置小立方体的个数,请解答下列问题: (l)a ,b ,c 各表示几?(2)这个几何体最少由几个小立方体搭成?最多由几个小立方体搭成? (3)当2,1===f e d 时,画出这个几何体的左视图.16.下图所示电线杆上有一盏路灯0,电线杆与三个等高的标杆整齐排列在马路一侧的一条直线上,AB 、CD 、EF 是三个标杆,相邻的两个标杆之间的距离都是2m ,已知AB 、CD 在灯光下的影长分别为.6.0,6.1m DN m BM ==(1)请画出路灯0的位置和标杆EF 在路灯灯光下的影子. (2)求标杆EF 的影长,中 考 链 接17.(2012.湖北成宁)中央电视台有一个非常受欢迎的娱乐节目:墙来了!选手需按墙上的空洞造型摆出相同姿势,才能穿墙而过,否则会被墙推入水池,类似地,有一个几何体恰好无缝隙地以三个不同形状的“姿势”穿过“墙”上的三个空洞,如下左图所示,则该几何体为( ).18.(2013.湖北荆门)过正方体上底面的对角线和下底面一顶点的平面截去一个三棱锥所得到的几何体如下左图所示,则它的俯视图为( ).19.(2012.湖南衡阳)一个圆锥的三视图如下图所示,则此圆锥的底面积为( ).230.cm A π 225.cm B π 250.cm C π 2100.cm D π巅 峰 突 破20.如下图所示,一根直立于水平地面上的木杆AB 在灯光下形成影子,当木杆绕A 按逆时针方向旋转直至到达地面时,影子的长度发生变化.设AB 垂直于地面时的影长为AC (假定AC>AB ),影长的最大值为m ,最小值为n ,那么下列结论:;;;AB n AC m AC m ==>③②①④影子的长度先增大后减小.其中,正确的结论的序号是21.学习投影后,小明、小颖利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律,如下图所示,在同一时间,身高为1.6m 的小明(AB)的影子BC 长是3m ,而小颖(EH)刚好在路灯灯泡的正下方H 点,并测得HB=6m.(1)请在图中画出形成影子的光线,并确定路灯灯泡所在的位置G . (2)求路灯灯泡的垂直高度GH. (3)如果小明沿线段BH 向小颖(点H)走去,当小明走到BH 中点1B 处时,求其影子11C B 的长;当小明继续走剩下路程的31到2B 处时,求其影子22C B 的长;当小明继续走剩下路程的41到3B 处,……按此规律继续走下去,当小明走剩下路程的11+n 到n B 处时,其影子n n C B 的长为 m(直接用n的代数式表示).。
九年级数学下册第二十九章《投影与视图》综合经典题(专题培优)

学校:__________ 姓名:__________ 班级:__________ 考号:__________一、选择题1.由m个相同的正方体组成一个立体图形,下面的图形分别是从正面和上面看它得到的平面图形,则m能取到的最大值是()A.6 B.5 C.4 D.32.下列说法错误的是()A.高矮不同的两个人在同一盏路灯下同一时刻的影子有可能一样长B.对角线互相垂直的四边形是菱形C.方程x2=x的根是x1=0,x2=1D.对角线相等的平行四边形是矩形3.从上面看下图能看到的结果是图形()A.B.C.D.4.如图,把一个棱长为3的正方体的每个面等分成9个小正方形,然后沿每个面正中心的一个正方形向里挖空(相当于挖去7个小正方体),所得到的几何体的表面积是()A.78 B.72 C.54 D.485.某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有()A.4个B.5个C.6个D.7个6.如图是由6个大小相同的立方体组成的几何体,在这个几何体的三视图中,是中心对称图形的是()A.主视图B.左视图C.俯视图D.主视图和左视图7.如图,身高为1.6m的某学生想测量一棵大树的高度,她沿着树影BA由B向A走去,当走到C点时,她的影子顶端正好与树的影子顶端重合,测得BC=3.2m",CA=0.8m,则树的高度为()A.4.8m B.6.4m C.8m D.10m8.小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是()A.三角形B.线段C.矩形D.平行四边形9.如图所示几何体的主视图是()A.B.C.D.10.下面的三视图对应的物体是()A.B.C.D.11.如图所示是某几何体从三个方向看到的图形,则这个几何体是()A.三棱锥B.圆柱C.球D.圆锥12.某展厅要用相同的正方体木块搭成一个展台,从正面、左面、上面看到的形状如图所示,请判断搭成此展台共需这样的正方体()A.3个B.4个C.5个D.6个13.如图,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20 m到达Q点时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5 m,两个路灯的高度都是9 m,则两路灯之间的距离是()A.24 m B.25 m C.28 m D.30 m14.如图是由若干个相同的小立方体搭成的几何体的俯视图和左视图,则小立方体的个数不可能是()A.6个B.7个C.8个D.9个第II卷(非选择题)请点击修改第II卷的文字说明参考答案二、填空题15.已知某几何体的三视图如图所示,其中俯视图为等边三角形,则该几何体的左视图的面积为_____.16.如图是由一些相同的小正方体构成的立体图形从三个方向看到的图形,那么构成这个立体图形的小正方体有_______个.17.如图,数学兴趣小组的小颖想测量教学楼前的一棵树的树高,下午课外活动时她测得一根长为1m的竹竿的影长是0.5m,但当她马上测量树高时,发现树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图),她先测得留在墙壁上的影高为1m,又测得地面的影长为1.5m,请你帮她算一下,树高为______.18.一个几何体由一些完全相同的小立方块搭成,从正面和从上面看到的这个几何体的形状如下,那么搭成这样一个几何体,最少需要_____个这样的小立方块,最多需要_____个这样的小立方块.19.如图,已知路灯离地面的高度AB为4.8m,身高为1.6m的小明站在D处的影长为2m,那么此时小明离电杆AB的距离BD为_____m.20.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块.21.如图:在桌上摆有一些大小相同的正方体木块,其从正面和从左面看到的形状图如图所示,则要摆出这样的图形至少需要_____块正方体木块,至多需要_____块正方体木块.22.如图,是一个几何体的三视图(含有数据)则这个几何体的侧面展开图的面积等于__.23.一个几何体由几个大小相同的小正方体搭成,这个几何体的俯视图和左视图如图所示,则这个几何体中小正方体的个数最少是________个.24.用小立方块搭成的几何体从正面和上面看的视图如图,这个几何体中小立方块的个数最多有_________个.25.如图,将19个棱长为a的正方体按如图摆放,则这个几何体的表面积是_____.26.写出两个三视图形状都一样的几何体:__________、__________.三、解答题27.用小立方体搭一个几何体,使它的主视图和俯视图如图所示,俯视图中小正方形中字母表示在该位置小立方体的个数,请解答下列问题:(1)直接写出a,b,c的值;(2)这个几何体最少有几个小立方体搭成,最多有几个小立方体搭成;(3)当d=1,e=2,f=1时画出这个几何体的左视图.28.如图1,是由一些棱长为单位1的相同的小正方体组合成的简单几何体:(1)图中有_____个小正方体;(2)请在图1右侧方格中分别画出几何体的主视图和左视图.29.如图所示的几何体是由若干个相同的小正方体组成的.(1)填空:这个几何体由个小正方体组成;(2)画出它的三个视图.(作图必须用黑色水笔描黑)30.用六个小正方体搭成如图的几何体,请画出该几何体从正面,左面,上面看到的图形.参考答案【参考答案】一、选择题1.B2.B3.D4.B5.B6.C7.C8.A9.D10.D11.D12.B13.D14.D二、填空题15.3cm2【分析】由三视图想象几何体的形状首先应分别根据主视图俯视图和左视图想象几何体的前面上面和左侧面的形状然后综合起来考虑整体形状【详解】解:该几何体是一个三棱柱底面等边三角形边长为2cm底面三角16.7【分析】利用主视图左视图中每列中正方形的个数判断俯视图中正方形的个数然后得出结果【详解】解:主视图从左往右2列正方形的个数依次为33;左视图从左往右2列正方形的个数依次为31;则俯视图中正方形的个17.4m【分析】首先要知道在同一时刻任何物体的高与其影子的比值是相同的所以竹竿的高与其影子的比值和树高与其影子的比值相同利用这个结论可以求出树高【详解】解:如图所示:过点D作DC⊥AB于点C连接AE由题18.68【解析】【分析】易得这个几何体共有2层由俯视图可得第一层立方体的个数由主视图可得第二层立方体的可能的个数相加即可【详解】综合主视图和俯视图这个几何体的底层有4个小正方体第二层最少有2个最多有4个19.4【解析】【分析】根据题意得△ABC∽△EDC相似三角形成比例得解【详解】∵△ABC∽△EDC∴CB=6BD=6-2=4故BD为4m【点睛】本题考查相似三角形解题的关键是清楚相似三角形的性质20.54【解析】试题21.616【解析】试题分析:由物体的主视图和左视图易得第一层最少有4块正方体最多有12块正方体;第二层最少有2块正方体最多有4块正方体故总共至少有6块正方体至多有16块正方体考点:几何体的三视图22.【解析】易得此几何体为圆柱底面直径为1高为2圆柱侧面积=底面周长×高代入相应数值求解即可解:主视图和左视图为长方形可得此几何体为柱体俯视图为圆可得此几何体为圆柱故侧面积=π×1×2=2π故答案为2π23.5【分析】易得这个几何体共有2层由俯视图可得第一层立方体的个数由左视图可得第二层所须小正方体最少的个数相加即可得答案【详解】由俯视图和左视图可知此几何体有2层第一层有4个小正方体第二层最少有1个小正24.10【分析】根据俯视图和主视图确定每一层正方体可能有的个数最后求和即可【详解】解:从俯视图可以看出下面的一层有6个由主视图可以知道在中间一列的一个正方体上面可以放2个或在一个上放2个另一个上放1或225.54a2【分析】求这个几何体的表面积就要数出这个几何体中小正方体漏在外面的面的个数从前后左右上下方向上来数然后用一个面的面积乘面的个数即可【详解】解:从前后左右上下方向看到的面数分别为:10108826.球;正方体【分析】找到从物体正面左面和上面看得到的图形全等的几何体即可答案不唯一【详解】解:三视图形状都一样的几何体为球正方体故答案为球正方体(答案不唯一)【点睛】考查三视图的有关知识注意三视图都相三、解答题27.28.29.30.【参考解析】一、选择题1.B解析:B【分析】根据主视图和俯视图分析每行每列小正方体最多的情况,即可得出答案.【详解】由题中所给出的主视图知物体共两列,且左侧一列高两层,右侧一列最高一层;由俯视图可知左侧两行,右侧一行,于是,可确定右侧只有一个小正方体,而左侧可能是一行单层一行两层,可能两行都是两层.最多的情况如图所示,所以图中的小正方体最多5块.故选:B.【点睛】本题考查根据三视图判断小正方体个数,需要一定空间想象力,熟练掌握主视图与俯视图的定义是解题的关键.2.B解析:B【分析】根据中心投影的性质、菱形的判定定理、矩形的判定定理及解一元二次方程的方法对各选项进行判断即可.【详解】A.高矮不同的两个人在同一盏路灯下同一时刻的影子有可能一样长,正确,不符合题意,B.对角线互相垂直且平分的四边形是菱形,故该选项错误,符合题意,C.方程x2=x的根是x1=0,x2=1,正确,不符合题意,D. 对角线相等的平行四边形是矩形,正确,不符合题意,故选B.【点睛】本题考查中心投影的性质、菱形和矩形的判定及解一元二次方程,熟练掌握相关性质及判定定理是解题关键.3.D解析:D【分析】先细心观察原立体图形中的圆锥体和长方体的位置关系,结合四个选项选出答案.【详解】从上面往下看到左边一个长方形,右边一个圆,因此只有D的图形符合这个条件.故选:D.【点睛】本题考查了三视图的知识,解题的关键是熟知俯视图是从上面往下的视图.4.B解析:B【解析】【分析】如图所示,一、棱长为3的正方体的每个面等分成9个小正方形,那么每个小正方形的边长是1,所以每个小正方面的面积是1;二、正方体的一个面有9个小正方形,挖空后,这个面的表面积增加了4个小正方形,减少了1个小正方形,即:每个面有12个小正方形,6个面就是6×12=72个,那么几何体的表面积为72×1=72.【详解】如图所示,周边的六个挖空的正方体每个面增加4个正方形,减少了1个小正方形,则每个面的正方形个数为12个,则表面积为12×6×1=72.故选:B.【点睛】主要考查学生的空间想象能力,解决本题的关键是能够想象出物体表面积的变化情况. 5.B解析:B【分析】由主视图和左视图确定俯视图的形状,再判断最少的正方体的个数.【详解】由主视图和左视图可确定所需正方体个数最少时俯视图(数字为该位置小正方体的个数)为:则搭成这个几何体的小正方体最少有5个,故选B.【点睛】本题考查了由三视图判断几何体,根据主视图和左视图画出所需正方体个数最少的俯视图是关键.【详解】请在此输入详解!【点睛】请在此输入点睛!6.C解析:C【解析】【分析】根据所得到的主视图、俯视图、左视图结合中心对称图形的定义进行判断即可.【详解】观察几何体,可得三视图如图所示:可知俯视图是中心对称图形,故选C.【点睛】本题考查了三视图、中心对称图形,正确得到三视图是解决问题的关键. 7.C解析:C【解析】解:因为人和树均垂直于地面,所以和光线构成的两个直角三角形相似,设树高x米,则1.6ACAB x=,即0.8 1.60.8 3.2x=+∴x=8故选C.8.A解析:A【分析】根据平行投影的性质进行分析即可得出答案.【详解】将长方形硬纸的板面与投影线平行时,形成的影子为线段;将长方形硬纸板与地面平行放置时,形成的影子为矩形;将长方形硬纸板倾斜放置形成的影子为平行四边形;由物体同一时刻物高与影长成比例,且长方形对边相等,故得到的投影不可能是三角形.故选A.【点睛】本题考查了投影与视图的有关知识,是一道与实际生活密切相关的热点试题,灵活运用平行投影的性质是解题的关键.9.D解析:D【解析】【分析】主视图是正面看去所得图形.【详解】解:由图可知,该几何体的主视图为D选项所示图形,故选择D.【点睛】本题考查了立体图形三视图的概念.10.D解析:D【解析】解:从俯视图可以看出直观图的下面部分为三个长方体,且三个长方体的宽度相同.只有D 满足这两点.故选D .点睛:本题主要考查学生对图形的三视图的了解及学生的空间想象能力.11.D解析:D【解析】试题∵主视图和左视图都是三角形,∴此几何体为椎体,∵俯视图是一个圆,∴此几何体为圆锥.故选D .12.B解析:B【解析】试题根据俯视图而得出,第一行第一列有2个正方形,第二列有1个正方体,第二行第二列有1个正方体,共需正方体2+1+1=4.故选B.13.D解析:D【解析】由题意可得:EP ∥BD ,所以△AEP ∽△ADB ,所以AP EP AP PQ BQ BD=++,因为EP =1.5,BD =9,所以1.59220AP AP =+,解得:AP =5,因为AP=BQ ,PQ =20,所以AB=AP+BQ+PQ =5+5+20=30,故选D. 点睛:本题主要考查相似三角形的对应边成比例在解决实际问题中的应用,应用相似三角形可以间接地计算一些不易直接测量的物体的高度和宽度,解题时关键是找出相似三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.14.D解析:D【解析】由俯视图可得得最底层有5个立方体,由左视图可得第二层最少有1个立方体,最多有3个立方体,所以小立方体的个数可能是6个或7个或8个,小立方体的个数不可能是9.故选D .点睛:本题主要考查了三视图的应用,掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.注意俯视图中有几个正方形,底层就有几个立方体.二、填空题15.3cm2【分析】由三视图想象几何体的形状首先应分别根据主视图俯视图和左视图想象几何体的前面上面和左侧面的形状然后综合起来考虑整体形状【详解】解:该几何体是一个三棱柱底面等边三角形边长为2cm底面三角解析:33cm2.【分析】由三视图想象几何体的形状,首先,应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.【详解】解:该几何体是一个三棱柱,底面等边三角形边长为2cm,底面三角形的高为3cm,三棱柱的高为3cm,∴其左视图为长方形,长为3cm,宽为3cm,∴面积为:3×3=33(cm2),故答案为:33cm2.【点睛】本题考查了三视图,三视图是中考经常考查的知识内容,难度不大,但要求对三视图画法规则要熟练掌握,对常见几何体的三视图要熟悉.16.7【分析】利用主视图左视图中每列中正方形的个数判断俯视图中正方形的个数然后得出结果【详解】解:主视图从左往右2列正方形的个数依次为33;左视图从左往右2列正方形的个数依次为31;则俯视图中正方形的个解析:7【分析】利用主视图、左视图中每列中正方形的个数,判断俯视图中正方形的个数,然后得出结果.【详解】解:主视图从左往右2列正方形的个数依次为3,3;左视图从左往右2列正方形的个数依次为3, 1;则俯视图中正方形的个数如下图示:即小正方体有7个,故答案为:7.【点睛】考查对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,主视图疯狂盖,左视图拆违章”就更容易得到答案.17.4m【分析】首先要知道在同一时刻任何物体的高与其影子的比值是相同的所以竹竿的高与其影子的比值和树高与其影子的比值相同利用这个结论可以求出树高【详解】解:如图所示:过点D作DC⊥AB于点C连接AE由题解析:4m【分析】首先要知道在同一时刻任何物体的高与其影子的比值是相同的,所以竹竿的高与其影子的比值和树高与其影子的比值相同,利用这个结论可以求出树高.【详解】解:如图所示:过点D作DC⊥AB于点C,连接AE,由题意可得:DE=BC=1m,BE=1.5m,∵一根长为1m的竹竿的影长是0.5m,∴AC=2CD=3m,故AB=3+1=4(m).故答案为4m.【点睛】此题主要考查了平行投影,解题的关键要知道竹竿的高与其影子的比值和树高与其影子的比值相同.18.68【解析】【分析】易得这个几何体共有2层由俯视图可得第一层立方体的个数由主视图可得第二层立方体的可能的个数相加即可【详解】综合主视图和俯视图这个几何体的底层有4个小正方体第二层最少有2个最多有4个解析:6 8【解析】【分析】易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由主视图可得第二层立方体的可能的个数,相加即可.【详解】综合主视图和俯视图,这个几何体的底层有4个小正方体,第二层最少有2个,最多有4个,因此搭成这样的一个几何体至少需要小正方体木块的个数为:4+2=6个,至多需要小正方体木块的个数为:4+4=8个,故答案为6,8.【点睛】此题主要考查了几何体的三视图,考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.如果掌握口诀“俯视图打地基,正视图疯狂盖,左视图拆违章”就更容易得到答案.19.4【解析】【分析】根据题意得△ABC∽△EDC相似三角形成比例得解【详解】∵△ABC∽△EDC∴CB=6BD=6-2=4故BD为4m【点睛】本题考查相似三角形解题的关键是清楚相似三角形的性质解析:4.【解析】【分析】根据题意得△ABC∽△EDC,相似三角形成比例得解.【详解】∵△ABC∽△EDC,∴ED CD=AB CB ,1.62=4.8CB,CB=6,BD=6-2=4.故BD为4m.【点睛】本题考查相似三角形,解题的关键是清楚相似三角形的性质.20.54【解析】试题解析:54【解析】试题由主视图可知,搭成的几何体有三层,且有4列;由左视图可知,搭成的几何体共有3行;第一层有7个正方体,第二层有2个正方体,第三层有1个正方体,共有10个正方体,∵搭在这个几何体的基础上添加相同大小的小正方体,以搭成一个大正方体,∴搭成的大正方体的共有4×4×4=64个小正方体,∴至少还需要64-10=54个小正方体.【点睛】先由主视图、左视图、俯视图求出原来的几何体共有10个正方体,再根据搭成的大正方体的共有4×4×4=64个小正方体,即可得出答案.本题考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查,关键是求出搭成的大正方体共有多少个小正方体.21.616【解析】试题分析:由物体的主视图和左视图易得第一层最少有4块正方体最多有12块正方体;第二层最少有2块正方体最多有4块正方体故总共至少有6块正方体至多有16块正方体考点:几何体的三视图解析:6 16【解析】试题分析:由物体的主视图和左视图易得,第一层最少有4块正方体,最多有12块正方体;第二层最少有2块正方体,最多有4块正方体,故总共至少有6块正方体,至多有16块正方体.考点:几何体的三视图.22.【解析】易得此几何体为圆柱底面直径为1高为2圆柱侧面积=底面周长×高代入相应数值求解即可解:主视图和左视图为长方形可得此几何体为柱体俯视图为圆可得此几何体为圆柱故侧面积=π×1×2=2π故答案为2π 解析:【解析】易得此几何体为圆柱,底面直径为1,高为2.圆柱侧面积=底面周长×高,代入相应数值求解即可.解:主视图和左视图为长方形可得此几何体为柱体,俯视图为圆可得此几何体为圆柱, 故侧面积=π×1×2=2π.故答案为2π. 23.5【分析】易得这个几何体共有2层由俯视图可得第一层立方体的个数由左视图可得第二层所须小正方体最少的个数相加即可得答案【详解】由俯视图和左视图可知此几何体有2层第一层有4个小正方体第二层最少有1个小正 解析:5【分析】易得这个几何体共有2层,由俯视图可得第一层立方体的个数,由左视图可得第二层所须小正方体最少的个数,相加即可得答案.【详解】由俯视图和左视图可知此几何体有2层,第一层有4个小正方体,第二层最少有1个小正方体,∴这个几何体中小正方体的个数最少是5个,故答案为:5【点睛】本题考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.24.10【分析】根据俯视图和主视图确定每一层正方体可能有的个数最后求和即可【详解】解:从俯视图可以看出下面的一层有6个由主视图可以知道在中间一列的一个正方体上面可以放2个或在一个上放2个另一个上放1或2 解析:10.【分析】根据俯视图和主视图,确定每一层正方体可能有的个数,最后求和即可.【详解】解:从俯视图可以看出,下面的一层有6个,由主视图可以知道在中间一列的一个正方体上面可以放2个或在一个上放2个,另一个上放1或2个.所以小立方块的个数可以是628+=个,6219++=个,62210++=个.所以最多的故答案为10.【点睛】本题主要考查了通过三视图确定立方体的数量,正确理解俯视图和主视图以及较好的空间想象能力是解答本题的关键.25.54a2【分析】求这个几何体的表面积就要数出这个几何体中小正方体漏在外面的面的个数从前后左右上下方向上来数然后用一个面的面积乘面的个数即可【详解】解:从前后左右上下方向看到的面数分别为:101088解析:54a2【分析】求这个几何体的表面积,就要数出这个几何体中小正方体漏在外面的面的个数,从前、后、左、右、上、下方向上来数,然后用一个面的面积乘面的个数即可.【详解】解:从前、后、左、右、上、下方向看到的面数分别为:10,10,8,8,9,9所以表面积为(10+10+8+8+9+9 )a2=54a2,故答案为:54a2.【点睛】本题主要考查组合体的表面积,分析图形,掌握表面积的计算公式是解题的关键.26.球;正方体【分析】找到从物体正面左面和上面看得到的图形全等的几何体即可答案不唯一【详解】解:三视图形状都一样的几何体为球正方体故答案为球正方体(答案不唯一)【点睛】考查三视图的有关知识注意三视图都相解析:球;正方体.【分析】找到从物体正面、左面和上面看得到的图形全等的几何体即可,答案不唯一,【详解】解:三视图形状都一样的几何体为球、正方体.故答案为球、正方体(答案不唯一).【点睛】考查三视图的有关知识,注意三视图都相同的常见的几何体有球或正方体.三、解答题27.(1)a=3,b=1,c=1;(2)最少9个,最多11个;(3)见解析.【分析】(1)由主视图可得,俯视图中最右边一个正方形处有3个小立方体,中间一列两个正方形处各有1个小立方体;(2)依据d,e,f处,有一处为2个小立方体,其余两处各有1个小立方体,则该几何体最少有9个小立方体搭成;d,e,f处,各有2个小立方体,则该几何体最多有11个小立(3)依据d=1,e=2,f=1,以及a=3,b=1,c=1,即可得到几何体的左视图.【详解】解:(1)由主视图可得,俯视图中最右边一正方形处有3个小立方体,中间一列两个正方形处各有1个小立方体,∴a=3,b=1,c=1;(2)若d,e,f处,有一处为2个小立方体,其余两处各有1个小立方体,则该几何体最少有9个小立方体搭成;若d,e,f处,各有2个小立方体,则该几何体最多有11个小立方体搭成;(3)当d=1,e=2,f=1时,几何体的左视图为:【点睛】此题主要考查了三视图,用到的知识点为:三视图分为主视图、左视图、俯视图,分别是从物体正面、左面和上面看,所得到的图形;俯视图决定底层立方块的个数,易错点是由主视图得到其余层数里最少的立方块个数和最多的立方块个数.28.(1)7,(2)见解析.【分析】(1)根据几何体有2层,将2层的小正方体的个数相加即可;(2)主视图有3列,每列小正方数形数目分别为1,2,1;左视图有3列,每列小正方形数目分别为2,1,1;据此可画出图形.【详解】解:(1)由图可得,图中有7个小正方体;故答案为:7;(2)如图所示:【点睛】本题考查了三视图,在画图时一定要将物体的边缘、棱、顶点都体现出来,看得见的轮廓线都画成实线,看不见的画成虚线,不能漏掉.29.(1)7个,(2)图形见详解【分析】。
《常考题》初中九年级数学下册第二十九章《投影与视图》知识点总结(含答案解析)

一、选择题1.如图,正方形ABCD 的边长为3cm ,以直线AB 为轴,将正方形旋转一周,所得几何体的主视图的面积是( )A .29cmB .29πcmC .218πcmD .218cm 2.如图所示的几何体的俯视图是( )A .B .C .D . 3.如图是一个由多个相同小正方体搭成的几何体的俯视图,图中所标数字为该位置小正方体的个数,则这个几何体的主视图是( )A .B .C .D . 4.如图,是一个由若干个小正方体组成的几何体的主视图和左视图,则该几何体最多可由多少个小正方体组合而成?( )A .12个B .13个C .14个D .15个 5.一张矩形纸片在太阳光的照射下,在地面上的投影不可能是( ) A .正方形 B .平行四边形 C .矩形 D .等边三角形 6.由m 个相同的正方体组成一个立体图形,下面的图形分别是从正面和上面看它得到的平面图形,则m 能取到的最大值是( )A.6 B.5 C.4 D.37.一个几何体由若干大小相同的小立方块搭成,从它的正面、左面看到的形状图完全相同(如下图所示),则组成该几何体的小立方块的个数至少有()A.3个B.4个C.5个D.6个8.下列各立体图形中,自己的三个视图都全等的图形有()个①正方体;②球;③圆柱;④圆锥;⑤正六棱柱.A.1个B.2个C.3个D.4个9.如图是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是( )A.(1)(2)(3)(4) B.(4)(3)(2)(1) C.(4)(3)(1)(2) D.(2)(3)(4)(1)10.圆桌面(桌面中间有一个直径为1m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图所示的圆环形阴影.已知桌面直径为2m,桌面离地面1m,若灯泡离地面2m,则地面圆环形阴影的面积是()A.2πm2B.3πm2C.6πm2D.12πm211.如图所示是某几何体从三个方向看到的图形,则这个几何体是()A.三棱锥B.圆柱C.球D.圆锥12.如图是一个由若干个相同的小正方体组成的几何体的三种形状图,则组成这个几何体的小正体的个数是( )A .7B .8C .9D .1013.如图是由一些完全相同的小立方块搭成的几何体的三种视图.搭成这个几何体所用的小立方块的个数是( )A .5个B .6个C .7个D .8个14.如图是一个几何体的三视图,根据图中所示数据求得这个几何体的侧面积是( )A .12πB .6πC .12π+D .6π+ 15.下面四个立体图形,从正面、左面、上面对空都不可能看到长方形的是( ) A . B . C . D .二、填空题16.如图是由一些相同的小正方体构成的立体图形从三个方向看到的图形,那么构成这个立体图形的小正方体有_______个.17.棱长是1cm 的小立方体组成如图所示的几何体,那么这个几何体的表面积是____________.18.如图是由几个小立方块所搭成几何体的从上面、从正面看到的形状图.这样搭建的几何体最多需要__________个小立方块.19.如图,用棱长为1cm的小立方块组成一个几何体,从正面看和从上面看得到的图形如图所示,则这样的几何体的表面积的最小值是__cm2.20.如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为_____ m.21.已知一个物体由x个相同的正方体堆成,它的正视图和左视图如图所示,那么x的最大值是_____.22.将若干个正方体小方块堆放在一起,形成一个几何体,分别从正面看和从上面看,得到的图形如图所示,则这对小方块共有____________块.23.如图,当太阳光与地面上的树影成45°角时,树影投射在墙上的影高CD等于2米,若树根到墙的距离BC等于8米,则树高AB等于___米.24.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要________个小立方块.25.如图,是由一些相同的小正方体构成的立体图形的三视图这些相同的小正方体的个数是______.26.如图,在A 时测得某树的影长为4米,在B 时测得该树的影长为9米,若两次日照的光线互相垂直,则该树的高度为___________米.三、解答题27.晚上,小亮在广场乘凉,图中线段AB 表示站立在广场上的小亮,线段PO 表示直立在广场上的灯杆,点P 表示照明灯.(1)请你在图中画出小亮在照明灯P 照射下的影子BC (请保留作图痕迹,并把影子描成粗线);(2)如果小亮的身高 1.6AB m =,测得小亮影长2BC m =,小亮与灯杆的距离13BO m =,请求出灯杆的高PO .28.树AB 和木杆CD 在同一时刻的投影如图所示,木杆CD 高2m ,影子DE 长3m ;若树的影子BE 长7m ,则树AB 高多少m ?29.由几个相同的边长为1的小立方块搭成的几何体的俯视图如图①,格中的数字表示该位置的小立方块的个数.(1)请在下面方格纸图②中分别画出这个几何体的主视图和左视图.(2)根据三视图,这个组合几何体的表面积为多少个平方单位?(包括底面积)(3)若上述小立方块搭成的几何体的俯视图不变,如图③,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大(包括底面积)仿照图①,将数字填写在图③的正方形中.30.如图1,是一个由正方体截成的几何体,请在图2的网格中依次画出这个几何体从正面、上面、和左面看到的几何体的平面图形.。
第二十九章投影与视图单元教学计划

第二十九章投影与视图单元教学计划英文回答:Chapter 29: Teaching Plan for Projection and View Units.In this chapter, I will outline my teaching plan forthe topic of projection and view units. This is animportant topic in the field of engineering and design, asit involves the representation of three-dimensional objects on a two-dimensional surface.To begin the lesson, I will introduce the concept of projection and explain its significance in engineering and design. I will use examples such as architectural drawings and technical schematics to illustrate how projection is used to represent objects in different views.Next, I will discuss the different types of projections, such as orthographic projection and perspective projection.I will explain the differences between these two types andprovide examples to help students understand the concept.After covering the basics of projection, I will move on to discussing view units. I will explain what view units are and how they are used to represent different views of an object. I will use examples of isometric views, top views, and side views to demonstrate how view units are used in engineering and design.To make the lesson more interactive, I will incorporate hands-on activities and exercises. For example, I will provide students with a set of three-dimensional objects and ask them to create different views using projection techniques. This will allow them to apply their knowledge and practice their skills.Furthermore, I will encourage classroom discussions and group work to promote collaboration and critical thinking.I will ask students to analyze and interpret different projections and view units, and explain their reasoning behind their interpretations.In addition to the theoretical aspects of projection and view units, I will also emphasize the practical applications of these concepts. I will discuss how projection is used in various industries, such as architecture, engineering, and product design. I will also highlight the importance of accuracy and precision in creating projections and view units.Overall, my teaching plan for the chapter on projection and view units aims to provide students with a comprehensive understanding of these concepts. By incorporating examples, hands-on activities, and practical applications, I hope to make the lesson engaging and informative.中文回答:第二十九章,投影与视图单元教学计划。
初中数学人教九年级下册第二十九章 投影与视图2 平行投影与中心投影(教案)

第二十九章投影与视图投影第1课时平行投影与中心投影教学目标【知识与技能】1.经历实践探索,了解投影、平行投影和中心投影的概念;2.了解平行投影和中心投影的区别.【过程与方法】经历观察、思考的过程,感受生活中的投影广泛存在着,从中体会平行投影与中心投影的联系和区别.【情感态度】使学生学会关注生活中有关投影的数学问题,提高数学应用意识.【教学重点】掌握投影的含义,体会中心投影与平行投影的联系和区别.【教学难点】中心投影与平行投影的联系与区别.教学过程一、情境导入,初步认识物体在日光或灯光的照射下,会在地面、墙壁等处形成影子.请观察下面三幅图片,感受日常生活中的一些投影现象,并引入教材练习以加深理解.二、思考探究,获取新知一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,照射光线叫做投影线,投影所在的平面叫做投影面.有时光线是一组互相平行的射线,如太阳光或探照灯光的一束光中的光线.由平行光线形成的投影是平行投影,例如物体在太阳光的照射下形成的影子(简称日影)就是平行投影.由同一点(点光源)发出的光线形成的投影叫做中心投影,如物体在灯泡发出的光照射下形成影子就是中心投影.如图所示的是三角尺在灯光(点光源)下的投影.由此可以看出点光源下物体的投影是物体的放大图形,这两个图形是位似图形.【思考】如何判断一个物体的投影是平行投影还是中心投影呢?【教学说明】学生间相互交流,进一步体验平行投影和中心投影的关系.【归纳结论】如果投影与物体的对应点连线互相平行,则此时的投影是平行投影,如果对应点的连线交于一点,则此时的投影为中心投影.三、典例精析,掌握新知(2) 当乙木杆移动到什么位置时,其影子刚好不落在墙上?(3)在(2)的情况下,如果测得甲、乙木杆的影子长分别为和1m,那么你能求出甲木杆的高度吗?例2 请举出生活中的投影现象,说说它们是平行投影还是中心投影?【教学说明】本环节的两个问题都可让学生自主探究或相互交流.教师巡视指导,听取学生的观点,加深对知识的理解.四、师生互动,课堂小结通过这节课的学习你有哪些收获?你还有什么疑问?【教学说明】师生共同回顾本节知识,在相互交流中巩固新知.当堂测评2. 下面属于中心投影的是 ( )A. 太阳光下的树影B. 皮影戏C. 月光下房屋的影子D. 海上日出3. 晚上,人在马路上走过一盏路灯的过程中,其影子长度的变化情况是( )A. 先变短后变长B. 先变长后变短C. 逐渐变短D. 逐渐变长4. 小玲和小芳两人身高相同,两人站在灯光下的不同位置,已知小玲的影子比小芳的影子长,则可以判定小芳离灯光较______.(填“远”或“近”) .5.小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察广场的旗杆随太阳转动的情况,无意之中,他发现这四个时刻广场的旗杆在地面上的影子的长度各不相同,那么影子最长的时刻为-----综合应用:如图,路灯(P点)距地面8米,身高米的小明从距路灯的底部(O点)20米的A点沿OA所在的直线行走14米到B点时,影子的长度是变长了还是变短了?变长或变短了多少米?教学反思本课时通过引入具体情境,让学生感受平行投影与中心投影的特征,进而探讨中心投影与平行投影的区别与联系,这进一步发展了学生的抽象概括能力.。
