北京市东城区(南片)2011-2012学年高一下学期期末考试_数学试题
北京东城区高一第二学期期末教学统一检测

东城区2012—2013学年度第二学期期末教学统一检测高一化学注意:1.考试时间100分钟,试卷满分100分。
2.本试卷分两部分,第I卷为选择题,共50分;第II卷为非选择题,共50分。
3.请将选择题的答案填写在第I卷最后的表格内。
可能用到的相对原子质量:H 1 O 16 S 32 Ba 137第I卷(选择题共50分)一、选择题(本题包括10小题,每小题3分,共30分,每小题只有一个选项符合题意)1.海水资源丰富,海水淡化问题已成为科学家的主要研究方向,若实行海水淡化来供应饮用水,下列方法不正确...的是( )A.利用太阳能,将海水蒸馏淡化B.加入明矾,使海水的盐份沉淀并淡化C.通直流电,采用电渗透法使海水淡化D.通过离子交换膜,除去所含的盐分使海水淡化2. 下列物质属于天然高分子化合物的是( )A.葡萄糖B.淀粉C.蔗糖D.油脂3.鉴别某种白色织物是否是蚕丝(主要成分蛋白质)制品,可选用的方法是( )A.滴加盐酸B.滴加浓硫酸C.滴加浓硝酸D.滴加氢氧化钠溶液4. 下列关于右图所示原电池装置的叙述正确的是( )A.铜片是负极B.铜片质量逐渐减少C.氢离子在铜片表面被还原D.电流从锌片经导线流向铜片5. 下列关于化学键的叙述正确的是A.离子化合物中只含离子键B.共价化合物一定不含离子键C.离子化合物一定不含共价键D.共价化合物可能含有离子键6.下列关于甲烷分子结构的叙述正确的是( )A.甲烷的结构式为CH4B.甲烷分子的空间结构是正方体C.甲烷分子中C、H原子间是离子键D.甲烷分子中4个碳氢键完全相同7.下列金属通常采用加热分解的方法来冶炼的是( )A.Na B.Al C.Fe D.Ag8.已知反应A+B=C+D的能量变化如右图所示,下列说法正确的是( )A.该反应为吸热反应B.A物质能量一定低于C物质能量C.该反应只有在加热条件下才能进行D.反应物的总能量高于生成物的总能量9. 糖类、脂肪和蛋白质是生命活动所必需的三大营养物质,下列叙述正确的是()A.植物油不能发生水解反应B.葡萄糖能发生氧化反应和水解反应C.淀粉水解的最终产物是葡萄糖D.蛋白质水解的最终产物产物为纯净物10.一定温度下的恒容密闭容器中,反应A2(g)+B2(g) 2AB(g)达到平衡的标志是()A.容器内n(A2): n(B2):n(AB)=1:1:2B.容器内气体的密度不随时间变化C.容器内气体的总压强不随时间变化D.单位时间内生成2n mol AB,同时生成n mol A2二、选择题(本题包括10小题,每小题2分,共20分,每小题只有一个选项符合题意)11.在同温同压条件下,已知:C+CO22CO(正反应是吸热),正反应的反应速率为v1;N2+3H22NH3(正反应是放热),正反应的反应速率为v2。
东城区2011——2012学第二学期期末教学统一检测.doc

东城区2011——2012学年度第二学期期末教学统一检测高二数学(理科)一、选择题(本大题共12小题,每小题4分,共48分.在每小题列出的四个选项中,选出符合题目要求的一项) 1.在复平面内,复数1iiz -=(i 是虚数单位)对应的点位于 A .第一象限 B .第二象限 C .第三象限D .第四象限2.若曲线2y x ax b =++在点(0,)b 处的切线方程是10x y +-=,则A .1,1a b ==B .1,1a b =-=C .1,1a b ==-D .1,1a b =-=-3.在6(2)x -的展开式中,3x 的系数是A .160B .160-C .120D .120- 4.类比“等差数列的定义”给出一个新数列“等和数列的定义”是 A .连续两项的和相等的数列叫等和数列B .从第一项起,以后每一项与前一项的和都相等的数列叫等和数列C .从第二项起,以后每一项与前一项的差都不相等的数列叫等和数列D .从第二项起,以后每一项与前一项的和都相等的数列叫等和数列 5.若函数()y f x =的导函数在区间[,]a b 上是增函数,则函数()y f x =在区间[,]a b 上的 图象可能是B. 6.某会议室第一排共有8个座位,现有3人就座,若要求每人左右均有空位,则不同的坐法种数为A .12B .16C .24D .327.某班有40名学生,其中有15人是共青团员.现将全班分成4个小组,第一组有学生10人,共青团员4人,从该班任选一个学生代表.在选到的学生代表是共青团员的条件下,他又是第一组学生的概率为 A .415B .514C .14D .348.若函数()ln f x x x x 2=-2-4的导函数为'()f x ,则'()f x >0的解集为 A. (,)0+∞ B. 102∞-+(,)(,) C. (,)2+∞ D. (,)-109.由曲线y =,直线2y x =-及y 轴所围成的图形的面积为密封线内不要答题区(县 学校 班 姓A .103B .4C .163D .6 10.已知随机变量ξ服从正态分布2(2)N σ,,(4)0.84P ξ=≤,则(0)P ξ≤等于A .0.16B .0.32C .0.68D ,0.8411.用总长14.8m 的钢条制作一个长方体容器的框架,若容器底面的长比宽多0.5m ,要使它的容积最大,则容器底面的宽为 A .0.5mB .0.7mC .1mD .1.5m12.设函数()y f x =在(,)-∞+∞内有定义.对于给定的正数K ,定义函数(),(),(),().k f x f x K f x K f x K ≤⎧=⎨>⎩取函数()2e xf x x -=--,若对任意的(,)x ∈-∞+∞,恒 有()()k f x f x =,则A .K 的最大值为2 B. K 的最小值为2C .K 的最大值为1 D. K 的最小值为1 二、填空题(本题共4小题,每小题4分,共16分) 13.6(1)x +的各二项式系数的最大值是 . 14.已知z 是纯虚数,21z i+-是实数,那么z = . 15根据上表可得回归方程ˆˆˆybx a =+中的ˆb 为9.4,则ˆa = . 16.设函数()(0)2xf x x x =>+,定义()n f x ,*n ∈N 如下:当1n =时,1()()f x f x =; 当*n ∈N 且2n ≥时,1()(())n n f x f f x -=.观察:1()(),2x f x f x x ==+ 21()(()),34xf x f f x x ==+32()(()),78xf x f f x x ==+43()(()),1516xf x f f x x ==+根据以上事实,由归纳推理可得:当*n ∈N 时,()n f x = .三、解答题(本大题共4个小题,其中第17题8分,第18,19题各9分,第20题10分,共36分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分8分)设函数32()2f x x x x =-+-(x ∈R ). (Ⅰ)求曲线()y f x =在点(2(2))f ,处的切线方程; (Ⅱ)求函数()f x 在区间[0,2]上的最大值与最小值.在数列{}n a 中,13a =,134n n a a n +=-,1,2,3,n =.(Ⅰ)计算2a ,3a ,4a 的值,(Ⅱ)根据(Ⅰ)的计算结果,猜想{}n a 的通项公式,并用数学归纳法加以证明.密封线内不要答题一个盒子中装有5张卡片,每张卡片上写有一个数字,数字分别是1,2,3,4,5,现从盒子中随机抽取卡片.(Ⅰ)若从盒子中有放回的抽取3次卡片,每次抽取一张,求恰有两次取到的卡片上数字为偶数的概率;(Ⅱ)若从盒子中依次抽取卡片,每次抽取一张,取出的卡片不放回,当取到一张记有偶数的卡片即停止抽取,否则继续抽取卡片,求抽取次数X的分布列和期望.题答要不内线封密外贸运动鞋的加工生产中,以美元为结算货币,依据数据统计分析,若加工产品订 单的金额为x 万美元,可获得加工费近似地为1ln(21)2x +万美元,由于生产加工签约 和成品交付要经历一段时间,收益将因美元贬值而损失mx 万美元,其中(0,1)m ∈为 该时段美元的贬值指数,从而实际所得的加工费为1()ln(21)2f x x mx =+-万美元. (Ⅰ)若美元贬值指数1200m =,为确保实际所得加工费随x 的增加而增加,加工产品 订单的金额x 应在什么范围内?(Ⅱ)若加工产品订单的金额为x 万美元时共需要的生产成本为120p x =万美元,已知 加工生产能力为[10,20]x ∈(其中x 为产品订单的金额),试问美元的贬值指数m 为何 范围时,加工生产将不会出现亏损(即当[10,20]x ∈时,都有()f x p ≥成立).东城区2011—2012学年度第一学期期末教学统一检测高二数学答案及评分参考(理科)一、选择题:本大题共12小题,每小题4分,共48分.在每小题列出的四个选项中,选出符合题目要求的一项.1.C 2.B 3.B 4.D 5.A 6. C 7.A 8.C 9.C 10.A 11.C 12.D 二.填空题:本题共4小题,每小题4分,共16分. 13.20 14.2i - 15.9.1 16.(21)2n nxx -+三.解答题:本大题共4个小题,共36分,解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分8分) 解:(Ⅰ)因为 32()2f x x x x =-+-,所以 2()341f x x x '=-+-,且(2)2f =-.………………………………… 2分 所以 (2)5f '=-. …………………………………………3分 所以 曲线()f x 在点(22)-,处的切线方程是25(2)y x +=--,整理得 580x y +-=. …………………………………………4分 (Ⅱ)由(Ⅰ)知2()341f x x x '=-+-(31)(1)x x =---. 令()0f x '=,解得13x =或1x =. …………………………………………6分 当[0,2]x ∈时,()f x ',()f x 变化情况如下表:因此,函数32()2f x x x x =-+-,[0,2]x ∈的最大值为0,最小值为2-. …………………………………………8分 18.(本小题满分9分) 解:(Ⅰ)由已知可得,25a =,37a =,49a =.………………………… 3分 (Ⅱ)猜想 21n a n =+.………………………………………………………… 4分证明:① 当1n =时,由已知,左边3=,右边2113=⨯+=,猜想成立.……………… 6分 ② 假设当()n k k =∈*N 时猜想成立,即21k a k =+.……………………… 7分 则1n k =+时,1343(21)4232(1)1k k a a k k k k k +=-=+-=+=++. 所以 当1n k =+时,猜想也成立.根据 ① 和 ②,可知猜想对于任何n ∈*N 都成立. ……………………………… 9分 19.(本小题满分9分) 解:(Ⅰ)设A 表示事件“有放回地抽取3次卡片,每次抽取一张,恰有两次取到的卡片上数字为偶数”, 由已知,每次取到的卡片上数字为偶数的概率为25, …………………1分 则2232336()()55125P A C =⨯=. ………………………………………………3分 (Ⅱ)依题意,X 的可能取值为1,2,3,4. …………………………………4分2(1)5P X ==. …………………………………………………………………5分 323(2)5410P X ⨯===⨯. ……………………………………………………6分3221(3)5435P X ⨯⨯===⨯⨯. …………………………………………………7分3211(4)54310P X ⨯⨯===⨯⨯. ………………………………………………8分12342510510EX =⨯+⨯+⨯+⨯=. ………………………………9分20.(本小题满分10分) 解:(Ⅰ)由已知1200m =, 11()ln(21)2200f x x x =+-,其中0x >.………………………………………1分所以'111992()21200200(21)xf x x x -=-=++.…………………………………………3分 由'()0f x >,即19920x ->, 解得099.5x <<.即加工产品订单的金额(0,99.5)x ∈(单位:万美元)时,实际所得加工费随x 的增加而增加. …………………………………………………………………………………4分 (Ⅱ)依题意,企业加工生产不出现亏损,则当[10,20]x ∈时,都有11()ln(21)220f x x mx x =+-≥.可得1ln(21)202x m x++≤.…………………………………………………5分 令ln(21)()2x g x x+=,[10,20]x ∈.则'22ln(21)21()2x x x g x x-++=22(21)ln(21)2(21)x x x x x -++=+.……………………7分 令()2(21)ln(21)h x x x x =-++. 则'2()2[2ln(21)(21)]21h x x x x =-+++⋅+2ln(21)0x =-+<.……………8分 可知()h x 在区间[10,20]上单调递减,()h x 最小值为(20)4041ln 410h =-<,最大值为(10)2021ln 210h =-<,所以当[10,20]x ∈时,'()0g x <,()g x 在区间[10,20]上单调递减,因此min ln 41()40g x =,即ln 4114020m ≤-.………………………………………10分 故当美元的贬值指数ln 412(0,)40m -∈时,加工生产不会亏损.。
练习-北京市东城区高一数学下学期期末考试新人教A版

北京市东城区(南片)-下学期高一年级期末统一测试数学试卷本试卷共100分O考试时间120分钟O一、选择题:本大题共10小题,每小题3分,共30分O在每小题列出的四个选项中,选出符合题目要求的一项O1O下列命题中正确的是A O=-B O 0=+C O=⋅D O=++2O函数()()R x x x f ∈⎪⎭⎫⎝⎛-=42sin 3π的最小正周期为A O2πB OπC Oπ2D Oπ43O已知向量()2,1=a ,()3,2=b ,()4,3=c ,且b a c 21λλ+=,则21λλ,的值分别为A O 2-,1B O1-,2C O2,1-D O1,2-4O已知542cos -=⎪⎭⎫⎝⎛-x π,且x 在第三象限,则()π-x tan 的值为A O34 B O34- C O43 D O43-5O不等式b a >和ba 11>同时成立的充要条件是A O0>>b a B O0,0<>b aC O0<<a b D O011>>ba 6O将函数x y sin =的图象上所有的点向右平移10π个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是A O ⎪⎭⎫ ⎝⎛-=102sin πx yB O⎪⎭⎫ ⎝⎛-=52sin πx yC O⎪⎭⎫ ⎝⎛-=1021sin πx yD O⎪⎭⎫ ⎝⎛-=2021sin πx y7O如图,()3,3=,()3,3-=,F E ,是AB 上的三等分点,则ECF ∠cos 的值为A O85852 B O23 C O21 D O54 8O已知等比数列{}n a 中,各项都是正数,且1a ,321a ,22a 成等差数列,则9871098a a a a a a ++++的值为A O 223+B O21-C O21+D O223-9O若有实数a ,使得方程2sin ax =在[)π2,0上有两个不相等的实数根21x x ,,则()21co sx x +的值为A O 1-B OC O 1D Oa 23 10O在ABC ∆中,内角C B A ,,的对边分别是c b a ,,,若bc b a 322=-,B C sin 32sin =,则A 的值为A O30° B O60° C O120° D O150°二、填空题:本大题共6小题,每小题3分,共18分O11O在区间[]2,1-上随机取一个数x ,则[]1,0∈x 的概率为____________O12O 在数列{}n a 中,01≠a ,()*1,22N n n a a n n ∈≥=-,前n 项和为n S ,则24a S =_______O13O若0>a ,20=+>b a b ,,则下列不等式对一切满足条件的b a ,恒成立的是______________(写出所有正确命题的编号)OO 1≤ab ;②2≤+b a ;③222≥+b a ;④333≥+b a⑤211≥+ba O14O 已知34tan -=⎪⎭⎫⎝⎛+απO则=α2tan ___________O15O如图所示,动物园要围成四间相同面积的长方形虎笼,一面可利用原有的墙,其它各面用钢筋网围成O现有36m 长的钢筋网材料,则可围成的每间虎笼面积最大为_________m 2O16O已知M 是ABC ∆内的一点,且︒=∠=⋅3032BAC ,O定义:()=M f()z y x ,,,其中z y x ,,分别为MAB MCA MBC ∆∆∆,,的面积,若()=M f ⎪⎭⎫ ⎝⎛21,,y x ,则yx 221+的最小值为______________________,此时()=M f __________________O三、解答题:本大题共6小题,共52分O解答应写出文字说明,演算步骤或证明过程O17O(本题9分)甲袋中有3只白球、7只红球、15只黑球;乙袋中有10只白球、6只红球、9只黑球O(1)从甲袋中任取一球,求取到白球的概率;(2)从两袋中各取一球,求两球颜色相同的概率; (3)从两袋中各取一球,求两球颜色不同的概率O18O(本题9分)在平面直角坐标系xOy 中,点()2,1--A 、()3,2B 、()1,2--C O(1)求以线段AC AB 、为邻边的平行四边形两条对角线的长; (2)当t 为何值时,t -与垂直;(3)当t 为何值时,t +与2-平行,平行时它们是同向还是反向O19O(本题8分)在ABC ∆中,角C B A 、、所对的边分别为c b a ,,,已知412cos -=C O(1)求C sin 的值; (2)当2=a ,C A sin sin 2=时,求b 及c 的长O20O(本题8分)已知等差数列{}n a 满足:267753=+=a a a ,,{}n a 的前n 项和为n S O(1)求n a 及n S ;(2)令n an C b =(其中C 为常数,且*0N n C ∈≠,),求证数列{}n b 为等比数列O21O(本题9分)设函数()[]ππ,02cos 232cos 2∈+⎪⎭⎫ ⎝⎛+=x xx x f ,O(1)求⎪⎭⎫⎝⎛3πf 的值; (2)求()x f 的最小值及()x f 取最小值时x 的集合; (3)求()x f 的单调递增区间O22O其中表有行,第1行的个数是1,3,5,…,,从第2行起,每行中的每个数都等于它肩上的两数之和O(1)写出表4,验证表4各行中数的平均数按从上到下的顺序构成等比数列,并将结论推广到表()3≥n n (不要求证明); (2)每个数表中最后一行都只有一个数,它们构成数列1,4,12,…,记此数列为{}n b ,求数列{}n b 的前n 项和O【试题答案】二、填空题:本大题共6小题,每小题3分,共18分O11O31 12O215 13OO ,③,⑤(少选一个扣1分)14O34-15O22716O9,⎪⎭⎫⎝⎛2131,61,(第一空2分,第二空1分)三、解答题:本大题共6小题,共52分O解答应写出文字说明,演算步骤或证明过程O17O解:(1)从甲袋中任取一球,取到白球的概率为253; ………………………3分(2)从两袋中各取一球,两球颜色相同的概率62520725925152562572510253=⨯+⨯+⨯=P ;………………………6分(3)从两袋中各取一球,两球颜色不同的概率6254186252071=-=P O……………9分 18O解:(1)(方法一)由题设知()5,3=AB ,()1,1-=AC ,则 ()6,2=+AC AB ,()4,4=-AC AB O102=+24=O故所求的两条对角线的长分别为24、102O……………………………………3分(方法二)设该平行四边形的第四个顶点为D ,两条对角线的交点为E ,则: E 为C B 、的中点,()1,0E又()1,0E 为D A 、的中点,所以()4,1D故所求的两条对角线的长分别为10224==AD BC 、; (2)由题设知:()1,2--=,()t t t ++=-523,O由t -与垂直,得:()0=⋅-t O即()()01,2523=--⋅++t t ,, 从而115-=t ,所以511-=t O…………………………………………………6分(3)由题设知:()t t t 23,2--=+,()8,52--=-O由t +//2-,得1681510-=-t t O解得:21-=t O此时,()8,5214,25---=⎪⎭⎫ ⎝⎛=+t ,所以它们方向相反O……………9分 19O(1)解:因为41sin 212cos 2-=-=C C ,及π<<C 0,所以410sin =C O………………………………………………………4分(2)解:当2=a ,C A sin sin 2=时,由正弦定理CcA a sin sin =,得4=c O由411cos 22cos 2-=-=C C ,及π<<C 0得46cos ±=C O由余弦定理C ab b a c cos 2222-+=,得01262=-±b b O解得6=b 或62O所以⎩⎨⎧==.4,6c b 或⎩⎨⎧==.4,62c b…………………………………………………8分20O解:(1)设等差数列{}n a 的公差为d ,因为73=a ,2675=+a a ,所以有 ⎩⎨⎧=+=+.26102,7211d a d a 解得231==d a ,O所以()12123+=-+=n n a n ;()n n n n n S n 222132+=⨯-+=O………4分 (2)由(1)知12+=n a n ,所以2111C C CC b b n n n na a a a n n ===----O(常数,*2N n n ∈≥,)所以,数列{}n b 是以31C b =为首项O2C 为公比的等比数列O…………………8分21O解:(1)2123216cos 2323cos 322=⎪⎪⎭⎫ ⎝⎛+-=+⎪⎭⎫ ⎝⎛+=⎪⎭⎫ ⎝⎛ππππf O………3分 (2)()2cos 232cos 2x x x f +⎪⎭⎫ ⎝⎛+=π 1c o s 32s i n s i n 32c o s c o s++-=x x x ππ 1s i n 23c o s 21+-=x x16s i n +⎪⎭⎫⎝⎛-=x πO因为[]π,0∈x ,所以6665πππ≤-≤-x ,所以216sin 1≤⎪⎭⎫ ⎝⎛-≤-x πO所以函数()x f 的最小值为0O此时26ππ-=-x ,即32π=x O所以x 的取值集合为⎭⎬⎫⎩⎨⎧32πO……………6分 (3)由(2)可知:()[]ππ,016sin ∈+⎪⎭⎫⎝⎛-=x x x f ,O设⎪⎭⎫ ⎝⎛≤≤--=6656πμππμx ,则原函数为1sin +=μy O因为x -=6πμ为减函数,所以1sin +=μy 的减区间就是复合函数()x f 的增区间O由2665πππ-≤-≤-x ,得ππ≤≤x 32O所以,函数()x f 的单调递增区间是⎥⎦⎤⎢⎣⎡ππ,32O………………………………………9分22O解:(1)表4为1 3 5 7 4 8 12 12 20 32它的第1,2,3,4行中的数的平均数分别是4,8,16,32,它们构成首项为4,公比为2的等比数列O将这一结论推广到表()3≥n n ,表n 的第1行是1,3,5,…,12-n ,其平均数是()n nn =-++++12531 O即表()3≥n n 各行中的数的平均数按从上到下的顺序构成首项为n ,公比为2的等比数列O…………………………………………………………………………………4分(2)由(1)知,表n 中最后一行的唯一一个数为12-⋅=n n n b O设n n b b b b S ++++= 3211212232221-⋅++⨯+⨯+⨯=n n O 设n n n S 22322212321⋅++⨯+⨯+⨯=②由O -②得,n n n n S 22222213210⋅-+++++=--整理,得()121+⋅-=n n n S…………………………………………………9分。
2011 2012年东城区第二学期高一期末考试南区
实用文档东城区(南片)2010—2011高一化学学年第二学期期末统一测试可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Al 27 S 32 Cl 35.5第I卷(选择题共50分)选择题(本题包括25小题,每小题2分,共50分。
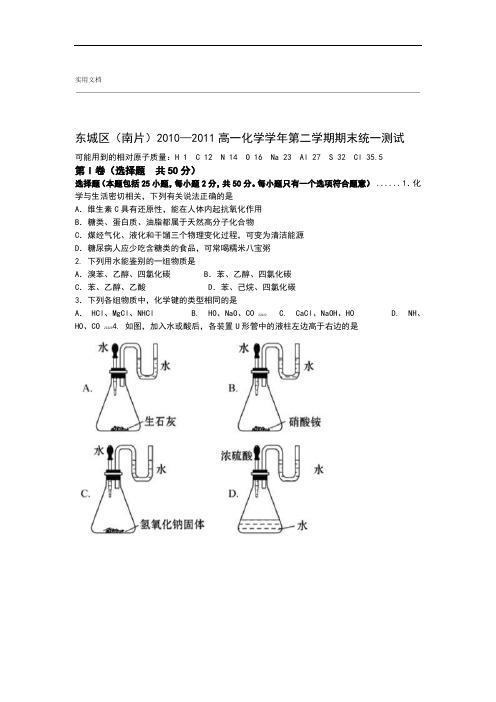
每小题只有一个选项符合题意)......1.化学与生活密切相关,下列有关说法正确的是A.维生素C具有还原性,能在人体内起抗氧化作用B.糖类、蛋白质、油脂都属于天然高分子化合物C.煤经气化、液化和干馏三个物理变化过程,可变为清洁能源D.糖尿病人应少吃含糖类的食品,可常喝糯米八宝粥2. 下列用水能鉴别的一组物质是A.溴苯、乙醇、四氯化碳 B.苯、乙醇、四氯化碳C.苯、乙醇、乙酸 D.苯、己烷、四氯化碳3.下列各组物质中,化学键的类型相同的是A. HCl、MgCl、NHCl B. HO、NaO、CO 22422 C. CaCl、NaOH、HO D. NH、HO、CO 222234. 如图,加入水或酸后,各装置U形管中的液柱左边高于右边的是.在元素周期表中,同周期元素原子具有相同的 5 .核电荷数A.电子层数B .最外层电子数C.核外电子数 D 的是.下列有关电池的叙述不正确6... A.水果电池是方便实用的家用电池 B.铅蓄电池是一种常用的二次电池C.氢氧燃料电池是一种高效、无污染的发电装置.锌锰干电池工作一段时间后,锌外壳逐渐变薄D的物质的量增加了NH,经一段时间后 2NH 3H+密闭容器中发生反应.在72LN3223大全.实用文档),则这段时间为L·s2.4 mol,这段时间内用氢气表示的反应速率为0.6mol /(2 s .4 s C.3 s D.A.6 s B .下列说法正确的是8 .反应条件是加热的反应都是吸热反应A .化学反应除了生成新的物质外,还伴随着能量的变化B .物质燃烧不一定是放热反应C .放热反应都不需要加热就能发生D .下列有关海水综合利用的说法正确的是9 .海水中含有钾元素,只需经过物理变化就可以得到钾单质A .海水蒸发制海盐的过程中只发生了化学变化BCl和可制备NaNaClC.从海水中可以得到,电解熔融NaCl2.从海带中提取碘单质的过程不涉及氧化还原反应D 的是 10.下列叙述中,不正确....乙烯和甲烷可用酸性高锰酸钾溶液鉴别 A .浓硝酸沾到皮肤上能使皮肤变黄,这是由于浓硝酸和蛋白质发生了颜色反应 B O三种元素组成的、.糖类、油脂、蛋白质都是只由C、H C D.利用油脂在碱性条件下的水解,可以制得肥皂和甘油11.下列表示正确的是2-++OO OH的电子式:-A.HClO的结构式:HO-ClB.HH2214C的原子结构示意图:. CO的比例模型: D C.212.过量铁与少量稀硫酸反应,为了加快反应速率,但是又不影响生成氢气的总量,可以采取的措施是A.加入适量镁粉 B.加入适量的水C.加入几滴硫酸铜溶液 D.再加入少量稀硫酸13.在恒温恒容的密闭容器中,有可逆反应2NO(g) + O(g)2NO(g)。
东城区(南片)2011-2012学年第一学期期末统一检测

x
(D) sin
(A) 2
(B)
1 2
(C)
1 3
(D)
1 4
第二部分(非选择题 共 70 分) 二、填空题共 6 小题,每小题 3 分,共 18 分。 (11) tan 690 . (12)已知幂函数 y f ( x) 的图象过点 (2, (13)已知 a, b R ,集合 {0,
(A) (1, 0) (B) (0, ) (C) ( ,1)
1 2
1 / 11
8 (7)函数 y log 1 x 2 的定义域为
(C) y sin(2 x ) , x R
2
(D) y sin(2 x
) , xR 8
(A) (0, ]
(8)若 是第二象限的角,则 (A) sin (C) sin
1 4
(B) [0, ]
1 4
(C) (0, 2)
(D) [ , )
1 4
2 2
0 cos
(B) tan
2
1 cos
2
2 2 (9)定义在 R 上的偶函数 f ( x) 满足:对任意的 x1 , x2 [0, ) ( x1 x2 ) , f ( x2 ) f ( x1 ) 有 0 ,则 x2 x1 (A) f (3) f (1) f (2) (B) f (1) f (2) f (3) (C) f (2) f (1) f (3) (D) f (3) f (2) f (1) (10)已知定义在 R 上的函数 f ( x) 满足下列条件:① f ( x) f ( x) ;② f ( x 2) f ( x) ;
北京市东城区2011-2012学年度第二学期高三综合练习(一)有答案-推荐下载

B. 四种物质中一定有 Ba(OH)2 C. 丙溶液中含有 NH4+ D. 丁溶液中含有 HCO325.(14 分) 卤化物和卤酸盐在工业生产中有着重要的作用。某小组为探究其中一些盐的性质,
查阅资料并进行实验。
查阅资料如下: ① BrO3- + 6I- + 6H+ = 3I2 + Br-+ 3H2O ③ IO3- + 5I- + 6H+ = 3I2 + 3H2O 实验如下:
11. 常温下,将某一元酸 HA 和 NaOH 溶液等体积混合,实验信息如下:
实验编号
甲
乙
下列判断不正确的是
A. c1 一定大于 0.2 mol·L-1 B. HA 的电离方程式是 HA
c(HA)/mol·L-1
C. 甲反应后溶液中:c(Na+) > c(OH-) > c(A-) > c(H+)
D. 乙反应后溶液中:c(Na+) < c(HA) + c(A-)
-2-
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
北京市东城区(南片)1112学年高一下学期期末统一检测数学(附答案) (1)

北京市东城区(南片)11-12学年高一下学期期末统一检测数学第一部分(选择题 共32分)一、选择题共8小题,每小题4分,共32分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1. 若a ,b 为实数,下列命题正确的是A. 若a>|b|,则a 2>b 2B. 若|a|>b ,则a 2>b 2C. 若a>b ,则a 2>b 2D. 若a 2>b 2,则a>b 2. 已知m ,n 是两条不同直线,α,β是两个不同平面。
下列命题中正确的是A. 若n ∥α,m ∥α,则n ∥mB. 若m ⊥α,α⊥β,则m ∥βC. 若m ⊥α,m ⊥β,则α∥βD. 若l ∥α,m ⊥l ,则m ⊥α3. 若非零向量a ,b 满足|a|=|b|,向量2a +b 与b 垂直,则a 与b 的夹角为A. 150°B. 120°C. 60°D. 30°4. 已知{a n }是由正数组成的等比数列,S n 表示{a n }的前n 项的和,若a 1=2,a 2a 4=64,则S 5的值是A. 30B. 61C. 62D. 635. 已知a ,b ∈R ,且ab ≠0,则在①222b a +≥ab ;②a b b a +≥2;③ab≤2)2(b a +;④2)2(b a +≤222b a +这四个不等式中,恒成立的个数为 A. 1B. 2C. 3D. 46. 在等差数列{a n }中,a 1>0且a 5=2a 10,S n 表示{a n }的前n 项的和,则S n 中最大的值是A. S 14B. S 15C. S 13或S 14D. S 14或S 157. 函数f (x )=2sin 2x +sin (2x +6π)在区间[0,2π]的最大值和最小值分别为 A. 2,21B.23,21C. 2,1-23 D. 1+23,1-23 8. 一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,四棱锥的底面为正方形,且底面边长与各侧棱长相等,三棱锥的底面边长与各侧棱长也都相等,设四棱锥、三棱锥、三棱柱的高分别为h 1,h 2,h ,则h 1:h 2:h =A. 1:1B. 2:2C. 2D.2第二部分(非选择题 共76分)二、填空题 共6小题,每小题3分,共18分。
北京市东城区2011-2012学年度第二学期高三综合练习(二)数学理科-推荐下载

(A) 70
(3) (2x 1 )4 的展开式中的常数项为 x
(A) 24
(B) 60
(B) 6
(4)若一个三棱柱的底面是正三角形,其正(主)视图如图所示,则它的体积为
(A) 3
(C) 2 3
(5)若向量 a , b 满足 a 1 , b 2 ,且 a (a + b) ,则 a 与 b 的夹角为
(1)下列命题中,真命题是
(A) x R , x2 1 0 (C) x R, x2 x 1 0
4
(2)将容量为 n 的样本中的数据分成 6 组,若第一组至第六组数据的频率之比为
2 : 3 : 4 : 6 : 4 :1,且前三组数据的频数之和等于 27 ,则 n 的值为
F n,2 F 2,n
3
(D) 或
2
(n N) ,
③ a2 b2 2 ;
④当 a 0 且 a 1, b 0 时, b 的取值范围为 ( , 5) ( 3 , ) .
其中,所有正确说法的序号是 .
a 1
三、解答题:本大题共 6 小题,共 80 分。解答应写出文字说明,演算步骤或证明过程。
(14) 已知点 A(a , b) 与点 B(1, 0) 在直线 3x 4 y 10 0 的两侧,给出下列说法:
① 3a 4b 10 0 ; ②当 a 0 时, a b 有最小值,无最大值;
2
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电通,力1根保过据护管生高线产中0不工资仅艺料可高试以中卷解资配决料置吊试技顶卷术层要是配求指置,机不对组规电在范气进高设行中备继资进电料行保试空护卷载高问与中题带资2负料2,荷试而下卷且高总可中体保资配障料置2试时32卷,3各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并25工且52作尽22下可护都能1关可地于以缩管正小路常故高工障中作高资;中料对资试于料卷继试连电卷接保破管护坏口进范处行围理整,高核或中对者资定对料值某试,些卷审异弯核常扁与高度校中固对资定图料盒纸试位,卷置编工.写况保复进护杂行层设自防备动腐与处跨装理接置,地高尤线中其弯资要曲料避半试免径卷错标调误高试高等方中,案资要,料求编试技5写、卷术重电保交要气护底设设装。备备置管4高调、动线中试电作敷资高气,设料中课并技3试资件且、术卷料中拒管试试调绝路包验卷试动敷含方技作设线案术,技槽以来术、及避管系免架统不等启必多动要项方高方案中式;资,对料为整试解套卷决启突高动然中过停语程机文中。电高因气中此课资,件料电中试力管卷高壁电中薄气资、设料接备试口进卷不行保严调护等试装问工置题作调,并试合且技理进术利行,用过要管关求线运电敷行力设高保技中护术资装。料置线试做缆卷到敷技准设术确原指灵则导活:。。在对对分于于线调差盒试动处过保,程护当中装不高置同中高电资中压料资回试料路卷试交技卷叉术调时问试,题技应,术采作是用为指金调发属试电隔人机板员一进,变行需压隔要器开在组处事在理前发;掌生同握内一图部线纸故槽资障内料时,、,强设需电备要回制进路造行须厂外同家部时出电切具源断高高习中中题资资电料料源试试,卷卷线试切缆验除敷报从设告而完与采毕相用,关高要技中进术资行资料检料试查,卷和并主检且要测了保处解护理现装。场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
北京市东城区(南片)2011-2012学年高一下学期期末考试 地理试题

北京市东城区(南片)2011-2012学年第二学期期末统一检测高一地理本试卷共100分,考试时长100分钟。
第一部分(选择题共50分)下列各小题均有四个选项,其中只有一项最符合题意要求。
(每小题1分,多选、错选、漏选,该小题均不得分)。
读图1,完成1~4题。
1. 图中人口自然增长率最高的国家是A. 甲B. 乙C. 丙D. 丁2. 乙与丙国的人口增长模式分别属于A. 原始型和传统型B. 现代型和传统型C. 原始型和现代型D. 传统型和原始型3. 与当前我国人口自然增长趋势相符的是A. 甲B. 乙C. 丙D. 丁4. 关于甲国人口问题现状的正确叙述是A. 人口老龄化日趋严重B. 青壮年劳动力过剩C. 人口素质偏低D. 城市人口比重较低5. 人口增长模式的原始型和传统型增长模式的共同点是A. 高自然增长率B. 低死亡率C. 高出生率D. 低出生率6. 决定某地区人口数量变化的主要是人口的①生育率②迁移③自然增长率④死亡率A. ①②B. ②③C. ③④D. ①④读图2,完成7-10题7. 关于图中说法正确的是A. 0-14岁人口比例下降,人口总数减少B. 15-59岁人口比例上升,年龄结构趋于年轻C. 60岁以上人口比例上升,老龄化进程加速D. 我国人口自然增长率已经出现负增长8. 关于人口流动的正确叙述是A. 2000年为1.5亿B. 2010年为1.5亿C. 2000年为3亿D. 2010年为5亿9. 近年来我国人口流动的主要方向,主要是A. 从城市流往农村B. 从平原流向山区C. 从沿海流向内地D. 从农村流往城市10. 近年来影响我国人口流动的主要因素是A. 政治B. 经济C. 生态环境D. 社会文化读图3,完成11-13题。
11. 与人口的合理容量呈正相关的有①地区开放程度②资源数量③科技发展水平④地区消费水平A. ①②③B. ①③④C. ①②④D. ②③④12. 关于一个地区人口合理容量的正确叙述是A. 只会升高,不会下降B. 不会变化C. 只会下降,不会升高D. 具有相对的确定性和绝对的不确定性13. 制约环境承载力的首要因素是A. 科技发展水平B. 人口的文化水平C. 资源状况D. 人口生活消费水平读图4,完成14-18题。
东城区2011-2012一模数学理科试题及答案

北京市东城区2011-2012学年度第二学期高三综合练习(一)数学 (理科)本试卷分第Ⅰ卷和第Ⅱ卷两部分,第Ⅰ卷1至2页,第Ⅱ卷3至5页,共150分。
考试时长120分钟。
考生务必将答案答在答题卡上,在试卷上作答无效。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷(选择题 共40分)一、本大题共8小题,每小题5分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
(1)若a ,b ∈R ,i 是虚数单位,且(2)i 1i a b +-=+,则a b +的值为(A )1 (B )2 (C )3 (D )4(2)若集合},0{2m A =,}2,1{=B ,则“1=m ”是“}2,1,0{=B A ”的 (A )充分不必要条件 (B )必要不充分条件 (C )充分必要条件 (D )既不充分也不必要条件(3)若实数x ,y 满足不等式组1,2,0,y x y x y +≤⎧⎪-≤⎨⎪≥⎩则y x z 2-=的最小值为(A )27-(B ) 2- (C )1 (D ) 25(4)右图给出的是计算1001...81614121+++++的一个程序框图, 其中判断框内应填入的条件是(A )50<i (B )50>i (C )25<i (D ) 25>i(5)某小区有排成一排的7个车位,现有3辆不同型号的车需要停放,如果要求剩余的4个车位连在一起,那么不同的停放方法的种数为(A )16(B )18(C )24(D )32(6)已知x ,y ,z ∈R ,若1-,x ,y ,z ,3-成等比数列,则xyz 的值为 C (A )3-(B )3±(C)-(D)±(7)在直角梯形ABCD 中,已知BC ∥AD ,AB AD ⊥,4AB =,2BC =,4AD =,若P 为CD 的 中点,则PA PB ⋅的值为(A )5- (B )4- (C )4 (D )5(8)已知函数21,0,()(1),0.x x f x f x x -⎧-≤=⎨->⎩若方程()f x x a =+有且只有两个不相等的实数根,则实数a的8 4 4 6 4 7m 9 35 4 5 5 10 7 9乙甲取值范围是(A )(),1-∞ (B )(],1-∞ (C )()0,1 (D )[)0,+∞第Ⅱ卷(共110分)二、填空题:本大题共6小题,每小题5分,共30分。
北京市东城区(南片)下学期高一数学期末考试

北京市东城区2010-2011学年下学期高一年级期末考试数学试卷本试卷共100分。
考试时间120分钟。
一、选择题:本大题共10小题,每小题3分,共30分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1. 下列命题中正确的是A. =-B. 0=+C. =⋅D. =++2. 函数()()R x x x f ∈⎪⎭⎫⎝⎛-=42sin 3π的最小正周期为A.2πB. πC. π2D. π43. 已知向量()2,1=a ,()3,2=b ,()4,3=c ,且b a c 21λλ+=,则21λλ,的值分别为A. 2-,1B. 1-,2C. 2,1-D. 1,2-4. 已知542cos -=⎪⎭⎫⎝⎛-x π,且x 在第三象限,则()π-x tan 的值为A. 34B. 34-C. 43D. 43-5. 不等式b a >和ba 11>同时成立的充要条件是A. 0>>b aB. 0,0<>b aC. 0<<a bD. 011>>ba6. 将函数x y sin =的图象上所有的点向右平移10π个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解读式是A. ⎪⎭⎫⎝⎛-=102sin πx yB. ⎪⎭⎫ ⎝⎛-=52sin πx y C. ⎪⎭⎫ ⎝⎛-=1021sin πx yD. ⎪⎭⎫ ⎝⎛-=2021sin πx y7. 如图,()3,3=,()3,3-=,F E ,是AB 上的三等分点,则ECF ∠cos 的值为A.85852B.23C.21 D. 54 8. 已知等比数列{}n a 中,各项都是正数,且1a ,321a ,22a 成等差数列,则9871098a a a a a a ++++的值为A. 223+B. 21-C. 21+D. 223-9. 若有实数a ,使得方程2sin ax =在[)π2,0上有两个不相等的实数根21x x ,,则()21cosx x +的值为 A. 1-B. 0C.1D.a 23 10. 在ABC ∆中,内角C B A ,,的对边分别是c b a ,,,若bc b a 322=-,B C sin 32sin =,则A 的值为A. 30°B. 60°C. 120°D.150°二、填空题:本大题共6小题,每小题3分,共18分。
北京市东城区10-11学年高一数学下学期期末考试新人教A版

北京市东城区(南片) 2010-2011 学年下学期高一年级期末统一测试数学试卷本试卷共 100 分。
考试时间 120 分钟。
一、选择题:本大题共 10 小题,每小题 3 分,共 30 分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1. 下列命题中正确的是A.OA OBABB. AB BA 0C. 0 AB 0D.AB BC CDAD2. 函数 f x3 sin xx R 的最小正周期为24A.2B.C. 2D. 43. 已知向量 a1,2 , b2,3 , c3,4 ,且 c1a2 b ,则 1, 2 的值分别为A.2 , 1B.1, 2C. 2, 1D. 1, 24. 已知 cos2x4,且 x 在第三象限,则 tan x的值为5A.4B.4C.3D.333441 15. 不等式 ab 同时成立的充要条件是和ba b 0 aa 0,b 0 A. B.C. ba 0D.1 1ab6. 将函数 ysin x 的图象上所有的点向右平移个单位长度,再把所得各点的横坐标伸10长到原来的 2 倍(纵坐标不变) ,所得图象的函数解析式是A. ysin 2xB.ysin 2x105C. ysin1 xD. y1 x2sin102207. 如图, AC3,3 , BC 3,3 , E , F 是 AB 上的三等分点,则 cos ECF 的值为2 853 1 4A.85B.C.D.2258. 已知等比数列 a n中,各项都是正数,且 a 1 ,1a 3 , 2a 2 成等差数列,则 a 8a 9 a 102a 7a 8a 9的值为A.3 2 2B. 12C. 12D.3 2 29. 若 有 实数 a , 使 得方程 sin xa 0,2 上 有 两 个 不 相 等 的实 数 根 x 1,x 2 在,则co sx 1x 22的值为A.1B. 0C.1D.3 a210. 在ABC 中 , 内 角 A , B , C 的 对 边 分 别 是 a , b , c , 若 a 2b23bc ,sin C 2 3sin B ,则 A 的值为A. 30°B. 60°C. 120°D. 150°二、填空题:本大题共6 小题,每小题 3 分,共 18 分。
北京高一下学期期末考试试题

2011-2012学年度数学期末卷试卷副标题考试范围:xxx ;考试时间:100分钟;命题人:xxx注意事项:1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上第I 卷(选择题)请点击修改第I 卷的文字说明一、选择题(题型注释)1,那么)2tan(αβ-的值为( ). .( ) 2倍(纵坐标不)..4.已知函数sin()y A x B ωφ=++(的周期为T ,在一个周期内的图象如图所示,则正确的结论是( ). A.3,2A T ==πB.2,1=-=ωB.5.在等差数列{}n a 中,若4612a a +=,n S 是数列{}n a 的前n 项和,则9S =( ) A .48 B .54 C .60 D .108 6的最小正周期为,且,则( )A 、在B 、在C 、在D 、在 7.则c o s (2)a π-= ( ) (A (B (C (D8( )A. B.C. D.、9.设实数满足,则 )A B C D 而x y 20x 2y 50y 20--≤⎧⎪+-≥⎨⎪-≤⎩x,y ()f x ()f x ()f x ()f x ()()f x f x -=π10.在数列{}n a 中,12a =,,则n a = ( )A .2ln n +B .2(1)ln n n +-C .2ln n n +D .1ln n n ++第II 卷(非选择题)请点击修改第II 卷的文字说明二、填空题(题型注释)11.若,则的最小值是________________________.12.已知xy y x R y x 则且,14,,=+∈+的最大值为 ; 13.已知点()b a P ,是直线14.设,x y 满足条件310x y y x y +≤⎧⎪≤-⎨⎪≥⎩,则22(1)x y w e ++=的最小值15.已知点P(x ,y )在不等式组⎪⎩⎪⎨⎧≥-+≤-≤-0220102y x y x 表示的平面区域内运动,则z =x -y 的取值范围是________________三、解答题(题型注释)16,且ON OM y ⋅=(其中O 为坐标原点).(1)求y 关于x 的函数关系式)(x f y =; (2)求函数)(x f y =的单调区间;24xy+21x y +=(3时,)(x f 的最大值为4,求a 的值.17.已知a 、b 、c 分别是ABC ∆的三个内角A 、B 、C 所对的边. ,求的值; (Ⅱ)若B c a cos =,且A c b sin =,试判断ABC ∆的形状.18.设n S 是正项数列{}n a 的前n 项和,且(*n N ∈). (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若2nn b =,设n n n c a b =,求数列{}n c 的前n 项和n T ..C sin19.已知数列{}n a 中,14a =,122n n n a a -=+(*2,n n N ≥∈).(Ⅰ)求2a 和3a 的值; (Ⅱ)求数列{}n a 的通项公式.20.某企业生产,A B 两种产品,每生产1吨产品所需的劳动力、煤、电消耗及利润如下表:产品品种劳动力(个) 煤(吨) 电(千瓦时) 利润(万元) A 产品4 9 3 7 B 产品541012因条件限制,该企业仅有劳动力200个,煤360吨,供电局最多供电300千瓦时,试问该企业生产,A B 两种产品各多少吨时能获得最大利润?并求最大利润.21.已知y x z +=2,使式中的x 、y 满足约束条件⎪⎩⎪⎨⎧-≥≤+≤.1,1,y y x x y(1)作出可行域; (2)求z 的最大值.22.(本题满分12分)设不等式组44330⎪⎩⎪⎨⎧≤+≥+≥y x y x x 表示的平面区域为D 。
北京市东城区(南片)2011-2012学年七年级数学下学期期末考试试题_人教新课标版

北京市东城区(南片)2011—2012学年第二学期期末统一检测初一数学一、选择题(共10个小题,每小题3分,共30分) 1. 在平面直角坐标系中,点)32(,P 在A. 第一象限B. 第二象限C. 第三象限D. 第四象限 2. 下列长度的三条线段能组成三角形的是A. 1,2,3B. 4,5,9C. 20,15,8D. 5,15,8 3. 不等式532≥+x 的解集在数轴上表示正确的是4. 若b a <,则下列不等式中成立的是A. 55+>+b aB. b a 55->-C. b a 33>D.33b a > 5. 如图,一把矩形直尺沿直线断开并错位,点E ,D ,B ,F 在同一条直线上。
若︒=∠125ADE ,则DBC ∠的度数为A. 55°B. 65°C. 75°D. 125°6. 为了解某校初一年级300名学生的体重情况,从中抽取50名学生的体重进行统计分析。
在这个问题中,总体是指A. 300名学生B. 被抽取的50名学生C. 300名学生的体重D. 被抽取50名学生的体重7. 为了让人感受丢弃塑料袋对环境的影响,某班环保小组10个同学记录了自己家中一天丢弃塑料袋的数量(单位:个):2,3,8,7,5,6,7,2,4,6,如果该班有50名学生,估计全班同学家中一周共丢弃塑料袋的数量约为A. 1000B. 1050C. 1350D. 17508. 如图,直线AB 与直线CD 相交于点O ,AB OE ⊥,垂足为O 。
若A O C EO D ∠=∠21,则=∠BOCA. 120°B. 130°C. 140°D. 150°9. 在平面直角坐标系中,线段AB 两端点的坐标分别为)0,1(A ,)2,3(B 。
将线段AB 平移后,A ,B 的对应点的坐标可以是A. )1,1(-,)3,1(--B. )1,1(,)3,3(C. )3,1(-,)1,3(D. )2,3(,)4,1(10. 在“五²一”黄金周期间,某超市推出如下购物优惠方案: (1)一次性购物在100元(不含100元)以内的,不享受优惠;(2)一次性购物在100元(含100元)以上,300元(不含300元)以内的,一律享受九折的优惠;(3)一次性购物在300元(含300元)以上时,一律享受八折的优惠。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市东城区(南片)2011-2012学年第二学期期末统一检测高一数学第一部分(选择题 共32分)一、选择题共8小题,每小题4分,共32分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1. 若a ,b 为实数,下列命题正确的是A. 若a>|b|,则a 2>b 2B. 若|a|>b ,则a 2>b 2C. 若a>b ,则a 2>b 2D. 若a 2>b 2,则a>b 2. 已知m ,n 是两条不同直线,α,β是两个不同平面。
下列命题中正确的是A. 若n ∥α,m ∥α,则n ∥mB. 若m ⊥α,α⊥β,则m ∥βC. 若m ⊥α,m ⊥β,则α∥βD. 若l ∥α,m ⊥l ,则m ⊥α3. 若非零向量a ,b 满足|a|=|b|,向量2a +b 与b 垂直,则a 与b 的夹角为A. 150°B. 120°C. 60°D. 30°4. 已知{a n }是由正数组成的等比数列,S n 表示{a n }的前n 项的和,若a 1=2,a 2a 4=64,则S 5的值是 A. 30B. 61C. 62D. 635. 已知a ,b ∈R ,且ab ≠0,则在①222b a +≥ab ;②a b b a +≥2;③ab≤2)2(b a +;④2)2(b a +≤222b a +这四个不等式中,恒成立的个数为A. 1B. 2C. 3D. 46. 在等差数列{a n }中,a 1>0且a 5=2a 10,S n 表示{a n }的前n 项的和,则S n 中最大的值是A. S 14B. S 15C. S 13或S 14D. S 14或S 157. 函数f (x )=2sin 2x +sin (2x +6π)在区间[0,2π]的最大值和最小值分别为 A. 2,21B.23,21 C. 2,1-23 D. 1+23,1-23 8. 一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,四棱锥的底面为正方形,且底面边长与各侧棱长相等,三棱锥的底面边长与各侧棱长也都相等,设四棱锥、三棱锥、三棱柱的高分别为h 1,h 2,h ,则h 1:h 2:h =A. 1:1B. 2:2C. 2D.2第二部分(非选择题 共76分)二、填空题 共6小题,每小题3分,共18分。
9. 若sin (2π+θ)=53,则cos2θ=______。
10. 若关于x 的不等式-21x 2+2x>ax 的解集为{x|0<x<2},则实数a 的值为______。
11. 如图,三棱柱ABC -A 1B 1C 1的侧棱长和底面边长均为2,且侧棱AA 1⊥底面ABC ,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为_______。
12. 已知两点A (-1,0),B (2,3),点C 满足2AC =CB ,则点C 的坐标是______,AB AC⋅ =______。
13. 121+241+381+…+101021=______。
14. 定义运算符合:“Π”,这个符号表示若干个数相乘。
例如:可将1×2×3×…×n 记作1ni i =∏,(n ∈N *),已知T n =1ni i a =∏(n ∈N *),其中a i 为数列{a n }(n ∈N *)中的第i 项。
①若a n =2n -1,则T 4=______。
②若T n =n 2(n ∈N *),则a n =____。
三、解答题共6小题,共50分。
解答应写出文字说明,演算步骤或证明过程。
15. (本小题共8分)如图,平行四边形ABCD 中,M 是DC 的中点,N 在线段BC 上,且NC =2BN 。
已知AM=c ,AN =d ,试用c ,d 表示AB 和AD 。
16. (本小题共8分) 已知cos (4π-α)=53,sin (45π+β)=-1312,α∈(4π,43π),β∈(0,4π),求sin(α+β)的值。
17. (本小题共8分)一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4t 、硝酸盐18t ;生产1车皮乙种肥料需要的主要原料是磷酸盐1t 、硝酸盐15t ,现库存磷酸盐10t 、硝酸盐66t ,在此基础上生产这两种混合肥料,若生产1车皮甲种肥料,产生的利润为10000元;生产1车皮乙种肥料,产生的利润为5000元,那么分别生产甲、乙两种肥料各多少车皮,能够产生最大利润?18. (本小题共8分)设△ABC 的内角A ,B ,C所对的边长分别为a ,b ,c ,且cosB =54,b =2。
(Ⅰ)当A =30°时,求a 的值;(Ⅱ)当△ABC 的面积为3时,求a +c 的值。
19. (本小题共8分)如图所示,正方形ABCD 与直角梯形ADEF 所在平面互相垂直,∠ADE =90°,AF ∥DE ,DE =DA =2AF 。
(Ⅰ)求证:AC ⊥平面BDE ;(Ⅱ)求证:AC ∥平面BEF 。
20. (本小题共10分)已知等差数列{an }中,公差d>0,其前n项和为Sn,且满足a2·a4=45,a1+a5=14。
(Ⅰ)求数列{an }的通项公式及其前n项和Sn;(Ⅱ)令bn =211na-(n∈N*),若数列{cn}满足c1=-41,nncc-+1=bn(n∈N*)。
求数列{cn }的通项公式cn;(Ⅲ)求f(n)=9n-nncb(n∈N*)的最小值。
【试卷答案】一、选择题(每小题4分,共32分) 1. A 2. C 3. B 4. C 5. C6. D7. A8. B二、填空题(每小题3分,共18分) 9. -25710. 1 11. 23 12. (0,1);6 13. 56-1021=102457343 14. 105;a n =21,1,21n n n n =⎧⎪⎨⎛⎫≥ ⎪⎪-⎝⎭⎩三、解答题(共50分) 15. (本小题8分)解:因为四边形ABCD 为平行四这形, M 为DC 的中点,NC =2BN ,所以AM =AD +DM =AD +21AB .2分 AN =AB +BN =AB +31AD.4分因为AM=c ,AN =d, 所以c =21AB+AD .d =AB +31AD .所以⎪⎪⎩⎪⎪⎨⎧+=+=.3121AD AB d AD AB c6分解得AB =52(3d -c ),AD =53(2c -d ).8分16. (本小题8分) 解:因为α∈(4π,43π),β∈(0,4π),所以4π-α∈(-2π,0),45π+β∈(45π,23π).又cos (4π-α)=53,sin (45π+β)=-1312, 2分所以sin (4π-α)=-54,cos (45π+β)=-135.4分 因为sin (π+α+β)=sin[(45π+β)-(4π-α)]6分=sin (45π+β)cos (4π-α)-cos (45π+β)sin (4π-α)=(-1312)·53-(-135)(-54)=-6556,所以sin (α+β)=-sin (π+α+β)=6556. 8分17. (本小题8分)解:设生产甲种肥料x 车皮、乙种肥料y 车皮,能够产生利润z 万元. 由题意满足以下条件:⎪⎪⎩⎪⎪⎨⎧≥≥≤+≤+.00661518104y ,x ,y x ,y x 可行域如图.4分目标函数为z =x +0.5y.由图可以看出,当直线y =-2x +2z 经过可行域上的点M 时,截距最大,即z 最大. 解方程组⎩⎨⎧=+=+,y x ,y x 104661518 得M 的坐标为 x =2,y =2.所以z max =x +0.5y =3.答:生产甲、乙两种肥料各2车皮,能够产生最大利润,最大利润为3万元. 8分18. (本小题8分) 解:(Ⅰ)因为cosB =54,所以sinB =53. 2分由正弦定理A a sin =B b sin ,可得 30sin a =532. 所以a =35.4分(Ⅱ)因为△ABC 的面积S =21acsinB ,sinB =53, 所以103ac =3,ac =10.5分由余弦定理b 2=a 2+c 2=-2accosB ,6分得4=a 2+c 2-58ac =a 2+c 2-16,即a 2+c 2=20. 所以(a +c )2-2ac =20,(a +c )2=40, 所以a +c =210.8分19. (本小题8分)(Ⅰ)证明:因为平面ABCD ⊥平面ADEF ,∠ADE =90°, 所以DE ⊥平面ABCD , 1分 所以DE ⊥AC.因为ABCD 是正方形, 所以AC ⊥BD , 3分 所以AC ⊥平面BDE. 4分(Ⅱ)证明:设AC BD =O ,取BE 中点G ,连结FG ,OG ,所以,OG21DE. 5分因为AF ∥DE ,DE =2AF ,所以AF OG , 从而四边形AFGO 是平行四边形,FG ∥AO. 6分 因为FG ⊂平面BEF ,AO ⊄平面BEF , 7分 所以AO ∥平面BEF ,即AC ∥平面BEF.8分20. (本小题10分)(Ⅰ)设数列{a n }的公差为d>0,且数列{a n }满足a 2·a 4=45,a 1+a 5=14. 因为数列{a n }是等差数列, 所以a 1+a 5= a 2+a 4=14. 因为d>0,所以解方程组⎩⎨⎧==+.45144242a a ,a a 得a 2=5,a 4=9.2分所以a 1=3,d =2. 所以a n =2n +1. 因为S n =na 1+21n (n -1)d , 所以S n =n 2+2n.数列{a n }的通项公式a n =2n +1,前n 项和公式S n =n 2+2n.4分(Ⅱ)因为b n =211n a -(n ∈N *),a n =2n +1, 所以b n =14(1)n n +.因为数列{c n }满足c 1=-41,c n +1-c n =14(1)n n -, 所以c n +1-c n =41(n 1-11+n ). c n - c n +1 =41(11+n -n1)… c 2-c 1=41(1-21) 以上各式相加得:c n +1-c 1=41(1-11+n )=)1(4+n n. 因为c 1=41, 所以.)1(411+-=+n c n所以.41nc n -=7分(Ⅲ)因为f (n )=9n -n n c b ,b n =)1(41+n n ,c n =-n 41, 所以f (n )=9n +11+n . 因为f (n )=9n +11+n =91+n +11+n -91,所以91+n +11+n -91≥211·91++n n -91 f (n )≥32-91=95,当且仅当91+n =11+n ,即n =2时等号成立. 当n =2时,f (n )最小值为95. 10分。
