基于时间序列的中国房地产价格走势预测
房地产市场中的房价预测模型比较

房地产市场中的房价预测模型比较引言:随着经济的发展和城市人口的增加,房地产市场一直都是一个备受关注的领域。
了解和预测房价走势对于投资者、开发商和政府来说都至关重要。
然而,由于房地产市场的复杂性和不确定性,准确预测房价一直都是一个具有挑战性的任务。
因此,为了解决这个问题,许多研究人员和机构开发了各种不同的房价预测模型。
本文将比较几种常见的房价预测模型,分析它们的优缺点和适用场景。
一、回归模型回归模型是最常见和广泛使用的房价预测方法之一。
它使用历史数据和相应的影响因素来建立一个数学模型,通过对未来一段时间的数据进行回归分析来预测房价。
回归模型可以分为线性回归和非线性回归两种。
1.1 线性回归模型线性回归模型假设价格与影响房价的因素之间存在线性关系。
它使用各种因素(如房屋面积、房龄、地理位置等)来建立数学模型,通过回归分析来预测未来的房价。
线性回归模型的优点是简单易用,计算效率高;缺点是无法处理非线性关系。
1.2 非线性回归模型非线性回归模型进一步拓展了线性回归模型的概念,它允许因素之间存在非线性关系。
非线性回归模型使用更复杂的数学函数来建立模型,并根据历史数据进行参数估计。
非线性回归模型的优点是可以更好地拟合实际数据,处理较复杂的关系;缺点是模型复杂度较高,计算成本较高。
二、人工神经网络人工神经网络是一种模拟人类神经系统工作方式的数学模型。
它通过训练算法从历史数据中提取模式,并学习建立预测模型。
人工神经网络模型在房价预测中表现出色,尤其是处理复杂非线性关系方面。
2.1 多层感知器(MLP)多层感知器是最常用的人工神经网络结构之一。
它由输入层、隐藏层和输出层组成。
多层感知器通过训练算法学习输入和输出之间的复杂关系,并通过这种关系进行预测。
多层感知器的优点是能够处理复杂的非线性关系,但模型的训练过程需要大量数据和计算资源。
2.2 循环神经网络(RNN)循环神经网络是一种具有循环连接的神经网络结构,可以处理时间序列数据。
2024年前三季度中国房地产市场总结与趋势分析

随着中国经济的快速增长和城市化的加快进程,房地产市场在过去的几年中一直是中国经济的支柱之一、2024年前三季度的中国房地产市场经历了一系列的调控政策和市场波动,下面将对这一时期的市场情况进行总结与分析。
总结:在2024年的前三个季度,中国房地产市场整体呈现出一定的波动和调整。
政府的楼市调控政策逐渐收紧,对房地产市场起到了一定的调控作用。
一方面,限购措施的实施有效控制了投机需求,抑制了房价的过快上涨;另一方面,调控政策对刚需购房者也产生了一定的影响,特别是购房难、购房贵的问题成为社会关注的焦点。
与此同时,国家经济的增长趋缓和金融危机的影响也对房地产市场产生了一定的压力。
金融危机导致大量资本外流,房地产市场的投资热情相对减弱,购房者的信心也受到一定的影响。
此外,政策调控对房地产开发商的影响较为明显,开发商面临融资压力和项目推广的困难。
趋势分析:未来的趋势中,中国房地产市场将继续面临一系列的挑战和机遇。
以下是其中几个重要的趋势:1.调控政策将继续收紧:中国政府将继续加强对房地产市场的调控力度,以维护市场的稳定和社会的平衡。
这将使得房地产市场价格上涨受到限制,对于投机炒房行为起到一定的遏制作用。
但是,政策的实施也可能会对市场的正常需求产生一定的负面影响。
2.商品房供应量将增加:为了稳定房价、保障刚需购房者的利益,政府将加大对住房建设的投资力度。
这将导致商品房供应量的增加,进一步释放市场需求。
同时,开发商也会提高房地产项目的推广力度和营销策略,寻找更多的购房者。
3.二手房市场将逐渐活跃:在政府调控政策的限制下,购房者可能会转向二手房市场来满足自己的住房需求。
这将带动二手房市场的活跃,对于房地产市场整体的稳定具有一定的积极影响。
4.城市化进程将继续推动市场需求:随着城市化进程的加快,人口流入一线和二线城市的速度将继续增加。
这将带动房地产市场需求的增加,尤其是中小型城市的房地产市场将迎来更多的机会。
总结起来,2024年前三季度的中国房地产市场呈现出了一定的波动和调整。
时间序列分析报告——VAR模型实验

基于VAR模型的我国房地产市场与汇率波动的因果关系————VAR模型实验第一部分实验分析目的及方法现选取人民币对美元汇率以及商品房房价作为变量构建VAR模型。
对于不满足单位根检验的序列采取对数化或差分处理,使其成为平稳序列再进行模型的拟合。
对于商品房房价这一变量,由于全国各省市差异较大,故此处采用全国房地产开发业综合景气指数这一变量。
此外,为了消除春节假期不固定因素带来的影响,增强数据的可比性,按照国家统计制度,从2012年起,不单独对1月份统计数据进行调查,1-2月份数据一起调查,一起发布。
所以国房景气指数p这一序列缺少每年一月份的相关数据,属于非随机、不可忽略缺失,在此采用平均值填充的方法,补足数据。
第二部分实验样本2.1数据来源数据来源于中经网统计数据库。
具体数据见附录表。
2.2所选数据变量由于我国于2005年7月实行第二次汇改,此次汇改以市场供求为基础、参考一篮子货币进行调节、有管理的浮动汇率制度取代了过去人民币汇率长达10年的紧盯美元的固定汇率体制。
故本实验拟选取2005年07月到2014年10月我国以月为单位的数据。
,用以上两个变量来构建VAR模型,并利用该模型进行分析预测。
第四部分模型构建4.1判断序列的平稳性4.1.1汇率E序列首先绘制出E的折线图,结果如下图:图4.1 汇率E的曲线图从图中可以看出,汇率E序列较强的趋势性,由此可以初步判断该序列是非平稳的。
为了减少m的变动趋势以及异方差性,先对m进行对数化处理,记为lm,其时序图如下:图4.2 lm的曲线图对数化后的趋势性减弱,但仍存在一定的趋势性,下面对lm进行一阶差分处理,去除趋势性,得到新变量dlm,观察dlm的曲线图。
图4.3 DLE的曲线图从图中可以看出,dle序列的趋势性基本已经消除,且新变量dle基本围绕0上下波动,因此选择形式为y t=y t-1+u t进行单位根检验:表4.1 单位根输出结果Null Hypothesis: DLE has a unit rootExogenous: ConstantLag Length: 2 (Automatic - based on SIC, maxlag=12)t-Statistic Prob.*Augmented Dickey-Fuller test statistic -3.031673 0.0351Test critical values: 1% level -3.4919285% level -2.88841110% level -2.581176*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(DLE)Method: Least SquaresDate: 11/15/14 Time: 20:20Sample (adjusted): 2005M11 2014M10Included observations: 108 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.DLE(-1) -0.353005 0.116439 -3.031673 0.0031 D(DLE(-1)) -0.502730 0.115417 -4.355768 0.0000 D(DLE(-2)) -0.311531 0.093265 -3.340258 0.0012C -0.000888 0.000470 -1.887592 0.0619R-squared 0.450240 Mean dependent var 1.15E-05 Adjusted R-squared 0.434382 S.D. dependent var 0.005058S.E. of regression 0.003804 Akaike infocriterion -8.269046 Sum squared resid 0.001505 Schwarz criterion -8.169708Log likelihood 450.5285 Hannan-Quinncriter. -8.228768F-statistic 28.39119 Durbin-Watson stat 2.061613Prob(F-statistic) 0.000000单位根统计量ADF=-3.031673小于临界值,且P为0.0351,因此该序列不是单位根过程,即该序列是平稳序列。
房地产市场的价格预测模型与建模分析

房地产市场的价格预测模型与建模分析房地产市场是一个重要的产业,对于政府经济政策的制定和投资者的决策具有重要影响。
因此,对于该市场的价格预测模型与建模分析显得尤为重要。
本文将讨论房地产市场价格预测模型的建立与分析方法,以帮助投资者和政府决策者更好地理解市场趋势和未来走势。
一、房地产市场价格预测模型的建立方法房地产市场价格预测模型的建立可以采用多种方法,包括回归分析、时间序列分析和机器学习等。
下面将分别介绍这些方法的原理和应用。
1. 回归分析回归分析是一种常用的统计方法,用于探索变量之间的关系。
在房地产市场中,可以选择影响房价的相关变量,如地理位置、楼层、面积、楼龄等,作为自变量,房价作为因变量,建立回归模型进行预测。
通过分析各个自变量的系数和显著性水平,可以了解各因素对房价的影响程度和方向。
2. 时间序列分析时间序列分析是一种用于研究时间序列数据的方法,适用于预测具有一定规律性和趋势性的数据。
在房地产市场中,可以将历史的房价数据作为时间序列数据,通过分析趋势、周期性和季节性等特征,建立时间序列模型进行预测。
3. 机器学习机器学习是一种基于数据的自动化建模方法,可以利用大量的历史数据进行模型训练和预测。
在房地产市场中,可以使用机器学习算法,如决策树、随机森林、神经网络等,根据房产特征数据和历史价格数据进行训练,建立预测模型。
机器学习有着良好的拟合能力和预测性能,可以提供较为准确的房价预测结果。
二、房地产市场价格模型的分析方法建立价格预测模型之后,需要对模型进行分析以评估其准确性和稳定性,进而为投资者和政府决策者提供决策支持。
下面将介绍几种常见的模型分析方法。
1. 模型拟合度分析模型拟合度分析用于评估模型对观测数据的拟合程度,可以通过计算拟合优度指标(如R方值)来衡量模型的拟合效果。
拟合度分析可以帮助我们了解模型的预测能力和稳定性。
2. 模型参数显著性检验模型参数显著性检验可以用于评估各个自变量对因变量的影响是否显著。
未来几年我国房价走势分析

2011年上学期期末考试论文写作试卷未来几年我国房价走势分析——房价是高还是低?提要:随着经济形势的紧张,国内通货膨胀的压力,这几年来,我国国内的房价不断上涨,虽有小幅度回落,但回升势头强劲。
一级城市量价齐升,幅度较大,二、三、四线城市微升,幅度较小。
随着市场销售的回升,房地产开发投资增速逐月提高。
通过德尔菲法、时间序列模型(定量分析法)和理论联系实际分析法来论证我国未来几年房价是上涨的,而且在未来很长一段时间内,上涨趋势明显。
总的来说,在政策没有大的调整情况下,2011年及今后房地产市场继续上涨是必然趋势。
关键词:房价上涨下跌一、引言2009年上半年房地产市场销售增长显著,一级城市量价齐升,幅度较大,二、三、四线城市微升,幅度较小。
随着市场销售的回升,房地产开发投资增速逐月提高。
楼王频频面世。
房地产市场下半年明显放慢速度,发展商和消费者都在疑惑中国的房地产何去何从,2007年的疯涨,2008年的低迷还会不会重现。
那么2007年疯涨、2008年低迷背后的玄机又在哪里呢。
未来几年中国房地产市场将走向何方?是涨还是跌?二.正文由于受我国传统思想影响,人们认为安家才能定天下,有了房,下半辈子就有了保障,因而我国房价居高不下,再者,由于“丈母娘现象”,房子是男女结婚的必备物品,没房就别想结婚。
最重要的是,房地产业也是我国的支柱产业,为了保证GDP逐年持续稳定上涨,除非有大的政策调整我国的房价将会继续上涨,是不会下跌的,即使有回落,也会那上回升的。
(1)目前人们对房价上升的心理预期普遍一致。
虽然希望下跌的人很多,但专家、舆论、媒体普遍看法是认为今年房价还会稳定上涨,而且以后也不会跌。
分析一下各个群体:第一,房地产商和地方政府是不希望房价下跌的,因为这和他们的利益和政绩紧密挂钩。
第二,中央政府的调控目标也仅仅是抑制房价过快上涨,并不是希望下跌。
第三,银行不希望房价下跌,否则可能出现大量坏账。
第四,有房人多,没房人少,有房的人自然是希望房价上涨的。
基于ARIMA模型对房地产行业分析与研究

基于ARIMA模型对房地产行业分析与研究一、引言房地产行业作为国民经济的支柱产业之一,在我国的经济发展中扮演着重要的角色。
随着经济的不断发展,房地产市场也一直保持着高速增长的态势,因此对房地产市场进行深入的分析与研究显得尤为重要。
传统的房地产市场研究方法主要依靠统计学方法,然而这些传统统计学方法在预测和分析方面存在较大的局限性。
本文将使用ARIMA模型对房地产行业进行分析与预测,以期能够提供更为准确的预测和分析结果。
二、ARIMA模型介绍自从Box和Jenkins于1970年提出了ARIMA模型以来,ARIMA模型被广泛应用于时间序列分析领域。
ARIMA模型是自回归、积分移动平均模型(Auto-Regressive Integrated Moving Average Model)的简称,是一种统计学模型,能够很好地处理非平稳时间序列。
ARIMA模型的主要特点是能够对时间序列数据进行拟合,然后通过预测来推断未来的走势。
ARIMA模型由AR模型(Auto-Regressive Model)、MA模型(Moving Average Model)和差分整合(Integrated)三个部分组成,其中AR模型用于描述时间序列数据的自相关结构,MA模型用于描述时间序列数据的反应结构,差分整合用于处理非平稳序列数据。
ARIMA模型可以从时间序列数据中提取趋势和周期性的信息,从而进行更为准确的预测。
三、房地产行业数据的获取与处理在本文中,我们将使用ARIMA模型对我国某地区房地产行业的数据进行分析与预测。
我们需要获取房地产行业的相关数据,包括房地产价格、销售数量、土地供应量等数据。
这些数据可以从国家统计局、房地产开发商、房地产中介机构等渠道进行获取。
然后,我们需要对这些数据进行处理,包括数据清洗、去除异常值、平稳性检验等工作。
这是为了确保我们所用的数据是可靠的、符合ARIMA模型的要求的。
四、房地产行业数据的分析与预测在获取并处理好房地产行业的数据之后,我们可以开始使用ARIMA模型进行分析与预测。
中国未来五年(2013-2017)住宅市场需求预测
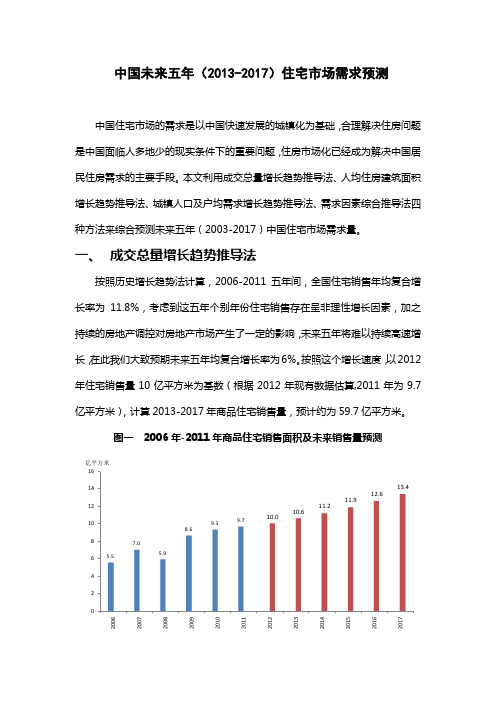
中国未来五年(2013-2017)住宅市场需求预测中国住宅市场的需求是以中国快速发展的城镇化为基础,合理解决住房问题是中国面临人多地少的现实条件下的重要问题,住房市场化已经成为解决中国居民住房需求的主要手段。
本文利用成交总量增长趋势推导法、人均住房建筑面积增长趋势推导法、城镇人口及户均需求增长趋势推导法、需求因素综合推导法四种方法来综合预测未来五年(2003-2017)中国住宅市场需求量。
一、成交总量增长趋势推导法按照历史增长趋势法计算,2006-2011五年间,全国住宅销售年均复合增长率为11.8%,考虑到这五年个别年份住宅销售存在呈非理性增长因素,加之持续的房地产调控对房地产市场产生了一定的影响,未来五年将难以持续高速增长,在此我们大致预期未来五年均复合增长率为6%。
按照这个增长速度,以2012年住宅销售量10亿平方米为基数(根据2012年现有数据估算,2011年为9.7亿平方米),计算2013-2017年商品住宅销售量,预计约为59.7亿平方米。
图一 2006年-2011年商品住宅销售面积及未来销售量预测二、人均住房建筑面积增长趋势推导法2006-2010年城镇人均居住建筑面积年均增长0.78平方米左右,且逐年放缓。
随着我国房地产市场持续调控,住宅市场进入到新的历史时期,国家更加注重住房保障工作,加强了对住房供应结构的调控,未来五年人均住房建筑面积的增长将继续放缓。
2004年,建设部政策研究中心发布了《2020我们住什么样的房子——中国全面小康社会居住目标研究》,这个课题研究公布了21项指标,主要包括城镇人均居住面积35平方米、城镇最低收入家庭人均住房面积大于20平方米等。
从目前的统计数据来看,我国应当可以提前实现城镇人均住房面积35平米的小康指标。
通过考虑已确定的住宅发展政策及近年的调控政策影响,结合历史增长的趋势分析,确定未来五年城镇人均住房面积年均增长0.6平方米,则2015年将实现小康指标,到2017年,城镇居民人均住房建筑面积达到36.3平米。
中国房价指数变化趋势分析及预测

中国房价指数变化趋势分析及预测中国房价指数变化趋势分析及预测提要:房地产市场呈现较快的下行趋势,市场信心明显不足,市场不确定性增加,稳定房地产市场压力很大。
汶川地震对中国房地产市场产生严重的负面影响中国房价指数变化趋势分析及预测着重分析了在次贷危机和2010年房产新政对中国房地产市场的双重影响下,房地产价格指数的变化趋势,并指出2008年之前房价非理性上涨和目前相对平稳的原因。
同时运用Gm(1,1)模型对次贷危机、房产新政后和没有次贷危机、房产新政情况下未来价格走势进行预测的对比。
中国房地产企业问题较多,如房地产开发企业鱼龙混杂,部分企业资金链管理能力和抗风险能力不强;房地产开发资金筹集方式不规范,缺乏风险控制机制;房地产开发企业债务负担过重,极易受到系统风险的影响;市场具有很强的垄断性同时房地产供求结构不均衡。
尤其是2008年上半年美国次货危机与全球经济减速,对房地产业产生了直接影响,房地产市场明显表现出信心不足,购房者持币观望,住房成交量缩减,房地产投资、新开工面积和土地购置面积持续下行。
这样造成房地产开发企业在前一阶段投资开发项目的实际收益率偏离了预期收益率,甚至有的企业将面临生存危机。
房地产市场呈现较快的下行趋势,市场信心明显不足,市场不确定性增加,稳定房地产市场压力很大。
汶川地震对中国房地产市场产生严重的负面影响,这种影响不仅在于对灾区的房地产市场造成毁灭性打击,而且在于改变目前国内居民对住房消费与投资的观念。
这些都会严重影响国内房产市场的供求关系,特别会影响房产市场的投资理念。
一、房地产价格指数变化分析图1为自2005年1月份以来中国房地产价格指数的变化图,从图中可以看出,从2005年1月起开始进入一个比较明显的下行周期,2006年初进入谷底,随后进入上行周期,2008年初中国房地产价格指数处于一个历史高位,但由于美国次货危机等因素的影响房地产价格指数一路下行,而且幅度颇大。
次贷危机的影响逐步消退,2009年底房地产价格开始回升,但是由于政府出台房地产新政策,房地产价格指数变动幅度很小,大部分投资者处于观望状态。
中国房地产周期波动研究——一个基于时序全局主成分方法的分析

作者简介: 唐志军(9 8一) 男 , 17 , 湖南永州人 , 怀化学院经济系副教授 , 东北财经 大学经济学博 士, 主要研究 方向为转轨 经济学 、 制度 新 经济学 、 宏观经济学 、 房地产业 、 产业经济学等。
l
科 学决 策 2 0 0 9年 第 6期
应用这种方法 , 我们可 以将原本用多个指标 描述 的某个复杂经济动态用一个综合指标在时间序列 图中反映并描绘 出来 , 从中看 出其发展态势。 在已有的研究中, 张红 , 谢娜 (0 8 利用主成 20 )
新疆区域综合经济实力进行 了比较分析 , 取得 了
期, 而在同样 的时间长度 内, 需求发展平稳且 不 存在周期性特征。这意味着从长期发展来看 , 市
研究提供 了一种快速 、 科学 的量化分析工具 。因 而, 我们打算利用 时序全局 主成分 分析 方法就我
国的房地产周期波动研究进行初步 的尝试 , 以期 得出一些新的结论。通过研究我们发现 自19 年 98
分分析与谱分析方法 , 于 19 -20 基 9 1 05的数据研 究了北京房地产 的周期波动情况 , 他们得 出结论
认为 19 -20 92 05年北京房地产市场的供给和需求 均存在明显的周期特征 , 中供给与需求 的主周 其 期时间长度一致。表明北京房地产市场基本保持
了供求关系的均衡发展。同时, 从较长的时间长 度来看 , 供给还存在一个较明显的为期 7 年的次周
与新疆区域经济发展水平 的实际情况非常一致 的 效果 ¨ 。鄢寒 , 吴群英 (08 利用时序全局主成 20 ) 分分析方法动态描绘广西 19 — 05 90 20 年的经济发 展历程。描绘结果与广西经济发展实际情况基本 吻合¨ 。然而 , 上述文献都未应用于我国房地产 周期的研究 中。目前利用时序全局主成分方法对 我国房地产周期进行研究的文献还不多见 。 而时序全局主成分分析方法能对多指标的经 济问题进行动态轨迹描绘及分析 , 为房地 产周期
基于时间序列的中国房地产价格走势预测

1 。擘 O.95 70 4 o OS S 5 1 0 0O o 2 8 趣 。 s 7. 7 o O∞ S3 ∞ OO o 3 46 .2 2 2 O 0 3 3 164 O∞ 4 - 5 02 3 8 1 S O 04 0 0 3 O n∞ S 2 3 .。6 417 2 6 o2 4 6 o硒 《 8 o .1 4185 O翻∞ 4O 19 1 . 7 5 ..o 4 OO 2 oo 7 2O阻 Oo O o 8 4 O O 3 4 08 o 2 1 OO o 9 O 2 . 4 4 ■0 , O o oo 3 2 9 ∞ O 国 9 . 6 4 3 OO 01 oO 4 21 0 ∞ 1 00 00 4 21 o o ’ 31 .0 4 。9 OO o 1 Oo 9 ,7 4241 0 2 5 0 8 3 ∞ 1 0 1 0 , 2 35 0 0锄时 3 3 , 4 5 . 5 { 0 缮 4 1 " 4 3 .o 3 4 0 7 0o O 2 1 00 9 0o 5 4 2 4 S 4 , 4 O∞} 8 o ’ 6∞ 8 0 4 4 I ,o 03 8 4 6 Oo O 1 ∞ 睁 00 8 54 9 0o} 7 羽 ,5 4 4 l o 1 12 .,51 6 8 1 oo 4 2§ Oo O o 1 O . 9 4 7 0o 日 9m 66 00 T 6 7 9 o 2 0 5 { 4 7 7 0 0 1 0 8 6.9 00
进行 预测 。
【 键 词】 地 产 价 格 ; 问序 列 ; RI A模 型 关 房 时 A M
19 年 实行 住 房 商 品化 以来 , 地 产 市 场 处 于 不成 熟 阶 段 , 98 房 我 国 房地 产 投 资规 模 不 断 扩 大 , 地 产 价 格 持 续 上 涨 。过 快 上 涨 的 房 房 价 不 仅 极 大 地 影 响 居 民 的 生 活 质 量 , 且 也影 响 了 我 国经 济 的 而 平稳 健 康 发 展 。因此 , 价 问题 已 经 成 为 一 个 重 要 的 经 济 问 题 和 房 社会 问题 本 文 旨在 通 过 时 间 序 列 模 型 的 建 立 , 未 来 房 价 走 势 对 进行 预 测
关于2024年中国房地产行业的预测和SWOT分析

关于2024年中国房地产行业的预测和SWOT分析1.政策调整与优化:预计2024年政府将继续对房地产市场相关政策进行优化调整,包括供需两端的支持措施,以稳定市场预期、缓解房企压力,并释放合理的购房需求。
2.融资环境改善:房企信用修复速度有望提升,随着金融支持政策的落地,企业融资环境将有所好转,有助于促进市场回暖。
3.基本面趋稳:有观点认为2024年二季度可能是房地产行业基本面企稳的重要时间点,房价不会持续下跌,而可能出现止跌回稳的趋势。
4.市场需求变化:中长期来看,尽管整体新增需求可能下降(如到2030年降至9.1亿平),但鉴于城镇化进程和人口结构的变化,房地产市场仍有一定发展空间。
5.细分市场机遇:商业地产领域如数据中心、养老地产等前景被看好,这些细分市场可能会成为新的增长点。
6.行业转型与升级:房地产行业在经历高速增长后步入存量时代,精细化运营、智能化服务、绿色建筑以及地产科技的应用将成为行业转型升级的重点方向。
SWOT分析Strengths(优势):•政策支撑:政府对市场的调控具有灵活性,能够适时推出支持性政策来稳定市场。
•行业整合:市场调整过程中,头部房企通过并购重组等方式提高行业集中度,增强抗风险能力。
•新兴领域潜力:如商业地产、养老地产等领域的发展空间大,为行业提供多元化发展路径。
Weaknesses(劣势):•高库存压力:过去几年的过度开发导致部分地区库存较高,消化周期较长。
•资金链紧绷:部分房企尤其是中小型房企依然面临严峻的资金流动性问题。
•消费者信心恢复缓慢:购房预期需要时间修复,短期之内市场信心可能难以快速提振。
Opportunities(机会):•新型城镇化:伴随着新型城镇化的推进,三四线城市和城市群建设带来新的市场需求。
•技术创新应用:智能建筑、大数据、物联网等技术为房地产业提供了创新升级的机会。
•可持续发展要求:绿色建筑标准提升和碳达峰、碳中和目标为行业发展注入绿色发展动力。
基于时间序列的趋势分析和预测

基于时间序列的趋势分析和预测近年来,随着经济的发展和社会的进步,越来越多的人们开始关注经济数据的变化,其中时间序列数据成为了经济研究的重要工具。
时间序列数据是按照时间顺序排列的观测值,例如股票价格、GDP增长率、汇率变化、气温等数据。
时间序列分析是一种对这些数据进行统计分析的方法,旨在揭示数据的规律性和趋势性,帮助人们做出科学合理的决策。
一、时间序列分析的基本方法时间序列分析的基本方法包括时序图、自相关图、偏自相关图、平稳性检验、白噪声检验、ARIMA模型等。
其中,时序图是最重要的方法之一,它可以直观地反映数据的趋势、季节性和随机性等特征。
自相关图和偏自相关图可以用来判断时间序列是否具有自相关性或偏自相关性,从而选择合适的模型。
平稳性检验和白噪声检验可以用来判断时间序列是否平稳、是否服从正态分布等,为模型的建立提供了依据。
ARIMA模型则是一种常用的自回归移动平均模型,它可以利用过去的数据来预测将来的数据。
二、时间序列分析的应用时间序列分析的应用非常广泛,主要应用于宏观经济预测、股票价格预测、商品价格预测、天气预测等方面。
下面,我们将以股票价格预测为例,来介绍时间序列分析的应用。
在股票交易中,准确地预测股票价格的变化趋势,可以帮助投资者做出正确的决策,避免投资风险。
时间序列分析可以通过建立ARIMA模型,对股票价格进行预测。
建立ARIMA模型的步骤如下:1、对时间序列进行多阶差分,使得时间序列变成平稳序列。
2、画出自相关图和偏自相关图,确定ARIMA模型的参数p、d、q。
3、采用极大似然估计法,对ARIMA模型进行拟合。
4、利用ARIMA模型进行预测。
以某股票为例,其时间序列数据如下:日期价格2010/1/4 10.202010/1/5 10.172010/1/6 10.412010/1/7 10.482010/1/8 10.59首先,我们对时间序列进行一阶差分,得到如下平稳序列:日期一阶差分2010/1/4 NA2010/1/5 -0.032010/1/6 0.242010/1/7 0.072010/1/8 0.11然后,我们画出一阶差分的自相关图和偏自相关图,确定ARIMA模型的参数。
基于时间序列的房地产价格指数预测方法探讨

[ 关键词]时间序 列; 房地产 ; 价格指数 [ 中图分类 号]F 9 .0 [ 2 33 文献标识码 ] [ A 文章编号 ]6 1— 12 2 0 )2— 0 0— 4 17 7 1 (0 8 0 0 8 0
The Fo e a tM e h d Dic s i n o a t e Prc nd x Ba e i Ti e S re r c s t o s u so f Re lEsat ie I e s d O l m e i s
ADF e a n t n T i ri l a i e e e ln mo y p rmee tte b g n i g o si t n h p rx mae ma i m ie i o d meh x mi a i . h sa t eh sgv n a s t h o g me r a a t ra e i n n f t o c t h e ma e a d t ea p o i t x mu lk l o t — h
记 忆 参数 d的 初 估 计 与近 似 极 大似 然 估 计 相 结合 , 时 间 序 列 长 记 忆 分 析 与 短 记 忆 分 析 相 结合 的 系统 性 的建 将 模 思路 。利 用 中 国房地 产价 格 指 数 , 行 了时 间序 列 长 记 忆性 判 断 以及 A FMA建 模 的 实证研 究 , 证 明 了该 进 RI 并
o si td u i e , nfe h i e e o g me  ̄ a ay i n h h f me  ̄ a ay i t e s se t d l g me t l y i al t ep p r d et ma e n f s u i st e t i i me s r sln mo i n l ssa d t e s o mo l n l ss h y tmai mo ei n ai F n l c n t y,h a e
房价预测数学建模

房价预测数学建模房价预测是指通过数学建模方法,对未来一定时期内的房价进行预测和分析。
房价预测在经济学和金融领域具有重要的应用价值,对政府、房地产市场参与者以及普通居民都有重要意义。
本文将介绍房价预测的数学建模方法,并探讨其应用和局限性。
房价预测的数学建模方法主要包括回归分析、时间序列分析和机器学习方法。
首先,回归分析是一种常用的房价预测方法。
它基于统计学原理,通过将房价作为因变量,收集并整理一系列可能影响房价的自变量数据,建立回归模型来分析它们之间的关系。
常用的回归模型包括线性回归、多项式回归和逻辑回归等。
通过对历史数据的回归分析,可以得到房价与自变量之间的数学关系,从而对未来的房价进行预测。
其次,时间序列分析也是一种常见的房价预测方法。
它基于时间序列数据的特点,通过分析房价随时间的变化趋势和周期性变动,建立时间序列模型来预测未来的房价。
常用的时间序列模型包括移动平均模型、自回归移动平均模型和季节性模型等。
时间序列分析方法对于具有一定规律性和周期性的房价数据预测较为有效。
此外,机器学习方法在房价预测领域也得到了广泛应用。
基于大数据和人工智能技术,机器学习方法可以通过对大量房价数据的学习和模式识别,建立复杂的预测模型来预测未来的房价。
常用的机器学习方法包括神经网络、支持向量机和决策树等。
机器学习方法在房价预测中具有较高的灵活性和准确性。
房价预测的数学建模方法具有一定的局限性。
首先,房价受到很多因素的影响,包括宏观经济因素、政策因素、地理因素等。
单一的数学模型并不能完全反映这些复杂的影响因素。
其次,房价预测存在一定的不确定性,无法完全准确预测未来的房价。
最后,数学模型的建立需要大量的房价数据和有效的指标,而这些数据并不总是容易获取。
综上所述,房价预测的数学建模方法包括回归分析、时间序列分析和机器学习方法。
这些方法在房价预测中发挥着重要作用,但仍然存在一定的局限性。
未来的研究可以进一步探索新的建模方法,提高房价预测的准确性和可靠性。
基于时域分析法的中国房地产市场和股票市场周期波动关系研究:1999—2009

关关 系, 在研 究方法上又有 区别 。如沈悦等 (0 8 运用时 间 但 20 ) 序 列相 关 方 法 对 我 国 股 票 市 场 与 房 地 产 市 场 的 关 系 进 行 了实 证 研 究 ,发 现 房 地 产 价 格 上 涨 对 股 票 价 格 上 升 有 显 著 影 响 , 而 反 之 影 响较 为 微 弱 。Q a un和 Tt n 19 ) 于 面板 数 据 分 析 i ma (9 9 基 l 个 国 家 的股 票 价 格 与 房 地 产 价 格 间 的 关 系 。得 出 除 E本 外 7 t 其 他 国家 房 地 产 价 格 与 股 票 价 格 的 变 化 没 有 同期 相 关 关 系 , 但 是 长期 而 言 股 票 收益 和房 租 、 价 的变 化存 在 显 著 的 正 向相 关 房
房价与股价关 系的研究成果 , 笔者归纳为三种类 型的观点 :
第 一 类 观 点 认 为 房 地 产 市 场 与 股 票 市 场 不 存 在 显 著 的相 关关 系。如 Z ag Li 2 0 ) hn ,i等( 0 7 利用协整模型检验 了我 国台湾 地 区 的房 地 产 市 场 与 股 票 市 场 的关 系 , 现 房 价 与 股 价 是 不 相 发
£: 1
为这 t1 原 时 间 序 列 增 量 的平 均 值 , 映 了 e 间 长 度 - 年 反 时
场 进行 有效 监 管 , 进 房 市 、 市 的持 续 稳 定 发 展 。 促 股
文献 综述 房地产价格 与股票价格 的关系及互 动机制 一直是学术 界 关 注的重点 ,早在 18 年 , b t n和 S gl 94 I oo b s i e 就对美 国的房 地 e 产 价格 和标 准普 尔 5 0股 票 指 数 之 间 的 相关 性 进 行 分 析 , 出 0 得 两者之 间的相关 系数仅为 一 . 00 6的结论 。针对 目前理论界关 于
基于ARIMA的房价预测研究

基于ARIMA的房价预测研究随着社会的发展,房地产已经成为了社会经济中不可或缺的一个组成部分。
随之,人们对于房价变化的关注和瞩目也越来越多。
尤其是在当前的市场环境下,房价的波动影响着每一个人的钱袋子。
那么,如何准确预测房价的变化呢?在这篇文章中,我们将讲述基于ARIMA的房价预测研究。
ARIMA是一个时间序列预测模型,它可以分析数据的趋势和周期性,并通过对历史数据进行拟合来预测未来数据的走势。
接下来,我们将详细介绍基于ARIMA的房价预测的过程和方法。
一、ARIMA模型简介ARIMA(Autoregressive Integrated Moving Average)模型是一种时间序列预测模型。
其核心思想是将历史数据进行拟合,分析出数据的趋势和周期性,然后利用这些信息来预测未来数据的走势。
ARIMA模型可以用于研究非平稳时间序列的性质。
所谓非平稳时间序列,指的是在时间轴上数据的统计性质随时间变化而变化的时间序列。
针对这种数据,我们可以通过差分的方式使其变得平稳,然后利用ARIMA模型进行拟合和预测。
ARIMA模型包含三个部分:自回归模型(AR)、差分模型(I)和移动平均模型(MA)。
其中,自回归模型用来表示当前数据与历史数据之间的关系;差分模型用来表示数据的趋势性和周期性;移动平均模型用来消除随机性的干扰。
二、ARIMA模型在房价预测中的应用基于ARIMA模型的房价预测研究,可以帮助我们更好地了解房价的走势,提前做出相应的应对措施。
在具体应用中,我们需要进行如下步骤:1.数据收集在进行预测之前,我们需要先收集历史的房价数据。
这些数据可以通过政府公示、各大房地产网站等途径获得。
收集到的数据越多,对于预测的准确性就有越大的帮助。
2.数据预处理在进行分析之前,我们需要对收集到的数据进行预处理。
具体包括:数据去重、数据清洗、缺失值填补等工作。
确保数据的稳定和准确。
3.数据分析我们需要对收集到的数据进行分析,分析数据的基本特征和规律,包括:房价的平均值、方差、标准差等统计信息;房价的趋势性和周期性分析等。
基于大数据的房地产市场走势分析与预测

基于大数据的房地产市场走势分析与预测随着科技的不断发展,大数据技术已经被越来越广泛的应用到各个领域。
房地产市场作为国家经济的重要组成部分,也成为了大数据技术应用的一个重要领域。
通过大数据技术的分析和预测,可以更好地了解房地产市场的走势,预测房价的变化趋势,提高市场参与者的风险预警能力,从而更好地发挥市场的作用。
本文将基于大数据技术,从多个角度对房地产市场进行分析与预测。
一、基于大数据的房地产市场概况分析首先,我们可以通过大数据技术,对房地产市场的整体概况进行分析。
大数据技术可以通过对大量的相关数据进行采集和分析,推测出市场的供求关系,预测房价的走势。
这里所说的数据并不限于房价、房源数量等基本数据,还包括人口、经济、政策、环境等多个维度的数据。
通过多方面的数据分析,可以更好的了解市场趋势,预测房价走势。
例如,深圳的房地产市场,可以通过大数据技术进行分析,获得以下一些数据:- 在深圳,房地产市场的人口需求占绝大部分,其次是企业需求,再是投资需求;- 2021年,深圳拥有的房源总量约为350万套,其中住宅占比达到70%以上;- 最新公布的数据显示,在深圳购房需求量近两月内一直保持“暴涨”,涨幅超过100%。
通过对这些数据的分析,可以推断出深圳房地产市场的供求关系紧张,市场需求旺盛,进一步加剧了房价的上涨。
二、基于大数据的房价预测分析基于大数据的预测分析是大数据技术在房地产市场中的一个重要应用领域。
该领域主要是通过对历史数据的分析、统计和预测分析来获得房价的变化趋势,制定相应的市场策略。
例如,我们可以使用如下策略来进行房价预测:- 收集过去5年的房价走势数据和当期的人口、经济、政策、环境等数据;- 基于收集到的数据,我们可以采用回归分析来推断在不同的条件下,房价的变化趋势;- 通过大量的模拟和对比,可以制定出房价预测模型,大大提高了预测的准确性。
三、基于大数据的风险预警与资产管理大数据技术还可以应用于风险预警与资产管理。
基于PVAR模型的中国房地产市场波动分析

基于PVAR模型的中国房地产市场波动分析中国房地产市场一直是国内外关注的热门话题,随着现代经济的迅速发展和城市化的不断推进,房地产市场的波动也越来越频繁和复杂。
由于房地产市场的波动会直接影响到整个经济体系的稳定性,因此对房地产市场的波动进行深入的分析和预测一直是学术界和政府部门的重要研究方向。
本文将基于PVAR模型,对中国房地产市场的波动进行分析。
一、PVAR模型简介PVAR模型是一种结构向量自回归模型,它将变量之间的相互影响和结构关系融合到了时间序列模型中。
PVAR模型的基本假设是,变量之间的关系分为两部分:一部分是直接的双向因果关系,另一部分是迂回的关系,可以用滞后项来捕捉。
PVAR模型不仅可以用于波动分析和预测,还可以用于政策评估和纠正。
二、中国房地产市场波动分析1.数据准备本文使用的数据来源于国家统计局和中国房地产统计年鉴。
选取的变量包括房地产开发投资、房价指数、人口密度、土地出让金等因素。
经过拟合分析,最终选取的波动因素包括房价指数、人口密度和土地出让金。
2.模型拟合首先,我们需要对选取的波动因素进行平稳性检验和差分处理,以满足模型拟合的要求。
接着,我们利用VAR模型进行参数估计,并对参数进行稳健性检验和误差项自相关性检验。
最终,我们得到PVAR模型的最优结构和参数。
3.模型评估和应用为了验证PVAR模型的预测效果,我们将模型拟合的结果与实际数据进行对比分析,并计算误差率和置信区间。
结果显示,PVAR模型可以较为准确地预测中国房地产市场的波动,预测结果与实际数据的拟合度较高。
在模型应用方面,我们可以利用PVAR模型进行政策评估和决策制定。
例如,如果政府出台了一项新的房地产政策,我们可以利用PVAR模型来评估其对房地产市场波动的影响,并做出相应的控制和调整。
三、结论与展望本文基于PVAR模型,对中国房地产市场的波动进行了深入分析和预测。
结果显示,PVAR模型可以很好地捕捉宏观经济因素和市场需求对房地产市场波动的影响,有效地预测房地产市场的发展趋势。
基于ARIMA模型的武汉房地产价格走势预测

基于ARIMA模型的武汉房地产价格走势预测本文运用《武汉房地产统计年鉴》中2005年第一季度到2013年第一季度的武汉商品住宅价格数据,建立ARIMA模型,并对武汉市未来三个季度的商品住宅价格进行预测与分析。
标签商品住宅价格;时间序列;ARIMA模型引言近十年来,中央出台了一系列房地产调控政策,经济手段和行政手段并用,从单一供给管理转向供给与需求综合管理,从防止房地产市场投资过热转向重点遏制房价过快上涨。
然而,虽然调控取得一定成绩,但调控多为定性的行政手段,量化调控方案很少。
本文旨在通过时间序列模型的建立,对武汉市未来房价走势进行预测。
一、数据来源及处理本文选取2005年第一季度到2013年第一季度的武汉商品住宅价格共33个数据进行研究。
因为ARIMA模型必须基于平稳数据,故对原始数据归一化处理后,先进行平稳性检验。
1、平稳性检验自相关图显示出序列有很强的短期相关性,所以初步认为2阶差分后的序列平稳。
2、对平稳的差分序列进行白噪声检验在检验的显著性水平取0.05的条件下,由于各阶的检验统计量的P值均小于0.05,所以该差分后序列不能视为白噪声序列,即差分后的序列还蕴含不容忽视的相关信息可以提取。
二、ARIMA模型建立1、模型定阶四、结论近几年来,国家通过出台一系列的经济措施,抑制房价过快增长,从而稳定房价。
但是,金融危机的阴影尚未彻底消退,未来经济走势还有待观察,一些政策还需视具体情形做必要的适应性调整。
国家在遏制楼市过热、房价上涨过快的同时,加大了经济适用房建设等方面的力度,通过多种途径来解决群众住房难的问题,从而保持中国经济稳步回升。
参考文献:[1]王燕.应用时间序列分析[M]. 北京:中国人民大学出版社,2005[2]姜启源,谢金星,叶俊.数学模型(第四版)[M]. 北京:高等教育出版社,2011。
基于ARIMA模型对房地产行业分析与研究

基于ARIMA模型对房地产行业分析与研究房地产行业是国民经济中重要的支柱产业之一,直接关系到国家经济和社会发展的稳定。
当前,我国房地产市场持续向好,房价也呈现出一定程度的上涨。
在这种背景下,通过数据分析与研究来预测未来市场变化,协助企业和政府进行决策,具有重要意义。
ARIMA模型是常用的时间序列预测模型,可以对某一时间序列进行趋势分析和季节性分析,并对未来的发展趋势进行预测。
在进行ARIMA模型预测之前,需要先对数据进行平稳化处理。
因为ARIMA模型要求数据是平稳的,即数据的均值、方差和自相关系数时间不变。
如果数据不平稳,就需要对数据进行差分或者拟合模型来使其平稳。
我们以2010-2020年中国房地产市场数据为例,进行ARIMA模型的分析预测。
首先,我们对数据进行平稳性判断,使用ADF和KPSS测试判断数据是否平稳。
下面是数据的ADF 和KPSS检验结果:ADF检验结果--------------------------------检验统计量 -2.33P值 0.16滞后数 3根据ADF和KPSS检验结果,我们判断房地产市场数据在5%的显著性水平下不是平稳的。
所以,我们需要对数据进行差分来使其变平稳。
差分后的数据经过ADF检验和KPSS检验后,P值均小于0.05,表明差分后的序列是平稳的。
接着,我们对差分后的数据进行时间序列模型的选择。
通过自相关图和偏自相关图的分析,我们选择了ARIMA(0,1,1)模型。
下面是该模型的参数解释:图1:历史数据与ARIMA预测结果从图中可以看出,在2010年到2020年之间,我国房地产行业整体呈现良好发展态势。
预计未来几年房地产市场仍将持续上升,但增幅不会太高。
综上所述,ARIMA模型是一种有效的时间序列预测模型,可以对房地产市场进行趋势分析和未来的发展趋势预测。
在实际操作中,我们也可以结合其他模型进行综合分析,以更好地预测未来市场变化和进行决策。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
选取 1998 年 第 1 季度 至 2009 年第 3 季度的全国房 屋销售价 格指数共 47 个数据进行研 究。由于原 数据是 以上一 期为基 期的 指数, 数 据 整体 没有 可 比性, 因 此 我们 对 其进 行处 理, 转 化 为以 1998 年第 1 季度为基期的指数数据, 用 Xt 表示( 原数据省略) 。
金融经济 Financial economy
基于时间序列的中国房地产价格走势预测
姜茜娅
( 西南财经大学 611130)
=摘 要> 本文采用5 2007 中国统计年鉴61998 年第 1 季度至 2009 年第 3 季度的全国房屋销售价格指数, 建立 ARIMA 模型, 并对未来房价走 势进行预测。 =关键词> 房地产价格; 时间序列; ARIM A 模型
1998 年实行住房商 品化 以来, 房 地产 市场 处于 不成 熟阶 段, 我国房地产投资规模 不断扩 大, 房 地产价 格持续 上涨。过快 上涨 的房价 不仅极大 地影响居民 的生活质量, 而且 也影响了 我国经济 的平稳健康发展。因此, 房价 问题已经 成为一 个重要 的经济 问题 和社会问题。本文旨在通 过时间 序列模 型的建 立, 对 未来房 价走 势进行预测。
2. 参数估计。运用最小二乘 法对 A RM A ( 2, 3) 模型 进行参数 估计, 通过结果我 们发 现的 系数 不显 著, 而且 存在 单位 圆以 外的 根, 因此将剔除, 得到最终参数 估计结果:
ý 2 Xt = 0. 7134+ 1. 3553 ý 2 X t- 1 - 0. 7836 ý 2 Xt- 2 + at + 0. 5643at- 1 + 0. 4172at- 3
二、建立 A RIM A 模型 1. 模型定阶。二阶差分序列 ý 2 Xt 的 自相关 函数( A CF ) 和偏 自相关函数( PA CF) 如图 1 所 示
图2
选取 A RIM A 模型。已知 I( d) 的阶数为 2, 即 d= 2, 因此, 对 ARM A 模型进行定阶分析, 考虑( p, q) 的 不同组合 p= 1, 2, 3, q= 1, 2, 3, 4, 再运用最小信息准则函数定价法, 即 AIC 准则, 在给出不同模型 的 A IC 计算公式基础上, 选取使 AIC 达到最小的那一组阶数为最佳模 型阶数, 运用 Eviews 软 件完 成这一 过程, 从 AIC 准 则函数 定阶 图 ( 图 2) 可以看出, 取 p= 2, q= 3 时模型 ARM A( 2, 3) 优于其他模型。
t= ( 2. 1000) ( 10. 4404) ( - 5. 5439) ( - 412.8378) ( - 2. 4507) R2 = 0. 7690, R 2 = 0. 7447, F= 31. 6289, DW = 2. 1636 由可决系数和相 关统计检验值可以看出, 模型估计结果较好。 3. 适应性检验。对模型 进行适 应性检 验, 即 检验残 差序 列{ } 是否是白噪声序列。做 出残差 的自相 关图和偏 自相关 图, 可得出 检验的相伴概率( p 值) 大于 0. 05, 表明模型是适合的。 三、. 房价预测及政策分析 我们由 1998 年第 1 季度到 2009 年第 3 季度的商 品房价格指 数 的历史数据拟合得来的模型, 向后做 4 期预测, 预测 2009 年第 4 季度到 2010 年第 3 季度, 预测值分别为 915. 6369、950. 1451、985. 3662、1021. 3030。由 预 测 结 果 可 以 看 出, 商 品 房 价 格 指 数 ( 以 1998 年第 1 季度数据为基期) 在未来一段时间内将平稳上升。 金融危机以来, 国家通过出台一系列刺激内需的经济 措施, 经 济开始回暖, 但是由于政策的滞后效应可能会造成房价泡 沫, 为了 抑制这一现象, 近期国家出台了抑制房价过快增长的政策, 以此确 保房价平稳上升。另外, 金融危机的阴影尚未彻底消退, 未来经济 走势还有待观察, 一些政策还需视具体情形做必要的适应 性调整。 国家在遏制楼市过热 、房价上涨过快的同时, 加大经济适用房建设 等方面的力度, 通过多种途径来解决群众住房难的问题, 而不是选 择直接硬性降低商品 房价格, 从而保持中国经济稳步回升。 四、结论
1. 平稳性检验。首先, 利用该时间序列做出一个时序图, 有此 我们发现时间 序列 存在 明显 的上 升趋 势, 即该 时间 序列 不平 稳。 我们依 此对该序 列进行一阶 差分和二阶 差分, 并分别进 行单位根 检验, 检验结果为在 1% 、5% 、10% 三 个显 著性 水平 下, 单位 根检 验的临界值分别为- 3. 5930、- 2. 9320、- 2. 6039, t 检验 统计量值 为- 6. 560517, 小于相应临 界值, 从而 拒绝原 假设, 表 明二阶 差分 序列 ý 2 Xt 不存在单位根, 是平稳时间序列。
本文通过时间序列分析方法, 对全国房地产价格未 来走势予以 预测。通过建立时间序列的 A RIMA 模型, 对未来房价走势进行 分 析, 并从预测结果中看出, 商品 阶截尾, 偏自相关 图是 3 阶截 尾, 我们
=参考文献> [ 1] 王振龙, 胡永宏. 应用时间序列分析[ M] . 科学出版社, 2007. [ 2] 尤梅芳, 黄敏, 程立. A RIM A 模型在房价预测中的应用[ J] . 中国物
价, 2009, ( 6) .
) 48 )
