26.2.4二次函数y=a(x-h)2+k的图象与性质 - 副本
二次函数y=a(x-h)2图像与性质

3、不画出图象,你能说明抛物线 y 3x 2
与 y 3(x 2)2 之间的关系吗?
4、已知函数y=4x2,y=4(x+1)2和y=4(x-1)2。 (1)在同一直角坐标系中画出它们的图象; (2)分别说出各个函数图象的开口方向,对称轴、
同;函数y= 1 (x一2)2的图象可以看作是函数
y=
1 2
2
x2的图象向右平移2个单位得到的,它
的对称轴是直线x=2,顶点坐标是(2,0)。
1 2、1 你(x+能2由)2的函图数象y与=性2质x吗2的? 图象与性质,得到函数y=
2
问题小结
一般地,由y=ax²的图象通过平移便 可得到二次函数y=a(x-h)²的图 象:y=a(x-h)²(a≠0) 的图象可以看成 y=ax²的图象沿x轴整体向左(右)平 移|h|个单位(当h>0时,向右平移;当 h<0时,向左平移)。
探究二
探究二次函数y=a(x-h)² 的性质。
y=a(x-h)²
a>o
a<o
开口方向 对称轴 顶点坐标
向上 直线x=h (h,0)
向下
直线x=h (h,0)
增减性
当x>h时,y随x增大而增 大;当x<h时,y随x增大 而减小
当x>h时,y随x增大而 减小;当x<h时,y随x 增大而增大
最值
最小值0
当a<0时,在对称轴左侧,y随x增大而减小,在对称轴右侧,y随x 增大而增大。
⑤当a>0时,有最小值0;当a<0时,有最大值0.
二次函数y=a(x-h)2 k的图象及其性质 PPT课件 5 人教版

(2)何时 y=3?
(3)根据图象回答:
当x
时,y>0。
3论( .二m)上次为函何数实y数=a,图(x象-m的)2+顶2m点,必无在活你用学答活对了
A)直线y=-2x上
B)x轴上 吗?
C)y轴上 y=2x上
D)直线
3.D 4. y3> y1 > y2
4.对于抛物线y=a(x-3)2+b其中
a>0,b 为常数,点( 3 ,y1) 点 ( 5 ,y2)点(8,y3)在该抛物线上, 试比较y1,y2,y3的大小
a<0 向下 x=h (h,k) x=h时, x<h时, y随x的增大而增 有最大 大; x>h时, y随x的增大而 值y=k 减小.
|a|越大开口越小.
返回
指出下列函数图象的开口方向,对称轴和顶点坐标. 开口 对称轴 顶点坐标
1y2x325 向上 直线x=3 (3,–5)
2 y 0.5x 12 向下 直线x= –1
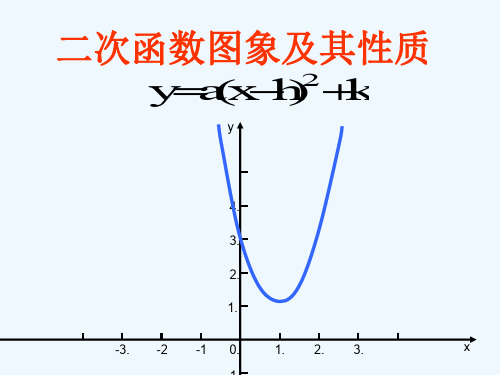
4.如图所示的抛物线: 当x=_0_或__-2_时,y=0; 当x<-2或x>0时, y__<___0; 当x在-_2_<__x_<0范围内时,y>0; 当x=___-1__时,y有最大值___3__.
3
5、试分别说明将抛物线的图象通 过怎样的平移得到y=x2的图象:
(1) y=(x-3)2+2 ;
•
17、第一个青春是上帝给的;第二个的青春是靠自己努力的。
•
18、励志照亮人生,创业改变命运。
•
19、就算生活让你再蛋疼,也要笑着学会忍。
•
20、当你能飞的时候就不要放弃飞。
•
21、所有欺骗中,自欺是最为严重的。
人教版初三数学上册二次函数y=a(x-h)2+k的图象与性质.4二次函数图像与性质(4)
6 y 3 x 32
4
向下 直线x=3
(–1,0) (0,–1) (2, 5) (– 4,2) (3,0)
各种形式的二次函数的关系
|k| |h|
左 个右 单平 位移
y = ax2 + k
y = a( x - h )2 + k
上 个下 单平 位移
y = a(x - h )2
上下平移 |k|个单位
左右平移
y = ax2 |h|个单位
结论: 一般地,抛物线 y = a(x-h)2+k与y = ax2形状 相同,位置不同。
及时总结
顶点式
y=a(x-h)2+k 开口方向 顶点坐标 对称轴 增 减 性 极值
a>0 向上
a<0 向下
(h ,k)
(h ,k)
直线 x=h
直线 x=h
当x<h时,
当x<h时,
2
-7
-8 -9
平移方法2:
-1x0=-1
y
1 2
x
2向1个左向下平移 1个单位
y1(x1)2 1 2
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时, 开口向上; 当a<0时,开口向下;
(2)对称轴是直线x=h; (3)顶点是(h,k).
指出下列函数图象的开口方向,对称轴和顶点坐标. 开口 对称轴 顶点坐标
二次函数图象及其性质
ya(xh)2k
y
4. 3. 2. 1.
-3. -2 -1 0.
1. 2. 3.
x
1)y=ax2 2)y=ax2+k 3)y=a(x-h)2
华东版九年级数学下册第26章26.226.2.2第2课时 二次函数y=a(x-h)2的图象与性质

4. 在函数 y=(x-3)2 中,当 x >3 时,函数值 y 随 x 的增大而增大;当 x <3 时,函数值 y 随 x 的增大 而减小; 当 x= 3 时, 函数值 y 取最 小 值, 是 0 .
1 2的开口向 5. 抛物线 y=-3x-2 1 1 直线 x= , 0 2 ,顶点坐标为 是 2
.
9. 若二次函数 y=x2-mx+1 的图象顶点在 x 轴上, 则 m 的值是( D ) A.2 C.0 B.-2 D.±2
10. 在平面直角坐标系中,函数 y=-x+1 与 y=- 3 (x-1)2 的图象大致是( D ) 2
11. 抛物线 y=3(x-1)2 的图象上有三点 A(-1,y1), B( 2,y2),C(2,y3),则 y1,y2,y3 的大小关系是( D ) A.y1>y2>y3 C.y3>y2>y1 B.y2>y1>y3 D.y1>y3>y2
16. 如图所示,二次函数 y1=a(x-h)2 的图象与直线 y2=kx+b 交于 A(0,-1),B(1,0)两点.
(1)确定二次函数与一次函数的解析式; (2)当 y1<y2,y1=y2,y1>y2 时,根据图象分别确定 自变量 x 的取值范围.
解:(1)y1=-(x-1)2, y2=x-1; (2)当 y1<y2 时, x<0 或 x>1, 当 y1=y2 时,x=0 或 x=1, 当 y1>y2 时,0<x<1.
18. 如图,抛物线的顶点 M 在 x 轴上,抛物线与 y 轴交于点 N,且 OM=ON=4,矩形 ABCD 的顶点 A、B 在抛物线上,C、D 在 x 轴上.
(1)求抛物线的解析式; (2)设点 A 的横坐标为 t(t>4), 矩形 ABCD 的周长为 l, 求 l 与 t 之间的函数关系式. 1 解:(1)y=4(x-4)2;
26.2.4二次函数y=a(x-h)2+k的图象与性质

y 1 (x 1)2 1
2
1个单位
y 1 x2 2
1
个 单 位
向 下 平 移
y 1 x2 1 2
-5 -4 -3 -2 -1-1 O1 2 3 4 5 x
-2
-3 -4
-5
-6
-7
-8
-9
y 1 (x 1)2 1
-10
2
河南淮阳羲城中学
怎样移动抛物线 y 1 x2就可以得到抛物线 y 1 (x 1)2 1?
向下
直线x=h (h,k)
当x>h时,y随x 当x=h时, 的增大而减小;
y最大值=k x<h时,y随x的 增大而增大.
河南淮阳羲城中学
顶点式
y a x h2 k a 0
h 0, k 0 y ax2 h 0, k 0 y ax2 k
k 0, h 0 y a x h2
可以看作互相平移得到的.
平移规律
左 右 平 移 y = ax2 + k
y = a( x - h )2 + k 上 下 平 移
y = a(x - h )2
简记为:
上加下减常数项, 左加右减自变量。
上下平移
河南淮阳羲城中学
y = ax2 左右平移
练一练
1.请回答抛物线y = 4(x-3)2+7由抛物线y=4x2怎样平 移得到? 由抛物线向上平移7个单位再向右平移3个单位得到的. 2.如果一条抛物线的形状与 y 1 x2 2 形状相
3
同,且顶点坐标是(4,-2),试求这个函数关系式. 中考链接:
抛物线y=-3(x-1)2+2的图象如何得到y=-3x2 .
河南淮阳羲城中学
课堂小结
二次函数y=a(x-h)2+k 的图象和性质
华师版九年级下册数学第26章 二次函数 二次函数y=a(x-h)2+k的图象与性质

当点 B 与 O 重合时,-12m2+4=0, 解得 m=2 2或 m=-2 2, 当点 B 与点 D 重合时,如图②, 顶点 A 也与 B、D 重合,点 B 到达最高点, ∴点 B(0,4),∴-12m2+4=4,解得 m=0.
当抛物线从图②的位置继续向左平移 时,如图③,点 B 不在线段 OD 上, ∴B 点在线段 OD 上时,m 的取值范 围是 0≤m<1 或 1<m<2 2.
(1)当m=5时,求n的值;
解:当 m=5 时,y=-12(x-5)2+4, 当 x=1 时,n=-12×42+4=-4.
(2)当n=2时,若点A在第一象限内,结合图象,求当y≥2 时,自变量x的取值范围;
解:当 n=2 时,将 C(1,2)的坐标代入函数表达式 y=-12(x-m)2+4,得 2=-12(1-m)2+4, 解得 m=3 或 m=-1(舍去), ∴此时抛物线的对称轴为 x=3, 根据抛物线的对称性可知,当 y=2 时,x=1 或 x=5, ∴x 的取值范围为 1≤x≤5.
7 ∴tan ∠ABC=OOCB=37=13.
12.把二次函数 y=a(x-h)2+k 的图象先向左平移 2 个单位 长度,再向上平移 4 个单位长度,得到二次函数 y=12(x +1)2-1 的图象.
(1)试确定 a、h、k 的值; 解:a=12,h=1,k=-5.
(2)指出二次函数y=a(x-h)2+k图象的开口方向、对称轴 和顶点坐标.
【答案】①②④
10.【中考·舟山】二次函数 y=-(x-1)2+5,当 m≤x≤n 且
mn<0 时,y 的最小值为 2m,最大值为 2n,则 m+n 的
值为( )
A.52
二次函数y=a(x-h)2 k的图像和性质__教案新部编本

教师学科教案[ 20 – 20 学年度第__学期]任教学科:_____________任教年级:_____________任教老师:_____________xx市实验学校二次函数y=a(x-h)2+k 的图像和性质执教者:付义成教学目标:1、 会用描点法画二次函数y=a(x-h)2+k 的图像,并通过图像认识函数的性质。
2、 能运用二次函数的知识解决简单的实际问题。
重点难点:1、 二次函数y=a(x-h)2+k 的性质2、 把实际问题转化为数学问题情境引入:1、 由前面的知识我们知道,函数y=12 x 2的图像,向下平移1个单位,可以得到函数y=12 x 2-1的图象;函数y=12 x 2的图像,向左平移1个单位,可以得到函数y= 12(x+1)2的图象,那么函数y=12 x 2的图象,如何平移,才能得到函数y= 12(x+1)2-1的图象呢?2、 引出课题:二次函数y=a(x-h)2+k 的图象和性质及实际应用。
自主探究: 1、探究在同一坐标系中画出y=—12 x 2,y=—12 x 2-1,y=— 12(x+1)2-1的图象,指出它们的开口方向、对称轴、及顶点。
通过观察图象探究下列问题:1、 抛物线y=—12 x 2经过怎样的变换可以得到抛物线y=— 12(x+1)2-1? 2、 对于抛物线y=— 12(x+1)2-1,当x 时,函数值y 随x 的增大而减小;当x 时,函数值y 随x 的增大而增大;当x 时,函数值取得最 值,最 值y= 。
2. 观察归纳观察:(1)抛物线y=—12 x 2,y=—12 x 2-1,y=— 12(x+1)2-1的开口方向、对称轴以及顶点坐标,猜想抛物线y=a(x-h)2+k 的开口方向、对称轴以及顶点坐标。
(2)由y=— 12 (x+1)2-1与y=—12x 2的关系,推广到抛物线y=a(x-h)2+k与y=ax2的关系。
归纳:(1)抛物线y=a(x-h)2+k与y=ax2的形状相同,位置不同。
《二次函数y=a(x-h)2+k的图象和性质》教案、教学设计、导学案、同步练习

《第3课时二次函数y=a(x-h)2+k的图象和性质》教案【教学目标】1.会用描点法画出y=a(x-h)2+k的图象.2.掌握形如y=a(x-h)2+k的二次函数图象的性质,并会应用.3.理解二次函数y=a(x-h)2+k与y=ax2之间的联系.【教学过程】一、情境导入对于二次函数y=(x-1)2+2的图象,你能说出它的顶点坐标、对称轴和开口方向吗?你能再说出一个和这个函数图象的顶点坐标、对称轴和开口方向一致的二次函数吗?二、合作探究探究点一:二次函数y=a(x-h)2+k的图象和性质【类型一】二次函数y=a(x-h)2+k的图象求二次函数y=x2-2x-1的顶点坐标、对称轴及其最值.解析:把二次函数y=x2-2x-1化为y=a(x-h)2+k(a≠0)的形式,就会很快求出二次函数y=x2-2x-1的顶点坐标及对称轴.解:y=x2-2x-1=x2-2x+1-2=(x-1)2-2,∴顶点坐标为(1,-2),对称轴是直线x=1.当x=1时,y最小值=-2.方法总结:把二次函数y=ax2+bx+c(a≠0)化成y=a(x-h)2+k(a≠0)形式常用的方法是配方法和公式法.【类型二】二次函数y=a(x-h)2+k的性质如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y 1),(32,y2)是抛物线上两点,则y1>y2.其中正确的是( )A.①②③ B.①③④C.①②④ D.②③④解析:∵-b2a=-1,∴b=2a,即b-2a=0,∴①正确;∵当x=-2时点在x轴的上方,即4a-2b+c>0,②不正确;∵4a+2b+c=0,∴c=-4a-2b,∵b=2a,∴a-b+c=a-b-4a-2b=-3a-3b=-9a,∴③正确;∵抛物线是轴对称图形,点(-3,y1)到对称轴x=-1的距离小于点(32,y2)到对称轴的距离,即y1>y2,∴④正确.综上所述,选B.方法总结:抛物线在直角坐标系中的位置,由a、b、c的符号确定:抛物线开口方向决定了a的符号,当开口向上时,a>0,当开口向下时,a<0;抛物线的对称轴是x=-b2a;当x=2时,二次函数的函数值为y=4a+2b+c;函数的图象在x轴上方时,y>0,函数的图象在x轴下方时,y<0.【类型三】利用平移确定y=a(x-h)2+k的解析式将抛物线y=13x2向右平移2个单位,再向下平移1个单位,所得的抛物线是( )A.y=13(x-2)2-1 B.y=13(x-2)2+1C.y=13(x+2)2+1 D.y=13(x+2)2-1解析:由“上加下减”的平移规律可知,将抛物线y=13x2向下平移1个单位所得抛物线的解析式为:y=13x2-1;由“左加右减”的平移规律可知,将抛物线y=13x2-1向右平移2个单位所得抛物线的解析式为y=13(x-2)2-1,故选A.探究点二:二次函数y=a(x-h)2+k的应用【类型一】y=a(x-h)2+k的图象与几何图形的综合如图,在平面直角坐标系中,点A在第二象限,以A为顶点的抛物线经过原点,与x轴负半轴交于点B,对称轴为直线x=-2,点C在抛物线上,且位于点A、B之间(C不与A、B重合).若△ABC的周长为a,则四边形AOBC的周长为________.(用含a的式子表示)解析:如图,∵对称轴为直线x=-2,抛物线经过原点,与x轴负半轴交于点B,∴OB=4,∵由抛物线的对称性知AB=AO,∴四边形AOBC的周长为AO +AC+BC+OB=△ABC的周长+OB=a+4.故答案是:a+4.方法总结:二次函数的图象关于对称轴对称,本题利用抛物线的这一性质,将四边形的周长转化到已知的线段上去,在这里注意转化思想的应用.【类型二】二次函数y=a(x-h)2+k的实际应用心理学家发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间满足函数y=-110(x-13)2+59.9(0≤x≤30),y值越大,表示接受能力越强.(1)x在什么范围内,学生的接受能力逐步增强?x在什么范围内,学生的接受能力逐步降低?(2)第10分钟时,学生的接受能力是多少?(3)第几分钟时,学生的接受能力最强?解:(1)0≤x≤13时,学生的接受能力逐步增强;13≤x≤30时,学生的接受能力逐步降低.(2)当x=10时,y=-110(10-13)2+59.9=59.故第10分钟时,学生的接受能力是59.(3)当x=13时,y值最大,是59.9,故第13分钟时,学生的接受能力最强.三、板书设计【教学反思】教学过程中,强调学生自主探索和合作交流,在操作中探究二次函数y=a(x -h)2+k的图象与性质,体会数学建模的数形结合思想方法.22.1.3 二次函数y=a(x-h)2+k的图象和性质《第3课时二次函数y=a(x-h)2+k的图象和性质》教案【教学目标】:1.使学生理解函数y=a(x-h)2+k的图象与函数y=ax2的图象之间的关系。
2015开学北师大版九年级数学下26.2 (第3-1课时 二次函数y=a(x-h)2 的图像与性质)

3 2 y ( x 1) 4
倍 速 课 时 学 练
3 2 y ( x 3) 4
3 2 y ( x 5) 4
不画图直接填空
抛物线 y = 2(x+3)2 y = -3(x-1)2
倍 速 课 时 学 练
开口方向
对称轴
顶点坐标
向上
向下 向下
直线x=-3
直线x=1 直线x=3
( -3 , 0 )
1 y
即:
倍 速 课 时 学 练
在对称轴左侧递增 在对称轴右侧递减
-5 -4 -3 -2 -1 o 1 2 3 4 5 x -1 -2 1 2 y ( x 1 ) -3 2 -4 -5 -6 -7 -8 -9 1 2 1 y x -10 y ( x 1) 2
2
2
一般地,抛物线y=a(x-h)2 有如下 特点:
h<0
h>0
h<0
对称性
顶点 增减性
开口向下 开口向上 a的绝对值越大,开口越小 直线x=h
(h,0)
顶点是最高点 在对称轴左侧递减 在对称轴左侧递增 在对称轴右侧递增 在对称轴右侧递减 顶点是最低点
例1. 填空题 (1)二次函数y=2(x+5)2的图像是 抛物线 ,开 口 向上 ,对称轴是直线x= -5 ,当x= -5 时,y有最 小 值, 是 0 . (2)二次函数y=-3(x-4)2的图像是由抛物线y= -3x2 向 右 平移 4 个单位得到的;开口 向下 ,对称轴 4 是直线x= ,当 x= 4 时,y有最 大 值,是 0 . 倍 速 课 时 学 练
… -3 -2 -1 0 1 2 3 … … -2 -0.5 0 -0.5 -2 -4.5 -8 … … -8 -4.5 -2 -0.5 0 -0.5 -2 …
二次函数y=a(x-h)2的图象与性质 华东师大版九年级数学下册课时练习(含答案)

26.2.2 第2课时 二次函数y =a (x -h )2的图象与性质【基础练习】知识点 1 二次函数y =a (x -h )2的图象与y =ax 2的图象的关系1.将抛物线y=x 2向 平移 个单位得到抛物线y=(x+5)2;将抛物线y=x 2向 平移 个单位得到抛物线y=(x -5)2.2.要得到函数y=x 2的图象,只要把函数y=(x -3)2的图象 ( )A .向左平移3个单位B .向右平移3个单位C .向上平移3个单位D .向下平移3个单位3.顶点是(-2,0),开口方向、形状与抛物线y=12x 2相同的抛物线是 ( )A .y=12(x -2)2B .y=12(x+2)2C .y=-12(x -2)2D .y=-12(x+2)2知识点 2 二次函数y =a (x -h )2的图象与性质4.二次函数y=13(x -3)2的图象开口 ,对称轴是 ,当x 时,y 随x 的增大而增大;当x 时,y 随x 的增大而减小.当x= 时,y 有最 值,是 .5.下列抛物线中,对称轴是直线x=3的是 ( ) A .y=-3x 2-3B .y=3x 2-3C .y=-12(x+3)2 D .y=3(x -3)26.抛物线y=x 2-4x+4的顶点坐标为 ( ) A .(-4,4)B .(-2,0)C .(2,0)D .(-4,0) 7.比较抛物线y=x 2,y=2x 2-1,y=12(x -1)2的共同点,其中说法正确的是 ( )A .顶点都是原点B .对称轴都是y 轴C .开口方向都向上D .开口大小相同8.二次函数y=-(x -2)2的图象不经过第 象限.9.已知函数y=-(x -1)2的图象上的两点A (2,y 1),B (a ,y 2),其中a>2,则y 1与y 2的大小关系是 y 1 y 2.(填“<”“>”或“=”)10. 在平面直角坐标系中画出函数y=-12(x -3)2的图象. (1)指出该函数图象的开口方向、对称轴和顶点坐标; (2)说明该函数图象与二次函数y=-12x 2的图象的关系; (3)根据图象说明,何时y 随x 的增大而减小.【提升训练】11.同一坐标系中,抛物线y=(x-a)2与直线y=a+ax的位置可能是()图1312.将抛物线y=a(x+2)2平移后与抛物线y=a(x-1)2重合,抛物线y=a(x+2)2上的点A(2,3)同时平移到点A'的位置,那么点A'的坐标为()A.(5,3)B.(-1,3)C.(2,0)D.(3,4)13.已知二次函数y=-(x-h)2,当x<-3时,y随x的增大而增大;当x>-3时,y随x的增大而减小,则当x=0时,y的值为()A.-1B.-9C.1D.914.已知抛物线y=a(x-h)2的形状及开口方向与抛物线y=-2x2相同,且顶点坐标为(-2,0),则a+h=.15.二次函数y=a(x-h)2的图象如图14所示,若A(-2,y1),B(-4,y2)是该图象上的两点,则y1y2.(填“>”“<”或“=”)图14x2+3的顶点A和抛物线y=3(x-2)2的顶点B,求该直线的16.已知直线y=kx+b经过抛物线y=-12函数关系式.17.已知二次函数y=(x-3)2.(1)写出该二次函数图象的开口方向、对称轴、顶点坐标和该函数的最值.(2)若点A(x1,y1),B(x2,y2)位于对称轴右侧的抛物线上,且x1<x2,试比较y1与y2的大小关系.(3)抛物线y=(x+7)2可以由抛物线y=(x-3)2平移得到吗?如果可以,请写出平移的方法;如果不可以,请说明理由.第2课时 二次函数y =a (x -h )2的图象与性质1.左 5 右 52.A3.B4.向上 直线x=3 >3 <3 3 小 05.D6.C [解析] 因为y=x 2-4x+4=(x -2)2, 所以抛物线的顶点坐标为(2,0). 故选C .7.C [解析] 抛物线y=x 2的顶点为原点,对称轴是y 轴,开口向上;抛物线y=2x 2-1的顶点坐标为(0,-1),对称轴是y 轴,开口向上;抛物线y=12(x -1)2的顶点坐标为(1,0),对称轴是直线x=1,开口向上.综合判断开口方向都向上,故选C . 8.一、二9.> [解析] 因为二次项系数为-1,小于0,所以在对称轴直线x=1的左侧,y 随x 的增大而增大;在对称轴直线x=1的右侧,y 随x 的增大而减小.因为a>2>1,所以y 1>y 2.故答案为>. 10.解:图略.(1)该函数图象的开口向下,对称轴为直线x=3,顶点坐标为(3,0).(2)二次函数y=-12(x -3)2的图象是由二次函数y=-12x 2的图象向右平移3个单位得到的.(3)当x>3时,y 随x 的增大而减小. 11.D 12.A13.B [解析] 由题意知二次函数y=-(x -h )2的图象的对称轴为直线x=-3,故h=-3.把h=-3代入二次函数y=-(x -h )2可得y=-(x+3)2,当x=0时,y=-9.故选B . 14.-415.= [解析] 由图象可知抛物线的对称轴为直线x=-3,所以点A 和点B 关于对称轴对称,所以y 1=y 2.16.解:抛物线y=-12x 2+3的顶点A 的坐标为(0,3),抛物线y=3(x -2)2的顶点B 的坐标为(2,0). 因为直线y=kx+b 经过点A ,B , 所以{b =3,2k +b =0,解得{k =-32,b =3, 所以该直线的函数关系式为y=-32x+3.17.解:(1)因为a=1>0,所以该二次函数的图象开口向上,对称轴为直线x=3,顶点坐标为(3,0);当x=3时,y 最小值=0,没有最大值.(2)因为当x>3时,y 随x 的增大而增大, 又因为3<x 1<x 2,所以y 1<y 2.(3)可以.将抛物线y=(x -3)2向左平移10个单位可以得到抛物线y=(x+7)2.。
华师版九年级下册数学第26章 二次函数 二次函数y=a(x-h)2的图象与性质

26.2 二次函数的图象与性质
第3课时 二次函数y=a(x-h)²
的图象与性质
1 课堂讲解 y=a( x-h) 2 的图象与性质
二次函数y=a(x-h)2与y=ax2之间的关系
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
通过上节课的学习我们知道,抛物线y=ax2+c可 以通过沿y轴平移y=ax2得到,那么y=a(x-h)2型的抛物 线能否通过平移得到呢?
A.y1<y2<0
B.0<y1<y2
C.0<y2<y1
D.y2<y1<0
知3-讲
知识点 3 二次函数y=a(x-h)2+c与y=ax2之间的关系
知3-讲
例2 将抛物线y=-x2向左平移2个单位后,得到的抛
物线对应的函数关系式是( A )
A.y=-(x+2)2
B.y=-x2+2
C.y=-(x-2)21, 2来自所以应选D.总结
知1-讲
本题运用了性质判断法和数形结合思想,运用二 次函数的性质,画出图象进行判断.
知1-练
1 抛物线y=-5(x-2)2的顶点坐标是( )
A.(-2,0)
B.(2,0)
C.(0,-2)
D.(0,2)
2 (中考·兰州)在下列二次函数中,其图象的对称轴为
直线x=-2的是( )
D.y=-x2-2
导引:本题依据“左加右减”解题,即抛物线向左平移几
个单位,x就加几,抛物线向右平移几个单位,x
就减几.
总结
知3-讲
y=ax2的图象左右平移时,顶点的横坐标发生变 化.平移的方向决定加减,平移的距离决定加减的数 值.
知3-练
1 试说明:分别通过怎样的平移,可以由抛物线y =
26.2.3 二次函数y=a(x-h)2+k的图象与性质 (2) 公开课一等奖课件

三、解答题(共 32 分) 17.(10 分)已知抛物线 y=a(x+2)2+k 过点(1,-3),且 其顶点的纵坐标为 3. (1)求抛物线的解析式; (2)画出函数的图象,写出抛物线的对称轴及顶点坐标; (3)从图象上观察当 x 为何值时,y 随 x 的增大而增大?
解:(1)由题意有 k=3,把(1,-3)代入 y=a(x+2)2+3 2 2 2 得:-3=a(1+2) +3,a=- ,∴y=- (x+2)2+3 (2)图 3 3 象略.对称轴:直线 x=-2,顶点坐标是(-2,3) (3)从图 象可以看出当 x<-2 时,y 随 x 的增大而增大
二、填空题(每小题 4 分,共 16 分) 1 13.抛物线 y= (x-2)2+5,当 x=__2__时,y 有最__小 2 __值为__5__. 14.二次函数 y=-3(x-2)2,当 x__>2__时,y 随 x 的 增大而减小;当 x__<2__时,y 随 x 的增大而增大. 15.将抛物线 C1 向左平移 1 个单位,再向下平移 3 个单 位,得到抛物线 C2:y=2(x+2)2-6,则原抛物线 C1 的表达 式为__y=2(x+1)2-3__. 16.把二次函数 y=(x-1)2+2 的图象绕原点旋转 180° 后得到的图象的解析式为__y=-(x+1)2-2__.
【综合运用】 19.(12 分)如图,排球运动员站在点 O 处练习发球,将 球从 O 点正上方 2 m 的 A 处发出,把球看成点,其运行的高 度 y(m)与运行的水平距离 x(m)满足关系式 y=a(x-6)2+h.已 知球网与 O 点的水平距离为 9 m,高度为 2.43 m,球场的边 界距 O 点的水平距离为 18 m. (1)当 h=2.6 时,求 y 与 x 的关系式;(不要求写出自变量 x 的取值范围) (2)当 h=2.6 时,球能否越过球网?球会不会出界?请说 明理由.
27.2.4二次函数y=a(x-h)^2+k的图象与性质___课件

例2.按下列要求求出二次函数的解析式: (1)已知抛物线y=a(x-h)2经过点(-3,2)(-1,0)求该抛物 线的解析式; (2)形状与y=-2(x+3)2的图象形状相同,但开口方向不同,顶点 坐标是(1,0)的抛物线解析式; (3)已知二次函数图像的顶点坐标(1,-8),且图像经过点(2, -2)。求此函数解析式;
9
例1:根据箭头叙述下列函数的平移关系
3 2 y ( x 1) 4
向上平移 3个单位 向右平移 4个单位 向下平移
向上平移
2个单位
3 2 y ( x 1) 2 4
向右平移 4个单位
3 2 y ( x 3) 3 4
5个单位
向左平移 8个单位
3 2 y ( x 5) 2 4
向左(右)平移 2 向上(下)平移y=a(x-h)2+k |h|个单位 y=a(x-h) |k|个单位 向上(下)平移 y=ax2+k 向左(右)平移 y=a(x-h)2+k |h|个单位 |k|个单位
思考:抛物线y=a(x-h)2+k开口、对称轴、顶点、极值有何特点? (1)当a>0时, 开口向上; 当a<0时,开口向下; (2)对称轴是直线x=h; (3)顶点是(h,k). (4)当x=h时,y极值=k;(a>0,有最小值;a<0有最大值)
5
1.完成下列表格: 二次函数 y=2(x+3)2+5 开口方向 向上 对称轴 顶点坐标
直线x=-3 (-3, 5 ) 直线x=1 ( 1 , -2 )
y=-3(x-1)2-2
y = 4(x-3)2+7
向下
向上 向下
直线x=3
直线x=2
2.2.4二次函数y=a(x-h)2的图象与性质

7.二次函数y=-5(x+m)2中,当x<-5时,y随x的增
大而增大,当x>-5时,y随x的增大而减小,则m
5 =________ .此时,二次函数的图象的顶点坐标
(-5,0) ,当x=________ -5 时,y取最________ 大 为________
0 值,为________ .
返回
8.关于二次函数y=-2(x+3)2,下列说法正确的是 ( D ) A.其图象的开口向上 B.其图象的对称轴是直线x=3 C.其图象的顶点坐标是(0,3)
第二章 二次函数
2.2
二次函数的图象与性质
第4课时
二次函数y=a(x-h)2的图 象与性质
1 6 11 16
2 7 12 17
3 8 13
4 9 14
5 10 15
知识点
1
二次函数y=a(x-h)2的图象
抛物线 ,它与 1.二次函数y=a(x-h)2的图象是__________ 位置 不同; 抛物线y=ax2的形状相同,只是________
点,边OA在x轴上,OA=AB=1个
单位长度,把Rt△OAB沿x轴正方
向平移1个单位长度后得△AA1B1.
(1)求以A为顶点,且经过点B1的抛物线的函数表达式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点
D,C的坐标.
【思路点拨】(1)由几何知识先求B1的坐标,再设抛 物线的函数表达式为 y = a(x - 1)2 即可求出; (2) 先 求直线 OB 的函数表达式,而 C 为直线与抛物线的 交点,其坐标为直线、抛物线的函数表达式组成 的方程组的解.
解: (1)易知A(1,0),B1(2,1). 设抛物线的函数表达式为y=a(x-1)2,将B1(2,1)
2.2.4二次函数y=a(x-h)2+k的图象与性质wyc

复习引入
y=ax2
左加 右减
上加 下减
y=ax2+k
左加 右减
y=a(x-h)2
上加 下减
y=a(x-h)2+k
温故知新 二次函数y=a(x-h)2的性质
y=a(x-h)2
a>0
a<0
图象
开口 对称轴
顶点 增减性
最值
h>0
h<0
h>0
的增大而小
y (x 2)2 3
当x= - 1时, y最大值= - 2
练习
1.已知二次函数 y (x 2)2 3, 当x_____2______时,y随x的增大而减小。 2.抛物线 y 4(x 3)2 12 的对称轴是____x_____3___,顶点是___(_-3__,__1_2__)_______. 3.抛物线 y 2(x 5)2 4 的对称轴是___x______5___,当_______x_____5______时,
y 1 (x 1)2 2 2
向下
当x≤1时, y随x的
x=1
(1,2)
增大而增大; 当x> 1时, y随x
当x= 1时, y最大值=2
的增大而减小
y 1 (x 1)2 2 2
向下
y 2(x 5)2 4 y 4(x 3)2 12
x=-1
当x≤-1时, y随x的
(-1,-2)
增大而增大; 当x> - 1时, y随x
直线x=1 (1,2)
当x≤0时, y随x的增大而减小; 当x≤1时, y随x的增大而减小; 当x>0时, y随x的增大而增大 当x>1时, y随x的增大而增大
二次函数y=a(x-h)2 k图象和性质课件

C组
10. 对于二次函数y=
+1,有下列说法:
①其图象的开口向上;②其图象的对称轴为直线x=
- ;③其图象的顶点坐标为
;④当x<
时,y随x的增大而减小.其中正确的说法有
(B )
A. 1个
B. 2个
C. 3个
D. 4个
直线x=1 (1,2)
y轴
(0,0)
直线x=-2 (-2,-4)
9. 已知二次函数y=-3(x-3)2+2. (1)写出该函数图象的顶点坐标; (2)判断点(1,-12)是否在这个函数的图象上.
解:(1)∵二次函数的解析式为 y=-3(x-3)2+2, ∴顶点坐标是(3,2). (2)当x=1时,y=-3×4+2=-10≠-12. ∴点(1,-12)不在这个函数的图象上.
向上平移3个单位 y=-2x2+3 3.把y=-2x2的图像
向左平移2个单位 y=-2(x+2)2 4.请猜测一下,二次函数y=-2(x+2)2+3的图象是否可 以由y=-2x2平移得到?你认为该如何平移呢?
y
y2x223 3
y
y2x223
3
-2 O
X
-2 O
X
y2x23
y 2 x2y 2x22
A. (-3,2)
B. (3,2)
C. (-3,-2)
D. (3,-2)
5. 将抛物线y=-x2向右平移1个单位,再向上平移2 个单位后,得到的抛物线的解析式为 _____y_=_-__(_x_-__1_)_2+_2________.
6. 将抛物线y=- (x-5)2+3向左平移5个单位, 再向上平移3个单位后得到的抛物线的解析式为 _____y_=_-____x_2_+_6__________.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
1个单位
y 1 x2 2
1
个 单 位
向 下 平 移
y 1 x2 1 2
-5 -4 -3 -2 -1-1 O1 2 3 4 5 x
-2
-3 -4
-5
-6
-7
-8
-9
y 1 (x 1)2 1
-10
2
河南淮阳羲城中学
怎样移动抛物线 y 1 x2就可以得到抛物线 y 1 (x 1)2 1?
课堂小结
二次函数y=a(x-h)2+k 的图象和性质
图象特点 平移规律
当a>0,开口向上;当 a<0,开口向下. 对称轴是x=h, 顶点坐标是(h,k).
左右平移:括号内左 加右减; 上下平移:括号外上 加下减.
一般地,抛物线 y = a(x-h)2+k与y = ax2形状相同,位置不同.
河南淮阳羲城中学
河南淮阳羲城中学
方法总结:
已知函数图象上的点,则这点的坐标 必满足函数的表达式,代入即可求得函数 解析式.
河南淮阳羲城中学
3、 要修建一个圆形喷水池,在池中心竖直安装一根水 管.在水管的顶端安装一个喷水头,使喷出的抛物线形 水柱在与池中心的水平距离为1m处达到最高,高度为 3m,水柱落地处离池中心3m,水管应多长?
3
同,且顶点坐标是(4,-2),试求这个函数关系式. 中考链接:
抛物线y=-3(x-1)2+2的图象如何得到y=-3x2 .
河南淮阳羲城中学
达标检测
1.完成下列表格: 二次函数
y=2(x+3)2+5
开口方向
y=-3(x-1)2-2
对称轴
顶点坐标
y = 4(x-3)2+7
y=-5(2-x)2-6
3.抛物线y=-3x2+2的图象向右平移2个单位,再向上平移1 个单位,得到抛物线的解析式为-------------------_2_.把___抛__物__线__y_=_-_3x2先向上平移2个单位,再向右平移1个单 位,那么所得抛物线是___________________.
2
2
平移方法2
y 1 (x 1)2 2
向左平移 1个单位
y 1 x2 2
1
个 单 位
向 下 平 移
y 1 (x 1)2 1 2
y 1
-5 -4 -3 -2 -1-1 O1 2 3 4 5 x
-2
-3 -4
-5
-6
-7
-8
-9
y 1 (x 1)2 1
-10
2
河南淮阳羲城中学
要点归纳
二次函数y=ax2 与y=a(x-h)2+k的关系
河南淮阳羲城中学
达标检测
1.完成下列表格:
二次函数
y=2(x+3)2+5
y=-3(x-1)2-2
y = 4(x-3)2+7 y=-5(2-x)2-6
开口方向 对称轴 顶点坐标 向上 直线x=-3 (-3, 5 )
向下
直线x=1 ( 1, -2 )
向上
直线x=3 ( 3 , 7)
向下 直线x=2 ( 2 , -6 )
(0≤x≤3)
当x=0时,y=2.25.
答:水管长应为2.25m.
河南淮阳羲城中学函数y=a(x-h)2+k与y=ax2的关系
探究归纳
怎样移动抛物线 y 1 x2就可以得到抛物线 y 1 (x 1)2 1 ?
2
2
平移方法1
y 1
向左平移
y 1 (x 1)2 1
河南淮阳羲城中学
解:如图建立直角坐标系,
点(1,3)是图中这段抛物线的顶点. y
因此可设这段抛物线对应的函数是 3
y=a(x-1)2+3 (0≤x≤3).
A 2
∵这段抛物线经过点(3,0), 1
∴ 0=a(3-1)2+3.
B(1,3)
解得:
a=-
3 4
O 12
因此抛物线的解析式为:
y=
-3 4
(x-1)2+3
河南淮阳羲城中学
华师大版《义务教育教科书》 九年级数学
26.2.3二次函数y=a(x-h)2+k的 图象与性质
单位:河南省淮阳羲城中学 数学教研组
河南淮阳羲城中学
26.2 .3 二次函数的图象与性质
第3课时 二次函数y=a(x-h)2+k的图象与性质
导入新课
讲授新课
当堂练习
课堂小结
河南淮阳羲城中学
可以看作互相平移得到的.
平移规律
左 右 平 移 y = ax2 + k
y = a( x - h )2 + k 上 下 平 移
简记为: 上下平移, 括号外上加下减;
y = a(x - h )2 左右平移,
上下平移
河南淮阳羲城中学
y = ax2 左右平移
括号内左加右减. 二次项系数a不变.
练一练
1.请回答抛物线y = 4(x-3)2+7由抛物线y=4x2怎样平 移得到? 由抛物线向上平移7个单位再向右平移3个单位得到的. 2.如果一条抛物线的形状与 y 1 x2 2 形状相
h 0, k 0 y ax2 h 0, k 0 y ax2 k
k 0, h 0 y a x h2
河南淮阳羲城中学
巩固训练
1.已知二次函数y=a(x-1)2-c的图象如图所示,则 一次函数y=ax+c的大致图象可能是( )
2. 已知二次函数y=a(x-1)2-4的图象经过点(3,0). (1)求a的值; (2)若A(m,y1)、B(m+n,y2)(n>0)是该函数图象上的两 点,当y1=y 2时,求m、n之间的数量关系.
河南淮阳羲城中学
学习目标
1.会用描点法画出y=a(x-h)2+k (a ≠0)的图象. 2.掌握二次函数y=a(x-h)2+k (a ≠0)的图象的性质并会应 用.(重点) 3.理解二次函数y=a(x-h)2+k (a ≠0)与y=ax2 (a ≠0)之间 的联系.(难点)
河南淮阳羲城中学
河南淮阳羲城中学
河南淮阳羲城中学
2.把抛物线y=-3x2先向上平移2个单位,再向右平移1
个单位,那么所得抛物线是__y_____3_(_x___1_)_2___2__.
3.抛物线y=-3x2+2的图象向右平移2个单位,再向上平
移1个单位,得到抛物线的解析式为___y____3__x___2_2_ 3
河南淮阳羲城中学
2
再描点、连线
y 1 (x 1)2 1 2
开口方向向下; 对称轴是直线x=-1; 顶点坐标是(-1,-1)
-1.5 -1 -1.5 -3 -5.5 …
y 1
-5 -4 -3 -2 -1-1 O1 2 3 4 5 x
-2
-3 -4
-5
-6
-7
直线x=-1
-8 -9
-10
y 1 (x 1)2 1 2
向上平移3个单位 y=-2x2+3 3.把y=-2x2的图像
向左平移2个单位 y=-2(x+2)2 4.请猜测一下,二次函数y=-2(x+2)2+3的图象是否可 以由y=-2x2平移得到?你认为该如何平移呢?
河南淮阳羲城中学
讲授新课
探究一 二次函数y=a(x-h)2+k的图象和性质
例1 画出函数
y 1 (x 1)2 1的图像.指出它的开口
a>0
a<0
开口方向
向上
向下
对称轴
直线x=h
直线x=h
顶点坐标
(h,k)
(h,k)
最值 增减性
河南淮阳羲城中学
当x=h时,y最小值=k
当x=h时,y最大值=k
当x<h时,y随x的增大 当x>h时,y随x的增大
而减小;x>h时,y随x 而减小;x<h时,y随x
的增大而增大.
的增大而增大.
顶点式
y a x h2 k a 0
2
方向、顶点与对称轴.
河南淮阳羲城中学
解: 先列表
x
… -4 -3 -2 -1 0 1 2 …
y 1 (x 1)2 1 … -5.5 -3 -1.5 -1 -1.5 -3 -5.5 …
2
再描点、连线
河南淮阳羲城中学
解: 先列表
x
… -4 -3 -2 -1 0 1 2 …
y 1 (x 1)2 1 … -5.5 -3
河南淮阳羲城中学
试一试 画出函数y= 2(x+1)2-2图象,并说出抛物线的
开口方向、对称轴、顶点.
y
开口方向向下; 对称轴是直线x=-1; 顶点坐标是(-1,-2)
8
6
4
2
-4 -2 O 2 4
x
-2
河南淮阳羲城中学
知识要点 二次函数 y=a(x-h)2+k(a ≠ 0)的性质
y=a(x-h)2+k
导入新课
复习引入
1.说出下列函数图象的开口方向,对称轴,顶点,最值和
增减变化情况:
y
y
(1)y=ax2 (2)y=ax2+c
Ox
y
y
O
x
y
O xO x
Ox
y
Ox
(3)y=a(x-h)2
河南淮阳羲城中学
y
y
Ox O x
yy
Ox O
x
河南淮阳羲城中学
2.请说出二次函数y=-2x2的开口方向、顶点坐标、 对称轴及最值?
