材料力学第六章简单的超静定问题
合集下载
材料力学-力法求解超静定结构
3 优化结构设计
力法求解超静定结构时，可以根据计算结果优化结构设计，提高结构的强度和稳定性。
结论与总结
力法是求解超静定结构的有效方法，通过合理应用材料力学基础和力法的原理，我们能够准确求解反力分布并 分析结构的应力情况。
样例分析
结构：桥梁
使用力法求解桥梁上的悬臂梁，计算主梁的支座反 力和悬臂梁的应力分布。
结构：楼房
将力法应用于楼房结构，确定楼板的支座反力并分 析楼梯的受力情况。
实用提示和技巧
1 标定自由度
在应用力法时，正确标定结构的自由度是成功求解反力的重要步骤。
2 验证计算结果
对计算得到的反力进行验证，确保结果的准确性，避免错误的设计决策。
材料力学-力法求解超静 定结构
超静定结构的定义
超静定结构是指具有不止一个不可靠支持反力的结构。它们挑战了传统的结构分析方法，需要使用力法进行求 解。
材料力学基础
材料力学研究材料的受力和变形规律，包括弹性力学、塑性力学和损伤力学。 这些基础理论为力法求解超静定结构提供了必要的工具。
力法的原理
力法是一种基于平衡原理和支座反力法则的结构分析方法。它通过对超静定结构施加虚位移，建立受力平衡方 程，求解未知反力。
超静定结构应用力法求解的步骤
1
确定结构类型
了解结构是否为超静定结构，并确定不
计算反力
2
可靠支持反力的个数。
根据力法原理，建立并求解受力平衡方
程，计算未知反力。
3
验证平衡
通过检查受力平衡方程是否满足等式的
确定应力分布
4
要求，验证计算的反力是否正确。
பைடு நூலகம்
根据已知反力和结构的几何特性，计算 并绘制应力分布图。
力法求解超静定结构时，可以根据计算结果优化结构设计，提高结构的强度和稳定性。
结论与总结
力法是求解超静定结构的有效方法，通过合理应用材料力学基础和力法的原理，我们能够准确求解反力分布并 分析结构的应力情况。
样例分析
结构：桥梁
使用力法求解桥梁上的悬臂梁，计算主梁的支座反 力和悬臂梁的应力分布。
结构：楼房
将力法应用于楼房结构，确定楼板的支座反力并分 析楼梯的受力情况。
实用提示和技巧
1 标定自由度
在应用力法时，正确标定结构的自由度是成功求解反力的重要步骤。
2 验证计算结果
对计算得到的反力进行验证，确保结果的准确性，避免错误的设计决策。
材料力学-力法求解超静 定结构
超静定结构的定义
超静定结构是指具有不止一个不可靠支持反力的结构。它们挑战了传统的结构分析方法，需要使用力法进行求 解。
材料力学基础
材料力学研究材料的受力和变形规律，包括弹性力学、塑性力学和损伤力学。 这些基础理论为力法求解超静定结构提供了必要的工具。
力法的原理
力法是一种基于平衡原理和支座反力法则的结构分析方法。它通过对超静定结构施加虚位移，建立受力平衡方 程，求解未知反力。
超静定结构应用力法求解的步骤
1
确定结构类型
了解结构是否为超静定结构，并确定不
计算反力
2
可靠支持反力的个数。
根据力法原理，建立并求解受力平衡方
程，计算未知反力。
3
验证平衡
通过检查受力平衡方程是否满足等式的
确定应力分布
4
要求，验证计算的反力是否正确。
பைடு நூலகம்
根据已知反力和结构的几何特性，计算 并绘制应力分布图。
材料力学 简单的超静定问题
l1 F N 1l1 E 1 A1
FN 3 l 3 E 3 A3
FN1
FN3
a a A
A1 FN2
l3
FN 3l3 E 3 A3
(3)
(4)补充方程：由几何方程和物理方程得：
F N 1l1 E1 A1
2
cos a
(5)联解（1）、（2）、（3）式，得:
FN 1 FN 2 E1 A1 F cos a 2 E1 A1 cos a E 3 A3
第六章
简单的超静定问题
1
第六章
§6-1
§6-2
简单的超静定问题
超静定问题及其解法
拉压超静定问题
§6-3 §6-4
扭转超静定问题 简单超静定梁
2
§6-1
超静定问题及其解法
1.单纯依靠静力平衡方程能够确定全部未知力（支反 力、内力）的问题，称为静定问题。 相应的结构称为静定结构。
2.单纯依靠静力平衡方程不能确定全部未知力（支反 力、内力）的问题，称为超静定问题。 相应的结构称为超静定结构。
3
F N3 A3 9F 14 A [ ]
F
[F ]
14 9
14 9
[ ] A
[ ] A
11
[例6-2-4]木制短柱的四角用四个40404的等边角钢 加固，角钢和木材的许用应力分别为[]1=160MPa和 []2=12MPa，弹性模量分别为E1=200GPa 和 E2 =10GPa；求许可载荷P。 解：（1）以压头为研究对象, 设每 个角钢受力为FN1，木柱受力为FN2.
14
B
1
D
C
3 2
(2) 几何方程
l1 ( l 3 ) cos a
FN 3 l 3 E 3 A3
FN1
FN3
a a A
A1 FN2
l3
FN 3l3 E 3 A3
(3)
(4)补充方程：由几何方程和物理方程得：
F N 1l1 E1 A1
2
cos a
(5)联解（1）、（2）、（3）式，得:
FN 1 FN 2 E1 A1 F cos a 2 E1 A1 cos a E 3 A3
第六章
简单的超静定问题
1
第六章
§6-1
§6-2
简单的超静定问题
超静定问题及其解法
拉压超静定问题
§6-3 §6-4
扭转超静定问题 简单超静定梁
2
§6-1
超静定问题及其解法
1.单纯依靠静力平衡方程能够确定全部未知力（支反 力、内力）的问题，称为静定问题。 相应的结构称为静定结构。
2.单纯依靠静力平衡方程不能确定全部未知力（支反 力、内力）的问题，称为超静定问题。 相应的结构称为超静定结构。
3
F N3 A3 9F 14 A [ ]
F
[F ]
14 9
14 9
[ ] A
[ ] A
11
[例6-2-4]木制短柱的四角用四个40404的等边角钢 加固，角钢和木材的许用应力分别为[]1=160MPa和 []2=12MPa，弹性模量分别为E1=200GPa 和 E2 =10GPa；求许可载荷P。 解：（1）以压头为研究对象, 设每 个角钢受力为FN1，木柱受力为FN2.
14
B
1
D
C
3 2
(2) 几何方程
l1 ( l 3 ) cos a
第6章超静定问题
T =7 kN.m d1=0.1 m
2m
A
1m
B
1m
C 2m d2
材料力学电子教案
例 7 答案 解：联立三式求出 FN ,即可得结果：
∆l = FN ⋅2 8FN = π d 22 Eπd 2 E 4 ∆l 2 ⋅∆l = = d1 d1 2 T ⋅1 FN d1 ⋅2 = − GI P GI P
材料力学电子教案
对(c)图: (1) 平衡方程
A
1
a
2 C
a
3 B
l
∑F
y
= 0, F1 + F2 + F3 − F = 0
A
F
∑M
= 0, aF2 + 2aF3 = 0
F1
F2
F3
(2) 变形协调方程
∆l1 − ∆l2 = ∆l2 − ∆l3
即∆l1 − 2∆l2 + ∆l3 = 0 (3) 物理方程 F1l ∆l1 = E1 A1
(4)补充方程变为 (4)
FN1 = FN 3
EA cos 2 α E3 A3
材料力学电子教案
联立平衡方程、补充方程，求解得
FN1 = FN 2 =
F E3 A3 2 cos α + EA cos 2 α
FN 3
F = EA 3 1+ 2 cos α E3 A3
在超静定杆系中，各杆轴力的大小和该杆的刚度与其它杆 的刚度的比值有关，杆系中任一杆刚度的改变都将引起杆系各 轴力的重新分配。这些特点在静定杆系中是不存在的。
F N3
α
FN2
A F
x
ΣFy = 0, FN3 + FN1 cos α + FN2 cos α − F = 0
材料力学第六章静不定
FHale Waihona Puke 5、列补充方程将物理方程代入几何方程得补充方程
材料力学
.
6
FN2l2FN3l3FN1l1cos
E2A2 E3A3 E1A1
解得
FN1
1
F 2E2A2l1
cos2
E1 A1l2
FN2 FN3 2cosE F2A E21l1 Ac1lo2s
材料力学
.
7
OAB为刚性梁，写几何方程。
450
①
②
O
A
B
l
l1 l l2
l
OAB为刚性梁， ①、②两杆材料相同， 抗弯刚度相等，求两杆轴力之比。
F
①
F
O
B l1 C
bA
l2 sin 45o
2l1
②
l
l
l
EAsF in N 1 2 clos2EAsiF nN b2closb
FN1 sin 2 FN2 sin 2b
l1 2 l2
sin sin b
l1F E N A 1(co 2 sl)， l2F E N A 2(colsb)
材料力学
.
8
OAB为刚性梁，①、②两杆材料相同，
EA2=2EA1。求②杆与①杆的应力之比。
解：变形协调关系
O
l2 sin 450
2l1
即 l2 2l1
450
①
②
a
A l1
a
l2
B
F
由物理关系建立补充方程，考虑对O取矩得平衡方程，联 立求出两杆轴力，再求应力后得结果。
小技巧
2
l2 l2
2l1 2l1
变形协调方程 。
材料力学——6简单的超静定问题
M
(x)
X
1
x
X1x, P(x
x l ), 2
l 2
x
l 2
B
l 0
M
(x)M EI
( x)dx
0
如果B处支撑为弹簧 （弹簧系数K） ？
例 P
A
l
l
2
2
BA
P
B
l
l
2
2
X1
解
M
(x)
X1
x
X1x, P(x
x l ), 2
l 2
x
静定基
l 2
x
B
l 0
M (x)M EI
(x)dx
X1 K
求解 线性方程
未知力
以一例说明解法
q
12 3
X1 X2 X3
• 静定基（含未知数）
1 0, 2 0, 3 0
• 位移协调条件
建立方程的过程
以1为例说明
X1 X2 X3
1
M (x)M1(x) dx EI
(M X1 M X2 M X3 M q )M1(x) dx EI
M X1M1 dx M X2 M1(x) dx M X3 M1(x) dx M qM1(x) dx
A
P0 =1 B
M (x) x
解： 协调条件——D截面转
角为零
A
静定基
D
/2
0
M
( )M
EI
()Rd
0
DX
P 2
二、装配应力
1、静定问题无装配应力
B
C
2、静不定问题存在装配应力
1
2
A
下图，3号杆的尺寸误差为，
《材料力学》第6章 简单超静定问题 习题解
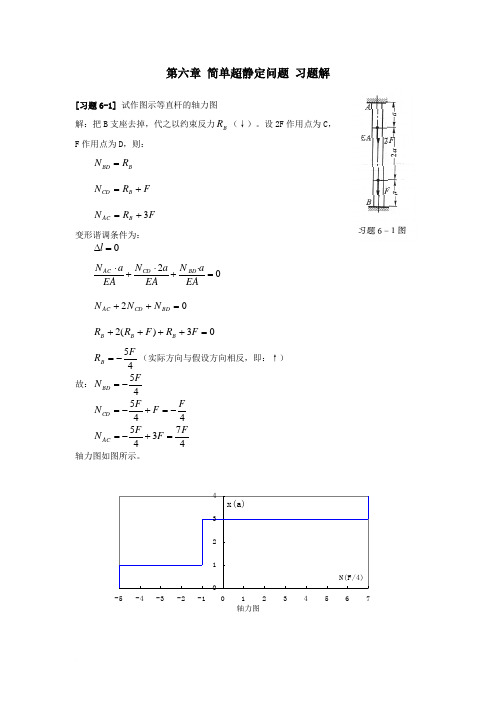
第六章 简单超静定问题 习题解[习题6-1] 试作图示等直杆的轴力图解：把B 支座去掉，代之以约束反力B R （↓）。
设2F 作用点为C ， F 作用点为D ，则：B BD R N = F R N B CD += F R N B AC 3+=变形谐调条件为：0=∆l02=⋅+⋅+⋅EA aN EA a N EA a N BD CD AC 02=++BD CD AC N N N03)(2=++++F R F R R B B B45FR B -=（实际方向与假设方向相反，即：↑） 故：45FN BD-= 445F F F N CD -=+-=47345FF F N AC=+-= 轴力图如图所示。
[习题6-2] 图示支架承受荷载kN F 10=，1，2，3各杆由同一种材料制成，其横截面面积分别为21100mm A =，22150mm A =，23200mm A =。
试求各杆的轴力。
解：以节点A 为研究对象，其受力图如图所示。
∑=0X030cos 30cos 01032=-+-N N N0332132=-+-N N N 0332132=+-N N N (1)∑=0Y030sin 30sin 0103=-+F N N2013=+N N (2)变形谐调条件：设A 节点的水平位移为x δ，竖向位移为y δ，则由变形协调图（b ）可知：00130cos 30sin x y l δδ+=∆x l δ=∆200330cos 30sin x y l δδ-=∆03130cos 2x l l δ=∆-∆2313l l l ∆=∆-∆设l l l ==31，则l l 232=223311233EA l N EA lN EA l N ⋅⋅=- 22331123A N A N A N =- 15023200100231⨯=-N N N23122N N N =-21322N N N -= (3)(1)、(2)、(3)联立解得：kN N 45.81=；kN N 68.22=；kN N 54.111=（方向如图所示，为压力，故应写作：kN N 54.111-=）。
第六章静不定
刚性梁AB悬挂于三根平行杆上。l=2m，a=1.5m，b=1m，c=0.25m， d=0.2m。1杆由黄铜制成，E1=100GPa，A1=2cm2，a1=16.5×10-6/ 0C。 2和3杆由碳钢制成，E2=E3=200GPa，A2=1cm2， A3=3cm2 ， a2=a3=12.5×10-6/0C，F=40kN。 设温度升高20 0C，求各杆的应力。
9
中南大学土木工程学院
OAB为刚性梁，①、②两杆材料相同， EA2=2EA1。求②杆与①杆的应力之比。
解：变形协调关系
450 ① ②
Dl 2 2Dl1 0 sin 45
即
O a
D l1
A a
D l2
B
F
Dl2 2Dl1
由物理关系建立补充方程，考虑对O取矩得平衡方程，联 立求出两杆轴力，再求应力后得结果。
∆l2
（ c）
∆l3
材料力学
中南大学土木工程学院
5
还可列出其它变形图，但必须保证变形图与受力图一致。 FN1
∆l1
FN2
FN3
∆l2
∆l3
（a）
∆l1 ∆l2 ∆l3
（a）
F FN3
对应受力图
FN1
FN2
（b）
（b）
F FN3
FN1
∆l1 ∆l2
FN2
（ c）
∆l3
（ c）
F
6
材料力学
中南大学土木工程学院
5、列补充方程：物理方程代入几何方程即得补充方程。
材料力学
中南大学土木工程学院
4
图示静不定结构， 可列如右变形图。
几何方程
∆l1
∆l2
∆l3
材料力学-第六章 简单的超静定问题
变形协调条件：
l1 l 3 cos
F N1
F N3
F N2
l3
l1
A
A
l2
例2.图示AB为刚性梁，1、2两杆的抗拉（压）
刚度均为EA，制造时1杆比原长l短，将1杆装
到横梁后，求两杆内力。
解: 装配后各杆变形 1杆伸长 l1 2杆缩短 l 2 变形协调条件
A
1
l1
4、联解方程
FN 1 F E3 A3 2 cos 2 E1 A 1 cos
FN 3
F E1 A 3 1 1 2 cos E3 A3
●装配应力的计算
装配应力：超静定结构中由于加工误差， 装 配产生的应力。 平衡方程：
FN 1 FN 2
1
3 2
A
l
FN 3 ( FN1 FN 2 ) cos
2、AC和BC材料相同，面积不同，外力作用在 连接界面处，在外力不变的情况下，要使AC上 轴力增加，错误的方法有（ ）。 A、 增加AC的横截面积 B、 减小BC的横截面积 C、 增加AC的长度 D、 增加BC的长度
A l1 C F B l2
3、AB为等截面杆，横截面面积为A，外力F作 用在中间，则AC和BC上应力分别（ ）。
2
l 2
B
2( l1 ) l 2
解: 分析AB
A
aF 1 2aF 2 0
F1l 物理方程 l1 EA 变形协调条件
FA
F1
F2
B
F2 l l 2 (缩短) EA
2( l1 ) l 2
4EA 2EA F1 (拉力) F2 (压力) 5l 5l
材料力学(I)第六章
N2 y N1 N2 N3
(2) 几何方程
L2
( L3 ) cos L1
材料力学(Ⅰ)电子教案
简单的超静定问题
15
(3)、物理方程及补充方程：
FN 1L1 FN 3 L3 ( ) cos E1 A1 E3 A3
(4) 、解平衡方程和补充方程，得:
FN1 FN 2
E1 A1 cos2 L3 1 2 cos3 E1 A1 / E3 A3
FN 1L FN 3 L 得: cos E1 A1 cos E3 A3
5）联立①、④求解：
FN ! F
④
E 3 A3 2 co s E1 A1 co s2
FN 3
F E1 A1 1 2 co s3 E A
材料力学(Ⅰ)电子教案
简单的超静定问题
[例2-19]刚性梁AD由1、2、3杆悬挂，已知三杆材料 相同，许用应力为[σ ]，材料的弹性模量为 E，杆长 均为l，横截面面积均为A，试求各杆内力。
5
1.比较变形法 把超静定问题转化为静定问题解，但 必须满足原结构的变形约束条件。
[例2-16] 杆上段为铜,下段为钢杆，
E1 A1
A
1
上段长 1 , 截面积A1 , 弹性模量E1 下段长 2 , 截面积A2 , 弹性模量E2
杆的两端为固支,求两段的轴力。
C
E 2 A2
F
FB
B
2
（1）选取基本静定结构（静定基如图），B 解： 端解除多余约束，代之以约束反力RB
2E1 A1 cos3 FN 3 3 L3 1 2 cos E1 A1 / E3 A3
例2-22
材料力学(Ⅰ)电子教案
(2) 几何方程
L2
( L3 ) cos L1
材料力学(Ⅰ)电子教案
简单的超静定问题
15
(3)、物理方程及补充方程：
FN 1L1 FN 3 L3 ( ) cos E1 A1 E3 A3
(4) 、解平衡方程和补充方程，得:
FN1 FN 2
E1 A1 cos2 L3 1 2 cos3 E1 A1 / E3 A3
FN 1L FN 3 L 得: cos E1 A1 cos E3 A3
5）联立①、④求解：
FN ! F
④
E 3 A3 2 co s E1 A1 co s2
FN 3
F E1 A1 1 2 co s3 E A
材料力学(Ⅰ)电子教案
简单的超静定问题
[例2-19]刚性梁AD由1、2、3杆悬挂，已知三杆材料 相同，许用应力为[σ ]，材料的弹性模量为 E，杆长 均为l，横截面面积均为A，试求各杆内力。
5
1.比较变形法 把超静定问题转化为静定问题解，但 必须满足原结构的变形约束条件。
[例2-16] 杆上段为铜,下段为钢杆，
E1 A1
A
1
上段长 1 , 截面积A1 , 弹性模量E1 下段长 2 , 截面积A2 , 弹性模量E2
杆的两端为固支,求两段的轴力。
C
E 2 A2
F
FB
B
2
（1）选取基本静定结构（静定基如图），B 解： 端解除多余约束，代之以约束反力RB
2E1 A1 cos3 FN 3 3 L3 1 2 cos E1 A1 / E3 A3
例2-22
材料力学(Ⅰ)电子教案
材料力学
5 Pa RD a RD a 6 EI 3EI 3EI
如何得到？
A D
P
B
自行完成
C D
RD
例题 6
图示结构AB梁的抗弯刚度为EI，CD杆的抗拉刚度为EA，
已知P、L、a。求CD杆所受的拉力。
D
a
A
C
L
2
L
B
2
P
解：变形协调条件为 wC lCD
D
a
C
FC
A
( P FC ) L wC 48EI FC L lCD EA
温度应力：
FB E t A
6 1 12 . 5 10 碳素钢线胀系数为 C0
温度应力：超静定结构中，由于温度变化，使构
件膨胀或收缩而产生的附加应力。
不容忽视！！！
路、桥、建筑物中的伸缩缝 高温管道间隔一定距离弯一个伸缩节
例题 11
图示阶梯形杆上端固定，下端与支座距离=1mm， 材料的弹性模量E=210GPa，上下两段杆的横截 面面积分别为600平方毫米和300平方毫米。试 作杆的轴力图。
C
A
FA
B
L2
FC
FA FB FC qL 0
L2
M
A
0
FB
变形协调方程
L qL2 FC FB L 0 2 2
3 FB qL 16
FA 3 qL 16
C q C FC 0
7.5kNm
5qL4 FC L3 5 0 FC qL 8 384 EI Z 48EI Z
由于超静定结构能有效降低结构的内力及变形，在 工程上（如桥梁等）应用非常广泛。
●超静定问题的解法：
材料力学第六章静不定
FN2
FN3
（c） F
材料力学
中南大学土木工程学院
13
静不定结构的特点（1）
内力按刚度比分配。 思考：静定结构是否也是这样？
B
C
D
B
刚度较大 内力较大
A
F
材料力学
中南大学土木工程学院
C
刚度增加 内力不变
A
F
14
静不定结构的特点（2） 配应力
——装
B
C
B
D
C
A
静定结构 ——无装配应力
A
中南大学土木工程学院
8
OAB为刚性梁，①、②两杆材料相同，
EA2=2EA1。求②杆与①杆的应力之比。
解：变形协调关系
O
l2 sin 450
2l1
即 l2 2l1
450
①
②
a
A l1
a
l2
B
F
由物理关系建立补充方程，考虑对O取矩得平衡方程，联
立求出两杆轴力，再求应力后得结果。
小技巧
l1
FN1
2 3
EA
l ，l2
1F.5NE2lA，l3
FN3
2 3
2EA
l
代入变形协调方程得补充方程
2FN2 2FN1 FN3
联立平衡方程求得
14 2 3 FN1 23 F 0.76F
FN2 3
3 2 F 0.14F 23
求拉压静 不定结构 注意事项
32 2 3 FN3 23 F 1.24F ()
材料力学
未知力：4个 平衡方程：2个 静不定次数 = 4－2 = 2 需要补充2个方程 此结构可称为2次静不定结构
材料力学超静定全版
结构与支承物的连接处只 能发生转动，不能发生刚 性位移。
按几何特征分类
连续性
Hale Waihona Puke 结构在各个方向上都是连 续的。非连续性
结构在某些方向上存在间 断，如梁的弯曲变形。
平面性
结构在某个平面内发生变 形，如薄板弯曲。
按求解方法分类
解析法
01
近似法
02
03
实验法
通过数学解析的方法求解超静定 问题，需要建立复杂的数学模型。
THANKS FOR WATCHING
感谢您的观看
解决超静定问题的技术和方法在工程 实践中具有广泛的应用价值，为复杂 结构的分析和设计提供重要的理论支 持和技术指导。
02 超静定问题的分类
按支承情况分类
01
02
03
固定支承
结构与支承物的连接处不 能发生任何方向的位移， 只能发生转动。
弹性支承
结构与支承物的连接处既 有刚性位移，又有弹性位 移。
铰支承
机械装置超静定问题分析
总结词
保障机械运转稳定性
详细描述
机械装置在运转过程中会受到各种外力和内 力的作用，导致其发生变形和位移。超静定 问题分析能够评估机械装置在不同工况下的 稳定性，预防因变形和位移引起的故障，提 高机械运转的可靠性和效率。
05 超静定问题的未来研究方 向
新型材料的超静定问题研究
详细描述
复杂结构如高层建筑、大跨度桥梁、空间结构等，其 超静定问题涉及到多个自由度和多种非线性因素，需 要深入研究其静力、动力和稳定性等问题。
多场耦合的超静定问题研究
要点一
总结词
要点二
详细描述
多场耦合的超静定问题研究将成为一个重要方向。
按几何特征分类
连续性
Hale Waihona Puke 结构在各个方向上都是连 续的。非连续性
结构在某些方向上存在间 断，如梁的弯曲变形。
平面性
结构在某个平面内发生变 形，如薄板弯曲。
按求解方法分类
解析法
01
近似法
02
03
实验法
通过数学解析的方法求解超静定 问题，需要建立复杂的数学模型。
THANKS FOR WATCHING
感谢您的观看
解决超静定问题的技术和方法在工程 实践中具有广泛的应用价值，为复杂 结构的分析和设计提供重要的理论支 持和技术指导。
02 超静定问题的分类
按支承情况分类
01
02
03
固定支承
结构与支承物的连接处不 能发生任何方向的位移， 只能发生转动。
弹性支承
结构与支承物的连接处既 有刚性位移，又有弹性位 移。
铰支承
机械装置超静定问题分析
总结词
保障机械运转稳定性
详细描述
机械装置在运转过程中会受到各种外力和内 力的作用，导致其发生变形和位移。超静定 问题分析能够评估机械装置在不同工况下的 稳定性，预防因变形和位移引起的故障，提 高机械运转的可靠性和效率。
05 超静定问题的未来研究方 向
新型材料的超静定问题研究
详细描述
复杂结构如高层建筑、大跨度桥梁、空间结构等，其 超静定问题涉及到多个自由度和多种非线性因素，需 要深入研究其静力、动力和稳定性等问题。
多场耦合的超静定问题研究
要点一
总结词
要点二
详细描述
多场耦合的超静定问题研究将成为一个重要方向。
材料力学第5版(孙训方编)第六章
100106 Pa 100 MPa
（压应力）
30
第六章 简单的超静定问题
§6-3 扭转超静定问题
例题6-5 两端固定的圆截面等直杆AB，在截面C处受 扭转力偶矩Me作用，如图a。已知杆的扭转刚度为GIp。试 求杆两端的约束力偶矩以及C截面的扭转角。
(a)
31
第六章 简单的超静定问题
MA (a)
FN l EAt
6. 杆的横截面上的温度应力为 FN l Et A
29
第六章 简单的超静定问题
FN l Et A
若该杆为钢杆而l =1.2×10-5/(˚C)，E=210GPa，则当
温度升高t =40˚时有
l Et 1.2 105 / C 210109 GPa40 C
4. 将补充方程与平衡方程联立求解得：
FN1 FN 2
eEA 1 ， l 1 2 EA E3 A3
FN 3
eE3 A3 1 EA l 1 3 3 2 EA
所得结果为正，说明原先假定杆1,2的装配内力为拉
力和杆3的装配内力为压力是正确的。 5. 各杆横截面上的装配应力如下：
FN1 1 2 74.53 MP a A FN3 3 19.51 MP a A3
（拉应力） （压应力）
25
第六章 简单的超静定问题
(2) 温度应力 也是由于超静定杆系存在“多余”约束，杆件会因温 度变化产生的变形受到限制而产生温度内力及温度应力。 铁路上无缝线路的长钢轨在温度变化时由于不能自由伸缩，
的弹性模量E=210 GPa，铜的弹
性模量E3=100 GPa。
22
第六章 简单的超静定问题
（压应力）
30
第六章 简单的超静定问题
§6-3 扭转超静定问题
例题6-5 两端固定的圆截面等直杆AB，在截面C处受 扭转力偶矩Me作用，如图a。已知杆的扭转刚度为GIp。试 求杆两端的约束力偶矩以及C截面的扭转角。
(a)
31
第六章 简单的超静定问题
MA (a)
FN l EAt
6. 杆的横截面上的温度应力为 FN l Et A
29
第六章 简单的超静定问题
FN l Et A
若该杆为钢杆而l =1.2×10-5/(˚C)，E=210GPa，则当
温度升高t =40˚时有
l Et 1.2 105 / C 210109 GPa40 C
4. 将补充方程与平衡方程联立求解得：
FN1 FN 2
eEA 1 ， l 1 2 EA E3 A3
FN 3
eE3 A3 1 EA l 1 3 3 2 EA
所得结果为正，说明原先假定杆1,2的装配内力为拉
力和杆3的装配内力为压力是正确的。 5. 各杆横截面上的装配应力如下：
FN1 1 2 74.53 MP a A FN3 3 19.51 MP a A3
（拉应力） （压应力）
25
第六章 简单的超静定问题
(2) 温度应力 也是由于超静定杆系存在“多余”约束，杆件会因温 度变化产生的变形受到限制而产生温度内力及温度应力。 铁路上无缝线路的长钢轨在温度变化时由于不能自由伸缩，
的弹性模量E=210 GPa，铜的弹
性模量E3=100 GPa。
22
第六章 简单的超静定问题
拉压超静定问题
第六章 超静定问题
(a)
(b)
图a所示静定杆系,为减小杆1、2中的内力或节点A的
位移，而增加了杆3 ，构成超静定杆系(如图b) 。
河南理工大学万方科技学院
材料力学
第六章 超静定问题
(b)
此时有3个未知内力FN1 、FN2 、FN3，但只有两个独立
的平衡方程── 一次超静定问题。
河南理工大学万方科技学院
(拉力）
材料力学
第六章 超静定问题
F N 1F N 22c F N 3 o s2co E sl33 A 3 e2E 1A 1 l1 co 2 s （压力）
至于各杆横截面上的装配应力，只需将装配内力(轴力) 除以杆的横截面面积即可。
由此可见，求解超静定杆系(结构)中的装配内力的关键， 仍在于根据变形几何相容条件，并结合应用物理关系列出补充 方程。
材料力学
第六章 超静定问题
例6-4 图示结构，AB为刚性梁，1、2两杆刚度相同。 求1、2杆的受力。
1l A
a
a
30o 2 B
A
FAX
a
FN1 a
30o FN2 B
P
FAY
P
平衡方程: m A 0F N 1 a F N 2 co 2 a s P 2 3 a 0 0
变形关系: coLs2302L1 物理关系: L1FEN1L A
P 假设均受拉力。
河南理工大学万方科技学院
材料力学
第六章 超静定问题
变形几何相容方程：
l1l32l2
1
2
3
a
a
即 l12l2l30（2） A
B
物理方程：
l1
孙训方《材料力学》(第6版)笔记和课后习题(含考研真题)详解-简单的超静定问题(圣才出品)
图 6-2-4 （2）补充方程 作铰 A 的位移图，由几何关系可得变形协调方程： Δl1/sin30°＝2Δl2/tan30°＋Δl3/sin30°③ 其中，由胡克定律可得物理关系：
8 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
Δl1＝FN1l1/EA1＝FN1l/（EA1cos30°） Δl2＝FN2l2/EA2＝FN2l/（EA2） Δl3＝FN3l3/EA3＝FN3l/（EA3cos30°） 代入式③可得补充方程： FN1l/（EA1sin30°·cos30°）＝2FN2l/（EA2tan30°）＋FN3l/（EA3sin30°·cos30°）④ （3）求解 联立式①②④，可得各杆轴力：FN1＝8.45kN，FN2＝2.68kN，FN3＝11.55kN。
9 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
MB = 0
FN2 Leabharlann 2 2a+
FN4
2 2
a
+
FN3
2a − F ( 2 a + e) = 0 2
②
根据结构的对称性可得 FN2＝FN4③
（2）补充方程
如刚性板的位移图所示，根据几何关系可得：Δl1＋Δl3＝2Δl2④
由结构对称可知 Δl2＝Δl4，其中，由胡克定律可得各杆伸长量：
Δl1＝FN1l/EA，Δl2＝FN2l/EA，Δl3＝FN3l/EA
代入式④，整理可得补充方程：FN1＋FN3＝2FN2⑤
（3）求解
联立式①②③⑤，解得各杆轴力：
FN1
=
(1 4
−
e )F(压) 2a
FN2
=
FN4
=
F 4
8 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
Δl1＝FN1l1/EA1＝FN1l/（EA1cos30°） Δl2＝FN2l2/EA2＝FN2l/（EA2） Δl3＝FN3l3/EA3＝FN3l/（EA3cos30°） 代入式③可得补充方程： FN1l/（EA1sin30°·cos30°）＝2FN2l/（EA2tan30°）＋FN3l/（EA3sin30°·cos30°）④ （3）求解 联立式①②④，可得各杆轴力：FN1＝8.45kN，FN2＝2.68kN，FN3＝11.55kN。
9 / 42
圣才电子书 十万种考研考证电子书、题库视频学习平台
MB = 0
FN2 Leabharlann 2 2a+
FN4
2 2
a
+
FN3
2a − F ( 2 a + e) = 0 2
②
根据结构的对称性可得 FN2＝FN4③
（2）补充方程
如刚性板的位移图所示，根据几何关系可得：Δl1＋Δl3＝2Δl2④
由结构对称可知 Δl2＝Δl4，其中，由胡克定律可得各杆伸长量：
Δl1＝FN1l/EA，Δl2＝FN2l/EA，Δl3＝FN3l/EA
代入式④，整理可得补充方程：FN1＋FN3＝2FN2⑤
（3）求解
联立式①②③⑤，解得各杆轴力：
FN1
=
(1 4
−
e )F(压) 2a
FN2
=
FN4
=
F 4
材料力学-简单超静定
1
建立力学模型
根据实际情况，选择适当的力学模型来描述系统的行为。
2
应用适当的计算方法
使用强大的计算方法，如有限元分析或解析方法，来解决超静定问题。
3
验证和优化
通过验证和优化计算结果，确保超静定结构的设计合理和可靠性。
简单超静定的应用范围和意义
建筑和桥梁设计
通过应用简单超静定材料 力学理论，可以设计出更 加稳定和安全的建筑和桥 梁结构。
2 材料创新
将超静定理论与热力学、 电磁学等领域相结合， 探索多物理场耦合的复 杂问题。
研究新型材料的超静定 特性，推动材料创新和 应用领域的进步。
3 智能结构设计
结合超静定理论和智能 材料，开发具有适应性 和自修复能力的结构。
简单超静定的相关实例分析和工程应用
实例1：桥梁设计 实例2：机械零件 实例3：材料性能
分析简单超静定桥梁的受力特点和优化设计方 法。
研究简单超静定机械零件的强度和刚度，优化 设计方案。
通过简单超静定力学模型，改进材料的性能和 可靠性。
总结和展望材料力学-简单超静定的未来 研究方向
1 多物理场耦合
材料力学-简单超静定
材料力学-简单超静定为你揭示了材料力学中的重要概念、计算方法和工程应 用。通过分析简单超静定问题，你将深入了解超静定结构的力学特性和解决 步骤。
分析简单超静定问题的背景
1 需求的复杂性
2 对刚体的限制
现实世界中，材料力学 问题往往涉及多种约束 条件和复杂的外力情况。
刚体假设无法适用于所 有情况，因此需要超静 定理论来帮助分析。
机械工程
简单超静定分析对于设计 高精度机械零件和装置具 有重要作用。
材料研究
了解材料力学的超静定现 象有助于开发新型材料和 改进现有材料的性能。
材料力学第五版课后习题答案修订版
材料力学第五版课后习题答案Company number：【WTUT-WT88Y-W8BBGB-BWYTT-19998】二、轴向拉伸和压缩2-1试求图示各杆1-1和2-2横截面上的轴力，并作轴力图。
（a）解：；；（b）解：；；（c）解：；。
(d)解：。
2-2 试求图示等直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。
若横截面面积，试求各横截面上的应力。
解：2-3试求图示阶梯状直杆横截面1-1，2-2和3-3上的轴力，并作轴力图。
若横截面面积，，，并求各横截面上的应力。
解：2-4 图示一混合屋架结构的计算简图。
屋架的上弦用钢筋混凝土制成。
下面的拉杆和中间竖向撑杆用角钢构成，其截面均为两个75mm×8mm的等边角钢。
已知屋面承受集度为的竖直均布荷载。
试求拉杆AE和EG横截面上的应力。
解：=1）求内力取I-I分离体得（拉）取节点E为分离体，故（拉）2）求应力75×8等边角钢的面积A=11.5 cm2(拉)（拉）2-5(2-6)图示拉杆承受轴向拉力，杆的横截面面积。
如以表示斜截面与横截面的夹角，试求当，30，45，60，90时各斜截面上的正应力和切应力，并用图表示其方向。
解：2-6(2-8) 一木桩柱受力如图所示。
柱的横截面为边长200mm的正方形，材料可认为符合胡克定律，其弹性模量E=10 GPa。
如不计柱的自重，试求：（1）作轴力图；（2）各段柱横截面上的应力；（3）各段柱的纵向线应变；（4）柱的总变形。
解：（压）（压）2-7(2-9)一根直径、长的圆截面杆，承受轴向拉力，其伸长为。
试求杆横截面上的应力与材料的弹性模量E。
解：2-8(2-11)受轴向拉力F作用的箱形薄壁杆如图所示。
已知该杆材料的弹性常数为E，，试求C与D两点间的距离改变量。
解：横截面上的线应变相同因此2-9(2-12) 图示结构中，AB为水平放置的刚性杆，杆1，2，3材料相同，其弹性模量E=210GPa，已知，，，。
材料力学第五版课件 主编 刘鸿文 第六章 简单的超静定问题
例题： 试判断下图结构是静定的还是超静定的？若是超静定， 则为几次超静定？
B
DE
A
C
FP
(a)静定。 未知内力数：3 平衡方程数：3
B
D
A
C
F
P
(b)超静定。 未知力数：5 平衡方程数：3 静不定次数=2
(c)静不定。
未知内力数：3
平衡方程数：2
FP
静不定次数=1
静不定问题的解法： （1）建立静力平衡方程； （2）由变形协调条件建立变形协调方程； （3）应用物理关系，代入变形协调方程，得到补充方程；
基本静定基的选取：
(1)解除B支座的约束,以约束反力
代替，即选择一端固定一端自由
的悬臂梁作为基本静定基。
(2)解除A端阻止转动的约束，以 约束反力代替，即选择两端简支 的梁作为基本静定基。
基本静定基选取可遵循的原则：
(1) 基本静定基必须能维持静力平衡，且为几何不变系统； (2) 基本静定基要便于计算，即要有利于建立变形协调条
E3 A3
F FN3 = 1+ 2E1 A1 cos3 a
E3 A3
(拉力) (拉力)
温度应力和装配应力
一、温度应力
在超静定结构中，由于温度变化引起的变形受到约束的限制， 因此在杆内将产生内力和应力，称为温度应力和热应力。
杆件的变形 ——
由温度变化引起的变形 温度内力引起的弹性变形
例：阶梯钢杆的上下两端在T1=5℃时被固 定,上下两段的面积为
=-
[13EI
32(1+
24
I Al
2
)
]
M
M
A
C
B D
l
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
列静力平衡方程 MA0
F NC 1 E k 3N 53F NBD
变形协调方程
D
F LN DB 31 m C LC 3 E k E / m 0 2 N 3 m F N 0 1 1 . 5 FB 6 m 1 m N0 0 . 8 B2 D l D F N E 65 F 4 N3 m B C3 E 0 1 0 F N D 6 m 0 0 C 2 l E E
EAcos
3P-2N2cos-N1＝0
l2
cos
=
2l1
所以
N2l
EAcos2
=2
N1l
EA
最后解得
N1 =
3P
4cos3+1
N2 =
6Pcos2
4cos3+1
L
1.8L LDB
例5
图示刚性梁AB受均布载荷作用，梁在A端铰支，在B点和C点由
两根钢杆BD和CE支承。已知钢杆的横截面面积ADB=200mm2， ACE=400mm2，其许用应力[σ]=170MPa，试校核钢杆的强度。
250 250
查表知40mm×40mm×4mm等边角钢 Ast3.08c6m 2 故 A st4A s t1.3 2c42 m , A W2 5 2 562 cm 2 5
代入数据，得 F W 0 .7F 1F 7 s t 0 .2F 83
F
根据角钢许用应力，确定F
st0.2As8tF3st F69k8N
水平杆缩短 l2 F E N 2 2 A l2 2 2 1 . 3 0 1 7 9 1 2 0 2 3 1 0 .7 5 1 6 3 0 0 .6 2 1 3 m 0 0 .6 mm
l1
FN1l1 E1A1
1mm
l2
FN2l2 E2A2
0.6mm
3、节点A的位移（以切代弧）
处受荷载F作用，试求B点的位移δB。
αD
B1B B2C1C
FNCD
F
A
C
a
CC1 ccoCoLssCCD
C
C1
L/2
L/2
B
mA0
FNCDc2oFs
B1
LC F D LF N1 2 C E L D c L A CoDs F CD
E2A F c o2as
BE4 A cFo3 as
二、拉压超静定问题解法
FN 1
FN 2
300
A2
A
y
A2
A
Ax
F A1
A3
A
A A4
A1A l11mm
A2A l20.6mm
A1
xl20.6mm
yA3 AA 3A 4s i3 l1 n0 t al3 2n0
21.0 339 .0 3 m9m
AAx2y2 0.623.032 9
3.1mm
图所示结构，刚性横梁AB由斜杆CD吊在水 例2 平位置上，斜杆CD的抗拉刚度为EA，B点
材料力学第六章简单 的超静定问题
§6-1 超静定问题
静定结构：
约束反力 可由静力平 衡方程全部 求得
超静定结构：结构的强度和刚度均得到提高 约束反力不能全 部由平衡方程求得 超静定次数：
约束反力多于 独立平衡方程的数
独立平衡方程数： 平面任意力系：
3个平衡方程 平面共点力系：
2个平衡方程
平面平行力系：2个平衡方程 共线力系：1个平衡方程
固， 已知角钢的许用应力[σst]=160MPa，Est=200GPa；木材
的许用应力[σW]=12MPa，EW=10GPa，求许可载荷F。
解： 平衡方程:FFWFst （1）
F
F
变形协调关系: lstlw
物理关系:
lW
FWl EWAW
FW
lst
ห้องสมุดไป่ตู้
Fst l EstAst
Fst
补充方程: Fst FW （2） EstAst EWAW
一、小变形放大图与位移的求法。
求各杆的变形量△Li ，如图；
A
B
变形图精确画法，图中弧线；
L1
L2
C
变形图近似画法，图中弧之切线。
L2 P L1 C' C"
例1
AB长2m, 面积为200mm2。AC面积为250mm2。 E=200GPa。F=10kN。试求节点A的位移。
解：1、计算轴力。（设斜杆为1杆，水
根据木柱许用应力，确定F
W0.7AW 1F7W F10k4N 6 许可载荷 F69k8N
250 250
例4
AB为刚性梁， 1、2两杆的横 截面面积相等。 求1、2两杆的 内力。
解
由平衡方程得 3P-2N2cos-N1＝0
由变形协调条件得
l2
cos
=
2l1
由物理关系
l1 =
N1l
EA
l2 =
N2l
超静定结构的求解方法：
1、列出独立的平衡方程
F x 0F N 1 F N 2
F y 0 2 F N 1 c o F N 3 s F
2、变形几何关系
l1 l2
l1 l2 l3co s
l3
3、物理关系
l1
FN1l
EAcos
l3
FN3l EA
4、补充方程
EFcA N1losF E N3lA cos FN1FN3co2s
5、求解方程组得
FN1FN21 F2 cco2o 3 ss FN312cFo3s
超静定问题的方法步骤：
平衡方程； 几何方程——变形协调方程； 物理方程——弹性定律； 补充方程：由几何方程和物理方程得； 解由平衡方程和补充方程组成的方程组。
例题3
木制短柱的四角用四个40mm×40mm×4mm的等边角钢加
平杆为2杆）取节点A为研究对象
Fx 0 F N 1co s F N 20
FN 1
FN 2 300
y
Ax
Fy 0 F N 1sin F0 F N 1 F /sin 2 F 2k0N
F N 2 F N 1 co s3 F 1 .3 7 k 2N
2、根据胡克定律计算杆的变形。
斜杆伸长 l1 F F E N 1 A 1 l1 1 2 0 2 1 9 1 0 0 0 2 3 0 2 0 1 6 0 0 1 1 3 m 0 1mm
D
FN 1 FN 2
FN 3
3杆材料相同，AB杆面积为200mm2，AC
杆面积为300 mm2，AD杆面积为400 mm2，
若F=30kN，试计算各杆的应力。
A 解：设AC杆杆长为 l，则AB、AD杆长为
F
lABlAD
2l 3
列出平衡方程：
y
Fx 0 F N 1 c3 o 0 0 sF N 2 F N 3 c3 o 00 s
30kN/m
B
A
C
1m
2m
E
FNB D32.2kN
FNCE38.4kN
BD
FNBD ADB
31 22.20M 6 m 010m32N 1 Pa
D
30kN/m
FBD B
A
C
B FBD
1m
CE
FNCE ACE
39 8.4M 6 103 NPa
40m 0 m2
2m
E LCE
例题6
B 1
C2 30 30 3