山东省枣庄市2008届高三第一次调研考试(数学理)
2008届新课标高三第一次调查测试数学试卷理20079

2008届新课标高三第一次调查测试数学试卷(理)2007.9一、选择题(每题5分,共40分)1、设全集U=R ,A={x|x<-3或x ≥2}、B={x|-1<x<5}则集合{x|-1<x<2}是 ( )A 、(CuA)∪(CuB ) B 、Cu (A ∪B )C 、(CuA )∩BD 、A ∩B 2、函数)13lg(13)(22++-=x xx x f 的定义域是 ( )A 、);31,(--∞B 、);31,31(-C 、);1,31(-D 、).,31(+∞-3、下列函数中,在其定义域内既是奇函数又是减函数的是( )A 、);()21(R x y x∈= B 、);0(1≠=x xy C 、y=x (x ∈R ); D 、).(3R x x y ∈-= 4、在同一平面直角坐标系中,函数x x f +=12)(与x x g -=12)(的图象关于( )A 、原点对称;B 、y 轴对称;C 、x 轴对称;D 、直线x=-1对称。
5、已知集合},2|),{(},123|),{(+===--=kx y y x N x y y x M 则k=1是M ∩N=φ的( )A 、 充分不必要条件;B 、必要不充分条件;C 、充要条件;D 、既不充分也不必要条件。
6、函数)1)(1(log >-=a a y x a 的图象只能位于 ( )A 、第一象限;B 、第二象限;C 、第三象限;D 、第四象限。
7、已知函数),30(42)(2<<++=a ax ax x f 若21x x <且ax x -=+121;则( )A 、)()(21x f x f <;B 、)()(21x f x f =;C 、)()(21x f x f >;D 、)(1x f 与)(2x f 的大小不能确定。
8、方程lnx=6-2x 的根所在大致区间是 ( )A 、(1,2);B 、(2,3);C 、(3,4);D 、(5,6). 二、填空题(每题5分,共40分)9、已知f(x)=|log 2x|,则=+)23()43(f f ; 10、已知命题"1,:"xx R x p >∈∃+,命题p 的否定为命题q ,则q 是“ ”;q 的真假为 (填真,假)。
2008年高考理科数学试题及参考答案(山东卷)

绪论马克思主义是关于无产阶级和人类解放的科学一、单项选择题1、马克思主义理论从狭义上说是(C)A、无产阶级争取自身解放和整个人类解放的学说体系B、关于无产阶级斗争的性质、目的和解放条件的学说C、马克思和恩格斯创立的基本理论、基本观点和基本方法构成的科学体系D、关于资本主义转化为社会主义以及社会主义和共产主义发展的普遍规律的学说2、马克思主义理论从广义上说是(A)A、不仅指马克思恩格斯创立的基本理论、基本观点和学说的体系,也包括继承者对它的发展。
B、无产阶级争取自身解放和整个人类解放的学说体系C、关于无产阶级斗争的性质、目的和解放条件的学说D、马克思和恩格斯创立的基本理论、基本观点和基本方法构成的科学体系3、作为中国共产党和社会主义事业指导思想的马克思主义是指(A)A、不仅指马克思恩格斯创立的基本理论、基本观点和学说的体系,也包括继承者对它的发展。
B、无产阶级争取自身解放和整个人类解放的学说体系C、关于无产阶级斗争的性质、目的和解放条件的学说D、列宁创立的基本理论、基本观点和基本方法构成的科学体系4、在19世纪三大工人运动中,集中反映工人政治要求的是(B)A、法国里昂工人起义B、英国宪章运动C、芝加哥工人起义D、德国西里西亚纺织工人起义5、马克思主义产生的经济根源是(C)A、工业革命B、资本主义经济危机C、资本主义社会生产力和生产关系的矛盾运动D、阶级斗争6、马克思主义产生的阶级基础和实践基础是(B)A、资本主义的剥削和压迫B、无产阶级作为一支独立的政治力量登上了历史舞台C、工人罢工和起义D、工人运动得到了“农民的合唱”7、马克思和恩格斯进一步发展和完善了英国古典经济学理论是(C)A、辩证法B、历史观C、劳动价值论D、剩余价值论8、马克思把黑格尔的辩证法称为(A)A、合理内核B、基本内核C、精髓D、核心9、在第一次世界大战中成为东西方矛盾焦点和帝国主义政治体系最薄弱环节的国家是(D)A、德国B、奥地利C、中国D、俄国10、“哲学把无产阶级当作自己的物质武器,同样,无产阶级把哲学当作自己的精神武器”,这个论断的含义是(A)A、马克思主义是无产阶级的世界观和方法论B、哲学的存在方式是物质C、无产阶级的存在方式是精神D、无产阶级掌握哲学就由自为阶级转变为自在阶级11、马克思主义生命力的根源在于(A)A、以实践为基础的科学性与革命性的统一B、与时俱进C、科学性与阶级性的统一D、科学性12、无产阶级的科学世界观和方法论是(C)A、辩证唯物主义B、历史唯物主义C、辩证唯物主义和历史唯物主义D、唯物主义13、马克思主义最重要的理论品质是(D)A、吐故纳新B、科学严谨C、博大精深D、与时俱进14、马克思主义最崇高的社会理想(A)A、实现共产主义B、消灭阶级、消灭国家C、实现个人的绝对自由D、实现人权15、学习马克思主义基本原理的根本方法(C)A、认真学习马克思主义的著作B、一切从实际出发C、理论联系实际D、实事求是第一章世界的物质性及其发展规律一、单选题1.列宁对辩证唯物主义物质范畴的定义是通过( A )。
2008高考山东数学理科试卷含详细解答及试题分析

2008年普通高等学校招生全国统一考试(山东卷)理科数学第Ⅰ卷(共60分)参考公式:球的表面积公式:24πS R =,其中R 是球的半径.如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好发生k 次的概率:()(1)(012)k k n k n n P k C p p k n -=-= ,,,,.如果事件A B ,互斥,那么()()()P A B P A P B +=+. 如果事件A B ,相互独立,那么()()()P AB P A P B = .一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.满足{}1234M a a a a ⊆,,,,且{}{}12312M a a a a a = ,,,的集合M 的个数是( ) A .1B .2C .3D .4解析:本小题主要考查集合子集的概念及交集运算。
集合M 中必含有12,a a ,则{}12,M a a =或{}124,,M a a a =.选B.2.设z 的共轭复数是z ,若4z z +=,8z z = ,则z z等于( )A .iB .i -C .1±D .i ±解析:本小题主要考查共轭复数的概念、复数的运算。
可设2z bi =+,由8z z ⋅=得248, 2.b b +==±()2222.88i z zi z±===±选D.3.函数ππln cos 22y x x ⎛⎫=-<<⎪⎝⎭的图象是( )xx A . B . C . D .解析:本小题主要考查复合函数的图像识别。
ln cos ()22y x x ππ=-<<是偶函数,可排除B 、D ,由cos 1ln cos 0x x ≤⇒≤排除C,选A.4.设函数()1f x x x a =++-的图象关于直线1x =对称,则a 的值为( ) A .3B .2C .1D .1-解:1x +、x a -在数轴上表示点x 到点1-、a 的距离,他们的和()1f x x x a =++-关于1x =对称,因此点1-、a 关于1x =对称,所以3a =(直接去绝对值化成分段函数求解比较麻烦,如取特殊值解也可以) 5.已知πcos sin 6αα⎛⎫-+= ⎪⎝⎭7πsin 6α⎛⎫+ ⎪⎝⎭的值是( )A.5-B.5C .45- D .45解::3cos()sin sin 622παααα-+=+=14cos 225αα+=,714sin()sin()cos .66225ππαααα⎛⎫+=-+=-+=- ⎪ ⎪⎝⎭6.右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .9πB .10πC .11πD .12π解:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面及为 22411221312.S ππππ=⨯+⨯⨯+⨯⨯=7.在某地的奥运火炬传递活动中,有编号为12318 ,,,,的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成以3为公差的等差数列的概率为( )A .151B .168C .1306D .1408解:古典概型问题,基本事件总数为31817163C =⨯⨯。
2008年数学(理科)试卷(山东卷)(word版 详细解析)

中学学科网2008年普通高等学校招生全国统一考试(山东卷)理科数学全解全析解析作者:孙宜新第I 卷一、选择题:本大题共12小题,每小题5分,共60分。
(1)满足M ⊆{}1234,,,a a a a 且{}{}12312,,,M a a a a a ⋂=的集合M 的个数是().1A ().2B ().3C ().4D2.设z 的共轭复数是z ,若4z z +=,8z z ⋅=,则zz等于 ().A i ().B i - ().1C ± ().D i ±【标准答案】:D 。
【试题分析】 可设2z bi =+,由8z z ⋅=得248, 2.b b +==±()2222.88i z z i z ±===± 【高考考点】: 共轭复数的概念、复数的运算。
【易错提醒】: 可能在以下两个方面出错:一是不能依据共轭复数条件设2z bi =+简化运算;二是由248b +=只求得 2.b =【学科网备考提示】: 理解复数基本概念并进行复数代数形式的四则运算是复数内容的基本要求,另外待定系数法、分母实数化等解题技巧也要引起足够重视。
3函数ln cos ()22y x x ππ=-<<的图象是5.已知4cos()sin 365παα-+=,则7sin()6πα+的值是 23().5A -23().5B 4().5C - 4().5D 【标准答案】:C 。
【试题分析】:334cos()sin cos sin 36225παααα-+=+=,134cos sin 225αα+=, 7314sin()sin()sin cos .66225ππαααα⎛⎫+=-+=-+=- ⎪ ⎪⎝⎭【高考考点】: 三角函数变换与求值。
【易错提醒】: 不能由334cos()sin cos sin 36225παααα-+=+=得到134cos sin 225αα+=是思考受阻的重要体现。
2008级(高三)第一次诊断性测试理科数学试题

山东省实验中学2008级第一次诊断性测试数学试题(理科)(2010.10)说明:本试卷分第I 卷(选择题)和第II 卷(非选择题)共两卷。
其中第一卷共60分,第II 卷共90分,两卷合计150分。
答题时间为120分钟.第Ⅰ卷(选择题 共60分)一.选择题:(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,)1.sin600°的值是A.12B. -12C. 32D. -322.设集合{}22,A x x x R =-≤∈,{}2|,12B y y x x ==--≤≤,则()R C A B 等于 A.R B. {},0x x R x ∈≠ C. {}0 D .∅3. ()2tan cot cos x x x += A.tan x B.sin x C.cos x D.cot x4.下列四个条件中,p 是q 的必要不充分.....条件的是 A.:p a b >,22:q a b > B.:p a b >,:22a b q >C.22:p ax by c +=为双曲线,:0q ab <D.2:0p ax bx c ++>,2:0c b q a x x ++> 5.在同一坐标系内,函数aax y a x y a 1)0(-=≠=和的图象可能是6.若曲线4y x =的一条切线l 与直线480x y +-=垂直,则l 的方程为A .430x y --= B. 450x y +-=C .430x y -+= D. 430x y ++=7.若,5sin 2cos -=+a a 则a tan = A.21 B.2 C.21- D.2- 8.设奇函数()f x 在(0,+∞)上为增函数,且(1)0f =,则不等式()()0f x f x x--<的解集是 A .(1,0)(1,)-+∞ B .(,1)(0,1)-∞-C .(,1)(1,)-∞-+∞D .(1,0)(0,1)- 9. 0203sin 702cos 10--=A . 12 C.2 10.函数20()(4)[1,5]xf x t t dt =--⎰在上的最大和最小值情况是A .有最大值0,但无最小值 B. 有最大值0和最小值-323 C .有最小值-323,但无最大值 D .既无最大值又无最小值 11. 设|13|)(-=x x f ,a b c <<且)()()(b f a f c f >>,则下列关系中一定成立的是A .b c 33> B.a b 33> C .233>+a cD .233<+a c 12.函数)1,0( )(log )(3≠>-=a a ax x x f a 在区间)0,21(-内单调递增,则a 的取值范围是 A .)1,41[ B. )1,43[ C. ),49(+∞ D. )49,1(第Ⅱ卷(非选择题 共90分)注意事项:1.用钢笔或圆珠笔直接答在试题卷上,考试结束后将答题卡和第Ⅱ卷一并交上。
2008年山东省高考数学试卷(理科)

2008年山东省高考数学试卷(理科)一、选择题(共12小题,每小题5分,满分60分)1.(5分)(2008•山东)满足1{M a ⊆,2a ,3a ,4}a ,且1{M a ⋂,2a ,31}{a a =,2}a 的集合M 的个数是( ) A .1B .2C .3D .42.(5分)(2008•山东)设z 的共轭复数是z ,若4z z +=,8z z =,则zz等于( ) A .iB .i -C .1±D .i ±3.(5分)(2008•山东)函数cos ()22y ln x x ππ=-<<的图象是( )A .B .C .D .4.(5分)(2008•山东)设函数()|1|||f x x x a =++-的图象关于直线1x =对称,则a 的值为( ) A .3B .2C .1D .1-5.(5分)(2008•山东)已知4cos()sin 365παα-+=,则7sin()6πα+的值是( )A .235-B .235 C .45-D .456.(5分)(2008•山东)如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .9πB .10πC .11πD .12π7.(5分)(2008•山东)在某地的奥运火炬传递活动中,有编号为1,2,3,⋯,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成以3为公差的等差数列的概率为( ) A .151B .168C .1306D .14088.(5分)(2008•山东)如图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为()A .304.6B .303.6C .302.6D .301.69.(5分)(2008•山东)123(x x展开式中的常数项为( )A .1320-B .1320C .220-D .22010.(5分)(2008•山东)4.设椭圆1C 的离心率为513,焦点在x 轴上且长轴长为26,若曲线2C 上的点到椭圆1C 的两个焦点的距离的差的绝对值等于8,则曲线2C 的标准方程为()A .2222143x y -=B .22221135x y -=C .2222134x y -=D .222211312x y -=11.(5分)(2008•山东)已知圆的方程为22680x y x y +--=,设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为( ) A .106B .206C .306D .40612.(5分)(2008•山东)设二元一次不等式组2190802140x y x y x y +-⎧⎪-+⎨⎪+-⎩所表示的平面区域为M ,使函数(0,1)x y a a a =>≠的图象过区域M 的a 的取值范围是( )A .[1,3]B .[2,10]C .[2,9]D .[10,9]二、填空题(共4小题,每小题4分,满分16分)13.(4分)(2008•山东)执行如图所示的程序框图,若0.8p =,则输出的n = .14.(4分)(2008•山东)设函数2()(0)f x ax c a =+≠,若100()()f x dx f x =⎰,001x ,则0x 的值为 .15.(4分)(2008•山东)已知a ,b ,c 为ABC ∆的三个内角A ,B ,C 的对边,向量(3m =,1)-,(cos ,sin )n A A =.若m n ⊥,且cos cos sin a B b A c C +=,则角B = .16.(4分)(2008•山东)若不等式|3|4x b -<的解集中的整数有且仅有1,2,3,则b 的取值范围 .三、解答题(共6小题,满分74分) 17.(12分)(2008•山东)已知函数()3i n ()c o s ()(0,0)f x x x ωϕωϕϕπω=+-+<<>为偶函数,且函数()y f x =图象的两相邻对称轴间的距离为2π. (Ⅰ)求()8f π的值;(Ⅱ)将函数()y f x =的图象向右平移6π个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数()y g x =的图象,求()g x 的单调递减区间. 18.(12分)(2008•山东)甲、乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者对本队赢得一分,答错得零分.假设甲队中每人答对的概率均为23,乙队中3人答对的概率分别为221,,332,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.(Ⅰ)求随机变量ξ的分布列和数学期望;(Ⅱ)用A 表示“甲、乙两个队总得分之和等于3”这一事件,用B 表示“甲队总得分大于乙队总得分”这一事件,求()P AB .19.(12分)(2008•山东)将数列{}n a 中的所有项按每一行比上一行多一项的规则排成如下数表:12345678910a a a a a a a a a a ⋯记表中的第一列数1a ,2a ,4a ,7a ,⋯构成的数列为{}n b ,111b a ==.n S 为数列{}n b 的前n 项和,且满足221(2)nn n nb n b S S =-. (Ⅰ)证明数列1n S ⎧⎫⎨⎬⎩⎭成等差数列,并求数列{}n b 的通项公式;(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当81491a =-时,求上表中第(3)k k 行所有项的和.20.(12分)(2008•山东)如图,已知四棱锥P ABCD -,底面ABCD 为菱形,PA ⊥平面ABCD ,60ABC ∠=︒,E ,F 分别是BC ,PC 的中点.(Ⅰ)证明:AE PD ⊥;(Ⅱ)若H 为PD 上的动点,EH 与平面PAD 所成最大角的正切值为62,求二面角E AF C --的余弦值.21.(12分)(2008•山东)已知函数1()(1)(1)nf x aln x x =+--,其中*n N ∈,a 为常数.(Ⅰ)当2n =时,求函数()f x 的极值;(Ⅱ)当1a =时,证明:对任意的正整数n ,当2x 时,有()1f x x -.22.(14分)(2008•山东)如图,设抛物线方程为22(0)x py p =>,M 为直线2y p =-上任意一点,过M 引抛物线的切线,切点分别为A ,B . (Ⅰ)求证:A ,M ,B 三点的横坐标成等差数列;(Ⅱ)已知当M 点的坐标为(2,2)p -时,||410AB =.求此时抛物线的方程;(Ⅲ)是否存在点M ,使得点C 关于直线AB 的对称点D 在抛物线22(0)x py p =>上,其中,点C 满足(OC OA OB O =+为坐标原点).若存在,求出所有适合题意的点M 的坐标;若不存在,请说明理由.2008年山东省高考数学试卷(理科)参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.(5分)满足1{M a ⊆,2a ,3a ,4}a ,且1{M a ⋂,2a ,31}{a a =,2}a 的集合M 的个数是( ) A .1B .2C .3D .4【考点】16:子集与真子集;1E :交集及其运算 【专题】11:计算题【分析】首先根据1{M a ⋂,2a ,31}{a a =,2}a 可知1a ,2a 是M 中的元素,3a 不是M 中的元素,由子集的定义即可得出答案. 【解答】解:1{M a ⋂,2a ,31}{a a =,2}a 1a ∴,2a 是M 中的元素,3a 不是M 中的元素 1{M a ⊆,2a ,3a ,4}a1{M a ∴=,2}a 或1{M a =,2a ,4}a ,故选:B .【点评】此题考查了交集的运算,属于基础题.2.(5分)设z 的共轭复数是z ,若4z z +=,8z z =,则zz等于( ) A .iB .i -C .1±D .i ±【考点】4A :复数的代数表示法及其几何意义【分析】可设,z a bi z a bi =+=-则,根据222,z z a z z a b +==+即得.【解答】解:本小题主要考查共轭复数的概念、复数的运算.可设2z bi =+,由8z z =得248b +=,22(22)2.88z z i b i z ±=±===±.选D【点评】本题中注意到复数与共轭复数的联系,利用这点解题,可更加简洁. 3.(5分)函数cos ()22y ln x x ππ=-<<的图象是( )A .B .C .D .【考点】3A :函数的图象与图象的变换 【专题】31:数形结合 【分析】利用函数cos ()22y ln x x ππ=-<<的奇偶性可排除一些选项,利用函数的有界性可排除一些个选项.从而得以解决. 【解答】解:cos()cos x x -=,∴cos ()22y ln x x ππ=-<<是偶函数,可排除B 、D ,由cos 1cos 0x ln x ⇒排除C , 故选:A .【点评】本小题主要考查复合函数的图象识别.属于基础题.4.(5分)设函数()|1|||f x x x a =++-的图象关于直线1x =对称,则a 的值为( ) A .3B .2C .1D .1-【考点】3A :函数的图象与图象的变换【分析】函数()||||f x x a x b =-+-的图象为轴对称图形,其对称轴是直线2a bx +=,可利用这个性质快速解决问题【解答】解:|1|x +、||x a -在数轴上表示点x 到点1-、a 的距离, 他们的和()|1|||f x x x a =++-关于1x =对称, 因此点1-、a 关于1x =对称, 所以3a = 故选:A .【点评】中学常见的绝对值函数一般都具有对称性:函数()||f x x a =-的图象为轴对称图形,其对称轴是直线x a =, 函数()||||f x x a x b =-+-的图象为轴对称图形,其对称轴是直线2a bx +=, 函数()||||f x x a x b =---的图象为中心对称图形,其对称中心是点(2a b+,0). 5.(5分)已知4cos()sin 365παα-+=,则7sin()6πα+的值是( )A .235-B .235 C .45-D .45【考点】GG :同角三角函数间的基本关系;GP :两角和与差的三角函数【分析】从表现形式上看不出条件和结论之间的关系,在这种情况下只有把式子左边分解再合并,约分整理,得到和要求结论只差π的角的三角函数,通过用诱导公式,得出结论. 【解答】解:334cos()sin cos sin 36225παααα-+=+=,∴134cos sin 225αα+=, ∴7314sin()sin()(sin cos )66225ππαααα+=-+=-+=-. 故选:C .【点评】已知一个角的某个三角函数式的值,求这个角的或和这个角有关的角的三角函数式的值,一般需用三个基本关系式及其变式,通过恒等变形或解方程求解.而本题应用了角之间的关系和诱导公式.6.(5分)如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )A .9πB .10πC .11πD .12π【考点】!L :由三视图求面积、体积 【专题】11:计算题【分析】由题意可知,几何体是由一个球和一个圆柱组合而成的,依次求表面积即可. 【解答】解:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面为22411221312S ππππ=⨯+⨯⨯+⨯⨯=故选:D .【点评】本题考查学生的空间想象能力,是基础题.7.(5分)在某地的奥运火炬传递活动中,有编号为1,2,3,⋯,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成以3为公差的等差数列的概率为( ) A .151B .168C .1306D .1408【考点】6C :等可能事件和等可能事件的概率 【专题】11:计算题【分析】由题意知本题是古典概型问题,试验发生的基本事件总数为318C ,选出火炬手编号为13(1)n a a n =+-,分类讨论当11a =时可得4种选法;12a =时得4种选法;13a =时得4种选法.【解答】解:由题意知本题是古典概型问题,试验发生的基本事件总数为31817163C =⨯⨯. 选出火炬手编号为13(1)n a a n =+-,11a =时,由1,4,7,10,13,16可得4种选法; 12a =时,由2,5,8,11,14,17可得4种选法; 13a =时,由3,6,9,12,15,18可得4种选法.∴44411716368P ++==⨯⨯. 故选:B .【点评】本题主要考查古典概型和等差数列数列,理解古典概型的特征:试验结果的有限性和每一个试验结果出现的等可能性,体现了化归的重要思想,掌握列举法,学会运用数形结合、分类讨论的思想解决概率的计算问题.8.(5分)如图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字.从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为( )A .304.6B .303.6C .302.6D .301.6【考点】BA :茎叶图 【分析】平均数=总数样本容量,总数的计算可分成个位数字的和,百位数字与十位数字的和两部分分别计算. 【解答】解:290430023104115826247303.610⨯+⨯+⨯+++++++++=故选:B .【点评】本题考查由茎叶图计算平均值问题,属基本题. 9.(5分)123(x x展开式中的常数项为( )A .1320-B .1320C .220-D .220【考点】DA :二项式定理 【专题】11:计算题【分析】利用二项展开式的通项公式求出第1r +项,令x 的指数为0求出常数项. 【解答】解:41212123311212123((1)(1)r r r r r rr r rr r T C x C xxC xx----+==-=-,令41203r-=得9r = ∴993101212121110(1)220321T C C ⨯⨯=-=-=-=-⨯⨯常数项.故选:C .【点评】本题考查二项展开式的通项公式是解决二项展开式的特定项问题的工具. 10.(5分)4.设椭圆1C 的离心率为513,焦点在x 轴上且长轴长为26,若曲线2C 上的点到椭圆1C 的两个焦点的距离的差的绝对值等于8,则曲线2C 的标准方程为( )A .2222143x y -=B .22221135x y -=C .2222134x y -=D .222211312x y -=【考点】4K :椭圆的性质;KB :双曲线的标准方程【专题】11:计算题【分析】在椭圆1C 中,由题设条件能够得到135a c =⎧⎨=⎩,曲线2C 是以1(5,0)F -,2(5,0)F ,为焦点,实轴长为8的双曲线,由此可求出曲线2C 的标准方程. 【解答】解:在椭圆1C 中,由226513a c a =⎧⎪⎨=⎪⎩,得135a c =⎧⎨=⎩椭圆1C 的焦点为1(5,0)F -,2(5,0)F ,曲线2C 是以1F 、2F 为焦点,实轴长为8的双曲线,故2C 的标准方程为:2222143x y -=,故选:A .【点评】本题考查圆锥曲线的性质和应用,解题时要注意公式的灵活运用,注意区分椭圆和双曲线的性质.11.(5分)已知圆的方程为22680x y x y +--=,设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为( ) A.B.C.D.【考点】8J :直线与圆相交的性质 【专题】16:压轴题【分析】根据题意可知,过(3,5)的最长弦为直径,最短弦为过(3,5)且垂直于该直径的弦,分别求出两个量,然后利用对角线垂直的四边形的面积等于对角线乘积的一半求出即可. 【解答】解:圆的标准方程为222(3)(4)5x y -+-=, 由题意得最长的弦||2510AC =⨯=,根据勾股定理得最短的弦||BD =AC BD ⊥, 四边形ABCD的面积11||||1022S AC BD ==⨯⨯. 故选:B .【点评】考查学生灵活运用垂径定理解决数学问题的能力,掌握对角线垂直的四边形的面积计算方法为对角线乘积的一半.12.(5分)设二元一次不等式组2190802140x y x y x y +-⎧⎪-+⎨⎪+-⎩所表示的平面区域为M ,使函数(0,1)x y a a a =>≠的图象过区域M 的a 的取值范围是( ) A .[1,3]B .[2,10]C .[2,9]D .[10,9]【考点】49:指数函数的图象与性质;7B :二元一次不等式(组)与平面区域 【专题】11:计算题;16:压轴题【分析】先依据不等式组2190802140x y x y x y +-⎧⎪-+⎨⎪+-⎩,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用函数(0,1)x y a a a =>≠的图象特征,结合区域的角上的点即可解决问题.【解答】解析:平面区域M 如如图所示. 求得(2,10)A ,(3,8)C ,(1,9)B .由图可知,欲满足条件必有1a >且图象在过B 、C 两点的图象之间. 当图象过B 点时,19a =, 9a ∴=.当图象过C 点时,38a =, 2a ∴=.故a 的取值范围为[2,9]. 故选:C .【点评】本题主要考查了用平面区域二元一次不等式组、指数函数的图象与性质,以及简单的转化思想和数形结合的思想,属中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础,纵观目标函数包括线性的与非线性,非线性问题的介入是线性规划问题的拓展与延伸,使得规划问题得以深化.二、填空题(共4小题,每小题4分,满分16分)13.(4分)执行如图所示的程序框图,若0.8p =,则输出的n = 4 .【考点】EF :程序框图【分析】根据流程图所示的顺序,逐框分析程序中各变量、各语句的作用可知:该程序的作用是判断1110.8242n S =++⋯+>时,1n +的值. 【解答】解:根据流程图所示的顺序, 该程序的作用是判断1110.8242n S =++⋯+>时,1n +的值. 当2n =时,110.824+< 当3n =时,1110.8248++>, 此时14n +=. 故答案为:4【点评】根据流程图(或伪代码)写程序的运行结果,是算法这一模块最重要的题型,其处理方法是::①分析流程图(或伪代码),从流程图(或伪代码)中既要分析出计算的类型,又要分析出参与计算的数据(如果参与运算的数据比较多,也可使用表格对数据进行分析管理)⇒②建立数学模型,根据第一步分析的结果,选择恰当的数学模型③解模.14.(4分)设函数2()(0)f x ax c a =+≠,若100()()f x dx f x =⎰,001x ,则0x 的值为 3. 【考点】69:定积分的应用【分析】求出定积分1()f x dx ⎰,根据方程12()ax c f x dx +=⎰即可求解.【解答】解:2()(0)f x ax c a =+≠,31100()()[]33ax af x f x dx cx c ∴==+=+⎰.又200()f x ax c =+.2013x ∴=,0[0x ∈,01]x ∴. 【点评】本题考查了积分和导数的公式,属于基本知识基本运算.同时考查了恒等式系数相等的思想.15.(4分)已知a ,b ,c 为ABC ∆的三个内角A ,B ,C 的对边,向量(3m =,1)-,(cos ,sin )n A A =.若m n ⊥,且cos cos sin a B b A c C +=,则角B =6π. 【考点】9T :数量积判断两个平面向量的垂直关系;GX :三角函数的积化和差公式 【专题】1:常规题型;16:压轴题【分析】由向量数量积的意义,有3cos sin 0m n A A ⊥⇒-=,进而可得A ,再根据正弦定理,可得sin cos sin cos sin A B B A C += sin C ,结合和差公式的正弦形式,化简可得2sin sin C C =,可得C ,由A 、C 的大小,可得答案.【解答】解:根据题意,3cos sin 03m n A A A π⊥⇒-=⇒=,由正弦定理可得,sin cos sin cos sin sin A B B A C C +=, 又由sin cos sin cos sin()sin A B B A A B C +=+=, 化简可得,2sin sin C C =, 则2C π=, 则6B π=,故答案为6π. 【点评】本题考查向量数量积的应用,判断向量的垂直,解题时,注意向量的正确表示方法. 16.(4分)若不等式|3|4x b -<的解集中的整数有且仅有1,2,3,则b 的取值范围 57b << . 【考点】5R :绝对值不等式的解法 【专题】11:计算题;16:压轴题【分析】首先分析题目已知不等式|3|4x b -<的解集中的整数有且仅有1,2,3,求b 的取值范围,考虑到先根据绝对值不等式的解法解出|3|4x b -<含有参数b 的解,使得解中只有整数1,2,3,即限定左边大于0小于1,右边大于3小于4.即可得到答案.【解答】解:因为44|3|443433b b x b x b x -+-<⇒-<-<⇒<<, 又由已知解集中的整数有且仅有1,2,3, 故有40147357458343b b b b b -⎧<⎪<⎧⎪⇒⇒<<⎨⎨+<⎩⎪<⎪⎩. 故答案为57b <<.【点评】此题主要考查绝对值不等式的解法问题,题目涵盖知识点少,计算量小,属于基础题型.对于此类基础考点在高考中属于得分内容,同学们一定要掌握. 三、解答题(共6小题,满分74分)17.(12分)已知函数())cos()(0,0)f x x x ωϕωϕϕπω=+-+<<>为偶函数,且函数()y f x =图象的两相邻对称轴间的距离为2π. (Ⅰ)求()8f π的值;(Ⅱ)将函数()y f x =的图象向右平移6π个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数()y g x =的图象,求()g x 的单调递减区间. 【考点】GL :三角函数中的恒等变换应用;GP :两角和与差的三角函数;HJ :函数sin()y A x ωϕ=+的图象变换【专题】11:计算题【分析】(Ⅰ)先用两角和公式对函数()f x 的表达式化简得()2sin()6f x x πωϕ=+-,利用偶函数的性质即()()f x f x =-求得ω,进而求出()f x的表达式,把8x π=代入即可.(Ⅱ)根据三角函数图象的变化可得函数()g x 的解析式,再根据余弦函数的单调性求得函数()g x 的单调区间. 【解答】解:(Ⅰ)1())cos())cos()]2sin()26f x x x x x x πωϕωϕωϕωϕωϕ=+-+=+-+=+-. ()f x 为偶函数,∴对x R ∈,()()f x f x -=恒成立, ∴sin()sin()66x x ππωϕωϕ-+-=+-.即sin cos()cos sin()sin cos()cos sin()6666x x x x ππππωϕωϕωϕωϕ--+-=-+-,整理得sin cos()06x πωϕ-=. 0ω>,且x R ∈,所以cos()06πϕ-=.又0ϕπ<<,故62ππϕ-=.∴()2sin()2cos 2f x x x πωω=+=.由题意得222ππω=,所以2ω=.故()2cos2f x x =.∴()2cos84f ππ=(Ⅱ)将()f x 的图象向右平移6π个单位后,得到()6f x π-的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到()46x f π-的图象.∴()()2cos[2()]2cos()464623x x x g x f πππ=-=-=-.当22()23x k k k Z ππππ-+∈,即2844()33k x k k Z ππππ++∈时,()g x 单调递减,因此()g x 的单调递减区间为28[4,4]()33k k k Z ππππ++∈.【点评】本题主要考查了三角函数的恒等变换和三角函数图象的应用.属基础题. 18.(12分)甲、乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者对本队赢得一分,答错得零分.假设甲队中每人答对的概率均为23,乙队中3人答对的概率分别为221,,332,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.(Ⅰ)求随机变量ξ的分布列和数学期望;(Ⅱ)用A 表示“甲、乙两个队总得分之和等于3”这一事件,用B 表示“甲队总得分大于乙队总得分”这一事件,求()P AB .【考点】5C :互斥事件的概率加法公式;CG :离散型随机变量及其分布列;CH :离散型随机变量的期望与方差 【专题】11:计算题【分析】(1)由题意甲队中每人答对的概率均为23,故可看作独立重复试验,故2~(3,)3B ξ,2323E ξ=⨯= (2)AB 为“甲、乙两个队总得分之和等于3”和“甲队总得分大于乙队总得分”同时满足,有两种情况:“甲得(2分)乙得(1分)”和“甲得(3分)乙得0分”这两个事件互斥,分别求概率,再取和即可.【解答】解:(Ⅰ)解法一:由题意知,ξ的可能取值为0,1,2,3,且03321(0)(1)327P C ξ==⨯-=,123222(1)(1)339P C ξ==⨯⨯-=,223224(2)()(1)339P C ξ==⨯⨯-=,33328(3)()327P C ξ==⨯=. 所以ξ的分布列为ξ的数学期望为124801232279927E ξ=⨯+⨯+⨯+⨯=. 解法二:根据题设可知,2~(3,)3B ξ,因此ξ的分布列为3333222()()(1)333k kk k kP k C C ξ-==⨯⨯-=⨯,0k =,1,2,3.因为2~(3,)3B ξ,所以2323E ξ=⨯=.(Ⅱ)解法一:用C 表示“甲得(2分)乙得(1分)”这一事件,用D 表示“甲得(3分)乙得分”这一事件,所以AB CD =,且C ,D 互斥,又22342221112111110()()(1)[]333323323323P C C =⨯⨯-⨯⨯⨯+⨯⨯+⨯⨯=,333521114()()()33323P D C =⨯⨯⨯⨯=,由互斥事件的概率公式得4551043434()()()333243P AB P C P D =+=+==. 解法二:用k A 表示“甲队得k 分”这一事件,用k B 表示“乙队得k 分”这一事件,0k =,1,2,3.由于事件30A B ,21A B 为互斥事件,故有30213021()()()()P AB P A B A B P A B P A B ==+.由题设可知,事件3A 与0B 独立,事件2A 与1B 独立,因此23213021302132222221121111234()()()()()()()()()()332332323243P AB P A B P A B P A P B P A P B C C =+=+=⨯⨯+⨯⨯⨯+⨯⨯=.【点评】本题考查独立重复试验、二项分布、期望、及互斥事件、独立事件的概率问题,同时考查利用概率知识分析问题解决问题的能力.在求解过程中,注意()P AB P =(A )P (B )只有在A 和B 独立时才成立.19.(12分)将数列{}n a 中的所有项按每一行比上一行多一项的规则排成如下数表:12345678910a a a a a a a a a a ⋯记表中的第一列数1a ,2a ,4a ,7a ,⋯构成的数列为{}n b ,111b a ==.n S 为数列{}n b 的前n 项和,且满足221(2)nn n nb n b S S =-. (Ⅰ)证明数列1n S ⎧⎫⎨⎬⎩⎭成等差数列,并求数列{}n b 的通项公式;(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当81491a =-时,求上表中第(3)k k 行所有项的和.【考点】8B :数列的应用;1F :归纳推理 【专题】29:规律型【分析】(Ⅰ)由题意所给的已知等式特点应考虑应用已知数列的前n 项和求其通项这一公式来寻求出路,得到Sn 与1n SS -之间的递推关系,先求出n S 的通项公式即可得证,接下来求{}n b 的通项公式;(Ⅱ)由题意第一列数1a ,2a ,4a ,7a ,⋯构成的数列为{}n b ,111b a ==,又已知{}n b 的通项公式和81a 的值,应该现有规律判断这一向位于图示中的具体位置,有从第三行起,第一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数进而求解. 【解答】解:(Ⅰ)证明:由已知,当2n 时,221nn n nb b S S =-,又12n n S b b b =++⋯+, 所以1121112()2()11111()2n n n n n n n n n n n n S S S S S S S S S S S S -------=⇒=⇒-=---,又1111S b a ===.所以数列1n S ⎧⎫⎨⎬⎩⎭是首项为1,公差为12的等差数列.由上可知1111(1)22n n n S +=+-=,21n S n ⇒=+. 所以当2n 时,12221(1)n n n b S S n n n n -=-=-=-++. 因此1,12,2(1)n n b n n n =⎧⎪=⎨-⎪+⎩(Ⅱ)设上表中从第三行起,每行的公比都为q ,且0q >. 因为12131212782⨯++⋯+==, 所以表中第1行至第12行共含有数列{}n a 的前78项,故81a 在表中第13行第三列, 因此28113491a b q ==-.又1321314b =-⨯,所以2q =. 记表中第(3)k k 行所有项的和为S ,则(1)2(12)2(12)(3)1(1)12(1)k k k k b q S k q k k k k --==-=--+-+. 【点评】(1)此问重点考查了数列中的已知前n 项的和求解通项这一公式,还考查了等差数的定义;(2)此问重点考查了由题意及图形准确找规律,还考查了等比数列的通向公式及有数列通向求其所有项和,同时还考查了方程的思想.20.(12分)如图,已知四棱锥P ABCD -,底面ABCD 为菱形,PA ⊥平面ABCD ,60ABC ∠=︒,E ,F 分别是BC ,PC 的中点.(Ⅰ)证明:AE PD ⊥;(Ⅱ)若H 为PD 上的动点,EH 与平面PAD 所成最大角的正切值为62,求二面角E AF C --的余弦值.【考点】LO :空间中直线与直线之间的位置关系;LQ :平面与平面之间的位置关系 【专题】11:计算题;14:证明题【分析】(1)要证明AE PD ⊥,我们可能证明AE ⊥面PAD ,由已知易得AE PA ⊥,我们只要能证明AE AD ⊥即可,由于底面ABCD 为菱形,故我们可以转化为证明AE BC ⊥,由已知易我们不难得到结论.(2)由EH 与平面PAD ,我们分析后可得PA 的值,由(1)的结论,我们进而可以证明平面PAC ⊥平面ABCD ,则过E 作EO AC ⊥于O ,则EO ⊥平面PAC ,过O 作OS AF ⊥于S ,连接ES ,则ESO ∠为二面角E AF C --的平面角,然后我们解三角形ASO ,即可求出二面角E AF C --的余弦值.【解答】证明:(Ⅰ)证明:由四边形ABCD 为菱形,60ABC ∠=︒,可得ABC ∆为正三角形. 因为E 为BC 的中点,所以AE BC ⊥. 又//BC AD ,因此AE AD ⊥.因为PA ⊥平面ABCD ,AE ⊂平面ABCD ,所以PA AE ⊥. 而PA ⊂平面PAD ,AD ⊂平面PAD 且PA AD A =,所以AE ⊥平面PAD .又PD ⊂平面PAD , 所以AE PD ⊥.解:(Ⅱ)设2AB =,H 为PD 上任意一点,连接AH ,EH . 由(Ⅰ)知AE ⊥平面PAD ,则EHA ∠为EH 与平面PAD 所成的角.在Rt EAH ∆中,AE 所以当AH 最短时,EHA ∠最大, 即当AH PD ⊥时,EHA ∠最大.此时tan AE EHA AH ∠===,因此AH =2AD =,所以45ADH ∠=︒, 所以2PA =.因为PA ⊥平面ABCD ,PA ⊂平面PAC , 所以平面PAC ⊥平面ABCD .过E 作EO AC ⊥于O ,则EO ⊥平面PAC ,过O 作OS AF ⊥于S ,连接ES ,则ESO ∠为二面角E AF C --的平面角, 在Rt AOE ∆中,3sin 302EO AE =︒=,3cos302AO AE =︒=, 又F 是PC 的中点,在Rt ASO ∆中,32sin 454SO AO =︒=, 又223930484SE EO SO =+=+=, 在Rt ESO ∆中,32154cos 5304SO ESO SE ∠===, 即所求二面角的余弦值为155.【点评】求二面角的大小,一般先作出二面角的平面角.此题是利用二面角的平面角的定义作出ESO ∠为二面角E AF C --的平面角,通过解AOC ∠所在的三角形求得ESO ∠.其解题过程为:作ESO ∠→证ESO ∠是二面角的平面角→计算ESO ∠,简记为“作、证、算”.21.(12分)已知函数1()(1)(1)nf x aln x x =+--,其中*n N ∈,a 为常数. (Ⅰ)当2n =时,求函数()f x 的极值;(Ⅱ)当1a =时,证明:对任意的正整数n ,当2x 时,有()1f x x -. 【考点】3R :函数恒成立问题;6D :利用导数研究函数的极值 【专题】11:计算题;14:证明题;16:压轴题 【分析】(1)欲求:“当2n =时,21()(1)(1)f x aln x x =+--”的极值,利用导数,求其导函数的零点及单调性进行判断即可; (2)欲证:“()1f x x -”,令1()1(1)(1)ng x x ln x x =-----,利用导函数的单调性,只要证明函数()f x 的最大值是1x -即可.【解答】解:(Ⅰ)解:由已知得函数()f x 的定义域为{|1}x x >,当2n =时,21()(1)(1)f x aln x x =+--,所以232(1)()(1)a x f x x --'=-.(1)当0a >时,由()0f x '=得111x =+>,211x =, 此时123()()()(1)a x x x x f x x ---'=-.当1(1,)x x ∈时,()0f x '<,()f x 单调递减; 当1(x x ∈,)+∞时,()0f x '>,()f x 单调递增. (2)当0a 时,()0f x '<恒成立,所以()f x 无极值. 综上所述,2n =时,当0a >时,()f x 在1x =2(1(1)2a f ln a=+. 当0a 时,()f x 无极值.(Ⅱ)证法一:因为1a =,所以1()(1)(1)nf x ln x x =+--.当n 为偶数时, 令1()1(1)(1)ng x x ln x x =-----,则1112()10(2)(1)11(1)n n n x n g x x x x x x ++-'=+-=+>----.所以当[2x ∈,)+∞时,()g x 单调递增, 又g (2)0=, 因此1()1(1)(2)0(1)ng x x ln x g x =----=-恒成立,所以()1f x x -成立.当n 为奇数时,要证()1f x x -,由于10(1)nx <-,所以只需证(1)1ln x x --,令()1(1)h x x ln x =---, 则12()10(2)11x h x x x x -'=-=--, 所以当[2x ∈,)+∞时,()1(1)h x x ln x =---单调递增,又h (2)10=>, 所以当2x 时,恒有()0h x >,即(1)1ln x x -<-命题成立. 综上所述,结论成立. 证法二:当1a =时,1()(1)(1)nf x ln x x =+--.当2x 时,对任意的正整数n ,恒有11(1)nx -,故只需证明1(1)1ln x x +--.令()1(1(1))2(1)h x x ln x x ln x =--+-=---,[2x ∈,)+∞, 则12()111x h x x x -'=-=--, 当2x 时,()0h x ',故()h x 在[2,)+∞上单调递增, 因此当2x 时,()h x h (2)0=,即1(1)1ln x x +--成立. 故当2x 时,有1(1)1(1)nln x x x +---.即()1f x x -.【点评】本题主要考查函数的导数、不等式等知识,以及不等式的证明,同时考查逻辑推理能力.22.(14分)如图,设抛物线方程为22(0)x py p =>,M 为直线2y p =-上任意一点,过M 引抛物线的切线,切点分别为A ,B .(Ⅰ)求证:A ,M ,B 三点的横坐标成等差数列;(Ⅱ)已知当M 点的坐标为(2,2)p -时,||410AB =.求此时抛物线的方程;(Ⅲ)是否存在点M ,使得点C 关于直线AB 的对称点D 在抛物线22(0)x py p =>上,其中,点C 满足(OC OA OB O =+为坐标原点).若存在,求出所有适合题意的点M 的坐标;若不存在,请说明理由.【考点】8K :抛物线的性质;KH :直线与圆锥曲线的综合 【专题】15:综合题;16:压轴题;2A :探究型【分析】(Ⅰ)根据题意先设出A ,B 和M 的坐标,对抛物线方程求导,进而表示出AM ,BM 的斜率,则直线AM 和BM 的直线方程可得,联立后整理求得0122x x x =+.推断出A ,M ,B 三点的横坐标成等差数列.(Ⅱ)利用(Ⅰ)的结论,02x =代入抛物线方程整理推断出1x ,2x 是方程22440x x p --=的两根,利用韦达定理求得12x x +的值,表示出直线AB 的方程,利用弦长公式求得||AB ,进而求得p ,则抛物线的方程可得.(Ⅲ)设出D 点的坐标,进而表示出C 的坐标,则CD 的中点的坐标可得,代入直线AB 的方程,把D 点坐标代入抛物线的方程,求得3x ,然后讨论00x =和00x ≠时,两种情况,分析出答案.【解答】解:(Ⅰ)证明:由题意设221212120(,),(,),,(,2)22x x A x B x x x M x p p p<-.由22x py =得22x y p =,得x y p'=,所以1MA x k p =,2MB x k p=. 因此直线MA 的方程为102()x y p x x p+=-, 直线MB 的方程为202()x y p x x p+=-. 所以211102()2x x p x x p p +=-,①222202()2x x p x x p p+=-.② 由①、②得121202x x x x x +=+-, 因此1202x x x +=,即0122x x x =+. 所以A ,M ,B 三点的横坐标成等差数列. (Ⅱ)解:由(Ⅰ)知,当02x =时,将其代入①、②并整理得:2211440x x p --=,2222440x x p --=, 所以1x ,2x 是方程22440x x p --=的两根, 因此124x x +=,2124x x p =-,又222101221222ABx x x x x p p k x x p p-+===-, 所以2AB k p=.由弦长公式得||AB ==又||AB =, 所以1p =或2p =,因此所求抛物线方程为22x y =或24x y =.(Ⅲ)解:设3(D x ,3)y ,由题意得12(C x x +,12)y y +, 则CD 的中点坐标为123123(,)22x x x y y y Q ++++, 设直线AB 的方程为011()xy y x x p-=-,由点Q 在直线AB 上,并注意到点1212(,)22x x y y ++也在直线AB 上, 代入得033x y x p=. 若3(D x ,3)y 在抛物线上,则2330322x py x x ==, 因此30x =或302x x =.即(0,0)D 或202(2,)x D x p. (1)当00x =时,则12020x x x +==,此时,点(0,2)M p -适合题意.(2)当00x ≠,对于(0,0)D ,此时22120(2,)2x x C x p+,2212221200224CD x x x x pk x px ++==,又0AB x k p=,AB CD ⊥, 所以22220121220144AB CDx x x x x k k p px p ++===-, 即222124x x p +=-,矛盾. 对于2002(2,)x D x p ,因为22120(2,)2x x C x p+,此时直线CD 平行于y 轴, 又00AB x k p=≠, 所以直线AB 与直线CD 不垂直,与题设矛盾, 所以00x ≠时,不存在符合题意的M 点.综上所述,仅存在一点(0,2)适合题意.M p【点评】本题主要考查了直线与圆锥曲线的关系的综合问题.考查了学生分析推理和分类讨论思想的运用.考点卡片1.子集与真子集【知识点的认识】1、子集定义:一般地,对于两个集合A,B,如果集合A中任意一个元素都是集合B中的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集(subset).记作:A⊆B(或B⊇A).2、真子集是对于子集来说的.真子集定义:如果集合A⊆B,但存在元素x∈B,且元素x不属于集合A,我们称集合A是集合B的真子集.也就是说如果集合A的所有元素同时都是集合B的元素,则称A是B的子集,若B中有一个元素,而A中没有,且A是B的子集,则称A是B的真子集,注:①空集是所有集合的子集;②所有集合都是其本身的子集;③空集是任何非空集合的真子集例如:所有亚洲国家的集合是地球上所有国家的集合的真子集.所有的自然数的集合是所有整数的集合的真子集.{1,3}⊂{1,2,3,4}{1,2,3,4}⊆{1,2,3,4}3、真子集和子集的区别子集就是一个集合中的全部元素是另一个集合中的元素,有可能与另一个集合相等;真子集就是一个集合中的元素全部是另一个集合中的元素,但不存在相等;注意集合的元素是要用大括号括起来的“{}”,如{1,2},{a,b,g};另外,{1,2}的子集有:空集,{1},{2},{1,2}.真子集有:空集,{1},{2}.一般来说,真子集是在所有子集中去掉它本身,所以对于含有n个(n不等于0)元素的集合而言,它的子集就有2n个;真子集就有2n﹣1.但空集属特殊情况,它只有一个子集,没有真子集.【解题方法点拨】。
2008年普通高等学校招生全国统一考试理科数学试题及答案-山东卷

2008年普通高等学校招生全国统一考试(山东卷)理科数学第Ⅰ卷(共60分)参考公式:球的表面积公式:S =4πR 2,其中R 是球的半径.如果事件A 在一次试验中发生的概率是p ,那么n 次独立重复试验中事件A 恰好发生k 次的概率:P n (k )=C kn p k (1-p )n-k (k =0,1,2,…,n ).如果事件A 、B 互斥,那么P (A +B )=P (A )+P (B ). 如果事件A 、B 相互独立,那么P (AB )=P (A )·P (B ).一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)满足M ⊆{a 1, a 2, a 3, a 4},且M ∩{a 1 ,a 2, a 3}={ a 1,a 2}的集合M 的个数是(A )1 (B)2 (C)3 (D)4 (2)设z 的共轭复数是z ,若z +z =4, z ·z =8,则zz等于 (A )i (B )-i (C)±1 (D) ±i (3)函数y =lncos x (-2π<x <2π=的图象是 ( A )(4)设函数f (x )=|x +1|+|x -a |的图象关于直线x =1对称,则a 的值为(A) 3 (B)2 (C)1 (D)-1(5)已知cos (α-6π)+sin α7sin()6πα+则的值是 (A )-532 (B )532 (C)-54 (D) 54(6)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是(A)9π (B )10π (C)11π (D) 12π(7)在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手。
若从中任选3人,则选出的火炬手的编号能组成以3为公差的等差数列的概率为(A )511 (B )681 (C )3061 (D )4081(8)右图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎 叶图,图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表 示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数 的平均数为(A )304.6 (B )303.6 (C)302.6 (D)301.6 (9)(X -31x)12展开式中的常数项为(A )-1320 (B )1320 (C )-220 (D)220 (10)设椭圆C 1的离心率为135,焦点在X 轴上且长轴长为26.若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为(A )1342222=-y x (B)15132222=-y x(C)1432222=-y x (D)112132222=-y x(11)已知圆的方程为X 2+Y 2-6X -8Y =0.设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为(A )106 (B )206 (C )306 (D )406(12)设二元一次不等式组⎪⎩⎪⎨⎧≤-+≥+-≥-+0142,080192y x y x y x ,所表示的平面区域为M ,使函数y =a x (a >0,a ≠1)的图象过区域M 的a 的取值范围是(A )[1,3] (B)[2,10] (C)[2,9] (D)[10,9]第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分.(13)执行右边的程序框图,若p =0.8,则输出的n = 4 . (14)设函数f (x )=ax 2+c (a ≠0),若)()(01x f dx x f =⎰,0≤x 0≤1,则x 0的值为33. (15)已知a ,b ,c 为△ABC 的三个内角A ,B ,C 的对边,向量m =(1,3-),n =(cos A , sin A )。
2008年高考理科数学试题及参考答案(山东卷)

2
(A)
1,3
(B) 2, 10
(C) 2,9
(D) 10,9
第二 卷(共 90 分) 二、境空题:本大题共 4 小题,每小题 4 分,共 16 分 ( 13 )执行右边的程序框图,若 P=0. 8 ,则输出的 n= 4 ( 14 ) 设函数 f ( x ) ax 2 c ( a 0) ,若
(2)设 Z 的共轭复数是 z ,若 z z 4, z z 8 ,则 A. i B. -i C.
z ( z
)
1
D.
i
)
y
(3)函数 y ln cos x (
x ) 的图像是( 2 2
y
y
y
x
x
x
x
A.
B.
C.
D. )
(4)设函数 f ( x ) x 1 x a 的图像关于直线 x=1 对称,则 a 的值为( A. 3 B. 2 C. 1 D. -1
俯视图
2
3
3
2 正(主)视图
2 侧(左)视图
(7)在某地的奥运火炬传递活动中,有编号为 1 , 2 , 3…18 的 18 名火炬手,若从中任选 3 人,则选出的火炬手的编号能组成以 3 为公差的等差数列的概率为( ) (A)
1 5
(B)
1 68
(C)
1 308
(D)
1 408
2 3 3 9 0 1 1 2 0 1 6 2 4 7 5 8
有互斥事件的概率得 P ( AB ) P (C ) P ( D )
34 243
解法二:用 A 表示“甲队得 k 分” 这一事件、用 B 表示“乙队得 k 分”这一事件,k=0, k k 1,2,3,由于事件 A3 B0 与 A2 B1 为互斥事件故有
2008年山东高考数学理科试题及答案1
2008年山东高考数学理科 第Ⅰ卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)满足M ⊆{a 1, a 2, a 3, a 4},且M ∩{a 1 ,a 2, a 3}={ a 1·a 2}的集合M 的个数是 (A )1 (B)2 (C)3 (D)4 (2)设z 的共轭复数是z ,或z +z =4,z ·z =8,则zz 等于(A )1 (B )-i (C)±1 (D) ±i (3)函数y =lncos x (-2π<x <)2π的图象是(4)设函数f (x )=|x +1|+|x -a |的图象关于直线x =1对称,则a 的值为 (A) 3 (B)2 (C)1 (D)-1 (5)已知cos (α-6π)+sin α=473,sin()56πα+的值是 (A )-532 (B )532 (C)-54 (D) 54(6)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是(A)9π (B )10π (C)11π (D)12π(7)在某地的奥运火炬传递活动中,有编号为1,2,3,…,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成3为公差的等差数列的概率为(A )511 (B )681(C )3061 (D )4081(8)右图是根据《山东统计年整2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图.图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为 (A )304.6(B )303.6 (C)302.6 (D)301.6(9)(X -31x)12展开式中的常数项为(A )-1320(B )1320(C )-220 (D)220(10)设椭圆C 1的离心率为135,焦点在X 轴上且长轴长为26.若曲线C 2上的点到椭圆C 1的两个焦点的距离的差的绝对值等于8,则曲线C 2的标准方程为(A )1342222=-y x (B)15132222=-y x (C)1432222=-y x (D)112132222=-y x (11)已知圆的方程为X 2+Y 2-6X -8Y =0.设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为(A )106(B )206(C )306(D )406(12)设二元一次不等式组⎪⎩⎪⎨⎧≤-+≥+-≥-+0142,080192y x y x y x ,所表示的平面区域为M ,使函数y =a x(a >0,a ≠1)的图象过区域M 的a 的取值范围是 (A )[1,3] (B)[2,10] (C)[2,9] (D)[10,9]第Ⅱ卷(共90分)二、填空题:本大题共4小题,每小题4分,共16分.(13)执行右边的程序框图,若p =0.8,则输出的n = 4 . (14)设函数f (x )=ax 2+c (a ≠0).若)()(010x f dx x f =⎰,0≤x 0≤1,则x 0的值为33. (15)已知a ,b ,c 为△ABC 的三个内角A ,B ,C 的对边,向量m =(1,3-),n =(cos A ,sin A ).若m ⊥n ,且a cos B +b cos A =c sin C ,则角B =6π. (16)若不等式|3x -b |<4的解集中的整数有且仅有1,2,3,则b 的取值范围为(5,7).三、解答题:本大题共6小题,共74分.(17)(本小题满分12分) 已知函数f (x )=)0,0)(cos()sin(3><<+-+ωϕϕωϕωπx x 为偶函数,且函数y =f (x )图象的两相邻对称轴间的距离为.2π(Ⅰ)求f (8π)的值; (Ⅱ)将函数y =f (x )的图象向右平移6π个单位后,再将得到的图象上各点的横坐标舒畅长到原来的4倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )的单调递减区间. 解:(Ⅰ)f (x )=)cos()sin(3ϕωϕω+-+x x=⎥⎦⎤⎢⎣⎡+-+)cos(21)sin(232ϕωϕωx x=2sin(ϕω+x -6π) 因为 f (x )为偶函数,所以 对x ∈R ,f (-x )=f (x )恒成立,因此 sin (-ϕω+x -6π)=sin(ϕω+x -6π). 即-sin x ωcos(ϕ-6π)+cos x ωsin(ϕ-6π)=sin x ωcos(ϕ-6π)+cos x ωsin(ϕ-6π),整理得 sin x ωcos(ϕ-6π)=0.因为 ω>0,且x ∈R ,所以 cos (ϕ-6π)=0.又因为 0<ϕ<π,故 ϕ-6π=2π.所以 f (x )=2sin(x ω+2π)=2cos x ω.由题意得.2,222 = 所以 ωπωπ⋅=故 f (x )=2cos2x . 因为 .24cos 2)8(==ππf(Ⅱ)将f (x )的图象向右平移个6π个单位后,得到)6(π-x f 的图象,再将所得图象横坐标伸长到原来的4倍,纵坐标不变,得到)64(ππ-f 的图象.).32(cos 2)64(2cos 2)64()(ππππππ-=⎥⎦⎤⎢⎣⎡-=-=f f x g 所以 当 2k π≤32ππ-≤2 k π+ π (k ∈Z),即 4k π+≤32π≤x ≤4k π+38π (k ∈Z)时,g (x )单调递减.因此g (x )的单调递减区间为 ⎥⎦⎤⎢⎣⎡++384,324ππππk k (k ∈Z)(18)(本小题满分12分)甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分, 答错得零分。
山东省枣庄市2007—2008学年度高三模拟考试数学理测试

山东省枣庄市2007—2008学年度高三模拟考试数学试题(理工类)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分. 共150分,测试时间120分钟.第Ⅰ卷(选择题 共60分)注意事项: 1.答第1卷前,考生务必将自己的姓名、准考证号、考试科目写在答题卡上.2.每小题选出答案后,用HB 或者2B 铅笔把答题卡上的对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.不能答在试题卷上.一、选择题:本大题共12个小题. 每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若ii m -+1是纯虚数,则实数m 的值为( )A .-1B .0C .1D .22.若以连续掷两次骰子分别得到的点数m ,n 作为点P 的横、纵坐标,则点P 在直线x +y=5下方的概率为 ( )A .61 B .41 C .121 D .913.若⎰⎰⎰===22232,si n ,,则xdx c dx x b dx x a a 、b 、c 大小关系是 ( ) A .a <c <b B .a <b <cC .c <b <aD .c <a <b4.如图所示给出的是计算201614121++++ 的值的一个程序框图,其中判断框内填入的条件是 ( ) A .10>i B .10<iC .20>iD .20<i5.如右图,一个空间几何体的主视图和侧视图(左视图)都是边长为1的正三角形,俯视图是一个圆,那么该几何体的侧面积( )A .4πB .π42C .π22 D .π216.已知函数]3,3[sin ππω-=在x y 上是减函数,则实数的ω的取值范围是 ( )A .]23,(--∞B .)0,23[-C .]23,0(D .),23[+∞7.一船向正北匀速行驶,看见正西方两座相距10海里的灯塔恰好与该船在同一直线上,继续航行半小时后,看见其中一座灯塔在南偏西60°方向上,另一灯塔在南偏西75°方向上,则该船的速度应该是( )A .10海里/小时B .103海里/小时C .5海里/小时D .53海里/小时 8.函数|2|||ln --=x e y x 的图象大致是( )9.已知直线x +y=a 与圆x 2+y 2=4交于A 、B 两点,且||||OB OA OB OA -=+,其中O 为坐标原点,则实数a 的值为 ( )A .2B .±2C .-2D .2±10.已知L 、M 、N 是平面α内的三点,点P 在平面α外,有三个命题 ①若PL ⊥α,LN ⊥MN ,则PN ⊥MN ②若PL ⊥α,PN ⊥MN ,则LN ⊥MN ③若LN ⊥MN ,PN ⊥MN ,则PL ⊥α 对这三个命题的正确评价是( )A .仅①是真命题B .仅②是假命题C .仅③是假命题D .全是真命题11.已知F 1、F 2是两个定点,点P 是以F 1和F 2为公共焦点的椭圆和双曲线的一个交点,并且PF 1⊥PF 2,e 1和e 2分别是上述椭圆和双曲线的离心率,则有 ( )A .4112221=+eeB .2112221=+eeC .42221=+e eD .22221=+e e12.设函数)(x f 在定义域为D ,如果对任意的D x ∈1,存在唯一的D x ∈2,使Cx f x f =+2)()(21(C 为常数)成立,则称函数)(x f 在D 上的均值为C . 给出下列四个函数:①y=x 3;②y=4sin x ;③y=lg x ;④y=2x,则满足在其定义域上的均值为2的所有函数是( ) A .①②B .③④C .②④D .①③第II 卷(非选择题 共90分)二、填空题:本大题共4个小题,每小题4分,共16分, 13.观察下列式子: ,474131211,3531211,2321122222<+++<++<+,则可以猜想:当2≥n 时,有 .14.若二项式6)sin (x x-θ展开式中的常数项为20,则θ的值为 .15.在两个实数间定义一种运算“#”,规定⎩⎨⎧≥-<=)(1)(1#b a b a b a ,则方程12|#21|=-x的解集是 .16.给出下列四个结论:①函数)10(log)10(≠>=≠>=a a a y a a a y xax且与函数且在其各自定义域上具备相同单调性;②函数k k y k (3⋅=为非零常数)的图象可由函数y=3x的图象经过平移得到;③函数)0)(21131()0(12121≠+-=≠-+=x x y x y xx是奇函数且函数是偶函数;④函数y=cos|x |是周期函数. 其中正确结论的序号是 .(填写你认为正确的所有结论序号)三、解答题:本大题共6个小题,共74分. 解答应写出文字说明,证明过程或演算步骤. 请 17.(12分)已知△ABC 的面积S 满足.,6,333θ的夹角为与且BC AB BC AB S =⋅≤≤(I )求θ的取值范围;(2)求函数θθθθθ22cos 3cos sin 2sin )(+⋅+=f 的最大值.18.(12分)如图,在四棱锥P —ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E 、F 分别是AB ,PB 的中点.(I )求证:EF ⊥CD ;(II )求DB 与平面DEF 所成角的正弦值;(III )在平面PAD 内是否存在一点G ,使G 在平面PCB 上的射影为△PCB 的外心,若存在,试确定点G 的位置;若不存在,说明理由.19.(12分)某班从6名干部中(其中男生4人,女生2人),选3人参加学校的义务劳动. (I )设所选3人中女生人数为ξ,求ξ的分布列及E ξ; (II )求男生甲或女生乙被选中的概率;(III )在男生甲被选中的情况下,求女生乙也被选中的概率.20.(12分)已知在曲线点项和为的前数列))(1,(,}{,14)(*12N n a a P S n a xx f n n n n n ∈+=+.0,1,)(1>==n a a x f y 且上(I )求数列{n a }的通项公式n a ;(II )数列{n b }的首项b 1=1,前n 项和为T n ,且381622121--+=++n n a T a T n n nn ,求数列{n b }的通项公式b n .21.(12分) 设M 是由满足下列两个条件的函数)(x f 构成的集合:①议程0)(=-x x f 有实根;②函数)(x f 的导数)(x f '满足0<)(x f '<1.(I )若4sin 2)(x x x f +=,判断方程0)(=-x x f 的根的个数;(II )判断(I )中的函数)(x f 是否为集合M 的元素;(III )对于M 中的任意函数)(x f ,设x 1是方程0)(=-x x f 的实根,求证:对于)(x f 定义域中任意的x 2,x 3,当| x 2-x 1|<1,且| x 3-x 1|<1时,有.2|)()(|23<-x f x f22.(14分)过点T (2,0)的直线2:+=my x l 交抛物线y 2=4x 于A 、B 两点.(I )若直线l 交y 轴于点M ,且,,21BT MB AT MA λλ==当m 变化时,求21λλ+的值; (II )设A 、B 在直线n x g =:上的射影为D 、E ,连结AE 、BD 相交于一点N ,则当m 变化时,点N 为定点的充要条件是n =-2.参考答案一、选择题:本大题共12小题,每小题5分,共60分. 1—5CADAD 6—10BACBC 11—12BD二、填空题:本大题共4个小题,每小题4分,共16分.13.nn n12131211222-<++++14.)(22Z k k ∈-ππ 15.),41(+∞ 16.③④三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分) 解:(I )由题意知.6cos ||||==⋅θBC AB BC AB ……………………1分θθθθtan cos ||||21sin ||||21)sin(||||21BC AB BC AB x BC AB S ==-=.tan 3tan 621ϑθ=⨯=………………………………………………………6分.3tan 1.33tan 33,333≤≤∴≤≤≤≤θθ即S].3,4[],,0[ππθπθ∈∴∈ 又………………………………………………8分(II )θθθθθθθ222cos 22sin 1cos 3cos sin 2sin )(++=++=f ).42sin(222cos 2sin 2πθθθ++=++=…………………………10分].1211,43[42],3,4[πππθππθ∈+∈)(,4,4342θπθππθf 时即当==+∴最大,其最大值为3.………………12分18.(本小题满分12分) 解:以DA ,DC ,DP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系(如图). 设AD =a ,则D (0,0,0),A (a ,0,0),B (a ,a ,0),C (0,a ,0),E (a ,2a ,0),P (0,0,a ),F (2a ,2a ,2a ).………………2分(I ),0)0,,0()2,0,2(=⋅-=⋅a a a DC EF.DC EF ⊥∴…………………………………………4分(II )设平面DEF 的法向量为⎪⎩⎪⎨⎧=⋅=⋅=00),,,(DE n DF n z y x n 由得⎪⎪⎩⎪⎪⎨⎧=+=++⎪⎪⎩⎪⎪⎨⎧=⋅=⋅.02,0)(2,0)0,2,(),,(,0)2,2,2(),,(y a ax z y x aa a z y x a a a z y x 即 取x =1,则y=-2,z=1.).1,2,1(-=∴n ………………………………………………6分.6362,cos =⋅=>=<∴a a n BD设DB 与平面DEF 所成角为.63sin ,=θθ则……………………………………8分(III )假设存在点G 满足题意因为).,0,(,z x G PAD G 点坐标为可设平面∈ .0,0)2(2),,0()2,2,2(.2,0)2()0,0,()2,2,2()2,2,2(10.)2,2,2(,,.,0),,0()0,0,(2==-+=-⋅---=⋅==-=⋅---=⋅---=∆∴∆⊥∴=-⋅=⋅z a x a aa a a z a a x CP FG a x a x a a a z a a x CB FG a x a a x FG PBC Rt aa a F PB F PBC Rt PC BC a a a CP CB 得由得由分的外心为中点为中在∴存在点G ,其坐标为(2a ,0,0),即G 点为AD 的中点.……………………12分19.(本小题满分12分) 解:(I )ξ的所有可能取值为0,1,2,依题意得:;51)2(;53)1(;51)0(3622143612243634=========CC C P Cc C P CC P ξξξ…………3分∴ξ的分布列为∴E ξ=0×51+1×53+2×51=1.…………………………………………4分(II )设“甲、乙都不被选中”的事件为C ,则.51204)(3634===C C C P ……6分∴所求概率为.54511)(1)(=-=-=C P C P …………………………………8分(III )记“男生甲被选中”为事件A ,“女生乙被选中”为事件B ,.51)(;212010)(36143625==⋂===C C A B P C C A P ………………………………10分)52104)|(.(52)()()|(2514=====CC A B P A P BA P A B P 或直接得……………12分20.(本小题满分12分)解:(I )由题意知.141.14122121nn nn aaaa +=∴+=++}1{,4112221nnn aa a即=-∴+是等差数列.…………………………………………2分.34441)1(411212-=-+=-+=∴n n n a a n.341,0.3412-=∴>-=∴n a a n a n n n 又………………………………5分(II )由题设知).34)(14()14()34(1-+++=-+n n T n T n n n.1,34.1341411=-=-=--+∴++n n n n n n c c c n T n T n T 则上式变为设}{n c ∴是等差数列.…………………………………………………………8分.1111111n n b n T n c c n =-+=-+=-+=∴.34)34(.342n n n n T n n T n n -=-==-∴即………………………………10分∴当n =1时,11==T b n ;当.78)1(3)1(434,2221-=-+---=-=≥-n n n n n T T b n n n n 时经验证n=1时也适合上式. ).(78*N n n b n ∈-=∴…………………………12分21.(本小题满分12分) 解:(I )令.24sin )(,)()(x x x F x x f x F -=-=即则.0)(,1cos 1.214cos )(≤'∴≤≤--='x F x x x Fx x f x F -=∴)()(是单调递减函数.……………………………………2分又取).)((02)(,,02)(,为奇函数或说明取x F F x F x <-==>=--=ππππππ0)(=-∴x x f 方程在其定义域上有唯一实根.……………………………4分(II )由(I )知方程0)(=-x x f 有实根(或者由0)(=-x x f ,易知x =0就是方程的一个根),)(x f 满足条件①.………………………………………………5分 .43)(41,1cos 1,4cos 21)(≤'≤≤≤-+='x f x x x f 得由又)(x f ∴满足条件②.故)(x f 是集合M 中的元素.……………………………7分(III )不妨设)(,1)(0,32x f x f x x 知由<'<<在其定义域上是增函数. ).()(32x f x f <∴………………………………………………………………8分x x f x f -∴<-')(,01)(又是其定义域上的减函数.23233322)()(0,)()(x x x f x f x x f x x f -<-<->-∴即.………………10分 |)()(||||)()(|12132323x x x x x x x f x f ---=-<-∴.211||||1213<+<---≤x x x x …………………………………………12分22.(本小题满分14分)解:(I )设),(),,(2211y x B y x A由.0844222=--⎩⎨⎧=+=my y xy my x 得.8,42121-==+∴y y m y y ………………………………………………2分又),,2()2,(,),2,0(111111y x my x AT MA nM --=+=-λλ即.21,211111my y my --=-=+∴λλ得同理,由.21,222my BT MB --==λλ得………………………………4分.1882)(22)11(2221212121-=+-=+--=+--=+∴mm y my y y y y mλλ…………6分(II )方法一:当m =0时,A (2,22),B (2,-2),D (n ,22),E (n ,-22). ∵ABED 为矩形,∴直线AE 、BD 的交点N 的坐标为().0,22+n ………………8分当),,22(),,22(),,(),,(,021121y n NE y x n AN y n E y n D m -=--+=≠ 时(*))2(28)2(2)(2222)222(22)22(2112121121n m mn m y my y y n y n y my n y n y x n +=+-=-+-=-+--+=-+-+则同理,对BN 、ND 进行类似计算也得(*)式.………………………………12分 即n =-2时,N 为定点(0,0).反之,当N 为定点,则由(*)式等于0,得n =-2.…………………………14分方法二:首先n =-2时,则D (-2,y 1),A (),,2(),,2(),,222211y my B y E y my +-+)2(4:2121++-=-x myy y y y l DB ①)2(4:1212++-=-x my y y y y l EA ②…………………………………………8分11①-②得,).4141)()(2(12121212y y my my y y x y y ≠+++-+=-.04884241411222121212=+-=++=-+++=∴my m m myy my y y m my my x.)0,0(为定点N ∴…………………………………………………………10分反之,若N 为定点N (0,0),设此时),,(),,(21y n E y n D 则).,2(),,(221y my NB y n ND +==由D 、N 、B 三点共线,.022121=-+∴ny y y my ③同理E 、N 、A 三点共线,.021221=-+∴ny y y my ④………………12分 ③+④得,0)()(22212121=+-++y y n y y y my 即-16m +8m -4m =0,m (n +2)=0.故对任意的m 都有n =-2.……………………………………………………14分。
2007-2008学年枣庄高三模拟考试理

2007-2008学年度山东省枣庄市高三模拟考试数学试题(理工类)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分. 共150分,测试时间120分钟.第Ⅰ卷(选择题 共60分)注意事项: 1.答第1卷前,考生务必将自己的姓名、准考证号、考试科目写在答题卡上.2.每小题选出答案后,用HB 或者2B 铅笔把答题卡上的对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.不能答在试题卷上.一、选择题:本大题共12个小题. 每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若iim -+1是纯虚数,则实数m 的值为 ( )A .-1B .0C .1D .22.若以连续掷两次骰子分别得到的点数m ,n 作为点P 的横、纵坐标,则点P 在直线x +y=5下方的概率为 ( )A .61B .41 C .121 D .91 3.若⎰⎰⎰===220232,sin ,,则xdx c dx x b dx x a a 、b 、c 大小关系是 ( )A .a <c <bB .a <b <cC .c <b <aD .c <a <b4.如图所示给出的是计算201614121++++ 的值的一个程序框图,其中判断框内填入的条件是 ( )A .10>iB .10<iC .20>iD .20<i5.如下图,一个空间几何体的主视图和侧视图(左视图)都是边长为1的正三角形,俯视图是一个圆,那么该几何体的侧面积( )A .4πB .π42 C .π22 D .π216.已知函数]3,3[sin ππω-=在x y 上是减函数,则实数的ω的取值范围是 ( )A .]23,(--∞B .)0,23[-C .]23,0(D .),23[+∞7.一船向正北匀速行驶,看见正西方两座相距10海里的灯塔恰好与该船在同一直线上,继续航行半小时后,看见其中一座灯塔在南偏西60°方向上,另一灯塔在南偏西75°方向上,则该船的速度应该是 ( )A .10海里/小时B .103海里/小时C .5海里/小时D .53海里/小时 8.函数|2|||ln --=x e y x 的图象大致是( )9.已知直线x +y=a 与圆x 2+y 2=4交于A 、B 两点,且||||-=+,其中O 为坐标原点,则实数a 的值为 ( )A .2B .±2C .-2D .2±10.已知L 、M 、N 是平面α内的三点,点P 在平面α外,有三个命题 ①若PL ⊥α,LN ⊥MN ,则PN ⊥MN ②若PL ⊥α,PN ⊥MN ,则LN ⊥MN ③若LN ⊥MN ,PN ⊥MN ,则PL ⊥α对这三个命题的正确评价是( )A .仅①是真命题B .仅②是假命题C .仅③是假命题D .全是真命题11.已知F 1、F 2是两个定点,点P 是以F 1和F 2为公共焦点的椭圆和双曲线的一个交点,并且PF 1⊥PF 2,e 1和e 2分别是上述椭圆和双曲线的离心率,则有 ( )A .4112221=+e e B .2112221=+e e C .42221=+e eD .22221=+e e12.设函数)(x f 在定义域为D ,如果对任意的D x ∈1,存在唯一的D x ∈2,使C x f x f =+2)()(21(C 为常数)成立,则称函数)(x f 在D 上的均值为C . 给出下列四个函数:①y=x 3;②y=4sin x ;③y=lg x ;④y=2x ,则满足在其定义域上的均值为2的所有函数是 ( )A .①②B .③④C .②④D .①③第II 卷(非选择题 共90分)二、填空题:本大题共4个小题,每小题4分,共16分, 13.观察下列式子: ,474131211,3531211,2321122222<+++<++<+,则可以猜想:当2≥n 时,有 . 14.若二项式6)sin (x x-θ展开式中的常数项为20,则θ的值为 . 15.在两个实数间定义一种运算“#”,规定⎩⎨⎧≥-<=)(1)(1#b a b a b a ,则方程12|#21|=-x 的解集是 . 16.给出下列四个结论:①函数)10(log )10(≠>=≠>=a a a y a a a y xa x 且与函数且在其各自定义域上具备相同单调性; ②函数k k y k(3⋅=为非零常数)的图象可由函数y=3x 的图象经过平移得到; ③函数)0)(21131()0(12121≠+-=≠-+=x x y x y x x 是奇函数且函数是偶函数; ④函数y=cos|x |是周期函数.其中正确结论的序号是 .(填写你认为正确的所有结论序号)三、解答题:本大题共6个小题,共74分. 解答应写出文字说明,证明过程或演算步骤. 请 17.(12分)已知△ABC 的面积S 满足.,6,333θ的夹角为与且S =⋅≤≤(I )求θ的取值范围;(2)求函数θθθθθ22cos 3cos sin 2sin )(+⋅+=f 的最大值. 18.(12分)如图,在四棱锥P —ABCD 中,PD ⊥底面ABCD ,底面ABCD 为正方形,PD =DC ,E 、F 分别是AB ,PB 的中点.(I )求证:EF ⊥CD ;(II )求DB 与平面DEF 所成角的正弦值;(III )在平面P AD 内是否存在一点G ,使G 在平面PCB 上的射影为△PCB 的外心,若存在,试确定点G 的位置;若不存在,说明理由.19.(12分)某班从6名干部中(其中男生4人,女生2人),选3人参加学校的义务劳动.(I )设所选3人中女生人数为ξ,求ξ的分布列及E ξ; (II )求男生甲或女生乙被选中的概率;(III )在男生甲被选中的情况下,求女生乙也被选中的概率. 20.(12分)已知在曲线点项和为的前数列))(1,(,}{,14)(*12N n a a P S n a xx f n n n n n ∈+=+.0,1,)(1>==n a a x f y 且上(I )求数列{n a }的通项公式n a ;(II )数列{n b }的首项b 1=1,前n 项和为T n ,且381622121--+=++n n a T a T n n n n ,求数列{n b }的通项公式b n .21.(12分) 设M 是由满足下列两个条件的函数)(x f 构成的集合:①议程0)(=-x x f 有实根;②函数)(x f 的导数)(x f '满足0<)(x f '<1.(I )若4sin 2)(xx x f +=,判断方程0)(=-x x f 的根的个数; (II )判断(I )中的函数)(x f 是否为集合M 的元素;(III )对于M 中的任意函数)(x f ,设x 1是方程0)(=-x x f 的实根,求证:对于)(x f 定义域中任意的x 2,x 3,当| x 2-x 1|<1,且| x 3-x 1|<1时,有.2|)()(|23<-x f x f22.(14分)过点T (2,0)的直线2:+=my x l 交抛物线y 2=4x 于A 、B 两点.(I )若直线l 交y 轴于点M ,且,,21BT MB AT MA λλ==当m 变化时,求21λλ+的值;(II )设A 、B 在直线n x g =:上的射影为D 、E ,连结AE 、BD 相交于一点N ,则当m变化时,点N 为定点的充要条件是n =-2.。
枣庄市2008届高三第一次调研考试

枣庄市2008届高三第一次调研考试英语2007.11本试卷分第一卷(选择题)和第二卷(非选择题)两部分。
第一卷1至12页。
第二卷13至16页。
共150分。
考试用时120分钟。
第一卷(三部分,共105分)注意事项:1.答第一卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
不能答在试卷上。
3.考试结束,考生将本试卷和答题卡一并交回。
第一部分:听力(共两节,满分30分)做题时,先将答案标在试卷上。
录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上。
第一节(共5小题;每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1. What does the woman mean?A. She’s learned a lot from the literat ure class.B. She’s written some books on the world classics.C. She’s met some of the world’s best writers.2. How does the woman feel about driving to work?A. She is tired of driving in the heavy traffic.B. She doesn’t mind as the roa d conditions are good.C. She is unhappy to drive such a long way every day.3.What does the man take the picture for?A. For a newspaper.B. For a magazine.C. For a book.4. Where will the speakers possibly have their meal?A. At a McDonald.B. In a friend’s house.C. At home.5. How long has the woman stayed in the country?A. For two months.B. For three months.C. For three weeks.第二节(共15小题;每小题1.5分,满分22.5分)听下面5段对话或独白。
修改版2008届高三调研考试数学试题(理科)答案及评分标准校对版
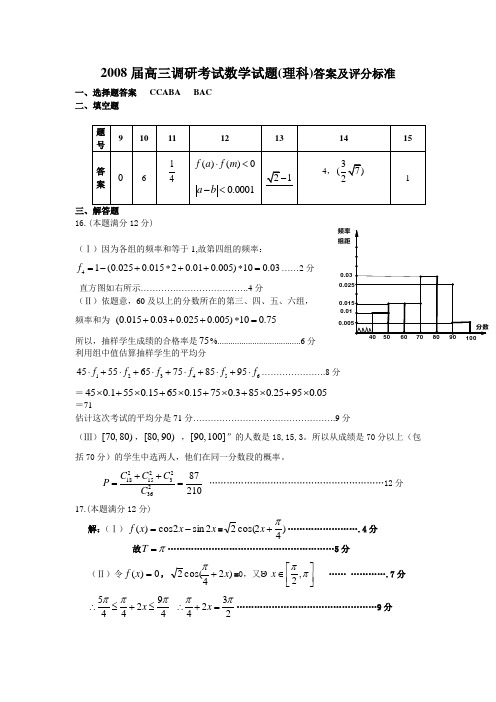
0.030.0250.0150.010.005频率组距2008届高三调研考试数学试题(理科)答案及评分标准一、选择题答案 CCABA BAC 二、填空题16.(本题满分12分)(Ⅰ)因为各组的频率和等于1,故第四组的频率:41(0.0250.01520.010.005)100.03f =-+*++*=……2分直方图如右所示……………………………….4分(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组, 频率和为 (0.0150.030.0250.005)100.75+++*=所以,抽样学生成绩的合格率是75%......................................6分 利用组中值估算抽样学生的平均分123456455565758595f f f f f f ⋅+⋅+⋅+⋅+⋅+⋅………………….8分=450.1550.15650.15750.3850.25950.05⨯+⨯+⨯+⨯+⨯+⨯=71估计这次考试的平均分是71分………………………………………….9分(Ⅲ)[70,80),[80,90) ,[90,100]”的人数是18,15,3。
所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
22218153236C C C P C ++==87210……………………………………………………12分17.(本题满分12分)解:(Ⅰ)x x x f 2sin 2cos )(-==)42cos(2π+x …………………….4分故π=T …………………………………………………5分 (Ⅱ)令0)(=x f ,)24cos(2x +π=0,又 ,2x ππ⎡⎤∈⎢⎥⎣⎦…… ………….7分 592444x πππ∴≤+≤3242x ππ∴+=…………………………………………9分故58x π=函数)(x f 的零点是58x π=……………. 12分18.(本题满分12分)证(Ⅰ)因为AB ⊥侧面11BB C C ,故1AB BC ⊥ 在1BC C 中,1111,2,3B C C C B B B C Cπ===∠=由余弦定理有1BC ==故有 222111B C B C C C C B B C +=∴⊥而 B C A B B = 且,AB BC ⊂平面ABC∴1C B A B C ⊥平面(Ⅱ)由11,,,,EA EB AB EB AB AE A AB AE ABE ⊥⊥=⊂ 平面从而1B E ABE ⊥平面 且BE ABE ⊂平面 故1BE B E ⊥ 不妨设 C E x =,则12C E x =-,则221BE x x =+- 又1123B C C π∠=则2211B E x x =++在1Rt BEB 中有 22114x x x x +++-+= 从而1x =±(舍负)故E 为1C C 的中点时,1EA EB ⊥ 法二:以B为原点1,,BC BC BA为,,x y z 轴,设C E x =,则11(0,0,0),(),1,3,0),(0,0,2)2B E x -- 由1EA EB ⊥得 10E A E B ⋅=即11(1,2)(,3,222211(1)(2)302222x x x xx x x x ----⎛⎫---=⎪⎪⎝⎭化简整理得 2320x x -+= 1x = 或 x = 当2x =时E 与1C 重合不满足题意EC 1B 1A 1CBA111当1x =时E 为1C C 的中点 故E 为1C C 的中点使1EA EB ⊥(Ⅲ)取1E B 的中点D ,1A E 的中点F ,1B B 的中点N ,1A B 的中点M 连D F 则11//DF A B ,连D N 则//D N B E ,连M N 则11//M N A B 连M F 则//M F B E ,且M N D F 为矩形,//M D AE又1111,A B EB BE EB ⊥⊥ 故M D F ∠为所求二面角的平面角在Rt D FM 中,111(22D F A B BCE ==∆ 为正三角形)111222M F B E C E ===1tan 22M D F ∴∠==法二:由已知1111,EA EB B A EB ⊥⊥, 所以二面角11A EB A --的平面角θ的大小为向量11B A 与EA的夹角因为11(0,B A BA ==1(,22EA =--故 1111cos tan 2E A B A E A B A θθ⋅==⇒=⋅.19. (本题满分14分)解:(Ⅰ)依题意知,直线l 的方程为:1x =-.点R 是线段F P 的中点,且RQ ⊥F P ,∴RQ 是线段F P 的垂直平分线.…………………….2分∴P Q 是点Q 到直线l 的距离.∵点Q 在线段F P 的垂直平分线,∴PQ QF =.…………4分 故动点Q 的轨迹E 是以F 为焦点,l 为准线的抛物线,其方程为:24(0)y x x =>.…………………………………………………….7分(Ⅱ) 设()()B B A A y x B y x A ,,,,()()N N M M y x N y x M ,,,,直线AB 的方程为)1(-=x k y…………………………………………………….8分则⎪⎩⎪⎨⎧==)2(4)1(422BB AA x y x y(1)—(2)得k y y B A 4=+,即ky M 2=,……………………………………9分代入方程)1(-=x k y ,解得122+=kx M .所以点M的坐标为222(1,)k k+.……………………………………10分同理可得:N 的坐标为2(21,2)k k +-. 直线MN 的斜率为21kk x x y y k NM N M MN -=--=,方程为)12(1222---=+k x kkk y ,整理得)3()1(2-=-x k k y ,………………12分显然,不论k 为何值,(3,0)均满足方程,所以直线MN 恒过定点R (3,0). (14)20. (本题满分14分) .解:11n na kn a +=+故2211a a k a ==+,.……………………………………1分又因为()211111,,2n n n n na a a a a a n N n +--+==+∈≥则3121a a a a =22a +,即3322221,21,2a a a k a k a a =+=+∴=又.………………………3分所以212,1k a k k +==∴=, ……………………………………4 (2)11,n n a n a +=+121121nn n n n a a a a a a a a ---=⋅⋅⋅⋅⋅⋅⋅⋅=()1...21!n n n ⋅-⋅⋅⋅= (6)因为()()11!n n a xg x n -=-=1n nx-所以,当1x =时,()()()11123 (2)n n f x f n +==++++= (7)当1x ≠时,()21123...n f x x x nx-=++++ (1)()1x ⋅得()()23123...1n nxf x x x x n xnx -=++++-+ (2)()()()()2112:11...n n x f x x x x nx ---=++++-=11nnxnx x ---()()2111n nxnxf x xx -∴=--- (9)综上所述:2(1),12()1,1(1)1n nn n x f x x nx x x x +⎧=⎪⎪=⎨-⎪-≠⎪--⎩……………………………10 (3)因为()()()212221211212n nnn f n -∴=-=-+--又()333ng n=,易验证当1,2n =,3时不等式不成立; (11)假设()3n k k =≥,不等式成立,即()3121kkk >-+两边乘以3得:()()111331232131222k kk kk k k k k +++>-+=⋅++--+又因为()()()131222233223220kk kkk k k k k +--⋅+=--+=-+>所以()11113213122221k k kk k k k k k ++++>⋅++--+>⋅+即1n k =+时不等式成立.故不等式恒成立. (14)21. (本题满分14分)解:(Ⅰ) ()ln(1)(1),xf x a e a x =+-+(1)()(1)011x xxxaea e f x a ee-+-'∴=-+=<++恒成立,…………………………所以函数()f x 在(,)-∞+∞上是单调减函数. …………………………4分(Ⅱ) 证明:据题意1,12233(()),(,()),(,())A x f x B x f x C x f x 且x 1<x 2<x 3,由(Ⅰ)知f (x 1)>f (x 2)>f (x 3), x 2=231x x +…………………………6分12123232(,()()),(,()()BA x x f x f x BC x x f x f x ∴=--=--12321232()()[()()][()()]BA BC x x x x f x f x f x f x ∴⋅=--+--…………………8分123212320,0,()()0,()()0x x x x f x f x f x f x -<->->-< 0,(,)2B A BC B ππ∴⋅<∴∠∈即⊿ABC 是钝角三角形……………………………………..9分(Ⅲ)假设⊿ABC 为等腰三角形,则只能是BA BC =即2132()()()f x f x f x =+3212132ln(1)2(1)[ln(1)(1)(1)()xx x a e a x a e e a x x ⇔+-+=++-++ 321222ln(1)2(1)[ln(1)(1)2(1)xxxa e a x a e e a x ⇔+-+=++-+3212ln(1)ln(1)(1)xx x e e e ⇔+=++31332122122(1)(1)(1)2xx x xxxx x x e e e eeeee +⇔+=++⇔+=++3212xx x ee e ⇔=+ ① …………………………………………..12分而事实上, 3122x xxe ee +≥= ②由于31x x e e <,故(2)式等号不成立.这与(1)式矛盾. 所以⊿ABC 不可能为等腰三角形..14分222212123232()[()()]()[()()]x x f x f x x x f x f x -+-=-+-即:2221321232[()()][()()]x x x x f x f x f x f x -=-∴-=-。
2008年高考山东卷(理科数学)
2008年普通高等学校招生全国统一考试理科数学(山东卷)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.满足1234{,,,}M a a a a ⊆,且12312{,,}{,}Ma a a a a =的集合M 的个数是A .1B .2C .3D .4 2.设z 的共轭复数是z ,若4z z +=,8z z ⋅=,则zz等于 A .i B .i - C .1± D .i ±3.函数ln cos y x =(22ππx -<<)的图象是4.设函数()1f x x x a =++-的图象关于直线1x =对称,则a 的值为 A .3 B .2 C .2 D.1-5.已知cos()sin 6παα-+=7sin()6πα+的值是A ..532 C .45- D .54 6.下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是 A .9π B .10π C .11π D .12π7.在某地的奥运火炬传递活动中,有编号为1,2,3,,18的18名火炬手.若从中任选3人,则选出的火炬手的编号能组成以3为公差的等差数列的概率为A .511B .681C .3061D .40818.右图是根据《山东统计年鉴2007》中的资料作成的1997年至2006年我省城镇居民百户家庭人口数的茎叶图,图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字,右边的数字表示城镇居民百户家庭人口数的个位数字,从图中可以得到1997年至2006年我省城镇居民百户家庭人口数的平均数为A .304.6B .303.6C .302.6D .301.69.12(x -展开式中的常数项为 A .1320- B .1320 C .220- D .22010.设椭圆1C 的离心率为135,焦点在x 轴上且长轴长为26.若曲线2C 上的点到椭圆1C 的两个焦点的距离的差的绝对值等于8,则曲线2C 的标准方程为正(主)视图俯视图侧(左)视图 29 30 31 1 1 5 8 2 6 0 2 4 7A .1342222=-y x B .15132222=-y xC .1432222=-y x D .112132222=-y x11.已知圆的方程为22680x y x y +--=.设该圆过点(3,5)的最长弦和最短弦分别为AC 和BD ,则四边形ABCD 的面积为A.. C..12.设二元一次不等式组2190802140x y x y x y +-≥⎧⎪-+≥⎨⎪+-≤⎩所表示的平面区域为M ,使函数xy a =(0a >,1a ≠)的图象过区域M 的a 的取值范围是A .[1,3] B. C .[2,9] D. 二、填空题:本大题共4小题,每小题4分,共16分. 13.执行右边的程序框图,若0.8p =,则输出的n = .14.设函数2()f x ax c =+(0a ≠),若)()(010x f dx x f =⎰,001x ≤≤,则0x 的值为 . 15.已知ABC ∆中,A ,B ,C 所对的边分别为a ,b ,c .向量(3,1)m =-,(cos ,sin )n A A =.若0m n ⋅=,且cos cos sin a B b A c C +=,则角B = .16.若不等式34x b -<的解集中的整数有且仅有1,2,3,则b 的取值范围为 . 三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.三、解答题:本大题共6小题,共74分. 17.(本小题满分12分)已知函数())cos()f x x x ωϕωϕ=+-+(0πϕ<<,0ω>)为偶函数,且函数()y f x =图象的两相邻对称轴间的距离为2π. (Ⅰ)求()8πf 的值;(Ⅱ)将函数()y f x =的图象向右平移6π个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数()y g x =的图象,求()g x 的单调递减区间.18.(本小题满分12分)甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为32,乙队中3人答对的概率分别为23,23,12,且各人回答正确与否相互之间没有影响.用ξ表示甲队的总得分.(Ⅰ)求随机变量ξ分布列和数学期望;(Ⅱ)用A 表示“甲、乙两个队总得分之和等于3”这一事件,用B 表示“甲队总得分大于乙队总得分”这一事件,求()P AB . 19.(本小题满分12分)将数列{}n a 中的所有项按每一行比上一行多一项的规则排成如下数表:记表中的第一列数1a ,2a ,4a ,7a ,构成的数列为{}n b ,111b a ==,n S 为数列{}n b 的前n 项和,且满足221nn n nb b S S =-(2n ≥). (Ⅰ)证明数列1{}nS 成等差数列,并求数列{}n b 的通项公式; 1a2a 3a 4a 5a 6a 7a 10a9a 8a(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当91481-=a 时,求上表中第k (3k ≥)行所有项的和.20.(本小题满分12分)如图,已知四棱锥P ABCD -,底面ABCD 为菱形,PA ⊥平面ABCD ,60ABC ∠= ,E ,F 分别是BC ,PC 的中点. (Ⅰ)证明:AE PD ⊥;(Ⅱ)若H 为PD 上的动点,EH 与平面PAD面角E AF C --的余弦值.21.(本小题满分12分) 已知函数1()ln(1)(1)nf x a x x =+--,其中n N *∈,a 为常数. (Ⅰ)当2n =时,求函数()f x 的极值;(Ⅱ)当1a =时,证明:对任意的正整数n ,当2x ≥时,有()1f x x ≤-. 22.(本小题满分14分)如图,设抛物线方程为22x py =(0p >),M 为直线2y p =-上任意一点,过M 引抛物线的切线,切点分别为A ,B .(Ⅰ)求证:A ,M ,B 三点的横坐标成等差数列;(Ⅱ)已知当M 点的坐标为(2,2)p -时,AB = (Ⅲ)是否存在点M ,使得点C 关于直线AB 的对称点D 在抛物线22x py = (0p >)上,其中,点C 满足OC OA OB =+(O 为坐标原点).若存在,求出所有适合题意的点M 的坐标;若不存在,请说明理由.A BCDEF P。
2008届枣庄高三第一次调研考试

2008届山东省枣庄市高三第一次调研考试地 理 试 题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分。
考试时间100分钟。
第Ⅰ卷(选择题 共90分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型(A 或B )用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试卷上。
3.考试结束,将本试卷和答题卡一并交回。
4.第Ⅰ卷共30小题,每小题3分,共计90分。
在每小题列出的四个选项中,只有一 项是符合题目要求的。
图1示意北半球某地某日的太阳视运动路径,图中椭圆为地平圈,太阳位于正南方天空。
图中α∠=23°26′,β∠=32°34′。
据图完成1—3题。
1.若该地西侧为东半球,东侧为西半球,则此时北京时间是( )A .9时20分B .21时20分C .15时40分D .6时40分2.此日是( ) A .6月22日 B .12月22日C .3月21日D .9月23日3.与该地正午太阳高度相同的另一地点的 纬度为 ( )A .80°52′NB .34°NC.80°52′S D.34°S图2为“北半球某区域近地面900hPa等压面空间高度分布图”,图中数值表示等压面高度(单位:m)。
据图完成4—5题。
4.图3四幅图中,与沿图2的XY方向作900hPa等压面剖面相符的是()5.关于图2中A、B两处风向的说法,正确的是()A.A处吹偏北风,B处吹偏南风B.A外吹偏南风,B处吹偏北风C.A、B两处均吹偏北风D.A、B两外均吹偏南风图4为“一万年来挪威雪线高度和五千年来中国气温距平(与平均气温的差值)变化图”。
读图完成6—7题。
6.图中显示全球气候有两次较大的波动,这两个时期是()①公元前5000年—公元前1500年②公元前500年—公元1000年③公元1450年—公元1850年④公元1000年—公元1500年A.①④B.①③C.②③D.②④7.图示公元后挪威雪线降低时期,我国可能出现的现象是()A.水稻种值范围向北扩展B.野象栖息的最北界北迁C.竹类分布向黄河流域扩展D.江淮一带遭受寒潮侵袭次数增加图5示意我国某内陆湖(海拔3800米)的水位变化情况,据图完成8—10题。
2008年高考理科数学试题及参考答案(山东卷)

理科数学本试卷分第I卷和第II卷两部分,共4页。
满分150分。
考试用时120分钟,考试结束,务必将试卷和答题卡一并上交。
注意事项:1.答题前,考生务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号、县区和科类填写在答题卡上和试卷规定的位置上。
2.第I卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;如需改动,用橡皮擦干净后,再选涂其他答案标号,答案不能答在试卷上。
3.第II卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的答案,然后再写上新的答案;不能使用涂改液、胶带纸、修正带。
不按以上要求作答的答案无效。
4.填空题请直接填写答案,解答题应写出文字说明、证明过程或演算步骤。
参考公式:锥体的体积公式:V= Sh,其中S是锥体的底面积,h是锥体的高。
如果事件A,B互斥,那么P(A+B)=P(A)+P(B);如果事件A,B独立,那么P(AB)=P(A)?P(B)。
第I卷(共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1 若复数x满足z(2-i)=11+7i(i为虚数单位),则z为A3+5i B3-5i C-3+5i D -3-5i2已知全集={0,1,2,3,4},集合A={1,2,3,},B={2,4} ,则(CuA)B为A {1,2,4}B{2,3,4}C{0,2,4}D{0,2,3,4}3设a>0a≠1 ,则“函数f(x)= a3在R上是减函数”,是“函数g(x)=(2-a)在R 上是增函数”的A 充分不必要条件B必要不充分条件C充分必要条件D既不充分也不必要条件(4)采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,……,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[1,450]的人做问卷A,编号落入区间[451,750]的人做问卷B,其余的人做问卷C.则抽到的人中,做问卷B的人数为(A)7(B)9(C)10(D)15(5)的约束条件,则目标函数z=3x-y的取值范围是(A)(B)(C)[-1,6](D)(6)执行下面的程序图,如果输入a=4,那么输出的n的值为(A)2(B)3(C)4(D)5(7)若,,则sin =(A)(B)(C)(D)(8)定义在R上的函数f(x)满足f(x+6)=f(x),当-3≤x<-1时,f(x)=-(x+2),当-1≤x<3时,f(x)=x。
山东省枣庄市高三数学理科第一次调研考试卷

山东省枣庄市2008届高三第一次调研考试数学试题(理科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
共150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试卷上。
3.考试结束,监考人将本试卷和答题卡一并收回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集B C A B A I I ⋂===则集合集合},4,1{},5,4,3,1{},6,5,4,3,2,1{等于 ( )A .{1,4}B .{2,6}C .{3,5}D .{2,3,5,6}2.圆0144:0882:222221=---+=-+++y x y x C y x y x C 与圆的位置关系是( )A .外离B .外切C .相交D .内含3.已知函数)1),41((,),(,log )(22f F y x y x F x x f 则+==等于 ( )A .-1B .5C .-8D .3 4.若b a b a 在则),7,4(),3,2(-==方向上的投影为( )A .13B .513 C .565 D .655.在△ABC 中,A=60°,AB=2,且△ABC 的面积23=∆ABC S ,则边BC 的长为( )A .3B .3C .7D .76.在同一坐标系内,函数aax y a x y a1)0(-=≠=和的图象可能是 ( )7.已知ααπαππαcos sin ,43)7tan(),23,2(+-=-∈则的值为 ( )A .51±B .51-C .51D .57-8.已知S n 是等比数列685,16,2,}{S a a n a n 等项和的前=-=等于 ( )A .821 B .-821 C .817 D .-817 9.已知点),(y x 构成的平面区域如图所示,)(为常数m y mx z +=在平面区域内取得最大值的最优解有无数多个,则m 的值为 ( )A .207-B .207 C .21 D .21207或 10.已知直线l 的倾斜角为π43,直线l 1经过点l l a B A 与且1),1,(),2,3(-垂直,直线l 2:b a l by x +=++平行,与直线1012等于 ( )A .-4B .-2C .0D .211.若},31)(|{,2)2(,4)1(,)(<++==-=-t x f x P f f x f 设且上的增函数是R }4)(|{-<=x f x Q ,若“P x ∈”是“Q x ∈”的充分不必要条件,则实数t 的取值范围是( )A .1-≤tB .1->tC .3≥tD .3>t12.给出下列四个结论:①当a 为任意实数时,直线012)1(=++--a y x a 恒过定点P ,则过点P 且焦点在y 轴上的抛物线的标准方程是y x 342=;②已知双曲线的右焦点为(5,0),一条渐近线方程为02=-y x ,则双曲线的标准方程是120522=-y x ;③抛物线a y a ax y 41)0(2-=≠=的准线方程为;④已知双曲线1422=+my x ,其离心率)2,1(∈e ,则m 的取值范围是(-12,0)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省枣庄市2008届高三第一次调研考试数学试题(理科)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
共150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)注意事项:1.答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号,不能答在试卷上。
3.考试结束,监考人将本试卷和答题卡一并收回。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知全集B C A B A I I ⋂===则集合集合},4,1{},5,4,3,1{},6,5,4,3,2,1{等于 ( )A .{1,4}B .{2,6}C .{3,5}D .{2,3,5,6}2.圆0144:0882:222221=---+=-+++y x y x C y x y x C 与圆的位置关系是( )A .外离B .外切C .相交D .内含3.已知函数)1),41((,),(,log )(22f F y x y x F x x f 则+==等于 ( )A .-1B .5C .-8D .3 4.若b a b a 在则),7,4(),3,2(-==方向上的投影为( )A .13B .513C .565 D .655.在△ABC 中,A=60°,AB=2,且△ABC 的面积23=∆ABC S ,则边BC 的长为( )A .3B .3C .7D .76.在同一坐标系内,函数aax y a x y a1)0(-=≠=和的图象可能是 ( )7.已知ααπαππαcos sin ,43)7tan(),23,2(+-=-∈则的值为 ( )A .51±B .51-C .51D .57-8.已知S n 是等比数列685,16,2,}{S a a n a n 等项和的前=-=等于 ( )A .821 B .-821 C .817 D .-817 9.已知点),(y x 构成的平面区域如图所示,)(为常数m y mx z +=在平面区域内取得最大值的最优解有无数多个,则m 的值为 ( )A .207-B .207 C .21 D .21207或 10.已知直线l 的倾斜角为π43,直线l 1经过点l l a B A 与且1),1,(),2,3(-垂直,直线l 2:b a l by x +=++平行,与直线1012等于 ( )A .-4B .-2C .0D .211.若},31)(|{,2)2(,4)1(,)(<++==-=-t x f x P f f x f 设且上的增函数是R }4)(|{-<=x f x Q ,若“P x ∈”是“Q x ∈”的充分不必要条件,则实数t 的取值范围是( )A .1-≤tB .1->tC .3≥tD .3>t12.给出下列四个结论:①当a 为任意实数时,直线012)1(=++--a y x a 恒过定点P ,则过点P 且焦点在y 轴上的抛物线的标准方程是y x 342=;②已知双曲线的右焦点为(5,0),一条渐近线方程为02=-y x ,则双曲线的标准方程是120522=-y x ;③抛物线a y a ax y 41)0(2-=≠=的准线方程为;④已知双曲线1422=+my x ,其离心率)2,1(∈e ,则m 的取值范围是(-12,0)。
其中所有正确结论的个数是( )A .1B .2C .3D .4第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
13.若b a b a b a 41,14,0,0+=+>>则且的最小值是 . 14.如图,由曲线x x x x y 与π23,0,sin ===轴围成的阴影部分的面积是 。
15.已知函数a a f x x x x f x的则满足21)(.0,2,0,log )(2<⎩⎨⎧<>= 的取值范围是 (用区间的形式表示)。
16.设函数1)3sin(sin )3cos(cos )(++⋅-+⋅=ππx x x x x f ,有下列结论:①点)0,125(π-是函数)(x f 图象的一个对称中心;②直线3π=x 是函数)(x f 图象的一条对称轴;③函数)(x f 的最小正周期是π;④将函数)(x f 的图象向右平移6π个单位后,对应的函数是偶函数。
其中所有正确结论的序号是 。
三、解答题:本大题共6小题,共74分,解答应写出文字说明、证明过程并演算步骤。
17.(本小题满分12分) 已知向量.)(),1,(cos ),1sin 2cos ,1cos 2(OQ OP x f x OQ x x x OP ⋅=-=+-+=定义(1)求函数)(x f 的单调递减区间;(2)求函数)(x f 的最大值及取得最大值时的x 的取值集合。
18.(本小题满分12分)已知数列.12}{2n n S n a n n -=项和的前 (1)求数列}{n a 的通项公式;(2)求数列.|}{|n n T n a 项和的前 19.(本小题满分12分)已知01:2=++mx x p 方程有两个不相等的负实根;q p q p R x m x q ∧∨>+-+,,01)2(44:2为真命题若的解集为不等式为假命题,求m 的取值范围。
20.(本小题满分12分)已知函数)(,32,)(23x f y x c bx ax x x f ==+++=时若有极值,曲线))1(,1()(f x f y 在点=处的切线l 不过第四象限且斜率为3,又坐标原点到切线l 的距离为.1010 (1)求a ,b ,c 的值;(2)求]1,4[)(-=在x f y 上的最大值和最小值。
21.(本小题满分12分)在对口扶贫活动中,为了尽快脱贫(无债务)致富,企业甲将经营状态良好的某种消费品专卖店以5.8万元的优惠价格转让给了尚有5万元无息贷款没有偿还的小型残疾人企业乙,并约定从该店经营的利润中,在保证企业乙的全体职工每月最低生活费的开支3600元后,逐步偿还转让费(不计息),在甲提供资料中:①这种消费品的进价每件14元;②该店月销量Q (百件)与销售单价P (元/件)的关系如右图所示;③该店每月需各种开支2000元。
(1)写出月销量Q (百件)与销售单价P (元/件)的关系,并求该店的月利润L (元)关于销售单价P (元/件)的函数关系式(该店的月利润=月销售利润-该店每月支出);(2)当商品的价格为每件多少元时,该店的利润最大?并求该店的月利润的最大值; (3)若企业乙只依靠该店,最早可望在多少年后脱贫(无债务)?22.(本小题满分14分)已知椭圆C 过点)0,2(),26,1(-F M 是椭圆的左焦点,P 、Q 是椭圆C 上的两个动点,且|PF|、|MF|、|QF|成等差数列。
(1)求椭圆C 的标准方程;(2)求证:线段PQ 的垂直平分线经过一个定点A ;(3)设点A 关于原点O 的对称点是B ,求|PB|的最小值及相应点P 的坐标。
参考答案一、选择题:本大题共12小题,每小题5分,共60分。
CCCA ACBA BBDD二、填空题:本大题共4小题,每小题4分,共16分。
13.16 14.3 15.)2,0()1,(⋃--∞ 16.②③④ 三、解答题: 17.(本小题满分12分)解:(1))1,(cos )1sin 2cos ,1cos 2()(-⋅+-+=⋅=x x x x x f 1sin 2cos cos cos 22-+-+=x x x x …………2分 x sin cos +=…………4分 )4sin(2π+=x…………6分.45242,,232422πππππππππ+≤≤+∈+≤+≤+k x k k k x k 解得令Z所以,函数.],452,42[)(Z ∈++k k k x f ππππ的单调递减区间为 …………9分(2)函数.42,224,2)(πππππ+=+=+k x k x x f 即此时的最大值是 所以,函数}.,42|{2)(Z ∈+=k k x x x x f ππ的取值集合为时的取得最大值…………12分18.(本小题满分12分)解:(1)当111112,1211=-⨯===S a n 时;…………1分当.213])1()1(12[)12(,2221n n n n n S S a n n n n -=-----=-=≥-时…………3分 .213}{,.213111n a a n a n n -=-=的通项公式为数列所以的形式也符合…………4分 (2)令.6,,0213*≤∈≥-=n n n a n 解得又N…………5分当2212112||||||,6n n S a a a a a a T n n n n n -==+++=+++=≤ 时;…………8分当||||||||||,67621n n a a a a a T n ++++++=> 时 n a a a a a a ----+++= 87621.7212)12()6612(222226+-=---⨯⨯=-=n n n n S S n…………11分 综上,⎪⎩⎪⎨⎧>+-≤-=.6,7212,6,1222n n n n n n T n…………12分19.(本小题满分12分)解:.2.01,0,042>⇒⎪⎩⎪⎨⎧><->-=∆⇔m m m p 为真命题 …………3分.310144)]2(4[2<<⇒<⨯⨯--=∆⇔m m q 为真命题 …………6分 .,,一真一假与为假为真q p q p q p ∴∧∨…………7分 若.3,31,2,≥≥≤>m m m m q p 所以或且则假真…………9分 若.21,31,2,≤<<<≤m m m q p 所以且则真假 …………11分 综上所述,m 的取值范围为}.3,21|{≥≤<m m m 或…………12分20.(本小题满分12分)解:(1).23)(2b ax x x f ++='…………1分由题意,得⎩⎨⎧-==⎪⎩⎪⎨⎧=+⨯+⨯='=+⨯+⨯='.4,2.31213)1(,0322)32(3)32(22b a b a f b a f 解得 …………4分设切线l 的方程为1010.3的距离为由原点到切线l m x y +=,则 .1.101013||2±==+m m 解得 .13.1,+=∴=∴x y l m l 的方程为切线不过第四象限切线…………5分由于切点的的横坐标为x =1,∴切点坐标为(1,4),.5,41.4)1(=∴=+++∴=∴c c b a f…………6分(2)由(1)知542)(23+-+=x x x x f ,.32,2,0)(),23)(2(443)(212=-=='-+=-+='x x x f x x x x x f 得令所以…………10分 )(x f ∴在[-4,1]上的最大值为13,最小值为-11。
