初二动点问题及中考压轴题
人教版八年级上册数学期末动点问题压轴题专题训练(含答案)

人教版八年级上册数学期末动点问题压轴题专题训练1.如图,△ABC是等边三角形,点D是边BC上一个动点(点D不与点B,C重合),连接AD,点E在边AC的延长线上,且DA=DE.(1)求证:△BAD=△EDC:(2)用等式表示线段CD,CE,AB之间的数量关系,并证明.2.如图,已知△ ABC是边长为10cm的等边三角形,点F为AC的中点,动点D,E同时从A,B两点出发,分别沿AB,BC匀速运动,其中点D运动的速度是1cm/s,点E运动的速度是2cm/s,设运动时为t 秒.(1)当t为何值时,△ AFD与△ CFE全等;(2)当t为何值时,△ BDE为直角三角形.3.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.(1)如图1,当点D在边BC上时,求证:△BD=CE,△AC=CE+CD;(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CE+CD是否成立?若不成立,请写出AC、CE、CD之间存在的数量关系,并说明理由.4.在等边△ABC中,(1)如图1,P,Q是BC边上两点,AP=AQ,△BAP=20°,求△AQB的度数;(2)点P,Q是BC边上的两个动点(不与B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.△依题意将图2补全;△求证:P A=PM.5.如图,在三角形ABC中,D是射线BC上一动点.(1)如图1,点D在BC边上(不与点B,C重合),△ 按要求作图:分别过点D作DE BA∥交边AB于点F;∥交边AC于点E,作DF CA△ 在△的条件下,判断△EDF与△A的数量关系,并说明理由;(2)如图2,若点D在BC的延长线上,DF CA∥,△EDF=△A,试判断DE与BA的位置关系,并说明理由.6.如图1,等腰Rt△ABC中,△BAC=90°,AB=AC,D,E分别是AC和BC上的动点,BD△AE,垂足为F.(1)求证△CAE=△ABD;(2)连接DE,满足△AEB=△DEC,求证:BD=DE+AE;(3)点G在BD的延长线上,连接EG,满足△AEB=△GEC,试写出AE,EG,BG之间的数量关系,并证明.7.已知:如图,ABC是边长为6cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P,Q两点停止运动,设点P的运动时间为()s t,解答下列各问题:(1)ABC的面积为多少?△是等边三角形?(2)当t为何值时,PBQ△是直角三角形时,求t的值.(3)当PBQA a,将点A向右平移b个单位得到点B,其中a,b满足8.如图△所示,点A的坐标为(0,)+-=.a b50(2)如图△,坐标轴上有两个动点P ,Q ,点P 从A 点出发沿y 轴负方向以每秒1个单位长度的速度运动,点Q 从O 点出发以每秒2个单位长度的速度沿x 轴正方向运动,点P 、Q 同时出发,点P 到达O 点时整个运动结束.设运动时间为t 秒,问t 为何值时,使得12OBP BOQ S S =△△?并求出此时点P 和点Q 的坐标; (3)如图△所示,点F 为x 轴上一点,作△BOF 的平分线OG ,且OG △FB ,垂足为G ,△AOB 的平分线OE 与射线FB 交于点E ,求△E 的度数.9.如图,在平面直角坐标系中,点A ,B 的坐标分别为(a ,0),(b ,0),且a ,b 满足()23-20a b ++=.现同时将点A ,B 分别向左平移2个单位,再向上平移2个单位,得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)直接写出A ,B 两点的坐标为:A ___________, B ___________.(2)若点P 是线段AC 上的一个动点,Q 是线段CD 的中点,连接PQ ,PO ,当点P 在线段AC 上移动时(不与点A ,C 重合),请找出PQD ∠,OPQ ∠,POB ∠的数量关系,并证明你的结论.(3)在坐标轴上是否存在点M ,使三角形MAD 的面积与三角形ACD 的面积相等?若存在,请求出点M 的坐标;若不存在,试说明理由.10.已知:直线AD BC ∥,动点P 在直线EF 上运动,探究ADP ,DPC ∠,BCP ∠之间的关系.(1)【问题发现】若25ADP ∠=︒,35BCP ∠=︒,求DPC ∠的度数.(2)【结论猜想】当点P 在线段AB 上时,猜想ADP ,DPC ∠,BCP ∠三个角之间的数量关系,并说明理(3)【拓展延伸】若点P 在射线AE 上或者在射线BF 上时(不包括端点),试着探究ADP ,DPC ∠,BCP ∠之间的关系是否会发生变化,请挑选一种情形画出图形,写出结论,并说明理由.11.ABC 中,70C ∠=︒,点D ,E 分别是ABC 边AC ,BC 上的点,点P 是一动点,令1PDA ∠=∠,2PEB ∠=∠,DPE α∠=∠.初探:(1)如图1,若点P 在线段AB 上,且60α∠=︒,则12∠+∠=_____________; (2)如图2,若点P 在线段AB 上运动,则△1,△2,α∠之间的关系为_____________; (3)如图3,若点P 在线段AB 的延长线上运动,则△1,△2,α∠之间的关系为_____________; 再探:(4)如图4,若点P 运动到ABC 的内部,写出此时△1,△2,α∠之间的关系,并说明理由.12.如图,AB 、CD 被AC 所截,AB CD ∥,△CAB =108°,点P 为直线AB 上一动点(不与点A 重合),连CP ,作△ACP 和△DCP 的平分线分别交直线AB 于点E 、F .(1)当点P 在点A 的右侧时△若△ACP =36°,则此时CP 是否平分△ECF ,请说明理由. △求△ECF 的度数.(2)在点P 运动过程中,直接写出△APC 与△AFC 之间的数量关系.(1)求证:AB CD ∥;(2)如图2,若3ABE EBF ∠=∠,120BFD ∠=︒,试求CDFBDF∠∠的值;(3)如图3,若H 是直线CD 上一动点(不与D 重合),BI 平分HBD ∠,则EBI ∠与BHD ∠的数量关系为______.14.如图1,在△ABC 中,BO AC ⊥于点O ,3,1AO BO OC ===,过点A 作AH BC ⊥于点H ,交BO 于点P .(1)求线段OP 的长度;(2)连接OH ,求证:点O 到△AHC 的两边距离相等;(3)如图2,若点D 为AB 的中点,点M 为线段BO 延长线上一动点,连接MD ,过点D 作DN DM ⊥交线段OA 延长线于N 点,则BDM ADN S S ∆∆-的值是否发生改变,如改变,求出该值的变化范围;若不改变,求该式子的值.15.在ABC 中,BAC ABC ∠>∠,三个内角的平分线交于点O .(1)填空:如图1,若80BCA ∠=︒,则BOA ∠的大小为________度;(3)如图2,CO 的延长线交AB 于点E ,点M 是AB 边上的一动点(不与点E 重合),过点M 作MN CE ⊥于点N ,请探索AMN ∠、ABC ∠、BAC ∠三者之间的数量关系.16.如图1,CE 平分ACD ∠,AE 平分BAC ∠,90EAC ACE ∠+∠=︒(1)请判断AB 与CD 的位置关系并说明理由;(2)如图2,在(1)的结论下,当90E ∠=︒保持不变,移动直角顶点E ,使MCE ECD ∠=∠,当直角顶点E 点移动时,问BAE ∠与MCD ∠是否存在确定的数量关系?(3)如图3,在(1)的结论下,P 为线段AC 上一定点,点Q 为直线CD 上一动点,当点Q 在射线CD 上运动时(点C 除外),CPQ CQP ∠+∠与BAC ∠有何数量关系?17.如图,在△ABC 中,D 为AB 的中点,AB =AC =10cm ,BC =8cm ,动点P 从点B 出发,沿BC 方向以每秒3cm 的速度向点C 运动;同时动点Q 从点C 出发,沿CA 方向以每秒3cm 的速度向点A 运动,运动时间是t 秒.(1)在运动过程中,当点C 位于线段PQ 的垂直平分线上时,求出t 的值;(2)在运动过程中,是否存在某一时刻t ,使△BPD 和△CQP 全等,若存在,求出t 的值.若不存在,请说明理由.18.如图,△ABC是边长是12cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:(1)当点Q到达点C时,PQ与AB的位置关系如何?请说明理由.(2)在点P与点Q的运动过程中,△BPQ是否能成为等边三角形?若能,请求出t,若不能,请说明理由.(3)则当t为何值时,△BPQ是直角三角形?2,0,以线段OA为边在第四象限内作等边AOB,点C 19.如图,在平面直角坐标系中,点A的坐标为()OC>,连接BC,以线段BC为边在第四象限内作等边CBD,连接DA.为x轴正半轴上一动点()2(1)求证:OBC ABD≌;(2)是否存在点C,使得ACD△为直角三角形.若存在,请求出点C的坐标;若不存在,请说明理由;(3)是否存在点C,使得ACD△为等腰三角形.若存在,请求出AC的长;若不存在,请说明理由.B-(0,4)点4(6,)A -.(1)如图1,动点P 从点B 出发,以每秒2个单位长度的速度沿BA 方向运动,同时动点Q 从点O 出发,以每秒3个单位长度的速度沿y 轴向上运动,当点P 运动到点A 时,P 、Q 同时停止运动,设点P 运动时间为t 秒.用含t 的式子表示P ,Q 两点的坐标.(2)如图2,点D 为线段OA (端点除外)上某一点,当点D 在线段上运动时,过点D 作直线EF 交x 轴正半轴于E ,交直线AB 于F ,,EOD AFD ∠∠的平分线相交于点N ,若ODF α∠=,请用含α的式子表示ONF ∠的大小,并说明理由.答案1. (2)AB =CD +CE 2.(1)103t =(2)t =2或53.(2)AC+CD =CE ,4.(1)80°5.(1);△△EDF =△A , (2)DE BA ∥,6. (3)BG =AE +EG ,7.(1)2cm (2)3 (3)2或48.(1)(0,2)A ,(3,2)B (2)65t =,点0,54P ⎛⎫ ⎪⎝⎭,12,05Q ⎛⎫ ⎪⎝⎭ (3)△E =45°9.(1)(−3,0);(2,0)(2)△DQP +△QPO +△BOP =360°; (3)(0,163)或(0,−43)或(−8,0)或(2,0)10.(1)60°;(2)△DPC =△ADP +△PCB(3)△PCB =△DPC +△ADP ;或△ADP =△DPC +△PCB11.(1)130︒;(2)1270α∠+∠=︒+∠; (3)1270α∠-∠=︒+∠; (4)12430α∠+∠=︒-∠,12.(1)△平分,;△36°(2)当点P 在点E 的右侧时,2APC AFC ∠=∠;当点P 、点E 在点A 的左侧,点F 在点A 的右侧时,2180AFC APC ∠+∠=︒;当点P 、点E 、点F 均在点A 的左侧时, 2180AFC APC ∠-∠=︒.13. (2)4(3)△BHD =2△EBI 或△EBI =90°-12△BHD14.(1)OP =1;(3)不变,9415.(1)130(3)2360AMN ABC BAC ∠=∠-∠+︒或2AMN BAC ABC ∠=∠-∠16.(1)平行,(2)存在,1902BAE MCD ∠+∠=︒(3)BAC PQC QPC ∠=∠+∠17.(1)43t = (2)当1t =时,△BPD △△CQP18.(1)PQ 与AB 垂直,(2)能,当4s t =时,△BPQ 是等边三角形(3) 2.4s t =或6s t =,△BPQ 是直角三角形19. (2)C (4,0)(3)不存在,20.(1)P (2t ,-4),Q (0,3t ); (2)12ONF α∠=,。
初中数学压轴题,动点

压轴题库(之动点)1.如图,在Rt ABC△中,∠C=90°,AB=50,AC=30,D,E,F分别是AC,AB,BC的中点.点P从点D出发沿折线DE-EF-FC-CD以每秒7个单位长的速度匀速运动;点Q从点B出发沿BA方向以每秒4个单位长的速度匀速运动,过点Q作射线QKAB ,交折线BC-CA于点G.点PQ,同时出发,当点P绕行一周回到点D时停止运动,点Q也随之停止.设点PQ,运动的时间是t秒(0t ).(1)DF,两点间的距离是;(2)射线QK能否把四边形CDEF分成面积相等的两部分?若能,求出t的值.若不能,说明理由;(3)当点P运动到折线EFFC 上,且点P又恰好落在射线QK上时,求t的值;(4)连结PG,当PGAB∥时,请直接..写出t的值.2.如图,矩形ABCD中,AB=6,BC=23,点O是AB的中点,点P在AB的延长线上,且BP=3.一动点E从O点出发,以每秒1个单位长度的速度沿OA匀速运动,到达A点后,立即以原速度沿AO返回;另一动点F从P 点出发,以每秒1个单位长度的速度沿射线PA匀速运动,点E、F同时出发,当两点相遇时停止运动.在点E、F的运动过程中,以EF为边作等边△EFG,使△EFG和矩形ABCD在射线PA的同侧,设运动的时间为t秒(t≥0).(1)当等边△EFG的边FG恰好经过点C时,求运动时间t的值;(2)在整个运动过程中,设等边△EFG和矩形ABCD重叠部分的面积为S,请直接写出S与t之间的函数关系式和相应的自变量t的取值范围;(3)设EG与矩形ABCD的对角线AC的交点为H,是否存在这样的t,使△AOH是等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由.3.如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为y=−43x+163,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运动.动点Q自点B出发,在折线BCD上匀速运动,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P 运动t(秒)时,△OPQ的面积为S(不能构成△OPQ的动点除外).(1)求出点B、C的坐标;(2)求S随t变化的函数关系式;(3)当t为何值时S有最大值?并求出最大值.4.如图,在等腰梯形ABCD中,AD∥BC,AB=DC=50,AD=75,BC=135.点P从点B出发沿折线段BA-AD-DC以每秒5个单位长的速度向点C匀速运动;点Q从点C出发沿线段CB方向以每秒3个单位长的速度匀速运动,过点Q向上作射线QK⊥BC,交折线段CD-DA-AB于点E.点P、Q同时开始运动,当点P与点C 重合时停止运动,点Q也随之停止.设点P、Q运动的时间是t秒(t>0).(1)当点P到达终点C时,求t的值,并指出此时BQ的长;(2)当点P运动到AD上时,t为何值能使PQ∥DC(3)设射线QK扫过梯形ABCD的面积为S,分别求出点E运动到CD、DA上时,S与t的关系式;(4)△PQE能否成为直角三角形?若能,写出t的取值范围;若不能,请说明理由.。
八年级数学下册期末动点问题及压轴题带答案

1.(12分)已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.(1)求证:BD∥AC;(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.2.(12分)如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.一动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB 边向点B以3cm/s的速度运动.P,Q分别从点A和点C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t s,则(1)t为何值时,四边形PQCD为平行四边形?(2)t为何值时,四边形PQCD为等腰梯形?(3)AB边的长是否存在一数值,使四边形PQCD为菱形.如果存在,请求出AB 边的长,如果不存在,请说出理由.3.(本题10分)已知:在正方形ABCD 中,AB =6,P 为边CD 上一点,过P 点作PE ⊥BD 于点E ,连接BP(1) O 为BP 的中点,连接CO 并延长交BD 于点F① 如图1,连接OE ,求证:OE ⊥OC② 如图2,若53=EF BF ,求DP 的长 (2) CP EP 22+=___________4.(本题12分)如图1,直线333+-=x y 分别与y 轴、x 轴交于点A 、点B ,点C 的坐标为(-3,0),D 为直线AB 上一动点,连接CD 交y 轴于点E(1) 点B 的坐标为__________,不等式0333>+-x 的解集为___________(2) 若S △COE =S △ADE ,求点D 的坐标(3) 如图2,以CD 为边作菱形CDFG ,且∠CDF =60°.当点D 运动时,点G 在一条定直线上运动,请求出这条定直线的解析式.5.(11分)如图1,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点A 的坐标为(﹣3,4),点C 在x 轴的正半轴上,直线AC 交y 轴于点M ,AB 边交y 轴于点H ,连接BM .(1)菱形ABCO的边长是 ;(2)求直线AC 的解析式;(3)动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设△PMB 的面积为S (S≠0),点P 的运动时间为t 秒.①求S 与t 之间的函数关系式;②在点P 运动过程中,当S =3,请直接写出t 的值.6.(11分)如图,在直角梯形ABCD 中,AD ∥BC ,∠B=90°,且AD=12cm ,AB=8cm ,DC=10cm ,若动点P 从A 点出发,以每秒2cm 的速度沿线段AD 向点D 运动;动点Q 从C 点出发以每秒3cm 的速度沿CB 向B 点运动,当P 点到达D 点时,动点P 、Q 同时停止运动,设点P 、Q 同时出发,并运动了t 秒,回答下列问题:(1)BC= cm ;(2)当t 为多少时,四边形PQCD 成为平行四边形?(3)当t 为多少时,四边形PQCD 为等腰梯形?(4)是否存在t ,使得△DQC 是等腰三角形?若存在,请求出t 的值;若不存在,说明理由.7、如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、D Q、CQ、BQ,设AP=x.(1)BQ+DQ的最小值是_______,此时x的值是_______;(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.①求证:点E是CD的中点;②求x的值.(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x 的值.8、如图1,平面直角坐标系中,直线AB:y=﹣x+b交x轴于点A(8,0),交y轴正半轴于点B.(1)求点B的坐标;(2)如图2,直线AC交y轴负半轴于点C,AB=BC,P为线段AB上一点,过点P 作y轴的平行线交直线AC于点Q,设点P的横坐标为t,线段PQ的长为d,求d与t之间的函数关系式;(3)在(2)的条件下,M为CA延长线上一点,且AM=CQ,在直线AC上方的直线AB上是否存在点N,使△QMN是以QM为斜边的等腰直角三角形?若存在,请求出点N的坐标及PN的长度;若不存在,请说明理由.1.【解答】解:(1)∵A(0,4),B(0,2),∴OA=4,OB=2,点B为线段OA的中点,又点D为OC的中点,即BD为△AOC的中位线,∴BD∥AC;(2)如图1,作BF⊥AC于点F,取AB的中点G,则G(0,3),∵BD∥AC,BD与AC的距离等于1,∴BF=1,∵在Rt△ABF中,∠AFB=90°,AB=2,点G为AB的中点,∴FG=BG=AB=1,∴△BFG是等边三角形,∠ABF=60°.∴∠BAC=30°,设OC=x,则AC=2x,根据勾股定理得:OA==x,∵OA=4,∴x=∵点C在x轴的正半轴上,∴点C的坐标为(,0);(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,∴DE⊥OC,∵点D为OC的中点,∴OE=EC,∵OE⊥AC,∴∠OCA=45°,∴OC=OA=4,∵点C在x轴的正半轴上,∴点C的坐标为(4,0),设直线AC的解析式为y=kx+b(k≠0).将A(0,4),C(4,0)代入AC的解析式得:解得:∴直线AC的解析式为y=﹣x+4.2.【解答】解:(1)由运动知,AP=t,CQ=3t,∴DP=AD﹣AP=24﹣t,∵四边形PQCD为平行四边形,∴DP=CQ,∴24﹣t=3t,∴t=6;(2)如图2,过点D作DE⊥BC于E,过点P作PF⊥BC于F,∴四边形EFPD是矩形,∴DE=PF,[来源:Z|xx|]∵四边形PQCD是等腰梯形,∴∠PQC=∠DCQ,∵∠PFQ=∠DEC=90°,∴△PFQ≌△DEC,∴FQ=CE,∴BE=AD=24,∴CE=BC﹣BE=2,∵四边形PQCD为等腰梯形,∴CQ=DP+2CE,由运动知,AP=t,CQ=3t,∴DP=AD﹣AP=24﹣t,∴24﹣t+2×2=3t,∴t=7,(3)AB边的长是8时,四边形PQCD为菱形,理由:由(1)知,t=6时,四边形PQCD是平行四边形,∴DP=24﹣6=18,∵平行四边形PQCD是菱形,∴CD=DP=18,如图2,过点D作DE⊥BC于E,∴四边形ABED是矩形,∴AB=DE,在Rt△CDE中,CE=2,CD=18,∴DE==8.3.证明:(1) ① ∵∠PEB =∠PCB =90°,O 为BP 的中点∴OE =OB =OP =OC∴∠POE =2∠DBP ,∠POC =2∠CBP∴∠COE =∠POE +∠POC =2(∠DBP +∠CBP )=90°∴OE ⊥OC② 连接OE 、CE∵△COE 为等腰直角三角形∴∠ECF =45°在等腰Rt △BCD 中,BF 2+DE 2=EF 2设BF =3x ,EF =5x ,则DE =4x∴3x +4x +5x =26,解得x =22 ∴DP =2DE =424=x(2) ∵62==-+=+CD C DP CP EP ∴2322=+CP EP4.解:(1) (3,0)、x <3(2) ∵S △COE =S △ADE∴S △AOB =S △CBD 即33321621⨯⨯=⨯⨯D y ,y D =233 当y =233时,23233333==+-x x ,∴D (23323,) (3) 连接CF∵∠CDF =60°∴△CDF 为等边三角形连接AC∵AB =AC =BC =6∴△ABC 为等边三角形∴△CAF ≌△CBD (SAS )∴∠CAF =∠ACB =60°∴AF ∥x 轴设D (m ,333+-m )过点D 作DH ⊥x 轴于H∴BH =3-m ,DB =6-2m =AF∴F (2m -6,33)由平移可知:G (m -9,m 3-) 令⎪⎩⎪⎨⎧-=-=m y m x 39∴点G 在直线393--=x y 上6.解:根据题意得:PA=2t ,CQ=3t ,则PD=AD-PA=12-2t .(1)如图,过D 点作DE ⊥BC 于E ,则四边形ABED 为长方形,DE=AB=8cm ,AD=BE=12cm ,在直角△CDE 中,∵∠CED=90°,DC=10cm ,DE=8cm ,∴22DC DE -,∴BC=BE+EC=18cm .…………………………………………………………………2分(直接写出最后结果18cm 即可)(2)∵AD ∥BC ,即PD ∥CQ ,∴当PD=CQ 时,四边形PQCD 为平行四边形,即12-2t=3t ,解得t=125秒, 故当t=125秒时四边形PQCD 为平行四边形;………………………………………4分(3)如图,过D 点作DE ⊥BC 于E ,则四边形ABED 为长方形,DE=AB=8cm ,AD=BE=12cm ,当PQ=CD 时,四边形PQCD 为等腰梯形.过点P 作PF ⊥BC 于点F ,过点D 作DE ⊥BC 于点E ,则四边形PDEF 是长方形,EF=PD=12-2t ,PF=DE .在Rt △PQF 和Rt △CDE 中,PQ CD PF DE ==⎧⎨⎩, ∴Rt △PQF ≌Rt △CDE (HL ),∴QF=CE ,∴QC-PD=QC-EF=QF+EC=2CE ,即3t-(12-2t )=12,解得:t=245, 即当t=245时,四边形PQCD 为等腰梯形;……………………………………………8分(4)△DQC 是等腰三角形时,分三种情况讨论:①当QC=DC 时,即3t=10,∴t=103;②当DQ=DC时,36 2t=∴t=4;③当QD=QC时,3t×65 10=∴t=259.故存在t,使得△DQC是等腰三角形,此时t的值为103秒或4秒或259秒.………11分③在Rt△DMQ中,DQ2=DM2+QM2222 (3)8(38) t t=+-36t=100t=25 97.解:(1);-1;(2)①证明:在正方形ABCD中,AB=BC,∠A=∠BCD=90°∵Q点为A点关于BP的对称点∴AB=QB,∠A=∠PQB=90°∴QB=BC,∠BQE=∠BCE∴∠BQC=∠BCQ∴∠EQC=∠EQB-∠CQB=∠ECB-∠QCB=∠ECQ∴EQ=EC在Rt△ABC中∵∠QDE=90°-∠QCE,∠DQE=90°-∠EQC∴∠QDE=∠DQE∴EQ+ED∴CE=EQ=ED即E是CD的中点②(3)或或8.解:(1)∵y=﹣x+b交x轴于点A(8,0),∴0=﹣×8+b,b=6,∴直线AB解析式为y=﹣x+6,令x=0,y=6,B(0,6);(2)∵A(8,0),B(0,6),∴OA=8,OB=6,∵∠AOB=90°,∴AB=10=BC,∴OC=4,∴点C(0,﹣4),设直线AC解析式为y=kx+b’,∴,∴∴直线AC解析式为y=x﹣4,∵P在直线y=﹣x+6上,∴可设点P(t,﹣t+6),∵PQ∥y轴,且点Q在y=x﹣4 上,∴Q(t, t﹣4),∴d=(﹣t+6)﹣(t ﹣4)=﹣t+10;(3)过点M作MG⊥PQ于G,∴∠QGM=90°=∠COA,∵PQ∥y轴,∴∠OCA=∠GQM,∵CQ=AM,∴AC=QM,在△OAC与△GMQ中,,∴△OAC≌△GMQ,∴QG=OC=4,GM=OA=8,过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,∴∠MGH=∠RHG=∠MRH=90°,∴四边形GHRM是矩形,∴HR=GM=8,可设GH=RM=k,∵△MNQ是等腰直角三角形,∴∠QMN=90°,NQ=NM,∴∠HNQ+∠HQN=90°,∴∠HNQ+∠RNM=90°,∴∠RNM=∠HQN,∴△HNQ≌△RMN,∴HN=RM=k,NR=QH=4+k,∵HR=HN+NR,∴k+4+k=8,∴k=2,∴GH=NH=RM=2,∴HQ=6,∵Q(t,t﹣4),∴N(t+2,t﹣4+6)即 N(t+2,t+2)∵N在直线AB:y=﹣x+6上,∴t+2=﹣(t+2)+6,∴t=2,∴P(2,),N(4,3),∴PH=,NH=2,∴PN==.。
初二动点问题及中考压轴题
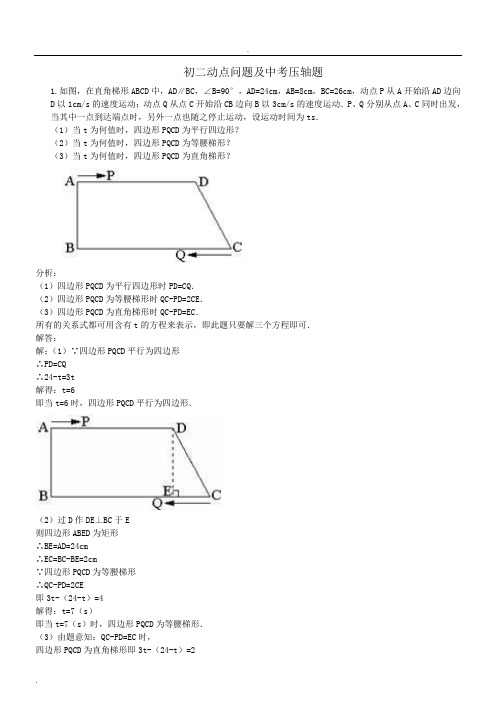
初二动点问题及中考压轴题1.如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A开始沿AD边向D以1cm/s的速度运动;动点Q从点C开始沿CB边向B以3cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts.(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形PQCD为等腰梯形?(3)当t为何值时,四边形PQCD为直角梯形?分析:(1)四边形PQCD为平行四边形时PD=CQ.(2)四边形PQCD为等腰梯形时QC-PD=2CE.(3)四边形PQCD为直角梯形时QC-PD=EC.所有的关系式都可用含有t的方程来表示,即此题只要解三个方程即可.解答:解:(1)∵四边形PQCD平行为四边形∴PD=CQ∴24-t=3t解得:t=6即当t=6时,四边形PQCD平行为四边形.(2)过D作DE⊥BC于E则四边形ABED为矩形∴BE=AD=24cm∴EC=BC-BE=2cm∵四边形PQCD为等腰梯形∴QC-PD=2CE即3t-(24-t)=4解得:t=7(s)即当t=7(s)时,四边形PQCD为等腰梯形.(3)由题意知:QC-PD=EC时,四边形PQCD为直角梯形即3t-(24-t)=2解得:t=6.5(s)即当t=6.5(s)时,四边形PQCD为直角梯形.点评:此题主要考查了平行四边形、等腰梯形,直角梯形的判定,难易程度适中.2.如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.(1)试说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.分析:(1)根据CE平分∠ACB,MN∥BC,找到相等的角,即∠OEC=∠ECB,再根据等边对等角得OE=OC,同理OC=OF,可得EO=FO.(2)利用矩形的判定解答,即有一个内角是直角的平行四边形是矩形.(3)利用已知条件及正方形的性质解答.解答:解:(1)∵CE平分∠ACB,∴∠ACE=∠BCE,∵MN∥BC,∴∠OEC=∠ECB,∴∠OEC=∠OCE,∴OE=OC,同理,OC=OF,∴OE=OF.(2)当点O运动到AC中点处时,四边形AECF是矩形.如图AO=CO,EO=FO,∴四边形AECF为平行四边形,∵CE平分∠ACB,∴∠ACE= ∠ACB,同理,∠ACF= ∠ACG,∴∠ECF=∠ACE+∠ACF= (∠ACB+∠ACG)= ×180°=90°,∴四边形AECF是矩形.(3)△ABC是直角三角形∵四边形AECF是正方形,∴AC⊥EN,故∠AOM=90°,∵MN∥BC,∴∠BCA=∠AOM,∴∠BCA=90°,∴△ABC是直角三角形.点评:本题主要考查利用平行线的性质“等角对等边”证明出结论(1),再利用结论(1)和矩形的判定证明结论(2),再对(3)进行判断.解答时不仅要注意用到前一问题的结论,更要注意前一问题为下一问题提供思路,有相似的思考方法.是矩形的判定和正方形的性质等的综合运用.3.如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P从B点出发,沿线段BC向点C 作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q 运动的时间为t秒.(1)求NC,MC的长(用t的代数式表示);(2)当t为何值时,四边形PCDQ构成平行四边形;(3)是否存在某一时刻,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;(4)探究:t为何值时,△PMC为等腰三角形.分析:(1)依据题意易知四边形ABNQ是矩形∴NC=BC-BN=BC-AQ=BC-AD+DQ,BC、AD已知,DQ就是t,即解;∵AB∥QN,∴△CMN∽△CAB,∴CM:CA=CN:CB,(2)CB、CN已知,根据勾股定理可求CA=5,即可表示CM;四边形PCDQ构成平行四边形就是PC=DQ,列方程4-t=t即解;(3)可先根据QN平分△ABC的周长,得出MN+NC=AM+BN+AB,据此来求出t的值.然后根据得出的t的值,求出△MNC的面积,即可判断出△MNC的面积是否为△ABC面积的一半,由此可得出是否存在符合条件的t值.(4)由于等腰三角形的两腰不确定,因此分三种情况进行讨论:①当MP=MC时,那么PC=2NC,据此可求出t的值.②当CM=CP时,可根据CM和CP的表达式以及题设的等量关系来求出t的值.③当MP=PC时,在直角三角形MNP中,先用t表示出三边的长,然后根据勾股定理即可得出t的值.综上所述可得出符合条件的t的值.解答:解:(1)∵AQ=3-t∴CN=4-(3-t)=1+t在Rt△ABC中,AC2=AB2+BC2=32+42∴AC=5在Rt△MNC中,cos∠NCM= = ,CM= .(2)由于四边形PCDQ构成平行四边形∴PC=QD,即4-t=t解得t=2.(3)如果射线QN将△ABC的周长平分,则有:MN+NC=AM+BN+AB即:(1+t)+1+t= (3+4+5)解得:t= (5分)而MN= NC= (1+t)∴S△MNC= (1+t)2= (1+t)2当t= 时,S△MNC=(1+t)2= ≠ ×4×3∴不存在某一时刻t,使射线QN恰好将△ABC的面积和周长同时平分.(4)①当MP=MC时(如图1)则有:NP=NC即PC=2NC∴4-t=2(1+t)解得:t=②当CM=CP时(如图2)则有:(1+t)=4-t解得:t=③当PM=PC时(如图3)则有:在Rt△MNP中,PM2=MN2+PN2而MN= NC= (1+t)PN=NC-PC=(1+t)-(4-t)=2t-3∴[ (1+t)]2+(2t-3)2=(4-t)2解得:t1= ,t2=-1(舍去)∴当t= ,t= ,t= 时,△PMC为等腰三角形点评:此题繁杂,难度中等,考查平行四边形性质及等腰三角形性质.考查学生分类讨论和数形结合的数学思想方法.4.如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.(1)当x为何值时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形;(2)当x为何值时,以P,Q,M,N为顶点的四边形是平行四边形;(3)以P,Q,M,N为顶点的四边形能否为等腰梯形?如果能,求x的值;如果不能,请说明理由.分析:以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边构成一个三角形的必须条件是点P、N重合且点Q、M不重合,此时AP+ND=AD即2x+x2=20cm,BQ+MC≠BC即x+3x≠20cm;或者点Q、M重合且点P、N不重合,此时AP+ND≠AD即2x+x2≠20cm,BQ+MC=BC即x+3x=20cm.所以可以根据这两种情况来求解x的值.以P,Q,M,N为顶点的四边形是平行四边形的话,因为由第一问可知点Q只能在点M的左侧.当点P在点N的左侧时,AP=MC,BQ=ND;当点P在点N的右侧时,AN=MC,BQ=PD.所以可以根据这些条件列出方程关系式.如果以P,Q,M,N为顶点的四边形为等腰梯形,则必须使得AP+ND≠AD即2x+x2≠20cm,BQ+MC≠BC即x+3x≠20cm,AP=ND即2x=x2,BQ=MC即x=3x,x≠0.这些条件不能同时满足,所以不能成为等腰梯形.解答:解:(1)当点P与点N重合或点Q与点M重合时,以PQ,MN为两边,以矩形的边(AD或BC)的一部分为第三边可能构成一个三角形.①当点P与点N重合时,由x2+2x=20,得x1= -1,x2=- -1(舍去).因为BQ+CM=x+3x=4(-1)<20,此时点Q与点M不重合.所以x= -1符合题意.②当点Q与点M重合时,由x+3x=20,得x=5.此时DN=x2=25>20,不符合题意.故点Q与点M不能重合.所以所求x的值为-1.(2)由(1)知,点Q只能在点M的左侧,①当点P在点N的左侧时,由20-(x+3x)=20-(2x+x2),解得x1=0(舍去),x2=2.当x=2时四边形PQMN是平行四边形.②当点P在点N的右侧时,由20-(x+3x)=(2x+x2)-20,解得x1=-10(舍去),x2=4.当x=4时四边形NQMP是平行四边形.所以当x=2或x=4时,以P,Q,M,N为顶点的四边形是平行四边形.(3)过点Q,M分别作AD的垂线,垂足分别为点E,F.由于2x>x,所以点E一定在点P的左侧.若以P,Q,M,N为顶点的四边形是等腰梯形,则点F一定在点N的右侧,且PE=NF,即2x-x=x2-3x.解得x1=0(舍去),x2=4.由于当x=4时,以P,Q,M,N为顶点的四边形是平行四边形,所以以P,Q,M,N为顶点的四边形不能为等腰梯形.点评:本题考查到三角形、平行四边形、等腰梯形等图形的边的特点.5.如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=15cm,BC=21cm,点M从点A开始,沿边AD向点D 运动,速度为1cm/s;点N从点C开始,沿边CB向点B运动,速度为2cm/s、点M、N分别从点A、C出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒.(1)当t为何值时,四边形MNCD是平行四边形?(2)当t为何值时,四边形MNCD是等腰梯形?分析:(1)根据平行四边形的性质,对边相等,求得t值;(2)根据等腰梯形的性质,下底减去上底等于12,求解即可.解答:解:(1)∵MD∥NC,当MD=NC,即15-t=2t,t=5时,四边形MNCD是平行四边形;(2)作DE⊥BC,垂足为E,则CE=21-15=6,当CN-MD=12时,即2t-(15-t)=12,t=9时,四边形MNCD是等腰梯形点评:考查了等腰梯形和平行四边形的性质,动点问题是中考的重点内容.6.如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21,动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,P、Q 分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,设运动时间为t(s).(1)设△BPQ的面积为S,求S与t之间的函数关系;(2)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形?分析:(1)若过点P作PM⊥BC于M,则四边形PDCM为矩形,得出PM=DC=12,由QB=16-t,可知:s= PM×QB=96-6t;(2)本题应分三种情况进行讨论,①若PQ=BQ,在Rt△PQM中,由PQ2=PM2+MQ2,PQ=QB,将各数据代入,可将时间t求出;②若BP=BQ,在Rt△PMB中,由PB2=BM2+PM2,BP=BQ,将数据代入,可将时间t求出;③若PB=PQ,PB2=PM2+BM2,PB=PQ,将数据代入,可将时间t求出.解答:解:(1)过点P作PM⊥BC于M,则四边形PDCM为矩形.∴PM=DC=12,∵QB=16-t,∴s= •QB•PM= (16-t)×12=96-6t(0≤t≤ ).(2)由图可知,CM=PD=2t,CQ=t,若以B、P、Q为顶点的三角形是等腰三角形,可以分三种情况:①若PQ=BQ,在Rt△PMQ中,PQ2=t2+122,由PQ2=BQ2得t2+122=(16-t)2,解得;②若BP=BQ,在Rt△PMB中,PB2=(16-2t)2+122,由PB2=BQ2得(16-2t)2+122=(16-t)2,此方程无解,∴BP≠PQ.③若PB=PQ,由PB2=PQ2得t2+122=(16-2t)2+122得,t2=16(不合题意,舍去).综上所述,当或时,以B、P、Q为顶点的三角形是等腰三角形.点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象.7.直线y=- 34x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q 沿线段OA运动,速度为每秒1个单位长度,点P沿路线O⇒B⇒A运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t(秒),△OPQ的面积为S,求出S与t之间的函数关系式;(3)当S= 485时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.分析:(1)分别令y=0,x=0,即可求出A、B的坐标;(2))因为OA=8,OB=6,利用勾股定理可得AB=10,进而可求出点Q由O到A的时间是8秒,点P的速度是2,从而可求出,当P在线段OB上运动(或0≤t≤3)时,OQ=t,OP=2t,S=t2,当P在线段BA上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,作PD⊥OA于点D,由相似三角形的性质,得 PD=48-6t5,利用S= 12OQ×PD,即可求出答案;(3)令S= 485,求出t的值,进而求出OD、PD,即可求出P的坐标,利用平行四边形的对边平行且相等,结合简单的计算即可写出M的坐标.解答:解:(1)y=0,x=0,求得A(8,0)B(0,6),(2)∵OA=8,OB=6,∴AB=10.∵点Q由O到A的时间是 81=8(秒),∴点P的速度是 6+108=2(单位长度/秒).当P在线段OB上运动(或O≤t≤3)时,OQ=t,OP=2t,S=t2.当P在线段BA上运动(或3<t≤8)时,OQ=t,AP=6+10-2t=16-2t,如图,做PD⊥OA于点D,由 PDBO=APAB,得PD= 48-6t5.∴S= 12OQ•PD=- 35t2+245t.(3)当S= 485时,∵ 485>12×3×6∴点P在AB上当S= 485时,- 35t2+245t= 485∴t=4∴PD= 48-6×45= 245,AD=16-2×4=8AD= 82-(245)2= 325∴OD=8- 325= 85∴P( 85, 245)M1( 285, 245),M2(- 125, 245),M3( 125,- 245)点评:本题主要考查梯形的性质及勾股定理.在解题(2)时,应注意分情况进行讨论,防止在解题过程中出现漏解现象.动点问题及四边形难题习题1如图1,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点A 的坐标为(-3,4),点C 在x 轴的正半轴上,直线AC 交y 轴于点M ,AB 边交y 轴于点H .(1)求直线AC 的解析式;(2)连接BM ,如图2,动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设△PMB 的面积为S (S ≠0),点P 的运动时间为t 秒,求S 与t 之间的函数关系式(要求写出自变量t 的取值范围);2.已知:如图,在直角梯形COAB 中,OC AB ∥,以O 为原点建立平面直角坐标系,A B C ,,三点的坐标分别为(80)(810)(04)A B C ,,,,,,点D 为线段BC 的中点,动点P 从点O 出发,以每秒1个单位的速度,沿折线OABD 的路线移动,移动的时间为t 秒.(1)求直线BC 的解析式;(2)若动点P 在线段OA 上移动,当t 为何值时,四边形OPDC 的面积是梯形COAB 面积的27? (3)动点P 从点O 出发,沿折线OABD 的路线移动过程中,设OPD △的面积为S ,请直接写出S 与t 的函数关系式,并指出自变量t 的取值范围;3.如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点. A BDC O P xy(1)如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动. ①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由;②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?4. 如图,已知AD 与BC 相交于E ,∠1=∠2=∠3,BD =CD ,∠ADB =90°,CH ⊥AB 于H ,CH 交AD 于F.(1)求证:CD ∥AB ;(2)求证:△BDE ≌△ACE ;(3)若O 为AB 中点,求证:OF =12BE.5、如图1―4―2l ,在边长为a 的菱形ABCD 中,∠DAB =60°,E 是异于A 、D 两点的动点,F 是CD 上的动点,满足A E +CF=a ,说明:不论E 、F 怎样移动,三角形BEF 总是正三角形.6、如图1-4-38,等腰梯形ABCD 中,AD ∥BC ,AB =CD ,∠ DBC =45○ ,翻折梯形使点B 重合于点 D ,折痕分别交边 AB 、BC 于点F 、E ,若AD=2,BC=8,求BE 的长.7、在平行四边形ABCD 中,E 为BC 的中点,连接AE 并延长交DC 的延长线于点F . A QC DB P(1)求证:CF AB ;(2)当BC 与AF 满足什么数量关系时, 四边形ABFC 是矩形,并说明理由.8、如图l -4-80,已知正方形ABCD 的对角线AC 、BD 相交于点O ,E 是AC 上一点,过点A 作AG ⊥EB ,垂足为G ,AG 交BD 于F ,则OE=OF . (1)请证明0E=OF(2)解答(1)题后,某同学产生了如下猜测:对上述命题,若点E 在AC 的延长线上,AG ⊥EB ,AG 交 EB 的延长线于 G ,AG 的延长线交DB 的延长线于点F ,其他条件不变,则仍有OE=OF .问:猜测所得结论是否成立?若成立,请给出证明;若不成立,请说明理由.9已知:如图4-26所示,△ABC 中,AB=AC ,∠BAC=90°,D 为BC 的中点,P 为BC 的延长线上一点,PE ⊥直线AB 于点E ,PF ⊥直线AC 于点F .求证:DE ⊥DF 并且相等.10已知:如图4-27,ABCD 为矩形,CE ⊥BD 于点E ,∠BAD 的平分线与直线CE 相交于点F .求证:CA=CF .FEDCBA11已知:如图4-56A .,直线l 通过正方形ABCD 的顶点D 平行于对角线AC ,E 为l 上一点,EC=AC ,并且EC 与边AD 相交于点F .求证:AE=AF .本例中,点E 与A 位于BD 同侧.如图4-56B .,点E 与A 位于BD 异侧,直线EC 与DA 的延长线交于点F ,这时仍有AE=AF .请自己证明.动点问题练习题1、已知:等边三角形ABC 的边长为4厘米,长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动(运动开始时,点M 与点A 重合,点N 到达点B 时运动终止),过点M N 、分别作AB 边的垂线,与ABC △的其它边交于P Q 、两点,线段MN 运动的时间为t 秒.1、线段MN 在运动的过程中,t 为何值时,四边形MNQP 恰为矩形?并求出该矩形的面积;(2)线段MN 在运动的过程中,四边形MNQP 的面积为S ,运动的时间为t .求四边形MNQP 的面积S 随运动时间t 变化的函数关系式,并写出自变量t 的取值范围.C P Q BA MNO M A N B C yx2、如图,在梯形ABCD 中,354245AD BC AD DC AB B ====︒∥,,,,∠.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒. (1)求BC 的长.(2)当MN AB ∥时,求t 的值.(3)试探究:t 为何值时,MNC △为等腰三角形.3、如图,在平面直角坐标系中,四边形OABC 是梯形,OA ∥BC ,点A 的坐标为(6,0),点B 的坐标为(4,3),点C 在y 轴的正半轴上.动点M 在OA 上运动,从O 点出发到A 点;动点N 在AB 上运动,从A 点出发到B 点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t (秒).(1)求线段AB 的长;当t 为何值时,MN ∥OC ?(2)设△CMN 的面积为S ,求S 与t 之间的函数解析式, 并指出自变量t 的取值范围;S 是否有最小值? 若有最小值,最小值是多少? (3)连接AC ,那么是否存在这样的t ,使MN 与AC 互相垂直?若存在,求出这时的t 值;若不存在,请说明理由.2、如图,在Rt △ABC 中,∠C =90°,AC =12,BC =16,动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动,动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动.P ,Q 分别从点A ,C 同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,△PCQ 关于直线PQ 对称的图形是△PDQ .设运动时间为t (秒).(1)设四边形PCQD 的面积为y ,求y 与t 的函数关系式; (2)t 为何值时,四边形PQBA 是梯形?(3)是否存在时刻t ,使得PD ∥AB ?若存在,求出t 的值;若不存在,请说明理由;(4)通过观察、画图或折纸等方法,猜想是否存在时刻t ,使得PD ⊥AB ?若存在,请估计t 的值在括号中的哪个时间段内(0≤t ≤1;1<t ≤2;2<t ≤3;3<t ≤4);若不存在,请简要说明理由.A D CB M NA P C QB DEDBCAQP3、如图,A 、B 分别为x 轴和y 轴正半轴上的点。
人教版八年级下册数学期末复习:动点问题压轴题

人教版八年级下册数学期末复习: 动点压轴题1. 如图, 在四边形ABCD中, ∠A=∠B=∠BCD=90°, AB=DC=3, AD=BC=7. 延长BC 到E, 使CE=4, 连接DE, 由直角三角形的性质可知DE=5. 动点P从点B出发, 以每秒2个单位的速度沿BC−CD−DA向终点A运动, 设点P运动的时间为t秒. (t>0)(1)当时, ______;(用含的代数式表示)(2)请用含t的代数式表示ABP△的面积S;(不包括点P与点A重合的情况)(3)当点在BC边上时, 直接写出点到四边形ABED任意相邻两边距离相等时的值.2. 如图, 在正方形ABCD中, E是边AB上的一动点(不与点A, B重合), 连接DE, 点A关于直线DE的对称点为F, 连接EF并延长交BC于点G, 且∠CGD=∠DGE, 连接DG, 过点E作EH⊥DE交DG的延长线于点H, 连接BH.(1)猜想: △DEH的形状, 并说明理由.(2)猜想BH与AE的数量关系, 并证明.3. 如图, 在中, , , AB=8cm, 动点从点开始以的速度向点运动, 动点从点开始以的速度向点运动, 两点同时运动, 同时停止, 运动时间为.(1)当为何值时, 是等边三角形?(2)当为何值时, 是直角三角形?(3)过点作交于点, 连接, 求证:四边形是平行四边形.4. 已知正方形, 点F是射线上一动点(不与C, D重合), 连接并延长交直线于点E, 交于点H, 连接, 过点C作交于点G.(1)若点F在边上, 如图1.①证明:⑤猜想线段CG与EF的数量关系并说明理由(2)取中点M, 连结, 若, 正方形边长为6, 求的长5. 已知: 如图, 在菱形ABCD中, ∠B=60°, 点E、F分别是AB.AD上的动点, 且BE=AF.(1)求证: △ECF是等边三角形(2)已知M为CD的中点, 仅用无刻度的直尺作出最短的EF(不写作法, 保留作图痕迹)6. 如图, 在矩形ABCD中, AB=9, 点E在边AB上, 且AE=5. 动点P从点A出发, 以每秒1个单位长度, 沿折线AD—DC运动, 到达点C后停止运动. 连接PE, 作点A关于直线PE的对称点F, 设点P的运动时间为t秒(t>0).(1)如图1, 在点P的运动过程中, 当F与点C重合时, 求BC的长;(2)如图2, 如果BC=4, 当点F落在矩形ABCD的边上时, 求t的值.7. 如图, 已知长方形的边AD=8, AB=4, 动点M从点A出发, 以每秒2个单位长度的速度沿A→D→A的路径匀速运动, 同时, 动点N从点C出发, 沿C→B方向以每秒1个单位长度的速度匀速运动, 当其中一个动点到达终点时, 另一点也随之停止运动, 设运动时间为t秒.(1)如(图一), 当运动时间为1秒时, 求MN的长度;(2)当0≤t≤4时, 直接写出AMN为直角三角形时的运动时间t的值;(3)如(图二), 当4<t<8时, 判断AMN的形状, 并说明理由.8. 如图1, 是正方形边上一点, 过点作, 交的延长线于点.(1)求证: ;(2)如图2, 若正方形边长为6, 线段上有一动点从点出发, 以1个单位长度每秒沿向运动. 同时线段上另一动点从点出发, 以2个单位长度每秒沿向运动, 当点到达点后点也停止运动. 连接, 点的运动时间为, 的面积为, 求关于的函数关系式;(3)如图3, 连接, 连接交于点, 连接并延长, 交于点, 已知, , 求的长.9. 在菱形中, , , 点E是边的中点, 点M是边上一动点(不与点A重合), 连接并延长交射线于点N, 连接、,(1)求证: 四边形是平行四边形;(2)当_______时, 四边形是矩形;(3)四边形能否成为菱形?若能, 求出的值, 若不能, 请说明理由.10. 已知正方形ABCD, 点F是射线DC上一动点(不与C.D重合), 连接AF并延长交直线BC于点E, 交BD于H, 连接CH, 过点C作CG⊥HC交AE于点G.(1)若点F在边CD上, 如图1.①证明: ∠DAH=∠DCH;②猜想GFC的形状并说明理由.(2)取DF中点M, 连结MG.若MG=5, 正方形边长为8, 求BE的长.11. 如图, 在△ABC中, ∠BAC=90°, AB=AC, 点D是直线BC上一动点(不与端点重合), 以AD为边在AD右侧作正方形ADEF, 连接CF.(1)如图1, 当点D在线段BC上时, 求证: CF⊥BC;(2)如图2, 当点D在线段BC延长线上时, CF⊥BC还成立吗?如成立请证明, 如不成立请说明理由;(3)在图1、图2中, 选择一个图形证明:BD2+CD2=2AD2.12. 如图, 在直角梯形中, , , , , , 动点P从点A开始沿AD边向点D以速度运动, 动点Q从点C开始沿CB边向点B以的速度运动. 点P、Q分别从点A.C同时出发, 当其中一点到达端点时, 另一点随之停止运动. 设运动时间为t秒. 求:(1)t为何值时, 四边形PQCD为平行四边形?(2)t为何值时, 四边形ABQP为矩形?(3)是否存在, 使梯形ABQP的面积为?若存在请求出, 若不存在请说明理由.13. 在中, 为锐角, 点D为射线BC上一动点, 连接AD, 以AD为一边且在AD的右侧作正方形ADEF. 解答下列问题:(1)如果,①如图1, 当点D在线段BC上时(与点B不重合), 线段CF、BD之间的位置关系为;数量关系为;②如图2, 当点D在线段BC的延长线上时, ①中的结论是否仍然成立, 并说明理由;(2)如图3, 如果, 点D在线段BC上运动(与点B不重合).试探究:当时, (1)中的CF, BD之间的位置关系是否仍然成立, 并说明理由.14. 如图, 在平面直角坐标系中, 点O是坐标原点, 四边形OABC是平行四边形, 点A的坐标为(14, 0), 点B的坐标为.(1)填空: 点C的坐标为;平行四边形OABC的对称中心的点的坐标为;(2)动点P从点O出发, 沿OA方向以每秒1个单位的速度向终点A匀速运动, 动点Q 从点A出发, 沿AB方向以每秒2个单位的速度向终点B匀速运动, 一点到达终点时, 另一点停止运动. 设点P运动的时间为t秒, 求当t为何值时, △PQC的面积是平行四边形OABC面积的一半?(3)当△PQC的面积是平行四边形OABC面积的一半时, 在平面直角坐标系中找到一点M, 使以M、P、Q、C为顶点的四边形是平行四边形, 请直接写出点M的坐标.15. 如图, 已知O是坐标原点, 点A的坐标是(5, 0), 点B是y轴正半轴上一动点, 以OB, OA为边作矩形OBCA, 点E, H分别在边BC和边OA上, 将△BOE沿着OE对折, 使点B落在OC上的F点处, 将△ACH沿着CH对折, 使点A落在OC上的G点处.(1)求证: 四边形OECH是平行四边形;(2)当点B运动到使得点F, G重合时, 求点B的坐标, 并判断四边形OECH是什么四边形?说明理由;(3)当点B运动到使得点F, G将对角线OC三等分时, 直接写出点B的坐标.16. 如图, 把矩形OABC放入平面直角坐标系xOy中, 使分别落在x, y轴的正半轴上, 其中, 对角线AC所在直线解析式为, 将矩形OABC沿着BE折叠, 使点A落在边OC 上的D处.(1)求点B的坐标;(2)求EA的长度;(3)点P是y轴上一动点, 是否存在点P使得△PBE的周长最小, 若存在, 请求出点P的坐标, 如不存在, 请说明理由.17. 【情境】某校数学兴趣小组尝试自制数学学具进行自主合作探究. 图①是一块边长为的等边三角形学具, 是边上一个动点, 由点向点运动, 速度为, 是边延长线上一动点, 与点同时以相同的速度由点向延长线方向运动, 连接, 交于点, 设点运动的时间为.(1)【问题】填空: _____;(2)【问题】当时, 求的值;(3)【探究】如图②, 过点作, 垂足为, 在点, 点运动过程中, 线段的长度是否发生变化?若不变, 请求出的长度;若变化, 请说明理由.18. 在长方形ABCD中, AB=4, BC=8, 点P、Q为BC边上的两个动点(点P位于点Q的左侧, P、Q均不与顶点重合), PQ=2(1)如图①, 若点E为CD边上的中点, 当Q移动到BC边上的中点时, 求证: AP=QE;(2)如图②, 若点E为CD边上的中点, 在PQ的移动过程中, 若四边形APQE的周长最小时, 求BP的长;(3)如图③, 若M、N分别为AD边和CD边上的两个动点(M、N均不与顶点重合), 当BP=3, 且四边形PQNM的周长最小时, 求此时四边形PQNM的面积.19. 如图, 长方形ABCD中, AB=4cm, BC=6cm, 现有一动点P从A出发以2cm/秒的速度, 沿矩形的边A—B—C—D—A返回到点A停止, 点P的运动时间为t秒.(1)当t=3秒时, BP=cm;(2)当t为何值时, 连结CP, DP, △CDP为等腰三角形;(3)Q为AD边上的点, 且DQ=5, 当t为何值时, 以长方形的两个顶点及点P为顶点的三角形与△DCQ全等.20. 在矩形ABCD中, AB=6, BC=8, 点E是射线BC上一个动点, 连接AE并延长交射线DC于点F, 将△ABE沿直线AE翻折到△AB'E, 延长AB'与直线CD交于点M.(1)求证: AM=MF;(2)当点E是边BC的中点时, 求CM的长;(3)当CF=4时, 求CM的长.参考答案:1. (1)2t−7;(2)S=;(3)点到四边形ABED任意相邻两边距离相等时的值为1.5秒或3秒.2. (1)等腰直角三角形,(2), 证明见解析3. (1)(2)4t=或8 5(3)见解析4. (1)①证明见解析;②结论,(2)BE的长为6+6-6. (1)BC的长为3;(2)t的值为6秒或12秒或14秒.7. (1)(2)83或4(3)⑤AMN是锐角三角形8. (2)(3)2.49. (2)1;(3)210. (1)②GFC是等腰三角形;(2)BE的长为14或2.11. (2)成立12. (1)6(2)13 2(3)不存在13. (1)①, ;②成立(2)成立14. (1), ;(2)当t为0或4时, △PQC的面积是平行四边形OABC面积的一半(3)或(10, -4)或或(18, 0)或或15. (2)B(0, );四边形OECH是菱形(3)点B的坐标是(0, )或(0, )16.(1)B(6, 10)(2)103 AE=(3)400,13 P⎛⎫ ⎪⎝⎭17. (1)24(2)4(3)线段DE的长度不改变, DE=618. (2)4(3)419. (1)2;(2)或或;(3)2.5或4.5或7.5或9.5 20.(2)8 3(3)215或21。
中考数学压轴题专题-动点综合问题
专题15动点综合问题【考点1】动点之全等三角形问题【例1】1.如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s 的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时,△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)【变式1-1】已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是线段OB、OC上的动点(1)如果动点E 、F 满足BE =OF (如图),且AE ⊥BF 时,问点E 在什么位置?并证明你的结论;(2)如果动点E 、F 满足BE =CF (如图),写出所有以点E 或F 为顶点的全等三角形(不得添加辅助线).【变式1-2】如图①,将长方形纸片沿对角线剪成两个全等的直角三角形ABC 、EDF ,其中AB =8cm ,BC =6cm ,AC =10cm .现将△ABC 和△EDF 按如图②的方式摆放(点A 与点D 、点B 与点E 分别重合).动点P 从点A 出发,沿AC 以2cm /s 的速度向点C 匀速移动;同时,动点Q 从点E 出发,沿射线ED 以acm /s (0<a <3)的速度匀速移动,连接PQ 、CQ 、FQ ,设移动时间为ts (0≤t ≤5).(1)当t =2时,S △AQF =3S △BQC ,则a =;(2)当以P 、C 、Q 为顶点的三角形与△BQC 全等时,求a 的值;(3)如图③,在动点P 、Q 出发的同时,△ABC 也以3cm /s 的速度沿射线ED 匀速移动,当以A 、P 、Q 为顶点的三角形与△EFQ 全等时,求a 与t 的值.【考点2】动点之直角三角形问题【例2】如图,在四边形纸片ABCD 中,//AB CD ,60A ∠=︒,30B ∠=︒,2CD =,4BC =,点E 是AB 边上的动点,点F 是折线A D C --上的动点,将纸片ABCD 沿直线EF 折叠,使点A 的对应点A '落在AB 边上,连接A C ',若A BC ' 是直角三角形,则AE 的长为________.【变式2-1】(2019·辽宁中考模拟)如图,已知二次函数y =ax 2+bx+4的图象与x 轴交于点A(4,0)和点D(﹣1,0),与y 轴交于点C ,过点C 作BC 平行于x 轴交抛物线于点B ,连接AC(1)求这个二次函数的表达式;(2)点M 从点O 出发以每秒2个单位长度的速度向点A 运动;点N 从点B 同时出发,以每秒1个单位长度的速度向点C 运动,其中一个动点到达终点时,另一个动点也随之停动,过点N 作NQ 垂直于BC 交AC 于点Q ,连结MQ.①求△AQM 的面积S 与运动时间t 之间的函数关系式,写出自变量的取值范围;当t 为何值时,S 有最大值,并求出S 的最大值;②是否存在点M ,使得△AQM 为直角三角形?若存在,求出点M 的坐标;若不存在,说明理由.【变式2-2】如图,在矩形OAHC 中,8,12OC OA ==,B 为CH 中点,连接AB .动点M 从点O 出发沿OA 边向点A 运动,动点N 从点A 出发沿AB 边向点B 运动,两个动点同时出发,速度都是每秒1个单位长度,连接,,CM CN MN ,设运动时间为t (秒)(010)t <<.则t =_____时,CMN ∆为直角三角形【考点3】动点之等腰三角形问题【例3】如图,AB 是⊙O 的直径,BC 是弦,10cm AB =,6cm BC =.若点P 是直径AB 上一动点,当PBC 是等腰三角形时,AP =__________cm .【变式3-1】如图①,已知正方形ABCD 边长为2,点P 是AD 边上的一个动点,点A 关于直线BP 的对称点是点Q ,连结PQ 、DQ 、CQ 、BQ .设AP=x.(1)当1x =时,求BP 长;(2)如图②,若PQ 的延长线交CD 边于E ,并且90CQD ∠=o ,求证:CEQ ∆为等腰三角形;(3)若点P 是射线AD 上的一个动点,则当CDQ ∆为等腰三角形时,求x 的值.【变式3-2】(2019·河南中考模拟)如图,抛物线y=ax 2+bx+3交y 轴于点A ,交x 轴于点B (-3,0)和点C (1,0),顶点为点M .(1)求抛物线的解析式;(2)如图,点E 为x 轴上一动点,若△AME 的周长最小,请求出点E 的坐标;(3)点F 为直线AB 上一个动点,点P 为抛物线上一个动点,若△BFP 为等腰直角三角形,请直接写出点P 的坐标.【变式3-3】(2019·广西中考真题)已知抛物线2y mx =和直线y x b =-+都经过点()2,4M -,点O 为坐标原点,点P 为抛物线上的动点,直线y x b =-+与x 轴、y 轴分别交于A B 、两点.(1)求m b 、的值;(2)当PAM ∆是以AM 为底边的等腰三角形时,求点P 的坐标;(3)满足(2)的条件时,求sin BOP ∠的值.【考点4】动点之相似三角形问题【例4】如图,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC 是相似三角形,求AP的长.【变式4-1】已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A,C的坐标分别为A(﹣3,0),C(1,0),BC=3 4AC(1)求过点A,B的直线的函数表达式;(2)在x轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;(3)在(2)的条件下,如P,Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m,使得△APQ与△ADB相似?如存在,请求出m的值;如不存在,请说明理由.【变式4-2】如图,正方形ABCD,点P为射线DC上的一个动点,点Q为AB的中点,连接PQ,DQ,过点P作PE⊥DQ于点E.(1)请找出图中一对相似三角形,并证明;(2)若AB=4,以点P,E,Q为顶点的三角形与△ADQ相似,试求出DP的长.【考点5】动点之平行四边形问题(含特殊四边形)【例5】如图,抛物线23y ax bx =++与x 轴交于(3,0),(1,0)A B -两点,与y 轴交于点C .(1)求抛物线的解析式;(2)点P 是抛物线上的动点,且满足2PAO PCO S S ∆∆=,求出P 点的坐标;(3)连接BC ,点E 是x 轴一动点,点F 是抛物线上一动点,若以B 、C 、E 、F 为顶点的四边形是平行四边形时,请直接写出点F 的坐标.备用图【变式5-1】(2019·江西中考真题)在图1,2,3中,已知,,点为线段上的动点,连接,以为边向上作菱形,且.(1)如图1,当点与点重合时,________°;(2)如图2,连接.①填空:_________(填“>”,“<”,“=”);②求证:点在的平分线上;(3)如图3,连接,,并延长交的延长线于点,当四边形是平行四边形时,求的值.【变式5-2】(2019·湖南中考真题)如图,二次函数213y x bx c =-++的图象过原点,与x 轴的另一个交点为()8,0(1)求该二次函数的解析式;(2)在x轴上方作x轴的平行线1y m=,交二次函数图象于A、B两点,过A、B两点分别作x轴的垂线,垂足分别为点D、点C.当矩形ABCD为正方形时,求m的值;(3)在(2)的条件下,动点P从点A出发沿射线AB以每秒1个单位长度匀速运动,同时动点Q以相同的速度从点A出发沿线段AD匀速运动,到达点D时立即原速返回,当动点Q返回到点A时,P、Q两点同时停止运动,设运动时间为t秒(0t>).过点P向x轴作垂线,交抛物线于点E,交直线AC于点F,问:以A、E、F、Q四点为顶点构成的四边形能否是平行四边形.若能,请求出t的值;若不能,请说明理由.【变式5-3】.如图,在平面直角坐标系中,AOB∆的顶点O是坐标原点,点A坐标为()1,3,A、B两点关于直线y x=对称,反比例函数()0ky xx=>图象经过点A,点P是直线y x=上一动点.(1)B点的坐标为______;(2)若点C是反比例函数图象上一点,是否存在这样的点C,使得以A、B、C、P四点为顶点的四边形是平行四边形?若存在,求出点C坐标;若不存在,请说明理由;(3)若点Q 是线段OP 上一点(O 不与O 、P 重合),当四边形AOBP 为菱形时,过点Q 分别作直线OA 和直线AP 的垂线,垂足分别为E 、F ,当QE QF QB ++的值最小时,求出Q 点坐标.【考点6】动点之线段面积问题【例6】如图,在平面直角坐标系中,平行四边形如图放置,将此平行四边形绕点O 顺时针旋转90°得到平行四边形.抛物线经过点A 、C 、A′三点.(1)求A 、A′、C 三点的坐标;(2)求平行四边形和平行四边形重叠部分的面积;(3)点M 是第一象限内抛物线上的一动点,问点M 在何处时,的面积最大?最大面积是多少?并写出此时M 的坐标.【变式6-1】(1)发现:如图1,点A 为线段BC 外一动点,且BC =α,AB b =(0)a b >>,当点A 位于时,线段AC 的长取得最大值,最大值为(用含,a b 的式子表示);(2)应用:如图2,点A 为线段BC 外一动点,4BC =,2AC =,以AB 为边作等边ABD ∆,连接CD ,求线段CD 的最大值;(3)拓展:如图3,线段3AB =,点P 为线段AB 外一动点,且2AP =,PM PB =,90BPM ∠=︒,求线段AM 长的最大值及此时PBM ∆的面积.【变式6-2】如图,矩形ABCD 中,3,4AD AB ==,点P 是对角线AC 上一动点(不与A C 、重合),连接PB ,过点P 作PE PB ⊥,交射线DC 于点E ,以线段,PE PB 为邻边作矩形BPEF ,过点P 作GH CD ⊥。
(完整版)初二动点问题(含答案)

动态问题一、所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想 数形结合思想 转化思想类型:1。
利用图形想到三角形全等,相似及三角函数2.分析题目,了解有几个动点,动点的路程,速度(动点怎么动)3.结合图形和题目,得出已知或能间接求出的数据4。
分情况讨论,把每种可能情况列出来,不要漏5.动点一般在中考都是压轴题,步骤不重要,重要的是思路6。
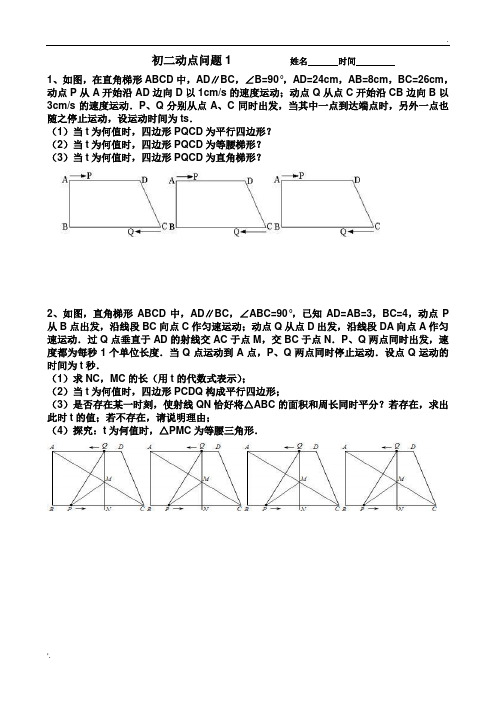
动点类题目一般都有好几问,前一问大都是后一问的提示,就像几何探究类题一样,如果后面的题难了,可以反过去看看前面问题的结论二、例题:1、如图1,梯形ABCD中,AD∥ BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从A开始沿AD边以1cm/秒的速度移动,点Q从C开始沿CB向点B以2 cm/秒的速度移动,如果P,Q分别从A,C同时出发,设移动时间为t秒。
当t= 时,四边形是平行四边形;当t= 时,四边形是等腰梯形.2、如图2,正方形ABCD的边长为4,点M在边DC上,且DM=1,N为对角线AC上任意一点,则DN+MN的最小值为.的长为 ;的长为 ;4、在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD—BE;(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.5、数学课上,张老师出示了问题:如图1,四边形ABCD是正方形,点E是边BCEFCF于点F,求证:AE=EF.AB的中点M,连接ME,则AM=EC在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E是边BC的中点"改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(2)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.ACBAED图1NMA BCDEMN图2ACBEDNM图36、如图, 射线MB上,MB=9,A是射线MB外一点,AB=5且A到射线MB的距离为3,动点P从M沿射线MB方向以1个单位/秒的速度移动,设P的运动时间为t.求(1)△ PAB为等腰三角形的t值;(2)△ PAB为直角三角形的t值;(3) 若AB=5且∠ABM=45 °,其他条件不变,直接写出△ PAB为直角三角形的t值(1)如果点P在线段BC上以3cm/s的速度由B点向CCA上由C点向A点运动①若点Q的运动速度与点P的运动速度相等,经过1②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能(2)若点Q以②中的运动速度从点C来的运动速度从点B边运动,求经过多长时间点P与点Q第一次哪条边上相遇?A DFC GEB图1A DFC GEB图3A DFC GEB图2。
八年级数学下册期末动点问题及压轴题带答案

1.(12分)已知:如图,平面直角坐标系中,A(0,4),B(0,2),点C是x轴上一点,点D为OC的中点.(1)求证:BD∥AC;(2)若点C在x轴正半轴上,且BD与AC的距离等于1,求点C的坐标;(3)如果OE⊥AC于点E,当四边形ABDE为平行四边形时,求直线AC的解析式.2.(12分)如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.一动点P从点A开始沿AD边向点D以1cm/s的速度运动,动点Q从点C开始沿CB 边向点B以3cm/s的速度运动.P,Q分别从点A和点C同时出发,当其中一点到达端点时,另一点也随之停止运动.设运动时间为t s,则(1)t为何值时,四边形PQCD为平行四边形?(2)t为何值时,四边形PQCD为等腰梯形?(3)AB边的长是否存在一数值,使四边形PQCD为菱形.如果存在,请求出AB 边的长,如果不存在,请说出理由.3.(本题10分)已知:在正方形ABCD 中,AB =6,P 为边CD 上一点,过P 点作PE ⊥BD 于点E ,连接BP(1) O 为BP 的中点,连接CO 并延长交BD 于点F① 如图1,连接OE ,求证:OE ⊥OC② 如图2,若53=EF BF ,求DP 的长 (2) CP EP 22+=___________4.(本题12分)如图1,直线333+-=x y 分别与y 轴、x 轴交于点A 、点B ,点C 的坐标为(-3,0),D 为直线AB 上一动点,连接CD 交y 轴于点E(1) 点B 的坐标为__________,不等式0333>+-x 的解集为___________(2) 若S △COE =S △ADE ,求点D 的坐标(3) 如图2,以CD 为边作菱形CDFG ,且∠CDF =60°.当点D 运动时,点G 在一条定直线上运动,请求出这条定直线的解析式.5.(11分)如图1,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点A 的坐标为(﹣3,4),点C 在x 轴的正半轴上,直线AC 交y 轴于点M ,AB 边交y 轴于点H ,连接BM .(1)菱形ABCO的边长是 ;(2)求直线AC 的解析式;(3)动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设△PMB 的面积为S (S≠0),点P 的运动时间为t 秒.①求S 与t 之间的函数关系式;②在点P 运动过程中,当S =3,请直接写出t 的值.6.(11分)如图,在直角梯形ABCD 中,AD ∥BC ,∠B=90°,且AD=12cm ,AB=8cm ,DC=10cm ,若动点P 从A 点出发,以每秒2cm 的速度沿线段AD 向点D 运动;动点Q 从C 点出发以每秒3cm 的速度沿CB 向B 点运动,当P 点到达D 点时,动点P 、Q 同时停止运动,设点P 、Q 同时出发,并运动了t 秒,回答下列问题:(1)BC= cm ;(2)当t 为多少时,四边形PQCD 成为平行四边形?(3)当t 为多少时,四边形PQCD 为等腰梯形?(4)是否存在t ,使得△DQC 是等腰三角形?若存在,请求出t 的值;若不存在,说明理由.7、如图①,已知正方形ABCD的边长为1,点P是AD边上的一个动点,点A关于直线BP的对称点是点Q,连接PQ、D Q、CQ、BQ,设AP=x.(1)BQ+DQ的最小值是_______,此时x的值是_______;(2)如图②,若PQ的延长线交CD边于点E,并且∠CQD=90°.①求证:点E是CD的中点;②求x的值.(3)若点P是射线AD上的一个动点,请直接写出当△CDQ为等腰三角形时x 的值.8、如图1,平面直角坐标系中,直线AB:y=﹣x+b交x轴于点A(8,0),交y轴正半轴于点B.(1)求点B的坐标;(2)如图2,直线AC交y轴负半轴于点C,AB=BC,P为线段AB上一点,过点P 作y轴的平行线交直线AC于点Q,设点P的横坐标为t,线段PQ的长为d,求d与t之间的函数关系式;(3)在(2)的条件下,M为CA延长线上一点,且AM=CQ,在直线AC上方的直线AB上是否存在点N,使△QMN是以QM为斜边的等腰直角三角形?若存在,请求出点N的坐标及PN的长度;若不存在,请说明理由.1.【解答】解:(1)∵A(0,4),B(0,2),∴OA=4,OB=2,点B为线段OA的中点,又点D为OC的中点,即BD为△AOC的中位线,∴BD∥AC;(2)如图1,作BF⊥AC于点F,取AB的中点G,则G(0,3),∵BD∥AC,BD与AC的距离等于1,∴BF=1,∵在Rt△ABF中,∠AFB=90°,AB=2,点G为AB的中点,∴FG=BG=AB=1,∴△BFG是等边三角形,∠ABF=60°.∴∠BAC=30°,设OC=x,则AC=2x,根据勾股定理得:OA==x,∵OA=4,∴x=∵点C在x轴的正半轴上,∴点C的坐标为(,0);(3)如图2,当四边形ABDE为平行四边形时,AB∥DE,∴DE⊥OC,∵点D为OC的中点,∴OE=EC,∵OE⊥AC,∴∠OCA=45°,∴OC=OA=4,∵点C在x轴的正半轴上,∴点C的坐标为(4,0),设直线AC的解析式为y=kx+b(k≠0).将A(0,4),C(4,0)代入AC的解析式得:解得:∴直线AC的解析式为y=﹣x+4.2.【解答】解:(1)由运动知,AP=t,CQ=3t,∴DP=AD﹣AP=24﹣t,∵四边形PQCD为平行四边形,∴DP=CQ,∴24﹣t=3t,∴t=6;(2)如图2,过点D作DE⊥BC于E,过点P作PF⊥BC于F,∴四边形EFPD是矩形,∴DE=PF,[来源:Z|xx|]∵四边形PQCD是等腰梯形,∴∠PQC=∠DCQ,∵∠PFQ=∠DEC=90°,∴△PFQ≌△DEC,∴FQ=CE,∴BE=AD=24,∴CE=BC﹣BE=2,∵四边形PQCD为等腰梯形,∴CQ=DP+2CE,由运动知,AP=t,CQ=3t,∴DP=AD﹣AP=24﹣t,∴24﹣t+2×2=3t,∴t=7,(3)AB边的长是8时,四边形PQCD为菱形,理由:由(1)知,t=6时,四边形PQCD是平行四边形,∴DP=24﹣6=18,∵平行四边形PQCD是菱形,∴CD=DP=18,如图2,过点D作DE⊥BC于E,∴四边形ABED是矩形,∴AB=DE,在Rt△CDE中,CE=2,CD=18,∴DE==8.3.证明:(1) ① ∵∠PEB =∠PCB =90°,O 为BP 的中点∴OE =OB =OP =OC∴∠POE =2∠DBP ,∠POC =2∠CBP∴∠COE =∠POE +∠POC =2(∠DBP +∠CBP )=90°∴OE ⊥OC② 连接OE 、CE∵△COE 为等腰直角三角形∴∠ECF =45°在等腰Rt △BCD 中,BF 2+DE 2=EF 2设BF =3x ,EF =5x ,则DE =4x∴3x +4x +5x =26,解得x =22 ∴DP =2DE =424=x(2) ∵62==-+=+CD C DP CP EP ∴2322=+CP EP4.解:(1) (3,0)、x <3(2) ∵S △COE =S △ADE∴S △AOB =S △CBD 即33321621⨯⨯=⨯⨯D y ,y D =233 当y =233时,23233333==+-x x ,∴D (23323,) (3) 连接CF∵∠CDF =60°∴△CDF 为等边三角形连接AC∵AB =AC =BC =6∴△ABC 为等边三角形∴△CAF ≌△CBD (SAS )∴∠CAF =∠ACB =60°∴AF ∥x 轴设D (m ,333+-m )过点D 作DH ⊥x 轴于H∴BH =3-m ,DB =6-2m =AF∴F (2m -6,33)由平移可知:G (m -9,m 3-) 令⎪⎩⎪⎨⎧-=-=m y m x 39∴点G 在直线393--=x y 上6.解:根据题意得:PA=2t ,CQ=3t ,则PD=AD-PA=12-2t .(1)如图,过D 点作DE ⊥BC 于E ,则四边形ABED 为长方形,DE=AB=8cm ,AD=BE=12cm ,在直角△CDE 中,∵∠CED=90°,DC=10cm ,DE=8cm ,∴22DC DE -,∴BC=BE+EC=18cm .…………………………………………………………………2分(直接写出最后结果18cm 即可)(2)∵AD ∥BC ,即PD ∥CQ ,∴当PD=CQ 时,四边形PQCD 为平行四边形,即12-2t=3t ,解得t=125秒, 故当t=125秒时四边形PQCD 为平行四边形;………………………………………4分(3)如图,过D 点作DE ⊥BC 于E ,则四边形ABED 为长方形,DE=AB=8cm ,AD=BE=12cm ,当PQ=CD 时,四边形PQCD 为等腰梯形.过点P 作PF ⊥BC 于点F ,过点D 作DE ⊥BC 于点E ,则四边形PDEF 是长方形,EF=PD=12-2t ,PF=DE .在Rt △PQF 和Rt △CDE 中,PQ CD PF DE ==⎧⎨⎩, ∴Rt △PQF ≌Rt △CDE (HL ),∴QF=CE ,∴QC-PD=QC-EF=QF+EC=2CE ,即3t-(12-2t )=12,解得:t=245, 即当t=245时,四边形PQCD 为等腰梯形;……………………………………………8分(4)△DQC 是等腰三角形时,分三种情况讨论:①当QC=DC 时,即3t=10,∴t=103;②当DQ=DC时,36 2t=∴t=4;③当QD=QC时,3t×65 10=∴t=259.故存在t,使得△DQC是等腰三角形,此时t的值为103秒或4秒或259秒.………11分③在Rt△DMQ中,DQ2=DM2+QM2222 (3)8(38) t t=+-36t=100t=25 97.解:(1);-1;(2)①证明:在正方形ABCD中,AB=BC,∠A=∠BCD=90°∵Q点为A点关于BP的对称点∴AB=QB,∠A=∠PQB=90°∴QB=BC,∠BQE=∠BCE∴∠BQC=∠BCQ∴∠EQC=∠EQB-∠CQB=∠ECB-∠QCB=∠ECQ∴EQ=EC在Rt△ABC中∵∠QDE=90°-∠QCE,∠DQE=90°-∠EQC∴∠QDE=∠DQE∴EQ+ED∴CE=EQ=ED即E是CD的中点②(3)或或8.解:(1)∵y=﹣x+b交x轴于点A(8,0),∴0=﹣×8+b,b=6,∴直线AB解析式为y=﹣x+6,令x=0,y=6,B(0,6);(2)∵A(8,0),B(0,6),∴OA=8,OB=6,∵∠AOB=90°,∴AB=10=BC,∴OC=4,∴点C(0,﹣4),设直线AC解析式为y=kx+b’,∴,∴∴直线AC解析式为y=x﹣4,∵P在直线y=﹣x+6上,∴可设点P(t,﹣t+6),∵PQ∥y轴,且点Q在y=x﹣4 上,∴Q(t, t﹣4),∴d=(﹣t+6)﹣(t ﹣4)=﹣t+10;(3)过点M作MG⊥PQ于G,∴∠QGM=90°=∠COA,∵PQ∥y轴,∴∠OCA=∠GQM,∵CQ=AM,∴AC=QM,在△OAC与△GMQ中,,∴△OAC≌△GMQ,∴QG=OC=4,GM=OA=8,过点N作NH⊥PQ于H,过点M作MR⊥NH于点R,∴∠MGH=∠RHG=∠MRH=90°,∴四边形GHRM是矩形,∴HR=GM=8,可设GH=RM=k,∵△MNQ是等腰直角三角形,∴∠QMN=90°,NQ=NM,∴∠HNQ+∠HQN=90°,∴∠HNQ+∠RNM=90°,∴∠RNM=∠HQN,∴△HNQ≌△RMN,∴HN=RM=k,NR=QH=4+k,∵HR=HN+NR,∴k+4+k=8,∴k=2,∴GH=NH=RM=2,∴HQ=6,∵Q(t,t﹣4),∴N(t+2,t﹣4+6)即 N(t+2,t+2)∵N在直线AB:y=﹣x+6上,∴t+2=﹣(t+2)+6,∴t=2,∴P(2,),N(4,3),∴PH=,NH=2,∴PN==.。
苏教版八年级上册复习专题练习一:动点问题压轴题(含答案)

初二数学期中复习专题一:动点问题3、动点中的旋转问题1、如图,在等边△ABC 中,AC=9,点O 在AC 上,且AO=3,点P 是AB 上一动点,连接OP,将线段OP 绕点O 逆时针旋转60°得到线段OD.要使点D 恰好落在BC 上,则AP 的长是.2、如图所示:一副三角板如图放置,等腰直角三角板ABC 固定不动,另一块三角板的直角顶点放在等腰直角三角形的斜边中点D 处,且可以绕点D 旋转,在旋转过程中,两直角边的交点G、H 始终在边AB、BC 上.(1)在旋转过程中线段BG 和CH 大小有何关系?证明你的结论.(2)若AB=BC=4cm,在旋转过程中四边形GBHD 的面积是否改变?若不变,求出它的值;若改变,求出它的取值范围.(3)若交点G、H 分别在边AB、BC 的延长线上,则(1)中的结论仍然成立吗?请画出相应的图形,直接写出结论.3、如图1,已知△ABC 是等腰直角三角形,∠BAC=90°,点D 是BC 的中点.作正方形DEFG,使点A、C 分别在DG 和DE 上,连接AE,BG.(1)试猜想线段BG 和AE 的数量关系是;(2)将正方形DEFG绕点D逆时针方向旋转α(0°<α≤360°),①判断(1)中的结论是否仍然成立?请利用图2 证明你的结论;②若BC=DE=4,当AE 取最大值时,求AF 的值.4、点的移动问题4、如图1,在△ABC 中,点P 为BC 边中点,直线a 绕顶点A 旋转,若B、P 在直线a 的异侧,BM⊥直线a 于点M,CN⊥直线a 于点N,连接PM、PN;(1)延长MP交CN于点E(如图2),①求证:△BPM≌△CPE;②求证:PM=PN;(2)若直线a 绕点A 旋转到图3 的位置时,点B、P 在直线a 的同侧,其它条件不变,此时PM=PN 还成立吗?若成立,请给予证明;若不成立,请说明理由.5、在△ABC 中,∠BAC=90°,AB=AC.点D 从点B 出发沿射线BC 移动,以AD 为边在AB 的右侧作△ADE,且∠DAE=90°,AD=AE.连接CE.(1)如图1,若点D 在BC 边上,则∠BCE=°;(2)如图2,若点D 在BC 的延长线上运动.①∠BCE 的度数是否发生变化?请说明理由;②若BC=3,CD=6,则△ADE 的面积为.6、在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D 在线段BC 上,如果∠BAC=90°,则∠BCE=度;(2)设∠BAC=α,∠BCE=β.①如图2,当点D 在线段BC 上移动,则α,β之间有怎样的数量关系?请说明理由;②当点D 在直线BC 上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.7、一个正方体物体沿斜坡向下滑动,其截面如图所示.正方形DEFH 的边长为1 米,∠B=90°,BC=4 米,AC=8 米,当正方形DEFH 运动到什么位置时,即当AE=米时,有DC2=AE2+BC2.8、【新知学习】如果一个三角形有一边上的中线等于这条边的一半,那么我们就把这样的三角形叫做“智慧三角形”.【简单运用】(1)下列三个三角形,是智慧三角形的是(填序号);(2)如图1,已知等边三角形ABC,请用刻度尺在该三角形边上找出所有满足条件的点D,使△ABD 为“智慧三角形”,并写出作法;【深入探究】(3)如图2,在正方形ABCD 中,点E 是BC 的中点,F 是CD 上一点,且CF=CD,试判断△AEF 是否为“智慧三角形”,并说明理由;【灵活应用】(4)如图3,等边三角形ABC 边长5cm.若动点P 以1cm/s 的速度从点A 出发,沿△ABC 的边AB ﹣BC﹣CA 运动.若另一动点Q 以2cm/s 的速度从点B 出发,沿边BC﹣CA﹣AB 运动,两点同时出发,当点Q首次回到点B时,两点同时停止运动.设运动时间为t(s),那么t为.(s)时,△PBQ为“智慧三角形”.动点问题压轴题1、【解答】解:∵∠A+∠APO=∠POD+∠COD,∠A=∠POD=60°,∴∠APO=∠COD,在△APO 和△COD 中,,∴△APO≌△COD(AAS),即AP=CO,∵CO=AC﹣AO=6,∴AP=6.故答案为6.2、【解答】解:(1)BG和CH为相等关系,如图1,连接BD,∵等腰直角三角形ABC,D 为AC 的中点,∴DB=DC=DA,∠A=∠DBH=45°,BD⊥AC,∵∠EDF=90°,∴∠ADG+∠GDB=90°,∴∠BDG+∠BDH=90°,∴∠ADG=∠HDB,∴在△ADG 和△BDH 中,,∴△ADG≌△BDH(ASA),∴AG=BH,∵AB=BC,∴BG =HC ,(2) ∵等腰直角三角形 ABC ,D 为 AC 的中点,∴DB =DC =DA ,∠DBG =∠DCH =45°,BD ⊥AC ,∵∠GDH =90°,∴∠GDB +∠BDH =90°,∴∠CDH +∠BDH =90°,∴∠BDG =∠HDC ,∴在△BDG 和△CDH 中,,∵△BDG ≌△CDH (ASA ),∴S 四边形 DGBH =S △BDH +S △GDB =S △ABD ,∵DA =DC =DB ,BD ⊥AC ,∴S △ABD = S △ABC ,∴S 四边形 DGBH =S △ABC =4cm 2,∴在旋转过程中四边形 GBHD 的面积不变,(3) 当三角板 DEF 旋转至图 2 所示时,(1)的结论仍然成立,如图 2,连接 BD ,∵BD ⊥AC ,AB ⊥BH ,ED ⊥DF ,∴∠BDG =90°﹣∠CDG ,∠CDH =90°﹣∠CDG ,∴∠BDG =∠CDH ,∵等腰直角三角形 ABC ,∴∠DBC =∠BCD =45°,∴∠DBG =∠DCH =135°,∴在△DBG 和△DCH 中,,∴△DBG ≌△DCH (ASA ),∴BG =CH .3、.【分析】(1)由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG 就可以得出结论;(2)①如图2,连接AD,由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG 就可以得出结论;②由①可知BG=AE,当BG 取得最大值时,AE 取得最大值,由勾股定理就可以得出结论.【解答】解:(1)BG=AE.理由:如图1,∵△ABC 是等腰直角三角形,∠BAC=90°,点D 是BC 的中点,∴AD⊥BC,BD=CD,∴∠ADB=∠ADC=90°.∵四边形DEFG 是正方形,∴DE=DG.在△BDG 和△ADE 中,,∴△ADE≌△BDG(SAS),∴BG=AE.故答案为:BG=AE;(2)①成立BG=AE.理由:如图2,连接AD,∵在Rt△BAC 中,D 为斜边BC 中点,∴AD=BD,AD⊥BC,∴∠ADG+∠GDB=90°.∵四边形EFGD 为正方形,∴DE=DG,且∠GDE=90°,∴∠ADG+∠ADE=90°,∴∠BDG=∠ADE.在△BDG 和△ADE 中,,∴△BDG≌△ADE(SAS),∴BG=AE;②∵BG=AE,∴当BG 取得最大值时,AE 取得最大值.如图3,当旋转角为270°时,BG =AE.∵BC=DE=4,∴BG=2+4=6.∴AE=6.在Rt△AEF 中,由勾股定理,得AF==,∴AF=2 .4、【解答】证明:(1)①如图2:∵BM⊥直线a 于点M,CN⊥直线a 于点N,∴∠BMA=∠CNM=90°,∴BM∥CN,∴∠MBP=∠ECP,又∵P 为BC 边中点,∴BP=CP,在△BPM 和△CPE 中,,∴△BPM≌△CPE,(ASA)②∵△BPM≌△CPE,∴PM=PE∴PM=ME,∴在Rt△MNE 中,PN=ME,∴PM=PN;(2)成立,如图3.延长MP 与NC 的延长线相交于点E,∵BM⊥直线 a 于点M,CN⊥直线a 于点N,∴∠BMN=∠CNM=90°∴∠BMN+∠CNM=180°,∴BM∥CN∴∠MBP=∠ECP,又∵P 为BC 中点,∴BP=CP,在△BPM 和△CPE 中,,∴△BPM≌△CPE,(ASA)∴PM=PE,∴PM=ME,则Rt△MNE 中,PN=ME,∴PM=PN.5、【解答】解:(1)∵△ABC和△ADE都是等腰Rt△,∴AB=AC,AD=AE,∠BAC=∠DAE=90°,∴∠BAD=∠CAE.在△ACE 和△ABD 中,,∴△ACE≌△ABD(SAS);∴∠ACE=∠ABD=45°,∴∠BCE=∠BCA+∠ACE=45°+45°=90°;故答案为:90;(2)①不发生变化.∵AB=AC,∠BAC=90°∴∠ABC=∠ACB=45°,∵∠BAC=∠DAE=90°∴∠BAC+∠DAC=∠DAE+∠DAC∴∠BAD=∠CAE,在△ACE 和△ABD 中∴△ACE≌△ABD(SAS)∴∠ACE=∠ABD=45°∴∠BCE=∠BCA+∠ACE=45°+45°=90°∴∠BCE 的度数不变,为90°;② 11746、【解答】解:(1)90°.理由:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC.即∠BAD=∠CAE.在△ABD 与△ACE 中,∴△ABD≌△ACE(SAS),∴∠B=∠ACE.∴∠B+∠ACB=∠ACE+∠ACB,∴∠BCE=∠B+∠ACB,又∵∠BAC=90°∴∠BCE=90°;(2)①α+β=180°,理由:∵∠BAC=∠DAE,∴∠BAD+∠DAC=∠EAC+∠DAC.即∠BAD=∠CAE.在△ABD 与△ACE 中,∴△ABD≌△ACE(SAS),∴∠B=∠ACE.∴∠B+∠ACB=∠ACE+∠ACB.∴∠B+∠ACB=β,∵α+∠B+∠ACB=180°,∴α+β=180°;②当点D 在射线BC 上时,α+β=180°;理由:∵∠BAC=∠DAE,∴∠BAD=∠CAE,∵在△ABD 和△ACE 中∴△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵∠BAC+∠ABD+∠BCA=180°,∴∠BAC+∠BCE=∠BAC+∠BCA+∠ACE=∠BAC+∠BCA+∠B=180°,∴α+β=180°;当点D 在射线BC 的反向延长线上时,α=β.理由:∵∠DAE=∠BAC,∴∠DAB=∠EAC,∵在△ADB 和△AEC 中,∴△ADB≌△AEC(SAS),∴∠ABD=∠ACE,∵∠ABD=∠BAC+∠ACB,∠ACE=∠BCE+∠ACB,∴∠BAC=∠BCE,即α=β.7、【解答】解:如图,连接CD,假设AE=x,可得EC=8﹣x.∵正方形DEFH 的边长为1 米,即DE=1 米,∴DC2=DE2+EC2=1+(8﹣x)2,AE2+BC2=x2+16,∵DC2=AE2+BC2,∴1+(8﹣x)2=x2+16,解得:x=,所以,当AE=米时,有DC2=AE2+BC2.故答案是:.8、【解答】解:(1)因为直角三角形的斜边上的中线等于斜边的一半,所以①是“智慧三角形”.故答案为①(2)用刻度尺分别量取AC、BC 的中点D、D′.点D、D′即为所求.(3)结论:△AEF 是“智慧三角形“.理由如下:如图,设正方形的边长为4a∵E 是BC 的中点∴BE=EC=2a,∵CF=CD∴FC=a,DF=4a﹣a=3a,在Rt△ABE 中,AE2=(4a)2+(2a)2=20a2在Rt△ECF 中,EF2=(2a)2+a2=5a2在Rt△ADF 中,AF2=(4a)2+(3a)2=25a2∴AE2+EF2=AF2∴△AEF 是直角三角形,∠AEF=90°∵直角三角形斜边AF 上的中线等于AF 的一半∴△AEF为“智慧三角形”.(4)如图3 中,①当点P 在线段AB 上,点Q 在线段BC 上时,若∠PQB=90°,则BP=2BQ,∴5﹣t=4t,解得t=1.若∠BPQ=90°,则BQ=2PB,∴2t=2(5﹣t)∴t=.②当点Q在线段AC上时,不存在“智慧三角形”.③当点P 在线段BC 上,点Q 在线段AB 上时,若∠PQB=90°,则BP=2BQ,∴t﹣5=2(15﹣2t),∴t=7,若∠QPB=90°,则BQ=2PB,∴15﹣2t=2(t﹣5),∴t=,综上所述,满足条件的t 的值为1 或或或7.故答案为1 或或或7.。
初二动点问题(非常经典)
初二动点问题1 姓名时间1、如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从A开始沿AD边向D以1cm/s的速度运动;动点Q从点C开始沿CB边向B以3cm/s的速度运动.P、Q分别从点A、C同时出发,当其中一点到达端点时,另外一点也随之停止运动,设运动时间为ts.(1)当t为何值时,四边形PQCD为平行四边形?(2)当t为何值时,四边形PQCD为等腰梯形?(3)当t为何值时,四边形PQCD为直角梯形?2、如图,直角梯形ABCD中,AD∥BC,∠ABC=90°,已知AD=AB=3,BC=4,动点P 从B点出发,沿线段BC向点C作匀速运动;动点Q从点D出发,沿线段DA向点A作匀速运动.过Q点垂直于AD的射线交AC于点M,交BC于点N.P、Q两点同时出发,速度都为每秒1个单位长度.当Q点运动到A点,P、Q两点同时停止运动.设点Q运动的时间为t秒.(1)求NC,MC的长(用t的代数式表示);(2)当t为何值时,四边形PCDQ构成平行四边形;(3)是否存在某一时刻,使射线QN恰好将△ABC的面积和周长同时平分?若存在,求出此时t的值;若不存在,请说明理由;(4)探究:t为何值时,△PMC为等腰三角形.3、如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21,动点P 从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,P、Q分别从点D、C同时出发,当点Q运动到点B时,点P随之停止运动,设运动时间为t(s).(1)设△BPQ的面积为S,求S与t之间的函数关系;(2)当t为何值时,以B、P、Q三点为顶点的三角形是等腰三角形?4、直线y=- 3/4x+6与坐标轴分别交于A、B两点,动点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿路线O⇒B⇒A 运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t(秒),△OPQ的面积为S,求出S与t之间的函数关系式;(3)当S= 48/5时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.5、如图,△ABC中,点O为AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的外角平分线CF于点F,交∠ACB内角平分线CE于E.(1)试说明EO=FO;(2)当点O运动到何处时,四边形AECF是矩形并证明你的结论;(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你的结论.。
(完整word版)初二数学动点问题归类复习(含例题、练习及答案)

初二数学动点问题归类复习(含例题、练习及答案)所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.关键:动中求静.数学思想:分类思想数形结合思想转化思想本文将初一至二学习过的有关知识,结合动点问题进行归类复习,希望对同学们能有所帮助。
一、等腰三角形类:因动点产生的等腰三角形问题例1:(2013年上海市虹口区中考模拟第25题)如图1,在Rt△ABC中,∠A=90°,AB=6,AC =8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC 上的一动点,且∠PDQ=90°.(1)求ED、EC的长;(2)若BP=2,求CQ的长;(3)记线段PQ与线段DE的交点为F,若△PDF为等腰三角形,求BP的长.图1 备用图思路点拨1.第(2)题BP=2分两种情况.2.解第(2)题时,画准确的示意图有利于理解题意,观察线段之间的和差关系.3.第(3)题探求等腰三角形PDF时,根据相似三角形的传递性,转化为探求等腰三角形CDQ.解答:(1)在Rt△ABC中,AB=6,AC=8,所以BC=10.在Rt△CDE中,CD=5,所以315tan544ED CD C=⋅∠=⨯=,254EC=.(2)如图2,过点D作DM⊥AB,DN⊥AC,垂足分别为M、N,那么DM、DN是△ABC的两条中位线,DM=4,DN=3.由∠PDQ=90°,∠MDN=90°,可得∠PDM=∠QDN.因此△PDM∽△QDN.所以43PM DMQN DN==.所以34QN PM=,43PM QN=.图2 图3 图4 ①如图3,当BP=2,P在BM上时,PM=1.此时3344QN PM==.所以319444CQ CN QN=+=+=.②如图4,当BP=2,P在MB的延长线上时,PM=5.此时31544QN PM ==.所以1531444CQ CN QN =+=+=. (3)如图5,如图2,在Rt △PDQ 中,3tan 4QD DN QPD PD DM ∠===.在Rt △ABC 中,3tan 4BA C CA ∠==.所以∠QPD =∠C .由∠PDQ =90°,∠CDE =90°,可得∠PDF =∠CDQ . 因此△PDF ∽△CDQ .当△PDF 是等腰三角形时,△CDQ 也是等腰三角形.①如图5,当CQ =CD =5时,QN =CQ -CN =5-4=1(如图3所示). 此时4433PM QN ==.所以45333BP BM PM =-=-=. ②如图6,当QC =QD 时,由cos CHC CQ =,可得5425258CQ =÷=. 所以QN =CN -CQ =257488-=(如图2所示). 此时4736PM QN ==.所以725366BP BM PM =+=+=. ③不存在DP =DF 的情况.这是因为∠DFP ≥∠DQP >∠DPQ (如图5,图6所示).图5 图6考点伸展:如图6,当△CDQ 是等腰三角形时,根据等角的余角相等,可以得到△BDP 也是等腰三角形,PB =PD .在△BDP 中可以直接求解256BP =. 二、直角三角形:因动点产生的直角三角形问题 例2:(2008年河南省中考第23题)如图1,直线434+-=x y 和x 轴、y 轴的交点分别为B 、C ,点A 的坐标是(-2,0).(1)试说明△ABC 是等腰三角形;(2)动点M 从A 出发沿x 轴向点B 运动,同时动点N 从点B 出发沿线段BC 向点C 运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M 运动t 秒时,△MON 的面积为S . ① 求S 与t 的函数关系式;② 设点M 在线段OB 上运动时,是否存在S =4的情形?若存在,求出对应的t 值;若不存在请说明理由;③在运动过程中,当△MON 为直角三角形时,求t 的值.图1思路点拨:1.第(1)题说明△ABC 是等腰三角形,暗示了两个动点M 、N 同时出发,同时到达终点. 2.不论M 在AO 上还是在OB 上,用含有t 的式子表示OM 边上的高都是相同的,用含有t 的式子表示OM 要分类讨论.3.将S =4代入对应的函数解析式,解关于t 的方程.4.分类讨论△MON 为直角三角形,不存在∠ONM =90°的可能. 解答:(1)直线434+-=x y 与x 轴的交点为B (3,0)、与y 轴的交点C (0,4). Rt △BOC 中,OB =3,OC =4,所以BC =5.点A 的坐标是(-2,0),所以BA =5. 因此BC =BA ,所以△ABC 是等腰三角形.(2)①如图2,图3,过点N 作NH ⊥AB ,垂足为H .在Rt △BNH 中,BN =t ,4sin 5B =,所以45NH t =. 如图2,当M 在AO 上时,OM =2-t ,此时211424(2)22555S OM NH t t t t =⋅⋅=-⨯=-+.定义域为0<t ≤2.如图3,当M 在OB 上时,OM =t -2,此时211424(2)22555S OM NH t t t t =⋅⋅=-⨯=-.定义域为2<t ≤5.图2 图3②把S =4代入22455S t t =-,得224455t t -=. 解得1211t =,2211t =.因此,当点M 在线段OB 上运动时,存在S =4的情形,此时211t = ③如图4,当∠OMN =90°时,在Rt △BNM 中,BN =t ,BM 5t =-,3cos 5B =,所以535tt-=.解得258t=.如图5,当∠OMN=90°时,N与C重合,5t=.不存在∠ONM=90°的可能.所以,当258t=或者5t=时,△MON为直角三角形.图4 图5考点伸展:在本题情景下,如果△MON的边与AC平行,求t的值.如图6,当ON//AC时,t=3;如图7,当MN//AC时,t=2.5.图6 图7三、平行四边形问题:因动点产生的平行四边形问题例3:(2010年山西省中考第26题)在直角梯形OABC中,CB//OA,∠COA=90°,CB=3,OA=6,BA=35.分别以OA、OC边所在直线为x轴、y轴建立如图1所示的平面直角坐标系.(1)求点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2EB,直线DE交x轴于点F.求直线DE的解析式;(3)点M是(2)中直线DE上的一个动点,在x轴上方的平面内是否存在另一点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.图1 图2思路点拨:1.第(1)题和第(2)题蕴含了OB与DF垂直的结论,为第(3)题讨论菱形提供了计算基础.2.讨论菱形要进行两次(两级)分类,先按照DO为边和对角线分类,再进行二级分类,DO与DM、DO与DN为邻边.解答:(1)如图2,作BH⊥x轴,垂足为H,那么四边形BCOH为矩形,OH=CB=3.在Rt△ABH中,AH=3,BA=35,所以BH=6.因此点B的坐标为(3,6).(2) 因为OE=2EB,所以223E Bx x==,243E By y==,E(2,4).设直线DE的解析式为y=kx+b,代入D(0,5),E(2,4),得5,2 4.bk b=⎧⎨+=⎩解得12k=-,5b=.所以直线DE的解析式为152y x=-+.(3) 由152y x=-+,知直线DE与x轴交于点F(10,0),OF=10,DF=55.①如图3,当DO为菱形的对角线时,MN与DO互相垂直平分,点M是DF的中点.此时点M的坐标为(5,52),点N的坐标为(-5,52).②如图4,当DO、DN为菱形的邻边时,点N与点O关于点E对称,此时点N的坐标为(4,8).③如图5,当DO、DM为菱形的邻边时,NO=5,延长MN交x轴于P.由△NPO∽△DOF,得NP PO NODO OF DF==,即51055NP PO==.解得5NP=,25PO=.此时点N的坐标为(25,5)-.图3 图4考点伸展如果第(3)题没有限定点N在x轴上方的平面内,那么菱形还有如图6的情形.图5 图6四、相似三角形:因动点产生的相似三角形问题例4:(2013年苏州中考28题)如图,点O为矩形ABCD的对称中心,AB=10cm,BC=12cm,点E、F、G分别从A、B、C三点同时出发,沿矩形的边按逆时针方向匀速运动,点E的运动速度为1cm/s,点F的运动速度为3cm/s,点G的运动速度为1.5cm/s,当点F到达点C(即点F与点C重合)时,三个点随之停止运动.在运动过程中,△EBF关于直线EF的对称图形是△EB′F.设点E、F、G运动的时间为t(单位:s).(1)当t=s时,四边形EBFB′为正方形;(2)若以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似,求t的值;(3)是否存在实数t,使得点B′与点O重合?若存在,求出t的值;若不存在,请说明理由.思路点拨:(1)利用正方形的性质,得到BE=BF,列一元一次方程求解即可;(2)△EBF与△FCG 相似,分两种情况,需要分类讨论,逐一分析计算;(3)本问为存在型问题.假设存在,则可以分别求出在不同条件下的t值,它们互相矛盾,所以不存在.解答:(1)若四边形EBFB′为正方形,则BE=BF,即:10﹣t=3t,解得t=2.5;(2)分两种情况,讨论如下:①若△EBF∽△FCG,则有,即,解得:t=2.8;②若△EBF∽△GCF,则有,即,解得:t=﹣14﹣2(不合题意,舍去)或t=﹣14+2.∴当t=2.8s或t=(﹣14+2)s时,以点E、B、F为顶点的三角形与以点F,C,G为顶点的三角形相似.(3)假设存在实数t,使得点B′与点O重合.如图,过点O作OM⊥BC于点M,则在Rt△OFM中,OF=BF=3t,FM=BC﹣BF=6﹣3t,OM=5,由勾股定理得:OM2+FM2=OF2,即:52+(6﹣3t)2=(3t)2解得:t=;过点O作ON⊥AB于点N,则在Rt△OEN中,OE=BE=10﹣t,EN=BE﹣BN=10﹣t﹣5=5﹣t,ON=6,由勾股定理得:ON 2+EN 2=OE 2,即:62+(5﹣t )2=(10﹣t )2解得:t =3.9.∵≠3.9,∴不存在实数t ,使得点B ′与点O 重合.考点伸展:本题为运动型综合题,考查了矩形性质、轴对称、相似三角形的判定性质、勾股定理、解方程等知识点.题目并不复杂,但需要仔细分析题意,认真作答.第(2)问中,需要分类讨论,避免漏解;第(3)问是存在型问题,可以先假设存在,然后通过推导出互相矛盾的结论,从而判定不存在. 拓展练习:1、如图1,梯形ABCD 中,AD ∥ BC ,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P 从A 开始沿AD 边以1cm/秒的速度移动,点Q 从C 开始沿CB 向点B 以2 cm/秒的速度移动,如果P ,Q 分别从A ,C 同时出发,设移动时间为t 秒。
中考压轴题十大类型之动点问题

第一讲 中考压轴题十大类型之动点问题一、解题策略和解法精讲解决动点问题的关键是“动中求静”.从变换的角度和运动变化来研究三角形、四边形、函数图像等图形,通过“对称、动点的运动”等研究手段和方法,来探索与发现图形性质及图形变化,在解题过程中渗透空间观念和合情推理。
在动点的运动过程中观察图形的变化情况,理解图形在不同位置的情况,做好计算推理的过程。
在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。
二、精讲精练1. (2011吉林)如图,梯形ABCD 中,AD ∥BC ,∠BAD =90°,CE ⊥AD 于点E ,AD =8cm ,BC =4cm ,AB =5cm .从初始时刻开始,动点P ,Q 分别从点A ,B 同时出发,运动速度均为1cm/s ,动点P 沿A -B -C -E 方向运动,到点E 停止;动点Q 沿B -C -E -D 方向运动,到点D 停止,设运动时间为x s ,△P AQ 的面积为y cm 2,(这里规定:线段是面积为0的三角形)解答下列问题:(1) 当x =2s 时,y =_____ cm 2;当x =92s 时,y =_______ cm 2.(2)当5 ≤ x ≤ 14时,求y 与x 之间的函数关系式.(3)当动点P 在线段BC 上运动时,求出154y S 梯形ABCD 时x 的值.(4)直接写出在整个..运动过程中,使PQ 与四边形ABCE 的对角线平行的所有x 的值.2. (2007河北)如图,在等腰梯形ABCD 中,AD ∥BC ,AB =DC =50,AD =75,BC =135.点P 从点B 出发沿折线段BA -AD -DC 以每秒5个单位长的速度向DCBA 点C 匀速运动;点Q 从点C 出发沿线段CB 方向以每秒3个单位长的速度匀速运动,过点Q 向上作射线QK ⊥BC ,交折线段CD -DA -AB 于点E .点P 、Q 同时开始运动,当点P 与点C 重合时停止运动,点Q 也随之停止.设点P 、Q 运动的时间是t 秒(t >0).(1)当点P 到达终点C 时,求t 的值,并指出此时BQ 的长; (2)当点P 运动到AD 上时,t 为何值能使PQ ∥DC ?(3)设射线QK 扫过梯形ABCD 的面积为S ,分别求出点E 运动到CD 、DA 上时,S 与t 的关系式;(4)△PQE 能否成为直角三角形?若能,写出t 的取值范围;若不能,请说明理由.备用图3. (2008河北)如图,在Rt ABC △中,∠C=90°,AB =50,AC =30,D ,E ,F 分别是AC ,AB ,B C 的中点.点P 从点D 出发沿折线DE -EF -FC -CD 以每秒7个单位长的速度匀速运动;点Q 从点B 出发沿BA 方向以每秒4个单位长的速度匀速运动,过点Q 作射线QK AB ,交折线BC -CA 于点G .点P Q ,同时出发,当点P 绕行一周回到点D 时停止运动,点Q 也随之停止.设点P Q ,运动的时间是t 秒(0t >). (1)D F ,两点间的距离是 ;(2)射线QK 能否把四边形CDEF 分成面积相等的两部分?若能,求出t 的值.若不能,说明理由;(3)当点P 运动到折线EF FC -上,且点P 又恰好落在射线QK 上时,求t 的值;(4)连结PG ,当PG AB ∥时,请直接..写出t 的值.4.(2011山西太原)如图,在平面直角坐标系中,四边形OABC 是平行四边形.直线l 经过O 、C 两点.点A 的坐标为(8,0),点B 的坐标为(11,4),动点P 在线段OA 上从点O 出发以每秒1个单位的速度向点A 运动,同时动点Q 从点A 出发以每秒2个单位的速度沿A →B →C 的方向向点C 运动,过点P 作PM 垂直于x 轴,与折线O -C -B 相交于点M .当P 、Q 两点中有一点到达终点时,另一点也随之停止运动,设点P 、Q 运动的时间为t 秒(0t >),△MPQ 的面积为S .(1)点C 的坐标为________,直线l 的解析式为__________.(2)试求点Q 与点M 相遇前S 与t 的函数关系式,并写出相应的t 的取值范围.(3)试求题(2)中当t 为何值时,S 的值最大,并求出S 的最大值. (4)随着P 、Q 两点的运动,当点M 在线段CB 上运动时,设PM 的延长线与直线l 相交于点N .试探究:当t 为何值时,△QMN 为等腰三角形?请直接写出t 的值.B备用图FE D C BA5.(2011四川重庆)如图,矩形ABCD 中,AB =6,BC =23,点O 是AB 的中点,点P 在AB 的延长线上,且BP =3.一动点E 从O 点出发,以每秒1个单位长度的速度沿OA 匀速运动,到达A 点后,立即以原速度沿AO 返回;另一动点F 从P 点出发,以每秒1个单位长度的速度沿射线P A 匀速运动,点E 、F 同时出发,当两点相遇时停止运动.在点E 、F 的运动过程中,以EF 为边作等边△EFG ,使△EFG 和矩形ABCD 在射线P A 的同侧,设运动的时间为t 秒(t ≥0).(1)当等边△EFG 的边FG 恰好经过点C 时,求运动时间t 的值; (2)在整个运动过程中,设等边△EFG 和矩形ABCD 重叠部分的面积为S ,请直接写出S 与t 之间的函数关系式和相应的自变量t 的取值范围; (3)设EG 与矩形ABCD 的对角线AC 的交点为H ,是否存在这样的t ,使△AOH 是等腰三角形?若存在,求出对应的t 的值;若不存在,请说明理由.备用图1备用图2三、测试提高1.(2011山东烟台)如图,在直角坐标系中,梯形ABCD的底边AB在x轴上,底边CD的端点D在y轴上.直线CB的表达式为41633y x=-+,点A、D的坐标分别为(-4,0),(0,4).动点P自A点出发,在AB上匀速运动.动点Q自点B出发,在折线BCD上匀速运动,速度均为每秒1个单位.当其中一个动点到达终点时,它们同时停止运动.设点P运动t(秒)时,△OPQ 的面积为S(不能构成△OPQ的动点除外).(1)求出点B、C的坐标;(2)求S随t变化的函数关系式;(3)当t为何值时S有最大值?并求出最大值.备用图。
初二数学动点问题专项试卷

一、选择题(每题3分,共30分)1. 在平面直角坐标系中,点P(a,b)在直线y=2x+1上运动,那么a与b的关系是:A. a+b=1B. a=2bC. a=2b+1D. a=2b-12. 已知点A(2,3),点B在x轴上,且AB=5,那么点B的坐标可能是:A. (7,0)B. (-3,0)C. (-7,0)D. (3,0)3. 在△ABC中,AB=AC,点D在BC上,且BD=CD,那么∠ADB与∠ADC的关系是:A. ∠ADB=∠ADCB. ∠ADB=∠BACC. ∠ADB=∠BAC/2D. ∠ADB=∠BAC/34. 在平面直角坐标系中,点M在直线y=x+1上运动,那么点M的坐标满足:A. x=y-1B. x=y+1C. y=x-1D. y=x+15. 已知直线l的方程为2x-3y+6=0,那么直线l与x轴的交点坐标是:A. (3,0)B. (-3,0)C. (0,2)D. (0,-2)6. 在△ABC中,AB=AC,点D在BC上,且BD=CD,那么∠ADB与∠ADC的关系是:A. ∠ADB=∠ADCB. ∠ADB=∠BACC. ∠ADB=∠BAC/2D. ∠ADB=∠BAC/37. 已知点P(a,b)在直线y=-2x+3上运动,那么a与b的关系是:A. a+b=3B. a=2bC. a=2b+3D. a=2b-38. 在平面直角坐标系中,点Q(m,n)在直线y=3/2x-2上运动,那么m与n的关系是:A. m=n+4B. m=2n-4C. m=n-4D. m=2n+49. 已知直线l的方程为x+4y-12=0,那么直线l与y轴的交点坐标是:A. (0,3)B. (0,-3)C. (4,0)D. (-4,0)10. 在△ABC中,AB=AC,点D在BC上,且BD=CD,那么∠ADB与∠ADC的关系是:A. ∠ADB=∠ADCB. ∠ADB=∠BACC. ∠ADB=∠BAC/2D. ∠ADB=∠BAC/3二、填空题(每题5分,共20分)11. 在平面直角坐标系中,点P(2,3)在直线y=mx+1上运动,那么m的取值范围是______。
人教版八年级上册数学期末动点问题压轴题专题训练(含解析)

人教版八年级上册数学期末动点问题压轴题专题训练(1)当时,点C 的坐标为 .(2)动点A 在运动的过程中,试判断发生变化,请说明理由.(3)当时,在坐标平面内是否存在一点若存在,请直接写出点P 的坐标;若不存在,请说明理由.(1)如图1,当点在边上时.①求证:;②求证:;(2)如图2,当点在边的延长线上时,其他条件不变,请写出2a =3a =D BC ABD ACE ≌△△BC DC CE =+D BC(1)请直接写出点A 和点B 的坐标;(2)请判断的形状并说明理由;(3)下列结论:①四边形为定值.请选择一个正确的结论并说明理由.(1)求证:;(2)求的面积;(3)点M ,N 分别是线段,上的动点,连接,求的最小值.DEF OEDF OEF DFE ∠+∠CD CE =CDE BC BD MN 12MN DN +(1)求出点的坐标.(2)求证:.(3)数学活动小组进行深入探究后发现变,你同意这个说法吗?请说明理由B OD BC =(1)如图①,请找出图中与相等的角,并说明理由;(2)如图②,交轴于点,过点作轴于点,求证:平分;(3)如图③,若,点在轴正半轴移动,且,取,连交轴OAB ∠BC x M C CD x ⊥,2D AM CD =AD BAC ∠()3,0A B y OB OA >()0,3P CP x边三角形,使其与点在直线的两侧,与直线相交于点(点与点A 不重合),连接.(1)如图,当时,①求证:;②在点A 运动的过程中,的度数是否会发生改变?如果会请说明理由,如果不会请求出的度数;(2)在点A 运动的过程中,试探究线段,,之间的数量关系.11.在平面直角坐标系中,点在轴的正半轴上,点在第一象限,,.(1)如图1,求证:是等边三角形;(2)如图1,若点M 为y 轴正半轴上一动点,以为边作等边三角形,连接并延长交轴于点,求证:;(3)如图2,若,,点为的中点,连接、交于,请问、与之间有何数量关系,并证明你的结论.12.在平面直角坐标系中,点A 为y 轴正半轴上一点,点B 为x 轴上一动点,连接ABD C AB DC l E E EB 120BAC ∠<︒ABE ACE =∠∠DCB ∠DCB ∠EA EB ED A y B OB AB =150BOP ∠=︒OAB BM BMN NA x P 2AP AO =BC BO ⊥BC BO =D CO AC DB E AE BE CE,以为腰作等腰,.(1)如图1,点B 在x 轴负半轴上,点C 的坐标是,直接写出点A 和点B 的坐标;(2)如图2,点B 在x 轴负半轴上,交x 轴于点D ,若平分.且点C 的纵坐标是,求线段的长;(3)如图3,点B 在x 轴正半轴上,以为边在左侧作等边,连接,,若,且,求的面积.13.等腰直角中,,,,点、分别是轴,轴上两个动点,直角边交轴于点,斜边交轴于点.(1)如图1,已知点的横坐标为,直接写出点的坐标;(2)如图2,若点为轴上的固定点,且,当点在轴正半轴运动时,分别以、为直角边在第一、二象限作等腰直角和等腰直角,连接交轴于点,问当点在轴的正半轴上运动时,的长度是否变化?若变化请说明理由;若不变化,请求出的长度.14.在平面直角坐标系中,点为坐标原点,点、分别位于轴和轴AB AB Rt ABC △90BAC ∠=︒(2,2)-AC BD ABC ∠3-BD BC BC BCE EO CO 60COE ∠=︒8CO =AOC ABC 90BAC ∠=︒AB AC =ABC C ∠=∠B A x y AC x D BC y E C 2-A A x ()6,0A -B y OB AB BOD ABC CD y P B y BP BP O ()6,0B -()0,6A x y上,连接,交轴于点.(1)求点的坐标;(2)动点从出发以个单位/秒的速度沿轴向终点运动,连接,将线段绕着点逆时针旋转后得到线段,与为对应点.连接、,为的面积,用含的式子表示;(3)在()的条件下,连接,过点作于,交轴于,交于,若,求点的坐标.15.如图①,在中,,现有一动点,从点出发,沿着三角形的边运动,回到点停止,速度为,设运动时间为秒.(1)如图①,当的面积等于面积的一半时,求的值:(2)如图②,点在边上,点在边上,在的边上,若另外有一个动点与点同时从点出发,沿着边运动,回到点停止.在两点运动过程中的某一时刻,以为顶点的三角形恰好与全等,求点的运动速度.16.如图,在平面直角坐标系中,,点在轴正半轴上,.AB CA AB ⊥x C C P B 2x C AP AP A 90︒AQ P Q PQ CQ S PCQ △t S 2BQ A AH BQ ⊥G x H PQ AC M :2:1APM AQM S S = H Rt ABC △90,12cm,16cm,20cm B AB BC AC ∠=︒===P A AB BC CA →→A 2cm /s t ABP ABC t D BC 4cm CD =E AC 5cm,,3cm CE ED BC ED =⊥=ABC Q P A AC CB BA →→A ,,A P Q EDC △Q ()0,9A B x 45OAB ∠=︒(1)求出点坐标;(2)动点从点出发,以每秒个单位长度的速度沿轴正半轴运动,同时点从点出发,以相同速度沿轴向左运动,连接,过点作交直线于点,连接,设点的运动时间为,请用含的式子表示的面积;(3)在(2)的条件下,直线与直线交于点,当时,求点坐标.17.已知中,,过点的直线交轴于,其中是方程组的解,(1)求的值(2)动点从点出发,沿线段以每秒1个单位的速度运动,运动时间为秒;请用含的式子表示线段的长度;并直接写出此时的取值范围;(3)在(2)的条件下,当为何值时,直线与直线互相垂直.18.在平面直角坐标系中,O 为坐标原点,直线交x 轴的正半轴于点A ,交y 轴的B P O 1y Q B x PQ O OG PQ ⊥AB G PG P t t OPG PQ AB H 72OPG S =△H AOB OA OB a ==A AM x (),0M b ,a b 3830a b a b +=⎧⎨+=⎩,a b P A AO t t OP t t BP AM AB(1)如图1求的长;(2)如图2动点E 在第二象限,点E 的坐标为,连接,,请写出面积s 与t 的关系;(3)在(2)的条件下,如图3点F 在第一象限,连接、、,,连接,当,求的值.OD (,)t m DE OE ODE FE FD FA 30ADF ∠=FE FA =EB 12,4EBO ODA ODA EFA EOB ∠=∠∠+∠=∠t m +参考答案:1.(1)(2)动点A 在运动的过程中,的值不变,(3)或或【分析】本题考查全等三角形判定及性质.(1)根据题意过点C 作轴于点,证明出,利用全等性质即可得到本题答案;(2)由(1)得,利用全等性质及点坐标表示线段长即可得到本题答案;(3)根据题意分3种情况讨论P 点位置,利用全等三角形性质及判定即可得到本题答案.【详解】(1)解:如下图,过点C 作轴于点E ,则,,∵是等腰直角三角形,∴,∴,∴.在和中,∴(AAS ),∵,∴,∴,∴;(2)解:动点A 在运动的过程中,的值不变.理由如下:(2,3)-+c d (4,)1-(3,2)--(2,1)-CE y ⊥E ACE BAO ≌ACE BAO ≌CE y ⊥CEA AOB ∠=∠ABC ,90AC BA BAC =∠︒=90ACE CAE BAO CAE ∠+∠=︒=∠+∠ACE BAO ∠=∠ACE △BAO CEA AOB ACE BAOAC BA ∠=∠⎧⎪∠=∠⎨⎪=⎩ACE BAO ≌(0,1),(0,2)B A -12BO AE AO CE ====,123OE =+=2,3C -()+c d由(1)知,,∵,,∴,∴,∴,又∵点C 的坐标为,∴,即的值不变;(3)解:存在一点P ,使与全等,符合条件的点P 的坐标是或或,分为三种情况讨论:①如下图,过点P 作轴于点E ,则,∴,∴,在和中,,∴(AAS ),∴,∴,即点P 的坐标是,②如下图,过点C 作轴于点M ,过点P 作轴于点E ,ACE BAO ≌(0,1)B (0,)A a -1,BO AE AO CE a ====1OE a =+(,1)C a a --(,)c d 11c d a a +=--=-+c d PAB ABC (4,)1-(3,2)--(2,1)-PE x ⊥90PBA AOB PEB ∠=∠=∠=︒90,90EPB PBE PBE ABO ∠+∠=︒∠+∠=︒EPB ABO ∠=∠PEB △BOA △EPB OBA PEB BOA PB BA ∠=∠⎧⎪∠=∠⎨⎪=⎩PEB BOA △≌△1,3PE BO EB AO ====314OE =+=(4,)1-CM x ⊥PE x ⊥则.∵,∴,∴,∴,∴,在和中,,∴(AAS ),∴.∵,∴,即点P 的坐标是;③如下图,过点P 作轴于点E ,则.∵,∴,∴,90CMB PEB ∠=∠=︒CAB PAB △≌△45,PBA CBA BC BP ∠=∠=︒=90CBP ∠=︒90,90MCB CBM CBM PBE ∠+∠=︒∠+∠=︒MCB PBE ∠=∠CMB BEP △MCB EBP CMB BEP BC PB ∠=∠⎧⎪∠=∠⎨⎪=⎩CMB BEP △≌△,PE BM CM BE ==3,4),10C B -((,)2,413PE OE BE BO ==-=-=(3,2)--PE x ⊥90BEP BOA ∠=∠=︒CAB PBA △≌△,90AB BP CAB ABP =∠=∠=︒90,90ABO PBE PBE BPE ∠+∠=︒∠+∠=︒∴.在和中,,∴(AAS ),∴,∴,即点P 的坐标是,综上所述,符合条件的点P 的坐标是或或.2.(1)①见解析;②见解析;(2),见解析【分析】本题主要考查了等边三角形,全等三角形.(1)①根据等边三角形的性质得出,,,根据得出,从而说明三角形全等;②根据全等的性质得出,然后根据即得;(2)根据等边三角形的性质得出,,,根据得出,从而说明,根据全等的性质得出,然后根据即得.【详解】(1)证明:①∵和是等边三角形,∴,,.∴,∴.在和中,,∴;②∵,ABO BPE ∠=∠BOA △PEB △ABO BPE BOA PEB BA PB ∠=∠⎧⎪∠=∠⎨⎪=⎩BOA PEB △≌△1,3PE BO BE OA ====312OE BE BO =-=-=(2,1)-(4,)1-(3,2)--(2,1)-BC CD CE +=AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠-∠=∠-∠BAD EAC ∠=∠BD CE =BC BD CD =+AB AC =AD AE =60BAC DAE ∠=∠=︒BAC DAC DAE DAC ∠+∠=∠+∠BAD EAC ∠=∠ABD ACE ≌△△BD CE =+=BC CD BD ABC ADE V 60BAC DAE ∠=∠=︒AB BC AC ==AD DE AE ==BAC DAC DAE DAC ∠-∠=∠-∠BAD CAE ∠=∠ABD △ACE △AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()SAS ABD ACE △≌△ABD ACE ≌△△∵,,∴,∴是等腰直角三角形,即∵点D 是线段中点,∴,,(0,6)A (6,0)B 6O A O B ==AOB ∠AB OD AB ⊥12OD AD AB ==∠∵,,∴在中,∵在(1)中已求出根据翻折可知:、∴N 点关于的对称点H 在根据对称性有:∴,∴是等边三角形,∵N 点关于的对称点是点H ,3BD =30CBD ∠=︒DG Rt BDG △12DG BD =CE CD =11BDC BKC △BE BK DBC KBC ∠=∠60BDK DBC KBC ∠=∠+∠=︒BDK BE NH如图,,即:,在中,PNC DNC∠=∠24PNC αβ∠==2αβ=MCN DCM DCN x β∠=∠+∠=+MCN △180MCN DCN NMC ∠+∠+∠=2180x βαα+++=︒3180x βα++=︒解得:,.II.当点在线段上时,如图,,,即:,在中,,,即:联立得:,解得:,此时:,不合题意舍去;III .当点在线段上时,如图,,52550x βα=︒⎧⎪=︒⎨⎪=︒⎩∴5DCM ∠=︒N PD 180PNC DNC ∠+∠=︒∴24180αβ+=︒290αβ+=︒∴MCN DCM DCN x β∠=∠+∠=+ CMN PCN MCN CMN x βα∠=∠+∠=++∴4180PCN NDC x βαβ∠+∠=+++=︒5180x βα++=︒2602905180x x ααββα+=︒⎧⎪+=︒⎨⎪++=︒⎩11.2526.2537.5x βα=︒⎧⎪=︒⎨⎪=︒⎩11.2526.5PCN DCN ∠=︒<∠=︒N DM PNC DNC ∠=∠【详解】(1)解:过点B 作轴于点D ,∵,∴,∵轴,∴,∵,∴,∴,在和中,,∴,∴,∵,∴;(2)解:∵,∴,∴,∵轴,∴,∴,∴,在和中,BD y ⊥()()6,0,0,3A C -6,3OA OC ==BD y ⊥90BCD CBD ∠+∠=︒90ACB ∠=︒90BCD ACO ∠+∠=︒ACO CBD ∠=∠ACO △CBD △90AOC CDB ACO CBDAC BC ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩≌ACO CBD 6,3OA CD OC BD ====()0,3C ()3,3B -90ACB ∠=︒90BCF ∠=︒90CBF F ∠+∠=︒BE y ∥90AEF ∠=︒90CAD F ∠+∠=︒CAD CBF ∠=∠CAD CBF V∴,∴,∵,∴∴.【点睛】本题主要考查了三角形综合,折叠的性质,全等三角形的判定和性质,角平分线的性质,解题的关键是掌握全等三角形的判定方法,全等三角形对应边相等,对应角相等;折叠前后对应角相等;角平分线上的点到两边距离相等.7.(1)(2)见解析(3)的度数总是保持不变,理由见解析【分析】本题考查了全等三角形的性质与判定,等腰三角形的性质,坐标与图形;(1)根据等腰三角形的性质解答即可;(2)根据等式的性质得出,进而利用证明与全等,进而解答即可;(3)根据全等三角形的性质得出,进而利用平角的定义解答即可.【详解】(1)解:如图所示,过作轴于,()Rt Rt HL EFO EFN ≌FN FO =(),0F t FO t=-2FG HG t +=-()2,0-COD ∠BAC OAD ∠=∠SAS BAC OAD AOD ABO ∠=∠A AE x ⊥E),点C 是的中点,,D 作轴于点F ,,,4=AB 114222AB ==⨯=DF x ⊥90DFO =︒90FDO DOF +∠=︒),的坐标为,关于x 轴的对称点,则的坐标为,交x 轴于点,则为定值,此时的周长最小.作轴于点Q ,114222AB '==⨯=M '()0,2M '''M ''M AM ''P PAM C AM AP ''=+ AM 'PAM '△()4,4A -AQ y ⊥对于(3),作轴,先证明,可得,再得出,进而得出,根据等腰直角三角形的性质和判定即可得出答案.【详解】(1).理由:,;(2)证明:如图②中,延长交的延长线于点..∵,,,.,即.垂直平分,平分.(3)的长度不变,.理由:如图③中,过点作轴于点...CH y ⊥≌CHB BOA △△,3===CH BO BH OA 3==OA OP ==OB PH CH OAB OBC ∠=∠90,90OAB OBA OBC OBA ∠+∠=∠+∠=︒︒ OAB OBC ∴∠=∠AB CD T ,90,90,AD CD ADT T BAM BCT BAM ⊥∴∠=∴∠+∠=∴∠=∠︒︒ BC BA ===90CB T A B M ∠∠︒()CBT ABM ASA ∴≌△△CT AM ∴=2,2AM CD CT CD =∴= CD DT =,AD CT AD ⊥∴ CT ,AC AT AD ∴=∴BAC ∠OQ 3OQ =C CH y ⊥H 90,90CHB BOA HBC HCB ∴∠=∠=∴∠+∠=︒︒90,90,ABC OBA HBC HCB OBA ∠=∴∠+∠=︒︒∴∠=∠..,..,.【点睛】本题主要考查了全等三角形的性质和判定,同角的余角相等,线段垂直平分线的性质,等腰直角三角形的性质和判定等,构造辅助线是解题的关键.10.(1)①见解析;②不变,(2)或【分析】(1)①根据垂直平分线的性质得出,再由等边对等角及各角之间的数量关系求解即可;②设与交于点M ,根据等边三角形的性质及各角之间的关系得出,即可求解;(2)分两种情况进行分析:当时,当时,分别利用全等三角形的判定和性质及等边三角形的判定和性质分析求解即可.【详解】(1)证明:①点A 、E 在线段的垂直平分线l 上,∴,∴,∴,即;②在点A 运动的过程中,的度数不变,理由如下:如图,设与交于点M ,(),CB AB CHB BOA AAS =∴ ≌△△,3∴===CH BO BH OA ()()3,0,0,3,3A P OA OP ∴== ,BH OP OB PH CH ∴=∴==90,45CHP CPH OPQ ∠=∴∠=∠=︒︒ 90,45∠=∴∠=︒=︒∠ POQ OQP OPQ 3OQ OP ∴==30DCB ∠=︒ED EB EA =+EB ED EA=+AC AB EC EB ==,AB CD 260ECB ∠=︒120BAC ∠<︒120BAC ∠>︒BC ,AC AB EC EB ==,ABC ACB EBC ECB ∠∠∠∠==ABC EBC ACB EBC ∠∠∠∠-=-ABE ACE ∠∠=DCB ∠AB CD∵是等边三角形,∴ ,∴,∴,∴,∴,∴,∵,∴,即;(2)当时,在上截取,连接,∵,∴,由(1)得直线,,∴,∴是等边三角形,∴ ,∴,即,ABD ,60AB AD BAD ∠==︒AD AC =ADC ACE ∠∠=,ABE ADC EBC ECB ∠∠∠∠==,180,180AMD EMB BED ABE EMB BAD ADC AMD ∠∠∠∠∠∠∠∠==︒--=︒--60BED BAD ∠∠==︒,EBC ECB BED EBC ECB ∠∠∠∠∠+==260ECB ∠=︒30DCB ∠=︒120BAC ∠<︒ED EF EA =AF ED DF EF =+ED DF EA =+l BC ⊥30DCB ∠=︒903060AED ∠=︒-︒=︒AEF 60,EAF BAD AE AF ∠∠==︒=–EAF BAF BAD BAF ∠∠∠∠=-BAE DAF ∠∠=∴,∴,∵,∴;当时,如图所示在上截取,连接,∵,∴,由(1)得直线,,,∴,∴F 是等边三角形,∴,∴,∴,∴,∴,∵,∴;综上可得:或.【点睛】题目主要考查线段垂直平分线的性质,全等三角形的判定和性质,等边三角形的判定和性质等,理解题意,作出相应辅助线是解题关键,同时注意进行分类讨论.11.(1)见解析(2)见解析(3),证明见解析【分析】(1)根据有一个角是的等腰三角形是等边三角形可得结论;(SAS)BAE DAF ≌ EB DF =ED DF EA =+ED EB EA =+120BAC ∠>︒EB EF EA =AF EB BF EF =+EB BF EA =+l BC ⊥30DCB ∠=︒BE BC =903060AEB AEC ∠∠==︒-︒=︒AE 60,EAF BAD AE AF ∠∠==︒=–EAF DAF BAD DAF ∠∠∠∠-=EAD BAF ∠∠=(SAS)BAF DAE ≌ BF ED =EB BF EA =+EB ED EA =+ED EB EA =+EB ED EA =+AE BE CE =+60︒(2)根据证明,得,由8字形可得,最后由含角的直角三角形的性质可得结论;(3)如图2,在上截取,先证,方法是根据题意得到三角形为等边三角形,三角形为等腰直角三角形,确定出度数,根据,且,得到度数,进而确定出为,再由,得到,再由,且夹角,利用得到三角形与三角形全等,利用全等三角形的对应边相等得到,得到三角形为等边三角形,得到,由,等量代换即可得证.【详解】(1)解:证明:,,,,是等边三角形;(2)证明:由(1)知:是等边三角形,,是等边三角形,,,,,,,,,,,,SAS MBO NBA ≌OMB ANB ∠∠=60FAM FBN ∠∠==︒30︒AC AG CE =60AEB ∠=︒ABO BOC ABD ∠AB BC =150ABC ∠=︒BAE ∠AEB ∠60︒AG CE =AE CG =AB CB =BAC BCA ∠=∠SAS BCG BAE BG BE =BEG BE EG =AE EG AG =+150BOP ∠=︒ 90AOP ︒=∠60AOB ∴∠=︒OB AB = OAB ∴ OAB 60ABO ∴∠=︒BMN BM BN ∴=60MBN ∠=︒MBO NBA ∴∠=∠AB OB = (SAS)MBO NBA ∴△≌△OMB ANB ∴∠=∠AFM BFN ∠=∠ 60FAM FBN ∴∠=∠=︒60OAP FAM ∠=∠=︒ 90AOP ︒=∠30APO ∴∠=︒;(3),理由如下:如图2,在上截取,连接,,即,,,,为的中点,平分,即,,,,,,,在和中,,,,为等边三角形,,.【点睛】本题是三角形综合题,考查了等腰直角三角形的性质和判定,等边三角形的性质和判定,全等三角形的判定和性质,以及含角的直角三角形的性质,添加辅助线.12.(1),2AP AO ∴=AE BE CE =+AC AG EC =BG AG EG CE EG +=+AE CG =BC BO ⊥ BC BO =90OBC ∴∠=︒D CO BD ∴OBC ∠45CBD OBD ∠=∠=︒60ABO ∠=︒ 105ABD ∴∠=︒150ABC ∠=︒AB OB BC == 15BAC BCA ∴∠=∠=︒154560AEB ∴∠=︒+︒=︒ABE CBG AB CB BAE BCG AE CG =⎧⎪∠=∠⎨⎪=⎩(SAS)ABE CBG ∴△≌△BG BE ∴=BEG ∴△BE EG ∴=AE AG EG CE BE ∴=+=+30︒()02A ,()40B -,∴,∵∴,∵,∴,,90ADC BOA ∠=︒=∠90CAD BAO ABO ∠+∠=︒=∠CAD ABO ∠=∠(2,2)C -2CD =2OD =∴,,∴,;(2)解:如图2,作轴,交轴于,交的延长线于,∴,∵平分,∴,,,∴,∴,∵,∴,∵,∴,∴,∵,,∴,∴,∴的长为6;(3)解:∵为等边三角形,∴,,如图3,在上截取,使,连接,2AO CD ==4BO AD AO OD ==+=()02A ,()40B -,CM x ⊥x N BA M 90BNM BNC ∠=︒=∠BD ABC ∠MBN CBN ∠=∠BN BN =90BNM BNC ∠=︒=∠()ASA MBN CBN ≌3MN CN ==∥CM AO ACM CAO ∠=∠90CAO BAO ABD BAO ∠+∠=︒=∠+∠CAO ABD ∠=∠ACM ABD ∠=∠AC AB =90MAC DAB ∠=︒=∠()ASA ACM ABD ≌6BD CM CN MN ==+=BD BCE BE CE =60BEC EBC ECB ∠=∠=∠=︒OC OF OF OE =EF∴是等边三角形,∴,∴∵,∴,∴,OEF OE EF =60OEF ∠=︒=∠OEF BEF BEC ∠-∠=∠-∠OE EF =BEO CEF ∠=∠()SAS BEO CEF ≌OBE FCE ∠=∠13.(1)(2)【分析】(1)如图①,过作 轴于, 证明可得从而可得答案;(2)如图①,过点作 轴于点.证明 ,可得 ,再证明,从而可得: .【详解】(1)解: 如图①,过作 轴于,∴,∵,∴,∴,∵,∴.∴,,∴,∴,故答案为 : .(2)的长度不变,理由如下:如图②, 过点作 轴于点.()0,23BP =C CF y ⊥F ,ACF BAO ≌CF AO =C CE y ⊥E CBE BAO ≌,6CE BO BE AO ===CPE DPB ≌3BP EP ==C CF y ⊥F 90,90CFA AOB ACF CAF ∠=∠=︒∠+∠=︒90BAC ∠=︒90CAF OAB ∠+∠=︒ACF OAB ∠=∠AC AB =()AAS ACF BAO ≌CF AO =2c x =- 2CF AO ==()0,2A ()0,2BP C CE y ⊥E∵ ,∴∵∴ .∵90ABC ∠=︒90CBE ABO ∠+∠=︒90BAO ABO ∠+∠=︒CBE BAO ∠=∠90CEB AOB ∠=∠=∵,∴,在和中,90BAC PAQ ∠=∠=︒BAP CAQ ∠=∠BAP △CAQ AB AQ =⎧∴四边形为正方形,∴,过作于点,∵AOCN 6OA CN OC ===T TL CN ⊥L AH BQ⊥AOH TLQ ≌∴,解得;②当点在上,点∴,解得;3AP DE cm AQ EC ===,352x =103x =cm/s P AB 5AP EC cm AQ ==,532x =65x =cm/s∴点P 的路程为∴点P 的路程为3AP ED AQ EC ===,AB +1216205AQ =++-=4543x =5AP EC cm AQ ==,AB +1216203AQ =++-=4345x =从出发,以每小时从出发,以相同速度沿,①当在线段上时,P O Q B OQ ∴=AP =t P AO,等腰,,设,,为的一个外角,RO PO ∴=∴POR 45R BAO ∴∠=∠=︒QPO α∠=45RPQ α∴∠=︒-QON BOG α∠==∠ABO ∠ OBG,,,,90HTA ∴∠=︒45HAT OAB ∠=∠=︒45HAT AHT ∴∠=∠=︒HT AT ∴=由(1)知,,则,∵直线与直线互相垂直,∴,()1.0M -1OM =BP AM 90MNB ∠=︒。
中考数学动点问题专题练习(含答案)

动点专题一、应用勾股定理建立函数解析式例1(2000年·上海)如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥O A,垂足为H,△OPH 的重心为G .(1)当点P在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设P Hx =,GP y =,求y 关于x 的函数解析式,并写出函数的定义域(即自变量x 的取值范围).(3)如果△PG H是等腰三角形,试求出线段PH 的长.二、应用比例式建立函数解析式例2(2006年·山东)如图2,在△ABC 中,AB=AC =1,点D,E在直线B C上运动.设BD=,x CE=y . (1)如果∠B AC=30°,∠DA E=105°,试确定y 与x 之间的函数解析式;(2)如果∠B AC的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.AEDCB 图2H M NG PO A B 图1 x yC三、应用求图形面积的方法建立函数关系式例4(2004年·上海)如图,在△A BC中,∠BAC =90°,AB=AC =22,⊙A 的半径为1.若点O在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A相切时, △AO C的面积.一、以动态几何为主线的压轴题 (一)点动问题.1.(09年徐汇区)如图,ABC ∆中,10==AC AB ,12=BC ,点D 在边BC 上,且4=BD ,以点D 为顶点作B EDF ∠=∠,分别交边AB 于点E ,交射线CA 于点F . (1)当6=AE 时,求AF 的长;(2)当以点C 为圆心CF 长为半径的⊙C 和以点A 为圆心AE 长为半径的⊙A 相切时,求BE 的长; (3)当以边AC 为直径的⊙O 与线段DE 相切时,求BE的长.AB C O 图8HAB CDEOlA ′(二)线动问题2,在矩形A BCD 中,AB =3,点O 在对角线A C上,直线l过点O ,且与AC 垂直交AD于点E .(1)若直线l 过点B,把△ABE 沿直线l 翻折,点A 与矩形A BCD的对称中心A '重合,求BC 的长; (2)若直线l 与AB 相交于点F,且AO=41AC,设AD 的长为x ,五边形BCDEF 的面积为S.①求S 关于x 的函数关系式,并指出x 的取值范围;②探索:是否存在这样的x ,以A 为圆心,以-x 43长为半径的圆与直线l 相切,若存在,请求出x 的值;若不存在,请说明理由.(三)面动问题3.如图,在ABC ∆中,6,5===BC AC AB ,D 、E 分别是边AB 、AC 上的两个动点(D 不与A 、B 重合),且保持BC DE ∥,以DE 为边,在点A 的异侧作正方形DEFG .(1)试求ABC ∆的面积;(2)当边FG 与BC 重合时,求正方形DEFG 的边长; (3)设x AD =,ABC ∆与正方形DEFG 重叠部分的面积为y ,试求y 关于x 的函数关系式,并写出定义域;(4)当BDG ∆是等腰三角形时,请直接写出AD 的长.解决动态几何问题的常见方法有:C一、 特殊探路,一般推证例2:(2004年广州市中考题第11题)如图,⊙O 1和⊙O2内切于A,⊙O1的半径为3,⊙O2的半径为2,点P为⊙O1上的任一点(与点A 不重合),直线PA 交⊙O2于点C,PB 切⊙O2于点B ,则PCBP的值为(A)2 (B)3 (C)23(D)26二、 动手实践,操作确认例4(2003年广州市中考试题)在⊙O中,C 为弧AB 的中点,D 为弧A C上任一点(与A 、C 不重合),则(A)A C+CB=AD+DB (B) A C+C B<AD+DB(C) AC+CB >A D+D B (D) AC+C B与AD+DB 的大小关系不确定例5:如图,过两同心圆的小圆上任一点C 分别作小圆的直径CA 和非直径的弦CD ,延长CA 和C D与大圆分别交于点B 、E,则下列结论中正确的是( * ) (A)AB DE = (B )AB DE >(C)AB DE <(D )AB DE ,的大小不确定三、 建立联系,计算说明例6:如图,正方形ABCD 的边长为4,点M在边DC 上,且DM=1,N为对角线A C上任意一点,则DN +MN 的最小值为 .BMND CBA以圆为载体的动点问题中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不重例1.在Rt ABC合),Q是BC边上的动点(与点B、C不重合),当PQ与AC不平行时,△CPQ可能为直角三角形吗?若有可能,请求出线段CQ的长的取值范围;若不可能,请说明理由。
2023年中考数学专题复习:二次函数综合压轴题(动点问题)

2023年中考数学专题复习:二次函数综合压轴题(动点问题)1.抛物线2y x bx c =-++与x 轴交于点()10A -,,()30B ,,与y 轴交于点C .(1)求抛物线的解析式;(2)点D 为第一象限内抛物线上的一动点,作DE x ⊥轴于点E ,交BC 于点F ,过点F 作BC 的垂线与抛物线的对称轴、x 轴、y 轴分别交于点G ,N ,H ,设点D 的横坐标为m .①当DF HF +取最大值时,求点F 的坐标;②连接EG ,若45GEH ∠=︒,求m 的值.2.如图,已知抛物线2y x bx c =-++与x 轴交于()1,0A -,()5,0B 两点(点A 在点B 的左侧),与y 轴交于点C .(1)求抛物线的解析式;(2)在抛物线的对称轴上存在一点P ,使得PA PC +的值最小,求此时点P 的坐标;(3)点D 是第一象限内抛物线上的一个动点(不与点C 、B 重合),过点D 作DF x ⊥轴于点F ,交直线BC 于点E ,连接BD ,直线BC 把BDF V 的面积分成两部分,若:3:2BDE BEF S S =V V ,请求出点D 的坐标.3.如图1,对于平面内小于等于90︒的MON ∠,我们给出如下定义:若点P 在MON ∠的内部或边上,作PE OM ⊥于点E ,PF ON ⊥于点F ,则将PE PF +称为点P 与MON ∠的“点角距”,记作(),d MON P ∠.如图2,在平面直角坐标系xOy 中,x 、y 正半轴所组成的角为xOy ∠.(1)已知点()5,0A 、点()3,2B ,则(),d xOy A ∠=______ ,(),d xOy B ∠=______.(2)若点P 为xOy ∠内部或边上的动点,且满足(),5d xOy P ∠=,在图2中画出点P 运动所形成的图形.(3)如图3,在平面直角坐标系xOy 中,抛物线212y x mx n =-++经过()5,0A 与点()3,4D 两点,点Q 是A 、D 两点之间的抛物线上的动点(点Q 可与A 、D 两点重合),求当(),d xOD Q ∠取最大值时点Q 的坐标.4.如图,抛物线2134y ax bx =++与x 轴交于点()30A -,和点B ,点D 是抛物线1y 的顶点,过点D 作x 轴的垂线,垂足为点()10C -,.(1)求抛物线1y 所对应的函数表达式;(2)如图1,点M 是抛物线1y 上一点,且位于x 轴上方,横坐标为m ,连接MC ,若MCB DAC ∠=∠,求m 的值;(3)如图2,将抛物线1y 平移后得到顶点为B 的抛物线2y .点P 为抛物线1y 上的一个动点,过点P 作y 轴的平行线,交抛物线2y 于点Q ,过点Q 作x 轴的平行线,交抛物线2y 于点R .当以点P ,Q ,R 为顶点的三角形与ACD V 全等时,请直接写出点P 的坐标.5.如图,抛物线()20y ax bx c a =++≠与x 轴交于A 、B 两点,与y 轴交于点()0,6C ,顶点为D ,且()1,8D .(1)求抛物线的解析式;(2)若在线段BC 上存在一点M ,过点O 作OH OM ⊥交BC 的延长线于H ,且MO HO =,求点M 的坐标;(3)点P 是y 轴上一动点,点Q 是在对称轴上一动点,是否存在点P ,Q ,使得以点P ,Q ,C ,D 为顶点的四边形是菱形?若存在,求出点Q 的坐标;若不存在,请说明理由.6.如图,已知二次函数24y x bx =+-的图像经过点()3,4A -,与x 轴负半轴交于点B ,与y 轴交于点C ,连接AB ,BC .(1)填空:b =______;(2)点P 是直线AB 下方抛物线上一个动点,过点P 作PT x ⊥轴,垂足为T ,PT 交AB 于点Q ,求线段PQ 的最大值;(3)点D 是y 轴正半轴上一点,若∠=∠BDC ABC ,求点D 的坐标.7.如图,抛物线2y x bx c =++(b ,c 是常数)的顶点为C ,与x 轴交于A ,B 两点,()1,0A ,4AB =(1)求该抛物线的解析式;(2)点P 为线段AB 上的动点,过P 作PQ BC ∥交AC 于点Q ,求CPQ V 面积的最大值,并求此时P 点坐标;(3)如图,设抛物线与y 轴交于点D ,平行于BD 的直线MN 交抛物线于点M ,N ,作直线MB ND 、交于点G ,问点G 是否在某一定直线上运动,若在求此直线的解析式,若不在说明理由.8.如图,已知抛物线23y ax bx =+-的图象与x 轴交于点A ()10,和B ()30,,与y 轴交于点C ,D 是抛物线的顶点,对称轴与x 轴交于E .(1)求抛物线的解析式;(2)如图1,在抛物线的对称轴DE 上求作一点M ,使A M C V 的周长最小,M 的坐标__________周长的最小值______.(3)如图2,点P 是x 轴上的动点,过P 点作x 轴的垂线分别交抛物线和直线BC 于F 、G .设点P 的横坐标为m .是否存在点P ,使FG 最长?若存在,求出m 的值;若不存在,请说明理由.9.如图1,抛物线()230y ax bx a =+->交x 轴于点A ,B (点A 在点B 左侧),交y 轴于点C ,且3O B O C O A ==,点D 为抛物线上第四象限的动点.(1)求抛物线的解析式.(2)如图1,直线AD 交BC 于点P ,连接AC BD ,,若ACP △和BDP △的面积分别为1S 和2S ,当12S S -的值最小时,求直线AD 的解析式.(3)如图2,直线BD 交抛物线的对称轴于点N ,过点B 作AD 的平行线交抛物线的对称轴于点M ,当点D 运动时,线段MN 的长度是否会改变?若不变,求出其值;若变化,求出其变化的范围.10.已知抛物线23y ax bx =++(0a ≠)交x 轴于()0A 1,和()30B -,,交y 轴于C .(1)求抛物线的解析式;(2)若M 为抛物线上第二象限内一点,求使MBC V 面积最大时点M 的坐标;(3)若F 是对称轴上一动点,Q 是抛物线上一动点,是否存在F 、Q ,使以B 、C 、F 、Q 为顶点的四边形是平行四边形?若存在,直接写出点Q 的坐标.11.如图,在平面直角坐标系中,二次函数的图象交坐标轴于()20A -,,()40B ,,()08C ,三点,点P 是直线BC 上方抛物线上的一个动点.(1)求这个二次函数的解析式;(2)动点P 运动到什么位置时,PBC V 的面积最大,求此时P 点坐标及PBC V 面积的最大值;(3)在y 轴上是否存在点Q ,使以O ,B ,Q 为顶点的三角形与AOC V 相似?若存在,请直接写出点Q 的坐标;若不存在,请说明理由.12.如图,抛物线2y x bx c =++与x 轴交于()1,0A -,()3,0B 两点,与y 轴交于点C .(1)求该抛物线的解析式;(2)若点E 是线段BC 上的一个动点,平行于y 轴的直线EF 交抛物线于点F ,求FBC V 面积的最大值;(3)设点P 是(1)中抛物线上的一个动点,是否存在满足6PAB S =△的点P ?如果存在,请求出点P 的坐标;若不存在,请说明理由.13.如图,抛物线2y ax bx =+经过()()3,0,2,10A B -两点.(1)求抛物线的解析式;(2)点P 是直线AB 下方抛物线上的一个动点,求PAB V 面积的最大值;(3)点M 是直线AB 上的一个动点,将点M 向左平移3个单位长度得到点N ,设点M 的横坐标为m ,若线段MN 与抛物线只有一个公共点,请直接写出m 的取值范围.14.如图,在平面直角坐标系中,直线122y x =-与x 轴交于点A ,与y 轴交于点C ,抛物线212y x bx c =++经过A ,C 两点,与x 轴的另一交点为点B ,点P 为抛物线上的一个动点.(1)求抛物线的函数表达式;(2)当ACP △的面积与ABC V 的面积相等时,求点P 的坐标;(3)是否存在点P ,使得ACP ABC BAC ∠=∠-∠,若存在,请直接写出点P 的横坐标;若不存在,请说明理由.15.如图,已知拋物线2y ax bx c =++与x 轴交于点()1,0A ,()3,0B -,与y 轴交于点()0,3C -.点P 是抛物线上一动点,且在直线BC 的下方,过点P 作PD x ⊥轴,垂足为D ,交直线BC 于点E .(1)求抛物线的函数解析式;(2)连接CP ,若45CPD ∠=︒,求点P 的坐标;(3)连接BP ,求四边形OBPC 面积的最大值.16.如图,在平面直角坐标系中,抛物线28y x bx =-++与x 轴交于点A ,B ,与y 轴交于点C ,直线y x t =-过点B ,与y 轴交于点D ,点C 与点D 关于x 轴对称.点P 是线段OB 上一动点,过点P 作x 轴的垂线交抛物线于点M ,交直线BD 于点N .(1)求抛物线的解析式;(2)当MDB △的面积最大时,求点P 的坐标;(3)在(2)的条件下,在y 轴上是否存在点Q ,使得以Q ,M ,N ,D 为顶点的四边形是平行四边形,若存在,求出点Q 的坐标;若不存在;说明理由17.如图,抛物线21262y x x =--与x 轴相交于点A 、点B ,与y 轴相交于点C .(1)请直接写出点A ,B ,C 的坐标;(2)若点P 是抛物线BC 段上的一点,当PBC V 的面积最大时求出点P 的坐标,并求出PBC V 面积的最大值.(3)点F 是抛物线上的动点,作FE AC ∥交x 轴于点E ,是否存在点F ,使得以A 、C 、E 、F 为顶点的四边形是平行四边形?若存在,请写出所有符合条件的点F 的坐标;若不存在,请说明理由.18.如图,在平面直角坐标系中,抛物线21=2y x bx c ++经过点()4,0A -,点M 为抛物线的顶点,点B 在y 轴上,直线AB 与抛物线在第一象限交于点()2,6C .(1)求抛物线的解析式;(2)连接OC ,点Q 是直线AC 上不与A 、B 重合的点,若2OAQ OAC S S =V V ,请求出点Q 的坐标;(3)在x 轴上有一动点H ,平面内是否存在一点N ,使以点A 、H 、C 、N 为顶点的四边形是菱形?若存在,直接写出点N 的坐标,若不存在,请说明理由.参考答案:1.(1)223y x x =-++(2)①点F 的坐标为⎝⎭;②1或952.(1)245y x x =-++(2)()2,3P (3)335,24D ⎛⎫ ⎪⎝⎭3.(1)5,5 (3)54,2⎛⎫ ⎪⎝⎭4.(1)21113424y x x =--+(2)2-(3)304⎛⎫ ⎪⎝⎭,或524⎛⎫- ⎪⎝⎭,5.(1)2246y x x =-++ (2)126,55⎛⎫ ⎪⎝⎭(3)(1,8或(1,8或271,4⎛⎫ ⎪⎝⎭6.(1)3-(2)PQ 的最大值是4 (3)50,3⎛⎫ ⎪⎝⎭7.(1)223y x x =+-(2)CPQ V 面积的最大值为2,此时P 点坐标为()1,0-(3)在,3y x =--8.(1)2=+43y x x --(2)()21-,(3)存在,m 的值为329.(1)2=23y x x --(2)22y x =--(3)不变,值为810.(1)223y x x =--+ (2)31524⎛⎫- ⎪⎝⎭, (3)存在,点Q 的坐标为()23-,或()45-,-或()25,-11.(1)228y x x =-++(2)当P 点坐标为()28,时,PBC V 的最大面积为8; (3)存在,点Q 的坐标为()016,或()016-,或()01,或()01-,.12.(1)2=23y x x -- (2)278(3)存在,点P 的坐标为()1或()1或()0,3-或()2,3-13.(1)23y x x =-(2)PAB S V 最大值为1258(3)23m -≤<或34m <<或338m =14.(1)抛物线的函数表达式为213222y x x =-- (2)点P 的坐标为(5,3)P(3)存在,点P 的横坐标为2911或7.15.(1)223y x x =+- (2)(14)--, (3)63816.(1)278y x x =-++(2)()3,0(3)存在,()0,17Q 或()0,33-17.(1)()2,0A -,()6,0B ,()0,6C - (2)点P 的坐标为153,2⎛⎫- ⎪⎝⎭时,PBC S V 有最大值272(3)存在,点F 的坐标为()4,6-或()2+或()2-18.(1)21=22y x x + (2)()8,12或()16,12--(3)()2N +或()2N -或()2,6N -或()4,6-。
初二动点问题及中考压轴题

初二动点问题及中考压轴题初二动点问题及中考压轴题2.如图,△ ABC中,点 O为 AC边上的一个动点,过点 O作直线MN∥BC,设MN交∠BCA的外角均分线CF于点F,交∠ACB内角均分线 CE于 E.(1)试说明 EO=FO;(2)当点 O运动到哪处时,四边形 AECF是矩形并证明你的结论;(3)若 AC边上存在点 O,使四边形 AECF是正方形,猜想△ABC的形状并证明你的结论.4.如图,在矩形ABCD中,BC=20cm,P,Q,M,N分别从A,B,C,D出发沿 AD,BC,CB, DA方向在矩形的边上同时运动,当有一个点先抵达所在运动边的另一个端点时,运动即停止.已知在同样时间内,若 BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.(1)当 x 为何值时,以 PQ,MN为两边,以矩形的边( AD 或 BC)的一部分为第三边组成一个三角形;(2)当 x 为何值时,以 P,Q,M,N 为极点的四边形是平行四边形;...6. 如图,在直角梯形 ABCD中,AD∥BC,∠ C=90°,BC=16,DC=12,AD=21,动点 P 从点 D出发,沿射线 DA的方向以每秒 2 个单位长的速度运动,动点 Q从点 C出发,在线段 CB 上以每秒 1 个单位长的速度向点 B 运动,P、Q分别从点 D、 C 同时出发,当点 Q运动到点 B 时,点 P随之停止运动,设运动时间为 t (s).(1)设△ BPQ的面积为 S,求 S 与 t 之间的函数关系;(2)当 t 为何值时,以 B、P、Q三点为极点的三角形是等腰三角形?1 如图 1,在平面直角坐标系中,点 O是坐标原点,四边形ABCO是菱形,点 A的坐标为(- 3,4),点 C 在 x 轴的正半轴上,直线 AC交 y 轴于点 M,AB边交 y 轴于点 H.(1)求直线 AC的分析式;(2)连结BM,如图2,动点P 从点A 出发,沿折线ABC 方向以 2 个单位/秒的速度向终点 C匀速运动,设△ PMB的面积为 S(S≠0),点 P 的运动时间为 t 秒,求 S 与 t 之间的函数关系式(要求写出自变量 t 的取值范围);3.如图,已知△ABC 中, AB AC 10厘米, BC 8厘米,点 D 为 AB 的中点.(1)假如点P在线段BC上以 3 厘米 / 秒的速度由B点向C 点运动,同时,点 Q在线段 CA上由 C点向 A 点运动.①若点Q的运动速度与点 P 的运动速度相等,经过1秒后,△BPD 与△CQP能否全等,请说明原因;②若点 Q的运动速度与点 P 的运动速度不相等,当点 Q的运动速度为多少时,可以使△BPD 与△CQP全等?(2)若点Q以②中的运动速度从点C出发,点PA以本来的运动速度从点 B 同时出发,都逆时针沿△ ABC 三边运动,求经过多长时间点P 与点 Q第一DQ 次在△ ABC 的哪条边上相遇?B P C4.如图,已知 AD与 BC订交于 E,∠ 1=∠ 2=∠ 3,BD=CD,∠ ADB=90°, CH⊥AB于 H,CH交 AD于 F.(1)求证: CD∥AB;(2)求证:△ BDE≌△ ACE;(3)若 O为 AB中点,求证: OF=1 BE.25、如图 1―4―2l ,在边长为 a 的菱形 ABCD中,∠ DAB=60°,E 是异于A、D两点的动点,F 是CD上的动点,知足 A E+CF=a,说明:无论 E、F 如何挪动,三角形 BEF老是正三角形.6、如图 1-4-38,等腰梯形 ABCD中, AD∥BC,AB =CD,∠ DBC=45○ , 翻折梯形使点 B 重合于点 D,折痕分别交边 AB、BC于点 F、E,若 AD=2,BC=8,求 BE的长.7、在平行四边形ABCD中,E为BC的中点,连结的延伸线于点 F .(1)求证: AB CF ;(2)当 BC 与 AF 知足什么数目关系时,B 四边形 ABFC 是矩形,并说明原因.AE 并延伸交 DCD ACEF8、如图 l -4-80,已知正方形 ABCD的对角线 AC、BD订交于点 O, E是 AC上一点,过点 A 作 AG⊥EB,垂足为 G,AG交 BD于 F,则 OE=OF.(1)请证明 0E=OF(2)解答(1)题后,某同学产生了以下猜想:对上述命题,若点 E 在 AC的延伸线上, AG⊥EB,AG交 EB 的延伸线于G,AG的延伸线交 DB的延伸线于点 F,其余条件不变,则仍有 OE=OF.问:猜想所得结论能否建立?若建立,请给出证明;若不建立,请说明原因.9 已知:如图4-26 所示,△ABC中,AB=AC,∠BAC=90°,D 为BC的中点,P 为BC的延伸线上一点,PE⊥直线AB于点 E,PF⊥直线 AC于点 F.求证: DE⊥DF而且相等.10 已知:如图 4-27 ,ABCD为矩形, CE⊥BD于点 E,∠BAD 的均分线与直线 CE订交于点 F.求证: CA=CF.11 已知:如图4-56A.,直线l 经过正方形ABCD的极点D 平行于对角线AC,E 为l 上一点,EC=AC,而且EC与边AD 订交于点 F.求证: AE=AF.本例中,点 E 与 A 位于 BD同侧.如图 4-56B.,点 E与A 位于 BD异侧,直线 EC与 DA的延伸线交于点 F,这时仍有 AE=AF.请自己证明.动点问题练习题1、已知:等边三角形ABC的边长为 4 厘米,长为 1 厘米的线段 MN 在△ABC的边 AB上沿 AB方向以1厘米/秒的速度向 B点运动(运动开始时,点 M 与点 A 重合,点 N 抵达点 B 时运动停止),过点 M 、N 分别作 AB 边的垂线,与△ ABC 的其余边交于P、Q两点,线段 MN 运动的时间为 t 秒.1、线段MN在运动的过程中,t为何值时,四边形MNQP恰为矩形?并求出该矩形的面积;(2)线段MN在运动的过程中,四边形MNQP的面积为S,运动的时间为t .求四边形MNQP的面积S 随运动时间t 变C化的函Q数关系式,并写出自变量t 的取值范围.PAMN B2、如图,在梯形ABCD中,AD∥BC,AD 3,DC 5,AB 4 2,∠B 45.动点 M 从 B 点出发沿线段BC 以每秒2个单位长度的速度向终点C运动;动点 N 同时从 C 点出发沿线段 CD 以每秒1个单位长度的速度向终点 D 运动.设运动的时间为 t 秒.(1)求BC的长.(2)当MN∥AB时,求t的值.(3)尝试究:t为何值时,△MNC为A等腰三角D形.NB M C3、如图,在平面直角坐标系中,四边形OABC是梯形,OA∥BC,点 A 的坐标为(6,0),点 B 的坐标为(4,3),点C在 y 轴的正半轴上.动点 M在 OA上运动,从 O点出发y BC到 A 点;动点 N在 AB上运动,从 A 点出发到 B 点.两个N动点同时出发,速度都是每秒 1 个单位长度,当此中一O M A x个点抵达终点时,另一个点也随即停止,设两个点的运动时间为 t (秒).(1)求线段 AB的长;当 t 为何值时, MN∥OC?(2)设△ CMN的面积为 S,求 S与 t 之间的函数分析式,并指出自变量 t 的取值范围; S 能否有最小值?如有最小值,最小值是多少?(3)连结 AC,那么能否存在这样的 t ,使 MN与 AC相互垂直?若存在,求出这时的t 值;若不存在,请说明原因.2、如图,在 Rt△ABC中,∠C=90°,AC=12,BC=16,动点 P 从点 A 出发沿 AC边向点 C以每秒3个单位长的速度运动,动点 Q从点 C出发沿 CB边向点 B 以每秒4个单位长的速度运动. P,Q分别从点 A,C同时出发,当此中一点抵达端点时,另一点也随之停止运动.在运动过程中,△ PCQ 对于直线PQ对称的图形是△ PDQ.设运动时间为 t (秒).(1)设四边形PCQD的面积为y,求y与t的函数关系式;(2)t为何值时,四边形PQBA是梯形?(3)能否存在时辰t,使得PD AB t∥?若存在,求出若不存在,请说明原因;(4)经过察看、绘图或折纸等方法,猜想是否存在时辰 t ,使得 PD⊥AB?若存在,请预计AP t的值在括号中的哪个时间段内( 0≤t≤1;1<t ≤2;2<t ≤3;3<t ≤4);若不存在,请C Q简要说明原因.的值;DB4、在ABC中,C Rt , AC 4cm, BC 5cm,点D在BC上,且以CD=3cm,现有两个动点 P、Q分别从点 A 和点 B 同时出发,此中点 P以 1cm/s 的速度,沿 AC向终点 C 挪动;点 Q以 1.25cm/s 的速度沿BC 向终点 C 挪动。
人教版八年级下册数学期末复习:动点问题压轴题

人教版八年级下册数学期末复习:动点问题压轴题1.如图,已知O是坐标原点,点A的坐标是(5,0),点B是y轴正半轴上一动点,以OB,OA为边作矩形OBCA,点E,H分别在边BC和边OA上,将△BOE沿着OE 对折,使点B落在OC上的F点处,将△ACH沿着CH对折,使点A落在OC上的G 点处.(1)求证:四边形OECH是平行四边形;(2)当点B运动到使得点F,G重合时,求点B的坐标,并判断四边形OECH是什么四边形?说明理由;(3)当点B运动到使得点F,G将对角线OC三等分时,直接..写出点B的坐标.2.如图1,正方形ABCD边长为4,点P是直线BC上的一动点,连接DP,以DP为边在直线DP右侧作等边三角形DPE.(1)请直接写出正方形ABCD的面积;(2)当BP为何值时,点C落在DPE的边上;(3)如图2,若点P在线段BC上从B向C运动,当BP为何值时,线段CE的长度最小?请求出CE的最小值,并直接写出点E所经过的路径的长度.3.如图,已知ABC 为等腰直角三角形,且面积为4.点D 是BC 的中点,点F 是直线AB 上一动点,连结DF .(1)求线段BC 的长;(2)当点E 在射线BC 上,且2CE BC =时,连结FE ,若3AF AB =,试判断DEF 是否为等腰三角形,并说明理由;(3)直线AB 上是否存在点F (F 不与AB 重合),使ACF 的其中两边之比为存在,求出BF 的长;若不存在,请说明理由.4.如图1,在平面直角坐标系中,点A 的坐标为(5,0),点B 在第一象限内,且AB =4,OB =3.(1)试判断△AOB 的形状,并说明理由.(2)点P 是线段OA 上一点,且PB -P A =1,求点P 的坐标;(3)如图2,点C 、点D 分别为线段OB 、BA 上的动点,且OC =BD ,求AC +OD 的最小值.5.如图,在平面直角坐标系中,直线AB为y=﹣34x+b交y轴于点A(0,3),交x轴于点B,直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).(1)求点B的坐标及点O到直线AB的距离;(2)求△ABP的面积(用含n的代数式表示);(3)当S△ABP=72时,在第一象限找点C,使△PBC为等腰直角三角形,直接写出点C的坐标.6.如图,直线y kx b=+经过点75,04A⎛⎫⎪⎝⎭,点()0,25B,与直线34y x=交于点C,点D为直线AB上一动点,过D点作x轴的垂线交直线OC于点E.(1)求点C的坐标;(2)当23DE OA=时,求△CDE的面积;(3)当OAD△沿着OD折叠,当点A落在直线OC上时,直接写出点D的坐标.7.点P为等边ABC的边AB延长线上的动点,点B关于直线PC的对称点为D,连接AD.(1)如图1,若2BP AB ==,依题意补全图形,并直接写出线段AD 的长度; (2)如图2,线段AD 交PC 于点E , △设BCP α∠=,求AEC ∠的度数; △求证:AE CE DE =+.8.如图,在平面直角坐标系中,直线l 1:y =﹣x +5与y 轴交于点A ,直线l 2与x 轴、y 轴分别交于点B (﹣4,0)和点C ,且与直线l 1交于点D (2,m ).(1)求直线l 2的解析式;(2)若点E 为线段BC 上一个动点,过点E 作EF △x 轴,垂足为F ,且与直线l 1交于点G ,当EG =6时,求点G 的坐标;(3)若在平面上存在点H ,使得以点A ,C ,D ,H 为顶点的四边形是平行四边形,请直接写出点H 的坐标.9.如图1,直线AB :y x b =-+分别与x ,y 轴交于()6,0A ,B 两点,过点B 的直线交x 轴负半轴于C ,且:3:1OB OC =.()1求直线BC的函数表达式;()2在x轴是否存在一点M,使得BCM是一个等腰三角形,若存在请求出点M的坐标,若不存在请说明理由;()3如图2,P为x轴上A点右侧的一动点,以P为直角顶点,BP为一腰在第一象限内作等腰直角三角形BPQ,连接QA并延长交y轴于点K.当P点运动时,K点的位置是否发生变化?如果不变请求出它的坐标;如果变化,请说明理由.10.如图,直线1与直线m交于点Q89,55⎛⎫⎪⎝⎭,直线m与坐标轴分别交于A、B两点,直线l与y轴交与点C,已知B、C两点关于x轴对称且BC=6.(1)求直线l和直线m的解析式;(2)若P为直线l上一动点,S△P AB=32S△OAB,求点P的坐标;(3)M为直线l上一动点,N为平面内一点,直接写出所有使得以A、B、M、N为顶点的四边形为菱形的点N的坐标,并把求其中一个点N的坐标的过程写出来.11.如图,在四边形ABCD 中,AD △BC ,△B =90°,△C =60°,AD =24cm ,CD =8cm .点P 从点D 出发,以1cm /s 的速度向点A 运动;点Q 从点B 同时出发,以3cm /s 的速度向点C 运动.规定其中一个动点到达端点时,另一个动点也随之停止运动.设点Q 的运动时间为x (s ). (1)BC = cm ,AB = cm ; (2)当PQ =CD 时,x = ;(3)当四边形ABQP 为矩形时,求x 的值.12.如图,正比例函数34y x =与一次函数7y ax =+的图像相交于点()4,P n ,过点(),0A t 作x 轴的垂线l ,且04t <<,交一次函数的图像于点B ,交正比例函数的图像于点C ,连接OB . (1)求a 值;(2)设OBP 的面积为s ,求s 与t 之间的函数关系式;(3)当2t =时,在正比例函数34y x =与一次函数7y ax =+的图像上分别有一动点M 、N ,是否存在点M 、N ,使CMN △是等腰直角三角形,且90CNM ∠=︒,若存在,请直接写出点M 、N 的坐标;若不存在,请说明理由.13.如图1,在Rt△ABC中,△ACB=90°,AC=BC,将点C绕点B顺时针旋转105°得到点D,连接BD,过点D作DE△BC交CB延长线于点E,点F为线段DE上的一点,且△DBF=45°,作△BFD的角平分线FG交AB于点G.(1)求△BFD的度数;(2)求BF,DF,GF三条线段之间的等量关系式;(3)如图2,设H是直线DE上的一个动点,连接HG,HC,若AB,求线段HG+HC的最小值(结果保留根号).14.如图所示,点A是平面直角坐标系内一点坐标为(1,AB是过点A的一条直线,B是直线与x轴的交点,以OA、OB为邻边作平行四边形AOBC.若OD是△AOB的平分线,且D是AC的中点.(1)求B、D两点的坐标;(2)求直线AB的解析式;S平行四边形AOBC,请直接写出满足条件(3)若P是直线AB上一动点,且S△POD 12的点P的坐标.15.如图,矩形OABC的顶点A、C分别在x轴、y轴的正半轴上,点B的坐标为(3,4),一次函数y=23x b-+的图象与边OC,AB分别交于点D,E,并且满足OD=BE,点M是线段DE上的一个动点.(1)求b的值;(2)当DM:ME=1:2时,求点M的坐标;(3)设点N是x轴上方的平面内的一点,当以点O,M,D,N为顶点的四边形是菱形时,直接写出点N的坐标.16.在矩形ABCD中,BC,点E、F分别是边AD、BC上的动点,且AE=CF,连接EF,将矩形ABCD沿EF折叠,点C落在点G处,点D落在点H处.(1)如图1,当EH与线段BC交于点P时,求证:PE=PF;(2)如图2,当点P在线段CB的延长线上时,交AB于点M,求证:点M在线段EF 的垂直平分线上;(3)当AB=5时,在点E由点A移动到AD中点的过程中,直接写出点G运动路线长.交△BCA的平分线于点E,交△BCA的外角平分线于点F.(1)探究OE与OF的数量关系并加以证明;(2)四边形BCFE会是菱形吗?若是,请加以证明;若不是,则说明理由;(3)当点O运动到什么位置时,四边形AECF是矩形?请说明理由;(4)在(3)问的基础上,△ABC满足什么条件时,四边形AECF是正方形?为什么?18.如图,在平面直角坐标系中,直线123y x=-+与x轴交于点C,与y轴交于点A.(1)求AOC△的面积;(2)点P是直线AC上的动点,过P作x轴,y轴的垂线,垂足分别为点F,E,若2PF PE=,请求出点P的坐标;(3)点117,39B⎛⎫⎪⎝⎭在直线AC上,坐标轴上存在动点M,使ABM是以AB为直角边的直角三角形,请直接写出点M的坐标.把△COB沿BC翻折,点O恰好落在AB边的点D处,BC为折痕.(1)求线段AB的长;(2)求直线BC的解析式;(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P 为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.20.如图,在平面直角坐标系中,直线y=12x+2与y轴、x轴分别交于点A,B,点M在线段AB上运动(不与点A,B重合),连接OM.(1)求线段OB的长;(2)设点M的横坐标为m,△BOM的面积为S,求S关于m的函数关系式(不必写出自变量m的取值范围);(3)若点M为线段AB的中点,点P为射线BO上的动点,将△APM沿直线PM折叠得到△A1PM,若以点A1、B、P、M为顶点的四边形是平行四边形,直接写出点A1的横坐标.参考答案:1. (2)B (0);四边形OECH 是菱形(3)点B 的坐标是(00, 2.(1)16(2)4或4343或4(3)4-;2;E 所经过的路线的长度是43.(1)线段BC 的长为4;(2)△DEF 是等腰三角形(3)存在,BF 的长为或或-2.4.(1)△AOB 是直角三角形,(2)P (4514,0)5.(1)B (4,0),125(2)922n -(3)(5,7)或(8,3)或(92,72) 6.(1)点C 的坐标为(12,9);(2)△CDE 的面积为752;(3)点D 的坐标为(15,5)或(-15,45). 7.(1)AD =(2)△60AEC ∠=︒;△证明见解析.8.(1)122y x =+;(2)(﹣2,7);(3)(2,0)或(2,6)或(﹣2,4).9.()136y x =+; ()2 存在,M 的坐标为()12M --,()22M -+,()38,0M ,()42,0M ; ()3不变化,()0,6K -.10.(1)直线l 的解析式为33y x =-,直线m 的解析式为334y x =-+;(2)P (25,95-)或P (145,275);(3)N 1(2910,2710)或N 2(295+,35-N 3(295-,35-)或N 4(4-,0)或N 5(75-,395) 11.(1)28,(2)5或7;(3)6.12.(1)1a =-;(2)7142s t =-+;(3)存在,1133,28M ⎛⎫ ⎪⎝⎭,3973,1616N ⎛⎫ ⎪⎝⎭或2053M ⎛⎫ ⎪⎝⎭,,7311,1212N ⎛⎫ ⎪⎝⎭.13.(1)120°;(2)BF +DF =GF ;(314.(1)B 点的坐标是(4,0),D 点的坐标是(3.(2)y (3)(4,0)或(0. 15.(1)3;(2)M (1,73);(3)N (3613,5413)或N (﹣94,32). 16.(1)见解析;(2)见解析;(3)103π 17.(1)OE =OF ,证明见解析;(2)不是;(3)点O 运动到AC 的中点;(4)△ACB 为直角18.(1)6;(2)612,77P ⎛⎫ ⎪⎝⎭或612,55P ⎛⎫- ⎪⎝⎭;(3)点M 的坐标为2,03⎛⎫- ⎪⎝⎭或92,027⎛⎫ ⎪⎝⎭或920,9⎛⎫- ⎪⎝⎭ 19.(1)AB =10;(2)y =2x +6;(3)存在,满足条件的P 点的坐标为(3,2)或(-4,8).20.(1)4;(2)S =m +4;(3)-1或-3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二动点问题及中考压轴题2.如图,△ABC 中,点O 为AC 边上的一个动点,过点O 作直线MN ∥BC ,设MN 交∠BCA 的外角平分线CF 于点F ,交∠ACB 内角平分线CE 于E .(1)试说明EO=FO ;(2)当点O 运动到何处时,四边形AECF 是矩形并证明你的结论;(3)若AC 边上存在点O ,使四边形AECF 是正方形,猜想△ABC 的形状并证明你的结论.4.如图,在矩形ABCD 中,BC=20cm ,P ,Q ,M ,N 分别从A ,B ,C ,D 出发沿AD ,BC ,CB ,DA 方向在矩形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm (x≠0),则AP=2xcm ,CM=3xcm ,DN=x2cm .(1)当x 为何值时,以PQ ,MN 为两边,以矩形的边(AD 或BC )的一部分为第三边构成一个三角形;(2)当x 为何值时,以P ,Q ,M ,N 为顶点的四边形是平行四边形;...6.如图,在直角梯形ABCD 中,AD ∥BC ,∠C=90°,BC=16,DC=12,AD=21,动点P 从点D 出发,沿射线DA 的方向以每秒2个单位长的速度运动,动点Q 从点C 出发,在线段CB 上以每秒1个单位长的速度向点B 运动,P 、Q 分别从点D 、C 同时出发,当点Q 运动到点B 时,点P 随之停止运动,设运动时间为t (s ).(1)设△BPQ 的面积为S ,求S 与t 之间的函数关系;(2)当t 为何值时,以B 、P 、Q 三点为顶点的三角形是等腰三角形?1如图1,在平面直角坐标系中,点O 是坐标原点,四边形ABCO 是菱形,点A 的坐标为(-3,4), 点C 在x 轴的正半轴上,直线AC 交y 轴于点M ,AB 边交y 轴于点H .(1)求直线AC 的解析式;(2)连接BM ,如图2,动点P 从点A 出发,沿折线ABC 方向以2个单位/秒的速度向终点C 匀速运动,设△PMB 的面积为S (S ≠0),点P 的运动时间为t 秒,求S 与t 之间的函数关系式(要求写出自变量t 的取值范围);3.如图,已知ABC △中,10AB AC ==厘米,8BC =厘米,点D 为AB 的中点.(1)如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动,同时,点Q 在线段CA 上由C 点向A 点运动.①若点Q 的运动速度与点P 的运动速度相等,经过1秒后,BPD △与CQP △是否全等,请说明理由; ②若点Q 的运动速度与点P 的运动速度不相等,当点Q 的运动速度为多少时,能够使BPD △与CQP △全等?(2)若点Q 以②中的运动速度从点C 出发,点P 以原来的运动速度从点B 同时出发,都逆 A QC D B P时针沿ABC △三边运动,求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇?4. 如图,已知AD 与BC 相交于E ,∠1=∠2=∠3,BD =CD ,∠ADB =90°,CH ⊥AB 于H ,CH 交AD 于F.(1)求证:CD ∥AB ;(2)求证:△BDE ≌△ACE ;(3)若O 为AB 中点,求证:OF =12BE. 5、如图1―4―2l ,在边长为a 的菱形ABCD 中,∠DAB =60°,E 是异于A 、D 两点的动点,F 是CD 上的动点,满足A E +CF=a ,说明:不论E 、F怎样移动,三角形BEF 总是正三角形.6、如图1-4-38,等腰梯形ABCD 中,AD ∥BC ,AB =CD ,∠ DBC =45○,翻折梯形使点B 重合于点 D ,折痕分别交边 AB 、BC 于点F 、E ,若AD=2,BC=8,求BE 的长.7、在平行四边形ABCD 中,E 为BC 的中点,连接AE 并延长交DC 的延长线于点F .(1)求证:CF AB ;(2)当BC 与AF 满足什么数量关系时,四边形ABFC 是矩形,并说明理由. 8、如图l -4-80,已知正方形ABCD 的对角线AC 、BD 相交于点O ,E 是AC 上一点,过点A 作AG ⊥EB,垂足为G ,AG 交BD 于F ,则OE=OF .(1)请证明0E=OF(2)解答(1)题后,某同学产生了如下猜测:对上述命题,若点E 在AC 的延长线上,AG ⊥EB ,AG 交 EB 的延长线于 G ,AG 的延长线交DB 的延长线于点F ,其他条件不变,则仍有OE=OF .问:猜测所得结论是否成立?若成立,请给出证明;若不成立,请说明理由.9已知:如图4-26所示,△ABC 中,AB=AC ,∠BAC=90°,D 为BC 的中点,P 为BC 的延长线上一点,PE ⊥直线AB 于点E ,PF ⊥直线AC 于点F .求证:DE ⊥DF 并且相等.10已知:如图4-27,ABCD 为矩形,CE ⊥BD 于点E ,∠BAD 的平分线与直线CE 相交于点F .求证:CA=CF . 11已知:如图4-56A .,直线l 通过正方形ABCD 的顶点D 平行于对角线AC ,E 为l 上一点,EC=AC ,并且EC 与边AD 相交于点F .求证:AE=AF .本例中,点E 与A 位于BD 同侧.如图4-56B .,点E 与A 位于BD 异侧,直线EC 与DA 的延长线交于点F ,这时仍有AE=AF .请自己证明.动点问题练习题1、已知:等边三角形ABC 的边长为4厘米,长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动(运动开始时,点M 与点A 重合,点N 到达点B 时运动终止),过点M N 、分别作AB 边的垂线,与ABC △的其它边交于P Q 、两点,线段MN 运动的时间为t 秒.1、线段MN 在运动的过程中,t 为何值时,四边形MNQP 恰为矩形?并求出该矩形的面积;(2)线段MN 在运动的过程中,四边形MNQP 的面积为S ,运动的时间为t .求四边形MNQP 的面积S 随运动时间t 变化的函数关系式,并写出自变量t 的取值范围.F E D C B A CQO M A NB C y x E D B CA Q P 2、如图,在梯形ABCD 中,354245AD BC AD DC AB B ====︒∥,,,,∠.动点M 从B 点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动.设运动的时间为t 秒.(1)求BC 的长.(2)当MN AB ∥时,求t 的值.(3)试探究:t 为何值时,MNC △为等腰三角形. 3、如图,在平面直角坐标系中,四边形OABC 是梯形,OA ∥BC ,点A 的坐标为(6,0),点B 的坐标为(4,3),点C 在y 轴的正半轴上.动点M 在OA 上运动,从O 点出发到A 点;动点N 在AB 上运动,从A点出发到B 点.两个动点同时出发,速度都是每秒1个单位长度,当其中一个点到达终点时,另一个点也随即停止,设两个点的运动时间为t (秒). (1)求线段AB 的长;当t 为何值时,MN ∥OC ? (2)设△CMN 的面积为S ,求S 与t 之间的函数解析式, 并指出自变量t 的取值范围;S 是否有最小值?若有最小值,最小值是多少? (3)连接AC ,那么是否存在这样的t ,使MN 与AC 互相垂直? 若存在,求出这时的t 值;若不存在,请说明理由.2、如图,在Rt △ABC 中,∠C =90°,AC =12,BC =16,动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动,动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动.P ,Q 分别从点A ,C 同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,△PCQ 关于直线PQ 对称的图形是△PDQ .设运动时间为t (秒).(1)设四边形PCQD 的面积为y ,求y 与t 的函数关系式;(2)t 为何值时,四边形PQBA 是梯形?(3)是否存在时刻t ,使得PD ∥AB ?若存在,求出t 的值;若不存在,请说明理由;(4)通过观察、画图或折纸等方法,猜想是否存在时刻t ,使得PD ⊥AB ?若存在,请估计t 的值在括号中的哪个时间段内(0≤t ≤1;1<t ≤2;2<t ≤3;3<t ≤4);若不存在,请简要说明理由. 4、在ABC ∆中,,4,5,D BC CD 3cm C Rt AC cm BC cm ∠=∠==点在上,且以=现有两个动点P 、Q 分别从点A 和点B 同时出发,其中点P 以1cm/s 的速度,沿AC 向终点C 移动;点Q 以1.25cm/s 的速度沿BC 向终点C 移动。
过点P 作PE ∥BC 交AD 于点E ,连结EQ 。
设动点运动时间为x 秒。
(1)用含x 的代数式表示AE 、DE 的长度;(2)当点Q 在BD (不包括点B 、D )上移动时,设EDQ ∆的面积为2()y cm ,求y 与月份x 的函数关系式,并写出自变量x 的取值范围;(3)当x 为何值时,EDQ ∆为直角三角形。
6、如图1,在平面直角坐标系中,已知点(043)A ,,点B 在x 正半轴上,且30ABO =∠.动点P 在线段AB 上从点A 向点B 以每秒3个单位的速度运动,设运动时间为t 秒.在x 轴上取两点M N ,作等边PMN △.(1)求直线AB 的解析式;(2)求等边PMN △的边长(用t 的代数式表示),并求出当等边PMN △的顶点M 运动到与原点O 重合时t 的值;(3)如果取OB 的中点D ,以OD 为边在Rt AOB △内部作如图2所示的矩A DC B M N APC Q BDA M O F NEB C D 形ODCE ,点C 在线段AB 上.设等边PMN △和矩形ODCE 重叠部分的面积为S ,请求出当02t ≤≤秒时S 与t 的函数关系式,并求出S 的最大值.8. 梯形ABCD 中,AD ∥BC ,∠B=90°,AD=24cm ,AB=8cm ,BC=26cm ,动点P 从点A 开始,沿AD 边,以1厘米/秒的速度向点D 运动;动点Q 从点C 开始,沿CB 边,以3厘米/秒的速度向B 点运动。
已知P 、Q 两点分别从A 、C 同时出发,,当其中一点到达端点时,另一点也随之停止运动。
假设运动时间为t 秒,问:(1)t 为何值时,四边形PQCD 是平行四边形?(2)在某个时刻,四边形PQCD 可能是菱形吗?为什么? (3)t 为何值时,四边形PQCD 是直角梯形? (4)t 为何值时,四边形PQCD 是等腰梯形?9. 如右图,在矩形ABCD 中,AB=20cm ,BC=4cm ,点P 从A 开始沿折线A —B —C —D 以4cm/s 的速度运动,点Q 从C开始沿CD 边1cm/s 的速度移动,如果点P 、Q 分别从A 、C 同时 出发,当其中一点到达点D 时,另一点也随之停止运动,设运动时间为t(s),t 为何值时,四边形APQD 也为矩形?10、 如图,在等腰梯形ABCD 中,AB ∥DC ,cm BC AD 5==,AB =12 cm,CD =6cm , 点P 从A 开始沿AB 边向B 以每秒3cm 的速度移动,点Q 从C 开始沿CD 边向D 以每秒1cm 的速度移动,如果点P 、Q 分别从A 、C 同时出发,当其中一点到达终点时运动停止。
