四年级数学思维训练——周长面积(一)【经典例题篇】
四年级数学周长面积练习题

四年级数学周长面积练习题一、填空题1. 一个正方形的边长是3厘米,它的周长是____厘米。
2. 一个长方形的长是6厘米,宽是4厘米,它的面积是____平方厘米。
3. 一个边长为5厘米的正方形,它的周长是____厘米。
4. 一个长方形的周长是26厘米,它的长为7厘米,它的宽是____厘米。
5. 一个三角形的底边长是9厘米,高是5厘米,它的面积是____平方厘米。
二、选择题1. 一个正方形的边长是4厘米,它的周长是:A. 8厘米B. 12厘米C. 16厘米D. 20厘米2. 一个长方形的周长是30厘米,它的长和宽的可能组合是:A. 10厘米和5厘米B. 8厘米和7厘米C. 6厘米和9厘米D. 12厘米和4厘米3. 一个矩形的面积是18平方厘米,它的长和宽的可能组合是:A. 6厘米和3厘米B. 4厘米和5厘米C. 9厘米和2厘米D. 12厘米和6厘米三、计算题1. 一个正方形的边长是8厘米,它的周长和面积分别是多少?2. 一个长方形的长是12厘米,宽是5厘米,它的周长和面积分别是多少?3. 一个边长为3厘米的正方形,它的周长和面积分别是多少?4. 一个长方形的周长是18厘米,它的长是4厘米,它的宽是多少?面积是多少?5. 一个三角形的底边长是7厘米,高是4厘米,它的面积是多少?四、解答题1. 一个正方形的周长是20厘米,它的边长是多少?面积是多少?2. 一个长方形的面积是15平方厘米,长和宽的可能组合有哪些?3. 一个正方形和一个矩形边长相同,它们的周长和面积之间有什么关系?五、综合运用题1. 小明要铺一块正方形的地砖,地砖的边长是6厘米,地面的边长是2米,他需要多少块地砖?2. 一个花坛是长方形的,长和宽分别是7米和4米,他们要围上铁丝网,请问需要多长的铁丝网?3. 一个长方形的长是15厘米,宽是8厘米,这个长方形的周长比一个边长为7厘米的正方形的周长长多少厘米?六、拓展思考题1. 请你设计一个多边形,并计算它的周长和面积。
四年级数学思维训练(二)

四年级数学思维训练(二)周长和面积1、有一块长8分米,宽4分米的长方形纸板与两块边长4分米的正方形拼也一个正方形。
拼成的正方形的周长是多少分米?2、两个大小数点相同的正方形拼成一个长方形后,周长比原来的两个正方形周长的和减少6厘米。
原来一个正方形的周长是多少厘米?3、求图1和图2的周长。
(单位:米)图1 图24、右图是一座厂房的平面图,求这座厂房平面图的周长。
5、右图是个多边形,图中每个角都是直角,它的周长是多少?6、一个正方形被分成3个大小、形状完全不一样的长方形(如图3),每个小长方形的周长都是24厘米,求这个正方形的周长。
图37、右图是由四个一样大的长方形和一个周长是4分米的小正方形拼成的一个边长是11分米的大正方形。
每个长方形的长和宽各是多少?周长是多少?118、一根铁丝长12厘米,能围成几种长和宽都是整厘米数的长方形,每咱长方形的长和宽各是几厘米?围成的正方形的边长是几厘米?9、把一个长10厘米,宽5厘米的长方形,分成两个大小一样的正方形,每个正方形的周长是多少?10、用一个长8厘米,宽4厘米的长方形与7个边长4厘米的正方形,拼成一个大正方形。
拼成的大正方形的周长是多少?11、求图12、图13的周长。
12、图14是一座楼房的平面图,这座楼房平面图的周长是多少米?13、把一个正方形分成甲、乙两个部分(如图15),比较甲、乙两个部分周长的长短,并求出乙的周长。
14、有两个相同的长方形,长7厘米,宽3厘米,把它们按图(16)的样子重叠在一起,这个图形的周长是多少厘米?15、一个正方形被分成6个大小、形状完全一样的长方形(如图17),每个长方形的周长都是14厘米。
原来正文武的周长是多少厘米?16、一块长方形布,周长是18米,长比宽多1米,这块布的长是几厘米?宽是几米?图17 1米17、用4个一样大的长方形和一个小正方形,拼成一个边长是16分米的大正方形(如图18),每个长方形的周长是多少?18、有一块长方形的木板,长22分米,宽8分米,如果长和宽分别减少10分米、3分米,面积比原来减少多少平方分米?19、一块长方形铁板,长18分米,宽13分米,如果长和宽各减少2分米,面积比原来减少多少平方分米?20、一块长方形地,长是80米,宽是45米,如果把宽增加5米,要使面积不变,长应减少多少米?21、一个长方形,如果宽不变,长减少3米,那么它的面积减少24平方米,如果长不变,宽增加4米,那么它的面积增加60平方米,这个长方形原来的面积是多少平方米?22、一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米,如果长不变,宽增加3米,那么它的面积增加48平方米,这个长方形原来的面积是多少平方米?23、一个长方形,如果它的长减少3米,或它的宽减少2米,那么它的面积都减少36平方米,求这个长方形原来的面积。
四年级数学思维训练——周长面积(一)【经典例题篇】

【经典例题2】一个正方形的花坛,四周有1米宽的水泥路。
如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?【经典例题3】如图,将相同的小长方形拼成一个大长方形,已知小长方形的宽是12厘米,求大长方形的面积。
【经典例题4】一张长方形纸片,在长边上剪下5厘米,宽边上剪下2厘米,余下的部分正好是一个正方形,已知正方形的面积比原来长方形面积少66平方厘米,求正方形面积。
【经典例题5】一块正方形的玻璃,一边截去12厘米,另一边截去8厘米,剩下的长方形面积比原来的正方形减少1764平方厘米,原正方形玻璃的周长是多少厘米?【经典例题6】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个,第四个,第五个正方形,求第五个正方形的面积。
【经典例题7】如图,是一个楼梯的截面图,高280厘米,每阶台阶的宽和高都是20厘米,这楼梯的截面积是多少平方厘米?【经典例题8】如图,一个长方形,用垂直长和宽的两条线段分成四块,其中三块面积分别为10平方米,14平方米,42平方米,第四块面积是多少平方米?【答案】一条边7 6 5 4 3 2 1另一条边 1 3 5 7 9 11 13【经典例题2】一个正方形的花坛,四周有1米宽的水泥路。
如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?已知12平方米是4个完全相同的长方形组成的,所以14÷4=3平方米,每个长方形是3平方米。
又知长方形宽是1米,可知3÷1=3米,长方形长是3米。
中间花坛的长应该是3-1=2米,所以2×2=4平方米。
【经典例题3】如图,将相同的小长方形拼成一个大长方形,已知小长方形的宽是12厘米,求大长方形的面积。
小长方形4条宽和小长方形3条长的长度是相等的,可以求出小长方形的长是:12×4÷3=16厘米大长方形的长是16×3=48厘米,宽是12+12+16=40厘米大长方形的面积是:48×40=1920【经典例题4】一张长方形纸片,在长边上剪下5厘米,宽边上剪下2厘米,余下的部分正好是一个正方形,已知正方形的面积比原来长方形面积少66平方厘米,求正方形面积。
小学四年级数学逻辑思维训练题目
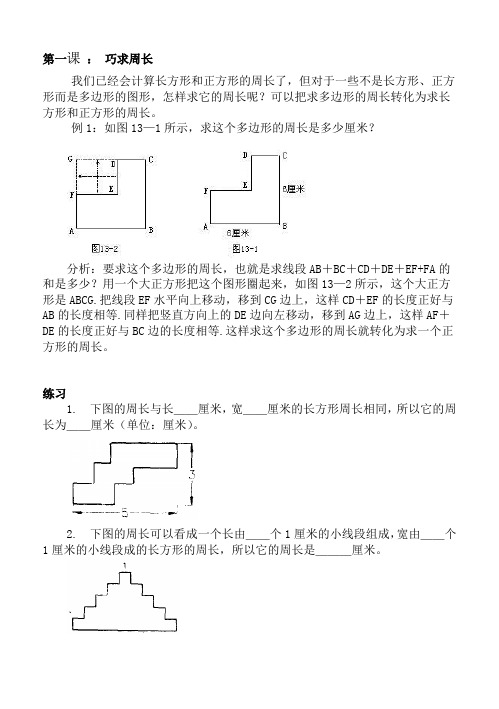
第一课:巧求周长我们已经会计算长方形和正方形的周长了,但对于一些不是长方形、正方形而是多边形的图形,怎样求它的周长呢?可以把求多边形的周长转化为求长方形和正方形的周长。
例1:如图13—1所示,求这个多边形的周长是多少厘米?分析:要求这个多边形的周长,也就是求线段AB+BC+CD+DE+EF+FA的和是多少?用一个大正方形把这个图形圈起来,如图13—2所示,这个大正方形是ABCG.把线段EF水平向上移动,移到CG边上,这样CD+EF的长度正好与AB的长度相等.同样把竖直方向上的DE边向左移动,移到AG边上,这样AF+DE的长度正好与BC边的长度相等.这样求这个多边形的周长就转化为求一个正方形的周长。
练习1.下图的周长与长__厘米,宽__厘米的长方形周长相同,所以它的周长为__厘米(单位:厘米)。
2.下图的周长可以看成一个长由__个1厘米的小线段组成,宽由__个1厘米的小线段成的长方形的周长,所以它的周长是___厘米。
3.求下列各图形的周长(单位:厘米)。
(围成图形的小线段长l厘米)。
②周长为多少厘米(每条小线段长度都是1厘米)?第二课:平均数问题求平均数问题是小学学习阶段经常接触的一类典型应用题,如“求一个班级学生的平均年龄、平均身高、平均分数……”。
解答这类应用题时,主要是弄清楚总数、份数、一份数三量之间的关系,根据总数除以它相对应的份数,求出一份数,即平均数。
一、算术平均数例1.用4个同样的杯子装水,水面高度分别是4厘米、5厘米、7厘米和8厘米,这4个杯子水面平均高度是多少厘米?分析:求4个杯子水面的平均高度,就相当于把4个杯子里的水合在一起,再平均倒入4个杯子里,看每个杯子里水面的高度。
解:(4+5+7+8)÷4=6(厘米)答:这4个杯子水面平均高度是6厘米。
练习1.机械厂前3天平均每天加工零件1259只,后4天共加工零件5379只,这星期内平均每天加工零件多少只?提示:平均数=总零件数÷总天数已知:前()天加工(),()天加工(),共()只,共加工()天要求:2.修路队4天修了两段公路,第一段长430米,第二段长250米,平均每天修多少米?提示:平均数=总长度÷多少段已知:第一段()米,第二段()米,共()米,共()段。
四年级面积周长练习题

四年级面积周长练习题1. 一个长方形的长是12米,宽是8米,求它的面积和周长。
解答:这个长方形的长是12米,宽是8米。
我们先来算一下它的面积。
长方形的面积等于长乘以宽,所以面积等于12米乘以8米,即12 × 8= 96 平方米。
所以这个长方形的面积是96平方米。
接下来我们计算一下长方形的周长。
长方形的周长等于长的两倍加宽的两倍,所以周长等于(12米 + 8米) × 2 = 40米。
所以这个长方形的周长是40米。
所以,这个长方形的面积是96平方米,周长是40米。
2. 一个正方形的边长是6厘米,求它的面积和周长。
解答:这个正方形的边长是6厘米。
我们先来算一下它的面积。
正方形的面积等于边长的平方,所以面积等于6厘米 × 6厘米 = 36平方厘米。
所以这个正方形的面积是36平方厘米。
接下来我们计算一下正方形的周长。
正方形的周长等于边长的四倍,所以周长等于6厘米×4 = 24厘米。
所以这个正方形的周长是24厘米。
所以,这个正方形的面积是36平方厘米,周长是24厘米。
3. 一个长方形的长是15米,宽是9米,求它的面积和周长。
解答:这个长方形的长是15米,宽是9米。
我们先来算一下它的面积。
长方形的面积等于长乘以宽,所以面积等于15米乘以9米,即15 × 9= 135 平方米。
所以这个长方形的面积是135平方米。
接下来我们计算一下长方形的周长。
长方形的周长等于长的两倍加宽的两倍,所以周长等于(15米 + 9米) × 2 = 48米。
所以这个长方形的周长是48米。
所以,这个长方形的面积是135平方米,周长是48米。
4. 一个正方形的边长是10厘米,求它的面积和周长。
解答:这个正方形的边长是10厘米。
我们先来算一下它的面积。
正方形的面积等于边长的平方,所以面积等于10厘米 × 10厘米 = 100平方厘米。
所以这个正方形的面积是100平方厘米。
接下来我们计算一下正方形的周长。
四年级周长与面积经典题库

四年级周长与面积经典题库(总3页)
--本页仅作为文档封面,使用时请直接删除即可--
--内页可以根据需求调整合适字体及大小--
第六讲图形的周长与面积
1.求图1和图2两个图形的周
长。
2.如图是由5个相同的小长方形拼成的大长方形,大长方形的周长是44厘米,求大长方
形的面积。
3.如右图是一个连长为20厘米的正方形和一个长方形组合,求
阴影部分的面积。
4.如右图所示,AD=4,BC=10,求四边形ABCD的面积。
(单位:厘
米)
5.如果一个长方形的宽增加2厘米,或长增加3厘米,它们的面积都增加120平方厘米,
原来长方形的面积是多少?
6.有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米,求小正方形
的面积是多少平方厘米?
7.如图,一个长方形苗圃,分别种有4种不同的树苗,其中三块的面积分别是400平方
米、560平方米、250平方米。
求第四块的面积是多少平方米?
400250
560
8.有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米,求小正方形
的面积是多少?
9.一个长方形的周长是22厘米,如果它的长和宽均为整数厘米,求这个长方形的面积
(单位:平方厘米)有多少种可能的值?
10.如右图所示,7个完全相同的长方形拼成了图中的阴影部分,图中空白部分的面积是多
少平方厘米?
11.如图,ABCD是边长为12厘米的正方形,E、F分别是AB、BC的中点,AF与CE交于
G,则四边形AGCD的面积是多少平方厘米。
数学思维拓展几何形面积与周长练习

数学思维拓展几何形面积与周长练习在学习数学的过程中,几何形是一个必不可少的内容。
几何形涉及到形状的面积与周长计算,对于培养学生的数学思维和观察能力有很大的帮助。
本文将通过几个练习题,帮助读者拓展数学思维,提高对几何形面积与周长的理解。
题目一:长方形和正方形的面积计算1. 已知一长方形的长为8cm,宽为4cm,请计算其面积。
2. 若一个正方形的边长为5cm,请计算其面积。
解答:1. 长方形的面积计算公式为:面积 = 长 ×宽。
根据题目给出的长方形的长和宽,可以得到:面积 = 8cm × 4cm = 32cm²。
2. 正方形的面积计算公式为:面积 = 边长 ×边长。
根据题目给出的正方形的边长,可以得到:面积 = 5cm × 5cm = 25cm²。
题目二:三角形的面积计算已知一个三角形的底边长为6cm,高为4cm,请计算其面积。
解答:三角形的面积计算公式为:面积 = 底边长 ×高 ÷ 2。
根据题目给出的三角形底边长和高,可以得到:面积 = 6cm × 4cm ÷ 2 = 12cm²。
题目三:圆形的面积计算已知一个圆的半径为3cm,请计算其面积。
解答:圆的面积计算公式为:面积= π × 半径²。
根据题目给出的圆的半径,可以得到:面积= 3.14 × 3cm × 3cm ≈ 28.26cm²(取近似值)。
题目四:矩形的周长计算一块矩形的长为5cm,宽为3cm,请计算其周长。
解答:矩形的周长计算公式为:周长 = 2 × (长 + 宽)。
根据题目给出的矩形的长和宽,可以得到:周长 = 2 × (5cm + 3cm) = 16cm。
题目五:正方形的周长计算已知一个正方形的边长为7cm,请计算其周长。
解答:正方形的周长计算公式为:周长 = 4 ×边长。
四年级奥数专题--图形周长与面积

第一讲图形周长和面积知识导航亲爱的同学们,我们已经学会长方形、正方形的周长与面积的计算,利用公式很容易算出它们的面积与周长。
但在遇到一些较复杂的有关长方形和正方形的周长和面积计算时,一些同学就会感到棘手。
这一讲我们将学习用平移、转化、分解、合并等技巧解决难题,使大家在解题中能顺利地找到突破口,化难为易,化繁为简。
精典例题例1:下图是由16个同样大小的正方形组成的,如果这个图形的面积是400平方厘米,那么它的周长是多少厘米?思路点拨每个正方形的面积为:400÷16=25(平方厘米),所以每个正方形的边长是5厘米。
从上下方向来看有14条边是周长的一部分,从左右方向来看有20条边是周长的一部分,所以……模仿练习计算右面图形的周长(单位:厘米)。
例2:有9个小长方形,它们的长和宽分别相等,用这9个小长方形拼成的大长方形(如图)的面积是45平方厘米,求这个大长方形的周长。
思路点拨从图上可以知道,小长方形的长的4倍等于宽的5倍,所以长是宽的5÷4=1.25倍。
每个小长方形的面积为45÷9=5平方厘米,所以1.25×宽×宽=5,所以宽为2厘米,长为2.5厘米。
模仿练习下图的长方形被分割成5个正方形,已知原长方形的面积为120平方厘米,求原长方形的长与宽。
例3:一块正方形的苗圃(如右图实线所示),若将它的边长各增加30米,则面积增加9900平方米,问原来这块正方形苗圃的面积是多少平方米?思路点拨通过画图可以算出:小正方形的面积为:30×30=900平方米。
用增加的面积减去小正方形的面积就得到增加的两个长方形的面积之和,9900-900=9000平方米。
而增加的两个长方形的面积相等,于是其中一个长方形的面积为9000÷2=4500平方米。
模仿练习喜阳阳小学的操场长90米,宽45米。
改造后,长增加10米,宽增加5米。
现在操场面积比原来增加了多少平方分米?例4:如下图,用标号为1,2,3,4,5的五种大小不同的正方形拼成一个大长方形,大长方形的长和宽分别是18,14,则标号为5的正方形的面积是多少?(2006年“希望杯”第二试)思路点拨如果标号为5的正方形的边长是a,那么1号比2号大a,2号比3号大a,所以1号比3号大2a,又因为2号和3号的边长之和是14,1号和2号的边长之和是18,所以1号比3号大18-14=4。
四年级数学下周长面积经典例题思维训练试题1

四年级数学下周长面积经典例题思维训练试题1【经典例题1】用15米长的木兰沿着围墙围一个种花草的长方形或者正方形的苗圃,其中一面利用围墙,如果每边的长度都是整数,那么有几种围法,怎样围才能使围成的面积最大?【经典例题2】一个正方形的花坛,四周有1米宽的水泥路。
如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?【经典例题3】如图,将相同的小长方形拼成一个大长方形,已知小长方形的宽是12厘米,求大长方形的面积。
【经典例题4】一张长方形纸片,在长边上剪下5厘米,宽边上剪下2厘米,余下的部分正好是一个正方形,已知正方形的面积比原长方形面积少66平方厘米,求正方形面积。
【经典例题5】一块正方形的玻璃,一边截去12厘米,另一边截去8厘米,剩下的长方形面积比原的正方形减少1764平方厘米,原正方形玻璃的周长是多少厘米?【经典例题6】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个,第四个,第五个正方形,求第五个正方形的面积。
【经典例题7】如图,是一个楼梯的截面图,高280厘米,每阶台阶的宽和高都是20厘米,这楼梯的截面积是多少平方厘米?【经典例题8】如图,一个长方形,用垂直长和宽的两条线段分成四块,其中三块面积分别为10平方米,14平方米,42平方米,第四块面积是多少平方米?【答案】【经典例题1】用15米长的木兰沿着围墙围一个种花草的长方形或者正方形的苗圃,其中一面利用围墙,如果每边的长度都是整数,那么有几种围法,怎样围才能使围成的面积最大?一条边7654321另一条边135791113【经典例题2】一个正方形的花坛,四周有1米宽的水泥路。
如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?已知12平方米是4个完全相同的长方形组成的,所以14÷4=3平方米,每个长方形是3平方米。
又知长方形宽是1米,可知3÷1=3米,长方形长是3米。
中间花坛的长应该是3-1=2米,所以2×2=4平方米。
发展数学思维三角形的面积与周长练习

发展数学思维三角形的面积与周长练习数学是一门基础学科,对于培养学生的数学思维能力和逻辑思维能力起着重要的作用。
而在数学的学习过程中,自然界中最普遍也最基础的图形——三角形,尤为重要。
三角形作为最简单的多边形,其面积和周长的计算是数学思维的重要内容之一。
在本文中,我们将通过一系列练习题来发展数学思维,加深对三角形面积和周长的理解。
一、面积相关练习1. 已知三角形的底边长为6cm,高为8cm,求三角形的面积。
解析:我们可以利用面积公式S=底边长×高/2进行计算。
带入已知数据,得出三角形的面积为S=6cm×8cm/2=24cm²。
2. 一个三角形的两边长分别为5cm和7cm,夹角为60°,求三角形的面积。
解析:可以利用三角形面积公式S=1/2×a×b×sinC进行计算。
其中a和b为两边长,C为夹角。
带入已知数据,得出三角形的面积为S=1/2×5cm×7cm×sin60°=17.1cm²。
3. 已知三角形的两个角分别为60°和90°,斜边长为8cm,求三角形的面积。
解析:可以利用正弦定理或余弦定理求得缺角的度数,再利用三角形面积公式进行计算。
这里我们使用余弦定理。
根据余弦定理可得c²=a²+b²-2abcosC,其中c为斜边长,a和b为两个已知边长,C为夹角。
带入已知数据,可求得缺角的度数为30°。
而正弦定理为a/sinA=b/sinB=c/sinC,利用已知数据可以求得缺角的度数为30°。
因此得出三角形的面积为S=1/2×a×b×sinC=1/2×8cm×8cm×sin30°=16cm²。
二、周长相关练习1. 已知正三角形的边长为4cm,求正三角形的周长。
4年级奥数边长,周长,面积的计算问题例题

涉及长方形、正方形、三角形、平行四边形和梯形的边长、周长与面积的计算问题.求多个图形覆盖总面积时宜分块处理.考察三角形面积时,需要选择恰当的高,并应注意三角形与等底等高平行四边形之间的关系.例题:1.图6-1由16个同样大小的正方形组成.如果这个图形的面积是400平方厘米,那么它的周长是多少厘米?[分析与解]正方形的面积是400÷16=25平方厘米,正方形边长是5厘米,整个图形的周长是170厘米.2.若干同样大小的长方形小纸片摆成了如图6-2所示的图形.已知小纸片的宽是12厘米,问阴影部分的总面积是多少平方厘米?[分析与解]从第一排与第二排看,五个小纸片的长等于三个小纸片的长加三个小纸片的宽,也就是说,二个小纸片的长等于三个小纸片的宽.已知小纸片的宽是12厘米,于是小纸片的长是12×3÷2=18厘米,阴影部分是三个正方形,边长正好是小纸片的长与宽的差18-12=6.于是,阴影部分的面积是6×6×3=108平方厘米.3.一个正方形,如果把它的相邻两边都增加6厘米,就可以得到一个新正方形,新正方形的面积比原正方形大120平方厘米.求原正方形的面积.[分析与解]如下图,有阴影部分是边长为6厘米的正方形,A、B部分均是长为原正方形边长,宽为6厘米的长方形.有120=6×6+6×原边长+6×原边长,即12×原边长=84,那么原边长为7,则原正方形面积为7×7=49(平方厘米).4.如图6-3,正方形客厅边长12米,若正中铺一块正方形纯毛地毯:外围铺化纤地毯,共需费用22455元.已知纯毛地毯每平方米250元,化纤地毯每平方米35元,问铺在外围的化纤地毯的宽度是多少分米?[分析与解]如果全铺化纤地毯,少用22455-35×122元,每平方米少用(250-35)元,所用纯毛地毯的面积为(22455-35×122)÷(250-35)=81平方米,从而纯毛地毯的边长为9米.因此,外围化纤地毯宽度是(12-9)÷2=1.5米=15分米.5.如图6-4,ABFE和CDEF都是长方形,AB的长是4厘米,BC的长是3厘米.那么图中阴影部分的面积是多少平方厘米?[分析与解]图中阴影部分的面积等于长方形ABCD的一半,即为4×3÷2=6平方厘米.6.如图6-5,有9个小长方形,其中编号为1,2,3,4,5的5个小长方形的面积分别为2,4,6,8,10平方米.求6号长方形的面积.[分析与解]如下图所示,将所有独立的小长方形标上号码:有①×④=②×⑦,⑦=2×8÷4=4;⑦×⑧=③×④,⑧=6×8÷4=12;④×⑥=⑤×⑧,⑥=10×12÷8=15.即6号长方形的面积等于15平方米.评注:在长方形中任意做一条线平行于长,一条平行与宽,将原长方形分成四个部分:左上角,左下角,右上角,右下角.则有左上角面积×右下角面积=左下角面积×右上角面积.7.如图6-6,直角三角形ABC的三边长分别为.AC=30分米,AB=18分米,BC=24分米,ED垂直于AC,且ED=95厘米.问正方形BFEG的边长是多少厘米?[分析与解]如下图所示,连接AE,BE,CE.以下均以厘米作单位,注意单位的转化.有△AFB底为AB时,高为EF;△BEC的底为BC时,高为EG;△AEC的底为AC时,高为ED;有它们的面积分别为180×EF×=90×EF,240×EG×=120EG,300×95×=14250;那么它们的面积和为14250+210×EG等于△ABC的面积180×240×=21600平方厘米,所以EG=35厘米.评注:有的同学如下求解这个问题:△ABC的面积为180×240×=21600平方厘米,有以AC为底时高为21600÷300×2=144,那么BE=144-95=49,正方形面积等于对角线平方的一半,从而BGEF的面积为49×49÷2,得出EG×EG=49×49÷2,EG不能用整数或分数表示.这是为什么呢?有错吗?8.如图6-7,一个平行四边形的一边长15厘米,这条边上的高为6厘米,一条线段将此平行四边形分成了两部分,它们的面积相差18平方厘米.那么其中梯形的上底是多少厘米?[分析与解]梯形面积+三角形面积=平行四边形面积=15×6=90(平方厘米).又已知两者的面积差是18平方厘米,所以梯形的面积为(90+18)÷2=54(平方厘米).于是梯形的上底是2×54÷6-15=3(厘米).9.一张长方形纸片,长7厘米,宽5厘米.把它的右上角往下折叠如图6-8所示,再把左下角往上折叠如图6-9所示.那么,未盖住的阴影部分的面积是多少平方厘米?[分析与解]图6-8中阴影部分的左边部分小长方形的长为5,宽为7-5=2,那么面积为5×2=10,而图6-9中左下角的对应的正方形的边长为2,所以面积为2×2=4.那么阴影部分的面积为10-4=6(平方厘米).10.有10张长3厘米,宽2厘米的纸片,将它们按照图6-10的样子摆放在桌面上,那么这l0张纸片所盖住的桌面的面积是多少平方厘米?[分析与解]第一张纸片盖住的面积是3×2=6平方厘米,后面每增加一张纸片,就多盖住(3-2)×2=2平方厘米.于是,这10张纸片盖住桌面上的面积是6+2×9=24平方厘米.11.三张正方形的纸片铺在桌面上如图6-11所示,其中任意两条相交线段之间的夹角都是直角,而各条线段的长度在图中标出,单位是厘米.那么它们一共遮盖的面积是多少平方厘米?[分析与解]62+42×2-[22+(4-1)×1×4]=36+32-(4+6)=58(平方厘米).12.如图6-12,直角梯形ABCD中,AB=15厘米,BC=12厘米,AE垂直于AB,阴影部分的面积为15平方厘米.问梯形ABCD的面积是多少平方厘米?[分析与解]延长AE交CD与F点,如下图所示.有△BFD,△AFD同底等高,所以面积相等,而△EFD为公共部分,两者都减去有,△BEF,△AED的面积相等为15平方厘米.而△BFA的面积为×15×12=90(平方厘米),所以△ABE的面积为90-15=75(平方厘米).那么△ABE,△EFD的面积之积等于△BEF,△ADE的面积之积.所以有所以△EFD的面积为15×15÷75=3,所以梯形ABCD的面积为75+15+15+90+3=198(平方厘米).13.如图6-13,ABCD是梯形,ABFD是平行四边形,CDEF是正方形,AGHF 是长方形.又知AD=14厘米,BC=22厘米,那么,阴影部分的面积是多少平方厘米?[分析与解]由题意知AD=BF=14,而FC=BC-BF=22-14=8.正方形EDFC的边FC为8,则EF也为8,那么△AFD的面积为×14×8=56(平方厘米).△AFD,△ABF均为平行四边形ABFD面积的一半,而△GBA与△BHF的面积和等于△ABF的面积,所以阴影部分面积为56平方厘米.14.图6-14是一块正方形的地板砖示意图,其中AA1=AA2=BB1=BB2=CC1=CC2=DD1=DD2,红色小正方形的面积是4,四块绿色小三角形的面积总和是18.求大正方形ABCD的面积.[分析与解]绿地可以拼成两个正方形,每一个面积是18÷2=9,所以绿色三角形的两条直角边的长都是3.△AA1A2,△BB1B2,△CC1C2,△DD1D2可以拼成一个正方形,与红色正方形一样大,面积是4.于是大正方形ABCD的面积是18+4+4+4×3×2=50.15.用l,2,3,4,5,7作为图6-15这样图形的6条边长,那么这个图形的最大面积是多少?[分析与解]显然当底部的边为7,右面的边为5时,这个图形的面积最大,但是经过尝试,发现无法组成六边形.于是将右面的边调整为4,发现有下图满足,此时图形的面积为4×7-2×1=26,为最大值.。
四升五思维训练一(周长问题)7.8
永嘉青少年素质拓展现代教育瓯北分中心
四升五思维训练一(周长问题)
班级: 姓名:
1、AB=12厘米,AC=6厘米,求图形的周长。
2、下图是由三个相同的长方形纸片组成的一个
图形,已知每个长方形纸片长7厘米,宽2厘米,这个图形周长是多少厘米?
3、如右图所示,一个正方形被分成了四个相同的长方形。
如
果其中一个长方形的周长是15米,那么这个正方形的周长是
多少米?
4、一个长方形的长是15厘米。
剪去一个最大的正方形后,
剩下的小长方形的周长是多少?
5、长方形ABCD 的周长是36厘米,小长方形CDEF 的宽CF 是8厘米, 阴影部分是正方形。
求原长方形的长和宽分别是多
少?
6
12厘米C
A
B。
四年级思维训练题

四年级思维训练题(全年级)一、周长面积计算1、一个周长为20厘米的正方形,从中间剪开成为两个大小相等的长方形。
这两个长方形周长共多少厘米?2、一张长方形纸,长为32厘米,宽为15厘米,先剪下一个最大的正方形,再从余下的纸片中,又剪下一个最大的正方形,最后余下的长方形周长是多少?3、一个长方形,长25厘米,如果长减少了5厘米,就变成了正方形,它的面积减少了多少平方厘米?4、一个长方形,如果宽不变,长增加5米,那么它的面积增加30平方米;如果长不变,宽增加3米,那么它的面积增加48平方米。
这个长方形原来的面积是多少平方米?5、正方形被分成了五个长方形,每个长方形的周长都是30厘米,求这个正方形的周长是多少厘米?6、用15米长的栅栏沿着围墙围一个种植花草的长方形苗圃,其中一面利用着墙。
如果每边的长度都是整数,怎样才能使围成的面积最大?7、一个正方形和一个长方形的周长相等,长方形长与宽的和是12分米,求正方形的周长和面积。
8、有两个相同的长方形,长是8厘米,宽是3厘米。
如果把它们按下图叠放,这个图形的面积是多少?二、简便运算1、计算:745+263+155-198 123456-78-822-155-4552、计算:22+20+18+16+14 9+99+999+999931+33+35+37+39+41 1+2+3+…+513、计算:999十998十997十996十1000十1004十1003十1002十10014、计算:2+4+6+8+……+18+205、计算:100-99+98-97+96-95+……+4-3+2-16、(100+98+97+………+4+2)-(99+97+95+……+3+1)7、在□里填上合适的数(1)28×225-2×225-225×6=225×□(2)39×8+□×39-11×39=39×208、999×6+111×46 68×32+64×169、306000÷125÷8 10、44444 × 9999911、某体育馆西侧看台有10排座位,后面一排都比前面一排多2个座位,最后一排有64个座位,体育馆西侧看台共有多少个座位?三、简单的搭配问题1、从上海到苏州的长途汽车中一共有5个车站,从上海到苏州一个来回需要为这趟长途汽车准备多少种不同的车票?2、从南通到上海有4条路可走,从上海到南京有3条路可走。
周长和面积专题训练(巧算面积)

周长和面积专题训练(巧算面积)一、知识梳理要想快速准确地将复杂的图形面积计算出来,首先要熟练的掌握最基础的图形面积计算公式。
任何一个复杂图形求面积,都要用到基础的公式逐步求解。
常用面积计算公式:长方形面积=长×宽,s=ab;正方形面积=边长×边长,s=a2;平行四边形面积=底×高,s=ah;三角形面积=底×高÷2,s=ah÷2;梯形面积=(上底+下底)×高÷2,s=(a+b)h÷2圆形面积=圆周率×半径的平方,s=∏r2;我们在计算复杂的图形面积时,经常会用到一些巧妙的方法,例如拆分组合图形、割补组合图形……。
本次专题还将带领同学接触一些更巧妙的算法。
二、例题精讲【例1】一个边长为40厘米的正方形,依次连接四边中点得到第二个正方形,这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积(图(a)).分析:第一个正方形的面积不难求出,第二个正方形的面积是多少呢?如图(b)所示,把大正方形平均分成8份,小正方形有4份,所以第二个正方形的面积是第一个正方形面积的一半.解:第二个正方形的面积为第一个正方形面积的一半.依此类推,第五个正方形的面积为:40×40÷2÷2÷2÷2=100(平方厘米)答:第五个正方形的面积为100平方厘米.【例2】如下图(a),大正方形比小正方形的面积大40平方厘米.求这两个正方形的面积.分析:将小正方形补成与大正方形一样(如图(a)),然后将所补的部分分成三块(如图(b)),并利用图(c)求得大、小、正方形的边长之差.解:如上图(b),大正方形比小正方形的面积多2块A和1块B.再将B下方的A旋转到如图(c).由A、B、A拼成的长方形,面积是40平方厘米,长是20厘米,所以宽是40÷20=2(厘米).即大正方形与小正方形边长的差是2厘米.所以大正方形边长为(20+2)÷2=11(厘米)小正方形边长:20-11=9(厘米)所以,大正方形面积为11×11=121(平方厘米)小正方形面积为9×9=81(平方厘米)答:大正方形面积为121平方厘米,小正方形面积为81平方厘米.【例3】一块长方形,用垂直于长和宽的两条线分成四块,其中三块面积分别为15、18、30平方米.第四块面积是多少平方米(如图(a))?解如图(b),长方形A的面积=a×b,长方形D的面积=c×d,因此长方形A的面积×长方形D的面积=a×b×c×d同样长方形B的面积×长方形C的面积=b×c×a×d所以长方形A的面积×长方形D的面积=长方形B的面积×长方形D的面积.在图(a)中,所求面积为15×30÷18=25(平方米)答:第四块面积是25平方米.发现:当一个长方形被分成四个小长方形时,对角的两个长方形面积的乘积一定相等.三、专题特训1.求图中的阴影部分的面积(单位:厘米).2.一个边长为80厘米的大正方形,称为第一个正方形.依次连接四边的中点,得到第二个正方形.这样继续下去,得到第三个,第四个,第五个,第六个,第七个,第八个正方形.求这八个正方形的面积的和.3.四个一样的长方形和一个小的正方形(如图所示)拼成一个面积为49平方米的大正方形.小正方形的面积是4平方米.长方形的短边是几米?4.一块长方形地被两条直线截成四块(如下图).其中三块长方形的面积是24、30、20平方米,第四块面积是多少平方米?5.如图所示,已知长方形ABCD,AD=8厘米,AB=5厘米,E、F分别为AB及BC边的中点.求阴影图形的面积.6.如图所示,已知正方形的边长为8厘米.求阴影部分的面积.7.如图所示,一块长方形草地,长100米,宽80米,中间有一条宽4米的道路.求草地(阴影部分)的面积.8.如图所示,一个长方形被两条直线分成三个长方形和一个正方形。
四数上册思维3

四年级思维训练 -图形的周长和面积
1.一个正方形的边长增加3厘米,面积就增加39平方厘米,原来正方形的面积是多少平方厘米?2.把一张边长24厘米的正方形对折4次后得到一个小正方形,这个小正方形的面积是多少平方厘米?3.图中阴影部分的面积是多少平方厘米?
5.大小两个正方形部分重合,重合部分的面积是9平方厘米,阴影部分的面积是多少平方厘米?
6.一个长方形,如果长增加4米,面积就增加24平方米;如果宽减少1米,面积就减少10平方米,原长方形的面积是多少平方米?
7.如图,四个同样的长方形和一个小正方形拼成一个大正方形(如下图).大正方形的面积是100平方米,小正方形面积是36平方米,求每个小长方形的周长.
8.已知大正方形比小正方形的边长多4厘米,大正方形比小正方形的面积大96平方厘米,分别求出大、小正方形的面积.
9.有一大一小两个正方形,对应边之间的距离是1厘米,如果夹在两正方形之间的面积是28平方厘米。
求大正方形的面积。
10.如图,正方形与阴影长方形的边分别平行,正方形的边长为10厘米,阴影长方形的面积为6平方厘米,那么图中四边形ABCD的面积是多少平方厘米?。
四年级周长与面积经典题库
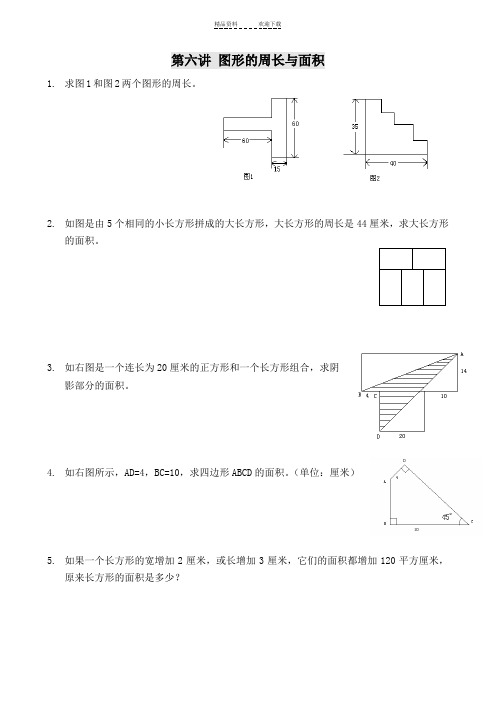
第六讲 图形的周长与面积
1. 求图1和图2两个图形的周长。
2. 如图是由5个相同的小长方形拼成的大长方形,大长方形的周长是44厘米,求大长方形
的面积。
3.
如右图是一个连长为20
厘米的正方形和一个长方形组合,求阴
影部分的面积。
4. 如右图所示,AD=4,BC=10,求四边形ABCD 的面积。
(单位:厘米)
5. 如果一个长方形的宽增加2厘米,或长增加3厘米,它们的面积都增加120平方厘米,
原来长方形的面积是多少?
6.有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米,求小正方形
的面积是多少平方厘米?
7.如图,一个长方形苗圃,分别种有4种不同的树苗,其中三块的面积分别是400平方米、
560平方米、250平方米。
求第四块的面积是多少平方米?
8.有一大一小两个正方形,它们的周长相差20厘米,面积相差55平方厘米,求小正方形
的面积是多少?
9.一个长方形的周长是22厘米,如果它的长和宽均为整数厘米,求这个长方形的面积(单
位:平方厘米)有多少种可能的值?
10.如右图所示,7个完全相同的长方形拼成了图中的阴影部分,图中空白部分的面积是多少
平方厘米?
11.如图,ABCD是边长为12厘米的正方形,E、F分别是AB、BC的中点,AF与CE交于G,
则四边形AGCD的面积是多少平方厘米?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【经典例题1】用15米长的木兰沿着围墙围一个种花草的长方形或者正方形的苗圃,其中一面利用围墙,如果每边的长度都是整数,那么有几种围法,怎样围才能使围成的面积最大?
【经典例题2】一个正方形的花坛,四周有1米宽的水泥路。
如果水泥路的总面积是12平方米,中间花坛的面积是多少平方米?
【经典例题3】如图,将相同的小长方形拼成一个大长方形,已知小长
方形的宽是12厘米,求大长方形的面积。
【经典例题4】一张长方形纸片,在长边上剪下5厘米,宽边上剪下2
厘米,余下的部分正好是一个正方形,已知正方形的面积比原来长方形面积少66平方厘米,求正方形面积。
【经典例题5】一块正方形的玻璃,一边截去12厘米,另一边截去8厘米,剩下的长方形面积
比原来的正方形减少1764平方厘米,原正方形玻璃的周长是多少厘米?
【经典例题6】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续
下去可得到第三个,第四个,第五个正方形,求第五个正方形的面积。
【经典例题7】如图,是一个楼梯的截面图,高280厘米,每阶台阶的宽和高都是20厘米,这楼梯的截面积是多少平方厘米?
【经典例题8】如图,一个长方形,用垂直长和宽的两条线段分成四块,其中三块面积分别为
10平方米,14平方米,42平方米,第四块面积是多少平方米?
【答案】
【经典例题1】用15米长的木兰沿着围墙围一个种花草的长方形或者正方形的苗圃,其中一面
平方米,中间花坛的面积是多少平方米?
已知12平方米是4个完全相同的长方形组成的,所以14÷4=3平方米,每个长方形是3平方米。
又知长方形宽是1米,可知3÷1=3米,长方形长是3米。
中间花坛的长应该是3-1=2米,所以2×2=4平方米。
【经典例题3】如图,将相同的小长方形拼成一个大长方形,已知小长
方形的宽是12厘米,求大长方形的面积。
小长方形4条宽和小长方形3条长的长度是相等的,可以求出小
长方形的长是:12×4÷3=16厘米
大长方形的长是16×3=48厘米,宽是12+12+16=40厘米
大长方形的面积是:48×40=1920
【经典例题4】一张长方形纸片,在长边上剪下5厘米,宽边上剪下2厘米,余下的部分正好是一个正方形,已知正方形的面积比原来长方形面积少66平方厘米,求正方形面积。
66-2×5=56,因为减去的两个图形有一条边是相等的(都是剩下正方形的边长),所以56÷(2+5)=8,8×8=64平方厘米。
【经典例题5】一块正方形的玻璃,一边截去12厘米,另一边截去8厘米,剩下的长方形面积
比原来的正方形减少1764平方厘米,原正方形玻璃的周长是多少厘米?
1764+12×8=1860平方厘米,即8×边长+12×边长=1860,故原来正
方形玻璃的边长是1860÷(12+8)=93厘米。
【经典例题6】一个边长为20厘米的正方形,依次连接四边中点得到第二个正方形,这样继续
下去可得到第三个,第四个,第五个正方形,求第五个正方形的面积。
20×20÷2÷2÷2÷2=25平方厘米
【经典例题7】如图,是一个楼梯的截面图,高280厘米,每阶台阶的宽和高都是20厘米,这楼梯的截面积是多少平方厘米?
把原图不成一个高280厘米,宽(280+20)=300厘米的长方形,它的面积
恰好是280×300÷2=42000平方厘米。
【经典例题8】如图,一个长方形,用垂直长和宽的两条线段分成四块,其中三块面积分别为10平方米,14平方米,42平方米,第四块面积是多少平方米?
比较42和14知道面积是3倍关系,那么长相同时,宽也是3倍关系
,所以在10和?之间也是满足长相同,宽是3倍关系,故面积也是
3倍关系,所以第四块面积是10×3=30平方米。
jkbjkbjkb。
