拟合曲线
计算机 曲线 拟合公式

计算机曲线拟合公式
拟合曲线是指在已知一组数据的前提下,通过一定的数学方法,找出一个代表这组数据的曲线方程。
这个曲线方程可以用于对数据进行预测、分析和优化等操作。
常见的曲线拟合公式包括线性拟合、多项式拟合、指数拟合等。
1. 线性拟合
线性拟合是指拟合一个一次函数y=kx+b,其中k和b分别为
拟合曲线的斜率和截距。
通常使用最小二乘法来求解k和b。
最小二乘法是指通过最小化误差平方值的方法来确定k和b的值,误差平方值=∑(yi-(kxi+b))^2,其中yi为实际的数据值,
xi为自变量的取值。
通过求解误差平方值的导数,可以得到k
和b的值。
2. 多项式拟合
多项式拟合是指将一个多项式函数拟合到一组数据上。
多项式函数的一般形式为y=a0+a1*x+a2*x^2+…+an*x^n。
多项式拟
合的主要目的是通过多项式来描述数据中的非线性趋势。
常见的拟合方法包括最小二乘法、牛顿法、拉格朗日法等。
3. 指数拟合
指数拟合是指将一个指数函数y=a*exp(b*x)拟合到数据上。
这
种拟合常用于数据呈现出指数增长或衰减趋势的情况。
指数拟合的关键是通过对数变换将指数函数转化为线性函数,然后再进行线性拟合。
具体方法是对数据进行对数变换,然后用线性拟合的方法求解出a和b的值,再通过指数函数进行反推,得
到拟合曲线的方程。
以上是常见的曲线拟合公式及方法,拟合的具体选择要根据不同的数据趋势和实际需求进行决定。
拟合曲线的

拟合曲线的拟合曲线是一种数学方法,通过寻找最符合给定数据集的数学模型,以近似描述数据的趋势或规律。
拟合曲线可以用于理解数据的变化趋势、预测未来趋势以及找出数据背后的规律。
常见的拟合曲线方法包括:1.线性拟合(Linear Regression):使用线性模型拟合数据,例如通过最小二乘法找到一条直线,使其在数据点附近误差最小化。
2.多项式拟合(Polynomial Regression):使用多项式函数来拟合数据,可以是二次、三次或更高次的多项式模型,适用于非线性数据。
3.最小二乘法(Least Squares Fitting):一种常用的拟合方法,通过最小化实际观测值和模型预测值之间的误差平方和来找到最佳拟合曲线。
4.非线性拟合(Non-linear Regression):使用非线性模型来拟合数据,例如指数函数、对数函数、高斯函数等,适用于复杂的非线性关系。
5.局部拟合(Local Regression):通过在数据的不同区域内分别拟合局部模型,来更好地适应数据的变化。
拟合曲线的步骤通常包括:●数据收集和准备:收集数据并对数据进行清洗和预处理,确保数据质量和一致性。
●选择模型:根据数据的特征和问题的需求选择合适的拟合模型。
●拟合曲线:使用所选的拟合方法,在数据集上拟合出最优的曲线或模型。
●评估拟合:对拟合模型进行评估,检查模型的拟合程度和预测能力。
●应用和解释:将拟合曲线应用于数据预测、分析趋势或发现数据背后的规律,并进行解释和应用。
拟合曲线是数据分析和建模中常用的技术之一,但在选择模型和解释结果时需要小心谨慎。
不同的拟合方法适用于不同类型的数据和问题,正确选择适合数据特征的模型是非常重要的。
拟合曲线公式

拟合曲线公式拟合曲线公式(CurveFittingFormula,简称CFF)指的是根据一组已知的数据点,以函数的形式得出拟合曲线的方法。
拟合曲线公式通常是以最小二乘法(Least Squares Method)来求解的。
最小二乘法是指将拟合曲线的数学表达式引入给定的点集中,并对给定点的离散程度进行最小化,以此达到拟合曲线的目的。
最小二乘法可以用于拟合线性函数,也可以用于拟合非线性函数。
拟合曲线公式包括多项式函数、指数函数、对数函数、函数和指节函数等。
多项式函数是指以x为自变量,系数构成的多项式为因变量的函数。
如常见的一元二次方程式:y=ax2+bx+c(a、b、c为系数)。
多项式函数可以拟合简单的数据,但当数据的起伏较大时,它的拟合性就不太好,此时可以考虑使用指数函数或其他更复杂的函数。
指数函数是指以x为自变量,以e为底数构成的指数式为因变量的函数。
如:y=2e^x(2为系数)。
指数函数一般用于拟合快速增长或下降的数据,它的优点是能够很好地拟合大范围的数据。
对数函数是指以x为自变量,以a为底数构成的对数函数为因变量的函数。
如:y=loga(x)(a为系数)。
对数函数一般用于拟合大范围的数据,它的优点是可以拟合大范围的数据,但是对数函数只能拟合正数,负数无法用对数函数拟合。
函数是指以x为自变量,构成的式为因变量的函数。
如:y=x^2(2为系数)。
函数可以拟合快速增长或下降的数据,但它只能拟合一个范围,如果要拟合多个范围的数据就需要使用多元函数了。
指节函数是指以x为自变量,构成的指节式为因变量的函数。
如:y=sin(x)(x为系数)。
指节函数可以拟合周期性的数据,它的优点是可以拟合大范围的数据。
除了上面介绍的几种拟合曲线公式,还有许多其他的拟合曲线公式,如勒让德曲线、五次多项式函数、数据密集拟合函数等等,这些拟合曲线公式都有比较好的拟合效果。
总之,拟合曲线公式是一种定性分析技术,能够更好地描述和分析给定数据点之间的联系,帮助人们更好地理解事物之间的关系和规律。
第5章-1 曲线拟合(线性最小二乘法)讲解
求所需系数,得到方程: 29.139a+17.9b=29.7076 17.9a+11b=18.25
通过全选主元高斯消去求得:
a=0.912605
b=0.174034
所以线性拟合曲线函数为: y=0.912605x+0.174034
练习2
根据下列数据求拟合曲线函数: y=ax2+b
x 19 25 31 38 44 y 19.0 32.3 49.0 73.3 97.8
∑xi4 a + ∑xi2 b = ∑xi 2yi
∑xi2 a + n b = ∑yi
7277699a+5327b=369321.5 5327a+5b=271.4
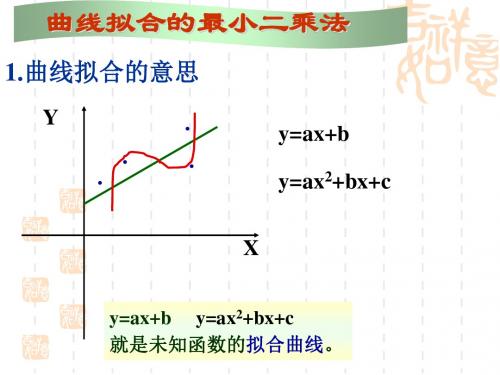
曲线拟合的最小二乘法
1.曲线拟合的意思
Y
.
.
.
.
y=ax+b y=ax2+bx+c
X
y=ax+b y=ax2+bx+c 就是未知函数的拟合曲线。
2最小二乘法原理
观测值与拟合曲线值误差的平方和为最小。
yi y0 y1 y2 y3 y4…… 观测值 y^i y^0 y^1 y^2 y^3 y^4…… 拟合曲线值
拟合曲线为: y=(-11x2-117x+56)/84
x
yHale Waihona Puke 1.61 1.641.63 1.66
1.6 1.63
1.67 1.7
1.64 1.67
1.63 1.66
1.61 1.64
1.66 1.69
1.59 1.62
excel中拟合曲线

excel中拟合曲线
在Excel 中,可以使用"趋势线" 功能来拟合曲线。
具体步骤如下:
1. 打开包含数据的工作表,选择要拟合曲线的数据范围。
2. 在Excel 菜单栏中选择"插入" -> "散点图" -> "散点图",在新的窗口中选择"第二个XY散点图"。
3. 在散点图中,右键单击数据点,选择"添加趋势线"。
4. Excel 会自动拟合曲线,并在图表下方显示拟合曲线的公式和R2值。
如果需要修改拟合曲线的样式或颜色,可以在图表选项中进行设置。
需要注意的是,Excel 中的拟合曲线功能只能用于简单的线性拟合,对于复杂的非线性关系则无法进行拟合。
此外,拟合曲线的精度和准确性也可能受到数据质量和拟合方法的影响。
因此,在使用Excel 进行拟合曲线时,需要谨慎评估结果的可靠性和适用性。
拟合曲线的方法(一)

拟合曲线的方法(一)拟合曲线拟合曲线是一种数据分析方法,用于找到最符合给定数据的函数曲线。
在实际应用中,拟合曲线广泛应用于计算机图形学、统计学和机器学习等领域。
不同的方法可以应用于不同类型的数据和问题,下面将介绍几种常见的拟合曲线方法。
线性拟合线性拟合是最简单也是最常见的拟合曲线方法之一。
其基本思想是通过一条直线来拟合数据点。
线性拟合常用于描述两个变量之间的线性关系。
线性拟合的数学模型可以表示为:y=a+bx,其中y是因变量,x是自变量,a是截距,b是斜率。
线性拟合的目标是通过最小化实际数据点和拟合直线之间的误差来确定最佳的a和b。
多项式拟合多项式拟合是一种通过多项式函数来拟合数据点的方法。
多项式函数是由多个幂函数组成的函数,可以适应各种形状的数据。
多项式拟合的数学模型可以表示为:y=a0+a1x+a2x2+⋯+a n x n,其中y是因变量,x是自变量,a0,a1,…,a n是拟合函数的系数。
多项式拟合的目标是通过最小化实际数据点和拟合曲线之间的误差来确定最佳的系数。
曲线拟合曲线拟合是一种通过曲线函数来拟合数据点的方法。
曲线函数可以是任意形状的函数,可以适应各种复杂的数据。
常见的曲线拟合方法包括:贝塞尔曲线拟合贝塞尔曲线拟合是一种用于拟合平滑曲线的方法。
贝塞尔曲线由控制点和节点构成,通过调整控制点的位置来改变曲线的形状。
贝塞尔曲线拟合的目标是通过最小化实际数据点和贝塞尔曲线之间的误差来确定最佳的控制点和节点。
样条曲线拟合样条曲线拟合是一种用于拟合光滑曲线的方法。
样条曲线由多个局部曲线段组成,每个曲线段由一组控制点和节点定义。
样条曲线拟合的目标是通过最小化实际数据点和样条曲线之间的误差来确定最佳的控制点和节点。
非线性拟合非线性拟合是一种用于拟合非线性关系的方法。
非线性关系在现实世界中很常见,例如指数函数、对数函数等。
非线性拟合的数学模型可以表示为:y=f(x,θ),其中y是因变量,x是自变量,θ是模型的参数。
拟合曲线数据

拟合曲线数据是通过对离散的数据点进行插值、逼近,绘制出一条光滑的曲线的过程。
曲线拟合的方法可以根据具体情况选择不同的曲线类型,常用的函数包括指数函数、对数函数等。
在拟合曲线时,通常需要先收集数据,并对数据进行清洗和预处理,然后选择适合的曲线类型进行拟合。
常用的拟合方法包括最小二乘法和多项式拟合等。
最小二乘法是一种常用的数学优化技术,通过最小化误差的平方和来寻找数据的最佳函数匹配。
多项式拟合则是通过多项式函数来逼近离散数据点,常用的多项式函数包括线性函数、二次函数、三次函数等。
在拟合曲线时,需要注意一些关键点。
首先,要选择合适的曲线类型,确保曲线的形态能够反映数据的内在规律;其次,要选择合适的多项式阶数,以避免过拟合或欠拟合的情况;最后,要注意处理异常值和缺失值,避免其对拟合结果的影响。
拟合曲线数据在许多领域都有应用,如工程设计、科学实验、社会活动等。
通过拟合曲线数据,可以更好地理解数据的内在规律和关系,为后续的数据分析和决策提供支持。
拟合曲线

拟合曲线就是把若干个已知座标的点,寻找某种曲线(二次,三次,等等)的参数,使寻找的曲线通过已知座标点,求出曲线的方程。
这样也可以计算已知座标的点外,曲线其它点的座标。
问题分析体重是一个人横向发育的指标,在一定程度上能反映骨骼、肌肉、皮下脂肪及内脏器官重量等综合情况和身体的充实度,它和身高的比便可以辅助说明人体的营养状况。
影响体重的因素很多,这里我们只分析身高与体重的关系,假设不同地区对身高和体重没有影响;假设季节的不同对身高和体重没有影响;假设气候的差异对身高和体重没有影响;假设运动量的多少对身高和体重没有影响;假设个体的遗传因素对身高和体重没有影响;假设个体的年龄对身高和体重没有影响;假设人体内分泌系统对身高和体重没有影响;假设在一天内人的身高和体重不变;假设是否刚吃过饭对身高和体重没有影响假设疾病对身高和体重没有影响;假设性别对身高和体重没有影响。
五.过程对于问题一,我们可以根据所提供的数据做出其散点图,然后拟合身高与体重间的关系式。
模型1(1)做出题中所给表的散点图,如下图1。
(2)由图1中我们可以发现身高体重的关系可选用二次函数的拟合曲线,也可采用指数函数的拟合曲线。
1.假设体重y与身高x的二次函数关系为2y ax bx c=++;二次函数利用最小二乘法原理,我们可以找出y与x的关系式;对于回归方程^^^i iXa b Y=+令:^i iiY eY-=式中ie--所占有数据iY与预测值^iY的误差;^^^222111min ()()n n i i i i i i Q ea b Y Y Y X =====-=--∑∑∑^^1^^12)02)0((ni ii ni i ii Y a bX Y a bX X ==---=---=∑∑解的: ^^^111111211;nniiii i nniii i n n iii i Y XXXX Y nna b X Y Yb XXXY=======--=-==∑∑∑∑∑∑利用MATLAB 软件,可以算出:a =0.0037 b=-0.4310 c=19.6973 ; 所以y 与x 间的二次函数解析式为:i x :第i 人的身高i y :第i 体重 x :i x 的平均值y :i y 的平均值σ:均方误差x m :为X 的均值x α,x β:为X 的左,右散度y m :为Y 均值y α,y β:为Y 左,右散度X,Y:为LR 模糊数2.假设体重y 与身高x 的函数关系为指数形式:xy ab=;根据最小二乘法原理,利用MATLAB 软件,可以算出:a=2.004 b=1.020 ;所以y 与x 间的函数关系为: 2.004 1.020;x y =⨯ 误差平方和为:2.19; 其函数图象如图3:将以上三图画到一起,则如下图4:由上图可以观察到:指数函数图形和散点图比较趋近,且起误差平方和较小;因此y与x间的模型为指数函数,其解析式为:y=⨯2.004 1.020;x。
拟合曲线的方法

拟合曲线的方法
拟合曲线是一种数据分析方法,用于找到最适合描述数据的数学函数或曲线。
这种方法主要用于通过已知数据点来估计未知数据点的数值。
在拟合曲线的过程中,有几种常见的方法可以使用。
下面是其中一些常见的方法:
1. 最小二乘法:最小二乘法是一种常见的拟合曲线方法,其目标是通过最小化观测数据点与拟合曲线之间的误差来找到最佳拟合曲线。
这种方法可以应用于线性和非线性函数。
2. 多项式拟合:多项式拟合是一种通过多项式函数来拟合数据的方法。
它通常用于拟合曲线比较平滑的数据集。
多项式拟合方法可以根据数据的复杂度选择合适的多项式阶数,例如线性、二次、三次等。
3. 样条插值:样条插值是一种通过多个分段多项式函数来拟合数据的方法。
这种方法通过将数据集划分为多个小段,并在每个小段上拟合一个多项式函数,从而得到整体的曲线拟合。
4. 非参数拟合:非参数拟合是一种不依赖于特定函数形式的拟合曲线方法。
这种方法主要通过使用核函数或直方图等技术来估计数据的概率密度函数,并从中得到拟合曲线。
总体而言,选择合适的拟合曲线方法取决于数据的特征和对拟合结果的要求。
需要根据数据的分布、噪声水平和所需精度等因素来选择合适的方法。
此外,还可以使用交叉验证等技术来评估拟合曲线的质量,并选择最佳的拟合曲线模型。
名词解释 曲线的拟合

名词解释曲线的拟合曲线的拟合是指通过一组已知的离散数据点,找到与这些数据点最匹配的数学函数曲线的过程。
它在许多领域有着广泛的应用,包括数学建模、统计学、机器学习和工程等。
曲线的拟合可以帮助我们理解数据之间的关系、预测未知数据点的值,以及寻找隐含在数据背后的规律和趋势。
在进行曲线的拟合之前,我们首先需要明确所使用的数据点以及期望的拟合函数类型。
常见的拟合函数包括线性函数、多项式函数、指数函数、对数函数等。
其中最简单的情况就是拟合一条直线,被称为线性回归。
而如果拟合的函数是一个高次的多项式,就被称为多项式拟合。
在实际应用中,我们根据数据的特点和需求选择合适的拟合函数类型。
曲线的拟合的关键在于确定拟合参数的取值,使得拟合函数与实际数据点尽可能地吻合。
我们使用拟合误差来衡量拟合的好坏。
拟合误差通常使用最小二乘法来计算,即将实际数据点到拟合函数曲线的距离平方求和最小化。
最小二乘法的优势在于能够将拟合误差平方化,避免正负误差相互抵消的情况产生。
在进行曲线的拟合过程中,我们可以使用一些常见的数学工具和算法。
例如,最小二乘法可以通过解线性方程组或最优化算法来求解最优拟合参数。
而在多项式拟合中,常常使用最小二乘多项式拟合,将实际数据点与多项式函数进行匹配。
此外,还有一些高级的拟合技术,如样条插值、非线性回归和神经网络等,可以在特定情况下提供更加精确和灵活的拟合结果。
曲线的拟合不仅仅是数学方法的应用,更是一门艺术。
在实际拟合过程中,我们需要不断地调整参数和拟合函数的选择,以寻找到最佳的拟合解。
拟合结果的质量取决于多个因素,包括数据的质量、调整参数的准确性,以及拟合函数的合理性等。
因此,拟合过程往往是一个经验丰富和反复试验的过程。
曲线的拟合还涉及到一些限制和问题。
例如,过度拟合是指拟合函数与实际数据点过于吻合,导致对未知数据的预测效果不佳。
解决过度拟合的方法之一是正则化,通过在拟合过程中引入惩罚项来控制模型参数的大小。
第五章 曲线拟合

泰勒展开
arctgx x x3 x5 .....取. arctgx x 35
R(x) | arctg11| 0.2146
以x=0,x=1 作线性插值
arctgx x 1 arctg0 x 0 arctg1 0.7854x
0 1
1 0
R(x) (1 2 ) x(x 1) 0.0711
n
ck j Pk (x j ) y j j 1
m
cik ai ck (k 0,1...m)
i0
写成方程组形式
c00a0 c01a1 c0mam c0 c10a0 c11a1 c1mam c1
cm0a0 cm1a1 cmmam cm
二、正交多项式的曲线拟合
1.) 概念:
)2
j 1
j 1 i0
对ak求偏导数(k=0,1…m)
ak
nm
2
(
ai
x
i j
j1 i0
y
j
)
x
k j
0
m
m
n
化简得
ai
xik j
y
j
x
k j
i0 j 1
j 1
n
n
记
x
k j
Sk
y
j
x
k j
Tk
j 1
j 1 m
aiSki Tk (k 0,1m)
i0
写成矩阵形式
S0 S1 S2 Sm S1 S2 S3 Sm1 S2 S3 S4 Sm2 Sm Sm1 Sm2 S mm
0 (k 0,1,m)
ak
n
m
j[ ai Pi (x j ) y j ]Pk (x j ) 0
拟合曲线算法

拟合曲线算法
拟合曲线算法是一种在平面上用连续曲线近似描述离散数据点之间函数关系的方法。
它可以用于分析和预测数据,从而在科学、工程和数学等领域解决一系列问题。
拟合曲线算法主要包括以下几种:
1.线性拟合:通过最小化误差平方和,找到一条直线或多项式,使得这条直线或多项式与数据点之间的误差最小。
线性拟合常用的工具有最小二乘法、多项式拟合等。
2.非线性拟合:对于非线性数据关系,可以采用非线性函数拟合方法。
常见的非线性拟合算法有:多项式拟合、指数拟合、对数拟合、贝塞尔基函数拟合等。
3.曲线拟合:通过寻找一个连续的函数来近似描述数据点之间的关系。
曲线拟合可以分为一线性曲线拟合和非线性曲线拟合。
线性曲线拟合通常采用最小二乘法,非线性曲线拟合可以采用de Boor算法、Navier-Stokes算法等。
4.插值拟合:插值拟合是通过在数据点之间插入新的点,然后用一个连续的函数来描述这些点之间的关系。
常见的插值方法有拉格朗日插值、牛顿插值、三次样条插值等。
5.优化算法:在拟合曲线过程中,可以使用优化算法来寻找最优的拟合参数。
常见的优化算法有梯度下降、牛顿法、拟牛顿法、信赖域反射算法等。
总的来说,拟合曲线算法是一种通过寻找一个数学函数来描述数据点之间关系的方法,可以根据实际问题和数据特点选择合适的拟合算法。
在实际应用中,曲线拟合算法可以帮助我们更好地理解数据,预测趋势,并为决策提供依据。
拟合曲线公式

拟合曲线公式拟合曲线公式是一种可以用来描述函数曲线的工具,它可以用来帮助我们更好地理解和探索数据中的规律和要素。
它的应用非常广泛,可以用在工程学,物理,生物,经济学,数学和其他学科领域中。
在本文中,我们将讨论拟合曲线公式的一般形式,分析它们如何将资料转换为可控的分类模型,以及如何改变拟合曲线公式以适应非线性的实际现象。
拟合曲线公式是一个基于数学理论的模型,它可以用来描述几何学曲线,也可以用来描述复杂的函数关系。
拟合曲线公式通过根据斜率来描述函数的曲线表现,拟合曲线的公式可以让我们根据实际现象来拟合我们想要的函数曲线。
拟合曲线公式的一般形式是:y = f(x) = a + b1x1 + b2x2 + ... + bnxn其中,a表示零点的偏移量,x1到xn表示各种变量,b1到bn表示与这些变量相关的系数。
拟合曲线公式可以用来描述复杂的非线性变化,而这些变化可以表示为一个简单的函数关系。
例如,如果我们要拟合曲线来对流体流量进行模拟,可以使用拟合曲线公式来描述流体的非线性变化,如流速和流量的关系。
拟合曲线公式的另一个应用是分类模型。
它可以将一个复杂的、不同条件下的实际现象抽象出来并精简为几个变量,而这些变量就可以用来表示复杂的现象。
通过使用拟合曲线公式,可以根据不同的变量构建出不同的函数曲线,并将这些不同函数曲线抽象成一些可以被控制的分类模型。
这样,拟合曲线公式就可以用来分析实际现象,从而更好地掌握实际现象的规律性,并帮助实现预测分析。
拟合曲线公式不仅可用于描述现象,也可以用来改变现象,以便更好地满足用户的要求。
例如,当需要模拟复杂的非线性现象时,可以改变拟合曲线公式以更适应实际现象。
通过调整拟合曲线公式中的参数和变量,可以让拟合曲线更好地描述实际变化,从而更加准确地模拟出实际现象。
总之,拟合曲线公式是一种非常有用的数学模型,它可以帮助我们更好地把握实际现象,将复杂的实际现象抽象成一些可以被控制的分类模型,也可以用来改变函数曲线以满足我们的要求。
拟合曲线算法

拟合曲线算法
拟合曲线是通过给定的一组数据点,找到一个函数或者曲线,使得这个函数/曲线能够尽可能地通过尽可能多的数据点。
常见的拟合曲线算法有:
1. 线性回归:通过最小二乘法,找到一条直线,在二维平面上尽可能地拟合数据点。
可以通过求解正规方程组或者梯度下降等方法得到线性回归模型。
2. 多项式拟合:通过多项式函数去拟合数据点,可以通过最小二乘法或者基于最小化误差的优化算法得到多项式的系数。
3. 插值:通过已知的数据点,构建一个插值函数,使得这个插值函数通过所有的数据点。
常用的插值方法有拉格朗日插值、牛顿插值、分段线性插值等。
4. 样条曲线拟合:将数据点拟合成一条光滑的曲线,常见的样条曲线拟合算法有B样条曲线、自然样条曲线等。
5. 参数拟合:通过拟合参数,调整函数中的参数值,使得函数能够最优地拟合数据点。
常见的参数拟合算法有最小二乘法、最大似然估计等。
这些算法根据不同的需求和数据特征选择,可以通过数学方法、最优化方法等得到拟合的结果。
数学中的曲线拟合

数学中的曲线拟合曲线拟合是数学中一种重要的数值分析方法,它主要用于研究数据点的关系,并通过建立适当的数学模型来预测未知数据或者分析数据间的相互影响。
在各个领域中,曲线拟合都扮演着重要的角色,从物理、生物到工程等多个学科都离不开曲线拟合技术的应用。
本文将简要介绍曲线拟合的基本概念、方法和实际应用。
一、曲线拟合概述曲线拟合是指通过建立数学模型,将数据点拟合在一条曲线上,在统计学中也称为回归分析。
在拟合过程中,我们试图找到最佳拟合曲线,使得所有数据点到拟合曲线的距离尽可能小,从而能够更好地描述数据间的规律。
常用的曲线模型包括线性回归、多项式拟合、指数拟合和对数拟合等。
二、曲线拟合方法1.线性回归线性回归是曲线拟合中最简单的一种方法,它假设数据点之间存在线性关系,即可以用一条直线来拟合数据。
线性回归的核心是最小二乘法,通过最小化实际观测值与拟合值之间的平方差来确定最佳拟合直线的斜率和截距。
2.多项式拟合多项式拟合是曲线拟合中常用的一种方法,它利用多项式函数来逼近数据点。
多项式拟合的核心是最小二乘法,通过最小化实际观测值与拟合值之间的平方差来确定最佳拟合曲线的系数。
多项式拟合可以根据数据点的特点选择合适的多项式阶数,从而更好地描述数据间的关系。
3.非线性拟合若数据点之间的关系不能通过线性函数或多项式函数来表示,就需要使用非线性拟合方法。
非线性拟合通过建立非线性模型来拟合数据点,常用的非线性模型包括指数函数、对数函数、幂函数等。
非线性拟合通常需要借助数值计算方法,如最小二乘法、牛顿法或Levenberg-Marquardt算法等。
三、曲线拟合应用举例曲线拟合广泛应用于各个领域,以下举例说明其实际应用:1.物理学中的运动学分析物理学中,我们常常使用曲线拟合的方法来研究运动学问题。
通过对物体在不同条件下运动的轨迹进行拟合,可以得到运动的规律和物体的运动参数,如位移、速度、加速度等。
2.生物学中的生长模型生物学研究中,曲线拟合方法可以用于分析生物体的生长过程。
拟合曲线公式

拟合曲线公式
拟合曲线公式,又称最小二乘法拟合,是用来拟合曲线的一种有效方法。
拟合曲线公式可以用来表示各种不同类型的曲线,如线性函数、指数函数、对数函数和多项式等。
此外,它也可以用来拟合一组数据,表示这组数据的走势,以及数据之间的关系。
拟合曲线的原理,可以从两个方面来说明。
一方面,它采用最小二乘法来拟合曲线,它是一种以统计学的方法,通过确定各变量之间的最佳拟合曲线,来解决最小可能误差的方法。
另一方面,拟合曲线也需要实际观察数据,并结合实际经验,通过确定曲线的起点、终点,以及曲线的形状等,实现最精确的拟合曲线。
首先,拟合曲线需要准备一组具有特定规律的数据点。
在这些数据点中,可以选择几个做为最小二乘法拟合所需的参数,这些参数会影响最终拟合曲线的形状。
并且还可以确定曲线的起点和终点,以及曲线的形状。
接下来,需要确定一个拟合曲线的公式,也就是用来拟合数据点的函数。
比如,对于线性函数,拟合曲线的公式可以表示为 y = ax + b,其中a和b分别表示线性函数的斜率和截距。
此外,还可以根据不同的类型的曲线,确定不同的拟合曲线公式。
最后,通过最小二乘法拟合实际观察到的数据点,从而求出各变量之间最佳拟合曲线,从而完成拟合曲线的过程。
总而言之,拟合曲线公式是一种有效的拟合曲线的方法。
它采用最小二乘法,充分结合实验结果,确定最佳拟合曲线,从而满足各种
不同曲线的拟合要求。
因此,拟合曲线公式在实际的统计分析中具有重要的意义,为我们提供了一种有效的曲线拟合方法。
曲线拟合的方法

曲线拟合的方法
1. 最小二乘法拟合呀,这就像是给一堆杂乱的数据穿上一件合身的衣服!比如说,你想知道一群人的身高和体重的关系,就可以用最小二乘法来找到那条最能代表它们的曲线。
哇塞,神奇吧!
2. 多项式拟合呢,就好像用不同形状的积木去搭建一个特定的模型。
比如要描述一条有起伏的道路,多项式拟合就能很好地做到。
不是很厉害吗?
3. 样条拟合呀,那简直就是数据的温柔管理者!像画一个美丽的曲线图案,比如模拟山脉的轮廓,样条拟合就能大展身手啦。
难道不吸引人吗?
4. 高斯拟合,哈哈,这就如同在黑暗中找到最亮的那颗星!比如分析一堆噪音中的主要信号,高斯拟合就能精准定位哦。
这多有意思呀!
5. 指数拟合,那可是揭示增长或衰减秘密的钥匙呢!像研究细菌的繁殖速度,指数拟合就能给出答案。
是不是特别酷?
6. 线性拟合呀,简单又直接,就像是走一条直直的路。
比如预测每天的步行距离,线性拟合就足够啦。
多方便呀!
7. 幂律拟合,它可是发现隐藏规律的小侦探哟!比如分析城市人口的分布,幂律拟合就能找到其中的奥秘。
哇哦!
8. 逻辑斯蒂拟合,就像是控制一个开关一样神奇呢!比如研究某种产品的市场饱和度,逻辑斯蒂拟合能起到大作用。
这多了不起啊!
我觉得这些曲线拟合方法都各有各的奇妙之处,能帮助我们更好地理解和处理各种数据呢!。
拟合曲线公式

拟合曲线公式拟合曲线公式是一个用来描述曲线的数学函数,有时也称为“曲线拟合”。
曲线拟合的基本原理是,给定一组数据,用尽可能最佳的参数来拟合出一个合适的函数,使数据能够尽量接近这个函数。
用拟合曲线公式来描述一组数据能够将这些数据放在数学上的统一模型中,这样就可以通过分析模型来得出关于数据的一些有用的信息,从而进行进一步的研究。
拟合曲线公式的应用广泛,常见的拟合曲线公式主要有一次曲线拟合、二次曲线拟合、三次曲线拟合、多项式拟合、Loi拟合和正弦拟合等。
它们可以用来描述温度、湿度、水压等大量复杂的各种物理和化学量,还可以用来描述用户活动、销售情况等信息,以及描述社会数量关系等过程之间的相互联系。
拟合曲线公式的基本思想是拟合出一个合适的方程来拟合变量之间的关系,即在给定的变量之间建立一个函数关系,其中函数的参数可以用来拟合数据,以求得数据拟合出来的最优关系。
拟合过程中主要采用最小二乘法、梯度下降法和其他机器学习算法,来求解出最优化参数,从而得到对应的拟合曲线。
一次曲线拟合是拟合曲线公式中最基本的一种,即用一次函数表达数据与拟合曲线之间的关系,它由一次函数y=kx+b组成,其中k 表示斜率,b表示y轴的截距,可以用此类拟合曲线描述直线的斜率和截距,从而可以获得某个模型的参数值,用于对该模型的进一步描述。
二次曲线拟合是拟合曲线公式中比较常见的一种,即用二次函数y=ax+bx+c来表达数据与拟合曲线之间的关系,它的特点是方程的参数a、b、c都可以调整,这样可以使拟合曲线明显变化,从而精确拟合出更准确的曲线,用于对图形的拟合与分析。
三次曲线拟合是拟合曲线公式中更为复杂的一种,即用三次函数y=ax+bx+cx+d来描述数据与拟合曲线之间的关系,它的特点是参数数量更多,拟合曲线更加复杂,可以用来拟合更加丰富的函数曲线,从而可以更准确地拟合出图形形状,有助于对数据进行更深入的分析。
多项式拟合是拟合曲线公式中更为复杂的一种,即用多项式y=a0+a1x+a2x+......+anx来描述数据与拟合曲线之间的关系,其中参数的个数可以任意设置,从而可以拟合出更复杂的函数曲线,用于对大量数据更为准确的拟合。
origin logistic拟合曲线

origin logistic拟合曲线拟合曲线是一种对实验数据进行数学模型拟合的方法,它可以帮助我们分析和预测实验数据的规律和趋势。
在物流行业中,拟合曲线在运输需求、货物流动和供应链管理等方面都有着重要的应用。
而Origin是一款功能强大的数据分析和绘图软件,它提供了多种拟合曲线的选项和工具,可以帮助我们优化运输和物流管理。
在物流领域,拟合曲线可以应用于货物运输需求的预测和优化。
通过对历史数据进行拟合曲线分析,我们可以了解货物的流动规律和趋势,从而更好地规划供应链和物流网络。
例如,我们可以通过拟合曲线来预测某个地区在未来一段时间内的货物运输需求量,从而合理调整运输资源和安排货运计划,以提高运输效率和降低成本。
拟合曲线还可以应用于货物运输路径的优化。
物流网络中存在着众多的运输路径选择,通过对各种路径进行数学模型的拟合曲线分析,可以找到最优的运输路径,以减少运输时间和成本。
例如,我们可以通过对不同路径的历史数据进行拟合曲线分析,来确定每条路径在不同时间段的运输效率和成本,从而选择最优的运输路径。
此外,拟合曲线在供应链管理中也有着广泛的应用。
供应链管理是一个涉及到多个环节和多个利益相关方的复杂系统,通过对供应链中各个环节的数据进行拟合曲线分析,可以帮助我们了解供应链的运作规律和瓶颈,从而进行优化和改进。
例如,我们可以通过对供应链中的订单、库存和交货时间等数据进行拟合曲线分析,来确定供应链中每个环节的效率和成本,以优化供应链管理和提升整体运作效率。
在Origin软件中,拟合曲线的方法有多种,如线性回归、多项式拟合、指数拟合、对数拟合等。
这些方法可以根据实际情况和实验数据的特点来选择合适的拟合方式。
另外,Origin还提供了丰富的数据可视化和分析工具,可以将拟合曲线绘制成直观清晰的图表,以帮助我们更好地理解和分析数据。
总的来说,拟合曲线是一种重要的数据分析方法,在物流行业中有着广泛的应用。
通过对实验数据进行拟合曲线分析,我们可以更好地了解和预测货物运输需求、优化货物运输路径和改进供应链管理。
拟合曲线与预测曲线

拟合曲线与预测曲线
拟合曲线和预测曲线是统计学和机器学习中常用的概念。
拟合
曲线是指根据已知的数据点,通过某种数学模型找到一条曲线来近
似表示这些数据点的分布规律。
常见的拟合曲线包括线性回归、多
项式回归、指数函数拟合等。
拟合曲线的目的是为了找到一个能够
最好地描述数据点分布的曲线,以便进行数据分析和预测。
预测曲线则是在拟合曲线的基础上进行未来数值的预测。
通过
已知的拟合曲线模型,可以对未来的数据进行预测,从而进行决策
和规划。
预测曲线在金融、经济、气象、环境科学等领域有着广泛
的应用,能够帮助人们做出合理的预测和规划。
拟合曲线和预测曲线的关系在于,拟合曲线是基于已知数据点
的分布规律得到的模型,而预测曲线则是利用这个模型对未来数据
进行预测。
拟合曲线的好坏直接影响到预测曲线的准确性和可靠性,因此在选择拟合曲线模型时需要根据具体的数据特点和预测需求进
行合理的选择。
总的来说,拟合曲线和预测曲线在统计学和机器学习中扮演着
重要的角色,通过对数据的分析和建模,能够帮助人们更好地理解
数据的规律并进行未来的预测和规划。
在实际应用中,需要结合具体的领域知识和数据特点来选择合适的拟合曲线模型,并对预测曲线的结果进行合理的解释和应用。
