初中奥数系列:13.1.1平行四边形的性质及判定.题库学生版
初中奥数讲义_平行四边形附答案

平行四边形平行四边形是一类特殊的四边形,它的特殊性体现在边、角、对角线上,矩形、菱形是特殊的平行四边形,矩形的特殊性体现在有一个角是直角,菱形的特殊性体现在邻边相等,所以,它们既有平行四边形的性质,又有各自特殊的性质.对角线是解决四边形问题的常用线段,对角线本身的特征又可以决定四边形的形状、大小,连对角线后,平行四边形就产生特殊三角形,因此解平行四边形相关问题时,既用到全等三角形法,特殊三角形性质,又要善于在乎行四边形的背景下探索问题,利用平行四边形丰富的性质为解题服务.熟悉以下基本图形、基本结论:例题求解【例1】如图,在矩形ABCD中,已知AD=12,AB=5,P是AD边上任意一点,PE⊥BD于E,PF⊥AC于F,那么PE+PF的值为.(全国初中数学联赛试题)思路点拨分别求出PE、PF困难,△AOD为等腰三角形,若联想“到等腰三角形底边上任一点到两腰距离的和等于腰上的高”这一性质,则问题迎刃而解.注特殊与一般是对立统一的,在一定条件下可以互相转化,相对于一般而言,特殊的事物往往更简单、更直观、更具体.因而人们常常通过特殊去认识一般;另一方面,一般概括了特殊,一般比特殊更为深刻地反映着事物的本质,所以人们也往往通过一般去了解特殊.一般与特殊,是知识之间联系的一种重要形式,知识常常在一般到特殊或特殊到一般的变化过程中,不斩地得到延伸与拓展.【例2】已知四边形ABCD,从下列条件中:(1)AB∠CD,(2)BC∥AD;(3)AB=CD;(4)BC=AD;(5)∠A=∠C;(6)∠B=∠D.任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况有()A.4种 B.9种 C.13种 D. 15种(山东省竞赛题)思路点拨根据平行四边形的判定方法及新的组合方式判定.【例3】】如图,在△ADC中,∠DAC=90°,AD⊥BC,DC、AF分别是∠ABC、∠DAC的平分线,BE和AD交于G,求证:GF∥AC.(湖北省荆州市中考题)思路点拨从角的角度证明困难,连结CF,在四边形AGFE的背景下思考问题,证明四边形AGFE为特殊平行四边形,证题的关键是能分解出直角三角形中的基本图形.【例4】如图,设P为等腰直角三角形ACB斜边AB上任意一点,PE⊥AC于点E,PF⊥BC于点F,PG ⊥EF于G点,延长GP并在其延长线上取一点D,使得PD=PC,求证:BC⊥BD,且BC=BD.(全国初中数学联赛试题)思路点拨尽管图形复杂,但证明目标明确,只需证明△CPB≌△DPB,应从图中分离出特殊三角形、特殊四边形,充分运用它们的性质为证题服务.【例5】如图,在等腰三角形ABC中,延长边AB到点D,延长边CA到点E,连结DE,恰有AD=BC=CE=DE.求∠BAC的度数.(北京市竞赛题)思路点拨 题设条件给出的是线段的等量关系,要求的却是角的度数,相等的线段可得到全等三角形、特殊三角形,为此需通过构造平行四边形改变它们的位置.注 课本中平行四边形的判定定理是从边、角、对角线三个方面探讨的,一般情况是,从四边形边、角、对角线三类元素任意选取两类,任意组合就产生许多判定平行四边形的命题.其中有真命题与假命题,对于假命题,要善于并熟悉构造反例.构造反例是学习数学的一种重要技能,可以帮助我们理解概念.培养推理能力,数学史上就曾有许多著名的论断被一个巧妙的反例推翻的实例.若题设条件中有彼此平行的线段或造成平行的因素,则通过作平行线,构造平行四边形,这是解四边形问题的常用技巧,这是由于平行四边形能使角的位置更理想,送线段到恰当的地方,使线段比良性传递.学力训练1.如图,BD 是平行四边形ABCD 的对角线,点E 、F 在BD 上,要使四边形AECF 是平行 四边形,还需要增加的一个条件是 (填上你认为正确的一个即可,不必考 虑所有可能情形) (宁波市中考题)2.(1)如图,已知矩形ABCD 中,对角线AC 、BD 相交于O ,AE ⊥BD 于E ,若∠DAE :∠BAE =3:1,则∠CAC = ; (河南省中考题)(2)矩形的一个角的平分线分矩形一边为lcm 和3cm 两部分,则这个矩形的面积 为 cm 2. (武汉市中考题)3.如图,以△ABC 的三边为边在BC 的同一侧分别作三个等边三角形,即△ABD 、△BCE 、△ACF . (1)四边形ADEF 是 ;(2)当△ABC 满足条件 时,四边形ADEF 为矩形;(3)当△ABC 满足条件 时,四边形ADEF 不存在. (2000年贵州省中考题)4.已知一个三角形的一边长为2,这边上的中线为1,另两边之和为1+3,则这两边之积为 . (2001年天津市选拔赛试题)5.四边形的四条边长分别是a 、b 、c 、d ,其中a 、c 为对边,且满足cd ab d c b a 222222+=+++,则这个四边形一定是( )A.平行四边形 B.两组对角分别相等的四边形C.对角线互相垂直的四边形 D.对角线相等的四边形6.如图,周长为68的矩形ABCD被分成7个全等的矩形,则矩形ABCD的面积为( )A.98 B.196 C.280 D. 284(湖北省荆州市中考题)7.如图,菱形花坛ABCD的边长为6m,∠B=60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长(粗线部分)为( )A.123 m B.20m C. 22m D.24m(吉林省中考题)8.在凸四边形ABCD中,AB∥CD,且AB+BC=CD+DA,则( )A.AD>BC B.AD<BCC.AD=BC D.AD与BC的大小关系不能确定(“希望杯”邀请赛试题)9.如图,△ABC为等边三角形,D、F分别是BC、AB上的点,且CD=BF,以AD为边作等边△ADC.(1)求证:△ACD≌△CNBF;(2)当D在线段BC上何处时,四边形CDEF为平行四边形,且∠DEF=30°?证明你的结论. (南通市中考题)10.如图,在Rt△ABC中,AB=AC,∠A=90°,点D为BC上任一点,DF⊥AB于F,DE⊥AC于C,M为BC的中点,试判断△MEF是什么形状的三角形,并证明你的结论.(黑龙江省中考题)11.如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.(1)求证:CO=FO;(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.(3)当△ABC满足什么条件时,四边形AECF是正方形?12.如图,在平行四边形ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在BD上,图中有对四边形面积相等,它们是.(常州市中考题)13.如图,菱形ABCD的对角线AC、BD相交于O,△AOB的周长为3+3,∠ABC=60°,则菱形ABCD的面积为.14.如图,矩形ABCD的对角线相交于O,AE平分∠BAD交BC于E,∠CAE=15°,则∠BOE= .15.如图,矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为. (山东省竞赛题)16.如图,平行四边形ABCD中,∠ABC=75°,AF⊥BC于F,AF交BD于E,若DE=2AB,则∠AED的大小是( )A.60° B.65° C.70° D.75° (“希望杯”邀请赛试题)17.如图,正△AEF 的边长与菱形ABCD 的边长相等,点E 、F 分别在BC 、CD 上,则∠B 的度数是( ) A .70° B .75° C .80° D .95° (重庆市竞赛题)18.如图,正方形ABCD 外有一点P ,P 在BC 外侧,并在平行线AB 与CD 之间,若PA=17,PB=2,PC=5,则PD=( )A .25B .19C .32D .17 (“五羊杯”竞赛题)19.如图,在平行四边形ABCD 中,BC=2AB ,CZ ⊥AB 于E ,F 为AD 的中点,若∠AEF=54°,则∠B=( )A .54°B .60°C .66°D .72° (武汉市选拔赛试题)20.如图,在Rt △ABC 中,∠ABC =90°,∠C=60°,BC =2,D 是AC 的中点,以D 作DE ⊥AC 与CB 的延长线交于E ,以AB 、BE 为邻边作长方形ABEF ,连结DF ,求DF 的长.21.如图,菱形的对角线AC 与BD 交于点O ,延长BA 到E ,使AE=21AB ,连结OE ,延长DE 交CA 的延长线于F .求证:OE=21DF . 22.阅读下面短文:如图1,△ABC 是直角三角形,∠C=90°,现将△ABC 补成矩形,使△ABC 的两个顶点为矩形一边的两个端点,第三个便点落在矩形这一边的对边上,那么符合要求的矩形可以画出两个:矩形ACBD 和矩形AEFB(如图2).解答问题;(1)设图2中矩形ACBD和矩形AEFB的面积分别为S l、S2,则S1 S2(填“>”,“=”或“<”);(2)如图3,△ABC是钝角三角形,按短文中的要求把它补成矩形,那么符合要求的矩形可以画出个,利用图3把它画出来;(3)如图4,△ABC是锐角三角形且三边满足BC>AC>AB,按短文中的要求把它补成矩形,则符合要求的矩形可以画出个,利用图4把它画出来;(4)在(3)中所画出的矩形中,哪一个的周长最小?为什么?(陕西省中考题)23.如图,在△ABC中,∠C=90°,点M在BC上,且BM=AC,N在AC上,且AN=MC,AM与BN相交于P,求证:∠BPM=45°.(杭州市“求是杯”竞赛题)24.如图,在锐角△ABC中,AD、CZ分别是BC、AB边上的高,AD、CE相交于F,BF的中点为P,AC的中点为Q,连结PQ、DE.(1)求证;直线PQ是线段DE的垂直平分线;(2)如果△ABC是钝角三角形,∠BAC>90°,那么上述结论是否成立?请按钝角三角形改写原题,画出相应的图形,并给予必要的说明.(“希望杯”邀请赛试题)。
(完整版)平行四边形的性质判定练习题

第一部分 平行四边形的性质练习题 例题1、平行四边形得周长为50cm ,两邻边之差为5cm,求各边长。
变题1.平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________. 变题2.四边形ABCD 是平行四边形,∠BAC=90°,AB=3,AC=4,求AD 的长。
例题2.平行四边形ABCD 中,∠A-∠B=20°,求平行四边形各内角的度数。
变题3.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=_________,∠B_________. 变题4.如图,在平行四边形ABCD 中,∠BAC=34°, ∠ACB=26°,求∠DAC 与∠D 的度数。
例题3.如图,在平行四边形ABCD 中,CE ⊥AD,CF ⊥BA 交BA 的延长线于F ,∠FBC=30°,CE=3cm,CF=5cm,求平行四边形ABCD 的周长。
变题5.如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
1、如图,四边形ABCD 是平行四边形,AB=6cm,BC=8cm ,∠B=70°,则AD=________,CD=______,∠D=_______,∠A=______,∠C=_______.2、平行四边形ABCD 的周长为40cm,两邻边AB 、AC 之比为2:3,则AB=_______,BC=________.3、平行四边形得周长为50cm ,两邻边之差为5cm,则长边是________ ,短边是__________.4、平行四边形ABCD 中,∠A-∠B=20°, 则∠A=_______ ∠B=________5、.平行四边形ABCD 中,AE 平分∠DAB, ∠DEA=20°,则∠C=____,∠B_____.6、平行四边形 ABCD 中,∠A+∠C=200°.则:∠A= _______,∠B= _________ .7、如图,平行四边形ABCD 的周长为50,其中AB=15,∠ABC=60°,求平行四边形面积。
平行四边形的性质与判定(含答案)

13.如图所示,平行四边形 的周长为 , , 相交于点 , 交 于点 ,则 的周长是.
14.如图,四边形 中, , 是 上一点,连接 并延长交 延长线于点 ,请你只添加一个条件:使得四边形 为平行四边形.
(1)求证: ;
(2)求证: .
19.已知四边形 是平行四边形(如图),把 沿对角线 翻折 得到 .
(1)利用尺规作出 .(要求保留作图痕迹,不写作法);
(2)设 与 交于点 ,求证: .
20.如图, , 是平行四边形 对角线 上的点, .请你想一想: 与 有怎样的位置关系和数量关系?并对你的猜想加以证明.
A. B.
C. D.
2.平行四边形的对角线一定具有的性质是( )
A.相等B.互相平分
C.互相垂直D.互相垂直且相等
3.如右图,将一张直角三角形纸片 沿中位线 剪开后,在平面上将 绕着 的中点 逆时针旋转 ,点 到了点 的位置,则四边形 是
A.平行四边形B.矩形C.菱形D.正方形
4.下列命题中,真命题的个数有
15.平行四边形相邻两边长之比为 ,它的周长为 ,则这个平行四边形较长的边长为 .
16.如图.在平行四边形 中,点 , 分别在边 , 上.请添加一个条件使四边形 是平行四边形(只填一个即可).
三、解答题(共6小题;共52分)
17.如图,平行四边形 中,点 , 分别在 , 上,且 ,求证: .
18.如图,四边形 是平行四边形, , 是对角线 上的点, .
第二部分
11.
12.
13.
14. (答案不唯一)
中考数学复习----《平行四边形的判定》知识点总结与专项练习题(含答案解析)

中考数学复习----《平行四边形的判定》知识点总结与专项练习题(含答案解析)知识点总结1.平行四边形的判定:①一组对边平行且相等的四边形是平行四边形。
∵AB∥DC,AB=DC,∴四边行ABCD是平行四边形②两组对边分别相等(两组对边分别平行)的四边形是平行四边形。
符号语言:∵AB=DC,AD=BC(AB∥DC,AD∥BC),∴四边行ABCD是平行四边形.③两组对角分别相等的四边形是平行四边形。
∵∠ABC=∠ADC,∠DAB=∠DCB,∴四边行ABCD是平行四边形④对角线相互平行的四边形是平行四边形。
∵OA=OC,OB=OD,∴四边行ABCD是平行四边形专项练习题1、(2022•河北)依据所标数据,下列一定为平行四边形的是()A.B.C.D.【分析】根据平行四边形的判定定理做出判断即可.【解答】解:A、80°+110°≠180°,故A选项不符合条件;B、只有一组对边平行不能确定是平行四边形,故B选项不符合题意;C、不能判断出任何一组对边是平行的,故C选项不符合题意;D、有一组对边平行且相等的四边形是平行四边形,故D选项符合题意;故选:D.2、(2022•达州)如图,在△ABC中,点D,E分别是AB,BC边的中点,点F在DE的延长线上.添加一个条件,使得四边形ADFC为平行四边形,则这个条件可以是()A.∠B=∠F B.DE=EF C.AC=CF D.AD=CF【分析】利用三角形中位线定理得到DE∥AC,DE=AC,结合平行四边形的判定定理对各个选项进行判断即可.【解答】解:∵D,E分别是AB,BC的中点,∴DE是△ABC的中位线,∴DE∥AC,DE=AC,A、当∠B=∠F,不能判定AD∥CF,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;B、∵DE=EF,∴DE=DF,∴AC=DF,∵AC∥DF,∴四边形ADFC为平行四边形,故本选项符合题意;C、根据AC=CF,不能判定AC=DF,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;D、∵AD=CF,AD=BD,∴BD=CF,由BD=CF,∠BED=∠CEF,BE=CE,不能判定△BED≌△CEF,不能判定CF∥AB,即不能判定四边形ADFC为平行四边形,故本选项不符合题意;故选:B.3、(2022•临沂)如图,在正六边形ABCDEF中,M,N是对角线BE上的两点.添加下列条件中的一个:①BM=EN;②∠F AN=∠CDM;③AM=DN;④∠AMB=∠DNE.能使四边形AMDN是平行四边形的是(填上所有符合要求的条件的序号).【分析】①连接AD,交BE于点O,证出OM=ON,由对角线互相平分的四边形是平行四边形可得出结论;②证明△AON≌△DOM(ASA),由全等三角形的性质得出AN=DM,根据一组对边平行且相等的四边形是平行四边形可得出结论;③不能证明△ABM与△DEN全等,则可得出结论;④证明△ABM≌△DEN(AAS),得出AM=DN,根据一组对边平行且相等的四边形是平行四边形可得出结论.【解答】解:①连接AD,交BE于点O,∵正六边形ABCDEF中,∠BAO=∠ABO=∠OED=∠ODE=60°,∴△AOB和△DOE是等边三角形,∴OA=OD,OB=OE,又∵BM=EN,∴OM=ON,∴四边形AMDN是平行四边形,故①符合题意;②∵∠F AN=∠CDM,∠CDA=∠DAF,∴∠OAN=∠ODM,∴AN∥DM,又∵∠AON=∠DOM,OA=OD,∴△AON≌△DOM(ASA),∴AN=DM,∴四边形AMDN是平行四边形,故②符合题意;③∵AM=DN,AB=DE,∠ABM=∠DEN,∴△ABM与△DEN不一定全等,不能得出四边形AMDN是平行四边形,故③不符合题意;④∵∠AMB=∠DNE,∠ABM=∠DEN,AB=DE,∴△ABM≌△DEN(AAS),∴AM=DN,∵∠AMB+∠AMN=180°,∠DNM+∠DNE=180°,∴∠AMN=∠DNM,∴AM∥DN,∴四边形AMDN是平行四边形,故④符合题意.故答案为:①②④.4、(2022•益阳)如图,在▱ABCD中,AB=8,点E是AB上一点,AE=3,连接DE,过点C作CF∥DE,交AB的延长线于点F,则BF的长为()A.5B.4C.3D.2【分析】根据平行四边形的性质可知CD=AB=8,已知AE=3,则BE=5,再判定四边形DEFC是平行四边形,则DC=EF=8,BF=EF﹣BE,即可求出BF.【解答】解:在▱ABCD中,AB=8,∴CD=AB=8,AB∥CD,∵AE=3,∴BE=AB﹣AE=5,∵CF∥DE,∴四边形DEFC是平行四边形,∴DC=EF=8,∴BF=EF﹣BE=8﹣5=3.故选:C.5、(2022•赤峰)如图,剪两张对边平行的纸条,随意交叉叠放在一起,重合部分构成一个四边形ABCD,其中一张纸条在转动过程中,下列结论一定成立的是()A.四边形ABCD周长不变B.AD=CDC.四边形ABCD面积不变D.AD=BC【分析】由条件可知AB∥CD,AD∥BC,可证明四边形ABCD为平行四边形,可得到AD=BC.【解答】解:由题意可知:AB∥CD,AD∥BC,∴四边形ABCD为平行四边形,∴AD=BC,故选:D.6、(2022•嘉兴)如图,在△ABC中,AB=AC=8,点E,F,G分别在边AB,BC,AC上,EF∥AC,GF∥AB,则四边形AEFG的周长是()A.8B.16C.24D.32【分析】由EF∥AC,GF∥AB,得四边形AEFG是平行四边形,∠B=∠GFC,∠C=∠EFB,再由AB=AC=8和等量代换,即可求得四边形AEFG的周长.【解答】解:∵EF∥AC,GF∥AB,∴四边形AEFG是平行四边形,∠B=∠GFC,∠C=∠EFB,∵AB=AC,∴∠B=∠C,∴∠B=∠EFB,∠GFC=∠C,∴EB=EF,FG=GC,∵四边形AEFG的周长=AE+EF+FG+AG,∴四边形AEFG的周长=AE+EB+GC+AG=AB+AC,∵AB=AC=8,∴四边形AEFG的周长=AB+AC=8+8=16,故选:B.。
(完整版)平行四边形性质和判定习题(答案详细)(可编辑修改word版)
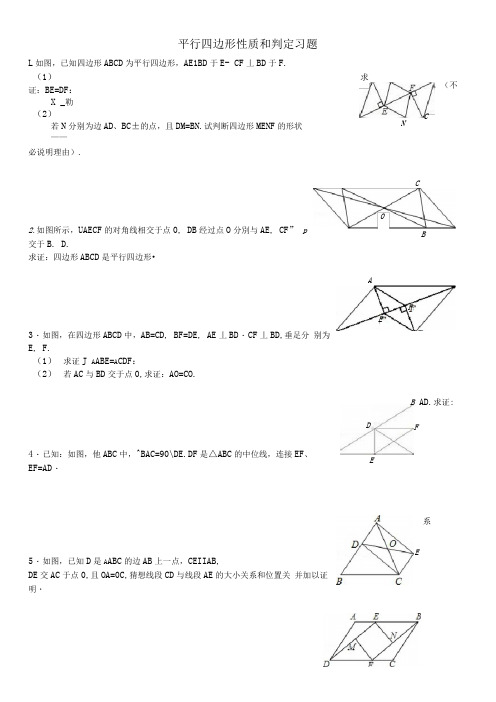
平行四边形性质和判定习题L如图,已知四边形ABCD为平行四边形,AE1BD于E- CF丄BD于F.(1)求证:BE=DF:X _勒(2)若N分别为边AD、BC±的点,且DM=BN.试判断四边形MENF的形状——必说明理由).2.如图所示,UAECF的对角线相交于点0, DB经过点O分別与AE, CF” p交于B. D.求证:四边形ABCD是平行四边形•3・如图,在四边形ABCD中,AB=CD, BF=DE, AE丄BD・CF丄BD,垂足分别为E, F.(1)求证J A ABE=A CDF:(2)若AC与BD交于点0,求证:AO=CO.4・已知:如图,他ABC中,^BAC=90\DE.DF是△ABC的中位线,连接EF、EF=AD・5・如图,已知D是A ABC的边AB上一点,CEIIAB,DE交AC于点0,且OA=0C,猜想线段CD与线段AE的大小关系和位置关并加以证明・B AD.求证:。
(不CNCBAFED FE系E6・如图,已知,UABCD中,AE=CF, M、N分别是DE、BF的中点.求证:四边形MFNE是平行四边形•7・如图,平行四边形ABCD, E 、F 两点在对角线BD 上,且BE=DF,连接AE. EG CF, FA ・求证:四边形AECF 是平行四边形•& 在UABCD 中,分别以AD 、BC 为边向内作等边△ADE 和等边△BCF,连接BE. DF ・求证:四边形BEDF 是平 行四边形・DBIIAC,且DB 丄AC. E 是AC 的中点,求证:BC=DE ・2如图,在梯形ABCD 中,ADIIBC, AD=24cm. BC=30cm,点P 自点A 向D 以IcmZs 的速度运动,到D 点Q 自点C 向B 以2cm/s 的速度运动,到B点即停止,直线PQ 截梯形为两个四边形•问当P. Q同时10. 已知脣 点即停止. 出发,几秒后其中一个四边形为平行四边形?IL 如图:已知D 、E 、F 分别是A ABC 各边的中点, 求证:AE 仃DF 互相平分.如图所示, 9・ED13.如图,已知四边形ABCD中,点E, F. G, H分别是AB、CD、AC. BD的中点,并且点E、F、G、H有在同一条直线上.求证:EF和GH互相平分・14.如图J oABCD 中,MNIIAC.试说明MQ=NP.15.已知:如图所示「平行四边形ABCD的对角线AC, BD柑交于点6 EF经过点0并且分别和AB. CD相交于点E, F,点G, H分别为OA, 0C的中点.求证:四边形EHFG是平行四边形.-46 如制已知的ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH. 连接GE、EH、HF、FG.(1)求证:四边形GEHF是平行四边形;(2)若点G、H分别在线段BA和DC上,尖余条件不变,则(1)中的结论是否成立?(不用说明理由)17.如图,在A ABC中,D是AC的中点,E是线段BC延长线一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.(1)求证J AF=CE:(2)如果AC=EF,且ZACB=135\试判断四边形AFCE是什么样的四边形,并证明你的结论・18,如图平行四边形ABCD 中.mBC=6(几 点E 、F 分別在CD.BC 的延长线上,AE||BD ・ EEhBB 垂足为点F, DF=2 (1) 求证:D 是EC 中点; (2) 求FC 的长.19.如图,已知A ABC 是等边三角形,点D 、F 分别在线段BC 、AB 匕 厶EFB=60。
平行四边形的性质与判定经典例题练习

平行四边形的性质与判定经典例题练习一、平行四边形的性质1. 定义:平行四边形是一种具有两对对边平行的四边形。
定义:平行四边形是一种具有两对对边平行的四边形。
2. 性质1:平行四边形的对边相等。
性质1:平行四边形的对边相等。
3. 性质2:平行四边形的对角线相等。
性质2:平行四边形的对角线相等。
4. 性质3:平行四边形的内角和为180度(即任意两个相邻内角之和为180度)。
性质3:平行四边形的内角和为180度(即任意两个相邻内角之和为180度)。
5. 性质4:平行四边形的两组对边分别互相平行并且相互等长。
性质4:平行四边形的两组对边分别互相平行并且相互等长。
二、平行四边形的判定1. 判定方法1:若一个四边形的对边分别平行且相等,则它是一个平行四边形。
判定方法1:若一个四边形的对边分别平行且相等,则它是一个平行四边形。
2. 判定方法2:若一个四边形的对角线互相相等,则它是一个平行四边形。
判定方法2:若一个四边形的对角线互相相等,则它是一个平行四边形。
三、经典例题练1. 例题1:已知四边形ABCD,AB = BC,且AD与BC互相平行,证明四边形ABCD是平行四边形。
例题1:已知四边形ABCD,AB = BC,且AD与BC互相平行,证明四边形ABCD是平行四边形。
2. 例题2:已知四边形EFGH,EF = GH,且EG与FH互相垂直,证明四边形EFGH是平行四边形。
例题2:已知四边形EFGH,EF = GH,且EG与FH互相垂直,证明四边形EFGH是平行四边形。
3. 例题3:判定以下四边形是否为平行四边形:(a)四边形ABCD,AB = CD,且AD与BC互相垂直;(b)四边形PQRS,PQ = SR,且PS与QR互相平行。
例题3:判定以下四边形是否为平行四边形:(a)四边形ABCD,AB = CD,且AD与BC互相垂直;(b)四边形PQRS,PQ = SR,且PS与QR互相平行。
- (a)根据对边平行和相等的判定方法,若AB = CD且AD与BC互相垂直,则四边形ABCD是平行四边形。
(完整版)平行四边形的性质和判定练习题.doc

初 2017 级寒假培训(八) A 层----平行四边形的性质与判定班级: 姓名:1.定 :两 互相平行的四 形叫做平行四 形,平行四 形 ABCD 作: □ ABCD几何 言:AB // CD , AD // BC , 四边形 ABCD 是平行四边形AD2.性 :平行四 形的 平行且相等, 角相等, 角互 , 角 互相平分;几何 言:∵四 形 ABCD 是平行四 形O∴ AD ∥ BC, _________ ( 平行); AD=BC ,__________( 相等);BCBAC BCD , _________( 角相等); BACABC 180 ⋯( 角互 ) ;OA OC ,( 角 互相平分) 。
平行四边形的判定:判定 1.两 分 平行的四 形是平行四 形 判定 2.两 分 相等的四 形是平行四 形 判定 3.两 角分 相等的四 形是平行四 形 判定 4. 角 互相平分的四 形是平行四 形 判定 5. 一 平行且相等的四 形是平行四 形; 几何 言判定 1.AB // CD , AD // BC , 四边形 ABCD 是平行四边形判定 2. AB DC , AD BC , 四边形 ABCD 是平行四边形判定 3. ABCADC , BADBCD , 四边形 ABCD 是平行四边形 判定 4. AO CO, BO DO , 四边形 ABCD 是平行四边形 判定 5.AB // CD , AB CD ,四边形 ABCD 是平行四边形夯 基 :1. 如 ,将 □ ABCD 的一 BC 延 至 E ,若∠ A =110°, ∠ 1=________.ADABADB E1 D C BCCE242. 如 ,在 □ ABCD 中, A 120,D =°.3. 在平行四 形ABCD 中, AB6cm , BC 8cm , 平行四 形ABCD 的周cm .4. 如 ,在 □ ABCD 中,已知 AD 8CM , AB 6CM , ,DE 平分 ADC 交 BC 于点 E ,则 BE 等于()A.2CMB.4CMC.6CM D .8CM5.平行四边形中一边的长为10cm,那么它的两条对角线的长度可以是()A.4cm和 6cmB.20cm和30cmC.6cm和8cmD.8cm和12cm6.在□ABCD中,对角线 AC,BD相交于点 O,若 BD与 AC的和为 18cm,CD: DA=2:3,AOB的周长为 13cm,那么 BC的长为()A. 6cmB. 9cm C .3cm D .12cm7.如图, ?ABCD 中, AC 、 BD 为对角线, BC=6 , BC 边上的高为4,则阴影部分的面积为.8. 在下面给出的条件中,能判定四边形ABCD是平行四边形的是()A. AB BC, AD CDB.AB // CD, AD BCC.AB // CD , B DD. AB, C D9. 一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是()A.88 ,108 ,88B.88 ,104 ,108 C .88 ,92 ,92 D.108 ,72 ,10810.点 A, B,C, D 在同一平面内,从①AB∥CD,② AB=CD,③ BC∥ AD,④ BC=AD 这四个条件中任选两个,能使四边形ABCD是平行四边形的选法有()种A. 3 B.4 C.5 D. 6 ADB C8.如图,在平行四边形 ABCD 中,若 AB=6 ,AD=10 ,?ABC 的平分线交 AD 于点 E,交 CD 的延长线于点 F,求 DF 的长.9. 已知:如图a,ABCD 的对角线 AC 、 BD 相交于点 O , EF 过点 O 与 AB 、 CD 分别相交于点 E 、 F .(1)求证:OE OF , AE CF , BE DF .(2)若上题中的条件都不变,将EF 转动到图 b 的位置,那么结论是否成立?若将EF向两方延长与平行四边形的两对边的延长线分别相交(图 c 和图 d),结论是否成立,说明你的理由.10.已知如图, O 为平行四边形 ABCD的对角线 AC 的中点, EF 经过点 O,且与 AB 交于 E,与 CD 交于 F,求证:四边形 AECF是平行四边形。
平行四边形的性质与判定

平行四边形的性质与判定一、平行四边形的性质1.对边平行且相等:平行四边形的对边分别平行且相等。
2.对角相等:平行四边形的对角线互相平分,且对角线交点将平行四边形分为两个相等的三角形,这两个三角形的角相等。
3.对角线互相平分:平行四边形的对角线互相平分,即平行四边形的对角线交点是对角线中点的两倍。
4.相邻角互补:平行四边形的相邻角互补,即它们的和为180度。
5.对边角相等:平行四边形的对边角相等,即平行四边形的对边上的角相等。
6.对角线所在的平行线间的距离相等:平行四边形的对角线所在的平行线间的距离相等。
二、平行四边形的判定1.两组对边分别平行的四边形是平行四边形。
2.两组对边分别相等的四边形是平行四边形。
3.一组对边平行且相等的四边形是平行四边形。
4.对角线互相平分的四边形是平行四边形。
5.相邻角互补的四边形是平行四边形。
6.对边角相等的四边形是平行四边形。
7.对角线所在的平行线间的距离相等的四边形是平行四边形。
8.矩形:矩形是四个角都是直角的平行四边形。
9.菱形:菱形是四条边都相等的平行四边形。
10.正方形:正方形是四个角都是直角且四条边都相等的平行四边形。
四、平行四边形的应用1.计算平行四边形的面积:平行四边形的面积可以通过底边长乘以高得到。
2.证明平行四边形的性质:利用平行四边形的性质证明四边形的形状或关系。
3.解决实际问题:应用平行四边形的性质解决生活中的实际问题,如设计图形、计算面积等。
知识点:__________习题及方法:1.习题:已知ABCD是平行四边形,AB=6cm,AD=4cm,求BC和CD 的长度。
答案:BC和CD的长度分别为6cm和4cm。
解题思路:根据平行四边形的性质,对边相等,所以BC=AD=4cm,CD=AB=6cm。
2.习题:在平行四边形ABCD中,∠B=60°,求∠D的度数。
答案:∠D的度数为120°。
解题思路:根据平行四边形的性质,相邻角互补,所以∠D=180°-∠B=120°。
平行四边形的性质与判定(练习)

E DCBA 平行四边形的性质与判定(练习)【知识点】:1. 平行四边形的定义:2.平行四边形性质:⑴边: ;⑵角: ; ⑶对角线: ;(3)对称性:___________________________. 3.平行四边形判定:边:①___________________ ___②_____________ ___________③ ; 角: ; 对角线: ; 【基础训练】一.填空题 (3分×10 = 30分)1.在□ABCD 中,如果∠A +∠C =120°,那么∠B = °.2.已知平行四边形的周长为56㎝,两邻边之比为3:1,则四边形较长的边长为 . 3.已知□ABCD 中,AB = 6,BC 、AB 边上的高分别为6、4,则BC 边长为 . 4.已知□ABCD 中,∠A =60°,AB = 4㎝,AD = 6㎝,则□ABCD 的面积为 . 5.已知□ABCD 中,若∠B 的2倍与∠A 的补角的和为90°,则∠B = 度.6.已知□ABCD 的周长为20cm ,对角线相交于点O ,且△BOC 的周长比△AOB 的周长多2cm ,则AB = cm .7.如图1,已知□ABCD 中,AE =CF ,则图中有 对全等三角形.8.如图2,已知□ABCD 中,BC =12,AB =10,AE ⊥BC 于点E ,且AE =8,则AB 与CD 两边之间的距离为 .9.如图3,已知□ABCD 中,AB =6,AD =8,AE 平分∠BAD 交BC 于E ,则EC = .图1 图2 图310.在四边形ABCD 中,AB =CD ,要使这个四边形成为平行四边形,则可添加的一个条件可以是 . 二.选择题 (3分×6 = 18分)E DCB A1.平行四边形是 ( )(A )轴对称图形 (B )既是轴对称图形,又是中心对称图形 (C )中心对称图形 (D )既不是轴对称图形,也不是中心对称图形2.用两个全等的三角形(三边互不相等)拼成不同的四边形,其中不同的平行四边形的个数是 ( ) (A )1个 (B )2个 (C )3 个 (D )4个 3.下列条件中,能判断四边形是平行四边形的条件是( ) (A )一组对边平行 (B )四条边相等 (C )一组对边平行,另一组对边相等 (D )两条对角线相等4.已知□ABCD 的周长为40cm ,△ABC 的周长为25cm ,则对角线AC 长为( ) (A )5cm (B )15cm (C )6cm (D )16cm 5.如图4,已知四边形ABCD 和CEFG 都是平行四边形, 则下列等式中正确的是( )(A )∠1+∠8=1800(B )∠1+∠5=180° (C )∠4+∠6=180° (D )∠2+∠8=180°6.已知P 为□ABCD 的边AB 上的任一点,则△PCD 与 图4□ABCD 的面积的比S △PCD :S □ABCD 为( )(A )1:2 (B )1:3 (C )1:4 (D )不能确定 三、几何证明1.已知:如图,D 、F 分别是ΔABC 的边BC 、AC 的中点,点E 在线段DF 的延长线上,FE =DF 。
平行四边形性质及判定练习题

平行四边形性质及判定练习题在几何学中,平行四边形是一种特殊类型的四边形,具有许多独特的性质。
本文将介绍平行四边形的性质,并提供一些判定平行四边形的练习题供读者练习。
一、平行四边形的定义和性质平行四边形定义:如果一组四边形的对边是平行的,那么这个四边形就是平行四边形。
平行四边形的性质如下:1. 对边性质:平行四边形的对边相等。
2. 对角线性质:平行四边形的对角线互相平分。
3. 内角和性质:平行四边形的内角和为180度。
4. 对顶角性质:平行四边形的对顶角相等。
二、判定平行四边形的方法1. 判定对边相等:如果一个四边形的对边相等,那么它是一个平行四边形。
2. 判定对角线平分:如果一个四边形的对角线互相平分,那么它是一个平行四边形。
3. 判定内角和:如果一个四边形的内角和为180度,那么它是一个平行四边形。
4. 判断对顶角相等:如果一个四边形的对顶角相等,那么它是一个平行四边形。
三、判定练习题1. 判断以下四边形是否是平行四边形:题目一:ABCD是一个四边形,AB = CD,AD = BC,AC = BD。
证明:ABCD是一个平行四边形。
解答一:由题意知,AB = CD,AD = BC,根据判定对边相等的方法可得,ABCD是一个平行四边形。
题目二:ABCD是一个四边形,AC是对角线,且AC平分∠BAD。
证明:ABCD是一个平行四边形。
解答二:由题意知,AC平分∠BAD,根据判定对角线平分的方法可得,ABCD是一个平行四边形。
题目三:ABCD是一个四边形,∠A + ∠C = 180°,∠B + ∠D = 180°。
证明:ABCD是一个平行四边形。
解答三:由题意知,∠A + ∠C = 180°,∠B + ∠D = 180°,根据判定内角和的方法可得,ABCD是一个平行四边形。
题目四:ABCD是一个四边形,∠A = ∠C,∠B = ∠D。
证明:ABCD是一个平行四边形。
平行四边形知识汇总练习及答案

平行四边形的知识点汇总练习与答案平行四边形定义:两组对边分别平行的四边形叫做平行四边形。
平行四边形是中心对称图形,对称中心是两条对角线的交点。
平行四边形性质1:平行四边形的两组对边分别相等。
平行四边形性质2:平行四边形的两组对角分别相等。
平行四边形性质3:平行四边形的两条对角线互相平分。
平行四边形判定1:两组对边分别平行的四边形是平行四边形。
平行四边形判定2:两组对边分别相等的四边形是平行四边形。
平行四边形判定3:两组对角分别相等的四边形是平行四边形。
平行四边形判定4:两条对角线互相平分的四边形是平行四边形。
平行四边形判定5:一组对边平行且相等的四边形是平行四边形。
平行线之间的距离与特征平行线之间的距离定义:假设两条直线互相平行,那么其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
平行线之间的距离特征1:平行线之间的距离处处相等。
平行线之间的距离特征2:夹在两条平行线之间的平行线段相等。
矩形矩形定义1:有一个角是直角的平行四边形叫做矩形矩形定义2:有三个角是直角的四边形叫做矩形矩形既是中心对称图形又是轴对称图形,对称中心是两条对角线的交点,对称轴是各边的垂直平分线。
矩形性质1:矩形的四个角都是直角。
矩形性质2:矩形的对角线相等且互相平分。
〔注意:矩形具有平行四边形的一切性质〕直角三角形的性质:直角三角形斜边上的中线等于斜边的一半矩形判定1:有一个角是直角的平行四边形是矩形。
矩形判定2:有三个角是直角的四边形是矩形。
矩形判定3:对角线相等的平行四边形是矩形。
菱形菱形定义1:有一组邻边相等的平行四边形叫做菱形.菱形定义2:四条边都相等的四边形叫做菱形。
菱形既是中心对称图形又是轴对称图形,对称中心是两条对角线的交点,对称轴是对角线所在的直线。
菱形性质1:菱形的四条边都相等。
菱形性质2:菱形的对角线互相垂直平分。
菱形性质3:菱形的每一条对角线平分一组对角。
菱形的面积:菱形的面积等于对角线乘积的一半。
平行四边形的性质与判定,附练习题含答案

平行四边形的性质与判定(讲义)一、知识梳理1.平行四边形的定义:两组对边分别平行的四边形叫做平行四边形.2.平行四边形的性质边:平行四边形的对边相等;角:平行四边形的对角相等;对角线:平行四边形的对角线互相平分.3.平行四边形的判定两组对边分别相等的四边形是平行四边形一组对边平行且相等的四边形是平行四边形对角线:两组对角分别相等的四边形是平行四边形.对角线互相平分的四边形是平行四边形4.夹在平行线之间的平行线段相等.例:已知:如图,在□ABCD中,E,F分别为AD,BC的中点.求证:四边形BFDE是平行四边形.【思路分析】①读题标注:②梳理思路:要证四边形BFDE是平行四边形,根据题目中已有的条件选择判定定理:一组对边平行且相等的四边形是平行四边形.在□ABCD中:AD∥BC,且AD=BC,根据条件E,F分别为AD,BC的中点,得ED=12AD,BF=12BC,从而可以得到ED=BF.又因为AD∥BC,即ED∥BF,所以四边形BFDE是平行四边形.【过程书写】证明:如图,∵四边形ABCD是平行四边形,∴AD∥BC,AD=BC.∵E,F分别为AD,BC的中点,∴ED=12AD,BF=12BC,∴ED=BF,∴四边形BFDE是平行四边形.FE DCBAFE DCBA二、练习题1. 已知□ABCD 的周长是100,且AB :BC =4:1,则AB 的长为______________.2. 如图,在□ABCD 中,∠DAB 的平分线AE 交CD 于点E ,若AB =5,BC =3,则EC 的长为( ) A .1B .1.5C .2D .33. 在□ABCD 中,∠A :∠B :∠C :∠D 的值可以是( )A .1:2:3:4B .1:2:2:1C .1:1:2:2D .2:1:2:14. 在□ABCD 中,对角线AC ,BD 相交于点O ,若△ABO 的周长为15,AB =6,则AC +BD =____________.5. 在周长为20cm 的□ABCD 中,AB <AD ,AC ,BD 相交于点O ,OE ⊥BD ,交线段AD 于点E ,连接BE ,则△ABE 的周长为_______.6. 如图,四边形ABCD 是平行四边形,已知AD =12,AB =13,BD ⊥AD ,求BC ,CD ,OB 的长以及□ABCD 的面积.7. 如图,已知四边形ABDE 是平行四边形,延长BD 至点C ,使AC=AB ,连接AD ,CE .(1)求证:△BAD ≌△ACE ;(2)若∠B =30°,∠ADC =45°,BD =10,求□ABDE 的面积.8. 下列说法:①如果一个四边形任意相邻的两个内角都互补,那么这个四边形是平行四边形; ②一组对边平行,另一组对边相等的四边形是平行四边形;③如果AC ,BD 是四边形ABCD 的对角线,且AC 平分BD ,那么四边形ABCD 是平行四边形;BCED AABCD O A BCD E④一组对边平行,一组对角相等的四边形是平行四边形. 其中正确的有( ) A .1个B .2个C .3个D .4个9. 已知四边形ABCD 是平行四边形,下列选项中,按照所给条件得到的四边形EFGH 不一定是平行四边形的是( )A .EF ⊥BC ,GH ⊥ADB .E ,F ,G ,H 分别是□ABCD 各边的中点C .AF ,BH ,CH ,DF 分别是D .EG ,FH 是过□ABCD□ABCD 各内角的角平分线 对角线交点的两条线段10. 如图,AB ∥CD ,AB =CD ,点E ,F 在BC 上,且BE =CF .试证明:以A ,F ,D ,E 为顶点的四边形是平行四边形.11. 上的两点,12. 如图,在□ABCD 中,点E ,F 分别在CD ,AB 的延长线上,且AE =AD ,CF =CB .求证:四边形AFCE 是平行四边形.13. 在□ABCD 中,若∠A :∠B =5:4,则∠C 的度数为( )A .80°B .120°C .100°D .110°H A CD E FGBHA CDE FG BFH A CDEG BHE FGA CDBABCDEF OABC DEF14. 在□ABCD 中,∠A :∠B :∠C :∠D 的值可以是( )A .1:2:3:4B .1:2:2:1C .1:1:2:2D .2:1:2:1 15. 若□ABCD 的周长为40,△ABC 的周长为25,则对角线AC 的长为( )A .5B .15C .6D .1616. 已知平行四边形的一边长为10,则其两条对角线的长可能是( )A .3,8B .20,30C .6,8D .8,1217. 已知四边形ABCD 的对角线相交于点O ,以下条件能判定四边形ABCD 为平行四边形的是( )A .AB ∥CD ,BC =ADB .AB ∥CD ,AO =COC .AB ∥CD ,∠DAC =∠CAB D .AB =CD ,∠B =∠C18. 如图,在平行四边形ABCD 中,EF ∥AD ,HN ∥AB ,则图中的平行四边形共有( )A .12个B .9个C .7个D .5个19. 已知平行四边形的周长为56,两邻边长之比为3:1,则这个平行四边形较长的边长为____________.20. 在□ABCD 中,已知AB ,BC ,CD 三条边的长度分别为3x +,4x -,16,则这个平行四边形的周长为___________.21. 如图,在□ABCD 中,CE ⊥AB 于点E ,CF ⊥AD 于点F .若∠B =60°,则∠ECF =___________.22. 若□ABCD 的周长为22,AC ,BD 相交于点O ,△AOD 的周长比△AOB 的周长小3,则AD =_________,AB =_________.F ED C B A N HFEDC B A参考答案1.402.C3.D4.185.10cm6.BC=12,CD=13,OB52=,□ABCD的面积为607.(1)证明(2)50+8.B9.A10.提示:证明△ABE≌△DCF11.提示:方法①,证明△AED≌△CFB,得到DE=BF,∠AED=∠CFB,则∠DEC=∠BF A,所以DE∥BF,进而可证明四边形EBFD是平行四边形方法②,连接BD,利用对角线互相平分可以证得四边形EBFD是平行四边形12.提示:证明△EAD≌△FCB13.C14.D15.A16.B17.B18.B19.2120.5021.60°22.4,7。
平行四边形的性质与判定练习题

E D C OF B A一、选择题1、下面各条件中,能判定四边形是平行四边形的是 〔 〕A 、对角线互相垂直B 、对角线互相平分C 、一组对角相等D 、一组对边相等2、以下四个命题:①一组对边平行且相等的四边形;②两组对角分别相等的四边形;③对角线相等的四边形;④对角线互相平分的四边形。
其中能判定平行四边形的命题的个数为 〔 〕A 、1个B 、2个C 、3个D 、4个3、以下说法中错误的选项是〔 〕A .平行四边形的对角线互相平分B .有两对邻角互补的四边形为平行四边形C .对角线互相平分的四边形是平行四边形D .一组对边平行,一组对角相等的四边形是平行四边形4、平行四边形的两条对角线及一边的长可依次取 〔 〕A 、6、6、6B 、6、4、3C 、6、4、6D 、3、4、55、以不共线三点为三个顶点作平行四边形,一共可作平行四边形的个数是 〔 〕A 、2个B 、3个C 、4个D 、5个6、 四边形ABCD 的四个角∠A ∶∠B ∶∠C ∶∠D 满足以下哪一条件时,四边形ABCD 是平行四边形?〔 〕A 、1∶2∶2∶1B 、2∶1∶1∶1C 、1∶2∶3∶4D 、2∶1∶2∶17、四边形ABCD 中,AD ∥BC ,要判定四边形ABCD 是平行四边形,还应满足〔 〕A 、∠A +∠C =180°B 、∠B +∠D =180°C 、∠A +∠B =180°D 、∠A +∠D =180°8、根据以下条件,得不到平行四边形的是〔 〕A 、AB =CD ,AD =BC B 、AB ∥CD ,AB =CD C 、AB =CD ,AD ∥BC D 、AB ∥CD ,AD ∥BC9、如图,在□ABCD 中,EF 过对角线的交点,假设AB =4,BC =7,OE =3,那么四边形EFDC 的周长是〔 〕A 、14B 、11C 、10D 、179题图 10题图 11题图 12题图10、如图,线段a 、b 、c 的端点分别在直线l 1、l 2上,那么以下说法中正确的选项是〔 〕A .假设l 1∥l 2,那么a=bB .假设l 1∥l 2,那么a=cC .假设a∥b,那么a=bD .假设l 1∥l 2,且a∥b,那么a=b11、如图,△ABC 中,AB=AC=15,D 在BC 边上,DE∥BA,DF∥CA,那么四边形AFDE 的周长是〔 〕A .30B . 25C . 20D .1512、如图,AB=CD ,BF=ED ,AE=CF ,由这些条件能得出图中互相平行的线段共有〔 〕A .1组 B . 2组 C . 3组 D . 4组13、假设□ABCD 的周长为40cm ,ΔABC 的周长为27cm ,那么AC 的长是〔 〕A 、13cmB 、3cmC 、7cmD 、14、平行四边形的对角线长分别是x 和y ,一边长为12,那么以下各组数据可能是x 与y 的值的是〔 〕A 、8与14B 、10与14C 、18与20D 、10与3615、□ABCD 中,∠A:∠B=13:5,那么∠A 和∠B 的度数分别为〔 〕A .80° ,100°B .130°,50°C .160°,20°D .60°,120°16、一个平行四边形的两条对角线把它分成的全等三角形的对数是( )A.2B.4 C17、E 、F 分别是□ABCD 的边AB 、DC 中点,DE 、BF 交AC 于M 、N ,那么( )⊥MD18、在□ABCD 中假设∠A >∠B ,那么∠A 的补角与∠B 的余角之和( )°°°19、从等腰三角形底边上任意一点分别作两腰的平行线与两腰所围成的平行四边形的周长等于三角形( )A B E C F DO A B D C20、平行四边形两条邻边的长分别是6厘米和4厘米,它们的夹角是60°,那么它的面积是( )A.123cm 2B.73cm 2C.63cm 2D.43cm 221、以下说法正确的有〔 〕①平行四边形的对角线相等;②平行四边形的对边相等;③平行四边形的对角线互相垂直;④平行四边形的对角线互相平分;⑤两组对边分别相等的四边形是平行四边形;⑥一组对边平行而且另一组对边相等的四边形是平行四边形.A .4个 B . 3个 C . 2个 D . 1个22、平行四边形的一条对角线与一边垂直,且此对角线为另一边的一半,那么此平行四边形两邻角之比为( )∶∶3 C.1∶∶523、如图,□ABCD 和□EAFC 的顶点D 、E 、F 、B 在一条直线上,那么以下关系中一定正确的选项是( )A.DE >BFB.DE=BFC.DE <BFD.DE=EF=BF23题图 24题图 25题图24、如图,□ABCD 中,∠ABC=60°,AE∥BD,EF⊥BC 交BC 的延长线于点F ,DF=2,那么EF 的长为〔 〕 A .2 B . 2 C . 4 D . 425、如图,∠BAC=120°,AD⊥AC,BD=CD ,那么以下结论正确的选项是〔 〕A . A D=ACB . A B=AC C . A B=2ACD . A B=AC二、填空题1、□ABCD 中,∠B -∠A =40°,那么∠D =________.2、□ABCD 的周长是44cm ,AB 比AD 大2cm ,那么AB =________cm ,AD =________cm.3、平行四边形的两个相邻内角的平分线相交所成的角的度数是________.4、平行四边形的两条邻边的比为2∶1,周长为60cm ,那么这个四边形较短的边长为________.5、如右上图,在□ABCD 中,AE ⊥BC 于E ,AF ⊥CD 于F ,∠BAD =120°,BE =2,FD =3,那么∠EAF =________,□ABCD 的周长为________.6、假设平行四边形的两邻边的长分别为16和20,两长边间的距离为8,那么两短边间的距离为________.7、□ABCD 中,AB=6cm,BC=8cm ,∠B=70°,那么AD=__________,CD=__________, ∠D=__________,∠A=__________,∠C=__________.8、平行四边形周长为50cm ,两邻边之差为5cm,各边长为 . 9、如右图,平行四边形ABCD 的周长为30cm,它的对角线AC 和BD 相交于O,且△AOB 的周长比△BOC 的周长大5cm,那么AB=________,BC=________. 10、□ABCD 的对角线AC 和BD 相交于O,那么其中全等的三角形有________对.(1)由平行四边形的一个顶点在形内向两边引垂线,二垂线夹角为65°,那么这个平行四边形各内角的度数分别为________.(2)在□ABCD 中,∠A 的补角与∠B 的和等于210°,那么∠A=________,∠B=________.(3)在□ABCD 中,AB ∶BC=1∶2,∠D=30°,AE ⊥BC 于E ,AE=3cm,那么AB=________cm.这个平行四边形的周长是________cm.(4)平行四边形周长是40cm ,二邻边的比为3∶2,那么两邻边长分别是________.(5)在□ABCD 中,两邻边AB 、AD 的比是1∶2,M 是大边AD 的中点,那么∠BMC 的度数是________.(6)平行四边形的周长为50厘米,那么它两邻边之和是______cm ,每条对角线的长不能超过______cm.(7)□ABCD 中,周长为50厘米,AB=15cm ,∠A=30°,那么此平行四边形的面积为______cm 2.(8)□ABCD 的周长为50厘米,对角线交于O 点,△AOB 的周长比△BOC 的周长大5厘米,那么AB 、BC 的长分别是______、______.(9)有五条平行的直线,每相邻两条的距离相等,有一条直线和这组平行线相交成30°角,它介于相邻两条平行线之间的线段长是10厘米,那么这一组平行线最外面两条之间的距离是______厘米.(10)平行四边形周长为68厘米,被两条对角线分成两个不同的三角形的周长的和等于82厘米,两条对角线A BF CD EA BE CFDA BFOC DE的长度比为2∶1,那么两条对角线的长分别为______厘米,______厘米.11、等腰△ABC底边上任意一点D,AB=AC=5cm,过D作DE∥AC交AB于E,DF∥AB交AC于F,那么四边形AEDF的周长为.12、如图〔在下页〕,等边△ABC的边长为8,P是△ABC内一点,PD∥AC,PE∥AD,PF∥BC,点D,E,F分别在AB,BC,AC上,那么PD+PE+PF= .第12题第13题第14题13、如图,在□ABCD中,E,F分别为AB,DC的中点,连接DE,EF,FB,那么图中共有个平行四边形.14、如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE这些结论中正确的选项是.15、如图,梯形ABCD,AD∥BC,∠B+∠C=90°,EF=10,E,F分别是AD,BC的中点,那么BC﹣AD= .第15题第16题第17题16、如图,六边形ABCDEF的每个内角都是120°,AB∥DE,BC∥EF,CD∥FA,且AB=4,BC=5,CD=6,DE=7,那么,六边形ABCDEF的周长是.17、如图,△ABC中,如果AB=30,BC=24,AC=27,DN∥GM∥AB,EG∥DF∥BC,FM∥EN∥AC,那么图中阴影局部的三个三角形周长之和为.18、如右图所示,木工师傅把曲尺的一边紧靠木板边缘,从曲尺的另一边上可以读出木板另一边缘的刻度,然后将曲尺移动到另一处〔紧靠木板边缘〕,如果两次读数一样,说明木板两个边缘平行,其中道理是 .三、解答题与证明题1、在□ABCD中,E、F分别在DC、AB上,且DE=BF。
第03讲 平行四边形的性质和判定(知识解读+达标检测)(解析版)

第03讲平行四边形的性质和判定【题型1 根据平行四边形的性质求边长】【题型2根据平行四边形的性质求角度】【题型3根据平行四边形的性质求周长】【题型4 平行四边形的判定】【题型5 平行四边形的判定与全三角形综合】【题型6 平行四边形的性质与判定综合】考点1:平行四边形的性质1.边的性质:两组对边分别平行且相等,如下图:AD∥BC,AD=BC,AB∥CD,AB=CD;2.角的性质:两组对角分别相等,如图:∠A=∠C,∠B=∠D3.对角线的性质:对角线互相平分。
如图:AO=CO,BO=DO【题型1 根据平行四边形的性质求边长】【典例1】(2023秋•龙口市期末)如图,平行四边形ABCD的对角线AC与BD相交于点O,AB⊥AC,若AB=8,AC=12,则BD的长是( )A.16B.18C.20D.22【答案】C【解答】解:∵四边形ABCD是平行四边形,AC=12,∴OB=OD,OA=OC=AC=6,∵AB⊥AC,由勾股定理得:OB===10,∴BD=2OB=20.故选:C.【变1-1】(2023春•历下区校级期中)如图,在平行四边形ABCD中,∠A的平分线AE交CD于E,AB=8,BC=6,则EC等于( )A.1B.1.5C.2D.3【答案】C【解答】解:∵四边形ABCD为平行四边形,∴CD=AB=8,AD=BC=6.CD∥AB,∵∠DAB的平分线AE交CD于E,∴∠DAE=∠BAE,∵CD∥AB,∴∠AED=∠BAE,∴∠DAE=∠AED.∴ED=AD=6,∴EC=CD﹣ED=8﹣6=2.故选:C.【变式1-2】(2022秋•牟平区期末)如图,在平行四边形ABCD中,∠ABC的平分线交AD 于点E,∠BCD的平分线交AD于点F,若AB=4,AD=5,则EF的长度( )A.1B.2C.3D.4【答案】C【解答】解:∵平行四边形ABCD,∴∠DFC=∠FCB,又CF平分∠BCD,∴∠DCF=∠FCB,∴∠DFC=∠DCF,∴DF=DC,同理可证:AE=AB,∵AB=4,AD=BC=5,∴2AB﹣BC=AE+FD﹣BC=EF=3.故选:C.【变式1-3】(2022秋•安化县期末)如图,F是平行四边形ABCD对角线BE上的点,若BF:FD=1:3,AD=12,则EC的长为( )A.6B.7C.8D.9【答案】C【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC,BC=AD=12,∵BF:FD=1:3,∴EB:AD=BF:FD,∴EB:12=1:3,∴EB=4,∴EC=BC﹣EB=12﹣4=8.故选:C.【题型2根据平行四边形的性质求角度】【典例2】(2023春•环翠区期末)如图,将一副三角板在平行四边形ABCD中作如下摆放,设∠1=30°,那么∠2=( )A.55°B.60°C.65°D.75°【答案】D【解答】解:延长EH交AB于N,∵△EFH是等腰直角三角形,∴∠FHE=45°,∴∠NHB=∠FHE=45°,∵∠1=30°,∴∠HNB=180°﹣∠1﹣∠NHB=105°,∵四边形ABCD是平行四边形,∴CD∥AB,∴∠2+∠HNB=180°,∴∠2=75°,故选:D.【变式2-1】(2023秋•二道区校级期末)如图,在▭ABCD中,∠A+∠C=80°,则∠D=( )A.80°B.40°C.70°D.140°【答案】D【解答】解:∵四边形ABCD是平行四边形,∴∠A=∠C,AB∥CD,∴∠A+∠D=180°,∵∠A+∠C=80°,∴∠A=∠C=40°,∴∠D=180°﹣∠A=140°,故选:D.【变式2-2】(2023春•北安市校级期中)如图,平行四边形ABCD中,∠ABC的平分线交AD于E,∠BED=155°,则∠A的度数为( )A.155°B.130°C.125°D.110°【答案】B【解答】解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AEB=∠CBE,∵∠ABC的平分线交AD于E,∠BED=155°,∴∠ABE=∠CBE=∠AEB=180°﹣∠BED=25°,∴∠A=180°﹣∠ABE﹣∠AEB=130°.故选:B.【变式2-3】(2023•巴东县模拟)四边形ABCD是平行四边形,∠ABC=70°,BE平分∠ABC交AD于点E,DF∥BE交BC于点F,则∠CDF的度数为( )A.55°B.50°C.40°D.35°【答案】D【解答】解:∵∠ABC=70°,BE平分∠ABC,∴∠CBE=∠ABC=35°,∵四边形ABCD是平行四边形,∴∠ADC=∠ABC=70°,AD∥BC,∴∠AEB=∠CBE=35°,∵DF∥BE,∴∠EDF=∠AEB=35°,∴∠CDF=∠ADC﹣∠EDF=70°﹣35°=35°,故选:D.【题型3根据平行四边形的性质求周长】【典例3】(2023春•光明区校级期中)如图,在平行四边形ABCD中,AE平分∠BAD交BC于E,BE=4,EC=3,则平行四边形ABCD的周长为( )cm.A.11B.18C.20D.22【答案】D【解答】解:∵四边形ABCD是平行四边形,∴AD与BC平行,AD=BC,AB=CD,∴∠DAE=∠AEB,∵AE平分∠BAD,∴∠BAE=∠DAE,∴∠BAE=∠AEB,∴BA=BE=4,∵BC=BE+EC=4+3=7=AD,∴平行四边形ABCD的周长为2×(7+4)=22(cm),故选:D.【变式3-1】(2023春•东港区校级期中)在平行四边形ABCD中,∠A的角平分线把边BC 分成长度为4和5的两条线段,则平行四边形ABCD的周长为( )A.13或14B.26或28C.13D.无法确定【答案】B【解答】解:设∠A的平分线交BC于点E,∵四边形ABCD是平行四边形,∴BC∥AD,∴∠BEA=∠DAE,∵∠BAE=∠DAE,∴∠BEA=∠BAE,∴AB=EB,当EB=5,EC=4时,如图1,则AB=EB=5,BC=EB+EC=9,∴2AB+2BC=2×5+2×9=28;当EB=4,EC=5时,如图2,则AB=EB=4,BC=EB+EC=9,∴2AB+2BC=2×4+2×9=26,∴平行四边形ABCD的周长为26或28,故选:B.【变式3-2】(2023春•沙坪坝区期中)如图,在▱ABCD中,对角线AC、BD交于点O,周长为18,过点O作OE⊥AC交AD于点E,连结CE,则△CDE的周长为( )A.18B.9C.6D.3【答案】B【解答】解:∵四边形ABCD是平行四边形,∴OA=OC,AB=CD,AD=BC,∵▱ABCD周长为18,∴AD+CD=9,∵OE⊥AC,OA=OC,∴AE=CE,∴△CDE的周长为:CD+CE+DE=CD+AE+DE=AD+CD=9.故选:B.【变式3-3】(2023秋•南关区校级期末)如图,在▱ABCD中,AD=10,对角线AC与BD 相交于点O,AC+BD=24,则△BOC的周长为 22 .【答案】22.【解答】解:∵四边形ABCD是平行四边形,∴AO=OC=AC,BO=OD=BD,AD=BC=10,∵AC+BD=24,∴OC+BO=12,∴△BOC的周长=OC+OB+BC=12+10=22.故答案为:22考点2:平行四边形的判定1.与边有关的判定:(1)两组对边分别平行的四边形是平行四边形(2)两组对边分别相等的四边形是平行四边形2.与角有关的判定:两组对角分别相等的四边形是平行四边形3.与对角线有关的判定:对角线互相平分的四边形是平行四边形【题型4 平行四边形的判定】【典例4】(2023秋•朝阳区校级期末)如图,四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )A.AB∥DC,AD∥BC B.AB∥DC,AD=BCC.AO=CO,BO=DO D.AB=DC,AD=BC【答案】B【解答】解:A、AB∥DC,AD∥BC可利用两组对边分别平行的四边形是平行四边形判定这个四边形是平行四边形,故此选项不合题意;B、AB∥DC,AD=BC不能判定这个四边形是平行四边形,故此选项符合题意;C、AO=CO,BO=DO可利用对角线互相平分的四边形是平行四边形判定这个四边形是平行四边形,故此选项不合题意;D、AB=DC,AD=BC可利用两组对边分别相等的四边形是平行四边形判定这个四边形是平行四边形,故此选项不合题意;故选:B.【变式4-1】(2022秋•泰山区期末)下列条件中,能判定四边形是平行四边形的是( )A.一组对边相等,另一组对边平行B.一组对边平行,一组对角互补C.一组对角相等,一组邻角互补D.一组对角互补,另一组对角相等【答案】C【解答】解:A、一组对边相等,另一组对边平行,也有可能是等腰梯形B、一组对边平行,一组对角互补,也有可能是等腰梯形C、一组对角相等,一组邻角互补可得到两组对角分别相等,所以是平行四边形D、一组对角互补,另一组对角相等,可能是含两个直角的一般四边形.故选:C.【变式4-2】(2023春•台山市校级期中)在四边形ABCD中,AB∥DC,要使四边形ABCD 成为平行四边形,还需添加的条件是( )A.∠A+∠C=180°B.∠B+∠D=180°C.∠A+∠D=180°D.∠A+∠B=180°【答案】D【解答】解:选项A,B中的两对角是对角关系,不能推出AD∥BC,选项C只能推出AB∥DC,选项D中两角是同旁内角,∵∠A+∠B=180°,∴AD∥BC,又∵AB∥DC,∴四边形ABCD为平行四边形,故选:D.【变式4-3】(2023•中牟县校级开学)小敏不慎将一块平行四边形玻璃打碎成如图的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,他带了两块碎玻璃,其编号应该是( )A.①②B.①④C.②④D.②③【答案】C【解答】解:∵只有②④两块碎玻璃的角的两边互相平行,且中间部分相连,角的两边的延长线的交点就是平行四边形的另两个顶点,∴带②④两块碎玻璃,就可以确定原来平行四边形玻璃的大小,能在商店配到一块与原来相同的平行四边形玻璃,故选:C.【题型5 平行四边形的判定与全三角形综合】【典例5】(2022秋•周村区期末)已知,如图,在▱ABCD中,点E、F分别在AD、BC上,且∠BAF=∠DCE.求证:(1)△ABF≌△CDE.(2)四边形AECF是平行四边形.【答案】(1)见解析过程;(2)见解析过程.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,∠B=∠D,AD=BC,在△ABF和△CDE中,,∴△ABF≌△CDE(ASA);(2)∵△ABF≌△CDE,∴AF=CE,BF=DE,∴AE=CF,∴四边形AECF是平行四边形.【变式5-1】(2023春•惠城区期末)如图,在▱ABCD中,点E,F在对角线BD上,且BE =DF.求证:(1)AE=CF;(2)四边形AECF是平行四边形.【答案】(1)见解答;(2)见解答.【解答】证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD.∴∠ABE=∠CDF.在△ABE和△CDF中,,∴△ABE≌△DCF(SAS).∴AE=CF.(2)∵△ABE≌△DCF,∴∠AEB=∠CFD,∴∠AEF=∠CFE,∴AE∥CF,∵AE=CF,∴四边形AECF是平行四边形.【变式5-2】(2023春•鱼台县期中)如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:(1)AE=CF;(2)四边形AECF是平行四边形.【答案】见试题解答内容【解答】证明:(1)∵四边形ABCD是平行四边形.∴AD∥BC,AD=BC.∴∠ADE=∠CBF.∵AE⊥BD,CF⊥BD,∴∠AED=∠CFB=90°.∵在△ADE与△CBF中,∴△ADE≌△CBF(AAS),∴AE=CF.(2)∵AE⊥BD,CF⊥BD,∴∠AEF=∠CFE=90°.∴AE∥CF.又∵AE=CF,∴四边形AECF是平行四边形.【变式5-3】(2023•新疆模拟)如图,在▱ABCD中,点E,F在对角线BD上,且BF=DE.证明:(1)△ABE≌△CDF;(2)四边形AECF是平行四边形.【答案】(1)见解答;(2)见解答.【解答】证明:(1)∵四边形ABCD为平行四边形,∴AB=CD,AB∥CD,∴∠ABD=∠CDB,∵BF=DE,∴BE=DF,在△ABE和△CDF中,,∴△ABE≌△CDF(SAS);(2)由(1)可知,△ABE≌△CDF,∴AE=CF,∠AEB=∠CFD,∴180°﹣∠AEB=180°﹣∠CFD,即∠AEF=∠CFE,∴AE∥CF,∵AE=CF,AE∥CF,∴四边形AECF是平行四边形.【题型6 平行四边形的性质与判定综合】【典例6】(2023春•温州月考)如图,在▱ABCD中,点E在AB上,点F在CD上,且AE =CF.(1)求证:四边形DEBF是平行四边形;(2)若DE为∠ADC的角平分线,且AD=6,EB=4,求▱ABCD的周长.【答案】(1)见解析;(2)32.【解答】(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD,∴DF∥BE,∵AE=CF,∴BE=DF,∴四边形DEBF是平行四边形;(2)解:∵DE为∠ADC的角平分线,∴∠ADE=∠CDE,∵CD∥AB,∴∠AED=∠CDE,∴∠ADE=∠AED,∴AE=AD=6,∵BE=4,∴AB=AE+BE=10,∴▱ABCD的周长=2(AD+AB)=2(6+10)=32.【变式6-1】(2023春•成都期末)如图,在▱ABCD中,点E,F在对角线AC上,且AF=CE,连接BE,DE,BF,DF.(1)求证:四边形BEDF是平行四边形;(2)若∠BAC=80°,AB=AF,DC=DF,求∠EBF的度数.【答案】(1)证明过程见解答;(2)30°.【解答】(1)证明:在▱ABCD中,AB=CD,AB∥CD,∴∠BAF=∠DCE,在△ABF和△CDE中,,∴△ABF≌△CDE(SAS),∴BF=DE,∠DEF=∠BFA,∴ED∥BF,∴四边形BEDF是平行四边形;(2)解:∵四边形BEDF是平行四边形,∴BE=DF,∵AB=DC=DF,∴AB=BE,∴∠BEA=∠BAC=80°,∴∠ABE=180°﹣2×80°=20°,∵AB=AF,∴∠ABF=∠AFB=(180°﹣80°)=50°,∴∠EBF=∠ABF﹣∠ABE=50°﹣20°=30°.【变式6-2】(2023秋•锦江区校级期末)如图,点E、F是平行四边形ABCD对角线AC上两点,BE∥DF.(1)求证:四边形BEDF是平行四边形;(2)若AC=8,BC=6,∠ACB=30°,求平行四边形ABCD的面积.【答案】(1)证明见解答过程;(2)24.【解答】(1)证明:平行四边形ABCD中,AD∥BC,AD=BC,∴∠ACB=∠CAD,又∵BE∥DF,∴∠BEC=∠DFA,在△BEC和△DFA中,,∴△BEC≌△DFA(AAS),∴BE=DF,又BE∥DF,∴四边形BEDF是平行四边形;(2)解:过A点作AG⊥BC,交CB的延长线于G,在Rt△AGC中,AC=8,∠ACB=30°,∴AG=4,∵BC=6,∴平行四边形ABCD的面积=BC•AG=4×6=24.【变式6-3】(2023春•和县校级期末)如图,BD是四边形ABCD的对角线,∠ADB=∠CBD,AD=BC,过点A作AE∥BD交C的延长于E.(1)求证:四边形ABDE是平行四边形;(2)过点E作EF⊥BC交BC的延长线于点F,连接DF,若,求DF的长.【答案】(1)见解析;(2)2.【解答】(1)证明:∵∠ADB=∠CBD,∴AD∥BC,∴∠ADE=∠BCD.∵AD=BC,∴四边形ABCD是平行四边形,∴AB∥CE,AB=CD,∵AE∥BD,∴∠EAD=∠BDA,∴∠EAD=∠DBC,在△EAD和△DBC中,,∴△EAD≌△DBC(ASA),∴DE=CD,∵AB=DE.∴四边形ABDE是平行四边形;(2)∵DE=CD=AB,∴FD是CE的中线,∵EF⊥BC,∴DF=CE==2.考点3:三角形的中位线三角形中位线:在△ABC 中,D,E 分别是A C,AC 的中点,连接DE.像DE 这样,连接三角形_两边中点的线段叫做三角形的中位线.B中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的二分之一。
(完整版)平行四边形的性质及判定典型例题

平行四边形的性质及判定 (典型例题)1.平行四边形及其性质例1如图,O 是卜二・ABCD 对角线的交点.△ OBC 的周长为59, BD=38 , AC=24,贝卩AD= __ 若厶OBC 与厶OAB 的周长之差为 15,贝y AB=QABCD 的周长= _____ .AC ,可得BC ,再由平行四边形对边相等知 AD=BC ,由平行四 边形的对角线互相平分,可知△ OBC 与厶OAB 的周长之差就为BC 与AB 之差,可得AB ,进而可得」ABCD 的周长.解 EBCD 中0A 二= OB = OD = |E D (平行四边形的对角线互相平分)•••△ OBC 的周长=0B + 0C +EC分析: 根据平行四边形对角线互相平先 所OC =1=19 + 12 + BC=59••• BC=28—ABCD 中,•BC=AD(平行四边形对边相等)•AD=28△ OBC的周长-△ OAB的周长=(OB + OC + BC)-(OB + OA+AB)=BC-AB=15•AB=13•••二ABCD的周长=AB + BC + CD + AD=2(AB + BC)=2(13 + 28)=82说明:本题条件中的△ OBC占厶OAB的周长之差为15”,用符号语言表示出来后,便容易发现其实质,即BC与AB之差是15 .例2判断题(1) 两条对边平行的四边形叫做平行四边形. ()(2) 平行四边形的两角相等.()(3) 平行四边形的两条对角线相等.()(4) 平行四边形的两条对角线互相平分. ()(5) 两条平行线中,一条直线上任一点到另一条直线的垂线段叫做两条平行线的距离.()(6) 平行四边形的邻角互补.()分析:根据平行四边形的定义和性质判断.解:(1) 错两组对边分别平行的四边形叫做平行四边形”是两组对边,而不是两条对边.如图四边形ABCD,两条对边AD // BC .显然四边形ABCD 不是平行四边形.(2) 错平行四边形的性定理1,“平行四边形的对角相等.”对角是指四边形中设有公共边的两个角,也就是相对的两个角.(3) 错平行四边形的性质定理3,“平行四边形的对角线互相平分.”一般地不相等.(矩形的两条对角线相等).(4) 对根据平行四边形的性质定理 3 可判断是正确的.(5) 错线段图形,而距离是指线段的长度,是正值正确的说法是:两条平行线中,一条直线上任一点到另一条直线的垂线段的长度叫做这两条平行线的距离.(6) 对由定义知道,平行四边形的对边平行,根据平行线的性质可知.平行四边形的邻角互补.例3 .如图1,在二ABCD中,E、F是AC上的两点.且AE=CF .求证:ED // BF .分析:欲址DE // BF,只需/ DEC二/ AFB,转证=/ ABF CDF, 因卜二,ABCD,则有AB丄CD,从而有/ BAC= / CDA .再由AF=CF 得AF=CE .满足了三角形全等的条件.证明:v AE=CFAE+EF二CF+EF••• AF=CE在二ABCD中AB // CD(平行四边形的对边平行)• / BAC= / DCA(两直线平行内错角相等)AB=CD(平行四边形的对边也相等)•••△ ABF刍乂 CDE(SAS)•••/ AFB= / DCE• ED // BF(内错角相等两直线平行)说明:解决平行四边形问题的基本思想是化为三角形问题不处理.例4如图已知在△ ABC中DE // BC // FG,若BD=AF、求证; DE + FG=BC .分析1:要证DE + FG=DC由于它们是平行线,由平行四边形定义和性质.考虑将DE平移列BC上为此,过E(或D)作EH // AB(或DM // AC),得至U DE=BH、只需证HC=FG ,因AF=BD=EH , / CEH=/ A. / AGF = Z C所以△ AFG幻/ EHC .此方法称为截长法.分析2:过C点作CK // AB交DE的延长线于K,只需证FG=EK , 转证△ AFG CKE .过E作EH // AB交于Hv DE // BC•••四边形DBHE是平行四边形(平行四边形定义)••• DB=EHDE=BH(平行四边形对边也相等)又BD=AF• AF=EHv BC // FGAGF= / C(两直线平行同位角相等)同理 / A= / CEH• △ AFG EHC(AAS)••• FG=HC••• BC二BH+HC二DE二FG.过C作CK // AB交DE的延长线于K.v DE // BC•四边形DBCK是平行四边形(平行四边形定义)•CK=BD DK=BC(平行四边形对边相等)又BD=AF•AF=CKv CK // AB• / A= / ECK(两直线平行内错角相等)v BC // FG•••/ AGF二/ AED(两直线平行同位角相等)又/ CEK二/ AED(对顶角相等)•••/ AGF= / CEK•••△ AFG S' CKE(AAS)FG=EKDE+EK=BC• DE+FG=BC例 5 如图I—ABCD 中,/ ABC=3 /A,点 E 在CD 上,CE=1 , EF丄CD交CB延长线于F,若AD=1,求BF的长.u --- ---------- r分析:根据平行四边形对角相等,邻角互补,可得/ C= / F=45°进而由勾股定理求出CF ,再根据平行四边形对边相等,得BF的长.解:在二ABCD 中,AD // BC•••/ A +/ ABC=180 (两直线平行同旁内角互补)vZ ABC=3 / A•••/ A=45 ,Z ABC=135•••Z C= Z A=45 (平行四边形的对角相等)•EF 丄CD•Z F=45°(直角三角形两锐角互余)•EF=CE=1在RtAOEF中,CF = JCE之》EF金=(勾股定理)v AD=BC=1二BF = CF”EC = Q[例6如图1,‘ ■ ABCD中,对角线AC长为10cm , Z CAB=30 , AB长为6cm,求一ABCD的面积.解:过点C作CH丄AB,交AB的延长线于点H .(图2)vZ CAB=30-■.CH 二丄= 1 X10=52 2••• S—ABCD = AB-CH = 6X5=30(cm2)答:二ABCD的面积为30cm2 .说明:由于二=底>高,题设中已知AB的长,须求出与底AB 相应的高,由于本题条件的制约,不便于求出过点D的高,故选择过点C 作高.例7如图,E、F分别在’・ABCD的边CD、BC上,且EF //求证:S△ ACE二S △ ABF分析:运用平行四形的性质,利用三角形全等,将其转化为等底同高的三角形.证明:将EF向两边延长分别交AD、AB的延长线于G、H.二ABCD DE // AB•••/ DEG= / BHF(两直线平行同位角相等)/ GDE= / DAB(同上)AD // BC•••/ DAB= / FBH(同上):丄 GDE= / FBHv DE // BH , DB // EH•四边形BHED是平行四边形V DE二BH(平行四边形对边相等)GDE 刍乂 FBH(ASA)••• S△ GDE=S △ FBH(全等三角形面积相等).GE=FH(全等三角形对应边相等).S△ ACE=S △ AFH(等底同高的三角形面积相等).S △ ADE = S △ ABF说明:平行四边形的面积等于它的底和高的积.即S二二a・ha .a 可以是平行四边形的任何一边,h必须是a边与其对边的距离.即对应的高,为了区别,可以把高记成ha,表明它所对应的底是a.例8如图,在二ABCD中,BE平分/ B交CD于点E, DF 平分/ D交AB于点F,求证BF=DE .分析EF二DE (目标)十BEDP 为口DF"d叫西3 ]1=Z 3 r Z 1=Z 2f t"S亠彩姑皤彩B口ABCD证明:T四边形ABCD是平行四边形二DE // FB,/ ABC= / ADC(平行四边形的对边也平行对角相等)•••/仁/ 3(两直线平行内错角相等)而Z]=^Z ADC,Z2=|ZABC•••/ 2= / 3• DF // BE(同位角相等两条直线平行)•四边形BEDF为平行四边形(平行四边形定义)• BF=DE .(平行四边形的对边相等)说明:此例也可通过△ ADF CBE来证明,但不如上面的方法简捷.例9如图,CD的Rt△ ABC斜边AB上的高,AE平分/ BAC 交CD于E, EF // AB,交BC于点F,求证CE=BF .分析作EG // BC,交AB于G,易得EG=BF .再由基本图, 可得EG=EC ,从而得出结论.过E点作EG // BC交AB于G点.v EF // AB••• EG=BFv CD为Rt△ ABC斜边AB上的高•/ BAC + / B=90°.Z BAC + / ACD = 90°•/ B= Z ACD•Z ACD=Z EGAv AE 平分Z BAC•Z 1= Z 2又AE=AE•△ AGE ACE(AAS)•CE=EG•CE=BF .说明:(1)在上述证法中,“平移”起着把条件集中的作用.(2)本题也可以设法平移AE .(连F点作FG // AE,交AB于G)例10如图,已知I —ABCD的周长为32cm , AB : BC=5 : 3, AE 丄BC 于E, AF 丄DC 于F,/ EAF=2 / C,求AE 和AF 的长.分析:从化简条件开始①由二ABCD的周长及两邻边的比,不难得到平行四边形的边长.口虹CD 的周长=321 fAB=10AB : BC-5 : 3 p |BC=6②/ EAF=2 / C告诉我们什么?AF i FC1 ZFAE^ZC=180°] oAE 1 EAF-2 Z C j討c=6°这样,立即可以看ADF、△ AEB都是有一个锐角为30°的直角三角形.于是有= = = 3再由勾股定理求出解:——ABCD的周长为32cm即AB+BC+CD+DA=32v AB=CD BC=DA(平行四边形的对边相等)/.AB + BC = - X32 = 16 2又AB : BC=5 : 35+3BC= —X3 = 65+3/ EAF+ / AFC+ / C+ / CEA=360 (四边形内角和等于360°v AE 丄BC / AEC=90AF 丄DC / AFC=90•••/ EAF+ / C=180/ EAF=2 / CT AB // CD(平行四边形的对边平行)•••/ ABE二/ C=60 (两直线平行同位角相等)同理/ ADF=60SRiAABE 中,ZBAE = 30* BE = |AB = 5£—■Al = ja =E^ = 5^3 (cm)在RtAADF中,ZDAF = 30° DF= ^AP = |B C=3■f-j d—iAF - 7A D3 -I>F a = M Ccm)说明:化简条件,化简结论,总之,题目中哪一部分最复杂就从化简那一部分开始,这是一种常用的解题策略,我们把这种解题策略称为:从最复杂的地方开始.它虽简单,却很有效.2 .平行四边形的判定例1填空题(1)如图1,四边形ABCD与四边形BEFC都是平行四边形,则四边形AEFD是—,理由是(2)如图2, D、E分别在△ ABC的边AB、AC上,DE=EF , AE=EC , DE // BC贝卩四边形ADCF是__,理由是__ ,四边形BCFD 是—,理由是—分析:判定一个四边形是平行四边形的方法较多,要从已知条件出发,具体问题具体分析:(1)根据平行四边形的性质可得AD平行且等于BC,BC平行且等于EF,从而得AD平行且等于EF,由判定定理4可得.(2)由AE=EC , DE=EF,由判定定理3可得四边形ADCF是平行四边形,从而得AD // CF即BD // CF,再由条件,可得四边形BCFD是平行四边形.解:(1)平行四边形,一组对边平行且相等的四边形是平行四边形(2)平行四边形,对角线互相平分的四边形是平行四边形,平行四边形,两组对边分别平行的四边形是平行四边形.说明:平行四边形的定义(两组对边分别平行的四边形叫做平行 四边形,既是平行四边形的一个性质,又是平行四边形的一个判定 方法.例 2 女口图,四边形 ABCD 中,AB=CD . / ADB 二 /CBD=90 .求 证:四边形ABCD 是平行四边形.分析:判定一个四边形是平行四边形,有三类五个判定方法, 这三类也是按边、角和对角线分类,具体的五个方法如下表:CIID 从对角钱看一(5 )对角线互相平分 因此必须根据已知条件与图形结构特点,选择判定方法.证法一:v AB=CD . Z ADB= / CBD=90 , BD=DB .••• Rt △ ABD 坐 Rt △ CDB .「( 1)两组对边分别平存C I )从边看 —(2)两组对边分别相等_(3)-组对边平行且相尊 (1)从边看 (II )从角看 (4)两组对角分别相等 的四边形绘平行四边形•••/ ABD= / CDB,/ A= / C.•/ ABD+ / CBD= / CDB+ / ADB即 / ABC= / CDA .•四边形ABCD 是平行四边形(两组对角分别相等的四边形是平行四边形).证法二:vZ ADB= / CBD=90 , AB=CD、BD=DB .•Rt△ ABD 坐Rt△ CDB .•Z ABD=Z CDB.•AB //CD.(内错角相等两直线平行)•四边形ABCD 是平行四边形(一组对边平行且相等的四边形是平行四边形).证法三:由证法一知,Rt △ ABD幻Rt △ CDB .••• DA=BC又T AB二CD•四边形ABCD是平行四边形(两组对边分别相等的四边形是平行四边形)说明:证明一个四边形是平行四边形,往往有多种证题思路,我们必须注意分析,通过比较,选择最简捷的证题思路.本题三种证法中,证法二与证法三比较简捷,本题还可用定义来证明.例3如图,‘「ABCD中,E、G、F、H分别是四条边上的点, 且AE=CF , BG=DH,求证:EF与GH互相平分.分析:只须证明EGFH为平行四边形.证明:连结EG 、GF、FH 、HE.T四边形ABCD是平行四边形•••/ A= / C, AD=CB .T BG=DH•AH=CG又AE=CF•△ AEH CFG(SAS)•HE=GF同理可得EG=FH•四边形EGFH 是平行四边形(两组对边分别相等的四边形是平行四边形)•EF 与GH 互相平分(平行四边形的对角线互相平分).说明:平行四边形的性质,判定的综合运用是解决有关线段和角问题基本方法.例4如图,二ABCD中,AE丄BD于E, CF丄BD于F.求证:四边形AECF是平行四边形.分析:由平行四边形的性质,可得△ ABE CDF••• AE= CF进而可得四边形AECF是平行四边形.证明:口ABCD中,AB屯CD(平行四边形的对边平行,对边相等)•/ ABD= / CDB(两直线平行内错角相等)AE 丄BD、CF 丄BD•AE // CF / AEB= / CFD=90•△ ABE CDF(AAS)•AE=CF•四边形AECF是平行四边形(一组对边平行且相等的四边形是平行四边形)说明:平行四边形的定义,既是平行四边形的一个性质,又是平行四边形的一个判定方法.例5如图,二ABCD中,E、F分别在AD、BC上,且AE=CF , AF、BE相交于G, CE、DF相交于H求证:EF与GH互相平分分析:欲证EF与GH互相平分,只需四边形EGFH为平行四边形,利用已知条件可知四边形AFCE、四边形EBFD都为平行四边形,所以可得AF // EC , BE // DF,从而四边形GEHF为平行四边形.证明:」ABCD中,AD丄BC(平行四边形对边平行且相等)v AE=CF /. DE=BFT四边形AFCE、四边形BFDE是平行四边形(一组对边平行且相等的四边形是平形四边形)二AF // CE , BE // DF(平行四边形对边平行)•••四边形EGFH是平行四边形(两组对边分别平行的四边形是平行四边形)••• GH与EF互相平分(平行四边形的对角线互相平分)说明:平行四边形问题,并不都是以求证某一个四边形为平行四边形的形式出现的.往往更多的是求证线段的相等、角的相等、直线的平行、线段的互相平分等等.要灵活地根据题中已知条件,以及定义、定理等.先判定某一四边形为平行四边形,然后再应用平行四边形的性质加以证明.例6如图,已知—ABCD中,EF在BD上,且BE=DF ,点G、H 在AD、CB上,且有AG=CH , GH与BD交于点0,求证EG丄HF分析:证EF 、GH 互相平分二GEHF 为平行四边形.证明:连 BG 、DH 、GF 、EHT ABCD 为平行四边形.••• AD 垒 BC又 AG=HC• DG 丄 BH•四边形BGDH 为平行四边形(一组对边平行且相等的四边形是平行四边形)• HO = GO , DO=BO (平行四边形的对角线互相平分) 又 BE=DF•OE=OF•四边形GEHF为平行四边形(对角线互相平分的四边形是平行四边形)••• EG丄HF.(平行四边形的对边平行相等)说明:由于条件BE=DF涉及到对角线BD,所以考虑用对角线互相平分来证明例7如图,——ABCD中,AE丄BD于E, CF丄BD于F, G、H分别为AD、BC的中点,求证:EF和GH互相平分.分析:连结EH , HF、FG、GE,只须证明EHFG为平行四边证法一:连结EH , HF、FG、GEv AE丄BD , G是AD中点.-■.GE=C J D =^AD2/ GED二 / GDE同理可得HF =HB =^EC,Z HFE =Z HEFV四边形ABCD是平行四边形••• AD 岂BC,/ GDE= / HBF••• GE=HF,/ GED= / HFB•GE // HF•四边形GEHF为平行四边形(一组对边平行且相等的四边形是平行四边形)•EF和GH互相平分.(平行四边形对角线互相平分)证法二:容易证明厶ABE CDF• BE=DFT四边形ABCD为平行四边形••• AD 些BCT G、H分别为AD、BC的中点•DG 丄BH•四边形BHDG为平行四边形(一组对边平行且相等的四边形是平行四边形)•BD和GH互相平分(平行四边形对角线互相平分)•OG=OH , OB=OD又BE=DF•OE=OF•EF和GH互相平分.例8如图,已知线段a、b与/ a,求作:—ABCD ,使/ ABC二/ a, AB=a , BC=b ,分析:已知两边与夹角,可先确定△ ABC,根据判定定理2(两组对边分别相等的四边形是平行四边形),再确定点D,从而平行四边形可作出.作法:(1) 作/ EBF二/ a,⑵在BE、BF上分别截取BA=a , BC=b ,⑶分别为A、C为圆心,b, a为半径作弧,两弧交于点D, 二四边形ABCD为所求.*证明:由作法可知AB=CD = aBC=AD=b二四边形ABCD 为平行四边形(两组对边分别相等的四边形为平 行四边形)且/ ABC 二 / a, AB=a , BC=b- ABCD 为所求说明:常见的平行四边形作图有以下几种:(1) 已知两邻边(AB 、BC)和夹角(/ B).(2) 已知一边(BC)和两条对角线(AC , BD).(3) 已知一边(BC)和这条边与两条对角线的夹角 (如/ DBC ,Z ACB).⑷已知一边(CD)和一个内角(/ ABC)以及过这个角的顶点的一条对角线(BD ,且BD > CD)求作平行四边形(如图)完成这些作图的关键点,都在于先作出一个三角形,然后再完成平行四边形的作图,体现了把平行四边形的问题化归为三角形问题的思想方法.。
平行四边形的性质及判定知识点与习题

平行四边形定义:两组对边分别平行的四边形是平行四边形.平行四边形的性质:(1)边:平行四边形的对边平行且相等(即:AB=CD,AD=BC,AB//CD,AD//BC)).(2)角:平行四边形的对角相等,邻角互补(即:∠A=∠C,∠B=∠D,∠A+∠B=180°等).(3)对角线:平行四边形的对角线互相平分(即:OA=OC,OB=OD).(4)对称性:平行四边形是中心对称图形,对角线的交点为对称中心.平行四边形的判定方法:1.两组对边分别平行的四边形是平行四边形(定义判定法);2.两组对边分别相等的四边形是平行四边形;3.一组对边平行且相等的四边形是平行四边形;4. 两组对角分别相等的四边形是平行四边形;5.对角线互相平分的四边形是平行四边形;面积:①S=底×高=ah;其中a可以是平行四边形的任何一边,h必须是a边到其对边的距离,即对应的高。
②平行四边形的对角线将四边形分成4个面积相等的三角形.③若一条直线过平行四边形对角线的交点,则直线被一组对边截下的线段以对角线的交点为中点,且这条直线二等分平行四边形的面积。
④平行四边形的面积一定,底与高成反比例.周长:四条边长的和或两邻边长和的2倍平行线之间的距离定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做两条平行线之间的距离。
性质:(1)两条平行线之间的任何两条平行线段都相等。
(2)两条直线平行,那么一条直线上所有的点到另一条直线的距离都相等。
平行线间的距离=平行线间的垂线段的长度1.在□ABCD中,已知AB=8,周长等于24,则BC=_________,CD=_________,AD=_________.2.□ABCD中,周长为20cm,对角线AC交BD于点O,△OAB比△OBC的周长多4,则边AB=____________,BC=____________.3.平行四边形的边长等于5和7,这个平行四边形锐角的平分线把长边分成两条线段长各是____________.4.一个平行四边形的一边长是8,一条对角线长是6,则它的另一条对角线x的取值范围为____________.5.如图.在□ABCD中.AB=13,AD=5,AC⊥BC,则S□ABCD=____________6.如下图.在□ABCD中.AB=9cm.AB边上的高DH=2cm.DF=3cm,则BC长为____________。
初二平行四边形的性质和判定知识点整理汇编

初二平行四边形的性质和判定专题1.平行四边形的定义(1)定义:两组对边分别平行的四边形叫做平行四边形.平行四边形的定义有两层意思:①是四边形;②两组对边分别平行.这两个条件缺一不可.(2)表示方法:平行四边形用符号“”表示.平行四边形ABCD记作“ABCD”,读作“平行四边形ABCD”.(3)平行四边形的基本元素:边、角、对角线.平行四边形的定义的作用:平行四边形的定义既是性质,又是判定方法.①由定义可知平行四边形的两组对边分别平行;②由定义可知只要四边形中有两组对边分别平行,那么这个四边形就是平行四边形.【例1】对于平行四边形ABCD,AC与BD相交于点O,下列说法正确的是().A.平行四边形ABCD表示为“ACDB”B.平行四边形ABCD表示为“ABCD”C.AD∥BC,AB∥CDD.对角线为AC,BO解析:两组对边分别平行的四边形是平行四边形,可知平行四边形的两组对边平行,故选C.答案:C2.平行四边形的性质(1)平行四边形的对边平行且相等.例如:如图①所示,在ABCD中,AB CD,AD BC.由上述性质可得,夹在两条平行线间的平行线段相等.如图2,直线l1∥l2.AB,CD是夹在直线l1,l2间的平行线段,则四边形ABCD是平行四边形,故AB CD.(2)平行四边形的对角相等,邻角互补.例如:如图①所示,在ABCD中,∠ABC=∠CDA,∠BAD=∠BCD.∠ABC+∠BAD=180°,∠ABC+∠BCD=180°,∠BCD+∠CDA=180°,∠BAD+∠CDA=180°.(3)平行四边形的对角线互相平分.例如:如图①所示,在ABCD中,OA=OC,OB =OD.图③(4)经过平行四边形对角线的交点的直线被对边截得的两条线段相等,并且该直线平分平行四边形的面积.例如:如图③所示,在ABCD 中,EF 经过对角线的交点O ,与AD 和BC 分别交于点E ,F ,则OE =OF ,且S 四边形ABFE =S 四边形EFCD .【例2】ABCD 的周长为30 cm ,它的对角线AC 和BD 交于O ,且△AOB 的周长比△BOC 的周长大5 cm ,求AB ,AD 的长.分析:依题意画出图形,如图,△AOB 的周长比△BOC 的周长大5 cm ,即AO +AB +BO -(BO +OC +BC )=5(cm).因为OA =OC ,OB 为公共边, 所以AB -BC =5(cm).由AB +BC =302=15(cm)可求AB ,BC ,再由平行四边形的对边相等得AD 的长. 解:∵△AOB 的周长比△BOC 的周长大5 cm , ∴AO +AB +BO -(BO +OC +BC )=5(cm). ∵四边形ABCD 是平行四边形, ∴AO =OC ,∴AB -BC =5(cm). ∵ABCD 的周长为30 cm , ∴AB +BC =15(cm).∴⎩⎪⎨⎪⎧ AB -BC =5,AB +BC =15,得⎩⎪⎨⎪⎧AB =10,BC =5.∴AB =10 cm ,AD =BC =5 cm.3.平行四边形的判定(1)方法一:(定义判定法)两组对边分别平行的四边形叫做平行四边形.平行四边形的定义是判定平行四边形的根本方法,也是其他判定方法的基础.关于边、角、对角线方面还有以下判定定理.(2)方法二:两组对边分别相等的四边形是平行四边形.如图,连接BD ,由AD =BC ,AB =CD ,可证明△ABD ≌△CDB ,所以∠CDB =∠ABD ,∠CBD =∠ADB ,从而得到AB ∥CD ,AD ∥BC .由定义得到四边形ABCD 为平行四边形.其推理形式为:∵AB=DC,AD=BC,∴四边形ABCD是平行四边形.(3)方法三:两组对角分别相等的四边形是平行四边形.如图,由∠A=∠C,∠B=∠D,∠A+∠B+∠C+∠D=360°,可得∠B+∠C=180°,∠A+∠B=180°.从而得到AB∥DC,AD∥BC.由定义得到四边形ABCD为平行四边形,其推理形式为:∵∠A=∠C,∠B=∠D,∴四边形ABCD是平行四边形.(4)方法四:对角线互相平分的四边形是平行四边形.其推理形式为:如图,∵OA=OC,OB=OD,∴四边形ABCD是平行四边形.(5)方法五:一组对边平行且相等的四边形是平行四边形.其推理形式为:如图,∵AD∥BC,AD=BC,∴四边形ABCD是平行四边形.(1)判定方法可作为“画平行四边形”的依据;(2)一组对边平行,另一组对边相等的四边形不一定是平行四边形.【例3】已知,如图,在四边形ABCD中,AC与BD相交于点O,AB∥CD,AO=CO.四边形ABCD是平行四边形,请说明理由.解:因为AB∥CD,所以∠BAC=∠DCA.又因为AO =CO ,∠AOB =∠COD , 所以△ABO ≌△CDO .所以BO =DO . 所以四边形ABCD 是平行四边形.4.三角形的中位线(1)定义:连接三角形两边中点的线段叫做三角形的中位线.(2)性质:三角形两边中点连线平行于第三边,并且等于第三边的一半.(1)一个三角形有三条中位线,每条中位线与第三边都有相应的位置关系和数量关系;(2)三角形的中位线不同于三角形的中线,三角形的中位线是连接两边中点的线段,而三角形的中线是连接三角形一边的中点和这边所对顶点的线段.【例4】如图所示,在△ABC 中,点D ,E ,F 分别是AB ,BC ,CA 的中点,若△ABC 的周长为10 cm ,则△DEF 的周长是__________cm.解析:由三角形的中位线性质得,DF =12BC ,EF =12AB ,DE =12AC ,所以△DEF 的周长=12×10=5(cm).答案:55.两条平行线间的距离定义:两条平行线中,一条直线上任意一点到另一直线的距离,叫做这两条平行线间的距离.如图所示,a ∥b ,点A 在直线a 上,过A 点作AC ⊥b ,垂足为C ,则线段AC 的长是点A 到直线b 的距离,也是两条平行线a ,b 之间的距离.(1)如图,过直线a 上点B 作BD ⊥b ,垂足为D ,则线段BD 的长也是两条平行线a ,b 之间的距离.于是由平行四边形的性质可知平行线的又一个性质:平行线间的距离处处相等.(2)两条平行线之间的距离是指垂线段的长度,当两条平行线的位置确定时,它们之间的距离也随之确定,它不随垂线段的位置的改变而改变,是一个定值.【例5】如图所示,如果l 1∥l 2,那么△ABC 的面积与△DBC 的面积相等吗?由此你还能得出哪些结论?解:△ABC的面积与△DBC的面积相等.因为l1∥l2,所以它们之间的距离是一个定值.所以△ABC与△DBC是同底等高的两个三角形.所以S△ABC=S△DBC.结论:l1上任意一点与B,C连接,构成三角形的面积都等于△ABC的面积,这样的三角形有无数个.6.平行四边形性质的应用平行四边形性质的应用非常广泛,可以利用它说明线段相等、证明线段平行、求角的度数、求线段的长度、求图形的周长、求图形的面积等.对平行四边形的性质、平行线的性质、勾股定理、含30°角的直角三角形、三角形的面积、三角形的内角和定理等知识点的理解和掌握,是解决此类问题的关键.【例6】如图,ABCD的对角线相交于点O,过O作直线EF,并与线段AB,CD的反向延长线交于E,F,OE与OF是否相等,阐述你的理由.解:OE与OF相等.理由:∵四边形ABCD是平行四边形,∴BE∥DF,OB=OD,∴∠FDO=∠EBO,∠E=∠F.∴△BOE≌△DOF.∴OE=OF.7.平行四边形的判定的应用熟练掌握判定定理是平行四边形的判定的关键.已学了平行四边形的五种判定方法,记忆时要注意技巧,其中三种方法都与边有关:(1)一种关于对边的位置关系(两组对边分别平行的四边形是平行四边形);(2)一种关于对边的数量关系(两组对边分别相等的四边形是平行四边形);(3)一种关于对边的数量与位置关系(一组对边平行且相等的四边形是平行四边形).平行四边形的判定方法是今后解决平行四边形问题的基础知识,应该熟练掌握.判定平行四边形的一般思路:①考虑对边关系:证明两组对边分别平行;或两组对边分别相等;或一组对边平行且相等;②考虑对角关系:证明两组对角分别相等;③考虑对角线关系:证明两条对角线互相平分.【例7】如图,请在下列四个关系中,选出两个恰当....的关系作为条件,推出四边形ABCD是平行四边形,并予以证明.(写出一种即可)关系:①AD∥BC,②AB=CD,③∠A=∠C,④∠B+∠C=180°.已知:在四边形ABCD中,__________,__________;求证:四边形ABCD是平行四边形.分析:选用①③关系时,证明两组对边分别平行的四边形是平行四边形;选用①④关系时,证明两组对边分别平行的四边形是平行四边形;选用②④关系时,证明一组对边平行并且相等的四边形是平行四边形;选用③④关系时,证明两组对边分别平行的四边形是平行四边形.解:已知:①③,①④,②④,③④均可,其余均不可以.举例如下:已知:在四边形ABCD中,①AD∥BC,③∠A=∠C,求证:四边形ABCD是平行四边形.证明:∵AD∥BC,∴∠A+∠B=180°.∵∠A=∠C,∴∠C+∠B=180°.∴AB∥CD.∴四边形ABCD是平行四边形.8.平行四边形的性质和判定的综合应用平行四边形的性质和判定的应用主要有以下几种情况:(1)直接运用平行四边形的性质解决某些问题,如求角的度数、线段的长、证明角相等或互补、证明线段相等或倍分关系;(2)判定一个四边形为平行四边形,从而得到两角相等、两直线平行等;(3)综合运用:先判定一个四边形是平行四边形,然后再用平行四边形的性质去解决某些问题;或先运用平行四边形的性质得到线段平行、角相等等,再判定一个四边形是平行四边形.【例8】如图所示,在ABCD中,E,F分别是AD,BC上的点,且AE=CF,AF 与BE交于G,DF与CE交于H,连接EF,GH,试问EF与GH是否互相平分?为什么?解:EF与GH互相平分.理由:在ABCD中,∵AD BC,AE=CF,∴AE CF.∴DE BF.∴四边形AFCE,BEDF都是平行四边形.(一组对边平行且相等的四边形是平行四边形)∴AF∥CE,BE∥DF.∴四边形EGFH是平行四边形.(平行四边形的定义)∴EF与GH互相平分.9.三角形的中位线性质的应用三角形的中位线的性质不仅反映了线段间的位置关系,而且还揭示了线段间的数量关系,借助三角形中位线的性质可以进行几何求值(计算角度、求线段的长度)、证明(证明线段相等、证明线段的不等、证明线段的倍分关系、证明两角相等)、作图,且能解决生活实际问题.应用三角形中位线定理解决问题时,已知条件中往往给出两个中点,若已知条件只给出一个中点,必须要证明另一个点也是中点,才能运用此定理.【例9】在△ABC 中,AB =12,AC =10,BC =9,AD 是BC 边上的高.将△ABC 按如图所示的方式折叠,使点A 与点D 重合,折痕为EF ,则△DEF 的周长为( ).A .9.5B .10.5C .11D .15.5 解析:∵△EDF 是△EAF 折叠而形成的图形, ∴△EDF ≌△EAF .∴∠AEF =∠DEF .∵AD 是BC 边上的高,由折叠可知AD ⊥EF , ∴EF ∥CB .∴∠AEF =∠B ,∠BDE =∠DEF . ∴∠B =∠BDE .∴BE =DE =AE .∴E 为AB 的中点.同理点F 是AC 的中点. ∴EF 是△ABC 的中位线.∴△DEF 的周长为△EAF 的周长,即AE +EF +AF =12×(AB +BC +AC )=12×(12+9+10)=15.5.答案:D10.平行四边形的性质探究题平行四边形是一类特殊的四边形,它的特殊性体现在对边相等、对角相等、邻角互补、对角线互相平分几方面,因此,由平行四边形可以得到很多相等线段、相等角.所以,要学会利用对比的方法正确区分平行四边形的判定定理和性质定理,正确地运用相关的结论解决相关的问题.平行四边形的探究型问题,关键是根据平行四边形的性质和判定,构造出平行四边形.【例10】如图,已知等边△ABC 的边长为a ,P 是△ABC 内一点,PD ∥AB ,PE ∥BC ,PF ∥AC ,点D ,E ,F 分别在AC ,AB ,BC 上,试探索PD +PE +PF 与a 的关系.解:如图,作DG∥BC交AB于点G,因为△ABC为等边三角形,所以∠A=∠B=∠C=60°.所以∠A=∠AGD=∠ADG=60°.所以GD=AG.又可得EP=GD,所以EP=AG,DP=GE.同理可得PF=EB,所以PD+PE+PF=a.11.平行四边形的判定的探究题平行四边形是一类特殊的四边形,并且它是学习矩形、菱形、正方形和梯形的基础.在有关平行四边形判定的探究型问题中,要会判定一个四边形是平行四边形,运动型问题的关键是把运动的问题转化为静止的问题.运动变化题,这类题的解决技巧是把“运动”的“静止”下来,以静制动,同时注意不同的情况.【例11】如图所示,已知在四边形ABCD中,AD∥BC(AD>BC),BC=6 cm,点P从A点以1 cm/s的速度向D点出发,同时点Q从C点以2 cm/s的速度向B点出发,设运动时间为t秒,问t为何值时,四边形ABQP是平行四边形?解:由题意知,AP=t,QC=2t,则BQ=6-2t,若四边形ABQP为平行四边形,因为AD∥BC,只需AP=BQ即可,即t=6-2t,解得t=2.答:当t为2秒时,四边形ABQP是平行四边形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
板块
考试要求 A 级要求
B 级要求
C 级要求
平行四边形
会识别平行四边形
掌握平行四边形的概念、判定和性质,会用平行四边形的性质和判定解决简单问题
会运用平行四边形的性质和判定解决有关问题
1.平行四边形的性质
平行四边形的边:平行四边形的对边平行且对边相等. 平行四边形的角:平行四边形的对角相等,邻角互补. 平行四边形的对角线:平行四边形的对角线互相平分. 平行四边形的对称性:平行四边形是中心对称图形. 平行四边形的周长:一组邻边之和的2倍. 平行四边形的面积:底乘以高. 2.平行四边形的判定
两组对边分别平行的四边形是平行四边形. 两组对边分别相等的四边形是平行四边形. 两条对角线互相平分的四边形是平行四边形. 两组对角分别相等的四边形是平行四边形 一组对边平行且相等的四边形是平行四边形.
一、平行四边形的性质
【例1】 如图,四边形ABCD 为平行四边形,即AB CD ∥,AD BC ∥.通过证明三角形全等来说明:
⑴AB CD =,AD BC =.(对边相等) ⑵AO CO =,BO DO =.(对角线互相平分)
O
D
C
B
A
例题精讲
知识点睛
中考要求
平行四边形的性质
及判定
【例2】 如图,点E F ,
是平行四边形ABCD 对角线上的两点,且BE DF =,那么AF 和CE 相等吗?请说明理由
2
1
F
E
D
C
B A
【例3】 如图所示,已知四边形ABCD ,从⑴AB DC ∥;⑵AB DC =;⑶AD BC ∥;⑷AD BC =;
⑸A C ∠=∠;⑹B D ∠=∠中取两个条件加以组合,能推出四边形ABCD 是平行四边形的有哪几种情形?请写出具体组合。
A
D
B
C
【例4】 如图,在平行四边形ABCD 中,EF BC GH AB EF ∥,
∥,与GH 相交于点O ,图中共有 个平行四边形
O H
G
F E
D
C B
A
【例5】 如图,在平行四边形ABCD 中,5AD =,3AB =,AE 平分BAD ∠交BC 边于点E ,则线段BE ,
EC 的长度分别为( )
A .2和3
B .3和2
C .4和1
D .1和4如图
D
C
E B A
【例6】 以三角形的三个顶点作平行四边形,最多可以作( )
A .2个
B .3个
C .4个
D .5个
【例7】 如图,平行四边形ABCD 中,AB AC ⊥.对角线AC ,BD 相交于点O ,将直线AC 绕点O 顺时
针旋转,分别交BC ,AD 于点E ,F .
⑴ 证明:当旋转角为90︒时,四边形ABEF 是平行四边形; ⑵ 试说明在旋转过程中,线段AF 与EC 总保持相等.。
