2012普通高校招生全国统一试卷文科数学(新课标卷)

2012年高考试题：文科数学(新课标卷)

2012年普通高等学校招生全国统一考试文科数学注息事项:1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.问答第Ⅰ卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动.用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效.3.回答第Ⅱ卷时。

将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

1、已知集合A={x |x 2－x －2<0}，B={x |－1<x <1}，则（A ）A ⊂≠B （B ）B ⊂≠A （C ）A=B （D ）A ∩B=∅（2）复数z ＝－3+i 2+i 的共轭复数是（A ）2+i （B ）2－i （C ）－1+i （D ）－1－i3、在一组样本数据（x 1，y 1），（x 2，y 2），…，（x n ，y n ）（n ≥2，x 1,x 2,…,x n 不全相等）的散点图中，若所有样本点（x i ，y i ）(i =1,2,…,n )都在直线y =12x +1上，则这组样本数据的样本相关系数为（A ）－1 （B ）0 （C ）12 （D ）1（4）设F 1、F 2是椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，P 为直线x =3a 2上一点，△F 1PF 2是底角为30°的等腰三角形，则E 的离心率为（）（A ）12 （B ）23 （C ）34 （D ）455、已知正三角形ABC 的顶点A(1,1)，B(1,3)，顶点C 在第一象限，若点（x ，y ）在△ABC 内部，则z =－x+y 的取值范围是（A ）(1－3，2) （B ）(0，2) （C ）(3－1，2) （D ）(0，1+3)（6）如果执行右边的程序框图，输入正整数N(N ≥2)和实数a 1,a 2,…,a N ，输出A,B ，则（A ）A+B 为a 1,a 2,…,a N 的和（B ）A ＋B 2为a 1,a 2,…,a N 的算术平均数（C ）A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数（D ）A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数（7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（A）6（B）9（C）12（D）18。

2012年全国高考文科数学试题及答案-新课标word版

绝密＊启用前2012年普通高等学校招生全国统一考试(新课标卷）文科数学注息事项:1。

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.问答第Ⅰ卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动。

用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效。

3。

回答第Ⅱ卷时。

将答案写在答题卡上.写在本试卷上无效·4.考试结束后。

将本试卷和答且卡一并交回.第Ⅰ卷一、选择题:本大题共12小题，每小题5分,在每小题给同的四个选项中，只有一项是符合题目要求的。

1、已知集合A=｛x｜x2－x－2<0｝，B={x｜－1<x〈1｝，则（A)A错误!B （B）B错误!A （C）A=B (D)A∩B=（2）复数z＝错误!的共轭复数是(A）2+i （B）2－i （C）－1+i (D）－1－i3、在一组样本数据（x1，y1）,（x2，y2），…,（x n，y n）（n≥2，x1,x2,…,x n不全相等）的散点图中，若所有样本点（x i，y i）(i=1，2，…，n）都在直线y=错误!x+1上，则这组样本数据的样本相关系数为（A）－1 （B)0 (C)错误!（D）1（4）设F1、F2是椭圆E:错误!＋错误!＝1（a〉b〉0)的左、右焦点，P为直线x=错误!上一点，△F1PF2是底角为30°的等腰三角形，则E的离心率为（）（A）错误!（B)错误!（C)错误!（D）错误!5、已知正三角形ABC的顶点A(1，1），B(1，3），顶点C在第一象限，若点(x,y）在△ABC内部,则z=－x+y的取值范围是（A）（1－错误!，2）(B)(0，2) （C）（错误!－1，2）(D)（0,1+错误!）（6)如果执行右边的程序框图,输入正整数N(N≥2）和实数a1，a2，…，a N，输出A,B,则(A)A+B为a1,a2，…，a N的和（B）错误!为a1,a2,…,a N的算术平均数(C）A和B分别是a1,a2,…,a N中最大的数和最小的数（D)A和B分别是a1，a2,…,a N中最小的数和最大的数（7）如图,网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图,则此几何体的体积为（A）6(B）9（C)12（D）18(8）平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为错误!，则此球的体积为（A ）错误!π （B ）4错误!π （C ）4错误!π （D ）6错误!π(9）已知ω>0,0<φ<π，直线x =错误!和x =错误!是函数f (x ）=sin （ωx +φ）图像的两条相邻的对称轴,则φ=(A ）错误! （B ）错误! (C ）错误! （D ）错误!（10）等轴双曲线C 的中心在原点,焦点在x 轴上，C 与抛物线y 2=16x 的准线交于A ，B 两点，|AB|=4错误!,则C 的实轴长为（A ）错误! （B ）2错误! （C ）4 （D)8(11)当0<x ≤错误!时，4x <log a x ,则a 的取值范围是（A ）（0，错误!) （B ）（错误!,1）（C ）(1，错误!) （D)（错误!，2)(12）数列{a n ｝满足a n +1＋(－1）n a n ＝2n －1,则{a n ｝的前60项和为(A ）3690 （B ）3660 （C)1845 （D)1830第Ⅱ卷本卷包括必考题和选考题两部分。

2012年全国统一高考数学试卷(文科)(新课标)(含解析版)

2012年全国统一高考数学试卷（文科）（新课标）一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A={x|x2﹣x﹣2＜0}，B={x|﹣1＜x＜1}，则（）A．A⊊B B．B⊊A C．A=B D．A∩B=∅2．（5分）复数z=的共轭复数是（）A．2+i B．2﹣i C．﹣1+i D．﹣1﹣i3．（5分）在一组样本数据（x1，y1），（x2，y2），…，（x n，y n）（n≥2，x1，x2，…，x n不全相等）的散点图中，若所有样本点（x i，y i）（i=1，2，…，n）都在直线y=x+1上，则这组样本数据的样本相关系数为（）A．﹣1B．0C．D．14．（5分）设F1、F2是椭圆E：+=1（a＞b＞0）的左、右焦点，P为直线x=上一点，△F2PF1是底角为30°的等腰三角形，则E的离心率为（）A．B．C．D．5．（5分）已知正三角形ABC的顶点A（1，1），B（1，3），顶点C在第一象限，若点（x，y）在△ABC内部，则z=﹣x+y的取值范围是（）A．（1﹣，2）B．（0，2）C．（﹣1，2）D．（0，1+）6．（5分）如果执行下边的程序框图，输入正整数N（N≥2）和实数a1，a2，…，a n，输出A，B，则（）A．A+B为a1，a2，…，a n的和B．为a1，a2，…，a n的算术平均数C．A和B分别是a1，a2，…，a n中最大的数和最小的数D．A和B分别是a1，a2，…，a n中最小的数和最大的数7．（5分）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（）A．6B．9C．12D．188．（5分）平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为，则此球的体积为（）A．πB．4πC．4πD．6π9．（5分）已知ω＞0，0＜φ＜π，直线x=和x=是函数f（x）=sin（ωx+φ）图象的两条相邻的对称轴，则φ=（）A．B．C．D．10．（5分）等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于点A和点B，|AB|=4，则C的实轴长为（）A．B．C．4D．811．（5分）当0＜x≤时，4x＜log a x，则a的取值范围是（）A．（0，）B．（，1）C．（1，）D．（，2）12．（5分）数列{a n}满足a n+1+（﹣1）n a n=2n﹣1，则{a n}的前60项和为（）A．3690B．3660C．1845D．1830二．填空题：本大题共4小题，每小题5分．13．（5分）曲线y=x（3lnx+1）在点（1，1）处的切线方程为．14．（5分）等比数列{a n}的前n项和为S n，若S3+3S2=0，则公比q=．15．（5分）已知向量夹角为45°，且，则=．16．（5分）设函数f（x）=的最大值为M，最小值为m，则M+m=．三、解答题：解答应写出文字说明，证明过程或演算步骤．17．（12分）已知a，b，c分别为△ABC三个内角A，B，C的对边，c=asinC ﹣ccosA．（1）求A；（2）若a=2，△ABC的面积为，求b，c．18．（12分）某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售．如果当天卖不完，剩下的玫瑰花做垃圾处理．（Ⅰ）若花店一天购进17枝玫瑰花，求当天的利润y（单位：元）关于当天需求量n（单位：枝，n∈N）的函数解析式．（Ⅱ）花店记录了100天玫瑰花的日需求量（单位：枝），整理得如表：（i）假设花店在这100天内每天购进17枝玫瑰花，求这100天的日利润（单位：元）的平均数；（ii）若花店一天购进17枝玫瑰花，以100天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于75元的概率．19．（12分）如图，三棱柱ABC﹣A1B1C1中，侧棱垂直底面，∠ACB=90°，AC=BC=AA1，D是棱AA1的中点．（Ⅰ）证明：平面BDC1⊥平面BDC（Ⅱ）平面BDC1分此棱柱为两部分，求这两部分体积的比．20．（12分）设抛物线C：x2=2py（p＞0）的焦点为F，准线为l，A∈C，已知以F为圆心，FA为半径的圆F交l于B，D两点；（1）若∠BFD=90°，△ABD的面积为，求p的值及圆F的方程；（2）若A，B，F三点在同一直线m上，直线n与m平行，且n与C只有一个公共点，求坐标原点到m，n距离的比值．21．（12分）设函数f（x）=e x﹣ax﹣2．（Ⅰ）求f（x）的单调区间；（Ⅱ）若a=1，k为整数，且当x＞0时，（x﹣k）f′（x）+x+1＞0，求k的最大值．22．（10分）如图，D，E分别为△ABC边AB，AC的中点，直线DE交△ABC的外接圆于F，G两点，若CF∥AB，证明：（1）CD=BC；（2）△BCD∽△GBD．23．选修4﹣4；坐标系与参数方程已知曲线C1的参数方程是（φ为参数），以坐标原点为极点，x轴的正半轴为极轴建立坐标系，曲线C2的坐标系方程是ρ=2，正方形ABCD的顶点都在C2上，且A，B，C，D依逆时针次序排列，点A的极坐标为（2，）．（1）求点A，B，C，D的直角坐标；（2）设P为C1上任意一点，求|PA|2+|PB|2+|PC|2+|PD|2的取值范围．24．已知函数f（x）=|x+a|+|x﹣2|①当a=﹣3时，求不等式f（x）≥3的解集；②f（x）≤|x﹣4|若的解集包含[1，2]，求a的取值范围．2012年全国统一高考数学试卷（文科）（新课标）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的．1．（5分）已知集合A={x|x2﹣x﹣2＜0}，B={x|﹣1＜x＜1}，则（）A．A⊊B B．B⊊A C．A=B D．A∩B=∅【考点】18：集合的包含关系判断及应用．【专题】5J：集合．【分析】先求出集合A，然后根据集合之间的关系可判断【解答】解：由题意可得，A={x|﹣1＜x＜2}，∵B={x|﹣1＜x＜1}，在集合B中的元素都属于集合A，但是在集合A中的元素不一定在集合B中，例如x=∴B⊊A．故选：B．【点评】本题主要考查了集合之间关系的判断，属于基础试题．2．（5分）复数z=的共轭复数是（）A．2+i B．2﹣i C．﹣1+i D．﹣1﹣i【考点】A1：虚数单位i、复数；A5：复数的运算．【专题】11：计算题．【分析】利用复数的分子、分母同乘分母的共轭复数，把复数化为a+bi的形式，然后求法共轭复数即可．【解答】解：复数z====﹣1+i．。

2012年高考数学试卷及解析新课标卷(文科)

2012年普通高等学校招生全国统一考试文科数学注息事项:1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.问答第Ⅰ卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动.用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效.3.回答第Ⅱ卷时。

将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回。

第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

1、已知集合A={x |x 2－x －2<0}，B={x |－1<x <1}，则（A ）A ⊂≠B （B ）B ⊂≠A （C ）A=B （D ）A∩B=∅（2）复数z ＝－3+i 2+i的共轭复数是（A ）2+i （B ）2－i （C ）－1+i （D ）－1－i3、在一组样本数据（x 1，y 1），（x 2，y 2），…，（x n ，y n ）（n ≥2，x 1,x 2,…,x n 不全相等）的散点图中，若所有样本点（x i ，y i ）(i =1,2,…,n )都在直线y =12x +1上，则这组样本数据的样本相关系数为（A ）－1 （B ）0 （C ）12（D ）1 4、设F 1、F 2是椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点，P 为直线x =3a 2上一点，△F 1PF 2是底角为30°的等腰三角形，则E 的离心率为（）（A ）12 （B ）23 （C ）34 （D ）455、已知正三角形ABC 的顶点A(1,1)，B(1,3)，顶点C 在第一象限，若点（x ，y ）在△ABC 内部，则z=－x+y 的取值范围是（A ）(1－3，2) （B ）(0，2) （C ）(3－1，2) （D ）(0，1+3)6、如果执行右边的程序框图，输入正整数N(N≥2)和实数a 1,a 2,…,a N ，输出A,B ，则（A ）A+B 为a 1,a 2,…,a N 的和（B ）A ＋B 2为a 1,a 2,…,a N 的算术平均数（C ）A 和B 分别是a 1,a 2,…,a N 中最大的数和最小的数（D ）A 和B 分别是a 1,a 2,…,a N 中最小的数和最大的数7、如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（A ）6（B ）9（C ）12（D ）188、平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π9、已知ω>0，0<φ<π，直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴，则φ= （A ）π4 （B ）π3 （C ）π2 （D ）3π410、等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 2=16x 的准线交于A ，B 两点，|AB|=43，则C 的实轴长为（A ） 2 （B ）2 2 （C ）4 （D ）811、当0<x ≤124x <log a x ，则a 的取值范围是（A ）(0，22) （B ）(22，1) （C ）(1，2) （D ）(2，2) 12、数列{a n }满足a n +1＋(－1)n a n ＝2n －1，则{a n }的前60项和为（A ）3690 （B ）3660 （C ）1845 （D ）1830第Ⅱ卷本卷包括必考题和选考题两部分。

2012年全国高考文科数学试题及答案-新课标word版

绝密*启用前2012年普通高等学校招生全国统一考试(新课标卷）文科数学注息事项:1。

本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题)两部分。

答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上.2.问答第Ⅰ卷时。

选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动。

用橡皮擦干净后，再选涂其它答案标号.写在本试卷上无效.3。

回答第Ⅱ卷时。

将答案写在答题卡上.写在本试卷上无效·4。

考试结束后。

将本试卷和答且卡一并交回。

第Ⅰ卷一、选择题:本大题共12小题，每小题5分，在每小题给同的四个选项中,只有一项是符合题目要求的。

1、已知集合A={x|x2－x－2〈0}，B=｛x|－1<x〈1｝，则(A)A错误!B （B)B错误!A (C）A=B (D）A∩B=（2）复数z＝错误!的共轭复数是(A)2+i （B)2－i （C）－1+i （D)－1－i3、在一组样本数据（x1，y1)，(x2，y2)，…,（x n,y n）(n≥2，x1，x2，…，x n不全相等)的散点图中，若所有样本点（x i，y i)(i=1，2，…,n）都在直线y=错误!x+1上，则这组样本数据的样本相关系数为（A）－1 （B)0 （C)错误!(D）1（4）设F1、F2是椭圆E：错误!＋错误!＝1（a〉b>0）的左、右焦点，P为直线x=错误!上一点,△F1PF2是底角为30°的等腰三角形，则E的离心率为（）(A）错误!(B)错误!（C）错误!(D）错误!5、已知正三角形ABC的顶点A（1,1），B(1，3）,顶点C在第一象限,若点（x，y)在△ABC内部，则z=－x+y的取值范围是（A）（1－错误!，2) （B)（0，2) （C）（错误!－1，2）（D)（0,1+错误!）（6）如果执行右边的程序框图，输入正整数N(N≥2)和实数a1,a2，…,a N，输出A,B,则（A）A+B为a1，a2,…,a N的和（B）错误!为a1，a2，…，a N的算术平均数(C）A和B分别是a1,a2，…,a N中最大的数和最小的数(D）A和B分别是a1，a2，…，a N中最小的数和最大的数(7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（A）6(B）9（C）12(D）18(8)平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为错误!，则此球的体积为（A）错误!π（B)4错误!π（C）4错误!π（D)6错误!π(9）已知ω〉0，0〈φ〈π，直线x=错误!和x=错误!是函数f(x）=sin（ωx+φ）图像的两条相邻的对称轴,则φ=(A)错误!(B）错误!(C）错误!（D）错误!（10)等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于A，B两点，｜AB|=43，则C的实轴长为（A）错误!(B）2错误!（C）4 （D）8(11)当0<x≤错误!时，4x〈log a x,则a的取值范围是（A)（0，错误!）（B）(错误!,1）（C）（1，错误!) （D)(错误!，2）（12)数列｛a n}满足a n+1＋（－1）n a n＝2n－1，则{a n｝的前60项和为（A)3690 （B）3660 (C）1845 （D）1830第Ⅱ卷本卷包括必考题和选考题两部分。

2012年高考新课标全国卷文科数学试题(附答案)

2012年普通高等学校招生全国统一考试（新课标全国卷）文科数学试题一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

（1）已知集合A={x |x 2−x −2<0}，B={x |−1<x <1}，则（A ）A ⊂≠B （B ）B ⊂≠A （C ）A=B （D ）A ∩B=∅ （2）复数z ＝32ii-++的共轭复数是（A ）2i + （B ）2i - （C ）1i -+ （D ）1i --（3）在一组样本数据（x 1，y 1），（x 2，y 2），…，（x n ，y n ）（n ≥2，x 1,x 2,…,x n 不全相等）的散点图中，若所有样本点（x i ，y i ）(i =1,2,…,n )都在直线112y x =+上，则这组样本数据的样本相关系数为（A ）−1 （B ）0 （C ）12（D ）1（4）设1F ,2F 是椭圆E ：2222x y a b+=1（a ＞b ＞0）的左、右焦点，P 为直线32ax =上一点，△21F PF 是底角为030的等腰三角形，则E 的离心率为（A ）12 （B ）23 （C ）34 D .45（5）已知正三角形ABC 的顶点A (1,1)，B (1,3)，顶点C 在第一象限，若点（x ，y ）在△ABC内部，则z x y =-+的取值范围是（A ）(1－3，2) （B ）(0，2) （C ）(3－1，2) （D ）(0，1+3) （6）如果执行右边的程序框图，输入正整数N (N ≥2)和实数1a ，2a ，…，N a ，输出A ，B ，则（A ）A +B 为1a ，2a ，…，N a 的和（B ）2A B+为1a ，2a ，…，N a 的算术平均数（C ）A 和B 分别为1a ，2a ，…，N a 中的最大数和最小数（D ）A 和B 分别为1a ，2a ，…，N a 中的最小数和最大数（7）如图，网格上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（A ）6 （B ）9 （C ）12 （D ）18(8)平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π （9）已知ω>0，0ϕπ<<，直线x =4π和x =54π是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴，则ϕ=（A ）π4 （B ）π3 （C ）π2 （D ）3π4（10）等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线216y x =的准线交于A 、B 两点，||AB =43，则C 的实轴长为（A ）2 （B ）22 （C ）4 （D ）8 (11)当0<x ≤12时，4log xa x <，则a 的取值范围是（A ）(0，22) （B ）(22，1) （C ）(1，2) （D ）(2，2) （12）数列{n a }满足1(1)21nn n a a n ++-=-，则{n a }的前60项和为（A ）3690 （B ）3660 （C ）1845 （D ）1830二．填空题：本大题共4小题，每小题5分。

2012年全国高考文科数学试题及答案-新课标word版

绝密＊启用前2012年普通高等学校招生全国统一考试（新课标卷）文科数学注息事项：1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题）两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2。

问答第Ⅰ卷时.选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动。

用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效。

3.回答第Ⅱ卷时。

将答案写在答题卡上。

写在本试卷上无效·4.考试结束后。

将本试卷和答且卡一并交回。

第Ⅰ卷一、选择题：本大题共12小题,每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

1、已知集合A={x|x2－x－2<0}，B={x|－1〈x〈1｝，则（A）A错误!B （B）B错误!A （C）A=B （D）A∩B=（2）复数z＝错误!的共轭复数是（A）2+i （B）2－i （C)－1+i （D）－1－i3、在一组样本数据(x1,y1),（x2，y2），…，(x n，y n）（n≥2，x1，x2，…，x n不全相等)的散点图中，若所有样本点（x i，y i)（i=1,2，…,n)都在直线y=错误!x+1上,则这组样本数据的样本相关系数为（A)－1 （B）0 （C)错误!（D）1（4）设F1、F2是椭圆E：错误!＋错误!＝1(a>b〉0)的左、右焦点，P为直线x=错误!上一点，△F1PF2是底角为30°的等腰三角形，则E的离心率为( )（A）错误!（B）错误!（C）错误!（D）错误!5、已知正三角形ABC的顶点A(1,1）,B(1，3)，顶点C在第一象限，若点(x,y)在△ABC内部，则z=－x+y的取值范围是（A）(1－错误!，2) （B)（0,2）（C）(错误!－1，2）（D）（0,1+错误!）（6）如果执行右边的程序框图,输入正整数N（N≥2）和实数a1,a2,…,a N，输出A,B，则（A）A+B为a1，a2，…,a N的和（B)错误!为a1,a2,…，a N的算术平均数（C)A和B分别是a1，a2,…,a N中最大的数和最小的数（D)A和B分别是a1，a2，…，a N中最小的数和最大的数(7）如图,网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图,则此几何体的体积为(A)6(B)9(C）12（D)18(8）平面α截球O的球面所得圆的半径为1,球心O到平面α的距离为错误!，则此球的体积为（A）错误!π（B）4错误!π（C）4错误!π（D)6错误!π（9）已知ω>0，0〈φ〈π，直线x=错误!和x=错误!是函数f（x）=sin（ωx+φ)图像的两条相邻的对称轴,则φ=（A）错误!(B）错误!（C）错误!(D）错误!（10）等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于A,B两点，｜AB｜=43,则C的实轴长为（A） 2 （B）2 2 (C）4 （D）8（11）当0<x≤错误!时，4x<log a x，则a的取值范围是(A）（0,错误!）（B）(错误!，1）（C）(1，错误!) (D)（错误!，2）（12）数列{a n｝满足a n+1＋（－1)n a n＝2n－1，则{a n}的前60项和为（A）3690 （B）3660 （C)1845 （D)1830第Ⅱ卷本卷包括必考题和选考题两部分.第13题—第21题为必考题，每个试题考生都必须作答，第22-24题为选考题，考生根据要求作答。

2012年高考新课标全国卷文科数学试题附答案

学习资料收集于网络，仅供参考 2012年普通高等学校招生全国统一考试（新课标全国卷）文科数学试题分，在每小题给同的四个选项中，只有一项是符一、选择题：本大题共12小题，每小题5 合题目要求的。

2 |?1<x<1}，则?x?2<0}，B={xx|A={（1）已知集合x??∩B=?（D）A （C）A=B （A）AA B （B）B??i?3?＝的共轭复数是（2）复数z i2?i1???i1?i?2?i2 C （））（D（A）（B）不全相等）的,xx,x,…，…，（x，y）（n≥2，，（3）在一组样本数据（x，y），（xy）n121nn12211y??x 上，则这组样本）(i=1,2,…,n)都在直线，散点图中，若所有样本点（xy ii2数据的样本相关系数为11）（D ）0 （C）B?（A）1 （222yxa b?FFE是椭圆＞：0=1（（4）设）的,＞2122baa3PFF?x P上一点，△为直线左、右焦点，122030E的离心率为的等腰三角形，则是底角为4231D.（B）C（A））（5423ABC在第一象限，若点（x，y）在△）已知正三角形ABC的顶点A(1,1)，B(1,3)，顶点C（5y??x?z内部，则的取值范围是3) (0，1+ （D）（C）(3－1，2) 2) B (1（A），－32) （）(0，NN和实2)≥（6）如果执行右边的程序框图，输入正整数(aaaBA，输出，数，，则，…，N12aaa BA+的和为，，…，（A）N12BA?aaa，…，B（），的算术平均数为N122aaa BA中的最大数，…，）（C和分别为，N12和最小数学习资料．学习资料收集于网络，仅供参考aaaBA，（D）中的最小数和最大数和，…，分别为N12，粗线画出的是）如图，网格上小正方形的边长为1（7某几何体的三视图，则此几何体的体积为（A）6B）9 （）12 （C18（D）??，则此球的体积2到平面(8)平面的距离为截球O的球面所得圆的半径为1，球心O 为（D）π6C（）346π（A（）6πB）43π??5?????xx)x?f(?x?)?sin(0图像的两条=是函数，直线9）已知和>0，=（44?=相邻的对称轴，则3ππππ（D））（C A（）（B）44322x CC x16y?A、的中心在原点，焦点在轴上，的准线交于与抛物线（10）等轴双曲线C34|AB|B两点，=，则的实轴长为2228 D））（（C）4 （A）（B1x xxlog4?，则a的取值范围是(11)当0<时，≤2a222) ，）( （D1) ，（C）2(1（A）(0，，) （B）2) (22n aa1n??1)a?2a?(项和为的前，则{60}（12）数列{}满足nnn1n?1830 D）（）（C1845 （A）3690 （B）36605分。

2012年全国高考文科数学试题及答案-新课标word版

绝密 * 启用前2012 年普通高等学校招生全国统一考试（新课标卷）文科数学注息事项 :1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题 )两部分。

答卷前，考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2.问答第Ⅰ卷时。

选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动 .用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效.3.回答第Ⅱ卷时。

将答案写在答题卡上.写在本试卷上无效·4.考试结束后 .将本试卷和答且卡一并交回。

第Ⅰ卷一、选择题：本大题共 12 小题，每小题 5 分，在每小题给同的四个选项中，只有一项是符合题目要求的。

1、已知集合 A={x| x 2－ x － 2<0}， B={x| －1<x<1}，则（ A ）A B（B ）B A（C ）A=B（D ）A ∩B=－ 3+i （ 2）复数z ＝的共轭复数是 2+i（ A ） 2+i（ B ）2－ i（ C ）－ 1+i（ D ）－ 1－ i3、在一组样本数据（ x 1 ，y 1 ），（x 2 ，y 2 ），⋯，（ x n ，y n ）（ n ≥ 2，x 1,x 2, ⋯ ,x n 不全相等）的散点图中，若所有样本点（ x i ， y i ） (i=1,2, ⋯ , n) 都在直线 1y= x+1 上，则这组样本数据的样本相关系数为2（A ）－ 1（B ）0（C ）1（ D ）12223a上一点，△ F（ 4）设 F 、 F 是椭圆 E ：x2y 2是底角12a ＋b＝ 1(a>b>0)的左、右焦点， P 为直线 x= 2 1PF 2为 30°的等腰三角形，则 E 的离心率为（）（ A ）12342 （B ）3 （ C ）4 （D ） 55、已知正三角形 ABC 的顶点 A(1,1)，B(1,3)，顶点 C 在第一象限，若点（ x ，y ）在△ ABC 内部，则z=－x+y 的取值范围是（ A ）(1－ 3， 2)（ B ） (0， 2) （ C ）( 3－1，2) （ D ） (0， 1+ 3)（ 6）如果执行右边的程序框图，输入正整数 N(N ≥2)和实数 a 1,a 2,⋯,a N ，输出 A,B ，则（ A ）A+B 为 a 1,a 2,⋯,a N 的和（ B ）A ＋ B为 a 1,a 2,⋯ ,a N 的算术平均数2（ C ）A 和 B 分别是 a 1,a 2,⋯ ,a N 中最大的数和最小的数（ D ） A 和 B 分别是 a 1,a 2,⋯ ,a N 中最小的数和最大的数开始输入 N ，a 1,a 2,⋯,a Nk=1,A=a 1,B=a 1x =a kk=k+1是x ＞ A否A=x是x<B否B=x否k ≥ N是输出 A ，B结束（ 7）如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（ A ）6 （ B ）9 （ C ）12（ D ） 18(8)平面 α 截球 O 的球面所得圆的半径为 1，球心 O 到平面 α的距离为 2，则此球的体积为（ A ） 6π （ B ） 4 3π （C ） 4 6π （D ） 6 3ππ 5π（ 9）已知 ω>0， 0<φ<π，直线 x= 和 x=是函数 f(x)=sin(ωx+φ)图像的两条相邻的对称轴，则φ=44（ A ）πππ3π4（B ） 3（C ） 2（D ） 4（ 10）等轴双曲线 C 的中心在原点，焦点在 x 轴上， C 与抛物线 y 2=16x 的准线交于 A ，B 两点，|AB|=4 3，则 C 的实轴长为（A ） 2（B ）2 2（C ）4（D ）8(11)当 0<x ≤1时， 4x <log a x ，则 a 的取值范围是2（ A ）(0， 22，1) （C ） (1， 2) （D ）( 2， 2) 2 ) （B ）( 2（ 12）数列 {a n }满足 a n+1 ＋ (－ 1)n a n ＝ 2n － 1，则 {a n }的前 60 项和为（ A ）3690（ B ） 3660（ C ）1845（ D ）1830第Ⅱ卷本卷包括必考题和选考题两部分。

2012年普通高等学校招生全国统一考试新课标卷(数学文)word有答案

绝密*启用前2012年普通高等学校招生全国统一考试文科数学注息事项:1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分·答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上·2.问答第Ⅰ卷时·选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑·如需改动.用橡皮擦干净后,再选涂其它答案标号·写在本试卷上无效.3.回答第Ⅱ卷时·将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回· 第Ⅰ卷一、选择题：本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的· 1、已知集合A={x |x 2－x －2<0},B={x |－1<x <1},则（A ）A ⊂≠B （B ）B ⊂≠A （C ）A=B （D ）A ∩B=∅ （2）复数z ＝－3+i 2+i的共轭复数是（A ）2+i （B ）2－i （C ）－1+i （D ）－1－i3、在一组样本数据（x 1,y 1）,（x 2,y 2）,…,（x n ,y n ）（n ≥2,x 1,x 2,…,x n 不全相等）的散点图中,若所有样本点（x i ,y i ）(i =1,2,…,n )都在直线y =12x +1上,则这组样本数据的样本相关系数为（A ）－1 （B ）0 （C ）12（D ）1（4）设F 1、F 2是椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点,P 为直线x =3a2上一点,△F 1PF 2是底角为30°的等腰三角形,则E 的离心率为（）（A ）12 （B ）23 （C ）34 （D ）455、已知正三角形ABC 的顶点A(1,1),B(1,3),顶点C 在第一象限,若点（x,y ）在△ABC 内部,则z=－x+y 的取值范围是（A ）(1－3,2) （B ）(0,2) （C ）(3－1,2) （D ）(0,1+3)（6）如果执行右边的程序框图,输入正整数N(N ≥2)和实数a 1,a 2,…,a N ,输出A,B,则（A ）A+B 为a 1,a 2,…,a N 的和（B ）A ＋B 2为a 1,a 2,…,a N 的算术平均数（C）A和B分别是a1,a2,…,a N中最大的数和最小的数（D）A和B分别是a1,a2,…,a N中最小的数和最大的数（7）如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为（A）6（B）9（C）12（D）18(8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π（9）已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=（A ）π4 （B ）π3 （C ）π2 （D ）3π4（10）等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A,B 两点,|AB|=43,则C 的实轴长为（A ） 2 （B ）2 2 （C ）4 （D ）8 (11)当0<x ≤12时,4x <log a x ,则a 的取值范围是（A ）(0,22) （B ）(22,1) （C ）(1,2) （D ）(2,2) （12）数列{a n }满足a n +1＋(－1)n a n ＝2n －1,则{a n }的前60项和为（A ）3690 （B ）3660 （C ）1845 （D ）1830 第Ⅱ卷本卷包括必考题和选考题两部分·第13题-第21题为必考题,每个试题考生都必须作答,第22-24题为选考题,考生根据要求作答·二．填空题：本大题共4小题,每小题5分·(13)曲线y =x (3ln x +1)在点（1,1）处的切线方程为________ (14)等比数列{a n }的前n 项和为S n ,若S 3+3S 2=0,则公比q =_______(15)已知向量a ,b 夹角为45°,且|a |=1,|2a －b |=10,则|b |=(16)设函数f (x )=(x +1)2+sin xx 2+1的最大值为M,最小值为m ,则M+m =____三、解答题：解答应写出文字说明,证明过程或演算步骤· （17）（本小题满分12分）已知a ,b ,c 分别为△ABC 三个内角A,B,C 的对边,c = 3a sinC －c cosA(1)求A(2)若a =2,△ABC 的面积为3,求b ,c18.（本小题满分12分）某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售·如果当天卖不完,剩下的玫瑰花做垃圾处理·（Ⅰ）若花店一天购进17枝玫瑰花,求当天的利润y (单位：元)关于当天需求量n （单位：枝,n ∈N ）的函数解析式·（Ⅱ）花店记录了100天玫瑰花的日需求量（单位：枝）,整理得下表：(1)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润（单位：元）的平均数； (2)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率·（19）（本小题满分12分）如图,三棱柱ABC －A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(Ｉ)证明：平面BDC 1⊥平面BDC（Ⅱ）平面BDC 1分此棱柱为两部分,求这两部分体积的比·B 1 DC 1A 1（20）（本小题满分12分）设抛物线C：x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D 两点·（I）若∠BFD=90°,△ABD的面积为42,求p的值及圆F的方程；（II）若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值·（21）（本小题满分12分）设函数f (x )= e x －ax －2 (Ⅰ)求f (x )的单调区间(Ⅱ)若a =1,k 为整数,且当x >0时,(x －k ) f ´(x )+x +1>0,求k 的最大值请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清楚题号·（22）（本小题满分10分）选修4-1：几何证明选讲如图,D,E 分别为△ABC 边AB,AC 的中点,直线DE 交△ABC 的外接圆于F,G 两点,若CF//AB,证明：FG(Ⅰ)CD=BC ； (Ⅱ)△BCD ∽△GBD(23)(本小题满分10分)选修4—4；坐标系与参数方程已知曲线C 1的参数方程是⎩⎪⎨⎪⎧x ＝2cos φy ＝3sin φ(φ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程是ρ=2.正方形ABCD 的顶点都在C 2上,且A 、B 、C 、D 以逆时针次序排列,点A 的极坐标为(2,π3)(Ⅰ)求点A、B、C、D 的直角坐标；(Ⅱ)设P为C1上任意一点,求|PA| 2+ |PB|2 + |PC| 2+ |PD|2的取值范围·（24）（本小题满分10分）选修4—5：不等式选讲已知函数f(x) = |x + a| + |x－2|.(Ⅰ)当a =－3时,求不等式f(x)≥3的解集；(Ⅱ)若f(x)≤|x－4|的解集包含[1,2],求a的取值范围·。

2012年普通高等学校招生全国统一考试新课标卷(数学文)word有答案

绝密*启用前2012年普通高等学校招生全国统一考试文科数学注息事项:1.本试卷分第Ⅰ卷（选择题）和第Ⅱ卷(非选择题)两部分·答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上·2.问答第Ⅰ卷时·选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑·如需改动.用橡皮擦干净后,再选涂其它答案标号·写在本试卷上无效.3.回答第Ⅱ卷时·将答案写在答题卡上.写在本试卷上无效·4.考试结束后.将本试卷和答且卡一并交回· 第Ⅰ卷一、选择题：本大题共12小题,每小题5分,在每小题给同的四个选项中,只有一项是符合题目要求的· 1、已知集合A={x |x 2－x －2<0},B={x |－1<x <1},则（A ）A ⊂≠B （B ）B ⊂≠A （C ）A=B （D ）A ∩B=∅ （2）复数z ＝－3+i 2+i的共轭复数是（A ）2+i （B ）2－i （C ）－1+i （D ）－1－i3、在一组样本数据（x 1,y 1）,（x 2,y 2）,…,（x n ,y n ）（n ≥2,x 1,x 2,…,x n 不全相等）的散点图中,若所有样本点（x i ,y i ）(i =1,2,…,n )都在直线y =12x +1上,则这组样本数据的样本相关系数为（A ）－1 （B ）0 （C ）12（D ）1（4）设F 1、F 2是椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点,P 为直线x =3a2上一点,△F 1PF 2是底角为30°的等腰三角形,则E 的离心率为（）（A ）12 （B ）23 （C ）34 （D ）455、已知正三角形ABC 的顶点A(1,1),B(1,3),顶点C 在第一象限,若点（x,y ）在△ABC 内部,则z=－x+y 的取值范围是（A ）(1－3,2) （B ）(0,2) （C ）(3－1,2) （D ）(0,1+3)（6）如果执行右边的程序框图,输入正整数N(N ≥2)和实数a 1,a 2,…,a N ,输出A,B,则（A ）A+B 为a 1,a 2,…,a N 的和（B ）A ＋B 2为a 1,a 2,…,a N 的算术平均数（C）A和B分别是a1,a2,…,a N中最大的数和最小的数（D）A和B分别是a1,a2,…,a N中最小的数和最大的数（7）如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为（A）6（B）9（C）12（D）18(8)平面α截球O 的球面所得圆的半径为1,球心O 到平面α的距离为2,则此球的体积为（A ）6π （B ）43π （C ）46π （D ）63π（9）已知ω>0,0<φ<π,直线x =π4和x =5π4是函数f (x )=sin(ωx +φ)图像的两条相邻的对称轴,则φ=（A ）π4 （B ）π3 （C ）π2 （D ）3π4（10）等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A,B 两点,|AB|=43,则C 的实轴长为（A ） 2 （B ）2 2 （C ）4 （D ）8 (11)当0<x ≤12时,4x <log a x ,则a 的取值范围是（A ）(0,22) （B ）(22,1) （C ）(1,2) （D ）(2,2) （12）数列{a n }满足a n +1＋(－1)n a n ＝2n －1,则{a n }的前60项和为（A ）3690 （B ）3660 （C ）1845 （D ）1830 第Ⅱ卷本卷包括必考题和选考题两部分·第13题-第21题为必考题,每个试题考生都必须作答,第22-24题为选考题,考生根据要求作答·二．填空题：本大题共4小题,每小题5分·(13)曲线y =x (3ln x +1)在点（1,1）处的切线方程为________ (14)等比数列{a n }的前n 项和为S n ,若S 3+3S 2=0,则公比q =_______(15)已知向量a ,b 夹角为45°,且|a |=1,|2a －b |=10,则|b |=(16)设函数f (x )=(x +1)2+sin xx 2+1的最大值为M,最小值为m ,则M+m =____三、解答题：解答应写出文字说明,证明过程或演算步骤· （17）（本小题满分12分）已知a ,b ,c 分别为△ABC 三个内角A,B,C 的对边,c = 3a sinC －c cosA(1)求A(2)若a =2,△ABC 的面积为3,求b ,c18.（本小题满分12分）某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售·如果当天卖不完,剩下的玫瑰花做垃圾处理·（Ⅰ）若花店一天购进17枝玫瑰花,求当天的利润y (单位：元)关于当天需求量n （单位：枝,n ∈N ）的函数解析式·（Ⅱ）花店记录了100天玫瑰花的日需求量（单位：枝）,整理得下表：(1)假设花店在这100天内每天购进17枝玫瑰花,求这100天的日利润（单位：元）的平均数； (2)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率·（19）（本小题满分12分）如图,三棱柱ABC －A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(Ｉ)证明：平面BDC 1⊥平面BDC（Ⅱ）平面BDC 1分此棱柱为两部分,求这两部分体积的比·B 1 DC 1A 1（20）（本小题满分12分）设抛物线C：x2=2py(p>0)的焦点为F,准线为l,A为C上一点,已知以F为圆心,FA为半径的圆F交l于B,D 两点·（I）若∠BFD=90°,△ABD的面积为42,求p的值及圆F的方程；（II）若A,B,F三点在同一直线m上,直线n与m平行,且n与C只有一个公共点,求坐标原点到m,n距离的比值·（21）（本小题满分12分）设函数f (x )= e x －ax －2 (Ⅰ)求f (x )的单调区间(Ⅱ)若a =1,k 为整数,且当x >0时,(x －k ) f ´(x )+x +1>0,求k 的最大值请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清楚题号·（22）（本小题满分10分）选修4-1：几何证明选讲如图,D,E 分别为△ABC 边AB,AC 的中点,直线DE 交△ABC 的外接圆于F,G 两点,若CF//AB,证明：FG(Ⅰ)CD=BC ； (Ⅱ)△BCD ∽△GBD(23)(本小题满分10分)选修4—4；坐标系与参数方程已知曲线C 1的参数方程是⎩⎪⎨⎪⎧x ＝2cos φy ＝3sin φ(φ为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程是ρ=2.正方形ABCD 的顶点都在C 2上,且A 、B 、C 、D 以逆时针次序排列,点A 的极坐标为(2,π3)(Ⅰ)求点A、B、C、D 的直角坐标；(Ⅱ)设P为C1上任意一点,求|PA| 2+ |PB|2 + |PC| 2+ |PD|2的取值范围·（24）（本小题满分10分）选修4—5：不等式选讲已知函数f(x) = |x + a| + |x－2|.(Ⅰ)当a =－3时,求不等式f(x)≥3的解集；(Ⅱ)若f(x)≤|x－4|的解集包含[1,2],求a的取值范围·。

2012年全国高考文科数学试题及答案-新课标word版

绝密＊启用前2012年普通高等学校招生全国统一考试（新课标卷）文科数学注息事项：1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。

答卷前,考生务必将自己的姓名、准考证号填写在本试卷和答题卡相应位置上。

2。

问答第Ⅰ卷时.选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动.用橡皮擦干净后，再选涂其它答案标号。

写在本试卷上无效。

3.回答第Ⅱ卷时。

将答案写在答题卡上。

写在本试卷上无效·4.考试结束后。

将本试卷和答且卡一并交回.第Ⅰ卷一、选择题：本大题共12小题，每小题5分，在每小题给同的四个选项中，只有一项是符合题目要求的。

1、已知集合A={x｜x2－x－2<0}，B={x|－1〈x<1｝，则(A)A错误!B （B)B错误!A （C）A=B （D）A∩B=(2）复数z＝错误!的共轭复数是（A）2+i （B）2－i （C)－1+i （D）－1－i3、在一组样本数据（x1，y1），（x2，y2),…，（x n，y n）（n≥2,x1,x2，…，x n不全相等）的散点图中，若所有样本点（x i，y i)（i=1,2,…，n）都在直线y=错误!x+1上，则这组样本数据的样本相关系数为（A）－1 (B）0 （C）错误!(D)1（4）设F1、F2是椭圆E：错误!＋错误!＝1(a〉b〉0)的左、右焦点，P为直线x=错误!上一点，△F1PF2是底角为30°的等腰三角形,则E的离心率为（）(A）错误!（B）错误!（C)错误!(D）错误!5、已知正三角形ABC的顶点A(1，1），B(1，3），顶点C在第一象限，若点（x，y）在△ABC内部，则z=－x+y的取值范围是（A)（1－3,2）（B）(0,2）（C）（错误!－1，2）（D）（0,1+错误!)（6）如果执行右边的程序框图,输入正整数N（N≥2)和实数a1,a2,…，a N,输出A,B，则(A）A+B为a1，a2，…，a N的和(B）错误!为a1，a2，…,a N的算术平均数（C）A和B分别是a1，a2，…,a N中最大的数和最小的数（D）A和B分别是a1,a2,…，a N中最小的数和最大的数（7)如图，网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图，则此几何体的体积为（A）6（B)9（C)12（D）18（8)平面α截球O的球面所得圆的半径为1，球心O到平面α的距离为错误!，则此球的体积为（A）错误!π（B）4错误!π（C）4错误!π(D）6错误!π（9）已知ω>0,0<φ<π，直线x=错误!和x=错误!是函数f(x）=sin（ωx+φ)图像的两条相邻的对称轴，则φ=(A）错误!（B)错误!（C）错误!（D）错误!（10)等轴双曲线C的中心在原点，焦点在x轴上，C与抛物线y2=16x的准线交于A,B两点,｜AB|=4错误!，则C的实轴长为（A）错误!（B)2错误!（C）4 （D）8（11）当0〈x≤错误!时,4x<log a x，则a的取值范围是（A）(0,错误!）（B）(错误!,1) （C）(1，错误!) (D）(错误!，2）（12）数列{a n}满足a n+1＋（－1）n a n＝2n－1，则{a n｝的前60项和为（A)3690 (B）3660 （C）1845 （D)1830第Ⅱ卷本卷包括必考题和选考题两部分.第13题—第21题为必考题，每个试题考生都必须作答,第22—24题为选考题，考生根据要求作答.二．填空题：本大题共4小题,每小题5分。

(完整word版)2012年全国高考新课标1卷数学文科高考试题

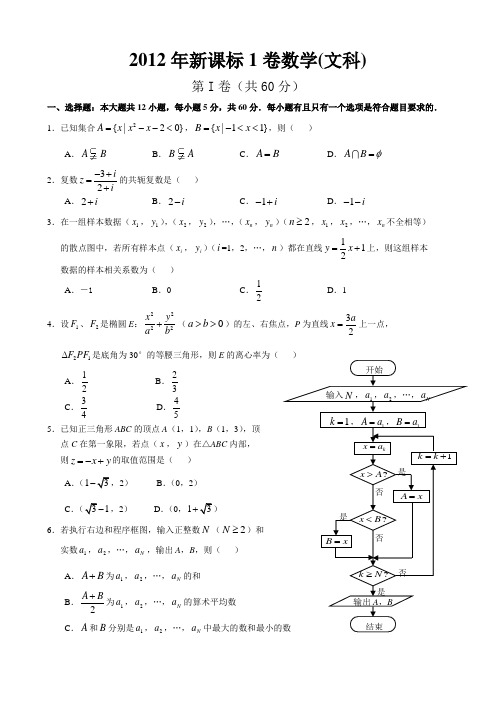
2012年新课标1卷数学(文科)第I 卷（共60分）一、选择题：本大题共12小题，每小题5分，共60分．每小题有且只有一个选项是符合题目要求的． 1．已知集合2{|20}A x x x =--<，{|11}B x x =-<<，则（）A ．AB B ．B AC ．A B =D ．A B φ=2．复数32iz i-+=+的共轭复数是（） A ．2i + B ．2i -C ．1i -+D ．1i --3．在一组样本数据（1x ，1y ），（2x ，2y ），…，（n x ，n y ）（2n ≥，1x ，2x ，…，n x 不全相等）的散点图中，若所有样本点（i x ，i y ）（i =1，2，…，n ）都在直线112y x =+上，则这组样本数据的样本相关系数为（） A ．－1B ．0C ．12D ．14．设1F 、2F 是椭圆E ：2222x y a b +（0a b >>）的左、右焦点，P 为直线32ax =上一点，21F PF ∆是底角为30°的等腰三角形，则E 的离心率为（）A ．12B ．23C ．34D ．455．已知正三角形ABC 的顶点A （1，1），B （1，3），顶点C 在第一象限，若点（x ，y ）在△ABC 内部，则z x y =-+的取值范围是（）A ．（13-，2）B ．（0，2）C ．（31-，2）D ．（0，13+）6．若执行右边和程序框图，输入正整数N （2N ≥）和实数1a ，2a ，…，N a ，输出A ，B ，则（）A ．AB +为1a ，2a ，…，N a 的和B ．2A B +为1a ，2a ，…，N a 的算术平均数C ．A 和B 分别是1a ，2a ，…，N a 中最大的数和最小的数否是是1k k =+B x=A x=结束输出A ，B ?k N ≥?x B <kx a =?x A >开始输入N ，1a ，2a ，…，N a1k =，1A a =，1B a =否是否D ．A 和B 分别是1a ，2a ，…，N a 中最小的数和最大的数7．如图，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则此几何体的体积为（）A ．6B ．9C ．12D ．158．平面α截球O 的球面所得圆的半径为1，球心O 到平面α的距离为2，则此球的体积为（） A ．6πB ．43πC ．46πD ．63π9．已知0ω>，0ϕπ<<，直线4x π=和54x π=是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴，则ϕ=（） A ．4π B ．3πC ．2πD ．34π 10．等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线216y x =的准线交于A ，B 两点，||43AB =，则C 的实轴长为（）A ．2B ．22C ．4D ．811．当102x <≤时，4log xa x <，则a 的取值范围是（） A ．（0，22） B ．（22，1） C ．（1，2） D ．（2，2） 12．数列{n a }满足1(1)21nn n a a n ++-=-，则{n a }的前60项和为（）A ．3690B ．3660C ．1845D ．1830第Ⅱ卷（共90分）本试卷包括必考题和选考题两部分。