6弯曲内力(习题课)
弯曲内力习题与答案

弯曲力1. 长l的梁用绳向上吊起,如图所示。
钢绳绑扎处离梁端部的距离为x。
梁由自重引起的最大弯矩|M|max为最小时的x值为:(A) /2l;(B) /6l;(C…) 1)/2l。
l;(D) 1)/22. 多跨静定梁的两种受载情况如图(a)、(b)所示。
下列结论中哪个是正确的?(A) 两者的剪力图相同,弯矩图也相同;(B) 两者的剪力图相同,弯矩图不同;(C) 两者的剪力图不同,弯矩图相同;(D….) 两者的剪力图不同,弯矩图也不同。
3. 图示(a)、(b)两根梁,它们的(A) 剪力图、弯矩图都相同;(B…) 剪力图相同,弯矩图不同;(C) 剪力图不同,弯矩图相同;(D) 剪力图、弯矩图都不同。
4. 图示梁,当力偶M e的位置改变时,有下列结论:(A) 剪力图、弯矩图都改变;(B…) 剪力图不变,只弯矩图改变;(C) 弯矩图不变,只剪力图改变;(D) 剪力图、弯矩图都不变。
5. 图示梁C截面弯矩M C = ;为使M C =0,则M e= ;为使全梁不出现正弯矩,则M e≥。
6. 图示梁,已知F、l、a。
使梁的最大弯矩为最小时,梁端重量P= 。
7. 图示梁受分布力偶作用,其值沿轴线按线性规律分布,则B端支反力为,弯矩图为 次曲线,|M |max 发生在 处。
8. 图示梁,m (x )为沿梁长每单位长度上的力偶矩值,m (x )、q (x )、F S (x )和M (x )之间的微分关系为:S d ();d F x x = d ()d M x x = 。
9. 外伸梁受载如图,欲使AB 中点的弯矩等于零时,需在B 端加多大的集中力偶矩(将大小和方向标在图上)。
10. 简支梁受载如图,欲使A 截面弯矩等于零时,则=e21e /M M 。
1-10题答案:1. C 2. D 3. B 4. B 5. 28e2M ql -;42ql ;22ql 6. ⎪⎭⎫⎝⎛-a l a F 24 7. m 0/2;二;l /28. q (x );F S (x )+ m (x ) 9. 10. 1/211-60题. 作图示梁的剪力图和弯矩图。
材料力学 弯曲内力习题课

习题课
[例6-13] 集中力F作用于A、B之间,问中间铰位于 F 何处最合理。 x1 C 解: A (1)F作用于AC段A B 处弯矩最大 l
(M A ) Fx1 max
Fx1
(2)F移动到CB段A处 弯矩及D处弯矩
F MD ( L x1 x2 ) x2 L x1 xx * MA 1 2 L x1 x2 F F M* M A D L x1
Q
G
FBy = 20 kN
由剪力图:x : 2 7 : 9 得到 (2)求极值弯矩
14 x 1.56 m 9
1.56m
30
20
M(kN .m)
-30
20
M G 30 70 1.56 / 2
M G 24.6kN m
20
5.求梁的最大剪力 和最大弯矩
FQ max 70 kN
l
2 9 ql 128
1 2 ql 8
作业: 4-10b,d 4-15f, 4-19
L x1 5
F ( L x1 ) Fx1 4
q
a
L 2a
a
二.面积法作内力图
30 kN
[例6-15]试作图示 外伸梁的FQ和M图。
1.求支反力 2.作FQ图 3.作M图
45 kN/m D
C
A
20 kN.m B E F 2m 1m 1m
G
1m 2m
FAy = 100 kN
70
FBy = 20 kN
FQ (kN)
1.56m
30
20
M(kN .m)
-30
20
20
4.求AD段的极值弯矩
材料力学典型例题及解析 4.弯曲内力典型习题解析

弯曲内力典型习题解析1 作图示简支梁的剪力图和弯矩图,并求出maxSF 和maxM。
解题分析:作剪力、弯矩图的基本方法是写出每一段梁上的剪力、弯矩方程,根据方程描点作图。
在能熟练地作剪力、弯矩图后,可采用如下简便作图法:在表中列出特殊截面(如有位移约束的截面、集中力作用截面等的剪力、弯矩值,再根据载荷集度与剪力、弯矩之间的微分关系判断各区段的内力图形状,连线相邻特殊截面对应的点。
下面按两种方法分别作图。
解I :1、求支反力qa F Ay =,qa F Cy 2=2、将梁分成AB 、BC 和CD 三个区段 以A 为原点,向右取x 坐标。
AB 段,如图d :qa F F Ay ==S ,()a x <<02qa(c)(b)(a)M(d)(e)MSSSM(f)题1图qax x F M Ay ==,()a x ≤≤0BC 段,如图e:)2()(S x a q a x q F F Ay −=−×−=,(a x a 2<<))/2()/2)((22a x q a x a x q x F M Ay +=−−+=,(a x a 2≤≤)CD 段,如图f:)()(S x a q F a x q F F Ay −=−−×−=,(a x a 32<<))/2()/2)((22a x q a x a x q x F M Ay +=−−+=,(a x a 32≤≤)3、按照步骤2所得各段梁的剪力、弯矩方程画出剪力图和弯矩图,如图b 和图c。
4、计算剪力和弯矩的最大值qa F 2maxS=, 2max23qa M=解II :1、计算支反力qa F Ay =,qa F Cy2=2、将梁分为AB 、BC 、CD 三个区段,计算每个区段起点和终点的力值。
3、根据载荷情况及微分关系,判断各力区的内力图形状,并以相应的图线连接起来,得到剪力图和弯矩图。
力区 A 截面 AB B 截面 BC C 截面 CD D 截面 载荷 F Ay 向上 q =0无集中力q =负常数 F 向下 q =负常数 F Dy 向上F S突跳F Ay水平(+)连续 下斜线(+) 突减F 下斜线(-) 突跳F DyM 0 上斜线 相切上凸抛物线转折上凸抛物线4、计算剪力弯矩最大值qa F 2maxS=, 2max23qa M=讨论:利用剪力弯矩方程作图时,注意坐标轴x 的正向一般由左至右。
02-弯曲内力-习题课

第5章弯曲内力5-1 选择题答: CmaxMS max F 如将图示的力F 平移到梁AD 的C 截面上,则梁上的与 。
FCBDAaaaA. 前者不变,后者改变B. 两者都改变C. 前者改变,后者不变D. 两者都不变 , 3A F F =23D F F =S max 23F F =max 24233B M M F a Fa ==⋅=max 22233C F M M a Fa==⋅=因为平移后支反力不变, , 不变。
,平移后 , 但平移前5-2 选择题答: D图示平面刚架ABC ,A 端固定,在其平面内施加图示集中力F ,其m-m 截面上的 内力分量不为零。
A. B. C. D. M S F NF 、 、 M NF、 M S F 、 S F NF、 F CBAmm力F 作用线过m-m 截面形心,弯矩M 为零。
5-3 选择题答: C图示简支梁上作用均布载荷q 和集中力偶M 0,当M 0在梁上任意移动时,梁的 。
A. M 、F S 图都变化B. M 、F S 图都不变化C. M 图改变、F S 图不变D. F S 图改变、M 图不变当M 0在梁上任意移动时,支反力不会改变,q 也不变, F S 只与横向外力有关,所以F S 图不变 。
M 0位置不同,M 图发生突变的截面改变了。
BqAM 05-4 选择题设梁的剪力图如图所示,则梁的 。
答:B33(kN)F S 5ABCA. AB 段有均布载荷,BC 段没有B. BC 段有均布载荷,AB 段没有C. 两段均有均布载荷D. 两段均无均布载荷S F =常数Sd ==0d F q xSd =0d F q x<AB 段, , BC 段为斜直线,5-5 选择题右端固定的悬臂梁长为4 m ,其 M 图如图所示,则在x =2m 处 。
答:AA. 既有集中力,又有集中力偶B. 只有集中力C. 既无集中力,也无集中力偶D. 只有集中力偶M (kN·m)332m2m该处M 有突变,说明有集中力偶;两边M 图斜率不同,说明F S 不同,是集中力作用引起的。
弯曲内力例题(0509)

和
M max 及其所
P
y
m=Pa
1、列出梁的剪力方程和弯矩方程
AB段:
A
x
x a
B a
C
x
FQ ( x) 0
(0 x a )
M ( x) m Pa (0 x a)
材料力学
弯曲内力/剪力方程和弯矩方程 剪力图和弯矩图 BC段: m=Pa P
FQ ( x) P
( a x 2a )
弯矩 立柱弯矩图为抛物线,左侧受压,1、2截面的弯矩值为
M1 0,
qa2/2
3
qa/2
4
2M4 0
qa/2
1
FAy
材料力学
M
FAx
1 2 1 2 M 2 qa a qa qa , 2 2 1 2 M 3 qa , M 4 0 2
作弯矩图。
弯曲内力/平面刚架内力图
x 3.1m
1 M E F 3.1 FAy 2.1 q 2.12 2
(-)
材料力学
1.41kN.m (+)
-3kN.m
(-)
-2.2kN.m
1.41kN.m M D左 2.2kN.m
q
P qa q
qa qa
a
FQ
a
a 2qa qa
M
qa 2 qa / 2
材料力学
弯曲内力/剪力和弯矩
M1 2qa
A
2
q
M 2 2qa2
B
C
a a 4a
FAy
FBy
取左段梁为研究对象:
取右段梁为研究对象:
FQc FAy q 2a qa
材料力学弯曲内力习题课

qL/2
qL/2
qx 2 MA 2
L L qL L MC q ( x) 2 4 2 2
M A MC
4 x 2 4 Lx L2 0
1 2 x L 2
x 0.207 L
(x为负值无意义)
( -)
x
在梁上行走的小车如图所示,两轮的轮压力均为F,设小 车的车轮距为c,大梁的跨度为l。试求小车行至何位置时, 梁内的弯矩最大?且求出最大弯矩的值。 x F c F
l
某工字型截面梁如图所示,一活动荷载P可以在全梁L上 移动。试问,如何布置中间铰B和可动铰C,才能充分利 用材料抗力。 P A B C D L
等截面杆AB,未受力时长L。将它竖起,上下端固定。当 上下端距离等于原长L时,求在自重作用下,(1)应力表 达式;(2)受拉区的位移表达式。设截面面积为A,材 料比重为γ,拉伸和压缩弹性模量分别为 E+ 和 E-。 A L B
作图示具有中间铰的组合梁的FS、M图。
qa2 qa2 /2
试画出图示有中间铰梁的 剪力图和弯矩图。
FDy qa / 2 FBy 3qa / 2 FAy qa / 2
M A qa 2 / 2
Fs qa/2
( +)AqaDBqC
a
a
a
qa
( +)
qa/2
qa2/2
( -)
M
( -)
qa2/2
弯曲内力课件

第八章弯曲内力【学时】6(其中习题课2)【基本要求】1.理解平面弯曲的概念[2]。
2.掌握剪力方程和弯矩方程[2]。
3.掌握剪力图和弯矩图弯矩的绘制[2]。
4.了解叠加法作弯矩图[3]。
【重点】梁在任一指定截面处的剪力和弯矩值的计算;剪力方程和弯矩方程;剪力图和弯矩图。
【难点】弯矩、剪力和荷载集度间的微分关系。
§8-1 平面弯曲的概念和实例一、弯曲的概念1. 弯曲: 杆受垂直于轴线的外力或外力偶矩矢的作用时,轴线变成了曲线,这种变形称为弯曲。
2. 梁:以弯曲变形为主的构件通常称为梁。
3. 工程实例4. 平面弯曲:杆发生弯曲变形后,轴线仍然和外力在同一平面内。
对称弯曲(如下图)——平面弯曲的特例。
二、梁的计算简图梁的支承条件与载荷情况一般都比较复杂,为了便于分析计算,应进行必要的简化,抽象出计算简图。
1. 构件本身的简化:通常取梁的轴线来代替梁。
2. 载荷简化:作用于梁上的载荷(包括支座反力)可简化为三种类型:集中力、集中力偶和分布载荷。
3. 支座简化①固定铰支座2个约束,1个自由度。
如:桥梁下的固定支座,止推滚珠轴承等。
②可动铰支座 1个约束,2个自由度。
如:桥梁下的辊轴支座,滚珠轴承等。
③固定端 3个约束,0个自由度。
如:游泳池的跳水板支座,木桩下端的支座等。
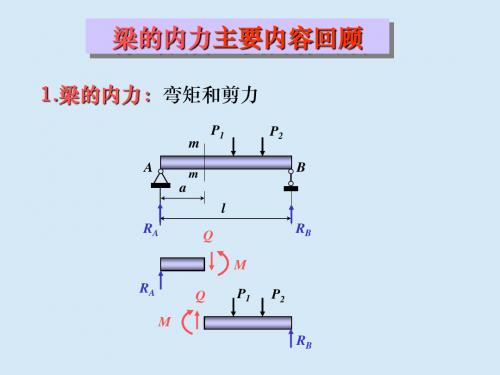
4.静定梁的三种基本形式③外伸梁§8-2 弯曲时的内力——剪力和弯矩一、弯曲内力[举例]已知:如图,P ,a ,l 。
求:距A 端x 处截面上内力。
解:①求外力la l P Y Y lPaR m X X A B A A )(, 0 ,00 , 0-=∑∴==∑∴==∑∴=②求内力——截面法X A Y AM Axx Y M m l a l P Y Q Y A C A ⋅=∑∴=-==∑∴=, 0)(, 0∴ 弯曲构件内力⎪⎩⎪⎨⎧弯矩剪力1. 弯矩:M构件受弯时,横截面上其作用面垂直于截面的内力偶矩。
2. 剪力:Q构件受弯时,横截面上其作用线平行于截面的内力。
弯曲内力习题课

0.5P
L
0.5P
0.5PL –
+
x
0.5P
L
L
0.5P
M2
0.5PL
[例3] 用简易作图法画下列各图示梁的内力图。
qa A a
q
解: 利用内力和外力的关系及
特殊点的内力值来作图。
a 特殊点(控制点):
端点、分区点(外力变化点)和
驻点等。
qa A a Fs
q
左端点: Fs qa; M 0 a x 线形:根据
例 题
[例1] qL 1 求图(a)所示梁1--1、2--2截面处的内力。 q 2 解:截面法求内力。 1--1截面处截取的分离体 2 b 如图(b)示。
1 a y qL A M1 x1 FS1
x
图(a)
Y qL F
S1
0
FS1 qL
mA( Fi ) qLx1 M1 0 M1 qLx1
dx
dFs x
dx 2 dM (x) d M ( x) ; q( x) FS (x) 2
dx
q x ;
– qa qa2
及集中载荷点的规律确定。
3 2 分区点A: F qa; M qa 2 qa S 2 3 2 M 的驻点: FS 0 ;M 2 qa
–
弯曲内力习题课
概念
平面弯曲——外力作用在梁的纵向对称平面内,使梁的 轴线弯曲后仍在此对称平面内的弯曲变形
P1 q P2
M
纵向对称面
弯曲内力
符号规定
剪力与弯矩的正负号规则
FS FS
剪力 FS一使截开部分梁段产生顺时针方向 弯矩M —— 使梁产生上凹、下凸变形的弯矩为 转动趋势者为正;逆时针方向转动者为负。 正;反之为负。
弯曲内力习题课

x MA
FAy
F’Dy
q
x
FDy
FBy
FDy qa / 2 FBy 3qa / 2
FAy qa / 2 M A qa2 / 2
Fs
15KN
O
(-)
1.5m 20KN
M
+
2.5m
(-)
x
25KN
O
(-)
8.75KN•m 20KN•m
x
40KN•m
Fs
qa 3qa 4 3qa 4
O
(+)
(+)
M B=0, M A=0
∴ FAy=8/9 kN , FBy=10/9 kN
2.确定控制面 在集中力、集中力偶以及支座的两侧截面均为控制
面。即A、C、D、E、F、B截面。
1KN.m
A
CD E F B
3.建立坐标系
8/9 kN=FAY
FS (KN)
O
1.5m
2kN
1.5m
1.5m
10/9
(+)
(-)
8/9
FBY 建立FS-x和M-x坐标系
=10/9 kN
4.应用截面法确定控制 x 面上的剪力和弯矩值,并
将 其 标 在 FS - x 和 M - x
坐标系中。再根据微分关
M (KN.m)
系连图线。
O (-)
(-)
x
1/3
4/3
5/3
试画出图示外伸梁的剪力图和弯矩图。
P1 =2kN q =1kN/m
一梁段上载荷图、剪力图、弯矩图三图的形状关系
q图
FS图
水平直线
斜直线
M图 斜直线
04章弯曲内力习题课
1KN 1KN
1KN
归纳:
1.根据微分关系作Q、M图步骤:
①求约束反力; ②确定分段,计算控制截面上的剪力和弯矩值;
③根据微分关系确定各段内力图形状;
④由② 、 ③作内力图。
2.控制截面的选择:
①分布荷载的起点和终点、集中力和集中力偶 作用点、支座点; ② M为极值(Q=0)的截面。
积分关系:
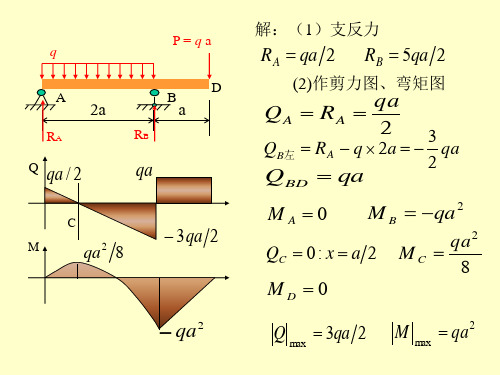
q(x) MA A QA QB B MB
q A
P=qa D
解:(1)支反力
R A qa 2
RB 5qa 2
2a
RB
B
a
RA
Q
qa / 2
C
qa
3 qa 2
qa QA RA 2 3 QB左 R A q 2a qa 2 QBD qa
MA 0
(2)作剪力图、弯矩图
M B qa 2
MC qa 2 8
②M 图 BC 段不为零 , 因为 BC
段Q=0,所以该段 M=常量。
Pa Pa P Q图 M图 Pa P
③在B、C点无集中力偶,M 图不应有突变;
Pa
例:已知梁的弯矩图,试画出梁的剪力图和荷载图。
1KN .m 1KN .m
A
B
2 KN .m 1m 3m
C
D
1m
2 KN 1KN
3KN .m
1KN .m
M D M A Q ( AD )
2a
a
qa / 3
1 5 5 25 2 0 qa a qa 2 3 3 18
M B左 M D Q ( DB ) 25 2 1 1 1 qa a qa 18 2 3 3 4 2 qa 3
第6章弯曲内力(1,2)

背口诀,快速记(42字)
剪力等于外力和;
弯矩等于力矩和; 左上右下剪为正;
左上右上弯为正;
左顺右逆弯为正; 与上不符皆为负。
3、简便法求梁内力的步骤 步骤: (1)先分别判断梁上各外力在截面上 引起的内力符号,并求出相应的内力数 值。 (2)由外力与内力大小规律,将截面 上的各内力代数和,即为所有外力作用 下梁截面的内力。
F 0, M 0,
y F
FSF FRB 0 M F FRB d 0
解得:
FSF FRB
-
M F FRB d +
(二)简便法求内力
1、外力与内力大小规律
a A
F1
m
F2 b B x
F
y
0:
m
FAy
a F1
x
F By
F2 b
FAy F1 FQ 0
FQ FAy F1
FAy
x
FQ
FQ
F By
任一横截面上的剪力等于该横截面任一侧所有外力的 代数和。
a
F1
m
F2 b B x
M
C
0:
A
m
x
FAy x F1 x a M 0 M FAy x F1 x a
FAy
FAy
a F1
F By
F2 b
M
M
x
四. 剪力方程和弯矩方程· 剪力图和弯矩图
剪力方程和弯矩方程实际上是表示梁的横截面上的剪力 和弯矩随截面位置变化的函数式,它们分别表示剪力和弯矩
随截面位置的变化规律,或称为内力方程。显示这种变化规
律的图形则分别称为剪力图和弯矩图,它们是梁配钢筋和承 载能力计算的依据。 梁剪力图的画法:取纵横坐标轴,横坐标轴与梁轴线平行,表 示梁的截面位置,纵坐标轴表示梁截面对应的剪力的大小,规 定正剪力画在横坐标轴的上方,负剪力画在横坐标轴的下方, 画出的图形即为梁的剪力图。 梁弯矩图的画法:取纵横坐标轴,横坐标轴与梁轴线平行,表 示梁的截面位置,纵坐标轴表示梁截面对应的弯矩的大小,规 定梁的弯矩图画在梁的受拉侧,因为正弯矩使梁下侧受拉,所 以正弯矩画在横坐标轴的下方;负弯矩使梁的上侧受拉,所以 负弯矩画在横坐标轴的上方,画出的图形即为梁的弯矩图。
材料力学第6章 弯曲内力

精品文档
6.1 梁的内力—剪力和弯矩
例题 6-2
(2)计算(jìsuàn)指定截面上的剪力和 弯矩
C截截面面C左(以侧梁的左力半:边为研究对象):
FAy 2 kN () (+)
FSC Fy FAy 2kN
C截面左侧的力矩:
FAy * 2m (+)
M e 8kN m (-)
M C
M F 2m - M -4kN m O
19
精品文档
6.2 剪力图和弯矩图
例题 6-3
(2) 作剪力图(lìtú)和弯矩图
由剪力、弯矩方程画剪力、弯矩图。
注意: 画图时应将剪力图、弯矩图与计算简图 对齐,并注明图名(FS图、M图)、 峰值点的值及正负号。
秦飞 编著《材料力学》 第6章 弯曲(wānqū)内
20
力
精品文档
6.2 剪力图和弯矩图
(plane bending)。当所有外力均作用在纵向对称面内时,梁只发生平面弯曲。
秦飞 编著《材料力学》 第6章 弯曲(wānqū)内力
6
精品文档
6.1 梁的内力(nèilì)—剪力和弯 矩
梁在外力作用下,其任一横截面上的内力可用截面法确定。
(1)截:在横截面m-m处假想地将梁分为两段
原来处于平衡状态的梁,被截出的任意段也处于平衡状态。
秦飞A编y 著《材料力学(cái lieào lìxué)》 第6章 弯
16
曲内力
精品文档
6.1 梁的内力(nèilì)—剪力和弯矩 例题 6-2
截面B(以梁右半边为研究对象):
B左截面
F 2kN (+)
FBy 4kN (-)
FSB左 F FBy -2kN
材料力学6弯曲内力

②悬臂梁
q(x)— 分布力
10
③外伸梁
q — 均布力
P — 集中力
5. 静定梁与超静定梁
静定梁:由静力学方程可求出支反力,如上述三种基本 形式的静定梁。
超静定梁:由静力学方程不可求出支反力或不能求出全 部支反力。
11
[例1]贮液罐如图示,罐长L=5m,内径 D=1m,壁厚t =10mm,
钢的密度为: 7.8g/cm³,液体的密度为:1g/cm³,液面高 0.8m,外伸端长 1m,试求贮液罐的计算简图。
2. 内力图规定: 弯矩图:画在各杆的受压一侧,不注明正、负号。
剪力图及轴力图:可画在刚架轴线的任一侧(普通正值
画在刚架的外侧),但须注明正、负号。
37
l P1 P1a
[例10] 试作图示刚架的内力图。
P2
a
P1
B
C
P2 A
+
+ Q图
P1
– N图
P1a
M图 P1a+ P2 l 38
二、曲杆:轴线为曲线的杆件。 内力状况及绘制办法与平面刚架相似。
M (x)
q0x 6L
(
L2
x2
)
③根据方程画内力图
23
§6–4 载荷集度、剪力和弯矩间的关系
一、 剪力、弯矩与分布荷载间的关系
q(x)
对dx 段进行平衡分析,有:
Y 0
Q( x ) q( x )dx Q( x ) dQ( x ) 0
x
dx
y
M(x) Q(x)
q(x) Q(x)+d Q(x) A dx M(x)+d M(x)
构造在反对称载荷作用下,Q图对称,M图反对称。
弯曲内力PPT课件专题培训

FAy=M / l FBy= -M / l
2.写出剪力和弯矩方程
AC FS x1 =M / l 0 x1 a
M x1 =Mx1 / l 0 x1 a
Mb / l
CB FS x2 =M / l 0 x2 b
M x2 = Mx2 / l 0 x2 b
3. 依方程画出剪力图和弯矩图。
目录
24
载荷集度、剪力和弯矩关系:
d
2M (x) dx2
dFs (x) dx
q(x)
1. q=0,Fs=常数, 剪力图为直线; 2. M(x) 为 x 旳一次函数,弯矩图为斜直线。
2.q=常数,Fs(x) 为 x 旳一次函数,剪力图为斜直线; M(x) 为 x 旳二次函数,弯矩图为抛物线。
分布载荷向上(q > 0),抛物线呈凹形;
b
b
a dFS
qdx
a
dM dx FS
dM FSdx
b
b
dM a
a FSdx
FS
b
FS
a
Aq
b a
M
b
M
a
AFS
b a
从左到右,向上(下)集中力作用处,剪力图向上(下) 突变,突变幅度为集中力旳大小。弯矩图在该处为尖点。
从左到右,顺(逆)时针集中力偶作用处,弯矩图向上
(下)突变,突变幅度为集中力偶旳大小。剪力图在该点没
q
A
FAy
9qa/4
B
4a
a
FBy
Fs (+)
9a / 4
(-) qa
7qa/4
81qa2/32 qa2
(+) M
4.求出剪力为零旳点 D 到A旳距离。 qa 5.从A截面左侧开始画弯
章弯曲内力习题课
4-6 刚架的内力图
刚架和曲杆可看作折线或曲线的梁,内力的计算和剪力 弯矩图的作法原理上与横梁相同。剪力的正负仍以外法线为 基准判断,弯矩图画在受压一侧。
注意:
横梁
1、在平面载荷作用下,组成刚 架的杆件横截面上一般存在轴力、 剪力和弯矩三个内力分量。
立柱
2、当杆件变形时,两杆连接处保 持刚性,弯矩保持不变,轴力和 剪力分量互换。
2(kNm)
M D 右 2 6 4 (km N )
•DB 段 M 图 是 二 次 曲 线 , 凸 向由q(x)确定。
5. 试判断Q、M图是否正确,画出正确的内力图。
P
P
BC
A
D
a
a
a
P
P
PP Q图
M图 Pa Pa
P Q图
P
M图
x 错误分析:
① Q图的正负号 “左上右下为 正, 且反对称;
q0a l Qc
Mc
RA
QcRA12q0laa M cR Aa1 2qo laaa 3
4. M(x)、Q(x)、q(x)的微分关系
q
P
Q Q
M
M
q
m
Q
Q
M
M
1. q=0 的区间,Q 水平直线, M为斜直线; Q>0,M的斜率为正, Q<0,M的斜率为负。
2.q为常数 (向下)的区间, Q 为斜向下的直线, M为向上凸的曲线。 Q=0 的位置对应于 M图 上的极值点位置 。
q=1kN/m m=6kNm
A
B
D
P=3kN C
4m 2m 3m
YA
YB
2.5
3
A
DB
第六章弯曲应力(习题解答)

216-3、图示矩形截面梁受集中力作用,试计算1-1横截面上a 、b 、c 、d 四点的正应力。
解:(1)外力分析,判变形。
荷载在纵向对称面内,与轴线垂直,梁发生平面弯曲。
中性轴z 轴过形心C 与载荷垂直,沿水平方向。
(2)内力分析,弯矩图如图(b )所示,1-1横截面的弯矩为:1115230(M-=-⨯=-⋅kN m )(3)应力分析,梁上边有弯矩图,上侧纤维受拉。
1-1横截面上的a 点处于拉伸区,正应力为正;c 点处于中性层上,正应力为零;b 、d 两点处于压缩区,正应力为负。
3111111m ax 2301011.1110.1800.36a a zzzM M M y y I I W σ---⨯=⋅=⋅===⨯⨯P a M P a 。
11.11b a σσ=-=-M Pa0c σ=31133010(0.1500.050)7.4110.1800.312d d zM y I σ-⨯=-⋅=-⨯-=-⨯⨯P a M P a37.5M kN ·m)V 图(kN )(a)(c)(b)30-(c)(e)(d)10102+q l /8M kN ·m)(f)20201z+25001150015bd (b)18015kNac (a)BqAlaz z az 22题6-3图 题6-5图6-5、两根矩形截面简支木梁受均布荷载q 作用,如图所示。
梁的横截面有两种情况,一是如图(b)所示是整体,另一种情况如图(c)所示是由两根方木叠合而成(二方木间不加任何联系且不考虑摩擦)。
若已知第一种情况整体时梁的最大正应力为10MPa ,试计算第二种情况时梁中的最大正应力,并分别画出危险截面上正应力沿高度的分布规律图示。
解:(1)外力分析,判变形。
荷载在纵向对称面内,与轴线垂直,梁发生平面弯曲。
第一种情况中性层为过轴线的水平纵向面,中性轴z 轴过整体形心C 与载荷垂直,沿水平方向。
而第二种情况,两根木梁以各自的水平纵向面为中性层发生弯曲,两根中性轴为与荷载垂直的水平形心主轴。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8
步骤: ①分别作出各项荷载单独作用下梁的弯矩图; ②将其相应的纵坐标叠加即可(注意:不是图 形的简单拼凑)。
9
F A F A
q B + M B
Fl ql 2 4 8
x
= +
q B
=
+
Fl 4xຫໍສະໝຸດ M1+m B 2m 2m q D
m=6kNm
A
C 2m
FA
FB
4 kN
+ _
2.5kN
4
m B 2m
q
q=2kN/m
D m=6kNm
A
C
2m
FA
2m
4 kN
FB
+
2.5kN
_
5kNm
4kNm
1kNm
5
[例] 改内力图之错。
A qa2 a Q qa/4 + – a qa/4 3qa/4 – 7qa/4 qa2/4 5qa2/4 3qa2/2 + x
A
M2
+ ql 2 8
x
10
[例] 绘制下列图示梁的弯矩图。
(1) a 2P a + Pa x
P M 2Pa –
=
2P
=
x
M1
+ M2 2Pa
+
P
+
x
11
a a q
q
qa2 –
qa2/2
M
x
=
=
q q M1 + qa2/2 x
+
3qa2/2 qa2/2 – M2
+
x 12
(3)
F
FL/2
M
FL/2 –
x
a
F
a
=
M1
=
+ FL/4 x FL/2 – M2 x
13
+
FL/2
+
20kNm 2m 20kNm
50kN
20kNm
20kNm +
20kNm x 30kNm
2m
M
=
20kNm M1
=
20kNm – x
+
M2
+
50kN
+ 50kNm
x
14
载荷单独作用于结构而引起的内力的代数和。
Fs ( F1F2 Fn ) Fs1 ( F1 ) Fs 2 ( F2 ) Fs n ( Fn )
M (F1F2 Fn ) M1 (F1 ) M 2 (F2 ) M n (Fn )
6
q B 2a x
FA
qa 7 qa ; FB 4 4
M
49qa2/32
[例9] 已知Fs图,求外载及M图(梁上无集中力偶) 。
Fs(kN) 2
+
1m 3 – 2m
1
+
1m
x
5kN
1kN
1.25 –
q=2kN/m
1 x
7
+
M(kN· m)
1
按叠加原理作弯矩图
一、叠加原理:
多个载荷同时作用于结构而引起的内力等于每个
1
载荷集度、剪力和弯矩间的关系
qa MA
A
q
B C
例题试画出图示有中间铰 梁的剪力图和弯矩图。
解:1.确定约束力 从铰处将梁截开
qa
D
FAy
a
a FBy
a
qa qa/2 Fs qa2/2
( -) ( +) ( +) MA FAy
FDy
q
qa/2
( -)
FDy
qa2/2
( -)
FDy qa / 2 FAy qa / 2
FBy
FBy 3qa / 2
M A qa 2 / 2
2
例: 利用M、Fs、q 之间的微分关系画图示梁 的Fs 、M图,已知:q=2KN/m,m=6kN· m。
m q
A 2m
C 2m
B
2m
D
FA
FB
解:求支反力
M B 0 FA 2.5kN M A 0 FB 6.5kN
3
q=2kN/m
