大学物理,相对论6-3 狭义相对论的基本原理 洛伦兹变换
大学物理(下册) 14.1 狭义相对论的基本原理 洛仑兹变换

u'x ux v u' y u y u'z uz
a' x a x
(4)
a' y a y
a' z a z
(5)
a a' F ma F ' ma '
结论:在相互作匀速直线运动的两惯性系中,牛顿 定律具有相同的形式!
s y
y
o
s'
y'
考察质点 P 的运动: 两个坐标系中质点 P 对应不同的坐标, 两套坐标之间的关 系为伽利略变换;
(oxyz ); 惯性系: S ' (o' x' y' z ' );
s y
y
o
s'
y'
y'
v
x'
x
*
P ( x, y , z ) ( x' , y ' , z ' )
vt
o' z' z'
z z
Albert Einstein ( 1879 – 1955 ) 20世纪 最伟大的物理学家,于1905、1915年 先后创立了狭义相对论、广义相对论。 于1905年提出光量子假设,为此获得 1921年度诺贝尔物理学奖。
爱因斯坦的哲学观念:自然界应当是 和谐而简单的。理论特色:出于简单 而归于深奥。
1. 狭义相对论建立的历史标志:1905年 Einstein 发 表的论文《论动体的电动力学》,以极其清晰和高 度简洁的观点叙述了相对性原理、光速不变原理, 狭义相对论建立在两原理基础之上。
以上结果说明:
在 S 系长为 x 的物体,在 S 系测量也为 x' x ; ' 在 S 系寿命为t 的生命,在 S ' 系测量也为t ' t ; 2.速度变换与加速度变换 注意:方程组(1)、(2)称为伽利略变换,反映了经典力学 时空观!将(1)对时间求导可得速度、加速度变换式: 速度变换公式: 加速度变换公式:
大学物理相对论 狭义相对论的基本原理 洛伦兹变换

洛伦兹变换
第八章 相对论
长度的测量是和同时性概念密切相关.
二 洛伦兹变换式
t 设 : t ' 0 时,o , o ' 重合 ; 事件 P 的时空 坐标如图所示 .
x' x vt 1
2
( x vt)
y
y'
P ( x, y, z, t)
s
z
s'
o
z'
v
* ( x', y ', z ', t ')
爱因斯坦的哲学观念:自然 界应当是和谐而简单的.
理论特色:出于简单而归于 深奥.
8 - 3 狭义相对论的基本原理
洛伦兹变换
第八章 相对论
一
狭义相对论的基本原理
1)爱因斯坦相对性原理:物理定律在所有的 惯性系中都具有相同的表达形式 . 相对性原理是自然界的普遍规律. 所有的惯性参考系都是等价的 . 2)光速不变原理: 真空中的光速是常量,它 与光源或观察者的运动无关,即不依赖于惯性系的 选择. 关键概念:相对性和不变性 .
1) x ' , t ' 与 x , t 成线性关系,但比例系数 1 .
2) 时间不独立, t 和
x
变换相互交叉. 伽利略变换。
3) v c 时,洛伦兹变换
意义:基本的物理定律应该在洛伦兹变换下保
持不变 . 这种不变显示出物理定律对匀速直线运动 的对称性 —— 相对论对称性 .
伽利略变换与狭义相对论的基本原理不符 .
8 - 3 狭义相对论的基本原理
洛伦兹变换
第八章 相对论
和光速不变紧密联系在一起的是:在某一惯性系 中同时发生的两个事件,在相对于此惯性系运动的另 一惯性系中观察,并不一定是同时发生的 .
简单推导洛伦兹变换(狭义相对论)

简单推导洛伦兹变换(狭义相对论)洛伦兹变换是狭义相对论的基本公式,从中我们可以进一步得到尺度缩减、时钟慢度、质能转换等奇妙有趣的推论。
值得一提的是,虽然洛伦兹变换最早是由洛伦兹得到的,但他并没有赋予这组变换方程组以相对论的内涵,他只是编造了一个数学观点来纠正错误的以太时空。
所以作者认为洛伦兹变换的结果应该还是属于爱因斯坦的。
1. 先导知识:波速取决于介质的速度,而不是波源的速度或许你听说过,光即是粒子又是波。
没错,但这个“粒子”已经不是我们日常理解的小微粒了,一定不能将发射一束光想象成手枪发射子弹。
许多困扰可能就来自于此,把光想象成子弹你可能永远也想不明白相对论的奇妙变换。
为了方便思考我们需要把光理解成波,发射光就像在水面触发一个涟漪。
我们先看看机械波,建立起对波的正确看法发射一波和发射一颗子弹有什么区别?根本区别在于,触发机械波实际上并不发射任何物理粒子,而是触发介质的传播振动,所以波速完全取决于介质,而不是波源的速度。
站在地上观察时,跑步时说话不会改变声音传播的速度,蜻蜓高速掠过水面也不会改变波纹扩散的速度,只会造成多普勒效应(仔细观察图1中最外层波纹的速度是否受波源速度影响)。
相反,考虑谈话的例子。
如果你站着不动,风在动,声速就会变。
比如逆风说话,声速会增加,逆风说话,声速会变慢。
仔细理解这里的区别,跑步不会改变波的传播速度,但空气运动会。
图1:一个运动的波源并不会导致波速的变化(观察最外层涟漪的速度)现在我们来考虑光的一个例子一列以速度v前进的火车在经过你的时候突然向前进方向发出了一个闪光,光是电磁波,不同于手枪发射子弹,不管这个光源运动情况怎么样,在你看来,这个闪光就像在水面上激起的一个涟漪,以不变的速度c前行。
(但是这里说的不变速度c还不是相对论说的光速不变,只是说光速与光源速度无关)2.光在真空中是通过什么介质传播的?从上面的分析我们看到波的速度,甚至波的性质似乎完全都取决于传递波的介质,波的行为似乎只与介质有关,完全由介质定义,完全由介质约束,波源在触发波之后好像就没有什么关系了。
狭义相对论的原理

狭义相对论的原理狭义相对论的原理狭义相对论是爱因斯坦于1905年提出的一种物理学理论,它是描述物质和能量之间关系的一种理论。
狭义相对论的原理可以分为以下几个方面:一、光速不变原理光速不变原理是狭义相对论的核心原理之一。
它认为在任何惯性参考系中,光速都是恒定不变的,即无论光源和观察者相对运动的状态如何,光速都保持不变。
这个原理可以用以下公式来表示:c = λf其中c代表光速,λ代表波长,f代表频率。
这个公式说明了在任何情况下,光速都是定值。
二、等效性原理等效性原理认为,在任何加速度下观察到的现象与在重力场中观察到的现象是等价的。
这个原理意味着重力可以被视为加速度。
三、时空相对性原理时空相对性原理认为,在所有惯性参考系中物理规律都应该具有相同的形式。
这个原理意味着时间和空间是相互关联且互不可分割的。
四、质能等价原则质能等价原则是狭义相对论的另一个核心原理。
它认为质量和能量是等价的,即E=mc²。
这个公式说明了质量和能量之间的转换关系。
五、洛伦兹变换洛伦兹变换是狭义相对论中最重要的数学工具之一。
它描述了不同惯性参考系之间时间和空间的变换关系。
洛伦兹变换包括时间、长度、速度和动量等方面。
六、相对性原理相对性原理是狭义相对论的基础之一。
它认为物理规律在所有惯性参考系中都应该具有相同的形式,而没有一个特定的惯性参考系是绝对正确的。
七、时间膨胀时间膨胀是狭义相对论中比较奇特的现象之一。
它指出,在高速运动状态下,时间会变慢,即观察到同一事件所需的时间会增加。
总结:以上就是狭义相对论的原理,其中包括光速不变原理、等效性原理、时空相对性原理、质能等价原则、洛伦兹变换、相对性原理以及时间膨胀等方面。
这些原理共同构成了狭义相对论的理论框架,为我们理解物质和能量之间的关系提供了重要的理论基础。
【大学物理】第一讲 狭义相对论基本原理 洛伦仑兹变换

v
G M1 G
ll t1 c v c v
c(1
2l v2
c2)
M2
M1
s G v T
G M2
c
- v
c2 v2
M2
-
v
c
G
c2 v2
(从 s'系看)
GM 2 GM 1 l
G
M2
G
t2 c
2l 1 v2
c2
t1
2l c(1 v2
c2) ,
2l
t2 c
1 v2
c2
两束光到达望远镜的时间差为
cv
1
vc c2
c
光速不变
光速在任何惯性 系中均为同一常量, 利用它可将时间测量 与距离测量联系起来.
§1.2 洛伦兹变换
寻找新的时空变换式来代替经典力学伽利略变换。
必需满足条件: (1)物理学定律都应该保持数学表达式不变。 (2)真空中光速在一切惯性系中保持不变。 (3)在低速运动条件下可转化为伽利略变换。
设 t t 0 时,o, o
重合 ; 同一事件 P 的
时空坐标如图所示。
s y s' y' v
t
t1
t2
2l
v2
c
1
c2
2l
v2
c
1
c2
1
2
=
2l c
1
v2 c2v2源自1 2c2v << c
t l v2 c c2
两束光汇合时的光程差为 ct l v2
c2
整个仪器旋转90度,那么两束光在前后两次测量
中光程差的该变量为
N 2 2l v2
大学物理下相对论-洛伦兹变换

100%
长度收缩
在相对论中,当物体以接近光速 运动时,其长度相对于静止观察 者会缩短,这种现象被称为长度 收缩。
80%
相对论的多普勒效应
当光源或观察者以接近光速运动 时,光波的频率或波长会发生改 变,这种现象被称为相对论的多 普勒效应。
相对论的速度合成法则
相对论的速度合成法则
当两个物体以接近光速相对运动时,它们的相对速度不能简单地通过矢量相加得到,而是需要使用洛伦兹变换进 行计算。
速度合成法则的应用
在高速运动和强引力场中,相对论的速度合成法则对于精确描述物体的运动状态非常重要。
相对论的质量-能量关系(E=mc^2)
质量-能量等效原理
在相对论中,物体的质量与能量是等效的,即存在一个固定的转换关系 E=mc^2。
质能方程的应用
质能方程在核能、粒子物理和宇宙学等领域有广泛的应用,如核反应释放能量、黑洞的形成和演化等 。
洛伦兹变换公式描述了不同参 考系之间的长度和时间的关系 ,是相对论中的基本公式之一 。
通过洛伦兹变换公式,可以推 导出相对论中的其他重要结论 ,如时间膨胀和长度收缩。
04
洛伦兹变换的应用
时间和空间的测量
80%
时间膨胀
在相对论中,当物体以接近光速 运动时,其内部的时间相对于静 止观察者会变慢,这种现象被称 为时间膨胀。
洛伦兹变换的性质
线性性质
洛伦兹变换是线性变换,即变换前后线性组合的结 果与单个变换的结果相同。
逆变换
如果知道从一个参考系到另一个参考系的洛伦兹变 换,则可以推导出从另一个参考系回到原参考系的 逆变换。
相对性
对于任意两个惯性参考系之间的变换,其逆变换与 原变换是等价的。
03
大学物理 狭义相对论

经
典
相对论
“同时”的相对性
时间延缓(膨胀) 长度收缩
14
时间独立于空间
时间间隔与坐标系无关 长度测量与坐标系无关
1. 同时的相对性 relativity of simultaneity ——在某惯性系中同时发生于不同地点的 两个事件,在另一相对运动惯性系中不一 定同时发生
x'
x2 , t2
x
17
y S y ' S'
O O
S ' 同时不同地
u
同时发生
, t x2
x1 , t
x1 , t1
x'
x2 , t2
先发生
x
后发生
t1 0 and x x2 x1 0 t t2
v v t1 2 ( x2 x1 ) x t2 2 c c 0 t t2 t1 2 2 1 v c 1 v2 c 2
x y z c t x y z c t
2 2 2 2 2 2 2 2
10
2 2
两个事件的空间间隔、时间间隔的变换:
x 2 x1 ( x 2 x1 ) u( t 2 t1 ) 1 u2 c 2
x 2 x1
( x 2 x1 ) u( t 2 t1 ) 1 u2 c 2
第六章 狭义相对论基础 Special Relativity
Albert Einstein (1879-1955)
1
本章: 伽利略相对性原理
狭义相对论基本原理
狭义相对论的基本原理 洛伦兹变换式

2、洛伦兹速度变换式
ux − v u′ = x u xv 1− 2 c
正变换
u y 1 − v 2 /c 2 ′ uy = u xv 1− 2 c
u z 1 − v 2 /c 2 ′ uz = u xv 1− 2 c
9
物理学
第五版
14-3 14-
狭义相对论的基本原理 洛伦兹变换式
逆变换
u′ + v ux = x u′ v 1 + x2 c u ′y 1 − v 2 / c 2 uy = u′ v 1 + x2 c
2 2
c ,0,0, 1 ) 点在K 中的时空坐标为( 即P1点在K'中的时空坐标为( 3 3
同理可得 P2点在K'中的时空坐标为(-3c,0,0,3) 点在K 中的时空坐标为(
12
物理学
第五版
14-3 14-
狭义相对论的基本原理 洛伦兹变换式
讨论: 讨论: ----同时 ∆t = 0 ----同时
物理学
第五版
14-3 14-
狭义相对论的基本原理 洛伦兹变换式
Qd x' =
d x −v dt 1−v c
2 2
dt' =
dt −v d x c 1−v c
2 2
2
d y' = d y
d z' = d z
ux −v d x' d x −v dt = ∴ux' = = 2 2 dt' dt −v d x c 1−vux c
8
16
= 2.99×10 m /s
15
物理学
第五版
14-3 14-
狭义相对论的基本原理 洛伦兹变换式
大学物理曲晓波-第6章 狭义相对论

x
x u t 1 u2 /c2
洛 仑
y
y
兹 z z
逆 变 换
t
t
ux c2
1 u2 /c2
洛伦兹逆变换只是把洛伦兹变换中的u→ - u,x与x’,
y与y’,z与z’交换位置。
说明:
①洛伦兹变换表示同一事件在不同惯性系中时空坐标的变换关系。 规定每个惯性系使用对该系统为静止的时钟和尺进行量度。
在所有惯性系中,物理定律的表达形式都相同。这就是爱因 斯坦相对性原理,即相对性原理。
此原理说明所有惯性系对于描述物理规律都是等价的,不存 在特殊的惯性系。可以看出,爱因斯坦相对性原理是力学相对 性原理的推广。
由此可得出,在任何惯性系中进行物理实验,其结果都是一 样的,运动的描述只有相对意义,而绝对静止的参考系是不存 在的。因此不论设计力学实验,还是电磁学实验,去寻找某惯 性系的绝对速度是没有意义的。
S 系v 中 x d d x t,v y d d y t,v z d d z t
v
x
vx 1
u
uvx c2
速 度 变 换
v
y
vy
1 u2 /c2
1
uvx c2
v
z
vz
1 u2 /c2
1
uvx c2
vx
v
x
1
u
u v x c2
速 度 逆 变 换
v
y
v
y
1 u2 /c2Biblioteka 1u v x c2
vz
v
z
1 u2 /c2
1
u v x c2
讨论:
①当u,v(vx,vy,vz)远小于光速c时,相对论速度变换式退化
经典时空观 狭义相对论的基本原理和洛伦兹变换 狭义相对论的基本原理和洛伦兹变换 相对论1

波动学知识点归纳 一.波动的基本概念 1.机械波:机械振动在弹性媒质中的传播. 横波:振动方向与波的传播方向垂直的波 纵波:振动方向与波的传播方向平行的波 2.波速、波长、周期、频率、波数之间的关系:u=λT= λν , k =2πλ=ωu二、波的描述 波阵面(波面)--在波传播的介质中,相位相同 的点所连成的面。
波前波线--波传播的方向线 均匀、各向同性媒质中波线 与波阵面垂直(1)平面波波函数:x y (x, t ) = A cos[ω (t m ) + ϕ 0 ] uy = A cos[ ω t − 2πλx + ϕ0 ]y = A cos[ωt − kx + ϕ0 ]明确波函数的物理意义(2)平面波波动的微分方程一维波动方程。
∂ y 1 ∂ y = 2 2 2 µ ∂t ∂x2 2三维波动方程1 ∂ 2ξ ∂ 2ξ ∂ 2ξ ∂ 2ξ + 2+ 2 = 2 2 2 ∂y ∂z µ ∂t ∂x三. 波的能量⎛ x⎞ dW = ρ A ω sin ω ⎜ t − ⎟dV ⎝ u⎠2 2 2波动可以传递能量,孤立振动系统并不能传递能量.1.能量密度:单位体 积媒质的波动能量 一周期内的平均值 称平均能量密度x w = ρω A sin ω (t − ) u2 2 21 w = ρω 2 A 2 22.平均能流密度(波强) :单位时间通 过垂直于传播方向单位面积的平均能 流1 I = ρω 2 A2u 2各向同性均匀介质中,平面波的强度不 变,球面波的强度与半径的平方成反比四、波的叠加原理: 几列波相遇之后, 仍然保持它们各自原有的特征不变继续前 进,好象没有遇到过其他波一样. 在相遇区域内,任一点的振动,为各列波单独存在时在该点 所引起的振动位移的矢量和. 五、波的干涉 相干条件 频率相同 振动方向相同 相位差恒定满足相干条件的两列波相遇叠加时,产生波的干涉现象.λ y = y1 + y2 = A cos(ωt + ϕ ) 2πr2 y2 = A2 cos(ωt + ϕ2 − ) λy1 = A1 cos(ωt + ϕ1 −2πr1)A = A + A2 + 2 A1 A2 cos ∆ϕ2 1 2tan ϕ =λ λ 2πr1 2πr2 ) + A2 cos(ϕ2 − ) A1 cos(ϕ1 − λ λA1 sin(ϕ1 −2πr1) + A2 sin(ϕ2 −2πr2)∆ϕ = (ϕ 2 − ϕ1 ) −2πλ(r2 − r1 )∆ϕ =±2k π k = 0 ,1, 2 ,L干涉加强± ( 2 k + 1 ) π k = 0 ,1 , 2 ,L 干涉减弱两个波源的相位相同时,干涉加强和减弱的条件也 可用波程差表示:∆ϕ =2πλδδ = r2 − r1干涉加强δ =±kλk = 0 ,1 , 2 ,L± ( k + 1 2 )λk = 0 ,1 , 2 ,L 干涉减弱六、驻波: 波形成条件: 振幅相同的相干波,在同一直线上沿相反方 向传播,叠加后就形成驻波 驻波的表达式: y ( x , t ) = 2 A cos 2πxx=k驻波振幅λ2λcos ω t, k = 0,±1,±2,...λ4波腹的位置x = ( 2k + 1), k = 0, ±1, ±2, ... 波节的位置驻波相位相邻两波节间的质点的振动同相, 波节两侧质点的振动反相;驻波的产生:入射波+反射波 固定端反射,界面处为波节L两列波自由端反射界面处为波腹λ x 驻波的表达式: y ( x , t ) = 2 A cos 2π cos ω t λ两列波λ x y 2 ( x, t ) = A cos( ω t + 2π )y1 ( x , t ) = A cos( ω t − 2πx)y1 ( x , t ) = A c o s (ω t + ϕ 1 − 2 πxλ x y 2 ( x , t ) = A cos[ω t + ϕ 2 + 2π ]x)y ( x , t ) = 2 A cos[ 2πλ+ϕ 2 − ϕ12λ]cos(ω t +ϕ 2 + ϕ12)s V u u u νλνS −=′=′s s V u u νν+='νλνSD V u V u u m ±=′′=′νννuu D ±=′*αB相对不同的参照系,长度和时间的测量结果都一样吗?§6.1 经典时空观一、牛顿相对性原理相对不同的参考系,基本力学定律的形式是完全一样的吗?力学概念,以及力学规律对一定的参考系才有意义的.因此,在任何惯性系中观察,同一力学现象将按同样的形式发生和演变。
狭义相对论的基本原理 洛伦兹变换

x
关键概念: 关键概念:相对性和不变性 .
0.80c
0.90c
二、狭义相对论的基本原理
洛伦兹变换
洛伦兹变换特点 洛伦兹变换特点 1) )
x ' , t ' 与 x, t
v << c
成线性关系, 成线性关系,但比例系数 γ
≠ 1.
2) 时间不独立, t 和 ) 时间不独立, 3) )
x 变换相互交叉 变换相互交叉.
二、狭义相对论的基本原理
洛伦兹变换
思路:用速度分量定义+ 思路:用速度分量定义+洛仑兹坐标变换公式 定义 系中: 在S系中: 系中 系中: 在S’系中: 系中
dx vx = dt dy vy = dt dz vz = dt
dx′ v′ = x dt′ dy′ v′ = y dt′ dz′ v′ = z dt′
洛伦兹变换
经典力学的相对性原理与麦氏电磁理论的矛盾
解决矛盾的可能方案: 解决矛盾的可能方案: (1)电磁学理论需要修正 ) (2)伽利略变换和牛顿力学的时空观有问题。 )伽利略变换和牛顿力学的时空观有问题。 (3)力学满足相对性原理只是偶然,相对性原理不 )力学满足相对性原理只是偶然, 是普遍原理,电磁学理论只在特殊的惯性系中成立。 特殊的惯性系中成立 是普遍原理,电磁学理论只在特殊的惯性系中成立。
二、狭义相对论的基本原理
洛伦兹变换
3. 洛伦兹变换式
t 设 : = t '= 0 时,o , o ' 重合 ; 事件 P 的时空 坐标如图所示 .
x' = x − ut 1− β
2
= γ ( x − ut )
s s'
z
y
y'
狭义相对论的基本原理洛伦兹变换
第一篇 力学基础
College Physics
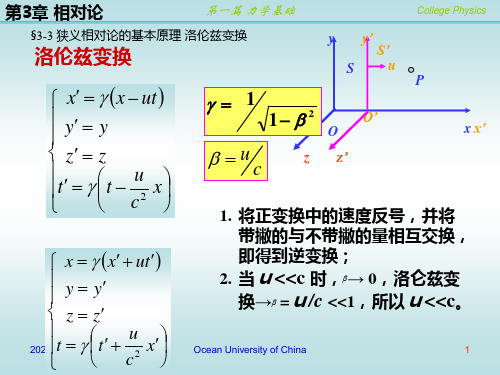
§3-3狭义相对论的基本原理 洛伦兹变换
在S系中,一个物体作匀速直线运动,那么必然有:
Ax Bt C 0
在S’系中,一个物体作匀速直线运动,那么必然有:
A' x' B' t 'C ' 0
y
y’
S
S’ u P
O z
2017/3/9 Ocean University of China
2017/3/9
z z t t
17
Ocean University of China
第3章 相对论
Examples:
第一篇 力学基础
College Physics
u x2 x1 2 c t1 t2 1 u 2 / c2 x2 x1 u t 2 t1 x2 x1 1 u 2 / c2 u
对
11
c tt (c u)t (c u)t
2017/3/9 Ocean University of China
第3章 相对论 洛伦兹变换推导
第一篇 力学基础
College Physics
§3-3 狭义相对论的基本原理 洛伦兹变换
y S
y’
x' ( x ut) x ( x'ut' )
y S
y’
x' ( x ut) x ( x'ut' )
以上推导仅使用了相对性原理
S’ u P
O z
Z’
O’
x
如何确定
2017/3/9
Ocean University of China
狭义相对论的基本原理与洛伦兹变换

物体不能超光速
则 变为虚数,时空变换式无实际意义。
时空不可分割 变换式揭示了时、空是相互依赖的。
例题 在约定惯性系中 系相对 系的速率 v = 0.6 c , 在 系中观察一事件发生的时 空坐标为 t = 2×10 - 4 s, x = 5×10 3 m , 则 该事件发生在 系中的时空坐标为
s, m。
变换式必须满足狭义相对论的两个基本假设。 时间和空间具有均匀性,变换性质应为线性变换。
对时间和空间不作绝对定义,允许其存在相互依赖的可能性。
模型 在约定惯性系中进行某一事件的时空坐标变换
约定惯性系
相对 沿 方向以匀速 重合开始计时 方向均无相对运动
运动
现推导有相对运动的 X 方向的时空坐标变换式:
推导
相对 沿 方向以匀速
运动
求待定系数变换式推导 Nhomakorabea重合开始计时
得
对任一事件,变换式均应满足 线性变换
相对性原理 重合时原点处沿OX方向发 若在 分别观察此光信号 出一光信号, 传播到达的X坐标和时间关系应满足:
光速不变原理
则
及
结果
洛仑兹变换
洛沦兹变换式
其中
或写成
高低速兼容 当
时,
,且
,回到伽利略变换式。
第一节两个基本假设 5-1
对所有惯性系, 物理规律都是相同的。
principle of special relativity and
在任何惯性系中, Lorentz transformation 光在真空中的速率 都等于同一量值 c 。
洛仑兹变换序
含义 洛仑兹变换是狭义相对论中联系任意两个惯性参考系之间时 空坐标的变换。对高、低速物质运动兼容。 来由 洛仑兹在研究速度小于光速运动系统中的电磁现象时,曾提 出解决时空变换问题的法则及数学形式,但仍受“以太”观 念束缚。爱因斯坦以狭义相对论的两个基本假设为前提,重 新导出这个变换,并赋予明确的物理意义 ,仍称为洛仑兹变 换。 条件
6A 狭义相对论的基本原理 洛伦兹变换

x k ( x Vt ) x k ( x Vt )
狭义相对论的基本假设
x k ( x Vt ) x k ( x Vt )
2
洛伦兹变换
第五章 相对论
根据相对性原理,惯性系S和S’是等价的,上 两式众k和k’应该相等:
xx k ( x Vt )(x Vt )
狭义相对论的基本假设
洛伦兹变换
第五章 相对论
例2 在惯性系S中,有两个事件同时发生在 x轴相距1000m的两点,而在另一惯性系S’ 中测得这两个事件发生地相距2000m,求在 S’系中测得这两个事件的时间间隔。 解:从S系到S’系的时空坐标间隔的变换式为
狭义相对论的基本假设
洛伦兹变换
第五章 相对论
(2)以太的假设
“以太”是人们假想的,充满宇宙空间 的一种绝对静止的物质。 为了测量地球相对于“以太”的运动 , 1881年迈克尔孙用他自制的干涉仪进行测量, 没有结果 .1887年他与莫雷以更高的精度重 新做了此类实验,仍得到零结果, 即未观测 到地球相对“以太”的运动 .
狭义相对论的基本假设
洛伦兹变换
第五章 相对论
在 S系中, x 100m, t 10s 从S系到S’系的时空坐标间隔的变换式为
x (x Vt )
V 0.98c
x 1.477 10 m V t ( t 2 x ) c
10
t 50 .25s
球 投 出 前 球 投 出 后
c
d
d t1 c
v cv
d t2 cv
t1 t 2
结果:观察者先看到投出后的球,后看到投出前的球.
狭义相对论的基本假设
洛伦兹变换
大学物理狭义相对论知识点总结

大学物理狭义相对论知识点总结
大学物理狭义相对论知识点总结
1.狭义相对论基本原理
(1)相对性原理:在所有惯性系中物理定律的表达形式都相同;
(2)光速不变原理:在所有惯性系中,真空中的光速具有相同的量值c.
2.洛伦兹变换 逆变换为:3.相对论的时空观(1) 同时的相对性;(2)时间延缓 ;(3)尺度缩短
4.相对论中的质量、动量和能量:(1)质量与速度的关系:
(2)动量的定义: ;(3)静止能量: 总能量:
动能: 当 时,即是经典力学中的动能。
(4)能量和动量的关系:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
伽利略变换与狭义相对论的基本原理不符。
6
第6章 相对论 6.3 狭义相对论的基本原理 洛仑兹变换 和光速不变紧密联系在一起的是:在某一惯性系 中同时发生的两个事件,在相对于此惯性系运动的另 一惯性系中观察,并不一定是同时发生的。
说明同时具有相对性,时间的量度是相对的。
长度的测量是和同时性概念密切相关。
(3)即在低速情况下可以转化为伽利略变换。
10
6.3 狭义相对论的基本原理 二 洛伦兹变换
洛仑兹变换
第6章 相对论
设有两个惯性系 S 系和 S’ 系,各坐标轴相互 平行。 S’ 系相对S系以 u的速度沿 ox 轴运动。 设: t
t' 0
时,
o, o ' 重合。
事件 P 的时空坐标为:
s
o z
7
6.3 狭义相对论的基本原理 明确几点:
洛仑兹变换
第6章 相对论
Hale Waihona Puke 1)第一条原理是对力学相对性原理的推广。 否定了绝对静止参照系的存在。
它表明不论在哪个惯性系中做物理实验(不仅 仅是力学实验),都不能确定该惯性系是静止的、 还是在作匀速直线运动。即对运动的描述只有相 对意义,绝对静止的参考系是不存在的。 2)第二条原理实际上是对实验结果的总结。 它表明:在任何惯性系中测得的真空中的光速都相 等。说明光速与观察者及光源的运动状态无关。
x
x ut 1 (u / c )
t xu / c 2 1 (u / c )
2
2
1 106 0.75 3 108 0.02 1 0.75
2
5.29 10 m
6
t
0.0265 s
6 x x ut 3.5 10 m t t 0.02s
6.3 狭义相对论的基本原理
洛仑兹变换
第6章 相对论
6.3 狭义相对论的基本原理 洛仑兹变换
1
6.3 狭义相对论的基本原理
洛仑兹变换
第6章 相对论
伽利略变换与电磁理论是互不相容的。“为 什么看起来如此正确的两件事却互不相容呢?” 爱因斯坦曾经苦苦地思索。
伽利略变换和电磁规律的矛盾引导人们去思考:
是伽利略变换正确而电磁现象的基本规律
8
6.3 狭义相对论的基本原理
洛仑兹变换
第6章 相对论
3)爱因斯坦理论带来了观念上的变革。 牛顿力学: 时间、长度、质量的测量, 均与参照系无关。 狭义相对论: 时间、长度、质量的测量, 均与参照系有关。 我们不应当以适用于低速情况的伽利略变 换为根据去讨论光速应该如何如何,而应当反 过来,用光速不变这个实验提供的事实作为前 提和基础,去讨论正确的时空变换。
3)在洛仑兹变换中,时间、空间都是 u 的函数, 说明时间与空间的测量都与参照系有关。这种 新的时空观叫做狭义相对论的时空观。
14
6.3 狭义相对论的基本原理
4)相对论因子:
第6章 相对论 洛仑兹变换 1 1 (v / c)2 总是大于1。
u > c 变换无意义, 存在极限速度 c 。 真空中的光速 c 是真实世界一切物体运动速率 的极限。两个惯性系的相对运动速度不能等于或大 于 c ,任何物体的速度也不能大于 c 。 x x ut 5)当 u << c 时, u / c = 0, γ →1 y y z z 洛仑兹变换回到了伽利略变换。 t t 表明伽利略变换只是洛仑兹变换在低速 情况下的近似。 15
9
6.3 狭义相对论的基本原理 ★ 意义:
洛仑兹变换
第6章 相对论
1)承认相对性原理,必须否定绝对静止参照系。 2)承认光速不变原理,必须否定伽利略变换, 否定绝对时空观。 满足狭义相对论基本原理的变换就是洛仑兹变换: 物理定律通过这种变换应做到: (1)都应该保持自己的数学表达形式不变; (2)真空中光的速率在一切惯性系中保持不变;
y
s'
o'
z'
y'
u
* ( x ' , y' , z ' , t )
x'
P ( x, y, z, t )
x, y, z , t
x , y , z , t
x
寻找对同一客观事件 P,在两个惯性系 中相应的时空坐标值之间的关系。
11
6.3 狭义相对论的基本原理
洛仑兹变换
20
6.3 狭义相对论的基本原理
洛仑兹变换
第6章 相对论
由洛仑兹变换可以得到两个事件在不同惯性 系中的时间间隔,空间间隔之间的变换关系。
两个事件
事件1
(如闪光到达A端)
S
( x1 , t1 ) ( x2 , t 2 )
S
( x1 ' , t1 ' )
事件2
(如闪光到达B端)
( x2 ' , t 2 ' )
若按伽利略变换,则:
17
6.3 狭义相对论的基本原理
洛仑兹变换
第6章 相对论
例:设S’系以速率 u = 0.6c 相对于S系沿 xx’ 轴运动,且在 t = t’ = 0 时,x = x’ = 0。 1)若在S系中有一事件发生于 t1 = 2.0×10–7s,x1 = 50m 处,该事件在S’系中发生于何时 刻?2)如有另一事件发生于S系中,t2=3.0×10–7s, x2=10m处,在S’系中测得这两个事件的时间间隔为多少? 解:1)u = 0.6c , ∴ γ = 5/4 由洛仑兹坐标变换可得: 第一个事件发生的时刻为: 1 2 u 7 1 ( u / c ) t' (t x ) 1.25 10 s
6.3 狭义相对论的基本原理
洛仑兹变换
第6章 相对论
5) 洛仑兹变换是有爱因斯坦狭义相对论的 两条基本原理推导出来的,以后在讨论问题 时可以直接用洛仑兹变换。
1904年,洛仑兹提出了洛仑兹变换用于解释迈克 尔逊——莫雷实验的结果。 根据他的设想,观察者相对于以太以一定速度运 动时,长度在运动方向上发生收缩,抵消了不同方向 上由于光速差异,这样就解释了迈克尔逊——莫雷实 验的零结果。并且证明了麦克斯韦方程组在洛仑兹变 换下保持形式不变。 当时只是作为一种假设提出来的,并没有相对论 的思想。爱因斯坦从新的观点出发,独立地推导出这 个变换式,仍然用洛仑兹的名字来命名。
后果:伽利略变换代表牛顿力学的时空观,否定 它必然否定牛顿力学的时空观。
4
6.3 狭义相对论的基本原理 ◆ 爱因斯坦的观点:
洛仑兹变换
第6章 相对论
相信自然界有其内在的和谐规律。
(必定存在和谐的力学和电磁学规律。)
相信自然界存在普遍性的相对性原理。
(必定存在更普遍的相对性原理,对和谐的力学和电磁学规律都适用。)
后果:必须否定力学的相对性原理。也就是 说,物理规律在不同惯性系下应当具有不同 的物理形式。
3
6.3 狭义相对论的基本原理
洛仑兹变换
第6章 相对论
方案二:坚持力学的相对性原理和光速不变的实验 事实,进而否定麦克斯韦理论遵从伽利略变换。
理由:光速不变是实验事实,不容否定。 力学的相对性原理是一种自然观,与其否定 一种科学观念不如否定一种特定的变换——伽利 略变换。因为所有证明伽利略变换的科学事实都 来自于宏观、低速物体的运动;而电磁场是一种 高速运动,没有理由断言适合于低速物体运动的 变换一定对高速运动的物体同样适用!
t1 t t 2
两事件时间间隔 两事件空间间隔
t t 2 t1
x x2 x1
x x 2 x1
21
6.3 狭义相对论的基本原理 由洛伦兹变换:
x' x ut 1 (u / c)
2
洛仑兹变换
第6章 相对论
x
x' ut '
2
y' y
1 1
c
2
1
2)第二事件发生的时刻为:
∴ 在S’系中测得这两个事件的时间间隔为:
7 Δt' t' t' 2.25 10 s 2 1
18
u t '2 ( t 2 2 x2 ) 3.5 10 7 s c
6.3 狭义相对论的基本原理
洛仑兹变换
第6章 相对论
例:地面观察者测得地面上甲、乙两地相距8.0×106 m ,一列火车由甲到乙作匀速运动,历时 2.0 秒。 求:在与列车同向对地运行且u= 0.6 c 的宇宙飞船中 观测,该列车由甲到乙的路程、时间和速率。
第6章 相对论
由光速不变原理和狭义相对性原理,可得 到洛仑兹坐标变换:
x' x ut 1 (u / c )2
y' y z' z
t'
s
2
y
s'
o'
z'
y'
u
* ( x ' , y' , z ' , t )
x'
P ( x, y, z, t )
t ux / c 2 1 (u / c )
6.3 狭义相对论的基本原理 一
洛仑兹变换
第6章 相对论
狭义相对论的基本原理
1)爱因斯坦相对性原理:一切物理定律 在所有的惯性系中都具有相同的表达形式。
相对性原理是自然界的普遍规律。
所有的惯性参考系对物理规律等价。 2)光速不变原理:在所有的惯性系中,真空 中的光速是常量,与光源或观察者的运动无关。 关键概念:相对性和不变性。
16
6.3 狭义相对论的基本原理
洛仑兹变换
第6章 相对论
例:地面参照系 S 中,在 x = 1.0×106 m 处,于 t = 0.02s 时刻爆炸一颗炸弹。一沿 x 轴正方向以速率 u = 0.75 c 运动 飞船上的观察者测得这颗炸弹爆炸的地点和时间? 解: 设飞船为S’系,则可求出炸弹爆炸的空间、 时间坐标分别为:
