2018-2019学年最新浙教版九年级数学上册《相似三角形》同步练习及答案-精编试题
浙教版九年级上册数学第4章 相似三角形含答案(查漏补缺)
浙教版九年级上册数学第4章相似三角形含答案一、单选题(共15题,共计45分)1、如图所示是一个直角三角形的苗圃,由一个正方形花坛和两块直角三角形的草皮组成.如果两个直角三角形的两条斜边长分别为4米和6米,则草皮的总面积为()平方米.A.3B.9C.12D.242、如图,在中,,以其三边为边向外作正方形,过点作于点,再过点作分别交边,于点,.若,,则的长为A.14B.15C.D.3、如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为()A.1:2B.1:4C.2:1D.4:14、如图,在△ABC中,D是BC的中点,DE⊥BC交AC与E,已知AD=AB,连接BE交AD于F,下列结论:①BE=CE;②∠CAD=∠ABE;③AF=DF;④S△ABF =3S△DEF;⑤△DEF∽△DAE,其中正确的有()个.A.5B.4C.3D.25、如图①,在边长为的正方形中,点以每秒的速度从点出发,沿的路径运动,到点停止.过点作,与边(或边)交于点,的长度与点的运动时间(秒)的函数图象如图②所示.当点运动秒时,的长是().A. B. C. D.6、如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH,④CH2=HO•HD中,正确的有()个.A.1B.2C.3D.47、如图,在△ABC 中,点E 是线段AC 上一点,AE∶CE=1∶2,过点C 作CD∥AB 交BE 的延长线于点D,若△ABE 的面积等于 4,则△BCD 的面积等于()A.8B.16C.24D.328、如图,△ABC与△DEF是位似图形,点A(﹣1,2)和点D(2,﹣4)是对应点,则△ABC内的点P(m,n)的对应点P′的坐标为()A.(2m,2n)B.(﹣2m,﹣2n)C.(2m,﹣2n)D.(﹣2m,2n)9、如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是()A.BO:BC=1:2B.CD:AB=2:1C.CO:BC=1:2 D.AD:DO=3:110、如图,在▱ABCD中,E是AB的中点,EC交BD于点F,那么EF与CF的比是()A.1:2B.1:3C.2:1D.3:111、已知三个数为3,4,12,若再添加一个数,使这四个数能组成一个比例,那么这个数可以是()A.1B.2C.3D.412、如下图,以某点为位似中心,将△AOB进行位似变换得到△CDE,记△AOB 与△CDE对应边的比为k,则位似中心的坐标和k的值分别为()A. B. C. D.13、△ABC与△DEF满足下列条件,其中能使△ABC∽△DEF的是( )A.AB=1,BC=1.5,AC=2,DE=8,EF=12,DF=16B.AB=,BC=,AC=,DE=,EF=3,DF=3 C.AB=3,BC=4,AC=6,DE =6,EF=8,DF=16 D.AB=3,BC=4,AC=5,DE=,EF=2,DF=14、如图,在△ABC中,点D、E分别在AB、AC上,DE∥BC.若AD=6,DB=3,则的值为()A. B. C. D.215、如图,在矩形ABCD中,AB=12,P是AB上一点,将△PBC沿直线PC折叠,顶点B的对应点是G,过点B作BE⊥CG,垂足为E,且在AD上,BE 交PC于点F,则下列结论,其中正确的结论有()①BP=BF;②若点E是AD的中点,那么△AEB≌△DEC;③当AD=25,且AE<DE时,则DE=16;④在③的条件下,可得sin∠PCB=;⑤当BP=9时,BE•EF=108.A.2个B.3个C.4个D.5个二、填空题(共10题,共计30分)16、已知Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D是AB中点,点E是直线AC上一点,若以C、D、E为顶点的三角形与△ABC相似,则AE的长度为________.17、若,则________.18、如图,已知△ABC中,∠C=90°,BC=3,AC=4,BD平分∠ABC,将△ABC绕着点A旋转后,点B、C的对应点分别记为B1、C1,如果点B1,落在射线BD上,那么CC1的长度为 ________ .19、如图,在矩形中,,E是CD延长线上一点,连接BE交AD于点F,连接CF,若与的面积相等,则DE长为________.20、如图,直线AA1∥BB1∥CC1,如果, AA1=2,CC1=6,那么线段BB1的长是________ .21、如图,在▱ABCD中,AB=10,AD=6,点E是AD的中点,在AB上取一点F,使△CBF与△CDE相似,则BF的长是________.22、如图,AG:GD=4∶1, BD :DC=2∶3,则AE∶EC的值为________.23、如图,在中,点E在边AD上,AE:AD=2:3,BE与AC交于点F.若AC=20,则AF的长为________.24、已知在△ABC和△DEF中,,且△DEF与△ABC的周长之差为,则△ABC的周长为________.25、如图,四边形ABCD中,AD∥BC,CM是∠BCD的平分线,且CM⊥AB,M为垂足,AM= AB.若四边形ABCD的面积为,则四边形AMCD的面积是________.三、解答题(共5题,共计25分)26、22.若==≠0,求的值.27、如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.(1)求EC的值;(2)求证:AD•AG=AF•AB.28、某校九(2)班学生在一次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量,下面是他们通过测量得到的一些信息:甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm;乙组:如图2,测得学校旗杆的影长为900 cm;丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200 cm,影长为156 cm.请你根据以上信息,解答下列问题:(1)计算学校旗杆的高度.(2)如图3,设太阳光线NH与⊙O相切于点M,请根据甲、丙两组得到的信息,求景灯灯罩的半径.(友情提示:如图3,景灯的影长等于线段NG的影长,需要时可采用等式1562+2082=2602)29、理解与应用小明在学习相似三角形时,在北京市义务教育课程改革实验教材第17册书,第37页遇到这样一道题:如图1,在△ABC中,P是边AB上的一点,联结CP.要使△ACP∽△ABC,还需要补充的一个条件是____________,或_________.请回答:(1)小明补充的条件是____________________,或_________________.(2)请你参考上面的图形和结论,探究、解答下面的问题:如图2,在△ABC中,∠A=60°,AC2= AB2+AB.BC.求∠B的度数.30、如图,已知P是正△ABC外接圆的上的任一点,AP交BC于D.求证:PA2=AC2+PB•PC.参考答案一、单选题(共15题,共计45分)1、C2、A3、B4、B5、B6、D7、C8、B9、B10、A11、A12、C13、A14、A15、C二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、27、29、。
浙教版数学九年级上册 第四章 相似三角形 单元练习(含答案)

浙教版数学九年级上册第四章相似三角形一、选择题1.如果2a =5b ,那么下列比例式中正确的是( )A .a b =25B .a 5=2b C .a 2=b 5D .a 5=b 22.如图,直线l 1∥l 2∥l 3,AC =6,DE =3,EF =2,则AB 的长为( )A .3B .125C .165D .1853.如图,点P 是线段AB 的黄金分割点,且PA >PB ,若AB =2,则PA 的长度是( )A .5−1B .3−5C .25−4D .14.如图, 在▱ABCD 中, E 是边AB 上一点, 连结AC ,DE 相交于点F . 若AE EB =23,则 AF CF 等于( )A .13B .23C .25D .355.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC 相似的是( )A .B .C.D.6.△ABC和△DEF是两个等边三角形,AB=2,DE=4,则△ABC与△DEF的面积比是( ) A.1:2B.1:4C.1:8D.1:27.如图,在△ABC中,BC=6,AC=8,∠C=90°,以B为圆心,BC长为半径画弧,与AB交于点D,再分别以点A,D为圆心,大于12AD的长为半径画弧,两弧交于点M,N,作直线MN,分别交AC,AB于点E,F,则AE的长度为( )A.52B.103C.3D.228.如图,△ABC和△A1B1C1是以点O为位似中心的位似图形,点A在线段O A1上,若OA:A A1=1:2,则△ABC和△A1B1C1的周长之比为( )A.1:2B.2:1C.1:3D.3:19.如图,在△ABC中,D为线段AC上一点,点E在AC的延长线上,过点D作DF∥AB交BC于点F,连结BE,EF,若A C2+D E2=A E2,则△BEF与△DCF的面积比为( )A.1:2B.1:3C.2:3D.2:510.如图,矩形ABCD中,AB=4,AD=2,E为边AD上一个动点,连接BE,取BE的中点G,点G绕点E逆时针旋转90°得到点F,连接CF,则△CEF面积的最小值是( )A .4B .154C .3D .114二、填空题11.如图,AC 、BD 交于点O ,连接AB 、CD ,若要使△AOB ∽△COD ,可以添加条件 .(只需写出一个条件即可)12.已知△ABC ∽△DEF ,且AB:DE =1:3,△ABC 与△DEF 的周长比是 .13.如图,在这架小提琴中,点C 是线段AB 的黄金分割点(BC >AC ).若AB =60cm ,则BC = cm .14.如图,在Rt △ABC 中,∠ABC =90°,AB =4,AC =5,AE 平分∠BAC ,点D 是AC 的中点,AE 与BD交于点O ,则的值AOOE .15.如图,矩形ABCD 中,AB =3 6 ,BC =12,E 为AD 中点,F 为AB 上一点,将△AEF 沿EF 折叠后,点A 恰好落到CF 上的点G 处,则折痕EF 的长是 .16.如图,正方形ABCD 中,BF =FG =CG ,BE =2AE ,CE 交DF 、DG 于M 、N 两点,有下列结论:①DF ⊥EC ;②S △MFC =59S 四边形MFBE ;③DM :MF =2:1;④MN NC =913.其中,正确的有 .三、解答题17.(1)已知线段a =2,b =6,求线段a ,b 的比例中项线段c 的长.(2)已知x :y =3:2,求2x−yx的值.18.如图,已知D 、E 分别是△ABC 的边AB 、AC 上的点,DE ∥BC ,AD BD =32,求DE BC 的值.19.如图,AD 、BC 相交于点P ,连接AC 、BD ,且∠1=∠2,AC =6,CP =4,DP =2,求BD 的长.20. 如图,在平行四边形ABCD 中,E 为DC 边上一点,∠EAB =∠EBC .(1)求证:△ABE∽△BEC ;(2)若AB=4,DE=3,求BE的长.21.如图,在四边形ABCD中,OA=OC,OB=OD,AB=BC,AC=12,BD=16.(1)求证:四边形ABCD时菱形;(2)延长BC至点M,连接OM交CD于点N,若∠M=12∠BAC,求MNOM.22.如图,AB∥CD,且AB=2CD,E是AB的中点,F是边BC上的动点(F不与B,C重合),EF与BD相交于点M.(1)求证:△FDM∽△FBM;(2)若F是BC的中点,BD=18,求BM的长;(3)若AD=BC,BD平分∠ABC,点P是线段BD上的动点,是否存在点P使DP⋅BP=BF⋅CD,若存在,求出∠CPF的度数;若不存在,请说明理由.23.如图,在平面直角坐标系中,已知抛物线y=12x2+bx+c与x轴交于A、B两点,与y轴交于C点,且OB=OC=4.(1)求抛物线的解析式;(2)在抛物线上是否存在点M,使∠ABC=∠BCM,如果存在,求M点的坐标,如果不存在,说明理由;(3)若D是抛物线第二象限上一动点,过点D作DF⊥x轴于点F,过点A、B、D的圆与DF交于E点,求△ABE的面积.答案解析部分1.【答案】D2.【答案】D3.【答案】A4.【答案】C5.【答案】B6.【答案】B7.【答案】A8.【答案】C9.【答案】A10.【答案】B11.【答案】∠A=∠C(答案不唯一)12.【答案】1:313.【答案】(305−30)14.【答案】9415.【答案】21516.【答案】①④17.【答案】(1)解:∵线段a=2,b=6,线段c是线段a、b的比例中项,∴c2=ab=12,∴c=23(负值舍去);(2)解:∵x:y=3:2,∴可设x=3k,y=2k(k≠0),∴2x−yx=6k−2k3k=43.18.【答案】3519.【答案】BD=320.【答案】(1)证明:∵平行四边形ABCD,∴AB//CD,∴∠EBA=∠BEC,又∵∠EAB=∠EBC,∴△ABE∽△BEC.(2)解:∵四边形ABCD 平行四边形,∴AB =DC =4,∵DE =3,∴CE =1,∵△ABE∽△BEC ,∴AB EB =EBEC,∴AB ⋅CE =B E 2=4×1=4,∴BE =2.21.【答案】(1)证明:∵ 在四边形ABCD 中,OA=OC ,OB=OD∴ 四边形ABCD 是平行四边形 ∵ AB=BC∴ 平行四边形ABCD 是菱形。
(基础题)浙教版九年级上册数学第4章 相似三角形含答案

浙教版九年级上册数学第4章相似三角形含答案一、单选题(共15题,共计45分)1、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=2,BD=1,则AD的长是()A.1B.C.2D.42、如图,在四边形ABCD中,BD平分∠ABC,∠BAD=∠BDC=90°,E为BC的中点,AE与BD相交于点F.若BC=4,∠CBD=30°,则DF的长为()A. B. C. D.3、如图,在平行四边形中,F为BC中点,延长AD至E,连结EF交DC 于点G,若,则()A.1:2B.1:3C.1:4D.2:94、如图,锐角△ABC的高CD和BE相交于点O,图中与△ODB相似的三角形有()A.4个B.3个C.2个D.1个5、已知线段a、b、c,其中c是a、b的比例中项,若a=9cm,b=4cm,则线段c长()A.18cmB.5cmC.6cmD.±6cm6、如图,已知点A、B分别是反比例函数y= (x>0),y= (x<0)的图象上的点,且,∠AOB=90°,则的值为()A.4B.C.2D.7、下列条件,不能判定△ABC与△DEF相似的是()A.∠C=∠F=90°,∠A=55°,∠D=35°B.∠C=∠F=90°,AB=10,BC=6,DE=15,EF=9C.∠C=∠F=90°,D.∠B=∠E=90°,=8、如图,平行四边形ABCD中,点E为AD边中点,连接AC、BE交于点,若的面积为关于的一元二次方程的解,则的面积为().A.4B.5C.6D.79、小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为30°,同一时刻,一根长为1米且垂直于地面放置的标杆在地面上的影长为2米,则树的高度为()A.(6+ )米B.12米C.(4﹣2 )米D.10米10、如图,已知△ABO与△DCO位似,且△ABO与△DCO的面积之比为1:4,点B的坐标为(﹣3,2),则点C的坐标为( )A.(3,﹣2)B.(6,﹣4)C.(4,﹣6)D.(6,4)11、如图,I是△ABC的内心,AI的延长线与△ABC的外接圆相交于点D,与BC 交于点E,连接BI、CI、BD、DC.下列说法中正确的有()①∠CAD绕点A顺时针旋转一定的角度一定能与∠DAB重合;②I到△ABC三个顶点的距离相等;③∠BIC=90°+ ∠BAC;④线段DI是线段DE与DA的比例中项;⑤点D是△BIC的外心.A.1个B.2个C.3个D.4个12、如图,已知△ABC,P是边AB上的一点,连结CP,以下条件中不能确定△ACP与△ABC相似的是()A.∠ACP=∠BB.∠APC='∠ACB'C.AC 2=AP·ABD.13、如图,△ABC是⊙O的内接三角形,把沿BC折叠后,与弦AB交于点P,恰好OP⊥AB.若OP=1,AB=4,则BC:AC等于()A. B. C. D.14、如右图所示为农村一古老的捣碎器,已知支撑柱的高为0.3米,踏板长为1.6米,支撑点到踏脚的距离为0.6米,原来捣头点着地,现在踏脚着地,则捣头点上升了()A.1.2米B.1米C.0.8米D.1.5米15、生活中到处可见黄金分割的美.如图,在设计人体雕像时,使雕像的腰部以下a与全身b的高度比值接近0.618,可以增加视觉美感.若图中b为2米,则a约为()A.1.24米B.1.38米C.1.42米D.1.62米二、填空题(共10题,共计30分)16、如图,矩形ABCD中,AB=3cm,AD=6cm,点E为AB边上的任意一点,四边形EFGB也是矩形,且EF=2BE,则S△AFC =________cm2.17、如图,B、C、D依次为一直线上4个点,BC=3,△BCE为等边三角形,⊙O 过A、D、E三点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系式为________.18、如图,已知Rt ABC中,AC=b,BC=a,D1是斜边AB的中点,过D1作D 1E1⊥AC于E1,连结BE1交CD1于D2;过D2作D2E2⊥AC于E2,连结BE2交CD1于D3;过D3作D3E3⊥AC于E3,…,如此继续,可以依次得到点D4,D 5,…,Dn,分别记BD1E1,BD2E2,BD3E3,…,BDnEn的面积为S1, S2, S3,…Sn.则(1)=________,(2)Sn=________.19、如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,已知AE=6,,则EC的长是________.20、如图,要使△ABC与△DBA相似,则只需添加一个适当的条件是________(填一个即可).21、如图,n+1个边长为2的等边三角形有一条边在同一直线上,设△B2D1C1的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则Sn=________(用含n的式子表示).22、如图,在菱形中,是的中点,连接,,将沿直线翻折,使得点落在上的点处,连接并延长交于点,则的值为________.23、如果,∠C=∠F=90°,AB=5,BC=3,DE=15,则DF=________.24、若线段MN的长为1,P是MN的黄金分割点(MP<NP),则MP的长为________.25、如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=________三、解答题(共5题,共计25分)26、已知x:y:z=2:3:4,求的值.27、如图,AB是⊙O的直径,C,P是上两点,AB=13,AC=5.(1)如图(1),若点P是的中点,求PA的长;(2)如图(2),若点P是的中点,求PA的长.28、周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D,竖起标杆DE,使得点E与点C. A共线.已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.29、已知:= = ,x﹣y+z=6,求:代数式3x﹣2y+z的值.30、如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后点D的对应点D2的坐标.参考答案一、单选题(共15题,共计45分)1、D2、D3、B4、B5、C6、C7、D9、A10、B11、D12、D13、B14、C15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、28、29、30、。
【浙教版】九年级数学上册第四章相似三角形能力提升训练(一)及答案

第四章相似三角形单元培优训练(一)一. 选择题1.如图,A , B 两地被池塘隔开,小明通过下列方法测出了 AB 间的距离:先在AB 外选一点C,然后测出AC BC 的中点M N,并测量出MN 勺长为12m 由此他就知道了 AB 间的距离. 有关他这次探究活动的描述错误的是( )A. AB=24mB.MN//ABiT : H i图2甲:将边长为3.4.5的三角形按图1的方式向外扩张,得到 新三角形,它们的对应边间距为1,则新三角形与原三角形相 似.乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新 的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似.2.如图,在△ ABC 中, D.E 分别是ABBC 上的点,且DE/AC 右 S A BD E S A CD =1 : 4, S A BDE S A AC =()A.1 : 16B. 1 :18C.1 : 20D.1:243.在研究相似问题时,甲 .乙同学的观点如下:图1第1题 第2题C. CMN s CABD. CM : MA 1:2对于两人的观点,下列说法正确的是()A.两人都对B.两人都不对C.甲对,乙不对D.甲不对,乙对4. 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S,S2,则S i S2的值为()A.16B.17C. 18D.195. 如图,已知直线I : y仝x,过点A (0, 1 )作y轴的垂3线交直线I于点B,过点B作直线I的垂线交y轴于点A;过点A作y轴的垂线交直线I于点B,过点B作直线I的垂线交y轴于点A;…;按此作法继续下去,则点A的坐标为( )A. (0, 64)B. (0, 128)C. (0, 256)D. (0, 512)=NM= 2 , ME二 3,贝卩AN =( )A.3B.4C.5D.67. 已知△ ABC的三边长分别为20cm , 50cm 60cm,现要利用长度分别为30cm和60cm的细木条各一根,做一个三角形木架与三角形相似,要求以其中一根为一边,将另一根截成两段(允许有余料)作为另外两边.那么另两边的长度(单位:cm分别为()A.10,25B.10 ,36 或12,36C.12,36D.10 ,25或12,368. 如图,Rt△ ABC中,/ ACB90°,Z AB(=60°, BC=2cm D为BC的中点,若动点E以1cn/s的速度从A点出发,沿着2B^A 的方向运动,设E点的运动时间为t秒(0W t v6), 连接DE当厶BDE是直角三角形时,t的值为()A.2B.2.5 或3.5C.3.5 或4.5D.2 或3.5 或4.59. 已知:在厶ABC中, BO10, BC边上的高h=5,点E在边AB 上,过点E作EF// BC,交AC边于点F.点D为BC上一点,连接DEDF 设点E到BC的距离为X,则厶DEF的面积S关于x的函数图象大致为()5② 乂 ABE^ ACD③ BEFDO DE ④ B E +D C =D E , 其中正确的有( )个. A.1B.2C.3D.4二. 填空题11. 如图,在?ABCDK E 在 AB 上, CEBD 交于 F ,若 AE BE=4:E12. 如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点020米的A 处,则小明的影子AM 长为 _____ 米. 13. 如图,小明在打网球时,使球恰好能打过网,而且落在离网4米的位置上,则球拍击球的高度 h 为 ______________ 14. 将一副三角尺如图所示叠放在一起,则的值是_______10. 如图,/ BAC / DA =90° 上的两点,且/ DAE 45° 连接EFBF,则下列结论: ① 厶 AED^ AEFAB=AQ ADAF,点 DE 为 BC i3,且 BF =2,贝H DF= _____第11题第12题第13题15. 劳技课上小敏拿出了一个腰长为8厘米,底边为6厘米的等腰三角形,她想用这个等腰三角形加工成一个边长比是1: 2的平行四边形,平行四边形的一个内角恰好是这个等 腰三角形的底角,平行四边形的其它顶点均在三角形的边 上,则这个平行四边形的较短的边长为 _______________若厶AEF 勺面积为2,则四边形EBCF 勺面积为 _________ 17.如图,在平面直角坐标系中,四边形OAB 是边长为2的正 方形,顶点AC 分别在x , y 轴的正半轴上•点Q 在对角线的坐标为 __________________ 18.如图,正方形ABCDK 过点D 作DP 交AC 于点M 交AB于点N,交CB 的延长线于点P,若MN 1, PN =4,则DM 勺20. 如图,在△ ABC 中, AB=2, AG=4,将厶ABC 绕点C按逆OB 上且Q OO 连接CC 并延长CC 交边AB 于点P.则点P时针方向旋转得到△ A B C,使CB // AB,分别延长AB, CA 相交于点D,则线段BD的长为 _____________三.解答题21. 如图,口ABCDK E是CD勺延长线上一点,BE与AD交于点F, DE 〔CD .2(1)求证:△ ABF^A CEB(2)若厶DEF的面积为2,求口ABCD勺面积“厂22. 矩形OAB啲顶点AC分别在x轴和y轴上,点B的坐标为4,6,双曲线y k(x 0)的图象经过BC的中点D,且于AB交x于点E(1)求反比例函数解析式和E点坐标;(2)若F是OC上一点,且以/ OAF和/ CFD为对应角的厶FDC WA AFC相似,求F点的坐标.23.如图,抛物线y ax2bx c a 0与x轴交于点A 1,0 ,B 3,0两点,与y轴交于点C 0, 3 . (1)求该抛物线的解析式及顶点M的坐标;(2)求厶BCM面积与△ ABC面积的比;(3)若P是x轴上一个动点,过P作射线PQ/ AC交抛物线于点Q随着P点的运动,在抛物线上是否存在这样的点Q使以A P QC为顶点的四边形为平行四边形?若存在请求出QM参考答案.选择题二填空题L11. —12.513-1 1.5米 14. —L5. 2.4cm sE —cm3 31116. IS 17(2, 4 - 2723 IS. 丄20.6三.解答题21.解:⑴证明:T 四边形 ABC [是平行四边形,•••/ A =Z C, AB// C [ •••/ ABF ^Z CEBABI ^A CEB⑵T 四边形ABC [是平行四边形,••• AD// BC AB £ C[T DE 丄CD2 ,22-SDEFDE 1 S DEF DE 1 SCEBEC 9,SABFAB4T S DEF2,…SCEB18, SABF8, • -S四边形BCDFSBCE…S四边形ABCD S四边形BCDFSABF16 8 24•••△ DEI ^A CEB △ DEI ^A ABF ,SDEF16 ,22.解:(1)四边形ABC [是矩形,D 是BC 中点,B 4,6二D 2,6设反比例函数解析式为y k V 6 - ••• k 12 y 12 x2 x 当 x 4 时,y 123 二 E 4,3 4(2)设 F 0,yV / OAF / DFC △ AOM FDC...O F CD 即 y _2_ OA CF 4 6 y.y 2 6y 8 0 解得:y i 2 y ? 4n訂.給 ⑴设抛物魏解析式为尸二必托+1)(兀—耳T 抛物娃过点(0誇)—<4小)[0-孑)■ Q —1抛物线解析式 ^^ = (^+1)(^3)=・・•严二/-2才一呂=("1『-4 上 财(1,4)(2) iSBCs B 皿 CM,作 K> 丄* 轴于 D■/弋一….=E... 亠尺 …__弋=1乂代亠4人1亠丄弱九』_12“ =]亠?_? =2S ABC 14 3 62 (3)存在①当Q 点在x 轴下方时,作 QEL x 轴于Ev AC/ PQ M A(=PQ 二 0CEQ 33 X 2 2x 3 解得:X , 0 (舍) X 2 2 Q 2, 3②当Q 点在x 轴上方时,作 QH x 轴于F v AC/ PQ M A(=PQ . Rt A 0AC2 Rt A FPQ . 0CFQ=3 3 x 2 2x 3 解得:x , 1 .7 x 2 1 . 7.Q 1 7,3 或 Q 1 .7,3S BCM :S ABC 3:6 1:2综上,满足条件的Q 点为2, 3或1.7,3或1 7,3。
(基础题)浙教版九年级上册数学第4章 相似三角形含答案

浙教版九年级上册数学第4章相似三角形含答案一、单选题(共15题,共计45分)1、已知,若,,则的度数为()A.30°B.70°C.80°D.120°2、如图,在中,,点是的中点,连接,将沿翻折得到与交于点,连接.若,则点到的距离为()A. B. C. D.3、如图,在▱ABCD中,E是AB的中点,EC交BD于点F,那么()A.1:2B.1:3C.1:4D.2:34、若将一个正方形的各边长扩大为原来的4倍,则这个正方形的面积扩大为原来的()A.16倍B.8倍C.4倍D.2倍5、如图,五边形ABCDE和五边形A1B1C1D1E1是位似图形,且PA1=PA,则AB∶A1B1=( )A. B. C. D.6、在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加美感,按此比例,如果雕像的身高为3米,设雕像的上部为x米,根据其比例关系可得其方程应为()A. B. C. D.7、如图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R应是甲、乙、丙、丁四点中的()A.甲B.乙C.丙D.丁8、如图,在中,,分别是和上的点,且,若,,则的长是()A.12B.10C.8D.69、勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉,生活中到处可见黄金分割的美.如图,点将线段分成两部分,且,如果,那么称点为线段的黄金分割点.若是线段的黄金分割点,,则分割后较短线段长为()A. B. C. D.10、如图,D,E分别是△ABC的边AB,AC上的点,DE∥BC,若=,则等于()A. B. C. D.11、已知2x=3y,则下列比例式成立的是( )A. B. C. D.12、如图,点在反比例函数上,连接分别交轴于点D、点E,且,将沿翻折,点D刚好落在y轴上的点F处,与x轴交于点G,已知,则k的值为()A.3B.4C.5D.613、具备下列各组条件的两个三角形中,不一定相似的是().A.有一个角是40°的两个等腰三角形;B.两个等腰直角三角形;C.有一个角为100°的两个等腰三角形;D.两个等边三角形14、已知,如图一张三角形纸片ABC,边AB长为10cm,AB边上的高为15cm,在三角形内从左到右叠放边长为2的正方形小纸片,第一次小纸片的一条边都在AB上,依次这样往上叠放上去,则最多能叠放的正方形的个数是( ).A.12B.13C.14D.1515、如图的两个四边形相似,则∠α的度数是()A.87°B.60°C.75°D.120°二、填空题(共10题,共计30分)16、如图,锐角三角形ABC的边AB,AC上的高线EC,BF相交于点D,请写出图中的两对相似三角形________.(用相似符号连接)17、如图,在矩形中,点是的中点,点为射线上的一个动点,沿着折叠得到,连接,分别交和直线于点和,已知,,若与相似,则的长度是________.18、《九章算术》是中国古代的数学专著,它奠定了中国古代数学的基本框架,以计算为中心,密切联系实际,以解决人们生产、生活中的数学问题为目的.书中记载了这样一个问题:“今有勾五步,股十二步,问勾中容方几何?”其大意是:如图,Rt△ABC的两条直角边的长分别为5和12,则它的内接正方形CDEF的边长为________.19、如图,在△ABC中,点D,E分别在AB,AC上,∠AED=∠B,AB=2AE,若△ADE的面积为2,则四边形BCED的面积为________.20、把一矩形纸片对折,如果对折后的矩形与原矩形相似,则原矩形纸片的长与宽之比为________21、如图,上体育课,甲、乙两名同学分别站在C、D的位置时,乙的影子恰好在甲的影子里边,已知甲,乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是________米.22、若= = =0.5,则=________.23、点P是线段AB的黄金分割点(AP>BP),则=________.24、如图,在边长为3的等边△ABC中,点D在AC上,且CD=1,点E在AB上(不与点A、B重合),连接DE,把△ADE沿DE折叠,当点A的对应点F落在等边△ABC的边上时,AE的长为________.25、在矩形中,,,点,分别为,上的两个动点,将沿折叠,点的对应点为,若点落在射线上,且恰为直角三角形,则线段的长为________.三、解答题(共5题,共计25分)26、已知=k,求k2-3k-4的值.27、如图,已知矩形OABC中,OA=2,AB=4,双曲线y=(k>0)与矩形两边AB、BC分别交于E、F.(1)若E是AB的中点,求F点的坐标;(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,请证明△EGD∽△DCF,并求出k的值.28、为了测量水平地面上一棵不可攀的树的高度,某学校数学兴趣小组做了如下的探索:根据光的反射定律,利用一面镜子和一根皮尺,设计如图所示的测量方案:把一面很小的镜子放在与树底端B相距8米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=2米,观察者目高CD=1.5米,则树AB的高度.29、我们通常用到的一种复印纸,整张称为A1纸,对折一分为二裁开成为A2纸,再一分为二成为A3纸,…,它们都是相似的矩形.求这种纸的长与宽的比值(精确到千分位).30、如图,AD是Rt△ABC斜边上的高,若AB=4cm,BC=10cm,求BD的长.参考答案一、单选题(共15题,共计45分)1、C2、D3、A4、A5、B6、A7、C8、A9、B11、C12、D13、A14、C15、A二、填空题(共10题,共计30分)16、17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)27、29、30、。
九年级数学上册第四章《相似三角形》练习题-浙教版(含答案)

九年级数学上册第四章《相似三角形》练习题-浙教版(含答案)一.选择题:(本题共10小题,每小题3分,共30分)温馨提示:每一题的四个答案中只有一个是正确的,请将正确的答案选择出来!1.如图,ABC △与DEF △位似,点O 为位似中心,相似比为2:3.若ABC △的周长为4,则DEF △的周长是( ) A.4B.6C.9D.162.若ABC ∆∽DEF ∆,6BC =,4EF =,则ACDF=( ) A.49B.94C.23D.323.两个相似三角形的面积之比为1:4,较小的三角形的周长为4,则另一个三角形的周长为( ) A .16 B .8C .2D .14.设32yx =,则y x y x 523+-的值为( )A .113B .199 C .193 D .167 5.如图,矩形EFGH 的四个顶点分别在菱形ABCD 的四条边上,BE BF =.将AEH △,CFG △分别沿边EH ,FG 折叠,当重叠部分为菱形且面积是菱形ABCD 面积的116时,则EB AE 为( ) A .53B .2C .25D .356.如图,△ABC 内接于⊙O ,AB 为⊙O 的直径,D 为⊙O 上一点(位于AB 下方),CD 交AB 于点E ,若∠BDC =45°,BC =62 ,CE =2DE ,则CE 的长为( ) A .22B .24C .53D .547.如图平行四边形ABCD 中,F 为BC 中点,延长AD 至E ,使4:3:=AE AD ,连结EF 交DC 于点G ,则=∆∆CPG DEG S S :( ) A .2∶3B .4∶9C .9∶4D .3∶28.如图,在四边形ABCD 中,以AB 为直径的O 恰好经过点C ,AC ,DO 交于点E ,已知AC 平分BAD ∠,90ADC ∠=︒,:25CD BC =:CE AE 的值为( )A .2:5B .4:5C .5:22D .5:89.由四个全等的直角三角形和一个小正方形组成的大正方形ABCD 如图所示.过点D 作DF 的垂线交小正方形对角线EF 的延长线于点G ,连结CG ,延长BE 交CG 于点H .若AE =2BE ,则BHCG的值为( ) A .23 B .2C .7103 D .553 10.将一张以AB 为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD ,其中90A ∠=︒,9AB =,7BC =,6CD =,2AD =,则剪掉的两个直角三角形的斜边长不可能是( ) A.252B.454C.10D.354二.填空题(本题共6小题,每题4分,共24分) 温馨提示:填空题必须是最简洁最正确的答案!11.如图,线段AB 两个端点的坐标分别为()12,12A ,()4,16B ,以原点O 为位似中心,在第一象限内将线段AB 缩小为原来的21后得到线段CD ,则端点D 的坐标为12.如图,在梯形ABCD 中,AD ∥EF ∥BC ,且AE :EB =2:3,CD =15,则FC = 13.如图,M 是Rt △ABC 的斜边BC 上异于B 、C 的一定点,过M 点作直线截△ABC ,使截得的三角形与△ABC 相似,这样的直线共有______________14.如图,在△ABC 中,∠ACB =90°,边BC 在x 轴上,顶点A ,B 的坐标分别为(-2,6)和(7,0).将正方形OCDE 沿x 轴向右平移,当点E 落在AB 边上时,平移的距离为_____________ 15.如图,在锐角三角形ABC 中,6cm AB =,12cm AC =,动点D 从点A 出发到点B 停止,动点E 从点C 出发到点A 停止,点D 运动的速度为1cm/s ,点E 运动的速度为2cm/s ,如果两点同时开始运动,那么以点A ,D ,E 为顶点的三角形与ABC 相似时的运动时间为_______________16.如图,四边形ABCD 是正方形,点E 在边AD 上,BEF △是以E 为直角顶点的等腰直角三角形,EF ,BF 分别交CD 于点M ,N ,过点F 作AD 的垂线交AD 的延长线于点G .连接DF ,请完成下列问题:(1)FDG ∠=_______°;(2)若1DE =,22DF =,则MN =________.三.解答题(共6题,共66分)温馨提示:解答题应将必要的解答过程呈现出来!17.(本题6分)如图,在△ABC 中,D 、E 分别是AB ,AC 上的点,∠AED =∠B ,△ABC 用平分线AF 交DE 于点G ,交BC 于点F .(1)求证:△AED ∽△ABC .(2)设23AD AC,求AG AF的值.18.(本题8分)如图,在平行四边形ABCD 中,对角线AC 、BD 交于点O .M 为AD 中点,连接CM 交BD 于点N .(1)求DN :BN 的值;(2)若△OCN 的面积为2,求四边形AONM 的面积.19(本题8分)如图,在ABC △中,点D ,E ,F 分别在边AB ,AC ,BC 上,连接DE ,EF ,已知四边形BFED 是平行四边形,14DE BC =.(1)若8AB =,求线段AD 的长.(2)若ADE △的面积为1,求平行四边形BFED 的面积.20.(本题10分)如图,锐角三角形ABC 内接于⊙O ,∠BAC 的平分线AG 交⊙O 于点G ,交BC 边于点F ,连接BG .(1)求证:△ABG ∽△AFC .(2)已知AB =a ,AC =AF =b ,求线段FG 的长(用含a ,b的代数式表示).(3)已知点E 在线段AF 上(不与点A ,点F 重合),点D 在线段AE 上(不与点A ,点E 重合),∠ABD =∠CBE ,求证:BG 2=GE •GD .21.(本题10分)如图,在平行四边形ABCD 中,点E 是AC 上一点,射线BE 与CD 的延长线交于点P ,与边AD 交于点F ,连接FC .(1)若∠ABF =∠ACF ,求证:CE 2=EF •EP ; (2)若点D 是CP 中点,BE =32,求EF 的长.22(本题12分).如图,已知△ABC 是边长为6cm 的等边三角形,动点P 、Q 同时从A 、B 两点出发,分别沿AB 、BC 匀速运动,其中点P 运动的速度是1cm /s ,点Q 运动的速度是2cm /s ,当点Q 到达点C 时,P 、Q 两点都停止运动,设运动时间为t (s ),解答下列问题:(1)当t =2时,判断△BPQ 的形状,并说明理由;(2)设△BPQ 的面积为S (cm 2),求S 与t 的函数关系式;(3)作QR ∥BA 交AC 于点R ,连接PR ,当t 为何值时,△APR ∽△PRQ .23(本题12分)如图,已知抛物线24y ax ax =-交x 轴于点A ,与直线12y x =交于点B (非原点),过点B 作BC ∥x 轴交抛物线于点C ,6BC =.(1)求a 的值.(2)若P 是线段BC 上一点,过点P 作x 轴的垂线分别交直线OB 与抛物线于E ,F .求线段EF 的最大值.(3)若P 是射线BC 上一点,作点F 关于直线BC 的对称点G ,连结PG ,BG .是否存在BPG ∆与PBE ∆相似,若不存在请说明理由,若存在请求出点G 的坐标.参考答案一、选择题:(本题共10小题,每小题3分,共30分)温馨提示:每一题的四个答案中只有一个是正确的,请将正确的答案选择出来!1.答案:B解析:由两个位似图形的周长比等于位似比可知,23ABC DEF C C =△△, 334622DEF ABC C C ∴==⨯=△△.故选B.2.答案:D解析:~ABC DEF △△, BC ACEF DF∴=, 6BC =,4EF =,6342AC DF ∴==. 故选择:D3.答案:B解析:设另一个三角形的周长为x ,则 4:x =41, 解得:x =8.故另一个三角形的周长为8, 故选:B .4.答案:C 解析:∵32y x = ∴y x 32=,∴19331953425322323523==+-=+⨯-⨯=+-y y y y y y y y yy y x y x . 故选:C .5.答案:D解析:设重叠的菱形边长为x ,BE =BF =y ,由矩形和菱形的对称性以及折叠的性质得:四边形AHME 、四边形BENF 是菱形, ∴AE =EM ,EN =BE =y ,EM =x +y ,∵当重叠部分为菱形且面积是菱形ABCD 面积的116,且两个菱形相似, ∴AB =4MN =4x , ∴AE =AB -BE =4x -y , ∴4x -y =x +y , 解得:x =23y ,∴AE =53y ,∴5533yAE EB y ==, ∴35BE AE =, 故选:D .6.答案:D解析:连接CO ,过点D 作DG ⊥AB 于点G ,连接AD ,∵∠BDC =45°, ∴∠CAO =∠CDB =45°, ∵AB 为⊙O 的直径, ∴∠ACB =∠ADB =90°, ∴∠CAB =∠CBA =45°, ∵BC =62, ∴AB = 2BC =12, ∵OA =OB , ∴CO ⊥AB ,∴∠COA =∠DGE =90°, ∵∠DEG =∠CEO , ∴△DGE ∽△COE , ∴CDDGOE GE CE DE ===21, ∵CE =2DE ,设GE =x ,则OE =2x ,DG =3, ∴AG =6﹣3x ,BG =6+3x , ∵∠ADB =∠AGD =90°, ∠DAG =∠BAD , ∴△AGD ∽△ADB , ∴DG 2=AG •BG ,∴9=(6﹣3x )(6+3x ), ∵x >0, ∴x =3, ∴OE =23 ,在Rt △OCE 中,由勾股定理得:CE =34361222=+=+OC OE ,故答案为:D .7.答案:B解析:∵4:3:=AE AD ∴设x AE x AD 4,3==, ∴x x x AD AE DE =-=-=34, ∵四边形ABCD 是平行四边形, ∴x AD BC BC AD 3,//==,∵点F 是BC 的中点,xBC CF 2321==∴BC AD //FCG EDG CFG DEG ∠=∠∠=∠∴,∴△DEG ∽△CFG,942322=⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=∴∆∆x x CF DE S S CFGDEG故答案为:B .8.答案:D解析:如图所示,连接OC ∵AB 是圆的直径, ∴∠ACB =∠ADC =90°, ∵AC 平分∠BAD ,∴∠DAC =∠CAB ,∠DAB =2∠CAB , ∴△ADC ∽△ACB , ∴5CD AC ADBC AB AC==, ∴25AC AB =, ∴225BC AB AC AB =-=,455AD AC AB == ∴255CD AB ==,又∵∠BOC =2∠CAB , ∴∠BOC =∠DAB , ∴AD ∥OC , ∴△OCE ∽△DAE ,∴152485AB CE OC AE DA AB ===,故选D .9.答案:C解析:如图,过点G 作GT ⊥CF 交CF 的延长线于T ,设BH 交CF 于M ,AE 交DF 于N .设BE =AN =CM =DF =a ,则AE =BM =CF =DN =2a , ∴EN =EM =MF =FN =a , ∵四边形ENFM 是正方形,∴∠EFH =∠TFG =45°,∠NFE =∠DFG =45°, ∵GT ⊥TF ,DF ⊥DG ,∴∠TGF =∠TFG =∠DFG =∠DGF =45°, ∴TG =FT =DF =DG =a , ∴CT =3a ,CG =()a a a 10322=+,∵MH ∥TG , ∴△CMH ∽△CTG , ∴CM :CT =MH :TG =1:3, ∴MH =a 31, ∴BH =a a a 37312=+, ∴71033710==a a BH CG ,故选:C .10.答案:A 解析:如图1所示,由已知可得,~DFE ECB △△, 则DF FE DEEC CB EB==, 设DF x =,CE y =, 则9672x yy x+==+, 解得274214x y ⎧=⎪⎪⎨⎪=⎪⎩,2145644DE CD CE ∴=+=+=,故选项B 不符合题意; 2735244EB DF AD =+=+=,故选项D 不符合题意; 如图2所示,由已知可得,DCF FEB △△, 则DC CF DF FE EB FB==, 设FC m =,FD n =, 则6927m nn m ==++, 解得810m n =⎧⎨=⎩,10FD ∴=,故选项C 不符合题意; 8614BF FC BC =+=+=,如图3所示:此时两个直角三角形的斜边长为6和7; 故选A.二、填空题(本题共6小题,每题4分,共24分)温馨提示:填空题必须是最简洁最正确的答案!11.答案:(8,2)解析:∵线段AB 端点B 的坐标分别为B (16,4),以原点O 为位似中心,在第一象限内将线段AB 缩小为原来的21后得到线段CD , ∴端点D 的横坐标和纵坐标都变为B 点的一半,∴端点D 的坐标为:(8,2).故答案是:(8,2).12.答案:9解析:∵AD ∥BC ∥EF ,AE :EB =2:3,∴32==EB AE FC DF , ∴35=FC DC , ∵CD =15,∴FC =9.故答案为:9.13.答案:三条解析:过点M 作直线与另一边相交,使所得的三角形与原三角形有一个公共角,只要再作一个直角就可以.因此,∵截得的三角形与△ABC 相似,∴过点M 作AB 的垂线,或作AC 的垂线,或作BC 的垂线,所得三角形满足题意∴过点M 作直线l 共有三条.15.答案:4解:如图,设正方形D ′C ′O ′E ′是正方形OCDE 沿x 轴向右平移后的正方形,∵顶点A ,B 的坐标分别为(-2,6)和(7,0),∴AC =6,OC =2,OB =7,∴BC =9,∵四边形OCDE 是正方形,∴DE =OC =OE =2,∴O ′E ′=O ′C ′=2,∵E ′O ′⊥BC ,∴∠BO ′E ′=∠BCA =90°,∴E ′O ′∥AC ,∴△BO ′E ′∽△BCA , ∴E O BO AC BC =''', ∴269BO '=, ∴BO ′=3,∴OO ′=7-3=4,15.答案:3s 或4.8s .解析:设以点A ,D ,E 为顶点的三角形与ABC 相似时的运动时间为s t , 根据题意得:cm AD t = ,2cm CE t = ,则()122cm AE t =- ,当ADE ABC ,即AD AE AB AC = 时, ∴122612t t -=,解得:3t = ; 当ADE ACB ,即AD AE AC AB = 时, ∴122126t t -=,解得: 4.8t = , 综上所述,以点A ,D ,E 为顶点的三角形与ABC 相似时的运动时间为3s 或4.8s .16.答案:045 1526 解析:(1)90A BEF G ∠=∠=∠=︒,BE EF =,易证ABE GEF ≅△△,EG AB AD ∴==,GF AE =,DG AE GF ∴==,DFG ∴△是等腰直角三角形,45FDG ∴∠=︒.(2)由(1)可知DFG △是等腰直角三角形.又22DF =,2DG GF ∴==,123CD BC AB EG ED DG ∴====+=+=.如图,分别延长GF ,BC ,两线交于点H ,则//CD GH ,3GH CD ==,2CH DG ==,EDM EGF ∴△△,BNC BFH △△,MD ED GF EG ∴=,NC BC FH BH=, 即123MD =,33232NC =-+, 23MD ∴=,35NC =, 232633515MN CD MD NC ∴=--=--=.三.解答题(共6题,共66分)温馨提示:解答题应将必要的解答过程呈现出来!17.解析:(1)∵∠AED =∠B ,∠BAC =∠DAE ,∴△AED ∽△ABC ;(2)∵△AED ∽△ABC ,∴∠ADE =∠ACB ,∵AF 平分∠BAC ,∴∠DAG =∠CAF ,∴△ADG ∽△ACF , ∴2=3AG AD AF AC =.18.解析:(1)∵四边形ABCD 是平行四边形,∴AD ∥BC ,且AD =BC ,∴∠MDN =∠CBN ,又∵∠BNC =∠DNM ,∴△MND ∽△CNB ,∴BNDN BC DM =, ∵M 为AD 的中点, ∴BC AD DM 2121==, ∴DN :BN =1:2;(2)连接OM ,∵△MND ∽△CNB ,DN :BN =1:2;∴MN :CN =1:2,∴MC :CN =3:2,∴S △OCM :S △OCN =3:2,∵S △OCN =2,∴S △OCM =3,∴S △ACM =2S △OCM =6,∴S 四边形AONM =S △ACM ﹣S △OCN =6﹣2=4.19.解析:(1)由题意,得//DE BC ,所以ADE ABC ∽△△, 所以14AD DE AB BC ==. 因为8AB =,所以2AD =.(2)设ABC △的面积为S ,ADE △的面积为1S ,CEF △的面积为2S . 因为14AD AB =, 所以21116S AD S AB ⎛⎫== ⎪⎝⎭. 因为11S =,所以16S =.因为34CE CA =, 所以同理可得29S =,所以平行四边形BFED 的面积126S S S =--=.20.解析:(1)证明:∵AG 平分∠BAC ,∴∠BAG =∠FAC ,又∵∠G =∠C ,∴△ABG ∽△AFC ;(2)由(1)知,△ABG ∽△AFC ,∴ACAG AF AB =, ∵AC =AF =b ,∴AB =AG =a ,∴FG =AG ﹣AF =a ﹣b ;(3)∵∠CAG =∠CBG ,∠BAG =∠CAG ,∴∠BAG =∠CBG ,∵∠ABD =∠CBE ,∴∠BDG =∠BAG +∠ABD =∠CBG +∠CBE =∠EBG ,又∵∠DGB =∠BGE ,∴△DGB ∽△BGE , ∴GE BG BG GD =, ∴GD GE BG ⨯=2.21.解析:(1)∵平行四边形ABCD ,射线BE 与CD 的延长线交于点P , ∴AB ∥CD ,∴∠ABF =∠P ,∵∠ABF =∠ACF ,∴∠ACF =∠P ,∵∠CEF =∠PEC ,∴△CEF ∽△PEC ,∴CEEF PE CE =, 即CE 2=EF •PE ;(2))∵平行四边形ABCD ,射线BE 与CD 的延长线交于点P , ∴AB ∥CD ,AB =CD ,AD ∥BC ,∴∠ABF =∠P ,∵∠AEB =∠CEP ,∴△BEA ∽△PEC ,∴CPAB PE BE =, ∵点D 是CP 的中点, ∴CP =2CD =2AB ,点F 是BP 的中点,∴2132=PE解得:34=PE ,∴PF =21BP =21(BE +PE )=33 ∴EF =PE ﹣PF =322.解析:(1)△BPQ 是等边三角形当t =2时AP =2×1=2,BQ =2×2=4∴BP =AB ﹣AP =6﹣2=4∴BQ =BP又∵∠B =60°∴△BPQ 是等边三角形;(2)过Q 作QE ⊥AB ,垂足为E在Rt △BEQ 中,∠BQE =90°﹣∠B =30°,QB =2t , ∴BE =t ,QE =3t 由AP =t ,得PB =6﹣t∴S △BPQ =21×BP ×QE =21(6﹣t )×3t =t t 33232+- ∴t t s 33232+-=; (3)∵QR ∥BA∴∠QRC =∠A =60°,∠RQC =∠B =60°∴△QRC 是等边三角形∴QR =RC =QC =6﹣2t∵BE =BQ •cos60°=21×2t =t ∴EP =AB ﹣AP ﹣BE =6﹣t ﹣t =6﹣2t∴EP ∥QR ,EP =QR∴四边形EPRQ 是平行四边形∴PR =EQ =3t又∵∠PEQ =90°,∴∠APR =∠PRQ =90°∵△APR ∽△PRQ , ∴AP PR PR QR =, ∴t t tt 3326=- 解得t =56 ∴当t =56时,△APR ∽△PRQ .23.解析:(1)抛物线24y ax ax =-,令120,0,4y x x === , 抛物线对称轴为422a x a-=-= , ∵B 点在抛物线上,且BC =6,∴B 点横坐标为6252+= , ∵B 点在直线12y x =上, ∴代入B 点横坐标求得52y =,即55,2B ⎛⎫ ⎪⎝⎭ , 将55,2B ⎛⎫ ⎪⎝⎭代入24y ax ax =-,得:525202a a =-,解得12a = ; (2)由(1)知12a =,所以抛物线为2122y x x =- , ∵P 是线段BC 上一点,PF x ⊥轴,∴E 、F 的横坐标15x -≤≤ , 设EF 的最大值为M ,E 、F 横坐标相同,则22111522222M x x x x x ⎛⎫=--=-+ ⎪⎝⎭,为开口向下的抛物线,有最大值,2215404252214842ac b M a ⎛⎫⎛⎫⨯-⨯- ⎪ ⎪-⎝⎭⎝⎭===-⨯,∴EF 的最大值为258; (3)存在, 如图:EF 交x 轴于点M∵//BC x 轴,∴OEM BEP , ∵BEP GBP , ∴OEM GBP , ∴OM EM GP BP= , ∵P 在射线BC 上且可形成△GPB ,55,2B ⎛⎫ ⎪⎝⎭, 设P 点横坐标为x ,∴P 点横坐标5x < ,∴5PB x =- ,G 点、E 点、F 点横坐标都为x , ∵E 在直线12y x =上, ∴1,2OM x EM x == , ∵G 为点F 关于直线BC 的对称点,且F 在抛物线2122y x x =-上, ∴21,22F x x x ⎛⎫- ⎪⎝⎭, 即2122MF x x =- , ∴215222PF x x =-+ , ∴215222PG x x =-+ , ∴OM EM GP BP ==212155222x x xx x =--+ 解得:123,5x x == ,∵5x <,∴取3x = , ∴2152422PG x x =-+= , ∴G 点纵坐标为513422+= ,∴133,2G ⎛⎫ ⎪⎝⎭.。
浙教版九年级数学上册:4.5 相似三角形的性质及应用 同步练习(含答案)

4.5 相似三角形的性质及其应用一.填空题1.(2019•奉贤区一模)联结三角形各边中点,所得的三角形的周长与原三角形周长的比是.2.(2019•南关区一模)利用标杆CD测量建筑物的高度的示意图如图所示,若标杆CD的高为1.5米,测得DE=2米,BD=18米,则建筑物的高AB为米.3.(2019•曲阜市二模)学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,BD 足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为.4.(2019春•广陵区校级期末)如图,∠ACB=90°,CD是Rt△ABC斜边上的高,已知AB=25cm,BC=15cm,则BD=.5.(2019春•滨湖区期末)如图,平行四边形ABCD中,点E为BC边上一点,AE和BD交于点F,已知△ABF的面积等于6,△BEF的面积等于4,则四边形CDFE的面积等于.二.选择题(共10小题)6.(2019春•海州区校级月考)若P是Rt△ABC斜边BC上异于B,C的一点,过点P作直线截△ABC,截得的三角形与原△ABC相似,满足这样条件的直线有()条.A.1 B.2 C.3 D.47.(2018秋•嘉兴期末)如图,有一块三角形余料ABC,BC=120mm,高线AD=80mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM:PQ=3:2,则PM的长为()A.60mm B.mm C.20mm D.mm8.(2019•新乐市二模)“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=()A.1.2 里B.1.5 里C.1.05 里D.1.02 里9.(2018春•南票区期末)如图,在平行四边形ABCD中,O1、O2、O3分别是对角线BD上的三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于点F,则AF:DF等于()A.19:2 B.9:1 C.8:1 D.7:110.(2018秋•秀洲区期末)如图,点G是△ABC的重心,下列结论中正确的个数有()①=;②=;③△EDG∽△CBG;④=.A.1个B.2个C.3个D.4个11.若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则△ABC与△DEF的周长比为()A.3:4 B.4:3 C.:2 D.2:12.(2018秋•道里区期末)如图,△ABC∽△ADE,且BC=2DE,则的值为()A.B.C.D.13.(2018秋•南岗区校级月考)两个相似三角形的一组对应边的长分别是15和23,它们周长的差是40,则这两个三角形的周长分别为()A.75,115 B.60,100 C.85,125 D.45,8514.(2019•毕节市)如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为()A.100cm2B.150cm2C.170cm2D.200cm215.(2018秋•襄州区期末)如图是小明设计用手电筒来测量某古城墙高度的示意图.在地面上点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=18米,那么该古城墙的高度是()A.6米B.8米C.12米D.24米三.解答题16.(2019•余杭区二模)如图,在△ABC中,AD、BE是中线,它们相交于点F,EG∥BC,交AD于点G.(1)求证:△FGE∽△FDB;(2)求的值.17.(2018秋•梁溪区校级期中)(1)如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点P是边AB上一点,若△PAD∽△CBP,请利用没有刻度的直尺和圆规,画出满足条件的所有点P;(2)在(1)的条件下,若AB=8,AD=3,BC=4,则AP的长是.18.(2018秋•德清县期末)如图,点C,D在线段AB上,CD2=AC•DB,且△PCD是等边三角形.(1)证明:△ACP∽△PDB;(2)求∠APB的度数.19.(2018秋•昌图县期末)如图,路灯(点P)距地面6m,身高1.5m的学生小明从路灯的底部点O处,沿射线OH走到距路灯底部9m的点B处,此时小明的身影为BN,接着小明走到点N处,此时的身影为AM.求学生小明的身影长度变长了多少米.(小明如图中BD、AC所示)20.(2018秋•番禺区期末)如图,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,设EG=xmm,EF=ymm.(1)写出x与y的关系式;(2)用S表示矩形EGHF的面积,某同学说当矩形EGHF为正方形时S最大,这个说法正确吗?说明理由,并求出S的最大值.参考答案一.填空题1.(2019•奉贤区一模)联结三角形各边中点,所得的三角形的周长与原三角形周长的比是1:2.【思路点拨】根据D、E、F分别是AB、BC、AC的中点,求证△DEF∽△ABC,然后利用相似三角形周长比等于相似比,可得出答案.【答案】解:如图,∵D、E、F分别是AB、BC、AC的中点,∴DE=AC,DF=BC,EF=AB,∴DE+DF+EF=AC+BC+AB,∵△DEF∽△ABC,∴所得到的△DEF与△ABC的周长之比是:1:2.故答案为:1:2.【点睛】此题考查了相似三角形的判定与性质和三角形中位线定理的理解和掌握,解答此题的关键是利用了相似三角形周长比等于相似比.2.(2019•南关区一模)利用标杆CD测量建筑物的高度的示意图如图所示,若标杆CD的高为1.5米,测得DE=2米,BD=18米,则建筑物的高AB为15米.【思路点拨】根据同一时刻同一地点物高与影长成正比列式求得CD的长即可.【答案】解:∵AB∥CD,∴△EBA∽△ECD,∴=,即=,∴AB=15(米).故答案为:15.【点睛】本题考查了相似三角形的应用,解题的关键是从实际问题中整理出直角三角形,难度不大.3.(2019•曲阜市二模)学校门口的栏杆如图所示,栏杆从水平位置BD绕O点旋转到AC位置,已知AB⊥BD,BD 足分别为B,D,AO=4m,AB=1.6m,CO=1m,则栏杆C端应下降的垂直距离CD为0.4m.【思路点拨】由∠ABO=∠CDO=90°、∠AOB=∠COD知△ABO∽△CDO,据此得=,将已知数据代入即可得.【答案】解:∵AB⊥BD,CD⊥BD,∴∠ABO=∠CDO=90°,又∵∠AOB=∠COD,∴△ABO∽△CDO,则=,∵AO=4m,AB=1.6m,CO=1m,∴=,解得:CD=0.4,∴栏杆C端应下降的垂直距离CD为0.4m.故答案为:0.4.【点睛】本题主要考查相似三角形的应用,解题的关键是熟练掌握相似三角形的判定与性质.4.(2019春•广陵区校级期末)如图,∠ACB=90°,CD是Rt△ABC斜边上的高,已知AB=25cm,BC=15cm,则BD=9cm.【思路点拨】根据相似三角形的判定和性质即可得到结论.【答案】解:∵CD⊥AB,∴∠CDB=∠ACB=90°,∵∠B=∠B,∴△ACB∽△CDB,∴,∴,解得:BD=9cm,故答案为:9cm.【点睛】本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.5.(2019春•滨湖区期末)如图,平行四边形ABCD中,点E为BC边上一点,AE和BD交于点F,已知△ABF的面积等于6,△BEF的面积等于4,则四边形CDFE的面积等于11.【思路点拨】利用三角形面积公式得到AF:FE=3:2,再根据平行四边形的性质得到AD∥BE,S△ABD=S△CBD,则可判断△AFD∽△EFB,利用相似的性质可计算出S△AFD=9,所以S△ABD=S△CBD=15,然后用△BCD的面积减去△BEF的面积得到四边形CDFE的面积.【答案】解:∵△ABF的面积等于6,△BEF的面积等于4,即S△ABF:S△BEF=6:4=3:2,∴AF:FE=3:2,∵四边形ABCD为平行四边形,∴AD∥BE,S△ABD=S△CBD,∴△AFD∽△EFB,∴=()2=()2=,∴S△AFD=×4=9,∴S△ABD=S△CBD=6+9=15,∴四边形CDFE的面积=15﹣4=11.故答案为11.【点睛】本题考查了相似三角形的判定与性质:在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形,灵活运用相似三角形的性质表示线段之间的关系;也考查了平行四边形的性质.二.选择题6.(2019春•海州区校级月考)若P是Rt△ABC斜边BC上异于B,C的一点,过点P作直线截△ABC,截得的三角形与原△ABC相似,满足这样条件的直线有()条.A.1 B.2 C.3 D.4【思路点拨】过点P作直线与另一边相交,使所得的三角形与原三角形有一个公共角,只要再作一个直角就可以.【答案】解:由于△ABC是直角三角形,过P点作直线截△ABC,则截得的三角形与△ABC有一公共角,所以只要再作一个直角即可使截得的三角形与Rt△ABC相似,过点P可作AB的垂线、AC的垂线、BC的垂线,共3条直线.故选:C.【点睛】本题主要考查三角形相似判定定理及其运用.解题时运用了两角法(有两组角对应相等的两个三角形相似)来判定两个三角形相似.7.(2018秋•嘉兴期末)如图,有一块三角形余料ABC,BC=120mm,高线AD=80mm,要把它加工成一个矩形零件,使矩形的一边在BC上,点P,M分别在AB,AC上,若满足PM:PQ=3:2,则PM的长为()A.60mm B.mm C.20mm D.mm【思路点拨】利用相似三角形的性质构建方程即可解决问题.【答案】解:如图,设AD交PN于点K.∵PM:PQ=3:2,∴可以假设MP=3k,PQ=2k.∵四边形PQNM是矩形,∴PM∥BC,∴△APM∽△ABC,∵AD⊥BC,BC∥PM,∴AD⊥PN,∴=,∴=,解得k=20mm,∴PM=3k=60mm,故选:A.【点睛】本题考查相似三角形的应用,解题的关键是学会利用参数构建方程解决问题,属于中考常考题型.8.(2019•新乐市二模)“今有邑,东西七里,南北九里,各开中门,出东门一十五里有木,问:出南门几何步而见木?”这段话摘自《九章算术》.意思是说:如图,矩形城池ABCD,东边城墙AB长9里,南边城墙AD长7里,东门点E、南门点F分别是AB、AD中点,EG⊥AB,FH⊥AD,EG=15里,HG经过A点,则FH=()A.1.2 里B.1.5 里C.1.05 里D.1.02 里【思路点拨】首先根据题意得到△GEA∽△AFH,然后利用相似三角形的对应边的比相等列出比例式求得答案即可.【答案】解:如图所示:∵EG⊥AB,FH⊥AD,HG经过A点,∴FA∥EG,EA∥FH,∴∠HFA=∠AEG=90°,∠FHA=∠EAG,∴△GEA∽△AFH,∴=.∵AB=9里,DA=7里,EG=15里,∴FA=3.5里,EA=4.5里,∴=,解得:FH=1.05里.故选:C.【点睛】本题考查了相似三角形的应用,解题的关键是从实际问题中整理出相似三角形.9.(2018春•南票区期末)如图,在平行四边形ABCD中,O1、O2、O3分别是对角线BD上的三点,且BO1=O1O2=O2O3=O3D,连接AO1并延长交BC于点E,连接EO3并延长交AD于点F,则AF:DF等于()A.19:2 B.9:1 C.8:1 D.7:1【思路点拨】根据题意,易得△BO3E∽△DO3F和△BO1E∽△DO1A,利用相似的性质得出DF:BE的值,再求出BE:AD的值,进而求出AF:DF.【答案】解:根题意,在平行四边形ABCD中,易得△BO3E∽△DO3F∴BE:FD=3:1∵△BO1E∽△DO1A∴BE:AD=1:3∴AD:DF=9:1∴AF:DF=(AD﹣FD):DF=(9﹣1):1=8:1故选:C.【点睛】考查了平行四边形的性质,对边相等.利用相似三角形三边成比例列式,求解即可.10.(2018秋•秀洲区期末)如图,点G是△ABC的重心,下列结论中正确的个数有()①=;②=;③△EDG∽△CBG;④=.A.1个B.2个C.3个D.4个【思路点拨】根据三角形的重心的概念和性质得到AE,CD是△ABC的中线,根据三角形中位线定理得到DE∥BC,DE=BC,根据相似三角形的性质定理判断即可.【答案】解:∵点G是△ABC的重心,∴AE,CD是△ABC的中线,∴DE∥BC,DE=BC,∴△DGE∽△BGC,∴=,①正确;=,②正确;△EDG∽△CBG,③正确;=()2=,④正确,故选:D.【点睛】本题考查的是三角形的重心的概念和性质,相似三角形的判定和性质,三角形中位线定理,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.11.若△ABC∽△DEF,且S△ABC:S△DEF=3:4,则△ABC与△DEF的周长比为()A.3:4 B.4:3 C.:2 D.2:【思路点拨】由△ABC∽△DEF,S△ABC:S△DEF=3:4,根据相似三角形的面积比等于相似比的平方,即可求得答案.【答案】解:∵△ABC∽△DEF,S△ABC:S△DEF=3:4,∴△ABC与△DEF的相似比为::2,∴△ABC与△DEF的周长比为::2.故选:C.【点睛】此题考查了相似三角形的性质.注意相似三角形面积的比等于相似比的平方.12.(2018秋•道里区期末)如图,△ABC∽△ADE,且BC=2DE,则的值为()A.B.C.D.【思路点拨】根据相似三角形的性质解答即可.【答案】解:∵△ABC∽△ADE,且BC=2DE,∴,∴,故选:B.【点睛】此题考查相似三角形的性质,关键是根据相似三角形的面积之比等于相似比的平方解答.13.(2018秋•南岗区校级月考)两个相似三角形的一组对应边的长分别是15和23,它们周长的差是40,则这两个三角形的周长分别为()A.75,115 B.60,100 C.85,125 D.45,85【思路点拨】根据两个相似三角形的对应边的长,可求出它们的相似比,也就求出了它们的周长比,再根据它们的周长差为40,即可求出两三角形的周长.【答案】解:∵两相似三角形的一组对应边为15和23,∴两相似三角形的周长比为15:23,设较小的三角形的周长为15a,则较大三角形的周长为23a,依题意,有:23a﹣15a=40,a=5,∴15a=75,23a=115,因此这两个三角形的周长分别为75,115.故选:A.【点睛】本题考查对相似三角形性质的理解:相似三角形周长的比等于相似比.14.(2019•毕节市)如图,在一块斜边长30cm的直角三角形木板(Rt△ACB)上截取一个正方形CDEF,点D在边BC上,点E在斜边AB上,点F在边AC上,若AF:AC=1:3,则这块木板截取正方形CDEF后,剩余部分的面积为()A.100cm2B.150cm2C.170cm2D.200cm2【思路点拨】设AF=x,根据正方形的性质用x表示出EF、CF,证明△AEF∽△ABC,根据相似三角形的性质求出BC,根据勾股定理列式求出x,根据三角形的面积公式、正方形的面积公式计算即可.【答案】解:设AF=x,则AC=3x,∵四边形CDEF为正方形,∴EF=CF=2x,EF∥BC,∴△AEF∽△ABC,∴==,∴BC=6x,在Rt△ABC中,AB2=AC2+BC2,即302=(3x)2+(6x)2,解得,x=2,∴AC=6,BC=12,∴剩余部分的面积=×12×6﹣4×4=100(cm2),故选:A.【点睛】本题考查的是相似三角形的应用、正方形的性质,掌握相似三角形的判定定理和性质定理是解题的关键.15.(2018秋•襄州区期末)如图是小明设计用手电筒来测量某古城墙高度的示意图.在地面上点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=18米,那么该古城墙的高度是()A.6米B.8米C.12米D.24米【思路点拨】因为小明和古城墙均和地面垂直,且光线的入射角等于反射角,因此构成一组相似三角形,利用对应边成比例即可解答.【答案】解:由题意知:∠APB=∠CPD,∠ABP=∠CDP=90°,∴Rt△ABP∽Rt△CDP,∴=,∴CD==12(米).故选:C.【点睛】本题考查了相似三角形的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问.三.解答题16.(2019•余杭区二模)如图,在△ABC中,AD、BE是中线,它们相交于点F,EG∥BC,交AD于点G.(1)求证:△FGE∽△FDB;(2)求的值.【思路点拨】(1)由GE∥BC,可得出∠GEF=∠DBF,再结合对顶角相等即可得出△FGE∽△FDB;(2)根据三角形中位线定理以及中线的定义得出GE=BD、AG=DG,再利用相似三角形的性质得出DF=DG,进而即可得出=.【答案】(1)证明:∵GE∥BC,∴∠GEF=∠DBF.又∵∠GFE=∠DFB,∴△FGE∽△FDB;(2)∵AD、BE是中线,EG∥BC,∴GE为△ADC的中位线,BD=DC,∴GE=DC=BD,AG=DG.∵△FGE∽△FDB,∴==,∴DF=DG,∴==.【点睛】本题考查了相似三角形的判定与性质、三角形中线的定义以及中位线定理,解题的关键是:(1)由GE(2)根据相似三角形的性质结合中位线定理得出DF=DG、∥BC利用相似三角形的判定定理证出△EGF∽△BDF;AG=DG.17.(2018秋•梁溪区校级期中)(1)如图,在四边形ABCD中,AD∥BC,∠ABC=90°,点P是边AB上一点,若△PAD∽△CBP,请利用没有刻度的直尺和圆规,画出满足条件的所有点P;(2)在(1)的条件下,若AB=8,AD=3,BC=4,则AP的长是2或6.【思路点拨】(1)先作CD中垂线得出CD的中点,再以中点为圆心,CD为半径作圆,与AB的交点即为所求;(2)证△APD∽△BPC得=,即=,解之可得.【答案】解:(1)如图所示,点P1和点P2即为所求.(2)∵AB⊥BC,∴∠B=90°.∵AD∥BC,∴∠A=180°﹣∠B=90°,∴∠PAD=∠PBC=90°.∴∠ADP+∠APD=90°,由(1)知,∠CPD=90°,∴∠APD+∠BPC=90°,∴∠ADP=∠BPC,∴△APD∽△BPC,∴=,即=,解得:AP=2或AP=6.故答案为:2或6.【点睛】本题主要考查作图﹣相似变换,解题的关键是掌握线段中垂线的尺规作图及圆周角定理,相似三角形的判定与性质等知识点.18.(2018秋•德清县期末)如图,点C,D在线段AB上,CD2=AC•DB,且△PCD是等边三角形.(1)证明:△ACP∽△PDB;(2)求∠APB的度数.【思路点拨】(1)根据PC=PD=CD,以及CD2=AC•DB,可得,又∠ACP=∠PDB,则△ACP∽△PDB;(2)根据(1)的结论求出∠APC+∠BPD度数,最后加上∠CPD度数即可.【答案】(本小题8分)解:(1)∵△PCD是等边三角形,∴∠PCD=∠PDC=60°,∴∠ACP=∠PDB=120°,∵CD2=AC•DB,由PC=PD=CD可得:PC•PD=AC•DB,即,∴△ACP∽△PDB;(2)∵△ACP∽△PDB,∴∠APC=∠PBD.∵∠PDB=120°,∴∠DPB+∠DBP=60°,∴∠APC+∠BPD=60°.∴∠APB=∠CPD+∠APC+∠BPD=120°.【点睛】本题主要考查了相似三角形的判定和性质、等边三角形的判定和性质,三角形相似的判定一直是中考考查的热点之一,在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形;或依据基本图形对图形进行分解、组合;或作辅助线构造相似三角形,判定三角形相似的方法有事可单独使用,有时需要综合运用,无论是单独使用还是综合运用,都要具备应有的条件方可.19.(2018秋•昌图县期末)如图,路灯(点P)距地面6m,身高1.5m的学生小明从路灯的底部点O处,沿射线OH走到距路灯底部9m的点B处,此时小明的身影为BN,接着小明走到点N处,此时的身影为AM.求学生小明的身影长度变长了多少米.(小明如图中BD、AC所示)【思路点拨】根据相似三角形的性质解答即可.【答案】解:由题意知,∠PON=∠DBN=90°,△PON∽△DBN∴又∵OB=9∴BN=3,OA=12由题意知,∠POM=∠CAM=90°,△POM∽△CAM∴又∵OA=12∴AM=4,OM=16∴身影长BN=3,AM=4,AM﹣BN=4﹣3=1∴小明的身影长度变长了1米.【点睛】此题考查相似三角形的应用,关键是根据相似三角形的性质解答.20.(2018秋•番禺区期末)如图,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD=80mm,把它加工成矩形零件,使矩形的一边在BC上,其余两个顶点分别在AB、AC上,设EG=xmm,EF=ymm.(1)写出x与y的关系式;(2)用S表示矩形EGHF的面积,某同学说当矩形EGHF为正方形时S最大,这个说法正确吗?说明理由,并求出S的最大值.【思路点拨】(1)证明△AEF∽△ABC,利用相似比得到=,从而得到y与x的关系式;(2)计算矩形的面积S=xy=﹣x2+120x,则S=﹣(x﹣40)2+2400,根据二次函数的性质得到当x=40时,S有最大值2400,由于y=60,此时矩形不为正方形,所以这个同学的说法错误.【答案】解:(1)易得四边形EGDK为矩形,则KD=EG=x,∴AK=AD﹣DK=80﹣x,∵EF∥BC,∴△AEF∽△ABC,∴=,即=,∴y=﹣x+120(0<x<80);(2)这个同学的说法错误.理由如下:S=xy=﹣x2+120x=﹣(x﹣40)2+2400,当x=40时,S有最大值2400,此时y=﹣×40+120=60,即矩形EGHF的长为60mm,宽为40mm时,矩形EGHF的面积最大,最大值为2400mm2,此时矩形不为正方形,所以这个同学的说法错误.【点睛】本题考查了相似三角形的应用:常常构造“A”型或“X”型相似图,用相似三角形对应边的比相等的性质求相应线段的长.也考查了二次函数的性质和矩形的性质.。
浙教版九年级上《第四章相似三角形》期末复习试题(有答案)

期末复习:浙教版九年级数学学上册第四章相似三角形一、单选题(共10题;共30分)1.若△ABC∽△DEF,顶点A、B、C分别与D、E、F对应,且AB:DE=1:4,则这两个三角形的面积比为()A. 1:2B. 1:4C. 1:8D. 1:162.如图,在△ABC中,点D,E分AB,AC边上,DE∥BC,若AD:AB=3:4,AE=6,则AC等于()A. 3B. 4C. 6D. 83.△ABC和△DEF相似,且相似比为,那么它们的周长比是()A. B. C. D.4.如图,△ABC中,AD⊥BC于D ,下列条件:①∠B+∠DAC=90°;②∠B=∠DAC;③ = ;④AB2=BD•BC .其中一定能够判定△ABC是直角三角形的有()A. 1B. 2C. 3D. 45.若把△ABC的各边扩大到原的3倍后,得△A′B′C′,则下列结论错误的是()A. △ABC∽△A′B′C′B. △ABC与△A′B′C′的相似比为14C. △ABC与△A′B′C′的对应角相等D. △ABC与△A′B′C′的相似比为136.如果两个相似三角形对应边之比是1:4,那么它们的对应中线之比是()A. 1:2B. 1:4C. 1:8D. 1:167.如图,斜靠在墙上的梯子AB,梯脚B距墙面1.6米,梯上一点D距墙面1.4米,BD长0.55米,则梯子AB 的长为( )米A. 3.85B. 4.00C. 4.4D. 4.50.8.两个相似多边形的一组对分别是3cm和4.5cm,如果它们的面积之和是,那么较大的多边形的面积是()A. 44.8B. 42C. 52D. 549.在同一时刻,身高1.6米的小强在阳光下的影长为0.8米,一棵大树的影长为4.8米,则树的高度为()A. 10米B. 9.6米C. 6.4米D. 4.8米10.如图,正方形ABCD中,O为BD中点,以BC为边向正方形内作等边△BCE,连接并延长AE交CD于F,连接BD分别交CE、AF于G、H,下列结论:①∠CEH=45°;②GF∥DE;③2OH+DH=BD;④BG=√2DG;⑤S△BEC:S△BGC=√3+1。
浙教版数学九年级上册第四章相似三角形 单元测试(含答案)

浙教版数学九年级上册第四章相似三角形一、选择题1.已知c 是a 和b 的比例中项,a =2,b =18,则c =( )A .±6B .6C .4D .±32.如图,DE ∥BC ,在下列比例式中,不能成立的是()A .AD DB =AEECB .DE BC =AEEC C .AB AD =AC AED .DB EC =ABAC3.如果两个相似三角形的周长之比为5:7,那么这两个三角形的面积之比为( )A .5:7B .7:5C .25:49D .49:254.如图,已知AB ∥CD ∥EF ,AE =9,AC =6,BD =4,则BF 的长是( )A .5B .6C .7D .85.小明在测量楼高时,先测出楼房落在地面上的影长BA 为15米(如图),然后在A 处树立一根高2米的标杆,测得标杆的影长AC 为3米,则楼高为( )A .10米B .12米C .15米D .22.5米6.如图所示,小正方形的边长均为1,则下列选项中阴影部分的三角形与△ABC 相似的是( )A .B .C.D.7.如图,△ABC与△DEF位似,点O为位似中心.已知OA:OD=1:2,则△ABC与△DEF的面积比为( ).A.1:2B.1:3C.1:4D.1:58.如图,在平行四边形ABCD中,E是AB的中点,CE和BD交于点O,设△OCD的面积为m,△OEB的面积为5,则下列结论中正确的是( )A.m=5B.m=45C.m=35D.m=109.如图,已知AB=AC,∠B<30°,BC上一点D满足∠BAD=120°,BDCD =73,则ADAC的值为( )A.12B.33C.13D.3210.如图,在边长为2的正方形ABCD中,对角线AC与BD相交于点O,点P是BD上的一个动点,过点P作EF∥AC,分别交正方形的两条边于点E,F,连接OE,OF,设BP=x,△OEF的面积为y,则能大致反映y与x之间的函数关系的图像为( )A .B .C .D .二、填空题11.如图,线段AC 、BD 交于点O ,请你添加一个条件: ,使△AOB ∽△COD .12.如图,点G 为△ABC 的重心,GE ∥AC ,若DE =2,则DC = .13.在某市建设规划图上,城区南北长为120cm ,该市城区南北实际长为36km ,则该规划图的比例尺是 .14.如图,在Rt △ABC 中,∠ABC =90°,AB =4,AC =5,AE 平分∠BAC ,点D 是AC 的中点,AE 与BD交于点O ,则的值AOOE .15.如图, EB 为驾驶员的盲区,驾驶员的眼睛点 P 处与地面 BE 的距离为1.6米,车头 FACD 近似看成一个矩形,且满足 3FD =2FA ,若盲区 EB 的长度是6米,则车宽 FA 的长度为 米.16.如图,在△ABC中,点D是AC边上一点,将△ABD沿BD翻折得到△EBD,BE与AC交于点F,设AF=x,EF=y.(1)当BE⊥AC,x=9,y=3时,AD的长是 ;(2)当BD=BF,2x=7y时,△DEF与△ABD的面积之比是 .三、解答题17.如图,已知D、E分别是△ABC的边AB、AC上的点,DE∥BC,ADBD =32,求DEBC的值.18.如图,在△ABC中,D为BC上一点,∠BAD=∠C.(1)求证:△ABD∽△CBA;(2)若AB=6,BD=3,求CD的长.19.在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部的(全身)的高度比,可以增加视觉美感,按比例,如果雕像的高为2m,那么它的下部设计为多高?(结果保留小数点后两位)参考数据:2=1.414,3=1.732,5=2.23620.如图,在矩形ABCD中,AB=6,BC=4,E是边BC上的一点(不与B、C重合),DF⊥AE,垂足为F.(1)求证:△ABE∽△DFA;S△ABE,求BE的长.(2)若S△DFA=1321.如图,在△ABC中,AD是BC上的高,且BC=3,AD=2,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB、AC上.(1)设EF=x(0<x<2),矩形EFGH的周长为y,求y关于x的函数解析式;(2)当EFGH为正方形时,求正方形EFGH的面积.22.如图,矩形ABCD中,点M在对角线BD上,过点A、B、M的圆与BC交于点E.(1)若AM=4,EB=EM=3,求BM.(2)若AB=6,BC=8,①求AM:ME.②若BM=7,求BE.23.如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O.点P从点A出发,沿AD方向匀速运动速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长交BC于点E,过点Q作QF//AC,交BD于点F,设运动时间为t(s)(0<t<6),解答下列问题:(1)当t为何值时,△AOP是等腰三角形;(2)设五边形OECQF的面积为S(c m2),试确定S与t的函数关系式;(3)在运动过程中,当S五边形OECQF:S△ACD=9:16时.直接写出t的值.答案解析部分1.【答案】A2.【答案】B3.【答案】C4.【答案】B5.【答案】A6.【答案】A7.【答案】C8.【答案】B9.【答案】A10.【答案】C11.【答案】AB∥CD(答案不唯一)12.【答案】6.13.【答案】1:3000014.【答案】9415.【答案】12716.【答案】5;1417.【答案】3518.【答案】(1)证明:∵∠BAD=∠C,∠B=∠B,∴△ABD∽△CBA(2)解:设DC=x,∵△ABD∽△CBA,∴ABBD=BCAB,∴63=2+x6,解得,x=9;即CD=719.【答案】1.24米.20.【答案】(1)证明:∵四边形ABCD是矩形,AB=6,BC=4,∴∠B=90°,AD∥BC,AD=BC=4,∴∠AEB=∠DAF,∵DF⊥AE,∴∠DFA=90°,∴∠B=∠DFA,∴△ABE∽△DFA;(2)解:∵△ABE∽△DFA,S△DFA=13S△ABE,∴(AEAD )2=S△ABES△DFA=3,∴AEAD=3或AEAD=−3(负数不符合题意,舍去),∴AE=3AD=43,∴BE=AE2−AB2=(43)2−62=12=23,∴BE的长为23.21.【答案】(1)解:设AD,EH交于点M,∵矩形EFGH,∴EH∥BC,AM⊥EH,∴△ABC∼△AEH,∴EHBC=AMAD∵EF=DM=x,AD=2∴AM=2−x∴EH3=2−x2∴EH=32(2−x)∴y=2(EH+EF)=2(3−32x+x)=−x+6(0<x<2)∴y关于x的函数解析式为∴y=−x+6(0<x<2)(2)解:当EFGH为正方形时,∴EF=EH,由(1)得:EF =x ,EH =32(2−x),∵EF =EH ,∴x =3(2−x)2,∴x =65,即EF =65.正方形EFGH 的面积=65×65=3625.22.【答案】(1)245(2)①43,②17423.【答案】(1)解:在矩形ABCD 中,AB =6cm ,BC =8cm ,∴AC =10,①当AP =PO =t ,如图1,过P 作PM ⊥AO 于点M ,∴AM =12AO =52,∵∠PMA =∠ADC =90°,∠PAM =∠CAD ,∴△APM∽△ACD ,∴AP AC =AM AD,∴AP =t =258,②当AP =AO =t =5,∴当t 为258或5时,△AOP 是等腰三角形;(2)解:如图2,过点O 作OH ⊥BC 交BC 于点H ,则OH =12CD =12AB =3cm ,由矩形的性质可知∠PDO =∠EBO ,DO =BO ,又得∠DOP =∠BOE ,∴△DOP≌BOE(ASA),∴BE =PD =8−t ,则S △BOE =12BE ⋅OH =12×3(8−t)=12−32t.∵FQ//AC ,∴△DFQ∽△DOC ,相似比为DQ DC =t6,∴S △DFQ S △DOC =t 236,∵S △DOC =14S 矩形ABCD =14×6×8=12c m 2,∴S △DFQ =12×t 236=t 23,∴S 五边形OECQF =S △DBC −S △BOE −S △DFQ =12×6×8−(12−32t)−t 23=−13t 2+32t +12;∴S 与t 的函数关系式为S =−13t 2+32t +12;(3)t =3或32。
浙教版九年级数学上册第四章:相似三角形基本模型练习题(含答案)
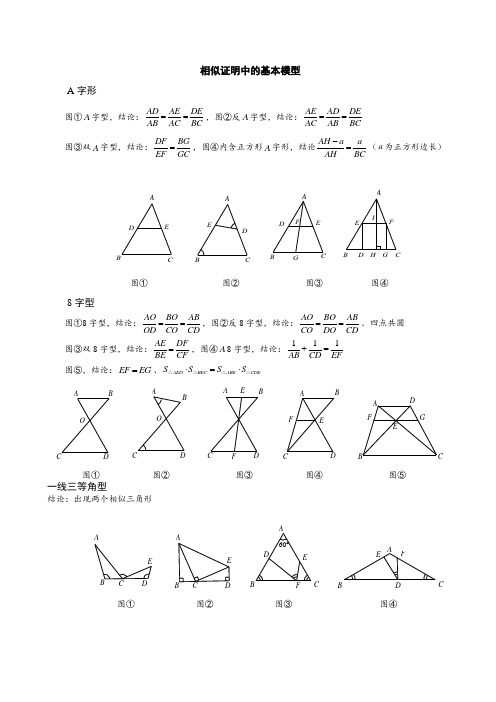
相似证明中的基本模型A 字形图①A 字型,结论:AD AE DE AB AC BC ==,图②反A 字型,结论:AE AD DEAC AB BC== 图③双A 字型,结论:DF BG EF GC =,图④内含正方形A 字形,结论AH a aAH BC-=(a 为正方形边长)IH G FED CB AGFEDC BAEDCB A ED C BA图① 图② 图③ 图④8字型图①8字型,结论:AO BO AB OD CO CD ==,图②反8字型,结论:AO BO AB CO DO CD==、四点共圆 图③双8字型,结论:AE DF BE CF=,图④A 8字型,结论:111AB CD EF += 图⑤,结论:EF EG =、AED BEC ABE CDE S S S S ⋅=⋅△△△△EFD C BA F ED C BAOD C BAODC BAGFED CB A图① 图② 图③ 图④ 图⑤一线三等角型结论:出现两个相似三角形HE DC B AE DC BAEDCBAC60°F E DCB AFED CB A图① 图② 图③ 图④角分线定理与射影定理图①内角分线型,结论:AB BD AC DC =,图②外角分线型,结论:AB BDAC CD= 图③斜射影定理型,结论:2AB BD BC =⋅,图④射影定理型,结论:1、2AC AD AB =⋅,2、2CD AD BD =⋅,3、2BC BD BA =⋅D C BD BCAEDB AD B A梅涅劳斯型常用辅助线G FEDCBAGFEDCBA G E DC B ADEFCBA四、相似证明中的面积法面积法主要是将面积的比,和线段的比进行相互转化来解决问题. 常用的面积法基本模型如下:如图:1212ABC ACDBC AHS BCS CD CD AH ⋅⋅==⋅⋅△△. 图1:“山字”型H DC B A如图:1212ABC BCDBC AHS AH AO S DG OD BC DG ⋅⋅===⋅⋅△△. 图2:“田字”型G HODCBA如图:ABD ABD AED ACE AED ACE S S S AB AD AB ADS S S AE AC AE AC⋅=⋅=⋅=⋅△△△△△△.图3:“燕尾”型CDEB A考点一:相似三角形【例1】 如图,D 、E 是ABC ∆的边AC 、AB 上的点,且AD AC ⋅=AE AB ⋅,求证:ADE B ∠=∠.EDCBA【答案】∵AD AC AE AB ⋅=⋅ ∴AD ABAE AC=∵DAE BAC ∠=∠∴DAE ∆∽BAC ∆∴ADE B ∠=∠ 【例2】 如图,在ABC ∆中,AD BC ⊥于D ,CE AB ⊥于E ,ABC ∆的面积是BDE ∆面积的4倍,6AC =,求DE 的长.ED CB A【答案】∵AD BC ⊥,CE AB ⊥,ABD CBE ∠=∠ ∴ABD ∆∽CBE ∆∴BE BCBD AB=∵EBD CBA ∠=∠ ∴BED ∆∽BCA ∆∴11322DEDE AC AC===⇒== 【例3】 如图,ABC △中,60ABC ∠=︒,点P 是ABC △内一点,使得APB BPC CPA ∠=∠=∠,86PA PC ==,,则PB =________.PCBA【解析】120APB BPC ∠=∠=︒,60BAP ABP ABC ABP CBP ∠=︒-∠=∠-∠=∠,故ABP BCP △∽△,2PB PA PC =⋅.【例4】 如图,已知三个边长相等的正方形相邻并排,求EBF EBG ∠+∠.HGFED CB A【答案】45︒ 【解析】连接DF 、CG ,则45EDF EBF DFB ∠=∠+∠=︒,若DFB EBG ∠=∠,则EBF EBG ∠+∠可求,问题的关键是证明BCG FDB △∽△.考点二:相似三角形与边的比例☞考点说明:可运用相似三角形模型,常用A 字形与8字形【例5】 在ABC ∆中,BD CE =,DE 的延长线交BC 的延长线于P , 求证:AD BP AE CP ⋅=⋅.PE D CBA MPED C BA【答案】过C 作CM AB ∥交DP 于M ,∵CM AB ∥,∴PCM PBD ∆∆∽, ∴CM PC BD PB =, ∵CM AB ∥,∴CEM AED ∆∆∽, ∴CM AD CE AE =, ∵BD CE =, ∴CM CM CE BD =, ∴PC AD PB AE=, ∴AD BP AE CP ⋅=⋅【例6】 如图,在ABC ∆的边AB 上取一点D ,在AC 取一点E ,使AD AE =,直线DE 和BC 的延长线相交于P ,求证:BP BDCP CE= PEDCBA4321MPE D CBA【答案】过C 作CM AB ∥交DP 于M ,∵CM AB ∥,∴PCM PBD ∆∆∽, ∴BP BD CP CM =, ∵CM AB ∥, ∴14∠=∠, 又∵AD AE =,∴12∠=∠,∴24∠=∠, ∵23∠=∠, ∴34∠=∠, ∴CM CE = ∴BP BD CP CE= 【例7】 如图,M 、N 为ABC △边BC 上的两点,且满足BM MN NC ==,一条平行于AC 的直线分别交AB 、AM 和AN 的延长线于点D 、E 和F .求证:3EF DE =.F NMED CBAK HF N MG ED CBA【答案】过M ,N 分别作AC 的平行线交AB 于H ,G 两点,NH 交AM 于K ,∵BM MN NC ==, ∴BG GH HA ==,易知12HK GM =,12GM HN =,∴14HK HN =,即13HK KN =,又∵DF HN ∥, ∴13DE HK EF KN ==,即3EF DE =. 考点三:相似三角形与内接矩形☞考点说明:内接矩形问题是相似三角形中比较典型的问题,考查了相似三角形对应高的比等于相似比【例1】 一块直角三角形木板的一条直角边AB 长为1.5米,面积为1.5平方米,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学进行设计加工方案。
【易错题】浙教版九年级数学上册《第四章相似三角形》单元测试卷含答案解析.doc

【易错题解析】浙教版九年级数学上册第四章相似三角形单元测试卷一、单选题(共10题;共30分)1•已知「夕,则?的值是()3 4 y2. 如图1, A ABC和4GAF是两个全等的等腰直角三角形,图屮相似三角形(不包括全等)共有()A. 1对B. 2对C. 3对D. 4对3. 图中的两个三角形是位似图形,它们的位似中心是()A.点PB.点OC.点MD.点N4. 在ZiABC 和△ DEF 屮,ZA=40°, ZD=60°, ZE=80°,字=器,那么ZB 的度数是()AC FEA.40°B.60°C.80°D.100°5. 如图,锐角AABC的高CD和BE相交于点0,图中与△ ODB相似的三角形有()6. 如图,在平行四边形ABCD中,AE: AD=2: 3,连接BE交AC于点F,若△ ABF和四边形CDEF的面积分别记为Si , S2 ,贝iJSi: S2% ()A. 2: 3B.4: 9C. 6: 11D. 6: 137. 如图,在AABC中,点D, E分别是AB, C的中点,则S AADE:S A ABC=()A. 1: 2B. 1: 3C. 1: 4D. 1: 58. (2017*淄惮)如图,在RtA ABC 中,ZABC=90°, AB=6, BC=8, ZBAC, ZACB 的平分线相交于点E,过点E作EF〃BC交AC于点F,则EF的长为()9.如图,点D是AABC的边AC的上一点,且ZABD=ZC;如果= |,那么譽=()CD 3 D LF八…! f►•10.如图,RtA ABC 中,BC=2V3 ,ZACB=90°, ZA=30°, 6 是斜边 AB 的中点,过 6 作 DiEi 丄AC 于 Ei二、填空题(共10题;共30分)AB=4, CD=3, OD=2,那么线段OA 的长为22.如果两个相似三角形周长的比是2:3 ,那么它们面积的比是 ____________ •13. 如图,已知直线 I] || l 2 II $,分别交直线 m 、n 于点 A^ C^ D 、E 、F, AB = 5cm, AC=15cm, DE = 3cm,则EF 的长为 ________ cm.14. ________________________________________________________________________________ 已知AABCsADEF,相似比为3:5, A ABC 的周长为6,则△ DEF 的周长为 ___________________________________ .15. ________________________________________________________________________________________________ 已知△ ABC^ADEF, △ ABC 的周长为1, △ DEF 的周长为3,则厶ABC 与氐DEF 的面积之比为 _________________ .16. 若两个相似三角形的周长之比为2:3,较小三角形的面积为8crY?,则较大三角形面积是 ____________ cm 2 . 17. 如图,在矩形ABCD 中,E 是边AB 的中点,连接DE 交对角线4C 于点F ,若AB = 4 f18. 如图,已知ZAOB=60。
4.3 相似三角形 浙教版九年级数学上册同步练习(含答案)

4.3 相似三角形一、选择题(共8小题)1. 如图所示,△ABC∽△CBD,CD=2,AC=3,BC=4,那么AB的值等于( )A. 5B. 6C. 7D. 42. 如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3,4及x,那么x的值为( )A. 7B. 5C. 7或5D. 无数个3. 如图所示,在平行四边形ABCD中,AB=10,AD=6,E是AD的中点,在AB上取一点F,使△CBF∽△CDE,则BF的长是( )A. 5B. 8.2C. 6.4D. 1.84. 已知△ABC和△DEF相似,且△ABC的三边长为3,4,5,如果△DEF的周长为6,那么△DEF中某条边的边长不可能是( )A. 1.5B. 2C. 2.5D. 35. 如图所示,点A,B,C,D的坐标分别是(1,7),(1,1),(4,1),(6,1),以C,D,E为顶点的三角形与△ABC相似,则点E的坐标不可能是( )A. (6,0)B. (6,3)C. (6,5)D. (4,2)6. 如图所示,在钝角三角形ABC中,AB=6 cm,AC=12 cm,动点D从点A出发到点B止,动点E从点C出发到点A止,点D运动的速度为1 cm/s,点E运动的速度为2 cm/s.如果两点同时运动,那么当以点A,D,E为顶点的三角形与△ABC相似时,运动的时间是( )A. 3 s或4.8 sB. 3 sC. 4.5 sD. 4.5 s或4.8 s7. 已知△ABC的三边长分别为2,6,2,△AʹBʹCʹ的两边长分别为1和3,如果△ABC与△AʹBʹCʹ相似,那么△AʹBʹCʹ的第三边长应该是( )A. 2B. 22C. 62D. 338. 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )A. AB2=BC⋅BDB. AB2=AC⋅BDC. AB⋅AD=BD⋅BCD. AB⋅AD=AD⋅CD二、填空题(共6小题)9. 已知△ABC的三边分别是4,5,6,与它相似的△AʹBʹCʹ的最长边为12,则△AʹBʹCʹ的周长是.10. 如图所示,在△ABC中,AB=8,AC=6,D是线段AC的中点,点E在线段AB上,且△ADE∽△ABC,则AE=.11. 如图所示,∠ACB=∠ADC=90∘,AB=5,AC=4,若△ABC∽△ACD,则AD=.12. 如图所示,在△ABC中,∠C=90∘,AC=3,BC=6,D为BC中点,E是线段AB上一动点,若△BDE∽△BAC,则BE=.13. 如图所示,在长方形ABCD中,AB=4,AD=3,E是AB边上一点(不与点A,B重合),F是BC边上一点(不与B,C重合).若△DEF和△BEF是相似三角形,则CF=.14. 如图所示,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=k(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若x△OCD∽△ACO,则直线OA的表达式为.三、解答题(共6小题)15. 如图所示,AD=2,AC=4,BC=6,∠B=36∘,∠D=107∘,△ABC∽△DAC.求:(1)AB 的长.(2)CD 的长.(3)∠BAD 的大小.16. 如图所示,在 △ABC 中,AD 平分 ∠BAC 交 BC 于点 D ,点 E ,F 分别在 AB ,AC 上,BE =AF ,FG ∥AB 交线段 AD 于点 G ,连接 BG ,EF .(1)求证:四边形 BGFE 是平行四边形;(2)若 △ABG ∽△AGF ,AB =10,AG =6,求线段 BE 的长.17. 如图所示,已知 △ABG ∽△FBD ,F 是 AB 的中点,求证:BD CD =AE EC .18. 如图所示,点 C ,D 在线段 AB 上,△PCD 是等边三角形,且 △ACP ∽△PDB .(1)求 ∠APB 的大小 ⋅(2)说明线段 AC ,CD ,BD 之间的数量关系.19. 如图所示,已知,在平面直角坐标系中有四点:A (―2,4),B (―2,0),C (2,―3),D (2,0),设 P 是 x 轴上的点,且 PA ,PB ,AB 所围成的三角形与 PC ,PD ,CD 所围成的三角形相似,请求出所有符合上述条件的点 P 的坐标.20. 如图,已知△ABC∽△A1B1C1,相似比为k(k>1),且△ABC的三边长分别为a,b,c(a>b>c),△A1B1C1的三边长分别为a1,b1,c1.(1)若c=a1,求证:a=kc;(2)若c=a1,试给出符合条件的一对△ABC和△A1B1C1,使得a,b,c和a1,b1,c1都是正整数,并加以说明;(3)若b=a1,c=b1,问:是否存在△ABC和△A1B1C1使得k=2 ?请说明理由.答案1. B2. C3. D4. D5. B6. A7. A8. A9. 3010. 9411. 16512. 65513. 53或3214. y=2x15. (1)∵△ABC∽△ADC,∴ABAD =BCAC,即AB2=64,∴AB=3.(2)∵△ABC∽△ADC,∴BCAC =ACDC,即64=4DC,∴CD=83.(3)∵△ABC∽△ADC,∴∠CAD=∠B=36∘,∠BAC=∠D=107∘,∴∠BAD=∠BAC+∠CAD=107∘+36∘=143∘.16. (1)∵FG∥AB,∴∠BAD=∠AGF.∵∠BAD=∠GAF,∴∠AGF=∠GAF,AF=GF.∵BE=AF,∴FG=BE.∵FG∥BE,∴四边形BGFE为平行四边形.(2)BE=3.6.17. ∵△ABG∽△FBD,∴∠G=∠BDF.∴DF∥AG.∵F是AB的中点,∴DF是△ABG的中位线.∴BD=DG.又∵DF∥AG,∴DGCD =AEEC.∴BDCD =AEEC.18. (1)因为△PCD是等边三角形,所以∠PCD=60∘.所以∠ACP=120∘.因为△ACP∽△PDB,所以∠APC=∠B.所以∠APC+∠CPB=∠B+∠CPB.所以∠APB=∠ACP=120∘.(2)因为△ACP∽△PDB,所以AC:PD=PC:BD.所以PD⋅PC=AC⋅BD.因为△PCD是等边三角形,所以PC=PD=CD.所以CD2=AC⋅BD.19. 设OP=x(x>0).(1)如图 1 所示,若点P在AB的左边,有两种可能:①若△ABP∽△PDC,则PB:CD≡AB:PD,∴(x―2):3=4:(x+2),解得x=4.∴点P的坐标为(―4,0).②若△ABP∽△CDP,则AB:CD=PB:PD,∴4:3=(x―2):(x+2),解得x=―14.不存在.(2)如图 2 所示,若点P在AB与CD之间,有两种可能:①若△ABP∽△CDP,则AB:CD=BP:PD,∴4:3=(x+2):(2―x),解得x=2.7∴点P的坐标为,0.②若△ABP∽△PDC,则AB:PD=BP:CD,∴4:(2―x)=(x+2):3,方程无解.(3)如图 3 所示,若点P在CD的右边,有两种可能:①若△ABP∽△CDP,则AB:CD=BP:PD,∴4:3=(2+x):(x―2).∴x=14.∴点P的坐标为(14,0).②若△ABP∽△PDC,则AB:PD=BP:CD,∴4:(x―2)=(x+2):3,∴x=4或x=―4(舍去).∴点P的坐标为(4,0).综止所述,点P的坐标为,0,(14,0),(4,0),(―4,0).20. (1)∵△ABC∽△A1B1C1,且相似比为k(k>1),∴aa1=k,∴a=ka1.又∵c=a1,∴a=kc.(2)取a=8,b=6,c=4,同时取a1=4,b1=3,c1=2.此时aa1=bb1=cc1=2,∴△ABC∽△A1B1C1且c=a1.(3)不存在这样的△ABC和△A1B1C1.理由如下:若k=2,则a=2a1,b=2b1,c=2c1,又∵b=a1,c=b1,∴a=2a1=2b=4b1=4c.∴b=2c.∴b+c=2c+c<4c=a,而b+c>a,故不存在这样的△ABC和△A1B1C1,使得k=2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4.3 相似三角形
1.已知△ABC∽△A′B′C′,且相似比为2,则(C)
A.∠A 是∠A′的2倍
B.∠A′是∠A 的2倍
C.AB是A′B′的2倍
D.A′B′是AB的2倍
2.已知△ABC∽△A′B′C′,∠A=45°,∠B=105°,则∠C′等于(D)
A.105°
B.80°
C.45°
D.30°
3.如图,已知△ADE∽△ABC,若AD=1,BD=2,则△ADE与△ABC的相似比是(B)
(第3题)
A.1∶2
B.1∶3
C.2∶3
D.3∶2
4.已知在△ABC中,AB=12,BC=18,CA=24,另一个和它相似的三角形的最长边是36,则最短边是(C)
A. 27
B. 12
C. 18
D. 20
5.如图,在△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论中,一定正确的是(A)
A. AB2=BC·BD
B. AB2=AC·BD
C. AB ·AD =BC ·BD
D. AB ·AC =AD ·BD
(第5题) (第6题) 6.如图,若△ADE ∽△ACB ,且AD AC =23
,DE =10,则BC =__15__. 7.如图,已知AB 与CD 交于点O ,△OBD ∽△OAC.若OD OC =23
,OB =4,求AB 的长.
(第7题)
【解】 ∵△OBD ∽△OAC ,
∴OD OC =OB OA ,即23=4OA
, ∴OA =6,∴AB =OA +OB =10.
8.已知三角形的三边之比是3∶5∶7,与它相似的三角形的最长边是21 cm ,求另两边之和.
【解】 ∵三角形的三边之比是3∶5∶7,
∴与之相似的三角形的三边之比也是3∶5∶7,
∵最长边是21 cm ,
∴另两边之和是21×3+57
=24(cm).
9.如图,AB 是斜靠在墙上的梯子,梯脚B 距墙80 cm ,梯上一点D 距墙60 cm ,AD 的长为100 cm ,且△ADE ∽△ABC ,试求梯子AB 的长.
(第9题)
【解】 由题意,得BC =80,DE =60,AD =100.
∵△ADE ∽△ABC ,
∴AD AB =DE BC ,即100AB =6080
, ∴AB =100×8060=4003
(cm).
10.如图,在平面直角坐标系中,已知点O(0,0),A(0,2),B(1,0),P 是反比
例函数y =-1x
图象上的一个动点,过点P 作PQ ⊥x 轴,垂足为Q.若以O ,P ,Q 为顶点的三角形与△OAB 相似,则相应的点P 共有(D)
(第10题)
A. 1个
B. 2个
C. 3个
D. 4个
【解】 ∵点P 在反比例函数y =-1x
的图象上,
∴设点P ⎝
⎛⎭⎪⎫x ,-1x . 易得OA =2,OB =1,OQ =|x|,PQ =⎪⎪⎪⎪
⎪⎪1x . 当△PQO ∽△AOB 时,则PQ AO =OQ BO
, ∴⎪⎪⎪⎪⎪⎪1x 2=|x|1,解得x =±22
. ∴点P 的坐标为⎝ ⎛⎭⎪⎫22,-2或⎝ ⎛⎭
⎪⎫-22,2. 同理,当△PQO ∽△BOA 时,
可求得点P 的坐标为⎝ ⎛⎭⎪⎫-2,22或⎝ ⎛⎭
⎪⎫2,-22. 综上所述,相应的点P 共有4个.
11.如果有一个直角三角形的两条边长分别是10和26,另一个与它相似的直角三角形的边长分别是5,13和x ,求x 的值.
【解】 ∵一个直角三角形的两条边长分别是10和26,
∴此直角三角形的第三边长为262-102或262+102,
即24或2194.
当510=x 24=1326
时,x =12; 当510=1326=x 2194
时,x =194. ∴x =12或194.
12.如图,在平面直角坐标系中,直线y =12
x +1交x 轴于点A ,交y 轴于点B.试在y 轴上找一点P ,使△AOP 与△AOB 相似,你能找出几个这样的点(点P 与点B 不重合)?分别求出对应AP 的长度.
(第12题)
【解】 可求得点A(-2,0),B(0,1),∴OB OA =12
. ∵点P 在y 轴上,且点P 与点B 不重合,
∴∠AOB =∠AOP =90°.
若△AOP 与△AOB 相似,
则OP OA =12或OP OA =21
, ∴OP =4或OP =1.
∴当OP =4时,点P(0,4)或P(0,-4),此时AP =22+42=2 5;
当OP =1时,点P(0,-1),此时AP =22+12= 5.
综上所述,共3个点满足条件,分别为点P 1(0,4),P 2(0,-4),P 3(0,-1),AP 1=AP 2=2 5,AP 3= 5.
13.如图,直线y =ax +1与x 轴,y 轴分别相交于A ,B 两点,与反比例函数y =k x
(x >0)相交于点P ,PC ⊥x 轴于点C ,且PC =2,点A 的坐标为(-2,0).
(第13题)
(1)求反比例函数的表达式.
(2)若Q 为反比例函数上点P 右侧的一点,且QH ⊥x 轴于点H ,当以Q ,C ,H 为顶点的三角形与△AOB 相似时,求点Q 的坐标.
【解】 (1)把点A(-2,0)的坐标代入y =ax +1,得a =12
, ∴y =12
x +1. ∵点P 在直线y =12
x +1上,且点P 的纵坐标为2, ∴2=12
x +1,解得x =2. ∴点P 的坐标为(2,2).
∵点P 在反比例函数y =k x
上, ∴k =2×2=4,
∴反比例函数的表达式为y =4x
. (2)设点Q(a ,b).
∵点Q(a ,b)在反比例函数y =4x
上, ∴b =4a
.
当△QCH ∽△BAO 时,可得CH AO =QH BO
, 即a -22=4a 1
, 整理,得a -2=8a
, 解得a =4或a =-2(不合题意,舍去).
∴b =44
=1. ∴点Q(4,1).
当△QCH ∽△ABO 时,可得CH BO =QH AO
, 即a -21=4a 2
, 整理,得a 2-2a =2,
解得a =1+3或a =1-3(不合题意,舍去).
∴b =41+3
=2 3-2. ∴点Q(1+3,2 3-2).
综上所述,点Q 的坐标为(4,1)或(1+3,2 3-2).。
