2008年北京市延庆县初中升学模拟练习数学试卷及答案
2008年初中毕业、升学统一考试数学模拟试题以及参考答案

2008年初中毕业、升学统一考试数学模拟试题 08.6.1(考试时间:120分钟 满分:150分)请注意:1.本试卷分选择题和非选择题两个部分。
2.考生答卷前,必须将自己的姓名、考试号、座位号用黑色或蓝色钢笔或圆珠笔填写在试卷和答题卡的相应位置,再用2B 铅笔将考试号、科目填涂在答题卡上相应的小框内。
第一部分 选择题(共36分)请注意:考生必须将所选答案的字母标号用2B 铅笔填涂在答题卡相应的题号内,答在试卷上无效。
一、选择题 1.2的绝对值是 A. 2B. -2C. 0.5D. -0.52.下列计算中,正确的是A .2a 3-3a =-a ;B .(-ab )2=-a 2b 2;C .a 2·a -3=a -1;D .-2a 3÷(-2a )=-a 2.3.为迎接2008年北京奥运会修建的鸟巢,将用于国际、国内体育比赛和文化、娱乐活动,鸟巢的建筑面积约为258000 平方米,将258000用科学记数法表示应为 A .62.5810⨯B .52.610⨯C .42.5810⨯D .52.5810⨯4.小明从正面观察下图所示的两个物体,看到的是5.右图可以看作是一个等腰直角三角形旋转若干次 而生成的则每次旋转的度数可以是A. 90°B. 60°C. 45°D. 30°6.在直角坐标系中,⊙O 的圆心在原点,半径为3,⊙A 的圆心A 的坐标为(3-,1),半径为1,那么⊙O 与⊙A 的位置关系是B A CDA .内含B 内切C 相交D 外切7. 如图,把一个边长为1的正方形经过三次对折后沿中位线(虚线)剪下,则右图展开得到 的图形的面积是A .34 B.12 C . 38D .3168.如图是一个电脑桌面背景图,左右 两个“京”字图的面积比约是A .2∶1B .4∶1C .8∶1D .16∶19.下列事件的概率是1的是A. 任意两个偶数的和是4的倍数 B. 任意两个奇数的和是2的倍数 C. 任意两个质数的和是2的倍数 D. 任意两个整数的和是2的倍数 10.如果不等式组212x m x m >+⎧⎨>+⎩,的解集是1x >-,那么m 的值是A.3 B.1 C.1- D.3-11.匀速向一个容器注满水,容器水面的高度变化过程如左图所示:则这个容器可能是A .B .C .D . 12.从A 点出发的一条光线在直线AD 与CD 之间反射了n 次以后,垂直地射到B 点(该点可能在AD 上,也 可能在CD 上),然后按原路返回点A ,如图所示是n =3时的光路图,若∠CDA =8°,则n 的最大值是沿虚线剪开635412A. 10B. 11C. 12D. 14 二.填空题 (每题3分,共24分)13.为支援南方雪灾地区,某校团委举行了“雪灾无情人有情”的捐资活动,其中6个班同学的人均捐款数分别为:6元、4.6元、4.1元、3.8元、4.8元、5.2元.则这组数据的中位数是 元.14.如图,一扇窗户打开后,用窗钩BC 可将其固定,•这里所运用的几何原理是__________.第14题 第18题 第20题15.已知一段公路在斜坡上,坡度i=1:3,若汽车在斜坡上行驶100米,则汽车升高_______________米. 16.时钟的时针长6㎝,经过80分钟时针扫过的面积为 ㎝2 (结果保留π) . 17.下表所描述的是1y 与2y 分别与x 的函数关系:若两个函数的图象只有一个交点,则交点坐标是_________.18. 一个均匀的立方体六个面上分别标有数1,2,3,4,5,6.如图是这个立方体表面的展开图.抛掷这个立方体,则朝上一面上的数恰好等于朝下一面上的数的21的概率是___________.19.晓莹按如图所示的程序输入一个数x ,最后从输出端得到的数为16,则晓莹输入的最大的负数为 .20.如图所示,已知反比例函数y =1x的图象上有一点P ,过点P 分别作x 轴和y 轴的垂 线,垂足分别为A 、B ,使四边形OAPB 为正方形,又在反比例函数的图象上有一点P 1,过点P 1分别作BP 和y 轴的垂线。
北京市延庆县中考数一模试卷 人教版
1E DCBAEDCB A 北京市延庆县中考数一模试卷一、选择题(本题共30分,每小题3分)1.清明小长假延庆县的旅游收入约为1900万,将1900用科记数法表示应为( ) A .21910⨯ B .31.910⨯ C .41.910⨯ D .40.1910⨯ 2. 23的倒数是( ) A .23- B .23 C .32- D . 323. 在一个不透明的口袋中装有5个完全相同的小球,把它们分别标号为1,2,3,4,5, 从中随机摸出一个小球,其标号是奇数的概率为( ) A.51 B. 52 C. 53 D. 54 4.如图,△ABC 中,∠A =90°,点D 在AC 边上,DE ∥BC , 若∠1=35°,则∠B 的数为( ) A . 25° B. 35° C. 55° D. 65°5.关于x 的方程0222=++m x x 有两个相等的实数根,那么m 的值为( ) A .2± B .1± C .1 D . 26.在下列交通标志中,既是轴对称图形,又是中心对称图形的是( )7.若把代数式223x x -+化为()2x m k -+的形式,其中m ,k 为常数,结果为( )A .2(1)4x ++B .2(1)2x -+C .2(1)4x -+D . 2(1)2x ++ 8.如图,在△ABC 中,点D E 、分别在AB AC 、边上,DE BC ∥,若AD =1,BD =2,则DEBC 的值为( )A .12 B .13 C .14 D .199完成引体向上的个数 10 9 8 7 人 数1135这 A .7和7.5 B .7和8 C .7.5和9 D .8和9CABED O10.如图,△ABC 中,∠ACB =90°,∠A =30°,AB =16.点P 是斜边AB 上一点.过点P 作PQ ⊥AB ,垂足为P ,交边AC (或边CB )于点Q ,设AP =x ,△APQ 的面积为y ,则y 与x 之间的函数图象大致是( )二、填空题(本题共18分,每小题3分) 11.分解因式:24x y y -= . 12.若分式1x x-的值为0,则x 的值等于_________ . 13.如图,⊙O 的直径CD 垂直弦AB 于点E ,且CE =2,DE =8,则AB 的长为 .14.请写出一个开口向上,并且与y 轴交于点(0,2)的抛物线的表达式__________ .15. 习勾股定理相关内容后,张老师请同们交流这样的一个问题:“已知直角三角形的两条边长分别为3,4,请你求出第三边.”张华同通过计算得到第三边是5,你认为张华的答案是否正确:________,你的理由是 _______________________________________.16. 将正方体骰子(相对面上的点数分别为1和6、2和5、3和4)放置于水平桌面上,如图161.在图162中,将骰子向右翻滚90°,然后在桌面上按逆时针方向旋转90°,则完成一次变换.若骰子的初始位置为图161所示的状态,那么按上述规则连续完成3次变换后,骰子朝上一面的点数是________;连续完成次变换后,骰子朝上一面的点数是________.三、解答题(本题共30分,每小题5分)17.如图,△ABC 中,∠ACB =90°,延长AC 到D ,使得CD=CB ,过点D 作DE ⊥AB 于点E ,交BC 于F .求证:AB =DF .FED C BA图161 图162向右翻滚90° 逆时针旋转90°18.计算:011(3)4cos 45()2π---︒++-.19.解不等式组: 32,12.3x x x x >-⎧⎪+⎨>⎪⎩20.已知2410x x +-=,求代数式22(2)(2)(2)x x x x +-+-+的值.21.如图,一次函数1y x =+的图象与反比例函数ky x=(k 为常数,且0k ≠)的图象都经过点A (m ,2).(1)求点A 的坐标及反比例函数的表达式;(2) 设一次函数1y x =+的图象与x 轴交于点B ,若点P 是x 轴上一点,且满足△ABP 的面积是2,直接写出点P 的坐标.22.列方程或方程组解应用题:八级的生去距校10千米的科技馆参观,一部分生骑自行车先走,过了20分钟,其余的生乘汽车出发,结果他们同时到达,已知汽车的速是骑自行车生速的2倍,求骑车生每小时走多少千米?四、 解答题(本题共20分,每小题5分)23. 如图,点O 是△ABC 内一点,连结OB 、OC ,并将AB 、OB 、OC 、AC 的中点D 、E 、F 、G 依次连结,得到四边形DEFG .(1)求证:四边形DEFG 是平行四边形;(2)如果∠OBC =45°,∠OCB =30°,OC =4,求EF 的长.G FOBCDE A24. 某区对市民开展了有关雾霾的调查问卷,调查内容是“你认为哪种措施治理雾霾最有效”,有以下四个选项:A .使用清洁能源B .汽车限行C .绿化造林D .拆除燃煤小锅炉调查过程随机抽取了部分市民进行调查,并将调查结果绘制了两幅不完整的统计图,请回答下列问题:(1)这次被调查的市民共有 人. (2)请你将统计图1补充完整.(3)已知该区人口为00人,请根据调查结果估计该市认同汽车限行的人数.25. 如图,AB 是⊙O 的直径,点C 在⊙O 上,过点C 作⊙O 的切线CM . (1)求证:∠ACM =∠ABC ;(2)延长BC 到D ,使CD = BC ,连接AD 与CM 交于点E ,若⊙O 的半径为2,ED =1,求AC 的长.ODCA BM E26. 阅读下面资料: 问题情境:(1)如图1,等边△ABC ,∠CAB 和∠CBA 的平分线交于点O ,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点与点O 重合,已知OA =2,则图中重叠部分△OAB 的面积是 . 探究:(2)在(1)的条件下,将纸片绕O 点旋转至如图2所示位置,纸片两边分别与AB ,AC 交于点E ,F ,求图2中重叠部分的面积.(3)如图3,若∠ABC =α(0°<α<90°),点O 在∠ABC 的角平分线上,且BO =2,以O 为顶点的等腰三角形纸片(纸片足够大)与∠ABC 的两边AB ,AC 分别交于点E 、F ,∠EOF =180°﹣α,直接写出重叠部分的面积.(用含α的式子表示)五、解答题(本题共22分,第27题7分、28题各7分,29题8分) 27. 二次函数2y x mx n =-++的图象经过点A (﹣1,4),B (1,0),12y x b =-+经过点B ,且与二次函数2y x mx n =-++交于点D .过点D 作DC ⊥x 轴,垂足为点C .(1)求二次函数的表达式;(2)点N 是二次函数图象上一点(点N 在BD 上方),过N 作NP ⊥x 轴,垂足为点P ,交BD 于点M ,求MN 的最大值.28. 已知,点P是△ABC边AB上一动点(不与A,B重合)分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系是;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.29. 对于平面直角坐标系xOy 中的点P 和线段AB ,给出如下定义:在线段AB 外有一点P ,如果在线段AB 上存在两点C 、D ,使得∠CPD =90°,那么就把点P 叫做线段AB 的悬垂点.(1)已知点A (2,0),O (0,0)①若1(1,)2C ,D (1,1),E (1,2),在点C ,D ,E 中,线段AO 的悬垂点是______; ②如果点P (m ,n )在直线1y x =-上,且是线段AO 的悬垂点,求m 的取值范围; (2)如下图是帽形M (半圆与一条直径组成,点M 是半圆的圆心),且圆M 的半径是1,若帽形内部的所有点是某一条线段的悬垂点,求此线段长的取值范围.延庆县毕业考试答案初三数题号 1 2 3 4 5 6 7 8 9 104分 4分 5分① ② 5分4分 2分5分5分 4分 2分1分011(3)4cos 45()2123π---︒++-=-+=3分 1分三、解答题(本题共30分,每小题5分) 17. 证明:证明:∵ DE ⊥AB ∴∠DEA=90° ∵∠ACB =90° ∴∠DEA=∠ACB ∴∠D=∠B在△DCF 和△ACB 中DCB ACB DC BC B D ∠=∠⎧⎪=⎨⎪∠=∠⎩∴DCF ACB ∆≅∆∴AB =DF18.解:19. 32,12.3x x x x >-⎧⎪+⎨>⎪⎩解:由①得:x>1 由①得:15x < ∴115x -<<22222220.(2)(2)(2)44448x x x x x x x x x x +-+-+=++-++=++ ∵2410x x +-=∴241x x +=∴原式=921. ⑴ ∵点A (m ,2)在一次函数1y x =+的图象上,5分3分 5分 4分4分 5分 3分2分4分2分60MA FG E BCD∴m=1.∴点A 的坐标为(1,2).∵点A 的反比例函数xky =的图象上,∴k=2.∴反比例函数的解析式为2y x=. ⑵ 点P 的坐标为(1,0)或(3,0).24.(1)200 (2)5分 1分 2分3分 5分O D C A BME(3)8020020000080000÷⨯=25.证明:(1)证明:连接OC . ∵ AB 为⊙O 的直径, ∴ ∠ACB = 90°.∴ ∠ABC +∠BAC = 90°. ∵ CM 是⊙O 的切线, ∴ OC ⊥CM .∴ ∠ACM +∠ACO = 90°. ·································································· 1分[来∵ CO = AO ,∴ ∠BAC =∠ACO . ∴ ∠ACM =∠ABC . ··············································································· 2分 (2)解:∵ BC = CD ,OB=OA ,∴ OC ∥AD. 又∵ OC ⊥CE ,∴CE ⊥AD . 3分[∵ ∠ACD =∠ACB = 90°,∴ ∠AEC =∠ACD . ∴ ΔADC ∽ΔACE .∴AD ACAC AE=. ····················································································· 4分[ 而⊙O 的半径为2, ∴ AD = 4. ∴43AC AC =. ∴ AC = 2 3 . ······················································································ 5分[ 26.(1) 3(2) 连接AO 、BO ,如图②,由题意可得:∠EOF =∠AOB ,则∠EOA =∠FOB . 在△EOA 和△FOB 中,EAO FBO OA OBEOA FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△EOA ≌△FOB . ∴S 四边形AEOF =S △OAB .过点O 作ON ⊥AB ,垂足为N ,如图, ∵△ABC 为等边三角形, ∴∠CAB =∠CBA =60°.∵∠CAB 和∠CBA 的平分线交于点O ∴∠OAB =∠OBA =30°. ∴OB=OA =2. ∵ON ⊥AB ,∴AN=NB ,ON =1.∴AN =N FEOCBA4分 5分D P ABCE FQPFEQD CBA ∴AB=2AN =2. ∴S △OAB =AB •ON =. S 四边形AEOF = (3) S 面积=4sincos.27. 解:(1)∵二次函数2y x mx n =-++的图象经过点A (﹣1,4),B (1,0) ∴4101m nm n=--+⎧⎨=-++⎩∴m=2,n=3∴二次函数的表达式为223y x x =--+ (2)12y x b =-+经过点B ∴12b = 画出图形()211(,),2322M m m m m m -+--+设,则N ∴21123()22MN m m m =--+--+设 ∴23522MN m m =--+∴2349()416MN m =-++ ∴MN 的最大值为491628.解:(1)AE ∥BF ,QE=QF , (2)QE=QF ,证明:如图2,延长EQ 交BF 于D , ∵AE ∥BF ,∴∠AEQ=∠BDQ , 在△BDQ 和△AEQ 中AEQ BDQ AQE BQD AQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△BDQ ≌△AEQ (ASA ), ∴QE=QD , ∵BF ⊥CP ,∴FQ 是Rt △DEF 斜边上的中线, ∴QE=QF=QD , 即QE=QF . (3)(2)中的结论仍然成立, 证明:如图3,延长EQ 、FB 交于D , ∵AE ∥BF ,7分 2分 6分 5分3分 4分2分3分5分4分∴∠AEQ =∠D ,在△AQE 和△BQD 中AEQ BDQ AQE BQD AQ BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩, 图3 ∴△AQE ≌△BQD (AAS ), ∴QE=QD ,∵BF ⊥CP ,∴FQ 是Rt △DEF 斜边DE 上的中线, ∴QE=QF . 说明:第三问画出图形给1分 29.(1)线段AO 的悬垂点是C ,D ;(2)以点D 为圆心,以1为半径做圆,设1y x =-与⊙D 交于点B ,C与x 轴,y 轴的交点坐标为(1,0),(0,1) ∴∠ODB=45° ∴DE=BE在Rt △DBE 中,由勾股定理得:DE=22∴2211122m m -≤≤+≠且 (3)设这条线段的长为a①当2a <时,如图1,凡是⊙D 外的点不满足条件; ②当2a =时,如图2,所有的点均满足条件; ③当2a >时,如图3,所有的点均满足条件; 综上所述:2a ≥以上答案仅供参考。
北京市延庆县中考一模数学试题及答案

延庆县初中毕业试卷 数 学(一模)一、选择题:(本题共32分,每小题4分)下列各题均有四个选项,其中只有一个是正确的,请将所选答案在答题卡相应位置涂黑。
1.9-的相反数是A .19-B .19C .9-D .92. 第27届龙庆峡冰灯节接待游客大约230000人次,将230000用科学记数法表示应为A .2.3×104B .23×104C .2.3×105D .0.23×1063.如图所给的三视图表示的几何体是A. 圆柱B. 长方体C. 圆锥D. 圆台4. 若一个多边形的每一个外角都等于40°,则这个多边形的边数是A .10B .9C .8D .75.小明将6本书分别放在6个完全相同的不透明礼盒中,准备将它们送给6位好朋友.这些书中3本是小说,2本是科普读物,1本英语小词典.小明的一个朋友从6个礼盒中随机取一份,恰好取到小说的概率是 A .16B .13C .12D .236.如图1,AD ∥BC ,BD 平分∠ABC , 且︒=∠110A ,则D ∠的度数为A .︒70B .︒35C .︒55D .︒1107.如图,在△ABC 中,点D 、E 分AB 、AC 边上, DE//BC ,若AD :AB=3:4,AE=6,则AC 等于A. 3B.4C. 6D.8考生须知:1.本试卷分试题和答题卡两部分. 满分120分, 考试时间120分钟.2.答题前,考生务必将自己的学校名称、姓名、班级填写清楚.3.本试卷中的选择题及作图题用2B 铅笔做答,其它题目用黑色或蓝色的签字笔或钢笔做答.4.修改时,选择题及作图用橡皮擦干净,不得使用涂改液。
请保持卡面清洁,不要折叠、弄破.5.请按照题号顺序在各题目的答题区域内做答,超出答题区域的答案无效.6.草稿一律不得写在答题卡上,考试结束后, 只上交答题卡.ADCB(图1)8. 在如图所示的棱长为1的正方体中, A 、B 、C 、D 、E 是正 方体的顶点,M 是棱CD 的中点. 动点P 从点D 出发,沿着D →A→B 的路线在正方体的棱上运动,运动到点B 停止运动. 设点P 运动的路程是x , y=PM +PE ,则y 关于x 的函数图象大致为( ) A B C D二、填空题(本题共16分,每小题4分) 9.分解因式:2327x -= __________ . 10.函数y =1x +5中,自变量x 的取值范围是 . 11.方程x (x ﹣2)=x 的根是 .12.观察下面一列数的规律并填空:0,3,8,15,24,…,则它的第个数是 .第n 个数是_________ .三、解答题(本题共30分,每小题5分) 13.(本题满分5分)计算:︱-2︱+3sin30°-12--(π-)0.14.(本题满分5分)解不等式组并把它的解集在数轴上表示出来.15.(本题满分5分)已知2230a a --=,求代数式2(1)(2)(2)a a a a --+-的值.16.(本题满分5分)已知:如图,E 为BC 上一点,AC ∥BD ,AC=BE ,BC=BD. 求证:AB=DE17.(本题满分5分)已知直线l 与直线y=2x 平行,且与直线y= -x+m 交于点(2,0), 求m 的值及直线的解析式.18.(本题满分5分)列方程或方程组解应用题:EDCBA学校举行“大家唱大家跳”文艺汇演,设置了歌唱与舞蹈两类节目,全校师生一共表演了30个节目,其中歌唱类节目比舞蹈类节目的3倍少2个,则全校师生表演的歌唱类节目多少个?四、 解答题(本题共20分,每小题5分) 19. (本题满分5分)如图,将矩形ABCD 沿直线AE 折叠,顶点D 恰好落在BC 边上F 点处,已知CE=6cm ,AB=16cm ,求BF 的长.20.(本题满分5分)莲花山的主峰海拔约为600米,主峰AB 上建有一座电信信号发射架BC ,现在山脚P 处测得峰顶的仰角为α,发射架顶端的仰角为β,其中35tan tan 58αβ==,,求发射架高BC .21. (本题满分5分)某校初三年级(1)班要举行一场毕业联欢会.规定每个同学分别转动下图中两个可以自由转动的均匀转盘A 、B (转盘A 被均匀分成三等份.每份分別标上1,2,3三个数字.转盘B 被均匀分成二等份.每份分别标上4,5两个数字).若两个转盘停止后指针所指区域的数字都为偶数(如果指针恰好指在分格线上.那么重转直到指针指向某一数字所在区域为止).则这个同学要表演唱歌节目.请求出这个同学表演唱歌节目的概率(要求用画树状图或列表方法求解)22. 操作与探究:(本题满分5分)阅读下面材料:将正方形ABCD (如图1)作如下划分:FEDCBA CB AP α β (第21题600米山顶发射架第1次划分:分别联结正方形ABCD 对边的中点(如图2),得线段HF 和EG ,它们交于点M ,此时图2中共有5个正方形;第2次划分:将图2左上角正方形AEMH 按上述方法再作划分,得图3,则图3中共有_______个正方形;若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有_______个正方形;继续划分下去,能否将正方形ABCD 划分成有个正方形的图形?需说明理由.图3图2图1MFGHEMFGHEABABABDCCDCD五、解答题(本题共22分,第23题、24题各7分,25题8分)23. (本题满分7分)如图,AB 是⊙O 的直径,AC 和BD 是它的两条切线,CO 平分∠ACD. (1)求证:CD 是⊙O 的切线; (2)若AC=2,BD=3,求AB 的长.24. (本题满分7分)如图,已知平面直角坐标系xOy ,抛物线y =-x 2+bx +c 过点A(4,0)、B(1,3) . (1)求该抛物线的解析式,并写出该抛物线的对称轴和顶点坐标;(2)记该抛物线的对称轴为直线l ,设抛物线上的点P(m,n)在第四象限,点P 关于直线l 的对称点为E ,点E 关于y 轴的对称点为F ,若四边形OAPF 的面积为20,求m 、n 的值.25. (本题满分8分)如图1,在四边形ABCD 中,AB CD ,E F 、分别是BC AD 、的中点,连结EF 并延长,分别与BA CD 、的延长线交于点M N 、,则BME CNE ∠=∠(不需证明).(温馨提示:在图1中,连结BD ,取BD 的中点H ,连结HE HF 、,根据三角形中位线定理,证明HE HF =,从而12∠=∠,再利用平行线性质,可证得BME CNE ∠=∠.)问题一:如图2,在四边形ADBC 中,AB 与CD 相交于点O ,AB CD =,E F 、分别是BC AD 、的中点,连结EF ,分别交DC AB 、于点M N 、,判断OMN △的形状,请直接写出结论.问题二:如图3,在ABC △中,AC AB >,D 点在AC 上,AB CD =,E F 、分别是BC AD 、的中点,连结EF 并延长,与BA 的延长线交于点G ,若60EFC ∠=°,连结GD ,判断AGD △的形状并证明.延庆县初中毕业试卷参考答案一、选择题:(本题共32分,每小题4分)题号 12345 6 7 8 答案DCAB C B D C二、填空题(本题共16分,每小题4分)题 号 9 10 11 12答 案 3(x +3)(x -3) x ≠-5 x 1=0,x 2=3.4052168(或2-1),n 2-1三、解答题(本题共30分,每小题5分) 13.解:原式1212132--⨯+= ………………………………………4分 2=. ………………………………………………………………5分14. 解:,解不等式①得,x≤1,………………………………………………………………2分 解不等式②得,x >﹣2, …………………………………………………………4分 在数轴上表示如下:故答案为:﹣1<x≤2.……………………………………………………5分 15.解:∵2230a a --=∴322=-a a----------------------------------------1分2(1)(2)(2)a a a a --+-=)4(2222---a a a ----------------------------------2分 =42222+--a a a ----------------------------------------3分 =422+-a a - ---------------------------------------4分=3+4=7 ----------------------------------------5分16. 证明:∵AC ∥BD ∴∠C=∠CBD---------------------------------------------1分在△ACB 和△EBD 中⎪⎩⎪⎨⎧=∠=∠=,,,BD BC CBD C BE AC ----------------------------------------3分∴△CBM ≌△DBM----------------------------------------4分∴AB=DE ------------------------------------------------------5分 EDCBA17.解:依题意,点(2,0)在直线y =-x +m 上,∴ 0=-2+m . …………………………………………………………………1分 ∴ m =2. …………………………………………………………………………2分 由直线l 与直线y =2x 平行,可设直线l 的解析式为y =2x +n . ………………3分 ∵ 点(2,0)在直线l 上,∴ 0=2×2+n .∴ n =-4 …………………………………………………………………4分 故直线l 的解析式为 y =2x -4. …………………………………………………5分 18. 设 歌唱类节目有x 个,舞蹈类节目有y 个,……………………1分由等量关系:共表演了30个节目,及歌唱类节目比舞蹈类节目的3倍少2个,可得,……………………3分 解得:,……………………4分答:歌唱类节目有22个.……………………5分 四、 解答题(本题共20分,每小题5分)19. 解:由题意可知△ADE ≌△AFE . ………………………………………………… 1分在矩形ABCD 中,16==AB CD ,CB AD =,︒=∠=∠=∠90D C B ,∵6=CE ,∴10=-==CE CD DE EF . ……………………………………………… 3分 在Rt △CEF 中,822=-=CE EF FC . …………………………………4分设x BF =,则x BF FC BC +=+=8, ∴x BC AD AF +===8.在Rt △ABF 中,222AF BF AB =+, 即222)8(16x x +=+,解得 12=x . ………………………………………………………………… 5分即12=BF .20. 解:在Rt PAB △中, ∵tan ABPA α=,∴6001000m 3tan 5AB PA α===.······ 3分 在Rt PAC △中,∵tan ACPAβ=,∴5tan 1000625m 8AC PA β===.···················· 4分 ∴62560025m BC =-=. ························· 5分 答:发射架高为25m .FEDCBACB APα β(第21题米山顶 发射架21. 解:画树状图得:…………………3分∵共有6种等可能的结果,两个转盘停止后指针所指区域的数字都为偶数的有1种情况, ∴这个同学表演唱歌节目的概率为:.…………………………………5分22. 解:第2次划分,共有9个正方形; …………………………………………1分 第100次划分后,共有401个正方形; ………………………………………2分 依题意,第n 次划分后,图中共有4n+1个正方形, …………………………3分而方程4n+1=有整数解,n = 503 …………………………………4分 所以,第503划分后次能得到个正方形. …………………………………5分 五、解答题(本题共22分,第23题、24题各7分,25题8分) 23.(1)证明:过O 点作OE⊥CD,垂足为E , ∵AC 是切线,∴OA⊥AC, ……………………………………………2分 ∵CO 平分∠ACD,OE⊥CD,∴OA=OE, ………………………………3分 ∴CD 是⊙O 的切线. ………………………………4分 (2)解:过C 点作CF⊥BD,垂足为F ,……………5分 ∵AC、CD 、BD 都是切线, ∴AC=CE=2,BD=DE=3,∴CD=CE+DE=5, …………………………6分∴四边形ABFC ∴BF=AC=2,DF=BD ﹣在Rt△CDF 中,CF 2=CD ∴AB=CF=2.24. 解:(1)将2244b 013c b c ⎧-++=⎪⎨-++=⎪⎩解之得:b=4,c=0 所以对称轴为x=2(2)点p (m ,n 为点F 坐标为(4-m,-n ),……………………………………5分则四边形的面积OAPF=4n =20所以n =5,因为点P 为第四象限的点,所以n<0,所以n= -5 ………6分 代入抛物线方程得m=5 …………………………………………………7分25. (1)等腰三角形 ···························· 1分 (2)判断出直角三角形 ··························· 2分 证明:如图连结BD ,取BD 的中点H ,连结HF HE 、, ············ 3分F 是AD 的中点,HF AB ∴∥,12HF AB =,13∴∠=∠.同理,12HE CD HE CD =∥,,2EFC ∴∠=∠.AB CD =,∴HF HE =,12∴∠=∠.-------4分 60EFC ∠=°,360EFC AFG ∴∠=∠=∠=°,AGF ∴△是等边三角形. ·························· 6分 AF FD =,GF FD ∴=,30FGD FDG ∴∠=∠=° 90AGD ∴∠=°即AGD △是直角三角形. ························· 8分A BC D F GH E12 3。
延庆县2008—2009年度第一学期初三期末统测试卷参考答案

延庆县2008—2009学年第一学期期末统测试卷初三数学参考答案与评分标准一、二、填空题:(本题共16分,每空4分)9.5110. 8 11. 5:1 12. 1或7 三、解答题:(本题共31分,13、14题各4分,15题5分,16、17、18各6分) 13.(本题4分) 解:原式=22)22(⨯+3∙23+21……………………3分 =1+23+21=3……………………4分14.(本题4分) 15.(本题5分)解:所有可能出现的结果如下:∴(1)P 甲乙在同一餐厅=2142=-----------------------------------------------------3分(2)P 甲乙至少有一人在B 餐厅=34---------------------------------------------------5分B 16.(本题6分) 解:(1)根据题意得,此二次函数的图象的顶点为(1,-4) ∴ 设此二次函数的解析式为:4)1(2--=x a y 二次函数图象过(3,0) ∴ 04)13(2=--a ∴ a=1∴ 所求二次函数的解析式为:4)1(2--=x y即:x x y 22-=-3 -------------------------- 3分 (2)图象(略) --------------------------------------------------5分 (3)根据图象可知:当-1<x <3时,y <0 -----------------6分 17.(本题6分) 解:联结BC ,由勾股定理求得: AB=AC=2,------------2分∴22180ππ==Rn l -----------------------------------4分∴213602n R S π==π. --------------------------------6分 18.(本题6分)(1)证明:在Rt △ABD 和Rt △ADC 中,∵tanB=AD BD ,cos ∠DAC=ADAC, -------------------------2分 又tanB=cos ∠DAC,∴ AD BD =AD AC, ∴AC=BD. -------------------------3分(2)解:在Rt △ADC 中,由sinC=1213,可设AD=12k,则AC=13k,由勾股定理,得CD=5k, --------------4分 又由(1)知BD=AC=13k,∴13k+5k=12,解得k=23, --------------------------------------------------5分∴AD=8. ---------------------------------------------------------------6分18题图D CBA四、解答题:(本题共21分,其中21题6分,其余每小题5分) 19.(本题5分)解:根据题意得: 30A ∠=︒ , 60PBC ∠=︒∴6030APB ∠=︒-︒,APB A ∠=∠ ,∴AB =PB --------------------------------2分在Rt BCP ∆中,90,60C PBC ∠=︒∠=︒,PC =450,∴PB =450sin 60==︒--------------------------------4分∴520AB PB ==≈(米)答:略.----------------------------------------------------------------5分20.(本题5分) 解:(1)1OA OB OD ===∵,∴点A ,B ,D 的坐标分别为(10)A -,,(01)B ,,(10)D ,(2)∵点A ,B 在一次函数(0)y kx b k =+≠上,01k b b -+=⎧⎨=⎩,,∴解得11.k b =⎧⎨=⎩, ----------------------------------------------------------------------2分 ∴一次函数解析式为1y x =+.------------------------------------------------------------------3分C ∵在一次函数1y x =+的图象上且CD x ⊥轴.(12)C ,∴.---------------------4分 又点C 在m y x=上,2m =∴.故反比例函数解析式为2y x =.-------------------5分21.(本题6分)证明:延长CG 交⊙O 交于点M ,--------1分 ∵直径AB ⊥CM∴弧AM AC 弧=∴F ACM ∠=∠ ------------------2分 ∵FAC CAG ∠=∠∴ACG ∆∽AFC ∆ ------------------4分∴ACAFAG AC = ∴AC 2=AG ∙AF --------------------6分 (若联结CB 或用其他方法证明,参照给分)QB CPA45060︒30︒19题图22.(本题5分)解:(1) y=(x-100) w=(x-100) (-2x+400)=-2x2+600x-40000,∴y与x的关系式为:y=-2x2+600x 40000.------ ------ ------------2分⑵y=-2 (x-150)2+5000,∴当西裤的销售价定为150元时,所获利润最大。
延庆县2008年初中毕业考试试卷

初三数学 第1页 (共8页 )FEDA21延庆县2008年初中毕业考试试卷初三数学第Ⅰ卷(选择题 共32分)答题卡:请将选择题的答案添在下面的答题卡内.一、选择题(共8个小题,每小题4分,共32分) 下列各题均有四个选项,其中只有一个..是符合题意的. 1.3的倒数是( )(A)3 (B) -3 (C) 13 (D) - 132. 2008年4月,首次实行清明节假期,延庆旅游景点在三天内接待中外游客的人数为45000人次,这个数字用科学记数法可表示为( )(A)4.5×105(B)4.5×104(C) 45×103(D) 0.45×1053.在函数y=2-x 中,自变量x 的取值范围是( ) (A) x>2(B) x<2 (C) x 2≥ (D) 2≤4.已知:如图,AD ∥EF ,∠1=80°,则∠2=( )(A) 20° (B) 100°(C) 10°(D) 80° 4题图 5.某小区为了了解居民用水情况,随机抽查了6户居民,其用水量分别为6,5,5,4, 6,6,(单位为吨),则这组数据的众数和中位数分别为( ) (A)3,5 (B) 3,5.5 (C)6,5 (D) 6,5.5初三数学 第2页 (共8页 )114133EDCBA6.如图是由几个小立方块所搭成的几何体,那么这个几何体的主视图是( )7.有6张写着数字的卡片,他们的背面相同,现将它们的背面朝上,从中任意抽取一张是数字3的概率是( ) (A) 13 (B) 12 (C)16 (D)238.如图,将一块含有60°的三角板ABC 绕着顶点B 旋转与△BDE 重合,若BC=3,则点A 走 过的路线长是( ) (A)π(B)2π (C) 4π (D) 6初三数学第Ⅱ卷(非机读卷共88分)二、填空题(共5个小题,每小题3分,共15分)9. 关于x 的一元二次方程x 2-2x+k=0无实数根。
二模参考答案

延庆县2008年初三模拟考试参考答案及评分标准英语试卷第I卷1 2 3 4 5 6 7 8 9 10 11 12 13 14 15C A B A C B B A C B B A C C A16 17 18 19 20 21 22 23 24 25 26 27 28 29 30B BC A BD B C A B A C D A B31 32 33 34 35 36 37 38 39 40 41 42 43 44 45C A A BD D A B C D B C D C D46 47 48 49 50 51 52 53 54 55 56 57 58 59 60A DBC B A B C A B第II卷一、听短文,按要求完成下面的表格。
1. Walton,2. March 13th/ March 13/ 13, March,3. doctor,4. morning二、词汇。
5. name,6. eyes,7. know,8. go,9. after 10. talk, 11. great三、根据中文意思完成句子。
12. It’s too hot in the room. You’d better open the window.1.5 0.513. There’s / There is something wrong with my computer and I can’t use it now.1 114. The soldiers didn’t leave until it was very late at night.0.515. It’s important for us to have/ do sports every day.1 116. I got up so late that I was late for school yesterday.1 1四、阅读短文,根据其内容回答下面的问题。
2008年北京市延庆县初中升学模拟练习(一)

2008年延庆县初中升学模拟练习(一)数学试卷第Ⅰ卷 (选择题 32分)一、选择题(本题共32分,每小题4分)下列各题均有四个选项,其中只有一个..是符合题意的. 1.-31的绝对值是 A . 31 B .-31 C .3 D .-3 2.为迎接2008年北京奥运会修建的鸟巢,将用于国际、国内体育比赛和文化、娱乐活动,鸟巢的建筑面积约为258000 平方米,将258000用科学记数法表示应为A .62.5810⨯B .52.610⨯C .42.5810⨯D .52.5810⨯3.如图, BC ∥DE,∠1=105°, ∠AED=65°, 则∠A 的大小是A .25°B .35°C .40°D .60°4.在函数21-=x y 中,自变量x 的取值范围是 A .0≠x B .2≠x C .2-≠x D .不确定5.一组数据:34,35,36,35,36,37,37,36,37,37,这组数据的平均数和众数分别是A.36,37B.37,36 C.36.5,37 D.35,37 6.把239ab a -因式分解正确的是A .a (9a+b )(9a-b )B .a 2)9(b a -C .a (3a+b )(3a-b )D .22)3(ab a -7. 有一只小狗,在如图所示的方砖上走来走去,最终停在深色方砖上的概率是.A. 12B. 13C. 19D. 598.如图,在矩形ABCD 中,AB =4,BC =3,点F 在DC 边上运动,连结AF ,过点B 作BE ⊥AF 于E ,设BE =y ,AF =x ,则能反映y 与x 之间函数关系的大致图象是第Ⅱ卷 (非选择题 88分)二、填空题(本题共16分,每小题4分)9.已知实数x ,y 满足x y -++=540,则代数式xy =_______10.关于x 的一元二次方程kx 2 -x +1=0有两个不相等的实数根,则k 的取值范围是_______11.如图,从左到右,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.可求得c=_______,第2009个格子中的数为_________12.如图,矩形ABCG 与矩形CDEF 全等,点BCD 在一条直线上,∠APE 的顶点P 在线段BD 上移动,使得∠APE 为直角的点P 的个数是 个三、解答题(本题共23分,14,15小题各4分,13,16,17小题各5分)13.计算:12 -4sin60°+(2-1)0+(- 12)-1 14.解不等式组⎪⎩⎪⎨⎧+<-≤-)1(32121x x x ,并求出它的最小负整数解。
延庆县2008年初中升学模拟二答案
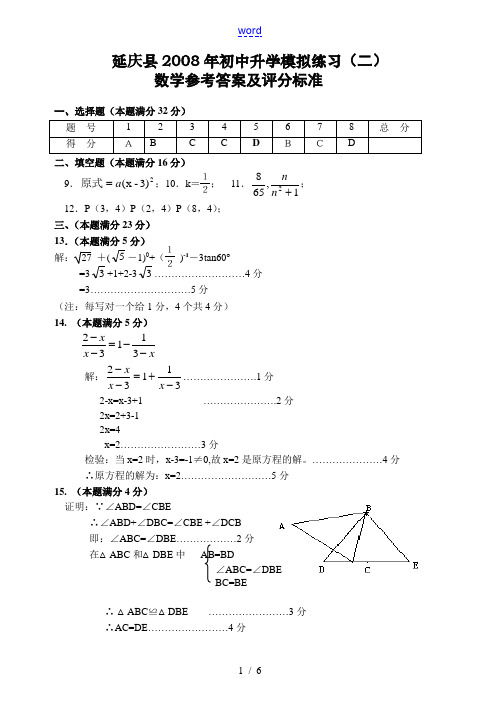
x x x --=--31132延庆县2008年初中升学模拟练习(二)数学参考答案及评分标准一、 选择题(本题满分32分) 题 号 1 2 3 4 5 6 7 8 总 分 得 分ABCCDBCD二、填空题(本题满分16分)9.2)3-x (a =原式;10.k =12; 11.1,6582+n n ; 12.P (3,4)P (2,4)P (8,4); 三、(本题满分23分) 13.(本题满分5分)解:27 +(5-1)0+(12)-1-3tan60°=33+1+2-33………………………4分=3…………………………5分 (注:每写对一个给1分,4个共4分) 14. (本题满分5分)解:31132-+=--x x x ………………….1分 2-x=x-3+1 ………………….2分 2x=2+3-1 2x=4x=2……………………3分检验:当x=2时,x-3=-1≠0,故x=2是原方程的解。
…………………4分 ∴原方程的解为:x=2………………………5分15. (本题满分4分) 证明:∵∠ABD=∠CBE∴∠ABD+∠DBC=∠CBE +∠DCB 即:∠ABC=∠DBE ………………2分在△ABC 和△DBE 中 AB=BD∠ABC=∠DBE BC=BE∴ △ABC ≌△DBE ……………………3分 ∴AC=DE ……………………4分解:11311332+-+•--x xx x x =1131)1)(1()1(3+-+•+--x x x x x x=111+-x x ………………2分 =)1(11+-+x x x=xx +21………………3分∵x 2+x -1=0, ∴x 2+x =1∴原式= 1…………………5分17.(本题满分4分)解:(1)由题意得:△=[-(m+1)]2-4×14m 2=m 2+2m+1-m 2=2m+1≥0∴m ≥-12………………2分(2)取m=0则原方程化为x 2-x=0 ∴x(x-1)=0∴x 1=0,x 2=1 ………………4分 18. (本题满分5分)解:过D 做DM ⊥BC 于M ,过A 做AN ⊥BC 于N 则∠DMC=∠ANB=90°∴四边形ANMD 为矩形 ∴AD=MN=5…………1分∵等腰梯形ABCD ,AD ∥BC ,AB=CD ,∠ADC=120° ∴∠DCB=60°AN=DM ,…………2分 在Rt △CDM, ∠CDM=30°,CD=6∴ CM=3 , DM=33…………3分 在Rt △ABN, tanB=3=BNAN设AN=3k , BN=k ∵DM=AN=33∴k=3 ……………………4分 ∴S 梯形ABCD =29339233)3535(2)(+=+++=+DM BC AD …………5分321OMED CBA(1)…………………1分(2)1.0…………………2分(3)80% …………………3分 (4)8000 …………………4分 (5)略…………………6分 20. (本题满分6分)(1)证明: ∵O M=OE∴∠1=∠2=°………………1分 ∵等腰梯形ABCD ∴∠1=∠2=°∴∠1=∠A ∴OE ∥AD ………………2分 ∵AD 与⊙O 相切于M ∴OM ⊥AD ∴OE ⊥OM∴△EOM 为等腰直角三角形 ………………3分 (2)设⊙O 的半径为r,OE=OM=r,由(1)可知,∴∠OEM=45°∴ME=2r, ………………4分 ∵∠3=180°—(∠OME+∠1)=180°°+45°°∴△AME ∽△EOB ………………5分 ∴BE:AE=OE:ME∴BE:AE=r:2r=1:2=2:2………………6分图6CBA解:(1)……………………..1分 (2)解:设A B ''与x 轴交于点M由题意可知:OA=2,∠A MO '=30°∴AM=1 …………………..3分 由勾股定理得:OM=3∴A 点的坐标为(3,-1) …………………..4分 ∵A '恰好落在双曲线)0(≠=k xky ∴k=-3∴双曲线的解析式为:xy 3-=…………………..5分 (3)30 …………………..6分 22. (本题满分4分) (1)…………3分(2)CM=AB …………4分 23.(本题满分7分)解:(1)联结PM ,因A 、B 、M 均在半圆P 上,且AB=10 ∴PM=PA=PB=5∴OP=OB-PB=3 ……………1分在Rt △POM 中,由勾股定理得:OM=4352222=-=-OP PM M 的坐标为(0,4) ……………2分 ∵正方形ABCD∴矩形OBCE ,AB=CB=10,∴CE=OB=8∴C 的坐标为(8,10) ……………3分 (2)直线CM 是半圆P 的切线 联结CM ,CP由(1)可知,BM=OB-OM=10-4=6在Rt △CEM 中,CM=10682222=+=+EC ME ……………4分 ∵BC=10 ∴BC=CM∵BP=PM,CP=CP ∴△CMP ≌△CBP∴∠CMP=∠CBP=90°∴直线CM 是半圆P 的切线。
北京市延庆县2008年初三第二次统一练习定稿

延庆县2008年初中升学模拟练习(二)数学 试 卷第Ⅰ卷 (机读卷32分)一、选择题(共8个小题,每小题4分,共32分) 下列各题均有四个选项,其中只有一个是符合题意的. 1.4的算术平方根是 A .2B .-2C .±2D.162.在“迎奥运,全民健身”活动中,据不完全统计,截至5月1日市延庆县参与的人数累 计达35000人,这个数用科学记数法表示正确的是 A. 5105.3⨯B. 4105.3⨯C. 31035⨯ D. 61035.0⨯3.下列各式,运算正确的是A . x 2·x 3=x 6B . x 3-x 2=x C . (-x)3(-x)=-x 3D . x 6÷x 2=x 3 4.下列函数中,自变量x 的取值X 围是x>2的函数是A .y =.y =C .y =D .y =5. 王华五次数学考试成绩分别为:86分,78分,80分,85分,92分,李老师想了解他数学学习变化情况,则李老师应最关注王华数学成绩的( ) A.平均数B.众数C.中位数D.方差6.已知实数x ,y 满足043=++-y x,则代数式()2008y x +的值为A. -1 B .1C . 2008D .-20087.如图1,电路图上有四个开关A ,B ,C ,D 和一个小灯泡, 闭合开关D 或同时闭合开关A ,B ,C ,都可使小灯泡发光. 任意闭合其中一个开关,则小灯泡发光的概率等于A .21B .31C .41D .438.如图2,是某一立方体的侧面展开图,则该立方体是第Ⅱ卷(非机读卷 共88分)二、填空题(共4个小题,每小题4分,共16分) 9.分解因式:ax 2-6ax+9a=.10. 已知关于x 的方程x 2+kx -3=0一个根是-2,则k 的值为. 11. 小王利用计算机设计了一个计算程序,输入和输出的数据如下表:当输入数据是8时,则输出的数据是;当输入数据是n 时,则输出的数据是 12.已知:如图3,在直角坐标系中,O 为坐标原点,四边形OABC 为矩形, A 、C 的坐标分别为A (10,0),C (0,4),点D是OA 的中点,点P 在 BC 上运动,当△ODP 是腰长为5的等腰三角形时, 则P 点的坐标为A.B.C.D.EDCBA三、解答题(共5个小题,共23分) 13.(本题满分5分) 27 +(5-1)0+(12 )-1-3tan60°14.(本题满分5分) 解方程:xx x --=--3113215.(本题满分4分)已知:如图4,BA=BD ,BC=BE ,∠ABD=∠CBE : 求证:AC=DE图4已知:x 2+x -1=0,求代数式的值:1332--x x ·1131+-+x x x17.(本题满分4分)已知:关于x 的方程041)1(22=++-m x m x (1)当m 取何值时,方程有两个实数根?(2)为m 选取一个合适的整数,使得方程有两个不相等的整数根,并求出这两个根。
2008中考数学模拟试题及答案(3)

2008年中考数学模拟试卷(3)本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷10小题,共30分,第Ⅱ卷90分,共120分.考试时间120分钟.第Ⅰ卷(选择题 共30分)一、选择题(每小题3分,共30分)1、世界文化遗产长城总长约6700000m ,用科学记数法可表示为 ( ) A 、6.7×105m B 、6.7×10-5m C 、6.7×106m D 、6.7×10-6m2、将一圆形纸片对折后再对折,得到图1,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是 ( )3、图2中几何体的正视图是 ( )4、在选取样本时,下列说法不正确的是 ( ) A 、所选样本必须足够大 B 、所选样本要具有普遍代表性C 、所选样本可按自己的爱好抽取D 、仅仅增加调查人数不一定能提高调查质量5、如图3,圆弧形桥拱的跨度AB =12M ,拱高CD =4M ,则拱桥的半径为 ( ) A 、6.5M B 、9M C 、13M D 、15M6、气象台预报“本市明天降水概率是80%”.对此信息,下列说法正确的是 ( ) A 、本市明天将有80%的地区降水 B 、本市明天将有80%的时间降水 C 、明天肯定下雨 D 、明天降水的可能性比较大7.若反比例函数ky x =的图象经过点(-1,2),则这个函数的图象一定经过点 ( ) A 、(2,-1) B 、(12-,2) C 、(-2,-1) D 、(12,2)8.钟表的轴心到分针针端的长为5cm ,那么经过40分钟,分针针端转过的弧长是 ( ) A 、103cm π B 、203cm π C 、253cm π D 、503cm π正面图2ABCD 图3A B CD图3图19.由几个小立方体搭成的一个几何体如图1所示,它的主(正)视图见图2,那么它的俯视图为( )10、下图是由10把相同的折扇组成的“蝶恋花”(图l )和梅花图案(图2)(图中的折扇无重叠),则梅花图案中的五角星的五个锐角均为 ( )A.36ºB.42ºC.45ºD.48º第Ⅱ卷(非选择题 共90分)二、填空题(每小题3分,共18分) 11、-7的绝对值是,21-的倒数是 ; 12、某果园有果树200棵,从中随机抽取5棵,每棵果树的产量如下(单位:千克) 98 102 97 103 105 这5棵果树的平均产量为千克, 估计这200棵果树的总产量约为千克;13、把抛物线2x y -=向上平移2个单位,那么所得抛物线与x 轴的两个交点之间的距离是; 14、用两块完全重合的等腰三角形纸片能拼出下列图形;15、已知22y mxy x +-是完全平方式,则=m ;16、如图,是一个简单的数值运算程序,当输入x 的值为-1时,则输出的数值为;三、解答题(共72分)17、(6分)计算:221245cos 4)21(81⨯÷-︒-+-18、(8分)先化简,在求值,11)1211(2+÷---+a a a a ,其中13+=a19、(8分)解不等式组⎪⎩⎪⎨⎧+<-≥--21x 51x 24)2x (3x ,并把解集在数轴上表示出来.20、(8分)为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x (min )与通话费y (元)的关系如图所示:(1)、分别求出通话费1y 、2y 与通话时间x 之间的函数关系式;(2)、请帮用户计算,在一个月内使用哪一种卡便宜? 21、(8分)等腰梯形一底的中点到另一底的两个端点的距离会相等吗?若相等,请给出证明。
延庆县2008-2009学年初三数学第一学期期末试卷

延庆县2008—2009学年第一学期期末统测试卷初三数学一、选择题:(每题4分,共32分)在下列各题的四个备选答案中,只有一个是正确的,请将所选答案在答题卡相应位置涂黑。
1.如图,ABC ∆中,DE ∥BC ,如果1=AD ,2=DB ,那么BCDE的值为()A .32 B .41 C .31D .212.如图,已知圆心角∠BOC =100°,则圆周角∠BAC 的度数为( ) A.130°B.50°C.80°D. 100°3.在Rt ABC ∆中,90C ︒∠=,sinA=35,则cosB=( ) A.53B.45C.34D. 354.如果反比例函数ky x=的图象经过点(-3,-4),那么函数的图象应在() A .第一、三象限 B .第一、二象限 C .第二、四象限 D .第三、四象限5.已知⊙O 1和⊙O 2的半径分别为3cm 和5 cm ,两圆的圆心距是6 cm ,则这两圆的位置关系是( )A .内含B .外离C .内切D .相交6.抛物线y=-x 2+x+7与x 轴的交点个数是( )A . 3B .2C . 1D . 02题图1题图考生须知:1.本试卷分试题卷和答题卷两部分. 满分120分, 考试时间120分钟.2.答题前,考生务必将自己的学校名称、某某、班级填写清楚。
3.本试卷中的选择题及作图题用2B 铅笔做答,其它题目用黑色的签字笔做答。
4.修改时,选择题及作图用橡皮擦干净,不得使用涂改液。
请保持卡面清洁,不要折叠、弄破。
5.请按照题号顺序在各题目的答题区域内做答,超出答题区域的答案无效。
6.草稿一律不得写在答题卡上,考试结束后, 只上交答题卷.想梦界世个个一一同同7.下列命题中为真命题的是( ) °的两个等腰三角形相似. B.三点一定可以确定一个圆.C.圆心角的度数相等,则圆心角所对的弧相等.D.三角形的内心到三角形三边距离相等.8.二次函数()20y ax bx c a =++≠的图象如图所示.有下列结论: ①240b ac -<;②0ab >;③0a b c -+=;④40a b +=; ⑤当2y =时,x 只能等于0.其中正确的是( ) A.①④B.②⑤C.③④D.③⑤二、填空题:(每空4分共16分)9.如图,有10X 正面写有2008年奥运会主题口号的卡片,它们的背面都相同. 将它们背面朝上洗匀后摆放,从中任意翻开一X 是汉字“同”的概率是_____ .10.如图,△ABC 三边与⊙O 分别切于D ,E ,F ,已知AB=7cm ,AC=5cm ,AD=2cm ,则BC=_______cm .11.x 3=y 5=z 70≠,则x z y x ++=.12.在⊙O 半径为5cm,弦AB ∥CD,且AB=8cm ,CD=6cm,那么AB 与CD 之间的距离是__________cm.三、解答题:(本大题共31分,13、14题各4分,15题5分,16、17、18各6分) 13.(本题4分)计算:2sin 245°+3sin60°+ cos60°14.(本题4分)已知: △ABC求作:△ABC 的外接圆. (要求:用尺规作图,保留痕迹,不写作法,不要求证明)0 2 5 x2y7题图AB 14题图DBE15.(本题5分)某校有A、B两个餐厅,甲、乙二名学生各自随机选择其中的一个餐厅用餐。
年延庆县初三升学模拟考试(二)

年延庆县初三升学模拟考试(二)数 学 试 卷第Ⅰ卷(机读卷 共44分)考 生 须 知1. 第Ⅰ卷为选择题,只有一道大题,共2页。
答题前要认真审题,看清题目要求,按要求认真作答。
2. 第Ⅰ卷各题均须按规定要求在“机读答题卡”上作答,题号要对应,填涂要规范。
3. 考试结束后,考生应将试卷和“机读答题卡”一并交监考老师收回。
一、选择题(共11个小题,每小题4分,共44分)下列各题均有四个选项,其中只有一个是符合题意的,用铅笔把”机读答题卡”上对应题目答案的相应字母处涂黑. 1. 若a 与2互为相反数,则2+a(A) 0 (B) 2- (C) 2 (D) 4 2. 函数 11+=x y 中自变量 x 的取值范围是 (A) 1-≠x (B) 1->x (C) 1≠x (D) 0≠x 3. 下列各式中,与2是同类二次根式的是(A) 3 (B)4 (C)21(D)12 4. 若⊙1O 和⊙2O 的直径分别为cm 4和cm 6,圆心距cm O O 821=,则两圆的公切线有(A) 1条 (B) 2条 (C) 3条 (D) 4条 5. 如果代数式mnm 1+-有意义,那么在直角坐标系中点()n m P ,的位置在(A) 第一象限 (B) 第二象限 (C) 第三象限 (D) 第四象限摩托车自行车4.50y/km x/h6050403020107654321HGFE D CBA 6. 用换元法解分式方程 123322++=+xx x x ,若设 y x x =+2,则原方程可化为关于 y 的整式方程是 (A) 123+=yy (B) 0232=++y y (C) 0232=-+y y (D) 0232=--y y7.如图1,在矩形ABCD 中,E ,F ,G ,H 分别为边AB ,BC , CD ,DA 的中点.若AB=2,AD=4,则四边形EFGH 的面积为 (A) 3 (B) 4 (C) 6 (D) 88.如图2,CD 是 Rt △ABC 斜边AB 上的高,将△BCD沿CD 折叠,B 点恰好落在AB 的中点E 处,则∠A 等于(A) 25° (B) 30° (C) 45° (D) 60°9. 如图3,AB 为⊙O 的直径,PB 、PC 分别切⊙O 于点B 、C ,如果∠ACE =40°,则∠P 等于 (A) 40° (B) 50° (C) 80° (D) 100°10.一个底面半径为5cm,母线长为16cm 的圆锥,它的侧面展开图 的面积是(A) 240cm (B) 240cm π(C) 280cm (D) 280cm π 11.如图4表示的是一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程中的函数图像.两地之间的距离是60km ,请你根据图像判断下列结论中错误..的是 (A)骑摩托车者的速度为40km/h (B) 骑自行车者的速度为10km/h (C) 两人相遇的时候距离乙地还有40km(D) 骑摩托车者比骑自行车者晚出发3小时,却早到1.5小时图4图1PO D BA 图2图3第Ⅱ卷 (非机读卷76分)考生须知 1. 考生认真填写密封线内的区县名、学校名、姓名、报名号、准考证号。
延庆县答案
2008年延庆县初三化学升学模拟考试(一)参 考 答 案一、选择题(每小题只有一个选项符合题意。
共30个小题,每小题1分,共30分。
)二、填空题(共5个小题,共26分) 31.(5分) (1)氮气 (或N 2) (2)(332.(7分)(1)①可燃物 ②氧气(或空气) ③达到着火点 (不要求顺序) (2)热量 混合物(3)①达到着火点 ②提供氧气33.(5分)(1)B(2)O 2 KOH K 2SO 4(3)HCl + KOH = KCl + H 2O(其他合理答案给分)34.(4分)⑴30℃时,a 、b 两物质的溶解度相等 (强调温度给分) ⑵a b c ⑶升温 ⑷有固体析出 35.(5分) (1) A :H 2O 2 甲:Fe (2)可燃性(或还原性)(3) 2H 2O 2MnO 2 2H 2O+O 2↑ (条件加热也可)4CO +Fe 3O 4 高温 3Fe +4CO 2 (反应物也可以是Fe 2O 3或FeO )三、实验题(共3个小题,共18分)36.(6分)(1)①铁架台 ②酒精灯(2)B ⑤将导管从水槽中取出 2KMnO 4=====K 2MnO 4+MnO 2+O 2↑(3)D 37.(6分)(1)足量..的一氧化碳 (2)验证有CO 2生成 Ca(OH)2+CO 2=CaCO 3↓+H 2O (3)尾气处理 (4)乙 90% 38.(6(其他方法合理得分) (表格中答案2分)⑵① 甲、乙装置中气球都变大,但甲中气球体积小于乙中气球体积;甲装置中石灰水变浑浊,乙装置中液体仍澄清 2NaOH + CO 2 == Na 2CO 3 + H 2O ② NaOH 溶液四、计算题(共2个小题,共6分。
)最后结果保留一位小数 39.(3分)(1)4; (2)14.3%; (3)45.5 40.(3分)解:(1) 设该厂每天至少需氯化钠固体的质量为x 。
2NaCl+2H 2O 通电Cl 2↑+H 2↑+2NaOH 117 71 x 7.1 t7.1t71x117=x =11.7 t ……………………………………………………………………(1分) (2)氯化钠溶液的质量:11.7 t ÷26.5%=44.15 t (或44.2 t ) ……………(1分) (3)设生成氢氧化钠的质量为y ,生成氢气的质量为z 。
延庆2008-2009初二第一学期期末试题

延庆县2008—2009学年第一学期期末统测试卷初二数学分数一、选择题:(共30分,每小题3分)下列各题只有一个正确答案,请把正确答案的序号填在题后的括号里 1、14的算术平方根是( ) A .12- B.12C.12±D.1162、下列四个算式中,正确的是( )A .a 3·a 2=2a 6 B. b 3+b 3=b 6 C. x ·x 4=x 4 D.y 5+y 5=2y 53、函数72-=x y 中自变量x 的取值范围是( )A .x >27 B.x ≥72 C. x ≥27 D. x >724、下列图案中是轴对称图形的是( )5、如图,已知△ABC 的六个元素,则下面甲、乙、丙三个三角形中和△ABC 全等的图形是( )A .甲和乙 B.乙和丙 C.只有乙 D.只有丙 6、已知等腰三角形的两边长分别为6㎝、3㎝,则这个三角形的周长为( )A .15㎝B.12㎝C.12㎝或15㎝ D.9㎝7、不借助计算器,估计76的大小应为( )A .7 —— 8之间B.8.0 —— 8.5之间C.8.5 —— 9.0之间 D.9 —— 10之间8、如图,直线l 是一条河,P 、Q 两地相距8千米,P 、Q 两地到l 的距离分别为2千米、5千米,欲在l 上的某点M 处修建一个水泵站,向P 、Q 两地供水,现有如下四种铺设管道的方案,图中实线表示铺设的管道,则铺设的管道最短的是( )9、如图,△ABC 中,∠A = 36°,AB = AC ,BD 平分∠ABC, DE ∥ BC, 则图中的等腰三角形的个数( ) A .1个 B.3个 C. 4个 D.5个10、小王于上午8时从甲地出发去相距50千米的乙地.下图中,折线OABC 是表示小王离开甲地的时间t (时)与路程s (千米)之间的函数关系的图象.根据图象给出的信息,下列判断中错误的是( ) A .小王11时到达乙地 B.小王在途中停了半小时C.出发后1小时,小王走的路程少于25千米 D.与8:00-9:30相比,小王在10:00-11:00前进的速度较慢EDCB A二、填空题:(共18分,每小题3分) 11、化简()32a-=_______ .12、点M(1,2)关于x 轴对称点的坐标为________. 13、如右图在ABC △中,点D 是BC 上一点,80BAD ∠=°,AB AD DC ==,则C ∠= .14、如右图所示,利用函数图象回答下列问题:(1)方程组3,2x y y x+=⎧⎨=⎩ 的解为__________;(2)不等式32+->x x 的解集为___________; (3)不等式32+-<x x 的解集为__________.15、如图,在ABC ∆中, ︒=∠90C ,AD 平分∠BAC ,DE ⊥AB ,垂足为E , BC=6, DE=2 , 则DB=________.16、观察下列各式:32343112==+;43494122==+;545165132==+;656256142==+……设n 为正整数,请用关于n 的等式表示这个规律为:______+______=______.ABCDCBEAD三、作图题(3分)17、为了美化环境,需要在一块正方形空地上分别种植四种不同的花草,现将这块地按下列要求分成四块:(1)四块地形状相同;(2)四块地面积相等。
2008年北京延庆初中升学模拟练习

2008年北京市延庆县初中升学模拟练习(二)语文试卷第Ⅰ卷(共60分)一、选择。
下面各题均有四个选项,其中只有一个..符合题意,请将该答案的字母序号填在题干后的括号内。
(共10分。
每小题2分)1.下列词语中加点字的读音都正确的是()A.败兴.xīng 勉强.qiǎng 卑鄙.bì煎熬.áoB.称.职chèn 惩.罚chéng 享.受xiǎng 修葺.qìC.订.正dìng 氛.围fèn 解剖.pāo 哽咽.yèD.倔.强juè暂.时zhǎn 避讳.huì祈.祷qí2.下列词语中没有错别字的是()A.伫藏虐待滥竽充数拔山涉水B.游戈细腻完壁归赵刻舟求剑C.忙碌讥刺买椟还珠不可救要D.逃窜捐款亡羊补牢再接再厉3. 下列词语中加点字的意思相同的是()A.茅.塞顿开三顾茅.庐B.油然而生.栩栩如生.C.触景.生情春和景.明D.新闻.联播鸡犬相闻.4.填入下面文字中横线上的语句最恰当的一项是()在天山的高处,可以看到巨大的天然湖,①,使湖光天影山色融为晶莹的一体。
在这秀美的湖上,唯一活动的就是天鹅。
②。
大地慷慨地赋予人类这宁静的自然环境。
A.①四周的雪峰和高空的白云被明净如镜、水清见底的湖水清晰的倒映出来。
②湖水的明净衬托了天鹅的洁白,湖面的幽静衬托了天鹅的叫声。
B.①湖面明净如镜,水清见底,高空的白云和四周的雪峰清晰的倒映在水中。
②湖水的明净衬托了天鹅的洁白,湖面的幽静衬托了天鹅的叫声。
C.①湖面明净如镜,水清见底,高空的白云和四周的雪峰清晰的倒映在水中。
②天鹅的洁白增添了湖水的明净,天鹅的叫声衬托了湖面的平静。
D.①四周的雪峰和高空的白云被明净如镜、水清见底的湖水清晰的倒映出来。
②天鹅的洁白增添了湖水的明净,天鹅的叫声衬托了湖面的幽静。
5. 下列作家作品均为同一朝代的是()①《行路难》②《醉翁亭记》③《钱塘湖春行》④《记承天寺夜游》⑤王安石⑥杜甫⑦柳宗元⑧辛弃疾A.①③⑤⑦B.②④⑤⑧C.③④⑥⑦D.②④⑥⑧二、填空(共8分)6.默写(6分)⑴采菊东篱下,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
延庆县2008年初中升学模拟练习(一)数 学 试 卷第Ⅰ卷 (选择题 32分)一、选择题(本题共32分,每小题4分)下列各题均有四个选项,其中只有一个..是符合题意的. 1.-31的绝对值是 A . 31 B .-31 C .3 D .-32.为迎接2008年北京奥运会修建的鸟巢,将用于国际、国内体育比赛和文化、娱乐活动,鸟巢的建筑面积约为258000 平方米,将258000用科学记数法表示应为A .62.5810⨯B .52.610⨯C .42.5810⨯D .52.5810⨯ 3.如图1,BC ∥DE,∠1=105°, ∠AED=65°, 则∠A 的大小是 A .25° B .35° C .40° D .60° 4.在函数21-=x y 中,自变量x 的取值范围是 A .0≠x B .2≠x C .2-≠x D .不确定5.一组数据:34,35,36,35,36,37,37,36,37,37,这组数据的平均数和众数分别是 A.36,37B.37,36 C.36.5,37 D.35,376.把239ab a -因式分解正确的是 A .a (9a+b )(9a-b )B .a 2)9(b a -C .a (3a+b )(3a-b )D .22)3(ab a -7. 有一只小狗,在如图2所示的方砖上走来走去,最终停在深色方砖上的概率是. A. 12 B. 13C. 19D. 598.如图3,在矩形ABCD 中,AB =4,BC =3,点AF ,过点B 作BE ⊥AF 于E ,设BE =y ,AF =x ,则能反映y 与x 之间函数关系的大致图象是A B C D二、填空题(本题共16分,每小题4分)9.已知实数x ,y 满足x y -++=540,则代数式xy =_______10.关于x 的一元二次方程kx 2 -x +1=0有两个不相等的实数根,则k 的取值范围是_______ 11.如图4,从左到右,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.可求得c=_______,第2009个格子中的数为_________12.如图5,矩形ABCG 与矩形CDEF 全等,点BCD 在一条直线 上,∠APE 的顶点P 在线段BD 上移动,使得∠APE 为直角的点P 的个数是 个图4三、解答题(本题共23分,14,15小题各4分,13,16,17小题各5分)13.计算:12 -4sin60°+(2-1)0+(- 12)-114.解不等式组⎪⎩⎪⎨⎧+<-≤-)1(32121x x x ,并求出它的最小负整数解。
15.计算:21422---a a a16.已知:如图6,点E 是正方形的边CD 上的点,点F 是边CB 的延长线上的点,且AE ⊥AF ,垂足为A , 求证:DE=BF17.已知:x 2+4x=0.求代数式1)2()2)(2()3(2-+--+++x x x x x 的值.四、解答题(本题共15分,每小题5分)18.如图7,等腰梯形ABCD 中,AD ∥BC ,AB=CD ,∠ACB=45°,翻折梯形ABCD ,使点C 重合于点A ,折痕分别交边CD 、BC 于点F 、E ,若AD=3,BC=12, 求:(1)CE 的长;(2)∠BAE 的正切值.19.北京市教委为增强中学生体质,开展了“每天锻炼一小时”的体育活动。
4月份对全市中小学生进行体质监测评价,专家组随机抽查了某区若干名初中学生。
我们对专家的测评数据作了适当处理,并将统计结果绘制了如下两幅不完整的统计图(图8),请你根据图中所给信息解答下列问题: (1)请将两幅统计图补充完整; (2)在这次监测评价中,一共抽查了名学生,如果全市有10万 名初中生,那么全市初中生中,可以 达到优秀的学生约有 人; (3)根据统计结果,请你简单谈谈自己的看法. 图7 图8C A20.如图9,以Rt △ABC 的一条直角边AB 为直径作⊙O ,与AC 交于点F ,在AB 的延长线上取一点E ,联结EF 与BC 交于点D ,且使得DF=CD 。
(1)求证:FE 是⊙O 的切线(2)如果sin ∠A= 12 ,AE=3 ,求AF 的长五、解答题(本题共10分,21小题6分,22小题4分)21.列方程或方程组解应用题某景点为在五一期间吸引更多的游客,推出集体购票优惠票价活动,其门票价目如下:有同一旅行社的甲、乙两个旅行团共60人(甲团人数多于乙团)准备去该景点旅游,如果甲、乙两团各自购票,那么一共要支付98元。
(1) 如果两团联合起来购票,那么比各自购票要节约多少钱? (2) 甲乙两团各有多少人?(3)如果甲团有12人因故不能前往旅游,那么旅行社该如何购票才能最省钱?A22. 现有一张长和宽之比为2:1的长方形纸片.将它折两次(•第一次折后也可以打开铺平再折第二次).使得折痕将纸片分为面积相等且不重叠的四个部分(称为一个操作),如图甲(虚线表示折痕).除图甲外,请你再给出四个不同的操作,分别将折痕画在图①至图③中(规定:一个操作得到的四个图形,和另一个操作得到的四个图形,如果能够“配对”得到四组全等的图形,那么就认为是相同的操作.如图乙和图甲是相同的操作). ① ② ③ ④六、解答题(本题共24分,23小题6分,24小题9分,25小题9分)23.(1)已知:有两块完全相同的含45°角的三角板,如图10-1,将Rt △DEF 的直角的=顶点D 放在Rt △ABC 斜边AB 的中点处,这时两块三角板重叠部分△DBC 的面 积是△ABC 的面积的 ;(2)如图10-2,点D 不动,将Rt △DEF 绕着顶点D 旋转α(0°<∠α<90°),这时两块三角板重叠部分为任意四边形DNCM ,这时四边形DNCM 的面积是△ABC 的面积的 ; (3)若Rt △DEF 的顶点D 在AB 上移动(不与点A 、B 重合),且两条直角边与Rt △ABC的两条直角边相交,是否存在一点,使得两块三角板重叠部分的面积是Rt △ABC的面积的49 ,如果存在,请在图10-3中画出此时的图形,并说明点D 在AB 上的位置。
如果不存在,说明理由。
图10-324.已知:抛物线n mx x y ++=2与x 轴交A 、B 两点(A 点在B 点左侧),B (3,0), 且经过C (2,-3),与y 轴交于点D , (1)求此抛物线的解析式及顶点F 的坐标;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物于E 点,求线段PE 长度的最大值;(3)在(1)的条件下,在x 轴上是否存在两个点G 、H (G 在H 的左侧),且GH=2,使得线段GF+FC+CH+HG 的长度和为最小;如果存在,求出G 、H的坐标;如果不存在,说明理由。
25.我们给出如下定义:如图12-2所示,若一个四边形的两组相邻两边分别相等,则称这个四边形为筝形四边形,把这两条相等的邻边称为这个四边形的筝边.(1)写出一个你所学过的特殊四边形中是筝形四边形的图形的名称_________; (2)如图12-1,已知格点(小正方形的顶点)(00)O ,,A (0,3),B (3,0),请你画出以格点为顶点,OA OB ,为边的筝形四边形OAMB ;(3)如图12-2,在筝形ABCD ,AD=CD ,AB=BC ,若∠ADC=60°,∠ABC=30°求证:2AB 2 =BD 2。
图12-2图12-1⎪⎩⎪⎨⎧+<-≤-)1(32121x x x 延庆县2008年初中模拟考试试卷(一)数学参考答案及评分标准一、 选择题(本题满分32分)9.-20; 10.k<14 且k≠0; 11.3,-1; 12.2个 ;三、(本题满分23分) 13.(本题满分5分)解: 12 -4sin60°+(2-1)0+(-12)-1=23-23+1-2…………………………4分 =-1…………………………5分 (注:每写对一个给1分,4个共4分) 14. (本题满分4分) ①②解:由①得,x≤3 ………………………1分 由②得,x>-2.5 ………………………2分∴原不等式组的解集为:-2.5<x≤3 ………………………3分 ∴原不等式组的最小负整数解为:-2 ………………………4分 15. (本题满分4分)解: 原式=21)2)(2(2---+a a a a ……………………1分=)2)(2(2)2)(2(2-++--+a a a a a a ……………………2分=)2)(2(22-+--a a a a=)2)(2(2-+-a a a ……………………3分=21+a ……………………4分 16. (本题满分5分)证明:∵正方形ABCD∴AB=AD ,∠ABC=∠ADC=∠ABF=∠BAD =90°………………2分 ∵AE ⊥AF ,∠BAD =90°∴∠1=∠2在△ABF 和△ADE 中 ∠ADE=∠ABF =90°AB=AD ∠1=∠2∴ △ABF ≌△ADE ……………………4分 ∴DE=BF ……………………5分17 (本题满分5分)解: 1)2()2)(2()3(2-+--+++x x x x x=x 2+6x +9+x 2-4-x 2-2x -1 …………………3分 = x 2+4x+4 ………………4分 ∵x 2+4x=0, ∴原式= x 2+4x+4=4 … ………………5分 18. (本题满分5分) 解:∵翻折梯形ABCD∴∠ACE=∠EAC=45°,AE=EC∴∠AEB=∠AEC=90° ……………1分过D 做DM ⊥BC 交BC 于M ,则∠DMB=90° ∴四边形AEMD 为矩形∴ AD=ME=3∵等腰梯形ABCD ,AD ∥BC ,AB=CD∴∠ABC=∠DCB AE=DM , …………2分 在△ABE 和△DMC ∠AEB=∠DMC =90°AB=CD AE=DM∴ △ABE ≌△DMC ∴BE=CM ∴BE=CM =(12-3)÷2=4.5 ……………………3分 ∴CE=7.5 ……………………4分在△BAE 中,tan ∠BAE=535.75.4===CE BE AE BE …………………5分19. (本题满分5分)(1)…………………2分………………2分(2)500;15000 …………………4分(3)略 …………………5分20. (本题满分5分)(1)证明:联结OF∵ OA=OF ∴ ∠OAF= ∠OFA∵DF=DC . ∴ ∠DFC=∠DCF ……………1分∵∠ABC=90°∴ ∠OAF+∠FCD=90°∴∠AFO+∠DFC=90°∴ ∠OFD =90°…………………………………2分∴CD 与⊙O 相切 …………………………3分(2)∵sin ∠A=12∴∠A= 30° ∴∠ACB= 60° 在Rt △ABC 和Rt △CBE 中,∠A= 30°,∠BEF= 30°设BD=x, 则BE=3x , BC=2x ,∴AC=4x ∴AB=2x 3 AE=3x 3∴ x=31,即BD=CD =31 ∴ AC=34 ……………….. 4分 联结BF ,则有DF=12BC 又∵∠BFC=90° ∴DB=DF=DC ,∵∠ACB= 60°∴△DFC 为等边三角形∴CF=DF=31 ∴AF=AC-CF=1 ………………5分21. (本题满分6分)解: (1)98-60×1=38 要节约38元。
