山东省威海市2014届下学期高三年级第一次模拟考试数学试卷(理科)
山东省2014届理科一轮复习试题选编25:空间几何体的三视图

山东省2014届理科数学一轮复习试题选编25:空间几何体的三视图、表面积与体积一、选择题 1 .(山东省临沂市2013届高三第三次模拟考试 理科数学)一个空间几何体的三视图如图,则该几何体的体积为( )A.B.CD【答案】D2 .(2013年山东临沂市高三教学质量检测考试理科数学)具有如图所示的正视图和俯视图的几何体中,体积最大的几何体的表面积为( )A .13B .C .72πD .14【答案】D 由正视图和俯视图可知,该几何体可能是四棱柱或者是水平放置的三棱柱,或水平放置的圆柱.由图象可知四棱柱的体积最大.四棱柱的高为1,底面边长分别为1,3,所以表面积为2(131131)14⨯+⨯+⨯=,选D . 3 .(山东省莱芜五中2013届高三4月模拟数学(理)试题)已知四面体S ABC -的所有棱长都相等,它的俯视图如下图所示,的正方形;则四面体S ABC -外接球的表面积为( )A . 6πB .4πC .8πD .3π【答案】A4 .(山东省临沂市2013届高三5月高考模拟理科数学)某几何体的三视图如图(其中侧视图中的圆弧是半圆),第7题图( )A .9214+πB .8214+πC .9224+πD .8224+π【答案】A 由几何体的三视图,知该几何体的下半部分是长方体,上半部分是半径为2,高为5的圆柱的一半. 长方体的中445EH HG GK ===,,,所以长方体的表面积为(去掉一个上底面)2(4445)45=92⨯+⨯+⨯.半圆柱的两个底面积为22=4ππ⨯,半圆柱的侧面积为25=10ππ⨯⨯,所以整个组合体的表面积为92+410=92+14πππ+,选( )A ..5 .(山东省菏泽市2013届高三5月份模拟考试数学(理)试题)如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积、体积分别是 ( )A .12832,3ππ B .3216,3ππ C .1612,3ππ D .168,3ππ【答案】C 6 .(山东省潍坊市2013届高三第二次模拟考试理科数学)有一平行六面体的三视图如图所示,其中俯视图和左视图均为矩形,则这个平行六面体的表面积为( )A .B .6+C .30+D .42【答案】C 由三视图可知该平行六面体的底面是个矩形,两个侧面和底面垂直.其中侧棱12AA =.底面第7题图边长3AD =,平行六面体的高为3.2BE =,又2222112(3)1AE AA A E =-=-=,所以123AB =+=.所以平行六面体的表面积为2(333332)=3063⨯+⨯+⨯+,选C .7 .(山东省兖州市2013高三9月入学诊断检测数学(理)试题)如右图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h 随时间t 变化的可能图象是【答案】 B . 8 .(山东省2013届高三高考模拟卷(一)理科数学)一个几何体的三视图如图所示,其正视图和侧视图都是底边长分别为2和4,腰长为4的等腰梯形,则该几何体的侧面积是( )A .π6B .π12C .π18D .π24【答案】B 【解析】结合三视图可知该几何体是一个圆台,其上,下底面的半径分别为2,1,其直观图如图所示.则该几何的侧面积⨯=2(πS π12)414=⨯+.9 .(山东省泰安市2013届高三上学期期末考试数学理)如图,若一个空间几何体的三视图中,正视图和侧视图都是直角三角形,其直角边均为1,则该几何体的体积为( )A .13B .12 C .16D .1【答案】A【解析】由三视图可知,该几何体是四棱锥,底面为边长为1的正方形,高为1的四棱锥,所以体积为1111133⨯⨯⨯=,选A . 10.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的( )AB1 CD .外接球的表面积为4π【答案】B11.(山东省济南市2013届高三3月高考模拟理科数学)一个几何体的三视图如右图所示,则它的体积为( )A .203 B .403C .20D .40【答案】B由三视图可知,该几何体是一个放到的四棱锥,其中四棱锥的底面是主视图,为直角梯形,直角梯形的上第11题图图图底为1,下底为4,高为 4.棱锥的高位4,所以四棱锥的体积为1144044323+⨯⨯⨯=,选B .12.(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)一个几何体的三视图如图所示,则该几何体的体积为( )A .1B .13 C.12D.32 【答案】B 由三视图可知,该几何体是四棱锥,以俯视图为底,高为1,俯视图的面积为11=1⨯,使用四棱锥的体积为111133⨯⨯=,选 B .13.(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)如图所示是以建筑物的三视图,现需将其外壁用油漆刷一遍,若每平方米用漆0.2k g,则共需油漆大约公斤数为(尺寸如图所示,单位:米 π取3)( )A .20B .22.2C .111D .110【答案】B【解析】由三视图可知,该几何体上面是个圆锥,下面是个长方体.长方体的底面是边长为3的正方形,高为4,所以长方体的表面积(去掉上下两个底面)为24(34)=48()m ⨯⨯.圆锥的底面半径为3,母线为5,所以圆锥的侧面积为2351545()m ππ⨯⨯==,底面积(去掉一个正方形)为29339918()m ππ-⨯=-=,所以该几何体的总面积为2484518111()m ++=,所以共需油漆0.211122.2⨯=公斤,选 B .14.(山东省济宁市2013届高三4月联考理科数学)已知某几何体的三视图如图所示,其中俯视图中圆的直径为4,该几何体的体积为1V ,直径为4的球的体积为2V ,则12:V V =( )A .1:2B .2:1C .1:1D .1:4【答案】A15.(2013届山东省高考压轴卷理科数学)右图是一个几何体的正(主)视图和侧(左)视图,其俯视图是面积为的矩形.则该几何体的表面积是( )A.20+B.24+C .8D .16【答案】( )A .【解析】由已知俯视图是矩形,则该几何体为一个三棱柱,根据三视图的性质,俯视图的矩形宽为由面积4,则1+2=24+2S S S =⨯⨯⨯⨯侧底()2 =2820+. 16.(山东省青岛市2013届高三第一次模拟考试理科数学)一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是( )A .16πB .14πC .12πD .8π【答案】A 由三视图可知,该几何体是一挖去12半球的球.其中两个半圆的面积为224ππ⨯=.34个球的表面积为2342124ππ⨯⨯=,所以这个几何体的表面积是12416πππ+=,选A. 17.(山东省枣庄市2013届高三3月模拟考试数学(理)试题)一个几何体的三视图如图所示,其中的长度单位为cm,则该几何体的体积为( )cm 3.( )正视图 俯视图左视图A .18B .48C .45D .54【答案】D由三视图可知,该几何体时底面是矩形的四棱柱,以俯视图为底,底面直角梯形的上底为4,下底为5,高为3.棱柱的高为4,所以四棱柱的体积为34534542cm +⨯⨯=,选 D .18.(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)一个几何体的三视图如图所示,则该几何体的体积为( )A .2B .1C .23D .13【答案】C 19.(2011年高考(山东理))右图是长和宽分别相等的两个矩形.给定下列三个命题:① 存在三棱柱,其正(主)视图、俯视图如右图;② 存在四棱柱,其正(主)视图、俯视图如右图; ③ 存在圆柱,其正(主)视图、俯视图如右图.其中真命题的个数是 ( ) A .3 B .2 C .1 D .0【答案】解析:①②③均是正确的,只需①底面是等腰直角三角形的直四棱柱, 让其直角三角形直角边对应的一个侧面平卧;②直四棱柱的两个侧面 是正方形或一正四棱柱平躺;③圆柱平躺即可使得三个命题为真, 答案选A . 20.(山东省济南市2013届高三上学期期末考试理科数学)一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是【答案】C【 解析】若俯视图为C,则俯视图的宽和左视图的宽长度不同,所以俯视图不可能是C .21.(山东省潍坊市2013届高三上学期期末考试数学理 ( )A .)一个几何体的三视图如图所示,其中主视图和左视图是腰长为4的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是 ( ) A .π12 B .π24 C .π32 D .π48 【答案】D【解析】该几何体的直观图如图1所示,它是有一条侧棱垂直于底面的四棱锥.其中底面ABCD 是边长为4的正方形,高为CC 1=4,该几何体的所有顶点在同一球面上,则球的直径为12AC R ==,所以球的半径为R =,,所以球的表面积是224448R πππ=⨯=,选D .22.(山东省威海市2013届高三上学期期末考试理科数学)某几何体的三视图如右图所示,则该几何体的体积不可能是( )A .1B .1.5C .2D .3【答案】D 由三视图可知,该几何体时一个侧面和底面垂直的的三棱锥,,其中底面三角形BAC为直径三角形,PA ABC ⊥,2AB =,4PC =,设,04AC x x =<<,则PA ==,所以三棱锥的体积为111168232363x ⨯⨯=≤==,当且仅当x =即28,x x ===,此时体积有最大值82233=,所以该三棱锥的体积不可能是3,选D .23.(山东省烟台市莱州一中2013届高三第三次质量检测数学(理)试题)如图是某一几何体的三视图,则这个几何体的体积为( )A .4B .8C .16D .20【答案】C 【解析】由三视图可知,该几何体是一个四棱锥,四棱锥的高为4,底面为俯视图对应的矩形,俯视图的面积为2612⨯=,所以四棱锥的体积为1124163⨯⨯=,选C .24.(山东省烟台市2013届高三上学期期末考试数学(理)试题)一个几何体的三视图如下所示,则该几何体的表面积是 ( )A .6+B .12+C .12+D .18+【答案】C【解析】由三视图可知,该几何体是一个直三棱柱,三棱柱的底面是一个腰长为2,底面上的高是1的等腰三角形,侧棱长是3,所以该几何体的表面积为1213(22122⨯⨯+++=+,选 C . 25.(山东师大附中2013届高三第四次模拟测试1月理科数学)已知某几何体的三视图如图,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )A .3242π-B .243π-C .24π-D .242π-【答案】A 【解析】由三视图可知该几何体是一个长方体去掉一个半圆柱.长方体的长宽高分别为3,2,4.所以长方体的体积为32424⨯⨯=.半圆柱的高为3,所以半圆柱的体积为13322ππ⨯⨯=,所以几何体的体积为3242π-,选 ( )A .26.(山东省泰安市2013届高三第二次模拟考试数学(理)试题)如右图,一个由两个圆锥组合而成的空间几何体的正视图和侧视图都是边长为1、一个内角为60°的菱形,俯视图是圆及其圆心,那么这个几何体的体积为( )A.12B .6ππC.12π D.6【答案】A27.(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))如图,正三棱柱ABC -111A B C 的各棱长均为2,其正(主)视图如图所示,则此三棱柱侧(左)视图的面积为( )A .22B .4C .3D .32【答案】D【解析】由正视图可知,此三棱柱的侧视图为,高为2,宽为3的矩形,所以面积为32,选 D . 28.(2009高考(山东理))一空间几何体的三视图如图所示,则该几何体的体积为( )A .2ππ D .4π+1,高为2,体积为2π,四棱2=所以该几何体的体积为2π.答案:C29.(山东省日照市2013届高三12月份阶段训练数学(理)试题)如右图,某几何体的主视图与左视图都是边长正(主)视图为1的正方形,且体积为12,则该几何体的俯视图可以是【答案】C 【解析】若俯视图为A,则该几何体为边长为1的正方体,体积为1,不成立.若俯视图为B,则该几何体为圆柱,体积为21()124ππ⨯=,不成立.若俯视图为C,则该几何体为三棱柱,体积为1111122⨯⨯⨯=,成立.若俯视图为D,则该几何体为14圆柱,体积为211144ππ⨯⨯=,不成立.所以只有C 成立,所以选 C .30.(山东省烟台市2013届高三3月诊断性测试数学理试题)如右图,某几何体的三视图均为边长为l 的正方形,则该几何体的体积是( ) A .65 B .32 C .1 D .21 【答案】A 由题意三视图对应的几何体如图所示,所以几何体的体积为正方体的体积减去一个三棱锥的体积,即31151111326-⨯⨯⨯⨯=,选 ( )A .31.(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的体积是( )A .1B .2C .3D .4【答案】B 由题设及图知,此几何体为一个四棱锥,其底面为一个对角线长为2的正方形,故其底面积为141122⨯⨯⨯=.由三视图知其中一个侧棱为棱锥的高,其相对的侧棱与高及底面正方形的对角线组成一个直角三角形由于此侧棱长为13,对角线长为2,故棱锥的高为22(13)293-==.此棱锥的体积为12323⨯⨯=,选B . 32.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)如图所示是一几何体的三视图,则该几何体外接球的表面积为( ) A .3π B .4π C .8π D .9π【答案】D二、填空题33.(山东省凤城高中2013届高三4月模拟检测数学理试题 )已知某几何体的三视图如图所示,其中正视图中半圆的直径为2,则该几何体的体积为____.【答案】3242π- 34.(山东省文登市2013届高三3月二轮模拟考试数学(理))如图,已知球O 的面上有四点,,,A B C D ,DA ⊥平面ABC ,AB BC ⊥,2DA AB BC ===,则球O 的体积与表面积的比为__________.【答案】35.(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)已知矩形ABCD 的顶点都在半径为5的球O 的球面上,且8,AB BC ==则棱锥O ABCD -的体积为______.【答案】球心在矩形的射影为矩形对角线的交点上.所以对角线长为=,所以棱锥的高为=,所以棱锥的体积为183⨯=. 36.(2012年山东理)(14)如图,正方体ABCD-A 1B 1C 1D 1的棱长为1,E,F 分别为线段AA 1,B 1C 上的点,则三棱锥D 1-EDF 的体积为____________.【答案】解析:61112113111=⨯⨯⨯⨯==--DE D F EDF D V V . 37.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )从如图所示的长方形区域内任取一个点M(x,y),则点M 取自阴影部分的概率为 ____________;【答案】31 38.(山东省济南市2013届高三4月巩固性训练数学(理)试题)已知某几何体的三视图如图所示,则该几何体的体积为_________.【答案】 4163π+ 39.(山东省德州市2013届高三3月模拟检测理科数学)一空间几何体的三视图如图所示,该几何体的体积为16π,则图中x 的值为_______________.【答案】3由三视图可知,该几何体下面是个圆柱,上面是个四棱锥.圆柱的体积为4416ππ⨯=,四棱锥的底面积为14482⨯⨯=,所以四棱锥的体积为18833h h ⨯⨯=,所以816163h ππ=+,所以四棱锥的高h =所以2222549x h =+=+=,即3x =. 40.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)一个几何体的三视图如图所示,则这个几何体的表面积与其外接球面积之比为________.【答案】π3 41.(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)一个几何体的三视图如右图所示,则正视图 侧视图俯视图该几何体的表面积为__________.【答案】242π+ 【解析】由三视图可知,该组合体下部是底面边长为2,高为3的正四棱柱,上部是半径为2的半球,所以它的表面积为224322221224πππ⨯⨯+⨯+⨯=+. 42.(山东济南外国语学校2012—2013学年度第一学期高三质量检测数学试题(理科))一个几何体的三视图如图所示(单位:m),则该几何体的体积为__________________3m .【答案】4 【解析】由三视图可知,该组合体是由两个边长分别为2,1,1和1,1,2的两个长方体,所以体积之和为2111124⨯⨯+⨯⨯=。
山东省2014届理科一轮复习试题选编38:算法初步(含解析)
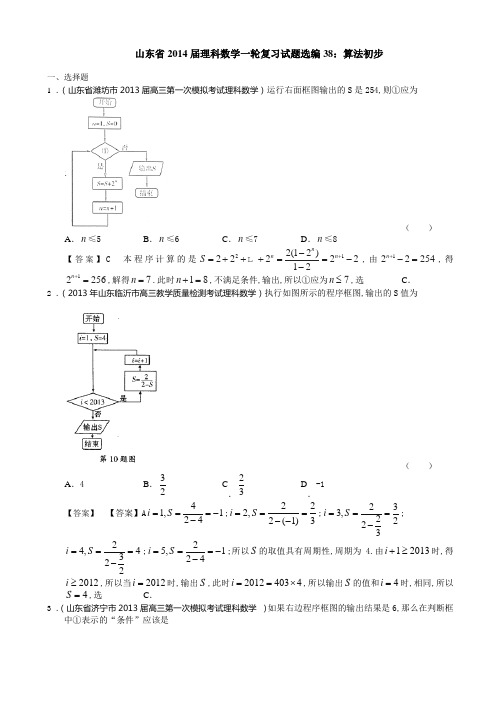
山东省2014届理科数学一轮复习试题选编38:算法初步一、选择题 1 .(山东省潍坊市2013届高三第一次模拟考试理科数学)运行右面框图输出的S 是254,则①应为( )A .n ≤5B .n ≤6C .n ≤7D .n ≤8【答案】C 本程序计算的是212(12)2222212n nn S +-=+++==-- ,由122254n +-=,得12256n +=,解得7n =.此时18n +=,不满足条件,输出,所以①应为7n ≤,选C . 2 .(2013年山东临沂市高三教学质量检测考试理科数学)执行如图所示的程序框图,输出的S 值为( )A .4B .32 C.23D .-1 【答案】 【答案】A 41,124i S ===--;222,2(1)3i S ===--;233,2223i S ===-;24,4322i S ===-;25,124i S ===--;所以S 的取值具有周期性,周期为 4.由12013i +≥时,得2012i ≥,所以当2012i =时,输出S ,此时20124034i ==⨯,所以输出S 的值和4i =时,相同,所以4S =,选 C .3 .(山东省济宁市2013届高三第一次模拟考试理科数学 )如果右边程序框图的输出结果是6,那么在判断框中①表示的“条件”应该是( )A .i≥3B .i≥4C .i≥5D .i≥6 【答案】D【解析】第一次循环,264,6410,2m s i =-+==+==;第二次循环,2262,10212,3m s i =-⨯+==+==;第三次循环,2360,12,4m s i =-⨯+===;第四次循环,2462,12210,5m s i =-⨯+=-=-==;第五次循环,2564,1046,6m s i =-⨯+=-=-==;此时满足条件输出6s =,所以条件应为,6i ≥选D .4 .(山东省泰安市2013届高三第二次模拟考试数学(理)试题)已知数列{}11,1,n n n a a a a n +==+中,若利用如图所示的程序框图计算并输出该数列的第10项,则判断框内的条件可以是( )A .11?n ≤B .10?n ≤C .9?n ≤D .8?n ≤【答案】C 5 .(山东省临沂市2013届高三5月高考模拟理科数学)执行如图所示的程序框图,输出的结果是( )A .11B .12C .13D .14【答案】C 第一次循环,1,2,123x y z ===+=;第二次循环,2,3,235x y z ===+=;第三次循环,3,5,358x y z ===+=;第四次循环,5,8,5813x y z ===+=,此时满足条件,输出13z =,选 C . 6 .(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)若程序框图如图所示,则该程序运行后输出k 的值是( )A .4B .5C .6D .7【答案】B第一次35116,1n k =⨯+==;第二次168,22n k ===;第三次84,32n k ===;第四次42,42n k ===;第五次21,52n k ===此时满足条件输出5k =,选 B . 7 .(山东省济南市2013届高三4月巩固性训练数学(理)试题)定义某种运算⊗,a b ⊗的运算原理如图 所示.设x x f ⊗=1)(.()f x 在区间[2,2]-上的最大值为. ( )A .-2B .-1C .0D .2【答案】D 8 .(山东省济宁市2013届高三4月联考理科数学)左图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到14次的考试成绩依次记为1214,,,.A A A 右图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是7.98.6 3 89.3 9 8 8 4 1 5 10.3 1 11.4 ( )A .7B .8C .9D .10【答案】D9 .(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)执行如图所示的程序框图,若输出结果为3,则可输入的实数x 值的个数为( )A .1B .2C .3D .4【答案】C 由题意知221,2log ,2x x y x x ⎧-≤=⎨>⎩.当2x ≤时,由213x -=,得24x =,解得2x =±.当2x >时,由2log 3x =,得8x =,所以输入的实数x 值的个数为3个,选 C .10.(山东省德州市2013届高三第二次模拟考试数学(理)试题)执行如图所示的程序框图,若输入n 的值为≤≥16,则输出s 的值为( )A .17B .16C .10D .9【答案】C 11.(山东省2013届高三高考模拟卷(一)理科数学)执行如图所示的程序框图,若输入5=p ,6=q ,则输出a ,i 的值分别为( )A .5,1B .30,3C .15.3D .30.6【答案】D 【解析】执行程序框图可知,当1=i 时,15⨯=a ;当2=i 时,25⨯=a ;;当6=i 时,65⨯=a ,即a 能被q 整除,退出循环,输出i a ,的值分别为30,6. 12.(山东省德州市2013届高三3月模拟检测理科数学)如图所示,程序框图运行后输出k 的值是( )A .4B .5C .6D .7【答案】B 第一次循环,35116,1n k =⨯+==;第二次循环,168,22n k ===; 第三次循环,84,32n k ===;第四次循环,42,42n k ===;第五次循环,21,52n k ===,此时输出5k =,选B . 13.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)阅读程序框图,若输出的S 的值等于16,那么在程序框图中的判断框内应填写的条件是( )A .i>5?B .i>6?C .i>7?D .i>8?【答案】A14.(山东省兖州市2013高三9月入学诊断检测数学(理)试题)右图给出的是计算111124620++++ 的值的一个框图,其中菱形判断框内应填入的条件是 ( )A .10>iB .10<iC .11>iD .11<i【答案】A15.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )若右边的程序框图输出的S 是254,则条件①可为( )A .5n ≤B .6n ≤C .7n ≤D .8n ≤【答案】C16.(山东省枣庄市2013届高三3月模拟考试数学(理)试题)如图是一个算法的流程图,若输出的结果是31,则判断框中整数M 的值是( )A .3B .4C .5D .6【答案】B本程序计算的是21222AS =++++ ,即11122112A A S ++-==--,由121=31A +-得12=32A +,解得4A =,则15A +=时,条件不成立,所以4M =,选B . 17.(山东省莱芜五中2013届高三4月模拟数学(理)试题)执行如图所示的程序框图,则输出的结果为( )A .2B .1C .21 D .1-【答案】C 18.(山东省凤城高中2013届高三4月模拟检测数学理试题 )阅读如图所示的程序框图,运行相应的程序,则输出的结果是( )ABC.D.【答案】A19.(山东省文登市2013届高三3月二轮模拟考试数学(理))右面的程序框图中,若输出S 的值为126,则图中应填上的条件为( ) A .5n ≤ B .6n ≤C .7n ≤D .8n ≤【答案】B 20.(2012年山东理)(6)执行下面的程序图,如果输入a=4,那么输出的n 的值为( )C .4D .5【答案】:312,140,00=+==+==q p n ;716,541,11=+==+==q p n ;15114,2145,22=+==+==q p n ,q p n >=,3.答案应选 B .21.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)右图是某算法的程序框图,则程序运行后输出的结果是( )A .6B .27C .124D .168【答案】B 22.(山东省潍坊市2013届高三第二次模拟考试理科数学)运行如图所示的程序,若结束时输出的结果不小于3,则t 的取值范围为( )A .14t ≥B .18t ≥C .14t ≤D .18t ≤ 【答案】B 第一次循环,2,2,211n x t a ===-=;第二次循环,4,4,413n x t a ===-=;第三次循环,6,8,633n x t a ===-=,此时满足条件输出83x t a =,由题意知833x t a =≥,解得81t ≥,即18t ≥,选B .23.(山东省济南市2013届高三3月高考模拟理科数学)阅读右边的程序框图,运行相应的程序,输出的结果为( )A .1311B .2113C .813D .138【答案】D第7题图第一次循环,112,1,2z x y =+===;第二次循环,123,2,3z x y =+===;第三次循环,235,3,5z x y =+===;第四次循环,358,5,8z x y =+===;第五次循环,5813,8,13z x y =+===;第六次循环,81321z =+=,不满足条件输出138y x =,选 D . 24.(山东省夏津一中2013届高三4月月考数学(理)试题)如图给出的是计算20121614121+⋅⋅⋅+++的值的程序框图,其中判断框内应填入的是( )A .2012i ≤B .i >2012C .1006≤iD .i >1006【答案】A 25.(山东省青岛即墨市2013届高三上学期期末考试数学(理)试题)如果执行下面的程序框图,输出的S=110,则判断框处为( )A .10<k ?B .11≥k ?C .10≤k ?D .11>k ?【答案】C【 解析】由程序可知该程序是计算(22)242(1)2k k S k k k +=+++==+ ,由(1)110S k k =+=得10k =,则当10k =时,110111k k =+=+=不满足条件,所以条件为10k ≤,选 C .26.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)右图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值.若要使输入的x 值与输出的y 值相等,则这样的x 值有( )A .1个B .2个C .3个D .4个【答案】C27.(山东威海市2013年5月高三模拟考试数学(理科))一算法的程序框图如右图所示,若输出的12y =,则输入的x 可能为 ( )A .1-B .1C .1或5D .1-或1【答案】 B . 二、填空题 28.(2013届山东省高考压轴卷理科数学)执行如右图的程序框图,那么输出S 的值是________.第5题图【答案】1-【解析】由框图知:12,1;1,2;,3;2S k S k S k ===-===2,4;1,5,S k S k ===-=不满足条件,输出S 的值是1-.29.(2013山东高考数学(理))执行右图的程序框图,若输入的ε的值为0.25,则输出的n 的值为_____.,10123,312,2F F n =+==-==,此时1110.253F =≤不成立.第二次循环,10235,523,3F F n =+==-==,此时1110.255F =≤成立,输出3n =. 30.(山东省济南市2013届高三上学期期末考试理科数学)已知程序框图如右图所示,则输出的i =________;【答案】9【 解析】第一次循环,133,5S i =⨯==;第二次循环,3515,7S i =⨯==;第三次循环,157105,9S i =⨯==;第四次循环,满足条件输出9i =. 31.(山东省德州市2013届高三上学期期末校际联考数学(理))执行如图所示程序框图,输出结果S=.【答案】1【解析】第一次循环1(1)2,3,2S T n =--===;第二次循环23(1)21,5,3S T n =--⨯===;第三次循环35(1)6,7,4S T n =--===;第四次循环47(1)61,9,5S T n =--⨯===,第五次循环,满足条件,输出1S =. 32.(2011年高考(山东理))执行右图所示的程序框图,输入2,3,5l m n ===,则输出的y 的值是______.【答案】解析:1406375278,y =++=278105173,17310568y y =-==-=.答案应填:68. 33.(山东省烟台市2013届高三3月诊断性测试数学理试题)执行如右图所示的程序框图,输出的S 值为___________【答案】10第一次循环,1,1,2i S i ==-=;第二次循环,22,123,3i S i ==-+==; 第三次循环,23,336,4i S i ==-=-=;第四次循环,24,6410,5i S i ==-+==,此时不满足条件,输出10S =. 34.(山东省菏泽市2013届高三5月份模拟考试数学(理)试题)执行如图所示的程序框图,输出S 的值为__________.【答案】-2 35.(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)执行如图所示的程序框图,若输出的结果是8,则输入的数是______.【答案】2或22- 由a b ≥得23x x ≥,解得1x ≤.所以当1x ≤时,输出2a x =,当1x >时,输出3b x =.所以当1x ≤时,由28a x ==,解得822x =-=-.若1x >,由38b x ==,得2x =,所以输入的数为2或22-. 36.(2010年高考(山东理))执行右图所示的程序框图,若输入10x =,则输出y 的值为_____________.【答案】54-【解析】当x=10时,y=110-1=42⨯,此时|y-x|=6; 当x=4时,y=14-1=12⨯,此时|y-x|=3;当x=1时,y=111-1=-22⨯,此时|y-x|=32;当x=12-时,y=115-1=-224⨯-(),此时|y-x|=3<14,故输出y 的值为54-.【命题意图】本题考查程序框图的基础知识,考查了同学们的试图能力.37.(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))如果执行右面的程序框图,那么输出的S =______.【答案】 20【解析】第一次循环:2,220==+=k S ;第二次循环:3,642==+=k S ;第三次循环:4,1266==+=k S ;第四次循环:5,20812==+=k S ;第五次循环:输出20=S .38.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)执行如图的程序框图,如果输入的n 是4,则输出的p 是______【答案】3 39.(山东省青岛市2013届高三第一次模拟考试理科数学)某程序框图如右图所示,若3a=,则该程序运行后,输出的x 值为【答案】31 第一次循环,2317,2x n =⨯+==;第二次循环,27115,3x n =⨯+==;第三次循环,215131,4x n =⨯+==.此时不满足条件,输出31x =. 40.(2009高考(山东理))执行右边的程序框图,输入的T= .【答案】【解析】:按照程序框图依次执行为S=5,n=2,T=2; S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30 答案:30。
山东省2014届理科一轮复习试题选编4:函数的奇偶性与周期性

山东省2014届理科数学一轮复习试题选编4:函数的奇偶性与周期性、对称性(教师版)一、选择题错误!未指定书签。
.(2013届山东省高考压轴卷理科数学)已知函数()f x 是R 上的奇函数,若对于0x ≥,都有()2()f x f x +=, [)()()20,2,log 1x f x x ∈=+当时时,()()20132012f f -+的值为 ( )A .2-B .1-C .1D .2【答案】B 【解析】由()2()f x f x +=知,函数()f x 的周期为2,所以()()20132012f f -+ .1)0()1()0()121006()21006()2013(-=+-=++⨯-=⨯+-=f f f f f f错误!未指定书签。
.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)已知函数()f x 对任意x R ∈都有(6)()2(3),(f x f x f y f x ++==-的图象关于点(1,0)对称,则(2013)f = ( )A .10B .5-C .5D .0【答案】D错误!未指定书签。
.(山东省威海市2013届高三上学期期末考试理科数学)已知函数()f x 的定义域为(32,1)a a -+,且(1)f x +为偶函数,则实数a 的值可以是( ) A .23 B .2 C .4 D .6【答案】B 因为函数(1)f x +为偶函数,所以(1)(1)f x f x -+=+,即函数()f x 关于1x =对称,所以区间(32,1)a a -+关于1x =对称,所以32112a a -++=,即2a =,所以选 B . 错误!未指定书签。
.(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)已知函数()f x 是定义在R 上的奇函数,当x >0时,()12x f x -=-,则不等式()f x <12-的解集是 ( )A .(),1-∞-B .(],1-∞-C .()1,+∞D .[)1,+∞ 【答案】A 【解析】因为()111122f -=-=,又因为函数为奇函数,所以1(1)(1)2f f -=-=-,所以不等式1()2f x <-等价于()(1)f x f <-,当0x >时,()1121()2x x f x -=-=-单调递增,且0()1f x <<,所以在(,0)-∞上函数也单调递增,由()(1)f x f <-得1x <-,即不等式的解集为(),1-∞-,选 ( )A .错误!未指定书签。
山东省2014届理科数学一轮复习试题选编7:函数的综合问题(学生版)

山东省2014届理科数学一轮复习试题选编7:函数的综合问题一、选择题 1 .(山东省潍坊市2013届高三第二次模拟考试理科数学)某学校要召开学生代表大会,规定根据班级人数每10人给一个代表名额,当班级人数除以10的余数大于6时,再增加一名代表名额.那么各班代表人数y与该班人数x 之间的函数关系用取整函数[]y x =([x]表示不大于*的最大整数)可表示为 ( )A .[]10x y = B .3[]10x y += C .4[]10x y += D .5[]10x y += 2 .(山东省寿光市2013届高三10月阶段性检测数学(理)试题)已知函数321,,1,12()111,0,.362x x x f x x x ⎧⎛⎤∈ ⎪⎥+⎪⎝⎦=⎨⎡⎤⎪-+∈⎢⎥⎪⎣⎦⎩函数π()sin()22(0)6g x a x a a =-+ ,若存在[]12,0,1x x ∈,使得12()()f x g x =成立,则实数a 的取值范围是 ( )A .14,23⎡⎤⎢⎥⎣⎦ B .10,2⎛⎤⎥⎝⎦ C .24,33⎡⎤⎢⎥⎣⎦D .1,12⎡⎤⎢⎥⎣⎦3 .(山东省德州市2013届高三第二次模拟考试数学(理)试题)若对于定义在R 上的函数f(x),存在常数()t t R ∈,使得f(x+t)+tf(x)=0对任意实数x 均成立,则称f(x )是阶回旋函数,则下面命题正确的是( )A .f(x)=2x是12-阶回旋函数 B .f(x)=sin(πx)是1阶回旋函数C .f (x)=x 2是1阶回旋函数D .f(x)=log a x 是0阶回旋函数4 .(山东省2013届高三高考模拟卷(一)理科数学)已知c b a ,,为互不相等的三个正实数,函数)(x f 可能满足如下性质:①)(a x f -为奇函数;②)(a x f +为奇函数;③)(b x f -为偶函数;④)(b x f +为偶函数;⑤()()f x c f c x +=-.类比函数2013sin y x =的对称中心、对称轴与周期的关系,某同学得到了如下结论:(i)若满足①②,则)(x f 的一个周期为4a ;(ii)若满足①③;则)(x f 的一个周期为||4b a -;(iii)若满足③④,则)(x f 的一个周期为||3b a -;(iv)若满足②⑤;则)(x f 的一个周期为||4c a +. 其中正确结论的个数为 ( ) A .1 B .2 C .3 D .45 .(山东省枣庄市2013届高三3月模拟考试数学(理)试题)已知函数2()1f x x =+的定义域为[,]()a b a b <,值域为[1,5],则在平面直角坐标系内,点(a,b)的运动轨迹与两坐标轴围成的图形的面积是 ( ) A .8 B .6 C .4 D .2 6 .(山东省德州市2013届高三3月模拟检测理科数学)已知函数(1)y f x =-的图象关于直线1x =对称,且当(,0),()'()0x f x xf x ∈-∞+<成立若a=(20.2)·0.2(2),(12)f b n =·121(12),(1)4f n c og =·121(1)4f og ,则a,b,c 的大小关系是 ( ) A .a b c >>B .b a c >>C .c a b >>D .a c b >>7 .(2012年山东理)(12)设函数f (x)=,g(x )=ax 2+bx 若y=f(x)的图像与y=g(x)图像有且仅有两个不同的公共点A(x 1,y 1),B(x 2,y 2),则下列判断正确的是 ( ) A .当a<0时,x 1+x 2<0,y 1+y 2>0 B .当a<0时, x 1+x 2>0, y 1+y 2<0 C .当a>0时,x 1+x 2<0, y 1+y 2<0 D .当a>0时,x 1+x 2>0, y 1+y 2>0 8 .(山东省2013届高三高考模拟卷(一)理科数学)我们定义若函数)(x f 为D 上的凹函数须满足以下两条规则:(1)函数在区间D 上的任何取值有意义;(2)对于区间D 上的任意n 个值n x x x ,,,21 ,总满足)()()()(2121nx x x nf x f x f x f n n +++≥+++ ,那么下列四个图象中在]2,0[π上满足凹函数定义的是9 .(山东省夏津一中2013届高三4月月考数学(理)试题)函数y=f(x),x∈D,若存在常数C,对任意的x l ∈D,仔在唯一的x 2∈D,使得C =,则称函数f(x)在D 上的几何平均数为C .已知f(x)=x 3,x∈[1,2],则函数f(x)=x 3在[1,2]上的几何平均数为 ( )AB .2C .4D . 10.(山东省威海市2013届高三上学期期末考试理科数学)对于函数(f x ,如果存在锐角θ使得()f x 的图象绕坐标原点逆时针旋转角θ,所得曲线仍是一函数,则称函数()f x 具备角θ的旋转性,下列函数具有角4π的旋转性的是 ( )A .y =B .ln y x =C .1()2x y =D .2y x =11.(山东省实验中学2013届高三第一次诊断性测试数学(理)试题)已知定义在R 上的函数()y f x =满足以下三个条件:①对于任意的x R ∈,都有(4)()f x f x +=;②对于任意的121212,,02,()();x x R x x f x f x ∈≤<≤<且都有③函数(2)y f x =+的图象关于y 轴对称,则下列结论中正确的是( )A .(4.5)(7)(6.5)f f f <<B .(7)(4.5)(6.5)f f f <<C .(7)(6.5)(4.5)f f f <<D .(4.5)(6.5)(7)f f f <<12.(山东省青岛市2013届高三上学期期中考试数学(理)试题)已知定义在R 上的奇函数()f x 满足(4)()f x f x -=-,且[]0,2x ∈时,2()log (1)f x x =+,甲、乙、丙、丁四位同学有下列结论:甲:()31f =;乙:函数()f x 在[]6,2--上是减函数;丙:函数()f x 关于直线4x =对称;丁:若()0,1m ∈,则关于x 的方程()0f x m -=在[]8,8-上所有根之和为8-,其中正确的是( )A .甲、乙、丁B .乙、丙C .甲、乙、丙D .甲、丙二、填空题:本大题共4小题,每小题4分,共16分.13.(山东省夏津一中2013届高三4月月考数学(理)试题)函数y = 1n|x-1|的图像与函数y=-2 cosπx(-2≤x≤4)的图像所有交点的横坐标之和等于( )A .8B .6C .4D .2 14.(山东省文登市2013届高三3月二轮模拟考试数学(理))对于正实数α,记M α为满足下述条件的函数()f x 构成的集合:12,x x R ∀∈且21x x >,有212121()()()()x x f x f x x x αα--<-<-.下列结论中正确的是( )A .若12(),()f x M g x M αα∈∈,则12()()f x g x M αα++∈B .若12(),()f x M g x M αα∈∈且12αα>,则12()()f x g x M αα--∈C .若12(),()f x M g x M αα∈∈,则12()()f x g x M αα⋅⋅∈D .若12(),()f x M g x M αα∈∈且()0g x ≠,则12()()f x M g x αα∈ 15.(2013年山东临沂市高三教学质量检测考试理科数学)已知集合M={(x,y )|y f (x )=},若对于任意11(x ,y )M ∈,存在22(x ,y )M ∈,使得12120x x y y +=成立,则称集合M 是“垂直对点集”.给出下列四个集合:①M={1(x,y )|y x=};②M={1(x,y )|y sin x =+}; ③M={2(x,y )|y log x =};④{(,)2}x M x y y e ==-.其中是“垂直对点集”的序号是 ( )A .①②B .②③C .①④D .②④二、填空题 16.(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)已知()f x 为R 上的偶函数,对任意x R ∈都有(6)()(3)f x f x f +=+且当[]12,0,3x x ∈, 12x x ≠ 时,有1212()()0f x f x x x ->-成立,给出四个命题:①(3)0f = ② 直线6x =-是函数()y f x =的图像的一条对称轴③ 函数()y f x =在[]9,6--上为增函数 ④ 函数()y f x =在[]9,9--上有四个零点 其中所有正确命题的序号为______________17.(山东省潍坊市2013届高三上学期期末考试数学理(A ))若函数)(x f 满足0,≠∈∃m R m ,对定义域内的任意)()()(,m f x f m x f x +=+恒成立,则称)(x f 为m 函数,现给出下列函数: ①xy 1=; ②x y 2=; ③x y sin =; ④nx y 1=其中为m 函数的序号是.(把你认为所有正确的序号都填上)18.(2009高考(山东理))已知定义在R 上的奇函数)(x f ,满足(4)()f x f x -=-,且在区间[0,2]上是增函数,若方程f(x)=m(m>0)在区间[]8,8-上有四个不同的根1234,,,x x x x ,则1234_________.x x x x +++=19.(山东省济宁市2013届高三第一次模拟考试理科数学 )函数(x)f 的定义域为D,若存在闭区间[a,b]⊆D,使得函数f (x )满足:(1) f (x )在[a,b]内是单调函数;(2)f (x )在[a,b]上的值域为[2a,2b],则称区间[a,b]为y=f (x )的“和谐区间”.下列函数中存在“和谐区间”的是_______ (只需填符合题意的函数序号) ①20f (x )x (x )=≥;②xf (x )e (x R )=∈; ③10f (x )(x )x =>;④2401xf (x )(x )x =≥+. 20.(山东省烟台市2013届高三上学期期中考试数学试题(理科))函数()f x 的定义域为A ,若12,x x A ∈且12()()f x f x =时总有12x x =,则称()f x 为单函数.例如:函数)(12)(R x x x f ∈+=是单函数.给出下列命题:①函数)()(2R x x x f ∈=是单函数; ②指数函数)(2)(R x x f x∈=是单函数;③若()f x 为单函数,12,x x A ∈且12x x ≠,则12()()f x f x ≠; ④在定义域上具有单调性的函数一定是单函数,其中的真命题是 ______________.(写出所有真命题的序号)21.(山东济南外国语学校2012—2013学年度第一学期高三质量检测数学试题(理科))具有性质:1()()f f x x=-的函数,我们称为满足“倒负”交换的函数,下列函数:①1;y x x =-②1;y x x=+ ③,(01)0,(1)1(1)x x y x x x⎧⎪<<⎪==⎨⎪⎪->⎩中满足“倒负”变换的函数是________________.22.(山东省日照市2013届高三12月份阶段训练数学(理)试题)定义在R 上的函数()yf x =,若对任意不等实数12,x x 满足()()12120f x f x x x -<-,且对于任意的,x y R ∈,不等式()()22220f x x f y y -+-≤成立.又函数()1y f x =-的图象关于点()1,0对称,则当14x ≤≤时,yx的取值范围为_______________. 23.(山东省青岛市2013届高三上学期期中考试数学(理)试题)已知函数()f x 的定义域为R ,若存在常数0m >,对任意R x ∈,有()f x m x ≤,则称函数()f x 为F -函数.给出下列函数:①2()f x x =;②2()1x f x x =+;③()2xf x =;④()sin 2f x x =. 其中是F -函数的序号为_________________.24.(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)已知函数()f x 在实数集R 上具有下列性质:①直线1x =是函数()f x 的一条对称轴;②()()2f x f x +=-;③当1213x x ≤<≤时,()()()21f x f x -⋅()210,x x -<则()2012f 、()2013f 从大到小的顺序为_______.25.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)如图,已知边长为8米的正方形钢板有一个角锈蚀,其中4AE =米,6CD =米. 为了合理利用这块钢板,将在五边形ABCDE 内截取一个矩形块BNPM ,使点P 在边DE 上. 则矩形BNPM 面积的最大值为_________平方米 .A MEPDCB N F三、解答题26.(2009高考(山东理))两县城A 和B 相距20km ,现计划在两县城外以AB 为直径的半圆弧上选择一点C 建造垃圾处理厂,其对城市的影响度与所选地点到城市的的距离有关,对城A 和城B 的总影响度为城A 与城B 的影响度之和,记C 点到城A 的距离为x km ,建在C 处的垃圾处理厂对城A 和城B 的总影响度为y,统计调查表明:垃圾处理厂对城A 的影响度与所选地点到城A 的距离的平方成反比,比例系数为4;对城B 的影响度与所选地点到城B 的距离的平方成反比,比例系数为k ,当垃圾处理厂建在的中点时,对城A 和城B 的总影响度为0.065.(1)将y 表示成x 的函数;(11)讨论(1)中函数的单调性,并判断弧上是否存在一点,使建在此处的垃圾处理厂对城A 和城B 的总影响度最小?若存在,求出该点到城A 的距离;若不存在,说明理由。
山东省威海市乳山一中2014届高三寒假开学检测数学(理)试题含答案

保密★启用前 试卷类型:A高三数学开学检测(理科)本试卷共4页,分第I 卷(选择题)和第II 卷(非选择题)两部分,共150分,考试时间120分钟。
第I 卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)全集U=R ,集合{}02|2≥+=x x x A ,则[U A= (A )[]0,2-(B )()0,2- (C )(][)+∞⋃-∞-,02,(D )[]2,0(2)已知,54cos ,23,-=⎪⎭⎫ ⎝⎛∈αππα则)4tan(απ-等于 (A )7 (B )71(C )71-(D )7-(3)如果等差数列{}n a 中,15765=++a a a ,那么943...a a a +++等于 (A )21(B )30(C )35(D )40(4)要得到函数)23sin(-=x y 的图象,只要将函数x y 3sin =的图象 (A )向左平移2个单位(B )向右平移2个单位 (C )向左平移32个单位(D )向右平移32个单位 (5)“1-=m ”是“直线02)12(=+-+y m mx 与直线033=++my x 垂直”的 (A )充分而不必要条件(B )必要而不充分条件(C )充要条件(D )既不充分也不必要条件(6)设,m n 是两条不同直线,,αβ是两个不同的平面,下列命题正确的是 (A )//,////,//m n m n αβαβ且则(B ),m n αβαβ⊥⊥⊥且,则m n ⊥ (C ),,m n m n αβ⊥⊂⊥,则αβ⊥(D ),,//,//m n m n ααββ⊂⊂,则//αβ (7)函数sin e()xy x =-π≤≤π的大致图象为(8)已知双曲线()0,012222>>=-babyax的一条渐近线的斜率为2,则该双曲线的离心率等于(A)2(B)3(C)2 (D)23(9)一个几何体的三视图如图所示,其中主视图和左视图是腰长为4的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则该球的表面积是(A)π12(B)π24(C)π32(D)π48(10)若()()()()()()92311 2012311132222 x x a a x a x a x a x+-=+-+-+-+⋅⋅⋅+-,则1211a a a++⋅⋅⋅+的值为(A)0 (B)5-(C)5 (D)255(11)某班同学准备参加学校在寒假里组织的“社区服务”、“进敬老院”、“参观工厂”、“民俗调查”、“环保宣传”五个项目的社会实践活动,每天只安排一项活动,并要求在周一至周五内完成.其中“参观工厂”与“环保宣讲”两项活动必须安排在相邻两天,“民俗调查”活动不能安排在周一.则不同安排方法的种数是A.48B.24C.36D.64(12)已知函数⎩⎨⎧>≤+=,1,2)(xnxxkxxf()k R∈,若函数()y f x k=+有三个零点,则实数k的取值范围是(A)2k≤(B)10k-<<(C)21k-≤<-(D)2k≤-(A) (B) (C) (D)第II 卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分。
山东省2014届理科数学一轮复习试题选编38:算法初步(教师版)
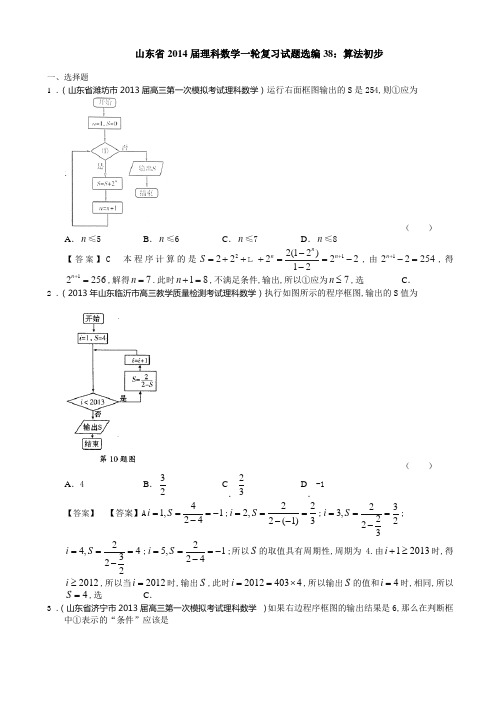
山东省2014届理科数学一轮复习试题选编38:算法初步一、选择题 1 .(山东省潍坊市2013届高三第一次模拟考试理科数学)运行右面框图输出的S 是254,则①应为( )A .n ≤5B .n ≤6C .n ≤7D .n ≤8【答案】C 本程序计算的是212(12)2222212n nn S +-=+++==-- ,由122254n +-=,得12256n +=,解得7n =.此时18n +=,不满足条件,输出,所以①应为7n ≤,选C . 2 .(2013年山东临沂市高三教学质量检测考试理科数学)执行如图所示的程序框图,输出的S 值为( )A .4B .32 C.23D .-1 【答案】 【答案】A 41,124i S ===--;222,2(1)3i S ===--;233,2223i S ===-;24,4322i S ===-;25,124i S ===--;所以S 的取值具有周期性,周期为 4.由12013i +≥时,得2012i ≥,所以当2012i =时,输出S ,此时20124034i ==⨯,所以输出S 的值和4i =时,相同,所以4S =,选 C .3 .(山东省济宁市2013届高三第一次模拟考试理科数学 )如果右边程序框图的输出结果是6,那么在判断框中①表示的“条件”应该是( )A .i≥3B .i≥4C .i≥5D .i≥6 【答案】D【解析】第一次循环,264,6410,2m s i =-+==+==;第二次循环,2262,10212,3m s i =-⨯+==+==;第三次循环,2360,12,4m s i =-⨯+===;第四次循环,2462,12210,5m s i =-⨯+=-=-==;第五次循环,2564,1046,6m s i =-⨯+=-=-==;此时满足条件输出6s =,所以条件应为,6i ≥选D .4 .(山东省泰安市2013届高三第二次模拟考试数学(理)试题)已知数列{}11,1,n n n a a a a n +==+中,若利用如图所示的程序框图计算并输出该数列的第10项,则判断框内的条件可以是( )A .11?n ≤B .10?n ≤C .9?n ≤D .8?n ≤【答案】C 5 .(山东省临沂市2013届高三5月高考模拟理科数学)执行如图所示的程序框图,输出的结果是( )A .11B .12C .13D .14【答案】C 第一次循环,1,2,123x y z ===+=;第二次循环,2,3,235x y z ===+=;第三次循环,3,5,358x y z ===+=;第四次循环,5,8,5813x y z ===+=,此时满足条件,输出13z =,选 C . 6 .(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)若程序框图如图所示,则该程序运行后输出k 的值是( )A .4B .5C .6D .7【答案】B第一次35116,1n k =⨯+==;第二次168,22n k ===;第三次84,32n k ===;第四次42,42n k ===;第五次21,52n k ===此时满足条件输出5k =,选 B . 7 .(山东省济南市2013届高三4月巩固性训练数学(理)试题)定义某种运算⊗,a b ⊗的运算原理如图 所示.设x x f ⊗=1)(.()f x 在区间[2,2]-上的最大值为. ( )A .-2B .-1C .0D .2【答案】D 8 .(山东省济宁市2013届高三4月联考理科数学)左图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到14次的考试成绩依次记为1214,,,.A A A 右图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是7.98.6 3 89.3 9 8 8 4 1 5 10.3 1 11.4 ( )A .7B .8C .9D .10【答案】D9 .(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)执行如图所示的程序框图,若输出结果为3,则可输入的实数x 值的个数为( )A .1B .2C .3D .4【答案】C 由题意知221,2log ,2x x y x x ⎧-≤=⎨>⎩.当2x ≤时,由213x -=,得24x =,解得2x =±.当2x >时,由2log 3x =,得8x =,所以输入的实数x 值的个数为3个,选 C .10.(山东省德州市2013届高三第二次模拟考试数学(理)试题)执行如图所示的程序框图,若输入n 的值为≤≥16,则输出s 的值为( )A .17B .16C .10D .9【答案】C 11.(山东省2013届高三高考模拟卷(一)理科数学)执行如图所示的程序框图,若输入5=p ,6=q ,则输出a ,i 的值分别为( )A .5,1B .30,3C .15.3D .30.6【答案】D 【解析】执行程序框图可知,当1=i 时,15⨯=a ;当2=i 时,25⨯=a ;;当6=i 时,65⨯=a ,即a 能被q 整除,退出循环,输出i a ,的值分别为30,6. 12.(山东省德州市2013届高三3月模拟检测理科数学)如图所示,程序框图运行后输出k 的值是( )A .4B .5C .6D .7【答案】B 第一次循环,35116,1n k =⨯+==;第二次循环,168,22n k ===; 第三次循环,84,32n k ===;第四次循环,42,42n k ===;第五次循环,21,52n k ===,此时输出5k =,选B . 13.(山东省菏泽市2013届高三第二次模拟考试数学(理)试题)阅读程序框图,若输出的S 的值等于16,那么在程序框图中的判断框内应填写的条件是( )A .i>5?B .i>6?C .i>7?D .i>8?【答案】A14.(山东省兖州市2013高三9月入学诊断检测数学(理)试题)右图给出的是计算111124620++++ 的值的一个框图,其中菱形判断框内应填入的条件是 ( )A .10>iB .10<iC .11>iD .11<i【答案】A15.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )若右边的程序框图输出的S 是254,则条件①可为( )A .5n ≤B .6n ≤C .7n ≤D .8n ≤【答案】C16.(山东省枣庄市2013届高三3月模拟考试数学(理)试题)如图是一个算法的流程图,若输出的结果是31,则判断框中整数M 的值是( )A .3B .4C .5D .6【答案】B本程序计算的是21222AS =++++ ,即11122112A A S ++-==--,由121=31A +-得12=32A +,解得4A =,则15A +=时,条件不成立,所以4M =,选B . 17.(山东省莱芜五中2013届高三4月模拟数学(理)试题)执行如图所示的程序框图,则输出的结果为( )A .2B .1C .21 D .1-【答案】C 18.(山东省凤城高中2013届高三4月模拟检测数学理试题 )阅读如图所示的程序框图,运行相应的程序,则输出的结果是( )ABC.D.【答案】A19.(山东省文登市2013届高三3月二轮模拟考试数学(理))右面的程序框图中,若输出S 的值为126,则图中应填上的条件为( ) A .5n ≤ B .6n ≤C .7n ≤D .8n ≤【答案】B 20.(2012年山东理)(6)执行下面的程序图,如果输入a=4,那么输出的n 的值为( )C .4D .5【答案】:312,140,00=+==+==q p n ;716,541,11=+==+==q p n ;15114,2145,22=+==+==q p n ,q p n >=,3.答案应选 B .21.(山东省枣庄市2013届高三4月(二模)模拟考试数学(理)试题)右图是某算法的程序框图,则程序运行后输出的结果是( )A .6B .27C .124D .168【答案】B 22.(山东省潍坊市2013届高三第二次模拟考试理科数学)运行如图所示的程序,若结束时输出的结果不小于3,则t 的取值范围为( )A .14t ≥B .18t ≥C .14t ≤D .18t ≤ 【答案】B 第一次循环,2,2,211n x t a ===-=;第二次循环,4,4,413n x t a ===-=;第三次循环,6,8,633n x t a ===-=,此时满足条件输出83x t a =,由题意知833x t a =≥,解得81t ≥,即18t ≥,选B .23.(山东省济南市2013届高三3月高考模拟理科数学)阅读右边的程序框图,运行相应的程序,输出的结果为( )A .1311B .2113C .813D .138【答案】D第7题图第一次循环,112,1,2z x y =+===;第二次循环,123,2,3z x y =+===;第三次循环,235,3,5z x y =+===;第四次循环,358,5,8z x y =+===;第五次循环,5813,8,13z x y =+===;第六次循环,81321z =+=,不满足条件输出138y x =,选 D . 24.(山东省夏津一中2013届高三4月月考数学(理)试题)如图给出的是计算20121614121+⋅⋅⋅+++的值的程序框图,其中判断框内应填入的是( )A .2012i ≤B .i >2012C .1006≤iD .i >1006【答案】A 25.(山东省青岛即墨市2013届高三上学期期末考试数学(理)试题)如果执行下面的程序框图,输出的S=110,则判断框处为( )A .10<k ?B .11≥k ?C .10≤k ?D .11>k ?【答案】C【 解析】由程序可知该程序是计算(22)242(1)2k k S k k k +=+++==+ ,由(1)110S k k =+=得10k =,则当10k =时,110111k k =+=+=不满足条件,所以条件为10k ≤,选 C .26.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)右图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值.若要使输入的x 值与输出的y 值相等,则这样的x 值有( )A .1个B .2个C .3个D .4个【答案】C27.(山东威海市2013年5月高三模拟考试数学(理科))一算法的程序框图如右图所示,若输出的12y =,则输入的x 可能为 ( )A .1-B .1C .1或5D .1-或1【答案】 B . 二、填空题 28.(2013届山东省高考压轴卷理科数学)执行如右图的程序框图,那么输出S 的值是________.第5题图【答案】1-【解析】由框图知:12,1;1,2;,3;2S k S k S k ===-===2,4;1,5,S k S k ===-=不满足条件,输出S 的值是1-.29.(2013山东高考数学(理))执行右图的程序框图,若输入的ε的值为0.25,则输出的n 的值为_____.,10123,312,2F F n =+==-==,此时1110.253F =≤不成立.第二次循环,10235,523,3F F n =+==-==,此时1110.255F =≤成立,输出3n =. 30.(山东省济南市2013届高三上学期期末考试理科数学)已知程序框图如右图所示,则输出的i =________;【答案】9【 解析】第一次循环,133,5S i =⨯==;第二次循环,3515,7S i =⨯==;第三次循环,157105,9S i =⨯==;第四次循环,满足条件输出9i =. 31.(山东省德州市2013届高三上学期期末校际联考数学(理))执行如图所示程序框图,输出结果S=.【答案】1【解析】第一次循环1(1)2,3,2S T n =--===;第二次循环23(1)21,5,3S T n =--⨯===;第三次循环35(1)6,7,4S T n =--===;第四次循环47(1)61,9,5S T n =--⨯===,第五次循环,满足条件,输出1S =. 32.(2011年高考(山东理))执行右图所示的程序框图,输入2,3,5l m n ===,则输出的y 的值是______.【答案】解析:1406375278,y =++=278105173,17310568y y =-==-=.答案应填:68. 33.(山东省烟台市2013届高三3月诊断性测试数学理试题)执行如右图所示的程序框图,输出的S 值为___________【答案】10第一次循环,1,1,2i S i ==-=;第二次循环,22,123,3i S i ==-+==; 第三次循环,23,336,4i S i ==-=-=;第四次循环,24,6410,5i S i ==-+==,此时不满足条件,输出10S =. 34.(山东省菏泽市2013届高三5月份模拟考试数学(理)试题)执行如图所示的程序框图,输出S 的值为__________.【答案】-2 35.(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)执行如图所示的程序框图,若输出的结果是8,则输入的数是______.【答案】2或22- 由a b ≥得23x x ≥,解得1x ≤.所以当1x ≤时,输出2a x =,当1x >时,输出3b x =.所以当1x ≤时,由28a x ==,解得822x =-=-.若1x >,由38b x ==,得2x =,所以输入的数为2或22-. 36.(2010年高考(山东理))执行右图所示的程序框图,若输入10x =,则输出y 的值为_____________.【答案】54-【解析】当x=10时,y=110-1=42⨯,此时|y-x|=6; 当x=4时,y=14-1=12⨯,此时|y-x|=3;当x=1时,y=111-1=-22⨯,此时|y-x|=32;当x=12-时,y=115-1=-224⨯-(),此时|y-x|=3<14,故输出y 的值为54-.【命题意图】本题考查程序框图的基础知识,考查了同学们的试图能力.37.(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))如果执行右面的程序框图,那么输出的S =______.【答案】 20【解析】第一次循环:2,220==+=k S ;第二次循环:3,642==+=k S ;第三次循环:4,1266==+=k S ;第四次循环:5,20812==+=k S ;第五次循环:输出20=S .38.(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)执行如图的程序框图,如果输入的n 是4,则输出的p 是______【答案】3 39.(山东省青岛市2013届高三第一次模拟考试理科数学)某程序框图如右图所示,若3a=,则该程序运行后,输出的x 值为【答案】31 第一次循环,2317,2x n =⨯+==;第二次循环,27115,3x n =⨯+==;第三次循环,215131,4x n =⨯+==.此时不满足条件,输出31x =. 40.(2009高考(山东理))执行右边的程序框图,输入的T= .【答案】【解析】:按照程序框图依次执行为S=5,n=2,T=2; S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30 答案:30。
山东省2014届理科数学一轮复习试题选编17:等差数列(学生版)

山东省2014届理科数学一轮复习试题选编17:等差数列一、选择题 1 .(山东省青岛市2013届高三第一次模拟考试理科数学)设n S 是等差数列{}n a 的前n 项和,1532,3a a a ==,则9S = ( )A .90B .54C .54-D .72- 2 .(山东省实验中学2013届高三第三次诊断性测试理科数学)在等差数列{}n a 中,20131-=a ,其前n 项和为n S ,若210121012=-S S ,则2013S 的值等于 ( )A .-2012B .-2013C .2012D .20133 .(山东省淄博市2013届高三上学期期末考试数学(理))如果等差数列{}n a 中,15765=++a a a ,那么943...a a a +++等于( )A .21B .30C .35D .404 .(山东省滨州市2013届高三第一次(3月)模拟考试数学(理)试题)已知{}n a 为等差数列,若34899,a a a S ++==则( )A .24B .27C .15D .545 .(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)等差数列{}n a 前n 项和为n S ,已知310061006(1)2013(1)1,a a -+-= 310081008(1)2013(1)1,a a -+-=-则( )A .2013100810062013,S a a =>B .2013100810062013,S a a =<C .2013100810062013,S a a =->D .2013100810062013,S a a =-<6 .(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)已知正项组成的等差数列{}n a 的前20项的和100,那么615a a ⋅最大值是 ( )A .25B .50C .100D .不存在 7 .(山东省威海市2013届高三上学期期末考试理科数学){}n a 为等差数列,n S 为其前n 项和,77521a S ==,,则10S =( )A .40B .35C .30D .288 .(山东省淄博市2013届高三复习阶段性检测(二模)数学(理)试题)已知等差数列{}n a 的前n 项和为n S ,满足1313113a S a ===,则 ( )A .14-B .13-C .12-D .11-9 .(山东省济南市2012届高三3月高考模拟题理科数学(2012济南二模))在等差数列}{na 中,1a =-2 012 ,其前n 项和为n S ,若10121210S S -=2,则 2 012S 的值等于 ( )A .-2 011B .-2 012C .-2 010D .-2 01310.(山东省日照市2013届高三12月份阶段训练数学(理)试题)已知数列{}n a ,若点()()*,n n a n N∈在经过点()8,4的定直线l 上,则数列{}n a 的前15项和15S = ( )A .12B .32C .60D .12011.(山东省济南市2013届高三4月巩固性训练数学(理)试题)等差数列{}n a 中,已知112a =-,130S =,使得0n a >的最小正整数n 为( )A .7B .8C .9D .10 12.(山东师大附中2013届级高三12月第三次模拟检测理科数学)等差数列{}n a 的前n 项的和为n S ,且A .2012B .-2012C .2011D .-201113.(山东省烟台市莱州一中2013届高三第三次质量检测数学(理)试题)设数列{}n a 是等差数列,且23415a a a ++=,则这个数列的前5项和5S( )A .10B .15C .20D .25 14.(山东省寿光市2013届高三10月阶段性检测数学(理)试题)如果等差数列{}n a 中,35712a a a ++=,那么129...a a a +++的值为( )A .18B .27C .36D .54二、填空题15.(山东省烟台市2013届高三上学期期末考试数学(理)试题)设直线(1)2(*)nx n y n N ++=∈与两坐标轴围成的三角形的面积为S n ,则S 1+S 2++S 2012的值为 16.(山东省泰安市2013届高三上学期期末考试数学理)下面图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第n 个图形中小正方形的个数是___________.17.(山东省潍坊市2013届高三第一次模拟考试理科数学)现有一根n 节的竹竿,自上而下每节的长度依次构成等差数列,最上面一节长为 10cm,最下面的三节长度之和为114cm,第6节的长度是首节与末节长度的等比中 项,则n=___________.三、解答题18.(山东省泰安市2013届高三上学期期末考试数学理)在等差数列{}n a 中,13a =,其前n 项和为n S ,等比数列{}n b 的各项均为正数,11b =,公比为q ,且222212,.S b S q b +==(I)求n a 与n b ; (II)设1121,n n n n T a b a b a b n N +-=++⋅⋅⋅+∈,求n T 的值.19.(山东省文登市2013届高三3月二轮模拟考试数学(理))已知数列{}n a 为公差不为0的等差数列,n S 为前n 项和,5a 和7a 的等差中项为11,且25114a a a a ⋅=⋅.令11,n n n b a a +=⋅数列{}n b 的前n 项和为n T .(Ⅰ)求n a 及n T ;(Ⅱ)是否存在正整数1,(1),,,m n m n m n T T T <<使得成等比数列?若存在,求出所有的,m n 的值;若不存在,请说明理由.20.(山东省莱芜市莱芜二中2013届高三4月模拟考试数学(理)试题)已知数列{}n a 是等差数列,()*+∈-=N n a a c n n n 212(1)判断数列{}n c 是否是等差数列,并说明理由;(2)如果()为常数k k a a a a a a 13143,130********-=+++=+++ ,试写出数列{}n c 的通项公式;(3)在(2)的条件下,若数列{}n c 得前n 项和为n S ,问是否存在这样的实数k ,使n S 当且仅当12=n 时取得最大值.若存在,求出k 的取值范围;若不存在,说明理由.21.(2013届山东省高考压轴卷理科数学)设数列{}n a 的前.n 项积..为n T ,且n na T 22-= ()n N *∈.(Ⅰ)求证数列1n T ⎧⎫⎨⎬⎩⎭是等差数列; (Ⅱ)设)1)(1(1+--=n n n a a b ,求数列{}n b 的前n 项和n S .22.(山东省实验中学2013届高三第一次诊断性测试数学(理)试题)已知等差数列{}n a 的首项11a =,公差0d >,且2514,,a a a 成等比数列.(1)求数列{}n a 的通项公式; (2)设*121(),(3)n n n n b n N S b b b n a =∈=++++ ,是否存在最大的整数t,使得对任意的n 均有36n tS >总成立?若存在,求出t;若不存在,请说明理由,23.(山东省青岛市2013届高三上学期期中考试数学(理)试题)设{}n a 是公差大于零的等差数列,已知12a =,23210a a =-.(Ⅰ)求{}n a 的通项公式;(Ⅱ)设{}n b 是以函数214sin ()12y x π=+-的最小正周期为首项,以3为公比的等比数列,求数列{}n n a b -的前n 项和n S .24.(山东省德州市2013届高三3月模拟检测理科数学)已知各项均不相等的等差数列{}n a 的前5项和为513235,1,1,1S a a a =+++成等比数列. (1)求数列{}n a 的通项公式;(2)设n T 为数列1n S ⎧⎫⎨⎬⎭⎩的前n 项和,问是否存在常数m,使12(2)n n n T n n n ⎡⎤=+⎢⎥++⎣⎦,若存在,求m 的值;若不存在,说明理由.25.(山东省威海市2013届高三上学期期末考试理科数学)已知数列{}n a ,15a =-,22a =-,记()A n =12n a a a +++ ,23()B n a a =+1n a +++ ,()C n =342+n a a a +++ (*N n ∈),若对于任意*N n ∈,()A n ,()B n ,()C n 成等差数列.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ) 求数列{}||n a 的前n 项和.26.(2010年高考(山东理))已知等差数列{}n a 满足:37a =,5726a a +=,{}n a 的前n 项和为n S .(Ⅰ)求n a 及n S ; (Ⅱ)令b n =211n a -(n ∈N *),求数列{}n b 的前n 项和n T .山东省2014届理科数学一轮复习试题选编17:等差数列参考答案一、选择题1. 【答案】 C 由1532,3a a a ==得1143(2)a d a d +=+,即12d a =-=-,所以919899298542S a d ⨯=+=⨯-⨯=-,选C. 2.B【解析】1211211122S a d ⨯=+,101109102S a d ⨯=+,所以112112111211212122a dS a d ⨯+==+,1019102S a d =+,所以101221210S S d -==,所以201312013201220132013(20132012)2012S a d ⨯=+=-+=-,选B 3. C【 解析】由15765=++a a a 得663155a a ==,.所以3496...77535a a a a +++==⨯=,选C.4. 【答案】B 在等差数列中,由3489a a a ++=得13129a d +=,即1543a d a +==,所以19599()9292327222a a a S +⨯⨯⨯====,选B. 5. B 6. A7. 【答案】A 设公差为d ,则由77521a S ==,得1777()2a a S +=,即17(5)212a +=,解得11a =,所以716a a d =+,所以23d =.所以1011091092101040223S a d ⨯⨯=+=+⨯=,选A. 8. 【答案】D 在等差数列中,1131313()132a a S +==,所以1132a a +=,即113221311a a =-=-=-,选D.9. 【答案】B【解析】设公差为d,则2)1(1dn n na S n -+=,2)1(1d n a n S n -+=,由ddd S S =---=-2)110(2)112(10121012,所以2=d ,所以)2013(-=n n S n ,2012)20132012(20122012-=-=S ,选B10. C 【解析】可设定直线为4(8)y k x -=-,知4(8),(8)4nn a k n a k n -=-=-+得,则{}n a 是等差数列84a =,所以11515815()15154602a a S a ⋅+==⋅=⨯=,选C.11. B12. D 【解析】在等差数列中,1201320132013()20132a a S +==,所以120132a a+=,所以120132220132011a a=-=-=-,选D.13. D 【解析】在等差数列中2343315a a a a ++==,所以35a =,所以选D.14. C 二、填空题 15. 【答案】20122013【解析】当0x =时,y =.当0y =时,y =,所以三角形的面积11112(1)1n S n n n n ===-++,所以1220121111112012112232012201320132013S S S +++=-+-++-=-= . 16. 【答案】(1)2n n +【解析】12341,3,6,10a a a a ====,所以2132432,3,4a a a a a a -=-=-=, 1n n a a n --=,等式两边同时累加得123n a a n -=+++ ,即(1)122n n n a n +=+++= ,所以第n 个图形中小正方形的个数是(1)2n n +.17. 【答案】16 设对应的数列为{}n a ,公差为,(0)d d >.由题意知110a =,12114n n n a a a --++=,261n a a a =.由12114n n n a a a --++=得13114n a -=,解得138n a -=,即2111(5)()n a d a a d -+=+,即2(105)10(38)d d +=+,解得2d =,所以11(2)38n a a n d -=+-=,即102(2)38n +-=,解得16n =.三、解答题 18.19.解:(Ⅰ)因为{}n a 为等差数列,设公差为d ,整理得111511212a d d a d a +==⎧⎧⇒⎨⎨==⎩⎩ 所以1(1)221n a n n =+-⨯=-由111111()(21)(21)22121n n n b a a n n n n +===-⋅-+-+所以111111(1)2335212121n nT n n n =-+-++-=-++ (Ⅱ)假设存在 由(Ⅰ)知,21n n T n =+,所以11,,32121m n m nT T T m n ===++ 若1,,m n T T T 成等比,则有222121()2132144163m n m n m nT T T m n m m n =⋅⇒=⋅⇒=+++++ 2222441633412m m n m m m n n m ++++-⇒=⇒=,.....(1) 因为0n >,所以2412011m m m +->⇒<<, 因为,1,2,m N m m *∈>∴=,当2m =时,带入(1)式,得12n =; 综上,当2,12m n ==可以使1,,m n T T T 成等比数列20.解:(1)设{}n a 的公差为d ,则22221121()()n n n n n n c c a a a a ++++-=---2221112()()n n n aa d a d +++=---+22d =-∴数列{}n c 是以22d -为公差的等差数列3 (2)1325130a a a +++=242614313a a a k+++=-∴两式相减:131313d k =- 1d k ∴=-113(131)1321302a d -∴+⨯=k a 1221+-=)313()1()1(1-+-=-+=∴k n k d n a a n22111()()n n n n n n n c a a a a a a +++∴=-=+-22)1)(12(63226k n k k -+-+-=53025)1(222+-+--=k k n k 8(3)因为当且仅当12n =时nS 最大12130,0c c ∴><有即2222224(1)2530501819036(1)25305022210k k k k k k k k k k ⎧⎧--+-+>+->⎪⎪⇒⎨⎨--+-+<-+>⎪⎪⎩⎩ 1191921k k k k ><-⎧⇒⇒<->或或21.【解析】(Ⅰ)1132T = 由题意可得:122n n n TT T -=-⇒1122n n n n T T T T --⋅=-(2)n ≥,所以11112n n T T --=(Ⅱ)数列1n T ⎧⎫⎨⎬⎩⎭为等差数列,122n n T +=,12nn a n +=+, 1(2)(3)n b n n =++,1113445(2)(3)n S n n =+++⨯⨯+⨯+ 111111()()()344523n n =-+-++-++113339nn n =-=++ 22.23.24.25.解:(Ⅰ)根据题意()A n ,()B n ,()C n 成等差数列∴()+()2()A n C n B n =整理得2121253n n a a a a ++-=-=-+= ∴数列{}n a 是首项为5-,公差为3的等差数列 ∴53(1)38n a n n =-+-=-(Ⅱ)38,2||38,3n n n a n n -+≤⎧=⎨-≥⎩记数列{}||a 的前n 项和为S .当2n ≤时,2(583)313222n n n n S n +-==-+当3n ≥时,2(2)(138)313714222n n n n S n -+-=+=-+综上,2231322231314322n n n n S n n n ⎧-+≤⎪⎪=⎨⎪-+≥⎪⎩ 26. 【解析】(Ⅰ)设等差数列{}n a 的公差为d,因为37a =,5726a a +=,所以有112721026a d a d +=⎧⎨+=⎩,解得13,2a d ==, 所以321)=2n+1n a n =+-(;n S =n(n-1)3n+22⨯=2n +2n .(Ⅱ)由(Ⅰ)知2n+1n a =,所以b n =211n a -=21=2n+1)1-(114n(n+1)⋅=111(-)4n n+1⋅,所以n T =111111(1-+++-)4223n n+1⋅- =11(1-)=4n+1⋅n 4(n+1), 即数列{}n b 的前n 项和n T =n4(n+1).【命题意图】本题考查等差数列的通项公式与前n 项和公式的应用、裂项法求数列的和,熟练数列的基础知识是解答好本类题目的关键.。
山东省威海市乳山一中2014届高三1月限时训练数学理试题(附答案)

高三数学理科限时训练(2014.1.5)一、选择题:(本大题共12个小题,每小题5分,共60分) 1. 已知集合11{2,1,0,1,2}{|28R}2x M N x x +=--=<<∈,,,则M N =( )A .{1,0,1}-B .{2,1,0,1,2}--C .{0,1}D .{10}-, 2.设复数z 的共轭复数为z ,若3(1)2,i z i -=-则复数z =( )A .iB .i -C .1i -+D .1i --3. 若1e u r ,2e u r 是夹角为3π的单位向量,且122a e e =--r u r u r ,1232b e e =-r u r u r ,则a b ⋅=r r ( )A .1B .4-C .72-D .724. 已知各项不为0的等差数列{}n a ,满足23711220a a a -+=,数列{}n b 是等比数列,且77b a =,则68b b =( ) A. 2 B. 4 C. 8 D. 165.已知命题p :1||<x ,命题q :062<-+x x ,则q 是p 成立的 ( )A .充分不必要条件 B.必要不充分条件 C. 充要条件 D.既不充分也不必要条件6.已知函数))((R x x f ∈为奇函数,(2)1,(2)()(2)f f x f x f =+=+,则(3)f 等于( )A .12B .1C .32D .2 7.一个几何体的三视图如图所示,则该几何体的体积为( )A .πB .2πC .πD .2π8. 已知m 、n 为两条不同的直线,α、β为两个不同的平面,则下列命题中正确的是( )A .若l m ⊥,l n ⊥,且,m n α⊂,则l α⊥B .若平面α内有不共线的三点到平面β的距离相等,则βα//C .若n m m ⊥⊥,α,则α//nD .若α⊥n n m ,//,则α⊥m 9.如果函数px nx y ++=21的图象关于点A (1,2)对称,那么( )A .p =-2,n =4B .p =2,n =-4C .p =-2,n =-4D .p =2,n =4 10.直线l 与圆22240(3)x y x y a a ++-+=<相交于A 、B 两点,若弦AB 的中点为(-2,3),则直线l 的方程为( )A.50x y -+=B. 10x y +-=C.50x y --=D.30x y +-=11.已知实数,x y 满足约束条件1,1,22x y x y x y +≥⎧⎪-≥-⎨⎪-≤⎩若函数()0,0z ax by a b =+>>的最大值为1,则11a b+的最小值为 ( )A.7+B.7+C.D.12.已知集合M={(x,y )|y f (x )=},若对于任意11(x ,y )M ∈,存在22(x ,y )M ∈,使得12120x x y y +=成立,则称集合M 是“垂直对点集”.给出下列四个集合:①M={1(x,y )|y x=}; ②M={1(x,y )|y sin x =+}; ③M={2(x,y )|y log x =};④M={2x(x,y )|y e =-}.其中是“垂直对点集”的序号是( ) A.①② B.②③ C.①④ D.②④第II 卷(共90分)二、填空题:(本大题共4小题,每小题4分,共16分)13.已知两条直线()23210y ax x a y =--++=和互相平行,则a 等于_______. 14.由直线ππ,,033x x y =-==与曲线cos y x =所围成的封闭图形的面积为 .15. 椭圆22221(0)x y a b a b+=>>的左、右顶点分别是A ,B ,左、右焦点分别是F 1,F 2.若|AF 1|,|F 1F 2|,|F 1B|成等比数列,则此椭圆的离心率为 .16.已知|||lg |,0()2,0x x x f x x >⎧=⎨≤⎩,则函数22()3()1y f x f x =-+的零点的个数为_______个.三、解答题:(本大题共有6个小题,共74分.解答应写出文字说明、演算步骤或证明过程.) 17.(本小题满分12分)已知向量(cos ,sin ),a x x =r,cos )b x x =r,若()a b f x =⋅r r(1)求函数()f x 的最小正周期和图象的对称轴方程; (2)求函数()f x 在区间5ππ,1212-⎡⎫⎪⎢⎣⎭上的值域. 18. (本题满分12分) 数列{}n a 的前n 项和为n S ,11a =,121n n a S +=+*()n N ∈,等差数列{}n b 满足353,9b b ==.(1)分别求数列{}n a ,{}n b 的通项公式; (2)设*22()n n n b c n N a ++=∈,求证113n n c c +<≤.19.(本小题满分12分) 设命题:p 关于x 的二次方程()2120x a x a +++-=的一个根大于零,另一根小于零;命题:q 不等式222x x ax +>+对(),1x ∀∈-∞-上恒成立,如果命题“p q ∨”为真命题, 命题“p q ∧”为假命题,求实数a 的取值范围.20. (本小题满分12分)三棱锥P ABC -,底面ABC为边长为PBC ⊥平面ABC ,2PB PC ==,D 为AP 上一点,2AD DP =,O 为底面三角形中心.(Ⅰ)求证DO ∥面PBC ; (Ⅱ)求证:BD AC ⊥;C(Ⅲ)设M 为PC 中点,求二面角M BD O --的余弦值.21.(本小题满分13分)已知中心在原点,焦点在x 轴上的椭圆C 的离心率为12,且椭圆经过点,(I)求椭圆C 的标准方程;(Ⅱ)是否存在过点P(2,1)的直线l 与椭圆C 交于不同的两点A,B 满足PA ·54PB =,若存在,求出直线l 的方程;若不存在,请说明理由.22.(本小题满分13分)已知函数32()f x ax bx =+在点(3,(3))f 处的切线方程为122270x y +-=,且对任意的[)0,x ∈+∞,()ln(1)f x k x '≤+恒成立.(Ⅰ)求函数()f x 的解析式; (Ⅱ)求实数k 的最小值; (Ⅲ)求证:1111ln(1)223n n++++<++K (*N n ∈) 附加题:在实数集R上定义运算:)()()(,2)(,)(,)((2x g x f x F x e x g e x f a R a y a x y x x x ⊗=+==∈-=⊗-为常数),若 (Ⅰ)求F(x )的解析式;山东中学联盟(Ⅱ)若F(x )在R 上是减函数,求实数a 的取值范围;(Ⅲ)若a =-3,在F(x )的曲线上是否存在两点,使得过这两点的切线互相垂直?若存在,求出切线方程;若不存在,说明理由.高三理科数学限时练习答案ADCDB CADAA AD -3或1;5.17.解:(1)()a b f x =⋅r r2sin cos x x x =++1cos 2sin 2222x x ++=πsin 232x ++⎛⎫ ⎪⎝⎭. 2ππ2T ∴==,图象的对称轴方程为ππ(212k x k =+∈Z ).(2)由于区间5ππ,1212-⎡⎫⎪⎢⎣⎭的长度为π2,为半个周期.又()f x 在5ππ,1212-处分别取到函数的最小值12-,最大值12+,所以函数()f x 在区间5ππ,1212-⎡⎫⎪⎢⎣⎭上的值域为1⎫-+⎪⎣⎭18. 解:(1)由121n n a S +=+----① 得121n n a S -=+----②,①-②得112()n n n n a a S S +--=-,13n n a a +∴=…………………………………………2分13n n a -∴=; ………………………………………………………………………………3分 5326,3b b d d ∴-==∴=………………4分36n b n ∴=- ……………………6分(2)因为 1223,3n n n a b n +++== ……8分所以 1333n n nn nc +== ………9分所以032111<-=-++n n n n c c ………10分1113n n c c c +<<⋅⋅⋅<= …………11分 所以113n n c c +<≤………………………………………………………12分19.解:令()2()12f x x a x a =+++-,因为关于x 的二次方程()2120x a x a +++-=的一个根大于零,另一根小于零,所以(0)0f <,即:20a -<,解得:命题p 为真时2;a <………3分因为(),1x ∈-∞-,所以由不等式222x x ax +>+可得:221a x x>-+,令()221g x x x=-+,由()g x 在(),1-∞-上单调递增,故()(),1g x ∈-∞.又不等式222x x ax +>+对(),1x ∀∈-∞-上恒成立,所以命题q 为真时1a ≥. ………7分因为命题“p q ∨”为真命题, 命题“p q ∧”为假命题,所以(1)若p 真q 假,得1;a < ………9分(2)若p 假q 真,得2a ≥. ………11分综上可得:1a <或2a ≥. ………12分 20.(本小题满分12分)证明:(Ⅰ)连结AO 交BC 于点E ,连结PE .O 为正三角形ABC 的中心,∴2AO OE =,且E 为BC 中点.又2AD DP =, ∴DO ∥PE , --------------2分DO ⊄平面PBC ,PE ⊂平面PBC∴DO ∥面PBC . --------------4分 (Ⅱ)PB PC =,且E 为BC 中点, ∴PE BC ⊥,又平面PBC ⊥平面ABC ,∴PE ⊥平面ABC , ------------5分由(Ⅰ)知,DO ∥PE ,∴DO ⊥平面PBC ,∴DO AC ⊥ ----------6分 连结BO ,则AC BO ⊥,又DO BO O =I , ∴AC ⊥平面DOB ,∴AC BD ⊥. -----------8分(Ⅲ)由(Ⅰ)(Ⅱ)知,,,EA EB EP 两两互相垂直,且E 为BC 中点,所以分别以,,EA EB EP所在直线为,,x y z 轴,建立空间直角坐标系,如图,则21(3,0,0),(0,0,1)(1,0,),(0,(0,)32A B P D C M ,------------9分∴12(0,),()23BM DB ==--uuu r uu u r 设平面BDM 的法向量为(,,)n x y z =u r ,则203102n DB x z n BM y z ⎧⋅=-+-=⎪⎪⎨⎪⋅=+=⎪⎩r uu ur r uuu r,令1y =,则(n =r. --------------10分由(Ⅱ)知AC ⊥平面DBO ,∴(3AC =-u u u r为平面DBO 的法向量,∴cos ,||||n AC n AC n AC ⋅<>===r uuu rr uuu r r uuu r由图可知,二面角M BD O --. --------------12分 21.解:(1)设椭圆C 的标准方程为22221(0)x y a b a b+=>>,由题意得b =由12c a =得2,1a c == 故椭圆C 的标准方程为22143x y +=. (2)若存在过点P(2,1)的直线l 满足条件,则l 的斜率存在 .22. (本小题满分13分)解:(Ⅰ)将3x =代入直线方程得92y =-,∴92792a b +=-① --------------1分 2()32,(3)6f x ax bx f ''=+=-,∴2766a b +=-② --------------2分①②联立,解得11,32a b =-=∴3211()32f x x x =-+ --------------3分 (Ⅱ)2()=f x x x '-+,∴2ln(1)x x k x -+≤+在[)0,x ∈+∞上恒成立;即2ln(1)0x x k x -++≥在[)0,x ∈+∞恒成立; --------------4分设2()ln(1)g x x x k x =-++,(0)0g =,∴只需证对于任意的[)0,x ∈+∞有()(0)g x g ≥ -5分[)221()21,0,11k x x k g x x x x x ++-'=-+=∈+∞++设2()21h x x x k =++-,1)当=18(1)0k ∆--≤,即98k ≥时,()0h x ≥,∴()0g x '≥ ()g x 在[)0,+∞单调递增,∴()(0)g x g ≥ --------------6分2)当=18(1)0k ∆-->,即98k <时,设12,x x 是方程2210x x k ++-=的两根且12x x < 由1212x x +=-,可知10x <,分析题意可知当20x ≤时对任意[)0,x ∈+∞有()(0)g x g ≥;∴10,1k k -≥≥,∴918k ≤<--------------7分综上分析,实数k 的最小值为1. --------------8分 (Ⅲ)令1k =,有2ln(1),x x x -+≤+即2ln(1)x x x ≤++在[)0,x ∈+∞恒成立----9分 令1x n=,得221111ln(1)ln(1)ln n n n n n n ≤++=++- --------------11分∴22211111111(ln 2ln1)(ln 3ln 2)(ln(1)ln )2323n n n n++++≤+++++-+-+++-K K L 222111111=1ln(1)1ln(1)231223(1)n n n n n ++++++<++++++⨯⨯-K K 12ln(1)2ln(1)n n n=-++<++,∴原不等式得证. --------------13分附加题解:(I )由题意,F(x )=f (x ) ⊗(a -g (x ))……………………………………2分=e x (a -e -x -2x 2)=a e x -1-2x 2e x .………………………………4分(II )∵F ′(x )=a e x -2x 2e x -4x e x =-e x (2x 2+4x -a ),………………6分 当x ∈R 时,F(x )在减函数, ∴F ′(x )≤0对于x ∈R 恒成立,即-e x(2x2+4x-a)≤0恒成立,…………………………………8分∵e x>0,∴2x2+4x-a≥0恒成立,∴△=16-8(-a) ≤0,∴a≤-2.……………………………………………………9分(III)当a=-3时,F(x)= -3e x-1-2x2e x,设P(x1,y1),Q(x2,y2)是F(x)曲线上的任意两点,∵F′(x)= -e x(2x2+4x+3)=-e x[2(x+1)2+1]<0,……………………………………11分∴F′(x1)·F′(x2)>0,∴F′(x1)·F′(x2)= -1 不成立.………………………………12分∴F(x)的曲线上不存的两点,使得过这两点的切线点互相垂直.…………13分。
山东省2014届理科数学一轮复习试题选编7:函数的综合问题

山东省2014届理科数学一轮复习试题选编7:函数的综合问题一、选择题错误!未指定书签。
.(山东省潍坊市2013届高三第二次模拟考试理科数学)某学校要召开学生代表大会,规定根据班级人数每10人给一个代表名额,当班级人数除以10的余数大于6时,再增加一名代表名额.那么各班代表人数y 与该班人数x 之间的函数关系用取整函数[]y x =([x]表示不大于*的最大整数)可表示为 ( ) A .[]10xy = B .3[]10x y += C .4[]10x y += D .5[]10x y += 【答案】B 法一:特殊取值法,若x=56,y=5,排除 C .D,若x=57,y=6,排除A,所以选B法二:设)90(10≤≤+=ααm x ,,时⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+≤≤10103103,60x m m x αα 1101103103,96+⎥⎦⎤⎢⎣⎡=+=⎥⎦⎤⎢⎣⎡++=⎥⎦⎤⎢⎣⎡+≤<x m m x αα时当,所以选B 错误!未指定书签。
.(山东省寿光市2013届高三10月阶段性检测数学(理)试题)已知函数321,,1,12()111,0,.362x x x f x x x ⎧⎛⎤∈ ⎪⎥+⎪⎝⎦=⎨⎡⎤⎪-+∈⎢⎥⎪⎣⎦⎩函数π()s i n ()22(0)6g x a x a a =-+ ,若存在[]12,0,1x x ∈,使得12()()f x g x =成立,则实数a 的取值范围是( )A .14,23⎡⎤⎢⎥⎣⎦ B .10,2⎛⎤⎥⎝⎦C .24,33⎡⎤⎢⎥⎣⎦ D .1,12⎡⎤⎢⎥⎣⎦【答案】B错误!未指定书签。
.(山东省德州市2013届高三第二次模拟考试数学(理)试题)若对于定义在R 上的函数f(x),存在常数()t t R ∈,使得f(x+t)+tf(x)=0对任意实数x 均成立,则称f(x )是阶回旋函数,则下面命题正确的是 ( ) A .f(x)=2x是12-阶回旋函数 B .f(x)=sin(πx)是1阶回旋函数 C .f (x)=x 2是1阶回旋函数 D .f(x)=log a x 是0阶回旋函数【答案】B错误!未指定书签。
山东省威海市乳山市乳山一中2014届高三12月份限时训练全科数学理及答案
高三阶段检测理科数学 2013.12.07一、选择题:每小题5分,共60分.在给出的四个选项中,只有一项是符合要求的.1.若113πα=,则ααcos tan = A.21 B.21- C. 23- D.232.已知集合4{|log 1}A x x =<,{|2}B x x =≥,则R A C B =A.(,2)-∞B.(0,2)C.(,2]-∞D.[2,4)3.已知向量(3,4)a =, (2,1)b =- ,如果向量a xb - 与b 垂直,则x 的值为A.233B.323C.25D. 25-4.函数||2()2x f x x =-的图像为5.如果若干个函数的图象经过平移后能够重合,则称这些函数为“同簇函数”.给出下列函数: ①()sin cos f x x x =;②()21f x x =+;③()2sin()4f x x π=+;④()sin f x x x =.其中“同簇函数”的是 A.①② B.①④ C.②③ D.③④ 6.若数列{}n a 的前n 项和2133n n S a =+,则数列{}n a 的通项公式n a = A.11()(2)2n -- B.1()(2)2n- C.2(2)n -- D.1(2)n --7.已知命题:,23xxp x R ∀∈<;命题32:,1q x R x x ∃∈=-,则下列命题中为真命题的是A.p q ∧B.p q ∧⌝C.p q ⌝∧D.p q ⌝∧⌝8.已知0a >,,x y 满足约束条件13(3)x x y y a x ≥⎧⎪+≤⎨⎪≥-⎩,若2z x y =+的最小值为32,则a =A.14B.12C.1D.29.在ABC ∆中,角,,A B C 的对边分别为,,a b c ,且22coscos sin()sin 2A BB A B B --- 4cos()5AC ++=-.则cos A = A .45-B .45C .35D .35-10.函数(1)f x -是R 上的奇函数,12,R,x x ∀∈1212()[()()]0x x f x f x --<,则(1)0f x -<的解集是 A .)0,(-∞ B. ),0(+∞ C. (,2)-∞ D. (2,)+∞11. 等比数列{}n a 中,12a =,84a =,128()()()()f x x x a x a x a =--⋅⋅⋅-,()f x '为函数()f x 的导函数,则(0)f '=( )A .0B .62C .92D .12212.空间中,l 、m 、n 是三条不同的直线,α、β、γ是三个不同的平面,则下列结论错误的是A.若//,//,αβαγ则//βγB.若//,//,,l l m αβαβ= 则//l mC.若,,l αβαγβγ⊥⊥= ,则l α⊥D.若,,,,,m l n l m l n αββγγα===⊥⊥ 则m n ⊥ 二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡中相应题的横线上.13.321221(2)x dx x+⎰= . 14.已知圆锥的母线长为5cm ,侧面积为15πcm 2,则此圆锥的体积为 cm 3.15.在ABC ∆中,BC = ,AD AB ⊥,1AD = ,则AC AD ⋅=.16.已知命题p :x 2+2x -3>0;命题q1<,若“非q 且p ”为真,则x 的取值范围是____________________.三、解答题:本大题共6小题,共74分. 把解答写在答题卡中.解答应写出文字说明,证明过程或演算步骤.17.记函数)2lg()(2--=x x x f 的定义域为集合A ,函数||3)(x x g -=的定义域为集合B .(1)求A B 和A B ;(2)若A C p x x C ⊆<+=},04|{,求实数p 的取值范围.18.(本小题满分12分)已知(2cos ,2sin )(cos ,sin )a b ααββ==,,02αβπ<<<. (Ⅰ)若a b ⊥ ,求|2|a b - 的值;(Ⅱ)设(2,0)c =,若2a b c += ,求βα,的值.19.(本小题满分12分)已知函数()y f x =和()y g x =的图象关于y 轴对称,且2()242f x x x =+-. (Ⅰ)求函数()y g x =的解析式;(Ⅱ)解不等式()()|21|2f xg x x +<-20. (本小题满分12分)已知数列{a n }中,a 1=1,a n+1=a n +2n +1,且n ∈N *。
山东省威海市2014届高三上学期期中考试理科数学含答案

理科数学试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页.考试时间120分钟.满分150分.答题前,考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、考号填写在答题纸规定的位置.第Ⅰ卷(选择题 共60分)注意事项:1.每小题选出答案后,用铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.2.第Ⅰ卷只有选择题一道大题.一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 300=3||1,||2,,60a b a b ==<>=,则|2|a b -=2 (B )4 (C )22 5.已知等差数列{}n a 的前n 项和为n S ,111a =-,564a a +=-,n S 取得最小值时n 的值为(A )6 (B )7 (C )8 (D )96.已知函数()y f x x =+是偶函数,且(2)1,f =则(2)f -=(A )1- (B )1 (C )5- (D )5(sin10,cos10)-,则α的可能取值为10 80 10 (D 80(A ) (B ) (C ) (D )第Ⅱ卷(非选择题 共90分)注意事项:1. 请用0.5毫米的黑色签字笔将每题的答案填写在答题纸的指定位置.书写的答案如需改动,要先划掉原来的答案,然后再写上新答案.2. 不在指定答题位置答题或超出答题区域书写的答案无效.在试题卷上答题无效.3. 第Ⅱ卷共包括填空题和解答题两道大题.二、填空题(本大题共4小题,每小题4分,共16分)13.0(sin )x x dx π-=⎰ ____________.14.公比为2的等比数列前4项和为15,前8项和为 .15.不等式534x x --+≥的解集为_______________.16.将函数[]sin(),0,23y x x ππ=-∈的图象上各点的纵坐标不变横坐标伸长到原来的2倍,再向左平移6π个单位,所得函数的单调递增区间为 .三、解答题(本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.)18.(本小题满分12分)19.(本小题满分12分)已知{}n a 为等差数列,且3745,21a a a ==-.(Ⅰ)求数列{}n a 的通项公式及其前n 项和n S ;(Ⅱ)若数列{}n b 满足212349n n b b b n b a ++++=求数列{}n b 的通项公式. 20.(本小题满分12分)21.(本小题满分12分)22.(本小题满分14分) 已知()xf x e =,()g x 为其反函数.(Ⅰ)说明函数()f x 与()g x 图象的关系(只写出结论即可);(Ⅱ)证明()f x 的图象恒在()g x 的图象的上方;(Ⅲ)设直线l 与()f x 、()g x 均相切,切点分别为(11,()x f x )、(22,()x g x ),且120x x >>,求证:11x >.高三理科数学参考答案一、选择题B AC A A,D D B D A, B C二、填空题 13.222π- 14. 25515.{|1}x x ≤- 16. 3723,,,6226ππππ⎡⎤⎡⎤-⎢⎥⎢⎥⎣⎦⎣⎦ 三、解答题17.(本小题满分12分)(Ⅰ)113 ------------------------------------6分 (Ⅱ)sin α- ------------------------------------12分18.(本小题满分12分)解:(1)根据正弦定理sin sin sin a b c A B C==,原等式可转化为: 222a b c ab +-= ------------------------------------2分2221cos 22a b c C ab +-== ------------------------------------4分 ∴60C = ------------------------------------6分(Ⅱ)11sin 22ABC S ab C ab ∆===∴6ab = ------------------------------------8分22222cos ()325187c a b ab C a b ab =+-⋅=+-=-= ------------10分∴c = ------------------------------------12分2n n b ++=1n ++-()21.(本小题满分12分)22.(本小题满分14分)解:(Ⅰ)()f x 与()g x 的图象关于直线y x =对称 --------------------------------2分 (Ⅱ)()ln g x x =,设()h x x = ------------------------------------4分 令()()x y f x h x e x =-=-,1x y e '=-令0y '=,解得0x =当0x <时0y '<,当0x >时0y '>∴当0x =时,0min 010y e =-=>∴x e x > ------------------------------------6分。
山东省2014届理科数学一轮复习试题选编19:等差与等比的综合问题(学生版)

山东省2014届理科数学一轮复习试题选编19:等差与等比的综合问题一、选择题 1 .(山东省实验中学2013届高三第三次诊断性测试理科数学)已知等差数列{}n a 的公差d 不为0,等比数列{}n b 的公比q 是小于1的正有理数.若d a =1,,21d b =且321232221b b b a a a ++++是正整数,则q 的值可以是( )A .71 B .-71 C .21 D .-21 2 .(山东省莱芜五中2013届高三4月模拟数学(理)试题)已知数列{},{}n n a b 满足113a b ==,113n n n nb a a b ++-==,n N +∈,若数列{}n c 满足n n a c b =,则2013c = ( )A .20129B .201227C .20139D .2013273 .(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)已知各项均不为零的数列{}n a ,定义向量()()1,,,1,n n n n c a a b n n n N *+==+∈ .下列命题中真命题是( )A .若n N *∀∈总有n n c b ⊥成立,则数列{}n a 是等比数列B .若n N *∀∈总有//n n c b 成立,则数列{}n a 是等比数列C .若n N *∀∈总有n n c b ⊥成立,则数列{}n a 是等差数列D .若n N *∀∈总有//n n c b 成立,则数列{}n a 是等差数列二、填空题 4 .(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)已知等差数列{}n a 中,有11122012301030a a a a a a ++++++=成立.类似地,在正项等比数列{}n b 中,有_____________________成立.三、解答题 5 .(山东省济南市2013届高三4月巩固性训练数学(理)试题)已知数列{}n a 满足13a =,*133()n n n a a n N +-=∈,数列{}n b 满足3nn na b =. (1)证明数列{}n b 是等差数列并求数列{}n b 的通项公式; (2)求数列}{n a 的前n 项和n S .6 .(山东省济宁市2013届高三第一次模拟考试理科数学 )已知数列{n a }的前n 项和1122n *n n S a ()(n N )-=--+∈,数列{n b }满足n b =2n n a .(I)求证数列{n b }是等差数列,并求数列{n a }的通项公式;(Ⅱ)设2n n n c log a =,数列{22n n c c +}的前n 项和为T n ,求满足2521*n T (n N )<∈的n 的最大值.7 .(山东省莱芜五中2013届高三4月模拟数学(理)试题)在等差数列{}n a 中,345842,30a a a a ++==.(1)求数列{}n a 的通项公式; (2)若数列{}n b满足2n a n b λ+=+(R λ∈),则是否存在这样的实数λ使得{}n b 为等比数列;(3)数列{}n c 满足112,1,2n n n n n c T a n --⎧⎪=⎨⎪⎩为奇数,为偶数为数列{}n c 的前n 项和,求2n T .8 .(山东省凤城高中2013届高三4月模拟检测数学理试题 )设等比数列{}n a 的前项和为n S ,已知122n n a S +=+,(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)在n a 与1n a +之间插入n 个数,使这2+n 数组成公差为n d 的等差数列,求1{}nd 的前n 项和n T .9 .(山东省莱芜市莱芜十七中2013届高三4月模拟数学(理)试题)已知数列{}n a 的前n 项和n S 满足21n n S a =-,等差数列{}n b 满足11b a =,43b S =.(1)求数列{}n a 、{}n b 的通项公式; (2)设11n n n c b b +=,数列{}n c 的前n 项和为n T ,问n T >10012012的最小正整数n 是多少?10.(山东省青岛即墨市2013届高三上学期期末考试数学(理)试题)等差数列}{n a 中,9,155432==++a a a a .(Ⅰ)求数列}{n a 的通项公式; (Ⅱ)设213+=n a n b ,求数列n n a 1{,b }2+的前n 项和n S .11.(山东省德州市2013届高三上学期期末校际联考数学(理))数列{a n }的前n 项和为1,2(1)n n n S S n +=-+,等差数列{}n b 的各项为正实数,其前n 项和为31122339,,,n T T a b a b a b =+++,且又成等比数列. (I)求数列{a n }、{}n b 的通项公式;(2)若.n n n c a b =,当n≥2时,求数列{}n c 的前n 项和A n .12.(山东省泰安市2013届高三第二次模拟考试数学(理)试题)已知等差数列{}n a 的首项13,0a d =≠公差,其前n 项和为n S ,且1413,,a a a 分别是等比数列{}n b 的第2项,第3项,第4项. (I)求数列{}n a 与{}n b 的通项公式;(II)证明1211113.34n S S S ≤++⋅⋅⋅+< 13.(山东省泰安市2013届高三第一轮复习质量检测数学(理)试题)设等比数列{}n a 的前n 项和为,415349,,,n S a a a a a =-成等差数列.(I)求数列{}n a 的通项公式;(II)证明:对任意21,,,k k k R N S S S +++∈成等差数列.14.(山东师大附中2013届高三第四次模拟测试1月理科数学)已知数列{}n a 是等差数列,{}n b 是等比数列,且112a b ==,454b =,12323a a a b b ++=+.(1)求数列{}n a 和{}n b 的通项公式(2)数列{}n c 满足n n n c a b =,求数列{}n c 的前n 项和n S .15.(山东省烟台市莱州一中2013届高三第二次质量检测数学(理)试题)已知{}n a 是公差为2的等差数列,且317111a a a +++是与的等比中项.(1)求数列{}n a 的通项公式;(2)令()12n n na b n N *-=∈,求数列{}n b 的前n 项和Tn. 16.(2012年山东理)(20)在等差数列{}n a 中,345984,73a a a a ++==.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)对任意*m ∈N ,将数列{}n a 中落入区间2(9,9)m m 内的项的个数记为{}n b ,求数列{}n b 的前m 项和m S .17.(山东省枣庄三中2013届高三上学期1月阶段测试理科数学)已知数列{}n a 的前n 项和为1,3n n n S a S n +=-+且,1,2n a ∈=+N .(Ⅰ)求数列{}n a 的通项; (Ⅱ)设()2n n nb n S n =∈-++N 的前n 项和为n T ,证明:n T <34. 18.(山东省日照市2013届高三12月份阶段训练数学(理)试题)已知{}n a 是公差不为零的等差数列,11391,,,a a a a =成等比数列.求: (I)数列{}n a 的通项公式; (II)数列{}2an n a ⋅的前n 项和n S19.(山东省莱钢高中2013届高三4月模拟检测数学理试题 )设数列{}n a 为等差数列,且145=a ,720a =,且132(2,)n n S S n n N -=+≥∈;, (Ⅰ(Ⅱ为数列{}n c 的前n 项和. T n <m 恒成立对N n *∈,求m 的最小值.20.(山东省莱芜市第一中学2013届高三12月阶段性测试数学(理)试题)已知数列n a 满足222121na a a n n =+⋅⋅⋅++- (Ⅰ)求数列{}n a 的通项; (Ⅱ)若nn a nb =,求数列{}n b 的前n 项的和n S .21.(山东师大附中2013届级高三12月第三次模拟检测理科数学)数列{}n a 的前n 项的和为n S ,对于任意的自然数0n a >,()241n n S a =+(Ⅰ)求证:数列{}n a 是等差数列,并求通项公式 (Ⅱ)设3nn na b =,求和12n n T b b b =+++ 22.(山东省兖州市2013高三9月入学诊断检测数学(理)试题)设等比数列{}n a 的前n 项和为n S ,已知122(n n a S n +=+∈N *).(1)求数列{}n a 的通项公式;(2)在n a 与1n a +之间插入n 个数,使这n+2个数组成公差为n d 的等差数列,求数列1n d ⎧⎫⎪⎨⎬⎪⎭⎩的前n 项和n T . 23.(山东省潍坊市四县一校2013届高三11月期中联考(数学理))已知各项均为正数的数列{}n a 前n 项和为n S ,首项为1a ,且n n S a ,,21等差数列. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若n b n a )21(2=,设n n n a b c =,求数列{}n c 的前n 项和n T .24.(山东省夏津一中2013届高三4月月考数学(理)试题)在等比数列}{n a 中,412=a ,512163=⋅a a .设22122log 2log 2nn n a a b +=⋅,n T 为数列{}n b 的前n 项和.(Ⅰ)求n a 和n T ;(Ⅱ)若对任意的*∈N n ,不等式n n n T )1(2--<λ恒成立,求实数λ的取值范围.25.(山东省济南市2013届高三3月高考模拟理科数学)数列{}n a 的前n 项和为n S ,11a =,121n n a S +=+*()n N ∈,等差数列{}n b 满足 353,9b b ==.(1)分别求数列{}n a ,{}n b 的通项公式; (2)设*22()n n n b c n N a ++=∈,求证113n n c c +<≤.26.(山东省济南市2013届高三上学期期末考试理科数学)已知等差数列{}n a 的前n 项和为n S ,365,36a S ==,(1)求数列{}n a 的通项公式;(2) 设2n an b =,求数列{}n b 的前n 项和n T .27.(山东省潍坊市2013届高三上学期期末考试数学理(A ))设数列{}n a 为等差数列,且9,553==a a ;数列{}n b 的前n 项和为n S ,且2=+n n b S .(I)求数列{}n a ,{}n b 的通项公式; (II)若()+∈=N n b a c nnn ,n T 为数列{}n c 的前n 项和,求n T .28.(山东威海市2013年5月高三模拟考试数学(理科))已知{}n a 为等差数列,n S 为其前n 项和,且222n n S a n =+.(Ⅰ)求,n n a S ;(Ⅱ)若2221,,k k k a a a -+成等比数列,求k 的值及公比.山东省2014届理科数学一轮复习试题选编19:等差与等比的综合问题参考答案一、选择题1. C 【解析】由题意知21312,23a a d d a a d d =+==+=,22222131,b b q d q b b q d q ====,所以2222221232222212349141a a a d d d b b b d d q d q qq++++==++++++,因为321232221b b b a a a ++++是正整数,所以令2141t q q=++,t 为正整数.所以2114t q q ++=,即21014t q q ++-=,解得5613t q +-+===,因为t 为正整数,所以当8t =时,12122q -+===.符合题意,选C2. D3. D 【解析】由//nn c b 得,1(1)n n na n a +=+,即11n n a a n n +=+,所以11n n a n a n ++=,所以1n a na =,故数列{}n a 是等差数列,选D.二、填空题4. 由算术平均数类比几何平均数,容易得出30302110201211b b b b b b =. 三、解答题5. 解(1)证明:由3n n n a b =,得1113n n n a b +++=, ∴1111333n n n n n n a a b b +++-=-=所以数列{}n b 是等差数列,首项11b =,公差为13∴121(1)33n n b n +=+-=(2)13(2)3n n n n a b n -==+⨯n n a a a S +++=∴ 2113)2(3413-⨯+++⨯+⨯=n n ----① n n n S 3)2(343332⨯+++⨯+⨯=∴ -------------------②①-②得n n n n S 3)2(33313212⨯+-++++⨯=--n n n 3)2(3331212⨯+-+++++=-n n n 3)2(233⨯+-+=23)2(433nn n n S +++-=∴6. 解:(Ⅰ)在2)21(1+--=-n n n a S 中,令n=1,可得1121a a S n =+--=,即211=a . 当2≥n 时,2)21(211+--=---n n n a S ∴111)21(---++-=-=n n n n n n a a S S a ,∴11)21(2--+=n n n a a ,即12211+=--n n n n a a .∵n n n a b 2=,∴11+=-n n b b ,即当2≥n 时,11=--n n b b . 又1211==a b ,∴数列{b n }是首项和公差均为1的等差数列.于是n n n a n n b 21)1(1==⋅-+=,∴nn n a 2= (Ⅱ)∵nn a nc 2log ==n n =2log 2, ∴22211(2)2n n+==-c c n n+n n+, ∴)211()1111()5131()4121()311(+-++--++-+-+-=n n n n T n =2111211+-+-+n n 由n T 2125<,得2111211+-+-+n n 2125<,即42132111>+++n n , =)(n f 2111+++n n 单调递减,∵4213)5(,209)4(==f f , ∴n 的最大值为47. 解:(1)因为{}n a 是一个等差数列,所以34544342,14a a a a a ++==∴=.设数列{}n a 的公差为d ,则84416d a a =-=,故4d =;故4(4)42n a a n d n =+-=-(2)29n a n n b λλ+=+=+.假设存在这样的λ使得{}n b 为等比数列,则212n n n b b b ++=⋅,即122(9)(9)(9)n n n λλλ+++=+⋅+,整理可得0λ=. 即存在0λ=使得{}n b 为等比数列(3)∵12,23,n n n c n n -⎧=⎨-⎩为奇数为偶数,∴242221(223)2(243)22(223)n n T n -=+⨯-++⨯-++++⨯- 242212224(12)3n n n -=++++++++-214(1)414321423n n n n n n n -+-=+⨯-=+-- 8. 解:(Ⅰ)由122(n n a S n +=+∈ N +)得122(n n a S n -=+∈N +,2n ≥), 两式相减得:12n n n a a a +-=, 即13(n n a a n +=∈N +,2n ≥),∵{}n a 是等比数列,所以213a a = ; 又2122,a a =+则11223a a +=,∴12a =, ∴132-⨯=n n a(Ⅱ)由(1)知132-⨯=n n a ,则nn a 321⨯=+∵1(1)n n n a a n d +=++ , ∴1341+⨯=-n d n n∵123111n T d d d =+++1nd + ∴1210341344343342-⨯+++⨯+⨯+⨯=n n n T ① nn n n n T 34134344343342311321⨯++⨯++⨯+⨯+⨯=- ② ①-②得nn n n T 3413413413413413423213210⨯+-⨯++⨯+⨯+⨯+⨯=-n n n 3413113113141211⨯+--⎪⎭⎫ ⎝⎛-⨯+=-n n 385285⨯+-= ∴1316521615-⨯+-=n n n T 9. 解:(1)当1n =时,11121a S a ==-,∴11a =当2n ≥时,111(21)(21)22n n n n n n n a S S a a a a ---=-=---=-, 即12nn a a -= ∴数列{}n a 是以11a =为首项,2为公比的等比数列,∴12,21n n n n a S -==- 设{}n b 的公差为,d 111b a ==,4137b d =+=,∴2d = ∴1(1)221n b n n =+-⨯=-(2)111111()(21)(21)22121n n n c b b n n n n +===--+-+ ∴11111111(1...)(1)2335212122121n n T n n n n =-+-++-=-=-+++ 由n T >10012012,得21n n +>10012012,解得n >100.1∴n T >10012012的最小正整数n 是10110.解:(Ⅰ)设数列{}由题意得首项的公差为,1a d a n且⎩⎨⎧=+=+⎩⎨⎧==++941563915115432d a d a a a a a 即 解得⎩⎨⎧==211d a所以数列{}12-=n a a n n 的通项公式为 (Ⅱ)由(Ⅰ)可得n n n ab 3231==+所以n n n n b a3..21=+所以+++=323.33.23.11n S 13.+n n两式相减得++++-=433333(22n S 13.)3+++n n n 10 分43).12(323..1233.31313111+++-+=-+=+---=n n n n n n S n n n 即)()(11.12.13.14. 【解析】:(Ⅰ)设{}n a 的公差为d ,{}n b 的公比为q由341b b q =,得354272q ==,从而3q = 因此11132--⋅=⋅=n n n q b b又123223361824a a a a b b ++==+=+=,28a ∴= 从而216d a a =-=,故466)1(1-=⋅-+=n n a a n (Ⅱ)13)23(4-⋅-⋅==n n n n n b a c令122103)23(3)53(373431--⋅-+⋅-++⨯+⨯+⨯=n n n n n Tn n n n n T 3)23(3)53(37343131321⋅-+⋅-++⨯+⨯+⨯=-两式相减得13)13(3313)23(333333331211321--⨯+=⋅--⨯++⨯+⨯+⨯+=---n nn n n Tnn 3)23(⋅--n 1n 9(31)13n 2)32--=+--⋅(73(67)44n n n T -∴=+,又n n n S 4T 7(6n 7)3==+-⋅15.16. (20)解:(Ⅰ)因为{}n a 是一个等差数列,所以3454384a a a a ++==,即428a =. 所以,数列{}n a 的公差9473289945a a d --===-, 所以,*4(4)289(4)98()n a a n d n n n =+-=+-=-∈N (Ⅱ)对*m ∈N ,若 299m m n a <<,则 298998m m n +<<+,因此 121919m m n --+≤≤, 故得 2199m m m b -=-(lb ylfx) 于是 123...m m S b b b b =++++35212121(999...9)(199...9)9(181)19181199109180m m m m m m --+=++++-++++⨯--=----⨯+=17.解:(Ⅰ)()113,213n n n n a S n n a S n +-=-+≥=--+ 时, ,,12,111-=-=-∴++n n n n n a a a a a 即 112(1),(2,),n n a a n n +∴-=-≥∈N* 2221(1)232n n n a a --∴-=-=∙=n a ⎩⎨⎧≥+∙=-2,1231,22n n n (Ⅱ)113322n n n S a n n -+=+-=∙+- ,123-∙=∴n n nb⎪⎭⎫⎝⎛++++=∴-1222322131n n n T⎪⎭⎫ ⎝⎛++++=n n n T 2232221312132 相减得,⎪⎭⎫⎝⎛-++++=-n n n n T 22121211312112 ,n n n nT 23221134∙-⎪⎭⎫ ⎝⎛-=∴﹤34∴结论成立.18.解:(Ⅰ)设等差数列{}n a 的公差为d ,由题设知0d ≠,由11391,,,a a a a =成等比数列,得1218112d dd++=+ 解得1,0d d ==(舍去).故{}n a 的通项公式为11)1=+(n a n n -⨯=(Ⅱ)由(I)知22n a n n a n ⋅=⋅,1231122232(1)22n n n S n n -=⨯+⨯+⨯++-⨯+⨯ , (1)23412122232(1)22n n n S n n +⨯=⨯+⨯+⨯++-⨯+⨯ ,(2) (1)(2)-,得123122222n n n S n +-=++++-⨯所以11222.12n n n S n ++--=-⨯-从而1(1)2 2.=nS n +-⨯+19.∵T n <m 恒成立对N n *∈∴2≥m ∴m 的最小值是220.解:(Ⅰ)2111==a n 时222213221na a a a n n =+++- (1)21222123221-=+++--n a a a a n n (2) (1)-(2)得2121=-n n a 即n n a 21=(n 2≥),又211=a 也适合上式∴n n a 21=21.解 :(1)令(2)-(1)是等差数列(2)---①---②①-②所以22. (1)由122(n n a S n +=+∈ Z *)得122(n n a S n -=+∈ Z *,2n ≥),两式相减得:12n n n a a a +-=, 即13(n n a a n +=∈ Z *,2n ≥),∵{}n a 是等比数列,所以213a a = ; 又2122,a a =+则11223a a +=,∴12a =, ∴132-⨯=n n a(2)由(1)知132-⨯=n n a ,则n n a 321⨯=+ ∵1(1)n n n a a n d +=++ ,∴1341+⨯=-n d n n∵123111n T d d d =+++1nd +∴1210341344343342-⨯+++⨯+⨯+⨯=n n n T ① nn n n n T 34134344343342311321⨯++⨯++⨯+⨯+⨯=- ② ①-②得nn n n T 3413413413413413423213210⨯+-⨯++⨯+⨯+⨯+⨯=- n n n 3413113113141211⨯+--⎪⎭⎫ ⎝⎛-⨯+=-nn 385285⨯+-= ∴1316521615-⨯+-=n n n T 23.解(1)由题意知0,212>+=n n n a S a当1=n 时,21212111=∴+=a a a当2≥n 时,212,21211-=-=--n n n n a S a S两式相减得1122---=-=n n n n n a a S S a整理得:21=-n n a a∴数列{}n a 是以21为首项,2为公比的等比数列.211122212---=⨯=⋅=n n n n a a(2)42222--==n b n n a∴n b n 24-=,nn n n n nn a b C 28162242-=-==-nn n nn T 28162824282028132-+-⋯+-++=- ① 13228162824202821+-+-+⋯++=n n n n n T ② ①-②得1322816)212121(8421+--+⋯++-=n n n nT 1112816)211442816211)2112184+-+----=----⋅-=n n n nn (( n n 24= .28n n n T =∴24.解:(Ⅰ)设}{n a 的公比为q ,由5121161552263==⋅=q q a a a 得21=q , ∴n n n q a a )21(22=⋅=-22211211()2122()2log 2log 2=log 2log 21111()(21)(21)22121n n nn n a a b n n n n -++=⋅⋅==--+-+∴)1211215131311(21+--++-+-=n n T n 111)22n 121nn =-=++( (Ⅱ)①当n 为偶数时,由2-<n T n λ恒成立得,322)12)(2(--=+-<nn n n n λ恒成立,即m in )322(--<nn λ, 而322--n n 随n 的增大而增大,∴2=n 时0)322(m in =--nn ,∴0<λ; ②当n 为奇数时,由2+<n T n λ恒成立得,522)12)(2(++=++<nn n n n λ恒成立,即m in )522(++<n n λ,而95222522=+⋅≥++n n n n ,当且仅当122=⇒=n nn 等号成立,∴9<λ综上,实数λ的取值范围0∞(-,)25.解:(1)由121n n a S +=+----① 得121n n a S -=+----②,①-②得112()n n n n a a S S +--=-,13n n a a +∴=13n n a -∴=;5326,3b b d d ∴-==∴= 36n b n ∴=-(2)因为 1223,3n n n a b n +++==所以 1333n n nn nc+==所以032111<-=-++n n n nc c1113n n c c c +<<⋅⋅⋅<=所以113n n c c +<≤26.解: (1)设{}n a 的公差为d , 36535a S =⎧∴⎨=⎩;则1125656362a d a d +=⎧⎪⎨⨯+=⎪⎩即112556a d a d +=⎧⎨+=⎩,解得112a d =⎧⎨=⎩,*12(1)21,()n a n n n N ∴=+-=-∈(2) 2122na n nb -==135212222n n T -∴=++++2(14)2(41)143n n --==-27.28.解:(Ⅰ)∵{}n a 为其等差数列,设公差为d1n =,则有11112a a =+,∴12a = 2n =,有122142a a a +=+,∴24a =,∴21422d a a =-=-=∴2+2(1)2n a n n =-=,(22)(1)2n n n S n n +==+ (Ⅱ)若2221,,k k k a a a -+成等比数列,则有22221k k k a a a -+= 即24(22)22(21)k k k -=⋅+,整理得22940k k -+=, 解得4k =或12k =(舍) ∴469,,a a a 成等比数列,6432a q a ==。
山东省各地市2014届高三一模数学试题

1.已知集合M={|ln(1)x y x =-},集合N={|,xy y e x =∈R}(e 为自然对数的底数) 则MN=(A ){|1x x <} (B) {|1x x >} (C) {|01x x <<} (D ) ∅2.复数1z i =-,则1z z+ (A ) 1322i + (B) 1322i - (C ) 3322i - (D ) 3122i -3.三棱柱的侧棱与底面垂直,且底面是边长为2的等边三角形,其正(主)视图(如图所示)的面积为8,则侧(左)视图的面积为 (A ) 8 (B ) 4 (C ) 43 (D) 34.函数sin(3)cos()cos(3)cos()3633y x x x x ππππ=+--++的图象的一条对称轴的方程是(A )12x π=(B) 6x π=(C ) 12x π=-(D) 24x π=-5.“22ab>"是“ln ln a b >”的(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D )既不充分也不必要条件 6.若P (2,—l)为圆22(1)25x y -+=的弦AB 的中点,则直线AB 的方程是(A ) 30x y --= (B ) 230x y +-= (C) 10x y +-= (D ) 250x y --= 7.从8名女生和4名男生中,抽取3名学生参加某档电视节目,如果按性别比例分层抽样,则不同的抽取方法数为(A ) 224 (B ) 112 (C) 56 (D ) 288.现有四个函数①y =x ·sin x ,②y =x ·cos x ,③y =x ·|cos x |,④y =x ·2x 的部分图象如下,但顺序被打乱,则按照图象从左到名,对应的函数序号正确的一组是(A ) ①④②③ (B) ①④③② (C ) ④①②③ (D ) ③④②① 9.已知三点A(2,1),B(1,-2),C(35,15-),动点P (a,b)满足0≤OP OA ≤2,且0≤OP OB ≤2,则点P 到点C 的距离大于14的概率为 (A) 1564π- (B) 564π (C ) 116π- (D ) 16π10.已知定义在R 上的函数()f x 满足:222,[0,1),()2,[1,0),x x f x x x ⎧+∈=⎨-∈-⎩且(2)()f x f x +=,25()2x g x x +=+,则方程()()f x g x =在区间[—5,1]上的所有实根之和为(A ) -5 (B) —6 (C) —7 (D ) —811.若*2()()n x n N x+∈展开式中的第5项为常数,则n 等于 . 12.执行右面的框图,若输出P 的值是24,则输入的正整数N 应为 .13.若双曲线22221(0,0)x y a b a b-=>>的实轴长、虚轴长、焦距成等差数列,则双曲线的离心率为 .14.已知双曲正弦函数2x x e e shx --=和双曲余弦函数2x xe e chx -+=与我们学过的正弦函数和余弦函数有许多类似的性质,请类比正、余弦函数的和角或差角.....公式,写出双曲正弦或双曲余弦函数的一个..类似的正确结论 . 15.若关于x 的不等式(组)2272209(21)9n n x x ≤+-<+对任意*n N ∈恒成立,则所有这样的解x 构成的集合是 .16.已知函数()2sin()sin(),63f x x x x ππ=-+∈R . (I )求函数f (x )的最小正周期; (II)在∆ABC 中,若A=4π,锐角C 满足1()262C f π+=,求BC AB 的值.17.寒假期间,我市某校学生会组织部分同学,用“10分制”随机调查“阳光花园”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):若幸福度分数不低于8.5分,则称该人的幸福度为“幸福”.(I )求从这16人中随机选取3人,至少有2人为“幸福”的概率;(II )以这l6人的样本数据来估计整个社区的总体数据,若从该社区(人数很多)任选3人,记ξ表示抽到“幸福"的人数,求ξ的分布列及数学期望.18.如图,等腰梯形ABCD ,AD//BC ,P 是平面ABCD 外一点,P 在平面ABCD 的射影O 恰在AD 上,PA=AB=BC=2AO=2,BO=3. (I )证明:PA ⊥BO ;(II)求二面角A-BP-D 的余弦值. 19.己知数列{n a }是首项为114a =,公比14q =的等比数列,设*1423log ()n n b a n N +=∈,数列{n c }满足n n n c a b =.(I )求数列{n c }的前n 项和n S ; (II )若2114n c m m ≤+-对一切正整数n 恒成立,求实数m 的取值范围. 20.已知椭圆C 2的方程为22221y x a b+= (a >b 〉0),离心率为22,且短轴一端点和两焦点构成的三角形面积为1,抛物线C 1的方程为22y px = (p >0),焦点F 与椭圆的一个顶点重合. (I )求椭圆C 2和抛物线C 1的方程;(II)过点F 的直线交抛物线C 1于不同两点A ,B,交y 轴于点N ,已知12,NA AF NB BF λλ==,求12λλ+的值;(III )直线l 交椭圆C 2于不同两点P ,Q ,P ,Q 在x 轴上的射影分别为P ',Q ',满足''10OP OQ OP OQ ++= (O 为原点),若点S 满足OS OP OQ =+,判定点S 是否在椭圆C 2上,并说明理由.21.已知函数(),()ln xxf x e axg x e x =+=(e=2.71828…).(I )设曲线()y f x =在x =1处的切线为l ,点(1,0)到直线l 的距离为22,求a 的值; (II)若对于任意实数x ≥0,f (x )〉0恒成立,试确定实数a 的取值范围;(III )当a =-1时,是否存在实数0x ∈[1,e ],使曲线C :()()y g x f x =-在点0x x =处的切线与y 轴垂直?若存在,求出0x 的值;若不存在,请说明理由.二〇一一级高三模块考试 理科数学答案 2014。
2014年山东省威海市文登市高考数学三模试卷(理科)

2014年山东省威海市文登市高考数学三模试卷(理科)学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共10小题,共50.0分)1.设全集U=R,集合A={x||x-1|≤1},B={x|y=2x,y>1},则A∩(∁U B)=()A.∅B.{0}C.{x|0≤x≤2}D.{x|x≤2}【答案】B【解析】解:A={x||x-1|≤1}={x|0≤x≤2},B={x|y=2x,y>1}={x|x>0},∴(∁U B)={x|x≤0},即A∩(∁U B)═{x|x=0}={0},故选:B求出集合A,B,利用集合的基本运算即可得到结论本题主要考查集合的基本运算,利用条件求出集合A,B是解决本题的关键,比较基础.2.袋中有40个小球,其中红色球16个、蓝色球12个,白色球8个,黄色球4个,从中随机抽取10个球作成一个样本,则这个样本恰好是按分层抽样方法得到的概率为()A. B. C. D.【答案】A【解析】解:∵这个样本要恰好是按分层抽样方法得到的概率依题意各层次数量之比为4:3:2:1,即红球抽4个,蓝球抽3个,白球抽2个,黄球抽一个,根据古典概型公式得到结果为;故选A因为这个样本要恰好是按分层抽样方法得到的概率,依题意各层次数量之比为4:3:2:1,即红球抽4个,蓝球抽3个,白球抽2个,黄球抽一个,所以红球抽4个,蓝球抽3个,白球抽2个,黄球抽一个是按分层抽样得到的概率.本题考查分层抽样和古典概型,分层抽样为保证每个个体等可能入样,需遵循在各层中进行简单随机抽样,每层样本数量与每层个体数量的比与这层个体数量与总体容量的比相等.3.空间几何体的三视图如图所示,则此空间几何体的直观图为()A. B. C. D.【答案】A【解析】解:由已知中三视图的上部分是锥体,是三棱锥,满足条件的正视图的选项是A与D,由左视图可知,选项D不正确,由三视图可知该几何体下部分是一个四棱柱选项都正确,故选A.根据已知中的三视图,结合三视图几何体由两部分组成,上部是锥体,下部为柱体,将几何体分解为简单的几何体分析后,即可得到答案.本题考查的知识点是由三视图还原实物图,如果三视图均为三角形,则该几何体必为三棱锥;如果三视图中有两个三角形和一个多边形,则该几何体为N棱锥(N值由另外一个视图的边数确定);如果三视图中有两个为矩形和一个多边形,则该几何体为N棱柱(N值由另外一个视图的边数确定);如果三视图中有两个为梯形和一个多边形,则该几何体为N棱柱(N值由另外一个视图的边数确定);如果三视图中有两个三角形和一个圆,则几何体为圆锥.如果三视图中有两个矩形和一个圆,则几何体为圆柱.如果三视图中有两个梯形和一个圆,则几何体为圆台.4.已知随机变量ξ服从正态分布N(0,σ2).则“P(-2≤ξ≤2)=0.9”是“P(ξ>2)>0.04”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】解:由随机变量ξ服从正态分布N(0,σ2)可知正态密度曲线关于y轴对称,∵P(-2≤ξ≤2)=0.9,∴P(ξ>2)==0.05>0.04∴“P(-2≤ξ≤2)=0.9”是“P(ξ>2)>0.04”的充分不必要条件.故选:A.由正态分布N(0,σ2),得其正态密度曲线关于y轴对称,再结合正态曲线的对称性即可得解.本题主要考查正态分布的概率求法,结合正态曲线,加深对正态密度函数的理解.5.按照如图的程序运行,已知输入x的值为1+log23,则输出y的值为()A. B. C. D.【答案】A【解析】解:根据框图的流程,输入x=1+log23<4,则x=2+log23,∴输出y=×=×=.故选:A.当输入x=1+log23<4,则x=2+log23,再利用对数公式及指数的运算法则计算可得答案.本题考查了选择结构的程序框图,根据框图的流程代入x值计算是解答此类问题的基本方法.6.某中学高三年级从甲、乙两个班级各选出8名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生成绩的平均分是86,乙班学生成绩的中位数是83,则x+y的值为()A.9B.10C.11D.13【答案】D【解析】解:∵班学生成绩的平均分是86,∴-8-7-4-6+x-1+0+8+10=0,即x=8.∵乙班学生成绩的中位数是83,∴若y≤1,则中位数为81,不成立.如y>1,则中位数为,解得y=5.∴x+y=5+8=13,故选:D.根据平均数和中位数的定义和公式,分别进行计算即可得到结论.本题主要考查茎叶图是应用,要求熟练掌握平均数和中位数的概念和计算公式,比较基础.7.在△ABC中,角A、B均为锐角,且cos A<sin B,则△ABC的形状是()A.直角三角形B.锐角三角形C.钝角三角形D.等腰三角形【答案】B【解析】解:因为cos A<sin B,所以cos A<cos(),又因为角A,B均为锐角,所以-B为锐角,又因为余弦函数在(0,π)上单调递减,所以A>,所以A+B>△ABC中,A+B+C=π,所以C<,即三角形的三个内角全为锐角.故选B.利用诱导公式cos(-α)=sinα及余弦函数的单调性可得答案.本题考查诱导公式及正弦函数的单调性及三角形的基本知识,属中档题.8.设二元一次不等式组所表示的平面区域为M,使函数y=a x(a>0,a≠1)的图象过区域M的a的取值范围是()A.[1,3]B.[2,]C.[2,9]D.[,9]【答案】C【解析】解析:平面区域M如如图所示.求得A(2,10),C(3,8),B(1,9).由图可知,欲满足条件必有a>1且图象在过B、C两点的图象之间.当图象过B点时,a1=9,∴a=9.当图象过C点时,a3=8,∴a=2.故a的取值范围为[2,9=.故选C.先依据不等式组,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用函数y=a x(a>0,a≠1)的图象特征,结合区域的角上的点即可解决问题.本题主要考查了用平面区域二元一次不等式组、指数函数的图象与性质,以及简单的转化思想和数形结合的思想,属中档题.巧妙识别目标函数的几何意义是我们研究规划问题的基础,纵观目标函数包括线性的与非线性,非线性问题的介入是线性规划问题的拓展与延伸,使得规划问题得以深化.9.抛物线C:y2=2px(p>0)的焦点为F,M是抛物线C上的点,若△OFM的外接圆与抛物线C的准线相切,且该圆面积为36π,则p=()A.2B.4C.6D.8【答案】D【解析】解:∵△OFM的外接圆与抛物线C的准线相切,∴△OFM的外接圆的圆心到准线的距离等于圆的半径∵圆面积为36π,∴圆的半径为6,又∵圆心在OF的垂直平分线上,|OF|=,∴+=6,∴p=8,故选:D.根据△OFM的外接圆与抛物线C的准线相切,可得△OFM的外接圆的圆心到准线的距离等于圆的半径,由此可求p的值.本题考查圆与圆锥曲线的综合,考查学生的计算能力,属于基础题.10.函数y=的图象与函数y=sin x(-4≤x≤8)的图象所有交点的横坐标之和等于()A.16B.12C.8D.4【答案】A【解析】解:作出函数y=的图象,则函数关于点(2,0)对称,同时点(2,0)也是函数y=sin x(-4≤x≤8)的对称点,由图象可知,两个函数在[-4,8]上共有8个交点,两两关于点(2,0)对称,设对称的两个点的横坐标分别为x1,x2,则x1+x2=2×2=4,∴8个交点的横坐标之和为4×4=16.故选:A.分别作出两个函数的图象,根据图象的对称性即可得到交点坐标问题.本题主要考查函数交点个数以及数值的计算,根据函数图象的性质,利用数形结合是解决此类问题的关键,综合性较强.二、填空题(本大题共5小题,共25.0分)11.已知复数z满足(+3i)z=3i,则z的虚部= ______ .【答案】【解析】解:由(+3i)z=3i,得:=,∴z的虚部为:.故答案为:.直接由复数代数形式的除法运算化简(+3i)z=3i,则z的虚部可求.本题考查了复数代数形式的除法运算,考查了复数虚部的求法,是基础题.12.设函数f(x)=3|x+1|+|x-1|-a,则使f(x)≥恒成立的a的取值范围为______ .【答案】(-∞,]【解析】解:∵f(x)=3|x+1|+|x-1|-a≥=恒成立,y=3x为增函数,∴|x+1|+|x-1|-a≥恒成立.∴a+≤|x+1|+|x-1|恒成立.令g(x)=|x+1|+|x-1|,则a+≤g(x)min,∵g(x)=|x+1|+|x-1|≥|x+1+1-x|=2,∴g(x)min=2,∴a+≤2,解得:a≤,即a的取值范围为(-∞,].故答案为:(-∞,].依题意,利用指数函数y=3x的单调性可得|x+1|+|x-1|-a≥恒成立.令g(x)=|x+1|+|x-1|,易求g(x)min=2,从而可得a的取值范围.本题考查绝对值不等式的解法,考查构造函数思想、等价转化思想与恒成立问题,求得g(x)=|x+1|+|x-1|的最小值是关键,考查运算求解能力,属于中档题.13.已知(1-2x)n展开式中,奇数项的二项式系数之和为64,则(1-2x)n(1+x)展开式中含x2项的系数= ______ .【答案】70【解析】解:∵(1-2x)n展开式中,奇数项的二项式系数之和为64,∴所有项的二项式系数和为2n=128,解得n=7,根据(1-2x)n(1+x)=(1+x)[1+++…+],可得展开式中含x2项的系数为+(-2)=84-14=70,故答案为:70.由题意可得,所有项的二项式系数和为2n=128,解得n=7,根据(1-2x)n(1+x)=(1+x)[1+++…+],可得展开式中含x2项的系数.本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.14.如图矩形ORTM内放置5个大小相同的正方形,其中A,B,C,D都在矩形的边上,若向量=x-y,则x-2y= ______ .【答案】-1【解析】解:根据图及向量的加法:;∴x=3,y=2,∴x-2y=-1.故答案为-1.根据图很容易用向量,来表示向量,对比条件中的向量,便可以求出x,y,从而求出x-2y.根据图及向量的加法不难做出本题,要注意的是向量的方向.15.已知f(x)是定义在R上的不恒为零的函数,且对于任意实数a、b∈R满足:f(a•b)=af(b)+bf(a),f(2)=2,a n=(n∈N*),b n=(n∈N*),考察下列结论:①f(0)=f(1);②f(x)为偶函数;③数列{b n}为等差数列;④数列{a n}为等比数列,其中正确的是______ .(填序号)【答案】①③④【解析】解:∵f(0)=f(0•0)=0,f(1)=f(1•1)=2f(1),∴f(1)=0,①正确;f(1)=f[(-1)•(-1)]=-2f(-1),∴f(-1)=0,f(-2)=f(-1×2)=-f(2)+2f(-1)=-2≠f(2),故f(x)不是偶函数,故②错;则f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,∴b n=b n-1+1,∴{b n}是等差数列,④正确;b1═1,b n=1+(n-1)×1=n,f(2n)=2n b n=n2n,a n═2n,故数列{a n}是等比数列,③正确.故答案为:①③④令x=y=0,得f(0)=f(0•0)=0,令x=y=1得f(1)=f(1•1)=2f(1),∴f(1)=0,可知正确;用特例,f(-2)=f(-1×2)=-f(2)+2f(-1)=-2≠f(2),故f(x)不是偶函数,f(2n)=f(2•2n-1)=2f(2n-1)+2n-1f(2)=2f(2n-1)+2n,有b n=b n-1+1,符合等差数列定义;b1═1,b n=1+(n-1)×1=n,f(2n)=2n b n=n2n,a n═2n,故数列{a n}是等比数列.本题主要考查数列与函数的综合运用,主要涉及了函数的奇偶性,赋值法,等差数列,等比数列的定义及通项.三、解答题(本大题共6小题,共75.0分)16.将函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象向右平移后得到g(x)图象,已知g(x)的部分图象如图所示,该图象与y轴相交于点F(0,1),与x轴相交于点B、C,点M为最高点,且S△MBC=.(Ⅰ)求函数g(x)的解析式,并判断(-,0)是否是g(x)的一个对称中心;(Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,g(A)=1,且a=,求S△ABC 的最大值.【答案】解:(Ⅰ)由题意,函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的图象向右平移后得到g(x)图象,∴g(x)=2sin[(ω(x-)+φ],∵S△MBC=,∴|BC|==,∴T=π,即ω=2,∵g(0)=2sin(φ-)=1,且-<φ-<,∴φ-=,∴φ=,∴g(x)=2sin[(2(x-)+]=2sin(2x+),∵g(-)=2sin[2•(-)+]=-2≠0,∴(-,0)不是g(x)的一个对称中心;(Ⅱ)∵g(A)=2sin(2A+)=1,2A+∈(,),∴2A+=,∴A=,由余弦定理可得5=b2+c2-2bccos A=b2+c2-bc≥bc,∴S△ABC=bcsin A≤,∴S△ABC的最大值为.【解析】(Ⅰ)利用S△MBC=,确定周期,可得ω,利用g(0)=2sin(φ-)=1,可求φ的值,尽快求函数g(x)的解析式,代入(-,0),即可判断(-,0)是否是g(x)的一个对称中心;(Ⅱ)先求出A,再由余弦定理可得5=b2+c2-2bccos A=b2+c2-bc≥bc,即可求S△ABC的最大值.本题考查函数解析式的确定,考查余弦定理的运用,考查基本不等式,确定函数的解析式,正确运用基本不等式是关键.17.已知正项数列{a n}的前n项和为S n,a1=,且满足2S n+1=4S n+1(n∈N*).(Ⅰ)求数列{a n}的通项公式;(Ⅱ)当1≤i≤n,1≤j≤n(i,j,n均为正整数)时,求a i和a j的所有可能的乘积a i a j 之和.【答案】解:(Ⅰ)∵,∴,,(1分)两式相减得a n+1=2a n,∴,,(2分)由2S2=4S1+1得2(a1+a2)=4a1+1,又,∴,.(3分)∴数列{a n}是首项为,公比为2的等比数列,∴.(5分)(Ⅱ)由a i和a j的所有可能乘积(1≤i≤n,1≤j≤n)(6分)可构成下表:21+1-4,21+2-4,21+3-4,…,21+n-4,22+1-4,22+2-4,…,22+n-4,2n+1-4,2n+2-4,2n+3,…,2n+n-4,(8分)设上表第一行的和为T1,则(10分)于是…+2n-1)==(12分)【解析】(Ⅰ)由2S n+1=4S n+1,再写一式,两式相减,确定数列{a n}是首项为,公比为2的等比数列,即可求出a n.(Ⅱ)由a i和a j的所有可能乘积a i•a j=2i+j(1≤i≤j≤n)可构成下表:21+1-4,21+2-4,21+3-4,…,21+n-4,22+1-4,22+2-4,…,22+n-4,2n+1-4,2n+2-4,2n+3,…,2n+n-4,即可求a i和a j的所有可能的乘积a i a j之和T n.考查等差数列、等比数列、不等式的证明、数列的求和等知识,考查推理论证能力和运算求解能力和化归转化数学思想.18.如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直.AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB.(Ⅰ)求直线EC与平面ABE所成角的正切值;(Ⅱ)线段EA上是否存在点F,使EC∥平面FBD?存在请确定具体位置,不存在说明理由.【答案】解:(Ⅰ)∵平面ABCD⊥平面ABE,且交线AB,BC⊥AB,BC⊂平面ABCD,∴BC⊥平面ABE,则∠CEB是直线EC与平面ABE所成角,∵在等腰三角形ABE中,AB=2,∴EB=EA=,在直角三角形CBE中,tan∠,∴直线EC与平面ABE所成角的正切值为.(Ⅱ)设O为AB的中点,连接OD,OE,则OE⊥AB,∵平面ABCD⊥平面ABE,∴OE⊥平面ABE,OE⊥OD,在直角梯形ABCD,由CD=OB,CD∥OB,可得OD⊥AB,由OB,OD,OE两两垂直,建立空间直角坐标系O-xyz,假设线段EA上存在点F,使EC∥平面FBD,设=(x,y,z)是平面PBD的一个法向量,则必需使⊥.∵E(0,0,1),C(1,-1,0),B(0,-1,0),D(1,0,0)则,,,,,,设F(0,a,1-a),,,∴,得令x=1,则,,.要使⊥,则有,∴.此时,,,,,,,,,∴则线段EA上存在点F,且是靠近点E的一个三等分点.【解析】(Ⅰ)根据线面所成角的定义,即可求直线EC与平面ABE所成角的正切值;(Ⅱ)建立空间直角坐标系,利用向量法结合EC∥平面FBD,即可得到结论.本题主要考查直线和平面所成角的计算,以及线面平行的判断,建立空间坐标系是解决本题的关键.19.现有正整数1,2,3,4,5,…n,一质点从第一个数1出发顺次跳动,质点的跳动步数通过抛掷骰子来决定:骰子的点数小于等于4时,质点向前跳一步;骰子的点数大于4时,质点向前跳两步.(Ⅰ)若抛掷骰子二次,质点到达的正整数记为ξ,求Eξ和Dξ;(Ⅱ)求质点恰好到达正整数6的概率.【答案】解:(Ⅰ)ξ的可能取值为3,4,5…(1分),P(ξ=4)=,…(4分)ξ的分布列为…(7分)(Ⅱ)质点恰好到达6有三种情形①抛掷骰子五次,出现点数全部小于等于4,概率;…(8分)②抛掷骰子四次,出现点数三次小于等于4,一次大于4,概率为;(9分)③抛掷骰子三次,出现点数一次小于等于4,二次大于4,概率…(10分)所以即质点恰好到达正整数6的概率为.…(12分)【解析】(I)由于ξ表示抛掷骰子二次,质点到达的正整数,由题意则ξ的取值有3,4,5,并利用随机变量得到定义求出每一个值下对应的事件的概率,有分布列定义求出其分布列,并根据期望定义求出期望.(II)由题意质点恰好到达正整数6有三种情形,①抛掷骰子五次,出现点数全部小于等于4;②抛掷骰子四次,出现点数三次小于等于4,一次大于4;③抛掷骰子三次,出现点数一次小于等于4,二次大于4.利用独立事件的概率公式各自的概率,最后相加即可;此题重在准确理解题意,主要考查了独立事件同时发生的概率公式,随机变量的定义及其分布列,并利用随机变量的分布列求其期望.20.已知圆M:(x-)2+y2=,椭圆C:=1(a>b>0)的右顶点为圆M的圆心,左焦点与双曲线x2-y2=1的左顶点重合.(Ⅰ)求椭圆C的方程;(Ⅱ)已知直线l:y=kx与椭圆C分别交于两点A,B,与圆M分别交于两点G,H(其中点G在线段AB上)且|AG|=|BH|,求k的值.【答案】解:(Ⅰ)由题意,圆心,,双曲线的左顶点(-1,0),(1分)所以,,,椭圆方程为::(3分)(Ⅱ)设A(x1,y1),B(x2,y2),由直线l与椭圆相交于两点A,B,则所以(1+2k2)x2-2=0,则,,(5分)所以(7分)点,到直线l的距离,则(9分)显然,若点H也在线段AB上,则由于对称性知,直线y=kx就是y轴,矛盾.因为|AG|=|BH|,所以|AB|=|GH|,(10分)即整理得4k4-3k2-1=0(12分)解得k2=1,即k=±1(13分)【解析】(Ⅰ)求出圆心,,双曲线的左顶点(-1,0),可得椭圆的几何量,即可求椭圆C的方程;(Ⅱ)直线l与椭圆联立,求出|AB|,|GH|,利用|AG|=|BH|,可得|AB|=|GH|,建立方程,即可求k的值.本题考查圆锥曲线的综合,考查直线与椭圆的位置关系,考查韦达定理,考查学生分析解决问题的能力,正确计算|AB|,|GH|是关键.21.设x=3是函数f(x)=(x2+ax+b)e3-x,(x∈R)的一个极值点.(Ⅰ)求a与b的关系式(用a表示b),并求f(x)的单调区间;(Ⅱ)设a>0,g(x)=(a2+)e x,若存在ξ1,ξ2∈[0,4],使得|f(ξ1)-g(ξ2)|<成立,求实数a的取值范围.【答案】解:(Ⅰ)∵f(x)=(x2+ax+b)e3-x∴f′(x)=(2x+a)e3-x-(x2+ax+b)e3-x=-[x2+(a-2)x+b-a]e3-x,由题意得:f′(3)=0,即32+3(a-2)+b-a=0,b=-2a-3,∴f(x)=(x2+ax-2a-3)e3-x且f′(x)=-(x-3)(x+a+1)e3-x令f′(x)=0得x1=3,x2=-a-1.∵x=3是函数f(x)=(x2+ax+b)e3-x,(x∈R)的一个极值点∴x1≠x2,即a≠-4故a与b的关系式b=-2a-3,(a≠-4).(1)当a<-4时,x2=-a-1>3,由f′(x)>0得单增区间为:(3,-a-1);由f′(x)<0得单减区间为:(-∞,3),(-a-1,+∞);(2)当a>-4时,x2=-a-1<3,由f′(x)>0得单增区间为:(-a-1,3);由f′(x)<0得单减区间为:(-∞,-a-1),(3,+∞).(Ⅱ)由(Ⅰ)知:当a>0时,x2=-a-1<0,f(x)在[0,3]上单调递增,在[3,4]上单调递减,∴,,f(x)max=f(3)=a+6.∴f(x)在[0,4]上的值域为[-2(a+3)e3,a+6].又g(x)=(a2+)e x,在x∈[0,4]上单调递增,∴g(x)在x∈[0,4]上的值域为,.由于≥0,∴若存在ξ1,ξ2∈[0,4],使得|f(ξ1)-g(ξ2)|<成立,必需><,解得0<a<3.∴a的取值范围是(0,3).【解析】(I)利用函数导数与极值的关系即可得出a与b的关系,对a分类讨论即可得出函数f (x)的单调性;(II)利用单调性分别求出函数f(x),g(x)的值域,f(x)在[0,4]上的值域为[-2(a+3)e3,a+6].g(x)在x∈[0,4]上的值域为,.由于≥0,可知:若存在ξ1,ξ2∈[0,4],使得|f(ξ1)-g(ξ2)|<成立,必需>,解得即可.<本题考查了利用函数导数研究函数的单调性极值与最值,考查了分类讨论的思想方法,考查了恒成立问题的等价转化方法,属于难题.。
数学_2014年山东省某校高考数学一模试卷(理科)_(含答案)

2014年山东省某校高考数学一模试卷(理科)一、选择题:本大题共12小题;每小题5分,共60分.在每小题给出的四个选项中,有且只有一项是符合题目要求的.1. 定义差集A −B ={x|x ∈A, 且x ∉B},现有三个集合A 、B 、C 分别用圆表示,则集合C −(A −B)可表示下列图中阴影部分的为( )A B C D2. 函数:f(x)=3+xlnx 的单调递增区间是( )A (0, 1e )B .(e, +∞)C (1e , +∞)D (1e , e) 3. 函数f(x)=sin 4x +cos 2x ,x ∈[0, π6]的最小值是( )A 34B 1316C 78D 1 4. 等差数列数列{a n }的公差为2,前n 项和为S n ,若a 1,a 3,a 4成等比数列,则S 20=( )A 180B 220C 580D 4105. 已知三棱锥P −ABC 的四个顶点均在半径为1的球面上,且满足PA →⋅PB →=0,PB →⋅PC →=0,PC →⋅PA →=0,则三棱锥P −ABC 的侧面积的最大值为( )A 2B 1C 12D 14 6. 一动圆圆心在抛物线x 2=4y 上,过点(0, 1)且与定直线l 相切,则l 的方程为( )A x =1B x =116C y =−1D y =−116 7. 在算式“4×□+1×△=30”的两个□,△中,分别填入两个正整数,使它们的倒数之和最小,则这两个数构成的数对(□,△)应为( )A (4, 14)B (5, 10)C (6, 6)D (3, 18)8. 如图是一个正方体纸盒的展开图,把1、−1、2、−2、√2、−√2分别填入六个正方形,使得按虚线折成正方体后,相对面上的两个数的绝对值相等,求不同填法的种数( )A 3B 6C 24D 489. 将甲、乙两颗骰子先后各抛掷一次,a ,b 分别表示抛掷甲、乙两颗骰子所掷出的点数,若M(a, b)落在不等式x 2+y 2≤m (m 为常数)所表示的区域内,设为事件C ,要使事件C 的概率P(C)=1,则m 的最小值为( )A 52B 61C 72D 710. 设z =1+i1−i +(1−i)2,则(1+x)4(1+zx)3展开式中x 5项的系数是( )A −2−3iB −12+3iC 1+21iD −35i11. 在平面直角坐标系中,x 轴的正半轴上有4个点,y 轴的正半轴上有5个点,这9个点任意两点连线,则所有连线段的交点落入第一象限的个数最多是( )A 30B 60C 120D 24012. 一个均匀小正方体的六个面中,三个面上标以数0,两个面上标以数1,一个面上标以数3,将这个小正方体抛掷两次,则向上的数之积的数学期望是( )A 49B 59C 736D 2536二、填空题:本大题共4小题,每小题4分,共16分.请把答案填写在题中横线上.13. 考察某种针剂对预防疾病的效果,进行的试验数据记录如下:注射针剂患病的有12例,未患病的有48例;没注射针剂患病的有22例,未患病的有35例,根据所学知识,你认为针剂无效这一结论的可能性约为________(百分数要为整数)14. 设有两个命题:①关于x 的不等式mx 2+1>0的解集是R ;②函数f(x)=log m x 是减函数,如果这两个命题有且只有一个真命题,则实数m 的取值范围是________.15. 某班有50个同学,其中男生30人,女生20人,某次导师要抽五位同学打扫环境,依性别按人数作分层抽样,则班上的男同学甲被抽中的概率是________.16. 给出以下几个命题:①由曲线y =x 2与直线y =2x 围成的封闭区域的面积为43; ②已知点A 是定圆C 上的一个定点,线段AB 为圆的动弦,若OP →=12(OA →+OB →),O 为坐标原点,则动点P 的轨迹为圆;③把5本不同的书分给4个人,每人至少1本,则不同的分法种数为A 54⋅A 41=480种;④若直线l // 平面α,直线l ⊥直线m ,直线l ⊂平面β,则β⊥α.其中,正确的命题有________.(将所有正确命题的序号都填在横线上)三.解答题17. 已知△ABC 中,a ,b ,c 分别是三个内角A ,B ,C 的对边,关于x 的不等式x 2cosC +4xsinC +6<0的解集是空集.(1)求角C 的最大值;(2)若c =72,△ABC 的面积S =32√3,求当角C 取最大值时a +b 的值. 18. 高考理科总分得640就能上北京大学,已知一名理科学生的语文、英语、理综合得分分别为135分,125分,260分.数学试卷中12个选择题每题5分,且每题答对的概率都是0.9,4个填空题每题4分且每题答对的概率都是0.8,6个大题前五个每题12分,最后一题14分,前两个大题估计能得满分,最后一个大题估计能得2分.已知第三、四、五个大题每题答对的概率都相等,且至少答对一题的概率为0.992.(1)求这名理科学生数学试卷得分的期望;(2)这名学生能否考上北京大学?19. 正△ABC 的边长为4,CD 是AB 边上的高,E 、F 分别是AC 和BC 边的中点,现将△ABC 沿CD 翻折成直二面角A −DC −B(Ⅰ)试判断直线AB 与平面DEF 的位置关系,并说明理由;(Ⅱ)求二面角E −DF −C 的余弦值;(Ⅲ)在线段BC 上是否存在一点P ,使AP ⊥DE ?证明你的结论.20. 东方庄家给游人准备了这样一个游戏,他制作了“迷尼游戏板”:在一块倾斜放置的矩形胶合板上钉着一个形如“等腰三角形”的八行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙,…,第8行9个铁钉之间有8个空隙(如图所示).东方庄家的游戏规则是:游人在迷尼板上方口放人一球,每玩一次(放入一球就算玩一次)先付给庄家2元.若小球到达①②③④号球槽,分别奖4元、2元、0元、−2元.(一个玻璃球的滚动方式:通过第1行的空隙向下滚动,小球碰到第二行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙.以后小球按类似方式继续往下滚动,落入第8行的某一个空隙后,最后掉入迷尼板下方的相应球槽内).恰逢周末,某同学看了一个小时,留心数了数,有80人次玩.试用你学过的知识分析,这一小时内庄家是赢是赔;通过计算,你想到了什么?21. 点A 是椭圆x 2a 2+y 2b 2=1(a >b >0)短轴位于x 轴下方的顶点,过A 作斜率为1的直线交椭圆于P 点,B 点在y 轴上且BP // x 轴,且AB →⋅AP →=9.(1)若B(0, 1),求椭圆的方程;(2)若B(0, t),求t 的取值范围.22. 已知f(x)是定义在R 上的不恒为零的函数,且对于任意的a ,b ∈R 都满足f(a ⋅b)=af(b)+bf(a).(1)求f(0),f(1)的值;(2)判断f(x)的奇偶性,并证明你的结论;(3)若f(12)=−12,令b n =2n f(2n ),S n 表示数列{b n }的前n 项和,试问:是否存在关于n 的整式g(n),使得S 1+S 2+S 3+...+S n−1=(S n −1)⋅g(n)对于一切不小于2的自然数n 恒成立?若存在,写出g(n)的解析式,并加以证明;若不存在,试什么理由.2014年山东省某校高考数学一模试卷(理科)答案1. A2. C3. A4. B5. A6. C7. B8. D9. C10. B11. B12. D13. 5%14. m=0或m≥115. 11016. ①②17.解:(1)∵ 不等式x2cosC+4xsinC+6<0的解集是空集.∴ {cosC>0,Δ≤0,即{cosC>0,16sin2C−24cosC≤0,即{cosC>0,cosC≤−2或cosC≥12,故cosC≥12,∴ 角C的最大值为60∘.(2)当C=60∘时,S△ABC=12absinC=√34ab=32√3,∴ ab=6,由余弦定理得c2=a2+b2−2abcosC=(a+b)2−2ab−2abcosC,∴ (a+b)2=c2+3ab=1214,∴ a+b=112.18. 解:(1)数学卷中,选择题得分的期望为12×0.9×5=54,…2分填空题得分的期望为4×0.8×4=12.8,…4分前两个大题得24分,设三,四,五是每题答对的概率为P,则至少答对一题的概率为1−(1−p)3=0.992,解得p=0.8.∴ 三,四,五题得分的期望为3×0.8×12=28.8.…7分最后一题得2分,54+12.8+24+28.8+2=121.2∴ 数学试卷得分的期望为121.2(分).…9分(2)得总分的期望为135+125+260+121.2=641.2,∵ 641.2>640,∴ 能考上北京大学.…12分19. 法一:(I)如图:在△ABC中,由E、F分别是AC、BC中点,得EF // AB,又AB ⊄平面DEF ,EF ⊂平面DEF .∴ AB // 平面DEF .(II)∵ AD ⊥CD ,BD ⊥CD∴ ∠ADB 是二面角A −CD −B 的平面角∴ AD ⊥BD∴ AD ⊥平面BCD取CD 的中点M ,这时EM // AD∴ EM ⊥平面BCD过M 作MN ⊥DF 于点N ,连接EN ,则EN ⊥DF∴ ∠MNE 是二面角E −DF −C 的平面角在Rt △EMN 中,EM =1,MN =√32 ∴ tan∠MNE =√32,cos∠MNE =y =−√3x +2√3.(Ⅲ)在线段BC 上存在点P ,使AP ⊥DE证明如下:在线段BC 上取点P .使BP =13BC ,过P 作PQ ⊥CD 与点Q , ∴ PQ ⊥平面ACD∵ DQ =13DC =2√33在等边△ADE 中,∠DAQ =30∘ ∴ AQ ⊥DE∴ AP ⊥DE .法二:(Ⅱ)以点D 为坐标原点,直线DB 、DC 为x 轴、y 轴,建立空间直角坐标系, 则A(0, 0, 2)B(2, 0, 0)C(0,2√3,0,),E(0,√3,1),F(1,√3,0)平面CDF 的法向量为DA →=(0,0,2)设平面EDF 的法向量为n →=(x,y,z)则{DF →⋅n →=0DE →⋅n →=0 即{x +√3y =0√3y +z =0 n →=(3,−√3,3)cos <DA →,n →>=DA →⋅n →|DA →||n →|=√217 所以二面角E −DF −C 的余弦值为√217(Ⅲ)在平面坐标系xDy 中,直线BC 的方程为y =−√3x +2√3设P(x,2√3−√3x,0),AP →=(x,2√3−√3x,−2)∴ AP ⊥DE ⇔AP →⋅DE →=0⇔x =43⇔BP →=13BC →所以在线段BC 上存在点P ,使AP ⊥DE另设P(x,y,0),AP →⋅DE →=√3y −2=0∴ y =2√33 又BP →=(x −2,y,0),PC →=(−x,2√3−y,0)∵ BP →∥PC →∴ (x −2)(2√3−y)=−xy ∴ √3x +y =2√3把y =2√33代入上式得x =43, ∴ BP →=13BC →所以在线段BC 上存在点P 使AP ⊥DE20. 庄家当然是赢家!我们应当学会以所学过的知识为武器,劝说人们不要被这类骗子的骗术所迷惑.21. 解:(1)直线AP 的方程为y =x −b ,联立{y =1y =x −b,解得{x =b +1y =1,∴ P(b +1, 1). ∴ AB →⋅AP →=(0, 1+b)⋅(b +1, b +1)=(1+b)2=9(b >0),解得b =2.∴ P(3, 1),代入椭圆的方程为32a 2+1b 2=1,解得a 2=12. ∴ 椭圆的方程为x 212+y 24=1. (2)由AB →⋅AP →=9,∴ (0, t +b)⋅(t +b, t +b)=(t +b)2=9(t >0, b >0),∴ t +b =3①.把P(3, t)代入椭圆的方程可得9a 2+t 2b 2=1,化为a 2=9b 2b 2−t 2.∵ a 2>b 2,∴ 9b 2b 2−t 2>b 2,∴ 9b 2−t 2>1,②由①可得b =3−t 代入②可得9(3−t)2−t 2>1,化为99−6t >1,解得0<t <32.∴ t 的取值范围是(0,32).22. 解:(1)令a =b =0,得f(0)=0⋅f(0)+0⋅f(0)=0.令a =b =1,得f(1)=1⋅f(1)+1⋅f(1),∴ f(1)=0.(2)令a =b =−1,得f(1)=f[(−1)⋅(−1)]=−f(−1)−f(−1)=−2f(−1),∴ f(−1)=0.令a =−1,b =x ,得f(−x)=f(−1⋅x)=−1⋅f(x)+x ⋅f(−1)=−f(x)+0=−f(x).∴ f(x)是奇函数.(3)当ab ≠0时,f(a⋅b)a⋅b =f(b)b +f(a)a . 令g(x)=f(x)x ,则g(a ⋅b)=g(a)+g(b),∴ g(a n )=ng(a).∴ f(a n )=a n ⋅g(a n )=n ⋅a n ⋅g(a)=n ⋅a n−1⋅f(a).∵ f(1)=f(2⋅12)=2f(12)+12f(2)=0,f(12)=−12∴ f(2)=2,∴ b n=2nf(2n)=1n∴ S n=1+12+13+⋯+1n,∴ S n−S n−1=1n(n≥2)即nS n−(n−1)S n−1=S n−1+1,∴ (n−1)S n−1−(n−2)S n−2=S n−2+1,…,2S2−S1=S1+1,∴ nS n−S1=S1+S2+...+S n−1+n−1,∴ S1+S2+...S n−1=nS n−n=(S n−1)⋅n(n≥2)∴ g(n)=n.故存在关于n的整式g (n)=n,使等式对于一切不小于2的自然数n恒成立。
山东省威海市2014届高三下学期第一次模拟考试化学试题及答案

高三化学试题本试卷分第I卷(选择题)和第II卷(非选择题)两部分,共8页。
考试结束后,将答题卡交回。
第I卷(选择题共46分)注意事项:1.答卷前,将答题卡内的相关项目填写清楚。
2.每题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号,不能答在试题上。
可能用到的相对原子质量:H 1 C 12 N 14 O 16 Na 23 Mg 24 Al 27 S 32 Cl 35.5 V 51 Fe 56 Cu 64选择题(本题包括18小题,1-8题每题2分,9-18题每题3分,共46分。
每小题只有一个选项符合题意)1.化学与社会、生产、生活密切相关。
下列说法正确的是A.可以用物理方法或化学方法从海水中提取所需物质B.用激光笔分别照射盛有牛奶、食盐水的玻璃杯,都有光亮的通路C.神舟10号飞船所用太阳能电池板可将光能转换为电能,所用转换材料是二氧化硅D.氯气溶于水生成次氯酸有强氧化性,可以起到除去水中杂质和杀菌消毒作用2. 下列叙述正确的是A. 沼气和水煤气都是可再生能源B.石油裂解和油脂皂化都有高分子生成小分子的过程C. 不能用植物油萃取溴水中的溴D. 可以用加热使蛋白质变性的方法分离提纯蛋白质3. 解释下列事实的方程式正确的是A.用碳酸钠溶液处理水垢中的硫酸钙:Ca2++CO32-=CaCO3↓B.SO2使紫色石蕊溶液变红色:SO2+H2O=2H++SO32-C.用石墨电极电解AlCl3溶液,阴极附近生成沉淀:2Al3++6H2O+6e-=2Al(OH)3↓+3H2↑D.工业上制取硅:SiO2+C高温Si+CO24.下列说法错误的是A.一定条件下,气体体积大小主要由气体的分子数目决定的B.有热量变化的过程一定有化学键的断裂与形成C.通过钠、镁、铝与水反应的实验,可以比较三种单质的金属性强弱D.轮船外壳连接锌块保护外壳不受腐蚀,是采用了牺牲阳极的阴极保护法5.铁和铁合金是生产、生活中常用的材料,下列说法中错误的是A.不锈钢比生铁抗腐蚀能力强B.以铁为阴极、铜片为阳极、硫酸铜为电镀液可以实现铁制品镀铜C.铁与稀硫酸反应,铁与浓硫酸不能反应D.铁轨焊接时可以用铝热反应的方法制取少量的铁CH CH OHH C 3336.C 、Si 、S 都是自然界中含量丰富的非金属元素,下列关于其单质及化合物的说法中正确的是 A .三种元素在自然界中既有游离态又有化合态B .二氧化物都属于酸性氧化物,能与碱反应而不能与任何酸反应C .最低价的气态氢化物都具有还原性,易与O 2发生反应D .其最高价氧化物对应水化物的酸性强弱:H 2SO 4>H 2SiO 3>H 2CO 37.主族元素M 、R 形成的简单离子M 2-离子与R +离子的核外电子数之和为20,下列说法正确的是A .M 原子的质子数一定大于R 原子的质子数B .M 可能存在16M 、18M 两种核素C .M 2-的离子与R +的电子层结构不可能相同D .两种离子结合形成的化合物中可能含有共价键 8.下列叙述和解释正确的是9A A .N A 个N 2分子与0.5 N A 个H 2分子所占的体积比一定是2 : 1 B .相同物质的量的OH -和CH 3+含有相同数目的电子C .25℃时,pH =13的Ba(OH)2溶液中含有OH -的数目为0.2N AD .常温常压下,NO 2与足量H 2O 反应生成0.1molNO ,则转移的电子数为0.2N A10.萜品醇可作为消毒剂、抗氧化剂、医药和溶剂。
山东省威海乳山一中2014届高三3月限时训练 数学理 含答案

高三理科数学综合练习一、选择题:本大题共10小题.每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. i 是虚数单位,复数ii+12的实部为 A .2 B .2- C .1 D .1- 2. 设全集R U =,集合{}2|lg(1)M x y x==-,{}|02N x x =<<,则()U NM =A .{}|21x x -≤<B .{}|01x x <≤C .{}|11x x -≤≤D .{}|1x x <3. 已知m 、n 为两条不同的直线,α、β为两个不同的平面,则下列命题中正确的是A .若l m ⊥,l n ⊥,且,m n α⊂,则l α⊥B .若平面α内有不共线的三点到平面β的距离相等,则βα//C .若n m m ⊥⊥,α,则α//nD .若α⊥n n m ,//,则α⊥m4. 一个几何体的三视图如图所示,其中俯视图与左视图均为半径是2的圆,则这个几何体的表面积是A .16πB .14πC .12πD .8π5。
已知抛物线x y 42=的焦点为F ,准线为l ,点P 为抛物线上一点,且在第一象限,l PA ⊥,垂足为A ,4PF =,则直线AF 的倾斜角等于 A .712π B.23π C .34π D.56π 6.若两个非零向量a ,b 满足||2||||a b a b a=-=+,则向量a b +与b a -的夹角A .6π B .3π C .32πD .65π正视图俯视图 左视图7。
已知函数2, 0(), 0x x f x x x x ≤⎧=⎨->⎩,若函数()()g x f x m =-有三个不同的零点,则实数m 的取值范围为A .1[,1]2- B .1[,1)2- C .1(,0)4- D .1(,0]4-8。
已知()|2||4|f x x x =++-的最小值为n ,则二项式1()nx x-展开式中2x 项的系数为A .15B .15-C .30D .30-9. 已知函数()f x 对定义域R 内的任意x 都有()f x =(4)f x -,且当2x ≠时其导函数()f x '满足()2(),xf x f x ''>若24a <<则 A .2(2)(3)(log)af f f a << B .2(3)(log )(2)a f f a f <<C .2(log)(3)(2)a f a f f <<D .2(log)(2)(3)a f a f f <<10. 定义区间(, )a b ,[, )a b ,(, ]a b ,[, ]a b 的长度均为d b a =-,多个区间并集的长度为各区间长度之和,例如, (1, 2)[3, 5)的长度(21)(53)3d =-+-=. 用[]x 表示不超过x 的最大整数,记{}[]x x x =-,其中R x ∈.设()[]{}f x x x =⋅,()1gx x =-,当0x k ≤≤时,不等式()()f x gx <解集区间的长度为5,则k 的值为A .6B .7C .8D .9二、填空题:本大题共5小题,每小题5分,共25分. 11。
山东省威海市数学高三理数4月第一次模拟考试试卷

山东省威海市数学高三理数4月第一次模拟考试试卷姓名:________ 班级:________ 成绩:________一、单选题 (共8题;共16分)1. (2分)设集合,或,则=()A .B .C .D . R2. (2分) (2016高一上·晋中期中) 已知函数f(x)=ax﹣1(a>0,且a≠1),当x∈(0,+∞)时,f(x)>0,且函数g(x)=f(x+1)﹣4的图象不过第二象限,则a的取值范围是()A . (1,+∞)B .C . (1,3]D . (1,5]3. (2分)圆的圆心坐标和半径分别为()A .B .C .D .4. (2分) (2019高一下·武宁期末) 按照程序框图(如图)执行,第4个输出的数是()A . 5B . 6C . 7D . 85. (2分) (2017高二上·佳木斯月考) 已知抛物线的焦点为,准线为,是上一点,是直线与的一个交点,若,则()A .B .C .D .6. (2分) (2019高三上·宁波月考) 若实数x,y满足x+y>0,则“x>0”是“x2>y2”的()A . 充分不必要条件B . 必要不充分条件C . 充分必要条件D . 既不充分也不必要条件7. (2分)(2017·蚌埠模拟) 如图,网格纸上小正方形的边长为1,粗实线画出的是某四棱锥的三视图,则该几何体的体积为()A . 15B . 16C .D .8. (2分)当1,2,3,4,5,6时,比较和的大小并猜想()A . 时,B . 时,C . 时,D . 时,二、填空题 (共6题;共6分)9. (1分) (2018高二下·聊城期中) 已知复数,,且,则 ________.10. (1分) (2018高二上·南京月考) 的内角所对的边为,则“ ”是“ ”的________条件.(填“充分不必要”、“必要不充分”、“充要”、“既不充分也不必要”中的一个)11. (1分) (2016高一下·钦州期末) 设变量x,y满足约束条件则z=3x﹣2y的最大值为________.12. (1分)给出下列命题;①设[x]表示不超过x的最大整数,则[log21]+[og22]+[log23]+…+[log2127]+[log2128]=649;②定义在R上的函数f(x),函数y=f(x﹣1)与y=f(1﹣x)的图象关于y轴对称;③函数f(x)=的对称中心为(﹣,﹣);④定义:若任意x∈A,总有a﹣x∈A(A≠∅),就称集合A为a的“闭集”,已知A⊆{1,2,3,4,5,6};且A为6的“闭集”,则这样的集合A共有7个.其中正确的命题序号是________13. (1分) (2016高二下·渭滨期末) 马路上有编号1,2,3,…,10共10盏灯,现要关掉其中的四盏,但不能关掉相邻的二盏或三盏,也不能关掉两端的两盏,则满足条件的关灯方案有________种.14. (1分)已知A={x|﹣2≤x≤5},B={x|m﹣1≤x≤m+1},B⊆A,则m的取值范围为________三、解答题 (共6题;共30分)15. (5分)已知cos(α+β)=﹣,cos 2α=﹣,α、β均为钝角,求cos(α﹣β)的值.16. (5分) (2015高二下·宜昌期中) 为了解某校高三毕业班报考体育专业学生的体重(单位:千克)情况,将从该市某学校抽取的样本数据整理后得到如下频率分布直方图.已知图中从左至右前3个小组的频率之比为1:2:3,其中第2小组的频数为12.(I)求该校报考体育专业学生的总人数n;(Ⅱ)若用这所学校的样本数据来估计该市的总体情况,现从该市报考体育专业的学生中任选3人,设ξ表示体重超过60千克的学生人数,求ξ的分布列和数学期望.17. (5分)已知E,F,G,H分别是空间四边形四条边AB,BC,CD,DA的中点,(1)求证四边形EFGH是平行四边形(2)若AC⊥BD时,求证:EFGH为矩形;(3)若AC、BD成30°角,AC=6,BD=4,求四边形EFGH的面积;(4)若AB=BC=CD=DA=AC=BD=2,求AC与BD间的距离.18. (5分) (2017高三上·河北月考) 已知椭圆C:的两个焦点和短轴的两个顶点构成的四边形是一个正方形,且其周长为 .(I)求椭圆C的方程;(II)设过点B(0,m)(m>0)的直线与椭圆C相交于E,F两点,点B关于原点的对称点为D,若点D总在以线段EF为直径的圆内,求m的取值范围.19. (5分)(2018·淮南模拟) 已知函数(为自然对数的底数)(Ⅰ)若函数的图像在处的切线与直线垂直,求的值;(Ⅱ)对总有≥0成立,求实数的取值范围.20. (5分) (2019高一下·上海月考) 是定义在上且满足如下条件的函数组成的集合:①对任意的,都有②存在常数使得对任意的,都有 .(1)设问是否属于?说明理由;(2)若如果存在使得证明:这样的是唯一的;(3)设且试求的取值范围.参考答案一、单选题 (共8题;共16分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、二、填空题 (共6题;共6分)9-1、10-1、11-1、12-1、13-1、14-1、三、解答题 (共6题;共30分)15-1、16-1、17-1、17-2、17-3、17-4、18-1、19-1、20-1、20-2、20-3、。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
山东省威海市2014届下学期高三年级第一次模拟考试数学试卷(理科)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共5页.考试时间120分钟.满分150分.答题前,考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、考号填写在答题纸规定的位置.第Ⅰ卷(选择题 共60分)注意事项:每小题选出答案后,用铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{1,2},{1,,}A B a b ==,则“2a =”是“A B ⊆”的 (A )充分不必要条件 (B )必要不充分条件 (C )充要条件 (D )既不充分也不必要条件2. 1i z i ⋅=-(i 为虚数单位),则z =(A )1i + (B )1i - (C )1i -+ (D )1i -- 3.若a b >,则下列不等式成立的是(A )ln ln a b > (B )0.30.3a b >(C )1122a b > (D >4.根据给出的算法框图,计算(1)(2)f f -+=(A )0 (B )1 (C )2 (D )45.某班级统计一次数学测试后的成绩,并制成了如下的频率分布表,根据该表估计该班级的数学测试平均分为(A )80 (B )81 (C )82 (D )836.已知,l m 是两条不同的直线,α是一个平面,且l ∥α,则下列命题正确的是 (A )若l ∥m ,则m ∥α (B )若m ∥α,则l ∥m (C )若l m ⊥,则m α⊥ (D )若m α⊥,则l m ⊥7.已知函数()sin 2f x x =向左平移6π个单位后,得到函数()y g x =,下列关于()y g x =的说法正确的是 (A )图象关于点(,0)3π-中心对称 (B )图象关于6x π=-轴对称(C )在区间5[,]126ππ--单调递增 (D )在[,]63ππ-单调递减 8.任取三个整数,至少有一个数为偶数的概率为 (A )0.125 (B )0.25 (C )0.5 (D )0.8759.二项式n的展开式中第4项为常数项,则常数项为 (A )10 (B )10- (C )20 (D )20-10.函数()(2)()f x x ax b =-+为偶函数,且在(0,)+∞单调递增,则(2)0f x ->的解集为 (A ){|22}x x x ><-或 (B ){|22}x x -<< (C ){|04}x x x <>或 (D ){|04}x x <<11.双曲线221x y m-=的离心率2e =,则以双曲线的两条渐近线与抛物线2y mx =的交点为顶点的三角形的面积为(A (B )(C )(D )12.已知1a >,设函数()4x f x a x =+-的零点为m ,()log 4a g x x x =+-的零点为n ,则mn 的最大值为(A )8 (B )4 (C )2 (D )1第Ⅱ卷(非选择题 共90分)注意事项:1. 请用0.5毫米的黑色签字笔将每题的答案填写在答题纸的指定位置.书写的答案如需改动,要先划掉原来的答案,然后再写上新答案.2. 不在指定答题位置答题或超出答题区域书写的答案无效.在试题卷上答题无效. 3. 第Ⅱ卷共包括填空题和解答题两道大题.中学联盟 二、填空题:本大题共4小题,每小题4分,共16分. 13.若函数cos22y x x a =+在0,2π⎡⎤⎢⎥⎣⎦上有两个不同的零点,则实数a 的取值范围为_______________________.14.已知圆O 过椭圆22162x y +=的两焦点且关于直线10x y -+=对称,则圆O 的方程为__________________.15.设,x y 满足约束条件22002x x y e y x +≥⎧⎪-≥⎨⎪≤≤⎩,则(,)M x y 所在平面区域的面积为___________.16.函数()y f x =的定义域为(,1)(1,)-∞-+∞,其图象上任一点(,)P x y 满足221x y -=,则给出以下四个命题:①函数()y f x =一定是偶函数; ②函数()y f x =可能是奇函数;③函数()y f x =在(1,)+∞单调递增;④若()y f x =是偶函数,其值域为(0,)+∞ 其中正确的序号为_______________.(把所有正确的序号都填上)三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17. (本小题满分12分)已知向量(cos ,sin )a αα=,(1+cos ,sin )b ββ=- .(Ⅰ)若3πα=,(0,)βπ∈,且a b ⊥,求β;(Ⅱ)若=βα,求a b ⋅的取值范围.18. (本小题满分12分)一个袋子中装有7个小球,其中红球4个,编号分别为1,2,3,4,黄球3个,编号分别为2,4,6,从袋子中任取4个小球(假设取到任一小球的可能性相等). (Ⅰ)求取出的小球中有相同编号的概率;(Ⅱ)记取出的小球的最大编号为X ,求随机变量X 的分布列和数学期望.19.(本小题满分12分) 如图,矩形ABCD 所在的平面和平面ABEF 互相垂直,等腰梯形ABEF 中,AB ∥EF ,AB =2,1AD AF ==,60BAF ∠=,O ,P 分别为AB ,CB的中点,M 为底面OBF ∆的重心. (Ⅰ)求证:PM ∥平面AFC ;(Ⅱ)求直线AC 与平面CBF 所成角的正弦值.20.(本小题满分12分)已知正项数列{}n a ,其前n 项和n S 满足2843,n n n S a a =++且2a 是1a 和7a 的等比中项. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ) 符号[]x 表示不超过实数x 的最大整数,记23[log ()]4n n a b +=,求1232n b b b b +++ .21.(本小题满分13分)过椭圆22221(0)x y a b a b+=>>的左顶点A 作斜率为2的直线,与椭圆的另一个交点为B ,与y 轴的交点为C ,已知613AB BC =. (Ⅰ)求椭圆的离心率;(Ⅱ)设动直线y kx m =+与椭圆有且只有一个公共点P ,且与直线4x =相交于点Q ,若x 轴上存在一定点(1,0)M ,使得PM QM ⊥,求椭圆的方程.22.(本小题满分13分)山东中学联盟设函数()(1)xf x ae x =+(其中 2.71828....e =),2()2g x x bx =++,已知它们在0x =处有相同的切线.(Ⅰ)求函数()f x ,()g x 的解析式;(Ⅱ)求函数()f x 在[,1](3)t t t +>-上的最小值;(Ⅲ)若对2,()()x kf x g x ∀≥-≥恒成立,求实数k 的取值范围.高三理科数学参考答案一、选择题1-12 A D D A C, D C D B C, C B 二、填空题13. (21]-,- 14. 22(1)5x y +-= 15. 22e - 16. ② 三、解答题17.(本小题满分12分)解:(Ⅰ)∵a b ⊥ ∴cos cos cos sin sin 0a b ααβαβ⋅=+-=--------------1分∵3πα=∴coscoscos sinsin 0333πππββ+-=整理得1cos()32πβ+=- --------------------3分 ∴2233k ππβπ+=+过42,33k k z ππβπ+=+∈ --------------------4分 ∵(0,)βπ∈∴3πβ=--------------6分(Ⅱ)222cos cos sin cos 2cos 1a b ααααα⋅=+-=+- --------------------8分令[]cos ,1,1t t α=∈- 2219212()48a b t t t ⋅=+-=+- --------------------9分∴当1t =时,max 2a b ⋅= ,当14t =-时,98min a b ⋅=- --------------------11分∴a b ⋅ 的取值范围为9[,2]8-. ----------------------12分18.(本小题满分12分)解(Ⅰ):设取出的小球中有相同编号的事件为A ,编号相同可分成一个相同和两个相同 ----------------------2分112233472()119()35C C C P A C ++==----------------------4分(Ⅱ) 随机变量X 的可能取值为:3,4,6 -----------------6分4711(3)35P X C === , ----------------------7分132244472(4)5C C C P X C +===, ------------------8分 36474(6)7C P X C ===----------------------9分 所以随机变量X 的分布列为:-----------10分所以随机变量X 的数学期望124179346355735EX =⨯+⨯+⨯= .----------------------12分 19.(本小题满分12分)解(Ⅰ)连结OM 延长交BF 于H ,则H 为BF 的中点,又P 为CB 的中点,∴PH ∥CF ,又∵AF ⊂平面AFC ,∴PH ∥平面AFC ---------------2分 连结PO ,则PO ∥AC ,AC ⊂平面AFC ,PO ∥平面AFC --------------4分1PO PO P = ∴平面1POO ∥平面AFC , -------------5分PM ⊂平面AFC//PM 平面AFC ----------------------6分(Ⅱ) 矩形ABCD 所在的平面和平面ABEF 互相垂直,CB AB ⊥所以CB ⊥平面ABEF ,又AF ⊂平面1BDC ,所以CB AF ⊥ --------------7分又2AB =,1AF =,60BAF ∠=,由余弦定理知BF ,222AF BF AB +=得AF BF ⊥ --------------8分AF CB B = ∴AF ⊥平面CFB ---------------------9分所以ACF ∠为直线AC 与平面CBF 所成的角, ---------------10分 在直角三角形ACF 中sin 5AF ACF AC ∠===---------------------12分法二:以O 为原点建立如图所示空间直角坐标系,1(1,0,0),(1,0,0),(1,0,1),(,0),2A B C F -- -----------------7分设平面CBF 的法向量为(,,)n x y z =,()3(,1),0,0,12FC CB =--=- , -------------------8分由0,0,n CB n FC ⎧⋅=⎪⎨⋅=⎪⎩所以0,0,z y =⎧⎪+= 令1x =,则10x y z =⎧⎪=⎨⎪=⎩,所以(1,n =-,-----------------10分()2,0,1AC =-∴cos ,n AC <>==分 ∴直线AC 与平面CBF分 20.(本小题满分12分) 解:(Ⅰ) 由2843n n n S a a =++①知2111843(2,)n n n S a a n n N ---=++≥∈② ------------------1分由①-②得1118()()44n n n n n n n a a a a a a a ---=-++-整理得11(4)()0(2,)n n n n a a a a n n N ----+=≥∈ ----------------------2分 ∵{}n a 为正项数列∴10,n n a a -+>,∴14(2,)n n a a n n N --=≥∈ ----------------------3分所以{}n a 为公差为4的等差数列,由2111843,a a a =++得13a =或11a = -------4分 当13a =时,277,27a a ==,不满足2a 是1a 和7a 的等比中项. 当11a =时,275,25a a ==,满足2a 是1a 和7a 的等比中项.所以1(1)443n a n n =+-=-. ----------------------6分 (Ⅱ) 由43n a n =-得223[log ()][log ]4n n a b n +==, --------------------7分 由符号[]x 表示不超过实数x 的最大整数知,当122mm n +≤<时,2[log ]n m =,----------8分所以令12322222[log 1][log 2][log 3][log 2]n n S b b b b =+++=+++0112341n n =+++++++++-++∴1234112223242(1)2n S n n -=⨯+⨯+⨯+⨯+-⨯+① ----------------9分2345212223242(1)22n S n n =⨯+⨯+⨯+⨯+-⨯+② ----------------------10分①-②得234112222...2(1)22(12)(1)2(2)2212n n n n nS n nn n n n ---=+++++----=---=---- (2)22n S n n ∴=-++即1232n b b b b +++ (2)22nn n =-++. ----------------------12分 21. (本小题满分13分)解:(Ⅰ)∵A (,0)a -,设直线方程为2()y x a =+,11(,)B x y令0x =,则2y a =,∴(0,2)C a , ----------------------2分∴1111(,),(,2)AB x a y BC x a y =+=------------------------3分∵613AB BC =∴1x a+=11166(),(2)1313x y a y -=-,整理得111312,1919x a y a =-= --------------------4分∵B 点在椭圆上,∴22221312()()11919a b +⋅=,∴223,4b a = ------------------5分∴2223,4a c a -=即2314e -=,∴12e = ----------------6分 (Ⅱ)∵223,4b a =可设223.4b t a t ==,∴椭圆的方程为2234120x y t +-= ----------------------7分由2234120x y t y kx m⎧+-=⎨=+⎩得222(34)84120k x kmx m t +++-= ---------------8分 ∵动直线y kx m =+与椭圆有且只有一个公共点P∴0∆=,即2222644(34)(412)0k m m m t -+-=整理得2234m t k t =+ ----------------------9分 设P 11(,)x y 则有122842(34)34km kmx k k =-=-++,112334m y kx m k =+=+ ∴2243(,)3434km mP k k-++ ----------------------10分又(1,0)M ,Q (4,4)k m +若x 轴上存在一定点(1,0)M ,使得PM QM ⊥, ∴2243(1,)(3,(4))03434km mk m k k +-⋅--+=++恒成立整理得2234k m +=, ----------------------12分∴223434k t k t +=+恒成立,故1t =所求椭圆方程为22143x y += ----------------------13分 22. (本小题满分13分)解:(Ⅰ) ()(2)xf x ae x '=+, ()2g x x b '=+ -------------------1分由题意,两函数在0x =处有相同的切线.(0)2,(0),2,(0)(0)2,2,4f a g b a b f a g a b ''∴==∴====∴==,2()2(1),()42x f x e x g x x x ∴=+=++. ----------------------3分 (Ⅱ) ()2(2)x f x e x '=+,由()0f x '>得2x >-,由()0f x '<得2x <-, ()f x ∴在(2,)-+∞单调递增,在(,2)-∞-单调递减. -------------------4分 3,12t t >-∴+>-① 当32t -<<-时,()f x 在[,2]t -单调递减,[2,1]t -+单调递增,∴2min ()(2)2f x f e -=-=-. ----------------------5分 ② 当2t ≥-时,()f x 在[,1]t t +单调递增,min ()()2(1)t f x f t e t ∴==+;22(32)()2(1)(2)t e t f x e t t -⎧--<<-⎪∴=⎨+≥-⎪⎩----------------------6分(Ⅲ)令2()()()2(1)42x F x kf x g x ke x x x =-=+---,由题意当min 2,()0x F x ≥-≥ ----------------------7分 ∵2,()()x kf x g x ∀≥-≥恒成立,(0)220,1F k k ∴=-≥∴≥ ---------------8分 ()2(1)2242(2)(1)x x x F x ke x ke x x ke '=++--=+-, ---------------9分 2x ≥- ,由()0F x '>得11,ln x e x k k >∴>;由()0F x '<得1ln x k< ∴()F x 在1(,ln ]k-∞单调递减,在1[ln ,)k +∞单调递增 --------------10分 ①当1ln 2k<-,即2k e >时,()F x 在[2,)-+∞单调递增, 22min 22()(2)22()0F x F ke e k e -=-=-+=-<,不满足min ()0F x ≥. --------11分 ② 当1ln 2k =-,即2k e =时,由①知,2min 22()(2)()0F x F e k e=-=-=,满足 min ()0F x ≥. ----------12分 ③当1ln 2k >-,即21k e ≤<时,()F x 在1[2,ln ]k -单调递减,在1[ln ,)k+∞单调递增min 1()(ln )ln (2ln )0F x F k k k==->,满足min ()0F x ≥. 综上所述,满足题意的k 的取值范围为2[1,]e . -------------------13分。
