初三数学中考试卷(北师大版,含答案)

合集下载

最新北师大版九年级中考数学模拟试题以及答案

最新九年级中考数学测试试卷一、选择题（本大题共12小题，每小题4分，共48分）1、4的算术平方根是（）A．2B．－2C．±2D． 22、如图所示的几何体，它的俯视图是（）A． B． C． D．3、2018年1月，“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发，这标志着“墨子号”具备了洲际量子保密通信的能力．数字7600用科学记数法表示为（）A．0.76×104B．7.6×103C．7.6×104D．76×1024、“瓦当”是中国古建筑装饰××头的附件，是中国特有的文化艺术遗产，下面“瓦当”图案中既是轴对称图形又是中心对称图形的是（）A B C D5、如图，AF是∠BAC的平分线，DF∥AC，若∠1＝35°，则∠BAF的度数为（）A．17.5°B．35°C．55°D．70°6、下列运算正确的是（）A．a2＋2a＝3a3B．(－2a3)2＝4a5 1ABC DFC ．(a ＋2)(a －1)＝a 2＋a －2 D ．(a ＋b )2＝a 2＋b 27、关于x 的方程3x －2m ＝1的解为正数，则m 的取值范围是（） A ．m ＜－12B ．m ＞－12C ．m ＞12D ．m ＜128、在反比例函数y ＝－2x图象上有三个点A （x 1，y 1）、B （x 2，y 2）、C （x 3，y 3），若x 1＜0＜x 2＜x 3，则下列结论正确的是（）A ．y 3＜y 2＜y 1B ．y 1＜y 3＜y 2C ．y 2＜y 3＜y 1D ．y 3＜y 1＜y 29、如图，在平面直角坐标系中，△ABC 的顶点都在方格线的格点上，将△ABC 绕点P 顺时针方向旋转90°，得到△A ′B ′C ′，则点P 的坐标为（） A ．（0，4） B ．（1，1） C ．（1，2） D ．（2，1）10、下面的统计图大致反应了我国2012年至2017年人均阅读量的情况．根据统计图提供的信息，下列推断不合理．．．的是（） A ．与2016年相比，2017年我国电子书人均阅读量有所降低 B ．2012年至2017年，我国纸质书的人均阅读量的中位数是4.57C ．从2014年到2017年，我国纸质书的人均阅读量逐年增长D ．2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多年份电子书纸质书6234511、如图，一个扇形纸片的圆心角为90°，半径为6．如图2，将这张扇形纸片折叠，使点A 与点O 恰好重合，折痕为CD ，图中阴影为重合部分，则阴影部分的面积为（） A ．6π－92 3B ．6π－9 3C ．12π－92 3D ．9π412、若平面直角坐标系内的点M 满足横、纵坐标都为整数，则把点M叫做“整点”．例如：P （1，0）、Q （2，－2）都是“整点”．抛物线y ＝mx 2－4mx ＋4m －2(m ＞0)与x 轴交于点A 、B 两点，若该抛物线在A 、B 之间的部分与线段AB 所围成的区域（包括边界）恰有七个整点，则m 的取值范围是（） A ．12≤m ＜1B ．12＜m ≤1C ．1＜m ≤2D ．1＜m ＜2AB CDO (A ) ABO二、填空题（本大题共6小题，每小题4分，共24分） 13、分解因式：m 2－4＝____________；14、在不透明的盒子中装有5个黑色棋子和若于个白色做子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑包棋子的概率是14，则白色棋子的个数是＝____________； 15、一个正多边形的每个内角等于108°，则它的边数是＝____________；16、若代数式x －2x －4的值是2，则x ＝____________；17、A 、B 两地相距20km ，甲乙两人沿同一条路线从A 地到B 地．甲先出发，匀速行驶，甲出发1小时后乙再出发，乙以2km/h 的速度度匀速行驶1小时后提高速度并继续匀速行驶，结果比甲提前到达．甲、乙两人离开A 地的距离s （km ）与时间t （h ）的关系如图所示，则甲出发____________小时后和乙相遇．18、如图，矩形EFGH的四个顶点分别在矩形ABCD的各条边上，AB＝EF，FG＝2，GC＝3．有以下四个结论：①∠BGF＝∠CHG；②△BFG≌△DHE；③tan∠BFG＝12；④矩形EFGH的面积是43．其中一定成立的是____________．（把所有正确结论的序号填在横线上）BF三、解答题（本大题共9小题，共78分）19、计算：2－1＋│－5│－sin30°＋(π－1)0．20、解不等式组：⎩⎪⎨⎪⎧3x ＋1＜2x ＋3 ① 2x ＞3x －12 ②21、如图，在□ABCD中，连接BD，E是DA延长线上的点，F是BC延长线上的点，且AE＝CF，连接EF交BD于点O．求证：OB＝O D．22、本学期学校开展以“感受中华传统买德”为主题的研学部动，组织150名学生多观历史好物馆和民俗晨览馆，每一名学生只能参加其中全顺活动，共支付票款2000元，票价信息如下：（1）请问参观历史博物馆和民俗展览馆的人数各是多少人？（2）若学生都去参观历史博物馆，则能节省票款多少元？23、如图AB是⊙O的直径，PA与⊙O相切于点A，BP与⊙O相较于点D，C为⊙O上的一点，分别连接CB、CD，∠BCD＝60°．(1)求∠ABD的度数；(2)若AB＝6，求PD的长度．C24、某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程，为了解学生对这四门校本课程的喜爱情况，对学生进行了随机问卷调查（问卷调查表如图所示），将调查结果整理后绘制例图 1 、图2两幅均不完整的统计图表．请您根据图表中提供的信息回答下列问题：（1）统计表中的a＝________，b＝_______；（2）“D”对应扇形的圆心角为_______度；（3）根据调查结果，请您估计该校2000名学生中最喜欢“数学史”校本课程的人数；（4）小明和小亮参加校本课程学习，若每人从“A”、“B”、“C”三门校本课程中随机选取一门，请用画树状图或列表格的方法，求两人恰好选中同一门校本课程的概率．25、如图，直线y ＝ax ＋2与x 轴交于点A (1，0)，与y 轴交于点B (0，b )．将线段AB 先向右平移1个单位长度、再向上平移t （t ＞0）个单位长度，得到对应线段CD ，反比例函数y ＝kx（x ＞0）的图象恰好经过C 、D 两点，连接AC 、B D ． (1)求a 和b 的值；(2)求反比例函数的表达式及四边形ABDC 的面积；(3)点N 在x 轴正半轴上，点M 是反比例函数y ＝kx（x ＞0）的图象上的一个点，若△CMN 是以CM 为直角边的等腰直角三角形时，求所有满足条件的点M 的坐标．第25题图第25题备用图26、在△ABC 中，AB ＝AC ，∠BAC ＝120°，以CA 为边在∠ACB 的另一侧作∠ACM ＝∠ACB ，点D 为射线BC 上任意一点，在射线CM 上截取CE ＝BD ，连接AD 、DE 、AE ．（1）如图1，当点D 落在线段BC 的延长线上时，直接写出∠ADE 的度数；（2）如图2，当点D 落在线段BC （不含边界）上时，AC 与DE 交于点F ，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；（3）在（2）的条件下，若AB ＝6，求CF 的最大值．M第26题图1 第26题图227、如图1，抛物线y ＝ax 2＋bx ＋4过A (2，0)、B (4，0)两点，交y轴于点C ，过点C 作x 轴的平行线与不等式抛物线上的另一个交点为D ，连接AC 、B C ．点P 是该抛物线上一动点，设点P 的横坐标为m （m ＞4）．(1)求该抛物线的表达式和∠ACB 的正切值； (2)如图2，若∠ACP ＝45°，求m 的值；(3)如图3，过点A 、P 的直线与y 轴于点N ，过点P 作PM ⊥CD ，垂足为M ，直线MN 与x 轴交于点Q ，试判断四边形ADMQ 的形状，并说明理由．第27题图1 第27题图2 第27题图3答案解析一、选择题（本大题共12小题，每小题4分，共48分）1．（2018济南，1，4分）4的算术平方根是（）A．2 B．－2 C．±2 D． 2 【答案】A2．（2018济南，2，4分）如图所示的几何体，它的俯视图是（）A． B． C． D．【答案】D3．（2018济南，3，4分）2018年1月，“墨子号”量子卫星实现了距离达7600千米的洲际量子密钥分发，这标志着“墨子号”具备了洲际量子保密通信的能力．数字7600用科学记数法表示为（）A．0.76×104 B．7.6×103 C．7.6×104 D．76×102【答案】B4．（2018济南，4，4分）“瓦当”是中国古建筑装饰××头的附件，是中国特有的文化艺术遗产，下面“瓦当”图案中既是轴对称图形又是中心对称图形的是（）A B CD【答案】D5．（2018济南，5，4分）如图，AF是∠BAC的平分线，DF∥AC，若∠1＝35°，则∠BAF的度数为（）A．17.5°B．35°C．55°D．70°【答案】B6．（2018济南，6，4分）下列运算正确的是（）A．a2＋2a＝3a3 B．(－2a3)2＝4a5C．(a＋2)(a－1)＝a2＋a－2 D．(a＋b)2＝a2＋b2【答案】C7．（2018济南，7，4分）关于x的方程3x－2m＝1的解为正数，则m 的取值范围是（）A．m＜－12B．m＞－12C．m＞121ABCDFD ．m ＜12【答案】B8．（2018济南，8，4分）在反比例函数y ＝－2x图象上有三个点A （x 1，y 1）、B （x 2，y 2）、C （x 3，y 3），若x 1＜0＜x 2＜x 3，则下列结论正确的是（）A ．y 3＜y 2＜y 1B ．y 1＜y 3＜y 2C ．y 2＜y 3＜y 1D ．y 3＜y 1＜y 2 【答案】C9．（2018济南，9，4分）如图，在平面直角坐标系中，△ABC 的顶点都在方格线的格点上，将△ABC 绕点P 顺时针方向旋转90°，得到△A ′B ′C ′，则点P 的坐标为（）A ．（0，4）B ．（1，1）C ．（1，2）D ．（2，1）【答案】C10．（2018济南，10，4分）下面的统计图大致反应了我国2012年至2017年人均阅读量的情况．根据统计图提供的信息，下列推断不．合理．．的是（） A ．与2016年相比，2017年我国电子书人均阅读量有所降低 B ．2012年至2017年，我国纸质书的人均阅读量的中位数是4.57C ．从2014年到2017年，我国纸质书的人均阅读量逐年增长D ．2013年我国纸质书的人均阅读量比电子书的人均阅读量的1.8倍还多【答案】B11．（2018济南，11，4分）如图，一个扇形纸片的圆心角为90°，半径为6．如图2，将这张扇形纸片折叠，使点A 与点O 恰好重合，折痕为CD ，图中阴影为重合部分，则阴影部分的面积为（）年份电子书纸质书62345A ．6π－92 3B ．6π－9 3C ．12π－92 3D ．9π4【答案】A12．（2018济南，11，4分）若平面直角坐标系内的点M 满足横、纵坐标都为整数，则把点M 叫做“整点”．例如：P （1，0）、Q （2，－2）都是“整点”．抛物线y ＝mx 2－4mx ＋4m －2(m ＞0)与x 轴交于点A 、B 两点，若该抛物线在A 、B 之间的部分与线段AB 所围成的区域（包括边界）恰有七个整点，则m 的取值范围是（） A ．12≤m ＜1 B ．12＜m ≤1 C ．1＜m ≤2 D ．1＜m＜2 【答案】B 【解析】解：∵y ＝mx 2－4mx ＋4m －2＝m (x －2)2－2且m ＞0,∴该抛物线开口向上，顶点坐标为(2，－2)，对称轴是直线x ＝2．由此可知点(2，0)、点(2，－1)、顶点(2，－2)符合题意．方法一：AB CDO (A ) ABO①当该抛物线经过点（1，－1）和（3，－1）时（如答案图1），这两个点符合题意．将（1，－1）代入y ＝mx 2－4mx ＋4m －2得到－1＝m －4m ＋4m －2．解得m ＝1．此时抛物线解析式为y ＝x 2－4x ＋2．由y ＝0得x 2－4x ＋2＝0．解得x 1＝2－2≈0.6，x 2＝2＋2≈3.4．∴x 轴上的点(1，0)、(2，0)、(3，0)符合题意．则当m ＝1时，恰好有 (1，0)、(2，0)、(3，0)、(1，－1)、(3，－1)、(2，－1)、(2，－2)这7个整点符合题意．∴m ≤1．【注：m 的值越大，抛物线的开口越小，m 的值越小，抛物线的开口越大，】答案图1(m ＝1时) 答案图2( m ＝12时)②当该抛物线经过点（0，0）和点（4，0）时（如答案图2），这两个点符合题意．此时x 轴上的点 (1，0)、(2，0)、(3，0)也符合题意．将（0，0）代入y ＝mx 2－4mx ＋4m －2得到0＝0－4m ＋0－2．解得m ＝12．此时抛物线解析式为y ＝12x 2－2x ．当x ＝1时，得y ＝12×1－2×1＝－32＜－1．∴点(1，－1)符合题意．当x ＝3时，得y ＝12×9－2×3＝－32＜－1．∴点(3，－1) 符合题意．综上可知：当m ＝12时，点(0，0)、(1，0)、(2，0)、(3，0)、(4，0)、(1，－1)、(3，－1)、(2，－2)、(2，－1)都符合题意，共有9个整点符合题意， ∴m ＝12不符合题．∴m ＞12．综合①②可得：当12＜m ≤1时，该函数的图象与x 轴所围城的区域（含边界）内有七个整点，故答案选B ．方法二：根据题目提供的选项，分别选取m ＝12，m ＝1，m ＝2，依次加以验证．①当m ＝12时（如答案图3），得y ＝12x 2－2x ．由y＝0得12x2－2x＝0．解得x1＝0，x2＝4．∴x轴上的点(0，0)、(1，0)、(2，0)、(3，0)、(4，0)符合题意．当x＝1时，得y＝12×1－2×1＝－32＜－1．∴点(1，－1)符合题意．当x＝3时，得y＝12×9－2×3＝－32＜－1．∴点(3，－1) 符合题意．综上可知：当m＝12时，点(0，0)、(1，0)、(2，0)、(3，0)、(4，0)、(1，－1)、(3，－1)、(2，－2)、(2，－1)都符合题意，共有9个整点符合题意，∴m＝12不符合题．∴选项A不正确．答案图3( m＝12时) 答案图4(m＝1时)答案图5(m＝2时)②当m＝1时（如答案图4），得y＝x2－4x＋2．由y＝0得x2－4x＋2＝0．解得x1＝2－2≈0.6，x2＝2＋2≈3.4．∴x轴上的点(1，0)、(2，0)、(3，0)符合题意．当x＝1时，得y＝1－4×1＋2＝－1．∴点(1，－1)符合题意．当x＝3时，得y＝9－4×3＋2＝－1．∴点(3，－1) 符合题意．综上可知：当m＝1时，点(1，0)、(2，0)、(3，0)、(1，－1)、(3，－1)、(2，－2) 、(2，－1)都符合题意，共有7个整点符合题意，∴m＝1符合题．∴选项B正确．③当m＝2时（如答案图5），得y＝2x2－8x＋6．由y＝0得2x2－8x＋6＝0．解得x1＝1，x2＝3．∴x轴上的点(1，0)、(2，0)、(3，0)符合题意．综上可知：当m＝2时，点(1，0)、(2，0)、(3，0)、(2，－2) 、(2，－1)都符合题意，共有5个整点符合题意，∴m＝2不符合题．二、填空题（本大题共6小题，每小题4分，共24分）13．（2018济南，13，4分）分解因式：m2－4＝____________；【答案】(m＋2)(m－2)14．（2018济南，14，4分）在不透明的盒子中装有5个黑色棋子和若于个白色做子，每个棋子除颜色外都相同，任意摸出一个棋子，摸到黑包棋子的概率是14，则白色棋子的个数是＝____________；【答案】1515．（2018济南，15，4分）一个正多边形的每个内角等于108°，则它的边数是＝____________；【答案】516．（2018济南，16，4分）若代数式x －2x －4的值是2，则x ＝____________；【答案】617．（2018济南，17，4分）A 、B 两地相距20km ，甲乙两人沿同一条路线从A 地到B 地．甲先出发，匀速行驶，甲出发1小时后乙再出发，乙以2km/h 的速度度匀速行驶1小时后提高速度并继续匀速行驶，结果比甲提前到达．甲、乙两人离开A 地的距离s （km ）与时间t （h ）的关系如图所示，则甲出发____________小时后和乙相遇．【答案】165．【解析】y 甲＝4t (0≤t ≤4)；y乙＝⎩⎪⎨⎪⎧2(t －1)(1≤t ≤2)9(t －2)t (2＜t ≤4)；由方程组⎩⎪⎨⎪⎧y ＝4ty ＝9(t －2)解得⎩⎪⎨⎪⎧t ＝165y ＝645. ∴答案为165．18．（2018济南，18，4分）如图，矩形EFGH 的四个顶点分别在矩形ABCD 的各条边上，AB ＝EF ，FG ＝2，GC ＝3．有以下四个结论：①∠BGF ＝∠CHG ；②△BFG ≌△DHE ；③tan ∠BFG ＝12；④矩形EFGH的面积是43．其中一定成立的是____________．（把所有正确结论的序号填在横线上）F【答案】①②④．【解析】设EH ＝AB ＝a ，则CD ＝GH ＝a ． ∵∠FGH ＝90°，∴∠BGF ＋∠CGH ＝90°. 又∵∠CGH ＋∠CHG ＝90°,∴∠BGF ＝∠CHG …………………………………故①正确．同理可得∠DEH ＝∠CHG . ∴∠BGF ＝∠DEH .又∵∠B ＝∠D ＝90°，FG ＝EH ,∴△BFG≌△DHE…………………………………故②正确．同理可得△AFE≌△CHG.∴AF＝CH.易得△BFG∽△CGH.∴BFCG ＝FGGH.∴BF3＝2a.∴BF＝6a.∴AF＝AB－BF＝a－6a.∴CH＝AF＝a－6a.在Rt△CGH中，∵CG2＋CH2＝GH2，∴32＋( a－6a)2＝a2.解得a＝2 3.∴GH＝2 3.∴BF＝a－6a＝ 3.在Rt△BFG中，∵cos∠BFG＝BFFG＝32，∴∠BFG＝30°.∴tan∠BFG＝tan30°＝33.…………………………………故③正确．矩形EFGH的面积＝FG×GH＝2×23＝43…………………………………故④正确．三、解答题（本大题共9小题，共78分）19．（2018济南，19，6分）计算：2－1＋│－5│－sin30°＋(π－1)0．解：2－1＋│－5│－sin30°＋(π－1)0．＝12＋5－12＋1＝620．（2018济南，20，6分）解不等式组：⎩⎪⎨⎪⎧3x ＋1＜2x ＋3 ① 2x ＞3x －12 ② 解：由① ，得3x －2x ＜3－1. ∴x ＜2. 由② ，得 4x ＞3x －1. ∴x ＞－1.∴不等式组的解集为－1＜x ＜2.21．（2018济南，21，6分）如图，在□ABCD 中，连接BD ，E 是DA 延长线上的点，F 是BC 延长线上的点，且 AE ＝CF ，连接EF 交BD 于点O ．求证：OB ＝O D ．证明：∵□ABCD 中，∴AD ＝BC ,AD ∥B C. ∴∠ADB ＝∠CB D. 又∵AE ＝CF ， ∴AE ＋AD ＝CF ＋B C. ∴ED ＝F B.又∵∠EOD＝∠FOB,∴△EOD≌△FO B.∴OB＝O D．22．（2018济南，22，8分）本学期学校开展以“感受中华传统买德”为主题的研学部动，组织150名学生多观历史好物馆和民俗晨览馆，每一名学生只能参加其中全顺活动，共支付票款2000元，票价信息如下：（1）请问参观历史博物馆和民俗展览馆的人数各是多少人？（2）若学生都去参观历史博物馆，则能节省票款多少元？解：（1）设参观历史博物馆的有x人，则参观民俗展览馆的有（150－x）人，依题意，得10x＋20(150－x)2000.10x＋3000－20x＝2000.－10x＝－1000.∴x＝100.∴150－x＝50.答：参观历史博物馆的有100人，则参观民俗展览馆的有50人．（2）2000－150×10＝500（元）.答：若学生都去参观历史博物馆，则能节省票款500元．23．（2018济南，23，8分）如图AB 是⊙O 的直径，PA 与⊙O 相切于点A ，BP 与⊙O 相较于点D ，C 为⊙O 上的一点，分别连接CB 、CD ，∠BCD ＝60°．(1)求∠ABD 的度数； (2)若AB ＝6，求PD 的长度．C【解析】解：(1)方法一：连接AD （如答案图1所示）． ∵BA 是⊙O 直径，∴∠BDA ＝90°． ∵⌒BD ＝⌒BD ，∴∠BAD ＝∠C ＝60°．∴∠ABD ＝90°－∠BAD ＝90°－60°＝30°．CC第23题答案图1 第23题答案图2方法二：连接DA、OD（如答案图2所示），则∠BOD＝2∠C＝2×60°＝120°．∵OB＝OD，∴∠OBD＝∠ODB＝12(180°－120°)＝30°．即∠ABD＝30°．(2)∵AP是⊙O的切线，∴∠BAP＝90°．在Rt△BAD中，∵∠ABD＝30°，∴DA＝12BA＝12×6＝3．∴BD＝3DA＝33．在Rt△BAP中，∵cos∠ABD＝ABPB，∴cos30°＝6PB＝32．∴BP＝43．∴PD＝BP－BD＝43－33＝3．24．（2018济南，24，10分）某校开设了“3D”打印、数学史、诗歌欣赏、陶艺制作四门校本课程，为了解学生对这四门校本课程的喜爱情况，对学生进行了随机问卷调查（问卷调查表如图所示），将调查结果整理后绘制例图 1 、图2两幅均不完整的统计图表．请您根据图表中提供的信息回答下列问题：（1）统计表中的a＝________，b＝_______；（2）“D”对应扇形的圆心角为_______度；（3）根据调查结果，请您估计该校2000名学生中最喜欢“数学史”校本课程的人数；（4）小明和小亮参加校本课程学习，若每人从“A”、“B”、“C”三门校本课程中随机选取一门，请用画树状图或列表格的方法，求两人恰好选中同一门校本课程的概率．解：（1）a＝36÷0.45＝80.b＝16÷80＝0.20.（2）“D”对应扇形的圆心角的度数为：8÷80×360°＝36°.（3）估计该校2000名学生中最喜欢“数学史”校本课程的人数为：2000×0.25＝500（人）．（4）列表格如下：共有9种等可能的结果，其中两人恰好选中同一门校本课程的结果有3种，所以两人恰好选中同一门校本课程的概率为：39＝13．25．（2018济南，25，10分）如图，直线y ＝ax ＋2与x 轴交于点A (1，0)，与y 轴交于点B (0，b )．将线段AB 先向右平移1个单位长度、再向上平移t （t ＞0）个单位长度，得到对应线段CD ，反比例函数y ＝kx（x ＞0）的图象恰好经过C 、D 两点，连接AC 、B D ． (1)求a 和b 的值；(2)求反比例函数的表达式及四边形ABDC 的面积；(3)点N 在x 轴正半轴上，点M 是反比例函数y ＝kx（x ＞0）的图象上的一个点，若△CMN 是以CM 为直角边的等腰直角三角形时，求所有满足条件的点M 的坐标．第25题图第25题备用图【解析】解：(1)将点A(1，0)代入y＝ax＋2，得0＝a＋2．∴a＝－2．∴直线的解析式为y＝－2x＋2．将x＝0代入上式，得y＝2．∴b＝2．∴点B(0，2)．(2)由平移可得：点C(2，t)、D(1，2＋t)．将点C(2，t)、D(1，2＋t)分别代入y＝kx ，得⎩⎪⎨⎪⎧t＝k22＋t＝k1．解得⎩⎪⎨⎪⎧k＝4t＝2．∴反比例函数的解析式为y＝4x，点C(2，2)、点D(1，4)．分别连接BC、AD（如答案图1）．∵B(0，2)、C(2，2)，∴BC∥x轴，BC＝2．∵A(1，0)、D(1，4)，∴AD⊥x轴，AD＝4．∴BC⊥A D．∴S四边形ABDC＝12×BC×AD＝12×2×4＝4．第25题答案图1(3)①当∠NCM＝90°、CM＝CN时（如答案图2所示），过点C作直线l∥x轴，交y轴于点G．过点M作MF⊥直线l于点F，交x轴于点H．过点N作NE⊥直线l于点E．设点N(m，0)（其中m＞0），则ON＝m，CE＝2－m．∵∠MCN＝90°，∴∠MCF＋∠NCE＝90°．∵NE⊥直线l于点E，∴∠ENC＋∠NCE＝90°．∴∠MCF＝∠EN C．又∵∠MFC＝∠NEC＝90°，CN＝CM，∴△NEC≌△CFM．∴CF＝EN＝2，FM＝CE＝2－m．∴FG＝CG＋CF＝2＋2＝4．∴x M＝4．将x＝4代入y＝4x，得y＝1．∴点M(4，1)．l第25题答案图2 第25题答案图3②当∠NMC＝90°、MC＝MN时（如答案图3所示），过点C作直线l ⊥y轴与点F，则CF＝x C＝2．过点M作MG⊥x轴于点G，MG交直线l与点E，则MG⊥直线l于点E，EG＝y C＝2．∵∠CMN＝90°，∴∠CME＋∠NMG＝90°．∵ME⊥直线l于点E，∴∠ECM＋∠CME＝90°．∴∠NMG＝∠ECM．又∵∠CEM＝∠NGM＝90°，CM＝MN，∴△CEM≌△MGN．∴CE＝MG，EM＝NG．设CE＝MG＝a，则y M＝a，x M＝CF＋CE＝2＋a．∴点M(2＋a，a)．将点M(2＋a，a) 代入y＝4x，得a＝42＋a．解得a1＝5－1，a2＝－5－1．∴x M＝2＋a＝5＋1．∴点M(5＋1，5－1)．综合①②可知：点M的坐标为(4，1)或(5＋1，5－1)．26．（2018济南，26，12分）在△ABC 中，AB ＝AC ，∠BAC ＝120°，以CA 为边在∠ACB 的另一侧作∠ACM ＝∠ACB ，点D 为射线BC 上任意一点，在射线CM 上截取CE ＝BD ，连接AD 、DE 、AE ．（1）如图1，当点D 落在线段BC 的延长线上时，直接写出∠ADE 的度数；（2）如图2，当点D 落在线段BC （不含边界）上时，AC 与DE 交于点F ，请问（1）中的结论是否仍成立？如果成立，请给出证明；如果不成立，请说明理由；（3）在（2）的条件下，若AB ＝6，求CF 的最大值．M第26题图1第26题图2 【解析】解：(1) ∠ADE ＝30°．(2) （1）中的结论是否还成立证明：连接AE（如答案图1所示）．∵∠BAC＝120°，AB＝AC，∴∠B＝∠ACB＝30°．又∵∠ACM＝∠ACB，∴∠B＝∠ACM＝30°．又∵CE＝BD，∴△ABD≌△ACE.∴AD＝AE,∠1＝∠2.∴∠2＋∠3＝∠1＋∠3＝∠BAC＝120°.即∠DAE＝120°.又∵AD＝AE,∴∠ADE＝∠AED＝30°．答案图 1 答案图2(3) ∵AB＝AC，AB＝6，∴AC＝6．∵∠ADE＝∠ACB＝30°且∠DAF＝∠CAD，∴△ADF ∽△AC D.∴AD AC ＝AF AD.∴AD 2＝AF ·A C ．∴AD 2＝6AF ．∴AF ＝AD 26．∴当AD 最短时，AF 最短、CF 最长．易得当AD ⊥BC 时，AF 最短、CF 最长（如答案图2所示），此时AD ＝12AB ＝3．∴AF 最短＝AD 26＝326＝32． ∴CF 最长＝AC － AF 最短＝6－32＝92.27．（2018济南，27，12分）如图1，抛物线y ＝ax 2＋bx ＋4过A (2，0)、B (4，0)两点，交y 轴于点C ，过点C 作x 轴的平行线与不等式抛物线上的另一个交点为D ，连接AC 、B C ．点P 是该抛物线上一动点，设点P 的横坐标为m （m＞4）．(1)求该抛物线的表达式和∠ACB 的正切值； (2)如图2，若∠ACP ＝45°，求m 的值；(3)如图3，过点A 、P 的直线与y 轴于点N ，过点P 作PM ⊥CD ，垂足为M ，直线MN 与x 轴交于点Q ，试判断四边形ADMQ 的形状，并说明理由．第27题图 1 第27题图 2第27题图3 【解析】解：（1）将点A (2，0)和点B (4，0)分别代入y ＝ax 2＋bx ＋4，得⎩⎪⎨⎪⎧0＝4a ＋2x ＋40＝16a ＋4b ＋4．解得⎩⎪⎨⎪⎧a ＝12b ＝－3．∴该抛物线的解析式为y＝12x 2－3x ＋4. 将x ＝0代入上式，得y ＝4.∴点C （0，4），OC ＝4．在Rt △AOC 中，AC ＝OA 2＋OC 2＝22＋42＝2 5.设直线AC 的解析式为y ＝kx ＋4,将点A (2，0)代入上式，得0＝2k ＋4．解得k ＝－2． ∴直线AC 的解析式为y ＝－2x ＋4．同理可得直线BC 的解析式为y ＝－x ＋4．求tan ∠ACB 方法一：过点B 作BG ⊥CA ，交CA 的延长线于点G （如答案图1所示），则∠G ＝90°．∵∠COA ＝∠G ＝90°，∠CAO ＝∠BAG ，∴△GAB ∽△OA C.∴BG AG ＝OC OA ＝42＝2.∴BG ＝2AG . 在Rt △ABG 中，∵BG 2＋AG 2＝AB 2,∴(2AG )2＋AG 2＝22.AG ＝255.∴BG ＝455,CG ＝AC ＋AG ＝25＋255＝125 5.在Rt △BCG 中，tan ∠ACB ＝BG CQ ＝455 1255＝13.第27题答案图1 第27题答案图2求tan ∠ACB 方法二：过点A 作AE ⊥AC ，交BC 于点E （如答案图2所示），则k AE ·k AC＝－1.∴－2k AE ＝－1.∴k AE ＝12.∴可设直线AE 的解析式为y ＝12x ＋m ．将点A (2，0)代入上式，得0＝12×2＋m ．解得m ＝－1．∴直线AE 的解析式为y ＝12x －1．由方程组⎩⎪⎨⎪⎧y ＝12x －1y ＝－x ＋4解得⎩⎪⎨⎪⎧x ＝103y ＝23．∴点E （103，23）．∴AE ＝⎝ ⎛⎭⎪⎪⎫2－1032＋⎝ ⎛⎭⎪⎪⎫0－232＝23 5. 在Rt △AEC 中，tan ∠ACB ＝AE AC ＝23525＝13.求tan ∠ACB 方法三：过点A 作AF ⊥BC ，交BC 点E （如答案图3所示），则k AF ·k BC＝－1.∴－k AF ＝－1.∴k AF ＝1.∴可设直线AF 的解析式为y ＝x ＋n ．将点A (2，0)代入上式，得0＝2＋n ．解得n ＝－2．∴直线AF 的解析式为y ＝x －2．由方程组⎩⎪⎨⎪⎧y ＝x －2y ＝－x ＋4 解得⎩⎪⎨⎪⎧x ＝3y ＝1 ．∴点F （3，1）．∴AF ＝(3－2)2＋(1－0)2＝2，CF ＝(3－0)2－(1－4)2＝3 2.在Rt △AEC 中，tan ∠ACB ＝AF CF ＝232＝13．第27题答案图3（2）方法一：利用“一线三等角”模型将线段AC 绕点A 沿顺时针方向旋转90°，得到线段AC ′，则AC ′＝AC ，∠C ′AC ＝90°，∠CC ′A ＝∠ACC ′＝45°．∴∠CAO ＋∠C ′AB ＝90°．又∵∠OCA ＋∠CAO ＝90°， ∴∠OCA ＝∠C ′A B ．过点C ′作C ′E ⊥x 轴于点E ．则∠C ′EA ＝∠COA ＝90°． ∵∠C ′EA ＝∠COA ＝90°，∠OCA ＝∠C ′AB ，AC ′＝AC ， ∴△C ′EA ≌△AO C ．∴C ′E ＝OA ＝2，AE ＝OC ＝4． ∴OE ＝OA ＋AE ＝2＋4＝6． ∴点C ′(6，2)．设直线C ′C 的解析式为y ＝hx ＋4．将点C ′(6，2)代入上式，得2＝6h ＋4．解得h ＝－13．∴直线C ′C 的解析式为y ＝－13x ＋4．∵∠ACP＝45°，∠ACC′＝45°，∴点P在直线C′C上．设点P的坐标为(x，y)，则x是方程12x2－3x＋4＝－13x＋4的一个解．将方程整理，得3x2－14x＝0．解得x1＝163，x2＝0（不合题意，舍去）．将x1＝163代入y＝－13x＋4，得y＝209．∴点P的坐标为(163，209)．第27题答案图4 第27题答案图5（2）方法二：利用正方形中的“全角夹半角”模型．过点B作BH⊥CD于点H，交CP于点K，连接AK．易得四边形OBHC 是正方形．应用“全角夹半角”可得AK＝OA＋HK．设K(4，h)，则BK＝h，HK＝HB－KB＝4－h，AK＝OA＋HK＝2＋(4－h)＝6－h．在Rt△ABK中，由勾股定理，得AB2＋BK2＝AK2．∴22＋h 2＝(6－h)2．解得h＝83．∴点K(4，83 )．设直线CK的解析式为y＝hx＋4．将点K(4，83)代入上式，得83＝4h＋4．解得h＝－13．∴直线CK的解析式为y＝－13x＋4．设点P的坐标为(x，y)，则x是方程12x2－3x＋4＝－13x＋4的一个解．将方程整理，得3x2－14x＝0．解得x1＝163，x2＝0（不合题意，舍去）．将x1＝163代入y＝－13x＋4，得y＝209．∴点P的坐标为(163，209)．（3）四边形ADMQ是平行四边形．理由如下：∵CD∥x轴，∴y C＝y D＝4．将y＝4代入y＝12x2－3x＋4，得 4＝12x2－3x＋4.解得x1＝0，x2＝6．∴点D（6，4）．根据题意，得P （m ，12m 2－3m ＋4），M （m ，4），H （m ，0）．∴PH ＝12m 2－3m ＋4），OH ＝m ，AH ＝m －2，MH ＝4．①当4＜m ＜6时（如答案图5所示），DM ＝6－m∵△OAN ∽△HAP ，∴ON PH ＝OAAH ．∴ON12m 2－3m ＋4＝2m －2． ∴ON ＝m 2－6m ＋8m －2＝(m －4)(m －2)m －2＝m －4．∵△ONQ ∽△HMP ，∴ON HM ＝OQ HQ ．∴ON 4＝OQm －OQ．∴m －44＝OQm －OQ．∴OQ ＝m －4．∴AQ ＝OA －OQ ＝2－(m －4)＝6－m ． ∴AQ ＝ DM ＝6－m ．又∵AQ ∥DM ，∴四边形ADMQ 是平行四边形．第27题答案图6 第27题答案图7 ②当m ＞6时（如答案图6所示），同理可得：四边形ADMQ是平行四边形．综合①、②可知：四边形ADMQ是平行四边形．。

北师大版九年级中考数学模拟考试试题(含答案)

九年级中考数学模拟试卷（满分150分时间120分钟）一.单选题。

（共40分） 1.√25等于（）A.5B.﹣5C.±5D.25 2.下列正面摆放的几何体中，左视图是三角形的是（）3.据推算，全国每年减少10%的过度包装纸用量，那么可排放二氧化碳3 120 000吨，数3 120 000用科学记数法表示为（）A.3.12×106B.31.2×105C.312×104D.3.12×1074.下列平面直角坐标系内的曲线中，既是中心对称图形，又是轴对称图形的是（）5.如图，下列结论正确的是（）A.b －a ＞0B.a+b ＜0C.|a |＞|b |D.ac ＞0（第5题图）（第9题图）6.计算x+1x－1x 的结果是（）A.1B.xC.1x D.x+1x 27.不透明袋子中装有10个球，其中有6个红球和4个白球，它们除了颜色其余都相同，从袋中随机摸出1个球，是红球的概率是（） A.15 B.25 C.35 D.3108.在平面直角坐标系中，一次函数y=kx－1的图象向上平移2个单位长度后经过点（2，3），则k的值是（）A.1B.﹣1C.﹣2D.29.如图，在△ABC中，AB=AC=2BC=4，以点B为圆心，BC长为半径画弧，与AC交于点D，则线段CD的长为（）A.12B.1 C.43D.210.二次函数y=﹣x2+2x+8的图像与x轴交于B，C两点，点D平分BC，若在x轴上侧的A点为抛物线的动点，且∠BAC为锐角，则AD的取值范围是（）A.3＜AD≤9B.3≤AD≤9C.4＜AD≤10D.3≤AD≤8二.填空题。

（共24分）11.因式分解：m2－4= .12.如图，是由7个全等的正六边形组成的图案，假设可以随机在图中取点，那么这个点取在阴影部分的概率是.（第12题图）（第13题图）13.如图，一个正方形剪去四个角后形成一个边长为√2的正八边形，则这个正方形的边长为.14.已知m是关于x的方程x2－2x－3=0的一个根，则m2－2m+2020= .15.学校食堂按如图方式摆放餐桌和椅子，若用x表示餐桌的张数，y表示椅子的把数，请你写出椅子数y（把）与餐桌数x（张）之间的函数关系式.（第15题图）（第16题图）16.如图，在△ABC中，AB=AC=15，点D是BC边上的一动点（不与B、C重合），∠ADE=∠B=∠α，DE与AB交于点E，且tan∠α=34，有以下结论：①△ADE∽△ACD；②当CD=9时，△ACD与△DBE全等；③△BDE为直角三角形时，BD为12或214；④0＜BE≤5，其中正确结论是（填序号）三.解答题。

(完整版)北师大版中考数学试题及答案

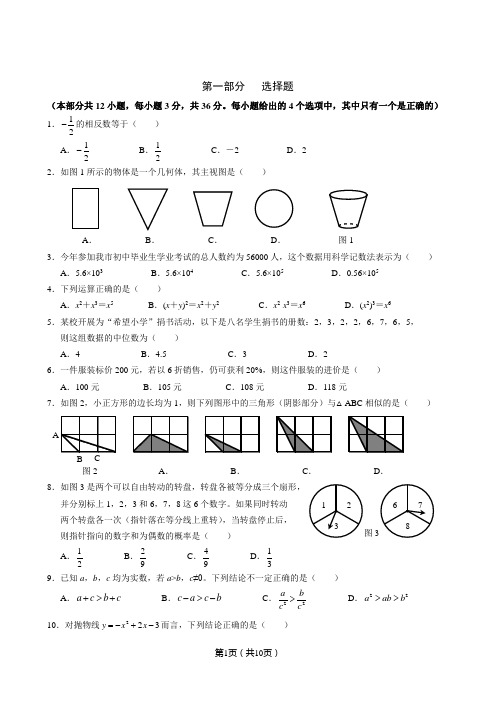
A B C31 23 6 78第一部分选择题（本部分共12小题，每小题3分，共36分。

每小题给出的4个选项中，其中只有一个是正确的）1．12-的相反数等于（）A ．12- B ．12 C ．－2 D ．22．如图1所示的物体是一个几何体，其主视图是（）A ．B ．C ．D ．图13．今年参加我市初中毕业生学业考试的总人数约为56000人，这个数据用科学记数法表示为（） A ．5.6×103 B ．5.6×104 C ．5.6×105 D ．0.56×105 4．下列运算正确的是（）A ．x 2＋x 3＝x 5B ．(x ＋y )2＝x 2＋y 2C ．x 2·x 3＝x 6D ．(x 2)3＝x 6 5．某校开展为“希望小学”捐书活动，以下是八名学生捐书的册数：2，3，2，2，6，7，6，5，则这组数据的中位数为（）A ．4B ．4.5C ．3D ．26．一件服装标价200元，若以6折销售，仍可获利20%，则这件服装的进价是（） A ．100元 B ．105元 C ．108元 D ．118元7．如图2，小正方形的边长均为1，则下列图形中的三角形（阴影部分）与△ABC 相似的是（）图2 A ． B ． C ． D ． 8．如图3是两个可以自由转动的转盘，转盘各被等分成三个扇形，并分别标上1，2，3和6，7，8这6个数字。

如果同时转动两个转盘各一次（指针落在等分线上重转），当转盘停止后，则指针指向的数字和为偶数的概率是（） A ．12 B ．29 C ．49D ．139．已知a ，b ，c 均为实数，若a >b ，c ≠0。

下列结论不一定正确的是（） A ．a c b c +>+ B ．c a c b ->- C ．22a b c c> D ．22a ab b >> 10．对抛物线223y x x =-+-而言，下列结论正确的是（）图7图5 A ．与x 轴有两个交点 B ．开口向上C ．与y 轴的交点坐标是（0，3）D ．顶点坐标为（1，－2） 11．下列命题是真命题的个数有（）①垂直于半径的直线是圆的切线； ②平分弦的直径垂直于弦；③若12x y =⎧⎨=⎩是方程x －ay ＝3的一个解，则a ＝－1；④若反比例函数3y x=-的图像上有两点（12，y 1），（1，y 2），则y 1<y2。

九年级中考北师大数学试卷

一、选择题（每小题3分，共30分）1. 已知函数f(x) = x^2 - 4x + 4，其图像的对称轴是：A. x = 1B. x = 2C. y = 1D. y = 42. 下列命题中正确的是：A. 等腰三角形的底角相等B. 平行四边形的对边平行C. 矩形的对角线相等D. 正方形的四条边相等3. 下列数中，不是有理数的是：A. 3.14B. -2/5C. √2D. 1/34. 已知等差数列{an}的公差为d，若a1 = 2，a5 = 12，则d的值为：A. 2B. 3C. 4D. 55. 在平面直角坐标系中，点A(2, 3)关于原点对称的点是：A. (2, 3)B. (-2, -3)C. (-2, 3)D. (2, -3)6. 已知等比数列{an}的公比为q，若a1 = 3，a3 = 27，则q的值为：A. 3B. 9C. 27D. 1/37. 在△ABC中，∠A = 60°，∠B = 45°，则∠C的度数是：A. 75°B. 105°C. 135°D. 150°8. 下列函数中，是反比例函数的是：A. y = 2x + 1B. y = 1/xC. y = x^2D. y = √x9. 已知一次函数y = kx + b（k≠0），若图象经过点(1, 3)和(2, 5)，则k和b 的值分别是：A. k = 2, b = 1B. k = 2, b = 3C. k = 1, b = 2D. k = 1, b = 310. 在△ABC中，若AB = AC，则△ABC是：A. 等腰三角形B. 等边三角形C. 直角三角形D. 锐角三角形二、填空题（每小题3分，共30分）11. 若|a| = 5，则a的值是______。

12. 已知等差数列{an}的公差为2，若a1 = 3，则第10项an的值为______。

13. 在平面直角坐标系中，点P(2, -3)关于x轴的对称点是______。

初三中考北师大版数学试卷

1. 下列各数中，有理数是（）A. √2B. πC. √-1D. 3.142. 已知a=5，b=-3，那么a²-b²的值为（）A. 4B. 14C. 16D. 223. 在△ABC中，∠A=45°，∠B=60°，则∠C的度数为（）A. 75°B. 90°C. 105°D. 120°4. 下列各图中，能组成三角形的是（）（图略）A. 图1B. 图2C. 图3D. 图45. 已知函数y=2x-3，当x=4时，y的值为（）A. 5B. 7C. 9D. 116. 若a、b是方程x²-3x+2=0的两根，则a+b的值为（）A. 2B. 3C. 4D. 57. 下列各式中，正确的是（）A. (a+b)²=a²+2ab+b²B. (a-b)²=a²-2ab+b²C. (a+b)²=a²-2ab+b²D. (a-b)²=a²+2ab-b²8. 已知x²-4x+4=0，则x的值为（）A. 2B. 4C. -2D. -49. 下列各数中，无理数是（）A. √9B. √16C. √-4D. √2510. 在△ABC中，若a=5，b=7，c=8，则△ABC的面积S为（）A. 14B. 21C. 28D. 3511. 若x=2，则x²-x+1的值为______。

12. 在△ABC中，若∠A=60°，∠B=45°，则∠C的度数为______。

13. 已知函数y=3x+2，当x=1时，y的值为______。

14. 若a、b是方程x²-5x+6=0的两根，则a²+b²的值为______。

15. 若（a+b）²=25，且a-b=5，则a的值为______。

初三北师版数学试卷及答案

1. 已知等腰三角形ABC中，AB=AC，AD是底边BC上的高，若∠BAC=40°，则∠BAD的度数是：A. 20°B. 40°C. 50°D. 80°答案：A2. 若a，b，c为三角形的三边，且满足a+b+c=10，则三角形面积的最大值为：A. 20B. 25C. 16D. 15答案：B3. 已知函数f(x)=2x+1，则函数f(x)的图象经过以下哪个点？A. (0,1)B. (1,3)C. (2,5)D. (3,7)答案：B4. 下列哪个图形不是轴对称图形？A. 正方形B. 等腰三角形C. 圆D. 梯形5. 已知二次函数y=ax^2+bx+c的图象开口向上，且顶点坐标为(1,3)，则下列哪个方程表示该二次函数？A. y=x^2+2x+2B. y=x^2-2x+2C. y=x^2+2x-2D. y=x^2-2x-2答案：B6. 若方程x^2+2ax+1=0的解为x1和x2，则x1+x2的值为：A. 2B. -2C. 0D. 1答案：B7. 已知函数f(x)=x^2-2x+3，则函数f(x)的图象的对称轴为：A. x=1B. x=2C. x=3D. x=4答案：A8. 在直角坐标系中，点A(2,3)，点B(-1,1)，则线段AB的中点坐标为：A. (1,2)B. (1,3)C. (2,1)答案：A9. 若方程2x-3=0的解为x1，则方程2x+3=0的解为：A. x1B. -x1C. x1/2D. -x1/2答案：B10. 已知等腰三角形ABC中，AB=AC，AD是底边BC上的高，若∠BAC=50°，则∠BAD的度数是：A. 25°B. 50°C. 75°D. 100°答案：A二、填空题（每题5分，共20分）11. 若等腰三角形ABC中，AB=AC，∠BAC=60°，则∠ABC的度数为______。

(北师大版)初中九年级数学下学期中考复习模拟考试试题卷(含答案详解)

（北师大版）初中九年级数学下学期中考复习模拟考试试题卷（含答案详解）（满分150分时间：120分钟）一.单选题。

（共40分） 1.16的算术平方根是（）A.±2B.2C.4D.±4 2.下面四个几何体中，左视图为圆的是（）A. B. C. D.3.据5月17日消息，全国各地约42600名医务人员支援湖北抗击新冠肺炎疫情，将42600用科学记数法表示为（）A.0.426×105B.4.26×105C.42.6×104D.4.26×1044.如图，直线a ∥b ，直线c 分别交a ，b 于点A ，C ，∠BAC 的平分线交直线b 于点D ，若∠1=50°，则∠2的度数是（）A.50°B.70°C.80°D.110°（第4题图）（第9题图）（第10题图） 5.下列图形中，既是轴对称图形又是中心对称图形的是（）A. B. C. D.6.化简a 2a －1－1－2a 1－a的结果为（）A.a+1a －1B.a ﹣1C.aD.17.从甲、乙、丙、丁四人中抽调两人参加“寸草心”志愿服务队，恰好抽到甲和乙的概率是（）A.112 B.18 C.16 D.128.在同一直角坐标系中，函数y=kx 和y=kx ﹣3的图象大致是（）A. B. C. D.9.在直角坐标系中，等腰直角三角形AOB 在如图所示的位置，点B 的横坐标为2，将△AOB 绕点O 按逆时针方向旋转90°，得到△A’OB’，则点A’的坐标为（） A.（1，1） B.（√2，√2） C.（﹣1，1） D.（﹣√2，√2）10.在平面直角坐标系内，已知点A （﹣1，0），点B （1，1）都在直线y ＝12x+12上，若抛物线y ＝ax 2﹣x+1（a ≠0）与线段AB 有两个不同的交点，则a 的取值范围是（） A.a ≤﹣2 B.a ＜98 C.1≤a ＜98或a ≤﹣2 D.﹣2≤a ＜98 二.填空题。

北师大初三数学中考试卷

一、选择题（每题4分，共40分）1. 下列数中，有理数是（）A. √2B. πC. -√3D. √92. 已知x^2 - 5x + 6 = 0，则x的值为（）A. 2B. 3C. 4D. 63. 在直角坐标系中，点P的坐标为（-2，3），则点P关于x轴的对称点坐标为（）A. (-2, -3)B. (2, 3)C. (-2, 3)D. (2, -3)4. 如果sinα = 1/2，那么cosα的值为（）A. √3/2B. -√3/2C. 1/2D. -1/25. 下列命题中，正确的是（）A. 平行四边形的对角线互相垂直B. 等腰三角形的底边上的高与底边垂直C. 矩形的对角线互相平行D. 正方形的四边相等，但对角线不相等6. 已知函数f(x) = 2x - 3，如果f(x) > 0，那么x的取值范围是（）A. x > 3/2B. x < 3/2C. x > 3D. x < 37. 下列各组数中，成等差数列的是（）A. 1, 3, 5, 7, 9B. 2, 4, 8, 16, 32C. 1, 4, 9, 16, 25D. 3, 6, 9, 12, 158. 下列函数中，是奇函数的是（）A. f(x) = x^2 + 1B. f(x) = |x|C. f(x) = x^3D. f(x) = x^2 - 19. 已知a > b > 0，则下列不等式中正确的是（）A. a + b > 2√abB. a - b > 2√abC. a + b < 2√abD. a - b < 2√ab10. 下列图形中，不是圆的内接四边形的是（）A. 矩形B. 菱形C. 正方形D. 等腰梯形二、填空题（每题4分，共40分）11. 已知方程2x - 5 = 3x + 1，解得x = ________。

12. 若∠ABC = 90°，AB = 6cm，BC = 8cm，则AC = ________cm。

初三北师大数学试题及答案

初三北师大数学试题及答案一、选择题（每题3分，共15分）1. 下列各数中，最小的数是（）A. -3B. -2C. -1D. 02. 若a < b < 0，且c > 0，那么ac + bc的值（）A. 一定大于0B. 一定小于0C. 可能为正，也可能为负D. 无法确定3. 一个圆的半径是5，那么这个圆的面积是（）A. 25πB. 50πC. 75πD. 100π4. 一个长方体的长、宽、高分别是a、b、c，若长方体的体积是120，那么a×b×c等于（）A. 120B. 60C. 30D. 155. 一个数的平方根是4，那么这个数是（）A. 16B. -16C. 8D. -8二、填空题（每题2分，共10分）6. 一个数的绝对值是3，这个数可能是_______。

7. 一个数的倒数是1/2，那么这个数是_______。

8. 一个直角三角形的两条直角边分别是3和4，那么斜边的长度是_______。

9. 若x² - 5x + 6 = 0，那么x的值是_______。

10. 一个数的立方是-27，那么这个数是_______。

三、解答题（共75分）11. 解方程：2x + 5 = 13。

（5分）12. 已知一个直角三角形的两条直角边长分别为6和8，求斜边的长度。

（5分）13. 一个长方体的长、宽、高分别是3米、4米和5米，求这个长方体的表面积和体积。

（10分）14. 某工厂生产一批零件，每件零件的成本是5元，售价是10元，如果工厂要获得10000元的利润，需要生产多少件零件？（10分）15. 一个圆的半径是7厘米，求这个圆的周长和面积。

（10分）16. 某班有40名学生，其中20名男生和20名女生。

如果随机挑选一名学生，求选出男生的概率。

（10分）17. 已知a + b = 10，a - b = 2，求a² - b²的值。

（10分）18. 某班有40名学生，其中20名男生和20名女生。

初三试卷数学北师大版答案

一、选择题（每题3分，共30分）1. 下列各数中，是整数的是（）A. √9B. -√16C. 2/3D. √25答案：D解析：A选项√9=3，B选项-√16=-4，C选项2/3不是整数，D选项√25=5，所以选D。

2. 已知x^2-5x+6=0，则x的值为（）A. 2或3B. 1或4C. 2或-3D. 1或-2答案：A解析：因式分解x^2-5x+6=(x-2)(x-3)=0，解得x=2或x=3，所以选A。

3. 在△ABC中，∠A=60°，∠B=45°，则∠C的度数为（）A. 45°B. 60°C. 75°D. 90°答案：C解析：三角形内角和为180°，所以∠C=180°-∠A-∠B=180°-60°-45°=75°，所以选C。

4. 下列各图中，平行四边形的是（）A.B.C.D.答案：C解析：平行四边形的对边平行且相等，只有C图符合条件，所以选C。

5. 已知一次函数y=kx+b（k≠0）的图象经过点（1，-2），则k的值为（）A. -3B. -2C. 2D. 3答案：A解析：将点（1，-2）代入一次函数，得-2=k1+b，解得k=-3，所以选A。

二、填空题（每题3分，共30分）6. -3的平方根是_________。

答案：±√3解析：-3的平方根是±√3，因为（±√3）^2=3。

7. 若a=5，b=2，则a^2-b^2的值为_________。

答案：21解析：a^2-b^2=(a+b)(a-b)，代入a=5，b=2，得21。

8. 下列各式中，完全平方公式是_________。

答案：a^2+2ab+b^2=(a+b)^2解析：完全平方公式是a^2+2ab+b^2=(a+b)^2。

9. 已知一次函数y=kx+b（k≠0）的图象经过点（0，-1），则b的值为_________。

九年级数学北师大版试卷答案

九年级数学北师大版试卷答案在学习九年级数学北师大版的过程中，试卷是检验我们知识掌握程度的重要工具。

而试卷答案则是帮助我们发现问题、纠正错误、深化理解的关键。

首先，让我们来看看选择题部分。

选择题通常考查的是一些基础知识和概念的理解。

比如，在某张试卷中，有这样一道题：“若关于 x 的方程 x² 2x ＋ m ＝ 0 有两个不相等的实数根，则 m 的取值范围是（）”。

答案是 m ＜ 1 。

这道题考查的是一元二次方程根的判别式。

对于一元二次方程 ax²＋ bx ＋ c ＝ 0（a ≠ 0），其判别式为Δ ＝ b²4ac 。

当Δ ＞ 0 时，方程有两个不相等的实数根。

在这道题中，a ＝ 1，b ＝－2，c ＝ m ，所以Δ ＝（－2)² 4×1×m ＞ 0 ，解得 m ＜ 1 。

再来看填空题。

填空题往往需要我们对知识点有较为准确的记忆和运用能力。

比如，“一个多边形的内角和是外角和的 2 倍，则这个多边形是_____边形”。

答案是六边形。

因为多边形的外角和是 360°，设这个多边形有 n 条边，则其内角和为（n 2)×180°。

由题意可得（n2)×180°＝ 2×360°，解得 n ＝ 6 。

接下来是计算题。

计算题要求我们具备扎实的运算能力和解题步骤的规范性。

例如，“计算：√18 √8 ＋√2 ”。

答案是：3√2 2√2 ＋√2 ＝2√2 。

在计算过程中，我们要先将根式化简，√18 ＝3√2 ，√8 ＝2√2 ，然后再进行计算。

解答题部分是试卷中的重点和难点。

比如，“在平面直角坐标系中，直线 y ＝ kx ＋ b 经过点（1，2）和点（－1，－4），求这条直线的解析式”。

首先，将点（1，2）和（－1，－4）分别代入直线方程 y ＝ kx ＋ b 中，得到方程组：｛ 2 ＝ k ＋ b ，－4 ＝ k ＋ b ｝，解这个方程组，可得 k ＝ 3 ，b ＝－1 ，所以直线的解析式为 y ＝ 3x 1 。

中考数学试卷北师版答案

一、选择题1. 下列各数中，正整数是（）A. -2.5B. 0.1C. -3D. 3答案：D解析：正整数是大于0的整数，只有选项D符合条件。

2. 下列各数中，有理数是（）A. √2B. πC. -√3D. √9答案：D解析：有理数是可以表示为两个整数之比的数，选项D可以表示为3/1，是有理数。

3. 若a=2，b=-1，则a²b=（）A. -4B. 4C. -2D. 2答案：B解析：将a和b的值代入公式，得a²b=2²×(-1)=4×(-1)=-4，故选B。

4. 下列函数中，一次函数是（）A. y=2x+3B. y=x²+1C. y=3/xD. y=√x答案：A解析：一次函数是指函数图像为一条直线的函数，只有选项A符合条件。

5. 下列三角形中，等边三角形是（）A. ABCB. DEFC. GHID. JKL答案：B解析：等边三角形的三边长度相等，只有选项B符合条件。

二、填空题6. 若x=5，则2x-3=（）答案：7解析：将x的值代入公式，得2x-3=2×5-3=10-3=7。

7. 下列各数中，绝对值最小的是（）A. -3B. 0C. 3D. -2答案：B解析：绝对值表示一个数与0的距离，只有0的绝对值为0，故选B。

8. 若a=2，b=-3，则a²+b²=（）答案：13解析：将a和b的值代入公式，得a²+b²=2²+(-3)²=4+9=13。

9. 下列各式中，分式有（）A. 2/xB. 3x+2C. 4x²-1D. 5/x+2答案：A解析：分式是指含有分母的代数式，只有选项A符合条件。

10. 下列各式中，正比例函数是（）A. y=2x+3B. y=x²+1C. y=3/xD. y=kx（k为常数）答案：D解析：正比例函数是指函数图像为一条通过原点的直线，只有选项D符合条件。

初三数学中考试卷北师大

一、选择题（每小题4分，共40分）1. 已知二次函数的图像开口向上，顶点坐标为（-1，3），则该函数的表达式为（）A. y = x^2 - 2x + 2B. y = x^2 + 2x + 2C. y = -x^2 + 2x + 2D. y = -x^2 - 2x + 22. 在直角坐标系中，点A（2，3）关于y轴的对称点坐标为（）A.（-2，3）B.（2，-3）C.（-2，-3）D.（2，3）3. 若等腰三角形的底边长为8，腰长为10，则该三角形的面积为（）A. 40B. 48C. 56D. 644. 下列关于函数y = -2x + 5的描述正确的是（）A. 图像是一条斜率为正的直线B. 图像是一条斜率为负的直线C. 图像是一条水平线D. 图像是一条垂直线5. 在直角三角形ABC中，∠A=30°，∠B=90°，若BC=4，则AB的长度为（）A. 2B. 2√3C. 4D. 86. 若等差数列的前三项分别为2，5，8，则该数列的公差为（）A. 1B. 2C. 3D. 47. 若a，b，c是等比数列的连续三项，且a + b + c = 21，abc = 27，则该等比数列的公比为（）A. 1B. 3C. 9D. 278. 在平行四边形ABCD中，若∠A=50°，则∠B的度数为（）A. 130°B. 50°C. 40°D. 30°9. 若等腰三角形ABC的底边BC=6，腰AB=AC=5，则该三角形的面积为（）A. 15B. 20C. 25D. 3010. 若一元二次方程x^2 - 3x + 2 = 0的两个根分别为a和b，则a + b的值为（）A. 1B. 2C. 3D. 4二、填空题（每小题3分，共30分）11. 已知函数y = -3x^2 + 6x + 1的图像开口向下，顶点坐标为（，）。

12. 在直角坐标系中，点P（3，-2）关于x轴的对称点坐标为（，）。

数学初三北师大版试卷答案

一、选择题（每题4分，共40分）1. 下列各数中，是正数的是（）A. -3/4B. -5C. 0D. 1/2答案：D解析：正数是指大于零的数，只有选项D中的1/2是大于零的。

2. 下列各式中，正确的是（）A. 3^2 = 9B. (-3)^2 = 9C. (-3)^3 = -27D. (-3)^4 = 81答案：B解析：平方是指一个数自乘一次，立方是指一个数自乘两次。

选项B中的(-3)^2表示-3乘以-3，结果为9。

3. 若a=2，b=3，则a^2+b^2的值为（）A. 5B. 7C. 11D. 13答案：D解析：将a和b的值代入公式a^2+b^2，得到2^2+3^2=4+9=13。

4. 下列各数中，是偶数的是（）A. 3B. 4C. 5D. 6答案：B解析：偶数是指能被2整除的数，只有选项B中的4是偶数。

5. 下列各数中，是质数的是（）A. 4B. 6C. 8D. 11答案：D解析：质数是指只有1和它本身两个因数的自然数，只有选项D中的11是质数。

6. 若x=2，则2x+3的值为（）A. 5B. 7C. 9D. 11答案：C解析：将x的值代入表达式2x+3，得到22+3=4+3=7。

7. 下列各式中，正确的是（）A. a+b=b+aB. a-b=b-aD. a/b=b/a答案：A解析：加法和乘法满足交换律，即a+b=b+a，ab=ba。

8. 若x=3，y=5，则x^2+y^2的值为（）A. 16B. 25C. 34D. 36答案：C解析：将x和y的值代入公式x^2+y^2，得到3^2+5^2=9+25=34。

9. 下列各数中，是正整数的是（）A. -2B. -1C. 0D. 1答案：D解析：正整数是指大于零的自然数，只有选项D中的1是正整数。

10. 若a=5，b=2，则a^2-b^2的值为（）A. 7B. 9C. 11D. 13解析：将a和b的值代入公式a^2-b^2，得到5^2-2^2=25-4=21。

初三数学试卷答案北师大版

一、选择题（每题4分，共20分）1. 若a > 0，b < 0，则下列不等式中正确的是（）A. a + b > 0B. a - b < 0C. -a + b > 0D. -a - b > 0答案：D2. 已知函数f(x) = 2x + 3，则f(-1)的值为（）A. -1B. 1C. 2D. 3答案：A3. 若等差数列{an}的公差为d，且a1 = 3，a4 = 9，则d的值为（）A. 2B. 3C. 4D. 6答案：A4. 下列各式中，不是一元二次方程的是（）A. x^2 - 2x + 1 = 0B. 2x + 3 = 5C. 3x^2 - 4x + 1 = 0D. x^2 + 2x - 3 = 0答案：B5. 在直角坐标系中，点P(2, -3)关于y轴的对称点为（）A. (-2, -3)B. (2, 3)C. (-2, 3)D. (2, -3)答案：A二、填空题（每题4分，共20分）6. 若x^2 - 5x + 6 = 0，则x的值为______。

答案：2，37. 已知函数f(x) = 3x - 2，则f(-1)的值为______。

答案：-58. 等差数列{an}的前n项和为S_n，若a1 = 1，d = 2，则S_10的值为______。

答案：1109. 若直角三角形的两个锐角分别为30°和60°，则该三角形的斜边长与直角边的比值为______。

答案：210. 已知一元二次方程x^2 - 4x + 3 = 0的解为x1和x2，则x1 + x2的值为______。

答案：4三、解答题（共60分）11. （12分）已知函数f(x) = x^2 - 4x + 3，求f(x)的图像与x轴的交点坐标。

解答：令f(x) = 0，得x^2 - 4x + 3 = 0，解得x1 = 1，x2 = 3。

所以f(x)的图像与x轴的交点坐标为(1, 0)和(3, 0)。