大学物理实验教案-驻波法测振动频率
大学物理实验讲义~弦振动和驻波研究方案

⼤学物理实验讲义~弦振动和驻波研究⽅案弦振动与驻波研究【实验⽬的】1.观察在弦上形成的驻波;2.确定弦线振动时驻波波长与张⼒的关系; 3.学习对数作图和最⼩⼆乘法进⾏数据处理。
【实验原理】在⼀根拉紧的弦线上,其中张⼒为T ,线密度为µ,则沿弦线传播的横波应满⾜下述运动⽅程:2222xyT t y ??=??µ (1) 式中x 为波在传播⽅向(与弦线平⾏)的位置坐标,y 为振动位移。
将(1)式与典型的波动⽅程 22222x y V t y ??=?? 相⽐较,即可得到波的传播速度: µTV =若波源的振动频率为f ,横波波长为λ,由于波速λf V =,故波长与张⼒及线密度之间的关系为:µλTf1=(2)为了⽤实验证明公式(2)成⽴,将该式两边取对数,得:11lg lg lg lg 22T f λµ=-- (3)固定频率f 及线密度µ,⽽改变张⼒T ,并测出各相应波长λ,作lg λ-lg T 图,若得⼀直线,计算其斜率值(如为21),则证明了λ∝21T的关系成⽴。
弦线上的波长可利⽤驻波原理测量。
当两个振幅和频率相同的相⼲波在同⼀直线上相向传播时,其所叠加⽽成的波称为驻波,⼀维驻波是波⼲涉中的⼀种特殊情形。
在弦线上出现许多静⽌点,称为驻波的波节。
相邻两波节间的距离为半个波长。
【实验仪器】1、可调频率数显机械振动源;2、振动簧⽚;3、弦线(铜丝);4、可动⼑⽚⽀架;5、可动⼑⼝⽀架;6、标尺;7、固定滑轮;8、砝码与砝码盘;9、变压器;10、实验平台;11、实验桌图1 实验装置⽰意图图2 可调频率数显机械振动源⾯板图(1、电源开关 2、频率调节 3、复位键 4、幅度调节 5、频率指⽰)实验装置如图1所⽰,⾦属弦线的⼀端系在能作⽔平⽅向振动的可调频率数显机械振动源的振簧⽚上,频率变化范围从0-200Hz 连续可调,频率最⼩变化量为0.01Hz ,弦线⼀端通过定滑轮⑦悬挂⼀砝码盘⑧;在振动装置(振动簧⽚)的附近有可动⼑⽚⽀架④,在实验装置上还有⼀个可沿弦线⽅向左右移动并撑住弦线的可动⼑⼝⑤。
2020年大学物理实验驻波实验(实用)
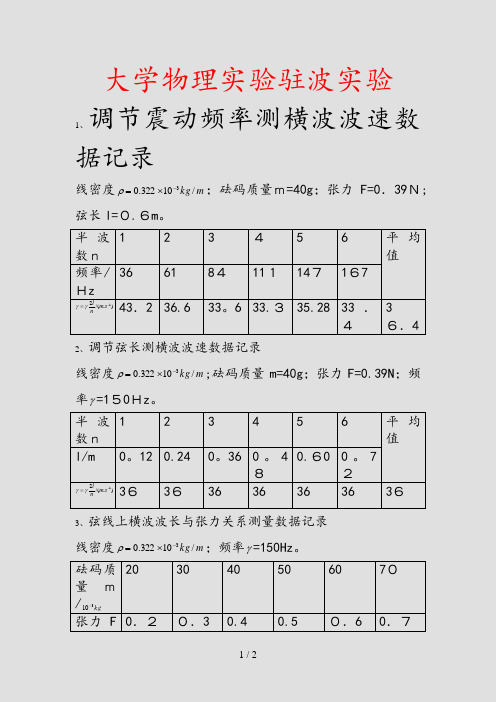
大学物理实验驻波实验1、调节震动频率测横波波速数据记录线密度m kg /10322.03-⨯=ρ;砝码质量m=40g ;张力F=0.39N;弦长l=0.6m 。
半波数n1 2 3 4 5 6 平均值频率/Hz36 61 84111147167)./(21-=s m nlγγ43.2 36.6 33。
6 33.3 35.28 33.4 36.42、调节弦长测横波波速数据记录线密度m kg /10322.03-⨯=ρ;砝码质量m=40g ;张力F=0.39N ;频率γ=150Hz 。
半波数n 1 23 4 5 6平均值l/m 0。
12 0.240。
36 0。
48 0.60 0。
72)./(21-=s m nlγγ36 3636 36 36 36 363、弦线上横波波长与张力关系测量数据记录线密度m kg /10322.03-⨯=ρ;频率γ=150Hz 。
砝码质量m/kg 310-2030 40 50 60 70张力F 0.20.3 0.40.5 0.6 0.7/N半波数n3 4 44 4 4弦长l/m0.216 0。
353 0。
3940.429 0.4770.498波长m /λ0.144 0。
17650.197 0。
21450。
2385 0.249 λln-1.9 -1.7 -1。
6 -1.5 -1.4 -1.3F ln—1.6—1。
2 -0。
9 -0。
7 —0。
5 —0.4思考题答案:1、13.8.3410322.039.0--=⨯==s m Fv ρ2、图略.由图得斜率53.07.11.10.2=-+-=a 截距b=-1。
1理论值a=0。
5 b =-0。
99相对误差:%6%1005.05.053.01=⨯-=E %11%10099.099.01.12=⨯-+-=E3、原因:存在空气阻力 弦长长度的精确度拨弦的方式和计算机采样的步数 改进:在真空环境下完成多次取值减少误差...谢阅...。
大学物理实验讲义-弦振动与驻波研究

大学物理实验讲义-弦振动与驻波研究弦振动与驻波研究【实验目的】1.观察在弦上形成的驻波;2.确定弦线振动时驻波波长与张力的关系; 3.学习对数作图和最小二乘法进行数据处理。
【实验原理】在一根拉紧的弦线上,其中张力为T ,线密度为μ,则沿弦线传播的横波应满足下述运动方程:2222x yT t y ∂∂=∂∂μ(1)式中x 为波在传播方向(与弦线平行)的位置坐标,y 为振动位移。
将(1)式与典型的波动方程22222x y V t y ∂∂=∂∂相比较,即可得到波的传播速度: μTV =若波源的振动频率为f ,横波波长为λ,由于波速λf V =,故波长与张力及线密度之间的关系为:μλTf1=(2)为了用实验证明公式(2)成立,将该式两边取对数,得:11lg lg lg lg 22T f λμ=-- (3)固定频率f 及线密度μ,而改变张力T ,并测出各相应波长λ,作lg λ-lg T 图,若得一直线,计算其斜率值(如为21),则证明了λ∝21T的关系成立。
弦线上的波长可利用驻波原理测量。
当两个振幅和频率相同的相干波在同一直线上相向传播时,其所叠加而成的波称为驻波,一维驻波是波干涉中的一种特殊情形。
在弦线上出现许多静止点,称为驻波的波节。
相邻两波节间的距离为半个波长。
【实验仪器】1、可调频率数显机械振动源;2、振动簧片;3、弦线(铜丝);4、可动刀片支架;5、可动刀口支架;6、标尺;7、固定滑轮;8、砝码与砝码盘;9、变压器;10、实验平台;11、实验桌9123456781011图1 实验装置示意图图2 可调频率数显机械振动源面板图 (1、电源开关 2、频率调节 3、复位键 4、幅度调节 5、频率指示)实验装置如图1所示,金属弦线的一端系在能作水平方向振动的可调频率数显机械振动弦线上驻波实验仪电 源ON复位 幅度 调节上海复旦天欣科教仪器有限公司频率调节H Z1 2 3 45FD-SWE-II源的振簧片上,频率变化范围从0-200Hz 连续可调,频率最小变化量为0.01Hz ,弦线一端通过定滑轮⑦悬挂一砝码盘⑧;在振动装置(振动簧片)的附近有可动刀片支架④,在实验装置上还有一个可沿弦线方向左右移动并撑住弦线的可动刀口⑤。
实验指导书(驻波)

上海电力学院物理实验指导书所属课程:大学物理实验实验名称:驻波(一)(二)面向专业:全院理工科实验室名称:物理实验室2006年2月驻波(一)一.实验目的:1.观察在弦线上形成的驻波;2.了解弦线振动时驻波波长与弦线所受张力的关系,并利用它来测定电动音叉的频率.二、实验仪器、设备:名称型号、规格备注电动音叉f=103.3Hz滑轮1个弦线μ=2.61×10-3g/cm砝码20g米尺1m劈形木板2个三、实验原理1.驻波:两个振幅相同的相干波,在同一直线上沿相反方向传播时。
叠加后直线上各质点形成稳定的振动状态,称此为驻波。
让相干前进的波与反射波叠加就能形成驻波。
2.在张紧的弦线上观察驻波:一根弦线横跨在音叉的一端A和劈形木块P的刀口B之间,在刀口右面通过滑轮H和砝码m给弦线施加一定的张力。
音叉由电磁策动力维持振幅恒定的振动。
当音叉振动时,在弦线上激起一横波,此波向右行进。
当此波遇到固定点B时又被反射,形成向左行进的反射波,这两个波在弦上相互叠加就形成驻波。
驻波从B开始就被分成几段,每段的两个端点的振幅为零,固定不动,这些点称为波节。
每段中的各质点则同步作上下振动。
两相邻的波节中间的点振幅最大,称为波腹。
相邻两波节(或波腹)之间的距离L等于形成这驻波的相干波波长的一半,即L=λ/2。
当弦线AB段的长度接近半波长的整数倍时,驻波振幅最大而且稳定。
由于B端是固定点,所以B端一定是波节。
3.当改变音叉频率或改变加上弦线的张力F时,就可改变半波长L。
在本实验中,采用改变张力F来改变L。
在弦线上传播的横波的波速u和张力F及弦线的单位长度的质量μ有如下关系:u2=F/μ又u=λf从上两式可知张力F的改变,引起u的变化。
由于音叉频率f不变,所以λ改变。
由上两式得f2=F/(μλ2)所以只要测得F、μ及λ就能求得电动音叉的频率f。
四.实验内容与步骤:1.记下弦线单位长度质量(由实验室给出)。
μ=2.45×10-4kg/m=2.45×10-3g/cm(原悬线值)μ=2.61×10-4kg/m=2.61×10-3g/cm(2001/9/10重测新悬线值)2.在弦线下垂端加砝码140克,记下张力(化为达因)。
音波的谐振与驻波实验

添加标题
操作人员的熟练程度:操作人员应熟练掌握实验操作流程,避免因操作不当导致的误差。
添加标题
实验设计的合理性:合理设计实验方案,避免因实验设计不合理导致的误差。
添加标题
实验环境的稳定性:保持实验环境的温度、湿度、气压等稳定,以减小环境因素对实验结果的影响。
添加标题
数据处理方法:采用适当的数据处理方法,如平均法、最小二乘法等,以减小数据误差。
音波的谐振与驻波实验在物理学中的其他领域也有应用,例如在光学、电磁学等领域,可以帮助我们理解波的传播和振动特性。
音波的谐振与驻波实验在工程技术中也有应用,例如在声学工程、电子工程等领域,可以帮助我们设计和优化各种声学系统。
音波谐振与驻波实验可以帮助音乐家更好地理解和控制声音的传播和接收
通过实验,音乐家可以调整乐器的音色和音量,以获得更好的音乐效果
实验还可以帮助音乐家理解声音在空间中的传播和接收,从而更好地设计和布置音乐厅和录音室
音波谐振与驻波实验还可以帮助音乐家理解和改进声音的合成和编辑技术,从而更好地创作和制作音乐作品
声波谐振器:用于滤波、放大、振荡等电路中
驻波测量:用于声学测量、无损检测等领域
声波谐振腔:用于声学器件的设计和优化
声波谐振天线:用于无线电通信、雷达等领域
音源的相位差为180度
音源的振幅相同
添加标题
添加标题
添加标题
添加标题
建筑设计:如教堂、音乐厅等建筑物的声学设计
乐器演奏:如吉他、小提琴等弦乐器的音调调整
医疗设备:如超声波治疗仪、听力测试仪等设备的使用
通信技术:如无线电、手机等设备的信号传输与接收
准备实验器材:音波发生器、共振腔、麦克风、示波器等
音波发生器:用于产生音波
大学物理实验教案-驻波法测振动频率 2
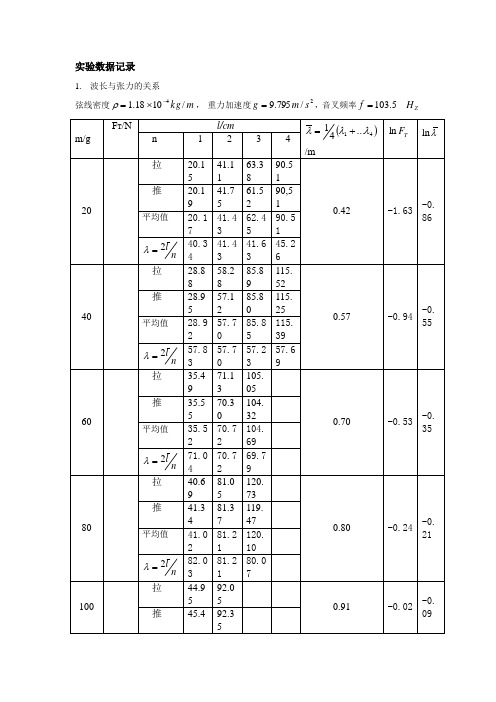
实验数据记录
1. 波长与张力的关系
弦线密度m kg /1018.14-⨯=ρ, 重力加速度2/795.9s m g =,音叉频率103.5
Z f H =
=⎪⎪⎭
⎫
⎝⎛ρf 1ln -0.03
实验数据处理
1
、
作
图
:
λ
ln ~
T
F ln 图
2、利用上表中的有关数据,最小二乘法求出斜率和截距,与公式(9)中的斜率和截距
比较,说明差异是否过大。
斜率=0.48 截距=-0.08
与公式9比较差异很小
3、用公式(1’)、(6)两种方法算出波速。
以20g一个半波区为例
(1)v=41.71
(2)v=41.17
用两种方法算出来的速度有较小的误差,原因是测量距离时有误差,还有驻波的震动频率可能没达到最大。
4、算出振动频率并与仪器标牌上的标称值相比较。
算出的振动频率与仪器标牌上的标称值误差较大,可能的原因是驻波的振幅没有达到最大。
驻波测频率实验报告

驻波测频率实验报告一、实验目的本实验旨在研究驻波现象与测量频率的关系,通过实际操作和数据分析,探究驻波测频率实验的原理和方法。
二、实验器材1. 准直器2. 振幅调节电源3. 信号发生器4. 振动发生器5. 波形发生器6. 示波器7. 可调电感8. 电阻盒三、实验原理3.1 驻波现象当一条电缆上有来自两个方向的波在反射时,交互干扰形成了干涉,此时产生了波沿电缆上的驻波。
3.2 驻波节和驻波腹在驻波状态下,波沿电缆上的某些部分振动最小,这些位置称为驻波的节。
而振动最大处则称为驻波的腹。
3.3 驻波节点和驻波腹节点是振幅最小处的位置,相邻节点之间相隔半个波长。
腹是振幅最大处的位置,相邻腹之间也相隔半个波长。
3.4 驻波测频率的方法测量电缆上的驻波数目,即可计算出波长,从而得出频率。
四、实验步骤1. 将准直器对准波形发生器,调节好振幅调节电源的电压,使其电流适中。
2. 将振幅调节电源连接至信号发生器和示波器。
3. 打开信号发生器和示波器,设置合适的频率和垂直、水平的缩放值。
4. 将振动发生器连接至电缆。
5. 逐渐调节振动发生器的频率,观察信号在示波器上的波形变化。
6. 当示波器上出现驻波现象时,记录下此时的频率和节点数目。
五、实验数据频率(Hz)节点数目10 220 430 640 850 10六、数据处理与分析根据表中数据,可以看出频率与节点数目之间呈一定的线性关系。
我们可以通过计算来进一步验证。
首先,根据节点的定义,相邻节点之间的距离等于半个波长。
所以,节点之间的距离可以表示为:d = \frac{\lambda}{2}其中,d 表示节点之间的距离,\lambda 表示波长。
由于相邻节点之间的距离相等,而频率是波长的倒数,即:f = \frac{c}{\lambda}其中,f 表示频率,c 表示波速。
所以,我们可以得出频率与节点数目的关系为:f = \frac{2c}{d}将实验数据带入上述公式,可以得到频率与节点数目之间的线性关系。
大学物理驻波实验报告

大学物理驻波实验报告大学物理驻波实验报告引言:驻波是物理学中一个重要的现象,它在很多领域都有广泛的应用。
本次实验旨在通过观察和测量驻波的特性,深入了解驻波现象及其相关的物理原理。
实验目的:1. 理解驻波的定义和基本特性;2. 学习使用仪器测量驻波的参数;3. 掌握驻波的数学表达式及其物理解释。
实验原理:驻波是由两个同频率、同振幅的相向传播的波叠加形成的。
当两个波相遇时,它们会相互干涉,形成驻波。
在一维情况下,驻波的表达式为y(x, t) = 2Asin(kx)sin(ωt),其中A为振幅,k为波数,x为位置,ω为角频率。
实验装置:1. 信号发生器:用于产生驻波的信号;2. 波形发生器:用于产生驻波所需的波形;3. 波形显示器:用于观察和测量驻波的参数;4. 测量工具:如尺子、计时器等。
实验步骤:1. 将信号发生器和波形发生器连接,并设置相同的频率和振幅;2. 将波形发生器的输出连接到波形显示器,并调整显示器的位置和角度,以便观察到驻波的现象;3. 通过调节波形发生器的相位差,观察驻波的变化,并记录下相应的数据;4. 使用尺子测量波形显示器上相邻两个节点(波峰或波谷)之间的距离,并记录下来;5. 重复步骤3和步骤4,直到获得足够的数据。
实验结果与分析:通过实验观察和测量,我们得到了一系列驻波的数据。
根据这些数据,我们可以计算出驻波的波长、频率和相速度等参数。
首先,我们可以通过测量相邻两个节点之间的距离来计算驻波的波长。
根据驻波的定义,相邻两个节点之间的距离应该等于波长的一半。
因此,我们可以将测得的距离乘以2,得到驻波的波长。
其次,我们可以通过测量信号发生器的频率和波长,计算出驻波的频率。
根据频率的定义,频率等于波速除以波长。
由于我们已经测得了波长,所以可以将波速除以波长,得到驻波的频率。
最后,我们可以通过测量两个相邻节点之间的时间间隔,计算出驻波的相速度。
相速度定义为波长除以周期。
由于周期等于时间间隔的倒数,所以可以将波长除以时间间隔,得到驻波的相速度。
驻波法

大学物理实验教案实验名称:空气中声速的测定1、实验目的(1)学会用驻波法和相位法测量声波在空气中传播速度。
(2)进一步掌握示波器、低频信号发生器的使用方法。
(3)学会用逐差法处理数据。
2、实验仪器超声声速测定仪、低频信号发生器DF1027B、示波器ST16B。
3、实验原理3.1 实验原理声速V、频率f 和波长λ之间的关系式为V f 。
如果能用实验方法测量声波的频率f和波长λ,即可求得声速V。
常用的测量声速的方法有以下两种。
3.2 实验方法3.2.1 驻波共振法(简称驻波法)S1 发出的超声波和S 2 反射的超声波在它们之间的区域内相干涉而形成驻波。
当波源的频率和驻波系统的固有频率相等时,此驻波的振幅才达到最大值,此时的频率为共振频率。
驻波系统的固有频率不仅与系统的固有性质有关,还取决于边界条件,在声速实验中,S1 、S 2 即为两边界,且必定是波节,其间可以有任意个波节,所以驻波的共振条件为:Ln n 123 2 (1)即当S1 和S 2 之间的距离L 等于声波半波长的整数倍时,驻波系统处于共振状态,驻波振幅最大。
在示波器上得到的信号幅度最大。
当L 不满足(1)式时,驻波系统偏离共振状态,驻波振幅随之减小。
移动S 2 ,可以连续地改变L 的大小。
由式(1)可知,任意两个相邻共振状态之间,即S 2 所移过的距离为:L L n 1 Ln n 1 n 2 2 2 (2)可见,示波器上信号幅度每一次周期性变化,相当于L 改变了 2 。
此距离 2 可由超声声速测定仪上的游标卡尺测得,频率可由低频信号发生器上的频率计读得,根据V f ,就可求出声速。
3.2.2 两个相互垂直谐振动的合成法(简称相位法)在示波器荧光屏上就出现两个相互垂直的同频率的谐振动的合成图形——称为李沙如图形。
其轨迹方程为:2 2 X Y Cos 2 1 Sin 2 2 1 2 XY A1 A2 A1 A2 (5)2 1 0 在一般情况下,此李沙如图形为椭圆。
大物实验报告 弦振动与驻波实验

物理实验报告哈工大物理实验中心班号33006学号1190501917姓名刘福田教师签字实验日期2020.4.19预习成绩学生自评分总成绩(注:为方便登记实验成绩,班号填写后5位,请大家合作。
)实验(三)弦振动和驻波实验一.实验目的1、在弦线张力不变时,用实验确定驻波波长与振动频率的关系;2、在振动源频率不变时,用实验确定驻波波长与张力的关系;3、观察弦振动及驻波的形成。
二.实验原理在一根拉紧的弦线上,张力为T,线密度为μ,则沿弦线传播的横波应满足运动方程其中x:波在传播方向(与弦线平行)的位置坐标;y:振动位移;而典型的波动方程为通过比较(1)、(2),可得到波的传播速度;若波源的振动频率为f,横波波长为λ,则横波沿弦线传播的速度可表示为波长与张力及线密度之间的关系可表示为两边取对数,得到公式波长的测量:驻波方法图像如图所示三.实验主要步骤或操作要点1、在弦线张力不变时,用实验确定驻波波长与振动频率的关系;①将弦线一端固定在鞋盒侧面,线跨过鞋盒沿,另一端下垂并悬挂一水瓶。
实验装置如图3-1图3-1②在保持张力不变的情况下,移动筷子位置,使半波长λ/2分别为10、15、20、25、30c m。
③用牙签波动弦线发出声音,利用P h y p h o x分别测出线的振动频率f2、在振动源频率不变时,用实验确定驻波波长与张力的关系①固定A B之间的距离并测量②利用小量杯等量地增加水瓶中水的体积,即等量地改变弦线的张力T③波动弦线,用软件p h y p h o x测量不同张力下弦线的振动频率f3、验证三分损益法①保持弦线张力不变,先将A B的距离固定,测出此时的频率,并将音调定为基准音D o,算出相应的F a,S o l,L a,高音D o的理论频率。
②移动筷子,缩短A B距离,波动弦线,先粗略听出F a音,再微调距离使得P h y p h o x 测出的频率恰为理论的F a音频率。
测出相应的A B距离。
标记F a位置。
物理驻波实验报告

物理驻波实验报告物理驻波实验报告引言:驻波是物理学中一个重要的现象,它在许多领域中都有广泛的应用。
本实验旨在通过驻波实验,探究驻波的形成原理、特性以及相关的物理量测量方法。
实验装置:本次实验采用的装置是一条绳子,两端固定在两个支架上。
实验中,我们通过手持绳子的一端,以一定频率振动绳子,观察并测量驻波的形成和特性。
实验步骤:1. 将绳子两端固定在支架上,确保绳子保持水平。
2. 用手持绳子的一端,以一定频率振动绳子。
3. 观察绳子上形成的驻波,并记录下观察到的现象。
4. 测量驻波的波长和频率。
实验结果:通过实验观察和测量,我们得到了以下结果:1. 驻波的形成:当我们以一定频率振动绳子时,产生的波向绳子的另一端传播,并在两端发生反射。
当传播波与反射波相遇时,它们叠加形成了驻波。
驻波的形成是由于传播波和反射波之间的干涉效应。
2. 驻波的节点和腹部:在驻波中,存在一些固定的位置,这些位置上的振动幅度为零,称为节点。
而在节点之间的位置上,振动幅度达到最大值,称为腹部。
3. 驻波的波长:通过测量绳子上相邻两个节点的距离,我们可以得到驻波的波长。
实验结果表明,驻波的波长是传播波长的两倍。
4. 驻波的频率:通过测量绳子振动的频率,我们可以得到驻波的频率。
实验结果表明,驻波的频率与传播波的频率相同。
实验分析:通过以上实验结果,我们可以得出以下结论:1. 驻波是由传播波和反射波之间的干涉效应形成的。
2. 驻波的节点和腹部位置是固定的,它们的位置与波长有关。
3. 驻波的波长是传播波长的两倍,频率与传播波的频率相同。
实验应用:驻波现象在许多领域中都有广泛的应用,例如:1. 乐器制作:驻波的特性可以用于调整乐器的音质和音高。
2. 声波传输:驻波可以用于声波在管道中的传输和扩散控制。
3. 振动测量:通过驻波的形成和特性,可以测量振动频率和波长,从而得到物体的振动状态。
结论:通过本次实验,我们深入了解了驻波的形成原理、特性以及相关的物理量测量方法。
物理教案驻波

物理教案驻波物理教案:驻波一、教学目标1.了解驻波的概念及产生条件;2.掌握驻波的节点、反节点和波长计算方法;3.能够应用驻波的知识进行问题求解。
二、教学重点1.驻波的概念和产生条件;2.驻波的节点、反节点和波长计算方法。
三、教学难点1.驻波节点和反节点的理解和计算方法;2.驻波波长的计算方法。
四、教学过程1.了解驻波的概念及产生条件驻波是指两个相同频率、振幅和波速的相反方向行进的波在空间重叠后,造成的一种特殊波形。
驻波的产生需要满足以下条件:波的频率和振幅相同;两个波在相反方向行进;两个波的相遇会发生干涉,干涉后形成固定不动的波形。
2.掌握驻波的节点、反节点和波长计算方法驻波的波形是由一系列节点和反节点组成的。
节点是波浪线上不动的部分,反节点是波浪线上振幅变化最大的部分。
波长是两个相邻方向的节点之间的距离,可以用以下公式计算:λ = 2L/n (n为节点个数,L为管长)3.应用驻波的知识进行问题求解驻波是一种波动现象,在音叉、单管短笛等乐器中都能够体现。
因此,学生们可以通过练习求解一些驻波相关的问题来更好地理解和应用驻波的知识。
五、教学方法1.讲授法:通过讲解、演示等方式让学生快速了解驻波的概念和产生条件。
2.实验法:通过设备的展示和操作,让学生自己亲身体验和观察驻波的产生和特点。
3.问题解决法:通过实际问题的解决,培养学生运用知识分析和解决问题的能力。
六、教学评价学习驻波的过程中,教师应该注重学生的亲身体验和思考能力的培养。
同时,对于重难点的内容,要及时进行讲解和练习,帮助学生掌握相关知识。
最后可以通过测试、作业等方式对学生的学习效果进行评估。
七、教学拓展1.了解声音的传播特性和音量的衰减规律;2.研究其他波动现象的性质,如机械波、电磁波等;3.开展相关实验和探究,加深对波动现象的认识。
线上的驻波实验

实验** 弦线上的驻波实验[引言]弦线上波的传播规律的研究是力学中的重要内容。
本实验重点在于观测弦线上形成的驻波,并用实验确定弦振动时,驻波波长与张力的关系,驻波波长与振动频率的关系,以及驻波波长与弦线密度的关系。
常用的实验方法有两种:一是采用振动频率固定的电动音叉,通过改变弦线长度或张力,形成稳定驻波;二是采用频率连续可调的振动体,改变弦长或张力,形成稳定驻波从而验证弦线上驻波的振动规律。
掌握驻波原理测量横波波长的方法。
这种方法不仅在力学中有重要应用,在声学、无线电学和光学等学科的实验中都有许多应用。
[预习提示]1.波的叠加原理。
2.驻波的形成原理。
3.弦线的共振频率和波速与哪些条件有关?[实验目的]1. 了解波在弦线上的传播及弦波形成的条件。
2.测量拉紧弦不同弦长的共振频率。
3. 测量弦线的密度。
4. 测量弦振动时波的传播速度。
[实验仪器]DH4618型弦振动研究实验仪,DH4618型弦振动实验仪信号源,双踪示波器 [实验原理]由波动理论知道,两列振幅和频率均相同、振动方向一致且传播方向相反的简谐波叠加后会产生驻波。
合成振幅为零的点称为波节,合成振幅最大的点称为波腹。
相邻两波节或波腹间的距离都是半个波长。
各种乐器,包括弦乐器、管乐器和打击乐器,都是由于产生驻波而发声。
在弦乐器中,沿弦线传播的行波在乐器一端被反射,反射波与入射波相互叠加,形成驻波,如图**-1所示。
图**-1 驻波示意图设沿轴正方向传播的波为入射波,沿轴负方向传播的波为反射波,则它们的波动方程可以写x x 为。
其中为简谐波的振幅,为频率,为波长,为弦线上质点的位置1,2cos 2()Y A ft x πλ=±A f λx 坐标。
两波叠加后的合成波为驻波,其方程为: (**-1)122cos 2()cos 2Y Y A x ft πλπ+=由此可见,入射波与反射波合成后,弦上各点都在以同一频率作简谐振动,它们的振幅为,只与质点的位置有关,与时间无关。
驻波实验指导书

驻波实验一、实验简介驻波在声学、无线电、雷达和激光等领域中都有重要的应用,可用它测量波长和确定振动系统的频率。
本实验是由金属弦线形成驻波,量度波长,测得弦线的线密度。
二、实验原理驻波是由两个同频率、同振动方向、振幅相等、传播方向相反的简谐波合成的。
他们的波动方程分别为:y1(x,t)=Acos(ωt−2πxλ)(1)y2(x,t)=Acos(ωt+2πxλ)(2)两列波叠加后,合成波为:y(x,t)=2Acos 2πxλcosωt(3)从式子(3)中看出,合成后各点都已角频率ω作简谐振动,但在不同的坐标x 处,各质点的振幅不等。
若2πx/λ=kπ,则x=kλ/2处振幅最大,为2A,该处称为波腹。
若2πx/λ=(2k+1)π/2,则x=(2k+1)λ/4处振幅最小,为零,该处称为波节。
两相邻的波节(或波腹)间的距离Δx=λ/2,如图所示:图1在弦线上产生驻波的装置如图所示。
金属弦线的一端系在能作水平方向振动的可调频率数显机械振动源的弹簧片上,另一端通过定滑轮悬挂一砝码盘;在振动装置(振动簧片)的附近有可动刀口,在实验装置上还有一个可沿弦线方向左右移动并撑住弦线的动滑轮。
当波源振动时,即在弦线上形成一维横波,波在弦线两端点发生全反射,叠加形成弦线上的驻波。
两固定点一定是驻波的波节,所以在弦线上形成稳定的驻波的条件为弦长是半波长的整数倍。
在一根拉紧的弦线上,其中张力为T ,线密度为μ,则沿弦线传播的横波应满足下述运动方程:∂2y ∂t 2=T ∂2y μ∂x 2(4) 式中x 为波在传播方向(与弦线平行)的位置坐标,y 为振动位移。
将(1)式与典型波动方程:∂2y ∂t 2=v ∂2y ∂x 2 (5) 相比较,即可得到波动传播速度:v =√T μ (6) 若波源的振动频率为f ,横波波长为λ,由于波速V=fλ,故波长与频率、波速之间的关系为:λf =v(7) 从而由式(6)、(7)可以得到弦线的线密度为:μ=(n −1)2mg 4L 2f 2 (8)三、 实验内容1. 通过实验观察和测量,加深对驻波的形成机理及其特征的认识(1) 调节弦振动仪的输出频率至合适值,移动可动滑轮的位置,观察弦线的振动及驻波的形成;(2) 调节至得到驻波后,逐渐改变频率的大小,观察驻波的变化。
驻波法

大学物理实验教案实验名称:空气中声速的测定1、实验目的(1)学会用驻波法和相位法测量声波在空气中传播速度。
(2)进一步掌握示波器、低频信号发生器的使用方法。
(3)学会用逐差法处理数据。
2、实验仪器超声声速测定仪、低频信号发生器DF1027B、示波器ST16B。
3、实验原理3.1 实验原理声速V、频率f 和波长λ之间的关系式为V f 。
如果能用实验方法测量声波的频率f和波长λ,即可求得声速V。
常用的测量声速的方法有以下两种。
3.2 实验方法3.2.1 驻波共振法(简称驻波法)S1 发出的超声波和S 2 反射的超声波在它们之间的区域内相干涉而形成驻波。
当波源的频率和驻波系统的固有频率相等时,此驻波的振幅才达到最大值,此时的频率为共振频率。
驻波系统的固有频率不仅与系统的固有性质有关,还取决于边界条件,在声速实验中,S1 、S 2 即为两边界,且必定是波节,其间可以有任意个波节,所以驻波的共振条件为:Ln n 123 2 (1)即当S1 和S 2 之间的距离L 等于声波半波长的整数倍时,驻波系统处于共振状态,驻波振幅最大。
在示波器上得到的信号幅度最大。
当L 不满足(1)式时,驻波系统偏离共振状态,驻波振幅随之减小。
移动S 2 ,可以连续地改变L 的大小。
由式(1)可知,任意两个相邻共振状态之间,即S 2 所移过的距离为:L L n 1 Ln n 1 n 2 2 2 (2)可见,示波器上信号幅度每一次周期性变化,相当于L 改变了 2 。
此距离 2 可由超声声速测定仪上的游标卡尺测得,频率可由低频信号发生器上的频率计读得,根据V f ,就可求出声速。
3.2.2 两个相互垂直谐振动的合成法(简称相位法)在示波器荧光屏上就出现两个相互垂直的同频率的谐振动的合成图形——称为李沙如图形。
其轨迹方程为:2 2 X Y Cos 2 1 Sin 2 2 1 2 XY A1 A2 A1 A2 (5)2 1 0 在一般情况下,此李沙如图形为椭圆。
物理教案驻波

物理教案驻波
教学目标
知识目标
1、认驻波现象,了解驻波产生的原理。
2、观察驻波的实验现象、能够解释现象的发生。
能力目标
1、通过实验,培养学生的实验动手能力和观察能力。
情感目标
通过对有趣物理现象的观察,培养学生对科学的探究精神
教学建议
关于驻波这一节内容较少,教师在讲解的时候,重点需要强调驻波产生实际是波的反射、波的叠加,教师可以通过两个有趣的物理实验:
1、用琴弦和打点计时器进行驻波的演示;
2、用音叉通过盛水玻璃管内的声波演示驻波。
培养学生对科学的探究精神,同时锻炼学生的动手实践的能力。
典型例题
关于驻波现象,下列说法正确的是:
a、相邻的两波节之间的各个质点的振幅都相等;
b、相邻的两波节之间的各个质点的振动方向都相同;
c、相邻的两波腹之间各个质点的振动方向不完全相同;
d、相邻的两个波腹之间的距离为半个波长
本题是考察驻波的基本知识:只有两个波节中点振幅为最大,两边这副逐渐减小,故不选a项;两波节间各个质点的振动方向都相同,故b选项是正确的;相邻的波腹以波节为界,一边振动方向向上,另一边质点振动方向向下,故选c选项;由波的干涉可知:驻波相邻的两个波腹之间的距离萎半个波长,故选项d正确,总之,本题的正确答案是b、c、d选项。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验名称:驻波法测振动频率 实验目的:
1、求出弦线线密度;
2、观察弦线上的驻波;
3、绘出弦线上横波波长与张力的关系;
4、测出弦振动的频率。
实验仪器:
电振音叉(频率约为Hz 100) 弦线 滑轮 砝码托 砝码(5个) 钢卷尺 螺丝刀 电子天平
实验原理:
1、 弦线上横波传播速度(一) 如图1所示,将细弦线的一端固定在电振音叉的一个叉子顶端上,另一端绕过滑轮挂上砝码。
闭合电源K 后,调节音叉断续器的接触点螺丝k ',使音叉维持稳定的振动,并将其振动沿弦线向滑轮一端传播,形成横波。
当横波到达B 点后产生反射,由于前进波与反射波能够满足相干条件,在弦线上形成驻波,而任意两个相邻的波节(或波腹)间的距离都为波长的一半。
适当调节砝码重量或弦长(音叉端到滑轮轴间的线长),在弦上将出现稳定的强烈的振动,即弦与音叉共振(弦振动频率应当和音叉的频率f 相等)。
弦共振时,驻波的振幅最大,音叉端为稍许振动的节点(非共振时,音叉端不是驻波的节点),若此时弦上有n 个半波区,则
n l 2=λ,弦上的波速v 则为: 图1
f v λ= (1)
即:f n
l
v 2= (1’) 2、 弦线上横波传播速度(二)
若横波在张紧的弦线上沿x 轴正方向传播,我们取ds AB =的微元段加以讨论(图2)。
设弦线的线密度(即单位长质量)为ρ,则此微元段弦线ds 的质量为ds ρ。
在A 、B 处受到左右邻段的张力分别为1T F 、2T F ,其方向为沿弦线的切线方向与x 轴交成1α、2α角。
由于弦线上传播的横波在x 方向无振动,所以作
用在微元段ds 上的张力的x 分量应该为零,即:0cos cos 1122=-ααT T F F (2) 又根据牛顿第二定律,在y 方向微元段的运动方程为:
221122sin sin dt
y
d ds F F T T ραα=- (3)
对于小的振动,可取dx ds ≈,而1α、2α都很小,所以1cos 1≈α,1cos 2≈α, 11sin ααtg ≈
,
x
y
图
2
22sin ααtg ≈。
又从导数的几何意义可知x dx dy tg ⎪⎭⎫ ⎝⎛=1α, dx
x dx dy tg +⎪
⎭⎫
⎝⎛=2α,式(2)将成为012=-T T F F ,即T T T F F F ==21表示张力不随时间和地点而变,为一定值。
式(3)将成为: 22dt y d dx dx dy F dx dy F x
T ds x T ρ=⎪⎭⎫
⎝⎛-⎪⎭⎫ ⎝⎛+ (4)
将dx x dx dy +⎪⎭⎫ ⎝⎛按泰勒级数展开并略去二级微量,得: dx dx y d dx dy dx dy x
x dx x ⎪⎪⎭⎫
⎝⎛+⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+22
将此式代入式(4),得: 2222dt y d dx dx dx y d F x
T ρ=⎪⎪⎭⎫ ⎝⎛ 即:x T
dx y d F dt y d ⎪⎪⎭⎫ ⎝⎛=2222ρ (5) 将式(5)与简谐波的波动方程22
222dx
y d v dt y d =相比较可知:在线密度为ρ、张力为T F 的弦线上,横波传播速度v 的平方等于: ρ
T
F v =2
即: ρ
T
F v =
(6)
3. 弦振动规律
将式(1)代入式(6),得出: ρ
λT
F f v =
= 即: ρ
λT
F f
1
=
(7)
又将式(1’)代入式(6),整理后可得: ρ
T
F l n f 2=
(8)
式(7)表示,以一定频率f 振动的弦,其波长λ将因张力T F 或线密度ρ的变化而变化的规律。
式(8)又表示出对于弦长l 、张力T F 、线密度ρ一定的弦,其自由振动的频率不只一个,而是包括相当于
3,2,1=n 的 321,,f f f 等多种频率,1=n 的频率称为基频,3,2=n 的频率称为第一、第二谐频,但基频较
其他谐频强得多,因此它决定弦的频率,而各谐频则决定它的音色。
振动体有一个基频和多个谐频的规律不只是弦线上存在,而是普遍的现象。
但基频相同的各振动体,其各谐频的能量分布可以不同,所以音色不同。
例如具有同一基频的弦线和音叉,其音调是相同的,但听起来声音不同就是这个道理。
当弦线在频率为f 的音叉策动下振动时,适当改变T F 、l 和ρ,则可能和强迫力发生共振的不一定是基频,而可能是第一、第二、第三、…谐频,这时弦上出现 4,3,2个半波区。
实验内容
1、 测量弦的线密度
将所用弦线取下来,用钢卷尺测出其长度,在分析天平上称其质量m ,求出线密度ρ。
或由(8)计算出线密度ρ。
2、 观察弦上的驻波
根据音叉频率f 和已知线密度ρ,求弦长在20~30cm 附近,若要弦的基频与音叉共振时,弦的张力?=T F 参照上述计算的FT 值,选适当的砝码挂在弦上(弦长在130cm 左右),给电振音叉的线圈上通以Hz 50,1~2V 的交流电,使音叉作受迫振动,进行以下的观测:
(1) 使弦长从20cm 左右开始逐渐增加,当在4,3,2,1=n 个半波区几种情况下,弦共振时,分别测出弦长并算出波长λ。
(2) 使弦长l 大于1=n 共振时的弦长,小于2=n 共振时的弦长,从这种情况振动的弦上,测出波长λ,
并和上面的测量相比较(注意,此时音叉端不是弦的节点)。
3、 弦上横波的波长与张力的关系 增加砝码的质量,再细调弦长使出现共振,测出弦长l ,算出波长λ。
重复测量取平均值。
T F 值改变6~8次。
将式(7)两侧取对数,得: T F f ln 21
1ln ln +⎪⎪⎭
⎫
⎝⎛=ρλ (9) 即λln 与T F ln 间是线性关系。
利用测量值,作T F ln ~ln λ图线,求出图线的纵轴截距和斜率,将截距和
)1
ln(
ρ
f 相比较,斜率和21
相比较,说明其差异是否过大?
4、 比较两种波速计算值
从以上测量中,选取合适的数据,代入式(1)和式(6)中,计算出理论上应当相等的两个速度值,说明其差异是否显著?
从测量记录中,选一组数据代入式(8),计算出弦振动的频率,说明它和已知音叉频率的差异是否显著。
实验数据记录
1. 波长与张力的关系
弦线密度m kg /1018.14
-⨯=ρ, 重力加速度2
/795.9s m g =,音叉频率Z H f =
最小二乘法求斜率和截距。
比较斜率b 是否等于1/2。
截距a 是否等于 =⎪⎪⎭
⎫
⎝⎛ρf 1ln 实验数据处理
1、作图: λln ~T F ln 图
2、利用上表中的有关数据,最小二乘法求出斜率和截距,与公式(9)中的斜率和截距比较,说明差异是否过大。
3、用公式(1’)、(6)两种方法算出波速。
4、算出振动频率并与仪器标牌上的标称值相比较。
