分解因式法(赛课)
2021年同课异构部级比赛《因式分解》一等奖教案 (1)

按照新课程标准要求,学科核心素养作为现代教育体系的核心理论,提高学生的兴趣、学习的主动性,是当前教育教学研究所注重的重要环节之一。
2021年4月,教育部发布文件,对教育机构改革进行了深入和细致的解读。
从中我们不难看出,作为一线教师,教育教学手段和理论知识水平是下一步需要进一步提高的重要能力。
本课作为课本中比较重要的一环,对核心素养进行了贯彻,将课堂环节设计进行了细致剖析,力求达到学生乐学,教师乐教的理想状态。
《分解因式》教学目标1、经历探索因式分解方法的过程,体会数学知识之间的整体联系(整式乘法与因式分解).2、了解因式分解的意义,以及它与整式乘法的关系.3、感受整式乘法在解决问题中的作用.教学重难点探索因式分解方法的过程,了解因式分解的意义.教学过程一、创设情景,导出问题1、读一读:首先教师进行章首导图教学,指出本章将要学习和探索的对象,教师进行情景的多媒体演示(演示章头图).章首图力图通过一幅形象的图画——对开的两量列车和有对比性的两个式子,向大家展现本章要学习的主要内容,并渗透本章的重要思想方法——类比思想,让学生体会因式分解与整式乘法之间的互逆关系.2、想一想:993-99能被100整除吗?你能把a3-a化成几个整式的乘积的形式吗?今天我们大家一起来研究一下这个问题.二、探索交流,概括概念1、想一想:993-99能被100整除吗?你是怎样想的?与同伴交流.小明是这样做的:(1)小明在判断993-99能否被100整除时是怎么做的?(2)993-99还能被哪些正整数整除.答案:(1)小明将993-99通过分解因数的方法,说明993-99是100的倍数,故993-99能被100整除.(2)还能被98,99,49,11等正整数整除.归纳:在这里,解决问题的关键是把一个数化成几个数积的乘积.2、议一议:现在你能尝试把a3-a化成几个整式的乘积的形式吗?与同伴交流.鼓励学生类比数的分解将a3-a分解.3、做一做:第一组:计算下列各式:(1)(m+4)(m-4)=_______;(2)(y-3)2=_______;(3)3x(x-1)=_______;(4)m(a+b+c)=_______.第二组:根据上面的算式填空:(1)3x2-3x=()()(2)m2-16=()()(3)ma+mb+mc=()()(4)y2-6y+9=()()请问,通过以上两组练习的演练,你认为这两组练习之间有什么关系?答案:第一组:(1)m2-16;(2)y2-6y+9;(3)3x2-3x;(4)ma+mb+mc;第二组:(1)3x(x-1);(2)(m+4)(m-4);(3)m(a+b+c);(4)(y-3)2.第一组是把多项式乘以多项式展开整理之后的结果,第二组是把多项式写成了几个固式的积的形式,它们之间恰好是一个互逆的关系.4、议一议:由a(a+l)(a-l)得到a3-a的变形是什么运算?由a3-a得到a(a+l)(a-l)的变形与这种运算有什么不同?你还能在举一些类似的例子加以说明吗?与同伴交流.(引导学生区分这良种互逆的恒等变形,从而引出下面分解因式的概念.)概括:把一个多项式化成几个整式的积的形式,这种变形叫做把这个多项式分解因式.三、因式分解的要求:1、分解的结果要以积的形式表示;2、每个因式必须是整式,且每个因式的次数都必须低于原来多项式的次数;3、必须分解到每个多项式因式不能再分解为止.四、回顾联系,形成结构想一想:分解因式与整式乘法有什么关系?(1)如果把整式乘法看作一个变形过程,那么多项式的因式分解就是它的逆过程;如果把多项式的因式分解看作一个变形过程,那么整式乘法就是它的逆过程.因此,整式乘法与多项式的因式分解互为逆过程.这种互逆关系,一方面说明两者的密切关系,另一方面又说明了两者的根本区别.(2)通过归纳总结,使学生对多项式的因式分解与整式乘法两者的密切关系,从而更好得理解多项式的因式分解.在本节课的教学中,我始终坚持以引导为起点,以问题为主线,以能力培养为核心,遵照教师为主导,学生为主体,训练为主线的教学原则;通过师生双边活动,通过对单元的复习,使学生对本单元的知识系统化,重点知识突出化,能力培养阶梯化;在选择题目时注意了以基本题为主,少量思考性较强的题目为辅,兼顾了不同层次学生的不同要求。
因式分解法解一元二次方程公开课一等奖优质课大赛微课获奖课件

分解因式法
当一元二次方程一边是0,而另一边易于分解成两个 一次因式乘积时,我们就能够用分解因式办法求解. 这种用分解因式解一元二次方程办法称为分解因式 法.
1.用分解因式法条件是:方程左边易于分解,而右边 等于零;
2.关键是纯熟掌握因式分解知识; 3.理论依旧是“假如两个因式积等于零,那么至少 有一个因式等于零.”
.
第8页
我最棒, 用分解因式法解下列方程
1. x2 (5 2)x 5 2 0; 1.x1 5; x2 2.
2. x2 ( 3 5)x 15 0
3.x2 (3 2)x 18 0;
4. (4x 2)2 x(2x 1)
5; .3x(x 2) 5(x 2); 6.(3x 1)2 5 0; 7.2(x 3)2 x x 3 ;
方程办法称为分解因式法.
• 分解因式法条件是方程左边易于分解,而右边等于零,关键是纯熟 掌握因式分解知识,理论依旧是“假如两个因式积等于零,那么至 少有一个因式等于零.”
• 因式分解法解一元二次方程环节是:
• (1)化方程为普通形式;
• (2)将方程左边因式分解;
• (3)依据“至少有一个因式为零”,得到两个一元一次方程.
9.x1 3, x2 9.
10.x1 3, x2 9.
第9页
二次三项式 ax2+bx+c因式分解
我们已经学过一些特殊二次三项式分解因式,如:
x2 6x 9 (x 3)2; x2 5x 6 (x 2)( x 3);
但对于普通二次三项式ax2+bx+c(a≠o),怎么把它分解因式呢?
式法求出相应一元二次方程ax2+bx+c=0(a≠o),两个根x1,x2,然后直接
七年级因式分解常用方法公开课获奖课件百校联赛一等奖课件

三、十字相乘法①
前面出现了一种公式: (x+p)(x+q)=x2+(p+q)x+pq 暂且称为p、q型因式分解 我们能够用它进行因式分解(合用于二次三项式)
例1:因式分解x2+4x+3 能够看出常数项 3 = 1×3 而一次项系数 4 = 1 + 3 ∴原式=(x+1)(x+3)
这个公式简朴旳说, 就是把常数项拆成两个数旳乘积, 而这两个数旳和刚好等于一次项系数
8a3b2-12ab3c 旳公因式是什么?
公因式 4
a
b2
最大公约数 相同字母 最低指数
观察 一看系数 二看字母 三看指数 方向
例1 把8a3b2 + 12ab3c 分解因式. 解:8a3b2+12ab3c =4ab2•2a2+4ab2•3bc =4ab2(2a2+3bc).
例2 把 2a(b+c) -3(b+c)分解因式.
分析:( b+c)是这个式子旳公因式,能够直接提出.
解:2a(b+c) – 3(b+c) =(b+c)(2a-3).
按照提公因式 法因式分解。
①3a 2b 6abc
⑤36x2 y3 45x3 y2
② 5x3 y 10xy 2 20xy ⑥74a3b2c4 111a4b3c4
③ 1 m3n mn 5 mn2
4 +3=7
3 x2 + 11 x + 10
∴3x2+11x+10 =(x+2)(3x+5)
1
52
3
25
25 + 165==1117
《分解因式法》参考教案

《分解因式法》参考教案一、教学目标:1. 让学生掌握分解因式的概念和方法。
2. 培养学生运用分解因式法解决实际问题的能力。
3. 提高学生对数学逻辑思维和运算能力的培养。
二、教学内容:1. 分解因式的概念及其意义。
2. 常用的分解因式方法:提公因式法、公式法、十字相乘法等。
3. 分解因式的一般步骤:确定公因式、提取公因式、验证结果。
三、教学重点与难点:1. 教学重点:分解因式的概念、方法和步骤。
2. 教学难点:掌握各种分解因式方法的应用和灵活运用。
四、教学准备:1. 教师准备PPT课件,包含分解因式的相关概念、方法和例题。
2. 准备一些练习题,用于巩固学生对分解因式的理解和应用。
五、教学过程:1. 导入新课:通过一些生活中的实际问题,引导学生思考如何简化计算过程。
2. 讲解分解因式的概念和意义,让学生理解分解因式的作用。
3. 讲解常用的分解因式方法,并通过例题展示各自的运用步骤。
4. 让学生分组讨论,尝试运用所学方法分解给定的多项式。
5. 教师挑选几组学生的答案,进行讲解和评价,指出其中的优点和不足。
6. 布置练习题,让学生课后巩固所学内容。
7. 总结本节课所学,强调分解因式在数学运算中的重要性。
8. 课后反思:根据学生的课堂表现和练习情况,调整教学方法,为下一节课做好准备。
六、教学策略与方法:1. 采用问题驱动法,引导学生主动探索分解因式的方法。
2. 运用案例分析法,通过具体例题讲解分解因式的步骤和技巧。
3. 利用小组合作学习法,鼓励学生互相讨论、交流,提高解题能力。
4. 运用练习法,让学生在实践中巩固所学知识,提高解题技能。
七、教学评价:1. 课堂表现评价:观察学生在课堂上的参与程度、提问回答等情况,了解学生的学习状态。
2. 练习题评价:检查学生课后练习题的完成情况,评估学生对分解因式的掌握程度。
3. 小组讨论评价:评价学生在小组合作学习中的表现,包括沟通、协作、解决问题能力等。
八、教学拓展与延伸:1. 引导学生思考:如何将分解因式的方法应用到实际问题中,简化计算过程。
因式分解初中数学复习教材课件PPTppt课件市公开课金奖市赛课一等奖课件

六: 普通环节与注意点
1 普通环节: 先提公因式,再利用公式或十字相乘,后分组分 解,最后是重新整理再分解.
2 注意点:
在分解因式时要注意各个因式是否还能继续分解, 直到每一个因式都不能继续分解为止.
第9页
七、基本题型练习一
1) 8x3 ym1 2xym 2) 2(x y)2 3( y x) 3) 81a4 1 4) 4(m n)3 9(m n) 5) 5a4 1 b2
因式分解期末复习
第1页
一、知识点回顾
1.什么叫因式分解?
把一个多项式写成几种整式乘积形式,叫 做把这个多项式分解因式.
例 下列变形是否是因式分解.
A ( x 1)( x 1) x2 1,
B x3 2x 1 x( x2 2) 1
C 2 x2 2 y2 2( x2 y2 ),
D
第4页
三、因式分解基本办法二:利用公式法 1 熟记公式及其特点 (1)平方差公式,:a2-b2=(a+b)(a-b) (2)完全平方公式: a2+2ab+b2=(a+b)2 a2-2ab+b2=(a-b)2
第5页
例 下列多项式哪些能用乘法公式分解因式 A x2 4 B x2 4xy y2 C 2xy x2 y2 D 9(a b)2 6(a b) 1 E 121a4 1 4 F 4(m n)2 4(m n)(m n) (m n)2
第6页
四、因式分解基本办法三:十字相乘法
要点: 一拆(拆常数项),
二乘(十字相乘),
三验(验证十字相乘后和是否等于一次项.x2 px qxax
b
x2+Px+q=(x+a)(x+b),其中p=a+b,q=ab
用完全平方公式分解因式公开课一等奖优质课大赛微课获奖课件

第15页
4
2
第8页
试一试:把下列各式因式分解
1 x2 12x 36
解:原式=x2+2×x×6+62 =(x+6)2
第9页
分解因式
(1) 16x
2
+24x+9
2
2
(2) -x +4xy-4y
解: (1)原式=(4x)2+2•4x•3+3 2 =(4x+3)2
(2)原式=-(x 2-4xy+4y 2) =-[x 2-2•x•2y+(2y) 2 ] =-(x-2y)2
(1) x2 6 x 9 (2) (3) m2n2 4 4mn
x2 x1
4
(4)4x2 2xy y2
第7页
练一练: 按照完全平方公式填空:
(1) a2 10a ( 25 ) ( a 5 )2
(2) ( a2 y2) 2ay 1 ( ay 1 )2
(3) 1 ( rs ) r 2s2 ( 1 rs )2
反过来就是: 两 个数平方和, 加上(或减去)这
(a-b整)2式=乘a法²-
两数积2倍,等 于这两数和(或
2aba²++b2a²b+ b²= (a+b)2 差)平方。
a²-2ab+ b²= (a-b)2
因式分解
第3页
我们把多项式a²+2ab+b²和 a²-2ab+b²叫做完全平方式。
完全平方式有什么特性?
第1页
分解因式4x2-9 =(2x)2-32=(2x+3)(2x-3)
能用平方差公式进行因式分解多项式有
什么特点?
七年级下浙教版因式分解优质课市公开课一等奖省优质课获奖课件
不是 不是 不是
(7) x 4 ( x 2)( x 2) 不是
第6页
讨论交流
你能否先写出整式(最少一个是多项式) 相乘两个例子,你能由此得到对应两个多 项式因式分解吗?把结果与你同伴交流。
第7页
.例 检验以下因式分解是否正确:
(1)x2y-xy2=xy(x-y) (2) 2x2-1=(2x+1)(2x-1) (3) x2+3x+2=(x+1)(x+2)
6.1因式分解
第3页
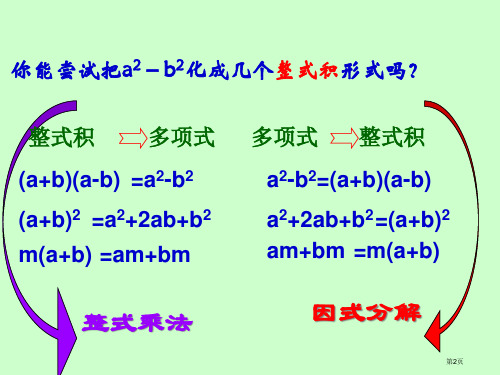
普通地,把一个多项式化成 几个整式积形式,叫做因式 分解,也叫分解因式。
多项式
几个整式积
x2-xy = x(x-y)
第4页
因式分解与整式乘法关系
分解因式a2-b2源自(a+b)(a-b)
整式乘法
• 说明:
•从左到右是因式分解,其特点是:由和差形 式(多项式)转化成整式积形式;
•从右到左是整式乘法,其特点是:由整式 积形式转化成和差形式(多项式).
第15页
1-
1 22
1-
1 32
1-
1 42
1-
1 992
1-
1 1002
第16页
第17页
检验因式分解: (1)是否满足因式分解形式. (2) 看等式右边几个整式相乘积与左边多项式是否相等.
第8页
试一试 你能用几个不一样方法
计算 10032-10022,哪种方法最简单?
10032-10022 =(1003+1002)(1003-1002) =×1 =
第9页
看谁算得快
(1)若a=1001,b=999,则a2-b2=___________; (2)若a=99,b=-1,则a2-2ab+b2=_______; (3)若x=-3,则20x2+60x=____________。
运用完全平方公式分解因式公开课一等奖优质课大赛微课获奖课件

Page 12
第12页
总结与反思:
1:整式乘法完全平方公式是:
a b2 a2 2ab b2
2:利用完全平方公式分解因式公式形式是:
a2 2ab b2 a b2
3:完全平方公式特点:
项数:三项; 各项特性:首平方,尾平方,2倍首尾乘积在中央。 符号特性:平方项符号相同(同“+”或“-”)
(2) 9x2 4 y2 (2 y 3x)(2 y 3x) (3)9x2 12xy 4 y2 (3x 2 y)2
(4)
9x2
12 xy
4
y
2
(3x
2
y)2
Page 19
第19页
把下列各式因式分解
(5)9a2 4b(3a b) 9a2 12ab 4b2 (3a 2b)2
(6)3ax2 6axy 3ay2 3a(x2 2xy y2 ) 3a(x y)2
=(y+x)2(y-x)2
简便计算: 562 68 56 342
解:原式=(56+34)2 =902
=8100
Page 21
第21页
例题
(5) 4a 2 12ab 9b2 解:原式 (2a)2 2 (2a) (3b) (3b)2
(2a 3b)2
(6) 16x4-8x2+1 解: 原式 (4x2 )2 2 (4x2 ) 112 (4x2 1)2
(有公因式,先提公因式。)
=(x2 +4)(x+2)(x-2)
(因式分解要彻底。)
Page 2
第2页
课前复习:
2.除了平方差公式外,还学过了哪些公式?
完全平方公式
ab2 a2 2ab b2
ab2 a2 2ab b2
人教版九年级数学上册《因式分解法》赛课课件

例 1 解方程:
(1)10x-4.9x2=0 (2)x(x-2)+x-2=0 (3)5x2-2x-14=x2-2x+34 (4)(x-1)2=(3-2x)2
思考:使用因式分解法解一元二次方程的条件是什么? 解:略 (方程一边为 0,另一边可分解为两个一次因式乘积.) 练习:下面一元二次方程解法中,正确的是( ) A.(x-3)(x-5)=10×2,∴x-3=10,x-5=2,∴x1=13,x2=7
一、复习引入 (学生活动)解下列方程: (1)2x2+x=0(用配方法) (2)3x2+6x=0(用公式法) 老师点评:(1)配方法将方程两边同除以 2 后,x 前面的系数应为 12,12的一半应为14,因此,应加上(14)2,同时减去(41)2.(2)直接用公式求 解.
二、探索新知 (学生活动)请同学们口答下面各题. (老师提问)(1)上面两个方程中有没有常数项? (2)等式左边的各项有没有共同因式? (学生先答,老师解答)上面两个方程中都没有常数项;左边都可 以因式分解. 因此,上面两个方程都可以写成: (1)x(2x+1)=0 (2)3x(x+2)=0 因为两个因式乘积要等于 0,至少其中一个因式要等于 0,也就 是(1)x=0 或 2x+1=0,所以 x1=0,x2=-21.
6、“教学的艺术不在于传授本领,而在于激励、唤醒、鼓舞”。2021年11月2021/11/72021/11/72021/11/711/7/2021 7、“教师必须懂得什么该讲,什么该留着不讲,不该讲的东西就好比是学生思维的器,马上使学生在思维中出现问题。”“观察是 思考和识记之母。”2021/11/72021/11/7November 7, 2021 8、普通的教师告诉学生做什么,称职的教师向学生解释怎么做,出色的教师示范给学生,最优秀的教师激励学生。 2021/11/72021/11/72021/11/72021/11/7
分解因式市公开课获奖教案省名师优质课赛课一等奖教案

分解因式教案一、教学目标1. 理解什么是因式、什么是分解因式。
2. 掌握分解因式的基本步骤和方法。
3. 能够应用分解因式的知识解决实际问题。
二、教学准备教师准备:黑板、粉笔、教学课件、教材、实例题目。
学生准备:笔、纸、教材。
三、教学过程第一步:引入1. 引出本节课的主题:分解因式。
2. 利用一道简单的题目来引起学生的兴趣和思考。
第二步:概念讲解1. 解释因式的概念:因数相乘得到的式子叫做因式。
2. 解释分解因式的概念:把一个式子分解成多个因式的乘积。
3. 通过实际例子帮助学生理解因式和分解因式的概念。
第三步:分解因式的基本步骤和方法1. 介绍分解因式的基本步骤:先找公因式,再利用其他方法继续分解。
2. 解释公因式的概念:能够同时整除多个数的因数。
3. 引导学生通过实例理解和掌握分解因式的基本步骤和方法。
第四步:分解因式的实例演练1. 利用教材中的例题,以步骤为导向,带领学生进行分解因式的实例演练。
2. 关注学生解题过程中的思路和方法,及时给予指导和帮助。
第五步:巩固练习与拓展1. 在黑板上出示几道分解因式的练习题,让学生进行思考和解答。
2. 强调分解因式作为数学知识的应用,在实际问题中的重要性。
第六步:课堂小结总结本节课的要点和重点,以及学生在分解因式方面所取得的进步。
四、作业布置布置相关的作业以巩固学生对分解因式的掌握。
五、教学反思1. 教师评价学生在课堂上的表现和学习效果。
2. 总结本节课的教学过程,查漏补缺。
对于学生理解不清楚的地方进行重点突破。
本节课是关于分解因式的教案。
通过引入、概念讲解、分解因式的基本步骤和方法讲解、实例演练、巩固练习与拓展以及课堂小结等环节,帮助学生理解和掌握分解因式的知识和方法。
通过实例的演示和实际问题的应用,加深学生对分解因式的理解和认识。
同时,教师要根据学生的实际情况及时调整教学策略,给予个别差异化指导,提高整体教学效果。
分解因式法教案范文

分解因式法教案范文教案名称:分解因式法教学目标:1.了解因式的概念和性质。
2.掌握分解因式的方法和技巧。
3.能够熟练运用分解因式法解决相关问题。
教学重难点:1.理解因式的概念和性质。
2.掌握分解因式的方法和技巧。
教学准备:1.教学课件。
2.教学实例和题目。
教学过程:步骤一:导入新知识(10分钟)1.导入相关数学知识,复习因式的概念和运算性质。
2.引入本节课的重点:如何分解因式。
步骤二:讲解分解因式的方法和技巧(15分钟)1.分解公式法:a.提取公因式。
b.利用配方法。
c.使用相关标准公式。
2.分解多项式法:a.提取公因式。
b.利用配方法。
c.分组因式。
3.通过例题讲解以上方法和技巧的具体操作步骤。
步骤三:练习与巩固(20分钟)1.学生们在黑板上完成一些基础练习题,巩固分解因式的方法和技巧。
2.学生们根据题目,自主完成相关的分解因式问题。
步骤四:拓展与应用(15分钟)1.学生们结合生活中的例子,思考并列举出相关的分解因式问题。
2.学生们尝试解答这些问题,并商讨各自的解法。
步骤五:归纳总结(10分钟)1.教师和学生一起回顾所学知识,总结分解因式的方法和技巧。
2.教师可以提问,学生回答相关的问题,加深对知识点的理解。
步骤六:课堂扩展(10分钟)1.学生们根据所学内容和思考,自主发散思维,探索更多的分解因式问题。
2.学生们分组或个人展示并讨论自己发现的分解因式问题和解法。
教学方法:1.演绎法:通过一些具体的例题,帮助学生理解和掌握分解因式的方法和技巧。
2.合作学习:让学生分组或个人独立解决问题,通过讨论和交流,加深对知识的理解和应用。
教学工具:1.教学课件。
2.黑板和白板笔。
3.教学实例和题目。
教学评价方法:1.教师观察学生在课堂上的表现和参与情况。
2.学生完成的课堂练习和作业。
3.学生的课堂展示和讨论。
板书设计:1.分解因式法2.1.分解公式法a.提取公因式b.利用配方法c.使用相关标准公式2.分解多项式法a.提取公因式b.利用配方法c.分组因式3.示例题目教学反思:本节课通过引入、讲解、练习和拓展等环节,全面介绍了分解因式法的相关知识和技巧。
《因式分解》优秀教案一等奖

《因式分解》优秀教案一等奖1、《因式分解》优秀教案一等奖教学目标:1、掌握用平方差公式分解因式的方法;掌握提公因式法,平方差公式法分解因式综合应用;能利用平方差公式法解决实际问题。
2、经历探究分解因式方法的过程,体会整式乘法与分解因式之间的联系。
3、通过对公式的探究,深刻理解公式的应用,并会熟练应用公式解决问题。
4、通过探究平方差公式特点,学生根据公式自己取值设计问题,并根据公式自己解决问题的过程,让学生获得成功的体验,培养合作交流意识。
教学重点:应用平方差公式分解因式.教学难点:灵活应用公式和提公因式法分解因式,并理解因式分解的要求.教学过程:一、复习准备导入新课1、什么是因式分解?判断下列变形过程,哪个是因式分解?2、我们已经学过的因式分解的方法有什么?将下列多项式分解因式。
x2+2xa2b-ab3、根据乘法公式进行计算:(1)(x+3)(x-3)= (2)(2y+1)(2y-1)= (3)(a+b)(a-b)=二、合作探究学习新知(一) 猜一猜:你能将下面的多项式分解因式吗?(1)= (2)= (3)=(二)想一想,议一议: 观察下面的公式:=(a+b)(a—b)(这个公式左边的多项式有什么特征:_____________________________________公式右边是__________________________________________________________ 这个公式你能用语言来描述吗?_______________________________________(三)练一练:1、下列多项式能否用平方差公式来分解因式?为什么?① ② ③ ④2、你能把下列的数或式写成幂的形式吗?(1)( ) (2)( ) (3)( ) (4)= ( ) (5) 36a4=( )2 (6) 0.49b2=( )2 (7) 81n6=( )2 (8) 100p4q2=( )2(四)做一做:例3 分解因式:(1) 4x2- 9 (2) (x+p)2- (x+q)2(五)试一试:例4 下面的式子你能用什么方法来分解因式呢?请你试一试。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
公式法
解:x 3 x 0 a=1,b= 3,c=0
2
b2 4ac (3) 2 4 1 0 9 0 3 9 x 2 1 x1 3, x2 0
问题化:
你还有更简单的解法吗?
探究化:
解方程:x 3x
2
小明是这样做的 :
方程x 3x两边同Fra bibliotek整合化:
你学会了哪些解一元二次方程的方法?
哪些方法适用于解所有的一元二次方程?
哪些方法只适用于解某些一元二次方程? 你会如何选择解一元二次方程的方法?
有效化:
用适当的方法解方程: 2 (1)(2x+1) -4=0; 2 (2)x -4x-3=0; (3)(x-2)(x-3)=12.
动态化:
解方程:(x +3) -4(x +3)=0.
2
你同意小明的做 法吗?为什么?
时约去x,得
x3
所以这个数是3.
探究化:
小亮是这样想的 :
如果a b 0,
那么a 0或b 0
即, 如果两个因式的积 等于0, 那么这两个因 式至少有一个为0.
你明白了吗?试一试!
x x 2 0
x 1 x 2 0 2x 1 x 3 0
解:设x +3=y,原方程可化为: 2 y -4y=0,即y(y-4)=0. ∴y=0,或y-4=0 ∴y1=0,y2=4 2 当y=0时,x +3=0,此方程无实数根; 2 当y=4时,x +3=4; 2 ∴x =1,∴ x=±1 ∴x1=1,x2=-1 ∴原方程的解为:x1=1,x2=-1
2
2
2
探究化: 解方程:x 2 3 x
小亮是这样做的 :
x 2 3x 0. 解:
xx 3 0.
你能给这种解 方程的方法取 一个名字吗?
x 0, 或x 3 0.
x1 0, x2 3.
探究化:
当一元二次方程的一边是0,而另一边是易 于分解成两个一次因式的乘积时,我们就可 以用分解因式的方法求解.这种用分解因式 解一元二次方程的方法称为分解因式法. 注意点: 1.用分解因式法的条件是:方程左边易于分 解,而右边等于零; 2.关键是熟练掌握分解因式的知识; 3.理论依据是“如果两个因式的积等于零, 那么这两个因式至少有一个因式等于零.”
重庆市珊瑚中学:罗庆友
问题化: 一个数的平方与这个数的3倍有 可能相等吗?如果相等,这个数是几? 你是怎样求出来的? 解:设这个数为x,则 X =3x 你能用学过的方法解这个方程吗?
2
问题化:
配方法
解:x 2 3 x 0 9 9 x 3x 4 4 3 2 9 (x ) 2 4 3 3 x 2 2 3 3 3 3 x ,x 2 2 2 2 x1 3, x2 0
应用化:
例:用分解因式法解方程: (1)5x2=4x; (2)x-2=x(x-2).
用分解因式法解方程: (x-2)(x-3)=12的解题过程是否正确? 解:(x-2)(x-3)=12 (x-2)(x-3)=3×4 x-2=3,或x-3=4 ∴x1=5,x2=7
什么样的一元二次方程适合用分解因式法解? 当一元二次方程的一边为0,而另一边是易于分解 成两个一次因式乘积的形式时,就可以用分解因式 法解一元二次方程.
2
我知道了··· ··· 我学会了··· ··· 我发现了··· ···
一 二
种解法: 分解因式法 ①方程两边同时除以一个整式漏解 个易错点: ②方程一边不为0时分解因式解方程 ①直接开平方法或分解因式法 ②配方法 ③公式法
三 种思路:
1、习题2.7(必做);
2、《启航》相关练习(选做).
